A tool for assessing the sensitivity of soil-based approaches for quantifying enhanced weathering: a US case study

Enhanced weathering (EW) of silicate rocks spread onto managed lands as agricultural amendments is a promising carbon dioxide removal (CDR) approach. However, there is an obvious need for the development of tools for Measurement, Reporting, and Verification (MRV) before EW can be brought to scale. Shifts in the concentration of mobile elements measured in the solid phase of soils after application of EW feedstocks can potentially be used to track weathering and provide an estimate of the initial carbon dioxide removal of the system. To measure feedstock dissolution accurately it is necessary to control for the amount of feedstock originally present in the sample being analyzed. This can be achieved by measuring the concentration of immobile detrital elements in soil samples after feedstock addition. However, the resolvability of a signal using a soil mass balance approach depends on analytical uncertainty, the ability to accurately sample soils, the amount of feedstock relative to the amount of initial soil in a sample, and on the fraction of feedstock that has dissolved. Here, we assess the viability of soil-based mass-balance approaches across different settings. Specifically, we define a metric for tracer-specific resolvability of feedstock mass addition (φ) and calculate the feedstock application rates (a) and dissolution fractions (b) required to resolve EW. Applying calculations of a, b, and φ to a gridded soil database from the contiguous USA in combination with known compositions of basalt and peridotite feedstocks demonstrates the importance of adequately capturing field heterogeneity in soil elemental concentrations. While EW signals should be resolvable after ~1–3 years of basalt feedstock addition at common application rates for most agricultural settings with adequate sampling protocols, resolving EW in the field is likely to be challenging if uncertainties in tracer concentrations derived from field-scale heterogeneity and analytical error exceed 10%. Building from this framework, we also present a simple tool for practitioners to use to assess the viability of carrying out soil-based EW MRV in a deployment-specific context.

1 Introduction

Enhanced weathering (EW) is a widely discussed method for carbon dioxide removal (CDR). Enhanced weathering involves accelerating natural silicate mineral weathering reactions, which convert carbonic acidity—ultimately sourced from atmospheric CO₂—to bicarbonate alkalinity (Seifritz, 1990; Schuiling and Krijgsman, 2006; Hartmann and Kempe, 2008; Köhler et al., 2010; ten Berge et al., 2012; Hartmann et al., 2013; Beerling et al., 2018, 2020; Strefler et al., 2018). EW has been discussed most prominently as an amendment practice in agricultural settings, where rock powder feedstocks are applied to fields (Beerling, 2017; Kantola et al., 2017; Beerling et al., 2018, 2020; Andrews and Taylor, 2019; Haque et al., 2019, 2020b,c; Goll et al., 2021; Kantzas et al., 2022; Larkin et al., 2022; Dietzen and Rosing, 2023). Many such rock powders (e.g., basalt) have long been used as agricultural additives due to their high concentrations of micronutrients, which can improve crop growth and yield (see Swoboda et al., 2022). Given that EW consumes acidity, the weathering of these feedstocks will raise soil pH, meaning they could replace more traditional liming agents (e.g., CaCO₃, CaO) in remediating soil acidification. Unlike conventional liming agents—which may act as CO₂ sources or sinks (West and McBride, 2005; Hamilton et al., 2007; Raymond et al., 2008)—silicate mineral weathering always results in net carbon removal. EW has a scale potential approaching gigatons of CO₂ per year (10⁹ tons of CO₂, GtCO₂) (Köhler et al., 2010; Taylor et al., 2016; Strefler et al., 2018; Beerling et al., 2020; Goll et al., 2021; Zhang et al., 2022; Baek et al., 2023), has lower cost and energy demands than most other forms of durable CDR (Fuss et al., 2018; Strefler et al., 2021), and has the potential to scale rapidly by utilizing existing infrastructure (Fuss et al., 2018).

Despite the potential promise of EW, there are still major gaps in our understanding of the process and how to track it in the field. Foremost, there are still significant uncertainties in weathering rates (e.g., Calabrese et al., 2022) and no widely implemented, scalable method of empirically tracking feedstock dissolution. The development and acceptance of robust Monitoring, Reporting, and Verification (MRV) frameworks will be required for EW to be brought to scale, including a cradle-to-grave (field to ocean) appraisal of carbon fluxes. Although it is likely that numerical modeling approaches will be needed to quantify whole-system CDR, there is growing consensus from multiple stakeholders in the EW space that empirical measurements are needed to constrain weathering rates in the field (Chay et al., 2022; Frontier, 2024). There are currently several potential methods for tracking initial weathering rates (Almaraz et al., 2022; Campbell et al., 2023; Clarkson et al., 2024). Reaction products of feedstock weathering (mobile major cations, alkalinity) can be measured in soil exchange phases, porewaters, and drainage waters (Renforth et al., 2015; Dietzen et al., 2018; Amann et al., 2020, 2022; Taylor et al., 2021; Larkin et al., 2022; Pogge von Strandmann et al., 2022; Vienne et al., 2022; Wood et al., 2022; Dietzen and Rosing, 2023; Holzer et al., 2023; Vanderkloot and Ryan, 2023), or the accumulation in secondary phases (Haque et al., 2019, 2020b,c; Khalidy et al., 2021; Jariwala et al., 2022; Larkin et al., 2022). Proxies for alkalinity in the dissolved phase have also been proposed—foremost electrical conductivity (Amann and Hartmann, 2022; Rieder et al., 2024). Isotope systems in soils and surface waters can also be used to disentangle enhanced from background weathering rates (Pogge von Strandmann et al., 2021; Knapp et al., 2023). All of these approaches are costly to implement over long periods of time as they provide snapshots rather than an integrated view of weathering rates. In contrast, in-situ weathering of feedstocks can potentially be measured using solid-phase mass balance approaches (e.g., Brimhall and Dietrich, 1987; Reershemius et al., 2023). These approaches are appealing as the solid phase in soils can potentially provide a time-integrated look at weathering rates, and solid-phase soil sampling can readily tie into existing agronomic practices (e.g., sampling for soil fertility). Therefore, in-situ solid-phase mass balance approaches for quantifying feedstock weathering potentially represent a labor-and cost-effective way to collect site-specific weathering rate data (Reershemius et al., 2023).

Solid-phase mass-balance approaches measure the amount of mobile cations lost from the feedstock added to soil, relative to the amount expected based on selected detrital trace elements that are assumed to be immobile during rock weathering. These approaches have long been used to quantify natural rock weathering rates in field and controlled settings (Brimhall and Dietrich, 1987; Chadwick et al., 1990, 1999; Brimhall et al., 1991; Kurtz et al., 2000; White et al., 2001; Anderson et al., 2002; Riebe et al., 2003; Tabor et al., 2004; Sheldon and Tabor, 2009; Brantley and Lebedeva, 2011; Fisher et al., 2017; Lipp et al., 2021; Kantola et al., 2023; Reershemius and Suhrhoff, 2023; Reershemius et al., 2023). Importantly, for soil-based mass balance approaches to be practicable for EW deployments, it must be demonstrated that representative soil sampling protocols can be designed such that samples taken before and after addition of EW feedstock can be directly compared and the outcome can be scaled to the whole field. Even so, sampling is likely to add significant uncertainty to weathering rate estimates calculated from soil samples; and even with ideal sampling, analytical uncertainty will dictate whether or not signals of feedstock addition and dissolution in soils can be detected (Reershemius et al., 2023).

Here, we construct a mass balance framework to evaluate how variable soil and feedstock compositions affect the resolvability and uncertainty of signals for feedstock addition and dissolution in the solid phase of soils. We use a theoretical mixing model between a soil and feedstock endmember (Reershemius et al., 2023) and impose an aggregated analytical and sampling uncertainty for the concentrations of immobile detrital trace elements and mobile cations in the soil, feedstock, and their mixture. We vary several key parameters over plausible ranges in order to test the effective detection sensitivity while quantifying enhanced weathering: (1) aggregated analytical and sampling uncertainty (e); (2) applied feedstock mass (a); (3) relative fraction of applied feedstock that dissolves (b); and (4) concentration of immobile tracer (i) and mobile cation (j) in both the soil and feedstock endmembers. Note that a here refers to total cumulative feedstock application amount and not annual feedstock application rate. We utilize a representative range of mafic and ultramafic rock feedstocks, including feedstocks used in EW trials (Pioneer Valley Basalt, Blue Ridge Basalt, and Almklovdalen Olivine (peridotite); Lewis et al., 2021; Kantola et al., 2023), together with the mean compositions of basalt and peridotite from the GEOROC database (Lehnert et al., 2000). Utilizing a database of semi-gridded soil samples (Smith et al., 2013), this investigation is framed in the context of topsoil compositions across the contiguous USA.

Our framework is designed to explore how sampling and analytical uncertainty (aggregated into one factor; e), and applied feedstock mass (a) and dissolution (b) control the resolvability of an EW signal for feedstock dissolution in the field. To compare between the resolvability of signals for feedstock addition using different detrital tracers, i, we define a metric for tracer-specific resolvability of feedstock mass addition, φ. Calculating φ for a range of tracers across soil and feedstock compositions, the impact of varying these parameters on the resolvability of feedstock amendments to soils using solid-phase mass balance can be evaluated. The framework also allows us to assess the utility of using multiple tracers in conjunction to improve signal strength, and the matching of specific tracers for use with specific feedstock and soil compositions—and to evaluate why some elements are not suitable for use as tracers for feedstock application with certain feedstock compositions.

Importantly, this framework is applicable to any setting where practitioners may wish to deploy EW. With that in mind, we also present an accompanying tool with an easy-to-use interface, where practitioners in the field can input soil and feedstock compositions specific to their site of interest to compute the requisite values of e, a, and b required to resolve a signal for feedstock application and weathering, given a number of tracers i. This work represents one step forward in the initial assessment of the feasibility of soil-based mass balance approaches to track weathering rates in EW deployments.

2 Materials and methods

2.1 A soil-based mass-balance framework for estimating weathering in EW deployments

Solid-phase mass balance approaches for estimating rock weathering rates rely on calculating the difference between the amount of a mobile element or cation, j (e.g., Mg, Ca, Na, K), present in the rock before and after weathering has occurred. For this calculation it must be assumed that the frame of reference is the same for measurements taken before and after weathering—i.e., that the same amount of rock is accounted for at both time steps (Reershemius et al., 2023). Given that feedstock application and mixing are unlikely to be perfectly homogeneous at the field scale, and that soil erosion can move material after application of feedstock, it is problematic to assume that a spatially uniform amount of feedstock mass applied in any given location can be perfectly resolved by sampling alone. Alternatively, the amount of rock accounted for in a sample can be estimated by referencing to the amount of a detrital trace element, i, measured in the sample, provided that this element is immobile during weathering (Brimhall and Dietrich, 1987; Chadwick et al., 1990, 1999; Brimhall et al., 1991; Kurtz et al., 2000; White et al., 2001; Anderson et al., 2002; Riebe et al., 2003; Tabor et al., 2004; Sheldon and Tabor, 2009; Brantley and Lebedeva, 2011; Fisher et al., 2017; Lipp et al., 2021; Kantola et al., 2023; Reershemius and Suhrhoff, 2023; Reershemius et al., 2023).

In order to facilitate the use of an immobile tracer i to calculate the amount of feedstock initially present in a sample, the addition of a feedstock to soil can be represented by a two-endmember mixing model between soil baseline (c_s) and feedstock (c_f) (Reershemius et al., 2023; see also Supplementary Figure S36). A mixture of composition c_m between soil and feedstock will fall along a mixing line in i vs. j space (Supplementary Figures S1, S36). Weathering will result in loss of j but not i from this mixture, and therefore the composition of the same mixture after weathering, c_n, will plot below the mixing line (Supplementary Figures S1, S36). Note that the compositional change due to weathering will likely be different for different cations j, as the mineral phases in rocks within which these cations are held may have different susceptibilities to weathering, and incongruent weathering or precipitation of secondary phases will result in preferential reincorporation of some cations j into solid phases. Assuming that feedstock dissolution has a negligible effect on [i] (but see section 4.4), the composition of c_m in i vs. j space can be reconstructed from [i] of c_n. The difference in [j] between c_m and c_n can then be used to calculate a sample-specific feedstock cation loss, which is directly proportional to dissolution.

2.2 A framework relating uncertainty, feedstock application, and dissolution to EW signal resolvability

This study builds upon the two-endmember mixing framework described above (Reershemius et al., 2023) to examine the impact of uncertainty in the compositions of a mixture post-weathering, c_n, and the soil (_s) and feedstock (_f) endmembers, c_s and c_f, on the calculation of dissolution using solid-phase mass balance (Supplementary Figures S1, S36). The derivations are laid out in more detail in the Supplementary material.

We first derive the uncertainty, e, for the mobile cation (j) concentration in a mixture of the initial soil and feedstock endmembers:

$\begin{array}{ll}{e}_{\mathrm{m}}^j=e_{\mathrm{s}}^j+\left(e_{\mathrm{f}}^j-e_{\mathrm{s}}^j\right)\ast \frac{{\left[j\right]}_{\mathrm{m}}-{\left[j\right]}_{\mathrm{s}}}{{\left[j\right]}_{\mathrm{f}}-{\left[j\right]}_{\mathrm{s}}}& (1)\end{array}$

Note that in these equations, uncertainties for feedstock, soil, or mixture are in concentration units, and for the soil and feedstock are calculated by multiplying concentrations with assumed % uncertainty for e (see section 2.3). For the purposes of this framework, we do not distinguish between analytical and sampling uncertainty, but present both as a aggregated uncertainty term.

Assuming that at field deployment scale no change in composition is resolvable if it does not exceed aggregated analytical and sampling uncertainty (see sections 4.2 and 4.4 for a discussion of this assumption), the limit of resolvability for Δ[j] due to dissolution is given by the expression:

$\begin{array}{ll}{e}_{\mathrm{n}}^j+e_{\mathrm{m}}^j<{\left[j\right]}_{\mathrm{m}}-{\left[j\right]}_{\mathrm{n}}& (2)\end{array}$

And therefore, substituting Eq. 1 into Eq. 2:

$\begin{array}{ll}{e}_{\mathrm{n}}^j+e_{\mathrm{s}}^j+\left(e_{\mathrm{f}}^j-e_{\mathrm{s}}^j\right)\ast \frac{{\left[j\right]}_{\mathrm{m}}-{\left[j\right]}_{\mathrm{s}}}{{\left[j\right]}_{\mathrm{f}}-{\left[j\right]}_{\mathrm{s}}}<{\left[j\right]}_{\mathrm{m}}-{\left[j\right]}_{\mathrm{n}}& (3)\end{array}$

Next, the relation of a (mass ratio of feedstock in a mixture based on the applied mass of feedstock) and b (the fraction of feedstock dissolved) to changes in mobile cation concentration is defined as follows:

$\begin{array}{ll}a\ast b\ast {\left[j\right]}_{\mathrm{f}}={\left[j\right]}_{\mathrm{m}}-{\left[j\right]}_{\mathrm{n}}& (4)\end{array}$

Combining Eqs. 3 and 4 gives an expression for the minimum resolvable a and b given uncertainty, which is solved with respect to either variable:

$\begin{array}{ll}a\ast b\ast {\left[j\right]}_{\mathrm{f}}>e_{\mathrm{n}}^j+e_{\mathrm{m}}^j& (5)\end{array}$

Substituting and rearranging gives the following expressions (see Supplementary material for full derivation):

$a>\frac{2\ast e_{\mathrm{s}}^j\ast {\left[j\right]}_{\mathrm{s}}}{\left(\begin{array}{l}{\left[j\right]}_{\mathrm{s}}\ast {\left[j\right]}_{\mathrm{f}}+\\ e_{\mathrm{s}}^j\ast {\left[j\right]}_{\mathrm{f}}\end{array}\right)\ast b-e_{\mathrm{s}}^j\ast {\left[j\right]}_{\mathrm{f}}+e_{\mathrm{f}}^j\ast {\left[j\right]}_{\mathrm{s}}+2\ast e_{\mathrm{s}}^j\ast {\left[j\right]}_{\mathrm{s}}}\text{ (6a)}$

$\begin{array}{ll}b>\frac{2\ast \frac{\left(1-a\right)}{a}\ast e_{\mathrm{s}}^j\ast {\left[j\right]}_{\mathrm{s}}+e_{\mathrm{s}}^j\ast {\left[j\right]}_{\mathrm{f}}+e_{\mathrm{f}}^j\ast {\left[j\right]}_{\mathrm{s}}}{{\left[j\right]}_{\mathrm{s}}\ast {\left[j\right]}_{\mathrm{f}}+e_{\mathrm{s}}^j\ast {\left[j\right]}_{\mathrm{f}}}& (6)\end{array}$

In order to compare between different detrital elemental tracers i in this mass-balance framework, we define a metric, φ, which denotes whether a signal from feedstock application is sufficient to overcome uncertainty, eⁱ, in the concentration of the immobile tracer i. Here φ is defined as:

$\begin{array}{ll}\phi =\frac{\left|\Delta {\left[i\right]}_{\mathrm{m}}-\Delta {\left[i\right]}_{\mathrm{s}}\right|}{e_{\mathrm{m}}^i+e_{\mathrm{s}}^i}& (7)\end{array}$

Thus, φ > 1 where feedstock addition is resolvable above uncertainty, and φ < 1 where it is not. Where i is a single element, this can be rewritten as follows (see Supplementary material for full derivation):

$\begin{array}{ll}\phi =\frac{\left|a\ast {\left[i\right]}_{\mathrm{f}}+\left(1-a\right)\ast {\left[i\right]}_{\mathrm{s}}-{\left[i\right]}_{\mathrm{s}}\right|}{2e_{\mathrm{s}}^i+\left(e_{\mathrm{f}}^i-e_{\mathrm{s}}^i\right)\ast a}& (8)\end{array}$

We can also employ the same framework to derive an expression for φ for a situation in which the ratio of multiple tracers ( $\frac{i^{\alpha }}{i^{\beta }}$ ) is used (see Supplementary material). Note that in this framework mixing in the shallow soil sampling horizon is assumed to be homogeneous. However, this does not imply that homogeneous mixing is necessarily required to resolve signals from EW deployments using mass-balance, but rather that in considering the role of uncertainty in resolving EW it is most instructive to consider perfect mixing of feedstock and soil in deployments on average, as feedstock may be over-or under-sampled spatially in real settings.

2.3 Data and spatial analysis

We use the expressions above to calculate values of applied feedstock mass a, dissolution b, and resolvability φ for a range of feedstocks and background soil compositions, given different scenarios for feedstock application a, feedstock dissolution b, and aggregated sampling and analytical uncertainty e. To allow comparison across a wide range of soil types and geographies, we use data for five feedstocks as well as soil compositions from across the coterminous US.

In the analysis presented here, we limit our selection of feedstocks to mafic and ultramafic rocks, which have been widely proposed for EW (Schuiling and Krijgsman, 2006; Hartmann and Kempe, 2008; Köhler et al., 2010; Hartmann et al., 2013; Taylor et al., 2016; Edwards et al., 2017; Beerling et al., 2018, 2020; Andrews and Taylor, 2019; Lewis et al., 2021). These lithologies contain the highest concentrations of weatherable cations of all abundant silicate rocks, and therefore have the highest CDR potential per mass deployed (see Supplementary Figure S34). These rock types also contain many trace elements in relative abundance compared with other silicate rocks, carbonates, and background soils (see Figure 1). This is useful when considering which detrital trace elements could be used as representative immobile tracer(s) i for feedstock addition in a mass-balance framework. We use specific compositions that are representative of feedstocks used in previous EW trials (Lewis et al., 2021; Kantola et al., 2023), as well as global average values for common rock types. Individual feedstocks considered here are Pioneer Valley Basalt (PVB), Blue Ridge Basalt (BRB), and Almklovdalen Olivine (AO) (see also Figures 1, 2; Supplementary Figures S2–S4, and Supplementary Datasheet 1). Elemental concentrations of these feedstocks were measured as laid out in detail previously (Reershemius et al., 2023), and are consistent with published values where available (BRB; Lewis et al., 2021). We stress that for this study, these serve purely as representative feedstocks for illustrative purposes. We also use mean compositions of basalt and peridotite from the GEOROC database (Lehnert et al., 2000) in our analysis to compare to the individual marketed feedstocks (see Figure 1). Only samples in the GEOROC database described as “whole rock” with data for all elements of interest are used. For the mean basalt composition, we restrict samples to those with “Rock Name” designated as “basalt”; those samples designated as “subaerial”; and those collected in the contiguous USA to be more representative of realistic source material for EW feedstocks, (limiting the range of longitude and latitude in the search criteria to those of the extremities of the contiguous USA; 24.52° to 49.38°N, and 66.9° to 124.7°W; n = 1,557). For the mean peridotite composition, samples were allowed to be globally distributed and were restricted to those with “Rock Name” designated as “peridotite,” “lherzolite,” “dunite,” “harzburgite,” or “wehrlite” (n = 257).

Figure 1

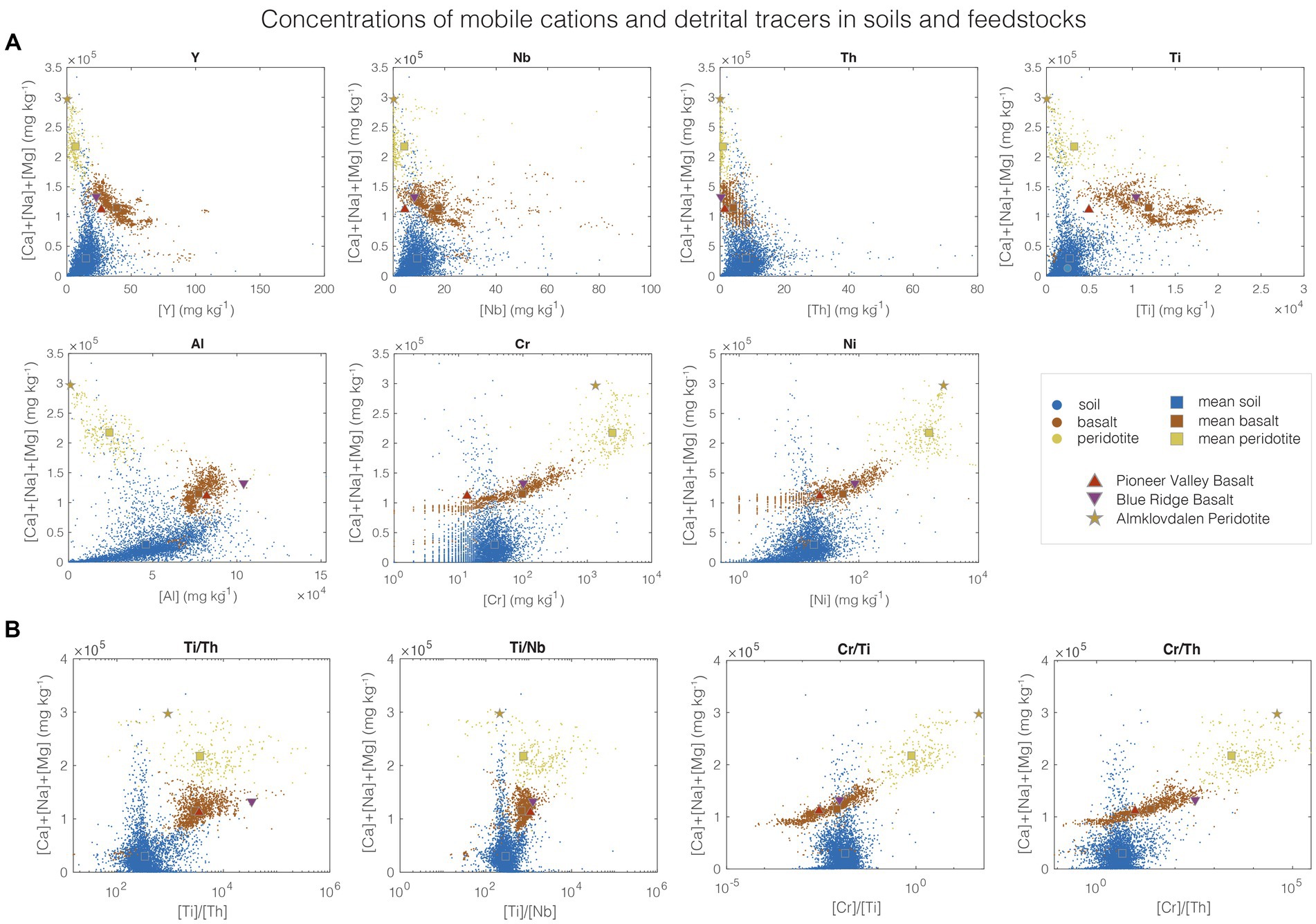
Figure 1. Cross-plots of sum mobile cation concentrations vs. the concentrations of different (partially) immobile detrital elements that may be used as tracers in mass-balance MRV approaches for ERW (A). Panels in (B) show plots of mobile cation concentrations vs. selected ratios of detrital elements. Soil data are from the USGS “Geochemical and mineralogical data for soils of the conterminous United States” database (n = 4,841) (Smith et al., 2013). Basalt and peridotite data (including AO) are extracted from the GEOROC database (Lehnert et al., 2000), see main text for more details on selection criteria and Supplementary Datasheet 1 for feedstock compositions.

Figure 2

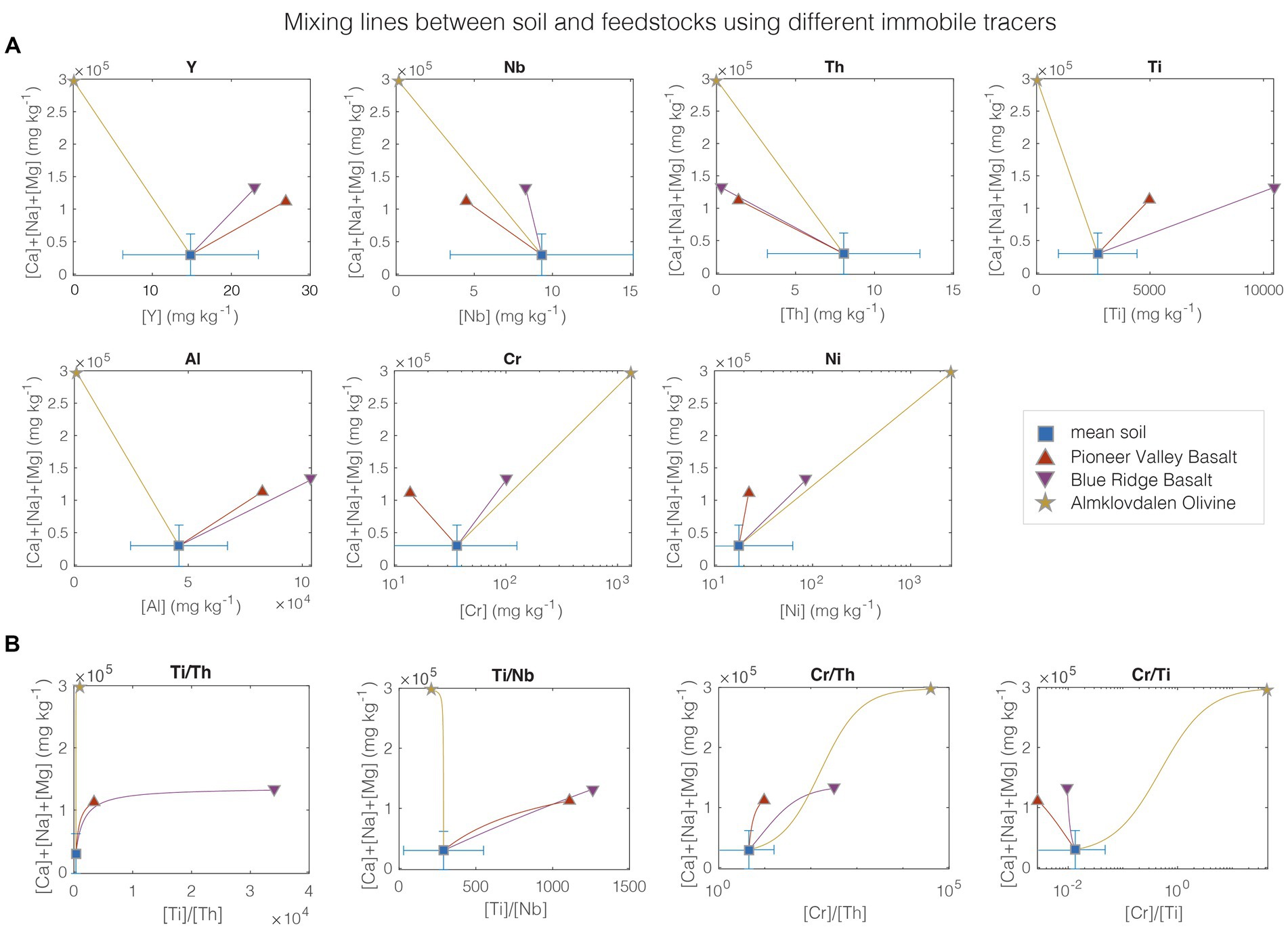
Figure 2. Mixing lines between soil and feedstock endmembers in mobile cation vs. detrital element space (A), and in mobile cation vs. detrital element ratio space (B). Shown are specific feedstock compositions (see Supplementary Datasheet 1), where AO is based on data from the GEOROC database (Lehnert et al., 2000). Soil data are mean soil concentrations based on the USGS “Geochemical and mineralogical data for soils of the conterminous United States” database (n = 4,841; shown is mean ± 1SD) (Smith et al., 2013). The panels demonstrate the lever between soil and feedstock compositions; the larger the difference in both cation and i space; the easier it is to quantify feedstock addition. Mixing lines for detrital element ratios form curves (note that Cr/Th and Cr/Ti have a different shape due to the logarithmic x-axis), as would be expected for soil-feedstock mixing with different concentrations of both detrital elements. The shape of the mixing curve has important implications for resolvability; the more vertical its trajectory from the mean soil composition, the more difficult feedstock addition resolvability based on φ because the detrital element ratio changes little in $\frac{i^{\alpha }}{i^{\beta }}$ space at low mixing ratios. See also Supplementary Figure S3 for additional i not contained in the USGS database.

These feedstock data are combined with soil data from a USGS dataset for soils of the coterminous US, utilizing the data for the top 5 cm of soil (Smith et al., 2013). The data are ideal for capturing large-scale soil variability because they are spatially balanced without adhering to a strict grid-based system (4,857 sample sites; 1 per 1,600 km²; see Figure 3; Supplementary Figures S5–S7 for maps of elemental and mineralogical concentrations) (Stevens and Olsen, 2000, 2003, 2004). Soil density data, relevant for the calculation of mass mixing ratios (a) based on feedstock application amounts in t ha⁻¹, were obtained from the National Soil Survey Geographic (gNATSGO) Database and the Gridded Soil Survey Geographic (gSSURGO) Databases (Boiko et al., 2021). The density data were interpolated using an inverse distance weighted interpolation algorithm (IDW) in ArcMap and extracted from the resulting layer for each sample site contained in the geochemical database (while capping data to the mean ± σ of all density data).

Figure 3

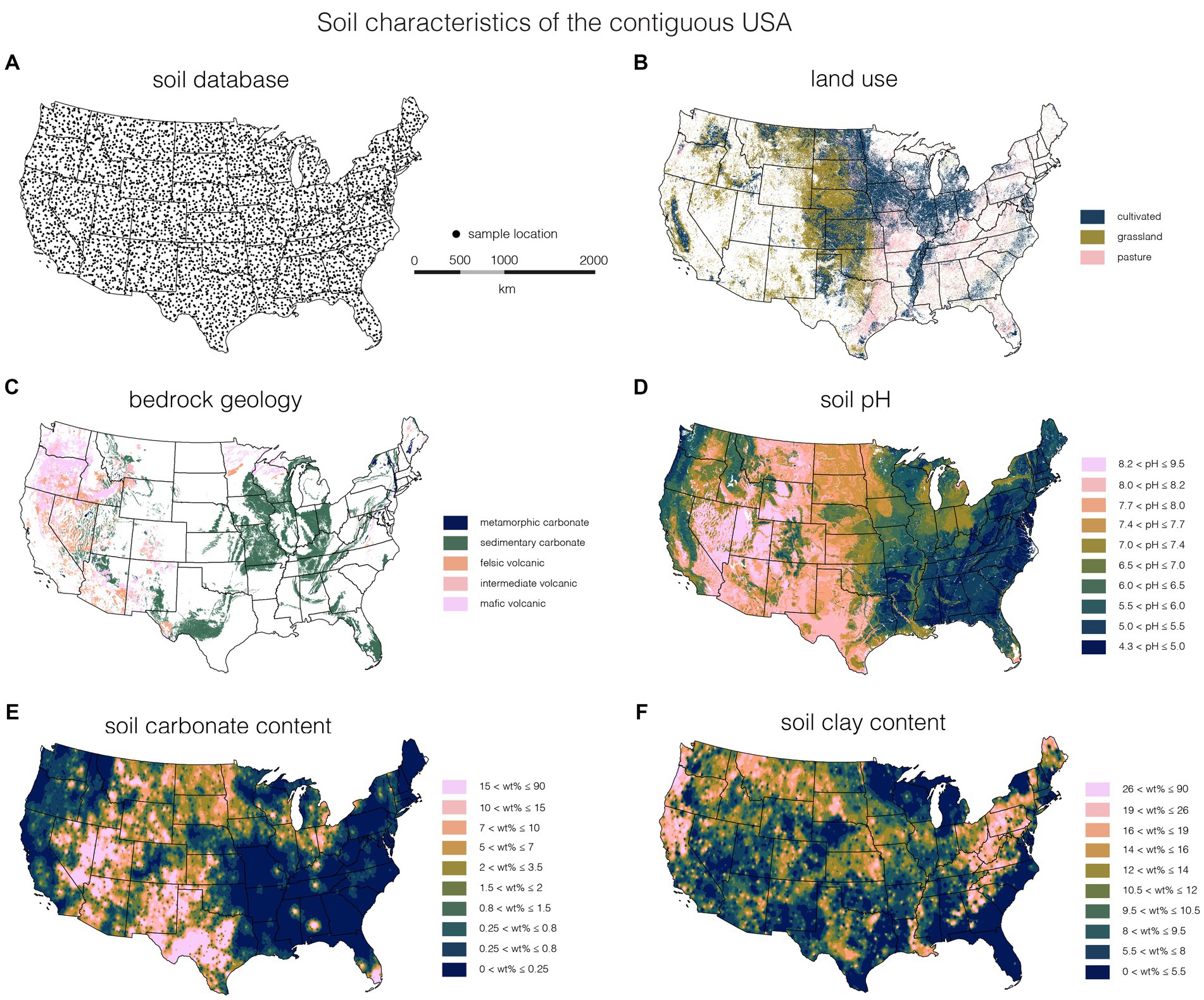
Figure 3. Panel (A) shows locations of topsoil samples contained in the USGS “Geochemical and mineralogical data for soils of the conterminous United States” database (Smith et al., 2013). The spatial sampling density corresponds to ~1 sample per 1,600 km2. Panel (B) shows “Culitvated Crops,” “Grassland/Herbaceous,” and “Pasture/Hay” spatial extent from the USGS National Land Cover Database (Yang et al., 2018). Panel (C) shows bedrock geology, with most data derived from the Global Lithological Map (GLiM) (Hartmann and Moosdorf, 2012) and additional metamorphic carbonate data from the USGS State Geologic Map Compilation (SGMC) (Horton et al., 2017). Soil pH data (D) is based on USGS STATSGO2 data (Wieczorek, 2019). Panels (E,F) show carbonate (carbonate + dolomite) and clay [total clays; sum of kaolinite, and 10 and 14 Å clays; see Smith et al. (2013) for discussion on uncertainties] content in top soils (A horizon) throughout the US, respectively. These latter data are sourced from the USGS “Geochemical and mineralogical data for soils of the conterminous United States” database (Smith et al., 2013), C horizon and average of A and C horizon is presented in the Supplementary Figure S7).

Using these data, a, b, and φ were calculated for each sample site using soil geochemical data and assuming a range of applied feedstock mass (a = 10, 25, 50, or 100 t ha⁻¹ total application); feedstock dissolution (b = 5, 15, or 30%); and aggregated sampling and analytical uncertainty (e = 1, 2, 5, 10, or 25%). Given that analytical uncertainty can be optimized to be <2% using isotope dilution, the lower end of these % uncertainty values represent cases where sampling uncertainty is neglected or has been reduced to the same order as analytical uncertainty (see discussion in sections 4.1, 4.2 and 4.4). Because of the greater ease of sampling from stockpiles, feedstock uncertainty was always assumed to be 1%. Although this is optimistic, the impact of the assumed feedstock uncertainty on parameters assessed here is low due to the low proportion of feedstock in soil-sampling mixtures at the feedstock application amounts considered here (generally <10% feedstock in soil-feedstock mixtures at application amounts < ~150 t ha⁻¹; see also Supplementary section S1.1 and Supplementary Figure S1). a and b were calculated in all cases using elements j (Mg + Ca + Na), excluding K which is a minor constituent in all feedstock compositions and is a major constituent of NPK fertilizers used in agriculture. φ was calculated separately for those elements i for which concentration data was present in the USGS soils database used: Ti, Al, Nb, Th, Y, Cr, and Ni. Additionally, φ was calculated for a subset of immobile element ratios $\frac{i^{\alpha }}{i^{\beta }}$ (see above): Ti/Th, Al/Th, Y/Th, Ti/Nb, Y/Nb, Cr/Ti, Cr/Th, Ni/Ti, and Ni/Th. The data from individual sites were interpolated (IDW) in ArcMap. Resulting maps utilize “scientific color maps” (Crameri et al., 2020).

3 Results

The minimum total mass of feedstock applied, a, required to resolve a fraction of feedstock dissolution b (in %) is shown in Figure 4A for mean basalt (maps for all other considered feedstocks can be found in the Supplementary Figures S8–S12). Although in our framework a is parameterized as the mass fraction of feedstock in a soil + feedstock mix, we report values for a in terms of t ha⁻¹ based on spatially explicit soil density data in order to facilitate comparison to feedstock application rates in field deployments (most commonly reported in t ha⁻¹). As relative feedstock dissolution (b) increases, the requisite feedstock application required for a given signal is reduced. Similarly, as uncertainty e (pertaining to the soil endmember and to the sample after weathering) is reduced, the requisite applied mass of feedstock drops. Depending on background soil chemistry and feedstock composition, our framework predicts a threshold value of high e and low b beyond which weathering signals become unresolvable regardless of the mass of applied feedstock. This is a function of Eq. 6a relating a, b, and e, and results from the fact that uncertainty in [j] for compositions c_n and c_m becomes greater than the difference in [j] between them.

Figure 4

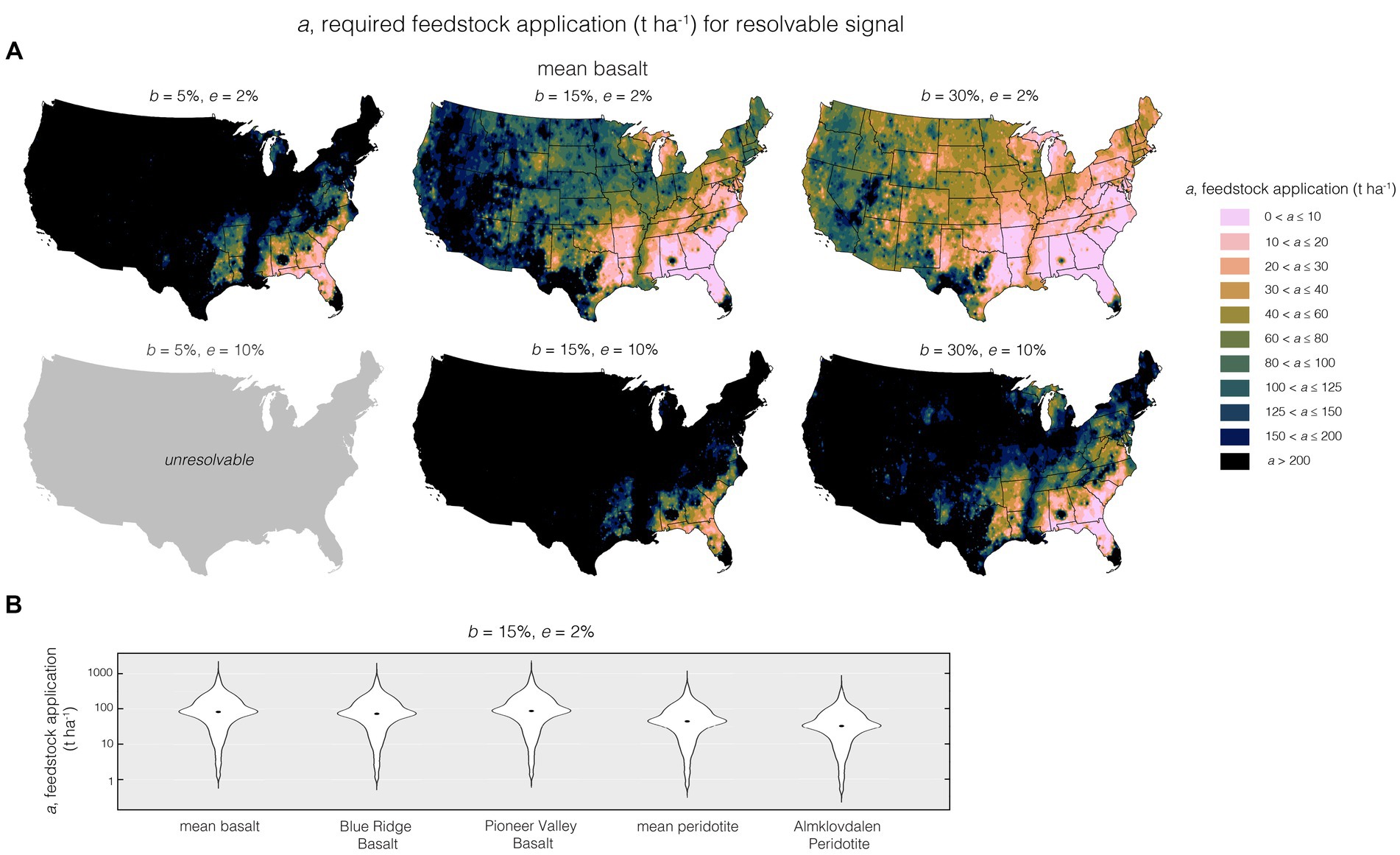
Figure 4. Requisite feedstock application (a) for enhanced weathering to be detectable through mobile cation loss based on assumed values of feedstock dissolution (b) and (aggregated analytical and sampling) uncertainty (e) (panels in A). For low dissolution rates and high uncertainties, feedstock dissolution cannot be resolved (panel with b = 5%, e = 10%; see main text for more detail). Panel (B) shows violin plots for requisite feedstock addition for the different assessed feedstocks using the data for each of the 4,857 sampling sites (using b = 15% and e = 2%).

The applied feedstock mass required to achieve a given signal varies by a factor of ~10³ across the dataset for topsoils from the coterminous US used here (Figures 4A,B). Much cultivated agricultural land in the US is in the Midwest “Corn Belt” (Figure 3B) (Yang et al., 2018). In the Corn Belt, with a low aggregated uncertainty and moderate weathering (i.e., b = 30%, e = 2%; Figure 4A), the minimum mass application of feedstock required for EW to be resolvable ranges from 10 t ha⁻¹ to over 100 t ha⁻¹. Feedstock application above 100 t ha⁻¹ is frequently required in order to resolve EW when there is an uncertainty of 10% (b = 30%). Owing to the higher cation content, the applied feedstock mass required to achieve a given signal is generally ~2 times lower for peridotites compared to basalts (Figure 4B). Pioneer Valley Basalt has similar requisite application amounts to average basalt, while BRB requires ~15% less feedstock application at the same values for a and e. Feedstock addition is generally easier to resolve in the southeast of the US, where generally <10 t ha⁻¹ is resolvable even at e = 10% (and b = 30%); we also note that in Pennsylvania, where BRB is sourced from, resolvability is generally favourable compared to the Corn Belt.

The minimum fraction of feedstock dissolution, b, required for a dissolution signal to be resolvable given prescribed a and e is shown in Figure 5 for mean basalt. Similarly to the patterns observed for required feedstock mass addition, the minimum feedstock dissolution required to achieve a given signal is reduced when a is increased and e is reduced. b also varies by a factor of ~10³ across the dataset of topsoils used in this analysis (Figures 5A,B, see Supplementary Figures S13–S17 for maps for all analyzed combinations of a, e, and feedstock). As shown in Figure 5B, in extreme cases b of >100% is required to resolve dissolution (for instance, a = 50 t ha⁻¹ and e = 2%), meaning that for some soil compositions even complete, congruent feedstock dissolution will be unresolvable.

Figure 5

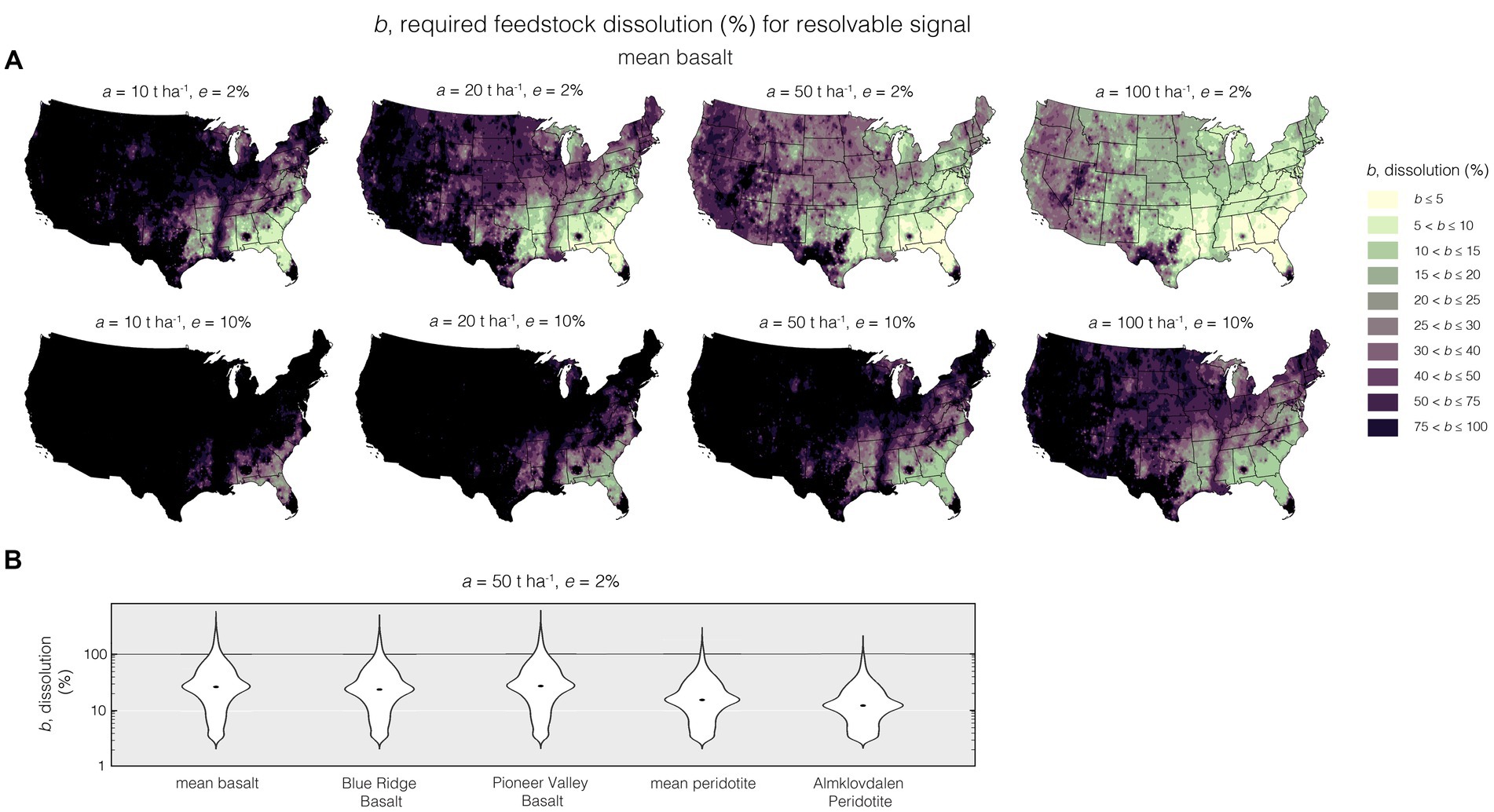
Figure 5. Requisite feedstock dissolution (b) for enhanced weathering to be detectable through mobile cation loss based on assumed values of feedstock application (a) and (aggregated analytical and sampling) uncertainty (e) (panels in A). Panel (B) shows violin plots for requisite feedstock dissolution for the different assessed feedstocks using the data for each of the 4,857 sampling sites (using a = 50 t ha⁻¹ and e = 2%).

Figure 6 shows the effect of varying a and e on φ (i.e., the resolvability of feedstock addition—which is independent from b as all i are assumed to be retained in soils) for a single tracer i for mean basalt (see Supplementary Figures S18–S22 for maps of all combinations of a, e and feedstock for i = Ti). The parameter φ defined here essentially refers to the difference in immobile element concentrations between soil and soil + feedstock over the sum of uncertainties on both measurements. Importantly, feedstock application measured using an immobile tracer i in this framework is only resolvable at or above threshold values of a and e such that φ > 1. This can be illustrated using Ti for i, which for mean basalt has the highest average resolvability φ. Resolvability φ increases as application a is increased and uncertainty e is reduced (Figure 6). For the corn belt, φ values are >2.5 for a = 100 t ha⁻¹ and e = 10% and are >1 (for most areas) for a = 100 t ha⁻¹ and e = 10%. It is clear that the concentration of Ti in the feedstock exerts a dominant control on the relative resolvability of applications of BRB (Figure 7; Supplementary Figure S19), PVB (Figure 7; Supploementary Figure S20), and in particular for the low-Ti mean peridotite and AO (Figure 7; Supplementary Figures S21, S22).

Figure 6

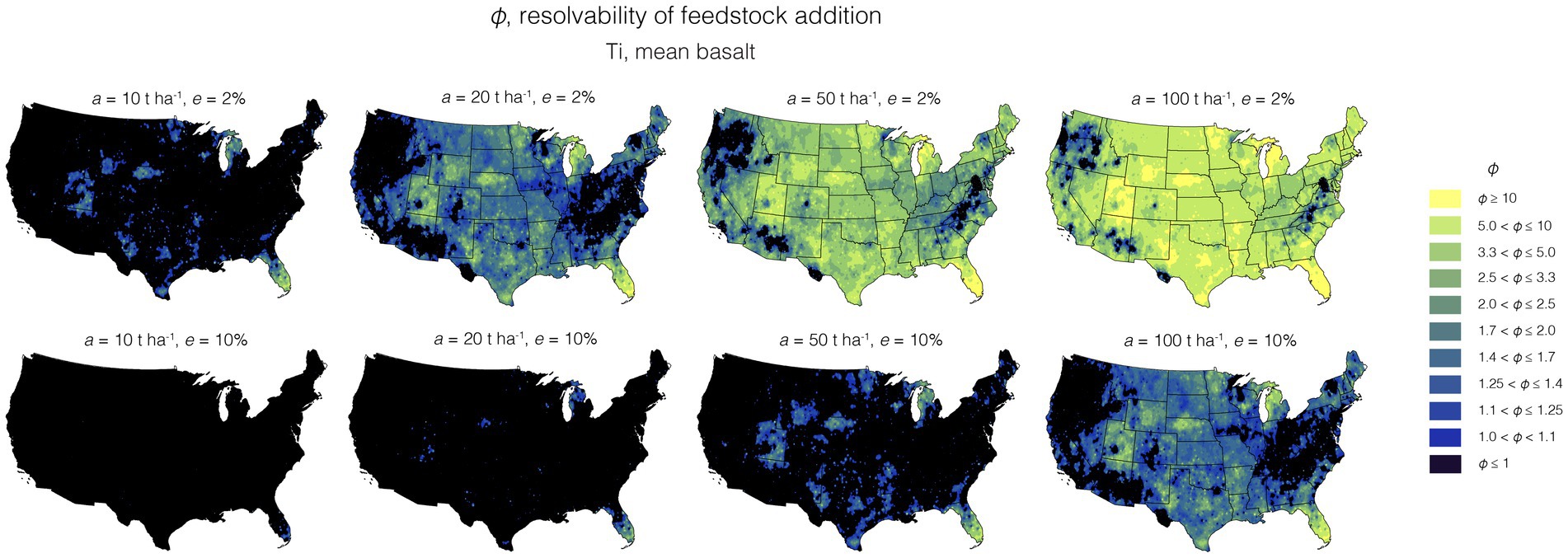
Figure 6. Resolvability of feedstock addition (φ) when using Ti as a proxy of the addition of mean basalt to US top soils. The resolvability increases with higher a and lower e.

Figure 7

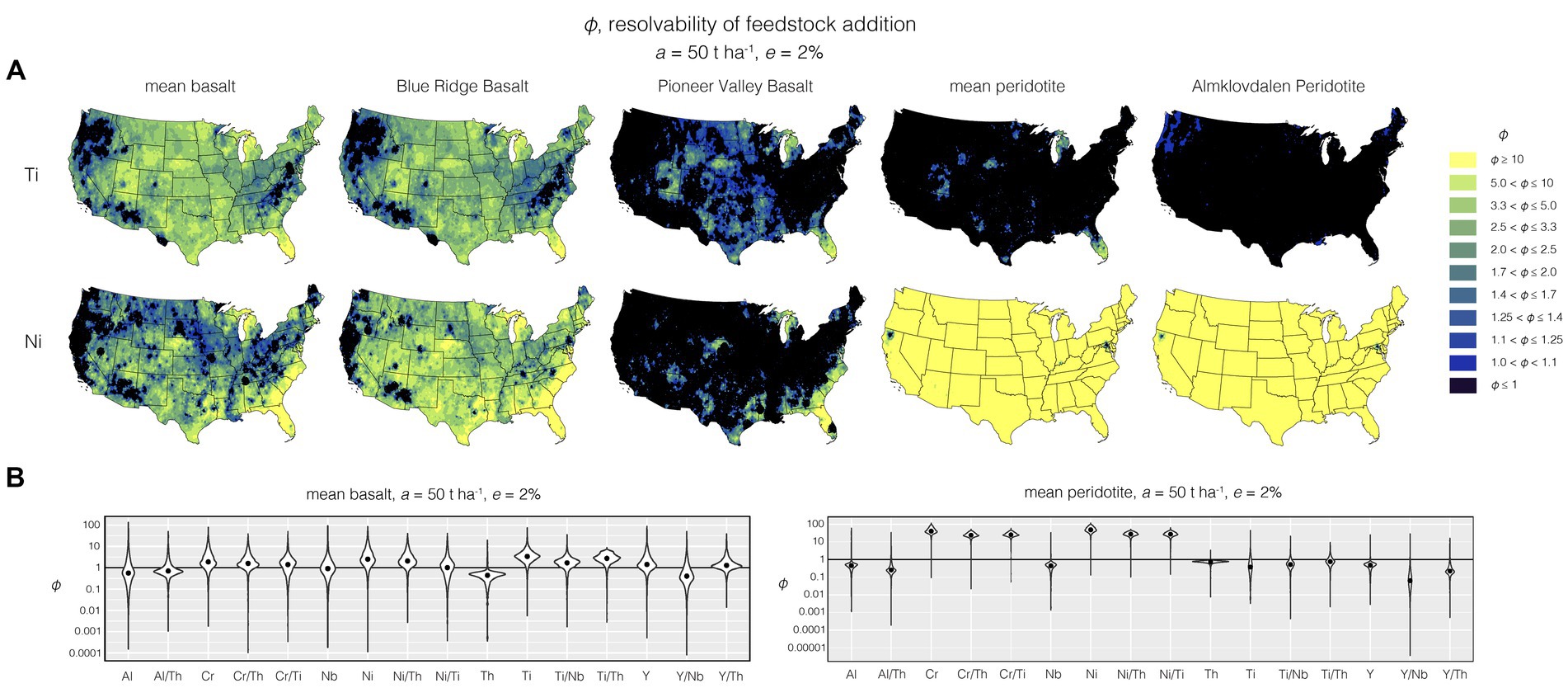
Figure 7. Comparison of the resolvability of feedstock addition (φ) between different feedstocks using Ti and Ni (A) and a range of different proxies for feedstock addition for mean basalt and peridotite (i; panels in B). Titanium works well as a proxy for feedstock addition for mean basalt and BRB, but is less effective for PVB and the peridotite feedstocks due to low Ti concentrations. Nickel, Cr, and their ratios to Ti and Th work particularly well for peridotite feedstocks. Note that higher aggregated analytical and sampling uncertainties would reduce φ values for all feedstocks, but do not impact the comparison between feedstocks.

The relative performance of different elements and elemental ratios as immobile tracers i are shown for mean basalt and mean peridotite compositions in Figure 7B. The difference in concentration of a specific immobile tracer i in different feedstocks means that values of φ also depend on feedstock composition (see Figure 7; maps for all i for all 5 feedstocks at a = 50 t ha⁻¹ and e = 2% and violin plots for PVB, BRB, and AO can be found in the Supplementary Figures S25–S29, S33). Titanium generally results in the highest resolvability for mean basalt (Figure 7B), closely followed by Ni, Cr, and Ti/Th. In the corn belt, φ values are typically >2.5 for Ti for mean basalt and BRB (at a = 50 t ha⁻¹ and e = 2%), but are considerably worse for PVB and both peridotite feedstocks. Nickel and Cr generally result in the highest resolvability for mean peridotite, followed by their ratios to Th and Ti, and have φ values >10 through the US (see Supplementary Figures S30, S31 for scaled Ni and Cr based φ values for peridotite feedstocks).

4 Discussion

We first discuss the representativeness of our chosen ranges for applied feedstock mass, relative dissolution, and aggregated uncertainty (section 4.1). Next, we discuss the implications of our findings for the viability of soil-based mass-balances approaches for MRV of EW, drawing on the resolvability of both feedstock dissolution and addition (section 4.2). The implications for the choice of EW feedstocks are discussed in section 4.3. Lastly, we discuss limitations of this approach, particularly if field heterogeneity and associated sampling uncertainty is high (section 4.4), before introducing a tool that EW practitioners may use to guide decision making regarding application amount and feedstock choice for EW deployment (section 4.5).

4.1 Choice of representative parameters

The framework we present here allows for the selection of arbitrary values for feedstock application amount (a), dissolution (b), and aggregated uncertainty on measurements (e). The usefulness of this discussion therefore depends on the selection of sensible criteria. Parameter values explored here were chosen to be realistic for early EW deployment scenarios.

Masses of applied feedstock (a), were chosen such that even the highest a values included here may be exceeded after 2–3 years of actual EW deployment. Academic enhanced weathering field trials commonly apply >40 t basalt ha⁻¹ per year (Larkin et al., 2022; Kantola et al., 2023; Beerling et al., 2024). Models estimating global CDR potential of EW have also used this application rate (Beerling et al., 2020, 2023; Kantzas et al., 2022), or alternatively cumulative addition of 150 t ha⁻¹ (Strefler et al., 2018). The lower application amounts are representative of basalt application as done purely for fertilization purposes (Swoboda et al., 2022), and are consistent with application amounts chosen in a modeling study focusing on the biological dimension of CDR from EW which uses 10, 30, and 50 t ha⁻¹ (Goll et al., 2021). However, application rates above 20 t ha⁻¹ will be a strong deviation from liming application rates (e.g., Mallarino et al., 2013).

The goal of EW is near complete dissolution of feedstock; achieving close to the full CDR potential of a feedstock will be important for EW to be cost effective. However, there are significant uncertainties regarding the timescales over which extensive dissolution will occur across settings. In practice, it has been difficult to relate field to lab or modeling based weathering rates for natural silicates (White and Brantley, 2003; Andrews and Taylor, 2019; Calabrese et al., 2022) because the former tend to be slower due to, e.g., surface passivation in soils through secondary precipitates and biofilms or fluctuating moisture content (Daval et al., 2018; Calabrese et al., 2022). In addition, factors such as grain size and, relatedly, specific surface area, likely exert a dominant influence on the rate in EW deployments (Strefler et al., 2018; Rinder and von Hagke, 2021; Amann et al., 2022; Rijnders et al., 2023; Vanderkloot and Ryan, 2023). As a result, it is difficult to predict a representative average value for b in EW deployments; and a trival portion of potential feedstocks have so far been tested. In mesocosm and field EW experiments, the fraction of applied feedstock that was weathered ranged for example from ~5.5% after 100 days (Vienne et al., 2022), 10% after 235 days (Reershemius et al., 2023) to ~22% after ~2.5 years average basalt residence time (Beerling et al., 2024). The values of 5 to 30% assessed here may therefore be seen as representative for a few months to years post-application, but will likely be exceeded over longer time horizons.

Our framework is agnostic as to the source of uncertainty e. It can therefore be seen as a aggregated measure of both analytical uncertainty and sampling uncertainty resulting from soil heterogeneity (also see section 4.2). Elemental concentrations of solid-phase samples can be measured using a variety of different methods, including X-ray fluorescence spectroscopy (XRF), inductively coupled plasma optical emission spectroscopy (ICP-OES), and ICP mass spectrometry (ICP-MS). Global analytical error for these methods varies, from <1% using isotope dilution to calculate concentrations using ICP-MS measurements, to >5% for typical XRF measurements (Reershemius et al., 2023). Hence, uncertainty deriving from spatial variability in background soil composition and soil + basalt mixture composition at the field scale are likely to be the larger source of uncertainty in real deployments. The scale of this uncertainty may also vary for different elements i and j depending on site-specific conditions. Importantly, uncertainty on an individual measurement of a sample will be much greater than the uncertainty of a mean calculated from many samples, when considering composition at the field scale. For example, in an EW field trial conducted in the US Corn Belt, Beerling et al. (2024) found that standard deviation of elemental concentration across pre-deployment soils was 7% for [Ti], 11% for [Ca], 13% for [Mg], 20% for [Al], 21% for [Na], and 25% for Th; however, standard error of the mean—an estimate of the variability of the sample mean—was 2% for [Ti], 3% for [Ca], 3% for [Mg], 5% for [Al], 5% for [Na], and 6% for Th. Regardless, it is clear that sampling methods will play a large role in determining uncertainty, and further systematic interrogation of this issue in the context of EW quantification and MRV is of critical importance. In our analysis, the smallest values chosen for e may be conceptualized as accounting for only analytical uncertainty, or for cases where sampling methods are successful in significantly limiting uncertainty that is a result of spatial variability, while larger e values (10–25%) may be seen as being more representative of aggregate uncertainty including both analytical and sampling uncertainties pertaining to individual measurements.

4.2 Viability of soil-based mass-balance approaches for quantifying EW

Differences in concentration of mobile (j) as well as immobile elements (or their ratios; i) between soil and feedstock are essential for detecting EW feedstock dissolution and addition, respectively. For a given feedstock, variability in EW signal resolvability is therefore driven by concentration gradients of relevant elements in soils (Figures 4–7). In terms of detecting feedstock dissolution (i.e., a and b; Figures 4, 5), areas where soil mobile cation concentrations are particularly low are ideal. These tend to be acidic soils in the southeastern US (compare with Figure 3D; Supplementary Figure S5). Importantly, this also implies that such soil-based methods may work better in sub-tropical and tropical soils, which are typically depleted in mobile cations due to intense chemical weathering (Brady and Weil, 2016), and which have been proposed as particularly promising sites for EW (e.g., Edwards et al., 2017). Soils enriched in j, where detecting feedstock dissolution is more challenging, are generally those with higher pH and therefore higher clay mineral and in some cases carbonate content (Figures 3C–F). These soil compositions should generally require less remediation of soil acidity than other arable lands that are depleted in j, and might therefore be less obvious targets for EW deployment from a purely agronomic perspective.

Similarly, the detection of feedstock addition (i.e., φ) also depends on the difference between soil and feedstock composition with respect to chosen immobile element tracers. Some connections to bedrock geology can be drawn here—for example Ti as a proxy for feedstock addition does not work well in the northwestern US (Figure 7), presumably because a higher prevalence of mafic volcanic rocks as protolith (Figure 3C) contributes to higher soil Ti concentrations. Interestingly, land use type does not have a clear impact on calculated φ parameters (Supplementary Figure S35). Spatial patterns of φ are more variable than for a and b. Concentrations of different immobile tracers i do not necessarily covary in soils, meaning that the immobile tracer i with the lowest threshold values of a and e on average may not be the best tracer to use in all sites. This variability is demonstrated in Figure 8, which shows that the immobile tracer i that results in the highest resolvability φ of a feedstock application varies greatly by geographic location (i.e., soil composition) and by choice of feedstock (maps for BRB, PVB, and AO can be found in the supplement together with larger maps for mean basalt and mean peridotite; Supplementary Figure S32).

Figure 8

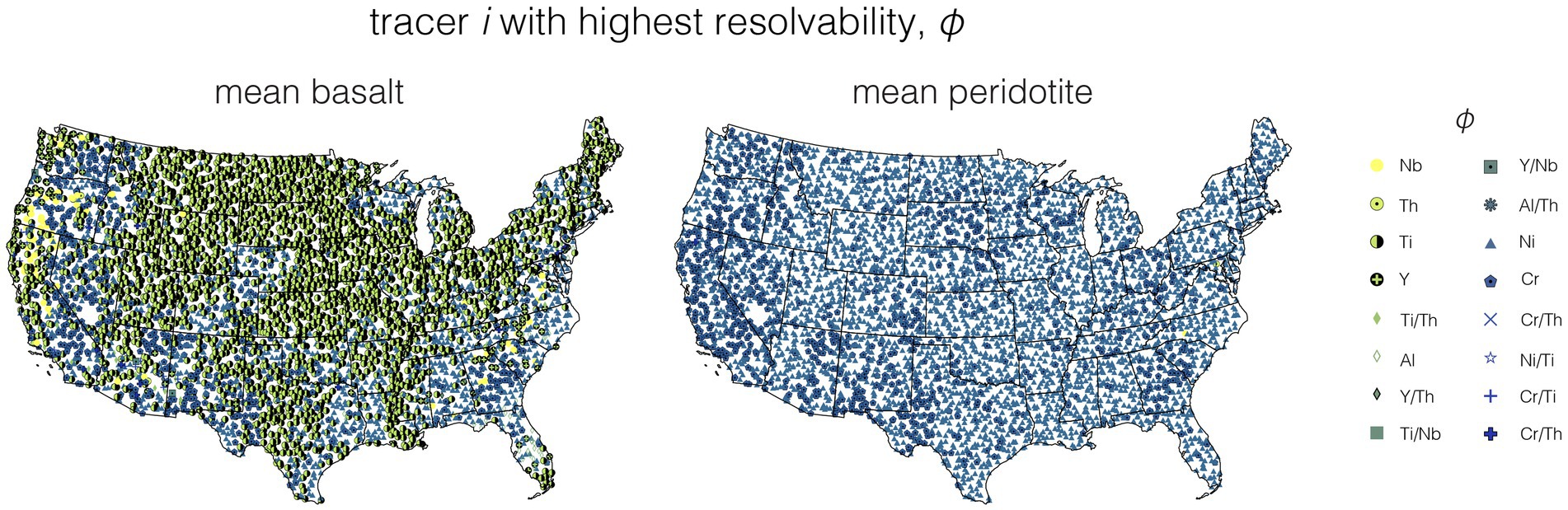
Figure 8. The immobile tracer i with the highest value of φ at each site contained in the USGS “Geochemical and mineralogical data for soils of the conterminous United States” database. (Smith et al., 2013) for two of the feedstocks considers: mean basalt and peridotite (maps for PVB, BRB, AO, and mean basalt and peridotite at higher resolution can be found in the Supplementary Figure S32). For basalt, Ti generally works best (particularly in the mid-west), followed by Ni and Cr. For peridotite, Ni and Cr yield the highest feedstock addition resolvability. Potential caveats for Ni and Cr in terms of mobility in the weathering zone are discussed in section 4.4.

In some cases, low resolvability of feedstock addition as a result of small Δ[i] may be overcome by comparing the ratio of immobile tracers in soils with that of feedstock, i.e., Δ( $\frac{{\left[i\right]}^{\alpha }}{{\left[i\right]}^{\beta }}$ ) where i^α is a tracer i that is more enriched in feedstock than in soil (e.g., Ti in most mafic rocks), and i^β is a tracer i that is more enriched in soil than feedstock (e.g., Th for most mafic rocks). As a result, immobile element ratios outperform single elements in many locations for PVB, which generally has lower immobile element concentrations (see Supplementary Figure S32; best φ for PVB; and Supplementary Figures S23, S24). However, while this measure amplifies the compositional difference between feedstock and soil, it also changes the form of the mixing line, such that it may not necessarily be beneficial to the resolvability of a signal for basalt addition in all cases (see Figure 2). An additional benefit of this approach is that if the concentrations of immobile tracers i^α and i^β are correlated, using a ratio of trace elements may help reduce sampling uncertainty because the variability of $\frac{{\left[i\right]}^{\alpha }}{{\left[i\right]}^{\beta }}$ in soils should be lower than variability of either i^α and i^β individually. As soil heterogeneity may be the main lever on aggregated uncertainties (e), this effect may be crucial in some cases for the detection of EW signals and should be considered in addition to mere optimization of φ values for a given location. A caveat for this approach is that the ratio of two detrital elements will change if one is more mobile than the other during weathering—i.e., if a larger relative amount of i^α is lost from the solid phase than i^β, or vice versa. If employing ratios of detrital tracers, this difference must be accounted for.

Crucially, the analysis presented here demonstrates the importance of successfully handling soil heterogeneity with appropriate sampling protocols and/or statistical resampling techniques, because otherwise spatial variability in soil elemental concentration at the field scale will be a major source of uncertainty relative to analytical uncertainty (see section 4.1). However, as noted above, the uncertainty of mean elemental concentration (i.e., the standard error of the mean) is significantly lower than that of individual measurements; and will decrease as the number of samples used to calculate a mean increases.

Broadly, our results suggest that depending on the quality of sampling and the size of analytical uncertainty, soil-based mass-balance approaches will often be useful for tracking EW in major agricultural regions of the US. Given that EW field trials usually apply large amounts of basalt each year (e.g., >40 t ha⁻¹) (Andrews and Taylor, 2019; Larkin et al., 2022; Kantola et al., 2023), feedstock addition and dissolution would be detectable even when considering aggregated analytical and sampling error of 10% (see Figures 4–6). However, these high rates may not be practical for many farmers and likely foster lower weathering efficiencies (for example due to clay formation). Similarly, feedstock addition is detectable in the Corn Belt using Ti for mean basalt and Ni or Cr for peridotite (Figures 7, 8; see section 4.4 for discussion of elemental immobility). However, if field-scale heterogeneity cannot be addressed adequately by sampling protocols (i.e., e ≥ 25%), addition and dissolution of feedstocks during EW deployments will be difficult to resolve. This is also the case for lower masses of total feedstock application than is commonly practiced in field trials to date—which, again, may be more realistic for deployments on farms. Nevertheless, it is important for EW practictioners to have the ability to assess resolvability of an EW deployment given their specific field conditions (see section 4.5).

4.3 Choice of feedstock

There is considerable overlap in the compositions of US top soils and potential EW feedstocks (see Figures 1, 2). However, Δ[i] and Δ[j] between feedstock and soil are key factors in determining the resolvability of a signal for feedstock application and dissolution, respectively. Given that most stakeholders (e.g., EW suppliers and farmers) are much more flexible with regards to feedstock composition than soil, the choice of feedstock and immobile tracer i must be informed by the specific soil composition of the site where soil-based mass-balance is being utilized.

In this context, maximizing Δ[j] through feedstock selection may already be in the interest of the EW supplier, because the concentration of mobile elements in feedstocks linearly scales with their CDR potential (Renforth, 2012, 2019; Supplementary Figure S34). Feedstocks should then be chosen that are enriched in a detrital element i that has low background concentrations in local soils. It should be noted here that not all of the “immobile” elements assessed here are immobile during weathering in all settings. To avoid underestimating CDR (see section 4.4), it is therefore in the interest of the stakeholder to ensure that the chosen tracer i is largely immobile during weathering on the relevant timescales. If this condition is not met, properly accounting for feedstock addition may require longer sediment cores (e.g., 1 m—to test for migration of i to below the ploughed layer) or testing effluent waters and harvested biomass.

The impact that feedstock choice may have on the resolvability of EW signals through soil-based mass-balance approaches is demonstrated by the difference in φ values between BRB and PVB (Figure 7; Supplementary Figures S19, S20). This is especially pronounced when comparing mafic to ultramafic feedstocks. Mafic rocks such as basalts generally have concentrations of some lithophile elements that can be used as immobile tracers, including Ti, Al, and Y, that are high relative to soils (Figure 1). By contrast, ultramafic rocks are depleted in these elements relative to soils and mafic rocks. As a result, there is a smaller selection of potential tracers i that may be used to track application of ultramafic rocks in EW deployments (e.g., Cr, Ni)—though given the much higher concentrations of these elements in peridotites than in soils resolvability φ for these elements in peridotite feedstocks is much greater (see also Supplementary Figures S30, S31). If EW suppliers are flexible with regards to feedstock type (basalt vs. peridotite), switching to peridotite may therefore be a viable strategy for soils where high concentration of lithophile elements may prevent detection of feedstock addition for basalt.

In any case, if soil-based mass balance approaches are to be widely used for the purpose of calculating EW rates in field deployments, care must be taken that feedstock application amount, feedstock choice, analytical methodology, and choice of immobile tracer are all selected with consideration of site-specific soil properties. Efficacy of soil-based mass balance approaches can be greatly improved by choosing a suitable feedstock. However, there may not be an optimal feedstock for all soils, particularly if concentrations of major and detrital elements in soils are high. In this context it is important to note that resolvability in this framework only refers to the efficacy of soil-based mass-balance approaches, not to the question of whether weathering and CDR occur. In other words, a given scenario below the resolvability threshold only means that soil-based mass-balance approaches will be inadequate for quantifying CDR in these settings, but CDR may still be occurring through EW.

4.4 Limitations of soil-based mass-balance approaches

Provided soils and feedstocks are matched in an effective way, and soil sampling is effective at constraining and minimizing uncertainty due to spatial heterogeneity in background soil and soil+basalt mixtures at the field scale, soil-based mass-balance approaches have clear potential for use in MRV of EW. However, there are some limitations to this class of MRV approaches that are important to consider.

One clear result of the feasibility assessment presented here is that soil heterogeneity needs to be addressed adequately for soil-based mass balances approaches to be able to quantify EW. At the largest aggregated sampling and analytical uncertainty assessed here (e = 25%), olivine weathering in most agricultural areas of the US requires very large masses of feedstock (a ≥ 100 t ha⁻¹) and extensive dissolution (b ≥ 40%) in order to be resolvable, while basalt dissolution will not be detectable even at 100 t ha⁻¹ (see Supplementary Figures S8–S17). At higher aggregated sampling and analytical uncertatinty and 50 t basalt application ha⁻¹, none of the detrital elements tested here would be reliable for assessing feedstock addition (Supplementary Figures S18–S24). These findings have fundamental implications for the utility of soil-based approaches. It is paramount for EW studies wishing to base MRV on soil-based approaches to successfully handle soil heterogeneity, an aspect not addressed in previous mesocosm experiments (Reershemius et al., 2023), or rigorously tested in large-scale field trials to date (e.g., Kantola et al., 2023; Beerling et al., 2024). Moving forward, EW deployments should prioritize testing and optimization of sampling protocols to capture in-field heterogeneity at multiple scales, which could potentially drive down the uncertainty derived from sampling a spatially heterogeneous background. Importantly, if the central tendency of soil elemental concentration at the field scale can be robustly and representatively determined through sampling (i.e., determining mean concentration with a small standard error of the mean), then spatial variability is not necessarily a barrier to resolvability. There is a clear need to test this hypothesis with additional field trials.

The effect of enrichment on the concentration of detrital elements i with dissolution of the feedstock is also an important issue that is not incorporated into the mass-balance frameworks presented here or elsewhere (Reershemius and Suhrhoff, 2023; Reershemius et al., 2023). However, a correction for feedstock dissolution can be easily applied that accounts for this concentration effect after loss of j has been calculated, given the ratio of mass soil:feedstock and the relative concentrations of i in soil and feedstock (Reershemius et al., 2023). As such, ignoring this concentration effect does not change the outcomes of our analyses. Furthermore, this concentration will cause the post-weathering soil+feedstock mixture to fall further away from the initial mixing line (see Supplementary Figure S36). Not accounting for it in this framework is therefore a conservative approach when estimating resolvability of EW signals where i in feedstock is greater than in soil.

There are some proposed EW feedstocks—notably wollastonite (Haque et al., 2019, 2020b,c; Paulo et al., 2021; Jariwala et al., 2022; Wood et al., 2022; Feng and Hicks, 2023)—that do not have significant concentrations of trace elements that can be used for the purposes of tracking feedstock application. The same is true for using carbonate feedstocks (Knapp and Tipper, 2022; Zhang et al., 2022). In these cases, using a detrital tracer i to track weathering rates is not workable. Addition of a feedstock that is more depleted in i than the soil to which it is deployed will result in the soil + feedstock mixture becoming more dilute in i. If this dilution effect overcame limitations of analytical and sampling uncertainty, an amount of feedstock application could be calculated as presented here. However, subsequent dissolution of this feedstock will result in an increase in the concentration of i such that the composition of soil + feedstock after weathering tracks the mixing line between the feedstock and soil (Supplementary Figure S36). This means that a signal for feedstock addition and subsequent weathering is indistinguishable from a signal for lower feedstock addition on its own, which defeats the purpose of using a detrital trace element to track weathering rates. Given this consideration, it should be noted that some potential detrital (or semi-immobile, detrital-like) elements i (Th, Zr, and REEs such as Pr, Nd, Sm—see Figures 1, 2; Supplementary Figure S3) on their own are unsuitable for this purpose for almost all mafic and ultramafic rocks. Moreover, despite apparent resolvability φ > 1 for AO when using Ti as a detrital tracer at high application a and low uncertainty e, it should be noted that given [Ti] is greater in most soils than in AO, the dissolution effect outlined above means that this result is erroneous (see Supplementary Figure S22). When performing these analyses, cases should therefore be excluded where [i]_s > [i]_f, which is also reflected in the online tool we present in section 4.5.

Furthermore, this framework is agnostic to potential mobility in certain detrital trace elements i during weathering. One practical measure of elemental (im-)mobility during weathering on a global scale is the ratio of world average river water concentration over the abundance of in the continental crust (Gaillardet et al., 2014). This measure indicates that Ti and Al may be among the most immobile elements. However, Ni, and Cr are more than 10 times more mobile. Given that parent material concentration rather than soil/leaching condition is the primary control on Ni and Cr concentrations in natural soils developing on both ultramafic (Kierczak et al., 2021) and basaltic (Suhrhoff, 2022) bedrocks, the assumption of immobility may be warranted for most soils to some degree. However, both Ni and Cr show higher mobility at low soil pH (Alloway, 2012). Specific caution should therefore be placed on the immobility of these tracers in acidic soils, though this also means that EW itself may positively impact Ni and Cr immobility. Furthermore, Cr mobility can also be promoted by elevated Cl-and F-concentrations (Seigneur and Constantinou, 1995; Alloway, 2012) as well as the presence of fulvic and organic colloids through formation of soluble Cr(III) complexes (James, 1996; Alloway, 2012). Mobility of Cr is further complicated through its redox sensitivity as Cr(VI) is generally more mobile than Cr(III) (Alloway, 2012). The oxidation of Cr(III) to Cr(VI) may be promoted by the presence of organic colloids (James, 1996; Alloway, 2012) and presence of Mn oxides in soils (Bartlett and James, 1979; James and Bartlett, 1988; Alloway, 2012). Importantly in the context of EW, elevated soil Cr(VI) concentrations have also been reported following P fertilization (Becquer et al., 2003; Alloway, 2012). Hence, the assumption of immobility should be a particular focus of EW employments in highly acidic soils, soils high in labile organic matter, and high P-fertilization regimes. Crucially, if detrital elements are lost from soils, this will cause underestimation of feedstock addition and of the fraction of weathering that has occurred. This is because the loss will not affect measured mobile cation concentrations but will reduce the amount of initial feedstock assumed to be present. Having a partially immobile tracer therefore means foregoing a part of earned CDR credits, but should not introduce the risk of exaggerating CDR.

Finally, some of the detrital elements discussed here—primarily Ni and Cr—may be toxic if available to plants and animals at elevated concentrations in soils. This has received extensive attention elsewhere in the context of EW (Haque et al., 2020a; Suhrhoff, 2022; Dupla et al., 2023; Vink and Knops, 2023) and is not the focus of this study. For these feedstocks and detrital elements, the need to quantify feedstock addition through the presence of a detrital element and the wish to avoid environmental risks lead to inherently contradictory feedstock choices, requiring a compromise between both. In this context we wish to stress that for these elements, the premise should not be to maximize φ as much as possible through the selection of high concentration feedstocks. Rather, assuming that other detrital elements are not viable tracers for feedstock addition, elemental concentrations in feedstocks should only be as high as necessary to detect feedstock addition (say, φ > 2), but as low as possible to avoid environmental risks.

4.5 From theory to practice

A key point we wish to emphasize is that although we present this framework in the context of a US case study, our approach can be applied to any dataset of soil composition, at any scale, and that the framework outlined here can be used as a tool for EW practitioners to use soil composition data from their fields as a guide for site-specific best practice in EW deployment. Moving forward, it will be particularly interesting to test the utility of soil-based approaches in tropical soils. These are also regions that may exhibit the potential for high weathering rates as a result of local climate (Edwards et al., 2017; Beerling et al., 2020), as well as the strongest potential for EW-driven fertilization effects (Goll et al., 2021). Tropical soils have very different background concentrations of mobile and immobile elements. Because mobile cations are typically depleted in such soils (Brady and Weil, 2016), soil-based approaches may be particularly sensitive in detecting dissolution of EW feedstock. Furthermore, because the ability of soil-based approaches to resolve EW signals scales directly with the concentration difference between soil and feedstock, the uncertainty imposed by sampling of soil heterogeneity may be lower in relation to the overall EW signal compared to temperate soils of high (mobile) cation concentrations. On the other hand, depending on site-specific conditions, tropical soils can have elevated immobile element concentrations or elevated mobility of immobile elements (e.g., Cornu et al., 1999; Du et al., 2012; Jiang et al., 2018), such that accurate detection of feedstock addition might be more challenging. In principle, although the utility of this framework will vary from site to site, the high potential for detection of both EW feedstock dissolution and addition in the southeastern US (Figures 4–8) is promising for soil-based approaches in tropical settings.

In order to facilitate practitioner use of site-specific data for individual deployments, we present this framework in a user-friendly online tool (Figure 9). This tool allows users to provide data on soil composition, expected aggregated analytical and sampling uncertainty, as well as different potential feedstock compositions, and reports information on the required mass of feedstock addition a,¹ relative feedstock dissolution b,² and resolvability of feedstock addition based on a single detrital tracer i³ and ratios of two detrital tracers i⁴ required to resolve EW feedstock application and dissolution using solid phase mass-balance. This tool is meant to help practitioners plan EW deployments where weathering rates and related CDR can be robustly monitored and verified. Additionally, this tool can also be used to vet reported weathering rates calculated using soil-based mass balance in EW deployments, given information on the use of tracers, feedstocks, and soil compositions, and could be used as part of efforts to standardize oversight in the growing market for carbon credits using EW.

Figure 9

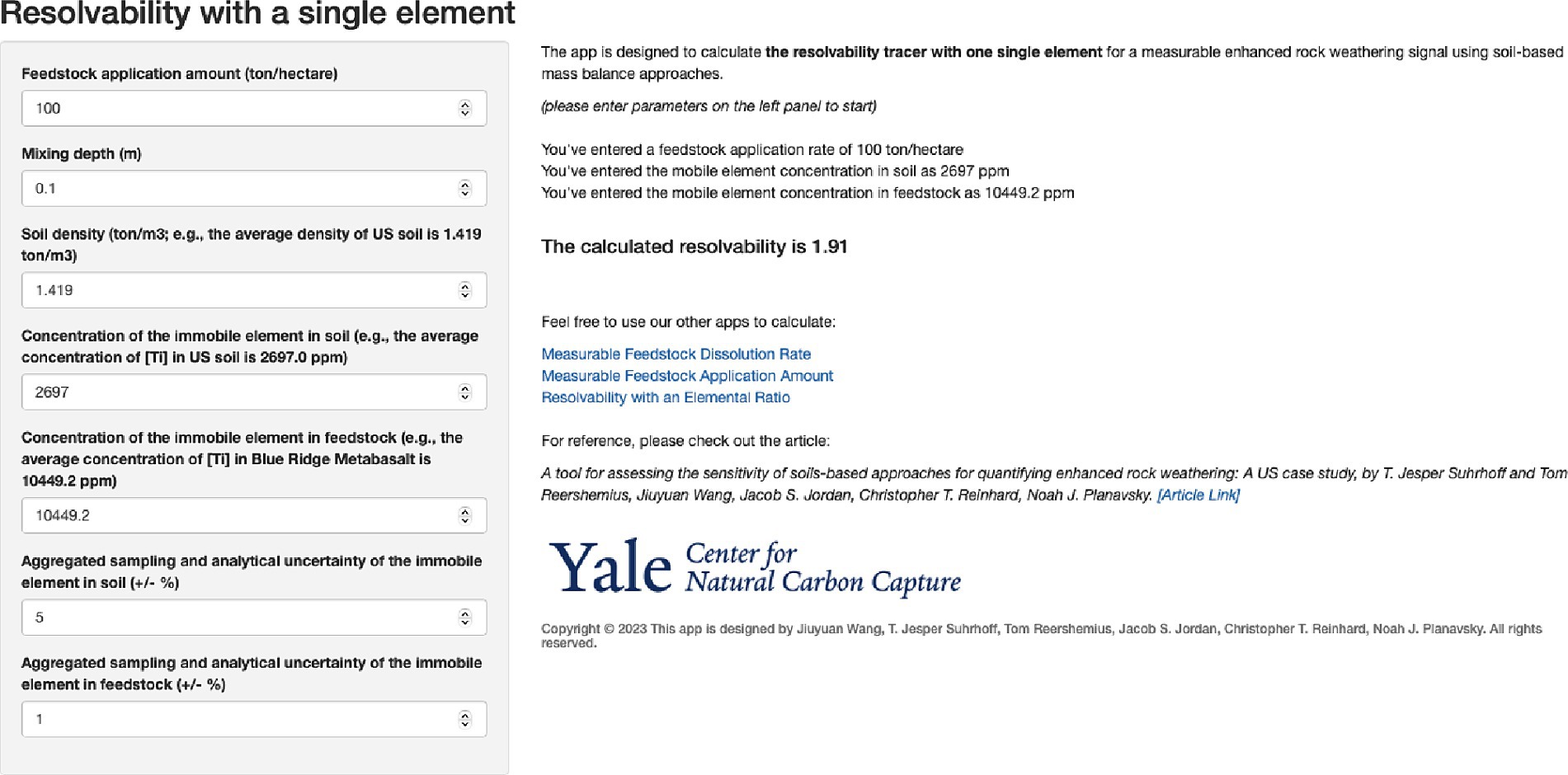
Figure 9. Preview of the tool provided to EW stakeholders. By inserting soil and feedstock composition, this tool can inform sensible feedstock application amounts and/or required (analytical) uncertainty for the detectability of EW signals. As an example, the figure shows a preview of the tool that can be used to estimate the resolvability of feedstock addition based on a single element. The tools can be found using the following links: Required dissolution rate: https://resolvability.shinyapps.io/dissolution-rate/. Required feedstock application: https://resolvability.shinyapps.io/application-amount/. Resolvability of feedstock addition using single i: https://resolvability.shinyapps.io/res-single/. Resolvability of feedstock addition using ratio of two i: https://resolvability.shinyapps.io/res-ratio/.

5 Conclusion

Using a simple two-endmember mixing framework with incorporation of uncertainty, we demonstrate how the resolvability of a signal for feedstock addition and dissolution in EW deployments depends on feedstock application and dissolution, aggregated analytical and sampling uncertainty, soil and feedstock composition, and the choice of detrital trace element i to track the amount of feedstock in samples. To ensure robust quantification of weathering rates in EW deployments using soil-based mass balance, EW stakeholders must successfully handle in-field variability of bulk elemental concentrations using adequate sampling protocols and statistical tools. Furthermore, they should consider site-specific soil properties when making choices about the amount of feedstock to apply, as well as which feedstock, analytical method, and immobile tracer i to use. When a specific methodology is chosen (e.g., using Ti as i), it is important to choose suitable EW feedstocks that are enriched in the respective immobile tracer, for example BRB rather than PVB in the case of i = Ti. Some detrital elements that may be useful as tracers of feedstock addition can be toxic at elevated soil concentrations, for example Ni and Cr (Haque et al., 2020a; Suhrhoff, 2022; Dupla et al., 2023). Where these are used to inform on feedstock addition, it may be necessary to compromise between feedstock resolvability (i.e., high concentrations) and environmental concerns. Elements with multiple stable isotopes are ideal tracers of feedstock addition (i) as this allow for isotope dilution methods which greatly decreases analytical uncertainty on concentration measurements (Reershemius et al., 2023).

In the context of optimal soil-feedstock matching, a public database of feedstock compositions would be of great help for practitioners. Scaling of EW would greatly benefit from quarries and EW suppliers publicly sharing their assessed feedstock data. Furthermore, a larger number of feedstock providers is desirable both from the perspective of feedstock composition variability (i.e., being able to match soils with a wide range of compositions with ideal feedstocks based on MRV approach) as well as to minimize transport distances and reduce technoeconomic barriers to scale. In this light, there are multiple reasons that many smaller quarries is advantageous over fewer large providers.

Lastly, we present a tool to enable practitioners to optimize parameters like feedstock addition and the choice of detrital elements as proxies for feedstock addition for their own site-specific soil composition. The framework presented here can be incorporated into MRV methods to vet reported weathering rates from EW deployments, and as such represents a way in which stakeholders can have confidence in reported claims of CDR from EW.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: Geochemical and Mineralogical Data for Soils of the Conterminous United States (https://pubs.usgs.gov/ds/801/). Additional data for feedstock compositions can be found in Supplementary Datasheet 1 in the Supplementary material.

Author contributions

TS: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Validation, Visualization, Writing – original draft, Writing – review & editing. TR: Conceptualization, Formal analysis, Investigation, Methodology, Validation, Visualization, Writing – original draft, Writing – review & editing. JW: Conceptualization, Formal analysis, Investigation, Methodology, Software, Validation, Writing – review & editing. JJ: Formal analysis, Investigation, Methodology, Writing – review & editing. CR: Conceptualization, Investigation, Writing – review & editing. NP: Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Supervision, Validation, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. TS is funded by the Swiss National Science Foundation (Grant P500PN_210790). NP and CR acknowledge funding from the Grantham foundation.

Acknowledgments

TS and NP acknowledge support from the Yale Center for Natural Carbon Capture.

Conflict of interest

JJ is funded through the public benefit corporation, Mati Carbon, a subsidiary of the not-for profit-Swaniti Initiative.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fclim.2024.1346117/full#supplementary-material

Footnotes

1. ^ https://resolvability.shinyapps.io/application-amount/

2. ^ https://resolvability.shinyapps.io/dissolution-rate/

3. ^ https://resolvability.shinyapps.io/res-single/

4. ^ https://resolvability.shinyapps.io/res-ratio/

References

Alloway, B. J. (2012). “Heavy metals in soils—trace metals and metalloids in soils and their bioavailability” in Heavy metals in soils: trace metals and metalloids in soils and their bioavailability (Dordrecht: Springer).

Google Scholar

Almaraz, M., Bingham, N. L., Holzer, I. O., Geoghegan, E. K., Goertzen, H., Sohng, J., et al. (2022). Methods for determining the CO removal capacity of enhanced weathering in agronomic settings. Front. Clim. 4:970429. doi: 10.3389/fclim.2022.970429

Crossref Full Text | Google Scholar

Amann, T., and Hartmann, J. (2022). Carbon accounting for enhanced weathering. Front. Clim. 4:849948. doi: 10.3389/fclim.2022.849948

Crossref Full Text | Google Scholar

Amann, T., Hartmann, J., Hellmann, R., Trindade Pedros, E., and Malik, A. (2022). Enhanced weathering potentials—the role of in situ CO and grain size distribution. Front. Clim. 4:929268. doi: 10.3389/fclim.2022.929268

Crossref Full Text | Google Scholar

Amann, T., Hartmann, J., Struyf, E., De Oliveira Garcia, W., Fischer, E. K., Janssens, I., et al. (2020). Enhanced weathering and related element fluxes—a cropland mesocosm approach. Biogeosciences 17, 103–119. doi: 10.5194/bg-17-103-2020

Crossref Full Text | Google Scholar

Anderson, S. P., Dietrich, W. E., and Brimhall, G. H. (2002). Weathering profiles, mass-balance analysis, and rates of solute loss: linkages between weathering and erosion in a small, steep catchment. Bull. Geol. Soc. Am. 114, 1143–1158. doi: 10.1130/0016-7606(2002)114<1143:WPMBAA>2.0.CO

Crossref Full Text | Google Scholar

Andrews, M. G., and Taylor, L. L. (2019). Combating climate change through enhanced weathering of agricultural soils. Elements 15, 253–258. doi: 10.2138/gselements.15.4.253

Crossref Full Text | Google Scholar

Baek, S. H., Kanzaki, Y., Lora, J. M., Planavsky, N., Reinhard, C. T., and Zhang, S. (2023). Impact of climate on the global capacity for enhanced rock weathering on croplands. Earth’s Future 11:e2023EF003698. doi: 10.1029/2023EF003698

Crossref Full Text | Google Scholar

Bartlett, R., and James, B. (1979). Behavior of chromium in soils: oxidation. J. Environ. Qual. 8, 31–35. doi: 10.2134/jeq1979.00472425000800010008x

Crossref Full Text | Google Scholar

Becquer, T., Quantin, C., Sicot, M., and Boudot, J. P. (2003). Chromium availability in ultramafic soils from New Caledonia. Sci. Total Environ. 301, 251–261. doi: 10.1016/S0048-9697(02)00298-X

Crossref Full Text | Google Scholar

Beerling, D. J. (2017). Enhanced rock weathering: biological climate change mitigation with co-benefits for food security? Biol. Lett. 13, 4–7. doi: 10.1098/rsbl.2017.0149

Crossref Full Text | Google Scholar

Beerling, D. J., Epihov, D. Z., Kantola, I. B., Masters, M. D., Reershemius, T., Planavsky, N. J., et al. (2024). Enhanced weathering in the U.S. Corn Belt delivers carbon sequestration with agronomic benefits. Proc. Natl. Acad. Sci. U.S.A. 120, 1–34. doi: 10.1073/pnas.2319436121

Crossref Full Text | Google Scholar

Beerling, D. J., Kantzas, E. P., Lomas, M. R., Wade, P., Eufrasio, R. M., Renforth, P., et al. (2020). Potential for large-scale CO₂ removal via enhanced rock weathering with croplands. Nature 583, 242–248. doi: 10.1038/s41586-020-2448-9

Crossref Full Text | Google Scholar

Beerling, D. J., Kantzas, E. P., Martin, M. V., Lomas, M. R., Lyla, L., Zhang, S., et al. (2023). Transforming U.S. agriculture with crushed rock for CO₂ sequestration and increased production. arXiv. 1–37. Available at: https://doi.org/10.48550/arXiv.2308.04302. [Epub ahead of preprint]

Google Scholar

Beerling, D. J., Leake, J. R., Long, S. P., Scholes, J. D., Ton, J., Nelson, P. N., et al. (2018). Farming with crops and rocks to address global climate, food and soil security. Nat. Plants 4, 138–147. doi: 10.1038/s41477-018-0108-y

Crossref Full Text | Google Scholar

Boiko, O., Kagone, S., and Senay, G. (2021). “Soil properties dataset in the United States” in USGS Data Release (Earth Resources Observation and Science (EROS) Center).

Google Scholar

Brady, N. C., and Weil, R. R. (2016). The nature and properties of soils. 15th Edn Columbus, OH, USA: Pearson.

Google Scholar

Brantley, S. L., and Lebedeva, M. (2011). Learning to read the chemistry of regolith to understand the critical zone. Annu. Rev. Earth Planet. Sci. 39, 387–416. doi: 10.1146/annurev-earth-040809-152321

Crossref Full Text | Google Scholar

Brimhall, G. H., Christopher, J. L., Ford, C., Bratt, J., Taylor, G., and Warin, O. (1991). Quantitative geochemical approach to pedogenesis: importance of parent material reduction, volumetric expansion, and eolian influx in lateritization. Geoderma 51, 51–91. doi: 10.1016/0016-7061(91)90066-3

Crossref Full Text | Google Scholar

Brimhall, G. H., and Dietrich, W. E. (1987). Constitutive mass balance relations between chemical composition, volume, density, porosity, and strain in metasomatic hydrochemical systems: results on weathering and pedogenesis. Geochim. Cosmochim. Acta 51, 567–587. doi: 10.1016/0016-7037(87)90070-6

Crossref Full Text | Google Scholar

Calabrese, S., Wild, B., Bertagni, M. B., Bourg, I. C., White, C., Aburto, F., et al. (2022). Nano-to global-scale uncertainties in terrestrial enhanced weathering. Environ. Sci. Technol. 56, 15261–15272. doi: 10.1021/acs.est.2c03163

Crossref Full Text | Google Scholar

Campbell, J., Bastianini, L., Buckman, J., Bullock, L., Foteinis, S., Furey, V., et al. (2023). Measurements in geochemical carbon dioxide removal. 1st Edn Edinburgh, UK: Heriot-Watt University.

Google Scholar

Chadwick, O. A., Brimhall, G. H., and Hendricks, D. M. (1990). From a black to a gray box—a mass balance interpretation of pedogenesis. Geomorphology 3, 369–390. doi: 10.1016/0169-555X(90)90012-F

Crossref Full Text | Google Scholar

Chadwick, O. A., Derry, L. A., Vitousek, P. M., Huebert, B. J., and Hedin, L. O. (1999). Changing sources of nutrients during four million years of ecosystem development. Nature 397, 491–497. doi: 10.1038/17276

Crossref Full Text | Google Scholar

Chay, F., Klitzke, J., Hausfather, Z., Martin, K., Freeman, J., and Cullenward, D. (2022). Verification confidence levels for carbon dioxide removal. Carbon, Available at: https://carbonplan.org/research/cdr-verification-explainer

Google Scholar

Clarkson, M. O., Larkin, C. S., Swoboda, P., Reershemius, T., Suhrhoff, T. J., Maesano, C. N., et al. (2024). A review of measurement for quantification of carbon dioxide removal by enhanced weathering in soil. Front. Clim., 1–44. Available at: https://eartharxiv.org/repository/view/6317/

Google Scholar

Cornu, S., Lucas, Y., Lebon, E., Ambrosi, J. P., Luizão, F., Rouiller, J., et al. (1999). Evidence of titanium mobility in soil profiles, Manaus, Central Amazonia. Geoderma 91, 281–295. doi: 10.1016/S0016-7061(99)00007-5

Crossref Full Text | Google Scholar

Crameri, F., Shephard, G. E., and Heron, P. J. (2020). The misuse of colour in science communication. Nat. Commun. 11, 1–10. doi: 10.1038/s41467-020-19160-7

Crossref Full Text | Google Scholar

Daval, D., Calvaruso, C., Guyot, F., and Turpault, M. P. (2018). Time-dependent feldspar dissolution rates resulting from surface passivation: experimental evidence and geochemical implications. Earth Planet. Sci. Lett. 498, 226–236. doi: 10.1016/j.epsl.2018.06.035

Crossref Full Text | Google Scholar

Dietzen, C., Harrison, R., and Michelsen-Correa, S. (2018). Effectiveness of enhanced mineral weathering as a carbon sequestration tool and alternative to agricultural lime: an incubation experiment. Int. J. Greenhouse Gas Control 74, 251–258. doi: 10.1016/j.ijggc.2018.05.007

Crossref Full Text | Google Scholar

Dietzen, C., and Rosing, M. T. (2023). Quantification of CO₂ uptake by enhanced weathering of silicate minerals applied to acidic soils. Int. J. Greenhouse Gas Control 125:103872. doi: 10.1016/j.ijggc.2023.103872

Crossref Full Text | Google Scholar

Du, X., Rate, A. W., and Gee, M. A. M. (2012). Redistribution and mobilization of titanium, zirconium and thorium in an intensely weathered lateritic profile in Western Australia. Chem. Geol. 330–331, 101–115. doi: 10.1016/j.chemgeo.2012.08.030

Crossref Full Text | Google Scholar

Dupla, X., Möller, B., Baveye, P. C., and Grand, S. (2023). Potential accumulation of toxic trace elements in soils during enhanced rock weathering. Eur. J. Soil Sci. 74, 1–14. doi: 10.1111/ejss.13343

Crossref Full Text | Google Scholar

Edwards, D. P., Lim, F., James, R. H., Pearce, C. R., Scholes, J., Freckleton, R. P., et al. (2017). Climate change mitigation: potential benefits and pitfalls of enhanced rock weathering in tropical agriculture. Biol. Lett. 13:20160715. doi: 10.1098/rsbl.2016.0715

Crossref Full Text | Google Scholar

Feng, D., and Hicks, A. (2023). Environmental, human health, and CO₂ payback estimation and comparison of enhanced weathering for carbon capture using wollastonite. J. Clean. Prod. 414:137625. doi: 10.1016/j.jclepro.2023.137625

Crossref Full Text | Google Scholar

Fisher, B. A., Rendahl, A. K., Aufdenkampe, A. K., and Yoo, K. (2017). Quantifying weathering on variable rocks, an extension of geochemical mass balance: critical zone and landscape evolution. Earth Surf. Process. Landf. 42, 2457–2468. doi: 10.1002/esp.4212

Crossref Full Text | Google Scholar

Frontier . (2024). Buyer principles for responsible procurement of carbon removal from enhanced weathering in working lands. Available at: https://frontierclimate.com/assets/enhanced-weathering-buyer-principles.pdf

Google Scholar

Fuss, S., Lamb, W. F., Callaghan, M. W., Hilaire, J., Creutzig, F., Amann, T., et al. (2018). Negative emissions—part 2: costs, potentials and side effects. Environ. Res. Lett. 13:063002. doi: 10.1088/1748-9326/aabf9f

Crossref Full Text | Google Scholar

Gaillardet, J., Viers, J., and Dupré, B. (2014). “Trace elements in river waters” in Treatise on geochemistry. eds. H. D. Holland and K. K. Turekian. 2nd ed (Columbus, OH, USA: Elsevier), 195–235.

Google Scholar

Goll, D. S., Ciais, P., Amann, T., Buermann, W., Chang, J., Eker, S., et al. (2021). Potential CO₂ removal from enhanced weathering by ecosystem responses to powdered rock. Nat. Geosci. 14, 545–549. doi: 10.1038/s41561-021-00798-x

Crossref Full Text | Google Scholar

Hamilton, S. K., Kurzman, A. L., Arango, C., Jin, L., and Robertson, G. P. (2007). Evidence for carbon sequestration by agricultural liming. Glob. Biogeochem. Cycles 21, 1–12. doi: 10.1029/2006GB002738

Crossref Full Text | Google Scholar

Haque, F., Chiang, Y. W., and Santos, R. M. (2020a). Risk assessment of Ni, Cr, and Si release from alkaline minerals during enhanced weathering. Open Agric. 5, 166–175. doi: 10.1515/opag-2020-0016

Crossref Full Text | Google Scholar

Haque, F., Santos, R. M., and Chiang, Y. W. (2020b). CO₂ sequestration by wollastonite-amended agricultural soils—an Ontario field study. Int. J. Greenhouse Gas Control 97:103017. doi: 10.1016/j.ijggc.2020.103017

Crossref Full Text | Google Scholar

Haque, F., Santos, R. M., and Chiang, Y. W. (2020c). Optimizing inorganic carbon sequestration and crop yield with wollastonite soil amendment in a microplot study. Front. Plant Sci. 11:1012. doi: 10.3389/fpls.2020.01012

Crossref Full Text | Google Scholar

Haque, F., Santos, R. M., Dutta, A., Thimmanagari, M., and Chiang, Y. W. (2019). Co-benefits of wollastonite weathering in agriculture: CO₂ sequestration and promoted plant growth. ACS Omega 4, 1425–1433. doi: 10.1021/acsomega.8b02477

Crossref Full Text | Google Scholar

Hartmann, J., and Kempe, S. (2008). What is the maximum potential for CO₂ sequestration by “stimulated” weathering on the global scale? Naturwissenschaften 95, 1159–1164. doi: 10.1007/s00114-008-0434-4

Crossref Full Text | Google Scholar

Hartmann, J., and Moosdorf, N. (2012). The new global lithological map database GLiM: a representation of rock properties at the earth surface. Geochem. Geophys. Geosyst. 13, 1–37. doi: 10.1029/2012GC004370

Crossref Full Text | Google Scholar

Hartmann, J., West, A. J., Renforth, P., Köhler, P., De La Rocha, C. L., Wolf-Gladrow, D. A., et al. (2013). Enhanced chemical weathering as a geoengineering strategy to reduce atmospheric carbon dioxide, supply nutrients, and mitigate ocean acidification. Rev. Geophys. 51, 113–149. doi: 10.1002/rog.20004

Crossref Full Text | Google Scholar

Holzer, I. O., Nocco, M. A., and Houlton, B. Z. (2023). Direct evidence for atmospheric carbon dioxide removal via enhanced weathering in cropland soil. Environ. Res. Commun. 5:101004. doi: 10.1088/2515-7620/acfd89

Crossref Full Text | Google Scholar

Horton, J. D., San Juan, C. A., and Stoesser, D. B. (2017). “State geologic map compilation (SGMC) geodatabase of the conterminous United States” in USGS ScienceBase Catalog. (USGS: USGS Data Release), 1–23.

Google Scholar

James, B. R. (1996). The challenge of remediating chromium-contaminated soils. Environ. Sci. Technol. 30, 248A–251A. doi: 10.1021/es962269h

Crossref Full Text | Google Scholar

James, B. R., and Bartlett, R. J. (1988). “Mobility and bioavailability of chromium in soil” in Chromium in natural and human environments. eds. J. O. Nriagu and E. Nieboer (New York, NY: Wiley Interscience), 265–305.

Google Scholar

Jariwala, H., Haque, F., Vanderburgt, S., Santos, R. M., and Chiang, Y. W. (2022). Mineral-soil-plant-nutrient synergisms of enhanced weathering for agriculture: short-term investigations using fast-weathering wollastonite skarn. Front. Plant Sci. 13:929457. doi: 10.3389/fpls.2022.929457

Crossref Full Text | Google Scholar

Jiang, K., Qi, H. W., and Hu, R. Z. (2018). Element mobilization and redistribution under extreme tropical weathering of basalts from the Hainan Island, South China. J. Asian Earth Sci. 158, 80–102. doi: 10.1016/j.jseaes.2018.02.008

Crossref Full Text | Google Scholar

Kantola, I. B., Blanc-Betes, E., Master, M. D., Chang, E., Marklein, A., Moore, C. E., et al. (2023). Improved net carbon budgets in the US Midwest through direct measured impacts of enhanced weathering. Glob. Change Biol. 29, 7012–7028. doi: 10.1111/gcb.16903

Crossref Full Text | Google Scholar

Kantola, I. B., Masters, M. D., Beerling, D. J., Long, S. P., and DeLucia, E. H. (2017). Potential of global croplands and bioenergy crops for climate change mitigation through deployment for enhanced weathering. Biol. Lett. 13:20160714. doi: 10.1098/rsbl.2016.0714

Crossref Full Text | Google Scholar

Kantzas, E. P., Martin, M. V., Lomas, M. R., Eufrasio, R. M., Renforth, P., Lewis, A. L., et al. (2022). Substantial carbon drawdown potential from enhanced rock weathering in the United Kingdom. Nat. Geosci. 15, 382–389. doi: 10.1038/s41561-022-00925-2

Crossref Full Text | Google Scholar

Khalidy, R., Haque, F., Chiang, Y. W., and Santos, R. M. (2021). Monitoring pedogenic inorganic carbon accumulation due to weathering of amended silicate minerals in agricultural soils. J. Vis. Exp. 2021:e61996. doi: 10.3791/61996

Crossref Full Text | Google Scholar

Kierczak, J., Pietranik, A., and Pędziwiatr, A. (2021). Ultramafic geoecosystems as a natural source of Ni, Cr, and Co to the environment: a review. Sci. Total Environ. 755:142260. doi: 10.1016/j.scitotenv.2020.142620

Crossref Full Text | Google Scholar

Knapp, W. J., Stevenson, E. I., Renforth, P., Ascough, P. L., Knight, A. C. G., Bridgestock, L., et al. (2023). Quantifying CO₂ removal at enhanced weathering sites: a multiproxy approach. Environ. Sci. Technol. 57, 9854–9864. doi: 10.1021/acs.est.3c03757

Crossref Full Text | Google Scholar

Knapp, W. J., and Tipper, E. T. (2022). The efficacy of enhancing carbonate weathering for carbon dioxide sequestration. Front. Clim. 4:928215. doi: 10.3389/fclim.2022.928215

Crossref Full Text | Google Scholar

Köhler, P., Hartmann, J., and Wolf-Gladrow, D. A. (2010). Geoengineering potential of artificially enhanced silicate weathering of olivine. Proc. Natl. Acad. Sci. U.S.A. 107, 20228–20233. doi: 10.1073/pnas.1000545107

Crossref Full Text | Google Scholar

Kurtz, A. C., Derry, L. A., Chadwick, O. A., and Alfano, M. J. (2000). Refractory element mobility in volcanic soils. Geology 28, 683–686. doi: 10.1130/0091-7613(2000)028<0683:REMIVS>2.3.CO;2

Crossref Full Text | Google Scholar

Larkin, C. S., Andrews, M. G., Pearce, C. R., Yeong, K. L., Beerling, D. J., Bellamy, J., et al. (2022). Quantification of CO₂ removal in a large-scale enhanced weathering field trial on an oil palm plantation in Sabah, Malaysia. Front. Clim. 4:959229. doi: 10.3389/fclim.2022.959229

Crossref Full Text | Google Scholar

Lehnert, K., Su, Y., Langmuir, C. H., Sarbas, B., and Nohl, U. (2000). A global geochemical database structure for rocks. Geochem. Geophys. Geosyst. 1. doi: 10.1029/1999gc000026

Crossref Full Text | Google Scholar

Lewis, A. L., Sarkar, B., Wade, P., Kemp, S. J., Hodson, M. E., Taylor, L. L., et al. (2021). Effects of mineralogy, chemistry and physical properties of basalts on carbon capture potential and plant-nutrient element release via enhanced weathering. Appl. Geochem. 132:105023. doi: 10.1016/j.apgeochem.2021.105023

Crossref Full Text | Google Scholar

Lipp, A. G., Shorttle, O., Sperling, E. A., Brocks, J. J., Cole, D. B., Crockford, P. W., et al. (2021). The composition and weathering of the continents over geologic time. Geochem. Perspect. Lett. 17, 21–26. doi: 10.7185/geochemlet.2109

Crossref Full Text | Google Scholar

Mallarino, A. P., Sawyer, J. E., and Barnhart, S. K. (2013). A general guide for crop nutrient and limestone recommendations in Iowa. Iowa State University. Available at: https://naturalresources.extension.iastate.edu/files/page/files/general_guide_for_nutrient_and_limestone_recommendations_in_iowa.pdf, and the location is Ames, IA, USA.

Google Scholar

Paulo, C., Power, I. M., Stubbs, A. R., Wang, B., Zeyen, N., and Wilson, S. A. (2021). Evaluating feedstocks for carbon dioxide removal by enhanced rock weathering and CO₂ mineralization. Appl. Geochem. 129:104955. doi: 10.1016/j.apgeochem.2021.104955

Crossref Full Text | Google Scholar

Pogge von Strandmann, P. A. E., Renforth, P., West, A. J., Murphy, M. J., Luu, T. H., and Henderson, G. M. (2021). The lithium and magnesium isotope signature of olivine dissolution in soil experiments. Chem. Geol. 560:120008. doi: 10.1016/j.chemgeo.2020.120008

Crossref Full Text | Google Scholar

Pogge von Strandmann, P. A. E., Tooley, C., Mulders, J. J. P. A., and Renforth, P. (2022). The dissolution of olivine added to soil at 4°C: implications for enhanced weathering in cold regions. Front. Clim. 4:827698. doi: 10.3389/fclim.2022.827698

Crossref Full Text | Google Scholar

Raymond, P. A., Oh, N. H., Turner, R. E., and Broussard, W. (2008). Anthropogenically enhanced fluxes of water and carbon from the Mississippi River. Nature 451, 449–452. doi: 10.1038/nature06505

Crossref Full Text | Google Scholar

Reershemius, T., Kelland, M. E., Davis, I. R., D’Ascanio, R., Kalderon-Asael, B., Asael, D., et al. (2023). Initial validation of a soil-based mass-balance approach for empirical monitoring of enhanced rock weathering rates. Environ. Sci. Technol. 57, 19497–19507. doi: 10.1021/acs.est.3c03609

Crossref Full Text | Google Scholar

Reershemius, T., and Suhrhoff, T. J. (2023). On error, uncertainty, and assumptions in calculating carbon dioxide removal rates by enhanced rock weathering in Kantola et al., 2023. Glob. Change Biol. 30:e17025. doi: 10.1111/gcb.17025

Crossref Full Text | Google Scholar

Renforth, P. (2012). The potential of enhanced weathering in the UK. Int. J. Greenhouse Gas Control 10, 229–243. doi: 10.1016/j.ijggc.2012.06.011

Crossref Full Text | Google Scholar

Renforth, P. (2019). The negative emission potential of alkaline materials. Nat. Commun. 10:1407. doi: 10.1038/s41467-019-09475-5

Crossref Full Text | Google Scholar

Renforth, P., Pogge von Strandmann, P. A. E., and Henderson, G. M. (2015). The dissolution of olivine added to soil: implications for enhanced weathering. Appl. Geochem. 61, 109–118. doi: 10.1016/j.apgeochem.2015.05.016

Crossref Full Text | Google Scholar

Riebe, C. S., Kirchner, J. W., and Finkel, R. C. (2003). Long-term rates of chemical weathering and physical erosion from cosmogenic nuclides and geochemical mass balance. Geochim. Cosmochim. Acta 67, 4411–4427. doi: 10.1016/S0016-7037(03)00382-X

Crossref Full Text | Google Scholar

Rieder, L., Amann, T., and Hartmann, J. (2024). Soil electrical conductivity as a proxy for enhanced weathering in soils. Front. in Clim. 5:1283107. doi: 10.3389/fclim.2023.1283107

Crossref Full Text | Google Scholar

Rijnders, J., Vicca, S., Struyf, E., Amann, T., Hartmann, J., Meire, P., et al. (2023). The effects of olivine fertilization on growth and elemental composition of barley and wheat differ with olivine grain size and rain regimes. Front. Environ. Sci. 11:117621. doi: 10.3389/fenvs.2023.1172621

Crossref Full Text | Google Scholar

Rinder, T., and von Hagke, C. (2021). The influence of particle size on the potential of enhanced basalt weathering for carbon dioxide removal—insights from a regional assessment. J. Clean. Prod. 315:128178. doi: 10.1016/j.jclepro.2021.128178

Crossref Full Text | Google Scholar

Schuiling, R. D., and Krijgsman, P. (2006). Enhanced weathering: an effective and cheap tool to sequester CO₂. Clim. Change 74, 349–354. doi: 10.1007/s10584-005-3485-y

Crossref Full Text | Google Scholar

Seifritz, W. (1990). CO₂ disposal by means of silicates. Nature 345:486. doi: 10.1038/345486b0

Crossref Full Text | Google Scholar

Seigneur, C., and Constantinou, E. (1995). Chemical kinetic mechanism for atmospheric chromium. Environ. Sci. Technol. 29, 222–231. doi: 10.1021/es00001a029

Crossref Full Text | Google Scholar

Sheldon, N. D., and Tabor, N. J. (2009). Quantitative paleoenvironmental and paleoclimatic reconstruction using paleosols. Earth Sci. Rev. 95, 1–52. doi: 10.1016/j.earscirev.2009.03.004

Crossref Full Text | Google Scholar

Smith, D. B., Cannon, W. F., Woodruff, L. G., Solano, F., Kilburn, J. E., and Fey, D. L. (2013). Geochemical and mineralogical data for soils of the conterminous United States. U.S. Geological Survey 801, 1–26. doi: 10.3133/ds801

Crossref Full Text | Google Scholar

Stevens, D. L., and Olsen, A. R. (2000). Spatially-restricted random sampling designs for design-based and model-based estimation. Accuracy 2000: Proceedings of the 4th International Symposium on Spatial Accuracy Assessment in Natural Resources and Environmental Sciences, 609–616.

Google Scholar

Stevens, D. L., and Olsen, A. R. (2003). Variance estimation for spatially balanced samples of environmental resources. Environmetrics 14, 593–610. doi: 10.1002/env.606

Crossref Full Text | Google Scholar

Stevens, D. L., and Olsen, A. R. (2004). Spatially balanced sampling of natural resources. J. Am. Stat. Assoc. 99, 262–278. doi: 10.1198/016214504000000250

Crossref Full Text | Google Scholar

Strefler, J., Amann, T., Bauer, N., Kriegler, E., and Hartmann, J. (2018). Potential and costs of carbon dioxide removal by enhanced weathering of rocks. Environ. Res. Lett. 13:034010. doi: 10.1088/1748-9326/aaa9c4

Crossref Full Text | Google Scholar

Strefler, J., Bauer, N., Humpenöder, F., Klein, D., Popp, A., and Kriegler, E. (2021). Carbon dioxide removal technologies are not born equal. Environ. Res. Lett. 16:074021. doi: 10.1088/1748-9326/ac0a11

Crossref Full Text | Google Scholar

Suhrhoff, T. J. (2022). Phytoprevention of heavy metal contamination from terrestrial enhanced weathering: can plants save the day? Front. Clim. 3:820204. doi: 10.3389/fclim.2021.820204

Crossref Full Text | Google Scholar

Swoboda, P., Döring, T. F., and Hamer, M. (2022). Remineralizing soils? The agricultural usage of silicate rock powders: a review. Sci. Total Environ. 807:150976. doi: 10.1016/j.scitotenv.2021.150976

Crossref Full Text | Google Scholar

Tabor, N. J., Montanez, I. P., Zierenberg, R., and Currie, B. S. (2004). Mineralogical and geochemical evolution of a basalt-hosted fossil soil (late Triassic, Ischigualasto formation, Northwest Argentina): potential for paleoenvironmental reconstruction. Bull. Geol. Soc. Am. 116, 1280–1293. doi: 10.1130/B25222.1

Crossref Full Text | Google Scholar

Taylor, L. L., Driscoll, C. T., Groffman, P. M., Rau, G. H., Blum, J. D., and Beerling, D. J. (2021). Increased carbon capture by a silicate-treated forested watershed affected by acid deposition. Biogeosciences 18, 169–188. doi: 10.5194/bg-18-169-2021

Crossref Full Text | Google Scholar

Taylor, L. L., Quirk, J., Thorley, R. M. S., Kharecha, P. A., Hansen, J., Ridgwell, A., et al. (2016). Enhanced weathering strategies for stabilizing climate and averting ocean acidification. Nat. Clim. Change 6, 402–406. doi: 10.1038/nclimate2882

Crossref Full Text | Google Scholar

ten Berge, H. F. M., van der Meer, H. G., Steenhuizen, J. W., Goedhart, P. W., Knops, P., and Verhagen, J. (2012). Olivine weathering in soil, and its effects on growth and nutrient uptake in ryegrass (Lolium perenne L.): a pot experiment. PLoS One 7:e42098. doi: 10.1371/journal.pone.0042098

Crossref Full Text | Google Scholar

Vanderkloot, E., and Ryan, P. (2023). Quantifying the effect of grain size on weathering of basaltic powders: implications for negative emission technologies via soil carbon sequestration. Appl. Geochem. 155:105728. doi: 10.1016/j.apgeochem.2023.105728

Crossref Full Text | Google Scholar

Vienne, A., Poblador, S., Portillo-Estrada, M., Hartmann, J., Ijiehon, S., Wade, P., et al. (2022). Enhanced weathering using basalt rock powder: carbon sequestration, co-benefits and risks in a mesocosm study with Solanum tuberosum. Front. Clim. 4:869456. doi: 10.3389/fclim.2022.869456

Crossref Full Text | Google Scholar

Vink, J. P. M., and Knops, P. (2023). Size-fractionated weathering of olivine, its CO₂-sequestration rate, and ecotoxicological risk assessment of nickel release. Fortschr. Mineral. 13, 1–11. doi: 10.3390/min13020235

Crossref Full Text | Google Scholar

West, T. O., and McBride, A. C. (2005). The contribution of agricultural lime to carbon dioxide emissions in the United States: dissolution, transport, and net emissions. Agric. Ecosyst. Environ. 108, 145–154. doi: 10.1016/j.agee.2005.01.002

Crossref Full Text | Google Scholar

White, A. F., and Brantley, S. L. (2003). The effect of time on the weathering of silicate minerals: why do weathering rates differ in the laboratory and field? Chem. Geol. 202, 479–506. doi: 10.1016/j.chemgeo.2003.03.001

Crossref Full Text | Google Scholar

White, A. F., Bullen, T. D., Schulz, M. S., Blum, A. E., Huntington, T. G., and Peters, N. E. (2001). Differential rates of feldspar weathering in granitic regoliths. Geochim. Cosmochim. Acta 65, 847–869. doi: 10.1016/S0016-7037(00)00577-9

Crossref Full Text | Google Scholar

Wieczorek, M. E. (2019). Area-and depth-weighted average of soil pH from STATSGO2 for the conterminous United States and District of Columbia : U.S. Geological Survey.

Google Scholar

Wood, C., Harrison, A. L., and Power, I. M. (2022). Impacts of dissolved phosphorus and soil-mineral-fluid interactions on CO₂ removal through enhanced weathering of wollastonite in soils. Appl. Geochem. 148:105511. doi: 10.1016/j.apgeochem.2022.105511

Crossref Full Text | Google Scholar

Yang, L., Jin, S., Danielson, P., Homer, C., Gass, L., Bender, S. M., et al. (2018). A new generation of the United States National Land Cover Database: requirements, research priorities, design, and implementation strategies. ISPRS J. Photogramm. Remote Sens. 146, 108–123. doi: 10.1016/j.isprsjprs.2018.09.006

Crossref Full Text | Google Scholar

Zhang, S., Planavsky, N. J., Katchinoff, J., Raymond, P. A., Kanzaki, Y., Reershemius, T., et al. (2022). River chemistry constraints on the carbon capture potential of surficial enhanced rock weathering. Limnol. Oceanogr. 67, S148–S157. doi: 10.1002/lno.12244

Crossref Full Text | Google Scholar