- 1Interdisciplinary Programme (IDP) in Climate Studies, Indian Institute of Technology Bombay, Mumbai, India
- 2Indian Institute of Tropical Meteorology, Ministry of Earth Sciences, Pune, India
- 3Department of Civil Engineering, Indian Institute of Technology Bombay, Mumbai, India
Rivers form an essential component of the earth system, with ~36,000 km3 of riverine freshwater being dumped into the global oceans every year. The role of rivers in controlling the sea-surface salinity and ensuing air-sea interactions in the Bay of Bengal (BoB) is well-known from observational studies; however, attempts to include rivers in coupled models used for seasonal prediction have been limited. This study reports the benefits of river routing in coupled models over prescribing observational river discharge and the impact on the Indian Summer Monsoon (ISM) simulation. Seasonal hindcasts are carried out using a state-of-the-art global coupled ocean-atmosphere-land-sea ice model, Climate Forecast System version 2, coupled to a runoff routing model. It is demonstrated that such a coupling leads to a better representation of the upper ocean stratification in northern BoB, causes mixed layer warming during July-August, and imparts a significant inter-annual variability to the mixed layer heat budget. The rainfall-runoff coupled feedback associated with ISM is captured better, and remote teleconnections with the equatorial Pacific are enhanced. Improved seasonal mean temperature and salinity profiles in the northern BoB lead to the formation of a thicker barrier layer, which is closely tied to the freshwater from rivers. These processes result in an overall enhancement of the ISM rainfall simulation skill, which stems from scale interactions between the sub-seasonal and seasonal variability of ISM. A significant community effort is required to reduce biases in land-surface processes to improve streamflow simulations, along with better parameterization of mixing of river water with the ocean.
Introduction
Rivers discharge ~36,000 km3 of freshwater into the global oceans (Dai et al., 2009). This riverine freshwater (RFW) directly impacts ocean salinity and stratification. Changes in ocean density can affect ocean circulation and currents and, hence, ocean temperature (Lagerloef, 2002; Seidov and Haupt, 2003; Huang and Mehta, 2010). Changes in sea surface salinity (SSS) directly impact the ocean's mixed layer depth (MLD). This layer interacts with the atmosphere, and MLD variability can impact the evolution of the coupled ocean-atmosphere system (Shenoi, 2002; de Boyer Montégut, 2004; Mignot et al., 2007). Salinity control on the mixed layer is much more critical for highly stratified ocean basins such as the Bay of Bengal (BoB) (Shetye et al., 1996), where RFW can cause sudden dips in SSS, thereby forming barrier layers and affecting mixed layer temperature (Lukas and Lindstrom, 1991; Vinayachandran et al., 2002; Rao and Sivakumar, 2003; Thadathil et al., 2007; Rao et al., 2011). These changes in upper ocean stratification can interact with vigorous monsoon intra-seasonal oscillations in the boreal summer and exhibit a classic example of the variability of the coupled ocean-atmosphere system. On monthly time scales, vertical mixing with the sub-surface is the main export pathway for freshwater plumes (Benshila et al., 2014); hence, it can also affect the seasonal mean.
The strong association of RFW with Indian Summer Monsoon (ISM) necessitates its representation in models. Many modeling studies have studied the impact of rivers on ocean salinity and circulation by prescribing observational river-runoff in ocean general circulation models (Howden and Murtugudde, 2001; OGCMs, Han et al., 2001; Durand et al., 2011; Jana et al., 2015; Behara and Vinayachandran, 2016; Srivastava et al., 2020). These studies report a better representation of salinity structure in the ocean model and warming of the mixed layer in response to river forcing in the northern BoB. Chowdary et al. (2016) reported significant salinity biases in long free runs of a coupled climate model due to the prescription of annual mean runoff. They have shown that prescribing local freshwater flux and seasonally varying river discharges reduces salinity bias in OGCM simulations. Prescribing runoff might be a suitable technique for standalone ocean model simulations but is not ideal in coupled ocean-atmosphere simulations, as runoff is a dynamically evolving component of the earth system. Furthermore, such standalone models cannot model the feedback that the atmosphere would have received in a coupled ocean-atmosphere system from the dynamically evolving runoff component. Seo et al. (2009) used a regional coupled model to study the impact of rivers by restoring SSS toward observations and reported realistic salinity distribution and warming near river mouths in the BoB, albeit with a limited impact on monsoon rainfall. Vinayachandran et al. (2015) used an earth system model to study the effects of blocking the rivers in 100-year-long simulations of an earth system model. They found an increase in global SSTs of ~0.5°C and a 10% increase in Indian Summer Monsoon Rainfall (ISMR), associated with increased frequency of La-Nina-type events. Masson et al. (2005) studied the effect of shallow salinity stratification on monsoon onset using a coupled model. They found that barrier layers in the south-eastern Arabian Sea enhance spring time SST warming and lead to early monsoon onset. The effect of El-Niño and Southern Oscillation (ENSO) on the Ganga-Brahmaputra river runoff is well established in the literature (Whitaker et al., 2001; Jian et al., 2009). Therefore, rivers affect ISMR not only on synoptic to intra-seasonal time scales but also interact with other modes of tropical variability, such as the ENSO. These interactions can bear significant implications for the seasonal predictability of ISMR, as it arises from these slowly varying boundary forcing events (Charney and Shukla, 1981).
A routing model is required to implement online river routing in coupled models. The hydrological modeling community has been using such routing models for a long time. Generally, meteorological fluxes from a general circulation model (GCM, such as CFSv2) are used to drive a macro-scale hydrological model such as the Variable Infiltration Capacity (VIC) model. A routing model is used as a post-processor to the hydrological model, providing streamflow predictions. One such model was developed by Lohmann et al. (1996, 1998) and has been used extensively as a post-processor for the VIC model (Nijssen et al., 2001a). This model belongs to the source to sink (STS) category of models. In STS models, the distribution and travel time of runoff between source and sink are parameterized without explicitly tracking the streamflow between grid cells. STS models have been used in coupled GCMs and are easier to parameterize for a wide range of spatial scales (Olivera et al., 2000; Hamman et al., 2017b). The other category of routing models are cell to cell (CTC) models, which parameterize the mass flux between neighboring grid cells, thereby explicitly tracking streamflow. The Community Earth System Model employs one CTC model referred to as the River Transport Model (RTM, Branstetter, 2003). CTC models are challenging to parameterize across wide spatial scales (Sushama et al., 2004). Various other river routing schemes have been developed in the past two decades. Shaad (2018) reviewed 18 routing schemes developed in the past two decades. Some of these models have been coupled to land models or hydrological models and have been utilized for uncoupled applications as well (Miller et al., 1994; Lohmann et al., 1996; Oki and Sud, 1998; Branstetter, 2001, 2003; Bell et al., 2007; Decharme et al., 2010; Pappenberger et al., 2010; David et al., 2011; Paiva et al., 2011; Yamazaki et al., 2011; Verzano et al., 2012; Wen et al., 2012; Lehner and Grill, 2013; Li et al., 2013; Ye et al., 2013; Getirana et al., 2014; Mizukami et al., 2016; Piccolroaz et al., 2016). Some of these routing schemes are used to validate global and regional models based on evaluation of the simulated discharge. These routing schemes differ in channel routing methods, resolution, and characterization of the routing network and have been evaluated for global/regional applications.
General circulation models participating in the Coupled Model Intercomparison Project Phase 5 (CMIP5), (Taylor et al., 2012) include river routing models. However, the climate projections of basin-scale freshwater fluxes derived from these models vary widely, and a significant community effort is required to improve basin-scale freshwater fluxes (Bring et al., 2015). Although rivers form a critical earth system component, many seasonal prediction models do not have an online river routing scheme. Climate Forecast System version 2 (CFSv2, Saha et al., 2014), used for operational forecasts at National Centers for Environmental Prediction (NCEP) and the India Meteorological Department (IMD), prescribes annual mean river runoff to an ocean model. It is worth noting that earlier studies (Han et al., 2001; Howden and Murtugudde, 2001; Vinayachandran et al., 2015; Behara and Vinayachandran, 2016; Chowdary et al., 2016; Jahfer et al., 2017) that studied the effect of river discharge on the ocean and Indian monsoon are sensitivity studies, an ocean model only studies or involves long free-runs of a climate model. To the best of our knowledge, the effects of river routing on ISMR simulation and prediction have not been studied in an operational seasonal prediction framework. Thus, the objective of this study is two-pronged. First, a runoff routing model is coupled to Climate Forecast System version 2 (CFSv2). Such coupling ensures that temporally evolving river freshwater flux is passed on to the ocean model. This represents an improvement over the current operational model, where climatological mean annual observational runoff is prescribed to the ocean model. Second, we intend to investigate the effect of temporally evolving runoff on ISMR simulation and value addition (if any) to the seasonal forecast skill. The analysis is focused primarily on the BoB, since it is thought to be the heart of the Indian monsoon (Goswami et al., 2016). Changes in upper ocean stratification, mixed layer characteristics, rainfall-runoff feedback, seasonal mean biases, and monsoon teleconnections are explored in this study. The synoptically varying nature of riverine freshwater flux can impact ISMR simulation on sub-seasonal time scales as well. This association with synoptic and intra-seasonal variability of the ocean-atmosphere system is also a major area of interest and is explored in Srivastava et al. (2022).
The study is organized as follows: Section Model Description, Data Used, and Methodology presents the model setup and the routing model and its coupling to CFSv2; Section Results and Discussion presents the simulation of river discharge by major river basins across the globe, changes in ocean mean state, stratification, and mixed layer characteristics, biases, skill, and teleconnections in the coupled model setup; the summary and conclusions are presented in Section Conclusions.
Model Description, Data Used, and Methodology
Climate Forecast System Version 2
CFSv2 primarily comprises four sub-models. The Global Forecast System (Moorthi et al., 2001) is the atmospheric core of the model and has a spectral resolution of T126, which amounts to ~110 km horizontal resolution in the tropics with 64 hybrid vertical levels. The land model is the Noah land surface model (Ek et al., 2003) with four soil layers and a snow layer. The ocean model is Modular Ocean Model version 4 (MOM4) (Griffies et al., 2004) and a dynamical sea-ice model (Winton, 2000). MOM4 used a tripolar grid (Murray, 1996) whose resolution is 0.5° × 0.5°poleward of 30°and the meridional resolution increases to 0.25°in between 10°S and 10°N latitudes. MOM4 has 40 vertical levels with a 10-m resolution in the upper 220 m. The Earth System Modeling Framework couples these four sub-models. CFSv2 is used for operational long-range forecasting at the National Centers for Environmental Prediction (NCEP), United States of America, and by the India Meteorological Department (Rao et al., 2019). The model is known to simulate the Indian Monsoon and its variability from synoptic to inter-annual time scales and other global phenomena such as the ENSO with a reasonable skill (Srivastava et al., 2015, 2017; Ramu et al., 2016; Pillai et al., 2018; Krishna et al., 2019; Rao et al., 2019). An annual mean river runoff value is prescribed in the ocean model of CFSv2, which is constant (one value) and is based on the Large and Yeager (2004) dataset, and is the same as in Saha et al. (2014). Figure 1A shows a schematic of the model setup.
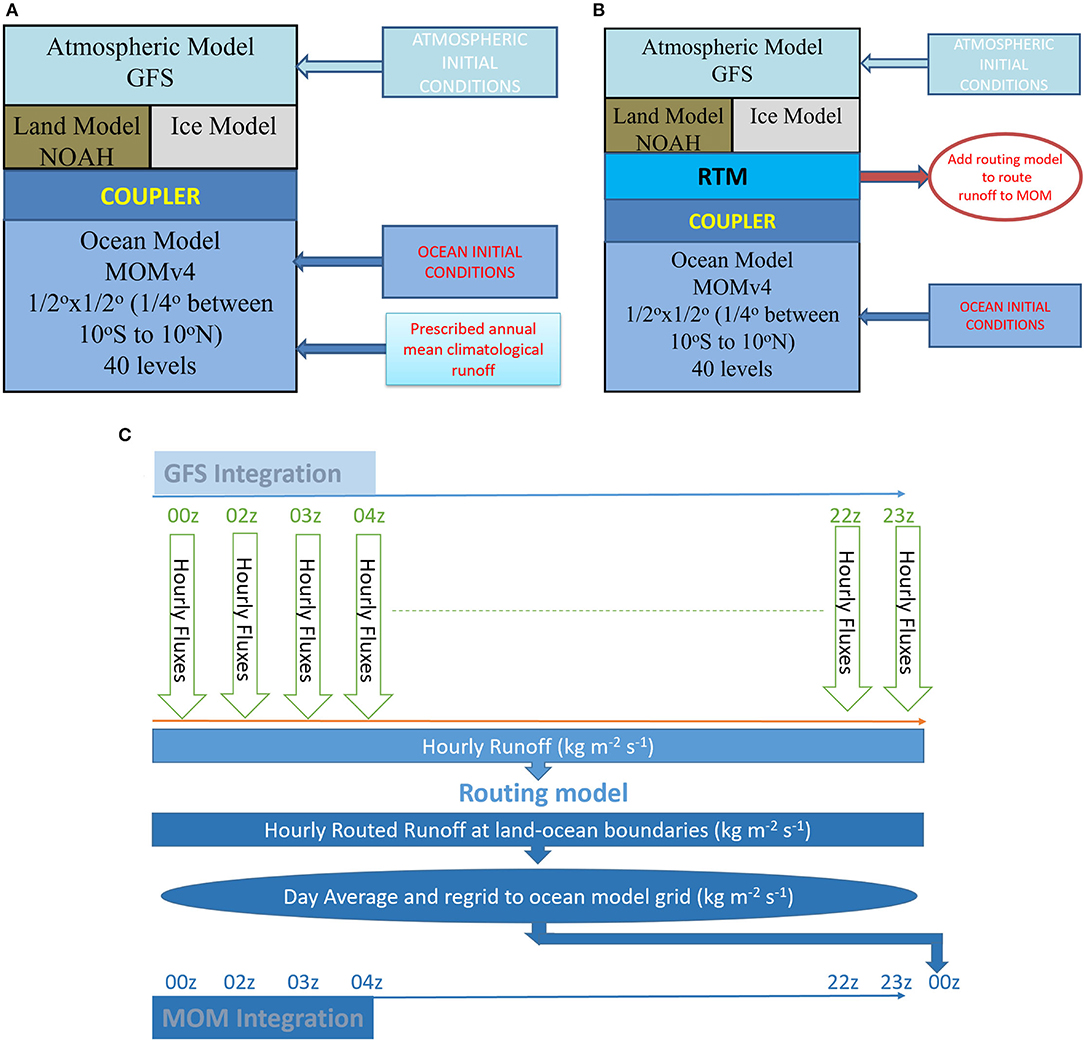
Figure 1. (A) Illustration depicting the model components of the control (CTL) run. (B) Model components of the sensitivity (RIV) run with the routing model added and (C) schematic illustrating the coupling of the routing model to atmospheric and ocean model components.
The Routing Model and Coupling With CFSv2
The land surface parameterization scheme used in the Noah land surface model (Ek et al., 2003) lacks the representation of water transport in the horizontal direction. Therefore, the surface runoff fluxes generated by the Noah land model are not routed to the ocean model. The intention is to route the runoff fluxes from the land model to the ocean model using a routing model. A modified version of the Lohmann et al. (1996) STS model, referred to as RVIC, was developed by the University of Washington Computational Hydrology Group (Hamman et al., 2017b). This source-to-sink model parameterizes the travel time and distribution of runoff between the source and outlet grid points. The code of the model is publicly available (doi: 10.5281/zenodo.269614). Hamman et al. (2017b) provided a detailed description of RVIC. It uses a linearized form of Saint-Venant equations, which are one-dimensional. A global flow direction raster forms the basis for the flow path and distance between each source to sink point. Such raster is developed from the topographic information taken from Wu et al. (2011, 2012) at a 1/16-degree resolution. They use a dominant river-tracing algorithm to extract and upscale river networks. The flow is parameterized as linear and time-invariant impulse response functions (IRFs, also referred to as unit hydrographs). Since flow directions are on a much finer grid compared to the land model resolution, IRFs are upscaled by conservative remapping to the land model grid. The convolution of the runoff from each grid cell with IRFs gives the streamflow at each outlet. RVIC was coupled to CFSv2. Figures 1B,C depict the model schematic and the coupling strategy of RVIC to CFSv2, respectively. RVIC runs at an hourly time step. RVIC routes hourly runoff fluxes from the land model to generate streamflow at land-ocean boundaries. This streamflow is conservatively remapped to the ocean model grid and passed on to the ocean model once every 24 hours. This CFSv2-RVIC coupled run is henceforth referred to as the RIV run. In the ocean model, freshwater flux changes the salinity of top grid cells by changing their volume. Transport of freshwater across ocean surface is enabled by adding it to the volume conservation equation, thereby conserving water mass (Griffies et al., 2005).
Figure 2A shows the annual mean runoff flux (shading) prescribed in the CTL. The red markers indicate the location of river outlets in the routing model setup of the RIV run. Other than the major rivers in this region (such as the Ganga, Brahmaputra, Mahanadi, Godavari, and Krishna), multiple small river basins exist. Along the coast, some small basins represent only one or two grid cells (because of the coarse resolution of the routing model), but they also discharge into the BoB. Figure 2A shows all the discharge locations. Dumping massive quantities of freshwater into just one model grid cell can cause problems because of the formation of strong halocline and vertical advection noise across the front (Griffies et al., 2004, 2005; Yin et al., 2010; Hamman et al., 2017b). Therefore, the runoff in the RIV run is spread horizontally and is discharged into a thick layer [upper 40 m, as in Yin et al. (2010)]. The diffusivity in river mouths is enhanced vertically up to a depth of 40 m to parameterize unresolved scales (Benshila et al., 2014). The gray halos around the red markers in Figure 2A denote the horizontal area over which the runoff is spread. Horizontal spreading was implemented for all river outlets globally between 50°S and 50°N, wherever the river discharge was >10 mm day−1, and for all outlets in the BoB. The prescribed runoff in CTL is pre-spread horizontally, as shown in Figure 2A, but vertical mixing was not enhanced. Also shown in Supplementary Figure 1 are major river basins identified from the DEM and used by the RVIC model.
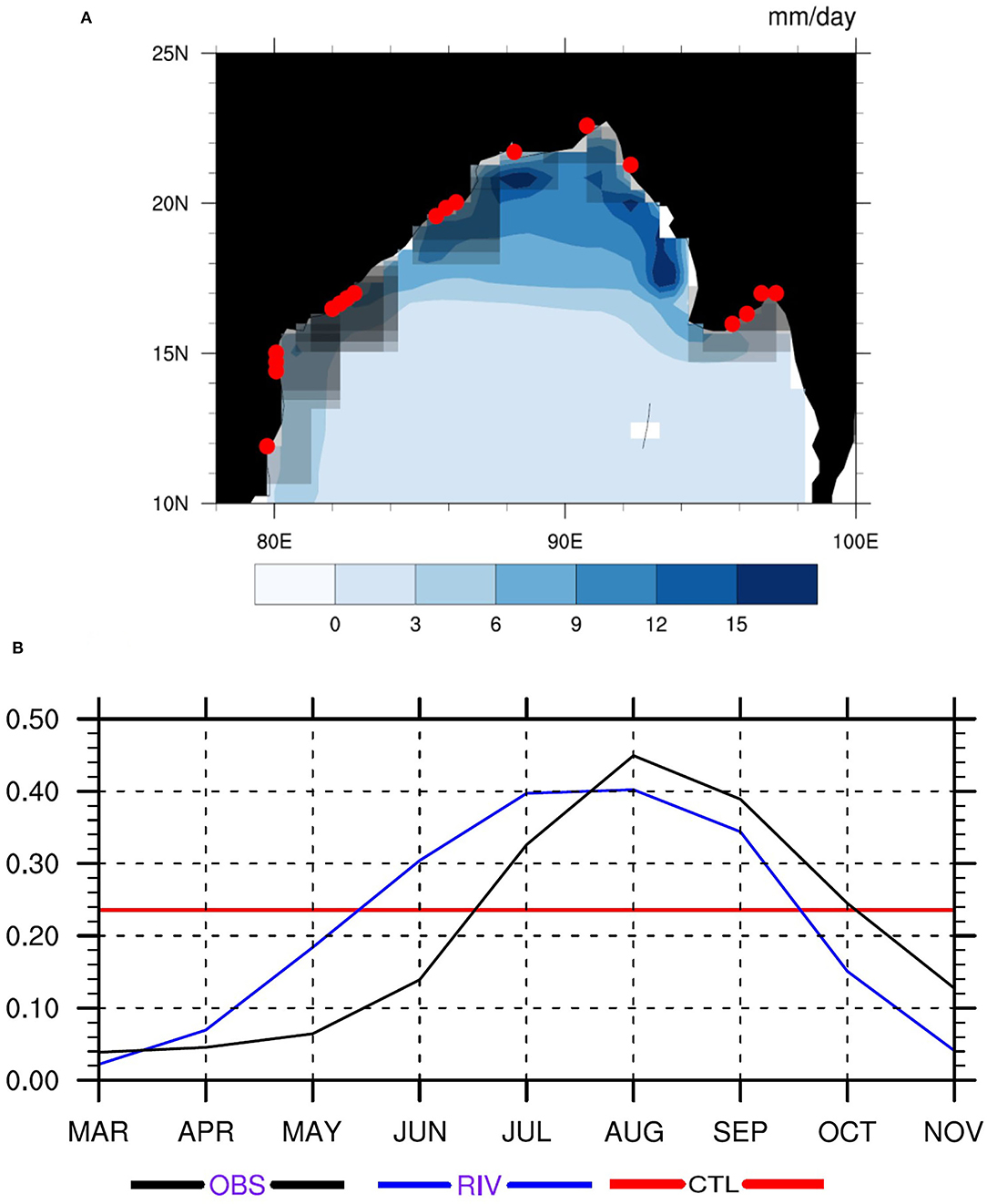
Figure 2. (A) Climatological annual mean values of river runoff (mm day−1) prescribed in the CTL run (shading). The runoff values are pre-spread over the basin before passing them to the ocean model. The red markers denote the river discharge points in the RIV run, and the gray halo around them depicts the area over which the discharge is spread in the ocean model for the RIV run. (B) Climatological annual cycle of river freshwater input (× 104 kg m−2 s−1) into the northern Bay of Bengal (10°N-25°N, 78°E-98°E) basin from the Large and Yeager (2009) dataset (black), the annual mean discharge prescribed in the CTL run (red), and the discharge simulated by the RIV run (blue).
Many refinements in routing models have been made in recent years to include parameterizations for irrigation withdrawal, reservoir operations, stream temperature, and other physical processes (Yamazaki et al., 2009, 2014; Li et al., 2013; Mizukami et al., 2016). Given the complex calibration and parameterization requirements for global-scale applications, a relatively simple global application of an STS model is sufficient for our purposes. The parameterization of other processes such as reservoir operations or irrigation withdrawal might be necessary for other applications where the intention is to predict the streamflow accurately. As in Hamman et al. (2017b), the primary objective of this study is to provide a first-order coupling between land hydrology and the ocean model. Seasonal prediction of streamflow is a challenging task even for offline simulations of hydrological models driven by GCM forecasts. Such forecasts are of value for management decisions on a seasonal or annual time scale at best (Sikder et al., 2016). Therefore, seasonal prediction of streamflow is not of interest in this study.
Model Hindcasts, Data Used, and Methodology
Model hindcasts for 37 years (1981–2017) with an ensemble of ten members are made using February initial conditions obtained from Climate Forecast System Reanalysis (Saha et al., 2010) and are integrated for 9 months lead time, i.e., from March to November. Details about model initialization and runs are mentioned in Supplementary Section 1. The control (CTL) run prescribes climatological annual mean river runoffs as shown in Figure 2B. The sensitivity (RIV) run is carried out using the CFS-RVIC coupled model.
The RIV simulated river discharge for some major river basins is compared against observations from the continental river discharge database produced by Dai and Trenberth (2002); Dai et al. (2009); Dai (2016) and has been recently updated to include river-flow gauge data from Global Runoff Data Centre, United States Geological Survey, Water Service of Canada, and Brazilian National Water Agency (Dai, 2021). Satellite altimeter-based discharge estimates for Ganga-Brahmaputra for 1993–2016 are also used (Papa et al., 2010). The model-simulated rainfall is evaluated against the Global Precipitation Climatology Project (GPCP) rainfall data [provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, United States, from their website at https://www.esrl.noaa.gov/psd/, Adler et al. (2003)] and the rainfall dataset obtained from the India Meteorological Department (IMD) at 1° resolution (Rajeevan et al., 2008). The Extended Reconstructed Sea Surface Temperature (ERSST) dataset (Huang et al., 2017) is used to verify model-simulated SSTs. Simulated ocean sub-surface variables are verified using the World Ocean Atlas dataset (Boyer et al., 2018).
ARGO data floats are a vital source of in situ temperature and salinity data (among other oceanic parameters) and are widely used in real-time data assimilation systems. They serve as a reliable source for model verification. ARGO profiles for 2005–2017 are obtained from the Coriolis Global Data Acquisition Center of France. The profiles have been pre-processed and quality controlled by the ARGO science team. ARGO floats collect temperature and salinity profiles from the upper 2,000 m of the global ocean in ice-free regions. About 51,361 profiles are present during boreal summer (May–October) in the study region of 50°E−105°E, 10°S−26°N. The profiles in the Arabian Sea, BoB, and eastern equatorial Indian basin are more abundant than those of other areas of the Indian Ocean. In the BoB interior, more than 40 profiles are available for a 1° × 1° grid box. In the BoB box, defined over 85°E−95°E, 7°N−21°N, which is important for our investigation, there are 5,147 profiles from May to October. At some grids, profile numbers can exceed 70, 80, or even 90.
To assess the salinity stratification in the BoB, mixed layer depth (MLD), isothermal layer depth (ILD), and barrier layer thickness (BLT) are defined mathematically using the method followed in MOM4 (Griffies et al., 2004). In the ocean model, MLD is defined using a stability criterion. Suppose a fluid parcel is displaced downward from the surface to a depth h without changing its temperature and salinity but feeling the in situ pressure. Let the density of this parcel be defined as:
where S, Θ, and P are the salinity, potential temperature, and pressure. The real in situ density can be defined as:
If the density of this displaced parcel is sufficiently far from the in situ density, then this mixing or displacement is not favored and implies that the parcel is below the mixed layer in the stratified interior ocean. The difference in these two densities is converted into a buoyancy criterion as defined below:
The depth at which δB exceeds a critical buoyancy difference of 0.0003 m s−2 (Conkright et al., 2002) is calculated. MLD is then defined by interpolating between this depth and the shallower level. Isothermal layer depth (ILD) is defined as the depth with a temperature decrease of ΔT = 0.5°C from surface temperature. BLT is calculated as the difference between ILD and MLD, i.e., BLT = ILD–MLD. For cases where ILD is less than MLD, BLT is set to zero.
Results and Discussion
Simulation of River Discharge
Before assessing model simulations, it is vital to verify the simulated annual cycle of river discharge by the RIV run, especially for the major rivers discharging in the Bay of Bengal (Ganga, Brahmaputra, and Irrawady). It must be noted that the accuracy of routed flow is largely governed by the performance of the model that produces the distributed runoff fields (GFS-Noah in this case) and not by the routing model itself (Mizukami et al., 2016). Calibration of routing model parameters can alter the timing and magnitude of peak flow (Mizukami et al., 2016; Hamman et al., 2017b). The distributed runoff fluxes generated by the land model can have large errors, thereby making direct comparison with observed streamflow less meaningful. As pointed out by Falloon et al. (2011), hydrologists and meteorologists have a widely different perception of what constitutes a valid river discharge simulation. For instance, correct simulation of the timing of peak flow is vital for hydrologists, whereas proper simulation of annual mean discharge volume might be sufficient to study the interaction of RFW with ocean circulation. The intention here is to gauge the performance of RIV simulation in terms of the shape of monthly mean hydrographs and mean discharge volume. As mentioned earlier, seasonal prediction of streamflow is not of interest in this study.
Figure 3 compares the monthly hydrographs simulated by RIV run with the satellite altimeter-derived runoff product for the period 1993-2016 (Papa et al., 2010) and the Dai (2004, D2021) database (for a common time period of January 1993-December 2016 for the Ganga-Brahmaputra and Irrawady rivers). Also shown in Figures 3C,D are the climatological monthly mean hydrographs, with the error bars representing the inter-annual standard deviation of the monthly hydrograph. The correlation between the observed and simulated hydrograph time series (r), relative root-mean-square error (RRMS), and percentage bias (PBIAS) is commonly used statistics to evaluate hydrological simulation (Lohmann et al., 1996; Nijssen et al., 2001a; Nohara et al., 2006; Falloon et al., 2011; Hamman et al., 2017b; Pan et al., 2021). Table 1 presents the statistics for major river basins. The high correlation for the Ganga-Brahmaputra (GB) and the Irrawady implies a good correspondence between the observed and modeled monthly hydrographs. The RRMS for Ganga is comparable to the values obtained by Nohara et al. (2006), who employed the TRIP routing model forced by the ensemble mean precipitation of CMIP5 models. The RRMS for the Ganga-Brahmaputra discharge compared against the Papa et al. (2010) dataset is lower than the RRMS values for the individual river basins (when compared against D2021 dataset). The PBIAS for Brahmaputra is significantly lower than that in Nijssen et al. (2001a), where runoff fluxes were generated by forcing a macro-scale hydrological model with meteorological forcing obtained from a reanalysis product. The RRMSE value for Ganga-Brahmputra and Irrawady is 40–50%, with a small PBIAS (−9 to −18%), and is comparable to that found in other global-scale studies. Figure 3C indicates a significant phase lag between the simulated Ganga-Brahmaputra discharge and the Papa et al. (2010) observations. This is partly because the basin averaged rainfall (shown in Supplementary Figure 2) also has a similar phase lag. It also makes us wonder whether reservoir water management can cause the observed discharge to peak later in the monsoon season. In the absence of the representation of man-made intervention, RIV simulation may cause the discharge to peak earlier. This cannot be verified with the current model setup and might be possible with advanced routing models that include parameterization of reservoirs. Studies have shown that the snowmelt contribution to the Ganga-Brahmaputra discharge is significant during spring (Bookhagen and Burbank, 2010; Siderius et al., 2013). The higher discharge values during March-April-May (Figure 3C) likely indicate a bias in snowmelt processes in the land model. The negative PBIAS value (−9%) for the Ganga and Brahmaputra rivers is due to the dry bias of rainfall in CFS over these basins (Supplementary Figure 2). The simulated climatological monthly hydrograph for Irrawady is better in terms of phase; however, the simulated discharge is lesser from August to November. The correct simulation of the magnitude and phase of the hydrographs are governed by the annual cycle of rainfall over the Irrawady river basin (Supplementary Figure 2). The major basins of interest, the Ganga-Brahmaputra basin (GB basin) and Irrawaddy, simulate a high correlation with observations. It should be noted that the observational river discharge data might be sparse and might not always be accurate. This is especially true for river basins such as Ganga-Brahmaputra that are shared by different countries. Nevertheless, the RIV model simulates a realistic shape of monthly mean hydrographs for the major basins discharging in the BoB, but with some phase lag. The phase lag and PBIAS are partly driven by similar biases in rainfall produced by the atmospheric model and by the routing model.
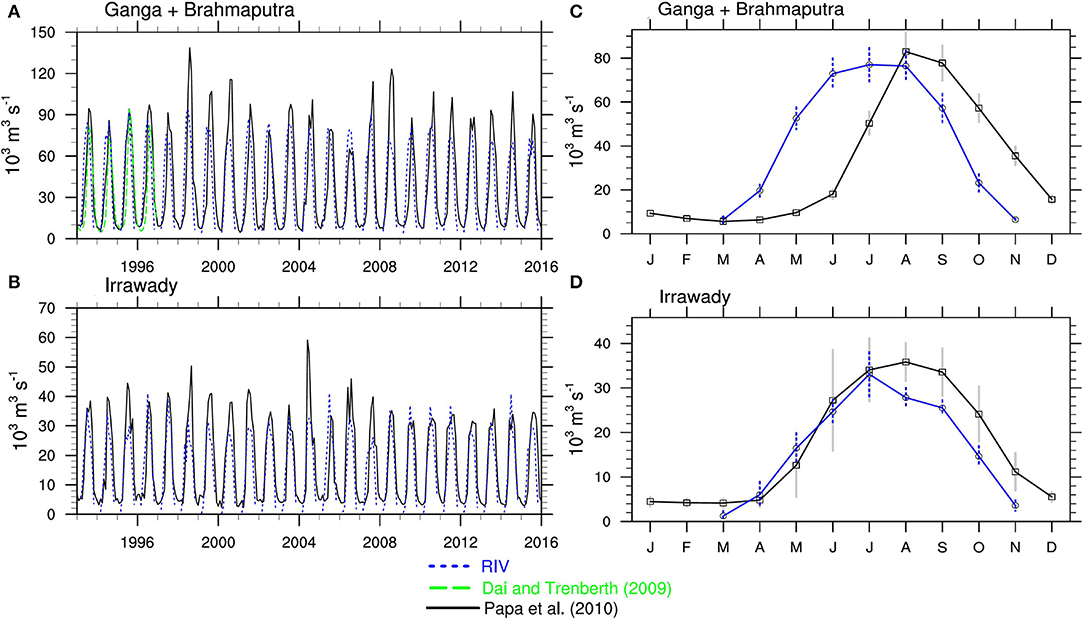
Figure 3. Monthly mean hydrographs in observations and RIV simulations during the period 1993–2016 for (A) Ganga + Brahmaputra and (B) Irrawady. The climatological annual cycle of the hydrographs depicted in (A,B) for (C) Ganga + Brahmputra and (D) Irrawady. Also shown as vertical error bars is the inter-annual standard deviation of the monthly mean hydrographs for the period 1993–2016.
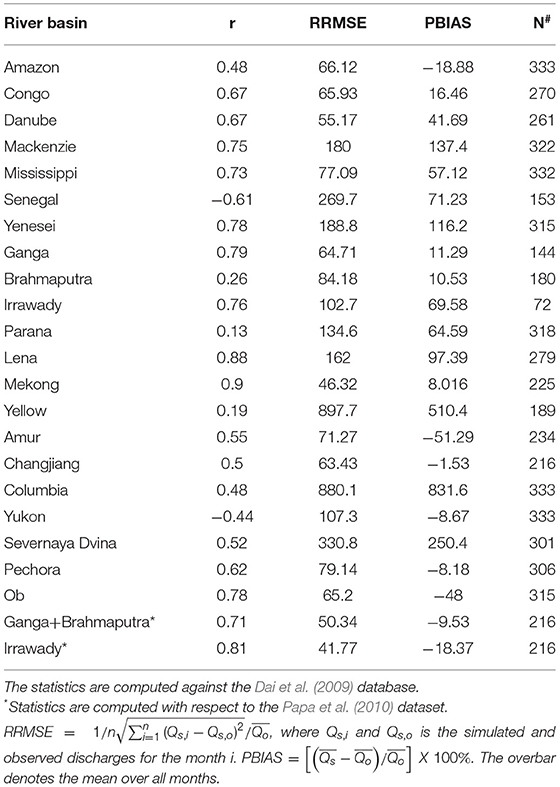
Table 1. The correlation coefficient (r), relative root mean square error (RRMSE), and percentage bias (PBIAS) for the major river basins. N denotes the number of monthly observations conducted to compute the statistics.
The climatological monthly hydrographs identical to Figures 3C,D but for the major rivers globally are shown in Supplementary Figure 3, and the statistics are listed in Table 1. Since the model simulation is for 9 months each year (March–November), the relevant 9-month observations are considered for comparison. The correlation values exceed 0.5 for many rivers such as the Congo, Danube, Mackenzie, Mississippi, Yenesei, Lena, Mekong, Yellow, Amur, Changjiang, Severnaya Dvina, Pechora, and Ob. For some other rivers such as Amazon and Columbia, correlation values are high (0.48). This indicates that the model captures the seasonality to some extent. The correlation is less for Parana and Yellow and is negative for Senegal and Yukon. The climatological monthly hydrographs indicate that the seasonality and amplitude are not well-captured for these rivers. The RRMS values for these rivers range from ~46 to 897%, comparable to other global-scale simulations (Nijssen et al., 2001b; Nohara et al., 2006; Falloon et al., 2011; Hamman et al., 2017b). For many rivers, PBIAS and phase errors are determined by the annual precipitation cycle over the basin (such as Amazon, Congo, Mississippi, Senegal, Changjiang and Severnaya Dvina; Supplementary Figure 2), while for other rivers, the magnitude and phase errors seem complex and not directly related to the annual cycle of precipitation (such as Mackenzie, Yenesei, Parana, Lena, Mekong, Yellow, Amur, and Yukon). The errors in phase and shape of the hydrograph can be corrected to some extent by calibrating the flow and diffusivity parameters of the routing model (Hamman et al., 2017a). The errors arising out of discrepancies in simulated runoff from CFSv2 will require better understanding and representation of basin-scale processes (such as soil moisture, floodplain processes, and snowmelt; Falloon et al., 2011). Improvements in the routing model (such as higher resolution, spatially varying velocity and diffusivity parameters, parameterization of reservoirs and irrigation) can improve the overall hydrological simulation and are suggested for future research.
Figure 2B shows the annual cycle of RFW input into the northern BoB basin (10N°–25°N; 78°E-98°E). The monthly mean runoff into the BoB from the Large and Yeager (2009) dataset (black curve) shows that the runoff starts building up in June, which coincides with the arrival of monsoon in India. Peak discharge occurs in the August and September months, after which it gradually decreases. The annual mean climatological runoff prescribed in the CTL run is a constant value (red line) and is higher than the observational discharge estimates during pre- and post-monsoon months. RIV simulates a marked seasonal variation in runoff similar to observational estimates, although there is a visible time lag and an under-estimation from August to November. Such seasonal variation in river discharge forcing can directly impact the upper ocean mean state and stratification and is discussed in the next section.
Impact on the Ocean Mean State and Upper Ocean Stratification
The Upper Ocean Structure
Figure 4 shows the monthly mean ocean salinity profile (shading) and the temperature profile (contours) from observations (in situ ARGO data) and model simulations in the northern BoB (14°N-22°N; 85°E-95°E; NBoB). Also shown is the MLD (blue curve) and the isothermal layer depth (ILD; red curve). The dotted curves in Figure 4 represent the MLD and ILD from the World Ocean Atlas (WOA) dataset. The ARGO data indicate that the upper 20 m of the northern BoB (NBoB) is relatively fresh (salinity < ~33 PSU) from March to November (Figure 4A). Salinity starts reducing in the upper ocean in mid June onward and reaches its minima in October. Such a seasonal cycle in salinity stems from the seasonality of freshwater forcing, which is particularly strong during monsoon and post-monsoon seasons and has been extensively reported (Shetye et al., 1996; Han et al., 2001; Rao and Sivakumar, 2003; Sengupta et al., 2006; Akhil et al., 2014; Chaitanya et al., 2014). The NBoB salinity is also less in the months of March-April. The CTL run has relatively low salinity values from March to November because of constant riverine freshwater flux (Figure 4B). Two centers of relatively lower salinities are evident in the CTL run, with the first occurring in March-April and the second occurring during the monsoon and post-monsoon months. However, the separation between the two salinity minima during June-July, as seen in the ARGO data, is not evident in the CTL run. RIV simulates a better salinity profile, which is comparable to observations. The minimum in salinity occurs during March-April-May, and subsequently August onward, with a clear separation between the two minima. In observations, the freshwater plume is restricted to the upper 20–25 m (Weller et al., 2016), while it is distributed over the upper 40 m in CFSv2. This can be due to the following reasons: CFSv2 over-estimates the mixing in the upper ocean (Chowdary et al., 2016), and the 10-m vertical resolution in the upper ocean is not sufficient to resolve the fine-scale salinity structure in the NBoB. The thickness of the column over which river water is discharged is another cause of concern and can cause biased salinity structure in the upper ocean. The upper ocean cold bias in CFSv2 is apparent in both runs. The 28°C isotherm hovers around a depth of ~45 m from May onward in observations, while in the model, it hovers around a depth of ~30 m.
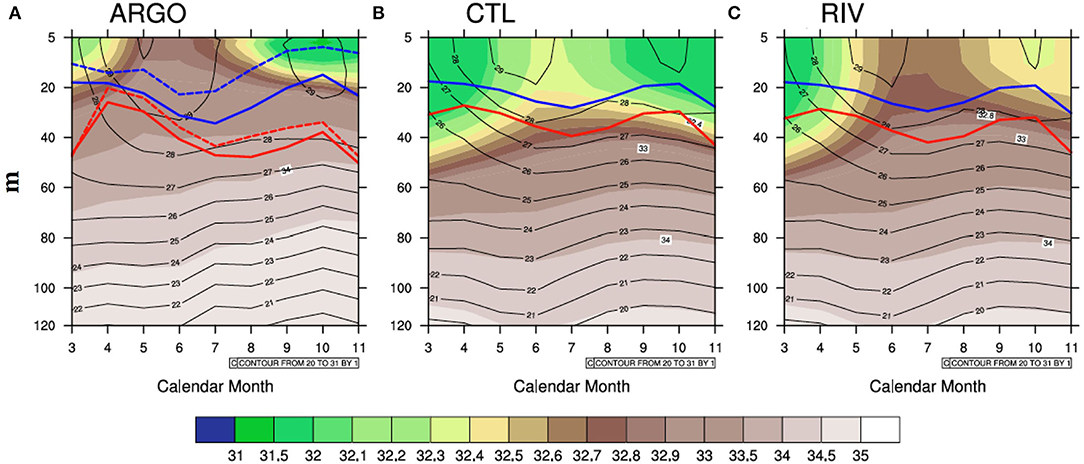
Figure 4. Monthly averaged salinity profiles (psu, shading) and temperature (contours, °C) for the North Bay of Bengal from (A) ARGO observations, (B) CTL run and (C) RIV run. Also depicted are the mixed layer depth (in meters, blue curve) and the isothermal layer depth (in m, red) curves. The broken blue and red curves in (A) denote the mixed layer depth (MLD) and isothermal layer depth (ILD), respectively, from the World Ocean Atlas (WOA) data, while the solid blue and red curves depict the MLD and ILD, respectively, from the ARGO data.
Simulation of Mixed Layer, Barrier Layer, and Isothermal Layer
Freshwater forcing in the ocean directly impacts MLD and can result in the formation of barrier layers. Therefore, the impact of RFW forcing on seasonal mean (June through September; JJAS) MLD, ILD, and barrier layer thickness (BLT) is evaluated in the CTL and RIV runs. The JJAS mean MLD, ILD, and BLT from the ARGO data, CTL, and RIV are shown in Figures 5A–I, top, middle, and bottom panels, respectively. The contours in Figures 5A–I denote the depths calculated from the WOA dataset. The differences (RIV-CTL) in MLD, ILD, and BLT are shown in the rightmost panel (Figures 5J–L). Due to the freshwater inflow from rain and rivers during the summer monsoon season, the MLD is very thin (~15–20 m) in the northern BoB. Due to the shallow mixed layers, thick barrier layers are seen in this region (Vinayachandran et al., 2002; Montégut C de et al., 2007; Thadathil et al., 2007). The barrier layers are comparatively thinner in the northwestern BoB because of excess evaporation (Sprintall and Tomczak, 1992; Pokhrel et al., 2012) and are thicker in the eastern BoB (>25 m, Figure 5). River runoff during the summer monsoon maintains the barrier layers along the northwestern BoB (Vinayachandran et al., 2002; Sengupta et al., 2006; Behara and Vinayachandran, 2016). This east-west difference in the BLT is clearly seen in observations (Figure 5G) and has been reported earlier (Thadathil et al., 2007; Rahaman et al., 2020). In agreement with observations, the model-simulated MLD is shallow in the NBoB (<24 m in the head BoB) and is relatively deep in the central bay (~30–40 m). The spatial patterns of the model-simulated MLD are consistent with observations. RIV simulates deeper MLD (~1.5–2 m) and ILD (~2–4 m) compared to the CTL run in the northern BoB. This is expected, since the vertical mixing was enhanced in the upper ocean in the RIV run in the vicinity of river mouths. Thicker isothermal layers in RIV indicate better simulation of seasonal (JJAS) mean temperature profiles. The variation of temperature with depth in the upper 35 m of the northern BoB is −0.01°C m−1 in observations, while the same for CTL and RIV is −0.04 °C m−1 and −0.02 °C m−1 respectively. Barrier layers are very thick in the eastern BoB (>20 m along the Myanmar coast, Figure 5G) while being relatively thinner along the coastal regions in the northwestern BoB in observations. The seasonal variability of the BLT is closely tied to the interaction of surface monsoon circulation with low salinity water and the associated Kelvin and Rossby wave activity (Thadathil et al., 2007). The RIV run simulates thicker barrier layers along the eastern coast of India, the head BoB, and along the Myanmar coast than the CTL run. The barrier layers are thinner along the north-western BoB and thicker along the Myanmar coast, thus making the east-west difference in BLT more prominent. Although the east-west gradient in BLT is not simulated well in CFSv2 compared to observations, the RIV run represents this gradient to some extent. This likely points toward better interaction of the surface circulation with the upper ocean in the RIV run. The seasonal cycle of MLD (blue curve in Figure 4) follows a shallow-deep-shallow evolution. MLD is shallower during March-April-May, deepens during the monsoon months, and shallows in the post-monsoon period. Both the CTL and RIV runs capture this well. In the NBoB, the barrier layers (BLs) are quite thick in March. The April, May, and June months exhibit the thinnest BLs. They start to thicken in July onward, which coincides with the monsoon months. BLs as thick as 20 m are seen from August to November. The barrier layer thickness and its variation in the northern BoB in CFSv2 is small as compared to observations (Figures 4A–C). Nevertheless, RIV simulates thicker BLs than the CTL run in the NBoB (Figure 5L). Rahaman et al. (2020) have shown that the MOM class of ocean models underestimates the BLT in comparison to the NEMO class of ocean models, which is thought to arise because of differences in the boundary layer parameterizations. Interestingly, increased horizontal resolution of the ocean model reduces this bias. CFSv2 is known to simulate thinner barrier layers compared to observations (Zhu and Kumar, 2019). Despite this limitation, the RIV run captures the east-west BLT gradients in the BoB better than the CTL run. Zhu et al. (2020) have shown that increasing the vertical resolution of the ocean model to 1 m near the ocean surface improves the salinity and barrier layer structure. Improvements to boundary layer parameterizations of the ocean model might improve barrier layer simulations and remains an area of active research. Improvements in boundary layer parameterizations in the ocean model might improve barrier layer simulations and remain an area of active research.
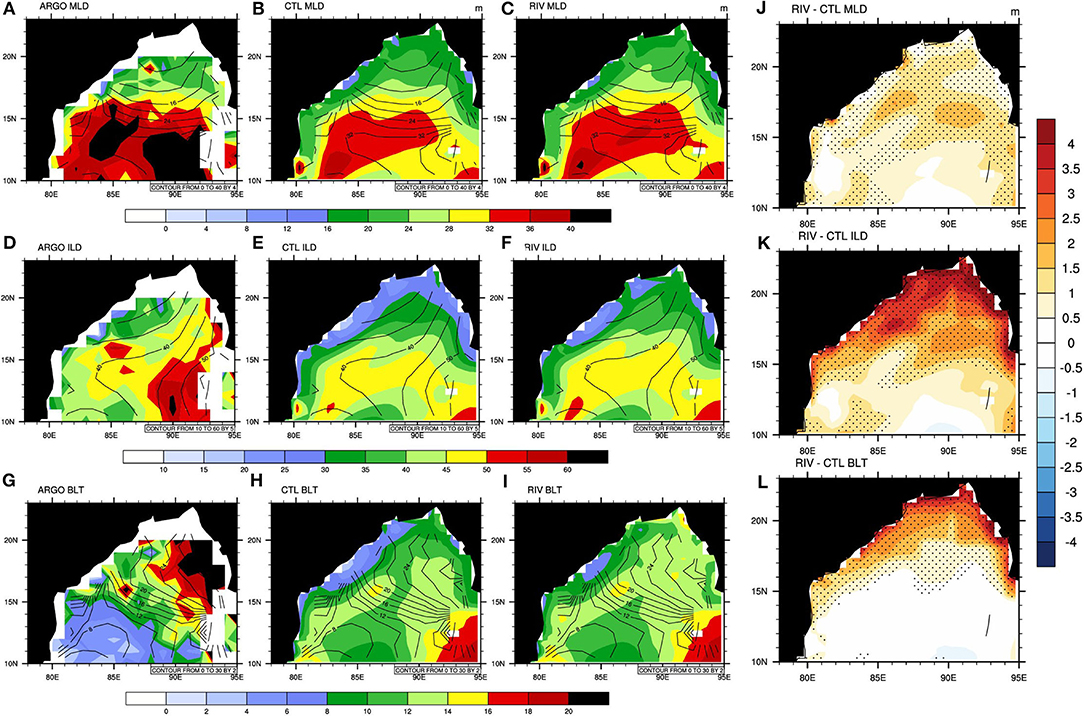
Figure 5. The JJAS mean MLD (in m, shading) for (A) ARGO, (B) CTL run and (C) RIV run. (D–F) and (G–I) Same as (A–C) but for ILD and BLT, respectively. The contours in (A–I) denote the parameters (MLD, ILD, and BLT) calculated from the WOA dataset. The JJAS mean RIV–CTL differences in (J) MLD, (K) ILD, and (L) BLT. Differences significant at 90% confidence level are stippled in (J–L).
Impact on Mixed Layer Characteristics
It is evident from the above discussion that RIV and CTL exhibit significantly different upper ocean characteristics in the seasonal mean sense. To understand the impact of river water on mixed layer processes and upper stratification, salinity and heat budgeting is performed and is discussed below.
The Mixed Layer Salinity Budget
The temporal evolution of mixed layer salinity is governed by freshwater (evaporation, precipitation, and river runoff), advection, entrainment, and mixing, and it has been studied extensively in the Indian Ocean (Rao and Sivakumar, 2003; Akhil et al., 2014; Moon and Song, 2014; Nyadjro and Subrahmanyam, 2014; Da-Allada et al., 2015; Schiller and Oke, 2015; Wilson and Riser, 2016; Zhang et al., 2016; Köhler et al., 2018). Following Schiller and Oke (2015), the salinity budget in the mixed layer is defined as follows:
where S is the mixed layer averaged salinity, E is evaporation, P is precipitation, R is river runoff, u is the horizontal velocity vector averaged over the mixed layer. H (we) is the Heaviside step function [H(we) = we if we > 0; H(we) = 0 if we < 0], and we is the entrainment velocity defined as ; where w is the vertical velocity at the base of the mixed layer. denotes the salinity tendency (ST), the terms on the right-hand side of equation (1) denote the contributions from freshwater flux (FWF), advection (ADV), entrainment (ENT), and residual. It is known that the minimum ST between June and September is driven by FWF, with a secondary contribution from ADV, and the positive contribution comes from the vertical processes (Akhil et al., 2014). The freshening effect during the summer months is attenuated by vertical diffusion and eddy processes (Köhler et al., 2018). The terms of the budget shown in equation (1) are computed from the daily mean outputs of the model. Multi-year monthly means of these terms are averaged over the northern BoB (15°-23° N, 80°-95°E) for CTL and RIV simulations and are shown in Figure 6. ST is positive during March-April-May and is negative from June to October for both CTL and RIV. In agreement with earlier studies, the FWF term governs the freshening of ST during summer months, followed by ADV. The magnitude of ENT is much smaller compared to FWF and ADV and attenuates the freshening effect of the FWF term during June-September. In CFSv2, the annual cycle of the sum of FWF, ADV, and ENT (Figure 6E) closely resembles ST (with the sum becoming negative during June). FWF, ADV, and ENT alone are not sufficient to explain ST. A significant residual exists in the budget during July-August-September, which attenuates the freshening effect, in agreement with Köhler et al. (2018). The constant river runoff prescribed in the CTL run makes the FWF forcing stronger during March-April-May and October-November. FWF terms for The RIV and CTL runs are almost similar in magnitude from June to September despite higher river runoff in the RIV run. This is because the FWF term has the MLD in the denominator, and the RIV-simulated MLD is deeper, making the overall term comparable in magnitude. ADV is stronger during pre-monsoon months in the CTL run. The sum of the terms (FWF+ADV+ENT) shows major differences between RIV and CTL during March–April (due to stronger ADV contribution in CTL) and toward the end of the monsoon season (August–September–October) owing to differences in FWF. The Residual term is stronger in RIV in summer monsoon months, indicating greater contribution from enhanced vertical diffusivity at river mouths and other unresolved processes. Realistic representation of the seasonal cycle of RFW in the RIV run causes significant differences in the evolution of ST during pre-monsoon and monsoon months, which better represents the upper ocean salinity structure in the northern BoB (Figure 4). As pointed out by Köhler et al. (2018), the representation of shear horizontal diffusion and eddy processes are vital to close the salinity budget. Some unresolved processes are accounted for in the RIV run (by enhancing vertical diffusivity at river mouths). Increased resolution of the ocean model and improved parameterization of mixing of river water with the ocean might further improve the simulation and should be considered in future studies.
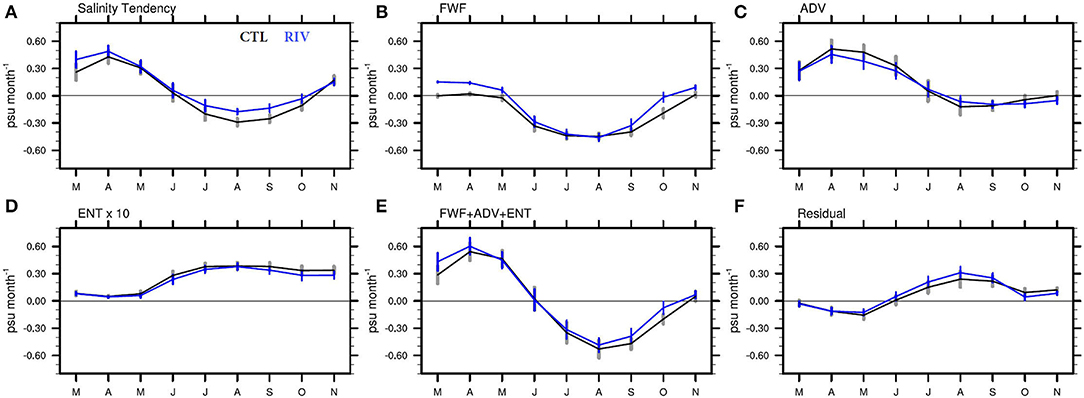
Figure 6. Climatological seasonal cycle of the mixed layer salinity budget terms (psu month−1) averaged over the northern Bay of Bengal (15 °N-23 °N; 80 °E-95 °E) for the CTL (black) and RIV (blue) runs. (A) Salinity tendency (ST), (B) freshwater forcing (FWF), (C) advection (ADV) term, (D) entrainment (ENT, × 10) term, (E) sum of FWF, ADV, and ENT, (F) residual term (ST-FWF-ADV-ENT). Also shown as vertical bars are the monthly standard deviations of the terms over the simulation period (1981–2017).
The Mixed Layer Heat Budget
The SST variability in the mixed layer can be ascertained using the mixed layer heat budget (MLHB) equation. The mixed layer averaged temperature tendency (TT) (where [ ] denotes vertical averaging up to the MLD) can be written as described in Li et al. (2017b):
where SHF is the surface heat flux forcing, ADV is the horizontal advection term; ENT is the vertical entrainment from the base of the mixed layer, and R is the residual. The methodology to compute these terms is the same as that in Li et al. (2017a); hence, it is not repeated here. The MLHB terms are computed from the daily mean outputs of CFSv2, and the monthly means of the MLHB terms are analyzed in this study.
It is known from earlier studies that the SHF term primarily drives the seasonal cycle of SST in the BoB, and that oceanic processes play a secondary role (De Boyer Montégut et al., 2007; Montégut C de et al., 2007; Behara and Vinayachandran, 2016). It has also been shown that on intra-seasonal time scales, the SHF term plays a dominant role in controlling the SST variability with the entrainment term playing a secondary role (Vialard et al., 2012; Li et al., 2017b). The SST tendency is similar to the temperature tendency term of the mixed layer (Girishkumar et al., 2017). In agreement with earlier studies, we note that the SHF term is the dominant term that controls SST variability on seasonal time scales (figure not shown). The advection and entrainment terms are an order of magnitude smaller than the SHF term. Recent in situ observational measurements of advection and entrainment indicate a greater contribution of these terms toward SST variability, but are, however, poorly resolved with models (Vijith et al., 2020). SST can change because of river water inflow in two ways. Shoaling of MLD because of freshening can increase SST, since the same amount of SHF forcing heats a lesser volume of water. On the other hand, shoaling of MLD can cause greater penetrative shortwave radiation, thereby cooling the mixed layer.
The difference between multi-year (1981–2017) monthly means computed from the daily MLHB terms for RIV and CTL (°C month−1) is shown in Figure 7. Behara and Vinayachandran (2016) have shown that during the monsoon season, the contribution of the SHF term toward heating the mixed layer dominates, and that there is a net gain in heat by the shallow mixed layer. The maximum river inflow in the BoB due to online river routing in the RIV run occurs during July-August. Also, the temperature tendency term shows a warming tendency of ~0.1–0.2°C month−1 during July and August. The signature of mixed layer warming is evident along the eastern coast of India during June and spreads southward during August, which must be because of the spreading of river water along the eastern coast of India. Such warming of the mixed layer is also noticed south of the discharge location of Irrawady during July-August. MLD is deeper in the RIV run than in the CTL run during June–August (Supplementary Figure 4A). Therefore, the SHF term is smaller in RIV than in CTL. Because of deeper MLD in RIV, the net loss of penetrative shortwave radiation from the mixed layer is less (Supplementary Figure 4B), hence causing the mixed layer temperature tendency to be greater during July–August. Toward the end of the monsoon season in September, the warming signal diminishes as the contribution from loss of penetrative shortwave radiation increases in RIV, which cools the mixed layer, as was noted by Behara and Vinayachandran (2016). The ADV term is responsible for the distribution of the mixed layer temperature by currents. The ADV term is stronger in the RIV run along the eastern coast of India and is responsible for spreading low-salinity warm water. The magnitude of the entrainment term shown in Figure 7d (scaled by a factor of 10) is relatively small compared to the other terms, indicating that its contribution to MLHB is small. The MLHB residual (figure not shown) is significant along the eastern coast of India and the southeastern BoB during July–October. This implies that other diffusive processes that are not accounted for in MLHB are also important and cannot be ignored in this region. The inclusion of temporally varying river runoff lends a seasonally varying character to the mixed layer heat budget.
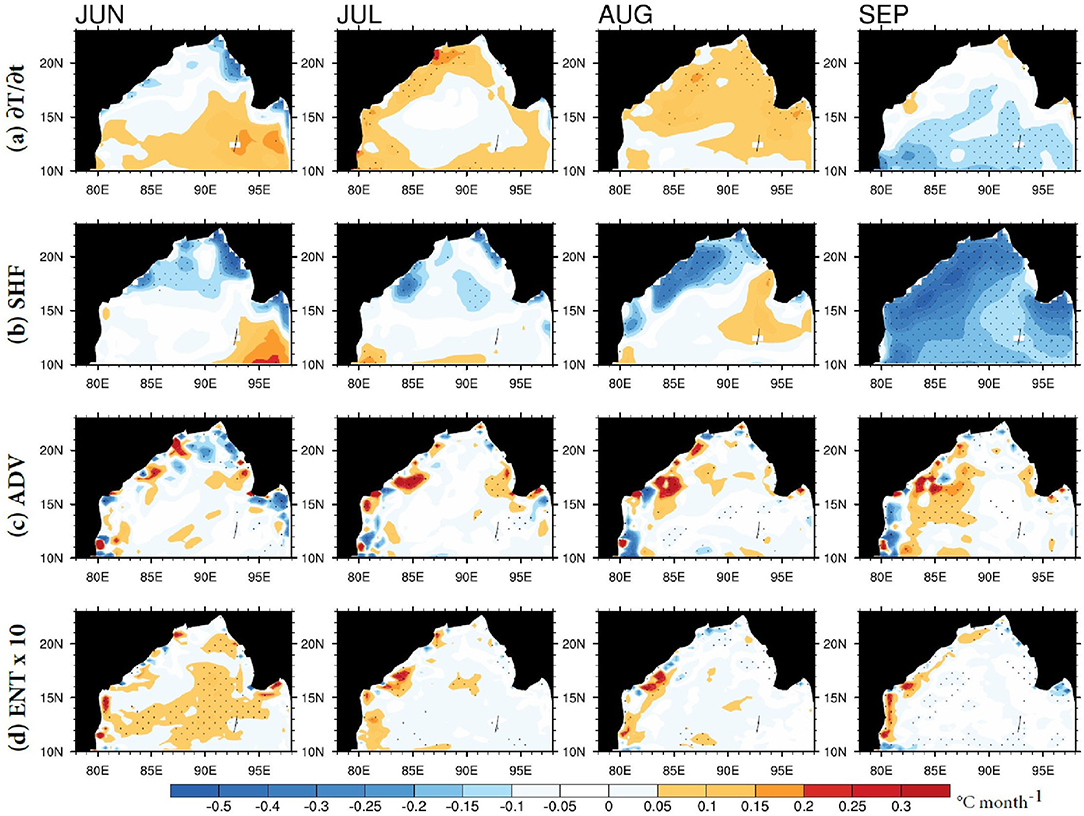
Figure 7. Difference (RIV-CTL) between the mixed layer heat budget terms (°C month−1) for panel (a) temperature tendency, (b) surface heat flux, (c) advection, (d) entrainment at the base of the mixed layer.
The interannual variability (IAV) of the MLD is rather small [~2–4 times smaller than the seasonal cycle, Keerthi et al. (2013)]. By conducting ocean model experiments, Valsala et al. (2018) have shown that a significant portion of MLD variability is controlled by surface momentum, heat, and freshwater fluxes, which are mostly controlled by the ENSO. They have also shown that the ENSO control on MLD in the BoB is maximum in the central BoB, and that the amplitude of IAV (defined as inter-annual standard deviation) of BLT is rather small. In agreement with earlier studies, the northern BoB averaged MLD has a small IAV (~1.6 m in ARGO data) and is much smaller in CFSv2 (~0.8 m). The IAV in upper ocean stratification due to freshwater (rain and rivers) is not explored much in the literature. The RIV-CTL differences in the IAV of seasonal (JJAS) mean MLD and BLT are shown in Supplementary Figure 5. Statistically significant variability of about 0.2–0.3 m is seen in the northern, north-western, and eastern BoB, consistent with the locations of maximum river discharge. The IAV of BLT, on the other hand, shows a much smaller amplitude (statistically insignificant), understandably because of the smaller amplitude of the mean itself. The impact of this change in IAV on the MLHB is explored further.
Figure 8 shows the RIV-CTL difference in the IAV of the monthly mean heat budget terms. The temperature tendency term shows stronger IAV over the CTL run (~0.1–0.15°C month−1) in the northern and northwestern BoB and in the Andaman Sea during June-July-August. These regions coincide with the discharge locations of major rivers, the Ganga, Brahmaputra, and Irrawady. The signal further spreads along the eastern coast of India during September. Irrawaddy's discharge also mixes with the saltier water in the Southern Bay, thereby diminishing the IAV of the TT term in August. The IAV of the SHF term partly governs TT term variability. During September, most of the river discharge simulated by these major rivers reduces, and the associated variability diminishes in the RIV run. The variability in the central BoB is smaller in RIV than CTL in July. This might indicate the weaker influence of remote forcing events such as the ENSO on the MLHB variability, which is dominant in the central BoB (Valsala et al., 2018), but requires further investigation. Thus, the temporally varying river discharge influences the IAV of mixed layer temperature tendency significantly.
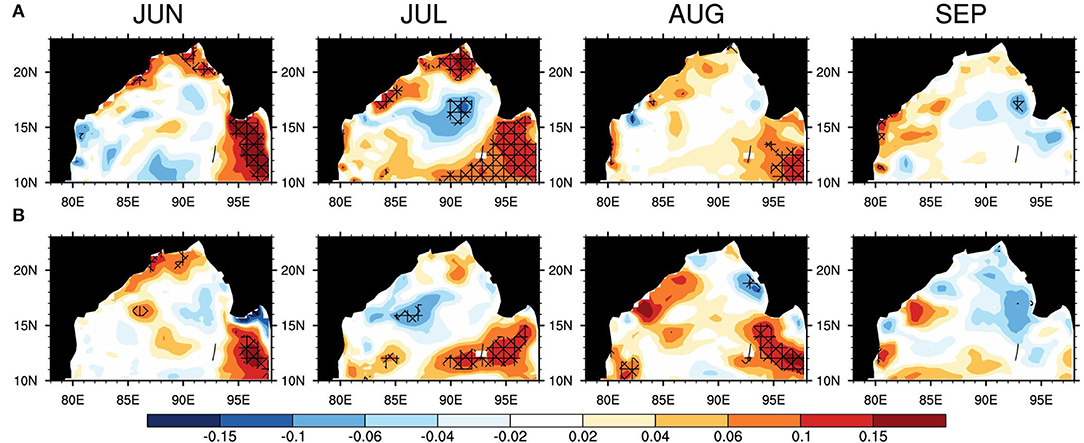
Figure 8. Difference (RIV-CTL) in the inter-annual standard deviation (°C month−1) of (A) the temperature tendency term and (B) the SHF term. Significant variability is observed in the RIV run compared to the CTL run. The hatched regions denote the area where variances are significantly different at 90% confidence level by F-test.
Link Between Runoff and Rainfall in the Bay of Bengal
Figure 9 shows the lag correlations of rainfall with river discharge, where monthly mean rainfall time-series lags/leads to discharge, and the lag frequency is in months. Since the runoff in the land model is primarily rainfall-driven, we expect good correspondence between the two parameters at lag 0. A statistically significant positive correlation between discharge and rainfall is seen in India's northern plains and central and northeastern India in observations. RIV also captures this relationship between rainfall and discharge, although the correlations are somewhat stronger. This indicates rapid conversion of rainfall over landmass to runoff in CFSv2. The runoff generated by rainfall events occurring over land takes some time to reach the ocean depending on the distance of the river mouth from the rainfall location. Observational studies have proven this aspect (Rao et al., 2011). Studies have also shown that the arrival of an RFW plume can affect the subsequent air-sea interactions (Vinayachandran et al., 2002), thereby having the potential to modulate the subsequent rainfall events (Goswami et al., 2016). A strong positive correlation between rainfall and runoff is observed at a lag of 2 months in observations (Figure 9A). This indicates that rainfall events that occurred 2 months earlier have some relationship with river discharge. Positive correlation at lead +1 implies that the discharge that occurred 1 month prior can affect rainfall events over the landmass. RIV also captures these positive correlations at lag −2, lag −1, and lag 0. They extend up to a lead of 1 month, albeit stronger than observations. This feedback between rainfall and runoff at different lags is an important component of the coupled ocean-atmosphere-hydrological system, which the CTL run cannot capture. This is well-represented in the RIV run.

Figure 9. Lag correlation of monthly rainfall with Ganga-Brahmaputra discharge for (A) observations and (B) RIV model simulation. Rainfall time-series leads/lags to discharge with a monthly lag frequency. Correlation values significant at 90% confidence level are stippled.
Systematic Biases, Model Skill, and Teleconnections
Since the ultimate goal is to study the implications of RFW on ISMR simulation, the seasonal (JJAS) mean biases and associated teleconnections are discussed in this section. Figure 10 shows the seasonal mean biases in rainfall and SST. The spatial patterns of the biases remain mostly unchanged, which implies that online river routing has a limited impact on seasonal mean systematic biases. There is slight cooling of SSTs in the tropical Indian Ocean and the BoB, along with slight warming in the tropical Pacific and cooling in the extra-tropical Pacific. Specification of temporally evolving RFW in RIV causes the equatorial Pacific to be warmer than the CTL run. Vinayachandran et al. (2015) have shown that shutting of river discharge in a coupled model causes cooling of SSTs in the equatorial central Pacific and causes the frequent occurrence of La Nina-type cooling events. Their model experiment (blocking river discharge globally) can be thought of as the extreme case of CTL run in this study (prescribing constant climatological runoff). In the absence of temporally varying river discharge, the equatorial central Pacific is colder than the RIV run. The pattern of rainfall bias also remains similar, although the dry bias over Indian landmass increases slightly in RIV (Figure 10H). This behavior has also been observed in earlier modeling studies where models with less cold bias in the central equatorial Pacific (equatorial Pacific is warmer in RIV than in CTL) can lead to stronger dry bias over India (Krishna et al., 2019; Pillai et al., 2021).
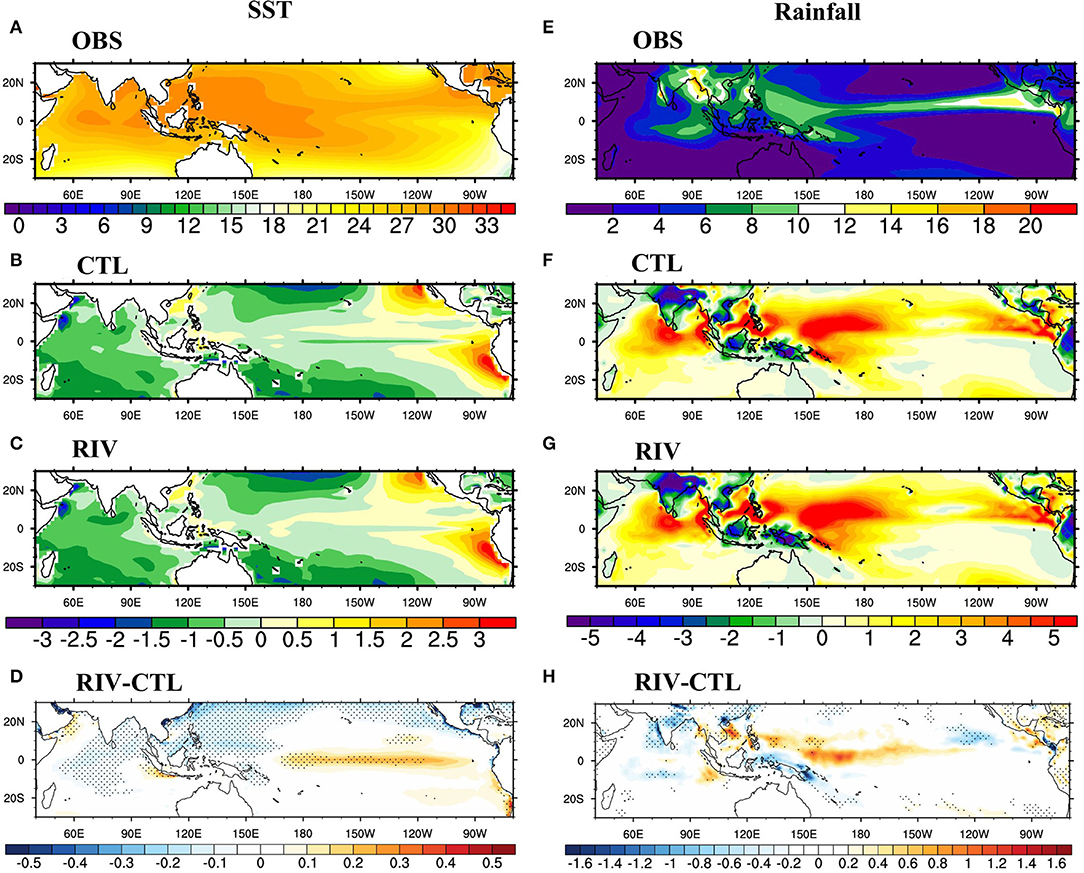
Figure 10. June-September (JJAS) mean SST (°C) in (A) observations (ERSST), and JJAS mean biases in model-simulated SST (°C) for (B) CTL run, (C) RIV run, and (D) RIV-CTL. (E–H) Same as (A–D) but for rainfall (mm day−1, observational rainfall from GPCP). Differences significant at 90% confidence level are stippled in (D,H). Biases are calculated for the period 1981–2017.
The IAV of RFW into the BoB is strongly tied to slowly varying modes of tropical variability such as the ENSO (Whitaker et al., 2001; Jian et al., 2009). The teleconnection of the ENSO with ISMR is predominantly strong in CFSv2 (George et al., 2015). Therefore, we expect a strong impact of the ENSO on simulated river discharge in the RIV run by modulation of rainfall. Furthermore, Vinayachandran et al. (2015) found an increased frequency of La Nina-type events in the presence of river discharge compared to zero discharge case in an earth system model. Supplementary Figure 6 shows the correlation of total runoff to the BoB with global SSTs in the RIV run. The runoff in May is strongly and positively correlated with basin-wide warm Indian Ocean SSTs, and a robust El-Nino type signal is evident in the tropical Pacific. June-July does not exhibit any significant global teleconnections. Warm SSTs in the western Arabian Sea and the BoB aid the runoff in July. From August onward, La Nina's influence becomes apparent. La Nina is known to cause abundant rainfall over the Indian subcontinent, which ultimately affects river discharge. The association between ENSO and RFW agrees with the observations (Figure not shown), indicating that the RIV run captures the remote teleconnections with the ENSO well.
Table 2 lists some parameters vital to quantify the performance of the model. The model-simulated mean ISMR and its standard deviation are quite similar. The skill for ISMR (defined as the anomaly correlation coefficient, ACC) increases from 0.28 in the CTL run to 0.41 in the RIV run, where GPCP is the reference, and it amounts to an improvement of skill of ~46%. When evaluated against the IMD dataset, the improvement is about 34%. Such a skill improvement is a welcoming result. The predictability in coupled dynamical models comes from slowly varying modes of variability such as the ENSO. The Nino 3.4 index simulation skill is slightly higher for the RIV run, while the Indian Ocean Dipole (IOD) east pole SST index skill is the same. The teleconnections of AISMR with the ENSO strengthen in RIV. Figure 11 shows the spatial ACC for rainfall. In the CTL run, positive correlations are restricted to the southern and southwestern parts of India (Figure 11C). However, in the RIV run, positive correlations extend northward to cover the western, western-central, northern, central, and northeastern parts of the country. From a global perspective, enhanced positive correlations are evident along the Myanmar coast, Maritime continent, IOD east pole region, parts of central Australia, and parts of South America. Supplementary Figure 7 shows the standardized AISMR anomalies from observations and model hindcasts. RIV simulation could correctly simulate the sign of the AISMR anomaly in 1984, 1987, 1993, and 2011. Furthermore, the magnitude of the simulated anomaly came closer to observations in 1983, 1986, 2001, 2003, 2004, 2007, 2009, 2012, and 2016. However, there are some years where CTL fared better than RIV. The overall improvement in skill points toward improvement in the variability simulated by RIV.

Table 2. The table lists the mean and standard deviation of All-India Summer Monsoon rainfall (AISMR) averaged over land region (column 1–2), the model skill defined as the anomaly correlation coefficient between the observed and simulated parameter, for AISMR (column 3 & 4), Nino 3.4 index (column 5) and the Indian Ocean Dipole's east (IODE) pole index (column 6), and the teleconnections between AISMR and Nino 3.4 index (column 7) and AISMR and IODE index (column 8).
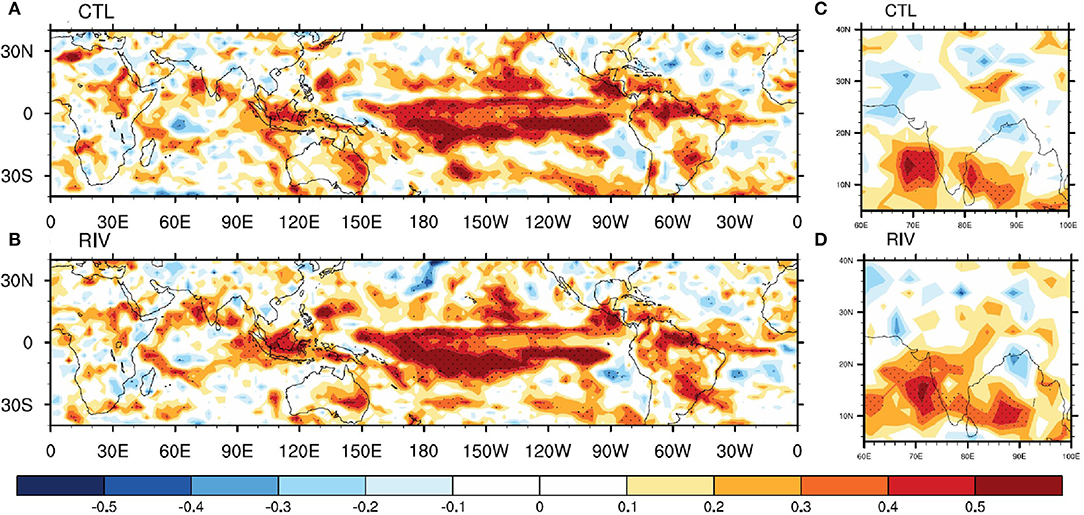
Figure 11. June-September (JJAS) mean anomaly correlation coefficient between GPCP and model simulations for (A) CTL run and (B) RIV run. (C) and (D) same as (A) and (B) but zoomed over India. Correlations significant at 90% confidence level are stippled.
Conclusions
Ocean salinity plays an important role in governing ocean circulation and can impact the SST and convection in highly stratified ocean basins such as the Bay of Bengal (BoB). Although the importance of riverine freshwater (RFW) is well understood, its effect on seasonal ISMR simulation and predictability has not been studied. In this study, a river routing model is coupled to a general circulation model, Climate Forecast System version 2 (CFSv2), which provides temporally evolving RFW to the ocean model. The implications of such coupling on ISMR simulation and its predictability are explored. Two sensitivity runs with CFSv2 are made. The CTL run has a prescribed climatological mean runoff. The RIV run, on the other hand, has a dynamically evolving discharge, which is produced by routing the land model's runoff to the ocean. The major findings are summarized below:
1. Online river routing in the RIV run causes a realistic simulation of the seasonal cycle of RFW input in the BoB. This causes improvements in upper ocean temperature and salinity compared to the CTL run.
2. Despite simulating deeper mixed layers, stronger warming of the mixed layer is noted during July-August, which is attributed to the simulation of thicker barrier layers in the RIV run. Apart from the seasonal variations, greater inter-annual variability in the mixed layer temperature tendency is noted in the RIV run, particularly in the vicinity of river discharge locations.
3. The salinity tendency in the mixed layer is dominated by freshwater input, which causes freshening of the mixed layer. Vertical diffusion and other eddy processes significantly attenuate the freshening signal and are better resolved by the RIV run by virtue of enhanced vertical mixing in the vicinity of river mouths.
4. The rainfall-runoff feedback is captured in the RIV run, along with remote teleconnections associated with the ENSO.
5. Srivastava et al. (2022) studied the interaction of RFW with the monsoon system on synoptic to intra-seasonal time scales. They found a better representation of convection and air-sea interaction in the RIV run. The scale interactions between the synoptic, intra-seasonal, and inter-annual modes of variability of ISMR lead to higher AISMR simulation skill in the RIV model setup. Hence, it is demonstrated that improvement in a particular model component propagates across various modes of variability of ISMR via the scale interactions among them.
This study has important implications for operational forecasting. It is demonstrated that rudimentary implementation of a routing model coupled with a state-of-the-art forecast system could improve ISMR simulation skill. Improvements in the routing model by involving other complexities in modeling river discharge and increasing the horizontal resolution to resolve the topography better, including reservoirs and dams, etc. can enhance the skill of the model further. Better parameterization of mixing of river water with the ocean, finer horizontal and vertical resolution, and changes in the vertical mixing scheme in the ocean model can improve the representation of upper ocean stratification. Most of the errors in the streamflow simulation are driven by biases from the land and atmospheric model, and significant community effort is required to address the biases.
Data Availability Statement
Publicly available datasets were analyzed in this study. The observational continental discharge dataset can be obtained from https://rda.ucar.edu/datasets/ds551.0/. The satellite altimeter-derived discharge estimates for Ganga-Brahmaputra were obtained through personal communication and can be obtained by contacting ZmFicmljZS5wYXBhQGlyZC5mcg== (F. Papa). The Global Precipitation Climatology Project (GPCP) rainfall data was provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA, from their Web site at https://www.esrl.noaa.gov/psd/. The gridded rainfall dataset provided by the India Meteorological Department can be obtained from their website at https://www.imdpune.gov.in/Clim_Pred_LRF_New/Grided_Data_Download.html. The Extended Reconstructed Sea Surface Temperature (ERSST) dataset can be obtained from their website at https://psl.noaa.gov/data/gridded/data.noaa.ersst.v5.html. The World Ocean Atlas dataset can be obtained from https://www.nodc.noaa.gov/OC5/woa18/woa18data.html. The ARGO dataset is obtained from the Coriolis Global Data Acquisition Center of France through http://www.coriolis.eu.org. Data processing and plots in this study were done using The NCAR Command Language Software (2019). The source code for the routing model can be obtained from doi: 10.5281/zenodo.269614. The Hydro1k dataset (Wu et al., 2012) used to generate RVIC parameters can be obtained from http://www.ntsg.umt.edu/project/drt.
Author Contributions
The model development, analysis, plotting, and preparation of the manuscript was conducted by AS. SR and SG contributed by formulating the problem and writing and editing the final manuscript. All authors contributed to the article and approved the submitted version.
Funding
The Ministry of Earth Sciences, Govt. of India, fully funds the Indian Institute of Tropical Meteorology.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors acknowledge all the dataset providers and the sources are duly cited. We thank Hamman et al. (2017a) for making the RVIC source code available.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fclim.2022.902586/full#supplementary-material
References
Adler, R. F., Huffman, G. J., Chang, A., Ferraro, R., Xie, P.-P., Janowiak, J., et al. (2003). The version-2 Global Precipitation Climatology Project (GPCP) monthly precipitation analysis (1979–Present). J. Hydrometeorol. 4, 1147–1167. doi: 10.1175/1525-7541(2003)004<1147:TVGPCP>2.0.CO;2
Akhil, V. P., Durand, F., Lengaigne, M., Vialard, J., Keerthi, M. G., Gopalakrishna, V. V., et al. (2014). A modeling study of the processes of surface salinity seasonal cycle in the Bay of Bengal. J. Geophys. Res. Oceans 119, 3926–3947. doi: 10.1002/2013JC009632
Behara, A., and Vinayachandran, P. N. (2016). An OGCM study of the impact of rain and river water forcing on the Bay of Bengal. J. Geophys. Res. Oceans 121, 2425–2446. doi: 10.1002/2015JC011325
Bell, V. A., Kay, A. L., Jones, R. G., and Moore, R. J. (2007). Development of a high resolution grid-based river flow model for use with regional climate model output. Hydrol. Earth Syst. Sci. 11, 532–549. doi: 10.5194/hess-11-532-2007
Benshila, R., Durand, F., Masson, S., Bourdallé-Badie, R., de Boyer Montégut, C., Papa, F., et al. (2014). The upper Bay of Bengal salinity structure in a high-resolution model. Ocean Model. 74, 36–52. doi: 10.1016/j.ocemod.2013.12.001
Bookhagen, B., and Burbank, D. W. (2010). Toward a complete Himalayan hydrological budget: Spatiotemporal distribution of snowmelt and rainfall and their impact on river discharge. J. Geophys. Res. 115, F03019. doi: 10.1029/2009JF001426
Boyer, T. P., Garcia, H. E., Locarnini, R. A., Zweng, M. M., Mishonov, A. V., Reagan, J. R., et al. (2018). World Ocean Atlas 2018. NOAA National Centers for Environmental Information. Dataset. Available online at: https://www.ncei.noaa.gov/archive/accession/NCEI-WOA18 (accessed May 26, 2020).
Branstetter, M. L. (2001). Development of a Parallel River Transport Algorithm and Applications to Climate Studies. The University of Texas at Austin. Available online at: https://repositories.lib.utexas.edu/handle/2152/10545 (accessed February 18, 2022).
Branstetter, M. L. (2003). Continental runoff dynamics in the Community Climate System Model 2 (CCSM2) control simulation. J. Geophys. Res. 108, 4550. doi: 10.1029/2002JD003212
Bring, A., Asokan, S. M., Jaramillo, F., Jarsjö, J., Levi, L., Pietroń, J., et al. (2015). Implications of freshwater flux data from the CMIP5 multimodel output across a set of Northern Hemisphere drainage basins. Earth's Fut. 3, 206–217. doi: 10.1002/2014EF000296
Chaitanya, A. V. S., Lengaigne, M., J. Vialard, V. V., Gopalakrishna, F., Durand, C., et al. (2014). Salinity measurements collected by fishermen reveal a “river in the sea” flowing along the Eastern Coast of India. Bull. Am. Meteorol. Soc. 95, 1897–1908. doi: 10.1175/BAMS-D-12-00243.1
Charney, J. G., and Shukla, J. (1981). Predictability of monsoons. Monsoon Dyn. 99–109. doi: 10.1017/CBO9780511897580.009
Chowdary, J., Srinivas, G., Fousiya, T. S., Parekh, A., Gnanaseelan, C., Seo, H., et al. (2016). Representation of bay of bengal upper-ocean salinity in general circulation models. Oceanography. 29, 38–49. doi: 10.5670/oceanog.2016.37
Conkright, M. E., Antonov, J. I., Baranova, O. K., Boyer, T. P., Garcia, H. E., Gelfeld, R., et al. (2002). NOAA Atlas NESDIS 42, World Ocean Database 2001 volume 1: introduction. Washington, DC: US Gov. Printing Office. Available online at: http://www.nodc.noaa.gov (accessed January 10, 2022).
Da-Allada, C. Y., Gaillard, F., and Kolodziejczyk, N. (2015). Mixed-layer salinity budget in the tropical Indian Ocean: seasonal cycle based only on observations. Ocean Dyn. 65, 845–857. doi: 10.1007/s10236-015-0837-7
Dai, A. (2016). “Historical and future changes in streamflow and continental runoff: A review,” in Terrestrial Water Cycle and Climate Change: Natural and Human-Induced Impacts. doi: 10.1002/9781118971772.ch2
Dai, A. (2021). Hydroclimatic trends during 1950–2018 over global land. Clim. Dyn. 56, 4027–4049. doi: 10.1007/s00382-021-05684-1
Dai, A., Qian, T., Trenberth, K. E., and Milliman, J. D. (2009). Changes in continental freshwater discharge from 1948 to 2004. J. Clim 22, 2773–2792. doi: 10.1175/2008JCLI2592.1
Dai, A., and Trenberth, K. E. (2002). Estimates of freshwater discharge from continents: latitudinal and seasonal variations. J. Hydrometeorol. 3, 660–687. doi: 10.1175/1525-7541(2002)003<0660:EOFDFC>2.0.CO;2
David, C. H., Maidment, D. R., Niu, G. Y., Yang, Z. L., Habets, F., and Eijkhout, V. (2011). River network routing on the NHDPlus dataset. J. Hydrometeorol. 12, 913–934. doi: 10.1175/2011JHM1345.1
de Boyer Montégut, C. (2004). Mixed layer depth over the global ocean: an examination of profile data and a profile-based climatology. J. Geophys. Res. 109, C12003. doi: 10.1029/2004JC002378
De Boyer Montégut, C., Vialard, J., Shenoi, S. S. C., Shankar, D., Durand, F., Eth,é, C., et al. (2007). Simulated seasonal and interannual variability of the mixed layer heat budget in the northern indian ocean. J. Clim 20, 3249–3268. doi: 10.1175/JCLI4148.1
Decharme, B., Alkama, R., Douville, H., Becker, M., and Cazenave, A. (2010). Global evaluation of the ISBA-TRIP continental hydrological system. Part II: uncertainties in river routing simulation related to flow velocity and groundwater storage. J. Hydrometeorol. 11, 601–617. doi: 10.1175/2010JHM1212.1
Durand, F., Papa, F., Rahman, A., and Bala, S. K. (2011). Impact of Ganges–Brahmaputra interannual discharge variations on Bay of Bengal salinity and temperature during 1992–1999 period. J. Earth Syst. Sci. 120, 859–872. doi: 10.1007/s12040-011-0118-x
Ek, M. B., Mitchell, K. E., Lin, Y., Rogers, E., Grunmann, P., Koren, V., et al. (2003). Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model. J. Geophys. Res.: Atmospheres. 108, 12–16. doi: 10.1029/2002JD003296
Falloon, P., Betts, R., Wiltshire, A., Dankers, R., Mathison, C., McNeall, D., et al. (2011). Validation of river flows in HadGEM1 and HadCM3 with the TRIP river flow model. J. Hydrometeorol. 12, 1157–1180. doi: 10.1175/2011JHM1388.1
George, G., Rao, D. N., Sabeerali, C. T., Srivastava, A., and Rao, S. A. (2015). Indian summer monsoon prediction and simulation in CFSv2 coupled model. Atmos. Ocean. Sci. Lett. 17, 57–64. doi: 10.1002/asl.599
Getirana, A. C. V., Boone, A., and Peugeot, C. (2014). Evaluating LSM-based water budgets over a west african basin assisted with a river routing scheme. J. Hydrometeorol. 15, 2331–2346. doi: 10.1175/JHM-D-14-0012.1
Girishkumar, M. S., Joseph, J., Thangaprakash, V. P., Pottapinjara, V., and McPhaden, M. J. (2017). Mixed layer temperature budget for the northward propagating summer monsoon intraseasonal oscillation (MISO) in the Central Bay of Bengal. J. Geophys. Res. Oceans 122, 8841–8854. doi: 10.1002/2017JC013073
Goswami, B. N., Rao, S., Sengupta, D., and Chowdary, S. (2016). Monsoons to mixing in the bay of bengal: multiscale air-sea interactions and monsoon predictability. Oceanography. 29, 18–27. doi: 10.5670/oceanog.2016.35
Griffies, S. M., Gnanadesikan, A., Dixon, K. W., Dunne, J. P., Gerdes, R., Harrison, M. J., et al. (2005). Formulation of an ocean model for global climate simulations. Ocean Sci. 1, 45–79. doi: 10.5194/os-1-45-2005
Griffies, S. M., Harrison, M. J., Pacanowski, R. C., and Rosati, A. (2004). A technical guide to MOM4. GFDL Ocean Group Tech. Rep. 5, 371. Available online at: https://www.gfdl.noaa.gov/bibliography/related_files/smg0301.pdf
Hamman, J., Nijssen, B., Clark, E., Matthews, D., and Veerman, B. (2017a). UW-Hydro/RVIC: RVIC 1.1.1 (rvic.1.1.1). Zenodo. doi: 10.5281/zenodo.269614
Hamman, J., Nijssen, B., Roberts, A., Craig, A., Maslowski, W., and Osinski, R. (2017b). The coastal streamflow flux in the regional arctic system model. J. Geophys. Res. Oceans 122, 1683–1701. doi: 10.1002/2016JC012323
Han, W., McCreary, J. P., and Kohler, K. E. (2001). Influence of precipitation minus evaporation and Bay of Bengal rivers on dynamics, thermodynamics, and mixed layer physics in the upper Indian Ocean. J. Geophys. Res. Oceans 106, 6895–6916. doi: 10.1029/2000JC000403
Howden, S. D., and Murtugudde, R. (2001). Effects of river inputs into the Bay of Bengal. J. Geophys. Res. Oceans 106, 19825–19843. doi: 10.1029/2000JC000656
Huang, B., and Mehta, V. M. (2010). Influences of freshwater from major rivers on global ocean circulation and temperatures in the MIT ocean general circulation model. Adv. Atmospheric Sci. 27, 455–468. doi: 10.1007/s00376-009-9022-6
Huang, B., Thorne, P. W., Banzon, V. F., Boyer, T., Chepurin, G., Lawrimore, J. H., et al. (2017). Extended reconstructed Sea surface temperature, Version 5 (ERSSTv5): Upgrades, validations, and intercomparisons. J. Clim. 30, 8179–8205. doi: 10.1175/JCLI-D-16-0836.1
Jahfer, S., Vinayachandran, P. N., and Nanjundiah, R. S. (2017). Long-term impact of Amazon river runoff on northern hemispheric climate. Scientific Rep. 7, 10989. doi: 10.1038/s41598-017-10750-y
Jana, S., Gangopadhyay, A., and Chakraborty, A. (2015). Impact of seasonal river input on the Bay of Bengal simulation. Continental Shelf Res. 104, 45–62. doi: 10.1016/j.csr.2015.05.001
Jian, J., Webster, P. J., and Hoyos, C. D. (2009). Large-scale controls on Ganges and Brahmaputra river discharge on intraseasonal and seasonal times-cales. Q. J. R. Meteorol. Soc. 135, 353–370. doi: 10.1002/qj.384
Keerthi, M. G., Lengaigne, M., Vialard, J., de Boyer Montégut, C., and Muraleedharan, P. M. (2013). Interannual variability of the Tropical Indian Ocean mixed layer depth. Clim. Dyn. 40, 743–759. doi: 10.1007/s00382-012-1295-2
Köhler, J., Serra, N., Bryan, F. O., Johnson, B. K., and Stammer, D. (2018). Mechanisms of mixed-layer salinity seasonal variability in the Indian Ocean. J. Geophys. Res. Oceans. 123, 466–496. doi: 10.1002/2017JC013640
Krishna, R. P. M., Rao, S. A., Srivastava, A., Kottu, H. P., Pradhan, M., Pillai, P., et al. (2019). Impact of convective parameterization on the seasonal prediction skill of Indian summer monsoon. Clim. Dyn. 6227–6243. doi: 10.1007/s00382-019-04921-y
Lagerloef, G. S. E. (2002). Introduction to the special section: The role of surface salinity on upper ocean dynamics, air-sea interaction and climate. J. Geophys. Res. Oceans. 107, SRF 1-1-SRF 1-2. doi: 10.1029/2002JC001669
Large, W. G., and Yeager, S. (2004). Diurnal to Decadal Global Forcing for Ocean and Sea-ice Models: The Data Sets and Flux Climatologies.
Large, W. G., and Yeager, S. G. (2009). The global climatology of an interannually varying air-sea flux data set. Clim. Dynam. 33, 341–364. doi: 10.1007/s00382-008-0441-3
Lehner, B., and Grill, G. (2013). Global river hydrography and network routing: baseline data and new approaches to study the world's large river systems. Hydrological Proc. 27, 2171–2186. doi: 10.1002/hyp.9740
Li, H., Wigmosta, M. S., Wu, H., Huang, M., Ke, Y., Coleman, A. M., et al. (2013). A physically based runoff routing model for land surface and earth system models. J. Hydrometeorol. 14, 808–828. doi: 10.1175/JHM-D-12-015.1
Li, Y., Han, W., Ravichandran, M., Wang, W., Shinoda, T., and Lee, T. (2017a). Bay of Bengal salinity stratification and Indian summer monsoon intraseasonal oscillation: 1. Intraseasonal variability and causes. J. Geophys. Res. Oceans 122, 4291–4311. doi: 10.1002/2017JC012691
Li, Y., Han, W., Wang, W., Ravichandran, M., Lee, T., and Shinoda, T. (2017b). Bay of Bengal salinity stratification and Indian summer monsoon intraseasonal oscillation: 2. Impact on SST and convection. J. Geophys. Res. Oceans 122, 4312–4328. doi: 10.1002/2017JC012692
Lohmann, D., Nolte-Holube, R., and Raschke, E. (1996). A large-scale horizontal routing model to be coupled to land surface parametrization schemes. Tellus A: Dyn. Meteorol. Oceanogr. 48, 708–721. doi: 10.3402/tellusa.v48i5.12200
Lohmann, D., Raschke, E., Nijssen, B., and Lettenmaier, D. P. (1998). Hydrologie à l'échelle régionale: I. Formulation du modèle VIC-2L couplé à un modèle du transfert de l'eau. Hydrol. Sci. J. 43, 131–141. doi: 10.1080/02626669809492107
Lukas, R., and Lindstrom, E. (1991). The mixed layer of the western equatorial Pacific Ocean. J. Geophys. Res. 96, 3343–3357. doi: 10.1029/90JC01951
Masson, S., Luo, J.-J., Madec, G., Vialard, J., Durand, F., Gualdi, S., et al. (2005). Impact of barrier layer on winter-spring variability of the southeastern Arabian Sea. Geophysical Research Lett. 32, 1–4. doi: 10.1029/2004GL021980
Mignot, J., de Boyer Montégut, C., Lazar, A., and Cravatte, S. (2007). Control of salinity on the mixed layer depth in the world ocean: 2. Tropical areas. J. Geophys. Res. 112, C10010. doi: 10.1029/2006JC003954
Miller, J. R., Russell, G. L., and Caliri, G. (1994). Continental-Scale River Flow in Climate Models. J. Clim. 7, 914–928. doi: 10.1175/1520-0442(1994)007<0914:CSRFIC>2.0.CO;2
Mizukami, N., Clark, M. P., Sampson, K., Nijssen, B., Mao, Y., McMillan, H., et al. (2016). mizuRoute version 1: a river network routing tool for a continental domain water resources applications. Geosci. Model Dev. 9, 2223–2238. doi: 10.5194/gmd-9-2223-2016
Montégut C de, B., Mignot, J., Lazar, A., and Cravatte, S. (2007). Control of salinity on the mixed layer depth in the world ocean: 1. general description. J. Geophys. Res. 112, C06011. doi: 10.1029/2006JC003953
Moon, J.-H., and Song, Y. T. (2014). Seasonal salinity stratifications in the near-surface layer from Aquarius, Argo, and an ocean model: focusing on the tropical Atlantic/Indian Oceans. J. Geophys. Res. Oceans. 119, 6066–6077. doi: 10.1002/2014JC009969
Moorthi, S., Pan, H. L., and Caplan, P. (2001). “Changes to the 2001 NCEP operational MRF/AVN global analysis/forecast system,” in Technical Procedures Bulletin: Vol. Ser. No. 4. National Oceanic and Atmospheric Administration, National Weather Service, Office of Meteorology.
Murray, R. J. (1996). Explicit generation of orthogonal grids for ocean models. J. Comput. Phys. 126, 251–273. doi: 10.1006/jcph.1996.0136
Nijssen, B., O'Donnell, G. M., Lettenmaier, D. P., Lohmann, D., and Wood, E. F. (2001a). Predicting the discharge of global rivers. J. Clim. 14, 3307–3323. doi: 10.1175/1520-0442(2001)014<3307:PTDOGR>2.0.CO;2
Nijssen, B., Schnur, R., and Lettenmaier, D. P. (2001b). Global retrospective estimation of soil moisture using the variable infiltration capacity land surface model, 1980-93. J. Clim. 14, 1790–1808. doi: 10.1175/1520-0442(2001)014<1790:GREOSM>2.0.CO;2
Nohara, D., Kitoh, A., Hosaka, M., and Oki, T. (2006). Impact of climate change on river discharge projected by multimodel ensemble. J. Hydrometeorol. 7, 1076–1089. doi: 10.1175/JHM531.1
Nyadjro, E. S., and Subrahmanyam, B. (2014). SMOS mission reveals the salinity structure of the Indian ocean dipole. IEEE Geosci. Remote. Sens. 11, 1564–1568. doi: 10.1109/LGRS.2014.2301594
Oki, T., and Sud, Y. C. (1998). Design of total runoff integrating pathways (TRIP)—a global river channel network. Earth Interact. 2, 1–37. doi: 10.1175/1087-3562(1998)002<0001:DOTRIP>2.3.CO;2
Olivera, F., Famiglietti, J., and Asante, K. (2000). Global-scale flow routing using a source-to-sink algorithm. Water Resour. Res. 36, 2197–2207. doi: 10.1029/2000WR900113
Paiva, R. C. D., Collischonn, W., and Tucci, C. E. M. (2011). Large scale hydrologic and hydrodynamic modeling using limited data and a GIS based approach. J. Hydrol. 406, 170–181. doi: 10.1016/j.jhydrol.2011.06.007
Pan, M., Lin, P., Beck, H. E., Zeng, Z., Yamazaki, D., David, C. H., et al. (2021). Global reach-level 3-hourly river flood reanalysis (1980–2019). Bull. Am. Meteorol. Soc. 102, E2086–E2105. doi: 10.1175/BAMS-D-20-0057.1
Papa, F., Durand, F., Rossow, W. B., Rahman, A., and Bala, S. K. (2010). Satellite altimeter-derived monthly discharge of the Ganga-Brahmaputra River and its seasonal to interannual variations from 1993 to 2008. J. Geophys. Res. 115, C12013. doi: 10.1029/2009JC006075
Pappenberger, F., Cloke, H. L., Balsamo, G., Ngo-Duc, T., and Oki, T. (2010). Global runoff routing with the hydrological component of the ECMWF NWP system. Int. J. Climatol. 30, 2155–2174. doi: 10.1002/joc.2028
Piccolroaz, S., Di Lazzaro, M., Zarlenga, A., Majone, B., Bellin, A., and Fiori, A. (2016). HYPERstream: a multi-scale framework for streamflow routing in large-scale hydrological model. Hydrol. Earth Syst. Sci. 20, 2047–2061. doi: 10.5194/hess-20-2047-2016
Pillai, P. A., Rao, S. A., Das, R. S., Salunke, K., and Dhakate, A. (2018). Potential predictability and actual skill of Boreal Summer Tropical SST and Indian summer monsoon rainfall in CFSv2-T382: Role of initial SST and teleconnections. Clim. Dyn. 51, 493–510. doi: 10.1007/s00382-017-3936-y
Pillai, P. A., Rao, S. A., Srivastava, A., Ramu, D. A., Pradhan, M., and Das, R. S. (2021). Impact of the tropical Pacific SST biases on the simulation and prediction of Indian summer monsoon rainfall in CFSv2, ECMWF-System4, and NMME models. Clim. Dyn. 56, 1699–1715. doi: 10.1007/s00382-020-05555-1
Pokhrel, S., Rahaman, H., Parekh, A., Saha, S. K., Dhakate, A., Chaudhari, H. S., et al. (2012). Evaporation-precipitation variability over Indian Ocean and its assessment in NCEP Climate Forecast System (CFSv2). Clim. Dyn. 39, 2585–2608. doi: 10.1007/s00382-012-1542-6
Rahaman, H., Srinivasu, U., Panickal, S., Durgadoo, J. V., Griffies, S. M., Ravichandran, M., et al. (2020). An assessment of the Indian Ocean mean state and seasonal cycle in a suite of interannual CORE-II simulations. Ocean Model. 145, 101503. doi: 10.1016/j.ocemod.2019.101503
Rajeevan, M., Bhate, J., and Jaswal, A. K. (2008). Analysis of variability and trends of extreme rainfall events over India using 104 years of gridded daily rainfall data. Geophys. Res. Lett. 35, L18707. doi: 10.1029/2008GL035143
Ramu, D. A., Sabeerali, C. T., Chattopadhyay, R., Rao, D. N., George, G., Dhakate, A. R., et al. (2016). Indian summer monsoon rainfall simulation and prediction skill in the CFSv2 coupled model: Impact of atmospheric horizontal resolution. J. Geophys. Res. Atmos. 1752–1775. doi: 10.1002/2015JD024629
Rao, R. R., and Sivakumar, R. (2003). Seasonal variability of sea surface salinity and salt budget of the mixed layer of the north Indian Ocean. J. Geophys. Res. 108, 3009. doi: 10.1029/2001JC000907
Rao, S. A., Goswami, B. N., Sahai, A. K., Rajagopal, E. N., Mukhopadhyay, P., Rajeevan, M., et al. (2019). Monsoon mission a targeted activity to improve monsoon prediction across scales. Bul.l Am. Meteorol. Soc. 100, 2509–2532. doi: 10.1175/BAMS-D-17-0330.1
Rao, S. A., Saha, S. K., Pokhrel, S., Sundar, D., Dhakate, A. R., Mahapatra, S., et al. (2011). Modulation of SST, SSS over northern Bay of Bengal on ISO time scale. J. Geophys. Res. 116, C09026. doi: 10.1029/2010JC006804
Saha, S., Moorthi, S., Pan, H. -L., Wu, X., Wang, J., Nadiga, S., et al. (2010). The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 91, 1015–1058. doi: 10.1175/2010BAMS3001.1
Saha, S., Moorthi, S., Wu, X., Wang, J., Nadiga, S., Tripp, P., et al. (2014). The NCEP climate forecast system version 2. J. Clim 27, 2185–2208. doi: 10.1175/JCLI-D-12-00823.1
Schiller, A., and Oke, P. R. (2015). Dynamics of ocean surface mixed layer variability in the Indian Ocean. J. Geophys. Res. Oceans 120, 4162–4186. doi: 10.1002/2014JC010538
Seidov, D., and Haupt, B. J. (2003). On sensitivity of ocean circulation to sea surface salinity. Glob Planet Change. 36, 99–116. doi: 10.1016/S0921-8181(02)00177-7
Sengupta, D., Bharath Raj, G. N., and Shenoi, S. S. C. (2006). Surface freshwater from Bay of Bengal runoff and Indonesian throughflow in the tropical indian Ocean. Geophy. Research Lett. 33, L22609. doi: 10.1029/2006GL027573
Seo, H., Xie, S. P., Murtugudde, R., Jochum, M., and Miller, A. J. (2009). Seasonal effects of Indian Ocean freshwater forcing in a regional coupled model. J. Clim. 22, 6577–6596. doi: 10.1175/2009JCLI2990.1
Shaad, K. (2018). Evolution of river-routing schemes in macro-scale models and their potential for watershed management. Hydrol. Sci. J. 63, 1062–1077. doi: 10.1080/02626667.2018.1473871
Shenoi, S. S. C. (2002). Differences in heat budgets of the near-surface Arabian Sea and Bay of Bengal: Implications for the summer monsoon. J. Geophys. Res. 107, 5–14. doi: 10.1029/2000JC000679
Shetye, S. R., Gouveia, A. D., Shankar, D., Shenoi, S. S. C., Vinayachandran, P. N., Sundar, D., et al. (1996). Hydrography and circulation in the western Bay of Bengal during the northeast monsoon. J. Geophys. Res. Oceans. 101, 14011–14025. doi: 10.1029/95JC03307
Siderius, C., Biemans, H., Wiltshire, A., Rao, S., Franssen, W. H. P., Kumar, P., et al. (2013). Snowmelt contributions to discharge of the Ganges. Sci. Total Environ. 468–469. doi: 10.1016/j.scitotenv.2013.05.084
Sikder, S., Chen, X., Hossain, F., Roberts, J. B., Robertson, F., Shum, C. K., et al. (2016). Are general circulation models ready for operational streamflow forecasting for water management in the ganges and brahmaputra river basins? J. Hydrometeorol. 17, 195–210. doi: 10.1175/JHM-D-14-0099.1
Sprintall, J., and Tomczak, M. (1992). Evidence of the barrier layer in the surface layer of the tropics. J. Geophys. Res. 97, 7305. doi: 10.1029/92JC00407
Srivastava, A., Gera, A., Momin, I. M., Mitra, A. K., and Gupta, A. (2020). The impact of northern Indian Ocean rivers on the Bay of Bengal using NEMO global ocean model. Acta Oceanologica Sinica 39, 45–55. doi: 10.1007/s13131-020-1537-9
Srivastava, A., Pradhan, M., George, G., Dhakate, A., Salunke, K., and Rao, S. A. (2015). “A Research Report on the 2015 Southwest Monsoon,” In, Mujumdar, M., Gnanaseelan, C., and Rajeevan, M. Pune: Indian Institute of Tropical Meteorology. ESSO/IITM/SERP/SR/02 (2015)/185. Available online at: http://www/tropmet.res.in. p. 58–62.
Srivastava, A., Rao, S. A., and Ghosh, S. (2022). Impact of riverine freshwater on synoptic and intra-seasonal variability of the Indian Summer Monsoon.
Srivastava, A., Rao, S. A., Rao, D. N., George, G., and Pradhan, M. (2017). Structure, characteristics, and simulation of monsoon low-pressure systems in CFSv2 coupled model. J. Geophys. Res. Oceans. 122, 6394–6415. doi: 10.1002/2016JC012322
Sushama, L., Laprise, R., Caya, D., Larocque, M., and Slivitzky, M. (2004). On the variable-lag and variable-velocity cell-to-cell routing schemes for climate models. Atmosphere-Ocean. 42, 221–233. doi: 10.3137/ao.420401
Taylor, K. E., Stouffer, R. J., and Meehl, G. (2012). An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 93, 485–498. doi: 10.1175/BAMS-D-11-00094.1
Thadathil, P., Muraleedharan, P. M., Rao, R. R., Somayajulu, Y. K., Reddy, G. V., et al. (2007). Observed seasonal variability of barrier layer in the Bay of Bengal. J. Geophys. Res. 112, C02009. doi: 10.1029/2006JC003651
The NCAR Command Language (Version 6.6.2). (2019). Boulder, CO: UCAR/NCAR/CISL/TDD. doi: 10.5065/D6WD3XH5
Valsala, V., Singh, S., and Balasubramanian, S. (2018). A modeling study of interannual variability of bay of bengal mixing and barrier layer formation. J. Geophys. Res. Ocean.s 123, 3962–3981. doi: 10.1029/2017JC013637
Verzano, K., Bärlund, I., Flörke, M., Lehner, B., Kynast, E., Vo,ß, F., et al. (2012). Modeling variable river flow velocity on continental scale: Current situation and climate change impacts in Europe. J. Hydrol. 424–425, 238–251. doi: 10.1016/j.jhydrol.2012.01.005
Vialard, J., Jayakumar, A., Gnanaseelan, C., Lengaigne, M., Sengupta, D., and Goswami, B. N. (2012). Processes of 30-90 days sea surface temperature variability in the northern Indian Ocean during boreal summer. Clim. Dyn. 38, 1901–1916. doi: 10.1007/s00382-011-1015-3
Vijith, V., Vinayachandran, P. N., Webber, B. G. M., Matthews, A. J., George, J., et al. (2020). Closing the sea surface mixed layer temperature budget from in situ observations alone: operation advection during BoBBLE. Sci. Rep. 10, 7062. doi: 10.1038/s41598-020-63320-0
Vinayachandran, P. N., Jahfer, S., and Nanjundiah, R. S. (2015). Impact of river runoff into the ocean on Indian summer monsoon. Environ. Res. Lett. 10, 054008. doi: 10.1088/1748-9326/10/5/054008
Vinayachandran, P. N., Murty, V. S. N., and Ramesh Babu, V. (2002). Observations of barrier layer formation in the Bay of Bengal during summer monsoon. J. Geophys. Res. Oceans. 107, 19–19. doi: 10.1029/2001JC000831
Weller, R., Farrar, J. T., Buckley, J., Matthew, S., Venkatesan, R., Lekha, J. S., et al. (2016). Air-Sea Interaction in the Bay of Bengal. Oceanography. 29, 28–37. doi: 10.5670/oceanog.2016.36
Wen, Z., Liang, X., and Yang, S. (2012). A new multiscale routing framework and its evaluation for land surface modeling applications. Water Resour. Res. 48, 8528. doi: 10.1029/2011WR011337
Whitaker, D. W., Wasimi, S. A., and Islam, S. (2001). The El Niño-Southern oscillation and long-range forecasting of flows in the ganges. Int. J. Climatol. 21, 77–87. doi: 10.1002/joc.583
Wilson, E. A., and Riser, S. C. (2016). An Assessment of the Seasonal Salinity Budget for the Upper Bay of Bengal. J. Phy. Oceanogr. 46, 1361–1376. doi: 10.1175/JPO-D-15-0147.1
Winton, M. (2000). A reformulated three-layer sea ice model. J. Atmos. Ocean. Technol. 17, 525–531. doi: 10.1175/1520-0426(2000)017<0525:ARTLSI>2.0.CO;2
Wu, H., Kimball, J. S., Li, H., Huang, M., Leung, L. R., and Adler, R. F. (2012). A new global river network database for macroscale hydrologic modeling. Water Resour. Res. 48, W09701. doi: 10.1029/2012WR012313
Wu, H., Kimball, J. S., Mantua, N., and Stanford, J. (2011). Automated upscaling of river networks for macroscale hydrological modeling. Water Resour. Res. 47, 1–18. doi: 10.1029/2009WR008871
Yamazaki, D., Kanae, S., Kim, H., and Oki, T. (2011). A physically based description of floodplain inundation dynamics in a global river routing model. Water Resour. Res. 47, 4501. doi: 10.1029/2010WR009726
Yamazaki, D., Oki, T., and Kanae, S. (2009). Deriving a global river network map and its sub-grid topographic characteristics from a fine-resolution flow direction map. Hydrol. Earth Syst. Sci. 13, 2241–2251. doi: 10.5194/hess-13-2241-2009
Yamazaki, D., Sato, T., Kanae, S., Hirabayashi, Y., and Bates, P. D. (2014). Regional flood dynamics in a bifurcating mega delta simulated in a global river model. Geophy. Res. Lett. 41, 3127–3135. doi: 10.1002/2014GL059744
Ye, A., Duan, Q., Zhan, C., Liu, Z., and Mao, Y. (2013). Improving kinematic wave routing scheme in Community Land Model. Hydrol. Res. 44, 886–903. doi: 10.2166/nh.2012.145
Yin, J., Stouffer, R. J., Spelman, M. J., and Griffies, S. M. (2010). Evaluating the uncertainty induced by the virtual salt flux assumption in climate simulations and future projections. J. Clim 23, 80–96. doi: 10.1175/2009JCLI3084.1
Zhang, N., Feng, M., Du, Y., Lan, J., and Wijffels, S. E. (2016). Seasonal and interannual variations of mixed layer salinity in the southeast tropical Indian Ocean. J. Geophys. Res. Oceans 121, 4716–4731. doi: 10.1002/2016JC011854
Zhu, J., and Kumar, A. (2019). Role of sea surface salinity feedback in MJO predictability: a study with CFSv2. J. Clim. 32, 5745–5759. doi: 10.1175/JCLI-D-18-0755.1
Keywords: fresh water river discharge, seasonal forecasts, coupled climate models, coupled system feedbacks, hydrology, monsoons
Citation: Srivastava A, Rao SA and Ghosh S (2022) Impact of Riverine Fresh Water on Indian Summer Monsoon: Coupling a Runoff Routing Model to a Global Seasonal Forecast Model. Front. Clim. 4:902586. doi: 10.3389/fclim.2022.902586
Received: 23 March 2022; Accepted: 05 May 2022;
Published: 14 June 2022.
Edited by:
Arun Kumar, National Oceanic and Atmospheric Administration (NOAA), United StatesReviewed by:
Bohua Huang, George Mason University, United StatesJieshun Zhu, University of Maryland, United States
Copyright © 2022 Srivastava, Rao and Ghosh. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Suryachandra A. Rao, c3VyeWFAdHJvcG1ldC5yZXMuaW4=
 Ankur Srivastava
Ankur Srivastava Suryachandra A. Rao
Suryachandra A. Rao Subimal Ghosh
Subimal Ghosh