Kinetics of Olivine Weathering in Seawater: An Experimental Study

Enhanced weathering of mafic and ultra-mafic minerals has been suggested as a strategy for carbon dioxide removal (CDR) and a contribution to achieve a balance between global CO₂ sources and sinks (net zero emission). This study was designed to assess CDR by dissolution of ultramafic sand (UMS) in artificial seawater (ASW). Fine grained UMS with an olivine content of ~75% was reacted in ASW for up to 134 days at 1 bar and 21.5–23.9°C. A decline in total alkalinity (TA) was observed over the course of the experiments. This unexpected result indicates that TA removal via precipitation of cation-rich authigenic phases exceeded the production of TA induced by olivine dissolution. The TA decline was accompanied by a decrease in dissolved inorganic carbon and Ca concentrations presumably induced by CaCO₃ precipitation. Temporal changes in dissolved Si, Ca, Mg, and TA concentrations observed during the experiments were evaluated by a numerical model to identify secondary mineral phases and quantify rates of authigenic phase formation. The modeling indicates that CaCO₃, FeOOH and a range of Mg-Si-phases were precipitated during the experiments. Chemical analysis of precipitates and reacted UMS surfaces confirmed that these authigenic phases accumulated in the batch reactors. Nickel released during olivine dissolution, a potential toxic element for certain organisms, was incorporated in the secondary phases and is thus not a suitable proxy for dissolution rates as proposed by earlier studies. The overall reaction stoichiometry derived from lab experiments was applied in a box model simulating atmospheric CO₂ uptake in a continental shelf setting induced by olivine addition. The model results indicate that CO₂ uptake is reduced by a factor of 5 due to secondary mineral formation and the buffering capacity of seawater. In comparable natural settings, olivine addition may thus be a less efficient CDR method than previously believed.

Introduction

The CO₂ content in the atmosphere has continuously increased over the last 120 years to a current maximum of 412 ppm (Keeling et al., 2001; MacFarling Meure et al., 2006; Howe, 2015). Since CO₂ acts as a greenhouse gas (Feldman et al., 2015), it is mainly responsible for the anthropogenic greenhouse effect (Lindzen, 2007; Solomon et al., 2009). The 2015 Paris Climate Change Conference COP21 agreed on limiting global warming to <2°C compared to the preindustrial level. Furthermore, it was stated that reaching this goal can only be reached if zero net emissions of CO₂ are attained between 2030 and 2050 (Rhodes, 2016). The 2018 IPCC (Intergovernmental Panel on Climate Change) special report “Global Warming of 1.5°C” has made clear that this goal is only achievable if in addition to the reduction of CO₂ emissions, CO₂ is actively sequestered from the atmosphere in form of negative emissions (Friedlingstein et al., 2011; IPCC, 2021).

A vast variety of carbon dioxide removal (CDR) techniques has been proposed and critically reviewed over the last 20 years (Lackner, 2003; Iizuka et al., 2004; Lal, 2004; Fuss et al., 2018; Saran et al., 2018). Amongst other methods, CO₂ sequestration by alkalinity enhancement through silicate weathering has been highlighted as an affordable and effective CDR technique (Oelkers, 2001; Hartmann and Kempe, 2008; Renforth and Henderson, 2014; Montserrat et al., 2017). The general concept behind this technique is the chemical reaction of an idealized magnesium silicate, i.e., forsterite (Mg₂SiO₄), with water, following:

$\begin{array}{ll}M{g}_{2}Si{O}_4+4H_{2}O+4C{O}_2\to 2M{g}^{2+}+H_{4}Si{O}_4+4{HC{O}_3}^{-}& (1)\end{array}$

This reaction has been thoroughly studied in soils on land (Oelkers, 1999; Olsen and Rimstidt, 2008; Oelkers et al., 2015; Amann et al., 2020) but to a smaller extent in seawater, despite the fact that enhanced olivine weathering would have a triple positive effect if applied in the ocean: (1) CO₂ would be sequestered from the atmosphere into the ocean, (2) the acidification of the oceans would be reduced, and (3) the supply of silica and iron, which are limiting nutrients in many parts of the ocean, would increase primary production and could lead to further CO₂ uptake (Hartmann et al., 2013; Montserrat et al., 2017).

The idea behind this concept is to distribute fine grained olivine (Strefler et al., 2018) in coastal areas, along beaches and/or on shelf regions (Meysman and Montserrat, 2017; Montserrat et al., 2017). Subsequently, olivine dissolves following Equation (1) and thus takes up CO₂ by contributing total alkalinity (TA) to the water column.

A vast number of studies have investigated or reviewed the dissolution kinetics of olivine in aqueous solutions (Pokrovsky and Schott, 2000; Oelkers, 2001; Davis et al., 2009; Rimstidt et al., 2012; Méheut and Schauble, 2014; Maher et al., 2016; Oelkers et al., 2018) including filtered seawater (FSW) (Montserrat et al., 2017) and artificial seawater (ASW) (Montserrat et al., 2017; Rigopoulos et al., 2018). Montserrat et al. (2017) showed that during the dissolution of olivine in SW and ASW the amount of TA increase is up to ~80% lower than theoretically expected. This TA deficit was left unexplained but loosely related to the possible but not observed formation of secondary minerals.

Other studies suggested that the low TA increase was caused by lower dissolution rates due to the formation of passivating surface layers that either consist of a deprotonated surface complex (Pokrovsky and Schott, 2000; Palandri and Kharaka, 2004) or repolymerized silicic acid (Maher et al., 2016) or the formation of secondary mineral phases on the olivine grains, which reduce the reactive surface (Béarat et al., 2006; King et al., 2010; Sissmann et al., 2013; Oelkers et al., 2018).

These secondary minerals, including the formation of CaCO₃, have also been linked to direct TA loss and thus low TA increase observed in several studies (Béarat et al., 2006; Hangx and Spiers, 2009; Köhler et al., 2013; Sissmann et al., 2013; Meysman and Montserrat, 2017; Montserrat et al., 2017). However, the rates and mechanisms of their formation are poorly constrained especially in SW and ASW.

Furthermore, the release of toxic elements such as nickel has been subject to speculations about a possible negative effect on the environment if olivine is applied in coastal ecosystems (Montserrat et al., 2017; Flipkens et al., 2021).

In this study, batch experiments were carried out in which ultramafic olivine sand was weathered in ASW. A special focus is laid on the formation of secondary phases and their impact on the CO₂ sequestration efficiency. The implications for the application of enhanced olivine weathering as a CDR measure for climate change mitigation are assessed. Furthermore, the release of potentially toxic elements such as nickel is investigated, which allows a better assessment of environmental risks associated with enhanced olivine weathering.

Materials and Methods

Materials

Commercially available ultra-mafic sand (UMS) was received from AdL Sandstrahltechnik, which, according to oral information from the company, ultimately derives from several quarries in northern Italy, presumably located in the mafic-ultramafic complex near Vidracco (Kremer et al., 2019). The olivine content of UMS was determined as 74.6 wt-%. For a detailed chemical composition see Table 1 and Supplementary Table 4.

TABLE 1

Table 1. Mineralogical model for UMS (bulk) combining XRD, WDX, and ICP-OES data.

The UMS was milled and subsequently sieved to separate grains with a diameter of 100–125 μm, based on the recommendation by Strefler et al. (2018). The 100–125 μm fraction was then thoroughly washed with ASW until the supernatant was clear. Subsequently, the diluted salts were removed by at least three wash cycles with deionized water (18.2 MΩ-Milli-Q system, hereafter: MQe) until the supernatant was clear. The composition of ASW was calculated for a salinity of 35.0 (Millero et al., 2008). Additionally, 2.3 mmol/l NaHCO₃ were added to reach an alkalinity of ~2.3 mmol/l. All chemical components listed in Supplementary Table 3 were dissolved in MQe. The initial Ca content was lower than listed (~320 mg/l instead of 422 mg/l). After day 50, the ASW used for replacement after sample taking contained the correct amount of Ca (422 mg/l). The lower initial Ca content was applied to keep the saturation state with respect to aragonite and calcite within natural ranges of the surface ocean (Feely et al., 2012) and to avoid strong oversaturation that can appear during the early stage of the experiment due to rapid dissolution of high-energy surface sites created during the milling process.

Experimental Setup

The UMS was permitted to react with artificial seawater in 250 ml polyethylene (PE) batch reactors. Three different batches with variable amounts of UMS were prepared, each containing three replicates (n = 3) to verify the reproducibility of the experiments. The amount of ASW was 200 ml for all replicates and batches. Fifty milliliter of ambient air were included to allow for equilibration with the atmosphere. The amount of UMS was varied from 20 g for Batch20 to 10 g for Batch10 and 5 g for Batch5 in order to investigate the effect of the solid/liquid ratio. The air was partly exchanged with the laboratory atmosphere every time samples were taken. All batch reactors with artificial seawater, UMS and gas phase were subjected to constant movement in Heidolph™ Reax2© over-head shakers at ~40 rpm. The experiment was conducted under controlled laboratory conditions (p = 1 bar, 21.5°C < T <23.9°C).

Sampling Procedure From Batch Reactors and Water Analysis

For each sample (23 in total), two aliquots (2 ml and 5 ml) were taken for further measurements and the same volume of artificial seawater was added to ensure a constant solid/liquid ratio. For the same reason it was made sure that no UMS grains were removed via sample taking. Sampling intervals increased from minutes to hours during day one to every 2 weeks between day 50 and day 134. The 5 ml aliquot was filtered through a 0.2 μm cellulose membrane filter and refrigerated in 5.2 ml Zinsser™ scintillation bottles. The 2 ml aliquot was used for direct pH measurements (see below) and not filtered to ensure a pristine chemical milieu. At the end of the experiments, the ASW in the batch reactors was carefully decanted over a 0.2 μm regenerated cellulose filter to recover the grayish suspended matter that had formed in the batch reactors during the experiment. Fine particles possibly stuck to the UMS grains were eluted by refilling the batch reactor with fresh ASW, shaking and decanting it. This procedure was repeated until the supernatant was clear. Withal, it was made sure that all precipitates, which left the bottles, were recovered on the filters. Subsequently, the wet cake was rinsed with pH neutral MQe to elute dissolved species (e.g., salinity). Furthermore, the UMS used in Batch20 was recovered, very carefully rinsed with pH neutral MQe (to only elute salinity), and dried for scanning electron microscope energy-dispersive X-ray spectroscopy (SEM–EDX).

The water samples were analyzed for pH following Dickson (1993). TA was analyzed by titration with diluted HCl to an end point of pH = 4.5 (Gieskes et al., 1991; Stumm and Morgan, 1996) and element concentrations were determined using inductively coupled plasma optical emission spectrometry (ICP-OES).

Solid Phase Analysis

Pristine (unused and washed) and weathered UMS as well as the precipitates recovered from the batch reactors were digested after a modified alkali-fusion method of van den Boorn et al. (2006), in order to preserve Si, which is lost using conventional HF digestion methods. In contrast to van den Boorn et al. (2006), we used Teflon beakers on a hot plate instead of an oven. Between 20 and 40 mg of NaOH (Merck™ Suprapure^®) and a drop of MQe were added and the sample set to reflux for 72 h at 120°C. Afterwards the sample was diluted with 1 ml MQe and transferred to a 1.5 ml save-lock tube and centrifuged at 11,000 rpm. The supernatant was separately stored and the undissolved residues retransferred to the Teflon vial, together with 200 μl of concentrated HNO₃ and set to reflux for 72 h at 120°C. After the second reflux 1 ml of MQe was added to the sample and the sample centrifuged and the supernatant removed, as described above. The entire procedure was then repeated. Subsequently, the dissolved samples (e.g., all aliquots of each sample) were retransferred to the Teflon beakers and measured with ICP-OES.

Additionally, major and trace elements were determined using the Panalytical Axios Plus X-ray spectrometer at the Institut für Chemie und Biologie des Meeres (ICBM) in Oldenburg. In brief, 700 mg of freeze-dried and homogenized ultra-mafic sand was mixed with 4,200 mg lithiumtetraborate (Li₂ B₄ O₇ Spektromelt) and fused to glass beads. The accuracy and precision were determined by simultaneous runs of certified sediment standards BE-N and BIR-1 (IGGE; e.g., Govindaraju, 1994) and in-house standard (PSS) with better than 2.6% RSD for major elements and 3.3% RSD for trace elements.

In order to determine the precise composition of the single mineral phases, the UMS before and after the experiment was investigated using a JXA-8200 SuperProbe high resolution SEM and a WDX/EDX Combined Electron Probe Microanalyzer (EPMA) at GEOMAR. For this purpose, a small portion of reacted UMS (see section Sampling Procedure From Batch Reactors and Water Analysis) and small portion of fresh UMS were poured on a self-sticking carbon plate. Thereby it was made sure that both samples did not mix and that the grains were placed solitarily. Furthermore, fresh UMS and reacted UMS were embedded in resin and the hardened samples were whetted to create a suitable surface for element analysis along a profile. Afterwards the samples were evaporated with carbon and placed in the EPMA. A large number of measuring points were evenly distributed along a profile with a distance between the measuring points of ~1.5 μm. The spatial resolution of each measuring point is ~5 μm. Hence, neighboring data points overlapped along the profile. The measured values were reported as atomic proportion normalized to 24 oxygen atoms with an RSD better than 0.7% for simultaneously measured standards and better than 1.5% for major elements. Finally, the element abundance was normalized to 100 wt.-% and the atomic proportion normalized to 24 oxygen. For the analysis of carbonate grains, the carbon content was pre-set to 12.01 wt.-%. Apart from quantitative measurements, scanning electron microscope (SEM) images were taken with the same device.

In order to verify the mineral composition, the pristine UMS as well as the precipitates recovered from the batch reactors were measured on a Phillips X-ray diffractometer (XRD) equipped with an automatic divergency slit, monochromator and a Co-cube at 40 kV and 35 mA. The samples were finely ground, pressed on an Si monocrystalline plate and measured with 2θ = [4;75] at 0.01° steps for 1 s at each step. The analysis of the XRD diffractograms was performed via the xPowder™ software and the standard PDF2 database. The results and interpretations are shown in Supplementary Figures 1–4.

Model Setup

A dissolution-precipitation model was set up with Wolfram Mathematica to simulate the chemical reactions for each batch experiment. The kinetic box model considers dissolution of olivine after Rimstidt et al. (2012), precipitation of the secondary phases aragonite/calcite, sepiolite, crysotile, talc and Fe(OH)₃ based on saturation state calculations (Supplementary Section 1). The model also calculates the concentration of dissolved Mg, Si, Ca, Fe as well as TA and is used to infer the overall reaction stoichiometry.

For each species in solution, ordinary differential equations (ODEs) were formulated as:

$\begin{array}{ll}\frac{dC}{dt}={\phi }_{ol}*r_{ol}-{\sum }_j{\phi }_{m,j}*r_{m,j}-r_s*(C-C_{in})& (2)\end{array}$

where C is concentration of the considered species in the dissolved phase, t is time, φ_ol represents the abundance of the species in olivine (ol) and r_ol is the olivine dissolution rate. Precipitation of secondary mineral phases (j) is calculated by multiplying the respective precipitation rate (r_{m, j}) with a corresponding stoichiometric coefficient (φ_{m, j}) defining the content of the considered element in the respective mineral. Sampling and replacement by fresh ASW are considered by applying the sampling rate r_S and the concentration difference between sample (C) and unreacted ASW (C_in).

The model is solved using the solver for ordinary differential equations of MATHEMATICA (version 11.3).

The precipitation rate of secondary minerals depends on the corresponding saturation state (Ω_i(t)):

$\begin{array}{ll}{r}_{pr{e}_i}={\epsilon }_{{pre1}_i}*UnitStep({\Omega }_i(t)-1)*{|{\Omega }_i(t)-1|}^{{\epsilon }_{{pre2}_i}}& (3)\end{array}$

UnitStep expresses a function that returns 0 for arguments smaller than or equal to 0 and 1 for all arguments larger than 0. Hence, precipitation was assumed to take place only when the solutions were oversaturated with respect to the considered mineral (Ω_i(t) > 1). ε_pre2i defines the order of the reaction and ε_pre1i is defined as

$\begin{array}{ll}{\epsilon }_{{pre1}_i}=k_{pr{e}_i}*\left(1-\frac{1}{1+e^{\frac{t-{\alpha }_i}{{\beta }_i}}}\right)& (4)\end{array}$

k_prei is a kinetic constant, α represents the time delay until the precipitation starts and β steers the speed with which the precipitation starts. ε_pre1i was introduced because the solids used in our experiments did not contain seed material for the precipitation of secondary minerals. Hence, the precipitation did not start immediately after oversaturation was reached but with a delay expressed by ε_pre1i. The kinetic constants k_prei (Equation 4) were employed to consider the fact that precipitation rates are not only determined by the degree of oversaturation but also by kinetic factors that may either slowdown or accelerate the precipitation reaction.

The oxidation of ferrous iron released during olivine dissolution was simulated applying the kinetic rate for abiotic iron oxidation (Millero et al., 1987).

The mineralogical composition of the UMS and the precipitates was determined with a simple mixing calculation. In a first step, element concentrations measured via ICP-OES were normalized to the measured Si content following:

$\begin{array}{ll}{C}_{i,S}=con{c}_i/S{i}_S& (5)\end{array}$

where $C_{i,S}\left(\frac{mo{l}_{element}}{mo{l}_{S{i}_S}}\right)$ is the concentration of an element normalized to the Si concentration in the respective solid S (UMS or precipitates), $con{c}_i\left(\frac{mo{l}_{element}}{m{g}_S}\right)$ is the concentration of an element per milligram solid and $S{i}_S\left(\frac{mo{l}_{S{i}_S}}{m{g}_S}\right)$ is the Si concentration in the solid.

In a second step, the composition was calculated following:

$\begin{array}{ll}{C}_{i,bulk}={\sum }_i(C_{i,min}*f_{bulk})/S{i}_{bulk}& (6)\end{array}$

$C_{i,bulk}\left(\frac{mo{l}_{element}}{mo{l}_{S{i}_{bulk}}}\right)$ represents the molar fraction of an element i in the calculated composition normalized to mol of Si; $C_{i,min}\left(\frac{mo{l}_{element}}{mo{l}_{mineral}}\right)$ is the molar content of the element in a certain mineral. $f_{bulk}\left(\frac{mo{l}_{mineral}}{mo{l}_{bulk}}\right)$ denotes the fraction of a certain mineral in the calculated composition and $S{i}_{bulk}\left(\frac{mo{l}_{S{i}_{bulk}}}{mo{l}_{bulk}}\right)$ represents the corresponding Si content (Table 1). The mineral phases used for this calculation were estimated from XRD and WDX measurements. The amount of each mineral (f_bulk) was then iterated until C_{i, bulk} values for each element were acceptably close to the measured C_{i, S} values. Normalization to Si was used to allow comparing concentrations (mol/mg) measured via ICP-OES to atomic proportions (normalized to 24 O) obtained via WDX and XRD.

Results

Composition of the Ultra-Mafic Sand (UMS)

The major and trace element measurements (ICP-OES and XRF) of the UMS are mainly in good agreement with the oxide composition provided by the manufacturer (Supplementary Table 6). Furthermore, 5% of the UMS consisted of accessory oxides such as MnO, K₂O, CaO, and Al₂O₃ which were not accounted for in the manufacturer information. According to WDX measurements the olivine used consists of 90.3% forsterite and 9.7% fayalite leading to the formula (M_{g0.90Fe0.10)2}SiO₄ (Fo90) and based on the simple mineral model accounts for 74.62% of the UMS (Table 1). The second largest fraction is Orthopyroxene (Opx) with the simplified structural formula (Mg_0.9Fe_0.1)₂(Al_0.15Si_0.85)₂O₆ accounting for 15.92% followed by an amphibole (Amph., likely tremolite) with the structural formula (Na_0.36K_0.14)(Ca_0.95Mg_0.05)₂(Cr_0.014Fe_0.079Mg_0.79Al_0.087Ti_0.03)₅(Si_7.4Al_0.6)O₂₂(OH)₂ (5.41%) and a Clinopyroxene (Cpx) with 3.5% and the structural formula (CaMg)₂(Si_0.9Al_0.1)₂O₆. Additionally, WDX measurements revealed the presence of accessory spinel and Ni and Fe sulfides. The abundance of these phases was estimated employing ICP-OES data and EDX observations.

Concentrations of Dissolved Species Measured During the Experiments

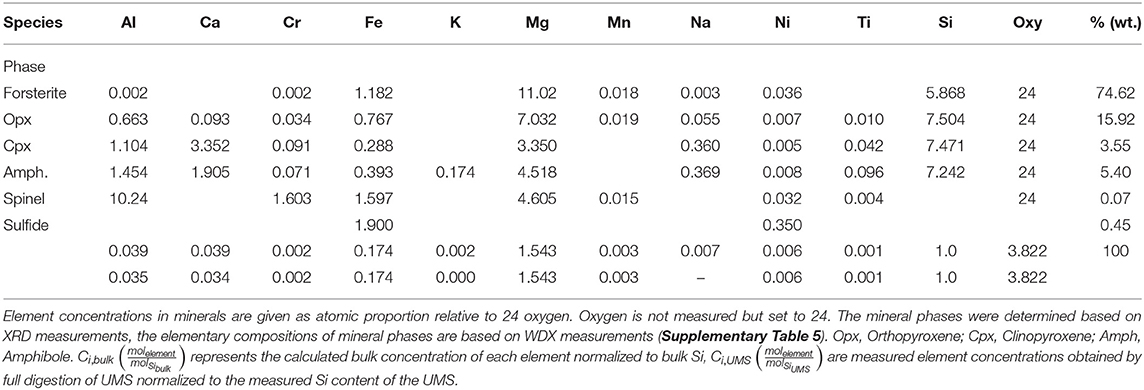
All experiments show a common trend of increasing TA in the early stage of the experiment and a decrease below initial values (2.36 ± 0.011 meq/l) after a certain period of time (Figure 1A). The highest and lowest values (2.65 ± 0.011 meq/l; 1.266 ± 0.019 meq/l), were measured in Batch20 (solid/liquid = 1/10) after 1 day (highest) and at the very end of the experiment (lowest). Batch5 (solid/liquid = 1/40) shows the lowest overall temporal gradient. The peak values occur the latest for Batch5, which also shows the highest final TA values, even though associated with the largest errors. Dissolved silicon concentrations [Si] increase persistently over the entire experiment (Figure 1B). The fastest increase is observed during the initial stage of the experiment (e.g., Supplementary Tables 8–10). The rate of [Si] increase then stabilizes during the experiment to nearly constant values toward the end. An exception to that trend is visible in Batch5. Here, the rate increases abruptly around day 78 (Supplementary Table 10) before a steady increase is attained. This rate change does not occur in all three replicates, which is reflected in high double standard deviation (2SD) values for [Si] toward the end of the experiment (Figure 1B). The highest concentrations are observed at the end of the experiment with a final [Si] of 421.8 ± 1.3 μmol/l (Batch20), 286.6 ± 6.4 μmol/l [Batch10 (solid/liquid = 1/20)] and 190.3 ± 42.1 μmol/l (Batch5). Calcium concentrations [Ca] (Figure 1C) show a common trend for all three batches: During the early stage of the experiment, [Ca] stays relatively constant, before the concentrations start to drop. Toward the end of the experiment, [Ca] increases again. Similar to TA values, the initial decrease appears latest in Batch5 and earliest and strongest in Batch20. Interestingly, until day three [Ca] follows a pattern that is similar to Mg concentrations ([Mg]) values (Supplementary Figure 5) with a well-pronounced peak in Batch20 after 115 min which, at the same time, represents the highest measured [Ca] value of all three batches ([Ca] = 8.26 ± 0.02 mmol/l). However, the temporal changes in [Mg] do not exceed the standard deviation of the three replicates due to the high [Mg] values in the ASW. In Batch20, [Ca] decreases constantly after 1 day from 8.10 ± 0.01 mmol/l to a minimum value of 6.58 ± 0.01 mmol/l at day 78. The decrease is weaker after day 50. For Batch10 and Batch5 the [Ca] decrease is less pronounced and occurs with a delay of 2 days in Batch10 and after 4 days in Batch5. After 50 days, the replenishment of ASW with high Ca concentrations (see section Materials) caused an increase in [Ca] in all three batches.

FIGURE 1

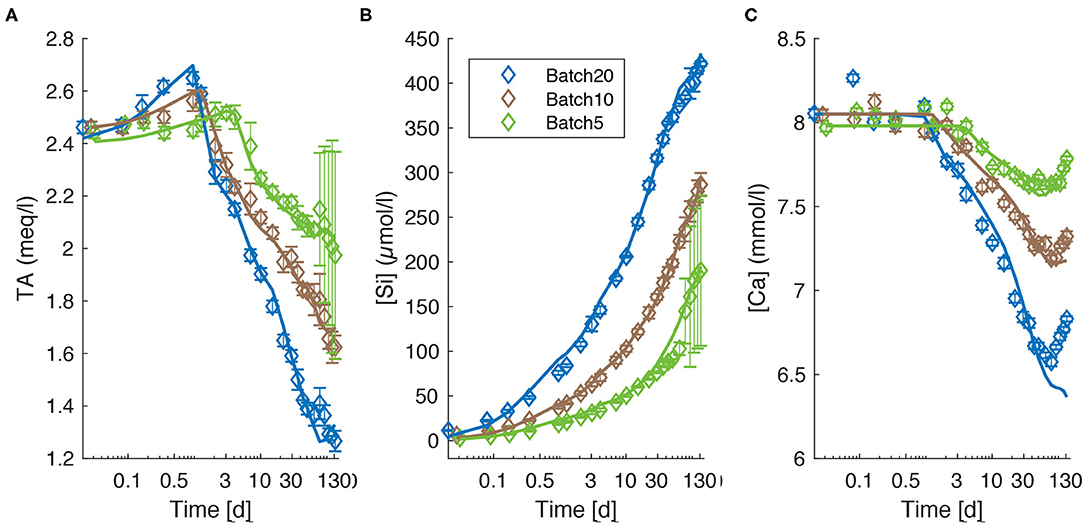
Figure 1. TA (A), [Si] (B), and [Ca] (C) values measured during the experiments. Symbols indicate mean values of three replicates for each batch. Error bars are reported as ± 2SD of the mean values. Lines represent modeled concentrations (blue; Batch20, brown: Batch10, green; Batch5). A logarithmic scale is used for the time axis.

Final experimental [Ca] is 6.83 ± 0.01 mmol/l for Batch20, 7.32 ± 0.01 mmol/l for Batch10 and 7.78 ± 0.01 mmol/l for Batch5. Overall, the behavior of [Si], [Ca], and TA reflects the amount of USM used in the experiments. Elevated solid/water ratios induce high [Si] and low [Ca] and TA values at the end of the experiments.

For all batches, the model used for the simulation was able to reproduce measured values very accurately (Figures 1A–C). The sum of squared errors ranged between 0.03 and 0.52 with highest errors in Batch5. Additional data used in the modeling are provided and described in detail in the Supplementary Section 1.

Secondary Mineral Formation and Precipitation Rates

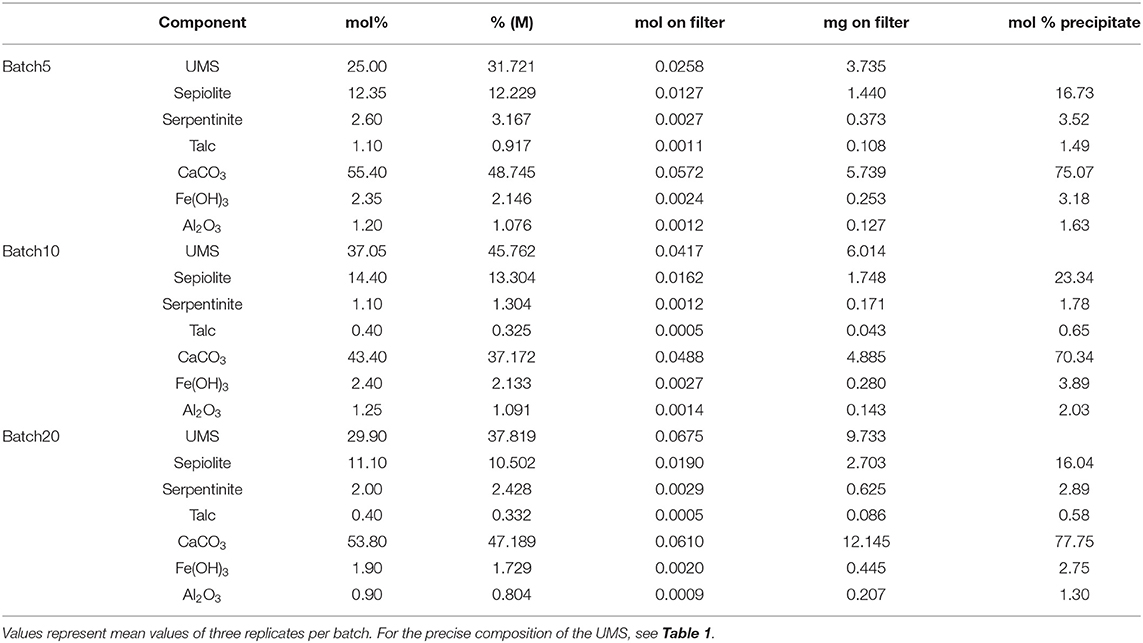
The change in water chemistry by dissolution of olivine and the subsequent accumulation of cations change the saturation state with respect to a variety of mineral phases containing these ions (Figure 2). Saturation states (Ω_i) were calculated using PHREEQ (Parkhurst and Appelo, 1999) where values above 1 indicate oversaturation (Supplementary Materials). During all experiments, DIC calculated from measured TA and pH values follows the same trend as TA (Figure 1A) and [Ca] (Figure 1C). In contrast, pH values (Figure 2B) follow a different trend. In all batches an initial increase in pH can be observed. This increase is strongest and appears earliest (until day 1) in Batch20. In Batch10 and Batch5 pH values rise less rapidly and highest values were measured latest in Batch5. Subsequently, the pH values decrease again in all batches. Again, this decrease ends first in Batch20 followed by Batch10 and is observed latest in Batch5. Contrary to the first increase, the subsequent drop has a similar magnitude in all batches which leads to lowest values in Batch5. After a well-pronounced peak, pH values decrease in Batch10 and Batch20 toward the end of the experiment. In Batch5 pH values plateau until day 78 before they slowly decrease toward the end. Note that the standard deviation of the three replicates in Batch5 becomes very large during the last days which leads to the assumption that an external input might have occurred in one of the Batch5 batch reactors.

FIGURE 2

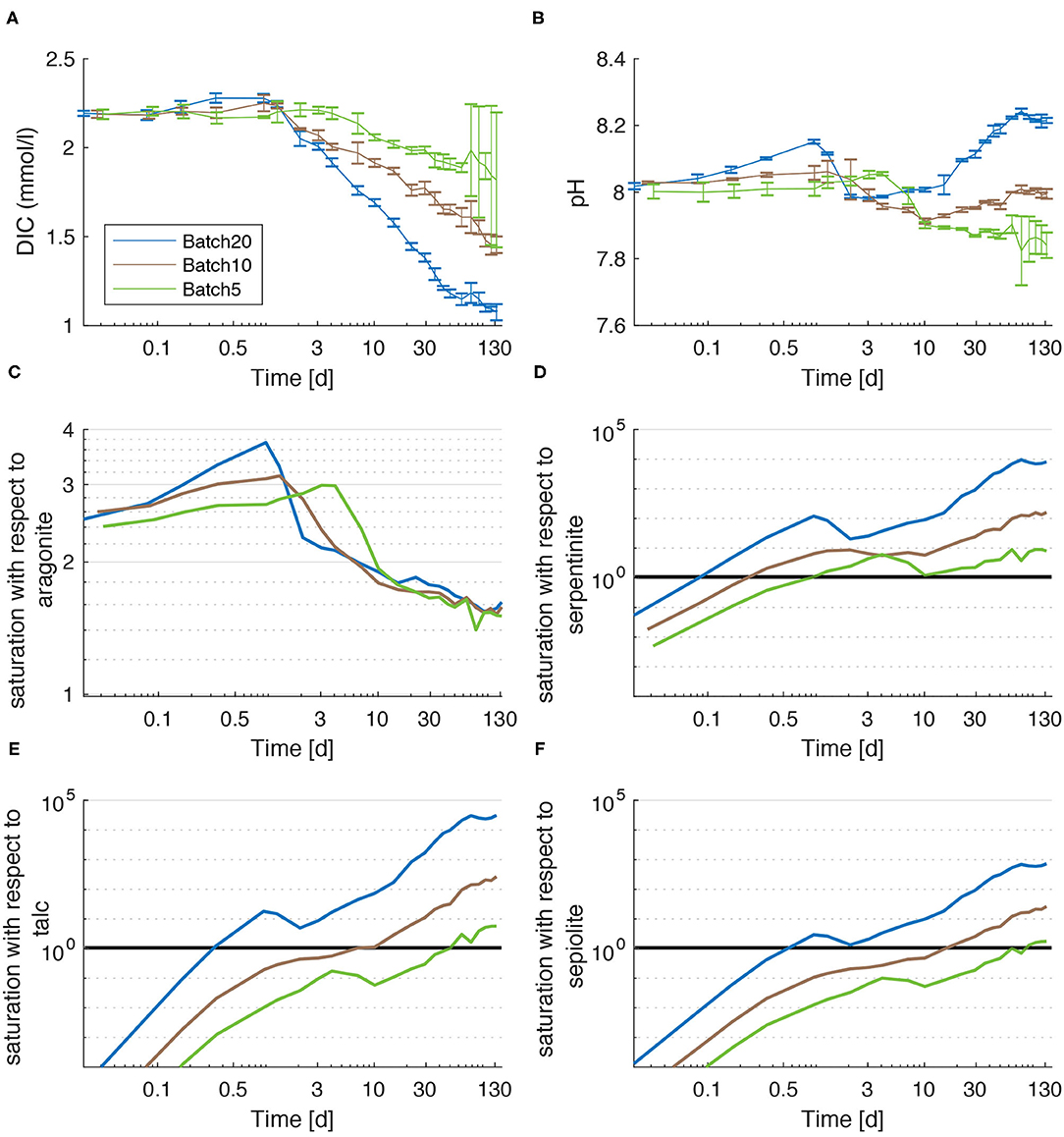
Figure 2. DIC (A), pH (B) and saturation states with respect to aragonite (C), serpentine (D), talc (E), and sepiolite (F) as calculated for Batch20 (blue), Batch10 (brown), and Batch5 (green). Error bars in (A) reflect ± 2SD that are calculated form the standard deviations of measured pH and TA values.

In all three batches, the system is oversaturated with respect to aragonite (saturation state >1) over the entire course of the experiment (Figure 2C). Following DIC (Figure 2A) and TA, the saturation states increase toward an initial peak that occurs first in Batch20, then Batch10 and less pronounced in Batch5. During the subsequent decrease that persists until the end of the experiment, the saturation states in all three batches converge toward a common value of ~1.5.

For the phyllosilicate phases considered in this study (serpentinite, talc, sepiolite), the saturation states, which depend on [Si], [Mg], and pH, develop differently from saturation with respect to aragonite. Since Si and Mg concentrations increase persistently, saturations follow this trend which is, though, overlain by changes in pH values (Figures 2D–F). The most striking features are the time after which the solution exceeds oversaturation with respect to the individual minerals (saturation values >1) and the extent of oversaturation attained at the end of experiments. Whilst serpentine saturation (Figure 2D) increases to a state of oversaturation very early in all batches (first Batch20 after ~0.1 day, latest Batch5 after ~1 day), saturations with respect to talc increase later and reveal higher differences between the batches (Figure 2E). A similar trend but with overall lower oversaturation is visible for sepiolite (Figure 2F). Thus, saturation with respect to both minerals (talc and sepiolite) rise above 1 in Batch5 only after day ~50 and day ~80 respectively.

Trace Metal Concentrations

Manganese concentrations [Mn] increase over the first 3 days during all experiments (Figure 3A). A well-pronounced peak is clearly visible in all batches at day 3, followed by a minimum at day 4. Subsequently, [Mn] values increase again but do not follow a common trend anymore. Important features are the strong increase in Batch5 between day 46 and day 78 which coincides with a strong increase in [Si] (Figure 1B) and the fact that lowest final values are observed in Batch20 (~0.3 μmol/l), whereas the concentrations in Btach10 and Batch5 are equal within the error (~0.5 μmol/l).

FIGURE 3

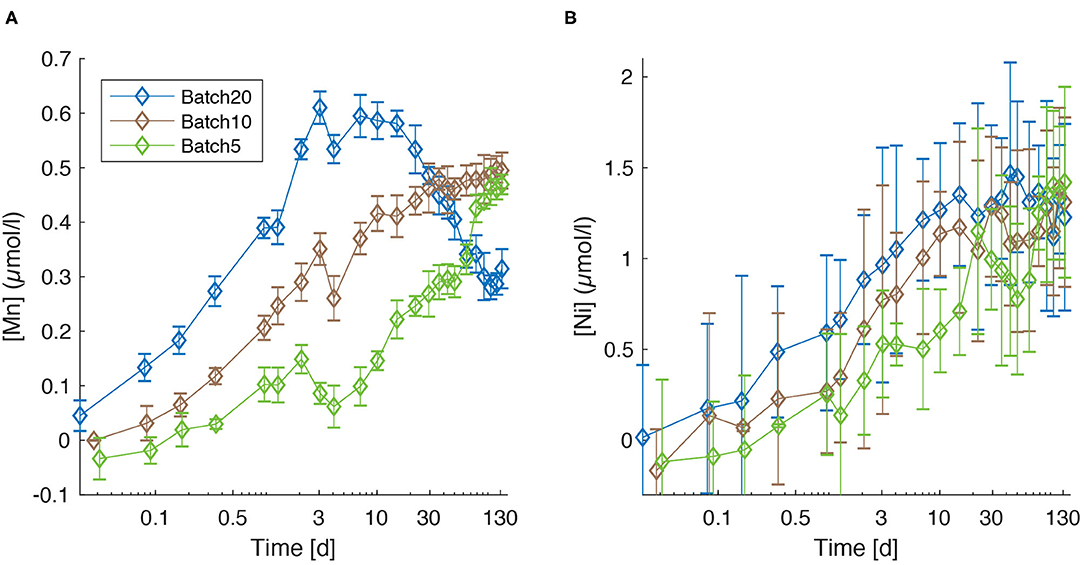
Figure 3. Concentration of dissolved Mn (A) and Ni (B) for Batch20 (blue), Batch10 (brown), and Batch5 (green). Error bars are reported as ± 2SD.

Despite the larger 2SD compared to [Mn], Ni concentrations show a clearly increasing trend throughout the experiment (Figure 3B) with a tendency toward highest values for Batch20 until day 22. A strong final increase for Batch5, that coincides with the increase in [Si], leads to values that are equal within the error for all batches (Batch201.23 ± 0.26 μmol/l, Batch10: 1.31 ± 0.23, Batch5: 1.42 ± 0.26 μmol/l).

Model Results: Composition of Precipitates and Overall Stoichiometry

The kinetic rate law employed in the model allows for secondary mineral precipitation only after the solutions reach oversaturation with respect to the considered mineral (Equations 3, 4). Precipitation does not start immediately after oversaturation is reached, since nucleation has to occur before precipitation can remove substantial amounts of solutes from solution. The time delay accounting for nucleation and the kinetic constants are derived by fitting the model to the measured dissolved species concentrations. The least deviation of modeled values from measured ones is reached with relatively low rates for talc and sepiolite precipitation compared to serpentine formation (Figures 4B–D). It also becomes clear that apparently phyllosilicate formation is less dependent on the saturation state compared to aragonite precipitation (Figure 4E; Equations 3, 4; Supplementary Table 1). The fastest precipitation is applied for Fe(OH)₃ because dissolved ferrous Fe released from olivine is rapidly oxidized to ferric iron and precipitated as iron hydroxide (Figures 4A,F).

FIGURE 4

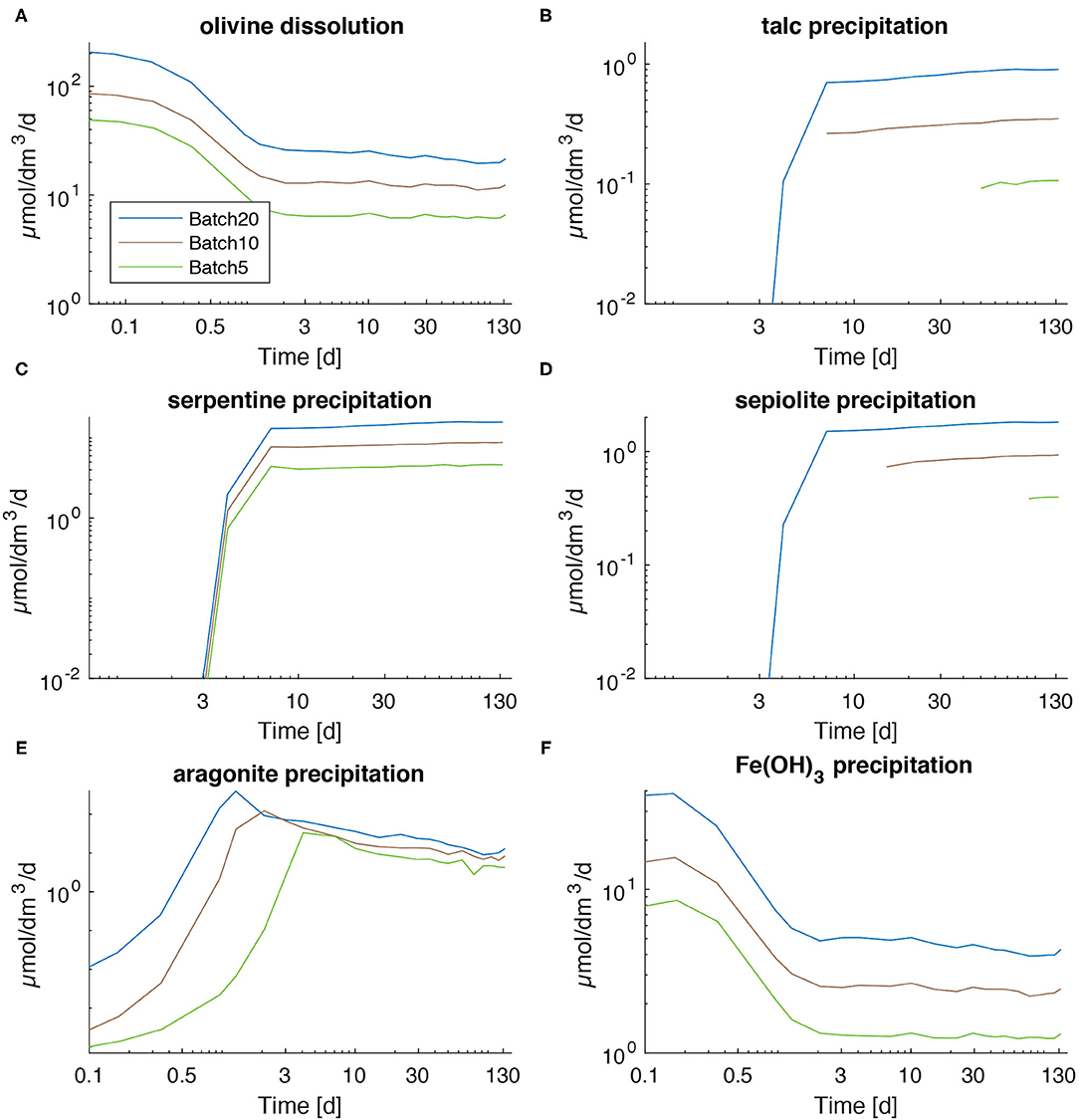
Figure 4. Dissolution rate for olivine (A) and precipitation rates for secondary phases (B–F) as calculated via the model for all batches.

The time-integrated rates of olivine dissolution and secondary phase precipitation calculated in the model are employed to derive the overall reaction stoichiometry for each of the three batches:

Batch20:

$\begin{array}{l}0.77H_{2}O+{(M{g}_{0.90}F{e}_{0.10})}_{2}Si{O}_4+0.055O_2+0.89C{a}^{2+}\\ +0.53C{O}_2+0.3{6HC{O}_3}^{-}\to 0.18Fe{(OH)}_3+0.25Si{(OH)}_4\\ +0.89CaC{O}_3+0.025M{g}_{2}S{i}_3{O}_{7.5}(OH){(H_{2}O)}_3\\ +0.32M{g}_{3}S{i}_2{O}_5{(OH)}_4+0.0090M{g}_{3}S{i}_4{O}_{10}{(OH)}_2+0.016F{e}^{3+}\\ +0.77M{g}^{2+}& (7)\end{array}$

Batch10:

$\begin{array}{l}0.79H_{2}O+{(M{g}_{0.90}F{e}_{0.10})}_{2}Si{O}_4+0.055O_2+0.98C{a}^{2+}\\ +0.45C{O}_2+0.53{HC{O}_3}^{-}\to 0.18Fe{(OH)}_3+0.27Si{(OH)}_4\\ +0.98CaC{O}_3+0.021M{g}_{2}S{i}_3{O}_{7.5}(OH){(H_{2}O)}_3\\ +0.32M{g}_{3}S{i}_2{O}_5{(OH)}_4+0.0061M{g}_{3}S{i}_4{O}_{10}{(OH)}_2+0.012F{e}^{3+}\\ +0.77M{g}^{2+}& (8)\end{array}$

Batch5:

$\begin{array}{l}0.79H_{2}O+{(M{g}_{0.90}F{e}_{0.10})}_{2}Si{O}_4+0.055O_2+0.98C{a}^{2+}\\ +0.51C{O}_2+0.47{HC{O}_3}^{-}\to 0.19Fe{(OH)}_3+0.32Si{(OH)}_4\\ +0.98CaC{O}_3+0.007M{g}_{2}S{i}_3{O}_{7.5}(OH){(H_{2}O)}_3\\ +0.32M{g}_{3}S{i}_2{O}_5{(OH)}_4+0.0025M{g}_{3}S{i}_4{O}_{10}{(OH)}_2+0.013F{e}^{3+}\\ +0.80M{g}^{2+}& (9)\end{array}$

To verify these model results, the composition of the grayish suspended matter that had formed in the batch reactors was determined applying a simple mixing calculation (Equations 3, 4). Especially the amount of fine-grained UMS in the suspended matter was scrutinized to subsequently estimate the composition of the actual precipitate. In contrast to the UMS procedure, no WDX measurements were performed on the precipitate. Hence, the mixing calculations are only based on XRD scans (Supplementary Figures 1–4) and full digestion, followed by ICP-OES measurements (Supplementary Table 6). The results of the calculations are presented in Table 2 and suggest a molar portion of UMS from 25% for Batch5 to 37.5% for Batch10. After the subtraction of these portions the result reveals very similar compositions for all batches with ~16–23% sepiolite and >70% aragonite as the major components. Minor phases are chrysotile (~3–4%), Fe(OH)₃ (~3–4%), and Al₂O₃. Even though Al₂O₃ is unlikely to have formed, it was included for the precipitates to match the measured compositions. It is most likely incorporated into the different partly amorphous Mg-Si-phases. Overall, the solid phase data and model results are broadly consistent as both indicate that CaCO₃ and a range of Mg-Si phases are the major secondary phases formed during the experiments.

TABLE 2

Table 2. Calculated composition of suspended matter filtered from batch reactors.

EDX/WDX Observations of Weathered UMS

After 134 days of agitation in batch reactors, grains of UMS were distinctively rounded with secondary mineral phases grown in indentations and fissures (Figure 5). The WDX measurement on the blank grain (Figure 5a2) revealed that the Mg/Si ratio was elevated for the olivine grain (Mg/Si = 2.33) compared to the pristine value (Mg/Si = 1.78) (Supplementary Table 5). The secondary mineral phase measured in inundations clearly indicates calcium carbonate and a very small contribution of iron (Figure 5a1).

FIGURE 5

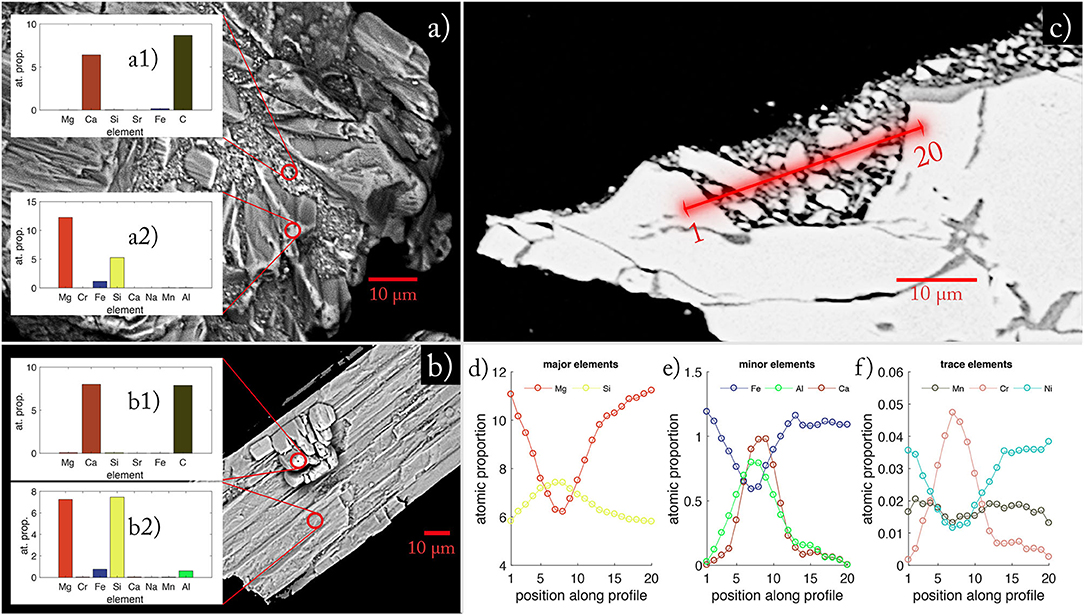
Figure 5. EDX images of reacted UMS grains taken at the end of the experiments. (a) Olivine grain with secondary mineral phases. (a1) Atomic proportions in secondary minerals grown on olivine. (a2) Atomic proportion of host mineral. (b) Orthopyroxene grain with on-grown aragonite crystal. (b1) Atomic proportion of secondary mineral grown on Orthopyroxene. (b2) Atomic proportion of host mineral for secondary phase (b1). Red circles indicate areas of WDX composition measurements. (c) Illustrates the transect through secondary minerals on an olivine grain. The red line denotes the measured transect. (d) Shows the atomic proportion of major elements measured along the profile shown in (c). (e) Shows the atomic proportion of minor elements measured along the profile shown in (c). (f) Shows the atomic proportion of trace elements measured along the profile shown in (c).

In Figure 5b, the elementary distribution suggests orthopyroxene as host mineral for secondary mineral formation (Figure 5b2). Here again, the data clearly indicate that the secondary phase is largely composed of calcium carbonate (Figure 5b1). The cross-section measured on an altered olivine grain (Figures 5c–e) illustrates that the material found on the grains not only consists of calcium carbonates. Instead, it is a heterogenous mixture of different phases with different densities (indicated by different shades of gray, Figure 5c). The atomic proportion (relative to 24 oxygen atoms) along the profile (Figures 5d,e) indicates a smooth transition from the host material olivine to different Mg-Si phases and back. The smoothness is an artifact of the measuring precision of the micro-probe indicated by the blurred area around the profile line. Hence the material is too fine grained to be examined in detail. Still, the asymmetric increase of Al and Ca indicates the presence of different phases along the profile which is underpinned by the jagged distribution of trace elements along the profile (Figure 5f). Overall, the measurements revealed that the agglomerations are most likely a mix of fine-grained UMS remnants cemented with a mix of calcium carbonate and hardly determinable secondary Mg-Si-phases. The examples in Figure 5 represent typical patterns obtained during a series of measurements.

Discussion

Robustness of Modeled and Measured Results

The consistency of measurements and model results suggests a step forward toward the precise understanding of the processes operating during olivine dissolution in seawater. For the interpretation of the results, however, it is necessary to shine a light on uncertainties. A crucial aspect is the surface area of the olivine grains. Rough edges that originate from the grinding process represent high energy sites which enhance the reactive surface of the grains but are worked off quickly during the early stage of the experiment. Even though, the initially enhanced reactive surface was considered in the kinetic model (Figure 4A, Supplementary Equation 11), all calculations are based on the geometrical surface area for spherical grains with a diameter of ~100 μm. Hence, the actual reactive surface is most certainly larger than assumed in the kinetic model of olivine dissolution. It is thus possible that the dissolution rates were actually higher than those calculated in the model. Moreover, idealized mineral phases were used in the modeling of authigenic mineral precipitation whereas the solid phase analyses indicate the formation of amorphous phases with a poorly defined composition (Figure 5).

Moreover, the model may not consider all processes occurring in the experiment. In general, olivine was assumed to be the only mineral phase that dissolves. Despite the considerably lower dissolution rates of other mineral phases (Lerman et al., 1975; Wolff-Boenisch et al., 2011; Gruber et al., 2019), their dissolution can play an important role at the beginning of the experiment due to the enhanced surface area. The admixture of very fine UMS particles that made up to 30% of the recovered precipitates (Table 2) and enhanced surface roughness can lead to a large number of possibly fast initial dissolution-precipitation reactions that might explain fluctuations in elementary concentrations in the early stage of the experiment.

Despite these uncertainties, the model is able to reproduce the concentrations of dissolved species measured over the course of the experiments (Figure 1). This and the fact that the same kinetic rate laws, functions and parameter values were used for all batches, suggests that the overall stoichiometries derived from the model are adequate.

Secondary Mineral Phases

The major goal of this study was to close the gaps in knowledge regarding the impact of secondary phases on the sequestration efficiency of ESW. Thus, the experiments were designed to allow investigating the precipitation of secondary phases under the following premises:

In order to reduce the number of unknown quantities, ASW was used instead of filtered seawater.

• Commercially available ultramafic sand was used since future large-scale applications of enhanced silicate weathering as CDR measure will rely on widely available rocks rather than purified olivine.

• Different solid-phase/water ratios were applied to investigate the dependency of secondary mineral formation on saturation states.

• A kinetic model was specifically designed to provide a deeper understanding of the kinetics and overall stoichiometry of authigenic mineral formation.

The most striking feature in the data presented in this study are the counterintuitively decreasing TA values (Figure 1A) as the weathering of olivine is supposed to lead to the exact opposite (Rimstidt et al., 2012; Köhler et al., 2013; Renforth and Henderson, 2014; Meysman and Montserrat, 2017; Montserrat et al., 2017; Fuss et al., 2018; Oelkers et al., 2018; Rigopoulos et al., 2018). The formation of secondary minerals has been invoked as a possible mechanism to reduce the net gain in TA during olivine weathering (Griffioen, 2017; Meysman and Montserrat, 2017; Montserrat et al., 2017; Oelkers et al., 2018; Torres et al., 2019) but to our knowledge have never been investigated in ASW in great detail. They appear in the form of phyllosilicates and carbonates. In seawater with a low rock/water ratio, the latter ones mainly exist in form of aragonite, calcite and Mg-calcite as these are the major authigenic carbonate phases that are formed in this chemical environment (Lein, 2004; Wallmann et al., 2008; Schrag et al., 2013; Torres et al., 2020). Mg-carbonates can be neglected as they only form under very special conditions mainly in highly alkaline facies with very high rock/water ratios, which do not match our experimental set-up (Moore et al., 2004; Ferrini et al., 2009; Power et al., 2013; Dehouck et al., 2014; Entezari Zarandi et al., 2017).

Precipitation of CaCO₃

The direct comparison of [Ca] and DIC (Figures 1C, 2A) reveals that the decrease in [Ca] is accompanied by a corresponding decrease in DIC. Meanwhile, [Mg] concentrations increased (Supplementary Figure 5). Combined with the low Mg/Si ratios in the recovered precipitates (Supplementary Tables 6, 7), the most likely explanation for these values is the formation of CaCO₃ either in the form of aragonite or calcite, as this process is the only one that has the potential to reduce both C and Ca to an equal amount. This is underlined by the composition of the precipitates (Table 2, Supplementary Table 7) that were calculated via Equations (5) and (6). Stockmann et al. (2014) suggest that forsterite has the potential to foster the nucleation of calcite on its surface. The major difference in the experimental design of Stockmann et al. (2014) and this study is the reagent in which forsterite was dissolved. Whilst in this study ASW with a pH of ~8 was used, Stockmann et al. (2014) dissolved forsterite in Na-carbonate and Ca-chlorite solutions at a pH of ~9. XRD measurements of precipitates recovered from the batch reactors in this study revealed no significant calcite content but indicated the presence of aragonite (Supplementary Figures 1–3). Despite the fact that these measurements have a very high noise/signal ratio and are therefore fraught with a very large error this is consistent with the findings of Rigopoulos et al. (2018), who found aragonite as the only CaCO₃ species in weathering experiments with dunite, and with the fact that aragonite is preferably precipitated in Mg rich solutions (De Choudens-Sánchez and González, 2009; Sun et al., 2015). Mixing calculations revealed that the precipitates recovered from the batch reactors consisted of ~72% (molar) CaCO₃ averaged over all batches, which is very close to the modeled values of ~65% (molar) as average for all batches. For natural seawater, Burton and Walter (1987) ascertained growth rates of aragonite 3 times higher compared to calcite at 25°C with highest aragonite dominance for calcite saturations of ~5, which corresponds to the values during the early stage of the experiment of this study. These findings are supported by Zhong and Mucci (1989) who used a different rate equation but found very similar total rates. In order to match measured and modeled [Ca] and TA values, aragonite precipitation needed to be considered in the model used in this study (Figures 4E, 6B). When comparing the rate parameters for aragonite precipitation which lead to the best model fit in this study, with the constants of Burton and Walter (1987), the values were higher compared to the values of Burton and Walter (1987) for Batch20 and Batch10 but matched for Batch5. The slightly higher values in this study indicate possible catalyzation of CaCO₃ precipitation on the surface of the UMS grains, as for the same saturation stronger precipitation takes place. Our data clearly show that, contrary to findings of Montserrat et al. (2017), calcium carbonate is formed during the experiments and is responsible for most of the observed TA loss.

FIGURE 6

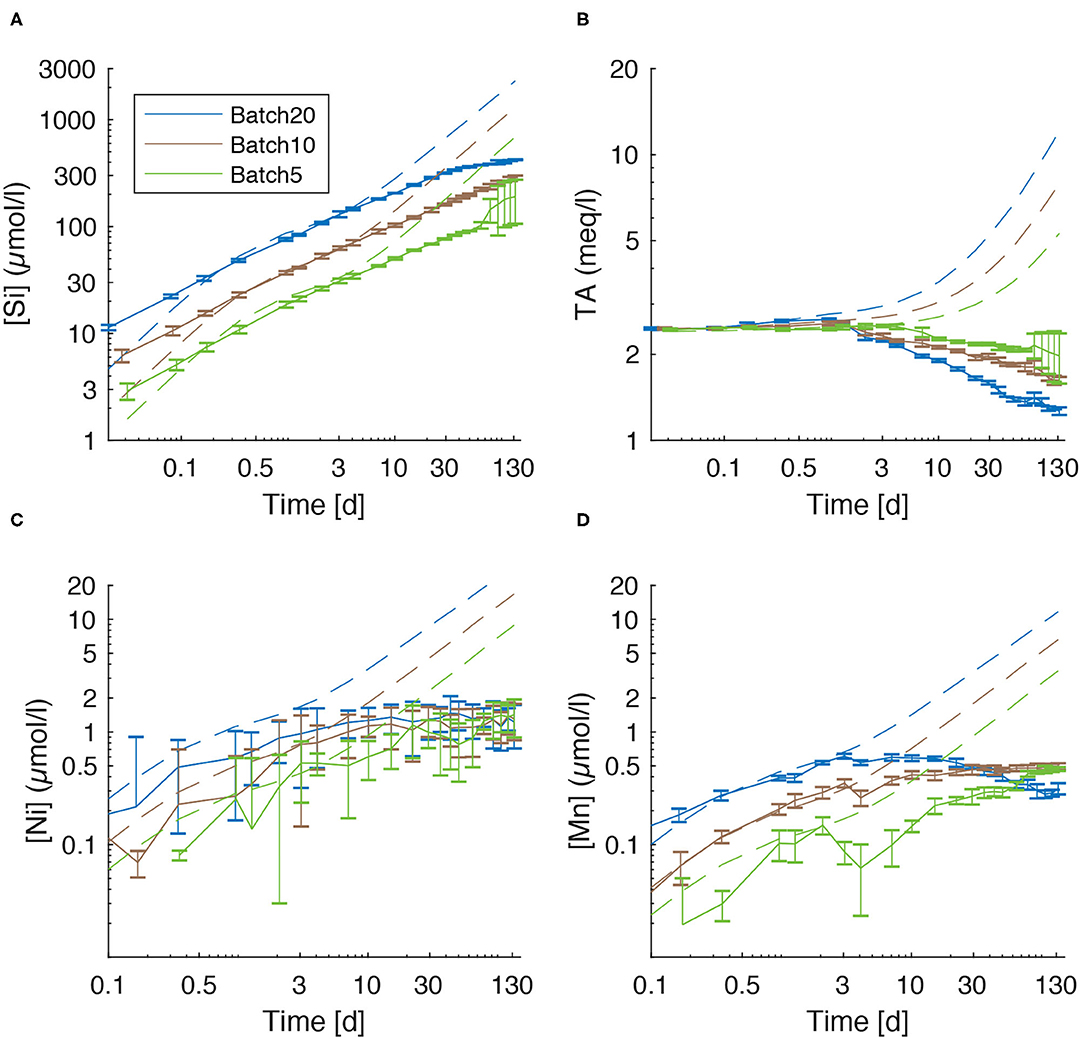
Figure 6. Comparison of measured values (solid lines) for dissolved species and modeled concentrations that would result from congruent dissolution of UMS without formation of secondary minerals (dashed lines). (A) silicon, (B) TA, (C) nickel, and (D) manganese.

Secondary Phyllosilicate and Fe(OH)₃ Phases

Next to calcium carbonate, phyllosilicates have the potential to form during olivine weathering (Delvigne et al., 1979; Buurman et al., 1988; Suárez et al., 2011; Hellmann et al., 2012; Sissmann et al., 2013; Griffioen, 2017; Montserrat et al., 2017; Rigopoulos et al., 2018). Hence, precipitation of serpentine, sepiolite and talc is investigated in this study (Figures 4B–D). Calculated saturation states vary largely for the different minerals (Figure 2). In the model, the precipitation of each mineral depends on the magnitude of oversaturation and a kinetic constant (Lasaga, 1998). The best fit to the Si, Mg, and TA data was reached applying a very small rate constant for talc precipitation compared to rate constants for serpentine and sepiolite. Hence, talc is least represented in the model results (0.25% (molar), averaged over all models). This is fairly congruent to the calculated composition of the recovered precipitates where the average content of talc was 0.89% (molar) (Table 2). Large discrepancies between the model and the calculated mineral composition based on measurements occur with regard to the ratio of sepiolite to serpentine $\left(\frac{sep}{serp}\right)$. The numerical model suggests a $\left(\frac{sep}{serp}\right)$ of ~0.066 (average of all batches) whereas the mineralogic model reveals a $\left(\frac{sep}{serp}\right)$ of 7.8. The saturation states (Figure 2) clearly show that ASW was least oversaturated with respect to sepiolite in all batches and undersaturated in Batch10 and Batch5 for at least half the experimental period. Thus, sepiolite appears highly unlikely to be the major precipitated phase (Figure 4D).

Hence, the remaining explanation is that a major portion of secondary phases with low Mg/Si ratios had stuck on the grains and was therefore not recovered. This is supported by EDS images (Figure 5). Several grains were found that were covered with secondary phases. Next to CaCO₃ the WDX analysis of these secondary phases indicates a large variety of Mg-Si-phases. Via their composition, though, these phases could hardly be identified as any of the Si-phases considered in the model.

Also, XRD measurements do not indicate high amounts of the phyllosilicate phases that were considered in the model. It is thus likely that the Mg-Si bearing phases in this study show the same amorphous character as the phases found by Davis et al. (2009) who described a “deweylite assemblage” which stands for a mix of different Mg-silicates whose precise chemical composition can vary strongly (Hövelmann et al., 2011). Thus, the mixed composition of all Si-bearing precipitates could be understood as the composition of a Si-Mg-rich partly amorphous bulk phase, which is well represented by the noisy XRD diffractograms (Supplementary Figures 1–3).

Similarly to secondary phyllosilicates, Fe(OH)₃ seems to have attached to UMS grains, as the measured (and subsequently calculated) content of Fe(OH)₃ in the suspended matter recovered from the batch reactors was ~3% on average and the model calculated ~13% (averaged over all batches). This is evidenced by little dense flakes that were found on the weathered grains during EDX/WDX measurements that consisted mainly of Fe and is supported by the fact that less precipitate was recovered, than the suggested by the model. Like the precipitation of phyllosilicates and carbonates, the formation of Fe(OH)₃ releases protons. It is therefore important to consider this process with regards to the overall efficiency of enhanced silicate weathering.

Dissolution Kinetics of Olivine

Over the first 2–4 days of the experiments dissolved [Si] and TA values are close to those predicted by the kinetic rate law for olivine dissolution used in our model (Rimstidt et al., 2012). However, the measured concentrations are significantly lower than the predicted value over the following period (Figures 6A,B) This observation could in principle either be explained by a decline in the olivine dissolution rate due to surface passivation/occupation by secondary minerals, or by the removal of Si and TA from solution via precipitation of secondary minerals.

Montserrat et al. (2017), whose experiment A3 was very similar to the experiments of this study, proposed a dissolution rate for olivine in dependence of the changing saturation state with respect to olivine that was calculated after Palandri and Kharaka (2004). For the validation of this hypothesis, they fitted their model to the accumulation of Si in solution $\left(\frac{d\left[Si\right]}{dT}\right)$, regardless of Si removal by secondary phases. The outcome is a good approximation of the apparent dissolution rate.

A passivation of the surface as a result of incongruent weathering has previously been invoked as one explanation for the decrease in dissolution rate over time (Wolff-Boenisch et al., 2011; Hellmann et al., 2012; Maher et al., 2016; Montserrat et al., 2017). Apart from Mg isotopes (Hellmann et al., 2012), which were not measured in this study, one indication for such processes is the cation depletion of the reactive surface of the olivine grains after the weathering process. Hellmann et al. (2012) as well as Maher et al. (2016) used HCl and NaCl solutions respectively which did not contain Mg. Likewise, Montserrat et al. (2017) reported highest Mg depletion on reactive surfaces for experiments with Mg-reduced ASW. Extensive WDX measurements applied in this study have not revealed such depletion. Instead, highest Mg/Fe ratios in olivine were measured on blank surfaces of weathered olivine that were not covered with secondary mineral phases (Figure 5a2). Thus, the depletion and subsequent passivation of forsterite surfaces observed in other studies during dissolution seems to be a result of diffusive equilibration between a depleted reagent and the crystal surface. This effect did not occur in in our study, as the background activity of Mg is very high in ASW (Millero et al., 2008). Hence, following the idea of an equilibrated steady state for surface layers (Maher et al., 2016), olivine grains might as well be considered a temporary sink for Mg, assuming the diffusive replacement of Fe²⁺ with Mg²⁺ supplied from the ambient seawater, similar to the process of Mg-replacement by H⁺ described by Oelkers et al. (2018). Additionally, elevated (Mg+Fe)/Si ratios point toward the results of Pokrovsky and Schott (2000), who described the preferential release of Si during the early stage of dissolution (100 days in their experiment) for non-acidic solutions.

Further passivation of the grain surface due to occupation with secondary minerals (Béarat et al., 2006; King et al., 2010; Sissmann et al., 2013; Oelkers et al., 2018) appears unlikely as the portion of reactive surface covered by authigenic phases was relatively small in this study (data not shown). Considering these observations and the solid phase data that were obtained in our experimental set-up, it is likely that most of the Si and TA deficit (Figures 6A,B) in the dissolved phase is induced by the precipitation of secondary phases rather than a decline in dissolution rate.

Fate of Nickel and Its Usability as a Dissolution Proxy

Ni concentrations were suggested as a possible proxy for olivine dissolution by Montserrat et al. (2017). The comparison of [Ni] values (Figures 3B, 6C), though, clearly shows that the accumulation of Ni is not proportional to the amount of dissolved olivine calculated by the model (Supplementary Tables 11–13) and not even proportional to the accumulation of [Si] in solution (Figures 1B, 6A). Incongruent weathering of olivine (Montserrat et al., 2017) can be excluded as, during the early stage of the experiment and thus before the precipitation of secondary minerals started, the accumulation of dissolved Si and Mn (which have a satisfyingly small 2SD) are proportional to the amount of olivine used in the experiments. Now under the assumption of congruent weathering, the expected [Ni] values would be 5.70 μmol/l for Batch20, 4.28 μmol/l for Batch10, and 2.26 μmol/l for Batch5. The measured values were significantly lower (Figure 3B). Therefore, some removal process must be operating, that is apparently strongest in Batch20 and weakest in Batch5, leading to values that are identical within the error in all batches at the end of the experiment. Ni and Mn can be adsorbed on the surface of phyllosilicate phases, FeOOH and CaCO₃ and incorporated in the crystal lattice of calcite and aragonite during carbonate precipitation (Hoffmann and Stipp, 2001; Lakshtanov and Stipp, 2007; Lazarević et al., 2010; Castillo Alvarez et al., 2020; Alvarez et al., 2021). Carré et al. (2017) even proposed aragonite precipitation as a way to remove dissolved Ni from seawater. Therefore, it is likely that the Ni and Mn deficits (Figures 6C,D) observed at the end of the experiments are due to uptake of these trace elements in authigenic CaCO₃, Mg-Si and FeOOH phases.

As a conclusion, it becomes clear that the variety of processes affecting Ni and Mn concentrations in batch experiments excludes both as a reliable proxy for olivine dissolution rate determination. However, the proposed strong Ni uptake in authigenic phases reduces toxic metal release that would limit the applicability of olivine weathering for CO₂ sequestration (Blewett and Leonard, 2017).

Sequestration Efficiency

In a first approach the CO₂ conversion observed in the experiments (R_ex) can be expressed as a function of total inorganic carbon (TIC) following:

$\begin{array}{l}{R}_{ex}=\Delta TIC=(DI{C}_{final}+PI{C}_{final})-(DI{C}_{ini}\\ +{\displaystyle \sum {}_j^{}}(DI{C}_{ini}\ast 0.007-DIC\left(t\right)\ast 0.007))& (10)\end{array}$

where DIC_final is the DIC at the end of the experiment, PIC_final is the amount of particulate inorganic carbon in form of CaCO₃ at the end of the experiment and DIC_ini is the initial DIC at the beginning of the experiment. ∑_j(DIC_ini * 0.007−DIC(t) * 0.007) represents the amount of DIC added during sample taking (0.007 l per sample).

PIC_final was calculated via the entire [Ca] loss during the experiment following,

$\begin{array}{l}PI{C}_{final}={\left[Ca\right]}_{ini}-{\left[Ca\right]}_{final}+{\displaystyle \sum {}_j^{}}({\left[Ca\right]}_{in}(t)\ast 0.007\\ -[Ca]\left(t\right)\ast 0.007)& (11)\end{array}$

where [Ca]_ini is the initial Ca concentration, [Ca]_final is the final concentration and [Ca]_in(t) is the function of the Ca input derived on sample taking that changes over time. The calculated net uptake was 0.21 mmol (Batch20), 0.166 mmol (Batch10), and 0.143 mmol (Batch5). Still, these values derive from a quasi-closed system with very limited CO₂ supply.

Hence, the efficiency of CO₂ uptake was investigated using a 1-box model where olivine with a grain diameter of 100 μm is dissolved in a 50 m deep water layer representative for the coastal ocean. The model box defines the seafloor at 50 m water depth. Hence, settling olivine grains that are rapidly deposited at the seafloor (Köhler et al., 2013) are kept within the system and continuously take part in the dissolution process. Hence, all olivine grains contribute equally to the overall dissolution rate whether they are kept in suspension or deposited at the seabed (Feng et al., 2017). Concentration and grain size of olivine were kept constant over the simulation period, for simplicity reasons. It is, thus, assumed that new olivine is added to the system to compensate for any olivine loss induced by dissolution. The concentration of olivine in the model box was set to a constant value of 10 mg dm⁻³ and the box was equilibrated with the atmosphere by applying a constant atmospheric pCO₂ of 400 μatm.

Mass balance equations (ordinary differential equations) for TA and DIC were set up and solved numerically to simulate temporal changes in DIC and TA. The TA mass balance considers TA production via olivine dissolution (4 × olivine dissolution rate) with the olivine dissolution rate depending on olivine concentration, grain size, temperature and pH (Rimstidt et al., 2012). TA consumption via authigenic mineral formation is considered applying the stoichiometry derived from dissolution experiments (Batch10, Equation 8). Rates of mineral precipitation were calculated from olivine dissolution rates applying the corresponding stoichiometric coefficient. The DIC mass balance considers DIC removal via CaCO₃ precipitation and DIC gain induced by CO₂ uptake from the atmosphere.

Initial values applied in the model (salinity: 34.77, temperature: 17.88°C, pressure: 1 bar, total alkalinity: 2,308 μmol kg⁻¹, total boron: 415 μmol kg⁻¹) correspond to the mean composition of surface water in the global ocean (Spivack and Edmond, 1987; Sarmiento and Gruber, 2006). The initial DIC concentration was set to 2,053 μmol kg⁻¹ to obtain an initial pCO₂ of 400 μatm in surface water. Equilibrium calculations were conducted using stability constants valid for seawater (Zeebe and Wolf-Gladrow, 2001). Total alkalinity (TA) was defined as:

$\begin{array}{ll}TA={HC{O}_3}^{-}+2{C{O}_3}^{-}+{B{(OH)}_4}^{-}+O{H}^{-}-H^{+}& (12)\end{array}$

while CO₂ uptake from the atmosphere was calculated as:

$\begin{array}{ll}FC{O}_2=v_p(C{O}_2(eq)-C{O}_2)& (13)\end{array}$

where v_P is the piston velocity [20 cm h⁻¹ (Sarmiento and Gruber, 2006)], CO₂(eq) is the concentration of dissolved CO₂ at equilibrium with the atmosphere and CO₂ is the time-dependent concentration calculated from TA and DIC (Sarmiento and Gruber, 2006).

In a first model run, olivine dissolution was simulated without secondary mineral formation to constrain the loss in CO₂ uptake efficiency induced by the buffer capacity of seawater (Middelburg et al., 2020). The efficiency (eff) is calculated as the ratio of the CO₂ uptake flux (FCO₂) and the depth-integrated rate of CO₂ consumption (RCO₂) induced by olivine dissolution (RCO₂ = 4 x olivine dissolution rate, eff = FCO₂/RCO₂). The model was run over a period of 10 years to equilibrate the water column with the overlying atmosphere (Figure 7). The shift in acid-base equilibria induced by olivine-driven CO₂ consumption (e.g., $2{HC{O}_3}^{-}\to C{O}_2+{C{O}_3}^{2-}+H_{2}O$) reduces the efficiency by about 42% at the end of the simulation period. TA and DIC increase continuously due to alkalinity release by olivine dissolution and CO₂ uptake from the atmosphere, respectively, while the CO₂ uptake flux approaches a plateau after the water column is equilibrated with the atmosphere. The depth-integrated rate of olivine dissolution was almost constant over the model run. The small increase in pH from 8.035 at the start to 8.075 at the end of simulation (data not shown) induced a small decrease in RCO₂ from an initial value of 147 mmol m⁻² yr⁻¹ to a final value of 145 mmol m⁻² yr⁻¹.

FIGURE 7

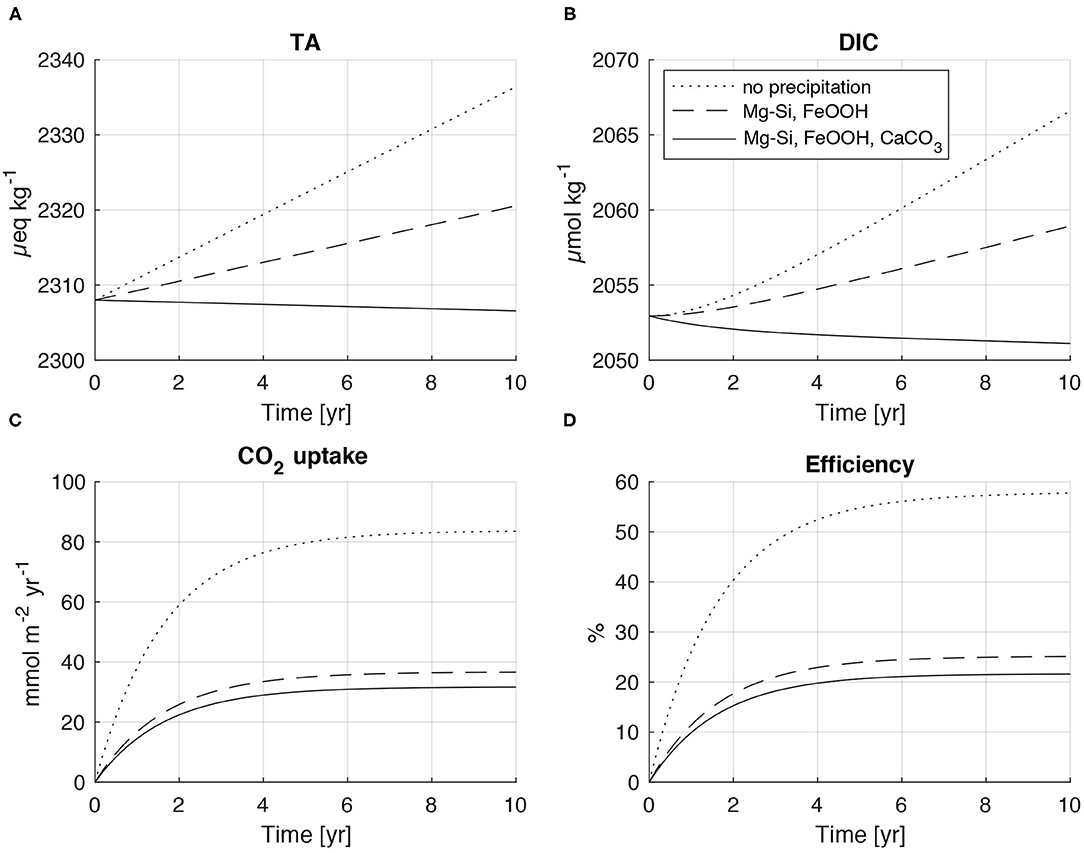
Figure 7. Model experiments simulating the effect of olivine dissolution on seawater composition and CO₂ uptake from the atmosphere. Dotted lines show results for a model run without secondary mineral formation. Broken lines represent model results for the precipitation of ferric iron oxides (FeOOH) and Mg-Si-phases (serpentinite, talc, sepiolite). Solid lines indicate the results for a model run where all authigenic phases (FeOOH, Mg-Si-phases, CaCO₃) precipitate according to the stoichiometry observed in our lab experiments. (A) Total alkalinity. (B) Dissolved inorganic carbon. (C) CO₂ uptake from the atmosphere (FCO₂). (D) Efficiency of CO₂ uptake is defined as FCO₂/RCO₂ where RCO₂ is the depth-integrated rate of CO₂ consumption induced by olivine dissolution (= 4 x olivine dissolution rate).

In a second model run, precipitation of ferric iron oxides and Si-Mg-phases was implemented employing the stoichiometry derived from batch experiments (batch10, Equation 8). Precipitation of ferric iron oxides and Si-Mg-phases strongly affects the model results. The increase in TA and DIC is reduced, whereas CO₂ uptake and CO₂ efficiency are strongly diminished since protons are released during the precipitation reactions. The efficiency at the end of the model period decreased from 0.58 in the model run without secondary mineral formation to only 0.25. Most of the efficiency loss is caused by the precipitation of Mg-Si-phases that consumes large amounts of alkalinity due to the strong proton release induced by these reactions (6 mol H⁺ per mol of serpentinite/talc, 4 mol H⁺ per mol of sepiolite).

In a final model run, all secondary phases including CaCO₃ are allowed to precipitate. CaCO₃ formation has a strong effect on solution composition and induces a decline in both TA and DIC. The CO₂ uptake is further reduced such that the efficiency drops to 0.21 after 10 years. CaCO₃ formation has a smaller effect on CO₂ fluxes than Mg-Si-phase precipitation even though CaCO₃ is the major secondary phase formed during the experiments. This somewhat surprising model result is related to the acid-base stoichiometry of carbonate precipitation where only two moles of alkalinity are removed per mol of CaCO₃, while the coeval DIC loss promotes CO₂ uptake from the atmosphere.

Additional model runs were conducted to explore the effects of olivine concentration (1–1,000 mg dm⁻³) and grain size (10–100 μM) on CO₂ uptake efficiency (data not shown). The experiments showed that olivine dissolution rates and CO₂ uptake fluxes strongly increase when higher concentrations and smaller grain sizes are applied. However, the CO₂ uptake efficiency was constant (0.21) over the explored parameter space when the stoichiometry derived from our lab experiments was applied. Hence, the low efficiency obtained in the box model simulations seems to be a robust result, if the overall stoichiometry that we observed in our lab experiments is also valid in the field. There are, however, a number of factors that may induce a change in the rates of olivine dissolution and secondary mineral precipitation. Hence, the solid/liquid ratio and the rates of water replacement, CO₂ uptake from the atmosphere and biological activity may affect the ratios between dissolution and precipitation reactions. These factors should be investigated in future lab and field experiments.

Implications for Field Application

The experimental results of this study show that precipitation of secondary minerals (CaCO₃, Mg-Si-phases, FeOOH) compromises the efficiency of CO₂ uptake by olivine dissolution. It should, however be noted that the stoichiometry that we observed in our lab experiments may not be valid for all field conditions. Moreover, we found higher rates of alkalinity removal than previous studies with pure olivine that were conducted under comparable experimental conditions (Montserrat et al., 2017). This observation may be due to the high solid/solution ratios applied in our experiments and could be related to the fact that we used commercially available olivine (UMS) that was not pure but contained a number of accessory minerals. Our use of ultramafic sand rather than pure olivine may be justified since large-scale CDR will probably not be conducted with pure olivine but with rocks containing other minerals and impurities. The range of dissolved Si concentrations attained in our experiments (Figure 1) is similar to the concentrations observed in bioturbated surface sediments (Dale et al., 2021). Since grains added to seawater will rapidly sink to the seafloor where they are mixed into surface sediments by benthic biota, the experimental conditions may be close to those in benthic habitats where most of the dissolution is expected to occur.

Precipitation rates of authigenic Mg-Si-phases may be lower than observed in our experiments, though, when olivine is applied to highly dynamic environments such as the coastal zone (beaches, surf zones), where dissolution products are rapidly removed (Hangx and Spiers, 2009; Meysman and Montserrat, 2017; Montserrat et al., 2017). It is, however, possible that CaCO₃ precipitation may also occur in these coastal environments since our data imply that carbonate precipitation is catalyzed by olivine surfaces even at low degrees of aragonite oversaturation. Further work is needed to scrutinize whether the abrasive effects of wave action may suppress CaCO₃ precipitation (Meysman and Montserrat, 2017).

Anyhow, fine-grained olivine added to the shelf environment will ultimately be transported by bottom currents to local depo-centers where low bottom current velocities allow for the permanent burial of sediments. These environments are marked by high accumulation rates of both sediments and organic matter (De Haas et al., 2002). The low pH values induced by the release of metabolic CO₂ during organic matter degradation largely inhibit CaCO₃ precipitation in these sedimentary environments while FeOOH formation is limited to surface sediments due to the reducing conditions prevailing in these deposits (Van Cappellen and Wang, 1996; Silburn et al., 2017). However, authigenic Mg-Si- phases and clays are formed in these benthic environments (Michalopoulos and Aller, 1995). Since the formation of cation-rich phases induces CO₂ release, the overall efficiency of CO₂ uptake might be strongly diminished as observed in our experiments. It is, hence, possible that, when applied in the field, olivine weathering is less efficient than previously believed. On the other hand, adverse environmental effects may be smaller than previously anticipated since data obtained during the experiments in this study indicate that Ni and other toxic metals will largely be fixed in authigenic phases. However, more work needs to be done to explore how variable conditions in pelagic and benthic environments may affect the ratio between olivine dissolution and authigenic mineral precipitation and, hence, the efficiency of CO₂ uptake from the atmosphere and the rate of toxic metal release.

Summary, Conclusion and Outlook

This study presents a first dedicated attempt to investigate the formation of secondary mineral phases in artificial seawater (ASW) during olivine weathering. For this purpose, ultra-mafic sand (UMS) was brought to reaction with ASW applying different solid/liquid ratios. The results strongly suggest the formation of CaCO₃, as evidenced by the congruent loss of Ca and DIC observed over the course of the experiments. XRD measurements suggest, that aragonite is the major CaCO₃ species precipitated which is underlined by the fact that this variation is more likely to be precipitated in Mg-rich solutions. This is further supported by WDX measurements that showed pure CaCO₃ crystals on the surface of weathered olivine grains. These observations are confirmed by the results of a numerical model that simulated the dissolution of olivine and the precipitation of several secondary mineral phases including aragonite. Moreover, the model results allowed estimating the overall stoichiometry of the combined dissolution-precipitation reaction. The thorough analysis of ASW and precipitates recovered from the batch reactors underline that Si-bearing phases must also have formed during the experiment. The precise character (amorphous or crystalline) and chemical composition of these phases, though, afford further dedicated studies. Via the different accumulation rates of Ni in the different batches, this study revealed that these secondary mineral phases most likely are a major sink for this toxic element, excluding it as a proxy for olivine dissolution rates. This makes the precise knowledge of secondary phase formation and characteristics crucial for the feasibility of enhanced olivine weathering on the one hand and for the understanding of the dissolution kinetics of olivine on the other. Experimental combined with modeling results suggest that the formation of secondary phases lowers the overall sequestration efficiency to ~20% during the application of enhanced olivine weathering in a shallow shelf sea. This bears implications for possible application sites, as not only physical parameters, but, more importantly, chemical parameters in the field steer secondary mineral formation and thus the overall efficiency.

Sandy shelf sediments and specifically the surf zone may be appropriate sites for enhanced olivine dissolution since the flushing of surface sediments by ambient bottom waters may mitigate the accumulation of dissolution products and the formation of secondary silicate and carbonate minerals in these permeable and physically dynamic deposits. Alternatively, application sites where pore and or bottom waters are undersaturated with respect to the major secondary phases would be a promising target for enhanced coastal weathering of olivine.

Our experimental and modeling results hence indicate that it may be promising to also investigate CaCO₃ as alkaline mineral for CO₂ removal since secondary mineral formation is usually not observed during CaCO₃ dissolution. CaCO₃ could be added to sediment depo-centers on the shelf where large amounts of metabolic CO₂ are formed (about 3 Pg yr⁻¹ at global scale) that can be converted into bicarbonate by CaCO₃ dissolution (Dunne et al., 2007). This process would accelerate the CO₂ shelf pump (Bozec et al., 2005) and promote further CO₂ uptake from the atmosphere. This approach may be most successful in marine environments where bottom waters are enriched in CO₂ and undersaturated with respect to calcite and aragonite. These conditions occur, e.g., in oxygen minimum zones and partly anoxic marginal basins such as the Baltic Sea (Tyrrell et al., 2008). The CO₂ release from Baltic Sea sediments amounts to 80 Tg yr⁻¹ (Nilsson et al., 2019). The addition of a corresponding amount of CaCO₃ may thus dramatically enhance CO₂ uptake from the atmosphere. Moreover, CaCO₃ addition may support the formation of authigenic carbonate fluorapatite and could thereby reduce benthic phosphate fluxes (Ruttenberg and Berner, 1993). Hence, CaCO₃ addition may mitigate eutrophication, which is a major problem in many shelf regions, while olivine addition would promote Si and Fe release and potentially amplify eutrophication. Further lab studies, field experiments and numerical modeling also focusing on the biological impact are needed to better constrain the efficiency and environmental effects of these CDR approaches and their large-scale applicability.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Author Contributions

MF carried out the experiments, processed most of the samples in the laboratory, and wrote the manuscript. SG helped with sample preparation in the clean-lab and contributed with discussions. MS supervised XRD interpretation and contributed with discussions. VL initiated and supervised EDX/WDX measurements and contributed with discussions. CV supported XRD interpretation. BL carried out additional XRD measurements and helped with XRD interpretation. KW designed the numerical models used in this study and contributed with discussions. All authors contributed to the article and approved the submitted version.

Funding

This study was funded by the Bundesministerium für Bildung und Forschung (BMBF) (Project RETAKE, granted to SG) in the framework of the Deutsche Allianz für Meeresforschung (DAM) mission CDRmare.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to thank Philipp Böning (ICBM, Oldenburg) for carrying out XRF measurements and interpretation. We also acknowledge Anke Bleyer (GEOMAR), Bettina Domeyer (GEOMAR), and Regina Surberg (GEOMAR) for their help with technical and analytical procedures in the clean laboratory, respectively. Additionally we thank Mario Thöner (GEOMAR) for his great support during EDX/WDX measurements. In deep mourning we commemorate our dear friend and highly respected and regarded colleague VL who deceased short before the publication of this study. Our thoughts are with his family and beloved ones.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fclim.2022.831587/full#supplementary-material

References

Alvarez, C. C., Quitté, G., Schott, J., and Oelkers, E. H. (2021). Nickel isotope fractionation as a function of carbonate growth rate during Ni coprecipitation with calcite. Geochim. Cosmochim. Acta 299, 184–198. doi: 10.1016/j.gca.2021.02.019

CrossRef Full Text | Google Scholar

Amann, T., Hartmann, J., Struyf, E., De Oliveira Garcia, W., Fischer, E. K., Janssens, I., et al. (2020). Enhanced weathering and related element fluxes - a cropland mesocosm approach. Biogeosciences 17, 103–119. doi: 10.5194/bg-17-103-2020

CrossRef Full Text | Google Scholar

Béarat, H. J, McKelvy, M. V. G, Chizmeshya, A., Gormley, D., et al. (2006). Carbon sequestration via aqueous olivine mineral carbonation: role of passivating layer formation. Environ. Sci. Technol. 40, 4802–4808. doi: 10.1021/es0523340

PubMed Abstract | CrossRef Full Text | Google Scholar

Blewett, T. A., and Leonard, E. M. (2017). Mechanisms of nickel toxicity to fish and invertebrates in marine and estuarine waters. Environ. Pollut. 223, 311–322. doi: 10.1016/j.envpol.2017.01.028

PubMed Abstract | CrossRef Full Text | Google Scholar

Bozec, Y., Thomas, H., Elkalay, K., and De Baar, H. J. W. (2005). The continental shelf pump for CO2 in the North Sea-evidence from summer observation. Mar. Chem. 93, 131–147. doi: 10.1016/j.marchem.2004.07.006

CrossRef Full Text | Google Scholar

Burton, E. A., and Walter, L. M. (1987). Relative precipitation rates of aragonite and Mg calcite from seawater: Temperature or carbonate ion control? Geology 15, 111–114. doi: 10.1130/0091-7613(1987)15<111:RPROAA>2.0.CO;2

CrossRef Full Text | Google Scholar

Buurman, P., Meijer, E. L., and Wijck, J. H. V. (1988). Weathering of chlorite and vermiculite in ultramafic rocks of Cabo Ortegal, northwestern Spain. Clays Clay Miner. 36, 263–269. doi: 10.1346/CCMN.1988.0360308

CrossRef Full Text | Google Scholar

Carré, C., Gunkel-Grillon, P., Serres, A., Jeannin, M., Sabot, R., and Quiniou, T. (2017). Calcareous electrochemical precipitation, a new method to trap nickel in seawater. Environ. Chem. Lett. 15, 151–156. doi: 10.1007/s10311-016-0602-2

CrossRef Full Text | Google Scholar

Castillo Alvarez, C., Quitté, G., Schott, J., and Oelkers, E. H. (2020). Experimental determination of Ni isotope fractionation during Ni adsorption from an aqueous fluid onto calcite surfaces. Geochim. Cosmochim. Acta 273, 26–36. doi: 10.1016/j.gca.2020.01.010

CrossRef Full Text | Google Scholar

Dale, A. W., Paul, K. M., Clemens, D., Scholz, F., Schroller-Lomnitz, U., Wallmann, K., et al. (2021). Recycling and burial of biogenic silica in an open margin oxygen minimum zone. Global Biogeochem. Cycles 35, e2020GB006583. doi: 10.1029/2020GB006583

CrossRef Full Text | Google Scholar

Davis, M. C., Brouwer, W. J., Wesolowski, D. J., Anovitz, L. M., Lipton, A. S., and Mueller, K. T. (2009). Magnesium silicate dissolution investigated by 29Si MAS, 1H-29Si CPMAS, 25Mg QCPMG, and 1H-25Mg CP QCPMG NMR. Phys. Chem. Chem. Phys. 11, 7013–7021. doi: 10.1039/b907494e

PubMed Abstract | CrossRef Full Text | Google Scholar

De Choudens-Sánchez, V., and González, L. A. (2009). Calcite and aragonite precipitation under controlled instantaneous supersaturation: elucidating the role of CaCO3 saturation state and Mg/Ca ratio on calcium carbonate polymorphism. J. Sediment. Res. 79, 363–376. doi: 10.2110/jsr.2009.043

CrossRef Full Text | Google Scholar

De Haas, H., Van Weering, T. C. E., and De Stigter, H. (2002). Organic carbon in shelf seas: sinks or sources, processes and products. Cont. Shelf Res. 22, 691–717. doi: 10.1016/S0278-4343(01)00093-0

CrossRef Full Text | Google Scholar

Dehouck, E., Gaudin, A., Mangold, N., Lajaunie, L., Dauzères, A., Grauby, O., et al. (2014). Weathering of olivine under CO2 atmosphere: a martian perspective. Geochim. Cosmochim. Acta 135, 170–189. doi: 10.1016/j.gca.2014.03.032

CrossRef Full Text | Google Scholar

Delvigne, J., Bisdom, E. B. A., Sleeman, J., and Stoops, G. (1979). Olivines, their pseudomorphs and secondary products. Pedologie 29, 247–309.

Google Scholar

Dickson, A. G.. (1993). pH buffers for sea water media based on the total hydrogen ion concentration scale. Deep Sea Res. Part I Oceanogr. Res. Pap. 40, 107–118. doi: 10.1016/0967-0637(93)90055-8

CrossRef Full Text | Google Scholar

Dunne, J. P., Sarmiento, J. L., and Gnanadesikan, A. (2007). A synthesis of global particle export from the surface ocean and cycling through the ocean interior and on the seafloor. Global Biogeochem. Cycles 21:GB4006. doi: 10.1029/2006GB002907

CrossRef Full Text | Google Scholar

Entezari Zarandi, A., Larachi, F., Beaudoin, G., Plante, B., and Sciortino, M. (2017). Nesquehonite as a carbon sink in ambient mineral carbonation of ultramafic mining wastes. Chem. Eng. J. 314, 160–168. doi: 10.1016/j.cej.2017.01.003

CrossRef Full Text | Google Scholar

Feely, R. A., Sabine, C. L., Byrne, R. H., Millero, F. J., Dickson, A. G., Wanninkhof, R., et al. (2012). Decadal changes in the aragonite and calcite saturation state of the Pacific Ocean. Global Biogeochem. Cycles 26:GB3001. doi: 10.1029/2011GB004157

CrossRef Full Text | Google Scholar

Feldman, D. R., Collins, W. D., Gero, P. J., Torn, M. S., Mlawer, E. J., and Shippert, T. R. (2015). Observational determination of surface radiative forcing by CO2 from 2000 to 2010. Nature 519, 339–343. doi: 10.1038/nature14240

PubMed Abstract | CrossRef Full Text | Google Scholar

Feng, E. Y., Koeve, W., Keller, D. P., and Oschlies, A. (2017). Model-based assessment of the CO2 sequestration potential of coastal ocean Alkalinization. Earth. Futur. 5, 1252–1266. doi: 10.1002/2017EF000659

CrossRef Full Text | Google Scholar

Ferrini, V., De Vito, C., and Mignardi, S. (2009). Synthesis of nesquehonite by reaction of gaseous CO2 with Mg chloride solution: Its potential role in the sequestration of carbon dioxide. J. Hazard. Mater. 168, 832–837. doi: 10.1016/j.jhazmat.2009.02.103

PubMed Abstract | CrossRef Full Text | Google Scholar

Flipkens, G., Blust, R., and Town, R. M. (2021). Deriving nickel (Ni(II)) and chromium (Cr(III)) based environmentally safe olivine guidelines for coastal enhanced silicate weathering. Environ. Sci. Technol. 55, 12362–12371. doi: 10.1021/acs.est.1c02974

PubMed Abstract | CrossRef Full Text | Google Scholar

Friedlingstein, P., Solomon, S., Plattner, G.-K., Knutti, R., Ciais, P., and Raupach, M. R. (2011). Long-term climate implications of twenty-first century options for carbon dioxide emission mitigation. Nat. Clim. Chang. 1, 457–461. doi: 10.1038/nclimate1302

CrossRef Full Text | Google Scholar

Fuss, S., Lamb, W. F., Callaghan, M. W., Hilaire, J., Creutzig, F., Amann, T., et al. (2018). Negative emissions - part 2: Costs, potentials and side effects. Environ. Res. Lett. 13:063002. doi: 10.1088/1748-9326/aabf9f

CrossRef Full Text | Google Scholar

Gieskes, J., Gamo, T., and Brumsack, H. (1991). Chemical Methods for Interstitial Water Analysis Aboard JOIDES Resolution. ODP Tech Note 15. doi: 10.2973/odp.tn.15.1991

CrossRef Full Text | Google Scholar

Govindaraju, K.. (1994). (1994). Compilation of working values and sample description for 383 geostandards. Geostand. Newsl. 18, 1–158. doi: 10.1046/j.1365-2494.1998.53202081.x-i1

CrossRef Full Text | Google Scholar

Griffioen, J.. (2017). Enhanced weathering of olivine in seawater: the efficiency as revealed by thermodynamic scenario analysis. Sci. Total Environ. 575, 536–544. doi: 10.1016/j.scitotenv.2016.09.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Gruber, C., Harlavan, Y., Pousty, D., Winkler, D., and Ganor, J. (2019). Enhanced chemical weathering of albite under seawater conditions and its potential effect on the Sr ocean budget. Geochim. Cosmochim. Acta 261, 20–34. doi: 10.1016/j.gca.2019.06.049

CrossRef Full Text | Google Scholar

Hangx, S. J. T., and Spiers, C. J. (2009). Coastal spreading of olivine to control atmospheric CO2 concentrations: a critical analysis of viability. Int. J. Greenh. Gas Control 3, 757–767. doi: 10.1016/j.ijggc.2009.07.001

CrossRef Full Text | Google Scholar

Hartmann, J., and Kempe, S. (2008). What is the maximum potential for CO 2 sequestration by “stimulated” weathering on the global scale? Naturwissenschaften 95, 1159–1164. doi: 10.1007/s00114-008-0434-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Hartmann, J., West, A. J., Renforth, P., Köhler, P., De La Rocha, C. L., Wolf-Gladrow, D. A., et al. (2013). Enhanced chemical weathering as a geoengineering strategy to reduce atmospheric carbon dioxide, supply nutrients, and mitigate ocean acidification. Rev. Geophys. 51, 113–149. doi: 10.1002/rog.20004

CrossRef Full Text | Google Scholar

Hellmann, R., Wirth, R., Daval, D., Barnes, J. P., Penisson, J. M., Tisserand, D., et al. (2012). Unifying natural and laboratory chemical weathering with interfacial dissolution-reprecipitation: a study based on the nanometer-scale chemistry of fluid-silicate interfaces. Chem. Geol. 294–295, 203–216. doi: 10.1016/j.chemgeo.2011.12.002

CrossRef Full Text | Google Scholar

Hoffmann, U., and Stipp, S. L. S. (2001). The behavior of Ni2+ on calcite surfaces. Geochim. Cosmochim. Acta 65, 4131–4139. doi: 10.1016/S0016-7037(01)00691-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Hövelmann, J., Austrheim, H., Beinlich, A., and Anne Munz, I. (2011). Experimental study of the carbonation of partially serpentinized and weathered peridotites. Geochim. Cosmochim. Acta 75, 6760–6779. doi: 10.1016/j.gca.2011.08.032

CrossRef Full Text | Google Scholar

Howe, J. P.. (2015). This is nature; This is un-nature: reading the keeling curve. Environ. Hist. Durh. N. C. 20, 286–293. doi: 10.1093/envhis/emv005

CrossRef Full Text | Google Scholar

Iizuka, A., Fujii, M., Yamasaki, A., and Yanagisawa, Y. (2004). Development of a new CO2 sequestration process utilizing the carbonation of waste cement. Ind. Eng. Chem. Res. 43, 7880–7887. doi: 10.1021/ie0496176

CrossRef Full Text | Google Scholar

IPCC (2021). “Climate change 2021: the physical science basis,” in Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, eds V. Masson-Delmotte, P. Zhai, A. Pirani, S.L. Connors, C. Péan, S. Berger, et al. (Cambridge: Cambridge University Press).

Google Scholar

Keeling, C. D., Stephen, C., Piper, S. C., Bacastow, R. B., Wahlen, M., Whorf, T. P., et al. (2001). Exchanges of atmospheric CO2 and 13CO2 with the terrestrial biosphere and oceans from 1978 to 2000. Glob. Asp. SIO Ref. Ser. Scripps Inst. Ocean (San Diego, CA), 01–06.

Google Scholar

King, E. H., Plümper, O., and Putnis, A. (2010). Effect of secondary phase formation on the carbonation of olivine. Environ. Sci. Technol. 44, 6503–6509. doi: 10.1021/es9038193

PubMed Abstract | CrossRef Full Text | Google Scholar

Köhler, P., Abrams, J. F., Völker, C., Hauck, J., and Wolf-Gladrow, D. A. (2013). Geoengineering impact of open ocean dissolution of olivine on atmospheric CO2, surface ocean pH and marine biology. Environ. Res. Lett. 8:014009. doi: 10.1088/1748-9326/8/1/014009

CrossRef Full Text | Google Scholar

Kremer, D., Etzold, S., Boldt, J., Blaum, P., Hahn, K. M., Wotruba, H., et al. (2019). Geological mapping and characterization of possible primary input materials for the mineral sequestration of carbon dioxide in Europe. Minerals 9:485. doi: 10.3390/min9080485

CrossRef Full Text | Google Scholar

Lackner, K. S.. (2003). A guide to CO2 sequestration. Science 300, 1677–1678. doi: 10.1126/science.1079033

PubMed Abstract | CrossRef Full Text | Google Scholar

Lakshtanov, L. Z., and Stipp, S. L. S. (2007). Experimental study of nickel(II) interaction with calcite: adsorption and coprecipitation. Geochim. Cosmochim. Acta 71, 3686–3697. doi: 10.1016/j.gca.2007.04.006

CrossRef Full Text | Google Scholar

Lal, R.. (2004). Soil carbon sequestration to mitigate climate change. Geoderma. 123, 1–22. doi: 10.1016/j.geoderma.2004.01.032

PubMed Abstract | CrossRef Full Text | Google Scholar

Lasaga, A. C.. (1998). Kinetic Theory in the Earth Sciences. Princeton, NJ: Princeton University Press. doi: 10.1515/9781400864874

CrossRef Full Text | Google Scholar

Lazarević, S., Janković-Castvan, I., Djokić, V., Radovanović, Z., Janaćković, D., and Petrović, R. (2010). Iron-modified sepiolite for Ni2+ sorption from aqueous solution: an equilibrium, kinetic, and thermodynamic study. J. Chem. Eng. Data 55, 5681–5689. doi: 10.1021/je100639k

CrossRef Full Text | Google Scholar

Lein, A. Y.. (2004). Authigenic carbonate formation in the ocean. Lithol. Miner. Resour. 39, 1–30. doi: 10.1023/B:LIMI.0000010767.52720.8f

CrossRef Full Text | Google Scholar

Lerman, A., Mackenzie, F. T., and Bricker, O. P. (1975). Rates of dissolution of aluminosilicates in seawater. Earth Planet. Sci. Lett. 25, 82–88. doi: 10.1016/0012-821X(75)90213-7

CrossRef Full Text | Google Scholar

Lindzen, R. S.. (2007). Taking greenhouse warming seriously. Energy Environ. 18, 937–950. doi: 10.1260/095830507782616823

PubMed Abstract | CrossRef Full Text | Google Scholar

MacFarling Meure, C., Etheridge, D., Trudinger, C., Steele, P., Langenfelds, R., van Ommen, T., et al. (2006). Law Dome CO2, CH4 and N2O ice core records extended to 2000 years BP. Geophys. Res. Lett. 33:L14810. doi: 10.1029/2006GL026152

CrossRef Full Text | Google Scholar

Maher, K., Johnson, N. C., Jackson, A., Lammers, L. N., Torchinsky, A. B., Weaver, K. L., et al. (2016). A spatially resolved surface kinetic model for forsterite dissolution. Geochim. Cosmochim. Acta 174, 313–334. doi: 10.1016/j.gca.2015.11.019

CrossRef Full Text | Google Scholar

Méheut, M., and Schauble, E. A. (2014). Silicon isotope fractionation in silicate minerals: Insights from first-principles models of phyllosilicates, albite and pyrope. Geochim. Cosmochim. Acta 134, 137–154. doi: 10.1016/j.gca.2014.02.014

CrossRef Full Text | Google Scholar

Meysman, F. J. R., and Montserrat, F. (2017). Negative CO2 emissions via enhanced silicate weathering in coastal environments. Biol. Lett. 13:20160905. doi: 10.1098/rsbl.2016.0905

PubMed Abstract | CrossRef Full Text | Google Scholar

Michalopoulos, P., and Aller, R. C. (1995). Rapid clay mineral formation in amazon delta sediments: reverse weathering and oceanic elemental cycles. Science 270, 614–617. doi: 10.1126/science.270.5236.614

CrossRef Full Text | Google Scholar

Middelburg, J. J., Soetaert, K., and Hagens, M. (2020). Ocean alkalinity, buffering and biogeochemical processes. Rev. Geophys. 58, e2019RG000681. doi: 10.1029/2019RG000681

PubMed Abstract | CrossRef Full Text | Google Scholar

Millero, F. J., Feistel, R., Wright, D. G., and McDougall, T. J. (2008). The composition of Standard Seawater and the definition of the Reference-Composition Salinity Scale. Deep. Res. Part I Oceanogr. Res. Pap. 55, 50–72. doi: 10.1016/j.dsr.2007.10.001

CrossRef Full Text | Google Scholar

Millero, F. J., Sotolongo, S., and Izaguirre, M. (1987). The oxidation kinetics of Fe(II) in seawater. Geochim. Cosmochim. Acta 51, 793–801. doi: 10.1016/0016-7037(87)90093-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Montserrat, F., Renforth, P., Hartmann, J., Leermakers, M., Knops, P., and Meysman, F. J. R. (2017). Olivine dissolution in seawater: implications for CO2 sequestration through enhanced weathering in coastal environments. Environ. Sci. Technol. 51, 3960–3972. doi: 10.1021/acs.est.6b05942

PubMed Abstract | CrossRef Full Text | Google Scholar

Moore, T. S., Murray, R. W., Kurtz, A. C., and Schrag, D. P. (2004). Anaerobic methane oxidation and the formation of dolomite. Earth Planet. Sci. Lett. 229, 141–154. doi: 10.1016/j.epsl.2004.10.015

CrossRef Full Text | Google Scholar

Nilsson, M. M., Kononets, M., Ekeroth, N., Viktorsson, L., Hylén, A., Sommer, S., et al. (2019). Organic carbon recycling in Baltic Sea sediments - an integrated estimate on the system scale based on in situ measurements. Mar. Chem. 209, 81–93. doi: 10.1016/j.marchem.2018.11.004

CrossRef Full Text | Google Scholar

Oelkers, E. H.. (1999). “A comparison of forsterite and enstatite dissolution rates and mechanisms,” in: Growth, Dissolution and Pattern Formation in Geosystems, eds B. Jamtveit, and P. Meakin (Dordrecht: Springer), 253–267. doi: 10.1007/978-94-015-9179-9_12

CrossRef Full Text | Google Scholar

Oelkers, E. H.. (2001). An experimental study of forsterite dissolution rates as a function of temperature and aqueous Mg and Si concentrations. Chem. Geol. 175, 485–494. doi: 10.1016/S0009-2541(00)00352-1

CrossRef Full Text | Google Scholar

Oelkers, E. H., Benning, L. G., Lutz, S., Mavromatis, V., Pearce, C. R., and Plümper, O. (2015). The efficient long-term inhibition of forsterite dissolution by common soil bacteria and fungi at Earth surface conditions. Geochim. Cosmochim. Acta 168, 222–235. doi: 10.1016/j.gca.2015.06.004

CrossRef Full Text | Google Scholar

Oelkers, E. H., Declercq, J., Saldi, G. D., Gislason, S. R., and Schott, J. (2018). Olivine dissolution rates: a critical review. Chem. Geol. 500, 1–19. doi: 10.1016/j.chemgeo.2018.10.008

CrossRef Full Text | Google Scholar

Olsen, A. A., and Rimstidt, J. D. (2008). Oxalate-promoted forsterite dissolution at low pH. Geochim. Cosmochim. Acta 72, 1758–1766. doi: 10.1016/j.gca.2007.12.026

CrossRef Full Text | Google Scholar

Palandri, J. L., and Kharaka, Y. K. (2004). A Compilation of Rate Parameters of Water-Mineral Interaction Kinetics for Application to Geochemical Modeling. USGS Open File Report.

Google Scholar

Parkhurst, D. L., and Appelo, C. A. J. (1999). User's Guide to PHREEQC (Version 2): A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations. Water-Resources Investigations Report, 99–4259.

Google Scholar

Pokrovsky, O. S., and Schott, J. (2000). Kinetics and mechanism of forsterite dissolution at 25°C and pH from 1 to 12. Geochim. Cosmochim. Acta 64, 3313–3325. doi: 10.1016/S0016-7037(00)00434-8

CrossRef Full Text | Google Scholar

Power, I. M., Wilson, S. A., and Dipple, G. M. (2013). Serpentinite carbonation for CO2 sequestration. Elements 9, 115–121. doi: 10.2113/gselements.9.2.115

CrossRef Full Text | Google Scholar

Renforth, P., and Henderson, G. (2014). Assessing ocean alkalinity for carbon sequestration. Rev. Geophys. 55, 636–674. doi: 10.1002/2016RG000533

CrossRef Full Text | Google Scholar

Rhodes, C. J.. (2016). The 2015 Paris climate change conference: COP21. Sci. Prog. 99, 97–104. doi: 10.3184/003685016X14528569315192

PubMed Abstract | CrossRef Full Text | Google Scholar

Rigopoulos, I., Harrison, A. L., Delimitis, A., Ioannou, I., Efstathiou, A. M., Kyratsi, T., et al. (2018). Carbon sequestration via enhanced weathering of peridotites and basalts in seawater. Appl. Geochem. 91, 197–207. doi: 10.1016/j.apgeochem.2017.11.001

CrossRef Full Text | Google Scholar

Rimstidt, J. D., Brantley, S. L., and Olsen, A. A. (2012). Systematic review of forsterite dissolution rate data. Geochim. Cosmochim. Acta 99, 159–178. doi: 10.1016/j.gca.2012.09.019

CrossRef Full Text | Google Scholar

Ruttenberg, K. C., and Berner, R. A. (1993). Authigenic apatite formation and burial in sediments from non-upwelling, continental margin environments. Geochim. Cosmochim. Acta 57, 991–1007. doi: 10.1016/0016-7037(93)90035-U

CrossRef Full Text | Google Scholar

Saran, R. K., Arora, V., and Yadav, S. (2018). CO2 sequestration by mineral carbonation: a review. Glob. Nest J. 20, 497–503. doi: 10.30955/gnj.002597

CrossRef Full Text | Google Scholar

Sarmiento, J. L., and Gruber, N. (2006). J. L. Sarmiento and N. Gruber 2006. Ocean Biogeochemical Dynamics. xiii + 503 pp. Princeton, Woodstock: Princeton University Press. 0 691 01707 7. Geol. Mag. 144, 1034. doi: 10.1017/S0016756807003755

CrossRef Full Text | Google Scholar

Schrag, D. P., Higgins, J. A., Macdonald, F. A., and Johnston, D. T. (2013). Authigenic carbonate and the history of the global carbon cycle. Science 339, 540–543. doi: 10.1126/science.1229578

PubMed Abstract | CrossRef Full Text | Google Scholar

Silburn, B., Kröger, S., Parker, E. R., Sivyer, D. B., Hicks, N., Powell, C. F., et al. (2017). Benthic pH gradients across a range of shelf sea sediment types linked to sediment characteristics and seasonal variability. Biogeochemistry 135, 69–88. doi: 10.1007/s10533-017-0323-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Sissmann, O., Daval, D., Brunet, F., Guyot, F., Verlaguet, A., Pinquier, Y., et al. (2013). The deleterious effect of secondary phases on olivine carbonation yield: Insight from time-resolved aqueous-fluid sampling and FIB-TEM characterization. Chem. Geol. 357, 186–202. doi: 10.1016/j.chemgeo.2013.08.031

CrossRef Full Text | Google Scholar

Solomon, S., Plattner, G.-K., Knutti, R., and Friedlingstein, P. (2009). Irreversible climate change due to carbon dioxide emissions. Proc. Natl. Acad. Sci. 106, 1704 LP−1709. doi: 10.1073/pnas.0812721106

PubMed Abstract | CrossRef Full Text | Google Scholar

Spivack, A. J., and Edmond, J. M. (1987). Boron isotope exchange between seawater and the oceanic crust. Geochim. Cosmochim. Acta 51, 1033–1043. doi: 10.1016/0016-7037(87)90198-0

CrossRef Full Text | Google Scholar

Stockmann, G. J., Wolff-Boenisch, D., Bovet, N., Gislason, S. R., and Oelkers, E. H. (2014). The role of silicate surfaces on calcite precipitation kinetics. Geochim. Cosmochim. Acta 135, 231–250. doi: 10.1016/j.gca.2014.03.015

CrossRef Full Text | Google Scholar

Strefler, J., Amann, T., Bauer, N., Kriegler, E., and Hartmann, J. (2018). Potential and costs of carbon dioxide removal by enhanced weathering of rocks. Environ. Res. Lett. 13:034101. doi: 10.1088/1748-9326/aaa9c4

CrossRef Full Text | Google Scholar

Stumm, W., and Morgan, J. J. (1996). Aquatic chemistry: chemical equilibria and rates in natural waters. Choice Rev. Online 33, 171–229. doi: 10.5860/CHOICE.33-6312

CrossRef Full Text | Google Scholar

Suárez, S., Nieto, F., Velasco, F., and Martín, F. J. (2011). Serpentine and chlorite as effective Ni-Cu sinks during weathering of the Aguablanca sulphide deposit (SW Spain). TEM evidence for metal-retention mechanisms in sheet silicates. Eur. J. Mineral. 23, 179–196. doi: 10.1127/0935-1221/2011/0023-2084

CrossRef Full Text | Google Scholar

Sun, W., Jayaraman, S., Chen, W., Persson, K. A., and Ceder, G. (2015). Nucleation of metastable aragonite CaCO₃ in seawater. Proc. Natl. Acad. Sci. U.S.A. 112, 3199 LP−3204. doi: 10.1073/pnas.1423898112

PubMed Abstract | CrossRef Full Text | Google Scholar

Torres, M. A., Dong, S., Nealson, K. H., and West, A. J. (2019). The kinetics of siderophore-mediated olivine dissolution. Geobiology 17, 401–416. doi: 10.1111/gbi.12332

PubMed Abstract | CrossRef Full Text | Google Scholar

Torres, M. E., Hong, W.-L., Solomon, E. A., Milliken, K., Kim, J.-H., Sample, J. C., et al. (2020). Silicate weathering in anoxic marine sediment as a requirement for authigenic carbonate burial. Earth Sci. Rev. 200, 102960. doi: 10.1016/j.earscirev.2019.102960

CrossRef Full Text | Google Scholar

Tyrrell, T., Schneider, B., Charalampopoulou, A., and Riebesell, U. (2008). Coccolithophores and calcite saturation state in the Baltic and Black Seas. Biogeosciences 5, 485–494. doi: 10.5194/bg-5-485-2008

CrossRef Full Text | Google Scholar

Van Cappellen, P., and Wang, Y. (1996). Cycling of iron and manganese in surface sediments; a general theory for the coupled transport and reaction of carbon, oxygen, nitrogen, sulfur, iron, and manganese. Am. J. Sci. 296, 197 LP−243. doi: 10.2475/ajs.296.3.197

CrossRef Full Text | Google Scholar

van den Boorn, S. H. J. M., Vroon, P. Z., van Belle, C. C., van der Wagt, B., Schwieters, J., and van Bergen, M. J. (2006). Determination of silicon isotope ratios in silicate materials by high-resolution MC-ICP-MS using a sodium hydroxide sample digestion method. J. Anal. At. Spectrom. 21, 734–742. doi: 10.1039/b600933f

CrossRef Full Text | Google Scholar

Wallmann, K., Aloisi, G., Haeckel, M., Tishchenko, P., Pavlova, G., Greinert, J., et al. (2008). Silicate weathering in anoxic marine sediments. Geochim. Cosmochim. Acta 72, 2895–2918. doi: 10.1016/j.gca.2008.03.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolff-Boenisch, D., Wenau, S., Gislason, S. R., and Oelkers, E. H. (2011). Dissolution of basalts and peridotite in seawater, in the presence of ligands, and CO₂: implications for mineral sequestration of carbon dioxide. Geochim. Cosmochim. Acta 75, 5510–5525. doi: 10.1016/j.gca.2011.07.004

CrossRef Full Text | Google Scholar

Zeebe, R. E., and Wolf-Gladrow, D. (2001). CO2 in Seawater: Equilibrium, Kinetics, Isotopes. Gulf Professional Publishing.

Google Scholar

Zhong, S., and Mucci, A. (1989). Calcite and aragonite precipitation from seawater solutions of various salinities: precipitation rates and overgrowth compositions. Chem. Geol. 78, 283–299. doi: 10.1016/0009-2541(89)90064-8

CrossRef Full Text | Google Scholar