Evidence for Increasing Frequency of Extreme Coastal Sea Levels

Projections of extreme sea levels (ESLs) are critical for managing coastal risks, but are made complicated by deep uncertainties. One key uncertainty is the choice of model structure used to estimate coastal hazards. Differences in model structural choices contribute to uncertainty in estimated coastal hazard, so it is important to characterize how model structural choice affects estimates of ESL. Here, we present a collection of 36 ESL data sets, from tide gauge stations along the United States East and Gulf Coasts. The data are processed using both annual block maxima and peaks-over-thresholds approaches for modeling distributions of extremes. We use these data sets to fit a suite of potentially non-stationary generalized extreme value distributions and generalized Pareto distributions by covarying the ESL statistics with multiple climate variables. For all of the sites and statistical model structures for tide surge considered here, we find that accounting for changes in the frequency of coastal extreme sea levels provides a better fit to data than using a stationary extreme value model. Further, when maximizing the a posteriori probability of the model parameters, given the available tide gauge data, generalized extreme value distribution structures with non-stationary scale parameter are preferred over non-stationary location parameter. These results have implications for how deep uncertainties in coastal flood hazards are characterized, particularly in how studies incorporate potential non-stationarity in storm surge statistics.

Introduction

Projections of the future coastal hazard posed by extreme sea levels are a key component of designing strategies to manage coastal flood risk, but probabilistic estimates of these hazards suffer from a number of intrinsic uncertainties. These uncertainties in coastal hazard estimates lead to uncertainty in the “correct” strategy to manage coastal risk (Buchanan et al., 2015; Wong and Keller, 2017). In turn, the uncertainty in flood defense strategy leads to potentially poorer performance of the risk management strategy in terms of economic losses (Oddo et al., 2017), size of inundated area (Fischbach et al., 2017), or loss of life (Jonkman et al., 2009). Thus, it is important to quantify how key uncertainties affect the estimated coastal flood height return levels, especially at the local scale (Durand et al., 2022).

The total extreme sea level height has three main components: mean sea level, astronomical tide levels and storm surge. The present work will focus on the total summed tide and storm surge level, termed “storm tide”, because this is the total hazard facing coastal zones. This approach also avoids the issue of biases that may arise when attempting to disentangle the tidal and non-tidal components of extreme sea level (Arns et al., 2020). For brevity's sake, we will interchangeably refer to the storm tide component as the “extreme sea level” (ESL), though what we are really referring to is the sea level in substantial excess of the mean. This approach runs the risk of missing the compounding effect on flood hazard of multiple drivers of risk (Wahl et al., 2015; Moftakhari et al., 2017a) and will not capture the potentially sizable costs of frequent minor, or “nuisance”, flood events (Vandenberg-Rodes et al., 2016; Moftakhari et al., 2017b). With these caveats in mind, this approach of modeling storm tides as a univariate hazard is effective for analyzing this particular key uncertainty, and is important for policy-making, as it represents the actual water level impacting the coastline during a flood event (Yu et al., 2019).

There exist multiple approaches for estimating storm tide return levels. These include the joint probability method (e.g., Pugh and Vassie, 1978; Tawn and Vassie, 1989; McMillan et al., 2011), process-based modeling (e.g., Orton et al., 2016; Garner et al., 2017), and statistical modeling (e.g., Coles, 2001; Tebaldi et al., 2012; Chen and Liu, 2016; Buchanan et al., 2017; Ceres et al., 2017; Lee et al., 2017; Wong and Keller, 2017; Ruckert et al., 2019). A key strength of process-based modeling is that explicitly resolving individual storms and physical processes permits an evaluation of the physical drivers of risk and their spatiotemporal dependence. However, process-based modeling comes at a higher computational cost. Joint probability method, by contrast, models the probabilities associated with flood events by estimating the conditional probabilities for the dependency relationships within the statistical model structure. While these other methods for estimating the hazards posed by coastal ESLs have their respective strengths, at present we restrict our attention to statistical modeling. Statistical modeling is another common and less computationally demanding approach for estimating the hazards posed by ESL. We elect to use statistical modeling because the focus of this work is on an accounting of uncertainty, for which the computational efficiency of statistical modeling is a strength.

Statistical modeling involves estimating the probability distribution of ESL heights from some observational data set that has been processed in such a way that it fulfills the assumptions of the fitted distribution (e.g., independent samples). Common choices for distributions include generalized extreme value distributions (GEV) and generalized Pareto distributions (GPD). A GEV is the limiting distribution for a sequence of independent block maxima, so it is a natural choice for sequences of sea-level extremes. However, GEV models are limited in that they do not resolve temporal variability or changes within a given time block. GPD models, on the other hand, give the distribution of exceedances of a given threshold height. These peaks-over-thresholds models are typically coupled to a Poisson process that gives the number of threshold exceedances per block of time. While of course no model can be expected to be a perfect representation of the real-world distribution of storm surge hazard, the literature is split on which distribution, GEV or GPD, provides the best mathematical representation of storm surge (Wahl et al., 2017). Thus, it is prudent to examine the impacts of model structural choice when making estimates of future coastal hazards.

Potential non-stationarity in the hazards posed by coastal storm surges presents another key uncertainty that is receiving an increasingly large share of attention in current research (Milly et al., 2008; Serinaldi and Kilsby, 2015; Lin et al., 2016; Rashid et al., 2019). Depending on geographic location, uncertainties in future ESLs may be within the range of natural variability and it can be difficult to say conclusively that storm surge statistics are changing (Cid et al., 2016; Haasnoot et al., 2020; Tebaldi et al., 2021). However, failure to account for potential non-stationarity (if it is in fact present) has both theoretical and practical consequences. On the theory side, non-stationarity can violate the assumption that ESL data for a given site are independent and identically distributed. In terms of practical consequences, neglecting non-stationarity can result in underestimation of storm surge return levels (Wong, 2018), leading to under-protection of coastal areas. In efforts to address this research need, recent work has examined the timescale on which non-stationary storm surge behavior can be confidently detected (Ceres et al., 2017; Lee et al., 2017), model averaging approaches to quantify the degree of belief that can be placed on non-stationary model structures (Wong, 2018) and quantification of indicators of changing ESL behavior (Rashid et al., 2019).

Non-stationarity can be incorporated into statistical models for storm surge return levels by allowing the parameters of the given distribution to covary with some climate conditions and/or indicator(s) (e.g., Haigh et al., 2010; Marcos et al., 2015; Wong et al., 2018). For example, previous studies have covaried ESL behavior with global mean surface temperature (Grinsted et al., 2013; Ceres et al., 2017; Lee et al., 2017), global mean sea level (Arns et al., 2013; Vousdoukas et al., 2018), the North Atlantic Oscillation (NAO) index (Haigh et al., 2010; Wong et al., 2018) and time (i.e., a linear change) (Grinsted et al., 2013). The work of Wong (2018) compared estimates for return levels using as a non-stationary covariate the winter mean (DJF) NAO index, global mean surface temperature, global mean sea level and a simple linear change with time. Here, we examine which of the covariates considered by Wong (2018) yields the best-fitting extreme value distributions for a set of tide gauge stations along the United States East and Gulf Coasts, and how the amount of data available affects the choice of best covariate.

The inherent dearth of data on environmental and climate extremes can lead to poorly constrained estimates of model parameters, which only worsens as the number of parameters that must be estimated increases. Consequently, the degree of confidence in those more complex model structures is reduced (c.f., Figure 1 from Wong, 2018). This paucity of observational data to constrain extremes frequently leads to a reliance on simpler non-stationary models with fewer parameters. For example, following this principle of parsimony, some previous work (e.g., Rashid et al., 2019) consider only non-stationarity in the location parameter for the GEV distribution, which governs the center of the distribution. Among the model structures considered by Lee et al. (2017), any non-stationarity in the scale parameter, which governs the width of the GEV distribution, is conditioned on the location parameter also being non-stationary. The model structures of Wong et al. (2018) suffer from a similar limitation, but in the context of the GPD class of models. However, changes to only the scale parameter of either a GEV distribution or GPD can also bring about changes to the medians for these distributions, as well as the distributions' tails. Previous research has generally neglected model structures in which only the scale parameter is non-stationary. Furthermore, the question of which covariate or non-stationary model structure fits the data the “best” depends on what goodness-of-fit metric one uses to compare the candidate model structures. Thus, it is important to examine how the selection of potentially non-stationary statistical model structure affects the estimated storm tide return levels and associated flood hazard.

Toward this end, we focus on two questions: First, what is the best-fitting form of potentially non-stationary extreme value statistical model for each site? We fit four candidate model structures for each of the GEV and GPD families of models. Among these structures, we vary which model parameters are considered to be potentially non-stationary. We do not include potential non-stationarity in the shape parameter due to the high sensitivity of the upper tails of the GP and GEV distributions to this parameter. We hypothesize that sites with shorter available data records will find better fits in extreme value models with fewer parameters. Second, we ask: how does uncertainty in the model structural choice affect the range of estimated storm tide return level? We expect that for some sites, the projected change in return level in non-stationary models will be similar in magnitude to the range in estimated changes across the set of candidate models (Haasnoot et al., 2020). We address these questions and characterize these uncertainties in a set of model experiments by examining all combinations of non-stationary/stationary statistical model parameters (keeping the shape parameters fixed) for both GEV and GPD model structures, and for each of the four candidate covariates used by Wong (2018).

Methods

Data

We use tide gauge data from 36 stations along the United States East and Gulf Coasts, obtained from the University of Hawaii Sea Level Center (Caldwell et al., 2015) (accessed March 21, 2020). The site names, locations and dates of available data are given in Table 1. Gaps exist in many of the data sets, which lead to the discarding of some data. Thus, the “Years of usable data” column does not always match the interval between “Start date” and “End date” in Table 1.

TABLE 1

Table 1. Tide gauge station name, latitude, longitude and years of available data.

We process the raw tide gauge data by first subtracting the annual block means using a moving 1-year window to account for changes in mean sea level. What remains is attributable to storm tides (astronomical tides and storm surges) and natural variability. For modeling using GEV distributions, we aggregate the detrended data into annual blocks and compute the annual maximum for each block. We discard any year that is missing more than 90% of its hourly data. Table 1 gives the final number of annual block maxima remaining for analysis for each tide gauge station.

The GPD family of models requires a time series of exceedances of some appropriately chosen threshold extreme sea level. We follow the same procedure as has been used extensively in previous work, so the interested reader is directed to Arns et al. (2013), Wahl et al. (2017), and Wong et al. (2018) for further details and a discussion of the associated uncertainties. For these models, we first detrend the data to account for mean sea-level change as described above. We then compute the time series of daily maximum sea levels for each location. We discard any days that are missing more than 90% of the hourly data (that is, 4 h or more are missing). For each site, we compute the 99th percentile of these daily maximum sea levels to use as the threshold for the GPD peaks-over-thresholds model. We collect a time series of exceedances of this threshold, which we then decluster in order to remove multiple extremes from the same ESL event. We use a declustering timescale of 3 days (Wong et al., 2018). Previous experiments suggest that results are not strongly sensitive to this choice of declustering timescale (Wong et al., 2018). The final declustered time series of threshold exceedances serves as the data for analysis and fitting a Poisson process/GPD model.

To account for gaps in the data for the GPD analysis, we use the following procedure. We fit an overall linear trend to the raw tide gauge data and subtract the fitted line. We fit a mean annual cycle to the detrended hourly sea levels. We then re-impose the linear trend and fill any gaps with this mean annual cycle plus a linear trend. We do not use any data that was gap-filled for analysis, only for detrending. Averaging is a smoothing operation, so this procedure will dampen extremes near these gaps. To partially account for this, the Poisson process rate parameter accounts for only the portion of the year of data that is present.

To incorporate non-stationarity by modulating the ESL statistical model parameters, we use the four time series covariates from a recent study (Wong, 2018): the winter mean (DJF) North Atlantic Oscillation (NAO) index, the global mean surface temperature, the global mean sea level and time. We compute the NAO index from sea-level pressure data following Stephenson et al. (2006). We use the historical monthly NAO index data from Jones et al. (1997) for the hindcast calibration and we use the CESM2 sea level pressure projection under the SSP5-85 scenario as part of the CMIP6 ensemble (O'Neill et al., 2016; Danabasoglu, 2019a,b; last accessed January 26, 2022). We take the historical global mean surface temperatures from the National Centers for Environmental Information data portal (NOAA, 2017) and the future projections from the CESM2 SSP5-85 CMIP6 scenario (O'Neill et al., 2016; Danabasoglu, 2019a,b; last accessed January 26, 2022). We use the historical sea level time series from Church and White (2011) and use the future projections of Wong and Keller (2017). We note that more recent sea-level rise projections exist, including those using the same model as Wong and Keller (2017), but we retain this sea-level time series for consistency with previous work (Wong, 2018). The time covariate is a simple identify function, representing a linear increase over time. Each covariate time series is normalized to the 0–1 range over the hindcast period.

Statistical Models for Storm Surge

Generalized Extreme Value Distribution

We consider two potential extreme value distributions: a generalized extreme value (GEV) distribution and a generalized Pareto distribution (GPD). The probability density function (pdf) for the GEV distribution is given by

$\begin{array}{ll}f(w(t)|\mu (t),\sigma (t),\xi (t))=\frac{1}{\sigma (t)}{r(t)}^{\xi (t)+1}{e}^{-r(t)}& (1)\end{array}$

where w(t) is the detrended annual maximum sea level in year t; μ(t) is the location parameter (mm), which governs the center of the distribution; σ(t) is the scale parameter (mm), which governs the width of the distribution; and ξ(t) is the shape parameter (unitless), which governs the tail of the distribution. The factor r(t) is given by $r(t)={\left(1+\xi (t)\frac{w(t)-\mu (t)}{\sigma (t)}\right)}^{-1/\xi (t)}$for ξ(t) ≠ 0 and exp[−(w(t)−μ(t))/σ(t)] if ξ(t) = 0. We assume that the model parameters can vary with time t and are constant within a given year. The general non-stationary form of the GEV model parameters is

$\begin{array}{l}\mu (t)={\mu }_0+{\mu }_1\varphi (t)\\ \sigma (t)=exp({\sigma }_0+{\sigma }_1\varphi (t))\\ \xi (t)={\xi }_0+{\xi }_1\varphi (t),& (2)\end{array}$

where μ₀, μ₁, σ₀, σ₁, ξ₀, and ξ₁ are all constant parameters that depend on location and φ(t) is a covariate time series. Our restriction that the shape parameter, ξ, is stationary amounts to the assumption that ξ₁ = 0, but we retain ξ₁ in the equations that follow for generality. For each of the four candidate covariates (time, temperature, sea level and NAO index), we consider four different possible GEV model structures to account for potential non-stationarity in each of the parameters, μ and σ (see Table 1). Note that the model structure in which μ₁ = σ₁ = ξ₁ = 0 corresponds to the assumption of stationarity in the GEV distribution, so there is a total of 13 distinct GEV model structures possible (four choices of covariate times three choices of non-stationary parameters, plus one stationary model).

The detrended series of annual block maxima, w, is assumed to be independent of one another. So, the likelihood function for the GEV distribution is given by

$\begin{array}{ll}L(w|{\mu }_0,{\mu }_1,{\sigma }_0,{\sigma }_1,{\xi }_0,{\xi }_1)={{\displaystyle \prod }}_{i=1}^{N}f(w_i|\mu (t),\sigma (t),\xi (t)),& (3)\end{array}$

where w_i denotes the annual block maximum for year i, for each of N years.

Generalized Pareto Distribution

The generalized Pareto distribution (GPD) model employs a peaks-over-thresholds approach in which the set of exceedances of a threshold, μ, is assumed to follow a generalized Pareto distribution. Following previous work, we take the threshold μ to be the 99th percentile of the time series of detrended daily block maxima (e.g., Tebaldi et al., 2012; Buchanan et al., 2017; Wong et al., 2018). The interested reader is directed to Arns et al. (2013) and Wong et al. (2018) for a more detailed discussion of the sensitivities surrounding the choice of this threshold and other structural choices. The pdf for the GPD is given by

$\begin{array}{ll}f(x(t)|\mu ,\sigma (t),\xi (t))=\frac{1}{\sigma (t)}{\left(1+\xi (t)\frac{x(t)-\mu }{\sigma (t)}\right)}^{-(1+\frac{1}{\xi (t)})},& (4)\end{array}$

where x(t) is sea level height at time t, σ(t) is the GPD scale parameter (mm) and ξ(t) is the GPD shape parameter (unitless), both of which are assumed to vary with time t, and are constant within a given year. Exceedances of the threshold μ are assumed to occur following a Poisson process with rate parameter λ(t) (units of exceedances per day). Supposing that there are n(t) exceedances in the time interval [t, t+Δt], the Poisson probability mass function (pmf) is then

$\begin{array}{ll}g(n(t)|\lambda (t))=\frac{{(\lambda (t)\Delta t)}^{n(t)}}{n(t)!}exp\left(-\lambda (t)\Delta t\right).& (5)\end{array}$

Like the GEV model parameters, the general non-stationary form of the GPD model parameters is

$\begin{array}{l}\lambda (t)={\lambda }_0+{\lambda }_1\varphi (t)\\ \sigma (t)=exp({\sigma }_0+{\sigma }_1\varphi (t))\\ \xi (t)={\xi }_0+{\xi }_1\varphi (t),& (6)\end{array}$

where λ₀, λ₁, σ₀, σ₁, ξ₀, and ξ₁ are all constant parameters that depend on the site location. We use the same candidate covariate times series φ(t) as with the GEV distributions (Section Generalized Extreme Value Distribution), and the four candidate GPD model structures with ξ stationary (ξ₁ = 0) are analogous to those considered for the GEV distributions, with the exception that the location parameter (GEV) is exchanged for the Poisson rate parameter (GPD) (see Table 2). Combining the pdf for the GPD, after conditioning on the number of threshold exceedances, n(y_i), for each year i=1, 2, …, N, the likelihood function for the data set of threshold exceedances x, given the model parameter set (λ₀, λ₁, σ₀, σ₁, ξ₀, ξ₁) is

$\begin{array}{l}L(x|{\lambda }_0,{\lambda }_1,{\sigma }_0,{\sigma }_1,{\xi }_0,{\xi }_1)={\displaystyle {\prod }_{i=1}^{N}g(n(y_i)|{\lambda }_0,{\lambda }_1)}\\ {\displaystyle {\prod }_{j=1}^{n(y_i)}f(x_j(y_i|\mu ,\sigma (t),\xi (t))}& (7)\end{array}$

where y_i denotes the year indexed by i and x_j(y_i) is the jth threshold exceedance in year y_i. The second product in this equation is replaced by one for any year with no exceedances. Note that the data used to fit the GEV models (w) and the GPD models (x) are different.

TABLE 2

Table 2. Candidate model parametric structures.

Model Calibration

For each site we calibrate each candidate model using a differential evolutionary algorithm (Storn and Price, 1997) to maximize the model goodness-of-fit for the time series of annual block maxima (GEV) or threshold exceedances (GPD), given the model parameters and covariate time series. Each annual block maximum or threshold exceedance, after appropriate declustering and detrending, is assumed to be independent of one another.

Goodness-of-Fit

Let NLL denote the negative of the maximal value of the log-likelihood function for a candidate extreme value model (that is, GEV or GPD, along with the specific parameters considered to be potentially non-stationary). Lower values of NLL correspond to better model fits to the available data. Suppose the model has k uncertain parameters that must be estimated as in Section Model Calibration and the data set for analysis has a total of N data points. Then the Akaike Information Criterion (Akaike, 1974) (AIC) and the Bayesian Information Criterion (Schwarz, 1978) (BIC) are given by the following:

$\begin{array}{l}AIC=2k+2NLL\\ BIC=kln(N)+2NLL.& (8)\end{array}$

Lower values of AIC and BIC correspond to better model fits to the available data. The three goodness-of-fit metrics, NLL, AIC and BIC, constitute a progressive increase in the penalty exacted for using too many model parameters (in that order). Using the likelihood function alone constitutes no penalty for the number of parameters, and the BIC penalizes each additional model parameter by a factor of ln(N). For data sets with more than exp(2) (about 7.4) data points, the AIC penalizes additional model parameters less harshly than the BIC. This is true for all of the data sets presented here. Thus, AIC and BIC embody the principle of parsimonious use of parameters and data.

Another perspective which penalizes profligate parameter usage is to apply a Bayesian approach. The model parameters, θ, are assigned a joint prior distribution, π, and instead of minimizing the negative log-likelihood, we minimize the negative log-posterior score, which is given by a gentle rearrangement of Bayes' theorem as

$\begin{array}{ll}NPS=-ln(L(x|\theta ))-ln(\pi (\theta )).& (9)\end{array}$

We note that the posterior score is proportional to the actual posterior probability from Bayes' theorem, so minimizing NPS is equivalent to maximizing the posterior probability of the parameters. We fit the prior distributions, π, by using the following procedure. We obtain and process the raw hourly tide gauge data for 27 sites from the University of Hawaii Sea Level Center (Caldwell et al., 2015) (accessed July 24, 2017) data repository. For each candidate model structure, for each site, we estimate maximum likelihood parameters. We pool the maximum likelihood parameters for all 27 sites and fit either a normal distribution or a gamma distribution to the set of parameters, depending on whether the parameter's support is theoretically infinite (e.g., the GEV/GPD shape parameter) or half-infinite (e.g., the GEV/GPD scale parameter). Note that these distributions are only (half-)infinite in theory; in practice, extreme values for these parameters are uncommon. However, the strength of using NPS for model selection lies in the prior distribution's function to penalize extreme parameter values that are unlikely a priori.

To examine the impacts of the amount of available data on the structure of the best-fitting statistical models, we use the median of the number of years of available data (55 years, c.f., Table 1) to separate the tide gauge sites into “long” and “short” records. There are no stations with exactly 55 years of data available, so each group contains 18 stations. Our use of the terms “long” and “short” are relative, and only meant to be used within the context of this study.

Estimates of Storm Tide Return Levels

For each site, we use all of the candidate model structures with stationary shape parameters (Table 2), conditioned separately on using a GPD (main text) or a GEV model (see Supplementary Figure 8), to estimate the 50-year return level between 2020 and the year 2050. We use NPS as the goodness-of-fit metric for model selection and highlight the best-fitting model for each of the tide gauge sites with more than 55 years of data available (Figure 4). To illustrate the model structural uncertainty associated with these storm tide statistical models, we show this best-fit model alongside all 12 of the other model structures considered in this work (4 covariates × 3 non-stationary parametric forms, plus a stationary model). The 10- and 100-year return levels are shown in Supplementary Figures 9–12, and other return levels are available in the data files accompanying this work (see Data Availability statement).

Results

Covariate Choices

When the number of model parameters is not penalized (NLL), all sites prefer some form of non-stationary model structure for both the GEV (Figure 1A) and GPD families of models (Figure 1E). For the GEV distribution, when either NLL (Figures 1A,E) or AIC (Figures 1B,F) is used for model selection, global mean surface temperature emerges as the most popular covariate choice for sites with short data records, while long-data sites generally prefer the sea level covariate (Figures 1A,B). For the GPD family of models, results are mixed; a sea level covariate is preferred by long-data sites much more frequently than by short-data sites across all goodness-of-fit metrics. Not surprisingly, if the number of model parameters is penalized by using the BIC for model selection, a stationary extreme value model fits best for both the GEV and GPD families (Figures 1C,G).

FIGURE 1

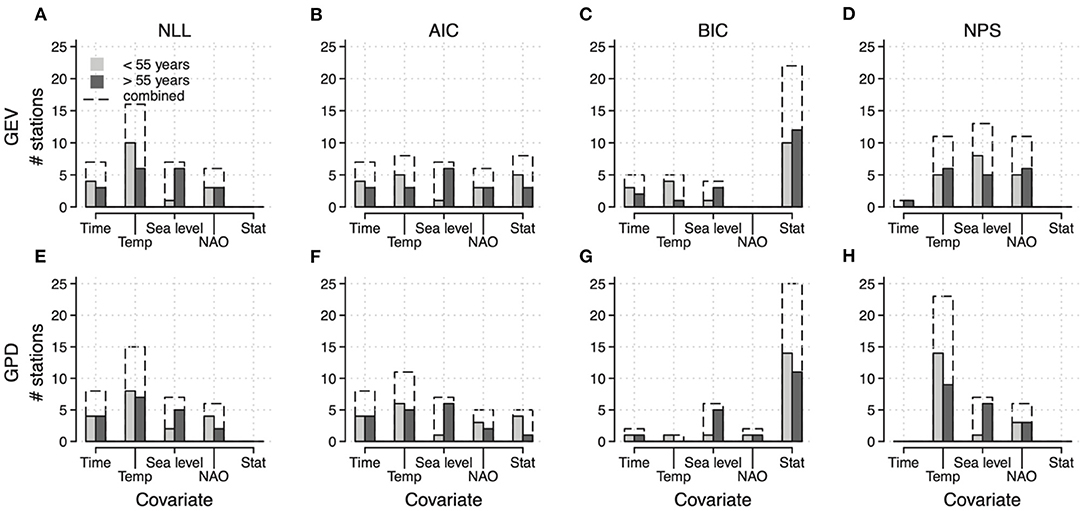
Figure 1. Frequency histograms of covariate choice. These figures aggregate over all 36 tide gauge stations, for each of the goodness-of-fit metrics: negative log-likelihood (A,E), Akaike information criterion (B,F), Bayesian information criterion (C,G), and negative posterior score (D,H). The top row corresponds to consideration of the four GEV model structures and the bottom row corresponds to the four GPD models. Sites are separated into long (>55 years, dark gray) and short (<55 years, light gray) data record lengths.

The essence of a Bayesian modeling approach is to update our a priori beliefs about a model and its parameters in light of the available tide gauge data. The NPS combines both these prior probabilities and the log-likelihood of the data, given the supposed values for model parameters. Taking the Bayesian approach leads to the temperature covariate as the overall most common choice for the GPD models (Figure 1H) but no decisive favorite among the GEV models (Figure 1D). For the remainder of the analysis presented in the main text, we provide results using NPS for model selection (see Supplementary Material for analogous results using the other goodness-of-fit measures).

The lack of a clear overall pattern to the choice of covariate by data length raises the question of whether a geographical pattern to these model structural choices might exist. The Gulf Coast shows some preference for all of the covariates (except time) at different locations when we use a GEV distribution (Figure 2A). When we use a GPD, however, more coherent spatial structure emerges (Figure 2B). Temperature is the preferred covariate along the Gulf Coast and eastern Florida, with some representation from NAO index on the western Gulf (Figure 2B). In the mid-Atlantic, there is a preference for non-stationary models modulated by temperature or sea level. In the Northeast (New England, east and north of New York City), the sea level covariate is the dominant best fit when using the GPD family of models, but there is no clear trend when using the GEV family.

FIGURE 2

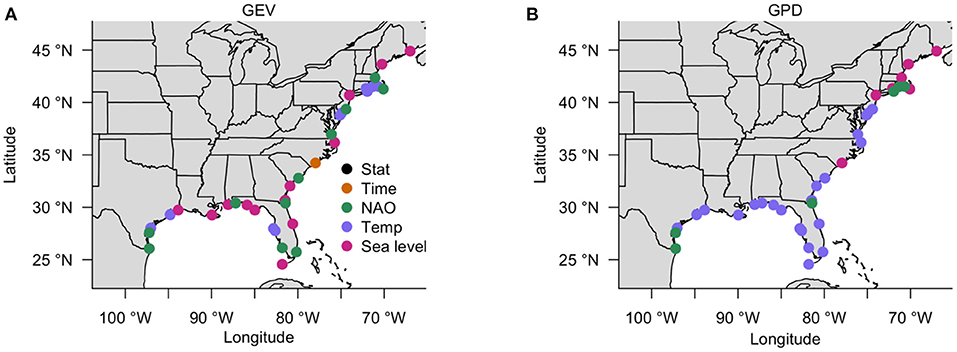
Figure 2. Geographical distribution of the preferred covariate time series. Best-fit models are selected using negative log-posterior score to evaluate goodness-of-fit, assuming a GEV model (A) or a GPD one (B).

Model Choice

When we select the best-fitting model using NPS, no sites prefer a stationary model (Figure 3). When considering only GEV models (Figures 3A–D), if only one parameter is to be non-stationary, then models with non-stationary scale parameter (σ) are clearly preferred over those with non-stationary location parameter (μ). No sites show preference for the GEV model with μ non-stationary (Figures 3A–D). Several sites with long data records prefer the GEV model wherein both σ and μ are non-stationary. This highlights the strict requirements placed on available data in order to fit more complex non-stationary extreme value models. For a GPD model, the preferred model structure is always the model with non-stationarity in both the Poisson rate parameter (μ) and the scale parameter (σ) (Figures 3E–H).

FIGURE 3

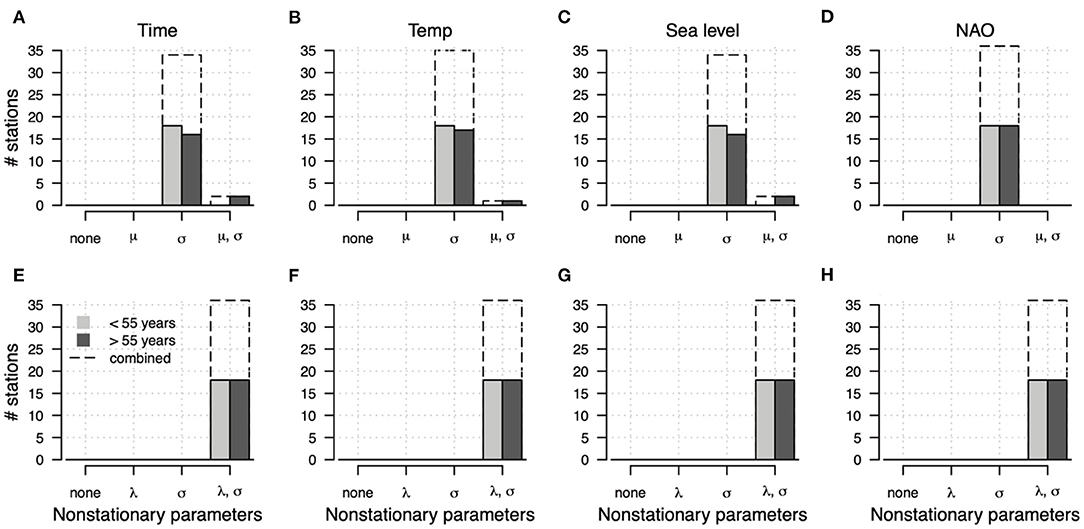
Figure 3. Frequency graphs of model choice. These figures aggregate over all 36 tide gauge stations, considering each covariate individually (time, A,E; temperature, B,F; sea level, C,G; and NAO index, D,H). Top row corresponds to consideration of the four GEV model structures and bottom corresponds to the four GPD models. Sites are separated into long (>55 years, dark gray) and short (<55 years, light gray) data record lengths. Negative log-posterior score is used to evaluate model goodness-of-fit.

Estimated Return Levels

We use all four potentially non-stationary GPD model structures with stationary shape parameter (ξ) and all four candidate covariates to fit a total of 13 distinct models for each tide gauge data site (4 covariates × 3 non-stationary models + 1 stationary model). We use these models to project the 50-year storm tide return level for each of the sites with at least 55 years of available data (Figure 4). In the Supplementary Material, we include analogous figures when the GEV family of models is used, and for other return periods.

FIGURE 4

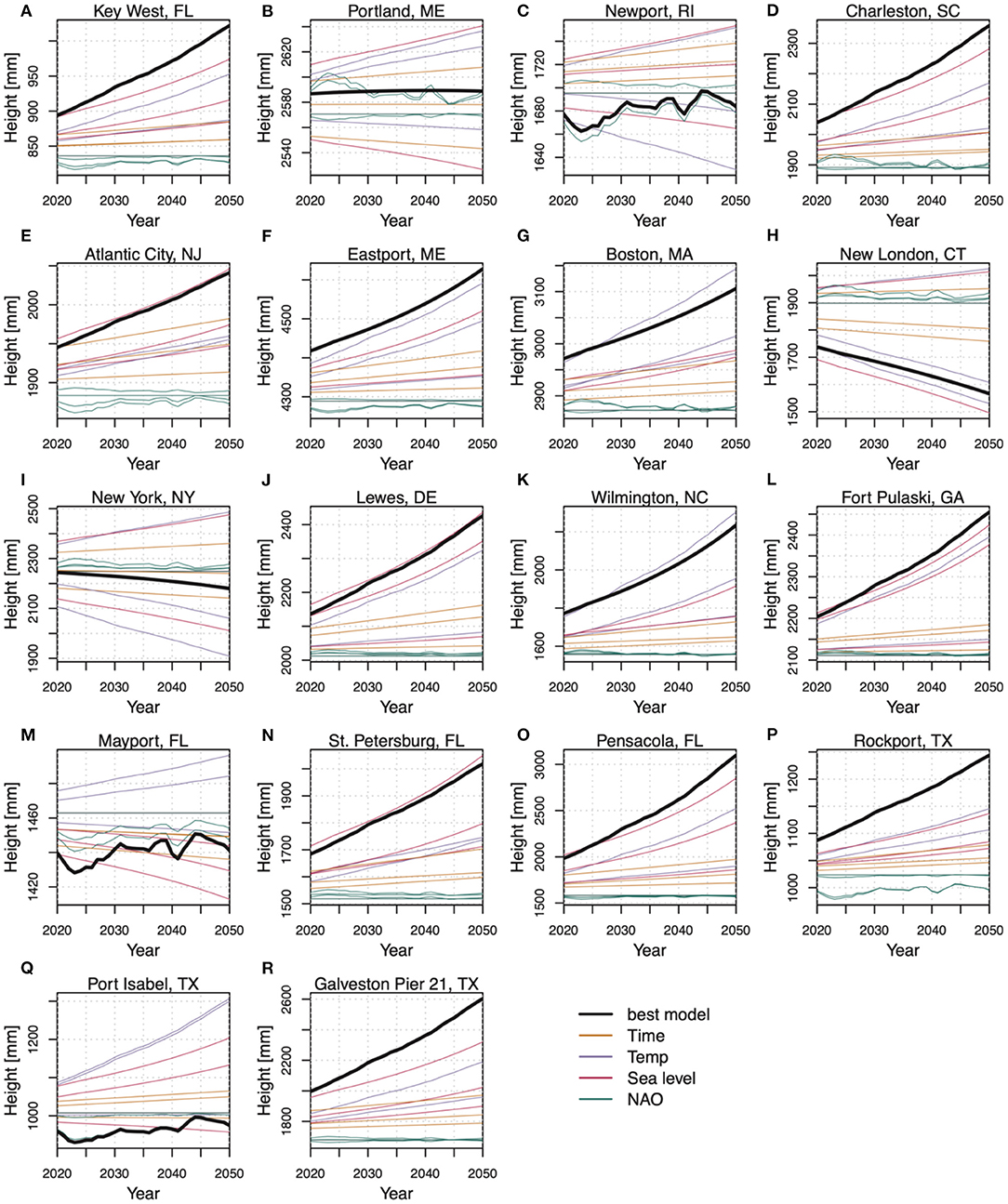
Figure 4. Projected 50-year return levels for the long-data sites (A–R). Uses a GPD model and a centered 21-year moving window average. The best-fitting model is selected by minimizing the negative log-posterior score and is shown in black. The four candidate models using as the covariate time series are shown with the same-colored lines: time (orange), temperature (purple), sea level (red), and NAO index (green). There is no visual distinction in each panel among the candidate model structures within the set using each covariate.

The ranges of these results for each tide gauge station demonstrate the diversity in estimates of flood hazards attributable to model structural uncertainty, and how this “cone of uncertainty” grows over time. As expected, for some sites, the signal can be roughly equal in magnitude to the noise. For example, in Pensacola, Florida, the 50-year storm tide return level using the best-fitting model (a non-stationary GPD with both λ and σ varying with temperature) increases from about 1980 mm in 2020 to about 3,100 mm by the year 2050 (Figure 4O). However, the range in 2050 between the minimum and maximum model projections is 1,500 mm. We are not arguing that the range is the appropriate measure of uncertainty, especially with skewed distributions as tend to arise in dealing with extremes. However, the range in model projections does shed light on the magnitude of the uncertainties present, and our intention is to provide a framework for better understanding these inherent decision-relevant uncertainties.

This wide range in projected return levels results in several sites displaying a range of projected changes in storm tide return levels that spans from potential decreases in return level to increases (e.g., Portland, Newport, New London, New York, Mayport, and Port Isabel; Figures 4B,C,H,I,M,Q). The Newport, Mayport, and Port Isabel sites use NAO index as the best-fitting model covariate and show little discernible overall trend in either direction (Figures 4C,M,Q). This is attributed to the NAO index being the noisiest covariate, and raises the possible question of to what degree these covariate models are really just fitting the noise in the data, as opposed to the covarying NAO-storm tide signal.

Discussion

We have presented a set of experiments to characterize uncertainty in projected ESL return levels for sites along the U.S. East and Gulf Coasts. In particular, we have focused our attention on three main questions: (i) in our sample of 36 tide gauge stations, which of the candidate covariates and which of the candidate (non-)stationary model parametric structures fits best for each site? (ii) what geographic patterns emerge based on those best-fitting models? and (iii) how does the projected 50-year return level compare to the uncertain range in future return levels, when looking across all of the plausible candidate model structures? We also examined whether the amount of available data has an impact on the choice of best-fitting model structure, with a specific focus on the number of parameters used (see Table 2).

For the GPD extreme value models, along the U.S. Gulf Coast and mid-Atlantic regions, global mean surface temperature emerges as the dominant best-fitting covariate (Figure 2). In the Northeast, global mean sea level is the dominant covariate for ESL. For the GEV models, in the Northeast, global mean sea level and temperature are the dominant covariates. Along the Gulf Coast, the GEV models show a preference for temperature and sea level as covariates, as well as the winter mean NAO index. However, we attribute the GEV models' relatively stronger preference for NAO index as a covariate to the reduced set of data as compared to the GPD models (see Section Estimated Return Levels). These geographic differences are likely attributable to the main drivers of ESL in different regions. For example, in the Gulf Coast region, the premise underlying previous work examining ESL in this region assumed a connection between tropical storm activity and changes in surface temperature (namely, in the tropical development region where storms may form) (Grinsted et al., 2013). The fact that temperature is favored as the best-fitting covariate for many of the sites considered here, and for both the GEV and GPD models, supports that premise. We emphasize that these models and methods employ temperature (or sea level, NAO index or time) as a covariate as opposed to a causal mechanism for changes in ESL.

We find that, in contrast to some previous studies (Lee et al., 2017; Wong et al., 2018; Rashid et al., 2019), a GEV model with only the scale parameter (σ) non-stationary fits the annual block maximum data sets better than a model with only the location parameter (μ) non-stationary (c.f., Figure 3). This result does not undermine these previous works, however. Both model structures lead to a change in the median of the distribution of ESL, but the σ-non-stationary structure also changes the width of the distribution. An increase in the width as we project return levels further into the future may well accurately reflect our imperfect understanding of precisely how climate change will affect environmental extremes (Seneviratne et al., 2012; Kossin et al., 2017). For GPD models, we find that the form with non-stationary rate and scale parameters (λ and σ) is the dominant best-fitting model structure. When we limit the model choices to only those with a single non-stationary parameter, GPD models with non-stationarity in only the rate parameter are the more popular choice (see Supplementary Figures 17–20). With GPD models, sites with more data tend to prefer non-stationarity in the rate parameter (λ), while sites with shorter data records prefer non-stationarity in the shape parameter (σ). We find the same preference among shorter-record sites for non-stationary σ is apparent when negative log-likelihood, AIC, or BIC are used for model selection, for both GEV and GPD models.

Note that we cannot, in general, directly compare goodness-of-fit measures across the GEV and GPD classes of models because the data sets (after processing) employed for the two types of models are different. However, the stationary form of each class of model (GPD or GEV) may be viewed as a baseline against which to compare the non-stationary model structures. For example, the mean differences in NPS among all sites for a global mean sea level, global mean surface temperature, or NAO index covariate, using a GPD model with the rate and scale parameters (λ and σ) non-stationary relative to a stationary GPD model, are 11.7, 11.8, and 10.1, respectively. By contrast, the use of a GEV model with only scale (σ) non-stationary, relative to a stationary GEV model, yields differences in NPS of 5.1, 5, and 5, respectively. Given that the use of GPD models can constrain two non-stationary parameters and provides a better fit relative to a stationary model, we conclude that a non-stationary GPD model is preferable to any of the available GEV-type models, or a stationary GPD.

A critical caveat is that these results for the optimal model choice (by whatever measure one wishes to use) do not depict the strength of the structural choice. For example, at the Chesapeake Bay Bridge Tunnel (Virginia) station, the range in AIC for the GEV models is 546.7–550.6. Differences in AIC and BIC this small do not indicate a strong preference among the model structural choices. Thus, in this particular case, there is effectively no significant preference between the best-fitting and the worst-fitting models. However, we include a stationary model in the set of candidate models, so our framework represents the hypothetical decision landscape that faces a modeler tasked with projecting storm tide hazard for these sites: a choice must be made among these (or other) possible model structures. Alternatively, this is an area where model averaging approaches have been shown to be a fruitful avenue to combine projections across model structures (Moftakhari et al., 2017c; Wong, 2018; Wong et al., 2018), or one might consider selecting a model that minimizes the potential regret if that choice turns out to be inappropriate (Lempert and Collins, 2007; Kasprzyk et al., 2013).

In light of these additional subjective modeling decisions and the uncertainty related to model structural choice illustrated by the results presented here, it is clear that there are many other cross-sections and extensions of these results. Further work will be of interest to researchers from the perspective of evaluating the practical implications of subjective choices that must be made regarding model structures employed. It is our aim that this work may provide a useful framework for these lines of inquiry into statistical modeling for extreme coastal sea levels, including a common set of processed tide gauge records for two common extreme value modeling approaches.

Data Availability Statement

All data supporting this work are freely available from Zenodo at https://doi.org/10.5281/zenodo.5934224 under the GNU general public open-source license. All modeling and analysis codes supporting this work are freely available from GitHub at https://github.com/tonyewong/surge_comparison, as well as on Zenodo alongside the data files at https://doi.org/10.5281/zenodo.5934224, both under the GNU general public open-source license. The authors assume no responsibility for the (mis)use of these codes.

Author Contributions

TT conducted the initial analysis, produced the figures, and contributed to the final version of the paper. MZ conducted the initial model calibration experiments, performed the final validation experiments, and contributed to the final version of the paper. HS assisted in the initial analysis, analyzed the data, produced the figures, and contributed to the final version of the paper. TW conceived the study, guided the research, generated the final analysis, produced figures, maintained the model and analysis codes, and wrote the initial version of the paper. All authors contributed to the article and approved the submitted version.

Funding

TT's portion of the work was supported by an Undergraduate Research Opportunities Program grant through the University of Colorado Boulder.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We gratefully acknowledge Frank Errickson, Klaus Keller, Radley Powers, Vivek Srikrishnan, Ryan Sriver, and Nathan Urban for fruitful conversations. We acknowledge the World Climate Research Programme, which, through its Working Group on Coupled Modelling, coordinated and promoted CMIP6. We thank the climate modeling groups for producing and making available their model output, the Earth System Grid Federation (ESGF) for archiving the data and providing access, and the multiple funding agencies who support CMIP6 and ESGF.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fclim.2022.796479/full#supplementary-material

References

Akaike, H. (1974). A new look at the statistical model identification. IEEE Trans. Automat. Contr. 19, 716–723.

Arns, A., Wahl, T., Haigh, I. D., Jensen, J., and Pattiaratchi, C. (2013). Estimating extreme water level probabilities: a comparison of the direct methods and recommendations for best practise. Coast Eng. 81, 51–66. doi: 10.1016/j.coastaleng.2013.07.003

CrossRef Full Text | Google Scholar

Arns, A., Wahl, T., Wolff, C., Vafeidis, A. T., Haigh, I. D., Woodworth, P., et al. (2020). Non-linear interaction modulates global extreme sea levels, coastal flood exposure, and impacts. Nat. Commun. 11, 1918. doi: 10.1038/s41467-020-15752-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Buchanan, M. K., Kopp, R. E., Oppenheimer, M., and Tebaldi, C. (2015). Allowances for evolving coastal flood risk under uncertain local sea-level rise. Clim. Change 137, 347–362. doi: 10.1007/s10584-016-1664-7

CrossRef Full Text | Google Scholar

Buchanan, M. K., Oppenheimer, M., and Kopp, R. E. (2017). Amplification of flood frequencies with local sea level rise and emerging flood regimes. Environ. Res. Lett. 12, 064009. doi: 10.1088/1748-9326/aa6cb3

CrossRef Full Text | Google Scholar

Caldwell, P. C., Merrfield, M. A., and Thompson, P. R. (2015). Sea Level Measured by Tide Gauges from Global Oceans - The Joint Archive for Sea Level holdings (NCEI Accession 0019568), Version 5.5. NOAA Natl Centers Environ Information.

Ceres, R., Forest, C. E., and Keller, K. (2017). Understanding the detectability of potential changes to the 100-year peak storm surge. Clim. Change 145, 221–235. doi: 10.1007/s10584-017-2075-0

CrossRef Full Text | Google Scholar

Chen, W.-B., and Liu, W.-C. (2016). Assessment of storm surge inundation and potential hazard maps for the southern coast of Taiwan. Nat. Hazards 82, 591–616. doi: 10.1007/s11069-016-2199-y

CrossRef Full Text | Google Scholar

Church, J. A., and White, N. J. (2011). Sea-level rise from the late 19th to the early 21st century. Surv. Geophys. 32, 585–602. doi: 10.1007/s10712-011-9119-1

CrossRef Full Text | Google Scholar

Cid, A., Menéndez, M., Castanedo, S., Abascal, A. J., Méndez, F. J., and Medina, R. (2016). Long-term changes in the frequency, intensity and duration of extreme storm surge events in southern Europe. Clim. Dyn. 46, 1503–1516. doi: 10.1007/s00382-015-2659-1

CrossRef Full Text | Google Scholar

Coles, S. G. (2001). An Introduction to Statistical Modeling of Extreme Values. London: Springer-Verlag.

Danabasoglu, G. (2019a). NCAR CESM2 Model Output Prepared for CMIP6 CMIP Historical [Internet]. Earth System Grid Federation.

Danabasoglu, G. (2019b). NCAR CESM2 Model Output Prepared for CMIP6 ScenarioMIP ssp585 [Internet]. Earth System Grid Federation. Available online at: https://doi.org/10.22033/ESGF/CMIP6.7768

Durand, G., van den Broeke, M. R., Le Cozannet, G., Edwards, T. L., Holland, P. R., Jourdain, N. C., et al. (2022). Sea-level rise: from global perspectives to local services. Front. Mar. Sci. 8, 709595. doi: 10.3389/fmars.2021.709595

CrossRef Full Text | Google Scholar

Fischbach, J. R., Johnson, D. R., and Molina-Perez, E. (2017). Reducing Coastal Flood Risk with a Lake Pontchartrain Barrier [Internet]. Santa Monica, CA. Available online at: https://www.rand.org/pubs/research_reports/RR1988.html

Garner, A. J., Mann, M. E., Emanuel, K. A., Kopp, R. E., Lin, N., Alley, R. B., et al. (2017). Impact of climate change on New York City's coastal flood hazard: increasing flood heights from the preindustrial to 2300 CE. Proc. Natl. Acad. Sci. U.S.A. 114, 11861–11866. doi: 10.1073/pnas.1703568114

PubMed Abstract | CrossRef Full Text | Google Scholar

Grinsted, A., Moore, J. C., and Jevrejeva, S. (2013). Projected Atlantic hurricane surge threat from rising temperatures. Proc. Natl. Acad. Sci. U.S.A. 110, 5369–5373. doi: 10.1073/pnas.1209980110

PubMed Abstract | CrossRef Full Text | Google Scholar

Haasnoot, M., Kwadijk, J., Van Alphen, J., Le Bars, D., Van Den Hurk, B., Diermanse, F., et al. (2020). Adaptation to uncertain sea-level rise; how uncertainty in Antarctic mass-loss impacts the coastal adaptation strategy of the Netherlands. Environ. Res. Lett. 15, 034007. doi: 10.1088/1748-9326/ab666c

CrossRef Full Text | Google Scholar

Haigh, I., Nicholls, R., and Wells, N. (2010). Assessing changes in extreme sea levels: application to the English Channel, 1900-2006. Cont. Shelf Res. 30, 1042–1055. doi: 10.1002/(SICI)1097-0088(19971115)17:13<1433::AID-JOC203>3.0.CO;2-P

CrossRef Full Text | Google Scholar

Jones, P. D., Jonsson, T., and Wheeler, D. (1997). Extension to the North Atlantic oscillation using early instrumental pressure observations from Gibraltar and south-west Iceland. Int. J. Climatol. 17, 1433–1450.

Jonkman, S. N., Maaskant, B., Boyd, E., and Levitan, M. L. (2009). Loss of life caused by the flooding of New Orleans after hurricane Katrina: analysis of the relationship between flood characteristics and mortality. Risk Anal. 29, 676–698. doi: 10.1111/j.1539-6924.2008.01190.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Kasprzyk, J. R., Nataraj, S., Reed, P. M., and Lempert, R. J. (2013). Many objective robust decision making for complex environmental systems undergoing change. Environ. Model Softw. 42, 55–71. doi: 10.1016/j.envsoft.2012.12.007

CrossRef Full Text | Google Scholar

Kossin, J. P., Hall, T., Knutson, T., Kunkel, K. E., Trapp, R. J., Waliser, D. E., et al. (2017). “Extreme storms,” in Climate Science Special Report: Fourth National Climate Assessment. US Global Change Research Program.

Lee, B. S., Haran, M., and Keller, K. (2017). Multi-decadal scale detection time for potentially increasing Atlantic storm surges in a warming climate. Geophys. Res. Lett. 44, 10617–10623. doi: 10.1002/2017GL074606

CrossRef Full Text | Google Scholar

Lempert, R. J., and Collins, M. T. (2007). Managing the risk of uncertain threshold responses: comparison of robust, optimum, and precautionary approaches. Risk Anal. 27, 1009–1026. doi: 10.1111/j.1539-6924.2007.00940.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, N., Kopp, R. E., Horton, B. P., and Donnelly, J. P. (2016). Hurricane Sandy's flood frequency increasing from year 1800 to 2100. Proc. Natl. Acad. Sci. U.S.A. 113, 12071–12075. doi: 10.1073/pnas.1604386113

PubMed Abstract | CrossRef Full Text | Google Scholar

Marcos, M., Calafat, F. M., Berihuete, Á., and Dangendorf, S. (2015). Long-term variations in global sea level extremes. J. Geophys. Res. Ocean 120, 8115–8134. doi: 10.1002/2015JC011173

CrossRef Full Text | Google Scholar

McMillan, A., Batstone, C., Worth, D., Tawn, J., Horsburgh, K., and Lawless, M. (2011). Coastal Flood Boundary Conditions for UK Mainland and Islands [Internet]. Bristol. Available online at: https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/291216/scho0111btki-e-e.pdf

Milly, P. C. D., Betancourt, J., Falkenmark, M., Hirsch, R. M., Kundzewicz, Z. W., Lettenmaier, D. P., et al. (2008). Stationarity is dead: whither water management? Science 319, 573–574. doi: 10.1126/science.1151915

PubMed Abstract | CrossRef Full Text | Google Scholar

Moftakhari, H., AghaKouchak, A., Sanders, B. F., Matthew, R. A., and Mazdiyasni, O. (2017c). Translating uncertain sea level projections into infrastructure impacts using a bayesian framework. Geophys. Res. Lett. 44, 11914–11921. doi: 10.1002/2017GL076116

CrossRef Full Text | Google Scholar

Moftakhari, H. R., AghaKouchak, A., Sanders, B. F., and Matthew, R. A. (2017b). Cumulative hazard: the case of nuisance flooding. Earths Future 5, 214–223. doi: 10.1002/2016EF000494

CrossRef Full Text | Google Scholar

Moftakhari, H. R., Salvadori, G., AghaKouchak, A., Sanders, B. F., and Matthew, R. A. (2017a). Compounding effects of sea level rise and fluvial flooding. Proc. Natl. Acad. Sci. U.S.A. 114, 9785–9790. doi: 10.1073/pnas.1620325114

PubMed Abstract | CrossRef Full Text | Google Scholar

NOAA (2017). National Centers for Environmental Information, Climate at a Glance: Global Time Series. Retrieved from: http://www.ncdc.noaa.gov/cag/

Oddo, P. C., Lee, B. S., Garner, G. G., Srikrishnan, V., Reed, P. M., Forest, C. E., et al. (2017). Deep uncertainties in sea-level rise and storm surge projections: implications for coastal flood risk management. Risk Anal. 40, 153–168. doi: 10.1111/risa.12888

PubMed Abstract | CrossRef Full Text | Google Scholar

O'Neill, B. C., Tebaldi, C., Van Vuuren, D. P., Eyring, V., Friedlingstein, P., Hurtt, G., et al. (2016). The scenario model intercomparison project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 9, 3461–3482. doi: 10.5194/gmd-9-3461-2016

CrossRef Full Text | Google Scholar

Orton, P. M., Hall, T. M., Talke, S. A., Blumberg, A. F., Georgas, N., and Vinogradov, S. (2016). A validated tropical-extratropical flood hazard assessment for New York Harbor. J. Geophys. Res. Ocean. 121, 8904–8929. doi: 10.1002/2016JC011679

PubMed Abstract | CrossRef Full Text | Google Scholar

Pugh, D. T., and Vassie, J. M. (1978). Extreme sea levels from tide and surge probability. Coast Eng. 1, 52. doi: 10.9753/icce.v16.52

CrossRef Full Text | Google Scholar

Rashid, M. M., Wahl, T., Chambers, D. P., Calafat, F. M., and Sweet, W. V. (2019). An extreme sea level indicator for the contiguous United States coastline. Sci. Data 6, 326. doi: 10.1038/s41597-019-0333-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruckert, K. L., Srikrishnan, V., and Keller, K. (2019). Characterizing the deep uncertainties surrounding coastal flood hazard projections: a case study for Norfolk, VA. Sci. Rep. 9:11373. doi: 10.1038/s41598-019-47587-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwarz, G. (1978). Estimating the dimension of a model. Ann. Stat. 6, 461–464.

Seneviratne, S. I., Nicholls, N., Easterling, D., Goodess, C. M., Kanae, S., Kossin, J., et al. (2012). “Changes in climate extremes and their impacts on the natural physical environment,” in Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the Intergovernmental Panel on Climate Change. Intergovernmental Panel on Climate Change.

Serinaldi, F., and Kilsby, C. G. (2015). Stationarity is undead: Uncertainty dominates the distribution of extremes. Adv. Water Resour. 77, 17–36. doi: 10.1016/j.advwatres.2014.12.013

CrossRef Full Text | Google Scholar

Stephenson, D. B., Pavan, V., Collins, M., Junge, M. M., and Quadrelli, R. (2006). North Atlantic Oscillation response to transient greenhouse gas forcing and the impact on European winter climate: A CMIP2 multi-model assessment. Clim. Dyn. 27, 401–420. doi: 10.1007/s00382-006-0140-x

CrossRef Full Text | Google Scholar

Storn, R., and Price, K. (1997). Differential evolution - a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 11, 341–359.

Tawn, J. A., and Vassie, J. M. (1989). Extreme sea levels: the joint probabilities method revisited and revised. Proc. Inst. Civ. Eng. 87, 429–442.

Tebaldi, C., Ranasinghe, R., Vousdoukas, M., Rasmussen, D. J., Vega-Westhoff, B., Kirezci, E., et al. (2021). Extreme sea levels at different global warming levels. Nat. Clim. Change 11, 746–751. doi: 10.1038/s41558-021-01127-1

CrossRef Full Text | Google Scholar

Tebaldi, C., Strauss, B. H., and Zervas, C. E. (2012). Modelling sea level rise impacts on storm surges along US coasts. Environ. Res. Lett. 7, 014032. doi: 10.1088/1748-9326/7/1/014032

CrossRef Full Text | Google Scholar

Vandenberg-Rodes, A., Moftakhari, H. R., AghaKouchak, A., Shahbaba, B., Sanders, B. F., and Matthew, R. A. (2016). Projecting nuisance flooding in a warming climate using generalized linear models and Gaussian processes. J. Geophys. Res. Ocean. 121, 8008–8020. doi: 10.1002/2016JC012084

CrossRef Full Text | Google Scholar

Vousdoukas, M. I., Mentaschi, L., Voukouvalas, E., Verlaan, M., Jevrejeva, S., Jackson, L. P., et al. (2018). Global probabilistic projections of extreme sea levels show intensification of coastal flood hazard. Nat. Commun. 9:1–12. doi: 10.1038/s41467-018-04692-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Wahl, T., Haigh, I. D., Nicholls, R. J., Arns, A., Dangendorf, S., Hinkel, J., et al. (2017). Understanding extreme sea levels for broad-scale coastal impact and adaptation analysis. Nat. Commun. 8:1–12. doi: 10.1038/ncomms16075

PubMed Abstract | CrossRef Full Text | Google Scholar

Wahl, T., Jain, S., Bender, J., Meyers, S. D., and Luther, M. E. (2015). Increasing risk of compound flooding from storm surge and rainfall for major US cities. Nat. Clim. Change 5, 1093–1097. doi: 10.1038/nclimate2736

CrossRef Full Text | Google Scholar

Wong, T. E. (2018). An integration and assessment of multiple covariates of nonstationary storm surge statistical behavior by Bayesian model averaging. Adv. Stat. Climatol Meteorol. Oceanogr. 4, 53–63. doi: 10.5194/ascmo-4-53-2018

CrossRef Full Text | Google Scholar

Wong, T. E., and Keller, K. (2017). Deep uncertainty surrounding coastal flood risk projections: a case study for New Orleans. Earths Future 5, 1015–1026. doi: 10.1002/2017EF000607

CrossRef Full Text | Google Scholar

Wong, T. E., Klufas, A., Srikrishnan, V., and Keller, K. (2018). Neglecting model structural uncertainty underestimates upper tails of flood hazard. Environ. Res. Lett. 13, 074019. doi: 10.1088/1748-9326/aacb3d

CrossRef Full Text | Google Scholar

Yu, Y.-C., Chen, H., Shih, H.-J., Chang, C.-H., Hsiao, S.-C., Chen, W.-B., et al. (2019). Assessing the potential highest storm tide hazard in Taiwan based on 40-year historical typhoon surge hindcasting. Atmosphere 10, 346. doi: 10.3390/atmos10060346

CrossRef Full Text | Google Scholar