- College of Law, Michigan State University, East Lansing, MI, United States
This article explores instinctive frames of human decision-making in environmental and resource economics. Higher-moment asset pricing combines rational, mathematically informed economic reasoning with psychological and biological insights. Leptokurtic blindness and skewness preference combine in particularly challenging ways for carbon mitigation. At their worst, human heuristics may generate perverse decisions. Information uncertainty and the innate preference for bonds-and-bullets portfolios may impair responses to catastrophic climate change.
1. Introduction
Climate change confronts humanity with the prospect of catastrophic harm. Indeed, the threat is sufficiently grave that it should be regarded as existential. Homo sapiens numbers among the species that the sixth great extinction of the Phanerozoic Eon may erase (Wake and Vredenburg, 2008; Ceballos et al., 2017).
Catastrophic climate change stems from human activity. The anthropogenic contribution to this calamitous state of affairs, however, also includes innately human frames for evaluating risk and making decisions under uncertainty. This article seeks to examine human decision-making and its impact on humanity's prospects for averting a climate catastrophe of its own device.
Environmental economics highlights the impact of emotion and cognitive bias on risk assessment and management. Like mathematical finance, environmental policymaking is a species of risk management. The treatment of physical uncertainty and behavioral heuristics in environmental economics differs from comparable factors in traditional finance more in degree than in kind. This article therefore evaluates the greatest challenge in environmental economics according to the tools that traditional finance applies to valuation problems.
Specifically, this article applies higher-moment asset pricing and related financial principles to problems in environmental and resource economics.
Part 2 of this article describes a higher-moment capital asset pricing model, or CAPM+. The Taylor series expansion of expected financial returns enables a generalization of conventional asset pricing models from its reliance on mean and variance to higher statistical moments. By extending financial analysis to skewness and kurtosis, higher-moment asset pricing harmonizes financial economics with prospect theory, a popular model of behavioral economics.
Avoiding catastrophic climate change can and should be evaluated as a valuation problem. Although environmental economics routinely requires the valuation of natural resources, including ecosystem services, explicit reliance on the CAPM and mathematically related models is less familiar. To bridge this gap, part 3 contextualizes CAPM+ and related aspects of environmental economics, particularly the spread between willingness to pay and willingness to accept.
After defining the difference between probabilistic risk and aleatory uncertainty, part 4 describes how uncertainty generates tension within foundational works in environmental economics. In earlier work with Robert Lind, Kenneth Arrow originally argued that the government's unique ability to absorb and finance risk permitted a purely risk-neutral approach to environmental decision-making. In later work with Anthony Fisher, however, Arrow acknowledged that irreversible commitments of resources might warranted a more circumspect approach. Evaluations of risk and uncertainty in environmental economics must account for this contradiction.
Part 5 describes an evidently universal set of financial preferences in the face of uncertainty. Psychologically informed models based on the work of Abraham Maslow predict that humans will respond differently to risk as they ascend a perceived hierarchy of needs and aspirations. In practical terms, higher-moment asset pricing of ecosystem services leads to an innate pairing of subsistence measures with highly speculative responses to threats perceived as remote.
The resulting “bonds-and-bullets” approach, this article concludes, bodes ill for effective responses to climate change and other challenges of the Anthropocene. Human psychology predisposes this species against preemptive, preventive mitigation measures, in the hope that miraculous feats of geoengineering may eventually prevail.
2. Higher-Moment Asset Pricing
2.1. The Taylor Series Expansion of Expected Logarithmic Returns
The conventional capital asset pricing model (CAPM) seeks to describe the cost of capital for firms and asset allocation choices by investors. In its canonical formulation, the CAPM relies principally upon the optimization of mean return relative to the variance of the market-wide portfolio (Fama and French, 2004). Among its many flaws, however, the CAPM fails to reflect human behavior (Shefrin and Statman, 1994).
A higher-moment capital asset pricing model may be derived from the Taylor series expansion of the logarithm of expected returns. Higher-moment CAPM (or CAPM+), once paired leading behavioral accounts of economics, explains seemingly “irrational” phenomena such as skewness preference and the bonds-and-bullets structure of financial decision-making.
A four-moment variant of CAPM+ is expressed in terms of mean, variance, skewness, and kurtosis (Jurczenko and Maillet, 2012). It can be derived from the Taylor series expansion of logarithmic returns from a continuously compounded financial series (Harvey and Siddique, 2000, p. 1269; Jondeau and Rockinger, 2006, p. 33; Harvey et al., 2010, pp. 469–470):
1. Let us express continuously compounded financial returns in logarithmic form:
2. The Taylor series expansion approximates f (x) at x = a:
3. The expansion of f (x) = ln(1 + x) at x = μ expresses that function in terms of mean, variance, skewness, and kurtosis:
where o[(x−μ)5] represents the fifth order and other remaining terms.
The formulation in ¶ 3 exhibits an alternating pattern of positive and negative signs. Modest assumptions such as positive marginal utility and decreasing risk aversion support this summary of CAPM+: Humans prefer high values for odd-numbered moments (mean and skewness), but low values for even-numbered moments (variance and kurtosis) (de Athayde and Flôres, 2004, p. 1336; Estrada, 2004, p. 241; Jondeau and Rockinger, 2006; Brunnermeier et al., 2007; Bali et al., 2011, p. 33). This trait enables higher-moment asset pricing models to provide effective guidance in advanced portfolio design and hedged trading applications (Brooks et al., 2012; Knif et al., 2020).
Exploring moments beyond variance explains many of the descriptive failures of conventional financial theory. The welfare implications of higher-moment asset pricing stem from disparate investor reactions to odd- and even-numbered moments. Behavioral departures from strict rationality begin with skewness, the first odd-numbered moment beyond variance. Kurtosis is properly associated with epistemic failures, with the inability to predict (let alone adapt to) previously unobserved phenomena. Consequently, skewness and kurtosis heavily influence environmental and resource economics.
Skewness preference arises when investors privilege skewness (the third moment) over expected return (the first). This departure from conventional rationality may represent the most obvious application of CAPM+. A wide range of behaviors of interest to various bodies of financial regulation reflects skewness preference: lotteries, prize-linked savings, private equity, crowdfunding, and initial public offerings. A preference for skewed outcomes, especially when the expected return is zero or negative, underlies many economic conditions thought to warrant regulatory intervention.
2.2. Flagging Prospect Theory
Especially in the cumulative formulation that acknowledges first- and second-order stochastic dominance, prospect theory gives behavioral meaning to skewness preference and its fourth-moment counterpart, leptokurtic blindness or insensitivity (Kahneman and Tversky, 1984; Tversky and Kahneman, 1992). Although Daniel Kahneman and Amos Tversky relied on a two-piece utility function to define prospective theory's value function, the cumulative distribution function of a right-skewed distribution such as the lognormal or the log-logistic illustrates all of that function's important properties.
Figure 1 displays three important properties of human decision-making under uncertainty. First, humans evaluate all decisions according to a fixed reference point. Second, humans are averse toward losses. All else being equal, losing hurts worse than winning feels good. Third, humans over time become less sensitive to changes in utility, no matter whether such changes are gains or losses. “If prospect theory had a flag,” the banner in Figure 1 would depict those three principles (Kahneman, 2011, p. 282).

Figure 1. Visualizing prospect theory as the cumulative distribution function of a right-skewed probability distribution.
Although volatility figures prominently in nearly every model in mathematical finance, even-numbered moments are harder to interpret. Starting with variance, however, finite higher moments cannot be assumed. If, as has been hypothesized for nearly six decades, financial returns follow a stable Paretian distribution (Fama, 1963, 1965; Ortobelli and Rachev, 2001), even variance (and, a fortiori, higher moments) may be infinite. This analytically debilitating mathematical property stems from the definition of a generalized Pareto distribution (Castillo and Hadi, 1997; Gençay and Selçuk, 2004, p. 291–292).
Leptokurtosis may be the most tractable statistical representation of tail risk and epistemic blindness. It provides a statistical basis for the longstanding distinction between probabilistic risk and aleatory uncertainty. Leptokurtosis likewise describes prospect theory's phenomenon of diminishing sensitivity at each extreme. These treatments of the fourth moment provide a mathematical bridge between rational and behavioral accounts of economic decision-making. This unity arises because human perception becomes duller precisely where information, as an empirical matter, becomes less attainable.
Combining these insights with behavioral finance explains the prevalence of “bonds and bullets” wealth allocations in numerous economic circumstances. Bifurcating even-numbered moments reveals the mathematical congruence between two seemingly divergent economic instincts. When forced to confront the loss of basic means of survival, humans do focus on downside risk. But once hope meets fear, even risk averse individuals will entertain upside gambles. Merging these insights expands the mathematical toolkit of finance and environmental economics.
3. Higher-Moment Asset Pricing in an Environmental Context
3.1. Matters of Housekeeping
Part 2 suggests how higher-moment asset pricing might affect environmental and resource economics. The Taylor series expansion of logarithmic returns counsels against simplistic reliance on the naked magnitude of expected gain or loss. Higher-moment pricing and valuation models reveal the opposite effects of odd- and even-numbered moments. But another boundary looms between mean and variance, on one hand, and the paucal moments of skewness and kurtosis. The most potentially treacherous decisions under uncertainty respond to internal asymmetry and extremity within the distribution of returns.
Ernst Haeckel is credited with introducing the term ecology from OiKOÇ, the ancient Greek word for house (Gould, 1977, p. 76 n.*). Economics and economy share the same root. By uniting human economy with natural ecology, environmental economics defines housekeeping in both social and biological terms (Caradonna, 2014, pp. 112–113).
Law and policy give voice to the idea of ecology as housekeeping through sustainability and the precautionary principle (Cameron and Abouchar, 1991; McIntyre and Mosedale, 1997; Sand, 2000). The definition of sustainability, at least, is contestable. The narrowest definition of environmental sustainability stems from strict notions of the human ecological footprint, which in turn dictate a definition of sustainability according to physical flows of energy and matter (Heal, 2012).
By contrast, the Hartwick principle holds that renewable environmental resources, non-renewable resources, and capital investments are subject to exchange (Hartwick, 1977). Because the Hartwick principle directly compares physical energy flows with financial returns, it is the starting point for any application of financial economics to environmental topics (Gowdy and McDaniel, 1999).
3.2. Contingent Valuation of Biodiversity and Ecosystem Services
Contingent valuation of ecosystem services is central to policy regarding climate change mitigation and related questions of natural resource economics (Carson et al., 2001; Champ and Bishop, 2001; Poe et al., 2002). Skewness preference and pricing premiums associated with uncertainty and kurtosis beset ecological valuation.
Perhaps the most striking application of higher-moment asset pricing to the valuation of ecosystem services involves biodiversity conservation, including the politically salient and controversial subfield of bioprospecting (Chen, 2014). A more outlandish instance of skewness preference in natural resource economics can scarcely be imagined. If the logic of bioprospecting is stretched to its absurd extreme, Costa Rica's biodiversity is worth saving only to the extent that endemic organisms with pharmaceutical potential can be profitably exploited.
Disputes over bioprospecting and its rhetorically rude cousin, “biopiracy” illustrate an extension of the rank effect from behavioral finance to resource economics. According to the “rank effect,” investors are likelier to sell their extreme winning and losing positions, even without considering the economic fundamentals of any firm in the portfolio (Hartzmark, 2015). Focusing exclusively on the best and worst positions, wholly without regard to the actual level of returns effectively ignores the rest of the portfolio (ibid.). Biodiversity, to say the least, vastly exceeds the genomic profitability of species of greatest commercial interest to humans.
3.3. Willingness to Pay vs. Willingness to Accept
Disaster law as a specialized branch of environmental law emphasizes downside risk and uncertainty (Chen, 2011). This emphasis highlights an anomaly in environmental economics. Stated preference studies often strive to quantify either respondents' willingness to pay (WTP) for environmental enhancements or their willingness to accept (WTA) compensation for environmental degradation.
Neoclassical economic theory presumes that WTP and WTA quantities should be equivalent. Experimental outcomes suggest otherwise. There is a considerable premium for willingness-to-accept compensation in cases of degradation, relative to willingness-to- pay bids in cases of enhancement (Hanemann, 1991; Shogren et al., 1994; Sayman and Öncüler, 2005). In addition, both WTA and WTP distributions are quite wide, in the sense their standard distributions are quite often multiples of the mean amount. This appears to be an artifact of numerous 0 responses in WTA surveys (Amigues et al., 2002, p. 25) and high bids in WTP surveys (Sillano and de Dios Ortúzar, 2005, p. 540).
The obvious behavioral explanation for the WTA/WTP premium lies in the endowment effect (Kahneman et al., 1990) and the closely related notion of myopic loss aversion (Benartzi and Thaler, 1995). Because losing hurts worse than winning feels good, willingness to accept on the downside should be expected to exceed willingness to pay on the upside. Behavioral accounts of finance, however, should never be detached from economic fundamentals (Zhang, 2005, p. 69). That admonition suggests that the WTA/WTP premium reveals more nuanced human judgment. That judgment is consistent with higher-moment asset pricing and related ideas of liquidity preference and comovement among asset classes.
Static, unconditional models of finance assume that agents live no longer than a single period (Merton, 1973). As a descriptive matter, this assumption is demonstrably false. Worse, the single-period assumption is normatively deficient, even morally repellent. One need not embrace notion of “deep ecology” to reach this prescriptive conclusion (Naess, 1988). Even Hartwick's rule of weak sustainability demands a commitment to compensate future generations for immediate consumption of exhaustible resources.
The WTA/WTP premium is most pronounced in two settings. First, there is a significant premium for public and non-marketable goods relative to “ordinary” goods readily available in private markets (Horowitz and McConnell, 2002). Second, consumers demand a high premium for goods whose future, contingent value is currently uncertain (Zhao and King, 2004).
In concert, the presence of a large premium in these contexts reveals an awareness (or at least an intuition) that assets have value only relative to the broader state of the economy. These principles suggest that instruments of exchange and storehouses of value within the human economy have worth only relative to the biological and abiotic condition of global ecology.
Under conditions of relative abundance and stability, Hartwick's assumptions regarding exchangeability and frictionless intergenerational bargaining may hold. In a manner of speaking, Merton (1973) meets Coase (1960). But finite carrying capacity and the potential disruption of physical flows within ecosystem services serve stern notice that the ecological basis of human economy cannot be treated as static and permanent. The premium for willingness to accept over willingness to pay thus represents the environmental equivalent of the liquidity and equity risk premiums in behavioral finance.
3.4. From Information Uncertainty to the Psychology of Bonds and Bullets
The balance of this article will address two additional aspects of higher-moment thinking in environmental economics. At this pivotal stage, a brief preview of parts 4 and 5 is warranted.
First, innate reactions to dispersion, ambiguity, and uncertainty are the domain of even-moment effects within CAPM+. In environmental economics, these effects explain the progression from the Arrow-Lind theorem of risk-neutral public investment to Kenneth Arrow's own partial repudiation of his own work in later work with Anthony Fisher. The tension in these treatments of information uncertainty leads naturally to the dismal theorem, which arises from the work of William Nordhaus, Martin Weitzman, and other economists evaluating the costs of anthropogenic climate change.
Second and perhaps even more pressingly, the ultimate question is how humans will handle ecosystem services and the terrestrial life support systems under attack in the Anthropocene. Highly risk-seeking behavior has been observed in settings such as subsistence farming and diamond mining. Wealthy actors are engaging in similar “shots-at-greatness” behavior with respect to fossil fuel and climate change policy. Because these preferences reflect expectations of high levels of kurtosis, higher-moment asset pricing helps explain why “bonds-and-bullets” portfolios have such universal appeal. Less optimistically, CAPM+ suggests that this heuristic approach to managing risk may disserve humanity in a moment of existential exigency.
4. Uncertainty and Leptokurtic Blindness
4.1. Probabilistic Risk vs. Aleatory Uncertainty
Purchases and sales within an exchange economy constitute a “central nervous system” (Supreme Court of the United States, 1940, p. 225, n. 59). Finance analyzes the market for capital to support speculative undertakings (Supreme Court of the United States, 1935, p. 689 [Stone, J., dissenting]). Prices as tools for transmitting economic knowledge within a collective “wisdom of prices” (Hayek, 1937, 1945; Grossman and Stiglitz, 1980).
An efficient capital market's very raison d'être is to reward investors who assume the risk of entrepreneurial failure (Ross, 1976). Indeed, the “first law of finance” dictates that excess return over a risk-free asset should correspond to volatility (Anderson et al., 2009, p. 233). Legal authorities recognize that abnormal returns are associated with elevated risk (Supreme Court of the United States, 1909, p. 49).
In environmental settings as elsewhere, the basic problem of finance becomes difficult, perhaps even intractable, when the investment horizon stretches into an indefinite future. Even without regard to temporal scales, risk management becomes virtually impossible where risks are poorly perceived and probabilities cannot be accurately estimated (Farber, 2011, p. 906).
A useful point of departure is “the impact of uncertainty on the behavior of investors and, ultimately, on market prices” (Campbell et al., 1997, p. 3). Knight (1921, pp. 19–20) and Keynes (1937, pp. 213–214) first recognized the theoretical difference between quantifiable, statistical risk and unknowable uncertainty. Situations where statistical probabilities can influence decision-making stand apart from truly aleatory circumstances where information is so vague that it eludes quantification (Epstein and Wang, 1994, p. 283; Runde, 1998, p. 539).
Uncertainty affects all economic activity (Bloom, 2009; Bachman et al., 2013; Baker et al., 2016), from household savings (Giavazzi and McMahon, 2012) and government borrowing (Pástor and Veronesi, 2012, 2013) to investment across the real economy (Born and Pfeifer, 2014; Fernández-Villaverde et al., 2015). When uncertainty clouds the economic outlook, risk averse consumers are the likeliest to realize option value from publicly supplied goods and services (Weisbrod, 1964; Cichetti and Freeman, 1971).
Ambiguity surrounding information affecting firm valuation has a powerful tendency to cast capital markets into uncertainty (Zhang, 2006, p. 105). Uncertainty exacts a far steeper toll on the downside, and not merely because the prospect of loss ground terrifies human decisionmakers. Coercion, after all, arises from “[t]hreat of loss” and not from “hope of gain” (Supreme Court of the United States, 1936, p. 82 [Stone, J., dissenting]). Economic retreat, whether attributable to an economy-wide recession or to bad news affecting an isolated sector or even a single firm, necessarily throttles the flow of information among buyers and sellers (Bloom, 2014, p. 162).
4.2. A Formal Model of Information Uncertainty
In all settings, economic agents prefer “known rather than unknown or vague probabilities” (Epstein and Wang, 1994, p. 284). Difficulty in judging the quality of information leads agents to “treat signals as ambiguous” (Epstein and Schneider, 2008, p. 197). All risk premiums rise alongside information uncertainty as investors ponder the probability of default, the amount at stake in potential business failures, transaction costs associated with bankruptcy, and even the size of the default premium itself (Christiano et al., 2014).
A specification of information uncertainty proceeds in two steps. First, an observed financial signal, or s, can be defined simply as s = v + e, where v indicates fundamental value implied by future cash flows or dividends, and e represents error or noise (Zhang, 2006, p. 105 n.2).
The second step consists of measuring the variance of the observed signal. Combining the variance of the firm's underlying volatility, or var(v), with var(e), the variance of the error term as an indicator of informational quality, enables information uncertainty to be expressed formally: var(s) = var(v) + var(e) (ibid.). This second formula recognizes the possibility that variance in cash flow or a series of returns may reflect not only fundamental economic variance, but also an additional premium based on information uncertainty.
The human reaction to uncertainty profoundly affects valuation and pricing. When agents face information uncertainty on top of risk, “they demand a higher premium” (Anderson et al., 2009, p. 234). This expression formalizes the relationship between risk and uncertainty (ibid., pp. 234–235):
where E designates the expectation operator, re indicates excess return over the risk-free baseline, V indicates market-wide conditional volatility, and M measures uncertainty throughout the economy. The temporal indexing variable t governs all of these variables as well as the expectation operator.
γ and θ, the coefficients in the foregoing formula, indicate aversion, respectively, to risk and uncertainty. Positive values for γ as well as θ imply that a positive premium for both risk and uncertainty (ibid., p. 234). In other words, investors will demand compensation bearing unknowable uncertainty as well as predictable risk. The expression, Et re, t+1 = γVt+θMt, should therefore be understood as a special instance of the more general formula, var(s) = var(v) + var(e).
In all events, it is crucial to distinguish between a fundamental economic signal (s = v + e) and information uncertainty as the sum of variance in informational quality and variance in the signal itself [var(s) = var(v) + var(e)]. The variability in many signals may stem from different sources of information, some less quantifiable than others. Uncertainty along economic, legal, scientific, and technological dimensions raises the cost of investing, by private actors as well as the government, in low- or zero-carbon generation and other responses to climate change.
4.3. Uncertainty's Arrow: From Risk-Neutrality to Irreversible Commitments
4.3.1. Risk-Neutrality
The economics of climate change demonstrates how uncertainty affects sunk costs and asset-specificity. Mitigation and adaptation efforts straddle Kenneth Arrow's divergent approaches to managing risk in public investments. Public ownership provides a neutral legal and economic baseline by which to gauge risk and uncertainty. A fifth of the United States' trillion-dollar electrical power industry remains publicly owned and continues to provide a viable alternative to private ownership (Bradley, 2003).
The spreading of risk among taxpayers reduces the costs of risk-bearing associated with public ownership to negligible levels (Arrow and Lind, 1970, pp. 374–375). In some circumstances, risk-adjusted return on a publicly owned investment might exceed that of a comparable private firm (Hirshleifer, 1965, 1966). Kenneth Arrow accordingly urged governments to “ignore uncertainty in evaluating public investments” (Arrow and Lind, 1970, p. 376).
According to the formula, var(s) = var(v) + var(e), the government's ability to eliminate the cost of risk-bearing collapses the definition of uncertainty into nothing more than variability in the underlying economic signal. Variability in fundamental value expresses the variability formula in its entirety. Critically, expected return on public investment serves as the exclusive yardstick of value (ibid., p. 374). In formal terms, var(s) = var(v) and s = v.
4.3.2. Irreversible Commitments
Befitting the contemporaneous emergence of intertemporal asset pricing (Merton, 1973) and the sustainability principle (Solow, 1974; Hartwick, 1977), Kenneth Arrow eventually took account of intergenerational differences (Arrow and Kurz, 1970, p. 12). Four years after devising his risk-neutral formula, Arrow reevaluated the role of public investment and ownership (Arrow and Fisher, 1974, p. 313). The rule of risk-neutrality yields in favor of a new cost-benefit analysis if public policy “involves some irreversible transformation of the environment” and permanent loss demands reevaluation of future “expected values” (ibid., pp. 313–314).
Arrow's later contribution to environmental and resource economics presciently anticipated many different types of irreversible events. In addition to biological extinction and the destruction of geological formations and phenomena, Arrow foresaw “increasing concentration[s] of carbon dioxide” and “attendant climatic changes” (ibid., p. 319). The legal Zeitgeist of the early 1970s likewise demanded environmental impact statements and interagency consultation before “any irreversible and irretrievable commitment of resources,” including endangered plant and animal species [National Environmental Policy Act of 1970, 42 U.S.C. § 4332(C)(v); Endangered Species Act of 1970, 16 U.S.C. § 1536(d)].
In stark contrast to his original hypothesis of risk-neutrality, Arrow's later approach to irreversibility effectively maximizes uncertainty. In the formula, var(s) = var(v) + var(e), presuming or detecting irreversibility is tantamount to assuming that var(e) ≫ 0. Accordingly, fundamental volatility in cash flow or dividends, conditioned on subjective aversion varying over time, serves as an adequate proxy for uncertainty (Bekaert et al., 2009).
5. Anthropocene Risk Management
5.1. The Dismal Theorem
On the other hand, severe uncertainty can drive variability, either in valuable flows of ecological services or in the quality information regarding those flows, effectively toward infinity. In other words, either var(s) → ∞ or var(e) → ∞. Alternatively, the value of those flows may implode within a foreseeable timeframe, such that v, s → 0. These are apocalyptic circumstances. A comparably cataclysmic approach to economic analysis is warranted.
The enormity of the Anthropocene catastrophe invites even more extreme approaches to uncertainty. When climate change inflicts an infinite amount of expected loss, the dismal theorem disables “standard economic analysis” altogether (Nordhaus, 2011, p. 240). More formally, since no amount of learning can prepare humanity for unlimited exposure to a fat-tailed risk, ordinary actuarial details such as risk assessment, social discounting, and the calibration of premiums to permit the smoothing of consumption all fall by the wayside (Weitzman, 2009, pp. 10–12, 18).
Risks contributing to the fat, leptokurtic tails associated with the dismal theorem bear many names. Whether it is described as variance risk (Carr and Wu, 2009; Bali and Zhou, 2016), tail risk (Bollerslev and Todorov, 2011; Kelly and Jiang, 2014), jump risk (Todorov, 2010; Dreschler and Yaron, 2011), or rare disaster risk (Gabaix, 2012), this risk resides at extremes where human epistemology exceeds its limits and outcomes observe no finite limits.
5.2. Rethinking Maslow's Hierarchy of Needs
5.2.1. The Original Hierarchy
No matter how dismal its prospects, humanity must choose. Even opting to take no action represents a choice. Human responses to risk and uncertainty are almost assuredly irrational in the rigid sense of Homo economicus (Faber et al., 1997; McMahon, 2015). But a closer look reveals that human decisions assume “orderly” rather than “chaotic and intractable” form (Tversky and Kahneman, 1992, p. 317).
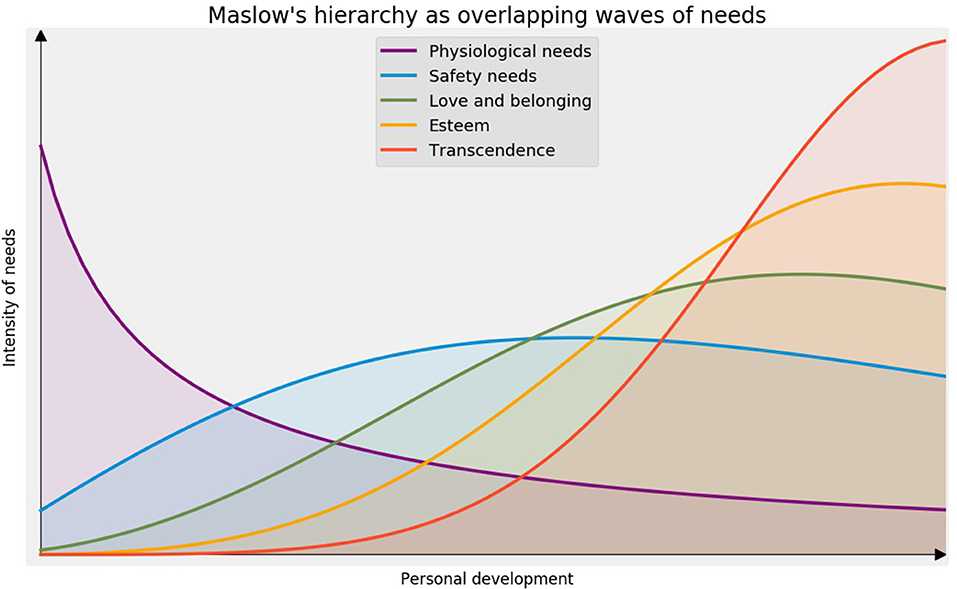
Abraham Maslow's hierarchy of needs (Maslow, 1943) has proved to be a durable if crude psychological model. The Maslowian hierarchy is often depicted as a pyramid with sequential layers of survival, safety, love and social standing, esteem, and self-realization (at the apex). Figure 2's alternative depiction, showing the hierarchy as overlapping and persisting waves, may be more accurate and persuasive (Krech et al., 1962, p. 77).
Maslow's enduring popularity intuitive appeal of his hierarchy of needs: It portrays human nature in a way that most people intuitively recognize and appreciate (Abulof, 2017, p. 508). In a study of innate frames of mind and decision-making heuristics, Maslow's hierarchy of needs—appropriately enough—stands atop the pyramid of ideas.
5.2.2. A Transcendent Adjustment
With a modest adjustment, Maslowian psychology continues to serve as a viable model of decision-making amid risk and uncertainty. By placing self-actualization atop his hierarchy, Maslow decoupled “the desire to fulfill one's own unique potential” from human biology (Kenrick et al., 2010; p. 297). As a matter of sociology, self-actualization can be affirmatively maladaptive to the extent it is decoupled from respect by and for other members of a community (ibid., p. 298; Kurzban and Aktipis, 2007).
At its most perverse, self-actualization might be nothing but overconfidence or even naked narcissism. Since it arises from the failure or refusal to look for evidence that might contradict one's own beliefs (Shefrin and Statman, 1994, p. 331, n. 21; Gervais and Odean, 2001), overconfidence is confirmation bias on stilts. Recognizing that an overemphasis on the individual violates the “functional logic of human evolutionary biology,” some psychologists have excised self-actualization from Maslow's hierarchy (Kenrick et al., 2010, p. 298). In later elaborations of his own work, Maslow himself revised the apex of his pyramid to include spirituality, altruism, and grander aspirations beyond the self (Maslow, 1969, 1996).
In place of self-actualization, Maslow ultimately inserted transcendence. He defined transcendence as “the very highest and most inclusive or holistic levels of human consciousness, behaving and relating… to human beings in general, to other species, to nature, and to the cosmos” (Maslow, 1971, p. 269). Even as the world collapses during the Anthropocene, individuals still strive for the transcendent. Everyone wants a shot at greatness. Environmental economics provides a channel by which humans may reassert their own ambition and expressive desires within the calculus of existential risk-taking.
5.3. Up From Subsistence
5.3.1. Bonds and Bullets in Bangladesh
As one of the earliest departures from the stiff formalism of classical mathematical finance, Roy's safety-first criterion counseled investors to minimize the probability of falling below their lowest acceptable level of returns (Roy, 1952). Safety-first portfolios depart in important ways from the methods of mean-variance optimization prescribed by the canonical capital asset pricing model. Human investors relying on intuitive risk management combine large, relatively safe positions, often consisting of cash and bonds, with a few speculative instruments with far greater upside potential. This approach to combining safe and speculative investments pairs the extremes in Maslow's hierarchy, from the strictly physiological to the transcendent.
The resulting “bonds-and-bullets” investment strategy transcends economic and cultural boundaries. It might even be a human universal. Agricultural and resource economists were among the first economists to embrace safety-first (Shahabuddin and Butterfield, 1986). Because their survival is at the mercy of pests, storms, floods, or even “invading armies,” subsistence farmers provide a prime illustration of the compatibility of survival-oriented and aspirational instruments (Lopes, 1987, p. 287).
A subsistence farmer seeking to optimize her or his prospects must allocate extremely scarce resources between two wildly different assets. On one hand, food crops guarantee survival, with as stable a level of variance as can be expected in agriculture. Such security comes at a price: It demands acceptance of ongoing, abject poverty. By contrast, less reliable, more volatile cash crops promise higher returns. Planting rice while pursuing one's dreams appears to be humanity's innate and perhaps universal plan for surviving while retaining a kernel of hope (ibid.).
At this point, however, formal financial economics and the psychology of subsistence part company—at least as a matter of framing. Behavioral economists simplify the narrative of subsistence agriculture as a “gamble on cash crops” in an aspirational, even desperate, bid “to escape poverty” (Shefrin and Statman, 2000, p. 137).
Subsistence farmers disagree. They do not regard the decision to plant a combination of rice and opium poppies as gambling (Kunreuther and Wright, 1979; Ortiz, 1979; Lopes, 1987, p. 287). Subsistence farmers' allocations between food and cash crops satisfy the same emotional mixture motivating rich as well as poor agents: fear, hope, and aspiration. Indeed, if conditions can be so dire that a higher allocation of acreage to cash crops may be an affirmatively rational bid “to maximize … chances of survival” (Shahabuddin, 1982, p. 95).
5.3.2. Digging for Diamonds
Diamond miners in Sierra Leone face a similar subsistence-driven dilemma (Davies, 2000, 2008). Miners throughout Africa work under arrangements similar to sharecropping: They borrow heavily from mine owners in exchange for a share of any mining profits. Should a mine fail, however, the owner never refunds loans net of laborers' earnings. All-or-nothing wagers on diamond mining has plunged Sierra Leone into economic and political turmoil for decades (Maconachie and Binns, 2007; Le Billon, 2008; Davies, 2010; Wilson, 2013).
Sierra Leone is hardly alone among developing countries that suffer the “resource curse” (Ross, 1999, 2015; Mehlum et al., 2006; Robinson et al., 2006). Lopsided bets on natural resource extraction stunt economic growth in countries whose mineral wealth should be a blessing.
As with subsistence farming in Bangladesh, however, diamond mining in Sierra Leone must not be relegated to a mythical category of risk management that is confined unique extremely poor countries. In affluent countries, firms on the verge of default routinely wager on their own resurrection by taking risks that might be condemned as excessive under ordinary conditions (White, 1989; Akerlof and Romer, 1993). Neither the managers of these firms nor their investors face a credible threat of starvation. Nevertheless, they combine the lowest and highest levels of Maslowian thinking in ways that are identical to the psychology of subsistence agriculture and mining on credit. In their own way, wealthy entrepreneurs and their backers in affluent countries are also digging for diamonds.
5.4. Shaping Bets for the End of the World
Translating bonds-and-bullets portfolio construction into the language of higher-moment asset pricing produces a convenient shorthand for this sort of risk-taking: Kurtosis preference. Affluent investors build layered portfolios according to opposite ends of Maslow's pyramid. While the bottom layer preserves capital as a bulwark against penury, the top layer takes “a shot at riches” (Shefrin and Statman, 2000, p. 141). This split portfolio assumes that the tails at either extreme will be fatter than the rest of the distribution of returns (ibid., p. 145). The combination of caution and optimism underlying this approach reflects the rank effect in behavioral finance (Hartzmark, 2015). It overestimates probabilities associated with the worst outcomes—and with the best (Shefrin and Statman, 2000, p. 141).
Kurtosis preference and bonds-and-bullets risk-taking appear to be innate frames for making decisions under conditions of extreme preference. But the innate optimism of the odd-numbered moments, especially skewness, lurks as a treacherous pitfall. Another existential threat to humanity illustrates the problem.
The Covid-19 pandemic, the greatest public health crisis in living memory, has killed millions around the world. Covid arguably poses a more immediate threat than climate change. At the very least, Covid-19 infection happens at the personal level and can reveal itself in hours rather than decades. Yet large swaths of the population perceive neither risk as urgent (Ruiu et al., 2020; Botzen et al., 2021). Indeed, at least in the United States, denying the threat has arguably become a badge of political allegiance. The same logic that urges Covid deniers to await deliverance through hydroxychloroquine, ivermectin, or some other miraculous therapeutic motivates a political preference to defer climate action. Justice delayed, as it were, is simply waiting for the deus ex machina of solar radiation management or geoengineering on the cheap.
In the opening passage to Their Eyes Were Watching God, Hurston (2006) distinguished those fortunate few whose ships “come in with the tide” from perpetual dreamers whose ships of dreams “sail forever on the horizon, never out of sight” (p. 1). Less wistfully, Nick the Greek lauded thrill-seeking gamblers who await the single “streak of luck” that might make up “for all the bad times” (Thackrey, 1968, p. 67).
Once the prospect of infinite loss has entered the casino, though, the dismal theorem counsels complete reconsideration of all approaches to risk management. That same principle also offers no guidance of its own. Humanity is consequently left to rely on its own instincts.
Those instincts may be quite destructive. In the context of Covid and other pandemic diseases, such instincts may defeat cooperative public health measures, as humans defer and avoid perceived risks associated with vaccination in favor of last-second therapeutic measures. To like effect, behaviorally influenced environmental decision-making often disfavors measures for mitigating climate change. The urgency of immediate sacrifices diminishes in the shadow of miraculous deliverance through future responses such as solar radiation management and other grandiose feats of geoengineering.
6. Conclusion
The dismal theorem forces humanity to confront an existential threat of its own creation: catastrophic climate change stemming from human activity. Because functioning, reliable flows of natural resources that sustain human life are the most vital of ecosystem services, the problem can and should be framed as one of resource valuation and risk assessment.
This article has approached what is arguably the greatest problem of environmental and resource economics according to tools normally applied to the valuation of financial assets. The existence of a premium for willingness-to-accept (WTA) valuations relative to their theoretical willingness-to-pay (WTP) equivalents suggests that resource valuation is as susceptible as financial risk management to innate heuristics and cognitive bias.
The resulting exercise bodes ill for humanity's prospects. The erasure of functional ecosystems and the contribution of climate change to mass extinctions represent the irreversible commitment of resources. Innate responses to skewed outcomes, especially under conditions of epistemic blindness associated with highly leptokurtic distributions, induce humans to assemble bonds-and-bullets portfolios laden with low-probability, high-payout instruments. Financial decisions ranging from corporate management in wealthy countries to subsistence farming and artisanal diamond mining in poor countries portend a similar approach to climate change mitigation and adaptation. The allure of last-minute rescue through heroic feats of geoengineering cripples efforts at cooperative and preemptive climate mitigation.
Long ago and in a seemingly distant setting, Oliver Wendell Holmes gave legal voice to decision-making in the face of uncertainty: “Every year, if not every day, we have to wager our salvation upon some prophecy based upon imperfect knowledge” (Supreme Court of the United States, 1919, p. 630 [Holmes, J., dissenting]). At its darkest hour, instinctive decision-making heuristics may serve humanity poorly. “This is the way the world ends/This is the way the world ends/This is the way the world ends”—not with a bang but bonds and bullets (Eliot, 1971, p. 59).
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
Charalampos Agiropoulos, George Galanos, and Thomas Poufinas provided helpful comments. Special thanks to Heather Elaine Worland Chen.
References
Abulof, U. (2017). Introduction: why we need Maslow in the twenty-first century. Society 54, 508–509. doi: 10.1007/s12115-017-0198-6
Akerlof, G. A., and Romer, P. M. (1993). Looting: The economic underworld of bankruptcy for profit. Brookings Pap. Econ. Act. 2, 1–73. doi: 10.2307/2534564
Amigues, J. P., Boulatoff, C., Desaigues, B., Gauthier, C., and Keith, J. E. (2002). The benefits and costs of riparian analysis habitat preservation: A willingness to accept/willingness to pay contingent valuation approach. Ecol. Econ. 43, 17–31. doi: 10.1016/S0921-8009(02)00172-6
Anderson, E. W., Ghysels, E., and Juergens, J. L. (2009). The impact of risk and uncertainty on expected returns. J. Financ. Econ. 94, 233–263. doi: 10.1016/j.jfineco.2008.11.001
Arrow, K. J., and Fisher, A. C. (1974). Environmental preservation, uncertainty, and irreversibility. Q. J. Econ. 88, 312–319. doi: 10.2307/1883074
Arrow, K. J., and Kurz, M. (1970). Public Investment, the Rate of Return, and Optimal Fiscal Policy. Baltimore, MD: John Hopkins University Press.
Arrow, K. J., and Lind, R. C. (1970). Uncertainty and the evaluation of public investment decisions. Am. Econ. Rev. 60, 366–378.
Bachman, R., Elstener, S., and Sims, E. R. (2013). Uncertainty and economic activity: evidence from business survey data. Am. Econ. J. Macroecon. 5, 217–249. doi: 10.1257/mac.5.2.217
Baker, S. R., Bloom, N., and Davis, S. J. (2016). Measuring economic policy uncertainty. Q. J. Econ. 131, 1593–1636. doi: 10.1093/qje/qjw024
Bali, T. G., Cakici, N., and Whitelaw, R. (2011). Maxing out: stocks as lotteries and the cross-section of expected returns. J. Financ. Econ. 99, 427–466. doi: 10.1016/j.jfineco.2010.08.014
Bali, T. G., and Zhou, H. (2016). Risk, uncertainty, and expected returns. J. Financial Quant. Anal. 11, 707–735. doi: 10.1017/S0022109016000417
Bekaert, G., Engstrom, E., and Xing, Y. (2009). Risk, uncertainty, and asset prices. J. Financ. Econ. 91, 59–82. doi: 10.1016/j.jfineco.2008.01.005
Benartzi, S., and Thaler, R. H. (1995). Myopic loss aversion and the equity premium puzzle. Q. J. Econ. 110, 73–92. doi: 10.2307/2118511
Bloom, N. (2014). Fluctuations in uncertainty. J. Econ. Perspect. 28, 153–176. doi: 10.1257/jep.28.2.153
Bollerslev, T., and Todorov, V. (2011). Tails, fears, and risk premia. J. Finance 66, 2165–2211. doi: 10.1111/j.1540-6261.2011.01695.x
Born, B., and Pfeifer, J. (2014). Policy risk and the business cycle. J. Monet. Econ. 68, 68–85. doi: 10.1016/j.jmoneco.2014.07.012
Botzen, W., Duijndam, S., and van Beukering, P. (2021). Lessons for climate policy from behavioral biases towards COVID-19 and climate change risks. World Dev. 137:105214. doi: 10.1016/j.worlddev.2020.105214
Bradley, R. L. Jr. (2003). “The origins and development of electric power regulation,” in The End of a Natural Monopoly: Deregulation and Competition in the Electric Power Industry, eds P. Z. Grossman and D. H. Cole (Kidlington: Taylor and Francis), 43–76.
Brooks, C., Cerný, A., and Miffre, J. (2012). Optimal hedging with higher moments. J. Futures Mark. 32, 909–944. doi: 10.1002/fut.20542
Brunnermeier, M. K., Gollier, C., and Parker, J. A. (2007). Optimal beliefs, asset prices, and the preference for skewed returns. Am. Econ. Rev. 97, 159–165. doi: 10.1257/aer.97.2.159
Cameron, J., and Abouchar, J. (1991). The precautionary principle: a fundamental principle of law and policy for the protection of the global environment. Boston College Int. Comp. Law Rev. 14, 1–27.
Campbell, J. Y., Lo, A. W., and MacKinlay, A. C. (1997). The Econometrics of Financial Markets. Princeton, NJ: Princeton University Press.
Carr, P., and Wu, L. (2009). Variance risk premiums. Rev.Financial Stud. 22, 1311–1341. doi: 10.1093/rfs/hhn038
Carson, R. T., Flores, N. E., and Meade, N. F. (2001). Contingent valuation: controversies and evidence. Environ. Resour. Econ. 19, 173–210. doi: 10.1023/A:1011128332243
Castillo, E., and Hadi, A. S. (1997). Fitting the generalized Pareto distribution to data. J. Am. Stat. Assoc. 92, 1609–1620. doi: 10.1080/01621459.1997.10473683
Ceballos, G., Ehrlich, P. R., and Dirzo, R. (2017). Biological annihilation via the ongoing sixth mass extinction signaled by vertebrate population losses and declines. Proc. Nat. Acad. Sci. U.S.A. 114, E6089–E6096. doi: 10.1073/pnas.1704949114
Champ, P. A., and Bishop, R. C. (2001). Donationa payment mechanisms and conting3ent valuation: an empirical study of hypothetical bias. Environ. Resour. Econ. 19, 383–402. doi: 10.1023/A:1011604818385
Chen, J. M. (2011). Modern disaster theory: evaluating disaster law as a portfolio of legal rules. Emory Int. Law Rev. 25, 1121–1143.
Christiano, L. J., Motto, R., and Rostagno, M. (2014). Risk shocks. Am. Econ. Rev. 104, 27–65. doi: 10.1257/aer.104.1.27
Cichetti, C. J., and Freeman, A. M. I. I. I. (1971). Option demand and consumer surplus: further comment. Q. J. Econ. 85, 528–539. doi: 10.2307/1885940
Davies, V. A. B. (2000). Sierra Leone: Ironic tragedy. J. Afr. Econ. 9, 349–369. doi: 10.1093/jae/9.3.349
Davies, V. A. B. (2008). “Sierra Leone's economic growth performance, 1961-2000,” in The Political Economy of Economic Growth in Africa, 1960-2000: Country Case Studies, Vol. 2, eds B. J. Ndulu, S. A. O'Connell, J.-P. Azam, R. H. Bates, A. K. Fosu, J. W. Gunning, and D. Njinkeu (Cambridge: Cambridge University Press), 660–696.
Davies, V. A. B. (2010). Development co-operation and conflict in Sierra Leone. Confl. Secur. Dev. 10, 57–76. doi: 10.1080/14678800903553886
de Athayde, G. M., and Flôres, R. G. (2004). Finding a maximum skewness portfolio—a general solution to three-moments portfolio choice. J. Econ. Dyn. Control 28, 1335–1352. doi: 10.1016/S0165-1889(02)00084-2
Dreschler, I., and Yaron, A. (2011). What's vol got to do with it? Rev. Financial Stud. 24, 1–45. doi: 10.1093/rfs/hhq085
Eliot, T. S. (1971). “The hollow men,” in The Complete Poems and Plays: 1909–1950, ed T. S. Eliot (New York, NY: Harcourt Brace and Co), 56–59.
Epstein, L. G., and Schneider, M. (2008). Ambiguity, information quality, and asset pricing. J. Finance 43, 197–228. doi: 10.1111/j.1540-6261.2008.01314.x
Epstein, L. G., and Wang, T. (1994). Intertemporal asset pricing under Knightian uncertainty. Econometrica 62, 283–322. doi: 10.2307/2951614
Estrada, J. (2004). Mean-semivariance behaviour: an alternative behavioural model. J. Emerg. Mark. Finance 3, 231–248. doi: 10.1177/097265270400300301
Faber, M., Manstetten, R., and Petersen, T. (1997). Homo Oeconomicus and Homo Politicus: political economy, constitutional interest and ecological interest. Kyklos 50, 457–483. doi: 10.1111/1467-6435.00026
Fama, E. F. (1963). Mandelbrot and the stable Paretian hypothesis. J. Bus. 36, 420–429. doi: 10.1086/294633
Fama, E. F. (1965). Portfolio analysis in a stable Paretian market. Manage. Sci. 11, 404–416. doi: 10.1287/mnsc.11.3.404
Fama, E. F., and French, K. R. (2004). The capital asset pricing model: theory and evidence. J. Econ. Perspect. 18, 25–46. doi: 10.1257/0895330042162430
Fernández-Villaverde, J., Guerrón-Quintana, P., Kuester, K., and Rubio-Ramirez, J. (2015). Fiscal volatility shocks and economic activity. Am. Econ. Rev. 105, 3352–3384. doi: 10.1257/aer.20121236
Gabaix, X. (2012). Variable rare disasters: an exactly solved framework for ten puzzles in macro-finance. Q. J. Econ. 127, 645–700. doi: 10.1093/qje/qjs001
Gençay, R., and Selçuk, F. (2004). Extreme value theory and value-at-risk: relative performance in emerging markets. Int. J. Forecast. 20, 287–305. doi: 10.1016/j.ijforecast.2003.09.005
Gervais, S., and Odean, T. (2001). Learning to be overconfident. Rev. Financial Stud. 14, 1–27. doi: 10.1093/rfs/14.1.1
Giavazzi, F., and McMahon, M. (2012). Policy uncertainty and household savings. Rev. Econ. Stat. 94, 517–534. doi: 10.1162/REST_a_00158
Gowdy, J. W., and McDaniel, C. N. (1999). The physical destruction of Nauru: an example of weak sustainability. Land Econ. 75, 333–338. doi: 10.2307/3147015
Grossman, S. J., and Stiglitz, J. (1980). On the impossibility of informationally efficient markets. Am. Econ. Rev. 70, 393–408.
Hanemann, W. M. (1991). Willingness to pay and willingness to accept: how much can they differ? Am. Econ. Rev. 81, 635–647.
Hartwick, J. M. (1977). Intergenerational equity and the investment of rents from exhaustible resources. Am. Econ. Rev. 67, 972–974.
Hartzmark, S. M. (2015). The Worst, the best, ignoring all the rest: the rank effect and trading behavior. Rev. Financial Stud. 28, 1024–1059. doi: 10.1093/rfs/hhu079
Harvey, C. R., Liechty, J. C., Liechty, M. W., and Müller, P. (2010). Portfolio selection with higher moments. Quant. Finance 10, 469–485. doi: 10.1080/14697681003756877
Harvey, C. R., and Siddique, A. (2000). Conditional skewness in asset pricing tests. J. Finance 55, 1263–1295. doi: 10.1111/0022-1082.00247
Heal, G. (2012). Reflections—defining and measuring sustainability. Rev. Environ. Econ. Policy 6, 147–163. doi: 10.1093/reep/rer023
Hirshleifer, J. (1965). Investment decision under uncertainty: choice-theoretic approaches. Q. J. Econ. 79, 509–536. doi: 10.2307/1880650
Hirshleifer, J. (1966). Investment decision under uncertainty: applications of the state-preference approach. Q. J. Econ. 80, 262–277. doi: 10.2307/1880692
Horowitz, J. K., and McConnell, K. E. (2002). A review of WTA/WTP studies. J. Environ. Econ. Manage. 44, 426–447. doi: 10.1006/jeem.2001.1215
Hurston, Z. N. (2006). Their Eyes Were Watching God. Danticat E., Foreword; Gates, H.L., Afterword. New York, NY: Harper Perennial/Modern Classics.
Jondeau, E., and Rockinger, M. (2006). Optimal portfolio allocation under higher moments. Eur. J. Financial Manag. 12, 29–55. doi: 10.1111/j.1354-7798.2006.00309.x
Jurczenko, E., and Maillet, B. (2012). “The four-moment capital asset pricing model: between asset pricing and asset allocation,” in Multi-Moment Asset Allocation and Pricing Models, eds E. Jurczenko and B. Maiilet (Hoboken, NJ: John Wiley and Sons), 113–163.
Kahneman, D., Knetsch, J., and Thaler, R. (1990). Experimental tests of the endowment effect and the Coase theorem. J. Polit. Econ. 98, 1325–1348. doi: 10.1086/261737
Kahneman, D., and Tversky, A. (1984). Choices, values, and frames. Am. Psychol. 39, 344–350. doi: 10.1037/0003-066X.39.4.341
Kelly, B., and Jiang, H. (2014). Tail risk and asset prices. Rev. Financial Stud. 27, 2841–2871. doi: 10.1093/rfs/hhu039
Kenrick, D.T., Griskevicius, V., and Schaller, M. (2010). Renovating the pyramid of needs: Contemporary extensions built upon ancient foundations. Perspect. Psychol. Sci. 5, 292–314. doi: 10.1177/1745691610369469
Keynes, J. M. (1937). The general theory of employment. Q. J. Econ. 51, 209–223. doi: 10.2307/1882087
Knif, J., Koutmos, D., and Koutmos, G. (2020). Higher co-moment CAPM and hedge fund returns. Atl. Econ. J. 48, 99–113. doi: 10.1007/s11293-020-09659-1
Krech, D., Crutchfield, R. S., and Ballachey, E. S. (1962). The Individual in Society: A Textbook of Social Psychology. New York, NY: McGraw-Hill Book Company.
Kunreuther, H., and Wright, G. (1979). “Safety first, gambling, and the subsistence farmer,” in Risk, Uncertainty, and Agricultural Development, eds J. A. Roumasset, J.-M., Boussard, and I. Singh (Los Baños: Southeast Asian Regional Center for Graduate Study and Research in Agriculture), 213–230.
Kurzban, R., and Aktipis, C. A. (2007). Modularity and the social mind: are psychologists too selfish? Pers. Soc. Psychol. Rev. 11, 131–149. doi: 10.1177/1088868306294906
Le Billon, P. (2008). Diamond wars? conflict diamonds and geographies of resource wars. Ann. Assoc. Am. Geogr. 98, 345–372. doi: 10.1080/00045600801922422
Lopes, L. L. (1987). Between hope and fear: the psychology of risk. Adv. Exp. Soc. Psychol. 20, 255–295. doi: 10.1016/S0065-2601(08)60416-5
Maconachie, R., and Binns, T. (2007). Beyond the resource curse? diamond mining, development and post-conflict reconstruction in Sierra Leone. Resour. Policy 32, 104–115. doi: 10.1016/j.resourpol.2007.05.001
Maslow, A. H. (1943). A theory of human motivation. Psychol. Rev. 50, 370–396. doi: 10.1037/h0054346
Maslow, A. H. (1996). “Critique of self-actualization theory,” in Future Visions: The Unpublished Papers of Abraham Maslow, ed E. Hoffman (Thousand Oaks, CA: Sage Publications), 26–32.
McIntyre, O., and Mosedale, T. (1997). The precautionary principle as a norm of customary international law. J. Environ. Law 9, 221–241. doi: 10.1093/jel/9.2.221
McMahon, J. (2015). Behavioral economics as neoliberalism: producing and governing homo economicus. Contemp. Polit. Theory 14, 137–158. doi: 10.1057/cpt.2014.14
Mehlum, H., Moene, K., and Torvik, R. (2006). Institutions and the resource curse. Econ. J. 116, 1–20. doi: 10.1111/j.1468-0297.2006.01045.x
Merton, R. C. (1973). An intertemporal capital asset pricing model. Econometrica 41, 867–887. doi: 10.2307/1913811
Nordhaus, W. D. (2011). The economics of tail events with an application to climate change. Rev. Environ. Econ. Polcy 5, 240–257. doi: 10.1093/reep/rer004
Ortiz, S. (1979). “The effect of risk aversion strategies on subsistence and cash crop decisions,” in Risk, Uncertainty, and Agricultural Development, eds J. A. Roumasset, J.-M. Boussard, and I. Singh (Los Baños: Southeast Asian Regional Center for Graduate Study and Research in Agriculture), 231–246.
Ortobelli, S., and Rachev, S. T. (2001). Safety-first analysis and stable Paretian approach to portfolio choice theory. Math. Comput. Model. 34, 1037–1072. doi: 10.1016/S0895-7177(01)00116-9
Pástor, L., and Veronesi, P. (2012). Uncertainty about government policy and stock prices. J. Finance 67, 1219–1264. doi: 10.1111/j.1540-6261.2012.01746.x
Pástor, L., and Veronesi, P. (2013). Political uncertainty and risk premia. J. Financ. Econ. 110, 520–545. doi: 10.1016/j.jfineco.2013.08.007
Poe, G. L., Clark, J. E., Rondeau, D., and Schulze, W. D. (2002). Provision point mechanisms and field validity tests of contingent valuation. Environ. Resour. Econ. 23, 105–131. doi: 10.1023/A:1020242907259
Robinson, J. A., Torvik, R., and Verdier, T. (2006). Political foundations of the resource curse. J. Dev. Econ. 79, 447–468. doi: 10.1016/j.jdeveco.2006.01.008
Ross, M. L. (1999). The political economy of the resource curse. World Polit. 51, 297–322. doi: 10.1017/S0043887100008200
Ross, M. L. (2015). What have we learned about the resource curse? Ann. Rev. Polit. Sci. 18, 239–259. doi: 10.1146/annurev-polisci-052213-040359
Ross, S. A. (1976). The arbitrage theory of capital asset pricing. J. Econ. Theory 13, 341–360. doi: 10.1016/0022-0531(76)90046-6
Roy, A. D. (1952). Safety first and the holding of assets. Econometrica 20, 431–449. doi: 10.2307/1907413
Ruiu, M. L., Ragnedda, M., and Ruiu, G. (2020). Similarities and differences in managing the Covid-19 crisis and climate change risk. J. Knowl. Manag. 24, 2597–2614. doi: 10.1108/JKM-06-2020-0492
Runde, J. (1998). Clarifying Frank Knight's discussion of the meaning of risk and uncertainty. Cambridge J. Econ. 22, 539–546. doi: 10.1093/cje/22.5.539
Sand, P. H. (2000). The precautionary principle: a European perspective. Hum. Ecol. Risk Assess. 6, 445–458. doi: 10.1080/10807030091124563
Sayman, S., and Öncüler, A. (2005). Effects of study design characteristics on the WTA-WTP disparity: a meta analytical framework. J. Econ. Psychol. 26, 289–312. doi: 10.1016/j.joep.2004.07.002
Shahabuddin, Q. (1982). Farmers' crop growing decisions under uncertainty—a safety-first approach. Bangladesh Dev. Stud. 10, 95–100.
Shahabuddin, Q., and Butterfield, D. (1986). The impact of risk on agricultural production decisions: Tests of a safety-first model in Bangladesh. Bangladesh Dev. Stud. 14, 13–37.
Shefrin, H., and Statman, M. (1994). Behavior capital asset pricing theory. J. Financial Quant. Anal. 29, 323–349. doi: 10.2307/2331334
Shefrin, H., and Statman, M. (2000). Behavioral portfolio theory. J. Financial Quant. Anal. 29, 127–151. doi: 10.2307/2676187
Shogren, J. F., Shin, S. Y., Hayes, D. J., and Kliebenstein, J. B. (1994). Resolving differences in willingness to pay and willingness to accept. Am. Econ. Rev. 84, 255–270.
Sillano, M., and de Dios Ortúzar, J. (2005). Willingness-to-pay estimation with mixed logit models: Some new evidence. Environ. Plan. A 37, 525–550. doi: 10.1068/a36137
Solow, R. M. (1974). The economics of resources or the resources of economics. Am. Econ. Rev. 62, 1–14.
Supreme Court of the United States (1909). Willcox v. Consolidated Gas Co. United States Rep. 212, 19–55.
Supreme Court of the United States (1919). Abrams v. United States. United States Rep. 250, 616–631.
Supreme Court of the United States (1935). West v. Chesapeake and Potomac Tel. Co. United States Rep. 295, 662–693.
Supreme Court of the United States (1940). United States v. Socony-Vacuum Oil Co. United States Rep. 310, 150–267.
Todorov, V. (2010). Variance risk premium dynamics: the role of jumps. Rev. Financial Stud. 23, 345–383. doi: 10.1093/rfs/hhp035
Tversky, A., and Kahneman, D. (1992). Advances in prospect theory: cumulative representation of uncertainty. J. Risk Uncertain. 5, 297–323. doi: 10.1007/BF00122574
Wake, D. B., and Vredenburg, V. T. (2008). Are we in the midst of the sixth mass extinction? a view from the world of amphibians. Proc. Natl. Acad. Sci. 105, 11466–11473. doi: 10.1073/pnas.0801921105
Weisbrod, B. A. (1964). Collective-consumption services of individual consumption goods. Q. J. Econ. 78, 471–477. doi: 10.2307/1879478
Weitzman, M. L. (2009). On modeling and interpreting the economics of catastrophic climate change. Rev. Econ. Stat. 91, 1–19. doi: 10.1162/rest.91.1.1
White, M. J. (1989). The corporate bankruptcy decision. J. Econ. Perspect. 3, 129–151. doi: 10.1257/jep.3.2.129
Wilson, S. A. (2013). Diamond exploitation in Sierra Leone 1930 to 2010: a resource curse? GeoJournal 78, 997–1012. doi: 10.1007/s10708-013-9474-1
Zhang, X. F. (2006). Information uncertainty and stock returns. J. Finance 61, 105–137. doi: 10.1111/j.1540-6261.2006.00831.x
Keywords: skewness, kurtosis, information uncertainty, irreversibility, environmental economics, asset pricing, portfolio theory, behavioral economics
Citation: Chen JM (2021) This Is the Way the World Ends, Not With a Bang but Bonds and Bullets. Front. Clim. 3:758021. doi: 10.3389/fclim.2021.758021
Received: 13 August 2021; Accepted: 08 November 2021;
Published: 02 December 2021.
Edited by:
Robin Kundis Craig, University of Southern California, United StatesReviewed by:
Guicai Ning, The Chinese University of Hong Kong, Hong Kong SAR, ChinaSurendra Singh, Central University of Jammu, India
Copyright © 2021 Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: James Ming Chen, Y2hlbmphbWVAbGF3Lm1zdS5lZHU=
 James Ming Chen
James Ming Chen