The Role of Surface Hydrophobicity on the Structure and Dynamics of CO2 and CH4 Confined in Silica Nanopores

Advancing a portfolio of technologies that range from the storage of excess renewable natural gas for distributed use to the capture and storage of CO₂ in geological formation are essential for meeting our energy needs while responding to challenges associated with climate change. Delineating the surface interactions and the organization of these gases in nanoporous environments is one of the less explored approaches to ground advances in novel materials for gas storage or predict the fate of stored gases in subsurface environments. To this end, the molecular scale interactions underlying the organization and transport behavior of CO₂ and CH₄ molecules in silica nanopores need to be investigated. To probe the influence of hydrophobic surfaces, a series of classical molecular dynamics (MD) simulations are performed to investigate the structure and dynamics of CO₂ and CH₄ confined in OH-terminated and CH₃-terminated silica pores with diameters of 2, 4, 6, 8, and 10 nm at 298 K and 10 MPa. Higher adsorption extents of CO₂ compared to CH₄ are noted on OH-terminated and CH₃-terminated pores. The adsorbed extents increase with the pore diameter. Further, the interfacial CO₂ and CH₄ molecules reside closer to the surface of OH-terminated pores compared to CH₃-terminated pores. The lower adsorption extents of CH₄ on OH-terminated and CH₃-terminated pores result in higher diffusion coefficients compared to CO₂ molecules. The diffusivities of both gases in OH-terminated and CH₃-terminated pores increase systematically with the pore diameter. The higher adsorption extents of CO₂ on OH-terminated and CH₃-terminated pores are driven by higher van der Waals and electrostatic interactions with the pore surfaces, while CH₄ adsorption is mainly due to van der Waals interactions with the pore walls. These findings provide the interfacial chemical basis underlying the organization and transport behavior of pressurized CO₂ and CH₄ gases in confinement.

Introduction

Scientific advancements that enable us to harness renewable energy resources and facilitate the removal and storage of greenhouse gas emissions are essential for meeting our energy and resource needs in a sustainable manner while responding to challenges associated with climate change. One approach in the portfolio of strategies needed to address this challenge is the storage of renewable energy carriers such as hydrogen and biomethane. Storage of excess renewable energy carriers in natural and engineered environments is critical to meeting our energy needs on demand. In this context, there is an emerging interest in exploring subsurface environments (Pfeiffer and Bauer, 2015; Berta et al., 2018; Shi et al., 2020) and engineered materials (Yun et al., 2002; Düren et al., 2004; Dündar-Tekkaya and Yürüm, 2016) to store clean energy carriers such as biomethane and hydrogen. Further, safe and permanent storage of CO₂ in geologic formations at the gigaton scale is essential if renewable and non-renewable carbon-bearing fuels continue to be used (Bachu et al., 2007; Aydin et al., 2010; Michael et al., 2010; Jiang, 2011; Zhang and Bachu, 2011). Resolving the physical and chemical adsorption of carbon dioxide (CO₂) and methane (CH₄) on porous silica is an area of increasing interest due to its relevance in various energy and environmental fields, including CO₂ capture and CO₂ utilization and storage coupled with enhanced oil and gas recovery from subsurface environments (Kuuskraa et al., 2013; Huo et al., 2017; Mohammed and Gadikota, 2019a; Farajzadeh et al., 2020; Klewiah et al., 2020).

While prior studies reported the link between functionalized silica surfaces and the structure of CO₂ and CH₄ for applications related to gas separations (Wiheeb et al., 2015; Mafra et al., 2018), the coupled effects of confinement and surface hydrophobicity have not been systematically probed. The surfaces of silica nanopores and nanoparticles can be either hydrophilic or hydrophobic depending on the surface polarity and the chemistry of the functional groups on the surface (Jin et al., 2019). The hydrophobicity of silica surfaces has significant impacts on the organization and flow of confined fluids, including water (Jin et al., 2021), hydrocarbons (Ghoufi et al., 2013) and gases. Given the interest in storing gases in subsurface environments, delineating the mechanisms underlying the storage of gases in oil-wet vs. water-wet environments is essential. Further, the influence of nano-scale confinement on the organization of these gases needs to be further delineated given the abundance of nanoporous-rich environments in subsurface environments and the anomalous thermodynamics and transport behavior of nano-confined fluids.

Extensive progress has already been made toward explaining the physical and chemical interactions of CO₂ with amine-functionalized porous silica using a wide range of experimental and computational characterization techniques (Chaikittisilp et al., 2011; Liu et al., 2014; Cogswell et al., 2015). Amine-functionalized porous silica provides the advantage of chemically binding CO₂ with the impregnated amines in the porous silica that enhance the gas uptake (Serna-Guerrero et al., 2008), as opposed to OH-functionalized porous silica in which CO₂ adsorbs physically through van der Waals interactions, electrostatic interactions, and hydrogen bonding. The chemical binding of CO₂ with the amine groups results in high CO₂ adsorption capacity, good selectivity, fast adsorption and desorption rates, and low energy consumption when compared to the porous materials that capture CO₂ through physical adsorption (Li et al., 2014). Despite these advancements in developing functional materials, there have been no efforts to contrast the organization of CO₂ and CH₄ in pores with hydrophobic and hydrophilic silica surfaces.

The structure, dynamics and flow of CH₄ in organic and inorganic confinement have also been studied using a range of experimental and computational tools, including small-angle neutron scattering (Chiang et al., 2016a,b; Mohammed et al., 2020b) and molecular simulations (Siderius et al., 2017; Xiong et al., 2017; Mohammed and Gadikota, 2020; Wang et al., 2020). The core-shell organization of pressurized CH₄ molecules in confinement and their associated dimensions can be successfully determined using small-angle neutron scattering (Chiang et al., 2016a,b; Mohammed et al., 2020b), and these measurements can be used to validate molecular simulations. The differences in the spatial organization of confined gases contribute to anisotropic variations in their diffusivities (Wu et al., 2015; Xiong et al., 2016, 2017; Mohammed and Gadikota, 2019a). Confined effects influence the desorption of bound species such as water and CO₂ (Baumgartner et al., 2019; Knight et al., 2019).

Prior work by Qin et al. (2008) used classical molecular dynamics (MD) simulations to show that supercritical CO₂ is preferentially adsorbed on hydroxylated silica surfaces [-Si(OH)] instead of silylated [-Si(CH₃)₃] silica pores due to the hydrogen bonding interactions between the confined CO₂ and -OH groups on the pore. Although these insights provided by Qin and co-workers provide a crucial link to the fate of confined CO₂ and the surface chemistry of silica pores, the effects of pore diameter remain unresolved.

To address this knowledge gap, we performed a series of classical MD simulations to investigate the structure, organization, dynamics, and energetics of CO₂ and CH₄ confined in OH-functionalized and CH₃-functionalized silica pores with diameters of 2, 4, 6, 8, and 10 nm. The hypothesis that the organization of CO₂ and CH₄ molecules is influenced by the hydrophobicity of the surfaces is investigated. The simulations are performed at 10 MPa and 298 K to mimic the mechanical and thermal conditions of subsurface environments.

Computational Methodology

CO₂, CH₄, and β-cristobalite silica unit cells are built using Avogadro software. The structure of isolated cristobalite unit cell is optimized using density functional theory implemented in Quantum Espresso (Giannozzi et al., 2017). A kinetic energy cutoff for wavefunctions of 36 Ry and K-points mesh of (6 × 6 × 6) are used to optimize the β-cristobalite silica unit cell. These values are chosen based on the convergence of the total energy of the silica structure. Ultrasoft pseudopotentials are implemented in which the generalized gradient approximation (GGA) (Perdew et al., 1996) is selected for the exchange correlation functional. The Broyden-Fletcher-Goldfarn-Shanno (BFGS) (Head and Zerner, 1985) algorithm is utilized to perform the structural optimization of the silica unit cell. BFGS has been widely used to optimize the electronic structure of a wide range of materials in DFT calculations (Han et al., 2019; Sharma et al., 2019; Neupane and Adhikari, 2020).

Silica surfaces are constructed by replicating the optimized β-cristobalite unit cell in x, y, and z directions. Slit-shaped pores with heights of 2, 4, 6, 8, and 10 nm are cleaved in the constructed surfaces. The non-bridging oxygens on the interior pore surfaces are functionalized with -OH and -CH₃ groups to tune the surface hydrophobicity of the constructed pores. Each pore has a length of 9.95 nm along the X-axis and a depth of 3.98 nm along the Y-axis, while the pore height varies from 2 to 10 nm along the Z-axis.

The pressures of CO₂ and CH₄ inside the pores is set to 10 MPa. The number of CO₂ and CH₄ molecules are 193, 385, 578, 771, and 964 in 2, 4, 6, 8, and 10 nm pores, respectively (see Figure 1). Silica pores are modeled using ClayFF forcefield (Cygan et al., 2004). The TraPPE forcefield (Potoff and Siepmann, 2001) is used to model -CH₃ functional group. The CO₂ molecules are modeled using TraPPE forcefield, while CH₄ molecules are modeled using OPLS/AA forcefield (Jorgensen et al., 1996). These forcefields have been widely used to study the properties of CO₂ and CH₄ on silica surfaces because the governed adsorption extents, organizations and dynamics agree with the experimental data (Phan et al., 2014; Le et al., 2015; Mohammed et al., 2020b, 2021).

FIGURE 1

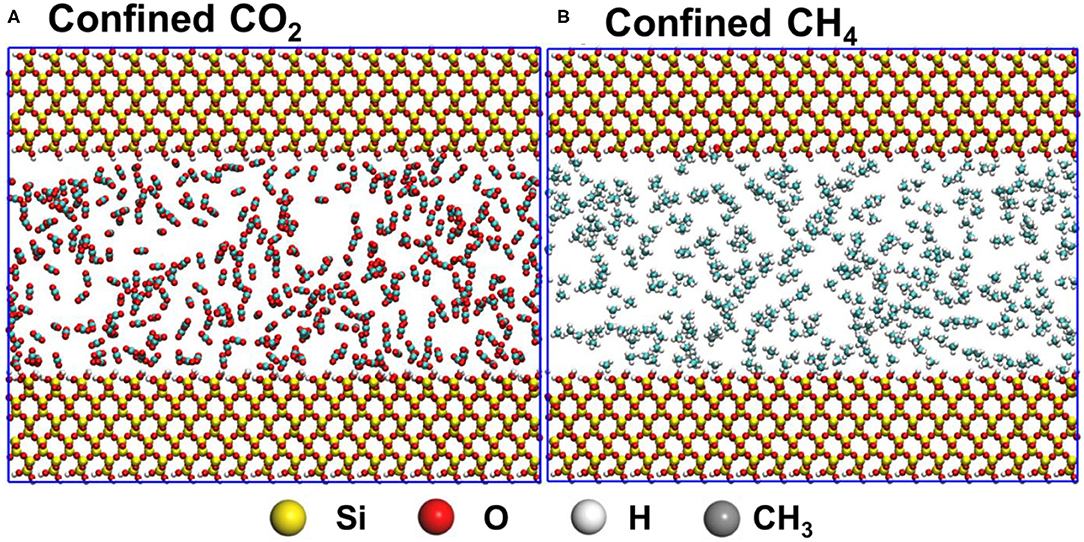
Figure 1. The initial configurations of confined CO₂ and CH₄ in silica pores with diameters 4 nm are shown in panels (A,B), respectively. Atoms in silica pores and confined gases molecules shown in CPK and VDW drawing methods, respectively, are implemented in VMD software.

Energy minimization is performed on the initial configurations for 50,000 steps using the steepest descent method to remove inappropriate geometries and reduce the high energy of the randomly distributed gas molecules in the pore space. Constant number of molecules, constant volume and constant temperature (NVT) ensemble are performed on the optimized cells for 50 ns under 298 K. The temperature is controlled using Nose-Hoover thermostat with a relaxation time of 1 ps (Evans and Holian, 1985). The short-range interaction is calculated in a cutoff of 1.4 nm, while the long-range electrostatic interactions are treated using Particle Mesh Ewald (PME). The equation of motion is integrated by leapfrog integrator with a time step of 2 fs. Non-bonding interactions are accounted for van der Waals and electrostatic potentials. Bonding interactions are calculated from bond stretching, angle bending, and dihedrals in CO₂ and CH₄ molecules while only O-H and O-CH₃ bond stretching are considered in silica pores. MD simulations are performed and analyzed using GROMACS 2018 code (Abraham et al., 2015) and the visualization of the simulations inputs and outputs are performed using VDM software (Humphrey et al., 1996). Further information on the simulation details can be found in Mohammed and Gadikota (2018, 2019a,b); Mohammed and Gadikota (2020) and Mohammed et al. (2020a,b).

Results and Discussions

Structural Properties of Confined CO₂ and CH₄

Insights into the organization of CO₂ and CH₄ molecules in silica nanopores are obtained from the density profiles of these gases. The density profiles of confined CO₂ and CH₄ along the pore height (z-axis) in OH-terminated and CH₃-terminated pores with diameter of 2 nm is shown in Figure 2 as a representative for the distribution of confined gases in slit pores with different pore hydrophobicity. The density profiles show a preferential adsorption of CO₂ and CH₄ on the pore surfaces in both OH-terminated and CH₃-terminated pores. The density profile of the confined gases decreases sharply on approaching the pore center where the minimum density values are observed for both gases. However, the number density of CO₂ molecules confined in OH-terminated pores is higher at the pore surface while the number density of CH₄ molecules is higher in the center of the pore (see Figures 2A,B). These observations suggest that CO₂ adsorbs preferentially on the OH-terminated silica pores compared to CH₄ at similar conditions of temperature, pressure and pore size. Prior studies probing the competitive adsorption of CO₂ on OH-terminated silica pores showed that CO₂ adsorbs preferentially over nonpolar aliphatic hydrocarbons (paraffins) such as ethane (C₂H₆) (Elola and Rodriguez, 2019), propane (C₃H₈) (Mohammed and Gadikota, 2019a), butane (C₄H₁₀) (Le et al., 2015) and octane (C₈H₁₈) (Le et al., 2016).

FIGURE 2

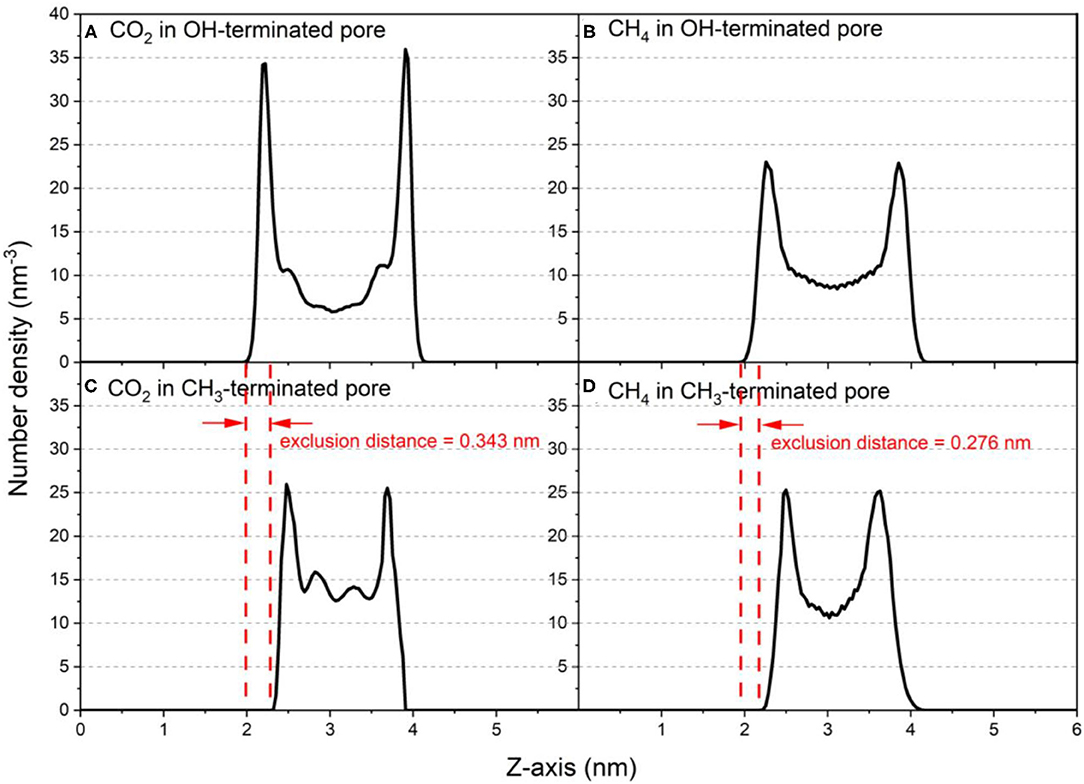
Figure 2. Number density profiles of confined CO₂ and CH₄ molecules along the vector normal to the pore surface (z-axis) in (A,B) OH-terminated pores and (C,D) CH₃-terminated pores in pore diameter of 2 nm. The density profiles are averaged over the last 10 ns of the simulation time.

The preferential adsorption of CO₂ and CH₄ on the surfaces of the OH-terminated and CH₃-terminated pores compared to the pore center is evident from the 2D density maps of the gases' distribution in the pore space (see Figures 3, 4). The density maps are averaged over the last 10 ns of the simulation time to ensure an equilibrium state. CO₂ showed higher density on the pore surfaces compared to CH₄ in OH-terminated and CH₃-terminated surfaces in all pore sizes. Further, the interactions with the functional groups on the pore surface influence the distribution of the interfacial molecules such that higher CO₂ densities are observed at the OH groups and higher CH₄ densities are noted at CH₃ groups.

FIGURE 3

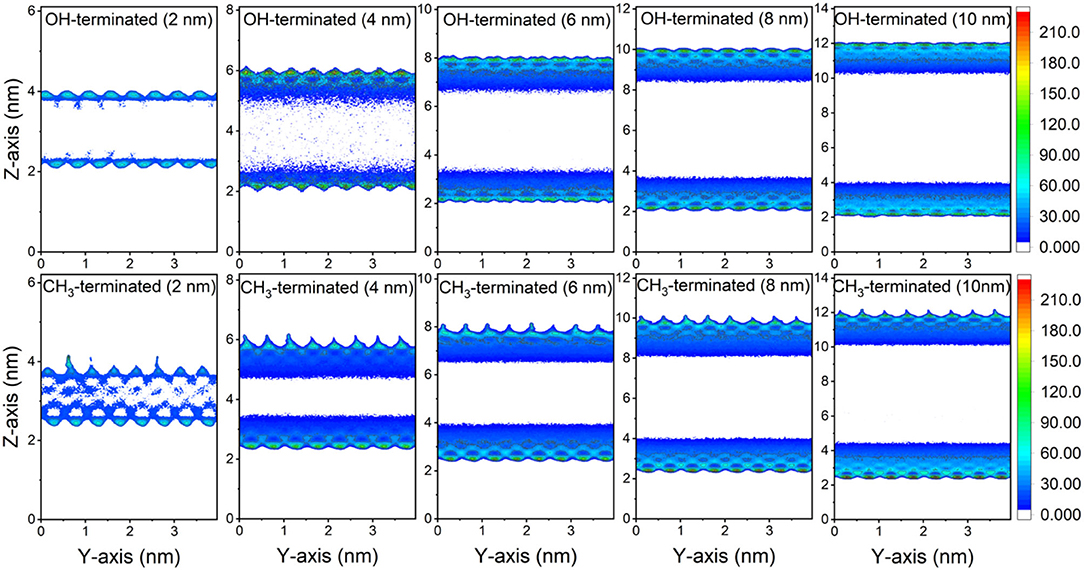
Figure 3. 2D density maps of CO₂ confined in OH-terminated and CH₃-terminated pores as a function of the pore diameter. The density maps are averaged over the last 10 ns of the simulation times.

FIGURE 4

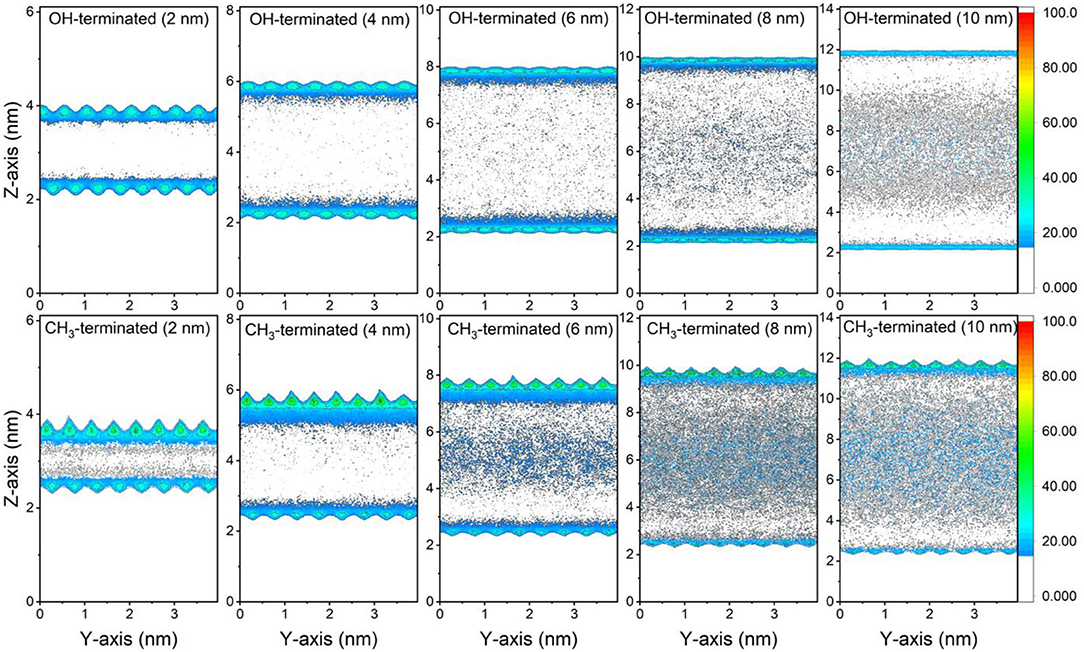
Figure 4. 2D density maps of CH₄ confined in OH-terminated and CH₃-terminated pores as a function of the pore diameter. The density maps are averaged over the last 10 ns of the simulation times.

Interestingly, the location of the adsorbed CO₂ and CH₄ peaks on the CH₃-terminated pores are shifted toward the pore center by about 0.34 and 0.27 nm, respectively, in 2 nm sized pores (see Table 1). The shift in the adsorbed peaks “exclusion region” in hydrophobic silica surfaces is evident for water (Jin et al., 2019), but studies on gases confined in CH₃-teriminated silica are scarce, making it difficult to compare such observations with previous studies. The exclusion of CO₂ and CH₄ from the CH₃-terminated pore surface is also shown by the snapshots taken from the silica-CO₂ and silica-CH₄ interfaces (see Figure 5). Figure 5 shows that the interfacial CO₂ and CH₄ molecules can reside between the dangling OH groups on the OH-terminated surfaces, while there is a finite distance between the dangling CH₃ groups and the interfacial CO₂ and CH₄ molecules.

TABLE 1

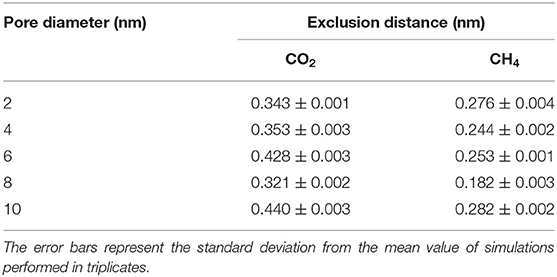
Table 1. The exclusion distance (nm) of CO₂ and CH₄ in CH₃-terminated pores as a function of the pore diameter.

FIGURE 5

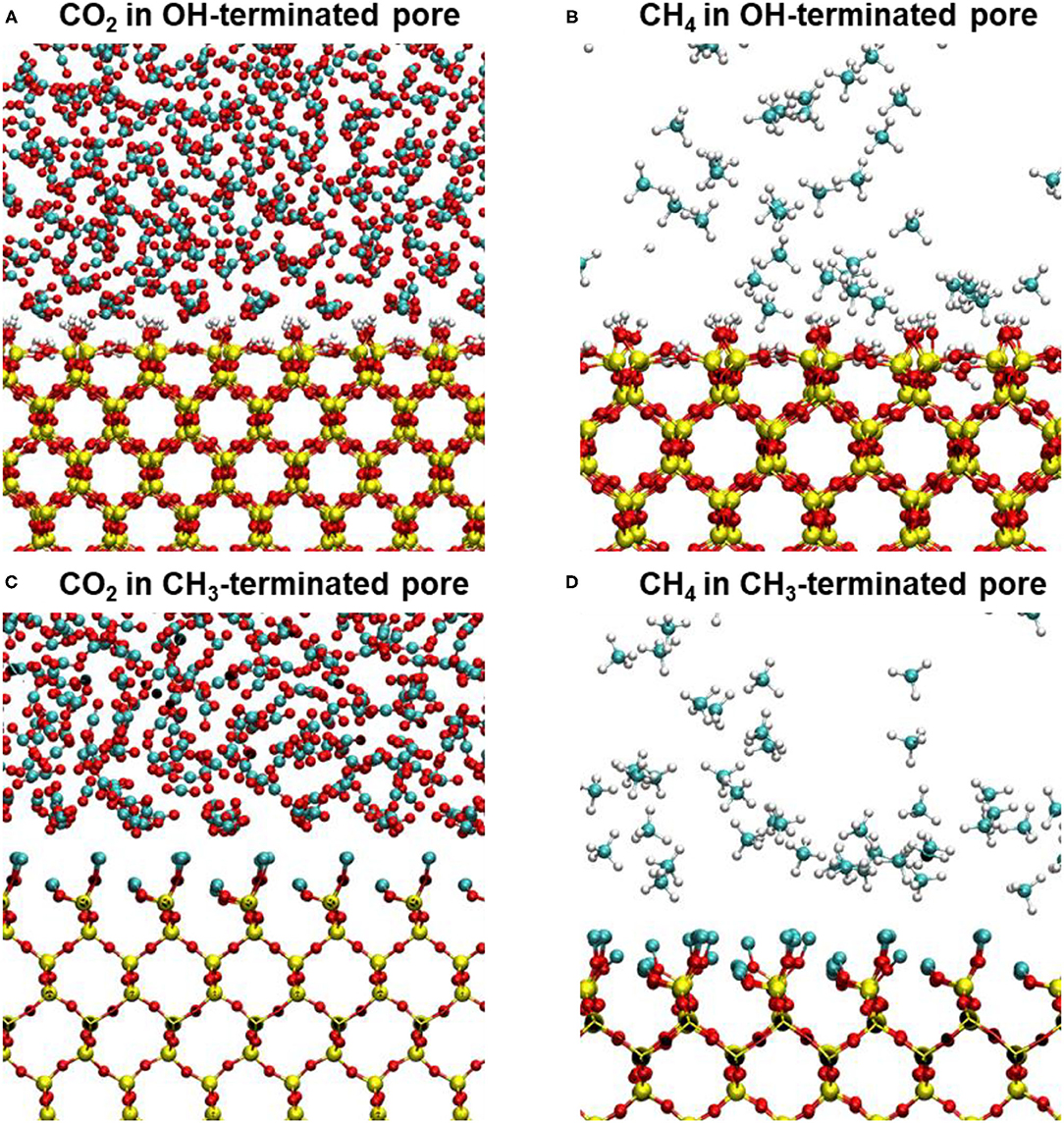
Figure 5. Snapshots showing the interfacial CO₂ and CH₄ molecules on (A,B) OH-terminated pore surfaces and (C,D) CH₃-terminated pore surfaces. The snapshots represent the last trajectory frame of CO₂ and CH₄ molecules confined in 10 nm pores. The exclusion regions of interfacial CO₂ molecules on CH₃-terminated pores are evident in panels (C,D).

To contrast the adsorption behavior of CO₂ and CH₄, the adsorption extents (mmol/m²) of CO₂ and CH₄ on the pore surfaces are calculated from the number density profiles in OH-terminated and CH₃-terminated pores and normalized by Avogadro number and the area of the pore surface (see Figure 6) as follows:

$\begin{array}{l}\begin{array}{c}Adsorption extent\left[\frac{mmol}{m^2}\right]\end{array}\\ \begin{array}{c}=\frac{Number of adsorbed molecules}{Avogadro number \times Pore surface area}\end{array}& (1)\end{array}$

FIGURE 6

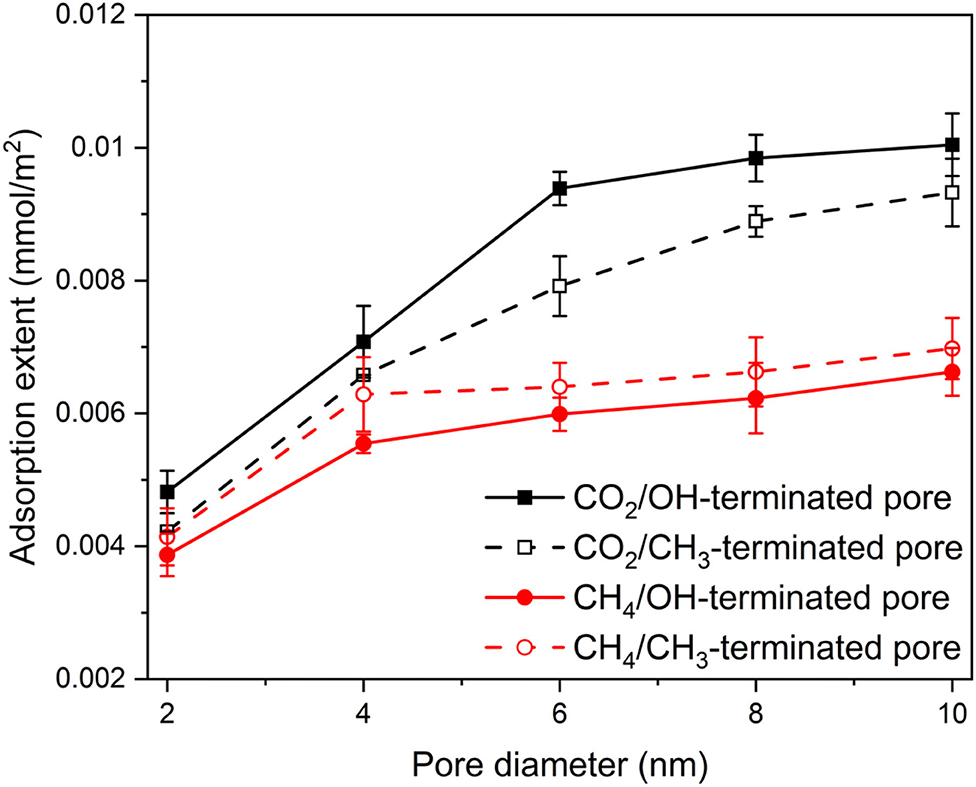
Figure 6. The adsorption extents of CO₂ and CH₄ on OH-terminated and CH₃-terminated pore surfaces as a function of the pore diameter and pore surface chemistry. The adsorption extents are determined as the number of adsorbed molecules by Avogadro number and the pore surface area. The adsorption extents are averaged over the last 10 ns of the simulation time. Error bars represent the standard deviation from the mean values of three different simulations.

The adsorbed molecules were considered as the first peak in the density profile adjacent to the pore surface. This approach is consistent with prior studies (Mohammed and Gadikota, 2019a). The adsorption extent of CO₂ and CH₄ in OH-terminated and CH₃-terminated pores increases systematically with the increase in the pore diameter. However, the adsorption extent of CO₂ is higher than that of CH₄ in OH-terminated and CH₃-terminated pores. Further, the adsorption extent of CO₂ in OH-terminated pores is higher than that in CH₃-terminated pores. In contrast, the CH₄ molecules adsorb preferentially on CH₃-terminated pores compared to that in OH-terminated pores. As the pore diameter increases from 2 nm to 10 nm, the adsorption extent of CO₂ in OH-terminated pores increases from 0.48 ± 0.03 to 1 ± 0.05 mmol/m², while CO₂ adsorption extent on CH₃-terminated pores increases from 0.42 ± 0.01 to 0.92 ± 0.05 mmol/m². Similarly, increasing the pore diameter from 2 to 10 nm causes the adsorption extent of CH₄ to increase from 0.38 ± 0.03 to 0.66 ± 0.03 mmol/m² in OH-terminated pores and from 0.41 ± 0.04 to 0.70 ± 0.04 mmol/m² in CH₃-terminated pores. The profiles of the adsorption extents are consistent with previous studies after accounting for the difference in the compositions of confined gases (Mohammed and Gadikota, 2019a).

The structural properties are further analyzed by calculating the radial distribution function (RDF) of the carbon atoms of CO₂ and CH₄ with respect to the -OH and -CH₃ groups on the pore surface (Figure 7). RDFs are averaged over the last 10 ns of the simulations time to ensure equilibrium structure of the interfacial CO₂ and CH₄ molecules. RDF of C atoms of CO₂ and CH₄ showed two peaks with respect to the -OH and -CH₃ groups on the silica pores surfaces. However, the first peak of OH-C_CO2 is higher than that of CH₃-C_CO2 (see Figures 7A,C). Further, the first peak of OH-C_CO2 is located at a radius of 0.34 nm while that of CH₃-C_CO2 is located at 0.41 nm. The lower first peak of C_CH4 compared to C_CO2 with respect to -OH and -CH₃ functional groups (Figures 7B,D) on the pore surfaces agrees with the lower adsorption extent of CH₄ on OH-terminated and CH₃-terminated pores. The peak values of all RDFs decrease systematically as the pore diameter increases due to the larger number of gas molecules residing in the pore center compared the molecules adsorbed on the pore surface. Previous studies showed similar trends in the RDF of confined CO₂ in OH-terminated and CH₃-terminated pore surfaces (Qin et al., 2008).

FIGURE 7

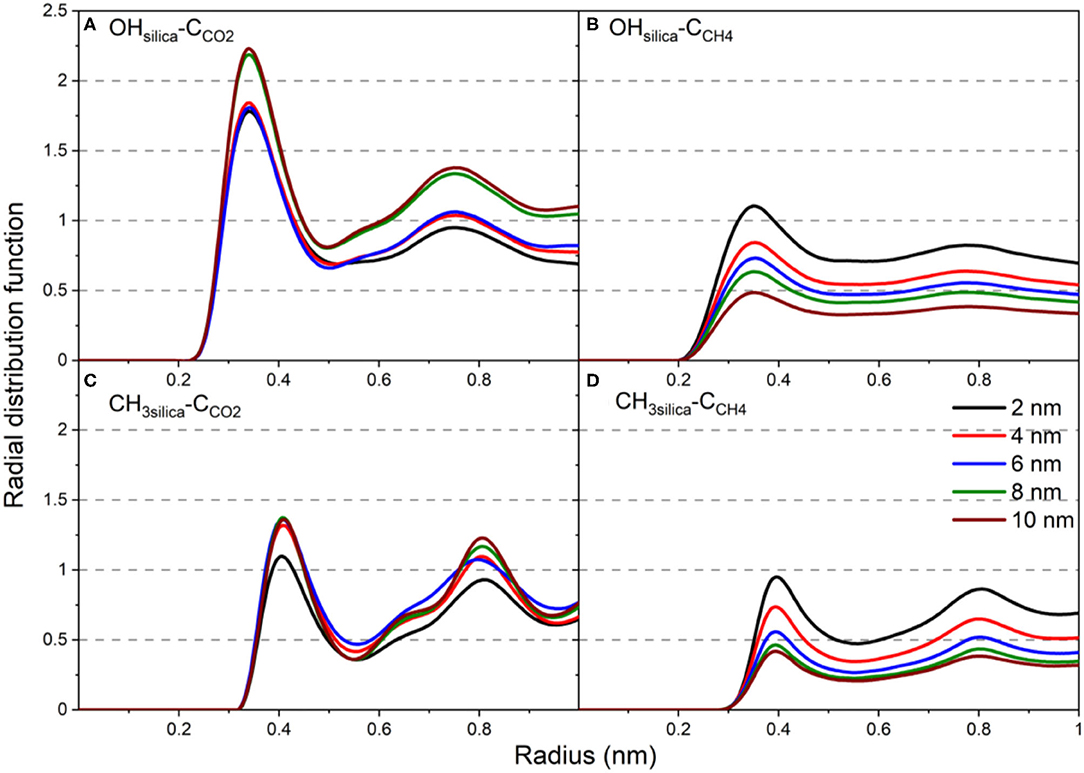
Figure 7. The radial distribution function of (A) OH_silica-C_CO2, (B) OH_silica-C_CH4, (C) CH_3silica-C_CO2, (D) CH_3silica-C_CH4 as a function of the pore diameter. Radial distribution functions are averaged over the last 10 ns of the simulation time.

The coordination numbers (n(r)) of C_CO2 and C_CH4 with respect to -OH and -CH₃ groups on the pore surfaces (Figure 8) are calculated by integrating the radial distribution function as follows:

$\begin{array}{ll}\begin{array}{c}n(r)=4\pi \rho {\displaystyle {\int }_0^{r}g(r)r^{2}dr}\end{array}& (2)\end{array}$

FIGURE 8

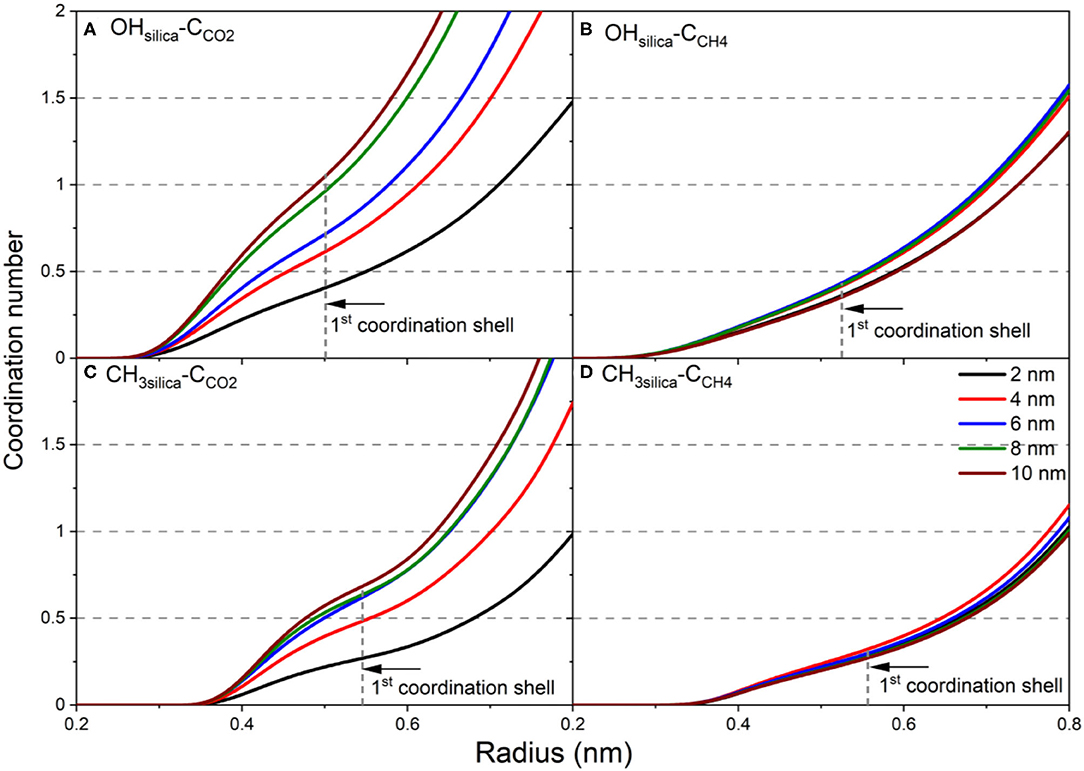
Figure 8. The coordination number of (A) C_CO2 from OH_silica, (B) C_CH4 from OH_silica, (C) C_CO2 from CH_3silica, and (D) C_CH4 from CH_3silica as a function of the pore diameter. The coordination number is calculated by integrating the radial distribution function and is averaged over the last 10 ns of the simulation time.

In the expression above, ρ is the density, r is the radius and g(r) is the radial distribution function. The number of C_CO2 atoms in the first coordination shell of -OH and -CH₃ increase significantly as the pore diameter increases from 2 nm to 10 nm (see Figures 8A,C). However, the number of C_CO2 in the first coordination shell of OH is higher than that of CH₃. In contrast, a slight increase is noted in the number of C_CH4 in the first coordination shell of -OH and -CH₃ groups on the silica surface (Figures 8B,D). In addition, the number of C_CO2 in the first coordination shell of -OH and -CH₃ is higher than C_CH4 in all the pore sizes. The denser packing of the first coordination shell of C_CO2 agrees with higher adsorption extent on OH-terminated and CH₃-terminated pore surfaces.

Diffusivity of Confined CO₂ and CH₄

The hypothesis that the structure of confined fluids influences their transport is investigated. The self-diffusion coefficient of confined CO₂ and CH₄ is calculated in the plane perpendicular to the pore diameter (xy plane) due to the negligible dimensionality of the pore diameter compared to xy plane (infinite) (see Figure 9). The self-diffusion coefficients are calculated based on the mean square displacement (l²) as follows (Gadikota et al., 2017):

$\begin{array}{ll}\begin{array}{c}D=\frac{1}{2n}\underset{t\to \infty }{\lim }\frac{d\langle l^2\rangle }{dt}\end{array}& (3)\end{array}$

FIGURE 9

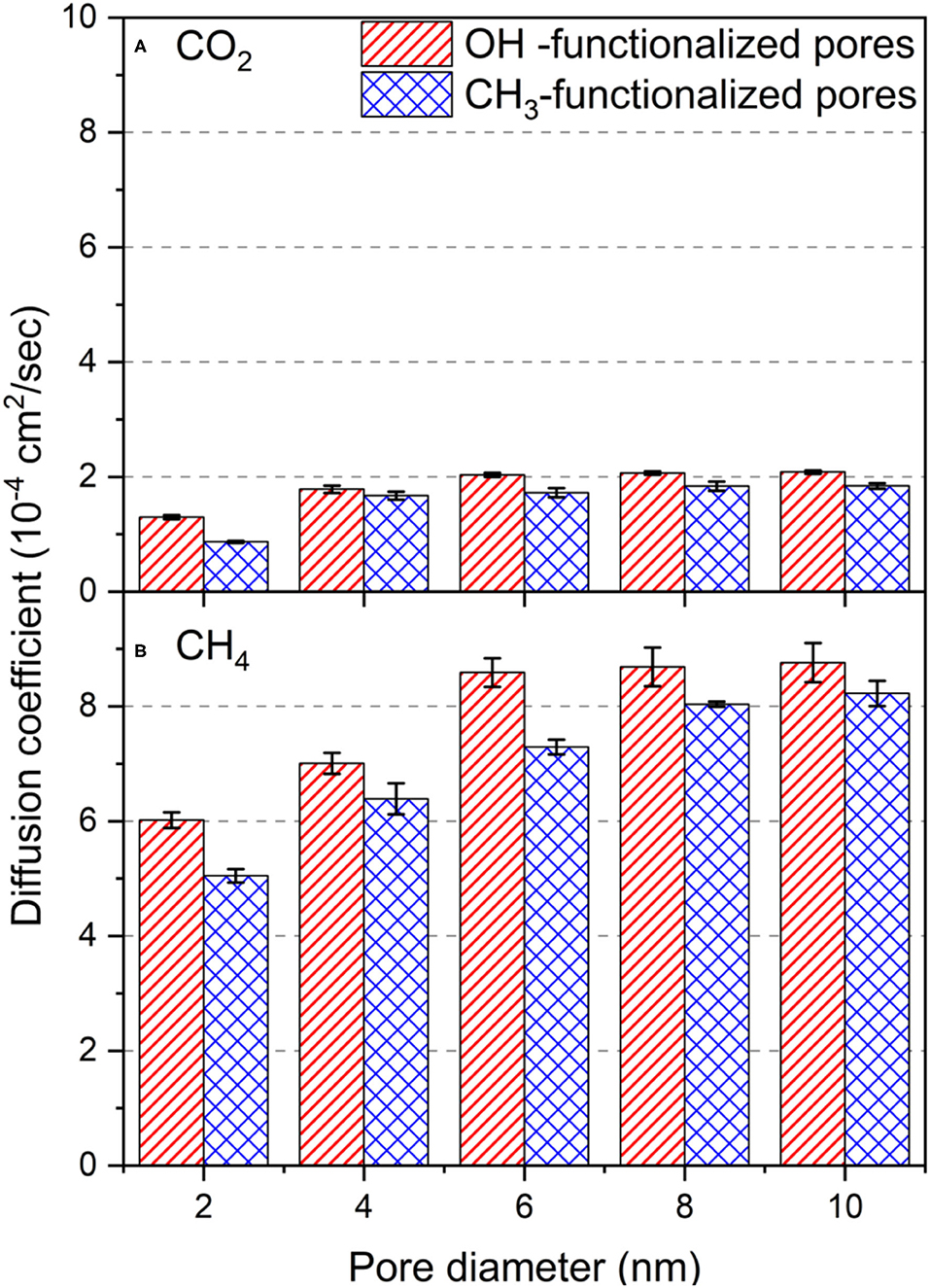
Figure 9. The self-diffusion coefficient of (A) CO₂ and (B) CH₄ molecules in OH-terminated and CH₃-terminated pores as a function of the pore diameter. Diffusion coefficients are averaged over the last 10 ns of the simulation time. Error bars represent the standard deviation from the mean values of the three different simulations.

In the expression above, l² was calculated in the xy plane (n = 2), and t is the time. The diffusion coefficients of confined CO₂ and CH₄ increase systematically with the pore diameter in OH-terminated and CH₃-terminated pores. The diffusion coefficients of CO₂ in OH-terminated pores increased from (1.29 ± 0.34) × 10⁻⁴ to (2.08 ± 0.29) × 10⁻⁴ cm²/sec as the pore diameter increases from 2 nm to 10 nm. Similarly, the diffusion coefficient of CO₂ in CH₃-terminated pores increased from (0.86 ± 0.16) × 10⁻⁴ to (1.84 ± 0.50) × 10⁻⁴ cm²/sec as the pore diameter increased from 2 to 10 nm. This increase in diffusivity with the pore diameter is attributed to the higher number of molecules confined in larger pores that occupy the adsorption sites on the pore surface and leave a large fraction of the confined molecules outside the attractive energy well near the pore surface. The non-adsorbed molecules on the pore surface can move freely along the xy direction due to the low molecular collisions and low steric hinderance in the pore center. The values of the self-diffusion coefficient of confined CO₂ match those predicted by previous studies after accounting for the differences in the pore diameter, CO₂ loading and the applied temperature (Qin et al., 2008; Le et al., 2015).

Interestingly, the diffusion coefficients in OH-terminated pores are higher than those confined in CH₃-terminated pores. The higher diffusion coefficients in OH-terminated pores can be linked to the higher adsorption extent of CO₂ molecules on the pore surface, such that it results in lower molecular density in the center of the pore. The lower molecular density in the center of the pore contributes to fewer molecular collisions in the OH-terminated pores compared to those in the CH₃-terminated pores.

The lower adsorption extent of CH₄ on OH-terminated and CH₃-terminated silica pores, relative to CO₂, result in higher in-plane self-diffusion coefficients in all the pore sizes. As the pore diameter increase from 2 nm to 10 nm, CH₄ diffusion coefficients increase from (6.01 ± 0.13) × 10⁻⁴ to (8.76 ± 0.34) × 10⁻⁴ cm²/sec, respectively, in OH-terminated pores and from (5.04 ± 0.12) × 10⁻⁴ to (8.22 ± 0.21) × 10⁻⁴ cm²/sec, respectively, in CH₃-terminated pores. The higher diffusion coefficient of CH₄ in confinement is also attributed to the lower molecular weight and the lower intermolecular interactions with the pore walls that enable even the adsorbed atoms to move faster in the xy plane compared to the adsorbed CO₂ molecules that bind strongly to the pore surfaces.

In addition, the diffusion coefficients of CO₂ and CH₄ in OH-terminated and CH₃-terminated pores vary across the pore space such that the adsorbed molecules on the pore surface diffuse slower than the molecules in the center of the pore (see Table 2). The lower diffusion coefficients in the adsorbed layers are derived by the intermolecular interactions with the pore surface that results in the domination of surface diffusion. In contrast, the absence of surface interactions and lower density profiles in the pore center enable the gas molecules to diffuse faster relative to the adsorbed layers. The confined free gas molecules diffuse faster than the adsorbed molecules on the pore surfaces by an order of magnitude in the simulated pores.

TABLE 2

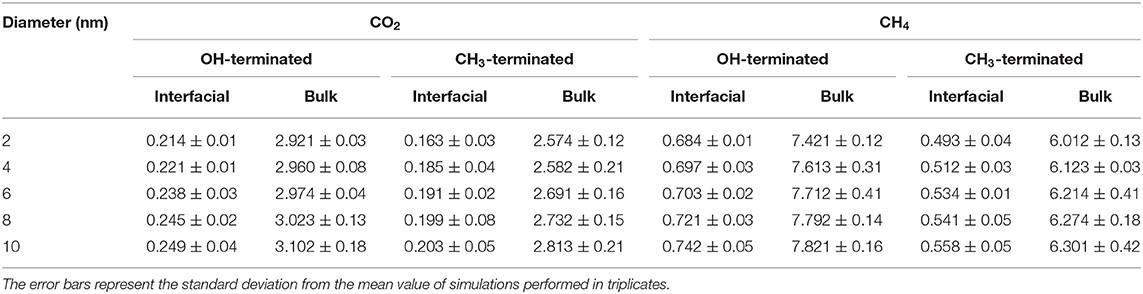
Table 2. Self-diffusion coefficients (10⁻⁴ cm⁻²/sec) of interfacial and confined free gas molecules (bulk) in OH-terminated and CH₃-terminated pores as a function of the pore diameter.

Energetics of Confined CO₂ and CH₄

The intermolecular interaction energies of CO₂ and CH₄ molecules with the silica surfaces are calculated to elucidate the energetic basis of the varying adsorption extents, organization of interfacial CO₂ and CH₄ molecules, and dynamics with changes in the functionalized surfaces and the pore diameter (see Figure 10). Van der Waals and electrostatic interactions are averaged over the last 10 ns of the simulations time as a function of the pore diameter. Error bars represent the standard deviation from the mean value of these three different simulations.

FIGURE 10

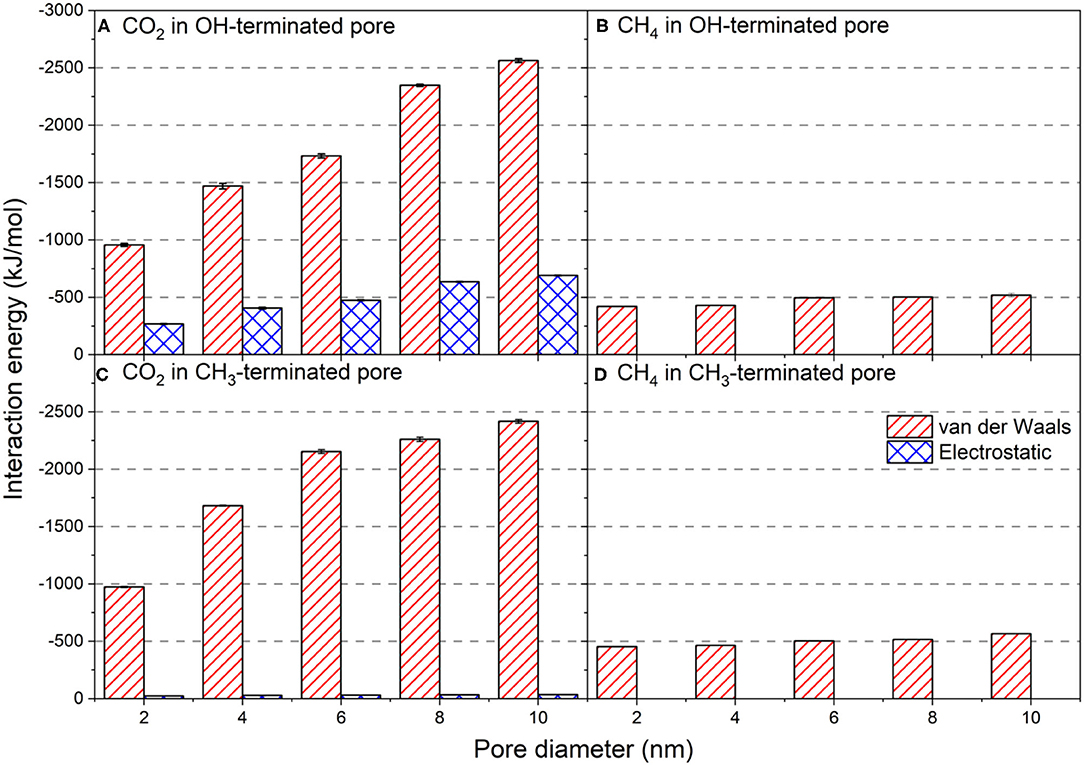
Figure 10. Van der Waals and electrostatic interaction energies of CO₂ and CH₄ with (A,C) OH-terminated and (B,D) CH₃-terminated pores as a function of the pore diameter. The intermolecular interactions are averaged over the last 10 ns of the simulation time. Error bars represent the standard deviation from the means values of three different simulations.

Van der Waals interactions of CO₂ with OH-terminated pores increase systematically with the pore diameter (Figure 10A). Van der Waals interactions in OH-terminated pores increased from −956.6 ± 13 to −2,563.5 ± 16 kJ/mol as the pore diameter increased from 2 to 10 nm. Similarly, van der Waals interactions between confined CO₂ molecules and CH₃-terminated pores have systematically increased from −972.6 ± 5 to −2,417.1 ± 16 kJ/mol as the pore diameter increase from 2 to 10 nm (Figure 10C). The increase in van der Waals interactions with the increase in pore diameter is attributed to the higher number of molecules in larger pores that are required to maintain the chemical potential. The larger number of molecules results in more intermolecular collisions between the interfacial CO₂ molecules and functional groups (OH and CH₃) on the pore surface. However, the difference in the magnitude of van der Waals interactions between the confined CO₂ molecules with OH-terminated and CH₃-terminated pores are not significant, suggesting that the intensity of intermolecular collisions between confined CO₂ and pore surfaces is independent of the type of functional group on the pore surface.

Electrostatic interactions, on the other hand, showed a profound difference in OH-terminated pores compared to CH₃-terminated pores. The electrostatic interactions between CO₂ and OH-terminated pores are higher compared to those between CO₂ and CH₃-terminated pores by an order of magnitude. The electrostatic interactions between OH-terminated pores and the confined CO₂ molecules increased from −267.5 ± 4 to −690.5 ± 4 kJ/mol as the pore diameter increased from 2 nm to 10 nm. The electrostatic interactions between CO₂ molecules and CH₃-terminated pores showed a slight increase from −23.0 ± 1 to −35.4 ± 1 kJ/mol as the pore diameter increased from 2 nm to 10 nm. Since the differences in the van der Waals interactions are insignificant, the profound difference in electrostatic interactions between CO₂ and silica pores drives the preferential adsorption of confined CO₂ on OH-terminated pores. The higher electrostatic interactions between CO₂ and OH-terminated pores stems from the quadruple moment of CO₂ molecules.

Further, CO₂ molecules form hydrogen bonds with the OH-group on the silica surfaces that contribute positively to the overall intermolecular interactions. The hydrogen bonds between the confined CO₂ molecules and OH-terminated surfaces increases from 33 ± 2 to 102 ± 4 as the pore diameter increases from 2 to 10 nm, respectively. The energy of a hydrogen bond can vary from 1 to 40 kcal/mol. The observed electrostatic interactions and hydrogen bonding between confined CO₂ and OH-terminated silica surfaces are consistent with previous studies (Mohammed and Gadikota, 2019a).

The intermolecular interactions between the confined CH₄ and pore walls are driven by van der Waals interactions with negligible contributions from the electrostatic interactions (see Figures 10B,D) due to the non-polar characteristics of CH₄ molecules, and they slightly with the pore diameter. The intermolecular interactions of CH₄ with the CH₃-teminated pores are slightly lower than compared to the OH-terminated pores, which explains the higher adsorption extents of CH₄ on CH₃-terminated pores (see Figure 6). The higher van der Waals interactions combined with the contribution of the electrostatic interactions of CO₂ with the OH-terminated and CH₃-terminated pores results in a preferential adsorption of CO₂ on the silica pores with different surface chemistries over non-polar hydrocarbons. This data suggests that the hydrophilic surfaces aid the preferential adsorption of CO₂ and the displacement of hydrocarbons, including CH₄, away from the silica surfaces.

Conclusions

The structure, dynamics and energetics of confined CO₂ and CH₄ in OH-terminated and CH₃-terminated silica pores with diameters ranging from 2 nm to 10 nm are investigated using classical molecular dynamics simulations. In this study, anisotropic distribution of CO₂ and CH₄ molecules in confinement is noted with higher number densities observed adjacent to the pore surfaces. Preferential adsorption of CO₂ on the surfaces of OH-terminated and CH₃-terminated pores over CH₄ is attributed to favorable intermolecular interactions with the hydroxyl functional groups. CO₂ and CH₄ molecules adsorb closer to the surfaces of OH-terminated pores than CH₃-terminated pores. Higher adsorption extents of CO₂ are noted compared to CH₄, and the adsorption extent increases with the pore diameter. The diffusion coefficients of confined CO₂ and CH₄ showed higher values in larger pores, and confined CH₄ diffuses faster than CO₂ in all pore sizes. The higher adsorption extent of CO₂ over CH₄ on the surfaces of OH-terminated and CH₃-terminated pores stems from significantly stronger van der Waals interactions with considerable contributions from electrostatic interactions. Thus, delineating the organization and transport behavior of CO₂ and CH₄ molecules in confinement in hydrophobic and hydrophilic pores provides the basis for tuning surface chemical interactions for storing gases in engineered materials and for predicting the fate of multicomponent fluids in porous environments in subsurface geologic formations.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

SM constructed the simulations and completed the first draft of the manuscript. AS and CW contributed to the simulations and data analyses. GG developed the concept and edited the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported as part of the Multi-Scale Fluid-Solid Interactions in Architected and Natural Materials (MUSE), an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award # DE-SC0019285.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors gratefully acknowledge the support from Akanksha Srivastava at Cornell University for assisting the effort.

References

Abraham, M. J., Murtola, T., Schulz, R., Páll, S., Smith, J. C., Hess, B., et al. (2015). GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 1, 19–25. doi: 10.1016/j.softx.2015.06.001

CrossRef Full Text | Google Scholar

Aydin, G., Karakurt, I., and Aydiner, K. (2010). Evaluation of geologic storage options of CO₂: applicability, cost, storage capacity, and safety. Energy Policy 38, 5072–5080. doi: 10.1016/j.enpol.2010.04.035

CrossRef Full Text | Google Scholar

Bachu, S., Bonijoly, D., Bradshaw, J., Burruss, R., Holloway, S., Christensen, N. P., et al. (2007). CO₂ storage capacity estimation: methodology and gaps. Int. J. Greenh. Gas Control 1, 430–443. doi: 10.1016/S1750-5836(07)00086-2

CrossRef Full Text | Google Scholar

Baumgartner, B., Hayden, J., Loizillon, J., Steinbacher, S., Grosso, D., and Lendl, B. (2019). Pore size-dependent structure of confined water in mesoporous silica films from water adsorption/desorption using ATR–FTIR spectroscopy. Langmuir 35, 11986–11994. doi: 10.1021/acs.langmuir.9b01435

PubMed Abstract | CrossRef Full Text | Google Scholar

Berta, M., Dethlefsen, F., Ebert, M., SchäFer, D., and Dahmke, A. (2018). Geochemical effects of millimolar hydrogen concentrations in groundwater: an experimental study in the context of subsurface hydrogen storage. Environ. Sci. Technol. 52, 4937–4949. doi: 10.1021/acs.est.7b05467

PubMed Abstract | CrossRef Full Text | Google Scholar

Chaikittisilp, W., Khunsupat, R., Chen, T. T., and Jones, C. W. (2011). Poly (allylamine)–mesoporous silica composite materials for CO₂ capture from simulated flue gas or ambient air. Ind. Eng. Chem. Res. 50, 14203–14210. doi: 10.1021/ie201584t

CrossRef Full Text | Google Scholar

Chiang, W. S., Fratini, E., Baglioni, P., Chen, J. H., and Liu, Y. (2016a). Pore size effect on methane adsorption in mesoporous silica materials studied by small-angle neutron scattering. Langmuir 32, 8849–8857. doi: 10.1021/acs.langmuir.6b02291

PubMed Abstract | CrossRef Full Text | Google Scholar

Chiang, W. S., Fratini, E., Baglioni, P., Georgi, D., Chen, J. H., and Liu, Y. (2016b). Methane adsorption in model mesoporous material, SBA-15, studied by small-angle neutron scattering. J. Phys. Chem. C 120, 4354–4363. doi: 10.1021/acs.jpcc.5b10688

CrossRef Full Text | Google Scholar

Cogswell, C. F., Jiang, H., Ramberger, J., Accetta, D., Willey, R. J., and Choi, S. (2015). Effect of pore structure on CO₂ adsorption characteristics of aminopolymer impregnated MCM-36. Langmuir 31, 4534–4541. doi: 10.1021/la505037f

PubMed Abstract | CrossRef Full Text | Google Scholar

Cygan, R. T., Liang, J. J., and Kalinichev, A. G. (2004). Molecular models of hydroxide, oxyhydroxide, and clay phases and the development of a general force field. J. Phys. Chem. B 108, 1255–1266. doi: 10.1021/jp0363287

CrossRef Full Text | Google Scholar

Dündar-Tekkaya, E., and Yürüm, Y. (2016). Mesoporous MCM-41 material for hydrogen storage: a short review. Int. J. Hydrogen Energ. 41, 9789–9795. doi: 10.1016/j.ijhydene.2016.03.050

CrossRef Full Text | Google Scholar

Düren, T., Sarkisov, L., Yaghi, O. M., and Snurr, R. Q. (2004). Design of new materials for methane storage. Langmuir 20, 2683–2689. doi: 10.1021/la0355500

PubMed Abstract | CrossRef Full Text | Google Scholar

Elola, M. D., and Rodriguez, J. (2019). Preferential adsorption in ethane/carbon dioxide fluid mixtures confined within silica nanopores. J. Phys. Chem. C 123, 30937–30948. doi: 10.1021/acs.jpcc.9b07969

CrossRef Full Text | Google Scholar

Evans, D. J., and Holian, B. L. (1985). The nose–hoover thermostat. J. Chem. Phys. 83, 4069–4074. doi: 10.1063/1.449071

CrossRef Full Text | Google Scholar

Farajzadeh, R., Eftekhari, A. A., Dafnomilis, G., Lake, L. W., and Bruining, J. (2020). On the sustainability of CO₂ storage through CO₂-enhanced oil recovery. Appl. Energy 261:114467. doi: 10.1016/j.apenergy.2019.114467

CrossRef Full Text | Google Scholar

Gadikota, G., Dazas, B., Rother, G., Cheshire, M. C., and Bourg, I. C. (2017). Hydrophobic solvation of gases (CO₂, CH₄, H₂, noble gases) in clay interlayer nanopores. J. Phys. Chem. C 121, 26539–26550. doi: 10.1021/acs.jpcc.7b09768

CrossRef Full Text | Google Scholar

Ghoufi, A., Hureau, I., Morineau, D., Renou, R., and Szymczyk, A. (2013). Confinement of tert-butanol nanoclusters in hydrophilic and hydrophobic silica nanopores. J. Phys. Chem. C 117, 15203–15212. doi: 10.1021/jp404702j

CrossRef Full Text | Google Scholar

Giannozzi, P., Andreussi, O., Brumme, T., Bunau, O., Nardelli, M. B., Calandra, M., et al. (2017). Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Mat. 29:465901. doi: 10.1088/1361-648X/aa8f79

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, Y., Liu, J., Huang, L., He, X., and Li, J. (2019). Predicting the phase diagram of solid carbon dioxide at high pressure from first principles. Npj Quantum Mater. 4, 1–7. doi: 10.1038/s41535-019-0149-0

CrossRef Full Text | Google Scholar

Head, J. D., and Zerner, M. C. (1985). A broyden—fletcher—goldfarb—shanno optimization procedure for molecular geometries. Chem. Phys. Lett. 122, 264–270. doi: 10.1016/0009-2614(85)80574-1

CrossRef Full Text | Google Scholar

Humphrey, W., Dalke, A., and Schulten, K. (1996). VMD: visual molecular dynamics. J. Mol. Graphics 14, 33–38. doi: 10.1016/0263-7855(96)00018-5

CrossRef Full Text | Google Scholar

Huo, P., Zhang, D., Yang, Z., Li, W., Zhang, J., and Jia, S. (2017). CO₂ geological sequestration: displacement behavior of shale gas methane by carbon dioxide injection. Int. J. Greenh. Gas Control 66, 48–59. doi: 10.1016/j.ijggc.2017.09.001

CrossRef Full Text | Google Scholar

Jiang, X. (2011). A review of physical modelling and numerical simulation of long-term geological storage of CO₂. Appl. Energy 88, 3557–3566. doi: 10.1016/j.apenergy.2011.05.004

CrossRef Full Text | Google Scholar

Jin, J., Asai, P., Wang, X., Miller, J. D., and Deo, M. (2021). Simulation and analysis of slip flow of water at hydrophobic silica surfaces of nanometer slit pores. Colloid. Surf. A 626:127032. doi: 10.1016/j.colsurfa.2021.127032

CrossRef Full Text | Google Scholar

Jin, J., Wang, X., Wick, C. D., Dang, L. X., and Miller, J. D. (2019). Silica surface states and their wetting characteristics. Surf. Innov. 8, 145–157. doi: 10.1680/jsuin.19.00053

CrossRef Full Text | Google Scholar

Jorgensen, W. L., Maxwell, D. S., and Tirado-Rives, J. (1996). Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 118, 11225–11236. doi: 10.1021/ja9621760

CrossRef Full Text | Google Scholar

Klewiah, I., Berawala, D. S., Walker, H. C. A., Andersen, P. Ø., and Nadeau, P. H. (2020). Review of experimental sorption studies of CO2 and CH4 in shales. J. Nat. Gas Sci. Eng. 73:103045. doi: 10.1016/j.jngse.2019.103045

CrossRef Full Text | Google Scholar

Knight, A. W., Kalugin, N. G., Coker, E., and Ilgen, A. G. (2019). Water properties under nano-scale confinement. Sci. Rep. 9, 1–12. doi: 10.1038/s41598-019-44651-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuuskraa, V. A., Godec, M. L., and Dipietro, P. (2013). CO₂ utilization from “next generation” CO₂ enhanced oil recovery technology. Enrgy Procedia 37, 6854–6866. doi: 10.1016/j.egypro.2013.06.618

CrossRef Full Text | Google Scholar

Le, T., Ogbe, S., Striolo, A., and Cole, D. R. (2016). N-octane diffusivity enhancement via carbon dioxide in silica slit-shaped nanopores–a molecular dynamics simulation. Mol. Simul. 42, 745–752. doi: 10.1080/08927022.2015.1089991

CrossRef Full Text | Google Scholar

Le, T., Striolo, A., and Cole, D. R. (2015). CO₂-C₄H₁₀ mixtures simulated in silica slit pores: relation between structure and dynamics. J. Phys. Chem. C 119, 15274–15284. doi: 10.1021/acs.jpcc.5b03160

CrossRef Full Text | Google Scholar

Li, K. M., Jiang, J. G., Tian, S. C., Chen, X. J., and Yan, F. (2014). Influence of silica types on synthesis and performance of amine–silica hybrid materials used for CO₂ capture. J. Phys. Chem. C 118, 2454–2462. doi: 10.1021/jp408354r

CrossRef Full Text | Google Scholar

Liu, F. Q., Wang, L., Huang, Z. G., Li, C. Q., Li, W., Li, R. X., et al. (2014). Amine-tethered adsorbents based on three-dimensional macroporous silica for CO₂ capture from simulated flue gas and air. ACS Appl. Mater. Interf. 6, 4371–4381. doi: 10.1021/am500089g

CrossRef Full Text | Google Scholar

Mafra, L., Cendak, T., Schneider, S., Wiper, P. V., Pires, J., Gomes, J. R., et al. (2018). Amine functionalized porous silica for CO₂/CH₄ separation by adsorption: which amine and why. Chem. Eng. J. 336, 612–621. doi: 10.1016/j.cej.2017.12.061

CrossRef Full Text | Google Scholar

Michael, K., Golab, A., Shulakova, V., Ennis-King, J., Allinson, G., Sharma, S., et al. (2010). Geological storage of CO₂ in saline aquifers—a review of the experience from existing storage operations. Int. J. Greenh. Gas Control 4, 659–667. doi: 10.1016/j.ijggc.2009.12.011

CrossRef Full Text | Google Scholar

Mohammed, S., Asgar, H., Kuzmenko, I., and Gadikota, G. (2020a). self-assembly of silica nanoparticles at water-hydrocarbon interfaces: insights from in-operando small-angle x-ray scattering measurements and molecular dynamics simulations. Energy Fuels 34, 12545–12555. doi: 10.1021/acs.energyfuels.0c02759

CrossRef Full Text | Google Scholar

Mohammed, S., and Gadikota, G. (2018). The effect of hydration on the structure and transport properties of confined carbon dioxide and methane in calcite Nanopores. Front. Energy Res. 6:86. doi: 10.3389/fenrg.2018.00086

CrossRef Full Text | Google Scholar

Mohammed, S., and Gadikota, G. (2019a). CO₂-Induced displacement and diffusive transport of shale geofluids in silica nanopores of varying sizes. J. CO₂ Utilizat. 32, 37–45. doi: 10.1016/j.jcou.2019.03.023

CrossRef Full Text | Google Scholar

Mohammed, S., and Gadikota, G. (2019b). The role of calcite and silica interfaces on the aggregation and transport of asphaltenes in confinement. J. Mol. Liq. 274, 792–800. doi: 10.1016/j.molliq.2018.10.163

CrossRef Full Text | Google Scholar

Mohammed, S., and Gadikota, G. (2020). Exploring the role of inorganic and organic interfaces on CO₂ and CH₄ partitioning: case study of silica, illite, calcite, and kerogen nanopores on gas adsorption and nanoscale transport behaviors. Energy Fuels 34, 3578–3590. doi: 10.1021/acs.energyfuels.0c00052

CrossRef Full Text | Google Scholar

Mohammed, S., Liu, M., and Gadikota, G. (2021). Resolving the organization of CO₂ molecules confined in silica nanopores using in situ small-angle neutron scattering and molecular dynamics simulations. Environ. Sci. Nano. 8, 2006–2018. doi: 10.1039/D0EN01282C

CrossRef Full Text | Google Scholar

Mohammed, S., Liu, M., Liu, Y., and Gadikota, G. (2020b). Probing the core-shell organization of nano-confined methane in cylindrical silica pores using in-situ small-angle neutron scattering and molecular dynamics simulations. Energy Fuels 34, 15246–15256. doi: 10.1021/acs.energyfuels.0c02237

CrossRef Full Text | Google Scholar

Neupane, H. K., and Adhikari, N. P. (2020). Structure, electronic and magnetic properties of 2D Graphene-Molybdenum diSulphide (G-MoS2) heterostructure (HS) with vacancy defects at Mo sites. Comput. Condens. Mater 24:e00489. doi: 10.1016/j.cocom.2020.e00489

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77:3865. doi: 10.1103/PhysRevLett.77.3865

CrossRef Full Text | Google Scholar

Pfeiffer, W. T., and Bauer, S. (2015). Subsurface porous media hydrogen storage–scenario development and simulation. Energy Procedia 76, 565–572. doi: 10.1016/j.egypro.2015.07.872

CrossRef Full Text | Google Scholar

Phan, A., Cole, D. R., and Striolo, A. (2014). Aqueous methane in slit-shaped silica nanopores: high solubility and traces of hydrates. J. Phys. Chem. C 118, 4860–4868. doi: 10.1021/jp500081t

CrossRef Full Text | Google Scholar

Potoff, J. J., and Siepmann, J. I. (2001). Vapor–liquid equilibria of mixtures containing alkanes, carbon dioxide, and nitrogen. AIChE J. 47, 1676–1682. doi: 10.1002/aic.690470719

CrossRef Full Text | Google Scholar

Qin, Y., Yang, X., Zhu, Y., and Ping, J. (2008). Molecular dynamics simulation of interaction between supercritical CO2 fluid and modified silica surfaces. J. Phys. Chem. C 112, 12815–12824. doi: 10.1021/jp711964e

CrossRef Full Text | Google Scholar

Serna-Guerrero, R., Da'na, E., and Sayari, A. (2008). New insights into the interactions of CO₂ with amine-functionalized silica. Ind. Eng. Chem. Res. 47, 9406–9412. doi: 10.1021/ie801186g

CrossRef Full Text | Google Scholar

Sharma, V., Kagdada, H. L., Jha, P. K., Spiewak, P., and Kurzydłowski, K. J. (2019). Halogenation of SiGe monolayers: robust changes in electronic and thermal transport. Phys. Chem. Chem. Phys. 21, 19488–19498. doi: 10.1039/C9CP03822A

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, Z., Jessen, K., and Tsotsis, T. T. (2020). Impacts of the subsurface storage of natural gas and hydrogen mixtures. Int. J. Hydrogen Energy 45, 8757–8773. doi: 10.1016/j.ijhydene.2020.01.044

CrossRef Full Text | Google Scholar

Siderius, D. W., Krekelberg, W. P., Chiang, W. S., Shen, V. K., and Liu, Y. (2017). Quasi-two-dimensional phase transition of methane adsorbed in cylindrical silica mesopores. Langmuir 33, 14252–14262. doi: 10.1021/acs.langmuir.7b03406

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, D., Wang, L., Zhang, L., Cai, C., Li, N., and Yang, M. (2020). A modified model for estimating excess adsorption of methane in moist nanoporous silica. Chem. Phys. 533:110740. doi: 10.1016/j.chemphys.2020.110740

CrossRef Full Text | Google Scholar

Wiheeb, A. D., Kim, J., and Othman, M. R. (2015). Highly perm-selective micro-porous hydrotalcite-silica membrane for improved carbon dioxide-methane separation. Sep. Sci. Technol. 50, 1701–1708. doi: 10.1080/01496395.2014.987300

CrossRef Full Text | Google Scholar

Wu, H., Chen, J., and Liu, H. (2015). Molecular dynamics simulations about adsorption and displacement of methane in carbon nanochannels. J. Phys. Chem. C 119, 13652–13657. doi: 10.1021/acs.jpcc.5b02436

CrossRef Full Text | Google Scholar

Xiong, J., Liu, K., Liu, X., Liang, L., and Zeng, Q. (2016). Molecular simulation of methane adsorption in slit-like quartz pores. RSC Adv. 6, 110808–110819. doi: 10.1039/C6RA22803H

CrossRef Full Text | Google Scholar

Xiong, J., Liu, X., Liang, L., and Zeng, Q. (2017). Adsorption of methane in organic-rich shale nanopores: an experimental and molecular simulation study. Fuel 200, 299–315. doi: 10.1016/j.fuel.2017.03.083

CrossRef Full Text | Google Scholar

Yun, J. H., Düren, T., Keil, F. J., and Seaton, N. A. (2002). Adsorption of methane, ethane, and their binary mixtures on MCM-41: experimental evaluation of methods for the prediction of adsorption equilibrium. Langmuir 18, 2693–2701. doi: 10.1021/la0155855

CrossRef Full Text | Google Scholar

Zhang, M., and Bachu, S. (2011). Review of integrity of existing wells in relation to CO₂ geological storage: what do we know? Int. J. Greenh. Gas Control 5, 826–840. doi: 10.1016/j.ijggc.2010.11.006

CrossRef Full Text | Google Scholar