Regime Shifts in Glacier and Ice Sheet Response to Climate Change: Examples From the Northern Hemisphere

Glaciers and ice sheets are experiencing dramatic changes in response to recent climate change. This is true in both mountain and polar regions, where the extreme sensitivity of the cryosphere to warming temperatures may be exacerbated by amplification of global climate change. For glaciers and ice sheets, this sensitivity is due to a number of non-linear and threshold processes within glacier mass balance and glacier dynamics. Some of this is simply tied to the freezing point of water; snow and ice are no longer viable above 0°C, so a gradual warming that crosses this threshold triggers the onset of melting or gives rise to an abrupt regime shift between snowfall and rainfall. Other non-linear, temperature-dependent processes are more subtle, such as the evolution from polythermal to temperate ice, which supports faster ice flow, a shift from meltwater retention to runoff in temperate or ice-rich (i.e., heavily melt-affected) firn, and transitions from sublimation to melting under warmer and more humid atmospheric conditions. As melt seasons lengthen, there is also a longer snow-free season and an expansion of glacier ablation area, with the increased exposure of low-albedo ice non-linearly increasing melt rates and meltwater runoff. This can be accentuated by increased concentration of particulate matter associated with algal activity, dust loading from adjacent deglaciated terrain, and deposition of impurities from industrial and wildfire activity. The loss of ice and darkening of glaciers represent an effective transition from white to grey in the world's mountain regions. This article discusses these transitions and regime shifts in the context of challenges to model and project glacier and ice sheet response to climate change.

Introduction

The IPCC (2019) special report on oceans and the cryosphere in a changing climate draws attention to a number of non-linear changes to the cryosphere that are under way as the climate warms (Collins et al., 2019). Sea ice loss and melting of the Greenland Ice Sheet have sometimes been described as “tipping elements,” vulnerable to irreversible decline beyond a particular climate threshold (e.g., Lenton et al., 2008; Ridley et al., 2010; King et al., 2020). Permafrost and mountain glaciers also have climatic thresholds for their long-term viability, while snow could be described as the definitive threshold feature of the climate system, existing below 0°C but in liquid phase above this value. Ecological and human systems have some degree of adaptive capacity and resilience to warming temperatures, but for snow and ice, the dependence on temperature is abrupt and non-negotiable.

The concept of irreversible climatic thresholds or tipping points is nonetheless uncertain in application to the global cryosphere. Snow and ice are present across a continuum of temporal and spatial scales, which smooths the cryospheric response to climate change. As a specific example, different sectors of the Greenland Ice Sheet have different climate sensitivities, so there can be large-scale decline of the ice sheet without a complete loss of ice. The survival of the central dome of the ice sheet in the last interglacial period is testament to this, as the core of the ice sheet proved resilient to temperatures 6 ± 2°C warmer than present, sustained for several millennia (NEEM Community Members, 2013; Yau et al., 2016). That is not to say that the Greenland Ice Sheet was insensitive to this warming; Yau et al. (2016) estimate that the ice sheet lost about 70% of its current volume, the equivalent of ~5 m of global sea level, before the ice sheet fully re-established itself during the early stages of the last glaciation. Hence, the Greenland Ice Sheet was greatly impacted by the Eemian warming, but ice sheet retreat was neither inexorable nor irreversible.

Most elements of the cryosphere are immediately responsive to climate fluctuations, inclusive of changes that drive either the accumulation or the loss of snow and ice (e.g., Armour et al., 2011). The Greenland Ice Sheet is projected to reach a condition of negative surface mass balance this century (e.g., van den Broeke et al., 2016; Muntjewerf et al., 2020), which will accelerate ice sheet thinning and decline. However, the complete demise of the ice sheet requires many centuries to millennia (e.g., Huybrechts and De Wolde, 1999; Aschwanden et al., 2019), and could be stabilised or reversed under cooler climate conditions in future centuries. Mountain glacier melt, sea ice decline, and permafrost thaw are all reversible as well, although there may be a lag of years to decades after the climate first stabilises, due to the current state of disequilibrium. Hysteresis in the system can also make it more difficult to recover from the decline or loss of some elements of the cryosphere (e.g., Ridley et al., 2010; Levermann and Winkelmann, 2016).

While cryospheric changes are reversible in principle and tipping points are not well-defined, there is no question that snow and ice lack resilience to a continually warming climate. Most parts of the cryosphere have responded dramatically to recent climate change (IPCC, 2019), and will continue to do so if subject to ongoing warming. There are also many non-linearities and “local” thresholds associated with the loss of snow and ice, associated with feedbacks and regime changes in the cryosphere-climate system. This article outlines several such processes associated with glacier and ice sheet melt. Improved monitoring and modelling of these regime changes will increase confidence in projections of glacier and ice sheet response to climate change and the associated consequences for sea level rise, water resources, and mountain hazards.

Field Sites and Methods

Field Sites

Examples of regime shifts in glacier and ice sheet response to climate change presented in this article are assessed from recent literature, involving established but incompletely-understood processes. I also draw from field studies of glacier-climate processes carried out at Haig and Kwadacha Glaciers in the Canadian Rocky Mountains, Kaskawulsh Glacier in the St. Elias Mountains, and DYE-2, Greenland, on the southwestern flank of the Greenland Ice Sheet (Figure 1, Table 1).

FIGURE 1

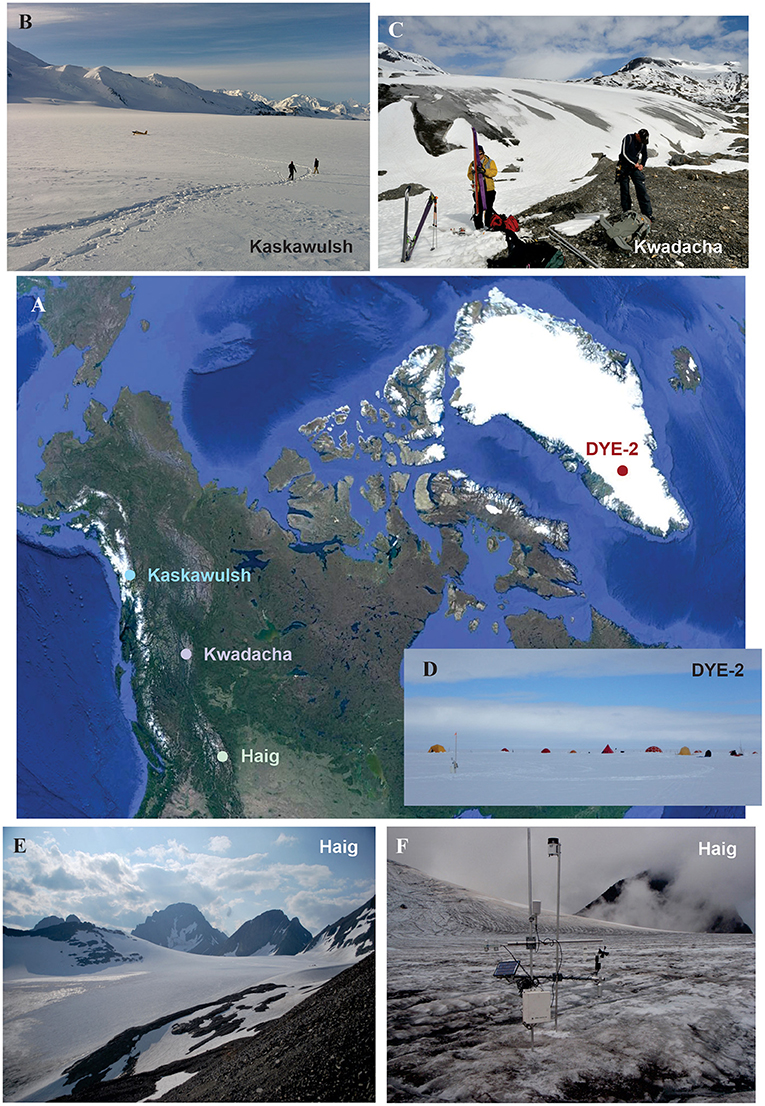
Figure 1. (A) Glacier locations for data used in this study and photographs depicting the general environment of each setting: (B) Kaskawulsh Glacier, St. Elias Mountains, (C) Kwadacha Glacier, Canadian Rocky Mountains, (D) DYE-2, Greenland Ice Sheet, and (E,F) Haig Glacier, Canadian Rocky Mountains, with (F) depicting the automatic weather station on the upper glacier. Photograph (C) is courtesy of David Roberts, photograph (E) is by Chris Szymiec, and all others by the author.

TABLE 1

Table 1. Field sites drawn from in the analyses of glacier-climate regime changes.

Glaciological and meteorological studies at Haig and Kwadacha Glaciers in the Canadian Rocky Mountains include measurement and modelling of surface energy and mass balance, climate downscaling studies, glacier flow modelling, and glacio-hydrological process studies (Marshall, 2014; Ebrahimi and Marshall, 2015). Automatic weather stations (AWSs) were installed in the glacier forefield and in the upper ablation zone of each glacier for several years, providing insight into high-elevation off- and on-glacier meteorological conditions as well as information concerning the lapse rates (elevation dependence) of different meteorological fields. Both sites have mixed continental and maritime influences, with precipitation sources dominated by Pacific air masses that transport moisture to the Canadian Rocky Mountains.

Additional data discussed within this paper are drawn from field studies at Kaskawulsh Glacier, Yukon Territory, Canada and DYE-2, Greenland over the period 2016–2018. These studies focus on firn processes, based on shallow firn coring (up to 35 m depth), field measurements of meltwater infiltration and refreezing, and numerical modelling of the coupled decadal-scale evolution of firn temperature, hydrology, density, and ice content in response to climate change.

Firn cores and firn modelling on Kaskawulsh Glacier are described in Ochwat et al. (2021). Kaskawulsh is a large (1,095 km²) glacier system within the St. Elias Mountains, and the field site for the firn cores is at an elevation of 2,640 m, in the upper accumulation area of the glacier. The site receives high amounts of precipitation delivered by Pacific storm tracks, ~1.8 m w.e. yr⁻¹, and has mean annual and mean summer (JJA) temperatures of about −11 and −2°C, respectively (Ochwat et al., 2021). The ablation zone of Kaskawulsh Glacier is temperate (ice is at the pressure melting point), but it is unknown whether conditions are polythermal or temperate in the upper accumulation area. The extent to which meltwater is refrozen and retained on the upper glacier is also uncertain.

DYE-2, Greenland is a very different glaciological setting, in the upper percolation zone of the southwestern Greenland Ice Sheet. A GC-Net automatic weather station (AWS) has been operational at this site since 1997 (Steffen and Box, 2001), and this location has been the subject of several firn studies in recent years (Machguth et al., 2016; Heilig et al., 2018; MacFerrin et al., 2019; Samimi et al., 2020; Vandecrux et al., 2020b). DYE-2 is located near the Arctic circle, at an elevation with relatively cold, dry conditions. Mean annual accumulation is ~0.36 m w.e. yr⁻¹ (Mosley-Thompson et al., 2001), with mean annual and mean summer temperatures of about −18 and −5°C. The site is in the accumulation area of the ice sheet, with low summer melt totals and sufficient pore space and cold content to refreeze and retain 100% of meltwater (Machguth et al., 2016; Vandecrux et al., 2020b). Firn cores and modelling at this site augur its likely 21st-century transition from the accumulation area to the ablation area of the ice sheet, which would be accompanied by a transition from meltwater retention to runoff.

Methods

Meteorological, surface mass balance, snow/firn hydrology, and firn-core data collected from these field sites. These data are used to constrain models of surface energy balance, snow and ice melt, and the coupled evolution of snow/firn thermodynamics and hydrology at each site. Details on the model physics and parameterizations are presented in Ebrahimi and Marshall (2016), Samimi et al. (2020), and Ochwat et al. (2021), and are summarised here to support the results and analysis in this study.

AWS data include incoming and outgoing longwave radiation, Q_L^↓ and Q_L^↑, incoming and reflected shortwave radiation, Q_S^↓ and Q_S^↑, air temperature, relative humidity, wind speed, barometric pressure, and snow surface height. Variables were typically measured at 10-s intervals, with 30-min averages saved to Campbell Scientific dataloggers. In addition to these measurements, vertical arrays of thermistors, and time-domain reflectometer (TDR) probes were installed in the supraglacial snow firn during field experiments at Haig Glacier and DYE-2, Greenland, to study the subsurface thermal and hydrological evolution through the melt season (Samimi and Marshall, 2017; Samimi et al., 2020). TDR probes measure dielectric permittivity, which is a proxy for liquid water content in the snow and firn. These data were also recorded continuously and saved to Campbell Scientific dataloggers.

For reconstructions of the long-term evolution of these glacier systems we use hourly meteorological data from ERA5 surface-level climate reanalyses for the period 1950–2020 (Hersbach et al., 2020), based on the ERA5 grid cell over the point of interest. ERA5 has a resolution of 0.25° (~28 km), so this is regionally and not locally representative. We therefore bias-adjust the ERA5 meteorological forcing using AWS data from each glacier. Where the AWS or ERA5 meteorological data are distributed over the glacier (horizontal distances of up to a few km), additional elevation adjustments are made using lapse rates for temperature and incoming longwave radiation, based on the elevation gradients measured on Haig and Kwadacha Glaciers: dT/dz = −6°C km⁻¹, dQ_L^↓/dz = −15 W m⁻² km⁻¹. Air pressure is adjusted following dP/dz = – ρ_a g, for gravitational acceleration g and air density ρ_a = P/RT. The gas law constant R = 287 J kg⁻¹ K⁻¹. In the absence of systematic observed variations, incoming shortwave radiation, wind speed, and relative humidity (RH) are assumed to be constant. Specific humidity is estimated from RH and from local air temperature and pressure.

Where upper-air analyses are included in this study, these are based on monthly mean ERA5 pressure-level data from 1950 to 2020. For the purpose of plotting the pressure-level data, altitude z_k is estimated from the pressure level, P_k, using ERA5 monthly temperature at each level, T_k. Temperature is used to calculate air density, ρ_k = P_k/RT_k, for the gas law constant R. The hydrostatic equation is then applied to estimate the elevation difference between pressure levels, dz = –dP_k/ρ_kg.

Meteorological and radiation data are used in the calculation of the surface energy balance,

$\begin{array}{ll}{Q}_N={Q_S}^{\downarrow }-{Q_S}^{\uparrow }+{Q_L}^{\downarrow }-{Q_L}^{\uparrow }+Q_H+Q_E+Q_C,& (1)\end{array}$

where Q_N is the net energy and Q_H, Q_E, and Q_C are the sensible, latent, and conductive heat fluxes, respectively, and energy fluxes are defined to be positive when they are directed toward the glacier surface. The surface energy balance model is coupled with a multi-layer subsurface model that simulates the snow, firn, and glacier temperature. Temperatures in the upper three layers are used in the calculation of the conductive heat flux, Q_C = –k_t dT/dz, for thermal conductivity k_t. The temperature of the surface layer is also used for the surface temperature and specific humidity in the sensible and latent heat flux calculations (Ebrahimi and Marshall, 2016).

When AWS data are available from the glacier, outgoing longwave, and shortwave radiation fluxes are directly available. When using climate reanalyses to drive Equation (1), these fluxes are parameterized. Outgoing longwave radiation follows Stefan-Boltzmann's equation, Q_L^↑= E_sσT_s⁴, for surface emissivity E_s = 0.98, Stefan-Boltzmann's constant σ, and absolute temperature of the surface layer, T_s. Reflected shortwave radiation Q_S^↑ = Q_S^↓ (1 – α_s), for surface albedo α_s. The albedo is modelled to decline through the melt season as a function of cumulative positive degree days, PDD,

$\begin{array}{ll}{\alpha }_s={\alpha }_{s0}-k_{\alpha }{\displaystyle \sum PDD},& (2)\end{array}$

where α_s0 is the initial (spring) albedo and k_α is a decay constant used in the modelling, which is calibrated from observed albedo data at each study site. This parameterization is meant to represent observed reductions in snow albedo that occur through the melt season due to several effects, including increases in snow grain size, rounding of grains, liquid water content, and the progressive concentration of impurities in melting snow (Brock et al., 2000). Fresh-snow events can temporarily reset the surface albedo to the dry-snow value, α_s0, during the summer melt season. I treat this as a stochastic process, simulating random summer snowfall events as described in Marshall and Miller (2020). Once the fresh snow has melted, the surface albedo is restored to its pre-snow value.

When the surface layer is at 0°C and Q_N > 0, net energy in Equation (1) goes to melting, following

$\begin{array}{ll}ṁ=Q_N/({\rho }_w{L}_f),& (3)\end{array}$

where ṁ is the melt rate (m s⁻¹), and L_f is the latent heat of fusion. If net energy is negative and the surface layer is 0°C, any liquid water that is present will refreeze, releasing latent heat, and the surface layer can then cool once all liquid water is refrozen. When surface layer temperatures are below the melting point, and surplus or deficit of energy drives warming or cooling, based on the energy balance solution within a one-dimensional model of subsurface temperature evolution:

$\begin{array}{ll}{\rho }_b{c}_b\frac{\partial T}{\partial t}=\frac{\partial }{\partial z}\left(-k_t\frac{\partial T}{\partial z}\right)+{\phi }_t+{\rho }_w{c}_w{q}_w\frac{\partial T_w}{\partial z}.& (4)\end{array}$

Here ρ_b, c_b, and k_t are the bulk density, specific heat capacity, and thermal conductivity of the snow or firn, ρ_w and c_w are the density and specific heat capacity of water, and q_w is the vertical rate of water percolation (m s⁻¹), with water temperature T_w. The right-hand terms in Equation (4) represent heat conduction, latent heat release from meltwater refreezing, and heat transport from advection of meltwater or rainwater, respectively. The thermal conductivity of the snow and firn is calculated after Calonne et al. (2019). The refreezing term in Equation (4) has units W m⁻³ and is calculated from

$\begin{array}{ll}{\phi }_t=\frac{{{\rho }_{w}L}_fṙ}{z},& (5)\end{array}$

where ṙ is the refreezing rate (m s⁻¹) and this heat is spread across the layer thickness, Δz.

The subsurface temperature model is coupled with a simple treatment of meltwater percolation. For a snow or firn layer with thickness Δz and the volume fraction of liquid water θ_w, the amount of water in the layer (m) is equal to θ_wΔz. Conservation of mass in each subsurface layer gives the expression for local water balance,

$\begin{array}{ll}\frac{d{\theta }_w}{dt}=-\nabla ·q_w-\frac{ṙ}{z}.& (6)\end{array}$

Water that refreezes is assumed to be distributed over the layer Δz. Refreezing in Equation (6) is calculated within the subsurface thermal model, as a function of cold content in the layer. The water balance is forced at the upper boundary, where q_w is equal to the melt rate. Below this, meltwater fluxes are calculated from Darcy's law,

$\begin{array}{ll}{q}_w=-k_h({\theta ,\theta }_w,d_g)\nabla \phi ,& (7)\end{array}$

where ∇ϕ is the hydraulic gradient and the hydraulic conductivity k_h is a function of the porosity, θ, liquid water content, θ_w, and snow/firn grain size d_g. The parameterization of hydraulic conductivity for unsaturated snow and firn follows that of Meyer and Hewitt (2017). Liquid water can also be retained within the pore space due to capillary forces, calculated after Coléou and Lesaffre (1998). Only excess water, beyond the irreducible water that is retained by capillary tension, is subject to vertical infiltration following Equation (7). Within this study, I assume purely vertical (gravitational) flow, such that the divergence and gradient terms in Equations (6) and (7) are replaced by vertical derivatives.

Ice layers in snow and firn can serve as impermeable barriers to meltwater infiltration, although this is not well-understood. Meltwater infiltration has been measured through continuous ice layers up to ~0.12 m in thickness (Samimi et al., 2020). Infiltration through such layers may depend on fractures or discontinuities (Humphrey et al., 2021), which could develop in association with diurnal cycles of thermal expansion and contraction in near-surface environments. Meltwater could also potentially erode such layers. In contrast, ice slabs with thicknesses of ~0.5 m or more may be impenetrable (Gascon et al., 2013; MacFerrin et al., 2019). In modelling presented here, I assume that ice layers <0.1 m thick are transmissive and ice layers more than 0.5 m thick act as impermeable barriers (k_h = 0). For ice layers with thickness t_i between 0.1 and 0.5 m, I prescribe a non-linear decrease in permeability by a factor κ_i = 10^{−γ(ti−0.1)}, with a reference value γ = 10. This reduces k_h by four orders of magnitude as ice-layer thickness increases from 0.1 to 0.5 m. Sensitivity experiments presented in section From Meltwater Retention to Runoff explore the effects of permeable vs. impermeable ice layers.

Regime Shifts in Glaciers and Ice Sheet Response to Climate Change

From Polythermal to Temperate Firn and Ice

The thermal regime of a glacier mass is a fundamental distinction in glaciology. Outside of the tropics, the upper several metres of ice, firn, and snow on a glacier typically experiences seasonal freezing through heat loss to the atmosphere. Through thermal diffusion, this results in a winter temperature wave that propagates to depths of up to ~10 m (Cuffey and Paterson, 2010). Below this, temperate glaciers are at the pressure-melting point throughout, while polythermal glaciers have a range of temperatures (Blatter, 1987; Blatter and Hutter, 1991). Ice temperatures in polythermal glaciers are generally warmer near the bed, due to the combined effects of geothermal heat fluxes and heat dissipation from creep deformation of the ice, which is concentrated in the lower glacier (Cuffey and Paterson, 2010). Heat can also be generated at the bed from frictional heat dissipation, where the glacier is sliding over the substrate.

In some cases, polythermal ice is warm-based (at the pressure-melting point), enabling the presence of liquid water in thermal equilibrium and supporting basal flow through either sliding or subglacial sediment deformation (Clarke, 1987). In other cases, polythermal ice masses can be frozen to the bed, a condition known as cold-based ice. Freezing conditions can be maintained if heat conducted upwards through the ice exceeds inputs of energy from geothermal heat flux, creep deformation, and frictional heat dissipation. Polar glaciers, icefields, and ice sheets are typically polythermal and have a mixture of warm- and cold-based ice. Basal ice temperatures do not follow a simple relationship with mean annual air temperature, so it is difficult to predict whether high-latitude or high-altitude glaciers and ice sheets will be warm- or cold-based. For instance, much of the plateau of the East Antarctic Ice Sheet, the coldest region in the world, is underlain by warm ice (e.g., Bell et al., 2007), because the ice is thick enough (~4 km) to insulate the base from cold surface temperatures. In contrast, the interior of the Greenland Ice Sheet is frozen to the bed (Huybrechts, 1996; Marshall, 2005) because it is thinner (~3 km) and snow accumulation rates are higher than in Antarctica. This results in effective downward advection of cold surface ice in Greenland, increasing the temperature gradient (hence, conductive energy loss) in the lower part of the ice sheet. On the flanks and in the marginal areas of Greenland, most of the ice sheet is believed to be warm-based, due to the combined influences of warmer air temperatures and strain heating in areas of active vertical shear deformation. Latent heat release from refreezing meltwater in the surface snow and firn also plays a significant thermodynamic role in parts of the Greenland Ice Sheet, as discussed in this study.

The thermal regime of glaciers is important for several reasons. Warm-based ice can flow more quickly via basal flow or ice surging (e.g., Clarke, 1987; Sevestre et al., 2015), and also enables a range of subglacial hydrological processes that differ from cold-based ice (e.g., exchanges with the groundwater system; chemical weathering, erosion, and mobilisation of sediments in well-developed drainage systems; subglacial water storage). Warmer ice has a lower effective viscosity (Glen, 1955), with variations by a factor of ~1,000 from temperatures of −50 to 0°C (Marshall, 2005); hence, deformational velocities in temperate ice are much higher (e.g., Phillips et al., 2010; Bell et al., 2014). Meltwater also cannot refreeze in temperate ice and firn, limiting the extent of meltwater retention through refreezing (Pfeffer et al., 1991), although meltwater can be retained as liquid water in temperate firn where there is adequate infiltration and pore space (e.g., Koenig et al., 2014; Christianson et al., 2015). Processes of meltwater refreezing and retention are important to glacier and ice sheet mass balance (section From Meltwater Retention to Runoff).

The transition from polythermal to temperate ice is expected in some glacier environments as a consequence of climate warming (e.g., Hoelzle et al., 2011). Sub-polar glaciers are good candidates to experience this transition in the coming decades, as these systems often lie close to the climatic threshold between polythermal and temperate conditions. Firn temperature observations on Lomonosovfonna, Svalbard (Marchenko et al., 2021) indicate that temperatures at ~12-m depth may have shifted from sub-freezing to temperate conditions over the past two decades. Such a transition may also be close at high elevations in the European Alps, where warming of cold firn has been measured over the last two decades (e.g., Hoelzle et al., 2011; Mattea et al., 2021; Colle Gnifetti on Monte Rosa). Climate change trends are strong at high latitudes (e.g., Zhang et al., 2019) and high elevations (Pepin et al., 2015; Williamson S. et al., 2020), which is likely to accelerate regime changes from polythermal to temperate ice.

Ochwat et al. (2021) report on a possible transition from polythermal to temperate conditions that was discovered during ice-coring work in May 2018 on the upper Kaskawulsh Glacier in the St. Elias Mountains. The drilling team was surprised to encounter temperate firn conditions with liquid water (i.e., a firn aquifer) at ~34 m depth. Based on density measurements in the firn core, this is near the base of the firn; the aquifer appears to be a few metres thick, representing a water table that is perched on the glacier ice. It is unclear whether or not the firn aquifer is new. Previous radar studies and ice-coring efforts in the region (Zdanowicz et al., 2014) provide no prior indication of the presence of perennial firn aquifers. It is possible that temperate conditions have existed for many decades at this site, but Ochwat et al. (2021) argue that the presence of deep, temperate, and water-saturated firn is a new development on Kaskawulsh Glacier.

Firn modelling at the drill site supports this hypothesis. Extending the results reported by Ochwat et al. (2021), Figure 2 plots simulated firn temperature evolution on upper Kaskawulsh Glacier for the period 1950–2020, using the coupled thermodynamic and hydrological model described in section Methods for the upper 35 m of firn. ERA5 meteorological fields are bias-adjusted using data from a nearby automatic weather station (Ochwat et al., 2021), and initial firn temperature and stratigraphy are based on a 30-year spin-up using the ERA5 climatology from 1950 to 1979. Based on these initial conditions, the climate forcing was restarted at 1950 for the 71-year simulation plotted in Figure 2.

FIGURE 2

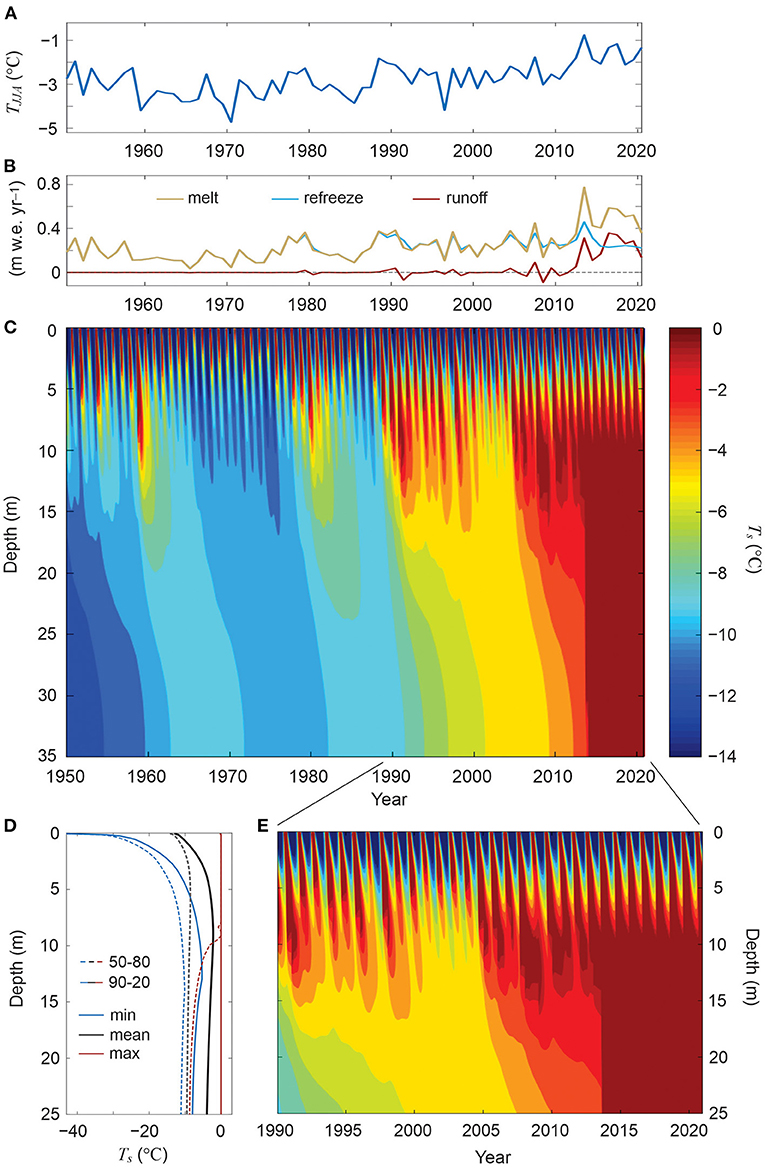
Figure 2. Modelled temperate firn development at Kaskawulsh Glacier, Yukon Territory over the period 1950–2020. (A) Mean summer air temperature in the ERA5 climate forcing. (B) Annual melt, refreezing, and runoff. Runoff is calculated from the annual melt minus refreezing. (C) Firn temperatures to 35 m depth. (D) Firn temperatures in the upper 25 m, 1990–2020 (E) Firn temperature envelope in the upper 25 m for the periods 1950–1980 (dashed) and 1990–2020 (solid lines). “Negative” runoff in (B) occurs when meltwater drainage to the deep firn from the prior summer refreezes in the subsequent calendar year.

Mean annual air temperature at the site over the period 1950–2020 was −11.2°C, increasing to an average of −10.3°C for the last decade (2010–2020), while mean summer (JJA) temperatures shifted from a long-term mean of −2.8 to −1.8°C for the last decade (Figure 2A). This decadal-scale warming was accompanied by increases in atmospheric humidity and incoming longwave radiation, as reported by Williamson S. et al. (2020), with overall increases in net energy driving an increase in surface melting at a rate of +0.03 m w.e. per decade (Figure 2B). The resulting intensification of meltwater infiltration and refreezing drove decadal-scale firn warming (Figures 2C–E), culminating in a transition from polythermal to temperate conditions in 2013–2014. Meltwater refreezing since this time provides sufficient latent heat release to maintain temperate firn, despite a mean annual air temperature of about −10°C. The climate conditions and firn processes governing this abrupt regime change are discussed in section Processes Governing Nonlinear Glacier and Ice Sheet Response to Climate Change.

This is a marked regime change for the glacier, as the glacier ice that forms from the firn will now develop into temperate ice. Glacier ice advecting downwards and downslope from the accumulation area will be more deformable than ice from earlier decades, when the firn column was cold. The importance of englacial and subglacial temperatures for ice dynamics is discussed in section Englacial and Subglacial Warming.

From Meltwater Retention to Runoff

Prior to 2013 at Kaskawulsh Glacier, all surface melt refroze within the firn (100% meltwater retention; Figure 2B). In summers with deep meltwater infiltration, liquid meltwater that is stored in the firn may not refreeze until the subsequent calendar year, as this requires penetration of the following winter's cold wave into the firn. Melting, refreezing, and runoff are calculated for the calendar year, with runoff calculated from melting minus refreezing. The lag in refreezing can give years with small amounts of positive runoff followed by years with “negative” runoff in Figure 2B; this is not a violation of conservation of mass, but an artefact of calculating this for calendar years.

Following the intensive melt season of 2013, which triggered the transition to temperate firn on Kaskawulsh Glacier, meltwater has begun to run off from this site (Figure 2B). Some summer meltwater still refreezes within the winter cold layer, which extends to about 8 m depth (Figures 2D,E), but for an average melt rate of 0.47 m w.e. yr⁻¹ from 2010 to 2020, 0.18 m w.e. yr⁻¹ (39%) is modelled to have drained to the deep firn. About half of this meltwater was retained within the firn aquifer (Ochwat et al., 2021), while the remainder is expected to have drained laterally, either as Darcian flow in the firn aquifer or at the firn-ice interface, where the glacier ice presents an impermeable barrier. This transition therefore impacts meltwater retention and surface mass balance on the upper Kaskawulsh Glacier.

This is an example of a wide-spread trend in the world's glaciers, ice caps, and ice sheets. Meltwater retention capacity is declining in response to loss of firn (e.g., Pelto, 2006) and increases in firn temperature, density, and ice content, all of which reduce the available cold content and pore space that is available for meltwater refreezing (e.g., van Angelen et al., 2013; Vandecrux et al., 2020a). Pfeffer et al. (1991) and Harper et al. (2012) describe the importance of meltwater refreezing and retention in the Greenland Ice Sheet. The firn layer acts as a buffer to sea level rise, as a large amount of meltwater stays within the ice sheet rather than running off to the ocean. Temperate snow, firn, and ice have limited capacity for meltwater retention, since liquid water cannot refreeze. Meltwater can be stored in the pore space of temperate snow and firn, but this generally drains effectively through gravitational percolation or Darcian flow in firn aquifers (e.g., Christianson et al., 2015), and water will run off once the available pore space is filled. Increases in meltwater runoff also result from reduced permeability in firn, through densification, and the development of thick near-surface ice layers (de la Peña et al., 2015; MacFerrin et al., 2019).

Noël et al. (2017) describe this transition from meltwater retention to runoff as a tipping point for glacier mass balance—from positive to negative—in glaciers and ice caps peripheral to the Greenland Ice Sheet. A similar mass balance regime change may have occurred in Svalbard, where a shift from meltwater retention to runoff has caused a large area of Svalbard's ice caps to transition from net accumulation to net ablation (Noël et al., 2020). Reductions in capacity for meltwater retention in firn have also been documented on the Barnes and Devon Ice Caps in Arctic Canada (Zdanowicz et al., 2012; Bezeau et al., 2013). This transition may also be occurring in the lower percolation zone of the Greenland Ice Sheet (Charalampidis et al., 2015; de la Peña et al., 2015). High melt rates can produce thick near-surface ice slabs which limit meltwater infiltration and refreezing (Machguth et al., 2016; MacFerrin et al., 2019). The percolation zone in Greenland is expanding to higher elevations of the ice sheet, but there is still sufficient cold content to support meltwater refreezing and retention in the vast interior regions of Greenland (Vandecrux et al., 2020a), as long as the permeability of the near-surface firn continues to permit meltwater infiltration. There is concern that strong episodic melt seasons, as observed in 2012 and 2019, may create ice layers that limit infiltration, and model projections suggest that Greenland could experience significant losses of firn meltwater retention capacity by the second half of this century (van Angelen et al., 2013).

Figure 3 plots the modelled increase in melting and meltwater runoff as a function of elevation in a simple future warming scenario on the southwestern flank of the Greenland Ice Sheet. This scenario is based on ERA5 climatology for the period 2000–2020 (Hersbach et al., 2020), followed by a linear warming rate of 0.5°C per decade from 2020 to 2100, superimposed on the climatology of the base period 2000 to 2020. This is a simplistic scenario, intended to examine the sensitivity of melting and meltwater retention processes to a hypothetical warming of 4°C in Greenland by the end of the century. The climate forcing drives a surface energy balance and firn model that have been calibrated for DYE-2 in southwest Greenland (Samimi et al., 2020), and the elevation range in Figure 3 is representative of the present-day percolation zone in southwest Greenland.

FIGURE 3

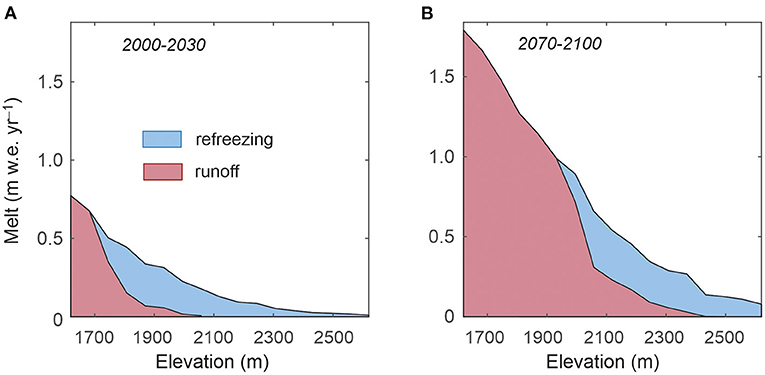
Figure 3. Mean annual surface melt rates as a function of elevation for a transect at 66.5°N in southwest Greenland for (A) 2000–2030 and (B) 2070–2100. The red shading indicates the surface runoff and the blue shading indicates the meltwater retained by refreezing.

For the period 2000–2030, the average melt rate from 1660 to 2640 m elevation in Figure 3A is 0.23 m w.e. yr⁻¹. This increases to 0.72 m w.e. yr⁻¹ for the period 2070–2100 (Figure 3B). The shading in Figure 3 indicates the fraction of meltwater runoff relative to the total meltwater production. Under a 4°C warming by end of the century, there is a transition from meltwater retention to runoff in the elevation range from ~1,800 to 2,100 m. The equilibrium line and percolation zone climb to higher elevations, and under the 4°C warming there is no longer a dry snow zone in southern Greenland. Above ~2,440 m, however, almost 100% of meltwater is still retained in 2,100. For the total elevation range represented in Figure 3, average runoff for the period 2000–2030 equals 0.08 m w.e. yr⁻¹ (33% of total melt). This increases to 0.45 m w.e. yr⁻¹ (62% of total melt) for 2070–2100 (Figure 3B). Melt rates in the present-day percolation zone of southwestern Greenland increase by a factor of ~3 under this warming scenario, but runoff increases by a factor of ~6.

This is a non-linear but continual change for Greenland Ice Sheet mass balance and meltwater runoff, rather than a threshold process. However, a given location on the ice sheet may experience a regime change such as the transition from the accumulation area to the ablation area of the ice sheet, or from meltwater retention to runoff (Charalampidis et al., 2015), similar to what was observed on Kaskawulsh Glacier in Figure 2. The nature of this regime change depends on the climate and firn conditions. As an example, Figure 4 plots the modelled firn temperature evolution at DYE-2, Greenland from 2000 to 2100 under the hypothetical warming scenario discussed in Figure 3. DYE-2 is situated at 2120 m elevation on the southwestern flank of the ice sheet. It is presently in the upper percolation zone, with moderate amounts of annual melt (~0.15 m w.e. yr⁻¹), 100% of meltwater retained as refrozen ice, a mean annual temperature of −17.4°C, and a 10-m firn temperature of about −15.5°C (Samimi et al., 2020; Vandecrux et al., 2020b). Under the imposed gradual warming scenario, the equilibrium line elevation climbs to ~2,050 m by 2100 and DYE-2 remains within the accumulation area of the ice sheet, with mean annual and summer (JJA) temperatures of −14.4 and −2.3°C for the period 2070–2100 (Figures 4A,C). Firn at DYE-2 is projected to remain polythermal through the century (Figure 4E), with 10-m temperatures of about −10°C by 2100 (Figure 4C).

FIGURE 4

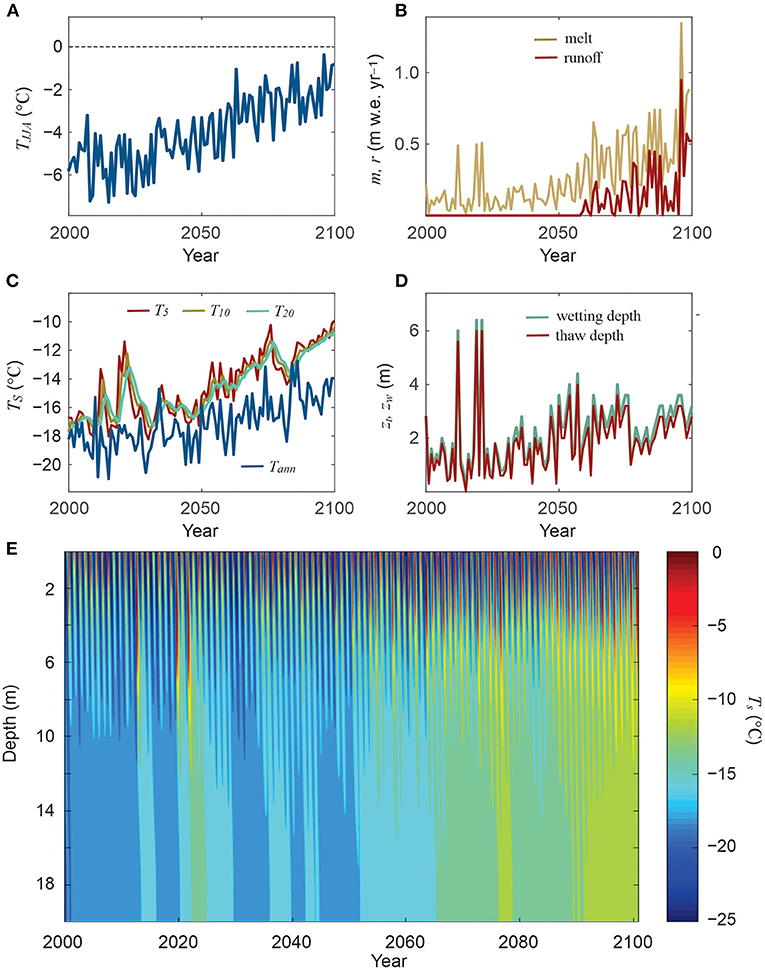
Figure 4. Modelled firn evolution at DYE-2, Greenland, 2000–2100, using ERA5 climate forcing from 2020 to 2020 and with a warming trend of 0.05°C yr⁻¹ for 2020–2100. (A) Mean summer air temperature. (B) Annual surface melt and runoff. (C) Mean annual snow/firn temperatures at the surface and at 5-, 10-, and 20-m depth. (D) Maximum annual thaw and meltwater infiltration depths. (E) Daily mean temperatures in the 20-m firn column from 2000 to 2100.

This projected firn evolution contrasts with that at Kaskawulsh Glacier for several reasons. In part, DYE-2 is colder, with less summer melt. This limits the latent heat release from meltwater refreezing, helping DYE-2 to remain polythermal. More importantly, however, deep meltwater infiltration events become less frequent in the second half of the century (Figure 5D), despite increasing melt rates (Figure 5B). Warming causes increased meltwater production in the 2050s, but much of this meltwater refreezes near the surface, driving the formation of dense firn with thick ice layers which impede meltwater infiltration. This triggers the onset of meltwater runoff from this site (Figure 5B). Hence, the site evolves from a location with 100% meltwater retention from 2000 to 2030 to an average meltwater retention of 58% from 2070 to 2100. Average net mass balance decreases from 0.38 to 0.16 m w.e. yr⁻¹ over these two periods.

FIGURE 5

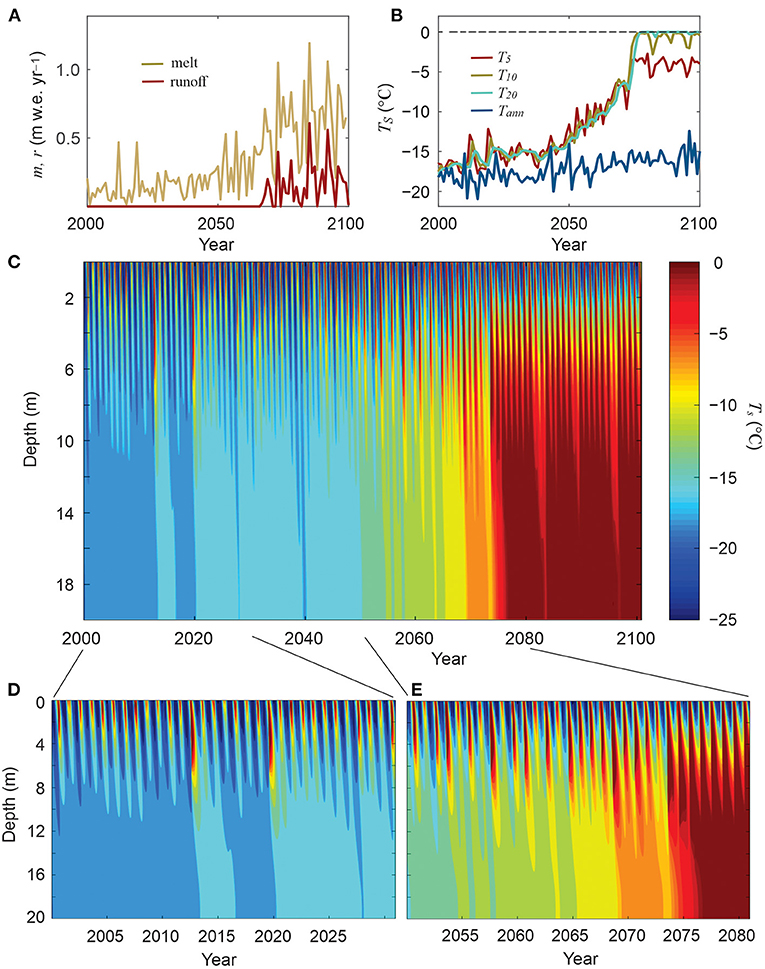
Figure 5. Modelled firn evolution at DYE-2, Greenland as per Figure 4 but prescribing a 50% increase in precipitation at DYE-2. (A) Modelled melt and runoff. (B) Mean annual air temperature and firn temperatures at 5-, 10-, and 20-m depth. (C–E) Daily mean temperatures in the 20-m firn column from 2000 to 2100, (D) 2000 to 2030, and (E) 2050 to 2080, showing the transition to deep temperate firn in 2077.

Limitations to meltwater infiltration are partly associated with the lack of near-surface cold content and pore space. As discussed by Kuipers Munneke et al. (2014), deep meltwater infiltration can be supported by high rates of snow accumulation, which increase the available pore space for meltwater refreezing and help to insulate the underlying firn, where liquid meltwater may be present from the previous melt season. As an illustration of this at DYE-2, snow accumulation rates (winter mass balance, b_w) were increased by 10% intervals from 100 to 200% of the present-day rate. The prescribed values of b_w range from an average of 0.37–0.74 m w.e. yr⁻¹ for the reference period 2000–2030. Combined with the prescribed increase in mean annual precipitation of +5%°C⁻¹ in the future warming scenario, the corresponding range in b_w for 2070–2100 is 0.44–0.87 m w.e. yr⁻¹.

The modelled 21st-century firn evolution is strongly dependent on accumulation rates (Figures 5, 6). Present-day firn conditions do not vary much in these numerical experiments, even for a doubling of accumulation, but a ~40% increase in accumulation is sufficient to give a dramatically different outcome by end of century. Figure 5 plots modelled firn temperature from 2000 to 2100 for a 50% increase in accumulation at DYE-2. All other climate and parameter settings in this experiment are identical to the baseline model shown in Figure 4. With the additional accumulation and meltwater refreezing capacity, firn at DYE-2 undergoes an abrupt transition from polythermal to temperate conditions in the late 2070s (Figures 5B,C). The transition is similar to the one observed on Kaskawulsh Glacier (Figure 2). Temperate firn from 10- to 20-m depth first develops in 2077, coinciding with meltwater infiltration through the full firn column. Modelled firn warming at 10-m depth is 1.2°C per decade, 3.4 times the rate of atmospheric warming (Figure 5B), although the firn warming is abrupt rather than linear. The winter cold wave at this site reaches a depth of about 8 m each year (Figure 5C), providing some meltwater refreezing capacity while this site remains in the accumulation area of the ice sheet. Similar to the baseline model in Figure 4, meltwater runoff from the site begins in the 2060s, associated with low-permeability near-surface ice layers.

FIGURE 6

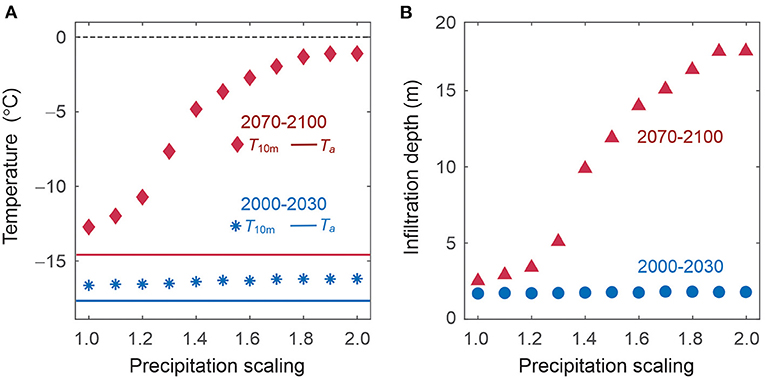
Figure 6. Effects of snow accumulation rate on modelled 21st-century (A) 10-m firn temperature and (B) meltwater infiltration depth at DYE-2, Greenland. Blue symbols are average values for the period 2000–2030 and red symbols are for 2070–2100. Lines in (A) indicate the mean annual air temperature for each period. Temperatures and infiltration depths are plotted for precipitation rates up to twice the present-day value at DYE-2, giving winter mass balances b_w ϵ [1, 2].

Figure 6 plots summary diagnostics for the precipitation sensitivity experiments, showing firn temperatures and meltwater filtrations depths for the reference period, 2000–2030 (blue symbols) and the end of the century, 2070–2100 (red symbols). The onset of deep meltwater corresponds with precipitation increases of ~40% or more, attended by deep firn warming. For 2000–2030, 10-m firn temperatures are 1.3°C warmer than the mean annual air temperature, on average. This differs only slight for 2070–2100 with the present-day accumulation rate, but for b_w values from 150 to 200% of present-day values, 10-m firn temperature is 11–14°C warmer than the mean annual air temperature. The transition to temperate conditions in the deep firn is difficult to reverse though (see section Processes Governing Nonlinear Glacier and Ice Sheet Response to Climate Change), such that this regime change leads to long-term reductions in firn meltwater retention capacity.

Meltwater Refreezing on Mountain Glaciers

Meltwater retention through refreezing is not a significant process on most mountain glaciers, due to temperate conditions, but meltwater refreezing still plays an important and more subtle effect in reducing the net energy that is available for melt. Meltwater that is stored in the pore space of near-surface snow/firn or in melt ponds on the glacier surface commonly refreezes overnight or during cold-weather episodes. This is a familiar process to mountaineers, who travel quickly and lightly over the refrozen snow and ice crust in the early morning hours. Energy is used to warm this crust to the melting point the following morning, and some of this energy is then used to “remelt” the refrozen meltwater. A significant amount of melt energy can be consumed by this recycled meltwater over several months of diurnal freeze-thaw cycles.

Samimi and Marshall (2017) estimate this process to reduce meltwater runoff by about 10% at Haig Glacier in the Canadian Rockies. Although the glacier and the supraglacial snowpack are temperate, the thin refreezing layer at the glacier surface consumes energy for the diurnal phase changes. This is consistent with the observed lag of meltwater production on the glacier surface and in the proglacial stream on a typical summer day. Diurnal increases in supraglacial streamflow commonly don't set in until late morning or early afternoon. As the climate warms and the glaciers experience less frequent overnight refreezing, diurnal freeze-thaw cycles will diminish in importance. Glaciers that are losing their firn will also see reductions in meltwater storage capacity. Collectively, these processes will result in “flashier” hydrological systems with reduced meltwater residence times.

Englacial and Subglacial Warming

Meltwater that infiltrates beyond the firn layer can also refreeze in cold glacier ice, with latent heat release directly warming up englacial or basal ice (Jarvis and Clarke, 1974). In Greenland, water that penetrates to depth through crevasses, moulins, and proglacial lake drainage (Das et al., 2008; Catania and Neumann, 2010) has been proposed as a mechanism to soften ice and increase flow rates through a process called cryo-hydrologic warming (Phillips et al., 2010). Latent heat release produces warmer ice, which has a lower effective viscosity, and liquid water content can further soften temperate ice (Cuffey and Paterson, 2010). Cryo-hydrologic warming and temperate ice therefore support greater rates of ice deformation, resulting in glacier thinning. Higher flow rates also increase the advection of ice to low elevations or the ocean, where there is surplus energy for ablation. This creates a more negative glacier mass balance and increases meltwater runoff.

Melting conditions at the glacier or ice sheet bed have the potential to induce higher rates of flow through sliding or sediment deformation, where sufficient meltwater is available to support basal flow through these processes (Iken and Bindschadler, 1986; Clarke, 1987). The transition from cold- to warm-based ice therefore represents a regime change that can fundamentally alter glacier dynamics. Increased ice fluxes through basal flow have a similar impact to low-viscosity ice: thinner ice masses, more negative mass balance, and a shorter response time to climate forcing. A transition from cold- to warm-based ice has been proposed as the trigger for deglaciation in the context of the 100-kyr glacial cycle (Marshall and Clark, 2002). The effects of basal flow have the potential to be dramatic, as observed in glacier surge cycles, since basal flow rates can greatly exceed those from internal ice deformation (e.g., Clarke, 1987; Sevestre et al., 2015).

Surging glaciers and ice streams provide clear examples of thermally-enabled, meltwater-lubricated fast flow in glaciers and ice sheets, but it is difficult to assess whether anthropogenic climate forcing can trigger changes in flow regimes. Subglacial thermal and hydrological conditions would need to evolve over large areas of the bed on annual to decadal timescales. The diffusive and advective timescales for atmospheric temperature changes to reach the subglacial environment are long: centuries for mountain glacier and millennia for ice sheets. Surface meltwater that reaches the bed has the potential to incite rapid change, through both latent heat release and impacts on subglacial hydrology (e.g., Zwally et al., 2002). Subglacial water that does not drain effectively can become pressurised, reducing basal friction (ice-bed coupling), and enabling speedups (Parizek and Alley, 2004; Colgan et al., 2012; Shannon et al., 2013).

These processes are not fully understood. The fate of meltwater that drains through crevasses, moulins, and proglacial lakes in Greenland is uncertain; some may refreeze near the surface and some may drain effectively from the ice sheet, through either englacial or subglacial pathways. To have a major effect on flow rates or on viscous softening, this water needs to penetrate to depth and remain within the ice sheet system, where it can lubricate the ice sheet bed or where refreezing can effectively warm and soften the deep ice. Das et al. (2008) and Catania and Neumann (2010) demonstrate that supraglacial water in Greenland can effectively reach the bed, so these processes have the potential to impact the ice sheet as the ablation area and wet-snow zones expand to higher elevations in Greenland in future decades. Previously frozen or dry parts of the ice sheet bed may become newly exposed to meltwater, with the potential to increase flow rates (Parizek and Alley, 2004; Shannon et al., 2013). On the other hand, efficient subglacial hydrological drainage systems typically develop in settings where large amounts of meltwater reach the bed. This effectively evacuates subglacial water rather than supporting the distributed, high-pressure water systems that support fast flow (e.g., Schoof, 2010; Sundal et al., 2011).

The net impact of climate warming and increasing amounts of meltwater on glaciers and ice sheet dynamics is uncertain. Based on ice sheet modelling, Shannon et al. (2013) conclude that the impacts of changing hydrology on basal flow are likely to be negligible in Greenland this century, in comparison with the direct impacts of climate change on surface mass balance and sea-level rise. Davison et al. (2019) reach a similar conclusion based on a review of recent literature analysing the relation between supraglacial water drainage and seasonal ice acceleration in Greenland. Models of englacial drainage and subglacial hydrology are becoming increasingly sophisticated (Flowers, 2015; Banwell et al., 2016; Hoffman et al., 2016), but challenges of scale, complexity, and the dearth of direct observations in subglacial environments limit understanding and modelling of ice-sheet scale hydrological and basal flow processes. For these reasons, ice sheet dynamical response to changing ice sheet hydrology remains an open question, and the possibility of widespread impacts of increasing meltwater supply to the bed cannot be ruled out.

Thawing at the Ice-Rock Interface

The transition from frozen to thawed conditions at the glacier bed is mirrored by thawing of the mountains themselves: reduced mountain permafrost as temperatures rise and active layers deepen. This interacts with glacier melting, as newly-exposed rock surfaces and circulating meltwater act collectively to increase mountain hazards associated with slope instabilities (Hock et al., 2019). The transition from frozen to thawed conditions can trigger rock and ice detachment processes in high-mountain regions (Gruber and Haeberli, 2007; Gilbert et al., 2015; Hock et al., 2019), through a combination of factors including decreased structural integrity (loss of ice bonding), lubrication from liquid water, and mechanical and thermal stresses from freeze-thaw cycles (Fischer et al., 2012; Haeberli et al., 2017). These processes have been linked with increasing frequency of rockfall and rock avalanches (e.g., Allen et al., 2011; Ravanel and Deline, 2011; Fischer et al., 2012; Allen and Huggel, 2013; Hock et al., 2019), and may play a role in glacier detachments (Fischer et al., 2013; Faillettaz et al., 2015; Gilbert et al., 2015). High-mountain slope failures are often associated with a mixture of ice, rock, and water. Glacier retreat can also directly influence slope stability (e.g., Allen et al., 2011; Hock et al., 2019), as fresh walls and debris become exposed and buttressing of steep slopes is reduced.

From White to Grey

The collection Darkening Peaks: Glacier Retreat, Science, and Society (Orlove et al., 2008) provides a compelling image of the transition from white to grey that is under way in the world's mountain regions. The demise of glaciers is changing the fundamental character of mountain landscapes, with direct impacts on regional weather, climate, hydrology, ecosystems, and tourism. Regional surface albedo also declines due to the loss of snow and ice, which may be contributing to elevation-dependent warming in some of the world's mountain regions (Pepin et al., 2015).

Changes in surface albedo in mountain regions can be subtle, and are less “binary” than the shift observed in polar regions when sea ice is replaced with open water. Highly-reflective seasonal snow still covers mountains for much of the year at high elevations, but there is a strong decline in albedo when seasonal snow on glaciers melts away to expose the underlying glacier ice. This transition is important to the surface energy balance and melt, and a shorter snow season contributes to regional reductions in albedo. Without snow cover, most mountain glaciers can already be described as “grey.” Glacier ice albedo varies from ~0.1 to ~0.6 (Bøggild et al., 2010; Cuffey and Paterson, 2010) but is commonly at the low end of this range on mountain glaciers. Low albedo values are associated with high concentrations of particulate matter on the ice, which can accumulate over many melt seasons. The photograph in Figure 1F illustrates this well, corresponding to an ice albedo of about 0.2.

There are numerous accounts of glaciers darkening in recent years due to increasing concentrations of particulate matter (e.g., Dumont et al., 2014; Ming et al., 2015; Tedesco et al., 2016; Stibal et al., 2017; Williamson et al., 2019). Impurities on glaciers have a variety of sources, some of which are linked to climate change. Mineral dust and aerosols make up the greatest mass fraction of particulate matter in many mountain glacier settings, associated with both local and long-range transport (e.g., Oerlemans et al., 2009; Dumont et al., 2014; Nagorski et al., 2019; Marshall and Miller, 2020). Actively deglaciating terrain typically exposes fresh sediment and rock surfaces at the glacier margins, some of which could be mobilised and deposited on the glacier. Oerlemans et al. (2009) suggest that this process may be causing an increase in dust concentrations and melt rates on the lower section of Morteratsch Glacier, Switzerland.

Organic material also constitutes a significant fraction of particulate matter on some glaciers, much of it associated with in situ algal populations (e.g., Takeuchi et al., 2001, 2006; di Mauro et al., 2020; Williamson, C. J. et al., 2020). There is an interaction between melting, mineral impurities, and biological activity, as algae and cyanobacteria require liquid water and nutrients. Warming temperatures, increase in liquid water, and longer melt seasons may be driving an increase in algal populations on glaciers and ice sheets. Albedo reductions due to algal activity have been reported at several sites (Stibal et al., 2017; Williamson et al., 2019; di Mauro et al., 2020; Williamson, C. J. et al., 2020).

Organic material and black carbon deposits on glaciers are also derived from incomplete combustion of fossil fuels, biomass burning, and forest fires (Ming et al., 2009; Keegan et al., 2014; de Magalhães Neto et al., 2019; Nagorski et al., 2019). Black carbon associated with industrial activity has been implicated in glacier darkening in the Himalayas (Ming et al., 2009, 2015). Albedo reductions have also been associated with the deposition of aerosols from wildfire activity (Keegan et al., 2014; de Magalhães Neto et al., 2019; Marshall and Miller, 2020). Wildfire represents a potential indirect effect of climate change on glaciers. There is a concern that increasing wildfire activity in western North America may be darkening glaciers in the region, contributing to increased glacier melt. Glaciers in the Canadian Rocky Mountains are vulnerable to this as they are situated downwind of wildfire activity in the U.S. Pacific Northwest and British Columbia. Marshall and Miller (2020) report ice-albedo values of as low as 0.07 during the summer of 2017, which was a record wildfire season in British Columbia at the time.

Regardless of its provenance, increased particulate matter is a positive feedback because it enhances melting, which concentrates impurities and further lowers the albedo. Indirect effects of climate change such as increasing wildfire and algal activity or increased dust deposition associated with glacier retreat exacerbate the melt-albedo feedback. While increasing concentrations of particulate matter are more of a gradual process than a regime change, the resulting melt-albedo feedbacks are accelerating the processes of deglaciation and the transition of the world's mountain regions from white to grey.

Seasonal Transition From Snow to Ice

Even in the absence of external darkening agents, climate change directly impacts surface albedo on glaciers. As noted above, the summer melt-season transition from seasonal snow to exposed glacier ice is attended by a sharp drop in surface albedo on most mountain glaciers. Reductions in winter snowpack, an earlier start to the melt season, and higher melt rates all lead to an earlier transition from seasonal snow to exposed glacier ice. In addition, transient increases in albedo from summer snow events has been shown to be important processes in reducing mass loss from the glacier (Marshall and Miller, 2020). These summer “refreshes” of the glacier surface will be less frequent under warmer conditions, as precipitation on the glacier shifts from snow to rain.

Figure 7 plots examples of these influences for the summer 2010 melt season at two different mid-latitude mountains glaciers in the Canadian Rocky Mountains. Automatic weather station (AWS) pairs were established for multi-year periods at each site: one on the glacier, in the upper ablation area, and one in the glacier forefield region (cf. Figure 7C). The off-glacier AWS at each site is situated on bare limestone. Marshall (2014) describes the Haig Glacier AWS records in detail. At Kwadacha Glacier, the forefield AWS was set up at an elevation of 1,670 m in August, 2007 and recorded continuously until August, 2011. The glacier AWS was set up at the same location on the glacier each year from 2008 to 2011, at an elevation of 2,005 m, and was established between mid-May and early June, while the glacier surface was still snow-covered.

FIGURE 7

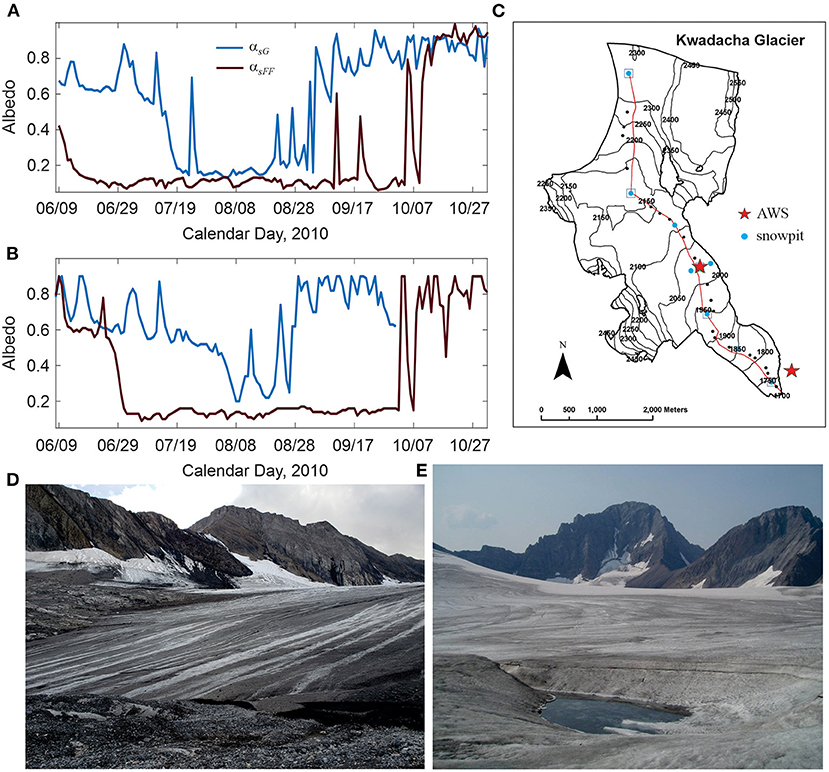
Figure 7. Mean daily surface albedo through the summer melt season as measured by paired on- and off-glacier automatic weather stations at (A) Kwadacha and (B) Haig Glaciers in the Canadian Rockies. Both plots show the albedo evolution from June 8 to November 1, 2010 from glacier sites in the upper ablation area (blue) and from proglacial sites in the glacier forefields (brown). (C) Contour map of Kwadacha Glacier, with the stars indicating the AWS locations. Photographs (D,E) are August, 2021 and August, 2006 images of Haig Glacier, providing visual examples of exposed glacier ice with an albedo of ~0.2 on the lower and upper glaciers. The end-of-summer seasonal snowline is visible in (E). Photographs by the author.

The two glaciers are about 1,010 km apart and are not subject to the same weather systems through the summer of 2010, but the melt-season albedo evolution is similar at the two locations (Figure 7). All four AWS sites were snow-covered in the first week of June. Snow at the off-glacier sites melted away by the end of June, exposing bare rock with an albedo of ~0.1. These sites remained mostly snow-free until mid-October. At Kwadacha Glacier the transition from seasonal snow to bare glacier ice took place in the second week of July, with bare ice (albedo of ~0.2) persisting until the first week of September (Figure 7A). Several summer snow events caused abrupt and transient increases in the glacier albedo, persisting for 1–3 days. Snow began to accumulate on the glacier in the second week of September, heralding the start of “winter” (i.e., the beginnings of the 2010–2011 winter snowpack). The Kwadacha forefield site experienced two transient September snow events in 2010, evidenced by short-lived albedo spikes (Figure 7A). These occurred after snow had already begun to accumulate on the glacier, and the main melt-season snow events on the glacier were not registered at the forefield AWS.

Summer albedo evolution at Haig Glacier was similar, with a drop in albedo from ~0.55 to ~0.2 marking the transition to exposed glacier ice in the first week of August (Figure 7B). Similar to Kwadacha Glacier, several summer snow events are evidenced by transient albedo spikes at the glacier AWS through the months of June to August. The bare-ice season was relatively short at Haig Glacier in 2010, with winter snow accumulation at the glacier AWS commencing on August 28. The Haig Glacier forefield AWS did not register any summer snow events in 2010, though there was one transient event in early October, before the off-glacier winter snowpack started to accumulate the following week (Figure 7B). Figures 7D,E provide a visual perspective of a glacier surface with an albedo of ~0.2, for the lower ablation area and the upper accumulation area of Haig Glacier. On the lower glacier, the glacier ice is difficult to discern from the limestone rock and till. On the upper glacier, particulate matter and melt ponds can both contribute to the low-albedo surface. The late-summer snowline is visible at the highest elevations of the glacier, near the top of the image.

This seasonal albedo evolution is typical of mid-latitude mountain glaciers, and illustrates the strong changes that attend both (a) the transition from seasonal snow cover to exposed glacier ice, and (b) transient summer snow events, which temporarily refresh the glacier surface (Oerlemans and Klok, 2003). Each of these conditions strongly affect the glacier energy and mass balance. Figure 8 illustrates this for four different summers on Kwadacha Glacier, 2008 to 2011, plotting the seasonal evolution of mean daily net radiation and albedo on the glacier. Net radiation is the sum of all incoming and outgoing shortwave and longwave radiation fluxes,

$\begin{array}{l}{Q}^{*}={Q_S}^{\downarrow }+{Q_S}^{\uparrow }+{Q_L}^{\downarrow }+{Q_L}^{\uparrow }={Q_S}^{\downarrow }(1-{\alpha }_s)+{Q_L}^{\downarrow }\\ -{\epsilon }_s\sigma {T_s}^4,& (8)\end{array}$

for surface albedo α_s, emissivity ε_s, and Stefan-Boltzmann's constant σ. Net radiation is positive during the summer melt season, and increases ~3-fold during the transition from seasonal snow to low-albedo glacier ice. This is the dominant term in the glacier surface energy balance, accounting for roughly 80% of the net energy available for glacier melt in these environments (e.g., Klok and Oerlemans, 2002; Marshall, 2014).

FIGURE 8

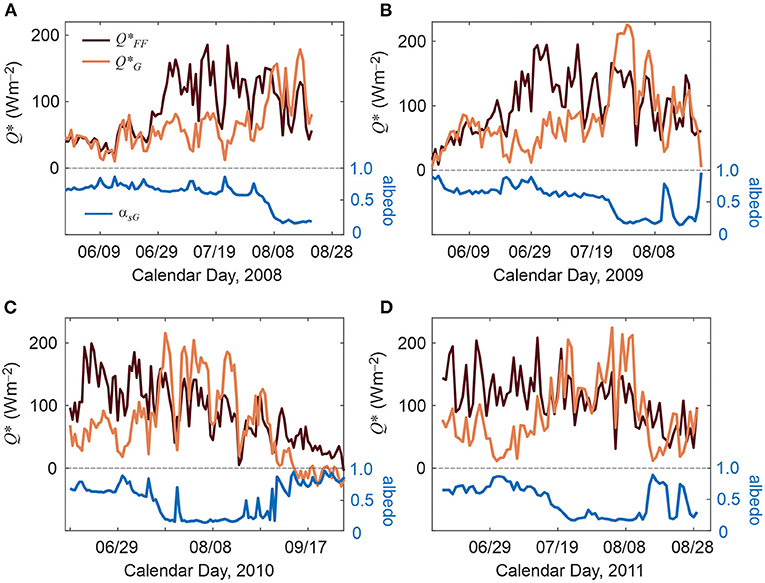
Figure 8. Mean daily net radiation, Q*, at the glacier forefield AWS and the glacier AWS for the (A) 2008, (B) 2009, (C) 2010, and (D) 2011 melt seasons at Kwadacha Glacier. The rapid decrease in mean daily glacier surface albedo, plotted in blue indicates the transition from seasonal snow to exposed glacier ice each summer.

Net radiation from the Kwadacha forefield AWS site provides an interesting comparison with net radiation on the glacier (Figure 8). The AWS records from 2008 and 2009 start in mid-May (Figures 8A,B), when the glacier forefield site was still snow-covered. At these times, net radiation on and off the glacier is nearly identical. The elevation difference between these sites is 335 m, which has a minor and off-setting influence on incoming radiation fluxes. Differences in net radiation between the sites are therefore associated with the albedo and surface temperature, via Stefan-Boltzmann's relation for outgoing longwave radiation in Equation (1). Net radiation increases strongly at the forefield site once it is snow-free, and greatly exceeds the net radiation available on the glacier while the glacier remains snow-covered. On average over the four summers (± 1 standard deviation), net radiation at the forefield site exceeds that on the glacier by 52 ± 39 Wm⁻² when there is snow cover at the glacier AWS (Table 2).

TABLE 2

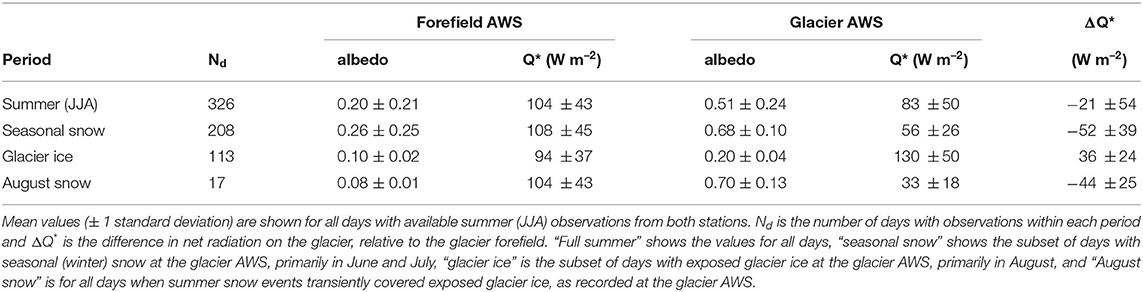
Table 2. Mean daily albedo and net radiation, Q^*, recorded at the glacier and off-glacier automatic weather stations on Kwadacha Glacier, 2008–2011.

The opposite is true when glacier ice is exposed; over bare ice, net radiation on the glacier exceeds that in the forefield by 36 ± 24 Wm⁻² (Table 2). Counter-intuitively, this means that there is more net radiative energy available on the glacier than in the proglacial environment. This is partially driven by the increase in absorbed shortwave radiation over bare ice. The ice albedo is higher than that of the proglacial environment, however, so this is not the full storey. Surplus energy on the glacier is also due to the fact that the surface temperature cannot exceed the melting point, 0°C. This limits the outgoing longwave radiation to 315 Wm⁻² on the glacier, whereas outgoing longwave radiation in the forefield increases as the rock warms up, averaging 353 Wm⁻² over the summer.

Summer Snowfall

The net radiation “inversion” on the glacier prevails in the ablation zone, where surface albedo is not much greater than that of the proglacial rock or sediments. This situation temporarily reverses during summer snow events on the glacier (Figure 8, Table 2). For the August snow events on Kwadacha Glacier from 2008 to 2011 (17 days in total), the average daily net radiation is 33 Wm⁻², compared with 104 Wm⁻² in the glacier forefield and 130 Wm⁻² for bare-ice days in late summer. These summer snow events on the glacier, evident in the albedo records in Figures 7, 8, all registered as rainfall in the glacier forefield.

Marshall and Miller (2020) assess the importance of summer snow events on Haig Glacier to total melt-season surface energy and mass balance. The impact varies from year to year, but on average, summer snow events increase the mean summer (JJA) albedo in the upper ablation area by about 0.07, from an estimated snow-free value of 0.48 to the observed mean value of 0.55. This results in a ~15% reduction in total summer melt and runoff. Summer snow events don't tend to involve much accumulation of mass, but their direct impact on albedo is significant to the glacier mass balance (Oerlemans and Klok, 2003). This effect is threatened by the likelihood that summer precipitation events will increasingly shift from snowfall to rainfall on glaciers. For the August snow events on Kwadacha Glacier from 2008 to 2011, the average daily forefield and glacier temperatures were 4.0 and 1.2°C, respectively. This is near the transition from liquid to solid-phase precipitation, where a slight warming will result in a shift from snow to rain on the glacier.

Multi-Decadal Perspective

The long-term evolution of surface albedo and net radiation can be modelled where AWS data or bias-adjusted climate reanalyses are available to drive a model of surface energy and mass balance. As an example, Figure 9 presents a historical reconstruction of mean summer (JJA) surface albedo and net radiation along the central flowline of Kwadacha Glacier, from the upper accumulation area to the terminus. Results are calculated from a surface energy balance model driven by ERA5 climate reanalyses for the period 1950–2020. Figure 9 illustrates the evolution of albedo and net radiation as a function of distance downglacier for the 1950s, 1980s, and 2010s.

FIGURE 9

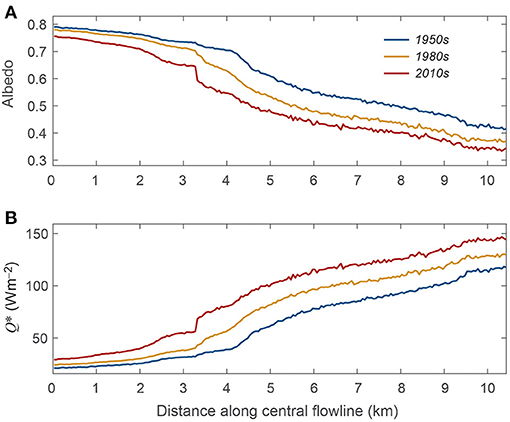
Figure 9. Mean summer (JJA) (A) albedo and (B) net radiation, Q*, along the Kwadacha Glacier central flowline for 1950–1960 (blue), 1980–1990 (orange), and 2010–2020, based on surface energy balance modelling from 1950 to 2020. The top of the flowline (x = 0) extends to Mt. Lloyd George, at an elevation of 2,938 m, and the terminus elevation (x = 10.4 km) is ~1,700 m.

The progressive decrease in surface albedo over these decades is evident, driven by the general trend of longer and warmer melt seasons. Averaged over the glacier, surface albedo has a trend of −0.012 per decade and net radiation has a trend of +3.7 W m⁻² per decade from 1950 to 2020, i.e., changes of −0.08 and +26 W m⁻² over this period. These changes are significant, relative to mean values (± 1σ) of 0.58 ± 0.05 and 72 ± 14 W m⁻² from 1950 to 2020. The linear correlation coefficient between time series of mean glacier albedo and net radiation (1950–2020) equals r = −0.98, indicating that interannual variability in net radiation is primarily governed by the albedo. Increases in net radiation over this 71-year period are therefore dominated by the albedo feedback. The decadal-scale decrease in albedo and increase in melt energy is partially associated with the up-glacier propagation of the ablation area and the relatively recent exposure of bare glacier ice at higher elevations. The flowline data from the 2010s illustrate this effect, with the abrupt step at x = 3.2 km. This aligns with the average elevation of the end-of-summer snowline through this decade.

The model results in Figure 9 do not include the potential effects of increased particulate loading or algal activity on the glacier, as these effects have yet to be interactively coupled in glacier mass balance models. The results are just due to the direct climate change effects of a longer and more spatially-extensive bare-ice season, along with a reduction in summer snow events. These direct albedo feedbacks are driving increased mass loss and accelerated glacier retreat (Ebrahimi and Marshall, 2016). Additional albedo reductions due to increased dust loading, wildfire or industrial activity, and algal development may be further hastening the transition from white to grey in some regions.

From White to Blue

Glacier and ice sheet retreat does not always expose bare rock. In polar regions at the ice-ocean interface, the collapse of floating glacier tongues and ice shelves represents a transition from white to blue. Where this is occurring, the loss of floating ice can have significant ecological impacts for local marine environments (e.g., Vincent and Mueller, 2020) and for oceanographic processes associated with ice-ocean interactions (e.g., mixing, stratification, sea ice and iceberg production, sedimentation). Catania et al. (2020) offer an excellent review of marine-terminating outlet glacier processes in Greenland and their ecological and oceanographic significance. Similar dynamics are impacting large sectors of the Antarctic Ice Sheet (e.g., Jenkins et al., 2018; Meredith et al., 2019).

Outlet glacier fluctuations at the ice sheet-ocean margin are complex and not fully understood (Catania et al., 2020). The inland retreat of tidewater glaciers and floating ice tongues causes short-term acceleration of ice sheet flow and higher rates of sea-level rise, as marginal thinning propagates upstream (Price et al., 2011; Catania et al., 2020; King et al., 2020). Following a transition period, however, outlet glacier margins may retreat to inland positions where they are more stable. In the absence of calving losses and marine melting at the ice-ocean interface, outlet glaciers that have lost touch with the ocean will have a more positive mass balance. This is one of the few negative feedbacks associated with glacier retreat processes, although it will require decades to centuries for some of the major outlets of the Greenland Ice Sheet to retreat to a stable terrestrial terminus position. Such a transition may help to reduce the rate and magnitude of sea-level rise from the Greenland Ice Sheet in the coming centuries, but marine-terminating outlet glaciers that have retreated inland will still be susceptible to ongoing atmospheric warming (Aschwanden et al., 2019).

This process of “self-stabilizing” glacier retreat is in fact common for mountain glaciers, which can retract to higher altitudes with less negative mass balance. This is well-manifest in north-facing cirque glaciers that have retreated to a topo-climatic niche where they are relatively stable. This can be thought of as a regime change from negative to neutral or positive mass balance. Glaciers can weather short-term warming through this process, but as in the polar regions, ongoing warming will make it difficult to reach a new and sustainable equilibrium.

In terrestrial environments, glacier retreat often exposes bedrock basins that have been over-deepened by glacial erosion, creating proglacial lakes in the wake of the retreating ice (e.g., Shugar et al., 2020). Proglacial lakes often pose a hazard, due to the risk of outburst floods (Carrivick and Tweed, 2016; Huggel et al., 2020), but they can also serve to moderate the hydrological impacts of diminished glacier ice, by acting as reservoirs to store water and release it slowly through the summer. Ice-marginal proglacial lakes also increase glacier mass loss through calving (Benn et al., 2007; Sakai et al., 2009; Maurer et al., 2016). This is another positive feedback process that can contribute to accelerated glacier mass loss (e.g., King et al., 2019).

From Sublimation to Melting

Meteorological conditions that are favourable to sublimation of snow and ice (high winds, low humidity, sub-zero temperatures) focus available sensible and radiative energy on sublimation rather than melting (e.g., Wagnon et al., 1999; Kaser, 2001; Mölg et al., 2008; MacDonell et al., 2013). Sublimation can serve as an effective energy sink, consuming significant amounts of net energy with minimal mass loss; compared with melting, it requires 8.5 times more energy to sublimate a molecule of ice (Cuffey and Paterson, 2010). This makes sublimation an ineffective ablation mechanism on glaciers, resulting in a more positive mass balance. This is well-documented for high-altitude glaciers in the Himalaya, the tropical Andes, and East Africa (e.g., Mölg et al., 2008; Ayala et al., 2017), and similar processes are important on the Greenland and Antarctic Ice Sheets.

Tropical glaciers spanning a large elevation range commonly experience a gradation in the dominant ablation regime from melting to sublimation as one moves to altitudes above ~5,000 m (e.g., Ayala et al., 2017). Cold and dry conditions that favour sublimation at high altitudes are sensitive to increases in both temperature and atmospheric moisture that are occurring with climate change (Trenberth et al., 2005; Hartmann et al., 2013; Gao et al., 2018; Ho et al., 2018). These changes increase incoming longwave radiation and latent heat flux in glacial environments, and could precipitate a transition from sublimation to melting at high elevations, non-linearly increasing ablation and mass loss. The partitioning of ablation processes between sublimation and melt is critical to glacier response to climate variability and change in high-elevation tropical environments (e.g., MacDonell et al., 2013), and shifts from sublimation to melt have been identified as a potential driving mechanism for glacier retreat on Mt. Kilimanjaro (Thompson et al., 2009) and in the tropical Andes (Réveillet et al., 2020).

Williamson S. et al. (2020) report positive trends in atmospheric humidity as the main manifestation of elevation-dependent climate change in the St. Elias Mountains of Yukon Territory, Canada. Climate reanalyses indicate marked increases in humidity at high elevations in this region, related to moisture advection from the North Pacific. Figure 10 shows an example of this from the pressure-level specific humidity data in the ERA5 grid cell over the Kaskawulsh Glacier field site (cf. Figure 2). Specific humidity at 700 mb (~2,810 m altitude) increased by about 14% from 1950 to 2020 (Figures 10A,B), with the strongest absolute changes in the summer months (JJA) and at the 700-mb level (Figure 10C). As a percentage, annual and summer changes are similar, with an average increase of 1.9% per decade over the pressure levels from 400 to 800 mb plotted in Figures 10B,C. Increases in atmospheric specific humidity reduce humidity gradients at the glacier surface, lowering sublimation rates and the energy sink association with latent heat flux. Together with influences on incoming longwave radiation, this is an important consideration for analyses of elevation-dependent climate change, with potential for non-linear impacts on glacier mass balance.

FIGURE 10

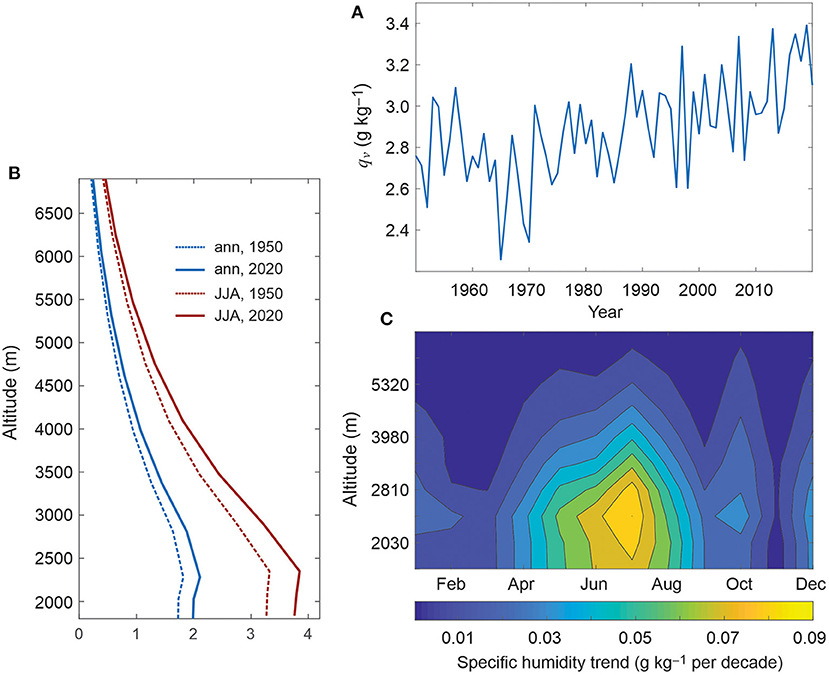
Figure 10. Specific humidity evolution from 1950 to 2020 in the ERA5 climate reanalysis in the grid cell over the upper Kaskawulsh Glacier, St. Elias Mountains, Yukon. (A) Mean annual specific humidity at the 700-mb level (~2,810 m). (B) Profiles of mean annual and summer (JJA) specific humidity in the 1950s (dashed lines) and the 2010s (solid lines). (C) Specific humidity trends over the period 1950–2020 as a function of pressure-level (altitude) and month.

Discussion

Processes Governing Non-Linear Glacier and Ice Sheet Response to Climate Change

The transitions discussed above are all under way as part of glacier and ice sheet response to climate change, but they are non-contemporaneous in space. There will not be a globally synchronous switch from polythermal to temperate ice masses or from meltwater retention to runoff, net accumulation to ablation, snow to rain, sublimation to melting, or white to grey. These transitions can nonetheless be rapid at any one point, representing a veritable regime shift.

Because these are non-linear, threshold processes, they can be difficult to predict with confidence in numerical models. As an example, the modelled transition from polythermal to temperate firn at Kaskawulsh Glacier in Figure 2 was an unanticipated model result, which may or may not reflect reality. There is temperate, water-saturated firn at 35 m depth at the site at present, discovered during drilling of a firn core in 2018, but the age of this firn aquifer is unknown. The modelling predicts that this developed over the past decade in response to increasing surface melt at the site, with high amounts of meltwater infiltration in 2013 exceeding the refreezing capacity of the firn. This triggered the rapid transition to temperate conditions. The atmospheric warming signal at this site is gradual and subtle, however. Mean annual air temperatures averaged −11.2°C from 1950 to 2020, with a long-term trend of +0.28°C per decade and a mean value of −10.3°C from 2010 to 2020. Mean summer (JJA) temperatures averaged −2.8°C, with a long-term trend of +0.21°C per decade and a mean value of −1.8°C from 2010 to 2020. Conditions in the last decade were therefore only ~1°C warmer than the long-term average. The coupled surface energy balance, firn thermodynamic, and firn hydrological system translated a gradual, linear atmospheric temperature forcing into the strongly non-linear response shown in Figure 2.

Latent heat release at this site is sufficient to produce temperate firn and ice despite mean annual air temperatures of about −10°C, but it is difficult to determine a threshold temperature which can trigger the transition from polythermal to temperate conditions. The regime change at Kaskawulsh Glacier was sudden, but the preconditioning for this transition developed over a number of years. Similar processes are seen in the modelled development of deep temperate firn at DYE-2, Greenland in Figure 5. Firn warming is gradual through the period 2000–2077, though at about twice the rate of the atmospheric warming, until a warm summer with above-average surface melting in 2077 triggers the transition to deep temperate conditions (Figures 5B,C). The years immediately preceding this pre-conditioned DYE-2 for this transition (Figure 5E). Following the transition to deep temperate conditions, air temperatures and melt rates at DYE-2 are high enough to sustain temperate firn.

This transition to temperate conditions at DYE-2 does not occur with the reference climatology of Figure 4, however; it requires significantly (> 40%) higher snow accumulation rates at DYE-2. It is more likely that this site will transition to an ablation area without developing temperate conditions in response to projected climate warming.

Latent heat of refreezing is the main factor that drives the development of temperate conditions and the magnitude of the difference between 10-m firn temperature and mean annual air temperature. In the simulations presented here, this is governed to first order by the amount of melt, and increasing melt rates provide the trigger for temperate firn development. It can develop abruptly and is difficult to reverse because once meltwater infiltrates to depths of >~8–10 m, it is below the depth of the annual winter cold wave. Wet and temperate conditions develop if deep firn has insufficient cold content to refreeze all of the meltwater. It would require sustained climate cooling over many years to restore sub-freezing conditions, limited by time scales of thermal diffusion from the surface. The latent heat release that drives this transition can be suppressed if the seasonal snowpack and near-surface firn do not have sufficient cold content, pore space, and permeability to support meltwater infiltration and refreezing. In particular, the development of thick, near-surface ice layers can inhibit meltwater infiltration (Bezeau et al., 2013; MacFerrin et al., 2019), potentially diverting meltwater to lateral runoff. There are numerous uncertainties in the firn system, particularly meltwater infiltration processes and the formation and permeability of ice layers (van As et al., 2016; Samimi et al., 2020; Vandecrux et al., 2020b).

Non-linear processes in glacier surface energy and mass balance are similarly hard to predict. Temperature strongly modulates multiple feedback processes that contribute to glacier response to climate change, including shifts from snowfall to rainfall, declines in glacier albedo, the magnitude and sign of latent heat fluxes, and the extent of meltwater refreezing. These interact to increase glacier sensitivity to warming beyond the direct effects of increases in sensible and incoming longwave radiation fluxes, which scale with temperature. These interactions help to explain the strong global glacier response to a warming of about 1°C over the past four decades (Marzeion et al., 2014; Hugonnet et al., 2021). Ebrahimi and Marshall (2016) analysed the sensitivity of glacier mass balance to a warming of 1°C at Haig Glacier with and without mass balance feedbacks, using an energy balance model calibrated to observations of glacier melt. For the period 2002–2012, the average summer (JJA) net energy and summer melt at the glacier AWS site were Q_N = 97 W m⁻² and ṁ = 2.32 m w.e. yr⁻¹. A temperature change of +1°C, with feedbacks suppressed, gives ΔQ_N = 8.3 W m⁻² and a 9% increase in summer melt (ṁ = 2.52 m w.e. yr⁻¹). Including humidity and albedo feedbacks in the surface energy balance, a 1°C-warming gives ΔQ_N = 27 W m⁻² and ṁ = 2.97 m w.e. yr⁻¹, a 28% increase in summer melt.

This is consistent with other studies on mid-latitude mountain glaciers, which report a ~30% reduction in net mass balance for a warming of 1°C (Klok and Oerlemans, 2002; Hirose and Marshall, 2013; Huss and Fischer, 2016). Feedbacks increase glacier mass balance sensitivity to a change in temperature by a factor of ~3. This implicitly includes some albedo feedbacks, such as a longer melt season with a greater duration of exposure of low-albedo glacier ice and more frequent summer rain events rather than snowfall as temperatures warm. This estimate does not include the potential effects of inheritance of impurities over many years, which can increase in concentration as meltwater runoff leaves some of the particulate load behind on the glacier surface. Additional albedo reductions that are not captured include the possible influences of increased glacier algal activity, dust loading from recently-deglaciated terrain, or increases in black carbon deposition. At Haig Glacier, for instance, the average long-term bare-ice albedo at the AWS site is 0.21 ± 0.06, but values of ~0.1 were measured for several weeks in August 2017, associated with intense wildfire activity upwind of the glacier (Marshall and Miller, 2020). Mean measured August albedo at the AWS site was 0.15 in 2017, compared with a long-term average of 0.38 (Ebrahimi and Marshall, 2016). This albedo reduction over the month of August equates to an additional melt of 0.38 m w.e., or a 16% increase in total summer runoff. Any additional darkening from increased particulate matter therefore serves to further increase the climate change sensitivity of ice masses.

Other direct consequences of the transition from white to grey or blue (exposed rock, melt ponds, and proglacial lakes) include sensible and radiative heat fluxes from exposed rock and open water. Glacier calving into marginal lakes can further accelerate glacier retreat (Watson et al., 2020). Observed increases in glacier mass loss over the past two decades testify to the current state of disequilibrium (Hugonnet et al., 2021).

Considerations for Glacier-Climate Modelling

Many of the feedback processes of glacier melt and retreat are not well-captured in glacier-climate models, which typically have one-way climate forcing and do not generally simulate the evolving environment (e.g., changes in proglacial terrain, lake development, ice-ocean conditions, transport, and deposition of impurities). Because many of these processes involve positive feedbacks, current model projections may underestimate glacier and ice sheet response to climate change. Process studies to advance understanding and modelling of some of these non-linear glacier mass balance processes can increase confidence in future projections.

It is important to understand mechanisms of elevation-dependent climate change and how these interact with glacier-climate processes on both mountain glaciers and polar ice sheets. Changes in the phase of precipitation with altitude, lapse rates of temperature, specific humidity, and longwave radiation, and overnight meltwater refreezing processes are all important to glacier surface energy balance, and will evolve in poorly-understood ways in response to ongoing climate warming. Coupled evolution of the glacier-climate system and explicit representation of the surface energy balance (vs. temperature index or degree-day melt models) may better capture many of these processes and feedbacks. An Earth-systems approach is also needed to represent the broader evolution of glacier, lake, ocean, and proglacial alpine/tundra environments as glaciers retreat from the landscape. This is important to regional energy fluxes and climate, as well as ecological and hydrological conditions and emerging hazards in deglaciating terrain.

While these processes are non-linear and can result in abrupt regime changes, it is difficult to identify the glaciological or glacio-climatic tipping points with confidence. The evolution from polythermal to temperate conditions and warming of the ice in glaciers and ice sheets may play a significant role in long-term ice-dynamical response to climate change, but the evolution of firn in Greenland and in parts of Antarctica which likely to experience surface melt this century is uncertain. Firn simulations like that shown in Figures 2–5 can be thought of as physically-plausible scenarios rather than predictions. These results are sensitive to uncertain process representations and parameter settings in the firn model, in particular concerning mechanisms of meltwater infiltration, capillary meltwater retention (irreducible water content in the pore space), and ice-layer formation (Samimi et al., 2020). These processes need to be better understood and represented in models before non-linear thresholds within firn temperature evolution and meltwater retention can be reliably predicted.

Ensemble modelling (multiple realisations) spanning a range of parameter space (e.g., Van Pelt et al., 2021) can arguably offer reasonable projections of how firn may evolve in response to climate change. For instance, firn conditions and meltwater runoff to retention ratios for different parts of the Greenland Ice Sheet could be expressed via probability distributions of conditions for the period 2070–2100 for a given climate scenario. This is a reasonable approach to future projections at this time, although averaging within ensemble modelling artificially smooths the projections and make regime changes appear like gradual system responses, rather than the rapid transitions that are expected in nature. Structural uncertainties within firn hydrological process models (Vandecrux et al., 2020b) may also bias ensemble modelling, giving distributions that don't fully represent the range of future conditions.

Concluding Thoughts

This review is not comprehensive in its identification of threshold processes and regime changes which glaciers experience as they respond to gradual climate forcing. In particular, several elements of glacier and ice sheet dynamics are non-linear and can either accelerate or help to stabilise glacier retreat. Marine grounding-line and tidewater glacier instabilities are two well-known examples of this, where an unstable state of retreat can be triggered for thinning ice on a reverse bed slope (e.g., Weertman, 1974; Schoof, 2007; Joughin et al., 2014). Climate-driven thinning at the margin of grounded ice masses also steepens glacier slopes, increasing flow rates and advection of ice to the ablation zone (e.g., Huybrechts and De Wolde, 1999; Schäfer et al., 2015), a positive feedback that accelerates mass loss. In other situations, retreating ice masses can stabilise inland or at higher elevations, if the climate permits a glacier to establish a new equilibrium with a neutral rather than negative mass balance.

The transitions from polythermal to temperate firn and ice, from meltwater retention to runoff, from solid to liquid phases of water (i.e., snow to rain; reduced overnight refreezing of meltwater), from bright snow to low-albedo ice surfaces and deglaciated terrain, and from sublimation to melting-dominated ablation at high altitudes all represent regime shifts within the glacier-climate system. These involve non-linear processes that accelerate glacier and ice sheet response to climate change once external forcing passes a particular threshold. Gradual forcing can translate to an abrupt change in system response or behaviour. These regime changes are not intrinsically irreversible, but hysteresis and inertia in the system mean that the original states can be difficult to restore. Latent heat release from meltwater refreezing immediately warms firn and ice (e.g., Figure 2), but thermal diffusion is the only mechanism for cooling and restoring polythermal conditions, on decadal timescales for deep firn. Similarly, glacier and ice sheet surfaces with high concentrations of particulate matter will remain dark until these advect through the system to the glacier margin. Alternatively, climate cooling could allow these surfaces to more effectively covered by reflective snow for a greater proportion of the melt season.

Stabilisation of climate change is not likely to restore polythermal conditions, refresh glacier surfaces, or halt glacier retreat, due to the current state of disequilibrium. Hence, while glaciers and ice sheets are not past a “tipping point” that guarantees their complete disappearance, it will be difficult to stop or reverse their demise in the face of ongoing climate change (e.g., King et al., 2020; Hugonnet et al., 2021). The non-linear feedbacks identified in this discussion are not fully understood or adequately modelled, but are likely to contribute to accelerated glacier and ice sheet response to climate change in the coming decades. Process studies and model development to better represent these processes in Earth system models will enable improved projections of future change and a better representation of the specific climate thresholds that will accelerate such changes.

Summary

Non-linear processes and feedbacks are contributing to the strong sensitivity of glacier and ice sheets to climate warming. This includes a number of threshold processes that can be triggered by a gradual climate forcing, such as regime shifts from polythermal to temperate glacier states and from snowfall to rainfall, sublimation to melting, and meltwater refreezing to runoff. Additional feedback mechanisms that can accelerate glacier mass loss include surface albedo reductions, increased calving losses, and increased heat flux from surrounding deglaciated terrain. These processes are not strictly irreversible but they create inertia in glacier retreat, such that it will be difficult to reverse the current state of disequilibrium in mountain glaciers and polar icefields. Many of the threshold processes involved in glacier-climate regime shifts are not well-understood and are still under development in modelling efforts. This includes meltwater routing and refreezing in firn and glacier systems, physically-based models of glacier surface albedo, and the evolving ice-atmosphere-land surface interactions in mountain and polar landscapes. This article identifies several regime shifts that are contributing to the extreme sensitivity of glaciers to climate change, which need to be better understood and modelled to permit improved projections of glacier change in the coming decades.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: Datasets and model code used in this study are publicly available in the Scholars Portal Dataverse data repository at the University of Calgary. Haig and Kwadacha Glacier AWS data are archived at https://doi.org/10.5683/SP2/7CXPPI and https://doi.org/10.5683/SP2/QIPI9W, respectively. DYE-2 AWS and firn hydrology data are available at https://doi.org/10.5683/SP2/2QY39K. The MATLAB code for the surface energy balance and firn modelling is available at https://doi.org/10.5683/SP2/WRWJAZ.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This research was supported by the Natural Sciences and Engineering Research Council (NSERC) of Canada through the Discovery Grant Modelling Glacier and Ice Sheet Response to Climate Change.

Author Disclaimer

Views and analyses presented in this manuscript are new and are the sole responsibility of SM.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

These ideas were first formulated for a presentation at the virtual High Mountain Summit hosted by the Colombian Ministry of the Environment and Sustainable Development in December 2020. I thank the Colombian National Meteorological and Hydrological Service (IDEAM) and the World Meteorological Organisation for co-ordinating this event and advancing understanding of the impacts of climate change in global mountain regions. I am grateful to the Natural Sciences and Engineering Research Council (NSERC) of Canada for support of my long-term research program studying glacier response to climate change. This has provided the foundation for the field studies and a host of exceptional graduate students that contributed to this work. Field studies at DYE-2, Greenland were also supported by NASA Award NNX15AC62G and the U.S. National Science Foundation. Thank you to the Editor and reviewers whose insights and suggestions improved this manuscript.

References

Allen, S., and Huggel, C. (2013). Extremely warm temperatures as a potential cause of recent high mountain rockfall. Glob. Planet. Change 107, 59–69. doi: 10.1016/j.gloplacha.2013.04.007

CrossRef Full Text | Google Scholar

Allen, S. K., Cox, S. C., and Owens, I. F. (2011). Rock avalanches and other landslides in the central Southern Alps of New Zealand: a regional study considering possible climate change impacts. Landslides 8, 33–48. doi: 10.1007/s10346-010-0222-z

CrossRef Full Text | Google Scholar

Armour, K., Eisenman, I., Blanchard-Wrigglesworth, E., McCusker, K., and Bitz, C. M. (2011). The reversibility of sea ice loss in a state-of-the-art climate model. Geophys. Res. Lett. 38:L16705. doi: 10.1029/2011GL048739

CrossRef Full Text | Google Scholar

Aschwanden, A., Fahnestock, M. A., Truffer, M., Brinkerhoff, D. J., Hock, R., Khroulev, C., et al. (2019). Contribution of the Greenland Ice Sheet to sea level over the next millennium. Sci. Adv. 5:eaav9396. doi: 10.1126/sciadv.aav9396

PubMed Abstract | CrossRef Full Text | Google Scholar

Ayala, A., Pelliccioti, F., Peleg, N., and Burlando, P. (2017). Melt and surface sublimation across a glacier in a dry environment: Distributed energy-balance modelling of Juncal Norte Glacier, Chile. J. Glaciol. 63, 803–822. doi: 10.1017/jog.2017.46

CrossRef Full Text | Google Scholar

Banwell, A., Hewitt, I., Willis, I., and Arnold, N. (2016), Moulin density controls drainage development beneath the Greenland ice sheet. J. Geophys. Res. Earth Surf. 121, 2248–2269. doi: 10.1002/2015JF003801

CrossRef Full Text | Google Scholar

Bell, R., Studinger, M., Shuman, C., et al. (2007). Large subglacial lakes in East Antarctica at the onset of fast-flowing ice streams. Nature 445, 904–907. doi: 10.1038/nature05554

PubMed Abstract | CrossRef Full Text | Google Scholar

Bell, R., Tinto, K., Das, I., et al. (2014). Deformation, warming and softening of Greenland's ice by refreezing meltwater. Nature Geosci. 7, 497–502. doi: 10.1038/ngeo2179

CrossRef Full Text | Google Scholar

Benn, D. I., Warren, C. R., and Mottram, R. H. (2007). Calving processes and the dynamics of calving glaciers. Earth Sci. Rev. 82, 143–179. doi: 10.1016/j.earscirev.2007.02.002

CrossRef Full Text | Google Scholar

Bezeau, P., Sharp, M., Burgess, D., and Gascon, G. (2013). Firn profile changes in response to extreme 21st-century melting at Devon Ice Cap, Nunavut, Canada. J. Glaciol. 59, 981–991. doi: 10.3189/2013JoG12J208

CrossRef Full Text | Google Scholar

Blatter, H. (1987). On the thermal regime of an Arctic valley glacier: a study of White Glacier, Axel Heiberg Island, N.W.T., Canada. J. Glaciol. 33, 200–211. doi: 10.3189/S0022143000008704

CrossRef Full Text | Google Scholar

Blatter, H., and Hutter, K. (1991), Polythermal conditions in Arctic glaciers, J. Glaciol. 37, 261–269. doi: 10.1017/S0022143000007279

CrossRef Full Text | Google Scholar

Bøggild, C. E., Brandt, R. E., Brown, K. J., and Warren, S. G. (2010). The ablation zone in northeast Greenland: ice types, albedos and impurities. J. Glaciol. 56, 101–113. doi: 10.3189/002214310791190776

CrossRef Full Text | Google Scholar

Brock, B. W., Willis, I. C., and Sharp, M. J. (2000). Measurement and parameterisation of albedo variations at Haut Glacier d'Arolla, Switzerland. J. Glaciol. 46, 675–688. doi: 10.3189/172756500781832675

CrossRef Full Text | Google Scholar

Calonne, N., Milliancourt, L., Burr, A., Philip, A., Martin, C. L., Flin, F., and Geindreau, C. (2019). Thermal conductivity of snow, firn and porous ice from 3-D image-based computations. Geophys. Res. Lett. 46, 13079–13089 doi: 10.1029/2019GL085228

CrossRef Full Text | Google Scholar

Carrivick, J. L., and Tweed, F. S. (2016). A global assessment of the societal impacts of glacier outburst floods. Glob. Planet. Change 144, 1–16. doi: 10.1016/j.gloplacha.2016.07.001

CrossRef Full Text | Google Scholar

Catania, G. A., and Neumann, T. A. (2010). Persistent englacial drainage features in the Greenland Ice Sheet. Geophys. Res. Lett. 37:L02501. doi: 10.1029/2009GL041108

CrossRef Full Text | Google Scholar

Catania, G. A., Stearns, L. A., Moon, T., Enderlin, E., and Jackson, R. H. (2020). Future evolution of Greenland's marine-terminating outlet glaciers. J. Geophys. Res. Earth Surf. 125:e2018JF004873. doi: 10.1029/2018JF004873

CrossRef Full Text | Google Scholar

Charalampidis, C., van As, D., Box, J. E., van den Broeke, M. R., Colgan, W. T., Doyle, S. H., et al. (2015). Changing surface–atmosphere energy exchange and refreezing capacity of the lower accumulation area, West Greenland. Cryosphere 9, 2163–2181. doi: 10.5194/tc-9-2163-2015

CrossRef Full Text | Google Scholar

Christianson, K., Kohler, J., Alley, R. B., Nuth, C., and Van Pelt, W. J. J. (2015). Dynamic perennial firn aquifer on an Arctic glacier. Geophys. Res. Lett. 42, 1418–1426. doi: 10.1002/2014GL062806

CrossRef Full Text | Google Scholar

Clarke, G. K. C. (1987). Fast glacier flow: Ice streams, surging, and tidewater glaciers, J. Geophys. Res. 92, 8835–8841. doi: 10.1029/JB092iB09p08835

CrossRef Full Text | Google Scholar

Coléou, C., and Lesaffre, B. (1998). Irreducible water saturation in snow: experimental results in a cold laboratory. Ann. Glaciol. 26, 64–68. doi: 10.3189/1998AoG26-1-64-68

CrossRef Full Text | Google Scholar

Colgan, W. T., Rajaram, H., Anderson, R. S., Steffen, K., Zwally, H. J., Phillips, T., et al. (2012). The annual glaciohydrology cycle in the ablation zone of the Greenland ice sheet: Part 2. observed and modeled ice flow. J. Glaciol. 58, 51–64. doi: 10.3189/2012JoG11J081

CrossRef Full Text | Google Scholar

Collins, M., Sutherland, M., Bouwer, L., Cheong, S.-M., Frölicher, T., Jacot Des Combes, H., et al. (2019). “Extremes, abrupt changes and managing risk,” in IPCC Special Report on the Ocean and Cryosphere in a Changing Climate, eds H.-O., Pörtner, D. C., Roberts, V., Masson-Delmotte, P., Zhai, M., Tignor, E. Poloczanska, et al. (Cambridge: Cambridge University Press).

Google Scholar

Cuffey, K. M., and Paterson, W. S. B. (2010). The Physics of Glaciers. Burlington, MA: Academic Press.

Google Scholar

Das, S. B., Joughin, I., Behn, M. D., Howat, I. M., King, M. A., Lizarralde, D., et al. (2008). Fracture propagation to the base of the Greenland Ice Sheet during supraglacial lake drainage. Science 320, 778–781. doi: 10.1126/science.1153360

PubMed Abstract | CrossRef Full Text | Google Scholar

Davison, B. J., Sole, A. J., Livingstone, S. J., Cowton, T. R., and Nienow, P. W. (2019). The influence of hydrology on the dynamics of land-terminating sectors of the Greenland Ice. Front. Earth Sci. 7:10. doi: 10.3389/feart.2019.00010

CrossRef Full Text | Google Scholar

de la Peña, S., Howat, I. M., Nienow, P. W., van den Broeke, M. R., Mosley-Thompson, E., Price, S. F., et al. (2015). Changes in the firn structure of the western Greenland Ice Sheet caused by recent warming. Cryosphere 9, 1203–1211. doi: 10.5194/tc-9-1203-2015

CrossRef Full Text | Google Scholar

de Magalhães Neto, N., Evangelista, H., Condom, T., Rabatel, A., and Ginot, P. (2019). Amazonian biomass burning enhances tropical Andean glaciers melting. Sci. Rep. 9:16914. doi: 10.1038/s41598-019-53284-1

PubMed Abstract | CrossRef Full Text | Google Scholar

di Mauro, B., Garzonio, R., Baccolo, G., Franzetti, A., Pittino, F., Leoni, B., et al. (2020). Glacier algae foster ice-albedo feedback in the European Alps. Sci. Rep. 10:4739. doi: 10.1038/s41598-020-61762-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Dumont, M., Brun, E., Picard, G., Michou, M., Libois, Q., Petit, J. R., et al. (2014). Contribution of light-absorbing impurities in snow to Greenland's darkening since 2009. Nat. Geosci. 7, 509–512. doi: 10.1038/ngeo2180

CrossRef Full Text | Google Scholar

Ebrahimi, S., and Marshall, S. J. (2015). Parameterization of incoming longwave radiation at glacier sites in the Canadian Rocky Mountains. J. Geophys. Res. Atmos. 120, 12536–12556. doi: 10.1002/2015JD023324

CrossRef Full Text | Google Scholar

Ebrahimi, S., and Marshall, S. J. (2016). Surface energy balance sensitivity to meteorological variability on Haig Glacier, Canadian Rocky Mountains. Cryosphere 10, 2799–2819. doi: 10.5194/tc-10-2799-2016

CrossRef Full Text | Google Scholar

Faillettaz, J., Funk, M., and Vincent, C. (2015). Avalanching glacier instabilities: review on processes and early warning perspectives. Rev. Geophys. 53, 203–224. doi: 10.1002/2014RG000466

CrossRef Full Text | Google Scholar

Fischer, L., Huggel, C., Kääb, A., and Haeberli, W. (2013). Slope failures and erosion rates on a glacierized high-mountain face under climatic changes. Earth Surf. Process. Landf. 38, 836–846. doi: 10.1002/esp.3355

CrossRef Full Text | Google Scholar

Fischer, L., Purves, R. S., Huggel, C., Noetzli, J., and Haeberli, W. (2012). On the influence of topographic, geological and cryospheric factors on rock avalanches and rockfalls in high-mountain areas. Nat. Hazard. Earth Sys. 12, 241–254. doi: 10.5194/nhess-12-241-2012

CrossRef Full Text | Google Scholar

Flowers, G. E. (2015). Modelling water flow under glaciers and ice sheets. Proc. R. Soc. A. 471:20140907. doi: 10.1098/rspa.2014.0907

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, Y., Chen, F., Lettenmaier, D. P., Xu, J., Xiao, L., and Li, X. (2018). Does elevation-dependent warming hold true above 5000 m elevation? Lessons from the Tibetan Plateau. Clim. Atmos. Sci. 1, 1–7. doi: 10.1038/s41612-018-0030-z

CrossRef Full Text | Google Scholar

Gascon, G., Sharp, M., Burgess, D., Bezeau, P., and Bush, A. B. G. (2013). Changes in accumulation-area firn stratigraphy and meltwater flow during a period of climate warming: Devon Ice Cap, Nunavut, Canada. J. Geophys. Res. 118, 2380–2391. doi: 10.1002/2013jf002838

CrossRef Full Text | Google Scholar

Gilbert, A., Vincent, C., Gagliardini, O., Krug, J., and Berthier, E. (2015). Assessment of thermal change in cold avalanching glaciers in relation to climate warming. Geophys. Res. Lett. 42, 6382–6390. doi: 10.1002/2015GL064838

CrossRef Full Text | Google Scholar

Glen, J. W. (1955). The creep of polycrystalline ice. Proc. Royal Soc. London Ser. A 228, 519–538. doi: 10.1098/rspa.1955.0066

CrossRef Full Text | Google Scholar

Gruber, S., and Haeberli, W. (2007). Permafrost in steep bedrock slopes and its temperature-related destabilization following climate change. J. Geophys. Res. Earth Surf. 112:F02S18. doi: 10.1029/2006JF000547

CrossRef Full Text | Google Scholar

Haeberli, W., Schaub, Y., and Huggel, C. (2017). Increasing risks related to landslides from degrading permafrost into new lakes in de-glaciating mountain ranges. Geomorph 293, 405–417. doi: 10.1016/j.geomorph.2016.02.009

CrossRef Full Text | Google Scholar

Harper, J., Humphrey, N., Pfeffer, W. T., Brown, J., and Fettweis, X. (2012). Greenland ice-sheet contribution to sea-level rise buffered by meltwater storage in firn. Nature 491, 240–243. doi: 10.1038/nature11566

PubMed Abstract | CrossRef Full Text | Google Scholar

Hartmann, D., Tank, A. K., Rusticucci, M., Alexander, L., Brönnimann, S., Charabi, Y., et al. (2013). “Observations: atmosphere and surface, in Climate Change 2013: The Physical Science Basis, Chap. 2, eds T., Stocker, D., Qin, G.-K., Plattner, M., Tignor, S., Allen, J. Boschung, et al. (Cambridge: Cambridge University Press), 159–254.

Google Scholar

Heilig, A., Eisen, O., MacFerrin, M., Tedesco, M., and Fettweis, X. (2018). Seasonal monitoring of melt and accumulation within the deep percolation zone of the Greenland Ice Sheet and comparison with simulations of regional climate modeling. Cryosphere 12, 1851–1866. doi: 10.5194/tc-12-1851-2018

CrossRef Full Text | Google Scholar

Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muñoz-Sabater, J., et al. (2020). The ERA5 global reanalysis. Quart. J. Royal Meteorol. Soc. 146, 1999–2049. doi: 10.1002/qj.3803

CrossRef Full Text | Google Scholar

Hirose, J. M. R., and Marshall, S. J. (2013). Glacier meltwater contributions and glacio-meteorological regime of the Illecillewaet River Basin, British Columbia, Canada. Atmos. Ocean 51, 416–435. doi: 10.1080/07055900.2013.791614

CrossRef Full Text | Google Scholar

Ho, S. P., Peng, L., Mears, C., and Anthes, R. A. (2018). Comparison of global observations and trends of total precipitable water derived from microwave radiometers and COSMIC radio occultation from 2006 to 2013. Atmos. Chem. Phys. 18, 259–274. doi: 10.5194/acp-18-259-2018

CrossRef Full Text | Google Scholar

Hock, R., Rasul, G., Adler, C., Cáceres, B., Gruber, S., Hirabayashi, Y., et al. (2019). “High mountain areas,” in IPCC Special Report on the Ocean and Cryosphere in a Changing Climate, eds H.-O., Pörtner, D. C., Roberts, V., Masson-Delmotte, P., Zhai, M., Tignor, E. Poloczanska, et al. (Cambridge: Cambridge University Press), 131–202.

Google Scholar

Hoelzle, M., Darms, G., Lüthi, M. P., and Suter, S. (2011). Evidence of accelerated englacial warming in the Monte Rosa area, Switzerland/Italy. Cryosphere 5, 231–243. doi: 10.5194/tc-5-231-2011

CrossRef Full Text | Google Scholar

Hoffman, M. J., Andrews, L. C., Price, S. A., Catania, G. A., Neumann, T. A., Lüthi, M. P., et al. (2016). Greenland subglacial drainage evolution regulated by weakly connected regions of the bed. Nat. Commun. 7:13903. doi: 10.1038/ncomms13903

PubMed Abstract | CrossRef Full Text

Huggel, C., Carey, M., Emmer, A., Frey, H., Walker-Crawford, N., and Wallimann-Helmer, I. (2020). Anthropogenic climate change and glacier lake outburst flood risk: local and global drivers and responsibilities for the case of lake Palcacocha, Peru. Nat. Hazards Earth Syst. Sci. 20, 2175–2193. doi: 10.5194/nhess-2020-44

CrossRef Full Text | Google Scholar

Hugonnet, R., McNabb, R., Berthier, E., Menounos, B., Nuth, C., Girod, L., et al. (2021). Accelerated global glacier mass loss in the early twenty-first century. Nature 592, 726–731, doi: 10.1038/s41586-021-03436-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Humphrey, N. F., Harper, J. T., and Meierbachtol, T. (2021). Physical limits to meltwater penetration in firn. J. Glaciol. 67, 952–960. doi: 10.1017/jog.2021.44

CrossRef Full Text | Google Scholar

Huss, M., and Fischer, M. (2016). Sensitivity of very small glaciers in the Swiss Alps to future climate change. Front. Earth Sci. 4:34. doi: 10.3389/feart.2016.00034

CrossRef Full Text | Google Scholar

Huybrechts, P. (1996). Basal temperature conditions of the Greenland ice sheet during the glacial cycles. Ann. Glaciol. 23, 226–236. doi: 10.3189/S0260305500013483

CrossRef Full Text | Google Scholar

Huybrechts, P., and de Wolde, J. (1999). The dynamic response of the Greenland and Antarctic Ice Sheets to multiple-century climatic warming. J. Clim. 12, 2169–2188. doi: 10.1175/1520-0442(1999)012<2169:TDROTG>2.0.CO;2

CrossRef Full Text | Google Scholar

Iken, A., and Bindschadler, R. A. (1986). Combined measurements of subglacial water pressure and surface velocity of Findelen- gletscher, Switzerland: conclusions about drainage system and sliding mechanism. J. Glaciol. 32, 101–119. doi: 10.1017/S0022143000006936

CrossRef Full Text | Google Scholar

IPCC (2019). “Summary for policymakers,” in IPCC Special Report on the Ocean and Cryosphere in a Changing Climate, eds H.-O. Portner, D. C. Roberts, V. Masson-Delmotte, P. Zhai, M. Tignor, E. Poloczanska, et al. (Geneva). Available online at: https://www.ipcc.ch/srocc/chapter/summary-for-policymakers/

Google Scholar

Jarvis, G., and Clarke, G. K. C. (1974). Thermal effects of crevassing on Steele Glacier, Yukon Territory, Canada. J. Glaciol. 13, 243–254. doi: 10.1017/S0022143000023054

CrossRef Full Text | Google Scholar

Jenkins, A., Shoosmith, D., Dutrieux, P., et al. (2018). West Antarctic ice sheet retreat in the Amundsen Sea driven by decadal oceanic variability. Nat. Geosci. 11, 733–738. doi: 10.1038/s41561-018-0207-4

CrossRef Full Text | Google Scholar

Joughin, I., Smith, B. E., and Medley, B. (2014). Marine ice sheet collapse potentially under way for the Thwaites Glacier Basin, West Antarctica. Science 344, 735–738. doi: 10.1126/science.1249055

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaser, G. (2001). Glacier-climate interaction at low latitudes, J. Glaciol. 47, 195–204. doi: 10.3189/172756501781832296

CrossRef Full Text | Google Scholar

Keegan, K. M., Albert, M. R., Mcconnell, J. R., and Baker, I. (2014). Climate change and forest fires synergistically drive widespread melt events of the Greenland ice sheet. Proc. Natl. Acad. Sci. U.S.A. 111, 7964–7967. doi: 10.1073/pnas.1405397111

PubMed Abstract | CrossRef Full Text | Google Scholar

King, M. D., Howat, I. M., Candela, S. G., Noh, M. J., Jeong, S., Noël, B. B. Y., et al. (2020). Dynamic ice loss from the Greenland Ice Sheet driven by sustained glacier retreat. Comm. Earth Env. 1, 1–7. doi: 10.1038/s43247-020-00019-0

CrossRef Full Text | Google Scholar

King, O., Bhattacharya, A., Bhambri, R., and Bolch, T. (2019). Glacial lakes exacerbate Himalayan glacier mass loss. Sci. Rep. 9:18145. doi: 10.1038/s41598-019-53733-x

PubMed Abstract | CrossRef Full Text

Klok, L., and Oerlemans, J. (2002). Model study of the spatial distribution of the energy and mass balance of Morteratschgletscher, Switzerland. J. Glaciol. 48, 505–518. doi: 10.3189/172756502781831133

CrossRef Full Text | Google Scholar

Koenig, L. S., Miège, C., Forster, R. R., and Brucker, L. (2014). Initial in situ measurements of perennial meltwater storage in the Greenland firn aquifer. Geophys. Res. Lett. 41, 81–85. doi: 10.1002/2013GL058083

CrossRef Full Text | Google Scholar

Kuipers Munneke, P., Ligtenberg, S. R. M., van den Broeke, M. R., van Angelen, J. H., and Forster, R. R. (2014). Explaining the presence of perennial liquid water bodies in the firn of the Greenland Ice Sheet. Geophys. Res. Lett. 41, 476–483. doi: 10.1002/2013GL058389

CrossRef Full Text | Google Scholar

Lenton, T. M., Held, H., Kriegler, E., Hall, J. W., Lucht, W., Rahmstorf, S., et al. (2008). Tipping elements in the Earth's climate system. Proc. Nat. Acad. Sci. U.S.A. 105, 1786–1793. doi: 10.1073/pnas.0705414105

PubMed Abstract | CrossRef Full Text | Google Scholar

Levermann, A., and Winkelmann, R. (2016). A simple equation for the melt elevation feedback of ice sheets. Cryosphere 10, 1799–1807. doi: 10.5194/tc-10-1799-2016

CrossRef Full Text | Google Scholar

MacDonell, S., Kinnard, C., Mölg, T., Nicholson, L., and Abermann, J. (2013). Meteorological drivers of ablation processes on a cold glacier in the semi-arid Andes of Chile. Cryosphere 7, 1513–1526. doi: 10.5194/tc-7-1513-2013

CrossRef Full Text | Google Scholar

MacFerrin, M., Machguth, H., van As, D., Charalampidis, C., Stevens, C. M., Heilig, A. et al. (2019). Rapid expansion of Greenland's low-permeability ice slabs. Nature 573, 403–407. doi: 10.1038/s41586-019-1550-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Machguth, H., Macferrin, M., van As, D., Box, J. E., Charalampidis, C., Colgan, W., et al. (2016). Greenland meltwater storage in firn limited by near-surface ice formation. Nat. Clim. Change 6, 390–393. doi: 10.1038/nclimate2899

CrossRef Full Text | Google Scholar

Marchenko, S., Van Pelt, W., Pettersson, R., Pohjola, V., and Reijmer, C. (2021). Water content of firn at Lomonosovfonna, Svalbard, derived from subsurface temperature measurements. J. Glaciol. 67, 921–932. doi: 10.1017/jog.2021.43

CrossRef Full Text | Google Scholar

Marshall, S. J. (2005). Recent advances in understanding ice sheet dynamics. Earth Planet. Sci. Lett. 240, 191–204. doi: 10.1016/j.epsl.2005.08.016

CrossRef Full Text | Google Scholar

Marshall, S. J. (2014). Meltwater runoff from Haig Glacier, Canadian Rocky Mountains, 2002–2013. Hydrol. Earth Syst. Sci. 18, 5181–5200. doi: 10.5194/hess-18-5181-2014

CrossRef Full Text | Google Scholar

Marshall, S. J., and Clark, P. U. (2002). Basal temperature evolution of North American ice sheets and implications for the 100-kyr cycle, Geophys. Res. Lett. 29:2214. doi: 10.1029/2002GL015192

CrossRef Full Text | Google Scholar

Marshall, S. J., and Miller, K. (2020). Seasonal and interannual variability of melt-season albedo at Haig Glacier, Canadian Rocky Mountains. Cryosphere 14, 3249–3267. doi: 10.5194/tc-14-3249-2020

CrossRef Full Text | Google Scholar

Marzeion, B., Cogley, J. G., Richter, K., and Parkes, D. (2014). Attribution of global glacier mass loss to anthropogenic and natural causes. Science 345, 919–921. doi: 10.1126/science.1254702

PubMed Abstract | CrossRef Full Text | Google Scholar

Mattea, E., Machguth, H., Kronenberg, M., van Pelt, W., Bassi, M., and Hoelzle, M. (2021). Firn changes at Colle Gnifetti revealed with a high-resolution process-based physical model approach. Cryosphere 15, 3181–3205. doi: 10.5194/tc-15-3181-2021

CrossRef Full Text | Google Scholar

Maurer, J. M., Rupper, S. B., and Schaefer, J. M. (2016). Quantifying ice loss in the eastern Himalayas since 1974 using declassified spy satellite imagery. Cryosphere 10, 2203–2215. doi: 10.5194/tc-10-2203-2016

CrossRef Full Text | Google Scholar

Meredith, M., Sommerkorn, M., Cassotta, S., Derksen, C., Ekaykin, A., Hollowed, A. et al. (2019). “Polar Regions,” in IPCC Special Report on the Ocean and Cryosphere in a Changing Climate, eds H.-O. Portner, D. C. Roberts, V. Masson-Delmotte, P. Zhai, M. Tignor, E. Poloczanska, et al. (Geneva). Available online at: https://www.ipcc.ch/site/assets/uploads/sites/3/2019/11/07_SROCC_Ch03_FINAL.pdf.

Google Scholar

Meyer, C. R., and Hewitt, I. J. (2017). A continuum model for meltwater flow through compacting snow. Cryosphere 11, 2799–2813. doi: 10.5194/tc-11-2799-2017

CrossRef Full Text | Google Scholar

Ming, J., Wang, Y., Du, Z., Zhang, T., Guo, W., Xiao, C., et al. (2015). Widespread albedo decreasing and induced melting of Himalayan snow and ice in the early 21st century. PLoS ONE 10:e0126235. doi: 10.1371/journal.pone.0126235

PubMed Abstract | CrossRef Full Text | Google Scholar

Ming, J., Xiao, C., Cachier, H., Qin, D., Qin, X., Li, Z., et al. (2009). Black Carbon (BC) in the snow of glaciers in west China and its potential effects on albedo. Atmos. Res. 92, 114–123. doi: 10.1016/j.atmosres.2008.09.007

CrossRef Full Text | Google Scholar

Mölg, T., Cullen, N. J., Hardy, D. R., Kaser, G., and Klok, L. (2008). Mass balance of a slope glacier on Kilimanjaro and its sensitivity to climate. Int. J. Climatol. 28, 881–892. doi: 10.1002/joc.1589

CrossRef Full Text | Google Scholar

Mosley-Thompson, E., McConnell, J. R., Bales, R. C., Lin, P. N., Steffen, K., Thompson, L. G., et al. (2001). Local to regional-scale variability of annual net accumulation on the Greenland ice sheet from PARCA cores. J. Geophys. Res. Atmos. 106, 33839–33851. doi: 10.1029/2001JD900067

CrossRef Full Text | Google Scholar

Muntjewerf, L., Petrini, M., Vizcaino, M., Ernani da Silva, C., Sellevold, R., Scherrenberg, M. D. W., et al. (2020). Greenland Ice Sheet contribution to 21st century sea level rise as simulated by the coupled CESM2.1-CISM2.1. Geophys. Res. Lett. 47:e2019GL086836. doi: 10.1029/2019GL086836

CrossRef Full Text | Google Scholar

Nagorski, S. A., Kaspari, S. D., Hood, E., Fellman, J. B., and Skiles, S. M. (2019). Radiative forcing by dust and black carbon on Juneau Icefield, Alaska. J. Geophys. Res. Atmos. 127, 3943–3959. doi: 10.1029/2018J.D.029411

CrossRef Full Text | Google Scholar

NEEM Community Members (2013). Eemian interglacial reconstructed from a Greenland folded ice core. Nature 493, 489–494. doi: 10.1038/nature11789

PubMed Abstract | CrossRef Full Text | Google Scholar

Noël, B., Jakobs, C. L., van Pelt, W. J. J., Lhermitte, S., Wouters, B., Kohler, J., et al. (2020). Low elevation of Svalbard glaciers drives high mass loss variability. Nat. Commun. 11:4597. doi: 10.5194/egusphere-egu2020-15184

PubMed Abstract | CrossRef Full Text | Google Scholar

Noël, B., van de Berg, W. J., Lhermitte, S., Wouters, B., Machguth, H., Howat, I., et al. (2017). A tipping point in refreezing accelerates mass loss of Greenland's glaciers and ice caps, Nat. Commun. 8:14730. doi: 10.1038/ncomms14730

PubMed Abstract | CrossRef Full Text

Ochwat, N. E., Marshall, S. J., Moorman, B. J., Criscitiello, A. S., and Copland, L. (2021). Evolution of the firn pack of Kaskawulsh Glacier, Yukon: meltwater effects, densification, and the development of a perennial firn aquifer. Cryosphere 15, 2021–2040. doi: 10.5194/tc-15-2021-2021

CrossRef Full Text | Google Scholar

Oerlemans, J., Giesen, R., and van den Broeke, M. R. (2009). Retreating alpine glaciers: increased melt rates due to accumulation of dust (Vadret de Morteratsch, Switzerland). J. Glaciol. 55, 729–736. doi: 10.3189/002214309789470969

CrossRef Full Text | Google Scholar

Oerlemans, J., and Klok, L. (2003). Effect of summer snowfall on glacier mass balance. Ann. Glaciol. 38, 97–100. doi: 10.3189/172756404781815158

CrossRef Full Text | Google Scholar

Orlove, B., Wiengandt, E., and Luckman, B., (Eds.) (2008). Darkening Peaks: Glacier Retreat, Science, and Society. Berkeley, Los Angeles, CA: University of California Press, 296.

Google Scholar

Parizek, B. R., and Alley, R. B. (2004). Implications of increased Greenland surface melt under global-warming scenarios: ice-sheet simulations. Quat. Sci. Rev. 23, 1013–1027. doi: 10.1016/j.quascirev.2003.12.024

CrossRef Full Text | Google Scholar

Pelto, M. S. (2006). The current disequilibrium of North Cascade glaciers. Hydrol. Process. 20, 769–779. doi: 10.1002/hyp.6132

CrossRef Full Text | Google Scholar

Pepin, N., Bradley, R. S., Diaz, H. F., Baraer, M., Caceres, E. B., Forsythe, N., et al. (2015). Elevation-dependent warming in mountain regions of the world. Nat. Clim. Change 5, 424–430. doi: 10.1038/nclimate2563

CrossRef Full Text | Google Scholar

Pfeffer, W. T., Meier, M. F., and Illangasekare, T. H. (1991). Retention of Greenland runoff by refreezing: implications for projected future sea-level change. J. Geophys. Res. 96, 22117–22124. doi: 10.1029/91JC02502

CrossRef Full Text | Google Scholar

Phillips, T., Rajaram, H., and Steffen, K. (2010). Cryo-hydrological warming: a potential mechanism for rapid thermal response of ice sheets. Geophys. Res. Lett. 37, 1–5. doi: 10.1029/2010GL044397

CrossRef Full Text | Google Scholar

Price, S. F., Payne, A., Howat, I. M., and Smith, B. E. (2011). Committed sea-level rise for the next century from Greenland ice sheet dynamics during the past decade. Proc. Nat. Acad. Sci. U.S.A. 108, 8978–8983. doi: 10.1073/pnas.1017313108

PubMed Abstract | CrossRef Full Text | Google Scholar

Ravanel, L., and Deline, P. (2011). Climate influence on rockfalls in high-Alpine steep rockwalls: the north side of the Aiguilles de Chamonix (Mont Blanc massif) since the end of the ‘Little Ice Age’. Holocene 21, 357–365. doi: 10.1177/0959683610374887

CrossRef Full Text | Google Scholar

Réveillet, M., MacDonell, S., Gascoin, S., Kinnard, C., Lhermitte, S., and Schaffer, N. (2020). Impact of forcing on sublimation simulations for a high mountain catchment in the semiarid Andes. Cryosphere 14, 147–163. doi: 10.5194/tc-14-147-2020

CrossRef Full Text | Google Scholar

Ridley, J., Gregory, J. M., Huybrechts, P., and Lowe, J. A. (2010). Thresholds for irreversible decline of the Greenland ice sheet, Clim. Dynam. 35, 1049–1057. doi: 10.1007/s00382-009-0646-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Sakai, A., Nishimura, K., Kadota, T., and Takeuchi, N. (2009). Onset of calving at supraglacial lakes on debris-covered glaciers of the Nepal Himalaya. J. Glaciol. 55, 909–917. doi: 10.3189/002214309790152555

CrossRef Full Text | Google Scholar

Samimi, S., and Marshall, S. J. (2017). Diurnal cycles of meltwater percolation, refreezing, and drainage in the supraglacial snowpack of Haig Glacier, Canadian Rocky Mountains. Front. Earth Sci. 5:6. doi: 10.3389/feart.2017.00006

CrossRef Full Text | Google Scholar

Samimi, S., Marshall, S. J., and MacFerrin, M. (2020). Meltwater penetration through temperate ice layers in the percolation zone at DYE-2, Greenland Ice Sheet. Geophys. Res. Lett. 47:e2020GL089211. doi: 10.1029/2020GL089211

CrossRef Full Text | Google Scholar

Schäfer, M., Möller, M., Zwinger, T., and Moore, J. (2015). Dynamic modelling of future glacier changes: mass-balance/elevation feedback in projections for the Vestfonna ice cap, Nordaustlandet, Svalbard. J. Glaciol. 61, 1121–1136. doi: 10.3189/2015JoG14J184

CrossRef Full Text | Google Scholar

Schoof, C. (2007). Ice sheet grounding line dynamics: Steady states, stability, and hysteresis. J. Geophys. Res. 112:F03S28. doi: 10.1029/2006JF000664

CrossRef Full Text | Google Scholar

Schoof, C. (2010). Ice-sheet acceleration driven by melt supply variability. Nature 468, 803–806. doi: 10.1038/nature09618

PubMed Abstract | CrossRef Full Text | Google Scholar

Sevestre, H., Benn, D. I., Hulton, N. R. J., and Bælum, K. (2015). Thermal structure of Svalbard glaciers and implications for thermal switch models of glacier surging. J. Geophys. Res. Earth Surf. 120, 2220–2236. doi: 10.1002/2015JF003517

CrossRef Full Text | Google Scholar

Shannon, S. R., Payne, A. J., Bartholomew, I. D., van den Broecke, M. R., Edwards, T. L., Fettweis, X., et al. (2013). Enhanced basal lubrication and the contribution of the Greenland ice sheet to future sea-level rise. Proc. Natl. Acad. Sci. U.S.A. 110, 14156–14161. doi: 10.1073/pnas.1212647110

PubMed Abstract | CrossRef Full Text | Google Scholar

Shugar, D. H., Burr, A., Haritashya, U. K., Kargel, J. S., Watson, C. S., Kennedy, M. C., et al. (2020). Rapid worldwide growth of glacial lakes since 1990. Nat. Clim. Chang. 10, 939–945. doi: 10.1038/s41558-020-0855-4

CrossRef Full Text | Google Scholar

Steffen, K., and Box, J. E. (2001). Surface climatology of the Greenland ice sheet: Greenland climate network 1995-1999. J. Geophys. Res. Atmos. 106, 33951–33964. doi: 10.1029/2001JD900161

CrossRef Full Text | Google Scholar

Stibal, M., Box, J. E., Cameron, K. A., Langen, P. L., Yallop, M. L., Mottram, R. H., et al. (2017). Algae drive enhanced darkening of bare ice on the Greenland ice sheet. Geophys. Res. Lett. 44, 11463–11471. doi: 10.1002/2017GL075958

CrossRef Full Text | Google Scholar

Sundal, A. V., Shepherd, A., Nienow, P., Hanna, E., Palmer, S., and Huybrechts, P. (2011). Melt-induced speed-up of Greenland ice sheet offset by efficient subglacial drainage. Nature 469, 521–524. doi: 10.1038/nature09740

PubMed Abstract | CrossRef Full Text | Google Scholar

Takeuchi, N., Kohshima, S., and Katsumoto, S. (2001). Structure, formation, and darkening process of albedo-reducing material (Cryoconite) on a Himalayan glacier: a granular algal mat growing on the glacier. Arct. Antarct. Alp. Res. 33, 115–122. doi: 10.1080/15230430.2001.12003413

CrossRef Full Text | Google Scholar

Takeuchi, N., Uetake, J., Fujita, K., Aizen, V., and Nikitin, S. (2006). A snow algal community on Akkem Glacier in the Russian Altai Mountains. Ann. Glaciol. 43, 378–384. doi: 10.3189/172756406781812113

CrossRef Full Text | Google Scholar

Tedesco, M., Doherty, S., Fettweis, X., Alexander, P., Jeyaratnam, J., and Stroeve, J. (2016). The darkening of the Greenland ice sheet: trends, drivers, and projections (1981–2100). Cryosphere 10, 477–496. doi: 10.5194/tc-10-477-2016

CrossRef Full Text | Google Scholar

Thompson, L., Brecher, H. H., Mosley-Thompson, E., Hardy, D. R., and Mark, B. G. (2009). Glacier loss on Kilimanjaro continues unabated. Proc. Natl. Acad. Sci. U.S.A. 106, 19770–19775. doi: 10.1073/pnas.0906029106

PubMed Abstract | CrossRef Full Text | Google Scholar

Trenberth, K. E., Fasullo, J., and Smith, L. (2005). Trends and variability in column-integrated atmospheric water vapor. Clim. Dyn. 24, 741–758. doi: 10.1007/s00382-005-0017-4

CrossRef Full Text | Google Scholar

van Angelen, J. H., Lenaerts, J. T. M., van den Broeke, M. R., Fettweis, X., and van Meijgaard, E. (2013). Rapid loss of firn pore space accelerates 21st century Greenland mass loss. Geophys. Res. Lett. 40, 2109–2113. doi: 10.1002/grl.50490

CrossRef Full Text | Google Scholar

van As, D., Box, J. E., and Fausto, R. S. (2016). Challenges of quantifying meltwater retention in snow and firn: an expert elicitation. Front. Earth Sci. 4:101. doi: 10.3389/feart.2016.00101

CrossRef Full Text | Google Scholar

van den Broeke, M. R., Enderlin, E. M., Howat, I. M., Kuipers Munneke, P., Noël, B. P. Y., van de Berg, W. J., et al. (2016). On the recent contribution of the Greenland ice sheet to sea level change. Cryosphere 10, 1933–1946. doi: 10.5194/tc-10-1933-2016

CrossRef Full Text | Google Scholar

Van Pelt, W., Schuler, T., Pohjola, V., and Pettersson, R. (2021). Accelerating future mass loss of Svalbard glaciers from a multi-model ensemble. J. Glaciol. 67, 485–499. doi: 10.1017/jog.2021.2

CrossRef Full Text | Google Scholar

Vandecrux, B., Fausto, R. S., van As, D., Colgan, W., Langen, P. L., Haubner, K., et al. (2020a). Firn cold content evolution at nine sites on the Greenland ice sheet between 1998 and 2017. J. Glaciol. 66, 591–602. doi: 10.1017/jog.2020.30

CrossRef Full Text | Google Scholar

Vandecrux, B., Mottram, R., Langen, P. L., Fausto, R. S., Olesen, M., Stevens, C. M., et al. (2020b). The firn meltwater Retention Model Intercomparison Project (RetMIP): evaluation of nine firn models at four weather station sites on the Greenland ice sheet. Cryosphere 14, 3785–3810. doi: 10.5194/tc-14-3785-2020

CrossRef Full Text | Google Scholar

Vincent, W. F., and Mueller, D. (2020). Witnessing ice habitat collapse in the Arctic. Science 370, 1031–1032. doi: 10.1126/science.abe4491

PubMed Abstract | CrossRef Full Text | Google Scholar

Wagnon, P., Ribstein, P., Francou, B., and Pouyaud, B. (1999). Annual cycle of energy balance of Zongo Glacier, Cordillera Real, Bolivia. J. Geophys. Res. 104, 3907–3923. doi: 10.1029/1998JD200011

CrossRef Full Text | Google Scholar

Watson, C. S., Kargel, J. S., Shugar, D. H., Haritashya, U. K., Schiassi, E., and Furfaro, R. (2020). Mass loss from calving in Himalayan proglacial lakes. Front. Earth Sci. 7:342. doi: 10.3389/feart.2019.00342

CrossRef Full Text | Google Scholar

Weertman, J. (1974). Stability of a junction of an ice sheet and an ice shelf. J. Glaciol. 13, 3–11. doi: 10.1017/S0022143000023327

CrossRef Full Text | Google Scholar

Williamson, C. J., Cameron, K. A., Cook, J. M., Zarsky, J. D., Stibal, M., and Edwards, A. (2019). Glacier algae: a dark past and a darker future. Front. Microbiol. 10:524. doi: 10.3389/fmicb.2019.00524

PubMed Abstract | CrossRef Full Text | Google Scholar

Williamson, C. J., Cook, J., Tedstone, A., Yallop, M., McCutcheon, J., Poniecka, E., et al. (2020). Algal photophysiology drives darkening and melt of the Greenland Ice Sheet, Proc. Natl. Acad. Sci. U.S.A. 117, 5694–5705. doi: 10.1073/pnas.1918412117

PubMed Abstract | CrossRef Full Text | Google Scholar

Williamson, S., Zdanowicz, C., Anslow, F. S., Clarke, G. K. C., Copland, L., Danby, R. K., et al. (2020). Evidence for elevation-dependent warming in the St. Elias Mountains, Yukon, Canada. J. Clim. 3253–3269. doi: 10.1175/JCLI-D-19-0405.1

CrossRef Full Text | Google Scholar

Yau, A. M., Bender, M. L., Robinson, A., and Brook, E. J. (2016). Reconstructing the last interglacial at Summit, Greenland: insights from GISP2. Proc. Nat. Acad. Sci. U.S.A. 113, 9710–9715. doi: 10.1073/pnas.1524766113

PubMed Abstract | CrossRef Full Text | Google Scholar

Zdanowicz, C., Fisher, D., Bourgeois, J., Demuth, M., Sheng, J., Mayewski, P., et al. (2014). Ice cores from the St. Elias Mountains, Yukon, Canada: Their significance for climate, atmospheric composition and volcanism in the North Pacific region. Arctic 67, 1–23. doi: 10.14430/arctic4352

CrossRef Full Text | Google Scholar

Zdanowicz, C., Smetny-Sowa, A., Fisher, D., Schaffer, N., Copland, L., Eley, J., et al. (2012). Summer melt rates on Penny Ice Cap, Baffin Island: past and recent trends and implications for regional climate, J. Geophys. Res. 117:F02006. doi: 10.1029/2011JF002248

CrossRef Full Text | Google Scholar

Zhang, X., Flato, G., Kirchmeier-Young, M., Vincent, L., Wan, H., Wang, X., et al. (2019). “Changes in temperature and precipitation across Canada,” in eds E. Bush, and D. S. Lemmen (Ottawa, ON: Canada's Changing Climate Report. Government of Canada), 112–193. doi: 10.4095/327811

CrossRef Full Text

Zwally, H. J., Abdalati, W., Herring, T., Larson, K., Saba, J., and Steffen, K. (2002). Surface melt-induced acceleration of Greenland ice-sheet flow. Science 297, 218–222. doi: 10.1126/science.1072708

PubMed Abstract | CrossRef Full Text | Google Scholar