Atul K. Sahai1*
Manpreet Kaur1,2
Susmitha Joseph1
Avijit Dey1
R. Phani1Raju Mandal1
Rajib Chattopadhyay1,3- 1Indian Institute of Tropical Meteorology, Ministry of Earth Sciences, Pune, India
- 2Department of Atmospheric and Space Sciences, Savitribai Phule Pune University, Pune, India
- 3India Meteorological Department, Ministry of Earth Sciences, Pune, India
In an endeavor to design better forecasting tools for real-time prediction, the present work highlights the strength of the multi-model multi-physics ensemble over its operational predecessor version. The exiting operational extended range prediction system (ERPv1) combines the coupled, and its bias-corrected sea-surface temperature forced atmospheric model running at two resolutions with perturbed initial condition ensemble. This system had accomplished important goals on the sub-seasonal scale skillful forecast; however, the skill of the system is limited only up to 2 weeks. The next version of this ERP system is seamless in resolution and based on a multi-physics multi-model ensemble (MPMME). Similar to the earlier version, this system includes coupled climate forecast system version 2 (CFSv2) and atmospheric global forecast system forced with real-time bias-corrected sea-surface temperature from CFSv2. In the newer version, model integrations are performed six times in a month for real-time prediction, selecting the combination of convective and microphysics parameterization schemes. Additionally, more than 15 years hindcast are also generated for these initial conditions. The preliminary results from this system demonstrate appreciable improvements over its predecessor in predicting the large-scale low variability signal and weekly mean rainfall up to 3 weeks lead. The subdivision-wise skill analysis shows that MPMME performs better, especially in the northwest and central parts of India.
1. Introduction
The Indian summer monsoon is an economically prodigious phenomenon accountable for the gross domestic product (GDP) of the world's second-largest populated country (Gadgil and Gadgil, 2006). A voluminous scientific literature unveils the manifold aspects and theories concatenating the events of this significant annual occurrence (Raghavan, 1973; Rao, 1976; Sikka and Gadgil, 1980; Parthasarathy et al., 1992; Webster and Yang, 1992; Goswami et al., 1999; Wang and Fan, 1999; Jiang et al., 2004; Joseph and Sijikumar, 2004; Goswami, 2005; Annamalai, 2010; Rajeevan et al., 2010). Apart from being a decisive economic factor, the monsoon has perpetuated the research in recent decades to undertake the emanating climate changes and accompanied extreme weather conditions (Goswami et al., 2006, 2019; Ajayamohan and Rao, 2008; Guhathakurta and Rajeevan, 2008; Rajeevan et al., 2008; Joseph et al., 2015; Parker et al., 2016; Sooraj et al., 2016; Houze et al., 2017; Roxy et al., 2017). In the above view, the prediction of monsoon is not only exigent but is highly inevitable. The significant rainfall contribution from intra-seasonal scale variability in the monsoon highlights the stature of sub-seasonal to seasonal (S2S) scale prediction (Abhilash et al., 2013, 2014b,c; Vitart and Robertson, 2018; Robertson et al., 2019).
The deterministic prediction on the S2S scale has limitations, and therefore probabilistic methods or ensemble prediction systems are considered (Molteni et al., 1996; Buizza et al., 2007, 2008; Vitart and Molteni, 2009; Rashid et al., 2011). The prediction from an ensemble of perturbed initial conditions (ICs) is one of the popular techniques. An idea initiated from the extra-tropical cyclogenesis problem (Bjerknes and Solberg, 1922) and an instigating theory of baroclinic instability (Charney, 1947; Eady, 1949), the perturbations in the atmospheric flows became a central solution to the initial value problem of numerical weather prediction (O'Malley, 1988). Later, it was polished into a well-versed technique to generate the ensemble of ICs to enhance prediction skill across various weather scales (Toth and Kalnay, 1993, 1997; Buizza and Palmer, 1995, 1998). The atmospheric lagged average is another traditional ensemble generation method (Hoffman and Kalnay, 1983; Kalnay and Dalcher, 1987; Chen et al., 2013) where the forecast from different initialization for the same target period is amalgamated into ensemble mean. These two techniques are famously known to address the uncertainties sourced from ICs.
Some of the recent literature incline toward grand ensemble based on multiple models (Krishnamurti et al., 2000; Sahai et al., 2013; Abhilash et al., 2015; Kalnay, 2019). The advantages in one or more aspects of one model formulation over the other could provide better assistant in the multi-model approach. The concept of inter-model diversity arises from the need to address another class of errors recognized as model-errors. Although there is a varying perspective on the nature and origin of these errors, they are largely attributed to the representation of physical processes in the model. The approximations considered while formulating parameterization schemes and misrepresentation of significant sub-grid scale phenomena in the model could cause biases in the predicted fields. Further, it is proposed that the multi-physics ensemble scheme can be an alternative to account for these model-errors (Richardson, 1997; Harrison et al., 1999; Orrell et al., 2001). The intra-model diversification introduced by using more than one physical parameterization showed significant improvement over single physics predictions (Stensrud and Fritsch, 1994; Berner et al., 2011; Tapiador et al., 2012; Greybush et al., 2017; Xu et al., 2020).
The above-mentioned ensemble prediction techniques have advantages as well as limitations when it comes to real-time prediction. For example, the perturbed initial conditions based ensemble could palliate the growth of initial errors, but such ensemble tends to be under dispersive, leading to presumptuous probabilistic prediction and underestimated larger weather anomalies (Stensrud et al., 2000). Similarly, lagged ensembles with improper weights from older initializations can debase the mean forecast (Abhilash et al., 2014b). Further, the model-error ensemble techniques require physical consistency among the members in terms of errors but are known to increase the ensemble spread (Green et al., 2017). Therefore, careful examination of these techniques is required to achieve the desired improvement.
The efficacy of any prediction tool is determined by its validity and reliability measured as the forecast skill (Murphy, 1991; Casati et al., 2008). Many skill assessment and verification methods are available to evaluate and compare various prediction strategies (Ghelli and Ebert, 2008; Jolliffe and Stephenson, 2011; Ebert et al., 2013). These methods increase the confidence in any prediction approach and motivate to understand and improve the limitations in the hypothesis formulation.
The skill analysis is vital, especially for the complex monsoon systems giving a significant annual rain share. In the present study, we evaluate the skill of a multi-model multi-physics ensemble prediction strategy for the Indian summer monsoon. This strategy is a part of developing a new extended range ensemble forecasting framework and here we will compare it to its current operational version. The functional version is only a multi-model ensemble prediction system (Sahai et al., 2013, 2016; Abhilash et al., 2014c, 2015) developed under the “National Monsoon Mission(NMM)” project (Rao et al., 2020) and has received acclaim on its successful implementation in 2016. This operational version is being used for extended range prediction (ERP) at the India Meteorological Department (IMD) and provides outlooks for rainfall, heatwaves, cyclones, and other meteorological parameters for various sectoral applications (Pattanaik et al., 2019). The next ERP version under development uses a multi-physics approach along with the multi-model framework. The results presented here are from the preliminary runs of this new version generated from unperturbed ICs. The comparison with the older version highlights its usefulness and drawbacks. This documentation will be handy for further improvements and modifications in the new framework.
The next section elaborates more on both the prediction systems as well as methodologies and datasets utilized in the study. The skill of ERP systems is discussed in the subsequent section, followed by conclusions.
2. Data and Methodology
The operational ERP system at IMD is a multi-model ensemble framework (Pattanaik et al., 2019). It comprises of two horizontal resolution variants (with 382 and 126 truncations) of two models; climate forecast system version 2 (CFSv2) and atmospheric global forecast system (GFS) from National Centers for Environmental Prediction (NCEP) (Saha et al., 2014). Further, this total of four variants run with a four-member ensemble of perturbed atmospheric ICs. These atmospheric ICs are obtained from National Center for Medium Range Weather Forecasting and oceanic ICs from Indian National Center for Ocean Information Services for CFSv2. Additionally, the real-time sea-surface temperature (SST) from CFSv2 after bias-correction is used as forcing to GFS (detailed technique can be seen in Abhilash et al., 2014a, Mandal et al., 2019, and Kaur et al., 2020). This ERP system was developed and thoroughly tested for skill at Indian Institute of Tropical Meteorology (IITM) under NMM. The operational forecasts are generated every week with Wednesday ICs for the next 32 days, also on the fly hindcast for 2003 to 2015 is produced for each IC. This system is henceforth addressed as ERPv1 in the paper.
The successor version of the above-mentioned prediction system is in the final development stage. This new ERP system also has two model variants CFSv2 and GFS, but the two resolution variants are now replaced with one seamless mode where the horizontal resolution of T574 transitions into the coarser T382 resolution after 15 days. Additionally, a multi-physics strategy is adopted for generating ensemble. We have used three convective parameterization permutations with two micro-physics parameterizations. These convection schemes include Simplified-Arakawa Shubert (SAS) (Pan and Wu, 1995), revised deep-convection SAS (NSAS) (Han and Pan, 2011), and revised SAS with modified shallow-convection (NSAS_SC) (Han and Pan, 2011). Zhao and Carr (ZC) (Zhao and Carr, 1997) and Ferrier (FER) (Ferrier et al., 2002) are the two micro-physics schemes incorporated in the new formulation. The resultant six physics combinations are SASZC, SASFER, NSASZC, NSASFER, NSASZC_SC, and NSASFER_SC. CFSv2 runs with all six combinations, whereas GFS has only four and does not include SASZC and SASFER. Similar to ERPv1, GFS is forced with bias-corrected CFSv2 real-time SST. The NCEP climate forecast system reanalysis ICs are utilized for both CFSv2 and GFS. The new multi-physics multi-model prediction contains 36 days forecast initialized on 1st, 6th, 11th, 16th, 21st, and 26th of each month for hindcast period 2001–2015. We are going to label this physics-based multi-model ensemble as MPMME hereafter.
The anomaly correlation coefficient (ACC), Pearson correlation, Heidke skill score (HSS) (Barnston, 1992), root mean square error (RMSE), root mean square skill score (RMSS), and Brier skill score (BSS) (Brier, 1950) are the verification matrices used to analogize MPMME skill with ERPv1. The verification is done for the weekly mean rainfall forecast at 4-week leads. The week 1 lead corresponds to the initial 7 days forecast, subsequent 8–14 days constitute week 2; similarly, 15–21 and 22–28 days forecast defines week 3 and 4, respectively, using common hindcast 2003–2015 from both the versions of ERP system. The sample size considered for ERPv1 is 22 weeks × 13 years = 286 forecasts for each lead. Similarly, MPMME has a sample of 24 weeks × 13 years = 312 forecasts. The skill scores are computed against observed daily rainfall from Tropical Rain Measure Mission (TRMM) merged rainfall provided by IMD (Mitra et al., 2009; Pai et al., 2014). The Monsoon Intraseasonal Oscillation (MISO) indices are computed following Sahai et al. (2013) and Suhas et al. (2013). It is specified that the MPMME includes only control runs (i.e., six members from CFSv2 and four members from GFS). Therefore, We have selected only 10 members from ERPv1 (three from each variant of CFS model and two from each GFS variant) for a fair comparison with 10-member MPMME.
3. Results
The hindcast from both ERPv1 and MPMME is analyzed for skill in predicting Indian summer monsoon weekly mean rainfall (ISMR) from June to September.
3.1. Monsoon Zone Weekly Rainfall Prediction Skill
ISMR exhibit large spatiotemporal heterogeneity during the season with positive (negative) rainfall anomalies over central India representing active (break) monsoon. A box defined in Rajeevan et al. (2010) over central India is the widely used prototypical monsoon region known as the core monsoon zone. Figure 1 and Table 1 illustrate the skill of predicted weekly mean rainfall averaged over the monsoon zone at 4-week leads. The ERPv1 has 0.78 and 0.63 ACC in week 1 and 2 lead, respectively. It is improved by almost a factor of 0.1 in MPMME for both the weeks. Although the skill is dropped in the third, it is still above 0.4, the practical skill limit. In the 4th week, the skill further declined. The difference between the deterministic prediction skill of both systems over the monsoon zone is statistically significant at 99.9, 95%, and above 90% confidence level for week 1, 2, and 3, respectively, and the difference in skill is not significant in the 4th week.
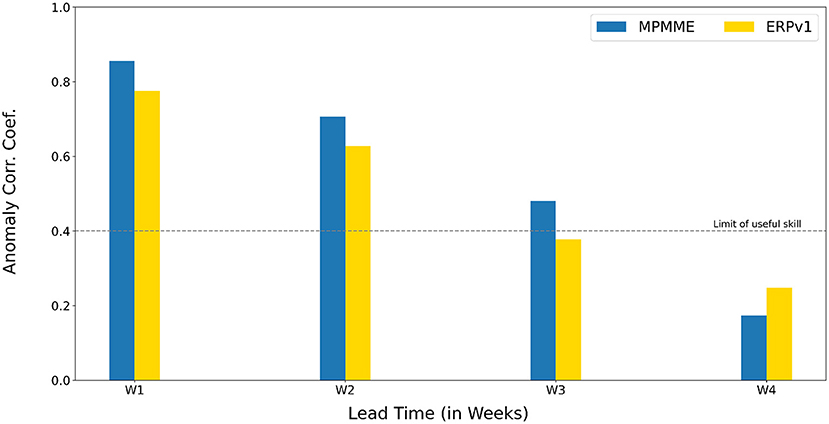
Figure 1. Anomaly correlation coefficient for weekly mean rainfall (mm/day) over Monsoon Zone of India during summer monsoon.
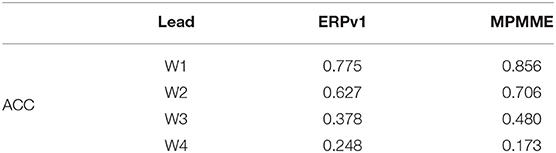
Table 1. Anomaly correlation coefficient (ACC) of predicted weekly mean rainfall over the monsoon zone.
Apart from spatial non-uniformity, the monsoonal rainfall has well-documented temporal variability that arises from intra-seasonal fluctuations. These fluctuations are recognized as spells of increased and minimum to no rain conditions over the monsoon zone. The transitions between these two spells are challenging but crucial, and models would have difficulties predicting such transitions, limiting the predictability of monthly rainfall. Figure 2 compares the monthly skill of weekly averaged rainfall over the monsoon zone for both systems. June and September have higher skill than July and August in both systems, which could be attributed to model inefficiency to predict frequent synoptic-scale systems in later months. However, the coefficient values are >0.6 for both systems in the first 2 weeks, which are reduced in following leads.
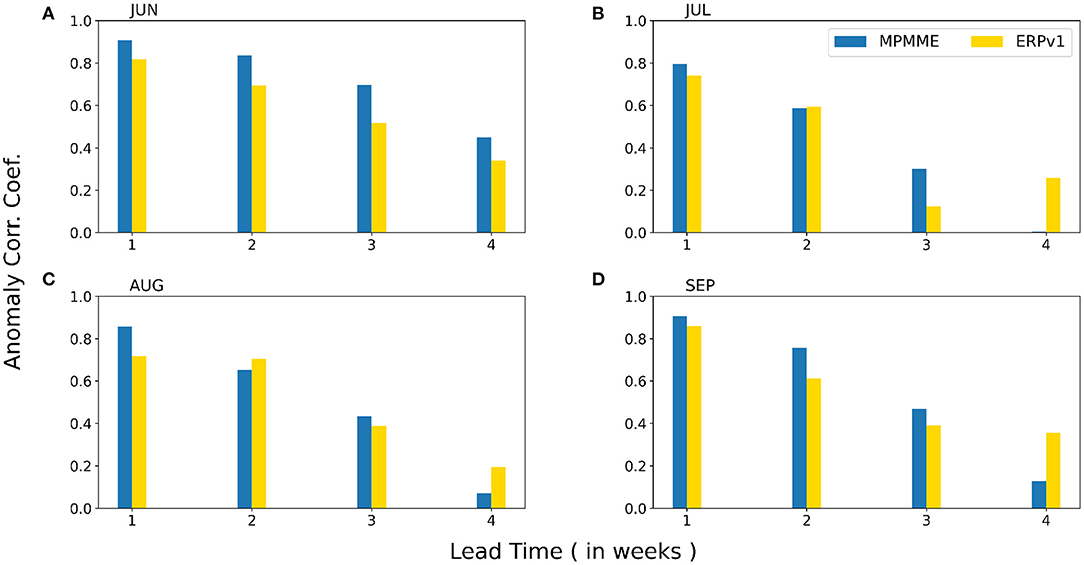
Figure 2. Anomaly correlation coefficient for weekly mean rainfall over monsoon zone of India for the month of (A) June, (B) July, (C) August, and (D) September at four week leads.
Regarding improvement, the month of June (Figure 2A) record the highest increase in the skill where at all 4 leads, MPMME shows 10, 18, 32, and 12% improvement over ERPv1, which is significant at 95% confidence level. The significant phenomena during June, such as monsoon onset and cyclonic system genesis impact the subsequent progress of the monsoon. These events are important to be predicted especially for dam management for releasing and storage planning of water, for agro-met services to begin sowing, and for disaster mitigation due to extreme rainfall activities. Hence, improvement in prediction skill of June will be highly beneficial for real-time ERP of monsoon onset and extreme rainfall conditions. Further, July, August, and September witness an increase in ACC up to week 3 lead (except week 2 lead during August) for MPMME. Relatively less skill is seen for the 4th week for these months than ERPv1, but the difference is insignificant as ERPv1 skill is also <0.4.
HSS gives fractional betterment of the forecast over a reference forecast, which is climatology in our case. HSS for deterministic forecast verification of various thresholds for weekly mean rainfall over monsoon zone is plotted in Figure 3. The skill decreases for higher rainfall thresholds at all weekly leads, indicating both versions' limitation in predicting heavy rainfall. However, the MPMME could perform better than reference forecast minimum up to 3 weeks leads for the given thresholds. The figure affirms the improvement in MPMME performance over ERPv1.
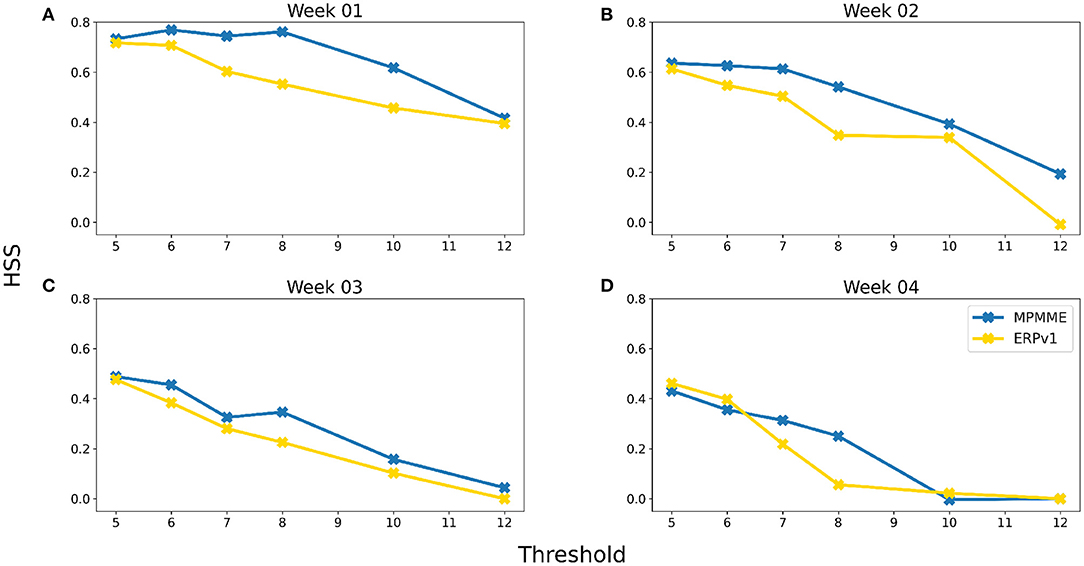
Figure 3. Heidke Skill score at different thresholds of weekly mean rainfall over Monsoon Zone of India for (A) week 1, (B) week 2, (C) week 3, and (D) week 4 lead.
3.2. Skill Assessment Over Meteorological Subdivisions
The ERP broadens the application spectrum of the meteorological forecast. These different sector-specific applications stipulate meteorological information at the finer spatial scale. However, the generation of stakeholder requisite forecast products requires skill assessment at the smaller spatial scale because the area-averaged precipitation skill will not be sufficient. Therefore, we will look into the skill for the meteorological subdivisions of India. There are 36 such subdivisions across the country; for further details, please refer Joseph et al. (2019).
The standard signal to noise ratio (SNR) is considered here to find out the limit of rainfall predictability (lead at which SNR becomes one) for these subdivisions. Figure 4 shows the spatial map of predictability with color indicating the number of predictable days. In both ERPv1 (Figure 4A) and MPMME (Figure 4B), maximum subdivisions show predictability of 10–14 days. A very few numbers of subdivisions, i.e., 5, have predictability >16 days. The number of such subdivisions with predictability higher than 16 days is almost doubled in MPMME. Simultaneously, the number is reduced by two for subdivisions with <8 predictable days in MPMME compared to ERPv1. In total, more than 12 subdivision show improvement in predictability by 2–4 days in MPMME, these subdivisions fall into north and northwest India. A similar increment is also seen for a few subdivisions in southern peninsular and northeast India. In contrast, for many subdivisions in central India, the predictability remains unchanged in MPMME, except a very few subdivision (i.e., 4) where predictability dropped by 1–2 days.
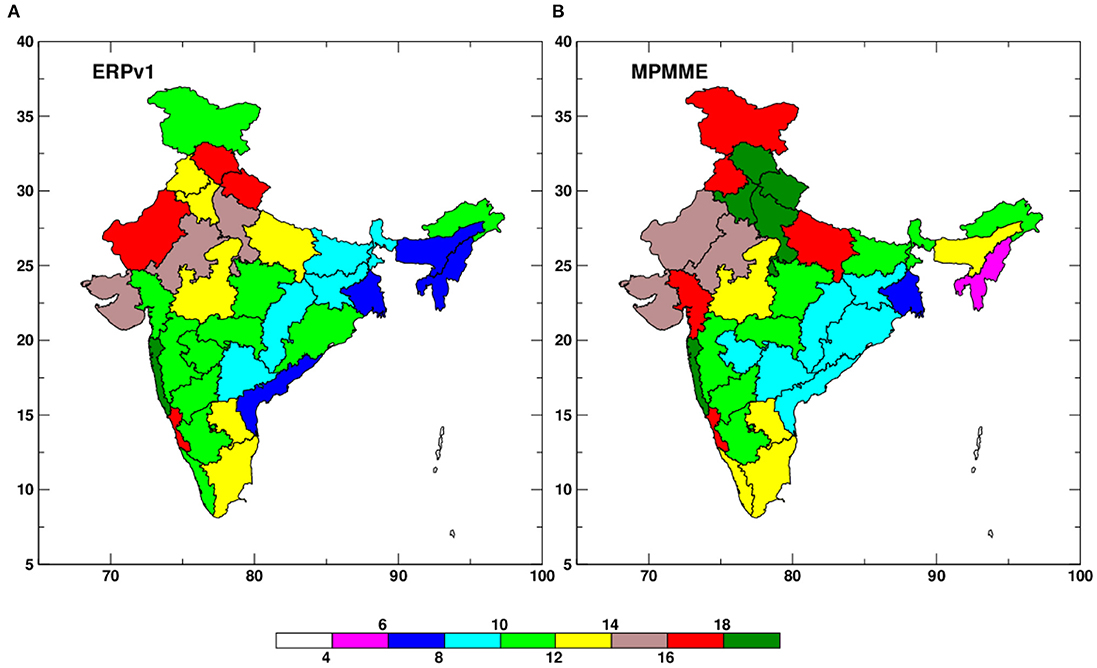
Figure 4. Subdivision-wise predictability limit for (A) extended range prediction system (ERPv1) and (B) multi-physics multi-model ensemble (MPMME) during monsoon.
The week-wise anomaly correlations for subdivisions are shown in Figure 5, where ACC>0.2 is statistically significant at a level of 99.9%. Both ERPv1 and MPMME have good skill in the week 1 and 2 forecast, with MPMME outperforming ERPv1 for maximum subdivisions. The lead-in prediction skill is maintained in week 3 by MPMME, where many subdivisions have ACC >0.2 and 0.3 in contrast to ERPv1. Week 4 is less skillful than the first 3 weeks in both ERPv1 and MPMME, where most of the subdivisions shows ACC smaller than 0.2. Figure 6 illustrates the RMSS values from ERPv1 and MPMME at 4 leads for meteorological subdivisions; the shaded values (i.e., >0) indicates reasonable prediction skill. Furthermore, similar to ACC, RMSS is also better in MPMME than ERPv1 for up to 3 weeks. Subdivisions in northeast India are less skillful in both ERPv1 and MPMME; the previous authors have linked lower predictability to more rainfall contribution from less predictable synoptic systems over the northeast regions (Abhilash et al., 2018; Joseph et al., 2019).
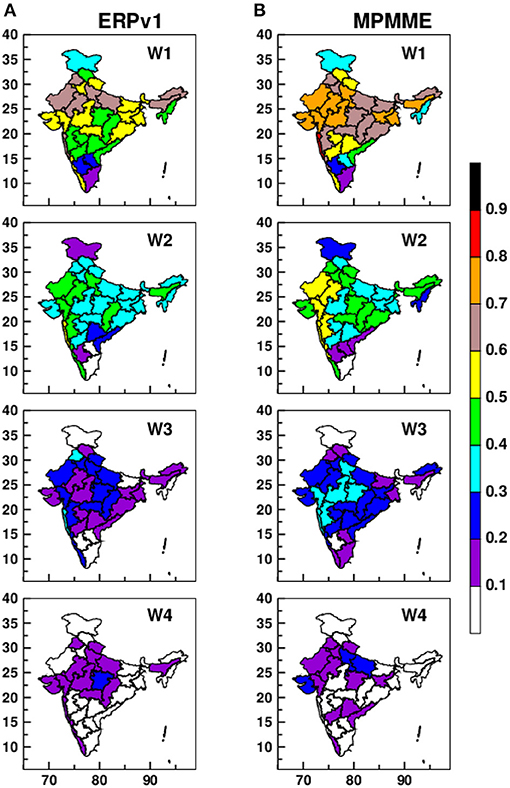
Figure 5. Sub-divisional skill in terms of anomaly correlation coefficient for (A) extended range prediction system (ERPv1) and (B) multi-physics multi-model ensemble (MPMME) during monsoon.
Figure 6. Sub-divisional skill in terms of root mean square score for (A) extended range prediction system (ERPv1) and (B) multi-physics multi-model ensemble (MPMME) during monsoon.
Overall, MPMME show reasonable improvement in deterministic skill over northwest and central India compared to ERPv1. The studies have reported the more frequent occurrence of extreme rainfall over these regions (Singh et al., 2011; Woo et al., 2019; Joseph et al., under revision; Rai et al., 2020). Therefore, improved predictability and prediction skill for these regions in MPMME can effectively improve the extreme event prediction (will be addressed in a separate study).
3.3. Prediction Skill for Monsoon Intraseasonal Oscillation
MISO is one of the most dominant mode of low-frequency intraseasonal variability, known to provide predictability in the extended range during the Indian summer monsoon. The enhanced skill witnessed in earlier sections could be explained by analyzing the model's ability to capture this large-scale signal.
The MISO prediction skill is computed in terms of bivariate anomaly correlation coefficient (BVCC) and root mean square error as mentioned in Rashid et al. (2011) of predicted MISO Indices from all ICs with the observed. The leading pair of model predicted MISO Indices from all ICs with the observed counterpart are utilized for ACC and RMSE computation. The BVCC is plotted in Figure 7 along with the RMSE for MISO indices as a function of lead days. We consider BVCC >0.5 and RMSE lower than 1.4 as a threshold for skillful MISO prediction. The horizontal line intersects the BVCC axis at 0.5 and RMSE axis at 1.41 to track the significant skill and error limit. The black line represents the combined skill for all MISO phases, whereas blue and cyan show the evolution of CC and RMSE for the transition to the active and break phase, respectively. The figure clearly shows a gain in skill for MPMME over ERPv1. The ERPv1 reaches the prediction limit in around 19 days, whereas the MPMME has this limit beyond 21 days.
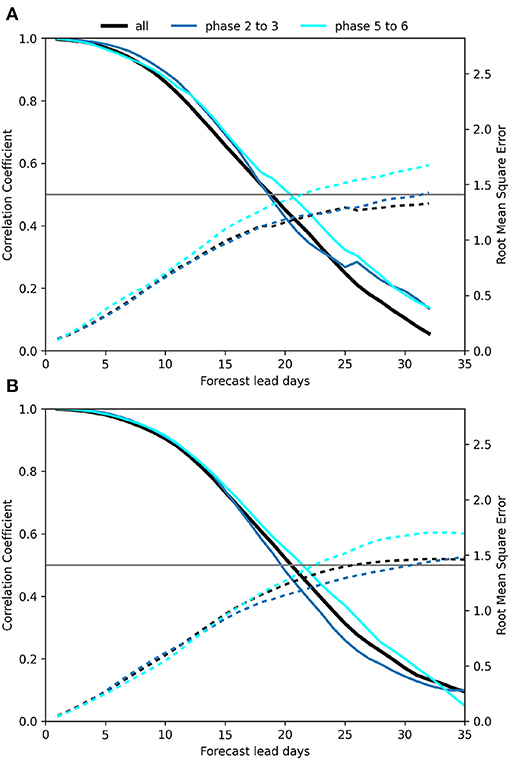
Figure 7. Monsoon Intraseasonal Oscillation (MISO) prediction skill for (A) extended range prediction system (ERPv1) and (B) multi-physics multi-model ensemble (MPMME), where solid lines are for bivariate anomaly correlation coefficient (BVCC) and dotted line represent root mean square error (RMSE).
The study from Goswami and Xavier (2003) reveals that the potential predictability for break (less to no rain) conditions during monsoon is high compared to the active. They also suggested that higher predictability of transition to break phase is due to governance of error growth in this phase by low frequency (30–60 days) signal. Abhilash et al. (2014b) also showed that ERP (from CFSv2-based 11-member ensemble) of breaks are more skillful. Similar inference can be made from Figure 7 for phase-dependent prediction skill of both systems; ERPv1 and MPMME also show slightly better predictability for break transition (Cyan line in Figures 7A,B) than active (blue). MPMME have improved skill for both (active and break) phases in comparison to ERPv1.
The higher predictability in northwest regions of India is associated with low-frequency monsoon oscillations (Joseph et al., 2019), which is evident in Figure 5. Therefore, the 2–4 days increase in predictability in MPMME over these regions can be attributed to about 2 days gain in the skill of this low variability signal skill, i.e., MISO.
3.4. Probabilistic Forecast Skill
In the previous sections, we have evaluated the deterministic prediction skill from ERPv1 and MPMME; in this section, we look into some probabilistic verification. The BSS is calculated for categorical rainfall probabilistic prediction (Figure 8). Based on the tercile method, three categories are defined as above normal (when the rainfall amount is more than upper tercile value), near normal (when it is between upper tercile and lower tercile values), and below normal (when it is below the lower tercile value). The probabilities for either category are 100% for the observation.
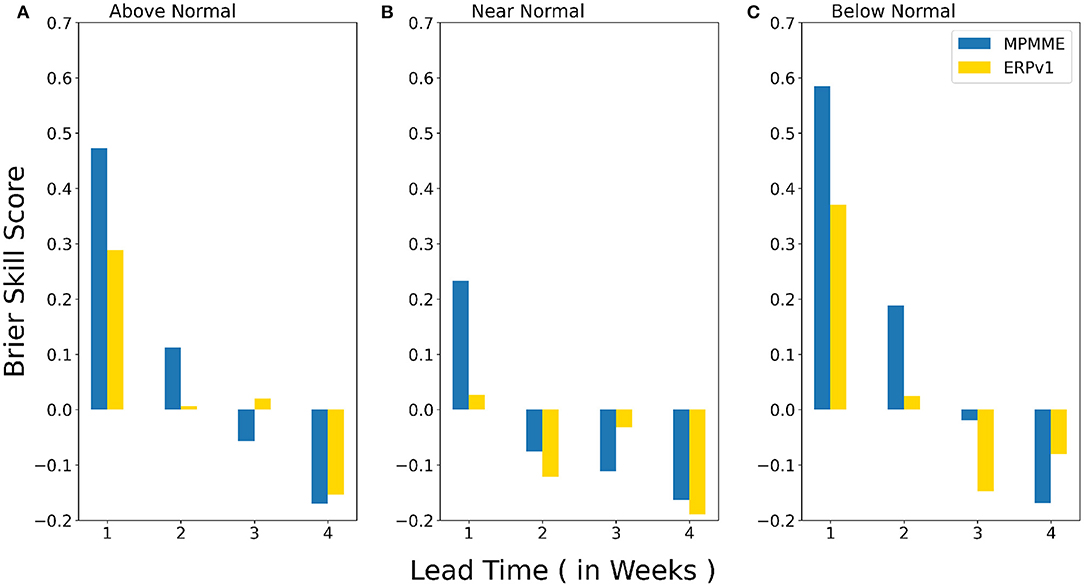
Figure 8. Brier skill score from extended range prediction system (ERPv1) and multi-physics multi-model ensemble (MPMME) for (A) above normal, (B) near normal, and (C) below normal categorical rainfall forecast over monsoon zone.
The BSS compares the brier score of the forecast with the reference forecast (climatology), assuming a 33% equal occurrence probability for each category. A BSS value >0 indicates an improvement over climatology. Both ERPv1 and MPMME have better skill in predicting the above normal (Figure 8A) and below normal (Figure 8C) categories up to 2 weeks. The near-normal (Figure 8B) rainfall predictions are comparatively less skillful in both systems. It is interesting to note from the figure that the considerable improvement is there for MPMME over ERPv1 in almost all categories in the first 2-week leads. The skill of both system reduces at longer leads.
The analysis presented in this section favors MPMME until almost 21-day lead. However, the current results are only from multi-physics ensemble, i.e., addressing model-errors to some extent. Nevertheless, the model also suffers from initial condition errors at longer leads. A few earlier studies have also concluded that physics ensemble along with perturbed initial conditions ensemble could provide better skill by addressing two major bias components (Stensrud and Fritsch, 1994; Stensrud et al., 2000). Therefore, the results of this study can be ameliorated further with the careful selection of physics and initial condition ensemble.
4. Conclusions
The present work highlights the improvements of a physics-based multi-model extended range ensemble prediction system over its predecessor operational version in predicting ISMR. This new MPMME framework distinguishes itself from the ERPv1 in its single seamless horizontal resolution, and most importantly, for considering multiple realizations of atmospheric dynamics achieved by permutations of convection and microphysics parameterizations.
The skill of MPMME and ERPv1 for ISMR is compared using different verification scores for spatiotemporal forecast evolution at weekly leads. ACC for hindcast of 2003–2015 from MPMME signifies an improvement for monsoon zone rainfall over ERPv1 up to 3-week lead. The MPMME prediction skill for 4 months from June to September also witnesses increment up to 3-week lead. The month of June has the highest skill for MPMME at all 4-week leads, which will come in handy for predicting monsoon onset and extreme rain-producing systems in the onset phase. The HSS for rainfall over monsoon zone elucidates the enhanced skill at all thresholds of the weekly mean rainfall for MPMME over ERPv1.
The MPMME extends the predictability limit by 2–4 days compared to ERPv1 as indicated by sub-division map. Similarly, the conclusion drawn from subdivision-wise ACC and RMSS favors MPMME in most regions through 7, 14, and 21-day leads. The subdivisions in the northwest and central parts of the country exhibit a maximum increase in the skill. All the phases of large-scale MISOs have a better prediction from MPMME than ERPv1, reflecting in the overall gain in predictability at the sub-division level. The tercile-based categorical rainfall prediction is verified for the probabilistic skill of both systems. BSS for these categorical rainfall occurrences exhibits the superiority of physics-based MPMME over ERPv1.
Although the results presented here are from the preliminary development stage, the different verifications used in the study support the MPMME over its operational version ERPv1 up to 21 days lead. Further assessment of signal and noise added per physics combination could assist in considering the weighted average of these ensembles to generate the forecast products. Since we have only considered the unperturbed control initial condition in MPMME, adding a few perturbed IC members could further help improve the prediction, especially at longer leads, by controlling the growth of initial condition uncertainty (Stensrud and Fritsch, 1994; Stensrud et al., 2000). The study proffers the utility of physics-based ensemble and finds its scope in further exploration. It is anticipated that the enhanced temporal skill for June and spatial skill for northwest and central regions of India could probably improve the extreme event prediction.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
AS, SJ, RP, and RC have conceptualized the MPMME strategy. RP, RM, AD, and MK were involved in the model runs, data-handling, and processing. MK has done the analysis, plotting, and structured the manuscript draft. All authors have contributed in writing and editing the final manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Research at IITM was fully supported by the Ministry of Earth Sciences and authors sincerely acknowledge it. The analysis and model integrations are performed on Aditya and Pratyush HPCS. We were thankful to Dr. D. R. Pattanaik for ERPv1 runs. The present work was part of Ph.D. thesis of MK. We express our gratitude to two reviewers for their insightful review, which contributed significantly to our manuscript's quality.
References
Abhilash, S., Mandal, R., Dey, A., Phani, R., Joseph, S., Chattopadhyay, R., et al. (2018). Role of enhanced synoptic activity and its interaction with intra-seasonal oscillations on the lower extended range prediction skill during 2015 monsoon season. Clim. Dyn. 51, 3435–3446. doi: 10.1007/s00382-018-4089-3
Abhilash, S., Sahai, A. K., Borah, N., Chattopadhyay, R., Joseph, S., Sharmila, S., et al. (2014a). Does bias correction in the forecasted SST improve the extended range prediction skill of active-break spells of Indian summer monsoon rainfall? Atmos. Sci. Lett. 15, 114–119. doi: 10.1002/asl2.477
Abhilash, S., Sahai, A. K., Borah, N., Chattopadhyay, R., Joseph, S., Sharmila, S., et al. (2014b). Prediction and monitoring of monsoon intraseasonal oscillations over Indian monsoon region in an ensemble prediction system using CFSv2. Clim. Dyn. 42, 2801–2815. doi: 10.1007/s00382-013-2045-9
Abhilash, S., Sahai, A. K., Borah, N., Joseph, S., Chattopadhyay, R., Sharmila, S., et al. (2015). Improved spread–error relationship and probabilistic prediction from the CFS-based grand ensemble prediction system. J. Appl. Meteorol. Climatol. 54, 1569–1578. doi: 10.1175/JAMC-D-14-0200.1
Abhilash, S., Sahai, A. K., Pattnaik, S., and De, S. (2013). Predictability during active break phases of Indian summer monsoon in an ensemble prediction system using climate forecast system. J. Atmos. Solar Terres. Phys. 100–101, 13–23. doi: 10.1016/j.jastp.2013.03.017
Abhilash, S., Sahai, A. K., Pattnaik, S., Goswami, B. N., and Kumar, A. (2014c). Extended range prediction of active-break spells of Indian summer monsoon rainfall using an ensemble prediction system in NCEP climate forecast system. Int. J. Climatol. 34, 98–113. doi: 10.1002/joc.3668
Ajayamohan, R. S., and Rao, S. A. (2008). Indian Ocean dipole modulates the number of extreme rainfall events over India in a warming environment. J. Meteorol. Soc. Jpn II 86, 245–252. doi: 10.2151/jmsj.86.245
Annamalai, H. (2010). Moist dynamical linkage between the equatorial Indian Ocean and the South Asian monsoon trough. J. Atmos. Sci. 67, 589–610. doi: 10.1175/2009JAS2991.1
Barnston, A. G. (1992). Correspondence among the correlation, RMSE, and Heidke forecast verification measures; refinement of the Heidke Score. Weather Forecast. 7, 699–709. doi: 10.1175/1520-0434(1992)007<0699:CATCRA>2.0.CO;2
Berner, J., Ha, S. Y., Hacker, J. P., Fournier, A., and Snyder, C. (2011). Model uncertainty in a mesoscale ensemble prediction system: stochastic versus multiphysics representations. Mon. Weather Rev. 139, 1972–1995. doi: 10.1175/2010MWR3595.1
Bjerknes, J., and Solberg, H. (1922). Life Cycle of Cyclones and the Polar Front Theory of Atmospheric Circulation. Geofysiske Publikationer. Cammermeyers Bogh.
Brier, G. W. (1950). Verification of forecasts expressed in terms of probability. Mon. Weather Rev. 78, 1–3. doi: 10.1175/1520-0493(1950)078<0001:VOFEIT>2.0.CO;2
Buizza, R., Bidlot, J. R., Wedi, N., Fuentes, M., Hamrud, M., Holt, G., et al. (2007). The new ECMWF VAREPS (variable resolution ensemble prediction system). Q. J. R. Meteorol. Soc. 133, 681–695. doi: 10.1002/qj.75
Buizza, R., Leutbecher, M., and Isaksen, L. (2008). Potential use of an ensemble of analyses in the ECMWF ensemble prediction system. Q. J. R. Meteorol. Soc. 134, 2051–2066. doi: 10.1002/qj.346
Buizza, R., and Palmer, T. N. (1995). The singular-vector structure of the atmospheric global circulation. J. Atmos. Sci. 52, 1434–1456. doi: 10.1175/1520-0469(1995)052<1434:TSVSOT>2.0.CO;2
Buizza, R., and Palmer, T. N. (1998). Impact of ensemble size on ensemble prediction. Mon. Weather Rev. 126, 2503–2518. doi: 10.1175/1520-0493(1998)126<2503:IOESOE>2.0.CO;2
Casati, B., Wilson, L. J., Stephenson, D. B., Nurmi, P., Ghelli, A., Pocernich, M., et al. (2008). Forecast verification: current status and future directions. Meteorol. Appl. 15, 3–18. doi: 10.1002/met.52
Charney, J. G. (1947). The dynamics of long waves in a baroclinic westerly current. J. Atmos. Sci. 4, 136–162. doi: 10.1175/1520-0469(1947)004<0136:TDOLWI>2.0.CO;2
Chen, M., Wang, W., and Kumar, A. (2013). Lagged ensembles, forecast configuration, and seasonal predictions. Mon. Weather Rev. 141, 3477–3497. doi: 10.1175/MWR-D-12-00184.1
Ebert, E., Wilson, L., Weigel, A., Mittermaier, M., Nurmi, P., Gill, P., et al. (2013). Progress and challenges in forecast verification. Meteorol. Appl. 20, 130–139. doi: 10.1002/met.1392
Ferrier, B. S., Jin, Y., Lin, Y., Black, T., Rogers, E., and DiMego, G. (2002). “Implementation of a new grid-scale cloud and precipitation scheme in the NCEP Eta model,” in Conference on Weather Analysis and Forecasting, Vol. 19 (AMS), 280–283.
Gadgil, S., and Gadgil, S. (2006). The Indian monsoon, GDP and agriculture. Econ. Polit. Weekly 41, 4887–4895.
Ghelli, A., and Ebert, E. (2008). Special issue on forecast verification. Meteorol. Appl. 15:1. doi: 10.1002/met.69
Goswami, B., Venugopal, V., Sengupta, D., Madhusoodanan, M., and Xavier, P. (2006). Earth by comets and meteorites. Further studies of these objects may elucidate whether their composition and membrane-like structures were important building blocks for the origin of life. Science 314, 1442–1445. doi: 10.1126/science.1132027
Goswami, B. N. (2005). “South Asian monsoon,” in Intraseasonal Variability in the Atmosphere-Ocean Climate System, eds W. K. M. Lau and D. E. Waliser (Berlin; Heidelberg: Springer Berlin Heidelberg), 19–61. doi: 10.1007/3-540-27250-X_2
Goswami, B. N., Krishnamurthy, V., and Annmalai, H. (1999). A broad-scale circulation index for the interannual variability of the Indian summer monsoon. Q. J. R. Meteorol. Soc. 125, 611–633. doi: 10.1002/qj.49712555412
Goswami, B. N., Venugopal, V., and Chattopadhyay, R. (2019). “Chapter 2–South Asian monsoon extremes,” in Tropical Extremes:Natural Variability and Trends, eds V. Venugopal, J. Sukhatme, R. Murtugudde, and R. B. T. T. E. Roca (Elsevier), 15–49. doi: 10.1016/B978-0-12-809248-4.00002-9
Goswami, B. N., and Xavier, P. K. (2003). Potential predictability and extended range prediction of Indian summer monsoon breaks. Geophys. Res. Lett. 30, 1–4. doi: 10.1029/2003GL017810
Green, B. W., Sun, S., Bleck, R., Benjamin, S. G., and Grell, G. A. (2017). Evaluation of MJO predictive skill in multiphysics and multimodel global ensembles. Mon. Weather Rev. 145, 2555–2574. doi: 10.1175/MWR-D-16-0419.1
Greybush, S. J., Saslo, S., and Grumm, R. (2017). Assessing the ensemble predictability of precipitation forecasts for the January 2015 and 2016 East Coast winter storms. Weather Forecast. 32, 1057–1078. doi: 10.1175/WAF-D-16-0153.1
Guhathakurta, P., and Rajeevan, M. (2008). Trends in the rainfall pattern over India. Int. J. Climatol. 28, 1453–1469. doi: 10.1002/joc.1640
Han, J., and Pan, H. L. (2011). Revision of convection and vertical diffusion schemes in the NCEP global forecast system. Weather Forecast. 26, 520–533. doi: 10.1175/WAF-D-10-05038.1
Harrison, M. S. J., Palmer, T. N., Richardson, D. S., and Buizza, R. (1999). Analysis and model dependencies in medium-range ensembles: two transplant case-studies. Q. J. R. Meteorol. Soc. 125, 2487–2515. doi: 10.1002/qj.49712555908
Hoffman, R. N., and Kalnay, E. (1983). Lagged average forecasting, an alternative to Monte Carlo forecasting. Tellus A 35, 100–118. doi: 10.3402/tellusa.v35i2.11425
Houze, R. A., McMurdie, L. A., Rasmussen, K. L., Kumar, A., and Chaplin, M. M. (2017). Multiscale aspects of the storm producing the June 2013 flooding in Uttarakhand, India. Mon. Weather Rev. 145, 4447–4466. doi: 10.1175/MWR-D-17-0004.1
Jiang, X., Li, T., and Wang, B. (2004). Structures and mechanisms of the northward propagating boreal summer intraseasonal oscillation. J. Clim. 17, 1022–1039. doi: 10.1175/1520-0442(2004)017<1022:SAMOTN>2.0.CO;2
Jolliffe, I. T., and Stephenson, D. B. (2011). Forecast Verification: A Practitioner's Guide in Atmospheric Science. John Wiley & Sons.
Joseph, P. V., and Sijikumar, S. (2004). Intraseasonal variability of the low-level jet stream of the Asian summer monsoon. J. Clim. 17, 1449–1458. doi: 10.1175/1520-0442(2004)017<1449:IVOTLJ>2.0.CO;2
Joseph, S., Sahai, A. K., Phani, R., Mandal, R., Dey, A., Chattopadhyay, R., et al. (2019). Skill evaluation of extended-range forecasts of rainfall and temperature over the meteorological subdivisions of India. Weather Forecast. 34, 81–101. doi: 10.1175/WAF-D-18-0055.1
Joseph, S., Sahai, A. K., Sharmila, S., Abhilash, S., Borah, N., Chattopadhyay, R., et al. (2015). North Indian heavy rainfall event during June 2013: diagnostics and extended range prediction. Clim. Dyn. 44, 2049–2065. doi: 10.1007/s00382-014-2291-5
Kalnay, E. (2019). Historical perspective: earlier ensembles and forecasting forecast skill. Q. J. R. Meteorol. Soc. 145, 25–34. doi: 10.1002/qj.3595
Kalnay, E., and Dalcher, A. (1987). Forecasting forecast skill. Monthly Weather Rev. 115, 349–356. doi: 10.1175/1520-0493(1987)115<0349:FFS>2.0.CO;2
Kaur, M., Krishna, R. P. M., Joseph, S., Dey, A., Mandal, R., Chattopadhyay, R., et al. (2020). Dynamical downscaling of a multimodel ensemble prediction system: application to tropical cyclones. Atmos. Sci. Lett. 21, 1–11. doi: 10.1002/asl.971
Krishnamurti, T. N., Kishtawal, C. M., Zhang, Z., LaRow, T., Bachiochi, D., Williford, E., et al. (2000). Multimodel ensemble forecasts for weather and seasonal climate. J. Clim. 13, 4196–4216. doi: 10.1175/1520-0442(2000)013<4196:MEFFWA>2.0.CO;2
Mandal, R., Joseph, S., Sahai, A. K., Phani, R., Dey, A., Chattopadhyay, R., et al. (2019). Real time extended range prediction of heat waves over India. Sci. Rep. 9:9008. doi: 10.1038/s41598-019-45430-6
Mitra, A. K., Bohra, A. K., Rajeevan, M. N., and Krishnamurti, T. N. (2009). Daily Indian precipitation analysis formed from a merge of rain-gauge data with the TRMM TMPA satellite-derived rainfall estimates. J. Meteorol. Soc. Jpn. A 87, 265–279. doi: 10.2151/jmsj.87A.265
Molteni, F., Buizza, R., Palmer, T. N., and Petroliagis, T. (1996). The ECMWF ensemble prediction system: methodology and validation. Q. J. R. Meteorol. Soc. 122, 73–119. doi: 10.1002/qj.49712252905
Murphy, A. H. (1991). Forecast verification: its complexity and dimensionality. Mon. Weather Rev. 119, 1590–1601. doi: 10.1175/1520-0493(1991)119<1590:FVICAD>2.0.CO;2
O'Malley, R. E. (1988). On nonlinear singularly perturbed initial value problems. SIAM Rev. 30, 193–212. doi: 10.1137/1030044
Orrell, D., Smith, L., Barkmeijer, J., and Palmer, T. N. (2001). Model error in weather forecasting. Nonlin. Process. Geophys. 8, 357–371. doi: 10.5194/npg-8-357-2001
Pai, D. S., Sridhar, L., Rajeevan, M., Sreejith, O. P., Satbhai, N. S., and Mukhopadhyay, B. (2014). Development of a new high spatial resolution (0.25° ×0.25°) long period (1901–2010) daily gridded rainfall data set over India and its comparison with existing data sets over the region. Mausam 1, 1–18.
Pan, H. L., and Wu, W. S. (1995). Implementing a mass flux convective parameterization package for the NMC medium-range forecast model. NMC Off. Note 409:40.
Parker, D. J., Willetts, P., Birch, C., Turner, A. G., Marsham, J. H., Taylor, C. M., et al. (2016). The interaction of moist convection and mid-level dry air in the advance of the onset of the Indian monsoon. Q. J. R. Meteorol. Soc. 142, 2256–2272. doi: 10.1002/qj.2815
Parthasarathy, B., Kumar, K. R., and Kothawale, D. R. (1992). Indian summer monsoon rainfall indices: 1871–1990. Meteorol. Mag. 121, 174–186.
Pattanaik, D. R., Sahai, A. K., Mandal, R., Phani Muralikrishna, R., Dey, A., Chattopadhyay, R., et al. (2019). Evolution of operational extended range forecast system of IMD: Prospects of its applications in different sectors. Mausam 70, 233–264.
Raghavan, K. (1973). Tibetan anticyclone and tropical easterly jet. Pure Appl. Geophys. 110, 2130–2142. doi: 10.1007/BF00876576
Rai, P. K., Singh, G. P., and Dash, S. K. (2020). Projected changes in extreme precipitation events over various subdivisions of India using RegCM4. Clim. Dyn. 54, 247–272. doi: 10.1007/s00382-019-04997-6
Rajeevan, M., Bhate, J., and Jaswal, A. K. (2008). Analysis of variability and trends of extreme rainfall events over India using 104 years of gridded daily rainfall data. Geophys. Res. Lett. 35, 1–6. doi: 10.1029/2008GL036105
Rajeevan, M., Gadgil, S., and Bhate, J. (2010). Active and break spells of the Indian summer monsoon. J. Earth Syst. Sci. 119, 229–247. doi: 10.1007/s12040-010-0019-4
Rao, S. A., Goswami, B. N., Sahai, A. K., Rajagopal, E. N., Mukhopadhyay, P., Rajeevan, M., et al. (2020). Monsoon mission: a targeted activity to improve monsoon prediction across scales. Bull. Am. Meteorol. Soc. 100, 2509–2532. doi: 10.1175/BAMS-D-17-0330.1
Rashid, H. A., Hendon, H. H., Wheeler, M. C., and Alves, O. (2011). Prediction of the Madden–Julian oscillation with the POAMA dynamical prediction system. Clim. Dyn. 36, 649–661. doi: 10.1007/s00382-010-0754-x
Richardson, D. (1997). “The relative effects of model and analysis differences on ECMWF and UKMO operational forecasts,” in Workshop on Predictability 20–22 October 1997 (Reading: ECMWF).
Robertson, A. W., Acharya, N., Goddard, L., Pattanaik, D. R., Sahai, A. K., Singh, K. K., et al. (2019). Subseasonal forecasts of the 2018 Indian summer monsoon over Bihar. J. Geophys. Res. Atmos. 124, 13861–13875. doi: 10.1029/2019JD031374
Roxy, M. K., Ghosh, S., Pathak, A., Athulya, R., Mujumdar, M., Murtugudde, R., et al. (2017). A threefold rise in widespread extreme rain events over central India. Nat. Commun. 8:708. doi: 10.1038/s41467-017-00744-9
Saha, S., Moorthi, S., Wu, X., Wang, J., Nadiga, S., Tripp, P., et al. (2014). The NCEP climate forecast system version 2. J. Clim. 27, 2185–2208. doi: 10.1175/JCLI-D-12-00823.1
Sahai, A. K., Chattopadhyay, R., Joseph, S., R, P., and S, A. (2016). Extended range prediction system and its application. Vayu Mandal 42, 75–96.
Sahai, A. K., Sharmila, S., Abhilash, S., Chattopadhyay, R., Borah, N., Krishna, R. P., et al. (2013). Simulation and extended range prediction of monsoon intraseasonal oscillations in NCEP CFS/GFS version 2 framework. Curr. Sci. 104, 1394–1408.
Sikka, D. R., and Gadgil, S. (1980). On the maximum cloud zone and the ITCZ over Indian, longitudes during the southwest monsoon. Mon. Weather Rev. 108, 1840–1853. doi: 10.1175/1520-0493(1980)108<1840:OTMCZA>2.0.CO;2
Singh, R., Kishtawal, C. M., Pal, P. K., and Joshi, P. C. (2011). Assimilation of the multisatellite data into the WRF model for track and intensity simulation of the Indian Ocean tropical cyclones. Meteorol. Atmos. Phys. 111, 103–119. doi: 10.1007/s00703-011-0127-y
Sooraj, K. P., Terray, P., and Xavier, P. (2016). Sub-seasonal behaviour of Asian summer monsoon under a changing climate: assessments using CMIP5 models. Clim. Dyn. 46, 4003–4025. doi: 10.1007/s00382-015-2817-5
Stensrud, D. J., Bao, J. W., and Warner, T. T. (2000). Using initial condition and model physics perturbations in short-range ensemble simulations of mesoscale convective systems. Mon. Weather Rev. 128, 2077–2107. doi: 10.1175/1520-0493(2000)128<2077:UICAMP>2.0.CO;2
Stensrud, D. J., and Fritsch, J. M. (1994). Mesoscale convective systems in weakly forced large-scale environments. Part III: numerical simulations and implications for operational forecasting. Mon. Weather Rev. 122, 2084–2104. doi: 10.1175/1520-0493(1994)122<2084:MCSIWF>2.0.CO;2
Suhas, E., Neena, J. M., and Goswami, B. N. (2013). An Indian monsoon intraseasonal oscillations (MISO) index for real time monitoring and forecast verification. Clim. Dyn. 40, 2605–2616. doi: 10.1007/s00382-012-1462-5
Tapiador, F. J., Tao, W. K., Shi, J. J., Angelis, C. F., Martinez, M. A., Marcos, C., et al. (2012). A comparison of perturbed initial conditions and multiphysics ensembles in a severe weather episode in Spain. J. Appl. Meteorol. Climatol. 51, 489–504. doi: 10.1175/JAMC-D-11-041.1
Toth, Z., and Kalnay, E. (1993). Ensemble forecasting at NMC: the generation of perturbations. Bull. Am. Meteorol. Soc. 74, 2317–2330. doi: 10.1175/1520-0477(1993)074<2317:EFANTG>2.0.CO;2
Toth, Z., and Kalnay, E. (1997). Ensemble forecasting at NCEP and the breeding method. Mon. Weather Rev. 125, 3297–3319. doi: 10.1175/1520-0493(1997)125<3297:EFANAT>2.0.CO;2
Vitart, F., and Molteni, F. (2009). Dynamical extended-range prediction of early monsoon rainfall over India. Mon. Weather Rev. 137, 1480–1492. doi: 10.1175/2008MWR2761.1
Vitart, F., and Robertson, A. W. (2018). The sub-seasonal to seasonal prediction project (S2S) and the prediction of extreme events. NPJ Clim. Atmos. Sci. 1, 1–7. doi: 10.1038/s41612-018-0013-0
Wang, B., and Fan, Z. (1999). Choice of South Asian summer monsoon indices. Bull. Am. Meteorol. Soc. 80, 629–638. doi: 10.1175/1520-0477(1999)080<0629:COSASM>2.0.CO;2
Webster, P. J., and Yang, S. (1992). Monsoon and Enso: selectively interactive systems. Q. J. R. Meteorol. Soc. 118, 877–926. doi: 10.1002/qj.49711850705
Woo, S., Singh, G. P., Oh, J. H., and Lee, K. M. (2019). Projection of seasonal summer precipitation over Indian sub-continent with a high-resolution AGCM based on the RCP scenarios. Meteorol. Atmos. Phys. 131, 897–916. doi: 10.1007/s00703-018-0612-7
Xu, Z., Chen, J., Jin, Z., Li, H., and Chen, F. (2020). Assessment of the forecast skill of multiphysics and multistochastic methods within the GRAPES regional ensemble prediction system in the East Asian monsoon region. Weather Forecast. 35, 1145–1171. doi: 10.1175/WAF-D-19-0021.1
Keywords: multi-physics, multi-model, extended range prediction, monsoon, ensemble prediction
Citation: Sahai AK, Kaur M, Joseph S, Dey A, Phani R, Mandal R and Chattopadhyay R (2021) Multi-Model Multi-Physics Ensemble: A Futuristic Way to Extended Range Prediction System. Front. Clim. 3:655919. doi: 10.3389/fclim.2021.655919
Received: 19 January 2021; Accepted: 30 March 2021;
Published: 21 May 2021.
Edited by:
Marcelo Barreiro, Universidad de la República, UruguayReviewed by:
Laura Ferranti, European Center for Medium-Range Weather Forecasts, United KingdomCarmen Alvarez-Castro, Universidad Pablo de Olavide, Spain
Copyright © 2021 Sahai, Kaur, Joseph, Dey, Phani, Mandal and Chattopadhyay. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Atul K. Sahai, c2FoYWkmI3gwMDA0MDt0cm9wbWV0LnJlcy5pbg==