Magnetocaloric effect in a high-spin ferromagnetic molecular cluster

The reaction of MnCl₂·4H₂O with HL ((1-methyl-1H-imidazol-2-yl)methanol) and pdH₂ (1, 3 propanediol) in a basic MeCN solution results in the formation of a mixed-valence [Mn₂₀] cationic cluster and two [Mn^IICl₄] counter anions. The metallic skeleton of the cluster describes two geometrically equivalent mixed-valent, linked [Mn^III₆Mn^II₄] supertetrahedra in which nearest-neighbor metal ions have a different oxidation state. Magnetic susceptibility, magnetization data and heat capacity measurements support evidence of predominant ferromagnetic correlations, leading to a s = 22 spin ground state for the [Mn^III₆Mn^II₄] supertetrahedra, which are pair-linked by a weak antiferromagnetic coupling. The properties are discussed in the context of the magnetocaloric effect and the potential application of this compound in cryogenic refrigeration.

1 Introduction

As early as the 1990s, seminal publications promoted the use of ferromagnetic particles for magnetic refrigeration (McMichael et al., 1992; Shull, 1993; Bennett et al., 1994). Clustering spin moments into noninteracting particles results in a net magnetic moment per particle. An applied magnetic field can align the large magnetic moments of ferromagnetic particles more easily than a magnetic domain of similar size in the bulk equivalent paramagnetic material, at least for certain temperatures and particle sizes. In a magnetocaloric material, the change of the applied magnetic field induces a change in the material’s magnetic entropy (ΔS_m) and adiabatic temperature (ΔT_ad). The magnetocaloric effect (MCE) can therefore be substantial, and enhanced, in ferromagnetic particles. However, interparticle interactions, size distributions, and the presence of non-active solvent, are all ingredients that negatively affect their performance in terms of the MCE.

Magnetic molecular clusters inherit the advantages of ferromagnetic particles and are in many ways superior because of ideal monodispersity in size, shape and magnetic moment. In addition, their molecular nature opens avenues for fine tuning properties (Evangelisti et al., 2011; Sharples et al., 2014; Tziotzi et al., 2023; Zhai et al., 2024). This last point is crucial for improving their MCE (Evangelisti and Brechin, 2010). Sought-after molecular clusters are those with a large spin ground state and a small magnetic anisotropy, because of their easier polarization by the applied magnetic field. At first, the archetypal “single-molecule magnets” such as [Mn₁₂] and [Fe₈] were proposed for magnetic refrigeration (Torres et al., 2000; Zhang et al., 2001; Spichkin et al., 2001), but their huge anisotropies limit their applicability as refrigerants despite the relatively large s = 10 spin ground state. The search for isotropic molecular clusters led to heterometallic Cr-based wheels, whose limitations are in the small value of their spin ground state (Affronte et al., 2004). The first high-spin and low-anisotropy molecular cluster was the highly symmetric supertetrahedron [Mn₁₀O₄Br₄(amp)₆(ampH₂)₃(HampH₂)]Br₃ (ampdH₂ = 2-amino-2-methyl-1,3-propanediol), a mixed-valent ([Mn^III₆Mn^II₄]) ferromagnetic cluster with a remarkable s = 22 ground state displaying negligible anisotropy (Manoli et al., 2007; Manoli et al., 2008). Most of the focus has shifted since then into gadolinium-containing molecular clusters, first in the form of mixed 3d-4f clusters (Karotsis et al., 2009), then as purely gadolinium-based clusters (Evangelisti et al., 2011). Gadolinium is nowadays considered as the standard element for any new molecular cluster for magnetic refrigeration, the advantage residing in its large s = 7/2 moment, zero orbital angular momentum and weak magnetic correlations that, together, facilitate record-high MCE values (Konieczny et al., 2022; Tziotzi et al., 2023). However, for commercial uptake, magnetocaloric materials should be made from safe, inexpensive, and abundant elements (Chaudhary et al., 2019). Since gadolinium is treated as critical because of the concerns surrounding its supply (Zhao et al., 2023), it could be replaced, for instance, by the earth abundant high spin, Fe^III and Mn^II ions without significantly deteriorating the MCE due to a not much smaller s = 5/2. Here, we show that the use of 1,3-propanediol in combination with the N,O-chelate (1-methyl-1H-imidazol-2-yl)methanol (HL) can be used to isolate the cluster [Mn^III₁₂Mn^II₈O₈(L)₁₆(HL)₂(pd)₄(pdH₂)Cl₈][Mn^IICl₄]₂·3MeCN·9C₂H₆O (1·3MeCN·9C₂H₆O), which is structurally related to [Mn₁₀O₄Br₄(amp)₆(ampH₂)₃(HampH₂)]Br₃ (Manoli et al., 2007). Compound 1 contains two analogous [Mn^III₆Mn^II₄] supertetrahedra carrying a s = 22 ground state, but on this occasion, they are covalently linked into a [Mn₁₀]₂ dimer through a single pdH₂ bridge. In comparison with [Mn₁₀O₄Br₄(amp)₆(ampH₂)₃(HampH₂)]Br₃ (Manoli et al., 2007), the structure of 1 is considerably lighter, which ultimately promotes a larger MCE, favored by the larger weight of magnetic elements with respect to nonmagnetic ones, which act passively (Lorusso et al., 2013; Tziotzi et al., 2023).

2 Experimental methods

2.1 Synthesis

MnCl₂·4H₂O (198 mg, 1 mmol), HL (112 mg, 1 mmol), pdH₂ (72 μL, 1 mmol) and NEt₃ (420 μL, 3 mmol) were dissolved in MeCN (15 mL) and stirred for 1 h. The solution was then filtered and diffused with acetone. Brown crystals of 1 were obtained after 2 days. Elemental analysis (%) calculated for Mn₂₂O₄₅N₅₆C₁₃₃H₂₁₆Cl₁₆: C, 31.35; H, 4.27; N, 15.39. Found: C, 31.42; H, 4.38; N, 15.27. Yield ≤40%.

2.2 Single-crystal X-ray diffraction

A suitable brown, blade-shaped crystal of 1·3MeCN·9C₂H₆O with dimensions 0.18 × 0.07 × 0.04 mm³ was selected and mounted on a MITIGEN holder in perfluoroether oil on a Rigaku Oxford Diffraction SuperNova diffractometer. The crystal was kept at a steady T = 100.00 K during data collection. The structure was solved with the ShelXT (Sheldrick, 2015a) solution program using dual methods and by using Olex2 1.5-beta (Dolomanov et al., 2009) as the graphical interface. The model was refined with ShelXL 2018/3 (Sheldrick, 2015b) using full matrix least squares minimization on F². Crystal Data. C_133.4H_216.41Cl₁₆Mn₂₂N_36.39O_45.32, M_r = 4,831.09, triclinic, P-1 (No. 2), a = 14.7918(17) Å, b = 18.444(2) Å, c = 19.275(2) Å, α = 82.653(5)^°, β = 69.696(5)^°, γ = 80.063(5)^°, V = 4,844.7(10) ų, T = 100.00 K, Z = 1, Z' = 0.5, m(MoK_a) = 1.675, 279539 reflections measured, 26124 unique (R_int = 0.0580) which were used in all calculations. The final wR₂ was 0.1620 (all data) and R₁ was 0.0558 (I ≥ 2σ(I)). CCDC = 2342033.

2.3 Physical properties measurements

Magnetization and magnetic susceptibility data were collected on a freshly prepared polycrystalline powder of 1 on a Quantum Design MPMS3 SQUID magnetometer, equipped with a 7 T magnet in the temperature range 2–300 K. Diamagnetic corrections were applied to the observed paramagnetic susceptibilities using Pascal’s constants. Heat capacity measurements were carried out using a Quantum Design PPMS, equipped with a ³He option and a 9 T magnet in the temperature range 0.3–30 K. The polycrystalline sample of 1 was in the form of a thin pressed pellet (ca. 1 mg), thermalized by ca. 0.2 mg of Apiezon N grease, whose contribution was subtracted by using a phenomenological expression.

3 Results and discussion

The reaction of MnCl₂·4H₂O with HL ((1-methyl-1H-imidazol-2-yl)methanol) and pdH₂ (1,3-propanediol) in a basic MeCN solution results in the formation of the mixed-valence compound [Mn^III₁₂Mn^II₈O₈(L)₁₆(HL)₂(pd)₄(pdH₂)Cl₈][Mn^IICl₄]₂·3MeCN·9C₂H₆O in (1), upon diffusion of acetone into the mother liquor (Figure 1). Compound 1 crystallizes in the triclinic space group P-1 with the asymmetric unit comprising half of the formula.

Figure 1

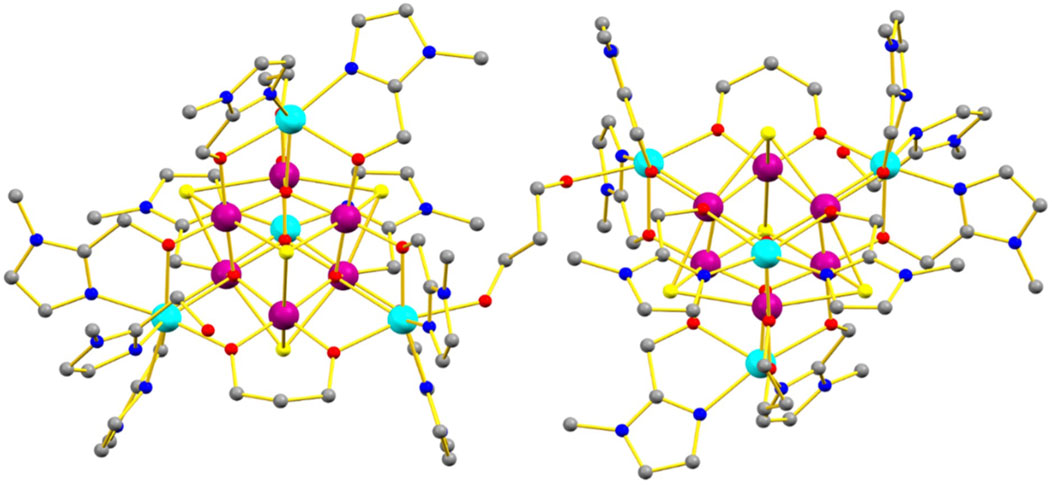
Figure 1. Molecular structure of 1. Color code: Mn^III = purple, Mn^II = cyan, O = red, N = blue, C = grey, Cl = yellow. Solvent molecules, anions and H atoms omitted for clarity.

The metallic skeleton of 1 (Figure 2) describes two geometrically equivalent mixed-valent [Mn^III₆Mn^II₄] supertetrahedra, bridged via a protonated pdH₂ ligand through Mn₈ (and symmetry equivalent (s. e.), Mn^II-Mn^II). Nearest neighbors within each supertetrahedron have a different oxidation state (Mn^II = Mn1, Mn6, Mn8, Mn10; Mn^III = Mn2, Mn3, Mn4, Mn5, Mn7, Mn9).

Figure 2

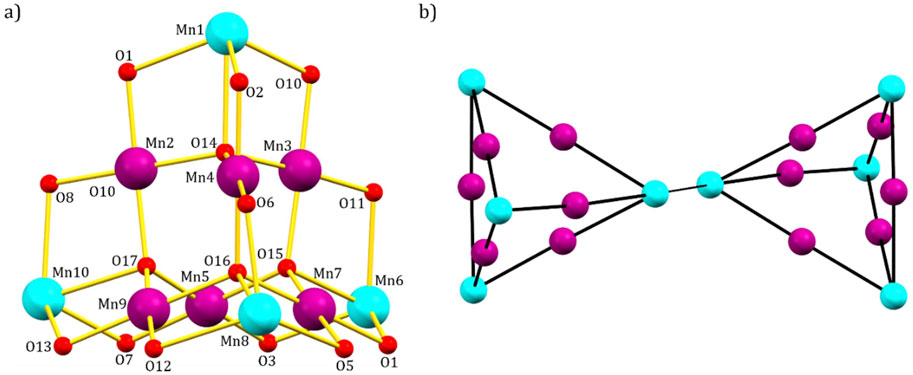
Figure 2. (A) Metal-oxygen core; (B) metallic skeleton of 1. Color code: Mn^III = purple, Mn^II = cyan, O = red.

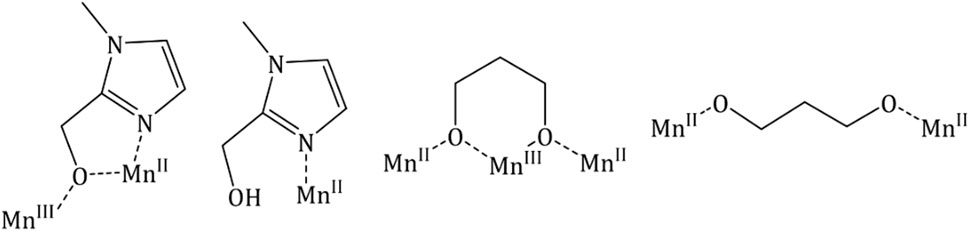
The Mn^II ions define the four apices of the tetrahedron while the six Mn^III ions lie along each edge, therefore describing a trigonal antiprism. The metal ions are connected via four μ₄-O²⁻ ions to give a [Mn^III₆Mn^II₄O₄]¹⁸⁺ core such that the supertetrahedron can be thought of as being built from four vertex-sharing [Mn^III₃Mn^IIO]⁹⁺ tetrahedra. Each chloride ion caps one face of the tetrahedron acting as a μ₃-bridge for the Mn^III ions (Mn-Br, ∼2.7 Å), while all L¹⁻ ligands display the same coordination mode, chelating to each Mn^II ion and bridging between two different Mn^III ions (Scheme 1).

Scheme 1

Scheme 1. Bridging modes displayed by HL³ and H₂diol in 1.

The two protonated HL ligands complete the coordination sphere of Mn10 (and s. e.), by terminally bonding to it through the N-atom. The metal ions are all six-coordinate and in distorted {MnO₄N₂} and {MnO₄Cl₂} octahedral geometries for the Mn^II and Mn^III ions, respectively. The only exceptions are Mn8 and Mn10, that are hepta-coordinated and in distorted {MnO₅N₂} and {MnO₄N₃} pentagonal bipyramidal geometries, respectively.

The pd²⁻ ligands chelate Mn3 and Mn9 (and s. e.) and bridge between two different Mn^II ions (Mn1/Mn6 and Mn8/Mn10, respectively), completing their coordination sphere. The Mn^III ions are Jahn-Teller distorted with the JT axes being defined by the {Cl-Mn-Cl} vectors. Charge balance is maintained by the presence of the two [Mn^IICl₄]²⁻ counter anions. The protonated pdH₂ ligands form intramolecular H-bonds to the acetone molecules of crystallization (O(H)⋯O, ∼2.9 Å), and the clusters pack in a brickwork like fashion in the extended structure (Figure 3).

Figure 3

Figure 3. Packing of the clusters of 1 in the extended structure viewed down the b-axis of the unit cell. H-bonds are highlighted with thin black dotted lines. Color code: Mn^III = purple, Mn^II = cyan, O = red, N = blue, C = grey. Solvent molecules and H atoms omitted for clarity.

Direct current (DC) magnetic susceptibility (χ) data on a sample of 1 were collected in the 2–300 K temperature range in an applied magnetic field of B = 0.1 T, and are plotted as χT versus T in Figure 4 (inset). The experimental χT value at room temperature (113.1 cm³ K mol⁻¹) is higher than the value expected for 10 Mn^II and 12 Mn^III noninteracting ions per formula unit (79.75 cm³ K mol⁻¹). More importantly, χT steadily increases on lowering the temperature, reaching a maximum of 476.4 cm³ K mol⁻¹ at 12.5 K, before dropping down to 356.8 cm³ K mol⁻¹ at 2.0 K. The magnetic behavior of 1 denotes predominant ferromagnetic interactions, likely associated with a s = 22 ground state for each [Mn^III₆Mn^II₄] supertetrahedron in close analogy with previous studies (Manoli et al., 2007). Indeed, assuming that all interactions within each super supertetrahedron are ferromagnetic, the effective spin at low temperatures is the sum of 4 s = 5/2 (Mn^II) and 6 s = 2 (Mn^III) spins, leading to a net s = 22. Weaker antiferromagnetic correlations between the supertetrahedra and/or Zeeman effects can account for the low-temperature χT decrease. Alternating current (AC) magnetic susceptibility measurements show no out-of-phase signal, hence no single-molecule magnet behavior for 1, as expected from the high symmetry of the supertetrahedron (Manoli et al., 2007). Isothermal magnetization (M) measurements were collected in the ranges 0–7 T and 2–10 K. The M data plotted versus B/T merge nicely into a single curve, except for the slight deviation of the data at the lowest temperature of 2 K (Figure 4). The relatively fast variation at low fields further confirms the predominant ferromagnetic interactions in 1. The saturation reached at low temperatures corresponds precisely to 98.0 Nμ_B, which is consistent with the value expected from 2 s = 22 [Mn^III₆Mn^II₄] supertetrahedra and 2 s = 5/2 [Mn^IICl₄] anions, all for g = 2.0 and negligible anisotropies. For T > 2 K, the experimental data are well modeled by the sum of the corresponding Brillouin functions (solid line in Figure 4).

Figure 4

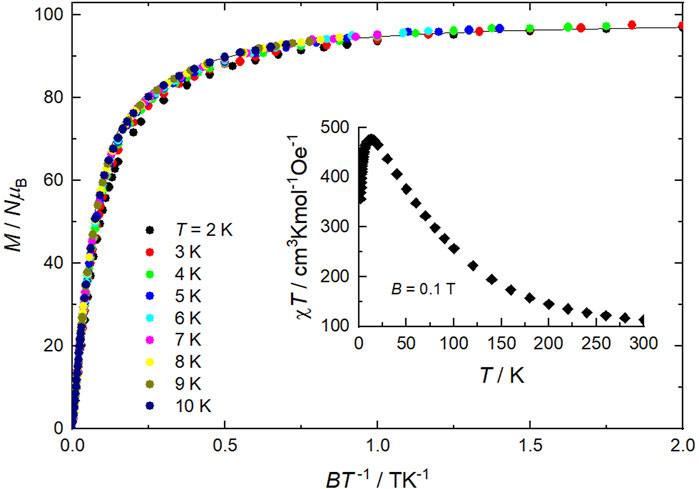
Figure 4. Isothermal low-temperature magnetization (M) curves versus B/T in the ranges T = 2–10 K and B = 0–7 T, and temperature dependence of the DC magnetic susceptibility at B = 0.1 T (as χΤ, inset) for 1. The solid line is the fit of the M data, see main text.

Calorimetry experiments were conducted on a pressed pellet sample of 1 for B up to 7 T and temperatures between 0.3 and 30 K. At high temperatures, the heat capacity (c_p, Figure 5) is dominated by the nonmagnetic contribution associated with lattice phonon vibrations, which follows Debye’s law (dashed line) that, below ca. 5 K, simplifies to c_p/R = aT ³, where a = 2.5 × 10⁻² K⁻³ and R is the gas constant. At low temperatures, c_p depends strongly on B, as expected in the case of ferromagnetic correlations. Note that the heat capacity of an equivalent system with ten Mn^II and twelve Mn^III ions per formula unit, but without any interaction, would be drastically different from the experimental data. We tentatively modeled the magnetic contribution to c_p for B $\ge$ 1 T as the sum of Schottky-like anomalies for two noninteracting s = 22 [Mn^III₆Mn^II₄] supertetrahedra, in addition to two noninteracting s = 5/2 [Mn^IICl₄] anions, per formula unit, with no anisotropies (dotted lines in Figure 5). While the agreement with the experimental data is acceptable, a better description can be achieved by adding an isotropic (super)exchange magnetic interaction between the two supertetrahedra in the form of a Hamiltonian of type $H=-J\overrightarrow{s_1}\cdot \overrightarrow{s_2}$, where $s_1=s_2=22$ and $J=-0.01$ K, denoting a weak but significant antiferromagnetic “intradimer” interaction (solid lines in Figure 5). The anomaly of the zero-field c_p is seen to increase up to values higher than the other anomalies, suggesting that “interdimer”/intercluster interactions, likely of dipolar origin and thus rather weak, are taking part in the ordering mechanism at such low temperatures below 1 K. From the experimental c_p, we evaluate the temperature and field dependence of the entropy (S, inset of Figure 5), according to

$\mathit{S}={\displaystyle \underset{\mathbf{0}}{\overset{\mathit{T}}{\int }}}\frac{{\mathit{c}}_{\mathit{p}}}{{\mathit{T}}^{\prime }}\mathit{d}{\mathit{T}}^{\prime }.$

Figure 5

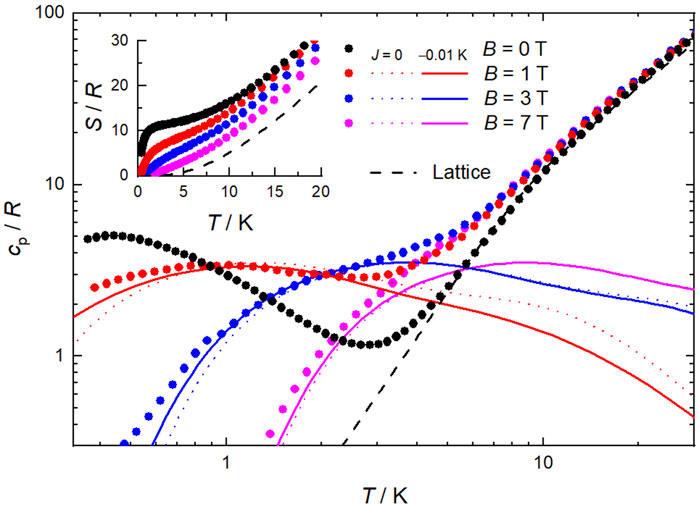
Figure 5. Temperature dependence of the heat capacity (c_p) and entropy (S, inset), both normalized to the gas constant, for selected applied field values for 1. Experimental data = symbols, modelling = lines, including the lattice contribution (dashed line).

The magnetic contribution to S at zero-applied field is seen to level off at temperatures between ca. 2–4 K to the value corresponding to 2 s = 22 [Mn^III₆Mn^II₄] supertetrahedra and 2 s = 5/2 [Mn^IICl₄] anions, i.e., S = 2×[ln(2 × 22 + 1)+ln(2 × 5/2 + 1)]R = 11.2R = 19.3 Jkg⁻¹ K⁻¹. At higher temperatures, S increases steadily with temperature, mainly because of the nonmagnetic lattice entropy.

Next, we evaluate the magnetocaloric effect, as differences between the entropy curves in Figure 5. The temperature dependencies of ΔS_m and ΔT_ad are depicted in Figure 6 for several applied-field changes ΔB = (B−0), i.e., full demagnetization from B = 1, 3 or 7 T. The entropy changes are also computed by applying the Maxwell relation to the magnetization data, namely

${\left(\frac{\mathbf{\partial }\mathit{S}}{\mathbf{\partial }\mathit{B}}\right)}_{\mathit{T}}={\left(\frac{\mathbf{\partial }\mathit{M}}{\mathbf{\partial }\mathit{T}}\right)}_{\mathit{B}},$

whose results are plotted in Figure 6. As can be seen, both sets of ΔS_m data, complementarily evaluated from S (hence c_p) and M data, respectively, agree very well with one another, therefore proving the validity of our approach. The strongest MCE takes place at low temperatures near 2 K. Specifically, the maximal −ΔS_m = 19.2 Jkg⁻¹K⁻¹ (which corresponds to the full entropy content for s = 22 spins) occurs at T = 2.1 K, while the maximal ΔT_ad = 9.6 K at T ≡ T_e = 1.4 K, both for ΔB = 7 T (Figure 6), where T_e is the ending temperature of the demagnetization process. The observed maximum of −ΔS_m is relatively large and compares positively with most Mn-based molecular clusters reported for magnetic refrigeration (Table 1), but less favorably with respect to selected Gd-containing molecular compounds (Evangelisti et al., 2011; Sharples et al., 2014; Konieczny et al., 2022; Tziotzi et al., 2023; Zhai et al., 2024). Where 1 excels is in the temperature range over which the entropy change remains fairly large, e.g., −ΔS_m = 10.5 Jkg⁻¹K⁻¹ at T = 20 K and −ΔS_m = 8.7 Jkg⁻¹ K⁻¹ at T = 30 K, which are equivalent to 54% and 45% of the observed maximal value, respectively. That is, the strength of the MCE decreases just by half after increasing the temperature by an order of magnitude. This behavior originates from the broad Schottky-like anomaly (Figure 5), which in turn results from the ferromagnetic interactions that are robust to the applied fields. Clusters with a high-spin ground state generated from strong ferromagnetic correlations, such as 1, are uncommon (Konieczny et al., 2022). These characteristics can be an advantage to MCE, if exploited properly. Clearly, the entropy of a hypothetical molecule having n spins s is smaller when the spins couple ferromagnetically, yielding a net spin ns at low temperature, than when they do not, i.e., ln(ns) < n×ln(s). Therefore, if one targets the largest MCE value, interactions should be avoided. However, the release of the entropy with temperature/field depends on the strength of the ferromagnetic interactions, or their lack thereof, being more abrupt when such interactions are important and hence facilitating a relatively large MCE with small changes of temperature/field (Evangelisti and Brechin, 2010). This behavior is clearly seen in 1, specifically in the temperature and field dependence of its −ΔS_m and ΔT_ad figures of merit that we plot in Figure 6 together with those calculated for a system of ten Mn^II and twelve Mn^III noninteracting ions per formula unit, for comparison. For any given ΔB, larger −ΔS_m and ΔT_ad can be produced at the lowest temperatures in the absence of interactions, while 1 outperforms the noninteracting system over a broad temperature/field range. For instance, to reach −ΔS_m = 4.5 Jkg⁻¹K⁻¹ at T = 8.4 K, or similarly ΔT_ad = 3.3 K at T = 5.0 K, an applied-field change of ΔB = 2 T would be needed with the noninteracting system, while just ΔB = 1 T would suffice with 1 (Figure 6).

Figure 6

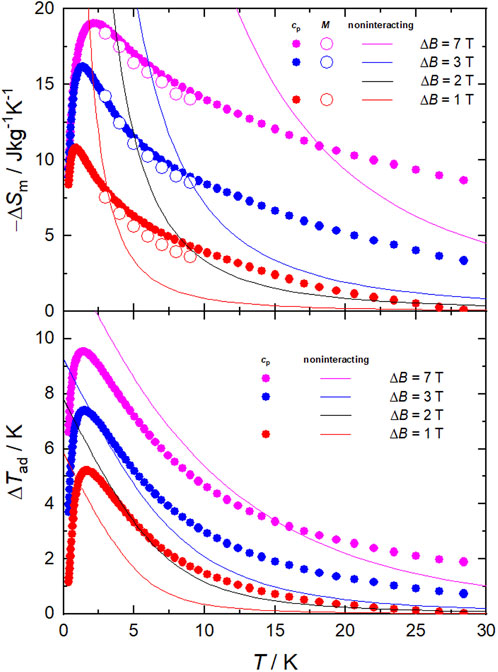
Figure 6. Temperature dependence of the magnetic entropy change (−ΔS_m, top) and adiabatic temperature change (ΔT_ad, bottom) for 1, obtained from the experimental magnetization (empty symbols) and heat capacity (filled symbols) data. Depicted for comparison are the calculated −ΔS_m and ΔT_ad (solid lines), at the indicated ΔB, for a hypothetical compound equivalent to 1 but with no magnetic interactions.

Table 1

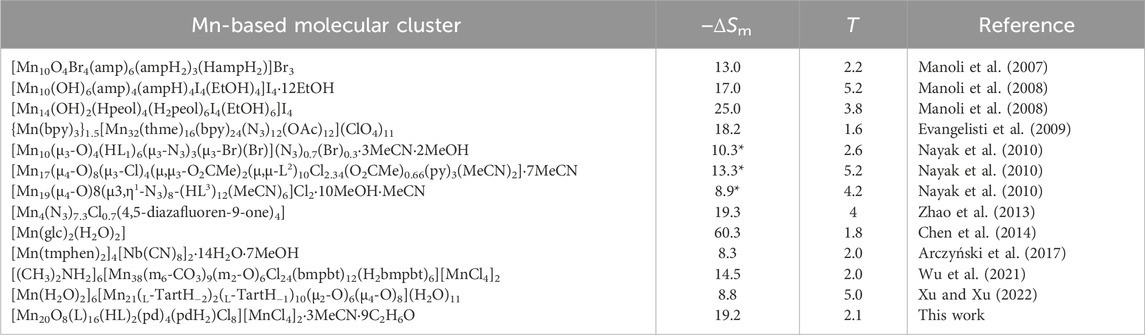
Table 1. Mn-based molecular clusters proposed for magnetic refrigeration; maximal magnetic entropy changes, −ΔS_m, in units of Jkg⁻¹K⁻¹ and for ΔB = 7 T (or 9 T, where indicated by *); temperatures of maximal −ΔS_m, in K; references.

Finally, we compare the magnetic and magnetocaloric properties of 1 with those of the structurally related cluster [Mn₁₀O₄Br₄(amp)₆(ampH₂)₃(HampH₂)]Br₃ (Manoli et al., 2007). Magnetically, both compounds behave similarly owing to the s=22 ground state of the ferromagnetic and isotropic [Mn^III₆Mn^II₄] supertetrahedra. The “dimer” coupling in 1 is relatively weak ($J=-0.01$ K) and marginally affects the properties at the lower temperatures. A further small difference comes from the presence of the noninteracting [Mn^IICl₄] anions in 1, which add a s = 5/2 paramagnetic contribution for every [Mn^III₆Mn^II₄] supertetrahedron. Given the close similarities from the magnetic standpoint, one would expect an equally similar MCE. However, their entropy changes differ drastically with respect to one another, e.g., the maximal values are −ΔS_m = 19.2 and 13.0 Jkg⁻¹K⁻¹ for 1 and [Mn₁₀O₄Br₄(amp)₆(ampH₂)₃(HampH₂)]Br₃, respectively, both for ΔB = 7 T and at ca. the same temperature (2.1 vs. 2.2 K, respectively). Such a difference is almost entirely ascribed to their molecular weights, namely 4,831.09 vs. 2,902.37 g/mol, respectively, which implies a significantly higher magnetic density in 1, which comprises two [Mn^III₆Mn^II₄] supertetrahedra and two [Mn^IICl₄] counter anions per formula unit. This apparent contradiction is resolved by reporting −ΔS_m in molar units, e.g., the maximal values reached by both compounds correspond to their full available entropy contents for s = 22 spins.

4 Concluding remarks

We have synthesized a molecular magnetic refrigerant, characterized by a mixed-valence [Mn₂₀] cationic cluster and two [Mn^IICl₄] counter anions. Each [Mn₂₀] unit can be magnetically described as formed by two ferromagnetic and isotropic [Mn^III₆Mn^II₄] supertetrahedra with s=22, coupled mutually by a weak antiferromagnetic interaction. Such a large spin ground state promotes an enhanced magnetocaloric response to the applied magnetic field and a MCE that remains relatively large over a broad temperature range, e.g., from −ΔS_m = 19.2 Jkg⁻¹K⁻¹ at 2.1 K to −ΔS_m = 8.7 Jkg⁻¹K⁻¹ at T = 30 K, for ΔB = 7 T, that is roughly a decrease by a factor of 2 upon increasing the temperature by an order of magnitude. Complex 1 differs from the closely related and previously reported cluster [Mn₁₀O₄Br₄(amp)₆(ampH₂)₃(HampH₂)]Br₃ (Manoli et al., 2007) because 1 is significant lighter, that is, its larger magnetic density makes it a better magnetic refrigerant.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

EA: Writing–review and editing, Investigation, Formal Analysis, Data curation. EC: Writing–review and editing, Investigation, Formal Analysis, Data curation. GN: Data curation, Formal Analysis, Investigation, Writing–review and editing. DG: Writing–review and editing, Investigation, Formal Analysis, Data curation. ME: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Supervision, Writing–original draft, Writing–review and editing. EB: Funding acquisition, Conceptualization, Data curation, Formal Analysis, Investigation, Supervision, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by MICINN (PID 2021-124734OB-C21) and Diputación General de Aragón (E11-23R, E12-23R). EKB thanks the EPSRC for funding grant EP/V010573/1. EKC and DG acknowledge financial supports from MICINN and the Gobierno de Aragón, respectively, through their doctoral fellowships.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Affronte, M., Ghirri, A., Carretta, S., Amoretti, G., Piligkos, S., Timco, G. A., et al. (2004). Engineering molecular rings for magnetocaloric effect. Appl. Phys. Lett. 84, 3468–3470. doi:10.1063/1.1737468

CrossRef Full Text | Google Scholar

Arczyński, M., Rams, M., Stanek, J., Fitta, M., Sieklucka, B., Dunbar, K. R., et al. (2017). A family of octahedral magnetic molecules based on [Nb^IV(CN)₈]^4–. Inorg. Chem. 56, 4021–4027. doi:10.1021/acs.inorgchem.6b03134

PubMed Abstract | CrossRef Full Text | Google Scholar

Bennett, L. H., McMichael, R. D., Tang, H. C., and Watson, R. E. (1994). Monte Carlo simulations of the magnetocaloric effect in superferromagnetic clusters having uniaxial magnetic anisotropy. J. Appl. Phys. 75, 5493–5495. doi:10.1063/1.355667

CrossRef Full Text | Google Scholar

Chaudhary, V., Chen, X., and Ramanujan, R. V. (2019). Iron and manganese based magnetocaloric materials for near room temperature thermal management. Prog. Mater. Sci. 100, 64–98. doi:10.1016/j.pmatsci.2018.09.005

CrossRef Full Text | Google Scholar

Chen, Y.-C., Guo, F.-S., Liu, J.-L., Leng, J.-D., Vrábel, P., Orendáč, M., et al. (2014). Switching of the magnetocaloric effect of Mn^II glycolate by water molecules. Chem. Eur. J. 20, 3029–3035. doi:10.1002/chem.201304423

PubMed Abstract | CrossRef Full Text | Google Scholar

Dolomanov, O. V., Bourhis, L. J., Gildea, R. J., Howard, J. A. K., and Puschmann, H. (2009). OLEX2: a complete structure solution, refinement and analysis program. J. Appl. Cryst. 42, 339–341. doi:10.1107/S0021889808042726

CrossRef Full Text | Google Scholar

Evangelisti, M., and Brechin, E. K. (2010). Recipes for enhanced molecular cooling. Dalton Trans. 39, 4672–4676. doi:10.1039/b926030g

PubMed Abstract | CrossRef Full Text | Google Scholar

Evangelisti, M., Candini, A., Affronte, M., Pasca, E., de Jongh, L. J., Scott, R. T. W., et al. (2009). Magnetocaloric effect in spin-degenerated molecular nanomagnets. Phys. Rev. B 79, 104414. doi:10.1103/PhysRevB.79.104414

CrossRef Full Text | Google Scholar

Evangelisti, M., Roubeau, O., Palacios, E., Camón, A., Hooper, T. N., Brechin, E. K., et al. (2011). Cryogenic magnetocaloric effect in a ferromagnetic molecular dimer. Angew. Chem. Int. Ed. 50, 6606–6609. doi:10.1002/anie.201102640

PubMed Abstract | CrossRef Full Text | Google Scholar

Karotsis, G., Evangelisti, M., Dalgarno, S. J., and Brechin, E. K. (2009). A calix[4]arene 3d/4f magnetic cooler. Angew. Chem. Int. Ed. 48, 9928–9931. doi:10.1002/anie.200905012

PubMed Abstract | CrossRef Full Text | Google Scholar

Konieczny, P., Sas, W., Czernia, D., Pacanowska, A., Fitta, M., and Pełka, R. (2022). Magnetic cooling: a molecular perspective. Dalton Trans. 51, 12762–12780. doi:10.1039/d2dt01565j

PubMed Abstract | CrossRef Full Text | Google Scholar

Lorusso, G., Sharples, J. W., Palacios, E., Roubeau, O., Brechin, E. K., Sessoli, R., et al. (2013). A dense metal-organic framework for enhanced magnetic refrigeration. Adv. Mater. 25, 4653–4656. doi:10.1002/adma.201301997

PubMed Abstract | CrossRef Full Text | Google Scholar

Manoli, M., Collins, A., Parsons, S., Candini, A., Evangelisti, M., and Brechin, E. K. (2008). Mixed-valent Mn supertetrahedra and planar discs as enhanced magnetic coolers. J. Am. Chem. Soc. 130, 11129–11139. doi:10.1021/ja802829d

PubMed Abstract | CrossRef Full Text | Google Scholar

Manoli, M., Johnstone, R. D. L., Parsons, S., Murrie, M., Affronte, M., Evangelisti, M., et al. (2007). A ferromagnetic mixed-valent Mn supertetrahedron: towards low-temperature magnetic refrigeration with molecular clusters. Angew. Chem. Int. Ed. 46, 4456–4460. doi:10.1002/anie.200701027

PubMed Abstract | CrossRef Full Text | Google Scholar

McMichael, R. D., Shull, R. D., Swartzendruber, L. J., Bennett, L. H., and Watson, R. E. (1992). Magnetocaloric effect in superparamagnets. J. Magn. Magn. Mater. 111, 29–33. doi:10.1016/0304-8853(92)91049-Y

CrossRef Full Text | Google Scholar

Nayak, S., Evangelisti, M., Powell, A. K., and Reedijk, J. (2010). Magnetothermal studies of a series of coordination clusters built from ferromagnetically coupled {Mn^II₄Mn^III₆} supertetrahedral units. Chem. Eur. J. 16, 12865–12872. doi:10.1002/chem.201001988

PubMed Abstract | CrossRef Full Text | Google Scholar

Sharples, J. W., Collison, D., McInnes, E. J. L., Schnack, J., Palacios, E., and Evangelisti, M. (2014). Quantum signatures of a molecular nanomagnet in direct magnetocaloric measurements. Nat. Commun. 5, 5321. doi:10.1038/ncomms6321

PubMed Abstract | CrossRef Full Text | Google Scholar

Sheldrick, G. M. (2015a). SHELXT-integrated space-group and crystal-structure determination. Acta Cryst. A71, 3–8. doi:10.1107/S2053273314026370

PubMed Abstract | CrossRef Full Text | Google Scholar

Sheldrick, G. M. (2015b). Crystal structure refinement with SHELXL. Acta Cryst. C71, 3–8. doi:10.1107/S2053229614024218

PubMed Abstract | CrossRef Full Text | Google Scholar

Shull, R. D. (1993). Magnetocaloric effect of ferromagnetic particles. IEEE Trans. Magn. 29, 2614–2615. doi:10.1109/20.280849

CrossRef Full Text | Google Scholar

Spichkin, Yu. I., Zvezdin, A. K., Gubin, S. P., Mischenko, A. S., and Tishin, A. M. (2001). Magnetic molecular clusters as promising materials for refrigeration in low-temperature regions. J. Phys. D. Appl. Phys. 34, 1162–1166. doi:10.1088/0022-3727/34/8/306

CrossRef Full Text | Google Scholar

Torres, F., Hernández, J. M., Bohigas, X., and Tejada, J. (2000). Giant and time-dependent magnetocaloric effect in high-spin molecular magnets. Appl. Phys. Lett. 77, 3248–3250. doi:10.1063/1.1325393

CrossRef Full Text | Google Scholar

Tziotzi, T. G., Gracia, D., Dalgarno, S. J., Schnack, J., Evangelisti, M., Brechin, E. K., et al. (2023). A {Gd₁₂Na₆} molecular quadruple-wheel with a record magnetocaloric effect at low magnetic fields and temperatures. J. Am. Chem. Soc. 145, 7743–7747. doi:10.1021/jacs.3c01610

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, T.-X., Tao, Y., He, Q.-J., Li, H.-Y., Bian, H.-D., and Huang, F.-P. (2021). Constructing an unprecedented {Mn^II₃₈} matryoshka doll with a [Mn₁₈(CO₃)₉] inorganic core and magnetocaloric effect. Chem. Commun. 57, 2732–2735. doi:10.1039/d0cc07884k

CrossRef Full Text | Google Scholar

Xu, X., and Xu, F. (2022). A heniconuclear {Mn₂₁} cluster-based coordination polymer with Manganese(II) linkers showing high proton conductivity. Inorg. Chem. 61, 16038–16044. doi:10.1021/acs.inorgchem.2c02441

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhai, Y.-Q., Chen, W.-P., Evangelisti, M., Fu, Z., and Zheng, Y.-Z. (2024). Gd-based molecular coolants: aggregating for better magnetocaloric effect. Aggregate 5, e520. doi:10.1002/agt2.520

CrossRef Full Text | Google Scholar

Zhang, X. X., Wei, H. L., Zhang, Z. Q., and Zhang, L. (2001). Anisotropic magnetocaloric effect in nanostructured magnetic clusters. Phys. Rev. Lett. 87, 157203. doi:10.1103/PhysRevLett.87.157203

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, J. P., Zhao, R., Yang, Q., Hu, B. W., Liu, F. C., and Bu, X. H. (2013). Magnetocaloric effect and slow magnetic relaxation in two only azido bridged ferromagnetic tetranuclear metal clusters. Dalton Trans. 42, 14509–14515. doi:10.1039/C3DT51655E

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, S., Wang, P., Chen, W., Wang, L., Wang, Q.-C., and Chen, W.-Q. (2023). Supply and demand conflicts of critical heavy rare earth element: lessons from gadolinium. Resour. Conserv. Recycl. 199, 107254. doi:10.1016/j.resconrec.2023.107254

CrossRef Full Text | Google Scholar