
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Chem., 12 October 2023
Sec. Theoretical and Computational Chemistry
Volume 11 - 2023 | https://doi.org/10.3389/fchem.2023.1295589
This article is part of the Research TopicTheoretical Study of Two-Dimensional Materials for Photocatalysis and PhotovoltaicsView all 8 articles
Monoelemental two-dimensional (2D) materials, which are superior to binary and ternary 2D materials, currently attract remarkable interest due to their fascinating properties. Though the thermal and thermoelectric (TE) transport properties of tellurium have been studied in recent years, there is little research about the thermal and TE properties of multilayer tellurium with interlayer interaction force. Herein, the layer modulation of the phonon transport and TE performance of monolayer, bilayer, and trilayer tellurium is investigated by first-principles calcuations. First, it was found that thermal conductivity as a function of layer numbers possesses a robust, unusually non-monotonic behavior. Moreover, the anisotropy of the thermal transport properties of tellurium is weakened with the increase in the number of layers. By phonon-level systematic analysis, we found that the variation of phonon transport under the layer of increment was determined by increasing the phonon velocity in specific phonon modes. Then, the TE transport properties showed that the maximum figure of merit (ZT) reaches 6.3 (p-type) along the armchair direction at 700 K for the monolayer and 6.6 (p-type) along the zigzag direction at 700 K for the bilayer, suggesting that the TE properties of the monolayer are highly anisotropic. This study reveals that monolayer and bilayer tellurium have tremendous opportunities as candidates in TE applications. Moreover, further increasing the layer number to 3 hinders the improvement of TE performance for 2D tellurium.
Two-dimensional (2D) nanomaterials have become a hotspot in research since the discovery of graphene (Geim, 2009; Abergel et al., 2010), hexagonal BN (Meziani et al., 2015; Zhang et al., 2017a), transition metal dichalcogenides (TMDs) (Zhang et al., 2017b), and so on (Meziani et al., 2015; Wang et al., 2023; Zhang et al., 2023). This can be attributed to their distinctive layer-related and thermal properties (Gu et al., 2017). As a newly proposed type of 2D material, monoelemental 2D materials (ME2DMs) have application potential in many fields (Zhou et al., 2021). These elements are placed between non-metals and metals and have different allotropes with intersectional electronic and chemical properties (Si and Niu, 2020). Besides, ME2DMs containing single elements provide a suitable model for studying the mechanisms of tractable chemistries (Borlido et al., 2019). The success of graphene in 2004 demonstrated the prospects of ME2DMs and sparked research on other ME2DMs with excellent electrical, mechanical, thermal, and optical properties (Novoselov et al., 2004). The combination of electrons confined in the 2D honeycomb lattice and peculiar energy electronic properties endow graphene with extreme electronic mobility (Du et al., 2008; Huang et al., 2023) and transparency (Nair et al., 2008), thereby realizing quantum phenomena (Novoselov et al., 2007). In addition, other ME2DMs such as black phosphorus, arsenene, antimonene, and bismuthene have also been widely reported (Pumera and Sofer, 2017).
Due to unique properties, monolayer tellurium has been proven to have potential applications in robust piezoelectricity for reliable memory (Rao et al., 2022) and optical properties for all-optical non-linear photonic devices (Wu et al., 2019). Especially, the ultra-low thermal conductivity and excellent thermoelectric (TE) performance (Gao et al., 2018a; Sang et al., 2019) of monolayer tellurium have been predicted by simulation. However, up to now, studies on the thermal and TE properties of multilayer tellurium are lacking. Besides, the method of constructing heterojunctions provides an idea to regulate and control electronic (Bediako et al., 2018; Hamer et al., 2018), optoelectronic (Geim and Grigorieva, 2013; Withers et al., 2015), and thermal (Tielrooij et al., 2018) properties. These properties are achieved not only by monolayer but also by multilayer structures and are promising to be applied in nanoscale optoelectronic or electronic equipment. More importantly, previous reports have provided references to layer-dependent phonon transport and TE properties (Sun et al., 2019; Lee et al., 2021). However, the impacts of layer numbers on phonon transport and TE properties of multilayer tellurium have not been studied explicitly enough.
Inspired by the above, phonon transport and TE properties of monolayer, bilayer, and trilayer tellurium have been investigated by first-principles calcuations at 300 K in our study. We first discuss phonon dispersion and energy electronic properties of the three materials and further obtain and discuss differences in phonon thermal conductivity and TE transport properties among them. We provide theoretical predictions of layer-dependent thermal transport and TE transport properties through different layer numbers of tellurium. This unexpected discovery may provide some theoretical references for future research on the application of multilayer 2D materials.
The first-principles calculations were completed within the method of density functional theory (DFT) using pseudopotentials as used in the Vienna Ab initio Simulation Package (VASP) code (Kresse and Furthmüller, 1996a; Kresse and Furthmüller, 1996b). The exchange-correlation energy function was treated using the Perdew-Burke-Ernzerhof (PBE) function of generalized gradient approximation (GGA) (Perdew et al., 1996). A kinetic energy cutoff of 500 eV was selected. The geometry-astringent tolerance for energy and force was less than 10–8 and 10–6 eV/Å. For all tellurium, the Monkhorst–Pack k-point grid was set to 13 × 13 × 1, and the vacuum region was set to 20 Å. The DFT-D3 methods for the vdW mechanism were also considered in our calculations. The interatomic force constants (IFCs) were obtained by the supercell (4 × 4 × 1 supercell) and Γ-point mesh method using the Phonopy (Togo et al., 2008). For the calculation of third-order IFCs in the thirdorder.py script (Li et al., 2014), a 4 × 4 × 1 supercell was also used. The cutoff was set for the 16th nearest number. The Q-grid of 60 × 60 × 1 was selected for obtaining the phonon properties. The lattice thermal conductivity (κp) and phonon transport properties were calculated using ShengBTE (Li et al., 2014). In the electronic transport part, the electrical conductivity was calculated using BoltzTraP (Madsen and Singh, 2006). The carrier mobility (μ) was calculated using the deformation potential theory. In 2D systems, the carrier mobility can be expressed as (Qiao et al., 2014; Zhang et al., 2014)
where C2D is the elastic modulus, m* is the electronic effective mass, and EDP is the deformation potential. In addition, the carrier relaxation time can be calculated by τ = μm*/e.
The performance of TE materials can be determined by the ZT value (Zhao et al., 2014):
where S, T, σ,
As shown in Figures 1A–C, monolayer tellurium consists of three atomic subplanes with buckling distances, while graphene has a planar structure. The calculated lattice constant of monolayer tellurium by us in the a and b directions is 5.62 and 4.23 Å, respectively. These values are very close to previously calculated values of 5.69 and 4.23 Å by Sang et al. (2019) and other reports (Gao et al., 2018a; Gao et al., 2018b). Different lattice constants in different directions usually indicate the directional dependence of the transport properties. Bilayer tellurium built on an AA stack and trilayer tellurium built on an AAA stack has the same characteristics as monolayer tellurium. As shown in Figures 1B, C, the stacking methods of bilayer and trilayer for our structures are AB and ABA types, respectively. The formation of dislocations between layers significantly affects their physical and chemical properties and further leads to differences in their TE performance.
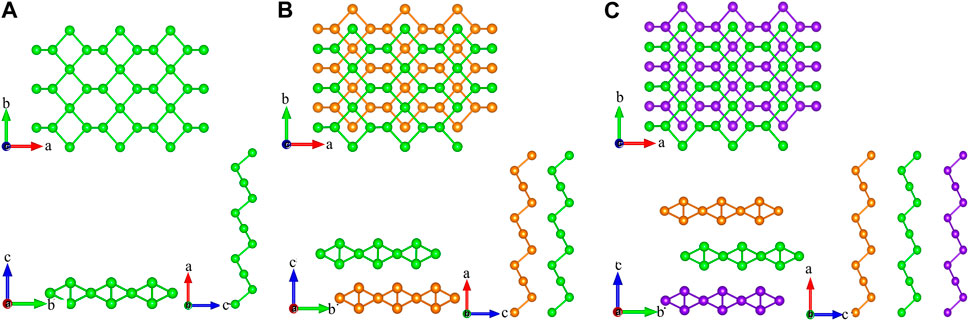
FIGURE 1. Crystal structures of the top and side views for (A) monolayer, (B) bilayer, and (C) trilayer tellurium.
Figures 2A–C show the phonon spectra of monolayer, bilayer, and trilayer tellurium. The frequency of the phonon spectra of the three structures is greater than 0, confirming the stability of the material. Through the three figures, we can also see that the frequencies of the acoustic branch of tellurium and some optical branches near the acoustic branch are very small, much smaller than those of many 2D materials (Geim, 2009; Abergel et al., 2010). The low-frequency distribution is similar to that reported for ultralow thermal conductivity 2D materials, such as triphosphides (Sun et al., 2020), monolayer Hf2Cl4 (Li et al., 2021), and XIS (X = Al, Ga, In) (Cheng et al., 2022). Our results show that the phonon harmonic vibration of tellurium is very weak with a small thermal conductivity, as is expected of a TE material with good application potential. Obviously, the increasing number of layers can reduce the vibration frequency of the optical branch but does not affect the frequency distribution of the acoustic branch. In addition, we find that multilayer tellurium has an indirect energy gap and significant asymmetry between the conduction and valence bands. Moreover, the number of layers can effectively regulate the electronic band structure of tellurium. Specifically, the indirect bandgap of tellurium decreases with an increasing number of layers, as shown in Figures 2D–F. The bandgaps of monolayer, bilayer, and trilayer tellurium are ∼1.7, ∼1.5, and ∼0.9 eV, respectively. The bandgap of monolayer tellurium is very close to the previous report of ∼1.5 eV by Sang et al. (2019).
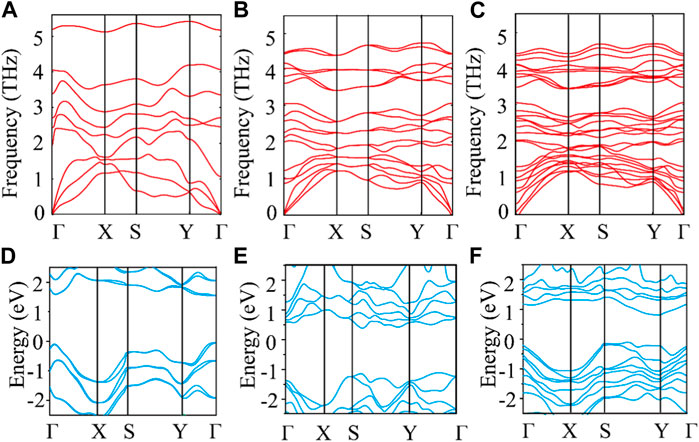
FIGURE 2. Phonon dispersion for (A) monolayer, (B) bilayer, and (C) trilayer tellurium. Electronic band structure for (D) monolayer, (E) bilayer, and (F) trilayer tellurium.
In Figure 3A, we test the convergence of thermal conductivity for three materials along different directions. It can be seen that the thermal transport shows good convergence when the Q grids exceed 50. The results in Figure 3B show that the thermal conductivity of monolayer, bilayer, and trilayer tellurium follows the 1/T law with temperature, and the layer-dependent thermal transport properties have obvious differences. The trend of thermal conductivity with the number of layers is an unusual non-monotonic behavior. Most importantly, as the number of layers increases, there is an unexpected difference in thermal conductivity between different numbers of layers. That is, the thermal conductivity of monolayer tellurium along the zigzag direction is much larger than that of bilayer and trilayer tellurium (twice), while the thermal conductivity of bilayer and trilayer tellurium is similar along the zigzag direction. However, in the armchair direction, both monolayer and bilayer tellurium exhibit ultralow thermal conductivity, while the thermal conductivity of trilayer tellurium is the highest relative to single and double layers. The lattice thermal conductivity depends, to some extent, on phonon anharmonicity. The phonon group velocity can be determined by the slope of the phonon dispersion curve. Since the acoustic branch contributes the most to thermal transport, here, the only focus is on the acoustic branch phonon. The detailed analysis of the phonon harmonicity and anharmonicity of the different layers of tellurium is as follows: the group velocities of phonons with high frequency along the armchair direction are similar, with the main difference being at low frequencies of 0–2 THz (Figure 3C). The values of the monolayer are the smallest at low frequencies, resulting in the lowest phonon thermal conductivity. The phonon group velocity of the bilayer and trilayer is similar. For the zigzag direction, in the 0–2 THz region (Figure 3D), the magnitude and distribution of the phonon group velocities for the bilayer and trilayer are similar, while the monolayer is significantly larger than the bilayer and trilayer, so the phonon transport of the monolayer along the zigzag direction is the strongest. We also analyzed the impact of layer number on anharmonicity. We find that interlayer interactions weaken the anharmonicity. In particular, trilayers exhibit higher phonon relaxation times at low frequencies (Figure 3E), and surface interlayer interactions weaken intrinsic phonon–phonon interaction and lead to the enhancement of anharmonicity.
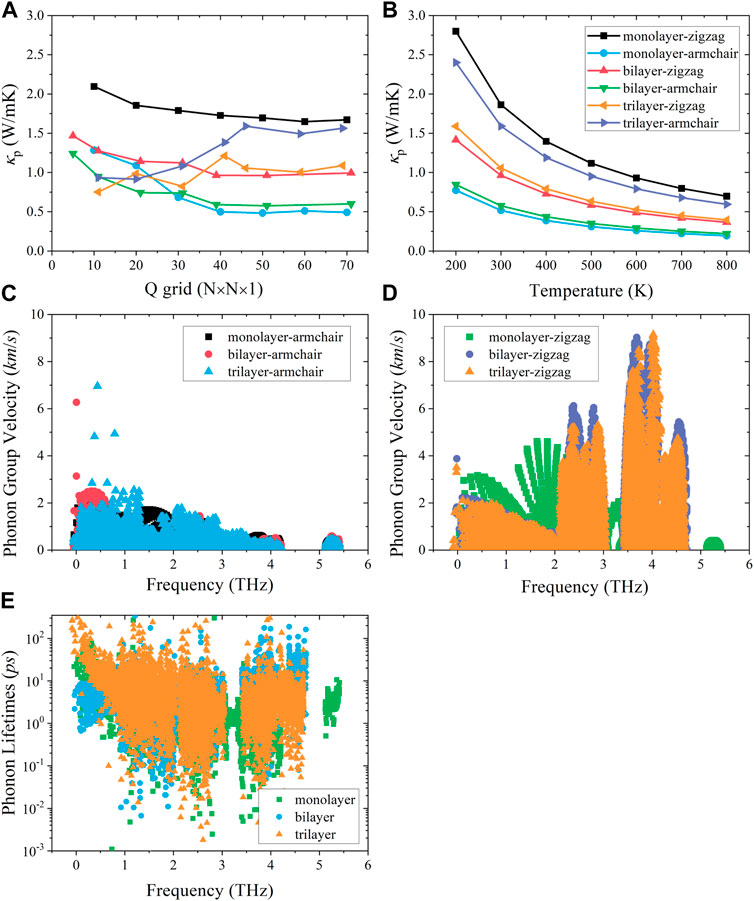
FIGURE 3. (A) Lattice thermal conductivity convergence test of the Q grid. (B) Lattice thermal conductivity of tellurium with different layer numbers at different temperatures along the zigzag and armchair directions. (C) Phonon group velocity along the armchair direction and (D) zigzag direction. (E) Phonon relaxation time.
As shown in Table 1, we have predicted the
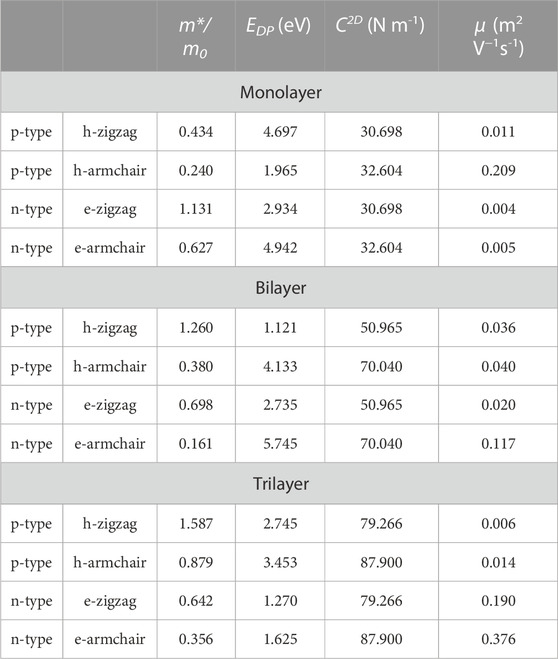
TABLE 1. Effective mass m*/m0, DP constant EDP, elastic constant C2D, and carrier mobility μ of monolayer, bilayer, and trilayer tellurium at room temperature.
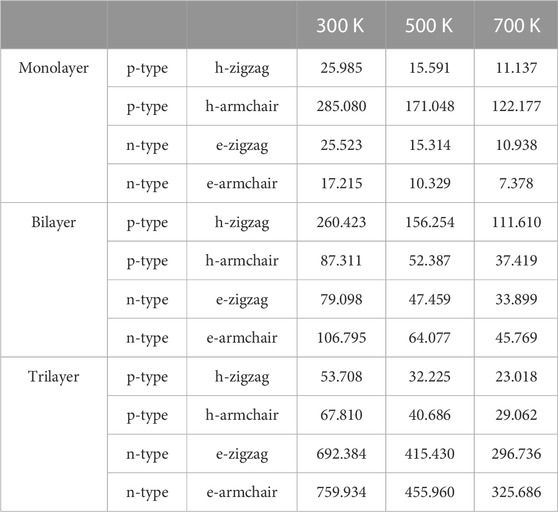
TABLE 2. Relaxation time τ (fs) of monolayer, bilayer, and trilayer tellurium at 300, 500, and 700 K.
The energy conversion efficiency of the TE materials can be assessed with the dimensionless figure of merit (ZT). The TE transport properties of tellurium with different layers are mainly explored. Figure 4 shows the calculated S of n-type and p-type doped tellurium with different layers as a function of the carrier concentration at 300, 500, and 700 K. The monolayer has anisotropic S. It can be found that S increases with the carrier concentration along the zigzag and armchair directions, almost similar to the bilayer. This phenomenon indicates that S is isotropic for bilayer tellurium, and S of n-type doped monolayer tellurium can reach ∼600 μV/K at a carrier concentration of 1 × 1011 cm-2 under 300 K, while that of n-type doped bilayer tellurium can reach ∼400 μV/K. When the environmental temperature reaches 700 K, S becomes larger. In fact, the S coefficient of typical TE materials is only between 200 and 300 μV/K, while the S coefficient of monolayer and multilayer tellurium is much better than that of the mature TE material SnSe (Guo et al., 2015). High values of S indicate that higher ZT may exist in the tellurium system. The origin of very high S values is related to the previously mentioned band structure. In Figure 1, the band graph has a multi-valley characteristic, which leads to a high slope of the density of states (DOS) near the Fermi energy, resulting in a high S. For monolayer n-type doped tellurium, S is greater than that of p-type tellurium at an effective carrier concentration n, mainly because the number of conduction band energy valleys is greater than the valence band. Contrary to S, σ increases with an increase in n, as shown in Figure 5. σ changes little at different temperatures, and bilayer and trilayer tellurium have their respective weaker anisotropies. When the carrier concentration increases, the σ of p-type doping is greater than that of n-type doping in monolayer and bilayer tellurium. However, the trilayers have similar electrical conductivities under the two different doping types. As we know, σ is directly proportional to the contributed κe, which means that the greater the σ, the higher the electronic thermal conductivity κe. In fact, TE properties not only depend on σ. This is because S, σ, and κe are interrelated in TE transport. In this work, using the abovementioned calculated TE transport parameters, we have predicted the TE performance for tellurium with different layers.
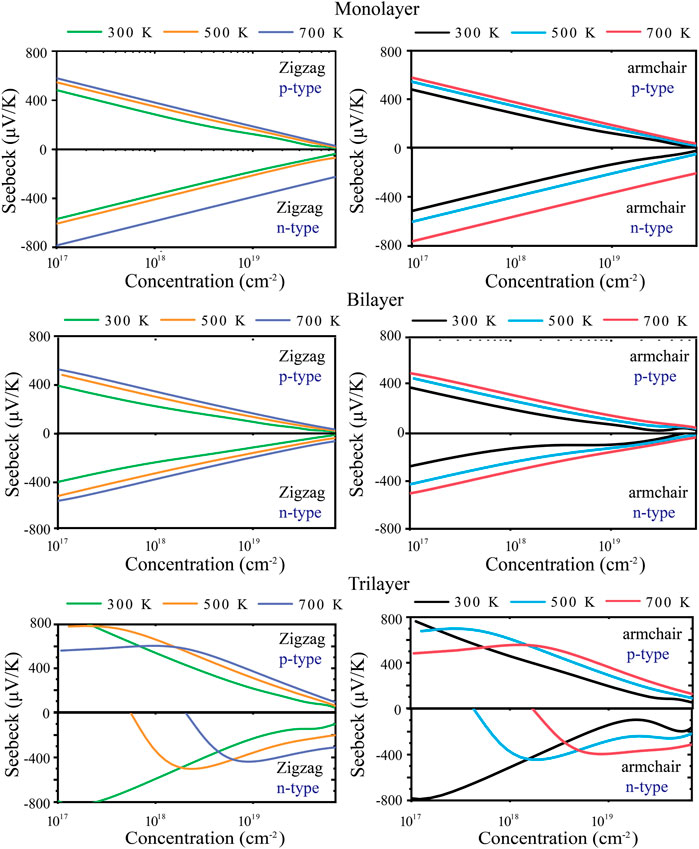
FIGURE 4. Calculated Seebeck coefficient S along zigzag and armchair directions at 300, 500, and 700 K.
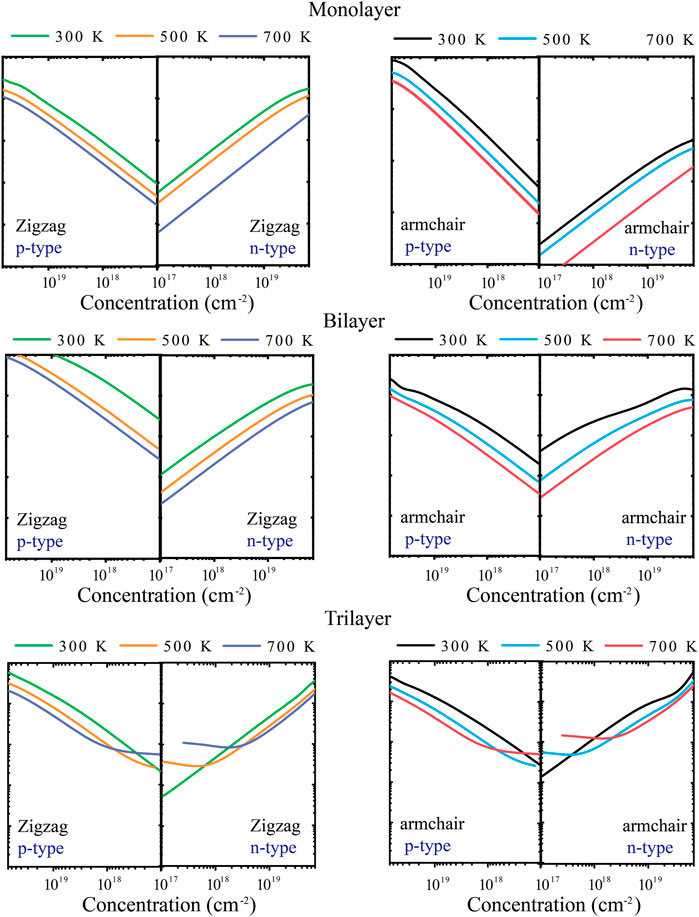
FIGURE 5. Calculated electrical conductivity σ along zigzag and armchair directions at 300, 500, and 700 K.
Figure 6 shows the relationship between the ZT value with different layers of tellurium and the carrier concentration under different types of doping. First of all, for the monolayer, the maximum ZT value of p-type doping along the armchair direction is 6.3 at a lower carrier concentration (1011–1012 cm−2). For the zigzag direction, the ZT value is not very high, so the p-type doping has a strong anisotropy. For n-type doping, the ZT value reaches 3.8 in the zigzag direction under 700 K at lower carrier concentrations (1011–1012 cm−2). For the bilayer, the ZT value along the armchair is not high, and the main reason is that the bilayer has stronger phonon thermal transport along the armchair direction. Its p-type doping has strong anisotropy, and the ZT value can reach 6.6 under 700 K along the zigzag direction at low carrier concentrations (1011–1012 cm−2). Such a high ZT value of bilayer tellurium is also larger than other typical 2D TE materials, such as ∼0.8 at 700 K for Bi2Te3 monolayer (Rashid et al., 2019), 3.46 at 500 K for SnP3 monolayer (Zhu et al., 2019), and 3.45 at 800 K for Bi2O2Se monolayer (Wang et al., 2019). For trilayer tellurium, the anisotropy of the ZT value is weakened, and the ZT value is lower than it is for monolayer and bilayer tellurium. The abovementioned calculations indicate that monolayer and bilayer tellurium are p-type TE materials with high ZT values and have broad practical application expectations in TE and energy-related applications in the future. When the structure has three layers, the TE performance of tellurium will decrease.
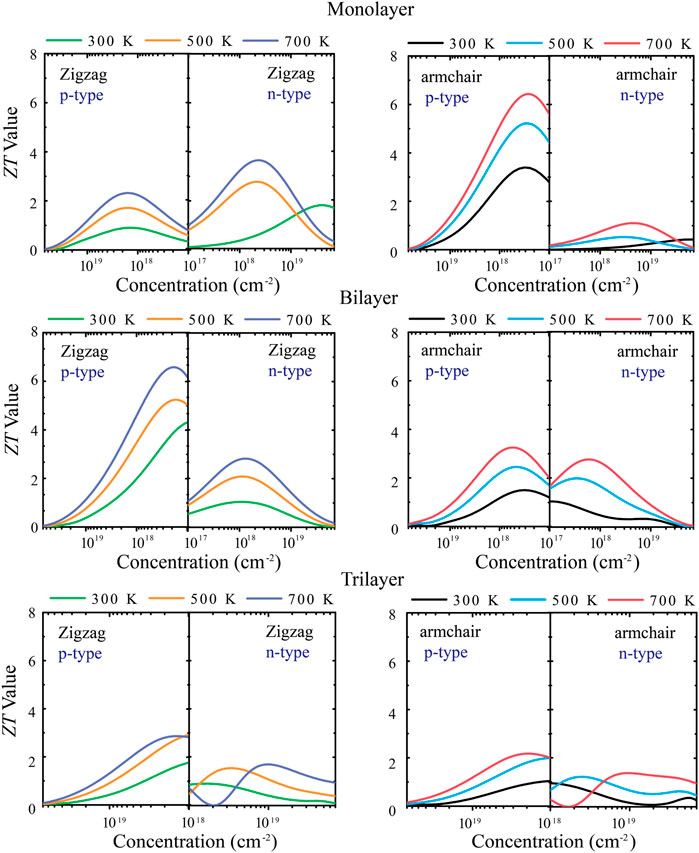
FIGURE 6. Calculated dimensionless figure of merit (ZT) along zigzag and armchair directions at 300, 500, and 700 K.
In this study, based on the Boltzmann transport equation and first-principles calculations, the TE transport parameters of monolayer, bilayer, and trilayer tellurium materials were comprehensively explored and compared. First, our results validate their thermal stability and determine the structural reliability by calculating the atomic second-order force constants. The three abovementioned 2D tellurium materials all have low lattice thermal conductivity. The lattice thermal conductivity does not change monotonically with the number of layers. Through analysis of phonon group velocity and relaxation time, it has been explained that phonon harmonicity dominates thermal conductivity. Unlike the phenomenon where the effective mass of holes in bilayer and trilayer structures is greater than that of electrons, for monolayer structures, the
The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding authors.
KZ: Manuscript writing–original draft. RY: manuscript writing–original draft. ZS: manuscript writing–original draft. XC: manuscript writing–original draft. SH: manuscript writing–review and editing. NW: manuscript writing–review and editing.
The authors declare that financial support was received for the research, authorship, and/or publication of this article. The work of XC has been supported by the Research Program of Chongqing Municipal Education Commission, China (Grant No. KJQN202201327).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, editors, and reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abergel, D., Apalkov, V., Berashevich, J., Ziegler, K., and Chakraborty, T. (2010). Properties of graphene: a theoretical perspective. Adv. Phys. 59, 261–482. doi:10.1080/00018732.2010.487978
Bediako, D. K., Rezaee, M., Yoo, H., Larson, D. T., Zhao, S. F., Taniguchi, T., et al. (2018). Heterointerface effects in the electrointercalation of van der Waals heterostructures. Nature 558, 425–429. doi:10.1038/s41586-018-0205-0
Borlido, P., Huran, A. W., Marques, M. A., and Botti, S. (2019). Structural prediction of stabilized atomically thin tin layers. Npj 2D Mat. Appl. 3, 21–25. doi:10.1038/s41699-019-0103-9
Cheng, S., He, Y., Chang, Z., Sun, Z., Zhang, X., Tang, D., et al. (2022). Structural, elastic, phononic, optical and electronic properties investigation of two-dimensional XIS (X= Al, Ga, In) for photocatalytic water splitting. Int. J. Hydrogen Energy 47, 41640–41647. doi:10.1016/j.ijhydene.2022.08.047
Du, X., Skachko, I., Barker, A., and Andrei, E. Y. (2008). Approaching ballistic transport in suspended graphene. Nat. Nanotechnol. 3, 491–495. doi:10.1038/nnano.2008.199
Gao, Z., Liu, G., and Ren, J. (2018b). High thermoelectric performance in two-dimensional tellurium: an ab initio study. ACS Appl. Mat. Interfaces. 10, 40702–40709. doi:10.1021/acsami.8b11836
Gao, Z., Tao, F., and Ren, J. (2018a). Unusually low thermal conductivity of atomically thin 2D tellurium. Nanoscale 10, 12997–13003. doi:10.1039/C8NR01649F
Geim, A. K. (2009). Graphene: status and prospects. Science 324, 1530–1534. doi:10.1126/science.1158877
Geim, A. K., and Grigorieva, I. V. (2013). Van der Waals heterostructures. Nature 499, 419–425. doi:10.1038/nature12385
Gu, X., Wei, Y., Yin, X., Li, B., and Yang, R. (2017). Colloquium: phononic thermal properties of two-dimensional materials. Rev. Mod. Phys. 90, 041002. doi:10.1103/RevModPhys.90.041002
Guo, R., Wang, X., Kuang, Y., and Huang, B. (2015). First-principles study of anisotropic thermoelectric transport properties of IV-VI semiconductor compounds SnSe and SnS. Phys. Rev. B 92, 115202. doi:10.1103/PhysRevB.92.115202
Hamer, M. J., Tóvári, E., Zhu, M., Thompson, M. D., Mayorov, A. S., Prance, J., et al. (2018). Gate-defined quantum confinement in InSe-based van der Waals heterostructures. Nano Lett. 18, 3950–3955. doi:10.1021/acs.nanolett.8b01376
Huang, Z., Ren, K., Zheng, R., Wang, L., and Wang, L. (2023). Ultrahigh carrier mobility in two-dimensional IV–VI semiconductors for photocatalytic water splitting. Molecules 28 (10), 4126. doi:10.3390/molecules28104126
Jonson, M., and Mahan, G. D. (1980). Mott's formula for the thermopower and the wiedemann-franz law. Phys. Rev. B Condens. Mat. 21, 4223–4229. doi:10.1103/physrevb.21.4223
Kresse, G., and Furthmüller, J. (1996a). Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mat. Sci. 6, 15–50. doi:10.1016/0927-0256(96)00008-0
Kresse, G., and Furthmüller, J. (1996b). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186. doi:10.1103/PhysRevB.54.11169
Lee, W. Y., Kang, M. S., Park, N. W., Kim, G. S., Nguyen, A. D., Choi, J. W., et al. (2021). Layer dependence of out-of-plane electrical conductivity and Seebeck coefficient in continuous mono-to multilayer MoS2 films. J. Mat. Chem. A 9, 26896–26903. doi:10.1039/D1TA07854B
Li, B., Yang, Y., Sun, Z., Qi, H., Xiong, Z., Wu, K., et al. (2021). First-Principles Investigation on the Significant Anisotropic Thermoelectric Transport Performance of a Hf2Cl4 Monolayer. J. Phys. Chem. C 126, 525–533. doi:10.1021/acs.jpcc.1c07301
Li, W., Carrete, J., Katcho, N., and Mingo, N. (2014). ShengBTE: A solver of the Boltzmann transport equation for phonons. Comput. Phys. Commun. 185, 1747–1758. doi:10.1016/j.cpc.2014.02.015
Madsen, G. K., and Singh, D. J. (2006). BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 175, 67–71. doi:10.1016/j.cpc.2006.03.007
Meziani, M. J., Song, W. L., Wang, P., Lu, F., Hou, Z., Anderson, A., et al. (2015). Boron nitride nanomaterials for thermal management applications. ChemPhysChem 16, 1339–1346. doi:10.1002/cphc.201402814
Nair, R. R., Blake, P., Grigorenko, A. N., Novoselov, K. S., Booth, T. J., Stauber, T., et al. (2008). Fine structure constant defines visual transparency of graphene. Science 320, 1308. doi:10.1126/science.1156965
Novoselov, K. S., Geim, A. K., Morozov, S. V., Jiang, D., Zhang, Y., Dubonos, S. V., et al. (2004). Electric field effect in atomically thin carbon films. Sci 306, 666–669. doi:10.1126/science.1102896
Novoselov, K. S., Jiang, Z., Zhang, Y., Morozov, S., Stormer, H. L., Zeitler, U., et al. (2007). Room-temperature quantum Hall effect in graphene. Science 315, 1379. doi:10.1126/science.1137201
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865
Pumera, M., and Sofer, Z. (2017). 2D monoelemental arsenene, antimonene, and bismuthene: beyond black phosphorus. Adv. Mat. 29, 1605299. doi:10.1002/adma.201605299
Qiao, J., Kong, X., Hu, Z. X., Yang, F., and Ji, W. (2014). High-mobility transport anisotropy and linear dichroism in few-layer black phosphorus. Nat. Commun. 5, 4475. doi:10.1038/ncomms5475
Rao, G., Fang, H., Zhou, T., Zhao, C., Shang, N., Huang, J., et al. (2022). Robust Piezoelectricity with Spontaneous Polarization in Monolayer Tellurene and Multilayer Tellurium Film at Room Temperature for Reliable Memory. Adv. Mat. 34, 2204697. doi:10.1002/adma.202204697
Rashid, Z., Nissimagoudar, A. S., and Li, W. (2019). Phonon transport and thermoelectric properties of semiconducting Bi2Te2X (X= S, Se, Te) monolayers. Phys. Chem. Chem. Phys. 21, 5679–5688. doi:10.1039/c8cp05793a
Sang, D. K., Ding, T., Wu, M. N., Li, Y., Li, J., Liu, F., et al. (2019). Monolayer β-tellurene: a promising p-type thermoelectric material via first-principles calculations. Nanoscale 11, 18116–18123. doi:10.1039/C9NR04176A
Si, N., and Niu, T. (2020). Epitaxial growth of elemental 2D materials: what can we learn from the periodic table? Nano Today 30, 100805. doi:10.1016/j.nantod.2019.100805
Stojanovic, N., Maithripala, D. H. S., Berg, J. M., and Holtz, M. (2010). Thermal conductivity in metallic nanostructures at high temperature: electrons, phonons, and the Wiedemann-Franz law. Phys. Rev. B 82, 075418. doi:10.1103/PhysRevB.82.075418
Sun, Z., Yuan, K., Chang, Z., Bi, S., Zhang, X., and Tang, D. (2020). Ultra-low thermal conductivity and high thermoelectric performance of two-dimensional triphosphides (InP3, GaP3, SbP3 and SnP3): a comprehensive first-principles study. Nanoscale 12, 3330–3342. doi:10.1039/C9NR08679J
Sun, Z., Yuan, K., Chang, Z., Zhang, X., Qin, G., and Tang, D. (2019). Efficient thermal conductivity modulation by manipulating interlayer interactions: A comparative study of bilayer graphene and graphite. J. Appl. Phys. 126, 125104. doi:10.1063/1.5115808
Tielrooij, K. J., Hesp, N. C., Principi, A., Lundeberg, M. B., Pogna, E. A., Banszerus, L., et al. (2018). Out-of-plane heat transfer in van der Waals stacks through electron–hyperbolic phonon coupling. Nat. Nanotechnol. 13, 41–46. doi:10.1038/s41565-017-0008-8
Togo, A., Oba, F., and Tanaka, I. (2008). First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 78, 134106. doi:10.1103/PhysRevB.78.134106
Wang, K., Ren, K., Hou, Y., Cheng, Y., and Zhang, G. (2023). Magnon–phonon coupling: from fundamental physics to applications. Phys. Chem. Chem. Phys. 25, 21802–21815. doi:10.1039/D3CP02683C
Wang, N., Li, M., Xiao, H., Gong, H., Liu, Z., Zu, X., et al. (2019). Optimizing the thermoelectric transport properties of Bi2O2Se monolayer via biaxial strain. Phys. Chem. Chem. Phys. 21, 15097–15105. doi:10.1039/C9CP02204J
Withers, F., Del, P. Z. O., Mishchenko, A., Rooney, A., Gholinia, A., Watanabe, K., et al. (2015). Light-emitting diodes by band-structure engineering in van der Waals heterostructures. Nat. Mat. 14, 301–306. doi:10.1038/nmat4205
Wu, L., Huang, W., Wang, Y., Zhao, J., Ma, D., Xiang, Y., et al. (2019). 2D tellurium based high-performance all-optical nonlinear photonic devices. Adv. Funct. Mat. 29, 1806346. doi:10.1002/adfm.201806346
Zhang, C., Ren, K., Wang, S., Luo, Y., Tang, W., and Sun, M. (2023). Recent progress on two-dimensional van der Waals heterostructures for photocatalytic water splitting: a selective review. J. Phys. D. Appl. Phys. 56, 483001. doi:10.1088/1361-6463/acf506
Zhang, W., Huang, Z., Zhang, W., and Li, Y. (2014). Two-dimensional semiconductors with possible high room temperature mobility. Nano Res. 7, 1731–1737. doi:10.1007/s12274-014-0532-x
Zhang, Z., Hu, S., Chen, J., and Li, B. (2017a). Hexagonal boron nitride: a promising substrate for graphene with high heat dissipation. Nanotechnol 28, 225704. doi:10.1088/1361-6528/aa6e49
Zhang, Z., Xie, Y., Ouyang, Y., and Chen, Y. (2017b). A systematic investigation of thermal conductivities of transition metal dichalcogenides. Int. J. Heat. Mass Transf. 108, 417–422. doi:10.1016/j.ijheatmasstransfer.2016.12.041
Zhao, L. D., Lo, S. H., Zhang, Y., Sun, H., Tan, G., Uher, C., et al. (2014). Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 508, 373–377. doi:10.1038/nature13184
Zhou, D., Li, H., Si, N., Li, H., Fuchs, H., and Niu, T. (2021). Epitaxial growth of main group monoelemental 2D materials. Adv. Funct. Mat. 31, 2006997. doi:10.1002/adfm.202006997
Keywords: layer-dependent, thermoelectric transport, tellurium, first-principles calculations, thermal transport
Citation: Zhang K, Yang R, Sun Z, Chen X, Huang S and Wang N (2023) Layer-dependent excellent thermoelectric materials: from monolayer to trilayer tellurium based on DFT calculation. Front. Chem. 11:1295589. doi: 10.3389/fchem.2023.1295589
Received: 16 September 2023; Accepted: 27 September 2023;
Published: 12 October 2023.
Edited by:
Kai Ren, Nanjing Forestry University, ChinaReviewed by:
Chen Shen, Darmstadt University of Technology, GermanyCopyright © 2023 Zhang, Yang, Sun, Chen, Huang and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kexin Zhang, 35769062@qq.com; Sizhao Huang, huangsz301@163.com; Ning Wang, ningwang0213@163.com
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.