
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Chem., 17 October 2023
Sec. Catalytic Reactions and Chemistry
Volume 11 - 2023 | https://doi.org/10.3389/fchem.2023.1286257
This article is part of the Research TopicElectrochemistry and Catalytic Reactions Editor's Pick 2024View all 10 articles
Low-dimensional carbon-based (LDC) materials have attracted extensive research attention in electrocatalysis because of their unique advantages such as structural diversity, low cost, and chemical tolerance. They have been widely used in a broad range of electrochemical reactions to relieve environmental pollution and energy crisis. Typical examples include hydrogen evolution reaction (HER), oxygen evolution reaction (OER), oxygen reduction reaction (ORR), carbon dioxide reduction reaction (CO2RR), and nitrogen reduction reaction (NRR). Traditional “trial and error” strategies greatly slowed down the rational design of electrocatalysts for these important applications. Recent studies show that the combination of density functional theory (DFT) calculations and experimental research is capable of accurately predicting the structures of electrocatalysts, thus revealing the catalytic mechanisms. Herein, current well-recognized collaboration methods of theory and practice are reviewed. The commonly used calculation methods and the basic functionals are briefly summarized. Special attention is paid to descriptors that are widely accepted as a bridge linking the structure and activity and the breakthroughs for high-volume accurate prediction of electrocatalysts. Importantly, correlated multiple descriptors are used to systematically describe the complicated interfacial electrocatalytic processes of LDC catalysts. Furthermore, machine learning and high-throughput simulations are crucial in assisting the discovery of new multiple descriptors and reaction mechanisms. This review will guide the further development of LDC electrocatalysts for extended applications from the aspect of DFT computations.
Environmental pollution and energy crisis are the two main critical issues of modern society caused by the excessive use of fossil fuels. Acid rain, haze, and greenhouse effects have disastrously affected the normal life of human beings (Turner John, 2004; Hubert and Nenad, 2009; Dai et al., 2015). On the one hand, great efforts have been devoted to the investigation and utilization of renewable clean energy and the efficient conversion between electrical and chemical energy, i.e., electrocatalytic hydrolysis and fuel cells (Chu and Majumdar, 2012; Abas et al., 2015). Greenhouse gas recycling, on the other hand, is also regarded as one of the most promising techniques to reduce air pollution, for example, the reduction of CO2. Therefore, effective electrochemical reactions, such as hydrogen evolution reaction (HER) and oxygen evolution reaction (OER) for water splitting, oxygen reduction reaction (ORR) for fuel cell, and carbon-dioxide reduction reaction (CO2RR) are highly expected to solve the above issues (Figure 1). (Karunadasa et al., 2010; Seh et al., 2017) However, the performance of these electrochemical reactions is severely hampered by their sluggish kinetics, which can be significantly improved with the introduction of efficient electrode catalysts (Liang et al., 2013; Zou and Zhang, 2015).
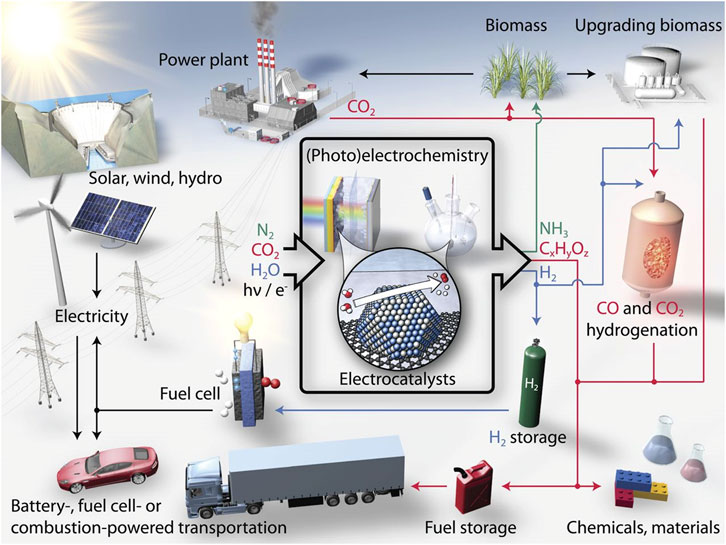
FIGURE 1. Schematic of a sustainable energy landscape based on electrocatalysis. Reproduced with permission (Seh et al., 2017). Copyright 2017, American Association for the Advancement of Science.
Noble metal-based materials such as platinum (Pt) and ruthenium (Ru) are widely used as benchmark catalysts. However, the scarcity and high cost impede their industrial mass production. Therefore, non-noble metals and even metal-free electrocatalysts have been intensively studied and remarkable progress has been reached (Yan X et al., 2016; Sui et al., 2017; Zhang L et al., 2018; Liu et al., 2019; Han et al., 2023a; He et al., 2023). Up to now, low-dimensional carbon materials, such as 2D graphene nanosheets (G), 1D carbon nanotubes (CNT), and 0D fullerenes, have been widely used for fabricating a series of non-noble metals and even metal-free catalysts for energy conversion. This is because of their unique properties such as tunable molecular structures, spatial confinement and surface effect, abundance and excellent oxidation, and corrosion resistance. Various defects and heteroatoms are embedded into carbon substrates, such as transition metals, nitrogen, and boron, which can greatly improve their catalytic efficiency (Kroto et al., 1985; Chen et al., 2002; Novoselov et al., 2004; Hsieh et al., 2009; Chen et al., 2013; Zhuo et al., 2013; Jia et al., 2016; Yan Y et al., 2016; He et al., 2017; Guo et al., 2018; Mao et al., 2019a).
It is difficult to reveal the catalytic mechanism and actual active sites of electrocatalysts only via experimental study. For instance, previous studies show that pyridinic nitrogen is responsible for the ORR in N-doped carbon-based metal-free catalysts (Wu et al., 2015; Liu and Dai, 2016), while other studies suggest that the active sites are graphitic nitrogen (Liu et al., 2010; Lin et al., 2013). Therefore, the current quest is to develop appropriate methodologies to provide a comprehensive understanding of the catalyst structures at electronic levels, which will promote the comprehension of the reaction mechanisms and guide future experimental studies (Bora et al., 2019). Nowadays, based on the first principles, the modern density functional theory (DFT) calculation has become an irreplaceable modeling toolkit for scientists in a variety of research areas. Two main strategies of DFT calculation-assisted design of electrocatalysts have been established by theoretical and experimental chemists. The first one is dominated by theoretical calculations, dedicated to achieving a rational design of high-performance catalysts. It is crucial to identify the most important parameters to reveal the relationships between structures and performance, which are the so-called descriptors and can considerably boost the traditional trial-and-error approach. Machine-learning and high-throughput calculations have also been developed to efficiently screen active sites and descriptors for the targeted catalysts. The second one is dominated by experimental testing and characterizations, assisted by calculating the change during the catalysis process such as step-energy, molecular and electronic structure, and electron transition that can reveal the reaction mechanism accurately. In this review, we will mainly summarize the history and concepts of modern DFT, the heterogeneous electrocatalytic surface-related descriptors, the combination of experiment and calculation, and recent achievements of low-dimensional carbon-based electrocatalysts for energy storage and conversion applications.
Quantum chemistry is mainly based on quantum mechanics principles, and the main goal of all first-principle calculations is to obtain the electronic wave function ψ that characterizes the state of the system, for which the Schrödinger equation must be solved. Theoretical computing has received increasing attention from the chemistry community as computer technology has progressed. However, the traditional Wave Function Theory (WFT) method has two fatal shortcomings. First, the wave function ψ of a system with N electrons will contain 3N coordinate variables. Therefore, a 3N-dimensional wave function image, which is difficult to describe visually, will be a stumbling block in solving the Schrödinger equation. Second, the Schrödinger equation for a multi-electron system is too computationally intensive to be calculated accurately. Modern DFT has become a viable option to solve these drawbacks.
The homogeneous electron-gas model, commonly known as the Thomas–Fermi model, was proposed by Thomas and Fermi in 1927, and it has established a firm foundation for DFT. The ground state energy of the electron system is directly represented in terms of electron density instead of the wave function, which drastically reduces the freedom degree of the system (Thomas, 1927). In 1964, Hohenberg and Kohn proposed an inhomogeneous electron-gas model based on the Thomas–Fermi model and proved that two theorems served as the fundamentals of modern DFT (Hohenberg and Kohn, 1964). The first theorem stated that the nuclear potential energy
Here,
Where,
Where,
Due to
And XC potential can be defined by:
Overall, there is no approximation and the Kohn–Sham equation is accurate. However, the
Typical approximations such as local density approximation (LDA), generalized gradient approximation (GGA), meta-GGA, and hybrid functional are shown in the well-known Jacob’s ladder from Hartree world to Chemical accuracy heaven (Figure 2). (Mattsson, 2002; Tao et al., 2003; Zhang and Xu, 2020)

FIGURE 2. Illustration of Jacob’s Ladder of DFT. Reproduced with permission. (Zhang et al., 2020). Copyright 2020, John Wiley and Sons.
The approximation for LDA is that the charge density changes slowly with position and behaves similarly to the local heterogeneous electron cloud, so the XC energy can be presented as:
The LDA method only considers local charge density, which is accurate for a uniform electron gas model but is clearly not applicable to real systems where the electron density is not perfectly uniform. Therefore, this method provides a rough approximation when computing the real systems and tends to overestimate binding energies.
To improve the accuracy of the LDA method, the GGA method describes electron density with the assistance of density gradient and can be presented as:
BLYP (Becke, 1988; Lee et al., 1988), PW91 (Perdew et al., 1992; White and Bird, 1994), and PBE (Perdew et al., 1996) are the commonly used approximated density functionals of the GGA method. The Becke exchange functional is a gradient-corrected exchange functional that considers the gradient of the electron density. The Lee-Yang-Parr (LYP) correlation functional incorporates the correlation energy of electrons. By combining these two components, BLYP aims to provide a more accurate description of electron-electron interactions and correlation effects in molecular systems. PW91 combines the Perdew-Wang exchange functional with the Perdew-Wang correlation functional. The exchange functional accounts for the exchange energy of electrons, while the correlation functional deals with electron-electron correlation effects. The PBE functional captures both the exchange and correlation effects in the electron-electron interaction. It has been found to perform well for a wide range of systems, including molecules, solids, and surfaces, making it a popular option in DFT calculations.
Based on the GGA method, meta-GGAs, such as TPSS, TPSSh, and M06-L (Zhao et al., 2006; Zhao and Truhlar, 2006; Zhao and Truhlar, 2008), introduced kinetic energy density variables but with better accuracy accompanied by a significant increase in computational cost.
By partially combining accurate XC functional in the DFT, the hybrid functional could improve the calculation accuracy. The most popular one is the B3LYP functional (Stephens et al., 1994), which can be described as:
Where A = 0.8, B = 0.72, and C = 0.81.
Calculations involving periodic systems frequently employ the HSE functional (Heyd and Scuseria, 2004), which is represented by the following equation:
Where A is the mixing parameter, and ω is an adjustable parameter controlling the short range of the interaction. The standard values of A = 0.25 and ω = 0.2 of HSE06 (Heyd et al., 2003) have been shown to give good results for most systems.
To deal with periodic systems, supercell models (primitive cells in three dimensions (X, Y, and Z) with periodic repetition) are frequently used. Vacuum space greater than 10 Å is added in the Z-direction to eliminate the interaction. In condensed matter physics, Bloch’s theorem states that solutions to the Schrödinger equation in a periodic potential take the form of a plane wave modulated by a periodic function and can be written as:
Where r is the position, Ψ is the wave function, and k is the wave vector. Based on the Bloch theorem, the electronic band structure is involved in investigating surface science, and electronic states at numerous k points should be calculated. In practical calculations, however, a finite number of k points is used; the higher the density of the k points, the lower the inaccuracy will be. In general, the number of k points for metal systems is higher than that of the oxide systems.
For periodic systems, the electron wave function can be expanded with numerous plane wave functions. However, only plane-wave basis sets with kinetic energy lower than the cut-off energy are considered in practical calculations, which would result in a systematic error (Kresse and Furthmüller, 1996a; Kresse and Furthmüller, 1996b). Therefore, a pseudopotential that can replace the true atomic potential of the nucleus and inner electrons is introduced to reduce systematic error. Currently, the most widely used plane-wave methods are the ultra-soft pseudopotential (US-PP) plane wave method and the projector augmented wave (PAW) method (Kresse and Joubert, 1999).
DFT calculations cannot adequately describe systems with physical properties that are controlled by many body electronic interactions (correlated systems) because it is typically challenging to model the dependence of the XC functional on electronic charge density. The over-delocalize valence electrons and over-stabilize metallic ground states are considered to be the main problems of DFT to describe correlated systems. Therefore, the DFT + U approach has been developed to enhance the description of the ground state of correlated systems (Dudarev et al., 1998). The key advantage of the DFT + U method is that it is within the realm of DFT, making it easy to implement in the existing DFT codes. Besides, its computational cost is only slightly higher than that of normal DFT computations. The local and semi-local density functionals that allow LDA + U and GGA + U computational operations can be enhanced with this ‘U’ correction. The primary function of the ‘U’ correction is to add an additional Hubbard-like term to the strong on-site Coulomb interaction of localized electrons. The on-site Coulomb term U and the site exchange term J are the two parameters that represent the strength of the on-site interactions for the purpose of practical DFT + U implementation in computational chemistry. Parameters ‘U and J’ are typically derived semi-empirically although ab initio computations can yield them (Tolba et al., 2018).
It has become a standard to use the parameter:
Molecular dynamics (MD) simulation, which is based on Newton’s laws of motion, can simulate the trajectory of each atom in a system at a certain temperature, thus the system’s dynamic properties can be calculated. However, the standard DFT can only be used to calculate a system’s static properties at 0 K. Briefly, for a given configuration and initial velocity of each atom, the MD simulation can be divided into three steps. Firstly, the forces acting on each atom in the system are calculated to determine the system’s acceleration. Secondly, the configuration of the system after Δt time can be obtained according to Newton’s three laws. Thirdly, the calculation of the forces in the first step is continued based on this configuration, and the results of the system evolving with time can be finally obtained by repeated recurrence. MD simulation can be further classified into two types: Classic MD simulation and ab initio MD (AIMD) simulation, depending on how the forces are calculated in the first step. Classic MD simulation builds the potential energy function from the empirical force field and calculates the force at each step using the gradient of the potential energy function. AIMD simulation, on the other hand, can be used to accurately calculate the force at each step by the ab initio quantum chemical method (Nosé, 1984; Hoover, 1985; Kresse and Hafner, 1993).
Unfortunately, AIMD is constrained by its suitability for small simulation systems and limited simulation durations. The utilization of force fields, however, can expedite the computation process. Nevertheless, for an extended period, there existed a gap between computationally demanding electronic structure-based DFT calculations and the more efficient yet less precise empirical potentials or force fields founded on physical approximations and intuition (Kocer et al., 2022). This situation witnessed substantial improvement with the emergence of machine learning potentials (MLPs) in 1995 (Blank et al., 1995). Modern MLPs have the capacity to discern the shape of multidimensional potential energy surfaces from high-level DFT calculations and subsequently incorporate the derived analytical atomic interactions (force fields) into large-scale simulations, such as MD, with negligible accuracy compromise (Handley and Popelier, 2010; Friederich et al., 2021; Unke et al., 2021). Over the last two decades, numerous types of MLPs have been introduced, including neural network potentials (NNPs) (Lorenz et al., 2004; Behler and Parrinello, 2007), Gaussian approximation potentials (GAPs) (Bartók et al., 2010), and gradient domain machine learning (GDML) (Chmiela et al., 2019). Among them, NNPs exhibit a formidable combination of neural network expressive capabilities and the availability of extensive datasets like the QM9 dataset (Ruddigkeit et al., 2012), Material Project (Jain et al., 2013), and Open Catalyst 2020 (Chanussot et al., 2021), rendering them exceptionally well-suited for expediting high-accuracy MD calculations (Takamoto et al., 2022). Additionally, beyond reliance on existing databases, on-the-fly machine learning enables the construction of precise force fields from newly sampled data with minimal training overhead (Jinnouchi et al., 2019; Jinnouchi et al., 2020). In this adaptive process, during each step, a decision is made whether to perform an ab initio calculation and potentially incorporate the data into the force field or to employ the existing force field and skip the learning phase for that specific step.
Furthermore, Metadynamics is an atomistic simulation technique based on MD that operates within the same system to expedite the exploration of rare events and calculate the free energies of intricate molecular systems (Laio and Parrinello, 2002; Iannuzzi et al., 2003). This technique functions by iteratively ‘filling’ the system’s potential energy surface using a series of Gaussian functions centered along its trajectory, all guided by a carefully selected set of collective variables (CVs). This process compels the system to transition from one energy minimum to another (Bussi and Laio, 2020). Metadynamics provides several advantages in free energy calculations. Firstly, it accelerates the sampling of high-energy events within the studied system by progressively moving it from low-energy regions to high-energy areas via the inclusion of a sequence of repulsive potentials. Secondly, it facilitates the establishment of high-dimensional reaction pathways, enabling the computation of multidimensional free energy data, including two-dimensional free energy potential surfaces. Thirdly, because it gradually elevates the studied system’s energy from low to high regions, this approach excels in discovering optimal reaction pathways. Lastly, this method does not require a prior prediction of the reaction pathway within the studied system (Barducci et al., 2011). One limitation of Metadynamics lies in the difficulty of determining the optimal point for terminating the simulation. Without proper termination, the bias potential keeps increasing, possibly leading the system intoreaction regions that hold no interest in our study. The application of Well-Tempered Metadynamics effectively mitigates this limitation (Barducci et al., 2008).
The transition state (TS), also known as the saddle point, is the highest energy point on the potential energy surface (PES) where the reactants (initial state, IS) generate products (final state, FS) along the minimum energy path. Within the transition state theory (TST), we assume that IS and TS are in quasi-equilibrium, and the main task is to find out the free energy barrier for the transition, which is the energy difference between IS and FS. Based on TST, the transition rate can also be calculated. The Dimer method (Henkelman and Jónsson, 1999) and the climbing image nudged elastic band (CINEB) approach (Henkelman et al., 2000) are the two most popular calculating techniques.
The dimer method can be used to find out the saddle points by two images of the system, which is the so-called ‘dimer’. Driven by the saddle point search algorithm, the dimer is moved uphill on the potential energy surface, away from the vicinity of the potential energy minimum of the IS and toward a saddle point. The dimer is rotated along the way to identify the potential energy mode with the lowest curvature at the dimer’s location. Since the Dimer technique only uses the first derivatives of the energy, the major benefit is not requiring the time-consuming computation of the minimal eigenvalue of the Hessian matrix. The Dimer technique also has the advantage of having less stringent initial configuration requirements.
The nudged elastic band (NEB) method is an efficient method for identifying the minimum energy path (MEP) between a given initial and the final state of a transition, which has also been widely used to estimate transition rates. A set of images between the IS and FS of the system are created, often on the order of 4–20. Then the adjacent images are contacted by a collection of spring interactions, which can form an elastic band and ensure the continuity of the path. The band is brought to the MEP by an optimization process that minimizes the force acting on the images. The drawback of the NEB method is that it requires the intermediates to be evenly spaced throughout the optimization process, and the predicted TS may be slightly deviated from the actual TS. The CINEB method was developed to address this issue. The force on the highest image is the full force resulting from the potential with the component along the elastic band inverted, showing that it will not be influenced by spring forces. As a result, the intermediates will gradually move to the higher energy direction and reach the actual TS.
Currently, the computational hydrogen electrode (CHE) model is the most commonly employed and straightforward model for assessing catalytic activity (Peterson et al., 2010). This model uses half of the chemical potential of H2 in the gas phase at 0 V to represent the chemical potential of a proton-electron pair (
Where e is the positive charge. Consequently, it becomes feasible to calculate the reaction-free energy (ΔG) of proton-coupled electron transfer (PCET) reactions, enabling a qualitative assessment of catalytic activity. Nonetheless, the CHE model falls short of representing the exact catalytic environment due to the neglection of sensitive parameters affecting catalytic performance, such as solvent, pH, and applied potential. To achieve a more precise simulation of electrochemical reactions, multiple approaches and tools have been developed and applied to consider the impact of the reaction environment.
Two primary approaches can be used to address the solvent effects: implicit and explicit solvation models. The implicit solvation model employs a polarizable medium, typically characterized by the dielectric constant (ε), to represent the solvent, while an electric field is constructed to depict the solvent’s charge distribution (Xu and Carter, 2019). Currently, two representative implicit solvation models are the solvation model based on solute electron density (SMD) (Marenich et al., 2009) and the conductor-like solution model (COSMO) (Klamt and Schüürmann, 1993). While the implicit solvation model permits a qualitative description of solvent effects at minimal computational cost, it falls short in describing specific interactions, such as hydrogen bonds (Ling et al., 2022).
On the other hand, the explicit solvation model precisely incorporates solvent molecules, atoms, and cations into the calculation systems, enabling direct observation of electrode/electrolyte and adsorbates/electrolyte interactions. When considering the most common water/electrode interfaces in electrocatalysis, two explicit solvation models are generally employed: icelike water bilayers and the electric double layer (Gross and Sakong, 2022). In the meantime, AIMD is typically employed to obtain reliable atomic configurations of the electrode/electrolyte interfaces, incurring significantly higher computational costs. Therefore, to strike a balance between computational accuracy and cost-effectiveness, the Quantum Mechanics/Molecular Mechanics (QMMM) method has been developed. With this approach, quantum mechanical (QM) computations are employed to simulate critical reaction components, such as adsorbates and electrode/electrolyte interfaces, while classical force fields or implicit solvation models are employed to handle the surrounding solvent environment. The primary challenge in the QMMM method is effectively partitioning the QM and MM fields to ensure an accurate representation of critical effects (Li et al., 2020).
In experimental macroscopic systems, both reaction temperatures and the chemical potential of the electrolyte and electrode remain constant throughout the reaction. However, in most common DFT calculations, a limited number of atoms is typically treated within the canonical (NVT) or NPT ensemble and the total number of electrons in the simulated cells remains constant. Consequently, this leads to significant variations in the electrochemical potential (Fermi level) during a reaction. To address this problem and achieve a setup closer to the fluctuating particle numbers found in experimental conditions, the combination of the grand-canonical (GC) ensemble (VTμ) with DFT emerges as a natural choice for atomistic simulations (Melander et al., 2018). GC-DFT provides a method to investigate electrochemical microscopic systems in thermodynamic equilibrium, offering insights into phenomena characterized by long-time and length scales (Groß, 2021). During the fixed-potential grand canonical calculations, varying the total charge of the system can result in the fixed electrode potential (Fermi level) (Gao and Wang, 2021). Furthermore, by the fixed-potential method, we can easily calculate the potential-dependent reaction barriers and avoid the inaccurate assumption about the charge transfer coefficients in the constant-charge calculations. Currently, great developments have been reached in the field of methodology and models, such as continuum charging methods (Gauthier et al., 2019) and constant-potential hybrid-solvation dynamical model (CP-HS-DM) (Zhao and Liu, 2021), making complicated NEB and AIMD simulations stable and possible.
Nowadays, a series of well-known carbon-based electrocatalysts have been fabricated through the combinations of various modification methods and substrate materials, such as heteroatom-doped graphene, defective graphene, Mxenes, heteroatom-doped carbon nanotubes/ribbons, and modified carbon dots (Yan et al., 2020; Zhou et al., 2020; Li et al., 2021; Ding et al., 2022; Song et al., 2022; Sun et al., 2022; Tang et al., 2022; Wu Q. et al., 2022; Wu Y. et al., 2022). However, the design of state-of-the-art electrocatalysts still relies on inefficient trial-and-error approaches, and the catalytic mechanism is still controversial and difficult to reveal only through experimental research. DFT calculations are thus utilized to address two issues: 1) predicting catalytic performance and guiding the synthesis of electrocatalysts and 2) investigating and corroborating the mechanism of electrocatalysis in conjunction with experimental study.
To predict the performance of electrocatalysts, computational scientists mainly focus on the most important microscopic properties of the catalysts that determine the macroscopic catalytic performance. Since the early 20th century, catalysts with high activity, according to the traditional Sabatier principle, should bind atoms and molecules with an ideal bond strength: not too weak to activate the reactants and not too strong to desorb the products. Therefore, a volcano-shape relationship between bond strength and catalytic activity has been proposed to represent the predictivity of many descriptors (Che, 2013). Due to the lack of quantitativeness and inability to undergo experimental validation, this principle is not very predictive. The “bond strength” between the relevant intermediates and the catalysts has been described during the past decades by the extraction of electronic and structural properties such as the descriptors.
The well-known d-band center theory proposed by Nørskov et al. has laid the foundation for a series of descriptors (Nørskov, 1991; Hammer and Norskov, 1995; Nilsson et al., 2005). It explains the interactions between atoms or molecules and the surface based on adsorbate orbitals and d-orbitals of atoms on the surface. The energy of the d states (the center of the d states) relative to the Fermi level is a good indicator of the bond strength. The higher the d states are in energy relative to the Fermi level, the higher in energy the antibonding states and the stronger the bond will be (Figure 3). Stamenkovic et al., for example, investigated the ORR activity of various Pt3M (M = Ti, V, Fe, Co, and Ni) alloys with Pt-skin and Pt-skeleton surface structures, employing both experimental and computational methods (Stamenkovic et al., 2007). They constructed a volcano plot using experimentally measured activity and theoretically calculated d-band center values. This analysis revealed that Pt3Co, Pt3Fe, and Pt3Ni exhibited significantly enhanced ORR activity compared to pure Pt.
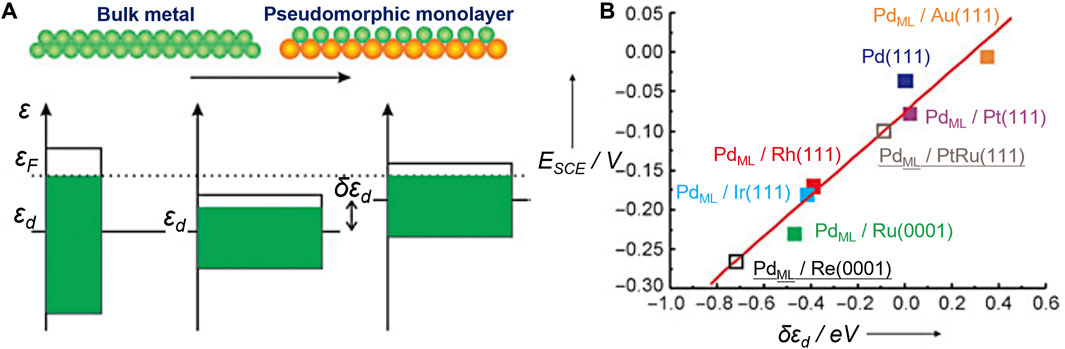
FIGURE 3. Illustration of the use of the d-band model. (A) The main origin of a shift in the d-band center εd is a change in the interatomic distances within an overlayer. (B) Electrochemically measured changes in the hydrogen adsorption energy (ESCE) for Pd overlayers on a number of metals are shown to scale well with the calculated shift of the d-band center (δεd). Reproduced with permission (Kibler et al., 2005). Copyright 2005, John Wiley and Sons.
The d-band center theory can also be applied to low-dimensional electrocatalysts (Wu et al., 2016; Gao G. et al., 2018; Tao et al., 2019; Ye et al., 2020; Jiao et al., 2022). For instance, Ling et al. established correlations between the d-band center and the adsorption strengths of *OH, *O, and *OOH, along with the potential of elementary reactions for OER on β12 boron monolayer (β12-BM)-supported single-atom catalysts (SACs) (Ling et al., 2017). Ni SACs supported on β12-BM exhibited a moderate energy level of the d-band center, resulting in a lower overpotential for OER compared to the other systems under study. Additionally, they proposed an optimal d-band center at −2.82 eV, at which β12-BM-supported SACs would theoretically have the lowest overpotential for OER. Deng et al. designed a series of N-doped graphene-supported transition metal atom-pair catalysts (TM APCs) models for efficient NRR (Deng et al., 2020). Twenty kinds of transition metal atoms were systematically studied and were proven by COHP and orbital interaction analysis; the d-band center can be used as a descriptor to describe the NRR performance of the TM APCs. For defective graphene-supported Fe and Al nanoparticles, Lim and co-workers found that the d-band center of the Fe and Al nanoparticles shifts closer to the Fermi level, indicating a potential increase in the catalytic reactivity associated with the graphene surface. Zhou et al. systematically explored the HER activity of transition metals, transition metal oxides, and carbide substrates covered by nitrogen-doped graphitic sheets and found that the HER activity is correlated to the C pz-band center, which is similar to the d-band center theory and determined in turn by the degree of electronic coupling between the graphitic sheet and the metal substrate, enabling the rational design of high-performance hybrid graphitic carbon/transition metal electrocatalysts (Zhou et al., 2018).
When oxygen atoms are adsorbed on Pt3Y (111) surface, even though the surface d-band center of Y is higher than that of Pt, the binding strength of Pt-O is stronger than Y-O, defying the d-band center theory. However, it can be reasonably explained by the “Fermi softness” (SF), which was developed by Huang and co-workers to describe the electronic structures of a solid surface (Huang et al., 2016). All the bands’ occupied and unoccupied states contribute to the bonding, but those closer to the Fermi level (EF) are more significant (Figure 4A). A reactivity weight function w(E) with a Fermi level peak is created to determine a weighted summation of the density of states of a solid surface (
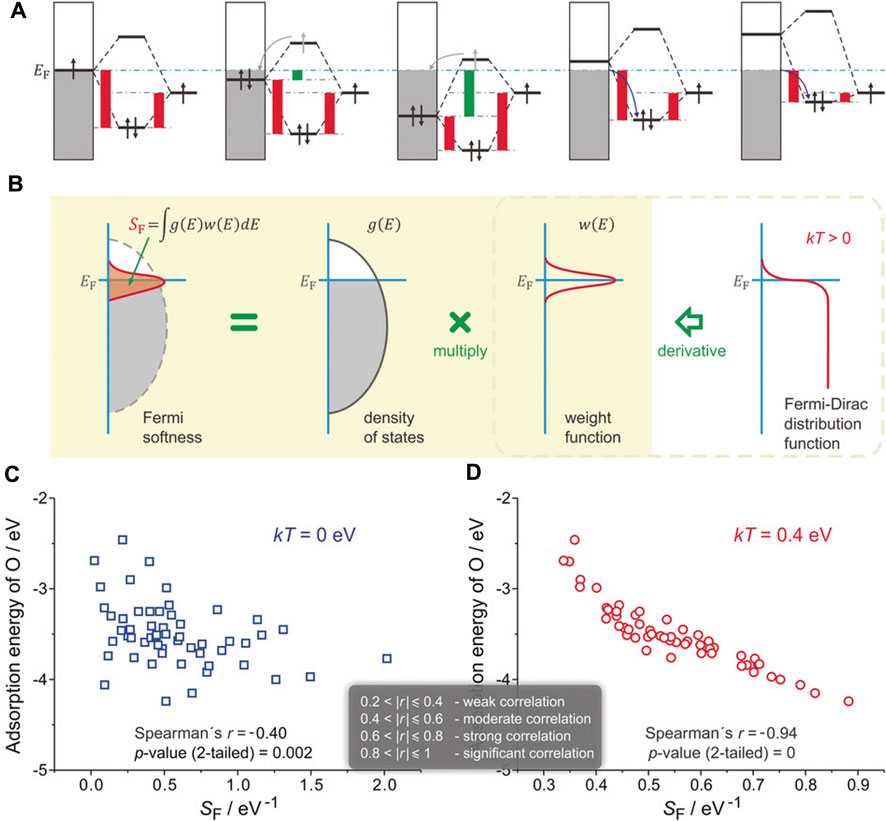
FIGURE 4. Definition of Fermi softness (SF) and its correlation with surface reactivity. (A) Energy analysis of surface bonding. (B) SF is defined as a weighted sum of the density of states. (C) SF that without and (D) with spreading. Reproduced with permission (Huang et al., 2016). Copyright 2016, John Wiley and Sons.
Fermi softness can also be an efficient descriptor to predict the catalytic performance of carbon-based catalysts (Gao R. et al., 2018; Gao Z. et al., 2018; Yang et al., 2018; Xiong et al., 2020; Wang and Zhang, 2022). Gao and co-workers designed a series of catalysts named Fe/GS, which are composed of Fe atom that serves as the active site and different graphene such as single and double vacancy graphene that serve as the substrate (Gao Z. Y. et al., 2018). They further found that the Fermi softness of Fe/GS and the O2 adsorption energy exhibit a strong positive linear correlation (R2 = 0.81) at kT = 1.15 eV. The Fermi softness is also used to describe the adsorption activity of Mn-modified graphene catalyst by Wu’s group (Xie et al., 2022). They discovered a substantial negative correlation (R2 = 0.93) between Fermi softness and adsorption energy at kT = 2.8 eV. The Fermi softness is increased with the increase of the adsorption energy.
Adsorption-free energies (ΔG) of key intermediates are utilized as activity descriptors for recognized reactions, including ΔGH for HER (Han et al., 2023b), ΔGO for ORR (Han et al., 2023a), ΔGCO for CO2RR (Chen et al., 2022a), and ΔGN for NRR (Fang et al., 2023). For instance, DFT calculations were conducted on the MoS2 edge, yielding a ΔGH of 0.08 eV, which closely approaches the optimal value of 0 eV (Hinnemann et al., 2005). Subsequently, experimental confirmation established that MoS2 edges serve as the catalytically active sites for HER (Jaramillo et al., 2007). Through the calculation of free energies of N2 adsorption and the formation energy of the key intermediate *NCON, Kou et al. found that V2N6 sites efficiently catalyze the cleavage of N-N bonds and the coupling of C-N bonds, facilitating effective urea production (Liu J. et al., 2023). Through calculating ORR energy profiles on various active sites within defective graphene, including pyridinic N sites, adjacent carbon atoms, and edge-located pentagon defects, Yao and colleagues determined that pentagon defects serve as the primary active sites for acidic ORR. Subsequent experimental studies have also validated these findings (Jia et al., 2019).
In multi-step catalytic processes, the adsorption and desorption of the intermediates occur during the concerted proton–electron transfer steps, and the adsorption energies of the intermediates follow a linear scaling relationship (Man et al., 2011; J. K. Nørskov et al., 2005; Nørskov et al., 2004). For example, the relationship between the adsorption energies of the intermediates of OER and ORR, such as *O, *OH, and *OOH, can be presented by:
Where
The excellent descriptors include eg-filling (Matsumoto et al., 1977a; Matsumoto et al., 1977b), average O-2p-state energy (
Different reaction mechanisms can be used to explain the complex NRR, including distal, alternating, and enzymatic (Figure 5A). To identify the viable routes and theoretical onset potentials by the classical approach, all chemical intermediates will be systematically investigated, which will be inefficient for large-scale catalyst screening. Ling et al. focused on two “stable to instable” transitions in the NRR process (Eq. 3.2 and 3.3). They set up a two-step method (Figure 5B) to efficiently and accurately screen the nitride-doped-graphene-supported single-atom catalysts (N-G-supported SACs) (Ling et al., 2018a).
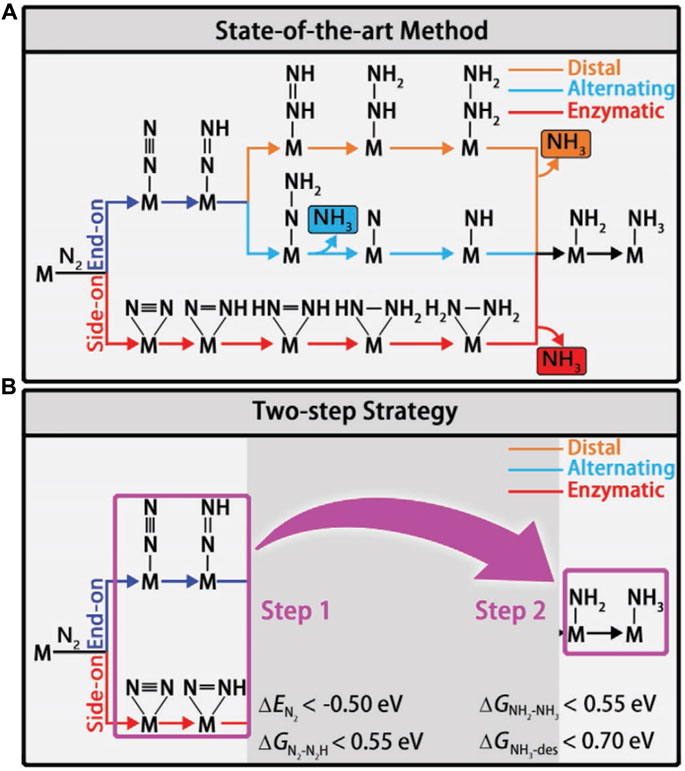
FIGURE 5. (A) Schematic depiction of different mechanisms for N2 reduction. (B) Flowchart of the two-step screening procedure for NRR catalysts. Reproduced with permission (Ling et al., 2018a). Copyright 2018, John Wiley and Sons.
In the first step, the systems with low activity are disregarded by using the descriptors
With the development of modern characterization techniques, an increasing number of in situ characterization tools are used to observe the catalytic reaction processes, aiming to accurately uncover the catalytic mechanism. However, it is still difficult to identify the actual active site and reaction intermediates of complex catalytic reactions by pure experimental study. In terms of CO2RR, through different reaction routes, the products of CO2RR can be carbon monoxide, formic acid, ethylene, or ethanol. Depending on whether the adsorption sites change or not during the catalytic processes, the actual reaction paths and intermediates and the competition between the carbon-carbon coupling reaction and HER are all unknown and difficult to elucidate experimentally (Zhang et al., 2021). For instance, Dual-atom catalysts (DACs) have been considered promising candidates for C2 product generation due to their ability to offer two metal sites that enhance *CO coverage on the surface. However, experimental results indicate that most DACs exhibit high Faradic efficiency for CO, while the formation of multi-carbon products is seldom observed (Gong et al., 2022; Hao et al., 2022; Zhao et al., 2022). Li and colleagues conducted DFT calculations and discovered a deviation from the conventional hypothesis, suggesting that C−C coupling typically does not occur at the metal-top sites (Yang et al., 2023). Surface Pourbaix analyses indicate that CO preferably occupies the bridge sites between two metals, potentially impeding subsequent C−C coupling reactions. Furthermore, based on energy variations, it is not feasible for C−C coupling to occur on the surface of a DAC, both in terms of thermodynamics and kinetics. In experimental settings, oxide-derived copper (OD-Cu) has demonstrated exceptional performance, displaying remarkable selectivity toward C2+ products even at low potentials (Cheng et al., 2021; Chen et al., 2022b). Nevertheless, the understanding of the atomic structures of active sites in OD-Cu remains limited due to its inherent complexity. Cheng et al. conducted multiscale computations based on first principles to simulate the synthesis, characterization, and performance assessment of Cu nanoparticles deposited on carbon nanotubes (CNTs) (Cheng et al., 2017). Their investigation identified two active sites that show an undercoordinated surface square structure adjacent to a subsurface stacking fault and exhibit lower formation energies for *COCOH compared to the Cu (100) surface sites.
Meanwhile, theoretical calculation is a key method to compensate for experimental shortcomings because it can investigate the electronic-scale change during the catalytic reaction. In the past decades, the use of theoretical simulations in defective electrocatalysis has greatly aided the catalytic mechanism analysis of novel catalysts (Hu et al., 2021; Khan et al., 2021; Lan et al., 2021; Liu A et al., 2021).
With the assistance of DFT calculations, Zhang et al. systematically investigated the origins of the high-performance atomic Co-Pt embedded into nitrogen-doped graphene (A-CoPt-NC) (Zhang B-W et al., 2018). A stable adsorption state of the intermediate in the HER is proved by the electron distribution calculations. The disappearance of charge depletion on the surface of the outer layer can improve the adsorption of protons to the catalyst. Li and co-workers synthesized a new HER electrocatalyst (Li M. et al., 2018). Carbon quantum dots were used to support ruthenium nanoparticles (Ru@CQDs). It shows superior catalytic activity and durability in alkaline conditions. DFT calculations provide compelling evidence of the excellent HER catalytic activity of Ru supported in the N-doped CQDs layer. The calculation results show the synergistic effect of doped N atoms and Ru clusters, and both are beneficial in reducing the dissociation energy of H2O. The electron transfer from Ru and H2O to C atoms, which is proved by the difference charge density analysis, can polarize Ru clusters, thus contributing to the dissociation of H2O. Meanwhile, the dissociated H atoms are held together by Ru and H interactions to form the H2 molecule (Figure 6).
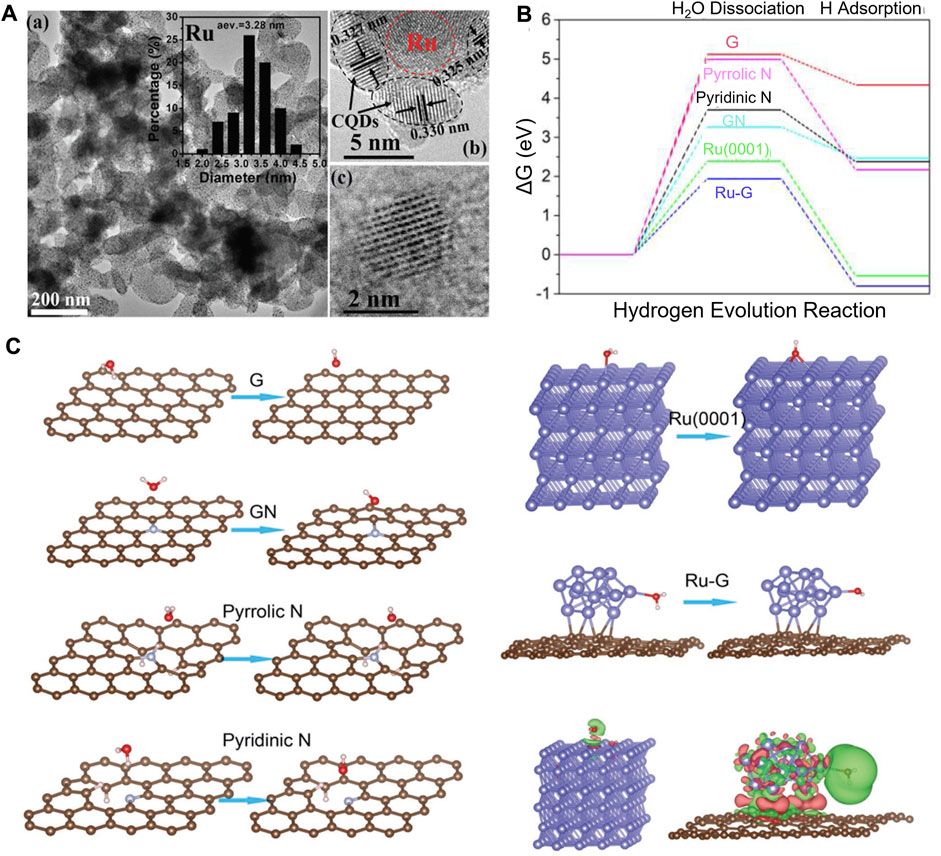
FIGURE 6. (A) TEM and HRTEM images of Ru@CQDs. (B) Calculated HER relative energy diagram. (C) Adsorption and dissociation of the H2O molecule on different surfaces. Reproduced with permission (Li M. et al., 2018). Copyright 2018, John Wiley and Sons.
As can be seen from the above discussions, theoretical calculation is an indispensable method to investigate the relationship between structures and performance. A reaction model will be built to thoroughly study the basic reaction path of the reaction, identify the crucial steps that determine the reaction rate, and then optimize the chemical reaction conditions. It is obvious that theoretical calculations are beneficial in identifying the basic process and reaction paths of electrocatalysis at the atomic level. Furthermore, the design of catalysts and the controllable synthesis of the desired structures can be aided by the DFT simulations, which can be utilized as a prediction tool. Theoretical modelings can also be used in catalyst structure optimization and validation of the design outcomes, as well as to support experimental study.
Hydrogen is one of the most promising clean energy sources to replace fossil fuels, and it also has the highest energy density among existing fuels. Water splitting is a sustainable way of producing hydrogen compared to industrial reduction of natural gas (CH4). Hydrogen evolution reaction (HER) is the cathodic half-cell reaction of water electrolysis (Karunadasa et al., 2010). The large overpotential restricts its practical application and high-performance electrocatalysts are needed to boost the HER. Noble metal-based catalysts such as Pt/C and RuO2 are commonly considered to be the most efficient HER electrocatalysts; however, scarcity and low durability limit their mass industrial production (Andreadis and Tsiakaras, 2006; Hao et al., 2016). To date, many high-performance low-dimensional carbon-based non-noble metals and even metal-free electrocatalysts have been designed and fabricated to be the alternatives of noble metal materials. In this part, the fundamental concepts and recent developments in HER electrocatalysts will be summarized.
HER is a two proton-electron transfer step (PETS) process. The first step is the Volmer reaction, i.e., the adsorption of hydrogen, which is presented in Eq. (4.1a) (acidic condition) and 4.1b (alkaline condition).
The second step can be the Heyrovsky reaction or the Tafel reaction. Equation (4.2a) (acidic condition) and 4.2b (alkaline condition) show the Heyrovsky reaction and Eq. (4.3) shows the Tafel reaction.
In which, * represents the active site on the catalyst surface.
For the design of low-cost and efficient electrocatalysts, it is crucial to reduce the amount of precious metals being used, which can be achieved in two ways. Firstly, the specific activity per metal atom usually increases with the downsize of metal particles (Figure 7). (Yang et al., 2013) Therefore, single-atom catalysts (SAC) that contain isolated metal atoms singly dispersed on supports have attracted extensive research attention. Alternatively, non-noble metal atoms or functional groups can also be anchored on the substrate to tune the electronic structures of noble-metal active sites (Sun et al., 2013; Gao G. et al., 2018; Li W. et al., 2018; Ren et al., 2020; Yang et al., 2022). Ye and co-workers designed a novel Pt SAC using aniline-stacked graphene as the support (Pt SASs/AG). It shows excellent HER performance with η = 12 mV at 10 mA cm−2 and a mass current density of 22,400
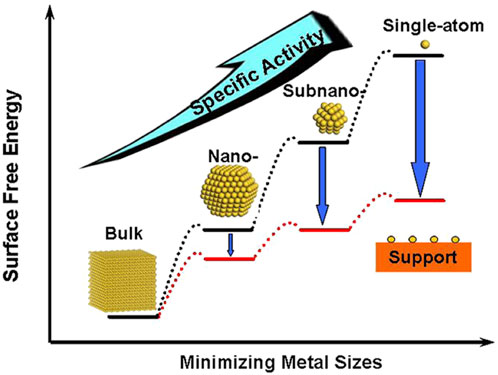
FIGURE 7. Schematic illustration of the changes of surface-free energy and specific activity per metal atom with metal particle size and the support effects on stabilizing single atoms. Reproduced with permission (Yang et al., 2013). Copyright 2013, American Chemical Society.
Secondly, non-noble metals such as transition metals are used as efficient HER catalysts, and even metal-free catalysts with excellent performance were designed and synthesized experimentally (Fan et al., 2016; He et al., 2017; Zhang L et al., 2018; He et al., 2019; Ahsan et al., 2021; Yasin et al., 2022; Han et al., 2023b; Yin and Du, 2023). For example, using the first principle DFT calculations, 3D, 4D, and 5D transition metal SACs in N-doped 2D graphene and nanographene of various sizes are screened for HER by Fung et al. (Fung et al., 2020) For most SACs, a d-band center downshift will occur when moving from graphene to nanographene, indicating that the hydrogen adsorption on metal SACs can be tuned by adjusting the size and dimension of the substrate. V, Rh, and Ir embedded in N-doped nanographene show much better HER activity than those on the extended 2D graphene. The machine learning models (kernel ridge regression, decision trees (random forest), and neural networks) and the SISSO (Sure Independence Screening and Sparsifying Operator) method are employed to accurately predict the
FIGURE 8. Comparison of DFT-calculated versus machine learning-predicted
Oxygen evolution reaction (OER,
Both the OER and ORR are restricted by the sluggish kinetic and high reaction energy barriers, thus electrocatalysts are needed to accelerate their reaction rates. However, the high cost and low abundance of current commercial noble metal-based catalysts, i.e., Pt/C for ORR, RuO2 and IrO2 for OER severely hinder their widespread applications. Similarly, the strategies of lowering the cost and improving the performance of the HER catalysts are also applicable to the OER and ORR electrocatalysts, and great achievements have been accomplished (Zhu et al., 2018; He et al., 2020a; Wang et al., 2020a; Yan et al., 2020; Yang et al., 2020; Yan et al., 2021; Xu et al., 2023). Zhang et al. anchored atomical distributed Ni atoms onto an N-doped hollow carbon matrix (HCM@Ni-N) (Zhang et al., 2019). In alkaline conditions, the HCM@Ni-N only requires an OER overpotential of 304 mV to reach the current density of 10 mA cm-2, which is much lower than that of the RuO2 (393 mV), suggesting excellent OER activity of the prepared catalyst. Through the calculated distributions of charge density, they found that the electronic distribution of N-doped HCM was changed obviously after the Ni decoration (Figure 9A). In addition, the 3d orbital of Ni in HCM@Ni-N shows a leftward shift, and the d-band center of the Ni was downshifted from −0.94 eV to −2.04 eV as a result of the Ni-N interaction (Figure 9B). According to the d-band center theory, this change could facilitate the desorption of adsorbates and reduce the energy barrier. The free energy pathways of the OER can also be calculated by DFT simulations and they are in good agreement with the experimental results (Figures 9C,D). By encapsulating Co and β-Mo2C into N-doped carbon nanotubes (Co/β-Mo2C@N-CNT), Ouyang and co-workers successfully fabricated a bifunctional electrocatalyst for the HER and OER in an alkaline electrolyte (Ouyang et al., 2019). Based on the heterointerface between Co and β-Mo2C, the OER activity of β-Mo2C is enhanced significantly. With the assistance of DFT calculations, they proved that the joint effect of N-CNTs, Co, and β-Mo2C resulted in the low energy barriers of the intermediates, thus greatly improving the HER and OER kinetics.
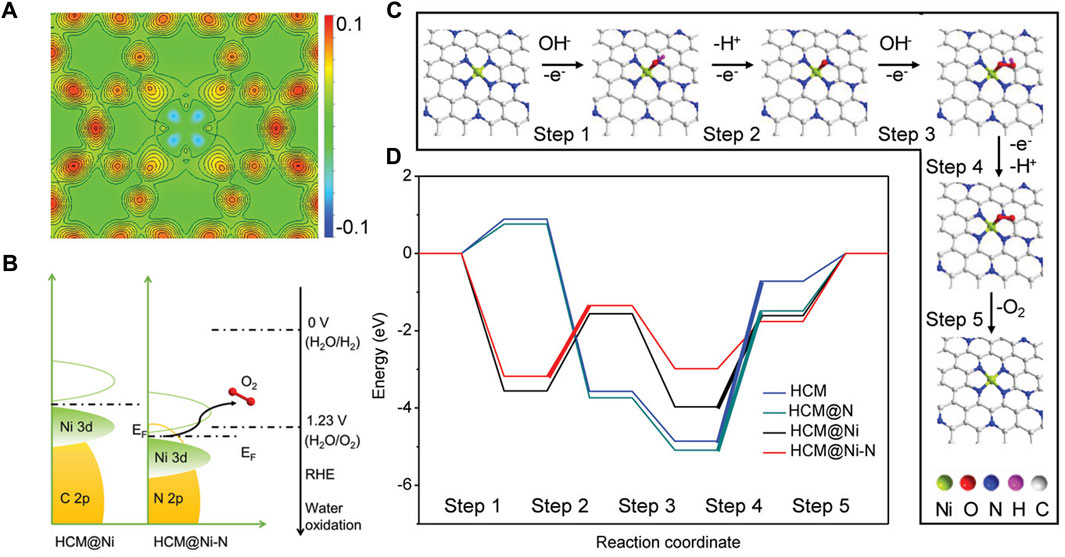
FIGURE 9. (A) Calculated distribution of charge density for HCM@Ni-N. (B) Schematic band diagrams of HCM@Ni and HCM@Ni-N. (C) Proposed mechanism of O2 evolution over HCM@Ni-N. (D) Free energy diagram at 0 V for OER over HCM, HCM@N, HCM@Ni, and HCM@Ni-N. The bold lines indicate the rate-determining step. Reproduced with permission (Zhang et al., 2019). Copyright 2019, John Wiley and Sons.
Under the guidance of DFT calculations, Wang et al. successfully synthesized a series of topological carbon defects through a facile N-removing strategy, among which adjacent pentagons (A-C5) show the best catalytic performance for the ORR and the edge divacancy defects (C585-2) are favorable for the HER (Wang et al., 2020b). DFT calculations were applied to investigate the relationship between the original carbon structure, the type of N configuration obtained, and the corresponding defect structures, for example, perfect carbon network versus graphitic-N versus C585 (Figure 10A), edge-rich hexagonal structure versus pyridinic-N versus S-C5 (Figure 10B), and edge-rich pentagon versus pyrrolic-N versus A-C5 (Figure 10C). By a spontaneous gas-foaming method, Jiang and co-workers fabricated a range of promising trifunctional electrocatalysts named defect-rich N-doped ultrathin carbon nanosheets for HER, OER, and ORR (Jiang et al., 2019). In rechargeable Zn-air batteries, NCN-1000-5 exhibits a high energy density (806 Wh/kg), a low charge/recharge voltage gap (0.77 V), and an extremely long cycle life (over 300 h). DFT calculations were used to identify the intrinsic active sites for the electrochemical reactions. The catalytic performance of various active sites for the ORR and OER was investigated, and the results are shown in the volcano plot (Figure 10D). The armchair edge carbon atoms, which are adjacent to the graphitic-N, possess the lowest overpotential, thus they should be the optimal catalytic active center for the specific electrocatalysis (Figures 10E–G).
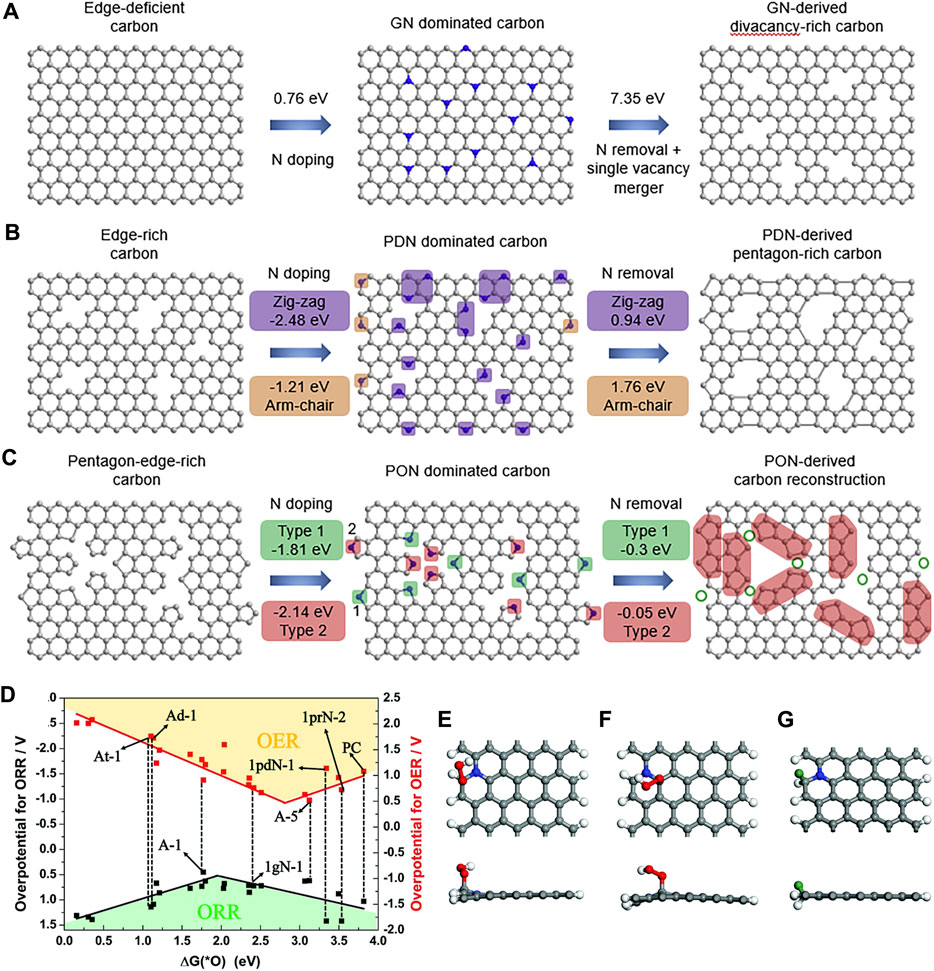
FIGURE 10. Computational simulation of specific N-doping and removing process in different carbon models: (A) Schematic and formation energy calculation of transformation from edge-deficient carbon to GN-dominated carbon and then to divacancy-rich carbon. (B) Schematic and formation energy calculations of transformation from edge-rich carbon to PDN-dominated carbon and then to pentagon-rich carbon. (C) Schematic and formation energy calculations of transformation from pentagon-edge-rich carbon to PON-dominated carbon and then to special carbon reconstruction. Reproduced with permission (Wang et al., 2020b). Copyright 2020, Elsevier. (D) The volcano plot for the ORR and OER by plotting the overpotential as a function of
Carbon dioxide reduction reaction (CO2RR) could convert CO2 to many value-added chemicals, such as CO, CH4, CH3OH, and C2H5OH (Eq. 4.6) (Whipple and Kenis, 2010; Chen J. et al., 2021; Chen S. et al., 2021), which can be directly used as fuels to replace fossil fuels like gasoline and natural gas. Therefore, the CO2RR could significantly relieve the greenhouse gas effect. However, the hydrogen atoms necessary for the reduction of CO2 molecules are transported from the aqueous solution, so the HER must be considered as the competitive reaction. The high cost of the currently used noble metal-based catalysts and the low selectivity of CO2RR are still the biggest obstacles to its industrialization. Therefore, developing highly efficient and selective non-noble metal CO2RR catalysts based on earth-abundant elements has attracted the most attention in this promising research field (Back et al., 2017; Mao et al., 2020a; He et al., 2020b; Er et al., 2021; Zha et al., 2021; Powar et al., 2022).
The initial stage of CO2 reduction is CO2 adsorption, which is a crucial step of the CO2RR. Zhu et al. systematically investigated the adsorption of CO2 on the g-C3N4 surface by DFT calculations (Zhu et al., 2017). Through analyzing the electronic properties such as the band gap, density of states, work function, HOMO, and LUMO, they found that the two-coordinated N atoms, which contributed to both valance band and conduction band edge, have the most negative adsorption energy (−0.4181) for CO2 molecule. CO2 can be effectively captured and activated on Si due to the “acceptance and back-donation” of electrons between the Si dopant and CO2 molecule. Accordingly, Mao and co-workers designed an experimentally synthesizable electrocatalyst called silicon-doped graphene edges (Si chain@G) (Mao et al., 2019b). The catalytic performance of the Si@ZZG (Si atoms doped into the zigzag edge of graphene) and Si@ACG (Si atoms doped into the armchair edge of graphene) was exhaustively studied through DFT calculations (Figure 11A). CO2 can be well captured and efficiently activated on Si@G. The binding energy at the zigzag and armchair edges is −0.65 eV and −0.83 eV, respectively. Remarkably, CO2 can be converted to CH3OH effectively when the Si@ACG is served as the active site. Moreover, Si chain@G with multiple Si active sites which are beneficial to product multiple-carbon productions was also investigated. They found that the Si chain@ZZG has a high selectivity to transform CO2 to C2H5OH with an extreme low limiting potential of −0.6 V under the optimal theoretical reaction pathway (Figures 11B,C).
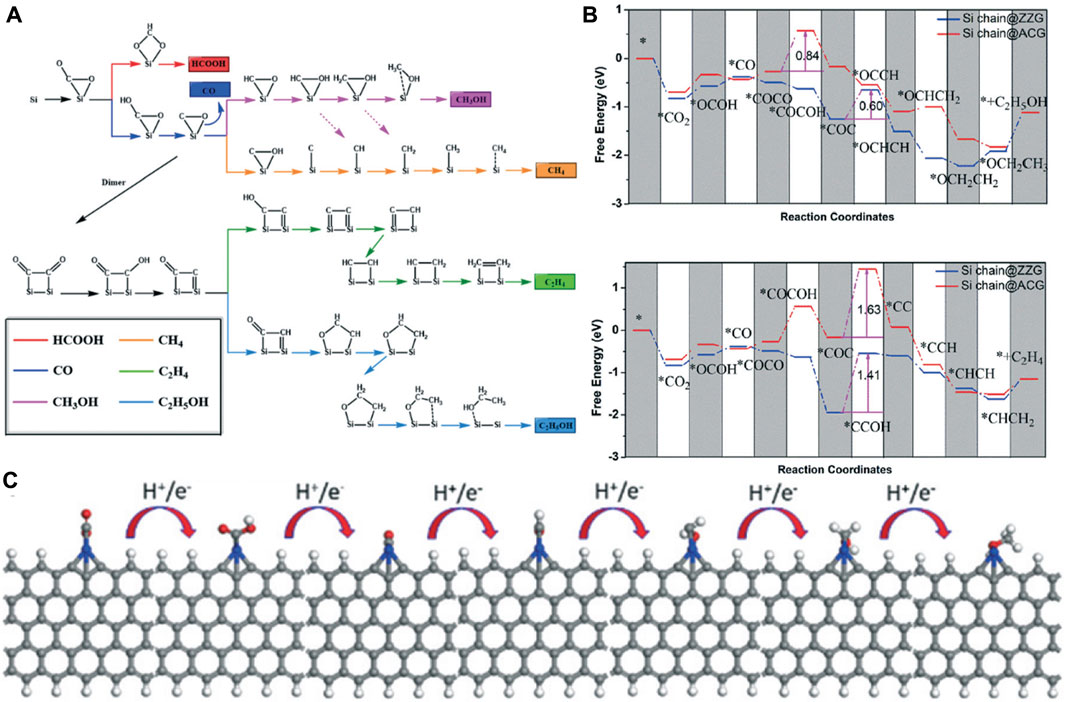
FIGURE 11. (A) Possible reaction pathways for the electrocatalytic reduction of CO2 to six different products. (B) Gibbs free energy diagrams of CO2 reduction reactions to CH3OH and C2H4 on Si chain@ZZG and Si chain@ACG. (C) The optimized structures for CO2 reduction to CH3OH on the zigzag edge. Reproduced with permission (Mao et al., 2019b). Copyright 2011, Royal Society of Chemistry.
Transition metal atoms can also be excellent CO2RR active centers. Guo et al. established calculation models with Fe, Co, and Ni single atoms embedded onto graphitic carbon nitride (Fe/Co/Ni-C3N4) and systematically investigated the structures of the electrocatalysts, CO2 adsorption configurations, and the reduction mechanisms (Guo X. et al., 2019). g-C3N4 with six-fold cavities was selected as the substrate, and the introduced Ni, Co, and Fe atoms are located from the corner to the center of the cavity. The PDOS of the metal d orbital and adsorbed CO2 indicated that CO2 could be chemically adsorbed on Co-C3N4 and Fe-C3N4 but physically adsorbed on Ni-C3N4 (Figures 12A,B). Guo et al. also probed the reaction pathway and mechanism of different C1 products and thoroughly calculated the limiting potentials for the production of CO, HCOOH, CH3OH, and CH4. They found that Co-C3N4 has superior CO2RR activity and selectivity for CH3OH (Figure 12C). Currently, copper (Cu) is found to be one of the best catalysts for achieving the high activity reduction of CO2 to hydrocarbons since *CO2 and *COOH can be effectively collected from Cu-based catalysts (Raciti and Wang, 2018). Due to the hydration of non-adsorbing CO2 molecules, Pb, Hg, Cd, and Bi also demonstrate good catalytic performance for producing formate (Mao et al., 2020b). Other transition metals such as Ni, Fe, Pd, and Ti exhibit low CO2RR selectivity because the HER is much more favorable due to the strong H-bonding (Back et al., 2017).
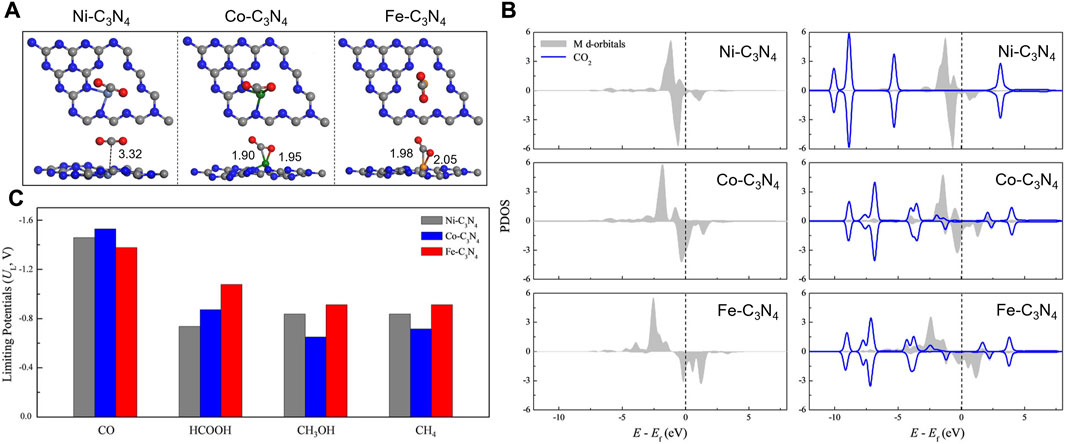
FIGURE 12. (A) The most stable CO2 adsorption configurations. (B) PDOS of the metal d orbital before and after adsorption (including the adsorbent CO2 total DOS). (C) Summary of the limiting potentials for the productions of CO, HCOOH, CH3OH, and CH4. Reproduced with permission (Guo X et al., 2019). Copyright 2019, John Wiley and Sons.
Nitrogen is the most abundant element on the earth, and it is essential for all organisms including animals and plants. Ammonia (NH3) is one of the most important industrial compounds due to its wide use in different fields. However, the ultra-stable N≡N triple bond greatly impedes the nitrogen fixation reaction. The industrial Haber-Bosch process uses N2 and H2 as the raw materials, consuming excessive energy because of the high reaction temperature (350°C–550°C) and pressure (150–350 atm) (van der Ham et al., 2014; Chen Jingguang et al., 2018). Therefore, the conversion of N2 to NH3 under ambient conditions is a promising research area. Recently, electrocatalytic nitrogen reduction reaction (NRR) has attracted increasing research attention because of its obvious advantages such as low energy consumption, reduced reaction temperature, and enhanced productivity (Li et al., 2016; Cui et al., 2018; He et al., 2020c; Liu Y et al., 2021; Ruiyi et al., 2021; Samal et al., 2021; Wang and Mao, 2021; Zhou et al., 2022; Fang et al., 2023; Liu H. et al., 2023). Figure 13 shows the possible reaction pathways of the catalytic conversion of N2 to NH3.
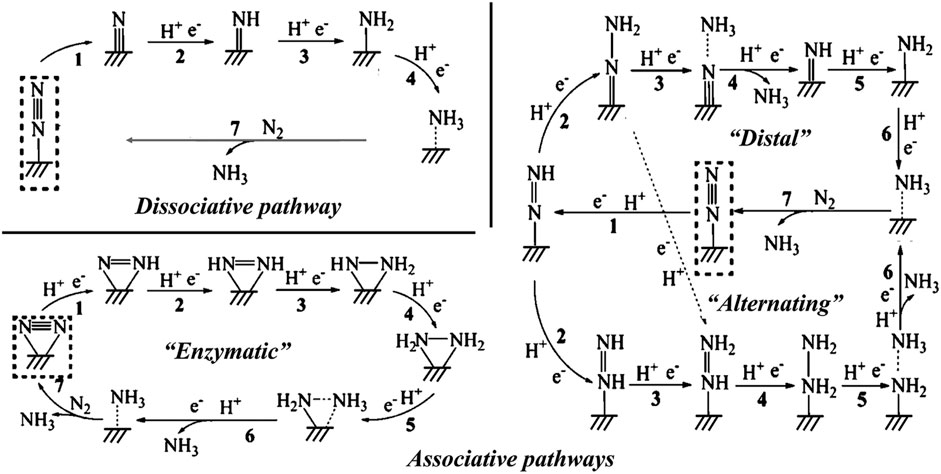
FIGURE 13. Schematic depiction of the dissociative pathways and the associative pathways (including distal, alternating, and enzymatic pathways) for catalytic conversion of N2 to NH3. Reproduced with permission (Li et al., 2016). Copyright 2016, American Chemical Society.
The first and most important step of the NRR is the adsorption of N2 to the active sites, which requires the atoms containing not fully occupied orbitals to accept the lone-pair electrons from the σ orbital of N2. Therefore, transition metals would be ideal electron acceptors due to their half-occupied d orbitals, and they have the potential to be promising NRR electrocatalysts (Lan et al., 2013; Le et al., 2014; Han et al., 2019). Ling and co-workers established a computational model that anchored Mo atoms onto N-doped carbon (Mo1-N1C2) and studied its NRR catalytic performance using the first principle calculations (Ling et al., 2018b). Firstly, the bonding energy of N2 adsorbed on M1-N1C2 (M = Cu, Pd, Pt, and Mo) is investigated; only Mo1-N1C2 shows strong adsorption of N2 with the adsorption energy of −1.19 and −1.18 eV for side-on and end-on adsorption, respectively. In addition, the N≡N bond length has increased from 1.12 Å (isolated N2 molecule) to 1.18 Å (side-on) and 1.14 Å (end-on) (Figures 14A–C). Accordingly, Mo is selected as the potential electrocatalyst, and the possible reaction pathways are calculated. As shown in Figure 14 D, Mo1-N1C2 has a low overpotential of 0.24 V and it can catalyze the NRR through an enzymatic pathway. It is worth noting that the generated NH3 can be removed quickly from the Mo1-N1C2 catalyst with a free-energy uphill of only 0.47 eV, which is much lower than that of the previously reported catalysts.
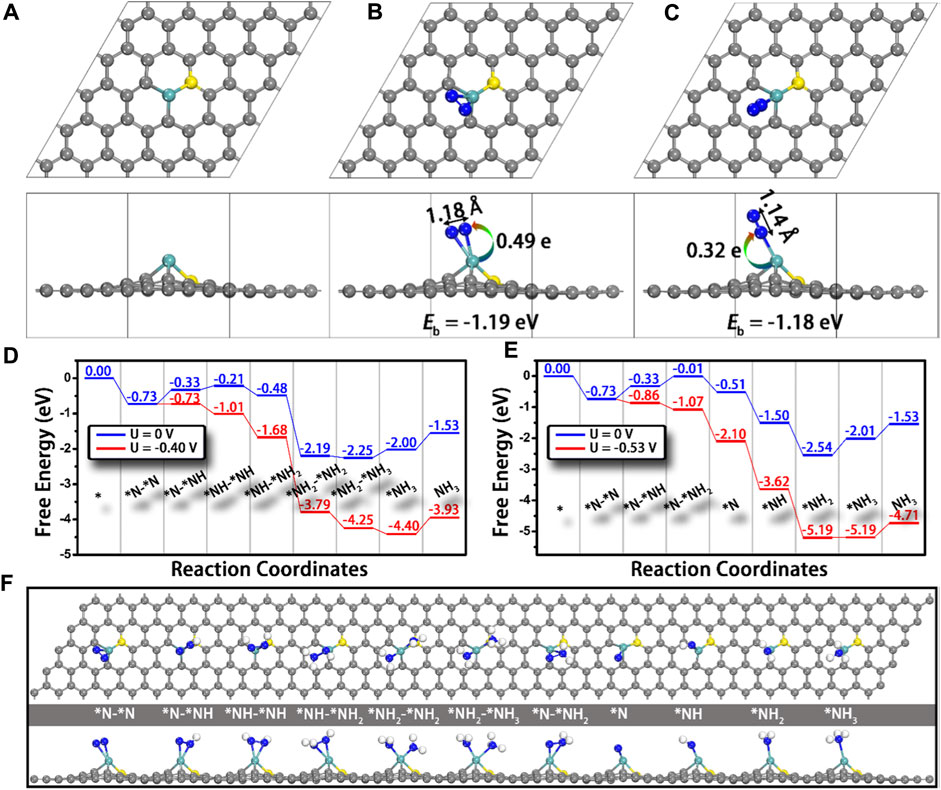
FIGURE 14. Top and side views of the structures of (A) Mo1-N1C2, and Mo1-N1C2 with N2 adsorption through (B) side-on and (C) end-on patterns. N−N bond lengths and charge transfer from Mo1-N1C2 to N2 are also presented. Free-energy diagrams for N2 reduction through (D) enzymatic and (E) consecutive mechanisms at different applied potentials as well as (F) the corresponding structures of the reaction intermediates. Gray, cyan, yellow, and blue balls represent the C, Mo, doped N, and adsorbed N atoms, respectively. Reproduced with permission (Ling et al., 2018b). Copyright 2018, American Chemical Society.
In recent years, metal-free catalysts have also emerged as an important category of electrocatalysts for ammonia formation. Boron (B) has the potential to be used in NRR processes because of its Lewis acid-like characteristics and electron-deficient nature, which is different from other main group elements. The outer orbital of B undergoes hybridization to produce sp2 orbitals, which can accept electrons from the N2 σ-bond and donate electrons from the filled 2p orbitals to the antibonding π*-orbitals of N2. This finding has been supported by a number of recent investigations (Ling et al., 2018c; Yu et al., 2018; Mao et al., 2019c). For instance, Yu’s group reported that B-doped graphene could effectively catalyze the NRR with a high Faradic efficiency of 10.8% for NH3 production in aqueous solutions under ambient conditions at −0.5 V (versus RHE), with the electron redistribution at the active site constituting the reduction process (Yu et al., 2018). However, the theoretically calculated overpotential remains very high, so there is still a great need for more suitable substrates to sustain B atoms. In addition, the detailed reaction mechanism of the N2 activation and reduction for non-metallic catalysts is yet to be uncovered, suggesting that new methods of nitrogen capture and activation should be exploited to increase the efficiency of nitrogen fixation.
In summary, the development of modern DFT was briefly introduced, and the applications of theoretical calculations such as descriptors suited to material screening and mechanism studies in carbon-based heterogeneous catalysts were reviewed. Afterward, recent achievements of carbon-based electrocatalysts were presented. As shown in Figure 15, the development of supercomputer technology could improve the accuracy of the theoretical calculations. With the assistance of machine learning and high-throughput computing, the prediction and screening ability of computational simulation has gradually enhanced and become more closely integrated with experimental work. Besides, DFT calculations can simulate a more realistic reaction environment and material structures, which could improve the efficiency and accuracy of the mechanism explanation. Particularly, low-dimensional carbon-based materials have demonstrated tremendous potential in electrocatalysis due to their distinctive features, including 1) diverse and controllable structures as well as excellent environmental tolerance; 2) inherent substrate materials can be easily doped by heteroatoms; 3) various defects can serve as the active sites. However, similar to other kinds of excellent electrocatalysts, carbon-based electrocatalysts also face severe limitations in the rational design and practical application. More universal, accurate, and measurable descriptors should be developed, and additional research attention should be focused on the synthesis of catalysts. The following important issues and challenges deserve further investigation.
(1) Microkinetic modeling is a bridge that can connect quantum-chemical data with macroscopic behaviors in surface reactions. However, the existing theoretical approaches and functionals describing interface charge cannot meet the requirement of evaluating kinetics and reaction barriers of elementary steps under realistic reaction environments. For example, the widely used CHE model can only obtain the reaction-free energies, without the consideration of the non-electrochemical processes, proton-electron transfer, and the recombination of electrons and holes. More advancements in kinetic modeling are needed to fully uncover the relationship between coverage, potential dependency of activation energies, adsorbate-adsorbate interactions, and pH effects. For interfacial catalytic processes, multiscale modeling can facilitate the understanding of the transport effects. Alternatively, assisted by advanced sampling methods, such as slow-growth (SG), metadynamics, and umbrella sampling, AIMD can compensate for the shortcomings of the CHE models. Meanwhile, grand-canonic fixed-potential DFT calculations offer a feasible way to evaluate the catalytic performance at equilibrium states, which is the same as the experimental setup.
(2) The combination of multiple descriptors to effectively describe the relationship between structures and performance is indispensable. This is because it may be impossible to accurately predict the activity trends of complicated multi-phase catalysts only using one descriptor. Meanwhile, the simulation results of completed calculations, such as explicit SG-AIMD simulation, are highly dependent on the selection of collective variables. Importantly, machine learning, high-throughput calculations, and force-field approaches should be applied to uncover more general descriptors and advanced models, leading to higher efficient reaction mechanisms investigation and catalytic performance prediction.
(3) In addition to kinetics and reaction barriers, the stability of the catalysts plays a pivotal role in practical applications. Several commonly employed simulation methods are used to assess the stability of designed catalysts. For instance, retaining a stable structure during AIMD simulations is often interpreted as a sign of catalyst stability; nevertheless, the limited simulation duration reduces the reliability of the results. Another commonly used method, Pourbaix diagrams, cannot fully overcome the limitation of thermodynamic formation energy, even considering factors such as pH and applied potential. Hence, there is a pressing need to develop a dependable approach for evaluating the stability of electrocatalysts, which deserves more attention in research.
(4) Selectivity is also a critical parameter in assessing the catalytic performance of electrocatalysts. In simulations, the selectivity of electrocatalysts is often evaluated by comparing formation energies, adsorption energies of reactants, or energy barriers of potential determining steps (PDS). However, these evaluations are typically based on the CHE model and do not consider the real reaction environment, which substantially impacts the selectivity of catalysts. Consequently, it is still unclear how to effectively assess the selectivity, while microkinetic models that consider various environmental factors may prove to be a successful solution.
(5) Synthesis of electrocatalysts with abundant active sites is also crucial, for instance, the formation process of specific defect structures and the synthesis of SACs with specific density are yet to be improved. Theoretical scientists have been focusing on improving the activity of electrocatalysts. However, rational design and synthesis strategies for large-scale production of carbon-based electrocatalysts are also one of the stumbling blocks for practical applications. More attention should be focused on the synthesis of electrocatalysts with the targeted active site for a specific reaction.
(6) The scaling relationship between oxygen adsorbates in OER, ORR, and CO2RR has the possibility to develop efficient descriptors. However, it also restricts the lowest overpotential of electrocatalytic reactions, for example, the predicted lowest overpotential is (3.2–2.46) eV/2e ≈ 0.4 V for both ORR and OER. Therefore, how to break the scaling relationship is also a prospective research topic in the near future. One possible solution is stabilizing the key intermediates, and the other method is exploring new reaction mechanisms to avoid the formation of key intermediates.
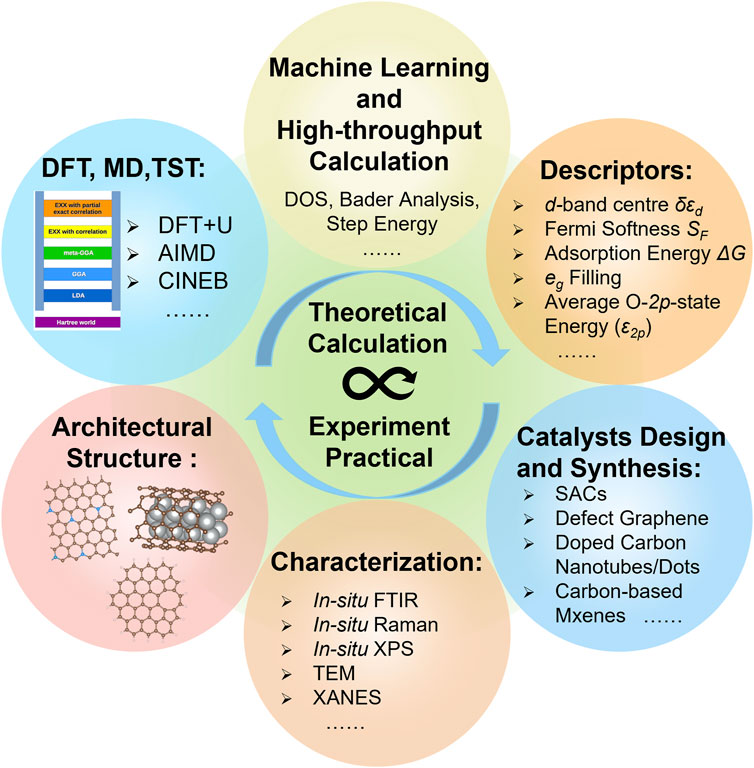
FIGURE 15. Schematic illustration showing the combination of theoretical calculations and experimental studies.
YH: Conceptualization, Writing–original draft. HX: Writing–review and editing. QL: Supervision, Writing–review and editing. AD: Conceptualization, Funding acquisition, Project administration, Supervision, Writing–review and editing. XY: Conceptualization, Funding acquisition, Project administration, Supervision, Writing–review and editing.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. Australian Research Council (DP200103043, DP210100721, and DP210100331).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abas, N., Kalair, A., and Khan, N. (2015). Review of fossil fuels and future energy technologies. Futures 69, 31–49. doi:10.1016/j.futures.2015.03.003
Abild-Pedersen, F., Greeley, J., Studt, F., Rossmeisl, J., Munter, T. R., Moses, P. G., et al. (2007). Scaling properties of adsorption energies for hydrogen-containing molecules on transition-metal surfaces. Phys. Rev. Lett. 99, 016105. doi:10.1103/PhysRevLett.99.016105
Ahsan, M. A., He, T., Eid, K., Abdullah, A. M., Curry, M. L., Du, A., et al. (2021). Tuning the intermolecular electron transfer of low-dimensional and metal-free BCN/C60 electrocatalysts via interfacial defects for efficient hydrogen and oxygen electrochemistry. J. Am. Chem. Soc. 143, 1203–1215. doi:10.1021/jacs.0c12386
Andreadis, G., and Tsiakaras, P. (2006). Ethanol crossover and direct ethanol PEM fuel cell performance modeling and experimental validation. Chem. Eng. Sci. 61, 7497–7508. doi:10.1016/j.ces.2006.08.028
Back, S., Lim, J., Kim, N. Y., Kim, Y. H., and Jung, Y. (2017). Single-atom catalysts for CO2 electroreduction with significant activity and selectivity improvements. Chem. Sci. 8, 1090–1096. doi:10.1039/c6sc03911a
Back, S., Tran, K., and Ulissi, Z. W. (2019). Toward a design of active oxygen evolution catalysts: insights from automated density functional theory calculations and machine learning. ACS Catal. 9, 7651–7659. doi:10.1021/acscatal.9b02416
Barducci, A., Bonomi, M., and Parrinello, M. (2011). Metadynamics. WIREs Comput. Mol. Sci. 1, 826–843. doi:10.1002/wcms.31
Barducci, A., Bussi, G., and Parrinello, M. (2008). Well-tempered metadynamics: a smoothly converging and tunable free-energy method. Phys. Rev. Lett. 100, 020603. doi:10.1103/PhysRevLett.100.020603
Bartók, A. P., Payne, M. C., Kondor, R., and Csányi, G. (2010). Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons. Phys. Rev. Lett. 104, 136403. doi:10.1103/PhysRevLett.104.136403
Becke, A. D. (1988). Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 38, 3098–3100. doi:10.1103/PhysRevA.38.3098
Behler, J., and Parrinello, M. (2007). Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 98, 146401. doi:10.1103/PhysRevLett.98.146401
Blank, T. B., Brown, S. D., Calhoun, A. W., and Doren, D. J. (1995). Neural network models of potential energy surfaces. J. Chem. Phys. 103, 4129–4137. doi:10.1063/1.469597
Bora, T., Dousse, A., Sharma, K., Sarma, K., Baev, A., Hornyak, G. L., et al. (2019). Modeling nanomaterial physical properties: theory and simulation. Int. J. Smart Nano Mater. 10, 116–143. doi:10.1080/19475411.2018.1541935
Bussi, G., and Laio, A. (2020). Using metadynamics to explore complex free-energy landscapes. Nat. Rev. Phys. 2, 200–212. doi:10.1038/s42254-020-0153-0
Calle-Vallejo, F., Loffreda, D., Koper, M. T., and Sautet, P. (2015a). Introducing structural sensitivity into adsorption-energy scaling relations by means of coordination numbers. Nat. Chem. 7, 403–410. doi:10.1038/nchem.2226
Calle-Vallejo, F., Martínez, J. I., García-Lastra, J. M., Sautet, P., and Loffreda, D. (2014). Fast prediction of adsorption properties for platinum nanocatalysts with generalized coordination numbers. Angew. Chem. Int. Ed. 53, 8316–8319. doi:10.1002/anie.201402958
Calle-Vallejo, F., Tymoczko, J., Colic, V., Vu Quang, H., Marcus, D. P., Morgenstern, K., et al. (2015b). Finding optimal surface sites on heterogeneous catalysts by counting nearest neighbors. Science 350, 185–189. doi:10.1126/science.aab3501
Chanussot, L., Das, A., Goyal, S., Lavril, T., Shuaibi, M., Riviere, M., et al. (2021). Open catalyst 2020 (OC20) dataset and community challenges. ACS Catal. 11, 6059–6072. doi:10.1021/acscatal.0c04525
Chattot, R., Le Bacq, O., Beermann, V., Kühl, S., Herranz, J., Henning, S., et al. (2018). Surface distortion as a unifying concept and descriptor in oxygen reduction reaction electrocatalysis. Nat. Mater 17, 827–833. doi:10.1038/s41563-018-0133-2
Che, M. (2013). Nobel prize in chemistry 1912 to sabatier: organic chemistry or catalysis? Catal. Today 218-219, 162–171. doi:10.1016/j.cattod.2013.07.006
Chen, B., Parker, G., Han, J., Meyyappan, M., and Cassell, A. M. (2002). Heterogeneous single-walled carbon nanotube catalyst discovery and optimization. Chem. Mater 14, 1891–1896. doi:10.1021/cm0116828
Chen, J., Wang, T., Li, Z., Yang, B., Zhang, Q., Lei, L., et al. (2021). Recent progress and perspective of electrochemical CO2 reduction towards C2-C5 products over non-precious metal heterogeneous electrocatalysts. Nano Res. 14, 3188–3207. doi:10.1007/s12274-021-3335-x
Chen Jingguang, G., Richard, M. C., Seefeldt Lance, C., L Bren Kara, R. M. B., Marcetta, Y. D., et al. (2018). Beyond fossil fuel–driven nitrogen transformations. Science 360, eaar6611. doi:10.1126/science.aar6611
Chen, S., Li, W.-H., Jiang, W., Yang, J., Zhu, J., Wang, L., et al. (2022a). MOF encapsulating N-heterocyclic carbene-ligated copper single-atom site catalyst towards efficient methane electrosynthesis. Angew. Chem. Int. Ed. 61, e202114450. doi:10.1002/anie.202114450
Chen, S., Wang, B., Zhu, J., Wang, L., Ou, H., Zhang, Z., et al. (2021). Lewis acid site-promoted single-atomic Cu catalyzes electrochemical CO2 methanation. Nano Lett. 21, 7325–7331. doi:10.1021/acs.nanolett.1c02502
Chen, S., Zhang, Z., Jiang, W., Zhang, S., Zhu, J., Wang, L., et al. (2022b). Engineering water molecules activation center on multisite electrocatalysts for enhanced CO2 methanation. J. Am. Chem. Soc. 144, 12807–12815. doi:10.1021/jacs.2c03875
Chen, Y., Wang, J., Meng, X., Zhong, Y., Li, R., Sun, X., et al. (2013). Pt–SnO2/nitrogen-doped CNT hybrid catalysts for proton-exchange membrane fuel cells (PEMFC): effects of crystalline and amorphous SnO2 by atomic layer deposition. J. Power Sources 238, 144–149. doi:10.1016/j.jpowsour.2013.03.093
Cheng, D., Zhao, Z.-J., Zhang, G., Yang, P., Li, L., Gao, H., et al. (2021). The nature of active sites for carbon dioxide electroreduction over oxide-derived copper catalysts. Nat. Commun. 12, 395. doi:10.1038/s41467-020-20615-0
Cheng, T., Xiao, H., and Goddard, W. A. (2017). Nature of the active sites for CO reduction on copper nanoparticles; suggestions for optimizing performance. J. Am. Chem. Soc. 139, 11642–11645. doi:10.1021/jacs.7b03300
Chmiela, S., Sauceda, H. E., Poltavsky, I., Müller, K.-R., and Tkatchenko, A. (2019). sGDML: constructing accurate and data efficient molecular force fields using machine learning. Comput. Phys. Commun. 240, 38–45. doi:10.1016/j.cpc.2019.02.007
Chu, S., and Majumdar, A. (2012). Opportunities and challenges for a sustainable energy future. Nature 488, 294–303. doi:10.1038/nature11475
Cui, X., Tang, C., and Zhang, Q. (2018). A review of electrocatalytic reduction of dinitrogen to ammonia under ambient conditions. Adv. Energy Mater 8. doi:10.1002/aenm.201800369
Dai, L., Xue, Y., Qu, L., Choi, H.-J., and Baek, J.-B. (2015). Metal-free catalysts for oxygen reduction reaction. Chem. Rev. 115, 4823–4892. doi:10.1021/cr5003563
Deng, T., Cen, C., Shen, H., Wang, S., Guo, J., Cai, S., et al. (2020). Atom-pair catalysts supported by N-doped graphene for the nitrogen reduction reaction: d-band center-based descriptor. J. Phys. Chem. Lett. 11, 6320–6329. doi:10.1021/acs.jpclett.0c01450
Ding, P., Song, H., Chang, J., and Lu, S. (2022). N-doped carbon dots coupled NiFe-LDH hybrids for robust electrocatalytic alkaline water and seawater oxidation. Nano Res. 15, 7063–7070. doi:10.1007/s12274-022-4377-4
Dudarev, S. L., Botton, G. A., Savrasov, S. Y., Humphreys, C. J., and Sutton, A. P. (1998). Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA+U study. Phys. Rev. B 57, 1505–1509. doi:10.1103/PhysRevB.57.1505
Er, C.-C., Tang, J.-Y., Fung, C.-M., Tan, L.-L., Medhekar, N. V., and Chai, S.-P. (2021). Atomistic insights into the reformation of CH4 with CO2 on metal-free gC3N4: unraveling the reaction mechanisms using first-principles DFT calculations. J. Phys. Chem. C 125, 23021–23028. doi:10.1021/acs.jpcc.1c06981
Fan, L., Liu, P. F., Yan, X., Gu, L., Yang, Z. Z., Yang, H. G., et al. (2016). Atomically isolated nickel species anchored on graphitized carbon for efficient hydrogen evolution electrocatalysis. Nat. Commun. 7, 10667. doi:10.1038/ncomms10667
Fang, Q., Yin, H., Mao, X., Han, Y., Yan, C., O’Mullane, A. P., et al. (2023). Theoretical evaluation of highly efficient nitrate reduction to ammonia on InBi. J. Phys. Chem. Lett. 14, 2410–2415. doi:10.1021/acs.jpclett.2c03900
Friederich, P., Häse, F., Proppe, J., and Aspuru-Guzik, A. (2021). Machine-learned potentials for next-generation matter simulations. Nat. Mater 20, 750–761. doi:10.1038/s41563-020-0777-6
Fung, V., Hu, G., Wu, Z., and Jiang, D.-E. (2020). Descriptors for hydrogen evolution on single atom catalysts in nitrogen-doped graphene. J. Phys. Chem. C 124, 19571–19578. doi:10.1021/acs.jpcc.0c04432
Gao, G., and Wang, L.-W. (2021). A potential and pH inclusive microkinetic model for hydrogen reactions on Pt surface. Chem. Catal. 1, 1331–1345. doi:10.1016/j.checat.2021.10.006
Gao, G., Bottle, S., and Du, A. (2018). Understanding the activity and selectivity of single atom catalysts for hydrogen and oxygen evolution via ab initial study. Catal. Sci. Technol. 8, 996–1001. doi:10.1039/C7CY02463K
Gao, R., Pan, L., Wang, H., Zhang, X., Wang, L., and Zou, J.-J. (2018). Ultradispersed nickel phosphide on phosphorus-doped carbon with tailored d-band center for efficient and chemoselective hydrogenation of nitroarenes. ACS Catal. 8, 8420–8429. doi:10.1021/acscatal.8b02091
Gao, Z., Sun, Y., Li, M., Yang, W., and Ding, X. (2018). Adsorption sensitivity of Fe decorated different graphene supports toward toxic gas molecules (CO and NO). Appl. Surf. Sci. 456, 351–359. doi:10.1016/j.apsusc.2018.06.112
Gao, Z. Y., Yang, W. J., Ding, X. L., Lv, G., and Yan, W. P. (2018). Support effects on adsorption and catalytic activation of O2 in single atom iron catalysts with graphene-based substrates. Phys. Chem. Chem. Phys. 20, 7333–7341. doi:10.1039/c7cp08301g
Gasteiger, H. A., Kocha, S. S., Sompalli, B., and Wagner, F. T. (2005). Activity benchmarks and requirements for Pt, Pt-alloy, and non-Pt oxygen reduction catalysts for PEMFCs. Appl. Catal. B Environ. 56, 9–35. doi:10.1016/j.apcatb.2004.06.021
Gauthier, J. A., Dickens, C. F., Heenen, H. H., Vijay, S., Ringe, S., and Chan, K. (2019). Unified approach to implicit and explicit solvent simulations of electrochemical reaction energetics. J. Chem. Theory Comput. 15, 6895–6906. doi:10.1021/acs.jctc.9b00717
Gong, Y.-N., Cao, C.-Y., Shi, W.-J., Zhang, J.-H., Deng, J.-H., Lu, T.-B., et al. (2022). Modulating the electronic structures of dual-atom catalysts via coordination environment engineering for boosting CO2 electroreduction. Angew. Chem. Int. Ed. 61, e202215187. doi:10.1002/anie.202215187
Grimaud, A., May, K. J., Carlton, C. E., Lee, Y.-L., Risch, M., Hong, W. T., et al. (2013). Double perovskites as a family of highly active catalysts for oxygen evolution in alkaline solution. Nat. Commun. 4, 2439. doi:10.1038/ncomms3439
Gross, A., and Sakong, S. (2022). Ab initio simulations of water/metal interfaces. Chem. Rev. 122, 10746–10776. doi:10.1021/acs.chemrev.1c00679
Groß, A. (2021). Grand-canonical approaches to understand structures and processes at electrochemical interfaces from an atomistic perspective. Curr. Opin. Electrochem. 27, 100684. doi:10.1016/j.coelec.2020.100684
Guan, D., Zhou, J., Hu, Z., Zhou, W., Xu, X., Zhong, Y., et al. (2019). Searching general sufficient-and-necessary conditions for ultrafast hydrogen-evolving electrocatalysis. Adv. Funct. Mater 29, 1900704. doi:10.1002/adfm.201900704
Guo, C., Zhang, T., Deng, X., Liang, X., Guo, W., Lu, X., et al. (2019). Electrochemical CO2 reduction to C1 products on single nickel/cobalt/iron-doped graphitic carbon nitride: a DFT study. ChemSusChem 12, 5126–5132. doi:10.1002/cssc.201902483
Guo, X., Lin, S., Gu, J., Zhang, S., Chen, Z., and Huang, S. (2019). Simultaneously achieving high activity and selectivity toward two-electron O2 electroreduction: the power of single-atom catalysts. ACS Catal. 9, 11042–11054. doi:10.1021/acscatal.9b02778
Guo, Y., Yuan, P., Zhang, J., Xia, H., Cheng, F., Zhou, M., et al. (2018). Co2P–CoN double active centers confined in N-doped carbon nanotube: heterostructural engineering for trifunctional catalysis toward HER, ORR, OER, and Zn–air batteries driven water splitting. Adv. Funct. Mater 28, 1805641. doi:10.1002/adfm.201805641
Hammer, B., and Norskov, J. K. (1995). Why gold is the noblest of all the metals. Nature 376, 238–240. doi:10.1038/376238a0
Han, L., Liu, X., Chen, J., Lin, R., Liu, H., Lü, F., et al. (2019). Atomically dispersed molybdenum catalysts for efficient ambient nitrogen fixation. Angew. Chem. Int. Ed. 58, 2321–2325. doi:10.1002/anie.201811728
Han, Y., Yan, X., Wu, Q., Xu, H., Li, Q., Du, A., et al. (2023a). Defect-derived catalysis mechanism of electrochemical reactions in two-dimensional carbon materials. Small Struct., 2300036. doi:10.1002/sstr.202300036
Han, Y., Mao, X., Yan, X., Wu, Q., Xu, H., Fang, Q., et al. (2023b). Carbon nanotubes encapsulated transition metals for efficient hydrogen evolution reaction: coupling effect of 3d orbital and π-bond. Mater. Today Chem. 30, 101573. doi:10.1016/j.mtchem.2023.101573
Handley, C. M., and Popelier, P. L. A. (2010). Potential energy surfaces fitted by artificial neural networks. J. Phys. Chem. A 114, 3371–3383. doi:10.1021/jp9105585
Hao, Q., Zhong, H.-X., Wang, J.-Z., Liu, K.-H., Yan, J.-M., Ren, Z.-H., et al. (2022). Nickel dual-atom sites for electrochemical carbon dioxide reduction. Nat. Synth. 1, 719–728. doi:10.1038/s44160-022-00138-w
Hao, Y., Wang, X., Shen, J., Yuan, J., Wang, A.-J., Niu, L., et al. (2016). One-pot synthesis of single-crystal Pt nanoplates uniformly deposited on reduced graphene oxide, and their high activity and stability on the electrocalalytic oxidation of methanol. Nanotechnology 27, 145602. doi:10.1088/0957-4484/27/14/145602
He, T., Gao, G., Kou, L., Will, G., and Du, A. (2017). Endohedral metallofullerenes (M@C60) as efficient catalysts for highly active hydrogen evolution reaction. J. Catal. 354, 231–235. doi:10.1016/j.jcat.2017.08.025
He, T., Kong, Y., Zhou, T., Zhang, J., Santiago, A. R. P., Du, A., et al. (2023). Rational modulation of single atom coordination microenvironments in a BCN monolayer for multifunctional electrocatalysis. Small, 2302429. doi:10.1002/smll.202302429
He, T., Santiago, A. R. P., and Du, A. (2020c). Atomically embedded asymmetrical dual-metal dimers on N-doped graphene for ultra-efficient nitrogen reduction reaction. J. Catal. 388, 77–83. doi:10.1016/j.jcat.2020.05.009
He, T., Zhang, C., and Du, A. (2019). Single-atom supported on graphene grain boundary as an efficient electrocatalyst for hydrogen evolution reaction. Chem. Eng. Sci. 194, 58–63. doi:10.1016/j.ces.2018.03.028
He, T., Zhang, C., Will, G., and Du, A. (2020b). Cobalt porphyrin supported on graphene/Ni (111) surface: enhanced oxygen evolution/reduction reaction and the role of electron coupling. Catal. Today 351, 113–118. doi:10.1016/j.cattod.2018.10.056
He, T., Zhang, L., Kour, G., and Du, A. (2020a). Electrochemical reduction of carbon dioxide on precise number of Fe atoms anchored graphdiyne. J. CO2 Util. 37, 272–277. doi:10.1016/j.jcou.2019.12.025
Henkelman, G., and Jónsson, H. (1999). A dimer method for finding saddle points on high dimensional potential surfaces using only first derivatives. J. Chem. Phys. 111, 7010–7022. doi:10.1063/1.480097
Henkelman, G., Uberuaga, B. P., and Jónsson, H. (2000). A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113, 9901–9904. doi:10.1063/1.1329672
Heyd, J., and Scuseria, G. E. (2004). Efficient hybrid density functional calculations in solids: assessment of the Heyd–Scuseria–Ernzerhof screened Coulomb hybrid functional. J. Chem. Phys. 121, 1187–1192. doi:10.1063/1.1760074
Heyd, J., Scuseria, G. E., and Ernzerhof, M. (2003). Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207–8215. doi:10.1063/1.1564060
Hinnemann, B., Moses, P. G., Bonde, J., Jørgensen, K. P., Nielsen, J. H., Horch, S., et al. (2005). Biomimetic hydrogen evolution: MoS2 nanoparticles as catalyst for hydrogen evolution. J. Am. Chem. Soc. 127, 5308–5309. doi:10.1021/ja0504690
Hohenberg, P., and Kohn, W. (1964). Inhomogeneous electron gas. Phys. Rev. 136, B864–B871. doi:10.1103/PhysRev.136.B864
Hoover, W. G. (1985). Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A 31, 1695–1697. doi:10.1103/PhysRevA.31.1695
Hsieh, C.-T., Lin, J.-Y., and Wei, J.-L. (2009). Deposition and electrochemical activity of Pt-based bimetallic nanocatalysts on carbon nanotube electrodes. Int. J. Hydrogen Energy 34, 685–693. doi:10.1016/j.ijhydene.2008.11.008
Hu, C., Hu, Y., Fan, C., Yang, L., Zhang, Y., Li, H., et al. (2021). Surface-enhanced Raman spectroscopic evidence of key intermediate species and role of NiFe dual-catalytic center in water oxidation. Angewandte Chemie Int. ed Engl. 60, 19774–19778. doi:10.1002/anie.202103888
Huang, B., Xiao, L., Lu, J., and Zhuang, L. (2016). Spatially resolved quantification of the surface reactivity of solid catalysts. Angew. Chem. Int. Ed. 55, 6239–6243. doi:10.1002/anie.201601824
Hubert, A. G., and Nenad, M. M. (2009). Just a dream—or future reality? Science 324, 48–49. doi:10.1126/science.1172083
Iannuzzi, M., Laio, A., and Parrinello, M. (2003). Efficient exploration of reactive potential energy surfaces using car-parrinello molecular dynamics. Phys. Rev. Lett. 90, 238302. doi:10.1103/PhysRevLett.90.238302
Jain, A., Ong, S. P., Hautier, G., Chen, W., Richards, W. D., Dacek, S., et al. (2013). Commentary: the Materials Project: a materials genome approach to accelerating materials innovation. Apl. Mater. 1, 011002. doi:10.1063/1.4812323
Jaramillo, T. F., Jørgensen, K. P., Bonde, J., Nielsen, J. H., Horch, S., and Chorkendorff, I. (2007). Identification of active edge sites for electrochemical H2 evolution from MoS2 nanocatalysts. Science 317, 100–102. doi:10.1126/science.1141483
Jia, Y., Zhang, L., Du, A., Gao, G., Chen, J., Yan, X., et al. (2016). Defect graphene as a trifunctional catalyst for electrochemical reactions. Adv. Mater 28, 9532–9538. doi:10.1002/adma.201602912
Jia, Y., Zhang, L., Zhuang, L., Liu, H., Yan, X., Wang, X., et al. (2019). Identification of active sites for acidic oxygen reduction on carbon catalysts with and without nitrogen doping. Nat. Catal. 2, 688–695. doi:10.1038/s41929-019-0297-4
Jiang, H., Gu, J., Zheng, X., Liu, M., Qiu, X., Wang, L., et al. (2019). Defect-rich and ultrathin N doped carbon nanosheets as advanced trifunctional metal-free electrocatalysts for the ORR, OER and HER. Energy Environ. Sci. 12, 322–333. doi:10.1039/c8ee03276a
Jiao, S., Fu, X., and Huang, H. (2022). Descriptors for the evaluation of electrocatalytic reactions: d-band theory and beyond. Adv. Funct. Mater 32, 2107651. doi:10.1002/adfm.202107651
Jinnouchi, R., Karsai, F., Verdi, C., Asahi, R., and Kresse, G. (2020). Descriptors representing two- and three-body atomic distributions and their effects on the accuracy of machine-learned inter-atomic potentials. J. Chem. Phys. 152, 234102. doi:10.1063/5.0009491
Jinnouchi, R., Lahnsteiner, J., Karsai, F., Kresse, G., and Bokdam, M. (2019). Phase transitions of hybrid perovskites simulated by machine-learning force fields trained on the fly with bayesian inference. Phys. Rev. Lett. 122, 225701. doi:10.1103/PhysRevLett.122.225701
Karunadasa, H. I., Chang, C. J., and Long, J. R. (2010). A molecular molybdenum-oxo catalyst for generating hydrogen from water. Nature 464, 1329–1333. doi:10.1038/nature08969
Khan, K., Liu, T., Arif, M., Yan, X., Hossain, M. D., Rehman, F., et al. (2021). Laser-irradiated holey graphene-supported single-atom catalyst towards hydrogen evolution and oxygen reduction. Adv. Energy Mater 11, 2101619. doi:10.1002/aenm.202101619
Kibler, L. A., El-Aziz, A. M., Hoyer, R., and Kolb, D. M. (2005). Tuning reaction rates by lateral strain in a palladium monolayer. Angew. Chem. Int. Ed. 44, 2080–2084. doi:10.1002/anie.200462127
Klamt, A., and Schüürmann, G. (1993). COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 2, 799–805. doi:10.1039/P29930000799
Kocer, E., Ko, T. W., and Behler, J. (2022). Neural network potentials: a concise overview of methods. Annu. Rev. Phys. Chem. 73, 163–186. doi:10.1146/annurev-physchem-082720-034254
Kohn, W., and Sham, L. J. (1965). Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138. doi:10.1103/PhysRev.140.A1133
Kresse, G., and Furthmüller, J. (1996a). Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater Sci. 6, 15–50. doi:10.1016/0927-0256(96)00008-0
Kresse, G., and Furthmüller, J. (1996b). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186. doi:10.1103/PhysRevB.54.11169
Kresse, G., and Hafner, J. (1993). Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561. doi:10.1103/PhysRevB.47.558
Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775. doi:10.1103/PhysRevB.59.1758
Kroto, H. W., Heath, J. R., O’Brien, S. C., Curl, R. F., and Smalley, R. E. (1985). C60: buckminsterfullerene. Nature 318, 162–163. doi:10.1038/318162a0
Laio, A., and Parrinello, M. (2002). Escaping free-energy minima. Proc. Natl. Acad. Sci. 99, 12562–12566. doi:10.1073/pnas.202427399
Lan, J., Luo, M., Han, J., Peng, M., Duan, H., and Tan, Y. (2021). Nanoporous B13C2 towards highly efficient electrochemical nitrogen fixation. Small 17, 2102814. doi:10.1002/smll.202102814
Lan, R., Irvine, J. T. S., and Tao, S. (2013). Synthesis of ammonia directly from air and water at ambient temperature and pressure. Sci. Rep. 3, 1145. doi:10.1038/srep01145
Le, Y. Q., Gu, J., and Tian, W. Q. (2014). Nitrogen-fixation catalyst based on graphene: every part counts. Chem. Commun. (Camb) 50, 13319–13322. doi:10.1039/c4cc01950d
Lee, C., Yang, W., and Parr, R. G. (1988). Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 37, 785–789. doi:10.1103/PhysRevB.37.785
Lee, Y.-L., Kleis, J., Rossmeisl, J., Shao-Horn, Y., and Morgan, D. (2011). Prediction of solid oxide fuel cell cathode activity with first-principles descriptors. Energy Environ. Sci. 4. doi:10.1039/c1ee02032c
Li, D., Wang, B., Long, X., Xu, W., Xia, Y., Yang, D., et al. (2021). Controlled asymmetric charge distribution of active centers in conjugated polymers for oxygen reduction. Angew. Chem. Int. Ed. 60, 26483–26488. doi:10.1002/anie.202109057
Li, M., Zhu, Y., Song, N., Wang, C., and Lu, X. (2018). Fabrication of Pt nanoparticles on nitrogen-doped carbon/Ni nanofibers for improved hydrogen evolution activity. J. Colloid Interface Sci. 514, 199–207. doi:10.1016/j.jcis.2017.12.028
Li, Q., Ouyang, Y., Lu, S., Bai, X., Zhang, Y., Shi, L., et al. (2020). Perspective on theoretical methods and modeling relating to electro-catalysis processes. Chem. Commun. 56, 9937–9949. doi:10.1039/D0CC02998J
Li, W., Liu, Y., Wu, M., Feng, X., Redfern, S. A. T., Shang, Y., et al. (2018). Carbon-quantum-dots-loaded ruthenium nanoparticles as an efficient electrocatalyst for hydrogen production in alkaline media. Adv. Mater 30, e1800676. doi:10.1002/adma.201800676
Li, X.-F., Li, Q.-K., Cheng, J., Liu, L., Yan, Q., Wu, Y., et al. (2016). Conversion of dinitrogen to ammonia by FeN3-embedded graphene. J. Am. Chem. Soc. 138, 8706–8709. doi:10.1021/jacs.6b04778
Liang, Y., Li, Y., Wang, H., and Dai, H. (2013). Strongly coupled inorganic/nanocarbon hybrid materials for advanced electrocatalysis. J. Am. Chem. Soc. 135, 2013–2036. doi:10.1021/ja3089923
Lin, Z., Waller, G. H., Liu, Y., Liu, M., and Wong, C.-P. (2013). 3D Nitrogen-doped graphene prepared by pyrolysis of graphene oxide with polypyrrole for electrocatalysis of oxygen reduction reaction. Nano Energy 2, 241–248. doi:10.1016/j.nanoen.2012.09.002
Ling, C., Bai, X., Ouyang, Y., Du, A., and Wang, J. (2018a). Single molybdenum atom anchored on N-doped carbon as a promising electrocatalyst for nitrogen reduction into ammonia at ambient conditions. J. Phys. Chem. C 122, 16842–16847. doi:10.1021/acs.jpcc.8b05257
Ling, C., Cui, Y., Lu, S., Bai, X., and Wang, J. (2022). How computations accelerate electrocatalyst discovery. Chem 8, 1575–1610. doi:10.1016/j.chempr.2022.03.015
Ling, C., Niu, X., Li, Q., Du, A., and Wang, J. (2018b). Metal-free single atom catalyst for N2 fixation driven by visible light. J. Am. Chem. Soc. 140, 14161–14168. doi:10.1021/jacs.8b07472
Ling, C., Ouyang, Y., Li, Q., Bai, X., Mao, X., Du, A., et al. (2018c). A general two-step strategy–based high-throughput screening of single atom catalysts for nitrogen fixation. Small Methods 3. doi:10.1002/smtd.201800376
Ling, C., Shi, L., Ouyang, Y., Zeng, X. C., and Wang, J. (2017). Nanosheet supported single-metal atom bifunctional catalyst for overall water splitting. Nano Lett. 17, 5133–5139. doi:10.1021/acs.nanolett.7b02518
Liu, , Smith, S. C., Gu, Y., and Kou, L. (2023). C─N coupling enabled by N─N bond breaking for electrochemical urea production. Adv. Funct. Mater 2305894. doi:10.1002/adfm.202305894
Liu, H., Qu, M., Du, A., and Sun, Q. (2023). N2 reduction in uranium-doped C2N/C3N4 monolayers: a DFT computational study. New J. Chem. 47, 13880–13887. doi:10.1039/D3NJ01668D
Liu, M., Zhao, Z., Duan, X., and Huang, Y. (2019). Nanoscale structure design for high-performance Pt-based ORR catalysts. Adv. Mater 31, 1802234. doi:10.1002/adma.201802234
Liu, R., Wu, D., Feng, X., and Müllen, K. (2010). Nitrogen-doped ordered mesoporous graphitic arrays with high electrocatalytic activity for oxygen reduction. Angew. Chem. Int. Ed. 49, 2565–2569. doi:10.1002/anie.200907289
Liu, X., and Dai, L. (2016). Carbon-based metal-free catalysts. Nat. Rev. Mater 1, 16064. doi:10.1038/natrevmats.2016.64
Liu, Y., Xue, Y., Hui, L., Yu, H., Fang, Y., He, F., et al. (2021). Porous graphdiyne loading CoOx quantum dots for fixation nitrogen reaction. Nano Energy 89, 106333. doi:10.1016/j.nanoen.2021.106333
Liu, A, , Yang, Y., Kong, D., Ren, X., Gao, M., Liang, X., et al. (2021). DFT study of the defective carbon materials with vacancy and heteroatom as catalyst for NRR. Appl. Surf. Sci. 536, 147851. doi:10.1016/j.apsusc.2020.147851
Lorenz, S., Groß, A., and Scheffler, M. (2004). Representing high-dimensional potential-energy surfaces for reactions at surfaces by neural networks. Chem. Phys. Lett. 395, 210–215. doi:10.1016/j.cplett.2004.07.076
Man, I. C., Su, H.-Y., Calle-Vallejo, F., Hansen, H. A., Martínez, J. I., Inoglu, N. G., et al. (2011). Universality in oxygen evolution electrocatalysis on oxide surfaces. ChemCatChem 3, 1159–1165. doi:10.1002/cctc.201000397
Mao, X., Kour, G., Zhang, L., He, T., Wang, S., Yan, C., et al. (2019a). Silicon-doped graphene edges: an efficient metal-free catalyst for the reduction of CO2 into methanol and ethanol. Catal. Sci. Technol. 9, 6800–6807. doi:10.1039/c9cy01709g
Mao, X., Ling, C., Tang, C., Yan, C., Zhu, Z., and Du, A. (2018). Predicting a new class of metal-organic frameworks as efficient catalyst for bi-functional oxygen evolution/reduction reactions. J. Catal. 367, 206–211. doi:10.1016/j.jcat.2018.09.012
Mao, X., Tang, C., He, T., Wijethunge, D., Yan, C., Zhu, Z., et al. (2020b). Computational screening of MN4 (M = Ti-Cu) based metal organic frameworks for CO2 reduction using the d-band centre as a descriptor. Nanoscale 12, 6188–6194. doi:10.1039/c9nr09529b
Mao, X., Wang, L., Xu, Y., Wang, P., Li, Y., and Zhao, J. (2021). Computational high-throughput screening of alloy nanoclusters for electrocatalytic hydrogen evolution. npj Comput. Mater. 7, 46. doi:10.1038/s41524-021-00514-8
Mao, X., Wijethunge, D., Zhang, L., Wang, S., Yan, C., Zhu, Z., et al. (2020a). Metal-free graphene/boron nitride heterointerface for CO2 reduction: surface curvature controls catalytic activity and selectivity. EcoMat 2, e12013. doi:10.1002/eom2.12013
Mao, X., Zhang, L., Kour, G., Zhou, S., Wang, S., Yan, C., et al. (2019c). Defective graphene on the transition-metal surface: formation of efficient bifunctional catalysts for oxygen evolution/reduction reactions in alkaline media. ACS Appl. Mater Interfaces 11, 17410–17415. doi:10.1021/acsami.9b02588
Mao, X., Zhou, S., Yan, C., Zhu, Z., and Du, A. (2019b). A single boron atom doped boron nitride edge as a metal-free catalyst for N2 fixation. Phys. Chem. Chem. Phys. 21, 1110–1116. doi:10.1039/c8cp07064d
Marenich, A. V., Cramer, C. J., and Truhlar, D. G. (2009). Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 113, 6378–6396. doi:10.1021/jp810292n
Matsumoto, H. Y., and Tamura, H. (1977b). Catalytic activity for electrochemical reduction of oxygen of lanthanum nickel oxide and related oxides. J. Electroanal. Chem. Interfacial Electrochem. 79, 319–326. doi:10.1016/S0022-0728(77)80453-1
Matsumoto, H. Y., and Tamura, H. (1977a). Influence of the nature of the conduction band of transition metal oxides on catalytic activity for oxygen reduction. J. Electroanal. Chem. Interfacial Electrochem. 83, 237–243. doi:10.1016/S0022-0728(77)80169-1
Mattsson, A. E. (2002). In pursuit of the "divine" functional. Science 298, 759–760. doi:10.1126/science.1077710
Melander, M. M., Kuisma, M. J., Christensen, T. E. K., and Honkala, K. (2018). Grand-canonical approach to density functional theory of electrocatalytic systems: thermodynamics of solid-liquid interfaces at constant ion and electrode potentials. J. Chem. Phys. 150, 041706. doi:10.1063/1.5047829
Nilsson, A., Pettersson, L. G. M., Hammer, B., Bligaard, T., Christensen, C. H., and Nørskov, J. K. (2005). The electronic structure effect in heterogeneous catalysis. Catal. Lett. 100, 111–114. doi:10.1007/s10562-004-3434-9
Nørskov, J. K. (1991). Electronic factors in catalysis. Prog. Surf. Sci. 38, 103–144. doi:10.1016/0079-6816(91)90007-Q
Nørskov, J. K., Rossmeisl, J., Logadottir, A., Lindqvist, L., Kitchin, J. R., Bligaard, T., et al. (2004). Origin of the overpotential for oxygen reduction at a fuel-cell cathode. J. Phys. Chem. B 108, 17886–17892. doi:10.1021/jp047349j
Nørskov, J. K., Bligaard, T., Logadottir, A., Kitchin, J. R., Chen, J. G., Pandelov, S., et al. (2005). Trends in the exchange current for hydrogen evolution. J. Electrochem Soc. 152. doi:10.1149/1.1856988
Nosé, S. (1984). A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 81, 511–519. doi:10.1063/1.447334
Novoselov, K. S., Geim, A. K., Morozov, S. V., Jiang, D., Zhang, Y., Dubonos, S. V., et al. (2004). Electric field effect in atomically thin carbon films. Science 306, 666–669. doi:10.1126/science.1102896
Ouyang, T., Ye, Y. Q., Wu, C. Y., Xiao, K., and Liu, Z. Q. (2019). Heterostructures composed of N-doped carbon nanotubes encapsulating cobalt and beta-Mo2C nanoparticles as bifunctional electrodes for water splitting. Angew. Chem. Int. Ed. 58, 4923–4928. doi:10.1002/anie.201814262
Parker, A. J., Opletal, G., and Barnard, A. S. (2020). Classification of platinum nanoparticle catalysts using machine learning. J. Appl. Phys. 128, 014301. doi:10.1063/5.0009129
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865
Perdew, J. P., Chevary, J. A., Vosko, S. H., Jackson, K. A., Pederson, M. R., Singh, D. J., et al. (1992). Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 46, 6671–6687. doi:10.1103/PhysRevB.46.6671
Peterson, A. A., Abild-Pedersen, F., Studt, F., Rossmeisl, J., and Nørskov, J. K. (2010). How copper catalyzes the electroreduction of carbon dioxide into hydrocarbon fuels. Energy Environ. Sci. 3, 1311–1315. doi:10.1039/C0EE00071J
Powar, N. S., Hiragond, C. B., Bae, D., and In, S.-I. (2022). Two-dimensional metal carbides for electro- and photocatalytic CO2 reduction: review. J. CO2 Util. 55, 101814. doi:10.1016/j.jcou.2021.101814 (
Raciti, D., and Wang, C. (2018). Recent advances in CO2 reduction electrocatalysis on copper. ACS Energy Lett. 3, 1545–1556. doi:10.1021/acsenergylett.8b00553
Ren, X., Lv, Q., Liu, L., Liu, B., Wang, Y., Liu, A., et al. (2020). Current progress of Pt and Pt-based electrocatalysts used for fuel cells. Sustain. Energy Fuels 4, 15–30. doi:10.1039/c9se00460b
Ruddigkeit, L., van Deursen, R., Blum, L. C., and Reymond, J.-L. (2012). Enumeration of 166 billion organic small molecules in the chemical universe database GDB-17. J. Chem. Inf. Model 52, 2864–2875. doi:10.1021/ci300415d
Ruiyi, L., Keyang, H., Pengwu, X., Wendong, W., Nana, L., Haiyan, Z., et al. (2021). Synthesis of a ruthenium–graphene quantum dot–graphene hybrid as a promising single-atom catalyst for electrochemical nitrogen reduction with ultrahigh yield rate and selectivity. J. Mater Chem. A 9, 24582–24589. doi:10.1039/d1ta07158k
Samal, P. P., Poonam, , and Krishnamurty, S. (2021). Substrate augmented catalytic activity towards NRR: a case study of Li doped Al clusters on defective graphene. Appl. Surf. Sci. 566, 150586. doi:10.1016/j.apsusc.2021.150586
Seh, Z. W., Kibsgaard, J., Dickens, C. F., Chorkendorff, I., Nørskov, J. K., and Jaramillo, T. F. (2017). Combining theory and experiment in electrocatalysis: insights into materials design. Science 355, eaad4998. doi:10.1126/science.aad4998
Song, H., Yu, J., Tang, Z., Yang, B., and Lu, S. (2022). Halogen-doped carbon dots on amorphous cobalt phosphide as robust electrocatalysts for overall water splitting. Adv. Energy Mater 12, 2102573. doi:10.1002/aenm.202102573
Stamenkovic, V. R., Mun, B. S., Arenz, M., Mayrhofer, K. J. J., Lucas, C. A., Wang, G., et al. (2007). Trends in electrocatalysis on extended and nanoscale Pt-bimetallic alloy surfaces. Nat. Mater 6, 241–247. doi:10.1038/nmat1840
Stephens, P. J., Devlin, F. J., Chabalowski, C. F., and Frisch, M. J. (1994). Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 98, 5. doi:10.1021/j100096a001
Sui, S., Wang, X., Zhou, X., Su, Y., Riffat, S., and Liu, C.-J. (2017). A comprehensive review of Pt electrocatalysts for the oxygen reduction reaction: nanostructure, activity, mechanism and carbon support in PEM fuel cells. J. Mater Chem. A 5, 1808–1825. doi:10.1039/C6TA08580F
Sun, S., Zhang, G., Gauquelin, N., Chen, N., Zhou, J., Yang, S., et al. (2013). Single-atom catalysis using Pt/graphene achieved through atomic layer deposition. Sci. Rep. 3, 1775. doi:10.1038/srep01775
Sun, Y., Cai, P., Yang, D., and Yao, X. (2022). Single-site catalysis in heterogeneous electro-Fenton reaction for wastewater remediation. Chem. Catal. 2, 679–692. doi:10.1016/j.checat.2022.02.002
Takamoto, S., Shinagawa, C., Motoki, D., Nakago, K., Li, W., Kurata, I., et al. (2022). Towards universal neural network potential for material discovery applicable to arbitrary combination of 45 elements. Nat. Commun. 13, 2991. doi:10.1038/s41467-022-30687-9
Tang, Y., Yang, C., Xu, X., Kang, Y., Henzie, J., Que, W., et al. (2022). MXene nanoarchitectonics: defect-engineered 2D MXenes towards enhanced electrochemical water splitting. Adv. Energy Mater 12, 2103867. doi:10.1002/aenm.202103867
Tao, J., Perdew, J. P., Staroverov, V. N., and Scuseria, G. E. (2003). Climbing the density functional ladder: nonempirical meta--generalized gradient approximation designed for molecules and solids. Phys. Rev. Lett. 91, 146401. doi:10.1103/PhysRevLett.91.146401
Tao, L., Qiao, M., Jin, R., Li, Y., Xiao, Z., Wang, Y., et al. (2019). Bridging the surface charge and catalytic activity of a defective carbon electrocatalyst. Angew. Chem. Int. Ed. 58, 1019–1024. doi:10.1002/anie.201810207
Thomas, L. H. (1927). The calculation of atomic fields. Math. Proc. Camb. Philosophical Soc. 23, 542–548. doi:10.1017/S0305004100011683
Tolba, S. A., Gameel, K. M., Ali, B. A., Almossalami, H. A., and Allam, N. K. (2018). The DFT+ U: approaches, accuracy, and applications. Density Funct. Calculations-Recent Progresses Theory Appl. 1, 5772.
Tran, K., and Ulissi, Z. W. (2018). Active learning across intermetallics to guide discovery of electrocatalysts for CO2 reduction and H2 evolution. Nat. Catal. 1, 696–703. doi:10.1038/s41929-018-0142-1
Turner John, A. (2004). Sustainable hydrogen production. Science 305, 972–974. doi:10.1126/science.1103197
Unke, O. T., Chmiela, S., Sauceda, H. E., Gastegger, M., Poltavsky, I., Schütt, K. T., et al. (2021). Machine learning force fields. Chem. Rev. 121, 10142–10186. doi:10.1021/acs.chemrev.0c01111
van der Ham, C. J., Koper, M. T., and Hetterscheid, D. G. (2014). Challenges in reduction of dinitrogen by proton and electron transfer. Chem. Soc. Rev. 43, 5183–5191. doi:10.1039/c4cs00085d
Wan, X., Zhang, Z., Niu, H., Yin, Y., Kuai, C., Wang, J., et al. (2021). Machine-learning-accelerated catalytic activity predictions of transition metal phthalocyanine dual-metal-site catalysts for CO2 reduction. J. Phys. Chem. Lett. 12, 6111–6118. doi:10.1021/acs.jpclett.1c01526
Wang, B., and Zhang, F. (2022). Main descriptors to correlate structures with the performances of electrocatalysts. Angew. Chem. Int. Ed. 61, e202111026. doi:10.1002/anie.202111026
Wang, F., and Mao, J. (2021). Effect of N-doping on graphene: NRR activity and N-source. Diam. Relat. Mater 118, 108494. doi:10.1016/j.diamond.2021.108494
Wang, X., Jia, Y., Mao, X., Liu, D., He, W., Li, J., et al. (2020a). Edge-rich Fe−N4 active sites in defective carbon for oxygen reduction catalysis. Adv. Mater 32, 2000966. doi:10.1002/adma.202000966
Wang, X., Jia, Y., Mao, X., Zhang, L., Liu, D., Song, L., et al. (2020b). A directional synthesis for topological defect in carbon. Chem 6, 2009–2023. doi:10.1016/j.chempr.2020.05.010
Wexler, R. B., Martirez, J. M. P., and Rappe, A. M. (2018). Chemical pressure-driven enhancement of the hydrogen evolving activity of Ni2P from nonmetal surface doping interpreted via machine learning. J. Am. Chem. Soc. 140, 4678–4683. doi:10.1021/jacs.8b00947
Whipple, D. T., and Kenis, P. J. A. (2010). Prospects of CO2 utilization via direct heterogeneous electrochemical reduction. J. Phys. Chem. Lett. 1, 3451–3458. doi:10.1021/jz1012627
White, J. A., and Bird, D. M. (1994). Implementation of gradient-corrected exchange-correlation potentials in Car-Parrinello total-energy calculations. Phys. Rev. B 50, 4954–4957. doi:10.1103/PhysRevB.50.4954
Wu, J., Ma, L., Yadav, R. M., Yang, Y., Zhang, X., Vajtai, R., et al. (2015). Nitrogen-doped graphene with pyridinic dominance as a highly active and stable electrocatalyst for oxygen reduction. ACS Appl. Mater Interfaces 7, 14763–14769. doi:10.1021/acsami.5b02902
Wu, J., Ma, S., Sun, J., Gold, J. I., Tiwary, C., Kim, B., et al. (2016). A metal-free electrocatalyst for carbon dioxide reduction to multi-carbon hydrocarbons and oxygenates. Nat. Commun. 7, 13869. doi:10.1038/ncomms13869
Wu, Q., Jia, Y., Liu, Q., Mao, X., Guo, Q., Yan, X., et al. (2022). Ultra-dense carbon defects as highly active sites for oxygen reduction catalysis. Chem. doi:10.1016/j.chempr.2022.06.013
Wu, Y., Wei, W., Yu, R., Xia, L., Hong, X., Zhu, J., et al. (2022). Anchoring sub-nanometer Pt clusters on crumpled paper-like MXene enables high hydrogen evolution mass activity. Adv. Funct. Mater 32, 2110910. doi:10.1002/adfm.202110910,
Xie, T., Wang, P., Tian, C., Zhao, G., Jia, J., He, C., et al. (2022). Adsorption characteristics of gas molecules adsorbed on graphene doped with Mn: a first principle study. Molecules 27. doi:10.3390/molecules27072315
Xiong, Y., Dong, J., Huang, Z.-Q., Xin, P., Chen, W., Wang, Y., et al. (2020). Single-atom Rh/N-doped carbon electrocatalyst for formic acid oxidation. Nat. Nanotechnol. 15, 390–397. doi:10.1038/s41565-020-0665-x
Xu, H., Han, Y., Wu, Q., Jia, Y., Li, Q., Yan, X., et al. (2023). Iridium-based electrocatalysts for the acidic oxygen evolution reaction: engineering strategies to enhance the activity and stability. Mater Chem. Front. 7, 1248–1267. doi:10.1039/D2QM01220K
Xu, S., and Carter, E. A. (2019). Theoretical insights into heterogeneous (Photo)electrochemical CO2 reduction. Chem. Rev. 119, 6631–6669. doi:10.1021/acs.chemrev.8b00481
Yan, X., Jia, Y., Chen, J., Zhu, Z., and Yao, X. (2016). Defective-activated-carbon-supported Mn-Co nanoparticles as a highly efficient electrocatalyst for oxygen reduction. Adv. Mater 28, 8771–8778. doi:10.1002/adma.201601651
Yan, X., Jia, Y., Wang, K., Jin, Z., Dong, C.-L., Huang, Y.-C., et al. (2020). Controllable synthesis of Fe–N4 species for acidic oxygen reduction. Carbon Energy 2, 452–460. doi:10.1002/cey2.47
Yan, X., Zhuang, L., Zhu, Z., and Yao, X. (2021). Defect engineering and characterization of active sites for efficient electrocatalysis. Nanoscale 13, 3327–3345. doi:10.1039/d0nr08976a
Yan, Y., Xia, B. Y., Zhao, B., and Wang, X. (2016). A review on noble-metal-free bifunctional heterogeneous catalysts for overall electrochemical water splitting. J. Mater Chem. A 4, 17587–17603. doi:10.1039/c6ta08075h
Yang, Q., Jia, Y., Wei, F., Zhuang, L., Yang, D., Liu, J., et al. (2020). Understanding the activity of Co-N4−xCx in atomic metal catalysts for oxygen reduction catalysis. Angew. Chem. Int. Ed. 59, 6122–6127. doi:10.1002/anie.202000324
Yang, Q., Liu, H., Yuan, P., Jia, Y., Zhuang, L., Zhang, H., et al. (2022). Single carbon vacancy traps atomic platinum for hydrogen evolution catalysis. J. Am. Chem. Soc. 144, 2171–2178. doi:10.1021/jacs.1c10814
Yang, W., Gao, Z., Ding, X., Lv, G., and Yan, W. (2018). The adsorption characteristics of mercury species on single atom iron catalysts with different graphene-based substrates. Appl. Surf. Sci. 455, 940–951. doi:10.1016/j.apsusc.2018.06.031
Yang, W., Jia, Z., Zhou, B., Chen, L., Ding, X., Jiao, L., et al. (2023). Why is C–C coupling in CO2 reduction still difficult on dual-atom electrocatalysts? ACS Catal., 9695–9705. doi:10.1021/acscatal.3c01768
Yang, X.-F., Wang, A., Qiao, B., Li, J., Liu, J., and Zhang, T. (2013). Single-atom catalysts: a new frontier in heterogeneous catalysis. Acc. Chem. Res. 46, 1740–1748. doi:10.1021/ar300361m
Yasin, G., Ibraheem, S., Ali, S., Arif, M., Ibrahim, S., Iqbal, R., et al. (2022). Defects-engineered tailoring of tri-doped interlinked metal-free bifunctional catalyst with lower gibbs free energy of OER/HER intermediates for overall water splitting. Mater. Today Chem. 23, 100634. doi:10.1016/j.mtchem.2021.100634
Ye, L., Ying, Y., Sun, D., Zhang, Z., Fei, L., Wen, Z., et al. (2020). Highly efficient porous carbon electrocatalyst with controllable N-species content for selective CO2 reduction. Angew. Chem. Int. Ed. 59, 3244–3251. doi:10.1002/anie.201912751
Ye, S., Luo, F., Zhang, Q., Zhang, P., Xu, T., Wang, Q., et al. (2019). Highly stable single Pt atomic sites anchored on aniline-stacked graphene for hydrogen evolution reaction. Energy Environ. Sci. 12, 1000–1007. doi:10.1039/c8ee02888e
Yin, H., and Du, A. (2023). Activating the hydrogen evolution reaction in low-dimensional carbon by partial hydrogenation: role of the hybrid sp2-sp3 orbital interface. ChemPhysMater. doi:10.1016/j.chphma.2022.12.001
Yu, X., Han, P., Wei, Z., Huang, L., Gu, Z., Peng, S., et al. (2018). Boron-doped graphene for electrocatalytic N2 reduction. Joule 2, 1610–1622. doi:10.1016/j.joule.2018.06.007
Zha, W., Liu, D., Ma, Z., Wang, Y., Wei, Y., Ma, X., et al. (2021). Efficient electrochemical CO2 reduction on C2N monolayer supported transition metals trimer catalysts: a DFT study. Appl. Surf. Sci. 564, 150331. doi:10.1016/j.apsusc.2021.150331
Zhang, B.-W., Yang, H.-L., Wang, Y.-X., Dou, S.-X., and Liu, H.-K. (2018). A comprehensive review on controlling surface composition of Pt-based bimetallic electrocatalysts. Adv. Energy Mater 8, 1703597. doi:10.1002/aenm.201703597
Zhang, H., Liu, Y., Chen, T., Zhang, J., Zhang, J., and D Lou, X. W. (2019). Unveiling the activity origin of electrocatalytic oxygen evolution over isolated Ni atoms supported on a N-doped carbon matrix. Adv. Mater 31, e1904548. doi:10.1002/adma.201904548
Zhang, I. Y., and Xu, X. (2020). On the top rung of Jacob's ladder of density functional theory: toward resolving the dilemma of SIE and NCE. WIREs Comput. Mol. Sci. 11. doi:10.1002/wcms.1490
Zhang, L., Fischer, J. M. T. A., Jia, Y., Yan, X., Xu, W., Wang, X., et al. (2018). Coordination of atomic Co–Pt coupling species at carbon defects as active sites for oxygen reduction reaction. J. Am. Chem. Soc. 140, 10757–10763. doi:10.1021/jacs.8b04647
Zhang, L., Jia, Y., Yan, X., and Yao, X. (2018). Activity origins in nanocarbons for the electrocatalytic hydrogen evolution reaction. Small 14, 1800235. doi:10.1002/smll.201800235
Zhang, N., Yang, B., Liu, K., Li, H., Chen, G., Qiu, X., et al. (2021). Machine learning in screening high performance electrocatalysts for CO2 reduction. Small Methods 5, 2100987. doi:10.1002/smtd.202100987
Zhao, X., and Liu, Y. (2021). Origin of selective production of hydrogen peroxide by electrochemical oxygen reduction. J. Am. Chem. Soc. 143, 9423–9428. doi:10.1021/jacs.1c02186
Zhao, X., Zhao, K., Liu, Y., Su, Y., Chen, S., Yu, H., et al. (2022). Highly efficient electrochemical CO2 reduction on a precise homonuclear diatomic Fe–Fe catalyst. ACS Catal. 12, 11412–11420. doi:10.1021/acscatal.2c03149
Zhao, Y., Schultz, N. E., and Truhlar, D. G. (2006). Design of density functionals by combining the method of constraint satisfaction with parametrization for thermochemistry, thermochemical kinetics, and noncovalent interactions. J. Chem. Theory Comput. 2, 364–382. doi:10.1021/ct0502763
Zhao, Y., and Truhlar, D. G. (2006). A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 125, 194101. doi:10.1063/1.2370993
Zhao, Y., and Truhlar, D. G. (2008). Density functionals with broad applicability in chemistry. Acc. Chem. Res. 41, 157–167. doi:10.1021/ar700111a
Zheng, J., Sun, X., Qiu, C., Yan, Y., Yao, Z., Deng, S., et al. (2020). High-throughput screening of hydrogen evolution reaction catalysts in MXene materials. J. Phys. Chem. C 124, 13695–13705. doi:10.1021/acs.jpcc.0c02265
Zheng, Y., Jiao, Y., and Qiao, S. Z. (2015). Engineering of carbon-based electrocatalysts for emerging energy conversion: from fundamentality to functionality. Adv. Mater 27, 5372–5378. doi:10.1002/adma.201500821
Zhou, S., Yang, X., Pei, W., Liu, N., and Zhao, J. (2018). Heterostructures of MXenes and N-doped graphene as highly active bifunctional electrocatalysts. Nanoscale 10, 10876–10883. doi:10.1039/c8nr01090k
Zhou, S., Yang, X., Xu, X., Dou, S. X., Du, Y., and Zhao, J. (2020). Boron nitride nanotubes for ammonia synthesis: activation by filling transition metals. J. Am. Chem. Soc. 142, 308–317. doi:10.1021/jacs.9b10588
Zhou, Y., Wei, B., Cao, H., An, Z., Li, M., Huo, Y., et al. (2022). Electroreduction of nitrogen to ammonia by single-atom catalysis with synergistic boron-carbon nitrogen nanotubes. J. Environ. Chem. Eng. 10, 107752. doi:10.1016/j.jece.2022.107752
Zhu, B., Zhang, L., Xu, D., Cheng, B., and Yu, J. (2017). Adsorption investigation of CO2 on g-C3N4 surface by DFT calculation. J. CO2 Util. 21, 327–335. doi:10.1016/j.jcou.2017.07.021
Zhu, M., Zhou, Y., Sun, Y., Zhu, C., Hu, L., Gao, J., et al. (2018). Cobalt phosphide/carbon dots composite as an efficient electrocatalyst for oxygen evolution reaction. Dalton Trans. 47, 5459–5464. doi:10.1039/c7dt04291d
Zhu, X., Yan, J., Gu, M., Liu, T., Dai, Y., Gu, Y., et al. (2019). Activity origin and design principles for oxygen reduction on dual-metal-site catalysts: a combined density functional theory and machine learning study. J. Phys. Chem. Lett. 10, 7760–7766. doi:10.1021/acs.jpclett.9b03392
Zhuo, J., Wang, T., Zhang, G., Liu, L., Gan, L., and Li, M. (2013). Salts of C60(OH)8 electrodeposited onto a glassy carbon electrode: surprising catalytic performance in the hydrogen evolution reaction. Angew. Chem. Int. Ed. 52, 10867–10870. doi:10.1002/anie.201305328
Keywords: density functional theory, descriptor, carbon-based materials, electrocatalysis, molecular dynamics
Citation: Han Y, Xu H, Li Q, Du A and Yan X (2023) DFT-assisted low-dimensional carbon-based electrocatalysts design and mechanism study: a review. Front. Chem. 11:1286257. doi: 10.3389/fchem.2023.1286257
Received: 31 August 2023; Accepted: 27 September 2023;
Published: 17 October 2023.
Edited by:
Guosong Zeng, Southern University of Science and Technology, ChinaReviewed by:
Cheng Zhan, Nanjing University of Science and Technology, ChinaCopyright © 2023 Han, Xu, Li, Du and Yan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xuecheng Yan, eC55YW5AZ3JpZmZpdGguZWR1LmF1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.