1 Introduction
A {(3,4),4}-fullerene graph G is a 4-regular plane graph with exactly eight triangular faces and other quadrangular faces. This concept of the {(3, 4), 4}-fullerene comes from Deza’s {(R,k)}-fullerene (Deza and Sikirić, 2012). Fixing R ⊂ N, a {(R, k)}-fullerene graph is a k-regular , and it is mapped on a sphere whose faces are i-gons . A {(a,b),k}-fullerene is {(R, k)}-fullerene with . The {(a, b), k}-fullerene draws attention because it includes the mostly widely researched graphs, such as fullerenes (i.e.,{(5, 6), 3}-fullerenes), boron–nitrogen fullerenes (i.e.,{(4, 6), 3}-fullerenes), and (3,6)-fullerenes (i.e.,{(3, 6), 3}-fullerenes) (Yang and Zhang, 2012).
The anti-Kekulé number of a graph was introduced by Vukičević and Trinajstić (2007). They introduced the anti-Kekulé number as the smallest number of edges that have to be removed from a benzenoid to remain connected but without a Kekulé structure. Here, a Kekulé structure corresponds to a perfect matching in mathematics; it is known that benzenoid hydrocarbon has better stability if it has a lower anti-Kekulé number. Veljan and Vukičević (2008) found that the anti-Kekulé numbers of the infinite triangular, rectangular, and hexagonal grids are 9, 6 and 4, respectively. Zhang et al. (2011) proved that the anti-Kekulé number of cata-condensed phenylenes is 3. For fullerenes, Vukičević (2007) proved that C60 has anti-Kekulé number 4, and Kutnar et al. (2009) showed that the leapfrog fullerenes have the anti-Kekulé number 3 or 4 and that for each leapfrog fullerene, the anti-Kekulé number can be established by observing the finite number of cases independent of the size of the fullerene. Furthermore, this result was improved by Yang et al. (2012) by proving that all fullerenes have anti-Kekulé number 4.
In general, Li et al. (2019) showed that the anti-Kekulé number of a 2-connected cubic graph is either 3 or 4; moreover, all (4,6)-fullerenes have the anti-Kekulé number 4, and all the (3,6)-fullerenes have anti-Kekulé number 3. Zhao and Zhang (2020) confirmed all (4,5,6)-fullerenes have anti-Kekulé number 3, which consist of four sporadic (4,5,6)-fullerenes (F12, F14, F18, and F20) and three classes of (4,5,6)-fullerenes with at least two and at most six pentagons.
Here, we consider the {(3, 4), 4}-fullerene graphs. In the next section, we recall some concepts and results needed for our discussion. In Section 3, by using Tutte’s Theorem on perfect matching of graphs, we determine the scope of the anti-Kekulé number of the {(3, 4), 4}-fullerene. Finally, we show that the {(3, 4), 4}-fullerene with anti-Kekulé number 4 consists of two kinds of graphs . As a consequence, we prove that if , then . Moreover, if , we give the condition to judge that the anti-Kekulé number of graph G is 4 or 5.
2 Definitions and preliminary results
Let be a simple and connected plane graph with vertex set V(G) and edge set E(G). For , G − V′ denotes the subgraph obtained from G by deleting the vertices in V′ together with their incident edges. If V′ = v, we write G − v. Similarly, for , G − E′ denotes the graph with vertex set V(G) and edge set . If E′ = e, we write G − e. Let V′ be a non-empty set; denotes the induced subgraph of G induced by the vertices of V′; similarly, if , denotes the induced subgraph of G induced by the edges of E′.
For a subgraph H of G, the induced subgraph of G induced by vertices of is denoted by . A plane graph G partitions the rest of the plane into a number of arcwise-connected open sets. These sets are called the faces of G. A face is said to be incident with the vertices and edges in its boundary, and two faces are adjacent if their boundaries have an edge in common. Let be the set of the faces of G.
An edge-cut of a connected plane graph G is a subset of edges such that G − C is disconnected. A k-edge-cut is an edge-cut with k edges. A graph G is k-edge-connected if G cannot be separated into at least two components by removing less than k edges. An edge-cut C of a graph G is cyclic if its removal separates two cycles. A graph G is cyclically k-edge-connected if G cannot be separated into at least two components, each containing a cycle, by removing less than k edges. A cycle is called a facial cycle if it is the boundary of a face.
For subgraphs H1 and H2 of a plane graph G, represents the set of edges whose two end vertices are in and separately. If and are two non-empty disjoint vertex subsets such that , then is an edge-cut of G, and we simply write or . We use to denote the boundary of G, that is, the boundary of the infinite face of G.
A matching M of a graph G is a set of edges of G such that no two edges from M have a vertex in common. A matching M is perfect if it covers every vertex of G. A perfect matching is also called a Kekulé structure in chemistry.
Let G be a connected graph with at least one perfect matching. For , we call S an anti-Kekulé set if G − S is connected but has no perfect matchings. The smallest cardinality of anti-Kekulé sets of G is called the anti-Kekulé number and denoted by .
For the edge connectivity of the {(3, 4), 4}-fullerene, we have the following results.
Lemma 2.1. ((Yang et al., 2023) Lemma 2.3) Every {(3, 4), 4}-fullerene is cyclically 4-edge-connected.
Lemma 2.2. ((Yang et al., 2023) Corollary 2.4) Every {(3, 4), 4}-fullerene is 4-edge-connected.
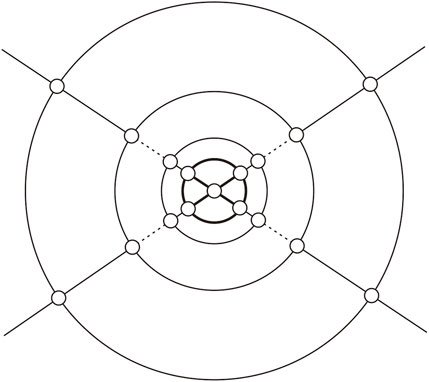
Qn is the graph consisting of n concentric layers of quadrangles, capped on each end by a cap formed by four triangles which share a common vertex as shown in Figure 2. In particular, Q0 is what we call an octahedron (see Figure 5F).
Lemma 2.3. ((Yang et al., 2023) Lemma 2.5) If G has a cyclical 4-edge-cut , then , where the four edges e1, e2, e3, and e4 form a matching, and each ei belongs to the intersection of two quadrilateral faces for i = 1, 2, 3, 4.
Tutte’s theorem plays an important role in the process of proof.
Theorem 2.4. (Lovász and Plummer, 2009) (Tutte’s theorem) A graph G has a perfect matching if and only if for any , , where denotes the number of odd components of G − X.
Here, an odd component of G − X is trivial if it is just a single vertex and non-trivial otherwise.
All graph-theoretical terms and concepts used but unexplained in this article are standard and can be found in many textbooks, such as Lovász and Plummer (2009).
3 Main results
From now on, let G always be a {(3, 4), 4}-fullerene; we called a 4-edge-cut E in G trivial if , that is, E consists of the four edges incident to v. By Lemma 2.3, if E is a cyclical 4-edge-cut, then the four edges in E form a matching. Moreover, if E is not a cyclical 4-edge-cut, then E is trivial. So, we have the following lemma.
Lemma 3.1. Let G be a {(3, 4), 4}-fullerene, be an 4-edge-cut, but it is not cyclical, then E is trivial.
Proof. Since is an 4-edge-cut, G − E is not connected. Then, G − E has at least two components. Moreover, as G is 4-edge-connected by Lemma 2.2, G − E has at most two components. So, G − E has exactly two components.
Let G1, G2 be two components of G − E. Since E is not cyclical, without loss of generality, we suppose that G1 is a forest; then, we have
where n, e, l is the number of vertices, edges, and trees in G1, respectively. Furthermore, since each vertex of G is of degree 4, we have
Combing with equalities 1) and 2), we know n = l = 1 and e = 0, which means G1 only consists of a single vertex. So, E is trivial. □
Lemma 3.1 plays an important role in the proof of the following theorem. Next, we explore the scope of the anti-Kekulé number of {(3, 4), 4}-fullerene.
Theorem 3.2. Let G be a {(3, 4), 4}-fullerene, then .
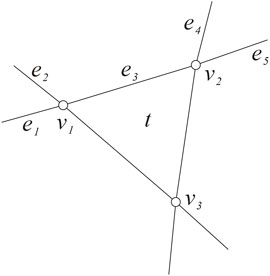
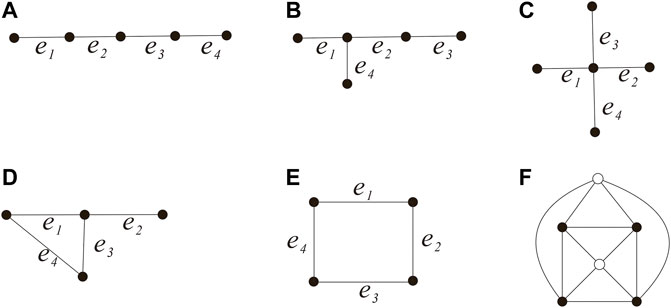
Proof. First, we show . Let t be any triangle in G and the boundary of t was labeled v1v2v3 along the clockwise direction. Denote the other two edges incident to by , set e3 = v1v2, then e1, e2, e3, e4, and e5 are pairwise different, set (see Figure 1) and G′ = G − E′.
In order to show , we only need to prove that G′ is connected and has no perfect matchings. Then, G′ has no perfect matchings since the two edges v1v3, v2v3 cannot be covered by a perfect matching at the same time in G′.
In the following, we show that G′ is connected. We proved this using reduction to absurdity, suppose G′ is not connected, then G′ has a component (say G1) containing vertices v1, v2, and v3, as v1, v2, and v3 are connected by the path v1v3v2 in G1. On the other hand, since e3 = v1v2 connects two vertices v1, v2 in G and is an edge cut of G, even if we remove five edges, e1, e2, e3, e4, and e5, to disconnect G, it is actually the same as removing four edges, e1, e2, e4, and e5 (see Figure 1); that is, is an 4-edge-cut. Moreover, due to Lemma 2.3, E1 cannot be a cyclical 4-edge-cut as e1, e2, e4, and e5 is not a matching. Then, according to Lemma 3.1, E1 is a trivial 4-edge-cut. Thus, G1 or is a single vertex, both of which are impossible by the definition of G. So G′ is connected. Thus,
Finally, we show . By the definition of an anti-Kekulé set, suppose was the smallest anti-Kekulé set of G, that is, . Then, was connected and has no perfect matching. Hence, according to Theorem 2.4, there exists a non-empty subset such that , since and is even, and have the same parity. Consequently,
For the sake of convenience, we let . If we chose an X0 with the maximum size, then has no even components. On the contrary, we suppose there exists an even component (say F) of . For any vertex , . Let , thus , which is a contradiction to the choice of X0.
In addition, is the smallest anti-Kekulé set of G, then has perfect matchings for any edge for 1 ≤ i ≤ k. On the other hand, the number of odd components of was not decreased or decreased by at most one or two if we add one edge to , that is,
By inequality (4), we have
Combined with inequalities (5) and (6), we have and each edge connects two odd components of . Let H1, H2, H3, …, Hα be the odd components of . Then, due to Lemma 2.2, ; therefore,
Thus, k ≥ 4, that is, . We know that .
By Theorem 3.2, we know that . Next, we give the characterization of {(3, 4), 4}-fullerenes with anti-Kekulé number 4. Before, we define , where Qn is shown in Figure 2. The structure of two adjacent triangles is called a diamond. In a diamond, the common edge of the two triangles is called the diagonal edge. The subgraph consisting of four diamonds such that the four diagonal edges form a matching is denoted by D, that is, (see Figure 7D for the four diamonds D1 − D4). Let . So, we have the following theorem.
Theorem 3.3. Let G be a {(3, 4), 4}-fullerene, if , then or .
Proof. Let E0 be the anti-Kekulé set of G such that , set G0 = G − E0. Then, G0 is connected without perfecting matchings. Thus, by Theorem 2.4, there exists a non-empty subset such that . For convenience, let , since α and have the same parity, that is,
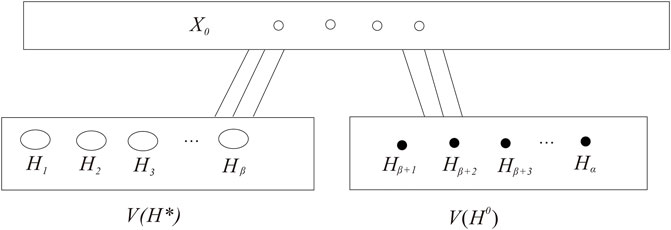
We choose an X0 satisfying Ineq. (8) with the maximum size. Then, a proof similar to the proof of Theorem 3.2 is used to prove . We can know G0 − X0 has no even components. Let H1, H2, H3, …, Hα be all the odd components of G0 − X0, set .
Let H1, H2, H3, …, Hβ be the non-trivial odd components of G0 − X0, set . Let Hβ+1, Hβ+2, Hβ+3, …, Hα be the trivial odd components of G0 − X0, set . Then, is divided into X0, , (see Figure 3 the partition of ).
Since , all equalities in Ineq. (7) of Theorem 3.2 hold. The first equality in Ineq. (7) holds if and only if , and the second equality in Ineq. 7) holds if and only if there is no edge in the subgraph ; that is, X0 is an independent set of G0. Moreover, each edge of E0 connects two components in H and . Since , is a cyclical 4-edge-cut of G or not.
Next, we distinguish the following two cases to complete the proof of Theorem 3.3.
Case 1: There exists one Hj such that is a cyclical 4-edge-cut.
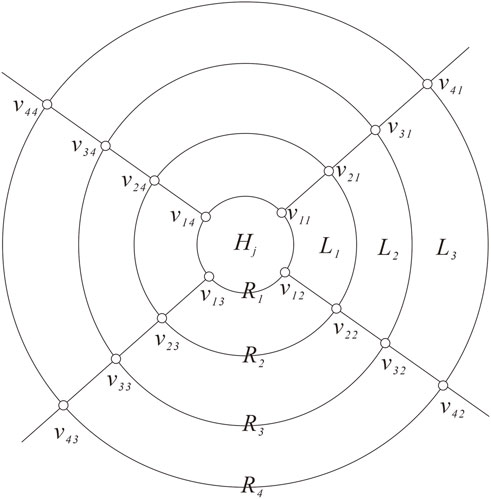
By Lemma 2.3, , which means the four edges of form a matching. Without loss of generality, we supposed Hj consists of s layers of quadrangular faces and the cap of Hj is entirely in the interior of the boundary cycle . Then, induced by the vertices of and the boundary of consists of n − s layers of quadrangular faces and a cap, for convenience, set m = n − s, let L1, L2, L3, …, Lm be all the layers and C be the cap of , where quadrangular layer Li is adjacent to Li−1 and Li+1 for 2 ≤ i ≤ m − 1, L1 is adjacent to Hj, and Lm is adjacent to C. Set R1 = Hj ∩ L1 and Rm+1 = C ∩ Lm. For 2 ≤ i ≤ m, let Ri = Li−1 ∩ Li. The vertices on are recorded as vi1, vi2, vi3, and vi4 (i = 1, 2, 3, …, m + 1) in a clockwise direction and vi1, vi3, and vi2, vi4, are on the same line, respectively (see Figure 4). Since is a cyclical 4-edge-cut, set . Without loss of generality, set . The vertices shared by the four triangles on the two caps are represented by v′, v″, respectively, such that v′ is in Hj and v″ is in .
Next, we analyze whether the edges of belongs to E0 or not, which is divided into the following five subcases.
Subcase 1.1: All the edges of belong E0.
That is, for all i = 1, 2, 3, 4. Since each edge of E0 connects two components of H and there are four edges belonging to E0. All the vertices of belong to , which means X0 = ∅, a contradiction.
Subcase 1.2: Exactly three edges of belong to E0.
Without loss of generality, suppose , then v24 ∈ X0 and , that is, v21, v22, v23 belong to or .
If all of v21, v22, and v23 belong to , then v21v22, v22v23 ∈ E0, immediately , which contradicts . This contradiction means at least one of v21, v22, and v23 belongs to (say ), then by Lemma 2.3 and Lemma 3.1, either is a cyclical 4-edge-cut and the four edges in form a matching or is trivial. However, since H1 is a non-trivial odd component of G0 − X0, . Thus, is not a trivial 4-edge-cut. That is, is a cyclical 4-edge-cut, and the four edges in form a matching. Now, if v21 (or v23) belong to , then v21v24, v21v11 (or v23v24, v23v13) belong to , but they do not form a matching, a contradiction. Thus, both and . Immediately, we have v21v22, v22v23 ∈ E0 and , which contradicts . This contradiction means there cannot be three edges of belonging to E0.
Subcase 1.3: Exactly two edges of belong to E0.
Then, by symmetry, or .
First, if , then v23, v24 ∈ X0 and , which contradicts that .
Claim 1: For a quadrangular face q with with clock direction such that , then or or .
Proof. Since , . If , then by Lemma 2.3 and Lemma 3.1, thus c ∈ X0 or .
If , then also by Lemma 2.3 and Lemma 3.1, we can know and the claim holds.
By Claim 1, next, if , then , . If all the vertices of v21, v22, v23, and v24 belong to the cap of , that is, all of v21, v22, v23, and v24 are adjacent to v″, then as and , we can know v″ ∈ H0 and v21v″, v23v″ ∈ E0, and we have the {(3, 4), 4}-fullerenes Qs+1, that is, m = 1.
If all the vertices of v21, v22, v23, and v24 do not belong to the cap of , that is, the layer L2 consists of four quadrangular faces, then, for the quadrangular face , the vertices on belong to X0, H0, H0, H0 or X0, H0, H*, H* or X0, H0, X0, H0 by Claim 1.
If the former case holds, that is, there exists one face such that the boundary of q is of the form X0, H0, H0, and H0, then immediately we can have , a contradiction.
If the second case holds, that is, there exists one face such that the boundary of q is of the form X0, H0, H*, and H*, then by Claim 1 and since , we can know all the faces of L2 are of the form X0, H0, H*, and H*, that is, all the vertices of belong to . In this case, we also have .
By the aforementioned discussion and Claim 1, next, we suppose all the quadrangular faces of L2 are of the form X0, H0, X0, and H0. Then, we can use the aforementioned same analysis to the layer L3 as L2, since G ≅ Qn and Hj consists of s layers of quadrangular faces; after finite steps (say t steps), we obtain t layers L2, L3, …, Lt+1 such that all the faces of are of form X0, H0, X0, and H0 and either the four vertices on are adjacent to or all the vertices of belong to .
If the four vertices on are adjacent to , then m = t + 1, n = s + t + 1 and . If all the vertices of belong to (say ), suppose H1 consists of p layers of quadrangular faces, then m = t + p + 2, n = s + t + p + 2, and also .
To sum up, if exactly two edges of belong to E0, then .
Subcase 1.4: Exactly one edge of belong to E0.
Without loss of generality, suppose , then v22, v23, v24 ∈ X0, , which contradicts that X0 is an independent set of G0.
Subcase 1.5: No edge of belongs to E0.
Thus, , so , which contradicts .
Case 2: is not a cyclical 4-edge-cut of G for all 1 ≤ j ≤ α.
For convenience, set . Here, first, we give the idea of proof, then we will show that G0 = G − E0 is bipartite by proving . Since G has exactly eight triangular faces and , which implies that each edge ei of E0 is the common edge of two triangles, by discussing all possible subgraphs formed by facial cycles containing an edge of E0, we show that or .
Since is not a cyclical 4-edge-cut of G for all 1 ≤ j ≤ α, Hj or is a singleton by Lemma 3.1. Since X0 is non-empty and , which means Hj is a singleton vertex, that is, .
Let Y0 denote the set of all singletons yi from each , and denote the vertices of X0 by , so is bipartite. For convenience, we color the vertices white in X0 and black in Y0.
Next, we consider possible subgraphs of G containing all edges of E0. By the Euler theorem, G has exactly eight triangular faces because is bipartite; each edge ei of E0 is the common edge of two triangles and connects two vertices in Y0, that is, every edge ei ∈ E0 belongs to a diamond, say Di, i = 1, 2, 3, 4 and .
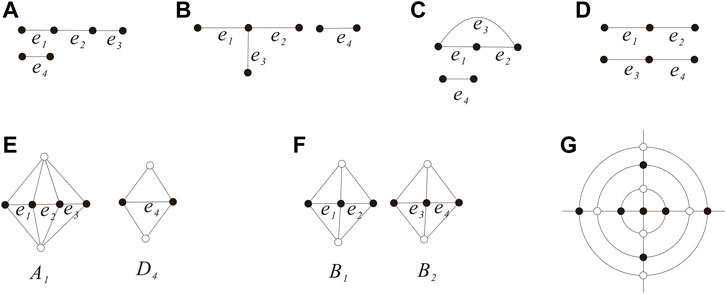
Claim 2: If has one component, then G ≅ Q0, where Q0 is the octahedron.
Proof. If has one component, then we have the subgraphs shown in Figures 5A, B, C) if is a tree and Figures 5D, E if has cycles. If is isomorphism to the graph shown in Figure 5A, then the two diamonds D1, D2 are adjacent and they form one cap of Qn. Set D12 = D1 ∪ D2, then forms an 4-edge-cut. On the other hand, by Lemma 2.3 and Lemma 3.1, is a cyclical 4-edge-cut and G ≅ Qp or is trivial. If is a cyclical 4-edge-cut, then and e3 belongs to a quadrangular face, which contradicts that the two faces containing e3 are triangles. If is a trivial 4-edge-cut, that is, is a singleton, which is impossible as the two vertices of e4 belong to . Thus, cannot be isomorphism to the subgraph shown in Figure 5A. All the situations of Figures 5B–D contradicts .
If is isomorphic to the graph shown in Figure 5E, then in order to guarantee , the four diamonds D1, D2, D3, and D4 forms two caps of Qn such that the cycle induced by E0 is exactly the intersecting of the two caps. Immediately, we have the graph Q0 (see Figure 5F the octahedron Q0), that is, G ≅ Q0 if has one component, so .
In accordance with Claim 2, next, we assume that is not connected, so has at least two and at most four components. Then, we have the following three cases.
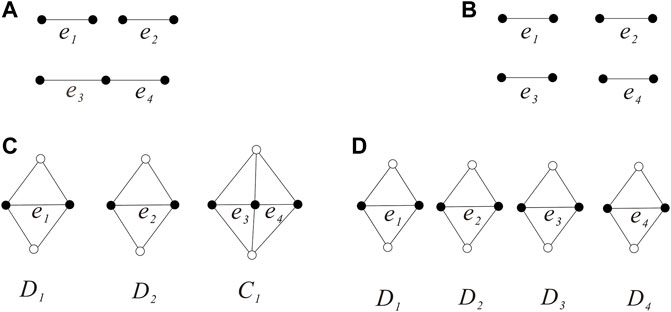
Subcase 2.1: has exactly two components.
By symmetry, the subgraph induced by E0 has four cases as shown in Figures 6A–D. Then, the graph G which contains the subgraphs shown in Figure 6B contradicts . If G contains the subgraph shown in Figure 6C, then the three edges e1, e2, and e3 belong to the same triangular face as every 3-length cycle of a {(3, 4), 4}-fullerene must be the boundary of a triangular face by Lemma 2.2, which contradicts that .
If is isomorphic to the graph as shown in Figure 6A, then the three edges e1, e2, and e3 belong to three diamonds D1, D2, and D3, respectively, and we have the subgraph A1 consisting of D1, D2, and D3 (see Figure 6E) such that and A1, D4 are disjoint. By the definition of G, we can know the two 3-degree vertices on must be adjacent and we obtain G ≅ Q0, which contradicts that A1, D4 are disjoint.
If is isomorphic to the graph as shown in Figure 6D, then D1, D2 are adjacent, and D3, D4 are adjacent. Set B1 = D1 ∪ D2, B2 = D3 ∪ D4. Since the two edges e1, e2 are disjoint, the edges e3, e4, B1, B2 are disjoint. Then, forms a cyclical 4-edge-cut (see Figure 6F), by Lemma 2.3, .
Since is bipartite, it should be noted that each edge ei of E0 is in these eight triangles and connects two vertices in Y0; thus, the edges of are X0Y0 − edges and G − B1 − B2 has only quadrangles (see Figure 6G). Moreover, by Lemma 2.3, we can know G − B1 − B2 consists of layers of quadrangles (each layer is made up of four quadrangles). Thus, we have .
Subcase 2.2: has exactly three components.
Then, both of the two components of are K2, and one component is K1,2 (see Figure 7A). Without loss of generality, we suppose the component K1,2 is induced by the edges e3, e4. Then, the two diamonds D3, D4 are adjacent, and D1, D2 are disjoint. Set C1 = D3 ∪ D4 (see Figure 7C).
Then, due to Lemma 2.3 and Lemma 3.1, forms a cyclical 4-edge-cut, thus, G≅Qs, where Qs is the tubular {(3, 4), 4}-fullerene as shown in Figure 2, which means each of the two caps of Qs must contain two adjacent diamonds, contradicts that D1, D2 are disjoint.
Subcase 2.3: has four components.
Then, the four diagonal edges e1, e2, e3, and e4 are disjoint (see Figure 7B), that is, the four diamonds D1, D2, D3, and D4 cannot intersect at the diagonal edges. We have the four diamonds D1, D2, D3, and D4 as shown in Figure 7D. Then, .
So far, we have completed the proof of Theorem 3.3.
Inspired by Theorem 3.3, we immediately get the following theorems.
Theorem 3.4. Let G be a {(3, 4), 4}-fullerene, if , then .
Proof. Let , that is, . By Theorem 3.2 and the definition of the anti-Kekulé number, we only need to find an anti-Kekulé set E0 of G such that .
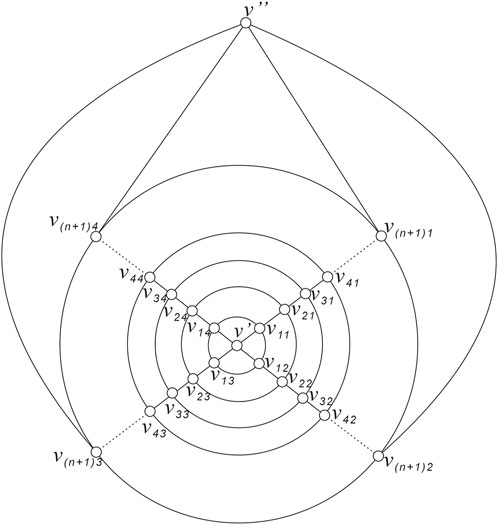
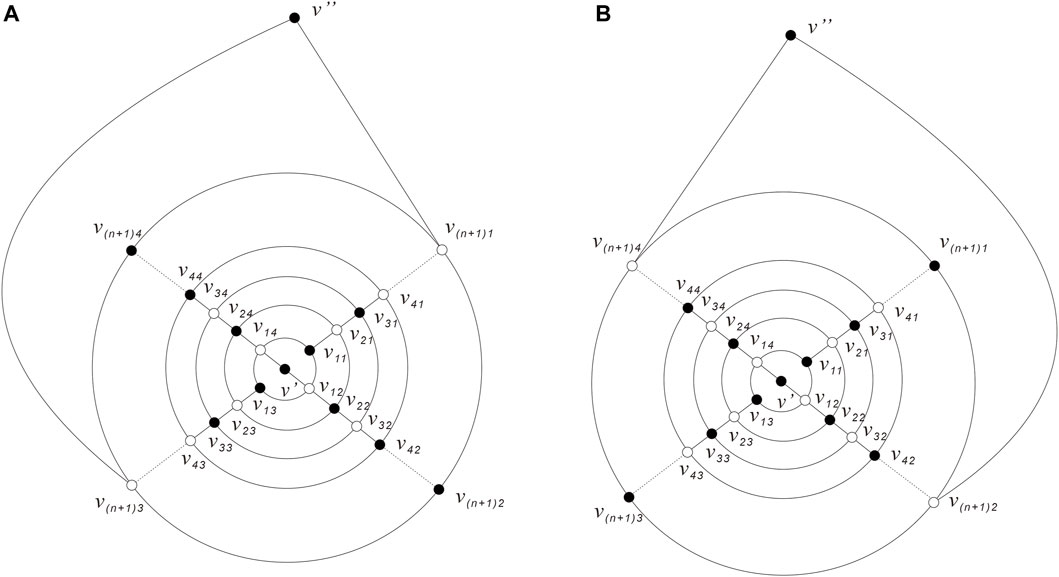
For convenience, let the plane embedding graph of Qn as shown in Figure 8. Qn consist of n + 1 concentric rings with four vertices on each ring and two vertices on two caps; these n + 1 concentric rings are recorded as R1, R2, R3, …, Rn+1 from the inside to the outside. Next, the vertices of Qn are labeled as follows: the vertices shared by the four triangles on the two caps are represented by v′, v″, respectively, and the vertices on are recorded as vi1, vi2, vi3, and vi4 (i = 1, 2, 3, …, n + 1) in a clockwise direction such that vi1, vi3 (vi2,, and vi4) are on the same line (see Figure 8 the labeling of Qn).
Next, we will prove Theorem 3.4 in two cases.
Case 1: n is an odd number.
Let (see Figure 9A), and set G1 = G − E0. Then, E0 is not a cyclically 4-edge-cut of G by Lemma 2.3. Moreover, E0 is not a trivial 4-edge-cut as the four edges in E0 are not incident with a common vertex. That is, G1 is connected.
Then, we prove that G1 = G − E0 has no perfect matching, and there are only quadrangular faces in G1, so, G1 is bipartite. We color the vertices of G1 with black and white such that adjacent vertices in G1 are assigned two distinct colors (see Figure 9A). Let M0 denote the set of white vertices and N0 denote the set of black vertices, then , , . In accordance with Theorem 2.4, there exist such that , so G1 has no perfect matching.
Case 2: n is an even number.
Let (see Figure 9B), and set G2 = G − E0. Also, G2 is connected.
There are only quadrangular faces in G2; so, G2 is also bipartite with one bipartition 2n + 2 vertices and the other bipartition 2n + 4 vertices, which means G2 has no perfect matching.
Therefore, we find the anti-Kekulé set E0 of G with , which means , if .
Due to Theorem 3.4, if , then . However, the anti-Kekulé number of G can be 4 or 5 if . Next, we use a method to judge whether the anti-Kekulé number of G can be 4 or 5 when . Before we give some definitions of G if . Let , the four diamonds of G be D1, D2, D3, and D4 and the four diagonal edges be e1, e2, e3, and e4 such that , i = 1, 2, 3, 4. Set and e1 = v1v2, e2 = v3v4, e3 = v5v6, and e4 = v7v8. The eight vertices of the four diagonal edges are called eight stars, and their union is denoted by .
Set G0 = G − E0. Then, G0 is bipartite, without loss of generality, we supposed the bipartitions of G0 were V1, V2. Then, by the proof of Theorem 3.3, we can know if , then V0 ⊂ V1 or V0 ⊂ V2, which means when V0⊄V1 and V0⊄V2. Thus, we have the following theorem.
Theorem 3.5. Let G be a {(3, 4), 4}-fullerene, , if V0 ⊂ V1 or V0 ⊂ V2, then , otherwise, .
Proof. By Theorem 3.2, we only need to show if V0 ⊂ V1 or V0 ⊂ V2, then . Without loss of generality, suppose V0 ⊂ V1. Then, consists of the four edges e1, e2, e3, and e4 and some singleton vertices. Since the four edges e1, e2, e3, and e4 cannot be incident with a common vertex, E0 is not a trivial 4-edge-cut. However, E0 also cannot be a cyclical 4-edge-cut by Lemma 2.3, as ei belongs to the intersection of two triangular faces for i = 1, 2, 3, 4. Thus, G0 = G − E0 is connected.
On the other hand, by the degree-sum formula , which means . Thus, G0 cannot have perfect matchings by Theorem 2.4. So, we find the anti-Kekulé set E0 with . Immediately, we have . Otherwise, by Theorem 3.2, .
By Theorem 3.5, for a {(3, 4), 4}-fullerene G with , we can give the method to judge the anti-Kekulé number of graph G is 4 or 5 as follows:
Step 1: Delete the four diagonal edges e1, e2, e3, and e4.
Step 2: Color the vertices of with black and white.
Step 3: If we find the eight stars are in the same color, then , otherwise, .
4 Conclusion
In this paper, we have obtained the scope of the anti-Kekulé number of {(3, 4), 4}-fullerenes in Theorem 3.2; at the same time, we characterized {(3, 4), 4}-fullerenes with anti-Kekulé number 4 in Theorem 3.3, which includes two kinds of graphs .
As a consequence, we proved that if , then . Interestingly, by the proof of Theorem 3.3, we found the {(3, 4), 4}-fullerene G belongs to , but the anti-Kekulé number of G is not always 4; therefore, at the end of this paper, we gave a condition for judging whether the anti-Kekulé number of graph G is 4 or 5.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
RY performed the ideas and the formulation of overarching research goals and aims. HJ wrote the first manuscript draft and performed the review and revision of the first draft.
Funding
This work was supported by the National Natural Science Foundation of China (grant nos. 11801148 and 11626089) and the Foundation for the Doctor of Henan Polytechnic University (grant no. B2014-060).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Deza, M., and Sikirić, M. (2012). Spheric analogs of fullerenes. Ecole Normale Superieure, Pairs, Rudjer Boskovic Inst. 16.
Google Scholar
Kutnar, K., Sedlar, J., and Vukičević, D. (2009). On the anti-Kekulé number of leapfrog fullerenes. J. Math. Chem. 45, 431–441. doi:10.1007/s10910-008-9416-1
CrossRef Full Text | Google Scholar
Li, Q., Shiu, W. C., Sun, P. K., and Ye, D. (2019). On the anti-Kekulé problem of cubic graphs. Art Discrete Appl. Math. 2, 1–14. doi:10.26493/2590-9770.1264.94b
CrossRef Full Text | Google Scholar
Lovász, L., and Plummer, M. D. (2009). Matching theory. Providence, RI, USA: American Mathematical Society.
Google Scholar
Veljan, D., and Vukičević, D. (2008). The anti-Kekulé number of the infinte triangular, rectangular, and hexagonal grids. Glas. Mat. 43, 243–252. doi:10.3336/gm.43.2.02
CrossRef Full Text | Google Scholar
Vukičević, D., and Trinajstić, N. (2007). On the anti-forcing number of benzenoids. J. Math. Chem. 42, 575–583. doi:10.1007/s10910-006-9133-6
CrossRef Full Text | Google Scholar
Vukičević, D. (2007). Anti-Kekulé number of C60. Australas. J. Comb. 38, 47–62.
Google Scholar
Yang, Q., Ye, D., Zhang, H., and Lin, Y. (2012). On the anti-Kekulé number of fullerenes. Match Commun. Math. Comput. Chem. 67, 281–288.
Google Scholar
Yang, R., Liu, C., and Wu, S. (2023). The facial resonance of {(3, 4), 4}-fullerene. J. Comb. Math. Comb. Comput. Accepted.
Google Scholar
Yang, R., and Zhang, H. (2012). Hexagonal resonance of (3,6)-fullerenes. J. Math. Chem. 50 (1), 261–273. doi:10.1007/s10910-011-9910-8
CrossRef Full Text | Google Scholar
Zhang, Q., Bian, H., and Vumar, E. (2011). On the anti-Kekulé and anti-forcing number of cata-condensed phenylenes. Match Commun. Math. Comput. Chem. 65 (3), 799–806.
Google Scholar
Zhao, L., and Zhang, H. (2020). On the anti-Kekulé number of (4,5,6)-fullerenes. Discrete Appl. Math. 283, 577–589. doi:10.1016/j.dam.2020.02.006
CrossRef Full Text | Google Scholar
 Rui Yang
Rui Yang Huimin Jia
Huimin Jia