Jianhua Wang
Dandan Wang*- School of Physical Science and Technology, Southwest University, Chongqing, China
In the past decade, two-dimensional (2D) materials and spintronic materials have been rapidly developing in recent years. 2D spin-gapless semiconductors (SGSs) are a novel class of ferromagnetic 2D spintronic materials with possible high Curie temperature, 100% spin-polarization, possible one-dimensional or zero-dimensional topological signatures, and other exciting spin transport properties. In this mini-review, we summarize a series of ideal 2D SGSs in the last 3 years, including 2D oxalate-based metal-organic frameworks, 2D single-layer Fe2I2, 2D Cr2X3 (X = S, Se, and Te) monolayer with the honeycomb kagome (HK) lattice, 2D CrGa2Se4 monolayer, 2D HK Mn–cyanogen lattice, 2D MnNF monolayer, and 2D Fe4N2 pentagon crystal. The mini-review also discusses the unique magnetic, electronic, topological, and spin-transport properties and the possible application of these 2D SGSs. The mini-review can be regarded as an improved understanding of the current state of 2D SGSs in recent 3 years.
1 Introduction
Due to their unique physical and chemical characteristics induced by low-dimensionality and electronic constraints, as well as their potential applications in spintronics, high-temperature ferromagnetic two-dimensional (2D) materials (Lee et al., 2010; Li and Yang, 2014; Wang et al., 2016a; Zhou et al., 2016; Ashton et al., 2017; Benmansour et al., 2017; Gong and Zhang, 2019; Kim et al., 2019; Zhou et al., 2019; Chen et al., 2020; Torelli et al., 2020; Xu et al., 2020; Zhang et al., 2021a; Tang et al., 2021; Miao and Sun, 2022) have attracted a great deal of attention in recent years. Nevertheless, the majority of prepared 2D materials that resemble graphene are not magnetic (Wang et al., 2012; Liu and Zhou, 2019), magnetic ordering has not been observed in the 2D material family for more than 10 years since the discovery of graphene (Hashimoto et al., 2004; Novoselov et al., 2004; Huang et al., 2017) in 2004. Recently, only some intriguing 2D magnetic materials, such as CrI3 (Huang et al., 2017), CrGeTe3 (Gong et al., 2017; Wang et al., 2018a), Fe3GeTe2 (Deng et al., 2018a; Fei et al., 2018), VSe2 (Bonilla et al., 2018) and CrTe2 (Sun et al., 2020a), have been experimentally realized. Furthermore, it should be noticed that, the 2D magnetic material is far from the actual spintronic application at room temperature due to the low Curie temperature Tc and low spin polarization. Thus, it is significant and urgent to develop ferromagnetic 2D materials with high spin-polarization and Tc via theory and experiment.
Among different types of 2D ferromagnetic materials, 2D spin-gapless semiconductors (SGSs) (Li et al., 2009; Zhang et al., 2015; Gao et al., 2016; Zhu and Li, 2016; Wang et al., 2017a; He et al., 2017; Lei et al., 2017; Wang, 2017; Deng et al., 2018b; Wang et al., 2018b; Wu et al., 2020a; Yang et al., 2020a; Wu et al., 2020b; Deng et al., 2020; Feng et al., 2020; Li et al., 2020; Nadeem et al., 2020; Rani et al., 2020; Wang et al., 2020; Yue et al., 2020; Şaşıoğlu et al., 2020; Feng et al., 2021; Phong and Nguyen, 2022) are ideal candidates for high-efficient spintronic devices. Wang (Wang, 2008) first proposed the concept of SGSs in 2008, and the SGSs can be viewed as a bridge to connect the magnetic semiconductors (Haas, 1970; Dietl, 2010; Sato et al., 2010) and half-metals (Wang et al., 2016b; Wang et al., 2017b; Wang et al., 2017c; Liu et al., 2017; Wang et al., 2018c; Han et al., 2019; Wang et al., 2019; Yang et al., 2020b; Tang et al., 2021; Yang et al., 2021). It is well known that the SGSs (Wang et al., 2018b) can host parabolic and linear dispersion between energy and momentum (see Figure 1A–H). Moreover, SGSs (Wang, 2017) can be categorized into four different types depending on the touching types of the valence band maximum (VBM) and the conduction band minimum (CBM) in both spin directions. We take the SGSs with parabolic dispersion as examples to introduce the above four types (see Figure 1A–D). In Figure 1A, one finds the CBM and VBM touch each other at the Fermi level (FL) in the spin-up (SU) channel, whereas a semiconducting gap appears in the spin-down (SD) channel. The VBM in the SD channel touches the FL. Figure 1B shows the semiconducting gaps in both spin channels. However, the VBM in the SU channel touches the CBM in the SD channel, forming an indirect zero-gap state. The case of Figure 1C is similar to that of Figure 1B. However, the CBM touches the FL in the SD channel. Figure 1D is the standard form of SGSs with parabolic dispersion: a zero-gap in the SU channel and a semiconducting gap in the SD channel. Similarly, the cases of SGSs with linear dispersion are listed in Figure 1E–H. Note that, for cases I, III and IV (see Figures 1A,C, D, E, G, F), depending on how the VBM and CBM touch each other, the zero-gap in one spin channel can be direct (VBM and CBM touch each other at the same k point) or indirect (they touch each other at different k points) (Wang et al., 2020).
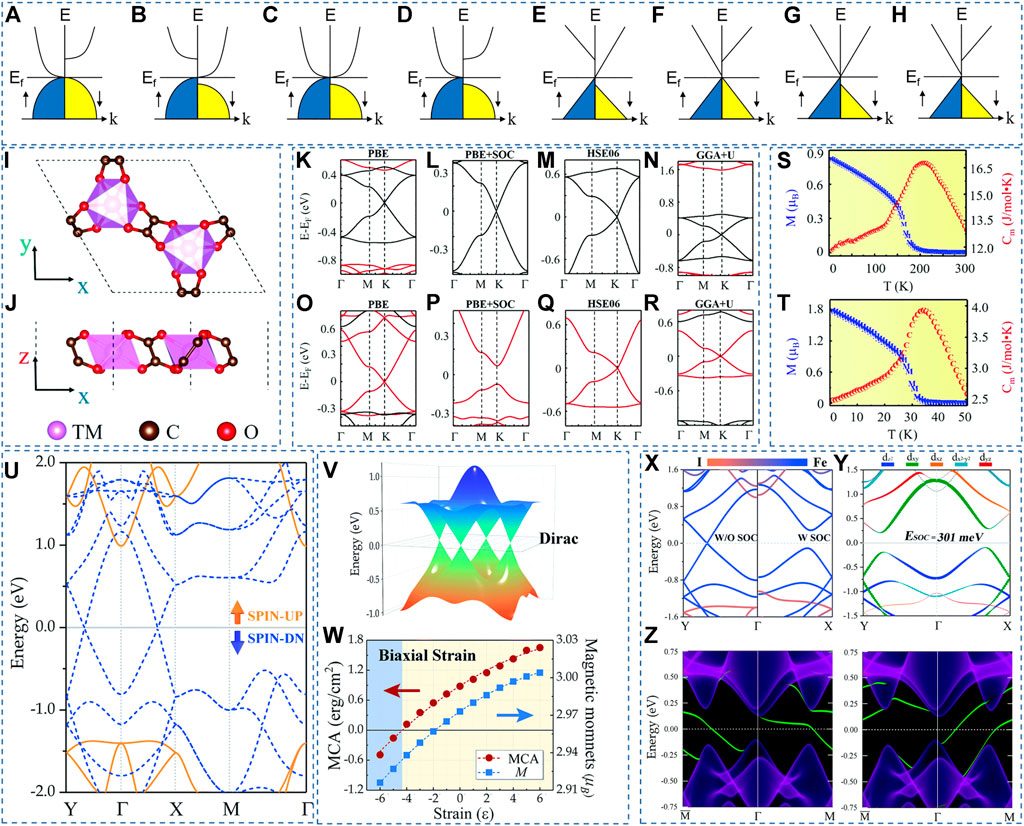
FIGURE 1. (A–H) Different SGSs. (I–J) Top and side views of the TM2(C2O4)3 structure. The calculated band structures (BSs) of Ni2(C2O4)3 (K–N) and Re2(C2O4)3 (O–R) with different methods. M and Cm of Ni2(C2O4)3 (S) and Re2(C2O4)3 (T) as a function of temperature. (I–T) Reproduced from (Xing et al., 2022) with permission from RSC publishing (U) BS of the Fe2I2 monolayer. (V) 3D plot of Dirac point (W) Magnetic anisotropy and magnetic moment of the Fe2I2 as a function of biaxial strain. (X) and (Y) atom-resolved BSs without and with SOC. (Z) Edge states of 2D Fe2I2 (U–Z) Reproduced from (Sun et al., 2020b) with permission from RSC publishing.
SGSs may host the following advantages: 1) the excitation of electrons from the valence band to the conduction band requires only a tiny amount of energy. 2) the excited carriers (electrons and holes) can be fully spin-polarized (S-P) simultaneously. 3) one can use the Hall effect to separate the 100% S-P electrons and holes. 4) for the case II SGSs (See Figure 1B and Figure 1F), one can control the gate voltage to manipulate the SU and SD electrons and holes. 5) researchers proposed nodal point SGSs and nodal line SGSs in 2D and 3D materials, which can be excellent candidates for studying the relationship between topological and spintronics. For example, Dirac SGSs may induce low energy consumption and ultrafast transport because of their unique linear band dispersion. Hence, Dirac SGSs can cohost 100% spin-polarization and linear Dirac point at the FL.
Although there were several reviews on the research topic of SGSs, these articles (Wang, 2017; Wang et al., 2020; Yue et al., 2020) all focused on SGSs from 2008 to 2020. To our best knowledge, other researchers have not reviewed the recent advances in 2D SGSs from 2020 to 2022. From 2020 to 2022, a series of ideal 2D SGSs are proposed via first-principles calculations, and the related novel properties are also investigated. Therefore, for spintronics and topology, a mini-review of 2D SGSs seems necessary. It is noteworthy that Dirac SGSs and nodal line SGSs are new cross concepts in spintronics and topology. Although in almost all the reported 2D (2D) materials, the twofold degenerate nodal points in their band structures are misused as “Dirac points” due to a historical issue (Yang, 2016). The correct naming of these nodal points should be “Weyl”, and then each twofold degenerate point is described by the Weyl model in 2D. This review follows the common practice of using “Dirac point” SGSs in 2D materials.
In this review, we divided 2D SGSs into four classes: 2D SGSs with direct band crossing points at high-symmetry (H-S) points and along the H-S paths, 2D SGSs with indirect zero-gap states, and 2D SGSs with zero-gap nodal ring states. Note that this is the first time to review SGSs based on classification as mentioned above.
Herein, we will review the most recent investigations of 2D SGSs from 2020 to 2022. Section 2 introduces the proposed 2D SGSs with band crossing points at the H-S point. Section 3 introduces the proposed 2D SGSs with band crossing points along the H-S paths and their unique behaviors. Section 3 reviews 2D SGSs with indirect zero-gap states and their possible application. Section 4 introduces the case of 2D SGSs with zero-gap nodal ring states. Section 5 is the conclusion.
2 2D SGSs with band crossing points at H-S points
In 2022, Xing et al. (Xing et al., 2022) proposed a family of 2D oxalate-based metal-organic frameworks (MOFs) that possed the SGS characteristic. Figures 1I,J show the structure and reciprocal lattice of a 2D MOF TM2(C2O4)3 with a honeycomb-kagome (HK) lattice. Figure 1K–R show the electronic BSs of Ni2(C2O4)3 and Re2(C2O4)3 calculated by different methods along the Γ-M-K-Γ high symmetry paths. Without SOC, the valence band and conduction band in one spin channel touch the FL at the K point, and the other spin channel has a semiconducting band gap of 1 eV (see Figure 1K, O). Meanwhile, spin-gapless Dirac points with linear dispersion appear at the FL in one spin channel, which is beneficial for dissipationless spin transport. The influence of SOC on the Dirac point at the K H-S point is considered, and the results are shown in Figure 1L, P. One finds that the SOC triggers a band gap of about 7.6 meV in Ni2(C2O4)3 and 143 meV in Re2(C2O4)3, respectively. Compared with Ni2(C2O4)3, the SOC-induced gap of Re2(C2O4)3 is more significant than that of Ni2(C2O4)3 because the relative atomic mass of the Re atom is heavier than that of the Ni atom, and the Dirac point of Re2(C2O4)3 only contributes the d orbital of Re atom. Figure 1M, Q show the BSs calculated by the HSE06 method, and Figure 1N, R show the BSs calculated by the GGA + U method. One finds that the spin-gapless Dirac point is still maintained at the K point under both HSE06 and GGA + U methods.
With the PBE functional, the calculated Fermi velocity (vF) values (Xing et al., 2022) are up to 2.0 × 105 m s−1 and 1.86 × 105 m s−1 for Ni2(C2O4)3 and Re2(C2O4)3, respectively. When using the HSE06 functional, the obtained vF values are relatively higher, up to 2.78 × 105 m s−1 and 2.58 × 105 m s−1 for Ni2(C2O4)3 and Re2(C2O4)3, respectively. As seen in Figure 1S, T, M and Cm exhibit a sudden change at a temperature of 208 K for Ni2(C2O4)3 and 34 K for Re2(C2O4)3, respectively. Note that the ultimate goals of spintronic or electronic devices in the future are ultra-fast transmission and extremely low energy consumption. The massless charge should ideally be fully S-P, and the (effective) mass of electrons or holes should be eliminated. Therefore, a class of magnetic materials called 2D SGSs with Dirac points at high symmetry points can be considered ideal for the use of next-generation spintronics (Wang et al., 2018b).
3 2D SGSs with band crossing points along the H-S paths
3.1 Example 1: 2D single-layer Fe2I2
In 2020, Sun, Ma, and Kioussis (Sun et al., 2020b) proposed single-layer Fe2I2, with space group P4/nmm (nop. 129) and calculated lattice constants a = b = 3.81 Å, is a 2D SGS. The calculated BSs for single-layer Fe2I2 without SOC and with GGA + U are shown in Figure 1U. One finds that the SU bands show a semiconducting behavior, whereas the SD bands show a zero-gap behavior. Two gapless band crossing points appear at the FL in the SD channel. Unlike the gapless point at the H-S point in Ni2(C2O4)3 and Re2(C2O4)3, the gapless points in Fe2I2 are along the H-S paths. As shown in Figure 1U, the gapless points appear along the Y-Γ-X H-S paths. The 3D plot of these gapless points (named as Dirac points in Ref. (Sun et al., 2020b)) is shown in Figure 1V. The obtained vF with the help of GGA + U and HSE06 is 4.66 × 105 m s−1 and 6.39 × 105 m s−1, respectively. As we all know, the massless Dirac fermions will lead to low effective masses and high carrier mobility. Further, as shown in Figure 1W, single-layer Fe2I2 undergoes a spin reorientation transition to an in-plane magnetization orientation beyond -4% compressive strain. As shown in Figure 1X, one finds that the SD bands arise from the Fe-d orbital, whereas the SU bands are from the I-p orbital. Hence, the Fe-d orbital contributes solely to the Dirac points at the FL. When SOC is added, significant band gaps (∼301 meV) appear along the Y-Γ-X H-S paths (see Figure 1Y) and a nonzero Chern number (|C| = 2). The edge states for the single-layer Fe2I2 are shown in Figure 1Z; one finds that two chiral topologically protected gapless edge states, which are consistent with the obtained |C| = 2. The SOC induces a physics nature transition from Driac SGS to quantum anomalous Hall (QAH) state in single-layer Fe2I2.
3.2 Example 2: 2D Cr2X3 monolayer with the HK lattice
In 2021, Feng, Liu, and Gao (Feng et al., 2021) proposed the spin-gapless semiconducting states in 2D Cr2X3 monolayers (X = S, Se, and Te) via first-principle calculations. The estimated Curie temperatures for these three monolayers are about 420, 480, and 510 K, respectively. The S-P BSs and the calculated MAE for these three monolayers are collected in Figures 2B–D. One finds these three monolayers belong to 2D SGSs with zero-gap Dirac points along the H-S paths, i.e., K-Γ-M. As shown in Figure 2A one finds that the MAEs for these three monolayers increase with the increasing tensile strains from 1% to 5%. Unfortunately, the SGS behaviors in Cr2Te3 at the FL are destroyed within HSE06. For the Cr2S3 and Cr2Se3, the Dirac points along the K-Γ-M paths are still maintained within PBE and HSE06. The effect of SOC to the Dirac points is also examined by Feng, Liu, and Gao (Feng et al., 2021); they stated that the SOC effect is weak for the proposed monolayers.
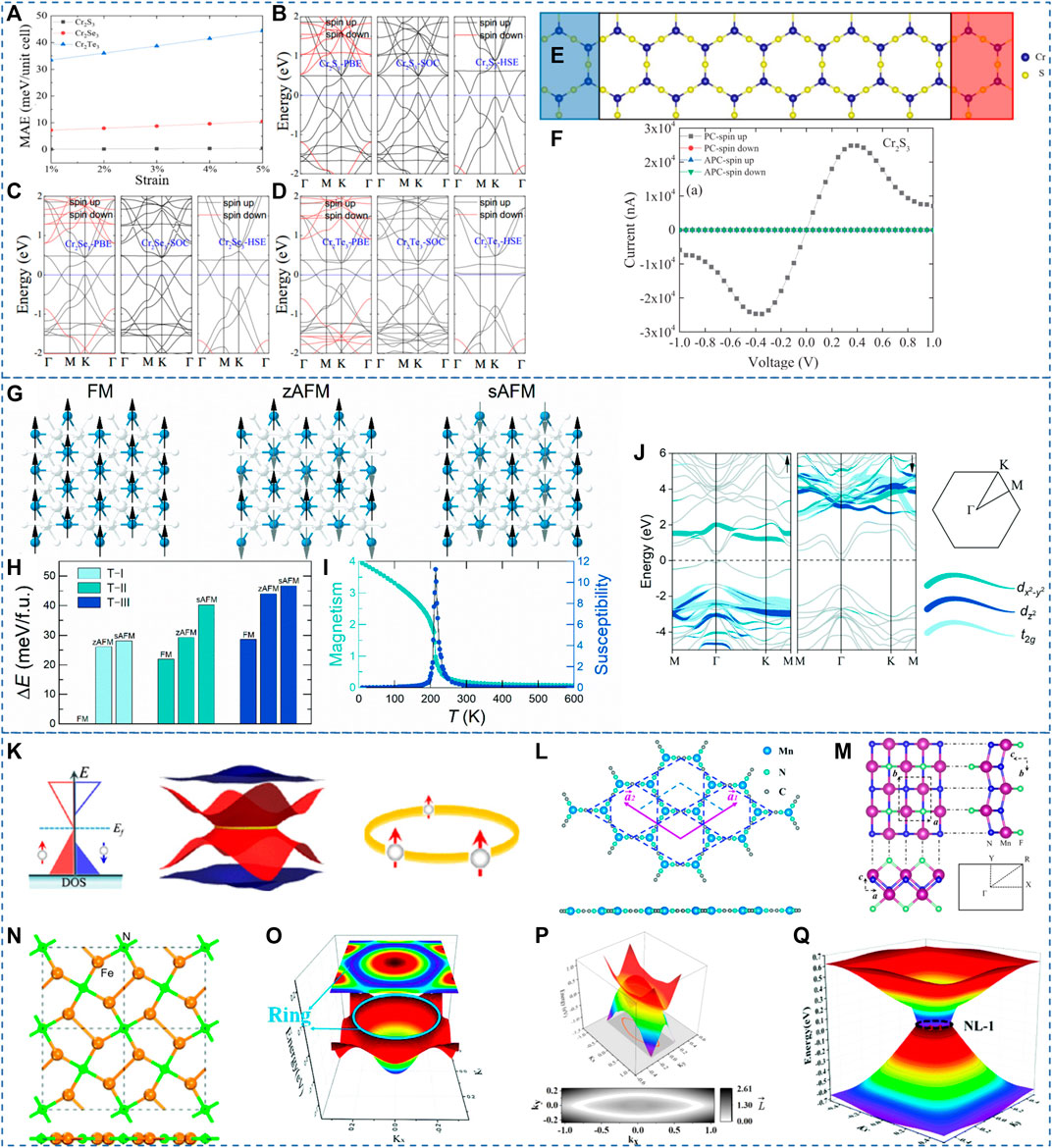
FIGURE 2. (A) The relationship between the MAE and strain. (B–D) BS of the Cr2X3 monolayers calculated with different methods. (E) The Cr2S3 device model. (F) The spin-resolved current-voltage curves for the PC and the APC of the device. (A–F) Reproduced from (Feng et al., 2021) with permission from AIP publishing. (G) Schematics for the FM and AFM states of the CrGa2Se4 monolayer. (H) Energy difference with respect to the ground state for T-I, T-II and T-III configurations. (I) The simulated Curie temperature (J) The calculated BSs by the HSE06 method. (G–J) Reproduced from (Chen et al., 2021) with permission from RSC publishing. (K) The schematic diagram of NRSGSs. Reproduced from (Zhang et al., 2020b) with permission from APS. (L–N) Structures of 2D HK Mn-cyanogen lattice, 2D MnNF monolayer, and 2D Fe4N2 pentagon crystal, respectively. (O–Q) 3D plot of the gapless NR states in 2D HK Mn–cyanogen lattice, 2D MnNF monolayer, and 2D Fe4N2 pentagon crystal, respectively. (L–Q) Reproduced from (Zhang et al., 2018; Hu et al., 2019; Zhang et al., 2021b) with permission from RSC and ACS publishing.
Feng, Liu, and Gao (Feng et al., 2021) also studied the nonequilibrium spin transport properties of monolayer Cr2S3, and the device model is shown in Figure 2E. From Figure 2F, for the APC in both spin directions, one finds the values of spin-currents are extremely small. For the PC, one finds the spin-current of the PC-spin down can be neglected, whereas the spin-current of PC-spin up increased at first and then decreased with the increase of voltage form 0.0 V–1.0 V. The maximum value of spin current of PC-spin up appears at about+/-0.35 V. Hence, the device model in Figure 2E should host a perfect spin filtering effect (Chen et al., 2019; Zhang et al., 2020a; Han et al., 2022).
4 2D SGSs with indirect zero-gap states
In 2021, Chen et al. (Chen et al., 2021) predicted a 2D spin gapless ferromagnetic semiconductor of CrGa2Se4 monolayer with indirect zero-gap state. As shown in Figures 2G,H, one finds that the magnetic ground state is the FM state with a T-I configuration. It can be seen from Figure 2I that the Curie temperature of the CrGa2Se4 monolayer is about 220 K. Chen et al. calculated the BSs of the CrGa2Se4 monolayer with HSE06 functional. The results are collected in Figure 2J. At first glance, one finds that the CrGa2Se4 monolayer is a ferromagnetic semiconductor. The bands in SU and SD channels host semiconducting gaps of 0.36 eV and 1.36 eV, respectively. Interestingly, the lowest conduction band state in the SD channel touches the FL, and the highest valence band states in the SU channel touch the FL, forming an indirect zero-gap state. Hence, the CrGa2Se4 monolayer can also be seen as an SGS with an indirect spin-gapless semiconducting state.
We would like to point out that the indirect zero gap states occur because the two spin components at different k points accidentally have their extreme values at the FL. Therefore, in general, they are not protected from the symmetry of systems due to the indirect band touching. However, the SGSs with indirect band touching usually host bipolar magnetic behavior. That is, by changing the sign of the applied gate voltage, one can achieve the electrical manipulation of spin-polarization orientation in SGSs (with indirect band touching).
5 2D SGSs with zero-gap nodal ring states
Compared to the Dirac SGSs with single or multiple nodal point states, Zhang et al. (Zhang et al., 2018) proposed a new class of 2D SGSs with a gapless nodal ring (NR) in the momentum space and 100% spin polarization. That is, the SGSs, with a one-dimensional topological signature, have zero-gap band crossing points that form a line in the momentum space. Typically, they are named as NRSGSs. The schematic diagram of NRSGSs is shown in Figure 2K. One finds that the SU channel shows a zero-gap NR state in the momentum space and the SD channel shows a semiconducting state.
To this date, 2D HK Mn–cyanogen lattice (Zhang et al., 2018), 2D MnNF monolayer (Hu et al., 2019), and 2D Fe4N2 pentagon crystal (Zhang et al., 2021b) are proposed to be 2D NR SGSs. The structural model and the 3D plot of the gapless NR state in one spin channel are shown in Figure 2L–Q. We would like to point out that the gapless NR state in one spin channel may suffer sizable SOC-induced gaps. Hence, searching for NRSGSs with light elements to reduce the value of SOC-induced gaps.
6 Conclusion and remarks
In this mini-review, we introduced a series of ideal 2D SGSs, including 2D SGSs with band-crossing points at H-S points or along the H-S paths, 2D SGSs with S-P NR states, and 2D SGSs with indirect zero-gap states.
The Dirac SGSs with band-crossing points at H-S points or along the H-S paths show massless fermions around the FL, ideal dissipation-less properties, and 100% spin-polarization. Furthermore, the band crossing points may not isolate in the momentum space and form an NR in 2D SGSs. The NRSGSs will exhibit more intensive nonlinear electromagnetic responses than a single Dirac point. It should be noted that the 2D SGSs are hopped to host a high Curie temperature and a robust FM state at room temperature. Finally, a major challenge for 2D SGSs is that no 2D SGSs has been experimentally realized. The reason is that the 2D SGSs are monolayer materials, and they are hard to synthesize. Moreover, some monolayer materials are not stable in the ambient environment. Thus, new nanotechnology is needed for fabricating 2D monolayer SGSs.
Author contributions
JW wrote the manuscript. DW revised and approved the manuscript.
Funding
This work is financially supported by the Fundamental Research Funds for the Central Universities (SWU019030).
Conflict of interest
The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor GW declared a past co-authorship with the author DW.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ashton, M., Gluhovic, D., Sinnott, S. B., Guo, J., Stewart, D. A., and Hennig, R. G. (2017). Two-dimensional intrinsic half-metals with large spin gaps. Nano Lett. 17 (9), 5251–5257. doi:10.1021/acs.nanolett.7b01367
Benmansour, S., Abhervé, A., Gómez-Claramunt, P., Vallés-García, C., and Gómez-García, C. J. (2017). Nanosheets of two-dimensional magnetic and conducting Fe(II)/Fe(III) mixed-valence metal-organic frameworks. ACS Appl. Mat. Interfaces 9 (31), 26210–26218. doi:10.1021/acsami.7b08322
Bonilla, M., Kolekar, S., Ma, Y., Diaz, H. C., Kalappattil, V., Das, R., et al. (2018). Strong room-temperature ferromagnetism in VSe2 monolayers on van der Waals substrates. Nat. Nanotech 13 (4), 289–293. doi:10.1038/s41565-018-0063-9
Chen, Q., Wang, R., Huang, Z., Yuan, S., Wang, H., Ma, L., et al. (2021). Two dimensional CrGa2Se4: A spin-gapless ferromagnetic semiconductor with inclined uniaxial anisotropy. Nanoscale 13 (12), 6024–6029. doi:10.1039/d0nr08296a
Chen, Z., Fan, X., Shen, Z., Luo, Z., Yang, D., and Ma, S. (2020). Two-dimensional intrinsic ferromagnetic half-metals: Monolayers Mn3X4 (X = Te, Se, S). J. Mat. Sci. 55 (18), 7680–7690. doi:10.1007/s10853-020-04582-x
Chen, Z., Li, T., Yang, T., Xu, H., Khenata, R., Gao, Y., et al. (2019). Palladium (III) fluoride bulk and PdF3/Ga2O3/PdF3 magnetic tunnel junction: Multiple spin-gapless semiconducting, perfect spin filtering, and high tunnel magnetoresistance. Nanomaterials 9 (9), 1342. doi:10.3390/nano9091342
Deng, Y. X., Chen, S. Z., Zeng, Y., Feng, Y., Zhou, W. X., Tang, L. M., et al. (2018). Spin gapless semiconductor and half-metal properties in magnetic penta-hexa-graphene nanotubes. Org. Electron. 63, 310–317. doi:10.1016/j.orgel.2018.09.046
Deng, Y. X., Chen, S. Z., Zhang, Y., Yu, X., Xie, Z. X., Tang, L. M., et al. (2020). Penta-hexa-graphene nanoribbons: Intrinsic magnetism and edge effect induce spin-gapless semiconducting and half-metallic properties. ACS Appl. Mat. Interfaces 12 (47), 53088–53095. doi:10.1021/acsami.0c14768
Deng, Y., Yu, Y., Song, Y., Zhang, J., Wang, N. Z., Sun, Z., et al. (2018). Gate-tunable room-temperature ferromagnetism in two-dimensional Fe3GeTe2. Nature 563 (7729), 94–99. doi:10.1038/s41586-018-0626-9
Dietl, T. (2010). A ten-year perspective on dilute magnetic semiconductors and oxides. Nat. Mater 9 (12), 965–974. doi:10.1038/nmat2898
Fei, Z., Huang, B., Malinowski, P., Wang, W., Song, T., Sanchez, J., et al. (2018). Two-dimensional itinerant ferromagnetism in atomically thin Fe3GeTe2. Nat. Mater 17 (9), 778–782. doi:10.1038/s41563-018-0149-7
Feng, Y., Liu, N., and Gao, G. (2021). Spin transport properties in Dirac spin gapless semiconductors Cr2X3 with high Curie temperature and large magnetic anisotropic energy. Appl. Phys. Lett. 118 (11), 112407. doi:10.1063/5.0045262
Feng, Y., Wu, X., and Gao, G. (2020). High tunnel magnetoresistance based on 2D Dirac spin gapless semiconductor VCl3. Appl. Phys. Lett. 116 (2), 022402. doi:10.1063/1.5128204
Gao, G., Ding, G., Li, J., Yao, K., Wu, M., and Qian, M. (2016). Monolayer MXenes: Promising half-metals and spin gapless semiconductors. Nanoscale 8 (16), 8986–8994. doi:10.1039/c6nr01333c
Gong, C., Li, L., Li, Z., Ji, H., Stern, A., Xia, Y., et al. (2017). Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 546 (7657), 265–269. doi:10.1038/nature22060
Gong, C., and Zhang, X. (2019). Two-dimensional magnetic crystals and emergent heterostructure devices. Science 363 (6428), eaav4450. doi:10.1126/science.aav4450
Haas, C. (1970). Magnetic semiconductors. C R C Crit. Rev. Solid State Sci. 1 (1), 47–98. doi:10.1080/10408437008243418
Han, J., Chen, X., Yang, W., Lv, C., Lin, X., Wang, X., et al. (2022). Promising spin caloritronics and spin diode effects based on 1T-FeCl2 nanotube devices. J. Mat. Chem. C 10 (2), 607–615. doi:10.1039/d1tc05094j
Han, Y., Chen, Z., Kuang, M., Liu, Z., Wang, X., and Wang, X. (2019). 171 scandium-based full heusler compounds: A comprehensive study of competition between xa and L21 atomic ordering. Results Phys. 12, 435–446. doi:10.1016/j.rinp.2018.11.079
Hashimoto, A., Suenaga, K., Gloter, A., Urita, K., and Iijima, S. (2004). Direct evidence for atomic defects in graphene layers. nature 430 (7002), 870–873. doi:10.1038/nature02817
He, J., Li, X., Lyu, P., and Nachtigall, P. (2017). Near-room-temperature chern insulator and Dirac spin-gapless semiconductor: Nickel chloride monolayer. Nanoscale 9 (6), 2246–2252. doi:10.1039/c6nr08522a
Hu, Y., Li, S. S., Ji, W. X., Zhang, C. W., Ding, M., Wang, P. J., et al. (2019). Glide mirror plane protected nodal-loop in an anisotropic half-metallic MnNF monolayer. J. Phys. Chem. Lett. 11 (2), 485–491. doi:10.1021/acs.jpclett.9b03320
Huang, B., Clark, G., Navarro-Moratalla, E., Klein, D. R., Cheng, R., Seyler, K. L., et al. (2017). Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 546 (7657), 270–273. doi:10.1038/nature22391
Kim, J., Kim, K. W., Kim, B., Kang, C. J., Shin, D., Lee, S. H., et al. (2019). Exploitable magnetic anisotropy of the two-dimensional magnet CrI3. Nano Lett. 20 (2), 929–935. doi:10.1021/acs.nanolett.9b03815
Lee, E. C., Choi, Y. C., Kim, W. Y., Singh, N. J., Lee, S., Shim, J. H., et al. (2010). A radical polymer as a two-dimensional organic half metal. Chem. Eur. J. 16 (40), 12141–12146. doi:10.1002/chem.201000858
Lei, J., Xu, M. C., and Hu, S. J. (2017). Anchoring transition metal elements on graphene-like ZnO monolayer by CO molecule to obtain spin gapless semiconductor. Appl. Surf. Sci. 416, 681–685. doi:10.1016/j.apsusc.2017.04.169
Li, L., Kong, X., Chen, X., Li, J., Sanyal, B., and Peeters, F. M. (2020). Monolayer 1T-LaN2: Dirac spin-gapless semiconductor of p-state and chern insulator with a high chern number. Appl. Phys. Lett. 117 (14), 143101. doi:10.1063/5.0023531
Li, X., and Yang, J. (2014). CrXTe3(X = Si, Ge) nanosheets: Two dimensional intrinsic ferromagnetic semiconductors. J. Mat. Chem. C 2 (34), 7071–7076. doi:10.1039/c4tc01193g
Li, Y., Zhou, Z., Shen, P., and Chen, Z. (2009). Spin gapless Semiconductor−Metal−Half-metal properties in nitrogen-doped zigzag graphene nanoribbons. ACS Nano 3 (7), 1952–1958. doi:10.1021/nn9003428
Liu, B., and Zhou, K. (2019). Recent progress on graphene-analogous 2D nanomaterials: Properties, modeling and applications. Prog. Mater. Sci. 100, 99–169. doi:10.1016/j.pmatsci.2018.09.004
Liu, J., Liu, Z., Song, T., and Cui, X. (2017). Computational search for two-dimensional intrinsic half-metals in transition-metal dinitrides. J. Mat. Chem. C 5 (3), 727–732. doi:10.1039/c6tc04490e
Miao, N., and Sun, Z. (2022). Computational design of two‐dimensional magnetic materials. WIREs Comput. Mol. Sci. 12 (2), e1545. doi:10.1002/wcms.1545
Nadeem, M., Hamilton, A. R., Fuhrer, M. S., and Wang, X. (2020). Quantum anomalous Hall effect in magnetic doped topological insulators and ferromagnetic spin‐gapless semiconductors-A perspective review. Small 16 (42), 1904322. doi:10.1002/smll.201904322
Novoselov, K. S., Geim, A. K., Morozov, S. V., Jiang, D. E., Zhang, Y., Dubonos, S. V., et al. (2004). Electric field effect in atomically thin carbon films. science 306 (5696), 666–669. doi:10.1126/science.1102896
Phong, P. N., and Nguyen, H. V. (2022). Spin gapless semiconductors in antiferromagnetic monolayer HC4N3BN under strain. Comput. Mater. Sci. 203, 111110. doi:10.1016/j.commatsci.2021.111110
Rani, D., Bainsla, L., Alam, A., and Suresh, K. G. (2020). Spin-gapless semiconductors: Fundamental and applied aspects. J. Appl. Phys. 128 (22), 220902. doi:10.1063/5.0028918
Şaşıoğlu, E., Aull, T., Kutschabsky, D., Blügel, S., and Mertig, I. (2020). Half-metal-spin-gapless-semiconductor junctions as a route to the ideal diode. Phys. Rev. Appl. 14 (1), 014082. doi:10.1103/physrevapplied.14.014082
Sato, K., Bergqvist, L., Kudrnovský, J., Dederichs, P. H., Eriksson, O., Turek, I., et al. (2010). First-principles theory of dilute magnetic semiconductors. Rev. Mod. Phys. 82 (2), 1633–1690. doi:10.1103/revmodphys.82.1633
Sun, Q., Ma, Y., and Kioussis, N. (2020). Two-dimensional Dirac spin-gapless semiconductors with tunable perpendicular magnetic anisotropy and a robust quantum anomalous Hall effect. Mat. Horiz. 7 (8), 2071–2077. doi:10.1039/d0mh00396d
Sun, X., Li, W., Wang, X., Sui, Q., Zhang, T., Wang, Z., et al. (2020). Room temperature ferromagnetism in ultra-thin van der Waals crystals of 1T-CrTe2. Nano Res. 13 (12), 3358–3363. doi:10.1007/s12274-020-3021-4
Tang, C., Zhang, L., Jiao, Y., Zhang, C., Sanvito, S., and Du, A. (2021). First-principles prediction of polar half-metallicity and out-of-plane piezoelectricity in two-dimensional quintuple layered cobalt selenide. J. Mat. Chem. C 9 (36), 12046–12050. doi:10.1039/d1tc02727a
Torelli, D., Moustafa, H., Jacobsen, K. W., and Olsen, T. (2020). High-throughput computational screening for two-dimensional magnetic materials based on experimental databases of three-dimensional compounds. npj Comput. Mat. 6 (1), 158. doi:10.1038/s41524-020-00428-x
Wang, A., Zhang, X., Feng, Y., and Zhao, M. (2017). Chern insulator and chern half-metal states in the two-dimensional spin-gapless semiconductor Mn2C6S12. J. Phys. Chem. Lett. 8 (16), 3770–3775. doi:10.1021/acs.jpclett.7b01187
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N., and Strano, M. S. (2012). Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotech 7 (11), 699–712. doi:10.1038/nnano.2012.193
Wang, X., Cheng, Z., Jin, Y., Wu, Y., Dai, X., and Liu, G. (2018). Magneto-electronic properties and tetragonal deformation of rare-earth-element-based quaternary heusler half-metals: A first-principles prediction. J. Alloys Compd. 734, 329–341. doi:10.1016/j.jallcom.2017.10.277
Wang, X., Cheng, Z., Liu, G., Dai, X., Khenata, R., Wang, L., et al. (2017). Rare earth-based quaternary Heusler compoundsMCoVZ(M= Lu, Y;Z= Si, Ge) with tunable band characteristics for potential spintronic applications. Int. Union Crystallogr. J. 4 (6), 758–768. doi:10.1107/s2052252517013264
Wang, X., Cheng, Z., Wang, J., and Liu, G. (2016). A full spectrum of spintronic properties demonstrated by a C1b-type Heusler compound Mn2Sn subjected to strain engineering. J. Mat. Chem. C 4 (36), 8535–8544. doi:10.1039/c6tc02526a
Wang, X., Cheng, Z., Yuan, H., and Khenata, R. (2017). L21 and XA ordering competition in titanium-based full-Heusler alloys. J. Mat. Chem. C 5 (44), 11559–11564. doi:10.1039/c7tc03909c
Wang, X., Cheng, Z., Zhang, G., Yuan, H., Chen, H., and Wang, X. L. (2020). Spin-gapless semiconductors for future spintronics and electronics. Phys. Rep. 888, 1–57. doi:10.1016/j.physrep.2020.08.004
Wang, X., Ding, G., Cheng, Z., Yuan, H., Wang, X. L., Yang, T., Khenata, W., and Wang, W. (2019). R3c-type LnNiO3(ln = La, Ce, Nd, Pm, Gd, Tb, Dy, Ho, Er, Lu) half-metals with multiple Dirac cones: A potential class of advanced spintronic materials. Int. Union Crystallogr. J. 6 (6), 990–995. doi:10.1107/s2052252519012570
Wang, X., Du, K., Fredrik Liu, Y. Y. F., Hu, P., Zhang, J., Zhang, Q., et al. (2016). Raman spectroscopy of atomically thin two-dimensional magnetic iron phosphorus trisulfide (FePS 3 ) crystals. 2D Mat. 3 (3), 031009. doi:10.1088/2053-1583/3/3/031009
Wang, X. L. (2017). Dirac spin-gapless semiconductors: Promising platforms for massless and dissipationless spintronics and new (quantum) anomalous spin Hall effects. Natl. Sci. Rev. 4 (2), 252–257. doi:10.1093/nsr/nww069
Wang, X., Li, T., Cheng, Z., Wang, X. L., and Chen, H. (2018). Recent advances in Dirac spin-gapless semiconductors. Appl. Phys. Rev. 5 (4), 041103. doi:10.1063/1.5042604
Wang, X. L. (2008). Proposal for a new class of materials: Spin gapless semiconductors. Phys. Rev. Lett. 100 (15), 156404. doi:10.1103/physrevlett.100.156404
Wang, Z., Zhang, T., Ding, M., Dong, B., Li, Y., Chen, M., et al. (2018). Electric-field control of magnetism in a few-layered van der Waals ferromagnetic semiconductor. Nat. Nanotech 13 (7), 554–559. doi:10.1038/s41565-018-0186-z
Wu, X., Feng, Y., Li, S., Zhang, B., and Gao, G. (2020). 2D Mn2C6Se12 and Mn2C6S6Se6: Intrinsic room-temperature Dirac spin gapless semiconductors and perfect spin transport properties. J. Phys. Chem. C 124 (29), 16127–16135. doi:10.1021/acs.jpcc.0c04786
Wu, X., Feng, Y., Li, S., Zhang, B., and Gao, G. (2020). 2D Mn2C6Se12 and Mn2C6Se12: Intrinsic room-temperature Dirac spin gapless semiconductors and perfect spin transport properties.
Xing, J., Jiang, X., Liu, Z., Qi, Y., and Zhao, J. (2022). Robust Dirac spin gapless semiconductors in a two-dimensional oxalate based organic honeycomb-kagome lattice. Nanoscale 14 (5), 2023–2029. doi:10.1039/d1nr07076b
Xu, J., Li, W., and Hou, Y. (2020). Two-dimensional magnetic nanostructures. Trends Chem. 2 (2), 163–173. doi:10.1016/j.trechm.2019.11.007
Yang, Q., Kou, L., Hu, X., Wang, Y., Lu, C., Krasheninnikov, A. V., et al. (2020). Strain robust spin gapless semiconductors/half-metals in transition metal embedded MoSe2 monolayer. J. Phys. Condens. Matter 32 (36), 365305. doi:10.1088/1361-648x/ab9052
Yang, S. A. (2016). Dirac and Weyl materials: Fundamental aspects and some spintronics applications. Spin, 6. World Scientific Publishing Company, 1640003. doi:10.1142/s2010324716400038
Yang, T., Cheng, Z., Surucu, G., and Wang, X. (2020). Coexistence of parabolic and linear band crossings and electron-doped spin-gapless properties in rhombohedral type YbBO3. J. Alloys Compd. 823, 153835. doi:10.1016/j.jallcom.2020.153835
Yang, T., Cheng, Z., Wang, X., and Wang, X. L. (2021). Nodal ring spin gapless semiconductor: New member of spintronic materials. J. Adv. Res. 28, 43–49. doi:10.1016/j.jare.2020.06.016
Yue, Z., Li, Z., Sang, L., and Wang, X. (2020). Spin‐gapless semiconductors. Small 16 (31), 1905155. doi:10.1002/smll.201905155
Zhang, K., Chen, M., Wang, D., Lv, H., Wu, X., and Yang, J. (2021). Nodal-loop half metallicity in a two-dimensional Fe4N2 pentagon crystal with room-temperature ferromagnetism. Nanoscale 13 (46), 19493–19499. doi:10.1039/d1nr06033c
Zhang, L., Li, T., Li, J., Jiang, Y., Yuan, J., and Li, H. (2020). Perfect spin filtering effect on Fe3GeTe2-based van der Waals magnetic tunnel junctions. J. Phys. Chem. C 124 (50), 27429–27435. doi:10.1021/acs.jpcc.0c09432
Zhang, L., Zhang, S. F., Ji, W. X., Zhang, C. W., Li, P., Wang, P. J., et al. (2018). Discovery of a novel spin-polarized nodal ring in a two-dimensional HK lattice. Nanoscale 10 (44), 20748–20753. doi:10.1039/c8nr05383a
Zhang, R. W., Zhang, Z., Liu, C. C., and Yao, Y. (2020). Nodal line spin-gapless semimetals and high-quality candidate materials. Phys. Rev. Lett. 124 (1), 016402. doi:10.1103/physrevlett.124.016402
Zhang, S., Xu, R., Luo, N., and Zou, X. (2021). Two-dimensional magnetic materials: Structures, properties and external controls. Nanoscale 13 (3), 1398–1424. doi:10.1039/d0nr06813f
Zhang, X., Wang, A., and Zhao, M. (2015). Spin-gapless semiconducting graphitic carbon nitrides: A theoretical design from first principles. Carbon 84, 1–8. doi:10.1016/j.carbon.2014.11.049
Zhou, X. F., Oganov, A. R., Wang, Z., Popov, I. A., Boldyrev, A. I., and Wang, H. T. (2016). Two-dimensional magnetic boron. Phys. Rev. B 93 (8), 085406. doi:10.1103/physrevb.93.085406
Zhou, X., Hang, Y., Liu, L., Zhang, Z., and Guo, W. (2019). A large family of synthetic two-dimensional metal hydrides. J. Am. Chem. Soc. 141 (19), 7899–7905. doi:10.1021/jacs.9b02279
Keywords: two-dimensional material systems, spin-gapless materials, Dirac point, nodal line, spin transport properties
Citation: Wang J and Wang D (2022) Two-dimensional spin-gapless semiconductors: A mini-review. Front. Chem. 10:996344. doi: 10.3389/fchem.2022.996344
Received: 17 July 2022; Accepted: 26 July 2022;
Published: 25 August 2022.
Edited by:
Guangzhao Wang, Yangtze Normal University, ChinaReviewed by:
Hao Guo, Hebei Normal University of Science and Technology, ChinaJunjie He, Charles University, Czechia
Copyright © 2022 Wang and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dandan Wang, d2FuZ2RhbmRhbkBzd3UuZWR1LmNu