- 1Department of Mathematics, Mohi-ud-Din Islamic University, Nerian Sharif, AJ&K, Pakistan
- 2Mechanical Engineering Department, College of Engineering and Islamic Architecture, Umm Al-Qura University, Makkah, Saudi Arabia
- 3Department of Mathematics, College of Science, King Khalid University, Abha, Saudi Arabia
- 4Faculty of Engineering and Technology, Future University in Egypt New Cairo, Mansoura, Egypt
- 5Departmment of Applied Mathematics and Statistics (AM&S), Institute of Space Technology (IST), Islamabad, Pakistan
- 6Department of Mathematics and Statistics, Hazara University Mansehra, Islamabad, Pakistan
- 7Mechanical Engineering Department, College of Engineering, Prince Sattam Bin Abdulaziz University, Wadi Addawaser, Saudi Arabia
- 8Production Engineering and Mechanical Design Department, Faculty of Engineering, Mansoura University, Mansoura, Egypt
Heat transfer and energy storage remain a core problem for industrialists and engineers. So, the concept of new heat transfer fluids, namely, nanofluids and hybrid nanofluids, has been introduced so far. Recently, a new third generation of heat transfer fluids has been developed known as modified hybrid nanofluids (MHNs), synthesized by ternary nanomaterials and the host fluid. Therefore, the study was conducted to investigate the energy storage efficiency between (Al2O3-CuO-Cu/H2O)mhnf and (Al2O3-CuO/H2O)hnf in the presence of novel viscous dissipation effects. The problem is developed for a channel with stretchable walls via thermophysical attributes of binary and ternary guest nanomaterials and the host liquid. The model is tackled numerically and furnished results for the dynamics, most specifically energy storage efficiency in (Al2O3-CuO-Cu/H2O)mhnf. It is examined that the third generation of heat transfer fluids (Al2O3-CuO-Cu/H2O)mhnf has high thermal energy storage efficiency than traditional nano and hybrid nanofluids. Therefore, these new insights in heat transfer would be beneficial and cope with the problems of energy storage in the modern technological world.
Introduction
The significance of heat transport in the modern technological world is unavoidable due to its remarkable applications. It is a bitter truth that conventional liquids have very limited thermal performance; therefore, these fluids have very limited applications in the modern world era. However, scientists and fluid dynamists thought that how to cope with this core problem. Finally, they introduced the concept of nanofluids. These fluids are the composition of host liquid and guest nanoparticles. The nanoparticles are stably suspended in the liquid and thermally compatible. The majority of issues of the modern world were tackled after the development of nanofluids. However, researchers did not stop their efforts and moved toward the second generation of nanofluids called hybrid nanofluids.
Lately, a superior class of hybrid nanofluids has developed called modified hybrid nanofluid. In this case, further nanoparticles of third guest metals were added to the conventional hybrid nanofluid. The newly suspended additives make the resultant suspension more efficient than hybrid nanofluid. These fluids attained much fame from fluid dynamists and industrialists because of their ultra-high thermal performance than conventional nano and hybrid nanofluids. However, we can categorize the heat transfer fluids into three categories to cope with the heat transfer problems of the modern technological world. These are:
Nanofluids (Choi, 1995) or first-generation heat transfer fluids.
Hybrid nanofluids (Ahmed et al., 2020; Mohyud-Din et al., 2020) or second-generation heat transfer fluids.
Modified hybrid Nanofluids (Abbasi et al., 2021) or third-generation heat transfer fluids.
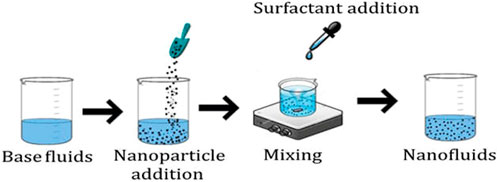
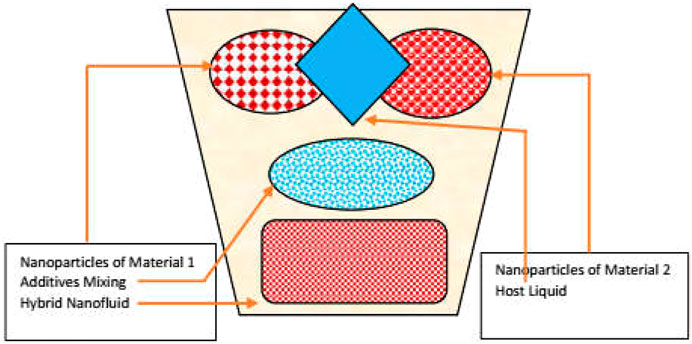
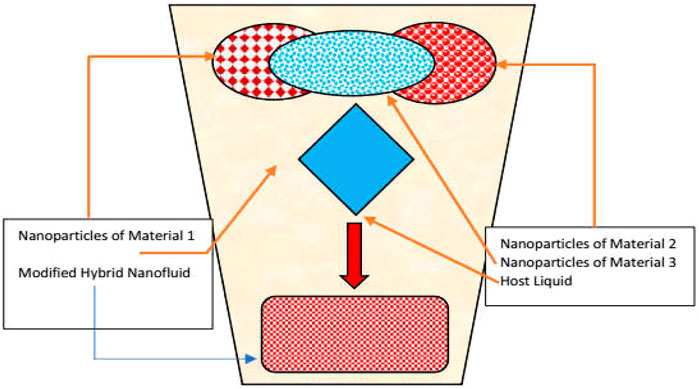
The synthetization process of the aforementioned classes is depicted in Figures 1–3 for nano, hybrid, and modified hybrid nanofluids, respectively.
The newly developed generation (first, second, and third generations) of the fluids strengthen their roots in modern world applications. These could be found in biomedical engineering, electronics, and cooling of the systems to save the drugs and different medicines from moisture in the stores, to check the interaction of biofluids in the human veins and arteries by injecting the hybrid and modified hybrid mixture of nanoparticles, aerodynamics, in the study of chemotherapy, to diagnose cancer symptoms, paint industries, and manufacturing of home appliances. Therefore, the study of heat transfer in nanofluids is significant to accomplish many industrial and engineering processes. In view of such a significant motive, the researchers and fluid dynamists started working in this direction with all of their potential.
The investigation of heat and mass transport mechanisms in opening/narrowing channel is of much interest owing to its applications in medical sciences and engineering as well. Therefore, fluid dynamists focused their attention on exploring the behavior of heat and mass transfer under certain flow assumptions. Such flows extensively appeared in different engineering systems and the flow of blood in human bodies. More specifically, these flows were named Jeffery–Hamel flows after the untiring efforts of Jeffery (1915) and Hamel (1916) during the era of 1915 and 1916, respectively. This concept of flow configuration became very prevalent and conferred the attention of researchers in this direction.
The exploration of thermal performance in the nanofluid under the impacts of internal heat generation/absorption source and viscous dissipation is reported in Akinshilo et al. (2020). The authors organized the study in converging/diverging walls by imposing Lorentz forces on them. The problem is modeled in a cylindrical polar frame, and a dimensionless version is attained via feasible similarity transforms. The mathematical section of the work is organized by using the homotopy perturbation method (HPM) and then plotting the results for the concerned flow parameters such as magnetic, Darcy, and Reynolds numbers. It is reported that by increasing the strength of Re, the fluid velocity drops and heat transfer declines at the high Darcy parameter. Although the study is fascinating, researchers performed the results with full consideration; however, it could be prolonged to the next nanofluid generation (hybrid nanofluids) by inducing the influences of Joule heating and thermal radiations.
An analytical study of JH flow for regular liquid is conducted by Patel and Meher (2018). They prolonged the concept of the traditional Adomian decomposition method (ADM) technique to modified Adomian decomposition method (MADM) and solved the problem and found satisfactory results regarding the implementation of the technique. The graphical results were explored and discussed in detail. From the critical review of the article, it is understood that the work has its own significance, but it lacks the important concept of nanofluids and other physical conditions such as slip, thermal jump, and Biot effects. Therefore, more interesting and novel results could be achieved by prolonging the work for hybrid and modified hybrid nanofluids. Further studies on JH flows by taking different physical conditions are reported in Sushila and Shishodia (2014) and Kumbinarasaiah and Raghunatha (2022), and the relevant studies are cited therein.
The applications of nanofluids and hybrid nanofluids attracted researchers and scientists to analyze these fluids for thermal performance, which is a primary element of the modern world. Therefore, numerous studies in this regard have been reported under different flow conditions by using nanofluids synthesized by various base liquids and multiple nano-additives, for instance, the studies by Turkyilmazoglu (2014), Zangooee et al. (2019); Kumar et al. (2021), and Rout et al. (2021). Furthermore, some significant studies related to hybrid nanofluids were reported in Ahmed et al. (2017), Khan et al. (2021) Kumar (2021), Saeed et al. (2021), and Shanmugapriya et al. (2021).
The careful literature survey reveals that comparative heat transfer efficiency of second-generation (Al2O3-CuO/H2O)hnf and third-generation (Al2O3-CuO-Cu/H2O)mhnf nanofluids between opening/narrowing walls subject to the stretching and shrinking conditions has not been reported so far. This type of flow has numerous applications in different engineering systems, most specifically in biomedical engineering. The blood flow at the junction of veins and arteries works under the principle of Jeffery–Hamel (JH) flow. Therefore, the study is organized to explore the velocity, heat transport mechanism, trends in shear stresses, and thermal conductivity in (Al2O3-CuO/H2O)hnf and (Al2O3-CuO-Cu/H2O)mhnf against various parameters, particularly the volumetric fraction. The efficiency of the studied nanofluids can be compared with other reported nanofluids.
Development of third-generation nanofluid model
Flow configuration
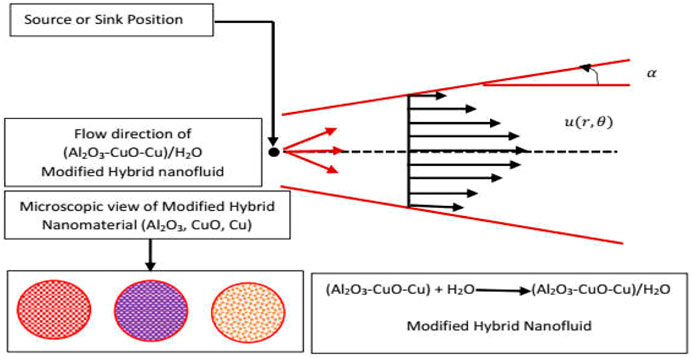
The flow of (Al2O3-CuO/H2O)hnf and (Al2O3-CuO-Cu/H2O)mhnf subject to viscous dissipation and flexible channel walls is organized between two non-parallel walls. It is supposed that the fluid flow is due to a source/sink positioned at the junction of these two walls. The walls are separated by an angle 2
• The guest hybrid nanomaterials Al2O3-CuO and H2O are thermally compatible.
• The guest hybrid nanomaterial Al2O3-CuO is uniformly suspended in H2O.
• The guest modified hybrid nanomaterials Al2O3-CuO-Cu and H2O are thermally compatible.
• The guest modified hybrid nanomaterial Al2O3-CuO-Cu is uniformly suspended in H2O.
The physical setup of the flow configuration is depicted in Figure 4.
Empirical correlations
The nanoparticles of aluminum oxide, copper oxide, and copper are used to synthesize the desired nanofluid (nf), hybrid nanofluid (hnf), and modified hybrid nanofluid (mhnf) in the presence of host liquid water. The empirical correlations for nanofluids, hybrid nanofluids, and modified hybrid nanofluids are given in Tables 1–3, respectively, whereas the shape factor is given in Table 4.

TABLE 2. Empirical correlations for second-generation heat transfer fluids (hybrid nanofluids) (Ahmed et al., 2021).

TABLE 3. Empirical correlations for third-generation heat transfer fluids (modified hybrid nanofluids).
The values of guest nanoparticles (Al2O3, CuO, and Cu) and the host liquid (water) are key ingredients in the study of newly generated heat transfer fluids. These attributes are given in Table 5 for the guest nanoparticles and the host liquid.
Development of modified hybrid nanofluid
The development of the model is based on well-known mass, momentum, and energy constitutive relations in a cylindrical polar frame. For the particular study, these relations are given as follows:
The flow conditions that are fixed on the flexible walls are described in the following expressions:
In the constitutive relations,
Furthermore, for non-dimensionalization of the model, the following similarity relations are introduced:
In the implementation of desired partial differentiation from Eq. 8, in the constitutive model, the following dimensionless model is acquired:
The functions
The parameters involved in the model are summarized in Table 6 with mathematical expressions.
Shear stresses and local energy storage
The investigation of shear stresses and local energy storage capability in (Al2O3-CuO-Cu/H2O)mhnf under multiple flow conditions is very imperative from an industrial and engineering point of view. The quantities can be described by the following mathematical formula in the dimensional form:
By endorsing the attributes of (Al2O3-CuO-Cu/H2O)mhnf and performing the calculation, the following version is obtained:
Mathematical investigation of [(Al2O3-CuO-Cu)/water]mhnf
The mathematical models appearing in the fields of medical sciences, engineering (deflection of beams, load over the bridge, etc.), and biomedical engineering are highly nonlinear in nature. For such models, it is almost impossible to handle the model in the form of an exact solution. However, numerical techniques are best suited to solve and analyze the impacts of various parameters on the dynamics of the model.
The under consideration model is very tedious due to the induction of ternary nanoparticles and their thermophysical attributes; therefore, the numerical technique is helpful to tackle the model and explore the results by altering the flow parameters. For said purpose, we adopted a numerical technique coupled with a shooting algorithm. Primarily, the setup of this technique is based on the development of a first-order initial value problem (IVP) from the higher-order model by means of feasible transformations. After that, the model is then solved by implementing the aforementioned algorithm. The calculation in the under consideration model is very lengthy; therefore, we omit the mathematical procedure. However, the results are plotted against various ranges of the flow parameters and discussed in the next section.
Results with discussion
(Al2O3-CuO-Cu/water)mhnf flow against Re
The Reynolds number, which is a quotient of viscous and inertial forces, is a significant parameter in the study of channel flow. The influences of this parameter on the flow behavior of (Al2O3-CuO/H2O)hnf and (Al2O3-CuO-Cu/H2O)mhnf in stretching/shrinking and opening/narrowing channels are pictured in Figure 2. It is worthy to mention that the values of the opening/narrowing parameter
The analysis of Figures 5A and B ensures that the fluid motion drops in a divergent channel for both stretching and shrinking walls. It is noticeable that a backflow phenomenon occurs near the walls because by increasing the Reynolds number, the fluid reverses its motion along the wall instead of mainstream
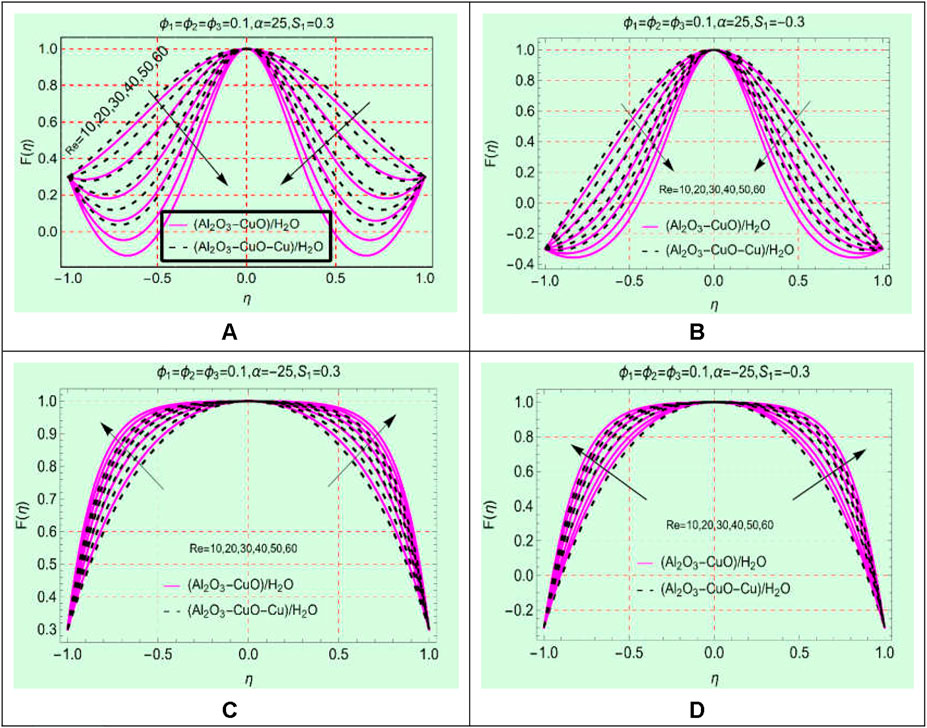
FIGURE 5.
Figures 5C and D elaborate on the behavior of (Al2O3-CuO/H2O)hnf and (Al2O3-CuO-Cu/H2O)mhnf in the narrowing channel. Physically, the flowing area reduces in the narrowing channel due to which force per unit area enhances which leads to an increment in the motion. The flow profile becomes more flattened at the central position due to the higher strength of Re and narrowing parameter
(Al2O3-CuO-Cu/water)mhnf thermal behavior against Ec
The viscous dissipation is an important physical phenomenon regarding the energy storage in (Al2O3-CuO/H2O)hnf and (Al2O3-CuO-Cu/H2O)mhnf. The Eckert number is a parameter that appeared due to viscous dissipation. Therefore, Figures 3A–D are organized to explore the influences of Ec on the thermal behavior
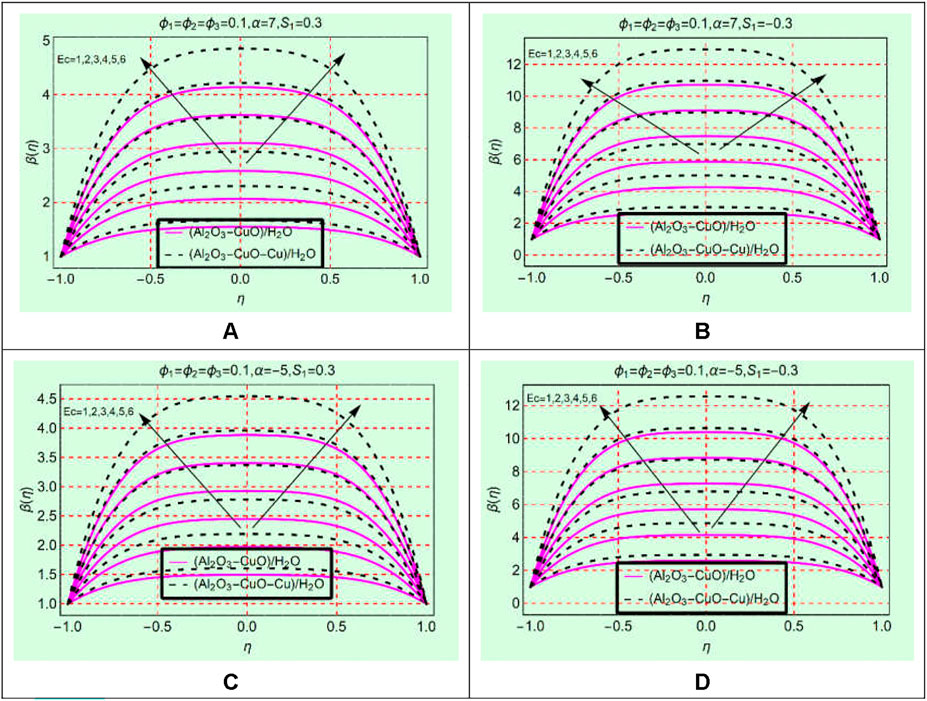
FIGURE 6.
The nanofluid containing ternary nanoparticles (Al2O3-CuO-Cu/H2O)mhnf has more capability to store energy than binary-based (Al2O3-CuO/H2O)hnf heat transfer fluids. Physically, the thermal conductivity of (Al2O3-CuO-Cu/H2O)mhnf becomes greater than (Al2O3-CuO/H2O)hnf which increases its energy storage ability. The maximum increasing behavior of binary- and ternary-based nanomaterial liquids is observed along the central line.
(Al2O3-CuO-Cu/water)mhnf thermal behavior against Re
The set of Figures 7A–D elaborates the thermal behavior of (Al2O3-CuO/H2O)hnf and (Al2O3-CuO-Cu/H2O)mhnf against Re. The keen study of Figure 7 reveals that the fluid temperature declines by strengthening Re within the physical domain. The temperature in (Al2O3-CuO/H2O)hnf reduces more abruptly than in (Al2O3-CuO-Cu/H2O)mhnf for both stretching/shrinking and opening/narrowing walls. Physically, (Al2O3-CuO-Cu/H2O)mhnf has high thermal conductivity due to the addition of the third additive Cu due to which its energy storage ability becomes maximum than (Al2O3-CuO/H2O)hnf. All these effects are elaborated in Figures 7A–D in both opening and narrowing channels.
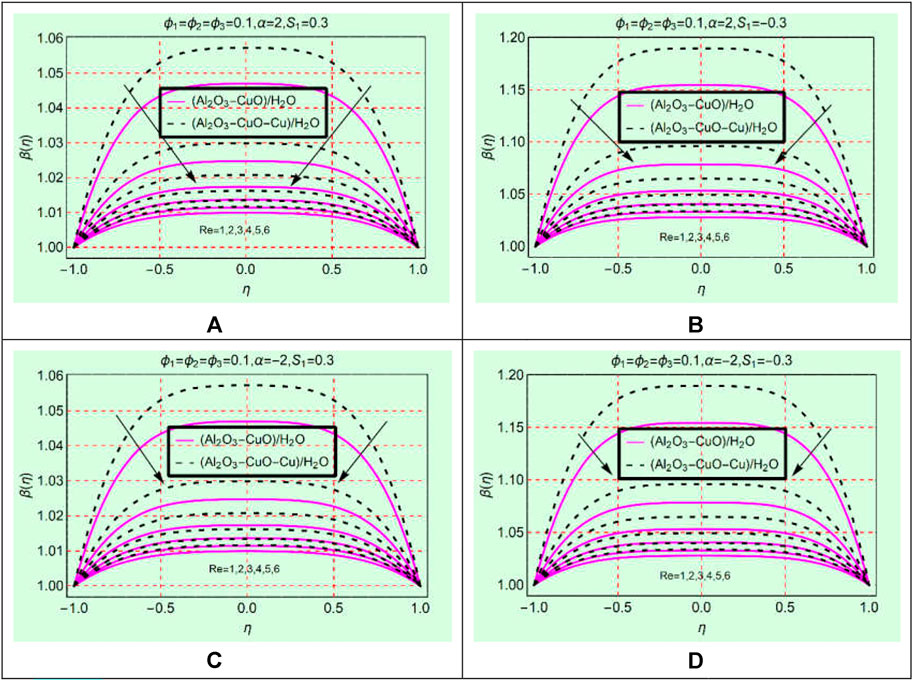
FIGURE 7.
Local energy storage in (Al2O3-CuO/water)hnf and (Al2O3-CuO-Cu/water)mhnf
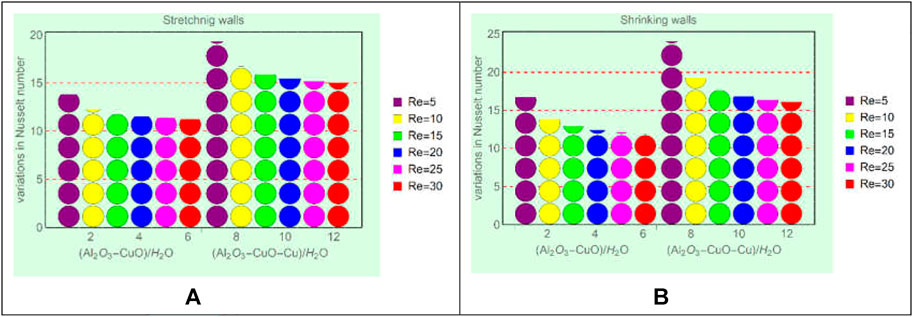
This subsection is devoted to analyzing the local energy storage in (Al2O3-CuO/H2O)hnf and (Al2O3-CuO-Cu/H2O)mhnf for varying flow parameters such as Ec, Re, and
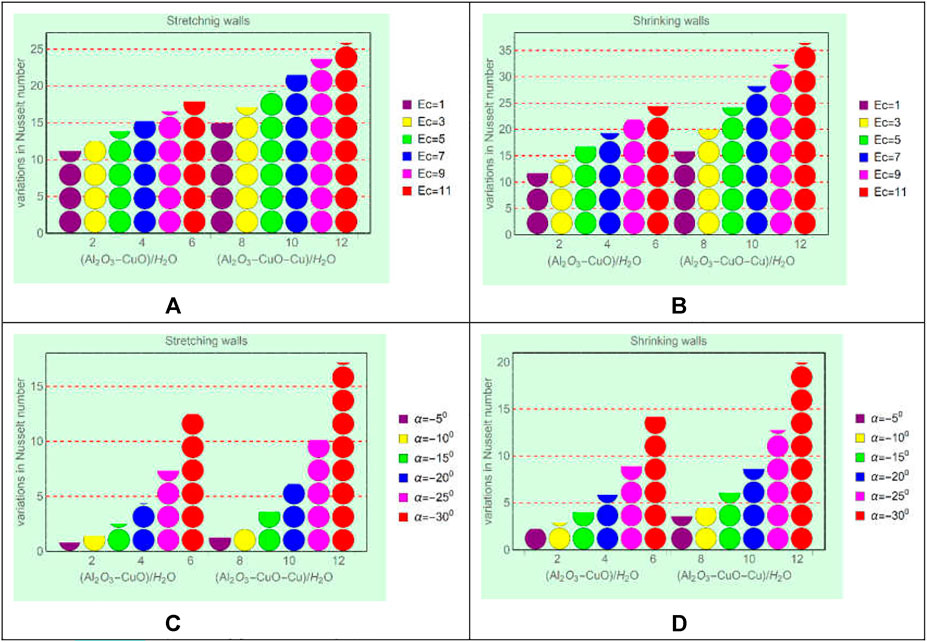
FIGURE 8. Local energy storage against (A) stretching and Ec, (B) shrinking and Ec, (C) stretching and
From Figures 8A–D, it is evident that the local energy storage in (Al2O3-CuO-Cu/H2O)mhnf is higher than that in (Al2O3-CuO/H2O)hnf. Physically, the ternary mixture of Al2O3, CuO, and Cu increases the thermal conductivity of (Al2O3-CuO-Cu/H2O)mhnf, while (Al2O3-CuO/H2O)hnf has low thermal conductivity due to the binary mixture of Al2O3 and CuO. Due to the high thermal conductance of (Al2O3-CuO-Cu/H2O)mhnf, the temperature increases rapidly. Moreover, imposed viscous dissipation effects provide extra energy to the fluid, which ultimately boosts the energy ability of (Al2O3-CuO-Cu/H2O)mhnf than (Al2O3-CuO/H2O)hnf. Similarly, from Figure 9, it can be seen that drops in the local energy storage in (Al2O3-CuO-Cu/H2O)mhnf is slower than (Al2O3-CuO/H2O)hnf. Therefore, modified hybrid nanofluids will be very effective for industrial and engineering applications because of their high energy storage capability.
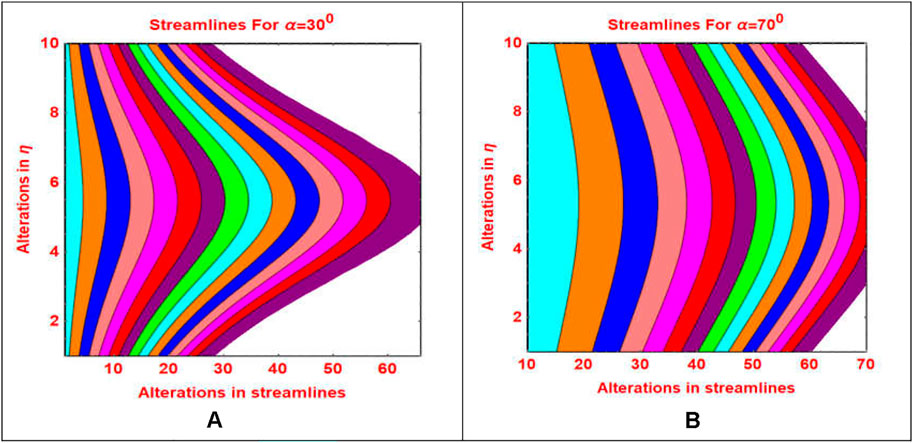
The streamlines pattern due to
Concluding remarks
The study of (Al2O3-CuO/H2O)hnf and (Al2O3-CuO-Cu/H2O)mhnf heat transfer fluids is organized between opening/narrowing channels. The channel walls are allowed to stretch/shrink to some physical extent. The model is developed via similarity and NS equations and then solved numerically. The results against the parameters that appeared due to physical phenomena are furnished and discussed deeply in the view of physics behind them. It is found that
• High Reynolds number causes backflow phenomena in the locality of channel walls, and maximum fluid motion is pointed out along the central line.
• The energy storage improved by strengthening viscous dissipation effects and reduces for multiple Re in the model.
• Ternary hybrid nanofluid (Al2O3-CuO-Cu/H2O)mhnf has outstanding heat transport than conventional hybrid due to the addition of the third particle’s volume concentration
• The optimum thermal behavior in both hybrid and ternary hybrid nanofluids is noticed for shrinking walls, and (Al2O3-CuO-Cu/H2O)mhnf is dominant over (Al2O3-CuO/H2O)hnf.
• The local Nusselt number is very high for ternary hybrid nanofluid at various locations inside the channel, and ultra-high thermal conductivity of trihybrid nanoparticles is a key element for this situation.
The presented study revealed that ternary hybrid nanofluid (Al2O3-CuO-Cu/H2O)mhnf has a high temperature featuring an under dissipation function and Reynolds number. Therefore, this class would play a vital role rather than normal hybrid and mono nanofluids in various industries to accomplish the products.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
A and WA formulated the model. A and UK solved the model and plotted the results. A and WA wrote the original draft. KG, ZR, ETE, and AG significantly contributed in revision process.
Acknowledgments
The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: 22UQU4331317DSR46. The author (ZR) extends her appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia, for funding this work through the Research Group Project Number (RGP.2/334/43).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abbasi, A., Al-Khaled, K., Khan, M. I., Khan, S. U., El-Refaey, A. M., Farooq, W., et al. (2021). Optimized analysis and enhanced thermal efficiency of modified hybrid nanofluid (Al2O3, CuO, Cu) with nonlinear thermal radiation and shape features. Case Stud. Therm. Eng. 28, 101425. doi:10.1016/j.csite.2021.101425
Ahmed, N., Adnan,, , Khan, U., Mohyud-Din, S. T., and Manzoor, R. (2017). Influence of viscous dissipation on a copper oxide nanofluid in an oblique channel: Implementation of the KKL model. Eur. Phys. J. Plus 132, 237. doi:10.1140/epjp/i2017-11504-y
Ahmed, N., Adnan,, , Mohyud-Din, S. T., Khan, U., Nisar, K. S., Baleanu, D., Khan, I., et al. (2020). A novel hybrid model for Cu–Al2O3/H2O nanofluid flow and heat transfer in convergent/divergent channels. Energies 13, 1686. doi:10.3390/en13071686
Ahmed, N., Mohyud-Din, S. T., Baleanu, D., Nisar, K. S., Khan, I., Sooppy Nisar, K., et al. (2021). Second law analysis of magneto radiative GO-MoS2/H2O–(CH2OH)2 hybrid nanofluid. Comput. Mater. Continua 68 (1), 213–228. doi:10.32604/cmc.2021.014383
Akinshilo, A. T., Ilegbusi, A., Ali, H. M., and Surajo, A. J. (2020). Heat transfer analysis of nanofluid flow with porous medium through Jeffery Hamel diverging/converging channel. J. Appl. Comput. Mech. 6 (3), 433–444. doi:10.22055/JACM.2019.29467.1601
Choi, S. U. S. (1995). Enhancing thermal conductivity of fluids with nanoparticles. ASME 66, 99–105.
Hamel, G. (1916). Spiralformige bewgungen zaher flussigkeiten. Jahresber. Dtsch. mathematiker-vereinigung 25, 34–60.
Jeffery, G. B. (1915). L. The two-dimensional steady motion of a viscous fluid. Lond. Edinb. Dublin Philosophical Mag. J. Sci. 629 (172), 455–465. doi:10.1080/14786440408635327
Khan, S. I., Khan, U., Ahmed, N., Mohyud-Din, S. T., Nisar, K. S., et al. (2021). Thermal transport investigation in AA7072 and AA7075 aluminum alloys nanomaterials based radiative nanofluids by considering the multiple physical flow conditions. Sci. Rep. 11, 9837. doi:10.1038/s41598-021-87900-w
Kumar, B., Seth, G. S., Singh, M. K., and Chamkha, A. J. (2021). Carbon nanotubes (CNTs)-based flow between two spinning discs with porous medium, Cattaneo–Christov (non-Fourier) model and convective thermal condition. J. Therm. Anal. Calorim. 146, 241–252. doi:10.1007/s10973-020-09952-w
Kumar, T. S. (2021). Hybrid nanofluid slip flow and heat transfer over a stretching surface. Partial Differ. Equations Appl. Math. 4, 100070. doi:10.1016/j.padiff.2021.100070
Kumbinarasaiah, S., and Raghunatha, K. R. (2022). Numerical solution of the Jeffery–Hamel flow through the wavelet technique. Heat. Trans. 51, 1568–1584. doi:10.1002/htj.22364
Mohyud-Din, S. T., Ahmed, N., Khan, U., Khan, I., Abdeljawad, T., Nisar, K. S., et al. (2020). Thermal transport investigation in magneto-radiative GO-MoS2/H2O-C2H6O2 hybrid nanofluid subject to cattaneo–christov model. Molecules 25, 2592. doi:10.3390/molecules25112592
Patel, H. S., and Meher, R. (2018). Analytical investigation of jeffery–hamel flow by modified adomian decomposition method. Ain Shams Eng. J. 9 (4), 599–606. doi:10.1016/j.asej.2016.02.007
Rout, H., Mohapatra, S. S., Shaw, S., Muhammad, T., Nayak, M. K., and Makinde, O. D. (2021). Entropy optimization for Darcy–Forchheimer electro-magneto-hydrodynamic slip flow of ferronanofluid due to stretching/shrinking rotating disk. Waves Random Complex Media. doi:10.1080/17455030.2021.1927238
Saeed, A., Jawad, M., Alghamdi, W., Nasir, S., Gul, T., and Kumam, P. (2021). Hybrid nanofluid flow through a spinning Darcy–Forchheimer porous space with thermal radiation. Sci. Rep. 11, 16708. doi:10.1038/s41598-021-95989-2
Shanmugapriya, M., Sundareswaran, R., and Kumar, P. S. (2021). Heat and mass transfer enhancement of MHD hybrid nanofluid flow in the presence of activation energy. Int. J. Chem. Eng., 2021, 9473226. doi:10.1155/2021/9473226
Sushila, S. J., and Shishodia, Y. S. (2014). A modified analytical technique for Jeffery–Hamel flow using sumudu transform. J. Assoc. Arab Univ. Basic Appl. Sci. 16, 11–15. doi:10.1016/j.jaubas.2013.10.001
Turkyilmazoglu, M. (2014). Nanofluid flow and heat transfer due to a rotating disk. Comput. Fluids 94, 139–146. doi:10.1016/j.compfluid.2014.02.009
Keywords: thermal energy storage, hybrid and modified hybrid nanofluids, thermophysical attributes, engineering applications, mathematical analysis, local energy storage
Citation: Adnan , Guedri K, Raizah Z, Tag-Eldin E, Ashraf W, Khan U and M. Galal A (2022) Thermal efficiency in hybrid (Al2O3-CuO/H2O) and tri-hybrid (Al2O3-CuO-Cu/H2O) nanofluids between converging/diverging channel with viscous dissipation function: Numerical analysis. Front. Chem. 10:960369. doi: 10.3389/fchem.2022.960369
Received: 02 June 2022; Accepted: 22 July 2022;
Published: 25 August 2022.
Edited by:
Hailong Wang, Ningxia University, ChinaCopyright © 2022 Adnan, Guedri, Raizah, Tag-Eldin, Ashraf, Khan and M. Galal. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Adnan, YWRuYW5fYWJiYXNpODlAeWFob28uY29t
 Adnan
Adnan Kamel Guedri2
Kamel Guedri2 Umar Khan
Umar Khan