
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Chem., 15 July 2022
Sec. Theoretical and Computational Chemistry
Volume 10 - 2022 | https://doi.org/10.3389/fchem.2022.951144
This article is part of the Research TopicFragment-Based Electronic Structure Methods for SolidsView all 4 articles
Embedded-cluster models of crystalline solids are important to allow accurate wave function methods to be applicable to solids. The ab-initio model potential method, in which the crystal is divided into three different fragments, one quantum fragment, one ab-initio model potential fragment and one point-charge fragment, has historically been shown to be a viable tool for describing the electronic structure in ionic solids. The optimal size of these regions is, of course, individual for each crystal. In this study we analyzed the convergence of the electronic structure properties with respect to an increase of the size of the quantum part and the layer of potentials. MgO crystal and Ni: MgO were used for this purpose as examples of an ideal crystal and a crystal with a point defect. We demonstrated that with an increase of the cluster size, the electron density in the inner part of the cluster becomes very similar to the electron density in the periodic model. Clusters, embedded into a layer of model potential and electrostatic field, are a good alternative to periodic description.
Metal oxides are important materials with many industrial applications in the areas of catalysis, glass manufacture, extractive metallurgy and many others (Jolivet et al., 2000; Di Cosimo et al., 2014; Arunadevi and Kirubavathy, 2022). Many metal oxides are characterized by highly ionic chemical bonds, which plays an important role in the properties of the materials and chemical reactions.
Alkali and alkaline earth metal oxides are good insulators with a very large optical gap, which makes them an ideal candidates for treatment by means of band theory in combination with density functional theory (DFT) (Schönberger and Aryasetiawan, 1995; Canney et al., 1999; Lany, 2014; Heo et al., 2015; Niedermeier et al., 2016). The interest to small alkaline earth metal oxides clusters is stimulated by a potential use of these materials for hydrogen storage (Srivastava et al., 2018; Mojica-Sánchez et al., 2019) and in biomedical applications (Awasthi et al., 2021). In the presence of dopants, for example, transition or rare metals in metal oxides (these compounds are most interesting from a scientific and industrial point of view), the electronic structure is much more complicated. First of all, in order to model a sparse distribution of the dopants in the host material, the unit cell has to be substantially increased to a so-called supercell. The accuracy of DFT might be insufficient to reproduce the electronic structure of highly correlated d- and f-elements. For these materials, the embedded cluster approach can be considered as an alternative to band structure calculations: 1) there is more flexibility in the selection of the size and the shape of a cluster, 2) the electronic structure calculations are not limited by DFT, but instead the full arsenal of accurate molecular methods from coupled cluster to multiconfigurational theory can be applied. These accurate methods provide a consistent way to include electron correlation effects, but only methods based on a single reference wavefunction were recently generalized for the periodic boundary conditions (Ayala et al., 2001; Hirata et al., 2004; McClain et al., 2017).
At the same time, DFT makes it possible to perform a detailed comparison between periodic models and cluster models of increasing size. Ideally, the inner part of a cluster should have the same electron density as in an infinite crystal. An increase of the cluster size should make the difference between the reference electron density (as in periodic model) and the electron density in the cluster smaller and smaller. In the current study we considered two systems: magnesium oxide (MgO) and magnesium oxide with sparse nickel substitution of magnesium atoms (Ni: MgO). Pure MgO is a wide gap insulator and thus one can expect very small dependence of the results on the amount k-points (or, similarly on the size of the supercell for a calculation with only the Γ point). For the cluster models, assuming non stoichiometric clusters made by the neighboring layers of atoms, there are two possibilities - clusters that are either centered at a magnesium atom or at an oxygen atom. Modeling sparse defects is different from modeling ideal crystals. Substitution of Mg to Ni in the cluster model (centered at magnesium atom) is a rather trivial change, but for periodic models it is necessary to increase the size of the supercell, in order to remove or reduce the interaction between dopant atoms.
The drawback of the cluster approach in electronic structure calculations is the cluster border. Using bare clusters, such as
Selection of clusters for ionic crystals is not an easy task. Stoichiometric clusters have complicated border structures and are generally not suitable for systems with a point defect. Clusters constructed by adding spheres of neighboring atoms starve from having an uncompensated electronic charge in the quantum region. Taking a cluster such as
The most reliable and straightforward method for construction of these potentials is AIMP (ab initio model potential) (Seijo and Barandiarán, 1999; Seijo and Barandiarán, 2013). In the Hartree-Fock equation, the Fock operator,
The MgO crystal has a rock-salt structure with 6 oxygen atoms surrounding a magnesium atom. We can build a set of clusters, centered on an atom, by adding the layers from the next neighbours. The smallest cluster has a composition MgO6. This cluster formally has a large electronic charge, however this charge will be compensated by terminating model potentials at the border and by a set of point charges, simulating the Madelung potential of a MgO crystal. Adding the next layer of neighboring atoms, we will get a cluster with composition MgO6Mg18, MgO6Mg18O38 and finally MgO6Mg18O38Mg66. One should not expect monotonic changes in local properties for these incrementally built clusters, since the electronic charge, associated with the quantum part, as well as the atoms on the border of the cluster are alternating between Mg and O depending on cluster size. The nomenclature of these clusters will be on the form
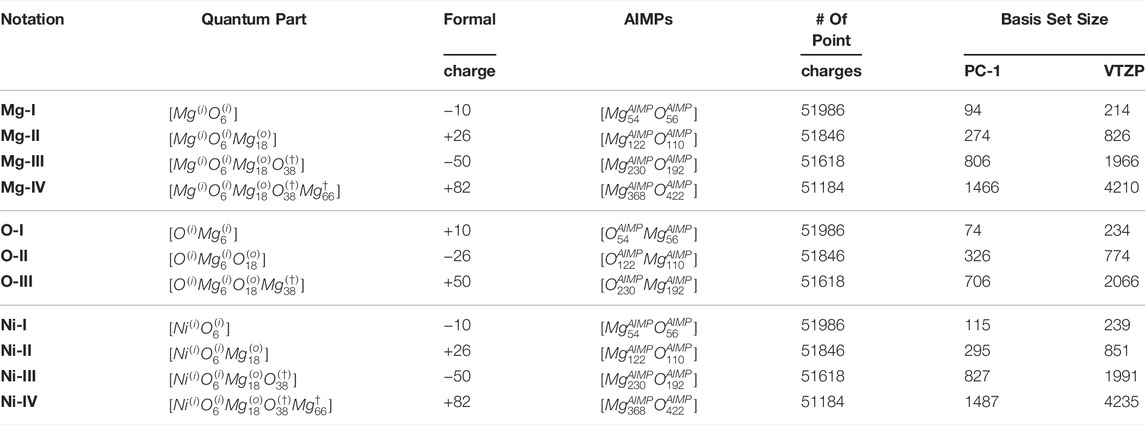
TABLE 1. Notations for the clusters, used in the study, indicating the quantum part, AIMPs and point charges. The basis set size is presented for PC-1 (used in the current study) and for a triple-ζ quality basis set.
Doping ionic metal oxides with transition metals or rare earth metals creates materials with interesting physicochemical properties. Many of these materials are active in chemical reactions, including catalytic. In practically interesting cases, the concentration of impurities is rather low. Ni: MgO is a compound where a Ni atom substitutes a Mg atom. Since the ionic radii of Mg2+ and Ni2+ are similar, we can construct corresponding clusters similar to those mentioned above with the center in magnesium atom. The smallest cluster, NiO6, has no Mg atoms at all, but the AIMP layer, as earlier, contains model potentials for magnesium and oxygen. The larger clusters will contain layer(s) of magnesium. In periodic model it is important to use relatively large supercells to provide a spatial separation between the defects.
Each cluster was surrounded by AIMPs up to a cutoff radius of the longest distance between two real atoms in the QM region plus the length of one unit-cell (4.26 Å) surrounding the central cluster, making the cluster plus AIMP-region spherical in shape. For instance, in
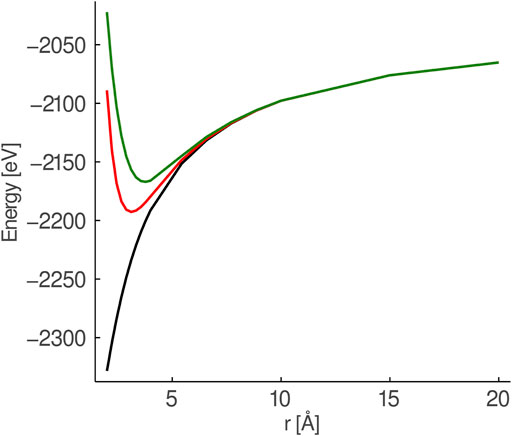
FIGURE 1. Comparison of the potential from a set of six point charges (black), six Mg2+-AIMPs (red) and six Ca2+-AIMPs (green) surrounding a O2−-ion. The surrounding charges/AIMPs are placed in an octahedral field and stretched symmetrically.
For the smallest cluster,

FIGURE 2. The structure of Mg-IV cluster. From left to right: the quantum part, AIMPs layer (model potentials are shown as pale spheres), point charges surrounding the embedded cluster.
All electronic structure calculations in this work utilized the Perdew–Burke–Ernzerhof (PBE) DFT functional with the pc-1 basis set Jensen, (2002). Cluster calculations were performed with OpenMolcas, with the embedding method described in Ref. Larsson et al. (2022). Periodic calculations were made with CP2K, using all-electron basis sets within the Gaussian and augmented plane wave (GAPW) framework, with a plane wave cutoff of 400 eV. The periodic calculations were based only on the Γ-point, using both a 2 × 2 × 2 supercell and a 3 × 3 × 3 supercell.
The electron density is a direct and a straightforward way to compare different cluster and periodic model calculations. Ideally, the electron density in a large enough cluster should be identical or close enough to the electron density obtained from a periodic calculation. Unphysical effects arising from the cluster–embedding border can be very strong and influence the central part of the quantum region. Simply increasing the cluster size might, however, not necessarily improve upon the results, as the number of broken bonds at the border of the cluster increases with cluster size. In principle, a large enough bare cluster would be the most realistic model of an ionic crystal. Unfortunately, the size required to reproduce the Madelung field from the extended crystal will in general prohibit such a route. One way to circumvent these problems is to use specially constructed potentials, designed to behave as similar as possible to the real atoms, at the border between the quantum region and the electrostatic embedding.
There are two options for comparing the electron density. First option includes the comparison of so-called local properties of the electronic structure: charges (Q), bond orders (W), covalency (C) and total valency (V). All these properties are computed from the population matrix (DS), where D is the density matrix and S is the overlap matrix. For molecular and cluster calculations the size of the matrix is determined by basis set size, but for periodic calculations it is determined by the basis set size in the supercell used in the calculation Veryazov et al. (1999). Although these properties depend on the atomic basis set, with a fixed basis set they can be used as an indicator of similarities between two electron densities. Atomic charges defined as a number of electrons, involved in ionic bonding and it is defined as a difference between nuclear charge ZA and the electron charge localized at the atomic region
To compute local properties from the wavefunctions produced by OpenMolcas and CP2K we used homemade scripts. For ionic crystals atomic charges are similar to formal charges, but never perfectly match them. The contributions to the covalent bonds are small and local: all bond indices between non-neighboring atoms are close to zero. It is important to compare the combination of all local properties to confirm the conclusion about the match between different electron densities.
Another alternative is to use spatial electron density ρ(r). Both OpenMolcas and CP2K can produce spatial electron density computed on a Cartesian grid. Since the electron density is a function of coordinates, the comparison can be performed in some arbitrary volume. For that purpose we used the union of seven spheres centered on the atomic positions of the MgO6 cluster, with radii of 1.6Å (3/4 of MgO bond length). This volume represents the density in the central part of the studied clusters, however for the smallest clusters (Mg-I, O-I) the border of this volume is too close to the cluster border. Different computational codes can use different approximations in computing electronic density in the regions close to atoms, for instance, the GAPW framework in CP2K, used in all-electron calculations, separate the electron density into a core (hard) density and valency (soft) density Ref Hutter et al. (1999). Only the valence region is dealt with in a similar fashion to standard molecular quantum chemistry codes, such as OpenMolcas. Thus, we removed spherical regions with the radius 0.8Å around each atom, which corresponds to the default value for the core density in CP2K.
Using Cartesian grid in the volume described above, we introduce the root mean square deviation (RMSD) of the density:
In this section we present the results for clusters centered on magnesium (Mg-I, Mg-II, Mg-III and Mg-IV) and clusters centered on oxygen (O-I, O-II, O-III). Calculation of the electronic structure of O-IV cluster diverges, for which reason it was excluded from this work. Periodic calculations were made for with both a 2 × 2 × 2 and a 3 × 3 × 3 MgO supercell.
The local properties of the electronic structure of MgO in periodic and embedded cluster models are presented in Table 2 Comparison of local properties between periodic calculations with different supercell sizes shows discrepancy for the individual descriptors, which one can consider as a threshold. For all local properties the difference is either in the second or in the third decimal point.
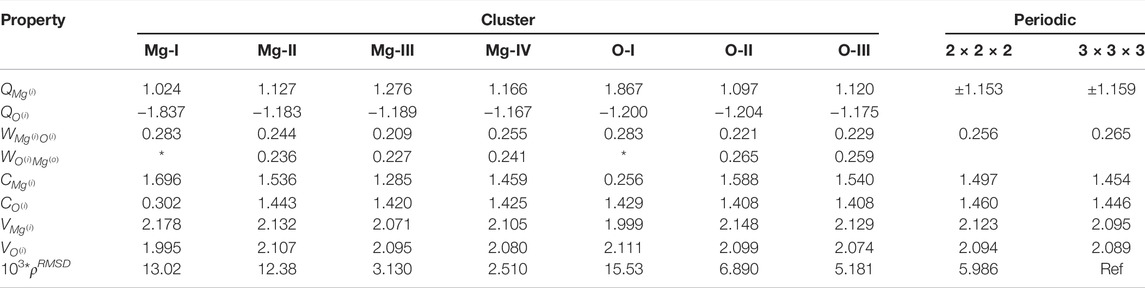
TABLE 2. Electronic structure of clusters with Mg- on O- center. Table showing the convergences of Mulliken charges (Q), Wiberg bond indices (W), covalency (C), total valency (V) and integrated density difference Δρ (multiplied by a factor of 103) with respect to periodic values. * indicates that the value is undefined for the particular cluster.
The smallest clusters, Mg-I and O-I have only one (central) atom with a proper atomic surrounding, thus, it is rather expected that the electronic structure even for the central region of these clusters is different within Mg-I–Mg-IV and O-I–O-III series. The atomic charge on the central Mg atom in Mg-I is 1.02e, while for larger clusters it is in the range 1.13–1.28 e. For the smallest clusters (Mg-I and O-I) the charges on the central atoms are ‘non symmetric’ for Mg in Mg-I it is 1.02 e, but for O in O-I it is −1.20 e. The difference between atomic charges on the central atoms for the larger clusters in by order of magnitude smaller (1.166 e for Mg-IV vs. −1.175 e for O-III). If we exclude the smallest clusters from consideration, the atomic charges are rather close to the charges in the periodic model. The difference between the absolute values of atomic charges on the central atom and on the nearest neighbor is also reducing with the increase of the cluster size. Increasing the cluster sizes from Mg-I to Mg-IV and from O-I to O-III does not result in a monotonic change in atomic charges. Instead of correlating with whether the central atom is Mg or O, the atomic charges correlate with the formal charge of the cluster. Thus, for a monotonic charge the clusters should be viewed in the order of Mg-I to O-II and finally Mg-III, which are all anionic clusters.
On the other hand, the variations of the atomic charges are relatively small: 0.02 e for oxygen atom in clusters O-II and O-III, and 0.1 e for Mg in clusters Mg-II–Mg-IV. The largest deviation is observed for Mg-III cluster, which in the quantum part has the largest negative charge.
The bond orders, also known as Wiberg indices, between Mg and O show only a small variation between clusters and they are similar to periodic values. Again the largest difference from the general trend is observed for the Mg-III cluster. Considering that the lowest bond index for Mg–O bond and largest atomic charge on Mg atom was obtained for the Mg-III cluster, we can conclude that this cluster is the has most ionic character of the clusters studied here. The covalency of central Mg atom in Mg-IV cluster (1.46) is almost the same as the covalency of Mg in periodic calculations (1.45). The covalency of O in O-II and O-III (1.41) is also close to corresponding value (1.45) in periodic calculations. Total valence of Mg and O in all clusters, except the smallest ones, is close to the corresponding values in periodic calculations.
In contrast, the RMSD of the electron density difference gave a smooth convergence towards the periodic limit for the central XY6 unit. For Mg-I, Mg-II and O-I clusters, the error is in the range of 0.012–0.015
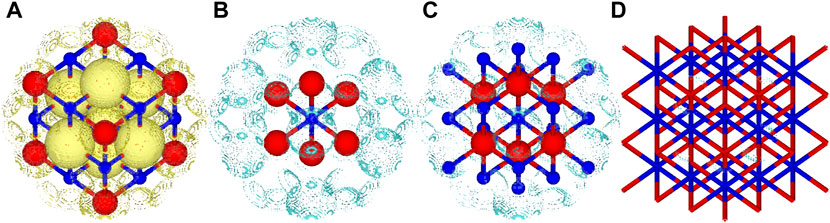
FIGURE 3. Total and difference density plots for MgO. (A) Total density retained from the 3 × 3 × 3 periodic calculation of MgO, only a small part of the total structure visualised for brevity, (B) density difference between the
Studies of single-ion dopants has been a major undertaking for AIMP studies. In this section, the convergence of the local electronic structure of Ni and O in Ni: MgO is presented. As in the previous sections, the results will be written for all three clusters on the order of Ni-I, Ni-II and Ni-III. We should note here that the calculations of these clusters were made with UHF Hamiltonian with triplet spin multiplicity. Periodic calculations were made by substituting a single Mg with Ni in both the 2 × 2 × 2 and 3 × 3 × 3 MgO supercells.
The local properties of the electronic structure of Ni: MgO in periodic and embedding cluster model are presented in Table 3. The difference between 2 × 2 × 2 and 3 × 3 × 3 periodic calculations is slightly larger, compared to pure MgO due to interaction between Ni atoms. Cluster models with a single nickel atom is free from this problem. Similar to MgO clusters, the smallest cluster (Ni-I) differs the most from the other clusters. The atomic charge on Ni increases when increasing the cluster size to Ni-II and Ni-III, but drops for the Ni-IV cluster, and becomes similar to the atomic charge in both periodic models. The atomic charge on Ni is smaller than the corresponding charge on Mg. But at the same time the covalent bonds between Ni–O are stronger than Mg–O bond. That results in larger, in comparison to Mg, covalency of nickel atom and the total valency 2.3. The ‘elevated’ total valency for nickel atom is not an unexpected result, since Ni atom can be found in different valence states Evarestov et al. (1994).
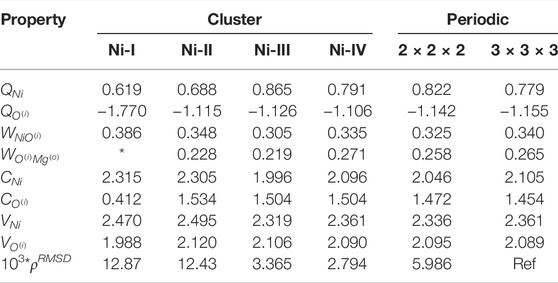
TABLE 3. Electronic structure of clusters Ni:MgO. Table showing the convergences of Mulliken charges (Q), Wiberg bond indices (W), covalency (C), total valency (V) and integrated density difference Δρ (multiplied by a factor of 103) with respect to periodic values. * indicates that the value is undefined for the particular cluster.
Comparison of electron density shows a similar trend as for MgO clusters. The electron density in Ni-I and Ni-II clusters is slightly different from density in the periodic calculations. But for the Ni-III and Ni-IV clusters, the difference is negligibly small.
In Figure 4, the projected density of states (PDOS) for Ni and O are plotted. The d-states of Ni are independent of the computational model used. In the α spin channel, the double peak closest to the Fermi level corresponds to the split between the t2g and eg Ni d-orbitals. Since no eg orbital is occupied in the β channel, there is only a single t2g peak near the Fermi level. The difference between the t2g and eg α peaks change as 0.72 eV, 0.67–0.69 eV when increasing the model size. From the periodic calculations, a split of 0.70 eV is predicted.
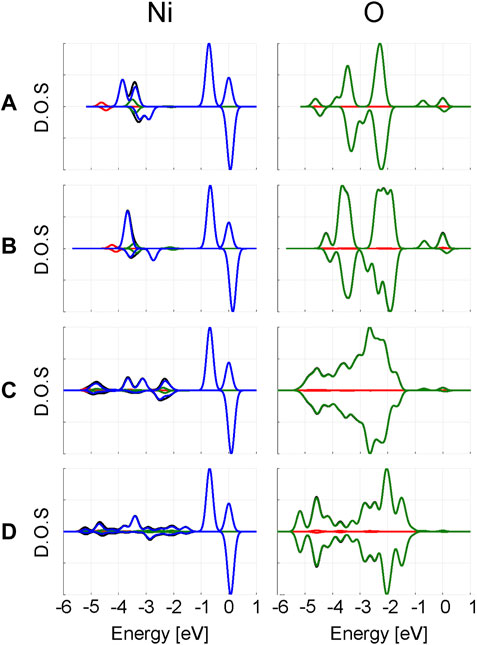
FIGURE 4. Projected density of states from clusters (A)
In addition to these two major peaks, there are several minor peaks at lower energies originating from the Ni d-orbitals. Comparison with the O PDOS at the same energy region suggests these are primarily caused by the Ni d-functions acting as additional polarizing basis functions for the oxygen p-band. Overall, larger changes are visible in the O PDOS compared to the Ni PDOS; primarily a broadening of the PDOS is observed when increasing the cluster size. This is an expected consequence of including more “real” oxygens in the model.
The advantage of embedded cluster model in comparison to periodic model is that all methods used in molecular quantum chemistry can be applied. It is very important for the properties, involving excited states, in particular excitation spectra. In Larsson et al. (2022) we presented the vibronic d–d transition in Ni: MgO, which was modeled as Ni-II embedded cluster. There, it was demonstrated that when using multiconfigurational theory and appropriate basis sets (ANO-RCC), the experimental spectrum of Ni: MgO could be reproduced to within 1000 cm−1 on average.
Obviously, one advantage of a material such as MgO is that, in comparison to transition metal oxides (e.g., TiO2), it is a relatively simple material. Adding additional layers of Mg or O does not increase the number of orbitals that might influence, for instance, the spectrum of single ion dopants. In materials like TiO2, the presence of valence d-orbitals, even if they are formally empty, potentially complicates the picture dramatically. More extensive studies are necessary to verify the applicability of multiconfigurational methods in such systems. At the present, the AIMP methodology is presented as a straightforward and accurate way of modelling ionic materials made from s or p group elements.
The computational cost to compute DFT density for these clusters consists of computing the integrals (in the compact form of RI/CD technique implemented in OpenMolcas) and self consistent field iterations. Even with the use of RI/CD technique the size of the temporary disk space is large and can easily reach several hundreds of Gb. The calculation of integrals is approximately one third of the total time. The size of AIMPs and electrostatic field has no effect on the timing. All calculations were performed at Tetralith cluster, with Intel Xeon Gold 6130 CPU and SSD hard drive. The calculations with 8 cores of Mg-I cluster take less than a minute, Mg-II—2 min, Mg-III—14 min and finally Mg-IV—2 h. The total timing also depends on the convergence of the optimal wavefunction. We should note here that a calculation with the periodic boundary conditions (performed with CP2K code with the same basis set and the same computational setup) takes even longer time. The computational resources will increase if a more accurate basis will be used, see Table 1. Using multiconfigurational theory for accurate calculations of the electronic structure will increase the timing in the order of magnitude.
Using PBE Hamiltonian and a relatively small basis set we investigated the convergence of the electron density with an increase of the size of embedded clusters. The results shown herein demonstrate that good agreement in both local properties and spatial electron density can be achieved for moderately sized clusters using AIMP embedding. Using the spatial electron density to assess the clusters gives a clearer convergence with increasing cluster size, compared to the local properties. One advantage with the local properties, however, is that they are generally faster to compute and therefore give an important first quality check of the clusters.
The smallest clusters considered accurate here (Mg-II, O-II and Ni-II) all achieve the following two criteria: 1) no single element in the material is described only by AIMPs and 2) in the central region, the co-ordination of all ions are completely saturated. This suggests that in future studies, minimal clusters should be constructed based on such criteria.
While the largest discrepancies were noted for the most anionic clusters (Mg-III and Ni-III, both with a formal charge of −50 e), the values are seemingly not far enough from periodic values to completely invalidate the use of anionic clusters with AIMPs. Even more anionic clusters, however, seem to give poor convergence and are thus discouraged from use in production calculations.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
VV thanks eSSENCE@LU grant 7:3 for financial support.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
We acknowledge support from Swedish National Infrastructure for Computing (SNIC). The computations were enabled by resources provided by SNIC at Tetralith partially funded by the Swedish Research Council through grant agreement no. 2018-05973 and LUNARC computer center.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2022.951144/full#supplementary-material
Abarenkov, I. V. (2007). Unit Cell for a Lattice Electrostatic Potential. Phys. Rev. B 76, 165127. doi:10.1103/physrevb.76.165127
Armstrong, D. R., Perkins, P. G., and Stewart, J. J. P. (1973). Bond Indices and Valency. J. Chem. Soc. Dalton Trans., 838–840. doi:10.1039/dt9730000838
Arunadevi, N., and Kirubavathy, S. J. (2022). “Chapter 2 - Metal Oxides: Advanced Inorganic Materials,” in Inorganic Anticorrosive Materials. Editors C. Verma, J. Aslam, and C. M. Hussain (Elsevier), 21–54. doi:10.1016/b978-0-323-90410-0.00002-7
Awasthi, S., Pandey, S. K., Arunan, E., and Srivastava, C. (2021). A Review on Hydroxyapatite Coatings for the Biomedical Applications: Experimental and Theoretical Perspectives. J. Mater. Chem. B 9, 228–249. doi:10.1039/d0tb02407d
Ayala, P. Y., Kudin, K. N., and Scuseria, G. E. (2001). Atomic Orbital Laplace-Transformed Second-Order Møller-Plesset Theory for Periodic Systems. J. Chem. Phys. 115, 9698–9707. doi:10.1063/1.1414369
Barandiarán, Z., and Seijo, L. (1988). The Ab Initio Model Potential Representation of the Crystalline Environment. Theoretical Study of the Local Distortion on NaCl:Cu+. J. Chem. Phys. 89, 5739–5746. doi:10.1063/1.455549
Canney, S. A., Sashin, V. A., Ford, M. J., and Kheifets, A. S. (1999). Electronic Band Structure of Magnesium and Magnesium Oxide: Experiment and Theory. J. Phys. Condens. Matter 11, 7507–7522. doi:10.1088/0953-8984/11/39/308
Di Cosimo, J. I., Díez, V. K., Ferretti, C., and Apesteguía, C. R. (2014). Chapter 1 Basic Catalysis on MgO: Generation, Characterization and Catalytic Properties of Active Sites. Catalysis 26, 1–28. doi:10.1039/9781782620037-00001
Evarestov, R. A., Tupitsin, I. I., and Veryazov, V. A. (1994). Quantum Chemical Calculation of Nickel and Copper Atomic Valencies in Crystalline Oxides. Int. J. Quantum Chem. 52, 295–299. doi:10.1002/qua.560520204
Evarestov, R. A., and Veryazov, V. A. (1991). Quantum-chemical Definition of the Atomic Valence in Molecules and Crystals. Theor. Chim. Acta 81, 95–103. doi:10.1007/bf01113380
Heo, S., Cho, E., Lee, H.-I., Park, G. S., Kang, H. J., Nagatomi, T., et al. (2015). Band Gap and Defect States of MgO Thin Films Investigated Using Reflection Electron Energy Loss Spectroscopy. AIP Adv. 5, 077167. doi:10.1063/1.4927547
Hirata, S., Podeszwa, R., Tobita, M., and Bartlett, R. J. (2004). Coupled-cluster Singles and Doubles for Extended Systems. J. Chem. Phys. 120, 2581–2592. doi:10.1063/1.1637577
Hutter, J., Parrinello, M., and Lippert, G. (1999). The Gaussian and Augmented-Plane-Wave Density Functional Method for Ab Initio Molecular Dynamics Simulations. Theor. Chem. Accounts 103, 124–140. doi:10.1007/s002149900042
Jensen, F. (2002). Polarization Consistent Basis Sets. II. Estimating the Kohn–Sham Basis set Limit. J. Chem. Phys. 116, 7372–7379. doi:10.1063/1.1465405
Jolivet, J.-P., Henry, M., and J, L. (2000). Metal Oxide Chemistry and Synthesis: From Solution to Solid State. Chichester, UK: Wiley.
Lany, S. (2014). “Polymorphism, Band-Structure, Band-Lineup, and Alloy Energetics of the Group II Oxides and Sulfides MgO, ZnO, CdO, MgS, ZnS, CdS,” in Oxide-based Materials and Devices V. Editors F. H. Teherani, D. C. Look, and D. J. Rogers (International Society for Optics and Photonics SPIE). doi:10.1117/12.2043587
Larsson, E. D., Krośnicki, M., and Veryazov, V. (2022). A Program System for Self-Consistent Embedded Potentials for Ionic Crystals. Chem. Phys., 111549. doi:10.1016/j.chemphys.2022.111549
McClain, J., Sun, Q., Chan, G. K.-L., and Berkelbach, T. C. (2017). Gaussian-based Coupled-Cluster Theory for the Ground-State and Band Structure of Solids. J. Chem. Theory Comput. 13, 1209–1218. doi:10.1021/acs.jctc.7b00049
Mojica-Sánchez, J. P., Zarate-López, T. I., Flores-Álvarez, J. M., Reyes-Gómez, J., Pineda-Urbina, K., and Gómez-Sandoval, Z. (2019). Magnesium Oxide Clusters as Promising Candidates for Hydrogen Storage. Phys. Chem. Chem. Phys. 21, 23102–23110. doi:10.1039/c9cp05075b
Niedermeier, C. A., Råsander, M., Rhode, S., Kachkanov, V., Zou, B., Alford, N., et al. (2016). Band Gap Bowing in NixMg1−xO. Sci. Rep. 6, 31230. doi:10.1038/srep31230
Schönberger, U., and Aryasetiawan, F. (1995). Bulk and Surface Electronic Structures of MgO. Phys. Rev. B 52, 8788–8793. doi:10.1103/physrevb.52.8788
Seijo, L., and Barandiarán, Z. (1999). The Ab Initio Model Potential Method: A Common Strategy for Effective Core Potential and Embedded Cluster Calculations. Comput. Chem. Rev. Curr. Trends 4, 55–152. doi:10.1142/9789812815156_0002
Seijo, L., and Barandiarán, Z. (2013). Host Effects on the Optically Active 4f and 5d Levels of Ce3+ in Garnets. Phys. Chem. Chem. Phys. 15, 19221–19231. doi:10.1039/c3cp53465k
Shi, B. X., Kapil, V., Zen, A., Chen, J., Alavi, A., and Michaelides, A. (2022). General Embedded Cluster Protocol for Accurate Modeling of Oxygen Vacancies in Metal-Oxides. J. Chem. Phys. 156, 124704. doi:10.1063/5.0087031
Srivastava, A. K., Misra, N., and Pandey, S. K. (2018). DFT Study on Planar (CaO) N Rings (N = 1-5) and Their Hydrogen Storage Behavior: Ca-O versus Mg-O Clusters. J. Clust. Sci. 29, 57–65. doi:10.1007/s10876-017-1306-x
Sushko, P. V., and Abarenkov, I. V. (2010). General Purpose Electrostatic Embedding Potential. J. Chem. Theory Comput. 6, 1323–1333. doi:10.1021/ct900480p
Veryazov, V. A., Leko, A. V., and Évarestov, R. A. (1999). Local Characteristics of Crystal Electronic Structure in the Hartree-Fock Method. Phys. Solid State 41, 1286–1290. doi:10.1134/1.1130983
Keywords: ionic solids, ab initio model potential, embedded clusters, fragment approach, electronic structure, valency
Citation: Larsson ED and Veryazov V (2022) Convergence of Electronic Structure Properties in Ionic Oxides Within a Fragment Approach. Front. Chem. 10:951144. doi: 10.3389/fchem.2022.951144
Received: 23 May 2022; Accepted: 23 June 2022;
Published: 15 July 2022.
Edited by:
Oleksandr Loboda, AC2T Research, AustriaReviewed by:
Ahmet Altun, Max Planck Institute for Coal Research, GermanyCopyright © 2022 Larsson and Veryazov. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Valera Veryazov, dmFsZXJhLnZlcnlhem92QHRlb2tlbS5sdS5zZQ==
†These authors have contributed equally to this work and share first authorship
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.