Strategies to Improve the Thermoelectric Figure of Merit in Thermoelectric Functional Materials

In recent years, thermoelectric functional materials have been widely concerned in temperature difference power generation, electric refrigeration and integrated circui, and so on. In this paper, the design and research progress of thermoelectric materials around lifting ZT value in recent years are reviewed. Optimizing the carrier concentration to improve the Seebeck coefficient, the steady improvement of carrier mobility and the influence of energy band engineering on thermoelectric performance are discussed. In addition, the impact of lattice thermal conductivity on ZT value is also significant. We discuss the general law that the synergistic effect of different dimensions, scales, and crystal structures can reduce lattice thermal conductivity, and introduce the new application of electro-acoustic decoupling in thermoelectric materials. Finally, the research of thermoelectric materials is summarized and prospected in the hope of providing practical ideas for expanding the application and scale industrialization of thermoelectric devices.

Introduction

With the progress of society, energy and environmental issues have become the most severe challenges for humanity in the new era. Especially for fossil energy, the large amount of waste heat generated in the combustion process cannot be reused, and the energy utilization rate is meager (Vining, 2009). To solve this problem, the research of a thermoelectric functional material that directly converts heat energy and electric energy to each other has received extensive attention. With their small size, high reliability, long life, high temperature sensitivity, and environmental friendliness, thermoelectric materials (TE) have become a current research hotspot (Figure 1). It is now mainly used in crucial new energy directions such as space probes, industrial waste heat utilization, and solar composite power generation (Poudel et al., 2008; Suarez et al., 2016). Since the middle of the last century, the performance of TE materials has been dramatically improved, which is the key to improving the energy conversion efficiency of TE devices. Solid-state TE devices can not only use the Seebeck effect to convert heat into electricity but also the Peltier effect to provide cooling.

FIGURE 1

FIGURE 1. Application and working mechanism of thermoelectric materials in aerospace.

The energy conversion efficiency of TE material power generation equipment is defined as the output electric energy (P) divided by the provided thermal energy (Q) (Yang and Caillat, 2006):

$\eta =\frac{P}{Q}=\frac{\mathrm{\Delta }T}{T_H}\left(\frac{\sqrt{1+\overline{ZT}}-1}{\sqrt{1+\overline{ZT}}+\frac{T_C}{T_H}}\right)(1)$

Where T_H is hot end temperature, T_C is cold end temperature, and ΔT is temperature difference, respectively. ZT is the average value of thermoelectric properties, which can be used as a dimensionless parameter to measure the properties of TE materials:

$ZT=\left(S^2\sigma /{\kappa }_e+{\kappa }_L\right)T(2)$

where S is the Seebeck coefficient, σ is the conductivity of the material, к_e is electronic thermal conductivity, к_L is lattice thermal conductivity, and T is the absolute temperature. Obviously, the larger the ZT value, the better the thermoelectric properties of the material. However, there is an intricate relationship between the Seebeck coefficient, electrical conductivity, and thermal conductivity, making it difficult for the thermoelectric figure of merit to be significantly improved for a long time (Bell, 2008; Snyder and Toberer, 2011). Therefore, our primary goal is to improve the electrical transmission performance (S²σ) of the material and reduce its heat transmission performance (к) through the coupling regulation of electrical transmission and heat transmission. According to Wiedemann-Franz law к_e=LσT, where L is the Lorentz constant. It can be seen that there is a positive correlation between electronic thermal conductivity and electrical conductivity. Therefore, as long as the thermal conductivity of the lattice with a small correlation is reduced, the thermoelectric figure of merit can be effectively optimized (Biswas et al., 2012; Zhao et al., 2014a; Kim et al., 2015; Li et al., 2017). Figure 2 summarizes the ZT statistical results of some typical TE materials in recent years (Ioffe et al., 1959; Cutler et al., 1964; Hicks and Dresselhaus, 1993; Horbach et al., 2001; Yang et al., 2001; Dashevsky et al., 2002; Kuznetsov et al., 2002; Hsu et al., 2004; Shutoh and Sakurada, 2005; Heremans et al., 2008; Poudel et al., 2008; Wang et al., 2008; Yang et al., 2008; Zhao et al., 2008; Xie et al., 2009; Du et al., 2011; Levin et al., 2011; Pei et al., 2011; Li et al., 2012; Liu et al., 2012; Chen et al., 2013; Gelbstein et al., 2013; Sui et al., 2013; Yamini et al., 2013; Yan et al., 2013; Hu et al., 2014; Lee et al., 2014; Tan et al., 2014; Wu et al., 2014; Zhao et al., 2014a; Zhao et al., 2014b; Zhong et al., 2014; Kim et al., 2015; Kraemer et al., 2015; Tan et al., 2015a; Tang et al., 2015; Huang et al., 2016; Liu et al., 2016; Tan et al., 2016a; Liu et al., 2017; Roychowdhury et al., 2017; Zhang et al., 2017; Li et al., 2018; Ren et al., 2018; Zhou et al., 2018; Xiang et al., 2019; Chong et al., 2020; Feng et al., 2020; Qin et al., 2020; Yvenou et al., 2020; Selimefendigil et al., 2021; Su et al., 2022).

FIGURE 2

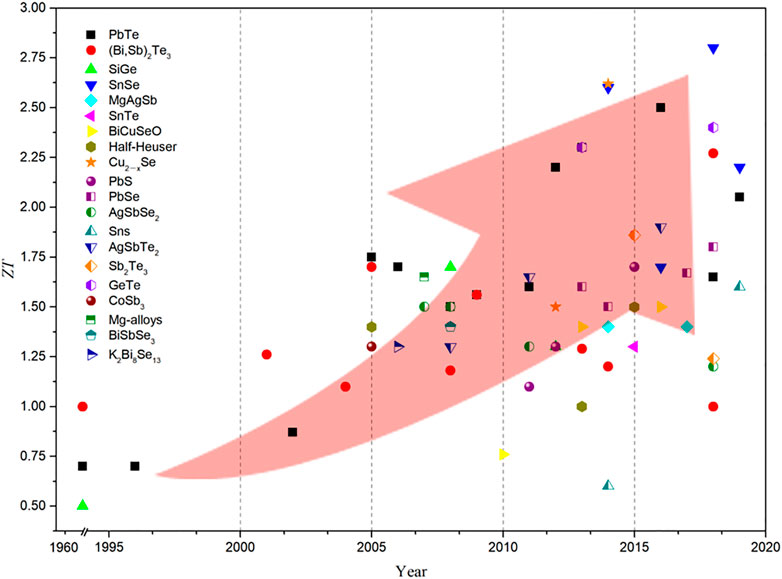
FIGURE 2. The figure of merit of TE, thermoelectricity in recent years (Ioffe et al., 1959; Cutler et al., 1964; Hicks and Dresselhaus, 1993; Horbach et al., 2001; Yang et al., 2001; Dashevsky et al., 2002; Kuznetsov et al., 2002; Hsu et al., 2004; Shutoh and Sakurada, 2005; Heremans et al., 2008; Poudel et al., 2008; Wang et al., 2008; Yang et al., 2008; Zhao et al., 2008; Xie et al., 2009; Bergum et al., 2011; Du et al., 2011; Levin et al., 2011; Pei et al., 2011; Li et al., 2012; Liu et al., 2012; Chen et al., 2013; Gelbstein et al., 2013; Sui et al., 2013; Yamini et al., 2013; Yan et al., 2013; Hu et al., 2014; Lee et al., 2014; Tan et al., 2014; Wu et al., 2014; Zhao et al., 2014a; Zhao et al., 2014b; Zhong et al., 2014; Kim et al., 2015; Kraemer et al., 2015; Tan et al., 2015a; Tang et al., 2015; Liu et al., 2016; Tan et al., 2016a; Liu et al., 2017; Roychowdhury et al., 2017; Zhang et al., 2017; Chang et al., 2018; Li et al., 2018; Zhou et al., 2018; Xiang et al., 2019; Chong et al., 2020; Feng et al., 2020; Qin et al., 2020; Yvenou et al., 2020; Selimefendigil et al., 2021; Su et al., 2022).

Figure 2 shows that the thermoelectric materials studied mainly include tellurides, layered chalcogenide compounds, oxides, clathrates, Half-Heusler, skutterudite, and copper chalcogenides. For example, telluride itself has good low thermal conductivity and is potential thermoelectric material. Kim et al. (2015) synthesized Bi_0.5Sb_1.5Te₃ by liquid-phase compression. The dense array of dislocations formed at the low-energy grain boundaries effectively scattered intermediate-frequency phonons, leading to a significant decrease in lattice thermal conductivity. The full-spectrum phonon scattering significantly increases the ZT to 1.86 at 320 K. Alkaline Earth oxides, such as cobalt compounds, have weak crystal symmetry and are also characterised by layered materials, which leads to a decrease in the lattice thermal conductivity of the material (Tang et al., 2015). The Cu₂Se of the copper chalcogenide has a layered monoclinic crystal structure at low temperatures, and its symmetry is also poor. At the same time, Cu ions can migrate freely in the sublattice like a liquid at high temperatures. The liquid-phase metal ions induce a specific deformation of the crystal structure and a significant increase in asymmetry, which facilitates the acquisition of solid anharmonicity and increases the phonon scattering ability, while having no effect on the electron mobility (Gelbstein et al., 2013). Zhong et al. (2014) used DC hot pressing process to prepare layered flake Cu_1.94Al_0.02Se, found that under the linkage of the disordered movement of the liquid phase of the Cu ion layer and the low symmetry, a maximum ZT value of 2.62 appeared. And SnSe, BiCuSeO, GeTe, and other materials have also found great thermoelectric figures of merit in recent studies (Gelbstein et al., 2013; Sui et al., 2013; Zhao et al., 2014a; Li et al., 2018; Qin et al., 2020). These materials are expected to further improve thermoelectric performance through methods, such as further parameter optimization, nanostructure design, and tape structure engineering.

For today’s rapid development of modern technology, it is necessary to improve the ZT value of thermoelectric materials through different strategies. It has been shown that the strategy to improve the ZT value are mainly focused on the design of defect engineering. The first one is the energy band engineering design by adding atomic or second phase doping (Bell, 2008; Pei et al., 2011), which is done to optimize the carrier concentration and to increase the carrier mobility and thus obtain a more significant power factor. The doping process inevitably introduces lattice defects and distortions, which greatly affect the physical properties of the material. It is worth noting that the electric field, magnetic field, and light radiation can also stimulate and control the carrier concentration by cooperating with thermal energy transmission (Horbach et al., 2001; Du et al., 2011; Levin et al., 2011; Chen et al., 2013; Kraemer et al., 2015). The second is to rely on phonon engineering through nanostructures of different scales or mesoscale materials to reduce the lattice thermal conductivity к_L through phonon scattering at the interface and crystal plane (Heremans et al., 2008; Biswas et al., 2012; Tan et al., 2014). Here we review recent advances in several aspects of thermoelectric materials, such as carrier concentration, carrier mobility, effective mass, lattice thermal conductivity and evidence of low thermal conductivity materials, and then summarise the effects of electro-acoustic decoupling effects on thermoelectric materials, finding commonalities in these materials through the above sections and refining rational design strategies for exploring materials with high thermoelectric efficiency.

Adjustments of Carrier Parameters to Improve ZT

Carrier Concentration

The fundamental challenge of high ZT thermoelectric material design stems from S, σ, and к. Through the strong correlation of carrier concentration n, the energy level can generally be adjusted by controlling the doping. Assuming that the dopant does not significantly change the scattering or band structure, the Seebeck coefficient can be derived from (Cutler et al., 1964):

$S=\frac{8{\pi }^2{k}_B^2}{3e{h}^2}{m}^{\ast }T{\left(\frac{\pi }{3n}\right)}^{2/3}(3)$

Among them, k_B is Boltzmann’s constant, m* is the effective carrier mass, h is Planck’s constant, and n is the carrier concentration. In semiconductor thermoelectric materials, according to the Kane energy band theory, the Hall carrier concentration can be expressed as (Ioffe et al., 1959; Cutler et al., 1964):

$n_H=\frac{1}{e{R}_H}=A^{-1}\frac{N_v{\left(2m_b^{\ast }{k}_{B}T\right)}^{3/2}}{3{\pi }^2{h}^3}{F}_0^{3/2}(4)$

where N_v is the degree of degeneration, ⁰F₀ is the Fermi integral function, which is the reduced Planck constant. Although the carrier concentration n has an inverse relationship with the Seebeck coefficient, the increase of n has a positive effect on the energy band degeneration and the increase of effective mass. Therefore, the current strategy of optimizing carrier concentration usually adopts the increasing carrier Concentration method to improve thermoelectric performance (Dashevsky et al., 2002; Kuznetsov et al., 2002; Pei et al., 2011).

The main strategy for optimizing the carrier concentration is doping, such as modulation doping, uniform doping, and gradient doping (Figure 3). Feng et al. (2020) systematically revealed the theoretical origin of high average ZT in GeTe-based alloys uniformly doped with Pb through theoretical simulations and experimental tests on GeTe-based alloys. On the one hand, the intrinsic high hole carrier density is reduced to a rough optimal range, and then the carrier density is fine-tuned by Pb doping. The lead-doped energy band convergence can maintain a higher power factor. On the other hand, lead causes a decrease in carrier density and can significantly reduce κ, and the combination of the two is almost the same. PF results in a maximum ZT at the corresponding carrier density, so that the average ZT is about 1.5 in the 300–773 K range and the peak ZT is about 2.0 at 573 K, indicating that Pb doping can be used over a wide temperature range (e.g., 300–800 K), rather than only for TE applications at higher temperatures (e.g., T > 600 K) (Feng et al., 2020). In the case of uniform doping, the carrier concentration is generally independent of temperature, so the best thermoelectric performance cannot be guaranteed in the entire temperature range. One way to deal with this problem is to use gradient doping. By integrating two or more different segments, a common method of preparing this graded material is the so-called spark plasma sintering or hot-pressed powder layer. Each powder layer has different carrier concentration (Dashevsky et al., 2002; Selimefendigil et al., 2021). Zhao et al. (2014c) take advantage of the low thermal conductivity of layered materials in the out-layer direction. The migration of carriers between layers is improved in the out-layer direction by adjusting the symmetry of the crystal structure, thereby promoting electron tunneling in the inter-layer direction. At 600–800 K, SnSe has a continuous phase transition process from low-symmetry Pnma (L-Pnma) phase to high-symmetry Pnma (H-Pnma) phase, and then to high-temperature high-symmetry Cmcm phase. In addition to temperature, introducing stress into SnSe crystals by doping/solid solution can also adjust the symmetry of the crystal structure, thereby optimizing the thermoelectric properties of the material, as shown in Figure 4 (Su et al., 2022).

FIGURE 3

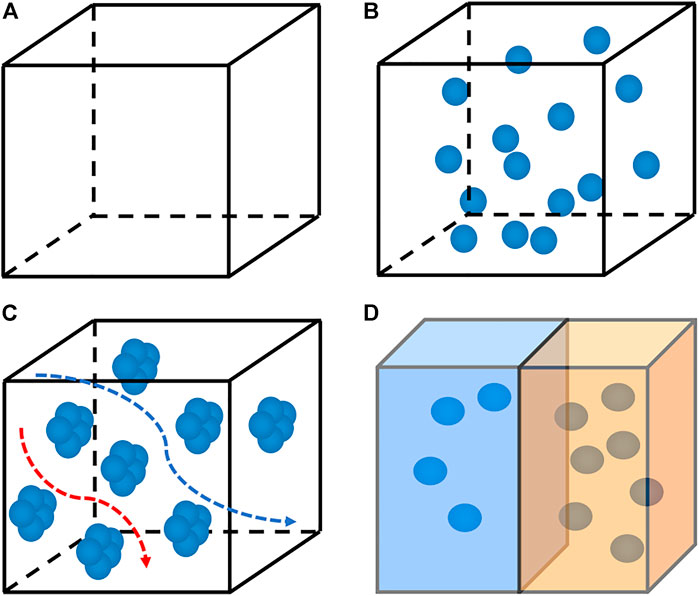
FIGURE 3. The schematic diagram of changing the carrier concentration by different doping methods; (A) undoped; (B) uniform doping; (C) modulated doping; (D) gradient doping.

FIGURE 4

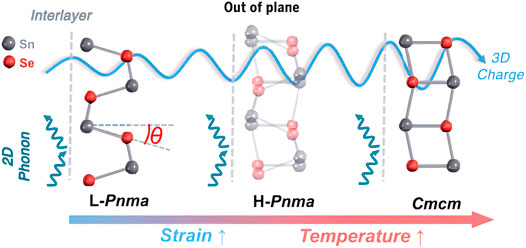
FIGURE 4. 3D electron-2D phonon transport properties outside the n-type SnSe layer: Layered SnSe crystals use their layer structure to suppress (lattice vibration) phonon transport, but electrons different from phonons can tunnel through overlapping electron orbital transport (Su et al., 2022).

However, with prolonged use, the initial carrier concentration gradient in the gradient material may decrease or disappear due to the homogenization effect induced by diffusion, thereby reducing the conversion efficiency. To solve this limitation, using the temperature dependence of the solubility of certain specific dopants (Yamini et al., 2013), a carrier concentration n is controlled only by temperature, and its gradient can be created in a single material. A well-known example is Cu, Ag, and excess Pb. They have negligible solubility in PbTe at room temperature but have high solubility at high temperatures (Bergum et al., 2011). Lidong Zhao et al. synthesized an n-type SnSe crystal with a two-dimensional layered structure using the temperature gradient method and bromine doping method. The electron doping promotes the hybridization of delocalized electrons and realizes the tunneling of electrons between the n-type SnSe layers. This “two-dimensional phonon/three-dimensional charge” transfer characteristic greatly improves the thermoelectric properties of n-type SnSe crystal materials, with a ZT as high as 2.8 (Chang et al., 2018). This temperature-dependent doping is reversible in the heating-cooling process and eliminates the diffusion problem of gradient doping, making it more suitable for practical applications. Polyatomic doping takes advantage of the synergistic effect to have a more significant change in carrier concentration (Zhu et al., 2002). Lixia Zhang et al. fabricated the Yb-filled CoSb₃ skutterudites with an ultra-high Yb filling fraction by melt-spinning methods, and they found a high ZT value of about 1.3 was achieved at 823 K for the nominal composition Yb_0.4Co₄Sb₁₂. An ultra-low lattice thermal conductivity approaching the glass limit was achieved due to the enhanced rattling effect from the ultra-high Yb filling fraction and extra phonon scattering from the ordered superstructures, nano-scale inhomogeneous Yb fillers, and high-density lattice strain caused by the ordered and modulated fillers (Ren et al., 2021). Shi et al. (2011) synthesized CoSb₃ with a variety of co-fillers such as Ba, La, and Yb. Finally, from single filling to double filling, and finally to multiple fillings to achieve continuous growth of ZT value, the maximum ZT at 850 K was increased to 1.7. Therefore, for thermoelectric material systems with different characteristics, it is particularly important to select a suitable doping method (the most current method is temperature-dependent doping) to optimize the carrier concentration in a broader temperature range.

Carrier Mobility

The improvement of carrier mobility is mainly through introducing impurity atoms in the intrinsic atomic vacancies. In most cases, the increase of m* will lead to a decrease in carrier mobility, and it will reduce the conductivity (Ioffe et al., 1959):

$\mu =\frac{e\tau }{m^{\ast }}(5)$

where τ is the relaxation time, so the improvement of carrier mobility also has a positive effect on the increase of ZT. Generally speaking, the smaller the electronegativity difference between the elements of the compound, the greater the mobility of the material, such as PbTe, Bi₂Se₃, etc. Lidong Zhao et al. further studied the effect of copper doping on n-type PbTe. The effective filling of Cu reduces the scattering of carriers in the gaps of Pb crystals, resulting in considerable carrier mobility and a high power factor (Xiao et al., 2017). The PbTe-2% Cu₂Te reaches a peak value of ZT ∼ 1.5 at 723 K, and the ZT_ave ∼ 1.0 of the n-type PbTe system achieves the highest value in history, as shown in Figure 5.

FIGURE 5

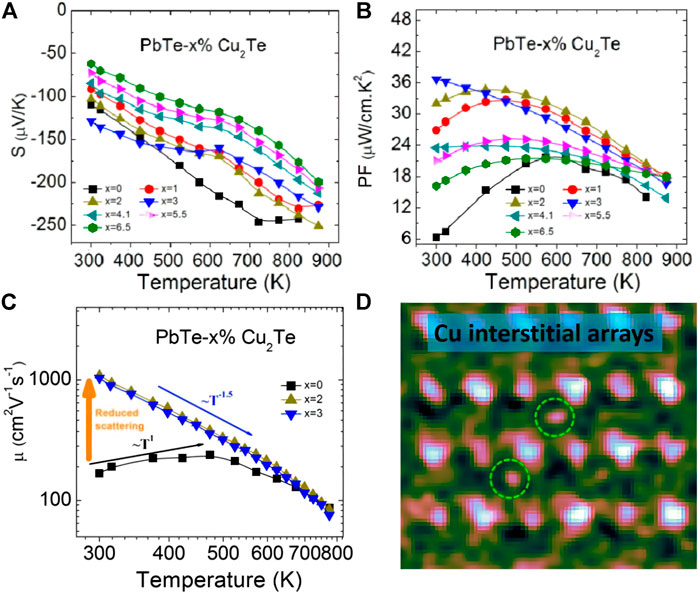
FIGURE 5. (A) Elimination of lead vacancies can reduce carrier scattering and significantly increase carrier mobility; (B) PbTe-Cu₂Te electrical transport properties change with temperature; (C) PbTe-Cu₂Te power factor change with temperature; (D) High magnification STEM HAADF image of Cu gap array (enlarged) (Xiao et al., 2017).

Studies have shown that to improve carrier mobility, three-dimensional modulation doping (mainly under low-temperature conditions) can effectively increase the ZT value of some important thermoelectric materials (Zebarjadi et al., 2011; Koirala et al., 2013; Pei et al., 2014). The modulated doped sample is a two-phase composite material composed of undoped and heavily doped. Undoped original samples have low carrier concentration but high carrier mobility, while uniformly doped and heavily doped samples have high carrier concentration but low carrier mobility. The Fermi level of undoped samples is usually in the middle of the energy gap, and the Fermi level of heavily doped samples goes deep into the conduction band (n-type doping) or valence band (p-type doping). With the energy imbalance between the undoped phase and the heavily doped phase, the carriers in the sample overflow from the heavily doped area to the undoped site, and this process enhances the carrier mobility (Valset et al., 2012).

In addition to modulating doping, the texture structure of the material can be used as another feasible way to improve carrier mobility, especially for some materials with anisotropic structures. In various heterostructures, the carrier mobility may only be higher in some specific crystal orientations (Zhao et al., 2014a). Li et al. (2018) proposed a method of high-efficiency thermoelectric materials that optimizes both electrical and heat transport performance. In (Bi, Sb)₂Te₃, the two-step sintering process with excess Te can increase mobility and reduce thermal conductivity at the same time. The two-step sintering process reduces the grain boundaries and defects that seriously hinder the transport of charge carriers, thereby increasing the mobility, and the maximum ZT of Bi_0.4Sb_1.6Te₃ can reach 1.3. Studies have shown that the two-step sintering technology is an effective method, which can control the existence and distribution of element inhomogeneity, so that the carrier transport and phonon transport have a special directionality. This has a specific guiding significance for other thermoelectric material systems with similar characteristics (Cha et al., 2019; Pan et al., 2019).

Improvement of Effective Quality

The effect of the local increase of the density of states on the Seebeck coefficient is given by Mott’s expression (Heremans et al., 2008). When semiconductors are doped or heavily doped with metals, according to the Mahan-Sofo theory, at a given carrier concentration, a high total density of states effective mass (m_d*) will determine a high Seebeck coefficient (Pei et al., 2012a), and then increase the ZT value of the material. To increase local DOS in a narrow energy range, md* can be effectively increased. Since the ZT value is related to the conductivity, the carrier concentration n cannot be too low. Most high-performance thermoelectric materials are heavily doped semiconductors, and the optimal carrier concentration n_opt varies with (m*T)^3/2. Therefore, n_opt can also be achieved by tuning the effective quality m_d* (Cha et al., 2019). According to m_d* = N_v^2/3m_b*, degeneracy (N_v) and effective mass (m_b*) play a decisive role in m_d*. In most cases, the increase in m_d* is due to the increase in m_b* (Pei et al., 2012b; Dutta et al., 2020), with the increase of the effective mass m_b* will result in a decrease in the carrier mobility μ and a decrease in the material conductivity (Tan et al., 2016b). Energy band engineering causes the density of states distortion by doping or changing symmetry, using energy band degeneration, increasing resonance states, hybridizing the energy gap, and doping Kondo atoms to change its effective mass essentially (Suwardi et al., 2019).

High energy band degeneracy is of great significance in thermoelectric materials because it can produce higher m_d* (as shown in Figure 6A), resulting in a more significant Seebeck coefficient, and has no deleterious effect on carrier mobility. N_v is closely related to the symmetry of the crystal structure. Low symmetry has very low к_L and poor thermoelectric performance. The current superior TE materials usually have a high symmetry crystal structure and symmetry-related multi-valley carrier structure (Zhang et al., 2014). To obtain more equivalent degenerate valleys and peaks, the N_v and Seebeck coefficients can be increased. For example, Zhao’s team found that due to the layered change of the crystal structure in the SnSe crystal structure, different N_v causes different m_b* in different directions, and the ZT value changes (Zhao et al., 2016). Then, Jiawei Zhang designs a constrained cubic structure by coexisting a long-range cubic frame and a partial short-range cubic lattice distortion (Zhang et al., 2014). By controlling the crystal structure of diamond distortion (Li et al., 2018), achieves low symmetry with convergence, while reducing the lattice thermal conductivity and increasing ZT values, it is shown that the symmetry breaking with degeneracy is small, and the high simplification and low lattice thermal conductivity can be realized simultaneously. This method of reconstructing the approximate cubic structure to obtain a highly symmetrical crystal structure is considered to be a feasible approach to obtaining a larger N_v and a higher Seebeck coefficient.

FIGURE 6

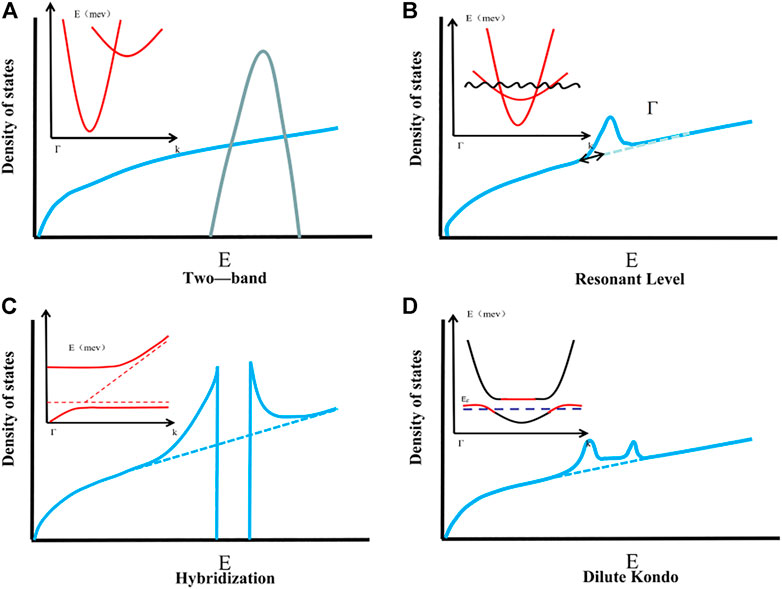
FIGURE 6. Four ways to improve effective mass: (A) Degenerate energy band; (B) Increase resonance state; (C) Hybrid energy gap; (D) Doping Kondo atoms.

Another effective method to improve N_v is to converge the different bands in the Brillouin region within the nk_BT of each other’s energy. The valley number in the conduction band and the peak number in the valence band increase, so that the mobility is not affected by N_v. For example, Su et al. (2017) regulates N_V according to the formation of Mg₂Si_1−xSn_x in the solid solution, when the concentration of Sn is close to x = 0.7, the band edges of the two conduction bands are guaranteed to overlap, and the band convergence is realized, as shown in Figure 7A. Due to the increase of m_d*, the Seebeck coefficient reaches its maximum value (as shown in Figure 7B), resulting in abnormally high TE performance at 700 K (ZT = 1.3). It is proved that by doping, the band structure with multiple extreme values can be formed at the top or bottom of the valence band, or the convergence of light band and heavy band can increase the degeneration of the band, so as to obtain better thermoelectric performance.

FIGURE 7

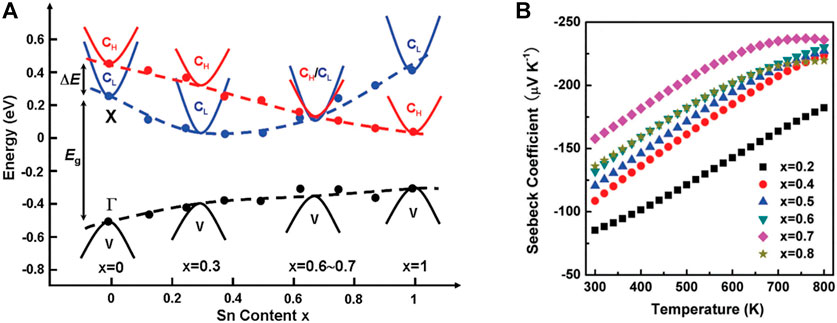
FIGURE 7. (A) The relationship between the tin content in the Mg₂Si_1−xSn_x solid solution and the relative position of the weight and light transmission bands and the highest valence band; (B) the temperature dependence of the Seebeck coefficient of the n-type Mg₂Si_1−xSn_x solid solution (Su et al., 2017).

The introduction of the resonance state can cause the density of states to be distorted (as shown in Figure 6B). If the Fermi energy E_F falls near the center of the resonance band, the PbTe density of states is distorted in Figure 6B, resulting in a large increase in the Seebeck coefficient. It is mainly achieved by doping, usually because after the resonant impurity atoms are introduced into the complete periodic structure, the same energy level and different energy states are superimposed so that the energy band of the doped impurity falls below the edge of the valence band or the host above the edge. In general, the lower the resonance level, the greater the distortion of the electronic density of states, and the Seebeck coefficient will increase (Dutta et al., 2020). Heremans et al. (2008) used PbTe doping with Ti and found that the electron DOS was enhanced near the Fermi level. Later, Tan et al. (2016a) used Na atoms to replace vacancies and defects in PbTe, which once again proved that doping can actually increase the effective mass of the density of states and increase the ZT value. However, Pei et al. (2012b) improved the effective mass by doping La in PbTe. They found that the effective mass is temperature-dependent, and the increase in the effective mass leads to an increase in the Seebeck coefficient, but it actually increases the ZT value significantly in the lower temperature range (Pei et al., 2012b), slightly deviating from the previous rule. Therefore, the core law of changing the effective mass of the density of states through the introduction of the resonance state to increase the ZT value needs further exploration.

The hybrid energy gap is another way to increase the effective mass of the density of states, as shown in Figure 6C. However, this method has great limitations on the change of the density of states. It will cause the carrier mobility of the material to drop to zero in a certain energy interval, and make the effective mass return to zero, which is fatal to the thermoelectric performance. However, the hybrid energy gap in its vicinity can effectively increase the effective mass of its density of states, and enhance the thermoelectric performance. For example, Tan et al. (2019) introduced an internal axis nanostructure into n-type PbTe, and they performed CdTe alloying and Sb doping on it, which enhanced the effective mass of state density by expanding the band gap, and increased the Seebeck coefficient. Improving the thermoelectric performance is also an effective method to enhance the Seebeck coefficient.

The Kondo effect may be triggered in some thermoelectric systems doped with magnetic atoms. The study found that the electrical conductivity of the material is higher when the Kondo temperature is near. The coupling of these Kondo atoms with nearby electrons will form a larger-scale Kondo cloud, which has an enhancement effect on the density of states, as shown in Figure 6D. Lu et al. (2015) maintains the additional valence band of the conductive spin-split Ni state by adding Ni-doped tetrahedral Cu₁₂Sb₄S₁₃, electrons fill holes in the valence band, and the resulting Kondo effect increases the thermoelectric performance by more than 30%. Qiu et al. (2014) used Fe doped Cu₂S at 900 K, the maximum ZT reaches 1.2, because Fe atoms are randomly distributed on the substrate to form a Kondo cloud, which leads to higher stability than Cu₂S (Tan et al., 2019). However, the Kondo effect will also reduce the electrical conductivity of the material when the Kondo temperature is far away, or the Kondo cloud-scale is too large, which is not suitable for increasing the ZT value. Therefore, it is generally used to dope Kondo atoms, while ensuring that the system application range is at the Kondo temperature. In the vicinity, the ZT value is guaranteed to increase. However, the current interpretation of the Kondo effect is still in its infancy, and there is a wide range of design prospects in the later period.

There have been extensive studies on improving the Seebeck coefficient by adjusting the effective mass through energy band engineering, but the improvement of the effective mass also means the reduction of carrier mobility, so blindly improving the effective mass is not necessarily beneficial to increasing the ZT value, even Some scholars believe that reducing the effective mass of energy bands in some systems can increase the ZT value (Pei et al., 2012a). Therefore, how to balance the relationship between effective mass and carrier mobility to achieve the maximum ZT value still needs further investigation and verification.

Reduction of Lattice Thermal Conductivity

The lattice thermal conductivity к_L is an independent influencing factor, and it is the most direct and effective means to optimize the thermal power figure.

According to the lattice thermal conductivity formula:

${\kappa }_L=\frac{1}{3}{C}_v{V}_{g}l=\frac{1}{3}{C}_v{V}_g^2\tau (6)$

(where C_v is the constant volume heat capacity, V_g is the group velocity of the phonon vibration mode, l is the mean free path, and τ is the phonon relaxation time) affects the lattice thermal conductivity. The main factors of the rate are heat capacity, speed of sound, and relaxation time. Therefore, by reducing any parameter, the lattice thermal conductivity can be reduced. The atomic point defects formed by element substitution and the nanostructures formed by the nucleation and growth of the second phase can significantly scatter short-wave phonons and medium-wave phonons, respectively. It is precise because the new structure generates an increased probability of phonon collisions, reduces the mean free path of phonons and the relaxation time of phonons, and enhances phonon scattering. And when the size of the defect in the material is close to the mean free path of the phonon, it will have a greater scattering effect on the phonon (Zhao et al., 2014c). According to the thermal conductivity model proposed by Klemens and Callaway (Callaway, 1959; Klemens, 1960), the degree of scattering reduction can be written by the scattering parameter evaluation (Γ) as:

$\Gamma =x(1-x)\left[{\left(\frac{\Delta M}{M}\right)}^2+\epsilon {\left(\frac{a_{disorder}-a_{pure}}{a_{pure}}\right)}^2\right](7)$

where x is the doping fraction, ΔM/M is the rate of change of relative atomic mass, α_disorder and α_pure represent the lattice constants of disordered and pure alloys, and ε is an elasticity-related adjustment parameter. Here we can find that maximizing Γ will result in the lowest lattice thermal conductivity. Generally, higher doping fractions, heavy element doping, and greater lattice mismatch can be used to reduce irritation. Next, we use several scattering mechanisms such as point defect scattering, dislocation scattering, interface scattering, and phonon resonance scattering to explain the influence of the above factors.

Point Defect Scattering

Introducing lattice point defects into the matrix lattice is an effective way to reduce the thermal conductivity of the lattice, as shown in Figure 8A. This is because phonons are more likely to be scattered by point defects rather than electrons, and thus have less impact on carrier mobility. Figures 8B–D show typical doping methods commonly used in thermoelectric materials research, namely single element doping, cross-substitution, and formation of lattice vacancies. In the case of single doping, the dopant can be the same valence as the main element, resulting in lattice disorder, or it can be heterovalent, so as to control the carrier concentration. However, this doping causes the system charge imbalance, which may hinder the reduction of к_L if done alone.

FIGURE 8

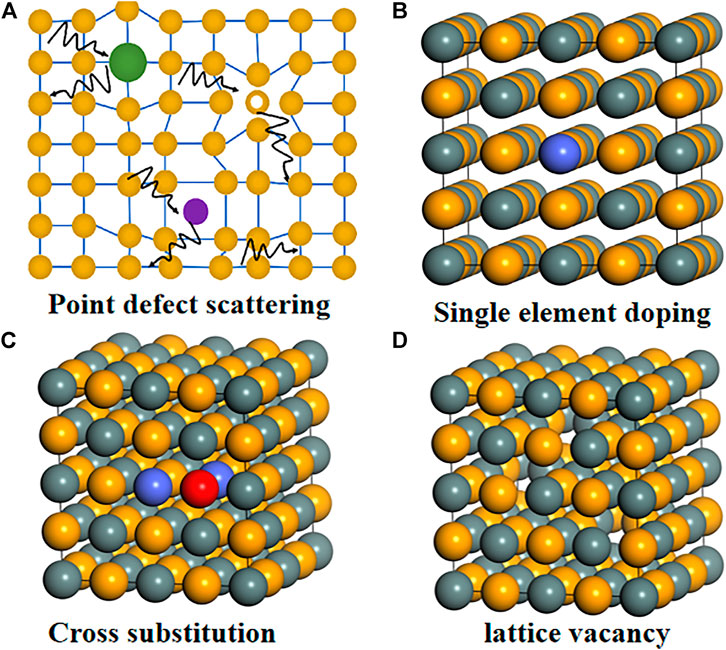
FIGURE 8. Schematic diagram of point defect scattering and atomic-scale doping methods; (A) Schematic diagram of point defect scattering; (B) single-atom doping; (C) polyatomic doping; (D) lattice vacancy.

To improve the solubility of different elements, cross-substitution is generally used. Cross-substitution refers to the pair-to-pair substitution of one or more main elements from other groups in the periodic table, while keeping the total number of valence electrons unchanged (Tan et al., 2013; Tan et al., 2015b).

Yu et al. (2018a) designed thermoelectric materials by isoelectronic substitution of the atom Ta for the atom Nb. By using isoelectronic substitution of atoms with similar size and chemical properties but the large mass difference, the lattice thermal conductivity of the alloy was greatly suppressed, but good electrical properties were maintained. As a result, the ZT reaches a peak of 1.6 at a Ta content of 0.4. It shows that the point defects caused by the substitute atoms will change the thermal conductivity of the lattice (Yu et al., 2018a). It is worth noting that the cross-substitution not only greatly affects the transport of phonons, but may also change the electronic structure (mainly the band gap), providing other ways to adjust the thermoelectric properties of the matrix material. Because only when these two heterogeneous elements exist together in a specific ratio, the amount of them entering the matrix will be greater. We call this effect synergistic alloying. In the Pb_0.98Na_0.02Te-8% SrTe sample, the ZT value is 2.5 at 923 K, and the average ZT value is 1.67 in the range of 300–900 K. It is further proved that by optimizing the Na concentration, a ZT of 2.5 can be obtained at a lower temperature of about 800 K (Xu et al., 2020a). Alloying is currently the most widely used method to enhance the scattering of point defects, in Bi₂Te₃ (Hu et al., 2014; Chen et al., 2015), Pb(Te, Se) (Pei et al., 2011), GeTe (Chen et al., 2020) and Half-Heusler (HH) alloys (Xue et al., 2016; Shen et al., 2018; Yu et al., 2018b) have applications.

In addition to alloying, vacancies and interstitial atoms also belong to a relatively special point defect scattering mechanism (Xue et al., 2016). Jiaqing He introduced double-vacancy defects by doping BiI₃ (Xu et al., 2020b) to improve the thermoelectric performance of Sb₂Te₃(GeTe)₁₇. The maximum value of ZT is 2.2 at 723 K. There are nearly 20% intrinsic Nb vacancies in the HH alloy Nb_0.8CoSb, which makes the Nb_0.8CoSb alloy have a relatively low lattice thermal conductivity (Xia et al., 2018). The same phenomenon exists in thermoelectric materials such as Cu₂SnSe₄ (Li et al., 2016). Like vacancies, interstitial atoms can also be generated by a solid solution method, but only compounds with a larger cation-anion ratio are applicable. The cations of such compounds need to have a smaller radius to fit the interstitial sites. Taking the solid solution (SnTe)_1−x (Cu₂Te)_x as an example (Li et al., 2017; Zheng et al., 2017), its lattice thermal conductivity is as low as 0.5 W m⁻¹ K⁻¹, which is close to the minimum lattice thermal conductivity limit of SnTe (About 0.4 W m⁻¹ K⁻¹).

Dislocation Scattering

Dislocations are a typical line defect, especially in metal materials. Dislocations and strain fields will scatter mid-and high-frequency phonons, so dislocations can effectively reduce the free path of phonons (Figure 9A). Kim et al. (2015) reported that by forming a high-density dislocation array at the grain boundary by extrusion, the lattice thermal conductivity of the Bi_0.5Sb_1.5Te₃ material could be significantly reduced, which is a dense dislocation array pair. The result of phonon scattering. In addition, dislocations can also be introduced through the precipitation of the second phase, where dislocations can play a role in reconciling the lattice mismatch at the phase boundary (Hu et al., 2015).

FIGURE 9

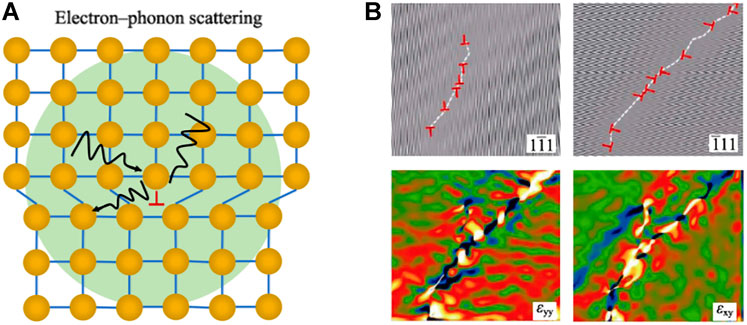
FIGURE 9. (A) Schematic diagram of dislocation scattering; (B) IFFT diagram of dislocation in Mg₂Si_0.5Sb_0.5 and the corresponding stress scan diagram (Xin et al., 2017).

In solid solution materials, due to the accumulation of vacancies, adjacent spaces collapse under external conditions to form vacancy dislocations. At the same time, vacancies will also spontaneously reduce energy. The released energy can promote dislocations to climb. The climbing motion of dislocations will increase the density of dislocations, and finally produce high-density and uniformly distributed dislocations in the crystal grain, thereby reducing к_L. In Mg₂Si_1−xSb_x materials (Xin et al., 2017), high-dose alloying of Sb has a large number of Mg vacancies, making the vacancy concentration much higher than the equilibrium vacancy density, and the excess Mg vacancies spontaneously aggregate to form dislocations, as shown in Figure 9B. In Mg₂Si_0.5Sb_0.5, the dislocation density is as high as 2.8 × 10¹⁶ m⁻². Besides, similar phenomena were also observed in the Na_yEu_0.03Pb_0.97−yTe system (Chen et al., 2017). Studies have shown that with the increase of Na doping, the main microscopic defects in the system gradually change from point defects to dislocations. Dislocation scattering reduces the lattice thermal conductivity of PbTe to below 0.4 W m⁻¹ K⁻¹.

Interface Scattering

Because atomic defects and dislocation defects can effectively scatter low- and mid-wavelength phonons, there are still some long-wavelength phonons that are not scattered and affect the thermal conductivity of the lattice. In polycrystalline materials, grain boundaries or phase boundaries can effectively scatter low-frequency phonons, and the scattering rate is inversely proportional to the grain size. Therefore, the effective method to effectively scatter long-wavelength phonons is to introduce micro-nano structures (Girard et al., 2010). The mechanism of action is shown in Figure 10A. In particular, nanostructures have been proven to be an effective method to enhance ZT by placing suitable nano-scale precipitates in the matrix to reduce к_L, such as AgPb_mSbTe_m+2 (Hsu et al., 2004), NaPb_xSbTe_2−x (Poudeu et al., 2006) and PbTe-Ag₂Te (Zhao et al., 2013a). In addition, p-type PbTe_1−xSe_x (Pei et al., 2011) and Tl-PbTe (Heremans et al., 2008) also have excellent thermoelectric properties, which come from the introduction of multiple valence bands and the density of states distortions in the valence band, respectively. Biswas et al. (2012), Liu et al. (2016), and others considered phonon scattering sources on all scales from the perspective of a layered approach, ranging from atomic-scale lattice disorder and nano-scale internal deposits to mesoscale crystals. The thermal conductivity of the crystal lattice is greatly reduced. Finally, the ZT of PbTe-SrTe is 2.2, and the ZT of Bi_0.88Ca_0.06Pb_0.06CuSeO is 1.5, which proves that the grain boundary scattering is important in reducing the thermal conductivity. Zhao et al. (2019) introduced the Ag₂Te phase into Cu₂Te. Due to multiple phase transitions, they show complex temperature dependence in the temperature range of 300–1000 K. As the Ag₂Te content increases, the interface scattering increases, and к_L decreases significantly (as shown in Figures 10B–D). At the same time, its highest ZT value reaches 1.8. It shows ultra-low lattice thermal conductivity at 900 K, and its value is about 0.3 W m⁻¹ K⁻¹ (Zhao et al., 2019).

FIGURE 10

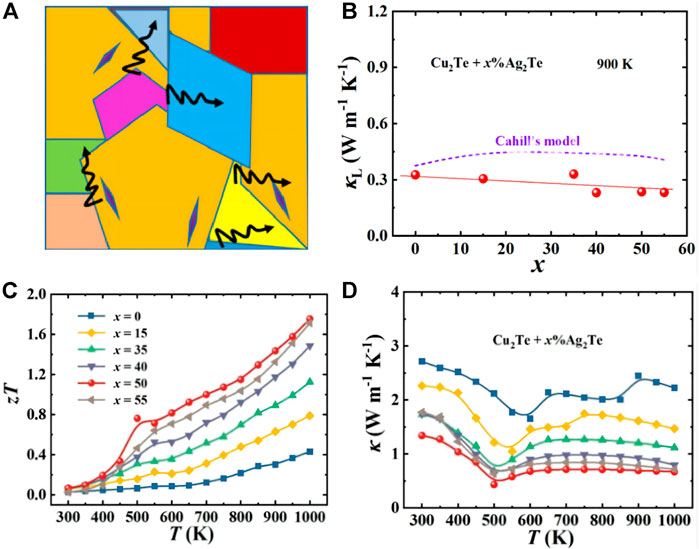
FIGURE 10. (A) Schematic diagram of interface scattering; (B) lattice thermal conductivity κ_L at 900 K for all samples of Cu₂Te + x% Ag₂Te; (C) and (D) are Cu₂Te + x% Ag₂Te(x = 0, 15, 35, 40, 50, and 55) thermal conductivity (к), thermoelectric figure of merit (ZT) varies with temperature (Zhao et al., 2019).

Commonly used methods to enhance grain boundary scattering include ball milling (Li et al., 2015) and plasma sintering (Xie et al., 2018), etc., to obtain finer or smaller grains from coarser-grained crystal powders to increase the grain boundary area. Li et al. (2015) prepared nanostructured Na_0.02Pb_0.98Te samples with a grain size of 20–100 nm through high-energy ball milling and semi-solid powder processing. Through observation, they found that the interface between the particles can be clearly seen. The size (0.1–1 μm) of the pores, so there is stronger phonon scattering at the grain boundary, which reduces the lattice thermal conductivity к_L to 0.74 W m⁻¹ K⁻¹ at 623 K. Similarly, Yu et al. (2017) combined melt spinning, ball milling and spark plasma sintering processes to construct a microstructure containing a large number of 60° twin grain boundaries in the Bi_0.5Sb_1.5Te₃ liquid alloy. The bilateral grain boundaries not only increase the current load mobility, and its scattering effect on phonons greatly reduces the thermal conductivity, so that ZT = 1.42 at 348 K (Yu et al., 2017).

In addition to the above methods, the process of separating the micro-nano phases to form twin crystals and dislocation network structures can also increase the grain boundary area, thereby enhancing phonon scattering and reducing thermal conductivity (Kim et al., 2015). Gelbstein et al. (2013) separated the p-type Ge_0.87Pb_0.13Te into two phases of GeTe and PbTe through spark plasma sintering, thereby generating the characteristics of multiple interfaces, enhancing the phonon scattering at the crystal plane, and achieving a relatively highly stable TE Performance.

It can be seen that defects of different sizes prepared by doping in materials and related physical and chemical methods can effectively scatter phonons of different wavelengths and different free paths, thereby reducing the thermal conductivity of the lattice. Therefore, the changes in energy band and structure (mass ratio and degree of distortion) caused by the coordinated effect of point defect scattering, dislocation scattering, and interface scattering will enhance the scattering of phonons at different wavelength levels simultaneously (Li et al., 2018; Lee et al., 2019).

Resonance Scattering

Resonance scattering is generally used in thermoelectric materials with special crystal structures, such as cage compounds (Christensen et al., 2008; Beekman and VanderGraaff, 2017), skutterudite (Duan et al., 2016), and some thermoelectric materials with topological insulation (Wei et al., 2016; Zeugner et al., 2019). By adding filler atoms, a strong local vibration close to the vibration frequency is generated, and a resonance spectrum of a specific frequency (shown in Figure 11) is introduced, thereby reducing the thermal conductivity.

FIGURE 11

FIGURE 11. Schematic spectrum of resonance scattering at a specific frequency.

Researchers fill CoSb₃ with S and Se as electronegative objects under equilibrium conditions. Because S and Se have unique localized “cluster vibrations,” a section can be introduced in the phonon spectrum. The optical branch with lower frequency is coupled with the acoustic branch, which significantly affects the lattice dynamics, greatly reduces the thermal conductivity of the lattice, and obtains S_0.26Co₄Sb_11.11Te_0.73 with ZT = 1.5 at 850 K (Zeugner et al., 2019). In recent years, research on topological insulating thermoelectric materials has gradually increased, and many studies have also shown that some of them have resonance scattering. Samanta et al. (2018) reported a layered structure of n-type BiSe (Se-Bi-Se-Bi-Se), the study found that the local vibration generated by the Bi layer can cause some low-energy optical branches to inhibit the propagation of the acoustic branches (i.e., photoacoustic coupling), and the sound wave branch with low cut-off frequency and strong anharmonic vibration Phonon interaction further reduces the thermal conductivity, and finally κ_L = 0.3 W m⁻¹ K⁻¹ at 300 K. Similarly, Wei et al. (2016), Christensen et al. (2008) predicted the minimum thermal conductivity of bismuth-based stacked structures with topological insulation and found that the NI layer has a strong influence on Bi₂TeI lattice dynamics and impedes phonon propagation, with low-frequency photo-phonon and phonon interactions arising from local vibrations of the NI layer causing a high degree of lattice anharmonicity and producing extremely low thermal conductivity. Moreover, Ying et al. (2017) studied the cause and physical mechanism of the intrinsic low thermal conductivity of α-MgAgSb thermoelectric materials and predicted a class of thermoelectric material systems with low thermal conductivity. The study found that α-MgAgSb has weak chemical bonds in addition to layering. In addition to the low sound velocity, the half-Heusler-like twisted lattice makes it form a Mg-Ag-Sb triple-center bond structure (Figures 12A,B). The Ag atoms in the Mg-Ag-Sb tri-center bond can move reciprocally in the direction of the arrow to a greater extent, forming a low-frequency optical branch in the phonon spectrum (Figure 12C). These low-frequency optical branches can generate resonance scattering and effectively reduce the thermal conductivity of the lattice (Ying et al., 2017). It can be seen from the above that the research on reducing thermal conductivity through resonance scattering is becoming more mature.

FIGURE 12

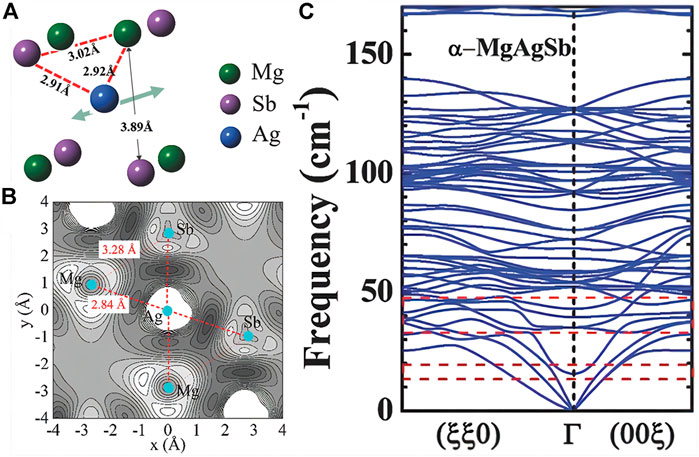
FIGURE 12. (A) Schematic diagram of the three-center bond structure in α-MgAgSb; (B) α-MgAgSb charge distribution diagram; (C) α-MgAgSb phonon spectrum (Ying et al., 2017).

Thermoelectric Materials With Low Thermal Conductivity

The use of low-dimensional defects and nanocomposite structures to reduce multi-scale phonon scattering and reduction of existing TE materials к_L does significantly increase the ZT value of thermoelectric materials, but existing methods at this stage will affect thermal stability and other issues. The search for thermoelectric materials with intrinsically low thermal conductivity is therefore also a necessary way to avoid the problems associated with reducing the thermal conductivity of existing materials. Most of the thermoelectric materials with an intrinsic low thermal conductivity that have been discovered so far have the characteristics of weak chemical bonding (Zhao et al., 2014a), strong anharmonic effects (Zhao et al., 2014d), liquid ionic properties (Liu et al., 2012), heavy molecular mass (Toberer et al., 2010), complex crystal structure (Kurosaki et al., 2005), etc. We will briefly describe the representative thermoelectric materials from the following five points.

Weak Chemical Bond

The lattice thermal conductivity is proportional to the speed of sound, so obtaining low sound speed performance often helps to improve the thermoelectric properties of the material. Materials with weak chemical bonds have a lower speed of sound, atoms have more space for movement near their equilibrium positions, and electron cloud distribution is more diffuse. In the phonon spectrum, weak chemical bonds often correspond to some low-frequency phonon models, which are easier to couple with the acoustic branch, thereby further reducing the contribution of the acoustic branch to the thermal conductivity.

SnSe is a typical simple thermoelectric material with weak chemical bonds and is very stable. SnSe has an orthogonal layer structure in the room temperature range. The Sn-Se bond in the bc direction is stronger and weaker in a direction. It is easy to cleave along the (100) plane and form a foldable projection in the b-axis direction. The structure contains a highly distorted SnSe₇ coordination polyhedron with three short Sn-Se bonds and four long Sn-Se bonds. Such a special structure makes it have strong non-resonance and high anisotropy, which essentially has ultra-low thermal conductivity. Lidong Zhao et al. prepared SnSe single crystal by the Briman method and found that the special crystal structure of SnSe (as shown in Figure 13A) made SnSe have a very low к_L, and the room temperature thermal conductivity of SnSe in the direction of the axis a was about 0.47 W m⁻¹ K⁻¹. With the increase of temperature, the thermal conductivity at 973 K decreased to about 0.23 W m⁻¹ K⁻¹ (as shown in Figures 13A, C), and a historic breakthrough was made at 923 K with a ZT of 2.6 along the b-axis (as shown in Figure 13B) (Zhao et al., 2014a). Subsequently, Zhao et al. (2014a) synthesized an n-type SnSe crystal with a two-dimensional layered structure with ZT up to 2.8 (Chang et al., 2018). Similarly, based on the low thermal conductivity of SnSe, Qin et al. (2020) introduced SnSe₂ as an extrinsic defect dopant to increase the carrier concentration to 6.55 × 10¹⁹ cm⁻³ while increasing the effective Mass and Seebeck coefficient, obtained an unusually high power factor at room temperature (about 5.4 × 10^–2 W m⁻¹ K⁻²), so that the maximum ZT value reached 2.2 and the average ZT value reached 1.7.

FIGURE 13

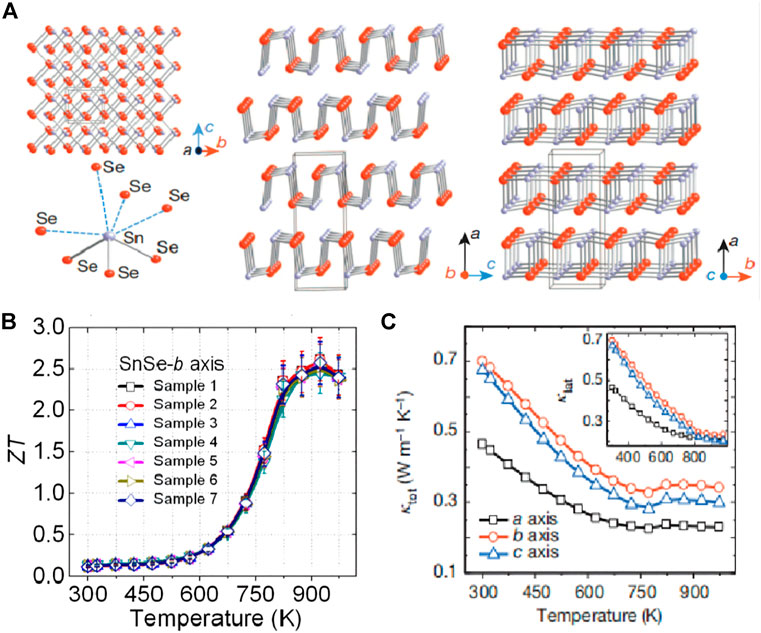
FIGURE 13. (A) SnSe crystal structure along the a-axis: gray, tin atoms; red, selenium atoms; highly distorted SnSe₇ coordination polyhedron with three short and four long Sn-Se bonds; structure along the b-axis; Structure along the c axis; (B) SnSe along the b axis ZT value changes with temperature (T); (C) SnSe single crystal lattice thermal conductivity (к_L) changes with temperature (T) in the a, b, and c directions (Zhao et al., 2014a).

In addition to single crystals SnSe, polycrystalline SnSe has gradually been widely used in research due to its thermal conductivity comparable to that of single crystals SnSe. Although SnSe crystals have strong anisotropy, polycrystalline materials have more carrier migration than single crystals SnSe materials. The rate is much lower, and the conductivity is very low, but therefore, increasing the conductivity has become an important way to improve the thermoelectric properties of polycrystalline SnSe. Zhang et al. (2015) prepared n-type SnSe polycrystalline powder by using I doping and SnS solid solution, and processed it in a vacuum device, and found that the thermal conductivity of polycrystalline SnSe would decrease, approaching 0.30 W m⁻¹ K⁻¹ at 773 K, which makes ZT = 1 finally.

Perhaps because polycrystalline materials have many dislocations, vacancies, bond deformations, and other defects in the grain boundary during the powder metallurgy process, they are in a state of stress distortion, and the energy is high, which makes the material in an unstable state at high temperatures, resulting in relatively poor performance. There are many speculations about the reason for the low thermal conductivity of SnSe. For example, the spring-type crystal structure of SnSe has a great shock-absorbing and buffering effect on the transmission of phonons in it (Heremans, 2014). Therefore, the thermal conductivity of SnSe still needs further investigation and verification.

Non-Resonance Effect

The resonance effect refers to the balance of external forces experienced by phonons during the transmission process. The sound wave transmits uniformly forward in the form of a parabola, which is similar to the transmission in a perfect lattice, but when the transmission of phonons is affected by external factors, it will deviate from the equilibrium position and cause non-resonance effects. The strength of anharmonicity is mainly related to the symmetry of chemical bonds and atomic equilibrium positions. During the vibration of an atom, the greater the deviation of its symmetry center, the stronger the asymmetry. Materials with lone pairs of electrons are often due to the uneven distribution of the electron cloud, the crystal structure will be deformed to a certain extent, and the asymmetry is significantly enhanced, which is beneficial to obtain strong anharmonicity.

Because there are two isolated electrons in the outermost layer of the Sb nucleus. The two lone electrons in the outermost layer of the nucleus will make the transmission of phonons unbalanced, resulting in non-resonance effects, resulting in Sb compounds with low heat transport properties. In the same way, compounds with Bi atoms belonging to the same group as Sb atoms should also have anharmonic effects. Therefore, the common thermoelectric materials with intrinsic low thermal conductivity of this kind are AgSbSe₂, BiCuSeO, and so on. The room temperature thermal conductivity of AgSbSe₂ is 0.48 W m⁻¹ K⁻¹ (Nielsen et al., 2013), which is lower than most thermoelectric materials at room temperature. In recent years, some people have introduced AgSbSe₂ into GeTe to prepare (GeTe)₈₀ (AgSbSe₂)₂₀. The introduction of hierarchical nano/mesoporous structure inside the material causes large-scale scattering of phonons, which reduces the lattice thermal conductivity к_L to 0.4 W m⁻¹ K⁻¹ at 300–700 K, which is close to the thermal conductivity of GeTe. The theoretical limit of the rate finally makes its ZT_max reach 1.9 at 660 K (Samanta et al., 2017). Later, Gao et al. (2018) used the method of mechanical alloying and rapid hot pressing to manufacture Ca doped AgSbSe₂ with the layered structure. Ca doping further optimized the carrier concentration and caused the point defect scattering of phonons, and obtained the ultra-low lattice thermal conductivity of 0.27 W m⁻¹ K⁻¹ at 673 K, thus increasing the ZT peak value to 1.2.

Since BiCuSeO was reported in 2010 (Zhao et al., 2010), BiCuSeO is considered to be one of the most promising oxygen-containing thermoelectric materials due to its special natural superlattice structure and corresponding ultra-low thermal conductivity. Later, researchers found that in BiCuSeO, modulating doping to increase carrier mobility can greatly improve thermoelectric performance. Modulating the heterostructure of the doped sample makes the carriers preferentially transport in the low carrier concentration region, which increases the carrier mobility by 2 times while maintaining the carrier concentration similar to the uniformly doped sample. The synergistic effect of the increased conductivity and the basically constant Seebeck coefficient results in a wide range of high power factors, about 5–10 × 10^–2 W cm⁻¹ K⁻². The combination of ultra-high power factor and extremely low thermal conductivity (about 0.25 W m⁻¹ K⁻¹) enables BiCuSeO to obtain a high ZT ≈ 1.4 at 923 K (Pei et al., 2014)^.

Later, with the widespread acceptance of simulation calculations, Saha (2015) used first-principles density functional theory calculations to propose the atomic displacement map of the lowest frequency optical mode of BiCuSeO, and systematically studied the correlation of BiCuSeO (such as dielectric and Anharmonic) characteristics, and compared with LaCuSeO of the same structure, it is found that the reason for the ultra-low thermal conductivity κ of BiCuSeO is that the Bi atom exhibits a significant displacement during the action, which indicates that it has a higher anharmonic effect. Furthermore, the calculated out-of-plane thermal conductivity of BiCuSeO is approximately twice that of the in-plane thermal conductivity, which indicates that BiCuSeO has a greater anisotropy of heat flow between in-plane and out-of-plane.

Ionic Liquid Characteristics

In solid, C_v = 3N_kB, while in liquid, most transverse vibration waves cannot be transmitted, C_v decreases to 2–2.5N_kB, and N_k is the total atomic number. Therefore, materials with liquid properties often have relatively low thermal conductivity due to their small heat capacity. Ionic conductors introduce some ions with “liquid” characteristics into solid materials to form an ionic liquid-like semiconductor, thus reducing the lattice thermal conductivity to a level lower than that of glass, which can not only reduce the mean free path of phonons but also eliminate lattice vibration. Cu_2−xSe compounds belong to this class of ion-electron composite conductors with special structures with two-phase structures at room temperature (transition from low-temperature α phase to high-temperature β phase at 400 K). The lattice network structure of Cu_2−xSe face-centred cubic Se atoms provides a good electrical transport pathway for the randomly distributed free movement of Cu ions in the interstitial positions, which enhances the scattered lattice phonons while reducing some lattice vibrational modes, so that the lattice heat capacity of the material decreases with increasing temperature and ultimately low thermal conductivity properties can be obtained.

Skomorokhov et al. (2006) experimentally found the local migration of Cu atoms in Cu₂Se. Later, Liu et al. (2012) found that the abnormal “liquid-like” behavior of copper ions around the crystalline sublattice of Se in Cu_2−xSe (Figure 3 shows the simple Face-centered cubic structure of Se atoms in the High-temperature β phase) leads to essentially very low lattice thermal conductivity (0.4–0.6 W m⁻¹ K⁻¹), thus achieving high ZT = 1.5 (T = 1,000 K) in this originally simple semiconductor. This unusual combination of properties resulted in ideal thermoelectric materials. The results show that exploring the network structure with electron conduction sublattices surrounded by liquid ions can provide new strategies and directions for High-efficiency thermoelectric materials.

Subsequently, Zhong et al. (2014) generated highly aligned wafers in the bulk Cu_1.94Al_0.02Se by the direct current hot pressing process according to the alternating arrangement of single disordered layers of Se ions and double disordered layers of Cu ions. The superionic mechanism in Cu_1.94Al_0.02Se was further enhanced by the enhancement of Cu ions and high crystal orientation. Finally, ZT = 2.62 was obtained at 756°C (Zhong et al., 2014). This study also provides a reliable way to use the superior mechanism. In the research process of Cu_2−xSe, the high fluidity of copper ions causes problems such as thermal stability during the preparation of Cu_2−xSe, which prevents the development of Cu_2−XSe. Therefore, it is also necessary to consider how to control such problems in the research process.

Molecular Weight

Heat capacity C_v is the important factor influencing the thermal conductivity and is proportional to the lattice thermal conductivity, based on the debye model for the heat capacity, the acoustic wave is the main source of contribution to the thermal conductivity, the assumption in a polyatomic system, the total number of the original cell of N, every cell in the atomic number is n, total system degrees of freedom to 3 nN, among them, the acoustic branch has 3N, optical 3(n−1)N, by the equipartition principle, the contribution of the acoustic branch heat capacity as the C/n, optical to C(n−1)/n (Toberer et al., 2011). Therefore, the total heat capacity remains unchanged. The more atoms in the primary cell, the less contribution of acoustic branches to the total heat capacity is, and the more conducive to obtaining low lattice thermal conductivity, which means that the thermoelectric materials with heavy molecular weight have certain advantages to obtain excellent thermoelectric properties. This has been demonstrated in many thermoelectric materials with complex crystal structures.

Zintl phase Yb₁₄MnSb₁₁ is a typical macromolecular mass material with a relative molecular weight of 3,783.088 g/mol, and its crystal structure is shown in Figure 14C (Wang Y. et al., 2018). Brown et al. (2006) found that electronic and thermal properties could be potentially modulated by doping at different locations in the A₁₄MPn₁₁ class of structures. Doped at cationic metal site A, the carrier concentration and phonon disordered scattering can be adjusted. Doped at cationic metal site A, the carrier concentration and phonon disordered scattering can be adjusted. Doping at a metal site M can adjust the electronic parameters, and for the first time by preparing Zintl phase Yb₁₄MnSb₁₁ to obtain the thermoelectric performance of the stability at high temperature, the thermal conductivity in about 0.7–0.9 W m⁻¹ K⁻¹ (400–1,300 K), the Seebeck coefficient reaches the maximum value of 185 μV/K at 1,275 K, and the ZT value reaches one at 1,223 K, which provides new guidance for the study of Zintl phase Yb₁₄MnSb₁₁.

FIGURE 14

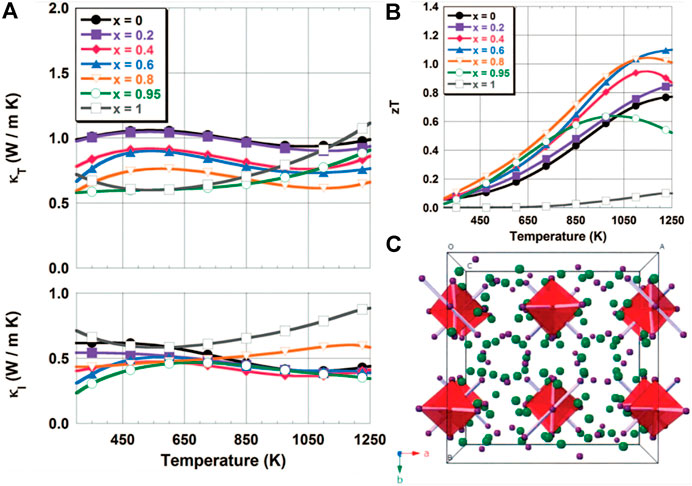
FIGURE 14. (A) Variation of total thermal conductivity and lattice thermal conductivity of Yb₁₄Mn_1-xAl_xSb₁₁ with x; (B) The change of ZT with the temperature at different x; (C) The crystal structure of Yb₁₄Mn_1-xAl_xSb₁₁ (Cox et al., 2009).

Then, Cox et al. (2009) began to conduct Al doping on the metal sites of Yb₁₄Mn_1−xAl_xSb₁₁ structure to regulate electronic parameters. Studies have shown that within a certain range of heat capacity (300–1,100 K), as the aluminum content increases, the unit cell volume increases, and the bond distance changes less than 2%, which means that the increase in cell volume is related to the decrease in the deformation of the tetrahedron with the increase in Al content. When the ZT peak appears at 1,223 K, it deviates from the measurement range, indicating that the lattice thermal conductivity here is extremely low (about 0.3–0.4 W m⁻¹ K⁻¹), as shown in Figure 14A. Subsequently, Uvarov et al. (2012) improved Seebeck’s coefficient and reduced thermal conductivity by replacing Yb²⁺ with equivalent Ca²⁺ in Yb₁₄MnSb₁₁, thus increasing ZT and obtaining higher thermoelectric performance. Therefore, it can be seen that the thermoelectric materials with similar heavy molecular weight can be adjusted at different sites to obtain low lattice thermal conductivity and stable thermoelectric properties with great exploration value.

Complex Crystal Structure

It is well known that the main factors affecting the thermal conductivity of materials are heat capacity, sound velocity, and phonon relaxation time. The complex crystal structure not only reduces the contribution of the acoustic branches to the total heat capacity, but also reduces the group velocity of the acoustic branches.

Due to its complex crystal structure, Ag₉TlTe₅ has a heavy molecular mass, and the number of atoms in a single cell is 298. Meanwhile, the low elastic modulus indicates that the chemical bond of the material is weak. The thermal conductivity of Ag₉TlTe₅ remains about 0.25 W m⁻¹ K⁻¹ from room temperature to 650 K (Kurosaki et al., 2005), which makes the ZT of the material reach 1.25 at 673 K. The ternary alkali metal-bismuth-chalcogenides exhibit extremely low thermal conductivity due to their more complex crystal structure, such as β-K₂Bi₈Se₁₃ (Figure 15A), CsBi₄Te₆ (Figure 15B), etc. The low symmetry monoclinic crystal structure of β-K₂Bi₈Se₁₃ makes it highly anisotropic. β-K₂Bi₈Se₁₃ was first proposed by Meng et al. (2003), and its thermal conductivity is as low as 1.28 W m⁻¹ K⁻¹. Afterwards, Kyratsi et al. (2011)prepared crystalline/amorphous β-K₂Bi₈Se₁₃ nanocomposites by ball milling the melt-synthesized polycrystalline β-K₂Bi₈Se₁₃ under an inert atmosphere. It was found that with the time of ball milling, the nanocrystalline phase gradually formed, the carrier concentration gradually decreased, the Seebeck coefficient gradually increased, and the thermal conductivity gradually decreased from the initial 1.28–0.3 W m⁻¹ K⁻¹, which greatly improved the thermoelectric properties of β-K₂Bi₈Se₁₃, and provided a new and reliable idea for the follow-up research. In addition, there are many materials with complex crystal structures, such as Bicuseo (Figure 15C) and Yb₁₄Mn_1-xAl_xSb₁₁ mentioned above, all of which are more or less affected by their structures. Therefore, given the many materials yet to be investigated, there is certainly much work ahead and promise for developing TE materials.

FIGURE 15

FIGURE 15. Crystal structure of complex thermoelectric materials: (A) Crystal structure of β-K₂Bi₈Se₁₃; (B) Crystal structure of CsBi₄Te₆; (C) Crystal structure of BiCuSeO.

Electron-Phonon Decoupling

In the above, we discussed that nanostructures in bulk materials greatly reduce thermal conductivity. However, due to the crystal mismatch or the electronic band of interface caused by the mismatch increased energy barrier, also can increase the carrier scattering, the carrier mobility and power factor have a negative effect, in other words, when doping material scale and the rise in the Numbers, thermal conductivity and electrical conductivity of coherence will increase, not conducive to improve the performance of thermoelectric (Zhao et al., 2013a). Therefore, ensuring high carrier mobility and wideband gap while fully regulating the thermal conductivity has become the key to the breakthrough of thermoelectric materials. The decoupling mode of electron and phonon transport is discussed below.

Slack proposed the concept of “Phonon glass and Electron Crystal” (PGEC), which can be used to guide the optimal design of thermoelectric materials. He believed that an ideal thermoelectric material should have phonon transport characteristics like glass and electron transport characteristics like crystal (Slack and Rowe, 1995). At present, the introduction of nano-sized precipitates can increase phonon scattering and produce very little electron scattering through interfacial interaction. When there is a coherent connection between the nano-precipitated phase and the matrix, but there is a certain tension around the interface (with nanostructure inside the tension), this interface is considered to promote the charge passing through, but strongly hinders the propagation of scattered phonons (Hsu et al., 2004; Cook et al., 2009). The coherent strain interface between the substrate and the nanometer precipitates results in strong phonon scattering, but the electron scattering is very small. Unfortunately, interfacial coherence can sometimes lead to asymmetry of energy band structure and generate potential barriers to hinder electron migration (Biswas et al., 2011). Although electron scattering can be minimized by improving the interfacial coherence of nanostructured materials, the energy barrier created by the asymmetry of electron bands hinders electron flow. Therefore, atomic fixation or nanometer phase minimization is generally used to increase electron migration. Huang et al. (2020) synthesized CuGaTe₂ + x wt.% CPS(x = 0, 0.3, 0.5, 1) composites. The results show that carbon particles (CPS) can be introduced into CuGaTe₂ matrix as electronic location center, and the conductivity and power factor of CuGaTe₂ matrix can be improved by adjusting its electrical transport performance. The results show that the introduction of CPS can be used as the local electron center, thus the hole concentration in the matrix is increased, and the electrical conductivity is increased by about 120% (300 K). Besides, the interface between carbon particles and matrix enhances the scattering of heat-carrying phonons and reduces the thermal conductivity of CuGaTe₂ + 0.5 wt.% CPS sample at 873 K, which significantly reduces the thermal conductivity of CuGaTe₂ sample by 37% compared with pure CuGaTe₂ (Huang et al., 2020).

To ensure the micro-transfer of energy bands and even form band alignment structure when embedded in nano-scale, the design of alloyed nano thermoelectric materials is also a good approach (Zhao et al., 2013b). The double alloying method of PbTe adopted by Sumanta Sarkar combines two different but identical structures, which can effectively improve the thermoelectric properties of PbTe from two aspects. First, in the presence of Bate, the solubility of Cate increases, leading to a widening of the band gap and a good convergence between L and ∑ bands, resulting in a record-high PF for the Seebeck coefficient. In addition, the point defects generated by alloying and the BaT-rich nanostructures contribute to the reduction of the lattice thermal conductivity of the system. This synergistic method generates a high ZT of 2.2 at 823 K (Sarkar et al., 2018). Makongo et al. (2011) proposed to obtain half-Heusler and Heusler nanocomposite phases in situ by atomic-scale regulation, which effectively improved the electrical conductivity and power factor of the material and reduced the lattice thermal conductivity of the material. At the same time, Jie Ma et al. studied the fundamental electron-phonon interaction using the chemical doping of ZrNis-based semi-Hessler materials as an example (Ren et al., 2020). This crossover between different major scattering mechanisms is achieved by shielding ionized impurities, grain boundary, and polarized phonon scattering, and enhanced phonon/alloy scattering. Based on the understanding of different carrier scattering, they derived the carrier scattering phase diagram, which can guide further improving the Te properties of semi-Hessler Te materials. This method can also be extended analogically to materials of different systems and may provide excellent guidance for electro-acoustic decoupling.

Organic materials would be a better choice purely from the direction of reducing thermal conductivity. However, the biggest disadvantage of organic materials is that their electrical properties are difficult to regulate, which greatly affects their thermoelectric properties. The thermal conductivity of organic thermoelectric materials is usually lower than 1 W m⁻¹ K⁻¹, close to the lower limit of the thermal conductivity of inorganic thermoelectric materials (Huang et al., 2016). Moreover, the electronic structure of the organic (semi) conductor can be appropriately adjusted by molecular chemistry and doping treatment, so that electron transport is not affected (Ren et al., 2018). Wang L. et al. (2018) not only reduced the thermal conductivity through flexible organic-inorganic hybridizationbut also improved the electrical performance, effectively realizing electro-acoustic decoupling. Therefore, organic thermoelectric materials have great prospects in Low-temperature applications.

The above is mainly by suppressing phonon transmission to ensure electron transport to improve the thermoelectric performance. The difference is that Zhimei Sun et al. discussed the thermoelectric properties of two-dimensional Nb₂C through first-principles calculations. It is found that when the density of electron states near the Fermi level is high and the phonon frequency is high, the anomalous strong E-P scattering will be generated, and the thermal conductivity of the lattice will be greatly reduced, which also provides a new idea for the design of two-dimensional metallic thermoelectric materials (Huang et al., 2019).

Conclusion

Although thermoelectric functional materials have a long history of research, from the discovery of narrow-band gap semiconductor materials to the vigorous development of wideband gap semiconductor thermoelectric materials, they still fail to achieve excellent ideal performance, so there is still a lot of room for exploration and improvement. This paper elaborates on the improvement of the thermoelectric optimal value ZT from the aspects of optimizing carrier concentration, improving carrier mobility, increasing effective mass, reducing lattice thermal conductivity, exploring intrinsic thermoelectric materials, and electro-acoustic decoupling, among which the relatively independent lattice thermal conductivity regulation has received extensive attention.

In energy band engineering, we can improve the effective mass by introducing resonant state density, increasing energy band degeneracy, controllable hybridization gap and doping Kondo atoms. However, increasing the Seebeck coefficient by increasing the effective mass tends to reduce carrier mobility. At the same time, the Seebeck coefficient can be improved by optimizing the carrier concentration and increasing carrier mobility by modulating doping and temperature-dependent gradient doping. In phonon engineering, the mechanism of point defect scattering, dislocation scattering, interface scattering and resonance scattering to reduce lattice thermal conductivity is summarized. It also reveals the structure-activity relationship of several influencing factors such as weak chemical bonding, strong anharmonic effects, liquid ionic properties, heavy molecular mass and complex crystal structure on the intrinsic low thermal conductivity thermoelectric materials. Finally, the electro-acoustic decoupling theory, such as how to block the transmission of electrons by phonons, is briefly explained.

It can be seen that further exploration of electro-acoustic synergy mechanism and design of intrinsic low thermal conductivity is still the mainstream research direction, but when making some breakthroughs, it is faced with challenges such as thermal dynamic stability and other issues. We can start with the following strategies: 1) new mechanism, new concept, and new theory of the synergy between band engineering and phonon engineering; 2) the influence mechanism of material defect engineering on thermoelectric properties; 3) the influence of synthesis methods, and characterization methods on the evolution of interface, and microstructure; 4) To design a comprehensive theoretical calculation module and establish a complete material genome database to screen new thermoelectric materials with high performance at a high speed and effectively. Although the influence conditions of thermoelectric performance are interlaced and complex, it is believed that breakthrough progress will be made under the rapid development of materials, physics, chemistry and computer science, and it is bound to play a role in the future reliable clean energy.

Author Contributions

YS and RL organized the data analysis, YaL and SB is responsible for the essays written, and YuL, YS, and YaL organized the whole idea.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Beekman, M., and VanderGraaff, A. (2017). High-temperature Thermal Conductivity of Thermoelectric Clathrates. J. Appl. Phys. 121 (20), 205105. doi:10.1063/1.4983817

CrossRef Full Text | Google Scholar

Bell, L. E. (2008). Cooling, Heating, Generating Power, and Recovering Waste Heat with Thermoelectric Systems. Science 321 (5895), 1457–1461. doi:10.1126/science.1158899

PubMed Abstract | CrossRef Full Text | Google Scholar

Bergum, K., Ikeda, T., and Jeffrey Snyder, G. (2011). Solubility and Microstructure in the Pseudo-binary PbTe-Ag₂Te System. J. Solid State Chem. 184 (9), 2543–2552. doi:10.1016/j.jssc.2011.07.012

CrossRef Full Text | Google Scholar

Biswas, K., He, J., Blum, I. D., Wu, C.-I., Hogan, T. P., Seidman, D. N., et al. (2012). High-performance Bulk Thermoelectrics with All-Scale Hierarchical Architectures. Nature 489 (7416), 414–418. doi:10.1038/nature11439

PubMed Abstract | CrossRef Full Text | Google Scholar

Biswas, K., He, J., Zhang, Q., Wang, G., Uher, C., Dravid, V. P., et al. (2011). Strained Endotaxial Nanostructures with High Thermoelectric Figure of Merit. Nat. Chem. 3 (2), 160–166. doi:10.1038/nchem.955

PubMed Abstract | CrossRef Full Text | Google Scholar

Brown, S. R., Kauzlarich, S. M., Gascoin, F., and Snyder, G. J. (2006). Yb₁₄MnSb₁₁: New High Efficiency Thermoelectric Material for Power Generation. Chem. Mat. 18 (7), 1873–1877. doi:10.1021/cm060261t

CrossRef Full Text | Google Scholar

Callaway, J. (1959). Model for Lattice Thermal Conductivity at Low Temperatures. Phys. Rev. 113 (4), 1046–1051. doi:10.1103/physrev.113.1046

CrossRef Full Text | Google Scholar

Cha, J., Zhou, C., Cho, S. P., Park, S. H., and Chung, I. (2019). Ultrahigh Power Factor and Electron Mobility in N-type Bi₂Te_3–x%Cu Stabilized under Excess Te Condition. ACS Appl. Mater. interfaces 11 (34), 30999. doi:10.1021/acsami.9b10394

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, C., Wu, M., He, D., Pei, Y., Wu, C.-F., Wu, X., et al. (2018). 3D Charge and 2D Phonon Transports Leading to High Out-Of-Plane ZT in N-type SnSe Crystals. Science 360 (6390), 778–783. doi:10.1126/science.aaq1479

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, S., Bai, H., Li, J., Pan, W., Jiang, X., Li, Z., et al. (2020). Vacancy-Based Defect Regulation for High Thermoelectric Performance in Ge₉Sb₂Te_12-X Compounds. ACS Appl. Mat. Interfaces 12 (17), 19664–19673. doi:10.1021/acsami.0c02155

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, S., Logothetis, N., Ye, L., and Liu, J. (2015). A High Performance Ag Alloyed Nano-Scale N-type Bi₂Te₃ Based Thermoelectric Material. Mater. Today Proc. 2 (2), 610–619. doi:10.1016/j.matpr.2015.05.083

CrossRef Full Text | Google Scholar

Chen, Z., Jian, Z., Li, W., Chang, Y., Ge, B., Hanus, R., et al. (2017). Lattice Dislocations Enhancing Thermoelectric PbTe in Addition to Band Convergence. Adv. Mat. 29 (23), 1606768. doi:10.1002/adma.201606768

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Z., Yang, J., Liu, R., Xi, L., Zhang, W., and Yang, J. (2013). Theoretical Study on Structural Stability of Fully Filled P-type Skutterudites RETM₄Sb₁₂ (RE = Rare Earth; TM = Fe, Ru). J. Elec Materi 42 (8), 2492–2497. doi:10.1007/s11664-013-2594-z

CrossRef Full Text | Google Scholar

Chong, X., Guan, P.-W., Wang, Y., Shang, S.-L., Soldan Palma, J. P., Drymiotis, F., et al. (2020). Correction to "Understanding the Intrinsic P-type Behavior and Phase Stability of Thermoelectric α-Mg₃Sb₂". ACS Appl. Energy Mat. 3 (1), 1249–1252. doi:10.1021/acsaem.9b02229

CrossRef Full Text | Google Scholar

Christensen, M., Abrahamsen, A. B., Christensen, N. B., Juranyi, F., Andersen, N. H., Lefmann, K., et al. (2008). Avoided Crossing of Rattler Modes in Thermoelectric Materials. Nat. Mater 7 (10), 811–815. doi:10.1038/nmat2273

PubMed Abstract | CrossRef Full Text | Google Scholar

Cook, B. A., Kramer, M. J., Harringa, J. L., Han, M.-K., Chung, D.-Y., and Kanatzidis, M. G. (2009). Analysis of Nanostructuring in High Figure-Of-Merit Ag1-xPbmSbTe2⁺mThermoelectric Materials. Adv. Funct. Mat. 19 (8), 1254–1259. doi:10.1002/adfm.200801284

CrossRef Full Text | Google Scholar

Cox, C. A., Toberer, E. S., Levchenko, A. A., Brown, S. R., Snyder, G. J., Navrotsky, A., et al. (2009). Structure, Heat Capacity, and High-Temperature Thermal Properties of Yb₁₄Mn_1−xAl_xSb₁₁. Chem. Mat. 21 (7), 1354–1360. doi:10.1021/cm803252r

CrossRef Full Text | Google Scholar

Cutler, M., Leavy, J. F., and Fitzpatrick, R. L. (1964). Electronic Transport in Semimetallic Cerium Sulfide. Phys. Rev. 133 (4A), A1143–A1152. doi:10.1103/physrev.133.a1143

CrossRef Full Text | Google Scholar

Dashevsky, Z., Shusterman, S., Dariel, M. P., and Drabkin, I. (2002). Thermoelectric Efficiency in Graded Indium-Doped PbTe Crystals. J. Appl. Phys. 92 (3), 1425–1430. doi:10.1063/1.1490152

CrossRef Full Text | Google Scholar

Du, B., Li, H., Xu, J., Tang, X., and Uher, C. (2011). Enhanced Thermoelectric Performance and Novel Nanopores in AgSbTe₂ Prepared by Melt Spinning. J. Solid State Chem. 184 (1), 109–114. doi:10.1016/j.jssc.2010.10.036

CrossRef Full Text | Google Scholar

Duan, B., Yang, J., Salvador, J. R., He, Y., Zhao, B., Wang, S., et al. (2016). Electronegative Guests in CoSb₃. Energy Environ. Sci. 9 (6), 2090–2098. doi:10.1039/c6ee00322b

CrossRef Full Text | Google Scholar

Dutta, M., Ghosh, T., and Biswas, K. (2020). Electronic Structure Modulation Strategies in High-Performance Thermoelectrics. Apl. Mater. 8 (4), 040910. doi:10.1063/5.0002129

CrossRef Full Text | Google Scholar

Feng, Y., Li, J., Li, Y., Ding, T., Zhang, C., Hu, L., et al. (2020). Band Convergence and Carrier-Density Fine-Tuning as the Electronic Origin of High-Average Thermoelectric Performance in Pb-Doped GeTe-Based Alloys. J. Mat. Chem. A 8 (22), 11370–11380. doi:10.1039/d0ta02758h

CrossRef Full Text | Google Scholar

Gao, W., Wang, Z., Huang, J., and Liu, Z. (2018). Extraordinary Thermoelectric Performance Realized in Hierarchically Structured AgSbSe₂ with Ultralow Thermal Conductivity. ACS Appl. Mat. Interfaces 10 (22), 18685–18692. doi:10.1021/acsami.8b03243

PubMed Abstract | CrossRef Full Text | Google Scholar

Gelbstein, Y., Davidow, J., Girard, S. N., Chung, D. Y., and Kanatzidis, M. (2013). Controlling Metallurgical Phase Separation Reactions of the Ge_0.87Pb_0.13Te Alloy for High Thermoelectric Performance. Adv. Energy Mat. 3 (6), 815–820. doi:10.1002/aenm.201200970

CrossRef Full Text | Google Scholar

Girard, S. N., He, J., Li, C., Moses, S., Wang, G., Uher, C., et al. (2010). In Situ nanostructure Generation and Evolution within a Bulk Thermoelectric Material to Reduce Lattice Thermal Conductivity. Nano Lett. 10 (8), 2825–2831. doi:10.1021/nl100743q

PubMed Abstract | CrossRef Full Text | Google Scholar

Heremans, J. P., Jovovic, V., Toberer, E. S., Saramat, A., Kurosaki, K., Charoenphakdee, A., et al. (2008). Enhancement of Thermoelectric Efficiency in PbTe by Distortion of the Electronic Density of States. Science 321 (5888), 554–557. doi:10.1126/science.1159725

PubMed Abstract | CrossRef Full Text | Google Scholar

Heremans, J. P. (2014). The Ugly Duckling. Nature 508 (7496), 327–328. doi:10.1038/508327a

PubMed Abstract | CrossRef Full Text | Google Scholar

Hicks, L. D., and Dresselhaus, M. S. (1993). Use of Quantum-Well Superlattices to Obtain a High Figure of Merit from Nonconventional Thermoelectric Materials. Cambridge: MRS Online Proceedings Library OPL, 326.

Google Scholar

Horbach, J., Kob, W., and Binder, K. (2001). Structural and Dynamical Properties of Sodium Silicate Melts: an Investigation by Molecular Dynamics Computer Simulation. Chem. Geol. 174 (1-3), 87–101. doi:10.1016/s0009-2541(00)00309-0

CrossRef Full Text | Google Scholar

Hsu, K. F., Loo, S., Guo, F., Chen, W., Dyck, J. S., and Uher, C. (2004). Cubic AgPb M SbTe 2⁺ M : Bulk Thermoelectric Materials with High Figure of Merit. Science 303 (5659), 818–821. doi:10.1126/science.1092963

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, L., Wu, H., Zhu, T., Fu, C., He, J., Ying, P., et al. (2015). Tuning Multiscale Microstructures to Enhance Thermoelectric Performance of N-type Bismuth-Telluride-Based Solid Solutions. Adv. Energy Mat. 5 (17), 1500411. doi:10.1002/aenm.201500411

CrossRef Full Text | Google Scholar

Hu, L., Zhu, T., Liu, X., and Zhao, X. (2014). Point Defect Engineering of High-Performance Bismuth-Telluride-Based Thermoelectric Materials. Adv. Funct. Mat. 24 (33), 5211–5218. doi:10.1002/adfm.201400474

CrossRef Full Text | Google Scholar

Huang, L., Zhang, J., Zhu, C., Ge, Z., Li, Y., Li, D., et al. (2020). Synergistically Optimized Electrical and Thermal Properties by Introducing Electron Localization and Phonon Scattering Centers in CuGaTe₂ with Enhanced Mechanical Properties. J. Mat. Chem. C 8 (22), 7534–7542. doi:10.1039/d0tc00795a

CrossRef Full Text | Google Scholar

Huang, Y., Qiao, J., He, K., Bliznakov, S., Sutter, E., Chen, X., et al. (2016). Interaction of Black Phosphorus with Oxygen and Water. Chem. Mat. 28 (22), 8330–8339. doi:10.1021/acs.chemmater.6b03592

CrossRef Full Text | Google Scholar

Huang, Y., Zhou, J., Wang, G., and Sun, Z. (2019). Abnormally Strong Electron-Phonon Scattering Induced Unprecedented Reduction in Lattice Thermal Conductivity of Two-Dimensional Nb₂C. J. Am. Chem. Soc. 141 (21), 8503–8508. doi:10.1021/jacs.9b01742

PubMed Abstract | CrossRef Full Text | Google Scholar

Ioffe, A. F., Stil'Bans, L. S., Iordanishvili, E. K., Stavitskaya, T. S., Gelbtuch, A., and Vineyard, G. (1959). Semiconductor Thermoelements and Thermoelectric Cooling. Phys. Today 12 (5), 42. doi:10.1063/1.3060810

CrossRef Full Text | Google Scholar

Kim, S. I., Lee, K. H., Mun, H. A., Kim, H. S., Hwang, S. W., Roh, J. W., et al. (2015). Dense Dislocation Arrays Embedded in Grain Boundaries for High-Performance Bulk Thermoelectrics. Science 348 (6230), 109–114. doi:10.1126/science.aaa4166

PubMed Abstract | CrossRef Full Text | Google Scholar

Klemens, P. G. (1960). Thermal Resistance Due to Point Defects at High Temperatures. Phys. Rev. 119 (2), 507–509. doi:10.1103/physrev.119.507

CrossRef Full Text | Google Scholar

Koirala, M., Zhao, H., Pokharel, M., Chen, S., Dahal, T., Opeil, C., et al. (2013). Thermoelectric Property Enhancement by Cu Nanoparticles in Nanostructured FeSb₂. Appl. Phys. Lett. 102 (21), 213111. doi:10.1063/1.4808094

CrossRef Full Text | Google Scholar

Kraemer, D., Sui, J., McEnaney, K., Zhao, H., Jie, Q., Ren, Z. F., et al. (2015). High Thermoelectric Conversion Efficiency of MgAgSb-Based Material with Hot-Pressed Contacts. Energy Environ. Sci. 8 (4), 1299–1308. doi:10.1039/c4ee02813a

CrossRef Full Text | Google Scholar

Kurosaki, K., Kosuga, A., Muta, H., Uno, M., and Yamanaka, S. (2005). Ag₉T_lTe₅: A High-Performance Thermoelectric Bulk Material with Extremely Low Thermal Conductivity. Appl. Phys. Lett. 87 (6), 061919. doi:10.1063/1.2009828

CrossRef Full Text | Google Scholar

Kuznetsov, V. L., Kuznetsova, L. A., Kaliazin, A. E., and Rowe, D. M. (2002). High Performance Functionally Graded and Segmented Bi₂Te₃-Based Materials for Thermoelectric Power Generation. J. Mater. Sci. 37 (14), 2893–2897. doi:10.1023/a:1016092224833

CrossRef Full Text | Google Scholar

Kyratsi, T., Hatzikraniotis, E., Ioannou, M., Chung, D. Y., and Tsiaoussis, I. (2011). Seebeck and Thermal Conductivity Analysis in Amorphous/crystallineβ-K2Bi8Se13nanocomposite Materials. J. Appl. Phys. 110 (3), 033713. doi:10.1063/1.3610393

CrossRef Full Text | Google Scholar

Lee, S., Kim, K., Kang, D.-H., Meyyappan, M., and Baek, C.-K. (2019). Vertical Silicon Nanowire Thermoelectric Modules with Enhanced Thermoelectric Properties. Nano Lett. 19 (2), 747–755. doi:10.1021/acs.nanolett.8b03822

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, Y., Lo, S. H., Chen, C., Sun, H., Chung, D. Y., Chasapis, T. C., et al. (2014). Contrasting Role of Antimony and Bismuth Dopants on the Thermoelectric Performance of Lead Selenide. Nat. Commun. 5 (1), 3640–3711. doi:10.1038/ncomms4640

PubMed Abstract | CrossRef Full Text | Google Scholar

Levin, E. M., Cook, B. A., Harringa, J. L., Bud’ko, S. L., Venkatasubramanian, R., and Schmidt-Rohr, K. (2011). Analysis of Ce- and Yb-Doped TAGS-85 Materials with Enhanced Thermoelectric Figure of Merit. Adv. Funct. Mat. 21 (3), 441–447. doi:10.1002/adfm.201001307

CrossRef Full Text | Google Scholar

Li, F., Li, J.-F., Zhao, L.-D., Xiang, K., Liu, Y., Zhang, B.-P., et al. (2012). Polycrystalline BiCuSeO Oxide as a Potential Thermoelectric Material. Energy Environ. Sci. 5 (5), 7188–7195. doi:10.1039/c2ee21274a

CrossRef Full Text | Google Scholar

Li, J., Zhang, X., Chen, Z., Lin, S., Li, W., Shen, J., et al. (2018). Low-symmetry Rhombohedral GeTe Thermoelectrics. Joule 2 (5), 976–987. doi:10.1016/j.joule.2018.02.016

CrossRef Full Text | Google Scholar

Li, W., Lin, S., Zhang, X., Chen, Z., Xu, X., and Pei, Y. (2016). Thermoelectric Properties of Cu2SnSe4 with Intrinsic Vacancy. Chem. Mat. 28 (17), 6227–6232. doi:10.1021/acs.chemmater.6b02416

CrossRef Full Text | Google Scholar

Li, W., Zheng, L., Ge, B., Lin, S., Zhang, X., Chen, Z., et al. (2017). Promoting SnTe as an Eco-Friendly Solution for P-PbTe Thermoelectric via Band Convergence and Interstitial Defects. Adv. Mat. 29 (17), 1605887. doi:10.1002/adma.201605887

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Mei, D., Wang, H., Yao, Z., Zhu, T., and Chen, S. (2015). Reduced Lattice Thermal Conductivity in Nanograined Na-Doped PbTe Alloys by Ball Milling and Semisolid Powder Processing. Mater. Lett. 140, 103–106. doi:10.1016/j.matlet.2014.11.015

CrossRef Full Text | Google Scholar

Liu, H., Shi, X., Xu, F., Zhang, L., Zhang, W., Chen, L., et al. (2012). Copper Ion Liquid-like Thermoelectrics. Nat. Mater 11 (5), 422–425. doi:10.1038/nmat3273

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y., Zhao, L.-D., Zhu, Y., Liu, Y., Li, F., Yu, M., et al. (2016). Synergistically Optimizing Electrical and Thermal Transport Properties of BiCuSeO via a Dual-Doping Approach. Adv. Energy Mat. 6 (9), 1502423. doi:10.1002/aenm.201502423

CrossRef Full Text | Google Scholar

Liu, Z., Zhang, Y., Mao, J., Gao, W., Wang, Y., Shuai, J., et al. (2017). The Microscopic Origin of Low Thermal Conductivity for Enhanced Thermoelectric Performance of Yb Doped MgAgSb. Acta Mater. 128, 227–234. doi:10.1016/j.actamat.2017.02.015

CrossRef Full Text | Google Scholar

Lu, X., Morelli, D. T., Xia, Y., and Ozolins, V. (2015). Increasing the Thermoelectric Figure of Merit of Tetrahedrites by Co-doping with Nickel and Zinc. Chem. Mat. 27 (2), 408–413. doi:10.1021/cm502570b

CrossRef Full Text | Google Scholar

Makongo, J. P. A., Misra, D. K., Zhou, X., Pant, A., Shabetai, M. R., Su, X., et al. (2011). Simultaneous Large Enhancements in Thermopower and Electrical Conductivity of Bulk Nanostructured Half-Heusler Alloys. J. Am. Chem. Soc. 133 (46), 18843–18852. doi:10.1021/ja206491j

PubMed Abstract | CrossRef Full Text | Google Scholar

Meng, J. F., Chandra Shekar, N. V., Chung, D.-Y., Kanatzidis, M., and Badding, J. V. (2003). Improvement in the Thermoelectric Properties of Pressure-Tuned β-K₂Bi₈Se₁₃. J. Appl. Phys. 94 (7), 4485–4488. doi:10.1063/1.1599049

CrossRef Full Text | Google Scholar

Nielsen, M. D., Ozolins, V., and Heremans, J. P. (2013). Lone Pair Electrons Minimize Lattice Thermal Conductivity. Energy Environ. Sci. 6 (2), 570–578. doi:10.1039/c2ee23391f

CrossRef Full Text | Google Scholar

Pan, Y., Qiu, Y., Witting, I., Zhang, L., Fu, C., Li, J.-W., et al. (2019). Synergistic Modulation of Mobility and Thermal Conductivity in (Bi,Sb)₂Te₃ towards High Thermoelectric Performance. Energy Environ. Sci. 12 (2), 624–630. doi:10.1039/c8ee03225d

CrossRef Full Text | Google Scholar

Pei, Y.-L., Wu, H., Wu, D., Zheng, F., and He, J. (2014). High Thermoelectric Performance Realized in a BiCuSeO System by Improving Carrier Mobility through 3D Modulation Doping. J. Am. Chem. Soc. 136 (39), 13902–13908. doi:10.1021/ja507945h

PubMed Abstract | CrossRef Full Text | Google Scholar

Pei, Y., LaLonde, A. D., Wang, H., and Snyder, G. J. (2012). Low Effective Mass Leading to High Thermoelectric Performance. Energy Environ. Sci. 5 (7), 7963–7969. doi:10.1039/c2ee21536e

CrossRef Full Text | Google Scholar

Pei, Y., Shi, X., LaLonde, A., Wang, H., Chen, L., and Snyder, G. J. (2011). Convergence of Electronic Bands for High Performance Bulk Thermoelectrics. Nature 473 (7345), 66–69. doi:10.1038/nature09996

PubMed Abstract | CrossRef Full Text | Google Scholar

Pei, Y., Wang, H., and Snyder, G. J. (2012). Band Engineering of Thermoelectric Materials. Adv. Mat. 24 (46), 6125–6135. doi:10.1002/adma.201202919

PubMed Abstract | CrossRef Full Text | Google Scholar

Poudel, B., Hao, Q., Ma, Y., Lan, Y., Minnich, A., Yu, B., et al. (2008). High-thermoelectric Performance of Nanostructured Bismuth Antimony Telluride Bulk Alloys. Science 320 (5876), 634–638. doi:10.1126/science.1156446

PubMed Abstract | CrossRef Full Text | Google Scholar

Poudeu, P. F. P., D'Angelo, J., Downey, A. D., Short, J. L., Hogan, T. P., and Kanatzidis, M. G. (2006). High Thermoelectric Figure of Merit and Nanostructuring in Bulk P-type Na_1−xPbmSbyTem+2. Angew. Chem. 118 (23), 3919–3923. doi:10.1002/ange.200600865

PubMed Abstract | CrossRef Full Text | Google Scholar

Qin, B., Zhang, Y., Wang, D., Zhao, Q., Gu, B., Wu, H., et al. (2020). Ultrahigh Average ZT Realized in P-type SnSe Crystalline Thermoelectrics through Producing Extrinsic Vacancies. J. Am. Chem. Soc. 142 (12), 5901–5909. doi:10.1021/jacs.0c01726

PubMed Abstract | CrossRef Full Text | Google Scholar

Qiu, P., Zhang, T., Qiu, Y., Shi, X., and Chen, L. (2014). Sulfide Bornite Thermoelectric Material: a Natural Mineral with Ultralow Thermal Conductivity. Energy Environ. Sci. 7 (12), 4000–4006. doi:10.1039/c4ee02428a

CrossRef Full Text | Google Scholar

Ren, Q., Fu, C., Qiu, Q., Dai, S., Liu, Z., Masuda, T., et al. (2020). Establishing the Carrier Scattering Phase Diagram for ZrNiSn-Based Half-Heusler Thermoelectric Materials. Nat. Commun. 11 (1), 3142–3149. doi:10.1038/s41467-020-16913-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Ren, W., Sun, Y., Zhang, J., Xia, Y., Geng, H., and Zhang, L. (2021). Doping Distribution in Skutterudites with Ultra-high Filling Fractions for Achieving Ultra-low Thermal Conductivity. Acta Mater. 209, 116791. doi:10.1016/j.actamat.2021.116791

CrossRef Full Text | Google Scholar

Ren, X., Yuan, L., Liang, Q., Xie, R., Geng, Z., Sun, Y., et al. (2018). Phase-Controlled Synthesis of High-Bi-Ratio Ternary Sulfide Nanocrystals of Cu_1.57Bi_4.57S₈ and Cu_2.93Bi_4.89S₉. ChemPlusChem 83 (8), 812–818. doi:10.1002/cplu.201800271

PubMed Abstract | CrossRef Full Text | Google Scholar

Roychowdhury, S., Panigrahi, R., Perumal, S., and Biswas, K. (2017). Ultrahigh Thermoelectric Figure of Merit and Enhanced Mechanical Stability of P-type AgSb_1-xZnxTe₂. ACS Energy Lett. 2 (2), 349–356. doi:10.1021/acsenergylett.6b00639

CrossRef Full Text | Google Scholar

Saha, S. K. (2015). Exploring the Origin of Ultralow Thermal Conductivity in Layered BiOCuSe. Phys. Rev. B 92 (4), 041202. doi:10.1103/physrevb.92.041202

CrossRef Full Text | Google Scholar

Samanta, M., Pal, K., Pal, P., Waghmare, U. V., and Biswas, K. (2018). Localized Vibrations of Bi Bilayer Leading to Ultralow Lattice Thermal Conductivity and High Thermoelectric Performance in Weak Topological Insulator N-type BiSe. J. Am. Chem. Soc. 140 (17), 5866–5872. doi:10.1021/jacs.8b02691

PubMed Abstract | CrossRef Full Text | Google Scholar

Samanta, M., Roychowdhury, S., Ghatak, J., Perumal, S., and Biswas, K. (2017). Ultrahigh Average Thermoelectric Figure of Merit, Low Lattice Thermal Conductivity and Enhanced Microhardness in Nanostructured (GeTe)x(AgSbSe₂)100−x. Chem. Eur. J. 23 (31), 7438–7443. doi:10.1002/chem.201701480

PubMed Abstract | CrossRef Full Text | Google Scholar

Sarkar, S., Zhang, X., Hao, S., Hua, X., Bailey, T. P., Uher, C., et al. (2018). A Dual Alloying Strategy to Achieve High Thermoelectric Figure of Merit and Lattice Hardening in P-type Nanostructured PbTe. ACS Energy Lett. 3 (10), 2593–2601. doi:10.1021/acsenergylett.8b01684

CrossRef Full Text | Google Scholar

Selimefendigil, F., Okulu, D., and Mamur, H. (2021). Numerical Analysis for Performance Enhancement of Thermoelectric Generator Modules by Using CNT-Water and Hybrid Ag/MgO-Water Nanofluids. J. Therm. Anal. Calorim. 143 (2), 1611–1621. doi:10.1007/s10973-020-09983-3

CrossRef Full Text | Google Scholar

Shen, J., Fu, C., Liu, Y., Zhao, X., and Zhu, T. (2018). Enhancing Thermoelectric Performance of FeNbSb Half-Heusler Compound by Hf-Ti Dual-Doping. Energy Storage Mater. 10, 69–74. doi:10.1016/j.ensm.2017.07.014

CrossRef Full Text | Google Scholar

Shi, X., Yang, J., Salvador, J. R., Chi, M., Cho, J. Y., Wang, H., et al. (2011). Multiple-filled Skutterudites: High Thermoelectric Figure of Merit through Separately Optimizing Electrical and Thermal Transports. J. Am. Chem. Soc. 133 (20), 7837–7846. doi:10.1021/ja111199y

PubMed Abstract | CrossRef Full Text | Google Scholar

Shutoh, N., and Sakurada, S. (2005). Thermoelectric Properties of the Ti_x(Zr_0.5Hf_0.5)_{1− x}NiSn Half-Heusler Compounds. J. alloys Compd. 389 (1-2), 204–208. doi:10.1016/j.jallcom.2004.05.078

CrossRef Full Text | Google Scholar

Skomorokhov, A. N., Trots, D. M., Knapp, M., Bickulova, N. N., and Fuess, H. (2006). Structural Behaviour of β-Cu₂-δ-Se (δ= 0, 0.15, 0.25) in Dependence on Temperature Studied by Synchrotron Powder Diffraction. J. alloys Compd. 421 (1-2), 64–71. doi:10.1016/j.jallcom.2005.10.079

CrossRef Full Text | Google Scholar

Slack, G. A., and Rowe, D. M. (1995). CRC Handbook of Thermoelectrics. Boca Raton: CRC Press.

Google Scholar

Snyder, G. J., and Toberer, E. S. (2011). Complex Thermoelectric Materials. London: Nature Publishing Group, 101.

Google Scholar

Su, L., Wang, D., Wang, S., Qin, B., Wang, Y., Qin, Y., et al. (2022). High Thermoelectric Performance Realized through Manipulating Layered Phonon-Electron Decoupling. Science 375 (6587), 1385–1389. doi:10.1126/science.abn8997

PubMed Abstract | CrossRef Full Text | Google Scholar

Su, X., Wei, P., Li, H., Liu, W., Yan, Y., Li, P., et al. (2017). Multi-Scale Microstructural Thermoelectric Materials: Transport Behavior, Non-equilibrium Preparation, and Applications. Adv. Mat. 29 (20), 1602013. doi:10.1002/adma.201602013

PubMed Abstract | CrossRef Full Text | Google Scholar

Suarez, F., Nozariasbmarz, A., Vashaee, D., and Öztürk, M. C. (2016). Designing Thermoelectric Generators for Self-Powered Wearable Electronics. Energy Environ. Sci. 9 (6), 2099–2113. doi:10.1039/c6ee00456c

CrossRef Full Text | Google Scholar

Sui, J., Li, J., He, J., Pei, Y.-L., Berardan, D., Wu, H., et al. (2013). Texturation Boosts the Thermoelectric Performance of BiCuSeO Oxyselenides. Energy Environ. Sci. 6 (10), 2916–2920. doi:10.1039/c3ee41859f

CrossRef Full Text | Google Scholar

Suwardi, A., Bash, D., Ng, H. K., Gomez, J. R., Repaka, D. V. M., Kumar, P., et al. (2019). Inertial Effective Mass as an Effective Descriptor for Thermoelectrics via Data-Driven Evaluation. J. Mat. Chem. A 7 (41), 23762–23769. doi:10.1039/c9ta05967a

CrossRef Full Text | Google Scholar

Tan, G., Shi, F., Hao, S., Zhao, L. D., Chi, H., Zhang, X., et al. (2016). Non-equilibrium Processing Leads to Record High Thermoelectric Figure of Merit in PbTe-SrTe. Nat. Commun. 7 (1), 12167–12169. doi:10.1038/ncomms12167

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, G., Chi, H., Liu, W., Zheng, Y., Tang, X., He, J., et al. (2015). Toward High Thermoelectric Performance P-type FeSb_2.2Te_0.8via In Situ Formation of InSb Nanoinclusions. J. Mat. Chem. C 3 (32), 8372–8380. doi:10.1039/c5tc01739d

CrossRef Full Text | Google Scholar

Tan, G., Shi, F., Hao, S., Chi, H., Zhao, L.-D., Uher, C., et al. (2015). Codoping in SnTe: Enhancement of Thermoelectric Performance through Synergy of Resonance Levels and Band Convergence. J. Am. Chem. Soc. 137 (15), 5100–5112. doi:10.1021/jacs.5b00837

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, G., Wang, S., and Tang, X. (2013). High Thermoelectric Figure of Merit of P-type Ternary Unfilled Skutterudite FeSb₂ Te via Ge Doping. Sci. Adv. Mat. 5 (12), 1974–1982. doi:10.1166/sam.2013.1665

CrossRef Full Text | Google Scholar

Tan, G., Zhang, X., Hao, S., Chi, H., Bailey, T. P., Su, X., et al. (2019). Enhanced Density-Of-States Effective Mass and Strained Endotaxial Nanostructures in Sb-Doped Pb_0.97Cd_0.03Te Thermoelectric Alloys. ACS Appl. Mat. Interfaces 11 (9), 9197–9204. doi:10.1021/acsami.8b21524

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, G., Zhao, L.-D., and Kanatzidis, M. G. (2016). Rationally Designing High-Performance Bulk Thermoelectric Materials. Chem. Rev. 116 (19), 12123–12149. doi:10.1021/acs.chemrev.6b00255

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, Q., Zhao, L.-D., Li, J.-F., Wu, C.-F., Wei, T.-R., Xing, Z.-B., et al. (2014). Thermoelectrics with Earth Abundant Elements: Low Thermal Conductivity and High Thermopower in Doped SnS. J. Mat. Chem. A 2 (41), 17302–17306. doi:10.1039/c4ta04462b

CrossRef Full Text | Google Scholar

Tang, Y., Gibbs, Z. M., Agapito, L. A., Li, G., Kim, H.-S., Nardelli, M. B., ., , Curtarolo, S., and Snyder, G. J. (2015). Convergence of Multi-Valley Bands as the Electronic Origin of High Thermoelectric Performance in CoSb3 Skutterudites. Nat. Mater 14 (12), 1223–1228. doi:10.1038/nmat4430

PubMed Abstract | CrossRef Full Text | Google Scholar

Toberer, E. S., May, A. F., and Snyder, G. J. (2010). Zintl Chemistry for Designing High Efficiency Thermoelectric Materials. Chem. Mat. 22 (3), 624–634. doi:10.1021/cm901956r

CrossRef Full Text | Google Scholar

Toberer, E. S., Zevalkink, A., and Snyder, G. J. (2011). Phonon Engineering through Crystal Chemistry. J. Mat. Chem. 21 (40), 15843–15852. doi:10.1039/c1jm11754h

CrossRef Full Text | Google Scholar

Uvarov, C. A., Ortega-Alvarez, F., and Kauzlarich, S. M. (2012). Enhanced High-Temperature Thermoelectric Performance of Yb_14-xCaxMnSb₁₁. Inorg. Chem. 51 (14), 7617–7624. doi:10.1021/ic300567c

PubMed Abstract | CrossRef Full Text | Google Scholar

Valset, K., Böttger, P. H. M., Taftø, J., and Finstad, T. G. (2012). Thermoelectric Properties of Cu Doped ZnSb Containing Zn₃P₂ Particles. J. Appl. Phys. 111 (2), 023703. doi:10.1063/1.3675505

CrossRef Full Text | Google Scholar

Vining, C. B. (2009). An Inconvenient Truth about Thermoelectrics. Nat. Mater 8 (2), 83–85. doi:10.1038/nmat2361

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, L., Zhang, Z., Liu, Y., Wang, B., Fang, L., Qiu, J., et al. (2018). Exceptional Thermoelectric Properties of Flexible Organic-Inorganic Hybrids with Monodispersed and Periodic Nanophase. Nat. Commun. 9 (1), 3817–3818. doi:10.1038/s41467-018-06251-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X. W., Lee, H., Lan, Y. C., Zhu, G. H., Joshi, G., Wang, D. Z., et al. (2008). Enhanced Thermoelectric Figure of Merit in Nanostructured N-type Silicon Germanium Bulk Alloy. Appl. Phys. Lett. 93 (19), 193121. doi:10.1063/1.3027060

CrossRef Full Text | Google Scholar

Wang, Y., Hu, Y.-J., Firdosy, S. A., Star, K. E., Fleurial, J.-P., Ravi, V. A., et al. (2018). First-principles Calculations of Lattice Dynamics and Thermodynamic Properties for Yb₁₄MnSb₁₁. J. Appl. Phys. 123 (4), 045102. doi:10.1063/1.5013601

CrossRef Full Text | Google Scholar

Wei, P., Yang, J., Guo, L., Wang, S., Wu, L., Xu, X., et al. (2016). Minimum Thermal Conductivity in Weak Topological Insulators with Bismuth-Based Stack Structure. Adv. Funct. Mat. 26 (29), 5360–5367. doi:10.1002/adfm.201600718

CrossRef Full Text | Google Scholar

Wu, H. J., Zhao, L. D., Zheng, F. S., Wu, D., Pei, Y. L., Tong, X., et al. (2014). Broad Temperature Plateau for Thermoelectric Figure of Merit ZT>2 in Phase-Separated PbTe_0.7S_0.3. Nat. Commun. 5 (1), 4515–4519. doi:10.1038/ncomms5515

PubMed Abstract | CrossRef Full Text | Google Scholar

Xia, K., Liu, Y., Anand, S., Snyder, G. J., Xin, J., Yu, J., et al. (2018). Enhanced Thermoelectric Performance in 18‐Electron Nb_0.8 CoSb Half‐Heusler Compound with Intrinsic Nb Vacancies. Adv. Funct. Mat. 28 (9), 1705845. doi:10.1002/adfm.201705845

CrossRef Full Text | Google Scholar

Xiang, B., Liu, J., Yan, J., Xia, M., Zhang, Q., Chen, L., et al. (2019). Local Nanostructures Enhanced the Thermoelectric Performance of N-type PbTe. J. Mat. Chem. A 7 (31), 18458–18467. doi:10.1039/c9ta06247e

CrossRef Full Text | Google Scholar

Xiao, Y., Wu, H., Li, W., Yin, M., Pei, Y., Zhang, Y., et al. (2017). Remarkable Roles of Cu to Synergistically Optimize Phonon and Carrier Transport in N-type PbTe-Cu₂Te. J. Am. Chem. Soc. 139 (51), 18732–18738. doi:10.1021/jacs.7b11662

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, J., Ohishi, Y., Ichikawa, S., Muta, H., Kurosaki, K., and Yamanaka, S. (2018). Naturally Decorated Dislocations Capable of Enhancing Multiple-Phonon Scattering in Si-Based Thermoelectric Composites. J. Appl. Phys. 123 (11), 115114. doi:10.1063/1.5019614

CrossRef Full Text | Google Scholar

Xie, W., Tang, X., Yan, Y., Zhang, Q., and Tritt, T. M. (2009). Unique Nanostructures and Enhanced Thermoelectric Performance of Melt-Spun BiSbTe Alloys. Appl. Phys. Lett. 94 (10), 102111. doi:10.1063/1.3097026

CrossRef Full Text | Google Scholar

Xin, J., Wu, H., Liu, X., Zhu, T., Yu, G., and Zhao, X. (2017). Mg Vacancy and Dislocation Strains as Strong Phonon Scatterers in Mg₂Si_1−xSb X Thermoelectric Materials. Nano Energy 34, 428–436. doi:10.1016/j.nanoen.2017.03.012

CrossRef Full Text | Google Scholar

Xu, Q., Xu, S.-M., Tian, R., and Lu, C. (2020). Significantly Enhanced Thermoelectric Properties of Organic-Inorganic Hybrids with a Periodically Ordered Structure. ACS Appl. Mat. Interfaces 12 (11), 13371–13377. doi:10.1021/acsami.0c00949

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, X., Huang, Y., Xie, L., Wu, D., Ge, Z., and He, J. (2020). Realizing Improved Thermoelectric Performance in BiI₃-Doped Sb₂Te₃(GeTe)₁₇ via Introducing Dual Vacancy Defects. Chem. Mat. 32 (4), 1693–1701. doi:10.1021/acs.chemmater.0c00113

CrossRef Full Text | Google Scholar

Xue, Q. Y., Liu, H. J., Fan, D. D., Cheng, L., Zhao, B. Y., and Shi, J. (2016). LaPtSb: a Half-Heusler Compound with High Thermoelectric Performance. Phys. Chem. Chem. Phys. 18 (27), 17912–17916. doi:10.1039/c6cp03211g

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamini, S. A., Ikeda, T., Lalonde, A., Pei, Y., Dou, S. X., and Snyder, G. J. (2013). Rational Design of P-type Thermoelectric PbTe: Temperature Dependent Sodium Solubility. J. Mat. Chem. A 1 (31), 8725–8730. doi:10.1039/c3ta11654a

CrossRef Full Text | Google Scholar

Yan, X., Liu, W., Chen, S., Wang, H., Zhang, Q., Chen, G., et al. (2013). Thermoelectric Property Study of Nanostructured P-type Half-Heuslers (Hf, Zr, Ti)CoSb_0.8Sn_0.2. Adv. Energy Mat. 3 (9), 1195–1200. doi:10.1002/aenm.201200973

CrossRef Full Text | Google Scholar

Yang, J., and Caillat, T. (2006). Thermoelectric Materials for Space and Automotive Power Generation. MRS Bull. 31 (3), 224–229. doi:10.1557/mrs2006.49

CrossRef Full Text | Google Scholar

Yang, J. Y., Aizawa, T., Yamamoto, A., and Ohta, T. (2001). Effects of Interface Layer on Thermoelectric Properties of a Pn Junction Prepared via the BMA-HP Method. Mater. Sci. Eng. B 85 (1), 34–37. doi:10.1016/s0921-5107(01)00630-4

CrossRef Full Text | Google Scholar

Yang, S. H., Zhu, T. J., Sun, T., He, J., Zhang, S. N., and Zhao, X. B. (2008). Nanostructures in High-Performance (GeTe)x(AgSbTe₂)100−xthermoelectric Materials. Nanotechnology 19 (24), 245707. doi:10.1088/0957-4484/19/24/245707

PubMed Abstract | CrossRef Full Text | Google Scholar

Ying, P., Li, X., Wang, Y., Yang, J., Fu, C., Zhang, W., et al. (2017). Hierarchical Chemical Bonds Contributing to the Intrinsically Low Thermal Conductivity in α-MgAgSb Thermoelectric Materials. Adv. Funct. Mat. 27 (1), 1604145. doi:10.1002/adfm.201604145

CrossRef Full Text | Google Scholar

Yu, J., Fu, C., Liu, Y., Xia, K., Aydemir, U., Chasapis, T. C., et al. (2018). Unique Role of Refractory Ta Alloying in Enhancing the Figure of Merit of NbFeSb Thermoelectric Materials. Adv. Energy Mat. 8 (1), 1701313. doi:10.1002/aenm.201701313

CrossRef Full Text | Google Scholar

Yu, J., Xia, K., Zhao, X., and Zhu, T. (2018). High Performance P-type Half-Heusler Thermoelectric Materials. J. Phys. D. Appl. Phys. 51 (11), 113001. doi:10.1088/1361-6463/aaaa58

CrossRef Full Text | Google Scholar

Yu, Y., He, D.-S., Zhang, S., Cojocaru-Mirédin, O., Schwarz, T., Stoffers, A., et al. (2017). Simultaneous Optimization of Electrical and Thermal Transport Properties of Bi_0.5Sb_1.5Te₃ Thermoelectric Alloy by Twin Boundary Engineering. Nano Energy 37, 203–213. doi:10.1016/j.nanoen.2017.05.031

CrossRef Full Text | Google Scholar

Yvenou, E., Sandroni, M., Carella, A., Gueye, M. N., Faure-Vincent, J., Pouget, S., et al. (2020). Spray-coated PEDOT:OTf Films: Thermoelectric Properties and Integration into a Printed Thermoelectric Generator. Mat. Chem. Front. 4 (7), 2054–2063. doi:10.1039/d0qm00265h

CrossRef Full Text | Google Scholar

Zebarjadi, M., Joshi, G., Zhu, G., Yu, B., Minnich, A., Lan, Y., et al. (2011). Power Factor Enhancement by Modulation Doping in Bulk Nanocomposites. Nano Lett. 11 (6), 2225–2230. doi:10.1021/nl201206d

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeugner, A., Nietschke, F., Wolter, A. U. B., Gaß, S., Vidal, R. C., Peixoto, T. R. F., et al. (2019). Chemical Aspects of the Candidate Antiferromagnetic Topological Insulator MnBi₂Te₄. Chem. Mat. 31 (8), 2795–2806. doi:10.1021/acs.chemmater.8b05017

CrossRef Full Text | Google Scholar

Zhang, J., Liu, R., Cheng, N., Zhang, Y., Yang, J., Uher, C., et al. (2014). High-Performance Pseudocubic Thermoelectric Materials from Non-cubic Chalcopyrite Compounds. Adv. Mat. 26 (23), 3848–3853. doi:10.1002/adma.201400058

CrossRef Full Text | Google Scholar

Zhang, J., Song, L., Pedersen, S. H., Yin, H., Hung, L. T., and Iversen, B. B. (2017). Discovery of High-Performance Low-Cost N-type Mg₃Sb₂-Based Thermoelectric Materials with Multi-Valley Conduction Bands. Nat. Commun. 8 (1), 1–8. doi:10.1038/ncomms13901

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Q., Chere, E. K., Sun, J., Cao, F., Dahal, K., Chen, S., et al. (2015). Studies on Thermoelectric Properties of N-type Polycrystalline SnSe1-xSxby Iodine Doping. Adv. Energy Mat. 5 (12), 1500360. doi:10.1002/aenm.201500360

CrossRef Full Text | Google Scholar

Zhao, H., Sui, J., Tang, Z., Lan, Y., Jie, Q., Kraemer, D., et al. (2014). High Thermoelectric Performance of MgAgSb-Based Materials. Nano Energy 7, 97–103. doi:10.1016/j.nanoen.2014.04.012

CrossRef Full Text | Google Scholar

Zhao, K., Liu, K., Yue, Z., Wang, Y., Song, Q., Li, J., et al. (2019). Are Cu₂Te‐Based Compounds Excellent Thermoelectric Materials? Adv. Mat. 31 (49), 1903480. doi:10.1002/adma.201903480

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, L.-D., Dravid, V. P., and Kanatzidis, M. G. (2014). The Panoscopic Approach to High Performance Thermoelectrics. Energy Environ. Sci. 7 (1), 251–268. doi:10.1039/c3ee43099e

CrossRef Full Text | Google Scholar

Zhao, L.-D., Hao, S., Lo, S.-H., Wu, C.-I., Zhou, X., and Lee, Y. (2013). High Thermoelectric Performance via Hierarchical Compositionally Alloyed Nanostructures. J. Am. Chem. Soc. 135 (19), 7364–7370. doi:10.1021/ja403134b

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, L.-D., He, J., Berardan, D., Lin, Y., Li, J.-F., Nan, C.-W., et al. (2014). BiCuSeO Oxyselenides: New Promising Thermoelectric Materials. Energy Environ. Sci. 7 (9), 2900–2924. doi:10.1039/c4ee00997e

CrossRef Full Text | Google Scholar

Zhao, L.-D., Lo, S.-H., Zhang, Y., Sun, H., Tan, G., Uher, C., et al. (2014). Ultralow Thermal Conductivity and High Thermoelectric Figure of Merit in SnSe Crystals. Nature 508 (7496), 373–377. doi:10.1038/nature13184

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, L.-D., Tan, G., Hao, S., He, J., Pei, Y., Chi, H., et al. (2016). Ultrahigh Power Factor and Thermoelectric Performance in Hole-Doped Single-Crystal SnSe. Science 351 (6269), 141–144. doi:10.1126/science.aad3749

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, L. D., Berardan, D., Pei, Y. L., Byl, C., Pinsard-Gaudart, L., and Dragoe, N. (2010). Bi1−xSrxCuSeO Oxyselenides as Promising Thermoelectric Materials. Appl. Phys. Lett. 97 (9), 092118. doi:10.1063/1.3485050

CrossRef Full Text | Google Scholar

Zhao, L. D., Wu, H. J., Hao, S. Q., Wu, C. I., Zhou, X. Y., Biswas, K., et al. (2013). All-scale Hierarchical Thermoelectrics: MgTe in PbTe Facilitates Valence Band Convergence and Suppresses Bipolar Thermal Transport for High Performance. Energy Environ. Sci. 6 (11), 3346–3355. doi:10.1039/c3ee42187b

CrossRef Full Text | Google Scholar

Zhao, L. D., Zhang, B.-P., Li, J.-F., Zhang, H. L., and Liu, W. S. (2008). Enhanced Thermoelectric and Mechanical Properties in Textured N-type Bi2Te3 Prepared by Spark Plasma Sintering. Solid State Sci. 10 (5), 651–658. doi:10.1016/j.solidstatesciences.2007.10.022

CrossRef Full Text | Google Scholar

Zheng, L., Li, W., Lin, S., Li, J., Chen, Z., and Pei, Y. (2017). Interstitial Defects Improving Thermoelectric SnTe in Addition to Band Convergence. ACS Energy Lett. 2 (3), 563–568. doi:10.1021/acsenergylett.6b00671

CrossRef Full Text | Google Scholar

Zhong, B., Zhang, Y., Li, W., Chen, Z., Cui, J., Li, W., et al. (2014). High Superionic Conduction Arising from Aligned Large Lamellae and Large Figure of Merit in Bulk Cu1.94Al0.02Se. Appl. Phys. Lett. 105 (12), 123902. doi:10.1063/1.4896520

CrossRef Full Text | Google Scholar

Zhou, C., Yu, Y., Lee, Y. K., Cojocaru-Mirédin, O., Yoo, B., Cho, S.-P., et al. (2018). High-Performance N-type PbSe-Cu₂Se Thermoelectrics through Conduction Band Engineering and Phonon Softening. J. Am. Chem. Soc. 140 (45), 15535–15545. doi:10.1021/jacs.8b10448

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, P. W., Jia, X., Chen, H. Y., Guo, W. L., Chen, L. X., Li, D. M., et al. (2002). A New Method of Synthesis for Thermoelectric Materials: HPHT. Solid state Commun. 123 (1-2), 43–47. doi:10.1016/s0038-1098(02)00182-5

CrossRef Full Text | Google Scholar