- 1MOE Key Laboratory for Non-equilibrium Synthesis and Modulation of Condensed Matter, School of Physics, Xi’an Jiaotong University, Xi’an, China
- 2State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute of Laser Spectroscopy, Shanxi University, Taiyuan, China
- 3Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan, China
In this work we quantitatively study the reliability of the frozen nuclei approximation for ultrafast dynamics. Specifically we study laser excitation of HCCI+ from its ground state to the first electronically excited state. The population of the first excited state is obtained by both the frozen nuclei approximation and by multidimensional nuclear dynamics. Detailed comparison of the results by the two methods are performed to provide quantitative criteria for the reliability of the frozen nuclei approximation for this system.
1 Introduction
The rapid advances of ultrafast science and technology have made it possible to manipulate electron dynamics in molecular systems with ultrashort laser pulses. In particular, laser induced electron density redistribution such as charge transfer (Marcus, 1956; May and Kühn, 2008) and charge migration (Weinkauf et al., 1996, 1997; Cederbaum and Zobeley, 1999; Calegari et al., 2014; Kraus et al., 2015) have been extensively investigated. In general, charge migration prefers frozen nuclei or small amplitude nuclear motions, while charge transfer is typically accompanied by large amplitude nuclear motions. The research of charge transfer processes has a relatively long history. While ultrafast charge migration emerged as a hot topic during the past two decades (Weinkauf et al., 1996, 1997; Remacle et al., 1998; Cederbaum and Zobeley, 1999; Remacle and Levine, 1999; Barth and Manz, 2006; Kanno et al., 2006; Yudin et al., 2006; Remacle et al., 2007; Kanno et al., 2010; Mineo et al., 2012; Calegari et al., 2014; Kraus et al., 2015; Li et al., 2015; Yamaki et al., 2016; Wörner et al., 2017; Mineo et al., 2021). It should be noted that the first attosecond charge migration phenomenon was already introduced in 1944 (Eyring et al., 1944) and was largely forgotten during the next decades. Surveys of the literature on ultrafast charge migration can be found in Ref. (Jia et al., 2017a; Wörner et al., 2017). Below we summarize some typical features of ultrafast charge migration and its connection to the frozen nuclei approximation (FNA).
Ultrafast charge migration typically represents quantum dynamics of a coherent superposition of more than one electronic state. The typical time scale of ultrafast charge migration ranges from several hundred attoseconds to a few femtoseconds which makes the experimental observation (Kraus et al., 2015) rather difficult. For such a short time, the frozen nuclei approximation has been widely used for theoretical work of ultrafast charge migration. There are also several theoretical investigations which include the effects of nuclear motions (Bandrauk et al., 2009; Kanno et al., 2010; Ulusoy and Nest, 2012; Mendive-Tapia et al., 2013; Mineo et al., 2014; Despré et al., 2015; Mineo et al., 2021). The amplitude of charge migration can be significantly modulated by nuclear motions, in particular for relatively long-time dynamics (Mendive-Tapia et al., 2013; Mineo et al., 2014; Jia et al., 2019a,b). In general, the FNA is widely believed to be only valid for short time pulses, but there are no quantitative criteria for how short the pulses should be. This serves as the motivation for the present work: to seek quantitative criteria for the reliability of the FNA. Specifically, we will investigate short-pulse excitations of HCCI+ by systematically varying the laser parameters in a sufficiently wide region.
The choice of HCCI+ as our model of interest is based on the availability of experimental data (Heilbronner et al., 1971; Kraus et al., 2015) and theoretical techniques (Jia et al., 2019b). The combined experimental and theoretical reconstruction of attosecond charge migration has been reported for ultrafast ionization of HCCI (Kraus et al., 2015). Coherent superposition of the ground and first excited states has been created and analyzed. Subsequent theoretical investigations of ultrafast charge migration in HCCI+ (Jia et al., 2017b; Ding et al., 2017) related to the experimental observation (Kraus et al., 2015) exploit the FNA. In-depth investigations of simulations and manipulations of charge migration in HCCI+ including multidimensional nuclear dynamics have been reported recently (Jia et al., 2019a,b). However, no comparisons between the results of multidimensional nuclear dynamics and the ones of the FNA are available.
In the present work, we will investigate the reliability of the FNA by comparing the FNA and multidimensional nuclear dynamics. The remainder parts of the paper are organized as follows. Section 2 contains the model and methods for numerical calculations. Section 3 presents the results and discussion. The conclusions are drawn in Section 4.
2 Model and Methods
We focus on laser excitations of HCCI+ from its ground state. Full dimensional simulations of the system involve sets of electronic coordinates r = {r1, r2, … } and nuclear coordinates R = {R1, R2, … }. Here ri and Rj are the spatial coordinates of the i-th electron and the j-th nucleus, respectively. It is convenient to use the Dirac notation for the electronic degrees of freedom. The total wavefunction of the system is thus
Using the Born-Huang expansion (Born and Oppenheimer, 1927; Born and Huang, 1954), the total wavefunction can be expressed in terms of the electronic eigenstates |k(R)⟩ which are the solutions of the standard time-independent electronic schrödinger equation
The corresponding electronic eigenenergy Vk(R) is the k-th potential energy surface (PES). Here Vk(R) and ⟨r|k(R)⟩ are the same as the ones used in Refs. (Jia et al., 2019a,b) which are calculated by Molpro (Werner et al., 2012) using the state-averaged CASSCF(15,13) with cc-pVQZ basis set (cc-pVQZ-pp for iodine).
According to (Kraus et al., 2015; Jia et al., 2019a,b), nonadiabatic couplings between different electronic states |k(R)⟩ are negligible. The total Hamiltonian for HCCI+ in an external laser field E(t) can be approximated as
where T(R) is the nuclear kinetic energy and μkk′(R) = ⟨k(R)|μ|k′(R)⟩ is the transition (or permanent) dipole moment. The laser pulse has a Gaussian shape with maximum amplitude Emax and carrier frequency ω
where ez is the direction of the electric field. For convenience, the electric field and the molecules are oriented along the z-axis. In the literature, there are different choices of the parameter a in Eq. 4. For the present work we set
for easier characterization of the pulse duration. We define the pulse duration as the full width at half maximum (FWHM) of s(t), which is just T in Eq. 4.
The quantum dynamics of the system can be simulated by the time-dependent schrödinger equation subject to initial condition at t = −∞
where χg,v=0(R) is the vibrational ground state wavefunction of the lowest potential energy surface Vg(R). For convenience we use k = g, e to represent the lowest and first excited electronic states, respectively. The wave packet is numerically propagated by means of the split operator method (Leforestier et al., 1991).
Subsequently, we can obtain the population of the electronic state |k(R)⟩ according to
where χk (R,t) = ⟨k(R)|Ψ(R, t)⟩ is the nuclear wave packet on the k-th PES Vk(R). It contains seven vibrational coordinates. According to Ref. (Jia et al., 2019a,b), one-dimensional (1D), three-dimensional (3D), and seven-dimensional (7D) calculations lead to essentially the same results. In the 3D calculations, the H-C, C-C and C-I bond lengths are explicitly taken into account and the four bending degrees of freedom are neglected. This kind of approximation is reasonable for linear molecules, such as HCCI+. In the present work we use the same 3D calculations for the nuclear wave packet χk (R,t) as in Ref. (Jia et al., 2019b). Then we mainly focus on the population of the first electronically excited state Pk(t) for k = e.
To check the reliability of the FNA, we further calculated the population of the first electronically excited state
the time dependent coefficient ck(t) can be obtained subject to the initial condition ck(t = −∞) = δkg. The corresponding population is
Throughout this work we fix the carrier frequency of the laser in Eq. 4 as ℏω = Ve (Req) − Vg (Req). We only focus on the final population at t = tf when the laser pulse is off. This leads to the following analytical expression (Jia et al., 2017a)
where
For all the subsequent numerical calculations we set tf = 5T. However, this should not be wrongly interpreted as the FNA is valid even for t = 5T. We choose tf = 5T just to make use of the property that the results presented in this work do not depend on different choices of tf as long as tf ≥ T.
3 Results and Discussion
The equilibrium structure Req of HCCI+ is linear with bond lengths RHC = 1.06 Å, RCC = 1.21 Å and RCI = 1.95 Å. The corresponding vertical excitation energy from ground state |g(Req)⟩ to the first excited state |e(Req)⟩ is ℏω = 2.41 eV. For typical pulse durations, there are sufficient numbers of cycles in E(t) to make the electronic transition resonant. The corresponding transition dipole has only a z-component, which is
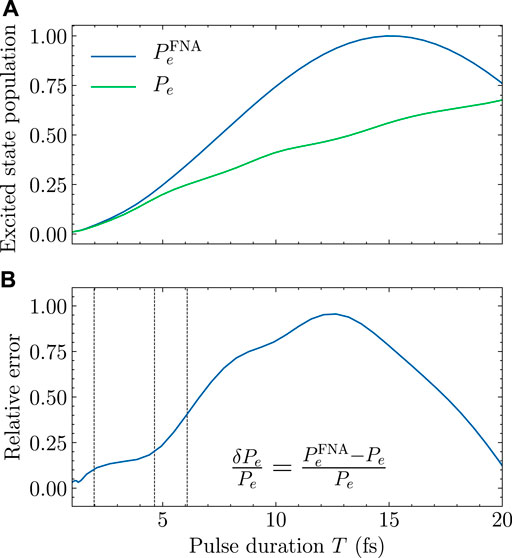
FIGURE 1. Population of the first electronically excited state of HCCI+ versus the pulse duration T, at t = tf when the laser pulse is switched off. The maximum-amplitude of the electric field Emax is 2 GV/m. (A) Pe (tf) and
As can be seen from Figure 1A, the deviation between
To quantitatively compare
Figure 2 shows the color-coded contour plots for the dependence of
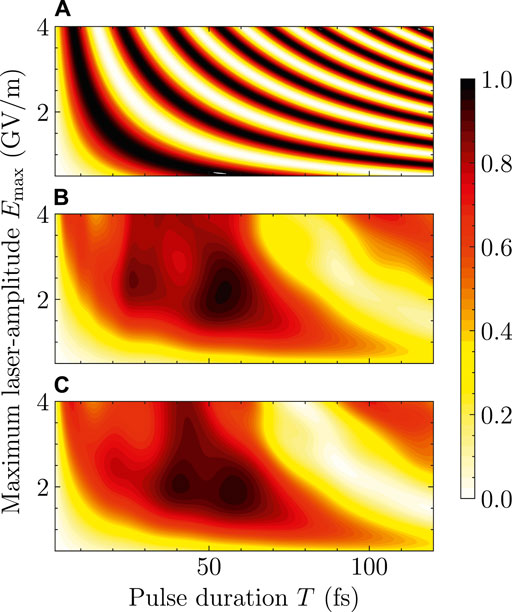
FIGURE 2. Population of the first electronically excited state of HCCI+ versus Emax and T illustrated by color-coded contour plots. (A)
To systematically study the reliability of the FNA for short pulses, the difference between

FIGURE 3. (A) Color-coded contour plots for the deviation
In the short pulse region, the relative error
For example, if we want to use the FNA to obtain results with relative errors smaller than 5%, we need to set the pulse durations of the lasers to be smaller than T95. Similarly for the meanings of T90, T80, and T60. According to our model the characteristic pulse durations T95, T90, T80, and T60 only depend on one parameter Emax, which will be investigated subsequently.
The detailed dependence of T95, T90, T80, and T60 on the maximum amplitude of the electric field Emax is shown in Figure 4. A quite good property for the characteristic pulse durations is that T95, T90, and T80 almost do not depend on Emax. The corresponding values are T95 = 1.32 fs, T90 = 1.97 fs, and T80 = 4.65 fs respectively. The value of T60 increases with Emax extremely slightly from 6.09 to 6.14 fs. For relatively high standard criteria, say relative errors below 20%, the corresponding characteristic pulse durations are quite robust with respect to different amplitudes of lasers. This greatly simplifies the criteria for choosing proper lasers for applications of short pulse excitations of HCCI+. Essentially, we only need to care about the durations of the laser pulses with quantitative guidance derived from Figure 4 for the reliability of the FNA.
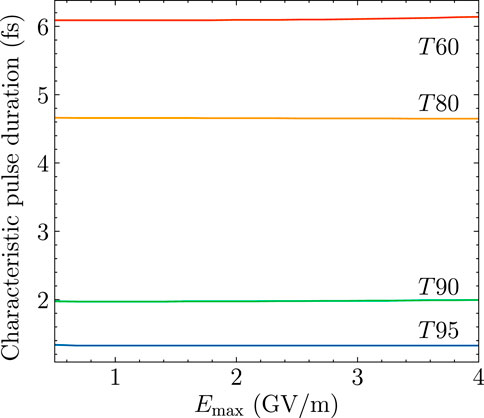
FIGURE 4. Characteristic pulse durations T95, T90, T80, and T60 for relative error
The FNA only considers the electronic degrees of freedom and neglects the nuclear motions. Mathematically this corresponds to a large overlap of the time-dependent and the initial nuclear wave packets. The overlap can be estimated as the product of the corresponding overlap for each normal mode. The overlap for a normal mode may be approximated as
4 Conclusion
We have systematically investigated the population of the first electronically excited state of HCCI+ excited by different laser pulses. The amplitudes and durations of the laser pulses span a rather large domain for typical applications. The deviations between the results obtained by the frozen nuclei approximation and the ones obtained by multidimensional nuclear dynamics are calculated and analyzed in detail to check the reliability of the FNA. As expected the validity of the FNA can be admitted for sufficiently short laser pulses. Quantitative criteria for the reliability of the FNA are obtained. Specifically if we want to limit the relative errors of the FNA within 5% (or 10, or 20, or 40%), the durations of the laser pulses should be less than T95 = 1.3 fs (or T90 = 2.0 fs, or T80 = 4.7 fs, or T60 = 6.1 fs). For example, ultrafast charge migration in HCCI+ is reconstructed in Ref. (Kraus et al., 2015). for the first period of 1.85 fs. By extrapolation of our results, the error of the reported charge migration in HCCI+ for the first period is less than 10%. For short pulses with durations up to T60, the relative errors of the FNA are found to be almost independent of the amplitudes of the laser pulses. The results of the present work are expected to provide valuable guidance to future investigations of short pulse excitations of HCCI+.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author Contributions
YY proposed the conception and design of the study. DJ carried out all the quantum chemical calculations and the quantum dynamics simulations, and prepared all Figures. YY wrote the zero-order draft. All the authors contributed to the submitted version of the manuscript.
Funding
This work was supported by the National Key Research and Development Program of China (2017YFA0304203), the Program for Changjiang Scholars and Innovative Research Team (IR_17R70), the National Natural Science Foundation of China (11904215), the 111 project (Grant No. D18001), the Fund for “Shanxi 1331 Project,” and the Hundred Talent Program of Shanxi Province.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We would like to express our gratitude to Professor Jörn Manz (Berlin) for stimulating discussions and careful reading of the manuscript.
References
Bandrauk, A. D., Chelkowski, S., Corkum, P. B., Manz, J., and Yudin, G. L. (2009). Attosecond Photoionization of a Coherent Superposition of Bound and Dissociative Molecular States: Effect of Nuclear Motion. J. Phys. B: Mol. Opt. Phys. 42, 134001. doi:10.1088/0953-4075/42/13/134001
Barth, I., and Manz, J. (2006). Periodic Electron Circulation Induced by Circularly Polarized Laser Pulses: Quantum Model Simulations for Mg Porphyrin. Angew. Chem. Int. Ed. 45, 2962–2965. doi:10.1002/anie.200504147
Born, M., and Oppenheimer, R. (1927). Zur Quantentheorie der Molekeln. Ann. Phys. 389, 457–484. doi:10.1002/andp.19273892002
Calegari, F., Ayuso, D., Trabattoni, A., Belshaw, L., De Camillis, S., Anumula, S., et al. (2014). Ultrafast Electron Dynamics in Phenylalanine Initiated by Attosecond Pulses. Science 346, 336–339. doi:10.1126/science.1254061
Cederbaum, L. S., and Zobeley, J. (1999). Ultrafast Charge Migration by Electron Correlation. Chem. Phys. Lett. 307, 205–210. doi:10.1016/S0009-2614(99)00508-4
Despré, V., Marciniak, A., Loriot, V., Galbraith, M. C. E., Rouzée, A., Vrakking, M. J. J., et al. (2015). Attosecond Hole Migration in Benzene Molecules Surviving Nuclear Motion. J. Phys. Chem. Lett. 6, 426–431. doi:10.1021/jz502493j
Ding, H., Jia, D., Manz, J., and Yang, Y. (2017). Reconstruction of the Electronic Flux during Adiabatic Attosecond Charge Migration in HCCI+. Mol. Phys. 115, 1813–1825. doi:10.1080/00268976.2017.1287967
Heilbronner, E., Muszkat, K. A., and Schäublin, J. (1971). An Estimate of the Interatomic Distances in Monohaloacetylene Radical Cations from Photoelectron-Spectroscopic Data. Hca 54, 58–76. doi:10.1002/hlca.19710540107
Jia, D., Manz, J., Paulus, B., Pohl, V., Tremblay, J. C., and Yang, Y. (2017a). Quantum Control of Electronic Fluxes during Adiabatic Attosecond Charge Migration in Degenerate Superposition States of Benzene. Chem. Phys. 482, 146–159. doi:10.1016/j.chemphys.2016.09.021
Jia, D., Manz, J., and Yang, Y. (2019a). De- and Recoherence of Charge Migration in Ionized Iodoacetylene. J. Phys. Chem. Lett. 10, 4273–4277. doi:10.1021/acs.jpclett.9b01687
Jia, D., Manz, J., and Yang, Y. (2017b). Generation of Electronic Flux during the Femtosecond Laser Pulse Tailored to Induce Adiabatic Attosecond Charge Migration in. J. Mod. Opt. 64, 960–970. doi:10.1080/09500340.2016.1269216
Jia, D., Manz, J., and Yang, Y. (2019b). Timing the Recoherences of Attosecond Electronic Charge Migration by Quantum Control of Femtosecond Nuclear Dynamics: A Case Study for HCCI+. J. Chem. Phys. 151, 244306. doi:10.1063/1.5134665
Kanno, M., Kono, H., and Fujimura, Y. (2006). Control of π-Electron Rotation in Chiral Aromatic Molecules by Nonhelical Laser Pulses. Angew. Chem. Int. Ed. 45, 7995–7998. doi:10.1002/anie.200602479
Kanno, M., Kono, H., Fujimura, Y., and Lin, S. H. (2010). Nonadiabatic Response Model of Laser-Induced Ultrafastπ-Electron Rotations in Chiral Aromatic Molecules. Phys. Rev. Lett. 104, 108302. doi:10.1103/physrevlett.104.108302
Kraus, P. M., Mignolet, B., Baykusheva, D., Rupenyan, A., Horný, L., Penka, E. F., et al. (2015). Measurement and Laser Control of Attosecond Charge Migration in Ionized Iodoacetylene. Science 350, 790–795. doi:10.1126/science.aab2160
Leforestier, C., Bisseling, R. H., Cerjan, C., Feit, M. D., Friesner, R., Guldberg, A., et al. (1991). A Comparison of Different Propagation Schemes for the Time Dependent Schrödinger Equation. J. Comput. Phys. 94, 59–80. doi:10.1016/0021-9991(91)90137-a
Li, H., Mignolet, B., Wachter, G., Skruszewicz, S., Zherebtsov, S., Süßmann, F., et al. (2015). Coherent Electronic Wave Packet Motion inC60Controlled by the Waveform and Polarization of Few-Cycle Laser Fields. Phys. Rev. Lett. 114, 123004. doi:10.1103/PhysRevLett.114.123004
Marcus, R. A. (1956). On the Theory of Oxidation‐Reduction Reactions Involving Electron Transfer. I. J. Chem. Phys. 24, 966–978. doi:10.1063/1.1742723
May, V., and Kühn, O. (2011). Charge and Energy Transfer Dynamics in Molecular Systems, Third, Revised and Enlarged Edition. Wiley-VCH, Weinheim.
Mendive-Tapia, D., Vacher, M., Bearpark, M. J., and Robb, M. A. (2013). Coupled Electron-Nuclear Dynamics: Charge Migration and Charge Transfer Initiated Near a Conical Intersection. J. Chem. Phys. 139, 044110. doi:10.1063/1.4815914
Mineo, H., Lin, S. H., and Fujimura, Y. (2014). Vibrational Effects on UV/Vis Laser-Driven π-electron Ring Currents in Aromatic Ring Molecules. Chem. Phys. 442, 103–110. doi:10.1016/j.chemphys.2014.02.011
Mineo, H., Phan, N.-L., La, D.-K., and Fujimura, Y. (2021). Theoretical Study of Dynamic Stark-Induced π-Electron Rotations in Low-Symmetry Aromatic Ring Molecules beyond the Frozen Nuclear Approximation. J. Phys. Chem. A. 125, 1476–1489. doi:10.1021/acs.jpca.0c10216
Mineo, H., Yamaki, M., Teranishi, Y., Hayashi, M., Lin, S. H., and Fujimura, Y. (2012). Quantum Switching of π-Electron Rotations in a Nonplanar Chiral Molecule by Using Linearly Polarized UV Laser Pulses. J. Am. Chem. Soc. 134, 14279–14282. doi:10.1021/ja3047848
Remacle, F., and Levine, R. D. (1999). Charge Migration and Control of Site Selective Reactivity: The Role of Covalent and Ionic States. J. Chem. Phys. 110, 5089–5099. doi:10.1063/1.478406
Remacle, F., Levine, R. D., and Ratner, M. A. (1998). Charge Directed Reactivity:. Chem. Phys. Lett. 285, 25–33. doi:10.1016/S0009-2614(97)01314-6
Remacle, F., Nest, M., and Levine, R. D. (2007). Laser Steered Ultrafast Quantum Dynamics of Electrons in LiH. Phys. Rev. Lett. 99, 183902. doi:10.1103/PhysRevLett.99.183902
Ulusoy, I. S., and Nest, M. (2012). Remarks on the Validity of the Fixed Nuclei Approximation in Quantum Electron Dynamics. J. Phys. Chem. A. 116, 11107–11110. doi:10.1021/jp304140r
Weinkauf, R., Schanen, P., Metsala, A., Schlag, E. W., Bürgle, M., and Kessler, H. (1996). Highly Efficient Charge Transfer in Peptide Cations in the Gas Phase: Threshold Effects and Mechanism. J. Phys. Chem. 100, 18567–18585. doi:10.1021/jp960926m
Weinkauf, R., Schlag, E. W., Martinez, T. J., and Levine, R. D. (1997). Nonstationary Electronic States and Site-Selective Reactivity. J. Phys. Chem. A. 101, 7702–7710. doi:10.1021/jp9715742
Werner, H.-J., Knowles, P. J., Knizia, G., Manby, F. R., Schütz, M., Celani, P., et al. (2012). Molpro, Version 2012.1, a Package of Ab Initio Programs. Available at http://www.molpro.net (accessed Feb 18, 2016)
Wörner, H. J., Arrell, C. A., Banerji, N., Cannizzo, A., Chergui, M., Das, A. K., et al. (2017). Charge Migration and Charge Transfer in Molecular Systems. Struct. Dyn. 4, 061508. doi:10.1063/1.4996505
Yamaki, M., Mineo, H., Teranishi, Y., Lin, S. H., and Fujimura, Y. (2016). Quantum Control of Coherent ρρ‐Electron Dynamics in Chiral Aromatic Molecules. Jnl Chin. Chem. Soc 63, 87–92. doi:10.1002/jccs.201500043
Keywords: frozen nuclei approximation, ultrashort laser pulses, nuclear quantum dynamics, electronic excitation, population transfer
Citation: Jia D and Yang Y (2022) Systematic Investigation of the Reliability of the Frozen Nuclei Approximation for Short-Pulse Excitation: The Example of HCCI+. Front. Chem. 10:857348. doi: 10.3389/fchem.2022.857348
Received: 18 January 2022; Accepted: 07 February 2022;
Published: 16 March 2022.
Edited by:
Yuichi Fujimura, Tohoku University, JapanReviewed by:
Hirobumi Mineo, Ton Duc Thang University, VietnamManabu Kanno, Tohoku University, Japan
Copyright © 2022 Jia and Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yonggang Yang, eWd5YW5nQHN4dS5lZHUuY24=
 Dongming Jia
Dongming Jia Yonggang Yang
Yonggang Yang