Abstract
The Zagreb connection indices are the known topological descriptors of the graphs that are constructed from the connection cardinality (degree of given nodes lying at a distance 2) presented in 1972 to determine the total electron energy of the alternate hydrocarbons. For a long time, these connection indices did not receive much research attention. Ali and Trinajstić [Mol. Inform. 37, Art. No. 1800008, 2018] examined the Zagreb connection indices and found that they compared to basic Zagreb indices and that they provide a finer value for the correlation coefficient for the 13 physico-chemical characteristics of the octane isomers. This article acquires the formulae of expected values of the first Zagreb connection index of a random cyclooctatetraene chain, a random polyphenyls chain, and a random chain network with l number of octagons, hexagons, and pentagons, respectively. The article presents extreme and average values of all the above random chains concerning a set of special chains, including the meta-chain, the ortho-chain, and the para-chain.
1 Introduction
Graph theory is vital to various disciplines, including the chemical and biological sciences. One of the objectives of chemical graph theory is its primary and significant role in studying physico-chemical reactions and biological activities and pointing out the structural properties of molecular graphs, etc., Topological descriptors have played a significant role in achieving the desired properties of molecular graphs. Topological descriptors are molecular structural invariants that theoretically and mathematically explain the connectivity characteristics of nano-materials and chemical compounds. Therefore, topological indices produce sharper approaches to measuring their behavior and characteristics.
For 20Â years, hydrocarbons and their derivatives have received attention from researchers because these compounds only have two members, carbon and hydrogen. We can acquire various types of hydrocarbon derivatives by replacing their molecular hydrogen atoms with different types of other atomic groups. A large number of valuable hydrocarbons are available in plants and some valuable characteristics of hydrocarbons are important to chemical raw materials and fuel.
Throughout this article, the vertex and edge sets of a graph are represented as and , respectively. We denote the degree of a vertex by , which is defined as the cardinality of edges joined with . Let the order and size of be n and m, respectively. The l-degree of a given vertex , presented by , is the cardinality of set of vertices of whose distance from is l, where and [this is known as the connection number of (Todeschini and Consonni, 2000)].
Suppose that is a collection of all connected simple graphs. There is a function that describes a topological invariant if for any two isomorphic members and of , we have . Thousands of degree and distance-related topological invariants have been proposed, but some are better known because of their high predictive power for many characteristics like density, boiling point, molecular weight, refractive index, etc., Topological invariants have so many implementations in numerous areas of sciences such as drug discovery, physico-chemical research, toxicology, biology, and chemistry. To date, topological indices are the most notable field of graphical research. For more discussion on numerous invariants, we refer readers to studies by (Gutman, 2013; Akhter et al., 2016; Akhter and Imran, 2016; Akhter et al., 2017; Akhter et al., 2018; Akhter et al., 2020).
The Zagreb indices are the most notable invariants, and they have many valuable applications in chemistry. In 1972 Gutman and Trinajstić (Gutman and Trinajstić, 1972) established the first vertex degree dependent Zagreb index of a graph . Two renowned Zagreb indices of a graph can be described in the following manner:
Motivated by how influential they have become and the many important applications of primary Zagreb indices, Naji et al. (Soner and Naji, 2016; Gutman et al., 2017) presented the concept of Zagreb connection indices (leap Zagreb indices), constructed from the second degrees of the vertices of a graph . The first, second, and modified Zagreb connection indices of can be defined as:
The chemical applications of ZC1 were presented in (8), indicating that the given index has a wide co-relation with the physical characteristics of chemical compounds, for instance, boiling point, enthalpy of evaporation, entropy, acentric factor, and standard enthalpy of vaporization. Let fl present the cardinality of the subset of vertices of with connection number l. The next formula for the first Zagreb connection index is equal to the above definition.Naji and Soner (2018), (Gutman et al., 2017) determined the leap Zagreb descriptors of some graph operations and families. Leap Zagreb indices are presented in a recently published survey (Gutman et al., 2020). In (39), the authors establish sharp bounds for the leap Zagreb indices of trees and unicyclic graphs and also determined the corresponding extremal graphs. For more studies on Zagreb connection indices, we refer the readers to (Ducoffe et al., 2018a; Ali and Trinajstić, 2018; Shao et al., 2018a; Basavanagoud and Chitra, 2018; Ducoffe et al., 2018b; Khalid et al., 2018; Manzoor et al., 2018; Du et al., 2019; Fatima et al., 2019; Tang et al., 2019; Ye et al., 2019; Raza, 2020a; Bao et al., 2020; Raza, 2020b; Cao et al., 2020; Naji et al., 2020; Raza, 2022).
Huang et al. (2014) determined the expected values for Kirchhoff indices of random polyphenyl and spiro chains. Ma et al. (2017), Yang and Zhang. (2012), and Qi et al. (2022) independently acquired the expected value of Wiener indices of random polyphenyl chain and random spiro chain. Zhang et al. (2020) have provided expected values of the Schultz, Gutman, multiplicative degree-Kirchhoff, and additive degree-Kirchhoff indices of random polyphenylene chains. Raza and Imran. (2021) obtained expected values of modified second Zagreb, symmetric difference, inverse symmetric, and augmented Zagreb indices in random cyclooctane chains. Zhang et al. (2021) established the formulae for expected values of Sombor indices of a general random chain. Recently, many studies have explored the expected values of different topological indices. For further information, we refer readers to the following studies (Raza, 2020b; Fang et al., 2021; Raza, 2021; Jahanbanni, 2022; Raza et al., 2022).
Motivated by the above research, the present study determined the explicit formulae for expected values of the first Zagreb connection index of the random cyclooctatetraene chain, random polyphenyls chain, and random chain network with l octagons, hexagons, and pentagons, respectively. Moreover, we examined the average and extreme values of the Zagreb connection index among all the above-mentioned random chains corresponding to their set.
2 The first Zagreb connection index of random cyclooctatetraene chain
Cyclooctatetraene, having chemical formula C8H8, is an organic compound whose full name is ‘1, 3, 5, 7 − cyclooctene. Its structure is a cyclic polyolefin-like benzene, but it is not aromatic, see (Willis et al., 1952; Mathews and Lipscomb, 1959; Traetteberg et al., 1970). It has the same chemical characteristics as unsaturated hydrocarbons and is easy to construct explosive organic peroxides, (Milas and NolanPetrus, 1958; Donald and Whitehead, 1969; Garavelli et al., 2002; Schwamm et al., 2019).
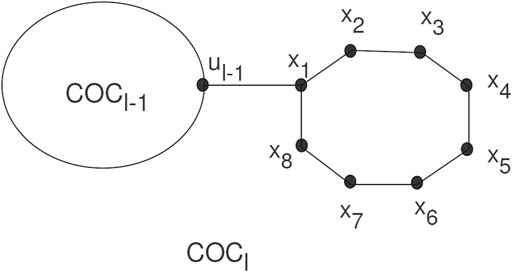
Spiro compounds are valuable types of cycloaltanes in organic chemistry. A spiro union is a join of two rings that have a common atom between both rings, and a join of a direct union among the rings is known as a free spiro union in spiro compounds. In a cyclooctatylene chain, octagons are joined by cut vertices or cut edges. A random cyclooctatetraene chain COCl, has l octagons, and can be constructed by a cyclooctatetraene chain COCl−1 with l−1 octagons attached to a new octagon Gl by a bridge (see Figure 1).
FIGURE 1
A random cyclooctatetraene chain COCl.
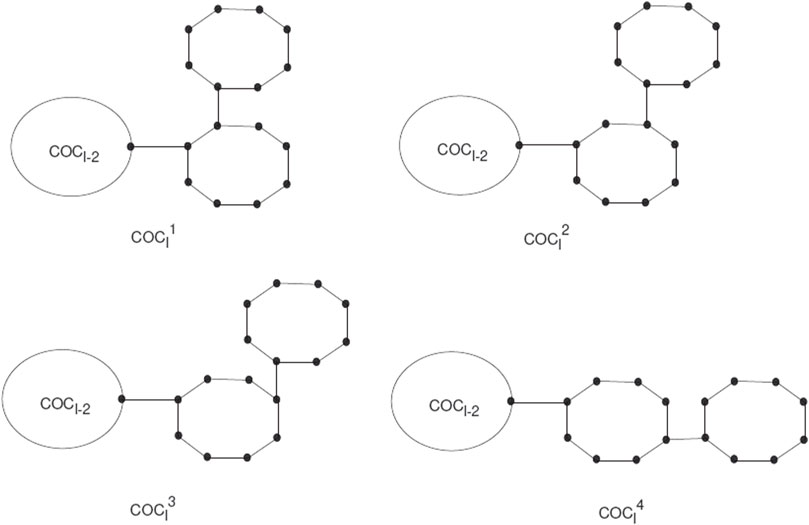
The COCl is a cyclooctatetraene chain with l ≥ 2 having G1, G2, … , Gl octagons. The new octagon can be joined by four different schemes, which give the local orderings. We use these as , , , (see Figure 2).
FIGURE 2
The four types of local arrangements of octagons , , and .
A random cyclooctatetraene chain
COCl(
k1,
k2,
k3) is a cyclooctatetraene chain constructed by step-by-step attachment of new octagons. At every step
p= 2, 3,
…,
la random choice is constructed from one of the four possible chains:
1 with probability k1,
2 with probability k2,
3 with probability k3,
4 with probability k4 = 1 − k1−k2−k3,
Where all the given probabilities are constant. In this section, we will discuss the expected value for the first Zagreb connection index among random cyclooctatetraene chains with l octagons.
For l ≥ 2, the expected value for the first Zagreb connection index of random cyclooctatetraene chainCOClis
Proof.
Case-I:When
l= 2, we get the result by direct calculations as:
Case-II:When
l≥ 3, it is obvious that
f2(
COCl),
f3(
COCl),
f4(
COCl) and
f5(
COCl) depends on the four possible cases as following:
1 If with probability k1, we acquire
By using the above values in Eq.
1.1, we get
2 If with probability k2, we acquire
By using the above values in Eq.
1.1, we get
3 If with probability k3, we acquire
By using the above values in Eq.
1.1, we get
4 If with probability 1 − k1−k2−k3, we acquire
By using above the values in Eq.
1.1, we get
NowNote that . By applying the expression operator to Eq. 2.1 and also l ≥ 3, we getThe Eq. 2.2 is a first-order non-homogeneous linear difference result with constant coefficients. We easily see that the general solution of the homogeneous equation of Eq. 2.2 is Ei = C. Suppose Ei′ = bl is a particular solution of Eq. 2.2, using Ei′ into Eq. 2.2, we acquireFinally the general solution of Eq. 2.2 isApplying the initial condition l = 3, we get the followingTherefore
If k1 = 1 (respectively, k2 = 1) and k2 = k3 = k4 = 0 (respectively, k1 = k3 = k4 = 0), then COCl = Ml (respectively, ). Similarly, if k3 = 1 (respectively, k4 = 1) and k1 = k2 = k4 = 0 (respectively, k1 = k2 = k3 = 0), then (respectively COCl = Ll). By Theorem 2.1, we can acquire the first Zagreb connection index of the cyclooctatetraene meta-chain Ml, ortho-chains , and para-chain Ll as:
Corollary 2.2. For a random cyclooctatetraene chainCOCl(l ≥ 3), the para-chainLland ortho chain, and the meta-chainMlachieves the minimum and the maximum ofE(ZC1(COCl)), respectively.Proof. Using Theorem 2.1, we acquireBy taking partial derivatives, we acquire , . When k1 = k2 = k3 = 0 (i.e. k4 = 1), the para-chain Ll and ortho chain achieve the minimum of E(ZC1(COCl)), that is COCl≅Ll or . If k3 = 1 − k1−k2 (0 ≤ k1, k2 ≤ 1), we haveBut k1 = k2 = 0 (when k3 = 1), E(ZC1(COCl)) can not attain the maximum value. If k1 = 1 − k2 (0 ≤ k2 ≤ 1), we acquireTherefore . Thus E(ZC1(COCl)) achieves the maximum value, if k2 = 0(k1 = 1), that is COCl≅Ml.
3 The first Zagreb connection index of a random polyphenyls chain
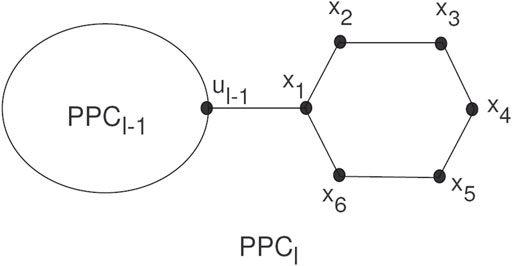
Polyphenyls showed a molecular graph corresponding to a type of macrocyclic aromatic hydrocarbons, and these molecular graphs of polyphenyls construct a polyphenyl structure. Polyphenyls and their derivatives have applications in drug synthesis, organic synthesis, heat exchangers, etc., and have received attention from chemists. A random polyphenyl chain PPCl with l hexagons can be constructed by a polyphenyl chain PPCl−1 using l−1 hexagons attached to a new hexagon Gl by a bridge (see Figure 3).
FIGURE 3
The three types of local arrangements of hexagons , , and .
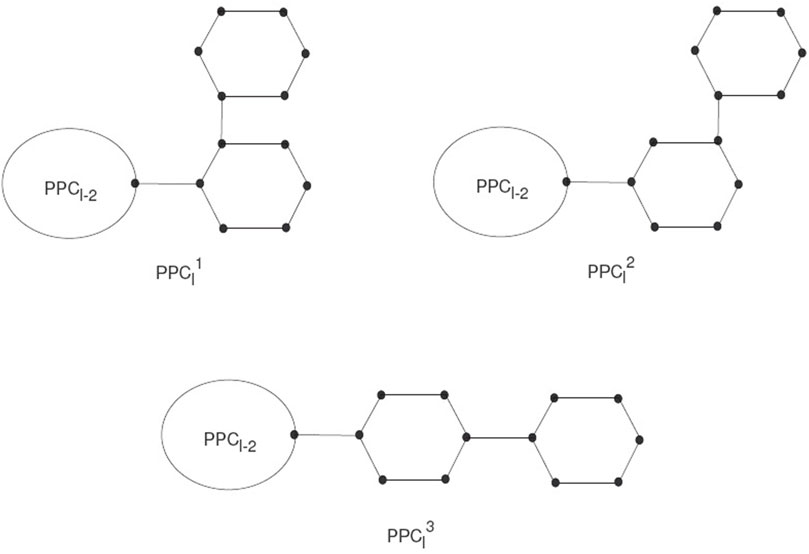
The PCCl will be a polyphenyl chain with l ≥ 2 having G1, G2, … , Gl hexagons. PPCl is the meta-chain Ml, the ortho-chain and the para-chain Ll. The new hexagon can be joined in three arrangements, which construct the local orderings. We use these as , , (see Figure 4).
FIGURE 4
A random polyphenyl chain PPCl.
A random polyphenyl chain
PPCl(
k1,
k2) is a polyphenyl chain constructed by step-by-step attachment of new hexagons. At every step
p= 2, 3,
…,
l, a random choice construct one of the three possible chains:
1 with probability k1,
2 with probability k2,
3 with probability k3 = 1 − k1−k2,
Where all the given probabilities are constant. In this section, we discuss the expected value for the first Zagreb connection index of the random polyphenyl chain with l hexagons.
For l ≥ 2, the expected value for the first Zagreb connection index of the random polyphenyl chainPPClis
Proof.
Case-I:When
l= 2, one can get
Case-II:When
l≥ 3, it is obvious that
f2(
PPCl),
f3(
PPCl),
f4(
PPCl) and
f5(
PPCl) depends on the four possible cases, as follows:
1 If having probability k1, we acquire
By using the above values in Eq.
1.1, we get
2 If having probability k2, we acquire
By using the above values in Eq.
1.1, we get
3 If having probability k3, we acquire
By using the above values in Eq.
1.1, we get
NowNote that . By applying the expression operator to Eq. 3.1 and also l ≥ 3, we getThe result Eq. 3.2 is a first-order non-homogeneous linear difference equation with constant coefficients. The general solution of the homogeneous side is Eq. 3.2 is Ei = C. Suppose Ei′ = bl is a particular result of Eq. 3.2, using Ei′ into Eq. 3.2, we acquireFinally the general solution of Eq. 3.2 is given byApplying the initial condition l = 3, we get followingTherefore
If k1 = 1 (respectively, k2 = 1) and k2 = k3 = 0 (respectively, k1 = k3 = 0), then PPCl = Ml (respectively, PPCl = Ol). Similarly, if k3 = 1 and k1 = k2 = 0, then PPCl = Ll. By Theorem 3.1, we can acquire the first Zagreb connection index of polyphenyl chains like meta Ml, ortho Ol, and para Ll, as
Corollary 3.2. For a random polyphenyl chainPPCl(l ≥ 3), the para-chainLland the meta-chainMlachieves the minimum and the maximumE(ZC1(PPCl)), respectively.Proof. From Theorem 3.1, we obtainBy taking partial derivatives, we acquire , . When k1 = k2 = 0 (i.e. k3 = 1), the para-chain Ll has the minimum of E(ZC1(COCl)), that is PPCl≅Ll. If k1 = 1 − k2 (0 ≤ k2 ≤ 1), we acquireTherefore . Thus E(ZC1(PPCl)) achieves the maximum value, if k2 = 0(k1 = 1), that is PPCl≅Ml.
4 The first Zagreb connection index of random chain network PGl
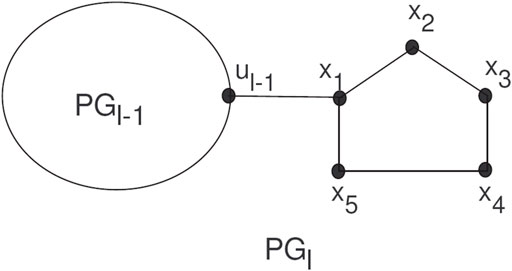
The random chain networks PGl with l pentagons can be constructed by PGl−1 having l−1 pentagons attached to a new pentagon Hl by a bridge (see Figure 5).
FIGURE 5
A random chain networks PGl.
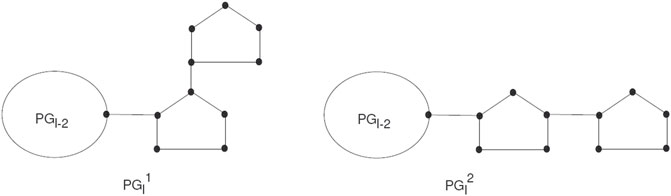
The
PGlwill be a random chain network with
l≥ 2, and
H1,
H2,
…,
Hlpentagons. For
l≥ 3, there are two ways to attach pentagons at the end and get
and
, (see
Figure 6). For such a random chain network, any step for
q= 2, 3, 4,
…,
lcan be constructed by two possible chains with given probabilities
k1and
k2, respectively:
1 with probability k1,
2 with probability k2 = 1 − k1,
FIGURE 6
The two types of local arrangements of pentagons and .
Where all the given probabilities are constant.
This section discusses the expected value for the first Zagreb connection index of the random chain network with l pentagons. The proof of Theorem 4.1 is the same as the proofs of Theorem 2.1 and Theorem 3.1; therefore, we omit it here.
For l ≥ 2, the expected value for the first Zagreb connection index of random chain networkPGlisE(ZC1(PGl)) = (6k1+66)L−12k1−48.
If k1 = 1 (respectively, k2 = 1) and k2 = 0 (respectively, k1 = 0), then (respectively, ). By Theorem 4.1, we can acquire the first Zagreb connection index of the meta-chain and para-chain , as
Corollary 4.2. For a random chain networkPGl(l ≥ 3), the para-chainand the meta-chainachieves the minimum and the maximum ofE(ZC1(PGl)), respectively.
5 The average values for the first Zagreb connection index
This section finds the average values for the first Zagreb connection index concerning the sets of all cyclooctatetraene chains with l octagons, polyphenyl chains with l hexagons, and chain networks with l pentagons. Let , and be the sets of all cyclooctatetraene chains, polyphenyl chains, and random chain network, respectively. The average values for the first Zagreb connection index for the sets , and are given below:The average value concerning sets , , and are expected values for the first Zagreb connection index of the random chains. From Theorem 2.1, Theorem 3.1 and Theorem 4.1, we have.
The average value for the first Zagreb connection index concerning the set is given as: After calculation, we acquire
The average value for the first Zagreb connection index concerningisAfter calculation, we acquire
The average value for the first Zagreb connection index concerning is . It is also:
6 Conclusion
This study computed the expected values of the first Zagreb connection index in a random cyclooctatetraene chain, random polyphenyls chain, and random chain network with l, octagons, hexagons, and pentagons, respectively. It has discussed the maximum chain and the minimum chain of the COCl, PPCl, and PGl, respectively, concerning the expected values of these chains. The average values discussed in all of the above are considered random chains for unique chains.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author contributions
Investigation: ZR, SA, and YS: Writing: ZR, SA, and YS; Review: ZR, SA, and YS.
Funding
This research was funded by the University of Sharjah.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2022.1067874/full#supplementary-material
References
1
Akhter S. Imran M. Farahan M. R. Javaid I. (2017). On topological properties of hexagonal and silicate networks. Hac. J. Math. Stat.48 (3), 1–13. 10.15672/hjms.2017.541
2
Akhter S. Imran M. Gao W. Farahani M. R. (2018). On topological indices of honeycomb networks and graphene networks. Hac. J. Math. Stat.47 (1), 19–35. 10.15672/hjms.2017.464
3
Akhter S. Imran M. Iqbal Z. (2020). Mostar indices of SiO2 nanostructures and melem chain nanostructures. Int. J. Quantum Chem.121 (5). 10.1002/qua.26520
4
Akhter S. Imran M. (2016). On molecular topological properties of benzenoid structures. Can. J. Chem.94 (8), 687–698. 10.1139/cjc-2016-0032
5
Akhter S. Imran M. Raza Z. (2016). On the general sum-connectivity index and general Randić index of cacti. J. Inequal. Appl.2016 (1), 300–309. 10.1186/s13660-016-1250-6
6
Ali A. Trinajstić N. (2018). A novel/old modification of the first Zagreb index. Mol. Inf.37 (6–7), 1800008. 10.1002/minf.201800008
7
Bao L. J. Raza Z. Javaid M. (2020). Zagreb connection numbers for cellular neural networks. Discrete Dyn. Nat. Soc.2020, 1–8. 10.1155/2020/8038304
8
Basavanagoud B. Chitra E. (2018). On the leap Zagreb indices of generalized xyz-point-line transformation graphs Txyz(G), when z = 1. Int. J. Math. Comb.2 (44–66).
9
Basavanagoud B. Jakkannavar P. (2018). Computing the first leap Zagreb index of some nanostructures. Inter. J. Appl. Math.6 (2–B), 141–150.
10
Cao J. Ali U. Javaid M. Huang C. (2020). Zagreb connection indices of molecular graphs based on operations. Complexity2020, 1–15. 10.1155/2020/7385682
11
Donald H. L. Whitehead M. A. (1969). Molecular geometry and bond energy. III. cyclooctatetraene and related compounds. J. Am. Chem. Soc.91 (2), 238–242. 10.1021/ja01030a003
12
Du Z. Ali A. Trinajstić N. (2019). Alkanes with the first three maximal/minimal modified first Zagreb connection indices. Mol. Inf.38 (4), 1800116. 10.1002/minf.201800116
13
Ducoffe G. Marinescu-Ghemeci R. Obreja C. (2018). International symposium on symbolic and numeric algorithms for scientific computing (SYNASC). Timisoara, Rom.141–148.
14
Ducoffe G. Marinescu-Ghemeci R. Obreja C. (2018). Proceedings of the 16th cologne-twente workshop on graphs and combinatorial optimization. Paris, Fr. CNAM65–68.
15
Fang X. You L. Liu H. (2021). The expected values of Sombor indices in random hexagonal chains, phenylene chains, and Sombor indices of some chemical graphs. Int. J. Quantum. Chem.121 (17). 10.1002/qua.26740
16
Fatima N. Bhatti A. A. Ali A. Gao W. (2019). Zagreb connection indices of two dendrimer nanostars. Acta Chem. Iasi27 (1), 1–14. 10.2478/achi-2019-0001
17
Garavelli M. Bernardi F. Cembran A. Castaño O. Frutos L. M. Merchán M. et al (2002). Cyclooctatetraene computational photo- and thermal chemistry: A reactivity model for conjugated hydrocarbons. J. Am. Chem. Soc.124 (46), 13770–13789. 10.1021/ja020741v
18
Gutman I. (2013). Degree-based topological indices. Croat. Chem. Acta.86, 351–361. 10.5562/cca2294
19
Gutman I. Milovanović E. Milovanović I. (2020). Beyond the Zagreb indices. AKCE Int. J. Graphs Comb.17 (1), 74–85. 10.1016/j.akcej.2018.05.002
20
Gutman I. Naji A. M. Soner N. D. (2017). The first leap Zagreb index of some graph operations. Commun. Comb. Optim.2 (2), 99–117.
21
Gutman I. Trinajstić N. (1972). Graph theory and molecular orbitals, Total π electron energy of alternant hydrocarbons. Chem. Phys. Lett.17 (4), 535–538. 10.1016/0009-2614(72)85099-1
22
Huang G. H. Kuang M. J. Deng H. Y. (2014). The expected values of Kirchhoff indices in the random polyphenyl and spiro chains. ARS Math. Contem.9 (2), 197–207. 10.26493/1855-3974.458.7b0
23
Jahanbanni A. (2022). The expected values of the first Zagreb and Randić indices in random polyphenyl chains. Polycycl. Aromat. Compd.42 (4), 1851–1860. 10.1080/10406638.2020.1809472
24
Khalid S. Kok J. Ali A. (2018). Zagreb connection indices of TiO2 nanotubes. Chem. Bulg. J. Sci. Edu.27 (1), 86–92.
25
Ma L. Bian H. Liu B. J. Yu H. Z. (2017). The expected values of the Wiener index in the random phenylene and spiro chains. ARS Comb.130, 267–274.
26
Manzoor S. Fatima N. Bhatti A. A. Ali A. (2018). Zagreb connection indices of some nanostructures. Acta Chem. Iasi26 (2), 169–180. 10.2478/achi-2018-0011
27
Mathews F. S. Lipscomb W. N. (1959). The structure of silver cyclooctatetraene nitrate. J. Phy. Chem.63 (6), 845–850. 10.1021/j150576a017
28
Milas N. NolanPetrus J. Jr. (1958). Notes-ozonization of cyclooctatetraene. J. Org. Chem.23 (4), 624–625. 10.1021/jo01098a611
29
Naji A. M. Davvaz B. Mahde S. S. (2020). A study on some properties of leap graphs. Commun. Comb. Optim.5 (1), 9–17.
30
Naji A. M. Soner N. D. (2018). The first leap Zagreb index of some graph operations. Int. J. Appl. Graph Theor.2 (1), 7–18.
31
Qi J. Fang M. Geng X. (2022). The expected value for the Wiener index in the random spiro chains. Polycycl. Aromat. Compd.1–11.
32
Raza Z. Imran M. (2021). Expected values of some molecular descriptors in random cyclooctane chains. Symmetry13 (11), 2197. 10.3390/sym13112197
33
Raza Z. (2020). Leap Zagreb connection numbers for some networks models. J. Chem.20 (6), 1407–1413. 10.22146/ijc.53393
34
Raza Z. Naz K. Ahmad S. (2022). Expected values of molecular descriptors in random polyphenyl chains. Emerg. Sci. J.6 (1), 151–165. 10.28991/esj-2022-06-01-012
35
Raza Z. (2020). The expected values of arithmetic bond connectivity and geometric indices in random phenylene chains. Heliyon6 (7), e04479. 10.1016/j.heliyon.2020.e04479
36
Raza Z. (2021). The expected values of some indices in random phenylene chains. Eur. Phys. J. Plus136 (11–15), 91. 10.1140/epjp/s13360-021-01082-y
37
Raza Z. (2022). Zagreb connection indices for some Benzenoid systems. Polycycl. Aromat. Compd.42 (4), 1814–1827. 10.1080/10406638.2020.1809469
38
Schwamm R. J. Anker M. D. Lein M. Coles M. P. (2019). Reduction vs. Addition: The reaction of an aluminyl anion with 1, 3, 5, 7 − cyclooctatetraene. Angew. Chem. Int. Ed.58 (5), 1489–1493. in English) 131. 10.1002/anie.201811675
39
Shao Z. Gutman I. Li Z. (2018). Leap Zagreb indices of trees and unicyclic graphs. Commun. Comb. Optim.3 (2), 179–194.
40
Shao Z. Gutman I. Li Z. Wang S. Wu P. (2018). Leap Zagreb indices of trees and unicyclic graphs. Commun. Comb. Optim.3 (2), 179–194.
41
Soner N. D. Naji A. M. (2016). The k-distance neighborhood polynomial of a graph. Int. J. Math. Comput. Sci.3 (9), 2359–2364.
42
Tang J. H. Ali U. Javaid M. Shabbir K. (2019). Zagreb connection indices of subdivision and semi-total point operations on graphs. J. Chem.
43
Todeschini R. Consonni V. (2000). Handbook of molecular descriptors. Weinheim: Wiley VCH.
44
Traetteberg M. Hagen G. Cyvin S. J. (1970). IV. 1, 3, 5, 7-Cyclooctatetraene. Z. Für Naturforsch. B25 (2), 134–138. 10.1515/znb-1970-0201
45
Willis B. P. George C. P. Kenneth S. P. (1952). The structure of cyclooctatetraene. J. Am. Chem. Soc.74 (13), 3437–3438. 10.1021/ja01133a524
46
Yang W. Zhang F. (2012). Wiener index in random polyphenyl chains. MATCH Commun. Math. Comp. Chem.68, 371–376.
47
Ye A. Qureshi M. I. Fahad A. Aslam A. Jamil M. K. Zafar A. et al (2019). Zagreb connection number index of nanotubes and regular hexagonal lattice. Open Chem.17 (1), 75–80. 10.1515/chem-2019-0007
48
Zhang L. Li Q. Li S. Zhang M. (2020). The expected values for the Schultz index, Gutman index, multiplicative degree Kirchhoff index, and additive degree Kirchhoff index of a random polyphenylene chain. Discrete Appl. Math.282, 243–256. 10.1016/j.dam.2019.11.007
49
Zhang W. You L. Liu H. Huang Y. (2021). The expected values and variances for Sombor indices in a general random chain. App. Math. Comp.411, 126521. 10.1016/j.amc.2021.126521
Summary
Keywords
average value, expected value, random cyclooctatetraene chain, random polyphenyls chain, zagreb connection indices
Citation
Raza Z, Akhter S and Shang Y (2023) Expected value of first Zagreb connection index in random cyclooctatetraene chain, random polyphenyls chain, and random chain network. Front. Chem. 10:1067874. doi: 10.3389/fchem.2022.1067874
Received
12 October 2022
Accepted
07 December 2022
Published
04 January 2023
Volume
10 - 2022
Edited by
Anakuthil Anoop, Indian Institute of Technology Kharagpur, India
Reviewed by
Parvez Ali, Qassim University, Saudi Arabia
Rogers Mathew, Indian Institute of Technology Hyderabad, India
Updates
Copyright
© 2023 Raza, Akhter and Shang.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zahid Raza, zraza@sharjah.ac.ae; Yilun Shang, yilun.shang@northumbria.ac.uk
This article was submitted to Theoretical and Computational Chemistry, a section of the journal Frontiers in Chemistry
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.