Abstract
The current work investigates the influence of porous media, homogeneous and heterogeneous reactions, and a heat source/sink on the hybrid nanoliquid circulation on three distinct surfaces (cone, plate, and wedge). The system of equations that describe the circulation issue and operating conditions is reduced to ordinary differential equations (ODEs) by using the proper similarity transformations. The Runge–Kutta–Fehlberg 45 order and the shooting approach are used to generate the numerical results. Graphs are used to show how various dimensionless limits affect the associated profiles. The results demonstrate that, in the presence of heat source/sink and porous medium characteristics, respectively, fluid velocity and heat dispersion are high in plate geometry and lower in cone geometry. The concentration profile shows the declination in the presence of both homogeneous and heterogeneous reaction intensities. The surface drag force decreases and the rate of heat dispersion rises with the addition of a porous attribute. Furthermore, cones sprinkle the heat more quickly than wedges, which disperse heat more slowly.
Introduction
A nanofluid (NF) is a mixture of nanosized particles and a base liquid. A colloidal dispersion of nanosized particles in a base liquid is employed to make nanofluids. Thermal conductivity is poor in these basic fluids. Nanosized particles are used for the long-term effectiveness of base fluid heat transfer, resulting in enhanced thermal conductivity. But base fluids have an extremely low thermophysical phenomenon. They have distinct physical and chemical features. In the last decades, a lot of research has been performed on heat transfer convection, modeling, and their programs. Eid (2022) investigated the magnetic rotating hybridizing nanoliquid flow over a solar collector with the Cattaneo–Christov heat flux (CCHF) theory and centripetal and Coriolis forces. Shahzad et al. (2022) examined Burger’s nanoliquid circulation with motile organisms and CCHF. Ghalambaz et al. (2015) scrutinized the impact of nanoparticle diameter and natural convection on a vertical cone in the presence of the porous medium. Veera Krishna and Chamkha (2019) studied the effects of hall and ion slip on the nanofluid rotating boundary layer flow across an infinite vertical plate encased in a porous medium. Reddy et al. (2017) considered the magnetohydrodynamic boundary layer flow of a rotating disk in the presence of the porous medium with nanofluid flow.
The NF exhibit a low heat transfer. So, in the context of NF, more than one nanosized particle is embedded with the base liquid, resulting in a hybrid nanofluid (HNF). When compared to NFs, HNFs have higher thermal conductivity. Over the past few decades, HNFs are constantly being studied experimentally and numerically. Khan et al. (2020) discussed the heat radiation upshot on the mixed convective movement of an HNF. Nisar et al. (2020) scrutinized the convective stream of an HNF with the suspension of magnetized ferroparticles between multiple disks. Madhukesh et al. (2021a) numerically examined the HNF flow across a curved sheet with stretching. Manohar et al. (2021) investigated the role of HNF via a semi-spherical permeable fin. Sreedevi et al. (2020) examined the analysis of unstable hybrid nanofluid flow across a stretched sheet with thermal radiation in terms of mass and heat transmission. Some of the useful works conducted on HNF are listed in Jamshed et al. (2022) and Sajid et al. (2022).
Porous media are solid materials made up of porous structures, which are often filled with fluid in biological applications. In fluid mechanics, the porous medium can be regarded as a solid structure with fluid-flowing channels. Engineering applications for porous medium heat transfer difficulties include separation processes in chemical industries, geothermal energy extraction, thermal energy storage, crude oil extraction, transpiration cooling, groundwater contamination, and fiber insulation. Umeshaiah et al. (2022) employed a porous medium to inspect the flow of dusty NF over a stretched cylinder with melting. Madhukesh et al. (2021b) analyzed the flow of Casson NF through a porous medium. Ramesh et al. (2022) used ternary NF to study the HSS and porosity effects in a stretched divergent/convergent channel. Chamkha and Ben-Nakhi (2008) examined the presence of Soret and Dufour effects and MHD mixed convection–radiation interaction along a permeable surface submerged in a porous medium. MHD heat and mass transfer oscillatory flow of a micropolar fluid across a vertical permeable plate in a porous medium through an analytical investigation was carried out by Modather et al. (2009).
Chemical reactions, both heterogeneous and homogeneous (H-H) are, especially important since many chemically reacting systems incorporate both H-H reactions, such as fog dispersion, cooling towers, biological systems, cooling towers, catalysis, and hydrometallurgical processes. The connection amid homogeneous processes in the bulk of the liquid and heterogeneous reactions on specific catalytic surfaces is fairly intricate. So, there is a three-way interaction among surface/liquid temperatures, and fluid and reactant species concentrations. Siddiqui et al. (2022) swotted the effect of H-H processes on the 3D flow of water-based NFs as well as the estimation of entropy generation. Mahato et al. (2022) explored the role of radiation and inclined magnetic field upshot in the stream of NFs with H-H reactions. Khashi’ie et al. (2021) educed the stream of a radiative HNF across a permeable shrinking/stretching sheet with a H-H reaction. Waseem et al. (2021) investigated the hydromagnetic stream of couple stress NHF past a heated plate using homogeneous–heterogeneous reactions. Rooman et al. (2021) used the Hall effect across a rotating disk to optimize the entropy of Jeffrey NF flow with H-H reactions.
Thermal conductivity, material thickness, specific heat capacity, flow rate, and other components all have an impact on heat transmission in heat exchange. Heat source/sink (HSS): a heat source is anything that generates or emits heat. Using a passive heat exchanger called a heat sink, heat from any liquids is transferred into a flowing cooling liquid. When an HSS is utilized, the heat distribution all over the entire field changes. It disperses the system’s surplus energy. Magyari and Chamkha (2010) scrutinized the combined impact of heat production or absorption and first-order chemical reaction on micropolar fluid flows across a uniformly stretched permeable surface. Madhukesh et al. (2022) investigated the dynamics of water-based NF with swimming microbes across a Riga sheet that was constrained to a heat source/sink. Ramesh et al. (2020) conferred the impact of aluminum alloy and magnetite graphene oxide heat transfer investigation through a permeability cylinder with a heat source/sink. Ahmed et al. (2019) discussed Maxwell NF flow across a porous radially shrinking/stretching rotating disk. Hayat et al. (2016) conducted extensive research on the HSS features in NF flow along with nonlinear thermal radiation.
Due to its wide range of uses in science and industry, scientists are paying special attention to fluid stream across many geometries, including a vertical plate, cone, and wedge, among many other geometries. Many scientists and scholars have analyzed this issue from diverse perspectives. Furthermore, there are several applications utilizing these geometries such as NF flow heat transport via plates and wedges. Recently, Rekha et al. (2022) carried out research on the flow of HNF via a wedge, cone, and plate. Chamkha (1996) scrutinized non-Darcy hydromagnetic free convection in porous media in the presence of a cone and a wedge. Hussain et al. (2022) swotted the stream and thermal properties of a moving stretched porous wedge in MHD Casson NF. Veera Krishna et al. (2020) pondered the exponentially accelerating plate and educed the unstable MHD rotating stream over a saturated porous material. Al-Harbi (2005) provided numerical research on natural convective heat transfer from a wedge and a cone with changing thermal radiation and viscosity.
According to the aforementioned literature, no research has been conducted on the HNF flow across three distinct geometries when a porous medium, H-H reactions, and HSS are present. The current work is to investigate the influence of the porous medium, H-H reactions, and HSS in the presence of HNF flow on three different geometries. The current investigation is carried out to find the answers to the following questions:
1) What is the role of the porous parameter in the flow profile?
2) What is the influence of solid volume fraction on the rate of thermal distribution?
3) What happens to the concentration profile when the values of homogeneous and heterogeneous parameter values are increased?
The current investigation can be useful in applications like thermal transportation via nanofluid over different geometries like a plate and wedge, and this impact can be used in fog dispersion, cooling towers, biological systems, catalysis, and hydrometallurgical processes. The current investigation can be extended to investigate thermal transportation by considering ternary nanoparticles/various non-Newtonian fluids in the presence of a non-uniform heat source/sink, zero mass flux conditions with the combination of concentration, and bioconvection.
Formulation
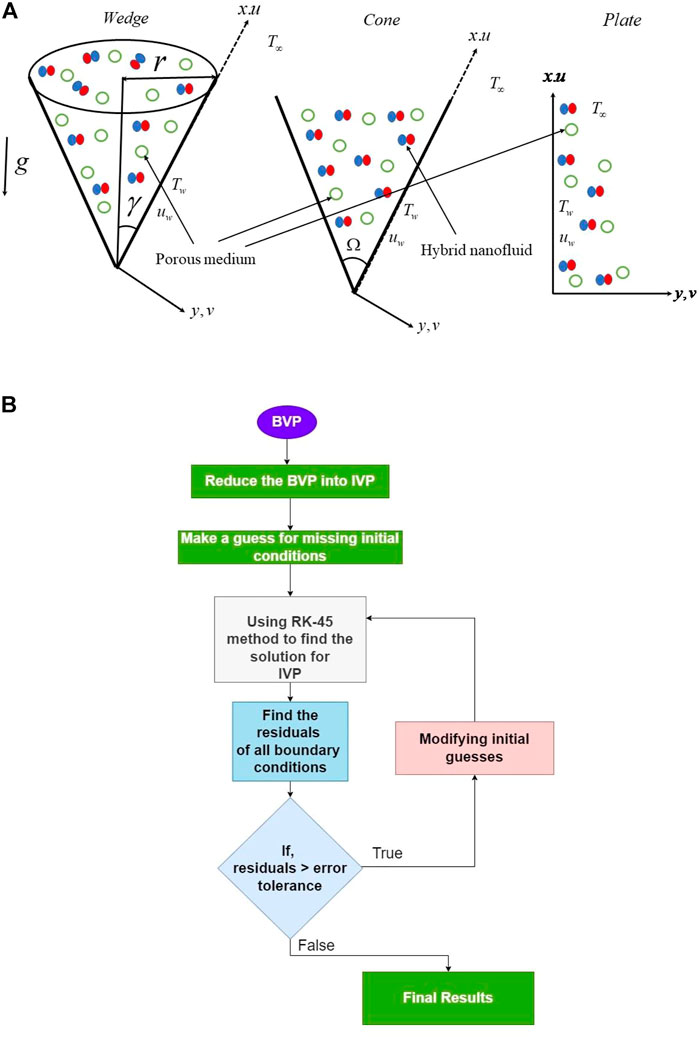
An incompressible HNF flow across wedge, cone, and plate geometries with a porous medium, HSS, and H–H reactions is considered. The coordinate x-axis is taken along the surface of the body, and is normal to its surface. Figure 1A illustrates the model’s physical manifestation. Let us assume is the half-angle of the cone/wedge, full angle of the wedge, and radius of the cone, respectively. Let us assume that is the far-field temperature, is the temperature near the surface, is the concentration near the surface, and is the far-field concentration.
FIGURE 1
(A) Flow geometry. (B) Flow chart of the numerical scheme.
The isothermal cubic autocatalytic model for H-H reactions involving two chemical species and , proposed by Merkin (1996) and Chaudhary and Merkin (1995a); Chaudhary and Merkin (1995b), is given by
Here, the concentration of the chemical species is given by , respectively. denotes the rate quantities. Both types of reactions are termed isothermal. Therefore, in Chamkha (1996), Chamkha (1997), and Chamkha and Ben-Nakhi (2008), the non-Darcy effect associated with the porous media inertia effect was considered to be infinitesimal and hence ignored. Furthermore, based on the aforementioned conditions, the equations for continuity, momentum, temperature, and concentration are as follows (Vajravelu and Nayfeh, 1992; Mahdy, 2019):with boundary conditions (Ali and Sandeep, 2017;Devi and Devi, 2016):
From the aforementioned expressions, denotes the velocity components along directions. is acceleration due to gravity; is the thermal expansion factor; is permeability of the porous medium; is kinematic viscosity; is the rate of heat generation/absorption; are the concentration of the chemical species ; and are the diffusivity; is the density; is the dynamic viscosity; , , and denotes temperature, wall temperature, and ambient temperature, respectively; is the geometric factor; is the specific heat; and the subscript denotes hybrid nanofluid.
The proposed issue provides three different geometries based on the following hypotheses:
1) Case 1: wedge and .
2) Case 2: cone and .
3) Case 3: plate and .
Following similarity variables are introduced:
The thermophysical properties of base fluid and nanoparticles are given in Table 1 (Devi and Devi, 2016). Furthermore, the correlations of the hybrid nanofluid are given as follows:
TABLE 1
| Property | ||||
|---|---|---|---|---|
| Al2O3 | 40 | 765 | 3970 | 0.85 |
| Water | 0.613 | 4179 | 997.1 | 21 |
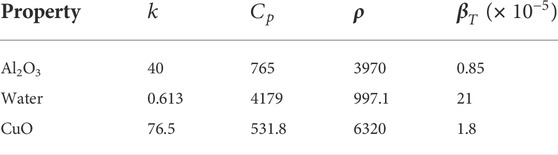
| CuO | 76.5 | 531.8 | 6320 | 1.8 |
Thermophysical properties of the base fluid and nanoparticle (Rana and Bhargava, 2011).
Here, the aforementioned Eqs 8–12 are used for the thermophysical features of the base fluid and the hybrid nanoparticles. The symbol corresponds to the solid nanoparticle volume fractions, and furthermore it is equal to the sum of two dissimilar nanoparticles (alumina) and (copper oxide). Meanwhile, the special case corresponds to the normal base fluid, and the subscripts 1 and 2 denote the solid nanoparticles, signifies the hybrid nanofluid, and denotes the normal base fluid.
After utilizing the similarity transformations, the following reduced equations are expressed:
We predict the diffusion coefficients of and to be equal in most situations. As a result, we must also assume that the diffusion factors and are identical, and this leads to (Chaudhary and Merkin, 1995a; Chaudhary and Merkin, 1995b). In this case, we get, . Thus, Eqs 15, 16 reduce to the form as follows:and the boundary conditions in the reduced form are:
in which:
The aforementioned equations required similarity equations comprising the distinct controlling influential constraints, which are listed as follows: is the Grashof number, is the porous parameter, is the Prandtl number, is the Schmidt number, is the heat source/sink parameter, is the homogeneous reaction strength, is the heterogeneous reaction strength, is the ratio of diffusion coefficient species, and is the geometric factor.
The important engineering factors and its reduced forms are given by Vajravelu and Nayfeh (1992) as follows:
Utilizing similarity variables and Eq. 20 into (19), the resultant equations are given in Eq. 21:
Numerical scheme and validation of the code
The shooting strategy was used to solve ODEs (13, 14, and 17) with associated constraints (18) using the RKF 45 order approach. The acquired ODEs, together with the boundary constraints, are turned into initial value problems in order to solve these equations (IVP). For this, we choose,and with known and unknown initial conditions becoming
The equations which are simplified to the first order are numerically solved with the help of the RKF-45 method by guessing the missing boundary values with the help of a shooting procedure by choosing the parameter values as with a calculation step size 0.1, mesh size is about 100, and convergence criteria are chosen nearly 9, so that the solution converges asymptotically with an error tolerance of roughly about . The present numerical code is validated with the available literature by limiting the values of the constraints. Figure 1B displays the flow chart of the numerical scheme.
The algorithm of the RKF-45 method is as follows:
Then, a Runge–Kutta technique of order 4 is used to approximate the IVP solution.
A Runge–Kutta technique of order 5 is used to find a better value for the solution:
Results and discussion
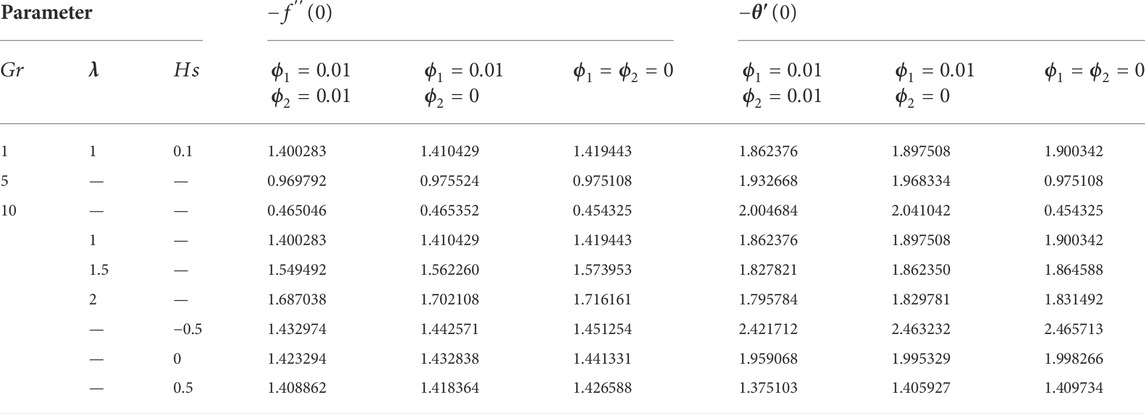
The properties of different dimensionless constraints on their corresponding profiles are described in detail in this section. The collection of governing equations is reduced into ODEs by employing apt similarity variables and thermophysical properties of nanoparticles mentioned in Table 1. The modified equations are numerically solved via the shooting approach and the RKF 45 process. The numerical findings are compared to the current works, and the best match is found (Table 2). Tables 3–5 demonstrate the main engineering factors on three different shapes in the manifestation of different constraints.
TABLE 2
| Salleh et al. (2010) | Present results | |
|---|---|---|
| 0.72 | 0.46317 | 0.46347 |
| 1 | 0.58198 | 0.58200 |
| 3 | 1.16522 | 1.16527 |
| 5 | 1.56806 | 1.56809 |
| 7 | 1.89548 | 1.89553 |
| 10 | 2.30821 | 2.30837 |
| 100 | 7.76249 | 7.76259 |
Validation of the code for with respect to some reduced cases.
TABLE 3
| Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.1 | 1.400283 | 1.410429 | 1.419443 | 1.862376 | 1.897508 | 1.900342 |
| 5 | — | — | 0.969792 | 0.975524 | 0.975108 | 1.932668 | 1.968334 | 0.975108 |
| 10 | — | — | 0.465046 | 0.465352 | 0.454325 | 2.004684 | 2.041042 | 0.454325 |
| 1 | — | 1.400283 | 1.410429 | 1.419443 | 1.862376 | 1.897508 | 1.900342 | |
| 1.5 | — | 1.549492 | 1.562260 | 1.573953 | 1.827821 | 1.862350 | 1.864588 | |
| 2 | — | 1.687038 | 1.702108 | 1.716161 | 1.795784 | 1.829781 | 1.831492 | |
| — | −0.5 | 1.432974 | 1.442571 | 1.451254 | 2.421712 | 2.463232 | 2.465713 | |
| — | 0 | 1.423294 | 1.432838 | 1.441331 | 1.959068 | 1.995329 | 1.998266 | |
| — | 0.5 | 1.408862 | 1.418364 | 1.426588 | 1.375103 | 1.405927 | 1.409734 | |
Change in and for various parameters in the cone when .
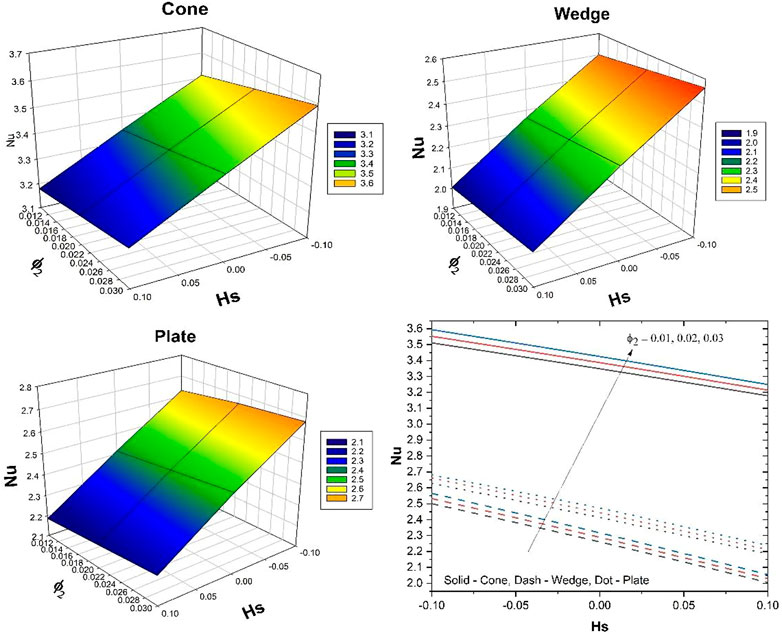
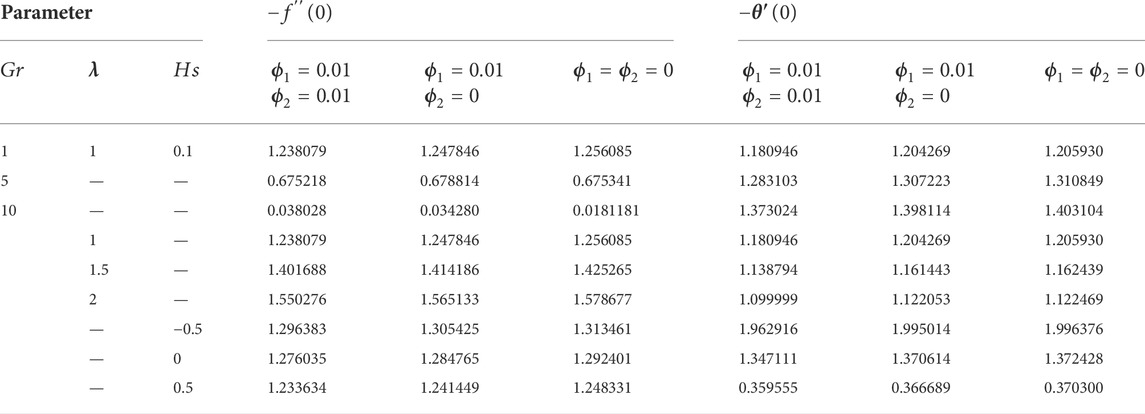
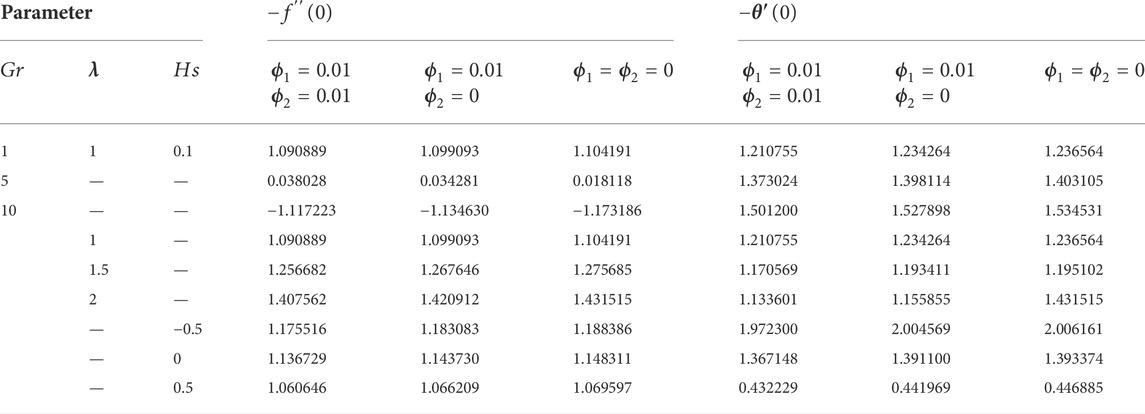
It is well understood that the velocity at which fluid passes onto a certain surface is fully influenced by the distribution of velocity; hence, velocity dispersion plays a significant role in researching variations in the fluid flow rate. Figure 2A displays the nature of the porosity constraint over the velocity profile. The figure shows that the fluid motion declines as the porosity constraint enhances. This is due to the fact that the existence of a porous material will improve the size of the pores which restricts the fluid flow, causing it to decelerate and hence diminish velocity. Here, fluid velocity is high in the case of the plate and low in the case of the cone.
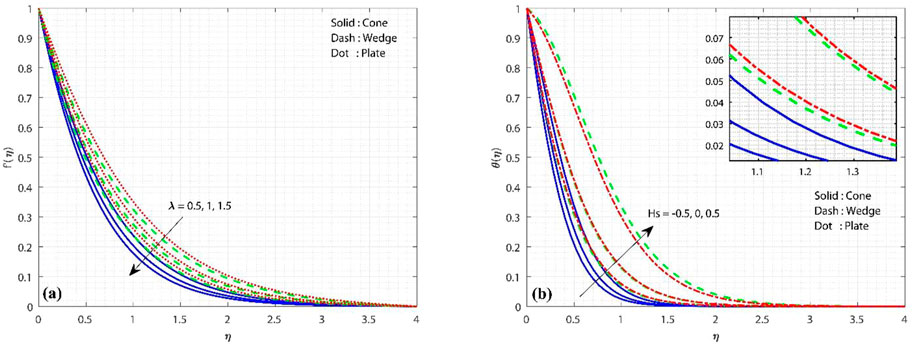
FIGURE 2
(A) Influence of porous constraint on the velocity profile, keeping constant, and (B) influence of the heat source/sink constraint on the temperature profile, keeping constant.
Figure 2B displays the variation in the thermal profile in the presence of . The value of , , and denotes the absence of HSS, heat source, and heat sink, respectively. As the values of improves, it gradually enlarges the thermal distribution in the system. This is owing to the fact that the outside surface of the geometry raises the temperature of the heat source. In the case of a heat sink, it acts as a heat exchanger, transferring the heat generated by the geometry’s surface into the fluid. From the diagram, it is clearly observed that thermal distribution is more in the case of the plate, and the least thermal distribution is observed in the cone.
Figures 3A,B show the variations in H–H reaction strengths over the concentration profile. The increase in the value of will diminish the mass transport, as shown in Figure 3A. The nanoscale particles and base liquid are in the same stage during a homogeneous reaction. In case of a heterogeneous reaction (reactions that occur on the surface of a distinct phase catalyst which improves the significant chemical reaction, which leads to reducing the chemical distribution in the flow system), a similar behavior is seen as in the homogeneous reaction. Figures 3A,B show that the concentration is lower in the wedge and higher in the cone in the presence of H-H reaction strengths.
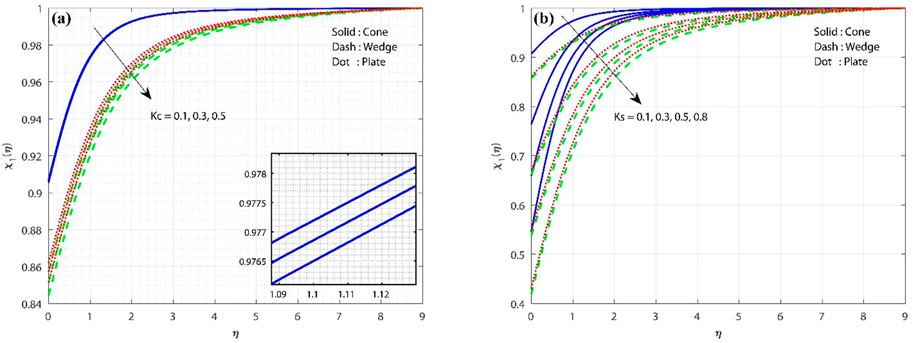
FIGURE 3
(A) Influence of homogeneous reaction strength on the concentration profile, keeping constant, and (B) influence of heterogeneous reaction strength on the concentration profile, keeping constant.
The impact of on for various values of is portrayed in Figure 4. Here, the surface drag force diminishes with increased and . This is due to the increment of , the permeable medium improves which creates the drag force that opposes the movement of the liquid. As a result, decreases. is less in a cone and more in a plate.
FIGURE 4
Behavior of over for various values of
The impact of on for various values of is illustrated in Figure 5. The rate of thermal distribution enhances with increased and . The improvement in will thicken the thermal boundary layer, and an increase in will improve the thermal distribution in the system. The rate of heat transport is more in the case of a cone and the least thermal distribution is seen in the case of a wedge.
FIGURE 5
Behavior of over for various values of
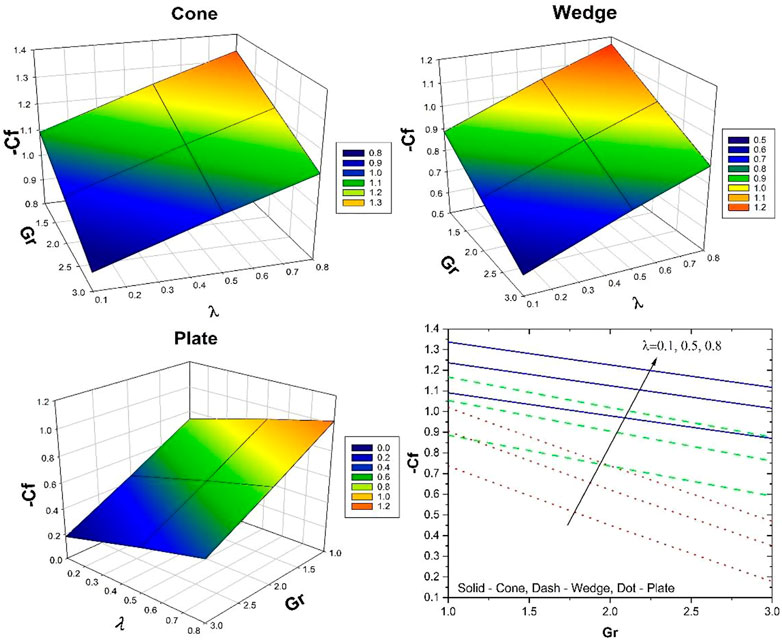
Table 3 displays the variation in for , , and in cone geometry when for hybrid fluid, nanofluid, and viscous fluid. Here, the coefficients of skin friction show improvement in the presence of and , and a reverse trend is observed in the case of . enhances with larger values of , but an opposite trend is established in . The HNF plays a more prominent role than the NF and viscous fluid. The same behavior is observed in wedge and plate geometries (Tables 4, 5).
TABLE 4
| Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.1 | 1.238079 | 1.247846 | 1.256085 | 1.180946 | 1.204269 | 1.205930 |
| 5 | — | — | 0.675218 | 0.678814 | 0.675341 | 1.283103 | 1.307223 | 1.310849 |
| 10 | — | — | 0.038028 | 0.034280 | 0.0181181 | 1.373024 | 1.398114 | 1.403104 |
| 1 | — | 1.238079 | 1.247846 | 1.256085 | 1.180946 | 1.204269 | 1.205930 | |
| 1.5 | — | 1.401688 | 1.414186 | 1.425265 | 1.138794 | 1.161443 | 1.162439 | |
| 2 | — | 1.550276 | 1.565133 | 1.578677 | 1.099999 | 1.122053 | 1.122469 | |
| — | −0.5 | 1.296383 | 1.305425 | 1.313461 | 1.962916 | 1.995014 | 1.996376 | |
| — | 0 | 1.276035 | 1.284765 | 1.292401 | 1.347111 | 1.370614 | 1.372428 | |
| — | 0.5 | 1.233634 | 1.241449 | 1.248331 | 0.359555 | 0.366689 | 0.370300 | |
Change in and for various parameters in the wedge when .
TABLE 5
| Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.1 | 1.090889 | 1.099093 | 1.104191 | 1.210755 | 1.234264 | 1.236564 |
| 5 | — | — | 0.038028 | 0.034281 | 0.018118 | 1.373024 | 1.398114 | 1.403105 |
| 10 | — | — | −1.117223 | −1.134630 | −1.173186 | 1.501200 | 1.527898 | 1.534531 |
| 1 | — | 1.090889 | 1.099093 | 1.104191 | 1.210755 | 1.234264 | 1.236564 | |
| 1.5 | — | 1.256682 | 1.267646 | 1.275685 | 1.170569 | 1.193411 | 1.195102 | |
| 2 | — | 1.407562 | 1.420912 | 1.431515 | 1.133601 | 1.155855 | 1.431515 | |
| — | −0.5 | 1.175516 | 1.183083 | 1.188386 | 1.972300 | 2.004569 | 2.006161 | |
| — | 0 | 1.136729 | 1.143730 | 1.148311 | 1.367148 | 1.391100 | 1.393374 | |
| — | 0.5 | 1.060646 | 1.066209 | 1.069597 | 0.432229 | 0.441969 | 0.446885 | |
Change in for various parameters in the plate when .
Conclusion
The current work looks into the upshot of the porous medium, H-H reactions, and HSS in the presence of HNF flow over three different geometries. Using similarity variables, the set of governing equations is converted into ODEs. Furthermore, these equations are numerically tackled with RKF-45 and shooting scheme. The important dimensionless constraints on their respective profiles are elucidated with the help of graphs. The important engineering coefficients are explained using tables. The major findings of the study are as follows:
1) The fluid velocity declines with improvement in the porous parameter.
2) The heat transport is more in the case of a heat source than a heat sink.
3) The H-H reaction strengths decline the concentration.
4) The fluid velocity and thermal distribution are high in plate geometry and less in cone geometry in the presence of and , respectively.
5) The rate of thermal distribution increases with the increase in the solid volume fraction and heat source sink factor.
6) The surface drag force minimizes with the escalating values in the porous parameter.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct and intellectual contribution to the work and approved it for publication. IH, RNK, RG, JKM, and UK wrote the original draft, ZR, NB, and AJ done the mathematical analysis, SME potentially contributed revision, language editing and study validation.
Funding
This work was partially funded by the Research Center of Future University in Egypt, 2022.
Acknowledgments
The author (ZR) extends her appreciation to the Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia, for funding this study through the Research Group Project under Grant Number (RGP.2/54/43).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Nomenclature
the concentration of the chemical species
- and
chemical species w
concentration near the surface
far-field concentration
specific heat
skin friction and Diffusivity
normal base fluid
acceleration due to gravity
Grashof number
heat source/sink parameter
permeability of the porous medium
homogeneous reaction strength
heterogeneous reaction strength
geometric factor
Nusselt number
Rate of heat generation/absorption
radius of the cone
Prandtl number
Schmidt number
Sherwood number
temperature
temperature near the surface
far-field temperature
velocity components
Cartesian coordinates
- Greek symbols:
half-angle of the cone/wedge
full-angle of the wedge
thermal expansion factor
kinematic viscosity
density
dynamic viscosity
similarity variable
dimensionless temperature profile
- and
dimensionless concentration profile
porous parameter
ratio of diffusion coefficient species
solid nanoparticle
- Subscripts:
hybrid nanofluid
alumina nanoparticle
copper oxide nanoparticle
References
1
Ahmed J. Khan M. Ahmad L. (2019). Stagnation point flow of Maxwell nanofluid over a permeable rotating disk with heat source/sink. J. Mol. Liq.287, 110853. 10.1016/j.molliq.2019.04.130
2
Al-Harbi S. M. (2005). Numerical study of natural convection heat transfer with variable viscosity and thermal radiation from a cone and wedge in porous media. Appl. Math. Comput.170, 64–75. 10.1016/j.amc.2004.10.093
3
Ali M. E. Sandeep N. (2017). Cattaneo-christov model for radiative heat transfer of magnetohydrodynamic casson-ferrofluid: A numerical study. Results Phys.7, 21–30. 10.1016/j.rinp.2016.11.055
4
Chamkha A. J. Ben-Nakhi A. (2008). MHD mixed convection–radiation interaction along a permeable surface immersed in a porous medium in the presence of Soret and Dufour’s Effects. Heat. Mass Transf.44, 845–856. 10.1007/s00231-007-0296-x
5
Chamkha A. J. (1997). Non-Darcy fully developed mixed convection in a porous medium channel with heat generation/absorption and hydromagnetic effects. Numer. Heat. Transf. Part A Appl.32 (6), 653–675. 10.1080/10407789708913911
6
Chamkha A. J. (1996). Non-Darcy hydromagnetic free convection from a cone and a wedge in porous media. Int. Commun. Heat Mass Transf.23, 875–887. 10.1016/0735-1933(96)00070-x
7
Chaudhary M. A. Merkin J. H. (1995). A simple isothermal model for homogeneous-heterogeneous reactions in boundary-layer flow. I Equal diffusivities. Fluid Dyn. Res.16, 311–333. 10.1016/0169-5983(95)00015-6
8
Chaudhary M. A. Merkin J. H. (1995). A simple isothermal model for homogeneous-heterogeneous reactions in boundary-layer flow. II Different diffusivities for reactant and autocatalyst. Fluid Dyn. Res.16, 335–359. 10.1016/0169-5983(95)90813-h
9
Devi S. P. A. Devi S. S. U. (2016). Numerical investigation of hydromagnetic hybrid Cu – Al2O3/water nanofluid flow over a permeable stretching sheet with suction. Int. J. Nonlinear Sci. Numer. Simul.17, 249–257. 10.1515/ijnsns-2016-0037
10
Eid M. R. (2022). 3-D flow of magnetic rotating hybridizing nanoliquid in parabolic trough solar collector: Implementing cattaneo-christov heat flux theory and centripetal and Coriolis forces. Mathematics10, 2605. 10.3390/math10152605
11
Ghalambaz M. Behseresht A. Behseresht J. Chamkha A. (2015). Effects of nanoparticles diameter and concentration on natural convection of the Al2O3–water nanofluids considering variable thermal conductivity around a vertical cone in porous media. Adv. Powder Technol.26, 224–235. 10.1016/j.apt.2014.10.001
12
Hayat T. Qayyum S. Alsaedi A. Shafiq A. (2016). Inclined magnetic field and heat source/sink aspects in flow of nanofluid with nonlinear thermal radiation. Int. J. Heat. Mass Transf.103, 99–107. 10.1016/j.ijheatmasstransfer.2016.06.055
13
Hussain M. Ali A. Ghaffar A. Inc M. (2022). Flow and thermal study of MHD Casson fluid past a moving stretching porous wedge. J. Therm. Anal. Calorim.147, 6959–6969. 10.1007/s10973-021-10983-0
14
Jamshed W. Safdar R. Ibrahim R. W. Nisar K. S. Eid M. R. Alam M. M. (2022). Shape-factor and radiative flux impacts on unsteady graphene–copper hybrid nanofluid with entropy optimisation: Cattaneo–Christov heat flux theory. Pramana -. J. Phys.96, 163. 10.1007/s12043-022-02403-1
15
Khan U. Shafiq A. Zaib A. Baleanu D. (2020). Hybrid nanofluid on mixed convective radiative flow from an irregular variably thick moving surface with convex and concave effects. Case Stud. Therm. Eng.21, 100660. 10.1016/j.csite.2020.100660
16
Khashi’ie N. S. Arifin N. M. Rosca N. C. Rosca A. V. Pop I. (2021). Three-dimensional flow of radiative hybrid nanofluid past a permeable stretching/shrinking sheet with homogeneous-heterogeneous reaction. Int. J. Numer. Methods Heat. Fluid Flow.32, 568–588. 10.1108/hff-01-2021-0017
17
Madhukesh J. K. Naveen Kumar R. Punith Gowda R. J. Prasannakumara B. C. Ramesh G. K. Ijaz Khan M. et al (2021). Numerical simulation of aa7072-aa7075/water-based hybrid nanofluid flow over a curved stretching sheet with Newtonian heating: A non-fourier heat flux model approach. J. Mol. Liq.335, 116103. 10.1016/j.molliq.2021.116103
18
Madhukesh J. K. Ramesh G. K. Prasannakumara B. C. Shehzad S. A. Abbasi F. M. (2021). Bio-Marangoni convection flow of Casson nanoliquid through a porous medium in the presence of chemically reactive activation energy. Appl. Math. Mech.42, 1191–1204. 10.1007/s10483-021-2753-7
19
Madhukesh J. K. Ramesh G. K. Aly E. H. Chamkha A. J. (2022). Dynamics of water conveying SWCNT nanoparticles and swimming microorganisms over a Riga plate subject to heat source/sink. Alexandria Eng. J.61, 2418–2429. 10.1016/j.aej.2021.06.104
20
Magyari E. Chamkha A. J. (2010). Combined effect of heat generation or absorption and first-order chemical reaction on micropolar fluid flows over a uniformly stretched permeable surface: The full analytical solution. Int. J. Therm. Sci.49, 1821–1828. 10.1016/j.ijthermalsci.2010.04.007
21
Mahato R. Das M. Nandkeolyar R. Mahala B. K. (2022). Inclined magnetic field and nonlinear thermal radiation effects on nanofluids flow with homogeneous-heterogeneous reactions. AIP Conf. Proc.2435, 020009.
22
Mahdy A. (2019). Aspects of homogeneous-heterogeneous reactions on natural convection flow of micropolar fluid past a permeable cone. Appl. Math. Comput.352, 59–67. 10.1016/j.amc.2019.01.049
23
Manohar G. R. Venkatesh P. Gireesha B. J. Madhukesh J. K. Ramesh G. K. (2021). Dynamics of hybrid nanofluid through a semi spherical porous fin with internal heat generation. Partial Differ. Equ. Appl. Math.4, 100150. 10.1016/j.padiff.2021.100150
24
Merkin J. H. (1996). A model for isothermal homogeneous-heterogeneous reactions in boundary-layer flow. Math. Comput. Model.24, 125–136. 10.1016/0895-7177(96)00145-8
25
Modather M. Rashad A. M. Chamkha A. J. (2009). An analytical study of MHD heat and mass transfer oscillatory flow of a micropolar fluid over a vertical permeable plate in a porous medium. Turkish J. Eng. Environ. Sci.33, 245–258.
26
Nisar K. S. Khan U. Zaib A. Khan I. Baleanu D. (2020). Numerical simulation of mixed convection squeezing flow of a hybrid nanofluid containing magnetized ferroparticles in 50%:50% of ethylene glycol–water mixture base fluids between two disks with the presence of a non-linear thermal radiation heat flux. Front. Chem.8, 792. 10.3389/fchem.2020.00792
27
Ramesh G. K. Shehzad S. A. Rauf A. Chamkha A. J. (2020). Heat transport analysis of aluminum alloy and magnetite graphene oxide through permeable cylinder with heat source/sink. Phys. Scr.95, 095203. 10.1088/1402-4896/aba5af
28
Ramesh G. K. Madhukesh J. K. Shehzad S. A. Rauf A. (2022). Ternary nanofluid with heat source/sink and porous medium effects in stretchable convergent/divergent channel. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng., 09544089221081344.
29
Rana P. Bhargava R. (2011). Numerical study of heat transfer enhancement in mixed convection flow along a vertical plate with heat source/sink utilizing nanofluids. Commun. Nonlinear Sci. Numer. Simul.16, 4318–4334. 10.1016/j.cnsns.2011.03.014
30
Reddy P. S. Sreedevi P. Chamkha Ali.J. (2017). MHD boundary layer flow, heat and mass transfer analysis over a rotating disk through porous medium saturated by Cu-water and Ag-water nanofluid with chemical reaction. Powder Technol.307, 46–55. 10.1016/j.powtec.2016.11.017
31
Rekha M. B. Sarris I. E. Madhukesh J. K. Raghunatha K. R. Prasannakumara B. C. (2022). Activation energy impact on flow of aa7072-aa7075/water-based hybrid nanofluid through a cone, wedge and plate. Micromachines13, 302. 10.3390/mi13020302
32
Rooman M. Jan M. A. Shah Z. Deebani W. Shutaywi M. (2021). Hall effect on the entropy optimization of radiative magnetized Jeffrey nanofluid flow with homogeneous and heterogeneous reaction by rotating stretching disk. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng., 09544089211065537.
33
Sajid T. Ayub A. Shah S. Z. H. Jamshed W. Eid M. R. El Din E. S. M. T. et al (2022). Trace of chemical reactions accompanied with arrhenius energy on ternary hybridity nanofluid past a wedge. Symmetry14, 1850. 10.3390/sym14091850
34
Salleh M. Z. Nazar R. Pop I. (2010). Boundary layer flow and heat transfer over a stretching sheet with Newtonian heating. J. Taiwan Inst. Chem. Eng.41, 651–655. 10.1016/j.jtice.2010.01.013
35
Shahzad F. Jamshed W. Sajid T. Shamshuddin M. D. Safdar R. Salawu S. O. et al (2022). Electromagnetic control and dynamics of generalized burgers’ nanoliquid flow containing motile microorganisms with cattaneo–christov relations: Galerkin finite element mechanism. Appl. Sci.12, 8636. 10.3390/app12178636
36
Siddiqui B. K. Batool S. mahmood ul Hassan Q. Malik M. Y. (2022). Repercussions of homogeneous and heterogeneous reactions of 3D flow of Cu-water and AL2O3-water nanofluid and entropy generation estimation along stretching cylinder. Ain Shams Eng. J.13, 101493. 10.1016/j.asej.2021.05.007
37
Sreedevi P. Sudarsana Reddy P. Chamkha A. (2020). Heat and mass transfer analysis of unsteady hybrid nanofluid flow over a stretching sheet with thermal radiation. SN Appl. Sci.2, 1222. 10.1007/s42452-020-3011-x
38
Umeshaiah M. Madhukesh J. Khan U. Rana S. Zaib A. Raizah Z. et al (2022). Dusty nanoliquid flow through a stretching cylinder in a porous medium with the influence of the melting effect. Processes10, 1065. 10.3390/pr10061065
39
Vajravelu K. Nayfeh J. (1992). Hydromagnetic convection at a cone and a wedge. Int. Commun. Heat Mass Transf.19, 701–710. 10.1016/0735-1933(92)90052-j
40
Veera Krishna M. Ameer Ahamad N. Chamkha A. J. (2020). Hall and ion slip effects on unsteady MHD free convective rotating flow through a saturated porous medium over an exponential accelerated plate. Alexandria Eng. J.59, 565–577. 10.1016/j.aej.2020.01.043
41
Veera Krishna M. Chamkha A. J. (2019). Hall and ion slip effects on MHD rotating boundary layer flow of nanofluid past an infinite vertical plate embedded in a porous medium. Results Phys.15, 102652. 10.1016/j.rinp.2019.102652
42
Waseem M. Gul T. Khan I. Khan A. Saeed A. Ali I. et al (2021). Gravity-driven hydromagnetic flow of couple stress hybrid nanofluid with homogenous-heterogeneous reactions. Sci. Rep.11, 17498. 10.1038/s41598-021-97045-5
Summary
Keywords
hybrid nanofluid, porous medium, homogeneous and heterogeneous reactions, heat source/sink, cone, wedge and plate
Citation
Haq I, Naveen Kumar R, Gill R, Madhukesh JK, Khan U, Raizah Z, Eldin SM, Boonsatit N and Jirawattanapanit A (2022) Impact of homogeneous and heterogeneous reactions in the presence of hybrid nanofluid flow on various geometries. Front. Chem. 10:1032805. doi: 10.3389/fchem.2022.1032805
Received
31 August 2022
Accepted
26 September 2022
Published
18 October 2022
Volume
10 - 2022
Edited by
Renjith Thomas, Mahatma Gandhi University, India
Reviewed by
Ioannis Sarris, University of West Attica, Greece
Ali Chamkha, Kuwait College of Science and Technology, Kuwait
Mohamed Eid, The New Valley University, Egypt
Updates
Copyright
© 2022 Haq, Naveen Kumar, Gill, Madhukesh, Khan, Raizah, Eldin, Boonsatit and Jirawattanapanit.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sayed M. Eldin, sayed.eldin22@fue.edu.eg
This article was submitted to Theoretical and Computational Chemistry, a section of the journal Frontiers in Chemistry
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.