Simulation study of inverse diffusion counterbalance method for super-resolution ion mobility spectrometry

Ion mobility spectrometer (IMS) is a powerful chemical composition analysis tool working at atmospheric pressure that can be used to separate complex samples and study molecular structures. Resolution is a key parameter for evaluating the performance of IMS. However, for the pulsed sampling technique used by drift tube IMS, there is an upper limit to the resolution due to the diffusion between ions and the drift gas. In this work, an inverse diffusion counterbalance method is proposed to break the resolution limit. The method is inspired by the stimulated emission depletion (STED). In optical microscopy systems, STED is used to break the optical diffraction limit by a ring of depleted light to counteract diffraction effects of the excited light. We modified this strategy and applied it to an IMS system for counteracting the diffusion effect of the pulsed ion packet. The method can increase the resolution up to 1.55 times through theoretical analysis, and the improvement is verified by simulations. The simulation results find that the initial width of the ion packet has an influence on the effectiveness of the method, and the narrower the initial width, the better the effect. The proposed inverse counterbalance strategy may also be applied to other spectral analysis instruments to break the resolution limit.

1 Introduction

Ion mobility spectrometer (IMS) (Eiceman et al., 2013; Sorribes-Soriano et al., 2018) is an analytical instrument working at atmospheric pressure. It has a wide range of applications in many fields, such as drug detection (Zou et al., 2018), medical diagnosis (Ruszkiewicz et al., 2020), and compound analysis (Han and Yao, 2020; Wu et al., 2021). IMS has many kinds of derivatives, such as Travelling wave ion mobility spectrometry (TW-IMS) (Giles et al., 2004; Pringle et al., 2007), Trapped ion mobility spectrometry (TIMS) (Fernandez-Lima et al., 2011b,a), Differential or field asymmetric ion mobility spectrometry (DMS/FAIMS) (Buryakov et al., 1993, 1991), Fourier transform ion mobility spectrometry (FT-IMS) (Knorr et al., 1985), Hadamard transform ion mobility spectrometry (HT-IMS) (Clowers et al., 2006; Szumlas et al., 2006), etc. The development of special configurations (Michelmann et al., 2014; Hernandez et al., 2014; Silveira et al., 2014) and post-processing technologies (Davis and Clowers, 2018; May et al., 2020) allows the instrument to reach a very high level of resolution. Because the mobility can be obtained directly without calibration (Kirk et al., 2019a), the conventional drift tube ion mobility spectrometry (DT-IMS) still has a wide range of applications. Unless otherwise indicated, all IMS mentioned in the following are DT-IMS. For conventional drift tube IMS, the ionized sample is sent into the drift region as a pulsed ion packet. The drift region is filled with neutral buffer gas, in which ions will drift a certain distance under the influence of electric field. Due to the difference in mobility, packets of different ion species are separated depending on their drift time. The separation capability can be quantified by the resolution of IMS (Rokushika et al., 1985), which is defined as the arrival time of a pulsed ion packet t_d divided by its full width at half maximum t_fwhm.

Lengthening the drift region while increasing the drift voltage is an effective way to improve the resolution (Siems et al., 1994; Watts and Wilders, 1992; Dugourd et al., 1997; Wu et al., 1998). However, a significant increase in drift length leads to a rather large and heavy device, and some short-lived ions will disappear due to the extended drift time. In recent years, reducing the initial width of the ion packet w_i has proven to be an effective way to improve the resolution. Since the ion gate is the key component to control the entry of ions, the w_i can be effectively shortened by making improvements to the ion gate. Du et al. (Du et al., 2012) studied three different effects that occur when a Bradbury-Nielsen gate is running, and used the compression effect to achieve a shortening of w_i. The compression effect was later shown to work also for the field switching gate IMS (Chen et al., 2019) and Tyndall-Powell gate IMS (Chen et al., 2015), both of which give an increase in resolution. Langejuergen et al. (Langejuergen et al., 2014; Reinecke et al., 2016) have proposed for the first time a three-grid shutter structure to control the entry of ions into the drift region. This type of ion gate can use the potential switching on the three metal grids to achieve precise ion control, which can make w_i much shorter. Combined with a high kinetic energy drift tube, a very high level of resolution can be achieved (Kirk et al., 2018; 2019b).

However, whether increasing the drift length or decreasing the w_i, these methods can only improve the resolution to a level close to the diffusion limit resolution (Siems et al., 1994; Wu et al., 1998; Revercomb and Mason, 1975). This resolution refers to the highest resolution that can be obtained by the instrument when the rest of the factors, such as the Coulomb repulsion between ions and the inhomogeneity of the electric field, are neglected and only the effect caused by diffusion is considered. To further improve the separation capacity of IMS, this limit needs to be broken from the principle.

In this work, an inverse diffusion counterbalance method is proposed. The strategy is similar to the stimulated emission depletion (STED) method, which uses a ring of depleted light to counteract diffraction effects of the excited light. In our method, an inverse diffusion of a dip in the ion beam is used to counteract the diffusion of the pulsed ion packet. The counteracting process can be implemented in three steps: the first step is to create a normal pulsed ion peak; the second step is to create an inverse blank peak (Tabrizchi and Jazan, 2009) and subtract the baseline; and the third step is to subtract the results obtained from the first and second steps. The exact value of the method in terms of resolution improvement ratio was obtained mathematically, and we verified this conclusion by finite element simulation. The effect of different w_i and diffusion coefficients on the degree of implementation of this method was also examined.

2 Method

2.1 Implementation steps

In the field of optical microscopy, the smaller the area of the excitation spot, the higher the resolution of the image. However, the area of the excitation spot has a minimum value because of the diffraction of light. Stefan W. Hell and Jan Wichmann (Hell and Wichmann, 1994) use ring light with quenching effect to counteract the excitation effect at the edge of the excitation spot. This results in a reduction of the actual excitation area and breaks the diffraction resolution limit. The method is called the stimulated-emission-depletion (STED). In the pulsed IMS, ion packet is put into the drift region in the form of pulses. The narrower the width of the ion packet, the higher the resolution. However, during the drift, the pulsed ion packet of the gas phase will diffuse towards the surrounding air, and the diffusion effect leads to an increase in width. In order to reduce the width, we adopt the strategy of STED, hoping to use diffusion in the opposite direction to counteract the diffusion of pulsed ion packet. For the inverse IMS (Tabrizchi and Jazan, 2009), the diffusion is in the opposite direction, which happens to be used to counteract it. By using the appropriate steps, this counteracting strategy can be applied in IMS.

The inverse diffusion counterbalance method can be accomplished through three steps. The first step is to generate a normal spectrum by putting ions in the form of a pulse into the drift tube. The pulsed ion packet diffuses from its center to the edge during the drift, and the process is shown in Figure 1A. Such diffusion leads to an increase in the width of the ion packet, which is the target we want to counteract afterwards. Figure 1B shows a schematic spectrum of the pulsed ion packet. The second step is to generate an inverse spectrum by a blocking pulse, as shown in Figure 1C. The ion dip generated in the second step has the same drift velocity and opposite diffusion direction (from the edge to the center) compared to the ion packet generated in the first step. Thus, the inverse spectrum can be used to counteract the diffusion part of the pulsed spectrum. In order to unify the minimum values of the spectrum obtained in the first and second steps, we subtracted a base parameter I_base from the inverse spectrum. The inverse spectrum is corrected to a minimum value of zero. The dashed and solid lines in Figure 1D show the original and corrected schematic spectra generated in the second step, respectively. The third step is to subtract the corrected inverse spectrum from the pulsed spectrum generated in the first step. For the pulsed spectrum, since what needs to be subtracted is only the intensity due to diffusion, the negative value in the spectrum after being subtracted should be set to zero. The equivalent drift process for this step is shown in Figure 1E, and the schematic spectrum is shown in Figure 1F. The area contained by the purple dashed line in Figure 1F is the remaining ion intensity after the diffusion has been counteracted.

FIGURE 1

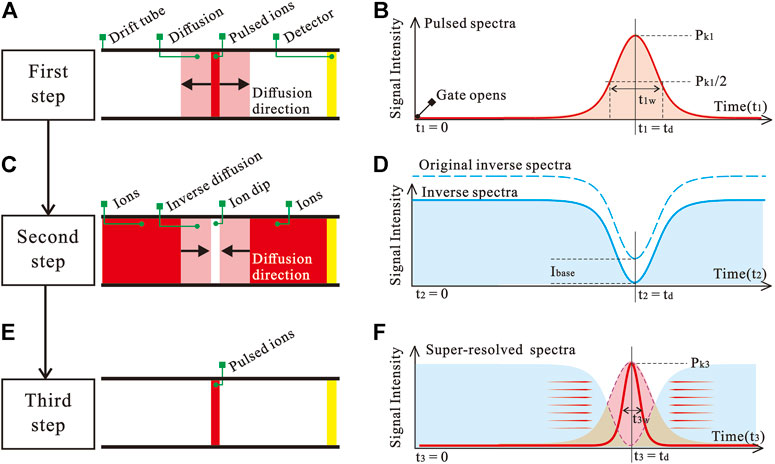
FIGURE 1. The steps of the inverse diffusion counterbalance method implementation. (A) Drift process of pulsed ion packet. (B) Schematic spectrum of a pulsed ion packet. (C) Drift process of inverse dip in ion beam. (D) Schematic inverse spectrum. (E) Pulsed ion packet after counterbalance. (F) Schematic spectrum that breaks the resolution limits.

In the actual experiment, the realization of this method relies mainly on the control of an ion gate. Ion gate generally consists of two sets of metal wires that control the opening and closing of the ion beam by the voltage difference between the wires (V_GVD. When V_GVD is greater than the closing voltage (V_Closing), the ions are pulled by the transverse electric field force and consumed on the lower voltage wires, which can cause the ion beam not to pass. In order to obtain the pulsed ion packet in the first step of the inverse diffusion counterbalance method, the ion gate needs to be opened (V_GVD = 0 V) for a short time (t_w) and then kept closed (V_GVD > V_Closing). The inverse dip in ion beam in the second step requires the ion gate to remain open at all times after a short time of closing.

2.2 Theoretical enhancement ratio

Here, we wish to derive the diffusion limit resolution of the spectrum obtained with the inverse diffusion counterbalance method. Similar to the preconditions (St. Louis et al., 1990; Siems et al., 1994) used in deriving the diffusion limit resolution of pulsed IMS, the following assumptions are made: space charge effects can be negligible; the diffusion motion is a gradient of concentration only along the x-axis; the normal and the inverse ion diffusion are symmetric and independent of the ion gate; and the width of ion packet at time zero is negligible.

We divide the derivation process into three parts. First we derive the relationship between the ion current (I₁) generated in the first step with time and drift distance based on Fick’s law. Then we derive the relationship between the ion current (I₂) generated in the second step with time and drift distance based on the symmetry of the diffusion. Finally, we obtain the relationship between the ion current (I₃) generated by the inverse diffusion counterbalance method with time and drift distance by subtracting the above two ion currents, and calculate resolution enhancement ratio of the method.

For pulsed ion packets formed in the first step, the one-dimensional concentration of ions C₁ versus time t₁ and distance x₁ is (Crank, 1975; Watts and Wilders, 1992)

$C_1=\frac{C_0}{{\left(4\pi D{t}_1\right)}^{1/2}}\exp \left[\frac{-{\left(x_1-K{\mathit{\text{E}}}_{\mathrm{d}}{t}_1\right)}^2}{4D{t}_1}\right],(1)$

where E_d is a constant electric field along the drift region, C₀ is the one-dimensional concentration of the ion packet at time zero, D is the diffusion coefficient, and K is the ion mobility. Eq. 1 mainly describes the relationship between the one-dimensional concentration (C₁) at different position (x₁) on the ion packet and time (t₁) when the ion packet moves along the x-axis. The ion concentration is an expression of the spatial distribution and cannot be used directly in the calculation of ion spectra. Therefore, we need to use the drift velocity of ions in an electric field to derive the ion concentration in the form of an ion current. Since the drift velocity v_d is lineraly related on E_d, which is

${\mathit{\text{v}}}_{\mathrm{d}}=K\cdot {\mathit{\text{E}}}_{\mathrm{d}}.(2)$

For a drift tube with a cross-sectional area of S, the current intensity of the received ions I₁ is

$I_1=C_{1}S{\mathit{\text{v}}}_{\mathrm{d}}=C_{1}SK{E}_d=\frac{C_{0}SK{E}_d}{{\left(4\pi D{t}_1\right)}^{1/2}}\exp \left[\frac{-{\left(x_1-K{E}_d{t}_1\right)}^2}{4D{t}_1}\right].(3)$

So far, the relationship between the ion current generated in the first step (ion packet) versus time and drift distance is obtained.

In the second step, the current generated by the continuous ions is

$I_0=C_{0}SK{E}_{\mathrm{d}}.(4)$

Due to the symmetry of diffusion, the inverse ion current I₂ with the base parameter subtracted versus time t₂ and distance x₂ is

$I_2=I_0-I_1\left(t_2,x_2\right)-I_{\text{base}},(5)$

where I_base is the base parameter to ensure that the minimum value of the inverse spectrum is zero. Suppose the peak height of the pulsed spectrum obtained in the first step is I_1pk, then I_base satisfies that,

$I_{\text{base}}=I_0-I_{\mathit{1pk}}.(6)$

According to Eqs 3–6, it can be obtained that

$I_2=I_{\mathit{1pk}}-\frac{C_{0}SK{E}_d}{{\left(4\pi D{t}_2\right)}^{1/2}}\exp \left[\frac{-{\left(x_2-K{E}_d{t}_2\right)}^2}{4D{t}_2}\right].(7)$

So far, the relationship between the ion current generated in the second step (inverse dip in ion beam) versus time and drift distance is obtained.

In the third step, the initial time of the pulsed spectrum and the inverse spectrum is aligned. The variables of time t₃ and distance x₃ are the same as the first two steps, which is t₃ = t₁ = t₂, x₃ = x₁ = x₂. The expression for the ion current I₃ of the spectrum is

$\begin{array}{cc}\hfill I_3& =I_1\left(t_3,x_3\right)-I_2\left(t_3,x_3\right)\hfill \\ \hfill & =\frac{2C_{0}SK{E}_d}{{\left(4\pi D{t}_3\right)}^{1/2}}\exp \left[\frac{-{\left(x_3-K{E}_d{t}_3\right)}^2}{4D{t}_3}\right]-I_{\text{pk}1}.\hfill \end{array}(8)$

t is noted here that there is a possibility that I₃ is negative in Eq. 8. According to the definition of our method, all negative values should be set to zero. Since the I₃ used in the subsequent calculations are all positive values, that why we do not restrict I₃ ≥ 0 here. For a drift region of length L, the magnitude of the peak happens at t_d, where

$t_d=L/K{E}_d.(9)$

According to Eq. 3, the peaks of the spectrum I_3pk is

$I_{\mathit{3pk}}=I_{\mathit{1pk}}=I_1\left(t_1=t_d,x_1=L\right)=\frac{C_{0}SK{E}_d}{{\left(4\pi D{t}_d\right)}^{1/2}}.(10)$

According to the concept of full width at half maxima, Eq. 8, and Eq. 10, when t₃ = t_d - t_w3/2, the current intensity at position x₃ = L is

$\begin{array}{c}\hfill \frac{2C_{0}SK{E}_d}{{\left(4\pi D{t}_d-t_{w3}/2\right)}^{1/2}}\exp \left[\frac{-{\left(L-K{E}_d\left(t_d-t_{w3}/2\right)\right)}^2}{4D\left(t_d-t_{w3}/2\right)}\right]-\frac{C_{0}SK{E}_d}{{\left(4\pi {\text{Dt}}_d\right)}^{1/2}}=I_{\mathit{3pk}}/2=\frac{C_{0}SK{E}_d}{2{\left(4\pi {\text{Dt}}_d\right)}^{1/2}},\end{array}(11)$

which yields:

$\frac{3}{4t_{w3}^{1/2}}=\frac{1}{{\left(t_d-t_{w3}/2\right)}^{1/2}}\exp \left[\frac{-{\left(K{E}_d{t}_{w3}/2\right)}^2}{4D\left(t_d-t_{w3}/2\right)}\right].(12)$

Since the drift time (t_d) is usually about 20 ms and the opening time (t_w) is usually less than 0.2 ms, it can be assumed that t_d is much larger than t_w. For t_d ≫ t_w, (t_d − t_w3/2) = t_d. The resolution R₃ of the inverse diffusion counterbalance method is

$R_3=\frac{t_d}{t_{w3}}={\left[\frac{K^2{E_d}^2{t}_d}{16Dln\left(4/3\right)}\right]}^{1/2}.(13)$

Since the diffusion coefficient and the mobility are determined by the Nernst-Einstein equation:

$D=K{k}_{\mathrm{B}}T/q,(14)$

where k_B is Boltzmann’s constant, T is the absolute temperature, q is the electrical charge of a particle. According to Eqs 9, 13, 14, the resolution R₃ is

$R_3={\left[\frac{E_d\mathit{\text{L}}\mathit{\text{q}}}{16k_{\mathrm{B}}Tln\left(4/3\right)}\right]}^{1/2}.(15)$

Under weak electric field conditions, the diffusion limit resolution (Cohen and Karasek, 1970; Watts and Wilders, 1992) of traditional pulsed IMS can be written as

${\mathit{\text{R}}}_{\mathrm{d}}={\left[\frac{E_d\mathit{\text{L}}\mathit{\text{q}}}{16{\mathit{\text{k}}}_{\mathrm{B}}Tln2}\right]}^{1/2}.(16)$

According to Eq. 15 and Eq. 16, the resolution enhancement ratio is

$\alpha =\frac{R_3}{R_{\mathrm{d}}}>1.55.(17)$

3 Experimental

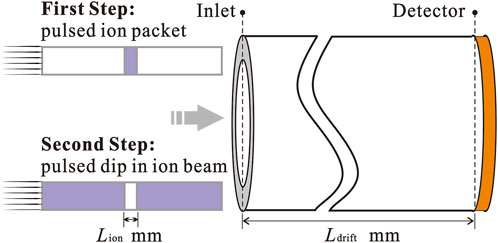
A model is built in the simulation environment using the finite element method, as shown in Figure 2. The entrance is at x = 0 mm and the detector is at x = L_drift. In order to divide the mesh in a more detailed way with limited computational power, the model is simplified in one-dimensional. A uniformly divided grid with a length of 5 µm is used. The cross-sectional area of the drift tube can be any value.

FIGURE 2

FIGURE 2. Schematic indicating the parameters of the drift tube.

The drift electric field was set to 50 V/mm with a high potential at the ion inlet and a low potential at the detector position. In the first step, the function of the ion gate is achieved by putting an ion sequence of blank-ion-blank into the drift tube in temporal order. In the second step, the ion sequence of the inverse spectrum is ion-blank-ion. The blank is the absence of ions. The width of the ion packet in the first step and the width of the blank in the second step are guaranteed to be same, denoted by L_ion. The initial moment of the spectrum is when the center of L_ion reaches x = 0 mm.

4 Results and discussion

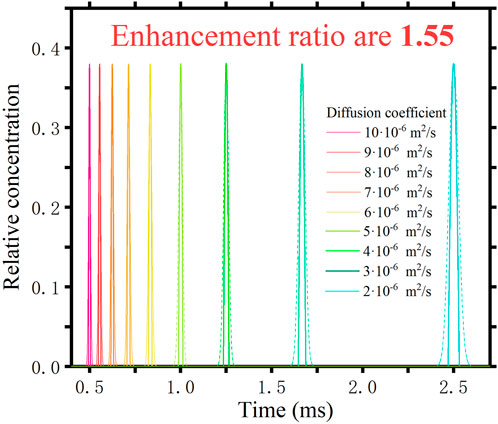
When L_drift = 10 mm and L_ion = 0.1 mm, the simulation spectrum of a single type of ion (D = 2.8⋅ 10⁻⁶ m²/s) is shown in Figure 3. The blue and the red curve are the pulsed and the inverse spectra generated in the first and second steps. The yellow curve is the counteracted spectrum obtained using the inverse diffusion counterbalance method. The drift time of the ion is 1.79 ms, and the resolution of the pulsed and the counteracted spectrum are 40 and 62, respectively. The resolution enhancement ratio α_r is 1.55, which is consistent with the theoretically calculated result.

FIGURE 3

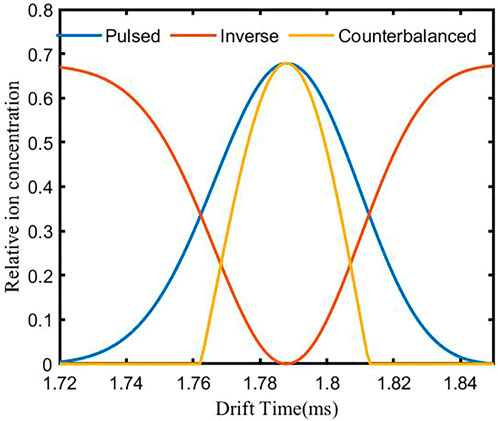
FIGURE 3. Simulation spectrum of a single type of ion using the inverse diffusion counterbalance method.

It is clear from the mathematical derivation that the beneficial effect of this method is independent of the diffusion coefficient of the ions themselves. We have also verified this in our simulations. Different species of ions (different D) are fed separately into the drift tube. Figure 4 shows the results. The dashed curve is the spectrum obtained using the traditional pulsed method and the solid line is the spectrum obtained using the inverse diffusion counterbalance method. The different colours correspond to the different D. It can be seen that ions with different diffusion coefficients arrive at the detection location at different times. We have tested nine different substances with diffusion coefficients ranging from 2 ⋅ 10⁻⁶ m²/s to 10 ⋅ 10⁻⁶ m²/s. They all have an resolution enhancement ratio of 1.55. Consistent with the theoretical derivation, the method does not have a differentiating effect depending on the diffusion coefficient of the sample.

FIGURE 4

FIGURE 4. Spectra obtained using two methods for ions with different diffusion coefficients.

When ions with different diffusion coefficients are sampled simultaneously, ions with close diffusion coefficients will form overlapping peaks. The inverse diffusion counterbalance method is supposed to have a better separation. In the simulation model, we put in five different ion packets at the same time. The values of the diffusion coefficients are from 2.30⋅ 10⁻⁶ m²/s to 2.50⋅ 10⁻⁶ m²/s in intervals of 0.05⋅ 10⁻⁶ m²/s. Results are shown in Figure 5. The gray curve is the spectrum obtained by using the conventional pulsed method. There is little valid information in the result due to the mutual overlap between the peaks. The red curve is obtained by using the inverse diffusion counterbalance method. Five peaks with different drift times have been presented. To achieve the same level of resolution as the inverse diffusion counterbalance method, the drift tube needs to be extended to more than 2.4 times the original length using the conventional method.

FIGURE 5

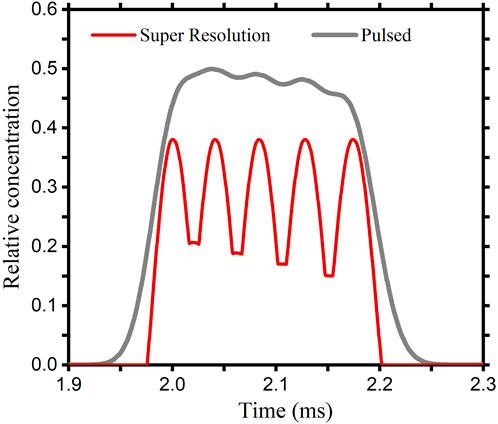
FIGURE 5. Results obtained by the pulsed method and the inverse diffusion counterbalance method, when ions with close diffusion coefficients are sampled simultaneously.

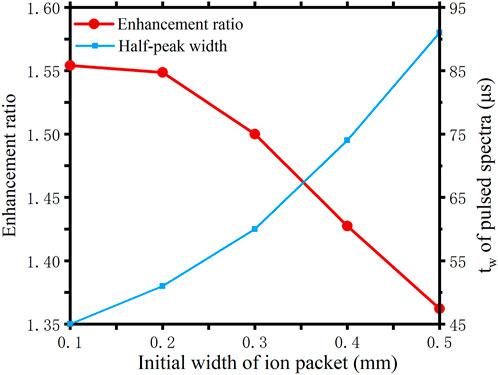
The equivalent open gate time for these results are 17.9 µs. Such a short opening time can be neglected compared to the total drift time. Under these conditions, the diffusion effect is the main cause of the resulting increase in half-peak width. Therefore, the method of reducing the half-peak width by counteracting diffusion can be extremely effective, showing the same result as the theoretical value. When the initial width of the ion packet increases, this situation will change.

The red curve in Figure 6 shows the variation of the enhancement when the initial width of the ion packet is increased. The blue curve shows the variation of the half-peak width of the pulsed spectrum. It can be seen that the wider the initial width of the ion packet, the less effective the method. This is easily understood because the method only works to counteract the effects caused by the diffusion. The larger the initial width as a percentage of the total ion packet width, the smaller the percentage of the diffusion width will be. Nevertheless, since the diffusion is inevitable, the method is also certain to result in an improvement in resolution.

FIGURE 6

FIGURE 6. Effect of different initial width on the inverse diffusion counterbalance method.

5 Conclusion

For drift tube IMS, different ion species are separated by their drift time, and the ability to separate them is characterized by resolution. Due to diffusion, the maximum resolution that an IMS system can achieve is the diffusion limit resolution. This limit constrains the analytical capability of IMS. In the current work, an inverse diffusion counterbalance method has been proposed to break the limit. Through theoretical analysis and mathematical calculation, the resolution obtained with this method can be 1.55 times better than the conventional pulsed method. Since the method cannot counteract the effect of the initial width of the ion packet, the larger the initial width, the less effective the method will be. For ions with different mobility, this method has the same effect on resolution enhancement.

In order to verify the effectiveness of this method, a simplified 1D model was built in a finite element simulation software. The simulation results are in general agreement with the calculation. This method is a simple but very effective way of increasing resolution, and breaks the diffusion limit resolution. In the practical application of IMS, even if the hardware improvements have taken the instrument to its diffusion resolution limit, the resolution can still be improved to 1.55 times by using this method. The strategy of ion counterbalance may be applied to more broad-spectrum analytical instruments by experimental verification.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

KG and YZ constructed the original idea and designed the experiments. KG wrote the manuscript. JL and HH proofread the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China under Grant U19B2030 and Grant 61976167, the Science and Technology Projects of Xi’an, China under Grant 201809170CX1 1JC12, and Natural Science Basic Research Program of Shaanxi Province (2022JQ-708), National Natural Science Foundation Youth Fund Grant XJS220208.

Acknowledgments

The authors express their sincere appreciation to Xu Zheng for help.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Buryakov, I., Krylov, E., Makas, A., Nazarov, E., Pervukhin, V., and Rasulev, U. K. (1991). Separation of ions according to their mobility in a strong alternating current electric field. Pis’ ma Zh. Tech. Fiz. Russ. 17, 61–65.

Google Scholar

Buryakov, I., Krylov, E., Nazarov, E., and Rasulev, U. K. (1993). A new method of separation of multi-atomic ions by mobility at atmospheric pressure using a high-frequency amplitude-asymmetric strong electric field. Int. J. Mass Spectrom. Ion Process. 128, 143–148. doi:10.1016/0168-1176(93)87062-w

CrossRef Full Text | Google Scholar

Chen, C., Tabrizchi, M., Wang, W., and Li, H. (2015). Field switching combined with bradbury-nielsen gate for ion mobility spectrometry. Anal. Chem. 87, 7925–7930. doi:10.1021/acs.analchem.5b01737

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, H., Chen, C., Li, M., Wang, W., Jiang, D., and Li, H. (2019). Achieving high gating performance for ion mobility spectrometry by manipulating ion swarm spatiotemporal behaviors in the vicinity of ion shutter. Anal. Chim. Acta 1052, 96–104. doi:10.1016/j.aca.2018.11.045

PubMed Abstract | CrossRef Full Text | Google Scholar

Clowers, B. H., Siems, W. F., Hill, H. H., and Massick, S. M. (2006). Hadamard transform ion mobility spectrometry. Anal. Chem. 78, 4474–4481. doi:10.1021/ac051743b

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen, M. J., and Karasek, F. W. (1970). Plasma chromatography™—A new dimension for gas chromatography and mass spectrometry. J. Chromatogr. Sci. 8, 330–337. doi:10.1093/chromsci/8.6.330

CrossRef Full Text | Google Scholar

Crank, J. (1975). The mathematics of diffusion. Oxford, UK: Oxford University Press.

Google Scholar

Davis, A. L., and Clowers, B. H. (2018). Leveraging spectral sparsity to realize enhanced separation of gas-phase ion populations. Int. J. Mass Spectrom. 427, 141–150. doi:10.1016/j.ijms.2017.11.008

CrossRef Full Text | Google Scholar

Du, Y., Wang, W., and Li, H. (2012). Resolution enhancement of ion mobility spectrometry by improving the three-zone properties of the bradbury-nielsen gate. Anal. Chem. 84, 1725–1731. doi:10.1021/ac203013u

PubMed Abstract | CrossRef Full Text | Google Scholar

Dugourd, P., Hudgins, R. R., Clemmer, D. E., and Jarrold, M. F. (1997). High-resolution ion mobility measurements. Rev. Sci. Instrum. 68, 1122–1129. doi:10.1063/1.1147873

CrossRef Full Text | Google Scholar

Eiceman, G. A., Karpas, Z., and Hill, H. H. (2013). Ion mobility spectrometry. Boca Raton, Florida: CRC Press.

Google Scholar

Fernandez-Lima, F., Kaplan, D. A., Suetering, J., and Park, M. A. (2011b). Gas-phase separation using a trapped ion mobility spectrometer. Int. J. Ion. Mobil. Spectrom. 14, 93–98. doi:10.1007/s12127-011-0067-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Fernandez-Lima, F., Kaplan, D., and Park, M. (2011a). Note: Integration of trapped ion mobility spectrometry with mass spectrometry. Rev. Sci. Instrum. 82, 126106. doi:10.1063/1.3665933

PubMed Abstract | CrossRef Full Text | Google Scholar

Giles, K., Pringle, S. D., Worthington, K. R., Little, D., Wildgoose, J. L., and Bateman, R. H. (2004). Applications of a travelling wave-based radio-frequency-only stacked ring ion guide. Rapid Commun. Mass Spectrom. 18, 2401–2414. doi:10.1002/rcm.1641

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, D. Q., and Yao, Z. P. (2020). Chiral mass spectrometry: An overview. TrAC Trends Anal. Chem. 123, 115763. doi:10.1016/j.trac.2019.115763

CrossRef Full Text | Google Scholar

Hell, S. W., and Wichmann, J. (1994). Breaking the diffraction resolution limit by stimulated emission: Stimulated-emission-depletion fluorescence microscopy. Opt. Lett. 19, 780–782. doi:10.1364/ol.19.000780

PubMed Abstract | CrossRef Full Text | Google Scholar

Hernandez, D. R., DeBord, J. D., Ridgeway, M. E., Kaplan, D. A., Park, M. A., and Fernandez-Lima, F. (2014). Ion dynamics in a trapped ion mobility spectrometer. Analyst 139, 1913–1921. doi:10.1039/c3an02174b

PubMed Abstract | CrossRef Full Text | Google Scholar

Kirk, A. T., Bohnhorst, A., Raddatz, C.-R., Allers, M., and Zimmermann, S. (2019a). Ultra-high-resolution ion mobility spectrometry—Current instrumentation, limitations, and future developments. Anal. Bioanal. Chem. 411, 6229–6246. doi:10.1007/s00216-019-01807-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Kirk, A. T., Bohnhorst, A., Raddatz, C.-R., Allers, M., and Zimmermann, S. (2019b). Ultra-high-resolution ion mobility spectrometry—Current instrumentation, limitations, and future developments. Anal. Bioanal. Chem. 411, 6229–6246. doi:10.1007/s00216-019-01807-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Kirk, A. T., Grube, D., Kobelt, T., Wendt, C., and Zimmermann, S. (2018). High-resolution high kinetic energy ion mobility spectrometer based on a low-discrimination tristate ion shutter. Anal. Chem. 90, 5603–5611. doi:10.1021/acs.analchem.7b04586

PubMed Abstract | CrossRef Full Text | Google Scholar

Knorr, F., Eatherton, R., Siems, W., and Hill, H. (1985). Fourier transform ion mobility spectrometry. Anal. Chem. 57, 402–406. doi:10.1021/ac50001a018

PubMed Abstract | CrossRef Full Text | Google Scholar

Langejuergen, J., Allers, M., Oermann, J., Kirk, A., and Zimmermann, S. (2014). High kinetic energy ion mobility spectrometer: Quantitative analysis of gas mixtures with ion mobility spectrometry. Anal. Chem. 86, 7023–7032. doi:10.1021/ac5011662

PubMed Abstract | CrossRef Full Text | Google Scholar

May, J. C., Knochenmuss, R., Fjeldsted, J. C., and McLean, J. A. (2020). Resolution of isomeric mixtures in ion mobility using a combined demultiplexing and peak deconvolution technique. Anal. Chem. 92, 9482–9492. doi:10.1021/acs.analchem.9b05718

PubMed Abstract | CrossRef Full Text | Google Scholar

Michelmann, K., Silveira, J. A., Ridgeway, M. E., and Park, M. A. (2014). Fundamentals of trapped ion mobility spectrometry. J. Am. Soc. Mass Spectrom. 26, 14–24. doi:10.1007/s13361-014-0999-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Pringle, S. D., Giles, K., Wildgoose, J. L., Williams, J. P., Slade, S. E., Thalassinos, K., et al. (2007). An investigation of the mobility separation of some peptide and protein ions using a new hybrid quadrupole/travelling wave ims/oa-tof instrument. Int. J. Mass Spectrom. 261, 1–12. doi:10.1016/j.ijms.2006.07.021

CrossRef Full Text | Google Scholar

Reinecke, T., Kirk, A. T., Ahrens, A., Raddatz, C. R., Thoben, C., and Zimmermann, S. (2016). A compact high resolution electrospray ionization ion mobility spectrometer. Talanta 150, 1–6. doi:10.1016/j.talanta.2015.12.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Revercomb, H. E., and Mason, E. A. (1975). Theory of plasma chromatography/gaseous electrophoresis. review. Anal. Chem. 47, 970–983. doi:10.1021/ac60357a043

CrossRef Full Text | Google Scholar

Rokushika, S., Hatano, H., Baim, M. A., and Hill, H. H. (1985). Resolution measurement for ion mobility spectrometry. Anal. Chem. 57, 1902–1907. doi:10.1021/ac00286a02310.1021/ac00286a02310.1021/ac00286a023

CrossRef Full Text | Google Scholar

Ruszkiewicz, D. M., Sanders, D., O’Brien, R., Hempel, F., Reed, M. J., Riepe, A. C., et al. (2020). Diagnosis of Covid-19 by analysis of breath with gas chromatography-ion mobility spectrometry-a feasibility study. EClinicalMedicine 29, 100609. doi:10.1016/j.eclinm.2020.100609

PubMed Abstract | CrossRef Full Text | Google Scholar

Siems, W. F., Wu, C., Tarver, E. E., Hill, H. H. J., Larsen, P. R., and McMinn, D. G. (1994). Measuring the resolving power of ion mobility spectrometers. Anal. Chem. 66, 4195–4201. doi:10.1021/ac00095a014

CrossRef Full Text | Google Scholar

Silveira, J. A., Ridgeway, M. E., and Park, M. A. (2014). High resolution trapped ion mobility spectrometery of peptides. Anal. Chem. 86, 5624–5627. doi:10.1021/ac501261h

PubMed Abstract | CrossRef Full Text | Google Scholar

Sorribes-Soriano, A., de La Guardia, M., Esteve-Turrillas, F. A., and Armenta, S. (2018). Trace analysis by ion mobility spectrometry: From conventional to smart sample preconcentration methods. a review. Anal. Chim. Acta 1026, 37–50. doi:10.1016/j.aca.2018.03.059

PubMed Abstract | CrossRef Full Text | Google Scholar

St. Louis, R. H., Hill, H. H., and Eiceman, G. A. (1990). Ion mobility spectrometry in analytical chemistry. Crit. Rev. Anal. Chem. 21, 321–355. doi:10.1080/10408349008050848

CrossRef Full Text | Google Scholar

Szumlas, A. W., Ray, S. J., and Hieftje, G. M. (2006). Hadamard transform ion mobility spectrometry. Anal. Chem. 78, 4474–4481. doi:10.1021/ac051743b

PubMed Abstract | CrossRef Full Text | Google Scholar

Tabrizchi, M., and Jazan, E. (2009). Inverse ion mobility spectrometry. Anal. Chem. 82, 746–750. doi:10.1021/ac902009c

PubMed Abstract | CrossRef Full Text | Google Scholar

Watts, P., and Wilders, A. (1992). On the resolution obtainable in practical ion mobility systems. Int. J. mass Spectrom. ion Process. 112, 179–190. doi:10.1016/0168-1176(92)80003-j

CrossRef Full Text | Google Scholar

Wu, C., Siems, W. F., Asbury, G. R., and Hill, H. H. (1998). Electrospray ionization high-resolution ion mobility spectrometry-mass spectrometry. Anal. Chem. 70, 4929–4938. doi:10.1021/ac980414z

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, X., Zhang, Y., Qin, R., Li, P., Wen, Y., Yin, Z., et al. (2021). Discrimination of isomeric monosaccharide derivatives using collision-induced fingerprinting coupled to ion mobility mass spectrometry. Talanta 224, 121901. doi:10.1016/j.talanta.2020.121901

PubMed Abstract | CrossRef Full Text | Google Scholar

Zou, W. B., Yin, L. H., and Jin, S. H. (2018). Advances in rapid drug detection technology. J. Pharm. Biomed. Analysis 147, 81–88. doi:10.1016/j.jpba.2017.08.016

PubMed Abstract | CrossRef Full Text | Google Scholar