- 1Department of Chemistry, Indian Institute of Technology Madras, Chennai, India
- 2Department of Chemistry, Indian Institute of Technology Ropar, Rupnagar, India
Collisional cross-sections of inelastic rotational excitations of CN in its ground electronic state (X2Σ+) by H+ scattering are studied by the exact quantum mechanical close-coupling (CC) method at very low collision energies (0–600 cm−1) relevant to interstellar atmospheres. Ab initio rigid rotor potential energy surface computed at MRCI/cc-pVTZ level of accuracy has been employed. Rate coefficients for the rotational excitations have also been calculated. The obtained results are compared with previous theoretical calculations and analyzed whether proton collisions could be significant sources for rotationally excited CN as a possible source for cosmic microwave background of about 3 K from the interstellar media.
Introduction
As early as 1965, cosmic microwave background radiation (CMBR) measurements were carried out, and an analysis of radio wave intensities revealed that there exists approximately isotropic CMBR corresponding to black body radiation of about 3 K (Penzias and Wilson, 1965; Dicke et al., 1965; Stokes et al., 1967)1. These radiations are considered as remnant radiation occurring due to falling out of the big-bang fireball. The near isotropic nature of CMBR also suggested that the Universe is full of 3 K CMBR (Dicke et al., 1965).
Subsequently, the rotational temperature of interstellar CN molecule was measured (Field and Hitchcock, 1966; Thaddeus and Clauser, 1966) in terms of the population ratio of the first rotationally excited state to the ground rotational state (n1/n0), which was found to be 0.55 ± 0.05. Using
The fact that the rotationally-excited (j’ = 1) CN molecule could be one of the primary sources for the CMBR (of about 3 K) has led to exploring various mechanisms and pathways that lead CN molecules to rotationally excited states. The CN radical has a permanent dipole moment, and therefore one expects it would have a higher probability for rotational excitations with electrons, protons, and ions. It can exist in two regions: 1) neutral hydrogen clouds (H-I region) and 2) ionized-hydrogen clouds (H-II region). In the H-I region, the cloud temperature can increase by several thousand degrees by cloud-cloud collisions, finally decreasing via infrared emissions. Here, the atomic hydrogen does not get ionized. However, minor constituents like Li, Mg, C, Si, Fe, etc., may get ionized liberating electrons through photoionization (Nishimura, 1968). Typically, the number density of these ions is approximated to be Nion = Ne = 1.6 × 10−3 cm−3. Therefore, the rate of collisions of the ions (with CN) is expected to be minimal compared to that of the electron because of the latter’s lighter (thousand times smaller) mass. Another energy source for the H-I cloud can be from the low-energy (in MeV range) component of the cosmic-ray protons. If the flux is appropriate, they can ionize the atomic hydrogen present as the principal constituent in the cloud. In such conditions, the cloud temperature is estimated to be around 100 K (Hayakawa et al., 1961)7 with Ne = Np = 0.03 cm−3.
In the H-II region, the gas exists in a completely ionized form. It gets heated up from lights emitted from stars up to a typical temperature of 104 K. The gas density varies, resulting in high and low-density regions. An estimate of the low density could be around Ne = Np < 0.1 cm−3.
Since the density of H+ is estimated to be an order of magnitude higher in the H-II region, it is appropriate to study the collisional excitation rates with CN molecules. Considering the temperature range of 100–1000 K of the gas in the H-II region, the collision energy (in the center of mass frame, Ec.m) corresponds to 0.01 and 1.0 eV, respectively. Takayanagi and Itikawa (1968) carried out early theoretical calculations of rotational excitation of CN molecule by electron collisions using the close-coupling and the Born-approximation methods at Ec.m = 0.01, 0.1, and 1.0 eV. The interaction potential has been modeled in terms of the dipole, polarization, and short-range electrostatic interactions. Excitations by protons were studied in the classical framework using the trajectory impact parameter method. Later, Jamieson et al. (1975) studied the rotational excitations of CN molecule by proton collisions by impact parameter method using a modified interaction potential used earlier for the e− + CN system (Crawford et al., 1969; Allison and Dalgarno, 1971). This interaction potential was based on dipole and polarization interactions. They obtained approximate solutions for rotational excitations based on Born and the “exponential” approximations, and the obtained integral cross sections were compared with those obtained from the close-coupling method. The calculations were carried out for Ec.m = 0.04—500 eV. Since long-range interactions are present in e−/H+ interactions with CN molecule leading to significant inelastic effects, it was desirable to test the validity of decoupling approximations of angular momenta to carry out efficient and reliable calculations. Subsequently, DePristo and Alexander (DePristo and Alexander, 1976) investigated decoupling approximations of angular momenta, namely decoupled l—dominant (DLD) method (DePristo and Alexander, 1975) using the model interaction potential. Various theoretical aspects were discussed, and cross-sections for rotational excitations were calculated at Ec.m = 0.04, 0.1 and 1.0 eV with dipole moments of CN, μ = 1.1 D and 1.45 D.
Potential Energy Surface
The bound HCN+ ion has a collinear geometry. There are two energetically low-lying electronic states in the collinear geometry: 12Σ+ and 12Π. Asymptotically, The former correlates to the inelastic channel, H+ + CN(X2Σ+), and the latter to charge transfer channel, H (2S) + CN+ (2Σ+). The computed energy for the asymptotic charge transfer channel is 0.278 eV higher than that of the inelastic channel. Around the equilibrium geometry and the Franck-Condon region, the 12Π state is lower in energy, and the computed energy difference between the 12Π and the 12∑ states is 0.979 eV (Anusuri and Kumar, 2016). For the off-collinear geometry, the 12Π state splits into the 2A′ and 2A″ states. The 2Σ+ state correlates to the 2A’ state. The nondegenerate states’ potential energy surfaces (PES) interact in the vicinity of collinear geometry with off-collinear distortions. Thus, the bound HCN+ constitutes a Renner-Teller system (see, KÖppel et al., 1979; Perić et al., 1983; and references therein), exhibiting strong vibronic interactions between the ground 2Π and the first excited 2Σ+states. The existence of Renner-Teller coupling complicates the assignment of vibrational progressions. For a brief account of the vibrational progression studies, see reference (Anusuri and Kumar, 2016) and the references therein.
For the scattering studies involving the inelastic channel, H+ + CN(X2Σ+), it is crucial to examine the (nonadiabatic) involvement of the 12Π state, which correlates to the endoergic charge transfer channel, H (2S) + CN+ (3Π). Since only the inelastic rotational excitations of the CN molecules upon collisions of H+ are studied, the potential energy surface is generated in the Jacobi scattering coordinates (Figure 1): r is the interatomic distance of the diatom BC (CN), R is the distance of H+ from the center of mass of BC (CN), and γ = cos−1 (R.r) is the angle between R and r. H+ approaching C-end is considered as γ = 0° and N-end as γ = 180°. Our earlier study (Anusuri and Kumar, 2016) found that the potential energy curve of 12Π state crosses with that of the 12Σ+ state around R = 5ao in the collinear geometry. For off-collinear geometry, the energy order is
Calculations were carried out in the C2υ symmetry for collinear geometries and the Cs symmetry for off-collinear geometries. The ground state RR surface was computed for the 12Σ+/12A′ symmetry for the collinear/off-collinear approaches. Computations were done at internally contracted multi-reference configuration interaction (Knowles and Werner, 1988; Werner and Knowles, 1988; Knowles and Werner, 1992) level of accuracy with Dunning’s (Dunning, 1989) cc-pVTZ basis set using MOLPRO 2010.1 (Werner et al., 2010) suite of programs. A total of 780 geometries were computed with r fixed at req = 2.23 ao: γ = 0°–180° (15°); R = 0.8–1.8 (0.2), 1.9–4.0 (0.1), 4.2–7.0 (0.2), 7.5–10.0 (0.5), 11.0–15.0 (1.0). R is in atomic units, and the numbers in the parentheses indicate the step size in the interval.
The computed basis set superposition error (BSSE) was small and varied systematically in the range 0.04–0.01 eV for R 3.0 ao to 5.0 ao, and falls off rapidly and becomes negligible (less than 10−4 eV) for R > 5.0 ao. R = 3.0 ao approximately signifies the bottom of the interaction well. We believe that the BSSE correction will still have a very small correction on the computed cross sections and rates, and therefore, we did not include them. The effect of the augmented basis set was also very small as interaction potential values varied on the second decimal places in eV. We believe that the potential energy surface generated using the cc-pVTZ basis set is sufficiently accurate for the scattering calculations.
The contour plot of the rigid-rotor surface is shown in Figure 2. To study the dynamics, we need the long-range asymptotic interaction potential up to large R values where the interaction potential dies down. For large values of R, the interaction potential is generally expanded in multipolar terms. Here, the charge on H+ interacts with the dipole, quadrupole, and polarizability components of CN, and the asymptotic interaction potential
where μ (−1.362 D) is the dipole moment, Q (0.368
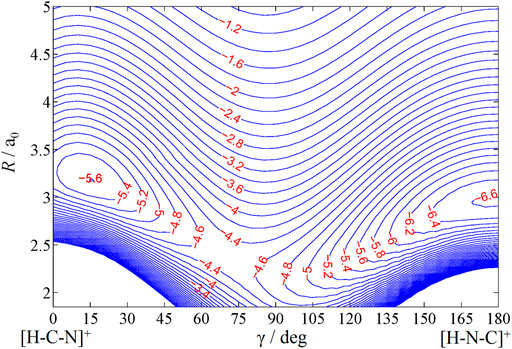
FIGURE 2. Contour plot of rigid-rotor PES of HCN+ (12Σ+/
Multipolar Expansion
The rigid-rotor interaction potential has been fitted to the following analytic expression:
where Vλ’s are expansion coefficients with λ varying from 0 to 12 (number of γ values) and Pλ’s are Legendre polynomials.
Vλ were numerically obtained at the computed grid points using the Legendre polynomials’ orthogonality. Once their dependence on grid points of R is known, each Vλ was fitted with a cubic spline fit. The interaction anisotropy can be examined in terms of Vλ’s plotted as a function of R and shown in Figure 3. V0, which gives spherically averaged interaction potential, exhibits a deep well and extends its strength beyond R = 10.0 a0 in long-range interactions given in charge-multipole interactions. Interestingly, V1, V3, and V4 components are very small throughout R, and they are repulsive and show their strength only at closer approaches. Next to V0, V2 only shows an interaction well. Therefore, it suggests that rotational excitations at low collision energies will be governed by only a few low Vλ’s.
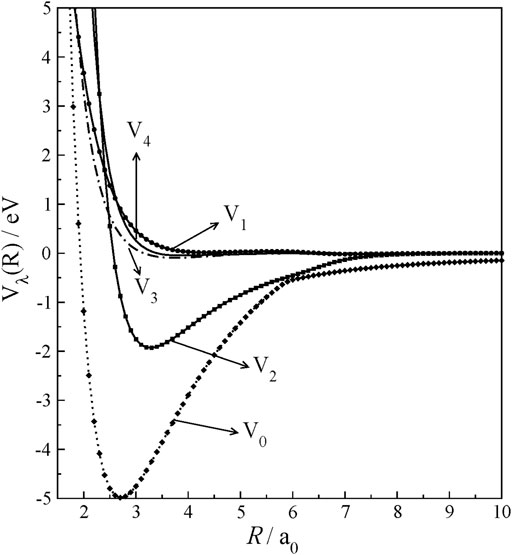
FIGURE 3. Radial multipolar expansion coefficients of HCN+ rigid-rotor potential as a function of R at r = req.
Scattering Calculations
The molecular energy levels in CN (X 2Σ+) are described by Hund’s case 2) limit. The theoretical framework for the scattering of a molecule in 2Σ+ electronic state was given by Alexander (Alexander, 1982). The rotational fine structure levels in the CN molecule here are labeled by the quantum numbers j and J. j is the rotational angular momentum, whereas J is the total angular momentum. J is given by J = j + s where s is the electronic spin angular momentum. For CN molecule in 2Σ+ electronic state, the J levels will be J = j + ½ (labeled as e) and J = j—½ (labeled as f).
Full close-coupling calculations have been carried in very low collision energy range of 0–600 cm−1 for rotational excitations from j = 0 to j' = one to four levels. Time-independent coupled scattering equations (Arthurs and Dalgarno, 1960) have been solved to compute cross-sections implemented in the HIBRIDON package (Alexander et al., 2011). The close-coupled radial equations were numerically integrated using the log derivative propagator (Manolopoulos, 1986). The following input parameters are taken in the calculation: rotational constant, Be = 1.89102 cm−1, D0 (centrifugal distortion constant) = 6.4 × 10−6 cm−1, spin-splitting constant γ0 = 7.2549 × 10−3 cm−1 (Huber and Herzberg, 1979) and reduced mass of the system, μ = 0.970,404 a.u. with values of Rmin and Rmax as 1.4 and 200 a0, respectively with ΔR = 0.1 a0. The value of CN bond length is fixed at 2.23 a0 (rigid-rotor approximation). The main focus of the present study is to have the first meaningful yet reliable estimates of the cross sections for rotational excitation for j = 0 - j′ = 1, using the full quantum calculations in vibrational manifold v = 0. Therefore, rigid-rotor calculations would capture the collision dynamics since there would hardly be any centrifugal distortions in the CN bond the small rotational excitation(s). The cross sections are computed for energies up to 600 cm−1. At least three energetically closed rotational channels were included in the calculations at a particular Ec.m to ensure numerical convergence of cross section within the acceptable limit (up to third decimal place). Maximum value of rotational quantum number taken is jmax = 18 at Ec.m = 600 cm−1. Also, the convergence of cross-sections is achieved through a sufficient number of partial waves; for instance, at Ec.m = 500 cm−1, l (total angular momentum) is kept at 580. The CC calculations have been performed from an energy value corresponding to the opening of the lowest inelastic channel to a total energy of 600 cm−1.
Integral Cross-Sections
The integral cross-sections for rotationally inelastic excitations obtained from the full close-coupling calculations in the energy range (5–600 cm−1) are shown as a function of Ec.m for excitations from the ground (j = 0, J = 1/2) rotational level to higher rotational levels for ΔJ = Δj transitions and ΔJ ≠ Δj transitions in Figure 4 and Figure 5, respectively. The rotational excitations are plotted for j = 0 → j' = one to four levels. In the case of j = 0 to j' = 1 transition, the cross sections oscillate at low energies for both ΔJ = Δj as well as for ΔJ ≠ Δj. The cross section for ΔJ = Δj from the energetic threshold rises to a maximum and shows a large decreasing plateau with increasing collision energy. For ΔJ ≠ Δj the cross sections show a monotonic increasing behavior with an increase in Ec.m. Near the threshold, all the cross sections show oscillatory behavior presumably due to the formation of scattering resonances. We have also observed a propensity for ΔJ = Δj transitions compared to that of ΔJ ≠ Δj transitions, which is a common feature in the scattering of molecules in 2S+1Σ electronic state (Alexander et al., 1986). This propensity is reported in He-CN scattering also (Lique et al., 2010).
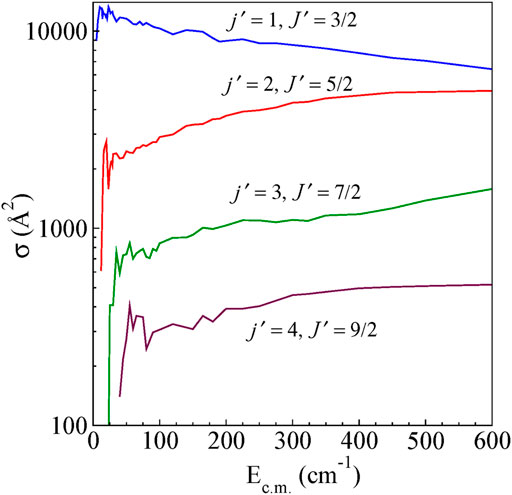
FIGURE 4. State-to-state integral cross sections for rotational excitations for ΔJ = Δj transitions from the initial level j = 0 and J = ½ for H+ + CN (j = 0, J = ½) → H+ + CN (j′, J′).
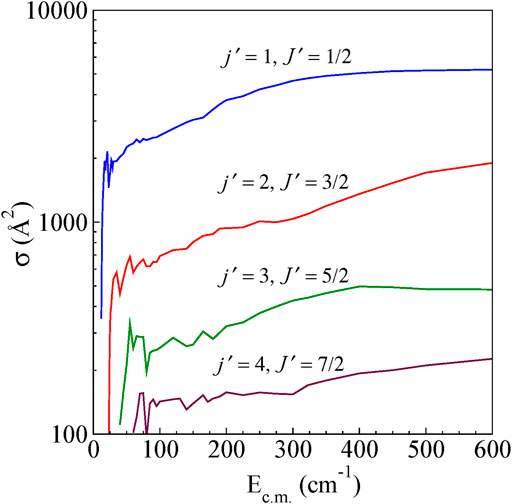
FIGURE 5. State-to-state integral cross sections for rotational excitations for ΔJ ≠ Δj transitions from the initial level j = 0 and J = ½ for H+ + CN (j = 0, J = ½) → H+ + CN (j′,J′).
The total state-to-state (j´) cross sections were obtained by summing the cross sections for the ΔJ = Δj and ΔJ ≠ Δj transitions. The computed integral cross sections for 0 → 1 and 0 → 2 are compared in Table 1 and earlier theoretical estimates. The earlier theoretical values were reported in units of cm2. Therefore, we also report our values in the same units for better comparison and convenience.
The cross sections are compared at three collision energies, Ec.m = 0.04, 0.06 and 0.08 eV. The 0 → 1 cross sections compare reasonably well with the previous calculations for these energies. The cross sections for 0 → 2 excitations are approximately two orders of magnitude less than that of 0 → 1 excitations. The present calculations yield consistently higher magnitudes for 0 → 2 excitations than those obtained in earlier calculations. The 0 → 1 cross sections are mostly governed by long-range effects (Harrison et al., 2012). Since the long-range interaction potential description is similar for the earlier and the present studies, there is an overall good agreement. But the direct 0 → 2 transitions are governed by the V2 multipolar term, the next strongest term after the V0 term in the interaction potential expansion.
Rate Coefficients
The computed rotational cross-sections are used to calculate rate-coefficient as a function of temperature:
where kB is the Boltzmann constant, μ is the reduced mass of the system, and E = Ec.m. The state-to-state rate coefficients for rotational transitions over a range of temperatures computed for both ΔJ = Δj and ΔJ ≠ Δj, up to T = 600 K, are shown in Figure 6 and Figure 7, respectively.
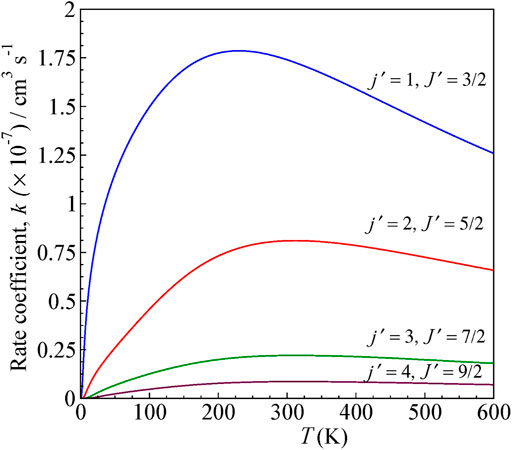
FIGURE 6. State-to-state rate as a function of temperature for 0–600 K computed for ΔJ = Δj transitions from the initial level j = 0 and J = ½ for H+ + CN (j = 0, J = ½) → H+ + CN (j', J′).
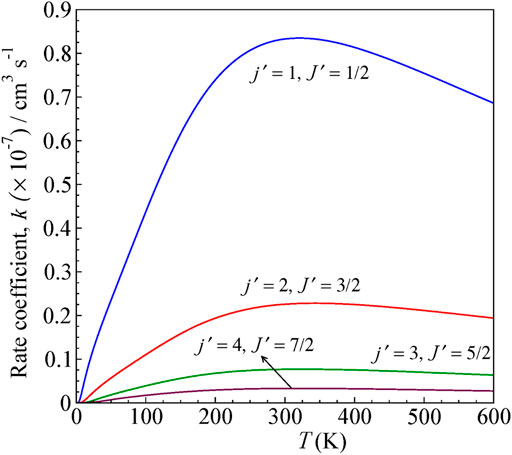
FIGURE 7. State-to-state rate as a function of temperature for 0–600 K computed for ΔJ ≠ Δj transitions from the initial level j = 0 and J = ½ for H+ + CN (j = 0, J = ½) → H+ + CN (j',J′).
The rates are higher for j = 0 → j′ = 1 transition, similar to cross sections, and decreases for other higher excitations. The rate coefficients are calculated by averaging the obtained cross section over a Boltzmann distribution of kinetic energy.
The rate coefficient for j = 0 to j′ = 1 excitation in CN by proton scattering was estimated to be about the order of 10−7 cm3 s−1 by Jamieson et al., 1975 at 80 K, which is the temperature of interstellar clouds. It is lower by a factor of ten compared to that obtained from the electron scattering calculations with CN. In our present calculation, we obtained a rate coefficient of 1.74 × 10−7 cm3 s−1.
Summary and Conclusions
Ab initio rigid-rotor PES obtained at MRCI/cc-pVTZ level of theory has been employed to study the inelastic rotational excitations in CN by H+ scattering. The ground electronic state PES asymptotically correlates to H+ (1S) + CN (2Σ+) for H+ + CN system. The contour plot of [HCN]+ shows deeper interaction wells corresponding to two collinear configurations. The long-range interaction potential is obtained in charge–dipole, -quadrupole, and polarizability interactions. The potential anisotropy of the system has been analyzed in terms of radial multipolar expansion. The rotational transitions are studied on the PES for low collision energies between 0—600 cm−1 by solving close-coupled equations. The cross-sections are calculated for inelastic rotational transitions for J = 0 → J' = 1-4 one to four using close-coupling method.
The rate coefficients in the temperature range 0–600 K have been calculated. The rate coefficients for j = 0 → j’ = 1 transition in H+ scattering of CN is found to be of the order of 10−7 cm3 s−1. It is an order of magnitude less than that of electron scattering at the average temperature of interstellar clouds (∼80 K). In clouds of the H-II region where H+ density could be relatively larger (>> 0.1 cm−3) H+ collision could lead to 0 → 1 rotational excitation of CN, which could become comparable to that obtained in collision with electrons.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
BA carried out the major computational work and analysis. He also prepared the first draft of the manuscript. TD was also involved in part for both computations and analysis. SK contributed to the conception and draft revisions. All authors contributed to manuscript revision, read and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
BA thanks IIT Madras and UGC, New Delhi, for fellowship. The calculations were performed using a high-power computing environment (HPCE) at IIT Madras.
Footnotes
1Dedicated to Professor Saurav Pal, Director, IISER Kolkata, India.
References
Alexander, M. H., Manolopoulos, D., Werner, H. J., Follmeg, B., Vohralik, P. F., Lemoine, D., et al. (2011). HIBRIDON (Version 4.3.7) Is a Package of Programs for the Time-independent Quantum Treatment of Inelastic Collisions and Photodissociation. Available at: http://www2.chem.umd.edu/groups/alexander/hibridon/hib43/hibhelp.html.
Alexander, M. H. (1982). Rotationally Inelastic Collisions between a Diatomic Molecule in a 2Σ+ Electronic State and a Structureless Target. J. Chem. Phys. 76, 3637–3645. doi:10.1063/1.443401
Alexander, M. H., Smedley, J. E., and Corey, G. C. (1986). On the Physical Origin of Propensity Rules in Collisions Involving Molecules In2Σ Electronic States. J. Chem. Phys. 84, 3049–3058. doi:10.1063/1.450286
Allison, A. C., and Dalgarno, A. (1971). Rotational Excitation of CN by Electron Impact. Astron.&Astrophys. 13, 331–332. Available at: https://ui.adsabs.harvard.edu/abs/1971A%26A.13.331A/abstract.
Anusuri, B., and Kumar, S. (2016). Ab Initio adiabatic and Quasidiabatic Potential Energy Surfaces of H++ CN System. J. Chem. Sci. 128, 287–296. doi:10.1007/s12039-015-1022-8
Arthurs, A. M., and Dalgarno, A. (1960). The Theory of Scattering by a Rigid Rotator. Proc. R. Soc. Lond. A. 256, 540–551. doi:10.1098/rspa.1960.0125
Crawford, O. H., Allison, A. C., and Dalgarno, A. (1969). Electron Impact Excitation of CN. Astron. Astrophys. 2, 451–452.
DePristo, A. E., and Alexander, M. H. (1975). Anl‐dominant Simplification of the Close‐coupled Equations for Collisions between Atoms and Diatomic Molecules. J. Chem. Phys. 63, 3552–3559. doi:10.1063/1.431794
DePristo, A. E., and Alexander, M. H. (1976). Decoupling Approximations for Rotationally Inelastic Collisions between Ions and Polar Molecules: H+-CN. J. Phys. B: Mol. Phys. 9, 2713–2721. doi:10.1088/0022-3700/9/15/020
Dicke, R. H., Peebles, P. J. E., Roll, P. G., and Wilkinson, D. T. (1965). Cosmic Black-Body Radiation. ApJ 142, 414–419. doi:10.1086/148306
Dunning, T. H. (1989). Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms boron through Neon and Hydrogen. J. Chem. Phys. 90, 1007–1023. doi:10.1063/1.456153
Field, G. B., and Hitchcock, J. L. (1966). The Radiation Temperature of Space at λ 2.6 MM and the Excitation of Interstellar CN. ApJ 146, 1–6. doi:10.1086/148853
Harrison, S., Tennyson, J., and Faure, A. (2012). Calculated Electron Impact Spin-Coupled Rotational Cross-Sections for2S+ 1Σ+linear Molecules: CN as an Example. J. Phys. B: Mol. Opt. Phys. 45, 175202–175209. doi:10.1088/0953-4075/45/17/175202
Hayakawa, S., Nishimura, S., and Takayanagi, T. (1961). Radiation from the Interstellar Hydrogen Atoms. Pub. Astro. Soc. Jpn. 13, 184–206. Available at: https://ui.adsabs.harvard.edu/abs/1961PASJ.13.184H/abstract.
Jamieson, M. J., Kalaghan, P. M., and Dalgarno, A. (1975). Rotational Excitation of CN Molecules by Proton Impact. J. Phys. B: Mol. Phys. 8, 2140–2148. doi:10.1088/0022-3700/8/12/025
Knowles, P. J., and Werner, H.-J. (1988). An Efficient Method for the Evaluation of Coupling Coefficients in Configuration Interaction Calculations. Chem. Phys. Lett. 145, 514–522. doi:10.1016/0009-2614(88)87412-8
Knowles, P. J., and Werner, H.-J. (1992). Internally Contracted Multiconfiguration-Reference Configuration Interaction Calculations for Excited States. Theoret. Chim. Acta 84, 95–103. doi:10.1007/BF01117405
Köppel, H., Cederbaum, L. S., Domcke, W., and von Niessen, W. (1979). Vibronic Coupling in Linear Molecules and Linear-To-Bent Transitions: HCN. Chem. Phys. 37, 303–317. doi:10.1016/0301-0104(79)85031-4
Lique, F., Spielfiedel, A., Feautrier, N., Schneider, I. F., Kłos, J., and Alexander, M. H. (2010). Rotational Excitation of CN(X Σ2+) by He: Theory and Comparison with Experiments. J. Chem. Phys. 132, 024303–024308. doi:10.1063/1.3285811
Manolopoulos, D. E. (1986). An Improved Log Derivative Method for Inelastic Scattering. J. Chem. Phys. 85, 6425–6429. doi:10.1063/1.451472
Nishimura, S. (1968). Cooling of Interstellar Clouds of Neutral Hydrogen and the Abundance of Molecular Hydrogen. Pub. Astro. Soc. Jpn. 20, 239–253. Available at: https://ui.adsabs.harvard.edu/abs/1968PASJ.20.239N/abstract.
Penzias, A. A., and Wilson, R. W. (1965). A Measurement of Excess Antenna Temperature at 4080 Mc/s. ApJ 142, 419–421. doi:10.1086/148307
Perić, M., Mladenović, M., Peyerimhoff, S. D., and Buenker, R. J. (1983). Ab Initio study of the Isomerization HNC → HCN. I. Ab Initio Calculation of the HNC ⇌ HCN Potential Surface and the Corresponding Energy Levels. Chem. Phys. 82, 317–336. doi:10.1016/0301-0104(83)85237-9
Stokes, R. A., Partridge, R. B., and Wilkinson, D. T. (1967). New Measurements of the Cosmic Microwave Background at λ=3.2cm and λ=1.58cm-Evidence in Support of a Blackbody Spectrum. Phys. Rev. Lett. 19, 1199–1202. doi:10.1103/physrevlett.19.1199
Takayanagi, K., and Itikawa, Y. (1968). Rotational Excitation of the Interstellar CN Molecule. Pub. Astro. Soc. Jpn. 20, 376–384. Available at: https://ui.adsabs.harvard.edu/abs/1968PASJ.20.376T/abstract.
Thaddeus, P., and Clauser, J. F. (1966). Cosmic Microwave Radiation at 2.63 Mm from Observations of Interstellar CN. Phys. Rev. Lett. 16, 819–822. doi:10.1103/physrevlett.16.819
Werner, H. J., and Knowles, P. J. (1988). An Efficient Internally Contracted Multiconfiguration-Reference Configuration Interaction Method. J. Chem. Phys. 89, 5803–5814. doi:10.1063/1.455556
Keywords: Proton-CN, collisions, quantum calculations, rotational excitations, cross sections, interstellar medium
Citation: Anusuri B, Dhilip Kumar TJ and Kumar S (2021) Quantum Dynamics of Rotational Transitions in CN (X 2Σ+) by H+ Collisions. Front. Chem. 9:790416. doi: 10.3389/fchem.2021.790416
Received: 06 October 2021; Accepted: 08 November 2021;
Published: 25 November 2021.
Edited by:
Sailaja Krishnamurty, National Chemical Laboratory (CSIR), IndiaReviewed by:
Riccardo Conte, University of Milan, ItalyTomás González-Lezana, Consejo Superior de Investigaciones Científicas (CSIC), Spain
Copyright © 2021 Anusuri, Dhilip Kumar and Kumar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sanjay Kumar, c2FuamF5QGlpdG0uYWMuaW4=
 Bhargava Anusuri
Bhargava Anusuri T. J. Dhilip Kumar
T. J. Dhilip Kumar Sanjay Kumar
Sanjay Kumar
