- 1Engineering and Technology Center, The Fourth Medical College of Harbin Medical University, Harbin, China
- 2Changchun Institute of Technology, Changchun, China
- 3Nanoscience and Engineering and Technology Electrophysiology Research Center, The Fourth Medical College of Harbin Medical University, Harbin, China
Searching for existing topological materials is a hot topic in quantum and computational chemistry. This study uncovers P63/mmc type TiTe compound—an existing material—is a newly discovered topological metal that hosts the various type of nodal line states. Different nodal line states normally exhibit different properties; they may have their individual applications. We report that TiTe hosts I, II, and hybrid type nodal line (NL) states at its ground state without chemical doping and strain engineering effects. Specifically, two type I NLs, two hybrid-type NLs, and one Γ—centered type II NL can be found in the kz = 0 plane. Moreover, the spin-orbit coupling induced gaps for these NLs are very small and within acceptable limits. The surface states of the TiTe (001) plane were determined to provide strong evidence for the appearance of the three types of NLs in TiTe. We also provide a reference for the data of the dynamic and mechanical properties of TiTe. We expect that the proposed NL states in TiTe can be obtained in future experiments.
Introduction
Searching for topological materials in realistic materials in quantum and computational chemistry is a hot research topic. Topological materials (TMs) (Cava et al., 2013; Kong and Cui, 2011; Xu et al., 2015; Strambini et al., 2016; Wang et al., 2017; Banik et al., 2018; Kageyama et al., 2018; Schoop et al., 2018; Culcer et al., 2020; Kumar et al., 2020; Li and Xia, 2020; Xu et al., 2020) enjoy nontrivial band-crossings (BCs) in their low-energy region, giving rise to novel fermionic excitations. A series of TMs, including nodal-point (Alcón et al., 2017; Fu et al., 2018a; Kong et al., 2018; Jin et al., 2019a; Jin et al., 2019b; Wang et al., 2019; Fang et al., 2020; Zhang et al., 2020), nodal-line (Chen et al., 2018; Zhou et al., 2018; Li et al., 2019; Liu et al., 2019; Sankar et al., 2019; Tang et al., 2019; Xu et al., 2019; Yi et al., 2019; Wang et al., 2020a; Zhao et al., 2020), and nodal-surface (Wu et al., 2018; Qie et al., 2019; Wang et al., 2020b) materials, have been predicted via symmetry and first-principle analysis. Some of them have been verified via experiment.
Recently, many chemists and physicists have focused on studying the nodal line (NL) type materials. The NL-type materials are very important because they can enjoy more sub-types than other types of topological materials; moreover, different sub-types generally have their physical behaviors. Many NL materials with different NL shapes have been proposed, including nodal ring (Zhang et al., 2018a), nodal chain (Bzdušek et al., 2016), nodal link (Yan et al., 2017), nodal knot (Bi et al., 2017; Ezawa, 2017), and nodal net materials (Wang et al., 2018a; Fu et al., 2018b; Feng et al., 2018). Different shapes of the NLs usually exhibit different electronic and optical behaviors. Moreover, NLs can normally be classified into the I, II, and hybrid types (Jin et al., 2020) according to the slope of the bands around the band-crossing points (BCPs).
The I type NL is composed of all the type I BCPs, and the II type NL is formed by the type II BCPs. However, the hybrid-type NL contains I and II type NLs simultaneously. The illustration of I and II type BCPs are shown in Figures 1A,B, respectively. The I type BCPs show a traditional conical dispersion, whereas the II type BCPs show a titled dispersion.
A series of materials (Wang et al., 2018b; Wang et al., 2020c; Jin et al., 2020), type I or II NLs, have been studied via symmetry analysis and first-principles calculations. However, materials with I and II type NLs have rarely been explored in the literature. It is fascinating to investigate if I, II, and hybrid NLs can coexist in one material without strain, chemical doping, or other controlling methods.
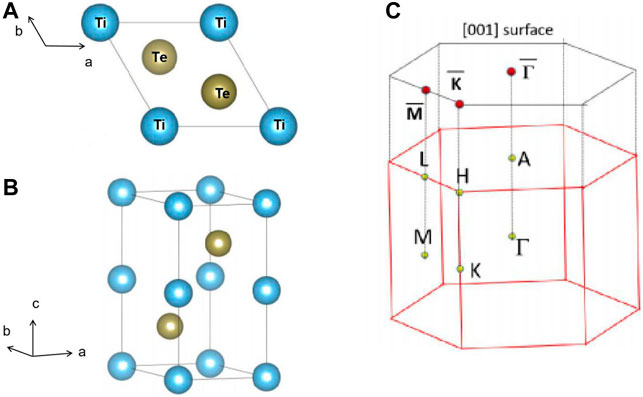
In this work, we select P63/mmc type TiTe material as an example and to show that the I, II, and hybrid types of NLs can coexist in realistic TiTe material (Ehrlish, 1949). The TiTe has already been realized in the experiment. We show that I, II, and hybrid NLs can be found in the kz = 0 plane of TiTe. The structural model of hexagonal P63/mmc type TiTe with a primitive cell is exhibited in Figures 2A,B under different view sides. TiTe contains two Ti and two Te atoms, located at the (0 0 0)/(0, 0, 0.5) sites and the (1/3, 2/3, 0.25)/(2/3, 1/3, 0.75) sites, respectively. We optimized the lattice constants and the atomic positions based on the first-principle calculation. The obtained lattice constants of TiTe were a = b = 3.66 Å and c = 7.27 Å, agreeing well with the calculated values in the database1.
This study reports the band structures, phonon dispersions, and topological signatures of TiTe. We uncover that TiTe is an NL metal with one pair of type I NLs, one type II NL, and one pair of hybrid NLs in the kz = 0 plane. We also examine the influence of spin-orbit coupling (SOC) on the band structures. Finally, we calculate the projected spectrum on the (001) surface of TiTe show the occurrence of drum-head-like surface states connected to the BCPs. More details about the computational methods can be found in Supplementary Material.
Dynamical Stability and Mechanical Stability
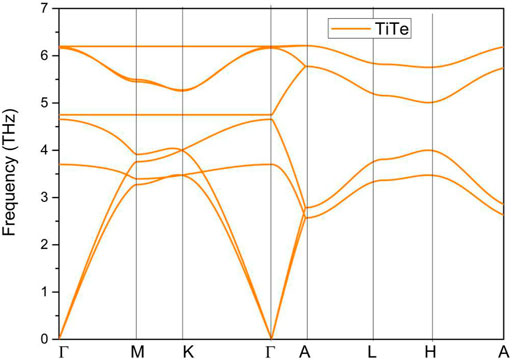
In this section, we present the study of the stabilities of TiTe with respect to dynamical and mechanical properties. Based on the bulk Brillouin zone and the selected symmetry points in Figure 2C. The phonon dispersion of TiTe was calculated through the force-constants method; the result is given in Figure 3. We conclude that the TiTe is dynamically stable because its phonon dispersion does not include imaginary frequencies.
Subsequently, the mechanical stability of TiTe is examined according to elastic stability criteria. TiTe has a P63/mmc structure with five elastic constants—C11, C12, C13, C33, C44, and C66. The computed values of C11, C12, C13, C33, C44, and C66 were 133.543, 47.021, 78.611, 173.304, 43.206, and 107.550 GPa, respectively. We conclude based on the obtained elastic constants that they meet the criteria for elastic stability, as mentioned below:
i) C11 > |C12|;
ii) 2 ×
iii) C44 > 0.
Hence, TiTe is mechanically stable theoretically.
Electronic Structures and Topological Signatures of Bulk TiTe
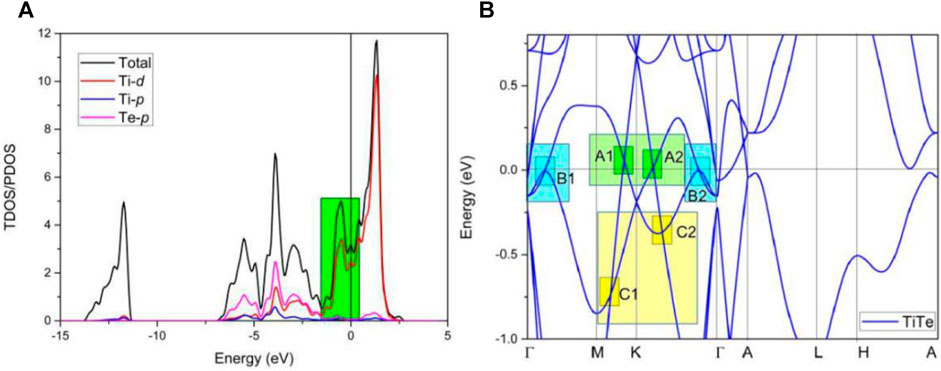
Figure 4A shows the calculated total and projected density of states (DOSs). We conclude that a small peak appears at the Fermi level (EF). Therefore, TiTe is a metallic material. The band structure of the TiTe metal is given in Figure 4B. We primarily focus on the bands closed to the EF. We observe that the Ti-d orbitals dominate the total DOSs in this region (-2 to 1 eV), as shown in Figure 4A with a green background. However, within the −5 to −2 eV energy range, the dominating factors contributing to the total DOSs are the Ti-d and Te-p orbitals. There exists a strong hybrid phenomenon between the Ti-d and Te-p orbitals in this energy range.
We show the band structure of the TiTe in Figure 4B ignoring the SOC. The band structure shows a series of BCPs above and below the EF. For clarity, we divided these BCPs into region A, region B, and region C, respectively. A, B, and C regions are marked by different colors. Two obvious BCPs—A1 and A2—located above the EF can be found in region A. Two BCPs—B1 and B2—located very close to and below the EF appear in region B. There are also two BCPs—C1 and C2—in region C. However, they are slightly further away from the EF than the other BCPs—A1, A2, B1, and B2.
Different types of BCPs are discussed in regions A, B, and C. The two BCPs in region A are I type nodal points (NPs). Weng et al. (Weng et al., 2015) stated that these doubly degenerated crossing points (A1 and A2) are not isolated points; they should belong to a line. We conclude based on the plotted Brillouin zone of 3D bulk TiTe in Figure 2C that the A1 and A2 NPs are located in the kz = 0 plane.
We show the K-centered 3D plotting of the band dispersion in region A of the kz = 0 plane in Figure 5A to demonstrate that the A1 and A2 NPs reside on an NL. We conclude that the energy variation of the NL in region A is very small. Such a flat NL is expected to host novel behaviors. Figures 5A,B show the highlighted NL (see the white dotted line) and the shape of the NL in region A, respectively. We conclude that the NL in region A is a type I. Furthermore, the NLs in region A are protected by two independent mechanisms: i) mirror symmetry and ii) inversion symmetry and time-reversal symmetry. TiTe possesses time-reversal symmetry; therefore, one more K′-centered NL should appear in the kz = 0 plane. The shape of one of the pairs of NLs, i.e., the K and K′ centered NLs, is shown in Figure 5C.
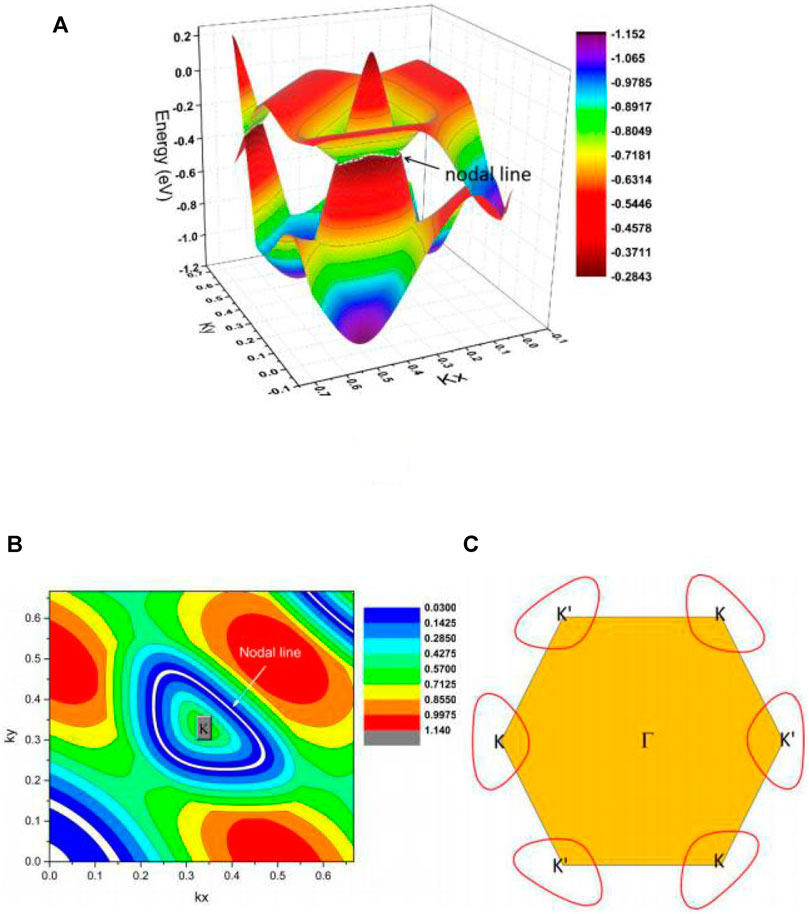
FIGURE 5. (A) 3D band dispersion in region A of the kz = 0 plane; (B) the shape of the NL in region A of the kz = 0 plane; and (C) illustration of one pair of type I NLs in the kz = 0 plane.
In region B, two type II NPs, B1 and B2, also belong to a single NL and the
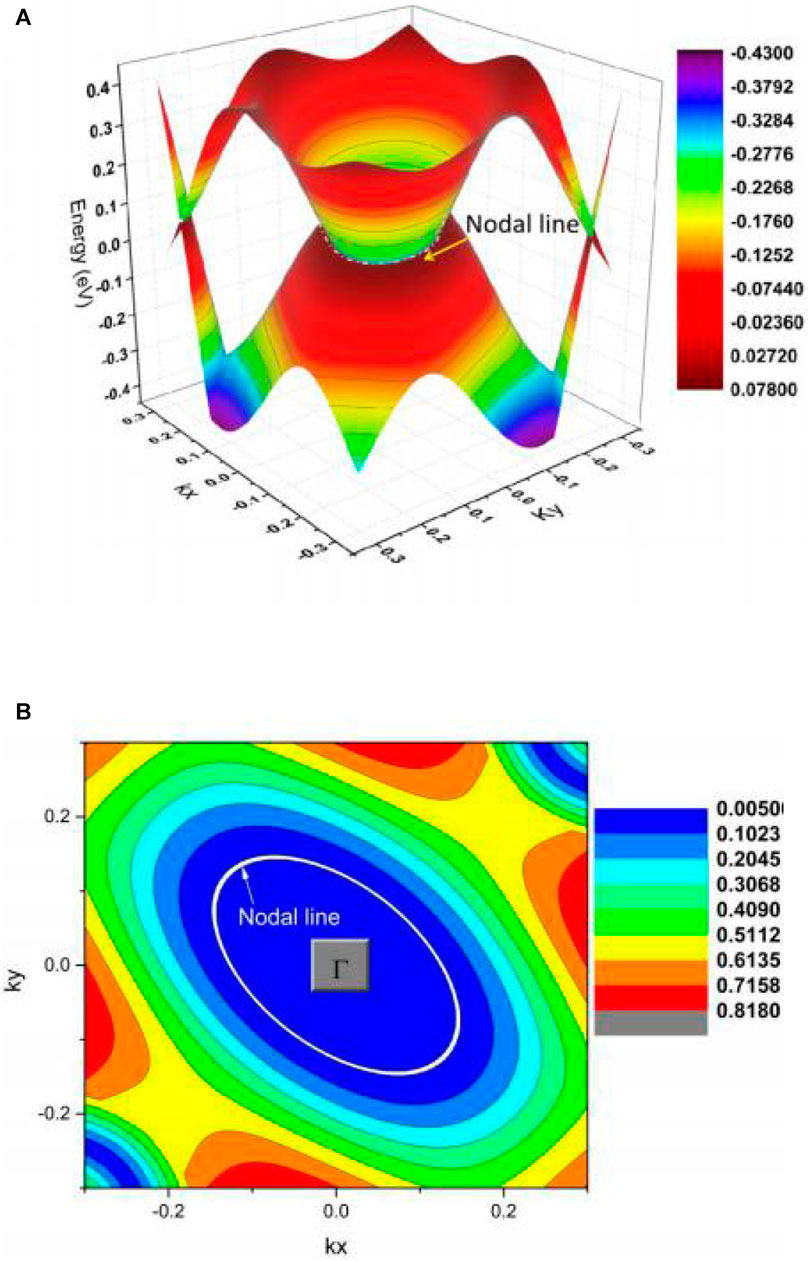
FIGURE 6. (A) Γ-centered 3D band dispersion in region B of the kz = 0 plane and (B) shape of the NL in region B of the kz = 0 plane.
Finally, the K-centered 3D band dispersion in region C of the kz = 0 plane and the shape of the NL in region C are exhibited in Figures 7A–C to determine the topological signatures of the C1 and C2 NPs in region C. We conclude from the different viewpoints of the K-centered 3-D band dispersion that the energy variation of the NL is significantly large (from −0.8 to −0.3 eV). The reason for such a large energy variation is because it is a hybrid NL (Zhang et al., 2018b), containing type I and type II NPs at the same time. Figure 4C shows that BCP C1 is a type I; however, BCP C2 is type II. Moreover, another K′-centered hybrid NL should be located in the kz = 0 plane as required by the time-reversal symmetry (Figure 7D).
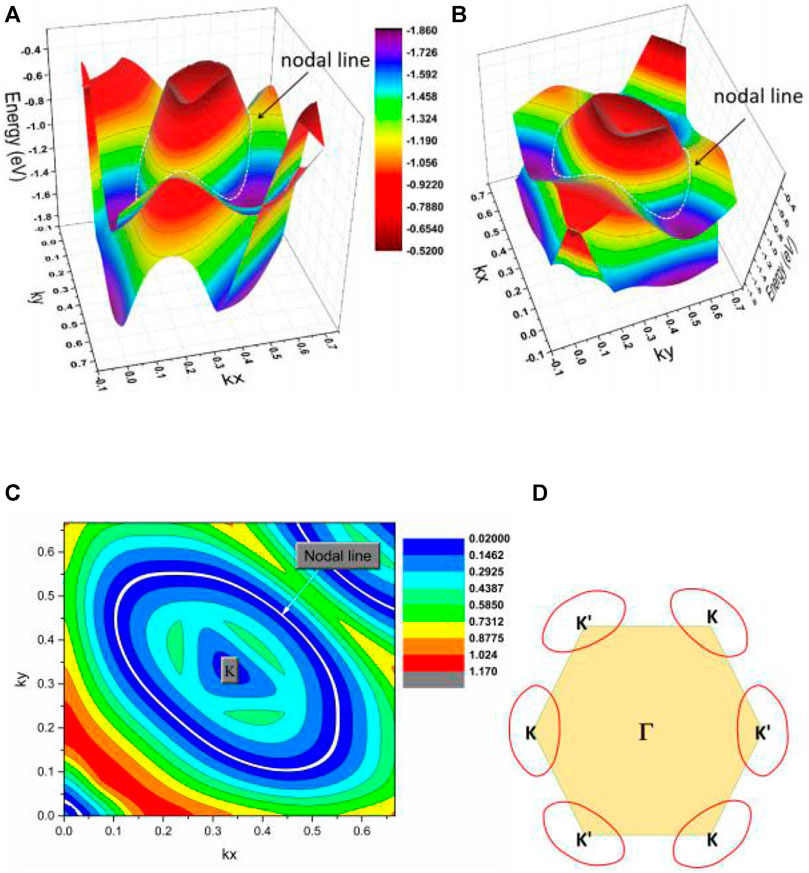
FIGURE 7. (A,B) K-centered 3D band dispersion in region C of the kz = 0 plane from different viewpoints. (C) The shape of the NL in region C of the kz = 0 plane. (D) Illustration of one pair of hybrid type NLs in the kz = 0 plane.
Projected Spectrum on the TiTe (001) Surface
In this section, we provide strong evidence for the appearance of the NLs in the three regions. NL materials usually host drum-head-like (D-H-L) surface states (Wang et al., 2020d) connected to the ban-crossing points, one of its most important characters. Figures 8A,B show the projected spectrum on the TiTe (001) surface. We use the black circles to indicate the positions of the BCPs. The D-H-L surface states, connected to the BCPs and marked by arrows, can be observed. Such obvious D-H-L surface states in TiTe benefit the experimental detection. It is expected that angle-resolved optical emission spectroscopy (ARPES) can be used to detect the D-H-L surface states in TiTe directly.
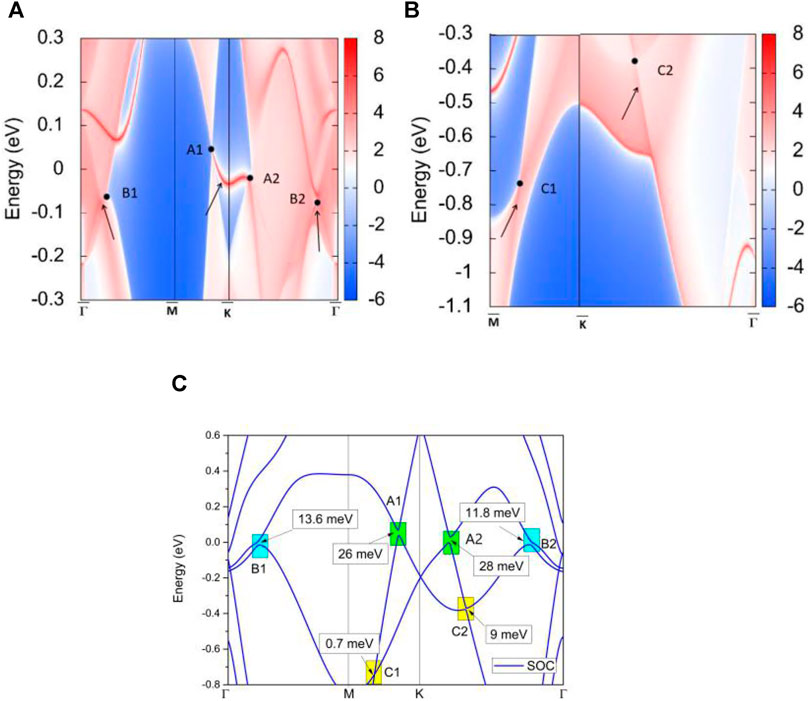
FIGURE 8. (A,B) The projected spectrum on the (001) surface of TiTe. The BCPs—A1, A2, B1, B2, C1, and C2—and the drum-head-like surface states are highlighted by the circles and arrows, respectively. (C) The band structure of TiTe under spin-orbit coupling.
Effect of SOC
The SOC usually induces a gap in the BCPs in most NL materials. The SOC-induced gap is particularly very large (50–200 meV) when the material contains heavy elements (Huang et al., 2016; Yamakage et al., 2016; Wang et al., 2020e), which significantly damages the intrinsic electronic properties of the NLs. Figure 8C shows the band structure with SOC. Therefore, we conclude that the SOC-induced gap for these band-crossings is smaller than 28 meV and within the acceptable limits, reflecting that TiTe is an ideal NL material with robust resistance to the effects of SOC.
Conclusion
We prove the existence of I, II, and hybrid types of NLs in TiTe at the ground state. Moreover, TiTe is shown to be a dynamic and mechanically stable material using first-principle calculations. Furthermore, it is proved to be an ideal NL material with two type I NLs: one Γ-centered type II NL and two hybrid-type NLs in the kz = 0 plane. The BCPs are robust to the SOC, and the SOC-induced gaps are quite small. The D-H-L surface states can be observed in (001) surface of the TiTe. We expect that the NLs and the (001) surface states of TiTe can be verified in an experiment.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author Contributions
LZ, PL, and FF: conceptualization, methodology, software, formal analysis, data curation, and writing. KW, YL, and LZ: investigation, funding, and project administration. All authors contributed to the article and approved the submitted version.
Funding
This work is supported by Topic Foundation of Changchun Institute of Technology (Grant No. 320200040), Young People Foundation of Changchun Institute of Technology (Grant No. 320200033), Doctor Foundation of Changchun Institute of Technology 2021, Natural Science Foundation of Heilongjiang Province (Grant No. LH2020H067), Heilongjiang Postdoctoral Program (LBH-Q16173), Science and Technology Program of Academy of Medical Sciences of Heilongjiang Province (Grant No. 201805), Research Foundation of Education Bureau of Jilin Province (Grant No. JJKH20210666KJ).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2021.755350/full#supplementary-material
Footnotes
1https://materialsproject.org/materials/mp-567832
References
Alcón, I., Viñes, F., Moreira, I. P. R., and Bromley, S. T. (2017). Existence of Multi-Radical and Closed-Shell Semiconducting States in post-graphene Organic Dirac Materials. Nat. Commun. 8 (1), 1957–1959. doi:10.1038/s41467-017-01977-4
Banik, A., Roychowdhury, S., and Biswas, K. (2018). The Journey of Tin Chalcogenides towards High-Performance Thermoelectrics and Topological Materials. Chem. Commun. 54 (50), 6573–6590. doi:10.1039/c8cc02230e
Bi, R., Yan, Z., Lu, L., and Wang, Z. (2017). Nodal-knot Semimetals. Phys. Rev. B 96 (20), 201305. doi:10.1103/physrevb.96.201305
Bzdušek, T., Wu, Q., Rüegg, A., Sigrist, M., and Soluyanov, A. A. (2016). Inventory Asset and Fixed Asset Frauds. Nature 538 (7623), 75–78. doi:10.4324/9781315576787-9
Cava, R. J., Ji, H., Fuccillo, M. K., Gibson, Q. D., and Hor, Y. S. (2013). Crystal Structure and Chemistry of Topological Insulators. J. Mater. Chem. C 1 (19), 3176–3189. doi:10.1039/c3tc30186a
Chen, H., Zhang, S., Jiang, W., Zhang, C., Guo, H., Liu, Z., et al. (2018). Prediction of Two-Dimensional Nodal-Line Semimetals in a Carbon Nitride Covalent Network. J. Mater. Chem. A. 6 (24), 11252–11259. doi:10.1039/c8ta02555j
Culcer, D., Cem Keser, A., Li, Y., and Tkachov, G. (2020). Transport in Two-Dimensional Topological Materials: Recent Developments in experiment and Theory. 2d Mater. 7 (2), 022007. doi:10.1088/2053-1583/ab6ff7
Ehrlish, P. (1949). Über Titanselenide und -telluride. Z. fuer Anorganische Allgemeine Chem. 260, 1–3.
Ezawa, M. (2017). Topological Semimetals Carrying Arbitrary Hopf Numbers: Fermi Surface Topologies of a Hopf Link, Solomon's Knot, Trefoil Knot, and Other Linked Nodal Varieties. Phys. Rev. B 96 (4), 041202. doi:10.1103/physrevb.96.041202
Fang, P., Shi, X., Liu, C., Zhai, X., Li, H., and Wang, L. (2020). Single- and Dual-Band Convertible Terahertz Absorber Based on Bulk Dirac Semimetal. Opt. Commun. 462, 125333. doi:10.1016/j.optcom.2020.125333
Feng, X., Yue, C., Song, Z., Wu, Q., and Wen, B. (2018). Topological Dirac Nodal-Net Fermions in AlB2-type TiB2 and ZrB2. Phys. Rev. Mater. 2 (1), 014202. doi:10.1103/physrevmaterials.2.014202
Fu, B., Fan, X., Ma, D., Liu, C. C., and Yao, Y. (2018). Hourglasslike Nodal Net Semimetal in Ag2BiO3. Phys. Rev. B 98 (7), 075146. doi:10.1103/physrevb.98.075146
Fu, C., Guin, S. N., Watzman, S. J., Li, G., Liu, E., Kumar, N., et al. (2018). Large Nernst Power Factor over a Broad Temperature Range in Polycrystalline Weyl Semimetal NbP. Energy Environ. Sci. 11 (10), 2813–2820. doi:10.1039/c8ee02077a
Huang, H., Liu, J., Vanderbilt, D., and Duan, W. (2016). Topological Nodal-Line Semimetals in Alkaline-Earth Stannides, Germanides, and Silicides. Phys. Rev. B 93 (20), 201114. doi:10.1103/physrevb.93.201114
Jin, K.-H., Huang, H., Wang, Z., and Liu, F. (2019). A 2D Nonsymmorphic Dirac Semimetal in a Chemically Modified Group-VA Monolayer with a Black Phosphorene Structure. Nanoscale 11 (15), 7256–7262. doi:10.1039/c9nr00906j
Jin, L., Zhang, X., Dai, X., Liu, H., Chen, G., and Liu, G. (2019). Centrosymmetric Li2NaN: a superior Topological Electronic Material with Critical-type Triply Degenerate Nodal Points. J. Mater. Chem. C 7 (5), 1316–1320. doi:10.1039/c8tc05930f
Jin, L., Zhang, X., He, T., Meng, W., Dai, X., and Liu, G. (2020). Intermetallic α-FeSi2: Realization of Type-I, Type-II, and Hybrid Nodal Line States in a Single Material via Tunable Valleys. J. Phys. Chem. C 124, 12311–12317. doi:10.1021/acs.jpcc.0c02967
Kageyama, H., Hayashi, K., Maeda, K., Attfield, J. P., Hiroi, Z., Rondinelli, J. M., et al. (2018). Expanding Frontiers in Materials Chemistry and Physics with Multiple Anions. Nat. Commun. 9 (1), 772–815. doi:10.1038/s41467-018-02838-4
Kong, D., and Cui, Y. (2011). Opportunities in Chemistry and Materials Science for Topological Insulators and Their Nanostructures. Nat. Chem 3 (11), 845–849. doi:10.1038/nchem.1171
Kong, X., Li, L., and Peeters, F. M. (2018). Topological Dirac Semimetal Phase in GexSny Alloys. Appl. Phys. Lett. 112 (25), 251601. doi:10.1063/1.5037121
Kumar, N., Guin, S. N., Manna, K., Shekhar, C., and Felser, C. (2020). Topological Quantum Materials from the Viewpoint of Chemistry. Chem. Rev. 121 (5), 2780–2815. doi:10.1021/acs.chemrev.0c00732
Li, X., Liu, J., Wang, F. Q., Wang, Q., and Jena, P. (2019). Rational Design of Porous Nodal-Line Semimetallic Carbon for K-Ion Battery Anode Materials. J. Phys. Chem. Lett. 10 (20), 6360–6367. doi:10.1021/acs.jpclett.9b02484
Li, Y., and Xia, J. (2020). Cubic Hafnium Nitride: A Novel Topological Semimetal Hosting a 0-Dimensional (0-D) Nodal point and a 1-D Topological Nodal Ring. Front. Chem. 8, 727. doi:10.3389/fchem.2020.00727
Liu, Q.-B., Fu, H.-H., Xu, G., Yu, R., and Wu, R. (2019). Categories of Phononic Topological Weyl Open Nodal Lines and a Potential Material Candidate: Rb2Sn2O3. J. Phys. Chem. Lett. 10 (14), 4045–4050. doi:10.1021/acs.jpclett.9b01159
Qie, Y., Liu, J., Wang, S., Sun, Q., and Jena, P. (2019). Tetragonal C24: a Topological Nodal-Surface Semimetal with Potential as an Anode Material for Sodium Ion Batteries. J. Mater. Chem. A. 7 (10), 5733–5739. doi:10.1039/c8ta11276b
Sankar, R., Muthuselvam, I. P., Babu, K. R., Murugan, G. S., Rajagopal, K., Kumar, R., et al. (2019). Crystal Growth and Magnetic Properties of Topological Nodal-Line Semimetal GdSbTe with Antiferromagnetic Spin Ordering. Inorg. Chem. 58 (17), 11730–11737. doi:10.1021/acs.inorgchem.9b01698
Schoop, L. M., Pielnhofer, F., and Lotsch, B. V. (2018). Chemical Principles of Topological Semimetals. Chem. Mater. 30 (10), 3155–3176. doi:10.1021/acs.chemmater.7b05133
Strambini, E., D'Ambrosio, S., Vischi, F., Bergeret, F. S., Nazarov, Y. V., and Giazotto, F. (2016). The ω-SQUIPT as a Tool to Phase-Engineer Josephson Topological Materials. Nat. Nanotech 11 (12), 1055–1059. doi:10.1038/nnano.2016.157
Tang, M., Shen, H., Qie, Y., Xie, H., and Sun, Q. (2019). Edge-State-Enhanced CO2 Electroreduction on Topological Nodal-Line Semimetal Cu2Si Nanoribbons. J. Phys. Chem. C 123 (5), 2837–2842. doi:10.1021/acs.jpcc.8b08871
Wang, A., Shen, L., Zhao, M., Wang, J., Zhou, W., Li, W., et al. (2019). Tungsten Boride: a 2D Multiple Dirac Semimetal for the Hydrogen Evolution Reaction. J. Mater. Chem. C 7 (29), 8868–8873. doi:10.1039/c9tc01862j
Wang, B., Gao, H., Lu, Q., Xie, W., Ge, Y., Zhao, Y.-H., et al. (2018). Type-I and Type-II Nodal Lines Coexistence in the Antiferromagnetic Monolayer CrAs2. Phys. Rev. B 98 (11), 115164. doi:10.1103/physrevb.98.115164
Wang, J. T., Nie, S., Weng, H., Kawazoe, Y., and Chen, C. (2018). Topological Nodal-Net Semimetal in a Graphene Network Structure. Phys. Rev. Lett. 120 (2), 026402. doi:10.1103/PhysRevLett.120.026402
Wang, X., Cheng, Z., Zhang, G., Kuang, M., Wang, X.-L., and Chen, H. (2020). Strain Tuning of Closed Topological Nodal Lines and Opposite Pockets in Quasi-Two-Dimensional α-phase FeSi2. Phys. Chem. Chem. Phys. 22, 13650–13658. doi:10.1039/d0cp02334e
Wang, X., Ding, G., Cheng, Z., Surucu, G., Wang, X.-L., and Yang, T. (2020). Novel Topological Nodal Lines and Exotic Drum-head-like Surface States in Synthesized CsCl-type Binary alloy TiOs. J. Adv. Res. 22, 137–144. doi:10.1016/j.jare.2019.12.001
Wang, X., Ding, G., Cheng, Z., Surucu, G., Wang, X.-L., and Yang, T. (2020). Rich Topological Nodal Line Bulk States Together with Drum-head-like Surface States in NaAlGe with Anti-PbFCl Type Structure. J. Adv. Res. 23, 95–100. doi:10.1016/j.jare.2020.01.017
Wang, X., Ding, G., Cheng, Z., Wang, X.-L., Zhang, G., and Yang, T. (2020). Intersecting Nodal Rings in Orthorhombic-type BaLi2Sn Compound. J. Mater. Chem. C 8 (16), 5461–5466. doi:10.1039/d0tc00504e
Wang, X., Zhou, F., and Chen, H. (2020). Organic-inorganic Hybrid Coordination Polymer C3H9CdCl3N Co-exhibiting superior Dirac point and Nodal Surface States. Results Phys. 17, 103159. doi:10.1016/j.rinp.2020.103159
Wang, Z. F., Jin, K. H., and Liu, F. (2017). Computational Design of Two‐dimensional Topological Materials. Wiley Interdiscip. Rev. Comput. Mol. Sci. 7 (4), e1304. doi:10.1002/wcms.1304
Weng, H., Liang, Y., Xu, Q., Yu, R., Fang, Z., Dai, X., et al. (2015). Topological Node-Line Semimetal in Three-Dimensional Graphene Networks. Phys. Rev. B 92 (4), 045108. doi:10.1103/physrevb.92.045108
Wu, W., Liu, Y., Li, S., Zhong, C., Yu, Z.-M., Sheng, X.-L., et al. (2018). Nodal Surface Semimetals: Theory and Material Realization. Phys. Rev. B 97 (11), 115125. doi:10.1103/physrevb.97.115125
Xu, S.-G., Zheng, B., Xu, H., and Yang, X.-B. (2019). Ideal Nodal Line Semimetal in a Two-Dimensional Boron Bilayer. J. Phys. Chem. C 123 (8), 4977–4983. doi:10.1021/acs.jpcc.8b12385
Xu, S.-Y., Liu, C., Kushwaha, S. K., Sankar, R., Krizan, J. W., Belopolski, I., et al. (2015). Observation of Fermi Arc Surface States in a Topological Metal. Science 347 (6219), 294–298. doi:10.1126/science.1256742
Xu, Y., Elcoro, L., Song, Z.-D., Wieder, B. J., Vergniory, M. G., Regnault, N., et al. (2020). High-throughput Calculations of Magnetic Topological Materials. Nature 586 (7831), 702–707. doi:10.1038/s41586-020-2837-0
Yamakage, A., Yamakawa, Y., Tanaka, Y., and Okamoto, Y. (2016). Line-Node Dirac Semimetal and Topological Insulating Phase in Noncentrosymmetric Pnictides CaAgX(X= P, as). J. Phys. Soc. Jpn. 85 (1), 013708. doi:10.7566/jpsj.85.013708
Yan, Z., Bi, R., Shen, H., Lu, L., Zhang, S. C., and Wang, Z. (2017). Nodal-link Semimetals. Phys. Rev. B 96 (4), 041103. doi:10.1103/physrevb.96.041103
Yi, X., Li, W. Q., Li, Z. H., Zhou, P., Ma, Z. S., and Sun, L. Z. (2019). Topological Dual Double Node-Line Semimetals NaAlSi(Ge) and Their Potential as Cathode Material for Sodium Ion Batteries. J. Mater. Chem. C 7 (48), 15375–15381. doi:10.1039/c9tc04096j
Zhang, L., Zhang, S.-f., Ji, W.-X., Zhang, C.-W., Li, P., Wang, P.-j., et al. (2018). Discovery of a Novel Spin-Polarized Nodal Ring in a Two-Dimensional HK Lattice. Nanoscale 10 (44), 20748–20753. doi:10.1039/c8nr05383a
Zhang, M.-H., Zhang, S.-F., Wang, P.-J., and Zhang, C.-W. (2020). Emergence of a Spin-valley Dirac Semimetal in a Strained Group-VA Monolayer. Nanoscale 12 (6), 3950–3957. doi:10.1039/c9nr09545d
Zhang, X., Yu, Z.-M., Lu, Y., Sheng, X.-L., Yang, H. Y., and Yang, S. A. (2018). Hybrid Nodal Loop Metal: Unconventional Magnetoresponse and Material Realization. Phys. Rev. B 97 (12), 125143. doi:10.1103/physrevb.97.125143
Zhao, Z., Zhang, Z., and Guo, W. (2020). A Family of All Sp2-Bonded Carbon Allotropes of Topological Semimetals with Strain-Robust Nodal-Lines. J. Mater. Chem. C 8 (5), 1548–1555. doi:10.1039/c9tc05470g
Keywords: DFT study, tite, nodal line states, surface states, SOC
Citation: Lin P, Fang F, Zhang L, Li Y and Wang K (2021) Various Nodal Lines in P63/mmc-type TiTe Topological Metal and its (001) Surface State. Front. Chem. 9:755350. doi: 10.3389/fchem.2021.755350
Received: 08 August 2021; Accepted: 10 September 2021;
Published: 28 September 2021.
Edited by:
Xiaotian Wang, Southwest University, ChinaReviewed by:
Chuanzhao Zhang, Yangtze University, ChinaRabah Khenata, University of Mascara, Algeria
Shoubing Ding, Chongqing Normal University, China
Copyright © 2021 Lin, Fang, Zhang, Li and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kai Wang, d2FuZ2thaUBocmJtdS5lZHUuY24=; Li Zhang, emhhbmdsaV9jaGVtaXN0cnlAMTI2LmNvbQ==; Yang Li, ZG9jdG9yeWFuZ2xpQGhyYm11LmVkdS5jbg==
 Peng Lin1
Peng Lin1 Li Zhang
Li Zhang Kai Wang
Kai Wang