Rui Yu1
Sudip Pan
Zhong-hua Cui- 1Institute of Atomic and Molecular Physics, Key Laboratory of Physics and Technology for Advanced Batteries (Ministry of Education), Jilin University, Changchun, China
- 2Wilhelm Ostwald Institute for Physical and Theoretical Chemistry, Leipzig University, Leipzig, Germany
- 3Fachbereich Chemie, Philipps-Universität Marburg, Marburg, Germany
- 4Beijing National Laboratory for Molecular Sciences, Beijing, China
Transition-metal-centered monocyclic boron wheels are important candidates in the family of planar hypercoordinate species that show intriguing structure, stability and bonding situation. Through the detailed potential energy surface explorations of MB9− (M = Fe, Ru, Os) clusters, we introduce herein OsB9− to be a new member in the transition-metal-centered borometallic molecular wheel gallery. Previously, FeB9− and RuB9− clusters were detected by photoelectron spectroscopy and the structures were reported to have singlet D9h symmetry. Our present results show that the global minimum for FeB9− has a molecular wheel-like structure in triplet spin state with Cs symmetry, whereas its heavier homologues are singlet molecular wheels with D9h symmetry. Chemical bonding analyses show that RuB9− and OsB9− display a similar type of electronic structure, where the dual σ + π aromaticity, originated from three delocalized σ bonds and three delocalized π bonds, accounts for highly stable borometallic molecular wheels.
Introduction
The pure and doped boron clusters have attracted great attentions because of their novel structures, intriguing chemical bonds and promising building blocks for boron-based nanomaterials (Alexandrova et al., 2006; Jian et al., 2019). Up to date, great achievements of boron-based clusters have been attained by extensive experimental and theoretical studies (Albert and Hillebrecht, 2009). They show a zoo of structural diversity ranging from planar (Pan et al., 2008; Piazza et al., 2014; Bai et al., 2019) or quasi-planar (Popov et al., 2013) configurations, tubular nanostructures (Kiran et al., 2005; Yang et al., 2008) to all-boron borospherenes/borophenes (Wang 2016; Li et al., 2017) with the increasing Bn size. On the other hand, the striking electronic properties, i.e., multiple aromaticity, nuclear dynamics, hydrocarbon analogues strongly enrich our knowledge of electronic theory. These unusual structural and electronic properties can be regarded as a consequence of the electron deficiency of boron atom, which gives rise to the extraordinary ability of boron to form delocalized multi-center bonds with itself and other elements. Indeed, the introduction of heteroatoms in boron clusters has created a variety of intriguing doped boron clusters, including metal-centered monocyclic ring/tubular/cage structures, (Romanescu et al., 2011; Jian et al., 2016; Dong et al., 2018; Liang et al., 2018; Chen et al., 2019; Lu et al., 2021), half-sandwich structures, (Chen et al., 2018; Ren et al., 2019), inverse sandwich structures, (Cui et al., 2020; Jiang et al., 2021), metallo-borophenes (Li et al., 2016; Zhang et al., 2016) and metallo-borospherenes, (Chen et al., 2020; Zhang et al., 2021), strongly leading to a new direction of research on boron chemistry and pushing the limit of structural chemistry as well as the record of coordination number in 2D and 3D environments for central metal atoms. (Islas et al., 2007; Liu et al., 2007; Miao et al., 2009; Li et al., 2012; Popov et al., 2014; Pan et al., 2018; Chen et al., 2019).
Amongst, the metal-centered monocyclic wheels represent a family of fascinating planar double aromatic borometallic compounds (Luo 2008; Pu et al., 2009; Romanescu et al., 2013; Romanescu et al., 2013). Such species were firstly found in the global minimum of CoB8− and FeB9− predicted by computational studies (Ito et al., 2008; Pu et al., 2009). After that, a set of MBn− monocyclic wheels (CoB8−, FeB8−, FeB9−, RuB9−, RhB9− and IrB9−) (Ito et al., 2008; Luo 2008; Romanescu et al., 2011; Li et al., 2012; Yang et al., 2015) have been characterized by the photoelectron spectroscopy supported by the computational studies. Thereafter, TaB10− and NbB10−, the largest member setting the new limit of maximum coordination number in planar form, were also experimentally detected (Galeev et al., 2012; Li et al., 2013). The extraordinary stability in planar structures in all these metal-centered monocyclic wheels can be rationalized by the presence of σ and π double aromaticity, making it an effective electronic design principle.
We noted that MBn− (M = group 8 and 9 elements) clusters have been detected and characterized to be the global monocyclic wheels except for M = Os. Thus, the question remains as to whether OsB9− is a real exception. To address this issue, the detailed potential energy surfaces (PESs) of MB9− (M = Fe, Ru, Os) were explored herein, and structural and electronic properties of the lowest-energy structures were systematically analyzed by coupling with various chemical bonding approaches. Interestingly, we found a new global minimum for FeB9−. A molecular wheel-like structure in triplet spin state with Cs symmetry is lower in energy than the previously reported singlet molecular wheel form with D9h symmetry (Romanescu et al., 2012). On the other hand, OsB9− is a singlet global monocyclic wheel that behaves similarly to RuB9−, where σ and π double aromaticity (three delocalized σ bonds and three delocalized π bonds) gives rise to their high stability, making it a suitable target for future experimental detection. (Romanescu et al., 2011).
Computational Methods
The CALYPSO (Wang et al., 2016) (Crystal structure AnaLYsis by Particle Swarm Optimization) code was used for the detailed structural explorations of MB9− (M = Fe, Ru, Os) in their singlet, triplet, and quintet spin states at the PBE0/def2-SVP level. For the low-lying energy isomers, further reoptimization followed by harmonic vibrational frequency calculation were done at the PBE0/def2-TZVPP level. For comparison, another level of theory, TPSSh/def2-TZVPP was also chosen. For further energetic refinement, singlet point calculations were further done at the CCSD(T) (Pople et al., 1987)/def2-TZVPP//PBE0/def2-TZVPP level. Total energies were corrected by the zero-point corrected energies (ZPE) of PBE0/def2-TZVPP level. The natural bond orbital (NBO), (Glendening et al., 2019), nucleus-independent chemical shift (NICS), (Mitchell 2001), adaptive natural density partitioning (AdNDP), (Zubarev and Boldyrev, 2008), quantum theory of atoms in molecules (QTAIM) and electron localization (ELF) analyses (Fuster et al., 2000) were performed for these global monocyclic molecular wheels using Multiwfn code (Lu and Chen, 2012). To facilitate future experimental characterization, the simulated photoelectron spectra of RuB9− and OsB9− were calculated at the BP86/def2-TZVPP level based on generalized Koopmans’ theorem (Tsuneda et al., 2010). The aromaticity was understood by the gauge including magnetically induced current (GIMIC) analysis (Fliegl et al., 2011) and the anisotropy of the current induced density (ACID) (Geuenich et al., 2005). All the calculations were performed using the Gaussian 09 package. (Frisch et al., 2016).
Structures and Energetics
The singlet PES of FeB9− was explored in 2008, (Ito et al., 2008), where the singlet D9h-symmetry planar nonacoordinate Fe-centered monocyclic boron wheel (isomer d in Figure 1) was reported to be the lowest-energy structure that lies 14.9 kcal/mol more stable than the second alternative at the BP86/TZVPP level. In 2012, the photoelectron spectroscopy of FeB9− was explained based on the singlet wheel isomer (Romanescu et al., 2012). However, by the detailed structural searches of singlet, triplet, and quintet states, we found that the triplet molecular wheel with Cs symmetry (a) is 19.5 kcal/mol lower in energy than d at the PBE0/def2-TZVPP level. Meanwhile, large T1 diagnostic values obtained with the coupled-cluster wave function indicate that FeB9− system is a multireference problem. Note that the broken-symmetry spin-unrestricted approach was used for the monocyclic boron wheel, which is still 2.1 kcal/mol lower in energy relative to the closed-shell one. Thus, the coexistence of triplet global state of the molecular wheel FeB9− could be the reason of the observed broad features in photoelectron spectrum, as assumed by the authors. (Romanescu et al., 2012).
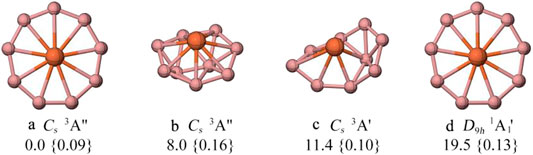
FIGURE 1. The low-lying energy isomers of FeB9− computed at the PBE0/def2-TZVPP level and T1 diagnostic values obtained with coupled-cluster wavefunction are given in curly braces. All energies are corrected from zero-point energies (ZPE) at the PBE0/def2-TZVPP level.
Figure 2 displays the low-lying energy isomers of RuB9− and OsB9−. The monocyclic boron wheel with D9h symmetry and 1A1’ electronic state is predicted to be a real global minimum having the lowest vibrational frequencies of 62.2 and 17.2 cm−1 for RuB9− and OsB9−, respectively. At the CCSD(T)/def2-TZVPP level, the monocyclic boron wheel is a global minimum that lies 30.4 and 37.1 kcal/mol more stable than the second alternative for RuB9− and OsB9−, respectively. The triplet monocyclic boron wheels are also located, but unlike FeB9−, they are significantly high-energy isomers. Note that the results at the TPSSh/def2-TZVPP level are very similar to the PBE0/def2-TZVPP level, except for the relative energy between isomer a and d of FeB9− (see Supplementary Figure S1). This is presumably because of the multireference character in these systems. The T1 diagnostic factors of RuB9− and OsB9− are within 0.05, suggesting that the single-reference method can be safely used for these two clusters. Given the fact that RuB9− was detected earlier by photoelectron spectroscopy, we believe that the monocyclic boron wheel OsB9− cluster is also a suitable target for the gas-phase experimental study.
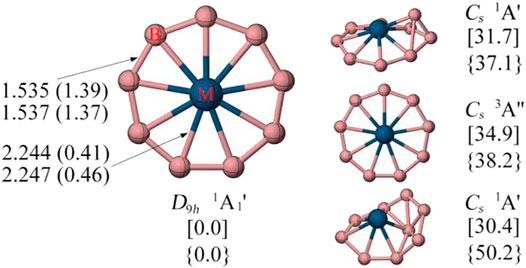
FIGURE 2. The minimum energy geometries and the corresponding bond distances in Å and WBI values in parentheses of RuB9− (top) and OsB9− (bottom) are given at the PBE0/def2-TZVPP level. Relative energies in kcal/mol of the low-lying energy isomers of [RuB9−] and {OsB9−} are given at the CCSD(T)/def2-TZVPP//PBE0/def2-TZVPP level with ZPE correction of PBE0. The T1 diagnostic are less than 0.05.
To understand the high stability of the MB9− monocyclic wheels, their detailed structural parameters are given in Figure 2. We found the MB9− (M = Ru, Os) clusters possess similar structural properties. In the case of OsB9−, like all other metal-centered monocyclic boron wheels, the B-B bonds show strong multiple bonding characteristic as indicated by the short bond distance of 1.54 Å and Wiberg bond indices (WBIs) value of 1.37, which is clearly shorter than the single B-B bond (1.70 Å) using the self-consistent covalent radius of Pyykkö (Pyykko and Atsumi, 2009). The strong peripheral B-B bonds is because each boron atom fully participate in the two-center two electron (2c-2e) B-B σ bonds and two sets of the delocalized σ and π bonds (see discussed below). The M-B bonds of OsB9− have the bond distance of 2.247 Å (WBI = 0.46), which is slightly longer than the M-B single bond using the self-consistent covalent radius of Pyykkö, a common characteristic for the multicentered bonds. (Pyykko and Atsumi, 2009).
Electronic Delocalization
The adaptive natural density partitioning (AdNDP) (Zubarev and Boldyrev, 2008) analyses were carried out for OsB9− to further understand its chemical bonding and electronic structure. As shown in Figure 3A, the first row displays three one center-two electrons (1c-2e) lone pair electrons associated with d orbitals of Os center, where the occupation number (ON) for the dz2 LP is 1.99 |e| and the same for others two are 1.49 |e|. Somewhat lower ON for these LPs are because of partial delocalization to boron rings. An alternative 10c-2e description gives ideal 2.00 |e| ON, but we continue it as 1c-2e LPs for similarity since in the previously reported AdNDP results for RuB9− the authors describe them as LPs (Romanescu et al., 2011). Nevertheless, even consideration of them as 10c-2e delocalized σ-bonds would not change the nature of aromaticity drawn based on the number of delocalized electrons. Nine 2c-2e bonds with ONs of 1.96 |e| account for the peripheral B-B bonds. The second row presents three delocalized 10c-2e σ bonds (left) and three delocalized 10c-2e π bonds (right), and they vividly satisfy the σ + π double aromaticity. The electron localization function (ELF) (Fuster et al., 2000) as shown in Figure 3B further confirms AdNDP results. The plot of ELF shows that the strong electron density is localized in the peripheral boron ring, but relatively lower electron density between M center and boron ring because of the delocalized σ and π clouds.
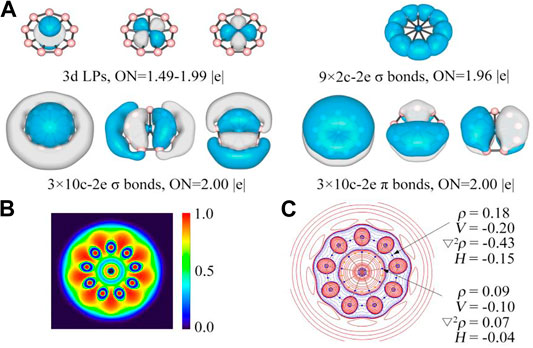
FIGURE 3. (A) AdNDP results, and (B) color-filled map of ELF and (C) contour plot of Laplacian of electron density of OsB9−. In c, the contour line map of Laplacian of electron density, red solid lines and blue dotted lines represent positive and negative regions, respectively. Blue and orange points correspond to position of bond critical points (BCPs) and ring critical point (RCP), respectively. Values of some real space functions at the BCP are given, including ρ (electron density), V (potential energy density), ∇2ρ, H (energy density).
We performed quantum theory of atom in molecules (QTAIM) analysis to shed additional light into the nature of Os-B interaction. The contour plot of Laplacian of the electron density (∇2ρ(r)) at the molecular plane is given in Figure 3C. There are nine bond paths and bond critical points (indicated by the small blue spheres) between Os and boron centers. The plot also shows that there are electron density accumulated regions (indicated by blue dotted lines) in between B and Os centers but BCPs just lie outside of the blue dotted regions because of polar nature of the bond giving positive ∇2ρ(rc) value at BCP. This is a very usual feature for the bonds involving heavier elements where the criterion of negative ∇2ρ(rc) value at BCP for covalent bond does not satisfy. For these cases, the total energy density H(rc) is more suitable descriptor for such cases which is negative for covalent bonds (Cremer and Kraka, 1984).55 The corresponding value of H(rc) at the BCP of Os-B bonds is −0.04 au, showing their covalent nature. On the other hand, for B-B bonds as expected both ∇2ρ(rc) and H(rc) are negative. Similar electron topology is noted in case of RuB9− as well (see Supplementary Figure S2 in supporting information).
Aromaticity
The dual σ + π aromaticity was further confirmed in the following discussion. The nucleus-independent chemical shift (NICS) (Mitchell 2001) is a key method to quantify aromaticity, where NICSzz values (the out-of-plane (“zz”) shielding tensor component of NICS). As shown in Figure 4A, the grids of NICSzz points are created at the center of wheels, the center of B-M-B ring and out of the ring associated with 1.0 Å vertical spacings from the wheel plane. The considerable negative NICSzz values vividly show aromatic boron wheels, especially the big NICS(1)zz of the wheel centers (−123.6 ppm) is consistent with the reported transition-metal-centered borometallic molecular wheel family. Figure 4B displays a gauge including magnetically induced current (GIMIC) map, (Fliegl et al., 2011), where the induced ring current is generated by employing an external magnetic field perpendicular to the molecular plane. The diatropic (clockwise) current comply with the left-handed rule. It is worthy of note that the inner and outside of the peripheral ring both show a diatropic and unidirectional current. This current behavior is similar to the C18 clusters with double aromaticity (σ + π) but sharply different from the benzene (π aromaticity only), where the ring current show a diatropic inside but paratropic outside of benzene ring. The induced current density (Jind) is integrated into a specific area, which starts at the center of the ring and intersects the B-B bond ending about 4 Å away for the current system. The ring-current strength of RuB9− (25.4 nA/T) and OsB9− (26.4 nA/T) is similar to C18 (Lu et al., 2020) (25.3 and 21.2 nA/T), and stronger than the benzene (11.5 nA/T) at the wB97XD/def2-TZVP level, which could be another indicator of dual σ + π aromaticity. The anisotropy of the current induced density (ACID) is able to describe the σ and π contribution for aromaticity as given in Figure 4C. Overall, the σ and π dual aromaticity is strongly confirmed by these analyses in Figure 4 and Supplementary Figure S3 for OsB9− and RuB9−, respectively.
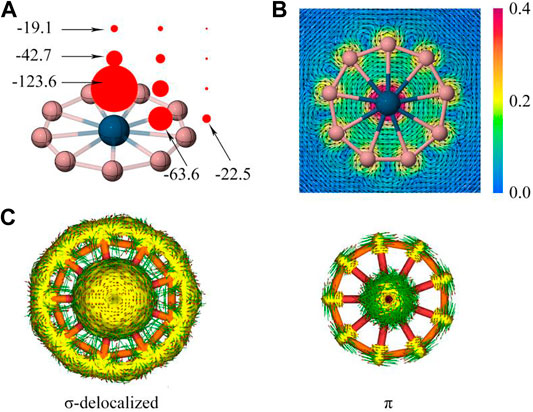
FIGURE 4. (A) NICSzz, and (B) GIMIC map and (C) induced ring current of the delocalized σ and π electrons based on ACID values of OsB9−. In b), the arrows indicate direction of induced current, the color correspond to magnitude of induced current.
Simulated Photoelectron Spectra
The simulated photoelectron spectra of RuB9− and OsB9− are given in Figure 5 based on the generalized Koopmans’ theorem (Tsuneda et al., 2010). The simulated spectrum for RuB9− is in good agreement with the experimental data as shown in Figure 5A. Thus, to facilitate the experimental confirmation, the simulated photoelectron spectrum of OsB9− cluster is illustrated in Figure 5B, where the well-resolved detachment transitions at the lower-binding-energy side, are labeled as X (4.08), A (5.31), B (5.67), C (6.24) in eV.
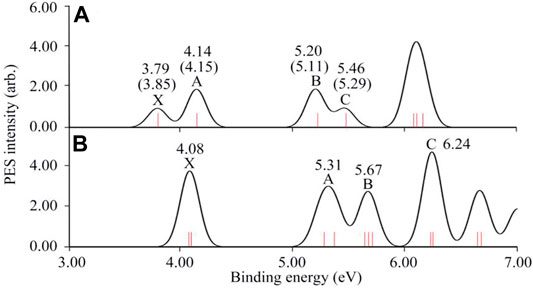
FIGURE 5. The simulated photoelectron spectrums of (A) RuB9− and (B) OsB9− were calculated at the BP86/def2-TZVPP level based on generalized Koopmans’ theorem. The experimental results of RuB9− are given in parenthesis.
Conclusion
The OsB9− cluster was found to be a new member of transition-metal-centered borometallic molecular wheel family. The detailed electronic structure analyses including the AdNDP, ELF, NICS, and ACID approaches all suggested that the dual σ + π aromaticity (three delocalized σ bonds and three delocalized π bonds) occurs in RuB9− and OsB9−, and it is a key factor to design highly stable borometallic molecular wheels. Additionally, we found a different picture relative to the previous work for FeB9−. The present results show that the global minimum for FeB9− has a molecular wheel-like structure in triplet spin state with Cs symmetry, whereas previously reported singlet molecular wheels with D9h symmetry is higher energy isomer.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author Contributions
RY performed all the calculations, SP and Z-HC designed the work, validated the results, and wrote the draft.
Funding
This work was funded by the National Natural Science Foundation of China (No. 11874178, 11922405, 91961204). This work was supported by Beijing National Laboratory for Molecular Sciences (BNLMS201910). The partial calculations in this work supported by High Performance Computing Center of Jilin University, China.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2021.751482/full#supplementary-material
References
Albert, B., and Hillebrecht, H. (2009). Boron: Elementary Challenge for Experimenters and Theoreticians. Angew. Chem. Int. Ed. 48, 8640–8668. doi:10.1002/anie.200903246
Alexandrova, A. N., Boldyrev, A. I., Zhai, H.-J., and Wang, L.-S. (2006). All-boron Aromatic Clusters as Potential New Inorganic Ligands and Building Blocks in Chemistry. Coord. Chem. Rev. 250, 2811–2866. doi:10.1016/j.ccr.2006.03.032
Bai, H., Chen, T.-T., Chen, Q., Zhao, X.-Y., Zhang, Y.-Y., Chen, W.-J., et al. (2019). Planar B41− and B42− Clusters with Double-Hexagonal Vacancies. Nanoscale 11, 23286–23295. doi:10.1039/c9nr09522e
Chen, B. L., Sun, W. G., Kuang, X. Y., Lu, C., Xia, X. X., Shi, H. X., et al. (2018). Structural Stability and Evolution of Medium-Sized Tantalum-Doped Boron Clusters: A Half-Sandwich-Structured TaB12 - Cluster. Inorg. Chem. 57, 343–350. doi:10.1021/acs.inorgchem.7b02585
Chen, T.-T., Li, W.-L., Bai, H., Chen, W.-J., Dong, X.-R., Li, J., et al. (2019). ReB8- and ReB9-: New Members of the Transition-Metal-Centered Borometallic Molecular Wheel Family. J. Phys. Chem. A. 123, 5317–5324. doi:10.1021/acs.jpca.9b03942
Chen, T. T., Li, W. L., Chen, W. J., Yu, X. H., Dong, X. R., Li, J., et al. (2020). Spherical Trihedral Metallo-Borospherenes. Nat. Commun. 11, 2766. doi:10.1038/s41467-020-16532-x
Cremer, D., and Kraka, E. (1984). Chemical Bonds without Bonding Electron Density - Does the Difference Electron-Density Analysis Suffice for a Description of the Chemical Bond?. Angew. Chem. Int. Ed. 23, 627–628. doi:10.1002/anie.198406271
Cui, Z.-h., Chen, C., Wang, Q., Zhao, L., Wang, M.-h., and Ding, Y.-h. (2020). Inverse sandwich Complexes of B7M2−, B8M2, and B9M2+ (M = Zr, Hf): the Nonclassical M-M Bonds Embedded in Monocyclic boron Rings. New J. Chem. 44, 17705–17713. doi:10.1039/d0nj03999c
Dong, X., Jalife, S., Vásquez-Espinal, A., Ravell, E., Pan, S., Cabellos, J. L., et al. (2018). Li2 B12 and Li3 B12 : Prediction of the Smallest Tubular and Cage-like Boron Structures. Angew. Chem. Int. Ed. 57, 4627–4631. doi:10.1002/anie.201800976
Fliegl, H., Taubert, S., Lehtonen, O., and Sundholm, D. (2011). The Gauge Including Magnetically Induced Current Method. Phys. Chem. Chem. Phys. 13, 20500–20518. doi:10.1039/c1cp21812c
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2016). Gaussian 09, Revision C.01. Wallingford CT: Gaussian, Inc..
Fuster, F., Sevin, A., and Silvi, B., (2000). Topological Analysis of the Electron Localization Function (ELF) Applied to the Electrophilic Aromatic Substitution, J. Phys. Chem. A. 104, 852–858. doi:10.1021/jp992783k
Galeev, T. R., Romanescu, C., Li, W.-L., Wang, L.-S., and Boldyrev, A. I. (2012). Observation of the Highest Coordination Number in Planar Species: Decacoordinated TaB10− and NbB10− Anions. Angew. Chem. Int. Ed. 51, 2101–2105. doi:10.1002/anie.201107880
Geuenich, D., Hess, K., Köhler, F., and Herges, R. (2005). Anisotropy of the Induced Current Density (ACID), a General Method to Quantify and Visualize Electronic Delocalization. Chem. Rev. 105, 3758–3772. doi:10.1021/cr0300901
Glendening, E. D., Landis, C. R., and Weinhold, F. (2019). NBO 7.0 : New Vistas in Localized and Delocalized Chemical Bonding Theory. J. Comput. Chem. 40, 2234–2241. doi:10.1002/jcc.25873
Islas, R., Heine, T., Ito, K., Schleyer, P. V. R., and Merino, G. (2007). Boron Rings Enclosing Planar Hypercoordinate Group 14 Elements. J. Am. Chem. Soc. 129, 14767–14774. doi:10.1021/ja074956m
Ito, K., Pu, Z., Li, Q.-S., and Schleyer, P. V. R. (2008). Cyclic Boron Clusters Enclosing Planar Hypercoordinate Cobalt, Iron, and Nickel. Inorg. Chem. 47, 10906–10910. doi:10.1021/ic800993b
Jian, T., Chen, X., Li, S.-D., Boldyrev, A. I., Li, J., and Wang, L.-S. (2019). Probing the Structures and Bonding of Size-Selected boron and Doped-boron Clusters. Chem. Soc. Rev. 48, 3550–3591. doi:10.1039/c9cs00233b
Jian, T., Li, W.-L., Popov, I. A., Lopez, G. V., Chen, X., Boldyrev, A. I., et al. (2016). Manganese-centered Tubular boron Cluster - MnB16−: A New Class of Transition-Metal Molecules. J. Chem. Phys. 144, 154310. doi:10.1063/1.4946796
Jiang, Z.-Y., Chen, T.-T., Chen, W.-J., Li, W.-L., Li, J., and Wang, L.-S. (2021). Expanded Inverse-Sandwich Complexes of Lanthanum Borides: La2B10- and La2B11-. J. Phys. Chem. A. 125, 2622–2630. doi:10.1021/acs.jpca.1c01149
Kiran, B., Bulusu, S., Zhai, H.-J., Yoo, S., Zeng, X. C., and Wang, L.-S. (2005). Planar-to-tubular Structural Transition in boron Clusters: B20 as the Embryo of Single-Walled boron Nanotubes. Proc. Natl. Acad. Sci. 102, 961–964. doi:10.1073/pnas.0408132102
Li, W.-L., Romanescu, C., Galeev, T. R., Piazza, Z. A., Boldyrev, A. I., and Wang, L.-S. (2012). Transition-Metal-Centered Nine-Membered Boron Rings: MⓒB9 and MⓒB9- (M = Rh, Ir). J. Am. Chem. Soc. 134, 165–168. doi:10.1021/ja209808k
Li, W.-L., Romanescu, C., Piazza, Z. A., and Wang, L.-S. (2012). Geometrical Requirements for Transition-Metal-Centered Aromatic boron Wheels: the Case of VB10−. Phys. Chem. Chem. Phys. 14, 13663–13669. doi:10.1039/c2cp42218b
Li, W. L., Ivanov, A. S., Federič, J., Romanescu, C., Černušák, I., Boldyrev, A. I., et al. (2013). On the Way to the Highest Coordination Number in the Planar Metal-Centred Aromatic Ta©B10- Cluster: Evolution of the Structures of TaB(n)- (N = 3-8). J. Chem. Phys. 139, 104312–104313. doi:10.1063/1.4820401
Li, W. L., Chen, X., Jian, T., Chen, T. T., Li, J., and Wang, L. S. (2017). From Planar boron Clusters to Borophenes and Metalloborophenes. Nat. Rev. Chem. 1, 1–9. doi:10.1038/s41570-017-0071
Li, W. L., Jian, T., Chen, X., Chen, T. T., Lopez, G. V., Li, J., et al. (2016). The Planar CoB 18 − Cluster as a Motif for Metallo‐Borophenes. Angew. Chem. Int. Ed. 55, 7358–7363. doi:10.1002/anie.201601548
Liang, W.-y., Das, A., Dong, X., and Cui, Z.-h. (2018). Lithium Doped Tubular Structure in LiB20 and LiB20−: a Viable Global Minimum. Phys. Chem. Chem. Phys. 20, 16202–16208. doi:10.1039/c8cp01376d
Liu, X., Zhao, G. F., Guo, L. J., Jing, Q., and Luo, Y. H. (2007). Structural, Electronic, and Magnetic Properties of MBn (M = Cr, Mn, Fe, Co, Ni, N≤7) Clusters. Phys. Rev. A. 75, 063201. doi:10.1103/physreva.75.063201
Lu, T., and Chen, F. (2012). Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 33, 580–592. doi:10.1002/jcc.22885
Lu, T., Chen, Q., and Liu, Z. (2020). A Thorough Theoretical Exploration of Intriguing Characteristics of Cyclo[18]carbon: Geometry, Bonding Nature, Aromaticity, Weak Interaction, Reactivity, Excited States, Vibrations, Molecular Dynamics and Various Molecular Properties. ChemRxiv, 468–475. doi:10.26434/chemrxiv.11320130
Lu, X.-Q., Gao, C.-Y., Wei, Z., and Li, S.-D. (2021). Cage-like La4B24 and Core-Shell La4B290/+/− : Perfect Spherically Aromatic Tetrahedral Metallo-Borospherenes. J. Mol. Model. 27, 130. doi:10.1007/s00894-021-04739-8
Luo, Q. (2008). Boron Rings Containing Planar Octa-And Enneacoordinate Cobalt, Iron and Nickel Metal Elements. Sci. China Ser. B-chem. 51, 607–613. doi:10.1007/s11426-008-0073-9
Miao, C., Guo, J., and Li, S. (2009). M@B9 and M@B10 Molecular Wheels Containing Planar Nona- and Deca-Coordinate Heavy Group 11, 12, and 13 Metals (M=Ag, Au, Cd, Hg, in, Tl). Sci. China Ser. B-chem. 52, 900–904. doi:10.1007/s11426-009-0086-z
Mitchell, R. H. (2001). Measuring Aromaticity by NMR. Chem. Rev. 101, 1301–1316. doi:10.1021/cr990359+
Pan, L.-L., Li, J., and Wang, L.-S. (2008). Low-lying Isomers of the B9− boron Cluster: The Planar Molecular Wheel versus Three-Dimensional Structures. J. Chem. Phys. 129, 024302. doi:10.1063/1.2948405
Pan, S., Kar, S., Saha, R., Osorio, E., Zarate, X., Zhao, L., et al. (2018). Boron Nanowheels with Axles Containing Noble Gas Atoms: Viable Noble Gas Bound MB10 − Clusters (M=Nb, Ta). Chem. Eur. J. 24, 3590–3598. doi:10.1002/chem.201705790
Piazza, Z. A., Hu, H.-S., Li, W.-L., Zhao, Y.-F., Li, J., and Wang, L.-S. (2014). Planar Hexagonal B36 as a Potential Basis for Extended Single-Atom Layer boron Sheets. Nat. Commun. 5, 3113. doi:10.1038/ncomms4113
Pople, J. A., Head‐Gordon, M., and Raghavachari, K. (1987). Quadratic Configuration Interaction. A General Technique for Determining Electron Correlation Energies. J. Chem. Phys. 87, 5968–5975. doi:10.1063/1.453520
Popov, I. A., Piazza, Z. A., Li, W. L., Wang, L. S., and Boldyrev, A. I. (2013). A Combined Photoelectron Spectroscopy and Ab Initio Study of the Quasi-Planar B24(-) Cluster. J. Chem. Phys. 139, 144307. doi:10.1063/1.4824156
Popov, I. A., Li, W.-L., Piazza, Z. A., Boldyrev, A. I., and Wang, L.-S. (2014). Complexes between Planar Boron Clusters and Transition Metals: A Photoelectron Spectroscopy and Ab Initio Study of CoB12- and RhB12-. J. Phys. Chem. A. 118, 8098–8105. doi:10.1021/jp411867q
Pu, Z., Ito, K., Schleyer, P. v. R., and Li, Q.-S. (2009). Planar Hepta-, Octa-, Nona-, and Decacoordinate First Row D-Block Metals Enclosed by Boron Rings. Inorg. Chem. 48, 10679–10686. doi:10.1021/ic901377h
Pyykkö, P., and Atsumi, M. (2009). Molecular Single-Bond Covalent Radii for Elements 1-118. Chem. Eur. J. 15, 186–197. doi:10.1002/chem.200800987
Ren, M., Jin, S., Wei, D., Jin, Y., Tian, Y., Lu, C., et al. (2019). NbB12−: a New Member of Half-sandwich Type Doped boron Clusters with High Stability. Phys. Chem. Chem. Phys. 21, 21746–21752. doi:10.1039/c9cp03496j
Romanescu, C., Galeev, T. R., Li, W.-L., Boldyrev, A. I., and Wang, L.-S. (2011). Aromatic Metal-Centered Monocyclic Boron Rings: CoB8− and RuB9−. Angew. Chem. Int. Ed. 50, 9334–9337. doi:10.1002/anie.201104166
Romanescu, C., Galeev, T. R., Li, W.-L., Boldyrev, A. I., and Wang, L.-S. (2013). Geometric and Electronic Factors in the Rational Design of Transition-Metal-Centered boron Molecular Wheels. J. Chem. Phys. 138, 134315. doi:10.1063/1.4798935
Romanescu, C., Galeev, T. R., Li, W.-L., Boldyrev, A. I., and Wang, L.-S. (2013). Transition-Metal-Centered Monocyclic Boron Wheel Clusters (MBn): A New Class of Aromatic Borometallic Compounds. Acc. Chem. Res. 46, 350–358. doi:10.1021/ar300149a
Romanescu, C., Galeev, T. R., Sergeeva, A. P., Li, W.-L., Wang, L.-S., and Boldyrev, A. I. (2012). Experimental and Computational Evidence of Octa- and Nona-Coordinated Planar Iron-Doped boron Clusters: FeB8− and FeB9−. J. Organomet. Chem. 721-722, 148–154. doi:10.1016/j.jorganchem.2012.07.050
Tsuneda, T., Song, J. W., Suzuki, S., and Hirao, K. (2010). On Koopmans' Theorem in Density Functional Theory. J. Chem. Phys. 133, 174101–174109. doi:10.1063/1.3491272
Wang, H., Wang, Y., Lv, J., Li, Q., Zhang, L., and Ma, Y. (2016). CALYPSO Structure Prediction Method and its Wide Application. Comput. Mater. Sci. 112, 406–415. doi:10.1016/j.commatsci.2015.09.037
Wang, L.-S. (2016). Photoelectron Spectroscopy of Size-Selected boron Clusters: from Planar Structures to Borophenes and Borospherenes. Int. Rev. Phys. Chem. 35, 69–142. doi:10.1080/0144235x.2016.1147816
Yang, L.-M., Ganz, E., Chen, Z., Wang, Z.-X., and Schleyer, P. v. R. (2015). Four Decades of the Chemistry of Planar Hypercoordinate Compounds. Angew. Chem. Int. Ed. 54, 9468–9501. doi:10.1002/anie.201410407
Yang, X. B., Ding, Y., and Ni, J. (2008). Ab Initio prediction of Stable boron Sheets and boron Nanotubes: Structure, Stability, and Electronic Properties. Phys. Rev. B. 77, 41402. doi:10.1103/physrevb.77.041402
Zhang, H., Li, Y., Hou, J., Tu, K., and Chen, Z. (2016). FeB6 Monolayers: The Graphene-like Material with Hypercoordinate Transition Metal. J. Am. Chem. Soc. 138, 5644–5651. doi:10.1021/jacs.6b01769
Zhang, Y., Lu, X.-Q., Yan, M., and Li, S.-D. (2021). Perfect Spherical Tetrahedral Metallo-Borospherene Ta4B18 as a Superatom Following the 18-Electron Rule. ACS. Omega. 6, 10991–10996. doi:10.1021/acsomega.1c00828
Keywords: molecular wheel, bonding, electron delocalization, dual aromaticity, electronic structure calculation
Citation: Yu R, Pan S and Cui Z-h (2021) OsB9−: An Aromatic Osmium-Centered Monocyclic Boron Ring. Front. Chem. 9:751482. doi: 10.3389/fchem.2021.751482
Received: 01 August 2021; Accepted: 24 August 2021;
Published: 10 September 2021.
Edited by:
Ambrish Kumar Srivastava, Deen Dayal Upadhyay Gorakhpur University, IndiaReviewed by:
Hong-Guang Xu, Chinese Academy of Sciences (CAS), ChinaJifu Sun, Shandong University of Science and Technology, China
Jin-Chang Guo, Shanxi University, China
Copyright © 2021 Yu, Pan and Cui. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sudip Pan, pans@chemie.uni-marburg.de; Zhong-hua Cui, zcui@jlu.edu.cn