
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Chem., 22 September 2021
Sec. Theoretical and Computational Chemistry
Volume 9 - 2021 | https://doi.org/10.3389/fchem.2021.739984
This article is part of the Research TopicDesign of Two-Dimensional Functional Materials and NanodevicesView all 18 articles
A heavy element is a special character for high thermoelectric performance since it generally guarantees a low lattice thermal conductivity. Here, we unexpectedly found a promising thermoelectric performance in a two-dimensional semiconducting monolayer consisting of a light boron element. Using first-principles combined with the Boltzmann transport theory, we have shown that in contrast to graphene or black phosphorus, the boron monolayer has a low lattice thermal conductivity arising from its complex crystal of hexagonal vacancies. The conduction band with an intrinsic camelback shape leads to the high DOS and a high n-type Seebeck coefficient, while the highly degenerate valence band along with the small hole effective mass contributes to the high p-type power factor. As a result, we obtained the p-type thermoelectric figure of merit up to 0.96 at 300 K, indicating that the boron monolayer is a promising p-type thermoelectric material.
In the past decade, people devoted themselves to improve the thermoelectric efficiency by trying to individually control the thermoelectric coefficients through low-dimensional crystals such as single layers, nanowires, 2D heterostructures, and nanotubes. The thermoelectric performance of a material is usually characterized by the dimensionless figure of merit ZT = S2σT/κ, where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the thermal conductivity including both electronic and lattice contributions, and T is the absolute temperature, respectively (Mohanraman et al., 2015; Hu et al., 2021). High ZT requires a superior electronic transport but a minimized phonon transport at the same time, the latter usually arises from heavy elements (Ding et al., 2016). For instance, the lattice thermal conductivity of traditional commercial bulk thermoelectric materials such as Bi2Te3 and PbTe are lower than 1 W/mK (Pei and Liu, 2012; Hellman and Broido, 2014). Although the thermoelectric coefficient in some cases can be individually controlled in a low-dimensional crystal, the high lattice thermal conductivity still prevents a striking improvement of ZT (Kumar and Schwingenschlögl, 2015).
Balandin et al. (2008) experimentally reported that the thermal conductivity of single-layer graphene is higher than 4000 W/mK at room temperature. For monolayer MoS2, it is about 100 W/mK at 300 K based on Yang’s report (Jin et al., 2015). Using a molecular dynamics simulation, Xu et al. (2015) obtained the lattice thermal conductivity of phosphorene along the zigzag direction that is higher than 150 W/mK at 300 K. Among these popular single-layer crystals, it was found that an extremely high thermal conductivity leads to poor ZT, which can be ascribed to the following two factors: 1) light elements with high vibration frequency and 2) large atomic weight difference forbids the anharmonic scattering. In this regard, we intended to think that is there possibility to achieve promising thermoelectric transport in other single-layer crystal consisting of light elements? In recent years, boron, one of the carbon’s nearest neighbors, demonstrated the polymorphism in two-dimensional crystals, which are called borophene. However, most of the boron monolayers were found to be metallic by experiment or theory. Interestingly, Hu et al. recently proposed a series of semiconducting boron monolayers formulated by the connected network of hexagonal vacancies (Xu et al., 2017). Such semiconducting phases of the boron monolayer are expected to achieve in experiments since the controlled synthesis of the boron monolayer is a mature technology (Kong et al., 2018; Kiraly et al., 2019).
The semiconducting
The first-principles calculations were performed within the framework of density function theory (DFT) using projector-augmented wave (PAW) (Perdew et al., 1997) pseudopotentials and Perdew–Burke–Ernzerhof (PBE) (Kresse and Furthmüller, 1996) exchange correlation functionals as implemented in VASP (Tran and Blaha, 2009). To construct the single-layer crystal, a 15-Å-thick vacuum slab was added along the z-direction. The plane-wave cutoff energy was set to 400 eV and the Monkhorst–Pack k mesh was 15 × 15 × 1. Geometry optimization was converged until the force acting on the ions become smaller than 10−3 eV/Å. When we calculated the electronic structure, a modified Becke–Johnson (mBJ) (Tran and Blaha, 2009) functional was also considered to yield the accurate effective mass and bandgap.
The electronic transport properties were calculated using the Boltzmann transport equation (BTE) under a constant relaxation time approximation as implemented in BoltzTraP (Madsen and Singh, 2006). A rigid band approximation is used to treat doping, and the Fermi level shifts up for n-type doping while down for the p-type. However, within this approximation, the Seebeck coefficient can be calculated independent of carrier relaxation time τ, while the evaluation of electrical conductivity still requires the knowledge of τ. In this regard, we employed deformation potential theory based on effective mass approximation to calculate τ (Herring and Vogt, 1956). At last, we performed phonon BTE solution as implemented in the ShengBTE (Li et al., 2014) package to calculate lattice thermal conductivity. Second- and third-order interatomic force constants (IFCs) are quite necessary inputs for pBTE, which were obtained from DFT calculations using a converged 4 × 4 × 1 supercell. The phonon spectrum was obtained from the Phonopy code (Togo et al., 2008), and a converged cutoff distance of 0.4 nm for interactive distance was used in calculating anharmonic IFCs.
Figure 1A shows the crystal structure of the
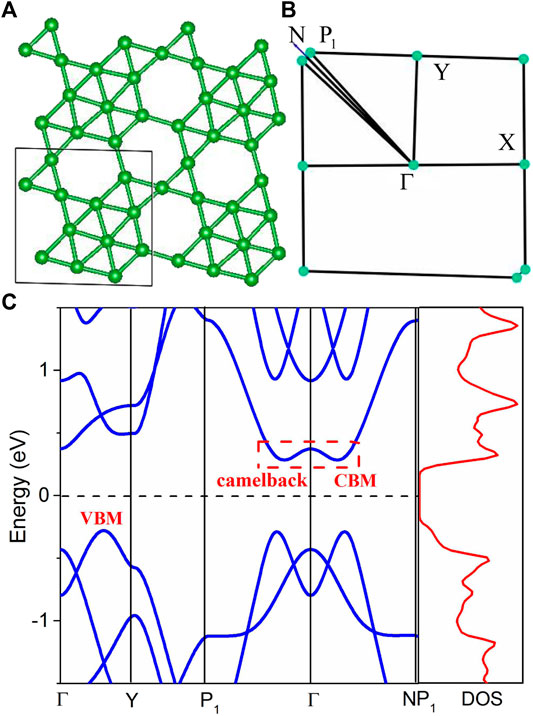
FIGURE 1. The atomic structure (A) and the Brillouin zone path (B) of the
As shown in Figure 1C, the calculated band structure of the
Interestingly, the band structure of the
Calculated electronic transport properties including the Seebeck coefficient, electrical conductivity, and the power factor at room temperature are shown in Figure 2. The Seebeck coefficient decreases while the electrical conductivity increases with the increase of carrier density since they are inversely related to carrier density. In this regard, the power factor cannot be improved infinitely but can be optimized by modulating carrier density. In Figure 2A, the higher n-type Seebeck coefficient can be attributed to the camelback-shaped band, as discussed above. To obtain the electrical conductivity as shown in Figure 2B, we employed deformation potential theory (Herring and Vogt, 1956) to calculate the carrier relaxation time. Calculated results are shown in Table 1. It is crucial to find that the lower deformation potential constant of holes reflects the minimal sensitivity of valence band maximum to deformation. Along with the smaller hole effective mass, a high hole mobility and long hole relaxation time were obtained, as compared to an electron. As a result, the p-type power factor is much higher than n-type, as shown in Figure 2C. The maximum power factor of the p-doped semiconducting boron monolayer reaches 121 mW/mK2 at an optimal carrier density of 3.14 × 1012 cm−2, while it is only about 17mW/mK2 in monolayer MoS2 (Jin et al., 2015). The Seebeck coefficient under this optimal carrier density for n- and p-type are 263 µV/K and 175 µV/K, respectively, which are the standard values of thermoelectric materials (Sun and Singh, 2016).
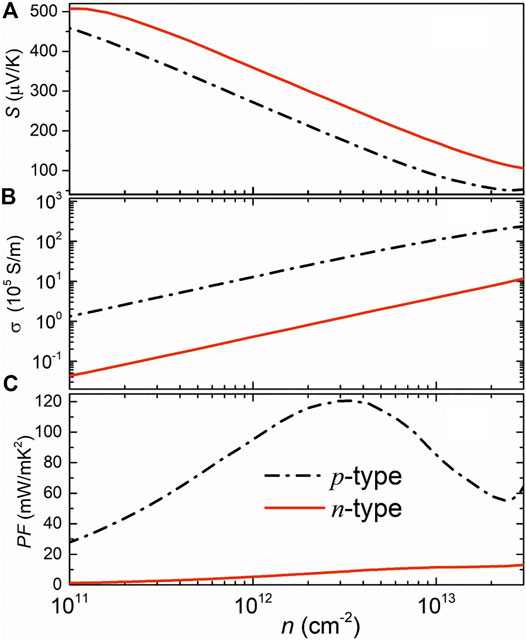
FIGURE 2. Calculated Seebeck coefficient (A), electrical conductivity (B), and the power factor (C) of the
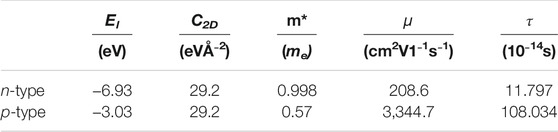
TABLE 1. Calculated DP constant, elastic modulus, carrier effective mass, carrier mobility, and carrier relaxation time at 300 K.
Calculated phonon dispersion of the
Figure 4A shows the calculated lattice thermal conductivity of the boron monolayer with respect to temperature. It can be seen that the BTE results are well fitted with κ∝1/T. The lattice thermal conductivity at room temperature is about 20 W/mK, which is much lower than that of graphene (above 4000 W/mK) (Balandin et al., 2008), phosphorene (above 150 W/mK along zigzag) (Xu et al., 2015) consisting of light element, and also monolayer MoS2 (about 100 W/mK) (Jin et al., 2015). Thus, the
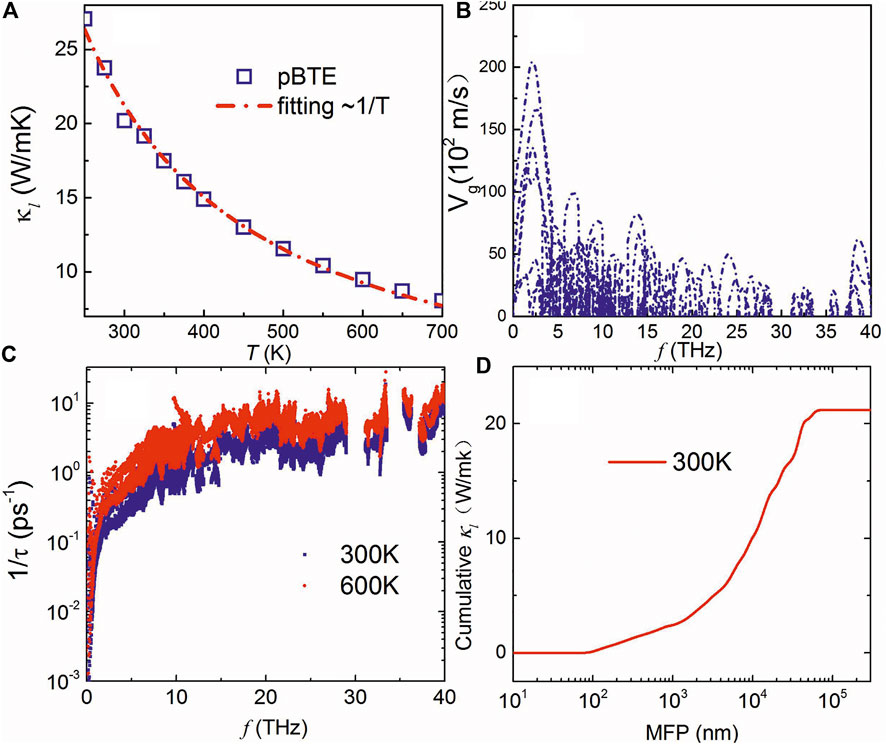
FIGURE 4. (A) Calculated lattice thermal conductivity with respect to temperature, phonon group velocity (B), and anharmonic scattering (C) of the
Combining the electronic and phonon transport properties, we evaluated the thermoelectric performance of the
We have investigated the thermoelectric performance of a semiconducting
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
GD developed the idea for the study. YH and GD did the analyses and wrote the study. DL, RL, SL, CF, and DFL conceived and designed the study. All authors analyzed the data and were involved in writing the manuscript.
This work is supported by the National Natural Science Foundation of China (Grant No.11804040).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer (HY) declared a past coauthorship with one of the authors (GD) to the handling editor.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Balandin, A. A., Ghosh, S., Bao, W., Calizo, I., Teweldebrhan, D., Miao, F., et al. (2008). Superior thermal Conductivity of Single-Layer Graphene. Nano Lett. 8, 902–907. doi:10.1021/nl0731872
Ding, G., Carrete, J., Li, W., Gao, G. Y., and Yao, K. (2016). Ultralow Lattice thermal Conductivity in Topological Insulator TlBiSe2. Appl. Phys. Lett. 108, 233902. doi:10.1063/1.4953588
Ding, G., He, J., Gao, G. Y., and Yao, K. (2018). Two-dimensional MoS2-MoSe2 Lateral Superlattice with Minimized Lattice thermal Conductivity. J. Appl. Phys. 124, 165101. doi:10.1063/1.5051067
Ding, G., Hu, Y., Li, D., and Wang, X. (2019). A Comparative Study of Thermoelectric Properties between Bulk and Monolayer SnSe. Results Phys. 15, 102631. doi:10.1016/j.rinp.2019.102631
Ding, G., Li, S., and He, J. (2019). Origins of Promising Thermoelectric Performance in Quaternary Selenide BaAg2SnSe4. Appl. Phys. Express 12, 071006. doi:10.7567/1882-0786/ab29e1
Eremeev, S. V., Koroteev, Y. M., and Chulkov, E. V. (2010). Ternary Thallium-Based Semimetal Chalcogenides Tl-V-VI2 as a New Class of Three-Dimensional Topological Insulators. JETP Lett. 91, 594–598. doi:10.1134/S0021364010110111
Fei, R., Faghaninia, A., Soklaski, R., Yan, J.-A., Lo, C., and Yang, L. (2014). Enhanced Thermoelectric Efficiency via Orthogonal Electrical and thermal Conductances in Phosphorene. Nano Lett. 14, 6393–6399. doi:10.1021/nl502865s
Ge, X.-J., Yao, K.-L., and Lü, J.-T. (2016). Comparative Study of Phonon Spectrum and thermal Expansion of Graphene, Silicene, Germanene, and Blue Phosphorene. Phys. Rev. B. 94, 165433. doi:10.1103/PhysRevB.94.165433
Hellman, O., and Broido, D. A. (2014). Phonon thermal Transport inBi2Te3from First Principles. Phys. Rev. B. 90, 134309. doi:10.1103/PhysRevB.90.134309
Herring, C., and Vogt, E. (1956). Transport and Deformation-Potential Theory for many-valley Semiconductors with Anisotropic Scattering. Phys. Rev. 101, 944–961. doi:10.1103/PhysRev.101.944
Hu, Y., Li, D., Yin, Y., Li, S., Ding, G., Zhou, H., et al. (2020). The Important Role of Strain on Phonon Hydrodynamics in diamond-like Bi-layer Graphene. Nanotechnology 31, 335711. doi:10.1088/1361-6528/ab8ee1
Hu, Y., Yang, T., Li, D., Ding, G., Dun, C., Wu, D., et al. (2021). Origins of Minimized Lattice thermal Conductivity and Enhanced Thermoelectric Performance in WS2/WSe2 Lateral Superlattice. ACS Omega 6, 7879–7886. doi:10.1021/acsomega.1c00457
Hu, Y., Yin, Y., Li, S., Zhou, H., Li, D., and Zhang, G. (2020). Three-Fold Enhancement of In-Plane Thermal Conductivity of Borophene through Metallic Atom Intercalation. Nano Lett. 20, 7619–7626. doi:10.1021/acs.nanolett.0c03135
Jin, Z., Liao, Q., Fang, H., Liu, Z., Liu, W., Ding, Z., et al. (2015). A Revisit to High Thermoelectric Performance of Single-Layer MoS2. Sci. Rep. 5, 1–7. doi:10.1038/srep18342
Kiraly, B., Liu, X., Wang, L., Zhang, Z., Mannix, A. J., Fisher, B. L., et al. (2019). Borophene Synthesis on Au(111). ACS Nano 13, 3816–3822. doi:10.1021/acsnano.8b09339
Kong, L., Wu, K., and Chen, L. (2018). Recent Progress on Borophene: Growth and Structures. Front. Phys. 13, 138105. doi:10.1007/s11467-018-0752-8
Kresse, G., and Furthmüller, J. (1996). Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B. 54, 11169–11186. doi:10.1103/PhysRevB.54.11169
Kumar, S., and Schwingenschlögl, U. (2015). Thermoelectric Response of Bulk and Monolayer MoSe2 and WSe2. Chem. Mater. 27, 1278–1284. doi:10.1021/cm504244b
Li, W., Carrete, J., A. Katcho, N., and Mingo, N. (2014). ShengBTE: A Solver of the Boltzmann Transport Equation for Phonons. Comp. Phys. Commun. 185, 1747–1758. doi:10.1016/j.cpc.2014.02.015
Madsen, G. K. H., and Singh, D. J. (2006). BoltzTraP. A Code for Calculating Band-Structure Dependent Quantities. Comp. Phys. Commun. 175, 67–71. doi:10.1016/j.cpc.2006.03.007
Mohanraman, R., Lan, T.-W., Hsiung, T.-C., Amada, D., Lee, P.-C., Ou, M.-N., et al. (2015). Engineering Nanostructural Routes for Enhancing Thermoelectric Performance: Bulk to Nanoscale. Front. Chem. 3, 63. doi:10.3389/fchem.2015.00063
Pei, Y.-L., and Liu, Y. (2012). Electrical and thermal Transport Properties of Pb-Based Chalcogenides: PbTe, PbSe, and PbS. J. Alloys Comp. 514, 40–44. doi:10.1016/j.jallcom.2011.10.036
Peng, H., Kioussis, N., and Snyder, G. J. (2014). Elemental Tellurium as a Chiralp-type Thermoelectric Material. Phys. Rev. B. 89, 195206. doi:10.1103/PhysRevB.89.195206
Perdew, J. P., Burke, K., and Ernzerhof, M. (1997). Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)]. Phys. Rev. Lett. 78, 1396. doi:10.1103/PhysRevLett.77.386510.1103/physrevlett.78.1396
Sun, J., and Singh, D. J. (2016). Thermoelectric Properties ofMg2(Ge,Sn): Model and Optimization ofZT. Phys. Rev. Appl. 5, 024006. doi:10.1103/PhysRevApplied.5.024006
Togo, A., Oba, F., and Tanaka, I. (2008). First-principles Calculations of the Ferroelastic Transition between Rutile-type andCaCl2-typeSiO2at High Pressures. Phys. Rev. B. 78, 134106. doi:10.1103/PhysRevB.78.134106
Tran, F., and Blaha, P. (2009). Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential. Phys. Rev. Lett. 102, 226401. doi:10.1103/PhysRevLett.102.226401
Xu, S.-G., Li, X.-T., Zhao, Y.-J., Liao, J.-H., Xu, W.-P., Yang, X.-B., et al. (2017). Two-Dimensional Semiconducting Boron Monolayers. J. Am. Chem. Soc. 139, 17233–17236. doi:10.1021/jacs.7b08680
Keywords: boron monolayer, thermoelectric, first-principles, Boltzmann, phonon
Citation: Hu Y, Li D, Liu R, Li S, Feng C, Li D and Ding G (2021) Promising Thermoelectric Performance in Two-Dimensional Semiconducting Boron Monolayer. Front. Chem. 9:739984. doi: 10.3389/fchem.2021.739984
Received: 12 July 2021; Accepted: 09 August 2021;
Published: 22 September 2021.
Edited by:
Guangzhao Wang, Yangtze Normal University, ChinaCopyright © 2021 Hu, Li, Liu, Li, Feng, Li and Ding. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guangqian Ding, ZGluZ2dxQGNxdXB0LmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.