Atomic Clusters: Structure, Reactivity, Bonding, and Dynamics

Atomic clusters lie somewhere in between isolated atoms and extended solids with distinctly different reactivity patterns. They are known to be useful as catalysts facilitating several reactions of industrial importance. Various machine learning based techniques have been adopted in generating their global minimum energy structures. Bond-stretch isomerism, aromatic stabilization, Rener-Teller effect, improved superhalogen/superalkali properties, and electride characteristics are some of the hallmarks of these clusters. Different all-metal and nonmetal clusters exhibit a variety of aromatic characteristics. Some of these clusters are dynamically stable as exemplified through their fluxional behavior. Several of these cluster cavitands are found to be agents for effective confinement. The confined media cause drastic changes in bonding, reactivity, and other properties, for example, bonding between two noble gas atoms, and remarkable acceleration in the rate of a chemical reaction under confinement. They have potential to be good hydrogen storage materials and also to activate small molecules for various purposes. Many atomic clusters show exceptional opto-electronic, magnetic, and nonlinear optical properties. In this Review article, we intend to highlight all these aspects.

Introduction

A cluster is defined as a finite aggregation of atoms, starting with as low as two atoms and extending up to an upper bound of some hundred thousand atoms (Herr, 1993; Corrigan and Dehnen, 2017). A theoretical study elucidates that cluster properties strongly depend on the geometry of the isolated cluster and the topology of the cluster sample. F. A. Cotton first used the term cluster for compounds with metal–metal bonds. Nonmetallic atomic clusters came into the limelight later, from both theoretical and experimental studies. The unique size-dependent properties of clusters are distinct from the molecules and bulk solids (Sergeeva et al., 2014). Experimental and theoretical methods on cluster research have seen substantial amount of improvement over the years in discovering a diversity of size-specific phenomena and physicochemical cluster properties (Jena and Castleman, 2010). Various physicochemical properties of metal clusters such as optical, magnetic, thermal, chemical properties differ remarkably from their bulk counterparts (Tsukuda and Hakkinen, 2015). In the last few decades, several studies have been reported on the ligand protected metal clusters, viz. phosphine-protected small Au cluster, thiolate (RS)-protected Au nanoparticles (Brust et al., 1994), etc. For small metal clusters (<∼100 atoms), the electronic structures are not continuous as in the bulk metals, but rather discretized, which is the primary reason for different physicochemical properties and functionalities in small clusters and bulk metal (Sharma et al., 2017). Studies have shown that clusters made of atoms with appropriate size and composition could potentially mimic the chemistry of elemental atoms in periodic table, and hence are known as superatoms (Li et al., 2008). Various experimental techniques such as laser ablation coupled with mass spectrometry, photoelectron spectroscopy have been employed to get insights into the atomic clusters. Along with experimental studies, theoretical investigations are required to get a better understanding of their geometric arrangement and corresponding properties (Srivastava, 2021).

A large number of theoretical studies have been reported dealing with finding the minimum energy structures of pure elemental clusters by using different optimization algorithms. The potential energy surface (PES) of various atomic clusters is explored to minimize their energy functional with the final objective of locating their global minimum (GM). Different optimization methods such as genetic algorithm (Holland, 1992) (GA), basin hopping (BH) algorithm (Wales and Doye, 1997), particle swarm optimization (PSO) algorithm (Bai, 2010), adaptive particle swarm optimization (APSO) (Zhan and Zhang, 2008), simulated annealing (SA) (Woodley et al., 1999), artificial bee colony optimization (ABC) (Karaboga and Basturk, 2007), honey bee mating optimization (HBMO) (Pham et al., 2005), ant colony optimization (ACO) (Colorni et al., 1991), heuristic algorithm combined with the surface and interior operators (HA-SIO), fast annealing evolutionary algorithm (FAEA), firefly algorithm (FA) (Yang, 2010). etc. are increasingly being used to solve the optimization problem in a time- and cost-efficient manner. Various models/empirical potentials (EPs) such as Lennard–Jones (LJ), Born–Mayer, Sutton–Chen, Gupta and Murrell–Mottram potentials can effectively explain the bonding within various clusters. A number of studies performed by Chattaraj et al. reveal that PSO is more efficient than commonly used techniques such as GA, SA, and BH for finding the GM of small clusters (Mitikiri et al., 2018; Jana et al., 2019). Further developments over PSO algorithm have been accomplished. Global optimization of boron clusters (B₅ and B₆) has been studied using an advanced PSO approach by Mitikiri et al. (2018). Jana et al. (2019) performed a similar study on carbon clusters, C_n (n = 3–6,10) by using a modified PSO algorithm. Mitra et al. (2020) reported the global optimization of Al₄^2- clusters by using firefly algorithm along with DFT.

The concept of trapping atoms and small molecules into the hollow cavity of clusters has shown several applications in biology (Cagle et al., 1996; Thrash et al., 1999; Wilson et al., 1999) and electrical engineering (Cioslowski and Nanayakkara, 1992). Pan et al. (2018) reported the encapsulation of noble gas (Ng) atoms into the B₄₀ host moiety, which is shown to have a fluxional character (Moreno et al., 2014). The dynamical study of the aforementioned system showed that the fluxional character persists even after the encapsulation. Smaller cages such as C₂₀H₂₀ (Cross et al., 1999; Jiménez-Vázquez et al., 2001), C₁₀H₁₆ (Haaland et al., 2004), BN cages (B₁₂N₁₂ and B₁₆N₁₆) (Khatua et al., 2014a), Pb₁₂^2-, and Sn₁₂^2- (Sekhar et al., 2017) can act as host molecules to endohedrally trapped noble gas atoms. Cucurbit[n]urils, abbreviated as CB[n]s, n being the number of gycoluril units, can also act as host for different guest molecules including metal cations, organic dyes, drugs, halide ions, etc. (Lagona et al., 2005; Pan et al., 2013a). CB[7] was also reported to bind different guest compounds such as organic dyes (e.g., Stilbenes, naphthalene), viologens, and metal complexes (e.g., Oxaliplatin) applicable in cancer treatment (Wagner et al., 2003). In 2017, Pan et al. (2017) have reported the adsorption of 14 molecules, viz., CH₄, C₂H₂, C₂H₄, C₂H₆, F₂, Cl₂, NO₂, NO, CO, CO₂, SO₂, H₂S, N₂, H₂ endohedrally within the hydrophobic inner cavity of CB[7]. CB[6] is also known to encapsulate noble gas atoms (Pan et al., 2015). Chakraborty et al. (Chakraborty and Chattaraj, 2015) reported the accommodation of noble gas atoms within the BN-doped (3, 3) single-walled carbon nanotubes. The Ng binding ability of BeX (X = SO₄, CO₃, O) has been reported by Saha et al. (2015). Pan et al. (2014) have explored the stability of Ng-bound SiH₃⁺ cluster ions. An emerging host molecule is the basket-shaped octa acid (OA) cavitand that can encapsulate different gas molecules (Chakraborty et al., 2016). Various steroids (Liu and Gibb, 2008), hydrophobic moieties such as ethane, ethylene, acetylene (Stang and Diederich, 2008; Hu et al., 2009; Florea and Nau, 2011; Zhang et al., 2011; Yang et al., 2015; Chong et al., 2016) have been confined inside OA. The encapsulation of gas molecules, especially the hazardous ones, by the cluster cavity has great applications in environmental chemistry. Encapsulation of greenhouse gases (CO₂) (Zhang and Chen, 2009; Jin et al., 2010; Kim et al., 2010; Jin et al., 2011; Mastalerz et al., 2011; Lü et al., 2014), air pollutants (NO₂) (Pan et al., 2017), and poisonous gases (CO, NO) using molecular cages has applications in reducing their negative impact on the atmosphere. N₂ encapsulation (Msayib et al., 2009; Akhtar et al., 2012; Schneider et al., 2012) is yet another important research topic in environmental chemistry. Chakraborty et al. (2016) reported a set of small gaseous molecules (C₂H₂, C₂H₄, C₂H₆, CO, CO₂, NO₂, NO, N₂, H₂⁻), and rare gas atoms as guest molecules for the OA host system. In fact, OA is a very efficient reaction vessel for accommodating various different guest molecules. Li⁺, Na⁺, K⁺, Be²⁺, Mg²⁺, Ca²⁺, Li₃O⁺, Na₃O⁺, K₃O⁺ and various nucleobases can occupy the basket-shaped octa acid cavitand as reported by Chakraborty and Chattaraj (2018).

In recent days, the conservation of the atmosphere and the desire to save up fuel for the upcoming generations has been a major concern in the scientific community that led to the search for alternatives of fossil fuel. Hydrogen, being renewable, recyclable, environment friendly, and abundantly available in nature, is now a globally acceptable fuel source with the potential to replace fossil fuels in the near future. The challenge, however, is designing compatible storage and transport materials. To that end, hydrogen-storing capacity of metal-organic-frameworks (MOF) (Rosi et al., 2003; Rowsell and Yaghi, 2005), covalent-organic-frameworks (COF) (Kuc et al., 2007; Cabria et al., 2008), clathrate hydrates (Lee et al., 2005; Chattaraj et al., 2011), polymers (McKeown et al., 2006), carbon nanotubes, BN cages, fullerene, grapheme-like materials (Froudakis, 2001; Deng et al., 2004; Heine et al., 2004; Sun et al., 2005; Wu et al., 2008), metal hydrides (Lee et al., 2005) have been explored. Pan et al. (2012a) performed a theoretical study on the H₂-storing capability of some Li-doped clusters and super-alkalis. Zhu et al. (2010) have shown cucurbiturils acting as a promising candidate for hydrogen storage. Pan et al. (2013a) have discussed the hydrogen storage capability of the CB[7] system. A different class of compound, alkali-doped carbon materials (graphene sheet and single-walled carbon nanotubes), have been designed for reversible hydrogen storage for transportation purposes by Wei-Qiao Deng et al. (2004). On the other hand, very explosive acetylene can be stored within the porous MOF-505 analogue as reported by Yunxia Hu et al. (2009).

The confinement effect on atoms and molecules has intrigued both theoreticians and experimentalists alike. It brings out interesting changes in the energy levels of the confined systems, their bonding, reactivity, and properties (Grochala et al., 2007; Schettino and Bini, 2007; Sabin and Brandas, 2009; Gubbins et al., 2011; Chakraborty and Chattaraj, 2019; Pal and Chattaraj, 2021). Khatua et al. (2014b) have performed a theoretical investigation on the entrapment of (HF)₂ in C_n (n = 60, 70, 80, 90) cages. Although CO and N₂ are isoelectric species, the latter is known to be pretty inert owing to its high ionization potential, low electron affinity, and high frontier orbital energy gap (ΔE_HOMO-LUMO). Thus, N₂ capture in various transition metal complexes has proven to induce bond activation that has various industrial applications (Chatt and Leigh, 1972; Yandulov and Schrock, 2003; Latysheva et al., 2012; Bergman et al., 2013; Hoffman et al., 2013). In this regard, Saha et al. (2017) reported the CO and N₂ bound metal supported boron clusters (MB₁₂^-, M = Co, Rh, Ir) which form a spinning umbrella-like structure and activate the bound molecules. Boron clusters have found profound applications in material science owing to their ability to act as nanomaterial building blocks. Their property to act as such is due to a bowl-like structure with an outer rim (B₉) and an inner well (B₃).

Along with the coordination and inorganic cages, various organic cavitands can also be considered host system for encapsulation. One such class of compounds is the cucurbiturils. Chemical reactions catalyzed by host–guest interactions are comparable to those catalyzed by enzymes (Dong et al., 2012). Hennig et al. (2007) successfully induced protease inhibition using the host–guest interaction with CB[7]. In addition to CB[7], ExBox⁺⁴ (Barnes et al., 2013) can also act as an organic host molecule that can encapsulate a wide array of guest moieties. Chakraborty et al. (2017) performed a theoretical study on [4+2] cycloaddition reaction confined within CB[7] and ExBox⁺⁴ host systems.

In recent times, low dimensional materials are being given more and more attention to be used as host moiety. Graphene has provided us with a plethora of highly efficient devices such as gas sensors, spintronic devices, nanoelectronics, and optoelectronic devices (Chakraborty and Chattaraj, 2017). An inorganic counterpart of graphene is the boron nitride doped system that can be functionalized with OLi₄, CLi₆, NLi₅, BLi₇, Al₁₂Be to achieve some interesting properties (Chakraborty and Chattaraj, 2017). The M₃O⁺ (M = Li, Na, K) functionalized graphene nanoflakes (Chakraborty and Chattaraj, 2016a) are known to sequestrate various polar molecules such as CO, NO, and CH₃OH. Sequestration of gas molecules such as H₂, O₂, O₃, CO, NO, and H₂O through bare boron nitride flakes (BNF) and metal oxide, MO (M = Cu, Ag, Au) functionalized BNF are also reported (Chakraborty and Chattaraj, 2016b). In this review we report some optimization techniques for the generation of minimum energy structures of some selected clusters and also the bonding, reactivity, and different properties of some selected confined systems. Aromatic behavior and electride properties of some clusters are also investigated.

Theoretical Background and Computational Details

Before optimizing the geometry of any system, we carefully ponder over the requirement of the study and select the level of theory maintaining a parity between the level of accuracy required and the computational cost to be incurred. Most often, the easiest way is to take into consideration the experimental data (if available) and select accordingly. The systems discussed in this article are optimized using the computational chemistry software package, Gaussian 09 (Frisch et al., 2009). We have used B3LYP (Lee et al., 1988; Becke, 1992), BP86 (Perdew, 1986a; Perdew, 1986b; Becke, 1988), ωb97X-D (Chai and Head-Gordon, 2008), PBE (Perdew et al., 1996; Perdew et al., 1997), TPSSTPSS (Staroverov and Scuseria, 2003; Tao et al., 2003), M06, M06-2X (Zhao and Truhlar, 2008), and M05-2X (Zhao et al., 2006) functionals for carrying out DFT calculations of various systems. The exact level of theory (method and basis set) chosen for the individual case studies is mentioned in the Results and Discussion section. Relativistic effects for heavier atoms are taken care of by effective core potentials (ECPs). The stationary states are better understood from the harmonic vibrational frequencies. The minimum energy structure and the transition state (TS) are identified with the presence of zero and one imaginary frequency, respectively.

The atomic charges, nature of interactions present within the systems, and the possible bond formation are analyzed with the help of natural population analysis (NPA) (Reed et al., 1985), Wiberg bond indices (WBI) (Wiberg, 1968) in the NBO scheme (Reed et al., 1988). The electron density topology is mapped using Bader’s quantum theory of atoms-in-molecules (QTAIM) (Bader, 1985) in Multiwfn (Lu and Chen, 2012). Parameters such as electron density [ρ(r_c)], total electron energy density [H(r_c)], local kinetic energy density [G(r_c)], local potential energy density [V(r_c)], and Laplacian of electron density [∇²ρ(r)] are computed at the bond critical points (BCPs) and they help analyze the extent of covalent or ionic character present along that bond path. The NCI index reveals the localized binding interaction in a system, and the plot can be visualized as red, blue, or green regions in the NCIPLOT program (Contreras-García et al., 2011) depending on whether the interaction is repulsive, H-bond, or van der Waals, respectively. The nonlinear optical (NLO) properties are evaluated in terms of average linear polarizability ($\overline{\alpha }$), first (β) and second (${\gamma }_{\mathrm{\Vert }}$) hyperpolarizabilities.

ADF 2013.01 software (Baerends et al., 2013) is utilized to perform the energy decomposition analysis (EDA) (Morokuma, 1971) with the natural orbitals for chemical valence (NOCV) (Mitoraj et al., 2009). The interaction between two selected fragments of the studied system is represented in terms of three attractive and one repulsive energy terms. The attractive term includes electrostatic energy (ΔE_elstat), orbital interaction energy (ΔE_orb), dispersion interaction energy (ΔE_disp), while the repulsive term is known as Pauli repulsion energy (ΔE_Pauli).

$\Delta E_{\mathrm{int}}=\Delta E_{\mathrm{elstat}}+\Delta E_{\mathrm{orb}}+\Delta E_{\mathrm{disp}}+\Delta E_{\mathrm{Pauli}}(1)$

In NOCV, the orbital term is represented as the sum of ΔE^k_orb (pairwise orbital energies) which is related to Δρ^k(r) (pairwise charge contributions).

$\Delta E_{orb}={\displaystyle \sum _k\Delta E_{orb}^k}(2)$

Atom-centered density matrix propagation (ADMP) (Iyengar et al., 2001; Schlegel et al., 2001; Schlegel et al., 2002) in Gaussian 09, and Born-Oppenheimer molecular dynamics (BOMD) in deMon2K software (Koster et al., 2011) are used to perform the dynamic study of the systems under discussion in this article.

For the global optimization study using PSO, ADMP-CNN-PSO, and FA, the algorithms are written in Python 3.7 programming language (Van Rossum and Drake, 2009). The single point energies (SPEs) are calculated using Gaussian 09 at the post-processing step. The calculations for all the clusters are performed using the B3LYP (Lee et al., 1988; Becke, 1992) functional of DFT. The basis set 6-311+G(d,p) (McLean and Chandler, 1980; Raghavachari et al., 1980) is used for the boron clusters, 6-311+G(d) for Al₄²⁻, C₅, and N₄^2-, 6-311G(d) for N₆^4-, and LANL2DZ (Dunning and Hay, 1977; Wadt and Hay, 1985; Hay and Wadt, 1985a; Hay and Wadt, 1985b) with ECPs for Au_n (n = 2–8) and Au_nAg_m (2 ≤ (n+m) ≤ 8). The algorithms are executed in a server with two Intel 2.70 GHz Xeon E5-2697 v2 processors (each with 12 cores and 30 threads) and a 256 GB RAM. The software Keras (Chollet, 2015) is used for interfacing with Python 3.7 with convolution neural networks (CNN).

Results and Discussion

Global Optimization Using Machine Learning Techniques

Minimization of a system’s energy functional is the most fundamental step in the determination of its ground state. Reaching the global minimum (GM) geometry, however, poses a number of challenges, the most important being the high probability of getting stuck in local minima in the PES. Swarm intelligence (SI)-based algorithms have turned out to be very effective in searching for optimal solutions in a given search space. Here we discuss three different techniques, PSO combined with DFT, PSO with CNN, and DFT-integrated FA. They do not need to implement any symmetry constraint, or consider bond characterization. DFT-PSO adjusts each particle’s trajectory at every time stamp while following the convergence criteria. We have successfully implemented these techniques to find the GM configurations for small-sized nonmetallic clusters such as Boron (B₅ and B₆) (Yuan et al., 2014), Carbon (C₅) (Jana et al., 2019), and polynitrogen clusters (N₄^2- and N₆^4-) (Mitra et al., 2021), and metallic clusters such as Al₄^2- (Mitra et al., 2020), Au_n (n = 2–8), and Au_nAg_m (2 ≤ n+m ≤ 8) (Mitra et al., 2021).

PSO Combined With DFT (DFT-PSO)

We start off with 14 and 15 random structures for B₅ and B₆ (Figure 1), respectively, with velocity set at zero and maximum number of iterations set at 1,000. No significant change in bond length is detected after reaching the global best configuration at the end of the PSO run. Following this, the optimization is performed at the B3LYP/6-311+G(d,p) level as the post-processing step that helps align the symmetry of the PSO-obtained final structure and obtain the corresponding exact energy. The post-processing in this case takes only 20 s to complete, and the final geometry obtained is energetically very close (0.0015 eV difference) to that obtained at the end of the PSO run. The zero-point energy (ZPE) corrected energy, free energy, and enthalpy for B₅ (C_2v) are −123.9873, −124.0135, and −123.9821 a.u., respectively, while those for B₆ (C_2h) are −148.8100, −148.8381, and −148.8038 a.u., respectively. A comparison drawn between our method and other popular algorithms such as DFT-SA and DFT-BH reveals that while these two require a CPU time of 369.64 and 455.43 min to locate the minimum energy structure of B₅, respectively, our method takes only 80.50 min. It is also observed that while the BH and the SA require 600 (unconverged) and 324 number of iterations, respectively, our modified PSO converges after only 138 number of iterations.

FIGURE 1

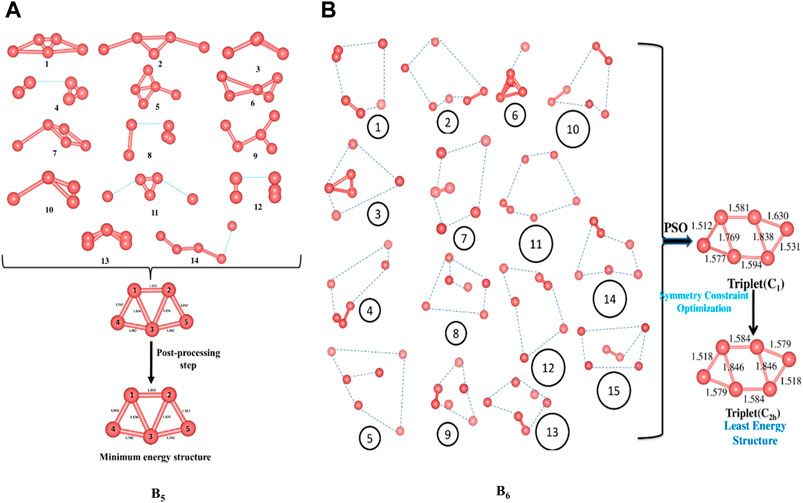
FIGURE 1. Randomly generated configurations of (A) B₅ and (B) B₆ and their convergence to their respective global minimum energy structures (Bond lengths are provided in Å). (Adapted with permission from Mitikiri et al., 2018. Copyright© 2021, John Wiley & Sons, Inc.).

For the carbon clusters, 10 random configurations are chosen with initial velocity zero and 1,000 number of iterations. For the C_n (n = 3–6) clusters, linear geometries are obtained with D_∞h point group as the GM. For n = 4–6, a cyclic isomer for each of them is also obtained with point groups D_2h, C_2v, and D_3h for C₄, C₅, and C₆, respectively, whereas for the relatively larger C₁₀ cluster, the GM geometry is a D_10h ring structure. It is to be noted that the geometries and corresponding energies reported here match with those obtained from the experimental reports (Raghavachari and Binkley, 1987; Watts et al., 1992; Hutter and Lüthi, 1994; Pless et al., 1994; Martin and Taylor, 1996; Van Orden and Saykally, 1998). Again, comparing with DFT-SA and DFT-BH, we get encouraging results for our modified PSO approach. The total execution time for our technique is 143.30 min versus 215.98 and 5085.67 min for DFT-SA and DFT-BH, respectively.

For N₄^2- and N₆^4- clusters, convergence takes place after 483 and 627 numbers of iterations with 228 and 323 min of execution time, respectively. The geometries obtained before and after the post-processing step are energetically very close (Figure 2). The N₆^4- cluster, however, shows a higher order saddle point at the post-processing symmetry constrained optimization with point group D_6h. In case of the binary gold–silver clusters (Au_nAg_m), AuAg₂ has a ring (C_s) doublet GM, those with n+m = 5 have trapezoidal GM, n+m = 6, 7 have triangular 3D geometry (C₁), and n+m = 8 failed to converge within the initial coordinates range of [−4, 4].

FIGURE 2

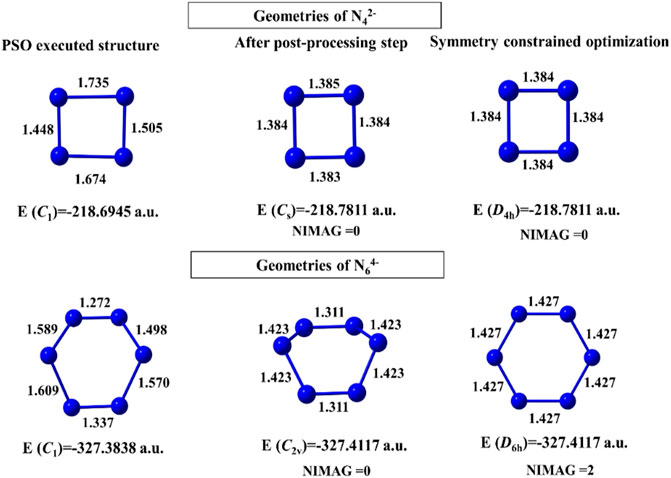
FIGURE 2. Structures of N₄^2- and N₆^4- clusters obtained at the end of the PSO run, post-processing step, and geometry-constrained optimization computed at the B3LYP/6-311 + G(d) level. (Reprinted from Mitra et al., 2021 with permission from Theoretical Chemistry Accounts, Springer Nature. Copyright© 2021, Springer-Verlag GmbH, DE.).

CNN With PSO (CNN-PSO)

Supervised learning (CNN) is performed on an initial guess set generated with the help of (ADMP) simulation. Their corresponding single point energies (SPEs) are calculated and stored to be read by the PSO to search for the GM geometry. Statistically relevant analysis is derived by making the method 8-fold (each with 30 files containing number of iterations and the SPEs). Remarkably high success rate (∼77–90%) is observed for this combined ADMP, CNN, PSO technique, indicating its efficiency in finding GMs. This technique is tested with the C₅ cluster and we have obtained the previously reported (Van Orden and Saykally, 1998) linear geometry as the GM with a higher convergence rate. However, two local minima are also detected due to a premature convergence (Figure 3).

FIGURE 3

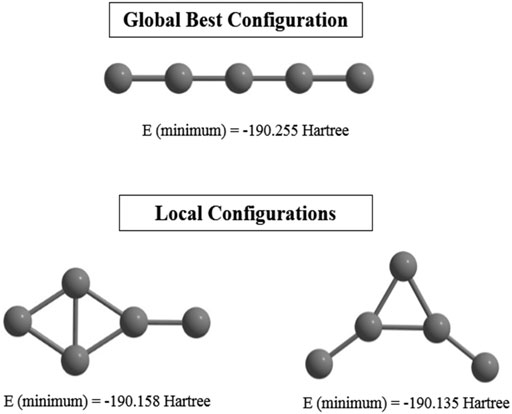
FIGURE 3. Global and local minimum energy structures of C₅ cluster obtained at the end of the post-processing step computed at the B3LYP/6-311+ G(d,p) level. (Reprinted from Mitra et al., 2021 with permission from Theoretical Chemistry Accounts, Springer Nature. Copyright© 2021, Springer-Verlag GmbH, DE.).

FA With DFT (DFT-FA)

A comparative study of the DFT-integrated FA algorithm with PSO is performed on Al₄^2- cluster considering planar and nonplanar structures, and it turns out that the former performs better than the PSO. The mean convergence times for the PSO and FA are 68.22 and 61.25 min for the planar, and 85.13 and 74.40 min for the nonplanar approach, respectively. The corresponding success rates are also higher for the FA. Since we know that the GM of Al₄^2- is planar, we have also investigated the search space of only the planar geometry to get a faster convergence since the number of variables decreases in this problem. Again, the modified FA performs better. A relation is also drawn between the stabilization energy of the system and the change in its aromaticity and number of iteration steps it takes to converge to the GM. The energy functional optimization and the NICS (0) value of Al₄²⁻ are scanned and depicted in Figure 4. It is observed that the aromaticity increases with the decrease in the energy, i.e., with the increase in the stability of the system.

FIGURE 4

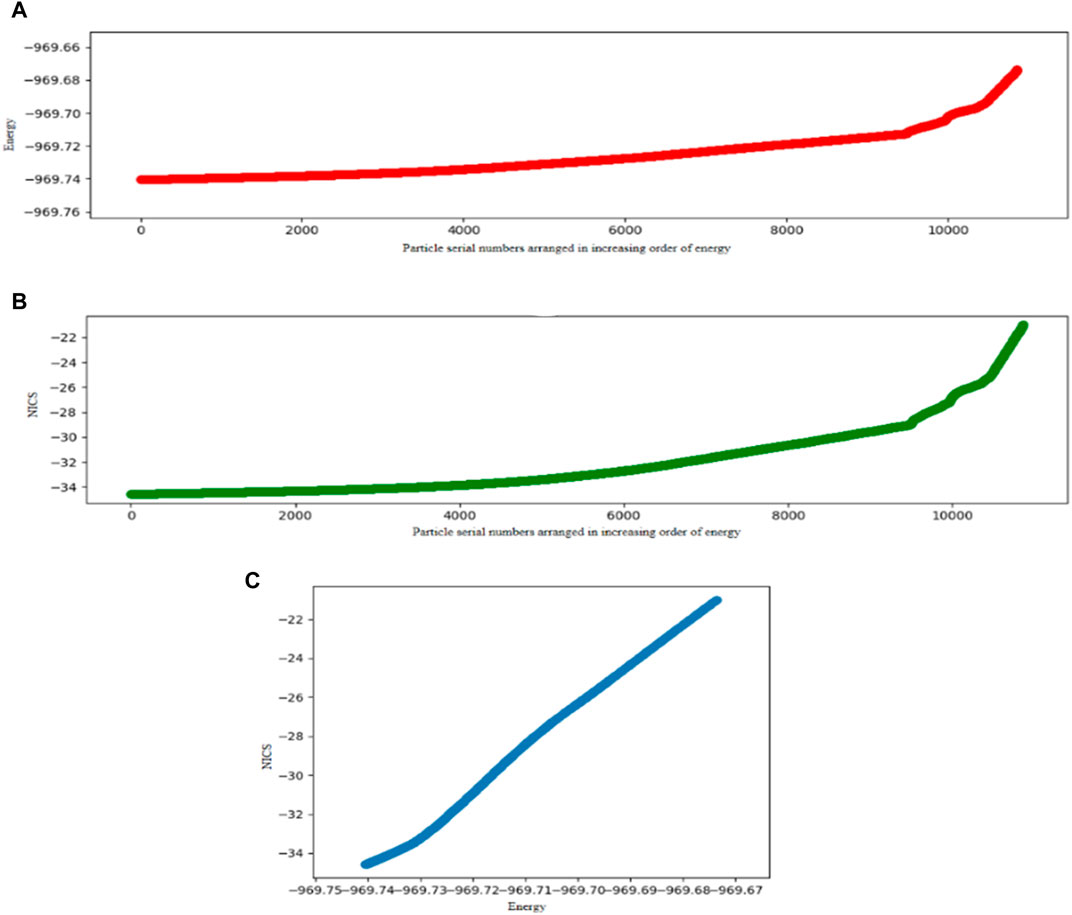
FIGURE 4. Energy profiles (in a.u.) and Nucleus-Independent Chemical Shift (NICS) values on Al₄^2- where 4(A), 4(B), and 4(C) represent plots of Energy vs. Particle serial numbers arranged in an increasing order of energy, NICS vs. Particle serial numbers arranged in an increasing order of energy and NICS vs. Energy, respectively. (Reprinted from Mitra et al., 2020 with permission from Theoretical Chemistry Accounts, Springer Nature. Copyright© 2020, Springer-Verlag GmbH Germany.).

Aromaticity of Clusters From a CDFT Perspective

It is well known from Hückel’s (4n+2) π electron theory (Hückel, 1931) and Pauling’s quantum mechanical description (Pauling and Sherman, 1933) that aromaticity of conjugated systems with cyclic and planar geometry is associated with their increased stability. Various structural, energetic, electronic, and magnetic behavior-based parameters are considered to analyze the aromaticity of the systems, among which the Nucleus-Independent Chemical Shift (NICS) (Schleyer et al., 1996) is, perhaps, the most widely used criterion for aromaticity. CDFT also plays an important role in aromaticity determination (Chattaraj et al., 2005; Chattaraj et al., 2006; Chattaraj et al., 2007), and it does so with the help of reactivity descriptors and associated electronic structure principles (Chattaraj et al., 1993; Chattaraj and Maiti, 2001; Pan et al., 2013b; Chakraborty and Chattaraj, 2021). The relative aromaticity index ΔX, where X could be energy (E), polarizability (α), electrophilicity (ω), or hardness (η), is defined as the difference between the respective indices in the cyclic and open (or localized) systems, i.e., ΔX = X_CYCLIC – X_{OPEN(/LOCALIZED)}. They are observed to show a similar performance as those of the NICS and MCI values. They also provide valuable insights into the stability, reactivity, and electronic properties of the associated cluster.

All-metal aromatic Al₄²⁻ (Li et al., 2001) and antiaromatic Al₄⁴⁻ (Kuznetsov et al., 2003) clusters are investigated at the B3LYP/6-311G(d, p) level of theory to analyze their aromaticity from a CDFT perspective (Chattaraj et al., 2005; Chattaraj et al., 2006; Chattaraj et al., 2007). While Δη > 0 represents aromaticity and Δη < 0 represents antiaromaticity, the reverse is true in the cases of E, α, and ω indices. Their values for the aluminum clusters are compared with those of benzene (C₆H₆) and cyclobutadiene (C₄H₄). While Al₄²⁻ and C₆H₆ show positive Δη and negative ΔE, Δα, and Δω values indicating an aromatic behavior, C₄H₄ shows an exact opposite trend to account for its antiaromaticity. For the Al₄⁴⁻ cluster, however, we have obtained somewhat contradictory results. ΔE and Δα values indicate the cluster’s antiaromatic nature, whereas Δη, Δω, and NICS values reflect its aromatic nature. It is in conformity with the current knowledge that this cluster exhibits conflicting aromaticity. Experimental synthesis and theoretical studies reported along with ELF analysis (Li et al., 2001; Santos et al., 2005) suggest the cluster to be antiaromatic. Its σ-aromaticity directs the overall aromaticity by dominating over its π-counterpart as studied through NICS (Chen et al., 2003) and magnetic field induced current density (Havenith et al., 2004) analyses. Such conflicting aromaticity, along with other varieties of multiple aromaticity and antiaromaticity, δ- and Φ-aromaticity, bond stretch isomerism, etc. are exhibited by several other all-metal clusters (Zubarev et al., 2009; Zubarev and Boldyrev, 2011). Be₃²⁻, Ca₃²⁻, and Mg₃²⁻ clusters are classified as aromatic in terms of the ΔX indices (Roy and Chattaraj, 2008; Giri et al., 2010). Other applications of aromatic clusters are studied by our group through molecular electronic transport (Khatua et al., 2008), hydrogen storage (Havenith et al., 2005; Giri et al., 2011a; Giri et al., 2011b; Das and Chattaraj, 2012; Srinivasu et al., 2012; Pan et al., 2012b), and Zn–Zn and Be–Be bond stabilization (Chattaraj et al., 2008; Roy and Chattaraj, 2008) in the domain of CDFT. The ΔX and NICS parameters show their versatility in quantifying the aromaticity of not just planar and cyclic systems, but also any other nonplanar closed structure. They are both easily computable and ΔX also has a conceptual lucidity since it originates from the electronic structure principles of CDFT.

Structure, Bonding, and Reactivity of Various Molecular Electrides

Certain chemical entities contain loosely bound electrons not directly connected to any atom(s) within the cluster, but trapped within a hollow space (cavity of cage compounds or packing void in crystals) that act as anions. Such entities are known as electrides and they are known for their nonlinear optical (NLO) properties. Besides showing NLO properties, which is considered to be an identifiable character of an electride, it is also widely applicable in electron emission, catalysis, reversible hydrogen storage, super conductivity, etc. (Toda et al., 2007; Xu et al., 2007; Kitano et al., 2012). Organic electrides of crown ethers and cryptands (Ellaboudy et al., 1983; Ward et al., 1988; Dawes et al., 1991; Xie et al., 2000), and inorganic electrides such as [Ca₂₄Al₂₈O₆₄]⁴⁺(4e⁻) (Matsuishi et al., 2003), Y₅Si₃ (Lu et al., 2016), [Ba₂N₂](e⁻), [Li₂Ca₃N₆](2e⁻) (Qu et al., 2019), [Ca₂N]⁺(e⁻) (Lee et al., 2013), [Y₂C]^1.8+·1.8e⁻ (Zhang et al., 2014), Sr₅P₃ (Wang et al., 2017), and Yb₅Sb₃ (Lu et al., 2018) are well reported in the literature. A different class of electrides, known as molecular electrides, are basically guest@host complexes containing a significant amount of localized electron cloud within the void of the host. Cavity-containing molecular structures such as decaborane (Muhammad et al., 2009; Muhammad et al., 2011), pyrrole (Chen et al., 2005), tetracyanoquinodimethane (TCNQ) (Li et al., 2009), fullerene cages (Das et al., 2020), C₂₀F₂₀ (Wang et al., 2012), C₆₀F₆₀, extended (3.1.3.1) porphyrin (EP) (Saha and Chattaraj, 2018), and many more are utilized for this purpose. The guest atoms are usually alkali and alkaline earth metals. For a guest@host complex to be characterized as a molecular or cluster electride, certain criteria need to be fulfilled such as the presence of a non-nuclear attractor/maximum (NNA/NNM) (a non-nuclear critical point with a local maximum of electron density), a negative Laplacian of electron density [∇²ρ(r_c)], presence of an ELF basin near the NNM, high NLO properties, and a green region in the NCI plot showing accumulation of electron density.

The Mg₂EP complex studied at the M06-2X-D3/6-311G(d,p) level of theory (Saha and Chattaraj, 2018) shows the presence of NNA in between the two Mg atoms where the value of ∇²ρ(r_c) < 0, with an ELF basin nearby. The electron population at said NNA is 1.02 e with 46% localization. The NLO properties in terms of $\overline{\alpha }$, β, and ${\gamma }_{\mathrm{\Vert }}$ are calculated and compared with other electride systems that show that $\overline{\alpha }$ is higher while β and ${\gamma }_{\mathrm{\Vert }}$ are lower in the studied systems. The donation of the loosely trapped electron to antibonding MOs of certain bonds in small molecules (H-H in H₂, C-O in CO₂, N-O in N₂O, and C-H in CH₄ and C₆H₆) results in the activation followed by the dissociation of the respective bonds (Saha and Chattaraj, 2018). Another study (Saha et al., 2019) performed by our group utilizes the modified form of β-diketiminate ligand (^DippNacnac) to hold four Mg atoms with two equivalent Mg(I)-Mg(I) bonds ([Mg₄(${}_{\mathrm{H}}{}^{\mathrm{Dipp}}\mathrm{L}$)₂]^2–) in its lower energy singlet state. Two NNAs are found to be present at the center of each Mg(I)-Mg(I) bond with an electron population of 1.18 |e| and 52% localization. The calculated values of $\overline{\alpha }$, β, and ${\gamma }_{\mathrm{\Vert }}$ are 891.7, 0.0, and 8.9 × 10⁵ a.u., respectively, which clearly indicate the system to be classified as an electride. This system is further stabilized by sandwiching it between two K@crown-6-ether⁺ [K@CE]⁺ counter cations. Again, the C₆₀ cage trapping a magnesium dimer (Mg₂@C₆₀) (Das et al., 2020) and a lithium trimer (Li₃@C₆₀) (Das and Chattaraj, 2021a) act as electrides as indicated by the presence of NNA at the center of the Mg-Mg bond path and Li₃ cluster in the respective complexes. The Li₃ cluster encapsulated within a B₄₀ cage (Li₃@B₄₀) (Das and Chattaraj, 2020) shows a similar behavior with a lower electron population at the corresponding NNA owing to the electron deficiency in the B cage atoms. Binuclear sandwich complexes formed with Be and Mg dimers with C₅H₅⁻, N₅⁻, P₅⁻, and As₅⁻ ligands forming M₂(η⁵-L)₂ complexes (Das and Chattaraj, 2020) contain NNAs at the center of the M-M bonds with population varying between 0.95 and 1.39 and percentage localization ranging within 43–62%. Discernible substituent effects on electride characterizers have also been reported (Das and Chattaraj, 2021b).

Noble Gas Encapsulated $B_{40}$ Cage

The encapsulation of noble gas (Ng) atoms in B₄₀ cavitand along with their structure and interactions of Ng with the Ng and B atoms in the host–guest complex is discussed with the help of DFT-based computations (Pan et al., 2018). Dissociation energy (∆E_diss) and Gibbs free energy change (∆G_diss) are calculated to study the stability of the encapsulated complexes. NBO, EDA, and NOCV calculations have been done for studying the nature of bonding. The optimized structure of the B₄₀ cage along with the Ng@B₄₀ and Ng₂@B₄₀ systems (at ωB97X-D/def2-TZVP level) are depicted in Figure 5. The size of the B₄₀ cage is suitable to accommodate He and Ne atoms at its center, whereas for heavier atom (Ar-Rn) encapsulation, the cavity diameter expands with the help of a certain amount of energy (preparation energy, ΔE_prep). Although these complexes are thermochemically unstable, they remain in their encapsulated form on account of their high kinetic barrier. Despite that, the lighter Ng encapsulated complexes have very low ∆E_diss (−1.8 kcal mol⁻¹ for He and −7.1 kcal mol⁻¹ for Ne) as compared with the experimentally identified He@C₂₀H₂₀ complex (−33.8 kcal mol⁻¹). For the heavier Ng atom-encapsulated Ng@B₄₀ systems (Ng = Kr-Rn), the ∆E_diss increases with the size of Ng. The possibility of releasing Ng atoms in the dissociation process is either through B₇ or B₆ holes for the lighter He-Ar atoms, whereas the heavier ones can only escape through the B₇ holes due to their larger size. Decapsulation through the B₇ hole has ΔG^≠ values ranging within 84.7–206.3 kcal mol⁻¹. The rate constant (k) calculated at 298 K for the dissociation through either the B₇ or the B₆ hole comes out to be pretty low suggesting that all the Ng@B₄₀ systems are kinetically stable.

FIGURE 5

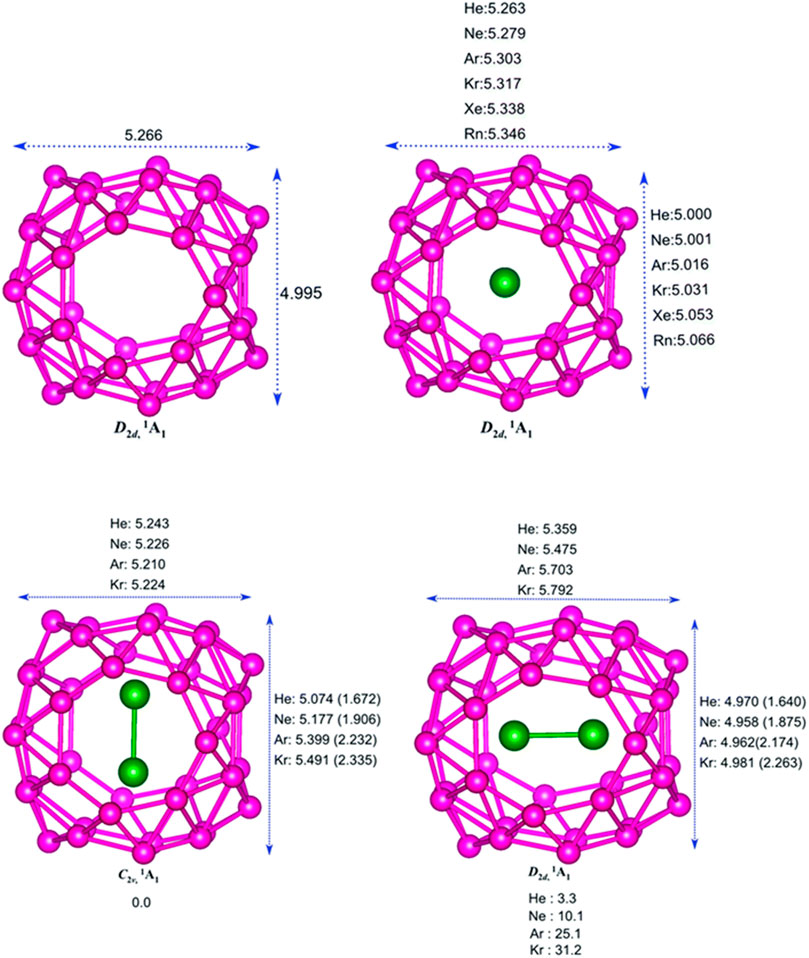
FIGURE 5. Optimized structures of B₄₀, Ng@B₄₀, C_2v, and D_2d isomers of Ng₂@B₄₀ optimized at the ωB97X-D/def2-TZVP level. (Adapted from Pan et al., 2018 with permission from the PCCP Owner Societies.).

In the case of two Ng atoms encapsulation, the inter atomic distance decreases from that of their free state. For Ar₂@B₄₀ and Kr₂@B₄₀, larger repulsion results in the exergonic dissociation of Ng₂@B₄₀ into Ng and Ng@B₄₀. Along with this, large ∆E_prep indicates the nonviability of Ar₂B₄₀ and Kr₂B₄₀. For even heavier Ng atoms (Xe and Rn), no minimum energy structures are obtained for the corresponding dimer encapsulation. The corresponding transition states of the Ng release process of Ng₂@B₄₀ (Ng = He-Ar) suggest that one Ng atom approaches and leaves through the B₇ rings, while the other remains near the center of the cavity. The associated ΔG^≠ values for the He and Ne dimer encapsulated complexes are high enough for them to be kinetically viable.

The B₄₀ cage exhibits a fluxional behavior due to the continuous interconversion between the B₆ and B₇ rings caused by the transfer of one B center from B₇ to B₆. The encapsulated system, Ng@B₄₀, also shows similar dynamic behavior as that of the bare B₄₀. The Ng atom inside the cage does not have any substantial influence on the fluxionality of the cage which is reflected in the free energy barrier values (16.4 kcal mol⁻¹ for the bare cage, and a range of 16–18.9 kcal mol⁻¹ for Ng@B₄₀). Topological analysis of Ng@B₄₀ explains the nature of the interactions therein. ∇²ρ(r_c) and H(r_c) values being positive at the BCPs of Ng-B bond suggest the presence of noncovalent character in most of the complexes except for Rn@B₄₀, Ar₂B₄₀, and Kr₂B₄₀, where H(r_c) < 0. For the encapsulation of Ng₂ (Ng = Ar₂ & Kr₂) the Ng-Ng bond becomes partially covalent in contrast to their noncovalent character in the free state, except in the cases of He₂@B₄₀ and Ne₂@B₄₀ where no covalency is imparted. From NBO analysis it has been shown that Ng → B₄₀ charge transfer increases with increasing the size of the Ng atoms. The electron transfer further increases in the case of Ng₂ encapsulation. Along He–Rn, an increase in WBI values indicates that the increasing size of Ng atoms increases the degree of covalency between the Ng and B centers. EDA analysis reveals a high positive ∆E_pauli which leads to positive ∆E_int suggesting the interaction to be repulsive in case of the heavier noble gas encapsulated B₄₀ systems. Also, both the attractive terms, ∆E_elstat and ∆E_orb, increase with the increasing size of Ng atoms.

Small Gas Molecule Encapsulation Within Octa Acid Cavitand

Small gas molecules such as C₂H₂, C₂H₄, C₂H₆, CO, CO₂, NO₂, NO, N₂, H₂, and Ng atoms (He_n-Xe_n, n = 1,2) are selected as guest molecules encapsulated in OA cavitand (Figure 6) and analyzed via DFT approach (Chakraborty et al., 2016). The systems under study are optimized at the ωB97X-D/6-311G(d,p) level of theory (LanL2DZ basis set with ECP is used for Xe). There are two possible cavities for the accommodation of the guest atoms, the inner cavity of OA is more suitable as it increases the host–guest interaction. In the case of Ng@OA, due to encapsulation of Ng atoms, no notable distortion is observed in the OA. For Ng₂@OA systems, one guest atom can occupy the center of the host cavity, whereas the other one remains in the outer cavity. The Ng–Ng bond distances inside OA are 3.6, 3.7, 3.8, 3.9, and 4.1 Ǻ, respectively, for He₂, Ne₂, Ar₂, Kr₂, and Xe₂. In the cases of CO@OA and NO@OA, the guest molecules prefer to stay in the inner cavity of OA. Their orientation with respect to the two nearest benzene-like fragments is almost perpendicular, whereas it is parallel to the rest of the benzene fragments of OA. The presence of these π electron clouds close to the encapsulated guests is expected to have a significant impact on the stability of the complexes, the nature of interaction, and dynamical behavior as well. For N₂@OA and H₂@OA, N₂ and H₂ remain well inside the inner cavity. Thermochemical study reveals that except for He@OA, in all cases, D₀ value is positive indicating the stability of the host–guest complexes concerning their dissociation into the corresponding individual components. Going from lighter to heavier Ng atoms (also for Ng₂@OA), D₀ value increases, i.e., the host–guest interaction increases. This could most likely be due to the increasing polarizability of the Ng atoms down the group. The dissociation channels for all the encapsulated complexes have positive D₀ values. Most of them, however, dissociate spontaneously at room temperature except in the cases of Kr, Kr₂, Xe, C₂H₂, C₂H₄, C₂H₆, and N₂ guest molecules. Thus, the encapsulation of the mentioned guest molecules is favorable at 298 K. In the cases of NO/NO₂@OA and CO/CO₂@OA, an increase in D₀ value is observed from NO to NO₂ and from CO to CO₂. It can thus be deduced that the encapsulation of NO₂ and CO₂ inside OA forms more stable complexes compared with NO and CO, respectively. Having said that, it is to be noted that all the four complexes have favorable dissociation channels at room temperature. The hydrocarbons have better interaction with the OA and hence are not prone to dissociation at ambient temperatures.

FIGURE 6

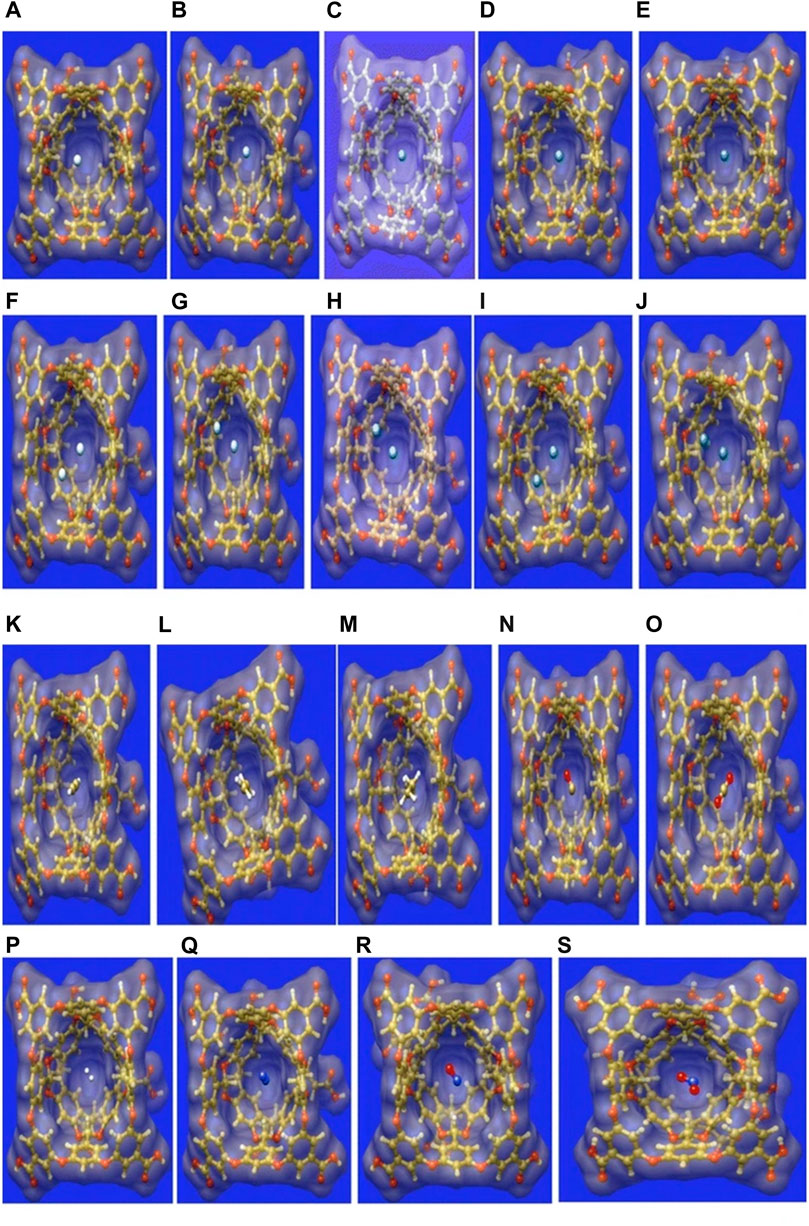
FIGURE 6. The surface representation of the optimized geometries of the guest encapsulated OA, where the guests are: (A) He, (B) Ne, (C) Ar, (D) Kr, (E) Xe, (F) He₂, (G) Ne₂, (I) Ar₂, (J) Kr₂, (K) Xe₂, (L) C₂H₂, (M) C₂H₄, (N) C₂H₆, (O) CO, (P) CO₂, (Q) H₂, (R) N₂, (S) NO, and (T) NO₂. (Adapted from Chakraborty et al., 2016 with permission from Theoretical Chemistry Accounts, Springer Nature. Copyright© 2016, Springer-Verlag Berlin Heidelberg.).

The interaction between the host and guest moieties is analyzed with the help of NBO, NCI, and EDA. All the Ng atoms acquire some positive charges, i.e., transfer of electron density occurs from the Ng atoms to the host OA surface. The donation primarily occurs from the lone pair (LP) of Ng to the C-H antibonding orbital of OA for all the Ng atoms [except Ne where it takes place from LP to antibonding Rydberg state (Ry*)] and for CO, NO, N₂, and CO₂ molecules. WBI values for Ng–Ng and Ng–OA interactions indicate a purely noncovalent character therein. From this discussion it is clear that the confinement brings about an increase in the reactivity of all the guest atoms/molecules within the OA. NCI isosurfaces show the presence of green surface around the guest molecules indicating van der Waals interaction that stabilizes the host–guest complexes. EDA results show that there exists closed shell type of interaction between guest Ng/H₂ and OA. The ΔE_disp and ΔE_orb are the largest and the smallest contributors toward the total attractive interaction, respectively. The former increases in magnitude with increasing size of the encapsulated Ng atoms. For the guest hydrocarbons, the contribution from ∆E_disp increases and ΔE_elstat decreases with the increasing number of H atoms. This is because the molecules such as C₂H₂ and C₂H₄ containing labile electron cloud can accumulate enough positive charge to favorably interact with the electron-rich fragments of the OA. This makes the contribution from ∆E_elstat very important in stabilizing these complexes. The contribution from charge transfer and polarization are very less toward ∆E_tot as indicated by the very low values of ΔE_orb. A similar type of situation is observed for CO/CO₂@OA complexes. For nitrogen-containing guests, the ∆E_orb outweighs the ∆E_elstat contribution toward ΔE_tot. Since the main stabilizing factor for all the complexes is ∆E_disp, the nitrogen-containing guest molecules are prone to be affected by the polarization or charge transfer by OA, in comparison with the other guest molecules. ADMP simulation performed at 298 K shows that all the Ng atoms (except Ne) are prone to leaving the cavity, whereas at 50 K they remain within the OA. Polar molecules such as CO, CO₂, NO, and NO₂ have a higher tendency to stay within the OA than the nonpolar H₂. Again, C₂H₂, C₂H₄, and N₂ containing π electron cloud also prefer to stay inside OA. From the above thermochemical, kinetic, and dynamical analyses, it can be said that OA makes a reasonably good choice for accommodating gas molecules.

Cucurbit[n]urils as a Host Moiety

Cucurbiturils are methylene-linked macrocyclic molecules having glycoluril unit [=C₄H₂N₄O₂=] as a building block. This repeating glycoluril unit can bind with hydrogen with sufficient amount of binding energy. Thus CB[n] can be designed as an effective hydrogen storage compound. The nitrogen and the oxygen centers are found to be the most active centers to bind with hydrogen with positive binding energy. It was found that (CH₃)₂C₄H₂N₄O₂(CH₃)₂ unit can interact with total 13H₂ atoms (Pan et al., 2013a). Since hydrogen has an electric quadrupole moment, a charge–quadrupole interaction plays a pivotal role in binding the hydrogen with the host. NPA charge analysis reveals that the charge transfer occurs from the N and O centers to the $\sigma$* orbital of $H_2$ molecule.

Among the CB[n] family, CB[7] can accommodate five H₂ molecules endohedrally. The O centers can adsorb a total of 28 $H_2$ molecules (two per O atom) and 19 H₂ molecules get adsorbed at the N centers exohedrally, making it a total of 52 hydrogen molecules. The binding energy and adsorption enthalpy are positive and negative, respectively, indicating CB[7] to be a potentially promising H₂ storage material. The gravimetric wt% of hydrogen for the CB[7] adsorbing 52 H₂ molecules comes out to be 8.3 with an average binding energy of 7.8 kJ mol⁻¹. These values are very encouraging when compared with various other potential hydrogen storage materials such as α-cyclodextrin (Zhu et al., 2010), COFs (Klontzas et al., 2008; Li et al., 2010), MOFs (Bhatia and Myers, 2006; Vitillo et al., 2008), Li-doped nanotubes (Wu et al., 2008), and polyacetylenes (Li and Jena, 2008), with average binding energies ranging within 5–8 kJ mol⁻¹.

The endohedral adsorption of gas molecules such as C₂H₂, C₂H₄, C₂H₆, CH₄, CO, CO₂, NO₂, NO, N₂, H₂, F₂, Cl₂, H₂S, and SO₂ into the CB[7] cavitand is depicted in Figure 7. Geometry optimizations are performed at the ωB97X-D/6-31G(d,p) and ωB97XD/6-311+G(d,p) levels (Pan et al., 2017). Both the CB[7] cage and the encapsulated gas molecules remain unaffected by the encapsulation. For SO₂ encapsulation, the binding enthalpy shows the highest value (14.3 kcal mol⁻¹) followed by Cl₂ and C₂H₂ (11.6 and 10.4 kcal mol⁻¹, respectively). CB[7] also encapsulates C₂H₄ and C₂H₆ more favorably than CO₂, NO₂, and H₂S. The binding enthalpies for NO/F₂/N₂/CO/CH₄@CB[7] systems vary from 4.7 to 5.8 kcal mol⁻¹, the highest value corresponding to CH₄. From the enthalpy values it is clear that CB[7] can selectively adsorb SO₂ among various gas molecules, and hence can be applicable in the SO₂ separation process from gas mixtures. ∆G value suggests that C₂H₆ is less prone to be encapsulated than CO₂ inside CB[7]. SO₂, Cl₂, and C₂H₂ adsorb with negative ΔG values, whereas those of C₂H₄ and CO₂ are slightly endergonic (0.6–0.7 kcal mol⁻¹). The corresponding ΔG values for the adsorption of C₂H₆, N₂, F₂, NO₂, NO, and H₂S vary within 1.3–2.8 kcal mol⁻¹ at 298 K temperature. EDA results show that for all the discussed complexes, ∆E_disp contributes more toward the stabilization of the host–guest systems. ∆E_elstat term also plays an important role here. In the hydrocarbons, as the number of H atoms increases, ∆E_elstat decreases gradually due to the reduction in the acidic character of the H atoms. Higher ∆E_elstat and lower ∆E_pauli values in the SO₂ encapsulated complex make the interaction between the host and the guest stronger than for C₂H₄ and C₂H₆ analogues. This again validates the higher SO₂ selectivity of CB[7].

FIGURE 7

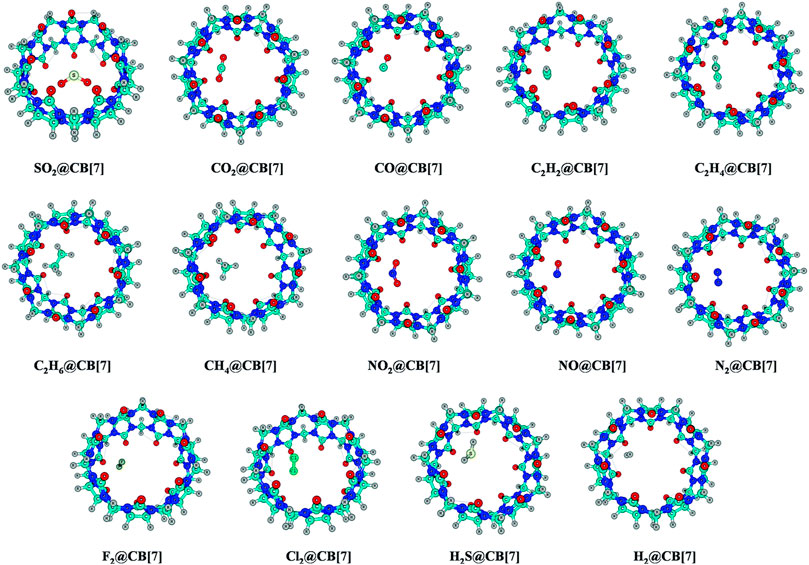
FIGURE 7. Optimized geometries of the guest encapsulated CB[7] systems at the ωB97X-D/6-311+G(d,p) level of theory. (Reproduced from Pan et al., 2017 with permission from the PCCP Owner Societies.).

Cucurbit[6]uril, among the CB[n] family, is found to be a compatible host for the encapsulation of Ngs within its cavity (Pan et al., 2015). The optimized geometries at the ωB97X-D/6-311G(2d,p) level of theory of the Ng_n@CB[6] complexes are provided in Figure 8. CB[6] effectively accommodates three Ne atoms, but can only trap two of the large Ar and Kr atoms. No significant distortion in the cage is observed for trapping all the three Ne atoms or for the first atom of Ar and Kr, whereas inserting a second atom deforms the shape of the host. The Ng dissociation process becomes more endothermic as we move from Ne to Kr. At 298 K, the dissociations of all Ng_n@CB[6] are exergonic except Kr@CB[6]. At 77 K, apart from the second Ng (Ar and Kr) atom dissociation from Ng₂ encapsulated CB[6], all dissociations become endergonic. Kr encapsulation at 298 K and 1 atm pressure is thermochemically favorable, whereas for Ne and Ar encapsulation, high pressure and moderately low temperature are preferred.

FIGURE 8

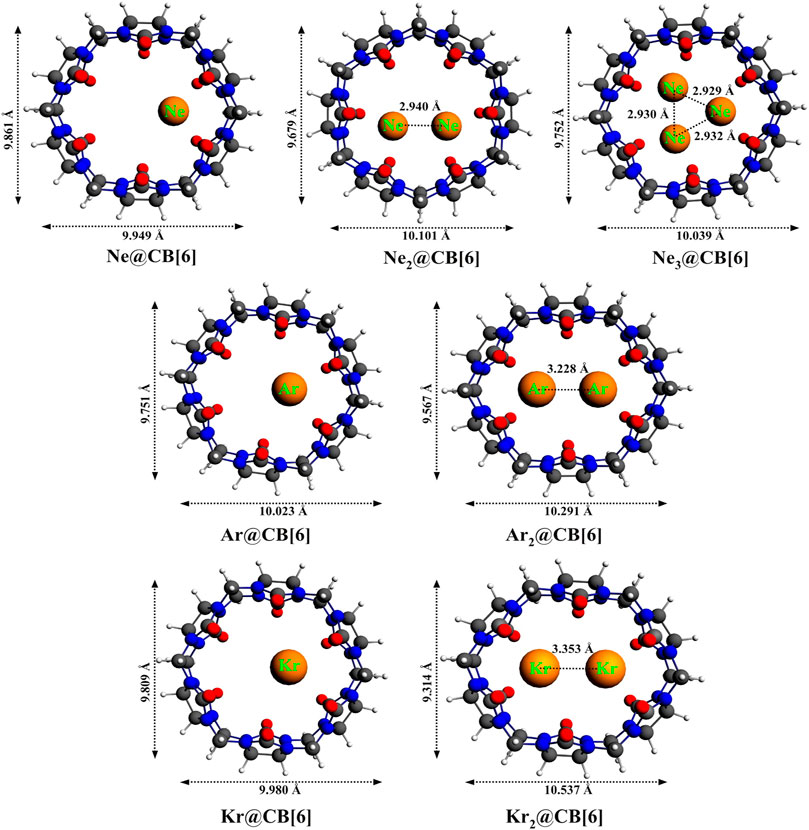
FIGURE 8. Optimized geometries of noble gas encapsulated CB[6] complexes at the ωB97X-D/6-311G(2d,p) level. (Reprinted with permission from Pan et al., 2015. Copyright© 2015, American Chemical Society.).

NPA charge analysis reveals N and O to be negatively charged in Ng_n@CB[6], while C and H have positive charges. Slight charge transfer (∼0.01 e^-) occurs from Ng→CB[6] moiety. Small ρ(r_c) value and positive ∇²ρ(r_c) and H(r_c) values from topological analysis suggest the interaction to be of closed shell type. ELF analysis shows an absence of electron localization between the Ng-Ng and Ng-cage atoms, corroborating the result obtained from AIM. EDA analysis reveals the contribution from ∆E_disp to be the largest, followed by ∆E_elstat, and the smallest contribution is from ∆E_orb, all of which gradually increases going from Ne to Kr. The green surfaces observed between the Ng and CB[6] units in the NCI isosurface (Figure 9) are an indication of a small van der Waals interaction, which increases with the size of the Ng atoms. The dynamical study (ab initio MD) for 1 ps and at 298 K reveals that Ne and Ar remain inside the cavity, whereas Kr and all the Ng₂ in Ng₂@CB[6] move toward the open end but do not leave the cage. At 77 K, all guests stay inside the host.

FIGURE 9

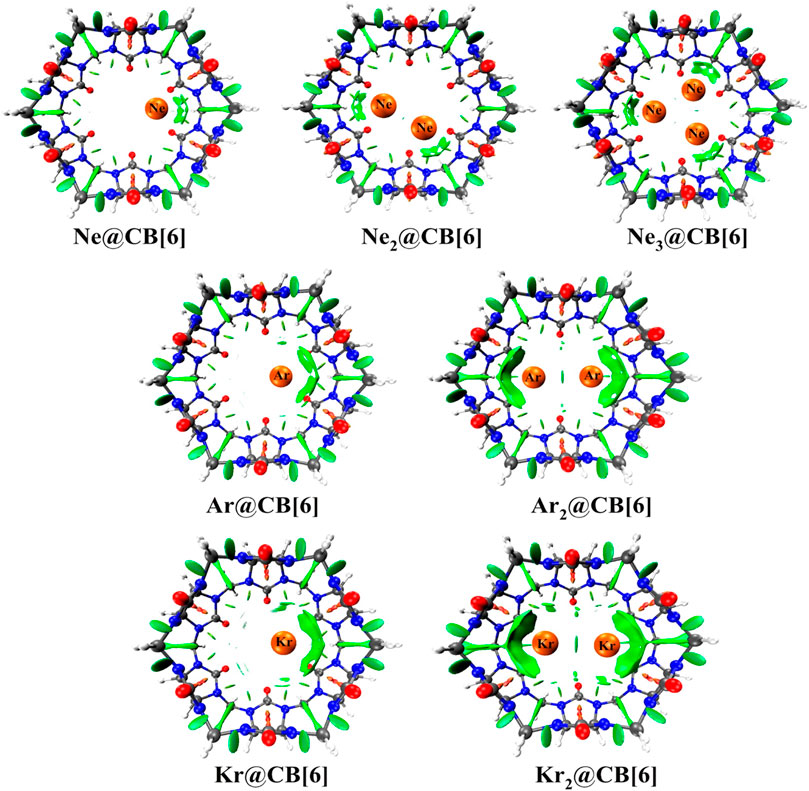
FIGURE 9. NCI plots of Ng_n@CB[6] complexes. (Reprinted with permission from Pan et al., 2015. Copyright© 2015, American Chemical Society.).

Small Molecules Bound Metal Coordinated Boron Cluster

The activation of small molecules by a metal-supported boron cluster is studied through DFT calculations (Saha et al., 2017). They are known to be applicable in nanomaterial building blocks, automobiles (Norbye, 1971; Jiménez‐Halla et al., 2010) etc. The global minimum energy structures calculated at PBE/def2-TZVPPD (Perdew et al., 1996; Weigend and Ahlrichs, 2005) level of MB₁₂^-, CO@MB₁₂^-, N₂@MB₁₂^- clusters and their corresponding TSs for the internal rotation of the B₃ ring are provided in Figure 10. The coordination of the small molecules with the MB₁₂^- cluster forms an umbrella-shaped structure in which the M-L bonds act like the stick of the umbrella. The coordination of CO with the metal center can take place through both the C and O ends, the former producing a more stable isomer. For both OCMB₁₂^_ and NNMB₁₂^_, the Ir-L bond has the highest strength, followed by Co and Rh, while for a particular M center, CO forms a stronger bond than N₂. ∆G values of these complexes are highly positive which suggest that the corresponding complexes are thermodynamically stable concerning the dissociation process. The O-side bound isomers, however, have low positive ∆G for Co and Ir, and become slightly negative for Rh. They can be made viable by lowering the temperature. The N−N and C–O bonds get lengthened due to complexation in the order COMB₁₂^- < N₂MB₁₂^- < OCMB₁₂^- causing a red shift in their bond stretching frequencies which is the highest for the Ir analogues.

FIGURE 10

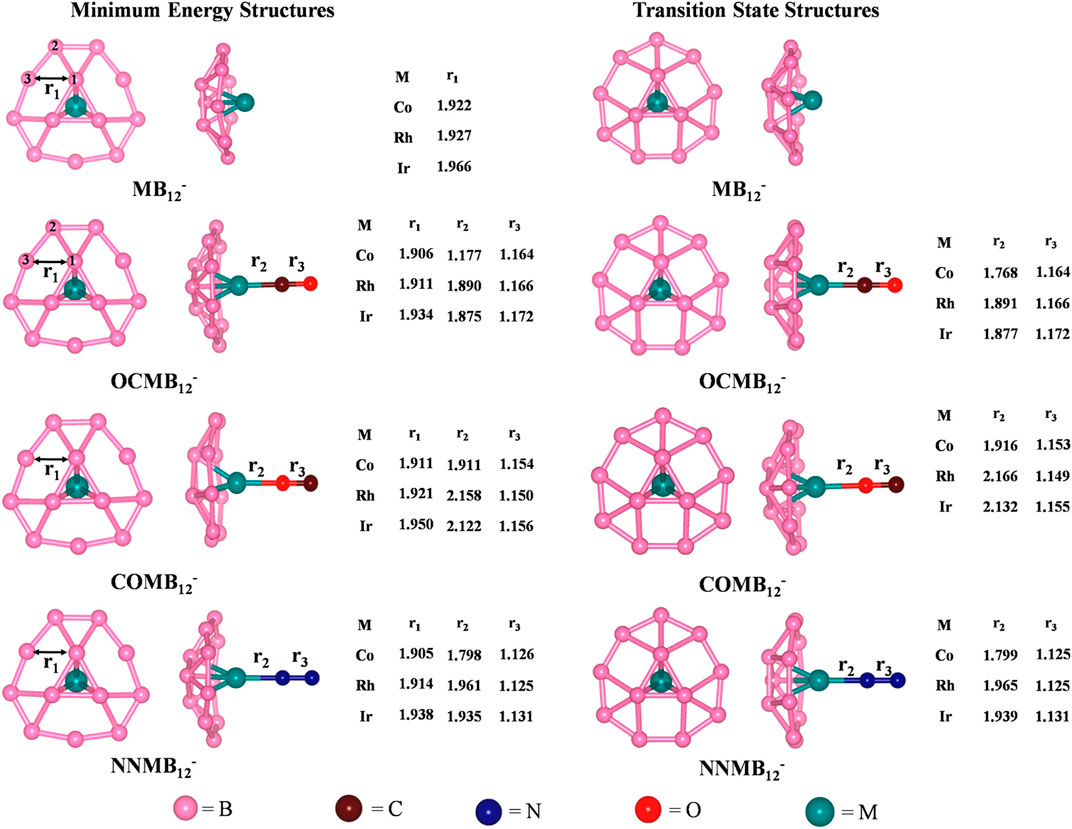
FIGURE 10. Optimized geometries of MB₁₂^- and ligand bound MB₁₂^- at the PBE/def2-TZVPPD level, and their transition state structures for the internal rotation of the B₃ ring. Bond distances are provided in Angstrom unit. (Reprinted with permission from Saha et al., 2017. Copyright© 2017, American Chemical Society.).

NBO analysis reveals that upon complexation, the metal centers get more negatively charged, apart from COIrB₁₂^_ and NNIrB₁₂^_, where Ir still contains positive charge (less than that in IrB₁₂⁻). L→M and M→L back transfers take place, and in certain complexes the latter completely compensates (or overcompensates) the former which is indicated by the zero (or negative) charge on the ligand. The Wiberg bond indices suggest that the covalent character follows the order M-C in OCMB₁₂^- > M-N in N₂MB₁₂^- > M-C in COMB₁₂^-. From EDA-NOCV, it is seen that the bonding between the metal and the ligand is predominantly orbital and electrostatic interactions (in more or less equal contributions), indicating the L-M bonds to have both covalent and ionic characters. For OCMB₁₂^-, however, the contribution from ∆E_elstat is higher than ∆E_orb. Figure 11 shows the deformation densities [Δρ(r)] for the pairwise orbital interactions for the LMB₁₂^_ complexes, where a shift in the electron density occurs from the red to the blue region. The Δρ(${\sigma }_1$) plot reveals that the shift of electron density occurs through the L→M→B scheme. Δρ(π₁) and Δρ(π₂) explain the π electron density shift from the d_L→M. The extent of L←M π-back-donation is greater than the L→M σ-donation, causing a red-shift in its stretching frequency. The σ-donation occurs from the HOMO_(CO) to the $\mathrm{LUM}{\mathrm{O}}_{\left(\mathrm{LM}{\mathrm{B}}_{12}^{-}\right)}$ fragment and π-back-donations occur from the degenerate $\mathrm{HOM}{\mathrm{O}}_{\left(\mathrm{M}{\mathrm{B}}_{12}^{-}\right)}$ to the degenerate π* LUMO_(CO).

FIGURE 11

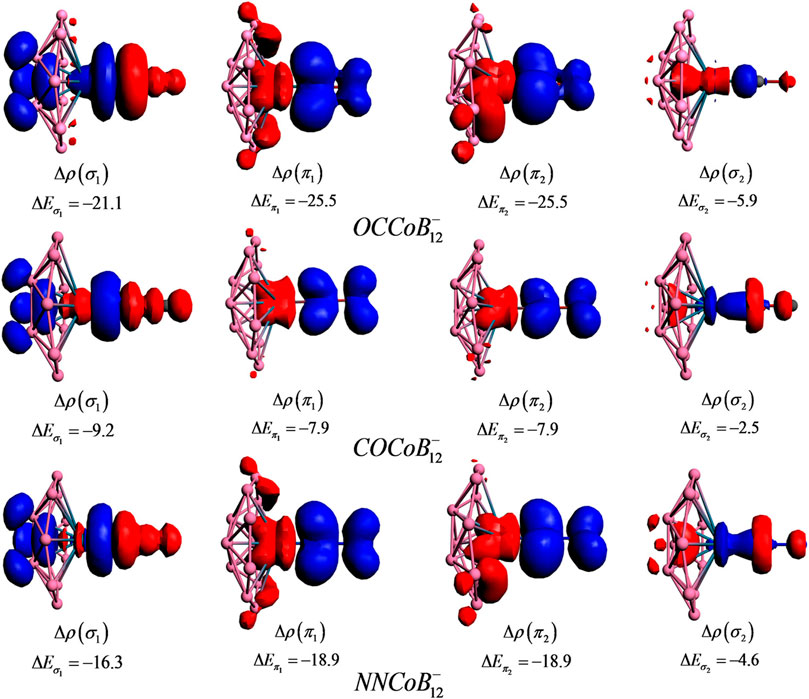
FIGURE 11. Deformation density plots of the pairwise orbital interactions in LCoB₁₂^- (OC, CO, and NN) systems at the revPBED3/TZ2P//PBE/def2-TZVPPD level. Energies are provided in kcal/mol. (Reprinted with permission from Saha et al., 2017. Copyright© 2017, American Chemical Society.).

An internal rotation of the inner B₃ ring with respect to the outer B₉ ring occurs within the MB₁₂^- cluster. The energy barrier associated with this rotation is reported (Popov et al., 2014; Liu et al., 2016) to follow the order Co > Rh > Ir. BOMD simulation at 800 K shows the L-M bonds to be intact during the rotation. This makes the complex seem like a spinning umbrella with the L-M bond as the stick.

Hydrogen Storage in Clathrate Hydrates, Li-Doped Clusters, and Super Alkalis

Clathrate hydrates, a class of inclusion compounds, are known to encapsulate guest compounds within its hydrogen bonded polyhedral cage (Mao et al., 2002; Mao and Mao, 2004; Lee et al., 2010). They constitute a very effective host for hydrogen storage. Four types of clathrate hydrates and their maximum possible hydrogen-encapsulated complexes studied at B3LYP/6-31G(d) level (Chattaraj et al., 2011) are depicted in Figure 12. 5¹² represents the cavity having 12 pentagonal faces, whereas 5¹²6^k (k = 2,4,8) represents 12 pentagonal faces along with k hexagonal faces. Here we discuss the structure, bonding, and stability of the bare and hydrogen-encapsulated complexes from a density functional theory perspective. For nH₂@5¹² complexes it is seen that for the first H₂ encapsulation, the process is energetically favorable although the overall nH₂ encapsulation is method dependent. Owing to the small size of 5¹² cavity, it can accommodate a maximum of five H₂ molecules, after which a deformation in the cavity is observed. The GM for H₂ confinement in the 5¹² cavity occurs endohedrally. The H₂ molecules favor the inside of 5¹² more than the outside. In the case of 5¹²6² cage, it can also take up a maximum of five H₂ molecules. Slight distortion is observed in the system that becomes more noticeable during the third H₂ encapsulation which slowly decreases for the fourth and the fifth hydrogen molecule encapsulation. This is reflected in the slightly conflicting trend in the corresponding interaction energies. Now in the case of 5¹²6⁴ clathrate, obtaining the minimum energy structure was difficult. It is fascinating to note that the encapsulation of one H₂ into the cage stabilizes the structure although it could not provide with the minimum energy structure. Further incorporation of guest molecules deforms the structure of the system. For 5¹²6⁸, the interaction energy for all the six H₂ encapsulation is negative making the process favorable. The large size of the host cavity makes it feasible to accommodate all the six guest molecules efficiently. Positive ∆G value suggests that the complexes are kinetically stable. Finally, it can be concluded that the 5¹² and 5¹²6² clathrates can encapsulate up to two hydrogen molecules without undergoing any structural distortions, whereas the 5¹²6⁸ clathrate may entrap up to six H₂ molecules depending upon the level of theory used. Calculation of CDFT-based reactivity descriptors of the complexes with and without H₂ encapsulation suggests that for most of the systems, stability increases with the increase in number of trapped hydrogen molecules. This is concluded from the increasing hardness and decreasing electrophilicity values.

FIGURE 12

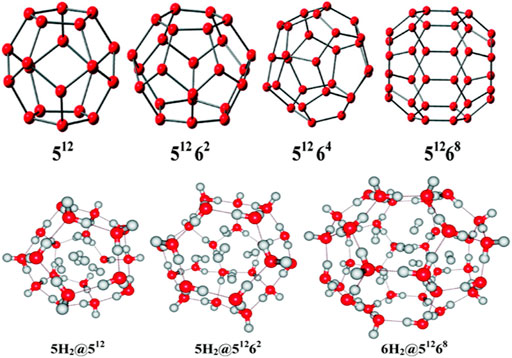
FIGURE 12. Optimized geometries of the clathrate hydrates along with their maximum possible H₂ molecule encapsulated complexes. (Adapted with permission from Chattaraj et al., 2011. Copyright© 2011, American Chemical Society.).

Li ion is popularly known to bind well with hydrogen molecule owing to its positive charge (Pan et al., 2012a). Inspired by this, a number of efforts have been made to effectively polarize the Li center of various clusters to increase its hydrogen adsorbing ability. Here we study the H₂ storage potential of the Li-doped clusters, M₅Li₇⁺ (M = C, Si, Ge), M₄Li₄ (M = Si, Ge) at the M06/6-311+G(d,p) level, and some super-alkali ions at the M052X/6-311+G(d) level (Figures 13, 14). The Li centers attain a net positive charge due to the high polarizability of the clusters, facilitating electrostatic interactions to bind with the H₂ molecules. The negative values of interaction energies and enthalpies indicate the efficacy of these clusters to be good H₂ storage materials. The gravimetric wt% of adsorbed H₂ are 28.0, 18.3, 9.3, 14.7, and 7.1 for C₂Li₇⁺, Si₅Li₇⁺, Ge₅Li₇⁺, Si₄Li₄, and Ge₄Li₄, respectively. For the super-alkali ions, the values range from 13.2 to 40.9%, with the highest being that for BLi₆⁺. On applying electric field, a gradual improvement is observed in the interaction energy value. Thus, in terms of gravimetric wt%, BLi₆⁺ is preferable whereas the interaction energy per H₂ molecule suggests B₂Li₁₁⁺ to be the preferred choice for hydrogen storage.

FIGURE 13

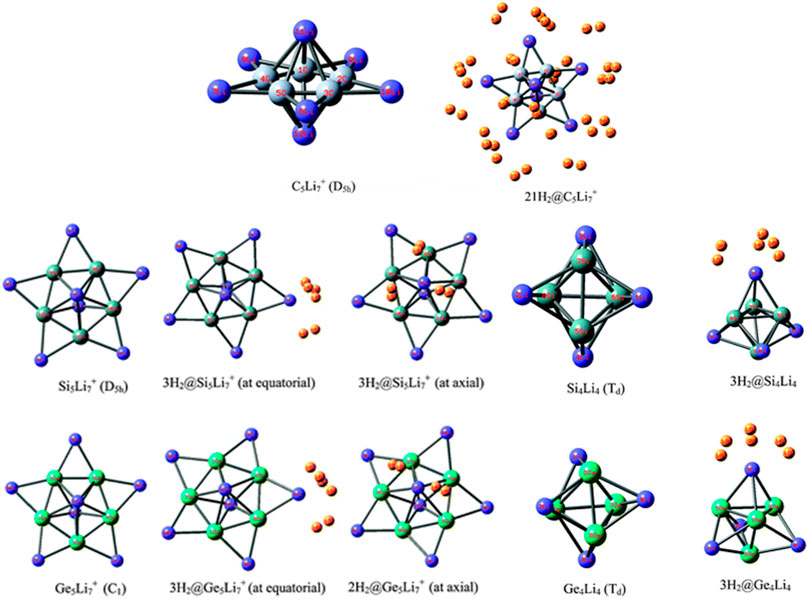
FIGURE 13. Optimized structures of C₅Li₇⁺, M₅Li₇⁺, M₄Li₄ (M = Si, Ge) and their H₂-trapped analogues at the M06/6-311+G(d,p) level. (Adapted from Pan et al., 2012b with permission from the PCCP Owner Societies.).

FIGURE 14

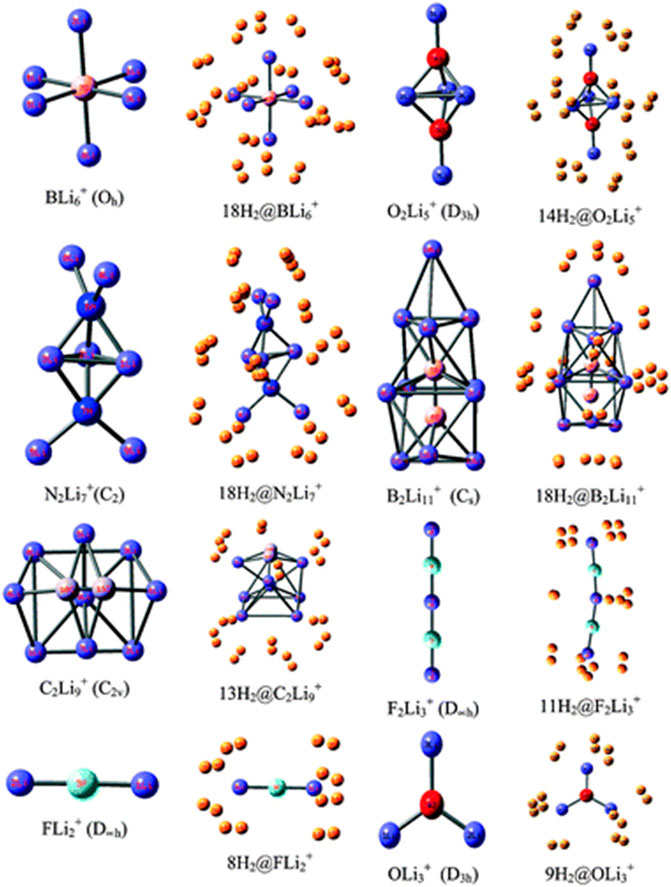
FIGURE 14. Optimized structures of studied super-alkali ions and their hydrogen-trapped analogues at the M052X/6-311+G(d) level. (Adapted from Pan et al., 2012b with permission from the PCCP Owner Societies.).

(HF)₂ Confinement in Fullerene Cages

The influence of encapsulation on the hydrogen bond strength in (HF)₂ within the fullerene cages is studied using DFT and ab initio MD (Khatua et al., 2014b). The optimized geometries of (HF)₂@C_n (n = 60, 70, 80, 90) complexes wB97X-D/6-31G are depicted in Figure 15. The dissociation energy, enthalpy, and change in free energy are negative for the (HF)₂@C₆₀ system which indicates that the encapsulation process is thermodynamically unfavorable, whereas positive values for the rest of the HF encapsulated C_n cages imply them to be favorable (highest being for the C₈₀ cage). Owing to the smaller size of the C₆₀, the HF units orient themselves antiparallelly to reduce repulsion at the cost of hydrogen bond strength. Thus, the energy associated with the HF-HF interaction is observed to be highest in the C₆₀ cage (positive, and hence repulsive in nature). For all the studied cases, upon encapsulation, the hydrogen bond distance reduces from that in the free state, the least being inside the C₇₀ cage. The EDA study reveals that the contribution from ∆E_pauli increases and the ∆E_int value decreases with decreasing the C_n cage cavity except for C₈₀ cage. For the C₆₀ cage, a very large value of ∆E_pauli makes the overall ∆E_int value positive. On account of the smaller H-bond distance within the C₇₀ and C₉₀ cages compared to the same within the C₈₀ cavity, both the ∆E_elstat and ∆E_orb contribute more to the attractive interaction than those in C₈₀. AIM analysis reveals that for all these confined systems, ∇²ρ(r_c) > 0 and H(r_c) < 0 implying the partial covalent nature of the hydrogen bonds. The hydrogen bond is mostly covalent in case of (HF)₂@C₇₀ ELF analysis that also supports this observation.

FIGURE 15

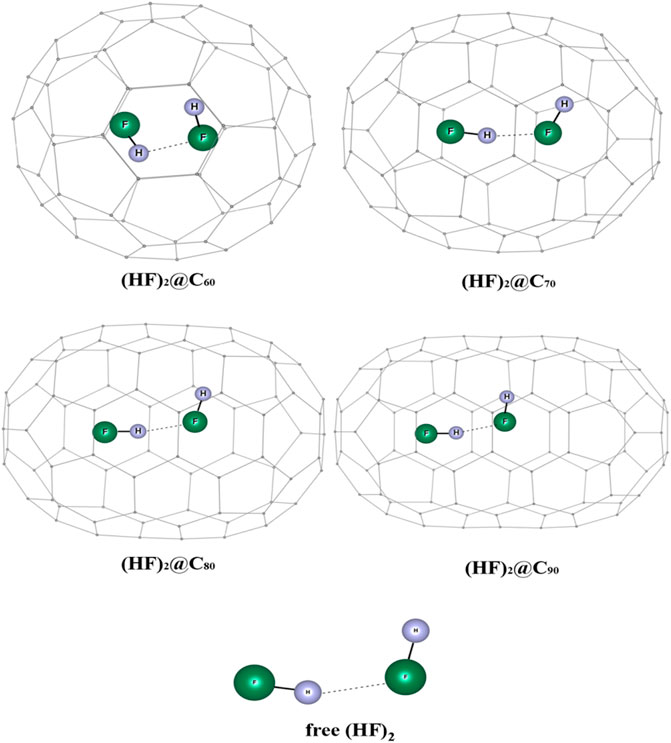
FIGURE 15. Optimized structures of (HF)₂@C_n (n = 60, 70, 80, 90) and free (HF)₂ at ωB97X-D/6-31G level. (Reprinted from Khatua et al., 2014b with permission from Elsevier. Copyright© 2014, Elsevier B.V.).

Concluding Remarks

There exists an appreciable amount of interest in the field of cluster chemistry, especially in the gas-phase and surface-adsorbed studies, and for good reasons. Common curiosities in this area include the difference between the properties exhibited by the bulk and individual clusters, how the cluster size affects the overall behavior of the bulk, etc. Other important branches of this cluster chemistry include solving their global optimization problem in a fast and cost-effective way, and investigating the effect of confinement on the cluster-encapsulated systems.

The global optimizers discussed in this review are shown to locate the global minimum configurations for small metallic and nonmetallic clusters with less execution time and higher success rate than commonly used optimization algorithms, without having the need to impose any symmetry constraint or any other external restrictions. The only requirement is to adjust the local and global best parameters at each iteration. Comparisons made between our modified PSO with other DFT-integrated BH and SA reveal the superiority of the former with respect to the total execution time and number of iterations the program takes to converge. Again, the DFT-integrated FA turns out to be more efficient than the modified PSO. Furthermore, the ADMP-CNN-PSO technique is well suited for locating the global solution from a huge dataset of initial configurations.

The effect of adsorption and confinement of hydrogen, noble gas atoms, and various other small molecules on their stability, reactivity, nature of interactions, and dynamics are studied from a DFT perspective. The concept of aromaticity is analyzed in terms of CDFT-based descriptors such as E, α, ω, and η, where a lower value of the first three parameters and a higher value of hardness in comparison with that of a reference system characterize an aromatic molecule. The reverse is true for antiaromatic compounds. Certain guest@host complexes containing loosely bound electrons acting as anions and showing high NLO properties, known as molecular electrides, are capable of bond activation in small molecules. Other host–guest complexes exhibit fluxionality. One such example is the B₄₀ cage whose fluxional property remains unaltered even after Ng atoms encapsulation. The complexation ability of the B₄₀ cage is also studied in some sandwich complexes and it is seen than the presence of Xe within the cage enhances its complexation ability. The gas molecules accommodated within the Octa acid cavitand become slightly more reactive compared to their free state. Most of the OA-guest complexes are stable with respect to dissociation. OA can thus be designated as a reasonably good storage material for a variety of small gas molecules. Cucurbiturils form another class of compounds which is well known for its hosting capabilities. CB[6] can act as an efficient noble gas carrier and CB[7] can bind up to 52 hydrogen molecules (8.3 wt%). CB[7] is also found to be highly selective toward the adsorption of SO₂ and hence can be used in separating SO₂ from a gas mixture. It is also known to accelerate the otherwise slow [4+2] cycloaddition reaction. The binding ability of the transition metal boron cluster (MB₁₂^-) with isoelectronic species, CO and N₂, is studied along with its fluxionality. Bond activation in both CO and N₂ is observed, and the rotation of the ligand-bound complex makes it look like a spinning umbrella. Hydrogen storage capabilities of clathrate hydrates, Li-doped clusters, and super alkali are investigated and it is found that the former can accommodate 2–6 hydrogen molecules, whereas the Li systems show a gravimetric wt% range of 7.1–28.0% for the star-like clusters and 13.2–40.9% for the super-alkali systems. The (HF)₂ encapsulation by the fullerene cages describes the confinement effect on the H-bond therein. Apart from C₆₀, all the cages form the complexes in a thermodynamically favorable process. Also, a partial covalent character is observed in the H-bonds upon confinement.

Author Contributions

PKC came up with the concept and design of the review, wrote the abstract, reviewed the final manuscript. RP and AP contributed towards the literature survey, writing the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer (SG) declared a past co-authorship with one of the authors (PKC) to the handling Editor.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

PKC would like to thank Ambrish Kumar Srivastava for kindly inviting him to contribute an article to the research topic “Atomic Clusters: Theory & Experiments” in the journal, Frontiers in Chemistry. He also thanks DST, New Delhi, for the J. C. Bose National Fellowship, grant number SR/S2/JCB-09/2009, and his students whose work is presented in this article. RP and AP thank CSIR and IIT Kharagpur, respectively, for their fellowships.

References

Akhtar, F., Liu, Q., Hedin, N., and Bergström, L. (2012). Strong and Binder Free Structured Zeolite Sorbents with Very High CO2-over-N2 Selectivities and High Capacities to Adsorb CO2 Rapidly. Energy Environ. Sci. 5, 7664–7673. doi:10.1039/C2EE21153J

CrossRef Full Text | Google Scholar

Bader, R. F. W. (1985). Atoms in Molecules. Acc. Chem. Res. 18, 9–15. doi:10.1021/ar00109a003

CrossRef Full Text | Google Scholar

Baerends, E. J., Ziegler, T., Autschbach, J., Bashford, D., Bérces, A., Bickelhaupt, F. M., and Ellis, D. E. (2013). “ADF2013. 01. SCM,” in Theo. Chem (Amsterdam, Netherlands: Vrije Universiteit).

Google Scholar

Bai, Q. (2010). Analysis of Particle Swarm Optimization Algorithm. Cis 3, 180. doi:10.5539/cis.v3n1p180

CrossRef Full Text | Google Scholar

Barnes, J. C., Juríček, M., Strutt, N. L., Frasconi, M., Sampath, S., Giesener, M. A., et al. (2013). ExBox: a Polycyclic Aromatic Hydrocarbon Scavenger. J. Am. Chem. Soc. 135, 183–192. doi:10.1021/ja307360n

PubMed Abstract | CrossRef Full Text | Google Scholar

Becke, A. D. (1988). Density-functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A. 38, 3098–3100. doi:10.1103/PhysRevA.38.3098

PubMed Abstract | CrossRef Full Text | Google Scholar

Becke, A. D. (1992). Density‐functional Thermochemistry. I. The Effect of the Exchange‐only Gradient Correction. J. Chem. Phys. 96, 2155–2160. doi:10.1063/1.462066

CrossRef Full Text | Google Scholar

Bergman, B., Sandh, G., Lin, S., Larsson, J., and Carpenter, E. J. (2013). Trichodesmium- a Widespread marine Cyanobacterium with Unusual Nitrogen Fixation Properties. FEMS Microbiol. Rev. 37, 286–302. doi:10.1111/j.1574-6976.2012.00352.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhatia, S. K., and Myers, A. L. (2006). Optimum Conditions for Adsorptive Storage. Langmuir 22, 1688–1700. doi:10.1021/la0523816

PubMed Abstract | CrossRef Full Text | Google Scholar

Brust, M., Walker, M., Bethell, D., Schiffrin, D. J., and Whyman, R. (1994). Synthesis of Thiol-Derivatised Gold Nanoparticles in a Two-phase Liquid-Liquid System. J. Chem. Soc. Chem. Commun. 7, 801–802. doi:10.1039/C39940000801

CrossRef Full Text | Google Scholar

Cabria, I., López, M. J., and Alonso, J. A. (2008). Hydrogen Storage Capacities of Nanoporous Carbon Calculated by Density Functional and Møller-Plesset Methods. Phys. Rev. B 78, 075415. doi:10.1103/PhysRevB.78.075415

CrossRef Full Text | Google Scholar

Cagle, D. W., Thrash, T. P., Alford, M., Chibante, L. P. F., Ehrhardt, G. J., and Wilson, L. J. (1996). Synthesis, Characterization, and Neutron Activation of Holmium Metallofullerenes. J. Am. Chem. Soc. 118, 8043–8047. doi:10.1021/ja960841z

CrossRef Full Text | Google Scholar

Chai, J.-D., and Head-Gordon, M. (2008). Long-range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 10, 6615–6620. doi:10.1039/B810189B

PubMed Abstract | CrossRef Full Text | Google Scholar

Chakraborty, D., and Chattaraj, P. K. (2019). Bonding, Reactivity, and Dynamics in Confined Systems. J. Phys. Chem. A. 123, 4513–4531. doi:10.1021/acs.jpca.9b00830

PubMed Abstract | CrossRef Full Text | Google Scholar

Chakraborty, D., and Chattaraj, P. K. (2021). Conceptual Density Functional Theory Based Electronic Structure Principles. Principles. Chem. Sci. 12, 6264–6279. doi:10.1039/D0SC07017C

Chakraborty, D., and Chattaraj, P. K. (2015). Confinement Induced Binding in noble Gas Atoms within a BN-Doped Carbon Nanotube. Chem. Phys. Lett. 621, 29–34. doi:10.1016/j.cplett.2014.12.053

CrossRef Full Text | Google Scholar

Chakraborty, D., and Chattaraj, P. K. (2017). Effect of Functionalization of boron Nitride Flakes by Main Group Metal Clusters on Their Optoelectronic Properties. J. Phys. Condens. Matter 29, 425201. doi:10.1088/1361-648X/aa8651

PubMed Abstract | CrossRef Full Text | Google Scholar

Chakraborty, D., and Chattaraj, P. K. (2018). Host-guest Interactions between Octa Acid and Cations/nucleobases. J. Comput. Chem. 39, 161–175. doi:10.1002/jcc.25097

PubMed Abstract | CrossRef Full Text | Google Scholar

Chakraborty, D., and Chattaraj, P. K. (2016a). Optical Response and Gas Sequestration Properties of Metal Cluster Supported Graphene Nanoflakes. Phys. Chem. Chem. Phys. 18, 18811–18827. doi:10.1039/C6CP02134D

PubMed Abstract | CrossRef Full Text | Google Scholar

Chakraborty, D., and Chattaraj, P. K. (2016b). Sequestration and Activation of Small Gas Molecules on BN-Flakes and the Effect of Various Metal Oxide Molecules Therein. J. Phys. Chem. C 120, 27782–27799. doi:10.1021/acs.jpcc.6b08404

CrossRef Full Text | Google Scholar

Chakraborty, D., Das, R., and Chattaraj, P. K. (2017). Does Confinement Always Lead to Thermodynamically And/or Kinetically Favorable Reactions? A Case Study Using Diels-Alder Reactions within ExBox+4 and CB[7]. ChemPhysChem 18, 2162–2170. doi:10.1002/cphc.201700308

PubMed Abstract | CrossRef Full Text | Google Scholar

Chakraborty, D., Pan, S., and Chattaraj, P. K. (2016). Encapsulation of Small Gas Molecules and Rare Gas Atoms inside the Octa Acid Cavitand. Theor. Chem. Acc. 135, 119. doi:10.1007/s00214-016-1876-y

CrossRef Full Text | Google Scholar

Chatt, J., and Leigh, G. J. (1972). Nitrogen Fixation. Chem. Soc. Rev. 1, 121–144. doi:10.1039/cs9720100121

CrossRef Full Text | Google Scholar

Chattaraj, P. K., Bandaru, S., and Mondal, S. (2011). Hydrogen Storage in Clathrate Hydrates. J. Phys. Chem. A. 115, 187–193. doi:10.1021/jp109515a

PubMed Abstract | CrossRef Full Text | Google Scholar

Chattaraj, P. K., and Maiti, B. (2001). Electronic Structure Principles and the Atomic Shell Structure. J. Chem. Educ. 78, 811–813. doi:10.1021/ed078p811

Chattaraj, P. K., Nath, S., and Sannigrahi, A. (1993). Ab Initio SCF Study of Maximum Hardness and Maximum Molecular Valency Principles. Chem. Phys. Lett. 212, 223–230. doi:10.1016/0009-2614(93)89318-C

Chattaraj, P. K., Roy, D. R., and Duley, S. (2008). Bonding and Aromaticity in an All-Metal sandwich-like Compound, Be₈²⁻. Chem. Phys. Lett. 460, 382–385. doi:10.1016/j.cplett.2008.06.005

CrossRef Full Text | Google Scholar

Chattaraj, P. K., Roy, D. R., Elango, M., and Subramanian, V. (2006). Chemical Reactivity Descriptor Based Aromaticity Indices Applied to and Systems. J. Mol. Struct. THEOCHEM 759, 109–110. doi:10.1016/j.theochem.2005.10.041

CrossRef Full Text | Google Scholar

Chattaraj, P. K., Roy, D. R., Elango, M., and Subramanian, V. (2005). Stability and Reactivity of All-Metal Aromatic and Antiaromatic Systems in Light of the Principles of Maximum Hardness and Minimum Polarizability. J. Phys. Chem. A. 109, 9590–9597. doi:10.1021/jp0540196

PubMed Abstract | CrossRef Full Text | Google Scholar

Chattaraj, P. K., Sarkar, U., and Roy, D. R. (2007). Electronic Structure Principles and Aromaticity. J. Chem. Educ. 84, 354. doi:10.1021/ed084p354

CrossRef Full Text | Google Scholar

Chen, W., Li, Z.-R., Wu, D., Li, Y., Sun, C.-C., and Gu, F. L. (2005). The Structure and the Large Nonlinear Optical Properties of Li@Calix[4]pyrrole. J. Am. Chem. Soc. 127, 10977–10981. doi:10.1021/ja050601w

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Z., Corminboeuf, C., Heine, T., Bohmann, J., and Schleyer, P. V. R. (2003). Do all-metal Antiaromatic Clusters Exist? J. Am. Chem. Soc. 125, 13930–13931. doi:10.1021/ja0361392

PubMed Abstract | CrossRef Full Text | Google Scholar

Chollet, F. (2015). Keras. GitHub. Available at: https://github.com/fchollet/keras. doi:10.2210/pdb4trn/pdb

CrossRef Full Text | Google Scholar

Chong, Z. R., Yang, S. H. B., Babu, P., Linga, P., and Li, X.-S. (2016). Review of Natural Gas Hydrates as an Energy Resource: Prospects and Challenges. Appl. Energ. 162, 1633–1652. doi:10.1016/j.apenergy.2014.12.061

CrossRef Full Text | Google Scholar

Cioslowski, J., and Nanayakkara, A. (1992). Endohedral Fullerites: a New Class of Ferroelectric Materials. Phys. Rev. Lett. 69, 2871–2873. doi:10.1103/PhysRevLett.69.2871

PubMed Abstract | CrossRef Full Text | Google Scholar

Colorni, A., Dorigo, M., and Maniezzo, V. (1991). “Distributed Optimization by Ant Colonies,” in Proceedings of the first European conference on artificial life. 142. Paris, France: Elsevier Publishing, 134–142.

Google Scholar

Contreras-García, J., Johnson, E. R., Keinan, S., Chaudret, R., Piquemal, J.-P., Beratan, D. N., et al. (2011). NCIPLOT: a Program for Plotting Noncovalent Interaction Regions. J. Chem. Theor. Comput. 7, 625–632. doi:10.1021/ct100641a

CrossRef Full Text | Google Scholar

Cross, R. J., Saunders, M., and Prinzbach, H. (1999). Putting Helium inside Dodecahedrane. Org. Lett. 1, 1479–1481. doi:10.1021/ol991037v

CrossRef Full Text | Google Scholar

Das, P., and Chattaraj, P. K. (2021a). Comparison between Electride Characteristics of Li3@B40 and Li3@C60. Front. Chem. 9, 638581. doi:10.3389/fchem.2021.638581

PubMed Abstract | CrossRef Full Text | Google Scholar

Das, P., and Chattaraj, P. K. (2020). Electride Characteristics of Some Binuclear Sandwich Complexes of Alkaline Earth Metals, M2(η5-L)2 (M = Be, Mg; L = C5H5-, N5-, P5-, As5-). J. Phys. Chem. A. 124, 9801–9810. doi:10.1021/acs.jpca.0c08306

PubMed Abstract | CrossRef Full Text | Google Scholar

Das, P., Saha, R., and Chattaraj, P. K. (2020). Encapsulation of Mg2 inside a C60 Cage Forms an Electride. J. Comput. Chem. 41, 1645–1653. doi:10.1002/jcc.26207

PubMed Abstract | CrossRef Full Text | Google Scholar

Das, P., and Chattaraj, P. K. (2021b). Substituent Effects on Electride Characteristics of Mg₂(η5-C₅H₅)2: A Theoretical Study. J. Phys. Chem. A. 125,6207–6220. doi:10.1021/acs.jpca.1c04605

Das, R., and Chattaraj, P. K. (2012). A (T-P) Phase Diagram of Hydrogen Storage on (N4C3H)6Li6. J. Phys. Chem. A. 116, 3259–3266. doi:10.1021/jp212472u

PubMed Abstract | CrossRef Full Text | Google Scholar

Dawes, S. B., Eglin, J. L., Moeggenborg, K. J., Kim, J., and Dye, J. L. (1991). Cesium(+1)(15-crown-5)2.cntdot.e-. A Crystalline Antiferromagnetic Electride. J. Am. Chem. Soc. 113, 1605–1609. doi:10.1021/ja00005a025

CrossRef Full Text | Google Scholar

Deng, W.-Q., Xu, X., and Goddard, W. A. (2004). New Alkali Doped Pillared Carbon Materials Designed to Achieve Practical Reversible Hydrogen Storage for Transportation. Phys. Rev. Lett. 92, 166103. doi:10.1103/PhysRevLett.92.166103

PubMed Abstract | CrossRef Full Text | Google Scholar

Dong, Z., Luo, Q., and Liu, J. (2012). Artificial Enzymes Based on Supramolecular Scaffolds. Chem. Soc. Rev. 41 (23), 7890–7908. doi:10.1039/C2CS35207A

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunning, T. H., and Hay, P. J. (1977). “Gaussian Basis Sets for Molecular Calculations,” in Modern Theoretical Chemistry. Editor H. F. Schaefer (New York: Plenum), Vol. 3, 1–27. doi:10.1007/978-1-4757-0887-5_1

CrossRef Full Text | Google Scholar

Ellaboudy, A., Dye, J. L., and Smith, P. B. (1983). Cesium 18-crown-6 Compounds. A Crystalline Ceside and a Crystalline Electride. J. Am. Chem. Soc. 105, 6490–6491. doi:10.1021/ja00359a022

CrossRef Full Text | Google Scholar

Florea, M., and Nau, W. M. (2011). Strong Binding of Hydrocarbons to Cucurbituril Probed by Fluorescent Dye Displacement: A Supramolecular Gas-Sensing Ensemble. Angew. Chem. 123, 9510–9514. doi:10.1002/ange.201104119

CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2009). Gaussian 09. Wallingford CT: Gaussian, Inc.

Froudakis, G. E. (2001). Hydrogen Interaction with Single-Walled Carbon Nanotubes: A Combined Quantum-Mechanics/molecular-Mechanics Study. Nano Lett. 1, 179–182. doi:10.1021/nl015504p

CrossRef Full Text | Google Scholar

Giri, S., Bandaru, S., Chakraborty, A., and Chattaraj, P. K. (2011a). Role of Aromaticity and Charge of a System in its Hydrogen Trapping Potential and Vice Versa. Phys. Chem. Chem. Phys. 13, 20602–20614. doi:10.1039/C1CP21752F

PubMed Abstract | CrossRef Full Text | Google Scholar

Giri, S., Chakraborty, A., and Chattaraj, P. K. (2011b). Potential Use of Some Metal Clusters as Hydrogen Storage Materials-A Conceptual DFT Approach. J. Mol. Model. 17, 777–784. doi:10.1007/s00894-010-0761-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Giri, S., Roy, D. R., Duley, S., Chakraborty, A., Parthasarathi, R., Elango, M., et al. (2009). Bonding, Aromaticity, and Structure of Trigonal Dianion Metal Clusters. J. Comput. Chem. 31, 1815–1821. doi:10.1002/jcc.21452

CrossRef Full Text | Google Scholar

Grochala, W., Hoffmann, R., Feng, J., and Ashcroft, N. W. (2007). The Chemical Imagination at Work inVery Tight Places. Angew. Chem. Int. Ed. 46 (20), 3620–3642. doi:10.1002/anie.200602485

PubMed Abstract | CrossRef Full Text | Google Scholar

Gubbins, K. E., Liu, Y.-C., Moore, J. D., and Palmer, J. C. (2011). The Role of Molecular Modeling in Confined Systems: Impact and Prospects. Phys. Chem. Chem. Phys. 13, 58–85. doi:10.1039/C0CP01475C

PubMed Abstract | CrossRef Full Text | Google Scholar

Haaland, A., Shorokhov, D. J., and Tverdova, N. V. (2004). Topological Analysis of Electron Densities: Is the Presence of an Atomic Interaction Line in an Equilibrium Geometry a Sufficient Condition for the Existence of a Chemical Bond? Chem. Eur. J. 10, 4416–4421. doi:10.1002/chem.200400663

PubMed Abstract | CrossRef Full Text | Google Scholar

Havenith, R. W. A., Fowler, P. W., Steiner, E., Shetty, S., Kanhere, D., and Pal, S. (2004). Aromaticity and Antiaromaticity of LixAl4clusters: Ring Current Patterns versus Electron Counting. Phys. Chem. Chem. Phys. 6, 285–288. doi:10.1039/B311559N

CrossRef Full Text | Google Scholar

Havenith, R. W., Proft, F. De., Fowler, P. W., and Geerlings, P. (2005). σ-Aromaticity in H₃⁺ and Li₃⁺: Insights from Ring-Current Maps. Chem. Phys. Lett. 407, 391–396. doi:10.1016/j.cplett.2005.03.099

CrossRef Full Text | Google Scholar

Hay, P. J., and Wadt, W. R. (1985b). Ab Initio effective Core Potentials for Molecular Calculations. Potentials for K to Au Including the Outermost Core Orbitals. J. Chem. Phys. 82, 299–310. doi:10.1063/1.448975

CrossRef Full Text | Google Scholar

Hay, P. J., and Wadt, W. R. (1985a). Ab Initio effective Core Potentials for Molecular Calculations. Potentials for the Transition Metal Atoms Sc to Hg. J. Chem. Phys. 82, 270–283. doi:10.1063/1.448799

CrossRef Full Text | Google Scholar

Heine, T., Zhechkov, L., and Seifert, G. (2004). Hydrogen Storage by Physisorption on Nanostructured Graphite plateletsElectronic Supplementary Information (ESI) Available: Fig. 1S: Potential Energy Surface of H2 Parallel to Benzene at the MP2 Level. See. Phys. Chem. Chem. Phys. 6, 980–984. doi:10.1039/B316209E

CrossRef Full Text | Google Scholar

Hennig, A., Ghale, G., and Nau, W. M. (2007). Effects of Cucurbit[7]uril on Enzymatic Activity. Chem. Commun. 16, 1614–1616. doi:10.1039/B618703J

PubMed Abstract | CrossRef Full Text | Google Scholar

Herr, W. A. D. (1993). The Physics of Simple Metal Clusters: Experimental Aspects and Simple Models. Rev. Mod. Phys. 65, 611. doi:10.1103/RevModPhys.65.611

CrossRef Full Text | Google Scholar

Hoffman, B. M., Lukoyanov, D., Dean, D. R., and Seefeldt, L. C. (2013). Nitrogenase: a Draft Mechanism. Acc. Chem. Res. 46, 587–595. doi:10.1021/ar300267m

PubMed Abstract | CrossRef Full Text | Google Scholar

Holland, J. H. (1992). Genetic Algorithms. Sci. Am. 267, 66–72. doi:10.1038/scientificamerican0792-66

CrossRef Full Text | Google Scholar

Hu, Y., Xiang, S., Zhang, W., Zhang, Z., Wang, L., Bai, J., et al. (2009). A New MOF-505 Analog Exhibiting High Acetylene Storage. Chem. Commun. 48, 7551–7553. doi:10.1039/B917046D

PubMed Abstract | CrossRef Full Text | Google Scholar

Hückel, E. (1931). Quantentheoretische Beiträge Zum Benzolproblem. Z. Phys. 70, 204–286. doi:10.1007/BF01339530

CrossRef Full Text | Google Scholar

Hutter, J., and Lüthi, H. P. (1994). The Molecular Structure of C6: A Theoretical Investigation. J. Chem. Phys. 101, 2213–2216. doi:10.1063/1.467661

CrossRef Full Text | Google Scholar

Iyengar, S. S., Schlegel, H. B., Millam, J. M., A. Voth, G. G., Scuseria, G. E., and Frisch, M. J. (2001). Ab Initio molecular Dynamics: Propagating the Density Matrix with Gaussian Orbitals. II. Generalizations Based on Mass-Weighting, Idempotency, Energy Conservation and Choice of Initial Conditions. J. Chem. Phys. 115, 10291–10302. doi:10.1063/1.1416876

CrossRef Full Text | Google Scholar

Jana, G., Mitra, A., Pan, S., Sural, S., and Chattaraj, P. K. (2019). Modified Particle Swarm Optimization Algorithms for the Generation of Stable Structures of Carbon Clusters, Cn (N = 3-6, 10). Front. Chem. 7, 485. doi:10.3389/fchem.2019.00485

PubMed Abstract | CrossRef Full Text | Google Scholar

Jena, P., and Castleman, A. W. (2010). Introduction to Atomic Clusters. Sci. Technol. At. Mol. Condensed Matter Biol. Syst. 1, 1–36. doi:10.1016/B978-0-444-53440-8.00001-X

CrossRef Full Text | Google Scholar

J. F. Corrigan, and S. Dehnen (Editors) (2017). Clusters-contemporary Insight in Structure and Bonding (Cham: Springer), 174.

Jiménez-Halla, J. O., Islas, R., Heine, T., and Merino, G. (2010). B19-: an Aromatic Wankel Motor. Angew. Chem. Int. Ed. Engl. 49, 5668–5671. doi:10.1002/anie.201001275

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiménez-Vázquez, H. A., Tamariz, J., and Cross, R. J. (2001). Binding Energy in and Equilibrium Constant of Formation for the Dodecahedrane Compounds He@C20H20 and Ne@C20H20. J. Phys. Chem. A. 105, 1315–1319. doi:10.1021/jp0027243

CrossRef Full Text | Google Scholar

Jin, Y., Voss, B. A., Jin, A., Long, H., Noble, R. D., and Zhang, W. (2011). Highly CO2-Selective Organic Molecular Cages: What Determines the CO2Selectivity. J. Am. Chem. Soc. 133, 6650–6658. doi:10.1021/ja110846c

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, Y., Voss, B. A., Noble, R. D., and Zhang, W. (2010). A Shape-Persistent Organic Molecular Cage with High Selectivity for the Adsorption of CO2 over N2. Angew. Chem. 122, 6492–6495. doi:10.1002/ange.201001517

CrossRef Full Text | Google Scholar

Karaboga, D., and Basturk, B. (2007). A Powerful and Efficient Algorithm for Numerical Function Optimization: Artificial Bee Colony (ABC) Algorithm. J. Glob. Optim. 39, 459–471. doi:10.1007/s10898-007-9149-x

CrossRef Full Text | Google Scholar

Khatua, M., Pan, S., and Chattaraj, P. K. (2014a). Confinement Induced Binding of noble Gas Atoms. J. Chem. Phys. 140, 164306. doi:10.1063/1.4871800

PubMed Abstract | CrossRef Full Text | Google Scholar

Khatua, M., Pan, S., and Chattaraj, P. K. (2014b). Confinement of (HF)2 in Cn (n= 60, 70, 80, 90).... Cages. Chem. Phys. Lett. 616-617, 49–54. doi:10.1016/j.cplett.2014.10.025

CrossRef Full Text | Google Scholar

Khatua, S., Roy, D. R., Bultinck, P., Bhattacharjee, M., and Chattaraj, P. K. (2008). Aromaticity in Cyclic Alkali Clusters. Phys. Chem. Chem. Phys. 10, 2461–2474. doi:10.1039/B718176K

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, H., Kim, Y., Yoon, M., Lim, S., Park, S. M., Seo, G., et al. (2010). Highly Selective Carbon Dioxide Sorption in an Organic Molecular Porous Material. J. Am. Chem. Soc. 132, 12200–12202. doi:10.1021/ja105211w

PubMed Abstract | CrossRef Full Text | Google Scholar

Kitano, M., Inoue, Y., Yamazaki, Y., Hayashi, F., Kanbara, S., Matsuishi, S., et al. (2012). Ammonia Synthesis Using a Stable Electride as an Electron Donor and Reversible Hydrogen Store. Nat. Chem 4, 934–940. doi:10.1038/nchem.1476

PubMed Abstract | CrossRef Full Text | Google Scholar

Klontzas, E., Tylianakis, E., and Froudakis, G. E. (2008). Hydrogen Storage in 3D Covalent Organic Frameworks. A Multiscale Theoretical Investigation. J. Phys. Chem. C 112, 9095–9098. doi:10.1021/jp711326g

CrossRef Full Text | Google Scholar

Koster, A. M., Geudtner, G., Calaminici, P., Casida, M. E., Dominguez, V. D., Flores-Moreno, R., and Salahub, D. R. (2011). DeMon2K, Version 3. Cinvestav, México: The deMon Developers.

Kuc, A., Zhechkov, L., Patchkovskii, S., Seifert, G., and Heine, T. (2007). Hydrogen Sieving and Storage in Fullerene Intercalated Graphite. Nano Lett. 7, 1–5. doi:10.1021/nl0619148

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuznetsov, A. E., Birch, K. A., Boldyrev, A. I., Li, X., Zhai, H. J., and Wang, L. S. (2003). All-Metal Antiaromatic Molecule: Rectangular Al44- in the Li3Al4- Anion. Science 300, 622–625. doi:10.1126/science.1082477

PubMed Abstract | CrossRef Full Text | Google Scholar

Lagona, J., Mukhopadhyay, P., Chakrabarti, S., and Isaacs, L. (2005). The Cucurbit[n]uril Family. Angew. Chem. Int. Ed. 44 (31), 4844–4870. doi:10.1002/anie.200460675

PubMed Abstract | CrossRef Full Text | Google Scholar

Latysheva, N., Junker, V. L., Palmer, W. J., Codd, G. A., and Barker, D. (2012). The Evolution of Nitrogen Fixation in Cyanobacteria. Bioinformatics 28 (5), 603–606. doi:10.1093/bioinformatics/bts008

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, C., Yang, W., and Parr, R. G. (1988). Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 37, 785–789. doi:10.1103/PhysRevB.37.785

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, H., Lee, J.-w., Kim, D. Y., Park, J., Seo, Y.-T., Zeng, H., et al. (2005). Tuning Clathrate Hydrates for Hydrogen Storage. Nature 434, 743–746. doi:10.1038/nature03457

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, H., Lee, J.-w., Kim, D. Y., Park, J., Seo, Y.-T., Zeng, H., Moudrakovski, I. L., Ratcliffe, C. I., and Ripmeester, J. A. (2010). “Tuning Clathrate Hydrates for Hydrogen Storage,” in Materials For Sustainable Energy: A Collection of Peer-Reviewed Research and Review Articles from Nature Publishing Group, 285–288. doi:10.1142/9789814317665_0042

CrossRef Full Text | Google Scholar

Lee, K., Kim, S. W., Toda, Y., Matsuishi, S., and Hosono, H. (2013). Dicalcium Nitride as a Two-Dimensional Electride with an Anionic Electron Layer. Nature 494, 336–340. doi:10.1038/nature11812

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, F., Zhao, J., Johansson, B., and Sun, L. (2010). Improving Hydrogen Storage Properties of Covalent Organic Frameworks by Substitutional Doping. Int. J. Hydrogen Energ. 35, 266–271. doi:10.1016/j.ijhydene.2009.10.061

CrossRef Full Text | Google Scholar

Li, S., and Jena, P. (2008). Li-and B-Decorated Cis-Polyacetylene: A Computational Study. Phys. Rev. B. 77, 193101. doi:10.1103/physrevb.77.193101

CrossRef Full Text | Google Scholar

Li, X., Kuznetsov, A. E., Zhang, H. F., Boldyrev, A. I., and Wang, L. S. (2001). Observation of All-Metal Aromatic Molecules. Science 291, 859–861. doi:10.1126/science.291.5505.859

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Wu, D., and Li, Z.-R. (2008). Compounds of Superatom Clusters: Preferred Structures and Significant Nonlinear Optical Properties of the BLi6-X (X = F, LiF2, BeF3, BF4) Motifs. Inorg. Chem. 47, 9773–9778. doi:10.1021/ic800184z

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Z.-J., Wang, F.-F., Li, Z.-R., Xu, H.-L., Huang, X.-R., Wu, D., et al. (2009). Large Static First and Second Hyperpolarizabilities Dominated by Excess Electron Transition for Radical Ion Pair Salts M2˙+TCNQ˙−(M = Li, Na, K). Phys. Chem. Chem. Phys. 11, 402–408. doi:10.1039/B809161G

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, L., Moreno, D., Osorio, E., Castro, A. C., Pan, S., Chattaraj, P. K., et al. (2016). Structure and Bonding of IrB12−: Converting a Rigid boron B12 Platelet to a Wankel Motor. RSC Adv. 6, 27177–27182. doi:10.1039/C6RA02992B

CrossRef Full Text | Google Scholar

Liu, S., and Gibb, B. C. (2008). High-definition Self-Assemblies Driven by the Hydrophobic Effect: Synthesis and Properties of a Supramolecular Nanocapsule. Chem. Commun. 32, 3709–3716. doi:10.1039/B805446K

PubMed Abstract | CrossRef Full Text | Google Scholar

Lü, J., Perez-Krap, C., Suyetin, M., Alsmail, N. H., Yan, Y., Yang, S., et al. (2014). A Robust Binary Supramolecular Organic Framework (SOF) with High CO2 Adsorption and Selectivity. J. Am. Chem. Soc. 136, 12828–12831. doi:10.1021/ja506577g

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, T., and Chen, F. (2012). Multiwfn: a Multifunctional Wavefunction Analyzer. J. Comput. Chem. 33, 580–592. doi:10.1002/jcc.22885

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, Y., Li, J., Tada, T., Toda, Y., Ueda, S., Yokoyama, T., et al. (2016). Water Durable Electride Y5Si3: Electronic Structure and Catalytic Activity for Ammonia Synthesis. J. Am. Chem. Soc. 138, 3970–3973. doi:10.1021/jacs.6b00124

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, Y., Wang, J., Li, J., Wu, J., Kanno, S., Tada, T., et al. (2018). Realization of Mott-insulating Electrides in Dimorphic Yb5Sb3. Phys. Rev. B 98, 125128. doi:10.1103/PhysRevB.98.125128

CrossRef Full Text | Google Scholar

Mao, W. L., and Mao, H.-k. (2004). Hydrogen Storage in Molecular Compounds. Proc. Natl. Acad. Sci. 101, 708–710. doi:10.1073/pnas.0307449100

CrossRef Full Text | Google Scholar

Mao, W. L., Mao, H. K., Goncharov, A. F., Struzhkin, V. V., Guo, Q., Hu, J., and Zhao, Y. (2002). Hydrogen Clusters in Clathrate Hydrate. Science 297, 2247–2249. doi:10.1126/science.1075394

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin, J. M. L., and Taylor, P. R. (1996). Structure and Vibrations of Small Carbon Clusters from Coupled-Cluster Calculations. J. Phys. Chem. 100, 6047–6056. doi:10.1021/jp952471r

CrossRef Full Text | Google Scholar

Mastalerz, M., Schneider, M. W., Oppel, I. M., and Presly, O. (2011). A Salicylbisimine Cage Compound with High Surface Area and Selective CO2/CH4 Adsorption. Angew. Chem. Int. Ed. 50, 1046–1051. doi:10.1002/anie.201005301

PubMed Abstract | CrossRef Full Text | Google Scholar

Matsuishi, S., Toda, Y., Miyakawa, M., Hayashi, K., Kamiya, T., Hirano, M., et al. (2003). High-Density Electron Anions in a Nanoporous Single Crystal: [Ca24Al28O64]4+(4e-). Science. 301, 626–629. doi:10.1126/science.1083842

PubMed Abstract | CrossRef Full Text | Google Scholar

McKeown, N. B., Gahnem, B., Msayib, K. J., Budd, P. M., Tattershall, C. E., Mahmood, K., et al. (2006). Towards Polymer-Based Hydrogen Storage Materials: Engineering Ultramicroporous Cavities within Polymers of Intrinsic Microporosity. Angew. Chem. Int. Ed. 45, 1804–1807. doi:10.1002/anie.200504241

PubMed Abstract | CrossRef Full Text | Google Scholar

McLean, A. D., and Chandler, G. S. (1980). Contracted Gaussian Basis Sets for Molecular Calculations. I. Second Row Atoms, Z=11-18. J. Chem. Phys. 72, 5639–5648. doi:10.1063/1.438980

CrossRef Full Text | Google Scholar

Mitikiri, P., Jana, G., Sural, S., and Chattaraj, P. K. (2018). A Machine Learning Technique toward Generating Minimum Energy Structures of Small boron Clusters. Int. J. Quan. Chem. 118, e25672. doi:10.1002/qua.25672

CrossRef Full Text | Google Scholar

Mitoraj, M. P., Michalak, A., and Ziegler, T. (2009). A Combined Charge and Energy Decomposition Scheme for Bond Analysis. J. Chem. Theor. Comput. 5, 962–975. doi:10.1021/ct800503d

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitra, A., Jana, G., Agrawal, P., Sural, S., and Chattaraj, P. K. (2020). Integrating Firefly Algorithm with Density Functional Theory for Global Optimization of Al42− Clusters. Theor. Chem. Acc. 139, 1–12. doi:10.1007/s00214-020-2550-y

CrossRef Full Text | Google Scholar

Mitra, A., Jana, G., Pal, R., Gaikwad, P., Sural, S., and Chattaraj, P. K. (2021). Determination of Stable Structure of a Cluster Using Convolutional Neural Network and Particle Swarm Optimization. Theor. Chem. Acc. 140, 1–12. doi:10.1007/s00214-021-02726-z

CrossRef Full Text | Google Scholar

Moreno, D., Pan, S., Zeonjuk, L. L., Islas, R., Osorio, E., Martínez-Guajardo, G., et al. (2014). B182−: a Quasi-Planar Bowl Member of the Wankel Motor Family. Chem. Commun. 50, 8140–8143. doi:10.1039/C4CC02225D

CrossRef Full Text | Google Scholar

Morokuma, K. (1971). Molecular Orbital Studies of Hydrogen Bonds. III. C=O···H-O Hydrogen Bond in H2CO···H2O and H2CO···2H2O. J. Chem. Phys. 55, 1236–1244. doi:10.1063/1.1676210

CrossRef Full Text | Google Scholar

Msayib, K. J., Book, D., Budd, P. M., Chaukura, N., Harris, K. D. M., Helliwell, M., et al. (2009). Nitrogen and Hydrogen Adsorption by an Organic Microporous Crystal. Angew. Chem. 121, 3323–3327. doi:10.1002/ange.200900234

PubMed Abstract | CrossRef Full Text | Google Scholar

Muhammad, S., Xu, H., Liao, Y., Kan, Y., and Su, Z. (2009). Quantum Mechanical Design and Structure of the Li@B10H14 Basket with a Remarkably Enhanced Electro-Optical Response. J. Am. Chem. Soc. 131, 11833–11840. doi:10.1021/ja9032023

PubMed Abstract | CrossRef Full Text | Google Scholar

Muhammad, S., Xu, H., and Su, Z. (2011). Capturing a Synergistic Effect of a Conical Push and an Inward Pull in Fluoro Derivatives of Li@B10H14Basket: Toward a Higher Vertical Ionization Potential and Nonlinear Optical Response. J. Phys. Chem. A. 115, 923–931. doi:10.1021/jp110401f

PubMed Abstract | CrossRef Full Text | Google Scholar

Norbye, J. P. (1971). The Wankel Engine: Design, Development, Applications. 1st Ed. Philadelphia, PA: Chilton Book Company.

Pal, R., and Chattaraj, P. K. (2021). Possible Effects of Fluxionality of a Cavitand on its Catalytic Activity through Confinement. Phys. Chem. Chem. Phys. 23, 15817–15834. doi:10.1039/D1CP01826D

CrossRef Full Text | Google Scholar

Pan, S., Ghara, M., Kar, S., Zarate, X., Merino, G., and Chattaraj, P. K. (2018). Noble Gas Encapsulated B40 Cage. Phys. Chem. Chem. Phys. 20, 1953–1963. doi:10.1039/C7CP07890K

PubMed Abstract | CrossRef Full Text | Google Scholar

Pan, S., Giri, S., and Chattaraj, P. K. (2012a). A Computational Study on the Hydrogen Adsorption Capacity of Various Lithium-Doped boron Hydrides. J. Comput. Chem. 33, 425–434. doi:10.1002/jcc.21985

PubMed Abstract | CrossRef Full Text | Google Scholar

Pan, S., Jana, G., Gupta, A., Merino, G., and Chattaraj, P. K. (2017). Endohedral Gas Adsorption by Cucurbit[7]uril: a Theoretical Study. Phys. Chem. Chem. Phys. 19, 24448–24452. doi:10.1039/C7CP03984K

PubMed Abstract | CrossRef Full Text | Google Scholar

Pan, S., Mandal, S., and Chattaraj, P. K. (2015). Cucurbit[6]uril: a Possible Host for noble Gas Atoms. J. Phys. Chem. B 119, 10962–10974. doi:10.1021/acs.jpcb.5b01396

PubMed Abstract | CrossRef Full Text | Google Scholar

Pan, S., Merino, G., and Chattaraj, P. K. (2012b). The Hydrogen Trapping Potential of Some Li-Doped star-like Clusters and Super-alkali Systems. Phys. Chem. Chem. Phys. 14, 10345–10350. doi:10.1039/C2CP40794A

PubMed Abstract | CrossRef Full Text | Google Scholar

Pan, S., Mondal, S., and Chattaraj, P. K. (2013a). Cucurbiturils as Promising Hydrogen Storage Materials: a Case Study of Cucurbit[7]uril. New J. Chem. 37, 2492–2499. doi:10.1039/C3NJ00399J

CrossRef Full Text | Google Scholar

Pan, S., Moreno, D., Merino, G., and Chattaraj, P. K. (2014). Stability of Noble-Gas-Bound SiH3+Clusters. ChemPhysChem 15, 3554–3564. doi:10.1002/cphc.201402370

PubMed Abstract | CrossRef Full Text | Google Scholar

Pan, S., Solà, M., and Chattaraj, P. K. (2013b). On the Validity of the Maximum Hardness Principle and the Minimum Electrophilicity Principle During Chemical Reactions. J. Phys. Chem. A 117, 1843–1852. doi:10.1021/jp312750n

Pauling, L., and Sherman, J. (1933). The Nature of the Chemical Bond. VI. The Calculation from Thermochemical Data of the Energy of Resonance of Molecules Among Several Electronic Structures. J. Chem. Phys. 1, 606–617. doi:10.1063/1.1749335

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1997). Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)]. Phys. Rev. Lett. 78, 1396. doi:10.1103/PhysRevLett.78.1396

CrossRef Full Text | Google Scholar

Perdew, J. P. (1986a). Density-functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Phys. Rev. B 33, 8822–8824. doi:10.1103/PhysRevB.33.8822

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P. (1986b). Erratum: Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Phys. Rev. B 34, 7406. doi:10.1103/PhysRevB.34.7406

CrossRef Full Text | Google Scholar

Pham, D. T., Ghanbarzadeh, A., Koc, E., Otri, S., Rahim, S., and Zaidi, M. (2005). “The Bees Algorithm,” in Technical Note (UK: Manufacturing Engineering Centre, Cardiff University).

Google Scholar

P. J. Stang, and F. Diederich (Editors) (2008). Modern Acetylene Chemistry (Hoboken, New Jersey, USA: John Wiley & Sons).

Pless, V., Suter, H. U., and Engels, B. (1994). Ab Initio study of the Energy Difference between the Cyclic and Linear Forms of the C6 Molecule. J. Chem. Phys. 101, 4042–4048. doi:10.1063/1.467521

CrossRef Full Text | Google Scholar

Popov, I. A., Li, W.-L., Piazza, Z. A., Boldyrev, A. I., and Wang, L.-S. (2014). Complexes between Planar Boron Clusters and Transition Metals: A Photoelectron Spectroscopy and Ab Initio Study of CoB12- and RhB12-. J. Phys. Chem. A. 118, 8098–8105. doi:10.1021/jp411867q

PubMed Abstract | CrossRef Full Text | Google Scholar

Qu, J., Zhu, S., Zhang, W., and Zhu, Q. (2019). Electrides with Dinitrogen Ligands. ACS Appl. Mater. Inter. 11, 5256–5263. doi:10.1021/acsami.8b18676

PubMed Abstract | CrossRef Full Text | Google Scholar

Raghavachari, K., Binkley, J. S., Seeger, R., and Pople, J. A. (1980). Self-Consistent Molecular Orbital Methods. 20. Basis Set for Correlated Wave-Functions. J. Chem. Phys. 72, 650–654. doi:10.1063/1.438955

CrossRef Full Text | Google Scholar

Raghavachari, K., and Binkley, J. S. (1987). Structure, Stability, and Fragmentation of Small Carbon Clusters. J. Chem. Phys. 87, 2191–2197. doi:10.1063/1.453145

CrossRef Full Text | Google Scholar

Reed, A. E., Curtiss, L. A., and Weinhold, F. (1988). Intermolecular Interactions from a Natural Bond Orbital, Donor-Acceptor Viewpoint. Chem. Rev. 88, 899–926. doi:10.1021/cr00088a005

CrossRef Full Text | Google Scholar

Reed, A. E., Weinstock, R. B., and Weinhold, F. (1985). Natural Population Analysis. J. Chem. Phys. 83, 735–746. doi:10.1063/1.449486

CrossRef Full Text | Google Scholar

Rosi, N. L., Eckert, J., Eddaoudi, M., Vodak, D. T., Kim, J., O'Keeffe, M., et al. (2003). Hydrogen Storage in Microporous Metal-Organic Frameworks. Science 300, 1127–1129. doi:10.1126/science.1083440

PubMed Abstract | CrossRef Full Text | Google Scholar

Rowsell, J. L. C., and Yaghi, O. M. (2005). Strategies for Hydrogen Storage in Metal-Organic Frameworks. Angew. Chem. Int. Ed. 44, 4670–4679. doi:10.1002/anie.200462786

PubMed Abstract | CrossRef Full Text | Google Scholar

Roy, D. R., and Chattaraj, P. K. (2008). Reactivity, Selectivity, and Aromaticity of Be32- and its Complexes. J. Phys. Chem. A. 112, 1612–1621. doi:10.1021/jp710820c

PubMed Abstract | CrossRef Full Text | Google Scholar

Sabin, J. R., and Brandas, E. J. (2009). Advances in Quantum Chemistry: Theory of Confined Quantum Systems-Part One. Cambridge: Academic Press.

Saha, R., and Chattaraj, P. K. (2018). Activation of Small Molecules (H2, CO2, N2O, CH4, and C6H6) by a Porphyrinoid-Based Dimagnesium(I) Complex, an Electride. ACS Omega 3, 17199–17211. doi:10.1021/acsomega.8b03006

PubMed Abstract | CrossRef Full Text | Google Scholar

Saha, R., Das, P., and Chattaraj, P. K. (2019). A Complex Containing Four Magnesium Atoms and Two Mg-Mg Bonds Behaving as an Electride. Eur. J. Inorg. Chem. 2019, 4105–4111. doi:10.1002/ejic.201900813

CrossRef Full Text | Google Scholar

Saha, R., Kar, S., Pan, S., Martínez-Guajardo, G., Merino, G., and Chattaraj, P. K. (2017). A Spinning Umbrella: Carbon Monoxide and Dinitrogen Bound MB12- Clusters (M = Co, Rh, Ir). J. Phys. Chem. A. 121, 2971–2979. doi:10.1021/acs.jpca.6b12232

PubMed Abstract | CrossRef Full Text | Google Scholar

Saha, R., Pan, S., Merino, G., and Chattaraj, P. K. (2015). Comparative Study on the Noble-Gas Binding Ability of BeX Clusters (X = SO4, CO3, O). J. Phys. Chem. A. 119, 6746–6752. doi:10.1021/acs.jpca.5b03888

PubMed Abstract | CrossRef Full Text | Google Scholar

Santos, J. C., Andres, J., Aizman, A., and Fuentealba, P. (2005). An Aromaticity Scale Based on the Topological Analysis of the Electron Localization Function Including σ and π Contributions. J. Chem. Theor. Comput. 1, 83–86. doi:10.1021/ct0499276

PubMed Abstract | CrossRef Full Text | Google Scholar

Schettino, V., and Bini, R. (2007). Constraining Molecules at the Closest Approach: Chemistry at High Pressure. Chem. Soc. Rev. 36, 869–880. doi:10.1039/B515964B

PubMed Abstract | CrossRef Full Text | Google Scholar

Schlegel, H. B., Iyengar, S. S., Li, X., Millam, J. M., Voth, G. A., Scuseria, G. E., et al. (2002). Ab Initio molecular Dynamics: Propagating the Density Matrix with Gaussian Orbitals. III. Comparison with Born-Oppenheimer Dynamics. J. Chem. Phys. 117, 8694–8704. doi:10.1063/1.1514582

CrossRef Full Text | Google Scholar

Schlegel, H. B., Millam, J. M., Iyengar, S. S., Voth, G. A., Daniels, A. D., Scuseria, G. E., et al. (2001). Ab Initiomolecular Dynamics: Propagating the Density Matrix with Gaussian Orbitals. J. Chem. Phys. 114, 9758–9763. doi:10.1063/1.1372182

CrossRef Full Text | Google Scholar

Schleyer, P. v. R., Maerker, C., Dransfeld, A., Jiao, H., and van Eikema Hommes, N. J. R. (1996). Nucleus-independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 118, 6317–6318. doi:10.1021/ja960582d

PubMed Abstract | CrossRef Full Text | Google Scholar

Schneider, M. W., Oppel, I. M., Ott, H., Lechner, L. G., Hauswald, H.-J. S., Stoll, R., et al. (2012). Periphery-Substituted [4+6] Salicylbisimine Cage Compounds with Exceptionally High Surface Areas: Influence of the Molecular Structure on Nitrogen Sorption Properties. Chem. Eur. J. 18, 836–847. doi:10.1002/chem.201102857

PubMed Abstract | CrossRef Full Text | Google Scholar

Sekhar, P., Ghosh, A., Joshi, M., and Ghanty, T. K. (2017). Noble Gas Encapsulated Endohedral Zintl Ions Ng@Pb122- and Ng@Sn122- (Ng = He, Ne, Ar, and Kr): A Theoretical Investigation. J. Phys. Chem. C 121, 11932–11949. doi:10.1021/acs.jpcc.7b03294

CrossRef Full Text | Google Scholar

Sergeeva, A. P., Popov, I. A., Piazza, Z. A., Li, W.-L., Romanescu, C., Wang, L.-S., et al. (2014). Understanding Boron through Size-Selected Clusters: Structure, Chemical Bonding, and Fluxionality. Acc. Chem. Res. 47, 1349–1358. doi:10.1021/ar400310g

PubMed Abstract | CrossRef Full Text | Google Scholar

Sharma, S., Kurashige, W., Niihori, Y., and Negishi, Y. (2017). Nanocluster Science. Supra-materials Nanoarchitectonics, 3–32. doi:10.1016/B978-0-323-37829-1.00001-8

CrossRef Full Text | Google Scholar

Srinivasu, K., Ghosh, S. K., Das, R., Giri, S., and Chattaraj, P. K. (2012). Theoretical Investigation of Hydrogen Adsorption in All-Metal Aromatic Clusters. RSC Adv. 2, 2914–2922. doi:10.1039/C2RA00643J

CrossRef Full Text | Google Scholar

Srivastava, R. (2021). Application of Optimization Algorithms in Clusters. Front. Chem. 9, 637286. doi:10.3389/fchem.2021.637286

PubMed Abstract | CrossRef Full Text | Google Scholar

Staroverov, V. N., Scuseria, G. E., Tao, J., and Perdew, J. P. (2003). Comparative Assessment of a New Nonempirical Density Functional: Molecules and Hydrogen-Bonded Complexes. J. Chem. Phys. 119, 12129–12137. doi:10.1063/1.1626543

CrossRef Full Text | Google Scholar

Sun, Q., Wang, Q., and Jena, P. (2005). Storage of Molecular Hydrogen in B−N Cage: Energetics and Thermal Stability. Nano Lett. 5, 1273–1277. doi:10.1021/nl050385p

PubMed Abstract | CrossRef Full Text | Google Scholar

Tao, J., Perdew, J. P., Staroverov, V. N., and Scuseria, G. E. (2003). Climbing the Density Functional Ladder: Nonempirical Meta-Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 91, 146401. doi:10.1103/PhysRevLett.91.146401

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsukuda, T., and Hakkinen, H. (2015). “Protected Metal Clusters: From Fundamentals to Applications,” in Frontiers of Nanoscience. 1st Ed. Editors R. E. Palmer (Amsterdam: Elsevier), Vol. 9.

CrossRef Full Text | Google Scholar

Thrash, T. P., Cagle, D. W., Alford, J. M., Wright, K., Ehrhardt, G. J., Mirzadeh, S., et al. (1999). Toward Fullerene-Based Radiopharmaceuticals: High-Yield Neutron Activation of Endohedral 165Ho Metallofullerenes. Chem. Phys. Lett. 308, 329–336. doi:10.1016/S0009-2614(99)00581-3

CrossRef Full Text | Google Scholar

Toda, Y., Yanagi, H., Ikenaga, E., Kim, J. J., Kobata, M., Ueda, S., et al. (2007). Work Function of a Room-Temperature, Stable Electride [Ca24Al28O64]4+(e-)4. Adv. Mater. 19, 3564–3569. doi:10.1002/adma.200700663

CrossRef Full Text | Google Scholar

Van Orden, A., and Saykally, R. J. (1998). Small Carbon Clusters: Spectroscopy, Structure, and Energetics. Chem. Rev. 98, 2313–2358. doi:10.1021/cr970086n

PubMed Abstract | CrossRef Full Text | Google Scholar

Van Rossum, G., and Drake, F. L. (2009). Python 3 Reference Manual. Scotts Valley, CA: CreateSpace. doi:10.1201/9781420049114.ch23

CrossRef Full Text

Vitillo, J. G., Regli, L., Chavan, S., Ricchiardi, G., Spoto, G., Dietzel, P. D. C., et al. (2008). Role of Exposed Metal Sites in Hydrogen Storage in MOFs. J. Am. Chem. Soc. 130, 8386–8396. doi:10.1021/ja8007159

PubMed Abstract | CrossRef Full Text | Google Scholar

Wadt, W. R., and Hay, P. J. (1985). Ab Initio effective Core Potentials for Molecular Calculations. Potentials for Main Group Elements Na to Bi. J. Chem. Phys. 82, 284–298. doi:10.1063/1.448800

CrossRef Full Text | Google Scholar

Wagner, B. D., Stojanovic, N., Day, A. I., and Blanch, R. J. (2003). Host Properties of Cucurbit[7]uril: Fluorescence Enhancement of Anilinonaphthalene Sulfonates. J. Phys. Chem. B 107, 10741–10746. doi:10.1021/jp034891j

CrossRef Full Text | Google Scholar

Wales, D. J., and Doye, J. P. K. (1997). Global Optimization by basin-hopping and the Lowest Energy Structures of Lennard-Jones Clusters Containing up to 110 Atoms. J. Phys. Chem. A. 101, 5111–5116. doi:10.1021/jp970984n

CrossRef Full Text | Google Scholar

Wang, J.-J., Zhou, Z.-J., Bai, Y., Liu, Z.-B., Li, Y., Wu, D., et al. (2012). The Interaction between Superalkalis (M3O, M = Na, K) and a C20F20 Cage Forming Superalkali Electride Salt Molecules with Excess Electrons inside the C20F20 Cage: Dramatic Superalkali Effect on the Nonlinear Optical Property. J. Mater. Chem. 22, 9652–9657. doi:10.1039/C2JM15405F

CrossRef Full Text | Google Scholar

Wang, J., Hanzawa, K., Hiramatsu, H., Kim, J., Umezawa, N., Iwanaka, K., et al. (2017). Exploration of Stable Strontium Phosphide-Based Electrides: Theoretical Structure Prediction and Experimental Validation. J. Am. Chem. Soc. 139, 15668–15680. doi:10.1021/jacs.7b06279

PubMed Abstract | CrossRef Full Text | Google Scholar

Ward, D. L., Huang, R. H., and Dye, J. L. (1988). Structures of Alkalides and Electrides. I. Structure of Potassium cryptand[2.2.2] Electride. Acta Crystallogr. C 44, 1374–1376. doi:10.1107/s0108270188002847

CrossRef Full Text | Google Scholar

Watts, J. D., Gauss, J., Stanton, J. F., and Bartlett, R. J. (1992). Linear and Cyclic Isomers of C4. A Theoretical Study with Coupled‐cluster Methods and Large Basis Sets. J. Chem. Phys. 97, 8372–8381. doi:10.1063/1.463407

CrossRef Full Text | Google Scholar

Weigend, F., and Ahlrichs, R. (2005). Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 7, 3297–3305. doi:10.1039/B508541A

PubMed Abstract | CrossRef Full Text | Google Scholar

Wiberg, K. B. (1968). Application of the Pople-Santry-Segal CNDO Method to the Cyclopropylcarbinyl and Cyclobutyl Cation and to Bicyclobutane. Tetrahedron 24, 1083–1096. doi:10.1016/0040-4020(68)88057-3

CrossRef Full Text | Google Scholar

Wilson, L. J., Cagle, D. W., Thrash, T. P., Kennel, S. J., Mirzadeh, S., Alford, J. M., et al. (1999). Metallofullerene Drug Design. Coord. Chem. Rev. 190–192, 199–207. doi:10.1016/S0010-8545(99)00080-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Woodley, S. M., Battle, P. D., Gale, J. D., and Richard A. Catlow, C. (1999). The Prediction of Inorganic crystal Structures Using a Genetic Algorithm and Energy Minimisation. Phys. Chem. Chem. Phys. 1, 2535–2542. doi:10.1039/A901227C

CrossRef Full Text | Google Scholar

Wu, X., Gao, Y., and Zeng, X. C. (2008). Hydrogen Storage in Pillared Li-Dispersed boron Carbide Nanotubes. J. Phys. Chem. C 112, 8458–8463. doi:10.1021/jp710022y

CrossRef Full Text | Google Scholar

Xie, Q., Huang, R. H., Ichimura, A. S., Phillips, R. C., Pratt, W. P., and Dye, J. L. (2000). Structure and Properties of a New Electride, Rb+(cryptand[2.2.2])e-. J. Am. Chem. Soc. 122, 6971–6978. doi:10.1021/ja9943445

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, H.-L., Li, Z.-R., Wu, D., Wang, B.-Q., Li, Y., Gu, F. L., et al. (2007). Structures and Large NLO Responses of New Electrides: Li-Doped Fluorocarbon Chain. J. Am. Chem. Soc. 129, 2967–2970. doi:10.1021/ja068038k

PubMed Abstract | CrossRef Full Text | Google Scholar

Yandulov, D. V., and Schrock, R. R. (2003). Catalytic Reduction of Dinitrogen to Ammonia at a Single Molybdenum center. Science 301, 76–78. doi:10.1126/science.1085326

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, C.-J., Leveen, L., and King, K. (2015). Ethane as a Cleaner Transportation Fuel. Environ. Sci. Technol. 49, 3263–3264. doi:10.1021/acs.est.5b00575

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, X. S. (2010). Firefly Algorithm, Stochastic Test Functions and Design Optimisation. Int. J. Bio-Inspired Comput. 2, 78–84. doi:10.1504/IJBIC.2010.032124

CrossRef Full Text | Google Scholar

Yuan, G.-N., Zhang, L.-N., Liu, L.-Q., and Wang, K. (2014). Passengers' Evacuation in Ships Based on Neighborhood Particle Swarm Optimization. Math. Probl. Eng. 2014, 1–10. doi:10.1155/2014/939723

CrossRef Full Text | Google Scholar

Zhan, Z.-h., and Zhang, J. (2008). “Adaptive Particle Swarm Optimization,” in International Conference on Ant Colony Optimization and Swarm Intelligence (Berlin, Germany: Springer), 227–234. doi:10.1007/978-3-540-87527-7_21

CrossRef Full Text | Google Scholar

Zhang, J.-P., and Chen, X.-M. (2009). Optimized Acetylene/carbon Dioxide Sorption in a Dynamic Porous crystal. J. Am. Chem. Soc. 131, 5516–5521. doi:10.1021/ja8089872

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Xiao, Z., Lei, H., Toda, Y., Matsuishi, S., Kamiya, T., et al. (2014). Two-Dimensional Transition-Metal Electride Y2C. Chem. Mater. 26, 6638–6643. doi:10.1021/cm503512h

CrossRef Full Text | Google Scholar

Zhang, Z., Xiang, S., and Chen, B. (2011). Microporous Metal-Organic Frameworks for Acetylene Storage and Separation. CrystEngComm 13 (20), 5983–5992. doi:10.1039/C1CE05437F

CrossRef Full Text | Google Scholar

Zhao, Y., Schultz, N. E., and Truhlar, D. G. (2006). Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Theor. Comput. 2, 364–382. doi:10.1021/ct0502763

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Y., and Truhlar, D. G. (2008). The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals. Theor. Chem. Account. 120, 215–241. doi:10.1007/s00214-007-0310-x

CrossRef Full Text | Google Scholar

Zhu, H., Liu, Y., Chen, Y., and Wen, Z. (2010). Cyclodextrins: Promising Candidate media for High-Capacity Hydrogen Adsorption. Appl. Phys. Lett. 96, 054101. doi:10.1063/1.3294631

CrossRef Full Text | Google Scholar

Zubarev, D. Y., and Boldyrev, A. I. (2011). “Multiple Aromaticity, Multiple Antiaromaticity, and Conflicting Aromaticity in Inorganic Systems,” in Encyclopedia of Inorganic and Bioinorganic Chemistry (Hoboken, NY, USA: John Wiley & Sons). doi:10.1002/9781119951438.eibc0396

CrossRef Full Text | Google Scholar

Zubarev, D. Y., Sergeeva, A. P., and Boldyrev, A. I. (2009). “Multifold Aromaticity, Multifold Antiaromaticity, and Conflicting Aromaticity: Implications for Stability and Reactivity of Clusters,” in Chemical Reactivity Theory (Boca Raton, FL, USA: CRC Press), 456–469.

CrossRef Full Text | Google Scholar