A Comparison of Order-Disorder in Several Families of Cubic Oxides

Order-disorder on both cation and oxygen sites is a hallmark of fluorite-derived structures, including pyrochlores. Ordering can occur on long- and short-range scales and can result in persistent metastable states. In various cubic oxide systems, different types of disorder are seen. The purpose of this paper is to review and compare the types and energetics of order-disorder phenomena in several families of cubic oxides having pyrochlore, weberite, defect fluorite, perovskite, rocksalt, and spinel structures. The goal is to better understand how structure, composition, and thermodynamic parameters (enthalpy and entropy) determine the feasibility of different competing ordering processes and structures in these diverse systems.

Introduction

Over the past two decades, there has been intense interest in defect chemistry, disorder, solid solution formation, and phase transitions in oxide pyrochlores (Glerup et al., 2001; Shlyakhtina et al., 2004; Liu et al., 2004; Knee et al., 2005; Mandal et al., 2006; Matsuhira et al., 2007; Zhang et al., 2008; Clements et al., 2011; Wang et al., 2011; de los Reyes et al., 2013; Zhang et al., 2013; Zhang et al., 2014; Popov et al., 2016; Paul et al., 2016; Rittman et al., 2017a; Rittman et al., 2017b; Simeone et al., 2017; Ponnilavan et al., 2019; Popov et al., 2020; Marlton et al., 2021; Panghal et al., 2021). Because the pyrochlore structure is a derivative of fluorite, it belongs to a large family of related structures. The interplay of short- and long-range order, especially in radiation-damaged pyrochlores, has drawn extensive attention as has amorphization and its recovery on annealing (Wang et al., 1998; Wang et al., 1999; Meldrum et al., 2001; Lian et al., 2002; Ewing et al., 2003; Lian et al., 2003a; Lian et al., 2004; Patel et al., 2008a; Patel et al., 2008b; Lang et al., 2009; Yudinsev et al., 2009; Lang et al., 2010; Xie et al., 2015; Shamblin et al., 2016a; Shamblin et al., 2016b; Kumari et al., 2016; Yang et al., 2017; Chung et al., 2018a; Chung et al., 2018b; Shamblin et al., 2018; Chung et al., 2019; Sherrod et al., 2021). Yet in a broader sense, pyrochlores are but one family of oxide materials.

Focusing on cubic structures, other families include defect fluorite ionic conductors such as yttria-stabilized zirconia (YSZ), weberites (both oxides and fluorides), rocksalt-based cation conducting oxides, perovskites, and spinels, all of which form the basis of numerous functional materials. Each of these families shows distinct and characteristic defect chemistry and order-disorder behavior.

Each simple structure (aristotype) is the parent of more complex structures showing ordering on anion and/or cation sublattices and the formation of layered structures. Modern diffraction and spectroscopy enable characterization of order on different length scales, with short-range order producing lower symmetry locally being detected increasingly often in nominally cubic structures (Radhakrishnan et al., 2011; Shamblin et al., 2016a; Shamblin et al., 2016b; Martel et al., 2017; Shamblin et al., 2018; Moran et al., 2019; Drey et al., 2020). The details of ordering are different in each structural family. Though at equilibrium at a given pressure, temperature, and composition, defect formation and order-disorder produce, by definition, the state of lowest Gibbs free energy, this macroscopic truism begs the question of why: why, in a structural sense, is one set of defects predominant while others are not, and why, in different structure types, does one get characteristic and distinct sets of defects. Such questions can be addressed by first-principles calculations (e.g., density functional theory and molecular dynamics) or by calculations using semiempirical interatomic potential. The results, though identifying the lowest energy configurations, are hard to compare for different structures and do not immediately give physical insight, in terms of identifiable structural parameters, to the question of why (Gunn et al., 2012; Xiao et al., 2015; Perriot et al., 2016; Solomon et al., 2016; Pilania et al., 2019; O’Quinn et al., 2020). Furthermore, many of the complex structures have too many elements and too large unit cells for meaningful computations. Computational approaches to different structures (possible or nonexistent) polymorphs for a given composition have also been very limited.

For more qualitative, but also more easily transferable, insight, solid-state chemists turn to concepts like ionic radius and tolerance factor, which fundamentally derive from optimizing local cation-anion coordination in terms of geometry and bond lengths (Goldschmidt, 1926; Cai et al., 2011; Mouta et al., 2013; Song and Liu, 2020). These concepts do not easily translate into describing order on the midrange scale, other than to say that it occurs to relieve “strain” in the lattice. At the same time, midrange order is challenging to attack by ab initio methods because of the large number of different atoms and large unit cells needed for realistic description.

A potentially useful step in understanding the “why” is understanding the “what” across different structure types and length scales. Thus, the goal of this paper is to describe the structures, defects, and order-disorder phenomena in the several classes of oxides mentioned above, linking, whenever possible, structural and thermodynamic behavior. By comparing these groups of materials, we propose some reasons why different types of defects and ordering schemes dominate in each group and suggest some areas for future research.

Specifically, we compare the occurrence and energetics of various types of defects and disorders in two groups of cubic oxides. The first group, as well as the one we spend most time on, consists of fluorite-related structures (pyrochlore, weberite, defect fluorite, and zirconolite) and perovskite and its derivatives. Both accommodate oxygen vacancies as well as cation disorder and cation vacancies. Their structures are not close-packed and relatively flexible, accommodating large cations with high coordination numbers (7–12), and some variability in oxidation state. The second group of cubic oxides consists of rocksalt-derived phases and spinels. Both are relatively dense structures based on cubic close packing of anions and they do not easily accommodate oxygen vacancies. They maintain charge balance by cation vacancies (and occasional cation interstitials) and variation in oxidation state of transition metal (TM) ions. They typically contain smaller ions with lower cation coordination numbers (4, 5, and 6) than the first group. We describe the various structures, compositions, and types of defects and disorder and their associated energetics for both groups of materials. In comparing these structures, disorder, and thermodynamics, we then turn to the why question, why does each structure type favor certain defects and not others.

Fluorite-Derived Structures

Pyrochlore

Pyrochlore oxides with idealized formula, A₂B₂O₇, are derivatives of the fluorite structure with ordered cations and vacancies (Subramanian et al., 1983; Chakoumakos, 1984; Ewing et al., 2004; Gardner et al., 2010). While cations with diverse valences can occupy A- and B-sites, the most common composition which has been widely studied with a focus on order-disorder phenomena is A₂B₂O₇ where A is a trivalent cation often rare earth and B is a tetravalent cation. The structure forms in cubic Fd-3m (no. 227) space group (Vanderah et al., 2005). It has five distinct Wycoff positions which are occupied by cations, anions, and vacancies. Bigger “A” cations occupy the 16d position with eight coordinated cation coordination with oxide anions, while smaller “B” cations occupy 16c position with six-coordinated geometry. Oxide anions go into 48f and 8b positions. Vacancies order in 8a positions. Structures of defect fluorite, pyrochlore, and weberite are shown schematically in Figure 1.

FIGURE 1

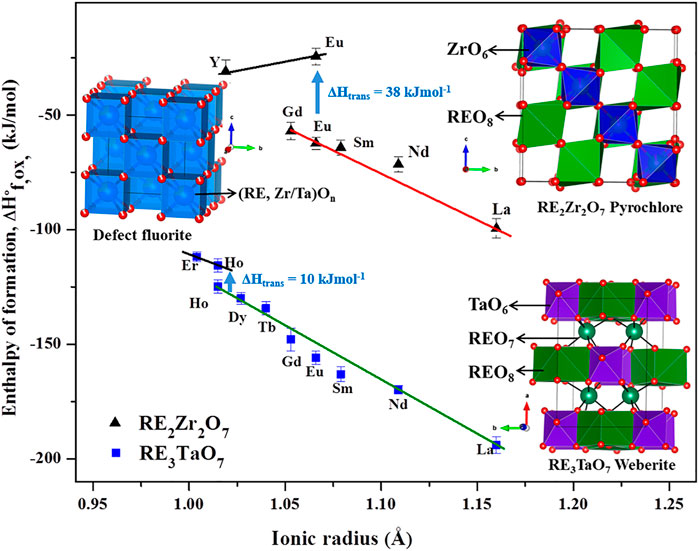
FIGURE 1. Structure and energetics of order-disorder transitions between ordered pyrochlore, weberite, and disordered defect fluorite structures with RE₂Zr₂O₇ and RE₃TaO₇ systems as examples. The figure has been made based on data from the literature (Saradhi et al., 2012; Subramani and Navrotsky, 2019).

The ordered pyrochlore structure disorders the defect fluorite structure under various conditions. The disordered defect fluorite structure of A₂B₂O₇ is basically the fluorite structure with cubic Fm-3m space group but with vacancies in O sites (Minervini et al., 2000; Wuensch and Eberman, 2000). Both A and B cations are distributed in 4a positions and both oxygen and vacancies occupy 8c positions, giving, as a limiting ideal case, complete disorder. All A and B cations are surrounded by seven oxide ions and a vacancy (7 + 1 coordination).

The process of disordering evolves through the formation of cation antisite pairs and Frenkel defects as discussed previously (Maram et al., 2015). The various conditions that induce disorder in pyrochlore are ionic radii of A and B cations, ball milling, temperature, pressure, and radiation damage (Subramanian et al., 1983; Heremans et al., 1995; Wuensch et al., 2000; Eberman et al., 2002; Lian et al., 2003b; Liu et al., 2004; Rushton et al., 2004; Fuentes et al., 2005; Zhang et al., 2005; Zhang and Saxena, 2005; Moreno et al., 2006a; Moreno et al., 2006b; Zhang et al., 2006; Mandal et al., 2007; Mandal and Tyagi, 2007; Zhang et al., 2007; Zhang et al., 2009; Zhang F. X. et al., 2010, Zhang et al., 2010 J; Lang et al., 2010; Sanjuán et al., 2011; Sayed et al., 2011; Shlyakhtina and Shcherbakova, 2011; Zhang et al., 2015; Rittman et al., 2017b; Turner et al., 2017; Fuentes et al., 2018; Wright et al., 2021).

Helean et al. (2004) reported enthalpies of formation for RE₂Ti₂O₇ systems which formed in ordered pyrochlore structure with RE = Sm - Lu. They also made similar measurements on GdTi₂-_xZr_xO₇ solid solution (Helean et al., 2000). Lian et al. (2006) published enthalpies of formation for RE₂Sn₂O₇ systems (RE = La, Nd, Sm, Eu, Dy, and Yb). The enthalpies of formation of RE₂Zr₂O₇ (RE = La, Ce, Nd, Sm, and Gd) system were also reported (Navrotsky and Ushakov, 2005; Radha et al., 2009). The enthalpies of formation became less exothermic with a decrease in ionic radii from La to Lu as the structure is more prone to disorder when the tetravalent and trivalent ions are more similar in size. The measurements on the above systems were made with a focus on their behavior upon irradiation, which is important in considering them as nuclear waste forms. It was concluded that a composition more susceptible to disorder is less likely to be amorphized by radiation damage (Ewing et al., 2004).

Enthalpies of formation of hafnium pyrochlores, RE2Hf2O7 (RE = Y, La, and Gd), were reported (Lee and Navrotsky, 2004; Ushakov et al., 2007). The enthalpy of the order-disorder transition for Hf₂Gd₂O₇ was 23.6 ± 3.1 kJmol⁻¹ and entropy of transition was calculated as 12 J K⁻¹mol⁻¹, which was half of the maximum possible configurational entropy, indicating possible local ordering in the long-range disordered fluorite phase. Enthalpies of formation of CaCeTi₂O₇ and Ca_1.5U_0.65Ti_1.85O₇ were measured (Helean et al., 2002). Recently, calorimetric data were obtained for iridium-based pyrochlores, RE₂Ir₂O₇ (RE = La, Gd, and Y) (Nenoff et al., 2021). In most of these systems, ionic radii of A or B cations play a dominant role in inducing disorder. Figure 1 shows formation enthalpies vs. ionic radii of different fluorite-related systems and enthalpy of an order-disorder transformation.

To understand the energetics of disordering, materials that disorder under different conditions must be studied. A disordered variant of Eu₂Zr₂O₇, which usually forms in ordered pyrochlore structure, was synthesized by soft chemical and laser melt quench methods, and the thermodynamics of the order-disorder transformation were determined (Saradhi et al., 2012). The transition enthalpy from ordered to disordered phase was 37.8 ± 3.1 kJmol⁻¹. In situ synchrotron diffraction coupled with aerodynamic levitation was performed on Eu₂Zr₂O₇ to study the structural progression of disorder upon increasing temperature (Maram et al., 2015). This was followed by in situ synchrotron diffraction on various zirconium and hafnium-based pyrochlores, RE₂Zr₂O₇ (RE = Sm, Eu, and Gd) and RE₂Hf₂O₇ (RE = La, Nd, and Sm), and modeling of the thermodynamics of disordering using configurational entropy calculations based on cation and anion site occupancies obtained from Rietveld refinement (Maram et al., 2018). This study extended early work on spinel disordering to fluorite-related systems (Navrotsky and Kleppa, 1967). The enthalpies of anion Frenkel disorder were found to be smaller than those of cation antisite disorder.

Hayun et al. (2012) investigated the energetics of highly disordered RE₂Ti₂O₇ (RE = Y, Gd, and Dy) formed by ball milling of their constituent binary oxides and of ordered variants formed by annealing the disordered materials at different temperatures. They found that the order-disorder transition upon annealing occurs through a two-step process.

With ionic radius, temperature, and ball milling already known to be important to induce disorder, radiation damage was then used as another “knob” to study the disorder energetics. Three different compositions in RE titanate and stannate pyrochlore systems were studied to understand the energetics of disordering induced by radiation damage (Chung et al., 2018b). Study of radiation damage, structural evolution upon annealing, and energetics of Dy₂Ti₂O₇ pyrochlore used a combination of nondestructive methods [pair distribution function (PDF) analysis of neutron total scattering] followed by destructive methods (high-temperature solution calorimetry and differential scanning calorimetry). The results showed that the radiation amorphized sample had been destabilized by 243 kJmol⁻¹. An important observation was that, upon annealing to 1,200°C, the amorphized sample never recovered completely structurally or energetically, with enthalpy of formation closer to that of disordered Dy₂Ti₂O₇ produced by ball milling (Hayun et al., 2012) than to that of pristine undamaged Dy₂Ti₂O₇, indicating a residual destabilization in the recrystallized pyrochlore. The neutron results showed that local disordered short-range domains containing a weberite-like structure (see below for discussion of weberites), present in the amorphized sample, persisted in the annealed material. The results were consistent with weberite-type short-range ordered domains observed in disordered pyrochlores (Shamblin et al., 2016a). Chung et al. (2018a) also studied the structural evolution and energetics in another pyrochlore Dy₂Sn₂O₇ and found residual destabilization similar to that in Dy₂Ti₂O₇. They then chose Er₂Ti₂O₇ and induced disorder by ball milling and radiation damage to study the energetics (Chung et al., 2019). They again found similar retention of local short-range weberite structure and concluded that the residual destabilization was a general phenomenon in radiation-damaged pyrochlores.

Thermodynamics of the composition dependence of order-disorder in pyrochlore solid solutions has been studied in Nd_xZr_1-xO_2-0.5x system (Finkeldei et al., 2017). They found that an order-disorder transition occurred at 0.30 < x < 0.33. Based on calorimetric data, they showed a disordering transition enthalpy of 30 kJmol⁻¹and transition entropy of 16 J K⁻¹mol⁻¹, yet again far less than the configurational entropy, showing evidence for local ordering.

Though order-disorder transitions have been induced by pressure in pyrochlores, not much thermodynamic work has been carried out on them. New pyrochlores with A₂B₂O₇ stoichiometry have been suggested to form under high pressure (Zhou and Wiebe, 2019). It will be interesting to study the energetics of pressure-induced order-disorder transformations to explore behavior under extreme conditions.

Weberite

The weberite structure with A₂B₂X₇ stoichiometry is also derived from the aristotype fluorite structure, with ordering in cation and anion sublattices. The weberite structure can include different cations with different charges in A- and B-sites and fluoride or oxide ions in the anion X sites. The structural and compositional diversity has been clearly described elsewhere (Cai and Nino, 2009; Cai and Nino, 2011). The discussion in this review will be limited to weberite oxides A₂³⁺B₂⁴⁺O₇ and A₃³⁺B⁵⁺O₇, which are currently the only systems studied for the structural and energetic evolution of order-disorder.

Fluorite-derived oxides with cation ratio 1:1 and molecular formula, A₂³⁺B₂⁴⁺O₇, usually form in the pyrochlore rather than the weberite structure (Subramanian et al., 1983). However, A₂³⁺B₂⁴⁺O₇ with weberite structure was discovered by Shamblin et al. (2016a), while analyzing the local structure of A₂B₂O₇ pyrochlores with disorder induced by various conditions, thus realizing that the weberite structure is a metastable form for this stoichiometry. A₃³⁺B⁵⁺O₇ phases form in the same orthorhombic space group as weberite A₂³⁺B₂⁴⁺O₇ (Allpress and Rossell, 1979; Wakeshima et al., 2004; Cai and Nino, 2007; Cai and Nino, 2009; Fu and IJdo, 2009; Cai et al., 2010; Cai and Nino, 2011; Nakamura et al., 2011; King et al., 2013). There has been some confusion on which space group (C2221 or Ccmm) best describes the structure. Gussev et al. (2020) recently showed that the space group C2221 describes the weberite structure based on the short-range and long-range structure using neutron total scattering data and DFT calculations.

The weberite structure (Figure 2) has three distinct sites for cations, namely, 4b, 4b, and 8c, and five different sites for oxide ions, 8c, 8c, 4a, 4a, and 4a. A³⁺ cations occupy one 4b and 8c sites and B⁵⁺ cations occupy other 4b sites in weberite-type A₃³⁺B⁵⁺O₇ oxides.

FIGURE 2

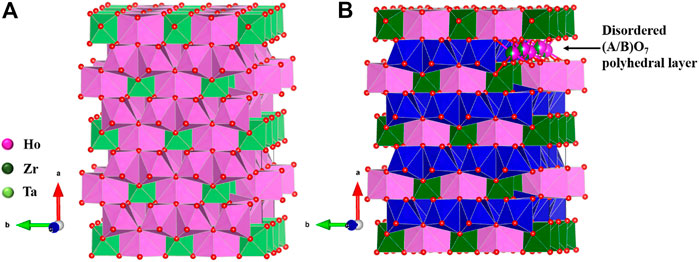
FIGURE 2. Structure of weberite-type (A) Ho₃TaO₇ and (B) Ho₂Zr₂O₇, both forming in orthorhombic C222₁ space group. The (A/B)O₇ layer in which partial disorder between A and B cations is marked with blue polyhedra for clarity in (B). Figure has been drawn based on the crystallographic data from the literature (Drey et al., 2020; Gussev et al., 2020). The crystal structures are drawn using the software VESTA (Momma and Izumi, 2008).

In A₂³⁺B₂⁴⁺O₇, A³⁺ and B⁴⁺ go into 4b sites, and 8c sites are occupied equally by both A³⁺ and B⁴⁺. 4b sites form a layer of the weberite-type structure in which the A cation takes eightfold coordination forming chains of edge-shared AO₈ cuboctahedra and B cations go into sixfold coordination forming chains of edge-shared BO₆ octahedra along the c axis. Then, both AO₈ and BO₆ chains share edges in an alternating arrangement along the b axis to form AO₈-BO₆ layers. The difference between A₃³⁺B⁵⁺O₇ and A₂³⁺B₂⁴⁺O₇ comes in the other layer having 8c sites which lead to sevenfold coordination with a distorted pentagonal bipyramidal geometry. The 8c sites are occupied completely by A³⁺ cations forming edge-shared AO₇ polyhedral chains along the c axis and the chains in turn share edges along the b axis to form the AO₇ layer. AO₈-BO₆ and AO₇ layers arrange alternately to form the overall structure (Gussev et al., 2020). However, in A₂³⁺M₂⁴⁺O₇, 8c sites are occupied equally by both A³⁺ and B⁴⁺ forming (A/B)O₇ polyhedral layer leading to disorder (Shamblin et al., 2016a; Drey et al., 2020). So, the structure can be seen as an alternating arrangement of ordered and disordered layers in weberite-type, A₂M₂O₇. In other words, the structure is intermediate between ideal pyrochlore (fully ordered) and defect fluorite (fully disordered), with, presumably, intermediate configurational entropy. This partially disordered weberite structure is found in the short-range ordered domains of disordered defect fluorite materials and annealed radiation-damaged materials, suggesting that a completely ordered state is difficult to achieve in these materials and may require annealing at higher temperatures for a longer time.

The thermochemistry of two systems with A₃BO₇ (A = RE; B = Nb, and Ta) composition has been studied. Mielewczyk-Gryn and Navrotsky (2015) reported enthalpies of formation of RE₃NbO₇ (RE = Y, La, Nd, Gd-Er, and Yb) with order-disorder occurring in compounds with RE ionic radii smaller than Tb. Energetics of another system, RE₃TaO₇ (La, Nd, Sm-Yb), was reported by Subramani and Navrotsky (2019). In both systems, enthalpies of formation became less exothermic as RE ionic radii decreased, showing a trend similar to RE₂M₂O₇ pyrochlores. The occurrence of ordered and disordered variants for a single composition, Ho₃TaO₇, enabled the study of the energetics of the order-disorder transition. It was found that the enthalpy of transition between ordered and disordered variants was near 10 kJmol⁻¹ (Figure 1). Based on configurational entropy calculations, substantial short-range ordering (SRO) in long-range disordered Ho₃TaO₇ was proposed.

Figure 3 shows enthalpies of formation vs. RE ionic radius. The data are based on high-temperature oxide melt solution calorimetry experiments performed by Navrotsky and coworkers over the past two decades. The plot clearly shows a trend of enthalpies of formation becoming less exothermic as RE ionic radii decrease for various fluorite-related systems. It is noteworthy that few systems have a single composition that exhibits both ordered and disordered polymorphs. A linear fit was used separately on enthalpies of formation of compositions with ordered and disordered structures in each system. The slopes show some scatter for ordered structures but are similar for ordered structures and are much less steep for disordered ones. In the future, one may be able to estimate enthalpies of formation for a whole series of rare earth by measuring the enthalpy of formation of a single composition in the system and applying the average slope.

FIGURE 3

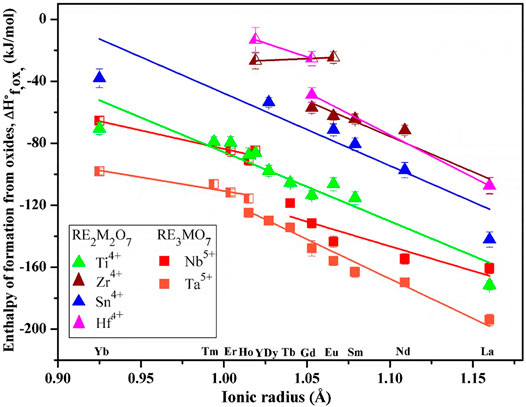
FIGURE 3. Enthalpies of formation vs. ionic radius of rare earth ions. The filled squares show compounds with weberite structure. The filled triangles represent compounds with ordered pyrochlore structure. The half-filled squares and triangles indicate compounds with disordered defect fluorite structure. The data for RE₂Ti₂O₇ and RE₂Sn₂O₇ are from Helean et al. (2004) and Lian et al. (2006). The data for RE₂Zr₂O₇ are from Navrotsky and Ushakov (2005), Radha et al. (2009), and Saradhi et al. (2012). The data for RE₂Hf₂O₇ are from Navrotsky and Ushakov (2005) and Ushakov et al. (2007). The data for RE₃MO₇ (M = Nb and Ta) are from (Mielewczyk-Gryn and Navrotsky (2015) and (Subramani and Navrotsky (2019).

Thermochemistry of pure weberite A₂B₂O₇ materials cannot be measured directly because such phases generally do not exist. The radiation-damaged and annealed samples that Chung et al. (2018a) measured contained weberite-like short-range ordered local domains, but the exact amount of such domains is hard to estimate. The thermochemical measurements made by Hayun et al. (2012) on disordered A₂B₂O₇ samples produced by ball milling might have had similar short-range ordered weberite domains, but there are no samples left for further studies. Drey et al. (2020a) described disordering in an unirradiated Ho₂(Ti_1-xZr_x)₂O₇ solid solution in which one of the end members, Ho₂Ti₂O₇, had the ordered pyrochlore structure and other, Ho₂Zr₂O₇, formed in the disordered defect fluorite structure. They investigated the long-range and short-range ordering using Rietveld refinement and PDF analysis of neutron scattering data. They found that an order-disorder transition occurred abruptly at the long-range crystallographic scale around x = 0.6, while order-disorder occurred gradually with increasing x on the short-range (nano)scale. The measured heats of mixing suggested that the solid solution could be considered a mixture of two phases at the nanoscale, agreeing with local structure studies. The structure of Ho₂Zr₂O₇ was reported to be completely weberite C2221 at the short-range scale by neutron PDF analysis. Thermochemical data for another related solid solution between pyrochlore Y₂Ti₂O₇ and defect fluorite Y₃NbO₇ were reported recently (Winiarz et al., 2020). Though niobium-rich members formed in a disordered structure based on XRD analysis, there were additional reflections indicating possible superstructure. More structural analysis is needed to delineate these order-disorder phenomena.

Understanding the energetics of order-disorder transitions induced by other parameters like temperature, radiation damage and pressure in weberite materials are open fields for future studies. Recently, a new oxide of composition MgTiSi₂O₇ with weberite structure in the MgO-SiO₂-TiO₂ system has been discovered under high pressure and high-temperature conditions similar to the ones found in the Earth’s transition zone and lower mantle (Bindi et al., 2017; Matrosova et al., 2020). MgTiSi₂O₇ weberite has cation occupancy disordering with Mg and Ti ions sharing the A cation sites and Si and Ti occupying the B cation sites (Bindi et al., 2017). This may lead to some “entropy stabilization.” The work suggests the possibility of finding various new compositions with fluorite-related structure in planetary interiors. Thus, thermochemistry of pressure-induced order-disorder transitions will be interesting for pyrochlores in view of understanding their formation, existence, and role in planetary interiors.

Other Fluorite-Related Structures

Y₂O₃ (YO_1.5) doping in zirconia (ZrO₂) introduces oxygen vacancies and leads to stabilization of zirconia in disordered cubic defect fluorite structure. These materials are called cubic yttria-stabilized zirconia (c-YSZ). The enthalpies of formation of disordered c-YSZ materials in the YO_1.5-ZrO₂ solid solution have been measured (Lee et al., 2003). They found that the enthalpy of mixing was negative with a very negative interaction parameter suggesting substantial SRO. Annealing produced an ordered δ-phase (Y₄Zr₃O₁₂) and enabled the study of the energetics of order-disorder. There is no difference in the enthalpy of solution of the δ-phase and the disordered c-YSZ solid solution. This suggests strong short-range order in the nominally disordered c-YSZ. The appearance of the δ-phase superstructure in XRD patterns may indicate growth of domain size in ordered regions rather than the onset of ordering. Lee and Navrotsky (2004) reported even more negative interaction parameters for YO_1.5-HfO₂ solid solution than for YO_1.5-ZrO₂ and suggested even stronger SRO. Simoncic and Navrotsky (2007a) studied different REO_1.5-HfO₂ solid solutions which formed in nominally disordered structure and again found strong negative interaction parameters indicating SRO (Simoncic and Navrotsky, 2007a). Simoncic and Navrotsky (2007b) found similar negative interaction parameter for other RE₂O₃(REO_1.5)-ZrO₂ and RE₂O₃(REO_1.5)-HfO₂ solid solutions, confirming and generalizing short-range order in these long-range disordered materials as well.

The enthalpies of formation of CeO₂ doped with La₂O₃, Gd₂O₃, and Y₂O₃, are positive (Chen and Navrotsky, 2006) in contrast to YO_1.5-ZrO₂ and YO_1.5-HfO₂ systems The reason for such behavior was attributed to the larger ionic radius of Ce⁴⁺ than that of Zr⁴⁺ and Hf⁴⁺ ions, making 7-fold coordination less favorable for the larger tetravalent ion and limiting the favorable energetics associated with oxide ion transfer (Chen et al., 2005). La₂O₃ and Y₂O₃-doped ThO₂ were studied by Aizenshtein et al. (2010). The energetics of these two systems were balanced by competition between a destabilizing factor due to cation size mismatch and a stabilizing factor due to defect clustering. The compositions with maximum endothermic enthalpies of formation in both La and Y doped ceria and thoria systems exhibited maximum ionic conductivity. As clustering became more pronounced at higher doping levels, ionic conductivity stayed constant or decreased while the mixing energetics became more favorable. Buyukkilic et al. (2012) and Buyukkilic et al. (2014) carried out a systematic study on the energetics of singly and doubly doped CeO₂ with Nd₂O₃ and Sm₂O₃. The doubly doped system had less average size mismatch, and the maxima in conductivity and heat of mixing were both shifted to higher doping levels, with heat of mixing smaller in magnitude. Enthalpies of defect association of the doubly doped (Nd.Sm) in a 1:1 ratio system were less exothermic than those of singly doped (Nd or Sm) systems. These studies show that ionic conductivity, defect association, and heats of mixing are closely related.

Zirconolites [CaMTi₂O₇ (M = Zr and Hf)] are another set of pyrochlore-related compounds derived from fluorite with defects but with lower symmetry and higher ordering for cations (Grey et al., 2003; Salamat et al., 2013; McCaugherty and Grosvenor, 2019). They are studied for the possible application as nuclear waste materials to host actinides in high-level waste (Vance et al., 1994; Ewing et al., 2004). Various types of disorder have been induced in the zirconolite structure using chemical substitution and high pressure (Whittle et al., 2012; Salamat et al., 2013). The enthalpies of formation of undoped CaMTi₂O₇ (M = Zr and Hf) and uranium doped CaZrTi₂O₇ have been reported (Putnam et al., 1999a; Putnam et al., 1999b; Subramani et al., 2020). However, energetics of disordering in zirconolites have not been explored in depth. Such studies would be very useful to understand the process of disordering in such highly ordered systems.

Perovskite and Related Structures

Structure and Occurrence

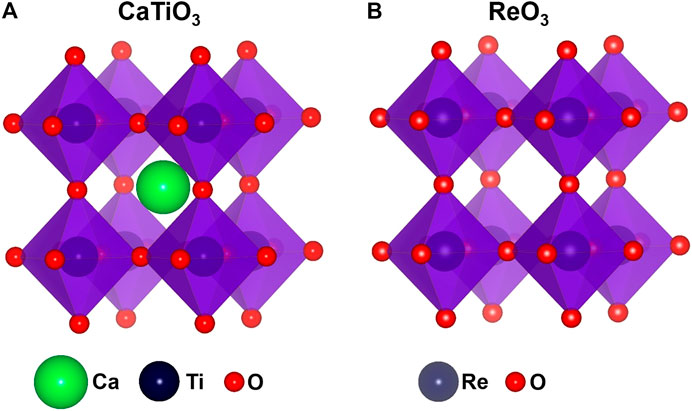
Perovskites derived from the ideal cubic aristotype structure are among the most, if not the most, rigorously investigated class of materials. Perovskite sensu stricto is a CaTiO₃ mineral and compounds with the isotypical crystal structures and ABX₃ (where A is an alkali, alkali earth, or lanthanide metal, B is a TM, and X is an oxygen or halogen atom) general formula are classified as inorganic perovskites. The perovskite structure is based on a corner-sharing array of octahedra which creates a large central site with room for a larger cation. This structure has flexibility in terms of rotation and distortion of the octahedra. The ideal cubic ABX₃ perovskite (space group Pm3m) has a large A cation at a twelve-coordinated site (A-site) by the X anions and a medium-size B cation at a six-coordinated site (B-site). The B-site cations are strongly bonded with the X anion, while A-site cations have weaker interactions. It forms a three-dimensional network of the corner-sharing BX₆ octahedra where A cations occupy empty cuboctahedral cavities (Figure 4A). If one removes all A cations from the twelve-coordinated sites, the simple ReO₃ structure is generated (Figure 4B).

FIGURE 4

FIGURE 4. (A) CaTiO₃ perovskite structure and (B) ReO₃ structure with empty cuboctahedral A-site.

In perovskite oxides, the A-site cation can have +1, +2, or +3 oxidation states, whereas the B-site cation can have a +3, +4, or +5 oxidation state to realize the charge neutrality of ionic structure. The presence of oxygen excess or deficiency in the lattice can cause the departure of stoichiometry from the ideal ABO₃. The strongly bonded framework of octahedra allows changing the elemental composition of A- and B-sites or partial substitution of cations without structural collapse. The presence of empty space in the perovskite structure can accommodate various octahedral tilts and distortions, reflecting the flexibility of the framework of octahedra. As a result, countless new perovskites with fascinating physical and chemical properties have been synthesized and have found applications in almost all areas of modern technology. Furthermore, the significance of perovskites extends to and beyond the Earth, since silicate perovskites based on MgSiO₃ are thermodynamically stable in the mantle of planets larger than Mars (Szuromi and Grocholski, 2017).

Reflecting the large flexibility of its crystal structure and its ability to show different properties depending upon the environment, perovskite can be well described as an “inorganic chameleon” (Stølen et al., 2006). The perovskite oxides commonly crystallize in a cubic structure, but, depending on the ionic radii and electronegativity of the corresponding cations, tilting or expansion/contraction of the octahedra occurs, leading to the formation of lower symmetry structures. The empirical prediction of whether the ABX₃ compound can form a stable cubic structure can be derived from a dimensionless number called the Goldschmidt tolerance factor t:

$t=\frac{(r_{a }+ r_b)}{\sqrt{2}(r_{b }+ r_x)}$

where r_a, r_b, and r_x are the ionic radii of A, B, and X ions, respectively (Goldschmidt, 1926). The closer this factor is to unity, the better the normal metal-oxygen bond lengths of both cations can be satisfied without distortions of the ideal structure. The tolerance factor possesses acceptable predictive power for oxide and fluoride structures. The ideal cubic perovskite SrTiO₃ has t = 1, and the closer the t value to unity, the greater the energetic stability of the structure (Navrotsky and Donald, 1989; Navrotsky, 1994). If t is between 0.9 and 1.0, predominantly cubic structures form, while below and above that limit significant distortions of the structure take place. When B is large and A is small, t < 1, the structure lowers its symmetry to fill the space, whereas if t > 1, hexagonal perovskite forms with face-sharing octahedra. The thermodynamic stability of various perovskites within a large compositional range has been extensively studied by high-temperature melt solution calorimetry in Navrotsky’s laboratory (Linton et al., 1998; Laberty et al., 1999; Xu et al., 2003; Cheng et al., 2005; Cheng and Navrotsky, 2005; Xu et al., 2005).

Perovskite properties can be tuned to a great degree by partial cation substitution. It can take place at either the A- or the B-site resulting in the double perovskites with A₂BB’X₆ or AA’B₂X₆ formula, respectively. The A/A’ and B/B’ cations may remain disordered at their corresponding sites, or they can order forming A-site or B-site ordered perovskites (Smyth, 1985; Anderson et al., 1993; Davies et al., 2008; King and Woodward, 2010; Vasala and Karppinen, 2015; Tilley, 2016). Three ordering patterns can be realized for either the A- or B-site cations. The most symmetric and most frequently encountered group is called rock salt or 1:1 ordering because the pattern of two different cations is equivalent to the anion and cation positions in the NaCl-type structure with Fm3m symmetry. This superstructure is also known as the elpasolite (K₂NaAlF₆) structure. Besides rocksalt ordering, cations can order into columns, or layers as shown in Figure 5 (King and Woodward, 2010).

FIGURE 5

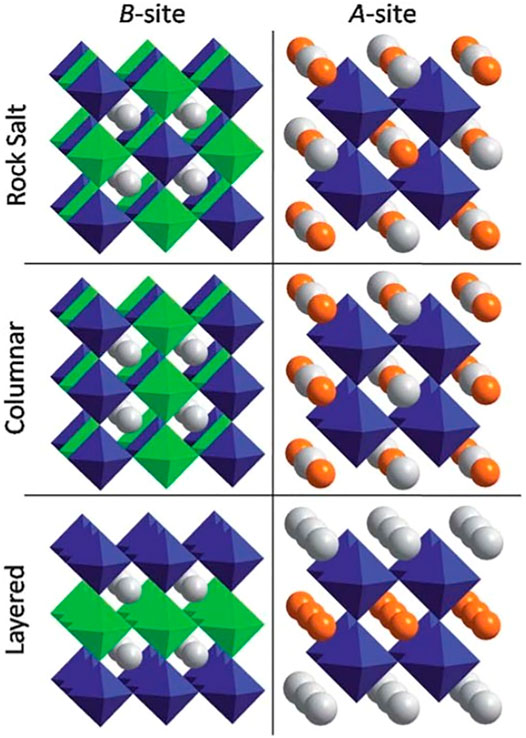
FIGURE 5. Cation ordering possibilities in perovskites for B-site ordering in A₂BB’X₆ and for A-site ordering in AA’B₂X₆ perovskites. Reproduced with permission from King and Woodward (2010), Copyright Royal Society of Chemistry.

These types of ordering are less common than the rocksalt-type ordering. The NaCl-type arrangement is 0D since two compositionally similar octahedra are alternating and separated from each other. The 1D and 2D ordering patterns result from columnar or layered ordering since it allows connectivity of the B’X₆ octahedra in one or two dimensions, respectively. The energetic stability of cation order is mainly driven by the charge and size difference of B/B’ or A/A’ cations. Among all three ordering patterns, the rocksalt-type ordering is usually thermodynamically most favorable because it increases the separation between highly charged B’ cations and hence decreases the Coulombic repulsive interactions. Then, it comes columnar configuration and 2D ordering is the least favorable due to the presence of four B’ cations neighboring with another B’ cation. Depending on the stoichiometric ratio of B:B’, the 1:2 and 1:3-layer ordering of cations can take place, which is the closest analog to the NaCl-type ordering (Davies et al., 2008). A-site ordering in perovskites is much less common compared to the B-site ordering. One way of achieving A-site ordering is by octahedral tilting which creates different size voids within the interconnected BX₃ network. The a⁺a⁺a⁺ tilting stabilization is the most commonly occurring type among the Glazer tilt systems (King and Woodward, 2010). The perovskites with this type of tilting usually contain larger cations such as an alkali, alkaline earth, or rare earth at the A-site, with much smaller cation at the A’-site. Cubic perovskites with AA₃’B₄O₁₂ general formula accommodate this type of cation ordering and compounds with this structure can form a metastable high pressure ζ-Mn₂O₃ phase (Ovsyannikov et al., 2013; Tilley, 2016). However, the number of reported A-site ordered perovskites is significantly smaller than the B-site ordered ones, and therefore the interesting question is why B-site ordering is more common than A-site ordering. This can be due to the small charge or size mismatch between A and A’ cations, while the difference of cation sizes and charges between B and B’ atoms can be larger. Generally, a large difference in valence, size, and coordination between two cations located at the same crystallographic site leads to the stabilization of a more ordered structure.

Oxygen Vacancy Formation

Another uniqueness of perovskite relative to many other crystal structures is its ability to accommodate a large concentration of oxygen vacancies (ABO_3-δ) without structural decomposition. The most oxygen deficiency is achieved close to δ = 0.5, although even nonstoichiometry higher than δ = 0.8 has been reported for Ba_1-xSr_xCo_1-yFe_yO_3-δ composition (Kubicek et al., 2017).

The ordering of oxygen vacancies along the (110) direction relative to the perovskite structure at δ= 0.5 often results in a new family of compounds known as brownmillerite (Ca₂AlFeO₅) with a layering of differently coordinated B and B’ cations (Smyth, 1985; King and Woodward, 2010; Tilley, 2016). The oxygen-deficient octahedra then transform into tetrahedra forming alternate layers of BO₆ octahedra and BO₄ tetrahedra in the … OTOT … sequence. The room temperature stable ordered brownmillerite transforms into perovskite with disordered oxygen vacancies at elevated temperatures (>800°C) (Shin et al., 1978). The transformation is gradual involving the coexistence of intermediate ordered and disordered phases or it may appear first order (Prasanna and Navrotsky, 1994). Disordering occurs through the formation of defect clusters which are statistically distributed in the cubic perovskite framework. Like in perovskites, B-site ordering is quite common for B-site substituted brownmillerites (King and Woodward, 2010). Also, the concentration of defects can be significantly altered through doping with different cations, often resulting in disordered cubic phases (Patrakeev et al., 2006). Another important parameter that affects the composition and phase formation is the oxygen partial pressure during the synthesis. If variable valence cations such as iron are present, low oxygen partial pressures brownmillerite and disordered perovskite phases can coexist, while at elevated temperatures transformation into disordered or ordered cubic structure takes place (Prado et al., 2004). The addition of oxygen to a brownmillerite structure can convert some of the tetrahedral layers into octahedral on forming intermediate intergrowth phases (A_nB_nO_3n-1) between pure perovskite and brownmillerite. For example, at n = 3, Grenier compounds with … OOTOOT … stacking can be generated. The whole range of oxygen-deficient intermediate compounds 0 < δ < 0.5 may be thermodynamically metastable relative to the stable perovskite and brownmillerite end members. Indeed, it has been shown that Ca₃Fe₂TiO₈ and Ca₄Fe₂Ti₂O₁₁ intermediate phases are energetically metastable relative to their parent CaTiO₃ and Ca₂Fe₂O₅ (Prasanna and Navrotsky, 1994).

Square pyramidal BO₅ coordination polyhedra can form if the oxygen vacancies are ordered in single octahedral sites rather than in two sites as in brownmillerite. These types of compounds include manganites (e.g., Sr₂Mn₂O₅), cobaltites (e.g., LaBaCo₂O_5.5), and ferrites (e.g., SrFeO_2.5+δ) (Tofield et al., 1975; Caignaert et al., 1985; Rautama et al., 2009). Another interesting family of oxygen-deficient perovskite is cuprates ACuO_3-δ in which copper atoms have square pyramidal and square planar coordination (Murphy et al., 1987; Rao and Raveu, 1989). Due to such unique structural geometry, these materials (e.g., YBa₂Cu₃O_x) exhibit high-temperature superconducting properties (Murphy et al., 1987).

Creating A-site deficiency, while retaining the corner-shared octahedral framework, can be realized in the so-called perovskite tungsten bronzes A_xWO₃, which undergo multiple structural changes upon increasing the concentration of A cations. For example, orthorhombic Ca_0.01WO₃ transforms into tetragonal phase at Ca_0.03WO₃ and eventually into cubic at Ca_0.12WO₃ (Tilley, 2016). Titanates, tantalates, and niobates are also capable of withstanding partially occupied A-sites if the charge neutrality is preserved (e.g., Ce_0.33NbO₃).

If the A-sites are completely empty in the perovskite structure and B cation has +6 oxidation state, cubic ReO₃ structure forms (Figure 4B). The slight reduction of anion content in some oxides with ReO₃ structure generates randomly distributed point defects, which undergo ordering and subsequent annihilation at high concentration of anion vacancies forming planar 2D defects known as crystallographic shear (CS) planes (Magneli, 1956; Wadsley, 1958; Voskanyan and Navrotsky, 2021). This suggests that the ordering of defects is thermodynamically favorable. Recently, Voskanyan and Navrotsky showed that TiO₂-Nb₂O₅ Wadsley-Roth CS phases are energetically metastable and stabilized via configurational entropy arising from the cation disorder at elevated temperatures (Voskanyan et al., 2020). In many oxides, defect clustering at the short-range scale is energetically more favorable and long-range ordering of vacancies does not take place. The reason for this is still not well understood and needs further theoretical and experimental investigations. In particular, the distribution and optimization of cluster size need further study.

Although some of the ReO₃ based compounds form CS phases, perovskites with occupied A-sites generally do not. This clearly indicates that the presence of filled A-sites hinders the formation of shear planes and at oxygen-deficient conditions, generation of BO₄ or BO₅ coordination polyhedra is more favorable in stabilizing the structure. From a kinetic viewpoint, shear plane formation involves cooperative migration of defects, which may be hampered in the presence of A cations.

Besides their high tolerance to oxygen deficiency, perovskites can also accommodate extra oxygen in their structure resulting in homologous series with A_nB_nO_3n+2 general formula (Nanot et al., 1974; Smyth, 1985). For example, with the addition of extra oxygen, SrTaO₃ perovskite can be converted into Sr₂Ta₂O₇ (n = 4) compound which belongs to the orthorhombic crystal system with space group Cmcm (Fu and Skrabalak, 2017). It consists of perovskite-type slabs four TaO₆ octahedra thick and two Sr sites, one within the slabs and the other between the slabs. The excess oxygen terminates one of the separated corners of the octahedra. Compared with perovskites, these compounds are likely to be also energetically metastable, and it will be of great interest to calculate the energetic penalty to form these structures from perovskites and how their energetics is compared with those of perovskite to brownmillerite transition.

Rocksalt Structures

Structures and Occurrence

Lithium TM oxides (LTMO) with rocksalt structure are formed when lithium and TM occupy the cation site and oxide ion occupy anion sites of structures derived from the simple rocksalt (NaCl) aristotype. The unique feature of this rocksalt structure is that both cation and anions occupy regular octahedral coordination. Close-packed oxygen atoms occupy sites of face-centered cubic (FCC) lattices; the lithium and TM occupy the FCC sublattice of octahedral interstices. The typical cation arrangement in LTMO structures was reviewed and later explained using atomistic modeling (Hewston and Chamberland, 1987; Wu et al., 1998). The arrangement of Li and TM in these LTMO structures may vary as shown in Figure 6 (Urban et al., 2014). Disordered rocksalt oxides (DRO) exhibit a random arrangement of Li and TM (at least at the long-range scale), leading to the α-LiFeO₂ structure shown in Figure 6A, while layered compounds exhibit an ordered arrangement of Li and TM in alternating planes along the (111) direction, leading to the α-NaFeO₂ structure shown in Figure 6B. The spinel-like low-temperature structure of LiCoO₂ and the γ-LiFeO₂ structure are two other cation-ordered variants of the rocksalt structure shown in Figures 6C,D (Clément et al., 2020).

FIGURE 6

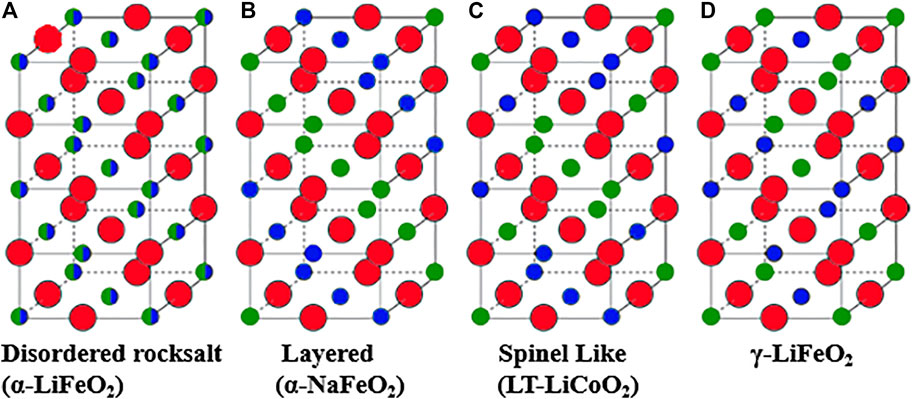
FIGURE 6. Rocksalt lithium transition metal oxides: (A) disordered rocksalt structure with equivalent cation sites, (B) layered structure with α-NaFeO₂ structure, (C) low-temperature spinel-like LiCoO₂ structure, and (D) γ-LiFeO₂ structure. Oxygen is indicated by red circles and Li and TM are indicated by small green and blue circles. Adapted with permission from Urban et al. (2014), Copyright Wiley-VCH.

DRS compounds can be composed of a wide variety of TM species, Ti, Cr, Mn Fe, Nb, and Mo with a large range of compositions in this structure space, whereas the layered LTMO appear to be restricted to Ni, Co, and Mn. However, there are extensive studies on the layered structure and its stability, which is attributed to its ability to independently relax the oxygen octahedra around each type of cation (Wu et al., 1998).

The electronic, optical, and magnetic properties exhibited by LTMO are governed by the type of Li-TM bond formed which in turn are dependent on the electronic configuration and size of the trivalent cation. Hewston and Chamberland (1987) investigated first-row TM (M) LMTO and showed that partially filled t_2g orbitals and t_2g-t_2g orbital overlap result in d electron delocalization in LiTiO₂ and Li_xVO₂ resulting in paramagnetic behavior of the former and semiconducting to metallic behavior of the latter. LiScO₂ with no d valence electrons is insulating, whereas the TM to the right of vanadium are characterized by contracted t_2g orbitals, prohibiting direct t_2g-t_2g orbital interactions and hence exhibiting localized d orbitals and semiconducting behavior.

Layered rocksalt structures form when the M³⁺ cation is significantly smaller than Li⁺, as observed in LiVO₂, LiCrO₂, (Rudorff and Becker, 1954), LiNiO₂, (Dyer et al., 1954), and LiCoO₂ (Orman and Wiseman, 1984); the structure is further stabilized by independent relaxation of bond length in LiO₆ and TMO₆ octahedra (Wu et al., 1998). However, in LiScO₂ (Wu et al., 1998), cations are of similar size, the relaxation effect is less significant, and the structure is dictated by electrostatic interactions resulting in γ- LiFeO₂ structure (Figure 6D). LiMnO₂ crystallizes in a low-temperature orthorhombic form with ordered Li⁺ and Mn³⁺ ions, unique among the other LTMO, and attributed this structure to the presence of Jahn-Teller distorted Mn³⁺ ion. However, at high temperature, the cation-ordered rocksalt structure forms (Dunitz and Orgel, 1957; Goodenough, 1959; Hoppe et al., 1975). LiCoO₂ adopts a spinel structure with cations in 16c and 16d octahedral sites when made by low-temperature synthesis routes (Gummow and Thackeray, 1992; Rossen et al., 1993; Lee et al., 2016). Although various combinations of TM can form the layered structure, only a few will remain layered when a significant amount of Li⁺ is removed from the structure. Only those TM which not only possess very high octahedral site preference but also retain such preference on oxidation as in Ni³⁺/Ni⁴⁺ (d⁷ to d⁶) and Co³⁺/Co⁴⁺ (d⁶ to d⁵) will have high enough thermodynamic and kinetic barriers to prevent disordering of the layered structure (Clément et al., 2020).

The cation disordered structure is the high-temperature and high-entropy form of the other structure types. Disorder in rocksalt structures can also be achieved, probably metastable, by ball milling (Dachille and Roy, 1964; Gutman, 1994).

First-principles computational studies are crucial in screening the compositional space for likely disordered structure and to shed light on the origin of cation disorder (Urban et al., 2017). For metallic alloys, Hume-Rothery and Powell (1935) rules predict that alloys are formed when species have similar electronegativities and difference in atomic radii is no more than 15%, and this rule is a possible guideline for ionic materials like oxides. Disorder in LMTO occurs with TM having larger ionic radius and charge differences, while current understanding would predict increasing disorder with smaller differences. The ability of the disordered structures to accommodate distortions in their octahedra may be a stabilizing factor.

Urban et al. (2017) suggested that the ability of the structure to accommodate disorder depends on the d- orbital occupancy in the TM. When cations are randomly distributed in the rocksalt structure, differences in ionic radii and charges create distortion in the O_h sites; these distortions must be shared by the neighboring octahedra. Thus, the energy benefit of distorting the octahedra to better fit various cations may determine the ability of the structure to accommodate cation disorder (Clément et al., 2020). Urban et al. (2017) have investigated the octahedral distortion modes in LTMO and concluded that the TM with d⁰ electrons accommodates octahedral distortion at the lowest energy. The band energy of d⁰ TM depends on the lower-lying oxygen-dominated orbitals that are always occupied and are insensitive to site distortions (Clément et al., 2020). Disorder in the rocksalt structures is best stabilized by TM having no valence d electron even when the ionic radius and charge differences are relatively large (Urban et al., 2017). These electronic structure studies show that the redox-inactive d⁰ metals (Ti⁴⁺, V⁵⁺, Nb⁵⁺, and Mo⁶⁺) in LTMO occupy the distorted O_h site, leaving the less distorted cation site for the other redox-active TM, thus stabilizing the disordered rocksalt structure. In other words, not only does the d⁰ cation have a low-energy penalty in distorted sites, but also their flexibility to distort allows the other TM cations with d electrons to optimize their distortions. Nevertheless, some DRO with no d⁰ TM have been synthesized (Freire et al., 2017; Freire et al., 2018; House et al., 2018). Li₂MnO₂F possesses a disordered rocksalt structure with cation vacancies (House et al., 2018), and Li₂MnO₃-disordered rocksalt with vacancies enhances the electrochemical properties of cathode materials (Freire et al., 2017; Freire et al., 2018).

Murphy et al. (1982) studied Li insertion in various close-packed titanate framework. LiTiO₂ spinel transforms to Li₂Ti₂O₄ on lithiation, which is accompanied by displacement of Li from Td sites to the O_h sites which are vacant in the spinel structure (Fd-3m space group) resulting in rocksalt structure (Fm-3m). Metastable Li₂Ti₂O₄ irreversibly transforms into the disordered rocksalt structure above 600°C (Murphy et al., 1982). The stable high-temperature form for LiTiO₂ is a disordered rocksalt structure. Hua et al. (2019) had investigated structural insights in the formation of Li- and Mn-rich layered oxides; in situ high-temperature synchrotron radiation diffraction reveals the transformation of the lithium-rich layered phase (R-3m) to a lithium poor spinel phase (Fd-3m) via an intermediate lithium-containing rocksalt phase (Fm-3m) which is accompanied by the release of oxygen and lithium.

Consequences of Cation Disorder

Ordered and disordered LMTO are cathode materials and changes in their chemical composition and structure affect the stability, capacity, energy density, and performance. Disordering results in radically different properties compared to the ordered rocksalt structure. Having excess lithium in the structure, diffusion processes are altered, easier anion redox, smaller and isotropic lattice expansion, and possible fluorine substitution, all leading to enhancement of electrochemical performance in lithium-ion battery applications.

LMTO cathode materials function by reversible extraction and insertion of Li⁺. To support continuous ion migration, the cathode material has to meet the following requirements: 1) the material must have facile ion diffusion via low-barrier channels and 2) the diffusion channels need to form a percolating network. The diffusion mechanism involves Li⁺ ions moving from the octahedral site to an adjacent edge-shared octahedral site through the empty face-shared tetrahedral site, referred to as o-t-o diffusion. The size of the T_d site and electrostatic interaction between Li⁺ in the activated T_d site and the four cations in the face-sharing octahedra forming a tetrahedral cluster has a major impact on the Li⁺ diffusion barrier. There are five types of tetrahedral cluster formed when the Li⁺ and TM species occupy the cation lattice: 0-TM, 1-TM, 2-TM, 3-TM, and 4-TM (Kang and Ceder, 2006; Kang et al., 2006). Li diffusion pathway requires at least two O_h Li connected via an activated T_d site; thus, 3-TM and 4-TM environments are excluded. In layered LTMO, every T_d site is coordinated by either 3 Li and 1-TM or 1 Li and 3 TM, out of which only 1 TM sustains Li migration. The size of the T_d site is dependent on the layers’ spacing of the Li slab (Kang and Ceder, 2006; Kang et al., 2006). In layered LMTO which has a separate Li layer and TM layer (Figure 7A), the ionic radius of Li is larger than that of TM, and the layer spacing of the Li slab lies in the range of 2.6–2.7 Å (Urban et al., 2014). All the Li sites are equivalent in layered LMTO and hence all are interconnected by 1-TM and form a 2D percolating network inside the Li slab. A migration barrier is associated with 1-TM diffusion during charging because of the increasing electrostatic repulsion when the TM is oxidized to higher valence and also due to a change in the slab distance. The electrostatic attraction between the Li and the oxygen atom decreases during charging. At the end of the charge when almost all the Li would be extracted and the Li slab collapses, the lithium mobility decreases.

FIGURE 7

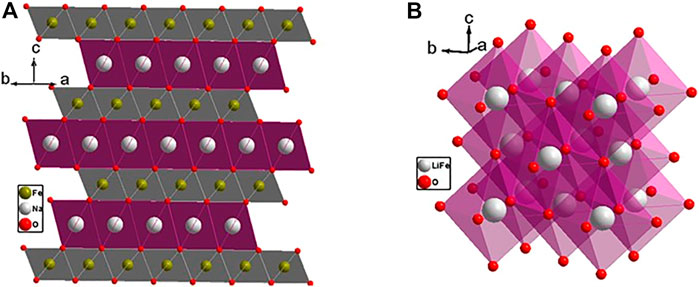
FIGURE 7. (A) Layered cation-ordered lithium transition metal oxide (R-3m space group); (B) cation disordered rocksalt structure (Fm-3m space group).

In cation disordered rocksalt structures, there are no separate layers for Li and TM and no defined slab distance (Figure 7B). Instead, there is a significant reduction in the slab spacing to 2.3–2.4 Å and the size of the T_d site due to cation mixing. The 2-TM channel is inactive and the 1-TM channel can support Li migration in cation disordered structures or if only 0-TM channels are available. In 0-TM, the absence of TM in face-sharing octahedra reduces electrostatic repulsion in the activated Li site, and the diffusion barrier is independent of the T_d height and the TM composition (Urban et al., 2014).

Long-range lithium diffusion depends on both the low-energy diffusion barrier and the percolating network formed by interconnecting the diffusion channel. In layered LMTO, all the Li ions are connected via 1-TM forming a 2D percolating network for Li conduction in Li slabs. Urban et al. (2014) have done Monte Carlo simulations to study the impact of cation disorder and Li content on Li percolation via the 0-TM channel. Though the amount of lithium is greater in the cation disordered structure, the percolation network of the 0-TM channel still forms at a critical Li concentration.

SRO in Defect Rocksalt Oxides

Nominally disordered rocksalt structures do exhibit some degree of SRO. SRO is known to control local transport (Ji et al., 2019). The SRO has previously been studied by a combination of experimental (electron diffraction, solid-state nuclear magnetic resonance, and 2D and 3D nanoscale X-ray spectro-microscopy), as well as by theoretical methods (DFT and MD simulations) (Clément et al., 2018; Kan et al., 2018; Ji et al., 2019; Jones et al., 2019).

Kan et al. (2018) proposed that local cation ordering redirects Li movement through nonequilibrium pathways, which results in the chemical heterogeneity evidenced by 2D and 3D maps of manganese valence state in Li_xNb_0.3Mn₀₄O₂. Ji et al. (2019) showed that SRO controls the Li transport by altering the distribution of 0-TM, 1-TM, and 2-TM channels as well as connectivity between them. Ji et al. (2019) explained the difference in the performance of Li_1.2Mn_0.4Ti_0.4O₂ and Li_1.2Mn_0.4Zr_0.4O₂ based on differences in SRO. Ji et al. (2019) had modeled SRO in a variety of Li_1.2M′_aM″_bO₂ structures (M′_a = V³⁺, Mn²⁺, Mn³⁺, Co²⁺, and Ni²⁺ and M″_b = Ti⁴⁺, Zr⁴⁺, Nb⁵⁺, and Mo⁶⁺) using DFT and rationalized SRO based on charge and size effects.

Spinels

Structure and Cation Distribution

The term “spinel” originates from the name of the naturally occurring mineral MgAl₂O₄, which is also well-known as a gemstone because of its variable color characteristics owing to the TM impurities (Malíčková et al., 2021). The spinel structural family consists of numerous materials with the basic formula AB₂X₄ where cation A can be either an alkali, alkaline earth, or a TM and cation B can be almost any TM or aluminum, gallium, and indium. The anion X is represented by O²⁻, S²⁻, Se²⁻, Te²⁻, F⁻, or CN⁻ species (Zhao et al., 2017). Fortunate conjunction of mixed valence, site preference, a remarkable variety of chemical compositions, and synthetic flexibility in spinels give rise to a wide range of useful functions such as magnetism (Gorter, 1950; Song and Zhang, 2004), catalytic activity (Dong et al., 2019; Kim et al., 2020), and superconductivity (Hagino et al., 1995; Moshopoulou, 2004) as well as electronic, optical, and electrochemical performance (Verwey et al., 1947; Ferg et al., 1994; Aizawa et al., 2002; Jouini et al., 2007; Kim et al., 2014).

The rich story of spinel structural chemistry began in 1915 when the crystal structure was determined for the first time in two independent works by Bragg and Nishikawa (Bragg, 1915; Nishikawa, 1915). At first glance, the structure is represented by a three-dimensional ensemble made of vertice/edge-sharing AX₄ tetrahedra and BX₆ octahedra (Figure 8A). A FCC unit cell ($Fd\overline{3}m$) accommodates 8 A, 16 B, and 32 X atoms resulting in eight formula units (Z = 8). Each anion X is tetrahedrally coordinated by one cation A situated in the tetrahedral cage and three cations B situated in octahedral cages (Figure 8B). A closer look at the unit cell reveals other important structural features. Specifically, the A sublattice possesses a diamond-like structure with a periodicity equal to the unit cell parameter. At the same time, both A and B sublattices together form a structure reminiscent of that in the Laves phase MgCu₂ (Stein et al., 2004). Thus, the overall spinel lattice can be imagined as a Laves phase structured AB₂ atomic array (Figure 8C) embedded into a matrix of a cubic close-packed (ccp) arrangement of X anions (Figure 8D). The ccp arrangement contains 96 available interstices in total (64 tetrahedral + 32 octahedral); however, only a fraction of them is populated by cations in the spinel structure. However, the ccp packing is imperfect, and the corresponding X layers are corrugated due to minor deviations of anion coordinates from the ideal position. From the crystallography viewpoint, these distortions originate from the flexibility of the Wyckoff site 32e; hence an additional parameter is required to describe atomic coordinates. It is denoted as the anion position parameter u (also known as the oxygen parameter in oxide spinels). Depending on the choice of origin, an ideal value of u for the perfect ccp arrangement can be either 0.250 or 0.375 for the origin at an octahedral vacancy ($\overline{3}m$) or an A-site cation ($\overline{4}3m$, such as in Figure 8), respectively. From geometric considerations, the anion position parameter is connected to both the cubic unit cell parameter a and cation-ligand distances in the tetrahedral (R_A-X) and octahedral (R_B-X) cages according to $R_{A-X}=\surd 3a(u-\frac{1}{4})$ and $R_{B-X}=a\sqrt{2{(u-\frac{3}{8})}^2+{(\frac{5}{8}-u)}^2}$, or $R_{A-X}=\surd 3a(u-\frac{1}{8})$ and $R_{B-X}=a\sqrt{2{(u-\frac{1}{4})}^2+{(\frac{1}{2}-u)}^2}$ for the $\overline{4}3m$ and $\overline{3}m$ origin settings, respectively. Therefore, distortions in the ccp arrangement of X result in corresponding changes in AX₄ and BX₆ polyhedra as the tetrahedra expand while the octahedra contract with increasing u. This optimization of tetrahedral and octahedral bond lengths to best fit the cations in the structure is the physical reason for the deviation from ideal cubic close packing.

FIGURE 8

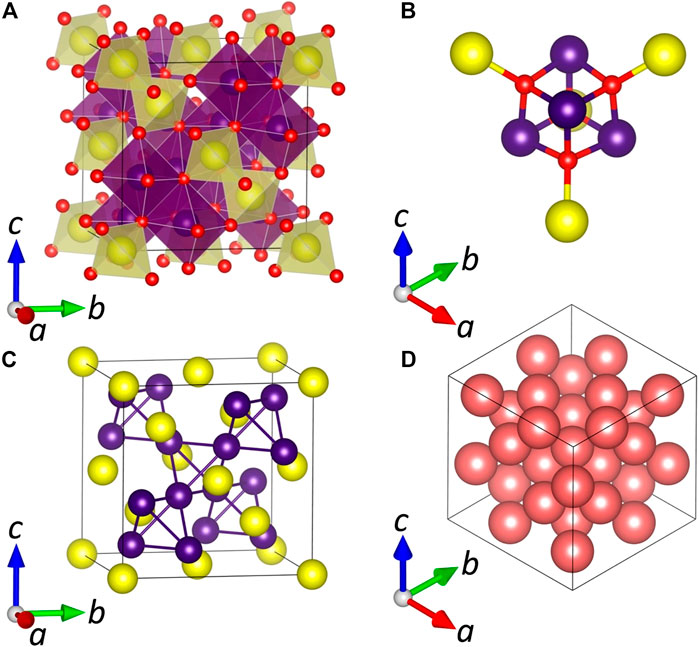
FIGURE 8. (A) A general view of the normal spinel unit cell ($Fd\overline{3}m$) with an origin on the A-site cation (Wyckoff site 8a). (B) A fragment of the crystal structure illustrating coordination surroundings of the X anion. (C) The metal sublattice AB₂ forming a framework of the Laves phase. (D) A cubic close-packed array of anions in the X sublattice. A, B, and X sites are shown as yellow, purple, and red spheres, respectively.

Figure 8 illustrates an ideal (normal) scenario in which distinct A and B cations are entirely separated in the tetrahedral and octahedral interstices; hence the chemical formula can be written as A(B)₂X₄ where brackets denote the octahedral site. However, as was initially shown in 1935 by Barth and Posnjak (1932), spinels may possess an inverse atomic layout in which the tetrahedral sites are fully occupied by B cations, while half of the octahedral sites are occupied by A cations and half by B cations so that the chemical formula is B(AB)X₄. Later, the terms “normal” and “inverse” spinel were proposed by Verwey and Heilmann (1947) to denote these two limiting scenarios. In some materials, the cation distribution is very close to the normal or inverse limits. For example, the naturally occurring mineral spinel, MgAl₂O₄ (which gives its name to the structure), is a nearly perfect normal spinel, while Fe(NiFe)O₄ is an example of the inverse structure (Zhao et al., 2017). The terms “normal” and “inverse” are also applicable to binary phases, in which the same TM cations with different oxidation states tend to occupy distinct crystallographic sites. As such, the mineral hausmannite (Mn₃O₄) has a normal spinel structure where Mn²⁺ cations occupy tetrahedral interstices, and Mn³⁺ cations occupy octahedral interstices; therefore, an accurate formula is Mn²⁺(Mn³⁺)₂O₄ (Garcês Gonçalves Jr. et al., 2018). In contrast, the minerals magnetite (Fe₃O₄) and greigite (Fe₃S₄) possess an inverse structure Fe³⁺(Fe³⁺Fe²⁺)X₄ (Chang et al., 2008).

In many spinel materials, the cation distribution falls between the normal and inverse limits, so different cation species are disordered and present in both types of sites. Taking such disorder into account, the general formula of spinel has to be written as A_1-i(B_2-iA_i)X₄, where i is a degree of inversion (the inversion parameter). Although it is clear that the normal spinel (i = 0) corresponds to the most ordered state, the inverse and intermediate distributions possess configurational entropy. If one assumes that the cations on each sublattice are randomly distributed, the composition of maximum entropy occurs at i = 0.667, and this may be thought of as the limiting case for disordering, with both initially normal and initially inverse spinels tending toward this random distribution at high temperature.

This assumption of randomness on each sublattice permits the construction of relatively simple thermodynamic models of cation disordering and the calculation of cation interchange energies and site preference energies. Understanding the long-range cation disorder in spinels is crucial because it substantially impacts physical properties. For example, Zhu et al. (2018) performed synthesis at variable temperatures to control the crystallinity and cation distribution in the photoanode ZnFe₂O₄, which can be used in the water-splitting reaction. ZnFe₂O₄ nanorods with a higher degree of disorder have enhanced charge carrier transport and higher photogenerated charge separation efficiency. Ndione et al. (2014) established a relation between cation disorder and conductivity in the ZnCo₂O₄ (normal) and NiCo₂O₄ (inverse) spinels, where increasing disorder leads to ZnO_h antisite defects and increase of the p-type conductivity for i < 0.5 in the former and a metal-insulator transition for 0.5 < i < 1.0 in the latter. The long-range cation disorder also influences principal magnetic properties in spinels, such as magnetic transition temperature, saturation magnetization, and magnetic exchange interactions (Willard et al., 1999).

Short-Range Order

The above considerations appear adequate for order/disorder which can be detected by commonly used techniques such as X-ray diffraction. However, there are also scenarios of the local (short-range) cation ordering that can be observed in the spinel structure. Ivanov et al. (2010) performed a study of NiFe₂O₄ single crystals via polarization Raman measurements in conjunction with lattice dynamics calculations. The number of observed Raman modes is significantly larger than one expected from the inverse spinel structure Fe(NiFe)O₄ in which Ni²⁺ and Fe³⁺ cations are mixed statistically in the octahedral site B. The obtained data were explained by the formation of local lower symmetry domains of α- (P4₁22/P4₃22) or β-type (Imma) having a size of ≤50 lattice constants. The domains can be organized in a twinned motif with the I, II, III, IV, V, or VI orientation for the α- and β-type, respectively. While the α-type is fully supported by the observed number of Raman bands and polarization rules, the β-type satisfies only a fraction of the obtained bands; however, it cannot be completely ruled out due to good agreement between calculated and observed bands at specific frequencies. Furthermore, the possible existence of both types of domains in superposition together with twinning complicates data interpretation. O’Quinn et al. (2020) proposed the Pauling rule as a base to understand the SRO phenomena in spinel, weberite, and pyrochlore structures. According to Pauling’s second rule, the sum of the bond strengths (a charge divided by coordination number) of the cations should be equal to the charge of the anion. In the normal spinel structure, each anion X is surrounded by three octahedrally coordinated cations B and one tetrahedrally coordinated cation A (Figure 8B). In the oxide spinel MgAl₂O₄, such arrangement leads to the sum of bond strengths 2.0, which is in excellent agreement with Pauling’s second rule. When inversion occurs, the number of possible anion coordinations extends to eight (Figure 8B). However, in MgAl₂O₄, only two of these configurations (with bond strength 2.083 and 1.917) are close to satisfying Pauling’s second rule and suggesting preference for these local clusters with such ion arrangement in the disordered MgAl₂O₄ samples (O’Quinn et al., 2020).

Discussion: Why Do Different Structures Have Different Modes of Disorder?

It is clear that, for any significant disorder to exist, the structure has to be flexible enough to accommodate it without exorbitant energetic penalty. In general, defects and disorder raise energy and entropy, and the balance of these terms determines the equilibrium extent of disorder at a given composition, temperature, and pressure. In largely ionic oxide systems, cation size and charge are major factors determining both structure and defect chemistry. In comparing the four groups of structures discussed here, one can draw the following inferences. The fluorite-derived structures are the most tolerant of disorder on both cation and anion sublattices. Its aristotype structure consists of alternating occupied and unoccupied cubes of anions (Subramanian et al., 1983; Chakoumakos, 1984; Ewing et al., 2004; Gardner et al., 2010). This means that a change in coordination or bonding in one filled cube has relatively little influence on the next filled cube because they do not directly share anion vertices. This structural feature may explain the easy formation of oxygen vacancies and the wide homogeneity ranges in AO₂-BO_1.5 systems like YSZ, but it does not readily explain the wealth of different ordered phases and the overwhelming evidence for clustering at various length scales. Such clustering and/or ordering involves cooperative interactions involving the lattice dynamics (and in some cases electron delocalization) at length scales of nanometers to micrometers, not just those involving nearest and next nearest-neighbor interactions. The wealth of structural phase transitions involving changes in symmetry but having very small thermodynamic consequence (enthalpies of transformation less than 5 kJ/mol in magnitude) in both fluorite and perovskite structures speaks to the closely balanced energetics and lattice dynamics of these structures.

The thermodynamic favorability of disordering has been associated with a decrease in the cation radii ratio (r_A/r_B) for most of the fluorite-related systems. However, this trend is not observed in rare earth titanate and stannate pyrochlore systems, RE₂M₂O₇ (M = Ti and Sn), in which only the ordered structure has been observed for all compositions all the way to RE = Yb, the smallest rare earth ion (Kennedy, 1996; Baroudi et al., 2015). One reason for such preference for the ordered structure might be the coordination geometry around Ti and Sn cations. They tend to prefer octahedral coordination as found in their natural binary oxide minerals TiO₂ and SnO₂ which crystallize in the rutile structure (Burdett et al., 1987; Bolzan et al., 1997). The ordered structure offers six-coordinated geometry for Ti and Sn cations, whereas seven-coordinated geometry is found for all cations in the disordered structure. The stronger covalency associated with tin may also be a factor favoring the ordered state.

For the idealized structures, configurational entropy increases in the order pyrochlore, weberite, and defect fluorite as disorder increases. The existence of short-range weberite domains within both amorphized and defect fluorite structures and their persistence into recrystallized pyrochlore is still somewhat a mystery and may represent a combination of thermodynamic and kinetic effects. The thermodynamic driver may be a compromise between energy and entropy, but the size distribution of the domains and interactions at their interfaces with the host structure (amorphous, defect fluorite, or pyrochlore) are still poorly known.

From the structural point of view, though the fully disordered structure has common seven coordination geometry for A and B cations and randomness for vacancies, the bigger A and smaller B cations prefer higher and lower coordination, respectively, leading to ordering of vacancies and consequently to locally ordered structure in nanoscale domains (Shamblin et al., 2016a). The occurrence of weberite nanodomains, which do not grow to macroscopic size and which represent a structure not seen in the equilibrium phase diagram, appears to be a unique feature of pyrochlore systems. From the kinetic point of view, annealing of such domains still needs study. Nor is it clear why certain A₂B₂O₇ materials crystallize as pyrochlore, others were weberite, though in both cases, as the cations become more similar, the defect fluorite structure becomes more favorable and may occur as a high-temperature equilibrium phase. The preference of A₂B₂O₇ and A₃BO₇ for pyrochlore and weberite structures, respectively, may reflect the different cationic charge and resulting differences in electrostatic energies, but these factors have not been explored quantitatively. In terms of coordination geometry and distortions, the weberite structure appears to be more flexible than the pyrochlore structure by accepting cations in different coordination geometries (six to eight) and being more tolerant of polyhedral distortions (Cai and Nino, 2009; Cai and Nino, 2011). This flexibility may be more important when the cation charge difference is greater.

Furthermore, the fluorite-based materials do not readily form layered or two-dimensional superstructures, and the oxygen vacancies are not coalesced into shear planes or ordered CS structures. Why are such structures unfavorable? One of the reasons may be that the vacancies tend to be separated from each other to reduce the destabilization due to electrostatic repulsion as the fluorite structure is compact without an open framework. Also, when the vacancies in fluorite-related systems are increased to stoichiometry A₂B₂O₆, the bixbyite structure with ordered vacancies forms (King et al., 2013). The bixbyite structure may “outcompete” other arrangements, including shear structures, in energy. Thus, the lack of the latter may reflect the existence of an even better structural arrangement rather than any intrinsic instability of shear. A computational approach to the stability and defect chemistry of these different hypothetical polymorphs is likely to be informative.

Perovskites are also tolerant of oxygen vacancies, but these often aggregate into specific ordered and layered structures or are essentially eliminated in CS structures. Within the perovskites, the framework of corner-linked octahedra is strongly bound yet flexible. The oxygen sublattice is far from being close-packed. In terms of distortions, both tilting of octahedra and off-centering of cations within them are mechanisms to adjust bond lengths. Much of this behavior is captured by the geometric arguments embedded in the Goldschmidt tolerance factor. Phase transitions involving these distortions are generally small in energy and entropy, and the more symmetrical structures occur with increasing temperature. If the volume of the perovskite increases with increasing symmetry, as is often the case, then the pressure will extend the temperature stability field of the more disordered structures.

From the thermodynamic point of view, the annihilation of oxygen vacancies should be an energetically favorable process since vacancy formation is energetically expensive. Following this argumentation, shear plane formation, involving vacancy elimination, should be a more prevalent type of defect accommodation in different crystal structures. However, it is not common, and one should also consider that the metal-metal distances become shorter in shear planes compared with their original positions. Therefore, to form shear planes, the exothermic energy released from annihilation of oxygen vacancies should be larger than the endothermic energy of cation repulsions in shear planes. So far, only a few oxides based on ReO₃ and rutile structures have been reported to form ordered shear structures. Based on this knowledge, it appears that the flexibility of the framework, some structural openness rather than close packing, high polarizability of atoms, octahedral coordination of metal atoms, and presence of corner-shared oxygen appear to all be essential for the formation of shear structures.

The clustering of vacancies into shear planes and their ordering into periodic structures diminishes the configurational entropy initially present on the anion sublattice. Presumably ordering is associated with a stabilizing energy (enthalpy) contribution and the formation of the shear phase reflects a balance between ΔH and TΔS. However, phases with ordered shear planes often appear to need another source of configurational entropy to stabilize them. This may arise from cation disorder in regions between the shear planes (Voskanyan and Navrotsky, 2021). This necessary and delicate balance of energetics within and between the shear planes may contribute to the relative rarity of shear structures.

The rocksalt and spinel structures contain (almost) cubic close-packed anion sublattices. Oxygen vacancies do not occur at appreciable levels but cation vacancies (and in some cases interstitials) are relatively easily accommodated. Charge balance occurs largely through variation in TM oxidation state. The cations are generally more similar in size than those occupying A- and B-sites in fluorite derivatives and perovskites. Though to a first approximation the ions on each sublattice are randomly mixed, there is increasing evidence of short-range order. Such local ordering, only beginning to be studied in detail, may suggest possible complexities in rocksalt and spinel structures analogous to those first discovered in pyrochlores and perovskites.

The discussion above reminds us how little we still know about short and midrange ordering, which appears to be a very general phenomenon in oxides. Cation radius and coordination number, as well as the openness and flexibility of the framework, appear to be the major factors influencing defect chemistry. To complement empirical trends and observations, rigorous first-principles calculations comparing different structures at the same composition would provide insight into the stability and defect chemistry in different, heretofore unsynthesized, polymorphs.

Conclusion

Fluorite-derived phases include a number of different structures, with high oxygen vacancy concentrations and varying degrees of cation disorder. SRO leading to cluster formation and nanoscopic weberite domains are common themes. The energetics of these phases and their solid solutions are complex because these materials are often neither completely ordered nor completely disordered, with the equilibrium degree of ordering depending on temperature, pressure, and composition. Nonequilibrium disorder can be produced by different means and its annealing appears to require long-term heating at temperatures above 1,200°C. The size, nature, and energetics of clusters and nanoscopic domains deserve additional systematic study.

Perovskites are very flexible in composition, cation ordering schemes, distortions, and the incorporation of oxygen vacancies. In addition to order-disorder on both A and B cation sites, the formation of clusters involving oxygen vacancies is possible. A unique way of ordering and eliminating oxygen vacancies, not seen in fluorite structures, is the development of shear planes and their ordering into various families of CS structures, not seen in the other structure types discussed here but observed in lower symmetry structures, such as those derived from rutile. Thermodynamically, ordering into shear planes decreases the entropy associated with oxygen vacancies, but disorder in other parts of the structure may add a stabilizing configurational entropy term, perovskite structures.

Both ordered and disordered rocksalt structures form a variety of systems. It is important to realize that the relation between ordered and disordered structures definitely is not a true order-disorder transition at the same chemical composition. Rather, ordered and disordered lithium TM oxides form having an entirely different composition. It is clear that a number of factors related to cation size and the nature of the TM affect the structure formed at a given composition. In contrast to fluorite and perovskite structures, oxygen vacancies do not play a significant role in either ordered or disordered rocksalt oxides. However, distortion of polyhedra and short-range order are important in nominally DRO. Much work remains to be done to understand these changes on an atomistic level and to optimize structures and compositions for battery operation.

Order-disorder in spinels is dominated by the exchange (disordering) of cations between octahedral and tetrahedral sites. Though interstitial cations may sometimes exist, oxygen vacancies are generally not incorporated. It is interesting that spinels, long considered to be “simple” in the sense of random cation arrangements on each sublattice, may in fact harbor ordering on different length scales analogous to that seen in fluorite, perovskite, and rocksalt phases.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary files; further inquiries can be directed to the corresponding author.

Author Contributions

AN conceptualized and designed the study. TS, AV, KJ, and MA wrote sections of the paper based on their prior published experimental work. All authors contributed to editing and coordinating the sections into a final manuscript but the major part of that work was done by AN.

Funding

The authors acknowledge the Department of Energy and the National Science Foundation for support over many years that allowed the thermodynamic and structural studies summarized here. The preparation of this review was supported by the Department of Energy, Office of Basic Energy Sciences, Grant DE-FG02-03ER46053.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aizawa, H., Ohishi, N., Ogawa, S., Watanabe, E., Katsumata, T., Komuro, S., et al. (2002). Characteristics of Chromium Doped Spinel Crystals for a Fiber-Optic Thermometer Application. Rev. Scientific Instr. 73 (8), 3089–3092. doi:10.1063/1.1491998

CrossRef Full Text | Google Scholar

Aizenshtein, M., Shvareva, T. Y., and Navrotsky, A. (2010). Thermochemistry of Lanthana- and Yttria-Doped Thoria. J. Am. Ceram. Soc. 93, 4142–4147. doi:10.1111/j.1551-2916.2010.04001.x

CrossRef Full Text | Google Scholar

Allpress, J. G., and Rossell, H. J. (1979). Fluorite-related Phases Ln3MO7, Ln = Rare Earth, Y, or Sc, M = Nb, Sb, or Ta. I. Crystal Chemistry. J. Solid State. Chem. 27, 105–114. doi:10.1016/0022-4596(79)90149-X10.1016/0022-4596(79)90149-x

CrossRef Full Text | Google Scholar

Anderson, M. T., Vaughey, J. T., and Poeppelmeier, K. R. (1993). Structural Similarities Among Oxygen-Deficient Perovskites. Chem. Mater. 5, 151–165. doi:10.1021/cm00026a003

CrossRef Full Text | Google Scholar

Baroudi, K., Gaulin, B. D., Lapidus, S. H., Gaudet, J., and Cava, R. J. (2015). Symmetry and Light Stuffing ofHo2Ti2O7, Er2Ti2O7, andYb2Ti2O7characterized by Synchrotron X-ray Diffraction. Phys. Rev. B 92, 24110. doi:10.1103/PhysRevB.92.024110

CrossRef Full Text | Google Scholar

Barth, T. F. W., and Posnjak, E. (1932). Spinel Structures: with and without Variate Atom Equipoints. Z. Kristallogr. Cryst. Mater. 82 (1-6), 325–341. doi:10.1524/zkri.1932.82.1.325

CrossRef Full Text | Google Scholar

Bindi, L., Sirotkina, E. A., Bobrov, A. V., Pushcharovsky, D., and Irifune, T. (2017). Discovery of MgTiSi2O7: a New High-Pressure Silicate with the Weberite Structure Synthesized at Transition-Zone Conditions. Phys. Chem. Minerals 44, 419–424. doi:10.1007/s00269-016-0868-8

CrossRef Full Text | Google Scholar

Bolzan, A. A., Fong, C., Kennedy, B. J., and Howard, C. J. (1997). Structural Studies of Rutile-type Metal Dioxides. Acta Crystallogr. Sect. B 53, 373–380. doi:10.1107/S0108768197001468

CrossRef Full Text | Google Scholar

Bragg, W. H. (1915). The Structure of the Spinel Group of Crystals. Lond. Edinb. Dublin Phil. Mag. J. Sci. 30, 305–315. doi:10.1080/14786440808635400

CrossRef Full Text | Google Scholar

Burdett, J. K., Hughbanks, T., Miller, G. J., Richardson, J. W., and Smith, J. V. (1987). Structural-electronic Relationships in Inorganic Solids: Powder Neutron Diffraction Studies of the Rutile and Anatase Polymorphs of Titanium Dioxide at 15 and 295 K. J. Am. Chem. Soc. 109, 3639–3646. doi:10.1021/ja00246a021

CrossRef Full Text | Google Scholar

Buyukkilic, S., Kim, S., and Navrotsky, A. (2014). Defect Chemistry of Singly and Doubly Doped Ceria: Correlation between Ion Transport and Energetics. Angew. Chem. Int. Ed. 53, 9517–9521. doi:10.1002/anie.201404618

PubMed Abstract | CrossRef Full Text | Google Scholar

Buyukkilic, S., Shvareva, T., and Navrotsky, A. (2012). Enthalpies of Formation and Insights into Defect Association in Ceria Singly and Doubly Doped with Neodymia and Samaria. Solid State Ionics 227, 17–22. doi:10.1016/j.ssi.2012.08.017

CrossRef Full Text | Google Scholar

Cai, L., Arias, A. L., and Nino, J. C. (2011). The Tolerance Factors of the Pyrochlore crystal Structure. J. Mater. Chem. 21, 3611–3618. doi:10.1039/C0JM03380D

CrossRef Full Text | Google Scholar

Cai, L., Denev, S., Gopalan, V., and Nino, J. C. (2010). Phase Transition in Weberite-type Gd3NbO7. J. Am. Ceram. Soc. 93, 875–880. doi:10.1111/j.1551-2916.2009.03494.x

CrossRef Full Text | Google Scholar

Cai, L., and Nino, J. C. (2009). Complex Ceramic Structures. I. Weberites. Acta Crystallogr. Sect. B Struct. Sci. 65, 269–290. doi:10.1107/S0108768109011355

PubMed Abstract | CrossRef Full Text | Google Scholar

Cai, L., and Nino, J. C. (2007). Structure and Dielectric Properties of Ln3NbO7 (Ln=Nd, Gd, Dy, Er, Yb and Y). J. Eur. Ceram. Soc. 27, 3971–3976. doi:10.1016/j.jeurceramsoc.2007.02.077

CrossRef Full Text | Google Scholar

Cai, L., and Nino, J. C. (2011). Synchrotron and Neutron Powder Diffraction Study of Phase Transition in Weberite-type Nd3NbO7 and La3NbO7. J. Solid State. Chem. 184, 2263–2271. doi:10.1016/j.jssc.2011.06.017

CrossRef Full Text | Google Scholar

Caignaert, V., Nguyen, N., Hervieu, M., and Raveau, B. (1985). Sr2Mn2O5, an Oxygen-Defect Perovskite with Mn(III) in Square Pyramidal Coordination. Mater. Res. Bull. 20, 479–484. doi:10.1016/0025-5408(85)90101-110.1016/0025-5408(85)90101-1

CrossRef Full Text | Google Scholar

Chakoumakos, B. C. (1984). Systematics of the Pyrochlore Structure Type, Ideal A2B2X6Y. J. Solid State. Chem. 53, 120–129. doi:10.1016/0022-4596(84)90234-2

CrossRef Full Text | Google Scholar

Chang, L., Roberts, A. P., Tang, Y., Rainford, B. D., Muxworthy, A. R., and Chen, Q. (2008). Fundamental Magnetic Parameters from Pure Synthetic Greigite (Fe3S4). J. Geophys. Res. 113 (B6), 104. doi:10.1029/2007JB005502

CrossRef Full Text | Google Scholar

Chen, W., Lee, T. A., and Navrotsky, A. (2005). Enthalpy of Formation of Yttria-Doped Ceria. J. Mater. Res. 20, 144–150. doi:10.1557/JMR.2005.0017

CrossRef Full Text | Google Scholar

Chen, W., and Navrotsky, A. (2006). Thermochemical Study of Trivalent-Doped Ceria Systems: CeO2– MO1.5 (M = La, Gd, and Y). J. Mater. Res. 21, 3242–3251. doi:10.1557/jmr.2006.0400

CrossRef Full Text | Google Scholar

Cheng, J., and Navrotsky, A. (2005). Energetics of La1−xAxCrO3−δ Perovskites (A=Ca or Sr). J. Solid State. Chem. 178, 234–244. doi:10.1016/j.jssc.2004.11.028

CrossRef Full Text | Google Scholar

Cheng, J., Navrotsky, A., Zhou, X. D., and Anderson, H. U. (2005). Thermochemistry of La1-xSrxFeO3-δ Solid Solutions (0.0 ≤ X ≤1.0, 0.0 ≤ δ ≤ 0.5). Chem. Mater. 17, 2197–2207. doi:10.1021/cm048613o

CrossRef Full Text | Google Scholar

Chung, C.-K., Lang, M., Xu, H., and Navrotsky, A. (2018a). Thermodynamics of Radiation Induced Amorphization and thermal Annealing of Dy2Sn2O7 Pyrochlore. Acta Materialia 155, 386–392. doi:10.1016/j.actamat.2018.06.003

CrossRef Full Text | Google Scholar

Chung, C.-K., O’Quinn, E. C., Neuefeind, J. C., Fuentes, A. F., Xu, H., Lang, M., et al. (2019). Thermodynamic and Structural Evolution of Mechanically Milled and swift Heavy Ion Irradiated Er2Ti2O7 Pyrochlore. Acta Mater. 181, 309–317. doi:10.1016/j.actamat.2019.09.022

CrossRef Full Text | Google Scholar

Chung, C.-K., Shamblin, J., O'Quinn, E. C., Shelyug, A., Gussev, I., Lang, M., et al. (2018b). Thermodynamic and Structural Evolution of Dy2Ti2O7 Pyrochlore after swift Heavy Ion Irradiation. Acta Materialia 145, 227–234. doi:10.1016/j.actamat.2017.12.044

CrossRef Full Text | Google Scholar

Clément, R. J., Kitchaev, D., Lee, J., and Gerbrand Ceder, G. (2018). Short-range Order and Unusual Modes of Nickel Redox in a Fluorine-Substituted Disordered Rocksalt Oxide Lithium-Ion Cathode. Chem. Mater. 30, 6945–6956. doi:10.1021/acs.chemmater.8b03794

CrossRef Full Text | Google Scholar

Clément, R. J., Lun, Z., and Ceder, G. (2020). Cation-disordered Rocksalt Transition Metal Oxides and Oxyfluorides for High Energy Lithium-Ion Cathodes. Energy Environ. Sci. 13, 345–373. doi:10.1039/C9EE02803J

CrossRef Full Text | Google Scholar

Clements, R., Hester, J. R., Kennedy, B. J., Ling, C. D., and Stampfl, A. P. J. (2011). The Fluorite-Pyrochlore Transformation of Ho2−yNdyZr2O7. J. Solid State. Chem. 184, 2108–2113. doi:10.1016/j.jssc.2011.05.054

CrossRef Full Text | Google Scholar

Dachille, F., and Roy, R. (1964). Effectiveness of Shearing Stresses in Accelerating Solid Phase Reactions at Low Temperatures and High Pressures. J. Geology. 72, 243–247. doi:10.1086/626979

CrossRef Full Text | Google Scholar

Davies, P. K., Wu, H., Borisevich, A. Y., Molodetsky, I. E., and Farber, L. (2008). Crystal Chemistry of Complex Perovskites: New Cation-Ordered Dielectric Oxides. Annu. Rev. Mater. Res. 38, 369–401. doi:10.1146/annurev.matsci.37.052506.084356

CrossRef Full Text | Google Scholar

de los Reyes, M., Whittle, K. R., Zhang, Z., Ashbrook, S. E., Mitchell, M. R., Jang, L.-Y., et al. (2013). The Pyrochlore to Defect Fluorite Phase Transition in Y2Sn2−xZrxO7. RSC Adv. 3, 5090–5099. doi:10.1039/C3RA22704A

CrossRef Full Text | Google Scholar

DongQu, C. Z., Qu, Z., Qin, Y., Fu, Q., Sun, H., and Duan, X. (2019). Revealing the Highly Catalytic Performance of Spinel CoMn2O4 for Toluene Oxidation: Involvement and Replenishment of Oxygen Species Using In Situ Designed-TP Techniques. ACS Catal. 9, 6698–6710. doi:10.1021/acscatal.9b01324

CrossRef Full Text | Google Scholar

Drey, D. L., O'Quinn, E. C., Subramani, T., Lilova, K., Baldinozzi, G., Gussev, I. M., et al. (2020a). Disorder in Ho2Ti2−xZrxO7: Pyrochlore to Defect Fluorite Solid Solution Series. RSC Adv. 10, 34632–34650. doi:10.1039/D0RA07118H

CrossRef Full Text | Google Scholar

Dunitz, J. D., and Orgel, L. E. (1957). Electronic Properties of Transition-Metal Oxides-II. J. Phys. Chem. Sol. 3, 318–323. doi:10.1016/0022-3697(57)90035-5

CrossRef Full Text | Google Scholar

Dyer, L. D., Borie, B. S., and Smith, G. P. (1954). Alkali Metal-Nickel Oxides of the Type MNiO2. J. Am. Chem. Soc. 76, 1499–1503. doi:10.1021/ja01635a012

CrossRef Full Text | Google Scholar

Eberman, K., Wuensch, B. J., and Jorgensen, J. D. (2002). Order-disorder Transformations Induced by Composition and Temperature Change in (SczYb1−z)2Ti2O7 Pyrochlores, Prospective Fuel Cell Materials. Solid State Ionics 148, 521–526. doi:10.1016/S0167-2738(02)00099-1

CrossRef Full Text | Google Scholar

Ewing, R. C., Lian, J., and Wang, L. M. (2003). Ion Beam-Induced Amorphization of the Pyrochlore Structure-type: a Review. MRS Proc. 792, 190–201. doi:10.1557/PROC-792-R2.1

CrossRef Full Text | Google Scholar

Ewing, R. C., Weber, W. J., and Lian, J. (2004). Nuclear Waste Disposal-Pyrochlore (A2B2O7): Nuclear Waste Form for the Immobilization of Plutonium and "minor" Actinides. J. Appl. Phys. 95, 5949–5971. doi:10.1063/1.1707213

CrossRef Full Text | Google Scholar

Ferg, E., Gummow, R. J., de Kock, A., and Thackeray, M. M. (1994). Spinel Anodes for Lithium‐ion Batteries. J. Electrochem. Soc. 141, 11–L147. doi:10.1149/1.2059324

CrossRef Full Text | Google Scholar

Finkeldei, S., Kegler, P., Kowalski, P. M., Schreinemachers, C., Brandt, F., Bukaemskiy, A. A., et al. (2017). Composition Dependent Order-Disorder Transition in Nd Zr1−O2−0.5 Pyrochlores: A Combined Structural, Calorimetric and Ab Initio Modeling Study. Acta Materialia 125, 166–176. doi:10.1016/j.actamat.2016.11.059

CrossRef Full Text | Google Scholar

Freire, M., Diaz-Lopez, M., Bordet, P., Colin, C. V., Lebedev, O. I., Kosova, N. V., et al. (2018). Investigation of the Exceptional Charge Performance of the 0.93Li4−xMn2O5-0.07Li2O Composite Cathode for Li-Ion Batteries. J. Mater. Chem. A. 6, 5156–5165. doi:10.1039/C8TA00234G

CrossRef Full Text | Google Scholar

Freire, M., Lebedev, O. I., Maignan, A., Jordy, C., and Pralong, V. (2017). Nanostructured Li2MnO3: a Disordered Rock Salt Type Structure for High Energy Density Li Ion Batteries. J. Mater. Chem. A. 5, 21898–21902. doi:10.1039/C7TA07476J

CrossRef Full Text | Google Scholar

Fu, J., and Skrabalak, S. E. (2017). Enhanced Photoactivity from Single‐Crystalline SrTaO 2 N Nanoplates Synthesized by Topotactic Nitridation. Angew. Chem. Int. Ed. 56 (45), 14169–14173. doi:10.1002/anie.201708645

PubMed Abstract | CrossRef Full Text | Google Scholar

Fu, W. T., and IJdo, D. J. W. (2009). On the crystal Structures of Ln3MO7 (Ln=Nd, Sm, Y and M=Sb, Ta)-Rietveld Refinement Using X-ray Powder Diffraction Data. J. Solid State. Chem. 182, 2451–2455. doi:10.1016/j.jssc.2009.06.028

CrossRef Full Text | Google Scholar

Fuentes, A. F., Boulahya, K., Maczka, M., Hanuza, J., and Amador, U. (2005). Synthesis of Disordered Pyrochlores, Ti2O7 (, Gd and Dy), by Mechanical Milling of Constituent Oxides. Solid State. Sci. 7, 343–353. doi:10.1016/j.solidstatesciences.2005.01.002

CrossRef Full Text | Google Scholar

Fuentes, A. F., Montemayor, S. M., Maczka, M., Lang, M., Ewing, R. C., and Amador, U. (2018). A Critical Review of Existing Criteria for the Prediction of Pyrochlore Formation and Stability. Inorg. Chem. 57, 12093–12105. doi:10.1021/acs.inorgchem.8b01665

PubMed Abstract | CrossRef Full Text | Google Scholar

Garcês Gonçalves, P. R., De Abreu, H. A., and Duarte, H. A. (2018). Stability, Structural, and Electronic Properties of Hausmannite (Mn3O4) Surfaces and Their Interaction with Water. J. Phys. Chem. C 122 (36), 20841–20849. doi:10.1021/acs.jpcc.8b06201

CrossRef Full Text | Google Scholar

Gardner, J. S., Gingras, M. J. P., and Greedan, J. E. (2010). Magnetic Pyrochlore Oxides. Rev. Mod. Phys. 82, 53–107. doi:10.1103/RevModPhys.82.53

CrossRef Full Text | Google Scholar

Glerup, M., Nielsen, O. F., and Poulsen, F. W. (2001). The Structural Transformation from the Pyrochlore Structure, A2B2O7, to the Fluorite Structure, AO2, Studied by Raman Spectroscopy and Defect Chemistry Modeling. J. Solid State. Chem. 160, 25–32. doi:10.1006/jssc.2000.9142

CrossRef Full Text | Google Scholar

Goldschmidt, V. M. (1926). Die Gesetze der Krystallochemie. Naturwissenschaften 14, 477–485. doi:10.1007/bf01507527

CrossRef Full Text | Google Scholar

Goodenough, J. B. (1959). On the Influence of 3d4 Ions on the Magnetic and Crystallographic Properties of Magnetic Oxides. J. Phys. Radium 20, 155–159. doi:10.1051/jphysrad:01959002002-3015500

CrossRef Full Text | Google Scholar

Gorter, E. W. (1950). Magnetization in Ferrites: Saturation Magnetization of Ferrites with Spinel Structure. Nature 165, 798–800. doi:10.1038/165798a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Grey, I. E., Mumme, W. G., Ness, T. J., Roth, R. S., and Smith, K. L. (2003). Structural Relations between Weberite and Zirconolite Polytypes-Refinements of Doped 3T and 4M Ca2Ta2O7 and 3T CaZrTi2O7. J. Solid State. Chem. 174, 285–295. doi:10.1016/S0022-4596(03)00222-6

CrossRef Full Text | Google Scholar

Gummow, R., and Thackeray, M. M. (1992). Lithium-cobalt-nickel-oxide Cathode Materials Prepared at 400$deg;C for Rechargeable Lithium Batteries. Solid State Ionics 53-56, 681–687. doi:10.1016/0167-2738(92)90447-W

CrossRef Full Text | Google Scholar

Gunn, D. S. D., Allan, N. L., Foxhall, H., Harding, J. H., Purton, J. A., Smith, W., et al. (2012). Novel Potentials for Modelling Defect Formation and Oxygen Vacancy Migration in Gd2Ti2O7 and Gd2Zr2O7 Pyrochlores. J. Mater. Chem. 22, 4675–4680. doi:10.1039/C2JM15264A

CrossRef Full Text | Google Scholar

Gussev, I. M., O'Quinn, E. C., Baldinozzi, G., Neuefeind, J., Ewing, R. C., Zhang, F., et al. (2020). Local Order of Orthorhombic Weberite-type Y3TaO7 as Determined by Neutron Total Scattering and Density Functional Theory Calculations✰. Acta Materialia 196, 704–709. doi:10.1016/j.actamat.2020.07.005

CrossRef Full Text | Google Scholar

Gutman, E. M. (1994). Mechanochemistry of Solid Surfaces. Singapore: World Scientific Publishing Co Inc. doi:10.1142/2373

CrossRef Full Text

Hagino, T., Seki, Y., Wada, N., Tsuji, S., Shirane, T., Kumagai, K.-i., et al. (1995). Superconductivity in Spinel-type compoundsCuRh2S4andCuRh2Se4. Phys. Rev. B 51, 12673–12684. doi:10.1103/PhysRevB.51.1267318

PubMed Abstract | CrossRef Full Text | Google Scholar

Hayun, S., Tran, T. B., Lian, J., Fuentes, A. F., and Navrotsky, A. (2012). Energetics of Stepwise Disordering Transformation in Pyrochlores, RE2Ti2O7 (RE=Y, Gd and Dy). Acta Materialia 60, 4303–4310. doi:10.1016/j.actamat.2012.04.007

CrossRef Full Text | Google Scholar

Helean, K. B., Begg, B. D., Navrotsky, A., Ebbinghaus, B., Weber, W. J., and Ewing, R. C. (2000). Enthalpies of Formation of Gd2(Ti2-xZrx)O7 Pyrochlores. MRS Proc. 663, 691. doi:10.1557/PROC-663-691

CrossRef Full Text | Google Scholar

Helean, K. B., Navrotsky, A., Vance, E. R., Carter, M. L., Ebbinghaus, B., Krikorian, O., et al. (2002). Enthalpies of Formation of Ce-Pyrochlore, Ca0.93Ce1.00Ti2.035O7.00, U-Pyrochlore, Ca1.46U4+0.23U6+0.46Ti1.85O7.00 and Gd-Pyrochlore, Gd2Ti2O7: Three Materials Relevant to the Proposed Waste Form for Excess Weapons Plutonium. J. Nucl. Mater. 303, 226–239. doi:10.1016/s0022-3115(02)00795-x

CrossRef Full Text | Google Scholar

Helean, K. B., Ushakov, S. V., Brown, C. E., Navrotsky, A., Lian, J., Ewing, R. C., et al. (2004). Formation Enthalpies of Rare Earth Titanate Pyrochlores. J. Solid State. Chem. 177, 1858–1866. doi:10.1016/j.jssc.2004.01.009

CrossRef Full Text | Google Scholar

Heremans, C., Wuensch, B. J., Stalick, J. K., and Prince, E. (1995). Fast-Ion Conducting Y2(Zr Ti1-)2O7 Pyrochlores: Neutron Rietveld Analysis of Disorder Induced by Zr Substitution. J. Solid State. Chem. 117, 108–121. doi:10.1006/jssc.1995.1253

CrossRef Full Text | Google Scholar

Hewston, T. A., and Chamberland, B. L. (1987). A Survey of First-Row Ternary Oxides LiMO2 (M = Sc-Cu). J. Phys. Chem. Sol. 48, 97–108. doi:10.1016/0022-3697(87)90076-X

CrossRef Full Text | Google Scholar

Hoppe, R., Brachtel, G., and Jansen, M. (1975). Zur Kenntnis der Oxomanganate(III):, Uber LiMnO2 und B NaMnO2. J. Anorg. Allg. Chem. 417, 1–10. doi:10.1002/zaac.19754170102

CrossRef Full Text | Google Scholar

House, R. A., Jin, L., Maitra, U., Tsuruta, K., Somerville, J. W., Förstermann, D. P., et al. (2018). Lithium Manganese Oxyfluoride as a New Cathode Material Exhibiting Oxygen Redox. Energ. Environ. Sci. 11, 926–932. doi:10.1039/C7EE03195E

CrossRef Full Text | Google Scholar

Hua, W., Wang, S., Knapp, M., Leake, S. J., Senyshyn, A., Richter, C., et al. (2019). Structural Insights into the Formation and Voltage Degradation of Lithium- and Manganese-Rich Layered Oxides. Nat. Commun. 10, 5365. doi:10.1038/s41467-019-13240-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Hume-Rothery, W., and Powell, H. M. (1935). On the Theory of Super-lattice Structures in Alloys. Z. Kristallogr. 91, 23–47. doi:10.1524/zkri.1935.91.1.23

CrossRef Full Text | Google Scholar

Ivanov, V. G., Abrashev, M. V., Iliev, M. N., Gospodinov, M. M., Meen, J., and Aroyo, M. I. (2010). Short-range B-site Ordering in the Inverse Spinel ferrite NiFe2O4. Phys. Rev. B 82, 024104. doi:10.1103/PhysRevB.82.024104

CrossRef Full Text | Google Scholar

Ji, H., Urban, A., Kitchaev, D. A., Kwon, D.-H., Artrith, N., Ophus, C., et al. (2019). Hidden Structural and Chemical Order Controls Lithium Transport in Cation-Disordered Oxides for Rechargeable Batteries. Nat. Commun. 10, 592. doi:10.1038/s41467-019-08490-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Jones, M. A., Reeves, P. J., Seymour, I. D., Cliffe, M. J., Dutton, S. E., and Grey, C. P. (2019). Short-range Ordering in a Battery Electrode, the ‘cation-Disordered' Rocksalt Li1.25Nb0.25Mn0.5O2. Chem. Commun. 55, 9027–9030. doi:10.1039/C9CC04250D

PubMed Abstract | CrossRef Full Text | Google Scholar

Jouini, A., Yoshikawa, A., Brenier, A., Fukuda, T., and Boulon, G. (2007). Optical Properties of Transition Metal Ion-Doped MgAl2O4 Spinel for Laser Application. Phys. Stat. Sol. (C) 4 (3), 1380–1383. doi:10.1002/pssc.200673872

CrossRef Full Text | Google Scholar

Kan, W. H., Deng, B., Xu, Y., Shukla, A. K., Bo, T., Zhang, S., et al. (2018). Understanding the Effect of Local Short-Range Ordering on Lithium Diffusion in Li1.3Nb0.3Mn0.4O2 Single-Crystal Cathode. Chem 4 (9), 2108–2123. doi:10.1016/j.chempr.2018.05.008

CrossRef Full Text | Google Scholar

Kang, K., and Ceder, G. (2006). Factors that Affect Li Mobility in Layered Lithium Transition Metal Oxides. Phys. Rev. B: Condens. Matter Mater. Phys. 74, 094105. doi:10.1103/PhysRevB.74.094105

CrossRef Full Text | Google Scholar

Kang, K., Meng, Y. S., Bréger, J., Grey, C. P., and Ceder, G. (2006). Electrodes with High Power and High Capacity for Rechargeable Lithium Batteries. Science 311, 977–980. doi:10.1126/science.1122152

PubMed Abstract | CrossRef Full Text | Google Scholar

Kennedy, B. J. (1996). Structural Trends in Pyrochlore Oxides. Msf 228-231, 753–758. doi:10.4028/www.scientific.net/msf.228-231.753

CrossRef Full Text | Google Scholar

Kim, J., Pieczonka, N. P. W., and Yang, L. (2014). Challenges and Approaches for Hhgh‐voltage Spinel Lithium‐ion Batteries. ChemPhysChem 15 (10), 1940–1954. doi:10.1002/cphc.201400052

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, Y., Kwon, S., Song, Y., and Na, K. (2020). Catalytic CO2 Hydrogenation Using Mesoporous Bimetallic Spinel Oxides as Active Heterogeneous Base Catalysts with Long Lifetime. J. CO2 Utilization 36, 145–152. doi:10.1016/j.jcou.2019.11.005

CrossRef Full Text | Google Scholar

King, G., Thompson, C. M., Greedan, J. E., and Llobet, A. (2013). Local Structure of the Vacancy Disordered Fluorite Yb3TaO7 from Neutron Total Scattering. J. Mater. Chem. A. 1, 10487–10494. doi:10.1039/C3TA12100C

CrossRef Full Text | Google Scholar

King, G., and Woodward, P. M. (2010). Cation Ordering in Perovskites. J. Mater. Chem. 20, 5785–5796. doi:10.1039/B926757C

CrossRef Full Text | Google Scholar

Knee, C. S., Holmlund, J., Andreasson, J., Käll, M., Eriksson, S. G., and Börjesson, L. (2005). Order-disorder-order Phase Transitions in the Pyrochlore superconductorCd2Re2O7. Phys. Rev. B 71, 214518. doi:10.1103/PhysRevB.71.214518

CrossRef Full Text | Google Scholar

Kubicek, M., Bork, A. H., and Rupp, J. L. M. (2017). Perovskite Oxides - a Review on a Versatile Material Class for Solar-To-Fuel Conversion Processes. J. Mater. Chem. A. 5, 11983–12000. doi:10.1039/C7TA00987A

CrossRef Full Text | Google Scholar

Kumari, R., Kulriya, P. K., Grover, V., Shukla, R., Saravanan, K., Mohapatra, S., et al. (2016). Radiation Stability of Gd2Zr2O7: Effect of Stoichiometry and Structure. Ceram. Int. 42, 103–109. doi:10.1016/j.Ceram.Int.2015.08.007

CrossRef Full Text | Google Scholar

Laberty, C., Navrotsky, A., Rao, C. N. R., and Alphonse, P. (1999). Energetics of Rare Earth Manganese Perovskites A1−xA′xMnO3 (A=La, Nd, Y and A′=Sr, La) Systems. J. Solid State. Chem. 145, 77–87. doi:10.1006/jssc.1999.8220

CrossRef Full Text | Google Scholar

Lang, M., Zhang, F. X., Ewing, R. C., Lian, J., Trautmann, C., and Wang, Z. (2009). Structural Modifications of Gd2Zr2-xTixO7 Pyrochlore Induced by swift Heavy Ions: Disordering and Amorphization. J. Mater. Res. 24, 1322–1334. doi:10.1557/jmr.2009.0151

CrossRef Full Text | Google Scholar

Lang, M., Zhang, F., Zhang, J., Wang, J., Lian, J., Weber, W. J., et al. (2010). Review of A2B2O7 Pyrochlore Response to Irradiation and Pressure. Nucl. Instr. Methods Phys. Res. Section B: Beam Interactions Mater. Atoms 268, 2951–2959. doi:10.1016/j.nimb.2010.05.016

CrossRef Full Text | Google Scholar

Lee, E., Blauwkamp, J., Castro, F. C., Wu, J., Dravid, V. P., Yan, P., et al. (2016). Exploring Lithium-Cobalt-Nickel Oxide Spinel Electrodes for ≥3.5 V Li-Ion Cells. ACS Appl. Mater. Inter. 8, 27720–27729. doi:10.1021/acsami.6b09073

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, T. A., and Navrotsky, A. (2004). Enthalpy of Formation of Cubic Yttria-Stabilized Hafnia. J. Mater. Res. 19, 1855–1861. doi:10.1557/JMR.2004.0234

CrossRef Full Text | Google Scholar

Lee, T. A., Navrotsky, A., and Molodetsky, I. (2003). Enthalpy of Formation of Cubic Yttria-Stabilized Zirconia. J. Mater. Res. 18, 908–918. doi:10.1557/JMR.2003.0125

CrossRef Full Text | Google Scholar

Lian, J., Chen, J., Wang, L. M., Ewing, R. C., Farmer, J. M., Boatner, L. A., et al. (2003a). Radiation-induced Amorphization of Rare-Earth Titanate Pyrochlores. Phys. Rev. B 68, 134107. doi:10.1103/PhysRevB.68.134107

CrossRef Full Text | Google Scholar

Lian, J., Helean, K. B., Kennedy, B. J., Wang, L. M., Navrotsky, A., and Ewing, R. C. (2006). Effect of Structure and Thermodynamic Stability on the Response of Lanthanide Stannate Pyrochlores to Ion Beam Irradiation. J. Phys. Chem. B 110, 2343–2350. doi:10.1021/jp055266c

PubMed Abstract | CrossRef Full Text | Google Scholar

Lian, J., Wang, L., Chen, J., Sun, K., Ewing, R. C., Matt Farmer, J., et al. (2003b). The Order-Disorder Transition in Ion-Irradiated Pyrochlore. Acta Materialia 51, 1493–1502. doi:10.1016/S1359-6454(02)00544-X10.1016/s1359-6454(02)00544-x

CrossRef Full Text | Google Scholar

Lian, J., Wang, L. M., Haire, R. G., Helean, K. B., and Ewing, R. C. (2004). Ion Beam Irradiation in La2Zr2O7-Ce2Zr2O7 Pyrochlore. Nucl. Instr. Methods Phys. Res. Section B: Beam Interactions Mater. Atoms 218, 236–243. doi:10.1016/j.nimb.2004.01.007

CrossRef Full Text | Google Scholar

Lian, J., Zu, X. T., Kutty, K. V. G., Chen, J., Wang, L. M., and Ewing, R. C. (2002). Ion-irradiation-induced Amorphization ofLa2Zr2O7pyrochlore. Phys. Rev. B 66, 54108. doi:10.1103/PhysRevB.66.054108

CrossRef Full Text | Google Scholar

Linton, J., Navrotsky, A., and Fei, Y. (1998). The Thermodynamics of Ordered Perovskites on the CaTiO3- FeTiO3 Join. Phys. Chem. Min. 25, 591–596. doi:10.1007/s002690050152

CrossRef Full Text | Google Scholar

Liu, Y., Withers, R. L., and Norén, L. (2004). The Pyrochlore to ‘defect Fluorite' Transition in the Y2(ZryTi1−y)2O7 System and its Underlying crystal Chemistry. J. Solid State. Chem. 177, 4404–4412. doi:10.1016/j.jssc.2004.09.014

CrossRef Full Text | Google Scholar

Magneli, A. (1956). Some Aspects of the crystal Chemistry of Oxygen Compounds of Molybdenum and Tungsten Containing Structural Elements of ReO3 or Perovskite Type. J. Inorg. Nucl. Chem. 2, 330–339. doi:10.1016/0022-1902(56)80086-9

CrossRef Full Text | Google Scholar

Malíčková, I., Bačík, P., Fridrichová, J., Hanus, R., Illášová, L., Štubňa, J., et al. (2021). Optical and Luminescence Spectroscopy of Varicolored Gem Spinel from Mogok, Myanmar and Lục Yên. Vietnam. Minerals. 11 (2), 169. doi:10.3390/min11020169

CrossRef Full Text | Google Scholar

Mandal, B. P., Banerji, A., Sathe, V., Deb, S. K., and Tyagi, A. K. (2007). Order-disorder Transition in Nd2−yGdyZr2O7 Pyrochlore Solid Solution: An X-ray Diffraction and Raman Spectroscopic Study. J. Solid State. Chem. 180, 2643–2648. doi:10.1016/j.jssc.2007.07.007

CrossRef Full Text | Google Scholar

Mandal, B. P., Garg, N., Sharma, S. M., and Tyagi, A. K. (2006). Preparation, XRD and Raman Spectroscopic Studies on New Compounds RE2Hf2O7 (RE=Dy, Ho, Er, Tm, Lu, Y): Pyrochlores or Defect-Fluorite? J. Solid State. Chem. 179, 1990–1994. doi:10.1016/j.jssc.2006.03.036

CrossRef Full Text | Google Scholar

Mandal, B. P., and Tyagi, A. K. (2007). Preparation and High Temperature-XRD Studies on a Pyrochlore Series with the General Composition Gd2−xNdxZr2O7. J. Alloys Comp. 437, 260–263. doi:10.1016/j.jallcom.2006.07.093

CrossRef Full Text | Google Scholar

Maram, P. S., Ushakov, S. V., Weber, R. J. K., Benmore, C. J., and Navrotsky, A. (2015). In Situ diffraction from Levitated Solids under Extreme Conditions - Structure and thermal Expansion in the Eu2O3 - ZrO2 System. J. Am. Ceram. Soc. 98, 1292–1299. doi:10.1111/jace.13422

CrossRef Full Text | Google Scholar

Maram, P. S., Ushakov, S. V., Weber, R. J. K., Benmore, C. J., and Navrotsky, A. (2018). Probing Disorder in Pyrochlore Oxides Using In Situ Synchrotron Diffraction from Levitated Solids-A Thermodynamic Perspective. Sci. Rep. 8. doi:10.1038/s41598-018-28877-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Marlton, F. P., Zhang, Z., Zhang, Y., Proffen, T. E., Ling, C. D., and Kennedy, B. J. (2021). Lattice Disorder and Oxygen Migration Pathways in Pyrochlore and Defect-Fluorite Oxides. Chem. Mater. 33, 1407–1415. doi:10.1021/acs.chemmater.0c04515

CrossRef Full Text | Google Scholar

Martel, L., Naji, M., Popa, K., Vigier, J.-F., and Somers, J. (2017). Fingerprint of Local Disorder in Long Range Ordered Isometric Pyrochlores. Sci. Rep. 7, 12269. doi:10.1038/s41598-017-12544-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Matrosova, E. A., Bobrov, A. V., Bindi, L., Pushcharovsky, D. Y., and Irifune, T. (2020). Titanium-rich Phases in the Earth’s Transition Zone and Lower Mantle: Evidence from Experiments in the System MgO - SiO2 -TiO2(±Al2O3) at 10-24 GPa and 1600 °C. Lithos 366–367, 105539. doi:10.1016/j.lithos.2020.105539

PubMed Abstract | CrossRef Full Text | Google Scholar

Matsuhira, K., Wakeshima, M., Nakanishi, R., Yamada, T., Nakamura, A., Kawano, W., et al. (2007). Metal-Insulator Transition in Pyrochlore Iridates Ln2Ir2O7 (Ln = Nd, Sm, and Eu). J. Phys. Soc. Jpn. 76, 043706–043727. doi:10.1143/JPSJ.76.043706

CrossRef Full Text | Google Scholar

McCaugherty, S., and Grosvenor, A. P. (2019). Low-temperature Synthesis of CaZrTi2O7 Zirconolite-type Materials Using Ceramic, Coprecipitation, and Sol-Gel Methods. J. Mater. Chem. C 7, 177–187. doi:10.1039/c8tc04560g

CrossRef Full Text | Google Scholar

Meldrum, A., White, C. W., Keppens, V., Boatner, L. A., and Ewing, R. C. (2001). Irradiation-induced Amorphization ofCd2Nb2O7pyrochlore. Phys. Rev. B 63, 104109. doi:10.1103/PhysRevB.63.104109

CrossRef Full Text | Google Scholar

Mielcewczyk-Gryn, A., and Navrotsky, A. (2015). Enthalpies of Formation of Rare Earth Niobates. Re3nbo7. Am. Mineral. 100, 1578–1583. doi:10.2138/am-2015-5210

CrossRef Full Text | Google Scholar

Minervini, L., Grimes, R. W., and Sickafus, K. E. (2000). Disorder in Pyrochlore Oxides. J. Am. Ceram. Soc. 83, 1873–1878. doi:10.1111/j.1151-2916.2000.tb01484.x

CrossRef Full Text | Google Scholar

Momma, K., and Izumi, F. (2008). VESTA: A Three-Dimensional Visualization System for Electronic and Structural Analysis. J. Appl. Crystallogr. 41, 653–658. doi:10.1107/S0021889808012016

CrossRef Full Text | Google Scholar

Moran, R. F., McKay, D., Tornstrom, P. C., Aziz, A., Fernandes, A., Grau-Crespo, R., et al. (2019). Ensemble-Based Modeling of the NMR Spectra of Solid Solutions: Cation Disorder in Y2(Sn,Ti)2O7. J. Am. Chem. Soc. 141, 17838–17846. doi:10.1021/jacs.9b09036

PubMed Abstract | CrossRef Full Text | Google Scholar

Moreno, K. J., Fuentes, A. F., Maczka, M., Hanuza, J., and Amador, U. (2006a). Structural Manipulation of Pyrochlores: Thermal Evolution of Metastable Gd2(Ti1−yZry)2O7 Powders Prepared by Mechanical Milling. J. Solid State. Chem. 179, 3805–3813. doi:10.1016/j.jssc.2006.08.023

CrossRef Full Text | Google Scholar

Moreno, K. J., Guevara-Liceaga, M. A., Fuentes, A. F., García-Barriocanal, J., León, C., and Santamaría, J. (2006). Room-temperature Synthesis and Conductivity of the Pyrochlore Type Dy2(Ti1−yZry)2O7 (0⩽y⩽1) Solid Solution. J. Solid State. Chem. 179, 928–934. doi:10.1016/j.jssc.2005.12.015

CrossRef Full Text | Google Scholar

Moshopoulou, E. G. (2004). Superconductivity in the Spinel Compound LiTi2O4. J. Am. Ceram. Soc. 82 (12), 3317–3320. doi:10.1111/j.1151-2916.1999.tb02245.x

CrossRef Full Text | Google Scholar

Mouta, R., Silva, R. X., and Paschoal, C. W. A. (2013). Tolerance Factor for Pyrochlores and Related Structures. Acta Crystallogr. Sect. B 69, 439–445. doi:10.1107/S2052519213020514

PubMed Abstract | CrossRef Full Text | Google Scholar

Murphy, D. W., Greenblatt, M., Zahurak, S. M., Cava, R. J., Waszczak, J. V., Hull, G. W., et al. (1982). Lithium Insertion in Anatase: a New Route to the Spinel LiTi2O4. Rev. Chim. Minor. 19, 441.

Google Scholar

Murphy, D. W., Sunshine, S., van Dover, R. B., Cava, R. J., Batlogg, B., Zahurak, S. M., et al. (1987). New Superconducting Cuprate Perovskites. Phys. Rev. Lett. 58, 1888–1890. doi:10.1103/PhysRevLett.58.1888

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakamura, A., Doi, Y., and Hinatsu, Y. (2011). Magnetic Properties of Barium Uranate Ba2U2O7. J. Solid State. Chem. 184, 531–535. doi:10.1016/j.jssc.2010.12.023

CrossRef Full Text | Google Scholar

Nanot, M., Queyroux, F., Gilles, J.-C., Carpy, A., and Galy, J. (1974). Phases multiples dans les systèmes Ca2Nb2O7-NaNbO3 et La2Ti2O7CaTiO3: Les séries homologues de formule AnBnO3n+2. J. Solid State. Chem. 11, 272–284. doi:10.1016/S0022-4596(74)80032-0

CrossRef Full Text | Google Scholar

Navrostky, A., and Kleppa, O. J. (1967). The Thermodynamics of Cation Distributions in Simple Spinels. J. Inorg. Nucl. Chem. 29 (11), 2701–2714. doi:10.1016/0022-1902(67)80008-3

CrossRef Full Text | Google Scholar

Navrotsky, A. (1994). Physics and Chemistry of Earth Materials. Cambridge University Press. doi:10.1017/cbo9781139173650

CrossRef Full Text

Navrotsky, A., and Ushakov, S. V. (2005). “Thermodynamics of Oxide Systems Relevant to Alternative Gate Dielectrics,” in Materials Fundamentals of Gate Dielectrics,”. Editors A. A. Demkov, and A. Navrotsky (Dordrecht: Springer Netherlands), 57–108.

Google Scholar

Navrotsky, A., and Weidner, D. J. (1989). 45. American Geophysical Union, 146.Perovskite: A Structure of Great Interest to Geophysics and Materials ScienceGeophys. Monogr. Ser.

CrossRef Full Text | Google Scholar

Ndione, P. F., Shi, Y., Stevanovic, V., Lany, S., Zakutayev, A., Parilla, P. A., et al. (2014). Control of the Electrical Properties in Spinel Oxides by Manipulating the Cation Disorder. Adv. Funct. Mater. 24 (5), 610–618. doi:10.1002/adfm.201302535

CrossRef Full Text | Google Scholar

Nenoff, T. M., Rademacher, D. X., Rodriguez, M. A., Garino, T. J., Subramani, T., and Navrotsky, A. (2021). Structure-property and Thermodynamic Relationships in Rare Earth (Y, Eu, Pr) Iridate Pyrochlores. J. Solid State. Chem. 299, 122163. doi:10.1016/j.jssc.2021.122163

CrossRef Full Text | Google Scholar

Nishikawa, S. (1915). Structure of Some Crystals of the Apinel Group. Proc. Math. Phys. Soc. Jpn. 8, 199–209. doi:10.11429/ptmps1907.8.7_199

CrossRef Full Text | Google Scholar

O'Quinn, E. C., Sickafus, K. E., Ewing, R. C., Baldinozzi, G., Neuefeind, J. C., Tucker, M. G., et al. (2020). Predicting Short-Range Order and Correlated Phenomena in Disordered Crystalline Materials. Sci. Adv. 6, eabc2758. doi:10.1126/sciadv.abc2758

PubMed Abstract | CrossRef Full Text | Google Scholar

Orman, H. J., and Wiseman, P. J. (1984). Cobalt(III) Lithium Oxide, CoLiO2: Structure Refinement by Powder Neutron Diffraction. Acta Crystallogr. C 40, 12–14. doi:10.1107/S0108270184002833

CrossRef Full Text | Google Scholar

Ovsyannikov, S. V., Abakumov, A. M., Tsirlin, A. A., Schnelle, W., Egoavil, R., Verbeeck, J., et al. (2013). Perovskite-like Mn2O3: A Path to New Manganites. Angew. Chem. Int. Ed. 52, 1494–1498. doi:10.1002/anie.201208553

PubMed Abstract | CrossRef Full Text | Google Scholar

Panghal, A., Kumar, Y., Kulriya, P. K., Shirage, P. M., and Singh, N. L. (2021). Atomic Order-Disorder Engineering in the La2Zr2O7 Pyrochlore under Low Energy Ion Irradiation. Ceramics Int. 47, 20248–20259. doi:10.1016/j.ceramint.2021.04.032

CrossRef Full Text | Google Scholar

Patel, M. K., Vijayakumar, V., Avasthi, D. K., Kailas, S., Pivin, J. C., Grover, V., et al. (2008a). Effect of swift Heavy Ion Irradiation in Pyrochlores. Nucl. Instr. Methods Phys. Res. Section B: Beam Interactions Mater. Atoms 266, 2898–2901. doi:10.1016/j.nimb.2008.03.135

CrossRef Full Text | Google Scholar

Patel, M. K., Vijayakumar, V., Kailas, S., Avasthi, D. K., Pivin, J. C., and Tyagi, A. K. (2008b). Structural Modifications in Pyrochlores Caused by Ions in the Electronic Stopping Regime. J. Nucl. Mater. 380, 93–98. doi:10.1016/j.jnucmat.2008.07.007

CrossRef Full Text | Google Scholar

Patrakeev, M. V., Kharton, V. V., Bakhteeva, Y. A., Shaula, A. L., Leonidov, I. A., Kozhevnikov, V. L., et al. (2006). Oxygen Nonstoichiometry and Mixed Conductivity of SrFe1−xO3−δ (M=Al, Ga): Effects of B-Site Doping. Solid State. Sci. 8, 476–487. doi:10.1016/j.solidstatesciences.2006.01.006

CrossRef Full Text | Google Scholar

Paul, B., Singh, K., Jaroń, T., Roy, A., and Chowdhury, A. (2016). Structural Properties and the Fluorite-Pyrochlore Phase Transition in La 2 Zr 2 O 7 : The Role of Oxygen to Induce Local Disordered States. J. Alloys Comp. 686, 130–136. doi:10.1016/j.jallcom.2016.05.347

CrossRef Full Text | Google Scholar

Perriot, R., Dholabhai, P. P., and Uberuaga, B. P. (2016). The Role of Surfaces, Chemical Interfaces, and Disorder on Plutonium Incorporation in Pyrochlores. Phys. Chem. Chem. Phys. 18, 22852–22863. doi:10.1039/C6CP03543D

PubMed Abstract | CrossRef Full Text | Google Scholar

Pilania, G., Puchala, B., and Uberuaga, B. P. (2019). Distortion-stabilized Ordered Structures in A2BB’O7 Mixed Pyrochlores. Npj Comput. Mater. 5, 7. doi:10.1038/s41524-018-0144-1

CrossRef Full Text | Google Scholar

Ponnilavan, V., Venkatesan, K., Nandha Kumar, P., and Kannan, S. (2019). Discrete Crystallization of Fluorite and Subsequent Pyrochlore Phase Transitions in Dy2Zr2O7 Facilitated by Ti4+ Additions. Mater. Chem. Phys. 236, 121788. doi:10.1016/j.matchemphys.2019.121788

CrossRef Full Text | Google Scholar

Popov, V. V., Menushenkov, A. P., Ivanov, A. A., Yastrebtsev, A. A., Gaynanov, B. R., d’Acapito, F., et al. (2020). A XAFS Investigation of Amorphous-To-Crystalline and Fluorite-To-Pyrochlore Phase Transitions in Ln2M2O7 (Ln = Gd, Tb, Dy; M = Ti, Zr). Radiat. Phys. Chem. 175, 108469. doi:10.1016/j.radphyschem.2019.108469

CrossRef Full Text | Google Scholar

Popov, V. V., Menushenkov, A. P., Yaroslavtsev, A. A., Zubavichus, Y. V., Gaynanov, B. R., Yastrebtsev, A. A., et al. (2016). Fluorite-pyrochlore Phase Transition in Nanostructured Ln2Hf2O7 (Ln = La-Lu). J. Alloys Comp. 689, 669–679. doi:10.1016/j.jallcom.2016.08.019

CrossRef Full Text | Google Scholar

Prado, F., Grunbaum, N., Caneiro, A., and Manthiram, A. (2004). Effect of La3+ Doping on the Perovskite-To-Brownmillerite Transformation in Sr1−xLaxCo0.8Fe0.2O3−δ (0≤x≤0.4). Solid State Ionics 167, 147–154. doi:10.1016/j.ssi.2003.12.006

CrossRef Full Text | Google Scholar

Prasanna, T. R. S., and Navrotsky, A. (1994). Energetics in the Brownmillerite-Perovskite Pseudobinary Ca2Fe2O5-CaTiO3. J. Mater. Res. 12, 3121–3124. doi:10.1557/JMR.1994.3121

CrossRef Full Text | Google Scholar

Putnam, R. L., Navrotsky, A., Woodfield, B. F., Boerio-Goates, J., and Shapiro, J. L. (1999a). Thermodynamics of Formation for Zirconolite (CaZrTi2O7) fromT=298.15 K toT=1500 K. The J. Chem. Thermodynamics 31, 229–243. doi:10.1006/jcht.1998.0445

CrossRef Full Text | Google Scholar

Putnam, R. L., Navrotsky, A., Woodfield, B. F., Shapiro, J. L., Stevens, R., and Boerio-Goates, J. (1999b). Thermochemistry of Hf-Zirconolite, CaHf Ti2O7. MRS Proc. 556, 11. doi:10.1557/PROC-556-11

CrossRef Full Text | Google Scholar

Radha, A. V., Ushakov, S. V., and Navrotsky, A. (2009). Thermochemistry of Lanthanum Zirconate Pyrochlore. J. Mater. Res. 24, 3350–3357. doi:10.1557/jmr.2009.0401

CrossRef Full Text | Google Scholar

Radhakrishnan, A. N., Rao, P. P., Linsa, K. S. M., Deepa, M., and Koshy, P. (2011). Influence of Disorder-To- Order Transition on Lattice thermal Expansion and Oxide Ion Conductivity in (CaxGd1−x)2(Zr1−xMx)2O7 Pyrochlore Solid Solutions. Dalt. Trans. 40, 3839–3848. doi:10.1039/C0DT01688H

CrossRef Full Text | Google Scholar

Rao, C. N. R., and Raveau, B. (1989). Structural Aspects of High-Temperature Cuprate Superconductors. Acc. Chem. Res. 22, 106–113.

CrossRef Full Text | Google Scholar

Rautama, E.-L., Caignaert, V., Boullay, P., Kundu, A. K., Pralong, V., Karppinen, M., et al. (2009). New Member of the "112" Family, LaBaCo2O5.5: Synthesis, Structure, and Magnetism. Chem. Mater. 21 (1), 102–109. doi:10.1021/cm8021775

CrossRef Full Text | Google Scholar

Rittman, D. R., Turner, K. M., Park, S., Fuentes, A. F., Park, C., Ewing, R. C., et al. (2017a). Strain Engineered Pyrochlore at High Pressure. Sci. Rep. 7, 1–10. doi:10.1038/s41598-017-02637-9

CrossRef Full Text | Google Scholar

Rittman, D. R., Turner, K. M., Park, S., Fuentes, A. F., Yan, J., Ewing, R. C., et al. (2017b). High-pressure Behavior of A2B2O7 Pyrochlore (A=Eu, Dy; B=Ti, Zr). J. Appl. Phys. 121, 045902. doi:10.1063/1.4974871

CrossRef Full Text | Google Scholar

Rossen, E., Reimers, J. N., and Dahn, J. R. (1993). Synthesis and Electrochemistry of Spinel LT-LiCoO2. Solid State Ionics 62, 53–60. doi:10.1016/0167-2738(93)90251-W

CrossRef Full Text | Google Scholar

Rüdorff, W., and Becker, H. (1954). Notizen: Die Strukturen von LiVO2, NaVO2, LiCrO2 und NaCrO2. Z. Naturforsch. B. 9, 614–615. doi:10.1515/znb-1954-0911

CrossRef Full Text | Google Scholar

Rushton, M. J. D., Grimes, R. W., Stanek, C. R., and Owens, S. (2004). Predicted Pyrochlore to Fluorite Disorder Temperature for A2Zr2O7 Compositions. J. Mater. Res. 19, 1603–1604. doi:10.1557/JMR.2004.0231

CrossRef Full Text | Google Scholar

Salamat, A., McMillan, P. F., Woodhead, K., Hector, A. L., Garbarino, G., et al. (2013). Structural Transformations and Disordering in Zirconolite (CaZrTi2O7) at High Pressure. Inorg. Chem. 52, 1550–1558. doi:10.1021/ic302346g

PubMed Abstract | CrossRef Full Text | Google Scholar

Sanjuán, M. L., Guglieri, C., Díaz-Moreno, S., Aquilanti, G., Fuentes, A. F., Olivi, L., et al. (2011). Raman and X-ray Absorption Spectroscopy Study of the Phase Evolution Induced by Mechanical Milling and thermal Treatments inR2Ti2O7pyrochlores. Phys. Rev. B 84, 104207. doi:10.1103/PhysRevB.84.104207

CrossRef Full Text | Google Scholar

Saradhi, M. P., Ushakov, S. V., and Navrotsky, A. (2012). Fluorite-pyrochlore Transformation in Eu2Zr2O7-Direct Calorimetric Measurement of Phase Transition, Formation and Surface Enthalpies. RSC Adv. 2, 3328–3334. doi:10.1039/C2RA00727D

CrossRef Full Text | Google Scholar

Sayed, F. N., Grover, V., Bhattacharyya, K., Jain, D., Arya, A., Pillai, C. G. S., et al. (2011). Sm2−xDyxZr2O7Pyrochlores: Probing Order−Disorder Dynamics and Multifunctionality. Inorg. Chem. 50, 2354–2365. doi:10.1021/ic200108u

PubMed Abstract | CrossRef Full Text | Google Scholar

Shamblin, J., Feygenson, M., Neuefeind, J., Tracy, C. L., Zhang, F., Finkeldei, S., et al. (2016a). Probing Disorder in Isometric Pyrochlore and Related Complex Oxides. Nat. Mater 15, 507–511. doi:10.1038/nmat4581

PubMed Abstract | CrossRef Full Text | Google Scholar

Shamblin, J., Tracy, C. L., Ewing, R. C., Zhang, F., Li, W., Trautmann, C., et al. (2016b). Structural Response of Titanate Pyrochlores to swift Heavy Ion Irradiation. Acta Materialia 117, 207–215. doi:10.1016/j.actamat.2016.07.017

CrossRef Full Text | Google Scholar

Shamblin, J., Tracy, C. L., Palomares, R. I., O'Quinn, E. C., Ewing, R. C., Neuefeind, J., et al. (2018). Similar Local Order in Disordered Fluorite and Aperiodic Pyrochlore Structures. Acta Materialia 144, 60–67. doi:10.1016/j.actamat.2017.10.044

CrossRef Full Text | Google Scholar

Sherrod, R., O’Quinn, E. C., Gussev, I. M., Overstreet, C., Neuefeind, J., and Lang, M. K. (2021). Comparison of Short-Range Order in Irradiated Dysprosium Titanates. Npj Mater. Degrad. 5, 19. doi:10.1038/s41529-021-00165-6

CrossRef Full Text | Google Scholar

Shin, S., Yonemura, M., and Ikawa, H. (1978). Order-disorder Transition of Sr2Fe2O5 from Brownmillerite to Perovskite Structure at an Elevated Temperature. Mater. Res. Bull. 13, 1017–1021. doi:10.1016/0025-5408(78)90166-610.1016/0025-5408(78)90166-6

CrossRef Full Text | Google Scholar

Shlyakhtina, A. V., Shcherbakova, L. G., Knotko, A. V., and Steblevskii, A. V. (2004). Study of the Fluorite?pyrochlore?fluorite Phase Transitions in Ln2Ti2O7 (Ln=Lu, Yb, Tm). J. Solid State. Electrochem. 8, 661–667. doi:10.1007/s10008-003-0491-8

CrossRef Full Text | Google Scholar

Shlyakhtina, A. V., and Shcherbakova, L. G. (2011). Polymorphism and High-Temperature Conductivity of Ln2M2O7 (Ln=Sm─Lu; M=Ti, Zr, Hf) Pyrochlores. Solid State Ionics 192, 200–204. doi:10.1016/j.ssi.2010.07.013

CrossRef Full Text | Google Scholar

Simeone, D., Thorogood, G. J., Huo, D., Luneville, L., Baldinozzi, G., Petricek, V., et al. (2017). Intricate Disorder in Defect Fluorite/pyrochlore: A concord of Chemistry and Crystallography. Sci. Rep. 7, 1–7. doi:10.1038/s41598-017-02787-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Simoncic, P., and Navrotsky, A. (2007a). Energetics of Rare-Earth-Doped Hafnia. J. Mater. Res. 22, 876–885. doi:10.1557/jmr.2007.0133

CrossRef Full Text | Google Scholar

Simoncic, P., and Navrotsky, A. (2007b). Systematics of Phase Transition and Mixing Energetics in Rare Earth, Yttrium, and Scandium Stabilized Zirconia and Hafnia. J. Am. Ceram. Soc. 90, 2143–2150. doi:10.1111/j.1551-2916.2007.01678.x

CrossRef Full Text | Google Scholar

Smyth, D. M. (1985). Defects and Order in Perovskite-Related Oxides. Annu. Rev. Mater. Sci. 15, 329–357. doi:10.1146/annurev.ms.15.080185.001553

CrossRef Full Text | Google Scholar

Solomon, J. M., Asta, M., Shamblin, J., Lang, M., Shamblin, J., and Navrotsky, A. (2016). Chemical Ordering in Substituted Fluorite Oxides: a Computational Investigation of Ho2Zr2O7 and RE2Th2O7 (RE=Ho, Y, Gd, Nd, La). Sci. Rep. 6, 38772. doi:10.1038/srep38772

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, Q., and Zhang, Z. J. (2004). Shape Control and Associated Magnetic Properties of Spinel Cobalt Ferrite Nanocrystals. J. Am. Chem. Soc. 126, 6164–6168. doi:10.1021/ja049931r

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, Z., and Liu, Q. (2020). Tolerance Factor, Phase Stability and Order–Disorder of the Pyrochlore Structure. Inorg. Chem. Front. 7, 1583–1590. doi:10.1039/D0QI00016G

CrossRef Full Text | Google Scholar

Stein, F., Palm, M., and Sauthoff, G. (2004). Structure and Stability of Laves Phases. Part I. Critical Assessment of Factors Controlling Laves Phase Stability. Intermetallics 12 (7-9), 713–720. doi:10.1016/j.intermet.2004.02.010

CrossRef Full Text | Google Scholar

Stølen, S., Bakken, E., and Mohn, C. E. (2006). Oxygen-deficient Perovskites: Linking Structure, Energetics and Ion Transport. Phys. Chem. Chem. Phys. 8, 429–447. doi:10.1039/B512271F

PubMed Abstract | CrossRef Full Text | Google Scholar

Subramani, T., Baker, J., Xu, H., and Navrotsky, A. (2020). Synthesis, Characterization, and Enthalpies of Formation of Uranium Substituted Zirconolites. ACS Earth Space Chem. 4, 1878–1887. doi:10.1021/acsearthspacechem.0c00182

CrossRef Full Text | Google Scholar

Subramani, T., and Navrotsky, A. (2019). Energetics of Formation and Disordering in Rare Earth Weberite RE3TaO7 Materials. Inorg. Chem. 58, 16126–16133. doi:10.1021/acs.inorgchem.9b02675

PubMed Abstract | CrossRef Full Text | Google Scholar

Subramanian, M. A., Aravamudan, G., and Rao, G. V. S. (1983). Oxide Pyrochlores: a Review. Chemistry 2, 55–143. doi:10.1016/0079-6786(83)90001-8

CrossRef Full Text | Google Scholar

Szuromi, P., and Grocholski, B. (2017). Natural and Engineered Perovskites. Science 358, 732–733. doi:10.1126/science.358.6364.732

PubMed Abstract | CrossRef Full Text | Google Scholar

Tilley, R. J. D. (2016). Perovskites: Structure-Property Relationships. Chichester: John Wiley & Sons.

Tofield, B. C., Greaves, C., and Fender, B. E. F. (1975). The SrFeO2.5/SrFeO3.0 System. Evidence of a New Phase Sr4Fe4O11 (SrFeO2.75). Mater. Res. Bull. 10, 737–745. doi:10.1016/0025-5408(75)90059-8

CrossRef Full Text | Google Scholar

Turner, K. M., Rittman, D. R., Heymach, R. A., Tracy, C. L., Turner, M. L., Fuentes, A. F., et al. (2017). Pressure-induced Structural Modifications of Rare-Earth Hafnate Pyrochlore. J. Phys. Condens. Matter 29, 255401. doi:10.1088/1361-648X/aa7148

PubMed Abstract | CrossRef Full Text | Google Scholar

Urban, A., Abdellahi, A., Dacek, S., Artrith, N., and Ceder, G. (2017). Electronic-structure Origin of Cation Disorder in Transition-Metal Oxides. Phys. Rev. Lett. 119, 176402. doi:10.1103/PhysRevLett.119.176402

PubMed Abstract | CrossRef Full Text | Google Scholar

Urban, A., Lee, J., and Ceder, G. (2014). The Configurational Space of Rocksalt-type Oxides for High-Capacity Lithium Battery Electrodes. Adv. Energ. Mater. 4, 1400478. doi:10.1002/aenm.201400478

CrossRef Full Text | Google Scholar

Ushakov, S. V., Navrotsky, A., Tangeman, J. A., and Helean, K. B. (2007). Energetics of Defect Fluorite and Pyrochlore Phases in Lanthanum and Gadolinium Hafnates. J. Am. Ceram. Soc. 90, 1171–1176. doi:10.1111/j.1551-2916.2007.01592.x

CrossRef Full Text | Google Scholar

Vance, E. R., Begg, B. D., Day, R. A., and Ball, C. J. (1994). Zirconolite-rich Ceramics for Actinide Wastes. MRS Proc. 353, 767. doi:10.1557/PROC-353-767

CrossRef Full Text | Google Scholar

Vanderah, T. A., Levin, I., and Lufaso, M. W. (2005). An Unexpected crystal-chemical Principle for the Pyrochlore Structure. Eur. J. Inorg. Chem. 2005, 2895–2901. doi:10.1002/ejic.200500234

CrossRef Full Text | Google Scholar

Vasala, S., and Karppinen, M. (2015). A2B′B″O6 Perovskites: A Review. Prog. Solid State. Chem. 43, 1–36. doi:10.1016/j.progsolidstchem.2014.08.001

CrossRef Full Text | Google Scholar

Verwey, E. J., Haayman, P. W., and Romeijn, F. C. (1947). Physical Properties and Cation Arrangement of Oxides with Spinel Structures II. Electronic Conductivity. J. Chem. Phys. 15, 181–187. doi:10.1063/1.174646410.1063/1.1746466174

CrossRef Full Text | Google Scholar

Verwey, E. J. W., and Heilmann, E. L. (1947). Physical Properties and Cation Arrangement of Oxides with Spinel Structures I. Cation Arrangement in Spinels. J. Chem. Phys. 15, 174–180. doi:10.1063/1.1746464

CrossRef Full Text | Google Scholar

Voskanyan, A. A., Abramchuk, M., and Navrotsky, A. (2020). Entropy Stabilization of TiO2-Nb2O5 Wadsley-Roth Shear Phases and Their Prospects for Lithium-Ion Battery Anode Materials. Chem. Mater. 32, 5301–5308. doi:10.1021/acs.chemmater.0c01553

CrossRef Full Text | Google Scholar

Voskanyan, A. A., and Navrotsky, A. (2021). Shear Pleasure: the Structure, Formation, and Thermodynamics of Crystallographic Shear Phases. Annu. Rev. Mater. Res. 51, 521–540. doi:10.1146/annurev-matsci-070720-013445

CrossRef Full Text | Google Scholar

Wadsley, A. D. (1958). "Modern Structural Inorganic chemistry.” Liversidge Research Lecture. J. Proc. Roy. Soc. N.S.W. 92, 25–35.

Google Scholar

Wakeshima, M., Nishimine, H., and Hinatsu, Y. (2004). Crystal Structures and Magnetic Properties of Rare Earth Tantalates RE3TaO7(RE = Rare Earths). J. Phys. Condens. Matter 16, 4103–4120. doi:10.1088/0953-8984/16/23/025

CrossRef Full Text | Google Scholar

Wang, J., Zhang, F., Lian, J., Ewing, R. C., and Becker, U. (2011). Energetics and Concentration of Defects in Gd2Ti2O7 and Gd2Zr2O7 Pyrochlore at High Pressure. Acta Materialia 59, 1607–1618. doi:10.1016/j.actamat.2010.11.025

CrossRef Full Text | Google Scholar

Wang, S. X., Wang, L. M., Ewing, R. C., and Govindan Kutty, K. V. (1998). Ion Irradiation Effects for Two Pyrochlore Compositions: Gd2Ti2O7 and Gd2Zr207. MRS Proc. 540, 355. doi:10.1557/PROC-540-355

CrossRef Full Text | Google Scholar

Wang, S. X., Wang, L. M., Ewing, R. C., Was, G. S., and Lumpkin, G. R. (1999). Ion Irradiation-Induced Phase Transformation of Pyrochlore and Zirconolite. Nucl. Instr. Methods Phys. Res. Section B: Beam Interactions Mater. Atoms 148, 704–709. doi:10.1016/S0168-583X(98)00847-7

CrossRef Full Text | Google Scholar

Whittle, K. R., Hyatt, N. C., Smith, K. L., Margiolaki, I., Berry, F. J., Knight, K. S., et al. (2012). Combined Neutron and X-ray Diffraction Determination of Disorder in Doped zirconolite-2M. Am. Mineral. 97, 291–298. doi:10.2138/am.2012.3848

CrossRef Full Text | Google Scholar

Willard, M. A., Nakamura, Y., Laughlin, D. E., and McHenry, M. E. (1999). Magnetic Properties of Ordered and Disordered Spinel-phase Ferrimagnets. J. Am. Ceram. Soc. 82 (12), 3342–3346. doi:10.1111/j.1151-2916.1999.tb02249.x

CrossRef Full Text | Google Scholar

Winiarz, P., Mielewczyk-Gryń, A., Lilova, K., Wachowski, S., Subramani, T., Abramchuk, M., et al. (2020). Conductivity, Structure, and Thermodynamics of Y2Ti2O7-Y3NbO7 Solid Solutions. Dalton Trans. 49, 10839–10850. doi:10.1039/d0dt02156c

PubMed Abstract | CrossRef Full Text | Google Scholar

Wright, A. J., Wang, Q., Hu, C., Yeh, Y.-T., Chen, R., and Luo, J. (2021). Single-phase Duodenary High-Entropy Fluorite/pyrochlore Oxides with an Order-Disorder Transition. Acta Materialia 211, 116858. doi:10.1016/j.actamat.2021.116858

CrossRef Full Text | Google Scholar

Wu, E. J., Tepesch, P. D., and Ceder, G. (1998). Size and Charge Effects on the Structural Stability of LiMO2 (M = Transition Metal) Compounds. Philosophical Mag. B 77, 1039–1047. doi:10.1080/13642819808206403

CrossRef Full Text | Google Scholar

Wuensch, B., Eberman, K. W., Heremans, C., Ku, E. M., Onnerud, P., Yeo, E. M. E., et al. (2000). Connection between Oxygen-Ion Conductivity of Pyrochlore Fuel-Cell Materials and Structural Change with Composition and Temperature. Solid State Ionics 129, 111–133. doi:10.1016/S0167-2738(99)00320-310.1016/s0167-2738(99)00320-3

CrossRef Full Text | Google Scholar

Wuensch, B. J., and Eberman, K. W. (2000). Order-disorder Phenomena in A2B2O7 Pyrochlore Oxides. JOM 52, 19–21. doi:10.1007/s11837-000-0155-4

CrossRef Full Text | Google Scholar

Xiao, H. Y., Weber, W. J., Zhang, Y., Zu, X. T., and Li, S. (2015). Electronic Excitation Induced Amorphization in Titanate Pyrochlores: an Ab Initio Molecular Dynamics Study. Sci. Rep. 5, 8265. doi:10.1038/srep08265

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, Q.-R., Zhang, J., Yin, D.-M., Guo, Q.-X., and Li, N. (2015). Krypton Ion Irradiation-Induced Amorphization and Nano-crystal Formation in Pyrochlore Lu 2 Ti 2 O 7 at Room Temperature. Chin. Phys. B 24, 126103. doi:10.1088/1674-1056/24/12/126103

CrossRef Full Text | Google Scholar

Xu, H., Navrotsky, A., Su, Y., and Balmer, M. L. (2005). Perovskite Solid Solutions along the NaNbO3−SrTiO3Join: Phase Transitions, Formation Enthalpies, and Implications for General Perovskite Energetics. Chem. Mater. 17, 1880–1886. doi:10.1021/cm047785i

CrossRef Full Text | Google Scholar

Xu, H., Su, Y., Balmer, M. L., and Navrotsky, A. (2003). A New Series of Oxygen-Deficient Perovskites in the NaTixNb1-xO3-0.5x System: Synthesis, Crystal Chemistry, and Energetics. Chem. Mater. 15, 1872–1878. doi:10.1021/cm020963s

CrossRef Full Text | Google Scholar

Yang, D., Xia, Y., Wen, J., Liang, J., Mu, P., Wang, Z., et al. (2017). Role of Ion Species in Radiation Effects of Lu2Ti2O7 Pyrochlore. J. Alloys Comp. 693, 565–572. doi:10.1016/j.jallcom.2016.09.227

CrossRef Full Text | Google Scholar

Yudinsev, S. V., Lukinykh, A. N., Tomilin, S. V., Lizin, A. A., and Stefanovsky, S. V. (2009). Alpha-decay Induced Amorphization of Cm-Doped Gd2TiZrO7. J. Nucl. Mater. 385, 200–203. doi:10.1016/j.jnucmat.2008.09.036

CrossRef Full Text | Google Scholar

Zhang, F. X., Lang, M., and Ewing, R. C. (2015). Atomic Disorder in Gd2Zr2O7 Pyrochlore. Appl. Phys. Lett. 106, 191902. doi:10.1063/1.4921268

CrossRef Full Text | Google Scholar

Zhang, F. X., Lang, M., Liu, Z., and Ewing, R. C. (2010a). Pressure-Induced Disordering and Anomalous Lattice Expansion inLa2Zr2O7Pyrochlore. Phys. Rev. Lett. 105, 15503. doi:10.1103/PhysRevLett.105.015503

CrossRef Full Text | Google Scholar

Zhang, F. X., Lang, M., Tracy, C., Ewing, R. C., Gregg, D. J., and Lumpkin, G. R. (2014). Incorporation of Uranium in Pyrochlore Oxides and Pressure-Induced Phase Transitions. J. Solid State. Chem. 219, 49–54. doi:10.1016/j.jssc.2014.07.011

CrossRef Full Text | Google Scholar

Zhang, F. X., Lian, J., Becker, U., Wang, L. M., Hu, J., Saxena, S., et al. (2007). Structural Distortions and Phase Transformations in Sm2Zr2O7 Pyrochlore at High Pressures. Chem. Phys. Lett. 441, 216–220. doi:10.1016/j.cplett.2007.05.018

CrossRef Full Text | Google Scholar

Zhang, F. X., Manoun, B., and Saxena, S. K. (2006). Pressure-induced Order-Disorder Transitions in Pyrochlore RE2Ti2O7 (RE=Y, Gd). Mater. Lett. 60, 2773–2776. doi:10.1016/j.matlet.2006.01.095

CrossRef Full Text | Google Scholar

Zhang, F. X., Manoun, B., Saxena, S. K., and Zha, C. S. (2005). Structure Change of Pyrochlore Sm2Ti2O7 at High Pressures. Appl. Phys. Lett. 86, 181906. doi:10.1063/1.1925307

CrossRef Full Text | Google Scholar

Zhang, F. X., and Saxena, S. K. (2005). Structural Changes and Pressure-Induced Amorphization in Rare Earth Titanates RE2Ti2O7 (RE: Gd, Sm) with Pyrochlore Structure. Chem. Phys. Lett. 413, 248–251. doi:10.1016/j.cplett.2005.07.094

CrossRef Full Text | Google Scholar

Zhang, F. X., Wang, J. W., Lian, J., Lang, M. K., Becker, U., and Ewing, R. C. (2008). Phase Stability and Pressure Dependence of Defect Formation inGd2Ti2O7andGd2Zr2O7Pyrochlores. Phys. Rev. Lett. 100, 2–5. doi:10.1103/PhysRevLett.100.045503

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, J., Lian, J., Fuentes, A. F., Zhang, F., Lang, M., Lu, F., et al. (2009). Enhanced Radiation Resistance of Nanocrystalline Pyrochlore Gd2(Ti0.65Zr0.35)2O7. Appl. Phys. Lett. 94, 243110. doi:10.1063/1.3155855

CrossRef Full Text | Google Scholar

Zhang, J., Lian, J., Zhang, F., Wang, J., Fuentes, A. F., and Ewing, R. C. (2010b). Intrinsic Structural Disorder and Radiation Response of Nanocrystalline Gd2(Ti0.65Zr0.35)2O7 Pyrochlore. J. Phys. Chem. C 114, 11810–11815. doi:10.1021/jp103371j

CrossRef Full Text | Google Scholar

Zhang, Z., Middleburgh, S. C., de los Reyes, M., Lumpkin, G. R., Kennedy, B. J., Blanchard, P. E. R., et al. (2013). Gradual Structural Evolution from Pyrochlore to Defect-Fluorite in Y2Sn2-xZrxO7: Average vs Local Structure. J. Phys. Chem. C 117, 26740–26749. doi:10.1021/jp408682r

CrossRef Full Text | Google Scholar

Zhao, Q., Yan, Z., Chen, C., and Chen, J. (2017). Spinels: Controlled Preparation, Oxygenreduction/evolution Reaction Application, and beyond, Chem. Rev. 117, 10121–10211. doi:10.1021/acs.chemrev.7b00051

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, H., and Wiebe, C. R. (2019). High-pressure Routes to New Pyrochlores and Novel Magnetism. Inorganics 7. doi:10.3390/inorganics7040049

CrossRef Full Text | Google Scholar

Zhu, X., Guijarro, N., Liu, Y., Schouwink, P., Wells, R. A., Le Formal, F., et al. (2018). Spinel Structural Disorder Influences Solar-Water-Splitting Performance of ZnFe2 O4 Nanorod Photoanodes. Adv. Mater. 30, 1801612. doi:10.1002/adma.201801612

PubMed Abstract | CrossRef Full Text | Google Scholar