Search for Global Minimum Structures of P2n+1+ (n = 1–15) Using xTB-Based Basin-Hopping Algorithm

A new program for searching global minimum structures of atomic clusters using basin-hopping algorithm based on the xTB method was developed here. The program can be performed with a much higher speed than its replacement directly based on DFT methods. Considering the structural varieties and complexities in finding their global minimum structures, phosphorus cluster cations were studied by the program. The global minimum structures of cationic ${\text{P}}_{2n+1}^{+}$ (n = 1–15) clusters are determined through the unbiased structure searching method. In the last step, further DFT optimization was performed for the selected isomers. For ${\text{P}}_{2n+1}^{+}$ (n = 1–4, 7), the found global minimum structures are in consistent with the ones previously reported; while for ${\text{P}}_{2n+1}^{+}$ (n = 5, 6, 8–12), newly found isomers are more energy-favorable than those previously reported. And those for ${\text{P}}_{2n+1}^{+}$ (n = 13–15) are reported here for the first time. Among them, the most stable isomers of ${\text{P}}_{2n+1}^{+}$ (n = 4–6, 9) are characterized by their C_3v, C_s, C_2v and C_s symmetry, in turn. But those of ${\text{P}}_{2n+1}^{+}$ (n = 7, 8, 10–12), no symmetry has been identified. The most stable isomers of ${\text{P}}_{29}^{+}$ and ${\text{P}}_{31}^{+}$ are characterized by single P-P bonds bridging units inside the clusters. Further analysis shows that the pnicogen bonds play an important role in the stabilization of these clusters. These results show that the new developed program is effective and robust in searching global minimum structures for atom clusters, and it also provides new insights into the role of pnicogen bonds in phosphorus clusters.

Introduction

Clusters bridge atoms, molecules and bulk matter (Johnstom, 2002; Castleman and Jena, 2006; Fehlner et al., 2007; Ha et al., 2019), showing their great potentials for applications in many research fields such as catalysis (Liu and Corma, 2018; Du et al., 2020) and energy storage (VanGelder et al., 2018; VanGelder et al., 2019). They are also characterized by their geometries and electronic structures in many cases (Johnstom, 2002; Fehlner et al., 2007; Ferrando, 2015; Luo et al., 2016; Jena and Sun, 2018; Ha et al., 2019). There are many wonderful examples, including the cage-like fused-ring structure (truncated icosahedron) of C₆₀ fullerene (Kroto et al., 1985), the tetrahedral structure of Au₂₀ (Li et al., 2003), C_6v symmetry boron cluster of B₃₆ (Piazza et al., 2014), the borospherene cluster of B₄₀ (Zhai et al., 2014; Li et al., 2017), and the protonated serine octamer (Cooks et al., 2001; Kong et al., 2006; Scutelnic et al., 2018). In lots of cases, the structural information of the clusters can hardly be obtained directly from experiments, and theoretical calculations are very important to provide structural candidates whose predicted properties should be further compared with the experimental results, in order to make the identification stable (Zhang and Glezakou, 2020).

Although the structural determination of small molecules based on density functional theory (DFT) or other methods has become a relatively routine task for computational chemists, the identification of the global minimum structures for clusters, especially those with large sizes, is still a great challenge. The reason is that the complexity of the searching space in their potential energy surface (PES) grows exponentially with the increasing number of atoms inside the clusters. Since the numbers of local minima grow quickly with the size of clusters, the global optimization becomes a very difficult task to overcome. Thus, different search algorithms and methodologies, including the genetic algorithm (GA) (Hartke, 1993; Deaven and Ho, 1995; Hartke, 1995; Daven et al., 1996; Rogan et al., 2013; Kanters and Donald, 2014; Shayeghi et al., 2015; Lazauskas et al., 2017; Rabanal-León et al., 2018; Jäger et al., 2019; Yañez et al., 2019) and relative evolutionary algorithm (EA) (Zhou et al., 2020), the swarm intelligence algorithm (Wang et al., 2012; Jana et al., 2019) and others, have been proposed and applied in the past decades (Zhang and Glezakou, 2020).

It is now accepted that the choosing of a suitable method for a special system based on its properties is very important. Usually, for clusters with tens of atoms, a very detailed investigation on their potential energy surfaces is still too difficult to be performed with reasonable computational cost. The Basin-Hopping (BH) algorithm, has been suggested as a good choice to solve global minima of Lennard–Jones clusters (Wales and Doye, 1997; Wales and Scheraga, 1999). Programs based on the BH algorithm have been developed based on empirical potentials (Zhan et al., 2005; Paz-Borbón et al., 2007) and DFT methods (Yoo et al., 2004.; Bai et al., 2006; Bulusu and Zeng, 2006; Huang et al., 2010; Jiang et al., 2012; Chen et al., 2017; Zhao et al., 2017; Chen et al., 2019). And the self-consistent charge density functional tight binding (SCC-DFTB) methods, including DFTB2, DFTB2-γh, DFTB2-γh + gaus and others, have been also applied (Choi et al., 2013).

Considering the success of the method of GFN-xTB, which was a DFTB3 variant developed by Grimme et al. (2017) (Bannwarth et al., 2019), the current work presents a new BH program named NKCS based on the Python, in conjunction with the xTB method for searching global minima of atomic clusters. Phosphorus clusters are selected to be studied, due to the two facts. The first one is that phosphorus exhibits a variety of structural phases, such as orthorhombic black, rhombohedral, violet, metallic, fibrous red, white, and amorphous. Thus, a better understanding about phosphorus clusters can deepen our knowledge about its structures and properties. The second fact is that although phosphorus cluster ions with wide size distributions have been observed in the laser ablation experiments for a long time (Martin, 1986; Mu et al., 2015; Yang et al., 2016; Kong et al., 2019), its structural studies are still limited for small to medium-sized clusters (Guo et al., 2004; Xue et al., 2010; Mu et al., 2015; Kong et al., 2019). And searching for the global minima in their PES is still a challenging task due to the diverse bonding patterns of the element.

Methods

The newly developed program NKCS described here is written in Python language. The procedure of the program is shown in Figure 1. It couples the xTB-based local optimization and BH global search algorithm. For all initially generated or distorted structures through the BH processes, xTB-based local optimization was applied. Then these structures were ranked according to their energies. In the last step, the selected isomers were further sent to high-level DFT calculations. The procedure of the program is shown in the middle part of the picture. According to the input parameters set by the user, initial structures of the clusters are randomly built for xTB optimization. Then the BH algorithm are employed to some selected isomers and during the process, the criteria to accept newly distorted isomers are judged according to their energies calculated by the xTB method. At last, some local minima are further selected to perform high-level DFT calculations to identify the global minimum.

FIGURE 1

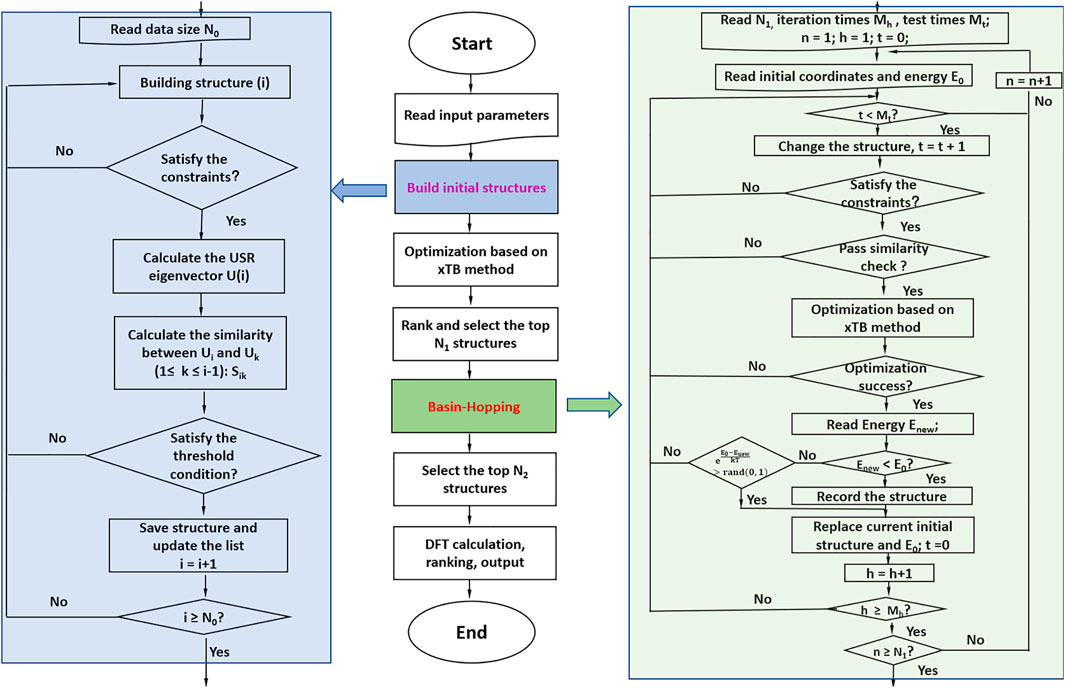
FIGURE 1. The procedure of the whole program is shown in the middle. The left side shows the process of building initial structures, and the right side shows the detail of the basin-hopping algorithm applied here.

To improve the efficiency of the program, the randomly generated or distorted geometries should be instantly checked according to their inter-atomic distances. Unreasonable structures with inter-atomic distances much smaller than the sum of their covalent radii are directly discarded. After that, a similarity check algorithm is applied to avoid duplicated structures. In this process, the ultrafast shape recognition (USR) algorithm is applied to compare the similarities of the randomly generated or distorted structures and the ones stored in the database (Ballester and Richards, 2007a; Ballester and Richards, 2007b; Ballester et al., 2009). For the homo atomic clusters studied here, the previously suggested 12 descriptors were applied here. The set of intra-cluster atomic distances from four locations are considered: the molecular centroid (ctd), the closest atom to ctd (cst), the farthest atom from ctd (fct) and the farthest atom from fct (ftf). So a molecule can be described as: $\overrightarrow{M}=\left({\mu }_1^{ctd},{\mu }_2^{ctd},{\mu }_3^{ctd},{\mu }_1^{cst},{\mu }_2^{cst},{\mu }_3^{cst},{\mu }_1^{fct} {\mu }_2^{fct},{\mu }_3^{fct},{\mu }_1^{ftf},{\mu }_2^{ftf},{\mu }_3^{ftf}\right)$. In this way, each structure can be described by the 12 numbers, and the similarity of two structures i and k can be calculated as:

$S_{ik}=\frac{1}{\left(1+\frac{1}{12}{{\displaystyle \sum }}_{l=1}^{12}\left(|M_l^i-M_l^k|\right)\right)}$

where $M_l^i$, $M_l^k$ are the lth USR descriptors of the ith and kth structures, respectively. The value of S_ik is limited between 0 and 1. A high value of S_ik indicates that the two isomers have close geometries, and a threshold can be selected in the program to distinguish two structures.

For the randomly constructed structure sets, the xTB method was applied to perform structural optimization and energy calculation. The parametrization in the method covers all spd-block elements and the lanthanides up to Z = 86 and it has been considered as a suitable method for dealing with various clusters with complex electronic structures (Grimme et al., 2017). The BH algorithm was then applied for the selected isomers based on their energies after the xTB optimization. Considering the BH method is one of the individual-based methods (Zhang and Glezakou, 2020), an initialized population with suitable size is applied here to improve its performance in the global optimization. After the selection of initial seed structures for BH algorithm based on their energies calculated by the xTB method, distorted structures are generated from the seeds by the displacement. The reasonability and similarity of the new structure should be checked and then optimized by the xTB method. For the acceptance of the newly distorted structure, the previously suggested criteria by Zhou et al. are applied here (Zhou et al., 2019). And the NKCS program also integrates the interface of Gaussian computing software (Frisch et al., 2009) to perform high-level structure optimization and frequency calculation for the selected isomers by the BH algorithm.

Results and Discussion

The NKCS program has been tested with the odd-numbered phosphorus cluster cations here. In order to make the process clear, an example for searching the global minimum of ${\text{P}}_{15}^{+}$ is displayed in Figure 2. The initial population size for clusters (N₀) with N atoms is set as ∼ N^2.8 for all the phosphorus clusters studied here. For ${\text{P}}_{15}^{+}$, after the reasonability and similarity check, 2000 structures were generated randomly. The distance between two adjacent phosphorus atoms is limited between 2 and 3 Å, and the USR threshold was selected to be 0.98. These 2000 structures were optimized by the xTB method and the top N₁ (30 in this case) structures were selected as seeds for BH processes. During the process, structural check for the new distorted isomers were also performed. If a new structure is more favorable in energy than the seed, it will be recorded and accepted as the new seed. Otherwise, the probability of accepting the structure, $e^{\frac{E_0-E_{new}}{kT}}$ , would be compared with a random number located in (0,1) to decide whether it should be taken as a new seed. For all the phosphorus cluster cations here, the temperature T was set at 273 K. After the BH process, the top N₂ (30 in this case) structures were further selected for DFT calculation. These isomers would be optimized and ranked at the level of B3LYP/6–311+G(d) by the Gaussian 09 program.

FIGURE 2

FIGURE 2. The process for searching the global minimum by the NKCS program.

Figures 3, 4 show the optimized global minimum geometries of ${\text{P}}_{2n+1}^{+}$ (n = 1 ∼ 15). To make sure that the results obtained are indeed global minima, the program has been run three times for each phosphorus cluster. For all reported cationic phosphorus clusters, frequency calculations are preformed to ensure that they are true minima on the potential energy surfaces. For small cationic clusters of ${\text{P}}_3^{+}$, ${\text{P}}_5^{+}$ and ${\text{P}}_7^{+}$, the most stable isomers with D_3h, C_4v and C_2v symmetries in turn, have been revealed by Guo et al. (2004), Xue et al. (2010) previously. These structures have also been reproduced here and are shown in Figure 3. For ${\text{P}}_9^{+}$, the previously suggested lowest-energy geometry with D_2d symmetry was reproduced too (Xue et al., 2010). The second stable isomer of ${\text{P}}_9^{+}-\text{II}$, has an energy 45.3 kJ/mol higher than that of the former one. It consists of a P₆ unit with a chair-like structure below and a triangle of P₃ unit above, characterized by its C_3v symmetry. For ${\text{P}}_{11}^{+}$, besides the previously reported structure (${\text{P}}_{11}^{+}-\text{II}$) (Xue et al., 2010), a new isomer of ${\text{P}}_{11}^{+}-\text{I}$ with a C_s symmetry, was found to be more stable by 9.8 kJ/mol than the former. For clusters with larger sizes, more stable isomers were found. To make them clear, the top eight isomers of ${\text{P}}_{2n+1}^{+}$ (n = 6–15) were all shown in Supplementary Figures S1, S2. For ${\text{P}}_{13}^{+},$ the previously suggested most stable isomer (${\text{P}}_{13}^{+}-\text{II})$ was found to be accompanied with a more stable isomer, ${\text{P}}_{13}^{+}-\text{I}$. The latter is characterized by its C_2v symmetry and has an energy 34.5 kJ/mol lower than that of ${\text{P}}_{13}^{+}-\text{II}$. For ${\text{P}}_{15}^{+}$, the found most stable isomer is the same as the one reported by Xue et al. (2020) previously. Another isomer of ${\text{P}}_{15}^{+}-\text{II}$ with C_2v symmetry was also found by the program, which has an energy 22.2 kJ/mol higher than ${\text{P}}_{15}^{+}-\text{I}$. Interestingly, this isomer ${\text{P}}_{15}^{+}-\text{II}$ can be formed by adding two P atoms in the middle of ${\text{P}}_{13}^{+}-\text{II}$. For ions of ${\text{P}}_{17}^{+}$, the previously reported isomer was found as the 10th most stable isomer (Xue et al., 2010). Nine more stable isomers have been identified and the three most stable isomers of ${\text{P}}_{17}^{+}-\text{I},\text{II}$ and III are shown in Figure 3. The isomer ${\text{P}}_{17}^{+}-\text{I}$, which has an energy 59.6 kJ/mol lower than the previously reported one, can be regarded as a P₈ cuneate unit connected with a P₇ norbornane though a P₂ unit, which has no symmetry. For ${\text{P}}_{19}^{+}$, 20 new isomers were found to have lower energies than the one previously reported. The top three isomers are shown in Figure 3, in which the most stable one has an energy 140.9 kJ/mol lower than the one reported before. And it is also characterized by a plane of symmetry.

FIGURE 3

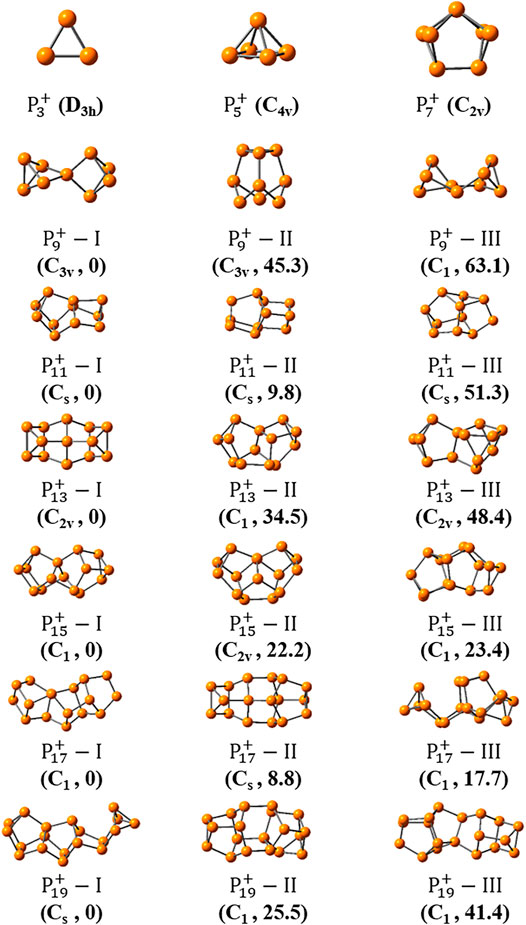
FIGURE 3. The most stable isomers of ${\text{ P}}_{2\text{n}+1}^{+}$ (n = 1–9) searched by the NKCS program. The three most stable isomers are identified as ${\text{P}}_{2\text{n}+1}^{+}-\text{I}$, ${\text{P}}_{2\text{n}+1}^{+}-\text{II}$, and ${\text{P}}_{2\text{n}+1}^{+}-\text{III}$, in turn. Their symmetries and relative energies (in kJ/mol) to corresponding global minima are shown below.

FIGURE 4

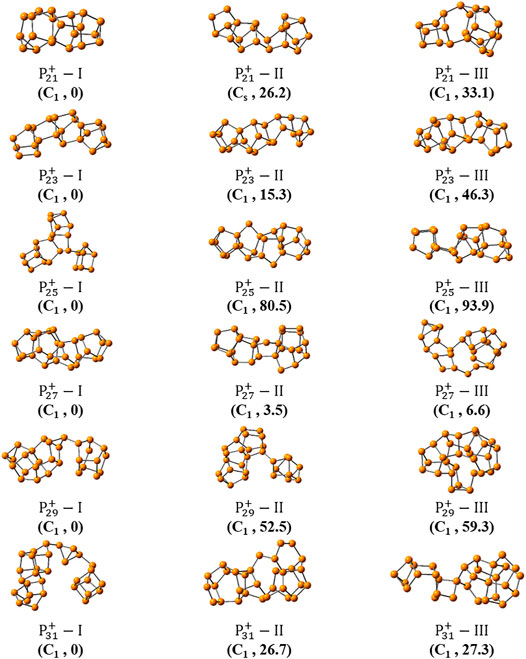
FIGURE 4. The three most stable isomers of ${\text{ P}}_{2\text{n}+1}^{+}$ (n = 10–15) searched by the NKCS program. Their symmetries and relative energies (in kJ/mol) to corresponding global minima are shown below.

As the size increased, the symmetry of the cluster ions decreases. The newly found most stable isomer of ${\text{P}}_{21}^{+}$ (${\text{P}}_{21}^{+}-\text{I}$), is more energy favorable than the previously reported one by 84.3 kj/mol. For ${\text{P}}_{23}^{+}$, the discovered isomer of ${\text{P}}_{23}^{+}-\text{I}$ has an energy 15.3 kJ/mol lower than the previously reported isomer of ${\text{P}}_{23}^{+}-\text{II}$ (Xue et al., 2010). Unlike other cluster ions of ${\text{P}}_{2\text{n}+1}^{+}$ (n = 7–11), the new isomer of ${\text{P}}_{25}^{+}-\text{I}$ does not has the chain-like geometry. There is a P₆ trigonal prism unit on the right side, suspended in the middle of the long P₁₈ unit on the left by a single bond. This isomer is energetically more preferred by 80.5 kJ/mol than the previously suggested one (${\text{P}}_{25}^{+}-\text{II}$ in Figure 4).

And the most stable isomers of ${\text{P}}_{27}^{+}$, ${\text{P}}_{29}^{+}$ and ${\text{P}}_{31}^{+}$ were suggested here for the first time. These structures are more complicated and show no symmetry (Figure 4). The most stable isomer of ${\text{P}}_{27}^{+}-\text{I}$ has a typical linear structure that likes that of ${\text{P}}_{23}^{+}-\text{I}$ or ${\text{P}}_{25}^{+}-\text{II}$. The structure of ${\text{P}}_{29}^{+}-\text{I}$, can be regarded as that its left and right sides are connected by a single P-P bond. The left side of the cluster ion has a compact unit of P₁₆, and right side has a unit of P₁₁ that can be regarded as a six-member ring connected with a five-member ring directly. For the second stable isomer ${\text{P}}_{29}^{+}-\text{II}$, the two units of P₂₀ and P₉ are also linked by a single bond. Interestingly, the structure of ${\text{P}}_{31}^{+}-\text{I}$ includes three parts of P_19, P₄, and P₉, in which the first and the latter two parts are both connected though P-P bonds, respectively. And the whole ion has a curved linear structure. In order to make the results more reliable, calculation based on the level of MP2/6–311+G(d)//B3LYP/6–311+G(d) were performed for the top three isomers of ${\text{P}}_{2\text{n}+1}^{+}$ (n = 12–15). Although the values of their relative energies are some different, their orders in energies keep unchanged (Supplementary Table S1 in the supporting information).

Briefly, the BH algorithm based on the xTB method has been developed for searching global minima of clusters. Considering the parametrization of xTB method covers all spd-block elements and the functional form of the xTB mostly avoids element-pair-specific parameters, the program developed here has a very wide range of applications. And compared with DFT-based methods, it significantly saves computing time. Medium-sized phosphorus cluster cations were studied here, and new energetically favored structures were identified. Based on these results, some structural rules of these cationic clusters should be further discussed, since it might be helpful to get some general pictures about these energetically preferred structures and structural tendency about large-sized clusters.

For one thing, it is interesting to find that symmetric structures are very important for small-sized clusters of ${\text{P}}_{2\text{n}+1}^{+}$ (n = 1–6). For ${\text{P}}_{19}^{+}$, the most stable isomer also has a C_s symmetry. For ${\text{P}}_{15}^{+},{\text{P}}_{17}^{+}$, and ${\text{P}}_{21}^{+}$, although none of their most stable isomers have symmetry, their second most stable isomers have C_2v, C_s, and C_s symmetry, in turn. For clusters with larger size of ${\text{P}}_{2\text{n}+1}^{+}$ (n = 11–15), all their top three stable isomers show no symmetry. Although this, the symmetry of local unit in the large-size clusters still exists. For example, both units in ${\text{P}}_{29}^{+}-\text{I}$ linked by a single bond have rough C_s symmetry. These results also suggest the importance of an unbiased method in searching the global minima of large-sized clusters, which can cannot be directly replaced by simple intuitions.

For the second point, most medium-sized globe minima of ${\text{P}}_{2\text{n}+1}^{+}$ (n = 5–15) exhibit chain-like configurations, expect that of ${\text{P}}_{25}^{+}$. And the common building units include P₇, P₈, and P₉ building blocks. For clusters with larger sizes, the chains become curved. A statistical view on the size of the energetically preferred structures may provide some clues. The USR parameter ftf that indicates the distance between the farthest atom from fct can be applied as an indicator of the length of the cluster. Based on the xTB calculation results of the initial population built up in the second step of Figure 2, a general picture descripting the relationship between energy and length can be obtained. Figure 5 shows the relative energy-fct diagrams for the xTB-optimized structures of the randomly generated populations of ${\text{P}}_9^{+},$${\text{P}}_{19}^{+}$, and ${\text{P}}_{31}^{+}$. It can be found that the most of energetically preferred structures for ${\text{P}}_9^{+}$ have a distribution of fct in the range of 4–6 Å. For ${\text{P}}_{19}^{+}$ and ${\text{P}}_{31}^{+}$, the lengths of energetically preferred structures were concentrated in the range of 7–10 and 8–12 Å, respectively. The results indicate that the lengths of the clusters grow with their sizes, but not linearly, and the curved structures will be more general for large-size clusters.

FIGURE 5

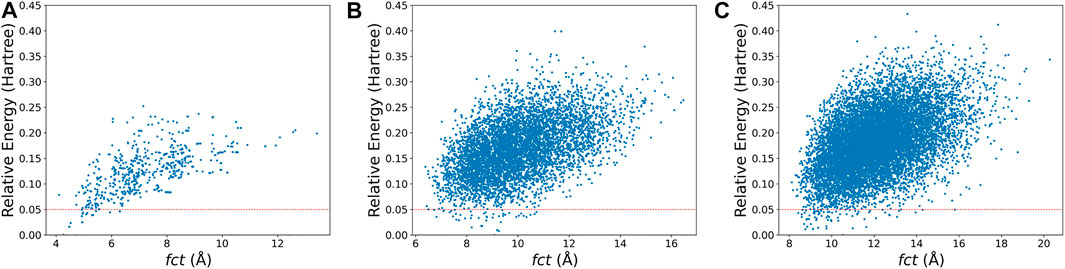
FIGURE 5. The relative energy-fct diagrams for the xTB-optimized structures of the randomly generated populations of (A)${\text{P}}_9^{+},$(B)${\text{P}}_{19}^{+}$ and (C)${\text{P}}_{31}^{+}$. Every dot in the picture corresponds one structure and the dots below the red line indicates the isomers have relative energies less than 0.05 hartree compared to the corresponding global minimum in each subgraph.

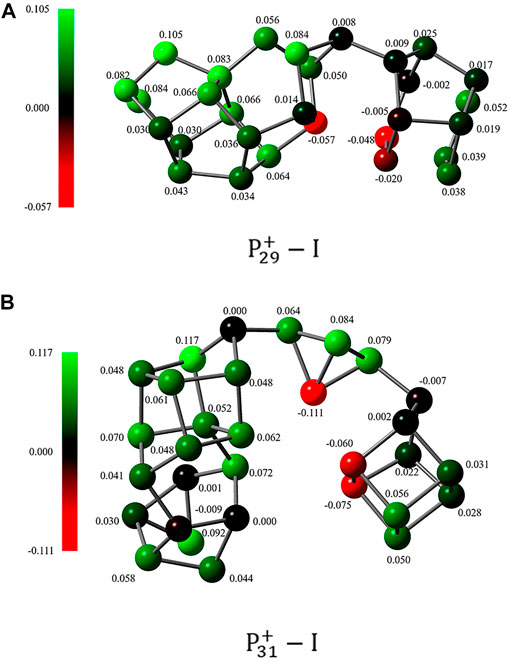
For the third point, it is interesting to found that both isomers of ${\text{P}}_{29}^{+}-\text{I}$ and ${\text{P}}_{31}^{+}-\text{I}$ are characterized by single P-P bonds bridging units inside the clusters. Although this kind of bridging bonds is reasonable in forming one- or two-dimensional phosphorus nanomaterials, it is lesser-known for middle- or large-size homoatomic clusters. For homoatomic clusters, it is usually to suggest that the clusters are inclined to take compact structures with high symmetry or consistent linear structures. So why these clusters are so different? A possible explanation is that the weak polarities of these intra-cluster covalent bonds are distributed in a way to stabilize the whole cluster by enhancing their charge-charge, charge-dipole, or dipole-dipole interactions. However, the natural bond orbital (NBO) charge distribution (Carpenter and Weinhold, 1988; Reed et al., 1988) of these clusters shows although this interaction may help to stabilize the isomer in some extent, it should not be the main reason (Figure 6).

FIGURE 6

FIGURE 6. The NBO charge distribution of (A)${\text{P}}_{29}^{+}-\text{I}$ and (B)${\text{P}}_{31}^{+}-\text{I}$.

On the other hand, the short distances between the nonbonding phosphorus atoms indicate that the pnicogen bonds (Zahn, et al., 2011; Scheiner, 2013) inside the clusters may play a very important role. In ${\text{P}}_{29}^{+}-\text{I}$, the distances of P5···P11 is 294 pm, which is below the sum of their van der Waals radii of 380 pm. Similarly, the distances of P2···P23 in ${\text{P}}_{31}^{+}-\text{I}$ is 333 pm. These attractive P···P interactions are very similar to those previously reported pnicogen bonds in carbaboranes. Chemical bonding analyses were also examined by electron localization function (ELF) analysis with the program of Multiwfn (Lu and Chen, 2012). As shown in Figure 7, regions between P11 and P5 in ${\text{P}}_{29}^{+}-\text{I}$, and between P2 and P23 in ${\text{P}}_{31}^{+}-\text{I}$, are both characterized by their electron-pair densities. The pnicogen interaction can be further investigated by the second-order perturbation approach. As the example of ${\text{P}}_{29}^{+}-\text{I}$ shown in Figure 8A and B, the interactions of LP(P5) →σ*(P11-P15) and LP(P11) →σ*(P5-P16) in ${\text{P}}_{29}^{+}-\text{I}$ have the stabilization energies of 9.34 and 3.70 kcal/mol, respectively, showing a very strong pnicogen bond. The second example of ${\text{P}}_{31}^{+}-\text{I}$ is shown in Figure 8C and D. The hyperconjugation of the lone pair of electrons at P2 with the adjacent phosphorus–phosphorus bond P23-P9 (LP(P2) →σ*(P23-P9)) was observed with a second-order perturbation stabilization energy of 2.66 kcal/mol. At the same time, the interaction of LP(P23) →σ*(P2-P29) also contributes 0.87 kcal/mol in stabilization the pnicogen bond.

FIGURE 7

FIGURE 7. ELFs of (A)${\text{P}}_{29}^{+}-\text{I}$ and (B)${\text{P}}_{31}^{+}-\text{I}$.

FIGURE 8

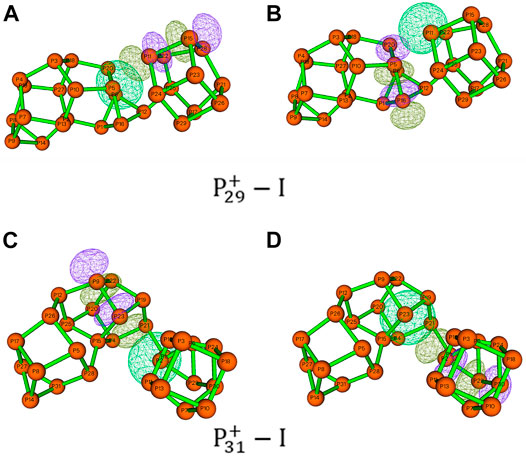
FIGURE 8. Hyperconjugation of LP(P) → σ*(P–P). The natural bonding orbits were obtained by NBO analysis of (A,B)${\text{P}}_{29}^{+}-\text{I}$ and (C,D)${\text{P}}_{31}^{+}-\text{I}$.

Both Wiberg bond index (WBI) and QTAIM topological analysis were employed to analyze the bonding nature of these bonds. The calculated total WBI values of the bonds P5···P11 in ${\text{P}}_{29}^{+}-\text{I}$, P2···P23 in ${\text{P}}_{31}^{+}-\text{I}$ are 0.14 and 0.04, respectively, supporting the existence of the pnicogen bonds. Table 1;Supplementary Table S2, show the results of AIM topology parameters, including electron density (ρ_e) at the pnicogen bond critical points and Laplacian (▽²ρ_e). The results suggest that intracluster pnicogen bonds play a very important role for their structural stabilization and isomerization. It is also found that the pnicogen bond is important for other curved clusters with small sizes (shown in Figure 4). For example, the structure of ${\text{P}}_{27}^{+}-\text{I}$ is characterized by a strong pnicogen bond with a P1 … P4 distance of 297 pm (with a WBI of 0.26). The NBO and QTAIM analysis also support the interaction (Supplementary Figures S3, S4; Table 1 and Supplementary Table S2).

TABLE 1

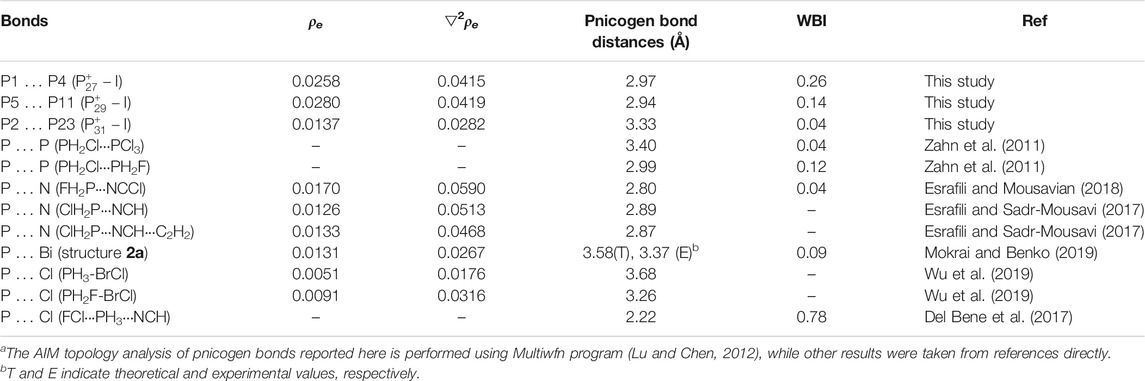
TABLE 1. Electron densities (ρ_e, a.u.), Laplacian of the electron densities (▽²ρ_e, a.u.), Pnicogen bond distances (Å), and Wiberg Bond Indexes (WBI) of the pnicogen bonds in ${\text{P}}_{27}^{+}-\text{I },{\text{ P}}_{29}^{+}-{\text{I and P}}_{31}^{+}-\text{I}$, compared with those of some pnicogen bonds previously reported.^a

Although pnicogen bonds have been previously reported and studied for different species by many research groups, this is still the first study showing that the pnicogen bonds can exist and play important roles in homoatomic phosphorus clusters without the help of other ligands or heteroatoms. By comparing the pnicogen bonds reported herein with other previously reported pnicogen bonds, the important roles of these interactions in phosphorus clusters can be further reflected. Thus, some typical pnicogen bonds were selected from relative references (Zahn, et al., 2011; Del Bene et al., 2017; Esrafili and Sadr-Mousavi, 2017; Esrafili and Mousavian, 2018; Mokrai, and Benko, 2019; Wu, et al., 2019) and were compared with those bonds reported here. Results were shown in Table 1. The P … P pnicogen bonds reported here have similar bond distances and WBIs with those previously reported (Zahn, et al., 2011) and similar to other type pnicogen bonds including PN, P … Bi and P … Cl interactions. And the bond of P1 … P4 in ${\text{P}}_{27}^{+}-\text{I}$ even has the highest WBI except to the special case of P … Cl in the ternary complex of FCl … PH₃ … NCH, in which the P … N pnicogen-bond was enhanced by the P … Cl halogen bond through the σ-hole (Del Bene, et al., 2017).

Briefly, these results reflected that the intracluster pnicogen bonds can greatly stabilize the cluster, thus play important roles in large-size phosphorus clusters and phosphorus-related materials. On the other hand, the ELF analysis shown in Figure 7 also indicates the possibility of the existence of multiple pnicogen bonds in large-size phosphorus clusters. And a very interesting topic is how the introduce of heteroatom can affect the pnicogen bonds and their most stable structures. So, we hope the result reported here can attract more researchers to focus on this issue.

Conclusion

A combined algorithm of BH and xTB to locate global minima in potential energy surface of atomic clusters has been developed here. Several strategies, including the similarity check, are considered in the algorithm. The $P_{2\text{n}+1}^{+}$ cluster cations are selected to be studied using the program due to their structural varieties and complexities. For cluster cations of ${\text{P}}_{2\text{n}+1}^{+}$ (n = 1–4) and ${\text{P}}_{15}^{+}$, the program reproduced the lowest-energy structures reported previously. For $P_{2\text{n}+1}^{+}$ (n = 5, 6, 8–12), new isomers with energies 10 ∼ 80 kJ/mol lower than those previously reported have been identified on the level of B3LYP/6–311+G(d). The most stable isomers of $P_{2\text{n}+1}^{+}$ (n = 13–5) are also reported here. Although symmetric structures dominate the most stable isomers of all small-sized clusters of ${\text{P}}_{2\text{n}+1}^{+}$ (n = 1–6), their importance decrease for the clusters of ${\text{P}}_{2\text{n}+1}^{+}$ (n = 7–10). And for clusters with larger sizes, no symmetry has been observed for all their top three isomers. The lengths of the clusters grow with their sizes, but only distinct for clusters up to ${\text{P}}_{23}^{+}$. Curved structures with single P-P bonds are found to be important for ${\text{P}}_{29}^{+}$ and ${\text{P}}_{31}^{+}$. Further analysis shows that the pnicogen bonds play important roles in these phosphorus clusters. The results show that the new developed xTB-based BH program is effective and robust in searching global minimum structures for atomic clusters. And for large-size phosphorus clusters, a systemic study for a better understanding about the pnicogen bonds is needed very much.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

MZ and YX designed the program and performed the calculations. YC participated in the calculation. XZ and XK directed the work, contributed to the interpretation of the data and wrote the paper. All authors have read and approved the content of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (21627810, 11704004).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2021.694156/full#supplementary-material

References

Bai, J., Cui, L.-F., Wang, J., Yoo, S., Li, X., Jellinek, J., et al. (2006). Structural Evolution of Anionic Silicon Clusters SiN(20 ≤N≤ 45). J. Phys. Chem. A. 110, 908–912. doi:10.1021/jp055874s

PubMed Abstract | CrossRef Full Text | Google Scholar

Ballester, P. J., Finn, P. W., and Richards, W. G. (2009). Ultrafast Shape Recognition: Evaluating a New Ligand-Based Virtual Screening Technology. J. Mol. Graphics Model. 27, 836–845. doi:10.1016/j.jmgm.2009.01.001

CrossRef Full Text | Google Scholar

Ballester, P. J., and Richards, W. G. (2007a). Ultrafast Shape Recognition for Similarity Search in Molecular Databases. Proc. R. Soc. A. 463, 1307–1321. doi:10.1098/rspa.2007.1823

CrossRef Full Text | Google Scholar

Ballester, P. J., and Richards, W. G. (2007b). Ultrafast Shape Recognition to Search Compound Databases for Similar Molecular Shapes. J. Comput. Chem. 28, 1711–1723. doi:10.1002/jcc.20681

PubMed Abstract | CrossRef Full Text | Google Scholar

Bannwarth, C., Ehlert, S., and Grimme, S. (2019). GFN2-xTB-An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-dependent Dispersion Contributions. J. Chem. Theor. Comput. 15, 1652–1671. doi:10.1021/acs.jctc.8b01176

PubMed Abstract | CrossRef Full Text | Google Scholar

Bulusu, S., and Zeng, X. C. (2006). Structures and Relative Stability of Neutral Gold Clusters: Aun (N=15-19). J. Chem. Phys. 125 (125), 154303. doi:10.1063/1.2352755

PubMed Abstract | CrossRef Full Text | Google Scholar

Carpenter, J. E., and Weinhold, F. (1988). Analysis of the Geometry of the Hydroxymethyl Radical by the “Different Hybrids for Different Spins” Natural Bond Orbital Procedure. J. Mol. Struct. THEOCHEM 169, 41–62. doi:10.1016/0166-1280(88)80248-3

CrossRef Full Text | Google Scholar

Castleman, A. W., and Jena, P. (2006). Clusters: a Bridge between Disciplines. Proc. Natl. Acad. Sci. 103, 10552–10553. doi:10.1073/pnas.0601783103

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., Zhao, Y.-F., Wang, L.-S., and Li, J. (2017). Recent Progresses of Global Minimum Searches of Nanoclusters with a Constrained Basin-Hopping Algorithm in the TGMin Program. Comput. Theor. Chem. 1107, 57–65. doi:10.1016/j.comptc.2016.12.028

CrossRef Full Text | Google Scholar

Chen, X., Zhao, Y. F., Zhang, Y. Y., and Li, J. (2019). TGMin: An Efficient Global Minimum Searching Program for Free and Surface‐supported Clusters. J. Comput. Chem. 40, 1105–1112. doi:10.1002/jcc.25649

PubMed Abstract | CrossRef Full Text | Google Scholar

Choi, T. H., Liang, R., Maupin, C. M., and Voth, G. A. (2013). Application of the SCC-DFTB Method to Hydroxide Water Clusters and Aqueous Hydroxide Solutions. J. Phys. Chem. B 117, 5165–5179. doi:10.1021/jp400953a

PubMed Abstract | CrossRef Full Text | Google Scholar

Cooks, R. G., Zhang, D., Koch, K. J., Gozzo, F. C., and Eberlin, M. N. (2001). Chiroselective Self-Directed Octamerization of Serine: Implications for Homochirogenesis. Anal. Chem. 73, 3646–3655. doi:10.1021/ac010284l

PubMed Abstract | CrossRef Full Text | Google Scholar

Daven, D. M., Tit, N., Morris, J. R., and Ho, K. M. (1996). Structural Optimization of Lennard-Jones Clusters by a Genetic Algorithm. Chem. Phys. Lett. 256, 195–200. doi:10.1016/0009-2614(96)00406-X

CrossRef Full Text | Google Scholar

Deaven, D. M., and Ho, K. M. (1995). Molecular Geometry Optimization with a Genetic Algorithm. Phys. Rev. Lett. 75, 288–291. doi:10.1103/PhysRevLett.75.288

PubMed Abstract | CrossRef Full Text | Google Scholar

Del Bene, J. E., Alkorta, I., Elguero, J., and Sánchez-Sanz, G. (2017). Lone-Pair Hole on P: P···N Pnicogen Bonds Assisted by Halogen Bonds. J. Phys. Chem. A. 121 (6), 1362–1370. doi:10.1021/acs.jpca.6b12553

PubMed Abstract | CrossRef Full Text | Google Scholar

Du, Y., Sheng, H., Astruc, D., and Zhu, M. (2020). Atomically Precise Noble Metal Nanoclusters as Efficient Catalysts: A Bridge between Structure and Properties. Chem. Rev. 120, 526–622. doi:10.1021/acs.chemrev.8b00726

PubMed Abstract | CrossRef Full Text | Google Scholar

Esrafili, M. D., and Mousavian, P. (2018). The Strengthening Effect of a Halogen, Chalcogen or Pnicogen Bonding on Halogen-π Interaction: a Comparative Ab Initio Study. Mol. Phys. 116, 526–535. doi:10.1080/00268976.2017.1406166

CrossRef Full Text | Google Scholar

Esrafili, M. D., and Sadr-Mousavi, A. (2017). Modulating of the Pnicogen-Bonding by a H⋯π Interaction: An Ab Initio Study. J. Mol. Graphics Model. 75, 165–173. doi:10.1016/j.jmgm.2017.04.017

CrossRef Full Text | Google Scholar

Fehlner, T., Halet, J. F., and Saillard, J. Y. (2007). Molecular Clusters: A Bridge to Solid-State Chemistry. Cambridge: Cambridge University Press.

Ferrando, R. (2015). Symmetry Breaking and Morphological Instabilities in Core-Shell Metallic Nanoparticles. J. Phys. Condens. Matter 27, 013003. doi:10.1088/0953-8984/27/1/013003

PubMed Abstract | CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2009). “Gaussian 09,” in Revision D.01 (Wallingford, CT: Gaussian, Inc).

Google Scholar

Grimme, S., Bannwarth, C., and Shushkov, P. (2017). A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All Spd-Block Elements (Z = 1-86). J. Chem. Theor. Comput. 13, 1989–2009. doi:10.1021/acs.jctc.7b00118

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, L., Wu, H., and Jin, Z. (2004). First Principles Study of the Evolution of the Properties of Neutral and Charged Phosphorus Clusters. J. Mol. Struct. THEOCHEM 677, 59–66. doi:10.1016/j.theochem.2004.02.014

CrossRef Full Text | Google Scholar

Ha, M., Kim, J.-H., You, M., Li, Q., Fan, C., and Nam, J.-M. (2019). Multicomponent Plasmonic Nanoparticles: From Heterostructured Nanoparticles to Colloidal Composite Nanostructures. Chem. Rev. 119, 12208–12278. doi:10.1021/acs.chemrev.9b00234

PubMed Abstract | CrossRef Full Text | Google Scholar

Hartke, B. (1995). Global Geometry Optimization of Clusters Using a Growth Strategy Optimized by a Genetic Algorithm. Chem. Phys. Lett. 240, 560–565. doi:10.1016/0009-2614(95)00587-T

CrossRef Full Text | Google Scholar

Hartke, B. (1993). Global Geometry Optimization of Clusters Using Genetic Algorithms. J. Phys. Chem. 97, 9973–9976. doi:10.1021/j100141a013

CrossRef Full Text | Google Scholar

Huang, W., Sergeeva, A. P., Zhai, H.-J., Averkiev, B. B., Wang, L.-S., and Boldyrev, A. I. (2010). A Concentric Planar Doubly π-aromatic B19− Cluster. Nat. Chem 2, 202–206. doi:10.1038/nchem.534

PubMed Abstract | CrossRef Full Text | Google Scholar

Jäger, M., Schäfer, R., and Johnston, R. L. (2019). GIGA: a Versatile Genetic Algorithm for Free and Supported Clusters and Nanoparticles in the Presence of Ligands. Nanoscale 11, 9042–9052. doi:10.1039/C9NR02031D

PubMed Abstract | CrossRef Full Text | Google Scholar

Jana, G., Mitra, A., Pan, S., Sural, S., and Chattaraj, P. K. (2019). Modified Particle Swarm Optimization Algorithms for the Generation of Stable Structures of Carbon Clusters, Cn (N = 3-6, 10). Front. Chem. 7, 65–77. doi:10.3389/fchem.2019.00485

PubMed Abstract | CrossRef Full Text | Google Scholar

Jena, P., and Sun, Q. (2018). Super Atomic Clusters: Design Rules and Potential for Building Blocks of Materials. Chem. Rev. 118, 5755–5870. doi:10.1021/acs.chemrev.7b00524

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, M., Zeng, Q., Zhang, T., Yang, M., and Jackson, K. A. (2012). Icosahedral to Double-Icosahedral Shape Transition of Copper Clusters. J. Chem. Phys. 136, 104501. doi:10.1063/1.3689442

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnstom, R. L. (2002). Atomic and Molecular Clusters. London: CRC Press.

Kanters, R. P. F., and Donald, K. J. (2014). Cluster: Searching for Unique Low Energy Minima of Structures Using a Novel Implementation of a Genetic Algorithm. J. Chem. Theor. Comput. 10, 5729–5737. doi:10.1021/ct500744k

PubMed Abstract | CrossRef Full Text | Google Scholar

Kong, X., Mu, L., Zhou, M., and Yang, S. (2019). “Phosphorus Clusters and Quantum Dots,” in Fundamentals and Applications of Phosphorous Nanomaterial. Editor H.-F. Ji (New York: ACS Symposium Series volume ACS Books), 79–102. doi:10.1021/bk-2019-1333.ch005

CrossRef Full Text | Google Scholar

Kong, X., Tsai, I.-A., Sabu, S., Han, C.-C., Lee, Y. T., Chang, H.-C., et al. (2006). Progressive Stabilization of Zwitterionic Structures in [H(Ser)2-8]+ Studied by Infrared Photodissociation Spectroscopy. Angew. Chem. Int. Ed. 45, 4130–4134. doi:10.1002/anie.200600597

PubMed Abstract | CrossRef Full Text | Google Scholar

Kroto, H. W., Heath, J. R., O’Brien, S. C., Curl, R. F., and Smalley, R. E. (1985). C60: Buckminsterfullerene. Nature 318, 162–163. doi:10.1038/318162a0

CrossRef Full Text | Google Scholar

Lazauskas, T., Sokol, A. A., and Woodley, S. M. (2017). An Efficient Genetic Algorithm for Structure Prediction at the Nanoscale. Nanoscale 9, 3850–3864. doi:10.1039/C6NR09072A

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Li, X., Zhai, H. J., and Wang, L. S. (2003). Au20: A Tetrahedral Cluster. Science 299, 864–867. doi:10.1126/science.1079879

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, W.-L., Chen, X., Jian, T., Chen, T.-T., Li, J., and Wang, L.-S. (2017). From Planar boron Clusters to Borophenes and Metalloborophenes. Nat. Rev. Chem. 1, 0071. doi:10.1038/s41570-017-0071

CrossRef Full Text | Google Scholar

Liu, L., and Corma, A. (2018). Metal Catalysts for Heterogeneous Catalysis: From Single Atoms to Nanoclusters and Nanoparticles. Chem. Rev. 118, 4981–5079. doi:10.1021/acs.chemrev.7b00776

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, T., and Chen, F. (2012). Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 33, 580–592. doi:10.1002/jcc.22885

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, Z., Castleman, A. W., and Khanna, S. N. (2016). Reactivity of Metal Clusters. Chem. Rev. 116, 14456–14492. doi:10.1021/acs.chemrev.6b00230

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin, T. P. (1986). Compound Clusters. Z. Phys. D - Atoms, Mol. Clusters 3, 211–217. doi:10.1007/BF01384809

CrossRef Full Text | Google Scholar

Mokrai, R., Barrett, J., Apperley, D. C., Batsanov, A. S., Benkő, Z., and Heift, D. (2019). Weak Pnictogen Bond with Bismuth: Experimental Evidence Based on Bi−P Through‐Space Coupling. Chem. Eur. J. 25, 4017–4024. doi:10.1002/chem.201900266

PubMed Abstract | CrossRef Full Text | Google Scholar

Mu, L., Yang, S., Bao, X., Yin, H., and Kong, X. (2015). Medium-sized Phosphorus Cluster cationsP+2m+1(6 ≤ M ≤ 32) Studied by Collision-Induced Dissociation Mass Spectrometry. J. Mass. Spectrom. 50, 1352–1357. doi:10.1002/jms.3705

PubMed Abstract | CrossRef Full Text | Google Scholar

Paz-Borbón, L. O., Mortimer-Jones, T. V., Johnston, R. L., Posada-Amarillas, A., Barcaro, G., and Fortunelli, A. (2007). Structures and Energetics of 98 Atom Pd-Pt Nanoalloys: Potential Stability of the Leary Tetrahedron for Bimetallic Nanoparticles. Phys. Chem. Chem. Phys. 9, 5202–5208. doi:10.1039/b707136a

PubMed Abstract | CrossRef Full Text | Google Scholar

Piazza, Z. A., Hu, H.-S., Li, W.-L., Zhao, Y.-F., Li, J., and Wang, L.-S. (2014). Planar Hexagonal B36 as a Potential Basis for Extended Single-Atom Layer boron Sheets. Nat. Commun. 5, 3113. doi:10.1038/ncomms4113

PubMed Abstract | CrossRef Full Text | Google Scholar

Rabanal-León, W. A., Tiznado, W., Osorio, E., and Ferraro, F. (2018). Exploring the Potential Energy Surface of Small lead Clusters Using the Gradient Embedded Genetic Algorithm and an Adequate Treatment of Relativistic Effects. RSC Adv. 8, 145–152. doi:10.1039/C7RA11449D

CrossRef Full Text | Google Scholar

Reed, A. E., Curtiss, L. A., and Weinhold, F. (1988). Intermolecular Interactions from a Natural Bond Orbital, Donor-Acceptor Viewpoint. Chem. Rev. 88, 899–926. doi:10.1021/cr00088a005

CrossRef Full Text | Google Scholar

Rogan, J., Varas, A., Valdivia, J. A., and Kiwi, M. (2013). A Strategy to Find Minimal Energy Nanocluster Structures. J. Comput. Chem. 34, 2548–2556. doi:10.1002/jcc.23419

PubMed Abstract | CrossRef Full Text | Google Scholar

Scheiner, S. (2013). The Pnicogen Bond: Its Relation to Hydrogen, Halogen, and Other Noncovalent Bonds. Acc. Chem. Res. 46, 280–288. doi:10.1021/ar3001316

PubMed Abstract | CrossRef Full Text | Google Scholar

Scutelnic, V., Perez, M. A. S., Marianski, M., Warnke, S., Gregor, A., Rothlisberger, U., et al. (2018). The Structure of the Protonated Serine Octamer. J. Am. Chem. Soc. 140, 7554–7560. doi:10.1021/jacs.8b02118

PubMed Abstract | CrossRef Full Text | Google Scholar

Shayeghi, A., Götz, D., Davis, J. B. A., Schäfer, R., and Johnston, R. L. (2015). Pool-BCGA: a Parallelised Generation-free Genetic Algorithm for the Ab Initio Global Optimisation of Nanoalloy Clusters. Phys. Chem. Chem. Phys. 17, 2104–2112. doi:10.1039/C4CP04323E

PubMed Abstract | CrossRef Full Text | Google Scholar

VanGelder, L. E., Kosswattaarachchi, A. M., Forrestel, P. L., Cook, T. R., and Matson, E. M. (2018). Polyoxovanadate-alkoxide Clusters as Multi-Electron Charge Carriers for Symmetric Non-aqueous Redox Flow Batteries. Chem. Sci. 9, 1692–1699. doi:10.1039/c7sc05295b

PubMed Abstract | CrossRef Full Text | Google Scholar

VanGelder, L. E., Pratt, H. D., Anderson, T. M., and Matson, E. M. (2019). Surface Functionalization of Polyoxovanadium Clusters: Generation of Highly Soluble Charge Carriers for Nonaqueous Energy Storage. Chem. Commun. 55, 12247–12250. doi:10.1039/C9CC05380H

PubMed Abstract | CrossRef Full Text | Google Scholar

Wales, D. J., and Doye, J. P. K. (1997). Global Optimization by Basin-Hopping and the Lowest Energy Structures of Lennard-Jones Clusters Containing up to 110 Atoms. J. Phys. Chem. A. 101, 5111–5116. doi:10.1021/jp970984n

CrossRef Full Text | Google Scholar

Wales, D. J., and Scheraga, H. A. (1999). Global Optimization of Clusters, Crystals, and Biomolecules. Science 285, 1368–1372. doi:10.1126/science.285.5432.1368

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Lv, J., Zhu, L., and Ma, Y. (2012). CALYPSO: A Method for crystal Structure Prediction. Comput. Phys. Commun. 183, 2063–2070. doi:10.1016/j.cpc.2012.05.008

CrossRef Full Text | Google Scholar

Wu, J., Yan, H., Zhong, A., Chen, H., Jin, Y., and Dai, G. (2019). Theoretical and Conceptual DFT Study of Pnicogen- and Halogen-Bonded Complexes of PH2X---BrCl. J. Mol. Model. 25, 28. doi:10.1007/s00894-018-3905-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Xue, T., Luo, J., Shen, S., Li, F., and Zhao, J. (2010). Lowest-energy structures of cationic P2m+1+ (m=1-12) clusters from first-principles simulated annealing. Chem. Phys. Lett. 485, 26–30. doi:10.1016/j.cplett.2009.12.019

CrossRef Full Text | Google Scholar

Yañez, O., Báez-Grez, R., Inostroza, D., Rabanal-León, W. A., Pino-Rios, R., Garza, J., et al. (2019). AUTOMATON: A Program That Combines a Probabilistic Cellular Automata and a Genetic Algorithm for Global Minimum Search of Clusters and Molecules. J. Chem. Theor. Comput. 15, 1463–1475. doi:10.1021/acs.jctc.8b00772

CrossRef Full Text | Google Scholar

Yang, S., Mu, L., and Kong, X. (2016). Collision-induced dissociation mass spectrometry of phosphorus cluster anionsP2m+1−(3 ≤ m ≤ 20). Int. J. Mass Spectrom. 399-400, 27–32. doi:10.1016/j.ijms.2016.02.006

CrossRef Full Text | Google Scholar

Yoo, S., Zhao, J., Wang, J., and Zeng, X. C. (2004). Endohedral Silicon Fullerenes SiN(27 ≤N≤ 39). J. Am. Chem. Soc. 126, 13845–13849. doi:10.1021/ja046861f

PubMed Abstract | CrossRef Full Text | Google Scholar

Zahn, S., Frank, R., Hey‐Hawkins, E., and Kirchner, B. (2011). Pnicogen Bonds: A New Molecular Linker?. Chem. Eur. J. 17, 6034–6038. doi:10.1002/chem.201002146

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhai, H.-J., Zhao, Y.-F., Li, W.-L., Chen, Q., Bai, H., Hu, H.-S., et al. (2014). Observation of an all-boron fullerene. Nat. Chem 6, 727–731. doi:10.1038/NCHEM.1999

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhan, L., Chen, J. Z. Y., Liu, W.-K., and Lai, S. K. (2005). Asynchronous multicanonical basin hopping method and its application to cobalt nanoclusters. J. Chem. Phys. 122, 244707. doi:10.1063/1.1940028

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, J., and Glezakou, V. A. (2020). Global optimization of chemical cluster structures: Methods, applications, and challenges. Int. J. Quan. Chem. 121, e26553. doi:10.1002/qua.26553

CrossRef Full Text | Google Scholar

Zhao, Y., Chen, X., and Li, J. (2017). TGMin: A global-minimum structure search program based on a constrained basin-hopping algorithm. Nano Res. 10, 3407–3420. doi:10.1007/s12274-017-1553-z

CrossRef Full Text | Google Scholar

Zhou, C., Ieritano, C., and Hopkins, W. S. (2019). Augmenting Basin-Hopping With Techniques From Unsupervised Machine Learning: Applications in Spectroscopy and Ion Mobility. Front. Chem. 7, 519. doi:10.3389/fchem.2019.00519

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, T., Ma, L., and Chen, H. (2020). Electronic structure and stability of Al6CMn (M = Li, Na, k; n = 2, 4, 6) clusters. Comput. Theor. Chem. 1178, 112780. doi:10.1016/j.comptc.2020.112780

CrossRef Full Text | Google Scholar