Low-Lying Electronic States of the Nickel Dimer

The generalized Van Vleck second order multireference perturbation theory (GVVPT2) method was used to investigate the low-lying electronic states of Ni₂. Because the nickel atom has an excitation energy of only 0.025 eV to its first excited state (the least in the first row of transition elements), Ni₂ has a particularly large number of low-lying states. Full potential energy curves (PECs) of more than a dozen low-lying electronic states of Ni₂, resulting from the atomic combinations ³F₄ + ³F₄ and ³D₃ + ³D₃, were computed. In agreement with previous theoretical studies, we found the lowest lying states of Ni₂ to correlate with the ³D₃ + ³D₃ dissociation limit, and the holes in the d-subshells were in the subspace of delta orbitals (i.e., the so-dubbed δδ-states). In particular, the ground state was determined as X ¹Γ_g and had spectroscopic constants: bond length (R_e) = 2.26 Å, harmonic frequency (ω_e) = 276.0 cm⁻¹, and binding energy (D_e) = 1.75 eV; whereas the 1 ¹Σ_g⁺ excited state (with spectroscopic constants: R_e = 2.26 Å, ω_e = 276.8 cm⁻¹, and D_e = 1.75) of the ³D₃ + ³D₃ dissociation channel lay at only 16.4 cm⁻¹ (0.002 eV) above the ground state at the equilibrium geometry. Inclusion of scalar relativistic effects through the spin-free exact two component (sf-X2C) method reduced the bond lengths of both of these two states to 2.20 Å, and increased their binding energies to 1.95 eV and harmonic frequencies to 296.0 cm⁻¹ for X ¹Γ_g and 297.0 cm⁻¹ for 1 ¹Σ_g⁺. These values are in good agreement with experimental values of R_e = 2.1545 ± 0.0004 Å, ω_e = 280 ± 20 cm⁻¹, and D₀ = 2.042 ± 0.002 eV for the ground state. All states considered within the ³F₄ + ³F₄ dissociation channel proved to be energetically high-lying and van der Waals-like in nature. In contrast to most previous theoretical studies of Ni₂, full PECs of all considered electronic states of the molecule were produced.

Introduction

Since Ni₂ has few holes in otherwise complete subshells, one might expect theoretical studies of Ni₂ to be less complicated than for other first row transition metal dimers, like Cr₂ where one has many more possibilities of distributing 12 electrons in 12 valence orbitals. Reported information on Ni₂, however, proves the contrary. For example, the exact symmetry of the ground electronic state of Ni₂ is still debated: Different studies have reported different space and spin symmetries for the molecule’s ground term.

Experimental data on Ni₂ is sparse and the true ground state of the molecule is not unequivocally accepted. From the analysis of electronic absorption bands of Ni₂ in the visible spectral region in argon matrices, De Vore et al. (De Vore et al., 1975) determined ω_e = 192 cm⁻¹, whereas a frequency of 380.9 cm⁻¹ was found in solid argon matrix (Ahmed and Nixon, 1979). The latter result was later criticized by Rasanen et al. (Rasanen et al., 1987) In photoelectron spectroscopic studies of Ni₂^-, ω_e = 280 ± 20 cm⁻¹ was determined for the lowest electronic state of Ni₂ (Ho et al., 1993). Second and third law analyses of information derived from a combination of Knudsen effusion and mass‐spectrometric techniques led to a binding energy of D₀ = 2.03 ± 0.30 eV (second law result) and D₀ = 2.36 ± 0.22 eV (third law result) for ground state Ni₂ (Kant, 1964). By using time-delayed resonant two-photon ionization, Morse et al. (Morse et al., 1984) determined D₀ = 2.068 ± 0.010 eV and R_e = 2.200 ± 0.007 Å for the lowest state of Ni₂, but assigned as either ³Γ_u or ¹Γ_g. Also from two-photon ionization studies on supersonic jet-cooled Ni₂ in argon carrier gas, Pinegar et al. (Pinegar et al., 1995) determined D₀ = 2.042 ± 0.002 eV and R_e = 2.1545 ± 0.0004 Å for the lowest state of Ni₂ but were unable to ascertain the symmetry of this state.

Theoretical studies of the electronic states of Ni₂ are complicated by the fact that the first excited state of the Ni atom, ³D₃ (3d⁹4s¹), is only 0.025 eV above the ³F₄ (3d⁸4s²) ground atomic state, which is the least excitation energy of any of the first row of transition elements (Harrison, 2000; Kramida et al., 2013). This low promotion energy supports the existence of several low-lying molecular states of the Ni₂ molecule resulting from the ³F₄ + ³F₄ and ³D₃ + ³D₃ atomic combinations. For example, limited configuration interaction (CI) calculations (Shim et al., 1979) found 84 states of Ni₂, corresponding to the ³F₄ + ³F₄ dissociation limit, to lie within an energy range of only 300 K (0.026 eV), and 45 states, also within a narrow energy range, to correlate with the ³D₃ + ³D₃ dissociation asymptote. Melius et al. (Melius et al., 1976) also noted that the manifold of electronic states within 0.50 eV of the ground state of Ni₂ was dense and complex.

Since the fully filled 4s-subshell of the ³F₄ (3d⁸4s²) ground state of Ni discourages significant bonding interaction, bonding in low-lying states of Ni₂ results largely from the coupling of excited state Ni atoms. In particular, the lowest states of the Ni₂ molecule can be expected to correlate with the ³D₃ (3d⁹4s¹) + ³D₃ (3d⁹4s¹) dissociation channel. At the generalized valence bond (GVB) and polarization CI (POL-CI) level of theory, (Upton and Goddard III, 1978) 30 of 45 low-lying states of Ni₂, within the ³D₃ + ³D₃ dissociation channel, were found (Shim et al., 1979) to be singlets and triplets ordered energetically as

δδ (6 states) < πδ (8 states) < δσ (4 states) < ππ (6 states) < πσ (4 states) < σσ (2 states), with the six lowest states (of symmetries ¹Γ_g, ¹Σ_g⁺, ³Σ_g⁻, ¹Σ_u⁻, ³Γ_u, and ³Σ_u⁺) being virtually degenerate and having an average equilibrium bond length, R_e, of 2.04 Å, and binding energy, D_e, of 2.29 eV. The designations δδ, πδ, et cetera, specify the positions of the holes in the dominant configurations of the 3d-orbitals at each atomic center which has a 3d⁹4s¹ configuration (Shim et al., 1979). In brief, the correct energy spacing of the low-lying states of the Ni dimer is problematic for both theory and experiment.

The determination of energy ordering and spacing is no less complicated for the Ni atom, and provides insight into necessary levels of experimental and theoretical approaches. The ³F₄ (3d⁸4s²) → ³D₃ (3d⁹4s¹) excitation energy has been determined by at least one experimental study (Moore, 1952) to be negative (-0.029 eV). This negative value was supported by ab initio wave function and density functional theory (DFT) calculations (Bauschlicher et al., 1982; Raghavachari and Trucks, 1989; Russo et al., 1994). A more recent study, (Schultz et al., 2005) that employed several functionals at all five rungs of Jacob’s ladder of DFT functionals, predicted the ground state configuration of the Ni atom as 3d⁹4s¹ (³D₃) with most of the functionals when using a triple-ζ quality basis set. On the other hand, multireference studies (Andersson and Roos, 1992; Murphy and Messmer, 1992) predicted a 3d⁸4s² (³F₄) ground state configuration for the Ni atom. Illustrating additional complexity, Upton and Goddard (Upton and Goddard III, 1978) found that averaging over J components (where J is the sum of spin and orbital angular momenta of the atom) of each state places the ³D₃ (3d⁹4s¹) state lower energetically than the ³F₄ (3d⁸4s²) state.

One of the earliest theoretical studies (Cooper et al., 1972) on Ni₂ employed the extended Hückel molecular orbital method and found a ³Σ_g^- ground state with R_e = 2.21 Å, ω_e = 370 cm⁻¹, and D_e = 2.45 eV, with dominant configuration 3dδ_g⁴ 3dδ_u⁴ 3dπ_u⁴ 3dπ_g² 3dσ_g² 3dσ_u² 4sσ_g². On the other hand, the self-consistent field (SCF) scattered-wave (X_α-sw) method (Rösch and Rhodin, 1974) found a ¹Σ_g⁺ ground state with configuration 3dδ_g⁴ 3dδ_u⁴ 3dπ_u⁴ 3dπ_g⁴ 3dσ_g² 4sσ_g²; whereas the generalized valence bond (GVB) method (Melius et al., 1976) also predicted a ¹Σ_g⁺ ground state for Ni₂, but with configuration 3dδ_g⁴ 3dδ_u² 3dπ_u⁴ 3dπ_g⁴ 3dσ_g² 3dσ_u² 4sσ_g². A Hartree-Fock followed by limited CI study, (Shim et al., 1979) which explored a variety of states of Ni₂ resulting from the ³F₄ + ³F₄ and ³D₃ + ³D₃ atomic combinations, found the ground state to be ¹Σ_g⁺ with the same configuration as was reported by the GVB study(Melius et al., 1976). The states ¹Γ_g and ¹Σ_u^- were reported to be in close proximity to the ¹Σ_g⁺ state in the CI study. Other theoretical studies found the six δδ–hole states (i.e., ¹Γ_g, ¹Σ_g⁺, ³Σ_g^-, ¹Σ_u^-, ³Γ_u, ³Σ_u⁺), resulting from the ³D₃ + ³D₃ atomic coupling, to be quasidegenerate(Basch et al., 1980; Noell et al., 1980; Wood et al., 1980).

Using an effective core potential basis set specifically optimized for the Ni atom in the ³D₃ state within the generalized valence bond CI (GVBCI) method, Noell et al. (Noell et al., 1980) found the splitting of the six δδ–hole states of Ni₂ to be quite small (≤0.1 eV), with the lowest states being ¹Γ_g and ¹Σ_g⁺. Inclusion of polarization configurations involving single and double excitations to the virtual space (POLSDCI) placed the triplet states (³Σ_g^-, ³Γ_u, ³Σ_u⁺) approximately 0.07 eV below the singlets. At the singles and doubles CI (SDCI) level of theory, these authors found the energy splitting of the six lowest δδ–hole states of Ni₂ to be less than 0.009 eV, with an average bond length of 2.26 Å and binding energy of 1.88 eV.

With a basis set similar to that used by Noell et al., (Noell et al., 1980) a contemporaneous restricted Hartree-Fock (RHF) and CI with single and double excitations (CISD) study predicted a ³Σ_u⁺ ground state for Ni₂, with spectroscopic data: R_e = 2.33 Å, ω_e = 211 cm⁻¹, and D_e = 1.43 eV(Basch et al., 1980). Calculations by these authors at the same levels of theory using an all electron basis set corroborated the prediction of the ground state symmetry as ³Σ_u⁺. On the other hand, a local spin density method (Harris and Jones, 1979) predicted a ³Σ_g^- ground state with R_e = 2.18 Å, ω_e = 320 cm⁻¹, and D_e = 2.70 eV. A slightly earlier CASSCF/CASPT2 study (Pou-Amérigo et al., 1994) that used an atomic natural orbital (ANO) type contraction of the (21s15p10d6f4g) primitive basis to [6s5p4d3f2g] for calculations without correlation of the semi-core 3s3p electrons, and a [10s9p8d3f2g] contracted basis for calculations involving the correlation of 3s3p electrons, likewise found the six lowest δδ–hole states of Ni₂ to lie within a particularly narrow energy gap (0.04 eV) with the triplet states higher in energy than the singlets. However, after inclusion of scalar relativistic effects, the ground term was predicted as ¹Γ_g, with the ¹Σ_g⁺ term lying only 0.01 eV higher at the equilibrium geometry. Correlating the 3s3p electrons in these calculations predicted the ¹Γ_g and ¹Σ_g⁺ states to be degenerate to the reported accuracy, with slightly improved spectroscopic constants relative to reference experimental values [i.e., R_e = 2.23 Å, D_e = 2.06 eV; and ω_e = 293 cm⁻¹ for ¹Γ_g versus ω_e = 294 cm⁻¹ for ¹Σ_g⁺ compared with experimental values of R_e = 2.1545 ± 0.0004 Å, (Pinegar et al., 1995) D₀ = 2.042 ± 0.002 eV, (Pinegar et al., 1995) and ω_e = 280 ± 20 cm⁻¹ (Ho et al., 1993)].

DFT studies of Ni₂ have also been inconclusive. Yanagisawa et al. (Yanagisawa et al., 2000) used various DFT functionals to study the ³Σ_g^- and ³Σ_u⁺ states of Ni₂ and found B3LYP (Becke, 1993) to predict the ³Σ_u⁺ state to lie lower than ³Σ_g^- whereas the rest of the functionals predicted the latter state to lie lower at the equilibrium geometry. However, the ³Σ_g^- state that they found had a configuration that corresponded to the ππ–hole manifold rather than the δδ. Gutsev et al. (Gutsev and Bauschlicher, 2003) also found a ³Σ_g^- ground state, with the same configuration as did Yanagisawa et al., (Yanagisawa et al., 2000) when using a variety of hybrid functionals. Contrarily, Diaconu et al. (Diaconu et al., 2004) found a singlet δδ–hole ground state (with a mixture of ¹Γ_g and ¹Σ_g⁺) for Ni₂ when using B3LYP with the (14s11p6d3f)/[8s6p4d1f] basis set, whereas use of the Stuttgart RSC ECP basis set (Dolg et al., 1987) with the same functional gave a triplet δδ–hole (with a mixture of ³Σ_g^- and ³Γ_u symmetries) that lay 0.001 eV lower than the singlet δδ–hole state at the equilibrium geometry. Using functionals at all levels of Jacob’s ladder of DFT functionals, Schultz et al. (Schultz et al., 2005) also found different functionals to predict different ground state symmetries for Ni₂, with all local spin density approximation (LSDA) functionals predicting a ³Σ_g^- ground state and all generalized gradient approximation (GGA) and meta GGA functionals predicting a ³Π_u ground state; whereas hybrid GGA and hybrid meta GGA functionals found either ³Σ_u⁺ or ³Σ_g^- to lie lowest energetically. Du et al. (Du et al., 2008) used various functionals to study the low-lying states of Ni₂. Their results that agreed best with experiment were obtained when using BLYP, which predicted a triplet σδ–hole (3d_z2 σ_u*¹ 3d_x2-y2 δ_u*¹) ground state. The space symmetry of this state was not reported. With the B3P86 functional, (Perdew, 1986; Becke, 1993) a quintet ground state was predicted for Ni₂, (Shi-Ying and Zheng-He, 2008) although the space symmetry was not reported. The Perdew-Burke-Ernzerhof (PBE) exchange correlation functional (Perdew et al., 1996) predicted a ³Σ_g^- ground state for Ni₂, (Kamal et al., 2012) with spectroscopic constants R_e = 2.93 Å, D_e = 3.09 eV, and ω_e = 334.08 cm⁻¹, which showed significant deviations from experimental values.

Some of the most recent wave function based calculations on Ni₂ include those due to Dong et al. (Dong et al., 2013) using the symmetry-adapted-cluster configuration interaction (SAC-CI) method (Nakatsuji, 1979) and Cheskidov et al. (Cheskidov et al., 2012) using the average coupled pair functional (ACPF), (Gdanitz and Ahlrichs, 1988) average quadratic coupled cluster (AQCC), (Szalay and Bartlett, 1993) internally contracted single and double multireference configuration interaction (MRCI or MRCI with Davidson corrections, i.e., MRCI + Q), (Werner and Knowles, 1990) and N-electron valence state second-order perturbation theory (NEVPT2) (Angeli et al., 2001) methods. The study by Dong et al. (Dong et al., 2013) predicted a ³B_1u ground state (with R_e = 2.56 Å) for Ni₂ in ${\mathrm{D}}_{2\mathrm{h}}$ symmetry which corresponds to ³Σ_u⁺, ³Δ_u or ³Γ_u in ${\mathrm{D}}_{\infty \mathrm{h}}$. The study by Cheskidov et al. (Cheskidov et al., 2012) used the Dunning-type quadruple-ζ quality basis set, cc-pVQZ-DK (22s18p11d3f2g1h/[8s7p6d3f2g1h]), (Balabanov and Peterson, 2005) and found the ¹Γ_g and ¹Σ_g⁺ δδ–hole states to be quasidegenerate for all five methods with the ¹Σ_g⁺ state lying lower when using AQCC, MRCI + Q, and MRCI methods and the two states fully degenerate (to the reported accuracy level) at the ACPF and NEVPT2 levels. At the ACPF level, the predicted ground state was instead ¹Σ_u^-; inclusion of spin-orbit relativistic corrections within ACPF calculations led to an $0_{\mathrm{g}}^{+}$ ground state (¹Σ_g⁺ + ³Σ_g^- δδ–hole states), whereas the $0_{\mathrm{u}}^{-}$ term (¹Σ_u^- + ³Σ_u⁺ δδ–hole states) lay at only 0.009 ± 0.004 eV above the predicted ground state.

The above synopsis of previous work on Ni₂ shows the difficulties involved in studying not only the spectroscopic constants, but even the ordering of the low-lying electronic states of Ni₂. Although wave function methods generally support δδ–hole states (¹Γ_g, ¹Σ_g⁺, ³Σ_g^-, ¹Σ_u^-, ³Γ_u, ³Σ_u⁺) as lying lowest energetically, the methods predict different ground state symmetries with some finding all six states to be degenerate. Similarly, experimental spectroscopic data have been obtained but most of the studies could not ascertain the ground state symmetry of the molecule. Our current study exploits the ability of the GVVPT2 method (Khait et al., 2002; Jiang et al., 2009) to describe well full PECs of ground- and excited-electronic states of complicated transition element dimers, such as has already been demonstrated on other problematic transition metal molecules [e.g., Cr₂ and Y₂ (Tamukong et al., 2012; Tamukong et al., 2014)]. It should be noted that of all previous theoretical work described above on electronic states of Ni₂, only six of the articles reported full PECs of the states they investigated. Consequently, where other data is available, this study also provides further assessment of the capabilities of the GVVPT2 method for difficult transition metal dimers, including the bond breaking regions. We have constructed full PECs of 21 states of Ni₂. All (nonrelativistic) calculations used the Dunning-type cc-pVTZ basis set (Balabanov and Peterson, 2005), and calculations were performed using ${\mathrm{D}}_{2\mathrm{h}}$ symmetry. Furthermore, low-lying ¹Γ_g and ¹Σ_g⁺ states were further studied with scalar relativistic effects included in GVVPT2 (Tamukong et al., 2014) through the spin-free exact two component (sf-X2C) method (Liu, 2010; Cheng and Gauss, 2011; Li et al., 2012; Li et al., 2013). Relativistic calculations used the cc-pVTZ-DK basis set (Balabanov and Peterson, 2005). The rest of the paper is organized as follows: Methods section briefly reviews key features of GVVPT2 and the spin-free exact two component (sf-X2C) methods, and describes computational details; the results are presented and discussed in Results and Discussion section; while conclusions are drawn in Conclusion section.

Methods

GVVPT2

The GVVPT2 method for electron correlation in molecules has been thoroughly described elsewhere, (Khait et al., 2002; Jiang et al., 2009) as has its application to some challenging systems (Mbote et al., 2010; Khait et al., 2012; Tamukong et al., 2012; Mokambe et al., 2013; Tamukong et al., 2014). Here, salient features of the GVVPT2 method relevant to the present study are reviewed. In GVVPT, the total Hilbert space of many-electron functions [e.g., configuration state functions (CSFs)] with appropriate molecular space and spin symmetry (L) is partitioned into a model space (L_M), and an external space (L_Q) whose electronic configurations are derived from configurations generated from the model space by single and double electron excitations into virtual orbitals, L = L_M ⊕ L_Q. The model space is further partitioned into a primary subspace, spanned by a set of reference functions that are linear combinations of CSFs (typically the lowest MCSCF or CASSCF states), and a secondary subspace. States within the primary subspace are then perturbatively corrected through primary-external (P–Q) interactions whereas the secondary subspace serves as a buffer energetically separating the primary and external subspaces. This energy buffer circumvents most intruder state problems that plague many multireference perturbation theory techniques. An effective Hamiltonian matrix $\left({\mathbf{H}}_{\mathrm{MM}}^{\mathrm{eff}}\right)$ is constructed with the same dimension as the model space, and its diagonalization includes both perturbatively corrected primary and unperturbed secondary subspace states. To guarantee continuity and smoothness of CSF responses (and ultimately PECs) even in situations of quasidegeneracies between primary and external states, GVVPT2 uses a continuously varying nonlinear denominator shift that arises from a resolvent that is both degeneracy-corrected and contains a hyperbolic tangent function as a switching function from nondegenerate to degenerate regimes (Khait et al., 2002). This resolvent can be written

${\mathrm{X}}_{qi}= \frac{\tanh \left({\Delta }_i\right)}{{\Delta }_i} {\mathrm{H}}_{qi}= \frac{\tanh \left({\Delta }_i\right)}{{\Delta }_i} {\displaystyle \sum _{m\in L_M}{\mathrm{H}}_{qm}{\mathrm{C}}_{mi}}(\mathrm{1a})$

${\Delta }_i=\frac{1}{2}\left({\epsilon }_q^i-{\epsilon }_i^{\left(0\right)}\right)+ \frac{1}{2} \sqrt{{\left({\epsilon }_q^i-{\epsilon }_i^{\left(0\right)}\right)}^2+4{\displaystyle \sum _{q\in e}{\mathrm{H}}_{qi}^2}}(\mathrm{1b})$

where the C_mi denote components of eigenvectors of the unperturbed model Hamiltonian; ${\epsilon }_i^{\left(0\right)}$ is the reference Møller-Plesset-type energy while ${\epsilon }_q^{\left(0\right)}$ is the state-specific zeroth-order energy of external CSF q. As with all studies of specific molecules with GVVPT2 since ca. 2005, semicanonical orbitals from the MCSCF are used. The mathematical robustness of GVVPT2 allows it to support both complete and incomplete model spaces. By construction, GVVPT2 is subspace-specific (N.B. excited states of the same symmetry as lower-lying states can be calculated) and is spin-adapted.

Spin-Free Exact Two Component Method

Matrix formulations of two-component relativistic methods have had significant successes in molecular electronic structure calculations, following Dyall’s seminal Normalized Elimination of Small Component (NESC) paper (Dyall, 1997) in 1997. For a summary of development of matrix two-component methods, we refer the reader to Ref. (Liu, 2014). In this work, we adopt the spin-free version of exact two component (sf-X2C) (Liu, 2010; Cheng and Gauss, 2011; Li et al., 2012; Li et al., 2013) that was previously used with GVVPT2 (Tamukong et al., 2014). The following Hamiltonian, written in second quantization form, incorporates scalar relativistic effects through the sf-X2C approach

$\mathrm{H}={\displaystyle \sum _{pq}{\left[{\mathbf{h}}_{+,\mathrm{sf}}^{\mathrm{X2C}}\right]}_{pq}{\mathrm{a}}_p^{+}{\mathrm{a}}_q} + \frac{1}{2} {\displaystyle \sum _{pqrs}\left(pr|qs\right){\mathrm{a}}_p^{+}{\mathrm{a}}_q^{+}{\mathrm{a}}_s{\mathrm{a}}_r}(2)$

where the first term is the one-electron spin-free part of the exact two-component (X2C) Hamiltonian, while the second is the unmodified Coulombic two-electron term. The sf-X2C Hamiltonian for positive energy states derives from a modified Dirac Hamiltonian, h^D which is decomposed into spin-free (sf) and spin-dependent (sd) parts.

${\mathbf{h}}^{\mathrm{D}}= {\mathbf{h}}_{\mathrm{sf}}^{\mathrm{D}}+{\mathbf{h}}_{\mathrm{sd}}^{\mathrm{D}}= \left(\begin{array}{cc}\mathbf{V}& \mathbf{T}\\ \mathbf{T}& \frac{{\alpha }^2}{4}{\mathbf{W}}_{\mathrm{sf}}-\mathbf{T}\end{array}\right)+ \left(\begin{array}{cc}\mathbf{0}& \mathbf{0}\\ \mathbf{0}& \frac{{\alpha }^2}{4}{\mathbf{W}}_{\mathrm{sd}}\end{array}\right)(3)$

where V is the matrix representation of the external nuclear attraction potential operator; T is the matrix representation of the kinetic energy operator; α is the fine-structure constant; while W is the matrix representation of the operator

$\mathrm{W}= \left(\overrightarrow{\mathrm{\sigma }} \cdot \overrightarrow{\mathrm{p}}\right)\mathrm{ V} \left(\overrightarrow{\mathrm{\sigma }} \cdot \overrightarrow{\mathrm{p}}\right)= \overrightarrow{\mathrm{p}} \cdot \mathrm{V} \overrightarrow{\mathrm{p}}+i \overrightarrow{\mathrm{\sigma }} \cdot \left(\overrightarrow{\mathrm{p}} \mathrm{V} \times \overrightarrow{\mathrm{p}}\right)= {\mathrm{W}}_{\mathrm{sf}}+ {\mathrm{W}}_{\mathrm{sd}}(4)$

The spin-free (sf) part of W, that is W_sf, describes scalar relativistic effects whereas the spin-dependent (sd) part, W_sd, incorporates spin-orbit coupling effects.

Computational Details

Unperturbed wavefunctions for GVVPT2 calculations were obtained from multiconfigurational self-consistent field (MCSCF) reference functions, using the local code “undmol.” The macroconfiguration approach (Khait et al., 2004) was used in all MCSCF and GVVPT2 calculations. In the macroconfiguration scheme, active orbitals are partitioned into orbital groups based on physical and mathematical intuition, such as orbital type or energy, and electrons are assigned to active orbital groups. Each unique assignment of electrons to active orbital groups defines a macroconfiguration, κ(n). Orbital rotations within each active orbital group are redundant (in MCSCF calculations), as all possible distributions of electrons within each group leading to the desired total spin and space symmetry are allowed. Each κ(n) generates a unique set of configurations, and hence configuration state functions (CSFs) that are orthogonal to those of all other κ(n). Additionally, the macroconfiguration approach permits a large number of noninteracting electronic configuration pairs to be efficiently screened by recognizing that all matrix elements resulting from configurations that differ by more than two electrons must be identically zero. The macroconfiguration formalism also provides an efficient way of generating excited configurations.

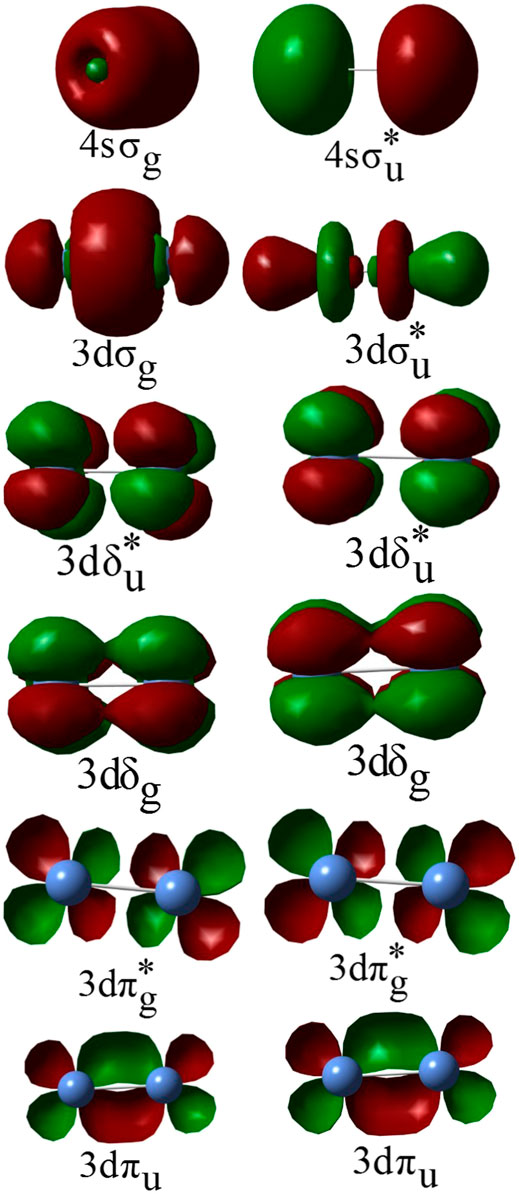
In all calculations, the active space consisted of 3d and 4s-derived molecular orbitals (MOs) of Ni₂ (Figure 1 shows representative 3d and 4s-derived MOs that were used to constitute the active spaces in this study). Depending on the specific state being investigated, some of the 3d-derived MOs and/or 4s-derived MOs were restricted to be doubly occupied in the MCSCF calculations, but were included with the 3s- and 3p-derived MOs in the active core and correlated at the GVVPT2 level of theory. For example, in all MCSCF calculations of δδ–hole states the 3dσ and 3dπ MOs were placed in the active core and only correlated at the GVVPT2 level. Similarly, the 3dσ and 3dπ electrons were kept doubly occupied in MCSCF calculations of ππ–hole states while only the 3dσ electrons were kept doubly occupied in MCSCF calculations of δπ–hole states, whereas the 4sσ, or 4sσ + 3dπ, or 4sσ + 3dσ orbitals were kept doubly occupied in MCSCF calculations of states within the ³F₄ (3d⁸4s²) + ³F₄ (3d⁸4s²) dissociation channel. The remaining orbitals in the active space were partitioned into sets (or so-called orbital groups), leading to configurations that describe δδ–, δπ–, δσ–, ππ–, πσ–, or σσ–hole states from the ³D₃ (3d⁹4s¹) + ³D₃ (3d⁹4s¹) atomic combination or configurations that describe ³D₃(3d⁹4s¹) +³F₄(3d⁸4s²) and ³F₄(3d⁸4s²) + ³F₄(3d⁸4s²) atomic couplings. In the present study, we indicate the positions of holes within the subspace of active 3d–derived MOs by specifying the active orbital types that qualitatively describe where holes exist (e.g., δδ–, δπ–, ππ–) as did Shim et al. (Shim et al., 1979) and Noel et al. (Noell et al., 1980)

FIGURE 1

FIGURE 1. Example of MCSCF 3d- and 4s-derived molecular orbitals of the Ni₂ molecule.

All δδ–states were computed using a single reference macroconfiguration,

${\mathrm{\kappa }}_1\left(\mathbf{n}\right)={\left(3\mathrm{d}{\mathrm{\delta }}_{\mathrm{g}}3\mathrm{d}{\mathrm{\delta }}_{\mathrm{u}}^{\ast }3\mathrm{d}{\mathrm{\delta }}_{\mathrm{g}}3\mathrm{d}{\mathrm{\delta }}_{\mathrm{u}}^{\ast }\right)}^6{\left(4\mathrm{s}{\mathrm{\sigma }}_{\mathrm{g}}4\mathrm{s}{\mathrm{\sigma }}_{\mathrm{u}}^{\ast }\right)}^2(5)$

where the superscripts denote the number of electrons in each orbital group. The semi-core 3s3p electrons were correlated together with those derived from 3d_z2, 3d_xz and 3d_yz at the GVVPT2 level. For four of the computed δδ–states, additional calculations were also performed in which the 3s3p were kept doubly occupied throughout (i.e., at both the MCSCF and GVVPT2 levels). When using the cc-pVTZ basis set, (Balabanov and Peterson, 2005) reference κ₁(n) generated 8 model and 27,891,120 total CSFs (in D_2h symmetry) for the 1 ³Σ_u⁺ and 1 ³Γ_u states; 8 model and 15,290,666 total space CSFs for the 1¹Σ_u⁻, 1¹Σ_g⁻, and 1¹Γ_u states; 10 model and 27,982,592 all space CSFs for the 1³Σ_g^- and 1³Σ_u^- states; and 12 model versus 15,270,687 all space CSFs for the X ¹Γ_g and 1 ¹Σ_g⁺ states. Without correlating the 3s3p electrons at the GVVPT2 level, the dimensions were: 12 model space CSFs versus 3,593,707 total CSFs for the X ¹Γ_g and 1 ¹Σ_g⁺ states; and 8 model versus 6,434,550 all space CSFs for the 1³Σ_u⁺ and 1³Γ_u states. Relativistic calculations on the X ¹Γ_g and 1 ¹Σ_g⁺ states utilized the same reference macroconfiguration, κ₁(n). A $\mathrm{\delta \delta }$³Γ_u state was computed with 4 active electrons in 4 orbitals using reference

${\mathrm{\kappa }}_2\left(\mathbf{n}\right)={\left(3{\mathrm{d}}_{{\mathrm{x}}^2-{\mathrm{y}}^2}{\mathrm{\delta }}_{\mathrm{g}}3{\mathrm{d}}_{{\mathrm{x}}^2-{\mathrm{y}}^2}{\mathrm{\delta }}_{\mathrm{u}}^{\ast }\right)}^6{\left(4\mathrm{s}{\mathrm{\sigma }}_{\mathrm{g}}4\mathrm{s}{\mathrm{\sigma }}_{\mathrm{u}}^{\ast }\right)}^2(6)$

which gave rise to 4 model space and 7,518,688 all space CSFs, using the cc-pVTZ basis set. The ππ–states were computed using reference

${\mathrm{\kappa }}_3\left(\mathbf{n}\right)={\left(3\mathrm{d}{\mathrm{\pi }}_{\mathrm{u}}3\mathrm{d}{\mathrm{\pi }}_{\mathrm{g}}^{\ast }3\mathrm{d}{\mathrm{\pi }}_{\mathrm{u}}3\mathrm{d}{\mathrm{\pi }}_{\mathrm{g}}^{\ast }\right)}^6{\left(4\mathrm{s}{\mathrm{\sigma }}_{\mathrm{g}}4\mathrm{s}{\mathrm{\sigma }}_{\mathrm{u}}^{\ast }\right)}^2(7)$

which is similar to κ₁(n) but with delta replaced with pi orbitals. This macroconfiguration gave rise to 12 model space and 15,267,629 all space CSFs for the 1¹Δ_g and 2¹Σ_g⁺ states when using the cc-pVTZ basis set and D_2h molecular space symmetry. The δπ–states were computed from

${\mathrm{\kappa }}_4\left(\mathbf{n}\right)={\left(3\mathrm{d}{\mathrm{\delta }}_{\mathrm{g}}3\mathrm{d}{\mathrm{\delta }}_{\mathrm{u}}^{\mathrm{\ast }}3\mathrm{d}{\mathrm{\delta }}_{\mathrm{g}}3\mathrm{d}{\mathrm{\delta }}_{\mathrm{u}}^{\mathrm{\ast }}\right)}^7{\left(3\mathrm{d}{\mathrm{\pi }}_{\mathrm{u}}3\mathrm{d}{\mathrm{\pi }}_{\mathrm{g}}^{\mathrm{\ast }}3\mathrm{d}{\mathrm{\pi }}_{\mathrm{u}}3\mathrm{d}{\mathrm{\pi }}_{\mathrm{g}}^{\mathrm{\ast }}\right)}^7{\left(4\mathrm{s}{\mathrm{\sigma }}_{\mathrm{g}}4\mathrm{s}{\mathrm{\sigma }}_{\mathrm{u}}^{\mathrm{\ast }}\right)}^2(8)$

κ₄(n) generated 16 model space and 27,178,852 total space CSFs for the 1¹Φ_g and 1¹Π_g states versus 20 model and 50,736,846 all space CSFs for the 1³Φ_g and 1³Π_g states, when using the cc-pVTZ basis set.

Within the ³F₄ + ³F₄ manifold, the 3¹Σ_g⁺, 1³Σ_g⁺, 2 ³Σ_g⁺, 1³Δ_u, and 2 ³Σ_u⁺ δπ–states were computed using

${\mathrm{\kappa }}_5\left(\mathbf{n}\right)={\left(3\mathrm{d}{\mathrm{\delta }}_{\mathrm{g}}3\mathrm{d}{\mathrm{\delta }}_{\mathrm{u}}^{\mathrm{\ast }}3\mathrm{d}{\mathrm{\delta }}_{\mathrm{g}}3\mathrm{d}{\mathrm{\delta }}_{\mathrm{u}}^{\mathrm{\ast }}\right)}^6{\left(3\mathrm{d}{\mathrm{\pi }}_{\mathrm{u}}3\mathrm{d}{\mathrm{\pi }}_{\mathrm{g}}^{\mathrm{\ast }}3\mathrm{d}{\mathrm{\pi }}_{\mathrm{u}}3\mathrm{d}{\mathrm{\pi }}_{\mathrm{g}}^{\mathrm{\ast }}\right)}^6(9)$

In these calculations, the 3s, 3p, 3d_z2, and 4s electrons were kept doubly occupied at the MCSCF level but correlated at the GVVPT2 level of theory. Reference κ₅(n) resulted in 40 model versus 55,053,638 total CSFs for the 3¹Σ_g⁺ state; 36 model and 103,306,512 all space CSFs for the 1³Σ_g⁺ and 2 ³Σ_g⁺ states; and 40 model versus 103,312,902 all space CSFs for the 1³Δ_u and 2 ³Σ_u⁺ states when using the cc-pVTZ basis set.

Two δπ–states, 2 ¹Γ_g and 2 ¹Δ_g, were computed within the ³F₄ + ³F₄ manifold using

${\mathrm{\kappa }}_6\left(\mathbf{n}\right)={\left(3\mathrm{d}{\mathrm{\delta }}_{\mathrm{g}}3\mathrm{d}{\mathrm{\delta }}_{\mathrm{u}}^{\mathrm{\ast }}3\mathrm{d}{\mathrm{\delta }}_{\mathrm{g}}3\mathrm{d}{\mathrm{\delta }}_{\mathrm{u}}^{\mathrm{\ast }}\right)}^6{\left(3\mathrm{d}{\mathrm{\sigma }}_{\mathrm{g}}3\mathrm{d}{\mathrm{\sigma }}_{\mathrm{u}}^{\mathrm{\ast }}\right)}^2(10)$

Reference κ₆(n) generated 12 model space and 15,270,687 all space CSFs for the computed states using the cc-pVTZ basis set. Two quintet δπσ–states (i.e., 1⁵Φ_u and 1⁵Π_u) were also computed within the ³F₄ + ³F₄ manifold, using

${\mathrm{\kappa }}_7\left(\mathbf{n}\right)={\left(3\mathrm{d}{\mathrm{\delta }}_{\mathrm{g}}3\mathrm{d}{\mathrm{\delta }}_{\mathrm{u}}^{\mathrm{\ast }}3\mathrm{d}{\mathrm{\delta }}_{\mathrm{g}}3\mathrm{d}{\mathrm{\delta }}_{\mathrm{u}}^{\mathrm{\ast }}\right)}^6{\left(3\mathrm{d}{\mathrm{\pi }}_{\mathrm{u}}3\mathrm{d}{\mathrm{\pi }}_{\mathrm{g}}^{\mathrm{\ast }}3\mathrm{d}{\mathrm{\pi }}_{\mathrm{u}}3\mathrm{d}{\mathrm{\pi }}_{\mathrm{g}}^{\mathrm{\ast }}\right)}^7{\left(3\mathrm{d}{\mathrm{\sigma }}_{\mathrm{g}}3\mathrm{d}{\mathrm{\sigma }}_{\mathrm{u}}^{\mathrm{\ast }}\right)}^3(11)$

This reference, κ₇(n), led to 12 model versus 69,738,914 total CSFs for the computed quintet states. Lastly, a limited study was done on two quintet states within the ³D₃(3d⁹4s¹) + ³F₄(3d⁸4s²) manifold at short bond lengths. While reference

${\mathrm{\kappa }}_8\left(\mathbf{n}\right)={\left(3\mathrm{d}{\mathrm{\delta }}_{\mathrm{g}}3\mathrm{d}{\mathrm{\delta }}_{\mathrm{u}}^{\mathrm{\ast }}3\mathrm{d}{\mathrm{\delta }}_{\mathrm{g}}3\mathrm{d}{\mathrm{\delta }}_{\mathrm{u}}^{\mathrm{\ast }}\right)}^7{\left(3\mathrm{d}{\mathrm{\pi }}_{\mathrm{u}}3\mathrm{d}{\mathrm{\pi }}_{\mathrm{g}}^{\mathrm{\ast }}3\mathrm{d}{\mathrm{\pi }}_{\mathrm{u}}3\mathrm{d}{\mathrm{\pi }}_{\mathrm{g}}^{\mathrm{\ast }}\right)}^6{\left(4\mathrm{s}{\mathrm{\sigma }}_{\mathrm{g}}4\mathrm{s}{\mathrm{\sigma }}_{\mathrm{u}}^{\mathrm{\ast }}\right)}^3(12)$

can describe the 1⁵Δ_g and 2 ⁵Δ_g δπσ–states resulting from the ³D₃(3d⁹4s¹) + ³F₄(3d⁸4s²) manifold of molecular states adequately at short internuclear distances, it cannot be expected to do so at long internuclear distances and our studies were restricted to the shorter bond lengths for these two states. Reference κ₈(n) generated 12 model CSFs versus 69,740,135 total space CSFs.

The reference macroconfigurations described above were used to define the active space, while all lower energy MOs were doubly occupied in MCSCF calculations. Initial MOs for MCSCF calculations were obtained from approximate natural orbitals of second-order restricted Møller−Plesset perturbation (RMP2) calculations from a closed-shell Hartree−Fock (HF) reference. At the GVVPT2 level, 3s, 3p, and all 3d and/or 4s electrons were correlated whether they were or were not at the MCSCF level. For comparison purposes, a few of the GVVPT2 calculations were performed without correlating the 3s and 3p electrons. Calculations that accounted for scalar relativistic effects employed the sf-X2C method described above. Finally, to aid in interpretation, the effective bond order (EBO) was computed, and used the following expression

$\eta = \frac{{\displaystyle \sum _i{\chi }_i{c}_i^2}}{{\displaystyle \sum _i{c}_i^2}}(13)$

where η is the EBO, χ_i is the EBO for the ith CSF, while c_i² is its corresponding weight. For each CSF used to estimate EBO, χ_i was determined as

${\chi }_i= \frac{1}{2 }\left(n_{\mathrm{b}}- n_{\mathrm{ab}}\right)(14)$

where n_b and n_ab are the numbers of bonding and antibonding electrons, respectively. Vibrational frequencies were obtained by 3-point finite differencing near the minima of the curves.

Results and Discussion

Where indicated, the letter “R” in parentheses following a molecular term denotes that scalar relativistic effects were included in the calculations, while the expression “no 3s3p” in parentheses after a molecular term symbol denotes that 3s and 3p electrons were not correlated in GVVPT2 calculations.

The δδ–Hole States

PECs of the δδ–hole states are shown in Figure 2 and the data describing them are in Table 1. In agreement with results from other high level ab initio methods, the lowest states of Ni₂ were found to be δδ–hole states of the ³D₃ (3d⁹4s¹) + ³D₃ (3d⁹4s¹) manifold. In particular, the ground state was found to be X ¹Γ_g, with the 1¹Σ_g⁺ state lying only 16.40 cm⁻¹ (0.002 eV) higher at the equilibrium geometry. After including scalar relativistic effects, the energy gap between these states slightly increased to 23.39 cm⁻¹ at equilibrium, with the X ¹Γ_g term having spectroscopic constants: R_e = 2.20 Å, D_e = 1.95 eV, and ω_e = 296 cm⁻¹. These results are in good agreement with experimental data (R_e = 2.1545 ± 0.0004 Å, (Cooper et al., 1972) $D_0^o$ = 2.042 ± 0.002 eV, (Cooper et al., 1972) and ω_e = 280 ± 20 cm⁻¹) (Rösch and Rhodin 1974) and with the relativistic CASSCF/CASPT2 results of Pou‐Amérigo et al. (Pou‐Amérigo et al., 1994) who also found the lowest ¹Γ_g and ¹Σ_g⁺ terms to be quasidegenerate (with R_e = 2.23 Å, D_e = 2.06 eV, and ω_e = 293 cm⁻¹ for the ¹Γ_g term). These results are also in good agreement with the time-delayed resonant two-photon ionization study of Morse and co-workers (Pinegar et al., 1995) that predicted either a ³Γ_u or ¹Γ_g state as the ground state of Ni₂ and the scalar relativistic calculations of Cheskidov et al. (Cheskidov et al., 2012) who found the lowest ¹Γ_g and ¹Σ_g⁺ terms to be degenerate at the ACPF and NEVPT2 levels of theory and the ¹Σ_g⁺ term to lie very slightly lower than the ¹Γ_g at the AQCC, MRCI, and MRCI + Q levels of theory. At 2.25 Å, we found the EBO to be 0.963 and 0.960 for the ¹Γ_g and ¹Σ_g⁺ states, respectively (using the largest dozen CSFs). In relativistic GVVPT2 calculations, these EBOs increased slightly to 0.975 for ¹Γ_g and 0.972 for ¹Σ_g⁺ at this geometry. The major configurations describing the X ¹Γ_g and 1¹Σ_g⁺ states involved two holes in the same δ–type; i.e., 0.445 × (3d_xyδ_g² 3d_xyδ_u^∗2 3d_x2-y2δ_g² 4sσ_g² + 3d_xyδ_g² 3d_x2-y2δ_g² 3d_x2-y2δ_u^∗2 4sσ_g²) and 0.077 × (3d_xyδ_g² 3d_xyδ_u^∗2 3d_x2-y2δ_u^∗2 4sσ_u^∗2 - 3d_xyδ_u^∗2 3d_x2-y2δ_g² 3d_x2-y2δ_u^∗2 4sσ_u^∗2), where coefficients are amplitudes and each term within parentheses denotes active orbitals of each leading CSF of the GVVPT2 wavefunction.

FIGURE 2

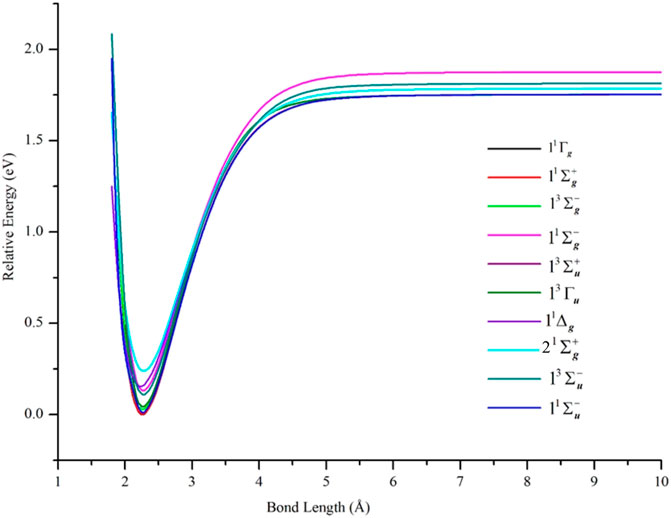
FIGURE 2. PECs of low-lying electronic states of Ni₂ computed at the GVVPT2 level of theory using the cc-pVTZ basis set. All energies are plotted relative to the lowest energy value of the ground X ¹Γ_g term. For all states, the holes are in the 3d delta orbitals (δδ–holes) except for 1¹Δ_g and 2 ¹Σ_g⁺ states which are ππ–hole states.

TABLE 1

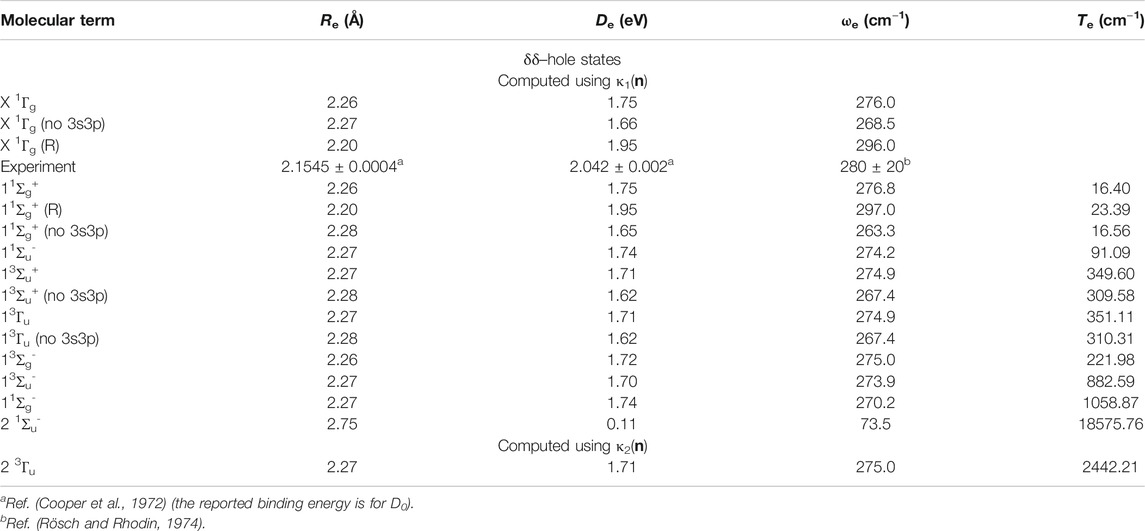
TABLE 1. Equilibrium bond lengths, R_e (Å), binding energies, D_e (eV), harmonic frequencies, ω_e (cm⁻¹), and adiabatic transition energies, T_e (cm⁻¹), of electronic states of Ni₂ calculated at the GVVPT2 level of theory using the cc-pVTZ basis set (or cc-pVTZ-DK for scalar relativistic calculations).

The semi-core 3s3p electrons were found to be important in the description of low-lying states of Ni₂. The inclusion of 3s3p electron correlation at the GVVPT2 level increased the binding energies by 0.09 eV for X ¹Γ_g, 0.10 eV for 1¹Σ_g⁺, and 0.09 eV for 1³Σ_u⁺ and 1³Γ_u states in non-relativistic calculations. As can be seen in Figure 3 and Table 1, the effects of the 3s3p electrons on the equilibrium bond lengths and harmonic frequencies for these states are minimal whereas inclusion of such core-valence correlation raises, for example, the binding energy of X ¹Γ_g from 1.66 to 1.75 eV compared to a reference D₀ value of 2.042 ± 0.002 eV (Cooper et al., 1972). Scalar relativistic effects shortened the bond length of X ¹Γ_g by 0.06 Å and further increased the bond energy by 0.20 to 1.95 eV which agreed even better with the reference experimental values (see Figure 4 and Table 1). The 3s3p electrons did not have any effect on the EBOs of X ¹Γ_g and 1¹Σ_g⁺; the EBOs were determined as 0.962 and 0.959 at 2.27 Å for X ¹Γ_g and 1¹Σ_g⁺, respectively, when the 3s3p electrons were not correlated compared to 0.963 vs. 0.960 when the semi-core electrons (3s3p) were correlated. Note the quasidegeneracy in the X ¹Γ_g and 1¹Σ_g⁺ states. For example, in Figure 4, the blue and green curves for the X ¹Γ_g and 1¹Σ_g⁺ states, respectively, lie on top of each other (only the green is visible). Also, the black and red curves for the X ¹Γ_g (R) and 1¹Σ_g⁺ (R) states lie on each other (only the red curve is visible).

FIGURE 3

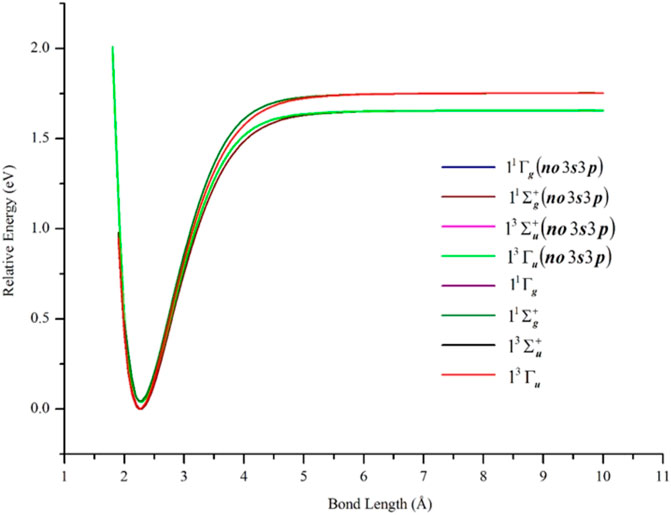
FIGURE 3. PECs of low-lying δδ–hole electronic states of Ni₂ computed at the GVVPT2 level of theory, with and without the correlation of 3s3p semi-core electrons, using the cc-pVTZ basis set. All energies are plotted relative to the lowest energy value of the ground X ¹Γ_g term.

FIGURE 4

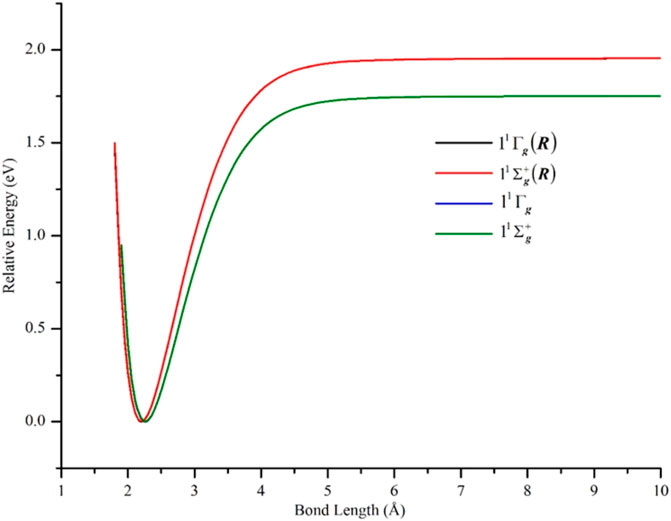
FIGURE 4. PECs of the lowest-lying δδ–hole X ¹Γ_g and 1¹Σ_g⁺ states of Ni₂ computed at the GVVPT2 level of theory, with and without scalar relativity included, using the cc-pVTZ (or cc-pVTZ-DK) basis set. Non-relativistic energies are plotted relative to the lowest energy value of the ground X ¹Γ_g term while relativistic energies are plotted relative to the lowest energy of the X ¹Γ_g (R) term.

The 1¹Σ_u^- state, which was predicted as the ground state of Ni₂ at the ACPF level of theory (Cheskidov et al., 2012) and found to lie quite close to a ¹Σ_g⁺ ground state in a limited CI study (Ahmed and Nixon, 1979), was found at the GVVPT2 level to lie 91.09 cm⁻¹ above the X ¹Γ_g state at equilibrium. The 2¹Σ_u^- state, however, lay much higher energetically (18,575.76 cm⁻¹ above the ground state at equilibrium).

As can be seen in Table 1, GVVPT2 predicted the triplet δδ–hole states, 1³Σ_g^-, 1³Σ_u⁺, and 1³Γ_u, to lie energetically in the order 1³Σ_g^-< 1³Σ_u⁺ < 1³Γ_u. Cheskidov et al. (Cheskidov et al., 2012) found this same ordering at the ACPF, AQCC, MRCI and MRCI + Q levels of theory, whereas their NEVPT2 calculations predicted the ordering 1³Σ_u⁺ < 1³Γ_u < 1³Σ_g^-, with the 1³Σ_g^- state lying at least 139 cm⁻¹ higher than the other two states. It should be noted that the vertical excitation energies in Ref. (Cheskidov et al., 2012) were not determined at the equilibrium geometries of the computed states. The 1³Σ_u⁺ state, which was predicted as the ground state of Ni₂ in some previous wavefunction (Wood et al., 1980; Schultz et al., 2005) and DFT (Diaconu et al., 2004; Kramida et al., 2013) studies, was found in our current study to lie 349.60 cm⁻¹ above the X ¹Γ_g state at the equilibrium geometry. Likewise, the 1³Σ_g^- state reported in other studies (Murphy and Messmer, 1992; Diaconu et al., 2004; Kramida et al., 2013) as the ground state of Ni₂ lay 221.98 cm⁻¹ higher at equilibrium. The 1³Σ_u^- state was found to have a bond length and bond energy comparable to those of 1³Σ_g^-, 1³Σ_u⁺, and 1³Γ_u but lying at least 531.48 cm⁻¹ higher in energy. The EBOs for these triplet states were 0.971 for 1³Σ_g^-, 0.933 for 1³Σ_u⁺ and 1³Γ_u, and 0.923 for 1³Σ_u^- in the vicinity of their equilibrium geometries (again computed with 10 leading CSFs). The major configurations for the δδ–hole triplet states involved a doubly occupied 4sσ_g bonding orbital.

The 1³Γ_u state, in which both δ–holes were in the 3d_x2-y2 δ_g and δ_u^∗ orbitals, was computed using reference κ₂(n). As can be seen in Table 1, this state was found to have spectroscopic constants comparable to other δδ–hole triplet states but lay much higher energetically (2442.21 cm⁻¹ above the ground state at equilibrium). The present results suggest that the 3dδ orbitals are indeed split in the bonding interaction. Since they are nondegenerate, the Aufbau principle suggests that energetically low-lying orbitals (the bonding 3dδ orbitals) be occupied before higher ones. Moreover, Hund’s rule suggests that orbitals with similar energies (in this case, 3dδ_u^∗ orbitals) be singly occupied before electron pairing occurs. This seems to bring qualitative understanding into why the 1³Σ_g^-, 1³Σ_u⁺, and 1³Γ_u states in which the 3d_x2-y2δ_u^∗ and 3d_xyδ_u^∗ are singly occupied lie energetically lower than the 2 ³Γ_u state for which the 3d_x2-y2δ_g and 3d_x2-y2δ_u^∗ are singly occupied.

The δπ–Hole and ππ–Hole States

The PECs of the computed ππ–hole states (1¹Δ_g and 2¹Σ_g⁺) are shown in Figure 2, while those for the δπ–hole states (1¹Φ_g, 1¹Π_g, 1³Π_g, and 1³Φ_g) are shown in Figure 5 and compared with the ground state PEC. The data describing these curves are in Table 2. GVVPT2 predicted the ππ–hole states to lie higher in energy than the δπ–hole states, in agreement with previous studies (Ahmed and Nixon, 1979; Rasanen et al., 1987; Russo et al., 1994). For all four δπ–hole states studied, the major CSFs involved a doubly occupied 4sσ_g bonding orbital. Thus, the main configurations of the 1¹Φ_g and 1¹Π_g states involved an unpaired spin-increasing electron in the 3dδ subspace and an unpaired spin-decreasing electron in the 3dπ subspace, e.g., 3dδ_g² 3dδ_u^∗2 3dδ_g² 3dδ_u^∗(↑) 3dπ_u² 3dπ_g^∗2 3dπ_u² 3dπ_g^∗(↓) 4sσ_g², whereas the major configurations of the 1³Φ_g and 1³Π_g states were similar to those of the corresponding singlet states but with two unpaired spin-increasing electrons: one in each of the 3dδ and 3dπ subspaces, e.g., 3dδ_g² 3dδ_u^∗2 3dδ_g² 3dδ_u^∗(↑) 3dπ_u² 3dπ_g^∗2 3dπ_u² 3dπ_g^∗(↑) 4sσ_g².

FIGURE 5

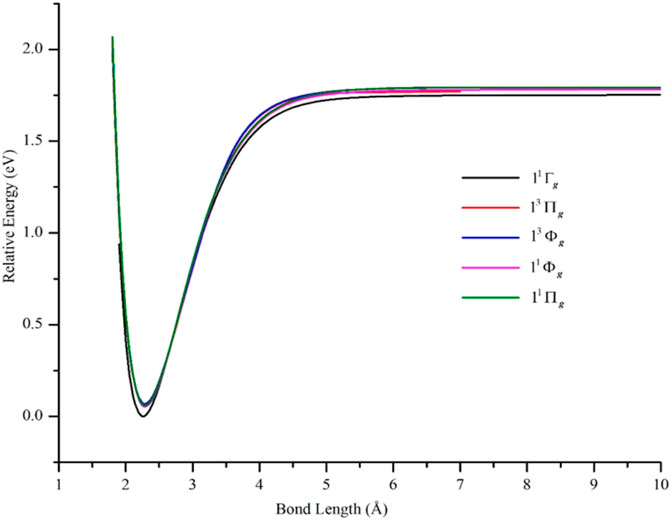
FIGURE 5. PECs of low-lying δπ–hole electronic states of Ni₂ computed at the GVVPT2 level of theory using the cc-pVTZ basis set compared with the PEC of the X ¹Γ_g ground term. All energies are plotted relative to the lowest energy value of the X ¹Γ_g ground term.

TABLE 2

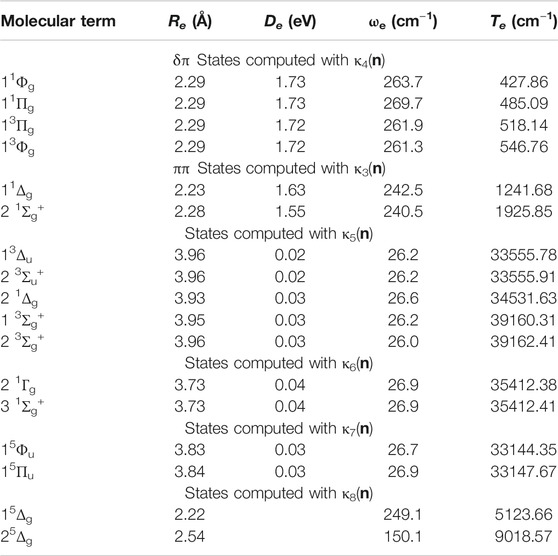
TABLE 2. Equilibrium bond lengths, R_e (Å), binding energies, D_e (eV), harmonic frequencies, ω_e (cm⁻¹), and adiabatic transition energies, T_e (cm⁻¹), of electronic states of Ni₂ calculated at the GVVPT2 level of theory using the cc-pVTZ basis set and reference macroconfigurations κ₃(n) to κ₈(n).

At the equilibrium geometries, the EBOs were 0.930 for the singlet 1¹Φ_g and 1¹Π_g states and 0.933 for the 1³Π_g and 1³Φ_g states. GVVPT2 predicted the four δπ–hole states to lie energetically in the order 1¹Φ_g < 1¹Π_g < 1³Π_g < 1³Φ_g, in agreement with the Ref. (Cheskidov et al., 2012) study at the scalar relativistic ACPF, AQCC, MRCI, and MRCI + Q levels of theory. However, our calculations found all three states considered in Ref. (Cheskidov et al., 2012) (i.e., 1¹Π_g, 1³Π_g, and 1³Φ_g) to lie some 500 cm⁻¹ closer to the ground state; e.g., at the scalar relativistic MRCI + Q level, the 1³Φ_g state was reported (Cheskidov et al., 2012) as lying 1238 cm⁻¹ above the ground state at 2.5 Å while non-relativistic GVVPT2 calculations predicted this state to lie 546.76 cm⁻¹ above the ground state at equilibrium. Based on our observation that including scalar relativistic effects increased the energy gap between the 1¹Σ_g⁺ and X ¹Γ_g states, it is likely that including such effects in GVVPT2 calculations on the δπ–hole states might lead to increases in corresponding adiabatic transition energies. It is not anticipated, however, that such effects would lead to any change in the energy ordering of the states.

Although lying higher in energy than the δπ–hole states, the ππ–hole states were found to have slightly shorter bond lengths and larger bond strengths than the δπ–hole states. The 1 ¹Δ_g state was 0.06 Å shorter while the 2 ¹Σ_g⁺ state was 0.01 Å shorter in bond length than the δπ–hole states. At 2.24 Å, the EBOs of 1 ¹Δ_g and 2 ¹Σ_g⁺ were 1.108 and 1.084 respectively (computed with a dozen CSFs); these were slightly higher than the EBOs of all computed δδ–hole and δπ–hole Ni₂ states. Near equilibrium, the major configurations of these ππ–hole states involved a doubly occupied 4sσ_g bonding orbital and a configuration of the 3dπ subspace that had the two π–holes in the same π–orbital; e.g., 3dπ_u² 3dπ_g^∗2 3dπ_u² 3dπ_g^∗0 4sσ_g².

States of the ³F₄ + ³F₄ and ³F₄ + ³D₃ Manifolds

Figure 6 contains PECs of states belonging to the ³F₄ + ³F₄ manifold. The data describing these curves are in Table 2. Irrespective of how the model space was partitioned into macroconfigurations [i.e., κ_i(n)], all such states were found to be van der Waals-like with interaction energies ≤0.04 eV. For example, near the equilibrium geometry (i.e., 3.77 Å), the 2 ¹Γ_g and 3 ¹Σ_g⁺ states had EBO of only 0.005, while the 1⁵Φ_u and 1⁵Π_u states had EBOs of 0.003 and 0.00, respectively, at 3.84 Å. These latter quintet states were computed using reference κ₇(n) and found to have the lowest total energies among the computed states of the ³F₄ + ³F₄ manifold; the 1⁵Π_u state is 3.312 cm⁻¹ less stable than the 1⁵Φ_u state at equilibrium. The rest of the PECs in Figure 6 were plotted relative to the 1⁵Φ_u PEC.

FIGURE 6

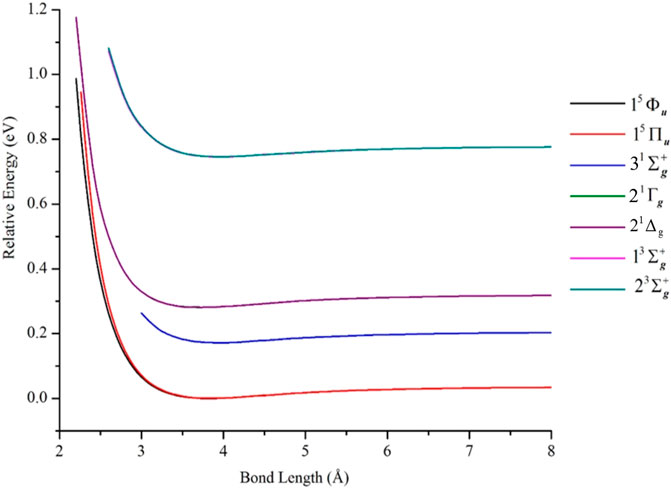
FIGURE 6. PECs of electronic states of Ni₂ from the ³F₄ (3d⁸4s²) + ³F₄ (3d⁸4s²) manifold, computed at the GVVPT2 level of theory using the cc-pVTZ basis set and reference macroconfigurations κ₅(n) to κ₇(n). All energies are plotted relative to the lowest energy value of the 1⁵Φ_u term.

Lastly, the 1⁵Δ_g and 2 ⁵Δ_g states of the ³F₄ + ³D₃ manifold were investigated, at short bond lengths only, using reference macroconfiguration κ₈(n). The data for these states are included in Table 2. Whereas the ³F₄ (3d⁸4s²) + ³F₄ (3d⁸4s²) states are van der Waals-like, the short bond length (2.22 Å) and high frequency (249.1 cm⁻¹) of the 1⁵Δ_g state is suggestive of significant bonding interaction. At 2.22 Å, the major configuration for this state was 3d_x2-y2δ_g² 3d_x2-y2δ_u^∗2 3d_xyδ_g² 3d_xyδ_u^∗1 3dπ_u² 3dπ_g^∗1 3dπ_u² 3dπ_g^∗1 4sσ_g² 4sσ_u^∗1, contributing 50% by weight to the total wave function. At this geometry, the EBO was found to be 1.186. However, one should approach these results for ³F₄ + ³D₃ derived states with some caution, as the macroconfiguration used cannot describe their dissociation limits.

Conclusion

The GVVPT2 method was used to study low-lying electronic states of Ni₂. The results indicate, in general, that bonding in these states involves predominantly the doubly occupied 4sσ_g bonding orbital with the 3d–3d electrons pairwise spin coupled (e.g., consistent with antiferromagnetism). This statement is corroborated by EBOs that were found to be approximately 1.0 for most states studied and, moreover, states that did not allow this type of interaction [e.g., belonging to the ³F₄ (3d⁸4s²) + ³F₄ (3d⁸4s²) manifold] were found to be bound only by weak polarization forces with bond orders close to zero. For computed states of the ³D₃ (3d⁹4s¹) + ³D₃ (3d⁹4s¹) dissociation limit, all major configurations involved a doubly occupied 4sσ_g bonding orbital and a vacant 4sσ_u^∗ antibonding orbital. The energy ordering of the computed states of the ³D₃ (3d⁹4s¹) + ³D₃ (3d⁹4s¹) manifold is in agreement with previous studies that found the δδ–hole states to lie lowest in energy followed by the δπ–hole and then the ππ–hole states (Rasanen et al., 1987). For the investigated δδ–hole states, the singlets were more stable than the triplet states at the GVVPT2 level of theory. As expected, based on previous GVVPT2 studies of transition metal dimers, all computed PECs are smooth and without unphysical artifacts (e.g., wiggles).

The ground state of Ni₂ was predicted as X ¹Γ_g in agreement with previous results from other high level ab initio methods (Cheskidov et al., 2012; Pou-Amérigo et al., 1994). The determined equilibrium spectroscopic constants of the X ¹Γ_g state, using a cc-pVTZ (or cc-pVTZ-DK) basis, were within the uncertainties of experimental results. The lowest ¹Σ_g⁺ state was found to be only 0.002 eV (16.40 cm⁻¹) higher than the ground state at the equilibrium geometry. Core-valence correlation was found to be important in the description of low-lying states of Ni₂ where the inclusion of 3s3p electron correlation at the GVVPT2 level was shown to improve harmonic frequencies and bond energies (e.g., by an increase of 7.5 cm⁻¹ in frequency and 0.09 eV in bond energy when 3s3p electron correlation was included in GVVPT2 calculations of the X ¹Γ_g state). Scalar relativistic effects were also shown to be important, especially for dissociation energy, where spectroscopic constants from relativistic calculations were predicted to agree better with reference data (e.g., a decrease of 0.06 Å in bond length, increase of 0.20 eV in bond energy, and an increase of 20.0 cm⁻¹ in harmonic frequency when including scalar relativistic effects in calculations of the X ¹Γ_g state). In our previous study (Tamukong et al., 2014) on electronic states of Y₂, Mn₂, and Tc₂, we did not find scalar relativistic effects to be as important for the Mn₂ molecule as they have proven to be in the present study. The inclusion of spin-orbit coupling effects was previously found (Cheskidov et al., 2012; Rasanen et al., 1987; Pou-Amérigo et al., 1994) to mix the low-lying states of Ni₂, leading to a 0_g⁺[¹Σ_g⁺(δδ) + ³Σ_g^-(δδ)] ground state. Since the two curves are close and nearly parallel for all internuclear separations in our study, we expect that including such effects after our scalar relativistic GVVPT2 treatment should lead to a similar mixing of states (i.e., and without change in spectroscopic constants).

The states investigated within the ³F₄ (3d⁸4s²) + ³D₃ (3d⁹4s¹) manifold suggested significant bonding interaction, giving large harmonic frequencies and short bond lengths in comparison with states correlating with the ³F₄ (3d⁸4s²) + ³F₄ (3d⁸4s²) dissociation limit. Further work on Ni₂ should explore the ³F₄ (3d⁸4s²) + ³D₃ (3d⁹4s¹) manifold more thoroughly, including possible expansion of the active space. It should be noted, however, that in the present study, we did not observe any significant electron excitations from the valence orbitals to 4p-dominated virtual orbitals. Also, while spin-free relativistic effects are noticeable (especially for bond dissociation energies), the parallelity and small energy separations for states in these manifolds are very similar to those in the ³D₃ (3d⁹4s¹) + ³D₃ (3d⁹4s¹) dissociation channel and, again, we do not expect that spin-dependent relativistic effects would change PECs appreciably, although current capabilities of our GVVPT2 code did not let us explore this.

In summary, the present study showed that Ni₂ does not form strong bonds with atomic configurations in which the 4s subshell is fully filled. This observation is consistent with other studies, by us and by others, of transition elements of the first row. Bonding in these systems is generally favored by atomic configurations that involve at least one of the participating atoms in an excited state (3dⁿ⁺¹4s¹). For example, in our previous study (Tamukong et al., 2012) of the low-lying electronic states of Sc₂, Cr₂, and Mn₂, the lowest states of Sc₂ were shown to correlate with the ²D (3d¹4s²) + ⁴F (3d²4s¹) dissociation asymptote, while those of Cr₂ correlated with the ⁷S (3d⁵4s¹) + ⁷S (3d⁵4s¹) dissociation limit. However, bonding in transition metal dimers is subtle and the most stable states of Mn₂ were obtained from weakly coupled ⁵D (3d⁵4s²) + ⁵D (3d⁵4s²) ground state Mn atoms, similar to the ³F₄ (3d⁸4s²) + ³F₄ (3d⁸4s²) coupling of ground state Ni atoms. Our results provide further evidence that GVVPT2, with sf-X2C treatment of relativistic effects, predict electronic excitation and bond energy trends in the first row transition metals consistent with experiment and the highest level ab initio calculations. In the present case, the quasidegeneracy of the ³F and ³D states of the Ni atom demonstrates that GVVPT2 can successfully be used for a system with an extraordinarily dense manifold of states, which generally requires computationally intensive variational treatments.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

MH and PT contributed to conception and design of the study. PT performed numerical calculations. MH and PT interpreted data and organized presentation. PT wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

The authors gratefully acknowledge the National Science Foundation (Grant No. EPS 0814442) for the financial support under which the project was started, and to North Dakota EPSCoR for support in later stages.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ahmed, F., and Nixon, E. R. (1979). The A→X System of Ni2 in Argon Matrices. J. Chem. Phys. 71 (8), 3547–3549. doi:10.1063/1.438750

CrossRef Full Text | Google Scholar

Andersson, K., and Roos, B. O. (1992). Excitation Energies in the Nickel Atom Studied with the Complete Active Space Scf Method and Second-Order Perturbation Theory. Chem. Phys. Lett. 191 (6), 507–514. doi:10.1016/0009-2614(92)85581-t

CrossRef Full Text | Google Scholar

Angeli, C., Cimiraglia, R., Evangelisti, S., Leininger, T., and Malrieu, J.-P. (2001). Introduction Ofn-Electron Valence States for Multireference Perturbation Theory. J. Chem. Phys. 114 (23), 10252–10264. doi:10.1063/1.1361246

CrossRef Full Text | Google Scholar

Balabanov, N. B., and Peterson, K. A. (2005). Systematically Convergent Basis Sets for Transition Metals. I. All-Electron Correlation Consistent Basis Sets for the 3d Elements Sc–Zn. J. Chem. Phys. 123 (6), 064107. doi:10.1063/1.1998907

CrossRef Full Text | Google Scholar

Basch, H., Newton, M. D., and Moskowitz, J. W. (1980). The Electronic Structure of Small Nickel Atom Clusters. J. Chem. Phys. 73 (9), 4492–4510. doi:10.1063/1.440687

CrossRef Full Text | Google Scholar

Bauschlicher, C. W., Walch, S. P., and Partridge, H. (1982). On Correlation in the First Row Transition Metal Atoms. J. Chem. Phys. 76 (2), 1033–1039. doi:10.1063/1.443095

CrossRef Full Text | Google Scholar

Becke, A. D. (1993). Density‐functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 98 (7), 5648–5652. doi:10.1063/1.464913

CrossRef Full Text | Google Scholar

Cheng, L., and Gauss, J. (2011). Analytic Energy Gradients for the Spin-free Exact Two-Component Theory Using an Exact Block Diagonalization for the One-Electron Dirac Hamiltonian. J. Chem. Phys. 135 (8), 084114. doi:10.1063/1.3624397

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheskidov, A. V., Buchachenko, A. A., and Bezrukov, D. S. (2012). Ab Initio Spin-Orbit Calculations on the Lowest States of the Nickel Dimer. J. Chem. Phys. 136 (21), 214304. doi:10.1063/1.4721624

PubMed Abstract | CrossRef Full Text | Google Scholar

Cooper, W. F., Clarke, G. A., and Hare, C. R. (1972). Molecular Orbital Theory of the Diatomic Molecules of the First Row Transition Metals. J. Phys. Chem. 76 (16), 2268–2273. doi:10.1021/j100660a016

CrossRef Full Text | Google Scholar

De Vore, T. C., Ewing, A., Franzen, H. F., and Calder, V. (1975). The Visible Absorption Spectra of Mn2, Fe2, and Ni2 in Argon Matrices. Chem. Phys. Lett. 35 (1), 78–81. doi:10.1016/0009-2614(75)85592-8

CrossRef Full Text | Google Scholar

Diaconu, C. V., Cho, A. E., Doll, J. D., and Freeman, D. L. (2004). Broken-Symmetry Unrestricted Hybrid Density Functional Calculations on Nickel Dimer and Nickel Hydride. J. Chem. Phys. 121 (20), 10026–10040. doi:10.1063/1.1798992

PubMed Abstract | CrossRef Full Text | Google Scholar

Dolg, M., Wedig, U., Stoll, H., and Preuss, H. (1987). Energy‐adjustedabinitiopseudopotentials for the First Row Transition Elements. J. Chem. Phys. 86 (2), 866–872. doi:10.1063/1.452288

CrossRef Full Text | Google Scholar

Dong, C. D., Lefkidis, G., and Hübner, W. (2013). Quantum Isobaric Process in Ni2. J. Supercond. Nov. Magn. 26 (5), 1589–1594. doi:10.1007/s10948-012-1948-8

CrossRef Full Text | Google Scholar

Du, J., Sun, X., and Wang, H. (2008). The Confirmation of Accurate Combination of Functional and Basis Set for Transition-Metal Dimers: Fe2, Co2, Ni2, Ru2, Rh2, Pd2, Os2, Ir2, and Pt2. Int. J. Quan. Chem. 108 (9), 1505–1517. doi:10.1002/qua.21684

CrossRef Full Text | Google Scholar

Dyall, K. G. (1997). Interfacing Relativistic and Nonrelativistic Methods. I. Normalized Elimination of the Small Component in the Modified Dirac Equation. J. Chem. Phys. 106 (23), 9618–9626. doi:10.1063/1.473860

CrossRef Full Text | Google Scholar

Gdanitz, R. J., and Ahlrichs, R. (1988). The Averaged Coupled-Pair Functional (ACPF): A Size-Extensive Modification of MR CI(SD). Chem. Phys. Lett. 143 (5), 413–420. doi:10.1016/0009-2614(88)87388-3

CrossRef Full Text | Google Scholar

Gutsev, G. L., and Bauschlicher, C. W. (2003). Chemical Bonding, Electron Affinity, and Ionization Energies of the Homonuclear 3d Metal Dimers. J. Phys. Chem. A. 107 (23), 4755–4767. doi:10.1021/jp030146v

CrossRef Full Text | Google Scholar

Harris, J., and Jones, R. O. (1979). Density Functional Theory and Molecular Bonding. III. Iron-Series Dimers. J. Chem. Phys. 70 (2), 830–841. doi:10.1063/1.437516

CrossRef Full Text | Google Scholar

Harrison, J. F. (2000). Electronic Structure of Diatomic Molecules Composed of a First-Row Transition Metal and Main-Group Element (H−F). Chem. Rev. 100 (2), 679–716. doi:10.1021/cr980411m

PubMed Abstract | CrossRef Full Text | Google Scholar

Ho, J., Polak, M. L., Ervin, K. M., and Lineberger, W. C. (1993). Photoelectron Spectroscopy of Nickel Group Dimers: Ni₂^-, Pd₂^-, and Pt₂^-. J. Chem. Phys. 99 (11), 8542–8551. doi:10.1063/1.465577

CrossRef Full Text | Google Scholar

Jiang, W., Khait, Y. G., and Hoffmann, M. R. (2009). Configuration-Driven Unitary Group Approach for Generalized Van Vleck Variant Multireference Perturbation Theory. J. Phys. Chem. A. 113 (16), 4374–4380. doi:10.1021/jp811082p

PubMed Abstract | CrossRef Full Text | Google Scholar

Kamal, C., Banerjee, A., Ghanty, T. K., and Chakrabarti, A. (2012). Interesting Periodic Variations in Physical and Chemical Properties of Homonuclear Diatomic Molecules. Int. J. Quan. Chem. 112 (4), 1097–1106. doi:10.1002/qua.23088

CrossRef Full Text | Google Scholar

Kant, A. (1964). Dissociation Energies of Diatomic Molecules of the Transition Elements. I. Nickel. J. Chem. Phys. 41 (6), 1872–1876. doi:10.1063/1.1726169

CrossRef Full Text | Google Scholar

Khait, Y. G., Song, J., and Hoffmann, M. R. (2002). Explication and Revision of Generalized Van Vleck Perturbation Theory for Molecular Electronic Structure. J. Chem. Phys. 117 (9), 4133–4145. doi:10.1063/1.1497642

CrossRef Full Text | Google Scholar

Khait, Y. G., Song, J., and Hoffmann, M. R. (2004). Macroconfigurations in Molecular Electronic Structure Theory. Int. J. Quan. Chem. 99 (4), 210–220. doi:10.1002/qua.10852

CrossRef Full Text | Google Scholar

Khait, Y. G., Theis, D., and Hoffmann, M. R. (2012). Nonadiabatic Coupling Terms for the GVVPT2 Variant of Multireference Perturbation Theory. Chem. Phys. 401, 88–94. doi:10.1016/j.chemphys.2011.09.014

CrossRef Full Text | Google Scholar

Kramida, A., Ralchenko, Y., and Reader, J. (2013). NIST Atomic Spectra Database (Ver. 5.1) [Online]. Gaithersburg, MD: National Institute of Standards and TechnologyAvailable at: http://physics.nist.gov/asd (Accessed Feb 7, 2014).

Li, Z., Suo, B., Zhang, Y., Xiao, Y., and Liu, W. (2013). Combining Spin-Adapted Open-Shell TD-DFT with Spin-Orbit Coupling. Mol. Phys. 111 (24), 3741–3755. doi:10.1080/00268976.2013.785611

CrossRef Full Text | Google Scholar

Li, Z., Xiao, Y., and Liu, W. (2012). On the Spin Separation of Algebraic Two-Component Relativistic Hamiltonians. J. Chem. Phys. 137 (15), 154114. doi:10.1063/1.4758987

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, W. (2010). Ideas of Relativistic Quantum Chemistry. Mol. Phys. 108 (13), 1679–1706. doi:10.1080/00268971003781571

CrossRef Full Text | Google Scholar

Liu, W. (2014). Advances in Relativistic Molecular Quantum Mechanics. Phys. Rep. 537 (2), 58–89. doi:10.1016/j.physrep.2013.11.006

CrossRef Full Text | Google Scholar

Mbote, Y. E. B., Khait, Y. G., Hardel, C., and Hoffmann, M. R. (2010). Multireference Generalized Van Vleck Perturbation Theory (GVVPT2) Study of the NCO + HCNO Reaction: Insight into Intermediates†. J. Phys. Chem. A. 114 (33), 8831–8836. doi:10.1021/jp102051p

PubMed Abstract | CrossRef Full Text | Google Scholar

Melius, C. F., Moskowitz, J. W., Mortola, A. P., Baillie, M. B., and Ratner, M. A. (1976). A Molecular Complex Model for the Chemisorption of Hydrogen on a Nickel Surface. Surf. Sci. 59 (1), 279–292. doi:10.1016/0039-6028(76)90305-8

CrossRef Full Text | Google Scholar

Mokambe, R. M., Hicks, J. M., Kerker, D., Jiang, W., Theis, D., Chen, Z., et al. (2013). GVVPT2 Multireference Perturbation Theory Study of Selenium Oxides. Mol. Phys. 111 (9-11), 1078–1091. doi:10.1080/00268976.2013.809163

CrossRef Full Text | Google Scholar

Moore, C. E. (1952). Atomic Energy Levels. Natl. Bur. Stand. U.S. Circ. 467.

Google Scholar

Morse, M. D., Hansen, G. P., Langridge‐Smith, P. R. R., Zheng, L. S., Geusic, M. E., Michalopoulos, D. L., et al. (1984). Spectroscopic Studies of the Jet‐cooled Nickel Dimer. J. Chem. Phys. 80 (11), 5400–5405. doi:10.1063/1.446646

CrossRef Full Text | Google Scholar

Murphy, R. B., and Messmer, R. P. (1992). Correlation in First-Row Transition Metal Atoms Using Generalized Mo/ller-Plesset Perturbation Theory. J. Chem. Phys. 97 (7), 4974–4985. doi:10.1063/1.463850

CrossRef Full Text | Google Scholar

Nakatsuji, H. (1979). Cluster Expansion of the Wavefunction. Electron Correlations in Ground and Excited States by Sac (Symmetry-Adapted-Cluster) and Sac Ci Theories. Chem. Phys. Lett. 67 (2), 329–333. doi:10.1016/0009-2614(79)85172-6

CrossRef Full Text | Google Scholar

Noell, J. O., Newton, M. D., Hay, P. J., Martin, R. L., and Bobrowicz, F. W. (1980). An Ab Initio Study of the Bonding in Diatomic Nickel. J. Chem. Phys. 73 (5), 2360–2371. doi:10.1063/1.440386

CrossRef Full Text | Google Scholar

Perdew, J. P. (1986). Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Phys. Rev. B 33 (12), 8822–8824. doi:10.1103/physrevb.33.8822

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77 (18), 3865–3868. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Pinegar, J. C., Langenberg, J. D., Arrington, C. A., Spain, E. M., and Morse, M. D. (1995). Ni2 Revisited: Reassignment of the Ground Electronic State. J. Chem. Phys. 102 (2), 666–674. doi:10.1063/1.469562

CrossRef Full Text | Google Scholar

Pou-Amérigo, R., Merchan, M., Nebot‐Gil, I., Malmqvist, P. Å., and Roos, B. O. (1994). The Chemical Bonds in CuH, Cu₂, NiH, and Ni₂ Studied with Multiconfigurational Second Order Perturbation Theory. J. Chem. Phys. 101 (6), 4893–4902.

Google Scholar

Raghavachari, K., and Trucks, G. W. (1989). Highly Correlated Systems. Excitation Energies of First Row Transition Metals Sc-Cu. J. Chem. Phys. 91 (2), 1062–1065. doi:10.1063/1.457230

CrossRef Full Text | Google Scholar

Rasanen, M., Heimbrook, L. A., and Bondybey, V. E. (1987). Rare Gas Matrix Studies of the Products of Vaporization of Nickel. J. Mol. Struct. 157 (1), 129–140. doi:10.1016/0022-2860(87)87088-6

CrossRef Full Text | Google Scholar

Rösch, N., and Rhodin, T. N. (1974). Bonding of Ethylene to Diatomic Nickel According to a Self-Consistent-Field,Xα, Scattered-Wave Model. Phys. Rev. Lett. 32 (21), 1189–1192. doi:10.1103/physrevlett.32.1189

CrossRef Full Text | Google Scholar

Russo, T. V., Martin, R. L., and Hay, P. J. (1994). Density Functional Calculations on First‐row Transition Metals. J. Chem. Phys. 101 (9), 7729–7737. doi:10.1063/1.468265

CrossRef Full Text | Google Scholar

Schultz, N. E., Zhao, Y., and Truhlar, D. G. (2005). Databases for Transition Element Bonding: Metal−Metal Bond Energies and Bond Lengths and Their Use to Test Hybrid, Hybrid Meta, and Meta Density Functionals and Generalized Gradient Approximations. J. Phys. Chem. A. 109 (19), 4388–4403. doi:10.1021/jp0504468

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi-Ying, Y., and Zheng-He, Z. (2008). Spin Polarization Effect of Ni 2 Molecule. Chin. Phys. B 17 (12), 4498–4503. doi:10.1088/1674-1056/17/12/028

CrossRef Full Text | Google Scholar

Shim, I., Dahl, J. P., and Johansen, H. (1979). Ab Initio Hartree-Fock and Configuration-Interaction Treatment of the Interaction between Two Nickel Atoms. Int. J. Quan. Chem. 15 (3), 311–331. doi:10.1002/qua.560150306

CrossRef Full Text | Google Scholar

Szalay, P. G., and Bartlett, R. J. (1993). Multi-Reference Averaged Quadratic Coupled-Cluster Method: A Size-Extensive Modification of Multi-Reference CI. Chem. Phys. Lett. 214 (5), 481–488. doi:10.1016/0009-2614(93)85670-j

CrossRef Full Text | Google Scholar

Tamukong, P. K., Hoffmann, M. R., Li, Z., and Liu, W. (2014). Relativistic GVVPT2 Multireference Perturbation Theory Description of the Electronic States of Y2and Tc2. J. Phys. Chem. A. 118 (8), 1489–1501. doi:10.1021/jp409426n

PubMed Abstract | CrossRef Full Text | Google Scholar

Tamukong, P. K., Theis, D., Khait, Y. G., and Hoffmann, M. R. (2012). GVVPT2 Multireference Perturbation Theory Description of Diatomic Scandium, Chromium, and Manganese. J. Phys. Chem. A. 116 (18), 4590–4601. doi:10.1021/jp300401u

PubMed Abstract | CrossRef Full Text | Google Scholar

Upton, T. H., and Goddard, W. A. (1978). The Electronic States of Ni2 and Ni2+. J. Am. Chem. Soc. 100 (18), 5659–5668. doi:10.1021/ja00486a014

CrossRef Full Text | Google Scholar

Werner, H.-J., and Knowles, P. J. (1990). A Comparison of Variational and Non-variational Internally Contracted Multiconfiguration-Reference Configuration Interaction Calculations. Theor. Chim. Acta 78 (3), 175–187.

Google Scholar

Wood, C., Doran, M., Hillier, I. H., and Guest, M. F. (1980). Theoretical Study of the Electronic Structure of the Transition Metal Dimers, Sc₂, Cr₂, Mo₂ and Ni₂. Faraday Symp. Chem. Soc. 14, 159–169. doi:10.1039/fs9801400159

CrossRef Full Text | Google Scholar

Yanagisawa, S., Tsuneda, T., and Hirao, K. (2000). An Investigation of Density Functionals: The First-Row Transition Metal Dimer Calculations. J. Chem. Phys. 112 (2), 545–553. doi:10.1063/1.480546

CrossRef Full Text | Google Scholar