- 1Department of Computer Science, University of Oxford, Oxford, United Kingdom
- 2School of Chemistry, Monash University, Clayton, VIC, Australia
- 3Department of Chemistry, University of York, Heslington, United Kingdom
This paper explores the impact of pH on the mechanism of reversible disulfide bond (CysS-SCys) reductive breaking and oxidative formation in Escherichia coli hydrogenase maturation factor HypD, a protein which forms a highly stable adsorbed film on a graphite electrode. To achieve this, low frequency (8.96 Hz) Fourier transformed alternating current voltammetric (FTACV) experimental data was used in combination with modelling approaches based on Butler-Volmer theory with a dual polynomial capacitance model, utilizing an automated two-step fitting process conducted within a Bayesian framework. We previously showed that at pH 6.0 the protein data is best modelled by a redox reaction of two separate, stepwise one-electron, one-proton transfers with slightly “crossed” apparent reduction potentials that incorporate electron and proton transfer terms (
Introduction
The redox chemistry of metalloenzymes and metalloproteins frequently occurs via multiple electron transfer events coupled to proton transfer (Hirst, 2006; Weinberg et al., 2012; Savéant and Costentin, 2019). For example, many of the enzymes which underpin photosynthesis and have application in artificial biological solar fuel production (i.e., Photosystem II, hydrogenases, and carbon monoxide dehydrogenases) rely on the efficient, concerted movement of protons and electrons to ensure product selectivity (Evans et al., 2019). Protein film electrochemistry (PFE) has been shown to be a powerful technique to probe the redox biochemistry of such proton-coupled electron transfer reactions (Armstrong et al., 1997; Hirst, 2006; Fourmond and Léger, 2017). As we have demonstrated previously (Adamson et al., 2017b), Escherichia coli hydrogenase maturation factor HypD (elsewhere “H2ase-MFHypD”), an enzyme which is important in the biosynthesis of hydrogenases (Nutschan et al., 2019), acts as a relatively simple example of such biological proton-coupled electron transfer redox chemistry. When H2ase-MFHypD was immobilized on a graphite electrode we could use both classical direct current cyclic voltammetry (DCV, involving a linear potential-time ramp) as well as large amplitude Fourier transform alternating current voltammetry (FTACV, utilizing a sine-wave plus linear-ramp voltage-time oscillation) to observe reversible disulfide bond reductive cleavage and oxidative formation (Supplementary Figure S1), a reaction that is considered to be a net two-proton, two-electron reaction at near-neutral pH (Figure 1A) (Adamson et al., 2017b).
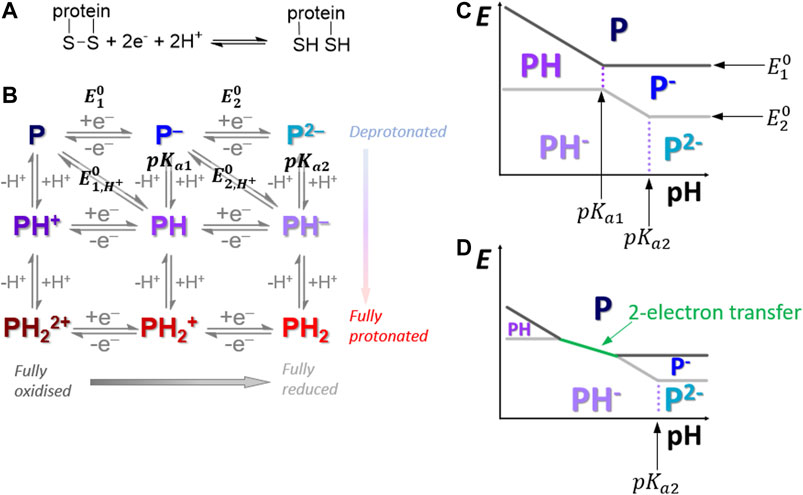
FIGURE 1. (A) Overall disulfide bond two-proton, two-electron oxidative-formation and reductive-cleavage reaction. (B) How the overall reaction separates into a square-scheme of vertical one-proton and horizontal one-electron transfers where “P” denotes the protein redox center. (C,D) Pourbaix diagrams depicting how pH can influence the reaction pathway across the top half of the Pourbaix diagram.
An advantage of using FTACV over DCV in dynamic electrochemical measurements is that the higher order harmonic current-time responses (isolated by the sequence of Fourier transformation of the total current, band selection of current at a certain frequency, and inverse Fourier transformation) emphasize the response of fast electron transfer processes, i.e., current from rapid electron transfer processes can be separated from that arising from slower processes (Zhang and Bond, 2007; Adamson et al., 2017a). The isolation of fast electron transfer current from other contributions becomes particularly powerful when FTACV is applied to PFE (Adamson et al., 2017a; Zouraris et al., 2018). This is attributed to the fact that in many PFE studies when looking at the DC/fundamental harmonic current there is a low ratio of Faradaic signal from non-catalytic electron transfer processes relative to the capacitive background charging current. This arises because the large footprint of the protein molecule only allows a low surface coverage of redox active biomolecules to be present on the electrode surface (Hirst, 2006; Adamson et al., 2017a; Fourmond and Léger, 2017). As a result of these benefits, large amplitude FTACV is beginning to be adopted by the electrochemical community and is now being used in multiple laboratories (Zhang et al., 2018; Zouraris et al., 2018; Kumari and Adeloju, 2019; Zheng et al., 2019). In this study, as well as exploiting access to the much improved faradaic-to-charging current ratio, we specifically demonstrate the utility of the technique in distinguishing reaction mechanisms of the kind showcased initially in our previous work (Adamson et al., 2017b). Use of AC techniques to distinguish mechanisms that give rise to similar voltammetric data is an area of increasing research as shown by the recent use of square-wave voltammetry to distinguish between one and two-step reaction mechanisms (Gulaboski, 2019; Gulaboski and Mirceski, 2020; Guziejewski, 2020).
In this study, although H2ase-MFHypD serves as an extremely useful test system for developing our data analysis techniques for probing disulfide mechanisms, it is not possible to conclude if this redox-driven bond making/breaking is relevant to the physiological function of the enzyme (Adamson et al., 2017b; Nutschan et al., 2019). However, there are a multitude of proteins and enzymes where the disulfide chemistry is vitally important and in vitro electrochemical studies do provide a useful insight into the in vivo biological chemistry, as demonstrated by the comprehensive study by Bewley et al. (Bewley et al., 2015).
In our previous publication (Adamson et al., 2017b), PF-FTACV H2ase-MFHypD data collected at pH 6.0 was analyzed using automated solver methods to address the inverse problem, i.e., return a set of reaction model parameter values which generated a simulated dataset that provides a “best fit” to the experimental data, as quantified by an objective function that measured the least squares distance between the experimental and simulated data (Adamson et al., 2017b). Based on this analysis we concluded that at pH 6.0 solution conditions the overall H2ase-MFHypD redox reaction was most accurately modelled as two separate one-electron, one-proton steps with very similar associated reversible potentials (Adamson et al., 2017b). We therefore considered that at pH 6.0 the overall reaction proceeded from the top-left to the bottom-right of the square scheme shown in Figure 1B (Adamson et al., 2017b).
The best fit parameters for modelling H2ase-MFHypD FTACV at pH 6.0 and low frequency were consistent with the reaction proceeding under equilibrium conditions and the second electron transfer having an apparent reversible potential value (Eapp, a potential term relating to the equilibrium point of an electrochemical-chemical “EC” process comprising electron transfer and chemical steps) more positive than for the first process by about 10 mV (Laviron, 1980; Adamson et al., 2017b). This is broadly observed across many two-electron transfer biological processes, and generally the redox crossover between the separate potential values is sufficiently small to permit a finite potential window to exist in which the intermediate one-electron state can be detected, as predicted by the Nernst equation (Supplementary Figure S2) (Lopez-Tenes et al., 2014; Evans et al., 2019).
As in Figure 1B, in proton-coupled electron transfer reactions the formal potential associated with an overall proton-electron equilibrium reaction is often denoted a value of
In our earlier work on H2ase-MFHypD (Adamson et al., 2017b), although we collected experimental data from pH 4.0 to pH 9.0 (Supplementary Figure S3), we did not explore the impact of proton availability on the conserved appropriateness of a stepwise two-sequential, one-electron transfer model, or on the tuning of the redox-potential crossover; this is the focus of the work presented here. We aim to establish if the same reaction model is appropriate under alkaline solution conditions (up to pH 9.0) and acidic solution conditions (down to pH 4.0) by comparing the accuracy with which a simulated dataset provides a “best fit” to the experimental data using either a two-stepwise one-electron transfer reaction model (n1 = n2 = 1) or a one-concerted two-electron transfer model (n3 = 2). We also explore if an equilibrium reaction model is appropriate across the entire pH range. Overall, we are therefore probing how proton availability in the bulk solution-phase impacts the mechanism of biological redox chemistry, as well as showcasing the power of FTACV in allowing differentiation between reaction models.
Materials and Methods
Electrochemistry Measurements
All data was collected in our previous study (Adamson et al., 2017b), all experiments were conducted at 25°C and all potentials are reported vs. the standard hydrogen electrode (SHE). An example of raw experimental data and verification of protein adherence can be seen in Supplementary Figure S11. In FTACV the input potential as a function of time,
The term
Mathematical Model of the Faradaic Current
Modelling has been undertaken to calculate the Faradaic current output from the FTACV interrogation of a two-sequential one-electron transfer process described by Reaction 1 and Reaction 2 (referred to as the n1 = n2 = 1 process), and a concerted two-electron process, as given by Reaction 3 (elsewhere designated n3 = 2). Other researchers have published work on the experimental measurement and theoretical modelling of solution phase voltammetry of such electrochemical-electrochemical stepwise multiple electron transfer processes (Evans, 2008; Lopez-Tenes et al., 2014). We, and others, have published a number of analogous studies on surface confined species such as the H2ase-MFHypD system we describe here (Finklea, 2001; Lee et al., 2011; Stevenson et al., 2012; Robinson et al., 2018; Robinson et al., 2019).
It is assumed that protonation reactions accompanying the electron transfer are reversible (diffusion controlled) which allows modelling to be undertaken by combining the Eo, Ka and pH terms of a reaction into an apparent
As detailed in the Results, an advantage of analyzing H2ase-MFHypD FTACV data compared to other proton coupled electron transfer protein systems is that we show that we are in a parameter regime where we do not have to incorporate kinetic dispersion into our simulation model; this avoids a substantial additional computational cost, as shown previously (Lloyd-Laney et al., 2021b). For simplicity, and as shown previously (Adamson et al., 2017b), we can also neglect a possible small contribution from thermodynamic dispersion (Léger et al., 2002; Morris et al., 2015); this is advantageous as it makes the data fitting computationally less demanding (and therefore faster), and it also decreases the number of models which must be compared (Lloyd-Laney et al., 2021b).
Two-step Approach to Solving the Inverse Problem
To extract the reaction model parameter values which gave the “best fit” between the experimental electrochemical data and either a simulation of the two-sequential one-electron transfer model (n1 = n2 = 1) or a simulation of the consecutive two-electron transfer model (n3 = 2) a two-step process was used, based on that described in our previous work (Adamson et al., 2017b). This two-step process takes advantage of the fact that the total current recorded in an experiment is a sum of both the Faradaic current arising from the redox reaction under interrogation and non-Faradaic background capacitive charging current contributions.
First, using analysis in the time-domain, we determined the parameter values which gave the best fit between a simulated non-Faradaic capacitance current trace (see Supplementary Material for details of the third order polynomial “capacitance” model) and regions of the experimental current trace with little or no Faradaic contribution (Supplementary Figures S5, S6) by performing 10 optimizations per experimental dataset and recording the parameter value combination which gave the minimal sum of square difference between the simulated capacitance current and the experimental current. Amongst other parameters, this enabled the determination of “best fit” values for the uncompensated resistance,
Full details of the mathematical model, as well as a more in-depth description of the optimization methods used to solve the inverse problem are provided in the Supplemantary Material (Gavaghan et al., 2018; Clerx et al., 2019; Harris et al., 2020; Gundry et al., 2021).
Results
Model Verification
The models and the inference methods used in this study were extensively verified based on synthetic data studies and the reproduction of results from the literature, as detailed in Verification of computational methods in the Supplementary Material.
Two-Sequential One-Electron Transfer Reaction Model Vs. Concerted Two Electron Transfer Model
The two-step fitting process described in the Materials and Methods was used to extract “best fit” parameter values for the pH 4.0, 5.0, 6.0, 7.0, 8.0, and 9.0 experimental H2ase-MFHypD FTACV data using the non-Faradaic capacitance-current model described in the Supplementary Material and both a two-sequential one-electron transfer reaction model (Reaction 1 and Reaction 2, n1 = n2 = 1) and the consecutive two-electron transfer model (Reaction 3, n3 = 2) to account for the Faradaic current. As previously (Adamson et al., 2017b), an objective function was used to quantify the distance between the total experimental current and the simulated data, denoted as
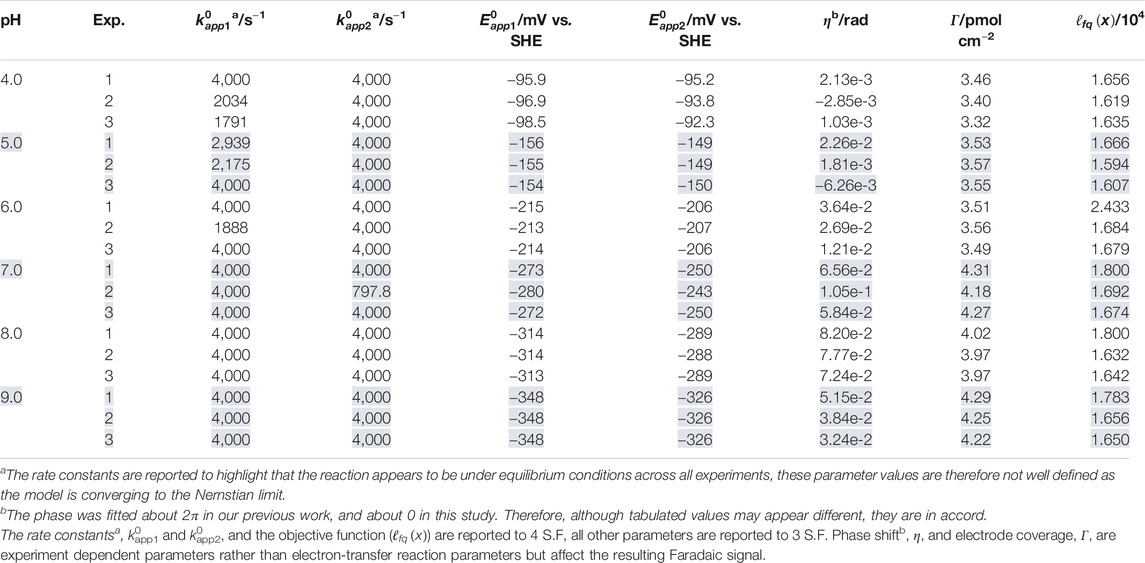
TABLE 1. Best fit parameter values extracted when the two-sequential one-electron transfer model (n1 = n2 = 1) is used to simulate three repeated ν = 22.4 mV s−1, f = 8.96 Hz, ΔE = 150 mV H2ase-MFHypD FTACV experiments (Exp. 1, 2, and 3) at each of the pH values 4.0, 5.0, 6.0, 7.0, 8.0, and 9.0.
As shown in Supplementary Tables S1, S2, the values of the objective function for the best fits from the two-sequential one-electron transfer model (n1 = n2 = 1) are consistently lower than those for the concerted two-electron transfer model (n3 = 2) across the entire pH range 4.0–9.0. The better fit of the n1 = n2 = 1 model can also be visualized via the residuals plotted in Figure 2 and Figure 3 for the pH 4.0, and 9.0 data, respectively; plots of the pH 5.0, 6.0, 7.0, and 8.0 data are shown in Supplementary Figure S8. The better fit of the n1 = n2 = 1 electron transfer model vs. the n3 = 2 electron reaction model in itself gives some confidence that this is the more likely of the two to be a correct reflection of physical reality, although it is not conclusive evidence since the better fitting model contains more free parameters (six vs. four). However, further strong evidence in favor of the correctness of the two-sequential one-electron transfer model can be seen by considering the higher harmonics of the experimental data as shown in Figures 2, 3, and Supplementart Figure S8. The fact that at least nine well defined harmonics are accessible for the reduction of surface confined H2ase-MFHypD is remarkable. This provides compelling evidence that the reduction of surface confined H2ase-MFHypD is an extremely fast process with both electron transfer and coupled protonation reactions being reversible or very close to reversible on the time scale of even the ninth harmonic of the AC voltammetric experiment. Thus, the data is strongly characteristic of a kinetic parameter approaching the reversible limit of Nernstian kinetics. This is consistent with the “best-fit” kinetic regime of the two-sequential one-electron transfer model (n1 = n2 = 1); as detailed below, all the electron transfer rates fall into the reversible regime (Table 1). Conversely, the concerted two-electron transfer model (n3 = 2) yields best-fit electron transfer (
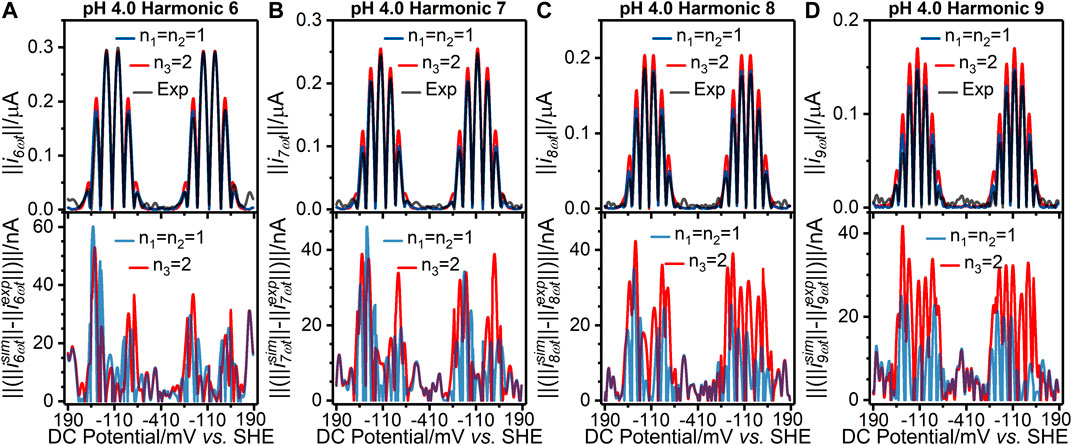
FIGURE 2. [(A–D) top panels] Current-potential plots of harmonics six to nine of (grey line) pH 4.0 experiment 3 (“Exp”) data and best fit simulated data using (red line) a concerted two-electron (n3 = 2) electron transfer model and (blue line) a stepwise two-sequential one-electron transfer reaction model (n1 = n2 = 1). (Bottom panels) Residual current-potential plots corresponding to the panel above. The parameter values used to generate the simulations are reported in Table 1, Supplementary Tables S3, S4.
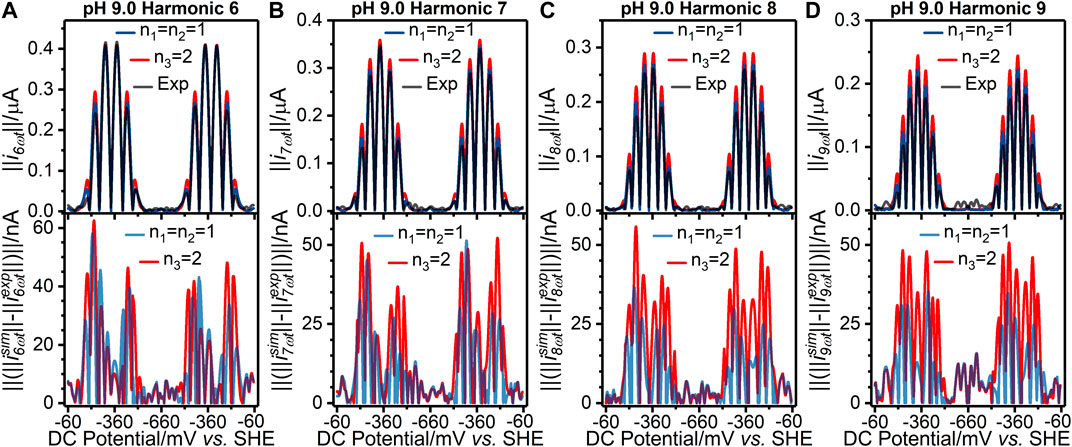
FIGURE 3. [(A–D) top panels] Current-potential plots of harmonics six to nine of (grey line) pH 9.0 experiment 3 (“Exp”) data and best fit simulated data using (red line) a concerted two-electron (n3 = 2) electron transfer model and (blue line) a stepwise two-sequential one-electron transfer reaction model (n1 = n2 = 1). (Bottom panels) Residual current-potential plots corresponding to the panel above. The parameter values used to generate the simulations are reported in Table 1, Supplementary Tables S3, S4.
Figure 4 further illustrates the mis-specification of the concerted two-electron transfer model (n3 = 2) by comparing data generated with a
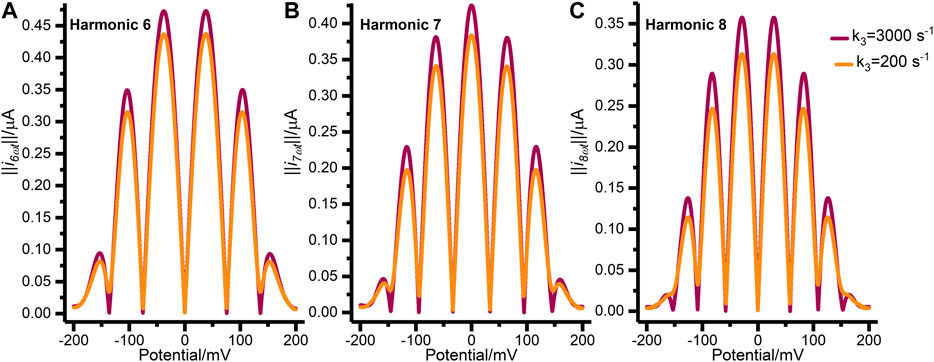
FIGURE 4. Synthetic FTACV data showing (A) harmonic 6, (B) harmonic 7, and (C) harmonic 8 generated by the concerted two-electron transfer model with
The best fit non-Faradaic capacitance-current parameters values give good estimates of background capacitance, as illustrated by Supplementary Figure S9. The polynomial parameters reported are not expected to be identical to our previous work as the model has been improved to better describe the underlying capacitance differences between the oxidative and reductive DC sweep directions (see Supplementary Material). However, the best fit values are of a comparable magnitude and as expected no significant trends are observed as a function of pH (Supplementary Table S4). In our previous work, the analysis of electrochemical impedance spectroscopy data collected at pH 6.0 was used to generate an estimate of the uncompensated resistance,
Within the three experimental measurements made at the same pH, the best fit n1 = n2 = 1 model parameter values are generally self-consistent. Results for
In our earlier work, we demonstrated that it was not possible to determine the electron transfer rate constants at pH 6.0 because the reaction reached equilibrium under the experimental conditions. This explains why experiment 1 and 3 of the pH 6.0 dataset return
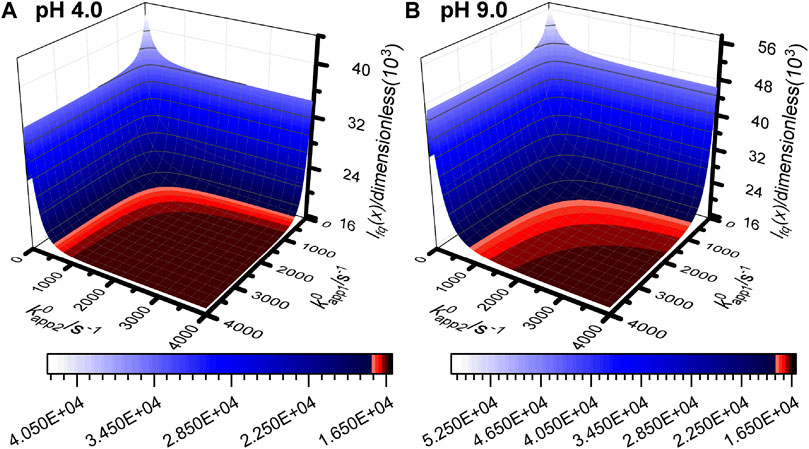
FIGURE 5. Objective function surface for (A) pH 4.0 experiment 3 and (B) pH 9.0 experiment 3 calculated using simulated data from the n1 = n2 = 1 reaction model with all input parameters set to the best fit values from Table 1 and Supplementary Table S4 except
We have not modelled the impact of either kinetic or thermodynamic dispersion when fitting the data in this work (Figures 2, 3, and Supplementary Figure S8). By definition, kinetic dispersion is not possible for a fully reversible electron transfer process that is fully described by the Nernst thermodynamic relationship. Furthermore, the experimental data shows none of the hallmarks of significant thermodynamic dispersion — a broadening of the harmonics, and substantial reduction in current amplitude of the higher harmonics relative to the non-dispersed case (Lloyd-Laney et al., 2021a). Since the harmonic simulations generated without dispersion in Figures 2, 3, and Supplementary Figure S8 provide such an excellent fit to the experimental harmonics, it is concluded that the contribution of thermodynamic dispersion is negligible.
Eapp Versus pH
Figure 6 shows how the
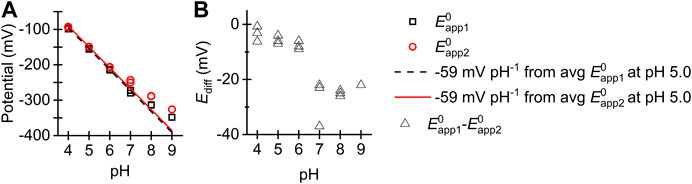
FIGURE 6. (A) Plot of (black square)
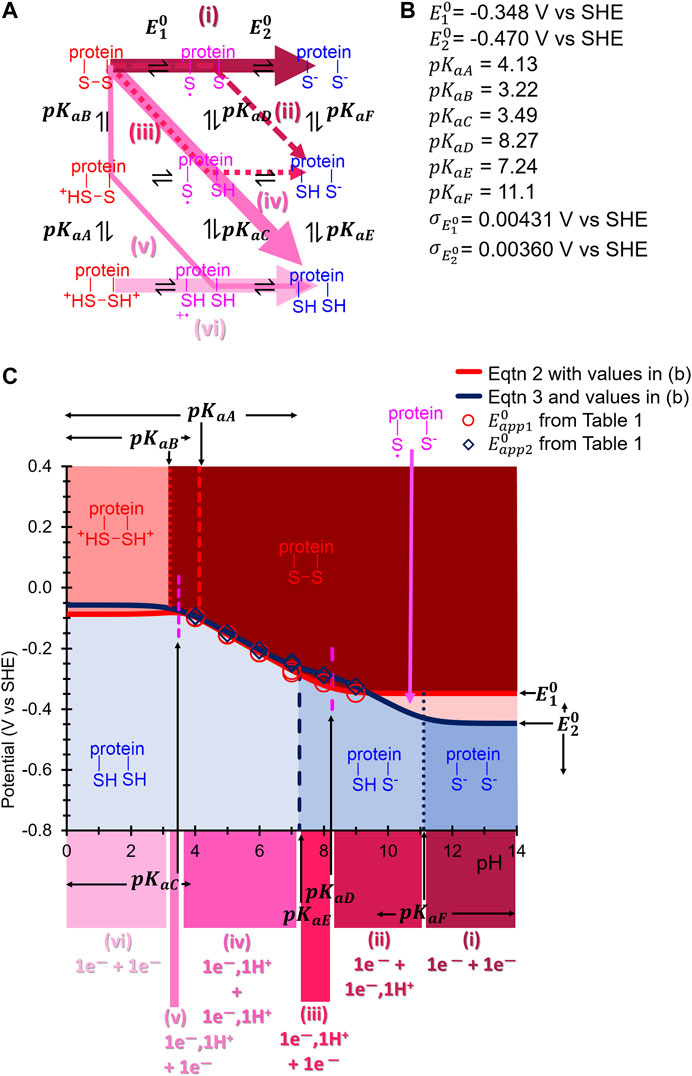
FIGURE 7. (A) Square scheme from Figure 1B updated to show the appropriate pKa and E0 symbols associated with each protonation and electron-transfer reaction, respectively, of H2ase-MFHypD. Coloured arrows indicate the suggested reaction path taken through the scheme at different pH values. (B) Best fit inferred
Discussion
Our Results indicate that across the pH range 4.0–9.0 H2ase-MFHypD maintains the same two-sequential one-electron transfer redox reaction, i.e., the Faradaic current detected in our FTACV experiments is attributable to the enzyme undergoing a redox process described by Reaction 1 and Reaction 2, converting from a fully oxidized state into a fully reduced state via the addition of one-electron to generate an intermediate state that accepts a second electron.
In the pH regime 4.0–6.0 the apparent potentials associated with the first and second electron transfer,
Although the net reaction is consistent with Figure 1A, we find that a concerted two-electron, two-proton mechanism is not appropriate, i.e., the classic double-headed arrow of organic chemistry does not accurately describe the reaction. A quasi-reversible concerted two-electron model is found to be mis-specified, as described in the Results. Figure 8 shows a theoretical comparison of the DCV and FTACV output from reversible concerted two-electron transfer compared to reversible two sequential one-electron transfers in the regimes of
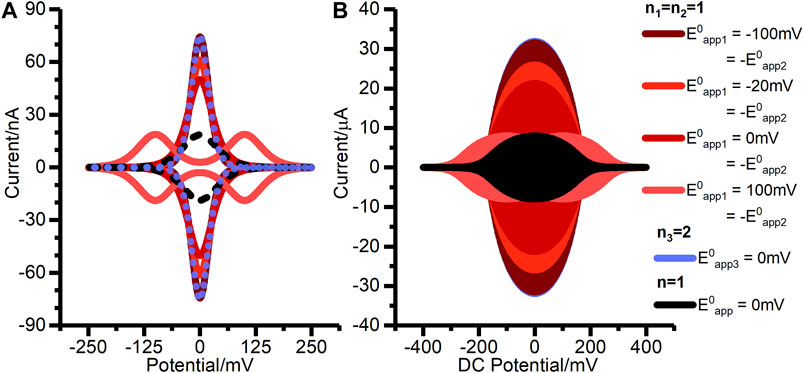
FIGURE 8. Simulated (A) DCV, and (B) FTACV outputs for two-stepwise one-electron transfer processes (n1 = n2 = 1) when (solid pink line)
When constructing Figure 8 we found that the magnitude of the electron transfer rate constant required to achieve model convergence in the
In amino acid reference tables, cysteine residues are ascribed an average pKa value of 8.5 (Poole, 2015), suggesting that under sufficiently alkali conditions the reductive cleavage of a disulfide linkage should collapse into a two-electron, zero-proton regime, equivalent to the top line of the Pourbaix diagram in Figure 1. The increased gap between
With this in mind, we wish to draw the reader’s attention to the incredible role that the protein matrix must play in ensuring a highly consistent redox reaction mechanism is maintained over a range of solution protonation values from 10-4 to 10-9 M. Clearly the secondary protein structure plays a vital role in mediating the protonation environment to enable Biology to precisely tune the disulfide chemistry so that the
There are examples of related voltammetric behaviour outside that of biologically relevant molecules. A well-studied example is the reduction of solution soluble and surface confined polyoxometalates as a function of acid concentration. For example, the DC cyclic voltammetry for reduction of [P2W18O62]6- in acetonitrile provides an extensive series of well separated one-electron reduction processes. On addition of sufficient acid, the processes converge into apparently multi-electron transfer processes (Prenzler et al., 1999). However, detailed voltammetry simulations based on one-electron transfer steps model the initial two reactions very well over the acid concentration range. The acid dependence and simulation details for this and related polyoxometalates have been reviewed (Bond, 2002). A fully analogous situation to the present study (Robinson et al., 2018; Robinson et al., 2019) has been demonstrated to apply for surface confined reduction of [PMo12O40]3-; in highly acid media it is shown to be well modelled by treatment as two closely spaced one-electron reduction steps rather than a simultaneous two-electron reduction processes. Conversely, more exotic electron-proton transfer schemes like the elegant “wedge” scenario are necessary for describing electron and proton transfer via an intermediate H-bond complex in some organic molecules (Clare et al., 2019).
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/alisterde/HypD_low_freq_pH_analysis
Author Contributions
AD-E carried out all the modelling work and wrote the first draft of the manuscript, MR and HL-L provided expertise in model construction and method verification. All authors contributed to the design of the project and the writing of the final paper.
Funding
This work was supported by funding from the Biotechnology and Biological Sciences Research Council (UKRI-BBSRC, grant number BB/T008784/1) which AD-E grateful acknowledges. MR and DG gratefully acknowledge support from the EPSRC SABS:R3 Centre for Doctoral Training (EP/S024093/1). HL-L gratefully acknowledges funding from the EPSRC and BBSRC Centre for Doctoral Training in Synthetic Biology (grant no. EP/L016494/1). AB, DG and AP thank the Australian Research Council for financial support that facilitated this international collaboration under the auspices of Discovery Program Grant No. DP170101535.
Acknowledgments
We thank Dr. Hope Adamson for her expert work in obtaining the original dataset.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2021.672831/full#supplementary-material
References
Adamson, H., Bond, A. M., and Parkin, A. (2017a). Probing Biological Redox Chemistry with Large Amplitude Fourier Transformed Ac Voltammetry. Chem. Commun. 53 (69), 9519–9533. doi:10.1039/C7CC03870D
Adamson, H., Robinson, M., Bond, P. S., Soboh, B., Gillow, K., Simonov, A. N., et al. (2017b). Analysis of HypD Disulfide Redox Chemistry via Optimization of Fourier Transformed Ac Voltammetric Data. Anal. Chem. 89 (3), 1565–1573. doi:10.1021/acs.analchem.6b03589
Armstrong, F. A., Heering, H. A., and Hirst, J. (1997). Reaction of Complex Metalloproteins Studied by Protein-Film Voltammetry. Chem. Soc. Rev. 26 (3), 169–179. doi:10.1039/CS9972600169
Bard, A. J., and Faulkner, L. R. (2001). Electrochemical Methods: Fundamentals and Applications. 2nd Edition. New York, NY: John Wiley & Sons, Incorporated.
Bewley, K. D., Dey, M., Bjork, R. E., Mitra, S., Chobot, S. E., Drennan, C. L., et al. (2015). Rheostat Re-wired: Alternative Hypotheses for the Control of Thioredoxin Reduction Potentials. PLOS ONE 10 (4), e0122466. doi:10.1371/journal.pone.0122466
Bond, A. M. (2002). Broadening Electrochemical Horizons: Principles and Illustration of Voltammetric and Related Techniques. Oxford, United Kingdom: Oxford University Press.
Chivers, P. T., Prehoda, K. E., and Raines, R. T. (1997). The CXXC Motif: A Rheostat in the Active Site. Biochemistry 36 (14), 4061–4066. doi:10.1021/bi9628580
Chobot, S. E., Hernandez, H. H., Drennan, C. L., and Elliott, S. J. (2007). Direct Electrochemical Characterization of Archaeal Thioredoxins. Angew. Chem. Int. Ed. 46 (22), 4145–4147. doi:10.1002/anie.200604620
Clare, L. A., Pham, T. D., Rafou, L. A., Buenaventura, A. G., Scott, T. R., Mikhaylova, V., et al. (2019). The Role of H-Bonding in Nonconcerted Proton-Coupled Electron Transfer: Explaining the Voltammetry of Phenylenediamines in the Presence of Weak Bases in Acetonitrile. J. Phys. Chem. C 123 (38), 23390–23402. doi:10.1021/acs.jpcc.9b06825
Clerx, M., Robinson, M., Lambert, B., Lei, C. L., Ghosh, S., Mirams, G. R., et al. (2019). Probabilistic Inference on Noisy Time Series (PINTS). J. Open Res. Softw. 7 (1), Article 23. doi:10.5334/jors.252
Costentin, C., Robert, M., Savéant, J.-M., and Teillout, A.-L. (2009). Concerted Proton-Coupled Electron Transfers in Aquo/hydroxo/oxo Metal Complexes: Electrochemistry of [OsII(bpy)2py(OH2)]2+ in Water. Proc. Natl. Acad. Sci. 106 (29), 11829. doi:10.1073/pnas.0905020106
Evans, D. H. (2008). One-Electron and Two-Electron Transfers in Electrochemistry and Homogeneous Solution Reactions. Chem. Rev. 108 (7), 2113–2144. doi:10.1021/cr068066l
Evans, R. M., Siritanaratkul, B., Megarity, C. F., Pandey, K., Esterle, T. F., Badiani, S., et al. (2019). The Value of Enzymes in Solar Fuels Research - Efficient Electrocatalysts through Evolution. Chem. Soc. Rev. 48 (7), 2039–2052. doi:10.1039/C8CS00546J
Finklea, H. O. (2001). Consequences of a Potential-dependent Transfer Coefficient in Ac Voltammetry and in Coupled Electron-Proton Transfer for Attached Redox Couples. J. Electroanalytical Chem. 495 (2), 79–86. doi:10.1016/S0022-0728(00)00399-5
Fourmond, V., and Léger, C. (2017). Modelling the Voltammetry of Adsorbed Enzymes and Molecular Catalysts. Curr. Opin. Electrochemistry 1 (1), 110–120. doi:10.1016/j.coelec.2016.11.002
Gavaghan, D. J., Cooper, J., Daly, A. C., Gill, C., Gillow, K., Robinson, M., et al. (2018). Use of Bayesian Inference for Parameter Recovery in DC and AC Voltammetry. ChemElectroChem 5 (6), 917–935. doi:10.1002/celc.201700678
Gulaboski, R., and Mirceski, V. (2020). Simple Voltammetric Approach for Characterization of Two-step Surface Electrode Mechanism in Protein-Film Voltammetry. J. Solid State. Electrochem. 24 (11), 2723–2732. doi:10.1007/s10008-020-04563-9
Gulaboski, R. (2019). Theoretical Contribution towards Understanding Specific Behaviour of "Simple" Protein‐film Reactions in Square‐wave Voltammetry. Electroanalysis 31 (3), 545–553. doi:10.1002/elan.201800739
Gundry, L., Guo, S.-X., Kennedy, G., Keith, J., Robinson, M., Gavaghan, D., et al. (2021). Recent Advances and Future Perspectives for Automated Parameterisation, Bayesian Inference and Machine Learning in Voltammetry. Chem. Commun. 57, 1855–1870. doi:10.1039/D0CC07549C
Guziejewski, D. (2020). Electrode Mechanisms with Coupled Chemical Reaction - Amplitude Effect in Square-Wave Voltammetry. J. Electroanalytical Chem. 870, 114186. doi:10.1016/j.jelechem.2020.114186
Harris, C. R., Millman, K. J., van der Walt, S. J., Gommers, R., Virtanen, P., Cournapeau, D., et al. (2020). Array Programming with NumPy. Nature 585 (7825), 357–362. doi:10.1038/s41586-020-2649-2
Hirst, J. (2006). Elucidating the Mechanisms of Coupled Electron Transfer and Catalytic Reactions by Protein Film Voltammetry. Biochim. Biophys. Acta (Bba) - Bioenerg. 1757 (4), 225–239. doi:10.1016/j.bbabio.2006.04.002
Hoffman, M. Z., and Hayon, E. (1972). One-electron Reduction of the Disulfide Linkage in Aqueous Solution. Formation, Protonation, and Decay Kinetics of the RSSR- Radical. J. Am. Chem. Soc. 94 (23), 7950–7957. doi:10.1021/ja00778a002
Kumari, P., and Adeloju, S. B. (2019). Fabrication of a Novel DNA Affinity Biosensor Based on Hybridisation Induced Current by Electrostatic Repulsion of Silicotungstic Acid as a Redox Indicator. Talanta 194, 127–133. doi:10.1016/j.talanta.2018.09.074
Laviron, E. (1983). Electrochemical Reactions with Protonations at Equilibrium. J. Electroanalytical Chem. Interfacial Electrochemistry 146 (1), 15–36. doi:10.1016/S0022-0728(83)80110-7
Laviron, E. (1980). Theoretical study of a 1e, 1H+ surface electrochemical reaction (four-member square scheme) when the protonation reactions are at equilibrium. J. Electroanalytical Chem. Interfacial Electrochemistry 109 (1), 57–67. doi:10.1016/S0022-0728(80)80106-9
Lee, C.-Y., Stevenson, G. P., Parkin, A., Roessler, M. M., Baker, R. E., Gillow, K., et al. (2011). Theoretical and Experimental Investigation of Surface-Confined Two-center Metalloproteins by Large-Amplitude Fourier Transformed Ac Voltammetry. J. Electroanalytical Chem. 656 (1), 293–303. doi:10.1016/j.jelechem.2010.08.012
Léger, C., Jones, A. K., Albracht, S. P. J., and Armstrong, F. A. (2002). Effect of a Dispersion of Interfacial Electron Transfer Rates on Steady State Catalytic Electron Transport in [NiFe]-Hydrogenase and Other Enzymes. J. Phys. Chem. B 106 (50), 13058–13063. doi:10.1021/jp0265687
Lloyd-Laney, H. O., Robinson, M. J., Bond, A. M., Parkin, A., and Gavaghan, D. J. (2021a). A Spotter's Guide to Dispersion in Non-catalytic Surface-Confined Voltammetry Experiments. J. Electroanalytical Chem. 894, 115204. doi:10.1016/j.jelechem.2021.115204
Lloyd-Laney, H. O., Yates, N. D. J., Robinson, M. J., Hewson, A. R., Firth, J. D., Elton, D. M., et al. (2021b). Using Purely Sinusoidal Voltammetry for Rapid Inference of Surface-Confined Electrochemical Reaction Parameters. Anal. Chem. 93 (4), 2062–2071. doi:10.1021/acs.analchem.0c03774
Lopez-Tenes, M., Gonzalez, J., and Molina, A. (2014). Two-Electron Transfer Reactions in Electrochemistry for Solution-Soluble and Surface-Confined Molecules: A Common Approach. J. Phys. Chem. C 118 (23), 12312–12324. doi:10.1021/jp5025763
Morris, G. P., Baker, R. E., Gillow, K., Davis, J. J., Gavaghan, D. J., and Bond, A. M. (2015). Theoretical Analysis of the Relative Significance of Thermodynamic and Kinetic Dispersion in the Dc and Ac Voltammetry of Surface-Confined Molecules. Langmuir 31 (17), 4996–5004. doi:10.1021/la5042635
Nutschan, K., Golbik, R. P., and Sawers, R. G. (2019). The Iron-Sulfur‐containing HypC‐HypD Scaffold Complex of the [NiFe]‐hydrogenase Maturation Machinery Is an ATPase. FEBS Open Bio 9 (12), 2072–2079. doi:10.1002/2211-5463.12743
Poole, L. B. (2015). The Basics of Thiols and Cysteines in Redox Biology and Chemistry. Free Radic. Biol. Med. 80, 148–157. doi:10.1016/j.freeradbiomed.2014.11.013
Prenzler, P. D., Boskovic, C., Bond, A. M., and Wedd, A. G. (1999). Coupled Electron- and Proton-Transfer Processes in the Reduction of α-[P2W18O62]6-and α-[H2W12O40]6-As Revealed by Simulation of Cyclic Voltammograms. Anal. Chem. 71 (17), 3650–3656. doi:10.1021/ac9814290
Robinson, M., Ounnunkad, K., Zhang, J., Gavaghan, D., and Bond, A. (2018). Integration of Heuristic and Automated Parametrization of Three Unresolved Two-Electron Surface-Confined Polyoxometalate Reduction Processes by AC Voltammetry. ChemElectroChem 5 (23), 3771–3785. doi:10.1002/celc.201800950
Robinson, M., Ounnunkad, K., Zhang, J., Gavaghan, D., and Bond, A. M. (2019). Models and Their Limitations in the Voltammmetric Parameterization of the Six‐Electron Surface‐Confined Reduction of [PMo 12 O 40 ] 3− at Glassy Carbon and Boron‐Doped Diamond Electrodes. ChemElectroChem 6 (21), 5499–5510. doi:10.1002/celc.201901415
Savéant, J. M., and Costentin, C. (2019). “Proton-Coupled Electron Transfers,” in Elements of Molecular and Biomolecular Electrochemistry. Editors J. M. Savéant, and C. Costentin, 259–284.
Stevenson, G. P., Lee, C.-Y., Kennedy, G. F., Parkin, A., Baker, R. E., Gillow, K., et al. (2012). Theoretical Analysis of the Two-Electron Transfer Reaction and Experimental Studies with Surface-Confined Cytochrome C Peroxidase Using Large-Amplitude Fourier Transformed AC Voltammetry. Langmuir 28 (25), 9864–9877. doi:10.1021/la205037e
Sutton, K. A., Black, P. J., Mercer, K. R., Garman, E. F., Owen, R. L., Snell, E. H., et al. (2013). Insights into the Mechanism of X-ray-induced Disulfide-Bond Cleavage in Lysozyme Crystals Based on EPR, Optical Absorption and X-ray Diffraction Studies. Acta Crystallogr. D Biol. Cryst. 69 (12), 2381–2394. doi:10.1107/S0907444913022117
Weinberg, D. R., Gagliardi, C. J., Hull, J. F., Murphy, C. F., Kent, C. A., Westlake, B. C., et al. (2012). Proton-Coupled Electron Transfer. Chem. Rev. 112 (7), 4016–4093. doi:10.1021/cr200177j
Zhang, J., and Bond, A. M. (2007). Theoretical Studies of Large Amplitude Alternating Current Voltammetry for a Reversible Surface-Confined Electron Transfer Process Coupled to a Pseudo First-Order Electrocatalytic Process. J. Electroanalytical Chem. 600 (1), 23–34. doi:10.1016/j.jelechem.2006.02.023
Zhang, Y., Zhang, X., Ling, Y., Li, F., Bond, A. M., and Zhang, J. (2018). Controllable Synthesis of Few‐Layer Bismuth Subcarbonate by Electrochemical Exfoliation for Enhanced CO 2 Reduction Performance. Angew. Chem. Int. Ed. 57 (40), 13283–13287. doi:10.1002/anie.201807466
Zheng, F., Lawrence, N. S., Hartshorne, R. S., and Fisher, A. C. (2019). Voltammetric and Electrosynthetic Triggered Gel Formation. Electrochimica Acta 296, 1095–1101. doi:10.1016/j.electacta.2018.11.146
Zouraris, D., Dimarogona, M., Karnaouri, A., Topakas, E., and Karantonis, A. (2018). Direct Electron Transfer of Lytic Polysaccharide Monooxygenases (LPMOs) and Determination of Their Formal Potentials by Large Amplitude Fourier Transform Alternating Current Cyclic Voltammetry. Bioelectrochemistry 124, 149–155. doi:10.1016/j.bioelechem.2018.07.009
Keywords: protein electrochemistry, ac voltammetry, surface confined voltammetry, proton-coupled electron-transfer, Escherichia coli HypD, disulfide redox
Citation: Dale-Evans AR, Robinson MJ, Lloyd-Laney HO, Gavaghan DJ, Bond AM and Parkin A (2021) A Voltammetric Perspective of Multi-Electron and Proton Transfer in Protein Redox Chemistry: Insights From Computational Analysis of Escherichia coli HypD Fourier Transformed Alternating Current Voltammetry. Front. Chem. 9:672831. doi: 10.3389/fchem.2021.672831
Received: 26 February 2021; Accepted: 25 May 2021;
Published: 14 June 2021.
Edited by:
Petra Imhof, University of Erlangen Nuremberg, GermanyReviewed by:
Rubin Gulaboski, Goce Delcev University, North MacedoniaVincent Fourmond, CNRS UMR7281 Bioénergétique et Ingénierie des Protéines, France
Copyright © 2021 Dale-Evans, Robinson, Lloyd-Laney, Gavaghan, Bond and Parkin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alison Parkin, YWxpc29uLnBhcmtpbkB5b3JrLmFjLnVr; David J. Gavaghan, ZGF2aWQuZ2F2YWdoYW5AY3Mub3guYWMudWs=; Alan M. Bond, YWxhbi5ib25kQG1vbmFzaC5lZHU=
 Alister R. Dale-Evans
Alister R. Dale-Evans Martin J. Robinson1
Martin J. Robinson1 Henry O. Lloyd-Laney
Henry O. Lloyd-Laney David J. Gavaghan
David J. Gavaghan Alan M. Bond
Alan M. Bond Alison Parkin
Alison Parkin