- College of Science, North China University of Science and Technology, Tangshan, China
In recent years, topological semimetals/metals, including nodal point, nodal line, and nodal surface semimetals/metals, have been studied extensively because of their potential applications in spintronics and quantum computers. In this study, we predict a family of materials, Zr3X (X = Al, Ga, In), hosting the nodal loop and nodal surface states in the absence of spin–orbit coupling. Remarkably, the energy variation of the nodal loop and nodal surface states in Zr3X are very small, and these topological signatures lie very close to the Fermi level. When the effect of spin–orbit coupling is considered, the nodal loop and nodal surface states exhibit small energy gaps (<25 and 35 meV, respectively) that are suitable observables that reflect the spin-orbit coupling response of these topological signatures and can be detected in experiments. Moreover, these compounds are dynamically stable, and they consequently form potential material platforms to study nodal loop and nodal surface semimetals.
Introduction
The exploration of non-trivial topologies in crystalline solids has attracted significant attention from chemists, physicists, and material scientists (Kong and Cui, 2011; Cava et al., 2013; Banik et al., 2018; Zhang et al., 2018a; Tang et al., 2019). The main features of these topological solids are enclosed in their electronic-band structures. Initially, research was conducted in the context of the insulating state (Zhang et al., 2011; Li et al., 2012; Peng et al., 2012; Rasche et al., 2013; Wang et al., 2013; Kambe et al., 2014; Chang et al., 2015; Walsh et al., 2017; Barton et al., 2019; Zeugner et al., 2019), and the concept of band topology has now been extended to the metallic and semi-metallic states (Bradlyn et al., 2017; Bernevig et al., 2018; Schoop et al., 2018; Zhou et al., 2018; Gao et al., 2019; Hu et al., 2019; Klemenz et al., 2020; Wang et al., 2020b,c; Zhao Z. et al., 2020) as well.
The dimensionality of band-crossings is a criterion used to classify topological semimetals/metals. The most famous topological semimetals/metals with zero-dimensional band-crossings, i.e., zero-dimensional nodal points, are Dirac semimetals/metals (Chen et al., 2015, 2020; Bradlyn et al., 2017; Zhong et al., 2017; Jing and Heine, 2018; Liu et al., 2018b; Zhang et al., 2018b; Khoury et al., 2019; Wang et al., 2020f; Xu et al., 2020) and Weyl semimetals/metals (Peng et al., 2016; Lin et al., 2017; Fu et al., 2018; Zhang et al., 2018c; Zhou et al., 2019; Gupta et al., 2020; Jia et al., 2020; Liu et al., 2020; Meng L. et al., 2020; Zhao B. et al., 2020). We selected Weyl semimetals/metals as examples here because there exists a band-crossing of the valance band and conduction band at an isolated nodal point in the momentum space of these solids. Particularly, around this isolated nodal point, the quasiparticle acts similarly to the behavior of Weyl fermions, which are particles of considerable interest in high-energy physics. We summarize some recent studies on Weyl materials as follows: (i) Zhao and Ma (2020) stated that hexagonal MnO ferromagnet is a magnetic Weyl semimetal with spin-gapless state; (ii) Meng W. et al. (2020b) predicted that HfCuP compound is a newly designed Weyl semimetal with different types of Weyl nodes; and (iii) Jia et al. (2020) reported that the VI3 monolayer hosts a Weyl fermion and 100% spin-polarization. Furthermore, under the protection from certain crystalline symmetries, two Weyl points of opposite chirality can be stable at the same point, forming a Dirac point.
In the case of three-dimensional materials, besides the zero-dimensional nodal point metals/semimetals, in principle, there should exist one-dimensional and two-dimensional band-crossing metals/semimetals as well. For three-dimensional materials with one-dimensional band-crossings, some members, named as nodal line/loop semimetal/metals, have garnered considerable attention owing to their rich properties. Based on the shape of the nodal lines, they may host various forms, such as nodal link (Yan et al., 2017), nodal chains (Bzdušek et al., 2016), nodal boxes (Sheng et al., 2017), nodal ring (Wang et al., 2020d), nodal knot (Bi et al., 2017), and nodal net (Feng et al., 2018; Wang et al., 2018). So far, numerous types of nodal-line semimetals/metals have been predicted (He et al., 2019, 2020; Jin et al., 2019a,b, 2020a,c; Zhang et al., 2019; Meng W. et al., 2020a; Wang et al., 2020a,e; Zhou et al., 2020), and it is assumed that the node-line states have interesting characteristics in terms of their electronic, transport, and magnetic properties.
Zhong et al. (2016) had first observed topological semimetals/metals with two-dimensional band-crossings, i.e., nodal surface states. However, investigations into nodal surface semimetals/metals are very rare (Wu et al., 2018), and the energy variation of the nodal surface state is great.
If one material hosts two or more types of band-crossings, it can be considered a good platform to investigate the relationship among different topological signatures. Very recently, tetragonal PtO was proposed by Li et al. (2020b) as an effective material to study the one-dimensional nodal line and zero-dimensional nodal point states. Furthermore, Li and Xia (2020) predicted that cubic HfN is a topological material that co-exhibits nodal line and nodal loop states.
Motivated by the above-mentioned information and based on the first principles, we report a new family of topological materials, Zr3X (X = Al, Ga, In) with one-dimensional nodal loop and two-dimensional nodal surface states. The progress in the field of nodal line/surface states, including the conceptual development, the character and classification of these nodal structures, and the material realization, can be found in Wang et al. (2019). Moreover, the dynamical stable as well as the effect of spin-orbit coupling on the electronic structures of these materials are discussed in detail.
Materials
In this study, we have focused on the hexagonal type Zr3X (X = Al, Ga, In). As an example, the primitive cell structure of hexagonal P63/mmc type Zr3Al from different sides are shown in Figures 1A,B. From the figures, it is evident that Zr3X has eight atoms, namely, two X atoms and six Zr atoms. The structures of Zr3X have been totally relaxed with the help of first principles. The equilibrium lattice parameters of Zr3X (X = Al, Ga, In) have been computed via minimizing the crystal total energy calculated for different values of lattice constant by means of Murnaghan's equation of state (EOS) (Murnaghan, 1944). The achieved lattice constants for these compounds are shown in Table 1.
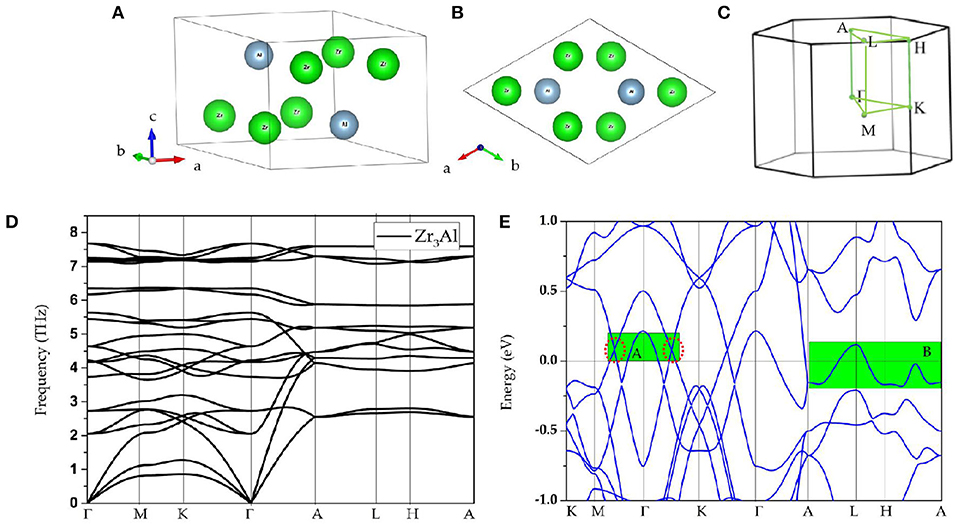
Figure 1. (A,B) Structures of Zr3Al as viewed from different sides; (C) Brillouin zone and the considered high-symmetry points; (D) calculated phonon dispersion of Zr3Al; (E) calculated band structure of Zr3Al; here, the obvious band-crossings can be found in region A and B.
Based on the Brillouin zone and considered high-symmetry points Γ-M-K-Γ-A-L-H-A (as shown in Figure 1C), dynamic stability was examined for these three compounds according to the calculated phonon dispersions, and the results are given in Figures 1D, 2A,B, respectively. These Zr3X compounds are obviously dynamically stable due to the absence of the imaginary frequency (Han et al., 2019; Wu et al., 2019; Li et al., 2020a). These materials are therefore proposed to be experimental platforms to study topological semimetals/metals.
Computational Methods
In this study, calculations have been carried out using the Vienna ab initio simulation package (VASP) (Kresse and Furthmüller, 1996) based on the first-principles density functional theory (DFT), and the generalized gradient approximation (GGA) (Perdew et al., 1996) of Perdew–Burke–Ernzerhof (PBE) (Perdew et al., 1998) functional is adopted for the exchange-correlation potential. During the calculations, the cutoff energy is set as 600 eV, and the Brillouin zone is sampled by the Monkhorst–Pack k-mesh with a size of 6 × 6 × 6. Furthermore, we set the energy/force convergence criteria as 10−6 eV/10−3 eV.
Results and Discussion
Observing the calculated band structure of Zr3Al in Figure 1E, we find that Zr3Al is a metal in which the bands and the Fermi level overlap. In addition to the metallic property, we find that there are several band-crossings near the Fermi level. These band-crossings are mainly located in two regions, named as region A and region B, which have been highlighted by green backgrounds. Similar properties are observed in Zr3Ga and Zr3In, as shown in Figures 2C,D, respectively.
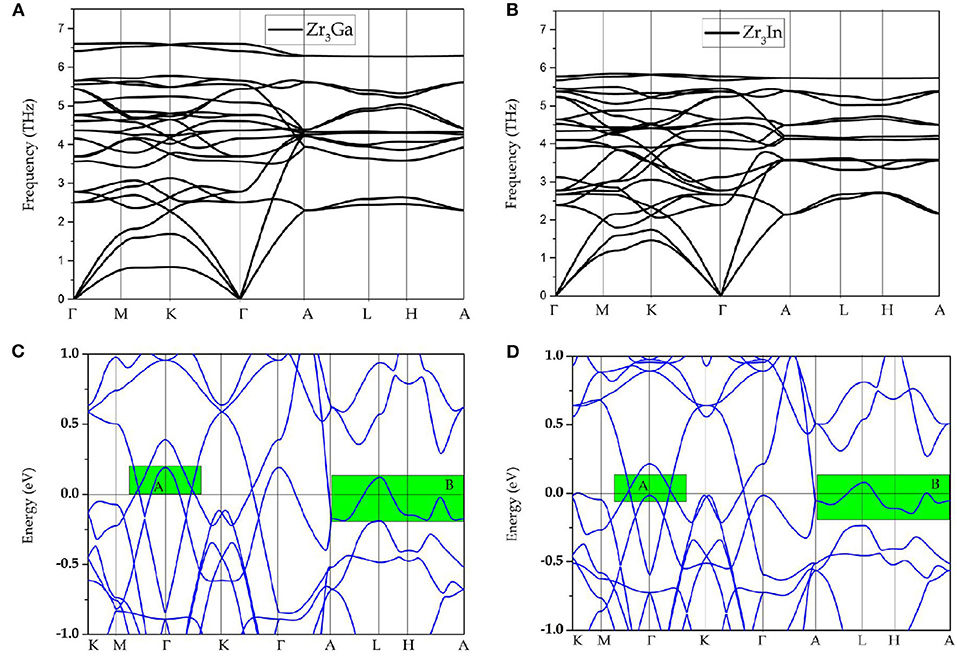
Figure 2. (A,B) Phonon dispersions of Zr3Ga and Zr3In, respectively; (C,D) calculated band structures of Zr3Ga and Zr3In, respectively; here, band-crossings around the Fermi level are highlighted by green rectangles.
In Figures 1E, 2C,D, one may notice that the band structures for these Zr3X compounds are approximately the same; hence, in the following discussion, Zr3Al was selected as an example with which to study the band topology of Zr3X compounds. As an example, the band structural of Zr3Al via GGA+U (U = 4 eV for Zr-d orbitals) is given in Supplementary Figure 1. One can find that the band topology of Zr3Al is still kept under GGA+U method.
In Figure 1E, we find that the band-crossings in region A and region B are quite close to the Fermi level. Specifically, the band-crossings in region A are along M-Γ-K paths, and the band-crossings in region B are along A-L-H-A paths. These band-crossings in both the regions may thus dominate the main features of Zr3Al.
As shown in Supplementary Figure 1, in region A, we observe two obvious band-crossings; one is along M-Γ, and the other one is along Γ-K. Zr3Al is a system with inversion P and time-reversal T symmetries; thus, the two band-crossings along M-Γ-K paths cannot be isolated points (Xu et al., 2017; Fu et al., 2019) on the plane kz = 0. To determine that the two band-crossings in region A belong to a nodal loop on the plane kz = 0, we selected Γ-a1, Γ-a2, Γ-a3, Γ-a4, and Γ-a5 paths (see Figure 3A) to further calculate the band structures of Zr3Al (a1, a2, a3, a4, and a5 are equally spaced between M and K). The calculated band structures are shown in Figure 3B, and we find that band-crossings (marked as yellow circles) appear along Γ-a1, Γ-a2, Γ-a3, Γ-a4, and Γ-a5 paths, implying that a nodal loop should occur on the plane kz = 0. The Γ-centered three-dimensional band dispersion in region A of the kz = 0 plane and the shape of Γ-nodal line in region A are shown in Figures 3C,D, respectively. As shown in Figures 3B,C, these band-crossings in region A host very little energy variation. That is, Zr3X materials can be seen as exceedingly flat in energy, which may exhibit special properties that have exceptional applications. For example, very recently, Wang et al. (2020e) proposed that a nearly flat nodal line around the Fermi level will induce an exceptional thermoelectric power factor in the Nb3GeTe6 monolayer. Moreover, as shown in Figure 3B, we find that all the band crossing points on the plane kz = 0 are type I (Liu et al., 2018a; see Supplementary Figure 2); this nodal line is thus type I.
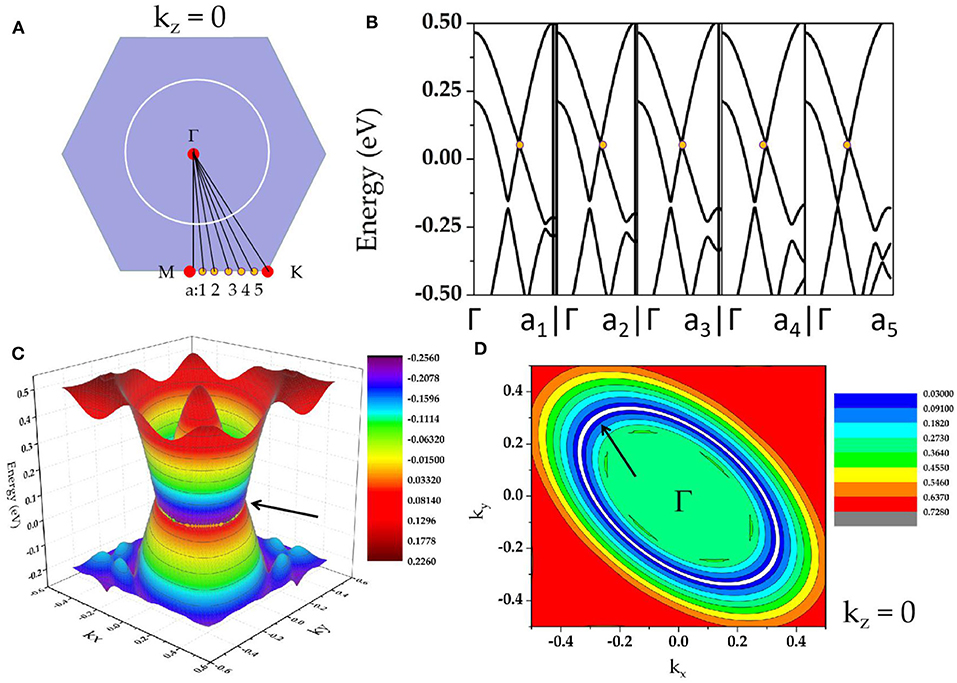
Figure 3. (A) Considered paths Γ-Q (Q = M, a1, a2, a3, a4, a5, K) in the kz = 0 plane; (B) calculated band structures along Γ-a1, Γ-a2, Γ-a3, Γ-a4, Γ-a5 paths; (C) Γ-centered three-dimensional band dispersion in region A of the kz = 0 plane; (D) shape of Γ-nodal line in region A of the kz = 0 plane (the nodal line is shown as white lines and marked by arrows).
In region B, one can see that there are degenerate bands along the A-L-H-A direction. This indicates that the bands in the plane kz = π are doubly degenerate, reflecting a nodal surface state that appeared in the plane kz = π. To further confirm that the two bands are degenerated in kz = π plane, we show the A-centered three-dimensional band dispersion in region B of the planes kz = 0.90 π, kz = 0.99 π, and kz = π in Figures 4A–C, respectively. In Figure 4C, the two bands are obviously totally degenerate, leading to a new topological signature, i.e., nodal surface state, in the kz = π plane (as shown in Figure 4D). Furthermore, as shown in Figure 4C, the energy variation of the nodal surface state is very small (range from −0.15 to 0.05 eV). Similar to the situation of the nearly flat nodal line state in the kz = 0 plane, the small energy variation of the nodal surface state in the kz = π plane may benefit the future experimental investigations.
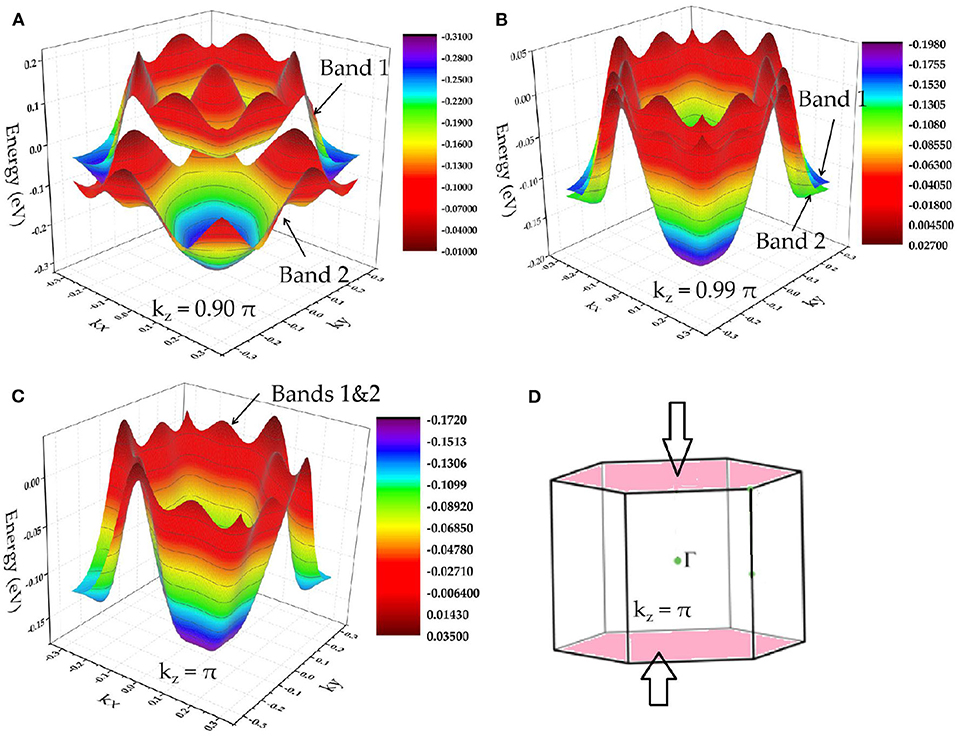
Figure 4. (A–C) A-centered three-dimensional band dispersion in region B of the planes kz = 0.90 π, kz = 0.99 π, and kz = π, respectively; (D) schematic diagram indicating the nodal surface state in the kz = π plane.
Finally, we discuss the electronic-band structure in the presence of spin–orbit coupling. The corresponding calculations results are shown in Figure 5. We find that Zr3Al is an excellent topological material whose band structure shows marked signatures (energy gaps) induced by the spin–orbit coupling effect (Fang et al., 2015). The spin–orbit coupling effect induces energy gaps of 23.05 and 20.08 meV (see Figure 5A) in region A. Furthermore, the band-crossings in region B have open energy gaps of 19.56 meV resulting from the spin–orbit coupling effect (see Figure 5B). The band structures of Zr3Ga and Zr3In with the effect of spin–orbit coupling are also exhibited in Figures 5C,D, respectively. The open energy gaps observed in these topological signatures, exhibited by Zr3X metal (X = Al, Ga, In), are very small compared to the other well-known topological semimetals/metals (Fang et al., 2016). A detailed collection of SOC gaps of typical nodal line materials can be found in the Supplementary Information of (Jin et al., 2020b).
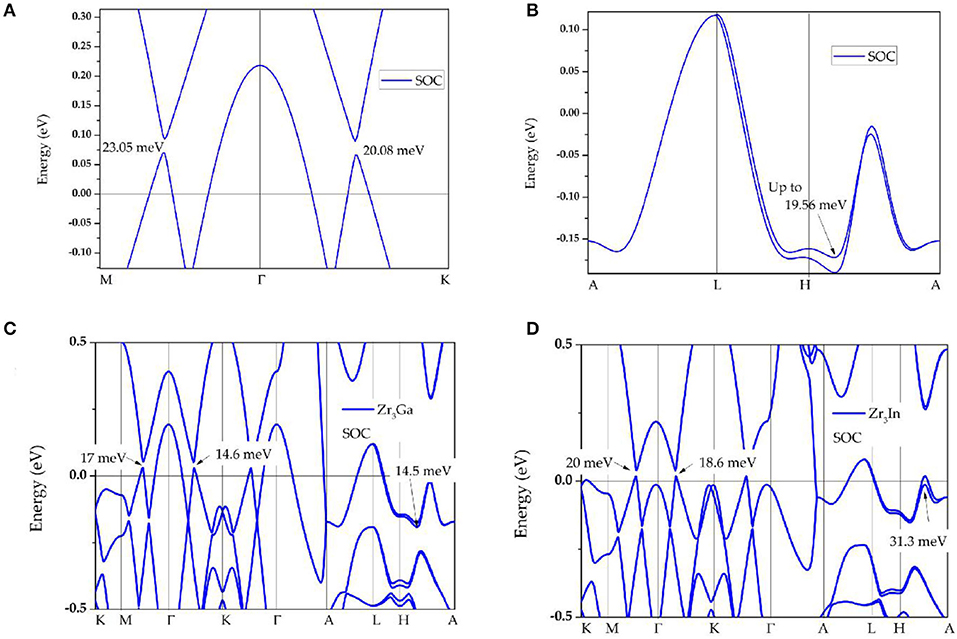
Figure 5. (A,B) Band structures of Zr3Al in the presence of spin–orbit coupling in region A and B, respectively; (C,D) band structures of Zr3Ga and Zr3In in the presence of spin–orbit coupling effect.
Summary
In summary, the topological band structures of Zr3X (X = Al, Ga, In) have been studied via DFT calculations in this study. Neglecting spin-orbit coupling, there is a nodal loop in the kz = 0 plane and nodal surface state in the kz = π plane. The rich topological signatures are quite near to the Fermi level, which can be detected experimentally. Remarkably, the loop is nearly flat and the nodal surface features small energy variation. These above-mentioned topological signatures are not sensitive to the effect of spin–orbit coupling. Further, these compounds are proved to be dynamically stable based on the calculated phonon dispersions and host simple and clear band structures. It is expected that these non-trivial band-crossings can be experimentally observed via angle-resolved photoemission spectroscopy (ARPES).
Data Availability Statement
The original contributions generated for the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author/s.
Author Contributions
HXu: investigation and writing-original draft. Y-CG: supervision. HXu and Y-CG: formal analysis. HXi: methodology. All authors contributed to the article and approved the submitted version.
Funding
This study has been funded by the Science and Technology Research Project of Hebei Province Colleges and Universities (Grant No. QN2020113), and Tangshan Applied Basic Research Project (Grant No. 19130227g).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2020.608398/full#supplementary-material
References
Banik, A., Roychowdhury, S., and Biswas, K. (2018). The journey of tin chalcogenides towards high-performance thermoelectrics and topological materials. Chem. Commun. 54, 6573–6590. doi: 10.1039/C8CC02230E
Barton, A. T., Walsh, L. A., Smyth, C. M., Qin, X., Addou, R., Cormier, C., et al. (2019). Impact of etch processes on the chemistry and surface states of the topological insulator Bi2Se3. ACS Appl. Mater. Interfaces 11, 32144–32150. doi: 10.1021/acsami.9b10625
Bernevig, A., Weng, H., Fang, Z., and Dai, X. (2018). Recent progress in the study of topological semimetals. J. Phys. Soc. Jpn. 87:041001. doi: 10.7566/JPSJ.87.041001
Bi, R., Yan, Z., Lu, L., and Wang, Z. (2017). Nodal-knot semimetals. Phys. Rev. B 96:201305. doi: 10.1103/PhysRevB.96.201305
Bradlyn, B., Elcoro, L., Cano, J., Vergniory, M. G., Wang, Z., Felser, C., et al. (2017). Topological quantum chemistry. Nature 547, 298–305. doi: 10.1038/nature23268
Bzdušek, T., Wu, Q., Rüegg, A., Sigrist, M., and Soluyanov, A. A. (2016). Nodal-chain metals. Nature 538, 75–78. doi: 10.1038/nature19099
Cava, R. J., Ji, H., Fuccillo, M. K., Gibson, Q. D., and Hor, Y. S. (2013). Crystal structure and chemistry of topological insulators. J. Mater. Chem. C 1, 3176–3189. doi: 10.1039/c3tc30186a
Chang, C. Z., Zhao, W., Kim, D. Y., Zhang, H., Assaf, B. A., Heiman, D., et al. (2015). High-precision realization of robust quantum anomalous Hall state in a hard ferromagnetic topological insulator. Nat. Mater. 14, 473–477. doi: 10.1038/nmat4204
Chen, X., Chen, W., Yu, S., Xu, S., Rong, X., Huang, P., et al. (2020). Designing Dirac semimetals with a honeycomb Na3Bi-lattice via isovalent cation substitution. J. Mater. Chem. C 8, 1257–1264. doi: 10.1039/C9TC05352B
Chen, Z. G., Zhang, C., Zou, Y., Zhang, E., Yang, L., Hong, M., et al. (2015). Scalable growth of high mobility dirac semimetal Cd3As2 microbelts. Nano Lett. 15, 5830–5834. doi: 10.1021/acs.nanolett.5b01885
Fang, C., Chen, Y., Kee, H. Y., and Fu, L. (2015). Topological nodal line semimetals with and without spin-orbital coupling. Phys. Rev. B 92:081201. doi: 10.1103/PhysRevB.92.081201
Fang, C., Weng, H., Dai, X., and Fang, Z. (2016). Topological nodal line semimetals. Chin. Phys. B 25:117106. doi: 10.1088/1674-1056/25/11/117106
Feng, X., Yue, C., Song, Z., Wu, Q., and Wen, B. (2018). Topological Dirac nodal-net fermions in AlB2-type TiB2 and ZrB2. Phys. Rev. Mater. 2:014202. doi: 10.1103/PhysRevMaterials.2.014202
Fu, B. B., Yi, C. J., Zhang, T. T., Caputo, M., Ma, J. Z., Gao, X., et al. (2019). Dirac nodal surfaces and nodal lines in ZrSiS. Sci. Adv. 5:eaau6459. doi: 10.1126/sciadv.aau6459
Fu, C., Guin, S. N., Watzman, S. J., Li, G., Liu, E., Kumar, N., et al. (2018). Large Nernst power factor over a broad temperature range in polycrystalline Weyl semimetal NbP. Energy Environ. Sci. 11, 2813–2820. doi: 10.1039/C8EE02077A
Gao, H., Venderbos, J. W., Kim, Y., and Rappe, A. M. (2019). Topological semimetals from first principles. Ann. Rev. Mater. Res. 49, 153–183. doi: 10.1146/annurev-matsci-070218-010049
Gupta, U., Rajamathi, C. R., Kumar, N., Li, G., Sun, Y., Shekhar, C., et al. (2020). Effect of magnetic field on the hydrogen evolution activity using non-magnetic Weyl semimetal catalysts. Dalton Trans. 49, 3398–3402. doi: 10.1039/D0DT00050G
Han, Y., Wu, M., Feng, Y., Cheng, Z., Lin, T., Yang, T., et al. (2019). Competition between cubic and tetragonal phases in all-d-metal Heusler alloys, X2−−xMn1+xV (X = Pd, Ni, Pt, Ag, Au, Ir, Co; x= 1, 0) a new potential direction of the Heusler family. IUCrJ 6, 465–472. doi: 10.1107/S2052252519004007
He, T., Zhang, X., Liu, Y., Dai, X., Liu, G., Yu, Z. M., et al. (2020). Ferromagnetic hybrid nodal loop and switchable type-I and type-II Weyl fermions in two dimensions. Phys. Rev. B 102:075133. doi: 10.1103/PhysRevB.102.075133
He, T., Zhang, X., Meng, W., Jin, L., Dai, X., and Liu, G. (2019). Topological nodal lines and nodal points in the antiferromagnetic material β-Fe2PO5. J. Mater. Chem. C 7, 12657–12663. doi: 10.1039/C9TC04046C
Hu, J., Xu, S. Y., Ni, N., and Mao, Z. (2019). Transport of topological semimetals. Annu. Rev. Mater. Res. 49, 207–252. doi: 10.1146/annurev-matsci-070218-010023
Jia, T., Meng, W., Zhang, H., Liu, C., Dai, X., Zhang, X., et al. (2020). Type-II Weyl state in VI3 monolayer. Front. Chem. 8:722. doi: 10.3389/fchem.2020.00722
Jin, L., Zhang, X., He, T., Meng, W., Dai, X., and Liu, G. (2019b). Topological nodal line state in superconducting NaAlSi compound. J. Mater. Chem. C 7, 10694–10699. doi: 10.1039/C9TC03464A
Jin, L., Zhang, X., He, T., Meng, W., Dai, X., and Liu, G. (2020a). Electronic structure, doping effect and topological signature in realistic intermetallics Li3−−xNaxM (x = 3, 2, 1, 0; M= N, P, As, Sb, Bi). Phys. Chem. Chem. Phys. 22, 5847–5854. doi: 10.1039/C9CP06033B
Jin, L., Zhang, X., He, T., Meng, W., Dai, X., and Liu, G. (2020b). Ferromagnetic two-dimensional metal-chlorides MCl (M= Sc, Y., and La) candidates for Weyl nodal line semimetals with small spin-orbit coupling gaps. Appl. Surface Sci. 520:146376. doi: 10.1016/j.apsusc.2020.146376
Jin, L., Zhang, X., Liu, Y., Dai, X., Shen, X., Wang, L., et al. (2020c). Two-dimensional Weyl nodal-line semimetal in a d0 ferromagnetic K2N monolayer with a high Curie temperature. Phys. Rev. B 102:125118. doi: 10.1103/PhysRevB.102.125118
Jin, L., Zhang, X. M., Dai, X. F., Wang, L. Y., Liu, H. Y., and Liu, G. D. (2019a). Screening topological materials with a CsCl-type structure in crystallographic databases. IUCrJ 6, 688–694. doi: 10.1107/S2052252519007383
Jing, Y., and Heine, T. (2018). Two-dimensional kagome lattices made of hetero triangulenes are Dirac semimetals or single-band semiconductors. J. Am. Chem. Soc. 141, 743–747. doi: 10.1021/jacs.8b09900
Kambe, T., Sakamoto, R., Kusamoto, T., Pal, T., Fukui, N., Hoshiko, K., et al. (2014). Redox control and high conductivity of nickel bis (dithiolene) complex π-nanosheet: a potential organic two-dimensional topological insulator. J. Am. Chem. Soc. 136, 14357–14360. doi: 10.1021/ja507619d
Khoury, J. F., Rettie, A. J., Khan, M. A., Ghimire, N. J., Robredo, I., Pfluger, J. E., et al. (2019). A new three-dimensional subsulfide Ir2In8S with Dirac semimetal behavior. J. Am. Chem. Soc. 141, 19130–19137. doi: 10.1021/jacs.9b10147
Klemenz, S., Hay, A. K., Teicher, S. M., Topp, A., Cano, J., and Schoop, L. M. (2020). The role of delocalized chemical bonding in square-net-based topological semimetals. J. Am. Chem. Soc. 142, 6350–6359. doi: 10.1021/jacs.0c01227
Kong, D., and Cui, Y. (2011). Opportunities in chemistry and materials science for topological insulators and their nanostructures. Nat. Chem. 3, 845–849. doi: 10.1038/nchem.1171
Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54:11169. doi: 10.1103/PhysRevB.54.11169
Li, H., Cao, J., Zheng, W., Chen, Y., Wu, D., Dang, W., et al. (2012). Controlled synthesis of topological insulator nanoplate arrays on mica. J. Am. Chem. Soc. 134, 6132–6135. doi: 10.1021/ja3021395
Li, Y., and Xia, J. (2020). Cubic hafnium nitride: a novel topological semimetal hosting a 0-Dimensional (0-D) triple nodal point and a 1-D topological nodal ring. Front. Chem. 8:727. doi: 10.3389/fchem.2020.00727
Li, Y., Xia, J., Khenata, R., and Kuang, M. (2020a). Insight into the topological nodal line metal YB2 with large linear energy range: a first-principles study. Materials 13:3841. doi: 10.3390/ma13173841
Li, Y., Xia, J., and Srivastava, V. (2020b). The tetragonal monoxide of platinum: a new platform for investigating nodal-line and nodal-point semimetallic behavior. Front. Chem. 8:704. doi: 10.3389/fchem.2020.00704
Lin, C. L., Arafune, R., Liu, R. Y., Yoshimura, M., Feng, B., Kawahara, K., et al. (2017). Visualizing type-II Weyl points in tungsten ditelluride by quasiparticle interference. ACS Nano 11, 11459–11465. doi: 10.1021/acsnano.7b06179
Liu, G., Jin, L., Dai, X., Chen, G., and Zhang, X. (2018a). Topological phase with a critical-type nodal line state in intermetallic CaPd. Phys. Rev. B 98:075157. doi: 10.1103/PhysRevB.98.075157
Liu, G. D., Zhai, X., Meng, H. Y., Lin, Q., Huang, Y., Zhao, C. J., et al. (2018b). Dirac semimetals based tunable narrowband absorber at terahertz frequencies. Opt. Exp. 26, 11471–11480. doi: 10.1364/OE.26.011471
Liu, J., Cheng, L., Zhao, D., Chen, X., Sun, H., Zhu, J. X., et al. (2020). Quenching of the relaxation pathway in the Weyl semimetal TaAs. Phys. Rev. B 102:064307. doi: 10.1103/PhysRevB.102.064307
Meng, L., Li, Y., Wu, J., Zhao, L., and Zhong, J. (2020). A type of novel Weyl semimetal candidate: layered transition metal monochalcogenides Mo2XY (X, Y = S, Se, Te, X≠ Y). Nanoscale 12, 4602–4611. doi: 10.1039/C9NR09123H
Meng, W., Zhang, X., Dai, X., and Liu, G. (2020a). IrSi as a superior electronic material with novel topological properties and nice compatibility with semiconductor Si. Phys. Status Solidi–Rapid Res. Lett. 14:2000178. doi: 10.1002/pssr.202000178
Meng, W., Zhang, X., He, T., Jin, L., Dai, X., Liu, Y., et al. (2020b). Ternary compound HfCuP: An excellent Weyl semimetal with the coexistence of type-I and type-II Weyl nodes. J. Adv. Res. 24, 523–528. doi: 10.1016/j.jare.2020.05.026
Murnaghan, F. D. (1944). The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. U.S.A. 30:244. doi: 10.1073/pnas.30.9.244
Peng, B., Zhang, H., Shao, H., Lu, H., Zhang, D. W., and Zhu, H. (2016). High thermoelectric performance of Weyl semimetal TaAs. Nano Energy 30, 225–234. doi: 10.1016/j.nanoen.2016.10.016
Peng, H., Dang, W., Cao, J., Chen, Y., Wu, D., Zheng, W., et al. (2012). Topological insulator nanostructures for near-infrared transparent flexible electrodes. Nat. Chem. 4, 281–286. doi: 10.1038/nchem.1277
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77:3865. doi: 10.1103/PhysRevLett.77.3865
Perdew, J. P., Burke, K., and Ernzerhof, M. (1998). Perdew, burke, and ernzerhof reply. Phys. Rev. Lett. 80:891. doi: 10.1103/PhysRevLett.80.891
Rasche, B., Isaeva, A., Ruck, M., Borisenko, S., Zabolotnyy, V., Büchner, B., et al. (2013). Stacked topological insulator built from bismuth-based graphene sheet analogues. Nat. Mater. 12, 422–425. doi: 10.1038/nmat3570
Schoop, L. M., Pielnhofer, F., and Lotsch, B. V. (2018). Chemical principles of topological semimetals. Chem. Mater. 30, 3155–3176. doi: 10.1021/acs.chemmater.7b05133
Sheng, X. L., Yu, Z. M., Yu, R., Weng, H., and Yang, S. (2017). A. d orbital topological insulator and semimetal in the antifluorite Cu2S family: contrasting spin Helicities, nodal box, and hybrid surface states. J. Phys. Chem. Lett. 8, 3506–3511. doi: 10.1021/acs.jpclett.7b01390
Tang, F., Po, H. C., Vishwanath, A., and Wan, X. (2019). Comprehensive search for topological materials using symmetry indicators. Nature 566, 486–489. doi: 10.1038/s41586-019-0937-5
Walsh, L. A., Smyth, C. M., Barton, A. T., Wang, Q., Che, Z., Yue, R., et al. (2017). Interface chemistry of contact metals and ferromagnets on the topological insulator Bi2Se3. J. Phys. Chem. C 121, 23551–23563. doi: 10.1021/acs.jpcc.7b08480
Wang, J. T., Nie, S., Weng, H., Kawazoe, Y., and Chen, C. (2018). Topological nodal-net semimetal in a graphene network structure. Phys. Rev. Lett. 120:026402. doi: 10.1103/PhysRevLett.120.026402
Wang, S. S., Wu, W. K., and Yang, S. Y. (2019). Progress on topological nodal line and nodal surface. Acta Phys. Sinica 68:227101. doi: 10.7498/aps.68.20191538
Wang, X., Cheng, Z., Zhang, G., Wang, B., Wang, X. L., and Chen, H. (2020a). Rich novel zero-dimensional (0D), 1D, and 2D topological elements predicted in the P63/m type ternary boride HfIr3B4. Nanoscale 12, 8314–8319. doi: 10.1039/D0NR00635A
Wang, X., Ding, G., Cheng, Z., Surucu, G., Wang, X. L., and Yang, T. (2020b). Novel topological nodal lines and exotic drum-head-like surface states in synthesized CsCl-type binary alloy TiOs. J. Adv. Res. 22, 137–144. doi: 10.1016/j.jare.2019.12.001
Wang, X., Ding, G., Cheng, Z., Surucu, G., Wang, X. L., and Yang, T. (2020c). Rich topological nodal line bulk states together with drum-head-like surface states in NaAlGe with anti-PbFCl type structure. J. Adv. Res. 23, 95–100. doi: 10.1016/j.jare.2020.01.017
Wang, X., Ding, G., Cheng, Z., Wang, X. L., Zhang, G., and Yang, T. (2020d). Intersecting nodal rings in orthorhombic-type BaLi2Sn compound. J. Mater. Chem. C 8, 5461–5466. doi: 10.1039/D0TC00504E
Wang, X., Ding, G., Khandy, S. A., Cheng, Z., Zhang, G., Wang, X. L., et al. (2020e). Unique topological nodal line states and associated exceptional thermoelectric power factor platform in Nb3GeTe6 monolayer and bulk. Nanoscale 12, 16910–16916. doi: 10.1039/D0NR03704D
Wang, X., Zhou, F., and Chen, H. (2020f). Organic-inorganic hybrid coordination polymer C3H9CdCl3N co-exhibiting superior Dirac point and nodal surface states. Results Phys. 17:103159. doi: 10.1016/j.rinp.2020.103159
Wang, Z. F., Su, N., and Liu, F. (2013). Prediction of a two-dimensional organic topological insulator. Nano Lett. 13, 2842–2845. doi: 10.1021/nl401147u
Wu, M., Han, Y., Bouhemadou, A., Cheng, Z., Khenata, R., Kuang, M., et al. (2019). Site preference and tetragonal distortion in palladium-rich Heusler alloys. IUCrJ 6, 218–225. doi: 10.1107/S2052252518017578
Wu, W., Liu, Y., Li, S., Zhong, C., Yu, Z. M., Sheng, X. L., et al. (2018). Nodal surface semimetals: theory and material realization. Phys. Rev. B 97:115125. doi: 10.1103/PhysRevB.97.115125
Xu, Q., Yu, R., Fang, Z., Dai, X., and Weng, H. (2017). Topological nodal line semimetals in the CaP3 family of materials. Phys. Rev. B 95:045136. doi: 10.1103/PhysRevB.95.045136
Xu, S. G., Chen, Z. J., Zhao, Y. J., Zhang, X., Xu, H., and Yang, X. B. (2020). Realizing graphene-like Dirac cones in triangular boron sheets by chemical functionalization. J. Mater. Chem. C 8, 2798–2805. doi: 10.1039/C9TC06464H
Yan, Z., Bi, R., Shen, H., Lu, L., Zhang, S. C., and Wang, Z. (2017). Nodal-link semimetals. Phys. Rev. B 96:041103. doi: 10.1103/PhysRevB.96.041103
Zeugner, A., Nietschke, F., Wolter, A. U., Ga,ß, S., Vidal, R. C., Peixoto, T. R., et al. (2019). Chemical aspects of the candidate antiferromagnetic topological insulator MnBi2Te4. Chem. Mater. 31, 2795–2806. doi: 10.1021/acs.chemmater.8b05017
Zhang, G., Qin, H., Chen, J., He, X., Lu, L., Li, Y., et al. (2011). Growth of topological insulator Bi2Se3 thin films on SrTiO3 with large tunability in chemical potential. Adv. Funct. Mater. 21, 2351–2355. doi: 10.1002/adfm.201002667
Zhang, M., Yang, Z., and Wang, G. (2018c). Coexistence of Type-I and Type-II Weyl points in the Weyl-semimetal OsC2. J. Phys. Chem. C 122, 3533–3538. doi: 10.1021/acs.jpcc.8b00920
Zhang, X., Fu, B., Jin, L., Dai, X., Liu, G., and Yao, Y. (2019). Topological nodal line electrides: realization of an ideal nodal line state nearly immune from spin–orbit coupling. J. Phys. Chem. C 123, 25871–25876. doi: 10.1021/acs.jpcc.9b08446
Zhang, X., Guo, R., Jin, L., Dai, X., and Liu, G. (2018a). Intermetallic Ca3Pb: a topological zero-dimensional electride material. J. Mater. Chem. C 6, 575–581. doi: 10.1039/C7TC04989G
Zhang, X., Liu, Q., Xu, Q., Dai, X., and Zunger, A. (2018b). Topological insulators versus topological Dirac semimetals in honeycomb compounds. J. Am. Chem. Soc. 140, 13687–13694. doi: 10.1021/jacs.8b06652
Zhao, B., Guo, C., Garcia, C. A., Narang, P., and Fan, S. (2020). Axion-field-enabled nonreciprocal thermal radiation in Weyl semimetals. Nano Lett. 20, 1923–1927. doi: 10.1021/acs.nanolett.9b05179
Zhao, X., and Ma, F. (2020). Hexagonal wurtzite MnO in ferromagnetic state: A magnetic topological spin-gapless Weyl semimetal. Phys. Lett. A 384:126494. doi: 10.1016/j.physleta.2020.126494
Zhao, Z., Zhang, Z., and Guo, W. (2020). A family of all sp2-bonded carbon allotropes of topological semimetals with strain-robust nodal-lines. J. Mater. Chem. C 8, 1548–1555. doi: 10.1039/C9TC05470G
Zhong, C., Chen, Y., Xie, Y., Sun, Y. Y., and Zhang, S. (2017). Semi-Dirac semimetal in silicene oxide. Phys. Chem. Chem. Phys. 19, 3820–3825. doi: 10.1039/C6CP08439G
Zhong, C., Chen, Y., Xie, Y., Yang, S. A., Cohen, M. L., and Zhang, S. B. (2016). Towards three-dimensional Weyl-surface semimetals in graphene networks. Nanoscale 8, 7232–7239. doi: 10.1039/C6NR00882H
Zhou, F., Ding, G., Cheng, Z., Surucu, G., Chen, H., and Wang, X. (2020). Pnma metal hydride system LiBH: a superior topological semimetal with the coexistence of twofold and quadruple degenerate topological nodal lines. J. Phys. 32:365502. doi: 10.1088/1361-648X/ab8f5d
Zhou, P., Ma, Z. S., and Sun, L. Z. (2018). Coexistence of open and closed type nodal line topological semimetals in two dimensional B2C. J. Mater. Chem. C 6, 1206–1214. doi: 10.1039/C7TC05095J
Keywords: nodal loop states, nodal surface states, first-principles, electronic structures, spin-orbit-coupling
Citation: Xu H, Xi H and Gao Y-C (2020) Hexagonal Zr3X (X = Al, Ga, In) Metals: High Dynamic Stability, Nodal Loop, and Perfect Nodal Surface States. Front. Chem. 8:608398. doi: 10.3389/fchem.2020.608398
Received: 20 September 2020; Accepted: 30 September 2020;
Published: 19 November 2020.
Edited by:
Zhenxiang Cheng, University of Wollongong, AustraliaReviewed by:
Songtao Li, North China Electric Power University, ChinaYajiu Zhang, Guangzhou University, China
Copyright © 2020 Xu, Xi and Gao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yong-Chun Gao, Z2FveWMxOTYzQG5jc3QuZWR1LmNu
 Heju Xu
Heju Xu Yong-Chun Gao
Yong-Chun Gao