The Cs2AgRhCl6 Halide Double Perovskite: A Dynamically Stable Lead-Free Transition-Metal Driven Semiconducting Material for Optoelectronics

A-Site doping with alkali ions, and/or metal substitution at the B and B′-sites, are among the key strategies in the innovative development of A₂BB′X₆ halide double perovskite semiconducting materials for application in energy and device technologies. To this end, we have investigated an intriguing series of five halide-based non-toxic systems, A₂AgRhCl₆ (A = Li, Na, K, Rb, and Cs), using density functional theory at the SCAN-rVV10 level. The lattice stability and bonding properties emanating from this study of A₂AgRhCl₆ matched well with those that have already been synthesized, characterized and discussed [viz. Cs₂AgBiX₆ (X = Cl, Br)]. Exploration of traditional and recently proposed tolerance factors has enabled us to identify A₂AgRhCl₆ (A = K, Rb and Cs) as stable double perovskites. The band structure and density of states calculations suggested that the electronic transition from the top of the valence band [Cl(3p)+Rh(4d)] to the bottom of the conduction band [(Cl(3p)+Rh(4d)] is inherently direct at the X-point of the first Brillouin zone. The (non-spin polarized) bandgap of these materials was found in the range 0.57–0.65 eV with SCAN-rVV10, which were substantially smaller than those computed with hybrid HSE06 and PBE0, and quasi-particle GW methods. This, together with the appreciable refractive index and high absorption coefficient in the region covering the range 1.0–4.5 eV, enabled us to demonstrate that A₂AgRhCl₆ (A = K, Rb, and Cs) are likely candidate materials for photoelectric applications. The results of our phonon calculations at the harmonic level suggested that the Cs₂AgRhCl₆ is the only system that is dynamically stable (no imaginary frequencies found around the high symmetry lines of the reciprocal lattice), although the elastic moduli properties suggested all five systems examined are mechanically stable.

GRAPHICAL ABSTRACT

Graphical Abstract. DFT modeling of the Cs₂AgRhCl₆ halide double perovskite (left) predicts a mechanically and dynamically stable material with reasonably high indices of refraction (right), suggesting possible application in optoelectronics.

Introduction

Dynamically and Mechanically Stable Halide Double Perovskites are an important class of light harvesting materials for application in solar energy technology and optoelectronics (Greul et al., 2017; Matthews et al., 2017; Xiao et al., 2017; Zhao X.-G. et al., 2017; Chen et al., 2018; Lei et al., 2018; Li H. et al., 2018; Li T. et al., 2018; Luo et al., 2018; Tan et al., 2018; Xu et al., 2018; Chu et al., 2019; Zhao et al., 2019; Zhou Y. et al., 2019). They are characterized by the chemical formula A₂BB′X₆, where A is generally a monocationic organic or alkali metal species such as MA⁺ (methyl ammonium), Cs⁺, Rb⁺; B is an alkali metal ion or a transition metal atom in its +1 oxidation state (for example, Cu⁺, Ag⁺, Na⁺); B′ is a transition or main group metal ion in the +3 oxidation state (In³⁺, Bi³⁺, Sb³⁺, Cr³⁺); and the X sites are occupied by halide ions. Examples of widely examined halide double perovskites include Cs₂AgSbBr₆ (Wei et al., 2019), Cs₂AgBiX₆ (Greul et al., 2017; Chen et al., 2018; Lei et al., 2018), Cs₂CuInX₆ (Zhao X.-G. et al., 2017), and Cs₂AgInX₆ (Volonakis et al., 2017), where A = Cs⁺, B = Ag⁺/Cu⁺, B′ = In³⁺, Bi³⁺, and X⁻ = Cl⁻, Br⁻, I⁻.

Many A₂BB′X₆ perovskites such as Cs₂AgSbBr₆ (Wei et al., 2019) and Cs₂AgBiX₆ (X = Cl, Br) (Mcclure et al., 2016) have been synthesized and their optoelectronic properties delineated. The great majority of them exhibited indirect bandgap transitions so they are not ideal for thin film photovoltaic applications (Mcclure et al., 2016; Volonakis et al., 2017; Zhao X.-G. et al., 2017; Wei et al., 2019). Many with direct bandgaps were also synthesized, but the first onset of optical absorption for several of them was beyond what might be expected from the Shockley–Queisser (S-Q) limit (Shockley and Queisser, 1961). For instance, Cs₂InAgCl₆ has a direct bandgap of 3.3 eV, in which the first onset of optical absorption was observed at 380 nm, with a second absorption at 585 nm (Volonakis et al., 2017); this is therefore not suitable for application in a solar cell because the S-Q limit suggests that the maximum theoretical efficiency of a solar cell can be achieved with materials that, among other properties, exhibit direct bandgaps between 1.1 and 1.4 eV (Rühle, 2016).

The search for ideal candidate materials for photovoltaics can be achieved through A, B, and B′-site doping (Yang et al., 2018) and this has already led to the discovery of many direct bandgap 2D and 3D semiconducting materials that are environmentally friendly and stable (Slavney et al., 2018; Jana et al., 2019; Yao et al., 2020; Belding et al.,). Doping assists in changing the characteristic properties of the resulting materials by modifying, inter alia, the lattice parameters, cell volume, lattice density and bonding environments that manipulate the bandgap and the character of the valence band maximum (VBM) and the conduction band minimum (CBM) (Zhao et al., 2018; Wang Z. et al., 2019). Examples of such doped materials include the sodium-based perovskites Cs₂NaB′X₆ (B′ = Sb, Bi; X = Cl, Br, I) that produced the iodide perovskites Cs₂NaSbI₆ and Cs₂NaBiI₆, with optimal bandgaps of 2.03 and 2.43 eV, respectively. Since Cs₂NaSbI₆, Cs₂NaBiI₆, and Cs₂NaSbBr₆ exhibited appreciable absorption coefficients in the visible range, accompanied by p-p valence to conduction band transitions, these have been suggested as materials for solar cell applications (Zhao et al., 2018). Similarly, others (Yang et al., 2018) have observed that the bandgap of Cs₂AgIn_xBi_1−xCl₆ can be tuned from indirect (x = 0, 0.25, and 0.5) to direct (x = 0.75 and 0.9) by manipulating the percentage of doping, and that they exhibited 3 times greater absorption cross section, lower sub-bandgap trap states, and more than 5 times the photoluminescence quantum efficiency (PLQE) compared to those observed for indirect bandgap nanocrystals such as Cs₂AgBiCl₆. Bandgap tuning by alloying of Cs₂AgBiCl₆ nanocrystals resulted in a series of Cs₂Na_xAg_1−xBiCl₆ (x = 0, 0.25, 0.5, 0.75, and 1) double perovskite nanocrystals that showed an increase in optical bandgap from 3.39 eV (x = 0) to 3.82 eV (x = 1) and a 30-fold increment in weak photoluminescence (Lamba et al., 2019). Other materials generated by replacing the B′-site species in A₂BB′X₆ with transition metals such as Mn³⁺ (Locardi et al., 2018; Nandha and Nag, 2018; Zhou J. et al., 2019), Cr³⁺ (Zhao et al., 2019), etc., via partial or heavy doping play a significant role in the discovery of innovative halide double perovskite materials for optoelectronics (Jain et al., 2017; Bartel et al., 2019; Cai et al., 2019; Li and Yang, 2019).

In this study, the electronic structures of a series of five double-halide perovskites A₂AgRhCl₆ (A = Li, Na, K, Rb, and Cs) are theoretically investigated using density functional theory at the SCAN-rVV10, PBE and PBEsol levels. We analyze their structural stability by means of the widely used octahedral and Goldsmith tolerance factors. An attempt is made to explore the same property using the Global Instability Index, as well as using a newly proposed tolerance factor, to demonstrate whether the traditionally-used octahedral and Goldsmith tolerance factors are adequate for identifying stable perovskites. The lattice constants, cell volume, cell density, density of states, and electronic structure properties are examined and discussed in light of the role that the A-site substitution (by the lighter alkali cations) plays in modifying the properties of Cs₂AgRhCl₆. The optical properties are investigated by calculating linear response characteristics such as the real and imaginary parts of the dielectric function, absorption coefficient, reflectivity and energy loss spectra. The reliability of electronic bandgaps of SCAN-rVV10 and those calculated using other GGA methods (GGA = Generalized Gradient Approximation) is assessed by comparing them with those calculated using HSE06, PBE0 and GW methods. The phonon modes, as well as the elastic properties, are calculated using density functional perturbation theory (DFPT) and finite difference method (FD) to probe the dynamical and mechanical stabilities, and the putative suitability of these materials for photovoltaic applications.

Computational Details

The conventional unit-cell structures (lattice parameters, ionic positions and volumes, etc.) of A₂AgRhCl₆ (each comprises 40 atoms) were fully optimized using DFT. The same calculations were performed on their primitive unit cells (each comprises 10 atoms). The k-point mesh 8 × 8 × 8 centered at Γ was used for sampling the first Brillouin zone. The projector augmented wave (PAW) method (Blöchl, 1994), together with an energy cut-off of 520 eV for a plane wave basis set, was used. The equilibrium positions of the ions were calculated by structural optimization, where the internal degrees of freedom and lattice constants, along with the volume of the unit cell, were allowed to vary until the residual forces per atom were <0.006 eV/Å. The maximum and average forces acting on each ion were minimized to 0.006 and 0.004 eV/Å, respectively. Instead of a default value of 10⁻⁴, the allowed error in the total energy for relaxation of the electronic degrees of freedom was set to 10⁻⁸ eV. Calculations involving both spin and non-spin polarizations were performed.

The three different DFT functionals employed for the relaxation of the geometry of A₂AgRhCl₆ were SCAN-rVV10 (Sun et al., 2015; Sun J. et al., 2016; Buda et al., 2017), PBE (Perdew et al., 1996) and PBEsol (Perdew et al., 2008). The reason for choosing three functionals is that we were interested in determining the extent to which the latter two functionals underestimate the bandgaps of the systems under investigation compared to SCAN-rVV10, since they generally underestimate the bandgap of halide single and double perovskites compared to both experiment and the computationally expensive GW and HSE06 (Volonakis et al., 2017; Lamba et al., 2019; Umadevi and Watson, 2019; Wang H.-C. et al., 2019). We note that the newly-proposed SCAN-rVV10 functional is one of the strongly constrained and appropriately normed meta-generalized gradient approximation (meta-GGA) functionals that is considered to model well metallic, insulating and semiconducting materials (Sun et al., 2015; Sun J. et al., 2016; Buda et al., 2017). The rVV10 part of the functional accounts for the non-local correlation part required to appropriately describe van der Waals (vdW) interaction (Peng et al., 2016; Chakraborty et al., 2018; Zhang et al., 2018; Anh et al., 2019). Bokdam et al. have demonstrated that the SCAN functional accounts for short range dispersion effects—which conventional hybrid functionals do not account for—and is the most suitable functional to study the atomic structure of hybrid perovskite materials (Bokdam et al., 2017). The Vienna Ab initio Simulation Package (VASP) was used for all calculations (Kresse and Furthmüller, 1996a,b).

The tetrahedron method with Blöchl corrections was used for the calculation of the density of states (DOS) of A₂AgRhCl₆. Their electronic band structures were calculated using a standard Self-Consistent (SC) procedure, followed by a subsequent non-SC calculation (VASP, 2020e). The 15 × 15 × 15 k-point mesh was used for sampling the Brillouin zone and the primitive cells were used. The DOS and band structures of A₂AgRhCl₆ were plotted using Pyband (Qijingzheng) and Sumo (Ganose et al., 2018).

The optical properties, such as the real and imaginary parts of the frequency dependent dielectric function, were computed on the SCAN-rVV10 geometries using the PBEsol functional (Perdew et al., 2008), a functional that has been extensively used to calculate the linear response properties of halide perovskites (Brivio et al., 2013; Frost et al., 2014; Savory et al., 2016b; Jong et al., 2018). In these calculations, the number of empty conduction band states were doubled, together with the number of frequency grid points, which was set to 2000. The Density Functional Perturbation Theory (DFPT) method was adopted (Gonze, 1997; Gonze and Lee, 1997; Baroni et al., 2001; VASP, 2020b). The Γ-centered k-point meshes 8 × 8 × 8, 10 × 10 × 10, and 18 × 18 × 18, blocked Davidson iteration scheme, energy cut-off of 520 eV, and a tightly converged electronic wavefunction (within 10⁻⁸ eV) were used.

Although the SCAN-rVV10 functional was used for the calculation of lattice properties, density of states, and electronic band structures, it cannot be combined with DFPT for the evaluation of linear response (optical) properties due to its lack of implementation in VASP 5.4. For this reason, and for comparison purpose with the DFPT/PBEsol results, a separate set of calculations was performed using the meta-GGA functional using a Γ-centered k-point mesh 12 × 12 × 12 that invoked an electronic minimization algorithm for an exact diagonalization of the matrix, in which the derivative of the cell-periodic part of the orbitals w.r.t. k, |∇_ku_nk>, was calculated using finite differences given by Equation (1) (VASP, 2020c),

$\begin{array}{ll}|{\nabla }_k{\overline{u}}_{nk}\rangle ={\displaystyle \sum _{n\ne n^{\prime }}|{\overline{u}}_{n^{\prime }k}\rangle \langle {\overline{u}}_{n^{\prime }k}|}\frac{\partial [H(k)-{\epsilon }_{nk}S(k)}{{\epsilon }_{nk}-{\epsilon }_{n^{\prime }k}}|{\overline{u}}_{nk}\rangle & (1)\end{array}$

where H(k) and S(k) are the Hamiltonian and overlap operator for the cell-periodic part of the orbitals, and the sum over n′ must include a sufficiently large number of unoccupied states.

The dynamical and mechanical stabilities of A₂AgRhCl₆ were examined using computed phonon band structures and elastic properties, respectively (Mouhat and Coudert, 2014; Togo and Tanaka, 2015; Kagdada et al., 2018). The former calculations were carried out using Phonopy (Togo and Tanaka, 2015). Both the DFPT/PBEsol and FD (Finite Difference) (Monserrat, 2018; VASP, 2020d) methods were used to calculate force constants in the reciprocal space. The 2 × 2 × 2 supercell structures (each 320 atoms) constructed using the conventional unit-cells of A₂AgRhCl₆ (A = Cs, Rb) (each 40 atoms) were supplied. The same practice was adopted to generate the supercell structures (each 80 atoms) using the primitive unit-cells of the system, and were used. Because the above calculations for systems with 320 atoms can be computationally very expensive, we used a 1 × 1 × 1 Γ-center scheme for k-point sampling integrations, together with an energy cut-off of 520 eV. For the latter supercells (80 atoms per supercell), a 4 × 4 × 4 k-mesh was used without changing other constraints.

The elastic coefficients (Mouhat and Coudert, 2014) of the stiffness matrix C_ij of A₂AgRhCl₆ (A = Cs, Rb, K, Li) were calculated within the harmonic approximation and finite differences to determine the second derivatives (Hessian matrix and phonon frequencies). A k-point mesh 6 × 6 × 6 was used. In all calculations referred to above, the SCAN-rVV10 optimized geometries of A₂AgRhCl₆ were used.

Results and Discussion

Geometrical Properties and Stability

The spin-polarized and spin non-polarized calculations gave very similar values for the total energies of each A₂AgRhCl₆. The calculated energy difference of the latter from the former (per formula unit) is −6.6, −7.3, −6.5, −5.2, and −3.6 meV for Cs₂AgRhCl₆, Rh₂AgRhCl₆, K₂AgRhCl₆, Na₂AgRhCl₆, and Li₂AgRhCl₆, respectively. Hence the spin-polarized systems were relatively more stable than the non-spin polarized systems. Unless otherwise stated, we report below the results of the most stable spin-polarized systems. We also confirm that the Rh³⁺ ions in A₂AgRhCl₆ had no local magnetic moments. Therefore, the chemical systems with perovskite stoichiometry examined in this work, A₂AgRhCl₆, contain low spin Rh³⁺ and are non-magnetic.

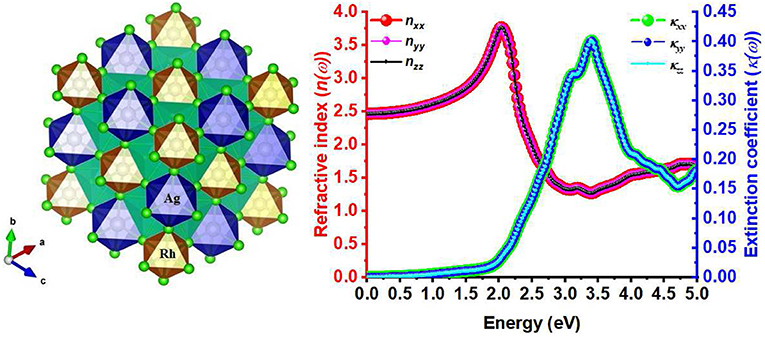
The selected lattice properties of A₂AgRhCl₆ obtained with SCAN-rVV10 are given in Table 1; those calculated using PBE and PBEsol are given in Table S1. As expected, the lattice constants are equal, a = b = c, for each member of the series A₂AgRhCl₆. The largest value of the lattice constants found with SCAN-rVV10 was for Cs₂AgRhCl₆, 10.087 Å (Table 1); the decrease across the series studied correlates with the decrease in the ionic radius of the A-site cation. This is accompanied by a decrease in the metal–Cl and A–Cl bond distances and a contraction in cell volumes (Table 2). All the structures preserved a face-centered cubic symmetry (space group Fm$\bar{3}$m, Figure 1).

TABLE 1

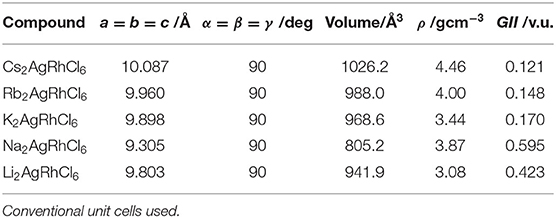
Table 1. Selected geometrical (lattice, volumetric, density, and stability) properties of A₂AgRhCl₆ (A = Cs, Rb, K, Na, Li) obtained with SCAN-rVV10.

TABLE 2

Table 2. Selected bond distances of A₂AgRhCl₆ (A = Li, Na, K, Rb, Cs).

FIGURE 1

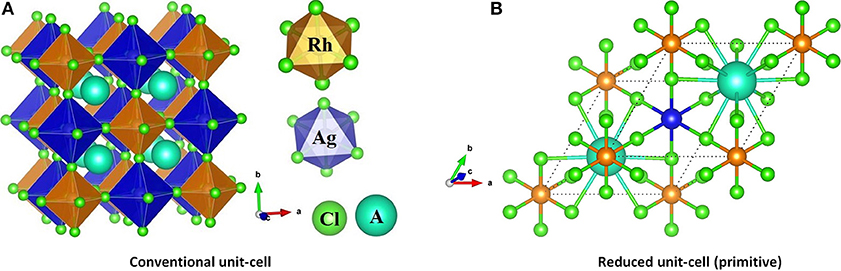
Figure 1. (A) SCAN-rVV10 relaxed polyhedral model of the conventional unit-cell of A₂AgRhCl₆, showing the coordination between the alkali metal anion and the halide anions. (B) The (reduced) primitive cell contains one unit of each of RhCl₆ and AgCl₆ octahedra in a face-centered cubic structure (space group Fm$\bar{3}$m).

The PBE and PBEsol functionals predicted larger and smaller cell volumes and lattice constants compared to those of SCAN-rVV10, respectively (see Table S1). There is no experimental data available for these systems for comparison. To verify the reliability of SCAN-rVV10, we optimized the geometry of Cs₂AgBiCl₆ (and Cs₂AgBiBr₆) using the same theoretical method, in conjunction with the same k-point mesh and convergence criteria used for A₂AgRhCl₆ as detailed above. Our calculations gave a value of 10.667 Å (and 11.234 Å) for a (= b = c) for these two systems, which is in good agreement with the experimental value of 10.77687 Å (and 11.27123 Å) (Mcclure et al., 2016). The predicted (and experimental) cell volumes for Cs₂AgBiCl₆ and Cs₂AgBiBr₆ were 1210.33 ų (1251.6356 ų) and 1417.87 ų (1431.904 ų), respectively. We note that there is variability in the reported experimental cell volumes and lattice constants of these halide double perovskites, possibly due to variability in sample preparation and the experimental procedures adopted. For instance, Slavney et al. have reported experimental a and V values of 11.2499 and 1423.7901 ų for Cs₂AgBiBr₆ (Slavney et al., 2016), somewhat different to those reported by others (Mcclure et al., 2016; Zhou et al., 2017); the values we obtained were similar to those reported by Mcclure et al. (2016). This demonstrates that the predictability SCAN-rVV10 is better than that of PBE and PBEsol, and that this method is useful for the prediction of 3D crystal structures of related compounds.

Whether compounds of the type ABO₃ (Li et al., 2004; Liu et al., 2008), ABX₃ and ABB′X₆ (Bartel et al., 2019) have a perovskite structure has often been judged based on the values of the octahedral factor μ and Goldschmidt tolerance factor, t, given by Equation (2):

$\begin{array}{ll}\mu =(r_{\text{B}}/r_X);t{=}^{r_A+r_{\text{X}}}{/}_{\sqrt{2}(r_B+r_{\text{X}})}& (2)\end{array}$

For ABX₃ and ABB′X₆ perovskite crystals, 0.813 < t < 1.107 and 0.415 < μ < 0.895. Structures with μ and t values outside these ranges (as generally found for non-perovskites) cannot be regarded as stable perovskites, and those close to 1.0 are cubic. We used Shannon's radii (Shannon, 1976) for the ions in A₂AgRhCl₆ and for calculated μ and t (Table 3). The value of μ = 0.50 for A₂AgRhCl₆ is constant because r_{X = Cl} and r_B [B=(r_Ag+r_Rh)/2] are the same for all five members of the series. This, and the values calculated for t, suggest that the first four members of the series form stable perovskite structures. Cs₂AgRhCl₆ was recently recognized to form a double perovskite structure (μ = 0.50 and t = 0.96) (Bartel et al., 2019); we found that three other members of the series studied (Rb₂AgRhCl₆, K₂AgRhCl₆ and Na₂AgRhCl₆) may also form stable perovskite structures. However, with t = 0.71, Li₂AgRhCl₆ is unlikely to have a perovskite structure. Such a low t value is generally observed for significantly distored perovskites (viz. orthorhombic).

TABLE 3

Table 3. Shannon's ionic radii (r) of ions, octahedral factor (μ), Goldschmidt tolerance factor (t), and new tolerance factor (τ) for A₂AgRhCl₆ (A = Cs, Rb, K, Na, Li).

Other approaches, such as energy phase diagrams (Filip et al., 2018) and the global instability index (GII) (Salinas-Sanchez et al., 1992; Yamada et al., 2018) have been used for examining the feasibility of a compound adopting a perovskite structure. We have also used GII to shed more light on the probable stability of A₂AgRhCl₆ as perovskites, as GII is a measure of geometrical stability.

GII = 0.0 valence units (v.u.) for geometrically stable perovskite structures without steric distortions, and for empirically unstable structures, GII > 0.2 v.u. (Yamada et al., 2018). By definition, GII is the root mean square of the bond discrepancy index in the unit cell given by Equation (3),

$\begin{array}{ll}GII=\sqrt{{\sum }_{i=1}^N{d}_i^2/N}& (3)\end{array}$

where N is the number of ions, and d is the bond discrepancy factor. The latter is defined as the deviation of the bond valence sum (BVS) from the formal valence (Salinas-Sanchez et al., 1992; Yamada et al., 2018) which can be calculated using the sum of bond valences (s_ij) around any specific ion. It is given by: $BVS={\sum }_{i=1}^n{s}_{ij}$, where s_ij = exp((l₀−l_ij)/b), l_ij is a bond length, l₀ is the bond valence parameter empirically determined using experimental room-temperature structural data, and b is the bond softness parameter. A detail of how this was done has been discussed in a number of previous studies (Brese and O'keeffe, 1991; Gagné and Hawthorne, 2015; Brown, 2017).

The GII values for A₂AgRhCl₆ (A = Cs, Rb, K, Na, Li) are given in Table 1. They are within the narrow range 0.12 v.u. < GII < 0.18 v.u. for A = Cs, Rb and K, but GII = 0.595 v.u. for A = Na and 0.423 v.u. for A = Li. This indicates that the first three are expected to form crystallographically stable perovskite structures, whereas the latter two are not. For comparison, SrTiO₃, CaTiO₃, NaTaO₃, LaAlO₃, and BaZrO₃, were reported to have GII values of 0.006, 0.273, 0.102, 0.027, and 0.003 v.u., respectively, and crystallized into cubic perovskite structures under ambient conditions (Yamada et al., 2018).

There is no mutual agreement on whether A₂AgRhCl₆ will form a stable perovskite when using GII or the μ and t combination. This is unsurprising since t is not always a good predictor as it gives a high false-positive rate (51%) in the region of t where a perovskite is expected (0.825 < t < 1.059). Bartel et al. have tested a set of 576 ABX₃ species and have found that t correctly predicted 94% of the known perovskites, but also 49% of the non-perovskites (Bartel et al., 2019). Because of this relatively poor predictability, these workers have proposed a new tolerance factor, τ, defined by Equation (4),

$\begin{array}{ll}\tau =r_X/r_{\text{B}}-n_A(n_A-(r_A/r_{\text{B}})/ln(r_A/r_{\text{B}}))& (4)\end{array}$

where n_A is the oxidation state of A, r_i is the ionic radius of ion i, and r_A > r_B by definition. Although the second term of τ is different to t, the first term incorporates the octahedral term μ that manifests itself in the probability maps, particularly in the lower bound on r_B where perovskites are expected as r_X is varied. As r_X increases, r_B must similarly increase to enable the formation of stable BX₆ octahedra. In particular, τ was shown to generalize outside the training set of 1034 experimentally observed single and double perovskites (91% accuracy) and was applied to identify 23,314 new double perovskites (A₂BB′X₆) ranked by their probability of being stable as perovskites based on the ranges of τ (τ < 4.18) that defines the decision boundary between a perovskite and a non-perovskite. Our results for τ are listed in Table 3; they indicate that A₂AgRhCl₆ (A = Cs, Rb, K) are stable perovskites (3.84 < τ < 4.05), but Na₂AgRhCl₆ (τ < 4.59) is only partially stable while Li₂AgRhCl₆ (τ < 75.10) is significantly unstable as a perovskite, and can be predicted to have a non-perovskite structure. These conclusions are in good agreement with the inferences drawn using GII.

It is worth mentioning that the coordination environment of Li⁺ in Li₂AgRhCl₆ is not remarkably different from that of the other A-site ions in the series A₂AgRhCl₆. The results of our calculations show that the alkali cations lie near the center of each cube in Figure 1 where they are involved in a dodecahedral arrangement with the coordinating Cl⁻ ions of A₂AgRhCl₆. This is evident in the data in Table 3; the Li–Cl bond distances are marginally smaller than those of the A–Cl (A = Cs, Rb, K) bond distances. The discrepancy in the trend in these distances between Li₂AgRhCl₆, Na₂AgRhCl₆ and K₂AgRhCl₆ is an artifact of the PAW potential in which the 3s and 2p semi-core states of Na were treated as valence states; consequently, the lattice constants and volume of Na₂AgRhCl₆ are predicted to be smaller than those of Li₂AgRhCl₆ (Table 1). It should also be noted that the indices μ, t, and τ were calculated using the ionic radii proposed by Shannon (1976), where the ionic radius of Li⁺ is for an 8-coordinate ion, whereas the ionic radii for the other ions are in a dodecahedral environment. This probably accounts for the very large τ value of 75.10 calculated for Li₂AgRhCl₆.

Bandgap, Band Dispersion and Density of States Analyses

Cs₂AgRhCl₆ is a direct bandgap material, as are the other members of the series. The bandgap (E_g) of Cs₂AgRhCl₆ with SCAN-rVV10 is 0.57 eV, indicating the possibility of electronic transition between the VBM and CBM. The A-site substitution in A₂AgRhCl₆ by lighter alkali atoms has a very small effect on the magnitude of E_g, and were found to vary between 0.57 and 0.65 (Table 4 and Table S3). On the other hand, the PBEsol and PBE functionals gave E_g of 0.42 and 0.55 eV for Cs₂AgRhCl₆ (Table S1), respectively. This shows how these two functionals slightly underestimate E_g compared to the SCAN-rVV10 functional, while retaining the direct nature of the bandgap transition between the VBM and CBM.

TABLE 4

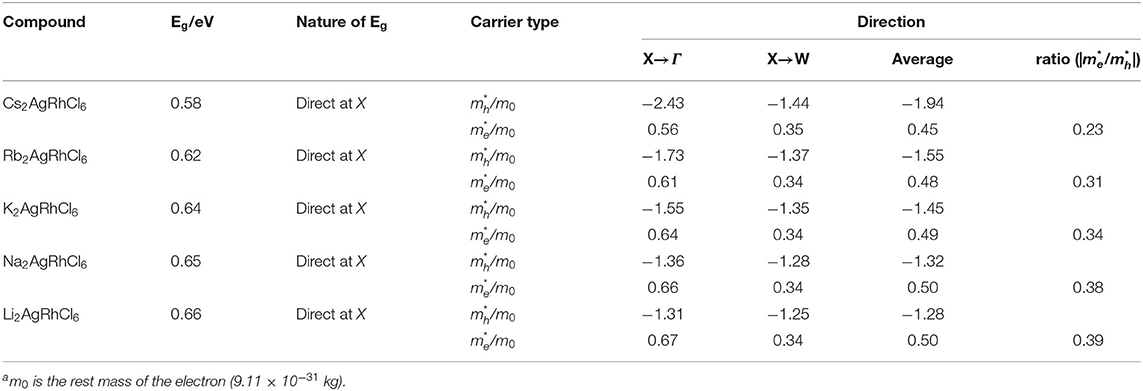
Table 4. Non-spin-polarized effective masses of electrons and holes obtained using the parabolic fitting of the lower conduction band and upper valence band for A₂AgRhCl₆ (A = Cs, Rb, K, Na, Li)^a. Primitive cells used.

From the plot of the density states (DOS) and electronic band structure of Cs₂AgRhCl₆ (Figures 2A,B, respectively), it was found that the VBM is of Cl(3p)–Rh (4d) character. In particular, the non-bonding orbital states t_2g (d_xy, d_yz, d_xz) of Rh and the 3p orbital states of Cl cause the dispersion of the valence band just below the Fermi level. The calculated normalized contribution of Rh(4d) and Cl(3p) to the VBM are 68.4 and 28.5%, respectively. The contribution of the alkali and Ag atoms to the VBM of Cs₂AgRhCl₆ are negligibly small (1–2%).

FIGURE 2

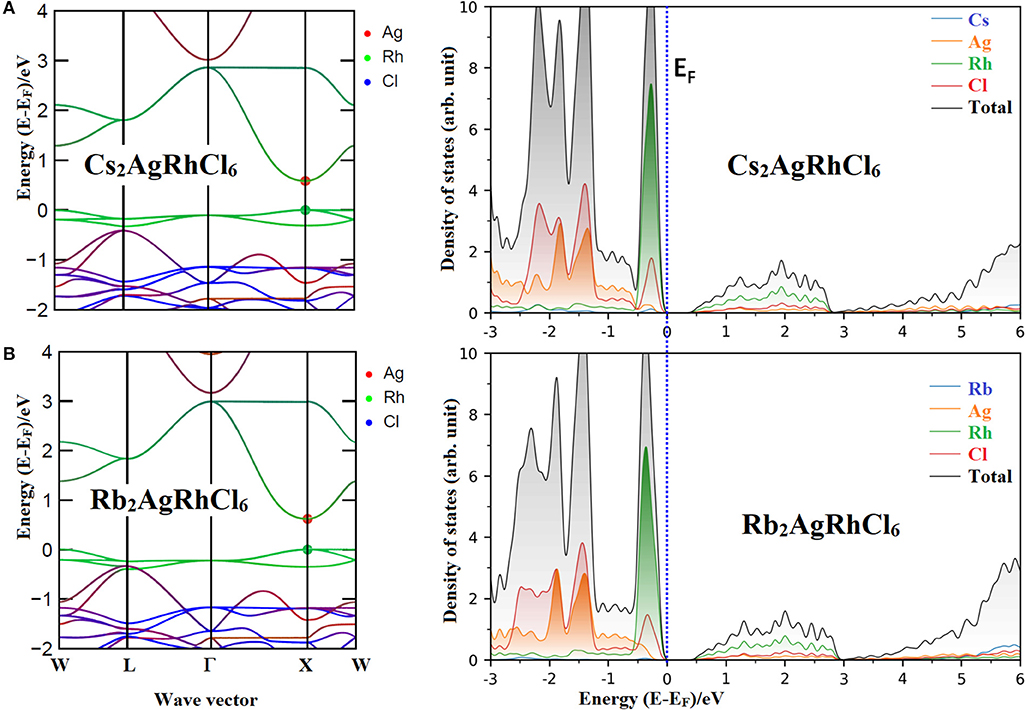
Figure 2. Comparison of the non-spin polarized atom-projected electronic band structure and partial (and total) density of states of (A) Cs₂AgRhCl₆ with (B) Rb₂AgRhCl₆. Different color codes were used for each plot. The k-vector types of space group Fm$\bar{3}$m were used for band structures.

By contrast, the edge associated with the CBM is largely derived from the Rh(4d) empty anti-bonding states e_g (d_z2, d_x2_−y2), but the entire band is formed using contributions from Ag, Rh and Cl states leading to its dispersion far above the Fermi level. For example, the normalized contribution of Rh(4d), Cl(3p), and Ag(5s) to the CBM of Cs₂AgRhCl₆ were 61.6, 23.3, and 6.3%, respectively. These vary marginally upon the replacement of the A-site cation by lighter elements of the alkali group. For instance, the contribution of Rh(4d), Cl(3p), and Ag(5s) to the CBM of Rb₂AgRhCl₆ was 61.0, 23.5, and 6.0%, respectively, whereas those of Rb₂AgRhCl₆ were 60.8, 23.6, and 6.0%, respectively. Since the CBM is far away, and at the same time, the VBM is just below the fermi level, one might conclude that A₂AgRhCl₆ are p-type conducting materials (Wang H.-C. et al., 2019). The spin-polarized DOS and band structures of the first three members of the series are shown in Figures S1–S3, revealing that spin-polarization does not have any marked impact on the orbital character of CBM and VBM.

We note that the qualitative nature of orbital character responsible for the HOMO and LUMO bands do not change when the conventional cells of the corresponding systems were used for the same analysis. This suggests that the 4d orbitals of Rh³⁺ do indeed play a predominant role in driving the HOMO and LUMO bands of the studied systems (Figure S4A). However, the nature of the dispersion associated with the valence and conduction bands is significantly affected (Figure S4B). As can be seen, the band structure resembles the presence of parabolic double bands along the line L → Γ → W → X evaluated using the same band labels defined for the Fm$\bar{3}$m point group for a conventional cell (Bilbao Crystallographic Server). The bands are symmetric with respect to the mid-point of the Γ-X path, and are significantly flatter along Γ-X-W path that are associated with the valence band. These are clearly the effects of the double cell which can be thought as a supercell of the cubic halide perovskite. The flat bands indicate that there is no direct interaction between halide atoms along those directions, and the empty band dispersion shows that there is little interaction between Rh and the other atoms. It is therefore expected that the mobility of electrons associated with the conduction band edge should be faster than those of the holes at the valence band edge. Although this is reflected on the effective masses of the charge carriers discussed in the following section, it should be noted that the high-symmetry k-point paths are all defined for the primitive cell, but not for conventional cells. This explains why the origin of the bandgap transition is shifted from the X-point (Figure 2) to the center of the Brilliouin zone Γ-point (Figure S4B). Accordingly, the band structure shown in Figure S4A could be misleading; band unfolding is likely to recover the actual nature of the HOMO and LUMO bands that are apparent in Figure 2 and Figures S1–S3.

Nature of Effective Masses and Their Mobility

We found that the top of the valence band is flatter than the bottom of the conduction band; the latter is appreciably parabolic. A similar flatter nature of the valence band was reported for bulk Cs₂AgInCl₆, which originated from Ag 4d and Cl 3p orbitals (Meng et al., 2017; Tran et al., 2017; Volonakis et al., 2017). In such a case, it is often observed that the hole effective mass (m_h^*) associated with the VBM is larger than the electron effective mass (m_e^*) of the CBM. Concomitantly, it is expected that the carrier mobility of the former is slower than that of the latter. The difference in the carrier masses arises from the nature of the curvature of the bottom of the conduction band (for electrons), or of the top of valence band (for holes); this is inversely proportional to the second derivative of the energy as a function of the wave vector k, and is described by the dispersion relationship shown in Equation (5),

$\begin{array}{ll}{m}^{*}=\pm \frac{{ħ}^2}{{\partial }^2\raisebox{1ex}{$E\left(\text{k}\right)$}\!\left/ \!\raisebox{-1ex}{$\partial {\text{k}}^2$}\right.}& (5)\end{array}$

where the + and – signs refers electrons and holes, respectively (Hartmann et al., 1982; Opoku et al., 2017). Using parabolic fitting of the band edges, it was found that the spin-up holes and electrons are the dominant charge carriers. The VBM comprises two degenerate bands. One of them is heavier than the other. This is arguably due to the fact that one of these bands is very flat along X → W and other is parabolic (see Figures 2A,B). For the lighter HOMO band, the hole masses are heavier along the X → Γ direction compared to the X → W direction, a feature that is consistent in all five A₂AgRhCl₆ systems examined (Tables 4 and S3). The same behavior is associated with the effective masses of electrons that are virtually isotropic (values between 0.45 and 0.50 m₀), suggesting that the charge transport would be predominant along the X → W direction.

The effective masses and bandgaps of A₂AgRhCl₆ obtained using non-spin polarized calculations were very similar to those calculated using the spin-polarized setting (see Table 4 and Table S3). Figure 3 illustrates the functional dependence of effective mass on the bandgap for the series A₂AgRhCl₆, which is independent of the nature of the spin- and non-polarized calculations performed. Nevertheless, the average effective mass of electrons is approximately 0.45 m₀, whereas that of the hole is 1.94 m₀ for Cs₂AgRhCl₆, where m₀ is the free electron mass. These values are, respectively, 0.48 and 1.55 m₀ for Rb₂AgRhCl₆; 0.49 and 1.45 m₀ for K₂AgRhCl₆; 0.50 and 1.32 m₀ for Na₂AgRhCl₆; and 0.50 and 1.28 m₀ for Li₂AgRhCl₆. As mentioned above, the hole masses for one of the flatter valence bands should be heavier, reducing the average hole mobility. Indeed, this is what we have observed. It is smaller along the X → Γ direction than X → W direction (viz. 2.43 m₀ vs. 27.0 m₀); they are therefore are not incorporated in the average values shown in Table 4 and Table S3. A similar result was reported elsewhere for the Cs₂InCuCl₆ double perovskite (Pham et al., 2019).

FIGURE 3

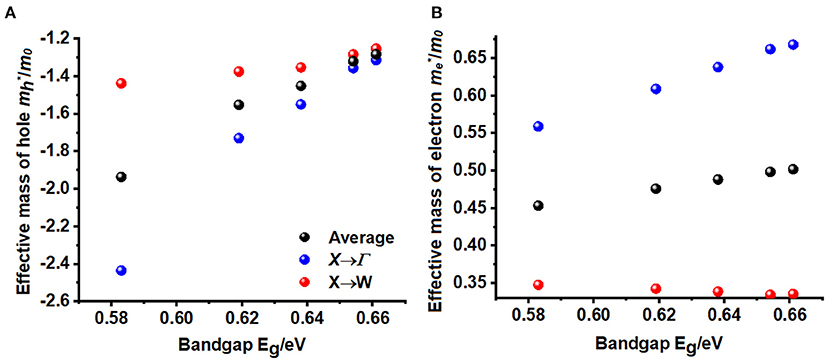
Figure 3. Dependence of non-spin polarized effective mass of (A) holes and (B) electrons holes on the bandgap E_g for A₂AgRhCl₆ (A = Cs, Rb, K, Na, Li).

These results not only suggest that the average spin-up holes are heavier than that of the spin-up electrons for A₂AgRhCl₆, but the relatively low electron effective mass also signifies the presence of n-type conductivity, as observed for the CdSe semiconductor, for example (Hartmann et al., 1982). Our result is consistent with Si, for which the electron mobilities are higher than hole mobilities. Since the hole mass for A₂AgRhCl₆ is comparable to that of other systems (Wang Z. et al., 2019), the contribution of the holes to charge transfer is unlikely to be very large (Park, 2019) and the lifetime of the charge carriers for these semiconductors is likely to be determined by electron-electron collisions (Kao, 2004; Morkoc, 2009; Fu and Zhao, 2018). The ratio $m_e^{*}$/m_h^* provides the nature of electron-hole (e-h) pair stability in a recombination process (Zhang et al., 2012a,b; Dong et al., 2015; Faraji et al., 2015; De Lazaro et al., 2017; Opoku et al., 2017). In general, the larger the m${}_e^{*}$/m_h^* ratio, the smaller the rate of recombination of the photoinduced charges. For instance, values of m${}_e^{*}$ and m_h^* were found to be 0.24 m₀ and 0.23 m₀, respectively, for MAPbI₃ (Filip et al., 2015). Similarly, they were 0.41 m₀ (0.34 m₀) and 0.35 m₀ (0.37 m₀) along the R to X direction for CsPbCl₃ (CsPbBr₃), respectively; 0.53 m₀ (0.37 m₀) along the L to W direction and 0.15 m₀ (0.14 m₀) along the X to Γ direction for Cs₂AgBiCl₆ (Cs₂AgBiBr₆), respectively (Mcclure et al., 2016). In all these cases, the ratio m${}_e^{*}$/m_h^* is in the range 0.28 and 1.09, which is consistent with the majority of charge carriers in halide perovskites being large polarons; the slow recombination of these polarons underlies long carrier lifetime and diffusion length (Hoye et al., 2018; Zhang et al., 2019).

Our calculations gave $m_h^{*}$/m_e^* values in the range between 2.6 (Li₂AgRhCl₆) and 4.4 (Cs₂AgRhCl₆), suggesting that these may be possible candidate materials for light-based device applications.

Optical Properties

Insight into the optical properties of a solid state system can be obtained using the frequency dependent complex dielectric function ε(ω), a property that has been widely used to provide insight into, among other properties, the extent of charge screening, electron-hole coupling, and the electronic and ionic contributions to chemical bonding (Brivio et al., 2013; Walsh, 2015; Luo et al., 2017; Kirchartz et al., 2018; Wilson et al., 2019). The difference between the electronic and ionic dielectric constants (ε_ionic and ε_electronic) assists to elucidate the polarity of the chemical bonds and the softness of the vibrations in a semiconducting material. The nature of the (picosecond) response of lattice vibrations (phonon modes) can be extracted, which can then be used to explain the extent of ionic and lattice polarizations required for a fundamental understanding of the photovoltaic performance of a material. If ε₁ (ω) = ${\epsilon }_{\alpha \beta }^{(1)}(\omega )$ is the real part, and ε₂(ω) = ${\epsilon }_{\alpha \beta }^{(2)}(\omega )$ is the imaginary part of the frequency dependent ε(ω), then ε(ω) can be written as ε(ω) = ε₁(ω) + iε₂(ω) = ${\epsilon }_{\alpha \beta }^{(1)}(\omega )$+i${\epsilon }_{\alpha \beta }^{(2)}(\omega )$. We used the Kubo-Greenwood relationship (Equation 6) for the calculation of the frequency dependent dielectric matrix associated with ${\epsilon }_{\alpha \beta }^{(2)}(\omega )$. This was determined upon summing over the empty states.

$\begin{array}{l}{\epsilon }_{\alpha \beta }^{(2)}(\omega )=\frac{4{\pi }^2{e}^2}{\Omega }{lim}_{q\to 0}\frac{1}{q^2}{\displaystyle \sum _{c,\upsilon ,k}}2w_k\delta ({\epsilon }_{ck}-{\epsilon }_{\upsilon k}-\omega )\\ \times \langle u_{ck+e\alpha q}|u_{\upsilon k}\rangle \langle u_{\upsilon k+e\beta q}|u_{\upsilon k}\rangle & (6)\end{array}$

In Equation (6), the subscripts c and υ refer to conduction and valence band states, respectively, and u_ck is the cell periodic part of the orbitals at the k-point k. The real part ${\epsilon }_{\alpha \beta }^{(1)}(\omega )$ of the dielectric function is related to ${\epsilon }_{\alpha \beta }^{(2)}(\omega )$ via the Kramers-Kronig transformation given given by Equation (7), where P denotes the Cauchy principal value, and η is a small complex shift.

$\begin{array}{ll}{\epsilon }_{\alpha \beta }^{(1)}(\omega )=1+\frac{2}{\pi }P{\displaystyle \underset{0}{\overset{\propto }{\int }}}\frac{{\epsilon }_{\alpha \beta }^{(2)}({\omega }^{\prime }){\omega }^{\prime }}{{{\omega }^{\prime }}^2-{\omega }^2+i\eta }d{\omega }^{\prime }& (7)\end{array}$

The energy (or frequency) dependence of the dielectric function of A₂AgRhCl₆ in depicted in Figure 4. The curves of the real part of the dielectric function suggest that the electronic contribution to the static dielectric constant ε(0) is appreciably large, where ε(0) = ε_∞ + ε₀ (the first and last terms represent the electronic and ionic constributions, respectively). ε_∞ is related to the vibrational polar phonons of the lattice (Yu, 2019), and is due to the (femtosecond) response of the electron density (Zangwill, 2019).

FIGURE 4

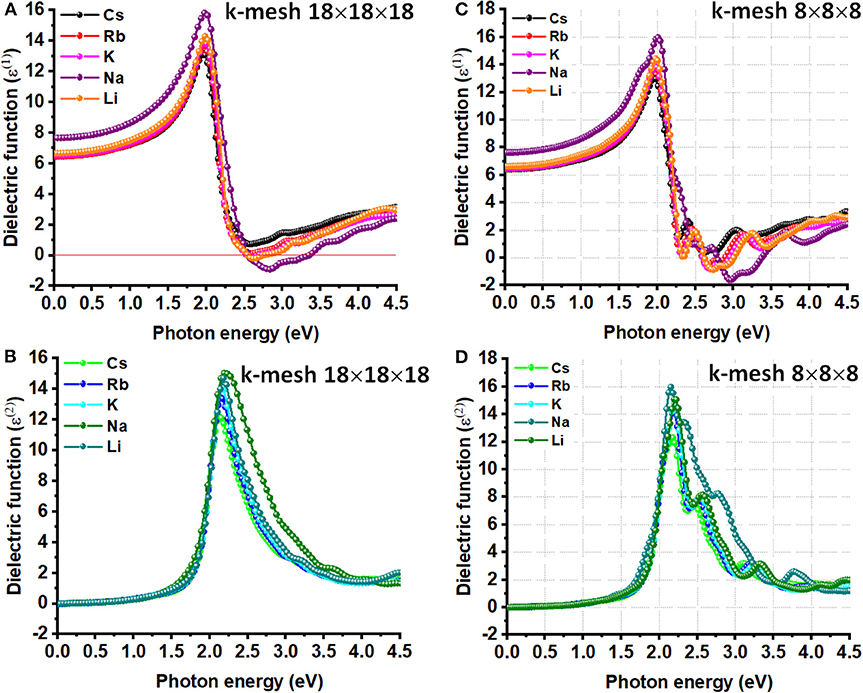
Figure 4. The (A) real and (B) imaginary parts of dielectric function ε(ω) plotted against the photon energy for A₂AgRhCl₆ (A = Li, K, Na, Rb, Cs), obtained using DFPT/PBEsol. Shown in (C) and (D) are the corresponding plots obtained using k-mesh 8x8x8. The primitive cells used.

The ionic contribution, ε₀, is due to the (picosecond) response of lattice vibrations (phonon modes); it is proportional to the polarity of the chemical bonds and the softness of the vibrations. The high frequency dielectric constant (ε_∞), which is also called the optical dielectric constant, is found to be isotropic because of the cubic nature of each of the five systems examined. Its value is around 6.5 for Cs₂AgRhCl₆, which is also the zero-frequency limit of ε₁(ω). This is the smallest across the series; of course, this is compared to the ε_∞ values of 6.5, 6.5, 7.7, and 6.7 calculated for Rb₂AgRhCl₆, K₂AgRhCl₆, Na₂AgRhCl₆ and Li₂AgRhCl₆, respectively. The size of the k-mesh has a very marginal effect on the zero-frequency limit of of ε₁(ω) (viz. Figure 4A vs. Figure 4C), regardless of the nature of the cell type used (Figure 4 vs. Figure S5). As noted above, the unusual trend in value of ε_∞ for Na₂AgRhCl₆ may be a consequence of the plane wave basis set or the spin-polarized setting. The former could be corrected if the p-type semi-core states were to be treated as valence states, among other cut-off settings.

The ε_∞ value of 6.5 found for Cs₂AgRhCl₆ is comparable to that reported for other absorbing materials (Wilson et al., 2019), e.g., CdTe (ε_∞ = 7.1), MAPbI₃ (ε_∞ = 6.0), MAPbBr₃ (ε_∞ = 5.2), MAPbCl₃ (ε_∞ = 4.2) and CsPbI₃ (ε_∞ = 5.3). It is well-known that ε_∞ is computationally sensitivity to the choice of electronic structure Hamiltonian and the level of geometry optimization; ε_∞ values between 4.0 and 7.1 have been reported for the same material (MAPbI₃), and experimentally determined to lie between 4.0 and 6.5 (Wilson et al., 2019). The experimental variability in ε_∞ is either due to surface effects (Leguy et al., 2016a), or the assumptions taken in data processing (Hirasawa et al., 1994), or indeed other factors (Wilson et al., 2019). Using spectrospic ellipsometry methods, the optical dielectric constant was reported to be 4.8–5.1 near the absorption edge of CH₃NH₃PbBr₃ organic-inorganic hybrid perovskite thin films, correspinding to a bandgap of 2.3 eV (Alias et al., 2016).

The maximum of ε₁(ω) is approximately 13.0 for Cs₂AgRhCl₆. It shows up in the region between 0 and 4.5 eV. This becomes 13.7, 14.1, 15.5, and 14.3 for Rb₂AgRhCl₆, K₂AgRhCl₆, Na₂AgRhCl₆ and Li₂AgRhCl₆, respectively. The first corresponds to a photon energy of 2.0 eV, whereas those for others correspond to an energy around 2.0 eV. The use of smaller k-grid has some effect on the height of the peak, but not on the position of its occurrence (Figure 4A vs. Figure 4C). These results suggest that decreasing the size of the alkali metal ion in the lattice increases the high frequency response behavior, but the nature of the transitions involved between the VBM and CBM is of similar character.

On the other hand, the transition peaks in the curves of ε₂(ω), which are directly related to the optical absorption process, occur at energies between 2.10 and 2.20 eV. These are located at higher energies than those in the ε₁(ω) curves (see above). Whereas the ε₂(ω) curves are quasi-symmetric and resemble a Lorentz-like resonant behavior that corresponds to bound electrons, the ε₁(ω) curves are anti-symmetric and show dispersion-like behavior. The ε₁(ω) spectra for K₂AgRhCl₆, Na₂AgRhCl₆, and Li₂AgRhCl₆ are strongly positive at low energies. It reaches a maximum value around 2.0 and then decreases. It becomes negative at the crossover energy around 2.5 eV and then becomes positive. The negative feature is likely to be a Drude-tail (Khatri et al., 2011; Eaton et al., 2018), thus indicating the quasi-metallic behavior of these materials in a specific region (Xu et al., 2008; Murtaza et al., 2011). This is not the case for Cs₂AgRhCl₆ and Rb₂AgRhCl₆. We note that the Drude feature appears in the ε₁(ω) spectra using DFPT, which is persisent regardless of the size the k-mesh and cell-type used [Figure 4 and Figure S5 (Top)], is not evident in that calculated using SCAN-rVV10 (Figure S6), suggesting that it could be an artifact of DFPT.

The appreciable dielectric features delineated above are also evidence of the spectra of absorption coefficient α(ω), reflectivity R(ω), and energy loss function L(ω), calculated using Equations (8), (9), and (10), respectively (Dresselhaus, 2001; Ma et al., 2014), where c and ω are the speed of light in vacuum and frequency of light wave, respectively. The calculated real and imaginary parts of the dielectric function of each system were used.

$\begin{array}{ll}\alpha (\omega )=\frac{\sqrt{2}\omega }{c}{\left\{{\left[{\epsilon }_1^2(\omega )+{\epsilon }_2^2(\omega )\right]}^{1/2}-{\epsilon }_1(\omega )\right\}}^{1/2}& (8)\end{array}$

$\begin{array}{ll}R(\omega )={\left|\frac{\sqrt{{\epsilon }_1(\omega )+i{\epsilon }_2(\omega )}-1}{\sqrt{{\epsilon }_1(\omega )+i{\epsilon }_2(\omega )}+1}\right|}^2,& (9)\end{array}$

$\begin{array}{ll}L(\omega )=Im(\frac{-1}{\epsilon (\omega )})=\frac{{\epsilon }_2(\omega )}{{\epsilon }_1^2(\omega )+i{\epsilon }_2^2(\omega )}& (10)\end{array}$

As noted elsewhere (Meng et al., 2017), absorption coefficients below 10⁴ cm⁻¹ are regarded as a weak absorption; this may lead to a tail in the absorption coefficient curve of a UV-Vis spectrum. However, inspection of Figure 5A shows that the absorption starts around the VBM to the CBM transition region for all A₂AgRhCl₆. The absorption coefficient increases with an increase of photon energy, and reaches a maximum at 2.2 eV, which is in reasonable agreement with the maximum oscillator peak of ε₂ as α is dependent on it (Equation 8). Since this occurs in the visible region, these systems could be useful in photovoltaic and photodetector applications (Wang et al., 2020). Specifically, the value of α at the highest peak varies between 6.4 × 10⁵ cm⁻¹ (Cs₂AgRhCl₆) and 8.3 × 10⁵ cm⁻¹ (Na₂AgRhCl₆); there should therefore be an appreciable absorption of light by these systems.

FIGURE 5

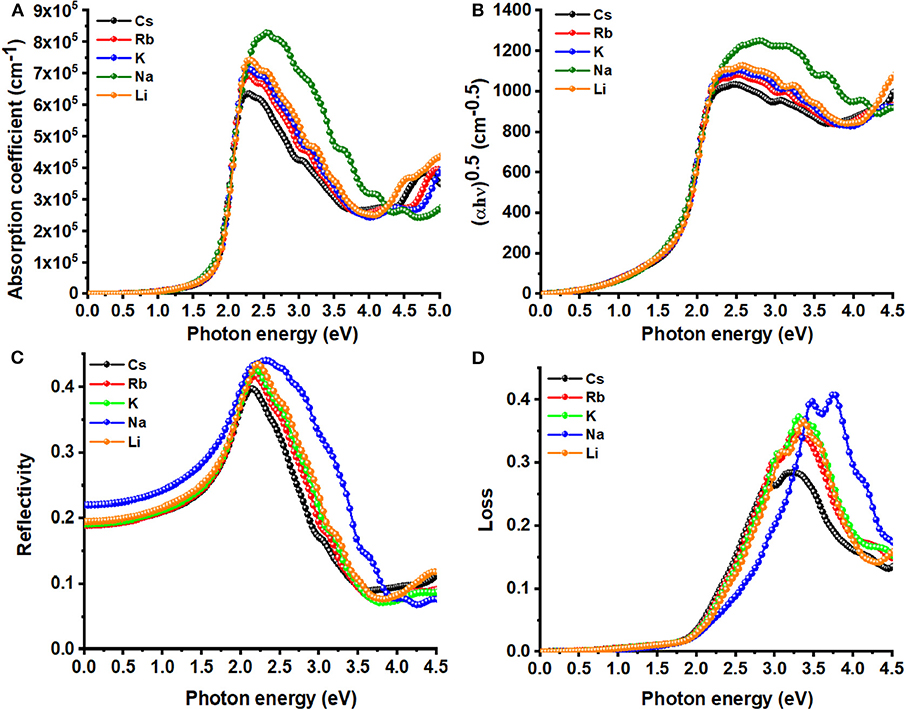
Figure 5. Dependence of the (A) absorption coefficient, (C) reflectivity, (D) energy-loss function on the photon energy of A₂AgRhCl₆ (A = Li, K, Na, Rb, Cs). Displayed in (B) is the Tauc plot for the corresponding systems. Primitive cells and k-mesh 18 × 18 × 18 used.

The computed absorption coefficient curves of A₂AgRhCl₆ show an onset around 1.1 and 1.3 eV; these are consistent with the SCF bandgaps predicted with SCAN-rVV10 (Table S2). The Tauc plot, Figure 5B, provides similar insight, since it is often used to extract the bandgaps from experimental absorption spectra (Eom et al., 2017; Tang et al., 2017; Habibi and Eslamian, 2018; Ji et al., 2018). The peak feature in the visible region with an appreciable absorption coefficient is a strong indication that A₂AgRhCl₆ are potential candidates for possible optoelectronic applications.

Since the VBM and CBM are substantially of Rh(4d) character, it is likely that the ligand field electronic transitions involved between them have d-d type metallic character (Ford, 2016). The Tanabe-Sugano diagram (Tanabe and Sugano, 1954) for a low spin d⁶ ion in an O_h environment indicates that the two lowest energy spin-allowed transitions from the ¹A_1g state of the ion are, in order of increasing energy, ¹A_1g → ¹T_1g and ¹A_1g → ¹T_2g. The spin-forbidden transitions ¹A_1g → ³T_1g and ¹A_1g → ³T_2g occur at longer wavelength. For instance, in some Rh³⁺-doped sodium borosilicate glasses thee spin-allowed transitions occur at 449 and 297 nm (2.76 and 4.17 eV, respectively) and the spin-forbidden transitions occur in the 600–2000 nm (2.0–0.62 eV) range (Wen et al., 2017). The emission onset and peak positions for Cs₂NaMCl₆:M' (M = Y, In, Sc; M′ = Rh³⁺) were reported between 1.3–1.4 and 1.04–1.07 eV, respectively, and ascribed to a ¹A₁ → ³T₁ transition (Campochiaro et al., 1992). The observation of a peak emission at ~1,600 nm (0.77 eV) of the single luminescence band in the infrared spectral region in Rh³⁺-doped AgBr crystals was also ascribed to this spin-forbidden transition (Spoonhower et al., 1986).

We observe an absorption envelope beginning around the fundamental bandgap and expending into the visible and UV regions for A₂AgRhCl₆ (see Figures 5A). The three principal peaks were found around 2.2, 2.5, and 3.2 eV for Cs₂AgRhCl₆. The dominant absorption, around 2.2 eV, is attributed to the lower energy, spin-allowed transition (¹A_1g → ¹T_1g); the higher energy spin-allowed transition (¹A_1g → ²T_1g) occurs around 3.2 eV. The lower energy shoulder on the main transition, around 2.5 eV, is ascribed to the spin-forbidden ¹A_1g → ³T_1g transition. These transitions are prominent in the dielectric spectra shown in Figure 4D.

The complex refractive index (n +iκ) is a fundamental property of a solid material that describes the propagation velocity of light in the medium, thus allowing one to recognize whether such a material is potentially useful for optoelectronics (Schubert et al., 2007). The real and imaginary parts of the complex refractive index, called the static refractive index (n(ω)) and extinction coefficient (κ(ω)), were calculated using Equations (11) and (12), respectively (Dresselhaus, 2001; Li et al., 2009; Jong et al., 2016; Dong et al., 2017). Depending on the nature of the bulk material, the value of n(ω) varies, but κ(ω) is generally small for semiconductors (Baranoski and Krishnaswamy, 2010).

$\begin{array}{ll}n(\omega )={\left[\frac{\sqrt{{\epsilon }_1^2+{\epsilon }_2^2}+{\epsilon }_1}{2}\right]}^{1/2}& (11)\end{array}$

$\begin{array}{ll}\kappa (\omega )={\left[\frac{\sqrt{{\epsilon }_1^2+{\epsilon }_2^2}-{\epsilon }_1}{2}\right]}^{1/2}& (12)\end{array}$

The static refractive index at the zero frequency limit of bulk Cs₂AgRhCl₆ is calculated to be 2.46, whereas that of Rb₂AgRhCl₆ is 2.47. Alkali introduction at the A-site caused a small increase in n, with values ranging between 2.46 and 2.50; this is caused by the contraction of the crystal lattice. As shown in Figure 6, n(ω) increases to a maximum value of 3.67 and 3.78 at the highest peaks, positioned at an energy of 2.03 eV for Cs₂AgRhCl₆ and Rb₂AgRhCl₆, respectively. Such large values of n(ω) are expected of optical ambient materials, with a typical refractive index of 2.5–3.5 (Schubert et al., 2007). For instance, the refractive index at the absorption edge was 2.29 and 2.61 for CH₃NH₃PbBr₃ (Alias et al., 2016) and CH₃NH₃PbI₃ (Löper et al., 2015) perovskites, respectively. CH₃NH₃PbI₃ (Löper et al., 2015) as a single crystal and thin film, has a refractive index of 2.45 [at 800 nm (1.55 eV)] and 1.95, respectively (Löper et al., 2015).

FIGURE 6

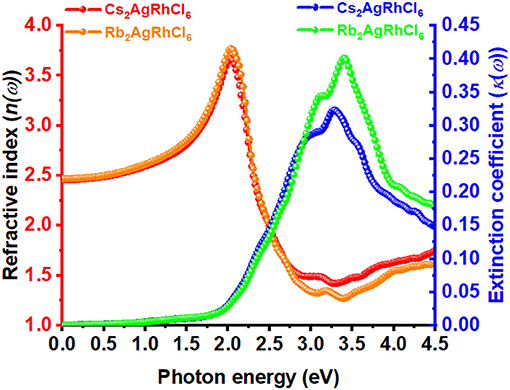
Figure 6. The dependence of the real and imaginary parts of the complex refractive index for Cs₂AgRhCl₆ and Rb₂AgRhCl₆. Although the corresponding spectra of A₂AgRhCl₆ (A = K, Na, Li) were of similar nature, they are not shown to avoid the complexity of the plot.

The value of n for halide perovskites is significantly larger than that of SiO₂ (1.09; Popova et al., 1972; Kitamura et al., 2007-−1.45; Malitson, 1965; Tan, 1998) or most polymers, making them a good material for resonant nanostructures due to their high optical contrast. Because n for Cs₂AgRhCl₆ is much lower than that of Si (n = 3.673; Refractiveindex.Info; Aspnes and Studna, 1983) or GaAs (3.4–3.7; Kachare et al., 1976; Aspnes et al., 1986; Jellison, 1992; Skauli et al., 2003), it provides high optical contrast with these materials in advanced hybrid structures (Makarov et al., 2019). By contrast, the extinction coefficient for Cs₂AgRhCl₆ is calculated to be very small and is close to 0.006 near the fundamental absorption edge of dispersion (Figure 6). This is comparable to the experimental κ values of 0.00014657, 0.08, and 0.005 reported for SiO₂ (Popova et al., 1972; Kitamura et al., 2007), GaAs (Aspnes et al., 1986), and Si (Aspnes and Studna, 1983), respectively.

As can be seen from Figure 6, the values of the real and imaginary parts of the refractive index for each A₂AgRhCl₆ are substantially different to each other. Since reflectivity R is related to the refractive indices via R = ((n² − κ²)/(n² + κ²))² and that n is several 100 orders of magnitude larger than κ at any specific critical point of the refractive index spectrum, it is clear that since n ≠ k the optical reflectivity will have a minimum value across the entire energy range investigated. This is seen in the reflectivity spectra calculated using the dielectric function (Equation 9), Figure 5C, in which a minimum reflection of <10% occurs in the region above 3.5 eV. The maximum of 38–45% light is likely to be reflected at the peak positions around 2.1 eV, and it is 15–25% around the onset of absorption. The reflectivity spectra of other systems reported elsewhere have similar characteristics (Peng et al., 2013; Ma et al., 2014; Saini et al., 2017; Mohamed et al., 2018). The energy loss function is plotted in Figure 5D. It is a measure of the loss of the energy of the electrons passing between energy bands. The maximum energy loss is calculated to lie between 32% (Cs₂AgRhCl₆) and 45% (Na₂AgRhCl₆) at energies of 3.2 and 3.6 eV, respectively.

Although the DFPT/PBEsol based optical properties described above were obtained using the primitive cells of A₂AgRhCl₆, the conventional cell geometries of these systems utilized for the same purpose using the same method did not significantly affect the location and height of peak features in the dielectric spectrum (Figure S5). However, when the same characteristics were investigated using SCAN-rVV10, it was found that although the nature of the transition features associated with the optical absorptions did not change markedly, the peak positions were blue-shifted. These were as large as 0.7–0.9 eV and the peak heights were reduced appreciably (Figure S6). In addition, the zero-frequency limit of ε⁽¹⁾ of A₂AgRhCl₆, which were found between 6.5 and 8.0 (Figure 4A), is reduced, so they are predicted around 5.0 (Figure S6), yet confirming that the electronic contribution to the static dielectric constant is reasonably high.

Because of the appreciable inconsistency between the onsets of optical absorption in the dielectric spectra calculated using SCAN-rVV10 and DFPT/PBEsol, we extended our calculations to compute the bandgap of the studied systems using quasiparticle G₀W₀ and GW₀ methods (Hedin, 1965; Van schilfgaarde et al., 2006; VASP, 2020a), based on Many-Body Perturbation Theory (MBPT), where G₀ is one-particle Green's function, W₀ is the screened Coulomb interaction, and GW₀ is the most usual step beyond single-shot GW (G₀W₀) to iterate the quasi-particle energies in the Greens functions. The G₀W₀ approach calculated the Green's function G₀ from the SCAN-rVV10 wavefunction in a non-self-consistent manner, and a perturbative scheme was utilized for the calculation of screened exchange in W₀. In general, G₀W₀ calculates the quasi-particle energies from a single GW iteration by neglecting all off-diagonal matrix elements of the self-energy and employing a Taylor expansion of the self-energy around the DFT energies. The self-energy and one-shot calculations were performed using a 6 × 6 × 6 k-mesh. Interestingly, the SCAN-rVV10 predicted optical absorption edges associated with the imaginary part of the dielectric spectra (Figure S6) are in good agreement with the nature of the G₀W₀ and GW₀ bandgaps of the corresponding systems. For instance, the G₀W₀ bandgaps were 2.43, 2.46 and 2.49 eV for Cs₂AgRhCl₆, Rb₂AgRhCl₆, and K₂AgRhCl₆ with the SCAN-rVV10 wavefunctions, respectively (Table S2). Similar calculations with the popular Heyd–Scuseria–Ernzerhof functional (HSE06) (Krukau et al., 2006; Savory et al., 2016a) and a 4 × 4 × 4 k-mesh gave bandgaps between 2.3 and 2.0 eV, showing an underestimation compared to G₀W₀ and GW₀ (Table S2). Table S7 compares the lattice and bandgap properties of Cs₂AgRhCl₆ obtained from various computational approaches with those experimentally reported and calculated in this work for Cs₂AgB′Cl₆ (B' = In, Bi, Sb, Tl) (Zhou et al., 2018; Zhou J. et al., 2019).

The large difference between the GGA/meta-GGA and GW/HSE06 bandgaps is not very surprising given that the former ones generally underestimate bandgaps for single and double perovskite semiconductors (Ganose et al., 2017; Umadevi and Watson, 2019). For example, the reported PBE bandgap for Cs₂AgInCl₆ is 0.95 eV (Kumar et al., 2020), compared to the experimental value of 3.3 eV (Volonakis et al., 2017). Similarly, the bandgaps of 0.89 eV (PBEsol) and 1.1.17–1.61 eV (PBE) (Lu et al., 2016; Sun P.-P. et al., 2016; Zhao Y.-Q. et al., 2017) were reported for CH₃NH₃GeI₃, and those of the hybrid functional range from 1.70 to 2.04 eV (Sun P.-P. et al., 2016; Zhao Y.-Q. et al., 2017), whereas the experimental value for which is 1.90 eV (Stoumpos et al., 2015). There is also precedence that the inclusion of dispersion correction further reduces the bandgaps, and this is likely the case with the GGA and HSE06 methods (Umadevi and Watson, 2019). The bandgaps found in the current study for A₂AgRhCl₆ are smaller/larger than, or comparable to, those of 2.19, 2.77, 2.33, and 3.00 eV reported for Cs₂AgBiCl₆, Cs₂AgBiBr₆, MAPbBr₃ and MAPbCl₃ (MA = methyl ammonium), respectively (Mcclure et al., 2016). There are other such double perovskite systems reported elsewhere (Jain et al., 2017; Zhao X.-G. et al., 2017; Locardi et al., 2018), which were stable and exhibited a direct bandgap in the spectral range relevant for solar energy conversion (1.5–2.5 eV), including Cs₂AgInX₆, Rb₂AgInX₆, and Rb₂CuInX₆ (X = Cl, Br). Clearly, the rhodium-based double perovskites examined in this study, which display excitonic features in the visible and UV regions, may be useful for applications in photoelectric detectors. MAPbBr₃ is an exemplar photovoltaic semiconductor, with an experimental bandgap of 2.33 eV (Niemann et al., 2016; Varadwaj et al., 2018), which has been recognized as a material for photovoltaics and photodetectors (Saraf and Maheshwari, 2018).

Phonon Features and Lattice Stability

The phonon band structures of Cs₂AgRhCl₆ and Rb₂AgRhCl₆ are illustrated in Figure 7 and Figure S7. The force constants defining the change in force on a reference atom in response to the displacement of another were used to construct a dynamics matrix. The matrix was then diagonalized. This gave the eigenvalues (normal mode phonon frequencies) and associated eigenvectors (phonon motion). As expected, there are three acoustic and several optical phonon modes. Although this is evidence of the dispersion curves shown in Figure S8, in which case, the conventional cells were used, two of these modes are found to be degenerate when the primitive cells used, showing the cell geometry plays an important role in unraveling the degeneracy involved. The acoustic modes are present below 1.5 THz and the optic modes are limited to the frequency interval 1.0–10.0 THz for Cs₂AgRhCl₆. These phonons are all stable across the Brillouin-zone boundary points, including the W, L, Γ, and X-points. This is true regardless of the nature of computational method employed (DFPT/PBEsol and FD, Figures 7A,B)—spin-polarized or non-spin polarized (see Figure S7). The only difference between the two theoretical approaches is that the phonon frequencies are somewhat different, with the FD method overestimating them compared to the DFPT/PBEsol method. However, all of them recognize the Cs₂AgRhCl₆ crystal lattice to be dynamically stable (Mouhat and Coudert, 2014).

FIGURE 7

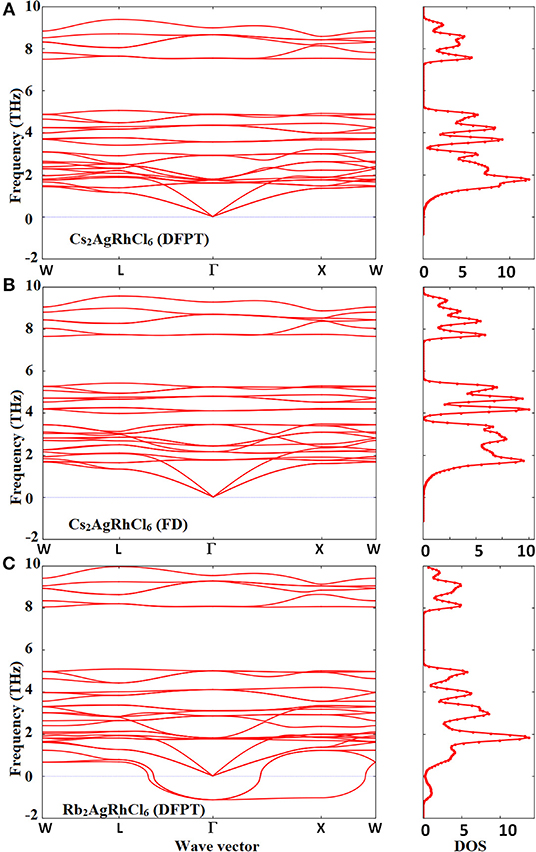
Figure 7. Comparison of the phonon dispersion and total phonon density of states (a.u.) of Cs₂AgRhCl₆ calculated using the (A) DFPT/PBEsol and (B) FD (finite difference) methods. Shown in (C) are the corresponding features for Rb₂AgRhCl₆, calculated using DFPT/PBEsol method with the supercell approach. Phonon “soft” modes are present around the Brillouin-zone boundary points and Γ → X → W for Rb₂AgRhCl₆.

For Rb₂AgRhCl₆ (Figure 7C), as well as the other three members of the A₂AgRhCl₆ series (not shown), the phonons are unstable along the entire path, especially along the paths L → Γ, Γ → X and X → W. They are associated with negative vibrational frequencies, which are due to the metastable lattice of the double perovskite induced by the alkali substitution at the A-site. The negative phonon modes are the so-called soft modes and are prominent, especially at the center of the Brillouin zone (Γ–point). This is evidence of the phonon density of states shown in Figure S9B (bottom), when compared against that shown in Figure S9A for Cs₂AgRhCl₆. The origin of such an instability for Rb₂AgRhCl₆ is probably a consequence of lattice softening induced by the softening of the shear constants for long wave phonons (Böni et al., 1988), and may not be ascribed to phonon instability that is generally caused by the softening of the transverse acoustic phonons near zone boundaries (Nakanishi et al., 1982; Liu et al., 2016). This is because the instability is primary associated with optical phonons, as the acoustic modes are unaffected. A somehow similar result was obtained for the other two members of the series, A₂AgRhCl₆ (A = Na, Li), but this is due to significant phonon and lattice instabilities tailored both by the acoustic phonons of low frequency and the optical modes of high frequency (not shown). Halide perovskites such as FAPbI₃, MAPbI₃, MAPbBr₃, and CsPbBr₃ were shown to exhibit phonon instabilities around the Brillouin-zone boundary points, which was significant at the R- and M-points; the imaginary frequency associated with the R-point was as large as 1.5 THz (for CsPbBr_3; Yang et al., 2017). This was attributed to the disorder introduced in the material by the anisotropic nature of the organic ion and octahedral tilting (Leguy et al., 2016b).

Mechanical (Elastic) Properties

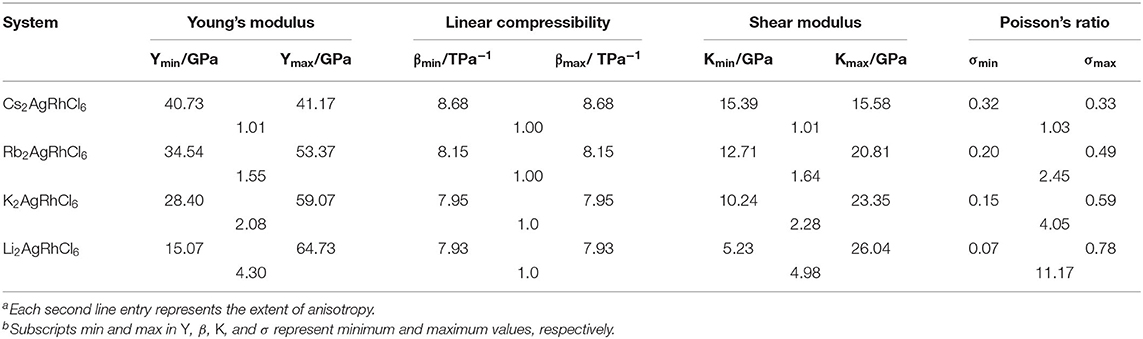
There are only three independent elastic constants (C₁₁, C₁₂, and C₄₄) associated with the stiffness matrix C_ij of cubic crystals that represent the directional mechanical responses of the crystals for different directions of applied forces (Mouhat and Coudert, 2014). The longitudinal distortion, C₁₁, is based on the longitudinal compression, and describes the hardness. The transverse distortion, C₁₂, is based on the transverse expansion, which is related to Poisson's ratio. The shear elastic parameter, C₄₄, is based on the shear modulus that represent the stiffness of the crystal. Our caclualtions gave all eigenvalues λ_i of the C_ij = C_ji matrix to be real and positive for all A₂AgRhCl₆ systems (Table S4). The Born criteria (Mouhat and Coudert, 2014) of the cubic system (i) C₁₁ – C₁₂ > 0; (ii) C₁₁ + 2C₁₂ > 0; (iii) C₄₄ > 0 are also satisfied (see Table S5 for values of the elastic constants). This, along with the real and positive character of all the six eigenvalues of the stiffness matrix, points to the mechanical stability of all the five A₂AgRhCl₆ systems (Mouhat and Coudert, 2014).

The three stiffness constants are found in the order C₁₁ > C₁₂ > C₄₄ (Table S5). The effect of the A-site cation on these constants is to increase C₁₁ along the series (Cs₂AgRhCl₆ > Rb₂AgRhCl₆ > K₂AgRhCl₆ > Li₂AgRhCl₆), consistent with the decreasing ionic radii of the alkali ions. There was a concomitant decrease of C₁₂ and C₄₄ along the same line. This shows that alkali substitution at the A-site has a marked effect on C₁₁ compared to C₁₂ and C₄₄; hence the longitudinal compression is increasingly larger compared to the transverse and shear distortions when passing from Cs⁺ through Rb⁺ to K⁺ to Li⁺. Because C₁₁ ≠ C₁₂ + 2C₄₄, which is undoubtedly the result of significant longitudinal distortion, especially for systems containing Rb⁺, K⁺ and Li⁺, we conclude that A₂AgRhCl₆ (A = Rb, K, Li) are not strictly isotropic.

The shear constant C₄₄, which measures plastic deformation, is less than (C₁₁ – C₁₂)/2 for each A₂AgRhCl₆. That is, the difference between them ([C₄₄ – ((C₁₁ – C₁₂)/2)]) is negative (see Table S5). It increases from Cs₂AgRhCl₆ to Rb₂AgRhCl₆ to K₂AgRhCl₆ to Li₂AgRhCl₆, and hence the shear softening increases in the order Cs₂AgRhCl₆ < Rb₂AgRhCl₆ < K₂AgRhCl₆ < Li₂AgRhCl₆. This trend is roughly preserved for the shear modulus (see K values in Table S6), although the value of K for Cs₂AgRhCl₆ is slightly smaller than that for Rb₂AgRhCl₆ (15.47 GPa vs. 15.50 GPa). Clearly, the softening in the shear constant that results in very large negative values of [C₄₄ – ((C₁₁ – C₁₂)/2)] (Table S4), except for Cs₂AgRhCl₆, probably explains the presence of the observed degenerate transverse branches shown in Figures 7A,B, and the lattice instability observed for Rb₂AgRhCl₆ and other members of the series (see Figure 7C and Figure S8).

There is no obvious trend observed between the mean values of Young's modulus (Y), Bulk modulus (B), and shear modulus (K) for any given A₂AgRhCl₆ (Table S6). For instance, the arithmetic mean values of these moduli were 40.91 (41.28), 38.39 (40.88), and 15.47 (15.50) GPa for Cs₂AgRhCl₆ (Rb₂AgRhCl₆), respectively, whereas such a trend is altered for the remaining two systems, with the corresponding values of 41.9 (42.01), 38.6 (29.23), and 14.3 (10.62), respectively. The Young's modulus, which is the ratio of stress to strain, and a measure of stiffness, is found to be largest, 41.28 (40.91) GPa, for Cs₂AgRhCl₆ (Rb₂AgRhCl₆), showing that they are relatively stiffer than K₂AgRhCl₆ and Li₂AgRhCl₆. This ultimately suggests that the contribution of covalence in chemical bonds is larger in the former two than in the latter two systems since stiffer solids usually feature significant covalent bond character. The bulk modulus B, which quantifies the resistance to fracture and was calculated using the expression B = (C₁₁ +2C₁₂)/3, shows a clear increasing trend in the series: Cs₂AgRhCl₆ (38.39 GPa) > Rb₂AgRhCl₆ (40.88 GPa) > K₂AgRhCl₆ (41.92 GPa) > Li₂AgRhCl₆ (42.01 GPa). This may lead to the interpretation that Cs₂AgRhCl₆ is relatively strengthened compared to other systems across the series and could be more resistant to external forces such as pressure and temperature.

From the values of the elastic properties listed in Table 5, it is quite clear that the anisotropy in Young's modulus, linear compressibility, Bulk modulus and Poisson's ratio is very marginal for Cs₂AgRhCl₆. This becomes very marked for Li₂AgRhCl₆, and the anisotropy increases in the series from Cs⁺ through Rb⁺ to K⁺ to Li⁺.

TABLE 5

Table 5. Some selected elastic constants of A₂AgRhCl₆ (A = Cs, Rb, K, Li) ^a,b.

The empirical measures of brittle/ductile response of mechanical solids are Pugh's criterion (K/B ratio) (Pugh, 1954) and the Cauchy pressure C_P (C_P = C₁₂ – C₄₄ for cubic crystals). (Johnson, 1988; Kamran et al., 2009). Materials with K/B > 1.75 are ductile while those with K/B < 1.75 are brittle (Pan and Guan, 2017; Singh et al., 2018). Our calculation gave a K/B value of 2.48 and 2.64 for Rb₂AgRhCl₆ and Rb₂AgRhCl₆, respectively, and a C_P value of 12.6 and 14.3 GPa, respectively. The former property unequivocally suggests the ductile nature of these materials, and the positive nature of C_P is expected of any ductile metals, such as Ni or Al, for example (Kamran et al., 2009; Ivanovskii, 2012). This may be consistent with the observation that materials that feature metallic bonding exhibit a positive Cauchy pressure (Thompson and Clegg, 2018). From the mean values of Poisson's ratio σ (values between 0.32 and 0.38 in Table S6), it is obvious that the chemical bonding between metal ions and Cl is increasingly ionic across the series from Cs₂AgRhCl₆ to Rb₂AgRhCl₆ to K₂AgRhCl₆ to Li₂AgRhCl₆, given that σ is close to 0.1 – 0.28 for covalent materials (Haines et al., 2001).

Conclusion

This study used density functional theory to describe the nature of the geometric stability, electronic, transport, optical, and dynamic lattice properties of the series A₂AgRhCl₆ (A = Li, Na, K, Rb, Cs). Although the bandgap of these systems was close to 0.57–0.65 eV with SCAN-rVV10, this was, as expected, appreciably underestimated with the traditionally recommended functionals PBE and PBEsol. All these GGA and meta-GGA methods have shown here to be consistently underestimated the bandgaps compared to the quasi-particle GW and hybrid functional HSE06/PBE0 methods, which predict the bandgaps in the visible region, revealing possible application of the studied systems in optoelectronics.

The use of the Global Instability Index suggested that Cs₂AgRhCl₆, Rb₂AgRhCl₆, and K₂AgRhCl₆ might possess perovskite-quality face-centered cubic structures. This was consistent with what emerged from the recommended combination of Goldsmith's tolerance and octahedral factors. However, with the application of the newly-proposed tolerance factor, the first three heavier members of the series were identified as perovskites and the remaining two lighter members as significantly unstable structures. Nevertheless, all showed nearly similar band structure, DOS, and bandgap features. It was shown that the CBM and VBM of A₂AgRhCl₆ originated mainly from the 4d states of the octahedron Rh³⁺ ion, with a non-negligible contribution from the 3p states of the 6-coordinate Cl⁻ ions.

The reasonably small effective masses of the charge carriers gave evidence of the presence of (quasi) bipolar conductivity and high mobility. These properties, together with the impressive electronic transition features in the dielectric function spectra, high refractive indices, and high absorption coefficients have enabled to us to conclude that the materials studied may be suitable for application in optoelectronics. However, the phonon and elastic properties examined in this study showed that A₂AgRhCl₆ (A = Li, Na, K, Rb) were dynamically unstable and mechanically stable. This was not the case for Cs₂AgRhCl₆, which was predicted to be both dynamically and mechanically stable; this suggests its experimental synthesis and an exploration of its properties appears to be justified.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

PV: conceptualization, problem design, investigation, literature survey, supervision, and writing—original draft. PV and HM writing—review and editing. All authors contributed to the article and approved the submitted version.

Funding

A part of this research was financially supported by the University of the Witwatersrand, RSA.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

PV thanks Prof. K. Yamashita for support. This work was conducted using the various facilities provided by the University of Tokyo.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2020.00796/full#supplementary-material

References

Alias, M. S., Dursun, I., Saidaminov, M. I., Diallo, E. M., Mishra, P., Ng, T. K., et al. (2016). Optical constants of CH₃NH₃PbBr₃ perovskite thin films measured by spectroscopic ellipsometry. Opt. Express 24, 16586–16594. doi: 10.1364/OE.24.016586

PubMed Abstract | CrossRef Full Text | Google Scholar

Anh, L. T., Wada, M., Fukui, H., Kawatsu, T., and Iitaka, T. (2019). First-principles calculations of the epsilon phase of solid oxygen. Sci. Rep. 9:8731. doi: 10.1038/s41598-019-45314-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Aspnes, D. E., Kelso, S. M., Logan, R. A., and Bhat, R. (1986). Optical properties of AlxGa1–x As. J. Appl. Phys. 60, 754–767. doi: 10.1063/1.337426

CrossRef Full Text | Google Scholar

Aspnes, D. E., and Studna, A. A. (1983). Dielectric functions and optical parameters of Si, Ge, GaP, GaAs, GaSb, InP, InAs, and InSb from 1.5 to 6.0 eV. Phys. Rev. B 27, 985–1009. doi: 10.1103/PhysRevB.27.985

CrossRef Full Text | Google Scholar

Baranoski, G. V. G., and Krishnaswamy, A. (2010). Light and Skin Interactions, Simulations for Computer Graphics Applications. Amsterdam: Elsevier Inc.

Google Scholar

Baroni, S., De Gironcoli, S., Dal Corso, A., and Giannozzi, P. (2001). Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 73, 515–562. doi: 10.1103/RevModPhys.73.515

CrossRef Full Text | Google Scholar

Bartel, C. J., Sutton, C., Goldsmith, B. R., Ouyang, R., Musgrave, C. B., Ghiringhelli, L. M., et al. (2019). New tolerance factor to predict the stability of perovskite oxides and halides. Sci. Adv. 5:eaav0693. doi: 10.1126/sciadv.aav0693

PubMed Abstract | CrossRef Full Text | Google Scholar

Belding, J., Gupta, S., and Kramer, R. Investigation of Direct Band Gap Solar Cells Through the Use of Cs-Sb-Halide Double Perovskites. Available online at: https://cpb-us-w2.wpmucdn.com/u.osu.edu/dist/e/45951/files/2018/04/hc3FinalReportPdf-v4s6d8.pdf (accessed April 19, 2020).

Google Scholar

Bilbao Crystallographic Server. Available online at: https://www.cryst.ehu.es/ (accessed July 24, 2020).

Blöchl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B. 50, 17953–17978. doi: 10.1103/PhysRevB.50.17953

PubMed Abstract | CrossRef Full Text | Google Scholar

Bokdam, M., Lahnsteiner, J., Ramberger, B., Schäfer, T., and Kresse, G. (2017). Assessing density functionals using many body theory for hybrid perovskites. Phys. Rev. Lett. 119:145501. doi: 10.1103/PhysRevLett.119.145501

PubMed Abstract | CrossRef Full Text | Google Scholar

Böni, P., Axe, J. D., Shirane, G., Birgeneau, R. J., Gabbe, D. R., Jenssen, H. P., et al. (1988). Lattice instability and soft phonons in single-crystal La_2−xSr_xCuO₄. Phys. Rev. B 38, 185–194. doi: 10.1103/PhysRevB.38.185

PubMed Abstract | CrossRef Full Text | Google Scholar

Brese, N. E., and O'keeffe, M. (1991). Bond-valence parameters for solids. Acta Cryst. B 47, 192–197. doi: 10.1107/S0108768190011041

CrossRef Full Text | Google Scholar

Brivio, F., Walker, A. B., and Walsh, A. (2013). Structural and electronic properties of hybrid perovskites for high-efficiency thin-film photovoltaics from first-principles. APL Mater. 1:042111. doi: 10.1063/1.4824147

CrossRef Full Text | Google Scholar

Brown, I. D. (2017). What is the best way to determine bond-valence parameters? IUCrJ 4, 514–515. doi: 10.1107/S2052252517011782

PubMed Abstract | CrossRef Full Text | Google Scholar

Buda, I. G., Lane, C., Barbiellini, B., Ruzsinszky, A., Sun, J., and Bansil, A. (2017). Characterization of thin film materials using SCAN meta-GGA, an accurate nonempirical density functional. Sci. Rep. 7:44766. doi: 10.1038/srep44766

PubMed Abstract | CrossRef Full Text | Google Scholar

Cai, Y., Xie, W., Teng, Y. T., Harikesh, P. C., Ghosh, B., Huck, P., et al. (2019). High-throughput computational study of halide double perovskite inorganic compounds. Chem. Mater. 31, 5392–5401. doi: 10.1021/acs.chemmater.9b00116

CrossRef Full Text | Google Scholar

Campochiaro, C., Mcclure, D. S., and Patterson, H. H. (1992). One- and two-photon spectroscopy of the hexafluoroplatinate(IV) ion. Inorg. Chem. 31, 2809–2813. doi: 10.1021/ic00039a027

CrossRef Full Text | Google Scholar

Chakraborty, A., Dixit, M., Aurbach, D., and Major, D. T. (2018). Predicting accurate cathode properties of layered oxide materials using the SCAN meta-GGA density functional. NPJ Comput. Mater. 4:60. doi: 10.1038/s41524-018-0117-4

CrossRef Full Text | Google Scholar

Chen, M., Ju, M.-G., Carl, A. D., Zong, Y., Grimm, R. L., Gu, J., et al. (2018). Cesium titanium(IV) bromide thin films based stable lead-free perovskite solar cells. Joule 2, 558–570. doi: 10.1016/j.joule.2018.01.009

CrossRef Full Text | Google Scholar

Chu, L., Ahmad, W., Liu, W., Yang, J., Zhang, R., Sun, Y., et al. (2019). Lead-free halide double perovskite materials: a new superstar toward green and stable optoelectronic applications. Nano-Micro Lett. 11:16. doi: 10.1007/s40820-019-0244-6

CrossRef Full Text | Google Scholar

De Lazaro, S. R., Ribeiro, R. A. P., and Lacerda, L. H. D. S. (2017). “Quantum chemistry applied to photocatalysis with TiO₂, titanium dioxide,” ed M. Janus (IntechOpen). Available online at: https://www.intechopen.com/books/titanium-dioxide/quantum-chemistry-applied-to-photocatalysis-with-tio2

Dong, L., Jia, R., Xin, B., Peng, B., and Zhang, Y. (2017). Effects of oxygen vacancies on the structural and optical properties of β-Ga2O3. Sci. Rep. 7:40160. doi: 10.1038/srep40160

PubMed Abstract | CrossRef Full Text | Google Scholar

Dong, M., Zhang, J., and Yu, J. (2015). Effect of effective mass and spontaneous polarization on photocatalytic activity of wurtzite and zinc-blende ZnS. APL Materials 3:104404. doi: 10.1063/1.4922860

CrossRef Full Text | Google Scholar

Dresselhaus, M. S. (2001). Solid State Physics. Part II. Optical Properties of Solids, Vol. 6. Lecture Notes, Massachusetts Institute of Technology, Cambridge, MA, USA.

Eaton, M., Catellani, A., and Calzolari, A. (2018). VO₂ as a natural optical metamaterial. Opt. Express 26, 5342–5357. doi: 10.1364/OE.26.005342

PubMed Abstract | CrossRef Full Text | Google Scholar

Eom, K., Kwon, U., Kalanur, S. S., Park, H. J., and Seo, H. (2017). Depth-resolved band alignments of perovskite solar cells with significant interfacial effects. J. Mat. Chem. A 5, 2563–2571. doi: 10.1039/C6TA09493G

CrossRef Full Text | Google Scholar

Faraji, M., Sabzali, M., Yousefzadeh, S., Sarikhani, N., Ziashahabi, A., Zirak, M., et al. (2015). Band engineering and charge separation in the Mo1–xWxS2/TiO2 heterostructure by alloying: first principle prediction. RSC Adv. 5, 28460–28466. doi: 10.1039/C5RA00330J

CrossRef Full Text | Google Scholar

Filip, M. R., Liu, X., Miglio, A., Hautier, G., and Giustino, F. (2018). Phase diagrams and stability of lead-free halide double perovskites Cs2BB′X6: B = Sb and Bi, B′ = Cu, Ag, and Au, and X = Cl, Br, and I. J. Phys. Chem. C 122, 158–170. doi: 10.1021/acs.jpcc.7b10370

CrossRef Full Text | Google Scholar

Filip, M. R., Verdi, C., and Giustino, F. (2015). GW band structures and carrier effective masses of CH3NH3PbI3 and hypothetical perovskites of the type APbI3: A = NH4, PH4, AsH4, and SbH4. J. Phys. Chem. C 119, 25209–25219. doi: 10.1021/acs.jpcc.5b07891

CrossRef Full Text | Google Scholar

Ford, P. C. (2016). From curiosity to applications. A personal perspective on inorganic photochemistry. Chem. Sci. 7, 2964–2986. doi: 10.1039/C6SC00188B

PubMed Abstract | CrossRef Full Text | Google Scholar

Frost, J. M., Butler, K. T., Brivio, F., Hendon, C. H., Van Schilfgaarde, M., and Walsh, A. (2014). Atomistic origins of high-performance in hybrid halide perovskite solar cells. Nano Lett. 14, 2584–2590. doi: 10.1021/nl500390f

PubMed Abstract | CrossRef Full Text | Google Scholar

Fu, H., and Zhao, Y. (2018). “9 - Efficiency droop in GaInN/GaN LEDs,” in Nitride Semiconductor Light-Emitting Diodes (LEDs), 2nd Edn, eds J. Huang, H.-C. Kuo, and S.-C. Shen (Cambridge: Woodhead Publishing), 299–325.

Google Scholar

Gagné, O. C., and Hawthorne, F. C. (2015). Comprehensive derivation of bond-valence parameters for ion pairs involving oxygen. Acta Cryst. B 71, 562–578. doi: 10.1107/S2052520615016297

PubMed Abstract | CrossRef Full Text | Google Scholar

Ganose, A. M., Jackson, A. J., and Scanlon, D. O. (2018). Sumo: command-line tools for plotting and analysis of periodic ab initio calculations. J. Open Source Software 3:717. doi: 10.21105/joss.00717

CrossRef Full Text | Google Scholar

Ganose, A. M., Savory, C. N., and Scanlon, D. O. (2017). Electronic and defect properties of (CH3NH3)2Pb(SCN)2I2 analogues for photovoltaic applications. J. Mat. Chem. A 5, 7845–7853. doi: 10.1039/C7TA01688C

CrossRef Full Text | Google Scholar

Gonze, X. (1997). First-principles responses of solids to atomic displacements and homogeneous electric fields: Implementation of a conjugate-gradient algorithm. Phys. Rev. B 55, 10337–10354. doi: 10.1103/PhysRevB.55.10337

CrossRef Full Text | Google Scholar

Gonze, X., and Lee, C. (1997). Dynamical matrices, born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory. Phys. Rev. B 55, 10355–10368. doi: 10.1103/PhysRevB.55.10355

CrossRef Full Text | Google Scholar

Greul, E., Petrus, M. L., Binek, A., Docampo, P., and Bein, T. (2017). Highly stable, phase pure Cs2AgBiBr6 double perovskite thin films for optoelectronic applications. J. Mater. Chem. A 5, 19972–19981. doi: 10.1039/C7TA06816F

CrossRef Full Text | Google Scholar

Habibi, M., and Eslamian, M. (2018). Facile and low-cost mechanical techniques for the fabrication of solution-processed polymer and perovskite thin film transistors. J. Phys. Commun. 2:075018. doi: 10.1088/2399-6528/aad3a6

CrossRef Full Text | Google Scholar

Haines, J., Léger, J. M., and Bocquillon, G. (2001). Synthesis and design of superhard materials. Ann. Rev. Mat. Res. 31, 1–23. doi: 10.1146/annurev.matsci.31.1.1

CrossRef Full Text | Google Scholar

Hartmann, H., Mach, R., and Selle, B. (1982). “Wide Gap II-VI compounds as electronic materials,” in Current Topics in Material Science, ed E. Kaldis (Amsterdam: Oxford: North-Holland), 18.

Google Scholar

Hedin, L. (1965). New method for calculating the one-particle green's function with application to the electron-gas problem. Phys. Rev. 139, A796–A823. doi: 10.1103/PhysRev.139.A796

CrossRef Full Text | Google Scholar

Hirasawa, M., Ishihara, T., Goto, T., Uchida, K., and Miura, N. (1994). Magnetoabsorption of the lowest exciton in perovskite-type compound (CH3NH3)PbI3. Phys. B Cond. Matter 201, 427–430. doi: 10.1016/0921-4526(94)91130-4

CrossRef Full Text | Google Scholar

Hoye, R. L. Z., Eyre, L., Wei, F., Brivio, F., Sadhanala, A., Sun, S., et al. (2018). Fundamental carrier lifetime exceeding 1 μs in Cs2AgBiBr6 double perovskite. Adv. Mater. Interfaces 5:1800464. doi: 10.1002/admi.201800464

CrossRef Full Text | Google Scholar

Ivanovskii, A. L. (2012). Mechanical and electronic properties of diborides of transition 3d−5d metals from first principles: Toward search of novel ultra-incompressible and superhard materials. Prog. Mat. Sci. 57, 184–228. doi: 10.1016/j.pmatsci.2011.05.004

CrossRef Full Text | Google Scholar

Jain, A., Voznyy, O., and Sargent, E. H. (2017). High-throughput screening of lead-free perovskite-like materials for optoelectronic applications. J. Phys. Chem. C 121, 7183–7187. doi: 10.1021/acs.jpcc.7b02221

CrossRef Full Text | Google Scholar

Jana, M. K., Janke, S. M., Dirkes, D. J., Dovletgeldi, S., Liu, C., Qin, X., et al. (2019). Direct-bandgap 2D silver–bismuth iodide double perovskite: the structure-directing influence of an oligothiophene spacer cation. J. Am. Chem. Soc. 141, 7955–7964. doi: 10.1021/jacs.9b02909

PubMed Abstract | CrossRef Full Text | Google Scholar

Jellison, G. E. (1992). Optical functions of GaAs, GaP, and Ge determined by two-channel polarization modulation ellipsometry. Opt. Mater. 1, 151–160. doi: 10.1016/0925-3467(92)90022-F

CrossRef Full Text | Google Scholar

Ji, C., Wu, Z., Lu, L., Wu, X., Wang, J., Liu, X., et al. (2018). High thermochromic performance of Fe/Mg co-doped VO2 thin films for smart window applications. J. Mat. Chem. C 6, 6502–6509. doi: 10.1039/C8TC01111G

CrossRef Full Text | Google Scholar

Johnson, R. A. (1988). Analytic nearest-neighbor model for fcc metals. Phys. Rev. B 37, 3924–3931. doi: 10.1103/PhysRevB.37.3924

PubMed Abstract | CrossRef Full Text | Google Scholar

Jong, U.-G., Yu, C.-J., Kim, Y.-S., Kye, Y.-H., and Kim, C.-H. (2018). First-principles study on the material properties of the inorganic perovskite Rb_1−xCs_xPbI₃ for solar cell applications. Phys. Rev. B 98:125116. doi: 10.1103/PhysRevB.98.125116

CrossRef Full Text | Google Scholar

Jong, U.-G., Yu, C.-J., Ri, J.-S., Kim, N.-H., and Ri, G.-C. (2016). Influence of halide composition on the structural, electronic, and optical properties of mixed CH₃NH₃Pb(I₁-_xBr_x)3 perovskites calculated using the virtual crystal approximation method. Phys. Rev. B 94:125139. doi: 10.1103/PhysRevB.94.125139

CrossRef Full Text | Google Scholar

Kachare, A. H., Spitzer, W. G., and Fredrickson, J. E. (1976). Refractive index of ion-implanted GaAs. J. Appl. Phys. 47, 4209–4212. doi: 10.1063/1.323292

CrossRef Full Text | Google Scholar

Kagdada, H. L., Jha, P. K., Spiewak, P., and Kurzydłowski, K.J. (2018). Structural stability, dynamical stability, thermoelectric properties, and elastic properties of GeTe at high pressure. Phys. Rev. B 97:134105. doi: 10.1103/PhysRevB.97.134105

CrossRef Full Text | Google Scholar

Kamran, S., Chen, K., and Chen, L. (2009). Ab initio examination of ductility features of fcc metals. Phys. Rev. B 79:024106. doi: 10.1103/PhysRevB.79.024106

CrossRef Full Text | Google Scholar

Kao, K. C. (2004). “3 - Optical and electro-optic processes,” in Dielectric Phenomena in Solids, ed K.C. Kao (San Diego, CA: Academic Press), 115–212.

Khatri, H., Aryae, K., Collins, R. W., and Marsillac, S. (2011). Electronic and Structural Properties of Copper Selenide (Cu2_xSe) Thin Films as Determined by in-situ Real-Time and ex-situ Characterization. IEEE. Available online at: https://www.researchgate.net/publication/261086174_Electronic_and_structural_properties_of_copper_selenide_Cu2-xSe_thin_films_as_determined_by_in-situ_real-time_and_ex-situ_characterization (accessed April 26, 2020).

Google Scholar

Kirchartz, T., Markvart, T., Rau, U., and Egger, D. A. (2018). Impact of small phonon energies on the charge-carrier lifetimes in metal-halide perovskites. J. Phys. Chem. Lett. 9, 939–946. doi: 10.1021/acs.jpclett.7b03414

PubMed Abstract | CrossRef Full Text | Google Scholar

Kitamura, R., Pilon, L., and Jonasz, M. (2007). Optical constants of silica glass from extreme ultraviolet to far infrared at near room temperature. Appl. Opt. 46, 8118–8133. doi: 10.1364/AO.46.008118

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996a). Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mat. Sci. 6, 15–50. doi: 10.1016/0927-0256(96)00008-0

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996b). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54:11169. doi: 10.1103/PhysRevB.54.11169

PubMed Abstract | CrossRef Full Text | Google Scholar

Krukau, A. V., Vydrov, O. A., Izmaylov, A. F., and Scuseria, G. E. (2006). Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 125:224106. doi: 10.1063/1.2404663

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, M., Jain, M., Singh, A., and Bhattacharya, S. (2020). Bandgap Engineering by Sublattice Mixing in Cs2AgInCl6: High-throughput Screening from First-principles. Available online at: https://arxiv.org/abs/2004.07991

Google Scholar

Lamba, R. S., Basera, P., Bhattacharya, S., and Sapra, S. (2019). Band gap engineering in Cs2(NaxAg1–x)BiCl6 double perovskite nanocrystals. J. Phys. Chem. Lett. 10, 5173–5181. doi: 10.1021/acs.jpclett.9b02168

PubMed Abstract | CrossRef Full Text | Google Scholar

Leguy, A. M. A., Azarhoosh, P., Alonso, M. I., Campoy-Quiles, M., Weber, O. J., Yao, J., et al. (2016a). Experimental and theoretical optical properties of methylammonium lead halide perovskites. Nanoscale 8, 6317–6327. doi: 10.1039/C5NR05435D

PubMed Abstract | CrossRef Full Text | Google Scholar

Leguy, A. M. A., Goñi, A. R., Frost, J. M., Skelton, J., Brivio, F., Rodríguez-Martínez, X., et al. (2016b). Dynamic disorder, phonon lifetimes, and the assignment of modes to the vibrational spectra of methylammonium lead halide perovskites. Phys. Chem. Chem. Phys. 18, 27051–27066. doi: 10.1039/C6CP03474H

PubMed Abstract | CrossRef Full Text | Google Scholar

Lei, L.-Z., Shi, Z.-F., Li, Y., Ma, Z.-Z., Zhang, F., Xu, T.-T., et al. (2018). High-efficiency and air-stable photodetectors based on lead-free double perovskite Cs2AgBiBr6 thin films. J. Mater. Chem. C 6, 7982–7988. doi: 10.1039/C8TC02305K

CrossRef Full Text | Google Scholar

Li, C., Soh, K. C. K., and Wu, P. (2004). Formability of ABO3 perovskites. J. Alloys Cmpds 372, 40–48. doi: 10.1016/j.jallcom.2003.10.017

CrossRef Full Text | Google Scholar

Li, H., Shan, X., Neu, J. N., Geske, T., Davis, M., Mao, P., et al. (2018). Lead-free halide double perovskite-polymer composites for flexible X-ray imaging. J. Mater. Chem. C 6, 11961–11967. doi: 10.1039/C8TC01564C

CrossRef Full Text | Google Scholar

Li, L., Wang, W., Liu, H., Liu, X., Song, Q., and Ren, S. (2009). First principles calculations of electronic band structure and optical properties of Cr-doped ZnO. J. Phys. Chem. C 113, 8460–8464. doi: 10.1021/jp811507r

CrossRef Full Text | Google Scholar

Li, T., Zhao, X., Yang, D., Du, M.-H., and Zhang, L. (2018). Intrinsic defect properties in halide double perovskites for optoelectronic applications. Phys. Rev. Appl. 10:041001. doi: 10.1103/PhysRevApplied.10.041001

CrossRef Full Text | Google Scholar

Li, Y., and Yang, K. (2019). High-throughput computational design of organic–inorganic hybrid halide semiconductors beyond perovskites for optoelectronics. Energy Environ. Sci. 12, 2233–2243. doi: 10.1039/C9EE01371G

CrossRef Full Text | Google Scholar

Liu, X., Gu, J., Shen, Y., and Li, J. (2016). Crystal metamorphosis at stress extremes: how soft phonons turn into lattice defects. NPG Asia Mater. 8:e320. doi: 10.1038/am.2016.154

CrossRef Full Text | Google Scholar

Liu, X., Hong, R., and Tian, C. (2008). Tolerance factor and the stability discussion of ABO3-type ilmenite. J. Mater. Sci. Mater. Electron. 20:323. doi: 10.1007/s10854-008-9728-8

CrossRef Full Text | Google Scholar

Locardi, F., Cirignano, M., Baranov, D., Dang, Z., Prato, M., Drago, F., et al. (2018). Colloidal synthesis of double perovskite Cs2AgInCl6 and Mn-doped Cs2AgInCl6 nanocrystals. J. Am. Chem. Soc. 140, 12989–12995. doi: 10.1021/jacs.8b07983

PubMed Abstract | CrossRef Full Text | Google Scholar

Löper, P., Stuckelberger, M., Niesen, B., Werner, J., Filipič, M., Moon, S.-J., et al. (2015). Complex refractive index spectra of CH3NH3PbI3 perovskite thin films determined by spectroscopic ellipsometry and spectrophotometry. J. Phys. Chem. Lett. 6, 66–71. doi: 10.1021/jz502471h

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, X., Zhao, Z., Li, K., Han, Z., Wei, S., Guo, C., et al. (2016). First-principles insight into the photoelectronic properties of Ge-based perovskites. RSC Adv. 6, 86976–86981. doi: 10.1039/C6RA18534G

CrossRef Full Text | Google Scholar

Luo, J., Wang, X., Li, S., Liu, J., Guo, Y., Niu, G., et al. (2018). Efficient and stable emission of warm-white light from lead-free halide double perovskites. Nature 563, 541–545. doi: 10.1038/s41586-018-0691-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, L., Men, L., Liu, Z., Mudryk, Y., Zhao, X., Yao, Y., et al. (2017). Ultrafast terahertz snapshots of excitonic Rydberg states and electronic coherence in an organometal halide perovskite. Nature Commun. 8:15565. doi: 10.1038/ncomms15565

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, X., Li, D., Zhao, S., Li, G., and Yang, K. (2014). The electronic and optical properties of quaternary GaAs1-x-yNxBiyalloy lattice-matched to GaAs: a first-principles study. Nanoscale Res. Lett. 9:580. doi: 10.1186/1556-276X-9-580

PubMed Abstract | CrossRef Full Text | Google Scholar

Makarov, S., Furasova, A., Tiguntseva, E., Hemmetter, A., Berestennikov, A., Pushkarev, A., et al. (2019). Halide-perovskite nanophotonics: halide-perovskite resonant nanophotonics. Adv. Opt. Mat. 7:1970002. doi: 10.1002/adom.201970002

CrossRef Full Text | Google Scholar

Malitson, I. H. (1965). Interspecimen comparison of the refractive index of fused silica^*,†. J. Opt. Soc. Am. 55, 1205–1209. doi: 10.1364/JOSA.55.001205

CrossRef Full Text | Google Scholar

Matthews, P. D., Lewis, D. J., and O'brien, P. (2017). Updating the road map to metal-halide perovskites for photovoltaics. J. Mater. Chem. A 5, 17135–17150. doi: 10.1039/C7TA04544A

CrossRef Full Text | Google Scholar

Mcclure, E. T., Ball, M. R., Windl, W., and Woodward, P. M. (2016). Cs2AgBiX6 (X = Br, Cl): new visible light absorbing, lead-free halide perovskite semiconductors. Chem. Mater. 28, 1348–1354. doi: 10.1021/acs.chemmater.5b04231

CrossRef Full Text | Google Scholar

Meng, W., Wang, X., Xiao, Z., Wang, J., Mitzi, D. B., and Yan, Y. (2017). Parity-forbidden transitions and their impact on the optical absorption properties of lead-free metal halide perovskites and double perovskites. J. Phys. Chem. Lett. 8, 2999–3007. doi: 10.1021/acs.jpclett.7b01042

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohamed, B., Allel, M., Bendouma, D., Miloud, B., and Baghdad, M. (2018). Improved electronic structure and optical performance of Bi2Te3-xSex from first-principle calculations within TB-mBJ exchange potential. Mater. Res. 21:e20170553. doi: 10.1590/1980-5373-mr-2017-0553

CrossRef Full Text | Google Scholar

Monserrat, B. (2018). Electron–phonon coupling from finite differences. J. Phys Condens. Matter 30:083001. doi: 10.1088/1361-648X/aaa737

PubMed Abstract | CrossRef Full Text | Google Scholar

Morkoc, H. (2009). Handbook of Nitride Semiconductors and Devices. Weinheim: Wiley-VCH GmbH and Co.

Google Scholar

Mouhat, F., and Coudert, F.-X. (2014). Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 90:224104. doi: 10.1103/PhysRevB.90.224104

CrossRef Full Text | Google Scholar

Murtaza, G., Ahmad, I., Amin, B., Afaq, A., Maqbool, M., Maqssod, J., et al. (2011). Investigation of structural and optoelectronic properties of BaThO3. Opt. Mater. 33, 553–557. doi: 10.1016/j.optmat.2010.10.052

CrossRef Full Text | Google Scholar

Nakanishi, N., Nagasawa, A., and Murakami, Y. (1982). Lattice stability and soft modes. J. Phys. Colloques 43, C4-35–C34-55. doi: 10.1051/jphyscol:1982403

CrossRef Full Text | Google Scholar

Nandha, K. N., and Nag, A. (2018). Synthesis and luminescence of Mn-doped Cs2AgInCl6 double perovskites. Chem. Commun. 54, 5205–5208. doi: 10.1039/C8CC01982G

PubMed Abstract | CrossRef Full Text | Google Scholar

Niemann, R. G., Kontos, A. G., Palles, D., Kamitsos, E. I., Kaltzoglou, A., Brivio, F., et al. (2016). Halogen effects on ordering and bonding of CH₃${\text{NH}}_3^{+}$ in CH₃NH₃PbX₃ (X = Cl, Br, I) hybrid perovskites: a vibrational spectroscopic study. J. Phys. Chem. C 120, 2509–2519. doi: 10.1021/acs.jpcc.5b11256

CrossRef Full Text | Google Scholar

Opoku, F., Govender, K. K., Van Sittert, C. G. C. E., and Govender, P. P. (2017). Understanding the mechanism of enhanced charge separation and visible light photocatalytic activity of modified wurtzite ZnO with nanoclusters of ZnS and graphene oxide: from a hybrid density functional study. New J. Chem. 41, 8140–8155. doi: 10.1039/C7NJ01942D

CrossRef Full Text | Google Scholar

Pan, Y., and Guan, W. M. (2017). Probing the balance between ductility and strength: transition metal silicides. Phys. Chem. Chem. Phys. 19, 19427–19433. doi: 10.1039/C7CP03182C

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, C. R. (2019). Advanced Thermoelectric Materials. Beverly, MA: Scrivener Publishing (Wiley).

Google Scholar

Peng, H., Yang, Z.-H., Perdew, J. P., and Sun, J. (2016). Versatile van der waals density functional based on a meta-generalized gradient approximation. Phys. Rev. X 6:041005. doi: 10.1103/PhysRevX.6.041005

CrossRef Full Text | Google Scholar

Peng, W., Li, X., and Du, J. (2013). First Principles investigations on structural, elastic, electronic, and optical properties of Li₂CdGeS₄. Mater. Trans. 54, 2167–2172. doi: 10.2320/matertrans.M2013186

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi: 10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Ruzsinszky, A., Csonka, G. I., Vydrov, O. A., Scuseria, G. E., Constantin, L. A., et al. (2008). Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100:136406. doi: 10.1103/PhysRevLett.100.136406

PubMed Abstract | CrossRef Full Text | Google Scholar

Pham, H. Q., Holmes, R. J., Aydil, E. S., and Gagliardi, L. (2019). Lead-free double perovskites Cs2InCuCl6 and (CH3NH3)2InCuCl6: electronic, optical, and electrical properties. Nanoscale 11, 11173–11182. doi: 10.1039/C9NR01645G

PubMed Abstract | CrossRef Full Text | Google Scholar

Popova, S., Tolstykh, T., and Vorobev, V. (1972). Optical characteristics of amorphous quartz in the 1400–200 cm⁻¹ region. Opt. Spectrosc. 33, 444–445.

Pugh, S. F. (1954). XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. London, Edinburgh, and Dublin. Phil. Mag. J. Sci. 45, 823–843. doi: 10.1080/14786440808520496

CrossRef Full Text | Google Scholar

Qijingzheng pyband. Available online at: https://github.com/QijingZheng/pyband (accessed April 20, 2020).

Refractiveindex.Info. Refractive Index Database. Available online at: https://refractiveindex.info/?shelf=mainandbook=Siandpage=Aspnes (accessed April 27, 2020).

Rühle, S. (2016). Tabulated values of the Shockley–Queisser limit for single junction solar cells. Solar Energy 130, 139–147. doi: 10.1016/j.solener.2016.02.015

CrossRef Full Text | Google Scholar

Saini, P. K., Ahlawat, D., and Singh, D. (2017). Study of electronic structure and optical properties of zinc-blende and rocksalt structures of HgSe : A DFT study. J. Metal. Mat. Sci. 59, 29–37.

Google Scholar

Salinas-Sanchez, A., Garcia-Muñoz, J. L., Rodriguez-Carvajal, J., Saez-Puche, R., and Martinez, J. L. (1992). Structural characterization of R2BaCuO5 (R = Y, Lu, Yb, Tm, Er, Ho, Dy, Gd, Eu and Sm) oxides by X-ray and neutron diffraction. J. Solid State Chem. 100, 201–211. doi: 10.1016/0022-4596(92)90094-C

CrossRef Full Text | Google Scholar

Saraf, R., and Maheshwari, V. (2018). Self-powered photodetector based on electric-field-induced effects in MAPbI3 perovskite with improved stability. ACS App. Mater. Interfaces 10, 21066–21072. doi: 10.1021/acsami.8b05860

PubMed Abstract | CrossRef Full Text | Google Scholar

Savory, C. N., Ganose, A. M., Travis, W., Atri, R. S., Palgrave, R. G., and Scanlon, D. O. (2016a). An assessment of silver copper sulfides for photovoltaic applications: theoretical and experimental insights. J. Mat. Chem. A 4, 12648–12657. doi: 10.1039/C6TA03376H

PubMed Abstract | CrossRef Full Text | Google Scholar

Savory, C. N., Walsh, A., and Scanlon, D. O. (2016b). Can Pb-free halide double perovskites support high-efficiency solar cells? ACS Energy Lett. 1, 949–955. doi: 10.1021/acsenergylett.6b00471

PubMed Abstract | CrossRef Full Text | Google Scholar

Schubert, E. F., Kim, J. K., and Xi, J.-Q. (2007). Low-refractive-index materials: a new class of optical thin-film materials. Phys. Stat. Sol. 244, 3002–3008. doi: 10.1002/pssb.200675603

CrossRef Full Text | Google Scholar

Shannon, R. D. (1976). Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. A32, 751–767. doi: 10.1107/S0567739476001551

CrossRef Full Text | Google Scholar

Shockley, W., and Queisser, H. J. (1961). Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 32, 510–519. doi: 10.1063/1.1736034

CrossRef Full Text | Google Scholar

Singh, S., Valencia-Jaime, I., and Romero, A. H. (2018). Effect of spin-orbit coupling on the elastic, mechanical, and thermodynamic properties of Bi-Sb binaries. Phys. Rev. B 97:054108. doi: 10.1103/PhysRevB.97.054108

CrossRef Full Text | Google Scholar

Skauli, T., Kuo, P. S., Vodopyanov, K. L., Pinguet, T. J., Levi, O., Eyres, L. A., et al. (2003). Improved dispersion relations for GaAs and applications to nonlinear optics. J. Appl. Phys. 94, 6447–6455. doi: 10.1063/1.1621740

CrossRef Full Text | Google Scholar

Slavney, A. H., Hu, T., Lindenberg, A. M., and Karunadasa, H. I. (2016). A Bismuth-Halide double perovskite with long carrier recombination lifetime for photovoltaic applications. J. Am. Chem. Soc. 138, 2138–2141. doi: 10.1021/jacs.5b13294

PubMed Abstract | CrossRef Full Text | Google Scholar

Slavney, A. H., Leppert, L., Saldivar Valdes, A., Bartesaghi, D., Savenije, T. J., Neaton, J. B., et al. (2018). Small-band-gap halide double perovskites. Angew Chem. Int. Edn. 57, 12765–12770. doi: 10.1002/anie.201807421

PubMed Abstract | CrossRef Full Text | Google Scholar

Spoonhower, J. P., Burberry, M. S., and Baxter, S. M. (1986). Infrared radiative recombination in Rh3+?doped AgBr. Solid State Commun. 59, 843–849. doi: 10.1016/0038-1098(86)90641-1

CrossRef Full Text | Google Scholar

Stoumpos, C. C., Frazer, L., Clark, D. J., Kim, Y. S., Rhim, S. H., Freeman, A. J., et al. (2015). Hybrid germanium iodide perovskite semiconductors: active lone pairs, structural distortions, direct and indirect energy gaps, and strong nonlinear optical properties. J. Am. Chem. Soc. 137, 6804–6819. doi: 10.1021/jacs.5b01025

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, J., Remsing, R. C., Zhang, Y., Sun, Z., Ruzsinszky, A., Peng, H., et al. (2016). Accurate first-principles structures and energies of diversely bonded systems from an efficient density functional. Nat. Chem. 8, 831–836. doi: 10.1038/nchem.2535

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, J., Ruzsinszky, A., and Perdew, J. P. (2015). Strongly constrained and appropriately normed semilocal density functional. Phys. Rev. Lett. 115:036402. doi: 10.1103/PhysRevLett.115.036402

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, P.-P., Li, Q.-S., Yang, L.-N., and Li, Z.-S. (2016). Theoretical insights into a potential lead-free hybrid perovskite: substituting Pb2+ with Ge2+. Nanoscale 8, 1503–1512. doi: 10.1039/C5NR05337D

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, C. Z. (1998). Determination of refractive index of silica glass for infrared wavelengths by IR spectroscopy. J. Non-Cryst. Solids 223, 158–163. doi: 10.1016/S0022-3093(97)00438-9

CrossRef Full Text | Google Scholar

Tan, Z., Li, J., Zhang, C., Li, Z., Hu, Q., Xiao, Z., et al. (2018). Highly efficient blue-emitting bi-doped Cs2SnCl6 perovskite variant: photoluminescence induced by impurity doping. Adv. Funct. Mater. 28:1801131. doi: 10.1002/adfm.201801131

CrossRef Full Text | Google Scholar

Tanabe, Y., and Sugano, S. (1954). On the absorption spectra of complex ions. I. J. Phys. Soc. Jpn. 9, 753–766. doi: 10.1143/JPSJ.9.753

CrossRef Full Text | Google Scholar

Tang, Z., Bessho, T., Awai, F., Kinoshita, T., Maitani, M. M., Jono, R., et al. (2017). Hysteresis-free perovskite solar cells made of potassium-doped organometal halide perovskite. Sci. Rep. 7:12183. doi: 10.1038/s41598-017-12436-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Thompson, R. P., and Clegg, W. J. (2018). Predicting whether a material is ductile or brittle. Curr. Opinion Solid State Mat. Sci. 22, 100–108. doi: 10.1016/j.cossms.2018.04.001

CrossRef Full Text | Google Scholar

Togo, A., and Tanaka, I. (2015). First principles phonon calculations in materials science. Scripta Mater. 108, 1–5. doi: 10.1016/j.scriptamat.2015.07.021

CrossRef Full Text | Google Scholar

Tran, T. T., Panella, J. R., Chamorro, J. R., Morey, J. R., and Mcqueen, T. M. (2017). Designing indirect–direct bandgap transitions in double perovskites. Mater. Horizons 4, 688–693. doi: 10.1039/C7MH00239D

CrossRef Full Text | Google Scholar

Umadevi, D., and Watson, G. W. (2019). Quasiparticle GW Calculations on lead-free hybrid germanium iodide perovskite CH3NH3GeI3 for photovoltaic applications. ACS Omega 4, 5661–5669. doi: 10.1021/acsomega.8b03291

PubMed Abstract | CrossRef Full Text | Google Scholar

Van schilfgaarde, M., Kotani, T., and Faleev, S. (2006). Quasiparticle self-consistent $GW$ theory. Phys. Rev. Lett. 96:226402. doi: 10.1103/PhysRevLett.96.226402

PubMed Abstract | CrossRef Full Text | Google Scholar

Varadwaj, A., Varadwaj, P. R., and Yamashita, K. (2018). Revealing the chemistry between band gap and binding energy for lead-/tin-based trihalide perovskite solar cell semiconductors. ChemSusChem 11, 449–463. doi: 10.1002/cssc.201701653

PubMed Abstract | CrossRef Full Text | Google Scholar

VASP (2020a). Bandgap of Si in GW. Available online at: https://www.vasp.at/wiki/index.php/Bandgap_of_Si_in_GW (accessed July 25, 2020).

VASP (2020b). Ionic Contributions to the Frequency Dependent Dielectric Function of NaCl. Available online at: https://www.vasp.at/wiki/index.php/Ionic_contributions_to_the_frequency_dependent_dielectric_function_of_NaCl#cite_note-gajdos:prb:2006-1 (accessed April 20, 2020).

VASP (2020c). LPEAD. Available online at: https://www.vasp.at/wiki/index.php/LPEAD (accessed July 26, 2020).

VASP (2020d). Phonons From Finite Differences. Available online at: https://www.vasp.at/wiki/index.php/Phonons_from_finite_differences (accessed July 28, 2020).

VASP (2020e). Si_Bandstructure. Available online at: https://www.vasp.at/wiki/index.php/Si_bandstructure (accessed April 20, 2020).

Volonakis, G., Haghighirad, A. A., Milot, R. L., Sio, W. H., Filip, M. R., Wenger, B., et al. (2017). Cs₂InAgCl₆: a new lead-free halide double perovskite with direct band gap. J. Phys. Chem. Lett. 8, 772–778. doi: 10.1021/acs.jpclett.6b02682

PubMed Abstract | CrossRef Full Text | Google Scholar

Walsh, A. (2015). Principles of chemical bonding and band gap engineering in hybrid organic–inorganic halide perovskites. J. Phys Chem. C 119, 5755–5760. doi: 10.1021/jp512420b

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H.-C., Pistor, P., Marques, M.a.L, and Botti, S. (2019). Double perovskites as p-type conducting transparent semiconductors: a high-throughput search. J. Mat. Chem. A 7, 14705–14711. doi: 10.1039/C9TA01456J

CrossRef Full Text | Google Scholar

Wang, Q., Hu, Z., and Shao, X. (2020). Exploring electronic, optoelectronic, and thermoelectric properties of ternary compound MgSrSe2 from first-principles study. AIP Adv. 10:045010. doi: 10.1063/5.0002946

CrossRef Full Text | Google Scholar

Wang, Z., Ganose, A. M., Niu, C., and Scanlon, D. O. (2019). Two-dimensional eclipsed arrangement hybrid perovskites for tunable energy level alignments and photovoltaics. J. Mat. Chem. C 7, 5139–5147. doi: 10.1039/C9TC01325C

CrossRef Full Text | Google Scholar

Wei, F., Deng, Z., Sun, S., Hartono, N. T. P., Seng, H. L., Buonassisi, T., et al. (2019). Enhanced visible light absorption for lead-free double perovskite Cs2AgSbBr6. Chem. Commun. 55, 3721–3724. doi: 10.1039/C9CC01134J

PubMed Abstract | CrossRef Full Text | Google Scholar

Wen, H., Cheng, B.-M., and Tanner, P. A. (2017). Optical properties of selected 4d and 5d transition metal ion-doped glasses. RSC Adv. 7, 26411–26419. doi: 10.1039/C7RA04062H

CrossRef Full Text | Google Scholar

Wilson, J. N., Frost, J. M., Wallace, S. K., and Walsh, A. (2019). Dielectric and ferroic properties of metal halide perovskites. APL Mater. 7:010901. doi: 10.1063/1.5079633

CrossRef Full Text | Google Scholar

Xiao, Z., Du, K.-Z., Meng, W., Wang, J., Mitzi, D. B., and Yan, Y. (2017). Intrinsic instability of Cs2In(I)M(III)X6 (M = Bi, Sb; X = Halogen) double perovskites: a combined density functional theory and experimental study. J. Am. Chem. Soc. 139, 6054–6057. doi: 10.1021/jacs.7b02227

CrossRef Full Text | Google Scholar

Xu, B., Li, X., Sun, J., and Yi, L. (2008). Electronic structure, ferroelectricity and optical properties of CaBi2Ta2O9. Eur. Phys. J. B 66, 483–487. doi: 10.1140/epjb/e2008-00461-9

CrossRef Full Text | Google Scholar

Xu, Q., Yang, D., Lv, J., Sun, Y.-Y., and Zhang, L. (2018). Perovskite solar absorbers: materials by design. Small Methods 2:1700316. doi: 10.1002/smtd.201700316

CrossRef Full Text | Google Scholar

Yamada, I., Takamatsu, A., and Ikeno, H. (2018). Complementary evaluation of structure stability of perovskite oxides using bond-valence and density-functional-theory calculations. Sci. Tech. Adv. Mater. 19, 101–107. doi: 10.1080/14686996.2018.1430449

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, B., Mao, X., Hong, F., Meng, W., Tang, Y., Xia, X., et al. (2018). Lead-free direct band gap double-perovskite nanocrystals with bright dual-color emission. J. Am. Chem. Soc. 140, 17001–17006. doi: 10.1021/jacs.8b07424

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, J., Wen, X., Xia, H., Sheng, R., Ma, Q., Kim, J., et al. (2017). Acoustic-optical phonon up-conversion and hot-phonon bottleneck in lead-halide perovskites. Nat. Commun. 8:14120. doi: 10.1038/ncomms14120

PubMed Abstract | CrossRef Full Text | Google Scholar

Yao, Y., Kou, B., Peng, Y., Wu, Z., Li, L., Wang, S., et al. (2020). (C3H9NI)4AgBiI8: a direct-bandgap layered double perovskite based on a short-chain spacer cation for light absorption. Chem. Commun. 56, 3206–3209. doi: 10.1039/C9CC07796K

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, C.-J. (2019). Advances in modelling and simulation of halide perovskites for solar cell applications. J. Phys. Energ 1:022001. doi: 10.1088/2515-7655/aaf143

CrossRef Full Text | Google Scholar

Zangwill, A. (2019). Modern Electrodynamics. Cambridge: Cambridge University Press.

Google Scholar

Zhang, H., Liu, L., and Zhou, Z. (2012a). First-principles studies on facet-dependent photocatalytic properties of bismuth oxyhalides (BiOXs). RSC Adv. 2, 9224–9229. doi: 10.1039/c2ra20881d

CrossRef Full Text | Google Scholar

Zhang, H., Liu, L., and Zhou, Z. (2012b). Towards better photocatalysts: first-principles studies of the alloying effects on the photocatalytic activities of bismuth oxyhalides under visible light. Phys. Chem. Chem. Phys. 14, 1286–1292. doi: 10.1039/C1CP23516H

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, M., Zhang, X., Lin, H.-Q., and Lu, G. (2019). Radiative recombination of large polarons in halide perovskites. J. Phys. Condens. Matter 31:165701. doi: 10.1088/1361-648X/ab0158

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Kitchaev, D. A., Yang, J., Chen, T., Dacek, S. T., Sarmiento-Pérez, R. A., et al. (2018). Efficient first-principles prediction of solid stability: towards chemical accuracy. NPJ Comput. Mater. 4:9. doi: 10.1038/s41524-018-0065-z

CrossRef Full Text | Google Scholar

Zhao, F., Song, Z., Zhao, J., and Liu, Q. (2019). Double perovskite Cs2AgInCl6:Cr3+: broadband and near-infrared luminescent materials. Inorg. Chem. Front. 6, 3621–3628. doi: 10.1039/C9QI00905A

CrossRef Full Text | Google Scholar

Zhao, S., Yamamoto, K., Iikubo, S., Hayase, S., and Ma, T. (2018). First-principles study of electronic and optical properties of lead-free double perovskites Cs2NaBX6 (B = Sb, Bi; X = Cl, Br, I). J. Phys. Chem. Solids 117, 117–121. doi: 10.1016/j.jpcs.2018.02.032

CrossRef Full Text | Google Scholar

Zhao, X.-G., Yang, D., Sun, Y., Li, T., Zhang, L., Yu, L., et al. (2017). Cu–In Halide perovskite solar absorbers. J. Am. Chem. Soc. 139, 6718–6725. doi: 10.1021/jacs.7b02120

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Y.-Q., Liu, B., Yu, Z.-L., Ma, J., Qiang, W., He, P.-B., et al. (2017). Strong ferroelectric polarization of CH3NH3GeI3 with high-absorption and mobility transport anisotropy: theoretical study. J. Mat. Chem. C 5, 5356–5364. doi: 10.1039/C7TC01166K

CrossRef Full Text | Google Scholar

Zhou, J., Rong, X., Molokeev, M. S., Zhang, X., and Xia, Z. (2018). Exploring the transposition effects on the electronic and optical properties of Cs2AgSbCl6via a combined computational-experimental approach. J. Mat. Chem. A 6, 2346–2352. doi: 10.1039/C7TA10062K

CrossRef Full Text | Google Scholar

Zhou, J., Rong, X., Zhang, P., Molokeev, M. S., Wei, P., Liu, Q., et al. (2019). Manipulation of Bi3+/In3+ transmutation and Mn2+-doping effect on the structure and optical properties of double perovskite Cs2NaBi1-xInxCl6. Adv. Opt. Mat. 7:1801435. doi: 10.1002/adom.201801435

CrossRef Full Text | Google Scholar

Zhou, J., Xia, Z., Molokeev, M. S., Zhang, X., Peng, D., and Liu, Q. (2017). Composition design, optical gap and stability investigations of lead-free halide double perovskite Cs2AgInCl6. J. Mater. Chem. A 5, 15031–15037. doi: 10.1039/C7TA04690A

CrossRef Full Text | Google Scholar

Zhou, Y., Askar, A. M., Pöhls, J.-H., Iyer, A. K., Oliynyk, A. O., Shankar, K., et al. (2019). Hexagonal double perovskite Cs2AgCrCl6. Z. Anorg. Allg. Chem. 645, 323–328. doi: 10.1002/zaac.201800351

CrossRef Full Text | Google Scholar