
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Chem. , 10 January 2020
Sec. Inorganic Chemistry
Volume 7 - 2019 | https://doi.org/10.3389/fchem.2019.00909
This article is part of the Research Topic Flux Crystal Growth: From Fundamentals to Crystal Functionality View all 8 articles
The flux growth method was successfully employed to synthesize millimeter-sized single crystals of the ternary barium vanadium pnictides Ba5V12As19+x (x ≈ 0.02) and Ba5V12Sb19+x (x ≈ 0.36), using molten Pb and Sb, respectively. Both compositions crystallize in space group P3m and adopt a structure similar to those of the barium titanium pnictides Ba5Ti12Pn19+x (Pn = Sb, Bi), yet with a subtly different disorder, involving the pnictogen and barium atoms. Attempts to obtain an arsenide analog of Ba5Ti12Pn19+x using a Pb flux technique yielded binary arsenides. High-temperature treatment of the elements Ba, Ti, and As in Nb or Ta tubes resulted in side reactions with the crucible materials and produced two isostructural compositions Ba8Ti13−xMxAs21 (M = Nb, Ta; x ≈ 4), representing a new structure type. The latter structure displays fcc-type metal clusters comprised of statistically distributed Ti and M atoms (M = Nb, Ta) with multi-center and two-center bonding within the clusters, as suggested by our first-principle calculations.
The application of molten metals as inert or reactive solvents for the crystal growth of intermetallic compounds is an actively used synthetic approach in solid-state chemistry. In a typical flux growth experiment, a mixture of selected metallic elements, along with a suitable flux material (also a metal or eutectic mixture of metals) are loaded in an inert container (graphite, alumina or other refractory materials, or high-melting metals from groups 5 or 6, such as Nb, Ta, and Mo). The reaction container can be equipped with some sort of filter or sieve for separating the molten flux from the grown crystals (Canfield and Fisk, 1992; Kanatzidis et al., 2005; Latturner, 2018). The as-prepared mixtures are then heated up, typically well above the melting point of the flux to achieve reasonably high diffusion rates and solubility. In general, complete dissolution is not necessary for production of small crystals, suitable for, e.g., single-crystal X-ray diffraction. However, obtaining larger crystals, which can be utilized for accurate physical property measurements, usually requires precipitation from homogeneous melts to assure a small number of crystallization centers (Wolff and Mlavsky, 1974). After the homogenization step, the temperature is lowered to allow formation of a solid phase. The flux material can then be removed by inverting the reactor at a temperature above the flux melting point and letting the molten flux pass through the filter, leaving the grown crystals behind. Alternatively, selective etching or evaporation of the flux can be used to recover the crystals from the reaction batch. In certain cases, single crystals can be mechanically isolated after breaking the solidified product (Canfield and Fisk, 1992; Kanatzidis et al., 2005). An important point that has to be taken into account when growing single crystals via the flux growth method is possible undesirable incorporation of the flux material into the crystal structure of the produced crystals. In such instances, the observed crystal structure may be inherently flux-stabilized and cannot be reproduced in a flux-free environment (Khan et al., 2018; Felder et al., 2019).
The flux growth process is well-suited for the production of incongruently-melting materials, but it can also be efficient for the growth of congruently-melting compounds when their melting points are prohibitory high. Since ternary and higher multicomponent phase diagrams are usually unknown, making the information about melting temperatures as well as phase relationships inaccessible, the flux method, owing to its wide applicability, offers a tool for explorative search for new materials. Various classes of intermetallics have been prepared by this route. In particular, numerous ternary (Ovchinnikov et al., 2017b; Baranets et al., 2019a; Childs et al., 2019; Nakamura et al., 2019; Ovchinnikov and Bobev, 2019a), quaternary (Ovchinnikov et al., 2017a, 2018a; Baranets and Bobev, 2019; Baranets et al., 2019b; Jayasinghe et al., 2019; Wakiya et al., 2019), and even quinary (Zaikina et al., 2010, 2017; Ma et al., 2012) compositions were successfully synthesized in the form of single crystals. Some examples of complex intermetallics which have been recently produced from metal fluxes include AE3Ti8Bi10 (Ovchinnikov and Bobev, 2019b), AELi2In2Ge2 (AE = Sr, Ba, Eu) (Ovchinnikov and Bobev, 2019c), Y7Ru4InGe12 (Bao et al., 2019), and R5Mg5Fe4AlxSi18−x (R = Gd, Dy, Y) (Ma et al., 2012).
Even apparently well-established binary systems may sometimes yield surprising new compositions, as it was the case for the RE–Bi (RE = Nd, Sm) systems (Ovchinnikov et al., 2018b), which host the isostructural RE3Bi7 phases, overlooked in the multiple early assessments of the corresponding phase diagrams. Careful optimization of the flux growth procedure resulted in large single crystals of these recently discovered compounds.
In this contribution, we explored the application of the metal flux approach to the synthesis of multinary vanadium pnictides. The choice of the elements was in part motivated by the lack of detailed experimental data on the ternary compounds in the A–V–Pn systems, where A stands for an electropositive metal, such as alkali, alkaline-earth, or rare-earth metal, and Pn is pnictogen, i.e., a group 15 element. From the physical property perspective, some of the early transition metal pnictides were reported to display interesting electronic behavior, such as superconductivity in K2Cr3As3 (Bao et al., 2015) and doped BaTi2Sb2O (Doan et al., 2012), and itinerant ferromagnetism in LaCrSb3 (Raju et al., 1998). In addition, our recent exploratory work in the field of titanium pnictides revealed several new phases in the AE–Ti–Bi systems (AE = Ca, Sr, Ba, Eu) (Ovchinnikov and Bobev, 2018a, 2019b). Taking into account pronounced structural similarities between multinary titanium and vanadium pnictides (Brylak and Jeitschko, 1994; Bie and Mar, 2009; Failamani et al., 2015; Ovchinnikov and Bobev, 2018a), the existence of yet unknown multinary vanadium pnictides can be foreseen.
We focused our studies on the ternary arsenides and antimonides of vanadium with alkaline-earth metals. Due to extremely low solubility of V in liquid Bi and the lack of stable binary bismuthides, Bi was excluded from our consideration, although it is conceivable that with suitably modified synthetic protocols, analogous bismuthides could also be found. The exploratory search resulted in two ternaries, Ba5V12As19+x (x ≈ 0.02) and Ba5V12Sb19+x (x ≈ 0.36), grown from liquid Pb and Sb, respectively. By high-temperature treatment of the elemental mixture with the nominal composition “Ba5Ti12As19” in Nb or Ta tubes, new isostructural compounds with the general formula Ba8Ti13−xMxAs21 (M = Nb, Ta) were produced. A striking structural peculiarity of these phases, adopting a new structure type, is the presence of fcc-type transition metal clusters with pronounced multi-center, as well as two-center, bonding.
Due to the air-sensitivity of the starting materials and the final products, most operations were performed in an argon-filled glovebox. All used materials had stated purity of at least 99.9 wt. %. Flux-assisted single crystal growth was employed for the synthesis of Ba5V12As19.02(1) and Ba5V12Sb19.36(2). For the former compound, metallic Pb was utilized as a flux. A mixture of Ba, V, As, and Pb with a molar ratio of 2:1:4:25, respectively, was placed in an alumina crucible topped with a piece of quartz wool and sealed in an evacuated fused silica tube. The reactor was heated up to 1173 K in a box furnace with a rate of 200 K/h. After the mixture was allowed to homogenize for 48 h, it was cooled down to 823 K with a rate of 5 K/h. At this final temperature, the fused silica tube was removed from the furnace, inverted, and subjected to centrifugation. The molten lead seeped through the quartz wool leaving the crystallized product on the wool and inside the crucible. The tube was break-opened inside the glovebox and the solid material was mechanically collected and inspected under an optical microscope. Besides some inhomogeneously looking powder, which was revealed by powder X-ray diffraction to be a mixture of binary Ba and V arsenides, well-formed single crystals of isotropic polyhedral shape and dimensions up to 1 mm were clearly visible. These crystals turned out to be a new compound with the composition Ba5V12As19.02(1) as was determined by single-crystal X-ray diffraction.
The single crystal growth of Ba5V12Sb19.36(2) was carried out applying a Sb self-flux approach. A similar experimental setup was used as detailed above. The starting mixture consisted of Ba, V, and Sb in a molar ratio of 2:1:4, respectively. The reactor was heated up to 1273 K with a rate of 50 K/h and kept at this temperature for 48 h. After that, the temperature was lowered to 1023 K with a rate of 5 K/h, and the excess of Sb was removed by centrifugation. Large crystals with dimensions up to 4–5 mm were the only solid product found in the crucible. Powder and single crystal X-ray diffraction analysis showed that the product was single phase Ba5V12Sb19.36(2).
Crystals of the new quaternary compound Ba8Ti9.24(6)Ta3.76As21 were discovered in the sample prepared by a direct reaction of the elements with the targeted composition Ba5Ti12As19. The starting mixture was placed in a weld-shut Ta tube under protective high-purity Ar atmosphere and sealed in an evacuated fused silica tube, which was subsequently loaded in a tube furnace. One end of the tube was left protruding out from the furnace to keep this part of the reactor at room temperature, as a safety measure: in the case of the Ta tube failure, the toxic As vapor would condense on the cold end without building dangerously high pressure inside the silica tube. The tube was heated up to 1273 K with a rate of 200 K/h, annealed at this temperature for 48 h, and cooled down to room temperature with a rate of 5 K/h. The resulting sample mostly consisted of binary Ba and Ti arsenides according to powder X-ray diffraction. However, strong peaks belonging to an unidentified phase were evident in the powder patterns. Visual inspection of the product under a microscope revealed the presence of single crystals with different morphologies. Among them, small submillimeter-sized crystals with cubic or octahedral shape could be easily distinguished. Subsequent single crystal data collection and refinement confirmed a new structure with the chemical formula Ba8Ti9.24(6)Ta3.76As21. The Ta in the composition obviously originated from the reactor. To indirectly cross check the results of the structural refinement, the reaction was repeated using the same protocol as described above, but in a Nb tube instead of Ta. The outcome of the synthesis with respect to the major phases was similar to the previous attempt. Single crystals with the refined composition Ba8Ti9.0(3)Nb4.0As21, isotypic with the Ta-containing phase, were found as a side product, thus confirming the crystal structure.
Powder X-ray diffraction measurements were done in the reflection mode on a Rigaku Miniflex diffractometer (Cu Kα radiation λ = 1.5418 Å) operating inside a nitrogen-filled glovebox to prevent sample deterioration upon contact with the ambient atmosphere. The powder patterns were recorded in a Θ–Θ scan mode with a step size of 0.05° and a 2 s per step acquisition time.
Suitable single crystals were selected and cut to desired dimensions under dry Paratone N oil using low-background plastic loops. Data were recorded in a cold nitrogen stream at T = 200 K on a Bruker SMART APEX CCD diffractometer equipped with monochromated Mo Kα radiation (λ = 0.71073 Å). The raw data were integrated using the program SAINT (SAINT, 2014). Semiempirical absorption corrections were performed with the SADABS software (SADABS, 2014). Crystal structures were solved by dual-space methods with SHELXT (Sheldrick, 2015a) and refined by full matrix least-squares methods on F2 using SHELXL (Sheldrick, 2015b). All studied compounds showed a certain degree of crystallographic disorder. Assignment of chemical types was straightforward, based on the interatomic distances and coordination environments. Atomic coordinates were standardized using STRUCTURE TIDY (Gelato and Parthé, 1987). Details of the data collection, crystallographic parameters, and selected interatomic distances are summarized in Tables 1–6.
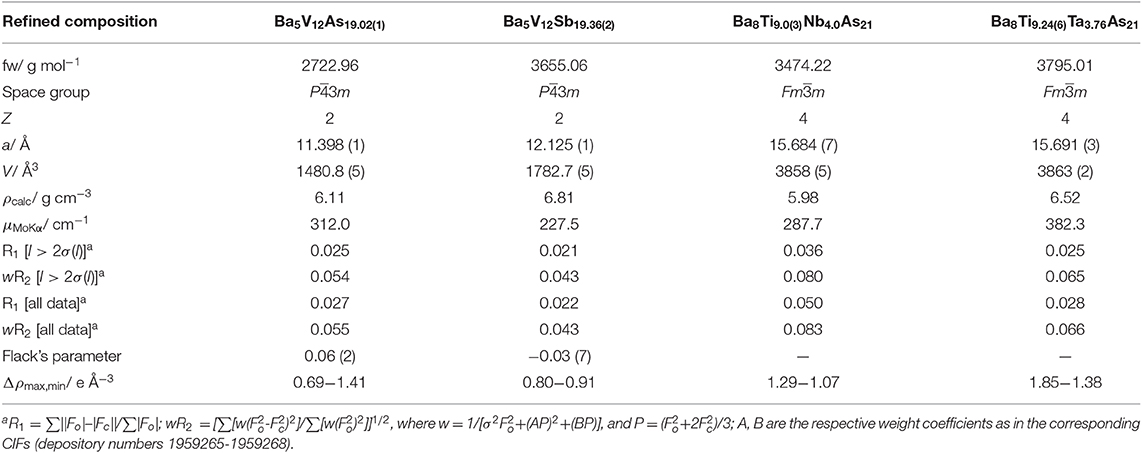
Table 1. Data collection details and selected crystallographic data (T = 200 K, Mo Kα, λ = 0.71073 Å).
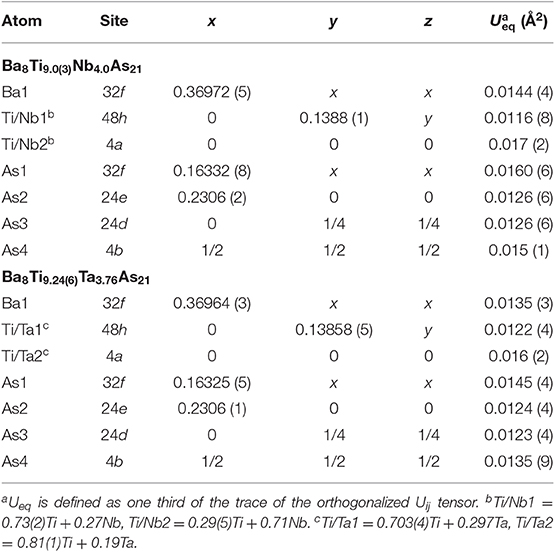
Table 4. Atomic coordinates and equivalent isotropic displacement parameters for Ba8Ti13−xMxAs21 (M = Nb, Ta).
For electronic structure calculations, a hypothetical disorder-free Ba5V12As19 model was employed. The split Ba1 site was treated as a single position with averaged atomic coordinates, and the partially occupied As6 and As7 sites were removed. An ordered model was also generated for Ba8Ti9.0(3)Nb4.0As21. For this purpose, the experimentally determined Fmm structure was transformed into a I4/mmm subgroup with half the original unit cell volume and the following transformation of the transition metal sites: 4a → 2a, 48h → 16m + 8i. The Nb atoms were placed exclusively in the 8i positions, resulting in the formula Ba8Ti9Nb4As21.
The calculations were executed with the TB-LMTO-ASA package (Jepsen and Andersen, 2000) at the local density approximation level applying the von Barth-Hedin exchange-correlation functional (von Barth and Hedin, 1972). Empty spheres were added to satisfy the Atomic Sphere Approximation (ASA). Chemical bonding was examined using Crystal Orbital Hamilton Population curves (COHP) (Steinberg and Dronskowski, 2018) and Electron Localization Function (ELF) (Savin et al., 1997), evaluated by the respective modules of the LMTO package. Electron density was integrated using the program Critic2 (Otero-de-la-Roza et al., 2014).
The use of Pb as a flux for the synthesis of arsenides provides considerable benefits over the high-temperature annealing of the elements. High solubilities of many elements in molten Pb and its low melting point enable single crystal growth at moderately high temperatures, without significant losses of the highly volatile As. In addition, owing to their dilution, the dissolved starting materials in the course of a flux growth process display reduced chemical activity toward the reaction container, thereby preventing side reactions, which are often inevitable in the conventional high-temperature approach (Chen and Corbett, 2004; Baranets et al., 2018). A particular advantage of the flux approach is the possibility to produce single crystals containing elements with significantly different melting points, providing that all of the elements are reasonably soluble in the flux. We applied this approach to synthesize new multinary vanadium arsenides, since in this case, too, the high melting point of V (Tm = 2183 K) and the low sublimation point of As (Tsubl = 883 K) make direct synthesis from the elements rather challenging.
Among the compositions in the AE–V–As–Pb systems (AE = Ca, Sr, Ba) used for single crystal growth attempts, only experiments with AE = Ba produced a new ternary phase, Ba5V12As19+x. For AE = Ca and Sr, binary arsenides were detected as products in all reactions. Although Ba5V12As19+x can be obtained from different starting elemental ratios, so far it has been observed as a side product, indicating that further optimization of the procedure is necessary. In all cases, binary metal arsenides have been detected alongside Ba5V12As19+x. The low yield of Ba5V12As19+xis suggestive that the reaction conditions used for AE = Ca and Sr may also be improved to ultimately afford ternary compounds. Due to high reactivity of As toward various metals used as container materials in high-temperature reactions, systematic studies of the potential homogeneity range in Ba5V12As19+x have been obstructed by side-reactions. However we would like to note that our investigations in the AE–Ti–Bi systems (AE = Sr, Ba), which host structurally related AE5Ti12Bi19+x compounds, revealed that the Bi content depends on the alkaline-earth metal chosen, but the respective homogeneity ranges for a given AE were found to be rather narrow (Ovchinnikov and Bobev, 2018a).
The relatively low melting point of Sb (Tm = 903 K) allows its application as a reactive flux for the synthesis of antimonides. Such “self-flux” approach prevents potential contamination of the grown crystals by foreign elements. Crystal growth attempts in the Ba–V–Sb system yielded well-formed single crystals of Ba5V12Sb19.36(2). It is worthwhile to mention that a very similar composition was found for the ternary Ba–V–Sb phase prepared by high-temperature annealing of an arc-melted sample with the nominal composition ≈ Ba5V12Sb25 (Failamani et al., 2015), suggesting that the obtained crystals are on the Sb-rich side of the homogeneity range. The crystal structure reported in Failamani et al. (2015) was refined as a Ba-deficient Ba5−δV12Sb19+x. Our refinement does not provide evidence for any Ba vacancies but confirms the previously described splitting of the Ba site. Furthermore, this splitting is correlated with the disorder in the Sb substructure.
To date, flux growth experiments in the Sr–V–Sb system have resulted in binary antimonides only. In the Ca–V–Sb system, the exploratory work so far has resulted in the phase CaV3Sb4 (Ovchinnikov and Bobev, 2020), which is structurally unrelated to Ba5V12Sb19+x.
Crystal growth experiments in the AE–Ti–As–Pb systems (AE = Ca, Sr, Ba) always produced binary arsenides. Since the ternary compounds Ba5Ti12Pn19+x (Pn = Sb, Bi), structurally related to Ba5V12Pn19+x (Pn = As, Sb), have been synthesized and characterized in detail (Bie and Mar, 2009; Ovchinnikov and Bobev, 2018a; Han et al., 2019), it may seem surprising that the isoelectronic “Ba5Ti12As19+x” could not be obtained. To address this issue, we attempted the synthesis of this nominal composition in Nb and Ta tubes, as described in the Experimental section. Synthesis of arsenides in metal containers is often complicated by possible side reactions with the reactor walls. As a matter of fact, many new compounds were originally discovered as unexpected outcomes of such reactions (He et al., 2012; Baranets et al., 2018). Although the desired Ba5Ti12As19+x was not detected in the products extracted from the Nb and Ta tubes after the high-temperature treatment, two isostructural compositions representing a new structure type were obtained – Ba8Ti9.0(3)Nb4.0As21 and Ba8Ti9.24(6)Ta3.76As21.
Ba5V12Pn19+x (Pn = As, Sb). The crystal structures of Ba5V12As19.02(1) and Ba5V12Sb19.36(2) are closely related to each other and to those of the Ti-antimonide Ba5Ti12Sb19+x (Bie and Mar, 2009) and Ti-bismuthide AE5Ti12Bi19+x (AE = Sr, Ba) ternaries (Ovchinnikov and Bobev, 2018a). Subtle structural variations are associated with different realization of disorder in the Pn sites. Similarly to Ba5Ti12Sb19+x and AE5Ti12Bi19+x (AE = Sr, Ba), Ba5V12Pn19+x (Pn = As, Sb) crystallize in the noncentrosymmetric space group P3m, with Pearson code cP72 (excluding the partially occupied sites). Refined Flack's parameter was close to zero for both compositions confirming correctness of the absolute configuration.
Analogously to the related Ti pnictides, in Ba5V12Pn19+x (Pn = As, Sb), the deficiency-free part of the Ba–Pn substructure resembles a γ-brass-type framework (Figure 1A). The nested 26-atom cluster centered around the unit cell corner can be described as two interpenetrating Ba4 and Pn4 tetrahedra placed inside an As6 octahedron, which is in turn accommodated within an As12 cuboctahedron. The structure of the second nested polyhedron, located in the center of the unit cell, deviates from a regular γ-brass-type type cluster, and comprises an As12 cuboctahedron hosting a Ba6 octahedron overlapped with an As4 tetrahedron. The said Ba-Pn framework and a three-dimensional V scaffold are interpenetrated (Figure 1B). All V atoms are six-fold coordinated by the Pn atoms, and the resulting octahedra link by corner- and face-sharing and form a cage-like substructure (Figure 1C).
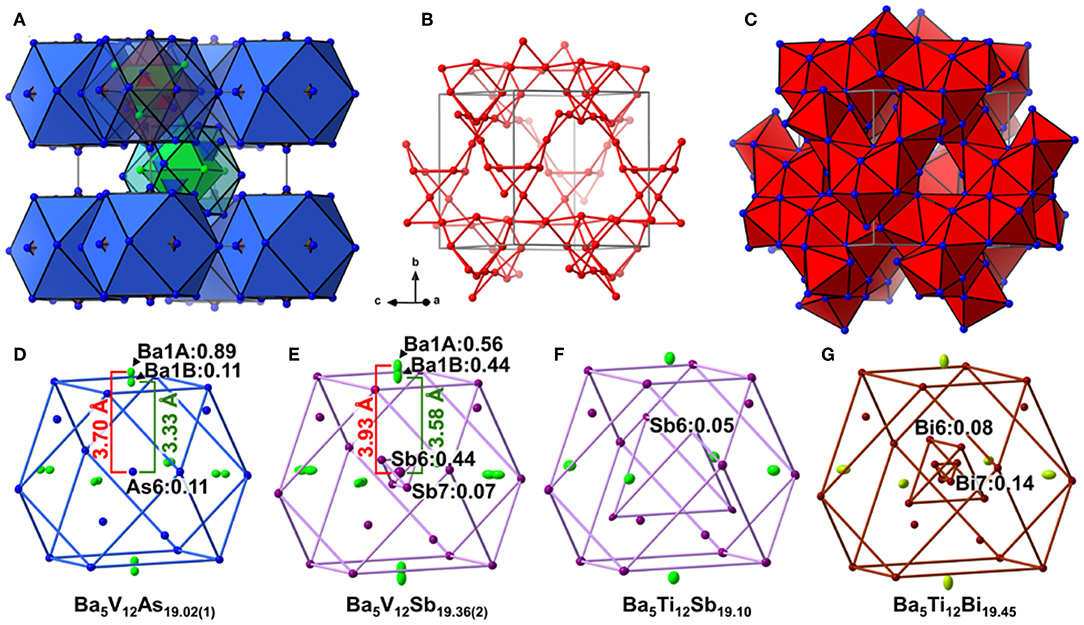
Figure 1. (A) Ba–Pn (Pn = As. Sb) substructure of Ba5V12Pn19+x represented as a γ-brass-like cluster assembly. Ba and Pn atoms are depicted in green and blue, respectively. (B) Three-dimensional framework of the V atoms in the structure. The V–V contacts with distances ≤ 3.2 Å are shown. (C) Cage-like interlinking of the VPn6 octahedra. The unit cell is outlined in gray. Close-up view of the central cuboctahedral cluster accommodating partially occupied Pn sites (Pn = As, Sb, Bi) in the structures of Ba5V12As19.02(1) (D), Ba5V12Sb19.36(2) (E), Ba5Ti12Sb19.10 (F), Ba5Ti12Bi19.45 (G). Partially occupied sites are indicated along with their occupancies. Thermal ellipsoids are drawn at the 50% probability level.
In all Ba5M12Pn19+x structures (M = Ti, V; Pn = As, Sb, Bi), partially occupied Pn sites are present in the central cuboctahedral cluster. However, the disorder pattern is strongly dependent on the transition metal and the pnictogen. In Ba5V12As19.02(1), extra As is located in the center of the unit cell (Figure 1D). The occupancy of this site refines to about 11 %. The adjacent Ba atoms in the corners of the octahedral shell show unphysically elongated thermal ellipsoids when refined as being positioned at a single crystallographic site. Splitting of this Ba position followed by independent refinement of the occupancies results in reasonable thermal parameters and occupation factors of about 89 and 11% for Ba1A and Ba1B, respectively. The splitting of Ba atom allows for two sets of distances to the center of the unit cell, where a partially occupied As atom (As6) is present −3.70 Å (Ba1A) and 3.33 Å (Ba1B), respectively. A good correlation of the Ba1B occupancy to that of the extra As site (As6) and the proximity of the total occupation of the two Ba atoms to unity implies the following account of the observed disorder: Whenever the As6 site is filled, the Ba6 octahedron “shrinks” to optimize the chemical interactions. Indeed, the Ba1B–As6 distance corresponds well to the typical Ba–As bonding contacts (He et al., 2010; Wang et al., 2011). When the center of the unit cell is empty, the Ba atoms in the octahedron move farther apart, likely due to electrostatic repulsion and optimization of the remaining Ba–As bonds.
A very similar picture is observed in Ba5V12Sb19.36(2) (Figure 1E). In this case, the position in the center of the unit cell is 44% occupied by Sb (Sb6), and the corresponding splitting pattern of the adjacent Ba site indicates the same mechanism of structural relaxation to accommodate the extra Sb atom. In contrast to the arsenide, an additional Sb site (Sb7) is found close to the unit cell center at a distance of 0.87(2) Å, giving rise to a split position with an occupancy of around 7 %. Due to short distances to the partially occupied Sb6 and Ba1B sites, this position can only reside in the octahedron composed of the Ba1A atoms, with no Sb in its center.
Interestingly, the realization of disorder is different in the Ba5Ti12Sb19+x and Ba5Ti12Bi19+x. In the former case (Figure 1F), only one partially occupied Sb site is present in the structure (Bie and Mar, 2009). This Sb position (Sb6) is filled only 5% of the time (for the experimentally determined composition Ba5Ti12Sb19.10) and is shifted from the center of the unit cell by 2.91 Å, forming a tetrahedron with an edge of 4.75 Å. Such a long interatomic separation renders any Sb6–Sb6 impossible. Yet a distance of 2.80 Å is observed between the Sb6 position and the Sb atoms on the triangular faces of the central cuboctahedral cluster, indicating covalent bonding. In Ba5Ti12Bi19+x(Figure 1G), there are two Bi sites with occupancies of about 8 and 14% (in Ba5Ti12Bi19.45), which are shifted from the center of the unit cell by 1.85 Å (Bi6) and 0.54 Å (Bi7), respectively (Ovchinnikov and Bobev, 2018a). The Bi6 atoms form a tetrahedron with an edge of 3.01 Å inside the central cuboctahedral cluster. Substitution studies provide evidence that the occupancy of this site can be increased up to 25% for the approximate composition SrEu4Ti12Bi20. This means that up to two Bi atoms can occupy the tetrahedron at a time, building a structural unit that is best viewed as a Bi2 dumbbell (Ovchinnikov and Bobev, 2018a).
To sum up, the Ba5M12Pn19+x (M = Ti, V; Pn = As, Sb, Bi) compositions display very similar structures, but the subtle differences of the disorder pattern vary strongly with the transition metal and the pnictogen. The general trend which can be discerned from the side-by-side comparison of these structures, is the increasing degree of disorder upon going from the arsenides to the bismuthides. Apparently, the more compact structure of Ba5V12As19.02(1) is not able to accommodate additional interstitial atoms. Another factor to be considered here is the lower stability of polyanions containing heavier pnictogens, due to the decrease of electronegativity in the order As–Sb–Bi (Ovchinnikov and Bobev, 2019d). The latter factor may call for additional stabilization by homoatomic bonding in antimonides and bismuthides, which is realized upon accommodating some extra pnictogen sites in the structure. Disregarding the disordered sites, the Pn atoms in Ba5M12Pn19+x (M = Ti, V; Pn = As, Sb, Bi) may participate in hypervalent bonding, as suggested by some relatively short Pn–Pn contacts, e.g., 2.910(4) Å and 2.965(1) Å in Ba5V12As19.02(1), and 3.266(3) Å and 3.2252(9) Å in Ba5V12Sb19.36(2).
Ba8Ti13−xMxAs21 (M = Nb, Ta). The isostructural Ba8Ti13−xNbxAs21 and Ba8Ti13−xTaxAs21 adopt a new structure type with space group Fmm and Pearson symbol cF168. The serendipitous incorporation of Nb and Ta metal from the crucible material into the structure, adds to many other instances of arsenides in particular (He et al., 2012; Baranets et al., 2018), where these typically high-melting and hard to activate elements prove to be quite reactive.
There are two symmetry-independent sites in the presented structures where the targeted transition metal atoms, Ti, and the atoms of group 5 element are found to be statistically mixed. These sites, hereafter referred to as TM1 and TM2 for brevity, are located in the vertices of a cuboctahedron and in its center, respectively, and account for isolated TM13 metal clusters (Figure 2A). The TM1–TM1 and TM1–TM2 distances are equal and measure dTM−TM = 3.078(2) Å and 3.075(1) Å for the Nb and Ta structures, respectively. The TM13 clusters can therefore be described as fragments of a perfect fcc-packing. The occurrence of such units is at first glance surprising, since the constituting transition metals form hexagonal close-packed (Ti) or bcc (Nb, Ta) structures at ambient conditions. A detailed account of the electronic interactions in the clusters will be given in the discussion of the electronic structure and chemical bonding (see below).
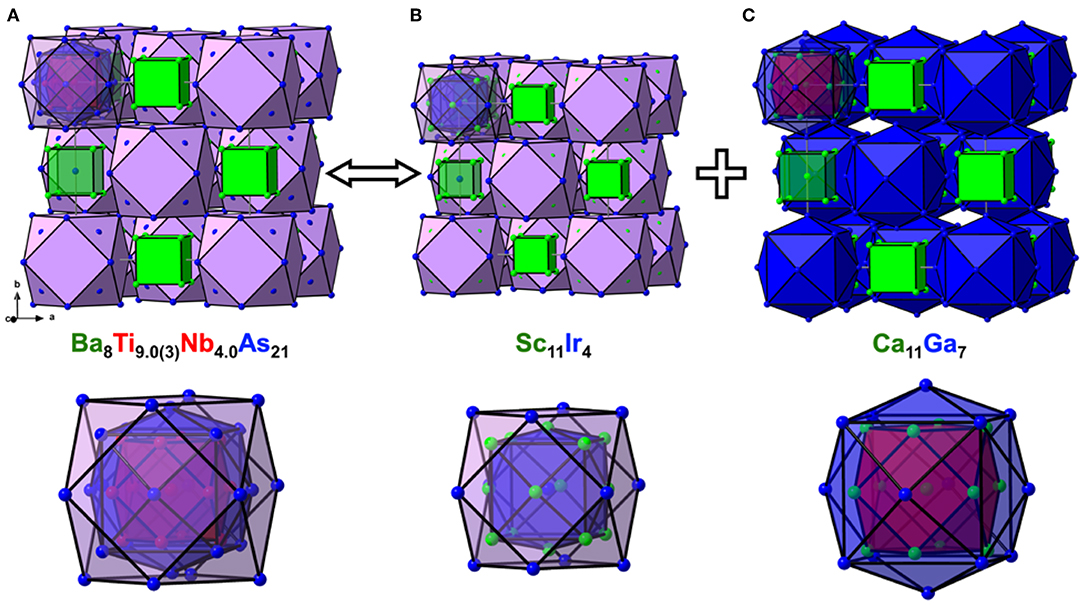
Figure 2. Crystal structures of Ba8Ti9.0(3)Nb4.0As21 (A), Sc11Ir4 (B), and Ca11Ga7 (C) in cluster representation, drawn at the same scale, along with the close-up view of the respective nested polyhedral clusters at the bottom. The shell structure of the nested and centered clusters is highlighted.
To simplify the description of the complex atomic arrangement in Ba8TM13As21 and highlight relationships with other cubic metal-rich compounds, it is convenient to represent the structure as a packing of polyhedra, in a similar manner as was previously described for Ba5V12Pn19+x. The TM1 sites are five-fold coordinated by As atoms, with the TM2 site completing a pseudo-octahedral coordination. The TM–As distances are very similar in both compounds and fall in the range 2.47–2.62 Å, in good agreement with the literature data on other titanium arsenides (Bachmayer et al., 1955; Nuss et al., 1996; Lee et al., 2001). The basal As atoms of the pseudo-octahedra are located in the vertices of an As14 tetrakis hexahedron around the central TM2 atom, whereas the apical As atoms can be viewed as forming a regular As12 cuboctahedron around the same center. The described geometrical construction yields a nested four-shell polyhedron, [TM2@TM112@As14@As12/2] (= TM13As20), where the innermost “shell” is built up of a single atom. The notation “As12/2” reflects the fact that each of the 12 As atoms in the outer cuboctahedral shell is shared between two symmetrically equivalent polyhedra. The shortest As–As distance in the structure is observed between the As atoms in the outermost and penultimate shells of the nested polyhedron and is found to be 3.203(2) Å and 3.2043(8) Å for the Nb and Ta representatives, respectively. The four-shell units form an fcc arrangement with the octahedral voids occupied by isolated As-centered [AsBa8] cubes.
The presented polyhedral description suggests that the structure of Ba8TM13As21 can be thought of as a combination of the Sc11Ir4 (Figure 2B) and Ca11Ga7 (Figure 2C) structure types (Villars and Calvert, 1991). All three structures adopt space group Fmm but show different populations of the Wyckoff sites. The nested polyhedron in Sc11Ir4, expressed as [Ir@Sc14@Ir12/2], lacks the inner cuboctahedral shell, hosted by the similar unit in Ba8TM13As21. The larger polyhedron in Ca11Ga7, on the contrary, accommodates a cuboctahedron, but represents a “peeled” version of the four-shelled cluster in the arsenide structure, with the following sequence of the shells: [Ca@Ca12@Ga14]. In both Sc11Ir4 and Ca11Ga7, centered cubes occupy the octahedral cavities in the fcc packing of the nested polyhedra.
The tetrahedral voids remain unoccupied in all three structures discussed above. Interestingly, in Ba8TM13As21, the distance between the center of the tetrahedral hole to the nearest As atoms measures 2.355(2) Å and 2.358(1) Å in the Nb and Ta representatives, respectively. These numbers imply that it might be possible to intercalate a small metal atom into this cavity, which would result in a reasonable tetrahedral coordination and could change/augment the valence electron count, as discussed in the next section.
Ba5V12As19. To interrogate the electronic structure and chemical bonding in the Ba5V12Pn19+x compounds, an idealized ordered Ba5V12As19 model was utilized. Total and projected electronic densities of states (DOS) are shown in Figure 3A. The Fermi level (EF) is located in the vicinity of a dip in the DOS: The electronic states close to EF are primarily composed of the hybridized V(3d) and As(4p) orbitals. The Ba–As bonding deviates significantly from a simple ionic character as indicated by the sizeable continuous contribution of the Ba electronic states around the Fermi level. The As(4s) orbitals are highly localized in a narrow energy interval around E – EF ≈ −11 eV. These states mainly manifest the presence of the As lone pairs in the structure.
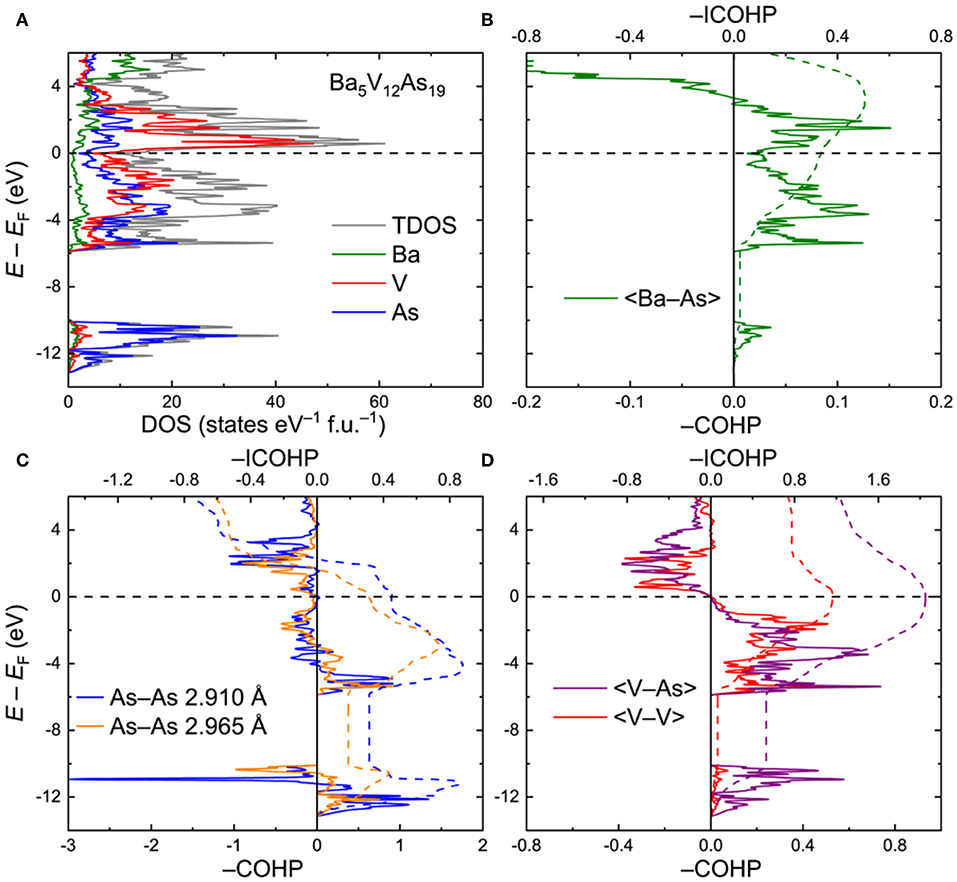
Figure 3. (A) Total and projected electronic densities of states (DOS) for Ba5V12As19. (B–D) Crystal Orbital Hamilton Population curves (COHP) for selected contacts. Dashed lines denote integrated COHP curves.
Crystal Orbital Hamilton Population graphs (COHP) for average selected interatomic interactions are plotted in Figures 3B–D. In line with the conclusion derived from the projected DOS, the Ba–As interactions do not display a typical ionic nature. The bonding is underoptimized at EF, with an energy window of unoccupied bonding states extending up to E – EF ≈ 2.9 eV (Figure 3B). The negative integrated COHP (–COHP) for the Ba–As amounts to about 0.34 eV/bond on average.
The two shortest As–As contacts demonstrate similar features in their COHP plots (Figure 3C). Both contacts are characterized by a combination of bonding and antibonding states below EF. The resulting attractive interaction is rather weak, yet the –ICOHP values of 0.31 and 0.45 eV/bond for the longer and shorter As–As contacts, respectively, are comparable with the numbers found for the Ba–As bonds. Altogether, the observed COHP pattern for the As–As contacts is in accordance with hypervalent (electron-rich) chemical bonding (Papoian and Hoffmann, 2000; Ovchinnikov and Bobev, 2018b,c).
In contrast, the V–As and V–V bonds are optimized at the Fermi level, with the respective average –ICOHP magnitudes of 2.05 and 1.16 eV/bond (Figure 3D). It is worth noting that in Ba5V12As19, only a small number of V–As and V–V bonding states are available in the near vicinity of EF down to E – EF ≈ −1.2 eV. This energy may correspond to the lowest electron count which would retain the structural stability. Indeed, upon lowering the Fermi level by more than 1.2 eV, the bonding V–As and V–V states get progressively vacated, perturbing the respective bonding. Introduction of small amounts of extra As, as in the experimentally determined composition Ba5V12As19.02(1), can be viewed as a mild oxidation of the discussed Ba5V12As19 composition and will have a very small effect on the V–As and V–V bonds. Furthermore, the hitherto unknown Ba5Ti12As19 would also fall in the stability region according to the suggested electronic considerations. If a rigid band model can be applied in this case, the electronic structure of Ba5Ti12As19 can be derived from that of Ba5V12As19 by shifting the Fermi level down by about 0.89 eV, which would correspond to removal of 12 electrons per formula unit with respect to the vanadium composition. In fact, the resulting hypothetical electronic structure would tolerate even further oxidation, e.g., by incorporation of extra pnictogen atoms. This prediction suggests that the apparent non-existence (or lower stability) of Ba5Ti12As19+xdoes not originate from electronic reasons. Atomic size factors or peculiarities of the reaction pathways in the Ba–Ti–As system should be examined in detail to resolve this conundrum.
Ba8Ti9Nb4As21. For analysis of the electronic interactions in the Ba8Ti13−xMxAs21 phases (M = Nb, Ta), an ordered model with composition Ba8Ti9Nb4As21 was generated. The electronic density of states (DOS) for this model is given in Figure 4A. In contrast to the Ba5V12As19 case, the Fermi level in Ba8Ti9Nb4As21 crosses a peak in the DOS, mainly composed of the transition metal d orbitals. The high density of states may indicate some electronic instabilities, warranting further experimental studies. In this respect, it is worthwhile to note that spin-polarized calculations did not indicate any localized magnetism, rendering magnetic instability quite improbable.
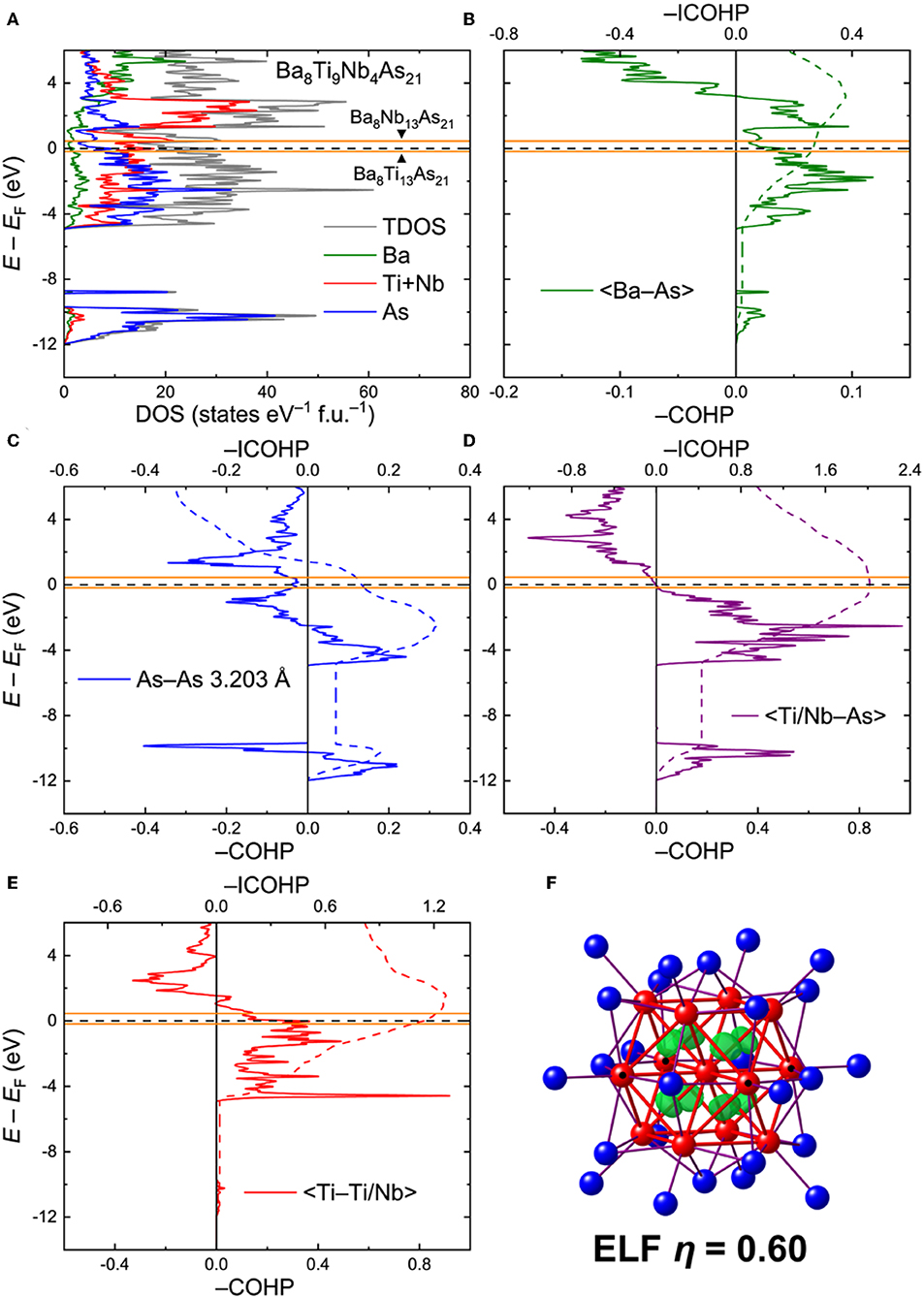
Figure 4. (A) Total and projected electronic densities of states (DOS) for Ba8Ti9Nb4As21. (B–E) Crystal Orbital Hamilton Population curves (COHP) for selected contacts. Positions of the Fermi level for the hypothetical ternary compositions Ba8Ti13As21 and Ba8Nb13As21 are given in orange. Dashed lines denote integrated COHP curves. (F) Isosurface of the Electron Localization Function (η = 0.60) inside the cuboctahedral transition metal cluster. Location of the Nb atoms in the ordered model is indicated with black dots.
The calculated COHP curves for averaged selected contacts in the structure are presented in Figures 4B–E. For the sake of simplicity, the contacts involving Ti and Nb in the ordered model were averaged. The Ba–As interactions bear resemblance to the respective contacts in Ba5V12As19, with somewhat underoptimized bonding at EF (Figure 4B). The average –ICOHP value for these contacts is 0.27 eV/bond.
The shortest As–As contact, despite a considerable interatomic separation, displays a non-negligible, yet underoptimized, bonding interaction, with a domain of occupied antibonding states just below EF (Figure 4C), akin to Ba5V12As19. In an idealized picture, these bonds can be treated as one-electron interactions (Papoian and Hoffmann, 2000). This very crude approximation allows assignment of formal charges to the As sites. An isolated As atom (i.e., with no short As–As contacts) has a formal charge of 3–, whereas every one-electron bond lowers the absolute negative charge by 0.5. In terms of such one-electron bonds, the As atoms in Ba8Ti9Nb4As21 are either isolated or three- and four-fold coordinated. The schematic representation of the As framework is shown in Figure S1. In the limit of full electron localization, the formula can be expressed as (Ba2+)8[Ti9Nb4]23+(As3−)7(As1.5−)8(As1−)6. Although this electronic distribution is an oversimplification, it will provide an insight into the metal-metal bonding in the clusters, as discussed below.
Quite notably, the transition-metal–arsenic bonds are perfectly optimized at the Fermi level (Figure 4D). The strong covalent nature of these bonds is evident from the high average—ICOHP magnitude of 2.02 eV/bond. Similarly to Ba5V12As19, the number of the occupied bonding states just below EF and the vacant antibonding states close to EF is rather small, suggesting that moderate changes in the electron count would not strongly affect the bonding. In particular, shifting the Fermi level down by 0.17 eV or lifting it up by 0.45 eV, corresponding to the positions of EF in the hypothetical Ba8Ti13As21 and Ba8Nb13As21, respectively (orange lines in Figure 4), will have virtually no influence on the transition-metal–arsenic interactions.
The situation is different for the metal–metal bonds, which appear to be underoptimized for the composition Ba8Ti9Nb4As21, owing to the availability of unoccupied bonding states above EF (Figure 4E). These states extend up to E – EF ≈ 1.54 eV, which would correspond to ~35 extra electrons per formula unit. This finding shows that electron doping in Ba8Ti9Nb4As21 is favorable and expected to enhance the metal-metal interactions, which are already quite strong for the examined composition, with an average –ICOHP of 1.14 eV/bond. The maximum –ICOHP value that can be achieved by filling up all the bonding states above EF amounts to 1.26 eV/bond. At this high electron count, however, some occupation of the antibonding transition-metal–arsenic states will be attained. Since the structure is dominated by the latter kind of bonds in terms of their number and relative strength, it is likely that these bonds will be pivotal for the overall stability.
Analysis of the Electron Localization Function (ELF) for the Ba–As contacts did not reveal any localization maxima but indicated small deviation of the ELF distribution from a spherical shape around the atoms, typical for highly polar bonds. A much more pronounced deviation was found for the TM–As contacts (Figure S2a). Increased values and flattening of the ELF was also observed for the short As–As contacts (Figure S2b). Clear localization domains are visible inside the tetrahedral voids of the cuboctahedral cluster, suggesting multi-center metal–metal bonding (Figure 4F). Detailed inspection of the ELF sections revealed the presence of additional ELF maxima on the lines connecting the central transition metal atom to the twelve vertices of the cuboctahedron, indicating two-center bonds (Figure S2c). In a very naïve picture of perfect electron localization, the formation of eight multi-center and 12 two-center bonds would require 40 electrons in total, if all these bonds are treated as two-electron. By considering the formula derived above, (Ba2+)8[Ti9Nb4]23+(As3−)7(As1.5−)8(As1−)6, the total number of valence electrons inside the [Ti9Nb4] cluster is 9 × 4 + 4 × 5 – 23 = 33. The limiting hypothetical compositions Ba8Ti13As21 and Ba8Nb13As21 would correspond to 29 and 42 cluster electrons, respectively. The proposed simple electron accounting is in line with the conclusion that electron doping of Ba8Ti9Nb4As21 will stabilize the bonding inside the clusters. A more accurate approach of determining the number of cluster electrons is direct integration of electron density inside the Bader basins of the transition metal atoms. This method yields 37.92 electrons in the [Ti9Nb4] cluster, which is somewhat below the optimal number obtained by the overly-simplified electron counting above. Since the bonding in the metallic Ba8Ti9Nb4As21 is rather delocalized, the valence electron considerations detailed above should be deemed a qualitative rationale for the stability of the discussed complex crystal structure. It seems very likely that Ba8Ti9Nb4As21 will show some flexibility with respect to the total electron count and definitely requires a more detailed experimental examination.
The metal flux method is a powerful approach for crystal growth of various kinds of intermetallic compounds. Its simple design and wide applicability makes it an efficient tool for exploratory synthetic research. Two ternary barium vanadium pnictides, Ba5V12As19.02(1) and Ba5V12Sb19.36(2) were successfully grown as mm-sized single crystals employing selected flux materials—Pb and Sb, respectively. The crystal structure of both compounds can be described as γ-brass-like cluster assemblies based on Ba and Pn (Pn = As, Sb), interpenetrated by three-dimensional V scaffolds. The observed non-stoichiometry results from additional partially occupied Pn positions, which show different disorder patterns depending on the pnictogen. First-principle calculations predict high flexibility of the structure with respect to the electron count, which explains the existence of the related electron-poorer Ti phases Ba5Ti12Sb19+x and AE5Ti12Bi19+x (AE = Sr, Ba). Following the analogy between the V and Ti pnictides, we attempted to obtain the hitherto unknown Ba5Ti12As19+x, employing the flux technique and conventional high-temperature annealing of the elements in metal tubes. The latter approach yielded two new compounds, Ba8Ti9.0(3)Nb4.0As21 and Ba8Ti9.24(6)Ta3.76As21, as a result of side-reactions with the container material. The quaternary compositions crystallize isotypically in a new structure type, which displays isolated fcc-type clusters composed of statistically mixed Ti and M atoms (M = Nb, Ta). First-principle calculations reveal that the bonding within these units displays two-center and multi-center features and complex electron distribution. The presented examples demonstrate that the field of early transition metal pnictides deserves additional study, as many new compounds with potentially interesting structures and properties are likely to be found. In this respect, the flux method proves to be a handy tool for exploration of these systems.
The datasets generated for this study can be found in the The Cambridge Crystallographic Data Centre (CCDC) under the deposition numbers 1959265-1959268.
AO designed and carried out the synthesis, performed crystallographic characterization and first-principle calculations, and prepared the initial draft of the manuscript. SB supervised the project and finalized the manuscript.
This work was funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, under Award No. DE-SC0008885.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2019.00909/full#supplementary-material
1. During the refinement of the Ba5V12As19.02(1) structure, a considerable residual electron density was detected in the corners of the unit cell. Modifications of the absorption correction did not result in disappearance of this feature. The only chemical species which would show reasonable local coordination when placed in this position was As. After ascribing the observed density peak to As (labeled here As7), the resulting Ba–As contacts were within the distance range found for other bonds of this sort in the structure. The refined occupancy of As7 was only about 2 %. Owing to an unphysically short As7–As4 distance of 2.217(1) Å, the occupancy of As4 was set to 100 – occupancy(As7) %. Acknowledging the possibility that the observed residual density peak is an artifact of the special position, we abstain from the discussion of this disorder until additional data are available. Due to the very small occupancy, the effect of the As7 site on the structure and composition is negligible.
Bachmayer, K., Nowotny, H., and Kohl, A. (1955). Die Struktur von TiAs. Monatsh. Chem. 86, 39–43. doi: 10.1007/BF00899271
Bao, J.-K., Bugaris, D. E., Zheng, H., Willa, K., Welp, U., Chung, D. Y., et al. (2019). Superconductivity in Y7Ru4InGe12. Phys Rev Mater. 3:024802. doi: 10.1103/PhysRevMaterials.3.024802
Bao, J.-K., Liu, J.-Y., Ma, C.-W., Meng, Z.-H., Tang, Z.-T., Sun, Y.-L., et al. (2015). Superconductivity in quasi-one-dimensional K2Cr3As3 with significant electron correlations. Phys. Rev. X. 5:011013. doi: 10.1103/PhysRevX.5.011013
Baranets, S., and Bobev, S. (2019). From the ternary phase Ca14Zn1+δSb11 (δ ≈ 0.4) to the quaternary solid solutions Ca14−xRExZnSb11 (RE = La–Nd, Sm, Gd, x ≈ 0.9). A tale of electron doping via rare-earth metal substitutions and the concomitant structural transformations. Inorg. Chem. 58, 8506–8516. doi: 10.1021/acs.inorgchem.9b00809
Baranets, S., Darone, G. M., and Bobev, S. (2019a). Synthesis and structure of Sr14Zn1+xAs11 and Eu14Zn1+xAs11 (x ≤ 0.5). New members of the family of pnictides isotypic with Ca14AlSb11, exhibiting a new type of structural disorder. J. Solid. State. Chem. 280:120990. doi: 10.1016/j.jssc.2019.120990
Baranets, S., He, H., and Bobev, S. (2018). Niobium-bearing arsenides and germanides from elemental mixtures not involving niobium: a new twist to an old problem in solid-state synthesis. Acta. Crystallogr. C. 74, 623–627. doi: 10.1107/S2053229618005739
Baranets, S., Voss, L., Stoyko, S., and Bobev, S. (2019b). Synthesis, crystal structure and physical properties of the solid solutions Ca14−xRExCdSb11 (RE = La–Nd, Sm, Gd–Yb, x ≈ 0.85 ± 0.15). J. Appl. Phys. 125:245101. doi: 10.1063/1.5099632
Bie, H., and Mar, A. (2009). Ba5Ti12Sb19+x, a polar intermetallic compound with a stuffed γ-brass structure. J. Solid. State. Chem. 182, 3131–3137. doi: 10.1016/j.jssc.2009.08.030
Brylak, M., and Jeitschko, W. (1994). U3TiSb5, U3VSb5, U3CrSb5, and U3MnSb5 with ‘Anti'-Hf5Sn3Cu Type Structure. Z Naturforsch. B. 49, 747–752. doi: 10.1515/znb-1994-0605
Canfield, P. C., and Fisk, Z. (1992). Growth of single crystals from metallic fluxes. Philos. Mag. B. 65, 1117–1123. doi: 10.1080/13642819208215073
Chen, L., and Corbett, J. D. (2004). R6TT‘2, New variants of the Fe2P structure type. Sc6TTe2 (T = Ru, Os, Rh, Ir), Lu6MoSb2, and the anti-typic Sc6Te0.80Bi1.68. Inorg. Chem. 43, 436–442. doi: 10.1021/ic0302581
Childs, A. B., Baranets, S., and Bobev, S. (2019). Five new ternary indium-arsenides discovered. Synthesis and structural characterization of the Zintl phases Sr3In2As4, Ba3In2As4, Eu3In2As4, Sr5In2As6 and Eu5In2As6. J. Solid. State. Chem. 278:120889. doi: 10.1016/j.jssc.2019.07.050
Doan, P., Gooch, M., Tang, Z., Lorenz, B., Möller, A., Tapp, J., et al. (2012). Ba1−xNaxTi2Sb2O(0.0 ≤ x ≤ 0.33): a layered titanium-based pnictide oxide superconductor. J. Am. Chem. Soc. 134, 16520–16523. doi: 10.1021/ja3078889
Failamani, F., Grytsiv, A., Giester, G., Polt, G., Heinrich, P., Michor, H., et al. (2015). Ba5{V,Nb}12Sb19+x, novel variants of the Ba5Ti12Sb19+x -type: crystal structure and physical properties. Phys. Chem. Chem. Phys. 17, 24248–24261. doi: 10.1039/C5CP04000K
Felder, J. B., Weiland, A., Hodovanets, H., McCandless, G. T., Estrada, T. G., Martin, T. J., et al. (2019). Law and disorder: special stacking units—building the intergrowth Ce6Co5Ge16. Inorg. Chem. 58, 6037–6043. doi: 10.1021/acs.inorgchem.9b00350
Gelato, L. M., and Parthé, E. (1987). STRUCTURE TIDY – a computer program to standardize crystal structure data. J. Appl. Crystallogr. 20, 139–143. doi: 10.1107/S0021889887086965
Han, F., Bao, J.-K., Malliakas, C. D., Sturza, M., Du, Y., Chung, D. Y., et al. (2019). Enormous electron-electron scattering in the filled-cage cubic compound Ba10Ti24Bi39. Phys. Rev. Mater. 3:105001. doi: 10.1103/PhysRevMaterials.3.105001
He, H., Stearrett, R., Nowak, E. R., and Bobev, S. (2010). BaGa2Pn2 (Pn = P, As): New semiconducting phosphides and arsenides with layered structures. Inorg. Chem. 49, 7935–7940. doi: 10.1021/ic100940b
He, H., Tyson, C., and Bobev, S. (2012). Synthesis and crystal structures of the quaternary zintl phases RbNa8Ga3Pn6 (Pn = P, As) and Na10NbGaAs6. Crystals 2, 213–223. doi: 10.3390/cryst2020213
Jayasinghe, A. S., Lai, Y., Baumbach, R., and Latturner, S. E. (2019). U1.33T4Al8Si2 (T = Ni, Co): complex uranium silicides grown from aluminum/gallium flux mixtures. Inorg. Chem. 58, 12209–12217. doi: 10.1021/acs.inorgchem.9b01627
Jepsen, O., and Andersen, O. K. (2000). The Stuttgart TB-LMTO-ASA Program, Version 4.7; Max-Planck-Institut für Festkörperforschung. Stuttgart.
Kanatzidis, M. G., Pöttgen, R., and Jeitschko, W. (2005). The metal flux: a preparative tool for the exploration of intermetallic compounds. Angew. Chem. Int. Ed. 44, 6996–7023. doi: 10.1002/anie.200462170
Khan, M. A., McCandless, G. T., Benavides, K. A., Martin, T. J., Palacios, A. M., Samuel, A. W. B., et al. (2018). Crystal Growth and Magnetic Properties of Pr3Co2+xGe7 and the Sn-Stabilized Ln3Co2+xGe7−ySny (Ln = Pr, Nd, Sm). Cryst. Growth. Des. 18, 6028–6034. doi: 10.1021/acs.cgd.8b00868
Latturner, S. E. (2018). Clusters, assemble: growth of intermetallic compounds from metal flux reactions. Acc. Chem. Res. 51, 40–48. doi: 10.1021/acs.accounts.7b00483
Lee, C. S., Dashjav, E., and Kleinke, H. (2001). Structure prediction using our semiempirical structure map: the crystal structure of the new arsenide ZrTiAs. Chem. Mater. 13, 4053–4057. doi: 10.1021/cm010433g
Ma, X., Chen, B., and Latturner, S. E. (2012). Synthesis and properties of new multinary silicides R5Mg5Fe4AlxSi18−x (R = Gd, Dy, Y, x ≈ 12) grown in Mg/Al Flux. Inorg. Chem. 51, 6089–6095. doi: 10.1021/ic202735b
Nakamura, S., Kano, T., and Ohara, S. (2019). Magnetic ordering in kondo lattice compound YbIr3Si7. J. Phys. Soc. Jpn. 88:093705. doi: 10.7566/JPSJ.88.093705
Nuss, J., Hönle, W., Peters, K., and Schnering, H. G. V. (1996). Tetrapnictidotitanate(IV) M4TiX4 (M = Sr, Ba; X = P, As), hierarchische Derivate der KGe-Struktur K4□Ge4. Z. Anorg. Allg. Chem. 622, 1879–1885. doi: 10.1002/zaac.19966221112
Otero-de-la-Roza, A., Johnson, E. R., and Luaña, V. (2014). Critic2: a program for real-space analysis of quantum chemical interactions in solids. Comput. Phys. Commun. 185, 1007–1018. doi: 10.1016/j.cpc.2013.10.026
Ovchinnikov, A., and Bobev, S. (2018a). Synthesis, crystal and electronic structure of the titanium bismuthides Sr5Ti12Bi19+x, Ba5Ti12Bi19+x, and Sr5−δ EuδTi12Bi19+x (x ≈ 0.5–1.0; δ ≈ 2.4, 4.0). Eur. J. Inorg. Chem. 2018, 1266–1274. doi: 10.1002/ejic.201701426
Ovchinnikov, A., and Bobev, S. (2018b). On the effect of Ga and In substitutions in the Ca11Bi10 and Yb11Bi10 bismuthides crystallizing in the tetragonal Ho11Ge10 structure type. Acta. Crystallogr. C. 74, 269–273. doi: 10.1107/S2053229618001596
Ovchinnikov, A., and Bobev, S. (2018c). Undistorted linear Bi chains with hypervalent bonding in La3TiBi5 from single-crystal X-ray diffraction. Acta. Crystallogr. C. 74, 618–622. doi: 10.1107/S205322961800565X
Ovchinnikov, A., and Bobev, S. (2019a). Multifaceted Sn–Sn bonding in the solid state. Synthesis and structural characterization of four new Ca–Li–Sn compounds. Dalton. Trans. 48, 14398–14407. doi: 10.1039/C9DT02803J
Ovchinnikov, A., and Bobev, S. (2019b). Synthesis, and crystal and electronic structures, of the titanium-rich bismuthides AE3Ti8Bi10 (AE = Sr, Ba, Eu). Inorg. Chem. 58, 2934–2941. doi: 10.1021/acs.inorgchem.8b01952
Ovchinnikov, A., and Bobev, S. (2019c). Layered quaternary germanides—synthesis and crystal and electronic structures of AELi2In2Ge2 (AE = Sr, Ba, Eu). Inorg. Chem. 58, 7895–7904. doi: 10.1021/acs.inorgchem.9b00588
Ovchinnikov, A., and Bobev, S. (2019d). Zintl phases with group 15 elements and the transition metals: a brief overview of pnictides with diverse and complex structures. J.Solid. State. Chem. 270, 346–359. doi: 10.1016/j.jssc.2018.11.029
Ovchinnikov, A., and Bobev, S. (2020). Bismuth as a reactive solvent in the synthesis of multicomponent transition-metal-bearing bismuthides. Inorg. Chem. doi: 10.1021/acs.inorgchem.9b02881. [Epub ahead of print].
Ovchinnikov, A., Darone, G., Saparov, B., and Bobev, S. (2018a). Exploratory work in the quaternary system of Ca–Eu–Cd–Sb: synthesis, crystal, and electronic structures of new zintl solid solutions. Materials 11:2146. doi: 10.3390/ma11112146
Ovchinnikov, A., Makongo, J. P. A., and Bobev, S. (2018b). Yet again, new compounds found in systems with known binary phase diagrams. Synthesis, crystal and electronic structure of Nd3Bi7 and Sm3Bi7. Chem. Commun. 54, 7089–7092. doi: 10.1039/C8CC02563K
Ovchinnikov, A., Prakash, J., and Bobev, S. (2017a). Crystal chemistry and magnetic properties of the solid solutions Ca14−xRExMnBi11 (RE = La–Nd, Sm, and Gd–Ho; x ≈ 0.6–0.8). Dalton. Trans. 46, 16041–16049. doi: 10.1039/C7DT03715E
Ovchinnikov, A., Saparov, B., Xia, S.-Q., and Bobev, S. (2017b). The ternary alkaline-earth metal manganese bismuthides Sr2MnBi2 and Ba2Mn1−xBi2 (x ≈ 0.15). Inorg. Chem. 56, 12369–12378. doi: 10.1021/acs.inorgchem.7b01851
Papoian, G., and Hoffmann, R. (2000). Hypervalent bonding in one, two, and three dimensions: extending the Zintl-Klemm concept to nonclassical electron-rich networks. Angew. Chem. Int. Ed. 39, 2408–2448. doi: 10.1002/1521-3773(20000717)39:14<2408::AID-ANIE2408>3.0.CO;2-U
Raju, N. P., Greedan, J. E., Ferguson, M. J., and Mar, A. (1998). LaCrSb3: a new itinerant electron ferromagnet with a layered structure. Chem. Mater. 10, 3630–3635. doi: 10.1021/cm9803758
Savin, A., Nesper, R., Wengert, S., and Fässler, T. F. (1997). ELF: the electron localization function. Angew Chem Int Ed Engl. 36, 1808–1832. doi: 10.1002/anie.199718081
Sheldrick, G. M. (2015a). SHELXT – Integrated space-group and crystal-structure determination. Acta. Crystallogr. A. 71, 3–8. doi: 10.1107/S2053273314026370
Sheldrick, G. M. (2015b). Crystal structure refinement with SHELXL. Acta. Crystallogr. C. 71, 3–8. doi: 10.1107/S2053229614024218
Steinberg, S., and Dronskowski, R. (2018). The Crystal Orbital Hamilton Population (COHP) method as a tool to visualize and analyze chemical bonding in intermetallic compounds. Crystals 8:225. doi: 10.3390/cryst8050225
Villars, P., and Calvert, L. D. (1991). Pearson's Handbook of Crystallographic Data for Intermetallic Phases, 2nd Edn. Materials Park, OH: American Society for Metals.
von Barth, U., and Hedin, L. (1972). A local exchange-correlation potential for the spin polarized case: I. J. Phys. C. Solid. State. Phys. 5, 1629–1642. doi: 10.1088/0022-3719/5/13/012
Wakiya, K., Sugiyama, Y., Komagata, T., Uehara, M., Sato, H., Gouchi, J., et al. (2019). Intermediate valence state of Ce in the novel quaternary compound CeRu2Sn2Zn18. J. Alloys. Compd. 797, 309–313. doi: 10.1016/j.jallcom.2019.04.345
Wang, J., Yang, M., Pan, M.-Y., Xia, S.-Q., Tao, X.-T., He, H., et al. (2011). Synthesis, crystal and electronic structures, and properties of the new pnictide semiconductors A2CdPn2 (A = Ca, Sr, Ba, Eu; Pn = P, As). Inorg. Chem. 50, 8020–8027. doi: 10.1021/ic200286t
Wolff, G. A., and Mlavsky, A. I. (1974). “Travelling solvent techniques,” in Crystal Growth: Theory and Techniques, Vol. 1, ed C. H. L. Goodman (Boston, MA: Springer US), 193–232.
Zaikina, J. V., Griffin, V. S., and Latturner, S. E. (2017). Switching on a spin glass: flux growth, structure, and magnetism of La11Mn13−x–yNixAlySn4−δ intermetallics. Inorg. Chem. 56, 15194–15202. doi: 10.1021/acs.inorgchem.7b02555
Keywords: flux growth, pnictides, crystal structure, electronic structure, metal clusters
Citation: Ovchinnikov A and Bobev S (2020) Exploration of Multi-Component Vanadium and Titanium Pnictides Using Flux Growth and Conventional High-Temperature Methods. Front. Chem. 7:909. doi: 10.3389/fchem.2019.00909
Received: 21 October 2019; Accepted: 16 December 2019;
Published: 10 January 2020.
Edited by:
Hans-Conrad zur Loye, University of South Carolina, United StatesReviewed by:
Arnold M. Guloy, University of Houston, United StatesCopyright © 2020 Ovchinnikov and Bobev. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Svilen Bobev, Ym9iZXZAdWRlbC5lZHU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.