Unexpected Routes of the Mutagenic Tautomerization of the T Nucleobase in the Classical A·T DNA Base Pairs: A QM/QTAIM Comprehensive View

In this paper using quantum-mechanical (QM) calculations in combination with Bader's quantum theory of “Atoms in Molecules” (QTAIM) in the continuum with ε = 1, we have theoretically demonstrated for the first time that revealed recently highly-energetic conformers of the classical A·T DNA base pairs – Watson-Crick [A·T(w_WC)], reverse Watson-Crick [A·T(w_rWC)], Hoogsteen [A·T(w_H)] and reverse Hoogsteen [A·T(w_rH)] – act as intermediates of the intrapair mutagenic tautomerization of the T nucleobase owing to the novel tautomerisation pathways: A·T(w_WC)↔A·T*(w^⊥_WC); A·T(w_rWC)↔A·${\text{T}}_{\text{O}2}^{*}$(w^⊥_rWC); A·T(w_H)↔A·T*(w^⊥_H); A·T(w_rH)↔A·${\text{T}}_{\text{O}2}^{*}$(w^⊥_rH). All of them occur via the transition states as tight ion pairs (A⁺, protonated by the N6H₂ amino group)·(T⁻, deprotonated by the N3H group) with quasi-orthogonal geometry, which are stabilized by the participation of the strong (A)N6⁺H···O4⁻/O2⁻(T) and (A)N6⁺H···N3⁻(T) H-bonds. Established tautomerizations proceed through a two-step mechanism of the protons moving in the opposite directions along the intermolecular H-bonds. Initially, proton moves from the N3H imino group of T to the N6H₂ amino group of A and then subsequently from the protonated N6⁺H₃ amino group of A to the O4/O2 oxygen atom of T, leading to the products – A·T*(w^⊥_WC), A·${\text{T}}_{\text{O}2}^{*}$(w^⊥_rWC), A·T*(w^⊥_H), and A·${\text{T}}_{\text{O}2}^{*}$(w^⊥_rH), which are substantially non-planar, conformationally-labile complexes. These mispairs are stabilized by the participation of the (A)N6H/N6H'···N3(T) and (T)O2H/O4H···N6(A) H-bonds, for which the pyramidalized amino group of A is their donor and acceptor. The Gibbs free energy of activation of these mutagenic tautomerizations lies in the range of 27.8–29.8 kcal·mol⁻¹ at T = 298.15 K in the continuum with ε = 1.

Introduction

Clarification at the microstructural level of the physico-chemical mechanisms underlying the formation of the mutagenic tautomers of the DNA bases via the mutagenic tautomerization of the classical Watson-Crick DNA base pairs is a matter of extreme importance for such branches of life science as molecular biophysics and molecular biology, since it enables us to understand the sources of the genome instability (Watson and Crick, 1953a,b; Löwdin, 1963, 1966; Topal and Fresco, 1976). Genome instability is frequently associated with mutations in DNA, playing role in cancer development due to DNA replication errors (Liu et al., 2014; Tomasetti et al., 2017).

Mutagenic tautomerization of the DNA bases attracts researchers' curiosity since the establishment of the spatial architecture of DNA molecule (Watson and Crick, 1953a) and further formulation of the tautomeric hypothesis of the origin of the spontaneous point mutations by Watson and Crick (Watson and Crick, 1953b).

Distinguished quantum chemist Per-Orlov Löwdin proposed original idea based on the electronic structure of the complementary A·T and G·C pairs of the DNA bases (Löwdin, 1963, 1966), which makes possible their conversion into the high-energy tautomerized states – A*·T*(L) and G*·C*(L) base pairs [currently known as Löwdin's base pairs; here and below rare, in particular mutagenic (Brovarets' and Hovorun, 2010a; Brovarets', 2015), tautomers are marked with an asterisk] causing origin of the transitions and transversions during the DNA replication. Löwdin believed that these transformations should be carried out by the double proton transfer (DPT) in the opposite directions along the neighboring intermolecular hydrogen (H) bonds through the quantum tunneling. These representations played an extremely important role in the formation of new visions in quantum biology and attracted the attention of a wide range of Löwdin's followers (Florian et al., 1994; Gorb et al., 2004; Bertran et al., 2006; Cerón-Carrasco and Jacquemin, 2013; Maximoff et al., 2017).

However, from the physico-chemical point of view it was established that generally accepted Löwdin's mechanism of the DPT along the intermolecular H-bonds in the Watson-Crick DNA base pairs cannot be the source of the formation of the mutagenic tautomers of the nucleobases due to the absence of the reverse barrier of tautomerization in the A·T(WC) pair of the DNA bases and its small value in comparison with kT (0.62 kcal·mol⁻¹ at T = 298.15 K) for the G·C(WC) DNA base pair (Gorb et al., 2004; Bertran et al., 2006; Brovarets' et al., 2012; Brovarets' and Hovorun, 2014a,b, 2015a).

Recently, we have proposed another mechanism of the mutagenic tautomerization of the A·T(WC) and G·C(WC) pairs of the DNA bases, which is alternative to Löwdin's approach, occurring via the sequential intrapair proton transfer and shifting of the bases relative each other, which ultimately leads to the wobble configuration (Brovarets' and Hovorun, 2015b). Moreover, we have discovered this intrinsic ability to perform wobble↔Watson-Crick / Watson-Crick↔wobble tautomeric transitions via the sequential intrapair proton transfer for all possible incorrect base mispairs, which are active players in the field of the spontaneous point mutagenesis: purine·pyrimidine – G·T and A·C (Brovarets' and Hovorun, 2009, 2015c,d, 2016), purine·purine – A·A, A·G and G·G (Brovarets' and Hovorun, 2015e,f) and pyrimidine·pyrimidine – C·C, C·T and T·T (Brovarets' and Hovorun, 2015f,g). Notably, these interconverisons are accompanied by a significant rebuilding of the base mispairs with Watson-Crick architecture into the mismatches wobbled toward both minor and major DNA grooves and vice versa. Moreover, it was established that these tautomerisation reactions occur non-dissociatively and are accompanied by the consequent replacement of the unique patterns of the intermolecular specific interactions along intrinsic reaction coordinate (IRC) (Brovarets' et al., 2013, 2017a,b).

These data allows to suggest that the intrapair tautomeric transition of the wobble pairs from the main tautomeric form into the rare, mutagenic, having a WC or close to its configuration, and vice versa, is the key to understanding of the microstructural mechanisms of the emergence of the spontaneous transitions and transversions at the DNA replication (Brovarets' and Hovorun, 2009, 2015b,c,d, 2016). Moreover, these theoretical approaches have been partly experimentally confirmed for some DNA/RNA purine·pyrimidine pairs (Nedderman et al., 1991, 1993; Kimsey et al., 2015, 2018).

In this study, we succeeded to further elaborate such approach and to reveal new mechanism of the mutagenic tautomerization of the classical A·T DNA base pairs (Scheme 1) as their intrinsic property, lying beyond classical representations at the microstructural level and which was not presented in the literature before. For the first time, it was theoretically shown using QM/QTAIM methods, that the transition of these pairs into the substantially non-planar, high-energy conformers (Brovarets' et al., 2018a) provokes intrapair mutagenic tautomerization of the T DNA base from the canonical, diketo into the rare, enol tautomeric forms T* and ${\text{T}}_{\text{O}2}^{*}$ (Brovarets' and Hovorun, 2014a, 2015b,d; Brovarets' et al., 2014a, 2015). Moreover, for the first time we have investigated in details conformationally-tautomeric properties of the classical A·T DNA base pairs (Brovarets' et al., 2018b,c,d,e).

SCHEME 1

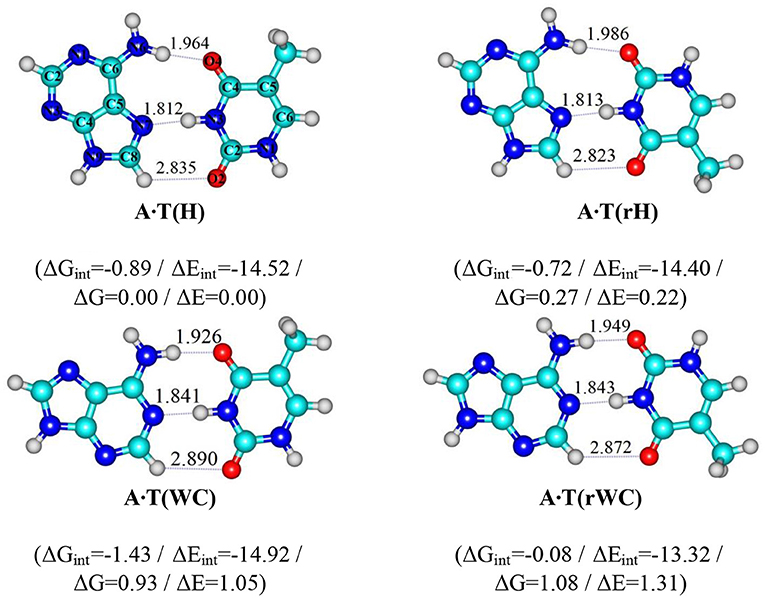
Scheme 1. Geometrical structures of the classical A·T DNA base pairs – Hoogsteen A·T(H), reverse Hoogsteen A·T(rH), Watson-Crick A·T(WC), reverse Watson-Crick A·T(rWC) (Brovarets', 2013b). Electronic ΔE_int and Gibbs free ΔG_int energies of the interaction (MP2/6-311++G(2df,pd)//B3LYP/6-311++G(d,p) level of theory, in kcal·mol-1), relative Gibbs free energies ΔG and electronic energies ΔE (MP2/aug-cc-pVDZ//B3LYP/6-311++G(d,p) level of theory in the continuum with ε = 1 at T = 298.15 K in kcal·mol-1) are presented below complexes in brackets. Dotted lines indicate AH··· B H-bonds – their lengths H··· B are presented in angstroms; carbon atoms are in light-blue, nitrogen – in dark-blue, hydrogen – in grey and oxygen – in red.

Transition states (TSs) of these mutagenic tautomerisations are tight ion pairs (A⁺, protonated by the N6H₂ amino group; T⁻, deprotonated by the N3H group) with quasi-orthogonal geometry, which are stabilized by the participation of the strong (A)N6⁺H··· O4⁻/O2⁻(T) and (A)N6⁺H··· N3⁻(T) H-bonds. Discovered reaction of the mutagenic tautomerization proceeds through the stepwise mechanism of the PT along the H-bonds: primarily proton moves from the imino group N3H of T to the N6H₂ amino group of A and then proton transfers from the protonated N6⁺H₃ amino group of A to the O4/O2 oxygen atom of T, leading to the products, which are substantially non-planar, conformationally-labile complexes. These complexes are stabilized by the participation of the (A)N6H/N6H′··· N3(T) and (T)O2H/O4H··· N6(A) H-bonds, for which the pyramidalized amino group of A DNA base acts as their donor and acceptor. The Gibbs free energy of the activation of the mutagenic tautomerizations lies in the range of 27.79–29.83 kcal·mol⁻¹ at T = 298.15 K in the continuum with ε = 1.

Also in this study, it was shown that the formed A·T*(w^⊥_WC), A·T*(w^⊥_H), A·${\text{T}}_{\text{O}2}^{*}$(w^⊥_rWC) and A·${\text{T}}_{\text{O}2}^{*}$(w^⊥_rH) complexes can conformationally interconvert according to the pathways A·T*(w^⊥_WC)↔A·T*(w^⊥_H) and A·${\text{T}}_{\text{O}2}^{*}$(w^⊥_rWC)↔A·${\text{T}}_{\text{O}2}^{*}$(w^⊥_rH) through three different TSs.

Computational Methods

Geometries of the investigated DNA base pairs and TSs of their mutual tautomeric and conformational transformations, as well as their harmonic vibrational frequencies were calculated at the B3LYP/6-311++G(d,p) level of theory (Hariharan and Pople, 1973; Krishnan et al., 1980; Lee et al., 1988; Parr and Yang, 1989; Tirado-Rives and Jorgensen, 2008), using Gaussian'09 package (Frisch et al., 2009) followed by the IRC calculations in the forward and reverse directions from each TS using Hessian-based predictor-corrector integration algorithm (Hratchian and Schlegel, 2005). A scaling factor that is equal to 0.9668 (Brovarets' and Hovorun, 2010b,c,d, 2011; El-Sayed et al., 2015) was applied in this study for the correction of the harmonic frequencies of all DNA base pairs and TSs of their tautomeric and conformational transitions. We have confirmed the TSs, localized by Synchronous Transit-guided Quasi-Newton method (Peng et al., 1996), on the potential energy landscape by the presence of one and only one imaginary frequency in the vibrational spectra of the complexes. We applied standard TS theory for the estimation of the activation barriers of the tautomeric transformations (Atkins, 1998). Single point electronic energy calculations have been performed using MP2 level of theory (Frisch et al., 1990) and aug-cc-pVDZ Dunning's cc-type basis set (Kendall et al., 1992), which was confirmed as appropriate level of theory for the analogous systems and tasks (Lozynski et al., 1998; Danilov et al., 2005; Matta, 2010; Rutledge and Wetmore, 2012; Brovarets' and Pérez-Sánchez, 2016, 2017; Brovarets' et al., 2016, 2018f; Brovarets' and Hovorun, 2018a).

All calculations were performed for the base pairs in the continuum with a dielectric constant of ε = 1 as their intrinsic property, that is adequate for modeling of the processes occurring in real systems (Bayley, 1951; Dewar and Storch, 1985; Petrushka et al., 1986; García-Moreno et al., 1997; Mertz and Krishtalik, 2000; Bebenek et al., 2011; Wang et al., 2011; Maximoff et al., 2017) without deprivation of the structurally functional properties of the bases in the composition of DNA (Brovarets' and Pérez-Sánchez, 2016, 2017; Brovarets' et al., 2016, 2018f).

The Gibbs free energy G for all structures was obtained in the following way:

$\begin{array}{ll}\text{G}={\text{E}}_{\text{el}}+{\text{E}}_{\text{corr}},& (1)\end{array}$

where E_el - electronic energy, while E_corr - thermal correction.

The Gibbs free energy of activation or barrier for the forward tautomeric/conformational transition was calculated as the difference between the Gibbs free energy of the TS and reactant of the reaction. The Gibbs free energy for the reverse tautomeric/conformational transition was calculated as the difference between the Gibbs free energy of the TS and product of the reaction.

Electronic interaction energies ΔE_int were calculated at the MP2/6-311++G(2df,pd) level of theory as the difference between the total energy of the base pair and energies of the monomers and corrected for the basis set superposition error (BSSE) (Boys and Bernardi, 1970; Gutowski et al., 1986) through the counterpoise procedure (Sordo et al., 1988; Sordo, 2001).

Bader's quantum theory of Atoms in Molecules (QTAIM) (Bader, 1990; Matta and Hernández-Trujillo, 2003; Matta, 2014; Lecomte et al., 2015) was applied to analyse the electron density distribution, using software package AIMAll (Keith, 2010). The presence of the bond critical point (BCP), namely (3,−1) BCP, and a bond path between hydrogen donor and acceptor or between two electronegative covalently bonded atoms, as well as the positive value of the Laplacian at this BCP (Δρ> 0), were considered as criteria for the H-bond or attractive van der Waals contact formation (Matta et al., 2006; Brovarets' and Hovorun, 2014c, 2018b; Brovarets' et al., 2014b). Wave functions were obtained at the level of theory used for geometry optimisation.

The energies of the attractive van der Waals contacts (Matta and Boyd, 2007; Brovarets' et al., 2018a) in the TSs of the conformational transitions of the tautomerized base pairs were calculated by the empirical Espinosa-Molins-Lecomte (EML) formula (Espinosa et al., 1998; Mata et al., 2011), based on the electron density distribution at the (3,−1) BCPs of the specific contacts:

$\begin{array}{ll}E=0.5·\text{V}(\text{r}),& (2)\end{array}$

in this formula V(r) is a value of a local potential energy at the (3,−1) BCP.

The energies of the conventional AH···B H-bonds were evaluated by the empirical Iogansen's formula (Iogansen, 1999):

$\begin{array}{ll}{E}_{AH···B}=0.33·\sqrt{△v-40},& (3)\end{array}$

in this formula Δν is a magnitude of the frequency shift of the stretching mode of the AH H-bonded group involved in the AH···B H-bond relatively the unbound group. The partial deuteration was applied in order to avoid the effect of vibrational resonances (Brovarets' and Hovorun, 2015h; Brovarets' et al., 2018a).

The atomic numbering scheme for the DNA bases was conventional (Saenger, 1984).

Obtained Results and Discussion

In our previous study, for the first time we have succeeded to establish in the classical biologically-important A·T DNA base pairs with C_s symmetry – Watson-Crick (WC), reverse Watson-Crick A·T(rWC), Hoogsteen A·T(H) and reverse Hoogsteen A·T(rH) DNA base pairs (Scheme 1) (Donohue and Trueblood, 1960; Haschemeyer and Sobell, 1963; Hoogsteen, 1963; Brovarets', 2013a,b; Yang et al., 2015; Poltev et al., 2016; Zhou, 2016; Szabat and Kierzek, 2017) – novel high-energetic, dynamically-stable, mirror-symmetrical A·T(w_WC)_{R, L}, A·T(w_H)_{R, L}, A·T(w_rWC)_{R, L} and A·T(w_rH)_{R, L} conformational states (Figure 1) (Brovarets' et al., 2018a). Their distinguished feature is significantly non-planar structure (C₁ symmetry), which is caused by the pyramidal structure of the ≥C6N6H₂ amino fragment of the A DNA base, which amino group acts simultaneously as a donor and an acceptor of the specific intermolecular interactions with T DNA base by two (T)N3H··· N6(A) and (A)N6H/N6H′··· O4/O2(T) H-bonds (the N6H′ bond has trans-orientation relatively the N1C6 bond of A). Each of the four A·T Watson-Crick DNA base pairs transfers into the aforementioned conformers via two mirror-symmetric pathways through the TS_{A·T(WC)↔A·T(wWC)R, L}, TS_{A·T(rWC)↔A·T(wrWC)R, L}, TS_{A·T(H)↔A·T(wH)R, L} and TS_{A·T(rH)↔A·T(wrH)R, L} (C₁ symmetry). At this, mirror-symmetrical complexes, which are enantiomers, are marked with the subscripts R and L. Notably, enantiomers in the achiral environment demonstrate identical scalar physico-chemical characteristics and differ only by the direction of the dipole moment.

FIGURE 1

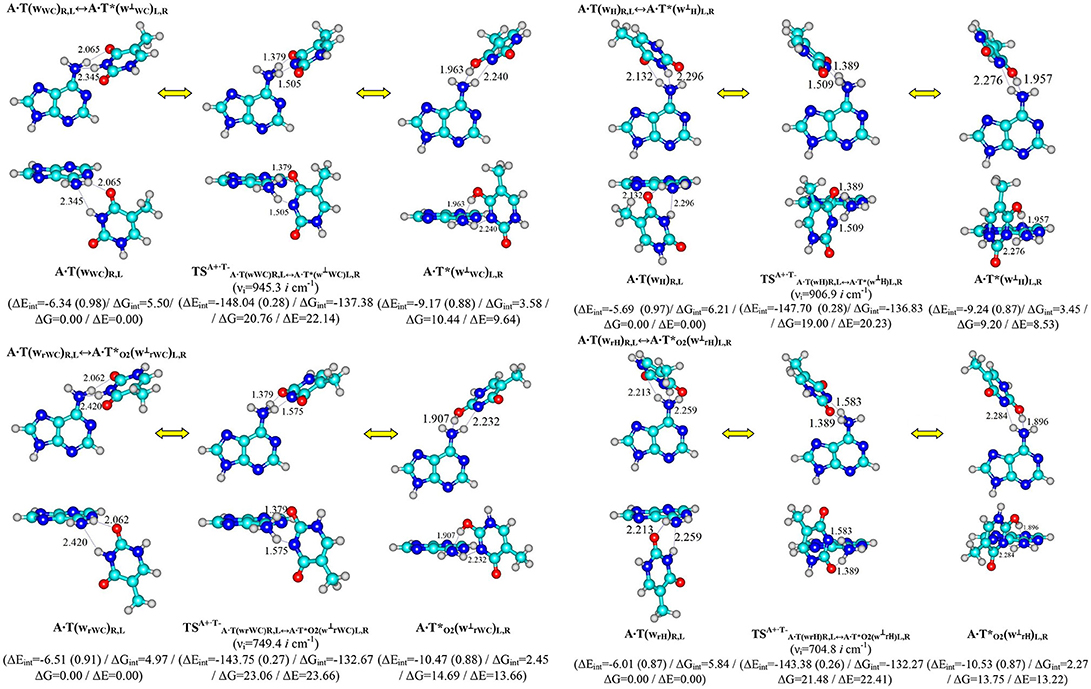
Figure 1. Discovered new reaction pathways of the T mutagenic tautomerization in the classical A·T DNA base pairs through the double proton transfer. νi – imaginary frequencies at the TSs of the conformational transitions. For more designations refer to Scheme 1.

Possible biological role of these conformers was also elucidated, in particular – their participation in the non-dissociative conformational interconversions of all four classical A·T DNA base pairs (Brovarets' et al., 2018b,e). Recently, we have identified novel pathway of the mutagenic tautomerisation of these structures through the quasi-orthogonal transition state as A⁻·T⁺ (Brovarets' et al., 2018c).

These data inspired us to elaborate further this novel point of view for the classical objects such as biologically-important A·T DNA base pairs and allow to suggest the possibility of the mutagenic tautomerization of T through the stepwise PT along the appropriate intermolecular H-bonds from the N3H imino group of T to the N6 atom of the N6H₂ amino group of A in the just-mentioned conformers and further – from the protonated amino group ${\text{NH}}_3^{+}$ of A to the O4/O2 oxygen atoms of T depending on the starting pair.

Performed quantum-chemical calculations completely confirm this assumption (Figures 1, 2 and Supplementary Information, Tables 1, 2).

FIGURE 2

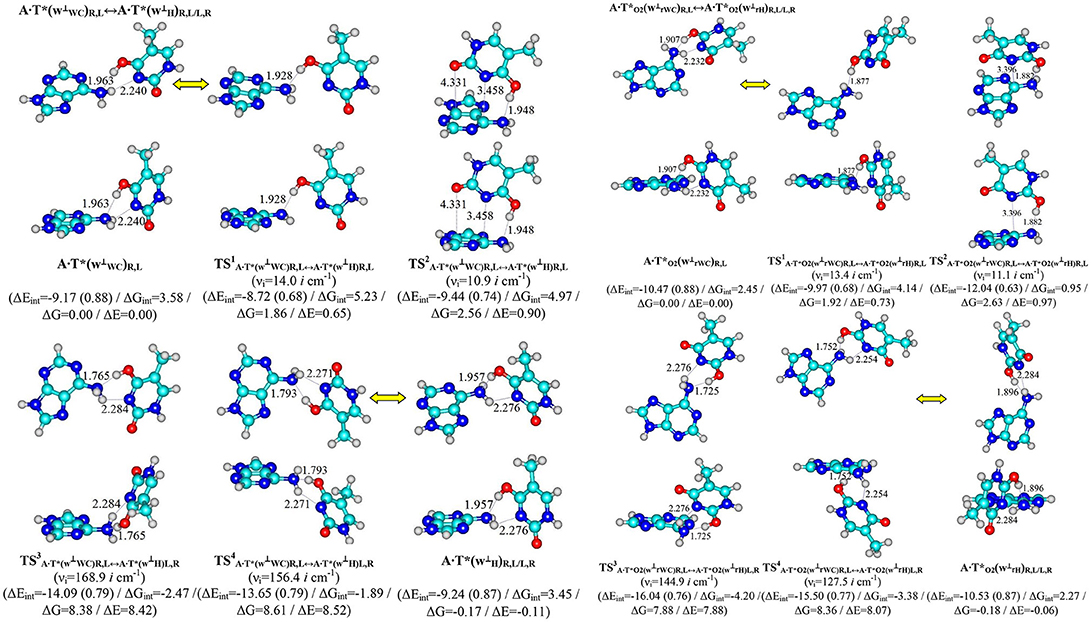
Figure 2. Pathways of the conformational transformations of the complexes - products of the T mutagenic tautomerization in the classical A·T DNA base pairs through the double proton transfer. For the designations see Figure 1.

It was established that novel pathways of the mutagenic tautomerization of the T DNA base in the classical A·T DNA base pairs (Scheme 1) are initiated by their spontaneous conformational transition into the high-energy A·T(w_WC)_{R, L}, A·T(w_H)_{R, L}, A·T(w_rWC)_{R, L} and A·T(w_rH)_{R, L} conformers as well as are controlled by the TSs as tight ion pairs (A⁺, protonated by the N6H₂ amino group)·(T⁻, deprotonated by the N3H imino group) with electronic energy of interaction ΔE_int ~145 kcal·mol⁻¹. These TSs – ${\text{TS}}^{{\text{A}}^{\text{+}}·{\text{T}}^{-}}{}_{\text{A}·\text{T}({\text{w}}_{\text{WC}})\text{R},\text{L}\leftrightarrow \text{A}·{\text{T}}^{\ast }({\text{w}}^{\perp }{}_{\text{WC}})\text{L},\text{R}}$ (20.76), ${\text{TS}}^{{\text{A}}^{\text{+}}·{\text{T}}^{-}}{}_{\text{A}·\text{T}({\text{w}}_{\text{rWC}})\text{R},\text{L}\leftrightarrow \text{A}·{\text{T}}^{\ast }{}_{\text{O}2}({\text{w}}^{\perp }{}_{\text{rWC}})\text{L},\text{R}}$ (23.06), ${\text{TS}}^{{\text{A}}^{\text{+}}·{\text{T}}^{\text{+}}}{}_{\text{A}·\text{T}({\text{w}}_{\text{H}})\text{R},\text{L}\leftrightarrow \text{A}·{\text{T}}^{\ast }({\text{w}}^{\perp }{}_{\text{H}})\text{L},\text{R}}$ (19.00) and ${\text{TS}}^{{\text{A}}^{+}·{\text{T}}^{-}}{}_{\text{A}·\text{T}({\text{w}}_{\text{rH}})\text{R},\text{L}\leftrightarrow \text{A}·{\text{T}}^{\ast }{}_{\text{O}2}({\text{w}}^{\perp }{}_{\text{rH}})\text{L},\text{R}}$ (21.48 kcal·mol⁻¹) are characterized by the quasi-orthogonal arrangement of the bases relatively each other and are stabilized by the participation of the two non-equivalent strong H-bonds (A)N6⁺H··· N3⁻(T) and (A)N6⁺H··· O4⁻/O2⁻(T) [the first of them is significantly weaker (~15.1–18.6 kcal·mol⁻¹), than the second one (~22.5–23.1 kcal·mol⁻¹)]. Protonated amino group N6⁺H₃ of A for these TSs acts simultaneously as donor and acceptor of the H-bonding and has such spatial orientation, that its N6⁺H/N6⁺H′ bond, which is not involved in the H-bonding with T, lies in the plane of the purine ring (Figure 1, Tables 1, 2).

TABLE 1

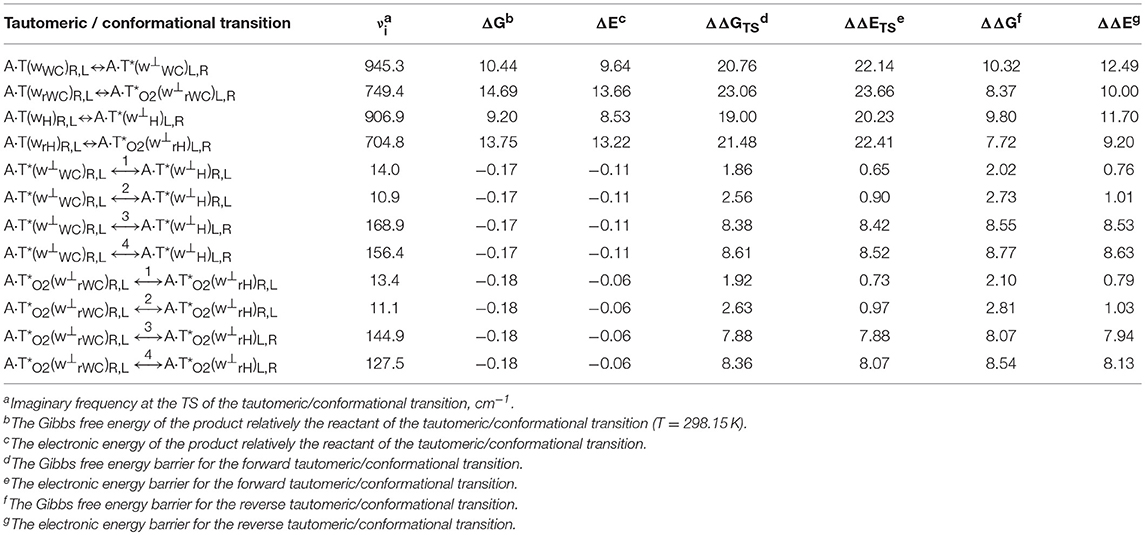
Table 1. Energetic characteristics (in kcal·mol⁻¹) of the discovered mutagenic tautomerizations of the T DNA base in the classical A·T DNA base pairs via the DPT and conformational transformations of their products obtained at the MP2/aug-cc-pVDZ//B3LYP/6-311++G(d,p) level of QM theory in the continuum with ε = 1 at T = 298.15 K (see Figures 1, 2).

TABLE 2

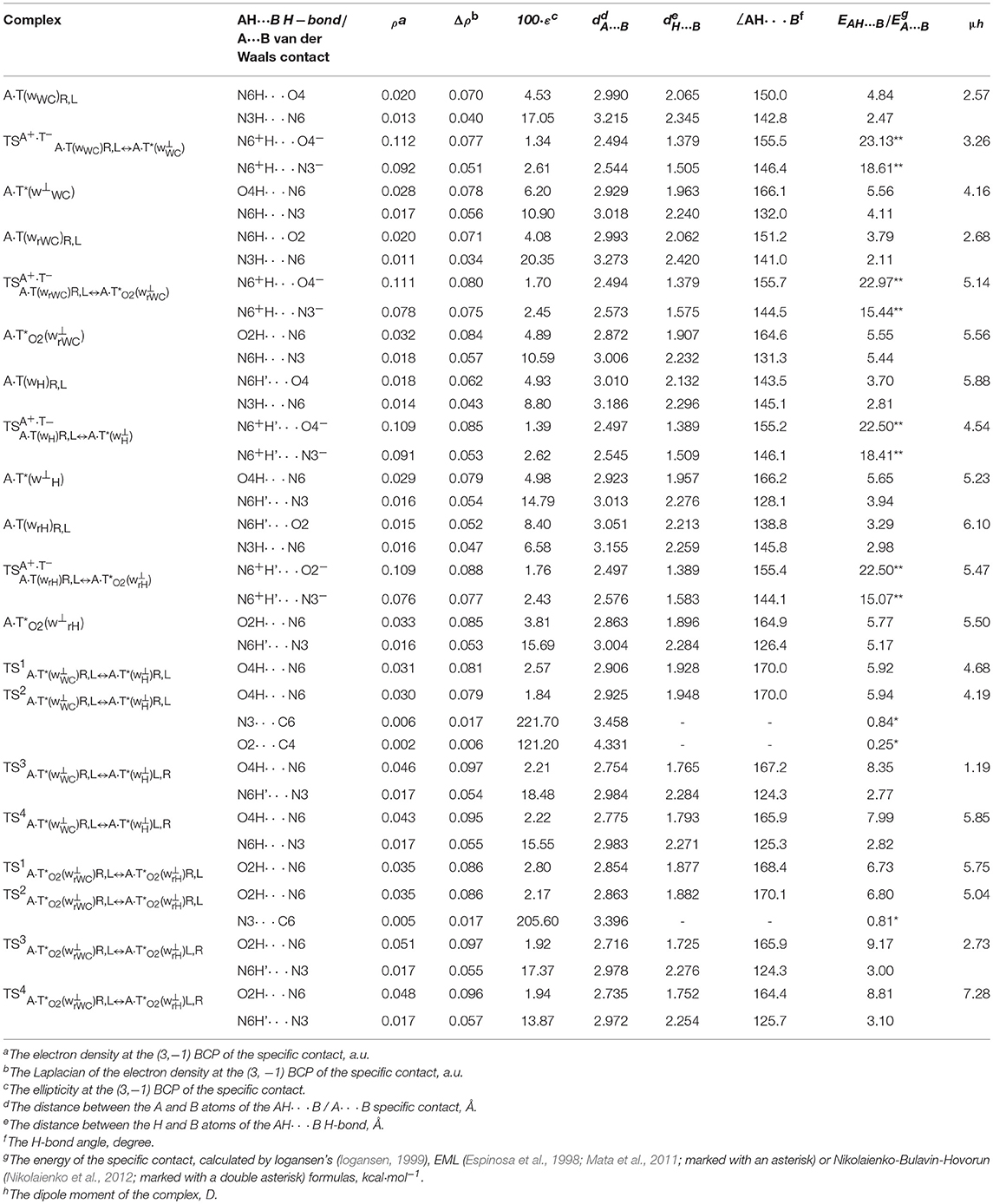
Table 2. Electron-topological, geometrical and energetic characteristics of the specific intermolecular contacts – H-bonds and attractive van der Waals contacts in the investigated DNA base pairs and TSs of their tautomeric and conformational transformations obtained at the B3LYP/6-311++G(d,p) level of QM theory in the continuum with ε = 1 at T = 298.15 K (see Figures 1, 2).

Significantly non-planar A·T*(w^⊥_WC)_{R, L} (10.44), A·T*(w^⊥_H)_{R, L} (14.69), A·${\text{T}}_{\text{O}2}^{*}$(w^⊥_rWC)_{R, L} (9.20) and A·${\text{T}}_{\text{O}2}^{*}$(w^⊥_rH)_{R, L} (13.75) kcal·mol⁻¹ complexes (C₁ symmetry), which are the products of these mutagenic tautomerizations, are stabilized by the two anti-parallel (T)O4H/O2H··· N6(A) (~5.5) and (A)N6H/N6H′··· N3(T) (~4.5 kcal·mol⁻¹) H-bonds (Figure 1 and Tables 1, 2).

It is worth to mention that each of the investigated tautomeric and conformational transitions proceed through two mirror-symmetric pathways and do not change cys/trans mutual orientation of the N1H and N9H glycosydic bonds of the bases. At the mutagenic tautomeric transformations of the DNA bases some R/L structures transfer into the other L/R structures and vice versa (Figures 1, 2).

Terminal tautomerized complexes are conformationally-labile and pairwise interconvert into each other according to four mechanisms (Tables 1, 2).

Two of these tautomerization reactions are controlled by the TSs – ${\text{TS}}^{1,2}{}_{\text{A}·{\text{T}}^{\ast }({\text{w}}^{\perp }{}_{\text{WC}})\text{R},\text{L}\leftrightarrow \text{A}·{\text{T}}^{\ast }({\text{w}}_{\text{H}}^{\perp })\text{R},\text{L}}$ (14.0, 10.9 cm⁻¹) and ${\text{TS}}^{1,2}{}_{\text{A}·{\text{T}}^{\ast }{}_{\text{O2}}({\text{w}}^{\perp }{}_{\text{rWC}})\text{R},\text{L}\leftrightarrow \text{A}·{\text{T}}^{\ast }{}_{\text{O2}}({\text{w}}^{\perp }{}_{\text{rH}})\text{R},\text{L}}$ (13.4, 11.1 cm⁻¹) with low values of the imaginary frequencies provided in the brackets. At this, one-single intermolecular (T)O4H/O2H··· N6(A) H-bond between the O4H/O2H hydroxyl groups of T*/${\text{T}}_{\text{O}2}^{*}$ and N6 nitrogen atom of the piramidalized amino group of A participates in the stabilization of the TS¹s. In the case of TS²s, when T hangs over A, the (T)O4H/O2H··· N6(A) H-bond coexists together with attractive van der Waals contacts with significantly increased ellipticity – N3··· C6 and O2··· C4 in the case of ${\text{TS}}^2{}_{\text{A}·{\text{T}}^{\ast }({\text{w}}^{\perp }{}_{\text{WC}})\leftrightarrow \text{A}·T^{\ast }({\text{w}}^{\perp }{}_{\text{H}})}$ and N3··· C6 in the case of ${\text{TS}}^2{}_{\text{A}·{\text{T}}^{\ast }{}_{\text{O}2}({\text{w}}^{\perp }{}_{\text{WC}})\leftrightarrow \text{A}·{\text{T}}^{\ast }{}_{\text{O}2}({\text{w}}^{\perp }{}_{\text{H}})}$ (Table 2). Notably, conformational transformations, which are controlled by the TS¹s are the most energetically favorable (1.86 and 1.92) in comparison with the TS²s (2.56 and 2.63 kcal·mol⁻¹) (Table 1). In these cases R/L structures are converted into the other R/L structures.

Two other mechanisms of the conformational transformations are accompanied by the anisotropic rotation of the A amino group around the exocyclic C6N6 bond, one R/L structures transform into the others L/R structures and vice versa. In these cases TSs – ${\text{TS}}^{3,4}{}_{\text{A}·{\text{T}}^{\ast }({\text{w}}^{\perp }{}_{\text{WC}})\text{R},\text{L}\leftrightarrow \text{A}·{\text{T}}^{\ast }({\text{w}}^{\perp }{}_{\text{H}})\text{L},\text{R}}$ (8.38 and 8.61 kcal·mol⁻¹) and ${\text{TS}}^{3,4}{}_{\text{A}·{\text{T}}^{\ast }{}_{\text{O}2}({\text{w}}^{\perp }{}_{\text{rWC}})\text{R},\text{L}\leftrightarrow \text{A}·{\text{T}}^{\ast }{}_{\text{O}2}({\text{w}}^{\perp }{}_{\text{rH}})\text{L},\text{R}}$ (7.88 and 8.36 kcal·mol⁻¹) are characterized by the considerably higher values of imaginary frequencies (168.9, 156.4, 144.9, 127.5 cm⁻¹) and stabilized by two antiparallel (T)O4/O2H··· N6(A) and (A)N6H/N6H′··· N3(T) H-bonds, the first of which is significantly stronger, then the other one (Table 2).

All tautomeric and conformational transitions without exceptions are dipole-active processes, since they are accompanied by a noticeable change in the dipole moment of the involved complexes (Table 2).

Interestingly, that among all without exception investigated in this work H-bonded structures, the total energy of the intermolecular specific contacts (H-bonds and attractive van der Waals contacts) contribute only a part of the electron energy of the monomer interactions (0.26–0.98; see Figures 1, 2). This result is in a good agreement with the previously published data for the others H-bonded pairs of nucleotide bases (Brovarets' and Hovorun, 2014d).

Notably, the methyl group of the T DNA base does not change its orientation during all, without exception, processes of the tautomeric and conformational transformations. Moreover, the heterocycles of the DNA bases remain planar, despite their ability for the out-of-plane bending (Govorun et al., 1992; Hovorun et al., 1999; Nikolaienko et al., 2011).

Finally, we would like to emphasize the fact that the presence of the conformational transitions between the complexes – products of the A·T*(w^⊥_WC)R,L↔ A·T*(w^⊥_H)R,L and A·T*_O2(${\text{w}}_{\text{rWC}}^{\perp }$)R,L↔ A·T*_O2(w^⊥_rH)R,L, tautomerizations indicating the close structural relationship between tautomerization the classical A·T(WC) and A·T(H) DNA base pairs, on the one hand, and A·T(rWC) and A·T(rH), on the other hand (Brovarets' et al., 2018b,e).

Conclusions

In this study, we came out from the existing framework of the mechanisms of the origin of the mutagenic tautomerization of the classical A·T DNA base pairs (Brovarets', 2013b; Brovarets' et al., 2018a,b,c,d,e).

Here we have shed light on the revealed for the first time physico-chemical mechanism of the intrapair mutagenic tautomerization of the T DNA base within the novel highly-energetic conformers of the classical A·T DNA base pairs – Watson-Crick [A·T(w_WC)], reverse Watson-Crick [A·T(w_rWC)], Hoogsteen [A·T(w_H)] and reverse Hoogsteen [A·T(w_rH)], which have been analyzed in details in our previous paper (Brovarets' et al., 2018a). These reactions – A·T(w_WC)↔ A·T*(w^⊥_WC), A·T(w_rWC)↔ A·${\text{T}}_{\text{O}2}^{*}$(w^⊥_rWC), A·T(w_H)↔ A·T*(w^⊥_H), A·T(w_rH)↔A·${\text{T}}_{\text{O}2}^{*}$(w^⊥_rH) – proceed through the stepwise proton transfer via the TSs as tight A⁺·T⁻ ion pairs, which Gibbs free energy of activation lies in the range of 27.79–29.83 kcal·mol⁻¹ at T = 298.15 K, thus creating the substantially non-planar, conformationally-labile complexes – A·T*(w^⊥_WC), A·${\text{T}}_{\text{O}2}^{*}$(w^⊥_rWC), A·T*(w^⊥_H) and A·${\text{T}}_{\text{O}2}^{*}$(w^⊥_rH). Furthermore, formed complexes involving mutagenic T*/${\text{T}}_{\text{O}2}^{*}$ tautomers are able to conformationally interconvert between each other according to reaction pathways – A·T*(w^⊥_WC)↔A·T*(w^⊥_H) and A·${\text{T}}_{\text{O}2}^{*}$(w^⊥_rWC)↔A·${\text{T}}_{\text{O}2}^{*}$(w^⊥_rH).

Author Contributions

OB, study conception and design, acquisition of data, drafting of manuscript analysis and interpretation of data, performance of calculations, discussion of the obtained data, preparation of the numerical data for Tables, graphical materials for Figures and text of the manuscript. KT, preparation of the numerical data for Tables and graphical materials for Figures, preparation of the text of the manuscript. AD, analysis and preparation of the current literature survey, discussion of the strategy of the current investigation, analysis of the obtained numerical data, discussion of the obtained data, preparation of the numerical data for Tables, graphical materials for Figures and text of the manuscript. DH, study conception, critical revision of manuscript, proposition of the task of the investigation, discussion of the obtained data, preparation of the text of the manuscript. All authors were involved in the proofreading of the final version of the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We gratefully appreciate technical support and computational facilities of joint computer cluster of SSI Institute for Single Crystals of the National Academy of Sciences of Ukraine (NASU) and Institute for Scintillation Materials of the NASU incorporated into Ukrainian National Grid. This work was partially supported by the Grant of the President of Ukraine to support the research of young scientists from the State Fund for Fundamental Research of Ukraine of the Ministry of the Education and Science of Ukraine given to OB. OB expresses sincere gratitude to organizing committee headed by Prof. Karl Kuchler (Medical University Vienna, Austria) for the kind invitation and financial support (ABC fellow) of the participation in the FEBS Special Meeting ATP-Binding Cassette (ABC) Proteins: From Multidrug Resistance to Genetic Disease (March 6–12, 2018, Innsbruck, Austria) and to Chemistry Biological Interface Division of the Royal Society of Chemistry (RSC, UK) for the RSC Travel Grant for the participation at the 3^rd Green and Sustainable Chemistry Conference (May 13–16, 2018, Hotel Intercontinental, Berlin, Germany).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2018.00532/full#supplementary-material

References

Atkins, P. W. (1998). Physical Chemistry. Oxford: Oxford University Press.

PubMed Abstract | Google Scholar

Bader, R. F. W. (1990). Atoms in Molecules: A Quantum Theory. Oxford: Oxford University Press.

Bayley, S. T. (1951). The dielectric properties of various solid crystalline proteins, amino acids and peptides. Trans. Faraday Soc. 47, 509–517. doi: 10.1039/tf9514700509

CrossRef Full Text | Google Scholar

Bebenek, K., Pedersen, L. C., and Kunkel, T. A. (2011). Replication infidelity via a mismatch with Watson–Crick geometry. Proc. Natl. Acad. Sci. U.S.A. 108, 1862–1867. doi: 10.1073/pnas.1012825108

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertran, J., Blancafort, L., Noguera, M., and Sodupe, M. (2006). “Proton transfer in DNA base pairs,” in Computational Studies of RNA and DNA, eds J. Šponer, and F. Lankaš, (Dordrecht: Springer), 411–432.

Google Scholar

Boys, S. F., and Bernardi, F. (1970). The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 19, 553–566. doi: 10.1080/00268977000101561

CrossRef Full Text | Google Scholar

Brovarets', O. O. (2013a). Under what conditions does G·C Watson-Crick DNA base pair acquire all four configurations characteristic for A·T Watson-Crick DNA base pair? Ukr. Biochem. J. 85, 98–103. doi: 10.15407/ubj85.04.098

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O. (2013b). Structural and energetic properties of the four configurations of the A·T and G·C DNA base pairs. Ukr. Biochem. J. 85, 104–110. doi: 10.15407/ubj85.04.104

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O. (2015). Microstructural Mechanisms of the Origin of the Spontaneous Point Mutations, DrSci Thesis: Taras Shevchenko National University of Kyiv, Kyiv, Ukraine.

Brovarets', O. O., and Hovorun, D. M. (2009). Physicochemical mechanism of the wobble DNA base pairs Gua·Thy and Ade·Cyt transition into the mismatched base Pairs Gua*·Thy and Ade·Cyt* formed by the mutagenic tautomers. Ukr. Bioorg. Acta 8, 12–18.

Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2010a). IR vibrational spectra of H-bonded complexes of adenine, 2-aminopurine and 2-aminopurine⁺ with cytosine and thymine: quantum-chemical study. Optics Spectr. 111, 750–757. doi: 10.1134/S0030400X11120058

CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2010b). Quantum-chemical investigation of tautomerization ways of Watson-Crick DNA base pair guanine-cytosine. Ukr. Biochem. J. 82, 55–60.

PubMed Abstract | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2010c). Quantum-chemical investigation of the elementary molecular mechanisms of pyrimidine·purine transversions. Ukr. Biochem. J. 82, 57–67.

PubMed Abstract | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2010d). Stability of mutagenic tautomers of uracil and its halogen derivatives: the results of quantum-mechanical investigation. Biopol. Cell 26, 295–298. doi: 10.7124/bc.000162

CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2011). Intramolecular tautomerization and the conformational variability of some classical mutagens – cytosine derivatives: quantum-chemical study. Biopol. Cell 27, 221–230. doi: 10.7124/bc.0000BD

CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2014a). Can tautomerisation of the A·T Watson-Crick base pair via double proton transfer provoke point mutations during DNA replication? A comprehensive, QM and QTAIM analysis. J. Biomol. Struct. Dyn. 32, 127–154. doi: 10.1080/07391102.2012.755795

CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2014b). Why the tautomerization of the G·C Watson–Crick base pair via the DPT does not cause point mutations during DNA replication? QM and QTAIM comprehensive analysis. J. Biomol. Struct. Dyn. 32, 1474–1499. doi: 10.1080/07391102.2013.822829

CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2014c). DPT tautomerisation of the G·A_syn and A*·${\text{G}}_{\text{syn}}^{*}$ DNA mismatches: a QM/QTAIM combined atomistic investigation. Phys. Chem. Chem. Phys. 16, 9074–9085. doi: 10.1039/c4cp00488d

PubMed Abstract | CrossRef Full Text

Brovarets', O. O., and Hovorun, D. M. (2014d). Does the G·${\text{G}}_{\text{syn}}^{*}$ DNA mismatch containing canonical and rare tautomers of the guanine tautomerise through the DPT? A QM/QTAIM microstructural study. Mol. Phys. 112, 3033–3046. doi: 10.1080/00268976.2014.927079

CrossRef Full Text

Brovarets', O. O., and Hovorun, D. M. (2015a). Proton tunneling in the A·T Watson-Crick DNA base pair: myth or reality? J. Biomol. Struct. Dyn. 12, 2716–2720. doi: 10.1080/07391102.2015.1092886

CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2015b). New structural hypostases of the A·T and G·C Watson-Crick DNA base pairs caused by their mutagenic tautomerisation in a wobble manner: a QM/QTAIM prediction. RSC Adv. 5, 99594–99605. doi: 10.1039/C5RA19971A

CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2015c). Tautomeric transition between wobble A·C DNA base mispair and Watson-Crick-like A·C* mismatch: microstructural mechanism and biological significance. Phys. Chem. Chem. Phys. 17, 15103–15110. doi: 10.1039/C5CP01568E

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2015d). How many tautomerisation pathways connect Watson-Crick-like G*·T DNA base mispair and wobble mismatches? J. Biomol. Struct. Dyn. 33, 2297–2315. doi: 10.1080/07391102.2015.1046936

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2015e). Wobble↔Watson-Crick tautomeric transitions in the homo-purine DNA mismatches: a key to the intimate mechanisms of the spontaneous transversions. J. Biomol. Struct. Dyn. 33, 2710–2715. doi: 10.1080/07391102.2015.1077737

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2015f). Novel physico-chemical mechanism of the mutagenic tautomerisation of the Watson–Crick-like A·G and C·T DNA base mispairs: a quantum-chemical picture. RSC Adv. 5, 66318–66333. doi: 10.1039/C5RA11773A

CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2015g). A novel conception for spontaneous transversions caused by homo-pyrimidine DNA mismatches: a QM/QTAIM highlight. Phys. Chem. Chem. Phys. 17, 21381–21388. doi: 10.1039/C5CP03211C

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2015h). The physicochemical essence of the purine·pyrimidine transition mismatches with Watson-Crick geometry in DNA: A·C* versa A*·C. A QM and QTAIM atomistic understanding. J. Biomol. Struct. Dyn. 33, 28–55. doi: 10.1080/07391102.2013.852133

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2016). By how many tautomerisation routes the Watson-Crick-like A·C* DNA base mispair is linked with the wobble mismatches? A QM/QTAIM vision from a biological point of view. Struct. Chem. 27, 119–131. doi: 10.1007/s11224-015-0687-4

CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2018a). Key microstructural mechanisms of the 2-aminopurine mutagenicity: results of extensive quantum-chemical research. J. Biomol. Struct. Dyn. 26, 1–39. doi: 10.1080/07391102.2018.1495577

CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2018b). Atomistic mechanisms of the double proton transfer in the H-bonded nucleobase pairs: QM/QTAIM computational lessons. J. Biomol. Struct. Dyn. 17, 1–28. doi: 10.1080/07391102.2018.1467795

CrossRef Full Text | Google Scholar

Brovarets', O. O., Kolomiets', I. M., and Hovorun, D. M. (2012). “Elementary molecular mechanisms of the spontaneous point mutations in DNA: a novel quantum-chemical insight into the classical understanding,” in Quantum Chemistry – Molecules for Innovations, ed Tomofumi Tada (Rijeka, Croatia: InTech Open Access).

Google Scholar

Brovarets', O. O., and Pérez-Sánchez, H. E. (2016). Whether the amino-imino tautomerism of 2-aminopurine is involved into its mutagenicity? Results of a thorough QM investigation. RSC Adv. 110, 108255–108264. doi: 10.1039/C6RA24277D

CrossRef Full Text | Google Scholar

Brovarets', O. O., and Pérez-Sánchez, H. E. (2017). Whether 2-aminopurine induces incorporation errors at the DNA replication? A quantum-mechanical answer on the actual biological issue. J. Biomol. Struct. Dyn. 35, 3398–3411. doi: 10.1080/07391102.2016.1253504

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O., Pérez-Sánchez, H. E., and Hovorun, D. M. (2016). Structural grounds for the 2-aminopurine mutagenicity: a novel insight into the old problem of the replication errors. RSC Adv. 6, 99546–99557. doi: 10.1039/C6RA17787E

CrossRef Full Text | Google Scholar

Brovarets', O. O., Tsiupa, K. S., and Hovorun, D. M. (2018a). Surprising conformers of the biologically important A·T DNA base pairs: QM/QTAIM proofs. Front. Chem. 6:8. doi: 10.3389/fchem.2018.00008

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O., Tsiupa, K. S., and Hovorun, D. M. (2018b). Non-dissociative structural transitions of the Watson-Crick and reverse Watson-Crick A·T DNA base pairs into the Hoogsteen and reverse Hoogsteen forms. Sci. Repts. 8:10371. doi: 10.1038/s41598-018-28636-y

CrossRef Full Text | Google Scholar

Brovarets', O. O., Tsiupa, K. S., and Hovorun, D. M. (2018c). Novel pathway for mutagenic tautomerization of classical A·T DNA base pairs via sequential proton transfer through quasi-orthogonal transition states: a QM/QTAIM investigation. PLoS ONE 13:e0199044. doi: 10.1371/journal.pone.0199044

CrossRef Full Text | Google Scholar

Brovarets', O. O., Tsiupa, K. S., and Hovorun, D. M. (2018d). The A·T(rWC)/A·T(H)/A·T(rH) ↔ A·T*(rw_WC)/A·T*(w_H)/A·T*(rw_H) mutagenic tautomerization via sequential proton transfer: a QM/QTAIM study. RSC Adv. 8, 13433–13445. doi: 10.1039/C8RA01446A

CrossRef Full Text | Google Scholar

Brovarets', O. O., Tsiupa, K. S., and Hovorun, D. M. (2018e). Unexpected A·T(WC)↔A·T(rWC)/A·T(rH) and A·T(H)↔A·T(rH)/A·T(rWC) conformational transitions between the classical A·T DNA base pairs: a QM/QTAIM comprehensive study. Int. J. Quantum. Chem. 118:e25674. doi: 10.1002/qua.25692

CrossRef Full Text | Google Scholar

Brovarets', O. O., Voiteshenko, I. S., and Hovorun, D. M. (2017b). Physico-chemical profiles of the wobble↔Watson-Crick G*·2AP(w)↔G·2AP(WC) and A·2AP(w)↔A*·2AP(WC) tautomerisations: a QM/QTAIM comprehensive survey. Phys. Chem. Chem. Phys. 20, 623–636. doi: 10.1039/C7CP05139E

CrossRef Full Text | Google Scholar

Brovarets', O. O., Voiteshenko, I. S., Pérez-Sánchez, H. E., and Hovorun, D. M. (2017a). A QM/QTAIM research under the magnifying glass of the DPT tautomerisation of the wobble mispairs involving 2-aminopurine. New J. Chem. 41, 7232–7243. doi: 10.1039/C7NJ00717E

CrossRef Full Text | Google Scholar

Brovarets', O. O., Voiteshenko, I. S., Pérez-Sánchez, H. E., and Hovorun, D. M. (2018f). A QM/QTAIM detailed look at the Watson-Crick↔wobble tautomeric transformations of the 2-aminopurine·pyrimidine mispairs. J. Biomol. Struct. Dyn. 36, 1649–1665. doi: 10.1080/07391102.2017.1331864

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O., Zhurakivsky, R. O., and Hovorun, D. M. (2013). The physico-chemical “anatomy” of the tautomerization through the DPT of the biologically important pairs of hypoxanthine with DNA bases: QM and QTAIM perspectives. J. Mol. Model. 19, 4119–4137. doi: 10.1007/s00894-012-1720-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O., Zhurakivsky, R. O., and Hovorun, D. M. (2014a). Structural, energetic and tautomeric properties of the T·T*/T*·T DNA mismatch involving mutagenic tautomer of thymine: a QM and QTAIM insight. Chem. Phys. Lett. 592, 247–255. doi: 10.1016/j.cplett.2013.12.034

CrossRef Full Text | Google Scholar

Brovarets', O. O., Zhurakivsky, R. O., and Hovorun, D. M. (2014b). Is the DPT tautomerisation of the long A·G Watson-Crick DNA base mispair a source of the adenine and guanine mutagenic tautomers? A QM and QTAIM response to the biologically important question. J. Comput. Chem. 35, 451–466. doi: 10.1002/jcc.23515

CrossRef Full Text | Google Scholar

Brovarets', O. O., Zhurakivsky, R. O., and Hovorun, D. M. (2015). DPT tautomerisation of the wobble guanine·thymine DNA base mispair is not mutagenic: QM and QTAIM arguments. J. Biomol. Struct. Dyn. 33, 674–689. doi: 10.1080/07391102.2014.897259

CrossRef Full Text | Google Scholar

Cerón-Carrasco, J. P., and Jacquemin, D. (2013). Electric field induced DNA damage: an open door for selective mutations. Chem. Commun. 49, 7578–7580. doi: 10.1039/c3cc42593b

PubMed Abstract | CrossRef Full Text | Google Scholar

Danilov, V. I., Anisimov, V. M., Kurita, N., and Hovorun, D. (2005). MP2 and DFT studies of the DNA rare base pairs: the molecular mechanism of the spontaneous substitution mutations conditioned by tautomerism of bases. Chem. Phys. Lett. 412, 285–293. doi: 10.1016/j.cplett.2005.06.123

CrossRef Full Text | Google Scholar

Dewar, M. J. S., and Storch, D. M. (1985). Alternative view of enzyme reactions. Proc. Natl. Acad. Sci. U.S.A. 82, 2225–2229. doi: 10.1073/pnas.82.8.2225

PubMed Abstract | CrossRef Full Text | Google Scholar

Donohue, J., and Trueblood, K. N. (1960). Base pairing in DNA. J. Mol. Biol. 2, 363–371. doi: 10.1016/S0022-2836(60)80047-2

PubMed Abstract | CrossRef Full Text | Google Scholar

El-Sayed, A. A., Tamara Molina, A., Alvarez-Ros, M. C., and Palafox, M. A. (2015). Conformational analysis of the anti-HIV Nikavir prodrug: comparisons with AZT and thymidine, and establishment of structure-activity relationships/tendencies in other 6‘-derivatives. J. Biomol. Struct. Dyn. 33, 723–748. doi: 10.1080/07391102.2014.909743

PubMed Abstract | CrossRef Full Text | Google Scholar

Espinosa, E., Molins, E., and Lecomte, C. (1998). Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 285, 170–173. doi: 10.1016/S0009-2614(98)00036-0

CrossRef Full Text | Google Scholar

Florian, J., Hrouda, V., and Hobza, P. (1994). Proton transfer in the adenine-thymine base pair. J. Am. Chem. Soc. 116, 1457–1460. doi: 10.1021/ja00083a034

CrossRef Full Text | Google Scholar

Frisch, M. J., Head-Gordon, M., and Pople, J. A. (1990). Semi-direct algorithms for the MP2 energy and gradient. Chem. Phys. Lett. 166, 281–289. doi: 10.1016/0009-2614(90)80030-H

CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2009). Gaussian 09, Revision, B.01; Wallingford, C. T: Gaussian, Inc.

García-Moreno, B. E., Dwyer, J. J., Gittis, A. G., Lattman, E. E., Spencer, D. S., and Stites, W. E. (1997). Experimental measurement of the effective dielectric in the hydrophobic core of a protein. Biophys. Chem. 64, 211–224. doi: 10.1016/S0301-4622(96)02238-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Gorb, L., Podolyan, Y., Dziekonski, P., Sokalski, W. A., and Leszczynski, J. (2004). Double-proton transfer in adenine–thymine and guanine–cytosine base pairs. A post-Hartree-Fock ab initio study. J. Am. Chem. Soc. 126, 10119–10129. doi: 10.1021/ja049155n

PubMed Abstract | CrossRef Full Text | Google Scholar

Govorun, D. M., Danchuk, V. D., Mishchuk, Y. R., Kondratyuk, I. V., Radomsky, N. F., and Zheltovsky, N. V. (1992). AM1 calculation of the nucleic acid bases structure and vibrational spectra. J. Mol. Struct. 267, 99–103. doi: 10.1016/0022-2860(92)87016-O

CrossRef Full Text | Google Scholar

Gutowski, M., Van Lenthe, J. H., Verbeek, J., Van Duijneveldt, F. B., and Caahalasinski, G. (1986). The basis set superposition error in correlated electronic structure calculations. Chem. Phys. Lett. 124, 370–375. doi: 10.1016/0009-2614(86)85036-9

CrossRef Full Text | Google Scholar

Hariharan, P. C., and Pople, J. A. (1973). The influence of polarization functions on molecular orbital hydrogenation energies. Theor. Chim. Acta 28, 213–222. doi: 10.1007/BF00533485

CrossRef Full Text | Google Scholar

Haschemeyer, A. E., and Sobell, H. M. (1963). The crystal structure of an intermolecular nucleoside complex: adenosine and 5-bromouridine. Proc. Natl Acad. Sci. U.S.A. 50, 872–877. doi: 10.1073/pnas.50.5.872

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoogsteen, K. (1963). The crystal and molecular structure of a hydrogen-bonded complex between 1-methylthymine and 9-methyladenine. Acta Cryst. 16, 907–916. doi: 10.1107/S0365110X63002437

CrossRef Full Text | Google Scholar

Hovorun, D. M., Gorb, L., and Leszczynski, J. (1999). From the nonplanarity of the amino group to the structural nonrigidity of the molecule: a post-Hartree-Fock ab initio study of 2-aminoimidazole. Int. J. Quantum. Chem. 75, 245–253. doi: 10.1002/(SICI)1097-461X(1999)75:3<245::AID-QUA14>3.0.CO;2-0

CrossRef Full Text | Google Scholar

Hratchian, H. P., and Schlegel, H. B. (2005). “Finding minima, transition states, and following reaction pathways on ab initio potential energy surfaces,” in Theory and Applications of Computational Chemistry: The First 40 Years, eds C. E. Dykstra, G. Frenking, K. S. Kim, and G. Scuseria (Amsterdam: Elsevier) 195–249.

Google Scholar

Iogansen, A. V. (1999). Direct proportionality of the hydrogen bonding energy and the intensification of the stretching ν(XH) vibration in infrared spectra. Spectrochim. Acta Part A55, 1585–1612. doi: 10.1016/S1386-1425(98)00348-5

CrossRef Full Text | Google Scholar

Keith, T. A. (2010). AIMAll,(Version 10.07.01). Available online at: aim.tkgristmill.com

Kendall, R. A., Dunning, T. H. Jr., and Harrison, R. J. (1992). Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 96, 6796–6806.

Google Scholar

Kimsey, I. J., Petzold, K., Sathyamoorthy, B., Stein, Z. W., and Al-Hashimi, H. M. (2015). Visualizing transient Watson-Crick-like mispairs in DNA and RNA duplexes. Nature 519, 315–320. doi: 10.1038/nature14227

PubMed Abstract | CrossRef Full Text | Google Scholar

Kimsey, I. J., Szymanski, E. S., Zahurancik, W. J., Shakya, A., Xue, Y., Chu, C. C., et al. (2018). Dynamic basis for dG·dT misincorporation via tautomerization and ionization. Nature 554, 195–201. doi: 10.1038/nature25487

PubMed Abstract | CrossRef Full Text | Google Scholar

Krishnan, R., Binkley, J. S., Seeger, R., and Pople, J. A. (1980). Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 72, 650–654. doi: 10.1063/1.438955

CrossRef Full Text | Google Scholar

Lecomte, C., Espinosa, E., and Matta, C. F. (2015). On atom–atom ‘short contact’ bonding interactions in crystals. IUCr J. 2, 161–163. doi: 10.1107/S2052252515002067

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, C., Yang, W., and Parr, R. G. (1988). Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B. 37, 785–789. doi: 10.1103/PhysRevB.37.785

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, T., Wang, N., Cao, J., Sofiadis, A., Dinets, A., Zedenius, J., et al. (2014). The age- and shorter telomere-dependent TERT promoter mutation in follicular thyroid cell-derived carcinomas. Oncogene 33, 4978–4984. doi: 10.1038/onc.2013.446

PubMed Abstract | CrossRef Full Text | Google Scholar

Löwdin, P.-O. (1963). Proton tunneling in DNA and its biological implications. Rev. Mod. Phys. 35, 724–732. doi: 10.1103/RevModPhys.35.724

CrossRef Full Text | Google Scholar

Löwdin, P.-O. (1966). “Quantum genetics and the aperiodic solid: some aspects on the biological problems of heredity, mutations, aging, and tumors in view of the quantum theory of the DNA molecule,” in Advances in Quantum Chemistry, ed P.-O. Löwdin (New York, NY, London: Academic Press) Vol. 2, 213–360.

Google Scholar

Lozynski, M., Rusinska-Roszak, D., and Mack, H.-G. (1998). Hydrogen bonding and density functional calculations: the B3LYP approach as the shortest way to MP2 results. J. Phys. Chem. A 102, 2899–2903. doi: 10.1021/jp973142x

CrossRef Full Text | Google Scholar

Mata, I., Alkorta, I., Espinosa, E., and Molins, E. (2011). Relationships between interaction energy, intermolecular distance and electron density properties in hydrogen bonded complexes under external electric fields. Chem. Phys. Lett. 507, 185–189. doi: 10.1016/j.cplett.2011.03.055

CrossRef Full Text | Google Scholar

Matta, C. F. (2010). How dependent are molecular and atomic properties on the electronic structure method? Comparison of Hartree-Fock, DFT, and MP2 on a biologically relevant set of molecules. J. Comput. Chem. 31, 1297–1311. doi: 10.1002/jcc.21417

PubMed Abstract | CrossRef Full Text | Google Scholar

Matta, C. F. (2014). Modeling biophysical and biological properties from the characteristics of the molecular electron density, electron localization and delocalization matrices, and the electrostatic potential. J. Comput. Chem. 35, 1165–1198. doi: 10.1002/jcc.23608

PubMed Abstract | CrossRef Full Text | Google Scholar

Matta, C. F., and Boyd, R. J. (2007). The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design. Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim.

Matta, C. F., Castillo, N., and Boyd, R. J. (2006). Extended weak bonding interactions in DNA: π-stacking (base-base), base-backbone, and backbone-backbone interactions. J. Phys. Chem. B 110, 563–578. doi: 10.1021/jp054986g

PubMed Abstract | CrossRef Full Text | Google Scholar

Matta, C. F., and Hernández-Trujillo, J. (2003). Bonding in polycyclic aromatic hydrocarbons in terms of the electron density and of electron delocalization. J. Phys. Chem. A 107, 7496–7504. doi: 10.1021/jp034952d

CrossRef Full Text | Google Scholar

Maximoff, S. N., Kamerlin, Sh. C. L., and Florián, J. (2017). DNA polymerase λ active site favors a mutagenic mispair between the enol form of deoxyguanosine triphosphate substrate and the keto form of thymidine template: a free energy perturbation study. J. Phys. Chem. B 121, 7813–7822. doi: 10.1021/acs.jpcb.7b04874

PubMed Abstract | CrossRef Full Text | Google Scholar

Mertz, E. L., and Krishtalik, L. I. (2000). Low dielectric response in enzyme active site. Proc. Natl. Acad. Sci. U.S.A. 97, 2081–2086. doi: 10.1073/pnas.050316997

PubMed Abstract | CrossRef Full Text | Google Scholar

Nedderman, A. N., Stone, M. J., Lin, P. K. T., Brown, D. M., and Williams, D. H. (1991). Base pairing of cytosine analogues with adenine and guanine in oligonucleotide duplexes: evidence for exchange between Watson-Crick and wobble base pairs using ¹H NMR spectroscopy. J. Chem. Soc. Chem. Commun. 1357–1359. doi: 10.1039/C39910001357

CrossRef Full Text | Google Scholar

Nedderman, A. N., Stone, M. J., Williams, D. H., Lin, P. K., and Brown, D. M. (1993). Molecular basis for methoxyamine initiated mutagenesis: ¹H nuclear magnetic resonance studies of oligonucleotide duplexes containing base-modified cytosine residues. J. Mol. Biol. 230, 1068–1076. doi: 10.1006/jmbi.1993.1219

PubMed Abstract | CrossRef Full Text | Google Scholar

Nikolaienko, T. Y., Bulavin, L. A., and Hovorun, D. M. (2011). How flexible are DNA constituents? The quantum-mechanical study. J. Biomol. Struct. Dyn. 29, 563–575. doi: 10.1080/07391102.2011.10507406

PubMed Abstract | CrossRef Full Text | Google Scholar

Nikolaienko, T. Y., Bulavin, L. A., and Hovorun, D. M. (2012). Bridging QTAIM with vibrational spectroscopy: the energy of intramolecular hydrogen bonds in DNA-related biomolecules. Phys. Chem. Chem. Phys. 14, 7441–7447. doi: 10.1039/c2cp40176b

PubMed Abstract | CrossRef Full Text | Google Scholar

Parr, R. G., and Yang, W. (1989). Density-Functional Theory of Atoms and Molecules. Oxford: Oxford University Press.

Peng, C., Ayala, P. Y., Schlegel, H. B., and Frisch, M. J. (1996). Using redundant internal coordinates to optimize equilibrium geometries and transition states. J. Comput. Chem. 17, 49–56. doi: 10.1002/(SICI)1096-987X(19960115)17:1<49::AID-JCC5>3.0.CO;2-0

CrossRef Full Text | Google Scholar

Petrushka, J., Sowers, L. C., and Goodman, M. F. (1986). Comparison of nucleotide interactions in water, proteins, and vacuum: model for DNA polymerase fidelity. Proc. Natl. Acad. Sci. U.S.A. 83, 1559–1562. doi: 10.1073/pnas.83.6.1559

CrossRef Full Text | Google Scholar

Poltev, V. I., Anisimov, V. M., Sanchez, C., Deriabina, A., Gonzalez, E., Garcia, D., et al. (2016). Analysis of the conformational features of Watson–Crick duplex fragments by molecular mechanics and quantum mechanics methods. Biophysics 61, 217–226. doi: 10.1134/S0006350916020160

PubMed Abstract | CrossRef Full Text | Google Scholar

Rutledge, L. R., and Wetmore, S. D. (2012). A computational proposal for the experimentally observed discriminatory behavior of hypoxanthine, a weak universal nucleobase. Phys. Chem. Chem. Phys. 14, 2743–2753. doi: 10.1039/c2cp23600a

PubMed Abstract | CrossRef Full Text | Google Scholar

Saenger, W. (1984). Principles of Nucleic Acid Structure. New York, NY: Springer.

Google Scholar

Sordo, J. A. (2001). On the use of the Boys–Bernardi function counterpoise procedure to correct barrier heights for basis set superposition error. J. Mol. Struct. 537, 245–251. doi: 10.1016/S0166-1280(00)00681-3

CrossRef Full Text | Google Scholar

Sordo, J. A., Chin, S., and Sordo, T. L. (1988). On the counterpoise correction for the basis set superposition error in large systems. Theor. Chim. Acta 74, 101–110. doi: 10.1007/BF00528320

CrossRef Full Text | Google Scholar

Szabat, M., and Kierzek, R. (2017). Parallel-stranded DNA and RNA duplexes-structural features and potential applications. FEBS J. 284, 3986–3998. doi: 10.1111/febs.14187

CrossRef Full Text

Tirado-Rives, J., and Jorgensen, W. L. (2008). Performance of B3LYP density functional methods for a large set of organic molecules. J. Chem. Theory Comput. 4, 297–306. doi: 10.1021/ct700248k

PubMed Abstract | CrossRef Full Text | Google Scholar

Tomasetti, C.r., Li, L., and Vogelstein, B. (2017). Stem cell divisions, somatic mutations, cancer etiology, and cancer preventions. Science 355, 1330–1334. doi: 10.1126/science.aaf9011

CrossRef Full Text | Google Scholar

Topal, M. D., and Fresco, J. R. (1976). Complementary base pairing and the origin of substitution mutations. Nature 263, 285–289. doi: 10.1038/263285a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, W., Hellinga, H. W., and Beese, L. S. (2011). Structural evidence for the rare tautomer hypothesis of spontaneous mutagenesis. Proc. Natl. Acad. Sci. U.S.A. 108, 17644–17648. doi: 10.1073/pnas.1114496108

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, J. D., and Crick, F. H. (1953a). Molecular structure of nucleic acids: a structure for deoxyribose nucleic acid. Nature 171, 737–738. doi: 10.1038/171737a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, J. D., and Crick, F. H. C. (1953b). The structure of DNA. Cold Spring Harb. Symp. Quant. Biol. 18, 123–131. doi: 10.1101/SQB.1953.018.01.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, C., Kim, E., and Pak, Y. (2015). Free energy landscape and transition pathways from Watson–Crick to Hoogsteen base pairing in free duplex DNA. Nucleic Acids Res. 43, 7769–7778. doi: 10.1093/nar/gkv796

CrossRef Full Text

Zhou, H. (2016). Occurrence and Function of Hoogsteen Base Pairs in Nucleic Acids. PhD Thesis: Department of Biochemistry, Duke University.