Surprising Conformers of the Biologically Important A·T DNA Base Pairs: QM/QTAIM Proofs

For the first time novel high-energy conformers–A·T(w_WC) (5.36), A·T(w_rWC) (5.97), A·T(w_H) (5.78), and A·T(w_rH) (ΔG = 5.82 kcal·mol⁻¹) (See Graphical Abstract) were revealed for each of the four biologically important A·T DNA base pairs – Watson-Crick A·T(WC), reverse Watson-Crick A·T(rWC), Hoogsteen A·T(H) and reverse Hoogsteen A·T(rH) at the MP2/aug-cc-pVDZ//B3LYP/6-311++G(d,p) level of quantum-mechanical theory in the continuum with ε = 4 under normal conditions. Each of these conformers possesses substantially non-planar wobble (w) structure and is stabilized by the participation of the two anti-parallel N6H/N6H′…O4/O2 and N3H…N6 H-bonds, involving the pyramidalized amino group of the A DNA base as an acceptor and a donor of the H-bonding. The transition states – TS_{A·T(WC)↔A·T(wWC)}, TS_{A·T(rWC)↔A·T(wrWC)}, TS_{A·T(H)↔A·T(wH)}, and TS_{A·T(rH)↔A·T(wrH)}, controlling the dipole-active transformations of the conformers from the main plane-symmetric state into the high-energy, significantly non-planar state and vice versa, were localized. They also possess wobble structures similarly to the high-energy conformers and are stabilized by the participation of the N6H/N6H′…O4/O2 and N3H…N6 H-bonds. Discovered conformers of the A·T DNA base pairs are dynamically stable short-lived structures [lifetime τ = (1.4–3.9) ps]. Their possible biological significance and future perspectives have been briefly discussed.

Introduction

Investigation of the dynamics of the isolated DNA base pairs by both the experimental and especially theoretical methods is urgent biophysical task of exceptional importance (Keepers et al., 1982; Pechenaya and Volkov, 1984; Volkov, 1995; Auffinger and Westhof, 1999). At this, the researchers are convinced that exactly the intrinsic conformational dynamics of the DNA base pairs largely determines the functionally important dynamical behavior of DNA and this approach has no reasonable alternatives.

GRAPHICAL ABSTRACT

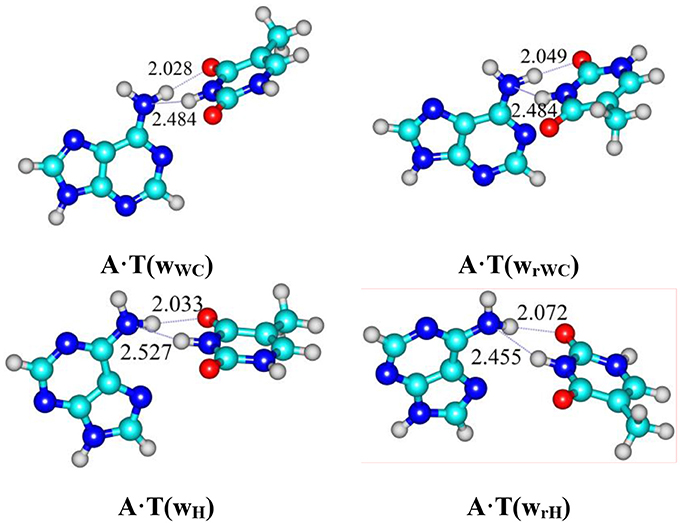
Graphical Abstract. For the first time it was revealed novel high-energy conformers A·T(w_WC) (5.36), A·T(w_rWC) (5.97), A·T(w_H) (5.78) and A·T(w_rH) (ΔG = 4.98 kcal/mol under normal conditions) at the MP2/aug-cc-pVDZ//B3LYP/6-311++G(d,p) level of quantum-mechanical theory in the continuum with ε = 4.

Spontaneous thermal fluctuations or breathing of DNA enables the opening of the DNA base pairs, making reactive their chemical groups, that are normally hidden inside the DNA double helix, available for hydrogen exchange involving imino and amino groups, chemical modification (e.g., by formaldehyde, that is a toxic, mutagenic and carcinogenic compound leading to fatal consequences or mutagenesis) and important protein-DNA interactions by the participation of the regulatory proteins (Lazurkin et al., 1970; Frank-Kamenetskii and Lazurkin, 1974; Lukashin et al., 1976; Chay, 1979; Frank-Kamenetskii, 1981, 1983, 1985; Guéron et al., 1987; Guéron and Leroy, 1995; von Hippel et al., 2013; Frank-Kamenetskii and Prakash, 2014). Notably, that reactions of the hydrogen exchange and formaldehyde interaction with DNA were the first documented cases evidencing the opening of the DNA base pairs (Lazurkin et al., 1970; Frank-Kamenetskii and Lazurkin, 1974; Lukashin et al., 1976; Chay, 1979; Guéron et al., 1987).

Moreover, it is believed that opening of the DNA base pairs with a defined probability ~10⁻⁵ (Lazurkin et al., 1970; Frank-Kamenetskii and Lazurkin, 1974; Lukashin et al., 1976; Frank-Kamenetskii, 1981, 1985; Guéron et al., 1987; Guéron and Leroy, 1995; von Hippel et al., 2013; Frank-Kamenetskii and Prakash, 2014) precedes the melting of DNA, that is represent the two-state model according to which each base pair is suggested to stay in the closed or open states (Frank-Kamenetskii and Lazurkin, 1974; Lukashin et al., 1976; Chay, 1979; Frank-Kamenetskii, 1981, 1983; Guéron et al., 1987; Singh and Singh, 2017). Exactly this model could quantitatively explain in details the melting of DNA processing in the multistate way due the different length and heterogeneous sequence (Vologodskii et al., 1984; Wartell and Benight, 1985; Wada and Suyama, 1986; SantaLucia, 1998). At this, predicted lifetimes of the open state of the base pairs lie in the sub microsecond range (~10⁻⁷ s) (Craig et al., 1971; Porschke and Eigen, 1971; Frank-Kamenetskii, 2011). However, according to the literature data it remains unknown, what the nature of the open state of the DNA base pairs is and whether there is a barrier on the potential energy surface for providing its existence (Lavery, 1994; Stofer et al., 1999; Yang et al., 2015).

It was also demonstrated by NMR experiment (Nikolova et al., 2011, 2013) a Hoogsteen breathing consisting in the flipping of the Watson-Crick DNA base pair from the usual anti-conformation to the less favorable syn-conformation with probability ~10⁻², representing another pathway for the reaction of formaldehyde attack on DNA (Bohnuud et al., 2012).

Since the model of two states—H-bonded base pair and opened base pair—is not able to describe in details the dynamical behavior of DNA, which experimentally manifests itself in a number of its physico-chemical properties (Lazurkin et al., 1970; Craig et al., 1971; Porschke and Eigen, 1971; Frank-Kamenetskii and Lazurkin, 1974; Lukashin et al., 1976; Chay, 1979; Frank-Kamenetskii, 1981, 1983, 1985, 2011; Vologodskii et al., 1984; Wartell and Benight, 1985; Wada and Suyama, 1986; Guéron et al., 1987; Lavery, 1994; Guéron and Leroy, 1995; SantaLucia, 1998; Stofer et al., 1999; Giudice et al., 2001; Ababneh et al., 2003; Coman and Russu, 2005; Nikolova et al., 2011, 2013; Bohnuud et al., 2012; von Hippel et al., 2013; Frank-Kamenetskii and Prakash, 2014; Yang et al., 2015; Singh and Singh, 2017), the searching of new conformational states of the DNA base pairs near their Watson-Crick global minima has been intensified (Keepers et al., 1982; Pechenaya and Volkov, 1984; Volkov, 1995; Giudice et al., 2003; Pérez et al., 2007; Lindahl et al., 2017).

The modeling of the conformational heterogeneity of the Watson-Crick A·T DNA base pair allowing the existence of the semiopen states in DNA, which is associated with the presence of the weak C2H…O2 H-bond in it, and their support by the semi-empirical quantum-chemical MNDO/H (Hovorun, 1997) and PM3 (Kryachko and Volkov, 2001) methods presented in the papers (Hovorun, 1997; Kryachko and Volkov, 2001) seems attractive. Moreover, none of these interesting ideas has been confirmed by ab initio methods.

Nowadays in the literature it does not present the data confirming the presence of the stable conformational states in the isolated Watson-Crick DNA base pairs, except canonical ones (Lavery, 1994; Stofer et al., 1999). It is obviously connected with the lack of the new ideas according as the structural features of the complementary foundations, so the nature of the intermolecular interactions, first of all of the H-bonds responsible for the presence of the conformers, which differs from the classical ones.

In present work basing on our previous data (Brovarets' and Hovorun, 2014a,b,c, 2015a,b; Glushenkov and Hovorun, 2016), we adhere to the idea that the pyramidalized amino group of the adenine (A) DNA base can simultaneously form two antiparallel N6H/N6H′…O4/O2 and N3H…N6 H-bonds with thymine (T) DNA base, thus supporting high-energy non-planar conformers of the biologically important A·T DNA base pairs. We succeeded to localize the transition states (TSs) connecting the main plane-symmetrical conformers of the A·T base pairs (global minimum) with the established significantly non-planar high-energy conformers. On the basis of the obtained data, we expressed the assumption according the possible biological importance of the discovered conformers of the canonical A·T DNA base pairs.

We chose as the object of the investigation of the biologically-important A·T DNA base pairs, in particular–Watson-Crick A·T(WC), reverse Watson-Crick A·T(rWC), Hoogsteen A·T(H) and reverse Hoogsteen A·T(rH) base pairs (Donohue and Trueblood, 1960; Haschemeyer and Sobell, 1963; Hoogsteen, 1963; Tchurikov et al., 1989; Liu et al., 1993; Parvathy et al., 2002; Sühnel, 2002; Zagryadskaya et al., 2003; Brovarets', 2013a,b; Alvey et al., 2014; Nikolova et al., 2014; Yang et al., 2015; Poltev et al., 2016; Zhou, 2016; Sathyamoorthy et al., 2017; Szabat and Kierzek, 2017; Ye et al., 2017).

Thus, the reverse A·T(rWC) Watson-Crick or so-called Donohue DNA base pair (Donohue and Trueblood, 1960), which is formed by the rotation of one of the bases according to the other by 180° around the N1–N3 axis of the Watson-Crick A·T(WC) DNA base pair, has been registered in the bioactive parallel-stranded DNA (Tchurikov et al., 1989; Parvathy et al., 2002; Brovarets', 2013a,b; Poltev et al., 2016; Szabat and Kierzek, 2017; Ye et al., 2017).

The A·T(H) Hoogsteen base pair (Hoogsteen, 1963) is formed due to the rotation on 180° of the A DNA base relative to the T DNA base around the C9-N9 axis from the anti (WC) to syn (H) conformation, representing itself alternative DNA conformation that is involved into a number of biologically important processes such as recognition, damage induction, replication and has been actively investigated in the literature (Hoogsteen, 1963; Brovarets', 2013a,b; Alvey et al., 2014; Nikolova et al., 2014; Yang et al., 2015; Zhou, 2016; Sathyamoorthy et al., 2017). In particular, in the canonical DNA double helix Watson–Crick base pairs exist in a dynamic equilibrium with sparsely populated (~0.02–0.4%) and short-lived (lifetimes ~0.2–2.5 ms) Hoogsteen base pairs (Zhou, 2016).

At this, the reverse A·T(rH) Hoogsteen or so-called Haschemeyer–Sobell base pair (Haschemeyer and Sobell, 1963), that is formed by the rotation of one of the bases by 180° around the N7–N3 axis of the base pair according the other base (Brovarets', 2013a,b), also plays important biological role (Liu et al., 1993; Sühnel, 2002; Zagryadskaya et al., 2003).

Computational Methods

Density Functional Theory Calculations of the Geometry and Vibrational Frequencies

Geometries of the main and high-energy conformers and transition states (TSs) of their mutual conformational transformations, as well as their harmonic vibrational frequencies have been calculated at the B3LYP/6-311++G(d,p) level of theory (Hariharan and Pople, 1973; Krishnan et al., 1980; Lee et al., 1988; Parr and Yang, 1989; Tirado-Rives and Jorgensen, 2008), using Gaussian'09 package (Frisch et al., 2010). Applied level of theory has proved itself successful for the calculations of the similar systems (Brovarets' and Hovorun, 2010a,b, 2015c; Matta, 2010; Brovarets' et al., 2015b). A scaling factor that is equal to 0.9668 has been applied in the present work for the correction of the harmonic frequencies of all conformers and TSs of their conformational transitions (Palafox, 2014; Brovarets' and Hovorun, 2015c; Brovarets' et al., 2015b; El-Sayed et al., 2015). We have confirmed the local minima and TSs, localized by Synchronous Transit-guided Quasi-Newton method (Peng et al., 1996), on the potential energy landscape by the absence or presence, respectively, of the imaginary frequency in the vibrational spectra of the complexes. We applied standard TS theory for the estimation of the activation barriers of the tautomerisation reaction (Atkins, 1998).

All calculations have been carried in the continuum with ε = 4, that adequately reflects the processes occurring in real biological systems without deprivation of the structurally functional properties of the bases in the composition of DNA and satisfactorily models the substantially hydrophobic recognition pocket of the DNA-polymerase machinery as a part of the replisome (Bayley, 1951; Dewar and Storch, 1985; Petrushka et al., 1986; García-Moreno et al., 1997; Mertz and Krishtalik, 2000; Brovarets' and Hovorun, 2014d,e).

Single Point Energy Calculations

We continued geometry optimizations with electronic energy calculations at the single point at the MP2/aug-cc-pVDZ level of theory (Frisch et al., 1990; Kendall et al., 1992).

The Gibbs free energy G for all structures was obtained in the following way:

$\begin{array}{cc}\text{G}={\text{E}}_{\text{el}}{+\text{E}}_{\text{corr}},& (1)\end{array}$

where E_el-electronic energy, while E_corr-thermal correction.

Evaluation of the Interaction Energies

Electronic interaction energies ΔE_int have been calculated at the MP2/6-311++G(2df,pd) level of theory as the difference between the total energy of the base pair and energies of the monomers and corrected for the basis set superposition error (BSSE) (Boys and Bernardi, 1970; Gutowski et al., 1986) through the counterpoise procedure (Sordo et al., 1988; Sordo, 2001).

Estimation of the Kinetic Parameters

The time τ_99.9% necessary to reach 99.9% of the equilibrium concentration of the reactant and product in the system of the reversible first-order forward (k_f) and reverse (k_r) reactions was estimated by the formula (Atkins, 1998):

$\begin{array}{cc}{\tau }_{99.9\%}=\frac{ln{10}^3}{k_f+k_r}.& (2)\end{array}$

The lifetime τ of the conformers has been calculated using the formula 1/k_r, where the values of the forward k_f and reverse k_r rate constants for the tautomerisation reactions were obtained as (Atkins, 1998):

$\begin{array}{cc}{k}_{f,r}=\Gamma ·\frac{k_{B}T}{h}{e}^{-\frac{\Delta \Delta G_{f,r}}{RT}},& (3)\end{array}$

where quantum tunneling effect has been accounted by Wigner's tunneling correction (Wigner, 1932), successfully used for the double proton reactions in DNA base pairs (Brovarets' and Hovorun, 2013, 2014c):

$\begin{array}{cc}\Gamma =1+\frac{1}{24}{\left(\frac{h{\nu }_i}{k_{B}T}\right)}^2,& (4)\end{array}$

where k_B–Boltzmann's constant, h–Planck's constant, ΔΔG_f,r–Gibbs free energy of activation for the conformational transition in the forward (f) and reverse (r) directions, ν_i–magnitude of the imaginary frequency associated with the vibrational mode at the TSs.

QTAIM Analysis

Bader's quantum theory of Atoms in Molecules (QTAIM) (Bader, 1990; Matta and Hernández-Trujillo, 2003; Matta et al., 2006a; Cukrowski and Matta, 2010; Matta, 2014; Lecomte et al., 2015), using program package AIMAll (Keith, 2010), was applied to analyse the electron density distribution. The presence of the bond critical point (BCP), namely the so-called (3,−1) BCP, and a bond path between hydrogen donor and acceptor, as well as the positive value of the Laplacian at this BCP (Δρ > 0), were considered as criteria for the H-bond formation (Bader, 1990; Matta and Hernández-Trujillo, 2003; Matta et al., 2006a; Cukrowski and Matta, 2010; Matta, 2014; Lecomte et al., 2015). Wave functions were obtained at the level of theory used for geometry optimisation.

Calculation of the Energies of the Intermolecular H-bonds

The energies of the intermolecular uncommon H-bonds (Brovarets' et al., 2013, 2015a) in the base pairs were calculated by the empirical Espinosa-Molins-Lecomte (EML) formula based on the electron density distribution at the (3,−1) BCPs of the specific contacts (Espinosa et al., 1998; Matta, 2006; Matta et al., 2006b; Mata et al., 2011; Brovarets' et al., 2014a):

$\begin{array}{cc}E=0.5·\text{V}(\text{r}),& (5)\end{array}$

where V(r) – value of a local potential energy at the (3,−1) BCP.

The energies of all other conventional AH···B H-bonds were evaluated by the empirical Iogansen's formula (Iogansen, 1999):

$\begin{array}{cc}{E}_{AH···B}=0.33·\sqrt{\Delta \nu -40},& (6)\end{array}$

where Δν—magnitude of the frequency shift of the stretching mode of the AH H-bonded group involved in the AH···B H-bond relatively the unbound group. The partial deuteration was applied to minimize the effect of vibrational resonances (Brovarets' and Pérez-Sánchez, 2016a, 2017; Brovarets' et al., 2016, 2017a,b, 2018; Brovarets' and Hovorun, in press).

The atomic numbering scheme for the DNA bases is conventional (Saenger, 1984).

Results and Their Discussion

For the first time we have detected on the potential (electronic) energy surface of each of the four biologically important A·T(WC), A·T(rWC), A·T(H) and A·T(rH) DNA base pairs the shallow local minima (ΔΔE < kT under normal conditions) corresponding to the dynamically stable A·T(w_WC), A·T(w_rWC), A·T(w_H) and A·T(w_rH) conformers, correspondingly, with shifted, wobble (w) architecture (Figure 1). These conformers possess significantly non-planar structure (see Table 1 with the selected angles of the non-planarity) and C₁ point group of symmetry. At this, the piramidalized amino group of the A DNA base is involved into the intermolecular H-bonding with T base through two anti-parallel N6H…O4/O2 and N3H…N6 H-bonds in the A·T(WC)/A·T(rWC) base pairs and N6H′…O4/O2 and N3H…N6 H-bonds in the A·T(H)/A·T(rH) DNA base pairs. In all conformers and TSs without exception the N3H…N6 H-bonds with significantly increased ellipticity are weaker than the N6H/N6H′…O4/O2 H-bonds (Table 2). These interactions should be attributed to the weak and medium H-bonds according to the existing classification (Saenger, 1984). Their most important characteristics are presented in Table 2. It should be noted that each of the four investigated A·T DNA base pairs in the basic plane-symmetric conformation is stabilized by the participation of the three intermolecular H-bonds, one of which, namely, the C2H/C8H…O4/O2 is non-canonical (Brovarets' et al., 2013, 2015a). For all A·T DNA base pairs without exception the middle N3H…N1/N7 H-bonds are the strongest (~7 kcal·mol⁻¹). At this, the total energy of the intermolecular H-bonds in each complex consists only some part of the total electronic energy of the interaction between the bases (Figure 1, Table 2). The same regularity is observed for the other DNA base pairs (Brovarets' et al., 2014b; Brovarets' and Hovorun, 2015d,e,f,g, 2016b). For all conformers without exception the amino H or H' atom of the A DNA base, that directly takes part in the H-bonding with T DNA base, significantly deviates from the plane of the purine ring in comparison with the other H′ or H hydrogen atom (Table 1). In all cases the high-energy conformers of the biologically important A·T base pairs are more polar than main conformers (Table 2).

FIGURE 1

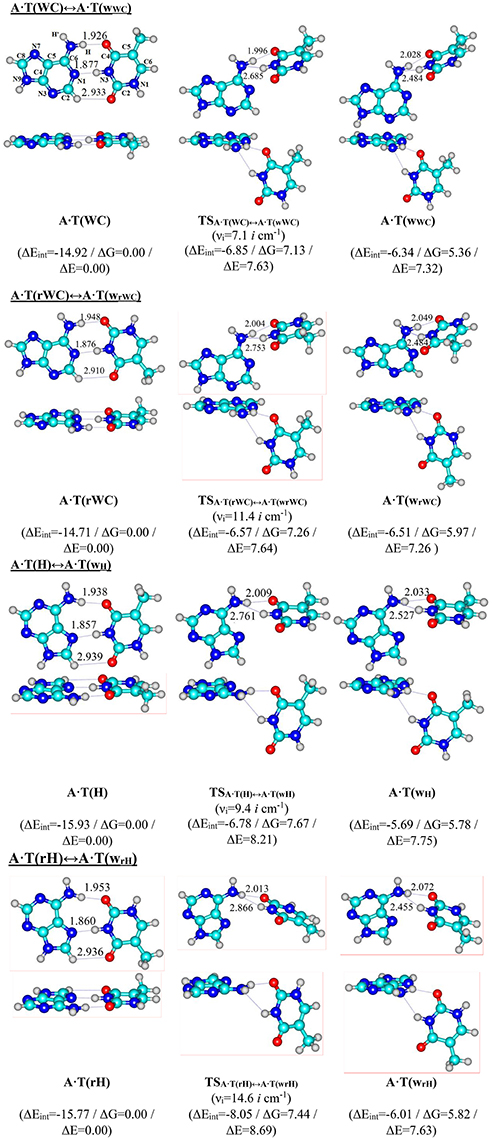
Figure 1. Reaction pathways of the discovered conformational transitions of the four biologically important A·T DNA base pairs. Electronic energies of the interaction ΔE_int (MP2/6-311++G(2df,pd)//B3LYP/6-311++G(d,p) level of theory, in kcal·mol⁻¹), relative Gibbs free energies ΔG and electronic energies ΔE (in kcal·mol⁻¹), imaginary frequencies ν_i at the TSs of the conformational transitions (MP2/aug-cc-pVDZ//B3LYP/6-311++G(d,p) level of theory in the continuum with ε = 4 at T = 298.15 K) are presented below pathways in brackets. Dotted lines indicate AH···B H-bonds – their lengths are presented in angstroms (for more detailed physico-chemical characteristics of the H-bonds see Table 2); carbon atoms are in light-blue, nitrogen – in dark-blue, hydrogen – in gray and oxygen – in red.

TABLE 1

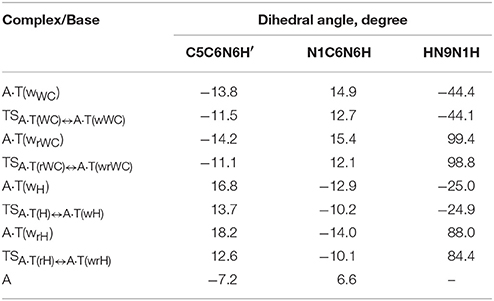
Table 1. Selected geometrical parameters characterizing the non-planarity of the discovered conformers of the four biologically important A·T DNA base pairs and TSs of their conformational transitions to the main conformers with plane symmetry, obtained at the B3LYP/6-311++G(d,p) level of theory in the continuum with ε = 4.

TABLE 2

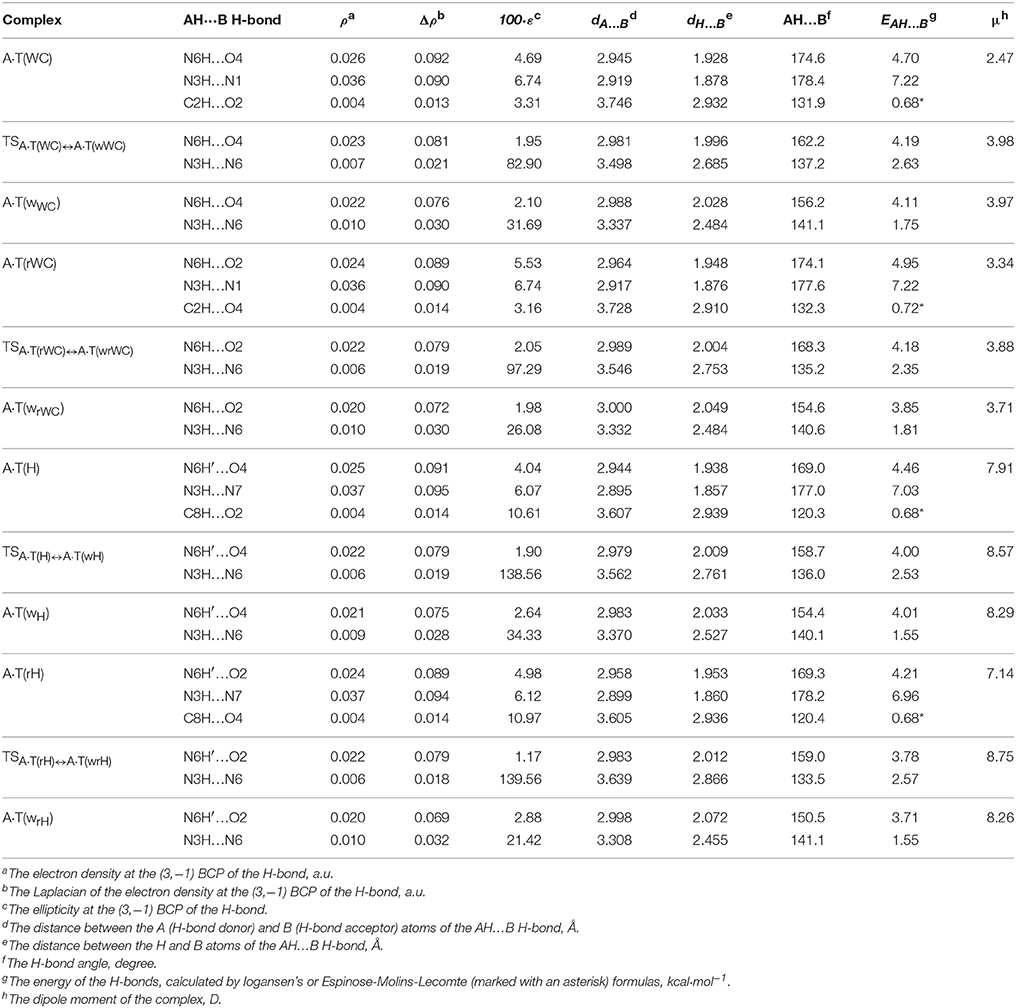
Table 2. Electron-topological, geometrical and energetic characteristics of the intermolecular H-bonds in the investigated conformers of the A·T DNA base pairs and TSs of their conformational transformations obtained at the B3LYP/6-311++G(d,p) level of theory (ε = 4) (see Figure 1).

We have also localized the non-planar transition states of the A·T(WC)↔A·T(w_WC), A·T(rWC)↔A·T(w_rWC), A·T(H)↔A·T(w_H) and A·T(rH)↔A·T(w_rH) conformational transitions - TS_{A·T(WC)↔A·T(wWC)}, TS_{A·T(rWC)↔A·T(wrWC)}, TS_{A·T(H)↔A·T(wH)} and TS_{A·T(rH)↔A·T(wrH)}, respectively, with low values of imaginary frequency (7.1, 11.4, 9.4 and 14.6 i cm⁻¹). These wobble structures (Table 1) are supported by the couple of the anti-parallel intermolecular H-bonds - N6H…O4/O2 and N3H…N6 H-bonds (A·T(WC)↔A·T(w_WC) and A·T(rWC)↔A·T(w_rWC), respectively), N6H′…O4/O2 and N3H…N6 H-bonds (A·T(H)↔A·T(w_H) and A·T(rH)↔A·T(w_rH), respectively) (Figure 1, Table 2). Characteristically, that all revealed conformational transitions without exception are dipole-active, since they are accompanied by the changing of the dipole moment of the initial and terminal base pairs. At this, TSs of each conformational transition have maximal value of the dipole moment (Table 2).

Main characteristics of the investigated conformational transitions are presented in Table 3. Analysis of these data points that short-lived conformers are dynamically-stable structures with the lifetimes (1.4–3.9) · 10⁻¹² s. Really, for all of them the energy of zero vibrations, which frequency become imaginary in the TS, is less than the electronic energy of the electronic energy barrier ΔΔE for the reverse conformational transition and Gibbs free energy barrier for the reverse conformational transition ΔΔG > 0 under normal conditions. Notably, the range of the six low-frequency intermolecular vibrations of the discovered conformers is significantly shifted to the low-frequency region comparably with the main conformational states. These data points on the fact that revealed conformers are quite soft structures, that could be easily deformed under the influence of the external forces, in particular, caused by the stacking interactions with the neighboring DNA bases.

TABLE 3

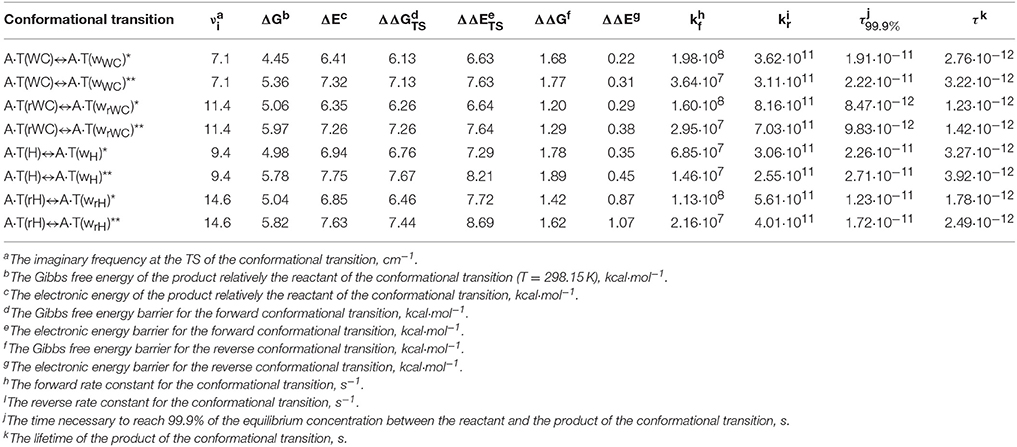
Table 3. Energetic and kinetic characteristics of the discovered conformational transitions of the four biologically important A·T DNA base pairs obtained at the MP2/6-311++G(2df,pd)//B3LYP/6-311++G(d,p) (marked by the asterisk) and MP2/aug-cc-pVDZ//B3LYP/6-311++G(d,p) (marked by the double asterisk) levels of theory in the continuum with ε = 4.

The methyl group of the T DNA base does not change its orientation during the process of the conformational transformations. Moreover, the heterocycles of the bases remain planar, despite their ability for the out-of-plane bending (Govorun et al., 1992; Hovorun et al., 1999; Nikolaienko et al., 2011).

Special attention should be payed to the characteristic specificities of the A·T(WC)↔A·T(w_WC), A·T(rWC)↔A·T(w_rWC), A·T(H)↔A·T(w_H) and A·T(rH)↔A·T(w_rH) conformational transformations. These reactions are non-dissociative, since they are accompanied by the transformation of the H-bonds and rupture of only some of them. Intermolecular N6H/N6H′…O4/O2 H-bonds exist along all intrinsic reaction coordinate opposite the N3H…N1/N7 H-bonds, that initially weaken and then rupture with a time delay in order to transform into the N3H…N6 H-bond. In other words, in the process of the conformational transformations the N3H group of the T DNA base as proton donor remain for some time free from the intermolecular H-bonding. This comes up with an opinion that discovered conformational transitions could be used for the explanation of the occurrence of the hydrogen-deuterium exchange in the A·T DNA base pairs. It is not excluded that revealed by us novel corridor of the spontaneous thermal fluctuations of the A·T DNA base pairs accompanied by the transformation of the base pair from the plane-symmetric geometry into the significantly non-planar wobble conformation could be useful for the explanation of the specificities of the blurriness of the transition at the DNA pre-melting enriched by the A·T DNA base pairs, that could not be explained in details in the framework of the two-states model.

We would continue to work in the direction of the elucidation of the biological importance of the revealed unusual conformers of the biologically important A·T DNA base pairs.

Conclusions

In general, in this work at the MP2/aug-cc-pVDZ//B3LYP/6-311++G(d,p) level of theory in the continuum with ε = 4 for the first time we have revealed the A·T(WC)↔A·T(w_WC), A·T(rWC)↔A·T(w_rWC), A·T(H)↔A·T(w_H) and A·T(rH)↔A·T(w_rH) conformational transformations in the biologically important A·T DNA base pairs and characterized their structural, energetic, polar and dynamical features. These data open new perspectives for the understanding of the physico-chemical mechanisms of the opening of the base pairs preceding DNA melting and also to describe in details the breathing of DNA, that has been experimentally registered. Moreover, it is also the subject for the investigation by using modern spectroscopic techniques such as two-dimensional fluorescent spectroscopy (2DFS) (Widom et al., 2013), time-resolved single molecule fluorescence resonant energy transfer (smFRET) (Lee et al., 2013), single molecule fluorescent linear dichroism (smFLD) (Phelps et al., 2013) and THz spectroscopy (Alexandrov et al., 2013).

Author Contributions

OB, performance of calculations, discussion of the obtained data, preparation of the text of the manuscript. DH, proposition of the task of the investigation, discussion of the obtained data, preparation of the text of the manuscript. KT, preparation of the numerical data for Tables and graphical materials for Figures, preparation of the text of the manuscript. All authors were involved in the proofreading of the final version of the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors gratefully appreciate technical support and computational facilities of joint computer cluster of SSI “Institute for Single Crystals” of the National Academy of Sciences of Ukraine (NASU) and Institute for Scintillation Materials of the NASU incorporated into Ukrainian National Grid. This work was partially supported by the Grant of the NASU for young scientists (contract N 50/17), Grant of the President of Ukraine to support the research of young scientists (project N F 70/17906/2017; contract N F 70/189-2017) from the State Fund for Fundamental Research of Ukraine of the Ministry of the Education and Science of Ukraine and by the Scholarship of Verkhovna Rada (Parliament) of Ukraine for the talented young scientists in 2017 year given to OB. OB expresses sincere gratitude to organizers [Prof. Daniel Otzen (Chairman) (Denmark) and Prof. M. Madan Babu (UK)] for financial support of the participation in the “EMBO/FEBS Lecture Course Spetsai Summer School 2017 for Proteins and Organized Complexity” (September 24–October 1, 2017, Spetses, Greece), to Lawyers Association “AVER Lex” (Kyiv, Ukraine) for the sponsorship of the presenting the plenary lecture as invited speaker at the “EMN Meeting on Computation and Theory 2017” (November 6–10, 2017, Dubai, United Arab Emirates) and to Max Plank Institute of Molecular Plant Physiology (hosted by Prof. Yariv Brotman) for the kind invitation and financial support of the invited lecture (November 29, 2017, Potsdam, Germany).

References

Ababneh, A. M., Large, C. C., and Georghiou, S. (2003). Solvation of nucleosides in aqueous mixtures of organic solvents: relevance to DNA open base pairs. Biophys. J. 85, 1111–1127. doi: 10.1016/S0006-3495(03)74548-2

CrossRef Full Text | Google Scholar

Alexandrov, B. S., Phipps, M. L., Alexandrov, L. B., Booshehri, L. G., Erat, A., Zabolotny, J., et al. (2013). Specificity and heterogeneity of terahertz radiation effect on gene expression in mouse mesenchymal stem cells. Sci. Rep. 3, 1184–1191. doi: 10.1038/srep01184

PubMed Abstract | CrossRef Full Text | Google Scholar

Alvey, H. S., Gottardo, F. L., Nikolova, E. N., and Al-Hashimi, H. M. (2014). Widespread transient Hoogsteen base-pairs in canonical duplex DNA with variable energetics. Nat. Comm. 5, 4786–4794. doi: 10.1038/ncomms5786

PubMed Abstract | CrossRef Full Text | Google Scholar

Atkins, P. W. (1998). Physical Chemistry. Oxford: Oxford University Press.

PubMed Abstract | Google Scholar

Auffinger, P., and Westhof, E. (1999). Singly and bifurcated hydrogen-bonded base-pairs in tRNA anticodon hairpins and ribozymes. J. Mol. Biol. 292, 467–483. doi: 10.1006/jmbi.1999.3080

PubMed Abstract | CrossRef Full Text | Google Scholar

Bader, R. F. W. (1990). Atoms in Molecules: A Quantum Theory. Oxford: Oxford University Press.

Bayley, S. T. (1951). The dielectric properties of various solid crystalline proteins, amino acids and peptides. Trans. Faraday Soc. 47, 509–517. doi: 10.1039/tf9514700509

CrossRef Full Text | Google Scholar

Bohnuud, T., Beglov, D., Ngan, C. H., Zerbe, B., Hall, D. R., Brenke, R., et al. (2012). Computational mapping reveals dramatic effect of Hoogsteen breathing on duplex DNA reactivity with formaldehyde. Nucl. Acids Res. 40, 7644–7652. doi: 10.1093/nar/gks519

PubMed Abstract | CrossRef Full Text | Google Scholar

Boys, S. F., and Bernardi, F. (1970). The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 19, 553–566. doi: 10.1080/00268977000101561

CrossRef Full Text | Google Scholar

Brovarets', O. O., Yurenko, Y. P., and Hovorun, D. M. (2015a). The significant role of the intermolecular CH…O/N hydrogen bonds in governing the biologically important pairs of the DNA and RNA modified bases: a comprehensive theoretical investigation. J. Biomol. Struct. Dynam. 33, 1624–1652. doi: 10.1080/07391102.2014.968623

CrossRef Full Text

Brovarets', O. O., Zhurakivsky, R. O., and Hovorun, D. M. (2015b). DPT tautomerisation of the wobble guanine·thymine DNA base mispair is not mutagenic: QM and QTAIM arguments. J. Biomol. Struct. Dynam. 33, 674–689. doi: 10.1080/07391102.2014.897259

CrossRef Full Text | Google Scholar

Brovarets', O. O. (2013a). Under what conditions does G·C Watson-Crick DNA base pair acquire all four configurations characteristic for A·T Watson-Crick DNA base pair? Ukr. Biochem. J. 85, 98–103. doi: 10.15407/ubj85.04.098

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O. (2013b). Structural and energetic properties of the four configurations of the A·T and G·C DNA base pairs. Ukr. Biochem. J. 85, 104–110. doi: 10.15407/ubj85.04.104

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2010a). Quantum-chemical investigation of tautomerization ways of Watson-Crick DNA base pair guanine-cytosine. Ukr. Biochem. J. 82, 55–60. Available online at: http://ubj.biochemistry.org.ua/images/stories/pdf/ubj3_2010/Brovarets_82_3.pdf

PubMed Abstract | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2010b). Quantum-chemical investigation of the elementary molecular mechanisms of pyrimidine-purine transversions. Ukr. Biochem. J. 82, 57–67. Available online at: http://ubj.biochemistry.org.ua/images/stories/pdf/UBJ_%20N%205_2010/Brovarets-2_82_5.pdf

PubMed Abstract | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2013). Atomistic nature of the DPT tautomerisation of the biologically important C·C* DNA base mispair containing amino and imino tautomers of the cytosine: a QM and QTAIM approach. Phys. Chem. Chem. Phys. 15, 20091–20104. doi: 10.1039/c3cp52644e

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2014a). Does the ${\text{G}·\text{G}}_{\text{syn}}^{*}$ DNA mismatch containing canonical and rare tautomers of the guanine tautomerise through the DPT? A QM/QTAIM microstructural study. Mol. Phys. 112, 3033–3046. doi: 10.1080/00268976.2014.927079

CrossRef Full Text

Brovarets', O. O., and Hovorun, D. M. (2014b). How the long G·G* Watson-Crick DNA base mispair comprising keto and enol tautomers of the guanine tautomerises? The results of the QM/QTAIM investigation. Phys. Chem. Chem. Phys. 6, 15886–15899. doi: 10.1039/C4CP01241K

CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2014c). DPT tautomerisation of the G·A_syn and A*·${\text{G}}_{\text{syn}}^{*}$ DNA mismatches: a QM/QTAIM combined atomistic investigation. Phys. Chem. Chem. Phys. 16, 9074–9085. doi: 10.1039/C4CP00488D

PubMed Abstract | CrossRef Full Text

Brovarets', O. O., and Hovorun, D. M. (2014d). Can tautomerisation of the A·T Watson-Crick base pair via double proton transfer provoke point mutations during DNA replication? A comprehensive QM and QTAIM analysis. J. Biomol. Struct. Dynam. 32, 127–154. doi: 10.1080/07391102.2012.755795

CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2014e). Why the tautomerization of the G·C Watson–Crick base pair via the DPT does not cause point mutations during DNA replication? QM and QTAIM comprehensive analysis. J. Biomol. Struct. Dynam. 32, 1474–1499. doi: 10.1080/07391102.2013.822829

CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2015a). How many tautomerisation pathways connect Watson-Crick-like G*·T DNA base mispair and wobble mismatches? J. Biomol. Struct. Dynam. 33, 2297–2315. doi: 10.1080/07391102.2015.1046936

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2015b). Novel physico-chemical mechanism of the mutagenic tautomerisation of the Watson–Crick-like A·G and C·T DNA base mispairs: a quantum-chemical picture. RSC Adv. 5, 66318–66333. doi: 10.1039/C5RA11773A

CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2015c). The nature of the transition mismatches with Watson-Crick architecture: the G*·T or G·T* DNA base mispair or both? A QM/QTAIM perspective for the biological problem. J. Biomol. Struct. Dynam. 33, 925–945. doi: 10.1080/07391102.2014.924879

CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2015d). New structural hypostases of the A·T and G·C Watson-Crick DNA base pairs caused by their mutagenic tautomerisation in a wobble manner: a QM/QTAIM prediction. RSC Adv. 5, 99594–99605. doi: 10.1039/C5RA19971A

CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2015e). Tautomeric transition between wobble A·C DNA base mispair and Watson-Crick-like A·C* mismatch: miscrostructural mechanism and biological significance. Phys. Chem. Chem. Phys. 17, 15103–15110. doi: 10.1039/C5CP01568E

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2015f). Wobble↔Watson-Crick tautomeric transitions in the homo-purine DNA mismatches: a key to the intimate mechanisms of the spontaneous transversions. J. Biomol. Struct. Dynam. 33, 2710–2715. doi: 10.1080/07391102.2015.1077737

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2015g). A novel conception for spontaneous transversions caused by homo-pyrimidine DNA mismatches: a QM/QTAIM highlight. Phys. Chem. Chem. Phys. 17, 21381–21388. doi: 10.1039/C5CP03211C

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O., and Hovorun, D. M. (2016b). By how many tautomerisation routes the Watson-Crick-like A·C* DNA base mispair is linked with the wobble mismatches? A QM/QTAIM vision from a biological point of view. Struct. Chem. 27, 119–131. doi: 10.1007/s11224-015-0687-4

CrossRef Full Text

Brovarets', O. O., and Hovorun, D. M. (in press). Key microstructural mechanisms of the 2-aminopurine mutagenicity: Results of thorough quantum-chemical research. Phys. Chem. Chem. Phys.

Brovarets', O. O., and Pérez-Sánchez, H. E. (2016a). Whether the amino-imino tautomerism of 2-aminopurine is involved into its mutagenicity? Results of a thorough QM investigation. RSC Adv. 110, 108255–108264. doi: 10.1039/C6RA24277D

CrossRef Full Text

Brovarets', O. O., and Pérez-Sánchez, H. E. (2017). Whether 2-aminopurine induces incorporation errors at the DNA replication? A quantum-mechanical answer on the actual biological issue. J. Biomol. Struct. Dynam. 35, 3398–3411. doi: 10.1080/07391102.2016.1253504

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O., Pérez-Sánchez, H. E., and Hovorun, D. M. (2016). Structural grounds for the 2-aminopurine mutagenicity: a novel insight into the old problem of the replication errors. RSC Adv. 6, 99546–99557. doi: 10.1039/C6RA17787E

CrossRef Full Text | Google Scholar

Brovarets', O. O., Voiteshenko, I. S., and Hovorun, D. M. (2018). Physico-chemical profiles of the wobble↔Watson-Crick G*·2AP(w)↔G·2AP(WC) and A·2AP(w)↔A*·2AP(WC) tautomerisations: a QM/QTAIM comprehensive survey. Phys. Chem. Chem. Phys. 20, 623–636. doi: 10.1039/C7CP05139E

CrossRef Full Text | Google Scholar

Brovarets', O. O., Voiteshenko, I. S., Pérez-Sánchez, H. E., and Hovorun, D. M. (2017b). A QM/QTAIM research under the magnifying glass of the DPT tautomerisation of the wobble mispairs involving 2-aminopurine. New J. Chem. 41, 7232–7243. doi: 10.1039/C7NJ00717E

CrossRef Full Text | Google Scholar

Brovarets', O. O., Voiteshenko, I. S., Pérez-Sánchez, H., and Hovorun, D. M. (2017a). A QM/QTAIM detailed look at the Watson-Crick↔wobble tautomeric transformations of the 2-aminopurine·pyrimidine mispairs. J. Biomol. Struct. Dynam. doi: 10.1080/07391102.2017.1331864. [Epub ahead of print].

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets', O. O., Yurenko, Y. P., and Hovorun, D. M. (2013). Intermolecular CH…O/N H-bonds in the biologically important pairs of natural nucleobases: a thorough quantum-chemical study. J. Biomol. Struct. Dynam. 32, 993–1022. doi: 10.1080/07391102.2013.799439

CrossRef Full Text

Brovarets', O. O., Zhurakivsky, R. O., and Hovorun, D. M. (2014a). Is the DPT tautomerisation of the long A·G Watson-Crick DNA base mispair a source of the adenine and guanine mutagenic tautomers? A QM and QTAIM response to the biologically important question. J. Comput. Chem. 35, 451–466. doi: 10.1002/jcc.23515

CrossRef Full Text | Google Scholar

Brovarets', O. O., Zhurakivsky, R. O., and Hovorun, D. M. (2014b). Structural, energetic and tautomeric properties of the T·T*/T*·T DNA mismatch involving mutagenic tautomer of thymine: a QM and QTAIM insight. Chem. Phys. Lett. 592, 247–255. doi: 10.1016/j.cplett.2013.12.034

CrossRef Full Text | Google Scholar

Chay, T. (1979). Mechanism for unwinding of double-helical polynucleotides by formaldehyde. Biopolymers 18, 1439–1464. doi: 10.1002/bip.1979.360180609

PubMed Abstract | CrossRef Full Text | Google Scholar

Coman, D., and Russu, I. M. (2005). A nuclear magnetic resonance investigation of the energetics of base pair opening pathways in DNA. Biophys. J. 89, 3285–3292. doi: 10.1529/biophysj.105.065763

CrossRef Full Text | Google Scholar

Craig, M. E., Crothers, D. M., and Doty, P. (1971). Relaxation kinetics of dimer formation by self complementary oligonucleotides. J. Mol. Biol. 62, 383–401. doi: 10.1016/0022-2836(71)90434-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Cukrowski, I., and Matta, C. F. (2010). Hydrogen–hydrogen bonding: a stabilizing interaction in strained chelating rings of metal complexes in aqueous phase. Chem. Phys. Lett. 499, 66–69. doi: 10.1016/j.cplett.2010.09.013

CrossRef Full Text | Google Scholar

Dewar, M. J., and Storch, D. M. (1985). Alternative view of enzyme reactions. Proc. Natl. Acad. Sci. U.S.A. 82, 2225–2229. doi: 10.1073/pnas.82.8.2225

PubMed Abstract | CrossRef Full Text | Google Scholar

Donohue, J., and Trueblood, K. N. (1960). Base pairing in DNA. J. Mol. Biol. 2, 363–371. doi: 10.1016/S0022-2836(60)80047-2

PubMed Abstract | CrossRef Full Text | Google Scholar

El-Sayed, A. A., Tamara Molina, A., Alvarez-Ros, M. C., and Alcolea Palafox, M. (2015). Conformational analysis of the anti-HIV Nikavir prodrug: comparisons with AZT and thymidine, and establishment of structure-activity relationships/tendencies in other 60-derivatives. J. Biomol. Struct. Dynam. 33, 723–748. doi: 10.1080/07391102.2014.909743

CrossRef Full Text | Google Scholar

Espinosa, E., Molins, E., and Lecomte, C. (1998). Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 285, 170–173. doi: 10.1016/S0009-2614(98)00036-0

CrossRef Full Text | Google Scholar

Frank-Kamenetskii, M. D. (1981). Fluctuations in DNA. Comm. Mol. Cell. Biophys. 1, 105–114.

Frank-Kamenetskii, M. D. (1983). Fluctuation mobility of DNA. Mol. Biol. 17, 639–652.

Frank-Kamenetskii, M. D. (1985). “Fluctutional motility of DNA,” in Structure & Motion: Membranes, Nucleic Acids & Proteins, eds E. Clementi, G. Corongiu, M. H. Sarma, and R. H. Sarma (New York. NY: Adenine Press), 417–32.

Frank-Kamenetskii, M. D. (2011). DNA breathes Hoogsteen. Artif. DNA PNA XNA 2, 1–3. doi: 10.4161/adna.2.1.15509

PubMed Abstract | CrossRef Full Text | Google Scholar

Frank-Kamenetskii, M. D., and Lazurkin, Y. S. (1974). Conformational changes in DNA molecule. Ann. Rev. Biophys. Bioeng. 3, 127–150. doi: 10.1146/annurev.bb.03.060174.001015

CrossRef Full Text | Google Scholar

Frank-Kamenetskii, M., and Prakash, S. (2014). Fluctuations in the DNA double helix: a critical review. Phys. Life Rev. 11, 153–170. doi: 10.1016/j.plrev.2014.01.005

CrossRef Full Text | Google Scholar

Frisch, M. J., Head-Gordon, M., and Pople, J. A. (1990). Semi-direct algorithms for the MP2 energy and gradient. Chem. Phys. Lett. 166, 281–289. doi: 10.1016/0009-2614(90)80030-H

CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2010). GAUSSIAN 09 (Revision, B.01). Wallingford CT: Gaussian Inc.

Google Scholar

García-Moreno, B., Dwyer, J. J., Gittis, A. G., Lattman, E. E., Spencer, D. S., and Stites, W. E. (1997). Experimental measurement of the effective dielectric in the hydrophobic core of a protein. Biophys. Chem. 64, 211–224. doi: 10.1016/S0301-4622(96)02238-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Giudice, E., Várnai, P., and Lavery, R. (2003). Base pair opening within B-DNA: free energy pathways for GC and AT pairs from umbrella sampling simulations. Nucleic Acids Res. 31, 1434–1443. doi: 10.1093/nar/gkg239

PubMed Abstract | CrossRef Full Text

Giudice, E., Várnai, P., and Lavery, R. (2001). Energetic and conformational aspects of A:T base-pair opening within the DNA double helix. Chem. Phys. Chem. 2, 673–677. doi: 10.1002/1439-7641(20011119)2:11<673::AID-CPHC673>3.0.CO;2-S

PubMed Abstract | CrossRef Full Text | Google Scholar

Glushenkov, A. N., and Hovorun, D. M. (2016). Can nucleobase pairs offer a possibility of a direct 3D self-assembly? Nan. Res. Lett. 11, 134–140. doi: 10.1186/s11671-016-1347-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Govorun, D. M., Danchuk, V. D., Mishchuk, Y. R., Kondratyuk, I. V., Radomsky, N. F., and Zheltovsky, N. V. (1992). AM1 calculation of the nucleic acid bases structure and vibrational spectra. J. Mol. Struct. 267, 99–103. doi: 10.1016/0022-2860(92)87016-O

CrossRef Full Text | Google Scholar

Guéron, M., Kochoyan, M., and Leroy, J. L. (1987). A single mode of DNA base-pair opening drives imino proton exchange. Nature 328, 89–92. doi: 10.1038/328089a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Guéron, M., and Leroy, J. L. (1995). Studies of base pair kinetics by NMR measurement of proton exchange. Meth. Enzymol. 261, 383–413. doi: 10.1016/S0076-6879(95)61018-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Gutowski, M., Van Lenthe, J. H., Verbeek, J., Van Duijneveldt, F. B., and Chalasinski, G. (1986). The basis set superposition error in correlated electronic structure calculations. Chem. Phys. Lett. 124, 370–375. doi: 10.1016/0009-2614(86)85036-9

CrossRef Full Text | Google Scholar

Hariharan, P. C., and Pople, J. A. (1973). The influence of polarization functions on molecular orbital hydrogenation energies. Theor. Chim. Acta 28, 213–222. doi: 10.1007/BF00533485

CrossRef Full Text | Google Scholar

Haschemeyer, A. E., and Sobell, H. M. (1963). The crystal structure of an intermolecular nucleoside complex: adenosine and 5-bromouridine. Proc. Natl Acad. Sci. U.S.A. 50, 872–877. doi: 10.1073/pnas.50.5.872

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoogsteen, K. (1963). The crystal and molecular structure of a hydrogenbonded complex between 1-methylthymine and 9-methyladenine. Acta Cryst. 16, 907–916. doi: 10.1107/S0365110X63002437

CrossRef Full Text | Google Scholar

Hovorun, D. M. (1997). A structural-dynamic model on spontaneous semiopen states in DNA. Biopolym. Cell 13, 39–45. doi: 10.7124/bc.000465

CrossRef Full Text | Google Scholar

Hovorun, D. M., Gorb, L., and Leszczynski, J. (1999). From the nonplanarity of the amino group to the structural nonrigidity of the molecule: a post-Hartree-Fock ab initio study of 2-aminoimidazole. Int. J. Quantum Chem. 75, 245–253. doi: 10.1002/(SICI)1097-461X(1999)75:3<245::AID-QUA14>3.0.CO;2-0

CrossRef Full Text | Google Scholar

Iogansen, A. V. (1999). Direct proportionality of the hydrogen bonding energy and the intensification of the stretching ν(XH) vibration in infrared spectra. Spectrochim. Acta A Mol. Biomol. Spectrosc. 55, 1585–1612. doi: 10.1016/S1386-1425(98)00348-5

CrossRef Full Text | Google Scholar

Keepers, J. W., Kollman, P. A., Weiner, P. K., and James, T. L. (1982). Molecular mechanical studies of DNA flexibility: coupled backbone torsion angles and base-pair openings. Proc. Natl. Acad. Sci. U.S.A. 79, 5537–5541. doi: 10.1073/pnas.79.18.5537

PubMed Abstract | CrossRef Full Text | Google Scholar

Keith, T. A. (2010). AIMAll (Version 10.07.01). Available online at: aim.tkgristmill.com.

Kendall, R. A., Dunning, T. H. Jr., and Harrison, R. J. (1992). Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 96, 6796–6806. doi: 10.1063/1.462569

CrossRef Full Text | Google Scholar

Krishnan, R., Binkley, J. S., Seeger, R., and Pople, J. A. (1980). Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 72, 650–654. doi: 10.1063/1.438955

CrossRef Full Text | Google Scholar

Kryachko, E. S., and Volkov, S. N. (2001). Preopening of the DNA Base Pairs. Int. J. Quantum Chem. 82, 193–204. doi: 10.1002/qua.1040

CrossRef Full Text | Google Scholar

Lavery, R. (1994). Modeling nucleic acids: fine structure, flexibility, and conformational transitions. Adv. Comput. Biol. 1, 69–145.

Lazurkin, Y. S., Frank-Kamanetskii, M. D., and Trifonov, E. N. (1970). Melting of DNA: its study and application as a research method. Biopolymers 9, 1253–1306. doi: 10.1002/bip.1970.360091102

PubMed Abstract | CrossRef Full Text | Google Scholar

Lecomte, C., Espinosa, E., and Matta, C. F. (2015). On atom–atom 'short contact' bonding interactions in crystals. IUCrJ 2, 161–163. doi: 10.1107/S2052252515002067

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, C., Yang, W., and Parr, R. G. (1988). Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 37, 785–789. doi: 10.1103/PhysRevB.37.785

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, W., Jose, D., Phelps, C., Marcus, A. H., and von Hippel, P. H. (2013). A Single-molecule view of the assembly pathway, subunit stoichiometry, and unwinding activity of the bacteriophage T4 primosome (helicase–primase) complex. Biochemistry 52, 3157–3170. doi: 10.1021/bi400231s

PubMed Abstract | CrossRef Full Text | Google Scholar

Lindahl, V., Villa, A., and Hess, B. (2017). Sequence dependency of canonical base pair opening in the DNA double helix. PLoS Comput. Biol. 13:e1005463. doi: 10.1371/journal.pcbi.1005463

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, K., Miles, H. T., Frazier, J., and Sasisekharan, V. (1993). A novel DNA duplex. A parallel-stranded DNA helix with Hoogsteen base pairing. Biochemistry 32, 11802–11809. doi: 10.1021/bi00095a008

PubMed Abstract | CrossRef Full Text | Google Scholar

Lukashin, A. V., Vologodskii, A. V., Frank-Kamenetskii, M. D., and Lyubchenko, Y. L. (1976). Fluctuational opening of the double helix as revealed by theoretical and experimental study of DNA interaction with formaldehyde. J. Mol. Biol. 108, 665–682. doi: 10.1016/S0022-2836(76)80111-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Mata, I., Alkorta, I., Espinosa, E., and Molins, E. (2011). Relationships between interaction energy, intermolecular distance and electron density properties in hydrogen bonded complexes under external electric fields. Chem. Phys. Lett. 507, 185–189. doi: 10.1016/j.cplett.2011.03.055

CrossRef Full Text | Google Scholar

Matta, C. F. (2006). “Chapter 9: Hydrogen–hydrogen bonding: the non-electrostatic limit of closed-shell interaction between two hydrogen atoms. A critical review,” in Hydrogen Bonding—New Insights, ed S. J. Grabowski (Dordrecht: Springer), 337–375.

Google Scholar

Matta, C. F. (2010). How dependent are molecular and atomic properties on the electronic structure method? Comparison of Hartree-Fock, DFT, and MP2 on a biologically relevant set of molecules. J. Comput. Chem. 31, 1297–1311. doi: 10.1002/jcc.21417

PubMed Abstract | CrossRef Full Text | Google Scholar

Matta, C. F. (2014). Modeling biophysical and biological properties from the characteristics of the molecular electron density, electron localization and delocalization matrices, and the electrostatic potential. J. Comput. Chem. 35, 1165–1198. doi: 10.1002/jcc.23608

PubMed Abstract | CrossRef Full Text | Google Scholar

Matta, C. F., Castillo, N., and Boyd, R. J. (2006a). Atomic contributions to bond dissociation energies in aliphatic hydrocarbons. J. Chem. Phys. 125, 20, 204103. doi: 10.1063/1.2378720

PubMed Abstract | CrossRef Full Text | Google Scholar

Matta, C. F., Castillo, N., and Boyd, R. J. (2006b). Extended weak bonding interactions in DNA: π-stacking (base-base), base-backbone, and backbone-backbone interactions. J. Phys. Chem. B 110, 563–578. doi: 10.1021/jp054986g

PubMed Abstract | CrossRef Full Text | Google Scholar

Matta, C. F., and Hernández-Trujillo, J. (2003). Bonding in polycyclic aromatic hydrocarbons in terms of the electron density and of electron delocalization. J. Phys. Chem. A 107, 7496–7504. doi: 10.1021/jp034952d

CrossRef Full Text | Google Scholar

Mertz, E. L., and Krishtalik, L. I. (2000). Low dielectric response in enzyme active site. Proc. Natl. Acad. Sci. U.S.A. 97, 2081–2086. doi: 10.1073/pnas.050316997

PubMed Abstract | CrossRef Full Text | Google Scholar

Nikolaienko, T. Y., Bulavin, L. A., and Hovorun, D. M. (2011). How flexible are DNA constituents? The quantum-mechanical study. J. Biomol. Struct. Dynam. 29, 563–575. doi: 10.1080/07391102.2011.10507406

PubMed Abstract | CrossRef Full Text | Google Scholar

Nikolova, E. N., Goh, G. B., Brooks, C. L., and Al-Hashimi, H. M. (2013). Characterizing the protonation state of cytosine in transient G·C Hoogsteen base pairs in duplex DNA. J. Am. Chem. Soc. 135, 6766–6769. doi: 10.1021/ja400994e

PubMed Abstract | CrossRef Full Text | Google Scholar

Nikolova, E. N., Kim, E., Wise, A. A., O'Brien, P. J., Andricioaei, I., and Al-Hashimi, H. M. (2011). Transient Hoogsteen base pairs in canonical duplex DNA. Nature 470, 498–504. doi: 10.1038/nature09775

PubMed Abstract | CrossRef Full Text | Google Scholar

Nikolova, E. N., Zhou, H., Gottardo, F. L., Alvey, H. S., Kimsey, I. J., and Al-Hashimi, H. M. (2014). A historical account of Hoogsteen base-pairs in duplex DNA. Biopolymers 99, 955–968. doi: 10.1002/bip.22334

PubMed Abstract | CrossRef Full Text | Google Scholar

Palafox, M. A. (2014). Molecular structure differences between the antiviral nucleoside analogue 5-iodo-2‘-deoxyuridine and the natural nucleoside 2‘-deoxythymidine using MP2 and DFT methods: conformational analysis, crystal simulations, DNA pairs and possible behavior. J. Biomol. Struct. Dynam. 32, 831–851. doi: 10.1080/07391102.2013.789402

CrossRef Full Text | Google Scholar

Parr, R. G., and Yang, W. (1989). Density-Functional Theory of Atoms and Molecules. Oxford: Oxford University Press.

PubMed Abstract | Google Scholar

Parvathy, V. R., Bhaumik, S. R., Chary, K. V., Govil, G., Liu, K., Howard, F. B., et al. (2002). NMR structure of a parallel-stranded DNA duplex at atomic resolution. Nucleic Acids Res. 30, 1500–1511. doi: 10.1093/nar/30.7.1500

PubMed Abstract | CrossRef Full Text | Google Scholar

Pechenaya, V. I., and Volkov, S. N. (1984). Mechanism of hydrogen exchange in DNA. Mol. Biol. 18, 1134–1140.

Peng, C., Ayala, P. Y., Schlegel, H. B., and Frisch, M. J. (1996). Using redundant internal coordinates to optimize equilibrium geometries and transition states. J. Comput. Chem. 17, 49–56. doi: 10.1002/(SICI)1096-987X(19960115)17:1<49::AID-JCC5>3.0.CO;2-0

CrossRef Full Text | Google Scholar

Pérez, A., Luque, F. J., and Orozco, M. (2007). Dynamics of B-DNA on the microsecond time scale. J. Am. Chem. Soc. 129, 14739–14745. doi: 10.1021/ja0753546

PubMed Abstract | CrossRef Full Text | Google Scholar

Petrushka, J., Sowers, L. C., and Goodman, M. F. (1986). Comparison of nucleotide interactions in water, proteins, and vacuum: model for DNA polymerase fidelity. Proc. Natl. Acad. Sci. U.S.A. 83, 1559–1562. doi: 10.1073/pnas.83.6.1559

CrossRef Full Text | Google Scholar

Phelps, C., Lee, W., Jose, D., von Hippel, P. H., and Marcus, A. H. (2013). Single-molecule FRET and linear dichroism studies of DNA breathing and helicase binding at replication fork junctions. Proc. Natl. Acad. Sci. U.S.A. 110, 17320–17325. doi: 10.1073/pnas.1314862110

PubMed Abstract | CrossRef Full Text | Google Scholar

Poltev, V. I., Anisimov, V. M., Sanchez, C., Deriabina, A., Gonzalez, E., Garcia, D., et al. (2016). Analysis of the conformational features of Watson–Crick duplex fragments by molecular mechanics and quantum mechanics methods. Biophysics 61, 217–226. doi: 10.1134/S0006350916020160

PubMed Abstract | CrossRef Full Text | Google Scholar

Porschke, D., and Eigen, M. (1971). Co-operative non-enzymic base recognition. III. Kinetics of the helix-coil transition of the oligoribouridylic · oligoriboadenylic acid system and of oligoriboadenylic acid alone at acidic pH. J. Mol. Biol. 62, 361–381. doi: 10.1016/0022-2836(71)90433-5

CrossRef Full Text

Saenger, W. (1984). Principles of Nucleic Acid Structure. New York, NY: Springer.

SantaLucia, J. Jr. (1998). A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl. Acad. Sci. U.S.A. 95, 1460–1465. doi: 10.1073/pnas.95.4.1460

PubMed Abstract | CrossRef Full Text | Google Scholar

Sathyamoorthy, B., Shi, H., Zhou, H., Xue, Y., Rangadurai, A., Merriman, D. K., et al. (2017). Insights into Watson–Crick/Hoogsteen breathing dynamics and damage repair from the solution structure and dynamic ensemble of DNA duplexes containing m¹A. Nucleic Acids Res. 45, 5586–5601. doi: 10.1093/nar/gkx186

PubMed Abstract | CrossRef Full Text | Google Scholar

Singh, A., and Singh, N. (2017). DNA melting in the presence of molecular crowders. Phys. Chem. Chem. Phys. 19, 19452–19460. doi: 10.1039/C7CP03624H

PubMed Abstract | CrossRef Full Text | Google Scholar

Sordo, J. A. (2001). On the use of the Boys–Bernardi function counterpoise procedure to correct barrier heights for basis set superposition error. J. Mol. Struct. 537, 245–251. doi: 10.1016/S0166-1280(00)00681-3

CrossRef Full Text | Google Scholar

Sordo, J. A., Chin, S., and Sordo, T. L. (1988). On the counterpoise correction for the basis set superposition error in large systems. Theor. Chim. Acta 74, 101–110. doi: 10.1007/BF00528320

CrossRef Full Text | Google Scholar

Stofer, E., Chipot, C., and Lavery, R. (1999). Free energy calculations of Watson–Crick base pairing in aqueous solution. J. Am. Chem. Soc. 121, 9503–9508. doi: 10.1021/ja991092z

CrossRef Full Text | Google Scholar

Sühnel, J. (2002). Beyond nucleic acid base pairs: from triads to heptads. Biopolymers 61, 32–51. doi: 10.1002/1097-0282(2001)61:1<32::AID-BIP10063>3.0.CO;2-B

PubMed Abstract | CrossRef Full Text | Google Scholar

Szabat, M., and Kierzek, R. (2017). Parallel-stranded DNA and RNA duplexes: structural features and potential applications. FEBS J. 284, 3986–3998. doi: 10.1111/febs.14187

PubMed Abstract | CrossRef Full Text | Google Scholar

Tchurikov, N. A., Chernov, B. K., Golova, Y. B., and Nechipurenko, Y. D. (1989). Parallel DNA: generation of a duplex between two Drosophila sequences in vitro. FEBS Lett. 257, 415–418. doi: 10.1016/0014-5793(89)81585-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Tirado-Rives, J., and Jorgensen, W. L. (2008). Performance of B3LYP Density Functional Methods for a large set of organic molecules. J. Chem. Theory Comput. 4, 297–306. doi: 10.1021/ct700248k

PubMed Abstract | CrossRef Full Text | Google Scholar

Volkov, S. N. (1995). Semi-open state of double-stranded spiral of DNA. Mol. Biol. 29, 1086–1094.

Vologodskii, A. V., Amirikyan, B. R., Lyubchenko, Y. L., and Frank-Kamenetskii, M. D. (1984). Allowance for heterogeneous stacking in the DNA helix-coil transition theory. J. Biomol. Struct. Dynam. 2, 131–148. doi: 10.1080/07391102.1984.10507552

PubMed Abstract | CrossRef Full Text | Google Scholar

von Hippel, P. H., Johnson, N. P., and Marcus, A. H. (2013). Fifty years of DNA “breathing”: reflections on old and new approaches. Biopolymers 99, 923–953. doi: 10.1002/bip.22347

PubMed Abstract | CrossRef Full Text | Google Scholar

Wada, A., and Suyama, A. (1986). Local stability of DNA and RNA secondary structure and its relation to biological functions. Prog. Biophys. Mol. Biol. 47, 113–157. doi: 10.1016/0079-6107(86)90012-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Wartell, R. M., and Benight, A. S. (1985). Thermal denaturation of DNA molecules: a comparison of theory with experiment. Phys. Rep. 126, 67–103. doi: 10.1016/0370-1573(85)90060-2

CrossRef Full Text | Google Scholar

Widom, J. R., Johnson, N. P., von Hippel, P. H., and Marcus, A. H. (2013). Solution conformation of 2-aminopurine (2-AP) dinucleotide determined by ultraviolet 2D fluorescence spectroscopy (UV-2D FS). New, J. Phys. 15:025028. doi: 10.1088/1367-2630/15/2/025028

PubMed Abstract | CrossRef Full Text | Google Scholar

Wigner, E. (1932). Über das Überschreiten von Potentialschwellen bei chemischen Reaktionen [Crossing of potential thresholds in chemical reactions]. Zeits. Physik. Chem. B 19, 203–216.

Google Scholar

Yang, C., Kim, E., and Pak, Y. (2015). Free energy landscape and transition pathways from Watson–Crick to Hoogsteen base pairing in free duplex DNA. Nucl. Acids Res. 43, 7769–7778. doi: 10.1093/nar/gkv796

PubMed Abstract | CrossRef Full Text | Google Scholar

Ye, M. Y., Zhu, R. T., Li, X., Zhou, X. S., Yin, Z. Z., Li, Q., et al. (2017). Adaptively recognizing parallel-stranded duplex structure for fluorescent DNA polarity analysis. Anal. Chem. 89, 8604–8608. doi: 10.1021/acs.analchem.7b02467

PubMed Abstract | CrossRef Full Text | Google Scholar

Zagryadskaya, E. I., Doyon, F. R., and Steinberg, S. V. (2003). Importance of the reverse Hoogsteen base pair 54–58 for tRNA function. Nucleic Acids Res. 31, 3946–3953. doi: 10.1093/nar/gkg448

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, H. (2016). Occurrence and Function of Hoogsteen Base Pairs in Nucleic Acids. Ph.D. Thesis, Department of Biochemistry, Duke University.