Time scale analysis of enzymatic reduction of uric acid in a microfluidic biomedical device

Time Scale Analysis (TSA) is an investigative tool used in engineering design to identify locations in processes that should be a focus of Process Intensification (PI). Furthermore, TSA points to process variables and parameters that could be used to advance and measure PI improvement. However, TSA cannot suggest any specific design solution to intensify process performance. Instead, design engineers should use their fundamental knowledge and creative intelligence to specify detailed design transformations. TSA will then provide a specific quantitative measure of the improvement. TSA implementation improves an explicitly defined process performance, thus helping achieve process intensification goals. TSA is based on first principles, and it utilizes Characteristic Times (CT) such as diffusion, mean residence, and reaction times to improve an existing process. In this study, we specifically consider microfluidic biomedical devices. To illustrate the genesis of CT and TSA, we start by developing a mathematical model of an enzymatic degradation process in a biomedical device called iCore based on mass, momentum, and kinetic equations. After introducing user-defined scaling parameters, we extract CTs pertinent to the enzymatic degradation of uric acid in this microfluidic biomedical device. Diffusion coefficients, microchannel architectural characteristics, enzyme loading, hydrogel thickness, and characteristic parameters of enzyme kinetics are the parameters and process variables incorporated in this analysis. Finally, we compared the extracted CTs with a COMSOL Multiphysics parametric study to demonstrate how time scale analysis as a design tool and adjusting design parameters, such as diffusion coefficient, hydrogel layer thickness, substrate concentration, and enzyme concentration, can enhance the enzymatic reaction process without a need for complex computational modeling. It is crucial to recognize that pertinent CTs can be determined by understanding the type and nature of the observed process, previous experience, published data, and other foundational engineering design work. There is no need for mathematical modeling and numerical simulations to identify and acknowledge the CTs relevant and essential to the observed process; in this work, we only illustrate the principal origin of CTs via a detailed mathematical model of the process, as previously reported by Jovanovic et al. Therefore, in a routine application of TSA, it is important to remember that mathematical modeling and detailed numerical simulations are not necessary. This is a very comforting fact when TSA is deployed as a tool in higher-level process design functions. The investigations on how best to apply TSA in these higher level design functions such as Process Intensification, scale-up/numbering-up, change of device architecture, change of operating conditions, change of process feed characteristics, change of material physical and chemical properties, parametric optimization of the system for various objective functions, and techno-economic analysis, are yet to be studied and reported.

1 Introduction

Biomedical engineering offers a dynamic platform for developing innovative solutions to transform healthcare practices. Researchers in this field continuously strive to enhance medical treatments and improve patient treatment outcomes. Time scale analysis (TSA) is a technique that serves as an analytical tool to identify phenomena in the reaction process where process intensification (PI) is needed and points to process variables and parameters to address these needs (Jovanovic et al., 2021a; Jovanovic et al., 2021b). Characteristic times (CTs) are the times (measured in seconds) associated with specific physical and chemical reaction process phenomena occurring within a therapeutic biomedical device. Understanding, interpreting, and suggesting changes in characteristic timescales enables enhancement of the process towards improved performance. Together, all the process CTs are the variables in TSA analysis, representing the timescale of constitutive processes such as mass transfer and reaction phenomena. TSA is a specifically vital design approach that can potentially transform biomedical devices by analyzing and enhancing biological processes via manipulating temporal and spatial characteristics to improve processes and treatment outcomes. When designing biomedical devices, especially in therapeutic procedures, researchers must consider various characteristic times associated with representative processes in the human body. For instance, one characteristic time that could be considered in hemodialysis is the characteristic time of water removal from the human body in renal patients. The characteristic time of accumulated water removal from the human body in a healthy adult male person is approximately 4 hours. Current treatment of renal patients via hemodialysis machines removes products of biological metabolic reactions at a 3-day time interval (Lacson and Brunelli, 2011). Other metabolites removed during hemodialysis, such as urea, creatinine, phosphates, etc., have substantially different CT requirements, thus making current hemodialysis practices relatively crude and inadequate (Himmelfarb and Ikizler, 2010). The TSA analysis of the hemodialysis characteristic times inevitably points to a design of a wearable biomedical device that can address these characteristic times in a substantially different manner. A wearable hemodialysis machine could provide selective, prolonged, and timely removal of hemodialysis compounds, each at a more adequate and different timescale. A design approach guided by CTs and TSA is technically feasible and would lead to medical treatments with improved patient outcomes.

TSA also has a crucial role in achieving process intensification (PI) goals. PI refers to any effort to design and develop more efficient systems via faster, smaller, and less energy-consuming processes (Jovanovic et al., 2021a; Jovanovic et al., 2021b; Tonkovich and Daymo, 2018; Boffito and Fernandez Rivas, 2020). In biomedical engineering, PI aims to improve the effectiveness of medical processes, such as drug delivery, cell separation (Asadi-Saghandi et al., 2023), enzyme reactions (Pantakitcharoenkul et al., 2024; Tamborini et al., 2018), and therapeutic intervention (Shallan and Priest, 2019). Optimizing treatment regimens and dosage protocols requires consideration of disease temporal characteristics and patient responses.

Microfluidics (momentum transport) is a basic, underlining, and uniquely successful technical approach to achieving process intensification goals (Santana et al., 2018). Microfluidics and predominantly associated laminar flow govern the behavior, control, and manipulation of fluids at the micrometer scale (Song, 2015). Microfluidic systems have several advantages, including sample and reagent volume reduction, enhancing heat and mass transfer rates (Singh et al., 2014), improving reaction kinetics, and providing precise control over process parameters at micrometer spatial and millisecond temporal scales. These fundamental advantages make microfluidic platforms pivotal in achieving PI goals in biomedical systems. Microfluidic devices offer compact designs, enabling the integration of multiple process steps and operations onto a single platform. This integration minimizes the footprint, reduces equipment and infrastructure requirements, and streamlines the overall process. In microfluidic devices, a high surface-to-volume ratio and effective transport at short distances in the laminar flow enhances reaction efficiency, enabling faster diffusion of species, and often improves reaction product yields.

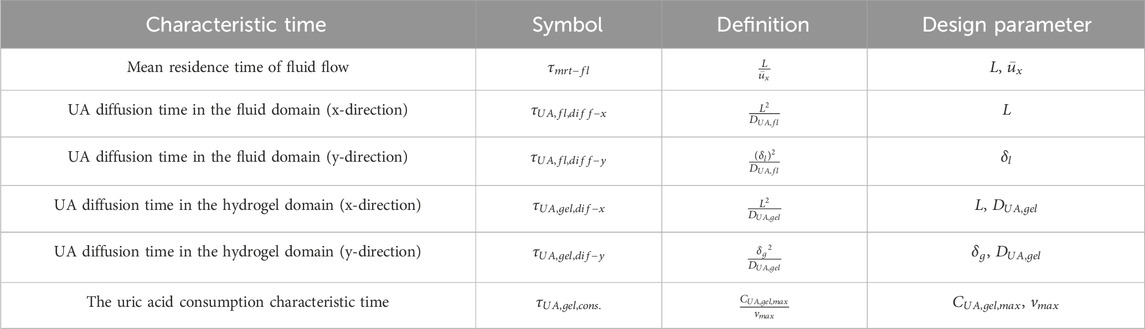
PI often encompasses the transition from large-scale to smaller modular processes (Stankiewicz and Moulijn, 2002). Microfluidics enables this scaled-down approach, which supports the translation of macroscale processes into micro/nanoscale platforms (Silva et al., 2024; Nazoktabar et al., 2014). For instance, iCore is a micro-scale-based blood processing biomedical device for capturing, separating, and enzymatic conversion applications (Pantakitcharoenkul et al., 2024). This device follows the fundamental advantages of microfluidic devices to achieve PI goals and is composed of an array of straight microchannels, which are accompanied by a thin hydrogel layer at the bottom of the device for therapeutics and diagnostics (see Figure 1) (Pantakitcharoenkul, 2022; Touma, 2022).

Figure 1

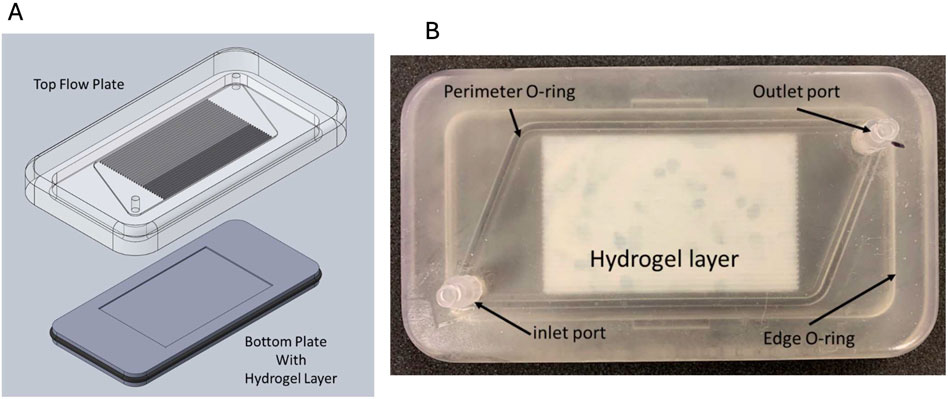
Figure 1. iCore extracorporeal blood processing device. (A) The computer-aided design (CAD) of iCore; (B) the 3D-printed iCore device, including the top flow plate and bottom plate loaded with a thin hydrogel layer. Courtesy from the Jovanovic lab.

However, numbering up becomes a requirement for implementing microfluidics in iCore and intensified processes. Numbering up, coupled with the automation capabilities of microfluidics, allows for high-throughput processing, leading to PI by reducing processing time and increasing processing capacity. In the healthcare realm, PI has the potential to enhance healthcare delivery significantly by producing small biomedical devices that reduce material costs and promote distributed additive manufacturing. Distributed additive manufacturing is especially important in remote areas where access to therapeutic devices may be limited. Shifting from institutional biomedical platforms toward home healthcare delivery is one of the primary goals of utilizing PI in biomedical device design and development. Enabling equal access to therapeutics facilitates improved community health, specifically in developing countries where being far from medical centers and physicians significantly decreases the level of health services and life quality.

In this study, we generated characteristic times by (first) creating a mathematical model that precipitated characteristic times for the uric acid reduction process. The uric acid reduction process was experimentally demonstrated in the microfluidic blood processing device, iCore, functionalized with a thin (500 µm) hydrogel film containing entrapped enzyme. Hyperuricemia occurs when the concentration of uric acid in the bloodstream exceeds 7 mg/dL, and it is often associated with gout disease. This arthritis-like disease causes severe joint inflammation and pain. To demonstrate how TSA could improve iCore design, we focused on the enzymatic (uricase) reduction of uric acid in the bloodstream. By considering pertinent CTs and TSA, we have shown one of the potential approaches to improve treatment outcomes by adjusting relevant process parameters.

2 Mathematical modeling and characteristic times

2.1 Development of the mathematical model

Creation of the characteristic times starts with developing a mathematical model of the design based on the mass and momentum equations, introducing assumptions, defining scaling factors and boundary conditions, and then recognizing the characteristic times. The detailed description of the characteristic times development based on the mathematical model is elaborated in the Supplementary Material. To initiate the development of the mathematical model equations, consider a 2D straight microchannel geometry, as shown in Figure 1, comprising two distinct domains. The top domain represents the fluid domain, with the thickness ${\delta }_l$, where a unidirectional $\left(u_x\ne 0,u_y=0,u_z=0\right)$., Newtonian, isothermal laminar flow of uric acid enters the microchannel, and the system is in a steady state condition $\left(\frac{\partial u_x}{\partial t}=0\right)$. The bottom domain comprises a thin hydrogel film designed to accommodate entrapped enzymes, for which we selected uricase as the enzyme to degrade uric acid for our study. Uricase catalyzes the enzymatic conversion of the diffused uric acid within the hydrogel layer into the desired products, such as allantoin and hydrogen peroxide. This study assumes that uricase is homogeneously immobilized within the hydrogel layer, no changes in enzyme activity during the process, and no convection occurs into the hydrogel domain. The uniform distribution of enzymes within a hydrogel layer has been demonstrated in a study by Pantakitcharoenkul et al., where multiple FTIR analyses of different sections of freeze-dried hydrogel samples demonstrated a consistent distribution of the enzyme within the hydrogel matrix (Pantakitcharoenkul et al., 2024). In another study by Khademhosseini et al., a uniform distribution of cells within an agarose gel has been shown, where CSFE-labeled fluorescence images of a cell encapsulation process demonstrated a uniform distribution of cells throughout the agarose gel (Ling et al., 2007). Due to the no-slip boundary condition selection, the fluid velocity equals zero at the top wall of the fluid domain and the fluid-hydrogel interface. The hydrogel layer is where the enzymatic reaction of uric acid degradation takes place. This involves the inflow of uric acid into the fluid domain, diffusion of uric acid into the hydrogel layer, meeting immobilized uricase within the hydrogel layer, and, consequently, the reaction product formation.

$UricAcid+O_2+\stackrel{Uricase}{\to }{H}_2{O}_2+Allantoin$

The momentum balance equation is crucial in creating the mean residence characteristic time for the fluid domain. Equation 1 is the simplified form of the momentum balance equation for the fluid layer and Equation 1 in the Supplementary Material is the momentum balance equation in the vector notation based on the Navier-Stokes equations for an incompressible Newtonian fluid, unidirectional flow, and a steady-state condition.

$\frac{\partial P}{\partial x}=\mu \frac{{\partial }^2{u}_x}{{\partial y}^2}(1)$

Additionally, the mass balance equation can be formulated for any species present in the fluid domain, such as uric acid. Equation 2 is the mass balance equation for uric acid and includes, from left to right, the convection term in the x-direction, the diffusion flux of uric acid in the x-direction, and the diffusion flux of uric acid in the y-direction, respectively, in the fluid domain. For the boundary conditions of the fluid domain, we considered the equal flux of uric acid perpendicular to the interface of hydrogel and fluid layers, no uric acid concentration changes at $y=H$ concerning the y-axis and at $x=L$ concerning the x-axis, and finally, the concentration of uric acid at the inlet of the fluid domain equals to the initial concentration of uric acid (see Figure 2).

$1.5{\overline{u}}_x\left[1-{\left(\frac{y}{{\delta }_l}\right)}^2\right].\frac{\partial C_{UA,fl}\left(x,y\right)}{\partial x}+D_{UA,fl}\frac{{\partial }^2{C}_{UA,fl}\left(x,y\right)}{\partial x^2}+D_{UA,fl}\frac{{\partial }^2{C}_{UA,fl}\left(x,y\right)}{{\partial y}^2}=0\left[\frac{{mol}_{UA,fl}}{m_{fl}^3.s}\right](2)$

Figure 2

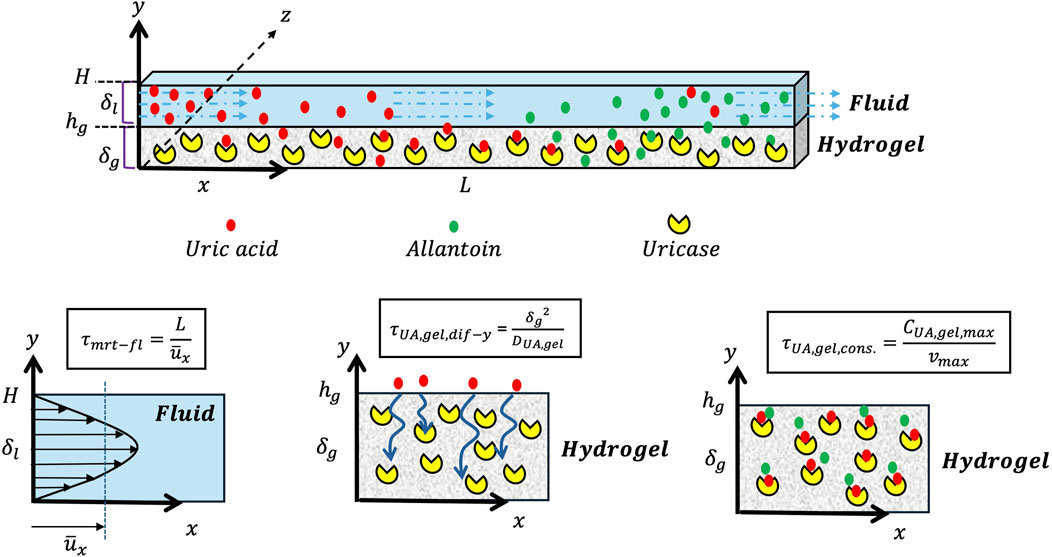
Figure 2. Schematic representation of the geometry in Cartesian coordinates (z∼x >>> y) used for the mathematical modeling, comprising the hydrogel layer (bottom domain), the fluid layer (top domain), and characteristic times.

At this step, scaling factors need to be introduced to derive characteristic times from the mass balance equation of a fluid domain. These scaling factors normalize the geometry dimensions and concentrations of the different species present in the fluid (e.g., uric acid). By normalizing these values, the unit consistency of the mass balance equation is obtained [1/s], and characteristic times could be extracted for further analysis (Equation 3).

$1.5\frac{{\overline{\mathrm{u}}}_{\mathrm{x}}}{\mathrm{L}}\left[1-{\left({\mathrm{y}}^{*}\right)}^2\right]\frac{\partial {\mathrm{C}}_{\text{UA},\text{fl}}^{*}}{\partial {\mathrm{x}}^{*}}+\frac{{\mathrm{D}}_{\text{UA},\text{fl}}}{{\mathrm{L}}^2}\frac{{\partial }^2{\mathrm{C}}_{\text{UA},\text{fl}}^{*}}{\partial {\left({\mathrm{x}}^{*}\right)}^2}+\frac{{\mathrm{D}}_{\text{UA},\text{fl}}}{{\left({\mathrm{\delta }}_{\mathrm{l}}\right)}^2}\frac{{\partial }^2{\mathrm{C}}_{\text{UA},\text{fl}}^{*}}{\partial {\left({\mathrm{y}}^{*}\right)}^2}=0\left[\frac{1}{\mathrm{s}}\right](3)$

Scaling factors:

$C_{UA,fl}^{*}=\frac{C_{UA,fl}}{C_{UA,fl}^0};y^{*}=\frac{y}{{\delta }_l};x^{*}=\frac{x}{L}$

Where $C_{UA,fl}^{*}$ is the normalized concentration of uric acid in the fluid phase $C_{UA,fl}$ and the normalizing uric acid concentration in the fluid phase is $C_{UA,fl}^0$, and $x^{*}$ is the normalized length and $y^{*}$ is the fluid layer normalized thickness.

Ultimately, the final form of the mass balance equation for the fluid domain is shown in Equation 4.

$1.5\frac{1}{{\mathrm{\tau }}_{\text{mrt}-\text{fl}}}\left[1-{\left({\mathrm{y}}^{*}\right)}^2\right]\frac{\partial {\mathrm{C}}_{\text{UA},\text{fl}}^{*}}{\partial {\mathrm{x}}^{*}}+\frac{1}{{\mathrm{\tau }}_{\text{UA},\text{fl},\text{diff}-\mathrm{x}}}\frac{{\partial }^2{\mathrm{C}}_{\text{UA},\text{fl}}^{*}}{\partial {\left({\mathrm{x}}^{*}\right)}^2}+\frac{1}{{\mathrm{\tau }}_{\text{UA},\text{fl},\text{diff}-\mathrm{y}}}\frac{{\partial }^2{\mathrm{C}}_{\text{UA},\text{fl}}^{*}}{\partial {\left({\mathrm{y}}^{*}\right)}^2}=0\left[\frac{1}{\mathrm{s}}\right](4)$

Where, ${\tau }_{mrt-fl}$ is the mean residence characteristic time of the fluid flow, and ${\tau }_{UA,fl,diff-x}$ and ${\tau }_{UA,fl,diff-y}$ are the x and y-direction characteristic times of uric acid diffusion in the fluid domain, respectively.

Equation 3 shows that the uric acid-containing fluid mean residence time depends on the average inlet fluid velocity and is inversely proportional to the channel length. Then, based on the design engineer’s choice, if a longer mean residence time is favorable in a bioprocess, designing a device by increasing the channel length or decreasing the average fluid velocity could suffice to achieve this goal.

The diffusion of uric acid in the x-direction depends on the diffusion coefficient of uric acid in the fluid and the channel length. Assuming a constant uric acid diffusion coefficient, the x-direction diffusion characteristic time can be varied by changing the channel length. However, convection could dominate diffusion as a mass transfer method within the fluid domain. Additionally, the derived characteristic time in the last part of Equation 3 (y-direction diffusion time) indicates that increasing the thickness of the fluid layer will result in an increase in the y-direction diffusion characteristic time. This means a thinner fluid layer could be chosen for faster y-direction diffusion. To accomplish this, micro/nanofabrication methods and additive manufacturing could be employed to construct desirable microfluidic geometries.

The mass balance equations for the hydrogel domain are explained in the next step. The complete process of expanding the mass balance equation, along with assumptions and scaling factors, can be found in the Supplementary Material. Since there is no fluid flow within the hydrogel layer, we only consider diffusion and the net reaction rate $∆r_{UA,gel}$ in the mass balance equation of the hydrogel layer. The boundary conditions associated with the mass balance of uric acid in the hydrogel domain include no uric acid flux at x = 0, x = L, and the bottom wall of the hydrogel domain (y = 0). Equation 5 is the mass balance equation of the uric acid species in the hydrogel. The first part of Equation 5 represents the diffusion flux of uric acid in the hydrogel in the x-direction. The second part represents the diffusion flux of uric acid in the gel layer in the y-direction. The final term denotes the net reaction rate of the species within the hydrogel domain (e.g., uric acid) using the Michaelis-Menten kinetics.

$\frac{{\mathrm{D}}_{\text{UA},\text{gel}}}{{\mathrm{L}}^2}\frac{{\partial }^2{\mathrm{C}}_{\text{UA},\text{gel}}^{*}}{\partial {\left({\mathrm{x}}^{*}\right)}^2}+\frac{{\mathrm{D}}_{\text{UA},\text{gel}}}{{{\mathrm{\delta }}_{\mathrm{g}}}^2}\frac{{\partial }^2{\mathrm{C}}_{\text{UA},\text{gel}}^{*}}{\partial {\left({\mathrm{y}}^{*}\right)}^2}-\frac{{\mathrm{v}}_{\max }}{{\mathrm{C}}_{\text{UA},\text{gel},\max }}\left(\frac{{\mathrm{C}}_{\text{UA},\text{gel}}^{*}}{{\mathrm{K}}_{\text{UA}}^{*}+{\mathrm{C}}_{\text{UA},\text{gel}}^{*}}\right)=0\left[\frac{1}{\mathrm{s}}\right](5)$

Scaling factors:

${∆r}_{UA}^{*}=\frac{{∆r}_{UA}}{C_{UA,gel,\mathit{max}}};C_{UA,gel}^{*}=\frac{C_{UA,gel}}{C_{UA,gel,\mathit{max}}};K_{UA}^{*}=\frac{K_{UA}}{C_{UA,gel,\mathit{max}}};x^{*}=\frac{x}{L};y^{*}=\frac{y}{{\delta }_g}$

Finally, Equation 6 shows the final form of the uric acid mass balance equation in the hydrogel domain, including the uric acid diffusion characteristic time in the x and y directions (${\tau }_{UA,gel,dif-x}$; ${\tau }_{UA,gel,dif-y}$) and the uric acid consumption characteristic time ${\tau }_{UA,gel,cons.}$.

$\frac{1}{{\mathrm{\tau }}_{\text{UA},\text{gel},\text{dif}-\mathrm{x}}}\frac{{\partial }^2{\mathrm{C}}_{\text{UA},\text{gel}}^{*}}{\partial {\left({\mathrm{x}}^{*}\right)}^2}+\frac{1}{{\mathrm{\tau }}_{\text{UA},\text{gel},\text{dif}-\mathrm{y}}}\frac{{\partial }^2{\mathrm{C}}_{\text{UA},\text{gel}}^{*}}{\partial {\left({\mathrm{y}}^{*}\right)}^2}-\frac{1}{{\mathrm{\tau }}_{\text{UA},\text{gel},\text{cons}.}}\left(\frac{{\mathrm{C}}_{\text{UA},\text{gel}}^{*}}{{\mathrm{K}}_{\text{UA}}^{*}+{\mathrm{C}}_{\text{UA},\text{gel}}^{*}}\right)=0\left[\frac{1}{\mathrm{s}}\right](6)$

The mathematical model uses mass balance equations to extract the characteristic times for uric acid species. A similar method can be applied to create a mathematical model for any other species involved in an enzymatic reaction. Equation 5 shows that the diffusion time of uric acid is directly proportional to the square of the channel’s length and the square of the hydrogel thickness. Thinner hydrogel layers would significantly reduce the diffusion characteristic time in the y-direction, which is favorable in uric acid reduction applications. However, creating thinner hydrogel films requires advanced tools, methods, and considering the mechanical strength of the film. Moreover, the characteristic time of uric acid reduction increases with increasing the uric acid concentration within the hydrogel layer. Notably, the maximum uric acid concentration in the hydrogel layer is equal to the initial (inlet) uric acid concentration entering the fluid domain.

2.2 Time scale analysis

In order to comprehend the technical significance of the characteristic times derived in biomedical device design, it is essential to examine each recognized characteristic time. Analyzing the time scale enables us to regulate and manage various design parameters based on our functional requirements and provides engineers with insight. These design parameters include the microchannel length, flow properties such as average fluid velocity, the thickness of the hydrogel and fluid layers, inlet substrate concentration, and enzyme concentration within the hydrogel layer. One can adjust these parameters by combining experimental data, literature references, and specific functional needs (Table 1).

Table 1

Table 1. List of characteristic times.

2.2.1 Mean residence characteristic time

As shown in Equation 3, the mean residence characteristic time is proportional to the average fluid velocity and the channel length. If one considers a microfluidic device with a length of 100 mm and a fluid flow with an average velocity of $0.5\left[mm/s\right]$, then the mean residence time equals 200 s. This is the time the inlet fluid containing substrate spends inside the device, ensuring the necessary time for species transport and reactions.

${\tau }_{mrt-fl}=\frac{L}{{\overline{u}}_x}=\frac{1\times {10}^{-1}\left[m\right]}{5\times {10}^{-4}\left[\frac{m}{s}\right]}=200.0\left[s\right]$

Often, a greater mean residence time compared to diffusion and reaction characteristic times (${\tau }_{mrt-fl}>{\tau }_{UA,gel,dif-y},{\tau }_{mrt-fl}>{\tau }_{UA,gel,cons.}$) is favorable for providing sufficient time for species to diffuse into the porous structure of the hydrogel hosting the entrapped enzymes and for the enzymatic reaction to occur. The length of the device as a design parameter is tunable by changing the computer-aided design (CAD) of the device. Additionally, adjusting the average fluid velocity by controlling the pump properties could be another choice for design engineers to manage the mean residence time. However, finding the optimum pumping conditions could be a more accessible option for mean residence time adjustments. As a result, one could optimize the mean residence time by determining the process aims and operational limitations. Dispersion due to the laminar velocity profile in the channel exists, but an advantage of operating in microscale is that the characteristic time for diffusion perpendicular to the flow direction (i.e., channel height direction) becomes significantly short, such that species in the fluid are able to sample a wide range of flow velocity regions. This dampens the laminar dispersion, but we aim for other important characteristic times to be significantly shorter than the mean residence time (e.g., three times shorter) to create some buffer. This has been investigated in previous work (Coblyn, 2015; Coblyn et al., 2016).

2.2.2 Diffusion characteristic times

Diffusion characteristic time in x-direction: The diffusion characteristic times of any species within the fluid domain depend on the diffusion length and the diffusion coefficient of species in the media. Using Equation 3 and by considering a device length of 100 mm and a uric acid diffusion coefficient of $2.0\times {10}^{-11}\left[\frac{m^2}{s}\right]$ (Pantakitcharoenkul et al., 2024), we find a long diffusion time in the fluid domain in the x-direction. This observation is convincing since convection is the dominant mass transfer mechanism within the fluid domain and in the x-direction. Therefore, diffusion characteristic time in the x-direction has less significance in any process optimization efforts.

The characteristic time of uric acid diffusion in the x-direction and for the hydrogel domain depends on the length of the hydrogel layer and the diffusion coefficient of uric acid in the hydrogel. Again, adjusting the length of the hydrogel layer is more accessible than enhancing the diffusion coefficient by various methods, such as employing an active transport mechanism (electric/magnetic fields) or increasing the temperature.

${\tau }_{UA,gel,dif-x}=\frac{L^2}{D_{UA,gel}}=\frac{{\left(1\times {10}^{-1}\left[m\right]\right)}^2}{2.0\times {10}^{-11}\left[\frac{m^2}{s}\right]}\cong 50\times {10}^7\left[s\right]$

Diffusion characteristic time in y-direction: The diffusion of uric acid into the hydrogel layer in the y-direction is crucial for facilitating mass transfer and reducing uric acid concentration in the device. It has been shown that the diffusion characteristic time in the hydrogel layer depends on the thickness of the hydrogel film and the species diffusion coefficient (e.g., uric acid). The square of the thickness of the hydrogel layer has a direct relation with the y-direction diffusion characteristic time, demonstrating how different hydrogel thicknesses could change the diffusion characteristic time. On the other hand, adjusting the thickness of the hydrogel as a design parameter is often more accessible than enhancing the diffusion coefficient. Thinner hydrogel films could lead to shorter diffusion times and improve the substrate reduction/product formation rate within a microfluidic device. Assuming a hydrogel layer thickness of 50 μm, the y-direction diffusion characteristic time is equal to:

${\tau }_{UA,gel,dif-y}=\frac{{{\delta }_g}^2}{D_{UA,gel}}=\frac{{\left(5\times {10}^{-5}\left[m\right]\right)}^2}{2.0\times {10}^{-11}\left[\frac{m^2}{s}\right]}=125\left[s\right]$

A characteristic time of 125 s for uric acid diffusion in the y-direction is generally considered unfavorable. This slow diffusion time may be associated with the high density of polymer crosslinks in the porous structure of the hydrogel. However, the diffusivity of hydrogels could be improved by adjusting specific properties such as porosity, crosslinking density, and swelling. Subsequently, this improvement can lead to shorter diffusion characteristic time and better overall reaction performance.

Now, assuming doubling the hydrogel thickness (100 µm), then we would have a y-direction diffusion characteristic time of 500 s ($\left.{\tau }_{UA,gel,dif-y}\gg {\tau }_{mrt-fl}\right)$, which is greater than the mean residence time and it means the more extended diffusion characteristic time can prevent the species from diffusing into the hydrogel layer before the fluid leaves the device. As a result, a process designer should consider greater mean residence time compared to diffusion time $\left({\tau }_{mrt-fl}>{\tau }_{UA,gel,dif-y}\right)$ to ensure sufficient time for species to diffuse into the hydrogel layer.

2.2.3 Uric acid consumption characteristic time

To illustrate the uric acid consumption characteristic time and based on the enzymatic reaction, we assume that uric acid consumption leads to the formation of allantoin, which is a product of the enzymatic reduction of uric acid by uricase. Based on Equation 5, there are two contributors in the uric acid consumption characteristic time, including the maximum rate of uric acid consumption $v_{\mathit{max}}$ and the maximum concentration of uric acid in the hydrogel layer $C_{UA,gel,\mathit{max}}$. The maximum uric acid concentration is the value of gout disease onset and is equal to the inlet (fluid domain) uric acid concentration.

${\tau }_{UA,gel,cons.}=\frac{C_{UA,gel,\mathit{max}}}{v_{\mathit{max}}}=\frac{0.575\left[\frac{{mol}_{UA,gel}}{m_{gel}^3}\right]}{1.28\times {10}^{-2}\left[\frac{{mol}_{UA,gel}}{m_{gel}^3.s}\right]}=44.9\left[s\right]$

The transport of uric acid in the hydrogel layer can be adjusted to increase by enhancing the diffusion of uric acid into the hydrogel layer from the fluid layer by tuning the hydrogel properties. However, a higher concentration of uric acid in the hydrogel could lead to longer uric acid consumption time. Ultimately, the maximum uric acid concentration in the hydrogel layer is equal to the inlet uric acid concentration in the fluid domain.

3 Conclusion

Time scale analysis, a powerful diagnostic tool, offers a fresh perspective on mass transfer and reaction kinetics in biochemical processes. It not only illuminates the inadequacies of a biochemical process by providing characteristic times of individual processes, but also allows to pinpoint process’s shortcomings through tunable design parameters such as channel length, enzyme concentrations, hydrogel and fluid layers thicknesses, and species concentrations.

This is particularly valuable in biological processes where access to biological samples is limited, and rapid treatments are crucial. By aiding in process improvement, time scale analysis paves the way for process intensification, a key goal in our field.

To highlight the value of TSA and CTs in estimating and targeting the bottlenecks of a bioprocess and observing the effect of design parameters extracted from characteristic times, we used a COMSOL Multiphysics^® model of the uric acid reduction in an iCore device. We selected various uric acid diffusion coefficients in the hydrogel layer with assumptions including a laminar, isothermal, Newtonian fluid flow and choice of physics comprising of the transport of diluted species, fluid flow and chemical reaction engineering modules. Four different uric acid diffusion coefficients within the hydrogel layer have been used. Figure 3 illustrates how increasing the diffusion coefficient enhances the transfer of uric acid species into the hydrogel layer and facilitates the enzymatic reaction within the iCore device. TSA and CTs, developed based on mass and momentum balance equations, target these engineering design parameters, and improve microfluidic device operations. The diffusion coefficient of species within the hydrogel layer could be adjusted by tuning the hydrogel properties, including the crosslinking density and porosity of the hydrogel. As a result, any effort to improve the diffusion process could significantly enhance the device function and, subsequently, the consumption of uric acid species.

Figure 3

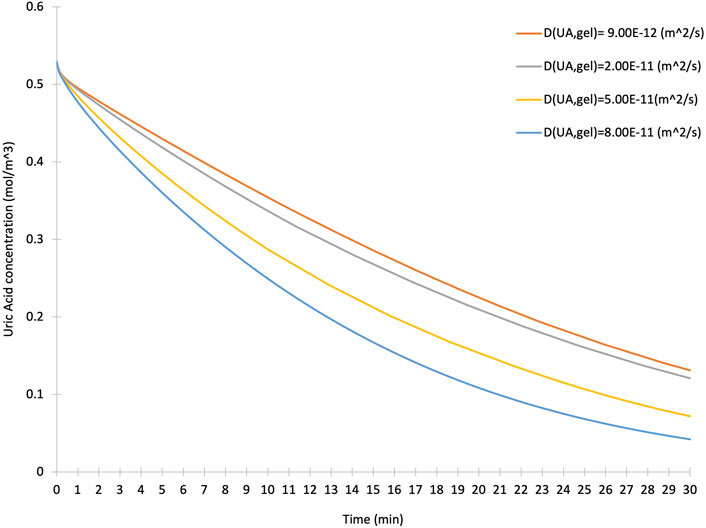
Figure 3. The effect of various uric acid diffusion coefficients in the hydrogel layer on the concentration of uric acid over time.

In summary, microfluidics is not just a tool but a necessity to meet the tenets of process intensification, and time scale analysis is not just a design tool but a catalyst for improving microfluidic devices and biochemical processes. This, in turn, leads to the attainment of process intensification tenets and aims. The advent of novel manufacturing methods such as additive manufacturing, coupled with the power of time scale analysis, is revolutionizing process intensification in biomedical research. This is an exciting time for the biomedical engineering field, and there are great opportunities to push the boundaries of current biomedical microfluidic devices and biochemical processes.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

AA: Investigation, Writing–original draft, Writing–review and editing. JP: Formal Analysis, Investigation, Software, Validation, Writing–review and editing. MC: Methodology, Project administration, Writing–review and editing. IP: Methodology, Writing–review and editing. GJ: Conceptualization, Funding acquisition, Methodology, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This project was partially funded by the RAPID Manufacturing Institute for Process Intensification and the School of Chemical, Biological, and Environmental Engineering at Oregon State University. The financial support from the Slovenian Research and Innovation Agency (Grants P2-0191, N2-0342, and L2-3161) is gratefully acknowledged.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fceng.2024.1451222/full#supplementary-material

References

Asadi-Saghandi, H., Karimi-Sabet, J., Ghorbanian, S., and Moosavian, S. M. A. (2023). Liquid-liquid extraction of calcium in a scaled-out microfluidic device: process intensification using a crown ether-ionic liquid system. Chem. Eng. Process - Process Intensif. 183 (December 2022), 109261. doi:10.1016/j.cep.2022.109261

CrossRef Full Text | Google Scholar

Boffito, D. C., and Fernandez Rivas, D. (2020). Process intensification connects scales and disciplines towards sustainability. Can. J. Chem. Eng. 98 (12), 2489–2506. doi:10.1002/cjce.23871

CrossRef Full Text | Google Scholar

Coblyn, M., Truszkowska, A., and Jovanovic, G. (2016). Characterization of microchannel hemodialyzers using residence time distribution analysis. J. Flow. Chem. 6 (1), 53–61. doi:10.1556/1846.2015.00041

CrossRef Full Text | Google Scholar

Coblyn, M. Y. (2015). An investigation of multiphase flow in complex microchannel geometries for hemodialysis systems using residence time distribution analysis. Corvallis, OR: Oregon State University. Available at: https://ir.library.oregonstate.edu/concern/graduate_thesis_or_dissertations/9019s732b?locale=en.

Google Scholar

Himmelfarb, J., and Ikizler, T. A. (2010). Hemodialysis. N. Engl. J. Med. 363 (19), 1833–1845. doi:10.1056/nejmra0902710

PubMed Abstract | CrossRef Full Text | Google Scholar

Jovanovic, G. N., Coblyn, M. Y., and Plazl, I. (2021a). Time scale analysis and characteristic times in microscale-based chemical and biochemical processes: Part I – concepts and origins. Chem. Eng. Sci. 238, 116502. doi:10.1016/j.ces.2021.116502

CrossRef Full Text | Google Scholar

Jovanovic, G. N., Coblyn, M. Y., and Plazl, I. (2021b). Time scale analysis and characteristic times in microscale-based bio-chemical processes: Part II – bioreactors with immobilized cells, and process flowsheet analysis. Chem. Eng. Sci. 236, 116499. doi:10.1016/j.ces.2021.116499

CrossRef Full Text | Google Scholar

Lacson, E., and Brunelli, S. M. (2011). Hemodialysis treatment time: a fresh perspective. Clin. J. Am. Soc. Nephrol. 6 (10), 2522–2530. doi:10.2215/cjn.00970211

PubMed Abstract | CrossRef Full Text | Google Scholar

Ling, Y., Rubin, J., Deng, Y., Huang, C., Demirci, U., Karp, J. M., et al. (2007). A cell-laden microfluidic hydrogel. Lab. Chip 7 (6), 756–762. doi:10.1039/b615486g

PubMed Abstract | CrossRef Full Text | Google Scholar

Nazoktabar, M., Zahedinejad, M., Heydari, P., and Reza, A. (2014) Fabrication and optical characterization of silicon nanostructure arrays by laser interference lithography and metal-assisted chemical etching, 4, 419–424.

Google Scholar

Pantakitcharoenkul, J. (2022). Extracorporeal treatment of hyperuricemia via enzymatic functionalized microchannel processing platform (iCore): experiment and modeling. Corvallis, OR: Oregon State University.

Google Scholar

Pantakitcharoenkul, J., Touma, J., Jovanovic, G., and Coblyn, M. (2024). Enzyme-functionalized hydrogel film for extracorporeal uric acid reduction. J. Biomed. Mater Res. Part B Appl. Biomater. 112 (2), e35375. doi:10.1002/jbm.b.35375

CrossRef Full Text | Google Scholar

Santana, H. S., Lopes, M. G. M., Silva, J. L., and Taranto, O. P. 2018. Application of microfluidics in process intensification 16(12). doi:10.1515/ijcre-2018-0038

CrossRef Full Text | Google Scholar

Shallan, A. I., and Priest, C. (2019). Microfluidic process intensification for synthesis and formulation in the pharmaceutical industry. Chem. Eng. Process - Process Intensif. 142, 107559. doi:10.1016/j.cep.2019.107559

CrossRef Full Text | Google Scholar

Silva, J. L., Calvo, P. V. C., Palma, M. S. A., Lopes, M. G. M., and Santana, H. S. (2024). Process intensification in flow chemistry using micro and millidevices: numerical simulations of the syntheses of three different intermediate API compounds for diabetes mellitus drug production. Chem. Eng. Res. Des. 205, 401–412. doi:10.1016/j.cherd.2024.04.007

CrossRef Full Text | Google Scholar

Singh, J., Kockmann, N., and Nigam, K. D. P. (2014). Novel three-dimensional microfluidic device for process intensification. Chem. Eng. Process Process Intensif. 86, 78–89. doi:10.1016/j.cep.2014.10.013

CrossRef Full Text | Google Scholar

Song, W. (2015). Encyclopedia of microfluidics and nanofluidics. Encycl. Microfluid. Nanofluidics. doi:10.1007/978-1-4614-5491-5

CrossRef Full Text | Google Scholar

Stankiewicz, A., and Moulijn, J. A. (2002). Process intensification. Ind. Eng. Chem. Res. 41 (8), 1920–1924. doi:10.1021/ie011025p

CrossRef Full Text | Google Scholar

Tamborini, L., Fernandes, P., Paradisi, F., and Molinari, F. (2018). Flow bioreactors as complementary tools for biocatalytic process intensification. Trends Biotechnol. 36 (1), 73–88. doi:10.1016/j.tibtech.2017.09.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Tonkovich, A. L., and Daymo, E. (2018). Process intensification. Handb. Therm. Sci. Eng. 34 (2), 1535–1592. doi:10.1007/978-3-319-26695-4_34

CrossRef Full Text | Google Scholar

Touma, J. G. (2022). Chemical and biochemical separation in high-throughput microfluidic systems: environmental, critical materials, and therapeutic applications. Corvallis, OR: Oregon State University.

Google Scholar

Nomenclature

List of subscripts

$\mathit{U}\mathit{A}$ Uric acid

$\mathit{m}\mathit{r}\mathit{t}$ Mean residence time

$\mathit{g}\mathit{e}\mathit{l}$ Hydrogel

$\mathit{f}\mathit{l}$ Fluid

$\mathit{d}\mathit{i}\mathit{f}$ Diffusion

$\mathit{c}\mathit{o}\mathit{n}\mathit{s}.$ Consumption

List of symbols

$\mathit{L}$ Microchannel length, $\left[m\right]$

$\mathit{H}$ Microchannel height, $\left[m\right]$

${\mathit{\delta }}_{\mathit{g}}$ Hydrogel layer thickness, $\left[m\right]$

${\mathit{\delta }}_{\mathit{l}}$ Fluid layer thickness, $\left[m\right]$

${\overline{\mathit{u}}}_{\mathit{x}}$ Average fluid velocity, $\left[\frac{m}{s}\right]$

${\mathit{D}}_{\mathit{U}\mathit{A},\mathit{f}\mathit{l}}$ Uric acid diffusion coefficient in the fluid, $\left[\frac{m^2}{s}\right]$

${\mathit{D}}_{\mathit{U}\mathit{A},\mathbf{gel}}$ Uric acid diffusion coefficient in the hydrogel, $\left[\frac{m^2}{s}\right]$

${\mathit{C}}_{\mathit{U}\mathit{A},\mathit{f}\mathit{l}}^{\mathbf{0}}$ initial uric acid concentration in the fluid, $\left[\frac{{mol}_{UA}}{m_{fl}^3}\right]$

${\mathit{C}}_{\mathit{U}\mathit{A},\mathit{g}\mathit{e}\mathit{l},\mathit{max}}$ Maximum uric acid concentration in the hydrogel layer, $\left[\frac{{mol}_{UA,gel}}{m_{gel}^3}\right]$

${\mathit{K}}_{\mathit{U}\mathit{A}}$ Michaelis-Menten constant for the uric acid species$\left[\frac{{mol}_{UA,gel}}{m_{gel}^3}\right]$

${\mathit{v}}_{\mathit{max}}$ Maximum rate of allantoin formation, $\left[\frac{{mol}_{Al}}{m_{gel}^3.s}\right]$

${\mathit{r}}_{\mathit{U}\mathit{A}}$ Rate of uric acid consumption, $\left[\frac{{mol}_{UA,gel}}{m_{gel}^3.s}\right]$