- 1Department of Chemical Engineering, University of Bath, Bath, United Kingdom
- 2Centre for Bioengineering and Biomedical Technologies (CBio), University of Bath, Bath, United Kingdom
Siphons have been used for thousands of years to transfer fluids without the use of pumps or power and are present in our daily lives. Paradoxically, it is only in recent decades that the operation of siphons has been fully clarified, which is now understood to be exclusively linked to gravity and molecular cohesion. Siphons are uniquely able to offer automatic, intermittent flow, yet present the main drawback of requiring a source of energy to induce initial flow. Our research team has recently disclosed a microfluidic siphon able to self-prime and deliver a sequence of bioanalytical reagents, previously demonstrated for high-performance, multi-reagents diagnostic testing. Here we show for the first time 2D and 3D computational fluid dynamics (CFD) modeling and the experimental characterization of fluid flow in a range of miniaturized hydrophilic siphons of varying hydraulic liquid height-to-length ratios, ΔH/LT = 0–0.9, using fluids of varying viscosities. CFD simulations using velocity- and pressure-driven inlet boundary conditions were generally in good agreement with experimental fluid flow rates and pressure-balance predictions for plastic ∼0.2 mm and glass ∼0.6 mm internal diameter microfluidic siphons. CFD predictions of fluid flow in “meso-scale” siphons with 1 and 2 mm internal diameters also fully matched normalized experimental data, suggesting that miniaturized siphons are scalable. Their discharge rate and pressure drop are readily predicted and fine-tunable through the physical properties of the fluid and some design parameters of the siphon. The wide range of experimental and numerical parameters studied here provide an important framework for the design and application of gravity-driven micro- and meso-fluidic siphons in many applications, including but not limited to life sciences, clinical diagnostics, and process intensification.
1 Introduction
There is currently a big global push for decentralizing high-performance diagnostic tests out of centralized labs. Diagnostic tests are now routinely informing 60%–70% of clinical decisions (Rohr et al., 2016; Sikaris, 2017), and many patient pathways already include a form of patient stratification or diagnosis based on the quantitation of at least one biomarker. However, the diagnosis of several infectious and non-communicable diseases is currently limited by long waiting periods, the need to access bulky and expensive centralized equipment, and the need to train medical professionals (Naghdloo et al., 2019). These limitations emphasize the need to develop new fluidic and bioanalytical capabilities suitable for point-of-care (POC) diagnostics. A key challenge from the perspective of fluidics for the development of high-performance POC tests is delivering a sequence of bioanalytical and washing reagents without the need for power. It is well established in the literature that any attempts in speeding up a diagnostic test towards a single step, away from multiple steps of incubation and/or washing, greatly compromises the performance of bioanalytical tests. Several studies have proposed fluid solutions for multi-step bioassays in lateral flow or paper strips (Lutz et al., 2013) using capillaries forces or capillary pumps (Juncker et al., 2002; Olanrewaju et al., 2016; Olanrewaju et al., 2018) with some success. Reis et al. (2021) introduced an innovative microfluidic siphon concept which was able to self-prime and deliver a sequence of bioassay reagents through a bioassay microcapillary based only on gravity. There is now a need to fully characterize fluid flow in microfluidic siphons, particularly by understanding how fluid flow is affected by the viscosity of reagents, which is key to the effective design of microfluidic siphons.
In recent years, the increasing popularity of microfluidics and nanotechnology has encouraged the development of microfluidic POC devices, such as lab-on-a-chip (LOC), lab-on-a-disc (LOAD), lateral flow, patterned paper, and miniaturized PCR devices (Holland and Kiechle, 2005; Sista et al., 2008; He et al., 2018). In comparison with traditional bioanalytical tools, microfluidics analysis is advantageous for a number of reasons, primarily due to fast reaction times, reduced volumes of specimens and reagents, and convenience. Fluid transport within microfluidic devices is predominantly driven by pressure forces, capillary action, or centrifugal forces. Pressure-driven devices are dependent on active components such as values and pumps to generate a pressure difference, such as in LOC devices (Ho et al., 2014; Reis et al., 2016; Kremers et al., 2020), limiting their application to in-house laboratory assays. Centrifugally driven devices have increased in popularity as they only require a low-power motor and frequently utilize microfluidic siphons to perform various unit operations, such as mixing, valving, liquid metering, and pumping (Kitsara et al., 2014; Hsu et al., 2020; Lapins et al., 2020; Woolf et al., 2020). In contrast, the portability and simplicity of capillary flow devices make them ideal for decentralized optical readouts; this includes ubiquitous lateral flow assays which use horizontal platforms and dipsticks which use vertical orientations.
Microfluidic siphons are an alternative POC platform that rely on gravity-driven flow and offer greater control over fluid flow as they are not limited by the frictional resistances present in capillary flow devices, as previously shown by our research team (Reis et al., 2021). Kitsara et al. (2012) and Ozaki et al. (2016) examined the use of siphon flow using paper and cotton yarn materials for controlling the flow of cell culture media through a microwell. The microfluidic siphon concept proposed by Reis et al. (2021) took its inspiration from conventional “macrofluidic” siphons that are ubiquitous in modern society. It is well established that siphons can have automatic, intermittent flow. However, a major limitation of a macrofluidic siphon is the need for a source of energy to start the flow. This has been addressed by Reis et al. (2021) using hydrophilic micro-bored capillaries which utilize surface tension forces in the self-priming of microfluidic siphons to offer full power-free operation combined with intermittent flow capability.
A siphon can be described as an inverted “J” tube, the highest point of which is above the liquid surface of the upper reservoir; it is used to transfer liquid from one vessel to another (Figure 1) at a lower elevation solely under the influence of gravity (Jeong et al., 2014). The hydraulic liquid height, ΔH, is the difference in height between the upper and lower reservoirs (Figure 1C) and acts as the driving force of fluid flow (Steigert et al., 2007). For centuries, the operation of a siphon was not fully understood; however, it is now fairly acknowledged in the literature that siphon flow is linked exclusively to molecular cohesion and gravity. The weight of the liquid reduces the pressure at the highest point of the siphon (“U-bend”), allowing for continuous flow thereafter (Figure 1A). For a liquid to be transported through the siphon-effect, it must have a density greater than that of the atmosphere and must have a surrounding pressure capable of opposing the gravitational pull on the short leg. However, macrofluidic siphon flow cannot be characterized as “power-free” as it requires initial energy for priming and elevating the liquid to the top of the “U” bend through Laplace pressure. Once the liquid level passes the neck of the siphon (the point of lowest pressure), there exists a positive ΔH driving fluid flow downwards.
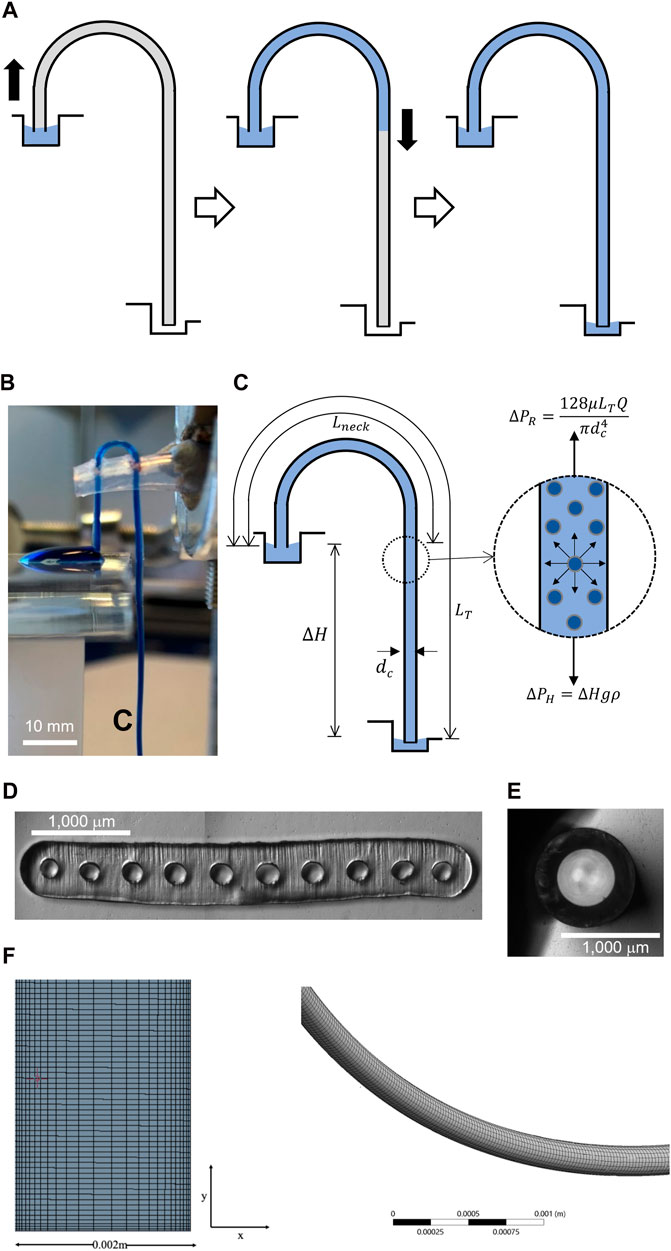
Figure 1. (A) Schematic diagram showing the operation of a microfluidic or mesofluidic siphon. Priming of siphon is triggered by capillary forces due to Laplace pressure generated in the hydrophilic (micro) capillary. Once the fluid passes through the top the siphon (lowest pressure point) and reaches the same liquid height of inlet, fluid flow is then driven solely by gravity. (B) Side view of an experimental 10-bore, 204 μm i.d. siphon in operation taking up a dyed water droplet though siphon action. (C) Flow in a siphon is entirely linked to gravity through hydrostatic height, ΔH, and cohesion forces. A pressure balance shows that discharge rate is linked to fluid properties of the inner diameter of the siphon and ΔH/LT ratio. (D) Microphotograph of the cross section of a 10-bore, 204 μm i.d. (E) Microphotograph of the cross section of a 578 μm i.d. glass capillary. (F) Details of meshing used in 3D, CFD simulations.
The concept of siphon-driven flow has previously been reported in terms of diagnostic medical testing, specifically using centrifugal microfluidics. Kitsara et al. (2012) induced siphon-driven flow by using centrifugal forces to drive the fluid across hydrophilic surfaces and distribute reagents. Mishra et al. (2018) developed a multiplex assay capable of measuring biomarkers associated with prostate cancer using a siphon-based centrifuge–pneumatic flow control scheme. However, it should be noted that the design of a siphon corresponding to a microfluidic channel with a J shape was correctly used in both Kitsara et al.(2012) and Mishra et al. (2018); however, in both cases the microfluidic channel operated horizontally and was therefore not truly experiencing the effect of gravity but only of induced centrifugal forces.
In this study, we experimentally measure discharge flow rates for fluids of varying viscosities and carry out pressure balance and numerical modeling using computational fluid dynamic (CFD) simulations in self-priming micro- and meso-fluidic siphons. In contrast to macrofluidic siphons, the self-priming of microfluidic siphons with an inner capillary diameter of dc < 1 mm and ideally below 0.5 mm was possible without the use of any external energy or power source due to capillary forces or Laplace pressure. We studied fluid flow in microfluidic siphons using 2D planar and 3D CFD simulations, validated experimentally using flow rates measured for a range of fluid viscosities composed of water–glycerol mixtures. A range of microfluidic siphon designs with a ratio of ΔH to total length LT, herein described by the ratio ΔH/LT between 0 and 0.9, were designed and experimentally tested based on a fully flexible 10-bore, ∼0.2 mm internal diameter (i.d.) plastic microfluidic material and single-bore ∼0.6 mm i.d. glass microcapillary. We compared pressure-driven with velocity-driven inlet boundary conditions to fully test the ability of the CFD models to predict pressure within the microcapillaries. Additional CFD simulation explored the ability to predict fluid flow in meso-fluidic channels (1–2 mm i.d.), demonstrating the fluidic concept and that CFD models are scalable. The wide range of experimental and numerical parameters studied here provide an important framework for gravity-driven micro- and meso-fluidic siphons in many applications, including life sciences, clinical diagnostics, and process intensification.
2 Materials and methods
2.1 Materials
High-molecular weight polyvinyl alcohol (PVOH, MW 146,000–186,000 g.mol−1 99% + hydrolyzed, catalogue no: 363065), Tween® 20 (Polysorbate 20), and ProclinTM 300 were sourced from Sigma-Aldrich (Dorset, United Kingdom), as was Indigo Carmine dye (concentration 85% and λmax of 608 nm). Micro-engineered, 10-bore MicroCapillary Film (MCF) melt-extruded (Hallmark et al., 2005) from Teflon® FEP with mean internal diameter dc = 203.7 ± 13.80 μm (Figure 1D) were supplied by Lamina Dielectrics Ltd. (Billinghurst, United Kingdom). The dimensions of individual capillaries are summarized in Supplementary Table S5. Single-bore glass capillaries, with an outer diameter of 1 mm and inner diameter of dc = 578 μm (Figure 1E) were sourced from World Precision Instruments (Sarasota, FL, United States).
2.2 Hydrogel-coating for hydrophilic MCF microfluidic strips
The MCF materials used to prepare microfluidic strips (supplied in reels of > 1,000 m) were trimmed into strips 1.0–1.5 m long. Since Teflon® FEP is hydrophobic, raw MCF siphons would be incapable of self-priming. This was overcome by coating the inner walls of the microcapillaries with high-molecular weight PVOH. A 20 mg⋅ml−1 solution of high molecular weight PVOH was prepared following the preparation guidelines suggested by SELVOL(TM). On a magnetic stirrer and hotplate, 4 g of PVOH were slowly added to 200 mL of ultra-pure water at < 38°C. The temperature was increased to 95°C until the solution had become homogeneous. Ultra-pure water was added throughout the process to maintain the liquid level and concentration of the solution. ProclinTM300, a preservative, was finally added to prevent microbial growth at 0.05% (w/w). The freshly prepared PVOH solution was then aspirated using a custom-built push-fit connector (Alves and Reis, 2019) and a plastic syringe until all ten capillaries were full. Following this, the microfluidic strips were incubated for 2 h, allowing the PVOH to solidify and bind the inner walls of the microcapillaries. Low-pressure air was used to flush excess PVOH solution. Finally, the MCF strips were thoroughly washed with ultrapure water. The process was repeated for air, Tween 20, 0.5% (w/w), and air one more time. The coated microfluidic MCF strips were then further trimmed into strips 100–150 mm long and fully dried by gently flushing with low pressure air or nitrogen.
2.3 Experimental measurement of flow rates in multi-bored microfluidic strips
We measured the discharge flow rate, Q, in the multi-bored MCF siphons for a range of ΔH/LT ratios (Figure 1A) fabricated from different combinations of LT and the length of the neck, Lneck (Supplementary Table S2). As the MCF material is flexible, the MCF strips could easily bend to form a siphon J-shape and was kept in shape using a plastic support. The upper reservoir was loaded with a 150 μL droplet of 0.05% (w/w) indigo carmine and the bottom reservoir consisted of a well containing 600 μL of water. Q was determined by recording the time taken to fully discharge 150 droplet μL into a cuvette placed at the MCF strip outlet, previously calibrated to deduce the volume of fluid discharged. This was repeated at least three times for each siphon in order to determine the mean Q value and standard deviation.
As the priming of empty siphons involves a receding gas–liquid interface, discharge flow measurements started by first priming the siphons using the working fluid (ultra-pure water or water–glycerol mixture). The siphon outlet was then submerged 2 mm below the liquid level of the bottom reservoir to keep the hydrostatic height constant throughout the experiment. The siphon inlet was then submerged into a 150 μL droplet of 0.05% (w/w) Indigo Carmine solution, and the time required to uptake the droplet was recorded. Adding Indigo Carmine solution to the working fluid facilitated imaging the flow in the transparent siphons. Considering that flow resistance depends on both Q and dynamic fluid viscosity μ, we also measured Q for fluids having a range of μ by combining a range of glycerol to ultra-pure water mixtures yielding 0%, 16%, 33%, and 50% (v/v) solutions, yielding values of μ, ρ, and θ (Supplementary Table S4) (Takamura et al., 2012; Volk and Kähler, 2018).
2.4 Experimental measurement of flow rate in glass capillaries
We fabricated a further set of siphons from single-bore hydrophilic glass microcapillaries yielding a range of ΔH/LT ratios by keeping LT constant (Supplementary Table S3). With borosilicate glass being naturally hydrophilic, there was no need to modify the inner wall of glass microcapillaries. A straight 142.4 mm-long glass microcapillary was bent above a Bunsen burner using heat to produce a J-shape. The siphon was then fastened into position using a sponge-covered clamp (Figure 1B). We optically measured the cross-section of the glass capillary, yielding an inner capillary diameter, dc = 578 μm (Figure 1C). The siphon inlet was then submerged 10 mm below the liquid level of a glass beaker containing ultra-pure water (upper reservoir), while a cuvette was placed under the siphon outlet. Once the first droplet of water was discharged from the siphon and the siphon was fully primed, the time required to uptake 2.5 mL of water was recorded from where the discharge flow rate was computed. This was repeated at least three times.
2.5 Equilibrium contact angle
The equilibrium contact angle, θ, was calculated for PVOH-coated MCF and single-bore glass capillary by submerging 100 mm of the microcapillary in a cuvette pre-loaded with ultra-pure water. Once the liquid within the capillary had reached equilibrium height, a photograph was taken and the vertical distance between the meniscus and air–liquid interface determined using ImageJ, which defined the equilibrium liquid height, Heq. The value of θ could be computed from Heq by taking into consideration the shape of each individual microcapillary and/or its inner dc. For circular microcapillaries (i.e. glass), pressure balance in equilibrium height yields the Laplace–Young Eq. 1:
where γ is surface tension (N m−1) and ρ is the specific mass (kg m−3) of the fluid. For elliptical microcapillaries, as is the case with the melt-extruded microcapillary film we used, a modified Laplace–Young equation given by Eq. 2 takes into consideration the shape of the microcapillaries by considering the major axis a and minor axis b:
Experimental measurements taking into consideration the inner dimensions of the microcapillaries, particularly the mean hydraulic diameter, dh, and/or the major and minor axis (Supplementary Table S5) yielded Heq of 57.7 mm for the 10-bore MCF (Supplementary Figure S1; Supplementary Table S6) and 32.5 mm for the glass microcapillary in DI water (results not shown), which reduced in the presence of glycerol. However, θ remained mostly independent on the concentration of glycerol, yielding ∼66° for the MCF and ∼51° for the glass microcapillary (Supplementary Figure S1; Supplementary Table S6).
2.6 CFD modeling in microfluidic and meso-fluidic siphons
ANSYS Fluent was used for 2D and 3D fluid flow simulations in microcapillary siphons with dc = 0.2 mm and mesofluidic siphons with dc = 1 and 2 mm, for ΔH/LT ratios up to 0.9. Dimensions of the various microfluidic siphons used in 2D and 3D CFD simulations are listed in Supplementary Table S1, all using a neck distance Lneck = 44 mm. A pressure-based SIMPLEC solver, gravity activated, with a pressure-correction-under-relaxation factor of 1, and the pressure-velocity coupling method was used to converge the steady-state flow solution (Jeon and Shin, 2009). A laminar transport model was applied and solved using the least-squares cell-based method, second-order pressure spatial discretization, and second-order upwind spatial discretization. CFD simulations were initialized using hybrid initialization. Convergence of the results was achieved once the steady state residual monitors reached below 10–4 for continuity and momentum equations in all 2D and 3D simulations. Under the assumption that fluid is Newtonian, incompressible, and abides by Fourier’s Law of heat conduction, fluid flow within the micro- and meso-fluidic siphons was governed by the continuity and Navier–Stokes equations, given by Eqs 3, 4, respectively:
where ū is the velocity vector, ρ is the fluid density, t is time, p is pressure, and µ is fluid viscosity. The angular momentum and continuity equations were satisfied by assuming the flow was steady, axisymmetric, and fully developed, and that there was no radial or axial mixing. The first and third momentum equations were reduced to Eqs 5, 6, respectively:
where r is the polar radial coordinate and z the axial (length) coordinate in the siphon. Eq. 4 was solved using the no-slip boundary condition, which requires uz = 0 at r = R, siphon inner radius, R = dc / 2, yielding a parabolic velocity profile given by Eq. 7:
The 2D and 3D micro- and meso-fluidic siphon geometries were meshed using quadrilateral and hexahedra structured grids which included a denser boundary layer along the walls of the siphon, allowing for a more accurate representation of the fluid flow along the boundary layers. The 2D and 3D CFD models contained grids ranging between 12,200 and 500,000 mesh elements, resulting from radial node sizes between 6 μm and 1 mm which were fully tested in the mesh independent study. In general, the 2D simulations ran relatively quickly, in the range of 10–15 min for full convergence for all ΔH/LT ratios simulated. The 3D simulations required longer computational times in the order of 1–2 h due to the more complex interaction of elements in three dimensions. CFD simulations were carried out for mixtures of 0%, 10%, 20%, 30%, and 40% (v/v) glycerol to DI water. Physical properties of glycerol–water mixtures were based on data gathered from literature (Takamura et al., 2012; Volk and Kähler, 2018) as summarized in Supplementary Table S4.
For the velocity-driven 2D and 3D microfluidic siphon simulations, the inlet boundary condition was set as a constant velocity determined using Eq. 8:
where vin is the inlet velocity, Q is the volumetric flow rate, and A is the cross-sectional area of the siphon. It was assumed that there was a no-slip boundary condition at the walls of the siphons. The outlet boundary condition was set at atmospheric pressure. For the pressure-driven 2D and 3D microfluidic siphon simulations, the inlet boundary condition was set as a constant pressure.
2.7 Pressure balance modeling of fluid flow in the siphons
For laminar flow in microcapillaries of length LT with a circular cross-section with inner capillary diameter dc = 2*R, the Navier-Stokes Eqs 5, 6 can be solved yielding the Hagen–Poiseuille equation shown in Eq. 9, which relates resistance pressure drop along the siphon, ΔPR, with discharge flow rate Q:
which can be rearranged for:
The pressure drop along the siphon can be described using Bernoulli’s equation:
where ΔH is the net hydraulic pressure head (i.e., vertical distance between the liquid levels in the inlet and outlet reservoirs—Figure 1A). Fluid transport in microfluidic devices is typically driven by a difference in pressure; hence for pressure-driven flow, Eq. 11 can be simplified to Pascal’s law:
Considering that the length of capillary/strip immersed in the inlet and outlet reservoirs is negligible, the discharge flow rate in the siphon can be shown to exclusively depend on the ratio ΔH/LT by substituting Eq. 12 into Eq. 10:
For the multi-bored MCF strips, having multiple N parallel microcapillaries, Q was assumed to be equally distributed across the whole array of microcapillaries, which can be estimated from:
Eqs 13, 14 show that Q is only dependent on the aspect ratio of the siphon and fluid properties and can be easily rearranged to units of acceleration (m s−2) as in Eq 15 to enable direct comparisons between different siphon systems:
Note there are an infinite number of combinations that produce a siphon with a given ΔH/LT ratio, yet two pragmatic approaches were devised: by keeping either i) LT or ii) Lneck constant. Thus the relationship between ΔP and ΔH/LT actually depends on the design approach to create the series of siphons. For a siphon with a given neck length Lneck (Figure 1C), it can be shown that:
Rearranging Eq. 16 in terms of the deltaH/Lt ratio yields:
For CFD simulation, Lneck was taken as a constant (44 mm—see Supplementary Table S1) coinciding with some of the design combinations used for experimental multi- and single-bored microfluidic siphons (Supplementary Tables S2, S3). When the length of the neck is negligible—Lneck << LT—it can be shown that ΔH ≈ LT, which would represent the ratio ΔP α ΔH/LT. However, in most designs, especially for short ΔH ≈ LT values, Lneck cannot be ignored, whence it can be shown that ΔP increases approximately with the square of the ΔH/LT ratio (Supplementary Figure S3).
3 Results and discussion
3.1 Mesh independence analysis and experimental validation of CFD model
By performing a detailed mesh independence analysis on single-capillary microfluidic siphons using 2D and 3D CFD models, we determined the optimum mesh size for subsequent CFD modeling. We controlled the number of nodes within the grids produced for the 2D and 3D models by directly decreasing the radial element size incrementally from 1,000 µm down to 5 µm (Supplementary Figure S4B), yielding 12,000–500,000 mesh elements (Supplementary Figure S4A). The number of nodes within the grids of the 3D models (Figure 1F) was controlled by decreasing both the element size and the number of divisions along the width of the siphon inlet and outlet. As independent criteria, we compared simulation results based on Q and ΔPH in order to determine the minimum number of elements that balanced computational time with the accuracy of CFD simulations (Figures 2A, B; Supplementary Figure S4). Note that in line with the pressure balance for single-phase flow in the microcapillaries, pressure drop through resistance ΔPR in the microcapillary should be equal to hydraulic liquid height ΔPH. We observed from simulations that an unrefined mesh could not produce an accurate solution; grids produced using element sizes of 1,000 μm, 500 μm, and 20 µm resulted in solutions that deviated by 0.50%, 0.10%, and 0.02%, respectively, from the pressure-balance model estimate (Figures 2A, B). Thus, all subsequent 2D and 3D CFD simulations were carried out using grids with ∼ 250,000 elements, corresponding to a radial node size of 20 µm (Supplementary Figure S4) combined with a boundary layer with a smoothing factor of 1.2. As expected, element sizes smaller than 20 µm gave a more accurate solution as the fluid velocity gradients could be better captured; however, element sizes of 10 µm or less resulted in element numbers exceeding 500,000, representing higher computational times (Supplementary Figure S4). We therefore capped the element size outside the boundary layer to 20 µm, but we noticed that this yielded a relatively coarse mesh in terms of axial distance at ΔH/LT ratios equal or above 0.6. As LT increased, the axial length of the mesh elements also increased, with CFD simulations overestimating pressure drop and consequently underestimating Q compared to both the analytical solution of the pressure balance model and experimental data in the microfluidic siphons.
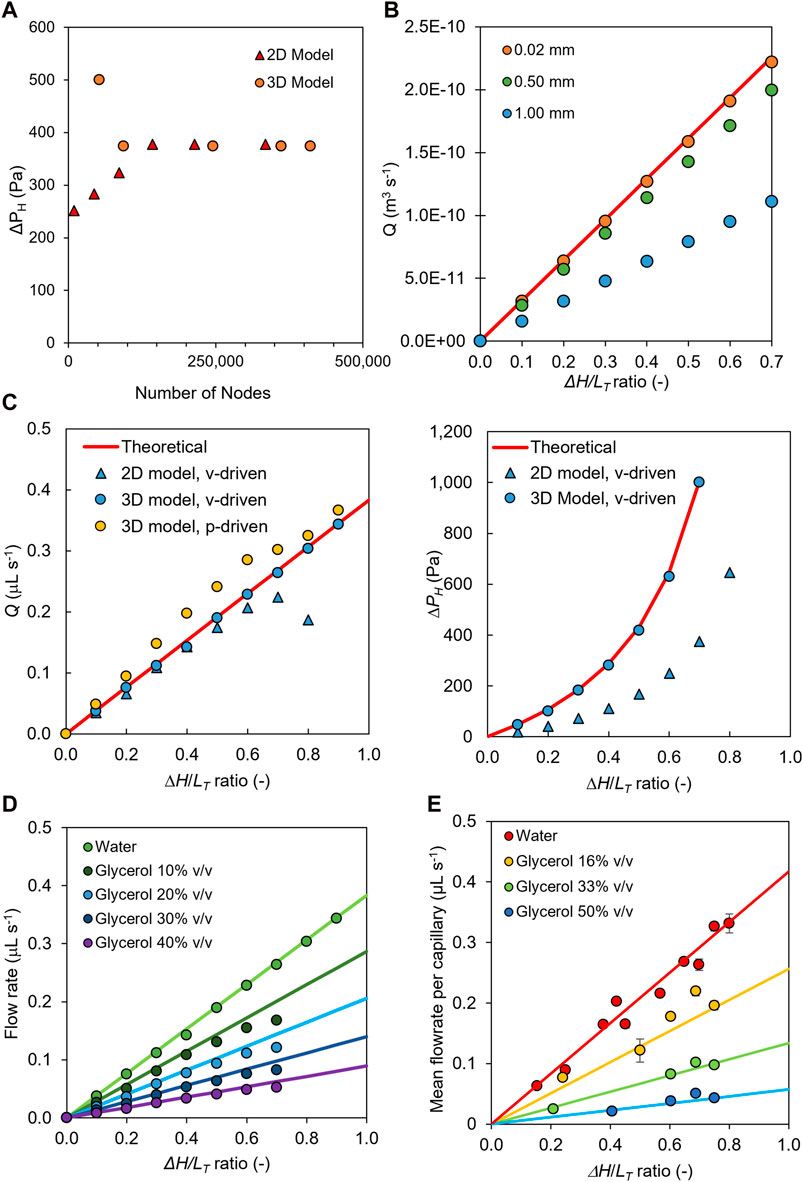
Figure 2. CFD simulations and experimental measurements of discharged flow rates and pressure drop in microfluidic siphons. (A) Mesh independence study performed for 2D and 3D simulation models, ΔH/LT = 0.5. (B) Effect of element size on the accuracy of the CFD output based on 2D model simulations, showing that a very fine mesh with a maximum node distance of 0.02 mm was required for matching CFD predictions with pressure balance model predictions. (C) Comparison of discharge flow rate and static pressure drop obtained with 2D and 3D velocity- and pressure-driven siphons with values predicted from pressure-balance. (D) Steady-state 3D CFD predictions (dotted data) for a microfluidic siphon operating with 0%, 10%, 20%, 30%, and 40% v/v water–glycerol mixtures, using pressure-inlet and -outlet boundaries, benchmarked against predictions from pressure balance (continuous lines), showing discharge flow rate increased linearly with increase in ΔH/LT ratio. (E) Experimental measurements (dotted data) of mean discharge flow rate obtained with a 10-bore microfluidic siphon (204 μm i.d.) as a function of the ΔH/LT ratio for 0%, 16%, 33%, and 50% v/v of glycerol in water solutions, and benchmark with predictions from pressure-balance model (continuous lines). Error bars represent ±1 standard deviation from at least three independent, experimental replicas. For all data shown, 2D simulations used dc = 206 μm, 3D simulations used dc = 200 μm, and experimental measurements used ten bored, dc = 204 μm microcapillaries.
3.2 Effect of ΔH, LT, and fluid properties on discharge flow rate
We experimentally observed that the ΔH/LT ratio and fluid viscosity μ are key parameters in setting the discharge rate of a microfluidic siphon. Consequently, we carried out systematic 2D and 3D simulations using velocity- and pressure-driven boundary conditions for microfluidic siphons with varying ΔH/LT of 0.1–0.9 (Figures 2C–E) which we initially validated against an analytical solution of a pressure balance model (Figure 2D) and experimental measurements (Figure 2E) of Q using a 10-bore MCF siphon dc = 203.7 ± 13.80 μm (Figure 2D) for DI water and glycerol–water mixtures. Note that the CFD simulations predicted a linear increase in Q with increasing ΔH/LT ratio and decreasing μ, in full agreement with predictions from the pressure balance model in Eq. 13. This demonstrates that Q is entirely driven by gravity and can be tuned for a given fluid by simply changing ΔH and/or LT. Overall, the CFD model was capable of predicting the discharge flow rate in microfluidic siphons relatively well across varying conditions (Figure 2D), thus providing a robust tool for optimizing fluid transport in microfluidic systems.
Unsurprisingly, fluid flow was observed to be parabolic and laminar for the entire length of the siphon, with the exception of initial length equivalent to 1 to 2*dc in both micro- (Figure 3A) and meso-fluidic (Figure 3B) siphons due to the smooth bend of the neck of the siphons. Q values measured with a 10-bored 204 μm plastic siphon (Figure 2D) and single-bored 575 μm glass siphon microcapillaries (Figures 3A, B) with various water–glycerol mixtures of 0%–50% (v/v) showed, as expected, an increase in μ reduced Q (Figures 2D, E) due to increased fluidic resistance (Nguyen and Wereley, 2006). A key application for microfluidic siphons is in point-of-care diagnostics, portable testing, or sustainable flow chemistry, which is likely to involve handling bioassay reagents and samples with a wide range of viscosities. For simplicity and taking into consideration the range of diameters and viscosities herein tested, we have normalized experimental and CFD numerical results to enable a direct comparison of normalized discharged flow rate in the y-axis, Q μ σ−1 dc−4 N−1 (m s−2), which helped confirm all sets of experiments. 2D and 3D CFD simulations closely follow predictions from the pressure balance model (Figure 4A). In general, the 3D CFD simulations fitted experimental data more closely as well as the analytical solution of the pressure balance model; this seems due to 2D planar model assuming a virtually infinite channel width (Chen and Liu, 2014). Consequently, to capture the laminar parabolic flow profile in three dimensions for the 3D model, we used finer nodes across the capillary where higher velocity gradients were expected. For longer siphon lengths, we increased the number of divisions along the length of the capillary to increase the number of elements, and yielding a solution that is independent of the quality of the mesh. However, at higher ∆H/LT values of 0.6 and above, the meshes produced failed to accurately capture the flow (Figure 4A) by overpredicting ΔP and consequently underpredicting Q. Keeping small node distances along the axial distance of the capillary at high ∆H/LT values would require the number of elements to exceed 500,000—a computational time of several hours.
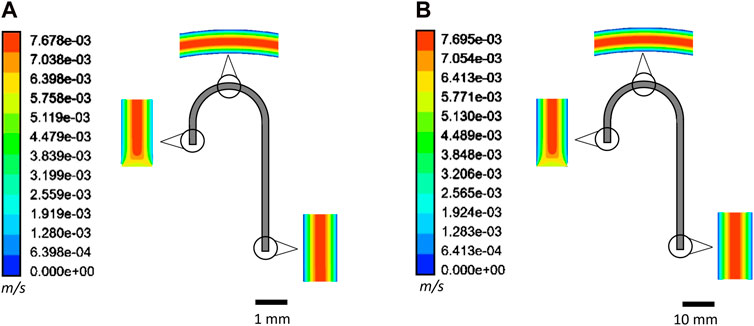
Figure 3. Velocity contour plots predicted for 10% water–glycerol solution within a pressure-driven 2D model using (A) microfluidic (dc = 206 μm) and (B) mesofluidic siphon (dc = 2 mm) with ΔH/LT = 0.4.
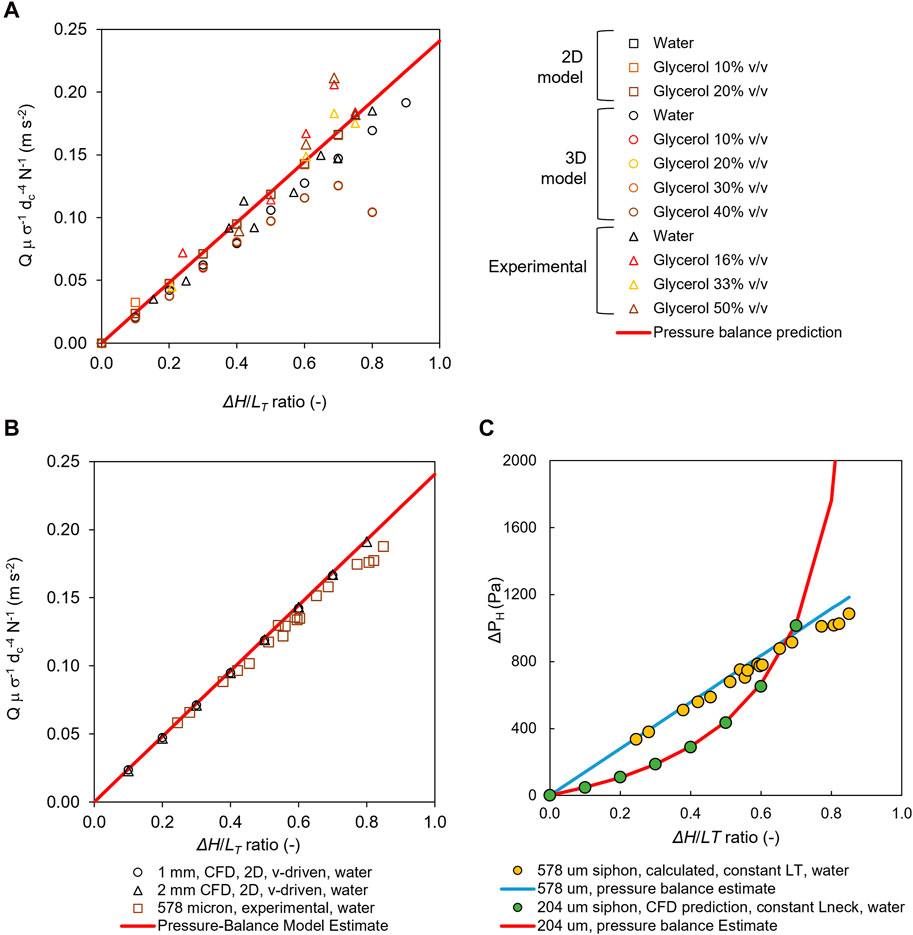
Figure 4. Normalized volumetric flow rates and corresponding pressure drops showing that CFD simulations could predict flow rates and pressure drops across a range of fluid viscosities and scales. (A) Comparison of 2D and 3D simulations and experimental results for a range of water–glycerol mixture microcapillary siphons, showing the normalized flow rate increasing linearly with ΔH/LT ratio. 2D simulations used dc = 206 μm, and 3D simulations used dc = 200 μm, (B) Normalized flow rates predicted by CFD model for “meso-scale” siphons with dc = 1 mm and dc = 2 mm, benchmarked against experimental measurements with dc = 578 μm glass microcapillary siphons, showing that CFD results predict increase in flow rate proportional to ΔH/LT ratio, in line with estimates from pressure balance. (C) Pressure drop as a function of ΔH/LT ratio, showing that pressure drop is independent of the scale or inner diameter of the siphon, yet the relationship is interconnected to the design rule used to scale-up the ΔH/LT ratio (i.e. keeping Lneck constant or LT constant).
3.3 Effect of pressure-driven and velocity-driven boundary conditions
CFD modeling of fluid flow was carried out using two sets of boundary conditions, being a velocity- or a pressure-driven inlet, based on Eq 8 and Eq 10 respectively. In practical terms, pressure inlet and outlet boundary conditions more closely replicated the gravity-driven flow in microfluidic siphons, yet we have experienced multiple challenges in converging solutions for some combination of ΔH/LT, with both 2D and 3D models, for some pressure-inlet velocity CFD simulations. This was presumably due to the difficulty of the CFD solver in considering gravitational effects and entry effects in a refined mesh, especially for siphons with long LT.
Nevertheless, in general, both velocity-driven and pressure-driven flows matched well with the Hagen–Poiseuille pressure balance calculations from experimental data in terms of normalized Q and pressure drop for a wide range of ΔH/LT (Figure 4C) based on data from 204 μm to 587 μm internal diameter microfluidic siphons. We have, however, noticed significant deviations as high as 50% in pressure drop predictions with velocity-driven 2D simulations (Figure 2C). In contrast, there was an excellent agreement for pressure drop with the 3D velocity driven model, suggesting that the third dimension is important for accurately computing the pressure field and avoiding assumptions which can be made for the U-bend in 2D simulations. In addition, we observed that both experimental and CFD pressure drop calculations followed the expected trend in terms of ΔP vs. ΔH/LT ratio (Figure 4C), independent of the boundary conditions. which in the case of the siphon series at constant LT, led to a linear relation. However, siphon series at constant Lneck led to a quadratic increase in pressure drop (Supplementary Figure S3). The ΔPH values determined using 2D and 3D CFD models deviated by up to only 11.8% and 18.3%, respectively, from pressure balance model estimates from experimental data. Overall, we have noticed good agreement between the pressure drop values estimated from the pressure head difference or Pascal’s law (Eq. 12) and pressure drop due to flow resistance computed from the Hagen–Poiseuille Eq. 9 (Supplementary Figure S2), validating the pressure-balance model. Perhaps not obviously, but changing the ΔH/LT ratio means that the hydrostatic head is changed in addition to the LT and/or shape of the microfluidic siphon, yet Q is automatically adjusted such that pressure drop due to flow resistance balances the pressure head difference—that is, ΔPH = ΔPR. This is only possible due to the molecular cohesion and suggests that as ΔH increases, Q increases linearly; also, as dc increases, Q should increase proportional to dc4, which makes longer and/or meso-fluidic siphons compelling for applications such as (green) flow chemistry. The CFD models presented here demonstrate the highly predictable flow of gravitationally driven fluids and can be used to easily design siphons based on the desired flow rates and sample volumes.
3.4 Prediction of flow in mesofluidic siphons
Using the fully validated CFD model, we performed additional sets of 2D CFD simulations for meso-fluidic siphons, with dc = 1 mm and dc = 2 mm, using 0%, 10%, and 20% w/w water–glycerol mixtures. As expected, we observed from velocity contour plots that the flow regime remains laminar regardless of fluid viscosity and siphon geometry (Figure 3B), with the Reynolds number, Re, remaining well within the laminar flow regime. The velocity profiles captured the parabolic flow characteristic of laminar flow, such that the maximum velocity was experienced at the center of the siphons and decreased radially as flow approached the walls, attributed to the high shear stresses present near the walls (Oh et al., 2012) linked to the no-slip boundary (Nguyen and Wereley, 2006). A study conducted by Hu et al. (2015) observed similar flow characteristics within T-shaped microchannels. Re remained below 700 for all siphon geometries and fluid viscosities simulated and experimentally tested, and so was well within the laminar flow regime observed for streamlined flow.
As LT was increased, yielding ΔH/LT values up to 0.8 (Supplementary Table S1), we observed a linear increase in Q with excellent agreement with the normalized experimental flow rate for microcapillaries with dc = 204 μm (data not shown) and 578 μm (Figure 4B). It also fully matched predictions from pressure balance in normalized Eq. 14, with deviations as low as 1.4%. These results suggest that CFD and the pressure balance modeling of microfluidic siphons can be equally used to predict fluid flow in meso-fluidic siphons with high accuracy using computationally low cost 2D models in a wider range of ΔH/LT values compared to microfluidic siphons. The siphons studied here are well suited to multi-step gravity-driven bioassays where continuous and constant flow is generally applied, in contrast with applications such as cell culture requiring dynamic flow or for sustainable flow chemistry operations.
4 Conclusion
To our knowledge, this is the first numerical and experimental study characterizing the flow of Newtonian fluids through microfluidic and mesofluidic siphons. 2D and 3D CFD simulations were able to predict to various levels of accuracy the discharge flow rate and pressure drops for a range of design, fluid properties, and inlet boundary conditions. In general, CFD results agreed well with predictions from the pressure-balance model and experimental estimates based on the Hagen–Poiseuille equation; however, the full prediction of resistance forces, particularly pressure drop in a microfluidic siphon for ΔH/LT values of 0.6 or above representing LT of 100 mm or longer, would have required extended computational efforts beyond 500,000 mesh elements. Although CFD simulations with velocity inlet/pressure outlet boundary conditions were able to capture fluid properties and pressure in the siphons well, we have succeeded in capturing fluid flow using a pressure inlet/ outlet that fully mimics the operation of a gravity-driven siphon working at atmospheric pressure. The CFD models were also able to predict fluid flow in mesofluidic siphons with internal diameters of 1 and 2 mm, demonstrating that utilizing both CFD and pressure balance equations that steady flow through microfluidic and mesofluidic siphons is fully scalable and predictable and is exclusively connected to gravity and molecular cohesion. We believe this detailed fluidic characterization of siphons provides a basis for the design of, for example, high performance POC diagnostic devices or sustainable flow chemistry micro- or meso-reactors only based on gravity.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
NA: Data curation, Formal Analysis, Investigation, Software, Visualization, Writing–original draft. GS: Data curation, Formal Analysis, Investigation, Software, Writing–original draft. KG: Investigation, Methodology, Software, Supervision, Writing–original draft. SB: Data curation, Formal Analysis, Writing–original draft. KA-H: Data curation, Formal Analysis, Investigation, Writing–original draft. NR: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.
Funding
The authors declare financial support was received for the research, authorship, and/or publication of this article. The authors are grateful to the University of Bath and ESPRC for funding a PhD studentship to KG.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fceng.2024.1443949/full#supplementary-material
References
Alves, I. P., and Reis, N. M. (2019). Immunocapture of Escherichia coli in a fluoropolymer microcapillary array. J. Chromatogr. A, 46–55. doi:10.1016/j.chroma.2018.11.067
Chen, X., and Liu, Y. (2014). Finite element modeling and simulation with ANSYS workbench. Finite Elem. Model. Simul. ANSYS Work. doi:10.1201/b17284
Hallmark, B., Gadala-Maria, F., and Mackley, M. R. (2005). The melt processing of polymer microcapillary film (MCF). J. Newt. Fluid Mech. 128, 83–98. doi:10.1016/j.jnnfm.2005.03.013
He, W., You, M., Wan, W., Xu, F., Li, F., and Li, A. (2018). Point-of-Care periodontitis testing: biomarkers, current technologies, and perspectives. Trends Biotechnol. 36, 1127–1144. doi:10.1016/j.tibtech.2018.05.013
Ho, H. P., Lau, P. m., Kwok, H. c., Wu, S. y., Gao, M., Cheung, A. K. l., et al. (2014). Allergen screening bioassays: recent developments in lab-on-a-chip and lab-on-a-disc systems. Bioanalysis 6, 2005–2018. doi:10.4155/bio.14.153
Holland, C. A., and Kiechle, F. L. (2005). Point-of-care molecular diagnostic systems - past, present and future. Curr. Opin. Microbiol. 8, 504–509. doi:10.1016/j.mib.2005.08.001
Hsu, C.-W., Shih, P.-T., and Chen, J. M. (2020). Enhancement of fluid mixing with U-shaped channels on a rotating disc. Micromachines 11 (12), 1110. doi:10.3390/mi11121110
Hu, R., Li, F., Lv, J., He, Y., Lu, D., Yamada, T., et al. (2015). Microfluidic analysis of pressure drop and flow behavior in hypertensive micro vessels. Biomed. Microdevices 17, 60. doi:10.1007/s10544-015-9959-4
Jeon, W., and Shin, C. B. (2009). Design and simulation of passive mixing in microfluidic systems with geometric variations. Chem. Eng. J. 152, 575–582. doi:10.1016/j.cej.2009.05.035
Jeong, G. S., Oh, J., Kim, S. B., Dokmeci, M. R., Bae, H., Lee, S. H., et al. (2014). Siphon-driven microfluidic passive pump with a yarn flow resistance controller. Lab a Chip 14, 4213–4219. doi:10.1039/c4lc00510d
Juncker, D., Schmid, H., Drechsler, U., Wolf, H., Wolf, M., Michel, B., et al. (2002). Autonomous microfluidic capillary system. Anal. Chem. 74 (24), 6139–6144. doi:10.1021/ac0261449
Kitsara, M., et al. (2012). “Hydrophilic polymeric coatings for enhanced, serial-siphon based flow control on centrifugal lab-on-a-disc platforms,” in Proceedings of the 16th International Conference on Miniaturized Systems for Chemistry and Life Sciences, USA, Jul 2014. MicroTAS 2012.
Kitsara, M., Nwankire, C. E., Walsh, L., Hughes, G., Somers, M., Kurzbuch, D., et al. (2014). Spin coating of hydrophilic polymeric films for enhanced centrifugal flow control by serial siphoning. Microfluid. Nanofluidics 16 (4), 691–699. doi:10.1007/s10404-013-1266-x
Kremers, T., Thelen, S., Bosbach, N., and Schnakenberg, U. (2020). PortaDrop: a portable digital microfluidic platform providing versatile opportunities for Lab-On-A-Chip applications. PLoS ONE 15, e0238581. doi:10.1371/journal.pone.0238581
Lapins, N., Kazemzadeh, A., and Russom, A. (2020). “Automated blood plasma separation and metering for clinical settings and centrifugal microfluidics devices,” in MicroTAS 2020 - 24th International Conference on Miniaturized Systems for Chemistry and Life Sciences, China, October 4-9, 2020, 378–379.
Lutz, B., Liang, T., Fu, E., Ramachandran, S., Kauffman, P., and Yager, P. (2013). Dissolvable fluidic time delays for programming multi-step assays in instrument-free paper diagnostics. Lab a chip 13 (14), 2840–2847. doi:10.1039/c3lc50178g
Mishra, R., Zapatero-Rodríguez, J., Sharma, S., Kelly, D., McAuley, D., Gilgunn, S., et al. (2018). Automation of multi-analyte prostate cancer biomarker immunoassay panel from whole blood by minimum-instrumentation rotational flow control. Sensors Actuators, B Chem. 263, 668–675. doi:10.1016/j.snb.2018.02.015
Naghdloo, A., Ghazimirsaeed, E., and Shamloo, A. (2019). Numerical simulation of mixing and heat transfer in an integrated centrifugal microfluidic system for nested-PCR amplification and gene detection. Sensors Actuators, B Chem. 283, 831–841. doi:10.1016/j.snb.2018.12.084
Nguyen, N. T., and Wereley, S. (2006). Fundamentals and applications of microfluidics. London: Artech House.
Oh, K. W., Lee, K., Ahn, B., and Furlani, E. P. (2012). Design of pressure-driven microfluidic networks using electric circuit analogy. Lab a Chip 12, 515–545. doi:10.1039/c2lc20799k
Olanrewaju, A., Beaugrand, M., Yafia, M., and Juncker, D. (2018). Capillary microfluidics in microchannels: from microfluidic networks to capillaric circuits’, Lab on a Chip. R. Soc. Chem. 18 (16), 2323–2347. doi:10.1039/c8lc00458g
Olanrewaju, A. O., Robillard, A., Dagher, M., and Juncker, D. (2016). Autonomous microfluidic capillaric circuits replicated from 3D-printed molds. Lab a Chip 16, 3804–3814. doi:10.1039/c6lc00764c
Ozaki, A., Arisaka, Y., and Takeda, N. (2016). Self-driven perfusion culture system using a paper-based double-layered scaffold. Biofabrication 8 (3), 035010. doi:10.1088/1758-5090/8/3/035010
Reis, N. M., Needs, S. H., Jegouic, S. M., Gill, K. K., Sirivisoot, S., Howard, S., et al. (2021). Gravity-driven microfluidic siphons: fluidic characterization and application to quantitative immunoassays. ACS Sensors 6 (12), 4338–4348. doi:10.1021/acssensors.1c01524
Reis, N. M., Pivetal, J., Loo-Zazueta, A. L., Barros, J. M. S., and Edwards, A. D. (2016). Lab on a stick: multi-analyte cellular assays in a microfluidic dipstick. Lab Chip. R. Soc. Chem. 16, 2891–2899. doi:10.1039/C6LC00332J
Rohr, U.-P., Binder, C., Dieterle, T., Giusti, F., Messina, C. G. M., Toerien, E., et al. (2016). The value of in vitro diagnostic testing in medical practice: a status report. PloS One. U. S. 11 (3), e0149856. doi:10.1371/journal.pone.0149856
Sikaris, K. A. (2017). Enhancing the clinical value of medical laboratory testing. Clin. Biochem. Rev. Aust. 38 (3), 107–114.
Sista, R., Hua, Z., Thwar, P., Sudarsan, A., Srinivasan, V., Eckhardt, A., et al. (2008). Development of a digital microfluidic platform for point of care testing. Lab a Chip 8, 2091. doi:10.1039/b814922d
Steigert, J., Brenner, T., Grumann, M., Riegger, L., Lutz, S., Zengerle, R., et al. (2007). Integrated siphon-based metering and sedimentation of whole blood on a hydrophilic lab-on-a-disk. Biomed. Microdevices 9, 675–679. doi:10.1007/s10544-007-9076-0
Takamura, K., Fischer, H., and Morrow, N. R. (2012). Physical properties of aqueous glycerol solutions. J. Petroleum Sci. Eng. 98–99, 50–60. doi:10.1016/j.petrol.2012.09.003
Volk, A., and Kähler, C. J. (2018). Density model for aqueous glycerol solutions. Exp. Fluids 59 (5), 75. doi:10.1007/s00348-018-2527-y
Keywords: microfluidics, siphon, gravity driven, pressure balance modeling, CFD, Hagen Poiseuille
Citation: Akhras N, Singh G, Gill KK, Bola S, Al-Hakeem K and Reis NM (2024) Numerical modeling and experimental validation of fluid flow in micro- and meso-fluidic siphons. Front. Chem. Eng. 6:1443949. doi: 10.3389/fceng.2024.1443949
Received: 04 June 2024; Accepted: 08 July 2024;
Published: 12 August 2024.
Edited by:
Volker Hessel, University of Adelaide, AustraliaReviewed by:
Chenguang Zhang, Sanofi Genzyme, United StatesVan Duc Long Nguyen, University of Adelaide, Australia
Copyright © 2024 Akhras, Singh, Gill, Bola, Al-Hakeem and Reis. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nuno M. Reis, n.m.reis@bath.ac.uk
 Nour Akhras1
Nour Akhras1 Kirandeep K. Gill
Kirandeep K. Gill Nuno M. Reis
Nuno M. Reis