Game theoretic optimisation in process and energy systems engineering: A review

Game theory is a framework that has been used by various research fields in order to represent dynamic correlation among stakeholders. Traditionally, research within the process and energy systems engineering community has focused on the development of centralised decision making schemes. In the recent years, decentralised decision-making schemes have attracted increasing attention due to their ability to capture multi-stakeholder dynamics in a more accurate manner. In this article, we survey how centralised and decentralised decision making has been facilitated by game theoretic approaches. We focus on the deployment of such methods in process systems engineering problems and review applications related to supply chain optimisation problems, design and operations, and energy systems optimisation. Finally, we analyse different game structures based on the degree of cooperation and how fairness criteria can be employed to find fair payoff allocations.

1 Introduction

Process and energy systems engineering problems inherently involve multiple stakeholders with potentially conflicting objectives. Game theory is among the different approaches that enables the representation of multi-level programming and multi-objective optimisation problems and at the same time evaluate different cooperation options. Game theory was developed as a conceptual framework and in the past century has served as a key methodological tool to economists, social scientists and engineers. Accordingly, process systems engineering (PSE) community has interpreted common process design and optimisation problems in a game theoretic framework with a growing rate over the past decades (Figure 1). The keywords used for this search in the Web of Science are: game theory, fairness, Nash, bargaining, Stackelberg, Cournot, process systems engineering and energy systems engineering. Note that papers based on fuzzy and evolutionary programming were excluded from the search. The publications were selected among the following journals: European Journal of Operational Research, Journal of Cleaner Production, Computers and Industrial Engineering, Energies, Omega, Energy, Computers and Chemical Engineering, Computer Aided Chemical Engineering, Chemical Engineering Journal, Sustainable Production and Consumption, Chemical Engineering Transaction, AIChE Journal and Chemical Engineering Research and Design.

FIGURE 1

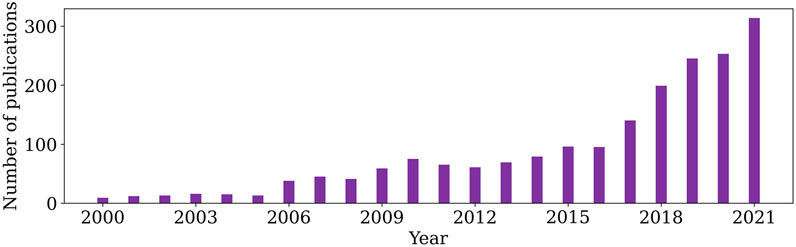
FIGURE 1. Number of papers published in journals including: European Journal of Operational Research, Journal of Cleaner Production, Computers & Industrial Engineering, Computers & Chemical Engineering, Sustainable Production and Consumption and AIChE Journal (Data obtained from Web of Science).

The aim of this article is to provide an overview of the existing publications in the field, and at the same time categorise them based on their application. The scope of this study entails only deterministic problems, which dominate PSE community. A graphical illustration of representative contributions of game theory in PSE can be found in Figure 2. Applications range from design of supply chains and planning, to heat and process integration, and process design. The rest of the article is organised as follows: initially we provide the background in game theory including game structures and fairness schemes, followed by the main body of the work which focuses on different fields of applications of game theory in PSE i.e., supply chain optimisation, process design and operation and finally energy systems optimisation. Finally, we summarise the conclusions of the review along with addressing the open questions in the field.

FIGURE 2

FIGURE 2. Graphic illustration of game theoretic applications in PSE.

2 Background in game theory

2.1 Types of games

The foundations of game theory were formed by von Neumann and Morgenstern (1944), when they generalised and put into a mathematical context notions that concerned economists since the 19th century. A game can be defined as any interaction between agents, that is restricted by set of rules dictating the allowed moves for each player and a set of outcomes for each possible combination of moves. However trivial this may seem, the theory of games mathematically reflects how the choice of an individual affect the choices of others (Hargreaves-Heap and Varoufakis, 2004). Let a strategic game be comprised of a set of players $\mathcal{N}≔\{1,\dots ,n\}$, and $X\subset {\mathcal{R}}^m$ be the set of feasible decisions players can make. Let the utility function $f_j:X\to {\mathcal{R}}_{+}$ of player $j\in \mathcal{N}$ be the mapping of a decision to a player’s payoff. Then the utility set $\mathcal{U}$ can be described as the set of all achievable utility allocations:

$\mathcal{U}≔\{u\in {\mathcal{R}}_{+}^n|\exists x\in X:f_j(x)=u_j,j\in \mathcal{N}\}(1)$

There exist various allocation schemes that propose the allocation of the utility among the players of the game. Such an allocation scheme is the choice of a function $\varphi :\mathcal{U}\to {\mathcal{R}}^n$ that selects a vector $u^{*}=\varphi (\mathcal{U})$. Following Moulin (1988), the axiomatic properties of allocation schemes can be summarised as follows.

1. Pareto optimality: An allocation scheme satisfies the Pareto optimality axiom, if there exists no other utility allocation that dominates the current one.

2. Symmetry: Let $\sigma :{\mathcal{R}}^2\to {\mathcal{R}}^2$ be a permutation operator such that σ((u₁, u₂)) = (u₂, u₁). Then, an allocation scheme is symmetric if the allocation under the permuted system $\varphi (\sigma (\mathcal{U}))$, is equal to the permutation of the original system, $\sigma \varphi (\mathcal{U})$. Thus, it satisfies $\sigma \varphi (\mathcal{U})=\varphi (\sigma (\mathcal{U}))$. The intuition behind this axiom is that under permuted identities, the equilibrium solution will not change.

3. Affine Invariance (AI): An allocation is AI if it satisfies $A\varphi (\mathcal{U})=\varphi (A(\mathcal{U}))$, where $A:{\mathcal{R}}^n\to {\mathcal{R}}^n$ is an affine operator. In this case, scaling the utilities will result in the affine transformation of the allocation acquired by the original game.

4. Independence of Irrelevant Alternatives (IIA): Let $\mathcal{U}$ and ${\mathcal{U}}^{\prime }$ be two utility sets such that $\mathcal{U}\subset {\mathcal{U}}^{\prime }$ and $\varphi ({\mathcal{U}}^{\prime })\in \mathcal{U}$. An allocation is IIA if it satisfies $\varphi (\mathcal{U})=\varphi ({\mathcal{U}}^{\prime })$.

5. Monotonicity: Let $\mathcal{U}$ and $\mathcal{W}$ be two utility sets, then an allocation satisfies monotonicity if it satisfies $\varphi (\mathcal{W})⪰\varphi (\mathcal{U})$.

The most common mean to define the solution of a strategic game with ordinal preferences is via the Nash equilibrium. The Nash equilibrium corresponds to a choice of strategy at which no player can achieve a greater utility function by changing their strategy. Let x* be the Nash equilibrium for a game consisting of players j, then Eq. 2 holds.

$u_j(x^{*})\ge u_j(x)\forall x,j(2)$

The stability and fairness of a Nash equilibrium is guaranteed under the following axioms: Pareto optimality, symmetry (anonymity), affine invariance (AI), independence of irrelevant alternatives (IIA) and monotonicity.

Inherent attributes of a strategic game entail different characteristics of the players and the decision making process. Among those are: 1) the number of players, 2) the set of decisions a player can make, 3) the level of cooperation, 4) the timing of the decision making, 5) the effect of a player’s decision to the others. In the context of PSE, the number of players and the set of decisions are part of the model formulation. Depending on the nature of collaboration among players, games can be divided in two categories: non-cooperative and cooperative games. In the former case, each player makes decision in order to maximise their individual payoff/utility function. Among the most widely used schemes for non-cooperative games are the Cournot (Cournot, 1838) and the Stackelberg games (von Stackelberg, 2011). The main difference between these two games, lies on the timing that decisions are made between players. In Cournot games the players make a simultaneous decision without communication. In contrast, following the Stackelberg scheme, the leader first makes a decision and then the follower responds to the leader’s choice. The Stackelberg games in which the leader has complete information on the follower can be formulated as bi-level programming problems (Sinha et al., 2018). Even though bi-level problems are proven to be NP-hard (Bard, 1991), different solution approaches have been proposed by the PSE community to address them (Djelassi et al., 2019; Yue et al., 2019). In cooperative games, players collaborate so as to make a decision that maximises the coalition’s payoff. Various fairness schemes have been proposed in the literature so as to allocate the coalition’s utility to the players of the game. The most prominent schemes are the Shapley value, social welfare and Nash bargaining which are discussed in detail in the following section. Finally, games can be divided in zero-sum (constant-sum games) or non-zero-sum-games depending on how the decision of a player affects the payoff of the others. In the zero-sum games the game is considered a closed system and each player wins what the other players loose. In contrast, in non-zero sum games the gain of a player is not always at the expense of the other players.

The study of firm coalitions has been in the interest of economists since establishment of the industrial sector at the end of industrial revolution. Cournot (1838) was the first to examine the impact of a strategic coalition between companies of the same industrial sector. Consider a market structure that consists of a small number of suppliers who provide their goods to demanding agents, either directly to end-consumers or retailers. In that case, the market corresponds to an oligopoly, if only two suppliers exist then the corresponding structure is a duopoly. Let n the number of firms which produce a single product and C_i(q_i) the cost of firm i ∈ 1, … , n to produce q_i units of that product. If all the produced quantity Q is sold at a single price, then the market price is P(Q) and firm i’s revenue is q_iP(q₁ + q_n⋯). Hence, the profit π of firm i is given by Eq. 3. From a game-theoretic perspective, the solution resulting by Cournot’s game corresponds to the Nash equilibrium.

${\pi }_i(q_1,\dots ,q_n)=q_{i}P(q_1+q_n\cdots )-C_i(q_i)\forall i(3)$

2.2 Fairness schemes

The question of fair player consideration is studied by social science by the theory of utilitarianism (Moulin, 1988). The two main doctrines are classical utilitarianism introduced by Bentham and egalitarianism. In the case of classical utilitarianism, the aim is to maximise the sum of individual profits in a coalition. In this approach the profit of an individual may be sacrificed for the sake of the collective profit. In contrast, egalitarianism seeks to equalise the individual profits, since all players should be treated equally. Let ${\underline{u}}_j$ be the utility of player j at disagreement with the other players. When evaluating cooperative games, a player will be incentivised to join a coalition only if they can achieve a greater payoff than operating alone, i.e., $u_j>{\underline{u}}_j$.

In the context of a cooperative game, different fairness schemes exist in the literature to allocate the profit of the coalition formation (Bertsimas et al., 2011). Fairness can be represented either as directly considering a fair objective function, or after an optimal solution is retrieved by deciding how the payoff allocation will be performed. Figure 3 presents the main fairness schemes and solution approaches that have been utilised in the PSE literature. Two of the most prominent post-optimisation fairness criteria used, are: 1) the Shapley value (Shapley, 1953) and 2) the Schmeidler’s nucleolus (Schmeidler, 1969). While the Shapley value is based on a utilitarian approach, nucleolus applies egalitarianism. Let S be a coalition of players, then u(S) is the utility function of the coalition, the Shapley value for a player σ_j reflects the contribution of the player to the overall cooperation and is formulated in Eq. 4. For convex games, the marginal contribution of a player to a coalition increases as the coalition expands, i.e., the coalition has increasing returns to scale (Moulin, 1988).

${\sigma }_j={\displaystyle \sum _{S\subseteq N\backslash \{j\}}}\frac{|S|!\times (n-|S|-1)!}{n!}(u(S\cup \{j\})-u(S)),j\in \mathcal{N}(4)$

From an optimisation perspective, the different fairness schemes that can be used in order to maximise the payoff of the coalition are summarised in the following section. An illustration of how the choice of fairness schemes affects the payoff in a two-player game can be found in Figure 4 for varying the scale of total payoff for each player.

FIGURE 3

FIGURE 3. Fairness schemes and proposed solution approaches.

FIGURE 4

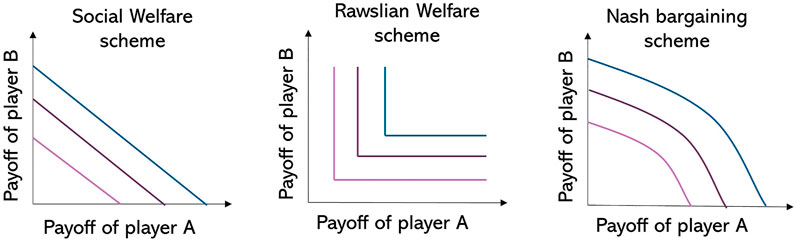
FIGURE 4. Payoff allocation for a two-player game under different fairness schemes. Pink contour corresponds to smaller total payoffs for both players, purple contour corresponds to higher payoffs, blue contour corresponds to the highest payoffs.

2.2.1 Social welfare scheme

The social welfare scheme seeks to maximise the total payoff of the coalition following the classical utilitarian approach.

${\varphi }_{SW}(\mathcal{U})≔\underset{u\in \mathcal{U}}{argmax}{\displaystyle \sum _{j\in \mathcal{N}}}{u}_j(5)$

The social welfare objective satisfies the Pareto optimality condition, weak AI and AII, however the resulting fairness allocation is often non-unique. Even if all the solutions where retrievable, an additional criterion would be needed to select the fairest allocation amongst them (Sampat and Zavala, 2019). Examples of utilisation of social welfare, also called as Naive scheme in some applications, can be found in Gjerdrum et al. (2002); Munguía-López et al. (2019); Charitopoulos et al. (2020).

2.2.2 Nash bargaining

Similarly to social welfare, the Nash bargaining scheme (Nash, 1950) is another utilitarian fairness scheme that can be perceived as the maximisation of the geometric mean of the players’ excess payoff by the coalition formation. Initially, Nash proposed the bargaining game for only two players and was later generalised by Harsanyi (1959) as an n-player game. Since the geometric mean is a strictly concave function, the allocation retrieved by the Nash scheme is optimal (Sampat and Zavala, 2019). Then, the Nash bargaining objective is introduced in Eq. 6.

${\varphi }_{NS}(\mathcal{U})≔\underset{u\in \mathcal{U}}{argmax}{\displaystyle \prod _{j\in \mathcal{N}}}{u}_j-{{\displaystyle \underline{u}}}_j(6)$

It can be proven that the Nash bargaining scheme satisfies all of the aforementioned axioms for the utility allocations schemes except of the monotonicity axiom. Using the Nash bargaining objective under different models can result in non-linear model formulations that have been widely studied in the PSE literature (Table 2). Different reformulation approaches have been used for its efficient computation such as: logarithmic transformation and SOS2 piecewise approximation (Gjerdrum et al., 2001; Ortiz-Gutiérrez et al., 2015; Carrero-Parreño et al., 2019; Charitopoulos et al., 2020), spatial Branch and Bound coupled with McCormick relaxations (McCormick, 1976) by Gjerdrum et al. (2002); Cruz-Avilés et al. (2021), and Branch and Refine with logarithmic transformation (Yue and You, 2014a; Charitopoulos et al., 2020).

2.2.3 Kalai-Smorodinsky solution

Kalai and Smorodinsky (1975) questioned the IIA axiom proposed by Nash (1950) for the Nash bargaining problem and proposed an alternative bargaining solution based on the monotonicity axiom. The aim of the Kalai-Smorodisnky bargaining focused on the player’s ideal payoffs, i.e., ${\bar{u}}_j$. At the KS solution, the fraction of the profit increase of the two players is equal to the fraction of the maximum profit increase they could achieve.

$\frac{u_1-{{\displaystyle \underline{u}}}_1}{u_2-{{\displaystyle \underline{u}}}_2}=\frac{{{\displaystyle \bar{u}}}_1-{{\displaystyle \underline{u}}}_1}{{{\displaystyle \bar{u}}}_2-{{\displaystyle \underline{u}}}_2}(7)$

2.2.4 Max-Min scheme

The Max-Min scheme is a mathematical representation of the Rawslian welfare principle. According to the Rawslian welfare (Rawls (1971)), the weakest agent of a coalition should be prioritised. Thus, the player with the lowest payoff should have the maximum gain from the game, as expressed in Eq. 8. In terms of axiomatic satisfaction, only the weak AI and the IIA are satisfied.

${\varphi }_{MM}(\mathcal{U})≔\underset{u\in \mathcal{U}}{argmax}\underset{j\in \mathcal{N}}{\mathit{min}}{u}_j(8)$

An extension of this scheme is the Lexicographic Max-Min scheme that seeks to maximise the payoff of the player with the lowest payoff, then maximise the payoff of the second lowest payoff, third lowest payoff and so on. Eq. 9 corresponds to the Lexicographic Max-Min scheme following the formulation of Liu and Papageorgiou (2018).

${\varphi }_{\mathit{LexMM}}(\mathcal{U})≔\underset{u\in \mathcal{U}}{argmax}\mathrm{\Theta }(g(u))(9)$

where g(u) = {g₁(u), g₂(u), …, g_N(u)} is a vector function on the decision space $u\in \mathcal{U}$, and $\mathrm{\Theta }:{\mathbb{R}}^N\to {\mathbb{R}}^N$ is a mapping function that re-orders the components of the vector in a increasing order such that Θ(g(u)) = (θ₁(g(u)), θ₂(g(u)), …, θ_N(g(u))), where θ₁(g(u)) ≤ θ₂(g(u)) ≤ ⋯ ≤ θ_N(g(u)).

2.2.5 Shannon entropy solution

This fairness scheme was introduced to bridge economic theory with statistics (Venkatasubramanian and Luo (2018)) and is obtained by maximising the entropy of a system.

${\varphi }_S(\mathcal{U})≔\underset{u\in \mathcal{U}}{argmax}{h}_S(p(u))=\underset{u\in \mathcal{U}}{argmax}-{\displaystyle \sum _{j\in \mathcal{N}}}{p}_j(u)log{p}_j(u)(10)$

where,

$p_j(u)=\frac{u_j-{{\displaystyle \underline{u}}}_j}{{\displaystyle \sum _{j\in \mathcal{N}}}(u_j-{{\displaystyle \underline{u}}}_j)}j\in \mathcal{N}(11)$

3 Classification of game theory applications in PSE problems

3.1 Supply chain optimisation

A growing interest for decentralised approaches in the decision making process for supply chains has been observed in the past decades (Papageorgiou (2009); Sahay and Ierapetritou (2013); Barbosa-Povoa and Pinto (2020)). The formulation of a supply chain (SC) design problem as a strategic game seems straightforward since the players can be the manufacturers, distributors and end consumers (Gjerdrum et al., 2002; Zamarripa et al., 2012; Yue and You, 2014b; Charitopoulos et al., 2020) aiming to maximise their profit. A conceptual representation of supply chains under different cooperation levels is showcased in Figure 5. To this end, supply chain optimisation problems have been widely studied through game theoretic lens (Leng and Parlar, 2005; Nagarajan and Sošić, 2008; Sohrabi and Azgomi, 2020). Game theory in conjunction with Data Envelopment Analysis (DEA) also constitutes another promising direction for evaluating SC efficiency (Liang et al., 2006; Halkos et al., 2014).

FIGURE 5

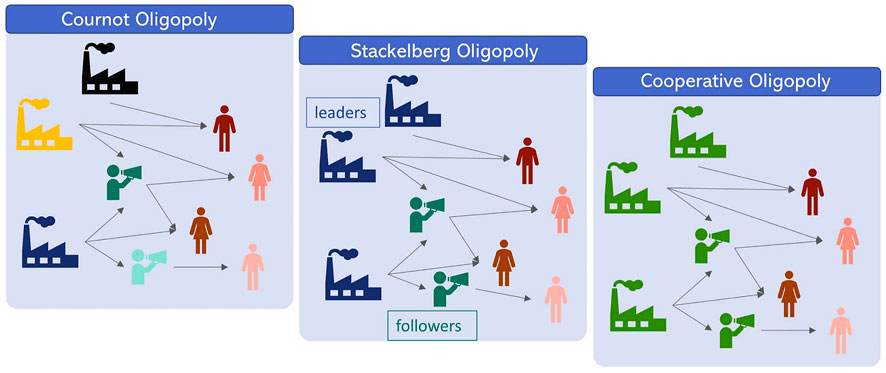
FIGURE 5. Conceptual representation of an Oligopolistic supply chain under different cooperation levels. Cournot Oligopoly: competitive game, Stackelberg Oligopoly: leader-follower game, Cooperative Oligopoly.

3.1.1 Non-cooperative supply chain optimisation

An overview of existing publications of non-cooperative supply chain optimisation is summarised in Table 1. An early work of supply chain design using the concept Nash equilibrium can be found in Sherali and Leleno (1988). The authors evaluated the nature of acquired equilibrium solutions for a non-cooperative two-stage supply chain under different behavioral structures among the players. In addition, Sherali and Leleno (1988) derived sufficient conditions for the existence of equilibira along with suitable solution methods. Levis et al. (2007) proposed the use of a Bertrand-type model to determine the Nash equilibrium prices in order to maximise the profit of the manufacturing firms in a duopoly. Bertrand model is a review of the Cournot model but in this case a firm should select a price that outperforms the competitor when their prices exceed the marginal cost. The model formulation of Levis et al. (2007) results in a series of NLP problems which are solved iteratively to determine the optimal decision making policy. From a similar perspective, Leng and Parlar (2010) aimed to find the optimal pair of lost-sales cost-sharing contracts in an assembly supply chain. At first they constructed two variations of non-cooperative games, Nash and Stackelberg, where the manufacturer and suppliers determine their retail price and production quantities. An alternative scenario was examined where the players collaborated. The computational results suggested that the suppliers were attributed equilibrium production quantities and the manufacturer adopted the equilibrium price, while the overall profit was maximised as well. Later on, Zamarripa et al. (2012) evaluated both a cooperative game to minimise the total operating cost of a supply chain as well as a non-zero sum game. While the cooperative game results in an MILP model, the non-zero sum game results in each player aiming to minimise their own cost disregarding the overall profit of the system. The non-cooperative model is represented by non-linear terms which require the computation of a payoff matrix for it’s solution. Sun et al. (2013) have formulated an agri-biomass supply chain as a Stackelberg game where the supplier initially decides the selling price of agri-biomass and then the industrial buyers determine their demands.

TABLE 1

TABLE 1. Representative contributions of non-cooperative supply chain problems.

Given the hierarchical structure of the examined markets, the supply chain problem can be addressed by different methods such as multi-level programming and decentralised game-theoretic methods. Yue and You (2014b) employed a Stackelberg game for modelling the interactions between manufacturers and suppliers of a bio-fuel supply chain and a bi-level programming for arrangements between manufacturers and customers that resulted in a non-convex MINLP. To tackle the non-linearities that aroused from considering capital cost economies of scale using a non-linear power function, they proposed an improved Branch and Refine algorithm (Bergamini et al., 2008) for the global optimal solution by iteratively solving a sequence of MILP subproblems. The subproblems are generated via a piecewise linear approximation, of the original MINLP, based on SOS1 variables (Padberg, 2000). The same authors have later on evaluated a different setting for reformulation and decomposition of a bi-level MILP problem representing a Stackelberg game (Yue and You, 2017). At first, the follower’s discrete decisions are fixed based on optimal value reformulation (Chen and Florian, 1995) and a pool of all decision permutations is generated. In the decomposition algorithm, only a subset of the combinations is evaluated in each iteration which correspond to the master problem, the solution of the relaxed master problem provides a set of the leader’s optimal decisions. Yue and You (2017) implemented the proposed algorithm in an integrated forestry and biofuel supply chain. In examined problem, the forestry company represents the leader, while the pulp company is the follower.

Often, supply chain design problems result in multi-objective formulations, such as in the case study of Gao and You (2017), where the non-cooperative shale gas supply chain is formulated as a multi-objective bi-level MILP. The shale gas producer is the leader aiming to maximise their net present value and at the same time minimise the life cycle greenhouse gas emissions. The shale gas processor is the follower aiming to maximise their net present value as well. To solve this problem the authors followed a reformulation and decomposition algorithm that was later published in detail (Yue et al., 2019). The effect of different game structures was evaluated by Noh et al. (2019). Noh and coworkers initially formulated a two-echelon supply chain as a Stackelberg game with decentralised decision making where they alternated the roles between the leader and the follower. They found that the choice that maximised the profit was when the retailer was the leader and manufacturer the follower. When examining the centralised approach in a cooperative game, Noh et al. reported that results where lying between those of the Stackelberg game.

Even though uncertainty is inherent in supply chain design problems, the majority of applications consider a deterministic model neglecting any uncertainties. Zamarripa et al. (2013) studied the problem of supply chain planning under uncertainty in cooperative and no-cooperative multi-objective scenarios. The uncertainty was manifested in the competitor’s behaviour and was formulated as a payoff matrix. For each scenario realisation Zamarripa et al. (2013) solved a multi-objective problem representing a non-zero sum game using the ϵ-constraint approach. Hjaila et al. (2016), proposed a Scenario-Based Negotiation (SBDN) coordination assuming a non-cooperative non-zero-sum game with non-symmetrical roles among the stakeholders of a multi-enterprise supply chain. One of the aims of the work is to attribute all the uncertainty factors of the examined supply chain to the follower’s decisions. In this model, the client acts as the leader of the game while the supplier is the follower. While maintaining the roles of the players, Hjaila et al. (2017) proposed a non-zero-sum Stackelberg game and search for Nash equilibrium solutions. The uncertainty in this case is accounted both for the clients and providers of the supply chain. In both of the aforementioned papers, the final model is an MINLP which is solved using off-the-shelf global optimisation solvers, while uncertainty is addressed indirectly via Monte Carlo sampling approach. In contrast, Gao and You. (2019) propose a two-stage stochastic method to address a single-leader multiple follower Stackelberg game formulated as MIBP. The solution approach used is similar to Yue and You. (2014b) with an additional Glover’s linearisation to tackle the bi-linear terms in the upper-level problem.

3.1.2 Cooperative supply chain optimisation

Even though competitive games are used to represent current supply chain formulations, the benefits of a coordination are evaluated by different researchers (Gjerdrum et al., 2001; Zamarripa et al., 2012). The study of cooperative games enables fairness considerations for the utility allocation between the collaborating parties. However, the selection of a fairness approach is not always straightforward, given that there may be conflicting objectives such as profit versus sustainability goals. Table 2 summarises representative contributions of fairness schemes in cooperative supply chains. The most common objective in cooperative games is the fair profit allocation via the Nash bargaining scheme. The formulations of the Nash scheme in Eq. 6 results in a non-linear formulation, hence the supply chain models are of NLP/MINLP type. The first publication in the field can be attributed to Gjerdrum et al. (2001), who examined the problem of the fair profit allocation in multi-enterprise supply chain. They formulated the objective function as a Nash bargaining problem which they approximated using separable programming via logarithmic transformation and SOS2 piecewise linearisation. In the following year the same authors (Gjerdrum et al., 2002), employed a spatial Branch and Bound (BB) algorithm, that is based on McCormick relaxations (McCormick, 1976), to solve the fair profit allocation in a two-echelon supply chain. Zhao et al. (2010) have studied a decentralised cooperative supply chain between manufacturers and suppliers to find the optimal wholesale contract selection. Zhao and coworkers (Zhao et al., 2010) suggested that a Nash bargaining model allowed both players to maximise their profit level under the selected wholesale price mechanism. Later on, Yue and You (2014a) optimised the operational decisions and profit allocation mechanism in a bioethanol supply chain by proposing the use of a logarithm transformation and Branch and Refine (BR) for the linearisation of the objective function. However, not all fairness evaluation approaches result in non-linear terms, Zheng et al. (2019) employed the Shapley, nucleolus and equal satisfaction mechanisms to find the optimal profit allocation in a three-echelon closed-loop supply chain. For all three of the examined fairness approaches the solution of the cooperative game results in increased profit for all players. Apart from typical economic design criteria; Toktaş-Palut (2022) evaluates the impact of Industry 4.0 technologies on the coordination and sustainability of supply chains. The proposed game-theoretic framework is a Nash bargaining scheme based on revenue-sharing contracts in a cooperative supply chain. The author conclude that under a coordinating framework the utilisation of Industry 4.0 technologies can provide significant improvements for in terms of overall supply chain sustainability (Toktaş-Palut, 2022).

TABLE 2

TABLE 2. Representative contributions of fairness schemes in cooperative games.

Logarithmic transformation and separable programming is the main reformulation approach selected by researches in the field over the last decade to tackle the non-linearities stemming from the Nash bargaining fairness, following the concepts initially introduced by Gjerdrum et al. (2001). Separable programming was utilised by Ortiz-Gutiérrez et al. (2015) to find the fair profit allocation in a biofuel supply chain under the Nash fairness scheme. Apart from Separable Programming and Nash fairness, Liu and Papageorgiou. (2018) have proposed a lexicographic max-min for the fair profit allocation in a multi-echelon supply chain of an active ingredient industry. Later on, Charitopoulos et al. (2020) investigated the impact of two different linearisation approaches for the Nash bargaining objective, i.e., approximation via SOS2 variables and BR algorithm. The authors also evaluated a Naïve fairness scheme that follows an utilitarian utility allocation such as the social welfare scheme (Eq. 5). Their results suggest that the use of Nash fairness provides a more viable solution since it accounts the market power dynamics, while in contrast the Naïve scheme maximises the total profit by disregarding the status quo dynamics. Carrero-Parreño et al. (2021) addressed the problem of fair cost distribution among various shale gas companies from a Nash bargaining perspective and linearised the Nash objective via Separable Programming and SOS2 variables. However, to determine the portion of the cost assigned to each company, bilinear terms were generated. To reformulate the additional non-linear constraints, Glover’s linearisation was proposed.

3.2 Process design and operations

The design of heat exchanger networks has been one of the primary fields of study in PSE. More recently, heat-integration has been studied under a game theoretic perspective in order to improve cost minimisation. Hiete et al. (2012) evaluated the fair shavings allocation in wood process industrial network. Both Alternate Cost Avoided method and Shapley value were used to fairly allocate the coallitions payoffs based on the contribution of each player to the savings of the coalition. Even though the results were similar between the two fairness approaches, they differed significantly with an alternative allocation scheme based on the actual energy prices. Similarly, Cheng et al. (2014) proposed a cooperative approach for heat-integration among different plants so as to maximise their savings under a social welfare scheme. In order to decide on the saving allocation from a cooperative heat-integration the use of Shapley value has been proposed both by Jin et al. (2018) and Wang et al. (2020). The problem of retrofit design of a synergistic heat exchange network was evaluated by Lo et al. (2021). The authors examined the core and Shapley values to find the fair payoff allocation among the different plants.

Torres and Stephanopoulos (2016) have studied the design of a multi-actor distributed processing systems under a decentralised scope. Two different games were studied: a Cournot competitive game using a 2-level Lagrangian approach and Nash bargaining cooperation. Tominac and Mahalec (2017), (2018) investigated the problem of strategic refinery production planning under Cournot games. In the former work they aimed to maximise the profit of the different plants, while in the second paper they introduced a multi-period framework and studied elimination scenarios for the player with the highest cost. The problem of production and utility coordination under incomplete information was studied by Leenders et al. (2019). The problem was formulated a Stackelberg game, where the leader was the power system and the follower the utility system. The proposed solution approach is based on iteratively finding the optimal production schedule and then minimise the operational cost of the utility system. The same authors (Leenders et al., 2021), generalised the approach for multi-leader-follower problems by taking into account multiple process units.

Liu and Papageorgiou (2013) have addressed the problem of capacity planning as a multi-objective MILP model targeting: total cost, total flow time and total lost sales in global supply chains. For the game theoretic formulation, two different approaches were used, that of ϵ-constraint and lexicographic minimax, so as to consider a fair payoff allocation. In the first approach only the cost was considered in the objective while the total flow time and total lost sales were transformed into constraints. From a competitive perspective, Garcia-Herreros et al. (2016) addressed the problem of capacity planing with rational markets as an MIBP problem. In the upper-level problem producers aim to maximise their profit while in lower-level the cost paid by the markets is minimised. The proposed solution method follows a Karush-Kuhn-Tacker (KKT) reformulation followed by a dual transformation. Florensa et al. (2017) introduced another level of decision makers resulting in tri-level linear problem of capacity planing under competitive decision makers. Two novel algorithms were introduced, however their implementation resulted in different degenerate solutions. The authors (Florensa et al., 2017) have defined the Optimistic and Pessimistic solutions to determine if multiple lower-level optima are resolved in favor or against the leader. In detail, if there are more than one solutions of the lower-level problem, the leader can select amongst those the one that results in the most favourable solution for the upper-level problem, i.e., the Optimistic solution.

An interesting integration of game theory and optimisation can be found in the studies of Faísca et al. (2007); Chu and You (2014); Ye et al. (2020). Faísca et al. (2007) proposed a global optimisation approach for multi-level problems that is based on considering the different optimisation levels using parametric programming in search for a Nash equilibrium. A tri-level programming problem and a bilevel programming problem with multiple-followers are evaluated, comprised of quadratic cost functions with linear constraints. In both cases the lower-level optimisation problems are considered as multi-parametric programming problems. In the tri-level case, the third-level problem is solved for parameters being the variables of the second and first-level. In the bilevel multi-follower problem, the lower-level problem comprises of two objectives for different decision variables while the upper-level variables are treated as parameters. In a later stage, the Nash equilibrium is employed to find and compare the set of the followers’ reaction sets. In a similar mentality, Chu and You (2014) have solved the design and scheduling of a batch process as a Stackelberg game. In the examined problem, the scheduling problem acts as the leader which affects the solution of the dynamic design optimisation problem. The gap between the leader and the follower is expressed through the dependence of processing costs to processing times via a linear function. The Stackelberg game problem is solved using a decomposition method based on cutting plane approximation. Ye et al. (2020) proposed an algorithm based on game theory to design an air separation unit. Their objective is to minimise the total cost by taking into account the penalty from product unavailability and the cost of installing parallel units and storage tanks. Large unit superstructures are coupled and perceived as players of a cooperative game. The algorithm proposed is built on the fact that the examined superstructures have limited correlation and by ignoring their interrelations provides an initial solution to the problem. The equilibrium conditions are checked iteratively followed by expansion of the pool of non-improving new designs.

3.2.1 Sustainability in process design

Even though traditionally the objective of optimisation problems in PSE concerned economic factors, i.e., profit maximisation or cost minimisation, the need to find sustainably viable solutions became prominent in the past decades. Zhao and You (2019) study how a waste-to-energy policy can be integrated with current operations in dairy farms. The authors, propose a Stackelberg game where the government is the leader and determine the incentive policy and investment factors of bio-electricity generation, while the dairy farms aim to maximise their net present value and select among different bio-energy conversion technologies. The objective of the game is formulated as a fractional MIBP which may render the problem intractable. The proposed solution is based on a hybrid algorithm combining a parametric algorithm, for fractional programming, along with a projection-based reformulation and decomposition algorithm, for MIBP.

Carbon sharing can be an efficient solution for greenhouse gas emission mitigation in the industrial sector. Zhang et al. (2017) have studied the fair design of Carbon Capture and Storage (CCS) infrastructure in Qatar under a carbon trading scheme with different fair objectives. While the first objective scheme followed a same saving ration, the second used the Nash bargaining objective, the authors noted that there is an impact of the fairness measure used on the optimal design of CCS infrastructure. In a similar spirit, Salcedo-Diaz et al. (2021) examined the problem of optimal supply chain design of chemical industries under a carbon trading policy framework. Different coalition formations were evaluated among the manufacturing firms aiming to maximise their profit while at the same time comply with CO₂ emissions targets. Their results suggested that a cooperative framework is beneficial both from an economic and environmental perspective. Fadzil et al. (2022) propose a carbon sharing scheme via the formation of an industrial symbiosis system. In the corresponding model, carbon permits are a shared resource among the cooperating plants aiming to maximise the total coalition’s profit, the allocation of the profit to each plant is dictated by their marginal contribution in the symbiotic system. The impact of carbon tax and consumer acceptance for the design of a low-carbon production line is studied by Wang and Wang (2022). The authors propose a Stackelberg game at which the manufacturer, leader, aims to maximise their profit while the retailer, follower, adjust their retail price to the end consumer.

3.2.2 Industrial symbiosis

Many studies have also been conducted for the formation of eco-industrial parks (EIP), resulting in integrating different production plants through resource, waste and emissions sharing schemes (Figure 6). An early paper in this field can be traced in the work of Lou et al. (2004), who used emergy analysis to find the optimal operation of an EIP under uncertainty. The authors, identified the Nash equilibrium of a matrix game and identified both the optimal profit and sustainability payoff of a two-plant case study. A series of papers have studied the problem of waste-sharing in a symbiotic manner. Xiao-Ping et al. (2009) studied an industrial symbiosis network for sulfur waste reduction under a multi-objective game. Tan and Aviso (2012) proposed an inverse optimisation approach to solve the problem of optimal waste integration in an EIP. A Stackelberg game was formulated as a bi-level programming problem, in which an EIP authority acted as a leader aiming to optimise incentives so as the followers, EIP, plants could have a positive payoff by joining the symbiotic network.

FIGURE 6

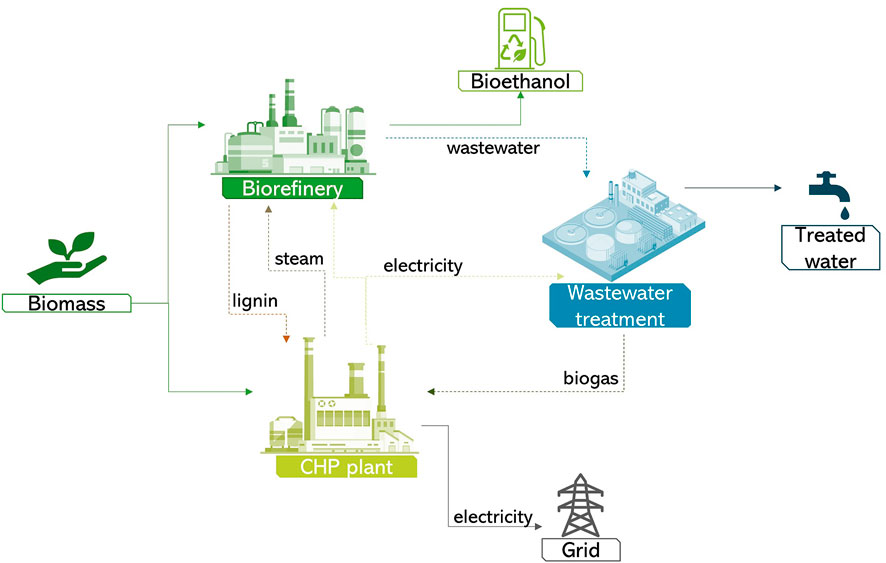
FIGURE 6. Eco-Industrial Park diagram for a three-plant symbiotic system. Based on data from Tan et al. (2016).

Later on, Tan et al. (2016) have studied a fair inter-plant process integration formulating a cooperative game based on Maali’s (Maali, 2009) max-min LP model, whose optimal solution is retrieved by maximising the least satisfied constraint. The authors have compared the results of Maali’s method with the Shapley value method and concluded that the former results in marginally more equitable profit distribution. A competitive multi-leader follower game for the design of utility network of in an EIP in Norway has been studied by Ramos et al. (2018). The enterprises of the park aim to minimise their annual cost while the EIP authority aims to minimise the coalitions CO₂ emissions. Ramos et al. (2018) have evaluated two variations for the leader/follower setting which results in different prioritisation of the game’s objectives. Since both games are bi-level problems, they authors employed KKT reformulation to guarantee the problems’ tractability.

The problem of water sharing in an EIP has been under the research interests of process engineers. Chew et al. (2009) formulated a problem of inter-plant water integration (IPWI) with equal bargaining power among plants and complete information sharing. Initially, the authors (Chew et al., 2009) evaluated a non-cooperative game which resulted in negative payoffs to some plants, however from a cooperative perspective the total profit of the system remained the same and all plants had positive payoffs. A cooperative approach was also applied in another IPWI problem by Chew et al. (2011) taking into account green incentives of an EIP authority. The green incentive introduced by Chew et al. (2011) facilitates the payoff allocation under different coalition formations. From a non-cooperative perspective, Ramos et al. (2016) proposed an alternative approach to solve a multi-leader-follower Stackelberg for IPWI. A solution approach to solve multi-leader-follower problems is based on stationary and KKT conditions, which results in non-convex problems with complementarity constraints. To address the non-convexities arising, Ramos et al. (2016) proposed the use of the so-called penalty formulation (Biegler, 2010) which transfers the complementarity constraints in the objective function. The fair and sustainable design of water supply chains under uncertainty has been studied by Koleva et al. (2018), both at a regional and national level. A multi-period and multi-objective model is introduced aiming to balance the trade-off between total cost minimisation and reliability maximisation. At first, Koleva and co-workers (Koleva et al., 2018) solved the problem with an ϵ-constraint method where the problem of cost minimisation was solved primarily followed by the reliability maximisation. The fair design was based on the Nash bargaining scheme resulting in an MINLP problem which was linearised using separable programming and SOS2 approximation. Uncertainty has been addressed via global sensitivity analysis. The impact of different fairness schemes i.e., social welfare, Rawslian welfare and Nash bargaining, on the design of water distribution networks for agricultural lands has been evaluated by Munguía-López et al. (2019). For the examined case studies, the authors highlighted that the Nash bargaining, after a logarithmic transformation, resulted in unique solutions and provided a favourable solution of all players regardless their contribution to the game. Recently, from a non-cooperative perspective, Salas et al. (2020) constructed an abstract single-leader multi-follower game where the leader is the authority that aims to minimise the water consumption and the industrial units (followers) minimise their operating cost, while the introduced problem is reformulated as an MILP. The main contribution of the work is the use of a Blind-Input contract, which binds the industrial units to participate in the EIP under the authority’s regulation. In contrast to this restrictive approach, Cruz-Avilés et al. (2021) considered a cooperative case among different plants in an EPI for water sharing. For the cost allocation of the coalition, they evaluated different fairness schemes such as social welfare, Nash scheme and Rawslian scheme. The objective of the Nash scheme was reformulated by a logarithmic transformation to concave non-linear problem which was further relaxed using McCormick relaxations. From a cooperative perspective, Chin et al. (2021) introduced a multi-stage game to decide on fair subsidies and incentive allocations towards the creation of an EIP. In the first stage of the game the objectives of a coalition are determined, at the later stage, the fair distribution of cost and benefits from the coalition is evaluated. It is noteworthy that the incentive allocation did not differ significantly with different fairness approaches (Shapley value, nucleolus, tau-value, min-max core).

3.3 Energy system optimisation

The energy sector is the predominant in contribution to greenhouse gas emissions (Ritchie et al., 2020) while at the same time holds a great decarbonisation potential. In this section we will provide a review of recent publications on the field of energy systems optimisation towards a renewable transition in existing energy markets based on the game theoretic scheme used. Recent reviews on power generation expansion planning can be found in Chen et al. (2018) and Churkin et al. (2021) were energy systems engineering tools are evaluated. Tsimopoulos and Georgiadis. (2020); Tsimopoulos and Georgiadis. (2021) examined the optimal conventional and wind generation investment portfolio of a producer in a pool-based electricity market. In the first study, (Tsimopoulos and Georgiadis, 2020), detect optimal physical and economic withholdings for dispatch and reserve procurements. In the second study, the authors model the strategies of the producers and identify the corresponding Nash equilibria. In both of the aforementioned papers, Tsimopoulos and Georgiadis represent the relation between energy producers and system operators as a Stackelberg game were the former is the leader and the latter the follower. The propsed model formulation results in an MIBP problem where in the upper level problem the negative expected profits of the producers are minimised while in the lower level the total expected cost of the system operation. The final problem is reformulated to a MILP class via the use of strong duality and disjunctive constraints. From a different viewpoint, Ma et al. (2022) regard the optimal planning and operation design of multi-agent energy system comprised by wind-hydrogen-heat producers as a cooperative game. The original optimisation problem is transformed into two subproblems: the cost minimisation problem and the payment bargaining problem which are solved using the algorithm of Alternating Direction Method of Multipliers (ADMM). For the fair payment allocation the Nash bargaining scheme is employed.

Previous sections indicate that game theoretic approach can be readily applied to represent real world supply chains and market structures. Liu et al. (2021) take advantage of a game theoretic framework to find the optimal energy system design and renewable subsidy strategies in four pilot plants in China. In their model, the government acts as the leader aiming to minimise the total subsidy while the towns (followers) aim to minimise their net present cost in response. Since the resulting model structure is MIBP with bi-linear terms in the lower level problem, a tractable reformulation of the problem is deemed necessary. At a first stage the problem is transformed in a single level MINLP using KKT conditions at the original problem, the use of Big M constraints along with auxiliary variables, results in the final MILP form of the problem. The fair investment portfolio in the energy system of town in Sweden has been examined by Fischer and Toffolo (2022). The authors juxtapose the results of a total cost minimisation objective against a Nash bargaining profit allocation among agents of the energy market and they highlight that the different games result in varying investment portfolios in terms of technology selected. Fisher and Toffolo argue that examining both game structures allowed them to identify the impact factors in each agent’s optimal strategy. Different game structures have also been studied for the sustainable growth of Iran’s electricity industry (Dehghan et al., 2022). The first game is a Cournot game were all the energy producers compete against each other to maximise their individual profit. The government is introduced as the leader in the second and third game, by determining the amount of subsidy or tax allocated at each producer. While in the second game producers act as independent followers, in the third game they cooperate aiming to maximise their total profit. The findings of this study suggest that the third game, with cooperating producers, results in the highest renewable share facilitating in Iran’s green transition until 2040.

The study of microgrids has attracted the researchers attention over the past decade. Zhang and co-workers Zhang et al., 2013, Zhang et al. (2014) have studied the fair electricity price and cost allocation for microgrids. In the first work, (Zhang et al., 2013), proposed a Nash bargaining objective to find the fair cost distribution among members in a general microgrid. The MINLP problem was reformulated using a logarithmic transformation and SOS2 approximation. The lexicographic max-min scheme was used in their second paper Zhang et al. (2014) where the corresponding model was of an MILP class.

4 Challenges and future directions

The aim of this review is to provide a basic background to game theoretic concepts and an overview of recent applications of game theory in process systems engineering problems. The examined applications vary from supply chain and process design and energy systems optimisation. The two main types of games encountered in the reviewed papers are non-cooperative Stackelberg games and Nash bargaining cooperative games. In the former case, the players make decisions sequentially, resulting in mixed integer bi-level programming problems, in many applications they also entail non-linear terms. Multi-parametric programming and different reformulation and decomposition methods are among the most common solution approaches. For the examined cooperative games with Nash bargaining objective, the resulting problem formulation was of MINLP class, where the non-linear term appeared only in the objective. The prevailing solution approaches entail logarithmic transformation coupled with different linearisation reformulations.

Since game theory traditionally has been studied by economists and social scientists, the existing textbooks focus mainly on these two directions. Hence, it can be challenging for an engineer to distill the necessary knowledge to apply game theoretic ideas to solve design and operation problems. To this end, the development of tutorials and textbooks focusing on practitioners are needed, which will facilitate an interdisciplinary dialogue. Many of the works reviewed here, result in non-tractable problem formulations. The intractability of the problems stems mainly from the limitations of existing computational resources to solve mixed-integer non-linear programming and multi-level programming problems. Tractability issues are surpassed by different approximations of the original problem, however any progress in solution methodologies for the aforementioned problem classes, will render the use of game theory even more appealing among process engineers. The use of game theory provides a useful tool in the PSE community to model multi-scale, multi-objective and multi-player games. One of the prominent advantages of using game theory in process and design problems, entails considering the payoff of conflicting objectives, such as environmental, economic and social agents.

Author contributions

Both AM and VC designed the outline and the content of this manuscript. AM finished the writing of this manuscript under the guidance of VC.

Acknowledgments

The authors gratefully acknowledge financial support from EPSRC grant EP/T022930/1.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Barbosa-Povoa, A. P., and Pinto, J. M. (2020). Process supply chains: Perspectives from academia and industry. Comput. Chem. Eng. 132, 106606. doi:10.1016/J.COMPCHEMENG.2019.106606

CrossRef Full Text | Google Scholar

Bard, J. F. (1991). Some properties of the bilevel programming problem. J. Optim. Theory Appl. 68, 371–378. doi:10.1007/BF00941574

CrossRef Full Text | Google Scholar

Bergamini, M. L., Grossmann, I., Scenna, N., and Aguirre, P. (2008). An improved piecewise outer-approximation algorithm for the global optimization of minlp models involving concave and bilinear terms. Comput. Chem. Eng. 32, 477–493. doi:10.1016/J.COMPCHEMENG.2007.03.011

CrossRef Full Text | Google Scholar

Bertsimas, D., Farias, V. F., and Trichakis, N. (2011). The price of fairness. Oper. Res. 59, 17–31. doi:10.1287/opre.1100.0865

CrossRef Full Text | Google Scholar

Biegler, L. T. (2010). Nonlinear programming. Philadelphia: Society for Industrial and Applied Mathematics Philadelphia. doi:10.1137/1.9780898719383

CrossRef Full Text | Google Scholar

Carrero-Parreño, A., Dua, V., and Papageorgiou, L. G. (2021). Fair shale gas water cost distribution using nash bargaining game. Chem. Eng. Res. Des. 176, 169–179. doi:10.1016/J.CHERD.2021.09.005

CrossRef Full Text | Google Scholar

Carrero-Parreño, A., Quirante, N., Ruiz-Femenia, R., Reyes-Labarta, J. A., Salcedo-Díaz, R., Grossmann, I. E., et al. (2019). Economic and environmental strategic water management in the shale gas industry: Application of cooperative game theory. AIChE J. 65, e16725. doi:10.1002/AIC.16725

CrossRef Full Text | Google Scholar

Charitopoulos, V. M., Dua, V., Pinto, J. M., and Papageorgiou, L. G. (2020). A game-theoretic optimisation approach to fair customer allocation in oligopolies. Optim. Eng. 21, 1459–1486. doi:10.1007/S11081-019-09482-X

CrossRef Full Text | Google Scholar

Chen, S., Guo, Z., Liu, P., and Li, Z. (2018). Advances in clean and low-carbon power generation planning. Comput. Chem. Eng. 116, 296–305. doi:10.1016/J.COMPCHEMENG.2018.02.012

CrossRef Full Text | Google Scholar

Chen, Y., and Florian, M. (1995). The nonlinear bilevel programming problem: Formulations, regularity and optimality conditions. Optimization 32, 193–209. doi:10.1080/02331939508844048

CrossRef Full Text | Google Scholar

Cheng, S. L., Chang, C. T., and Jiang, D. (2014). A game-theory based optimization strategy to configure inter-plant heat integration schemes. Chem. Eng. Sci.e 118, 60–73. doi:10.1016/J.CES.2014.07.001

CrossRef Full Text | Google Scholar

Chew, I. M. L., Tan, R. R., Foo, D. C. Y., and Chiu, A. S. F. (2009). Game theory approach to the analysis of inter-plant water integration in an eco-industrial park. J. Clean. Prod. 17, 1611–1619. doi:10.1016/J.JCLEPRO.2009.08.005

CrossRef Full Text | Google Scholar

Chew, I. M. L., Thillaivarrna, S. L., Tan, R. R., and Foo, D. C. Y. (2011). Analysis of inter-plant water integration with indirect integration schemes through game theory approach: Pareto optimal solution with interventions. Clean. Technol. Envir. 13, 49–62. doi:10.1007/s10098-010-0280-x

CrossRef Full Text | Google Scholar

Chin, H. H., Varbanov, P. S., Klemeš, J. J., and Bandyopadhyay, S. (2021). Subsidised water symbiosis of eco-industrial parks: A multi-stage game theory approach. Comput. Chem. Eng. 155, 107539. doi:10.1016/J.COMPCHEMENG.2021.107539

CrossRef Full Text | Google Scholar

Chu, Y., and You, F. (2014). Integrated scheduling and dynamic optimization by stackelberg game: Bilevel model formulation and efficient solution algorithm. Ind. Eng. Chem. Res. 53, 5564–5581. doi:10.1021/IE404272T

CrossRef Full Text | Google Scholar

Churkin, A., Bialek, J., Pozo, D., Sauma, E., and Korgin, N. (2021). Review of cooperative game theory applications in power system expansion planning. Renew. Sust. Energ. Rev. 145, 111056. doi:10.1016/J.RSER.2021.111056

CrossRef Full Text | Google Scholar

Cournot, A.-A. (1838). Recherches sur les principes mathématiques de la théorie des richesses par Augustin Cournot (chez L. Hachette).

Google Scholar

Cruz-Avilés, D. J., del Carmen Munguía-López, A., and Ponce-Ortega, J. M. (2021). Optimal design of water networks in eco-industrial parks incorporating a fairness approach. Ind. Eng. Chem. Res. 60, 8844–8860. doi:10.1021/ACS.IECR.1C00197

CrossRef Full Text | Google Scholar

Dehghan, H., Nahavandi, N., Chaharsooghi, S. K., Zarei, J., and Amin-Naseri, M. R. (2022). A hybrid game theory and system dynamics model to determine optimal electricity generation mix. Comput. Chem. Eng. 166, 107990. doi:10.1016/J.COMPCHEMENG.2022.107990

CrossRef Full Text | Google Scholar

Djelassi, H., Glass, M., and Mitsos, A. (2019). Discretization-based algorithms for generalized semi-infinite and bilevel programs with coupling equality constraints. J. Glob. Opt. 75, 341–392. doi:10.1007/s10898-019-00764-3

CrossRef Full Text | Google Scholar

Fadzil, F. A., Andiappan, V., Ng, D. K., Ng, L. Y., and Hamid, A. (2022). Sharing carbon permits in industrial symbiosis: A game theory-based optimisation model. J. Clean. Prod. 357, 131820. doi:10.1016/J.JCLEPRO.2022.131820

CrossRef Full Text | Google Scholar

Faísca, N. P., Saraiva, P. M., Rustem, B., and Pistikopoulos, E. N. (2007). A multi-parametric programming approach for multilevel hierarchical and decentralised optimisation problems. Comput. Manag. Sci. 6, 377–397. doi:10.1007/S10287-007-0062-Z

CrossRef Full Text | Google Scholar

Fischer, R., and Toffolo, A. (2022). Is total system cost minimization fair to all the actors of an energy system? Not according to game theory. Energy 239, 122253. doi:10.1016/J.ENERGY.2021.122253

CrossRef Full Text | Google Scholar

Florensa, C., Garcia-Herreros, P., Misra, P., Arslan, E., Mehta, S., and Grossmann, I. E. (2017). Capacity planning with competitive decision-makers: Trilevel milp formulation, degeneracy, and solution approaches. Eur. J. Oper. Res.h 262, 449–463. doi:10.1016/J.EJOR.2017.04.013

CrossRef Full Text | Google Scholar

Gao, J., and You, F. (2019). A stochastic game theoretic framework for decentralized optimization of multi-stakeholder supply chains under uncertainty. Comput. Chem. Eng. 122, 31–46. doi:10.1016/J.COMPCHEMENG.2018.05.016

CrossRef Full Text | Google Scholar

Gao, J., and You, F. (2017). Game theory approach to optimal design of shale gas supply chains with consideration of economics and life cycle greenhouse gas emissions. AIChE J. 63, 2671–2693. doi:10.1002/AIC.15605

CrossRef Full Text | Google Scholar

Garcia-Herreros, P., Zhang, L., Misra, P., Arslan, E., Mehta, S., and Grossmann, I. E. (2016). Mixed-integer bilevel optimization for capacity planning with rational markets. Comput. Chem. Eng. 86, 33–47. doi:10.1016/J.COMPCHEMENG.2015.12.007

CrossRef Full Text | Google Scholar

Gjerdrum, J., Shah, N., and Papageorgiou, L. G. (2002). Fair transfer price and inventory holding policies in two-enterprise supply chains. Eur. J. Oper. Res.h 143, 582–599. doi:10.1016/S0377-2217(01)00349-6

CrossRef Full Text | Google Scholar

Gjerdrum, J., Shah, N., and Papageorgiou, L. G. (2001). Transfer prices for multienterprise supply chain optimization. Ind. Eng. Chem. Res. 40, 1650–1660. doi:10.1021/IE000668M

CrossRef Full Text | Google Scholar

Halkos, G. E., Tzeremes, N. G., and Kourtzidis, S. A. (2014). A unified classification of two-stage dea models. Surv. Oper. Res. Manag. Sci. 19, 1–16. doi:10.1016/J.SORMS.2013.10.001

CrossRef Full Text | Google Scholar

Hargreaves-Heap, S., and Varoufakis, Y. (2004). Game theory: A critical text. Routledge, Taylor and Francis Group.

Google Scholar

Harsanyi, J. C. (1959). A bargaining model for the cooperative n-person game. Princeton University Press, 17.

Google Scholar

Hiete, M., Ludwig, J., and Schultmann, F. (2012). Intercompany energy integration. J. Ind. Ecol. 16, 689–698. doi:10.1111/J.1530-9290.2012.00462.X

CrossRef Full Text | Google Scholar

Hjaila, K., Laínez-Aguirre, J. M., Puigjaner, L., and Espuña, A. (2016). Scenario-based dynamic negotiation for the coordination of multi-enterprise supply chains under uncertainty. Comput. Chem. Eng. 91, 445–470. doi:10.1016/j.compchemeng.2016.04.004

CrossRef Full Text | Google Scholar

Hjaila, K., Puigjaner, L., Laínez, J. M., and Espuña, A. (2017). Integrated game-theory modelling for multi enterprise-wide coordination and collaboration under uncertain competitive environment. Comput. Chem. Eng. 98, 209–235. doi:10.1016/J.COMPCHEMENG.2016.11.041

CrossRef Full Text | Google Scholar

Jin, Y., Chang, C. T., Li, S., and Jiang, D. (2018). On the use of risk-based shapley values for cost sharing in interplant heat integration programs. Appl. Energy 211, 904–920. doi:10.1016/J.APENERGY.2017.11.097

CrossRef Full Text | Google Scholar

Kalai, E., and Smorodinsky, M. (1975). Other solutions to nash’s bargaining problem. Econometrica 43, 513–518. doi:10.2307/1914280

CrossRef Full Text | Google Scholar

Koleva, M. N., Calderón, A. J., Zhang, D., Styan, C. A., and Papageorgiou, L. G. (2018). Integration of environmental aspects in modelling and optimisation of water supply chains. Sci. Total Environ. 636, 314–338. doi:10.1016/J.SCITOTENV.2018.03.358

PubMed Abstract | CrossRef Full Text | Google Scholar

Leenders, L., Bahl, B., Hennen, M., and Bardow, A. (2019). Coordinating scheduling of production and utility system using a stackelberg game. Energy 175, 1283–1295. doi:10.1016/J.ENERGY.2019.03.132

CrossRef Full Text | Google Scholar

Leenders, L., Ganz, K., Bahl, B., Hennen, M., Baumgärtner, N., and Bardow, A. (2021). Scheduling coordination of multiple production and utility systems in a multi-leader multi-follower stackelberg game. Comput. Chem. Eng. 150, 107321. doi:10.1016/J.COMPCHEMENG.2021.107321

CrossRef Full Text | Google Scholar

Leng, M., and Parlar, M. (2005). Game theoretic applications in supply chain management: A review. INFOR 43, 187–220. doi:10.1080/03155986.2005.11732725

CrossRef Full Text | Google Scholar

Leng, M., and Parlar, M. (2010). Game-theoretic analyses of decentralized assembly supply chains: Non-cooperative equilibria vs. coordination with cost-sharing contracts. Eur. J. Oper. Res.h 204, 96–104. doi:10.1016/J.EJOR.2009.10.011

CrossRef Full Text | Google Scholar

Levis, A. A., Lazaros, ., and Papageorgiou, G. (2007). Active demand management for substitute products through price optimisation. OR Spectr. 29, 551–577. doi:10.1007/s00291-006-0064-1

CrossRef Full Text | Google Scholar

Liang, L., Yang, F., Cook, W. D., and Zhu, J. (2006). Dea models for supply chain efficiency evaluation. Ann. Oper. Res. 145, 35–49. doi:10.1007/s10479-006-0026-7

CrossRef Full Text | Google Scholar

Liu, S., and Papageorgiou, L. G. (2018). Fair profit distribution in multi-echelon supply chains via transfer prices. Omega 80, 77–94. doi:10.1016/J.OMEGA.2017.08.010

CrossRef Full Text | Google Scholar

Liu, S., and Papageorgiou, L. G. (2013). Multiobjective optimisation of production, distribution and capacity planning of global supply chains in the process industry. Omega 41, 369–382. doi:10.1016/J.OMEGA.2012.03.007

CrossRef Full Text | Google Scholar

Liu, Z., Wang, S., Lim, M. Q., Kraft, M., and Wang, X. (2021). Game theory-based renewable multi-energy system design and subsidy strategy optimization. Adv. Appl. Energy 2, 100024. doi:10.1016/J.ADAPEN.2021.100024

CrossRef Full Text | Google Scholar

Lo, F. Y., Hsu, C. H., and Chang, C. T. (2021). Practicable total-site heat integration plan for retrofitting multiple heat exchanger networks. Chem. Eng. Res. Des. 174, 137–157. doi:10.1016/J.CHERD.2021.07.032

CrossRef Full Text | Google Scholar

Lou, H. H., Kulkarni, M. A., Singh, A., and Huang, Y. L. (2004). A game theory based approach for emergy analysis of industrial ecosystem under uncertainty. Clean. Technol. Environ. Policy 6, 156–161. doi:10.1007/S10098-003-0235-6

CrossRef Full Text | Google Scholar

Ma, T., Pei, W., Deng, W., Xiao, H., Yang, Y., and Tang, C. (2022). A nash bargaining-based cooperative planning and operation method for wind-hydrogen-heat multi-agent energy system. Energy 239, 122435. doi:10.1016/J.ENERGY.2021.122435

CrossRef Full Text | Google Scholar

Maali, Y. (2009). A multiobjective approach for solving cooperative n-person games. Int. J. Electr. Power Energy Syst. 31, 608–610. doi:10.1016/J.IJEPES.2009.06.021

CrossRef Full Text | Google Scholar

McCormick, G. P. (1976). Computability of global solutions to factorable nonconvex programs: Part i — Convex underestimating problems. Math. Program. 10, 147–175. doi:10.1007/BF01580665

CrossRef Full Text | Google Scholar

Moulin, H. (1988). Axioms of cooperative decision making. Econometric Society Monographs (Cambridge University Press. doi:10.1017/CCOL0521360552

CrossRef Full Text | Google Scholar

Munguía-López, A. d. C., Sampat, A. M., Rubio-Castro, E., Ponce-Ortega, J. M., and Zavala, V. M. (2019). Fairness-guided design of water distribution networks for agricultural lands. Comput. Chem. Eng. 130, 106547. doi:10.1016/J.COMPCHEMENG.2019.106547

CrossRef Full Text | Google Scholar

Nagarajan, M., and Sošić, G. (2008). Game-theoretic analysis of cooperation among supply chain agents: Review and extensions. Eur. J. Oper. Res.h 187, 719–745. doi:10.1016/j.ejor.2006.05.045

CrossRef Full Text | Google Scholar

Nash, J. F. (1950). The bargaining problem. Econometrica 18, 155. doi:10.2307/1907266

CrossRef Full Text | Google Scholar

Noh, J., Kim, J. S., and Sarkar, B. (2019). Two-echelon supply chain coordination with advertising-driven demand under stackelberg game policy. Eur. J. Ind. Eng. 13, 213–244. doi:10.1504/EJIE.2019.098516

CrossRef Full Text | Google Scholar

Ortiz-Gutiérrez, R. A., Giarola, S., Shah, N., and Bezzo, F. (2015). An approach to optimize multi-enterprise biofuel supply chains including nash equilibrium models. Comput. Aided Chem. Eng. 37, 2255–2260. doi:10.1016/B978-0-444-63576-1.50070-4

CrossRef Full Text | Google Scholar

Padberg, M. (2000). Approximating separable nonlinear functions via mixed zero-one programs. Oper. Res. Lett. 27, 1–5. doi:10.1016/S0167-6377(00)00028-6

CrossRef Full Text | Google Scholar

Papageorgiou, L. G. (2009). Supply chain optimisation for the process industries: Advances and opportunities. Comput. Chem. Eng. 33, 1931–1938. doi:10.1016/j.compchemeng.2009.06.014

CrossRef Full Text | Google Scholar

Ramos, M. A., Boix, M., Aussel, D., Montastruc, L., and Domenech, S. (2016). Water integration in eco-industrial parks using a multi-leader-follower approach. Comput. Chem. Eng. 87, 190–207. doi:10.1016/J.COMPCHEMENG.2016.01.005

CrossRef Full Text | Google Scholar

Ramos, M. A., Rocafull, M., Boix, M., Aussel, D., Montastruc, L., and Domenech, S. (2018). Utility network optimization in eco-industrial parks by a multi-leader follower game methodology. Comput. Chem. Eng. 112, 132–153. doi:10.1016/J.COMPCHEMENG.2018.01.024

CrossRef Full Text | Google Scholar

Rawls, J. (1971). A theory of justice. Cambridge: Harvard University Press.

Google Scholar

Ritchie, H., Roser, M., and Rosado, P. (2020). co2 and greenhouse gas emissions. Our World in Data Available at: Https://ourworldindata.org/co2-and-other-greenhouse-gas-emissions.

Google Scholar

Sahay, N., and Ierapetritou, M. (2013). Supply chain management using an optimization driven simulation approach. AIChE J. 59, 4612–4626. doi:10.1002/aic.14226

CrossRef Full Text | Google Scholar

Salas, D., Van, K. C., Aussel, D., and Montastruc, L. (2020). Optimal design of exchange networks with blind inputs and its application to eco-industrial parks. Comput. Chem. Eng. 143, 107053. doi:10.1016/J.COMPCHEMENG.2020.107053

CrossRef Full Text | Google Scholar

Salcedo-Diaz, R., Ruiz-Femenia, J. R., Amat-Bernabeu, A., and Caballero, J. A. (2021). A cooperative game strategy for designing sustainable supply chains under the emissions trading system. J. Clean. Prod. 285, 124845. doi:10.1016/J.JCLEPRO.2020.124845

CrossRef Full Text | Google Scholar

Sampat, A. M., and Zavala, V. M. (2019). Fairness measures for decision-making and conflict resolution. Opt. Eng. 20, 1249–1272. doi:10.1007/s11081-019-09452-3

CrossRef Full Text | Google Scholar

Schmeidler, D. (1969). The nucleolus of a characteristic function game. SIAM J. Appl. Math. 17, 1163–1170. doi:10.1137/0117107

CrossRef Full Text | Google Scholar

Shapley, L. S. (1953). 17. A value for n-person games. Princeton University Press.

Google Scholar

Sherali, H. D., and Leleno, J. M. (1988). A mathematical programming approach to a nash-cournot equilibrium analysis for a two-stage network of oligopolies. Oper. Res. 36, 682–702. doi:10.1287/OPRE.36.5.682

CrossRef Full Text | Google Scholar

Sinha, A., Malo, P., and Deb, K. (2018). A review on bilevel optimization: From classical to evolutionary approaches and applications. IEEE Trans. Evol. Comput. 22, 276–295. doi:10.1109/TEVC.2017.2712906

CrossRef Full Text | Google Scholar

Sohrabi, M. K., and Azgomi, H. (2020). A survey on the combined use of optimization methods and game theory. Archives Comput. Methods Eng. 27, 59–80. doi:10.1007/s11831-018-9300-5

CrossRef Full Text | Google Scholar

Sun, J., Lin, J., and Qian, Y. (2013). Game-theoretic analysis of competitive agri-biomass supply chain. J. Clean. Prod. 43, 174–181. doi:10.1016/J.JCLEPRO.2012.12.026

CrossRef Full Text | Google Scholar

Tan, R. R., Andiappan, V., Wan, Y. K., Ng, R. T., and Ng, D. K. (2016). An optimization-based cooperative game approach for systematic allocation of costs and benefits in interplant process integration. Chem. Eng. Res. Des. 106, 43–58. doi:10.1016/J.CHERD.2015.11.009

CrossRef Full Text | Google Scholar

Tan, R. R., and Aviso, K. B. (2012). An inverse optimization approach to inducing resource conservation in eco-industrial parks. Comput. Aid. Chem. Eng. 31, 775–779. doi:10.1016/B978-0-444-59507-2.50147-5

CrossRef Full Text | Google Scholar

Toktaş-Palut, P. (2022). Analyzing the effects of industry 4.0 technologies and coordination on the sustainability of supply chains. Sustain. Prod. Consum. 30, 341–358. doi:10.1016/J.SPC.2021.12.005

CrossRef Full Text | Google Scholar

Tominac, P., and Mahalec, V. (2018). A dynamic game theoretic framework for process plant competitive upgrade and production planning. AIChE J. 64, 916–925. doi:10.1002/AIC.15995

CrossRef Full Text | Google Scholar

Tominac, P., and Mahalec, V. (2017). A game theoretic framework for petroleum refinery strategic production planning. AIChE J. 63, 2751–2763. doi:10.1002/AIC.15644

CrossRef Full Text | Google Scholar

Torres, A. I., and Stephanopoulos, G. (2016). Design of multi-actor distributed processing systems: A game-theoretical approach. AIChE J. 62, 3369–3391. doi:10.1002/AIC.15395

CrossRef Full Text | Google Scholar

Tsimopoulos, E. G., and Georgiadis, M. C. (2021). Nash equilibria in electricity pool markets with large-scale wind power integration. Energy 228, 120642. doi:10.1016/J.ENERGY.2021.120642

CrossRef Full Text | Google Scholar

Tsimopoulos, E. G., and Georgiadis, M. C. (2020). Withholding strategies for a conventional and wind generation portfolio in a joint energy and reserve pool market: A gaming-based approach. Comput. Chem. Eng. 134, 106692. doi:10.1016/J.COMPCHEMENG.2019.106692

CrossRef Full Text | Google Scholar

Venkatasubramanian, V., and Luo, Y. (2018). How much income inequality is fair? Nash bargaining solution and its connection to entropy. doi:10.48550/ARXIV.1806.05262

CrossRef Full Text | Google Scholar

von Neumann, J., and Morgenstern, O. (1944). Theory of games and economic behavior. Princeton University Press.

Google Scholar

von Stackelberg, H. (2011). Market structure and equilibrium/Heinrich von Stackelberg. Springer.

Google Scholar

Wang, H., and Wang, L. (2022). Product line strategy and environmental impact oriented to carbon tax constraints. Sustain. Prod. Consum. 32, 198–213. doi:10.1016/J.SPC.2022.04.015

CrossRef Full Text | Google Scholar

Wang, Y., Wan, Z., Chang, C., and Feng, X. (2020). A game theory based method for inter-plant heat integration considering cost allocation. Chin. J. Chem. Eng. 28, 1652–1660. doi:10.1016/J.CJCHE.2020.04.007

CrossRef Full Text | Google Scholar

Xiao-Ping, J., Fang, W., and Shu-Guang, X. (2009). Multi-objective game models for chemical industrial park. Comput. Aided Chem. Eng. 27, 2019–2024. doi:10.1016/S1570-7946(09)70727-8

CrossRef Full Text | Google Scholar

Ye, Y., Grossmann, I. E., Pinto, J. M., and Ramaswamy, S. (2020). Integrated redundancy and storage design optimization for reliable air separation units based on Markov chain-a game theoretic solution. Ind. Eng. Chem. Res. 59, 2491–2504. doi:10.1021/acs.iecr.9b04609

CrossRef Full Text | Google Scholar

Yue, D., Gao, J., Zeng, B., and You, F. (2019). A projection-based reformulation and decomposition algorithm for global optimization of a class of mixed integer bilevel linear programs. J. Glob. Optim. 73, 27–57. doi:10.1007/s10898-018-0679-1

CrossRef Full Text | Google Scholar

Yue, D., and You, F. (2014a). Fair profit allocation in supply chain optimization with transfer price and revenue sharing: Minlp model and algorithm for cellulosic biofuel supply chains. AIChE J. 60, 3211–3229. doi:10.1002/AIC.14511

CrossRef Full Text | Google Scholar

Yue, D., and You, F. (2014b). Game-theoretic modeling and optimization of multi-echelon supply chain design and operation under stackelberg game and market equilibrium. Comput. Chem. Eng. 71, 347–361. doi:10.1016/J.COMPCHEMENG.2014.08.010

CrossRef Full Text | Google Scholar

Yue, D., and You, F. (2017). Stackelberg-game-based modeling and optimization for supply chain design and operations: A mixed integer bilevel programming framework. Comput. Chem. Eng. 102, 81–95. doi:10.1016/J.COMPCHEMENG.2016.07.026

CrossRef Full Text | Google Scholar

Zamarripa, M. A., Aguirre, A. M., Méndez, C. A., and Espuña, A. (2012). Improving supply chain planning in a competitive environment. Comput. Chem. Eng. 42, 178–188. doi:10.1016/J.COMPCHEMENG.2012.03.009

CrossRef Full Text | Google Scholar

Zamarripa, M. A., Aguirre, A. M., Méndez, C. A., and Espuña, A. (2013). Mathematical programming and game theory optimization-based tool for supply chain planning in cooperative/competitive environments. Chem. Eng. Res. Des. 91, 1588–1600. doi:10.1016/J.CHERD.2013.06.008

CrossRef Full Text | Google Scholar

Zhang, D., Alhorr, Y., Elsarrag, E., Marafia, A. H., Lettieri, P., and Papageorgiou, L. G. (2017). Fair design of ccs infrastructure for power plants in Qatar under carbon trading scheme. Int. J. Greenh. Gas. Control 56, 43–54. doi:10.1016/J.IJGGC.2016.11.014

CrossRef Full Text | Google Scholar

Zhang, D., Liu, S., and Papageorgiou, L. G. (2014). Fair cost distribution among smart homes with microgrid. Energy Convers. Manag. 80, 498–508. doi:10.1016/J.ENCONMAN.2014.01.012

CrossRef Full Text | Google Scholar

Zhang, D., Samsatli, N. J., Hawkes, A. D., Brett, D. J., Shah, N., and Papageorgiou, L. G. (2013). Fair electricity transfer price and unit capacity selection for microgrids. Energy Econ. 36, 581–593. doi:10.1016/J.ENECO.2012.11.005

CrossRef Full Text | Google Scholar

Zhao, N., and You, F. (2019). Dairy waste-to-energy incentive policy design using stackelberg-game-based modeling and optimization. Appl. Energy 254, 113701. doi:10.1016/J.APENERGY.2019.113701

CrossRef Full Text | Google Scholar

Zhao, Y., Wang, S., Cheng, T. E., Yang, X., and Huang, Z. (2010). Coordination of supply chains by option contracts: A cooperative game theory approach. Eur. J. Oper. Res. 207, 668–675. doi:10.1016/j.ejor.2010.05.017

CrossRef Full Text | Google Scholar

Zheng, X. X., Liu, Z., Li, K. W., Huang, J., and Chen, J. (2019). Cooperative game approaches to coordinating a three-echelon closed-loop supply chain with fairness concerns. Int. J. Prod. Econ. 212, 92–110. doi:10.1016/J.IJPE.2019.01.011

CrossRef Full Text | Google Scholar