Editorial: Integration and optimization in the chemical process industry

Editorial on the Research Topic
Integration and optimization in the chemical process industry

Introduction

Process integration and optimization are important areas within process system engineering. It identifies targets and utilizes synergies in the overall production process, and minimizes the consumption of energy, raw materials, and natural resources, while reducing waste production and adverse environmental impacts. Process optimization is used to improve the design and operation of the entire plants or the standalone chemical processes, by maximizing the process performance and minimizing the production cost, using mathematical and computational techniques. Academicians and researchers have developed advanced process integration and optimization techniques, and applied them on a wide range of industrial chemical and related processes. In those applications, the consumption of raw materials, natural resources and the production of wastes should be minimized by designing sustainable processes, and determining the best operating conditions that minimize the environmental impact, investment and operating costs, and exergy destruction (Domingos et al., 2022).

Heuristics, thermodynamics and algorithmic approaches have been widely applied in process design and synthesis, although they are not exempt of drawbacks. The first two approaches do not guarantee that the optimum solution is obtained, as they do not use a systematic framework for synthetizing and integrating chemical plants, heat recovery networks and utility systems (Grossmann, 1985). Meanwhile, the algorithmic approach requires major computational effort and depends on the initial process superstructure. Thus, heuristics could be used in a preliminary screening to eliminate some alternatives or generate good estimates, whereas thermodynamic approaches could be used to develop bounds or eliminate energy inefficient alternatives. In turn, the algorithmic approaches could be useful to automatically generate integrated and optimized process flowsheets. In practice, the utilization of the heuristic and thermodynamic approaches for the improvement of the most important components represents a good starting value for a broader iterative optimization of industrial plants or clusters (Grossmann, 1985; Lazzaretto and Tsatsaronis, 2006). Moreover, when two or more optimization criteria are simultaneously imposed, different solutions can be acceptable, depending on the particular target. For this reason, the multi-objective optimization (MOO) appears as an attempt to reconcile the decision-making perspectives by conveniently displaying a set of optimal non-dominated solutions, known as Pareto optimal set. Thus, the optimal solution may not be unique and is only optimal in the strict mathematical sense, as the expertise of the engineers is still needed to weigh the alternatives and reach a final decision (Liew et al., 2014; Klemes, 2022).

Energy integration methods

A large portion of the energy consumed in the industrial facilities is eventually transformed and released as low-grade waste heat. As a result, the amount of useful products that can be obtained per unit of energy input is reduced. Thus, it would be desirable to reutilize most of the waste heat in order to preheat the cold streams of the production process and reduce the consumption of high-grade hot utility. Depending on the temperature levels of the waste heat, an additional amount of fuel input is often necessary in order to satisfy the heat demands of the industrial plants.

The classical energy integration (pinch analysis) method determines the maximum amount of waste heat that can be recovered, well before the final design of the heat exchanger network (HEN). By utilizing the waste heat that otherwise is irremediably dissipated by the cooling system to the environment, the energy integration (EI) method not only reduces the consumption of the costly external resources (e.g., fossil fuels) used in the utility systems, but also the wastes and emissions associated. The EI method requires 1) the number of cold and hot streams considered in the integration problem, 2) the corresponding supply and target temperatures, and 3) the value of either the heat capacity (m^.c_p) or the change in the enthalpy flow rate of each stream (ΔH).

The calculation of the minimum heating and cooling requirements starts by representing one cold and one hot process streams on a Temperature vs. Enthalpy flow rate (T vs. H) plot. By merging the representations of the cold and hot process streams, the cold and hot composite curves (CC) can be constructed. The vertical distances between the cold and hot composite curves correspond to the temperature difference along the overall heat exchange process. Moreover, the amount of the overlapping of the hot and cold composite curves along the horizontal axis indicates the extent of the heat transfer match between cold and hot process streams. Physical and economics restrictions are typically imposed on the minimum overall temperature difference allowed (ΔT_min). This fact ensures finding a HEN with the minimum utility consumptions that also achieves practical heat transfer rates in the industrial applications. The value of ΔT_min clearly depends on the nature of the fluids involved. Thus, an approach that separately assigns a contribution of each stream to the overall ΔT_min is recommendable (Marechal and Kalitventzeff, 2006). Typically, values of ΔT_min ranging between 10–100°C or more can be assumed, depending on the various characteristics of the substances studied (pressure, phase, etc.) (Couper et al., 2012).

The grand composite curve (GCC) represents the cascaded heat and proves to be a useful representation of the waste heat recovery potential. In effect, it aids in the choice and integration of one or more energy conversion technologies of the utility systems, aiming to improve the overall process performance. The minimum energy requirements (MER) can be understood as the horizontal distance between the T-axis and the GCC of the industrial process at the highest and lowest temperatures (Kemp, 2006). The point at which the GCC of the industrial process touches the T-axis is the pinch point temperature. The cascaded heat is null at the pinch point temperature. Thus, the location of this point serves to determine the extent of the penalty due to the transfer of heat across the pinch from a hot to a cold stream. If an operating condition with MER is aimed, the transfer of heat across the pinch point should be in principle avoided. Furthermore, the utilization of hot utility streams to heat below—and cold utility streams to cool above—the pinch point will only bring an increase in MER. A special case in which the heat transfer across the pinch may be thermodynamically advantageous is when low-grade waste heat below the pinch is upgraded to increase the amount of heat available above the pinch. The preheating of the reactants or the use of a mechanical vapor recompression system are examples of process that invert the transfer of waste heat across the pinch (Flórez-Orrego et al., 2020) (Figure 1).

FIGURE 1

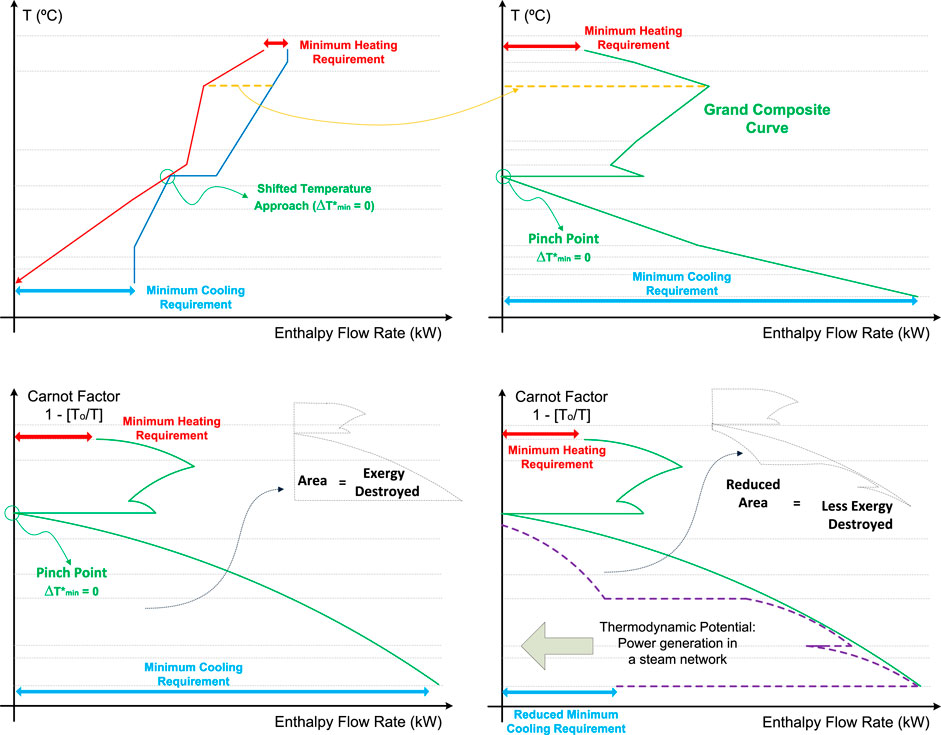
FIGURE 1. Plots of the (A) composite, (B) grand composite curve, and (C,D) Carnot grand composite curves applied to the waste heat recovery for power generation (Flórez-Orrego, 2018).

The concept of energy integration can be extended to represent the exergy destruction in the heat exchanger network (HEN). In fact, when the T-axis of the Grand Composite Curve GCC is substituted by the Carnot factor (1−T_o/T), the new representation obtained is called the Carnot Grand Composite curve (CGCC). The area enclosed between the CGCC of the chemical process and the vertical axis can be interpreted as a measure of the exergy destroyed in the HEN (Flórez-Orrego and Oliveira Junior, 2017). The CGCC can be used to determine the thermodynamic potential for exploiting the self-sufficient zones (pockets) or profit from the low-grade waste heat available below the pinch point. For this reason, it proves to be useful to propose the integration of a resourceful superstructure of energy technologies that allow to modify the area enclosed, in order to reduce the whole process irreversibility (Flórez-Orrego et al., 2019).

Mass integration methods

Industry is constantly seeking for on-site synergies to minimize the usage of the fresh resources, maximize the recycle of the process streams, and reduce the discharge of wastes. Many process designs rely on species characteristics and mass properties, such as toxicity, chemical and biological oxygen demand, hydrogen potential, density and viscosity, rather than on waste heat recovery. Thus, differently from the energy integration methods, mass integration methods focus on mass exchanger networks (MEN) (Short and Isafiade, 2021). These methods are used to conceive units that promote mass transfer between rich and lean process streams, as well as with external mass separation agents that selectively remove pollutants from waste process streams (Velázquez-Guevara et al., 2018). In order to synthesize a network of mass exchanger units, the supply and target mass flowrates and compositions of the streams are known, and the flowrates of the auxiliary lean streams are variables to be determined as part of the economic optimization problem (Short and Isafiade, 2021). An optimal synthesis of MEN, like that implemented in wastewater treatment networks, needs suitable strategies to design the mass transfer units that operate at minimum investment cost. Unlike the heat exchange network approach, in the synthesis of MEN, the composite curves touch each other in the point of closest approach.

Process optimization methods

Optimization methods are used to find the best possible solution in the feasible search space. The feasible search space is defined by the bounds on decision variables and equality and inequality constraints in the optimization problem. Optimization methods are classified into deterministic and stochastic methods. The deterministic method does not use random numbers, and they may or may not require derivatives (Smith, 2016). If the objective function and constraints are continuous and differentiable, the derivative-based methods (steepest descent, quasi-Newton and successive quadratic programming: SQP) are used. Conversely, derivative-free methods (e.g., Nelder-Mead or downhill simplex) are used when objective function and constraints have discontinuities. Deterministic methods are computationally efficient, and give the same solution in different runs if the initial point is the same. Some of them are for unconstrained optimization, whereas others fit better for problems with constraints. Nelder-Mead, steepest descent and quasi-Newton methods are for problems without constraints, whereas simplex, generalized reduced gradient and SQP methods are used for constrained optimization (Grossmann, 2021).

Stochastic optimization methods employ random numbers in their search strategies. Stochastic methods can be applied to any type of optimization problems including black-box problems, wherein only the effect of decision variables on the objective and/or constraints is known, but neither the underlying mathematical equations nor their nature. Stochastic optimization methods are based on a search that uses a single point/solution or population of points/solutions, and they are inspired by logic, physical and/or natural phenomena. Simulated annealing, genetic algorithms, differential evolution, particle swarm optimization and ant colony optimization are examples of stochastic methods (Rangaiah, 2017a). The optimization problem may have multiple conflicting objectives. A multi-objective optimization (MOO) problem can be converted into a single objective optimization (SOO) problem via weighted sum or epsilon constraint method. Next, the converted SOO problem can be solved using one of the above-mentioned optimization methods (Edgar et al., 2001). Some stochastic methods have been also developed for directly solving MOO problems (e.g. nondominated sorting genetic algorithms, multiobjective differential evolution, among others.) (Rangaiah, 2017b).

An overview of the articles published in this research topic

This Research Topic has featured five articles on process design, integration and optimization. In the following, their main contributions are highlighted:

⁃ A review of stochastic programming methods for optimization of process systems under uncertainty: This article presents mathematical framework based on stochastic programming that is used to optimize the process and energy systems under uncertainty. The article considers different types of uncertainties, and illustrates the use of the stochastic programming on several industrial case studies (Li and Grossmann).

⁃ Costs vs. flexibility of process heat recovery solutions considering short-term process variability and uncertain long-term development: This paper assess the trade-off between the annualized cost and the operating flexibility for heat exchanger network in short- and long-term perspectives. The proposed method identifies critical operating points to define flexibility targets, and then minimizes the annualized cost of heat exchanger network for each flexibility target. The approach is demonstrated on heat exchanger network retrofit for an oil refinery (Marton et al.).

⁃ Comparative techno-economic and exergetic analysis of circulating and dual bed biomass gasification systems: In this study, the authors perform a thermodynamic and economic analysis of two integrated gasification technologies aimed to produce combined heat and power from residual bagasse. The study demonstrates that a dual fluidized bed gasifier outperforms the circulating fluidized bed in terms of efficiency, when coupled with a combined cycle. The aforementioned technology also holds the lowest total production costs per unit of energy products. In this regard, the integration of more advanced technologies allows achieving a better configuration for applications such as cogeneration in the agro-industrial sector, which depends on lignocellulosic biomass to obtain the utilities (Silva Ortiz et al.).

⁃ Offshore utility systems for FPSOs: A techno-environomic assessment considering the uncertainty about the natural gas price: The main goal of this manuscript is to demonstrate that by optimizing certain operating parameters and other financial variables, the techno-economic feasibility of the floating, production, storage and offloading units (FPSOs) in deep waters could be improved, despite the opportunity cost arisen from the money depreciation and the variation of the natural gas price over time. The optimization strategy unveils the trade-offs between the best thermodynamic performance, the lowest environmental burden, and the most profitable operating conditions in floating power generation systems (Flórez-Orrego et al.).

⁃ Mass integration for rigorous process modelling: A sequential approach for direct recycling: This article discusses and proposes a solution to the challenges that arise with the use of process simulation tools for the mass integration problem. A sequential methodology is presented to devise a recycle network with rigorous process models. The violations of process constraints are handled at each sequential step through the concept of “tightening constant.” The proposed sequential methodology proves its ability to provide good approximations of the global optima with low computational effort (Marchione et al.).

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Couper, J., Penney, W. R., Fair, J. R., and Walas, S. M. (2012). Chemical process equipment. Third Edition. Boston: Butterworth-Heinemann.

Google Scholar

Domingos, M. E. G., Flórez-Orrego, D., Teles dos Santos, M., Oliveira Junior, S., and Maréchal, F. (2022). Techno-economic and environmental analysis of methanol and dimethyl ether production from syngas in a kraft pulp process. Comput. Chem. Eng. 163, 107810. doi:10.1016/j.compchemeng.2022.107810

CrossRef Full Text | Google Scholar

Edgar, T., Himmelblau, D., and Lasdon, L. (2001). Optimization of chemical processes. 2nd Edition. New york: McGraw-Hill, 651.

Google Scholar

Flórez-Orrego, D., Nascimento Silva, F., and Oliveira Junior, S. (2019). Syngas production with thermo-chemically recuperated gas expansion systems: An exergy analysis and energy integration study. Energy 178, 293–308. doi:10.1016/j.energy.2019.04.147

CrossRef Full Text | Google Scholar

Flórez-Orrego, D., and Oliveira Junior, S. (2017). Exergy assessment of single and dual pressure industrial ammonia synthesis units. Energy 141, 2540–2558. doi:10.1016/j.energy.2017.06.139

CrossRef Full Text | Google Scholar

Flórez-Orrego, D. (2018). “Process synthesis and optimization of syngas and ammonia production in nitrogen fertilizers complexes: Energy, energy integration and CO2 emissions assessment,” in Department of mechanical engineering, polytechnic school (Sao Paulo: University of Sao Paulo), 200.

Google Scholar

Flórez-Orrego, D., Sharma, S., Oliveira Junior, S., and Maréchal, F. (2020). Combined exergy analysis, energy integration and optimization of syngas and ammonia production plants: A cogeneration and syngas purification perspective. J. Clean. Prod. 244, 118647. doi:10.1016/j.jclepro.2019.118647

CrossRef Full Text | Google Scholar

Grossmann, I. (2021). Advanced optimization for process systems engineering. Cambridge: Cambridge University Press. Cambridge Series in Chemical Engineering.

Google Scholar

Grossmann, I. (1985). Mixed-integer programming approach for the synthesis of integrated process flowsheets. Comput. Chem. Eng. 9 (5), 463–482. doi:10.1016/0098-1354(85)80023-5

CrossRef Full Text | Google Scholar

Kemp, I. C. (2006). Pinch analysis and process integration: A user guide on process integration for the efficient use of energy. London. 2 ed ed.

Google Scholar

Klemes, J. (2022). Handbook of process integration. Minimisation of energy and water use, waste and emissions. Cambridge: Woodhead Publishing.

Google Scholar

Lazzaretto, A., and Tsatsaronis, G. (2006). SPECO: A systematic and general methodology for calculating efficiencies and costs in thermal systems. Energy 31 (8–9), 1257–1289. doi:10.1016/j.energy.2005.03.011

CrossRef Full Text | Google Scholar

Liew, P., Lim, J., Wan, S., Manan, Z., Varbanov, P., and Klemeš, J. (2014). A retrofit framework for Total Site heat recovery systems. Appl. Energy 135, 778–790. doi:10.1016/j.apenergy.2014.03.090

CrossRef Full Text | Google Scholar

Marechal, F., and Kalitventzeff, B. (2006). “Computer-aided integration of utility systems,” in Computer aided process and product engineering (Wiley-VCH Verlag GmbH), 327–381.

Google Scholar

Rangaiah, G. P. (2017). Differential evolution in chemical engineering: Developments and applications, 6. Singapur: World Scientific. Advances in Process Systems Engineering.

Google Scholar

Rangaiah, G. P. (2017). Multi-objective optimization: Techniques and applications in chemical engineering. Second Edition, 5. World Scientific. Advances in Process Systems Engineering.

Google Scholar

Short, M., and Isafiade, A. (2021). Thirty years of mass exchanger network synthesis – a systematic review. J. Clean. Prod. 304, 127112. doi:10.1016/j.jclepro.2021.127112

CrossRef Full Text | Google Scholar

Smith, R. (2016). Chemical process design and integration. 2 ed. Manchester: Wiley and Sons.

Google Scholar

Velázquez-Guevara, M., Uribe-Ramírez, A., Gómez-Castro, F., Ponce-Ortega, J., Hernández, S., Segovia-Hernández, J., et al. (2018). Synthesis of mass exchange networks: A novel mathematical programming approach. Comput. Chem. Eng. 115, 226–232. doi:10.1016/j.compchemeng.2018.04.012

CrossRef Full Text | Google Scholar