Stress Prediction of the Particle Structure of All-Solid-State Batteries by Numerical Simulation and Machine Learning

All-Solid-state batteries (ASSBs) are non-flammable and safe and have high capacities. Thus, ASSBs are expected to be commercialized soon for use in electric vehicles. However, because the electrode active material (AM) and solid electrolyte (SE) of ASSBs are both solid particles, the contact between the particles strongly affects the battery characteristics, yet the correlation between the electrode structure and the stress at the contact surface between the solids remains unknown. Therefore, we used the results of numerical simulations as a dataset to build a machine learning model to predict the battery performance of ASSBs. Specifically, the discrete element method (DEM) was used for the numerical simulations. In these simulations, AM and SE particles were used to fill a model of the electrode, and force was applied from one direction. Thus, the stress between the particles was calculated with respect to time. Using the simulations, we obtained a sufficient data set to build a machine learning model to predict the distribution of interparticle stress, which is difficult to measure experimentally. Promisingly, the stress distribution predicted by the constructed machine learning model showed good agreement with the stress distribution calculated by DEM.

1 Introduction

Global warming is a worldwide issue, and the reduction in the emission of greenhouse gases is key to combatting this problem. Therefore, electric vehicles (EV) and hybrid electric vehicles (HEV) have been attracting attention because they use batteries as their power sources, which reduces on-site carbon dioxide emissions and, if the electricity is sourced from renewable resources, overall carbon emissions. In recent years, all-solid-state batteries (ASSBs) have been attracting attention as next-generation batteries to power EVs and HEVs. ASSBs are superior to lithium-ion batteries that use liquid electrolytes in several ways. The first is safety because flammable organic electrolytes are not involved (instead, non-flammable inorganic electrolytes are used). Secondly, there is no need for a separator, and laminated structures can be used. Thus, high capacities can be expected. High energy densities and high output powers are key for practical use, and high-capacity anode active materials such as Si and Sn, and high-ionic-conductivity solid electrolytes such as sulfide crystals (Li_9.54Si_1.74P_1.44S_11.7Cl_0.3) (Kato et al., 2016) have been developed.

The battery performance of ASSBs naturally varies greatly depending on the materials used. Further, the contact between the solid particles also affects the battery characteristics. In a liquid lithium-ion battery, the liquid electrolyte surrounds the AM, so the entire surface of the AM acts as a reaction site. In contrast, in ASSBs, the electrolyte comprises solid particles, and only a section of the AM surface is a reaction field. The stress acting on the contact surface is strongly related to the contact state, but it is difficult to measure the stress on each particle in the electrode layer. In addition, even though it is possible to measure the stress during electrode fabrication, it is not possible to determine the stress on the particles by imaging the finished structure. Additionally, it is not possible to reproduce the formation of the exact microstructure via imaging.

In addition, the correlation between the microstructure and the contact state remains unknown, as is its relationship to structure fabrication. Therefore, with the aim of building a technology that can predict battery performance from the stress distribution in the electrode layer, we constructed a machine learning model to predict the stress distribution from cross-sectional images of particle-filled structures. Crucially, using machine learning, correlations that cannot be identified by humans can be isolated from a large number of data sets, and these correlations can be used to make predictions. As shown in Figure 1, in this study, to make predictions concerning the state of the electrode layer, we used a convolutional neural network (CNN), which is widely used in image recognition. To perform machine learning, a large amount of data is required. Therefore, to obtain sufficient stress distribution data to allow for adequate learning, we used the discrete element method (DEM). Further, we combined engineering modeling principles and machine learning.

FIGURE 1

FIGURE 1. Schematic image of concept of this study.

2 Simulation Method

This section describes the DEM, CNN dataset, and the CNN itself.

2.1 DEM

DEM is a method of determining the motion state of solid particles based on the temporal development and equations of forward motion and particle rotation. The stress between particles is calculated by assuming a spring–dashpot model that represents the damping of elasticity and viscosity, as shown in Figure 2.

FIGURE 2

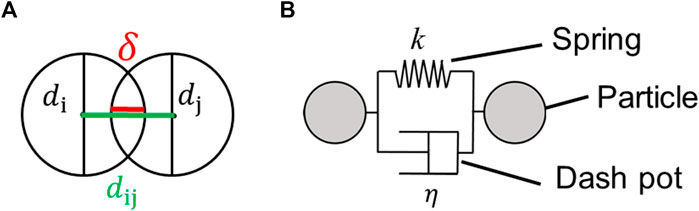
FIGURE 2. Schematic of particle handling in the DEM calculations. (A) The overlap, δ, used to calculate the contact force is the distance shown by the red line. (B) The DEM calculation assumes a spring and dashpot between the particles for the calculation of the contact force.

2.1.1 Creating a Particle-Filled Structure Before DEM Calculation

In preparation for performing a DEM calculation, the initial conditions and computational domain are determined. Therefore, in this section, we explain how to determine the initial particle array and particle size. First, the average particle size and SD of the particle size distribution of the AM particles (denoted AMs hereinafter) for one generated structure are randomly determined from set values (Bielefeld et al., 2019). Then, AMs with the particle size that achieves that size distribution are placed in randomly determined locations. In doing so, if a particle overlaps with a particle that has already been placed, the particle is discarded, and the process returns to determining the size and location of the new particle. If any particles protrude beyond the limits of the image, they are also discarded, and the process to determine the particle size and placement starts again. This process is repeated until the area ratio of the AMs becomes less than a specified value. In this study, we set five different values, 0.53, 0.58, 0.63, 0.68, and 0.73, to ensure sufficient variation between images and adequate feature extraction. The next step is to fill in the SE particles (denoted SEs); this is done in the following way For simplicity, the size of each SE particle was set to a fixed value of 1 μm, and the placement of the SEs was determined starting from the edge of the structure; as in the case of the AMs, if a particle was already placed or jumped out of the set range, we moved on to the placement of the next particle. In this way, the SE was filled exhaustively to create a particle-filled structure before the DEM calculation.

2.1.2 Calculation of Contact Force

Here, the calculation of the stress on the contact surface between particles i and j is used as an example. In DEM calculations, particles are assumed to be rigid and cannot deform. However, if we assume a completely rigid body, we cannot model multi-body contact. Therefore, we allow for an overlap of the particles in contact and define this overlap as δ [m].

$\text{δ}=\left(\left(d_i+d_j\right)/2\right)-d_{ij}.(1)$

Here, $d_{\mathrm{i}}$ [m] is the diameter of particle i, $d_{\mathrm{j}}$ [m] is the diameter of particle j, and d_ij[m] is the distance between the centers of particle i and j. Hereafter, the values used to calculate the force acting on the contact surface are derived from the equations shown below. R_eff [m] is the effective radius and is given by

$R_{\mathrm{eff}}=\frac{1}{2}\left(\frac{d_{\mathrm{i}}{d}_{\mathrm{j}}}{d_{\mathrm{i}}+d_{\mathrm{j}}}\right).(2)$

E_eff [Pa] is the effective Young’s modulus, which is calculated as

$E_{\mathrm{eff}}={\left(\frac{\left(1-{\mathrm{v}}_{\mathrm{i}}^2\right)}{E_{\mathrm{i}}}+\frac{\left(1-{\mathrm{v}}_{\mathrm{j}}^2\right)}{E_{\mathrm{j}}}\right)}^{-1}.(3)$

Here, $E$ is the Young’s modulus [Pa] of each particle, and $\text{υ}$ is the Poisson’s ratio [-] of each particle.

M_eff [kg] is the effective mass, as calculated below, where m_i [kg] is the mass of particle i, and m_j [kg] is the mass of particle j.

$M_{\mathrm{eff}}=\frac{1}{2}\left(\frac{m_{\mathrm{i}}{m}_{\mathrm{j}}}{m_{\mathrm{i}}+m_{\mathrm{j}}}\right)(4)$

$G_{\mathrm{eff}}$ [Pa] is the effective shear modulus:

$G_{\mathrm{eff}}={\left(\frac{\left(2-v_{\mathrm{i}}\right)}{G_{\mathrm{i}}}+\frac{\left(2-v_{\mathrm{j}}\right)}{G_{\mathrm{j}}}\right)}^{-1}.(5)$

In addition, k_N [N/m] is the spring constant:

$k_{\mathrm{N}}=\frac{4}{3}{E}_{\mathrm{eff}}\sqrt{\delta R_{\mathrm{eff}}}(6)$

Next, we explain how to derive the stress acting on the contact surface. The contact force, $F_{\mathrm{k}}$ [N], in a Hertzian nonlinear spring is usually expressed as

$F_{\mathrm{k}}=k_{\mathrm{N}}\delta \text{.}(7)$

Further, the viscous force, $F_{\mathrm{\eta }}$, arising from the dashpot in the normal direction is expressed as

$F_{\mathrm{\eta }}={\eta }_{\mathrm{N}}\dot{\delta }.(8)$

The viscosity coefficient, η_N, is given by

${\mathrm{\eta }}_{\mathrm{N}}=\sqrt{M_{\mathrm{eff}}{k}_{\mathrm{N}}}{\delta }^{0.25}.(9)$

Using the above equations, the contact force in the normal direction between particles can be expressed using the force of the spring, which represents elasticity, and the force of the dashpot, which represents viscous damping, as shown below.

$F_{\mathrm{N}}=k_{\mathrm{N}}\delta +{\eta }_{\mathrm{N}}\dot{\delta }(10)$

The calculation in the tangential direction was performed in the same way. However, in this case, the spring constant number, $k_{\mathrm{S}}$ [N/m], is given by

$k_{\mathrm{S}}=8G_{\mathrm{eff} }\sqrt{\delta R_{\mathrm{eff} }}.(11)$

The viscosity coefficient, η_S, is given by

${\eta }_{\mathrm{S}}={\eta }_{\mathrm{N}}.(12)$

In addition, the slippage arising from sliding in the tangential direction must be considered. A detailed explanation of this can be found in the original description of the DEM method (So et al., 2021a).

2.2 CNN Method

In this study, AM and SE are LiCoO₂ (LCO) and Li₁₀GeP₂S₁₂ (LGPS), respectively, and the values of the physical properties required for the DEM calculation are listed in Table 1 (Takahashi et al., 2006; Hao and Mukherjee, 2018; Wang et al., 2021). The size of the image after DEM calculation was 40 μm × 40 μm, and the size of the image before compression by DEM was fixed at 40 µm for the height and 46–55 µm for the width (Figures 3A,B. By varying the degree of compression, we were able to vary the stress applied to each particle in the data set. This improved the accuracy of feature extraction for machine learning. In the DEM calculation, the stress acting on the contact surface of each particle was calculated, and, from these results, the total stress acting on each particle was obtained. The stress distribution approximated a Gaussian distribution, so it was decided to express it using the average and SD. To train with CNN, we created a dataset consisting of 2D images of the particle structure obtained by DEM and structural parameters calculated from the DEM calculation results. For the 2D image of the particle image, AM was set to gray, SE to white, and voids to black (Figures 3C,D) based on the cross-sectional image of the electrode structure of an all-solid-state battery obtained at the Spring8 facility because the prediction accuracy is higher with a three-dimensional image than with a two-dimensional image and to enable matching of the image with future measurements. Thus, we created the images needed for machine learning. However, the particle array after calculation by DEM has voids concentrated at the edges, a feature not seen in the actual structure. Therefore, the actual images used for machine learning were cropped 2 µm from the edge of each of the four sides, and the center square was cut out. For each image, the structural parameters were set in the file name. The four structural property parameters are the mean value of stress on the AMs, its SD, the mean value of stress on the SEs, its SD. In addition, the reaction area, which is the contact area between AM and SE, was also calculated. This will be further discussed in Section 3.4.

TABLE 1

TABLE 1. Calculation conditions for DEM.

FIGURE 3

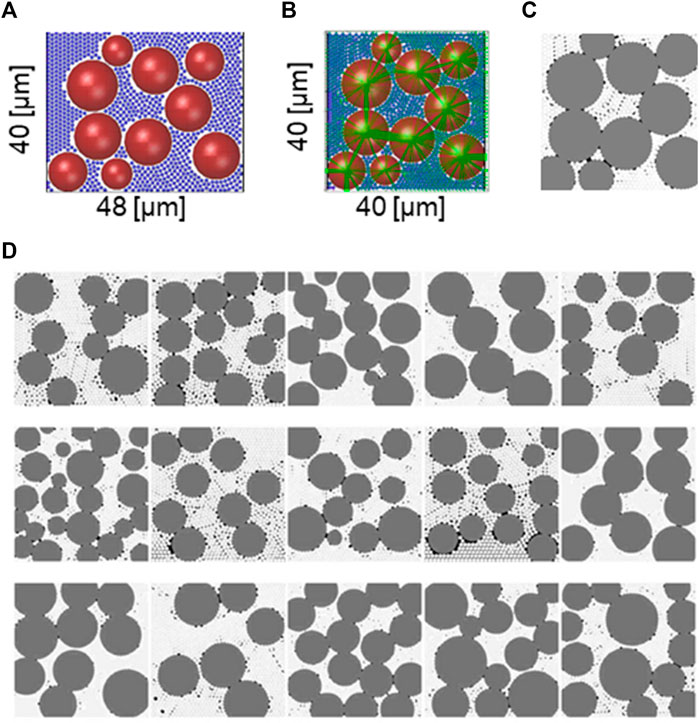
FIGURE 3. Part of the dataset created via DEM calculations. (A) Particle configuration before DEM calculation and (B) particle configuration after DEM calculation. Green lines indicate stress acting on the contact area, and the thickness of the line indicates the magnitude of the stress. (C) Triangulation of the structure in (B). Five-hundred such images were created to form a data set, and a part is shown in (D).

2.3 CNN

Machine learning is good at predicting static fields, but there are few examples of the prediction of actual operating environments such as flow, concentration, and reaction fields. However, in 2020 Raissi et al. predicted the flow phenomenon in an aneurysm of the carotid artery (Raissi et al., 2020). The authors predicted the flow field from computerized tomography images by combining operando measurements, numerical simulations of the flow, and machine learning. In this study, machine learning was also used to predict the stress distribution, which is also dynamic.

As described above, we used a CNN (Zhang et al., 2018) as the model for machine learning; this is a deep learning method used especially in the field of image recognition. CNNs extract features through multiple layers, including convolutional layers that perform sum-of-products operations and pooling layers that perform maximum value operations. The CNN then learns the correlation between the image and the output. As mentioned earlier, various structural parameters, including the stresses on each particle determined by DEM, were identified to create the dataset. For training, we used 500 images, of which 320 were used for training, 80 for validation, and 100 for testing. The CNN calculations were performed on a workstation equipped with three GeForce RTX 2080 Ti GPUs. When building a machine learning model from training data, the optimal weight parameters are automatically determined. The loss function, which used to determine the weighting parameter, has the minimum value in the final model and is a measure of the performance of a CNN. In this study, we used the mean square error (MSE) as the loss function, which is given by

$MSE=\frac{1}{N}{\displaystyle \sum }_{i=1}^N{\left(y_{\mathrm{i}}-\widehat{y_i}\right)}^2.(13)$

Here, $y_{\mathrm{i}}$ is actual value of the ith and $\widehat{y_{\mathrm{i}}}$ is predicted value of the ith.

Next, we repeatedly updated the parameters based on the gradient of the loss function and searched for the minimum value of the loss function. To calculate the gradient, backpropagation, which is one of the most mainstream learning methods, was used. In this method, the gradient of the loss function is obtained by backpropagating the loss between the output value and the training data in the direction of the input layer and applying the chain rule. The Adam algorithm (Kingma and Ba, 2017) was used to update the weighting parameters. The coefficient of determination (R²) was used to assess the accuracy of the created model. R² is given by

$R^2=1-\frac{{{\displaystyle \sum }}_{i=0}^{N-1}{\left(y_{\mathrm{i}}-\widehat{y_i}\right)}^2}{{{\displaystyle \sum }}_{i=0}^{N-1}{\left(y_{\mathrm{i}}-\overline{y}\right)}^2}.(14)$

R² is an indicator of the goodness of fit of a model, for which a perfect fit is represented by a value of 1. If R² is negative, the model is not functioning as a predictive model.

The CNN created in this study is a simple CNN consisting of convolutional and pooling layers based on VGG (SImonyan and Zisserman, 2015), which has a simple structure and high applicability.

The architecture of the constructed CNN is shown in Table 2. The convolution kernel size was set to (3, 3), and the pooling kernel size was set to (2, 2). In this study, the number of layers and parameters were reduced compared to those in the original VGG to prevent overtraining because of the limited dataset available. To implement the model, we used Keras and Tensorflow as the backend.

TABLE 2

TABLE 2. CNN summary.

3 Results and Discussion

3.1 Assessment of the CNN

Figure 4A shows the predictions obtained using the CNN model built for each structural parameter. In all figures, the horizontal axis is the value calculated from the DEMs and images, whereas the vertical axis is the value predicted by the CNN. Because the vertical and horizontal axes have the same range, the closer the data points are to the diagonal line, the higher the prediction accuracy; the coefficient of determination of the CNN model was positive for all items, indicating that it predicts the correlation with the images well.

FIGURE 4

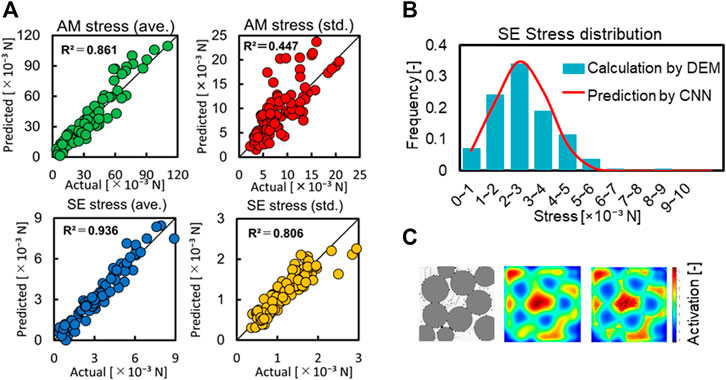
FIGURE 4. (A) Comparison between contact stresses predicted by CNN and calculated by DEM. (B) Stress distribution of SEs in Panel 2C. (C) Visualization of the region of interest. As shown by the red area, CNN training has taken place.

Figure 4B shows an example of the prediction of the distribution of stress on SE particles calculated by DEM. The light blue bars show the values calculated by DEM, whereas the red smooth lines show the values predicted using the constructed machine learning model. The predicted Gaussian distribution is almost identical to the calculated stress distribution.

3.2 Visualization of the Region of Interest

Machine learning is often described as a black box problem. Specifically, in machine learning, a model is trained using a large amount of data, but the application of the model simply provides an answer, and how the result was obtained is unknown. To solve this problem, we visualized which part of the image was being extracted as a feature during training. To do this, we used Grad-CAM (Gradient-Weighted Class Activation Mapping) (Selvaraju et al., 2017) as a reference for visualization. First, we fed the image to the CNN and extracted the feature map and output of the convolutional layer. The output results were then used to compute the gradient of the convolutional layer by backpropagation, and the average of the gradient of the convolutional layer was computed from the results. Finally, the sum of the weightings of the convolutional layers were superimposed on the original image to produce a heatmap, as shown in Figure 4C. In this way, the red area can be identified as the area that characterizes the structural properties. These results confirm that the CNN learns by focusing on the areas where the particles are in contact with each other, that is, the areas where interparticle stress is acting.

3.3 Prediction of the Reaction Boundary Area

As described above, CNN can predict the stress distribution on each particle. Next, we decided to use CNN to predict the reaction area, which is correlated with the stress. The reaction area here is the area of contact part between AM and SE particles, which is one of the indicators of battery performance because the reaction occurs between AM and SE. The reaction area was obtained from the stress on the contact surface and Hertz’s contact theory (Persson, 2006). When particles i and j are in contact and a pressure of P [N] is applied to the contact area, the radius (a) of the contact surface at that time is obtained by Hertz’s contact theory. P [N] is the interparticle stress, v_i [-] and v_j are Poisson’s ratio for each particle, E_i [MPa] and E_j [MPa] are the Young’s moduli, and R_i [mm] and R_j [mm] are the radii of curvature. The radius, a [mm], of the contact surface circle is given by

$a=\sqrt[3]{\frac{\frac{3P}{4}\left(\frac{1-{\text{ν}}_{\mathrm{i}}^2}{E_{\mathrm{i}}}+\frac{1-{\text{ν}}_{\mathrm{j}}^2}{E_{\mathrm{j}}}\right)}{\left(\frac{1}{R_{\mathrm{i}}}+\frac{1}{R_{\mathrm{j}}}\right)}}.(15)$

The area of the contact surface, S [mm²], is given by

$S=\mathrm{\pi }{a}^2\text{.}(16)$

Similar to Figures 4A, 5B shows the stress values calculated by DEM and the reaction area calculated from Hertz’s contact theory on the horizontal axis, and the predicted values by CNN on the vertical axis. The plotted points lie near the diagonal, and the coefficient of determination is 0.921, which is good. As mentioned in (Tian and Qi, 2017), the previous research most focused on the relationship between the applied pressure and the contact area and performed the prediction of the contact area loss during the degradation period of batteries. On the other hand, since this study uses images of the entire structure, we are able to predict reaction area that reflects the minute parts of the structure.

FIGURE 5

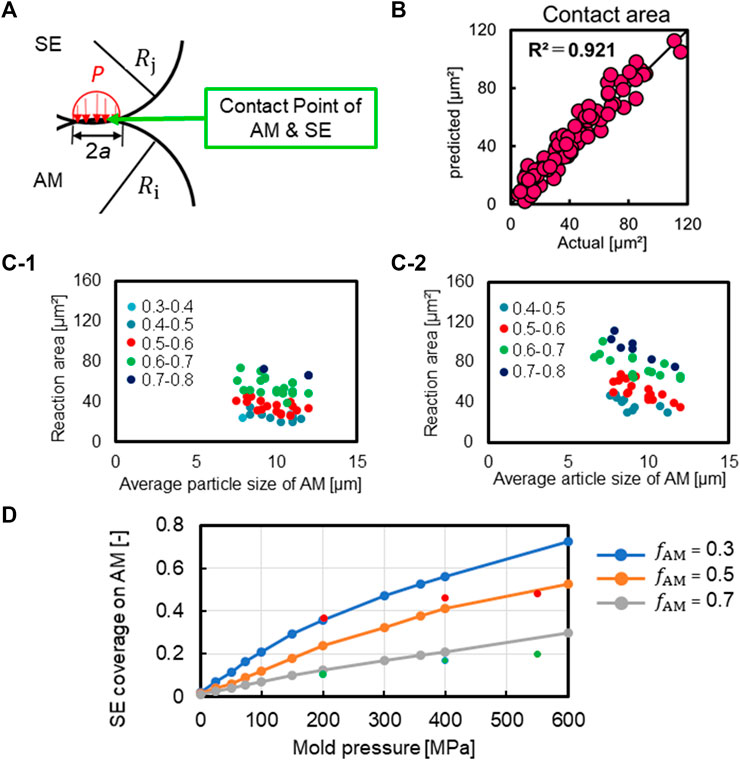
FIGURE 5. (A) Hertz’s contact theory and predicted contact area results. (B) Comparison between contact area predicted by CNN and calculated by DEM and Hertzian contact theory, indicating consistency between the predictions. (C-1,C-2) Relationship between particle size and reaction boundary area for each compression ratio and CNN results. (C-1) has a smaller compression ratio than (C-2), and the color coding of the dots on the graph is based on the volume fraction of AM. (D) Comparison with previously reported literature values. Here, $f_{AM}$ is volume fraction of AM Red circle represents $f_{AM}=0.5\text{\%}$, green circle represents $f_{AM}=0.7\text{\%}$.

3.4 Analysis of the Calculation Results of the Reaction Boundary Area

In this study, we created 10 compression width patterns as described earlier to provide a wide range to the data set. Fifty samples with the same compression widths were compared in terms of active material particle size and contact area. Some of the results are shown in Figures 5C-1,C-2. Under the conditions of this study, the smaller the active material particle size, the larger the reaction area. This can be attributed to the fact that the smaller the particle size is, the larger the surface area of the active material becomes when the active material volume fraction is the same. In addition, the larger the active material volume fraction, the larger the reaction boundary area. This is because the difference in the particle size ratio between the active material and the solid electrolyte in this study is large, approximately 10:1, allowing the solid electrolyte to enter even the smallest gaps. For example, when the active material and solid electrolyte particle sizes are similar, the larger the particle size, the more space the particles cannot enter, resulting in a decreased contact area between the active material and the solid electrolyte. Furthermore, the degree of change in the contact area owing to the particle size difference was greater for those with a larger width to compress in the DEM calculation compression process. We believe that this is also due to the solid electrolyte penetrating into the gaps between the particles when more external force is applied. Based on these considerations, we believe that the trend of the reaction area will change when the particle size difference between the solid electrolyte and the active material is changed.

3.5 Comparison With Elasto-Plastic Deformation Mode

From the cross-sectional view of the structure created by the DEM calculation incorporating previously reported elasto-plastic deformation (So et al., 2021b), we predicted the reaction area using the machine learning model constructed in this study. Subsequently, we verified what percentage of the active material surface area is in contact with the solid electrolyte. Figure 5D shows the relationship between the magnitude of the concluding pressure and the percentage of the active material surface area that is in contact with the SE, depending on the active material volume percentage.

$\text{SE coverage on AM }[-]=\frac{\mathrm{Predicted\; reaction\; area} \left[\mathrm{\mu }{\mathrm{m}}^2\right]}{\mathrm{Calculated\; total\; surface\; area\; of\; AM} \left[\mathrm{\mu }{\mathrm{m}}^2\right]}\times \text{f }[-](17)$

$\text{f}=2.44\times {10}^1(18)$

The correction factor f became a large value, and we think one reason for this is the difference in the cross-sectional structure of the previously reported structure and the data set used to create the original machine learning model. The dataset has a very small porosity, whereas the cross-section of the elasto-plastic deformation model has numerous voids. Furthermore, even in the AM-SE contact area, there are enough voids to clearly show the shape of the solid electrolyte, which is very different from the dataset. This is thought to be the reason why the reaction area is predicted to be very small.

Another factor is that with the DEM calculations used in this study, the active material and solid electrolyte are arranged such that the particle centers are aligned on the same plane. Therefore, the particles are in contact only in the cross-sectional view. However, in a three-dimensional structure, the active material is in contact with the solid electrolyte at every part of the surface. For the AM-SE ratio of the cross-sectional view obtained as a verification of this study, the reaction area is limited to the part in contact on the cross-sectional view. Conversely, the active material surface area was calculated by obtaining the grain size from the cross-sectional view. The figure in the reference paper used for the study uses the reaction field and surface areas of the active material for the entire three-dimensional structure; consequently, the number of solid electrolytes in contact with one active material is overwhelmingly large. As a result, the correction factor is considered to be large.

However, from this verification, we believe that the model constructed in this study captures the general trend of elasto-plastic deformation and can be applied to elasto-plastic deformation models. As a future improvement, we are considering using a data set that takes elasto-plastic deformation into account when constructing machine learning.

4 Conclusion

In this study, we developed a machine learning model to estimate the stress distribution of porous structures and investigated the correlation between the structural properties. Because it is difficult to measure the stress acting on the contact area between microparticles, DEM was used. Five-hundred images were obtained by DEM, and the dataset of the stress distribution was used to construct a machine learning model to predict the stress distribution acting on each particle that constitutes the porous electrode structure. From the machine learning model and using Hertzian contact theory, the contact area involved in the electrode reaction was estimated. Because the rapid commercialization of ASSBs is desirable, we plan to improve the charge–discharge and cycle characteristics by linking machine learning and measurements to enable structure design and develop a fundamental technology that will contribute to the rapid commercialization of ASSBs. For this purpose, we will also consider the in-situ stress distribution and lithium concentration distribution during charging and discharging period (Sakai et al., 2019) into our simulation model, and improve the DEM model by introducing elastic-plastic deformation (So et al., 2021b). In addition, the model established in this research can not only be applied to the performance evaluation of porous secondary batteries but also to other fields involving porous materials.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

Conceptualization, GI and CK; methodology, SI, KN and MS; formal analysis, NK, YT, SI and KN; writing—original draft preparation, CK; writing—review and editing, GI and CK. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by JSPS KAKENHI Grant-in-Aid for Scientific Research on Innovative Areas project “Science on Interfacial Ion Dynamics for Solid State Ionics Devices, Computational and Data Science” (Gp-A03, grant number 19H05815) and MEXT project “Program for Promoting Research on the Supercomputer Fugaku” (Fugaku Battery & Fuel Cell Project, Grant No. JPMXP1020200301).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bielefeld, A., Weber, D. A., and Janek, J. (2019). Microstructural Modeling of Composite Cathodes for All-Solid-State Batteries. J. Phys. Chem. C 123 (3), 1626–1634. doi:10.1021/acs.jpcc.8b11043

CrossRef Full Text | Google Scholar

Hao, F., and Mukherjee, P. P. (2018). Mesoscale Analysis of the Electrolyte-Electrode Interface in All-Solid-State Li-Ion Batteries. J. Electrochem. Soc. 165 (9), A1857–A1864. doi:10.1149/2.1251809jes

CrossRef Full Text | Google Scholar

Kato, Y., Hori, S., Saito, T., Suzuki, K., Hirayama, M., Mitsui, A., et al. (2016). High-power All-Solid-State Batteries Using Sulfide Superionic Conductors. Nat. Energ. 1, 16030. doi:10.1038/nenergy.2016.30

CrossRef Full Text | Google Scholar

Kingma, D., P., and Ba, J. (2017). Adam: A Method for Stochastic Optimization. arXiv. Available at: https://arxiv.org/abs/1412.6980v8.

Google Scholar

Persson, B. N. J. (2006). Contact Mechanics for Randomly Rough Surfaces. Surf. Sci. Rep. 61 (4), 201–227. doi:10.1016/j.surfrep.2006.04.001

CrossRef Full Text | Google Scholar

Raissi, M., Yazdani, A., and Karniadakis, G. E. (2020). Hidden Fluid Mechanics: Learning Velocity and Pressure fields from Flow Visualizations. Science 367 (6481), 1026–1030. doi:10.1126/science.aaw4741

PubMed Abstract | CrossRef Full Text | Google Scholar

Sakai, H., Taniguchi, Y., Uosaki, K., and Masuda, T. (2019). Quantitative Cross-Sectional Mapping of Nanomechanical Properties of Composite Films for Lithium Ion Batteries Using Bimodal Mode Atomic Force Microscopy. J. Power Sourc. 413, 29–33. doi:10.1016/j.jpowsour.2018.12.003

CrossRef Full Text | Google Scholar

Selvaraju, R., Cogswell, M., Das, A., Vedantam, R., Parikh, D., and Batra, D. (2017). “Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization,” in 16th IEEE International Conference on Computer Vision (ICCV), Venice, Italy, October 22-29, 2017. arXiv:1610. 02391 [cs.CV]. doi:10.1109/iccv.2017.74

CrossRef Full Text | Google Scholar

SImonyan, K., and Zisserman, A. (2015). Very Deep Convolutional Networks for Large-Scale Image Recognition. ICLR. arXiv: 1409. 1556 [cs.CV].

Google Scholar

So, M., Inoue, G., Hirate, R., Nunoshita, K., Ishikawa, S., and Tsuge, Y. (2021). Effect of Mold Pressure on Compaction and Ion Conductivity of All-Solid-State Batteries Revealed by the Discrete Element Method. J. Power Sourc. 508, 230344. doi:10.1016/j.jpowsour.2021.230344

CrossRef Full Text | Google Scholar

So, M., Inoue, G., Hirate, R., Nunoshita, K., Ishikawa, S., and Tsuge, Y. (2021). Simulation of Fabrication and Degradation of All-Solid-State Batteries with Ductile Particles. J. Electrochem. Soc. 168, 030538. doi:10.1149/1945-7111/abed23

CrossRef Full Text | Google Scholar

Takahashi, Y., Kijima, N., Nishizawa, M., Dokko, K., Uchida, I., and Akimoto, J. (2006). Structure and Electron Density Analysis of Electrochemically and Chemically Delithiated LiCoO2 Single Crystals. J. Solid State. Chem. 180 (1), 313–321. doi:10.1016/j.jssc.2006.10.018

CrossRef Full Text | Google Scholar

Tian, H.-K., and Qi, Y. (2017). Simulation of the Effect of Contact Area Loss in All-Solid-State Li-Ion Batteries. J. Electrochem. Soc. 164 (11), E3512–E3521. doi:10.1149/2.0481711jes

CrossRef Full Text | Google Scholar

Wang, Y., Hoang, B., Hoerauf, J., Lee, C., Lin, C.-F., Rubloff, G. W., et al. (2021). Hot and Cold Pressed LGPS Solid Electrolytes. J. Electrochem. Soc. 168, 010533. doi:10.1149/1945-7111/abdb44

CrossRef Full Text | Google Scholar

Zhang, M., Li, W., and Du, Q. (2018). Diverse Region-Based CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 27 (6), 2623–2634. doi:10.1109/tip.2018.2809606

PubMed Abstract | CrossRef Full Text | Google Scholar

Nomenclature

δ overlap (m)

d diameter (m)

R radius (m)

E Young’s modulus (Pa)

v Poisson’s ratio (-)

m mass (kg)

M mass (kg)

F Force (N)

G effective shear modulus (Pa)

k spring constant (N/m)

η viscosity coefficient (Pa・s)

P Stress (N)

a radius (mm)

S contact area (${\text{mm}}^2$)

$f_{AM}$ Volume fraction of AM (-)