Experimental Investigation of a Continuous Reactor for CO2 Capture and CaCO3 Precipitation

In a climate neutral world, the life cycle greenhouse gas (GHG) emissions of precipitated calcium carbonate (PCC) have to be reduced towards net-zero. Mineral carbonation processes allow to do so by replacing the carbon rich calcium source limestone by carbon free industrial mineral wastes. Various processes have been investigated in literature. They exhibit the benefit of little to no feedstock related emissions and high energy savings due to the avoidance of the CaCO₃ calcination step. However, the nature of the process changes significantly, which requires a fundamental understanding of the new mechanisms controlling the process of CO₂ absorption and CaCO₃ precipitation. Within this work, a CO₂ rich gas is contacted with a calcium rich aqueous feed in a continuous reactive crystallizor. The CO₂ selectively absorbs and precipitates as either vaterite or calcite. The effect of the liquid and gas feed flow rates, of the feed stoichiometric ratio and of the residence time on key performance indicators, such as the CO₂ capture efficiency the CaCO₃ precipitation efficiency and the features of the final product, is studied experimentally. As expected, these feed characteristics determine the effective stoichiometric ratio of reactants in the liquid phase, $\psi .$ The particle size increases strongly with $\psi$; vaterite represents the predominant solid phase at $\psi$ < 1 while otherwise a mix of vaterite and calcite was formed, whereas the latter one accounted for 13%–90% in mass of crystals collected. Moreover, $\psi$ of about one exhibits the highest CO₂ capture efficiency exceeding 80%.

1 Introduction

Today, the production of precipitated calcium carbonate (PCC), for use in products such as cleansing agents, paper or plastics, causes carbon dioxide emissions. Most of these emissions are inherent to the process, since the raw material limestone, CaCO₃, is calcinated at about 1,000°C to decompose it into calcium oxide, CaO, and carbon dioxide, CO₂. While CO₂ from limestone, about two thirds of the total, together with that resulting from the combustion of the fuel needed for calcination, about one third (Anantharaman et al., 2017), is usually released to the atmosphere, CaO is then reacted with water in the lime slaking process to form calcium hydroxide, Ca(OH)₂. Finally, a slurry of Ca(OH)₂ in water is carbonated with CO₂, in an amount exactly equal to that released during calcination, to form the final product, PCC. If the CO₂ for carbonation were sourced from the calcination flue gas itself, that part of the direct emissions would be avoided. However, since conventional products utilizing PCC are incinerated at their end of life, this CO₂ gets released again to the atmosphere (see the detailed life cycle analysis, LCA, presented in Mattila et al. (2014), and Mattila and Zevenhoven (2014a)). An option that has been proposed recently is the substitution of limestone as the calcium source with one that does not contain geogenic carbon. Such an approach would allow evolving the PCC production from a linear approach, to a circular approach that can reduce GHG emissions, save natural resources, and comply with the requirements that the future sustainable, carbon-neutral world prescribes.

There is plenty of literature about lab-scale processes, which utilize industrial mineral wastes to produce carbon neutral or even carbon negative PCC (see for a review (Sanna et al., 2014). Most promising approaches consist of indirect, two-step mineral carbonation processes. In step one, calcium is selectively extracted from an alkaline precursor material by a solvent. The residual of the precursor is removed by filtration. The filtrate, rich in calcium, is contacted with CO₂ in a second step where the PCC precipitates from the solution. Compared to the conventional lime slurry carbonation process described above, such processes use additives that enhance the solubility of the Ca containing minerals but at the same time lead to major disadvantages, for the reasons detailed below.

A constant liquid phase composition is critical to the quality of PCC, since this yields a constant supersaturation level, hence a constant driving force for crystal nucleation and growth, i.e., the processes controlling final particle size, shape and morphology (see Gullichsen et al. (2000)), for how these three features determine when PCC fulfills the requirements for industrial and commercial applications).

Conventional carbonation processes are operated in the batch mode. A constant liquid phase composition, hence a constant supersaturation, is maintained thanks to the interplay between dissolution of Ca(OH)₂ suspended in water and precipitation of PCC through reaction with the bubbling CO₂. The aqueous solution is rich in calcium ions thanks to the relatively high solubility of Ca(OH)₂ and in carbonate ions thanks to the speciation of CO₂; they are consumed by the precipitation of CaCO₃, which exhibits a very low solubility. The buffering effect just described lets the process operate at constant liquid phase composition until all Ca(OH)₂ is consumed. Note that calcium carbonate can precipitate as the metastable polymorphs vaterite and aragonite, or as the stable polymorph calcite.

Two-step processes, which utilize industrial wastes as a calcium source, tend to operate at calcium feed concentrations in the precipitation step an order of magnitude higher than in the case described above. This is necessary to maximize the cyclic capacity of the process and it is achieved by introducing additives that increase the solubility of the calcium containing minerals present, e.g., Ca(OH)₂, which is of high interest, since it is present in large amounts in the most abundant industrial mineral waste, i.e., demolition concrete. The consequence is that carbonation takes place in an aqueous solution rich in calcium ions, but without the buffering effect of suspended Ca(OH)₂. Such batch processes undergo a change in liquid phase composition as the carbonation progresses, thus leading to poor particle properties. Literature reviews about current process routes and effects of synthesis conditions on the particle properties have been conducted by Chang et al. (2017b) and Jimoh et al. (2018).

In order to exploit the benefits of both approaches, i.e., constant supersaturation and high calcium loading, a continuous carbonation process may be implemented, which is the subject and the novelty of this work. The design of such a process requires a thorough understanding of the thermodynamics and the kinetics involved. In this paper, we explore the design space of a continuous carbonation process through an experimental study.

2 Experimental

2.1 Materials

The synthetic feed stock was prepared from ultrapure de-ionized water (Millipore, 18.2 M Ω cm), calcium hydroxide (Sigma-Aldrich, ≥ 96%) as calcium source and ammonium nitrate (Sigma-Aldrich, ≥ 99%). As CO₂ source, synthetic gas mixtures (relative error ±1%) of 25 and 85% CO₂ in N₂ (Pangas AG, Switzerland) were used. The experiments were seeded with calcium carbonate seeds with a mean diameter of 27 μm. The seeds were synthetized in the lab and contained calcite, vaterite and aragonite phases.

2.2 Experimental Set-Up

A simplified flowsheet of the setup built for continuous calcium carbonate precipitation experiments is shown in Figure 1. An 850 ml, double walled glass, stirred (using a four bladed overhead stirrer, operated using a IKA, EUROSTAR, 40 digital electric engine, and rotated at 30–2000 RPM) crystallizer was used, which is thermostatted using a Huber CC 230 thermostat. To keep the reactor gas tight, the shaft of the stirrer was greased and inserted into a glass bearing sleeve (Möller AG), which was cooled with ice from the outside to maintain the viscous texture of the grease. A peristaltic pump (Watson-Marlow 502S) transferred the feed solution continuously from the storage tank into the reactor. The pump was calibrated a-priori and delivered flow rates of 10–50 g solution per minute. The suspension was discharged through periodically occurring pulses of 100–150 ml by means of a release valve installed at the bottom of the reactor. The suspension was transferred to a pressure filtration device (BHS Sonthofen, Taschenmessgerät PLF), where it was filtrated with compressed air at 6 bar. The particles were collected on paper filters (Macherey-Nagel, MN 625). The particle size was measured with a laser diffraction device (Sympatec, Helos BR). The particle morphology was determined by XRD (Bruker, D2 Phaser). Images of the particles were taken by SEM (Hitachi, S-4800). The mass of the filtrate and the dry mass of the particles were measured on a balance. The gas was fed into the reactor using a mass flow controller (F-201-CV, Bronkhorst High-Tech BV). A sparger (sintered metal, pores <10 μm), installed at the bottom of the reactor created very small gas bubbles which rose through the suspension towards the reactor’s gas overhead. A reflux condenser, connected to the cooling water circuit (cooling water temperature of about 15°C) reduced the water loss and dried the gas before it entered a gas mass flow meter (F-111-C, Bronkhorst High-Tech BV) and a mass spectrometer (ThermoStar GSD 301 C, Pfeiffer Vacuum Schweiz AG). The system pressure was kept at 1.25 bar using a back pressure regulator (LFO, Equilibar, United States), in combination with a pressure gauge. This slight overpressure facilitated the withdrawal of the suspension.

FIGURE 1

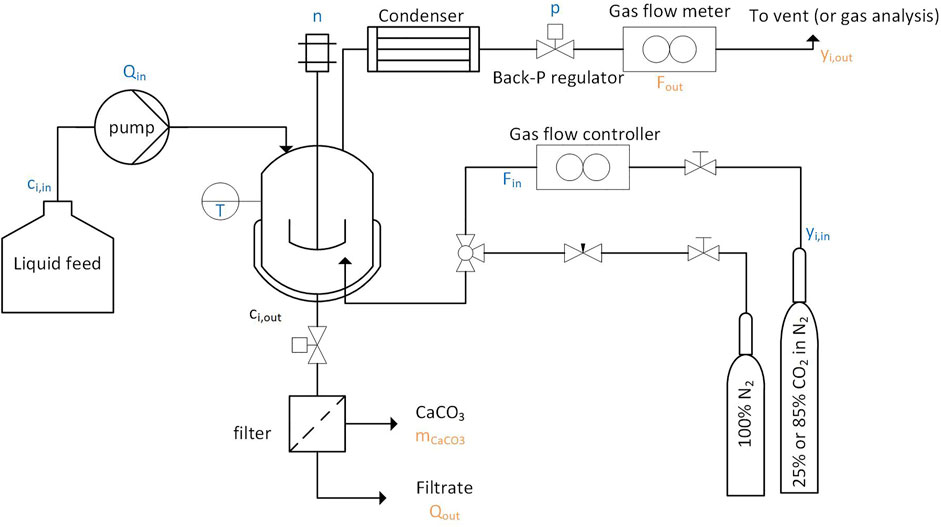
FIGURE 1. In the simplified flow sheet, the letters in blue specify the operating and feed conditions, while the organ letters specify the downstream data measured throughout the experiment.

2.3 Methods and Analytics

Prior to each experiment, the aqueous solutions with apparent calcium concentrations $c_{Ca,in}$ of 0.2, 0.25, 0.3 and 0.35 molal and an apparent ammonium nitrate concentration $c_{N{H}_{4}N{O}_3,in}$ of 0.4, 0.6 and 0.7 molal were prepared. To shorten the time until the system reached its cyclic steady state, the reactor was initially filled with 350 ml of aqueous solution with a composition close to that at steady state. In addition, the solution was seeded with 5 g of calcium carbonate seeds. Initial seeding with PCC crystals can reduce the transient phase significantly (Verdoes et al., 1992). Before the start of the experiment, the reactor’s gas overhead space was filled with nitrogen. In addition, the system was tested to make sure that there were no gas leakages. To conduct isothermal experiments, the thermostat was set to the set point temperature T, i.e., mostly 25°C.

At time zero, the peristaltic pump started feeding the feed solution at a rate $Q_{in}$ and at the desired composition. Simultanously, the overhead stirrer was switched to 250 rpm and the mass flow controller started feeding the CO₂ rich gas stream at a rate $F_{in}$ and at the desired composition, $y_{i,in}$. The back pressure regulator was set to 1.25 bar. Since the liquid outlet opened periodically, the liquid level was rising until it reached the upper level. At this point in time, the liquid outlet valve opened for a few seconds until the reactor suspension dropped to the lower level. The time averaged suspension volume was 0.4 L. The suspension was filtered and the solids were dried in an oven overnight at 70°C. The mass of the solids was measured to obtain $m_{CaC{O}_3}$. Furthermore, the particle size distribution was measured by laser diffraction and the polymorphs present were identified by XRD. Scanning electron microscopy (SEM) images were used to double check the type of polymorph present and to identify the different morphologies.

2.4 Experimental Planning

In the experimental campaign, the effect of varying feed conditions pertaining to both the gas and the liquid stream on the process outcome was investigated. Operating parameters are grouped in two categories, whereby the second consists of combined quantities that are called key operating parameters because of their importance.

2.4.1 Operating Parameters

The system’s operating conditions are determined by the temperature T, pressure P, gas inlet composition $y_{i,in}$, gas inlet flowrate $F_{in}$, liquid phase inlet composition $c_{i,in}$, liquid feed flow rate $Q_{in}$, geometry of the system and stirring rate n. Temperature, pressure and the geometry of the system were kept unchanged. More specifically, in the experiments, $Q_{in}$, $F_{in}$, $c_{i,in}$ and $y_{i,in}$ as well as n are varied (see Table 1), whereas it was assumed that the time averaged suspension volume $V_s$ in the reactor remained constant.

TABLE 1

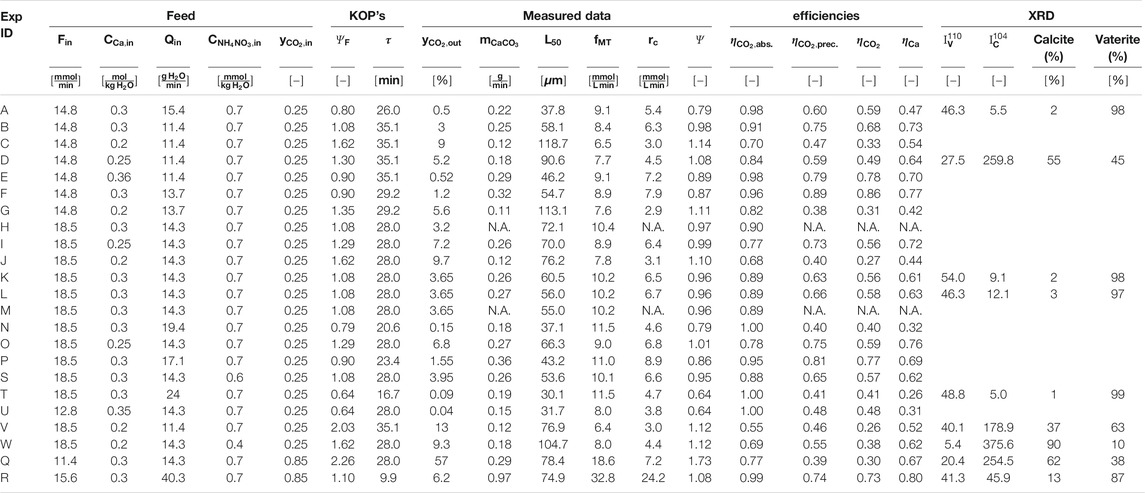
TABLE 1. The feed conditions, KOP as well as the downstream data and the process efficiencies are listed in the table below. All experiments listed were performed at 250 rpm, 25°C and a system pressure of 1.25 bars. Experiment m was conducted at a stirring rate of 350 rpm.

2.4.2 Key Operating Parameters

Calcium carbonate precipitates according to the following reaction:

${\text{Ca}}^{2+}+{\text{CO}}_3^{2-}\leftrightarrow {\text{CaCO}}_3$(2-1)

thus the reactants participate in the reaction with a stoichiometric ratio of one-to-one. The stoichiometric ratio in the feed to the reactor, ${\psi }_F$, is defined as:

${\psi }_F=\frac{F_{in}{y}_{C{O}_2,in}}{Q_{in}{c}_{Ca,in}}$(2-2)

While thermodynamics defines theoretical limits for crystal nucleation and growth, kinetics determines how close the system approaches such limits, as a function of the residence time $\tau$ of the suspension in the reactor, which is defined as:

$\tau =\frac{V_s{\rho }_s}{Q_{in}}$(2-3)

In the course of the experimental campaign, a wide range of operating conditions was screened in order to develop an understanding of how these influence the rate of CO₂ absorption, the rate of CaCO₃ crystal nucleation and growth, and the particles’ size and shape. To this aim, the values of ${\psi }_F$ and $\tau$ were varied by a factor 3.

2.5 Raw Data Treatment

In this section, we describe how the measured raw data is converted into more useful process data, from which process performances are calculated.

2.5.1 Measurements

During the experiments, the gas outlet flow rate $F_{out}$ and CO₂ concentration $y_{C{O}_2,out}$ are measured online. The mass of crystals exiting the reactor per unit time $m_{CaC{O}_3}$ is also measured. After filtration, the particle size and shape can be directly analyzed by laser diffraction, XRD and SEM. Under the assumption that the reflux condenser is drying the exiting gas stream completely, the exiting liquid flow rate $Q_{out}$ is equal to the feed liquid flow rate $Q_{in}$.

2.5.2 Calculations

From the measured data, the volume specific CO₂ absorption rate $f_{MT}$ and the volume specific CaCO₃ precipitation rate $r_c$ are determined. The former is calculated from the CO₂ material balance as:

$f_{MT}=\frac{\left(F_{in} y_{C{O}_2,in}-F_{out} y_{C{O}_2,out}\right)}{V_s}$(2-4)

Since the experiments are conducted with a binary CO₂—N₂ gas mixture, the exiting gas stream is assumed to be dry, and N₂ is assumed to not absorb in the solution, hence the N₂ material balance is:

$F_{in} y_{N_2,in}=F_{out} y_{N_2,out}$(2-5)

Finally, the rate of CO₂ absorption can be calculated from (Eqs 2-4, 2-5) as:

$f_{MT}=\frac{F_{in}}{V_s} \left(y_{C{O}_2,in}-\frac{1- y_{C{O}_2,in}}{1-y_{C{O}_2,out}} y_{C{O}_2,out}\right)$(2-6)

The volume specific rate of PCC precipitation $r_c$ can be calculated from the material balance over the solid phase as:

$r_c=\frac{m_{CaC{O}_3}}{V_s M_{CaC{O}_3}}$(2-7)

2.5.3. Process Efficiencies

The CO₂ absorption efficiency ${\eta }_{C{O}_2,abs.}$ is defined and calculated as:

${\eta }_{C{O}_2,abs.}= \frac{f_{MT}{V}_s}{F_{in}{y}_{C{O}_2,in}}$(2-8)

The product of the feed stoichiometry ${\psi }_F$ and the CO₂ absorption efficiency ${\eta }_{C{O}_2,abs.}$ determines the effective stoichiometric ratio of the two reactants that enters the aqueous solution, $\psi$, which is thus:

$\psi =\frac{f_{MT}{V}_s }{Q_{in} c_{Ca,in}}={\eta }_{C{O}_2,abs.} {\psi }_F$(2-9)

The efficiency of the precipitation of CO₂ from the aqueous solution, ${\eta }_{C{O}_2,prec.}$, is defined as:

${\eta }_{C{O}_2,prec.}=\frac{r_c }{f_{MT}}$(2-10)

Finally, the CO₂ mineralization efficiency of the process with respect to CO₂, ${\eta }_{C{O}_2}$, is defined as:

${\eta }_{C{O}_2}={\eta }_{C{O}_2,abs.} {\eta }_{C{O}_2,prec. }=\frac{r_c V_s}{F_{in} y_{C{O}_2,in}}$(2-11)

whilst the overall efficiency of the process with respect to calcium, ${\eta }_{Ca}$, is calculated as:

${\eta }_{Ca}=\frac{r_c{V}_s}{Q_{in} c_{Ca,in}}$(2-12)

Note that

${\eta }_{Ca}= {\eta }_{C{O}_2}{\psi }_F$(2-13)

These key performance indicators (KPIs) will be used to make a comparative assessment of the continuous precipitation process and of the effect of the operating conditions.

3 Results

We have conducted the twenty-three experiments listed in Table 1 according to the procedure described below. Afterwards, we analyze and discuss reproducibility first, then the effect of the operating parameters on $y_{C{O}_2,out}$, $m_{CaC{O}_3}$ and $L_{50}$, and finally that of the key operating parameters (KOP), i.e. ${\psi }_F$, $\tau$ and $p_{C{O}_2,in}$, on absorption of CO₂ and precipitation of CaCO₃ as well as on the final particle properties.

3.1 Phenomenology of Experiments

Figure 2 illustrates the transient and steady state behavior observed during three typical continuous precipitation experiments. Initially, the reactor is filled with a calcium ion rich solution in which CaCO₃ seed crystals are suspended, which is put in contact with a gas stream consisting of carbon dioxide and nitrogen, 25/75 v/v, and with a liquid stream. Part of the gas is not absorbed, and leaves the crystallizer with a flow rate and a CO₂ mole fraction that are plotted as function of time in Figures 2A,B. The difference between the CO₂ feed mole fraction, i.e., 0.25, and the values plotted indicates that CO₂ is indeed absorbed preferentially. Steady state is reached after between 30 and 60 min, while the gas phase goes from an initial CO₂ concentration of 0.5%, to about 4% (standard deviation 0.13%) (Figure 2B). Due to the fact that the liquid feed is continuous while the liquid outlet flow is pulsating, a cyclic steady state with period of 8 min is attained, as it can be observed both in the gas outlet flow rate (Figure 2A) and in the outlet CO₂ concentration (Figure 2B). Based on its definition (Eq. 2-6), the volume specific CO₂ absorption rate decreases when both the gas outlet flow rate and CO₂ concentration increase, as observed in Figures 2A,B and Figure 2B in the first 30 min of the experiment. This is a consequence of the fact that the initial solution is CO₂ free and calcium rich. The final steady state conditions, particulary the steady state gas outlet flow rate and the CO₂ concentration in the gas and in the solution, correspond to those where the CO₂ absorption rate and the calcium carbonate precipitation balance each other.

FIGURE 2

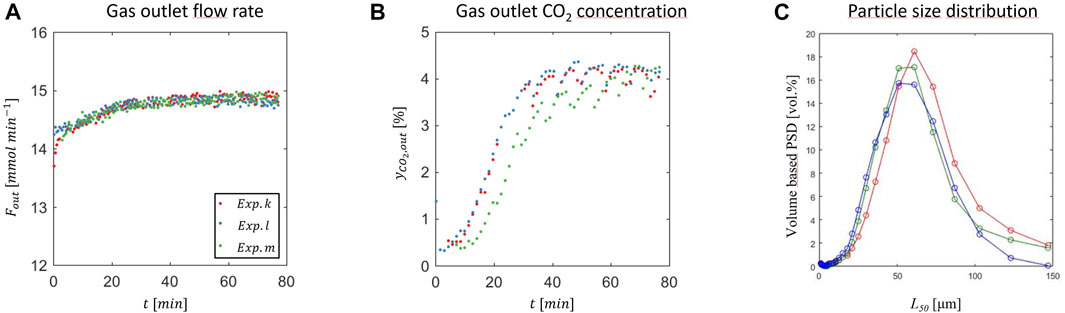
FIGURE 2. Precipitation of CaCO₃ at 25°C, 25% CO₂ in N₂, 1.25 bar, ${\psi }_F$ of 1.08 and a $r_{min}$ of 10.73 mmol/min/l: Three repetitions of (A) the outlet gas mass flow rate, (B) the CO₂ outlet concentration and (C) the particle size distribution of particles exiting the process.

When it absorbs, CO₂ speciates into bicarbonate and carbonate ions, thus generating supersaturation with respect to the formation of calcium carbonate in a solution that contains calcium ions in different forms. The mechanism of formation of PCC is still highly debated, though certainly complex and multi-step in nature, i.e., going through formation of amorphous calcium carbonate first that transforms then into a crystalline form. Which polymorph forms, either vaterite, aragonite or calcite (in increasing order of stability at ambient conditions) also depends on other factors beyond the absorption of CO₂ (Plummer and Busenberg 1982; Declet et al., 2016, Chang et al., 2017a). After precipitation, crystals are collected by filtration, dried in an oven, and characterized. Figure 2C shows the volume based particle size distributions in terms of particle diameter. In this case, most of the particles are in the range from 10 to 120 μm, with an average particle size of 57 μm (standard deviation 2.6 μm). Moreover, the precipitation rate in the presented experiments is 0.26 g per minute with a standard deviation of 0.0005 g per minute. This paper focuses on the steady state behavior of the carbonation reactor—therefore the transient phase will not be shown for any further experiments.

3.2 Dynamic and Steady-State Reproducibility

Experiments k and l correspond to two repetitions of the same experiment; as shown in Figures 2, 3, process parameters, both during the transient and at steady state, and product crystals’s properties, including the fact that they consist of agglomerates of spherical vaterite, are reproducible.

FIGURE 3

FIGURE 3. SEM images of the particles collected from reproducibility experiments are shown.

A third one, namely experiment m, has been carried at identical conditions except for the ammonium nitrate concentration, $c_{N{H}_{4}N{O}_3,in}$, that was decreased from 0.7 molal to 0.6 molal (green data points in Figure 2). The process behaves in a very similar way, as observed again in Figures 2, 3, which can be rationalized by the fact that though the concentration of NH₄NO₃ controls the solubility of Ca(OH)₂, under both these operating conditions the solution is undersaturated with respect to Ca(OH)₂, hence NH₄NO₃ in excess has only a minor effect on the pH of the solution. Experimental results show that this change in $c_{N{H}_{4}N{O}_3,in}$ has a negligible effect on the CO₂ absorption and CaCO₃ precipitation rate as well as on particle size and morphology.

3.3 Effect of the Inlet Operating Conditions

Figure 4 illustrates the effect of changing the features of the two inlet streams on the process outcome, in terms of rate of CO₂ absorbed, i.e., evaluated through the value of the CO₂ outlet concentration in the gas phase leaving the reactor, $y_{C{O}_2,out}$, of amount of calcium carbonate precipitated, $m_{CaC{O}_3}$, and of average particle size, $L_{50}$. The measurements are shown as a function of the liquid feed flow rate, $Q_{in}$, and of the calcium concentration in the liquid feed, in the top and in the bottom row, respectively, for two different gas feed flow rates, $F_{in}$; red and blue symbols refer to 14.8 and to 18.5 mmol min⁻¹, respectively. It is worth noting that increasing either the liquid feed flow rate or its calcium content yields an increase in the provision of calcium to the solution in the reactor, which increases its alkalinity hence its capacity of absorbing CO₂. However, only changing the liquid feed flow rate has an impact also on the residence time in the crystallizer, i.e., the latter decreases when the former increases.

FIGURE 4

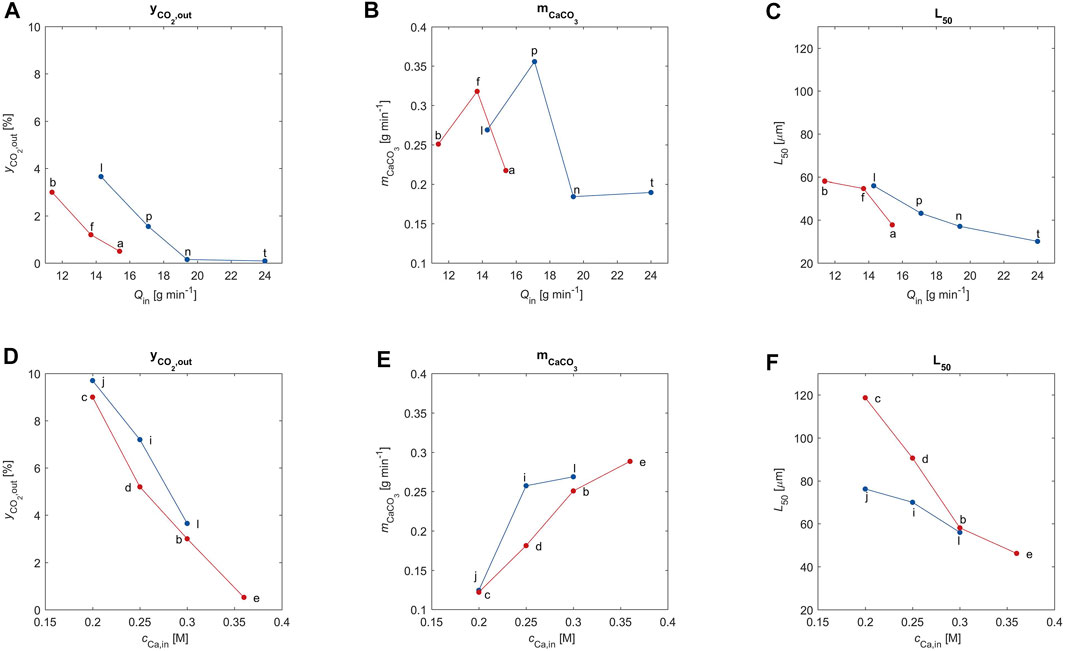
FIGURE 4. The CO₂ outlet concentration, the CaCO₃ outlet flow rate and the volume weighted average particle size are plotted as a function of the liquid feed rate (subplot A–C) and as a function of the calcium feed concentration (subplot D–F). The letters correspond to the experimental ID of the data point according to Table 1.

Figures 4A,D clearly show that indeed the outlet CO₂ concentration decreases to almost zero when the alkalinity of the solution increases; the CO₂, which is missing with respect to that in the feed, has been absorbed (see the column labeled $f_{MT}$ in Table 1) and ends up either in the product solid phase (see the column labelled $r_c$ in Table 1) or in the mother liquor leaving the crystallizer.

When it is due to an increase in calcium concentration in the feed, the increase in alkalinity causes an increase in amount of PCC formed (Figure 4E). However, increasing the liquid feed flow rate, $Q_{in}$, yields a maximum in the amount of PCC formed, which is arguably due to a competition between the positive effect of the increased alkalinity and the negative effect due to the corresponding decrease in residence time. It is also worth noting that increasing either $Q_{in}$ or $c_{Ca,in}$ causes the system to transition from calcium-limited conditions to a CO₂-limited regime, where the increase of alkalinity cannot bring additional benefits.

The average crystal size decreases monotonically with increasing alkalinity, as observed in Figures 4C,F. This is a combined effect of the reduced residence time for increasing values of $Q_{in}$ and of the change in the chemical environment where the precipitation takes place, when changing the composition of the solution by changing the $c_{Ca,in}$ values.

Finally, the effect of the inlet gas flow rate (red: 14.8 mmol min⁻¹; blue: 18.5 mmol min⁻¹) illustrated by the six plots of Figure 4 is less remarkable than that of the properties of the liquid stream, possibly also because all these experiments have been carried out with the same gas composition.

3.4 Effect of the Key Operating Parameters

The effect of the relative quantity ${\psi }_F$ on process efficiency and particle properties is investigated experimentally. Such understanding will allow to design a highly efficient process in terms of CO₂ and calcium to CaCO₃ conversion efficiency and solvent use. Moreover, the effect of these process parameters on the particle size, shape and morphology will be studied.

3.4.1 Role of the Stoichiometric Ratio in the Feed

In the precipitation reactor utilized in this study, the two reactants are fed in the liquid and in the gas phase, while the reaction leading to the precipitation of calcium carbonate takes place only in the solution. Such precipitation depends on the composition in solution, which in turn is affected by how much carbon dioxide is absorbed rather than by how much of it is fed to the reactor.

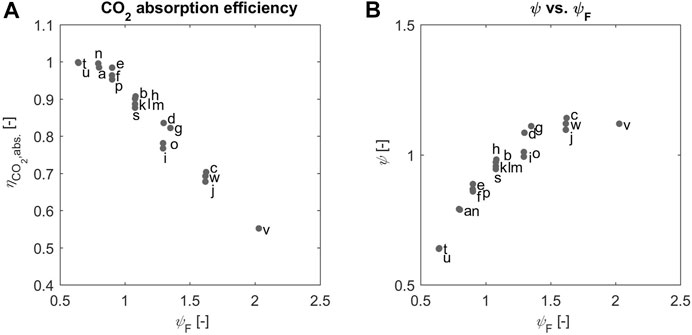
Such important feature of the continuous process studied here is illustrated in Figure 5A, where the CO₂ absorption efficiency, ${\eta }_{C{O}_2,abs.}$, is plotted as a function of the stoichiometric ratio in the feed. It can be readily observed that the CO₂ absorption efficiency is one when there is an excess of calcium in the feed, whereas it decreases steadily, in fact almost linearly, when there is a larger and larger excess of CO₂ in the feed, hence the alkalinity in solution is lower and lower. It is worth noting that all experiments have been carried with 25%v CO₂ in the gas feed, except experiments q and r where the CO₂ mole fraction was 0.85. It is also readily observed that the symbols corresponding to these two experiments are outliers with respect to an ideal trend line.

FIGURE 5

FIGURE 5. (A) The absorption efficiency and (B) the effective ratio of reactants is plotted over ${\psi }_F$.

Such considerations can be translated into the value of the effective stoichiometric ratio in solution, which is calculated from ${\eta }_{C{O}_2}$, and it is plotted in Figure 6B. It increases with ${\psi }_F$ when the latter is smaller than one (excess of calcium), while it flattens out at a value around 1.1 when the latter becomes larger than about 1.2. Such upper bound in effective stoichiometric ratio in solution reflects the fact that the solution capacity to absorb CO₂ is controlled essentially by its calcium concentration, for a given CO₂ mole fraction in the gas. Beyond a certain level of CO₂ excess in the feed, the solution has no capacity to absorb CO₂ any further. Only changing the CO₂ mole fraction in the gas (see exp labelled q) leads to an increase of the CO₂ uptake by the solution hence to a value of the effective stoichiometric ratio beyond 1.1 (about 1.7 in fact).

FIGURE 6

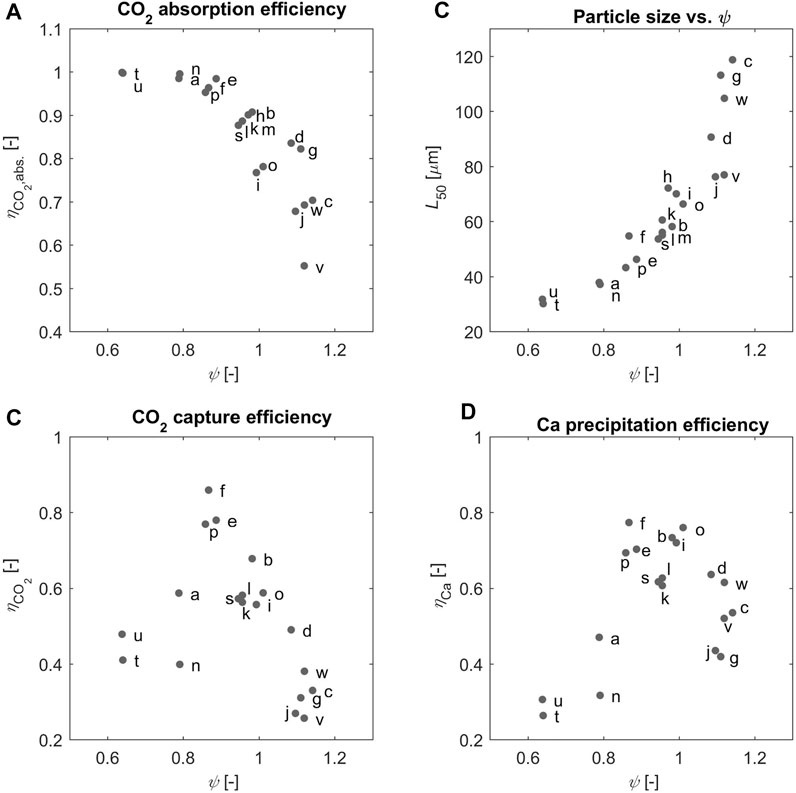
FIGURE 6. (A) The absorption efficiency (B) the $L_{50}$, (C) the CO₂ capture efficiency and (D) the calcium precipitation efficiency is plotted over $\psi$.

We believe that the experimental evidence about the KPIs of the process must be analyzed in light of the value of the effective stoichiometric ratio, which reflects the ratio of the amounts of the reactants that are present at the location of the reaction of interest. Accordingly, we expect that the region where both ${\psi }_F$ and $\psi$ are about one represents the most promising window of operation – since the stoichiometry in solution is equal to the reaction’s stoichiometry, which can result in an efficient use of both the solvent and the CO₂.

3.4.2 Role of the Effective Stoichiometric Ratio in Solution

Using the effective stoichiometric ratio of the reactants in solution, $\psi$, it is possible to conceptualize the trends observed 1) for the different efficiency indices of the process, 2) for the average product particle size and 3) for the product polymorph obtained.

The role of $\psi$ on the efficiency indices of the process, particularly the CO₂ absorption efficiency, ${\eta }_{C{O}_2,abs.}$, the CO₂ capture efficiency, ${\eta }_{C{O}_2}$, and the calcium precipitation efficiency, ${\eta }_{Ca}$, is illustrated in Figures 6A,C,D. First, in Figure 6A, ${\eta }_{C{O}_2,abs.}$ is at 1 for excess-Calcium conditions, where CO₂ fed with the gas is almost entirely absorbed in the calcium-rich solution; it decreases steadily for excess-CO₂ conditions for the same reasons discussed with reference to Figure 5B. Then, one can readily see that CO₂ capture efficiency (Figure 6C) and Calcium precipitation efficiency (Figure 6D) exhibit a similar qualitative trend, with a blunt maximum at $\psi$ approximately equal to 1. To explain this, we make the following remarks. It is not surprising that such indices depend on the conditions within the solution where precipitation occurs. On the one hand, when for $\psi$ >1 CO₂ is in excess, its capture is limited by the lack of a corresponding stoichiometric amount of calcium. On the other hand, when for $\psi$ <1 Calcium is in excess, its precipitation is limited by the lack of a stoichiometric amount of CO₂. Because of Eq. 2-13, which establishes a proportionality relationship between the two KPIs in Figures 6C,D, in the former case also the calcium precipitation efficiency decreases with increasing ${\psi }_F$, and in the latter case also the CO₂ capture efficiency decreases with decreasing ${\psi }_F$ . Moreover, this trend is in line with the observations of Nehrke et. Al., who observed a mixium in the growth rate at solution concentration ratio ([Ca²⁺]/CO₃²⁻]) equal to one (Han et al., 2006; Nehrke et al., 2007; Wolthers et al., 2012). Moreover, Han et. Al. also recognized the effect of $\psi$ on the particle morphology (Han et al., 2006).

Moreover, the average product particle size, $L_{50}$ (Figure 6B), exhibits a striking, rather smooth quasi-exponential evolution with $\psi$. It is worth noting that the measured average particle size reflects not only the size of primary particles, but also that of agglomerates, of which there are many, as one can see in the figure. Moreover, since the points exponentially aligned in Figure 6B correspond to experiments where the many operating parameters have been changed independently, it is not easy to identify the root-cause of such a regular behavior. This is possibly a situation where the model is indeed needed to appreciate the interdependencies among the operating parameters. This is, because the particle size is conventionally affected the interplay of various factors. Feng et. Al. studied the effect of CO₂ flow rate and CO₂ partial pressure, pH , reaction temperature and additives on the particle size. He identified that the particlie size was increasing with CO₂ concentration and decreasing with pH (Feng et al., 2007).

Among which are additives (reference), pH (reference), temperature (reference) CO₂ partial pressure (reference.

Finally, the composition of the solution, and particularly the ratio $\psi$, seem to be controlling which calcium carbonate polymorph forms. Calcium carbonate, CaCO₃, can precipitate as metastable vaterite, as aragonite or as stable calcite. Figure 7 reports the XRD patterns and the SEM images of PCC particles , which have been precipitated in representative experiments, namely experiments t, a, k, d, v and q, at increasing values of $\psi$ .

FIGURE 7

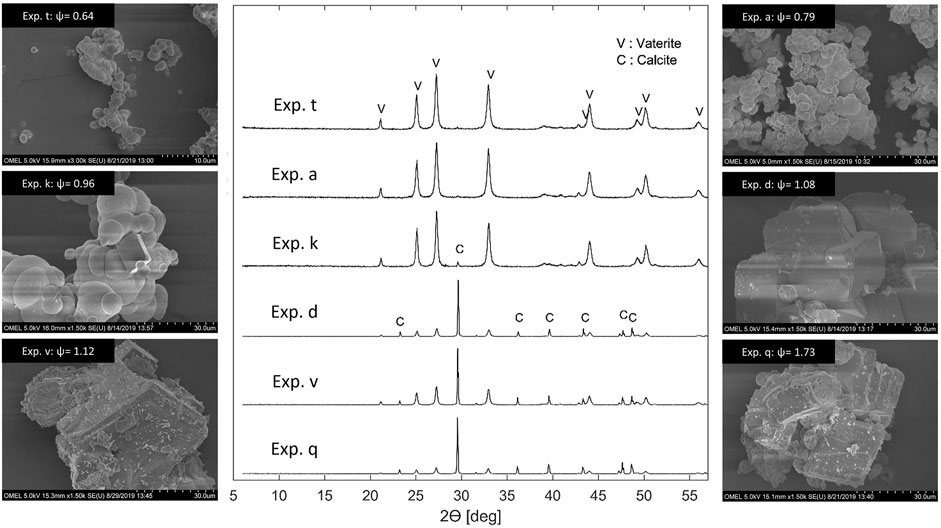
FIGURE 7. Selected XRD patterns and SEM images of precipitation experiments are plotted as a function of $\psi$. The spherical particles correspond to vaterite, while the cubes respresent calcite crystals.

Both XRD patterns and SEM microphotographs give a strong indication that vaterite forms at low $\psi$ values (experiments t, a, and k), at very high purity. On the contrary, at higher $\psi$ values (experiments d, v and q) also calcite forms, so as the final product crystals are a mix of vaterite and calcite, with a latter present in percentages between 37 and 62% (see Table 1). Note, that the composition of the solid phase has been estimated from the XRD patterns, using the method described in the literature (Kontoyannis and Vagenas 2000). It is also worth noting that supersaturation with respect to calcite exhibits a three-fold decrease when going from $\psi$ approximately equal to 0.65 to $\psi$ of about 1.15, whereas the pH of the solution decreases from above 9 to slightly above 8 in the same interval (data not shown here).

Note that a continuous carbonation experiment reported in the literature (Mattila and Zevenhoven 2014b) confirmed the trend illustrated in Figure 7. They operated their continuous precipitation reactor with an aqueous NH₄Cl solvent at an ${\psi }_F$ of 0.4 and 100% CO₂. Vaterite of a very small particle size (10 µm) precipitated from the solution. Moreover, at a pH below 9.5, mainly calcite precipitates while at a pH above 9.5, the predominant polymorph is vaterite (Hostomsky and Jones 1991; Jung et al., 2010). Both evidences are in accordance with the results reported in this paper. Also other reserachers identified, that the solution pH has a strong effect on the particle morphology and particle shape (Han et al., 2005; Ramakrishna et al., 2016). Chang et. Al. obtained at similar temperatures a mixture of calcite and vaterite crystals, while more and more calcite precipitated as the pH was reduced (Chang et al., 2017a).

3.4.3 Role of the CO₂ Partial Pressure

The experiments r and q have been conducted at elevated CO₂ partial pressure. Despite the limited data available, a few observations have been made. First, it is estonishing that at $\psi$ > 1, calcite is the predominant polymorph present – which is in agreement with observations at lower CO₂ partial pressures (see Figure 7). Moreover, the capacity to absorb CO₂ is significantly increased at high ${\psi }_F$. However, a large portion of this CO₂ is exiting the reactor with the mother liquer, without getting transformed to CaCO₃.

4 Concluding Remarks

In this work, we have operated a continuous crystallizer for the precipitation of calcium carbonate obtained via reaction of carbon dioxide, fed through an inlet gas stream and absorbed thereafter by the reacting solution, with calcium hydroxide, fed via an inlet solution. An experimental campaign has been performed, whereby crystallization has been conducted at constant temperature and pressure, but varying gas composition, and – most importantly – gas and liquid feed rate, and composition. The continuous reactive crystallization process has been operated successfully, and its operating conditions could be tuned so as to empirically optimize the key performance parameters of the process.

We have observed that—as expected—the absorption of CO₂ from the inlet gas stream to the solution plays a critical role, because it is the concentration of CO₂ in solution, and not just in the gas, that—together with calcium concentration hence pH—controls the conditions at which precipitation occurs. The key operating parameter here is—at constant inlet gas composition—the effective stoichiometric ratio of reactants in solution. Through the extensive experimental campaign it was possible to demonstrate that high levels of CO₂ capture efficiency and of calcium precipitation efficiency can be obtained. Interestingly such high levels occur at the conditions when the effective stoichiometric ratio in solution is close to one.

It was also possible to show that such ratio also controls the key features characterizing the product crystals. More specifically, on the one hand it was observed that at values of such parameter below 1, calcium carbonate precipitates as high purity vaterite (>97%) , whereas a mix of vaterite and calcite crystals is collected at values above one. The latter one accounts for 13% up to 90% in mass. On the other hand, the final average particle size increases strongly with the effective stoichiometric ratio in solution, though what we could measure was the size of the agglomerates rather than that of the primary particles. These observations are in line with the literature (Jung et al., 2000), though literature data refer generally to rather different processes and contexts.

The experimental measurements reported here represent very encouraging results. These will be followed by a simulation-based study of the same process, which will provide the basis for its model-based optimization aimed at exploring its application potential.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JT was responsible for the content and the writing of the publication. MM was involved in many detailed discussions about the content of the manuscript, reviewing and editing it.

Funding

This research was partially funded by the Swiss Competence Centre for Energy Research—Efficiency Industrial Processes and partially by ETH Zurich.

Conflict of Interest

JT, student in the Separation Processes Laboratory at ETH Zurich and Co-founder, member of the board and shareholder of the ETH-Spinoff neustark, which aims at scaling up and commercializing the presented technology. MM: Professor of the Separation Processes Laboratory at ETH Zurich and member of the advisory board of the ETH-Spinoff Neustark.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to acknowledge Daniel Trottmann for building the experimental setup, Markus Huber for the support with the analytics and Nazgol Razzaghi for a (not published) preliminary experimental study. Moreover, we would like to thank Yago Nel Vila Gracia for his contribution to the experimental campaign.

References

Anantharaman, R., David, B., Giovann, C., Lena, D., Manuele, G., Helmut, H., et al. (2017). CEMCAP Framework for Comparative Techno-Economic Analysis of CO2 Capture from Cement Plants. Energ. Proced. 114, 6175–6180. doi:10.1016/j.egypro.2017.03.1755

CrossRef Full Text | Google Scholar

Chang, R., Choi, D., Kim, M. H., and Park, Y. (2017a). Tuning crystal Polymorphisms and Structural Investigation of Precipitated Calcium Carbonates for CO₂ Mineralization. ACS Sustain. Chem. Eng. 5 (2), 1659–1667. doi:10.1021/acssuschemeng.6b02411

CrossRef Full Text | Google Scholar

Chang, R., Kim, S., Lee, S., Choi, S., Kim, M., and Park, Y. (2017b). Calcium Carbonate Precipitation for CO2 Storage and Utilization: a Review of the Carbonate Crystallization and Polymorphism. Front. Energ. Res. 5, 17. doi:10.3389/fenrg.2017.00017

CrossRef Full Text | Google Scholar

Declet, A., Reyes, E., and Suárez, O. (2016). Calcium Carbonate Precipitation: a Review of the Carbonate Crystallization Process and Applications in Bioinspired Composites. Rev. Adv. Mater. Sci. 44 (1), 87–107.

Google Scholar

Feng, B., Yong, A. K., and An, H. (2007). Effect of Various Factors on the Particle Size of Calcium Carbonate Formed in a Precipitation Process. Mater. Sci. Eng. A 445-446, 170–179. doi:10.1016/j.msea.2006.09.010

CrossRef Full Text | Google Scholar

Gullichsen, J., Paulapuro, H., and Lehtinen, E. (2000). Papermaking Science and Technology, Book 11: Pigment Coating and Surface Sizing of Paper. Jyväskylä: Fapet Oy.

Google Scholar

Han, Y. S., Hadiko, G., Fuji, M., and Takahashi, M. (2005). Effect of Flow Rate and CO2 Content on the Phase and Morphology of CaCO3 Prepared by Bubbling Method. J. Cryst. Growth 276 (3-4), 541–548. doi:10.1016/j.jcrysgro.2004.11.408

CrossRef Full Text | Google Scholar

Han, Y. S., Hadiko, G., Fuji, M., and Takahashi, M. (2006). Factors Affecting the Phase and Morphology of CaCO3 Prepared by a Bubbling Method. J. Eur. Ceram. Soc. 26 (4-5), 843–847. doi:10.1016/j.jeurceramsoc.2005.07.050

CrossRef Full Text | Google Scholar

Hostomsky, J., and Jones, A. G. (1991). Calcium Carbonate Crystallization, Agglomeration and Form during Continuous Precipitation from Solution. J. Phys. D: Appl. Phys. 24 (2), 165–170. doi:10.1088/0022-3727/24/2/012

CrossRef Full Text | Google Scholar

Jimoh, O. A., Ariffin, K. S., Hussin, H. B., and Temitope, A. E. (2018). Synthesis of Precipitated Calcium Carbonate: a Review. Carbonates Evaporites 33 (2), 331–346. doi:10.1007/s13146-017-0341-x

CrossRef Full Text | Google Scholar

Jung, W.-M., Hoon Kang, S., Kim, K.-S., Kim, W.-S., and Kyun Choi, C. (2010). Precipitation of Calcium Carbonate Particles by Gas-Liquid Reaction: Morphology and Size Distribution of Particles in Couette-Taylor and Stirred Tank Reactors. J. Cryst. Growth 312 (22), 3331–3339. doi:10.1016/j.jcrysgro.2010.08.026

CrossRef Full Text | Google Scholar

Jung, W. M., Kang, S. H., Kim, W.-S., and Choi, C. K. (2000). Particle Morphology of Calcium Carbonate Precipitated by Gas-Liquid Reaction in a Couette-Taylor Reactor. Chem. Eng. Sci. 55 (4), 733–747. doi:10.1016/s0009-2509(99)00395-4

CrossRef Full Text | Google Scholar

Kontoyannis, C. G., and Vagenas, N. V. (2000). Calcium Carbonate Phase Analysis Using XRD and FT-Raman Spectroscopy. Analyst 125 (2), 251–255. doi:10.1039/a908609i

CrossRef Full Text | Google Scholar

Mattila, H.-P., Hudd, H., and Zevenhoven, R. (2014). Cradle-to-gate Life Cycle Assessment of Precipitated Calcium Carbonate Production from Steel Converter Slag. J. Clean. Prod. 84, 611–618. doi:10.1016/j.jclepro.2014.05.064

CrossRef Full Text | Google Scholar

Mattila, H.-P., and Zevenhoven, R. (2014b). Design of a Continuous Process Setup for Precipitated Calcium Carbonate Production from Steel Converter Slag. ChemSusChem 7 (3), 903–913. doi:10.1002/cssc.201300516

PubMed Abstract | CrossRef Full Text | Google Scholar

Mattila, H.-P., and Zevenhoven, R. (2014a). “Production of Precipitated Calcium Carbonate from Steel Converter Slag and Other Calcium-Containing Industrial Wastes and Residues,” in Advances in Inorganic Chemistry (Turku, Finland: Elsevier), 66, 347–384. doi:10.1016/b978-0-12-420221-4.00010-x

CrossRef Full Text | Google Scholar

Nehrke, G., Reichart, G. J., Van Cappellen, P., Meile, C., and Bijma, J. (2007). Dependence of Calcite Growth Rate and Sr Partitioning on Solution Stoichiometry: Non-kossel crystal Growth. Geochimica et Cosmochimica Acta 71 (9), 2240–2249. doi:10.1016/j.gca.2007.02.002

CrossRef Full Text | Google Scholar

Plummer, L. N., and Busenberg, E. (1982). The Solubilities of Calcite, Aragonite and Vaterite in CO₂-H₂O Solutions between 0 and 90°C, and an Evaluation of the Aqueous Model for the System CaCO₃-CO₂-H₂O. Geochimica et cosmochimica acta 46 (6), 1011–1040. doi:10.1016/0016-7037(82)90056-4

CrossRef Full Text | Google Scholar

Ramakrishna, C., Thenepalli, T., Huh, J.-H., and Ahn, J. W. (2016). Precipitated Calcium Carbonate Synthesis by Simultaneous Injection to Produce Nano Whisker Aragonite. J. Korean Ceram. Soc. 53 (2), 222–226. doi:10.4191/kcers.2016.53.2.222

CrossRef Full Text | Google Scholar

Sanna, A., Uibu, M., Caramanna, G., Kuusik, R., and Maroto-Valer, M. M. (2014). A Review of mineral Carbonation Technologies to Sequester CO₂. Chem. Soc. Rev. 43 (23), 8049–8080. doi:10.1039/c4cs00035h

PubMed Abstract | CrossRef Full Text | Google Scholar

Verdoes, D., Kashchiev, D., and Van Rosmalen, G. (1992). Determination of Nucleation and Growth Rates from Induction Times in Seeded and Unseeded Precipitation of Calcium Carbonate. J. Cryst. Growth 118 (3-4), 401–413. doi:10.1016/0022-0248(92)90089-2

CrossRef Full Text | Google Scholar

Wolthers, M., Nehrke, G., Gustafsson, J. P., and Van Cappellen, P. (2012). Calcite Growth Kinetics: Modeling the Effect of Solution Stoichiometry. Geochimica et Cosmochimica Acta 77, 121–134. doi:10.1016/j.gca.2011.11.003

CrossRef Full Text | Google Scholar

Glossary

$c_{i,in}$ Apparent concentration of aqueous solute i entering the reactor (mol/kg H₂O)

$c_i$ Apparent concentration of aqueous solute i in the reactor (mol/kg H₂O)

$F_{in}$ Molar flow rate of the gas entering the reactor (mol/s)

$F_{out}$ Molar flow rate of the gas exiting the reactor (mol/s)

$f_{MT}$ CO₂ absorption rate (mol/m³/s)

$\psi$ Effective ratio of reactants in the liquid phase (-)

${\psi }_F$ Molar feed stoichiometric ratio (-)

$m_{CaC{O}_3}$ CaCO₃ outlet flow rate (g CaCO₃/s)

$M_{CaC{O}_3}$ Molar mass of CaCO₃ (kg/mol)

P Total pressure (bar)

$p_{C{O}_2,in}$ Partial pressure of CO₂ in the gas inlet (bar)

$Q_{in}$ Flow rate of aqueous solution (kg H₂O/s)

$r_C$ Precipitation rate (mol/m³/s)

T Temperature of aqueous solution (°C)

t Time (min)

$V_s$ Volume of the liquid phase (m³)

$y_{i,in}$ Mole fraction of component i in the gas entering the reactor (-)

$y_{i,out}$ Mole fraction of component i in the gas exiting the reactor (-)

${\eta }_{Ca}$ Precipitation efficiency of Ca (-)

${\eta }_{C{O}_2}$ CO₂ mineralization efficiency (-)

${\eta }_{C{O}_2, abs.}$ Absorption efficiency of CO₂ (-)

${\eta }_{C{O}_2, prec.}$ Precipitation efficiency of carbon (-)

${\rho }_s$ Density of the solution (kg/L)

τ Residence time of the aqueous solution (min)