- Department of Chemical Engineering and Materials Science, Wayne State University, Detroit, MI, United States
The controllers for a cyber-physical system may be impacted by sensor measurement cyberattacks, actuator signal cyberattacks, or both types of attacks. Prior work in our group has developed a theory for handling cyberattacks on process sensors. However, sensor and actuator cyberattacks have a different character from one another. Specifically, sensor measurement attacks prevent proper inputs from being applied to the process by manipulating the measurements that the controller receives, so that the control law plays a role in the impact of a given sensor measurement cyberattack on a process. In contrast, actuator signal attacks prevent proper inputs from being applied to a process by bypassing the control law to cause the actuators to apply undesirable control actions. Despite these differences, this manuscript shows that we can extend and combine strategies for handling sensor cyberattacks from our prior work to handle attacks on actuators and to handle cases where sensor and actuator attacks occur at the same time. These strategies for cyberattack-handling and detection are based on the Lyapunov-based economic model predictive control (LEMPC) and nonlinear systems theory. We first review our prior work on sensor measurement cyberattacks, providing several new insights regarding the methods. We then discuss how those methods can be extended to handle attacks on actuator signals and then how the strategies for handling sensor and actuator attacks individually can be combined to produce a strategy that is able to guarantee safety when attacks are not detected, even if both types of attacks are occurring at once. We also demonstrate that the other combinations of the sensor and actuator attack-handling strategies cannot achieve this same effect. Subsequently, we provide a mathematical characterization of the “discoverability” of cyberattacks that enables us to consider the various strategies for cyberattack detection presented in a more general context. We conclude by presenting a reactor example that showcases the aspects of designing LEMPC.
1 Introduction
Cyber-physical systems (CPSs) integrate various physical processes with computer and communication infrastructures, which allows enhanced process monitoring and control. Although CPSs open new avenues for advanced manufacturing (Davis et al., 2015) in terms of increased production efficiency, the quality of the production, and cost reduction, this integration also opens these systems to malicious cyberattacks that can exploit vulnerable communication channels between the different layers of the system. In addition to process and network cybersecurity concerns, data collection devices such as sensors and final control elements such as actuators (and signals to or from them) are also potential candidates that can be subject to cyberattacks (Tuptuk and Hailes, 2018). Sophisticated and malicious cyberattacks may affect industrial profits and even pose a threat to the safety of individuals working on site, which motivates attack-handling strategies that are geared toward providing safety assurances for autonomous systems.
There exist multiple points of susceptibility in a CPS framework ranging from communication networks and protocols to sensor measurement and control signal transmission, requiring the development of appropriate control and detection techniques to tackle such cybersecurity challenges (Pasqualetti et al., 2013). To better understand these concerns, vulnerability identification (Ani et al., 2017) has been studied by combining people, process, and technology perspectives. A process engineering-oriented overview of different attack events has been discussed in Setola et al. (2019) to illustrate the impacts on industrial control system platforms. In order to address concerns related to control components, resilient control designs based on state estimates have been proposed for detecting and preventing attacks in works such as Ding et al. (2020) and Cárdenas et al. (2011), wherein the latter cyberattack-resilient control frameworks compare state estimates based on models of the physical process and state measurements to detect cyberattacks. Ye and Luo (2019) address a scenario where actuator faults and cyberattacks on sensors or actuators occur simultaneously by using a control policy based on the Lyapunov theory and adaptation and Nussbaum-type functions.
Cybersecurity-related studies have also been carried out in the context of model-predictive control (MPC; Qin and Badgwell, 2003), an optimization-based control methodology that computes optimal control actions to a process. Specifically, for nonlinear systems, Durand (2018) investigated various MPC techniques with economics-based objective functions [known as economic model predictive controllers (EMPCs) (Ellis et al., 2014a; Rawlings et al., 2012)] when only false sensor measurements are considered. Chen et al. (2020) integrated a neural network-based attack detection approach initially proposed in Wu et al. (2018) with a two-fold control structure, in which the upper layer is a Lyapunov-based MPC designed to ensure closed-loop stability after attacks are flagged. A methodology that may be incorporated as a criterion for EMPC design has been proposed in Narasimhan et al. (2021), in which a control parameter screening based on a residual-based attack detection scheme classifies multiplicative sensor-controller attacks on a process as “detectable,” “undetectable,” and “potentially detectable” under certain conditions. In addition, a general description of “cyberattack discoverability” (i.e., a certain system’s capability to detect attacks) without a rigorous mathematical formalism has been addressed in Oyama et al. (2021).
Prior work in our group has explored the interaction between cyberattack detection strategies, MPC/EMPC design, and stability guarantees. In particular, our prior works have primarily focused on studying and developing control/detection mechanisms for scenarios in which either actuators or sensors are attacked (Oyama and Durand, 2020; Rangan et al., 2021; Oyama et al., 2021; Durand and Wegener, 2020). For example, Oyama and Durand (2020) proposed three cyberattack detection concepts that are integrated with the control framework Lyapunov-based EMPC (Heidarinejad et al., 2012a). Advancing this work, Rangan et al. (2021) and Oyama et al. (2021) proposed ways to consider cyberattack detection strategies and the challenges in cyberattack-handling for nonlinear processes whose dynamics change with time. In the present manuscript, we extend our prior work (which covered sensor measurement cyberattack-handling with control-theoretic guarantees and actuator cyberattack-handling without guarantees) to develop strategies for maintaining safety when actuator attacks are not detected (assuming that no attack occurs on the sensors). These strategies are inspired by the first detection concept in Oyama and Durand (2020) but with a modified implementation strategy to guarantee that even when an undetected actuator attack occurs, the state measurement and actual closed-loop state are maintained inside a safe region of operation throughout the next sampling period.
The primary challenge addressed by this work is the question of how to develop an LEMPC-based strategy for handling sensor and actuator cyberattacks occurring at once. The reason that this is a challenge is that some of the concepts discussed for handling sensor and actuator cyberattacks only work if the other (sensors or actuators) is not under an attack. A major contribution of the present manuscript, therefore, is elucidating which sensor and actuator attack-handling methods can be combined to provide safety in the presence of undetected attacks, even if both undetected sensor and actuator attacks are occurring at the same time. To cast this discussion in a broader framework, we also present a nonlinear systems definition of cyberattack “discoverability,” which provides fundamental insights into how attacks can fly under the radar of detection policies. Finally, we elucidate the properties of cyberattack-handling using LEMPC through simulation studies.
The manuscript is organized as follows: following some preliminaries that clarify the class of systems under consideration and the control design (LEMPC) from which the cyberattack detection and handling concepts presented in this work are derived, we review the sensor measurement cyberattack detection and handling policies from Oyama and Durand (2020), which form the basis for the development of the actuator signal cyberattack-handling and combined sensor/actuator cyberattack-handling policies subsequently developed. Subsequently, we propose strategies for detecting and handling cyberattacks on process actuators when the sensor measurements remain intact that are able to maintain safety even when actuator cyberattacks are undetected. We then utilize the insights and developments of the prior sections to clarify which sensor and actuator attack-handling policies can be combined to achieve safety in the presence of combined sensor and actuator cyberattacks. We demonstrate that there are combinations of methods that can guarantee safety in the presence of undetected attacks, even if these attacks occur on both sensors and actuators at the same time (though the other combinations of the discussed methods cannot achieve this). Further insights on the interactions between the detection strategies and control policies for nonlinear systems are presented via a fundamental nonlinear systems definition of discoverability. The work is concluded with a reactor study that probes the question of the practicality of the design of control systems that meet the theoretical guarantees for achieving cyberattack-resilience.
2 Preliminaries
2.1 Notation
The Euclidean norm of a vector is indicated by |⋅|, and the transpose of a vector x is denoted by xT. A continuous function α: [0, a) → [0, ∞) is said to be of class
2.2 Class of Systems
This work considers the following class of nonlinear systems:
where x ∈ X ⊂ Rn and w ∈ W ⊂ Rz (W≔{w ∈ Rz | |w| ≤ θw, θw > 0}) are the state and disturbance vectors, respectively. The input vector function u ∈ U ⊂ Rm, where U≔{u ∈ Rm| |u| ≤ umax}. f is locally Lipschitz on X × U × W, and we consider that the “nominal” system of Eq. 1 (w ≡ 0) is stabilizable such that there exist an asymptotically stabilizing feedback control law h(x), a sufficiently smooth Lyapunov function V, and class
∀ x ∈ D ⊂ Rn (D is an open neighborhood of the origin). We define Ωρ ⊂ D to be the stability region of the nominal closed-loop system under the controller h(x) and require that it be chosen such that x ∈ X, ∀x ∈ Ωρ. Furthermore, we consider that h(x) satisfies the following equation:
for all
Since f is locally Lipschitz and V(x) is a sufficiently smooth function, the following holds:
∀x1, x2 ∈ Ωρ, u, u1, u2 ∈ U and w ∈ W, where
We also assume that there are M sets of measurements
where ki is a vector-valued function, and vi represents the measurement noise associated with the measurements yi. We assume that the measurement noise is bounded (i.e.,
where zi is the estimate of the process state from the i-th observer, i = 1, … , M, Fi is a vector-valued function, and ϵi > 0. When a controller h(zi) with Eq. 7 is used to control the closed-loop system of Eq. 1, we consider that Assumption 1 and Assumption 2 below hold.
Assumption 1. Ellis et al. (2014b), Lao et al. (2015) There exist positive constants
Assumption 2. Ellis et al. (2014b), Lao et al. (2015) There exists
3 Economic Model Predictive Control
EMPC Ellis et al. (2014a) is an optimization-based control design for which the control actions are computed via the following optimization problem:
where N is called the prediction horizon, and u(t) is a piecewise-constant input trajectory with N pieces, where each piece is held constant for a sampling period with time length Δ. The economics-based stage cost Le of Eq. 8a is evaluated throughout the prediction horizon using the future predictions of the process state
Additional constraints that can be added to the formulation in Eq. 8 to produce a formulation of EMPC that takes advantage of the Lyapunov-based controller h(⋅), called Lyapunov-based EMPC [LEMPC Heidarinejad et al. (2012a)], are as follows:
where
4 Cyberattack Detection and Control Strategies Using LEMPC Under Single Attack-Type Scenarios: Sensor Attacks
The major goal of this work is to extend the strategies for LEMPC-based sensor measurement cyberattack detection and handling from Oyama and Durand (2020) to handle actuator attacks and simultaneous sensor measurement and actuator attacks. For the clarity of this discussion, we first review the three cyberattack detection mechanisms from Oyama and Durand (2020).
This section therefore considers a single attack-type scenario (i.e., only the sensor readings are impacted by attacks). The first control/detection strategy proposed in Oyama and Durand (2020) switches between a full-state feedback LEMPC and variations on that control design that are randomly generated over time to probe for cyberattacks by evaluating state trajectories for which it is theoretically known that a Lyapunov function must decrease between subsequent sampling times. The second control/detection strategy also uses full-state feedback LEMPC, but the detection is achieved by evaluating the state predictions based on the current and prior state measurements to flag an attack while maintaining the closed-loop state within a predefined safe region over one sampling period after an undetected attack is applied. The third control/detection strategy was developed using output feedback LEMPC, and the detection is attained by checking among multiple redundant state estimates to flag that an attack is happening when the state estimates do not agree while still ensuring closed-loop stability under sufficient conditions (which include the assumption that at least one of the estimators cannot be affected by the attack). In addition to reviewing the key features of this design, this section will provide several clarifications that were not provided in Oyama and Durand (2020) to enable us to build upon these methods in future sections.
4.1 Control/Detection Strategy 1-S Using LEMPC in the Presence of Sensor Attacks
The control/detection strategy 1-S, which corresponds to the first detection concept proposed in Oyama and Durand (2020), uses full-state feedback LEMPC as the baseline controller and randomly develops other LEMPC formulations with Eq. 9b always activated that are used in place of the baseline controller for short periods of time to potentially detect if an attack is occurring. We define specific times at which the switching between the baseline 1-LEMPC and the j-th LEMPC, j > 1, happens. Particularly, ts,j is defined as the switching time at which the j-LEMPC is used to drive the closed-loop state to the randomly generated j-th steady-state, and te,j is the time at which the j-LEMPC switches back to operation under the 1-LEMPC.
The baseline 1-LEMPC is formulated as follows, which is used if te,j−1 ≤ t < ts,j, j = 2, … , where te,1 = 0:
where x1(tk) is used, with a slight abuse of the notation, to reflect the state measurement in a deviation variable form from the operating steady state. In addition, in the remainder of this work, fi (i ≥ 1) represents the right-hand side of Eq. 1 when it is written in a deviation variable form from the i-th steady state. ui represents the input vector in a deviation variable form from the steady-state input associated with the i-th steady state. Xi and Ui correspond to the state and input constraint sets in a deviation variable form from the i-th steady state. In addition, ρi and
The j-th LEMPC, j > 1, which is used for t ∈ [ts,j, te,j), is formulated as follows:
where xj(tk) represents the state measurement in a deviation variable form from the j-th steady state.
The implementation strategy for this detection method is as follows (the stability region subsets are thoroughly detailed in Oyama and Durand (2020) but reviewed in Remark 1):
1) At a sampling time tk, the baseline 1-LEMPC receives the state measurement
2) At tk, a random number ζ is generated. If this number falls within a range that has been selected to start probing for cyberattacks, randomly generate a j-th steady state, j > 1, with a stability region
3) If
a) Compute control signals for the subsequent sampling period with Eq. 10f of the 1-LEMPC activated. Go to Step 6.
b) Compute control signals for the subsequent sampling period with Eq. 10g of the 1-LEMPC activated. Go to Step 6.
4) The j-LEMPC receives the state measurement
5) At te,j, switch back to operation under the baseline 1-LEMPC. Go to Step 6.
6) Go to Step 1 (k ← k + 1).
The first theorem presented in Oyama and Durand (2020) and replicated below guarantees the closed-loop stability of the process of Eq. 1 under the LEMPCs of Eqs 10–11 under the implementation strategy described above in the absence of sensor cyberattacks. To follow this and the other theorems that will be presented in this work, the impacts of bounded measurement noise and disturbances on the process state trajectory are characterized in Proposition 1 below, and the bound on the value of the Lyapunov function at different points in the stability region is defined in Proposition 2.
Proposition 1. Ellis et al. (2014b), Lao et al. (2015) Consider the systems below:
where
for all
Proposition 2. Ellis et al. (2014b) Let
where
Theorem 1. Oyama and Durand (2020) Consider the closed-loop system of Eq. 1 under the implementation strategy described above and in the absence of a false sensor measurement cyberattack where each controller
If
This expression indicates that
when the input is computed by the j-LEMPC (where θv,1 represents the measurement noise when the full-state feedback is available), then the state measurement must also be decreased by the end of the sampling period. However, at any given time instant, it is not guaranteed to be decreasing due to the noise. An unusual amount of increase could help to flag the attack before a sampling period is over, although this would come from recognizing atypical behavior (essentially pattern recognition).The reasoning behind the selection of the presented bound on
Remark 1. The following relation between the different stability regions has been characterized for Detection Strategy 1-S:
4.2 Control/Detection Strategy 2-S Using LEMPC in the Presence of Sensor Attacks
The control/detection strategy 2-S, which corresponds to the second detection concept in Oyama and Durand (2020), has been developed using only the 1-LEMPC of Eq. 10, and it flags false sensor measurements based on state predictions from the process model from the last state measurement. If the norm of the difference between the state predictions and the current measurements is above a threshold, the measurement is identified as a potential sensor attack. Otherwise, if the norm is below this threshold, even if the measurement was falsified, the closed-loop state can be maintained inside
1) At sampling time tk, if
a) Mitigating actions may be applied (e.g., a backup policy such as the use of redundant controller or an emergency shut-down mode).
b) Operate the process under the 1-LEMPC of Eq. 10 while implementing an auxiliary detection mechanism to attempt to flag any undetected attack at tk. tk ← tk+1. Go to Step 1.
The second theorem presented in Oyama and Durand (2020), which is replicated below, guarantees the closed-loop stability of the process of Eq. 1 under the 1-LEMPC of Eq. 10 under the implementation strategy described above before a sensor attack occurs and for at least one sampling period after the attack.
Theorem 2. Oyama and Durand (2020) Consider the system of Eq. 1 in closed loop under the implementation strategy described in Section 4.2 based on a controller
If an attack is not flagged at tk,
We note that Eqs 28, 29 assume that there is no attack or an undetected attack at tk−1, respectively, so that
Then, if an attack is not flagged at tk+1, following a procedure similar to that in Eq. 29 gives
It is reasonable to expect that ν would be set greater than θv,1 since it is reasonable to expect that
4.3 Control/Detection Strategy 3-S Using LEMPC in the Presence of Sensor Attacks
The Detection Strategy 3-S, which corresponds to the third detection concept proposed in Oyama and Durand (2020), utilizes multiple redundant state estimators (where we assume that not all of them are impacted by the false sensor measurements) integrated with an output feedback LEMPC and ensures that the closed-loop state is maintained in a safe region of operation for all the times that no attacks are detected. The output feedback LEMPC designed for this detection strategy receives a state estimate z1 from one of the redundant state estimators (the estimator used to provide state estimates to the LEMPC will be denoted as the i = 1 estimator) at tk, where the notation follows that of Eq. 10 with Eq. 10c replaced by
This implementation strategy assumes that the process has already been run successfully in the absence of attacks under the output feedback LEMPC of Eq. 8 for some time such that
1) At sampling time tk, if |zi(tk)−zj(tk)| > ϵmax, i = 1, … , M, j = 1, … , M, or z1(tk) ∉ Ωρ (where z1 is the state estimate used in the LEMPC design), flag that a cyberattack is occurring and go to Step 1a. Else, go to Step 1b.
a) Mitigating actions may be applied (e.g., a backup policy such as the use of redundant controller or an emergency shut-down mode).
b) Operate using the output feedback LEMPC of Eq. 10. tk ← tk+1. Go to Step 1.
Detection Strategy 3-S guarantees that any cyberattacks that would drive the closed-loop state out of
for all i ≠ j, i = 1, … , M, j = 1, … , M, as long as t ≥ tq = max{tb1, … , tbM}. Therefore, abnormal behavior can be detected if
The worst-case difference between the state estimate used by the output feedback LEMPC of Eq. 10 and the actual value of the process state under the implementation strategy above when an attack is not flagged is described in Proposition 3.
Proposition 3. Oyama and Durand (2020) Consider the system of Eq. 1 under the implementation strategy of Section 4.3 where
The third theorem presented in Oyama and Durand (2020), which is replicated below, guarantees the closed-loop stability of the process of Eq. 1 under the LEMPC of Eq. 10 under the implementation strategy described above when a sensor cyberattack is not flagged.
Theorem 3. Consider the system of Eq. 1 in a closed loop under the output feedback LEMPC of Eq. 10 based on an observer and controller pair satisfying Assumption 1 and Assumption 2 and formulated with respect to the i = 1 measurement vector, and formulated with respect to a controller
where
Remark 2. The role of
Remark 3. Assumption 1 and Assumption 2 are essentially used in Detection Strategy 3-S to imply the existence of observers with convergence time periods that are independent of the control actions applied (i.e., they converge, and stay converged, regardless of the actual control actions applied). High-gain observers are an example of an observer that can meet this assumption (Ahrens and Khalil 2009) for bounded x, u, and w. This is critical to the ability of the multiple observers to remain converged when the process is being controlled by an LEMPC receiving inputs based on the state feedback of only one of them, so that the others are evolving independently of the inputs to the closed-loop system.
Remark 4. We only guarantee in Theorem 3 that
Remark 5. Larger values of
Remark 6. The methods for attack detection (Strategies 1-S, 2-S, and 3-S) do not distinguish between sensor faults and cyberattacks. Therefore, they could flag faults as attacks (and therefore, it may be more appropriate to use them as anomaly detection with a subsequent diagnosis step). The benefit, however, is that they provide resilience against attacks if the issue is an attack (which can be designed to be malicious) and not a fault (which may be less likely to occur in a state that an attacker might find particularly attractive). They also flag issues that do not satisfy theoretical safety guarantees, which may make it beneficial to flag the issues regardless of the cause.
5 Cyberattack Detection and Control Strategies Using LEMPC Under Single Attack-Type Scenarios: Actuator Attacks
The methods described above from Oyama and Durand (2020) were developed for handling cyberattacks on process sensor measurements. In such a case, the actuators receive the signals that the controller calculated, but the signal that the controller calculated is not appropriate for the actual process state. This requires the methods to, in a sense, rely on the control actions to show that the sensor measurements are not correct. In contrast, when an attack occurs on the actuator signal, the controller no longer plays a role in which signal the actuators receive. This means that the sensor measurements must be used to show that the control actions are not correct. This difference raises the question of whether the three detection strategies of the prior section can handle actuator attacks or not. This section therefore seeks to address the question of whether it is trivial to utilize the sensor attack-handling techniques from Oyama and Durand (2020) for handling actuator attacks, or if there are further considerations.
We begin by considering the direct extension of all three methods, in which Detection Strategies 1-S, 2-S, and 3-S are utilized in a case where the sensor measurements are intact but the actuators are attacked. In this work, actuator output attacks will be considered to happen when 1) the code in the controller has been attacked and reformulated so that it no longer computes the control action according to an established control law; 2) the control action computed by a controller is replaced by a rogue control signal; or 3) a control action is received by the actuator but subsequently modified at the actuator itself.
When Detection Strategy 1-S is utilized but the actuators are attacked, then at random times, it is intended to utilize the j-LEMPC (however, because of the attack, the control actions from the j-LEMPC are not applied). For an actuator attacker to fly under the radar of the detection strategy, the attacker would need to force a net decrease in Vj along the measured state trajectory between the beginning and end of a sampling period and would need to ensure that the closed-loop state measurement does not leave
An improved version of Detection Strategy 1-S when there are actuator cyberattacks would only probe constantly for attacks (i.e., the implementation strategy would be the same as that in Section 4.1, except that the probing occurs at every sampling time, instead of at random sampling times; this implementation strategy assumes that the regions meeting the requirements in Step 2 in Section 4.1 can be found at every sampling time, although reviewing when this is possible in detail can be a subject of future work). In this case, since at every sampling time, the attacker would be constrained to choose inputs that cannot cause the state measurement to leave
To further explore how the sensor attack-handling strategies from Oyama and Durand (2020) extend to actuator cyberattack handling, we next consider the use of Detection Strategy 2-S for actuator attacks. This detection strategy is based on state predictions. These predictions must be computed under some inputs, so it is first necessary to consider which inputs these are for the actuator attack extension. Several options for inputs that could be used in making the state predictions include an input computed by a redundant control system, an approximation of the expected control output (potentially obtained via fitting the data between state measurements and (non-attacked) controller outputs to a data-driven model), or a signal from the actuator if it is reflective of what was actually implemented. If an actuator signal reflective of the control action that was actually implemented is received and a redundant control system is available, these can be used to cross-check whether the actuator output is correct. This would rapidly catch an attack if the signals are not the same. However, if there is no fully redundant controller (e.g., if actuator signals are available but only an approximation of the expected control output is also available) or if there is a concern that the actuator signals may be spoofed (and there is either a redundant control system or an approximation of the expected control output also available), then state measurements can be used (in the spirit of Detection Strategy 2-S as described in Section 4.2) to attempt to handle attacks.
The motivation for considering this latter case in which state measurements and predictions are used to check whether an actuator attack is occurring is as follows: the difference between the redundant control system output or approximation of the control system output and the control output of the LEMPC that is expected to be used to control the process can be checked a priori, before the controller is put online. This will result in a known upper bound ϵu between control actions that might be computed by the LEMPC and those of the redundant or approximate controller (for the redundant controller, ϵu = 0) for a given state measurement. If the state measurements are intact, then the state measurements and predictions under the redundant or approximate controller can be compared to assess the accuracy of the input that was actually applied. The redundant or approximate controller can be used to estimate the input that should be applied to the process, and state predictions can be made using the nominal model of Eq. 1 to check whether the input that was actually applied to the system seems to be sufficiently similar to the input that was expected (in the sense that it causes the control action that was actually applied to maintain the state measurement in an expected operating region), as it would have under the control action in the absence of an actuator attack, and keeps the norm of the difference between the state prediction and measurement below a bound. Even if ϵu = 0, process disturbances and measurement noise could cause the state prediction at the end of a sampling period over which a control action is applied to not fully match the measurement; however, if the error between the prediction and measurement is larger than a bound νu that should hold under normal operation considering the noise, value of ϵu, and plant/model mismatch, this signifies that there is another source of error in the state predictions beyond what was anticipated, which can be expected to come from the input applied to the process deviating more significantly from what it should have been than was expected (i.e., an actuator attack is flagged). Because the state measurements are correct, the state predictions are always initiated from a reasonably accurate approximation of the closed-loop state; therefore, with sufficient conservatism in the design of
So far, the extended versions of Detection Strategy 1-S and of 2-S to the actuator-handling case have been more powerful against actuator attacks than Detection Strategies 1-S and 2-S have been against sensor attacks. In contrast, attempting to utilize Detection Strategy 3-S, which enabled safety to be maintained for all times if a sensor measurement attack was undetected (and at least one redundant estimator was not), may result in a strategy that appears to be weaker in the face of actuator attacks. One of the assumptions of Detection Strategy 3-S in Section 4.3 is that an observer exists that satisfies the conditions in Assumption 1 and Assumption 2. High-gain observers can meet this assumption, and under sufficient conditions, they meet this assumption regardless of the actual value of the input (which was important for achieving the results in Theorem 3 as noted in Remark 3). However, this means that in the case that only the inputs are awry, the state estimates would still be intact because of the convergence assumption, such that they will not deviate from one another in the desired way and Detection Strategy 3-S could not be used as an effective detection strategy for actuator attacks with such estimators. Although a further investigation of whether other types of observer designs or assumptions could be more effective in designing an actuator attack-handling strategy based on Detection Strategy 3-S (to be referred to as Detection Strategy 3-A) could be pursued, these insights again indicate that there are fundamental differences between utilizing the detection strategies for actuator attack-handling compared to sensor attack-handling. The discussion throughout this section therefore seems to suggest that the integrated control and detection frameworks presented above have structures that make them more or less relevant to certain types of attacks and that also affect the extent to which they move toward flexible and lean frameworks with minimal redundancy for cyberattack detection, compared to relying on redundant systems. For example, Detection Strategy 3-S relies on redundant state estimators for detecting sensor attacks, but Detection Strategy 2-A relies on having a redundant controller for detecting actuator attacks. It is interesting in light of this that Detection Strategies 1-A and 1-S do not require redundant control laws but do require many different steady-states to be selected over time. We can also note that the strength of Detection Strategies 1-A and 2-A against actuator attacks above comes partially from the ability of the combined detection and control policies in those cases to set expectations for what the sensor signals should look like that, if not violated, indicate safe operation, and if violated, can flag an attack before safe operation is compromised. As will be discussed later, this has relevance to the notions of cyberattack discoverability in that to cause attacks to be discoverable, integrated detection and control need to be performed such that the control theory can set the expectations for detection to be different if there is an attack or impending safety issue from an attack compared to if not, to force attacks to show themselves. A part of the power of a theory-based control law like Detection Strategy 1-A or 2-A against actuator attacks is the ability to perform that expectation setting.
6 Motivation for Detection Strategies for Actuator and Sensor Attacks
The above sections addressed how LEMPC might be used for handling sensor attacks or actuator attacks individually. In this section, we utilize a process example to motivate further work on exploring how LEMPC might be used to handle both sensor and actuator attacks. Specifically, consider the nonlinear process model below, which consists of a continuous stirred tank reactor (CSTR) with a second-order, exothermic, irreversible reaction of the form A→B with the following dynamics:
where the states are the reactant concentration of species A (CA) and temperature in the reactor (T). The manipulated input is CA0 (the reactant feed concentration of species A). The values of the parameters of the CSTR model (F, V, k0, E, Rg, T0, ρL, ΔH, and Cp) are taken from (Heidarinejad et al., 2012b). The vectors of deviation variables for the states and input from their operating steady-state values,
The Lyapunov-based stability constraints in Eqs 9a, 9b were designed using a quadratic Lyapunov function V1 = xTPx, where P = [110.11 0; 0 0.12]. The Lyapunov-based controller utilized was a proportional controller of the form
We first seek to gain insight into the differences between single attack-type cases and simultaneous sensor and actuator attacks. To gain these insights, we will use the strategies inspired by the detection strategies discussed above, but not meeting the theoretical conditions, so that these are not guaranteed to have resilience against any types of attacks (some discussion of moving toward getting theoretical parameters for LEMPC, which elucidates that obtaining the parameters that guarantee cyberattack-resilience for LEMPC formulations in practice should be a subject of future work, will be provided later in this work). Despite the fact that there are no guarantees that any of the strategies used in this example that attempt to detect attacks will do so with the parameters selected, this example still provides a number of fundamental insights into the different characteristics of single attack types compared to simultaneous sensor and actuator attacks, providing motivation for the next results in this work. We also consider that the attack detection mechanisms are put online at the same time as the cyberattack occurs (0.4 h) so that we do not consider that they would have flagged, for example, the changes in the sensor measurements under a sensor measurement attack between the times prior to 0.4 and 0.4 h.
The case studies to be undertaken in moving toward understanding the differences between single and multiple attack-type scenarios involve an LEMPC where the constraint of Eq. 9b is enforced at the sampling time, followed by the constraints of the form of Eq. 9a enforced at the end of all sampling periods. The first study involves an attack monitoring strategy that involves checking whether the closed-loop state is overall driven toward the origin over a sampling period (if it is not, a possibility of an attack will be flagged). We implement attacks at 0.4 h; sensor attacks are implemented such that the measurement received by the sensor at 0.4 h would be faulty, and an actuator attack would be implemented by replacing the input computed for the time period between 0.4 and 0.41 h with an alternative input. When no attack occurs in the sampling period following 0.4 h of operation, the Lyapunov function evaluated at the actual state and at the state measurement decreases over the subsequent sampling period, as shown in Figures 1, 2.
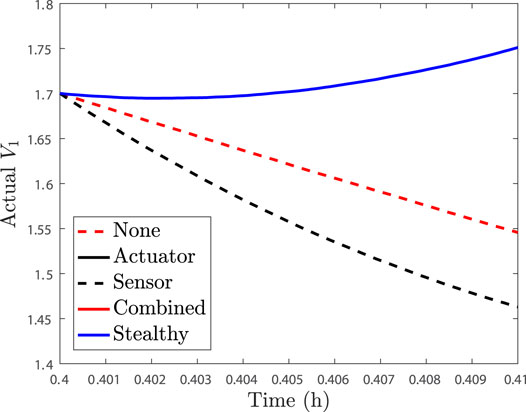
FIGURE 1. Actual V1 profiles over one sampling period after 0.4 h of operation for the process example described above in the presence of no attacks (“None”), only actuator cyberattacks (“Actuator”), only sensor attacks (“Sensor”), the baseline combined actuator and sensor attacks (“Combined”), and the stealthy combined sensor and actuator attack (“Stealthy”). The plots for the actuator attack, baseline combined actuator and sensor attack, and stealthy sensor and actuator attack are overlaid due to all having the same input (the false actuator signal) over the sampling period.
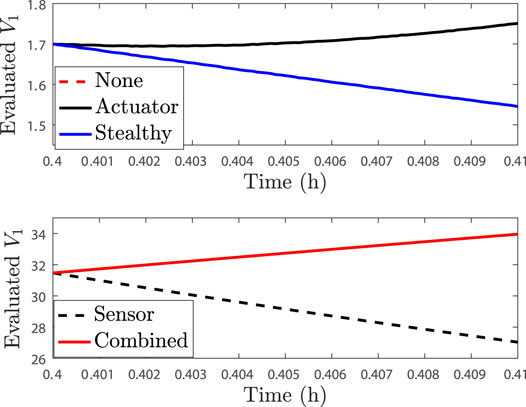
FIGURE 2. V1 profiles evaluated using the state measurements over one sampling period after 0.4 h of operation for the process example described above in the presence of no attacks (“None”), only actuator cyberattacks (“Actuator”), only sensor attacks (“Sensor”), the baseline combined actuator and sensor attacks (“Combined”), and the stealthy combined sensor and actuator attack (“Stealthy”). The plots for no attack and for the stealthy combined sensor and actuator attack are overlaid because the stealthy attack provides the no-attack sensor trajectory to the detection device to evade detection.
If instead we consider the case where only a rogue actuator output with the form u = 0.5 kmol/m3 is provided to the process for a sampling period after 0.4 h of operation, Figures 1, 2 show that the Lyapunov function profile increases over one sampling period after the attack policy is applied, when the Lyapunov function is evaluated for both the actual state and the measured state, and thus, this single attack event would be flagged by the selected monitoring methodology. Consider now the case where only a false state measurement for reactant concentration, with the form x1 + 0.5 kmol/m3, is continuously provided to the controller after 0.4 h of operation. This false sensor measurement causes the Lyapunov function value to decrease along the measurement trajectory, as can be seen in Figure 2, showing that this attack would not be detected by the strategy. However, it also decreases along the actual closed-loop state trajectory in this case (Figure 1) so that no safety issues would occur in this sampling period. This is thus a case when individual attacks would either be flagged over the subsequent sampling period or would not drive the closed-loop state toward the boundary of the safe operating region over that sampling period. Due to the large (order-of-magnitude) difference in the value of V1 evaluated along the measured state trajectory between the case that the sensor attack is applied and that no attack occurs, as shown in Figure 1, it could be argued that this type of attack could be flagged by the steep jump in V1 between the times prior to the sensor attack that occurs at 0.4 and 0.4 h. However, because we assumed that the method for checking V1 was not put online until 0.4 h, we assume that it does not have a record of the prior value of V1 so that we can focus on the trends in this single sampling period after the attacks.
We now consider two scenarios involving the combinations of sensor and actuator attacks. First, we combine the two attacks just described (i.e., false measurements are continuously provided to the controller and detection policies, which have the form x1 + 0.5 kmol/m3, and rogue actuator outputs with the form u = 0.5 kmol/m3 are provided directly to the actuators to replace any inputs computed by the controller). This attack is applied to the process after 0.4 h of operation and subsequently referred to as the “baseline” combined actuator and sensor attack because it is a straightforward extension of the two separate attack policies. In this case, the value of V1 increases along the measurement trajectory and also increases for the actual closed-loop state so that this attack would be flagged by the proposed policy. In some sense, the addition of the actuator attack made the fact that the system was under some type of attack “more visible” to this detection policy than in the sensor attack-only case (although the individual sensor attack was not causing the closed-loop state to move toward the boundary of the safe operating region so that the lack of detection of an attack in that case would not be considered problematic).
We next consider an alternative combined sensor and actuator attack policy, which we will refer to as a “stealthy” policy. In this case, the attacker provides the exact state trajectory to the detection device that would have been obtained if there was no attack, while at the same time falsifying the inputs to the process. In the case that this same false actuator trajectory was applied to the process and the sensor readings were accurate, we considered that it could be flagged. With the falsified sensor readings occurring at the same time, however, the attack is both undetected and driving the closed-loop state closer to the boundary of the safe operating region over a sampling period. From this, it can be seen that a major challenge arising from combining the attacks is that actuator attack detection policies based on state measurements may fail when attacks are combined, so that the state measurements may imply that the process is operating normally when problematic inputs are being applied.
This raises the question of whether there are alternative detection policies that might flag combined attacks, including those of the stealthy type just described that was “missed” by the detection policy described above where an overall decrease in the Lyapunov function value for the measured state across a sampling period was considered. For example, some of the detection methods described in the prior sections are able to flag actuator attacks before safety issues occur, whereas others flag sensor attacks. This suggests that detection strategies with different strengths might be combined into two-part detection strategies that involve multiple detection methods. To explore the concept of combining multiple methods of attempting to detect attacks (where again this example does not meet theoretical conditions required for resilience and is meant instead to showcase concepts underlying simultaneous attack mechanisms), we consider designing a state estimator for the process to use to compare state estimates against full-state feedback. If the difference between the state estimates and state measurements is larger than a threshold considered to represent abnormal behavior, we will flag that an attack might be occurring. In addition, we will monitor the decrease in the Lyapunov function evaluated along the trajectory of the state measurement over time, and flag a potential attack if it is noticeably increasing across a sampling period.
To implement such a strategy, we must first design a state estimator. We will use the high-gain observer from (Heidarinejad et al., 2012b) with respect to a transformed system state obtained via input–output linearization. This estimator (which is redundant because full-state feedback is available) will be used to estimate the reactant concentration of species A from continuously available temperature measurements. The observer equation using the set of new coordinates is as follows:
where
The next step in designing the detection strategy is to decide on a threshold for the norm of the difference between the state estimate and the state feedback. As a rough attempt to design one that avoids flagging measurement noise and process disturbances as attacks, the data from attack-free scenarios are gathered by simulating the process under different initial conditions and inputs within the input bounds. Particularly, we simulate attack-free events with an end time of 0.4 h of operation for initial conditions in the following discretization: x1 ranges from −1.5 to 3 kmol/m3 in the increments of 0.1 kmol/m3, with x2 ranging from −50 to 50 K in the increments of 5 K. When these initial conditions are within the stability region, the initial value of the state estimate is found in the transformed coordinates based on the assumption that the initial condition holds. Then, inputs must be generated to apply to the process with noise and disturbances. To explore what the threshold on the difference between the state measurement and estimate might be after 0.4 h to set a threshold to use when the state estimation-based attack detection strategy comes online at that time, we try several different input policies. One is to try h1(x) at every integration step; if this is done, then the maximum value of the norm of the difference between the state estimate and state measurement at 0.4 h among the scenarios tested is 0.026. If instead a random input policy is used (i.e., at every integration step, a new value of u is generated with mean zero and standard deviation of 2, and bounds on the input of −3.5 and 3.5 kmol/m3), then the maximum value of the difference between the state estimate and state measurement at 0.4 h among the scenarios tested is 0.122. If instead the random inputs are applied in sample-and-hold with a sampling period of length 0.01 h, the maximum value of the difference between the state estimate and state measurement at 0.4 h is 0.885. If the norm of the error between the state estimate and state measurement is checked at 1 h instead of 0.4 h in the three cases above, the results are 0.003, 0.107, and 0.923, respectively. Though a limited data set was used in these simulations and the theoretical principles of high-gain observer convergence were not reviewed in developing this threshold, 0.923 was selected for the cyberattack detection strategy based on the simulations that had been performed. One could also set the threshold by performing simulations for 0.4 h for a number of different initial states, specifically operated under the LEMPC, instead of the alternative policies above. Changing the threshold in the following discussion could have an impact on attack detection, although there would still be fundamental differences between single attack-type scenarios and simultaneous attack-type scenarios as discussed below.
We next consider the application of the same form of the baseline attacks as described in the prior example occurring at once, i.e., false measurements are continuously provided to the controller, which have the form x1 + 0.5 kmol/m3, and rogue actuator outputs with the form u = 0.5 kmol/m3 are provided to the process at 0.4 h of operation. In this combined attack scenario, the norm of the difference between the (falsified) state measurement and the state estimate at 0.4 h is 0.5016, and at 0.41 h is 0.5233, demonstrating that if the threshold is set to a larger number such as 0.923, the state estimate-based detection mechanism does not flag this attack at 0.4 or 0.41 h. Figure 3 plots the closed-loop state trajectory against the state estimate trajectory over one sampling period after 0.4 h of operation, showing the closeness of the trajectories in that time period despite the sensor and actuator attacks at 0.4 h. In fact, if this system is simulated with an actuator attack only, then the difference in the state estimate and state measurement at 0.41 h (the time at which the effects of the actuator attack could first be observed in the process data) is 0.05, showing that with the selected threshold for flagging an attack based on the difference between the state estimate and measurement, the actuator attack only would not be flagged at 0.41 h (despite that there is a net increase in the Lyapunov function value along the measured state trajectory in this case because that is not being checked with only the state estimate-based detection strategy). Considering that the threshold was set based on non-attacked measurements and many different input policies for the threshold set, it is reasonable to expect that an attack would not be flagged if only the input was to change.
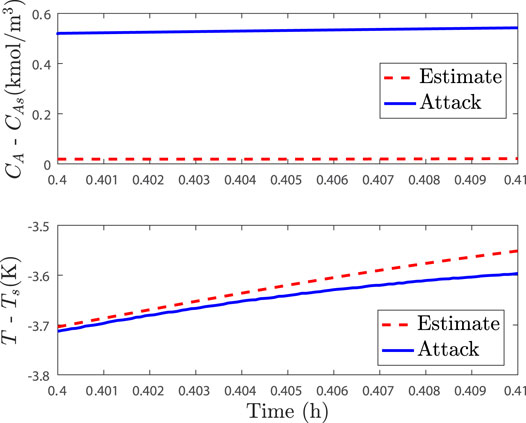
FIGURE 3. Comparison between the closed-loop state trajectory under attack (solid line) and the closed-loop state estimate trajectory (dashed lines) over one sampling period after 0.4 h of operation under the state feedback LEMPC.
For the baseline combined sensor and actuator case, Figure 4 shows that the Lyapunov function increases over the sampling period after 0.4 h along the measurement trajectory. Therefore, like the case where only the Lyapunov function was checked to attempt to flag this baseline combined attack, the baseline combined sensor and actuator attack can be detected here as well between 0.4 and 0.41 h. Though the attack occurs and is flagged, the closed-loop state was still kept inside the stability region
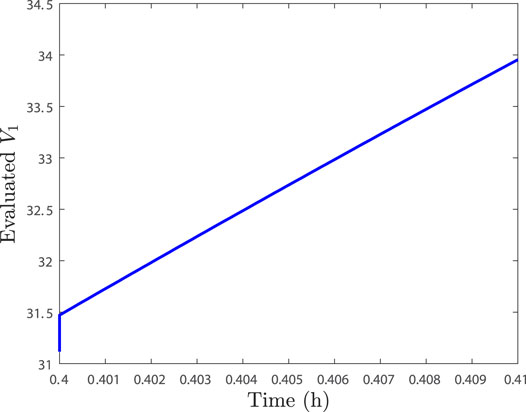
FIGURE 4. V1 profile along the measurement trajectory over one sampling period after 0.4 h of operation for the process example in the presence of multiple cyberattack policies (baseline case).
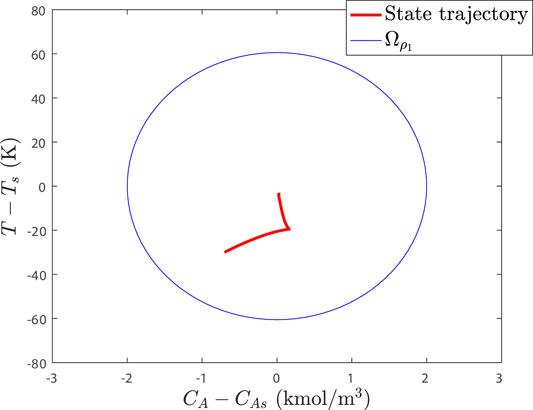
FIGURE 5. Stability region and closed-loop state trajectory for the process example in the presence of multiple cyberattack policies (baseline case).
If the stealthy combined sensor and actuator attack from the prior section is applied, the Lyapunov function value along the closed-loop state trajectory is again increasing, but again, it is decreasing along the estimated trajectory between 0.4 and 0.41 h. However, if this simulation is run longer, then the attack is eventually detected via the deviation of the state estimates from the state measurements exceeding the 0.923 threshold, at 0.45 h. In the case that only the Lyapunov function value along the measured state trajectories is checked until 0.45 h, no attack is yet detected, as the Lyapunov function value continues to decrease from 0.4 to 0.45 h along the measured state trajectory. These examples indicate the complexities of having combined sensor and actuator attacks, and also showcase that different detection policies may be better suited for detecting the combined attacks than others. This motivates a further study of the techniques and theory for handling the combined attacks, which is the subject of the next section.
Remark 7. The combined methods illustrated in the examples above do not determine the source of the attacks (e.g., the reason why the Lyapunov function increases could be either due to false sensors, incorrect actuator outputs, or both). However, the nature of a sensor attack differs from a sensor fault. A faulty sensor creates a state trajectory that is not inherently “dynamics based” and intelligently designed to harm a process.
7 Integrated Cyberattack Detection and Control Strategies Using LEMPC Under Multiple Attack Type Scenarios
The detection concepts described in the prior sections (and summarized in Table 1) have been developed to handle only single attack-type scenarios (i.e., either false sensor measurements or rogue actuator signals). However, to make a CPS resilient against different types of cyberattacks, the closed-loop system must be capable of detecting and mitigating scenarios where multiple types of attacks may happen simultaneously. As in the prior sections, detection approaches that not only enable the detection of attacks but that also prevent safety breaches when an attack is undetected are most attractive. This section extends the discussion of the prior sections to ask whether the detection strategies from Oyama and Durand (2020) that were developed for sensor cyberattack-handling and extended to actuator cyberattack-handling above can be used in handling simultaneous sensor and actuator attacks on the control systems.
We first note that based on the discussion in Section 5, we do not expect only a single method previously described (Detection Strategies 1-S, 2-S, 3-S, 1-A, 2-A, or 3-A) to be capable of handling both sensor and actuator cyberattacks occurring simultaneously. Instead, to handle the possibility that both types of attacks may occur, we expect that we may need to combine these strategies. However, care must be taken to select and design integrated control/detection strategies such that cyberattack detection and handling are guaranteed even when sensors and/or actuators are under attack. This is because the two types of attacks can interact with one another to degrade the performance of some of the attack detection/handling strategies that work for single attack types as suggested in the example of the prior section. For example, as noted in Section 5, in general, sensor measurement cyberattack-handling strategies may make use of correct actuator outputs in identifying attacks, and actuator attack-handling strategies may make use of “correct” (except for the sensor noise) sensor measurements in identifying attacks. If the actuators are no longer providing a correct output, it is then not a given that a sensor measurement cyberattack-handling strategy can continue to be successful, and if the sensors are attacked, it is not a given that an actuator cyberattack-handling strategy can continue to be successful. In this section, we analyze how the various methods in this work perform when these interactions between the sensor and actuator attacks may serve to degrade performance of strategies that worked successfully for only one attack type.
We discuss below the nine possible pairings of actuator and sensor attack-handling strategies based on the detection strategies discussed in this work. The goal of this discussion is to elucidate which of the combined strategies may be successful at preventing simultaneous sensor and actuator attacks from causing safety issues and which could not be based on counterexamples:
• Pairing Detection Strategies 1-S and 1-A: These two strategies essentially have the same construction (where when both are activated, there must be constant changing of the steady states around which the j-LEMPCs are designed for constant probing to satisfy the requirements of using Detection Strategy 1-A), in which a decrease in the Lyapunov function value along the measured state trajectories is looked for to detect both the actuator and sensor attacks. Consider a scenario in which an attacker provides sensor measurements that show a decrease in the Lyapunov function value when that would be expected, thus preventing the attack from being detected by the sensors. At the same time, the actuators may be producing inputs unrelated to what the sensors show, which could cause safety issues even if the sensors are not indicating any safety issues, due to attacks occurring on both the sensors and actuators. This pairing is therefore not resilient against combined attacks on the actuators and sensors (i.e., it is not guaranteed to detect attacks that would cause safety issues).
• Pairing Detection Strategies 1-S and 2-A: Detection Strategy 1-S relies on the value of the Lyapunov function decreasing between the beginning and end of a sampling period when the Lyapunov function is evaluated at the state measurement. Detection Strategy 2-A relies on the difference between a state prediction (from the last state measurement and under the expected input corresponding to that measurement) and a state measurement being less than a bound. This design faces a challenge for resilience against simultaneous sensor and actuator attacks in that the detection strategies for both types of policies depend on the state measurements. Since the state measurements here are falsified, this gives room for any actuator signal to be utilized, and then the sensors to provide readings that suggest that the Lyapunov function is decreasing and that the prediction error is within a bound. Thus, in this strategy, because there is no way to cross-check whether the sensor measurements are correct when there is also an actuator attack, safety is not guaranteed when there are undetected simultaneous attacks.
• Pairing Detection Strategies 1-S and 3-A: Detection Strategy 1-S relies on the state measurement creating a decrease in the Lyapunov function, while Detection Strategy 3-A relies on redundant state estimates being sufficiently close to one another. If Detection Strategy 1-S is not constantly activated (i.e., there is no continuous probing), then because Detection Strategy 3-A may not be guaranteed to detect actuator attacks and Detection Strategy 1-S may not detect them between probing times as described in Section 5, this strategy may not be resilient against actuator attacks (and thus also may not be against simultaneous actuator and sensor attacks). However, a slight modification to the strategy to achieve constant probing under Detection Strategy 1-S, forming the pairing of Detection Strategies 3-S and 1-A (because Detection Strategies 3-A and 3-S are equivalent in how they are performed) is resilient against simultaneous sensor and actuator attacks, as is further discussed below. If instead of probing,
• Pairing Detection Strategies 2-S and 1-A: This strategy faces similar issues to the combination of Detection Strategies 1-S and 2-A above. Specifically, these strategies again utilize state measurements only to flag attacks, allowing rogue actuator inputs to be applied at the same time as false state measurements without allowing the attacks to be flagged.
• Pairing Detection Strategies 2-S and 2-A: This is a case where only state measurements are being used to flag attacks, so like other methods above where this is insufficient to prevent the masking of rogue actuator trajectories by false sensor measurements, this strategy is also not resilient against attacks.
• Pairing Detection Strategies 2-S and 3-A: Detection Strategy 2-S is based on the expected difference between state predictions and actual states, and Detection Strategy 3-A is based on checking the difference between multiple redundant state estimates. If the threshold for Detection Strategy 2-S is redesigned (forming a pairing that we term as the combination of Detection Strategies 2-A and 3-S below since the threshold redesign must account for actuator attacks as described for Detection Strategy 2-A above to avoid false alarms), the strategy would be resilient to simultaneous actuator and sensor attacks. This is further detailed in the subsequent sections (although it requires that at least one state estimator is not impacted by the attacks).
• Pairing Detection Strategies 3-S and 1-A: This detection strategy can be made resilient against simultaneous actuator and sensor attacks and receives further attention in the following sections to demonstrate and discuss this (though at least one state estimator cannot be impacted by the attacks).
• Pairing Detection Strategies 3-S and 2-A: This strategy can be made resilient for adequate thresholds on the state prediction and state estimate-based detection metrics and will be further detailed below.
• Pairing Detection Strategies 3-S and 3-A: This strategy faces the challenge that it may not enable actuator attacks to be detected because both Detection Strategy 3-S and Detection Strategy 3-A are dependent only on state estimates, which may not reveal incorrect inputs as discussed in Section 5. Therefore, it would not be resilient for a case when actuator and sensor attacks could both occur if the redundant observer threshold holds regardless of the applied input.
The above discussion highlights that to handle both the sensor and actuator attacks, a combination strategy cannot be based on sensor measurements alone. In the following sections, we detail how the combination strategies using Detection Strategies 3-S and 1-A, and 3-S and 2-A, can be made resilient against simultaneous sensor and actuator attacks in the sense that, as long as at least one state estimate is not impacted by a false sensor measurement attack, the closed-loop state is always maintained within a safe operating region if attacks are undetected, even if both attack types occur at once. We note that the assumptions that the detectors are intact (e.g., that at least one estimator is not impacted by false sensor measurements or that a state prediction error-based metric is evaluated against its threshold) implies that other information technology (IT)-based defenses at the plant are successful, indicating that the role of these strategies at this stage of development is not in replacing IT-based defenses but in providing extra layers of protection if there are concerns that the attacks could reach the controller itself (while leaving some sensor measurements and detectors uncompromised).
7.1 Simultaneous Sensor and Actuator Attack-Handling via Detection Strategies 3-S and 1-A: Formulation and Implementation
In the spirit of the individual strategies Detection Strategy 3-S and Detection Strategy 1-A, a combined policy (to be termed Detection Strategy 1/3) can be developed that uses redundant state estimates to check for sensor attacks (assuming that at least one of the estimates is not impacted by any attack), and also uses different LEMPCs at every sampling time that are designed around different steady-states but contained within a subset of a safe operating region
The implementation strategy for Detection Strategy 1/3 assumes that the process has already been run successfully in the absence of attacks under the i = 1 output feedback LEMPC of Eq. 11 for some time (tq) such that
1) Before tq, operate the process under the 1-LEMPC of Eq. 11. Go to Step 2.
2) At sampling time tk, when the i-th output feedback LEMPC of Eq. 11 was just used over the prior sampling period to control the process of Eq. 1, if |zj,i(tk)−zp,i(tk)| > ϵmax, j = 1, … , M, p = 1, … , M, or
3) Mitigating actions may be applied (e.g., a backup policy such as the use of a redundant controller or an emergency shutdown mode).
4) Select a new i-th steady-state. This steady-state must be such that the closed-loop state measurement in deviation form from the new steady-state
5) The control actions computed by the i-LEMPC of Eq. 11 for the sampling period from tk to tk+1 is used to control the process according to Eq. 11. Go to Step 6.
6) Evaluate the Lyapunov function at the beginning and end of the sampling period, using the state measurements. If Vi does not decrease over the sampling period or if
7) (tk ← tk+1). Go to Step 2.
Remark 8. Though the focus of the discussions has been on preventing safety issues, it is possible that the detection and control policies described in this work may sometimes detect other types of malicious attacks that attempt to spoil products or cause a process to operate inefficiently to attack economics. The impacts of the probing strategies on process profitability (compared to routine operation) can be a subject of future work.
7.1.1 Simultaneous Sensor and Actuator Attack-Handling via Detection Strategies 3-S and 1-A: Stability and Feasibility Analysis
In this section, we prove recursive feasibility and safety of the process of Eq. 1 under the LEMPC formulations of the output feedback LEMPCs of Eq. 11 whenever no sensor or actuator attacks are detected according to the implementation strategy in Section 7.1 in the presence of bounded measurement noise. The theorem below characterizes the safety guarantees (defined as maintaining the closed-loop state in
Theorem 4. Consider the closed-loop system of Eq. 1 under the implementation strategy of Section 7.1 (which assumes the existence of a series of steady-states that can satisfy the requirements in Step 4), where the switching of the controllers at sampling times starts after
where
Proof 1. The proof consists of four parts. In Part 1, the feasibility of the i-th output feedback LEMPC of Eq. 11 is proven when
Part 1. The Lyapunov-based controller hi implemented in sample-and-hold is a feasible solution to the i-th output feedback LEMPC of Eq. 11 when
Part 2. To demonstrate boundedness of the closed-loop state in
for all t ∈ [t0, max{Δ, tz1}), where the latter inequality follows from Eqs 2, 5, and
Part 3. To demonstrate the boundedness of the closed-loop state and state estimate in
From
From Eqs 5, 54, 55, and considering
for all t ∈ [tk, tk+1). According to the implementation strategy in Section 7.1, when
Thus, when
When
Part 4. Finally, we consider the case that at some tk ≥ tq, the process is under either an undetected false sensor measurement cyberattack (Case 1), actuator cyberattack (Case 2) or both (Case 3).Part 4—Case 1. If the control system is under only a sensor attack, but it is not detected,
Remark 9. The proof for Part 4—Case 2 described above gives an indication of how the proof of closed-loop stability for actuator-only attacks on an LEMPC of the 1-A form would be carried out, but (noisy) state measurements then might be used in place of state estimates.
Remark 10. Several regions have been defined for the proposed detection strategy.
7.2 Simultaneous Sensor and Actuator Attack-Handling via Detection Strategies 3-S and 2-A: Formulation and Implementation
Following the idea of pairing single detection strategies above, another integrated framework, named Detection Strategy 2/3, can be developed that uses redundant state estimates to check for sensor attacks (again assuming that at least one of the estimates is not impacted by any attack) and relies on the difference between a state prediction based on the last available state estimate (obtained using an expected control action computed by either a fully redundant controller or an approximation of the controller output for a given state estimate) and a state estimate being less than a bound. The premise of checking the difference between the state estimate and the state prediction is that the state prediction should not be able to deviate too much from a (converged) state estimate (i.e., it approximates the actual process state to within a bound as in Assumption 2 after a sufficient period of time has passed since initialization of the state estimates) if there are no sensor or actuator attacks, and that therefore, seeing the estimate and prediction deviate by more than an expected amount is indicative of an attack.
If the actual state is inside a subset
To present the implementation strategy and subsequent proof in the next section that Detection Strategy 2/3 can be made cyberattack resilient in the sense that it can guarantee safety whenever no sensor or actuator attacks are flagged by this combined detection framework, it is necessary to determine the detection threshold for the difference between the state estimate and state prediction. Unlike in the case where a bound on the difference between state predictions and state measurements was derived for Detection Strategy 2-S for sensor attacks, we here need to set up mechanisms for detecting whether an actuator and/or sensor attack occurs. While state estimates are available to aid in detecting sensor attacks, a part of the mechanism for detecting whether actuator attacks occur is the use of a fully redundant controller (for which the input computed by the output feedback LEMPC of Eq. 10 is equivalent to the input computed by the redundant controller used in cross-checking the controller outputs) or the fast approximation of the control outputs (for which the input computed by the LEMPC would differ, within a bound, from the input computed by the algorithm used in cross-checking the controller outputs) for a given state measurement. The definition below defines the notation that will be used in this section to represent the actual state trajectory under the control input computed by the LEMPC and the state prediction obtained from the nominal (w ≡ 0) process model of Eq. 1 under the potentially approximate input used for cross-checking the control outputs.
Definition 1. Consider the state trajectories for the actual process and for the predicted state from t ∈ [t0, t1), which are the solutions of the systems:
where |xa(t0)−z1(t0)| ≤ γ. xa is the state trajectory for the actual process, where
where ϵu is the maximum deviation in the inputs computed for a given state estimate between the output feedback LEMPC of Eq. 10 and the method for cross-checking the controller inputs (if a fully redundant controller is utilized, ϵu = 0).The following proposition bounds the difference between xa and xb in Definition 1.
Proposition 4. Consider the systems in Definition 1 operated under the output feedback LEMPC of Eq. 10 and designed based on a controller h(⋅), which satisfies Eqs 2, 3. Then, the following bound holds:
and initial states
Proof 2. Integrating Eqs 59a, 59b from t0 to t, subtracting the second equation from the first, and taking the norm of both sides gives
for t ∈ [0, t1). Using Eqs 4a, 4c and the bound on w, the following bound is achieved:
for t ∈ [0, t1), where the last inequality follows from Eq. 60. Finally, using the Gronwall–Bellman inequality Khalil (2002), it is obtained that
Proposition 4 can be used to develop an upper bound on the maximum possible error that would be expected to be seen between a state prediction and a state estimate at a sampling time if no attacks occur. This bound is developed in the following proposition.
Proposition 5. Consider xa and xb defined as in Definition 1. If
Proof 3. Using Proposition 3 and Proposition 4 along with Eq. 32, we obtain
for all j = 1, … , M.
1) At sampling time tk, when the output feedback LEMPC of Eq. 10 is used to control the process of Eq. 1, if |zj(tk)−zp(tk)| > ϵmax or |zj(tk−1)−zp(tk−1)| > ϵmax, j = 1, … , M, p = 1, … , M, or
2) Mitigating actions may be applied (e.g., a backup policy such as the use of redundant controller or an emergency shutdown mode).
3) Control the process using the output feedback LEMPC of Eq. 10. Go to Step 4.
4) (tk ← tk+1). Go to Step 1.
7.2.1 Simultaneous Sensor and Actuator Attack-Handling via Detection Strategies 3-S and 2-A: Stability and Feasibility Analysis
In this section, we prove recursive feasibility and stability of the process of Eq. 1 under the proposed output feedback LEMPC of Eq. 10 whenever no sensor or actuator attacks are detected according to the implementation strategy in Section 7.2 in the presence of bounded plant/model mismatch, controller cross-check error, and measurement noise. The following theorem characterizes the safety guarantees of the process of Eq. 1 for all time under the implementation strategy of Section 7.2 when sensor and actuator cyberattacks are not detected. As for Detection Strategy 1/3, because the actuator cyberattacks would not be detected according to the implementation strategy in Section 7.2 until a sampling period after they had occurred (since they are being detected by their action on the state estimates, which would not be obvious until they have had a chance to impact the closed-loop state), it is necessary to define supersets
Theorem 5. Consider the closed-loop system of Eq. 1 under the implementation strategy of Section 7.2, in which no sensor or actuator cyberattack is detected using the proposed output feedback LEMPC of Eq. 10 based on an observer and controller pair satisfying Assumption 1 and Assumption 2 and formulated with respect to the i = 1 measurement vector and a controller h(⋅) that meets Eqs 2, 3. Let the conditions of Proposition 3 and Proposition 4 hold, and
where
Proof 4. The output feedback LEMPC of Eq. 10 has the same form as in Oyama and Durand (2020). Therefore, in the absence of attacks or in the presence of sensor attacks only, we obtain the same results as in Oyama and Durand (2020). Specifically, feasibility follows when z1(tk) ∈ Ωρ as proven in Oyama and Durand (2020). Since z1(tk) ∉ Ωρ flags an attack according to the implementation strategy of Section 7.2, there will not be a time before an attack is detected that z1(tk) ∉ Ωρ before an attack, so that the problem would not be infeasible before an attack. Also as demonstrated in Oyama and Durand (2020), the closed-loop state trajectory is contained in
Remark 11. The proof for actuator-only attacks for Theorem 5 described above gives an indication of how the proof of closed-loop stability for actuator-only attacks on an LEMPC of the 2-A form would be carried out, but state measurements might then be used in place of state estimates, with the bound developed on the difference between the state estimate and state prediction updated to be between the measurement and prediction.
8 Cyberattack Discoverability for Nonlinear Systems
The above sections reviewed a variety of cyberattack-handling mechanisms that rely on specific detection strategies designed in tandem with the controllers. None of those strategies, in the manner discussed, detects every attack, but some ensure that safety is maintained when the attacks are not detected. This raises the question of when detection mechanisms can detect attacks and when they cannot. This section is devoted to a discussion of these points. In Oyama et al. (2021), we first presented the notions of cyberattack discoverability for nonlinear systems in a discussionary sense (i.e., a stealthy attack is fundamentally “dynamics-based” or a “process-aware policy” and could fly under the radar of any reasonable detection method; on the other hand, a “non-stealthy” attack can be viewed as the one in which the attack policy is not within the bounds of a detection threshold and could promptly be flagged as a cyberattack using a reasonable detection method). In this section, we present the mathematical characterizations of nonlinear systems cyberattack discoverability that allow us to cast the various attack detection and handling strategies explored in this work in a unified framework and to more deeply understand the principles by which they succeed or do not succeed in attack detection.
We begin by developing a nonlinear systems definition of cyberattack discoverability as follows:
Definition 2. (Cyberattack Discoverability): Consider the state trajectories from t ∈ [t0, t1) that are the solutions of the systems:
where ua(x0 + va) and ub(x0 + vb) are the inputs to the process for t ∈ [t0, t1) computed from a controller when the controller receives a measurement
• If there are sensor attacks only, the functions ua and ub in Definition 2 may be the same, with the different arguments x0 + va and x0 + vb. If an actuator only is attacked, x0 + va and x0 + vb can be the same.
• The detection strategies presented in this work have implicitly relied on Definition 2. They have attempted, when an attack would cause a safety issue, to force that attack to be discoverable, by making, for example, the state measurement under an expected control action ua(x0 + va) different from the state measurement under a rogue policy ub(x0 + vb). We have seen methods fail to detect attacks when they cannot force this difference to appear. This fundamental perspective has the benefit of allowing us to better understand where the benefits and limitations of each of the methods arise from, which can guide future work by suggesting what aspects of strategies that fail would need to change to make them viable.
• The definition presented in this section helps to clarify the question of what the fundamental nature of a cyberattack is, in particular a stealthy attack, that may distinguish it from disturbances. Specifically, consider a robust controller designed to ensure that any process disturbance within the bounds of what is allowed for the control system should maintain the closed-loop state inside a safe region of operation for all time if no attack is occurring. In other words, the plant–model mismatch is accounted for during the control design stage and does not cause the feedback of the state to be lost. However, a stealthy attack is essentially a process-aware policy or an intelligent adversary that can modify the sensor measurements and/or actuator outputs through attack policies with a specific goal of making it impossible to distinguish between the actual and falsified data. The result of this is that stealthy attacks could fly under the radar of any reasonable detection mechanism and thus the control actions applied to the process may not be stabilizing. We have previously examined an extreme case of an undiscoverable attack in Oyama et al. (2021), where the attack was performed on the state measurements of a continuous stirred tank reactor by generating measurements that followed the state trajectory that would be taken under a different realization of the process disturbances and measurement noise and providing these to the controller. This would make the stealthy sensor attack, at every sampling time, appear valid to a detection strategy that is not generating false alarms.
• If a system is continuously monitored before and after an attack and the pair {wb, vb} does not follow the same disturbance and noise distribution as the pair {wa, va} in Definition 2, a cyberattack could conceivably be flagged by a detection method that is able to discern that.
• We note that although Definition 2 implies that if the attacker knows the process model and disturbance and noise distributions, they could implement an attack policy such that xa and xb trajectories cannot be distinguished (in the sense that one cannot be flagged as abnormal); cyberattack undiscoverability does not necessarily imply the loss of closed-loop stability. Specifically, if the closed-loop state trajectory (xa) and the false closed-loop state trajectory (xb) are “close enough” such that a Lyapunov function decreases along the closed-loop state trajectory in both cases under the inputs computed for both, then the closed-loop state may still be maintained within a desired operating region under the attack. This is implied by the fact that conservatively designed controllers can handle sufficiently small measurement noise (as, for example, in Detection Strategy 3-S described above). As a further example, consider that an attacker seeks to develop a falsified state measurement trajectory using disturbances w2 that are in the same distribution as those (w1) impacting the actual process for a closed-loop system under an explicit control policy h(x) with full-state feedback:
Depending on the trajectories of w1 and w2 (i.e., how the attacker’s simulated noise/disturbance profile deviates from that which is experienced by the true process over time), the closed-loop system of Eqs 78, 79 may maintain x1 in a bounded operating region (i.e., it may be stabilizing for the actual process system) or it may not. A nonlinear systems analysis [via, for example, the Lyapunov stability theory for the different potential functions of w1(t) and w2(t)] could be used to evaluate what types of disturbance/noise realizations and corresponding falsified conditions would enable a “dynamics-based” attack with this structure to be destabilizing. This is the same conclusion as was drawn in cases where one of the detection strategies described above was not effective at detecting an attack; many of the undetected attacks described did not prevent safety issues, which was the premise of the simultaneous actuator and sensor detection policies.
• Definition 2 assumes that no change in the process dynamics occurs. If the process dynamics change over time, the state trajectories, which are the solutions of the system indicated in the cyberattack discoverability definition, may significantly differ from the state trajectories prior to this change. If the detection scheme would then be set up to compare expectations under the old and new process models, the change in process dynamics may be erroneously flagged as a cyberattack. In Rangan et al. (2021), for example, we provide a two-fold control/detection mechanism to prevent false attack detection when the variations in the process dynamics are considered.
• Though methods for making cyberattacks discoverable might benefit from the knowledge of the distribution of the noise and disturbances (to better distinguish Eqs 76, 77), the various detection strategies developed in this work make no consideration for statistics; they look only at the bounds on disturbances and sensor measurements. The only requirements made on the attacks are that the sensor measurement cyberattacks keep the state measurements in the regions that do not flag the attacks (e.g., subsets of the stability region), and that the inputs remain in the input bounds (which must be true physically). Strategies such as those described in Sections 7.1, 7.2 were demonstrated to avoid false-positive detections of attacks by using these bounds instead of distributional information for the noise and disturbances.
9 Probing the Practicality of LEMPC-Based Cyberattack-Resilient Control Design
The results above suggest that if controllers can be designed to satisfy the theoretical requirements discussed in the prior sections, there would be benefits to using them from a cybersecurity perspective. However, an important question that arises from these studies is how easy it might be to design controllers satisfying the theoretical requirements (and if it would be practical at all) and what the answer to this question suggests about how the future work in cyberattack-resilient LEMPC should continue. In our prior work (Oyama et al. 2021), a number of simulations of a sensor measurement cyberattack-handling LEMPC that can also account for the changes in the process dynamics were performed. The results indicated that checking that the parameters of the control law and detection strategy (such as thresholds used in the detection policy or ρe) prevent cyberattacks from being successful can be challenging if it is performed using only a limited number of simulations. This suggests that either a significant number of simulations may be needed to design cyberattack-resilient LEMPCs (which would be expected to be a challenging way to design these controllers due to the interactions between the various parameters and could also still potentially leave system vulnerabilities if the simulations are not able to fully cover every possible issue), or a method for obtaining the parameters of the LEMPCs that meet the theory would be needed.
In this section, we seek to provide some initial insights into obtaining parameters for an LEMPC that meet the theory. To make progress on this, we remove some of the complexity of the problem by focusing on how to obtain the theoretical parameters not of the more specialized LEMPCs for cyberattack-resilient control discussed in this work, but instead for the original LEMPC developed in Heidarinejad et al. (2012a). This discussion is used to motivate future work in seeking to extend the initial results presented here on obtaining LEMPC parameters to more comprehensive methods for obtaining these parameters that could then be scaled to the cyberattack-resilient forms of LEMPC to eliminate the vulnerabilities.
9.1 LEMPC: Meeting Theoretical Requirements in Control Design
Before moving to a study working toward obtaining LEMPC parameters for a CSTR example, we first discuss a number of preliminaries regarding this topic. First, since this section will focus on the standard LEMPC of Eqs 8, 9, instead of its cyberattack-resilient form, we consider Proposition 2 (where in the remainder of this section; we will neglect the subscript i for the simplicity of notation) and the following proposition and theorem.
Proposition 6. Mhaskar et al. (2012), Heidarinejad et al. (2012a) Consider the following two systems:
with initial states of
Theorem 6. Heidarinejad et al. (2012a) Consider the system of Eq. 1 in closed loop under the LEMPC design of Eqs 8, 9 based on a controller h(x) that satisfies the conditions of Eq. 2. Let
and
where
for Mv as a positive constant. If
then the state x(t) of the closed-loop system is always bounded in Ωρ and is ultimately bounded in
Remark 12. As a comment on the last paragraph above, we remark that the requirements noted form a sort of optimization problem for h and V. To gain insight into the task, we could ask whether it would be possible to form the set of every possible h (Lipschitz continuous functions) and V (positive definite functions) and then to search within this set for h and V combinations that not only satisfy fundamental objectives of these functions (such as satisfaction of Eqs 2a, 2b) but which also enable the resulting h and V to cause all other parameters of the LEMPC to satisfy the two objectives of the LEMPC in the prior paragraph. We might begin by considering suggesting forms of h and V and then finding their form via optimization based on techniques in Brunton et al. (2016). Specifically, Brunton et al. (2016) develops potential dynamic models by guessing the terms that may appear on the right-hand side and then attempting to use a sparse regression to locate which of those should be used to represent the process dynamics. This begs the question of whether a form for h might be guessed, and then an optimization problem solved in which the coefficients of the terms of the form of h are the decision variables and the constraints enforce
9.1.1 Obtaining Control-Theoretic Parameters for LEMPC Applied to a CSTR
In this section, we provide a brute force-type method for exploring the parameters of an LEMPC that might be more aligned with the theory than assumed values. The brute force-type approach does not ensure that all of the parameters meet the theory, but it provides many insights into the shortcomings of this initial approach for attempting to obtain the parameters to motivate further studies on this topic and potential challenges with the parameters that might be obtained.
We consider the nonlinear process model of Eqs 40, 41. The manipulated inputs are CA0 (the reactant feed concentration of species A) and Q (the heat rate input), with the bounds of 0.5 ≤ CA0 ≤ 7.5 kmol/m3 and –5.0 × 105 ≤ Q ≤ 5.0 × 105 kJ/h. The values of the parameters of the CSTR model are presented in Table 2. An open-loop asymptotically stable steady-state occurs at CAs = 1.2 kmol/m3 and Ts = 438.2 K, where the subscript s indicates the steady-state values. In the control formulation, the state and input vectors are represented using deviation variables as xT = [CA−CAs T−Ts] and uT = [CA0–CA0s Q–Qs], respectively.
According to Theorem 6, the first step in finding the control-theoretic parameters for LEMPC is to find a controller h(x) satisfying Eq. 2 so that Ωρ, V, and h in the LEMPC of Eqs 8, 9 can be defined. In general, it may be challenging to find the functions α1, α2, α3, α4, and h(x) satisfying the requirements of Eq. 2. The input-affine form of Eqs 40, 41 allows Sontag’s formula (Lin and Sontag 1991) to be used for h(x) (assuming
The next function that we would like to obtain is α3. According to Eq. 2b, α3(|x|) should be a class
The first thing that we will check is that
The next function to be obtained is α4(|x|). We again here guess a form for α4(|x|) and then check whether Eq. 2c is satisfied at the points in the discretized stability region. Specifically, assuming that α4(|x|) = a4|x|2, we set a4 initially to −100 and then update it to be
Next, the value of Mf is determined to satisfy Eq. 5. In this case, it is necessary to discretize not only the state-space within the stability region but also the input space and disturbance space. Furthermore, the upper bound on the magnitude of the disturbances will play a role in determining not only Mf but also whether the conditions of Proposition 2 and Proposition 6 and Theorem 6 are satisfied for the controller parameters. Again, the larger the value of ρ, the larger the value of Mf. To obtain Mf in this simulation, the state-space was discretized in the manner described above, and, in addition, the range of CA0 was discretized in the units of 0.5 kmol/m3, while the range of Q was discretized in the units of 105 kJ/h. Furthermore, the disturbances used for this process had disturbance bounds of 2 kmol/m3 h and 5 K/h for the disturbances added to the right-hand sides of Eqs 40, 41, respectively. The disturbance space was therefore considered to go from −2 to 2 kmol/m3 h in the units of 0.1 kmol/m3 h for the disturbances added to the right-hand side of Eq. 40 in deviation form and from −5 to 5 K/h in the increments of 0.5 K/h for the disturbances added to the right-hand side of Eq. 41 in deviation form. Mf was originally set to 0, but then, it was changed to
Lx and Lw are the Lipschitz constants for f, as shown in Eq. 4a. To obtain these, first, Lx and Lw are obtained on their own by discretizing the state, input, and disturbance spaces, and finding the values that work when only the state is changed (for Lx) or when only the disturbances are changed (for Lw). Subsequently, it is checked that the resulting Lx and Lw satisfy Eq. 4a for the points in the discretized state-space. However, using the brute force method in this paper of checking many points (an aspect of this strategy that would scale poorly and therefore pose limitations for larger processes), the computation time can become many hours if the same discretization is used as was used above. Therefore, to obtain values for Lx and Lw more quickly, the discretization was made coarser; however, it should be understood that this also means that these parameter values (like the others above with other discretizations) are not necessarily the values that would be obtained with a finer discretization and therefore still leave the potential for safety vulnerabilities if the controller parameters are designed with these imperfect values of Lx and Lw. This also provides an insight into the challenges of using strategies like this for the safety-critical design of controllers, such as for the cyberattack-resilience extension.
Using a discretization of the input range of 1 kmol/m3 in CA0, of 105 kJ/h in Q, of 0.1 kmol/m3 in CA, of 1 K in T, and of 1 kmol/m3 h for the disturbance added to the right-hand side of Eq. 40 in a deviation form and of 1 K/h for the disturbance added to the right-hand side of Eq. 41 in a deviation form, and then only looking at points in the stability region, the value of Lx was initialized at −1 and then reset to |f(x, u, w)− f(x′, u, w)|/|x−x′| whenever |f(x, u, w)−f(x′, u, w)| > Lx|x−x′| among the points checked. This resulted in a value of Lx = 3,008.66 being selected. A similar procedure for Lw gave Lw = 1.00. Then, a code that checks that Eq. 4a is satisfied at the points in the discretization with Lx = 3,009 and Lw = 1.1 was utilized, and the points in the discretization satisfied it.
Subsequently, it is necessary to calculate
The final parameter to obtain is Mv in Eq. 16. This is obtained in a similar spirit to the methods above. Specifically, the range of CA is discretized in the units of 0.01 kmol/m3, while the range of T is discretized in the units of 1 K. Mv was originally set to 0. The points in this discretization in the stability region are examined. Subsequently, Mv is set to
The set of parameters obtained via these methods that is used in the first simulation is shown in Table 3. We note that many of these parameters were obtained within a given Ωρ, where if that region shrinks, it is possible that some values may change. To select the values of
In Eq. 86,
for t ∈ [tk, tk+1), according to Eq. 18 in Heidarinejad et al. (2012a). In a worst case, −α3(|x(tk)|) is close to zero near the origin, so that it can be neglected. From the requirement of Eq. 85,
Our first task is to analyze what values of the decision variables might satisfy these constraints, particularly those of interest in applying LEMPC (e.g., larger sampling periods and values of
If θw = 0, then values of
To investigate this, we can redo the procedure above for a different value of ρ that is smaller, to analyze the effects on the parameters of Table 3 and also on the feasible space of Eq. 86. Selecting ρ = 200 (i.e., ρ is about an order of magnitude smaller than above) and neglecting disturbances, we note that a1 and a2 are fixed by P for the selected form of V, α1(⋅), and α2(⋅), so that if these are still “large” in the resulting problem, V, α1(⋅), or α2(⋅) would need to change to make an impact on these. Though ρ is smaller here, we do not update the discretization of the stability region used, as the values that are obtained from the above procedure provide a best case (i.e., additional points in the stability region can only make a3 smaller, making it harder to find a larger Δ meeting Eq. 86c, and cannot make a4, Mf, Lx, Lw,
The new parameters from the above procedure with ρ = 200 are shown in Table 5. With these updated parameters, Eq. 86 gives a solution this time, specifically the solution in Table 6. The value of

TABLE 6. Equation 86 parameters from the second set of parameters for CSTR model in Table 5.
The maximum possible value of Δ from this procedure from the case with ρ = 200 is about 2 orders of magnitude smaller than the maximum possible value of Δ for the case with ρ = 1,800; this begs the question of whether a further reduction of ρ may improve the situation (we also note that the discretization could play a role in this, which was not further explored in the preliminary analyses of this study). We could consider ρ = 20 for which the parameters obtained via the method above and Eq. 86 are provided in Tables 7, 8. In this case, although a3 is increased compared to Table 5 (at least among the points in the discretization used), ρ is smaller so that the maximum possible value of ρs is smaller and therefore the negative term in Eq. 86c does not become as large as would be desired to raise Δ. In this case, the maximum possible value of Δ from the procedure described is 3.82 × 10–10 h, which again is very small.

TABLE 8. Equation 86 parameters from the third set of parameters for CSTR model in Table 7.
We see then that for the discretizations checked, decreasing the size of the stability region did not put the magnitude of Δ in a reasonable range for the selected for h, V, and αi, i = 1, 2, 3, 4. This gives a greater insight into Remark 12, which indicated that it is necessary to select h and V such that reasonable parameters can be obtained. Future work could explore other functions h, V, and αi, i = 1, 2, 3, 4 for this process to see whether there exists any that could result in more reasonable values of Δ or not. The results of this section also shed light on what changes could aid in making Δ larger (for example, it is seen above that a major reason why Δ is so small in each simulation is because a3 is small compared to a2 in each case and ρs is limited in magnitude by ρ, causing the only negative term in Eq. 86c to be small, and then since the terms that multiply Δ are large for the given shape of Ωρ, Δ must be small in each case to prevent the positive term containing Δ from overwhelming the negative term containing ρs and preventing
10 Conclusion
This work extended the control/detection strategies developed in Oyama and Durand (2020) to handle actuator attacks and cases where actuator and sensor attacks can occur simultaneously. For the event where multiple attacks are considered, several integrated control/detection frameworks that pair the detection strategies designed for single attack-type events were investigated. It was demonstrated that certain combinations of the detection strategies can be ineffective to flag both types of cyberattacks evaluated in this work, while others create a cyberattack-resilient structure that enables the detection of individual or simultaneous sensor and actuator attack types while ensuring safe operation even if undetected attacks occur. In particular, the pairing of Detection Strategies 1-A and 3-S and the pairing of Detection Strategies 2-A and 3-S were shown to be resilient against both types of cyberattacks. The major benefits of these methods are that multiple attack scenarios can be discovered, which adds a layer of protection, and closed-loop stability is guaranteed if an attack policy is not flagged by these two-piece structures. Finally, to characterize the fundamental nature of sensor and actuator attacks, we mathematically defined the concept of cyberattack discoverability in the context of process control and stealthy attack policies, which may provide insights for future detection strategy development. The potential practical challenges with designing LEMPCs meeting theoretical conditions, a precursor study for getting the parameters of cyberattack-resilient LEMPCs, elucidated some of the potential challenges with obtaining the parameters meeting the theory that could be addressed in future work.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation. The codes generated for this study will be uploaded to: https://durand.eng.wayne.edu/PublicationResources/index.html.
Author Contributions
HO worked on writing the manuscript and developing concepts and simulations for the manuscript. DM aided in developing simulations used for obtaining the results in the work and in writing portions of the work. KR aided in development of the actuator cyberattack-handling procedure. HD supervised the work and aided in writing and editing the manuscript and simulations and conceptualizing the methodology.
Funding
Financial support from the Air Force Office of Scientific Research (award number FA9550-19-1-0059), National Science Foundation CNS-1932026 and CBET-1839675, and Wayne State University is gratefully acknowledged.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We would like to thank the reviewers, who provided tremendous help and insights in their comments that aided us greatly in developing the final version of this manuscript.
References
Ahrens, J. H., and Khalil, H. K. (2009). High-gain Observers in the Presence of Measurement Noise: A Switched-Gain Approach. Automatica 45, 936–943. doi:10.1016/j.automatica.2008.11.012
Ani, U. P. D., He, H., and Tiwari, A. (2017). Review of Cybersecurity Issues in Industrial Critical Infrastructure: Manufacturing in Perspective. J. Cyber Security Technol. 1, 32–74. doi:10.1080/23742917.2016.1252211
Bemporad, A., Morari, M., Dua, V., and Pistikopoulos, E. N. (2002). The Explicit Linear Quadratic Regulator for Constrained Systems. Automatica 38, 3–20. doi:10.1016/s0005-1098(01)00174-1
Brunton, S. L., Proctor, J. L., and Kutz, J. N. (2016). Discovering Governing Equations from Data by Sparse Identification of Nonlinear Dynamical Systems. Proc. Natl. Acad. Sci. USA 113, 3932–3937. doi:10.1073/pnas.1517384113
Cárdenas, A. A., Amin, S., Lin, Z.-S., Huang, Y.-L., Huang, C.-Y., and Sastry, S. (2011). “Attacks against Process Control Systems: Risk Assessment, Detection, and Response,” in Proceedings of the ACM Asia Conference on Computer & Communications Security, Hong Kong, China.
Chen, S., Wu, Z., and Christofides, P. D. (2020). A Cyber-Secure Control-Detector Architecture for Nonlinear Processes. AIChE J. 66, e16907. doi:10.1002/aic.16907
Davis, J., Edgar, T., Graybill, R., Korambath, P., Schott, B., Swink, D., et al. (2015). Smart Manufacturing. Annu. Rev. Chem. Biomol. Eng. 6, 141–160. doi:10.1146/annurev-chembioeng-061114-123255
Ding, D., Han, Q.-L., Ge, X., and Wang, J. (2020). Secure State Estimation and Control of Cyber-Physical Systems: A Survey. IEEE Trans. Syst. Man, Cybernetics: Syst. 51, 176–190.
Durand, H. (2018). A Nonlinear Systems Framework for Cyberattack Prevention for Chemical Process Control Systems. Mathematics 6, 44. doi:10.3390/math6090169
Durand, H., and Messina, D. (2020). “Enhancing Practical Tractability of Lyapunov-Based Economic Model Predictive Control,” in Proceedings of the American Control Conference, Denver, Colorado, 2018–2023. doi:10.23919/acc45564.2020.9147880
Durand, H., and Wegener, M. (2020). Mitigating Safety Concerns and Profit/production Losses for Chemical Process Control Systems under Cyberattacks via Design/control Methods. Mathematics 8, 499. doi:10.3390/math8040499
Ellis, M., Durand, H., and Christofides, P. D. (2014a). A Tutorial Review of Economic Model Predictive Control Methods. J. Process Control. 24, 1156–1178. doi:10.1016/j.jprocont.2014.03.010
Ellis, M., Zhang, J., Liu, J., and Christofides, P. D. (2014b). Robust Moving Horizon Estimation Based Output Feedback Economic Model Predictive Control. Syst. Control. Lett. 68, 101–109. doi:10.1016/j.sysconle.2014.03.003
Griffith, D. W. (2018). “Advances in Nonlinear Model Predictive Control for Large-Scale Chemical Process Systems,”. Ph.D. thesis (Pittsburgh, Pennsylvania: Carnegie Mellon University).
Heidarinejad, M., Liu, J., and Christofides, P. D. (2012a). Economic Model Predictive Control of Nonlinear Process Systems Using Lyapunov Techniques. AIChE J. 58, 855–870. doi:10.1002/aic.12672
Heidarinejad, M., Liu, J., and Christofides, P. D. (2012b). State-estimation-based Economic Model Predictive Control of Nonlinear Systems. Syst. Control. Lett. 61, 926–935. doi:10.1016/j.sysconle.2012.06.007
Lao, L., Ellis, M., Durand, H., and Christofides, P. D. (2015). Real-time Preventive Sensor Maintenance Using Robust Moving Horizon Estimation and Economic Model Predictive Control. AIChE J. 61, 3374–3389. doi:10.1002/aic.14960
Lin, Y., and Sontag, E. D. (1991). A Universal Formula for Stabilization with Bounded Controls. Syst. Control. Lett. 16, 393–397. doi:10.1016/0167-6911(91)90111-q
Mhaskar, P., Liu, J., and Christofides, P. D. (2012). Fault-tolerant Process Control: Methods and Applications. Berlin, Germany: Springer Science & Business Media.
Muñoz de la Peña, D., and Christofides, P. D. (2008). Lyapunov-based Model Predictive Control of Nonlinear Systems Subject to Data Losses. IEEE Trans. Automat. Contr. 53, 2076–2089. doi:10.1109/tac.2008.929401
Narasimhan, S., El-Farra, N. H., and Ellis, M. J. (2021). Detectability-based Controller Design Screening for Processes under Multiplicative Cyberattacks. AIChE J. 68, e17430. doi:10.1002/aic.17430
Oyama, H., and Durand, H. (2020). Integrated Cyberattack Detection and Resilient Control Strategies Using Lyapunov-Based Economic Model Predictive Control. AIChE J. 66, e17084. doi:10.1002/aic.17084
Oyama, H., Rangan, K. K., and Durand, H. (2021). Handling of Stealthy Sensor and Actuator Cyberattacks on Evolving Nonlinear Process Systems. J. Adv. Manufacturing Process. 3, e10099. doi:10.1002/amp2.10099
Papachristodoulou, A., and Prajna, S. (2002). “On the Construction of Lyapunov Functions Using the Sum of Squares Decomposition,” in Proceedings of the IEEE Conference on Decision and Control (Las Vegas, Nevada: IEEE), Vol. 3, 3482–3487.
Pasqualetti, F., Dörfler, F., and Bullo, F. (2013). Attack Detection and Identification in Cyber-Physical Systems. IEEE Trans. Automat. Contr. 58, 2715–2729. doi:10.1109/tac.2013.2266831
Qin, S. J., and Badgwell, T. A. (2003). A Survey of Industrial Model Predictive Control Technology. Control. Eng. Pract. 11, 733–764. doi:10.1016/s0967-0661(02)00186-7
Rangan, K. K., Oyama, H., and Durand, H. (2021). Integrated Cyberattack Detection and Handling for Nonlinear Systems with Evolving Process Dynamics under Lyapunov-Based Economic Model Predictive Control. Chem. Eng. Res. Des. 170, 147–179. doi:10.1016/j.cherd.2021.03.024
Rawlings, J. B., Angeli, D., and Bates, C. N. (2012). “Fundamentals of Economic Model Predictive Control,” in Proceedings of the IEEE Conference on Decision and Control, Maui, Hawaii, 3851–3861. doi:10.1109/cdc.2012.6425822
Setola, R., Faramondi, L., Salzano, E., and Cozzani, V. (2019). An Overview of Cyber Attack to Industrial Control System. Chem. Eng. Trans. 77, 907–912.
Tuptuk, N., and Hailes, S. (2018). Security of Smart Manufacturing Systems. J. Manufacturing Syst. 47, 93–106. doi:10.1016/j.jmsy.2018.04.007
Wu, Z., Albalawi, F., Zhang, J., Zhang, Z., Durand, H., and Christofides, P. D. (2018). Detecting and Handling Cyber-Attacks in Model Predictive Control of Chemical Processes. Mathematics 6, 22. doi:10.3390/math6100173
Keywords: cyber-physical system, economic model predictive control, nonlinear systems, cyberattack detection, sensor attack, actuator attack
Citation: Oyama H, Messina D, Rangan KK and Durand H (2022) Lyapunov-Based Economic Model Predictive Control for Detecting and Handling Actuator and Simultaneous Sensor/Actuator Cyberattacks on Process Control Systems. Front. Chem. Eng. 4:810129. doi: 10.3389/fceng.2022.810129
Received: 06 November 2021; Accepted: 24 January 2022;
Published: 01 April 2022.
Edited by:
Gianvito Vilé, Politecnico di Milano, ItalyReviewed by:
Jinfeng Liu, University of Alberta, CanadaAlexander William Dowling, University of Notre Dame, United States
Copyright © 2022 Oyama, Messina, Rangan and Durand. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Helen Durand, aGVsZW4uZHVyYW5kQHdheW5lLmVkdQ==
 Henrique Oyama
Henrique Oyama Dominic Messina
Dominic Messina Keshav Kasturi Rangan
Keshav Kasturi Rangan Helen Durand
Helen Durand




