Computational design of quinone electrolytes for redox flow batteries using high-throughput machine learning and theoretical calculations

Molecular design of redox-active materials with higher solubility and greater redox potential windows is instrumental in enhancing the performance of redox flow batteries Here we propose a computational procedure for a systematic evaluation of organic redox-active species by combining machine learning, quantum-mechanical, and classical density functional theory calculations. 1,517 small quinone molecules were generated from the building blocks of benzoquinone, naphthoquinone, and anthraquinone with different substituent groups. The physics-based methods were used to predict HOMO-LUMO gaps and solvation free energies that account for the redox potential differences and aqueous solubility, respectively. The high-throughput calculations were augmented with the quantitative structure-property relationship analyses and machine learning/graph network modeling to evaluate the materials’ overall behavior. The computational procedure was able to reproduce high-performance cathode electrolyte materials consistent with experimental observations and identify new electrolytes for RFBs by screening 100,000 di-substituted quinone molecules, the largest library of redox-active quinone molecules ever investigated. The efficient computational platform may facilitate a better understanding of the structure-function relationship of quinone molecules and advance the design and application of all-organic active materials for RFBs.

Introduction

Large-scale, stationary energy storage techniques are imperative for the widespread applicability of green energy such as wind and solar power (Hasewend et al., 2020). A redox flow battery (RFB) is an electrochemical energy storage device (Eckroad and Gyuk, 2003), in which catholyte and anolyte are stored in separate external tanks and transported to the battery for energy conversions. The RFB power is determined by the capacity of electrodes while its energy density depends on the volume, the composition, and the concentration of the redox-active electrolytes (Zhou et al., 2006; Skyllas-Kazacos and Grossmith, 1987; Remick and Ang, 271984). The complete decoupling of the power and energy density makes RFBs ideal for high-capacity energy storage with operational flexibility.

Several types of RFBs have been proposed, such as all-vanadium flow batteries, Fe/Cr flow batteries, and zinc bromide flow batteries (Ye et al., 2019). All-vanadium RFBs utilize the same electrolytes for both half-cells and are advantageous in preventing contamination and thereby improving the battery life cycle (Skyllas-Kazacos and Grossmith, 1987; Hawkins and Robbins, 2001; Tsekouras et al., 2008). The cost and energy efficiency of all-vanadium RFBs, however, need to be improved for industrial applications (Li et al., 2011; Ma et al., 2012). Lithium-ion flow batteries (Pham-Truong et al., 2020) have the advantage of high current density, capacity, and flexibility, but their performance is often compromised by the availability of lithium conducting and storage materials. Aqueous organic redox flow batteries (AORFBs) may overcome some of the major hurdles of the metal ion-based RFBs by using Earth-abundant elements such as C, H, O, N, S. (Darling et al., 2014; Huskinson et al., 2014; Kwabi et al., 2018; Jin et al., 2019; Li J. et al., 2020; Allam et al., 2020). The tunability of redox-active molecules offers new avenues for engineering design and optimization by selecting materials with wider voltage windows, higher aqueous solubility, increased electrochemical stability, and faster electrode reaction kinetics (Sánchez-Díez et al., 2021). For example, quinones have a backbone structure that allows for a two-electron redox reaction in an aqueous solution. Their electrochemical properties and solution behavior can be tuned by substitutions at the benzene rings (Er et al., 2015). An open circuit voltage of 1.2V was achieved by utilizing 2,6-DHAQ (Kwabi et al., 2018) as the electrolyte under alkaline conditions, but the replacement of 2, 6-DHAQ with PEGAQs (Jin et al., 2019) reduces the voltage to 1.0V. Given the inexhaustible types of quinone organics that can be obtained by varying the substitution positions and substituent groups, a high-throughput molecular design method is needed for speeding up the development of all-quinone RFBs.

One key objective of molecular quinone design is to identify substitutions leading to a higher redox potential difference and higher solubility such that the RFBs can achieve a higher energy density. Whereas physics-based models are available to predict such properties, the direct application is often limited by their demanding computational cost in evaluating a large library of chemical species under diverse thermodynamic conditions. Exploring the chemical space requires new computational strategies to improve the design efficiency. The machine-learning (ML) methods provide complementary alternatives with particular strength in high-throughput screening and molecular design. To prepare the “big data” required for training ML models, we combine quantum-mechanical (QM) and classical density functional theory (cDFT) calculations with quantitative structure-property relationship (QSPR) analyses such that the physicochemical properties of quinones can be systematically evaluated.

A number of previous studies have reported the molecular design of redox-active materials for RFBs. (Narayan et al., 2019; Singh et al., 2019; Zhong et al., 2020). For example, Allam et al. (Allam et al., 2020) applied artificial neural networks (ANN), gradient-boosting regression (GBR), and kernel ridge regression (KRR) to predict the redox potentials of quinones based on the electron affinity and the number of bound lithium atoms. Li J. et al. (2020) applied ML methods to predict the cost and efficiency of all-vanadium flow batteries. Lin et al. (2017) used an extreme learning machine (ELM) model to predict the properties of a novel redox flow battery—the single flow Zinc-Nickle battery. However, there is still a lack of an accurate and efficient way to screen the huge virtual library of molecules for high-performance materials that can be applied to RFBs. In this work, we constructed 1,517 quinone molecules (except -SiH3 substituents) with benzoquinone, naphthoquinone and anthraquinone as building blocks, referring to the work of Aspuru-Guzik (Er et al., 2015). QM and cDFT calculations were performed on our own computational platform to calculate their HOMO-LUMO gaps and solvation free energies to quantitatively characterize the redox potential difference and solubility of molecules, respectively. Although the HOMO-LUMO gap and solvation free energy are not exactly the same concept as the redox potential difference and solubility of the active material in a battery system, they have a roughly positive correlation in general and it is feasible for our goal of rapidly screening potential performance molecules from a large library of molecules. We extracted molecular features from molecular descriptors and graph networks to build AI models to rapidly predict the above two properties and demonstrated the effectiveness of the proposed method with experimental results for the existing quinone electrolytes and its potential use for the computational design of redox-active materials by screening 100,000 di-substituted quinone molecules.

Models and methods

The computational scheme for quinone design

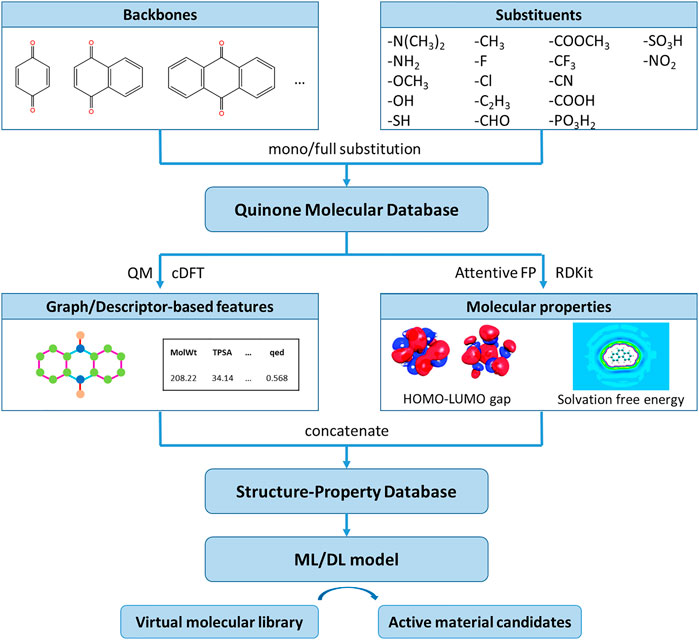
Figure 1 presents the overall computational scheme for the molecular design of quinones that may be used as catholytes in RFBs. Following previous work (Er et al., 2015; Li et al., 2016; Li T. et al., 2020; Li et al., 2021), we chose benzoquinone, naphthoquinone, and anthraquinone as the building blocks to construct a library of 1,517 mono- or fully-substituted quinone molecules by the addition of different substituent groups at different substitution positions. In terms of the choice of theoretical calculation methods, we have specifically compared the effects of different first-principles approaches, classical force field parameters, atomic charge distributions, and water model combinations on the accuracy of property calculations in our previous work (Li et al., 2016), and finally selected a combination of Hartree-Fork, GAFF force field, AM1-BCC charge, and SPC/E water models to calculate the solvation free energy of molecules. For most of the virtual quinone molecules, the experimental data for the solvation free energies and the HOMO-LUMO gaps have not been determined. Thus, we verified the prediction accuracy of the theoretical method on polycyclic aromatic hydrocarbons with similar structure to quinones aromatic hydrocarbons that are similar to quinones (Li T. et al., 2020). The calculated values agree well with the experimental data, the average error between the predicted and experimental values of solvation free energy obtained using cDFT is less than .5 kcal/mol. We conduct all QM calculations using the ORCA package (Neese, 2012). The solute structure is obtained from energy optimization in vacuum using HF-3c QM calculations. The molecular properties provide a quantitative measure of the redox potential difference and solubility of the electrolyte in RFBs, which in part reflect the capacity and performance of the flow battery. The theoretical results are then analyzed with the QSPR method and machine learning/graph network models. Next, surrogate models were constructed to reproduce the HOMO-LUMO gaps and solvation free energies of quinone molecules and analyze the dependence of such properties on substituents at different backbone positions. Compared with mono- and multi-substituted quinones, di-substituted quinones hold advantages in terms of a balance of stability, diversity, and synthesizability. Thus, our molecular design is focused on the properties of all possible di-substituents with the same backbone. Quinone molecules promising for AORFBs have been identified from over 100,000 di-substituted quinones.

FIGURE 1

FIGURE 1. The computational scheme for molecular quinone design.

The choice of AI models

We firstly constructed 1,517 quinone molecules with 17 different substituents using benzoquinone, naphthoquinone, and anthraquinone as building blocks (Supplementary Figure S1). The theoretical predictions for the solvation free energies and HOMO-LUMO gaps are used as a database for training two models, eXtreme Gradient Boosting (Xgboost) (Chen Q. et al., 2015) and Attentive Fingerprints (FP) (Xiong et al., 2019) because they have shown very outstanding performance in many nature prediction tasks (Zhang et al., 2020; Robles et al., 2021; Yang et al., 2022). The underlying Xgboost uses multiple simple base learners to continuously reduce the gap between the overall predicted and actual values of the model by continuously constructing new learners to learn the difference between the predicted value of the previous learner and the target. The underlying Xgboost uses multiple simple base learners to continuously reduce the gap between the overall predicted and actual values of the model by continuously constructing new learners to learn the difference between the predicted value of the previous learner and the target. Xgboost automatically assigns lower weights to features that are highly repetitive, which allows for some transferability when the model is applied to molecules with less similar structures, despite some loss in training efficiency. In some traditional molecular graph models, given a labeled atomic node, the influence of other atoms on the target node either decays severely with distance or defaults to the same influence of all other nodes on the target, lacking the flexibility to change. Attentive FP, while maintaining the intrinsic structure of the molecule, first adds an attention mechanism at the atomic level to learn local features of the molecule, then adds an attention mechanism at the whole molecular Attentive FP learns features from the molecular structure end-to-end and achieves the best performance in a very large number of prediction tasks compared to other similar graph neural network models (Xiong et al., 2019). The molecular properties, along with the predicted values from machine learning, are listed in Supplementary Table S2. In texting the ML models, the data are divided into a training set, a validation set, and a test set with a ratio of 8:1:1.

Results and discussion

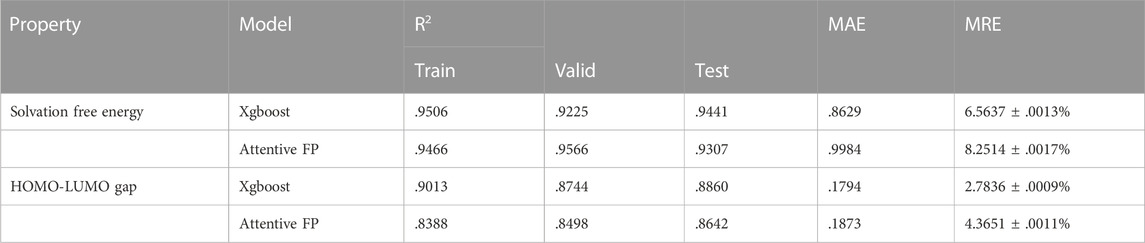
As shown in Figure 2, Xgboost is relatively accurate than Attentive FP for fitting both the solvation free energies and the HOMO-LUMO gaps. We performed a total of 30 model constructions for the random data distribution in the training, validation, and test samples, and obtained the average metrics of the model on the test set, including the R² (coefficient of determination), MAE (mean absolute error), and MRE (mean relative error), as listed in Table 1. In addition, the two methods have made higher-precision predictions of the solvation free energy, and the predicted value has a higher linear correlation with the value calculated by the theory. Attentive FP’s model gives a poor prediction of the HOMO-LUMO gap, in which most of the points formed by the calculated values and the predicted values deviated from the diagonal line. It is anticipated that the better prediction by the Xgboost model may attribute to feature selection.

FIGURE 2

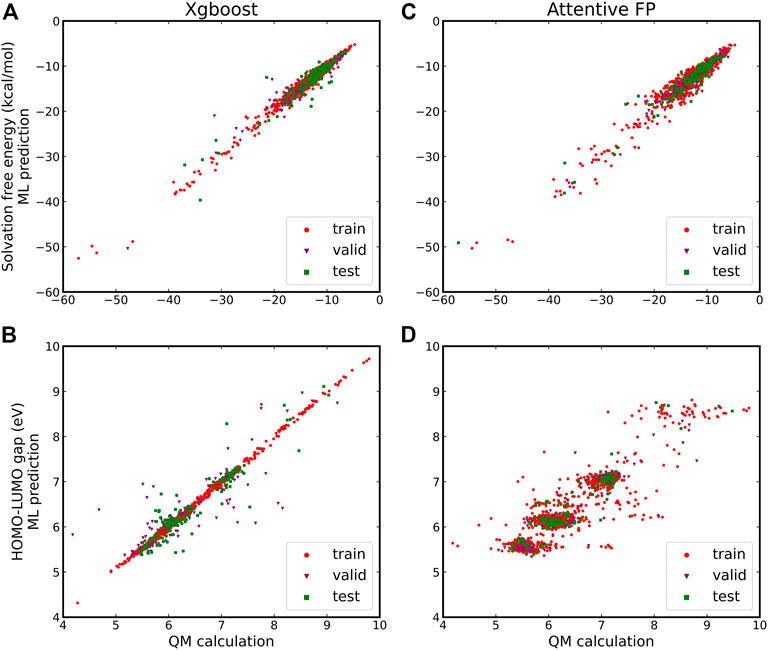
FIGURE 2. A comparison of Xgboost and Attentive FP methods to predict the solvation-free energies and HOMO-LUMO gaps of 1,517 quinone molecules. (A) Xgboost for predicting the solvation free energies; (B) Xgboost for predicting the HOMO-LUMO gaps; (C) Attentive FP for predicting the solvation free energies; and (D) Attentive FP for predicting the HOMO-LUMO gaps.

TABLE 1

TABLE 1. Various indicators of data fitting with Xgboost and Attentive FP methods.

In fitting the solvation free energies and the HOMO-LUMO gaps of quinone molecules with the Xgboost model, we have used 200 predefined molecular descriptors including molecular mass, elemental composition, alcohol-water partition coefficients, etc., to reflect numerically some simple properties of molecules physicochemically. These descriptors show good correlation with both the solubility and orbital properties of the quinone molecule. By contrast, the Attentive FP model is based on local environmental characteristics of individual atoms in a molecule (information about the atoms directly or indirectly connected to the central atom) constructed on the basis of the graph network. Such characteristics are more derived from the surrounding environment of each atom rather than the overall features of the molecule, which explains its relatively poor predictive ability in comparison with Xgboost. In general, the performance of the machine learning models depends on the choice of hyperparameters, the quality of the data, and the selection of features. As we can see in Figure 2, the selected features better reflect the solvation free energies of quinone molecules than their HOMO-LUMO gaps. It appears that the latter requires a larger data set or deeper feature engineering to have better correlations. Moreover, it can be seen from Table 1 that the prediction errors of the Xgboost model are acceptable for high-throughput screening. Compared to their actual values, the average relative error of the test set does not exceed 5%, implying that the predicted values are a good representation of the superiority or inferiority of the molecular properties. In the following, our analyses of quinone molecules for RFBs are all based on the Xgboost model.

The effects of substituent position, type and backbone

We have constructed 17 backbone molecules using benzoquinone, naphthoquinone, and anthraquinone as the building blocks. Xgboost also gives an assessment of the importance of molecular descriptor features in the modeling process. In the prediction of the HOMO-LUMO gap, the number of aromatic and aliphatic rings is the most important feature. Although our molecule has only one to three rings, in agreement with the results of similar experiments (Zade et al., 2011), the smaller the number of rings in the molecule, the larger its HOMO-LUMO gap, i.e., the molecule obtained by using benzoquinone as the backbone construction has a larger band gap. Some of the most important interpretable features for predicting the solvation free energy include TPSA (topological molecular polar surface area), the number of nitrogen and oxygen atoms, and the number of hydrogen bond acceptors. The lowest solvation free energy in the theoretically calculated results are also for molecules that have been substituted with some polar groups such as -SO3H and -PO3H2. The position of the substituent is less important for the above two properties, but we do not consider for the moment that it affects the stability of the molecular structure and thus causes practical experimental difficulties.

To study the influence of substituent position and substituent type on its molecular characteristics, we used the 1, 10-anthraquinone (AQ) as a representative backbone and compared the difference between theoretical results and ML correlation data according to the substituent position and substituent type. Although, the derivatives of 1, 10-AQ are very unstable and difficult to synthesize by chemical means, for our work we are currently considering only the target properties of the virtual molecule to determine whether it has potential as a battery-active material. Moreover, although the effect of substituents on different quinone backbones is not entirely consistent, given their structural similarity and our ultimate goal as described above, it does not matter which specific backbone is chosen to explore the effect of substituents on the properties, so we visualized the data on the properties of molecules constructed with 1, 10-AQ as a backbone. Figure 3 shows the results, and Table 2 presents the corresponding substituent positions.

FIGURE 3

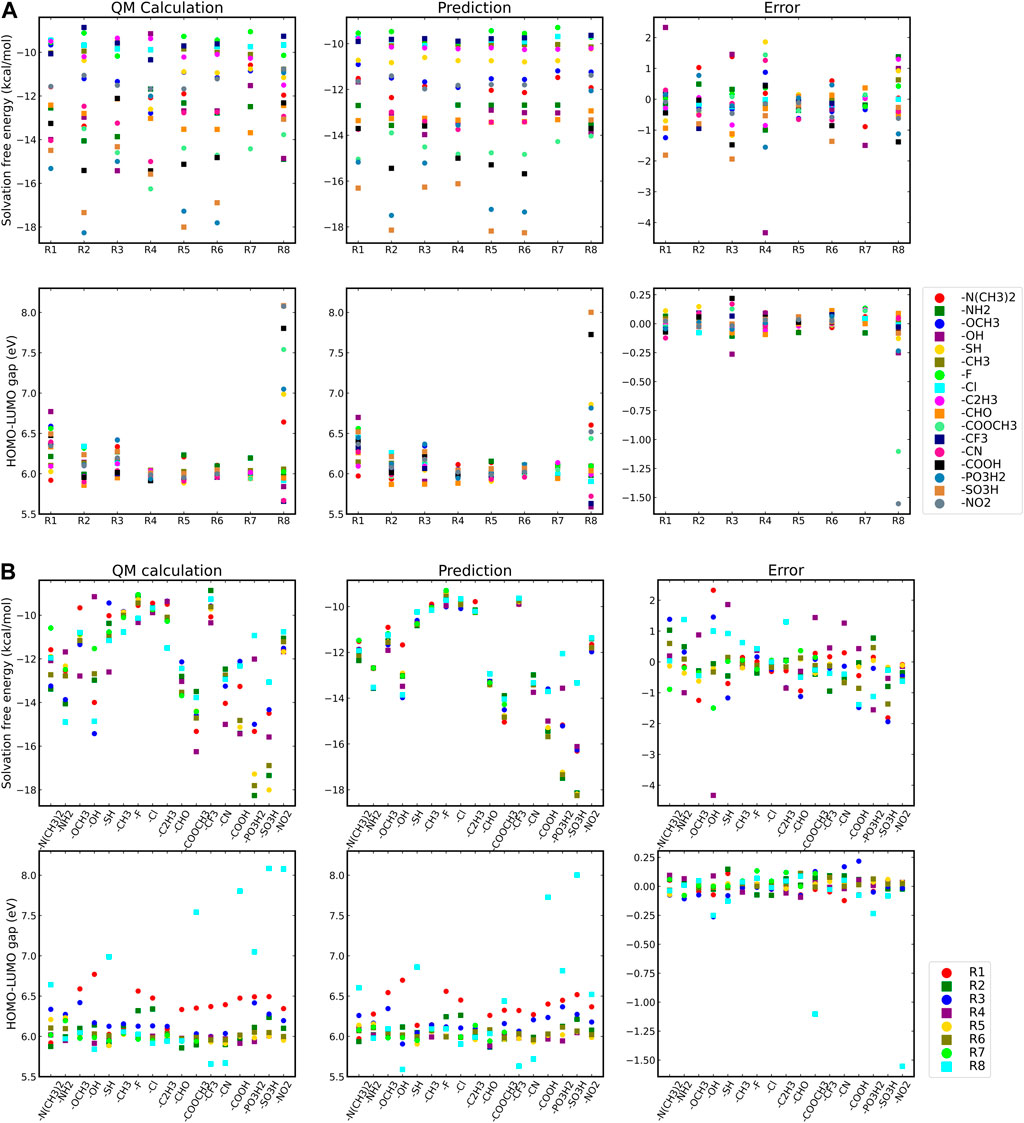
FIGURE 3. Solvation-free energies and HOMO-LUMO gaps of different quinones. (A) Effect of different substituent types on target properties. (B) Effect of different substituent positions on target properties.

TABLE 2

TABLE 2. The positions of substituent for a few representative quinone molecules.

Figure 3A shows the effects of different substituent groups at the same substitution position. It can be found that substitution with –PO₃H₂, –SO₃H, –COOCH₃, –COOH groups reduces the solvation free energy regardless of the substituent positions. The ranking of different substituents’s solvation free energy reproduces that by quantum-chemistry calculations. For the HOMO-LUMO gaps, different substituent groups have less influence on the target properties at the substitution positions of R1-R7, while at the R8 substitution position, the HOMO-LUMO gaps are sensitive to different substituent groups. Specifically, all substitutions at the R1 position result in a higher HOMO-LUMO gap compared to substitutions at other positions, while substitution with groups such as –COOCH₃, –COOH, –SO₃H, –NO₂ at the R8 position can greatly improve the HOMO-LUMO gap.

Figure 3B shows the molecular properties of quinones with the same substituent group but at different substitution positions. The results predicted by the ML model are similar to those from the physics-based calculations. Regardless of the substitution positions, substitution with –F, –Cl, and–CH₃ groups have little impact on the solvation free energies of the quinone molecules. On the other hand, substitution with–PO₃H₂ and –SO₃H groups leads to a significant reduction of the solvation free energy. In this case, the result is highly dependent on the position of the substituent. The lowest solvation free energy can be obtained when the substitution takes place on positions R2, R5, and R6. In terms of the HOMO-LUMO gaps, most of the substituents have better performance in the substitution positions R1 and R8. For some poorly performing substituent groups, satisfactory target properties cannot be obtained even if they are in the R8 substitution position. The above results indicate the substituents at the R1 position can improve the HOMO-LUMO gap, and the more refined selection of the substituents at the R8 position may achieve more extraordinary effects.

The error graphs in Figure 3 suggest that the machine-learning (ML) model has a fairly high level of fidelity in reproducing the theoretical results. In the mono-substituted quinones with 1, 10-AQ as the backbone, most of the prediction error of the ML model for the solvation free energy is within 5%, and the maximum prediction error is ranged between –3 and 2 kcal/mol. And the prediction error of the HOMO-LUMO gap is mostly between –.2 and .2 eV. However, the prediction error of the model for the R8 substitute HOMO-LUMO gap is relatively significant. For a high-throughput screening tool, this relative error is still within our acceptable range.

Screening from over 100,000 candidates

To demonstrate the high-through capabilities of our computational framework, we used the trained Xgboost model to predict the solvation free energies and the HOMO-LUMO gaps for over 100,000 di-substitutions derived from the 17 quinone-based backbones. It took about 10 s to complete the predictions and rank all molecules according to the predicted values based on an 8-core personal computer. In contrast, it took over 3 days to complete the QM calculation of the solvation free energy and HOMO-LUMO gap of a single di-substituted quinone molecule with a single CPU. We see an increase in calculation speed by 7 orders of magnitude!

The predicted results are shown in Figure 4. Here the predicted solvation free energies for all di-substituted quinone molecules is generally within –25 and –10 kcal/mol, and the predicted value of the HOMO-LUMO gap is between 5 and 9 eV. To normalize the evaluation of molecular properties and to make comparisons more easily, the potential of the molecule as a battery active material is scored by .5 × Solvation Free Energy/–30 + .5 × HOMO-LUMO gap/10. The detailed calculation results are available in Supplementary Table S3.

FIGURE 4

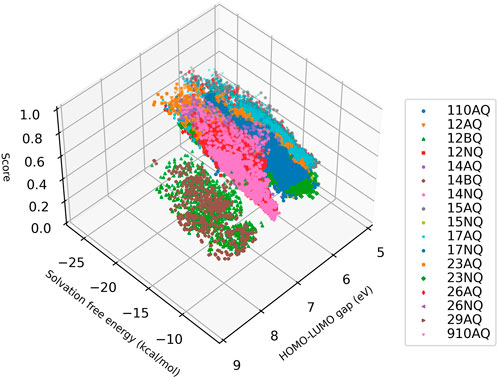
FIGURE 4. A score of over 100,000 virtual quinone molecules. The score is defined as .5 × Solvation Free Energy/–30 + .5 × HOMO-LUMO gap/10.

As shown in Figure 4, different quinone-based backbones have a great impact on molecular properties. The di-substituents of the 1, 2-benzoquinone (BQ) and 1, 4-BQ backbones generally yield high HOMO-LUMO gaps. However, the optimal value of solvation free energy they can achieve is not as good as the molecules produced by other backbones. The backbones with better overall performance include 1, 2-AQ, 1, 4-AQ, 1, 5-AQ. These quinone molecules can attain low solvation-free energy and high HOMO-LUMO gap simultaneously, and thus can be used as candidate materials for quinone-based flow batteries for experimental verification.

To further explore the common features of quinone-like molecules with different scores, we selected 10,000 molecules each with the highest, lowest and medium scores from more than 100,000 molecules, and analyzed the effects of backbones and substituents, as shown in Figure 5. We did not perform an in-depth analysis of the relationship between the score and the position of the substituents due to the difficulty in unifying the positions of the substituents on different backbones.

FIGURE 5

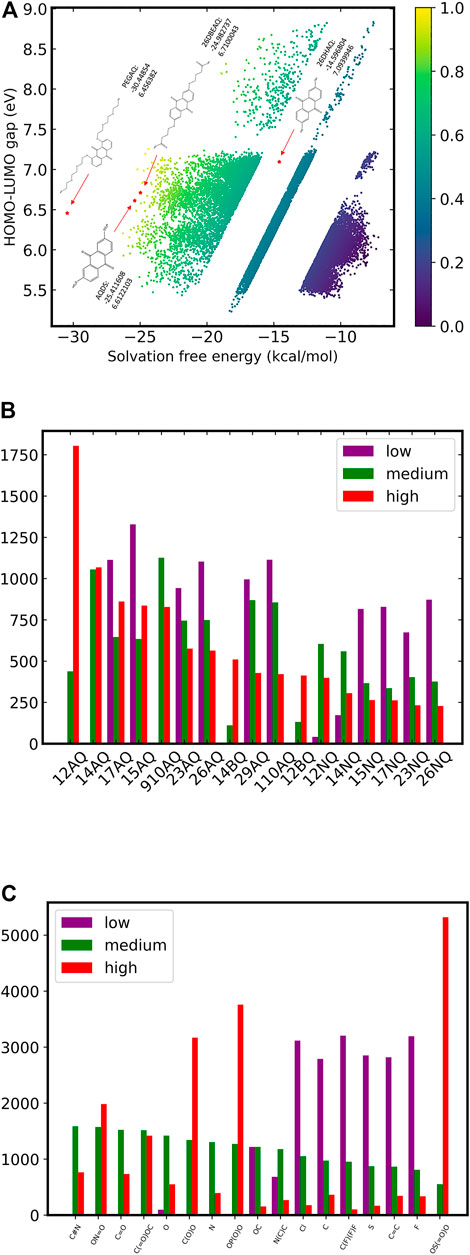
FIGURE 5. Virtual molecular library scoring and analysis of results. (A) Scoring chart for di-substituted quinones and reported quinone-based electrode materials; (B) Backbone distribution in three types of scoring molecules; (C) Distribution of substituent types in three types of scoring molecules.

Figure 5 shows the statistics of the backbones and substituent types according to three different levels of di-substituted molecule populations. As discussed above, most high-scoring molecules consist of the di-substitutions of 1, 2-AQ and 1, 4-AQ backbones. While all 17 backbones can get medium and high scores of quinone molecules, no di-substitutions constructed by the five backbones of 1, 2-AQ, 1, 4-AQ, 9, 10-AQ, 1, 4-BQ and 1, 2-BQ appear in the low-scoring group. In terms of the choice of substituent types, the large-scale tests can better reflect the influence of different substituents on molecular properties. In the high-scoring group, substituents with –SO₃H, –PO₃H and–COOH groups account for nearly half of the molecules, and the molecules obtained by their substitution will not be given low scores. The effect of –Cl, –CH₃, –CF₃, –SH, –F, –C₂H₃ is obviously not suitable substituents for quinone-based electrolytes, and the scores of molecules generated by their substitution are generally at a low level.

Combining the above two points, adjusting the –SO₃H, –PO₃H, and –COOH groups on the basis of the 1, 2-AQ or 1, 4-AQ backbone is expected to obtain battery materials with higher HOMO-LUMO gap and lower solvation free energy. From Figure 5A, we can also see that among all the above 100,000 quinone molecules, almost none have achieved satisfactory performance in terms of both solvation-free energy and the HOMO-LUMO gap at the same time. In terms of our scoring system for the entire di-substituted quinones, based on the statistical distribution of the two molecular properties, we believe that for a good alternative molecule as battery active material, it must be in at least the top 10% for each property, i.e., have a HOMO-LUMO gap of more than 7 eV and a solvation free energy of less than −20 kcal/mol, which means it must be in the top left corner of the scoring table in the gap region of the current material. Unfortunately, only a very few di-substituted molecules have been able to meet this criterion. In addition, we also used the same model to predict the corresponding properties of quinone-based battery materials that have been reported in the literature (Chen T. et al., 2015; Lin et al., 2015; Kwabi et al., 2018; Jin et al., 2019). The full cell performance data consisting of the above material-based composition is compiled in Supplementary Table S4. As shown in Figure 5A, all the materials that have been verified by experiments, but not in our data set samples, get high scores under the evaluation of this model, which means that our machine learning model has certain accuracy for the screening ability of battery materials. For PEGAQ {1, 8-bis [2- (2- (2- hydroxyethoxy) ethoxy) ethoxy] anthracene-9, 10-dione}, the modification of the PEG substitution greatly reduces the solvation free energy of the anthraquinone (AQ) molecules, which makes the molecule obtain a high evaluation score, but its HOMO-LUMO gap is actually in the lower-middle position in the whole evaluation system. For 26DHAQ (2, 6-dihydroxy-9, 10-anthraquinone), although it does not appear to be in a dominant position, it actually has the highest predicted voltage, except that the hydroxyl modification cannot bring a great improvement in solubility for the backbone molecule. In fact, it is reasonable to consider whether the modification of the molecule in the upper right corner of the scoring diagram with PEG could result in a new molecule that is good in both target properties. In addition, there are a number of molecules in the sample set of di-substituted substances that we have constructed to obtain scores comparable to them, showing that there is still a lot of room to find in the screening of battery materials, not to mention that the data set we constructed is only within the limited backbone and limited substituent types.

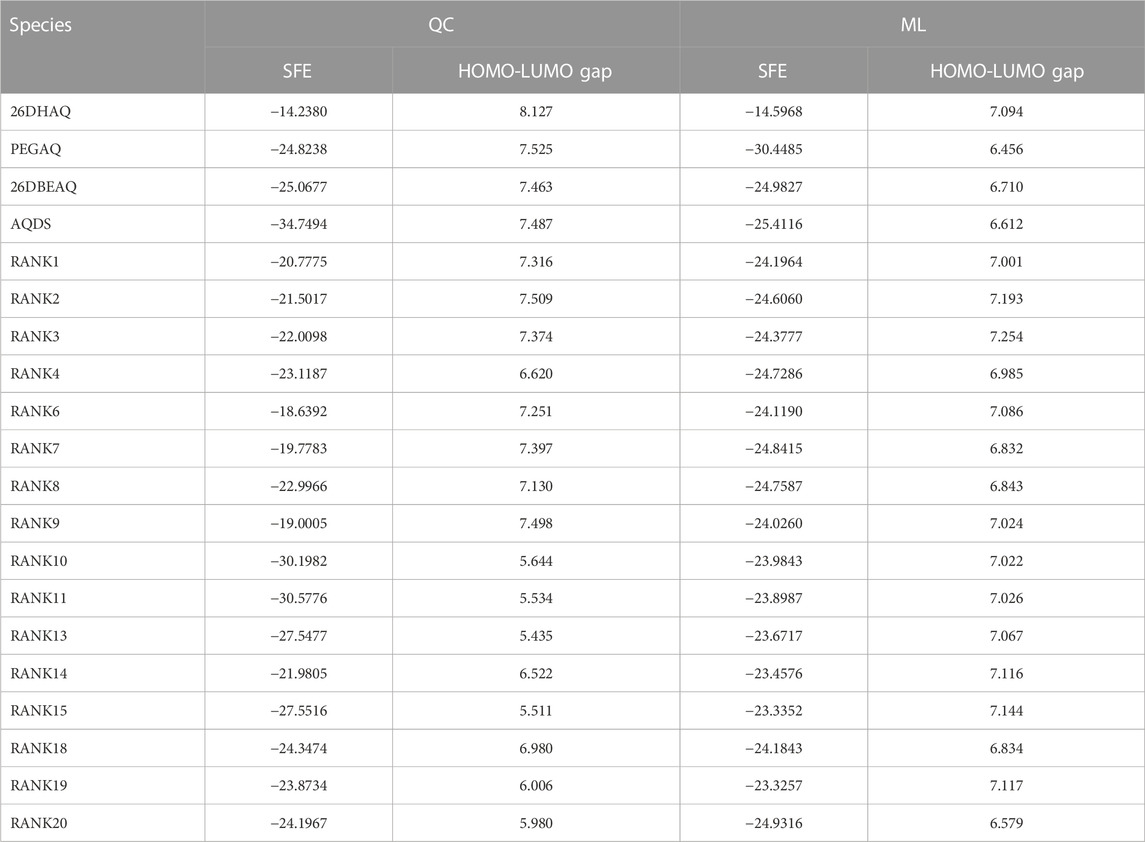
We also calculated the corresponding properties of the four molecules mentioned above and the top 20 high-scoring molecules in the virtual screening library using quantitative calculations (Li et al., 2016), where the molecules ranked 5th, 12th, 16th, and 17th were not optimized during the consistent quantitative calculations due to structural stability issues, and the final data are listed in Table 3. The properties obtained from ML predictions are generally highly comparable to quantitative calculations, and the average relative errors between the predicted and theoretically calculated values in the 20 samples are 13.73% and 11.77% for the solvation free energy and HOMO-LUMO gap, respectively, with some performance degradation compared to the results on the test set during modeling, which may be caused by the limitations of the data set itself. Since the samples used for modeling were mono-substituted quinone molecules and eventually used for predicting di-substituted molecules, slightly beyond the application domain of the model, resulting in a decrease in prediction accuracy. In principle, we should supplement the dataset by quantifying the properties of a large number of di-substituted quinone molecules to expand the application of the model, but the problem is that the structures of such molecules are not stable and their structures are difficult to converge during quantification, resulting in the inability to obtain the desired molecular properties, which is the biggest difficulty we face when doing further research.

TABLE 3

TABLE 3. Comparison of quantitative calculation results with ML predicted results.

Conclusion

In this work, we constructed a virtual database of quinone small molecules with quinone molecular backbones and predefined substituents, and further constructed a database of their structural properties by combining theoretical calculations. Then we combined machine learning tools to build an artificial intelligence model for fast prediction of target properties from molecular structure and verified the accuracy of the machine learning model for predicting the solvation free energy and HOMO-LUMO gap of quinone molecules, as well as its ability to reduce quantification and density functional theory calculation results. Through the analysis of the calculation results, we discussed the influence of the quinone backbone, the position of the substituent, and the type of the substituent on the characteristics of the quinone molecule, which proved that the machine learning method can be used as a high-throughput screening method for flow battery active materials with much higher efficiency than the theoretical calculation. Based on a model for rapid property prediction, we constructed over 100,000 virtual quinone molecules, evaluated their performance as active substances in redox flow batteries, and compared them with some molecules reported in the literature. Actually, all molecules, both virtual and real, have not been able to obtain sufficient advantages in solubility and open-circuit voltage at the same time, which also indicates that there is still much room for research on the development of active materials for redox flow batteries. The predictive model of molecular target properties and the effect of substituents and substitution positions on the properties of the backbone molecule can quickly help us to find the direction of molecular property improvement and assist in the design and development of new molecules with better performance.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

FW, JL, and DL contributed to conception and design of the study. FW and JL organized the database. FW performed the machine learning model construction. FW wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work is supported and sponsored by the National Natural Science Foundation of China (No. U1862204). The numerical calculations were performed at the “Tianhe-2” platform supported by Guangzhou Supercomputer Centre.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fceng.2022.1086412/full#supplementary-material

References

Allam, O., Kuramshin, R., Stoichev, Z., Cho, B., Lee, S., and Jang, S. (2020). Molecular structure–redox potential relationship for organic electrode materials: Density functional theory–machine learning approach. Mater. Today Energy 17, 100482. doi:10.1016/j.mtener.2020.100482

CrossRef Full Text | Google Scholar

Chen, T., He, T., Benesty, M., Khotilovich, V., Tang, Y., Cho, H., et al. (2015). Xgboost: Extreme gradient boosting. R package version 0.4-2 1 (4), 1–4.

Google Scholar

Chen, Q., Gerhardt, M. R., Hartle, L., and Aziz, M. J. (2015). A quinone-bromide flow battery with 1 W/Cm2 power density. J. Electrochem. Soc. 163 (1), A5010–A5013. doi:10.1149/2.0021601jes

CrossRef Full Text | Google Scholar

Darling, R. M., Gallagher, K. G., Kowalski, J. A., Ha, S., and Brushett, F. R. (2014). Pathways to low-cost electrochemical energy storage: A comparison of aqueous and nonaqueous flow batteries. Energy & Environ. Sci. 7 (11), 3459–3477. doi:10.1039/c4ee02158d

CrossRef Full Text | Google Scholar

Eckroad, S., and Gyuk, I. (2003). EPRI-DOE handbook of energy storage for transmission & distribution applications. Washington, DC: Electric Power Research Institute, Inc, 3–35.

Google Scholar

Er, S., Suh, C., Marshak, M. P., and Aspuru-Guzik, A. (2015). Computational design of molecules for an all-quinone redox flow battery. Chem. Sci. 6 (2), 885–893. doi:10.1039/c4sc03030c

PubMed Abstract | CrossRef Full Text | Google Scholar

Hasewend, B., and Jokic, T. (2020). “How the European green deal promotes sustainable energy research and innovation,” in Solar energy conversion in communities. Springer proceedings in energy. Editors I. Visa, and A. Duta (Cham: Springer International Publishing), 455–456. doi:10.1007/978-3-030-55757-7_32

CrossRef Full Text | Google Scholar

Hawkins, J. M., and Robbins, T. (2001). A field trial of a vanadium energy storage sys tem. Edinburgh, United Kingdom: IET, 652–656.

Google Scholar

Huskinson, B., Marshak, M. P., Suh, C., Er, S., Gerhardt, M. R., Galvin, C. J., et al. (2014). A metal-free organic–inorganic aqueous flow battery. Nature 505 (7482), 195–198. doi:10.1038/nature12909

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, S., Jing, Y., Kwabi, D. G., Ji, Y., Tong, L., De Porcellinis, D., et al. (2019). A water-miscible quinone flow battery with high volumetric capacity and energy density. ACS Energy Lett. 4 (6), 1342–1348. doi:10.1021/acsenergylett.9b00739

CrossRef Full Text | Google Scholar

Kwabi, D. G., Lin, K., Ji, Y., Kerr, E. F., Goulet, M.-A., De Porcellinis, D., et al. (2018). Alkaline quinone flow battery with long lifetime at PH 12. Joule 2 (9), 1907–1908. doi:10.1016/j.joule.2018.08.013

CrossRef Full Text | Google Scholar

Li, J., Fu, J., Huang, X., Lu, D., and Wu, J. (2016). Predicting hydration free energies of amphetamine-type stimulants with a customized molecular model. J. Phys. Condens. Matter 28 (34), 344001. doi:10.1088/0953-8984/28/34/344001

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Wang, J., Wang, Y., Lu, D., and Wu, J. (2020). A Multiscale procedure for predicting the hydration free energies of polycyclic aromatic hydrocarbons. J. Chem. Eng. Data 65 (4), 2206–2211. doi:10.1021/acs.jced.0c00061

CrossRef Full Text | Google Scholar

Li, T., Xing, F., Liu, T., Sun, J., Shi, D., Zhang, H., et al. (2020). Cost, performance prediction and optimization of a vanadium flow battery by machine-learning. Energy & Environ. Sci. 13 (11), 4353–4361. doi:10.1039/d0ee02543g

CrossRef Full Text | Google Scholar

Li, J., Xu, H., Wang, J., Wang, Y., Lu, D., Liu, J., et al. (2021). Theoretical insights on the hydration of quinones as catholytes in aqueous redox flow batteries. Chin. J. Chem. Eng. 37, 72–78. doi:10.1016/j.cjche.2021.06.016

CrossRef Full Text | Google Scholar

Li, S., Huang, K., Liu, S., Fang, D., Wu, X., Lu, D., et al. (2011). Effect of organic additives on positive electrolyte for vanadium redox battery. Electrochimica Acta 56 (16), 5483–5487. doi:10.1016/j.electacta.2011.03.048

CrossRef Full Text | Google Scholar

Lin, K., Chen, Q., Gerhardt, M. R., Tong, L., Kim, S. B., Eisenach, L., et al. (2015). Alkaline quinone flow battery. Science 349 (6255), 1529–1532. doi:10.1126/science.aab3033

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, X., Guo, Y., Cheng, J., Guo, Z., and Yan, X. (2017). An improved extreme learning machine model and state-of-charge estimation of single flow zinc-nickle battery. Springer, 613–622.

CrossRef Full Text | Google Scholar

Ma, X., Zhang, H., Sun, C., Zou, Y., and Zhang, T. (2012). An optimal strategy of electrolyte flow rate for vanadium redox flow battery. J. power sources 203, 153–158. doi:10.1016/j.jpowsour.2011.11.036

CrossRef Full Text | Google Scholar

Narayan, S. R., Nirmalchandar, A., Murali, A., Yang, B., Hoober-Burkhardt, L., Krishnamoorthy, S., et al. (2019). Next-generation aqueous flow battery chemistries. Curr. Opin. Electrochem. 18, 72–80. doi:10.1016/j.coelec.2019.10.010

CrossRef Full Text | Google Scholar

Neese, F. (2012). The ORCA Program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2 (1), 73–78. doi:10.1002/wcms.81

CrossRef Full Text | Google Scholar

Pham-Truong, T., Wang, Q., Ghilane, J., and Randriamahazaka, H. (2020). Recent advances in the development of organic and organometallic redox shuttles for lithium-ion redox flow batteries. ChemSusChem 13 (9), 2142–2159. doi:10.1002/cssc.201903379

PubMed Abstract | CrossRef Full Text | Google Scholar

Remick, R. J., and Ang, P. G. P. (US4485154ANovember 271984). Electrically rechargeable anionically active reduction-oxidation electrical storage-supply system. Available from: https://patents.google.com/patent/US4485154A/en (accessed 06 24, 2022).

Google Scholar

Robles, J., Sotelo, F., Rojas, C., Hurtado, J., and Lopez, J. (2021). “Performance analysis of XGBoost models with ultrafast shape recognition descriptors in ligand-based virtual screening,” in 2021 8th International Conference on Bioinformatics Research and Applications, 8–14.

CrossRef Full Text | Google Scholar

Sánchez-Díez, E., Ventosa, E., Guarnieri, M., Trovò, A., Flox, C., Marcilla, R., et al. (2021). Redox flow batteries: Status and perspective towards sustainable stationary energy storage. J. Power Sources 481, 228804. doi:10.1016/j.jpowsour.2020.228804

CrossRef Full Text | Google Scholar

Singh, V., Kim, S., Kang, J., and Byon, H. R. (2019). Aqueous organic redox flow batteries. Nano Res. 12 (9), 1988–2001. doi:10.1007/s12274-019-2355-2

CrossRef Full Text | Google Scholar

Skyllas-Kazacos, M., and Grossmith, F. (1987). Efficient vanadium redox flow cell. J. Electrochem. Soc. 134 (12), 2950–2953. doi:10.1149/1.2100321

CrossRef Full Text | Google Scholar

Tsekouras, G., Anastasopoulos, C., Kanellos, F., Kontargyri, V., Karanasiou, I., Salis, A., et al. A demand Side management Program of vanadium redox energy storage system for an interconnected power system; 2008; pp 26–28.

Google Scholar

Xiong, Z., Wang, D., Liu, X., Zhong, F., Wan, X., Li, X., et al. (2019). Pushing the Boundaries of molecular representation for Drug Discovery with the graph attention mechanism. J. Med. Chem. 63 (16), 8749–8760. doi:10.1021/acs.jmedchem.9b00959

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, D., Wang, L., Yuan, P., An, Q., Su, B., Yu, M., et al. (2022). Cocrystal virtual screening based on the XGBoost machine learning model. Chin. Chem. Lett., 107964. doi:10.1016/j.cclet.2022.107964

CrossRef Full Text | Google Scholar

Ye, J., Xia, L., Wu, C., Ding, M., Jia, C., and Wang, Q. (2019). Redox targeting-based flow batteries. J. Phys. D. Appl. Phys. 52 (44), 443001. doi:10.1088/1361-6463/ab3251

CrossRef Full Text | Google Scholar

Zade, S. S., Zamoshchik, N., and Bendikov, M. (2011). From short conjugated oligomers to conjugated polymers. Lessons from studies on long conjugated oligomers. Accounts Chem. Res. 44 (1), 14–24. doi:10.1021/ar1000555

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Deng, T., and Jia, G. (2020). Nuclear spin-spin coupling constants prediction based on XGBoost and LightGBM algorithms. Mol. Phys. 118 (14), e1696478. doi:10.1080/00268976.2019.1696478

CrossRef Full Text | Google Scholar

Zhong, F., Yang, M., Ding, M., and Jia, C. (2020). Organic electroactive molecule-based electrolytes for redox flow batteries: Status and challenges of molecular design. Front. Chem. 8, 451. doi:10.3389/fchem.2020.00451

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, H., Zhang, H., Zhao, P., and Yi, B. (2006). A comparative study of carbon felt and activated carbon based electrodes for sodium polysulfide/bromine redox flow battery. Electrochimica Acta 51 (28), 6304–6312. doi:10.1016/j.electacta.2006.03.106

CrossRef Full Text | Google Scholar