- 1Department of Chemical Engineering, Prairie View A&M University, Prairie View, TX, United States
- 2Oak Ridge National Laboratory, Oak Ridge, TN, United States
There is increased interest in many different processes based upon interactions between a charged solid surface and a liquid electrolyte. Energy storage in capacitive porous materials, ionic membranes, capacitive deionization (CDI) for water desalination, capacitive energy generation, removal of heavy ions from wastewater streams, and geophysical applications are some examples of these processes. Process development is driven by the production of porous materials with increasing surface area. Understanding of the physical phenomena occurring at the charged solid-electrolyte interface will significantly improve the design and development of more effective applied processes. The goal of this work is to critically review the current knowledge in the field. The focus is on concepts behind different models. We start by briefly presenting the classical electrical double layer (EDL) models in flat surfaces. Then, we discuss models for porous materials containing macro-, meso-, and micro-pores. Some of the current models for systems comprising two different pore sizes are also included. Finally, we discuss the concepts behind the most common models used for ionic transport and Faradaic processes in porous media. The latter models are used for simulation of electrosorption processes in porous media.
1 Introduction
In many scientific disciplines such as engineering, electrochemistry, biology, geophysics, and colloidal science the understanding of the physical phenomena related to processes in charged porous media is critical [(Johnson and Sen, 1988; Dukhin, 1995; Revil and Glover, 1997; Lyklema and Minor, 1998; Revil and Glover, 1998; Corry et al., 2003; Bazant et al., 2004), among others]. The first step to understand these phenomena is to have a clear physical picture. The charge present in a solid surface creates an equivalent charge of opposite sign in the electrolyte in contact. This charge arrangement is a common feature of many different natural or manufactured systems and receives the name of electrical double layer (EDL) (Helmholtz, 1853; Stern, 1924; Bockris et al., 1963; Bockris et al., 1998; Newman and Thomas-Alyea, 2004; IUPAC, 2019). The goal of the present article is to present a physical picture of transport processes in charged porous media with the intention of improving many important practical processes, such as, water desalination, ion separation, electrokinetics, sustainable energy systems, etc.
The article has been divided in three parts: electrical double layers (EDLs) in flat surfaces, qualitative model descriptions in porous materials, and transport models in porous carbon electrodes and intercalation materials. The first part is a review of the state of the art in this well-studied research area. The second attempts to present the qualitative picture of ionic distribution in porous media, and the third is a compilation of concepts related to porous electrodes and applications of porous electrodes. In the last part we introduce descriptions of new developed porous electrodes materials plus subsections focused on the simulation methods to describe the behavior of individual porous electrodes and desalination cells. In recent years, there has been a big increase in the number of articles dealing with theoretical and practical applications in this research area; therefore, it is very difficult to remain current on all the work continuously produced. The omission of some important articles and/or research groups is not intended as a judgement on the merit of these research groups work.
2 EDL models
2.1 EDLs in flat surfaces
The concepts presented in this section applies to flat electrodes and to porous materials where the pore size is much bigger than the curvature of the surface (big pores). The presence of a charged surface in contact with an electrolyte will produce a re-arrangement of charges in the liquid phase. Ions with the same charge as the solid surface (co-ions) will be repelled while ions of opposite charge (counter-ions) will be attracted to the surface. Molecules of the solvent, water for example, can also be oriented in a particular direction due to the presence of the surface charge. The level of orientation will depend upon the local electric field that is determined by the surface charge or the applied potential. Classical models of the EDL were originally derived for flat solid surfaces (Helmholtz, 1853; Stern, 1924; Bockris et al., 1963; Bockris et al., 1998; Newman and Thomas-Alyea, 2004; IUPAC, 2019). Critical understanding of the structure of the EDL was achieved through the work of Grahame (Grahame, 1947) who experimentally determined the differential capacity of mercury in contact with aqueous solutions of sodium fluoride as a function of concentration. Several different models were proposed to reproduce Grahame’s experimental data (Bockris et al., 1963; Bockris et al., 1998).
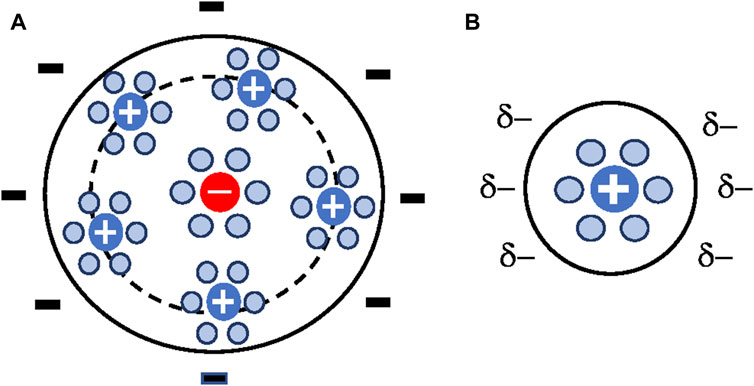
Presently, there is general agreement on the model depicted in Figure 1. The region between the solid surface and the inner Helmholtz plane contains a layer of solvent molecules and/or some specifically (chemically) adsorbed ions. According to IUPAC, the inner Helmholtz plane (IHP) is the locus of the electrical centers of specifically adsorbed ions (IUPAC, 2019). There is a layer of counterions located, on average, a distance from the electrode equal to the hydrated radius of the counterion. The outer Helmholtz plane (OHP) is the locus of the electrical centers of these ions (IUPAC, 2019). In the diffuse layer the ions follow a Boltzmann distribution and there is a net charge given by the counterions concentration (Landau and Lifshitz, 1980).
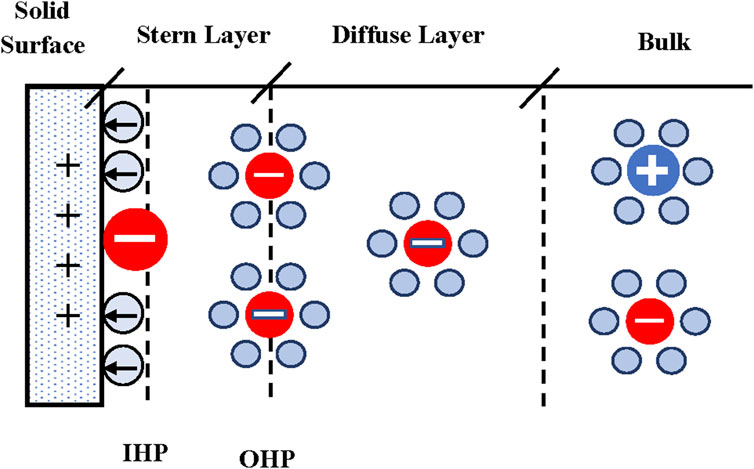
FIGURE 1. Flat surface EDL model schematic. Circles with signs represent ions, red circles represent chemically adsorbed ions, blue circles represent water molecules, blue circles with arrows represent electrically polarized water molecules, and ions surrounded by water molecules represent hydrated ions.
3 Ionic distribution in porous materials
According to the International Union of Pure and Applied Chemistry (IUPAC) (Rouquerol et al., 1994), pores sizes are classified according to effective pore diameters into macro (>50 nm), meso (between 50 and 2 nm), and micro (<2 nm). Presently, many porous materials are said to have nanopores. The characteristic dimension of a nanopore is 1 nm; however, nanopores can have effective diameter sizes up to 20 nm (Akeson et al., 1999). In this regard, according to the IUPAC classification nanopores sizes vary in a range from micropore size until medium mesopores sizes. Inside pores of any size EDLs will form in the interface between the solid wall and the liquid electrolyte. The EDL thickness can be estimated as a function of the solution ionic strength and the permittivity of the solution.
In the case of macropores, the EDL thickness is normally much smaller that the effective pore diameter, e.g., thin EDLs (Bockris et al., 1998; Newman and Thomas-Alyea, 2004; Biesheuvel and Bazant, 2010). Most of the pore volume is filled by an electroneutral electrolyte and there is small film (thin EDL) against the solid wall where there is a net ionic charge. The mathematical treatment of thin EDLs processes involves considering the EDL as a boundary condition and deals with the electroneutral bulk of the electrolyte (Bockris et al., 1998; Newman and Thomas-Alyea, 2004; Biesheuvel and Bazant, 2010). As we decrease the effective pore diameter, the EDL occupies an increasing part of the pore volume while the volume of the bulk of the solution decreases continuously. In the case of micropores, the EDLs occupy completely all the pore volume and strongly interact among themselves. This process is called EDL overlapping. Yang et al. (2001) presented an EDL model to predict electrosorption of ions from aqueous solutions by carbon aerogel electrodes. The carbon aerogel electrodes were treated as EDL capacitors, and electrosorption was modeled using classical EDL theory in slit-shaped pores. The authors concluded that when a pore has a width smaller than a specific value (cutoff pore width), it does not contribute to the total capacity because of the electrical double-layer overlapping effect. This effect would reduce the electrosorption capacity for electrodes with significant numbers of micropores. Ying et al. (2002) performed several equilibrium electrosorption experiments under various conditions of ion solution concentration and applied voltage. They considered the overlapping effect in their modeling by solving numerically the Poisson equation with appropriate boundary conditions. The authors modeling results agreed well with experimental data obtained at voltages up to 1.2 V, when the EDL overlapping correction was used. Several issues need to be considered regarding this study. Common hydrated ions have diameter sizes of the same order of magnitude of small nanopores; therefore, the assumption of a continuum solution is not valid anymore. Recognizing this shortcoming, Yang et al. (2002) studied the formation of the EDL in an aqueous solution in contact with the charged solid surfaces of a slit-type nanopore using grand canonical Monte Carlo (GCMC) and canonical Monte Carlo (CMC) methods. Their results were found to be slightly different from those predicted by the Gouy–Chapman model at low electrolyte concentrations and low surface charge densities. Yang et al. (2002) found, using a non-primitive model, that the walls are covered by water molecules and that the maximum counterion concentration in the nanopores occurs at the center of the pore, instead of the surfaces. These studies supported the idea that the best strategy for increasing capacitance of porous materials consisted in maximizing the EDL charging by using mesoporous carbon electrodes with the highest specific surface area. The authors’ work (Yang et al., 2002) reflected experimental data showing that the capacitance of porous materials decreases as the pore diameter decreases until being negligible for pores sizes smaller than 1 nm. However, Chmiola et al. (2006) discovered that their manufactured carbide-derived carbons (CDCs) electrodes with unimodal micropores smaller than 1.0 nm exhibit an anomalous increase in capacitance compared to similar materials with pore sizes above 2.0 nm. Therefore, Chmiola et al., 2006) results challenged the idea that pores smaller than the size of the solvated electrolyte ions do not contribute to the charge-storage process in porous electrodes. In their review on the fundamentals of supercapacitors Da Silva et al. (2020) stated that Koresh and Soffer (1977) were the first authors to report that the sub-nanometer micropores with average sizes as small as 0.37 nm could be accessed by the electrolyte ions due to the removal of the hydration shells of ions occurring during the charging process. However, the authors also stated that the mobility of ions inside the sub-nanometer micropores can be several orders of magnitude smaller than their mobility in the bulk solution outside the pores.
Feng et al. (2010a) studied ionic absorption in porous materials using organic ionic compounds. The authors experimental data indicated that organic ions tend to be desolvated before entering sub-nanometer pores, whereas aqueous electrolyte ions can retain their hydration shell in sub-nanometer pores. Grifn et al. (2014) used 19F NMR spectroscopy to study the local ionic environment in supercapacitor electrodes and to measure changes in the populations of adsorbed species during micropores charging. The authors reported that in absence of an applied potential, anionic species adsorbed within electrode micropores. Adsorption experiments and two-dimensional exchange experiments confirmed that anions are in dynamic equilibrium between the inside of the micropores and the outside solvent environment.
Grifn et al. (2014) proposed three mechanisms for ionic charging within the micropores of a porous electrode, Figure 2. One possible mechanism is the absorption of counter-ions from the solution outside the pores while the number of co-ions inside the pores remains unchanged. This is the traditional charging mechanism. Other possible mechanism is ion exchange between the inside of the pore and the outside solution where the combination of co-ion expulsion and counter-ion adsorption produces a net ionic charge inside the pores, while the total ionic population remains constant. Finally, a third possible mechanism is given by the expulsion of co-ions, thereby leaving an excess of counter ions within the pores at a reduced overall packing density (Grifn et al., 2014). The authors also concluded that a combination of the three mechanisms is also possible. Forse et al. (2016) presented a single model to consider the three mechanisms presented by Grifn et al. (2014). The authors introduced a charging mechanism parameter (X) that characterizes the charging process, a value X = 1 represents counter-ion absorption only, a value X = 0 represents ionic exchange, and X = −1 represents co-ion desorption only. As the parameter X is continuous, other values of X describe different combinations of the three mechanisms. Forse et al. (2016) concluded that the charging mechanism strongly depends on the polarization conditions, the electrolyte, and electrode materials. During the charging process the solution ions can lose partially, or totally, their solvated shell. This process consumes a significant amount of energy.
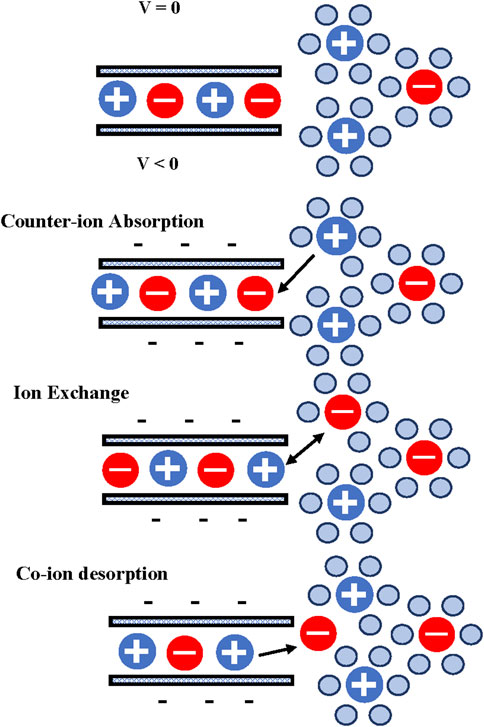
FIGURE 2. Charging mechanisms in micropores [adapted from Griffin et al. (Griffin et al., 2014)].
Kalluri et al. (2013) reported that the gain in storage capacity of ions in micropores pores comes with an efficiency penalty as the degree of charge compensation is lower in small pores than in bigger ones. The energy that is necessary to distort the solvation shell adds to the electrical work needed to charge the micropores. This effect may decrease the charging energy efficiency if the energy that is stored in the distortion of the solvation shell is dissipated as heat during the discharging step (Kalluri et al., 2013).
The findings of Chmiola et al. (2006) produced the desire to study ionic distributions inside micropores. Huang et al. (2008a), Huang et al. (2008b) proposed a heuristic theoretical model that takes pore curvature into account to replace EDL capacitors models (EDLC) based on a traditional parallel-plate capacitor. The authors studied pores of cylindrical shape. Huang et al. (2008a), Huang et al. (2008b) stated that when the pore diameter is of mesopore size (2–50 nm), counterions enter mesoporous carbon materials and approach the pore wall to form an electric double-cylinder capacitor (EDCC); for micropores (<2 nm), solvated/desolvated counterions line up along the pore axis to form an electric wire-in-cylinder capacitor (EWCC). In the case of macropores (>50 nm) the pore curvature is no longer significant and the EDCC model can be reduced naturally to the traditional EDLs model. The authors presented density functional theory calculations and analyses of available experimental data to show the significant effects of pore curvature on the supercapacitor properties of nanoporous carbon materials. A schematic of these models is shown in Figure 3.
The application of the “electric wire-in-cylinder capacitor” (EWCC) model has been questioned since the carbon micropores are actually ‘slit-shaped’ rather than “cylindrical” (Fryer, 1981). Thus, considering carbon micropores as slits with varying widths is more consistent with real experimental conditions, even considering that carbon electrodes have a strongly disordered structure (Hsieh et al., 2015). An alternative model for microporous carbons was presented by Feng et al. (2010b) studying the capacitance of slit-shaped micropores. The authors presented a model where the ions align at the center plane between the slit walls. This model was called “sandwich-type” (SP), Figure 4. Feng et al. (2010b) predicted the scaling of the slit pore capacitance as a function of pore width. The authors proposed that this model could predict the anomalous enhancement of capacitance verified for micropores with similar widths. However, Feng et al. (2010b) found that “curvature effects” cannot be neglected to quantitatively fit experimental data. Heimböckel et al. (2019) proposed a new model for the normalized capacitance depending on pore sizes, using a combination of a SP model for micropores and EDCC for larger pores. The model was called, “modified electric sandwich double-cylinder capacitor” (MESDCC). The model was validated by comparing the measured capacitance values of a set of prepared activated carbons in organic electrolytes with simulated values. The authors verified that pores below 1.0 nm provide the largest contribution to the overall capacitance, especially pores around 0.74 and 0.90 nm, thus confirming the effect of an anomalous increase of capacitance for pores with the size of bare tetraethylammonium ions (TEA+), while pores between 3.4 and 3.7 nm provide the lowest contribution to the capacitance (Heimböckel et al., 2019). These results confirmed that in preparing electrode materials increasing the proportion of micropores, compared to mesopores, will increase the capacitance. However, from the practical point of view, maximizing the capacitance is difficult, as an increase in specific surface area is associated with a simultaneous enlargement of pore sizes, which neutralizes the effect on the capacitance.
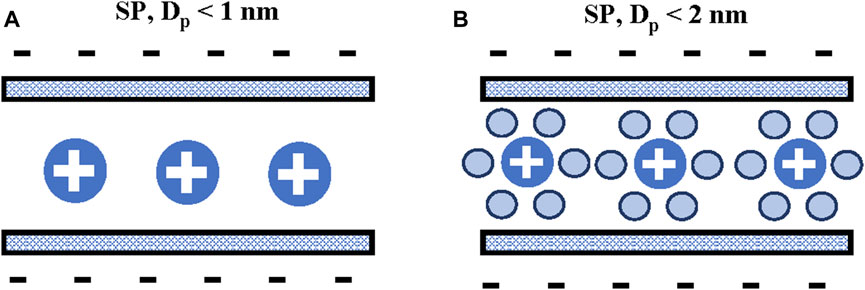
FIGURE 4. Sandwich-type capacitor (SP) in slit pores, (A) dehydrated ions in small pores and (B) hydrated ions in bigger pores.
At the same time, Da Silva et al. (2020) pointed out that the accessible surface area remains a key factor regarding the capacitance. There must be a large surface area, but this storage area should also be accessible by a big number of ions. It is now accepted that in porous electrodes micropores (<2 nm) provide a large surface area for ion storage, while mesopores (2–50 nm) and macropores (>50 nm) facilitate ion transport and act like sources of ions under ideal polarizations conditions (Saha et al., 2013; Zhang et al., 2013; Karthik et al., 2014; Hsieh et al., 2015).
Recently, Gamaethiralalage et al. (2021) reviewed ion storage mechanisms studying ionic removal selectivity in electrodes of different materials.
3.1 Equilibrium relationships in interphases
3.1.1 Carbon porous materials
In the case of carbon porous materials which exhibit a dual-porosity structure (macropores and micropores) Biesheuvel et al. (2011); Biesheuvel et al. (2012); Biesheuvel and Dykstra (2021) presented an equilibrium model that has become very popular, the Donnan model. This simple and elegant model relates the concentrations inside a porous material and in the bulk of the solution outside through the Donnan potential difference (
Here,
Similarly, to the case of “thin” EDLs the potential drop in the overlapped EDL in porous media has also two components, a charge-free Stern layer and the Donnan potential (
In the case of heavily overlapped EDLs there is charge neutrality between the charge at the electrode wall (
Here,
In the case of binary, monovalent salts, Eq. 3 can be written as:
Here,
The Donnan potential can be calculated from Eq. 4 as:
3.1.2 Functionalized carbon porous materials
Several authors have studied the concept of improving electrode performance by addition of chemical groups to the base electrode material [(Xu et al., 2011; Andelman, 2014; Biesheuvel et al., 2015; Mahmudov et al., 2015; Palko et al., 2018; Uwavid et al., 2022), among others]. The original idea came from similar practices used in functionalization of ion-exchange membranes (Xu et al., 2011). Cationic and anionic functionalized electrodes can be prepared by absorption of surfactant molecules on carbon materials (Andelman, 2014; Palko et al., 2018). A common procedure involves soaking the carbon electrode in separate surfactant solutions at room temperature. This procedure is based upon the fact that surfactants have hydrophobic tails which irreversibly adsorb onto carbon (Hei, 2006), thereby providing an easy and non-toxic technique to introduce the functional groups. Sulfate and carbonate groups are typically used as anionic chemical groups while quaternary amine chemical groups are used as cationic groups (Palko et al., 2018).
The charge efficiency describes the percentage of applied charge that goes to ion storage. Ionic membranes have been added to increase charge efficiency by excluding the co-ions from the electrode (Biesheuvel et al., 2010; Biesheuvel and van der Wal, 2010; Biesheuvel and Dykstra, 2021). During the process the externally provided charge is used to attract counterions and to eject co-ions (Biesheuvel and Bazant, 2010). Andelman (Andelman, 2014) stated that attached immobile ionic groups would exclude co-ions and increase coulombic (charge) efficiency without the need for an added charge barrier membrane. The author concluded that capacitive electrodes functionalized with ionic groups become polarized and are intrinsically more coulombically efficient (Andelman, 2014). Biesheuvel et al. (2015) presented a simple theoretical model to explain experiments that using chemically modified electrodes showed unexpected phenomena such as “inverted CDI, enhanced CDI, and inversion peaks.” The authors’ model explained these disparate experimental observations. In the case of classical CDI, the electrode charge is balanced by counterion absorption while co-ion rejection represents a non-useful “parasitic” process. However, the presence of immobile charges of the same sign as the electrode, negative for the cathode or positive for the anode, will suppress co-ion rejection during the charging step leading to improve electrode performance. In the case of immobile charges of different sign as the electrode, positive for the cathode or negative for the anode, during the charging step the main ionic transport mechanism will be co-ion rejection leading to the salt expulsion (inverted mode). Biesheuvel et al. (2015) also reported a previously undiscovered operational regime characterized by higher salt adsorption (extended voltage CDI).
The authors modified Eq. 2 according to semiconductor/water interface description and salinity gradient theory [(Jiang and Stein, 2011; Brogioli et al., 2013; Fleharty et al., 2014), among others] to obtain:
Here,
3.1.3 Intercalation materials
Ion storage inside porous electrodes can occur through two main mechanisms. The most common ion storage mechanism, known as non-Faradaic or capacitive adsorption, relies on the adsorption of ions inside the electrical double layers (EDLs) of carbon-based active materials with high specific surface area, 1,000–3,000 m2/g (Cheng et al., 2011). A second mechanism (Faradaic) uses accumulation of electrical charges mainly as the result of fast reversible redox reactions (Faradic pseudo-capacity) (Biesheuvel et al., 2021). A big increased in the total adsorption capacity has been observed by materials that combine both mechanisms (Lee et al., 2014; Yoon et al., 2017; Zhang et al., 2018). Porous carbon electrodes store ions mainly, by ion adsorption in EDLs while intercalation materials allow the absorption and free movement of ions through the interstitial pores inside the lattice structure of the material. In this way intercalation materials store electric charge in the crystal lattice structure (Biesheuvel and Dykstra, 2021). Among the most used intercalation materials are sodium transition metal oxides (NaTMO), sodium iron pyrophosphate, Prussian blue analogues, graphene, for the capture of cations and conductive polymers (polypyrrole or polyaniline), Ag/ACl, BiOCl, for the absorption of anions, among others (Biesheuvel et al., 2021).
The EDL models presented above are equilibrium relationships between the bulk of a solution and adsorbed chemical species on a thin volume or interface. In charged materials these models can be considered extensions of absorption isotherms due to the inclusion of potential as an extra variable (Biesheuvel and Dykstra, 2021). The Frumkin isotherm derived using regular solution theory describes the adsorption equilibrium for molecules in the bulk of a solution and adsorbed at an interface (Levi and Aurbach, 1999):
Here,
In the case of charged particles, Biesheuvel and Dykstra (2021) presented a derivation of the extended Frumkin isotherm. This isotherm is related to the Van der Waals equation of state (EOS) and similar EOSs, especially the Carnahan-Starling EOS.
Here,
The occupancy ratio of the adsorption layer can be defined as
Here,
4 Transport models in charged porous electrodes
4.1 Introduction
In the previous sections we have established a qualitative picture of ion storage in charged porous materials. In this section we try to review the most common models for ion transport and storage reported in the literature. The different theoretical models to simulate transport phenomena in charged porous media can be classified in two main groups, phenomenological models based on general and/or empirical assumptions, and models based on rigorous mathematical methods of upscaling transport phenomena in charged porous media. Several upscaling techniques can be used to study transport in porous media, multi-scale asymptotic expansions, mathematical homogenization, spatial averaging, moment methods, stochastic-convective approaches, various Eulerian and Lagrangian perturbation schemes, projection operators, renormalization group techniques, space transformational methods, continuous time random walks, etc. (Cushman et al., 2002). In this work we will concentrate on the volume averaging technique as there are several relevant applications published in literature (Whitaker, 1999; del Rìo and Whitaker, 2002a; Schmuck and Bazant, 2014; Gabitto and Tsouris, 2015; Gabitto and Tsouris, 2016; Gabitto and Tsouris, 2017; Gabitto and Tsouris, 2018; Gabitto and Tsouris, 2019).
4.2 General models in capacitive porous electrodes
The article by Johnson and Newman (Johnson and Newman, 1971) presented for the first time a porous electrode model that considered the characteristic properties of capacitive ionic transport. The authors considered adsorption of ions in electrical double layers and concluded that in the absence of concentration gradients the system behaves as a network of resistances and capacitances. The authors also suggested the important concept that a porous system could show different behavior at different length scales; for example, transient behavior at the macroscale and steady-state behavior at the microscale (Johnson and Newman, 1971).
Biesheuvel and Bazant (Biesheuvel and Bazant, 2010) presented a model for capacitive charging and desalination by ideally polarizable porous electrodes. This model excluded effects of Faradaic reactions or specific adsorption of ions. The authors discussed the theory for the case of a dilute, monovalent, binary electrolyte using the Gouy-Chapman-Stern (GCS) model of the EDL. The model is strictly valid in the limit of “thin EDLs” and applies to big pores (macropores and mesopores >10 nm). The authors mentioned in their paper the use of a volume averaging technique, but they did not present derivations that support this claim. Therefore, the model should be considered as based upon qualitative concepts of the volume averaging methodology (Whitaker, 1999). Biesheuvel and Bazant (Biesheuvel and Bazant, 2010) presented the following equations:
Here, zi is the ionic charge,
Here,
A charge balance for the same electrolyte leads to:
Here,
The last terms in Eqs 11, 12 can be replaced by the rate of change of the excess salt concentration in the EDL (
Gabitto and Tsouris (Gabitto and Tsouris, 2015) studied the ionic transport process in homogeneous porous electrodes using a volume averaging method formulation (Whitaker, 1999). The method of volume averaging is a homogenization technique that is used to derive continuum equations for multiphase systems. Equations that are valid in a particular phase can be spatially smoothed to produce equations that are valid everywhere in the domain (Whitaker, 1999). The volume averaging methodology not only allows for the derivation of the continuum equations but provides a way to estimate the transport coefficients appearing in the derived equations by solving the necessary closure problems.
Based upon the same constraints, the equations derived by Gabitto and Tsouris (Gabitto and Tsouris, 2015) were identical to the ones reported by Biesheuvel and Bazant (Biesheuvel and Bazant, 2010). The authors also derived an alternative formulation of the same problem.
The Biesheuvel and Bazant (Biesheuvel and Bazant, 2010) model was extended to include Faradaic reactions and a dual-porosity (macropores and micropores) approach (Biesheuvel et al., 2011; Biesheuvel et al., 2012) which considers that the electrodes are made of porous solid particles. This model has become very popular, and it has been used by many different researchers in many different studies [(Biesheuvel et al., 2010; Biesheuvel and van der Wal, 2010; Biesheuvel et al., 2011; Biesheuvel et al., 2012; Biesheuvel et al., 2014; Porada et al., 2014; Biesheuvel and Dykstra, 2021), among others]. It has also been extended to other research areas as ionic flow in membranes (Biesheuvel et al., 2010; Biesheuvel and van der Wal, 2010) and flow capacitive deionization [(Porada et al., 2014; Nativ et al., 2017), among others]. Suss et al. (2015) reviewed critically the CDI technology discussing these issues. The authors also discussed equilibrium and kinetic modeling aspects of the different CDI processes.
Biesheuvel et al. (2011), Biesheuvel et al. (2012) proposed the following equations:
Here,
Biesheuvel et al. (2014) improved the mD model by making the ionic attraction term dependent on total ion concentration in the carbon pores. The new model significantly improved the agreement of calculated results and experimental data for the operation of CDI processes. Gabitto and Tsouris (Gabitto and Tsouris, 2016) presented a model to simulate the CDI process in heterogeneous porous media comprising macro- and micropores. The authors used a two-step volume averaging technique to derive the averaged transport equations at both length scales. The authors derived a one-equation model, valid for both phases, based on the principle of local equilibrium [(del Rìo and Whitaker, 2002a; Whitaker, 1986; Whitaker, 1991; Quintard and Whitaker, 1995), among others] and approximate models for each phase (Gabitto and Tsouris, 2016). Gabitto and Tsouris (Gabitto and Tsouris, 2018) derived using a more precise theoretical procedure the two-equation model equations for the dual-porosity porous medium. The authors found out that these equations coincided with the equations originally proposed by them in their previous work (Gabitto and Tsouris, 2016).
Gabitto and Tsouris (Gabitto and Tsouris, 2018) derived the following equations for the liquid (γ-phase) and the solid (κ-phase) in the macropores:
Here,
Here,
The two-equation model derived by Gabitto and Tsouris (Gabitto and Tsouris, 2018) can be compared to the phenomenological formulation of Biesheuvel et al. (2011), Biesheuvel et al. (2012) by using the following assumptions:
• There are no transport processes inside the micropores. This assumption is justified on the grounds of the micropores sizes. The characteristic time for a transport process is proportional to the square of the micropores characteristic length, for example,
• The transport terms in Eq. 16 depend upon the average concentration in both phases. We can neglect the terms that depend on the solid (κ-phase) by using the classical assumption that the transport terms depend only upon the liquid (γ-phase) variables.
• Using the equality given by Eq. 20.
Introducing all the assumptions listed above into Eqs 16, 17 leads to:
Equation 21 is like Eq. 14 presented by Biesheuvel et al. (2011), Biesheuvel et al. (2012). However, these equations are not identical as the time variation of the average concentration in the solid (κ-phase) is not equal to the average concentration in the micropores (
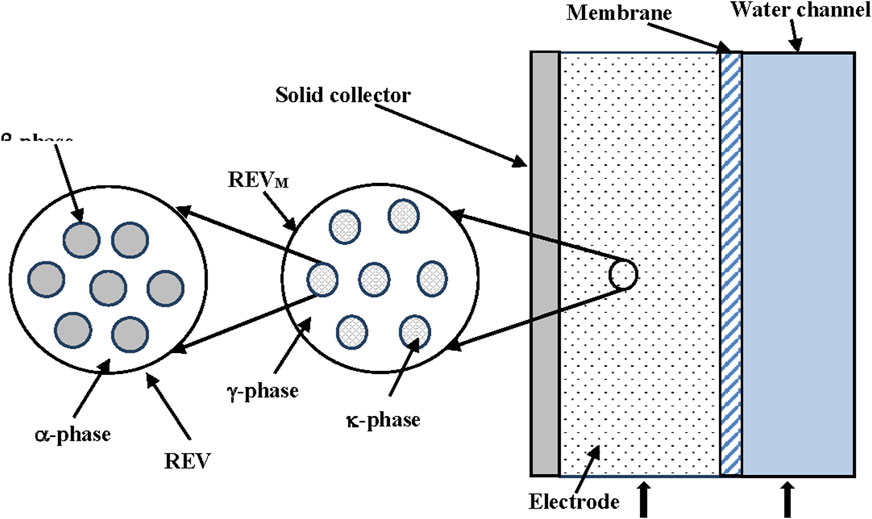
The two kinds of representative volumes (REVs) are shown in Figure 5.
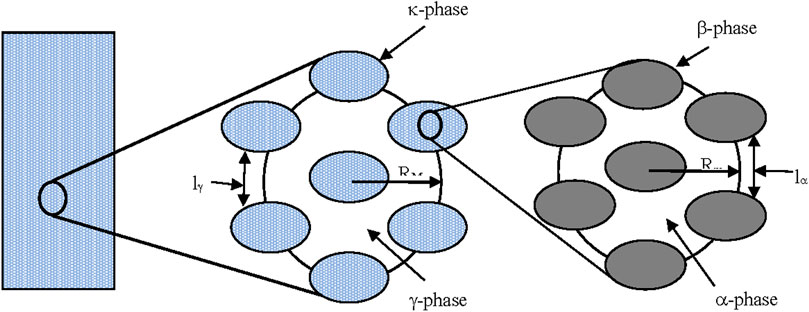
FIGURE 5. Schematic representation of the two-scales model, from ref. (Gabitto and Tsouris, 2018).
The small REV allows calculation of averaged concentrations inside the solid particles (Rm). Using the Donnan model we can assume that the ion concentrations are constant inside the solid particles (
It is important to stress that not only the three assumptions listed above must hold for Eq. 21 to be valid. Equation 16 and Equation 17 were derived by Gabitto and Tsouris (Gabitto and Tsouris, 2018) using also other constraints that are listed in reference (Gabitto and Tsouris, 2018). These constraints need also to be satisfied for Eq. 21 to be valid. Gabitto and Tsouris (Gabitto and Tsouris, 2018) also derived expressions to calculate the values of the transport coefficients appearing in Eq. 21 using the closure procedure in the volume average technique.
In recent years, there has been an exponential growth in the number of articles discussing different cell configurations and mechanisms to improve the CDI and related processes. Some researchers review critically the literature to summarize recent developments [(Suss et al., 2015; Tang et al., 2019a), among others]. New cell structures comprise the use of ion exchange membranes (MCDI) (Biesheuvel et al., 2010; Biesheuvel and van der Wal, 2010; Galama et al., 2016; Hassanvand et al., 2017; Tang et al., 2019b), flow through electrodes (FTE CDI) (Suss et al., 2012; Guyes et al., 2017), fluidization electrodes (Doornbusch et al., 2016), flow-electrode capacitive deionization (FCDI) without (Hatzell et al., 2014), and with membranes (Jeon et al., 2013; Porada et al., 2014; Choo et al., 2017; Rommerskirchen et al., 2017; Ma et al., 2018).
There has been increased interest in the use of ion exchange membranes in combination with porous electrodes. Several cell configurations have been proposed for water desalination using ion exchange membranes placed in front of porous electrodes allowing the passage of counterions while restricting the flow of co-ions. The process received the name membrane capacitive deionization (MCDI). Biesheuvel et al. (2010) proposed a theory for MCDI including the electrostatic EDLs inside the micropores of porous particles, but also incorporating the role of the macropores, i.e., the void space between the particles. In MCDI the macro porosity becomes a salt storage reservoir that increases the ion storage capacity of the electrodes. The authors used modified Donnan model to simulate ion transport between macro- and micropores. The cell configuration studied by the authors is shown in Figure 6. There is a central water channel, and each electrode is separated from the water channel by an ionic membrane. Horizontal (x-axis) mass flows were only considered by using an average flow while vertical (y-axis) were considered by dividing the domain into k-ideally stirred volumes without diffusion mass transport. This assumption is justified as the height of electrodes, membranes, and water channel is much higher than the respective thicknesses. Convective transport in the y-direction inside the water channel is also higher than the corresponding diffusive transport.
In the membrane Biesheuvel et al. (2010) assumed linear ionic mass flows. The total ionic flow through the membrane (
Here,
Here,
The ionic current flowing through the membrane is given by:
Here,
In the water channel the authors used the following equation:
Here,
In Eq. 26 the y-direction concentration changes by the convective transport in the y-direction, last term in the right-hand-side, and by the average ionic flow in the x-direction.
The flow in the electrodes was simulated by using a simplified version of Biesheuvel et al. (2014) model. For example, ionic mass flows are calculated by:
Here,
Galama et al. (2016) studied theoretically and experimentally the membrane potential generated by different ionic concentration in both sides of an ion exchange membrane. The authors reported an elegant derivation of the Teorell-Meyer-Sievers (TMS) equation The authors extended the theory considering the presence of stagnant layers on both sides of the membrane and differences in ionic mobility between co-ions and counterions inside the membrane.
Tang et al. (2019b) studied experimentally and theoretically saltwater desalination by an MCDI technique. The salt removal capacity of carbon electrodes is limited due to the high ionic concentration of seawater. The authors proposed to overcome this limitation by applying over-potentials, close to the Faradaic limit, and by reversing cell polarity in the ion-desorption step. The proposed technique (OP-MCDI-RP) was found to be acceptable for seawater desalination (Tang et al., 2019b). Tang et al. (2019b) used a cell like the one depicted in Figure 6. The authors simulated the process by a combined approach. They simulated the operation of the membrane by using Biesheuvel et al. (2010) membrane model, Eqs 23, 25. They simulated the flow inside the water channel by 1-D mass balance in the y-direction using the assumption of average x-direction ionic flows. The operation of the porous electrodes was simulated using the one-equation model presented by Gabitto and Tsouris (Gabitto and Tsouris, 2018).
Here,
Tang et al. (2019b) reported very good agreement between experimental data and simulation results using the capacity of the Stern layer (
Here,
Besides the use of membranes to improve the CDI process other configurations have been tried. Suss et al. (2012) proposed a cell configuration where the brackish feed flows through the electrodes in the direction of the applied electric field (FTE CDI). The authors used an electrode made up of carbon aerogel monoliths. They found that this configuration exhibits low flow resistance and high capacitance. They modelled the mass and charge balances using equations like the 1D heat equation, but the mass balance contains a sink term dependent on potential that couples both equations. Suss et al. (2012) concluded that the desalination process operates with a characteristic timescale equal to the cell’s RC constant.
Guyes et al. (2017) presented a 1-D model of water desalination by an FTE CDI cell based on the modified Donnan electric double layer theory and simplified boundary conditions. The authors reported good agreement for a comparison between experimental data measured using a laboratory FTE CDI cell and their simulation results. This agreement was obtained by simulating the experimental data using the capacity of the Stern layer, the micropore volume, and the attraction energy term as fitting parameters. Guyes et al. (2017) formulated mass balances for each ion species using Eq. 14 without a redox reaction and considering convective flow. In the case of a monovalent, binary electrolyte the total mass balance is calculated by adding the cation and anion differential equations while the net charge equation is derived by subtracting the anion equation from the cation one, to give:
where
Rommerskirchen et al. (2017) reported a constant voltage a process model for a continuous, steady state FCDI process. The process involves a single module device operating in single-pass model. The system comprises, a central water channel plus two flow-through electrodes each one separated from the water channel by an ion exchange membrane. The electrodes are made of flowing porous conductive porous particles. The membranes are considered ideally permselective so, only allow flow of the counterions into the flow electrodes. Reduction of flow through the membrane can occur due to mass transfer limitations in the water channel-membrane interphase [concentration polarization (Ma et al., 2018)]. A limiting current density occurs when the ion concentration on the membrane surface is reduced to zero. The authors allowed for this phenomenon by calculating the limiting flow in a stagnant boundary layer on the water channel side. This limiting flow is compared to the unlimited flow through the membrane and the smaller value is selected.
The electrodes are considered as homogeneous carbon suspensions with constant particle concentration and void fraction. Charge neutrality is assumed outside the particles, macropores volume, while there is net ionic charge inside the porous particles, micropores volume, balanced by the induced charge on the particles’ solid matrix. The storage of ions in the micropores of the carbon flowing particles was modeled using the modified Donnan model of Biesheuvel et al. (2011), Biesheuvel et al. (2012). Inside the porous particles the potential drop is divided between a Stern layer region without ionic charge and a region with potential drop given by the modified Donnan model. The potential drop through the various parts of the cell was considered by relating the cell potential to the sum of all ohmic potential losses.
Here,
Rommerskirchen et al. (2017) reported good agreement between experimental data and simulation results calculated using the Stern layer capacity as the only fitting parameter. The authors also studied an operating process comprising 2 cells one operating in charging mode and the other in discharging mode. They reported a strong influence of flow rate on the desalination performance.
Tang et al. (2019c), Tang et al. (2020) studied experimentally and theoretically the influence of applied potential and electrolyte concentration on the FCDI and electrodialysis (ED) desalination processes. The model presented by the authors relied upon the same general framework presented by Rommerskirchen et al. (2017) but the operation of the flow electrodes was based upon the “hybrid” model for flow electrodes by Gabitto and Tsouris (Gabitto and Tsouris, 2019), and the membrane operation was modelled after Galama et al. (2016).
Gabitto and Tsouris (Gabitto and Tsouris, 2019) simulated the operation of slurry carbon electrodes by combining a phenomenological approach for the point equations with a two-steps volume averaging method. This ‘hybrid approach’ led to the formulation of the equations describing the operation of flow electrodes. The authors used the macroscale REV shown in Figure 6. The γ-phase and κ-phase represent the liquid and solid particles, respectively.
Equation 34 and Eq. 35 are valid in the γ-phase. In Eq. 34 the authors defined a total mass parameter,
The system of Eqs 34, 35 requires calculation of the derivatives of cκ and ρκ. Gabitto and Tsouris (Gabitto and Tsouris, 2019) proposed that:
The Donnan potential (
Here, CStern is the surface capacitance of the Stern Layer,
4.3 General models in intercalation materials
4.3.1 Introduction
Recently, there has been an exponential increase on research projects using redox reactions, Faradaic processes, to improve different kinds of practical applications [(Johnson et al., 1970; Cheng et al., 2011; Pasta et al., 2012; Lee et al., 2014; Smith, 2016; Yoon et al., 2017; Zhang et al., 2018; Singh et al., 2019; Liu et al., 2020a; Wang and Lin, 2020; Younes and Zou, 2020; Biesheuvel et al., 2021; Liu et al., 2021); among others]. The authors will not attempt to cover all developments, but they will focus on the main ideas. It was already mentioned that ion storage inside porous electrodes occurs through two main mechanisms. Non-Faradaic or capacitive adsorption occurs by storage of ions inside the electrical double layers (EDLs) of carbon-based active materials. A second mechanism (Faradaic) uses accumulation of electrical charges inside the interstitial cavities of crystalline materials as the result of fast reversible redox reactions (Faradic pseudo-capacity) (Biesheuvel et al., 2021). A big increased in the total adsorption capacity has been observed by using materials that combine both mechanisms (Lee et al., 2014; Yoon et al., 2017; Zhang et al., 2018; Liu et al., 2020a). The use of Faradaic processes to increase the porous electrodes capacitance was first suggested by Johnson et al. (1970). Until recently however, no significant research has been carried out. Zhang et al. (2018) identified three types of Faradaic processes. Type I are anodic oxidation reactions. The most relevant is the oxidation of the carbon electrode matrix that decreases performance through time. Type II comprises reduction reactions that occur in the cathode. The most common is oxygen reduction. The third type includes all Faradaic ion storage processes in which pseudocapacitive/intercalation effects are used to store ions through reversible redox reactions (Zhang et al., 2018). The materials exhibiting this behavior receive the name of intercalation materials. Many of these materials are sodium oxides and sulfites of transition metals NaTiO2, NaMnO2, NaRuO2, NaIrO2, NaTiS2 or their combinations, sodium iron pyrophosphate, and Prussian blue analogues, among others. These materials are mostly used for the capture of cations due to their strong negative charge densities. Conductive polymers (polypyrrole or polyaniline), Ag/ACl, and BiOCl, are used for anions adsorption (Zhang et al., 2018). Intercalation materials trap ions in the interstitial pores inside the lattice structure of the material. In this way, an intercalation material stores electronic charge in the crystal lattice structure. The ions in the electrolyte are attracted and retained inside the crystal structure by fast redox reactions [(Zhang et al., 2018; Singh et al., 2019; Liu et al., 2020a; Wang and Lin, 2020; Liu et al., 2021); among others], as shown in Figure 7. The trapped ions can move by solid diffusion between different sites and leave the intercalation material if the applied charge is changed (Zhang et al., 2018).
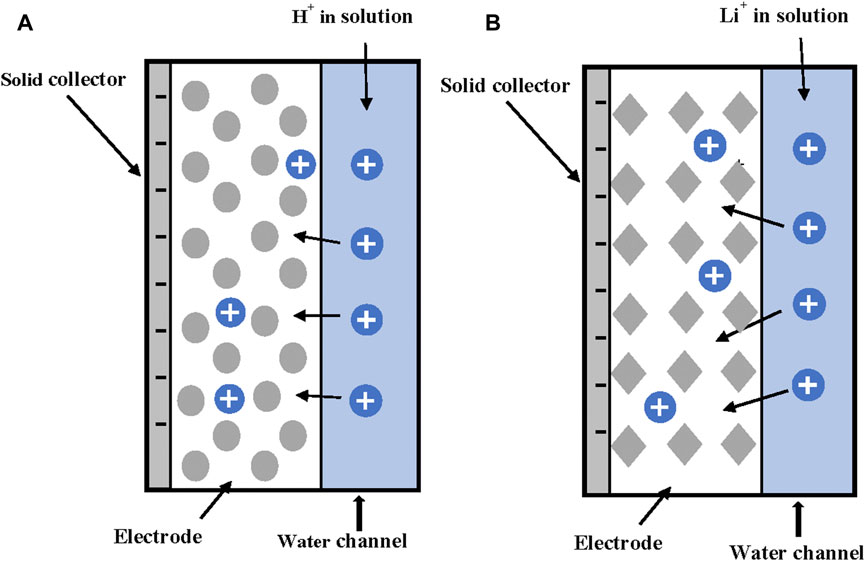
FIGURE 7. (A) Redox pseudocapacitance electrode and (B) Intercalation pseudocapacitance electrode. Adapted from ref. (Zhang et al., 2018).
Singh et al. (2019) presented a chronological review of the use of intercalation materials in water desalination by capacitive deionization technologies. The authors also provide some insights into cell architectures and values of operation parameters.
Improving ion capture has been the driving force for materials and process development (Biesheuvel et al., 2011; Singh et al., 2019; Liu et al., 2020a; Wang and Lin, 2020; Liu et al., 2021). Several cell configurations have been tried to achieve this goal (Pasta et al., 2012; Smith, 2016; Chen et al., 2017; Su et al., 2017; Su and Hatton, 2017; Kim et al., 2018; Younes and Zou, 2020). Pasta et al. (2012) were the first to propose the concept of a “desalination battery,” which operates by extracting sodium and chloride ions from seawater to produce fresh water. The desalination battery uses two Faradaic electrodes, a sodium-manganese oxide (Na2-xMn5O10) cathode and an Ag/AgCl anode electrode. The cathode is used for capturing sodium ions while the anode captures chloride ions. The authors reported high absorption ion capacity with acceptable energy consumption. Several attempts were made to combine Faradaic and non-Faradaic electrodes [(Biesheuvel and van der Wal, 2010; Biesheuvel et al., 2011; Biesheuvel et al., 2012; Chen et al., 2017; Su et al., 2017; Su and Hatton, 2017; Younes and Zou, 2020; Biesheuvel and Dykstra, 2021); among others]. These research studies combined a sodium-transition metal oxide Faradaic electrode with a porous carbon material electrode. These “hybrid” cell studies showed significant improvements in desalination capacity, long-term operation, and charge efficiency (Biesheuvel and van der Wal, 2010; Biesheuvel et al., 2011; Biesheuvel et al., 2012; Chen et al., 2017; Su et al., 2017; Su and Hatton, 2017; Younes and Zou, 2020; Biesheuvel and Dykstra, 2021). The addition of multi-channels and ion exchange membranes to the electrochemical cells allowed further improvements (Kim et al., 2018).
4.3.2 Simulation models
Two main approaches have been used to model CDI processes using cation intercalation materials (Liu et al., 2020b). One approach was based upon combining porous electrode theory formulations for rechargeable batteries with electrolyte flow (Fuller et al., 1994; Lai and Ciucci, 2011). These models coupled empirical reaction potentials with local intercalation rates using Butler-Volmer kinetics (Smith and Dmello, 2016; Smith, 2017; Liu and Smith, 2018) for different materials together with thin ion-exchange membranes. Smith and Dmello (Smith and Dmello, 2016) introduced the concept of a Na-Ion Desalination cell (NID) to desalinate NaCl from brackish and salt-water. The authors used a two-dimensional porous-electrode model to predict the performance of NID cells operating at medium and high salinity-levels by simulating electrolyte transport, membrane polarization, and electrochemical processes in the electrodes. The cell electrodes were separated by an anion selective membrane. The NID performance was calculated by neglecting side reactions, intercalant decomposition, membrane leakage, and competing cation-intercalation. Smith and Dmello (Smith and Dmello, 2016) reported improved performance, more salt adsorption, and less energy consumption, compared to traditional configurations.
Smith and Bazant (Smith and Bazant, 2017) presented a general multiphase porous electrode theory based on non-equilibrium thermodynamics to simulate battery operations. The authors used Cahn-Hilliard-type phase field models to describe the active materials with appropriate models of interfacial reaction kinetics. The ionic transport in the electrolyte phase was described by classical concentrated solution. Smith and Bazant (Smith and Bazant, 2017) showed that this formulation is compatible with Newman’s porous electrode theory with Butler-Volmer kinetics in the limit of solid solution active materials. The authors also included other models of faradaic reactions, such as Marcus-Hush-Chidsey kinetics for electron transfer at the electrodes. The full model was implemented in an open-source software package called “MPET.” Several example calculations were presented to illustrate the features of the developed software.
A second type of models based upon Nernst Planck theory describing ion transport across the porous electrode and inside the intercalation material has been presented (West et al., 1982; Ferguson and Bazant, 2012). The relation among solid electrode-electrolyte properties; electrode potential (relative to the electrolyte phase), ion concentration in solution, and intercalation degree (fraction of intercalation sites filled with cations), is given by the Frumkin isotherm (Biesheuvel et al., 2010; Heimböckel et al., 2019).
West et al. (1982) presented a model of a porous electrode made up by small particles, compared to the electrode thickness, of regular geometries homogeneously distributed assuring constant porosity and pore sizes. The authors assumed:
• The potential and concentration vary only along the length of the pores. Ionic transport in the electrolyte is represented by the one-dimensional Nernst-Planck equation.
• The ionic conductance of the solid phase is low compared to the electrolyte, so ionic transport by solid diffusion occurs only in the direction perpendicular to the pore length.
• Negligible space charge accumulation implying that electroneutrality can be applied in the derivation of the transport equations.
• Charge transfer overvoltages are negligible.
• Solid phase electronic conductivity is so high that the solid phase Fermi potential is constant.
• The insertion is described by an adsorption process with linear interaction term (Frumkin isotherm).
West et al. (1982) studied the dynamics of electrode charge or discharge using their model. The authors reported that electrolyte depletion produced by the ionic mobility of the not inserted ions is the main factor in the limitation of the capacity obtained during ionic discharge. Singh et al. (Nativ et al., 2017) presented a model for CDI using intercalation electrodes following Johnson and Newman (Johnson and Newman, 1971) and West et al. (1982). The authors neglected transport limitations within the intercalation material, a valid assumption for electrodes with small nanoparticles accessible on all sides by the ions in the electrolyte with fast insertion reactions (Ferguson and Bazant, 2012). Singh et al. (Nativ et al., 2017) studied a desalination cell which consists of two porous electrodes, two flow channels, and an anion-exchange membrane. A solution of monovalent ions was considered, with unequal diffusion coefficients for anions and cations. The authors solved the dynamic two-dimensional equations by assuming that advection of ions in the flow channel occurs only in the direction along the electrode and membrane. In all layers, diffusion and migration were only considered in the direction perpendicular to the water flow. The Frumkin isotherm was used to describe local chemical equilibrium of cations between the particles and electrolyte phases, for given electrode potentials. Singh et al. (Nativ et al., 2017) reported a dynamic variation of key parameters of the CDI process such as effluent salt concentration, the distribution of intercalated ions, cell voltage, and energy consumption.
5 Summary
Ion storage inside porous electrodes occurs through two main mechanisms. Non-Faradaic or capacitive adsorption occurs by storage of ions inside the electrical double layers (EDLs) of carbon-based active materials. A second mechanism (Faradaic) uses accumulation of electrical charges inside the interstitial cavities of crystalline materials as the result of fast reversible redox reactions (Faradic pseudo-capacity) (Mahmudov et al., 2015). Most of the published research has been done on capacitive processes on carbon or similar materials. The classical models of the EDL were derived for flat solid surfaces, or macropores. These models proposed the presence of a Stern layer between the solid surface and a layer of counterions located, on average, a distance from the electrode equal to the hydrated radius of the counterion. The outer Helmholtz plane (OHP) is the locus of the electrical centers of these ions. Inside the Stern layer there may be only water molecules and chemical adsorbed coions. Beyond the OHP there is a diffuse layer where the ions follow a Boltzmann distribution and there is a net charge given by the counterions concentration. The mathematical treatment of thin EDLs processes considers the EDL as a boundary condition and deals with an electroneutral bulk of the electrolyte. In the case of meso and micropores the EDLs increasingly occupy the pore volume and strongly interact among themselves leading to EDL overlapping.
In the early 2000s Ying et al. (2002) treated carbon aerogel electrodes as EDL capacitors, and electrosorption was modeled using classical EDL theory in slit-shaped pores. The authors concluded that when a pore has a width smaller than a specific value (cutoff pore width), it does not contribute to the total capacity because of the electrical double-layer overlapping effect. This conclusion was challenged by the work of Chmiola et al. (2006) who found that electrodes with unimodal micropores smaller than 1.0 nm exhibit an anomalous increase in capacitance compared to similar materials with bigger pore sizes. Chmiola et al. (2006) work led to several research projects that showed that ions can enter in micropores by partial/total removal of the solvation shell around hydrated ions. Grifn et al. (2014) proposed three mechanisms for ionic charging within the micropores of a porous electrode. The studies by Huang et al. (2008a), Huang et al. (2008b) on supercapacitors showed that for mesopores of cylindrical shape, counterions enter mesoporous carbon materials and approach the pore wall to form an electric double-cylinder capacitor (EDCC); for micropores of cylindrical shape, solvated/desolvated counterions line up along the pore axis to form an electric wire-in-cylinder capacitor (EWCC). However, carbon micropores are actually “slit-shaped” rather than “cylindrical” (Fryer, 1981). A model for slit-shaped microporous carbons was presented by Feng et al. (2010b) where the ions align at the center plane between the slit walls, “sandwich-type” (SP). The previous studies led to the currently accepted paradigm that in carbon porous electrodes micropores provide a large surface area for ion storage, while mesopores and macropores facilitate ion transport and act like sources of ions under ideal polarizations conditions (Saha et al., 2013; Zhang et al., 2013; Karthik et al., 2014; Hsieh et al., 2015).
The concept of improving electrode performance by addition of cationic and anionic chemical groups to the base electrode material has been studied [(Xu et al., 2011; Andelman, 2014; Biesheuvel et al., 2015; Mahmudov et al., 2015; Palko et al., 2018; Uwavid et al., 2022), among others]. Experimental studies showed performance improvement over classical CDI operation (Andelman, 2014; Palko et al., 2018; Uwavid et al., 2022). Biesheuvel et al. (2015) presented a simple theoretical model that showed that during the charging step the presence of immobile charges of the same sign as the electrode, negative for the cathode or positive for the anode, will suppress co-ion rejection leading to improve electrode performance. In the case of immobile charges of different sign as the electrode, positive for the cathode or negative for the anode, during the charging step the main ionic transport mechanism will be co-ion rejection leading to the salt expulsion (inverted mode).
In the case of carbon porous materials which exhibit a dual-porosity structure (macropores and micropores) Biesheuvel et al. (2011), Biesheuvel et al. (2012), Biesheuvel and Dykstra (2021) presented an equilibrium model, the Donnan model. This model relates the concentrations inside a porous material and in the bulk of the solution outside through the Donnan potential difference defined as the electrostatic potential inside the porous medium minus the potential in the solution outside the porous material. This model was extended to include Faradaic reactions and multi-ion transport in porous electrodes (Biesheuvel et al., 2011; Biesheuvel et al., 2012) and membranes (Biesheuvel et al., 2010; Biesheuvel and van der Wal, 2010). This model became very popular and was used to simulate operation of several different capacitive cell structures, for example, the use of ion exchange membranes (MCDI) (Biesheuvel et al., 2010; Biesheuvel and van der Wal, 2010; Galama et al., 2016; Hassanvand et al., 2017; Tang et al., 2019b), flow through electrodes (FTE CDI) (Suss et al., 2012; Guyes et al., 2017), fluidization electrodes (Doornbusch et al., 2016), flow-electrode capacitive deionization (FCDI) without (Hatzell et al., 2014), and with membranes (Jeon et al., 2013; Porada et al., 2014; Choo et al., 2017; Rommerskirchen et al., 2017), among others. Gabitto and Tsouris (Gabitto and Tsouris, 2015; Gabitto and Tsouris, 2016; Gabitto and Tsouris, 2017; Gabitto and Tsouris, 2018) used the method of volume averaging (Whitaker, 1999), to study several of the same systems studied by Biesheuvel et al. (2011), Biesheuvel et al. (2012), Biesheuvel and Dykstra (2021) using their phenomenological formulation. The equations derived using both methodologies generally coincided. However, in the case of dual-porosity materials, macro and micropores, Biesheuvel et al. (2011), Biesheuvel et al. (2012), Biesheuvel and Dykstra (2021) formulation should be used with care as the time variation of the average concentration in the porous solid is not equal to the average concentration in the micropores. Rommerskirchen et al. (2017) reported a constant voltage process model for a continuous, steady state FCDI desalination cell. This model was based on charge neutrality outside the particles, macropores volume, while there is net ionic charge inside the porous particles, micropores volume, balanced by the induced charge on the particles’ solid matrix. The storage of ions in the micropores of the carbon flowing particles was modeled using the modified Donnan model of Biesheuvel et al. (Feng et al., 2010b; Hsieh et al., 2015; Heimböckel et al., 2019). Tang et al. (2019c), Tang et al. (2020) studied experimentally and theoretically the influence of applied potential and electrolyte concentration on the FCDI and electrodialysis (ED) desalination processes. The authors used the general framework presented by Rommerskirchen et al. (2017) but the operation of the flow electrodes was based upon the “hybrid” model for flow electrodes by Gabitto and Tsouris (Gabitto and Tsouris, 2019) and the membrane model by Galama et al. (2016).
In recent years there have been many reports on development of Faradaic ion storage processes in which pseudocapacitive/intercalation effects are used to store ions through reversible redox reactions (Zhang et al., 2018). These intercalation materials trap ions in the interstitial pores inside the lattice structure of the material. Electrochemical cells that combine the use of capacitive and Faradaic electrodes show more efficient performances than those that use only capacitive electrodes. Singh et al. (2019) presented a chronological review of the use of intercalation materials in water desalination by capacitive deionization technologies and provided insights into cell architectures and values of operation parameters. Two main approaches have been used to model CDI processes using cation intercalation materials (Liu et al., 2020b). One approach was based upon combining porous electrode theory formulations for rechargeable batteries with electrolyte flow (Fuller et al., 1994; Lai and Ciucci, 2011). The other type of models is based upon Nernst Planck theory describing ion transport across the porous electrode and inside the intercalation material. The relation among electrode potential (relative to the electrolyte phase), ion concentration in solution, and intercalation degree (fraction of intercalation sites filled with cations), is given by an equilibrium equation [Frumkin isotherm (Levi and Aurbach, 1999; Biesheuvel and Dykstra, 2021)].
Further improvements in materials will lead to more efficient cells and new improved applications in this rapid developing field.
Author contributions
JG participated in methodology, literature search, and writing—original draft and CT participated in conceptualization, project supervision, and writing—review and editing.
Funding
This work was partially supported by a RISE Grant from the office of the Vice-President of Research at PVAMU and by the National Alliance for Water Innovation (NAWI), through funding from the U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy, Advanced Manufacturing Office, under Funding Opportunity Announcement DE-FOA-0001905.
Acknowledgments
Partial support to JG by a RISE Grant from the office of the Vice-President of Research at PVAMU is kindly acknowledged. Partial support to CT by NAWI is also acknowledged. This study was conducted at Prairie View A&M University and the Oak Ridge National Laboratory (ORNL). ORNL is managed by UT-Battelle, LLC under Contract No. DE-AC05-00OR22725 with the U.S. Department of Energy.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akeson, M., Branton, D., Kasianowicz, J. J., Brandin, E., and Deamer, D. W. (1999). Microsecond time-scale discrimination among polycytidylic acid, polyadenylic acid, and polyuridylic acid as homopolymers or as segments within single RNA molecules. Biophys. J. 77, 3227–3233. doi:10.1016/s0006-3495(99)77153-5
Andelman, M. (2014). Ionic group derivitized nano porous carbon electrodes for capacitive deionization. J. Mat. Sci. Chem. Eng. 2, 16–22. doi:10.4236/msce.2014.23002
Bazant, M. Z., Thornton, K., and Ajdari, A. (2004). Diffuse-charge dynamics in electrochemical systems. Phys. Rev. E. 70, 021506. doi:10.1103/physreve.70.021506
Biesheuvel, P. M., and Bazant, M. Z. (2010). Nonlinear dynamics of capacitive charging and desalination by porous electrodes. Phys. Rev. E. 81, 031502. doi:10.1103/physreve.81.031502
Biesheuvel, P. M., and Dykstra, J. E. Physics of electrochemical systems. http://www.physicsofeelectrochemicalprocesses.com (accessed August 11, 2021).
Biesheuvel, P. M., Fu, Y., and Bazant, M. Z. (2012). Electrochemistry and capacitive charging of porous electrodes in asymmetric multicomponent electrolytes. Russ. J. Electrochem. 48, 580–592. doi:10.1134/s1023193512060031
Biesheuvel, P. M., Hamelers, H. V. M., and Suss, M. E. (2015). Theory of water desalination by porous electrodes with immobile chemical charge. Colloid Interface Sci. Comm. 9, 1–5. doi:10.1016/j.colcom.2015.12.001
Biesheuvel, P. M., Porada, S., and Dykstra, J. E. (2021). The difference between Faradaic and non-Faradaic electrode processes. arXiv:1809.02930v4 [physics.chem-ph (accessed August 11, 2022).
Biesheuvel, P. M., Porada, S., Levi, M., and Bazant, M. Z. (2014). Attractive forces in microporous carbon electrodes for capacitive deionization. J. Solid State Electrochem. 18, 1365–1376. doi:10.1007/s10008-014-2383-5
Biesheuvel, P. M., and van der Wal, A. (2010). Membrane capacitive deionization. J. Membr. Sci. 546, 256–262. doi:10.1016/j.memsci.2009.09.043
Biesheuvel, P. M., Yu, F., and Bazant, M. Z. (2011). Diffuse charge and Faradaic reactions in porous electrodes. Phys. Rev. E 83, 061507. doi:10.1103/physreve.83.061507
Biesheuvel, P. M., Zhao, R., Porada, S., and van der Wal, A. (2010). Theory of membrane capacitive deionization including the effect of the electrode pore space. J. Colloid Interface Sci. 360, 239–248. doi:10.1016/j.jcis.2011.04.049
Bockris, J. O., Devanathan, M. A. V., and Müllen, K. (1963). On the structure of charged interfaces. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 274 (1356), 55–79.
Bockris, J. O., Reddy, A. K., and Gamboa-Aldeco, M. E. (1998). Modern electrochemistry 2B: Fundamentals of electrodics. Netherlands: Springer US.
Brogioli, D., Ziano, R., Rica, R. A., Salerno, D., and Mantegazza, F. (2013). Capacitive mixing for the extraction of energy from salinity differences: Survey of experimental results and electrochemical models. J. Colloid Interface Sci. 407, 457–466. doi:10.1016/j.jcis.2013.06.050
Chen, F., Huang, Y., Guo, L., Ding, M., and Yang, H. Y. (2017). A dual-ion electrochemistry deionization system based on AgCl-Na0.44MnO2 electrodes. Nanoscale 9, 10101–10108. doi:10.1039/c7nr01861d
Cheng, Q., Tang, J., Ma, J., Zhang, H., Shinya, N., and Qin, L.-C. (2011). Graphene and nanostructured MnO2 composite electrodes for supercapacitors. Carbon 49, 2917–2925. doi:10.1016/j.carbon.2011.02.068
Chmiola, J., Yushin, G., Gogotsi, Y., Portet, C., Simon, P., and Taberna, P. L. (2006). Anomalous increase in carbon capacitance at pore sizes less than 1 nanometer. Science 313, 1760–1763. doi:10.1126/science.1132195
Choo, K. Y., Yoo, C. Y., Han, M. H., and Kim, D. K. (2017). Electrochemical analysis of slurry electrodes for flow-electrode capacitive deionization. J. Electroanal. Chem. 806, 50–60. doi:10.1016/j.jelechem.2017.10.040
Corry, B., Kuyucak, S., and Chung, S.-H. (2003). Dielectric self-energy in Poisson-Boltzmann and Poisson-Nernst-Planck models of ion channels. Biophys. J. 84, 3594–3606. doi:10.1016/s0006-3495(03)75091-7
Cushman, J. H., Bennethum, L. S., and Hu, B. X. (2002). A primer on upscaling tools for porous media. Adv. Water Res. 25, 1043–1067. doi:10.1016/s0309-1708(02)00047-7
Da Silva, L. M., Cesar, R., Moreira, C. M. R., Santos, J. H. M., De Souza, L. G., Morandi Pires, B., et al. (2020). Reviewing the fundamentals of supercapacitors and the difficulties involving the analysis of the electrochemical findings obtained for porous electrode materialsculties involving the analysis of the electrochemical findings obtained for porous electrode materials. Energy Storage Mater. 27, 555–590. doi:10.1016/j.ensm.2019.12.015
del Rìo, J. A., and Whitaker, S. (2002a). Maxwell’s equations in two-phase systems I: Local electrodynamic equilibrium. Transp. Porous Media 39, 159–186. doi:10.1023/a:1006617029519
Doornbusch, G., Dykstra, J., Biesheuvel, P. M., and Suss, M. (2016). Fluidized bed electrodes with high carbon loading for water desalination by capacitive deionization. J. Mat. Chem. A 4, 3642–3647. doi:10.1039/c5ta10316a
Dukhin, S. S. (1995). Electrochemical characterization of the surface of a small particle and nonequilibrium electric surface phenomena. Adv. Colloid Interface Sci. 61, 17–49. doi:10.1016/0001-8686(95)00258-r
Feng, G., Huang, J., Sumpter, B. G., Meunier, V., and Qiao, R. (2010). Structure and dynamics of electrical double layers in organic electrolytes. Phys. Chem. Chem. Phys. 12, 5468. doi:10.1039/c000451k
Feng, G., Qiao, R., Huang, J., Sumpter, B. G., and Meunier, V. (2010). Ion distribution in electrified micropores and its role in the anomalous enhancement of capacitanceed micropores and its role in the anomalous enhancement of capacitance. ACS Nano 4, 2382–2390. doi:10.1021/nn100126w
Ferguson, T. R., and Bazant, M. Z. (2012). Nonequilibrium thermodynamics of porous electrodes. J. Electrochem. Soc. 159, A1967–A1985. doi:10.1149/2.048212jes
Fleharty, M. E., Van Swol, F., and Petsev, D. N. (2014). Manipulating semiconductor colloidal stability through doping. Phys. Rev. Lett. 113, 158302. doi:10.1103/physrevlett.113.158302
Forse, A. C., Merlet, C., Griffin, J. M., and Grey, C. P. (2016). New perspectives on the charging mechanisms of supercapacitors. J. Am. Chem. Soc. 138, 5731–5744. doi:10.1021/jacs.6b02115
Fryer, J. R. (1981). The micropore structure of disordered carbons determined by high resolution electron microscopy. Carbon 19, 431–439. doi:10.1016/0008-6223(81)90026-9
Fuller, T. F., Doyle, M., and Newman, J. (1994). Simulation and optimization of the dual lithium-ion insertion cell. J. Electrochem. Soc. 141, 1–10. doi:10.1149/1.2054684
Gabitto, J. F., and Tsouris, C. (2016). Modeling the capacitive deionization process in dual-porosity electrodes. Transp. Porous Media 113, 173–205. doi:10.1007/s11242-016-0688-9
Gabitto, J. F., and Tsouris, C. (2019). Modeling the operation of slurry carbon electrodes using a hybrid approach. hal-02412872v1.
Gabitto, J. F., and Tsouris, C. (2018). One- and two-equation models to simulate ion transport in charged porous electrodes. Colloids Interfaces 2, 4. doi:10.3390/colloids2010004
Gabitto, J. F., and Tsouris, C. (2017). Surface transport processes in charged porous media. J. Colloid Interface Sci. 498, 91–104. doi:10.1016/j.jcis.2017.03.009
Gabitto, J. F., and Tsouris, C. (2015). Volume averaging study of the capacitive deionization process in homogeneous porous media. Transp. Porous Media 109, 61–80. doi:10.1007/s11242-015-0502-0
Galama, A. H., Post, J. W., Hamelers, H. V. M., Nikonenko, V. V., and Biesheuvel, P. M. (2016). On the origin of the membrane potential arising across densely charged ion exchange membranes: How well does the Teorell-Meyer-Sievers theory work? J. Mem. Sci. Res. 2, 128–140.
Gamaethiralalage, J. G., Singh, K., Sahin, S., Yoon, J., Elimelech, M., Suss, M. E., et al. (2021). Recent advances in ion selectivity with c apacitive deionization. Energy Environ. Sci. 14, 1095–1120. doi:10.1039/d0ee03145c
Grahame, D. C. (1947). The electrical double layer and the theory of electrocapillarity. Chem. Rev. 41, 441–501. doi:10.1021/cr60130a002
Griffin, J. M., Forse, A. C., Wang, H., Trease, N. M., Taberna, P.-L., et al. (2014). Ion counting in supercapacitor electrodes using NMR spectroscopy. Faraday Discussions 176 (49), 49–68. doi:10.1039/c4fd00138a
Guyes, E. N., Shocron, A. N., Simanosvski, A., Biesheuvel, P. M., and Suss, M. E. (2017). A one-dimensional model for water desalination by flow-through electrode capacitive deionization. Desalination 415, 8–13. doi:10.1016/j.desal.2017.03.013
Hassanvand, A., Wei, K., Talebi, S., Chen, G. Q., and Kentish, S. E. (2017). The role of ion exchange membranes in membrane capacitive deionisation. Membranes 7, 54. doi:10.3390/membranes7030054
Hatzell, K. B., Iwama, E., Ferris, A., Daffos, B., Urita, K., Tzedakis, T., et al. (2014). Capacitive deionization concept based on suspension electrodes without ion exchange membranes. Electrochem. Comm. 43, 18–21. doi:10.1016/j.elecom.2014.03.003
Hei, H. H. (2006). Master of chemical engineering thesis. Hong Kong: Hong Kong University.Adsorption of ionic surfactants on active carbon cloth
Heimböckel, R., Hoffmann, F., and Fröba, M. (2019). Insights into the influence of the pore size and surface area of activated carbons on the energy storage of electric double layer capacitors with a new potentially universally applicable capacitor model. Phys. Chem. Chem. Phys. 21, 3122–3133. doi:10.1039/c8cp06443a
Helmholtz, H. (1853). Ueber einige gesetze der vertheilung elektrischer ströme in körperlichen leitern mit anwendung auf die thierisch-elektrischen versuche. Annalen der Physik und Chemie (in German) 165, 211–233. doi:10.1002/andp.18531650603
Hsieh, W., Horng, T.-L. A., Huang, H.-C., and Teng, H. (2015). Facile simulation of carbon with wide pore size distribution for electric double-layer capacitance based on Helmholtz models. J. Mat. Chem. A. 3, 16535–16543. doi:10.1039/c5ta04125b
Huang, J., Sumpter, B. G., and Meunier, V. (2008). A universal model for nanoporous carbon supercapacitors applicable to diverse pore regimes, carbon materials, and electrolytes. Chem. Eur. J. 14, 6614–6626. doi:10.1002/chem.200800639
Huang, J., Sumpter, B. G., and Meunier, V. (2008). Theoretical model for nanoporous carbon supercapacitors. Angew. Chem. Int. Ed. 47, 520–524. doi:10.1002/anie.200703864
Jeon, S., Park, H., Yeo, J., Yang, S. C., Cho, C. H., Han, M. H., et al. (2013). Desalination via a new membrane capacitive deionization process utilizing flow-electrodes. Environ. Sci. Technol. 47, 1471–1475. doi:10.1039/c3ee24443a
Jiang, Z., and Stein, D. (2011). Charge regulation in nanopore ionic field-effect transistors. Phys. Rev. E. 83, 031203. doi:10.1103/PhysRevE.83.031203
Johnson, A. M., and Newman, J. (1971). Desalting by means of porous carbon electrodes. J. Electrochem. Soc. 118, 510–517. doi:10.1149/1.2408094
Johnson, A. W., Venolia, A. W., Wilbourne, R. G., Newman, J., Wong, C. W., Gilliam, W. S., et al. (1970). The electrosorption process for desalting water. The office of saline water research and development progress report No. 516. Washington: U. S. Dept. of the Interior.
Johnson, D. L., and Sen, P. N. (1988). Dependence of the conductivity of a porous medium on electrolyte conductivity. Phys. Rev. B 37, 3502–3510. doi:10.1103/physrevb.37.3502
Kalluri, R. K., Biener, M. M., Suss, M. E., Merrill, M. D., Stadermann, M., Santiago, J., et al. (2013). Unraveling the potential and pore-size dependent capacitance of slit-shaped graphitic carbon pores in aqueous electrolytes. Phys. Chem. Chem. Phys. 15, 2309. doi:10.1039/c2cp43361c
Karthik, M., Redondo, E., Goikolea, E., Roddatis, V., Doppiu, S., and Mysyk, R. (2014). Effect of mesopore ordering in otherwise similar micro/mesoporous carbons on the high-rate performance of electric double-layer capacitors. J. Phys. Chem. C. 118, 27715–27720. doi:10.1021/jp508581x
Kim, C., Srimuk, P., Lee, J., Aslan, M., and Presser, V. (2018). Semi-continuous capacitive deionization using multi-channel flow stream and ion exchange membranes. Desalination 425, 104–110. doi:10.1016/j.desal.2017.10.012
Koresh, J., and Soffer, A. (1977). Double layer capacitance and charging rate of ultramicroporous carbon electrodes. J. Electrochem. Soc. 124, 1379–1385. doi:10.1149/1.2133657
Lai, W., and Ciucci, F. (2011). Mathematical modeling of porous battery electrodes-revisit of Newman's model. Electrochim. Acta. 56, 4369–4377. doi:10.1016/j.electacta.2011.01.012
Landau, L. D., and Lifshitz, E. M. (1980). “Statistical physics,” in Course of theoretical physic. s. 53 ed. (Oxford: Pergamon Press).
Lee, J., Kim, S., Kim, C., and Yoon, J. (2014). Hybrid capacitive deionization to enhance the desalination performance of capacitive techniques. Energy Environ. Sci. 7, 3683–3689. doi:10.1039/c4ee02378a
Levi, M. D., and Aurbach, D. (1999). Frumkin intercalation isotherm - a tool for the description of lithium insertion into host materials: A review. Electrochim. Acta. 45, 167–185. doi:10.1016/s0013-4686(99)00202-9
Liu, S., Do, V. Q., and Smith, K. C. (2020). Modeling of electrochemical deionization across length scales: Recent accomplishments and new opportunities. Current Opinion in Electrochemistry 22, 72–79. doi:10.1016/j.coelec.2020.05.003
Liu, S., and Smith, K. C. (2018). Quantifying the trade-offs between energy consumption and salt removal rate in membrane-free cation intercalation desalination. Electrochim. Acta. 271, 652–665. doi:10.1016/j.electacta.2018.03.065
Liu, Y., Jiang, S. P., and Shao, Z. (2020). Intercalation pseudocapacitance in electrochemical energy storage: Recent advances in fundamental understanding and materials development. Materials Today Advances 7, 100072. doi:10.1016/j.mtadv.2020.100072
Liu, Z., Shang, X., Li, H., and Liu, Y. (2021). A brief review on high-performance capacitive deionization enabled by intercalation electrodes. Global Challenges 5, 2000054. doi:10.1002/gch2.202000054
Lyklema, J., and Minor, M. (1998). On surface conduction and its role in electrokinetics. Colloid Surf. A. 140, 33–41. doi:10.1016/s0927-7757(97)00266-5
Ma, J., He, C., He, D., Zhang, C., and Waite, T. D. (2018). Analysis of capacitive and electrodialytic contributions to water desalination by flow-electrode CDI. Water Res 144, 296–303. doi:10.1016/j.watres.2018.07.049
Mahmudov, R., Chen, C., and Huang, C. (2015). Functionalized activated carbon for the adsorptive removal of perchlorate from water solutions. Front. Chem. Sci. Eng. 9, 194–208. doi:10.1007/s11705-015-1517-3
IUPAC (1997). “Compendium of chemical terminology,”. (the “Gold Book”). Blackwell Scientific Publications. Editors A. D. McNaught, and A. Wilkinson 2nd ed. (United Kingdom: Oxford).
Nativ, P., Badash, Y., and Gendel, Y. (2017). New insights into the mechanism of flow-electrode capacitive deionization. Electrochem. Comm. 76, 24–28. doi:10.1016/j.elecom.2017.01.008
Newman, J., and Thomas-Alyea, K. E. (2004). Electrochemical systems. 3rd Ed. Hobokea, NJ, US: John Wiley & Sons.
Palko, J, W., Oyarzun, D. I., Ha, B., Stadermann, M., and Santiago, J. G. (2018). Nitrate removal from water using electrostatic regeneration of functionalized adsorbent. Chem. Eng. J. 334, 1289–1296. doi:10.1016/j.cej.2017.10.161
Pasta, M., Wessells, C. D., Cui, Y., and La Mantia, F. (2012). A desalination battery. Nano Lett 12, 839–843. doi:10.1021/nl203889e
Porada, S., Weingarth, D., Hamelers, H. V. M., Bryjak, M., Presser, V., and Biesheuvel, P. M. (2014). Carbon flow electrodes for continuous operation of capacitive deionization and capacitive mixing energy generation. J. Mat. Chem. A. 2, 9313–9321. doi:10.1039/c4ta01783h
Quintard, M., and Whitaker, S. (1995). Local thermal equilibrium for transient heat conduction: Theory and comparison with numerical experiments. Int. J. Heat Mass Trans. 38, 2779–2796. doi:10.1016/0017-9310(95)00028-8
Revil, A., and Glover, P. W. J. (1998). Nature of surface electrical conductivity in natural sands, sandstones, and clays. Geophysical Research Letters 25, 691–694. doi:10.1029/98gl00296
Revil, A., and Glover, P. W. J. (1997). Theory of ionic-surface electrical conduction in porous media. Physical Review B 55, 1757–1773. doi:10.1103/physrevb.55.1757
Rommerskirchen, A. K. E., Ohs, B., and Wessling, M. (2017). Modelling continuous flow-electrodes capacitive deionization processes with ion-exchange membranes. J. Mem. Sci. 546, 188–196.
Rouquerol, J., Avnir, D., Fairbridge, C. W., Everett, D. H., Haynes, J. M., Pernicone, N., et al. (1994). Recommendations for the characterization of porous solids (Technical Report). Pure Appl. Chem. 66, 1739–1758. doi:10.1351/pac199466081739
Rubin, S., Suss, M. E., Biesheuvel, P. M., and Bercovici, M. (2016). Induced-charge capacitive deionization: The electrokinetic response of a porous particle to an external electric field. Phys. Rev. Lett. 117, 234502. doi:10.1103/physrevlett.117.234502
Saha, D., Payzant, E. A., Kumbhar, A. S., and Naskar, A. K. (2013). Sustainable mesoporous carbons as storage and controlled-delivery media for functional molecules. ACS Appl. Mat. Interf. 5, 5868–5874. doi:10.1021/am401661f
Schmuck, M., and Bazant, M. Z. (2014). Homogenization of the Poisson-Nernst-Planck equations for ion transport in charged porous media. arXiv:1202.1916v2.
Singh, K., Bouwmeester, H. J. M., de Smet, L. C. P. M., Bazant, M. P., and Biesheuvel, P. M. (2018). Theory of water desalination with intercalation materials. Phys. Rev. Applied. 9, 064036. doi:10.1103/physrevapplied.9.064036
Singh, K., Porada, S., de Gier, H. D., Biesheuvel, P. M., and de Smet, L. C. P. M. (2019). Timeline on the application of intercalation materials in capacitive deionization. Desalination 455, 115–134. doi:10.1016/j.desal.2018.12.015
Smith, K. C., and Dmello, R. D. (2016). Na-ion desalination (NID) enabled by Na-blocking membranes and symmetric Na-intercalation: Porous-electrode modeling. J. Electrochem. Soc. 163, A530–A539. doi:10.1149/2.0761603jes
Smith, K. C. (2016). Theoretical evaluation of electrochemical cell architectures using cation intercalation electrodes for desalination. Electrochimica Acta 230, 333–341. doi:10.1016/j.electacta.2017.02.006
Smith, K. C. (2017). Theoretical evaluation of electrochemical cell architectures using cation intercalation electrodes for desalination. Electrochim. Acta. 230, 333–341. doi:10.1016/j.electacta.2017.02.006
Smith, R. B., and Bazant, M. Z. (2017). Multiphase porous electrode theory. J. Electrochem. Soc. 164, E3291–E3310. doi:10.1149/2.0171711jes
Stern, O. (1924). Zur theorie der elektrolytischen doppelschicht. Zeitschrift für Elektrochemie. 30, 508.
Su, X., and Hatton, T. A. (2017). Redox-electrodes for selective electrochemical separations. Adv. Colloid Interface Sci. 244, 6–20. doi:10.1016/j.cis.2016.09.001
Su, X., Tan, K.-J., Elbert, J., Rüttiger, C., Gallei, M., Jamison, T. F., et al. (2017). Asymmetric Faradaic systems for selective electrochemical separations. Energy Environ. Sci. 10, 1272–1283. doi:10.1039/c7ee00066a
Suss, M. E., Baumann, T. F., Bourcier, W. L., Spadacini, C. M., Rose, K. A., Santiago, J. G., et al. (2012). Capacitive desalination with flow-through electrodes. Energy & Environ. Sci. 5, 9511–9519. doi:10.1039/c2ee21498a
Suss, M. E., Porada, S., Sun, X., Biesheuvel, P. M., Yoon, J., and Presser, V. (2015). Water desalination via capacitive deionization: What is it and what can we expect from it? Energy Environ. Sci. 8, 2296–2319. doi:10.1039/c5ee00519a
Tang, K., Kim, Y.-H., Chang, J., Mayes, R. T., Gabitto, J., Yiacoumi, S., et al. (2019). Seawater desalination by over-potential membrane capacitive deionization: Opportunities and hurdles. Chem. Eng. J. 357, 103–111. doi:10.1016/j.cej.2018.09.121
Tang, K., Yiacoumi, S., Li, Y., Gabitto, J., and Tsouris, C. (2020). Optimal conditions for efficient flow-electrode capacitive deionization. Sep. Sci. & Technol. 240, 116626. doi:10.1016/j.seppur.2020.116626
Tang, K., Yiacoumi, S., Li, Y. P., and Tsouris, C. (2019). Enhanced water desalination by increasing the electroconductivity of carbon powders for high performance flow-electrode capacitive deionization. ACS Sustain. Chem. Eng. 7, 1085–1094. doi:10.1021/acssuschemeng.8b04746
Tang, W., Liang, J., He, D., Gong, J., Tang, L., Liu, Z., et al. (2019). Various cell architectures of capacitive deionization: Recent advances and future trends. Water Res 150, 225–251. doi:10.1016/j.watres.2018.11.064
Uwavid, R., Diesendruck, C. E., and Suss, M. E. (2022). Emerging investigator series: A comparison of strong and weak-acid functionalized carbon electrodes in capacitive deionization. Environ. Sci. Water Res. Technol. 8, 949–956. doi:10.1039/d1ew00967b
Wang, R., and Lin, S. (2020). Thermodynamic reversible cycles of electrochemical desalination with intercalation materials in symmetric and asymmetric configurations. J. Colloid Interface Sci. 574, 152–161. doi:10.1016/j.jcis.2020.04.032
West, K., Jacobsen, T., and Atlung, S. (1982). Modeling of porous insertion electrodes with liquid electrolyte. J. Electrochem. Soc. 129, 1480–1485. doi:10.1149/1.2124188
Whitaker, S. (1991). Improved constraints for the principle of local thermal equilibrium. Ind. Eng. Chem. Res. 30, 983–997. doi:10.1021/ie00053a022
Whitaker, S. (1986). Local thermal equilibrium: An application to packed bed catalytic reactor design. Chem. Eng. Sci. 41, 2029–2039. doi:10.1016/0009-2509(86)87119-6
Whitaker, S. (1999). Theory and application of transport in porous media: The method of volume averaging. London: Kluwer Academic.
Xu, J. H., Gao, N. Y., Deng, Y., Sui, M. H., and Tang, Y. L. (2011). Perchlorate removal by granular activated carbon coated with cetyltrimethyl ammonium chloride. Desalination 275, 87–92. doi:10.1016/j.desal.2011.02.036
Yang, K.-L., Yiacoumi, S., and Tsouris, C. (2002). Monte Carlo simulations of electrical double-layer formation in nanopores. J. Chem. Phys. 117, 8499–8507. doi:10.1063/1.1511726
Yang, K.-L., Ying, T.-Y., Yiacoumi, S., Tsouris, C., and Vittoratos, E. S. (2001). Electrosorption of ions from aqueous solutions by carbon Aerogel: an electrical double-layer model. Langmuir 17, 1961–1969. doi:10.1021/la001527s
Ying, T.-Y., Yang, K.-L., Yiacoumi, S., and Tsouris, C. (2002). Electrosorption of ions from aqueous solutions by nanostructured carbon aerogel. J. Colloid Interface Sci. 250, 18–27. doi:10.1006/jcis.2002.8314
Yoon, H., Lee, J., Kim, S., and Yoon, J. (2017). Hybrid capacitive deionization with Ag coated carbon composite electrode. Desalination 422, 42–48. doi:10.1016/j.desal.2017.08.010
Younes, H., and Zou, L. (2020). Asymmetric configuration of pseudocapacitive composite and rGO electrodes for enhanced capacitive deionization. Environ. Sci. Water Res. Technol 6, 392–403. doi:10.1039/C9EW01033E
Zhang, C., He, D., Ma, J., Tang, W., and Waite, T. D. (2018). Faradaic reactions in capacitive deionization (CDI) – problems and possibilities: A review. Water Res 128, 314–330. doi:10.1016/j.watres.2017.10.024
Keywords: CDI, porous medium/fluid interface, EDL, ionic transport, intercalation materials
Citation: Gabitto JF and Tsouris C (2023) A review of transport models in charged porous electrodes. Front. Chem. Eng. 4:1051594. doi: 10.3389/fceng.2022.1051594
Received: 23 September 2022; Accepted: 09 December 2022;
Published: 10 January 2023.
Edited by:
Lewei Zeng, Shenzhen University, ChinaReviewed by:
Yusufu Abeid Chande Jande, Nelson Mandela African Institution of Science and Technology, TanzaniaChen Hu, Southern University of Science and Technology, China
Copyright © 2023 Gabitto and Tsouris. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jorge Federico Gabitto, amZnYWJpdHRvQHB2YW11LmVkdQ==
 Jorge Federico Gabitto
Jorge Federico Gabitto Costas Tsouris
Costas Tsouris