- Instituto de Física, Universidad Nacional Autónoma de México, Mexico City, Mexico
We describe the use of artificial intelligence techniques in heterogeneous catalysis. This description is intended to give readers some clues for the use of these techniques in their research or industrial processes related to hydrodesulfurization. Since the description corresponds to supervised learning, first of all, we give a brief introduction to this type of learning, emphasizing the variables X and Y that define it. For each description, there is a particular emphasis on highlighting these variables. This emphasis will help define them when one works on a new application. The descriptions that we present relate to the construction of learning machines that infer adsorption energies, surface areas, adsorption isotherms of nanoporous materials, novel catalysts, and the sulfur content after hydrodesulfurization. These learning machines can predict adsorption energies with mean absolute errors of 0.15 eV for a diverse chemical space. They predict more precise surface areas of porous materials than the BET technique and can calculate their isotherms much faster than the Monte Carlo method. These machines can also predict new catalysts by learning from the catalytic behavior of materials generated through atomic substitutions. When the machines learn from the variables associated with a hydrodesulfurization process, they can predict the sulfur content in the final product.
Introduction
The creation of predictive models in the oil industry is of the utmost importance. For example, models have been developed for oil production (Li and Horne, 2003; Irisarri et al., 2016; Hutahaean et al., 2017) and oil transformation (Farrusseng et al., 2003; Wang et al., 2019). These models, however, have not been entirely successful (Cai et al., 2021). Therefore, they have been constantly evolving and have now included artificial intelligence techniques. Examples of this are the models to find new catalysts (Günay and Yıldırım, 2021; Goldsmith et al., 2018; Lamoureux et al., 2019; Yang et al., 2020), the models to control oil exploitation (Davtyan et al., 2020; Liu et al., 2020; Tsvaki et al., 2020), and the models to analyze oil transformation (Al-Jamimi et al., 2019; Sircar et al., 2021).
In recent decades, models based on artificial intelligence techniques have performed impressive predictions in different knowledge fields. For example, in exact sciences (Sauceda et al., 2021; Hajibabaei and Kim, 2021; Cerioti et al., 2021; Bahlke et al., 2020; Chmiela et al., 2020; Saar et al., 2021; Artrith and Urban, 2016; Ch’ng et al., 2017; Shallue and Vanderburg, 2018; Sadowski et al., 2016), in social sciences (Ng et al., 2020; Lattner and Grachten, 2019), in technology (Bae et al., 2021; Cunneen et al., 2019; Feldt et al., 2018; Huang et al., 2014), and health sciences (Bashyam et al., 2020; Zhou et al., 2019; Themistocleous et al., 2021; Lagree et al., 2021).
The models based on artificial intelligence techniques contrast with the traditional models used for predictions in the oil industry. These techniques learn from the data associated with the process under study and generate relationships between the variables representing the process. It is important to remark that the learning mechanisms in artificial intelligence are generic, as it is the calculus, regardless of the source of the data to which it is applied. For example, the data to feed the learning system can be images of different types of objects (Wang et al., 2021; Torralba et al., 2008), or people´s tastes in movies (Keshava et al., 2020; Lash and Zhao, 2016), or the buyer behavior of shopping (Overgoor et al., 2019). The data may also come from words in a text (Devlin et al., 2019) or be associated with virus detection assays of people with Covid-19 (Zaobi et al., 2021), or come from a set of hydrodesulfurization experiments (Al-Jamimi et al., 2019).
The manuscript presents some applications of artificial intelligence techniques in heterogeneous catalysis. It includes the use of these techniques in the study of the hydrodesulfurization process. First, we present a brief overview of these techniques to give the reader, without experience in these techniques, the essential elements to understand the applications.
The first application shows the use of artificial intelligence techniques to predict the binding energy when a molecule interacts with a solid. In particular, the binding energy of CO or H when adsorbed by metals. The following application describes a learning machine that predicts surface areas and compares them with those obtained with the BET technique. The subsequent application searches for new nanoporous materials of interest in catalysis. The data comes from modeling the surface area of 6,500 zeolite structures.
In the following applications, the data come from experiments in research laboratories or production plants. First, we describe a learning machine that predicts new catalysts based on Ru for ammonia decomposition. In this case, to generate the data, ruthenium is replaced with three different elements (one at a time) to create catalysts that decompose ammonia under different experimental conditions. These experiments produced a data set to train the learning machine that predicts new Ru-based catalysts.
The applications that follow are related to the process of hydrodesulfurization. These kinds of applications were the first to be used in heterogeneous catalysis. For example, in 1996, one of these applications (Berger et al., 1996) predicted the hydrodesulfurization of atmospheric gas oil.
The last described application in the manuscript refers to the control of the hydrodesulfurization process in a production plant. In this case, the control occurs by using an online prediction based on time sequences.
Materials and Methods
A Basic Introduction to Machine Learning
As mentioned above, artificial intelligence techniques generate learning machines using data sets produced during the analysis of a topic of interest. As a result, these machines predict events that could occur in this topic.
Of the learning techniques, two stand out: supervised learning and unsupervised learning. Since everything presented in the paper is related to supervised learning, we describe the essential elements of this learning method for the non-specialist in artificial intelligence. Our presentation of this learning method does not follow any traditional way of presenting it. Instead, we explain the method using an example of heterogeneous catalysis, where the reader is a specialist.
When we develop a new catalyst for hydrodesulfurization, the goal is to bring out a product with low sulfur content. This content (which we describe as the variable Y) is the variable that determines the formulation of the catalyst, as well as the temperature, pressure, amount of hydrogen, and other variables related to the process that will use the catalyst. We mark out these last quantities with the vector X = (X1, X2, X3,…, Xn).
The use of artificial intelligence techniques to develop a new hydrodesulfurization catalyst requires a set of events, called samples, with values (X, Y). They can be obtained by modeling the hydrodesulfurization process or performing experiments in a laboratory or from the variables associated with the process in an industrial plant. Typically, 80% of the samples are used for training the machine, and the rest for testing the machine’s effectiveness to predict new catalysts.
The basic principle of learning is the following. First, we construct the function F(W, X), which estimates the sulfur content and is defined by the parameters W = (W1, W2, W3…). We create a metric to estimate the difference between the prediction of the sulfur content, F(W, X), and their values, Y, in the samples. With the average of these differences, we construct the loss function, J (W, X, Y), whose gradients with respect to each parameter permit updating the parameters. This updating continues until the loss function reaches its minimal value. Figure 1 depicts a general sketch of such a learning machine.
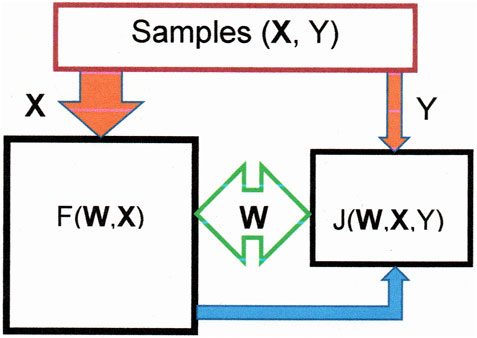
FIGURE 1. Sketch representing a learning machine. F(W, X), fed with the variable X, is represented by the left square. Its output (blue arrow) provides the right square, together with the variable Y, to form the error function, J(W, X, Y), during training . The parameters W are modified in this square to bring the function F(W, X) up to date.
There exist various algorithms to construct a learning machine (Breiman, 2001; Dhillon and Verma, 2020; Scherer et al., 2020; Schütt et al., 2018; Shazeer et al., 2018; Shawe-Taylor and Sun, 2011), from the simplest ones like the Random Forest (Breiman, 2001) which requires only a few samples, to algorithms based on artificial neural networks (Shazeer et al., 2018), which could require a large number samples for training. These last algorithms could contain millions of parameters (Krizhevsky et al., 2017). Going into detail on these algorithms is beyond the purpose of the present manuscript. However, the references for these algorithms are a good start for readers who want to dabble in them.
Results and Discussion
Adsorption Energy Prediction
When a molecule nears a solid, its interaction with the atoms on the solid’s surface determines the adsorption energy. If the solid is a catalyst, this energy determines many catalytic properties. Consequently, the analysis of this energy could help to develop new catalysts.
Although quantum mechanical calculations can provide this energy, they require long calculation times and much computing power. Therefore, the use of only this methodology to search for new catalysts generates a bottleneck.
An alternative to avoid this bottleneck is to generate these energies with the techniques of artificial intelligence. For example, through supervised learning using the Deep Learning technique. In this case, the constructed learning machine correlates the local atomic distribution and the properties of the atoms with the adsorption energy through the function F(W, X).
In this type of learning, it is necessary to define the target variable (the variable Y), which, in the present case, is the adsorption energy. It is also important to propose the variables from the system that determine this energy. For example, these variables can be the atomic properties of the atoms and their local atomic order (Behler, 2011; Back et al., 2019; Gómez-Peralta and Bokhimi, 2021). These variables can also correspond to relationships between the atomic radii (Gómez – Peralta and Bokhimi, 2020).
The function, F(W, X), generated with the Deep Learning technique, contains many parameters with values optimized during the training. Therefore, this learning procedure requires a considerable number of samples obtained from experiments or models. In the present case, each sample (X, Y) contains information related to the local distribution of the atoms and their chemical properties (variable X). In addition, it also includes the adsorption energy generated by quantum mechanical calculations (variable Y).
Thousands of samples (X, Y) are created by building atomic distributions used to perform quantum mechanical computations. The function F(W, X) maps X in Y through the relationship that lies between them without explicit modeling; for one sample, this function outputs a value that compares with the adsorption energy Y generating a difference value. For all samples, the average difference value gives the loss function J (W, X, Y), used to update the parameters W of the function F(W, X). This process repeats until the loss function reaches its minimal value to complete the learning process. It is important to note that the computations include the interaction between the molecule with catalytic and non-catalytic sites.
Of the samples, a percentage, about 80%, is used for training, and the rest to check the ability of the function F(W, X) to predict adsorption energies. This prediction allows finding new catalysts for specific catalytic processes related to the molecule adsorbed on the solid.
As an example of this methodology, (Back et al., 2019) used the Deep Learning technique to predict the adsorption energy (variable Y) of CO or H when they interact, each separately, with various surfaces of pure metals, metal alloys, or intermetallic compounds. Their model is a modification of the previously reported model for the prediction of the physicochemical properties of crystalline compounds (Xie and Grossman, 2018; Chen et al., 2019).
Back et al. identified (variable X) each atom with the group and period to which it belongs, its electronegativity, its covalent radius, its number of valence electrons, its first ionization energy, its electron affinity, the block to which they belong, and its atomic volume. They model the interaction between an atom with its local environment with its associated Voronoi polygon (Blatov, 2004).
The number of samples used by Back et al. for training was 43,237 for each adsorbate on the solid. Each sample had 37 different elements and 96 stoichiometries. In these samples, the number of different spatial groups was 110, while the number of crystal facets was 41.
The learning machine for CO adsorption had 4,938 parameters W, while the machine used for H adsorption utilized 6,738 parameters W.
For 12,000 samples excluded from the training set, the learning machine predicts adsorption energies for CO and H with a Mean Absolute Error (MAE) of only 0.15 eV. This value is lower than that obtained in previous studies by the authors using many alloys as the solid (Tran and Ulissi, 2018).
Surface Area Prediction
In heterogeneous catalysis, nanoporous materials are of particular interest because they have a large surface area. Hence, to help to understand the catalytic properties, this area should be determined accurately. The traditional method to get this area is the Brunauer-Emmett-Teller (BET) method, where for measuring this area, the material adsorbs inert molecules at low temperatures. But, the surface area estimation using this method is not always precise, especially for materials with large surface areas, where some of the adsorbed molecules are no more on a monolayer. Thus, for example, the reported surface areas of metal-organic frameworks (MOFs) are exaggerated (Gómez-Gualdrón et al., 2016; Sinha et al., 2019).
Datar et al. (Datar et al., 2020) developed a machine learning approach for estimating surface area to correct this problem. They combine machine learning with molecular modeling to derive argon isotherms at 87 K for over 300 metal-organic frameworks from the CoRE-MOF database (Chung et al., 2014; Chung et al., 2019). They use a Lennard-Jones potential with a cut radius of 12 Å (Rappe et al., 1992). Finally, they applied the BET theory to these isotherms to determine the surface area of these MOFs by using the SESAMI algorithm (Sinha et al., 2019), focusing primarily on the true monolayer area (Gómez-Gualdrón et al., 2016).
Their machine learning model relates the features that describe the adsorption isotherms and the surface area (variable Y). The isotherm features (variable X) were constructed by dividing the pressure into seven regions on a logarithmic scale. These regions are related linearly to the true monolayer areas. The model parameters were optimized using the Least Absolute Shrinkage and Selection Operator (Tibshirani, 1996). It includes regularization to reduce overfitting. For the training, Datar et al. used 40% for the samples for the training and 60% for the testing. The training evolution was analyzed using the cross-validation method (Zhang, 1993).
The learning machine predicts more precise surface areas than the BET method. For example, for samples with surface areas greater than 3,500 m2/ g, with the learning machine, only 2% of the structures were predicted with surface area errors more significant than 20%, while for the BET method, the latter figure was 54%.
With the trained learning machine, the surface area of 68 MOF structures of the CoRE-MOF database was obtained, modeling the isotherms with the adsorption of N2 (77 K). The predictions of the surface area using these isotherms with the learning machine trained with the isotherms generated with the adsorption of Ar also gave better results than those obtained by the BET approach. The estimated areas with the learning machine were scaled to a ratio of 1.148 since the area associated with the N2 molecule is 0.163 nm2, while the one associated with the Ar atom is 0.142 nm2 (Mikhail and Brunauer, 1975).
Adsorption Isotherm Prediction
Discovering new materials is of the utmost importance from both technological and scientific points of view. That is why, in recent years, the use of artificial intelligence techniques to speed up their search has proliferated (Goldsmith et al., 2018; Gupta et al., 2018; Gómez-Peralta and Bokhimi 2020; Chen et al., 2021; Cho and Lin, 2021; Konno et al., 2021). Of particular interest is the finding of nanoporous materials because they have a large surface area that is attractive in heterogeneous catalysis (Cho and Lin, 2021).
These materials can exist in hundreds of thousands. However, nowadays, selecting those with an attractive surface area for heterogeneous catalysis occurs through the slow procedure of trial and error. As an alternative to this discovery procedure, Cho et al. (Cho and Lin, 2021) developed a learning machine based on convolution neural networks (CNN) that predicts the surface area of such materials.
Their methodology analyzes methane adsorption on zeolites, but it applies to any molecule adsorption in any nanoporous material. In their research, Cho et al. used 6,500 zeolite structures with lattice parameters less than 24 Å, selected from the Predicted Crystallography Database (Pophale et al., 2011).
They calculated the methane adsorption isotherm (variable Y) at 300 K on every zeolite structure for 14 different pressure values between 0.0005 and 200 bar. For that, they employed the Monte Carlo method approach, using a Lennard-Jones type interaction potential (García-Pérez et al., 2007) with a cut-off radius of 12 Å. Their learning machine had the LeNet-5 architecture (LeCun et al., 1998), commonly used to detect objects in two-dimensional images (Qin et al., 2020; Jain et al., 2021).
Each zeolite structure was modeled with a three-dimensional image equivalent to a cubic cell with 24 Å per side. Each of the 24 × 24 × 24 image voxel values (variable X) corresponded to its potential as a methane adsorption active site. Filters of 2 × 2 × 2, 3 × 3 × 3, and 5 × 5 × 5 voxels built the different layers of the convolutional neural network. Of the total samples, 90% were for training and 10% for testing the model. The use of data augmentation techniques (Shorten and Khoshgoftaar, 2019) decreased the loss values, achieving squared means errors of up to 0.015 mol/ kg.
Their learning machine predicts adsorption isotherms in fractions of seconds, which contrasts with the times required by using the Monte Carlo method, where to calculate the adsorption isotherm in a zeolite requires dozens of CPU hours. This difference in time is significant since there are hundreds of thousands of such zeolite structures from which it is interesting to obtain their adsorption isotherms.
These studies show the potential of convolutional neural networks to develop other applications in heterogeneous catalysis. For example, for the capture of carbon dioxide or removing H2S or SO2 during sour gas sweetening.
Prediction of Novel Catalysts
The learning machines described above, for their learning, were fed with features defined by the properties of the elements and features obtained with calculations based on the atomic distribution. This methodology allowed generating a considerable number of samples for the training.
In contrast, Williams et al. (Williams et al., 2020) describe a learning machine in which part of the content of the samples comes from experiments, which limited the number of samples to less than 500.
In Machine Learning, when the number of samples is tiny, and the goal is to have a minor error in the predictions, it is convenient to choose an algorithm that learns correctly with this number of samples. One of these algorithms is the Random Forest (Breiman, 2001), which Williams et al. used to create their learning machine based on 100 tree predictors.
Their learning machine looked for new catalysts based on ruthenium for ammonia decomposition. They started with the ruthenium catalyst Ru4K12, promoted with potassium, and supported on gamma-alumina. Their research sought to predict new catalysts by substituting Ru with 33 different elements (Mg, Ca, Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Sr, Y, Zr, Nb, Mo, Rh, Pd, Ag, Cd, In, Sn, Hf, Ta, W, Re, Os, Ir, Pt, Au, Pb, Bi).
To develop their first learning machine, they prepared catalysts by replacing one Ru atom with an M atom (M = Ca, Mn, In). The composition of the catalysts was 3 wt% Ru, 1 wt% M and 12 wt% K. For each catalyst, they measured the ammonia conversion at 250, 300, and 350°C; this conversion is the target variable (variable Y) that supervises the learning. It is to notice that selecting these elements to replace Ru maximizes the difference between the features used in the learning.
The features (variable X) used to characterize the ammonia decomposition process were the catalyst composition, the operating conditions, the synthesis variables, and the atomic properties. Only five of these features were necessary to get accurate predictions, being the reactor temperature the most important. The other four features were related to the electronic structure of the atoms: the number of d-shell valence electrons, the electronegativity, the covalent radius, and the adjusted work function. It is important to remember that in 1985 Falicov et al. proposed that the number of d-shell valence electrons was essential to describe the catalytic activity (Falicov and Somorjai, 1985).
When evaluating the learning machine by replacing Ru with an atom M of the remaining 30 elements, the best ammonia conversions occurred with M = Sr, Mg, Sc, or Y.
These predictions motivated the authors to synthesize different catalysts by substituting Ru with the following 19 elements: Cu, Ni, Cr, W, Hf, Zn, Bi, Pd, Mo, Y, Sc, Sr, Mg, Os, Pt, Au, Nb, Fe, and Rh. When they catalyzed ammonia conversion, the highest conversions corresponded to the substitution of Ru with Sr, Mg, Sc, or Y, which matches the learning machine’s predictions, and demonstrates the usefulness of this machine to predict novel catalysts.
Williams et al. extended their model by generating new sets of catalysts using, for each set, three different atoms to replace Ru, selecting the atoms from the 19 elements mentioned in the previous paragraph, plus Ca, Mg, and In.
With these 22 elements replacing Ru, 60 different sets of three catalysts were built, generating 60 different learning machines. These machines predominantly predict that the catalysts that produce a high ammonia conversion are those in which Ru is replaced by Ca, Sr, Sc, Y, and Mg. These predicted conversions have a 10% error compared with those measured in experiments.
The results show that artificial intelligence techniques and relatively few experiments are sufficient to save both cost and time to discover new catalysts.
Sulfur Content Prediction After Hydrodesulfurization
Since the inception of machine learning techniques, they have been used to predict sulfur content after hydrodesulfurization (HDS). In 1996, Berger et al. (1996) constructed a learning machine based on a Feed-Forward Neural Network with only one hidden layer containing three nodes. Their experiments provided the 25 samples utilized to train and test this learning machine. Eighteen of them were for its training and seven to test it. For all the hydrodesulfurization experiments, they employed a catalyst with 4.2 wt% Co, 16.7 wt% Mo and 0.4 wt% S, with a hydrogen to oil volume ratio of 500.
The target variable (variable Y) was the sulfur content after the hydrodesulfurization process, with values between 10 and 1870 ppm. The features (variable X) that characterized the process were: temperature, with values between 348 and 360°C, pressure, with values between 600 and 1,200 psi, liquid hourly space velocity with values between 0.4 and 6.0 h−1, and the sulfur content of the heavy atmospheric gas oil, with values between 7,500 and 12,000 ppm. Since, in this study, the experimental sulfur output values have little change in the pressure range used, the study shows that, in this case, the pressure does not have a significant effect on the sulfur output predictions.
Despite the tiny number of samples used in training, the sulfur content predictions with the test samples were within 10% of the experimental values.
Another learning machine, developed by Al-Jamimi et al. (Al-Jamimi et al., 2019), predicts the sulfur content after an HDS process. They used a Support Vector Machine (Shawe-Taylor and Sun, 2011) combined with a genetic algorithm (Katoch et al., 2021) as the learning technique.
The ultimate sulfur content in the product (variable Y), with values between 0.0 and 1,258 ppm, is the variable that supervises the learning. The features (variable X) that characterized the HDS process were temperature, with values of 200 300 and 400°C, pressure, with values between 25 and 75 bar; hydrogen dosage, with values between 0.4 and 0.8 g, the initial sulfur concentration, with values between 439 and 1,500 ppm and the type of fuel. The authors generated 34 samples performing HDS experiments, 24 to train the learning machine, and 10 to test its prediction capability. After its training, the machine delivered predictions regarding the product’s sulfur content within 5.5 percent of the experimental results.
In the literature, some publications also report the use of artificial intelligence techniques to examine the evolution of the HDS process in industrial plants over time (Ma et al., 2020) or the evolution of this process in a refinery, with temperature, pressure, and hydrogen dosage (Arce-Medina and Paz-Paredes, 2009; Al-Jamimi et al., 2018). The literature also covers the use of these techniques for predictions in other oil industry processes (Sagheer and Kotb, 2019; Liu et al., 2020).
Conclusions
We describe some applications of artificial intelligence techniques in heterogeneous catalysis. Since they all correspond to supervised learning, first, we give a brief introduction to this kind of learning, emphasizing the variables X and Y that define it. Then, when we use this learning to analyze a problem, the essential point is to find these variables to represent it. Therefore, for each of the described applications, there is a particular emphasis on finding these variables. This emphasis will help extract this information when one is interested in a new application. In the end, the description intends to give readers some clues for using these techniques in their research or the industrial applications related to hydrodesulfurization.
The reported applications describe the building of learning machines that infer adsorption energies, surface areas, adsorption isotherms of nanoporous materials, novel catalysts, and the sulfur content after hydrodesulfurization.
The learning machine that predicts the adsorption energy learns from the interaction of CO or H on surfaces of pure metals, metal alloys, or intermetallic compounds. The one that predicts surface areas learns from the adsorption of argon on 300 different metal-organic frameworks. The machine that forecasts adsorption isotherms learn from the adsorption of methane on 6,500 zeolite structures. The machine that infers novel catalysts based on ruthenium learns from the ammonia decomposition using catalysts generated by the partial substitution of Ru with 22 different atoms. Finally, the machine inferring the sulfur content after hydrodesulfurization learns from the variables used to perform the experiments: temperature, pressure, hydrogen dosage, and initial oil sulfur concentration.
Learning machines can predict adsorption energies with mean absolute errors of 0.15 eV for a diverse chemical space. They predict more precise surface areas of porous materials than the BET technique and can calculate their isotherms much faster than the Monte Carlo method. These machines can also predict new catalysts by learning from the catalytic behavior of materials generated through atomic substitutions. When the machines learn from the variables associated with a hydrodesulfurization process, they can predict the sulfur content in the final product.
Author Contributions
XB. Conceptualization, Methodology, Resources, Writing-original draft, review and editing.
Funding
This work was financial supported by the laboratory, LAREC, from the Instituto de Física, Universidad Nacional Autónoma de México. Mexico.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
Mr. Antonio Morales provided technical assistance to the author.
References
Aizenberg, I., Sheremetov, L., Villa-Vargas, L., and Martinez-Muñoz, J. (2016). Multilayer Neural Network with Multi-Valued Neurons in Time Series Forecasting of Oil Production. Neurocomputing 175, 980–989. doi:10.1016/j.neucom.2015.06.092
Al-Jamimi, H. A., Al-Azani, S., and Saleh, T. A. (2018). Supervised Machine Learning Techniques in the Desulfurization of Oil Products for Environmental protection: A Review. Process Saf. Environ. Prot. 120, 57–71. doi:10.1016/j.psep.2018.08.021
Al-Jamimi, H. A., Bagudu, A., and Saleh, T. A. (2019). An Intelligent Approach for the Modeling and Experimental Optimization of Molecular Hydrodesulfurization over AlMoCoBi Catalyst. J. Mol. Liquids 278, 376–384. doi:10.1016/j.molliq.2018.12.144
Arce-Medina, E., and Paz-Paredes, J. I. (2009). Artificial Neural Network Modeling Techniques Applied to the Hydrodesulfurization Process. Math. Comp. Model. 49, 207–214. doi:10.1016/j.mcm.2008.05.010
Artrith, N., and Urban, A. (2016). An Implementation of Artificial Neural-Network Potentials for Atomistic Materials Simulations: Performance for TiO2. Comput. Mater. Sci. 114, 135–150. doi:10.1016/j.commatsci.2015.11.047
Back, S., Yoon, J., Tian, N., Zhong, W., Tran, K., and Ulissi, Z. W. (2019). Convolutional Neural Network of Atomic Surface Structures to Predict Binding Energies for High-Throughput Screening of Catalysts. J. Phys. Chem. Lett. 10, 4401–4408. doi:10.1021/acs.jpclett.9b01428
Bae, G., Kim, M., Song, W., Myung, S., Lee, S. S., and An, K.-S. (2021). Impact of a Diverse Combination of Metal Oxide Gas Sensors on Machine Learning-Based Gas Recognition in Mixed Gases. ACS Omega 6, 23155–23162. doi:10.1021/acsomega.1c02721
Bahlke, M. P., Mogos, N., Proppe, J., and Herrmann, C. (2020). Exchange Spin Coupling from Gaussian Process Regression. J. Phys. Chem. A. 124, 8708–8723. doi:10.1021/acs.jpca.0c05983
Bashyam, V. M., Erus, G., Doshi, J., Habes, M., Nasrallah, I. M., Truelove-Hill, M., et al. (2020). MRI Signatures of Brain Age and Disease over the Lifespan Based on a Deep Brain Network and 14 468 Individuals Worldwide. BRAIN 143, 2312–2324. doi:10.1093/brain/awaa32810.1093/brain/awaa160
Behler, J. (2011). Atom-centered Symmetry Functions for Constructing High-Dimensional Neural Network Potentials. J. Chem. Phys. 134, 074106. doi:10.1063/1.3553717
Berger, D., Landau, M. V., Herskowitz, M., and Boger, Z. (1996). Deep Hydrodesulfurization of Atmospheric Gas Oil; Effects of Operating Conditions and Modelling by Artificial Neural Network Techniques. Fuel 75, 907–911. doi:10.1016/0016-2361(96)00005-1
Blatov, V. A. (2004). Voronoi-dirichlet Polyhedra in crystal Chemistry: Theory and Applications. Crystallogr. Rev. 10, 249–318. doi:10.1080/08893110412331323170
Cai, G., Liu, Z., Zhang, L., Shi, Q., Zhao, S., and Xu, C. (2021). Systematic Performance Evaluation of Gasoline Molecules Based on Quantitative Structure-Property Relationship Models. Chem. Eng. Sci. 229, 116077. doi:10.1016/j.ces.2020.116077
Ceriotti, M., Clementi, C., and Anatole von Lilienfeld, O. (2021). Machine Learning Meets Chemical Physics. J. Chem. Phys. 154, 160401. doi:10.1063/5.0051418
Chen, C., Ye, W., Zuo, Y., Zheng, C., and Ong, S. P. (2019). Graph Networks as a Universal Machine Learning Framework for Molecules and Crystals. Chem. Mater. 31, 3564–3572. doi:10.1021/acs.chemmater.9b01294
Chen, Z. W., LuChen, Z. L. X., Chen, L. X., Jiang, M., Chen, D., and Singh, C. V. (2021). Machine-learning-accelerated Discovery of Single-Atom Catalysts Based on Bidirectional Activation Mechanism. Chem. Catal. 1, 183–195. doi:10.1016/j.checat.2021.03.003
Chmiela, S., Sauceda, H. E., Tkatchenko, A., and Müller, K.-R. (2020). “Accurate Molecular Dynamics Enabled by Efficient Physically Constrained Machine Learning Approaches,” in Machine Learning Meets Quantum Physics. Lecture Notes in Physics. Editors K. Schütt, S. Chmiela, O. von Lilienfeld, A. Tkatchenko, K. Tsuda, and K. R. Müller (Springer), 129–154. doi:10.1007/978-3-030-40245-7_7
Ch’ng, K., Carrasquilla, J., Melko, R. G., and Khatami, E. (2017). Machine Learning Phases of Strongly Correlated Fermions. Phys. Rev. X 7, 031038. doi:10.1103/PhysRevX.7.031038
Cho, E. H., and Lin, L.-C. (2021). Nanoporous Material Recognition via 3D Convolutional Neural Networks: Prediction of Adsorption Properties. J. Phys. Chem. Lett. 12, 2279–2285. doi:10.1021/acs.jpclett.1c00293
Chung, Y. G., Camp, J., Haranczyk, M., Sikora, B. J., Bury, W., Krungleviciute, V., et al. (2014). Computation-Ready, Experimental Metal-Organic Frameworks: A Tool to Enable High-Throughput Screening of Nanoporous Crystals. Chem. Mater. 26, 6185–6192. doi:10.1021/cm502594j
Chung, Y. G., Haldoupis, E., Bucior, B. J., Haranczyk, M., Lee, S., Zhang, H., et al. (2019). Advances, Updates, and Analytics for the Computation-Ready, Experimental Metal-Organic Framework Database: CoRE MOF 2019. J. Chem. Eng. Data 64, 5985–5998. doi:10.1021/acs.jced.9b00835
Cunneen, M., Mullins, M., and Murphy, F. (2019). Autonomous Vehicles and Embedded Artificial Intelligence: the Challenges of Framing Machine Driving Decisions. Appl. Artif. Intelligence 33, 706–731. doi:10.1080/08839514.2019.1600301
Datar, A., Chung, Y. G., and Lin, L.-C. (2020). Beyond the BET Analysis: the Surface Area Prediction of Nanoporous Materials Using a Machine Learning Method. J. Phys. Chem. Lett. 11, 5412–5417. doi:10.1021/acs.jpclett.0c01518
Davtyan, A., Rodin, A., Muchnik, I., and Romashkin, A. (2020). Oil Production Forecast Models Based on Sliding Window Regression. J. Pet. Sci. Eng. 195, 107916. doi:10.1016/j.petrol.2020.107916
Devlin, J., Chang, M.-W., Lee, K., and Toutanova, K. (2019). BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. Proc. Naacl-htl 2019, 4171–4186. doi:10.18653/v1/N19-1423
Dhillon, A., and Verma, G. K. (2020). Convolutional Neural Network: a Review of Models, Methodologies and Applications to Object Detection. Prog. Artif. Intell. 9, 85–112. doi:10.1007/s13748-019-00203-0
Erdem Günay, M., and Yıldırım, R. (2021). Recent Advances in Knowledge Discovery for Heterogeneous Catalysis Using Machine Learning. Catal. Rev. 63, 120–164. doi:10.1080/01614940.2020.1770402
Falicov, L. M., and Somorjai, G. A. (1985). Correlation between Catalytic Activity and Bonding and Coordination Number of Atoms and Molecules on Transition Metal Surfaces: Theory and Experimental Evidence. Proc. Natl. Acad. Sci. 82, 2207–2211. doi:10.1073/pnas.82.8.2207
Farrusseng, D., Baumes, L., and Mirodatos, C. (2003). “Data Management for Combinatorial Heterogeneous Catalysis: Methodology and Development of Advanced Tools,” in High-Throughput Analysis. Editors R. A. Potyrailo, and E. J. Amis (Boston, MA: Springer). doi:10.1007/978-1-4419-8989-5_25
Feldt, R., de Oliveira Neto, F. G., and Torkar, R. (2018). “Ways of Applying Artificial Intelligence in Software Engineering,”in 2018 IEEE/ACM 6th International Workshop on Realizing Artificial Intelligence Synergies in Software Engineering (RAISE), Gothenburg, Sweden, 27 May-3 June 2018 (IEEE), 35–41. doi:10.1145/3194104.3194109
García-Pérez, E., Parra, J. B., Ania, C. O., García-Sánchez, A., van Baten, J. M., Krishna, R., et al. (2007). A Computational Study of CO2, N2, and CH4 Adsorption in Zeolites. Adsorption 13, 469–476. doi:10.1007/s10450-007-9039-z
Goldsmith, B. R., Esterhuizen, J., Liu, J. X., Bartel, C. J., and Sutton, C. (2018). Machine Learning for Heterogeneous Catalyst Design and Discovery. Aiche J. 64, 2311–2323. doi:10.1002/aic.16198
Gómez – Peralta, J. I., and Bokhimi, X. (2020). Discovering New Perovskites with Artificial Intelligence. J. Solid State. Chem. 285, 121253. doi:10.1016/j.jssc.2020.121253
Gómez-Gualdrón, D. A., Moghadam, P. Z., Hupp, J. T., Farha, O. K., and Snurr, R. Q. (2016). Application of Consistency Criteria to Calculate BET Areas of Micro- and Mesoporous Metal-Organic Frameworks. J. Am. Chem. Soc. 138, 215–224. doi:10.1021/jacs.5b10266
Gómez-Peralta, J. I., and Bokhimi, X. (2021). Ternary Halide Perovskites for Possible Optoelectronic Applications Revealed by Artificial Intelligence and DFT Calculations. Mater. Chem. Phys. 267, 124710. doi:10.1016/j.matchemphys.2021.124710
Gupta, A., Müller, A. T., Huisman, B. J. H., Fuchs, J. A., Schneider, P., and Schneider, G. (2018). Generative Recurrent Networks for De Novo Drug Design. Mol. Inf. 37, 1700111. doi:10.1002/minf.201700111
Hajibabaei, A., and Kim, K. S. (2021). Universal Machine Learning Interatomic Potentials: Surveying Solid Electrolytes. J. Phys. Chem. Lett. 12, 8115–8120. doi:10.1021/acs.jpclett.1c01605
Huang, W., Song, G., Hong, H., and Xie, K. (2014). Deep Architecture for Traffic Flow Prediction: Deep Belief Networks with Multitask Learning. IEEE Trans. Intell. Transport. Syst. 15, 2191–2201. doi:10.1109/TITS.2014.2311123
Hutahaean, J., Demyanov, V., and Christie, M. A. (2017). On Optimal Selection of Objective Grouping for Multiobjective History Matching. SPE J. 22, 1296–1312. doi:10.2118/185957-PA
Irisarri, E., García, M. V., Pérez, F., Estévez, E., and Marcos, M. (2016). “A Model-Based Approach for Process Monitoring in Oil Production Industry,” in IEEE 21st International Conference on Emerging Technologies and Factory Automation (ETFA), Berlin, Germany, 6-9 Sept. 2016 (IEEE), 1–4. doi:10.1109/ETFA.2016.7733633
Jain, S., Smit, A., Truong, S. Q., Nguyen, C. D., Huynh, M.-T., Jain, M., Young, V. A., Ng, A. Y., Lungren, M. P., and Rajpurkar, P. (2021). “VisualCheXbert,” in Proc. Conf. on Health, Inference and Learning, Virtual Event USA, April 8 - 10, 2021 (ACM), 105–115. doi:10.1145/3450439.3451862
Katoch, S., Chauhan, S. S., and Kumar, V. (2021). A Review on Genetic Algorithm: Past, Present, and Future. Multimed. Tools Appl. 80, 8091–8126. doi:10.1007/s11042-020-10139-6
Keshava, M. C., Srinivasulu, S., Reddy, P. N., and Naik, B. D. (2020). Machine Learning Model for Movie Recommendation System. Int. J. Eng. Res. Tech. 9, 800–801. doi:10.17577/ijertv9is040741
Konno, T., Kurokawa, H., Nabeshima, F., Sakishita, Y., Ogawa, R., Hosako, I., et al. (2021). Deep Learning Model for Finding New Superconductors. Phys. Rev. B 103, 014509. doi:10.1103/PhysRevB.103.014509
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2017). ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 60, 84–90. doi:10.1145/3065386
Lagree, A., Mohebpour, M., Meti, N., Saednia, K., Lu, F.-I., Slodkowska, E., et al. (2021). A Review and Comparison of Breast Tumor Cell Nuclei Segmentation Performances Using Deep Convolutional Neural Networks. Sci. Rep. 11, 8025. doi:10.1038/s41598-021-87496-1
Lash, M. T., and Zhao, K. (2016). Early Predictions of Movie success: the Who, what, and when of Profitability. J. Manag. Inf. Syst. 33, 874–903. doi:10.1080/07421222.2016.1243969
Lattner, S., and Grachten, M. (2019). “High-level Control of Drum Track Generation Using Learned Patterns of Rhythmic Interaction,” in 2019 IEEE Workshop and Applications of Signal Processing to Audio, New Paltz, NY, USA, 20-23 Oct. 2019 (IEEE), 35–39. doi:10.1109/WASPAA.2019.8937261
LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). Gradient-Based Learning Applied to Document Recognition, Proc. IEEE, 86, 2278–2324. doi:10.1109/5.726791
Li, K., and Horne, R. N. (2003). A Decline Curve Analysis Model Based on Fluid Flow Mechanisms. Proc. Li2003adc, Spe-83470-ms. doi:10.2118/83470-MS
Liu, W., Liu, W. D., and Gu, J. (2020). Forecasting Oil Production Using Ensemble Empirical Model Decomposition Based Long Short-Term Memory Neural Network. J. Pet. Sci. Eng. 189, 107013. doi:10.1016/j.petrol.2020.107013
Ma, J., Li, N., Huang, Y., and Ma, Y. (2020). Smart Online Fuel Sulfur Prediction in Diesel Hydrodesulfurization Process. IEEE Access 8, 100974–100988. doi:10.1109/ACCESS.2020.2998515
Mikhail, R. S., and Brunauer, S. (1975). Surface Area Measurements by Nitrogen and Argon Adsorption. J. Colloid Interf. Sci. 52, 572–577. doi:10.1016/0021-9797(75)90282-9
Ng, V., Rees, E. E., Niu, J., Zaghlool, A., Ghiasbeglou, H., and Verster, A. (2020). Application of Natural Language Processing Algorithms for Extracting Information from News Articles in Event-Based Surveillance. Ccdr 46, 186–191. doi:10.14745/ccdr.v46i06a06
Overgoor, G., Chica, M., Rand, W., and Weishampel, A. (2019). Letting the Computers Take over: Using AI to Solve Marketing Problems. Calif. Manag. Rev. 61, 156–185. doi:10.1177/0008125619859318
Pophale, R., Cheeseman, P. A., and Deem, M. W. (2011). A Database of New Zeolite-like Materials. Phys. Chem. Chem. Phys. 13, 12407–12412. doi:10.1039/C0CP02255A
Qin, J., Pan, W., Xiang, X., Tan, Y., and Hou, G. (2020). A Biological Image Classification Method Based on Improved CNN. Ecol. Inform. 58, 101093. doi:10.1016/j.ecoinf.2020.101093
Rappe, A. K., Casewit, C. J., Colwell, K. S., Goddard, W. A., and Skiff, W. M. (1992). UFF, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations. J. Am. Chem. Soc. 114, 10024–10035. doi:10.1021/ja00051a040
Saar, K. L., Morgunov, A. S., Qi, R., Arter, W. E., Krainer, G., Lee, A. A., et al. (2021). Learning the Molecular Grammar of Protein Condensates from Sequence Determinants and Embeddings. Proc. Natl. Acad. Sci. USA 118, e2019053118. doi:10.1073/pnas.2019053118
Sadowski, P., Fooshee, D., Subrahmanya, N., and Baldi, P. (2016). Synergies between Quantum Mechanics and Machine Learning in Reaction Prediction. J. Chem. Inf. Model. 56, 2125–2128. doi:10.1021/acs.jcim.6b00351
Sagheer, A., and Kotb, M. (2019). Time Series Forecasting of Petroleum Production Using Deep LSTM Recurrent Networks. Neurocomputing 323, 203–213. doi:10.1016/j.neucom.2018.09.082
Sauceda, H. E., Vassilev-Galindo, V., Chmiela, S., Müller, K.-R., and Tkatchenko, A. (2021). Dynamical Strengthening of Covalent and Non-covalent Molecular Interactions by Nuclear Quantum Effects at Finite Temperature. Nat. Commun. 12, 442. doi:10.1038/s41467-020-20212-1
Scherer, C., Scheid, R., Andrienko, D., and Bereau, T. (2020). Kernel-based Machine Learning for Efficient Simulations of Molecular Liquids. J. Chem. Theor. Comput. 16, 3194–3204. doi:10.1021/acs.jctc.9b01256
Schlexer Lamoureux, P., Winther, K. T., Garrido Torres, J. A., Streibel, V., Zhao, M., Bajdich, M., et al. (2019). Machine Learning for Computational Heterogeneous Catalysis. ChemCatChem 11, 3581–3601. doi:10.1002/cctc.201900595
Schütt, K. T., Sauceda, H. E., Kindermans, P.-J., Tkatchenko, A., and Müller, K.-R. (2018). SchNet - A Deep Learning Architecture for Molecules and Materials. J. Chem. Phys. 148, 241722. doi:10.1063/1.5019779
Shallue, C. J., and Vanderburg, A. (2018). Identifying Exoplanets with Deep Learning: a Five-Planet Resonant Chain Around Kepler-80 and an Eighth Planet Around Kepler-90. Aj 155, 94. doi:10.3847/1538-3881/aa9e09
Shawe-Taylor, J., and Sun, S. (2011). A Review of Optimization Methodologies in Support Vector Machines. Neurocomputing 74, 3609–3618. doi:10.1016/j.neucom.2011.06.026
Shazeer, N., Cheng, Y., Parmar, N., Tran, D., Vaswani, A., Koanantakool, P., et al. (2018). “Mesh-tensorflow: Deep Learning for Supercomputers,” in NIPS’18: Proc. 32nd Int. Conf. on Neural Information Processing Systems, Montréal, Canada, December 3 - 8, 2018 (Curran Associates Inc), 10435–10444. doi:10.5555/3327546.3327703
Shorten, C., and Khoshgoftaar, T. M. (2019). A Survey on Image Data Augmentation for Deep Learning. J. Big Data 6, 60. doi:10.1186/s40537-019-0197-0
Sinha, P., Datar, A., Jeong, C., Deng, X., Chung, Y. G., and Lin, L.-C. (2019). Surface Area Determination of Porous Materials Using the Brunauer-Emmett-Teller (BET) Method: Limitations and Improvements. J. Phys. Chem. C 123, 20195–20209. doi:10.1021/acs.jpcc.9b02116
Sircar, A., Yadav, K., Rayavarapu, K., Bist, N., and Oza, H. (2021). Application of Machine Learning and Artificial Intelligence in Oil and Gas Industry. Pet. Res. doi:10.1016/j.ptlrs.2021.05.009
Themistocleous, C., Ficek, B., Webster, K., den Ouden, D.-B., Hillis, A. E., and Tsapkini, K. (2021). Automatic Subtyping of Individuals with Primary Progressive Aphasia. Jad 79, 1185–1194. doi:10.3233/JAD-201101
Tibshirani, R. (1996). Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B (Methodological) 58, 267–288. doi:10.1111/j.2517-6161.1996.tb02080.x
Torralba, A., Fergus, R., and Freeman, W. T. (2008). 80 Million Tiny Images: A Large Data Set for Nonparametric Object and Scene Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 30, 1958–1970. doi:10.1109/TPAMI.2008.128
Tran, K., and Ulissi, Z. W. (2018). Active Learning across Intermetallics to Guide Discovery of Electrocatalysts for CO2 Reduction and H2 Evolution. Nat. Catal. 1, 696–703. doi:10.1038/s41929-018-0142-1
Tsvaki, J. J., Tailakov, D. O., and Pavlovskiy, E. N. (2020). Development of Water Flood Model for Oil Production Enhancement. Sci. Artif. Intelligence Conf. (S.A.I.ence), 46–49. doi:10.1109/s.a.i.ence50533.2020.9303200
Wang, K., Niu, X., Dou, Y., Xie, D., and Yang, T. (2021). A Siamese Network with Adaptive Gated Feature Fusion for Individual Knee OA Features Grades Prediction. Sci. Rep. 11, 16833. doi:10.1038/s41598-021-96240-8
Wang, Y., Shang, D., Yuan, X., Xue, Y., and Sun, J. (2019). Modeling and Simulation of Reaction and Fractionation Systems for the Industrial Residue Hydrotreating Process. Processes 8, 32. doi:10.3390/pr8010032
Williams, T., McCullough, K., and Lauterbach, J. A. (2020). Enabling Catalyst Discovery through Machine Learning and High-Throughput Experimentation. Chem. Mater. 32, 157–165. doi:10.1021/acs.chemmater.9b03043
Xie, T., and Grossman, J. C. (2018). Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys. Rev. Lett. 120, 145301. doi:10.1103/PhysRevLett.120.145301
Yang, W., Fidelis, T. T., and Sun, W. H. (2020). Machine Learning in Catalysis, from Proposal to Practicing. ACS Omega 5, 83–88. doi:10.1021/acsomega.9b03673
Zaobi, Y., Deri-Rozov, S., and Shomron, N. (2021). Machine Learning-Based Prediction of COVID-19 Diagnosis Based on Symptoms. Npj Digit. Med. 4, 3. doi:10.1038/s41746-020-00372-6
Zhang, P. (1993). Model Selection via Multifold Cross Validation. Ann. Statist. 21, 299–313. doi:10.1214/aos/1176349027
Keywords: artificial intelligence, heterogeneous catalysis, hydrodesulfurization, supervised learning, machine learning
Citation: Bokhimi X (2021) Learning the Use of Artificial Intelligence in Heterogeneous Catalysis. Front. Chem. Eng. 3:740270. doi: 10.3389/fceng.2021.740270
Received: 12 July 2021; Accepted: 28 September 2021;
Published: 20 October 2021.
Edited by:
Jose Escobar, Mexican Institute of Petroleum, MexicoReviewed by:
Adnan Alsalim, University of Technology, IraqMaría Barrera, Universidad Veracruzana, Mexico
Copyright © 2021 Bokhimi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xim Bokhimi, Ym9raGltaUBmaXNpY2EudW5hbS5teA==
 Xim Bokhimi
Xim Bokhimi