Multiparametric Programming in Process Systems Engineering: Recent Developments and Path Forward

Pappas, Iosif; Kenefake, Dustin; Burnak, Baris; Avraamidou, Styliani; Ganesh, Hari S.; Katz, Justin; Diangelakis, Nikolaos A.; Pistikopoulos, Efstratios N.

doi:10.3389/fceng.2020.620168

REVIEW article

Front. Chem. Eng., 21 January 2021

Sec. Computational Methods in Chemical Engineering

Volume 2 - 2020 | https://doi.org/10.3389/fceng.2020.620168

Multiparametric Programming in Process Systems Engineering: Recent Developments and Path Forward

Iosif Pappas^1,2

Dustin Kenefake^1,2

Baris Burnak^1,2

Styliani Avraamidou²

Hari S. Ganesh²

Justin Katz^1,2

Nikolaos A. Diangelakis^1,2

Efstratios N. Pistikopoulos^1,2*

¹Artie McFerrin Department of Chemical Engineering, Texas A&M University, College Station, TX, United States
²Texas A&M Energy Institute, Texas A&M University, College Station, TX, United States

The inevitable presence of uncertain parameters in critical applications of process optimization can lead to undesirable or infeasible solutions. For this reason, optimization under parametric uncertainty was, and continues to be a core area of research within Process Systems Engineering. Multiparametric programming is a strategy that offers a holistic perspective for the solution of this class of mathematical programming problems. Specifically, multiparametric programming theory enables the derivation of the optimal solution as a function of the uncertain parameters, explicitly revealing the impact of uncertainty in optimal decision-making. By taking advantage of such a relationship, new breakthroughs in the solution of challenging formulations with uncertainty have been created. Apart from that, researchers have utilized multiparametric programming techniques to solve deterministic classes of problems, by treating specific elements of the optimization program as uncertain parameters. In the past years, there has been a significant number of publications in the literature involving multiparametric programming. The present review article covers recent theoretical, algorithmic, and application developments in multiparametric programming. Additionally, several areas for potential contributions in this field are discussed, highlighting the benefits of multiparametric programming in future research efforts.

1 Introduction

What is the impact of varying parameters in mathematical optimization problems? Optimal decision-making under parametric uncertainty is a fundamental area of research within the Process Systems Engineering community since its presence in practical applications is unavoidable. Reaction kinetic constants, mass transfer coefficients, demand volumes, feedstock prices, process disturbances, appear in optimization models, and comprise sources of uncertainty in the form of parameters that can lead to inaccurate or infeasible decisions. As a result, the derivation of the optimal solution which incorporates uncertainty considerations becomes challenging.

Among the various techniques that have been proposed in the open literature to solve this problem, multiparametric programming has emerged as a powerful tool to explain how parametric uncertainty and variability influence optimal decisions. The case of single-parameter problems (i.e. parametric programming) had been investigated since the 1950s. However, the computational complexity associated with the presence of numerous parameters in the problem formulation, hindered the development of algorithms for its solution. In one of these early efforts, Barnett (1968) demonstrated how the range of allowable changes of parameters appearing on the optimal basis of a linear program can be calculated, along with the form of the optimal solution. Multiparametric programming attracted significant interest, most notably following the efforts of Gal and Nedoma (1972), who considered multiple parameters, and introduced a systematic strategy to solve multiparametric linear programming problems (mpLPs), and explore all optimal active sets. In their formulation, the uncertain parameters appear solely in the right-hand side of the constraints, and the solution of the aforementioned program offered an explicit relationship between the decision variables and the varying parameters. This relationship constitutes the foundation of multiparametric programming and provides a holistic view to perform uncertainty analysis in optimization problems. Hence, the optimizer solves a single mathematical programming problem to describe the impact of the uncertainty for its whole range, without the assumption of a given probability distribution. Subsequently, uncertainty in the objective function was included in the problem definition (Gal, 1975).

The seminal papers by Pistikopoulos et al. (2000) and Bemporad et al. (2002b) that demonstrated the first exact strategy for the solution of convex multiparametric quadratic programming problems (mpQPs) represent another major milestone. In addition to that, they proved that a model predictive control problem (MPC), with a quadratic cost function, can be exactly reformulated and solved as a mpQP. In this work, the optimal control actions of a system — dictated by a discrete linear time-invariant state-space model — within a MPC framework are expressed as affine functions of the initial states which partially comprise the uncertainty vector of the optimal control problem. The immediate benefits of the offline nature of the solution of the multiparametric/explicit model predictive control (mpMPC) problem are captured by the following statements

(1) The computational burden associated with solving the MPC problem is dramatically reduced since the online repetitive solution of a quadratic optimization problem is substituted by a function evaluation.

(2) The feasible state-space of the control problem is explicitly created, offering a clear picture of the operability boundaries of the system to the engineer before the start of a closed-loop simulation.

(3) The understanding of the impact of the initial states of the system to the corresponding optimal control law and the objective function value for any optimal active set.

This research breakthrough motivated a new research direction in the process control community due to the capabilities of the approach for real-time optimization problems, where the computational power is limited. Nevertheless, the aforementioned benefits of having an explicit solution come at a cost. Namely, the computational effort in deriving the full multiparametric solution depends on the number of decision variables, parameters, and constraints, and as a result, as the problem size grows, the construction of the full solution becomes challenging. Additionally, for large-scale problems the procedure of finding which optimal active set corresponds to a feasible parameter value — the point location problem — can be complex. Nowadays, research efforts could be categorized into theoretical developments to derive and store the solution of new classes of multiparametric programming problems, the construction of efficient algorithms for the exploration of the parameter space which is described by the optimal active sets, and finally, their application in engineering problems. mpMPC is by far the most well-studied and explored application of multiparametric programming. Nevertheless, this exciting field captures a generous number of applications, beyond process control. To this end, researchers adopted multiparametric programming to solve other classes of receding horizons problems, most prominently, process scheduling and moving-horizon estimation. In recent years, the area of multiparametric programming has burgeoned with advances that include its integration with data-driven modeling and optimization techniques, the interactions of process design, control, and scheduling, robust MPC, and strategies for multilevel optimization.

Several reviews have been published in the field of multiparametric programming and mpMPC (Dua et al., 2008; Alessio and Bemporad, 2009; Pistikopoulos, 2012; Oberdieck et al., 2016a). The objective of this article is to provide an update on the recent developments in theory, algorithmic strategies, and applications, which have appeared in the open literature. Additionally, the aim is to also offer a perspective on potential future research pathways which will utilize multiparametric programming-based strategies to solve challenging engineering problems, and act as a roadmap for a researcher in this field. The remainder of this work is organized as follows: In Section 2, the fundamentals of multiparametric programming are introduced, while in Section 3 recent theoretical and algorithmic contributions are presented. In Section 4 applications which have multiparametric programming in their core to solve critical engineering problems are discussed. Section 5 serves as a future outlook, and in Section 6, we conclude.

2 Background

2.1 Multiparametric Programming

Consider a general multiparametric programming problem, described by the following formulation

\begin{array}{l} z (θ) = min_{x} & f (x, θ) \\ s . t . & g (x, θ) \leq 0 \\ h (x, θ) = 0 \\ x \in ℝ^{n} \\ θ \in ℝ^{m} \end{array} (1)

where x is the vector of the decision variables, θ the vector of the uncertain parameters, and $g (x, θ)$ and $h (x, θ)$ the inequality and equality constraints respectively. Multiparametric programming is founded on the assumptions and principles of the Basic Sensitivity Theorem as presented in Fiacco (1983). Based on that, the active set in the neighborhood of a nominal parameter vector, $θ *$ , with a corresponding optimal solution and Lagrange multipliers $(x *, λ *)$ of an optimization program, remains unchanged. Consequently, parametric areas with the same active set are created — critical regions — each characterized with a distinct set of Karush-Kuhn-Tucker (KKT) conditions. Since the optimality conditions remain the same, the resulting system of equations derived from the KKT conditions can be analytically solved, and hence the optimal solution with respect to the varying parameters for the whole parameter space is explicitly constructed. This statement can be expressed as

x * (θ) = {\begin{matrix} x^{1} (θ), & i f & θ \in C R^{1} \\ x^{2} (θ), & i f & θ \in C R^{2} \\ . \\ . \\ . \\ x^{v} (θ), & i f & θ \in C R^{v} \end{matrix} (2)

where the $i^{t h}$ critical region, $C R^{i}$ , corresponds to the parameter space described by the $i^{t h}$ active set. Consequently, the full solution of this optimization problem is obtained beforehand, and by identifying a given parameter value, the optimal solution is reduced to a simple function evaluation. The procedure of finding in which region a measured value of parameters lies, is termed as the point location problem. A schematic of a map of critical regions is shown in Figure 1.

Depending on the structure of problem 1, the functions describing the multiparametric solution and the structure of the critical regions can drastically change. General closed-forms for the optimal solutions are known for mpLPs, mpQPs, and their mixed-integer counterparts (mpMILPs, mpMIQPs). Specifically, assume the following mpMIQP that includes both continuous optimization variables, x, and binary variables, y

\begin{array}{l} z (θ) = min_{x, y} & {(Q ω + H θ + c)}^{T} ω \\ s . t & W_{i} x + E_{i} y \leq b_{i} + F_{i} θ \\ W_{e} x + E_{e} y = b_{e} + F_{e} θ \\ x \in ℝ^{n}, y \in {0,1}^{p}, ω = {[x^{T} y^{T}]}^{T} \\ θ \in ℝ^{m} \end{array} (3)

where the problem is defined by the matrices of appropriate dimensions.

Table 1 demonstrates the properties of the multiparametric solution depending on the problem type. Please note that problem 3 includes all the aforementioned problem formulations.

2.2 Connecting Multiparametric Programming and Model Predictive Control

A model predictive control problem, whose goal is to drive the system to the origin, can be described by the following formulation, assuming that ${\hat{x}}_{k}$ is the vector of the states of the system, ${\hat{y}}_{k}$ the outputs, and ${\hat{u}}_{k}$ are the control actions to be found at time instant k

\begin{array}{l} min_{{\hat{u}}_{0}, \dots, {\hat{u}}_{N - 1}} & {\hat{x}}_{N}^{T} P {\hat{x}}_{N} + \sum_{k = 0}^{N - 1} {\hat{x}}_{k}^{T} Q_{R} {\hat{x}}_{k} + {\hat{u}}_{k}^{T} R {\hat{u}}_{k} \\ s . t . & {\hat{x}}_{k + 1} = A {\hat{x}}_{k} + B {\hat{u}}_{k} & k = 0, \dots, N \\ {\hat{y}}_{k} = C {\hat{x}}_{k} & k = 0, \dots, N \\ {\hat{x}}_{k} \in X & k = 0, \dots, N \\ {\hat{u}}_{k} \in U & k = 0, \dots, N - 1 \\ {\hat{x}}_{0} = \hat{x} (0) \\ {\hat{x}}_{N} \in T \end{array} (4)

where $Q_{R}$ and R are the weights of the objective function, and P is the stabilizing matrix derived by the solution of the Riccati equation for discrete systems, and N is the prediction horizon of the problem. It is assumed that the sets $X, U$ , and $T$ are compact, the matrices $Q_{R}$ and P are positive semi-definite, while R is positive definite. Problem 4 is dictated by a discrete linear state-space model. Hence, future state vectors can be expressed as a function of the initial state of the system and the control actions, by utilizing the following relationship

{\hat{x}}_{k} = A^{k} {\hat{x}}_{0} + \sum_{q = 0}^{k - 1} A^{q} B {\hat{u}}_{k - 1 - q} (5)

Assuming that the initial state vector ${\hat{x}}_{0}$ is a vector of uncertain parameters, problem 4 can be reformulated to 3, and the optimal control policy can be calculated as an affine function of this uncertainty vector. Through mpMPC additive disturbances, setpoints, and outputs can also be part of the problem formulation.

3 Theoretical and Algorithmic Developments

The benefits of multiparametric programming-based solutions in practical applications have created a dynamic interest by the research community over the years, and resulted in multiple theoretical and algorithmic developments. Specifically, these contributions were focused on 1) the solution of new classes of multiparametric programming problems, and 2) the derivation of algorithms for the exploration of the parameter space.

3.1 Multiparametric Nonlinear Programming

The need to tackle more complex problems, described by nonlinear functions, is a central area of research within the multiparametric programming community. Even though linear models are shown to perform well in a wide range of optimization applications, such as model predictive control, various processes are inherently nonlinear. Apart from that, the required fluctuations in operation, together with stricter environmental and financial targets, lead to the need of incorporating nonlinear terms in these optimization formulations. Researchers focused on the impact of a single parameter to calculate how that would affect the behavior of a nominal solution of general nonlinear programs (Kojima, 1979; Benson, 1982; Kojima and Hirabayashi, 1984). The foundations of modern algorithms in nonlinear multiparametric programming have been based on the results of Fiacco and their coworkers, who provided local regularity and local sensitivity conditions for the general case involving multiple parameters (Fiacco, 1976; Fiacco, 1983; Fiacco and Kyparisis, 1986). More recent efforts in multiparametric nonlinear programming problems (mpNLPs) concentrated on developing approximations of the mpNLP to a form that exact solution strategies exist, by creating linear or quadratic approximations of the objective function and linearization of the constraints (Dua and Pistikopoulos, 1999; Johansen, 2002; Domínguez and Pistikopoulos, 2013). Apart from that geometric-based strategies have been utilized by creating parameter space approximation through hypercubes, simplicies, and hyperrectangles (Johansen, 2004; Bemporad and Filippi, 2006; Narciso, 2009), the utilization of a partially offline solution (Fotiou et al., 2006), or the approximation of the solution manifold based on the Fritz John conditions of optimality (Hale and Qin, 2004; Hale, 2005).

Dua (2015) considered general multiparametric mixed-integer nonlinear programming problems (mpMINLPs) described by polynomial functions. The author derived and solved the system of polynomial equations resulting from the KKT conditions, where the integer variables are treated as uncertain parameters. Since the problems include integer and nonconvex functions, the solutions of the KKT system are checked to identify whether the inactive inequality constraints, the slack complementary slackness and the constraint qualifications are satisfied. In Charitopoulos and Dua (2016) hybrid nonlinear model predictive control problems were considered, and the problem is reformulated as a mixed-integer polynomial programming problem. The algorithmic approach is based on the analytical solution of the system of equations arising from the KKT conditions. After performing feasibility and constraint qualification investigations of the solutions, a dominance check is performed for overlapping critical regions, leading to an exact multiparametric solution.

In another contribution, the focus was on controlling spatially distributed systems described by partial differential equations (PDEs) (Petsagkourakis and Theodoropoulos, 2018). A reduced-order digital twin of the process was constructed using proper orthogonal decomposition followed by a neural network. Given the challenges of directly solving the resulting mpNLP, multiple linearizations of the nonlinear problem were created, resulting in mpQPs. A model approximation checking mechanism was also employed that verifies whether the produced approximation error bound was satisfied, or further refinement of the model was required. A different perspective in solving mpNLPs in the form of mpMPC was given in Bayer et al. (2016). The authors created a grid of the state-space and assume a control law parametrization. A suboptimal control law, valid for a set of initial conditions, is computed through robust tube-based MPC techniques (Langson et al., 2004). As a result, hyperrectangular regions are created. However, the proposed approach has also an online cost, associated with finding the region with the desired control law.

In contrast to other efforts which consider general mpNLPs, in Diangelakis et al. (2018); Pappas et al. (2020b) the authors restricted themselves to multiparametric quadratically constrained quadratic programming problems (mpQCQPs), motivated by the applications described by this class of problems. However, the given structure of the problem allowed them to systematically show how the explicit solution for this class of problems can be generated without a post-processing step. The approach is based on a second-order Taylor approximation of the Basic Sensitivity Theorem, which allows for the existence and derivation of the multiparametric solution. In addition to the case where only convex constraints are included in the problem description, the authors expanded to the case where nonconvex constraints are part of the optimization formulation. The incorporation of quadratic terms in the constraints results in the construction of nonlinear and nonconvex critical regions. Hence, the adoption of a geometric strategy is challenging due to the absence of facets to utilize to explore new critical regions. For this reason, the authors utilize an active set-based exploration algorithm to guarantee the complete characterization of the parameter space. A crucial point in this procedure is also the fact that the comparison of overlapping critical regions is avoided, since the resulting Lagrange function is guaranteed to be convex. This development has been utilized for the solution of quadratically constrained model predictive control problems and the flexibility index problems with quadratic constraints and design considerations (Pappas et al., 2020a; Pappas et al., 2020b).

Based on the presented solution strategies for mpNLPs, there are two main routes that this class of problems has been approached. Firstly, an approximate solution, founded on a mpLP or mpQP, can be derived which has advantages in solving larger-scale problems. However, an approximation step will potentially encompass inaccuracies that can lead to undesirable behavior or infeasibility when applied to an actual problem. On the other hand, exact solution approaches result into an accurate solution. The fundamental challenge with exactly dealing with mpNLPs is the required analytical solution of the resulting system of nonlinear equations derived from the KKT conditions, which will express the decision variables as a function of the uncertain parameters. In Dua (2015); Charitopoulos and Dua (2016); Pappas et al. (2020b), Gröbner bases have been utilized — which scale with the number of decision variables — to build the parametric solution. However, among the computational algebra techniques, they have shown to be effective in solving nonlinear equations analytically, and further developments in parallel computing will encourage their wider adoption in multiparametric programming.

3.2 Parameter Space Exploration

A critical point in the multiparametric programming solution construction process is the efficiency of exploring the parameter space. Strategies to achieve that still remains an active area of research. Initially, approaches that solely observe the parameter space had been suggested. Namely, assuming that a single critical region is discovered, these exploration algorithms identify geometrically adjacent critical regions. The procedure is repeated until all regions are found. On the other hand, active set-based strategies exploit the fact that the optimal solution is defined by the active constraints, and hence by considering every active set in the parameter space, all critical regions are found. As the former techniques scale unfavorably with the number of parameters of the problem, and the latter with the number of decision variables and constraints, the selection of the exploration algorithm depends on the structure of the optimization problem. Moreover, note that that geometric-based techniques do not guarantee the full parameter space exploration. In the past three years, hybrid algorithms that blend the benefits of both approaches have been published, and have been extensively used in various applications. In Table 2 the algorithms that can solve the classes of problems that have general closed-form solutions are presented.

FIGURE 1

Figure 1. Schematic representation of critical regions resulting from the solution of a multiparametric programming problem. Each region is described by a different optimal active set.

TABLE 1

Table 1. Properties of multiparametric programming problems that have general closed-form solutions.

TABLE 2

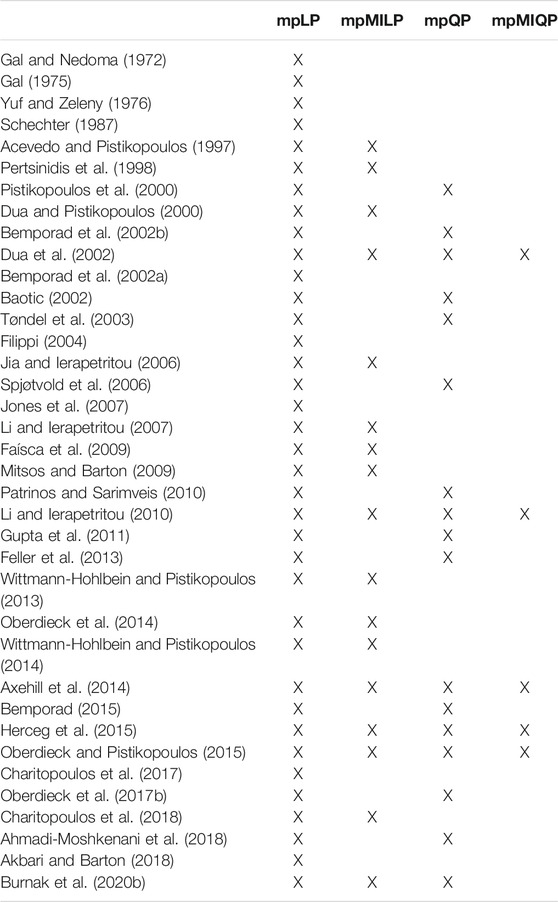
Table 2. Multiparametric programming algorithms for the solution of mpLPs, mpMPs, mpMILPs, and mpMIQPs.

Ahmadi-Moshkenani et al. (2018) proposed a hybrid multiparametric exploration approach for mpQPs, in a similar spirit to the one proposed by Oberdieck et al. (2017b). In particular, the devised algorithm is an active set-based in its core, and as a result, assumes a candidate active set to be potentially optimal. Subsequently, it asks the question whether there is a parameter vector value that the optimality assumption holds true. Additionally, to reduce the computational complexity, the authors take advantage of the facet-to-facet property, which states that two adjacent critical regions differ by a single constraint in their active set. Hence, for an already explored critical region, they add or remove a constraint in the construction of the optimality conditions and verify if that holds.

In Akbari and Barton (2018), multiparametric programming was studied through the lenses of metabolic networks and flux balance analysis. A key focus of this contribution is primal degeneracy and multiplicity of mpLPs. By exploiting the structure of the studied problems, the authors show that the issue of having an overdetermined KKT system with respect to the decision variables can be solved through generalized inverses, with enhanced computational complexity to the already published approaches. Moreover, the case where there are multiple primal solutions was addressed through an auxiliary objective or by solving a lexicographic linear program. An extensive discussion in degeneracy in multiparametric programming, and ways to tackle it is also presented in Oberdieck et al. (2016a).

Burnak et al. (2020b) proposed a space exploration algorithm for mpLPs, mpQPs, and mpMILPs. Their approach is facilitated by constructing simplices of the parameter space through Delaunay triangulation. Deterministic optimization problems are solved at the vertices of these simplices based on which parameter areas described by the same optimality conditions are identified. As a result, optimal parameter space partitions are created. Furthermore, it is shown that through the proposed algorithm volumetrically significant critical regions are prioritized to be discovered.

4 Applications

Multiparametric programming theory has been utilized to tackle various challenging problems. In this section, application areas that have utilized multiparametric programming at their heart for their solution are presented.

4.1 Multiparametric/Explicit Model Predictive Control

Multiparametric/explicit model predictive control is the most well-studied application of multiparametric programming. Since its inception (Pistikopoulos et al., 2000; Bemporad et al., 2002b), countless implementations and variations of the approach have been published in the literature both in simulations and in practical applications, which contribute to the thousands of citations of the original papers. Extensive reviews in mpMPC have been published in the literature to capture the use of multiparametric programming in process control (Dua et al., 2008; Alessio and Bemporad, 2009; Pistikopoulos et al., 2015). It is to be highlighted that large-scale industrial applications have utilized and will continue to utilize an online optimization algorithm for MPC. These implementations are used to control slow processes such as oil refineries and chemical manufacturing plants, which have already invested in installing a form of online MPC (Qin and Badgwell, 2000; Qin and Badgwell, 2003). Also, the scale of the problem for such implementations makes the derivation of the full multiparametric solution substantially challenging, given that they are comprised by a significant number of variables, states, and constraints. Nevertheless, the benefits of mpMPC are amplified in small to medium-scale applications. In these cases, there might exist some control hardware and software infrastructure to achieve the control objective, but due to lack of computational power or other constraints (e.g. power requirements, cost), the use of online MPC is not suitable. For such processes, whose dynamics are typically fast, mpMPC (or MPC-on-a-chip) can be an advantageous choice (Alessio and Bemporad, 2009; Pistikopoulos, 2009). Hence, numerous applications of mpMPC on simulation and real-life laboratory and pilot problems have been recorded in the published literature. The latter include biomedical systems (Dua, 2005), separation units (Grancharova et al., 2004; Mandler et al., 2006), automotive systems (Di Cairano et al., 2008; Naus et al., 2008), power electronics (Linder and Kennel, 2005; Mariéthoz and Morari, 2008), and energy systems (Arce et al., 2011). Accounting to its potential and recent advancements, mpMPC has continued to be applied in several fields and realistic problems, that are highlighted on Table 3.

TABLE 3

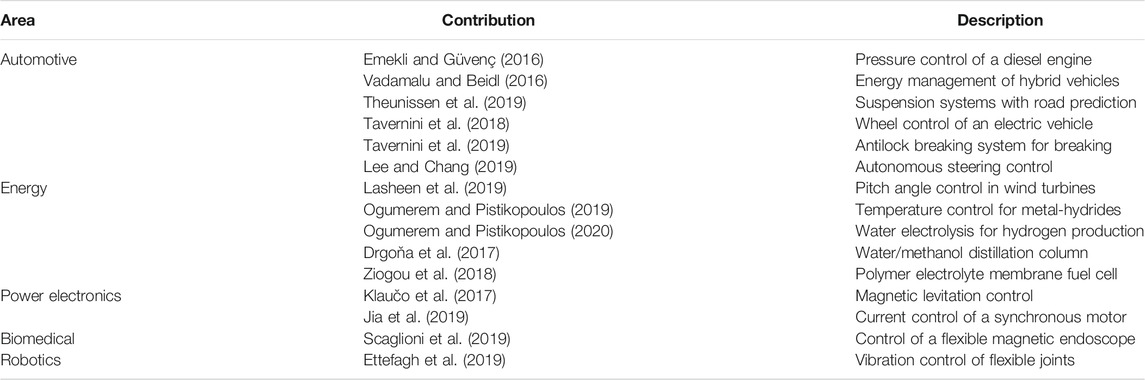
Table 3. List of recent real-life laboratory and pilot-scale applications of multiparametric/explicit model predictive control.

It is expected that mpMPC, similarly to the online MPC, will continue to find success and applicability in various fields (Mayne, 2014). Particular emphasis will be paid on areas that do not have the capability of having a powerful computer machine to perform online calculations to solve the optimal control problem.

4.2 Design, Control, and Scheduling

The Process Systems Engineering community has considered the seamless integration of process design and operational decisions a vital direction to achieve improved process efficiency and reliability (Burnak et al., 2019b). Conventional techniques for process decisions are usually isolated from each other with a hierarchical order in the time scales they span. Such isolation yields suboptimal, even infeasible operations when the decisions are applied in real time, due to lack of perfect information flow across different decision layers (Mohideen et al., 1996; Pistikopoulos and Diangelakis, 2016; Caspari et al., 2020). The integrated problem is mathematically casted as a multilevel dynamic optimization problem, hence conventional global optimization techniques are unable to solve this class of problems without simplifying assumptions or approximations. Furthermore, the time scale differences between each level exacerbate the tractability of the integrated problem (Rafiei and Ricardez-Sandoval, 2020). Multiparametric programming has been shown to be an effective tool to develop a simultaneous framework for here-and-now design decisions and operational decisions including process control, scheduling, and planning. The explicit solution set, described by Eq. 2, provides an offline map of optimal operational decisions that can be integrated in a dynamic optimization problem that governs longer time horizons. Therefore, the faster time scale decisions can be formulated as a multiparametric programming problem, where the unrealized system parameters at their respective levels can be explicitly accounted for, and incorporated into an overarching optimization problem with slower process dynamics (Burnak et al., 2020a).

Sakizlis et al. (2003) presented one of the first significant attempts to use multiparametric programming for the integration of process design and operational optimization problems. The authors integrated the explicit solution of an mpMPC into a mixed integer dynamic optimization problem that simultaneously minimizes the capital and operating costs. Although the approach proposed by Sakizlis et al. (2003) was shown to be effective as showcased on a binary distillation column and an evaporator, it relied on repetitive linearizations and solving a multiparametric programming problem at every iteration. Diangelakis et al. (2017) improved this approach by deriving a “design dependent offline controller”, which accepted the design variable as a parameter in the mpMPC problem, allowing for the formulation of a single mixed integer dynamic optimization formulation to determine the optimal design and closed loop control strategies. Tian et al. (2020) showed that a similar systematic approach is also applicable for much more complex intensified systems, namely a reactive distillation process.

On the integration of the operational decisions, Zhuge and Ierapetritou (2014) integrated the explicit MPC expressions in a continuous time, event point based scheduling problem for a batch process. Burnak et al. (2018) derived the offline expressions both for the scheduling and the MPC problems, and addressed the time scale gap by developing offline scale bridging models. Charitopoulos et al. (2019) incorporated nonlinear mpMPC, and extended the problem to include the planning problem.

A complete theory and framework for the integration of process design, scheduling, and control decisions was recently proposed by Burnak et al. (2019a), where the authors derived design dependent offline control and scheduling strategies that are embedded exactly in a mixed integer dynamic design optimization problem via multiparametric programming. Burnak and Pistikopoulos (2020) extended this framework to batch processes, where the scheduling of the multipurpose batch units is represented by a State Equipment Network (SEN).

4.3 Multilevel Optimization

Optimization problems involving a set of nested optimization problems over a single feasible region are referred to as multilevel programming problems. The control over the decision variables is divided among different optimization levels, but all decision variables can affect the objective function and constraints of all optimization levels. This class of problems has attracted considerable attention across a broad range of research communities, including economics, sciences, and engineering, and has been applied to many diverse problems that require hierarchical decision making.

Since the early 1980s, many algorithms have been proposed for the solution of continuous bilevel problems with many approaches exploiting the KKT optimality conditions of the lower level problem, to transform the multilevel problem into a single level problem. The main idea behind the development of multiparametric algorithms for the solution of multilevel programming problems came out through the observation that in a multilevel optimization setting, the lower level optimization problems are parametric in terms of the upper level variables (Dempe, 2002). This observation gave rise to the development of several algorithms for the solution of multilevel problems with the key idea to solve the lower level problem parametrically in terms of the upper level variables and transform the multilevel problem into a set of single-level reformulations.

Bilevel programming has attracted the most attention amongst other classes of multilevel programming problems due to its simplicity (compared to other multilevel problems) and great applicability. Multiparametric programming-based approaches for the solution of linear and quadratic bilevel problems were firstly introduced (Ryu et al., 2004; Faísca et al., 2007; FaÃsca et al., 2011). For classes of problems where the lower level problems also involve discrete variables, multiparametric solution algorithms can alleviate the need for global optimization methods and offer the exact global solution to bilevel mixed-integer linear and quadratic optimization problems (Domínguez and Pistikopoulos, 2010; Oberdieck et al., 2017a; Avraamidou and Pistikopoulos, 2019d).

The solution of optimization problems with more than two optimization levels has been addressed only for a restricted class of problems, mainly continuous trilevel linear problems, with only a few attempts to solve problems with more than three optimization levels or integer variables. The developed algorithms mainly fall in two categories: 1) data driven approaches (Pramanik and Roy, 2007; Sakawa and Matsui, 2014) that cannot guarantee neither feasibility nor optimality, and 2) multiparametric based approaches (Faísca et al., 2009; Kassa and Kassa, 2013; Kassa and Kassa, 2016; Avraamidou and Pistikopoulos, 2019b; Avraamidou and Pistikopoulos, 2019c) that can find the exact global optimum for mixed-integer linear and quadratic optimization problems.

The extension to multilevel problems with multiple followers has not received a lot of attention from the research community with some attempts to solve the linear and quadratic continuous case (Faísca et al., 2009), and limited heuristic approaches for the solution of nonlinear mixed-integer multifollower problems (Kassa and Kassa, 2017; Avraamidou and Pistikopoulos, 2018).

Most recently, Avraamidou and Pistikopoulos (2019a) have developed a freely accessible toolbox for the solution of bilevel and trilevel, continuous and mixed-integer, linear and quadratic optimization problems through multiparametric programming, and presented applications in hierarchical model predictive control (Avraamidou and Pistikopoulos, 2017a), supply chain planning (Avraamidou and Pistikopoulos, 2017b) and planning and scheduling integration (Avraamidou and Pistikopoulos, 2018).

4.4 Integration of Machine Learning and Multiparametric Programming

Apart from the aforedescribed developments, the explosion of interest in state-of-the-art data science strategies has been translated into the multiparametric programming community, making it arguably one of the most active research areas in the field. One major category of efforts are focused on approximating an MPC policy through machine learning techniques (Parisini and Zoppoli, 1995; Åkesson and Toivonen, 2006). It is crucial to note that in these types of methodologies, even though an explicit form of the control law can be created such as through a neural network, they do not capture all benefits of mpMPC, such as the development of a map of solutions. In Shokry et al. (2016), Shokry et al. (2017), the authors utilized sampling strategies to pass various parameter values to the optimizer whose output is collected. Subsequently, machine learning algorithms are used to learn optimal decisions as a function of the varying parameters. Another strategy to use data-driven techniques to approximate the explicit optimal control law of a MPC problem is presented in Chen et al. (2018). Deep reinforcement learning is applied to train a deep neural network with rectified linear units (ReLU) which is used to approximate the optimal piecewise control law. Karg and Lucia (2020) utilized ReLU-based neural networks to represent the piecewise affine law of a linearly constrained mpMPC. Lovelett et al. (2020) presented a framework to learn the optimal control policy as a function of the system by using diffusion maps. The authors demonstrate that the proposed approach can be used to control both linear and nonlinear models.

The impact of machine learning models to approximate nonlinear functions for modeling purposes in the context of mpMPC has also been explored. Most notably, Katz et al. (2020b) presented a framework for the integration of deep neural networks with ReLU as activation functions and multiparametric programming. Given that a ReLU-based neural network includes max operators which are challenging to be introduced in multiparametric optimization formulation, the authors reformulated the neural network as a mixed-integer linear model that can be readily solved through existing multiparametric programming algorithms. Because the neural network to the mixed-integer linear reformulation is exact, no information is lost in the approximation step (Grimstad and Andersson, 2019), which assists in achieving a high-quality optimal multiparametric solution. The authors also applied the approach to a solar field (Katz et al., 2020a).

Apart from that, multiparametric programming has been coupled with machine learning techniques for process monitoring, in a contribution by Onel et al. (2019). In particular, support vector machine feature-based selection and modeling is used to identify potential faults that exist in a given process. This information is then processed by a random forest algorithm that calculates the magnitude of the present fault. Additionally, these faults are treated in the mpMPC design stage as uncertain parameters, and consequently, the controller acts accordingly based on the existence/absence and the magnitude of a process fault, resulting to an enhanced closed-loop performance of the system.

Finally, multiparametric programming has found application as a means to enhance the capabilities of machine learning itself. A connection between hyperparameter optimization strategies, where the aim is to optimally find the algorithm parameters that control how a machine learning model learns from data, and parametric optimization has been established. Specifically, it has been shown that there is a piecewise linear parametric relationship of the model weights and the regularization term in LASSO regression (Efron et al., 2004) and support vector machine (SVM) classification (Hastie et al., 2004). Extensions for the case of multiple parameters in hyperparameter optimization problems have subsequently been presented in Karasuyama et al. (2012); Zhou and Spanos (2016). In a more recent effort, Tso et al. (2020) demonstrated that K-fold cross-validation in hyperparameter optimization can be cast as a bilevel optimization program, and exactly solved in a single formulation through multiparametric programming (Avraamidou and Pistikopoulos, 2019a). One of the key benefits of the aforementioned technique is that it can be applied to any machine learning problem that is described by a LP/QP/MILP/MIQP model.

Machine learning and data science techniques will continue to be a major part of future developments in the field of multiparametric programming. Data-driven techniques can provide assistance in solving mpNLPs, reducing the complexity from a derived multiparametric solution, solving large-scale problems, and many more.

5 Future Outlook

5.1 Software

Rapid progress in computational hardware has led to a widespread adoption of parallel programming and heterogeneous compute in the last 2 decades (Fang et al., 2020). Multi-core and many-core compute paradigms will be essential for performance improvements to be realized for new software. Multiparametric solvers will need to be written so that they are able to scale with hardware. Recently there has been activity in the use of parallel techniques in a multiparametric programming context (Oberdieck and Pistikopoulos, 2016; Jiang et al., 2020), however these are the solitary examples that integrate multiparametric programming and parallel computing in the open literature. There is still a large amount of work to be done in developing parallel algorithms to utilize multicore CPUs, as well as algorithms that distribute work across multiple compute nodes. Currently, the literature on Field Programmable Gate Arrays (FPGA) MPC is based on solving the optimization problem online (McInerney et al., 2018). Software support of heterogeneous compute platforms such as FPGA and Application Specific Integrated Circuits (ASIC) for accelerating the solution of the point location problem has an opportunity to surpass the fastest MPC implementations by exchanging the optimization problem with the point location problem.

The major multiparametric solvers, POP and MPT3 (Oberdieck et al., 2016b; Herceg et al., 2013), are both written in MATLAB. This presents challenges with inter-operability of leading software packages in data science. Implementing code generation techniques that allow the multiparametric solver to export solutions to different code environments for example C code for microcontrollers, Javascript code for scripting interfaces, or Python for software interfacing. The MPT3 solver implements C and Python generation (Takács et al., 2016). This is an important feature as it allows for the deployment of multiparametric solutions to multiple different hardware and software platforms.

Region-free multiparametric programming solutions are based on storing the active set combinations defining solution and not constructing the explicit critical regions. Instead of a more typical point location algorithm, a direct enumeration of the primal and dual constraints of each active set is carried out, as opposed to checking the reduced primal constraints in typical point location problem (Kvasnica et al., 2015). This approach makes a trade off between memory required to store the solution and the computational requirement to solve the region-free online point location problem. Methods like this could be effective for multiparametric programming on memory constrained systems.

5.2 Complexity Reduction

The complexity in deriving the full multiparametric programming solution is non-polynomial in nature, due to the possible combinatorial number of critical regions that define the solution of multiparametric programming problems. However, for many multiparametric programming problems the number of fully-dimensional critical regions usually not scale combinatorially, such as in generating mpMPCs. Recent algorithmic developments are based on reducing the number of deterministic optimization subproblems that need to be considered (Gupta et al., 2011). The graph-based algorithms of (Oberdieck et al., 2016a) and (Ahmadi-Moshkenani et al., 2018) greatly reduce the required number of subproblems, however they both have cases where a combinatorial number of subproblems would need to be considered for the construction of a single critical region. The development of a multiparametric programming algorithm that is output sensitive to the number of solution critical regions without the aforementioned behavior would be a significant development for the field. For specific multiparametric programming problem types, there are possibly ways to exploit the problem structure to reduce the number of deterministic optimization subproblems required to fully solve the problem, in a similar manner to the exploitation of symmetries in the constraint matrix in (Feller et al., 2013). Additionally, the online cost associated with multiparametric methods is primarily derived from solving the point location problem. There are promising results that reduce the algorithmic complexity of this operation by using bounding volume hierarchies (Tøndel and Johansen, 2002), or hash functions (Bayat et al., 2010). Further exploration of different hierarchical data structures or mathematical reformulations of the point location problem could further these results. Results from the universal approximation theorem show that any piecewise affine function can be represented by a ReLU neural network of sufficient depth (Hanin and Sellke, 2018). Advances in machine learning has enabled the construction of ReLU-based well fitting approximations of multiparametric programming solutions (Chen et al., 2018; Karg and Lucia, 2020), that will continue to be part of future developments.

5.3 Robust Optimization and Robust Model Predictive Control

Multiparametric programming theory has assisted in developing solution algorithms for other classes of optimization problems under uncertainty. Classical robust optimization (RO) assumes that all decisions must be made before the realization of uncertainty, a strategy that may be overly conservative, as it aims to immunize against any uncertainty. A less conservative approach is adjustable robust optimization (ARO) which involves recourse decisions (i.e. reactive actions after the realization of the uncertainty) as functions of the uncertainty (Ben-Tal et al., 2004). Solving ARO problems is challenging, therefore ways to reduce the computational effort have been proposed, with the most popular being the affine decision rules, where the recourse decisions are approximated as affine adjustments of the uncertainty (Kuhn et al., 2011); an approximation which can be overly conservative for general ARO problems. Multiparametric programming has been used to develop the exact and optimum generalized piecewise affine decision rule for mixed-integer linear ARO problems with a decision dependant uncertainty set (Avraamidou and Pistikopoulos, 2020). This offered a theoretical justification – via multiparametric programming – on why affine rules can be suboptimal (or even optimal at limited cases).

Applications of RO techniques have also been used in mpMPC. Model predictive control, being a model-based control technique, requires an accurate process to drive a given system to the desired state. Nevertheless, the underlying model in the MPC application includes uncertainty in its dynamics, since it will never be an exact representation of the real process Mohideen et al. (1997). For this reason, robustness considerations have been introduced in mpMPC studies to address this issue, as a means to hedge against model uncertainty (Kothare et al., 1996; Bemporad and Morari, 1999; Mayne et al., 2005). The field of robust MPC through multiparametric programming has not seen extensive developments due to the inherent computational complexity stemming from the need to obtain feasible operation. Sakizlis et al. (2004) included a feasibility constraint in the mpMPC formulation assuming linear models with additive uncertainty, and $1 / \infty$ or quadratic performance indices. Tejeda-Iglesias et al. (2019) utilized ARO to develop a mpMPC policy for discrete linear state-space plants with additive disturbances. On the other hand, Bemporad et al. (2003) considered linear uncertain systems (problems with multiplicative uncertainty) with a linear objective function. Kouramas et al. (2013) proposed a solution for uncertain linear systems with a quadratic performance criterion, using dynamic programming, which required the solution of a multiparametric programming problem at each stage of the prediction horizon. The solution of multiple multiparametric programs poses a significant challenge in the derivation of the solution. Hence, an open question in this area is the development of an approach for robust mpMPC problems with a quadratic objective function avoiding the need of dynamic programming. Furthermore, since the robust control formulation considers a larger number of uncertainty sources compared to the conventional MPC, solution techniques that would be able to efficiently manage the complexity stemming from the increased parameter space dimensionality is needed.

5.4 Multiparametric Programming for Online Optimization

A significant number of researchers have solved multiparametric programming problems without developing the full map of solutions. Instead, the utilized concepts of multiparametric programming theory to shrink the online cost associated with the solution of the original problem. This strategy has been preferred in large scale online applications, where the derivation of the full multiparametric solution is prohibitive.

An approach that utilizes concepts of multiparametric programming for large-scale optimization applications is shown in Pannocchia et al. (2007), which is a combination of online and offline optimization. A table comprised of multiparametric solutions for multiple parameter values are created. In the online phase of the algorithm, an optimality check is performed. If none of the precomputed solutions satisfy the optimality conditions, an online step is followed to calculate the optimal solution is found. Ziogou et al. (2013) utilized multiparametric programming to speed-up the online solution time of nonlinear MPC. Specifically, an mpQP problem is formulated, based on which tighter bounds for the nonlinear program are constructed, which accelerate the computational performance.

Ferreau et al. (2008) demonstrated this concept for the solution of convex QPs in MPC. Based on their approach, it is assumed that the optimal control policy is found for an initial state vector. Given that 1) the current active set is known, 2) the optimal control actions are described by known piecewise affine functions with respect to the initial state vector, 3) a new initial state vector whose optimal solution is sought, and 4) guaranteeing primal and dual feasibility hold, the same KKT matrix is used to find the optimal solution for the new state vector dramatically reducing the online cost. The authors of the approach extended their findings and published an open source software package (Ferreau et al., 2014). The aforedescribed strategy was extended by Katz and Pistikopoulos (2020), where sampling is employed to uniformly build multiple critical regions that are used as a hot start for online MPC. An open question is whether such an approach can be extended to nonlinear systems, given that they have an increased complexity compared to convex QPs.

Multiparametric programming has also the potential to be utilized to solve dynamic optimization problems. To the knowledge of the authors, this topic has only been explored and published by Sakizlis (2003). Specifically, for problems described by a set of linear ordinary differential equations, it is demonstrated how the explicit continuous-time control laws can be obtained, as well as the switching points of the solution. The presented methodology was applied to relatively small-scale problems. Nevertheless, it can be used as the foundation for further developments in this field. Unlocking the capabilities of multiparametric programming in dynamic optimization is a substantially challenging task, however the benefits of having an explicit solution are remarkable and applicable in a wide range of problems in Process Systems Engineering.

5.5 Multiparametric Distributed Model Predictive Control

To minimize consumption of scarce resources and energy, integrated process systems with material recycling streams and energy integration are designed and operated in the chemical industry. Control of such systems using multiple single-loop proportional‐integral‐derivative (PID) controllers or MPC controllers by the conventional decentralized control system (DCS) architecture, will not capture the interactions between different control loops controlling the different subsystems of the process. The control system, hence, will not achieve the best possible closed-loop performance. On the other hand, a centralized control system, typically a single MPC controller capturing the interactions through a model, will not be able to respond within the time limit set by process dynamics and operating conditions when the number of controlled, manipulated, or process variables exceeds a particular threshold. The need to strike a balance between keeping the number of variables within acceptable limits like in DCS and capturing inter-loop interactions like in centralized MPC lead to the development of distributed model predictive control (DMPC) (Camponogara et al., 2002; Stewart et al., 2010). In this architecture, the DCS is improved to also pass on actuator settings of local controller(s) as inputs to controller(s) of other subsystems in the process. The MPC is the controller of choice as it takes advantage of a mathematical model. The MPC controllers in DMPC are not independent but interact with each other to optimize a centrally driven control objective (Christofides et al., 2013). Therefore, the model of a local MPC should not only be a function of the local manipulated variables but also a function of the variables that are being passed on as inputs from other controllers. This model can then be used to predict the local states over a finite time horizon into the future and calculate the optimal control move of the local controller by the conventional MPC control algorithm.

A major challenge in DMPC is the prohibitive online computational costs of exchanging data and solving the optimal control problems of the multiple MPC controllers to converge to a solution. Another challenge is identifying the optimal distributed control structure based on either minimizing the number of inter-loop variables, improving robustness, or enhancing fault tolerant capabilities (Richards and How, 2007; Venkat et al., 2007; Jogwar, 2019). The optimal distributed control structure could also change during process operation as the conditions or operating modes change. Multiparametric programming helps shift the DMPC control and decomposition optimization problems offline, thereby keeping online computational loads manageable. The combined control algorithm will be referred to as “multiparametric distributed model predictive control” or mpDMPC.

While there are several studies reported in the literature on DMPC and on mpMPC, publications on mpDMPC are limited. Koehler and Borrelli (2013) formulated a one-step explicit DMPC for a building heating, ventilation and air conditioning (HVAC) system and compared the control performance against heuristic, ”trim and respond” control. Kirubakaran et al. (2014) studied the feasibility, disturbance rejection capability, and robustness of cooperative mpDMPC for a benchmark quadruple tank problem. The authors reported improved state vector trajectory tracking, disturbance rejection, and robustness under cooperative mpDMPC compared to utilizing game theory DMPC.

The recent advancements in multiparametric programming algorithms reviewed in this paper and interest from the industry on energy-efficient integrated processes make mpDMPC a promising control strategy for applications to such systems and further research.

6 Concluding Remarks

In this contribution the background and recent developments in multiparametric programming have been presented. Advances focused in multiparametric programming theory, algorithms and applications have been discussed. In the former group of research efforts, particular attention has been paid on incorporating nonlinearity in the constraints of the problem, and solving the resulting multiparametric nonlinear programming problem. As far as solution algorithms are concerned, both geometric-based and active set-based strategies have been proposed. Further developments on hybrid solution algorithms which balance the advantages of both approaches will be necessary to tackle large-scale problems. In the latter group of research contributions, mpMPC remains the most studied application, motivated by its benefits in solving online optimization problems. However, it is highlighted through this paper that multiparametric programming is much broader than mpMPC, with exciting applications such as in solving multiscale, and multilevel optimization programs. Additionally, an outlook in future developments in the field of multiparametric programming has been included. The integration of data science and multiparametric programming, robust optimization and control, as well as complexity reduction techniques are still areas of development. It is expected that these fields, together with the aforedescribed recently published developments, will be at the heart of research within this fascinating world.

Author Contributions

IP: Methodology, Formal Analysis, Data Collection, Writing - original draft, DK: Data Collection, Formal Analysis, Writing - review and editing, BB: Data Collection, Formal Analysis, Writing - review and editing, SA: Data Collection, Formal Analysis, Writing - review and editing, HG: Data Collection, Formal Analysis, Writing - review and editing, JK: Writing - review and editing, ND: Writing - review and editing, EP: Conceptualization, Supervision, Project administration, Funding acquisition.

Funding

Financial support from the National Science Foundation (Grant No. 1705423), Texas A&M Energy Institute, the Clean Energy Smart Manufacturing Innovation Institute (CESMII), and the Rapid Advancement in Process Intensification Deployment (RAPID SYNOPSIS Project - DE-EE0007888-09-04) Institute is gratefully acknowledged.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Åkesson, B. M., and Toivonen, H. T. (2006). A neural network model predictive controller. J. Process Contr. 16, 937–946. doi:10.1016/j.jprocont.2006.06.001