Neuronal and Astrocytic Regulations in Schizophrenia: A Computational Modelling Study

According to the tripartite synapse model, astrocytes have a modulatory effect on neuronal signal transmission. More recently, astrocyte malfunction has been associated with psychiatric diseases such as schizophrenia. Several hypotheses have been proposed on the pathological mechanisms of astrocytes in schizophrenia. For example, post-mortem examinations have revealed a reduced astrocytic density in patients with schizophrenia. Another hypothesis suggests that disease symptoms are linked to an abnormality of glutamate transmission, which is also regulated by astrocytes (glutamate hypothesis of schizophrenia). Electrophysiological findings indicate a dispute over whether the disorder causes an increase or a decrease in neuronal and astrocytic activity. Moreover, there is no consensus as to which molecular pathways and network mechanisms are altered in schizophrenia. Computational models can aid the process in finding the underlying pathological malfunctions. The effect of astrocytes on the activity of neuron-astrocyte networks has been analysed with computational models. These can reproduce experimentally observed phenomena, such as astrocytic modulation of spike and burst signalling in neuron-astrocyte networks. Using an established computational neuron-astrocyte network model, we simulate experimental data of healthy and pathological networks by using different neuronal and astrocytic parameter configurations. In our simulations, the reduction of neuronal or astrocytic cell densities yields decreased glutamate levels and a statistically significant reduction in the network activity. Amplifications of the astrocytic ATP release toward postsynaptic terminals also reduced the network activity and resulted in temporarily increased glutamate levels. In contrast, reducing either the glutamate release or re-uptake in astrocytes resulted in higher network activities. Similarly, an increase in synaptic weights of excitatory or inhibitory neurons raises the excitability of individual cells and elevates the activation level of the network. To conclude, our simulations suggest that the impairment of both neurons and astrocytes disturbs the neuronal network activity in schizophrenia.

1. Introduction

Astrocytes contribute to the complex cognitive function in humans (Santello et al., 2019), whereby they have structural, homeostatic, and metabolic roles. Astrocytes are connected to each other via gap junctions and form non-overlapping domains in complex networks. This glial cell type composes, together with a pre- and a postsynaptic neuron, the so-called tripartite synapse (Araque et al., 1999). They take up glutamate rapidly from the synaptic cleft to ensure a short glutamate exposition to the postsynaptic neuron for precise synaptic transmission. Subsequently, astrocytes respond to neuronal activity with intracellular calcium (Ca²⁺) elevations and release ions and transmitter molecules in return.

Seemingly neurons and astrocytes play a role in psychiatric diseases such as schizophrenia (SCZ) (Uhlhaas and Singer, 2010; Takahashi and Sakurai, 2013; Moraga-Amaro et al., 2014; Mei et al., 2018). SCZ is associated with positive (such as delusions and hallucinations), negative (such as social withdrawal and lack of motivation), and cognitive symptoms (difficulties in memory and attention).

Due to the success of first generation antipsychotics, the dopamine hypothesis of SCZ was formed. The underlying assumption of this hypothesis is that excessive transmission of subcortical dopamine causes the positive symptoms of SCZ (Grnder and Cumming, 2016). While research has found significant support of this hypothesis, it is not pathognomonic and does not sufficiently account for the negative symptoms of SCZ.

Post-mortem examinations, human induced pluripotent stem cell experiments, and animal studies have revealed a reduced astrocytic and neuronal synaptic density in SCZ patients (Cotter et al., 2001; Brennand et al., 2011; Dietz et al., 2020; Naujock et al., 2020). Cell death is associated with excitotoxicity due to excessive glutamate amounts and glutamate receptor activation (Drouin-Ouellet et al., 2011). However, the mechanisms and pathways of this developmental brain disorder are not well understood yet. Different studies reach conflicting conclusions. Some papers report an upregulation in glial fibrillary acidic protein (GFAP) in SCZ astrocytes (review by Moraga-Amaro et al., 2014), whereas in other studies, a reduced GFAP expression has been described (review by Takahashi and Sakurai, 2013).

Koskuvi et al. (2020) found that human stem cell-derived astrocytes from SCZ patients show highly sex-specific alterations in gene expression. The Gene Ontology pathways related to neuronal wiring and inflammation are altered in SCZ astrocytes. Healthy neurons co-cultured with SCZ astrocytes of either sex exhibited a significantly increased response to glutamate. Transplanted hiPSC-astrocyte progenitors from SCZ patients developed into matured astrocytes in a mouse model and led to subtle behavioural changes. Furthermore, they induced demyelination, synaptic dysfunction and affected the inflammation pathways (Koskuvi et al., 2020). Several studies have shown that the expression of the metabotropic glutamate receptor (mGluR) type 5 is increased in astrocytes in the prefrontal cortex (Ohnuma et al., 1998; Kosten et al., 2016).

For neurons, the glutamate hypothesis of SCZ has been established (de Bartolomeis et al., 2005; Moghaddam and Javitt, 2012; Takahashi and Sakurai, 2013; Cohen et al., 2015; Mei et al., 2018): a hypofunction of NMDA receptors (NMDARs) leads to excessive glutamate release, mainly prevalent in the hippocampus and prefrontal cortex. However, the underlying mechanisms are not yet clarified. A decreased level of D-serine, which is mainly released by astrocytes, affects the NMDAR function in neurons. Both glutamate and either D-serine or glycine are co-agonists to the NMDAR binding sites. The astrocyte-derived NDMAR antagonist kynurenic acid (KYNA) shows increased levels in SCZ patients (Takahashi and Sakurai, 2013; Cohen et al., 2015). Interneurons might react to changes in NMDAR function with inhibition, leading to disinhibition and a hyperexcitation of glutamate levels in SCZ (Moghaddam and Javitt, 2012; Mei et al., 2018). Alternatively, Schobel et al. (2013) suggested that excess synaptic glutamate release results in a reduction of the interneuronal function and hippocampal disinhibition. The abnormality of glutamate transmission is also related to astrocytes since they regulate the glutamate uptake and release from and to the extracellular space (Danbolt, 2001; Kondziella et al., 2007). While the glutamate hypothesis is more recent and less well studied than the dopamine hypothesis, it has the advantage of being able to account for a wider range of SCZ symptoms (Hu et al., 2015; Mei et al., 2018).

A third hypothesis is that, instead, the excessive glutamate release leads to the NMDAR hypofunction. Higher glutamate levels may result in a rise of astrocytic Ca²⁺ levels. Subsequently, astrocytes may release higher concentrations of the gliotransmitter adenosine triphosphate (ATP). Lalo et al. (2016) suggested that the activation of postsynaptic purinergic P2X receptors (P2XRs) by ATP downregulates NMDARs.

These findings indicate that different neuronal and astrocytic malfunctions could lead to the same disease, despite different underlying mechanisms. This poses a major challenge to effective treatments for psychiatric diseases (Herman et al., 2012; Stephan et al., 2016). Computational models can complement or supersede experimental studies (Manninen et al., 2018; Oschmann et al., 2018), where the latter are not feasible or too expensive. They can guide experimental researchers to the relevant pathways that are altered in disease and thus predict pharmaceutical responses (Moran et al., 2016). Siekmeier and Hoffman (2002) proposed a computational model in which they reduced the number of synapses in a neuronal network. This synaptic pruning leads to semantic priming and difficulties in accessing memories in SCZ patients. Mahdavi et al. (2014) developed a tripartite synapse model focusing on the dysregulation of D-serine released by the astrocyte. To our best knowledge, no biophysical neuron-astrocyte network models have been published that explore the role of astrocytes in SCZ.

In this study, we investigate how changes in mechanisms and topology in neuron-astrocyte networks alter the functional state, i.e., spike and burst rate of neurons as well as glutamate levels in astrocytes, in health and SCZ. For this, we use the previously published computational model called INEXA (Lenk et al., 2020) to test the following four SCZ-related hypotheses: we alter (1) the number of neurons or astrocytes in the network, (2) the effect of astrocytic ATP on the postsynaptic activity, (3) the release of glutamate from the presynapse and the uptake of glutamate by the astrocyte, and (4) the excitatory and/or inhibitory synaptic strength.

2. Materials and Methods

To study the three aspects mentioned above in SCZ, we used the published model INEXA (Lenk et al., 2020) with the main components as shown in Figure 1. In section 2.1, we describe the governing equations of the INEXA model. In section 2.2, we explain how the model is used to simulate neuron-astrocyte networks in healthy and SCZ states. In sections 2.3, 2.4, the statistical analysis of the resulting neuronal and astrocytic activity is described.

FIGURE 1

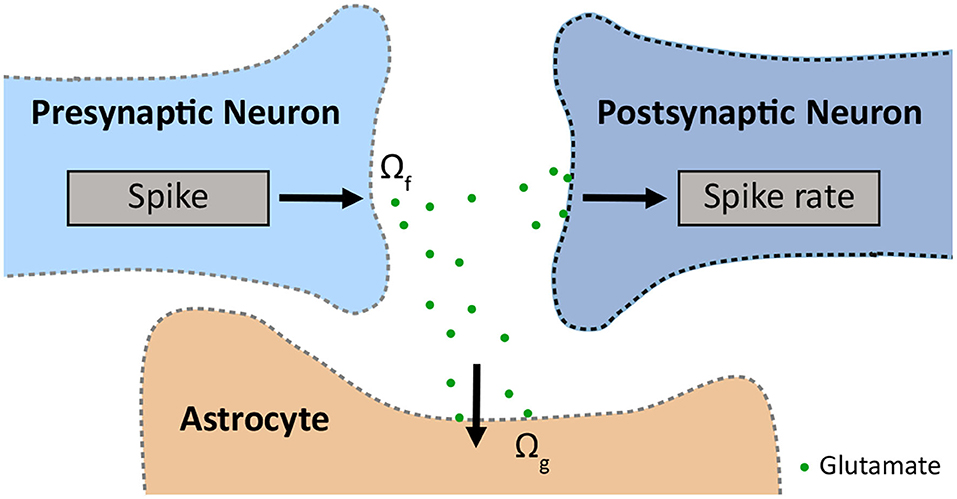
Figure 1. Schematic of the tripartite synapse, which consists of a pre- and a postsynapse and an astrocyte, modelled with INEXA (Lenk et al., 2020). The presynapse releases glutamate with release rate Ω_f. The glutamate is taken up by the astrocyte with uptake rate Ω_g.

2.1. Governing Equations of the INEXA Model

The phenomenological model INEXA (Lenk et al., 2020) includes both excitatory and inhibitory neurons and was initially developed to study the astrocytes' effect on neuronal firing rates in the cortex. The governing equation for simulating neurons is the one for the firing rate λ_i of a postsynaptic neuron i for each time step t_k of 5 ms:

$\begin{array}{ll}{\lambda }_i(t_k)=max\left(0,c_i+{\displaystyle \sum _j}{y}_{ij}·s_j(t_{k-1})-{\displaystyle \sum _j}{y}_{\text{Astro}}·A_{ija}(t_{k-1})\right),& (1)\end{array}$

where c_i is the stochastic noise of neuron i. The term y_ij denotes the synaptic weight between the presynaptic neuron j and a postsynaptic neuron i, which can vary at each time step. The synapse can be either excitatory (y_ij ∈ [0, 1], representing glutamatergic neurons) or inhibitory (y_ij ∈ [−1, 0], representing GABAergic interneurons). The parameter s_j is a binary term indicating whether neuron j transmitted a spike in the previous time step t_k−1. The second term in the equation denotes the depressing effect caused by astrocytes. The variable A_ija is binary, indicating whether a synapse ij is enclosed by astrocyte a and if astrocyte a was active at the previous time step. If this is the case, the astrocyte applies a depressing effect, y_Astro, on the synapse. Otherwise, A_ija is zero, removing the astrocytic effect on neuronal activity.

Due to limited experimental data on the interaction between GABAergic neurons and astrocytes, the INEXA model currently only connects astrocytes with glutamatergic synapses. These excitatory synapses release glutamate into the synaptic cleft with rate Ω_f. The released glutamate binds to astrocytic mGluRs with rate Ω_g causing the inositol 1,4,5-trisphosphate (IP₃)-mediated release of Ca²⁺ from the endoplasmic reticulum (ER) into the astrocytic cytoplasm (Figure 1).

The governing equation for astrocyte dynamics describes the intracellular calcium dynamics ${\left[C{a}^{2+}\right]}_{ija}$ in an astrocyte a that encloses the synapse ij:

$\begin{array}{l}{[C{a}^{2+}]}_{ija}(t_k)={[C{a}^{2+}]}_{ija}(t_{k-1})+{\Omega }_{acc}\cdot ({[I{P}_3]}_{ija}(t_k)\\ -{[C{a}^{2+}]}_{ija}(t_{k-1})).& (2)\end{array}$

The calcium concentration is composed of the calcium concentration left from the last time step ($C{a}_{ija}^{2+}(t_{k-1})$), the IP₃-mediated Ca²⁺-induced Ca²⁺-release from the ER stores, and the Ca²⁺ uptake back to the ER by the SERCA (sarco/endoplasmic reticulum Ca²⁺-ATPase) pumps. To reflect the slow dynamics of the calcium release (which can take up to multiple seconds), we multiplied the ER term by the time scale Ω_acc. A more detailed description of the INEXA model can be found in the original article (Lenk et al., 2020).

2.2. Simulated Experimental Setups

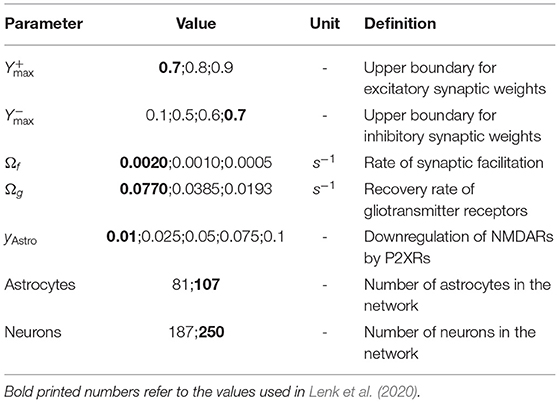
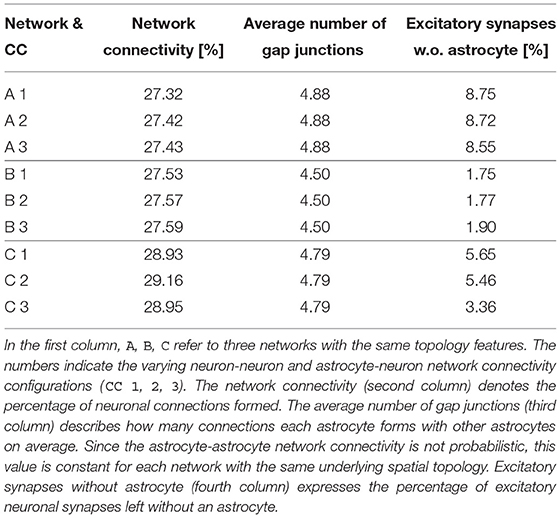
The topology and connectivity of the neuron-astrocyte network models were generated as described in Lenk et al. (2020) (see parameters in Table 1). Hence, 107 astrocytes and 250 neurons were placed uniformly at random on a planar area of 750 × 750 × 10 μm³, resembling the electrode field of an in vitro multielectrode array (MEA). Neurons and astrocytes within a distance of 30 μm were reallocated to account for the cell sizes. Astrocyte-astrocyte connections were formed whenever the distance was smaller than 100 μm. Neuron-neuron and astrocyte-neuron connections were created according to a truncated Gaussian distribution based on their distance.

TABLE 1

Table 1. Used parameters for simulating healthy and SCZ neuron-astrocyte networks.

To study the effects of various spatial network topologies and network connectivities, we generated three spatially different network topologies A, B, and C. For each network A, B, C, we computed three independent connectivity configurations (CC 1, 2, 3) according to the rules described above, resulting in a total of nine different networks. We considered those networks to represent the healthy, non-pathological baseline. Different topological properties of these initial networks are described in Table 2. The stochastic noise c_i was set to 0.02 in all simulations.

TABLE 2

Table 2. Different connectivity properties of the nine initial networks used in this paper.

To simulate healthy, non-pathological neuron-astrocyte network activity, we tuned the parameters of the INEXA model so that they resemble in vitro MEA recordings. Thereby, we used a reference spike rate of 30–200 spikes per minute as measured from mouse neurons (Gramowski et al., 2006; Jenkinson et al., 2017) and human-derived neurons (Tukker et al., 2018; Kizner et al., 2019).

Based on hypotheses and experimental evidence about SCZ described in the Introduction, we modified four different sets of INEXA parameters and examined their effect on neuronal and astrocytic activity. More specifically, we simulated the following four pathological changes in the neuron-astrocyte interaction:

1. We stochastically removed 25% of astrocytes or 25% of neurons from premade network configurations to account for the reduced astrocytic and neuronal synaptic density in SCZ patients.

2. We amplified the depressing signal y_Astro of astrocytes to study the effect of astrocytic ATP on the postsynaptic activity.

3. We scaled the two parameters Ω_f and Ω_g by the factors 0.5 and 0.25, which control glutamate release from presynapses and glutamate uptake by astrocytes, respectively (Figure 1). Simulations were performed for each combination of the distorted and unmodified parameter values Ω_f and Ω_g.

4. We increased the maximal synaptic weight $Y_{max}^{+}$ and $Y_{max}^{-}$ for excitatory and inhibitory neurons, which both result in a higher excitability of the cells.

The latter two manipulations allowed us to simulate the excessive release of glutamate in excitatory neurons and astrocytes as well as the dysfunctional interneurons assumed in the glutamate hypothesis of SCZ. A summary of the modified parameters can be found in Table 1. All other model parameters not listed in this table were used as described in the original paper by Lenk et al. (2020). Each simulation consisted of T = 5min simulated time and was repeated 10 times to account for the statistical variability of our results.

2.3. Quantifying Neuronal and Astrocytic Activity Features

To analyze the neuronal activity, we calculated spike and burst describing features. Bursts are cascades of spikes (i.e., action potentials). The features were determined using a modified version of the cumulative moving average (CMA) algorithm (Kapucu et al., 2012; Välkki et al., 2017). Therewith, we calculated the mean spike rate in spikes per minute and the mean burst rate in bursts per minute across all neurons, respectively. Additionally, we quantified the astrocytic activity by calculating how often an astrocyte changes its state to ‘active’ during the simulated time T and denoted the count as mean number of activations per astrocyte. We will refer to these three features as response variables below. The results were depicted as box plots.

2.4. Testing the Effects of Different Neuronal and Astrocytic Dysfunctions

The objective of this section is twofold: we quantify the effects of the four simulated pathological changes in SCZ (see section 2.2) on the neuronal and astrocytic response variables and estimate how much the effects vary for different network configurations. In the previously described simulated experimental setups, there were two sources of stochasticity. One came from the stochastic nature of the INEXA model, e.g., when creating the excitatory and inhibitory synaptic weights and in the update equations. The other was due to the fact that neuron-neuron and astrocyte-neuron connections were formed stochastically in our setup. To estimate the average random effect from both sources of stochasticity, we performed all simulations on the nine initial networks, as described in section 2.2. We analysed the data with linear mixed-effects (LME) models using the lme4-package (Bates et al., 2015) in R, version 3.6.3 (2020-02-29). In order to satisfy the LME model requirements, it was sometimes necessary to transform the response variable Z by some function φ:ℝ → ℝ. In the following subsections, we decomposed the variance of φ(Z) into intra-network terms Σ, which capture the stochasticity from different network connectivity configurations, and the residual error variance σ². We note that these are the variance terms for the transformed response φ(Z). If one is interested in prediction intervals for Z, these must first be computed for φ(Z) and then back-transformed.

2.4.1. Hypothesis 1: Astrocyte or Neuron Removal

In the first set of simulated experiments, we quantified the average effect of stochastically removing 25% of the astrocytes or neurons, respectively. In order to estimate the random effect of different network configurations, we made three identical copies of each of the nine networks described in section 2.2 and Table 2. Then, we either randomly removed 25% of astrocytes or 25% of neurons including their connections to other cells, which resulted in 27 cell-reduced networks per cell type.

For all of these networks, we ran 10 simulations and fit the resulting data using an LME model with a fixed effect for cell removal and a random effect for different network configurations. Using contrasts to distinguish the full network from reduced networks (Oehlert, 2010) (see Supplementary Material), we then determined the average reduction δ_rem of the response variables resulting from cell removal in percent. Moreover, we decomposed the variance of the transformed response φ(Z) into an inter-network term ${\sigma }_{\mathrm{\text{rem}}}^2$ and the residual error variance σ². For each response variable, we report the restricted maximum likelihood (REML) estimates, 95% confidence intervals (CIs) of δ_rem as well as the p-value for the null-hypothesis that the mean response of reduced and default networks A, B and C coincides. We also present the REML estimates and the 95% CIs for the standard deviations ${\sigma }_{\mathrm{\text{rem}}}/\widehat{\mu }$ and $\sigma /\widehat{\mu }$, which have been normalised by the mean $\widehat{\mu }$ of the transformed response φ(Z), when no cells were removed. A more detailed description of the reported quantities mentioned in this section and the LME model can be found in the Supplementary Material.

2.4.2. Hypothesis 2: Effect of Astrocytic ATP

In this part, we altered the impact of astrocytic ATP on the postsynaptic P2XR and NMDAR activity by modifying the parameter y_Astro. Therefore, we first performed 10 simulations with y_Astro ∈ {0.01, 0.025, 0.05, 0.075, 0.1} for each of the nine networks described in section 2.2. To analyze our simulated data, we used the LME model

$\begin{array}{ll}log(Z_{ij})=(\mu +u_{i,\mu })+({\beta }_a+u_{i,a})·y_{\text{Astro}}+{\beta }_{a^2}·y_{\text{Astro}}^2+{\epsilon }_{ij},& (3)\end{array}$

where the index i enumerates the nine network configurations and j ∈ {1, …, 10} indices the 10 independent repetitions. The variable μ is the average value of log(Z) if y_Astro was equal to zero. The coefficients ${\beta }_a,{\beta }_{a^2}$ correspond to the average increase of log(Z) in dependence of y_Astro and $y_{\mathrm{\text{Astro}}}^2$, respectively. Random effects are captured in the vectors u_i: = (u_{i, μ}, u_i,a) for each i, which are independent with multivariate Gaussian distribution $u_i~{N}(0,\Sigma )$ with mean 0 and diagonal covariance matrix $\Sigma =diag({\sigma }_{\mu }^2,{\sigma }_a^2)\in {ℝ}^{2\times 2}$. This means that we assumed the individual components to be independent. The stochasticity of the INEXA model and the residual error is captured in ε_ij, which we assumed to be normally distributed with mean 0, equal variance σ² and independent of u_i for all indices i. We reported REML estimates and CIs for $\mu ,{\beta }_a,{\beta }_{a^2},\Sigma$ and σ².

2.4.3. Hypothesis 3: Glutamate Dynamics Parameters

Following the glutamate hypothesis of SCZ, we tested the effect of changing the parameters regulating the glutamate dynamics in neurons and astrocytes. The parameters w_f and w_g for the glutamate dynamics are defined as follows: running the LME model with parameter values w_f and w_g corresponds to the scaling of the presynaptic glutamate release rate by a factor w_f (equivalent to a multiplication of Ω_f by w_f) and scaling the astrocyte glutamate uptake rate by a factor w_g (equivalent to multiplying Ω_g by w_g) compared to the default rates of the INEXA model. For every response variable Z = Z(w_f, w_f), we used the LME model

$\begin{array}{l}{Z}_{ij}=(\mu +u_{i\mu })+({\beta }_f+u_{i,f})w_f+({\beta }_g+u_{i,g})w_g+{\beta }_{f^2}{w}_f^2\\ +{\beta }_{g^2}{w}_g^2+({\beta }_{fg}+u_{i,fg})w_f{w}_g+{\epsilon }_{ij},& (4)\end{array}$

where the index i enumerates the nine network configurations described in section 2.2 and j ∈ {1, …, 10} denotes 10 independent repetitions. The variable μ stands for the average value of the response Z if w_f and w_g were equal to zero. The coefficients ${\beta }_f,{\beta }_g,{\beta }_{f^2},{\beta }_{g^2},{\beta }_{fg}\in ℝ$ correspond to the average increase of Z in dependence of the parameters they are multiplied by. Random effects were captured in vectors u_i: = (u_{i, μ}, u_i,f, u_i,g, u_i,fg), which are independent with multivariate Gaussian distribution $u_i~{N}(0,\Sigma )$ with mean 0 and covariance matrix Σ. We assumed $\Sigma =diag({\sigma }_{\mu }^2,{\sigma }_f^2,{\sigma }_g^2,{\sigma }_{fg}^2)\in {ℝ}^{4\times 4}$ was a diagonal matrix with positive entries, which means that the individual components were assumed to be independent. The random effects u_i are specific to each network configuration i, however we assumed them to be identically distributed. The estimates for ${\sigma }_{\mu }^2,{\sigma }_f^2,{\sigma }_g^2,{\sigma }_{fg}^2$ quantify the variance of Z as a stochastic function of parameter values w_f and w_g, considering the stochasticity from random network connectivities. The stochasticity of the INEXA model as well as the residual error was captured in ${\epsilon }_{ij}~{N}(0,{\sigma }^2)$, which we assumed to be normally distributed with mean 0, equal variance σ² and independent of u_i for all indices i.

We performed 10 simulations with the INEXA model for each of the nine networks described in section 2.2 and every combination of the parameter values w_f, w_g ∈ {1, 1/2, 1/4}. The corresponding values for Ω_f, Ω_g are listed in Table 1. Fitting this data in R, we reported the REML estimates and CIs for $\mu ,{\beta }_f,{\beta }_g,{\beta }_{f^2},{\beta }_{g^2},{\beta }_{fg},\Sigma$, and σ². We created contour plots for the response Z(w_f, w_g) as a function of w_f and w_g using the estimates provided by the LME model fit and setting all stochastic terms equal to 0.

2.4.4. Hypothesis 4: Changes in the Excitatory and Inhibitory Synaptic Weights

In this set of simulated experiments, we tested the dependency of neuronal and astrocytic activity on the inhibitory and excitatory synaptic weight boundaries $Y_{max}^{-}$ and $Y_{max}^{+}$ (see section 2.1). In our statistical LME model, we considered first and second order fixed effects of synaptic weight boundaries on the response variables as well as a random effect term to account for the variation caused by different network configurations. For ease of notation, let y_in and y_ex denote the parameter values for $Y_{max}^{-}$ and $Y_{max}^{+}$, respectively. For every response variable Z = Z(y_in, y_ex), we assumed the statistical model

$\begin{array}{l}{Z}_{ij}=\mu +{\beta }_{in}{y}_{\text{in}}+{\beta }_{ex}{y}_{\text{ex}}+{\beta }_{{in}^2}{y}_{\text{in}}^2+{\beta }_{{ex}^2}{y}_{\text{ex}}^2+{\beta }_{in,ex}{y}_{\text{in}}{y}_{\text{ex}}\\ +{\gamma }_i+{\epsilon }_{ij},& (5)\end{array}$

where the index i enumerates the nine network configurations described in section 2.2 and j ∈ {1, …, 10} denotes 10 independent repetitions. The variable μ refers to the estimated mean of Z if y_in and y_ex were equal to zero. The coefficients ${\beta }_{in},{\beta }_{ex},{\beta }_{{in}^2},{\beta }_{{ex}^2},{\beta }_{in,ex}\in ℝ$ correspond to the average increase of Z in dependence of the parameters they are multiplied by. Random effects were captured in the random variables γ_i, which we assumed to be independent with zero-mean Gaussian distribution and equal variance ${\sigma }_{net}^2$. The variance term ${\sigma }_{net}^2$ quantifies how much the response varies between different stochastically chosen network connectivities if all other parameters are held constant. The residual error was captured in ε_ij, which we assumed to be normally distributed with mean 0, equal variance σ² and independent of γ_i for all indices i.

We performed 10 simulations with the INEXA model for each of the nine networks described in section 2.2 and every combination of the parameter values for $Y_{max}^{-},Y_{max}^{+}$ listed in Table 1. Fitting this data in R, we reported the REML estimates and 95% CIs for $\mu ,{\beta }_{in},{\beta }_{ex},{\beta }_{{in}^2},{\beta }_{{ex}^2},{\beta }_{in,ex},{\sigma }_{net}$ and σ. Moreover, we created contour plots for the response Z(y_in, y_ex) as a function of y_in and y_ex using the estimates provided by the LME model fit while setting all stochastic terms equal to 0.

3. Results

3.1. Hypothesis 1: Astrocyte or Neuron Removal Leads to Reduction of the Network Activity

In our first set of simulations, we reduced the cell density of either astrocytes or neurons by 25%. The cell removal resulted in a general decrease of mean spike rate, mean burst rate and mean number of astrocyte activations (Figure 2A). Overall, the decline of the response variables was larger when the neurons were removed from the network. In Figure 2B, the average amount of glutamate prevalent in astrocytes is shown at each time step. While both forms of reduction caused a decrease in astrocytic glutamate, the effect was more pronounced in the case of neuron removal. The p-values for the null-hypothesis that the mean response of reduced and default networks coincide were smaller than 10⁻¹⁰ for all response variables and both simulated experiments.

FIGURE 2

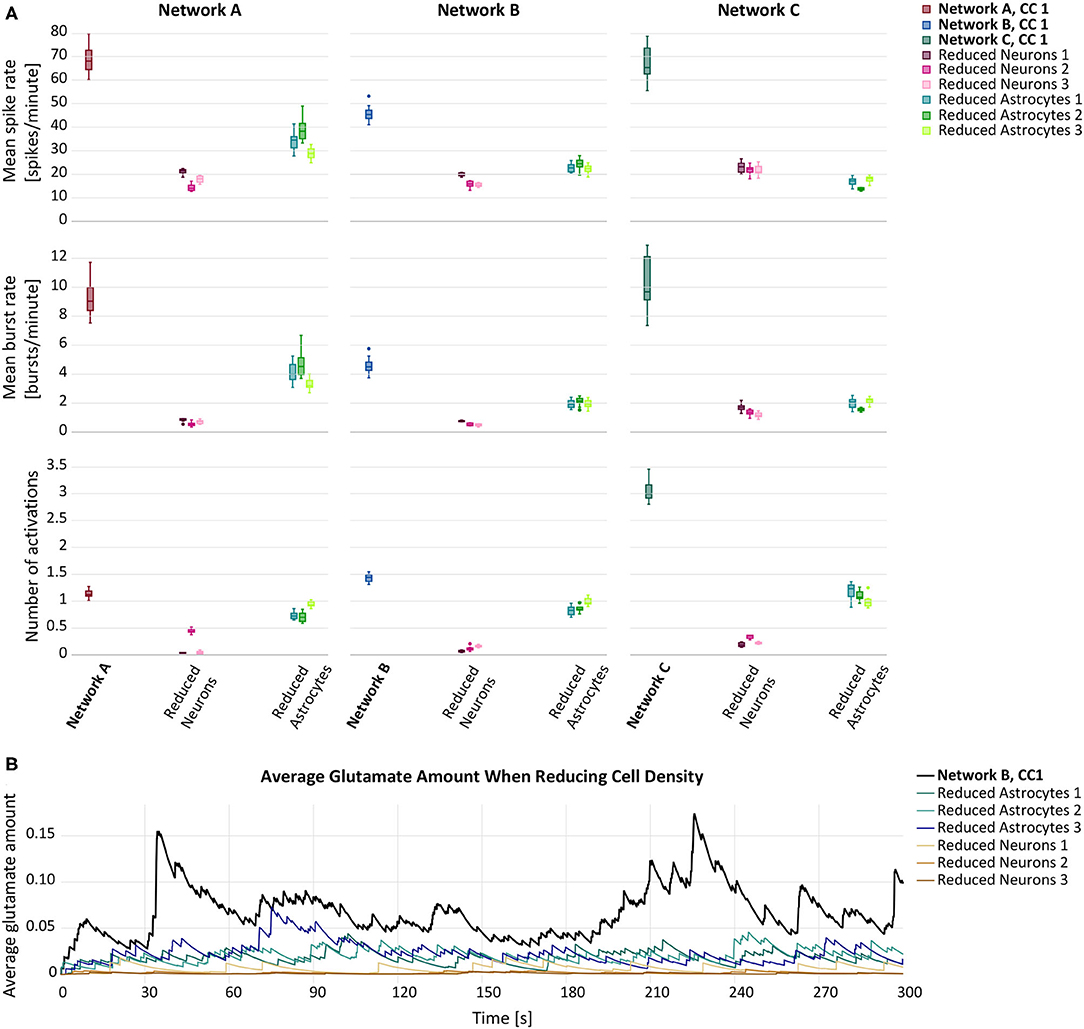
Figure 2. (A) Mean spike rate (top), mean burst rate (middle) and mean number of activations per astrocyte (bottom) resulting from the networks with reduced astrocyte or neuron density compared to the default networks A–C with connectivity configuration CC 1 (bold). (B) Average glutamate amount in astrocytes when randomly removing 25% of either astrocytes (blue lines) or neurons (brown lines) from a premade network configuration B,CC 1 (black line).

The results of the LME model fit are listed in Table 3 for the astrocyte removal and in Table 3 for the neuron removal. They show that cell removal leads to statistically significant activity reduction. The 95% CIs of δ_rem are tighter for the neuron removal than for astrocyte removal, indicating that the neuron removal data was fit more accurately by the LME model. The results highlight stark differences between the inter-network standard deviations ${\sigma }_{rem}/\widehat{\mu }$ of the transformed responses φ(Z). While in the astrocyte removal experiments, the inter-network variance of the logarithm of the mean spike rate is relatively low, the standard deviation term for the logarithm of the mean number of astrocyte activations is estimated to be at around 50%. This shows that the robustness to changing network configurations varies significantly for the different response variables considered. Similarly, the standard deviation $\sigma /\widehat{\mu }$ of the residual error varies considerably between different response variables, but is consistently smaller than the inter-network standard deviation ${\sigma }_{rem}/\widehat{\mu }$.

TABLE 3

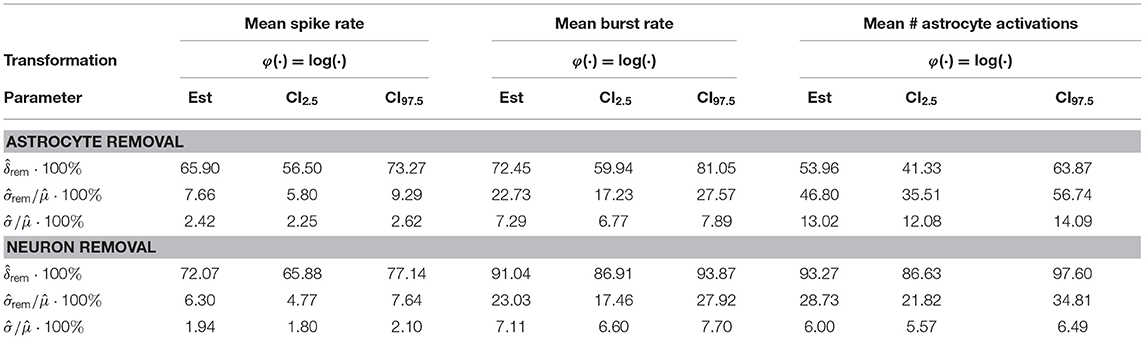
Table 3. Estimates and 95% confidence intervals for the quantities estimated in the astrocyte (upper part) and neuron (lower) removal experiments in percent.

3.2. Hypothesis 2: Effect of Astrocytic ATP

For our second hypothesis, we increased the depressing effect of the astrocytic gliotransmitter ATP on excitatory postsynapses. As can be seen in Figure 3A, the depressing effect results in a decreased mean spike rate. In networks A and C, the activity reduction can also be observed for the other two response variables, mean burst rate and astrocyte activity. The increase of the depression, y_Astro, from 0.01 to 0.025 has the proportionally largest effect. In network B, the behaviour of the mean burst rate and the astrocyte activity follows no clear tendency. Figure 3B depicts the average amount of astrocytic glutamate ready for release in presence with an ATP release from the astrocyte. Compared to the baseline level, we observed temporary higher levels of glutamate when amplifying the depressing effect.

FIGURE 3

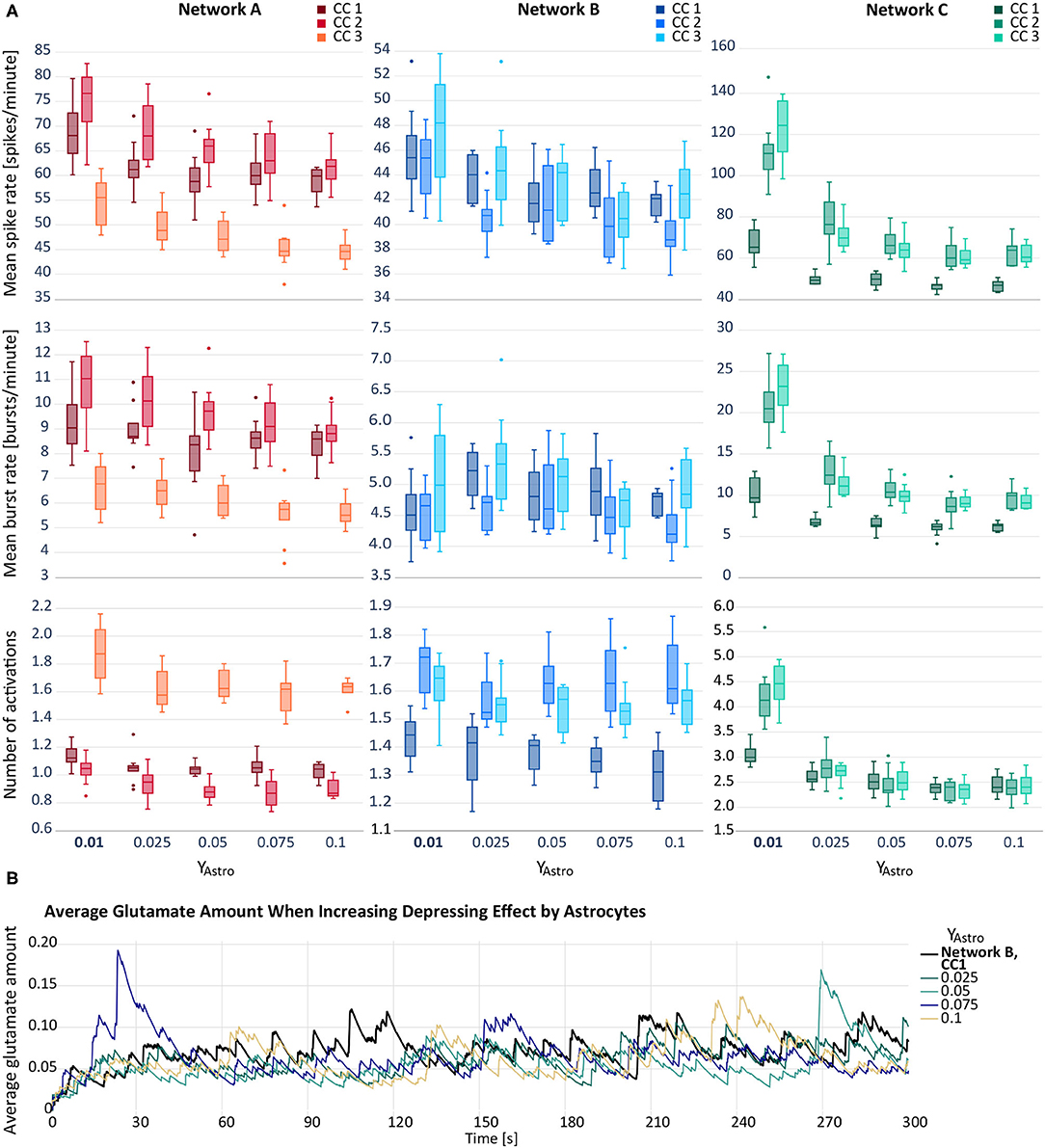
Figure 3. (A) Mean spike rate (top), mean burst rate (middle) and mean number of activations per astrocyte (bottom) resulting from the networks with increased astrocytic depression compared to the default networks A–C with y_Astro = 0.01 (bold). Note that the y-axes differ for each subfigure. (B) Average glutamate amount in astrocytes when applying a depressive effect on the postsynapse by releasing ATP from the astrocyte. The black line resembles the baseline activity from network B, CC 1. The remaining lines represent deviating values of y_Astro.

In Table 4, we listed the REML estimates and confidence intervals of the parameters of the LME model described in section 2.4.2. We observed a positive second order fixed effect (${\widehat{\beta }}_{a^2}$) and a negative first-order one (${\widehat{\beta }}_a$) for all logarithmically transformed responses log(Z_ij). While we obtain tight confidence intervals for the baseline activity $\widehat{\mu }$, the first and second order coefficients ${\widehat{\beta }}_a,{\widehat{\beta }}_{a^2}$ have comparatively wider confidence intervals. The standard deviation term ${\widehat{\sigma }}_{\mu }$ of log(Z_ij) associated with μ is considerably lower than the standard deviation term ${\widehat{\sigma }}_a$ associated with ${\widehat{\beta }}_a$, moreover the confidence intervals of ${\widehat{\sigma }}_{\mu }$ are narrower than those of ${\widehat{\sigma }}_a$, indicating that the first order term is difficult to fit by our model. The error standard deviation $\widehat{\sigma }$ is comparatively low and has tight confidence intervals for all responses.

TABLE 4

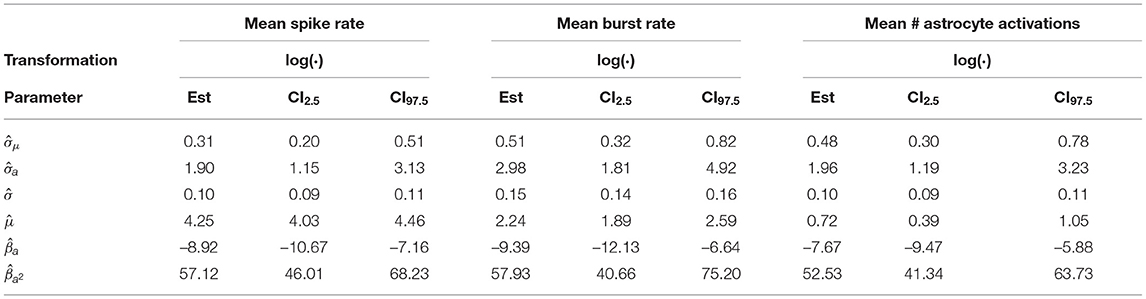
Table 4. Restricted maximum likelihood estimates, lower and upper ends of 95% confidence intervals for the astrocyte depressing effects experiment.

3.3. Hypothesis 3: Reducing the Glutamate Release and Uptake Rate Results in Higher Network Activity

Figure 4A depicts the behaviour of the response variables with respect to varying rates of synaptic facilitation, Ω_f, and varying recovery rates of the gliotransmitter receptors, Ω_g. In general, a reduction in both, Ω_g and Ω_f, resulted in an elevation of the response variables. However, the increase between two consecutive values for Ω_f was larger than between two values of Ω_g. An exception was observed for network B, for which the modification of Ω_g did not result in any considerable changes of the response variables.

FIGURE 4

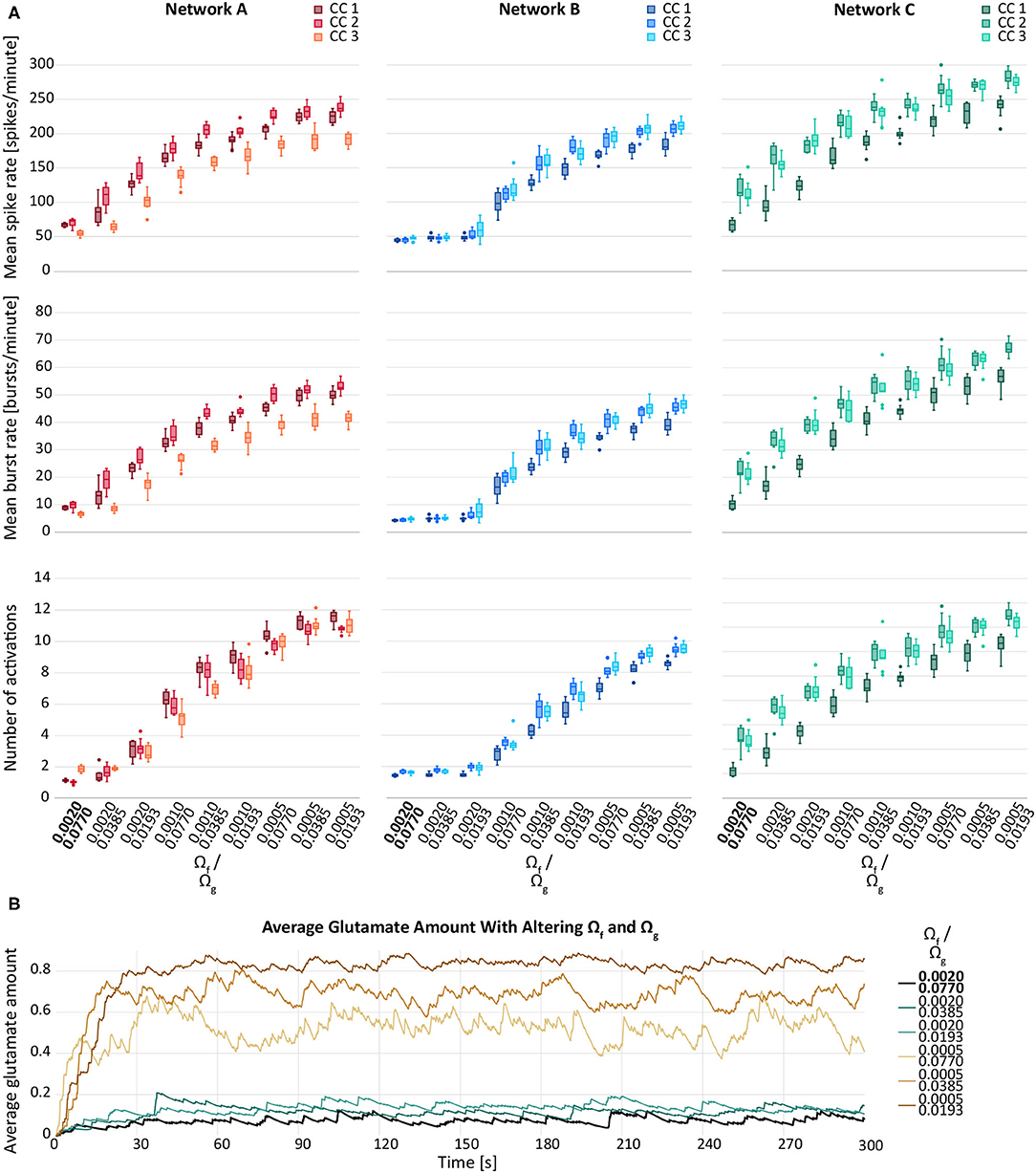
Figure 4. (A) Mean spike rate (top), mean burst rate (middle) and mean number of activations per astrocyte (bottom) for varying rates of synaptic facilitation, Ω_g, and varying recovery rates of the gliotransmitter receptors, Ω_g, for networks A–C and their connectivity configurations CC 1, 2, 3. The default values are indicated in bold. (B) Average glutamate amount in astrocytes when varying the synaptic facilitation rate, Ω_g, and the recovery rate of the gliotransmitter receptors, Ω_g. The black line resembles the baseline activity from network B, CC 1. The brown lines represent the changes by Ω_f and the blue lines the changes by Ω_g.

We observed a similar behaviour for the average glutamate level when varying Ω_f and Ω_g. Figure 4B shows a larger effect of Ω_g compared to the effect of Ω_f. Decreasing either parameter resulted in elevated response variables compared to the default network. Also in this case, the effect of Ω_f was larger compared the effect of Ω_g.

The results of the LME model fit are reported in Table 5. We observed that the average response μ fitted for values w_f = w_g = 0 (baseline activity) was difficult to estimate, indicated by the wide confidence intervals. Also the estimated standard deviation ${\widehat{\sigma }}_{\mu }$ of the baseline activity due to different network configurations was large relative to μ for all response variables, particularly for the mean number of astrocyte activations. For most response variables, the estimated standard deviation $\widehat{\sigma }$ of the residual error was at around 10% of the baseline activity, significantly smaller than ${\widehat{\sigma }}_{\mu }$.

TABLE 5

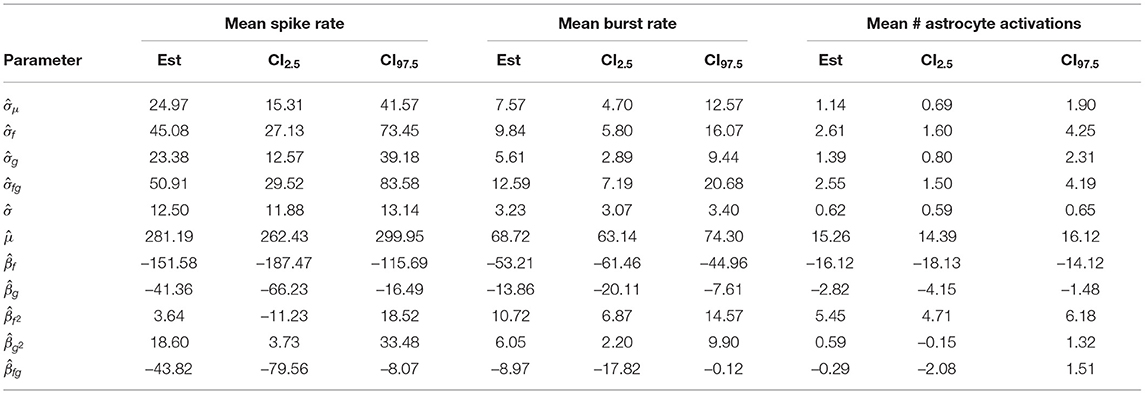
Table 5. Restricted maximum likelihood estimates, lower and upper ends of 95% confidence intervals for the glutamate dynamics experiment.

The parameters ${\beta }_f,{\beta }_{f^2}$ had tight confidence intervals, indicating that the estimates were reliable. We saw a strong negative first order effect of the rate of presynaptic glutamate uptake w_f on all responses and a positive second-order effect. For all responses, the standard deviation estimate σ_f of the first order effect was small relative to ${\widehat{\beta }}_f$. Similarly, we found a negative first order and a positive second-order effect of the astrocyte glutamate uptake on all variables with small estimated standard deviation ${\widehat{\sigma }}_g$. The corresponding 95% CIs for the parameters ${\beta }_g,{\beta }_{g^2}$ were slightly wider than those of β_f and ${\beta }_{f^2}$. The first-order interaction coefficient β_fg of the parameters w_f and w_g was significant, but with a small effect for all responses. The fact that ${\widehat{\sigma }}_{fg}$ and β_fg lay in a similar range indicates that the interaction terms might vary considerably for different network configurations. However, these effects were all small compared to β_f or β_g. Contour plots of the response variables derived from the LME model fit are shown in Figure 5.

FIGURE 5

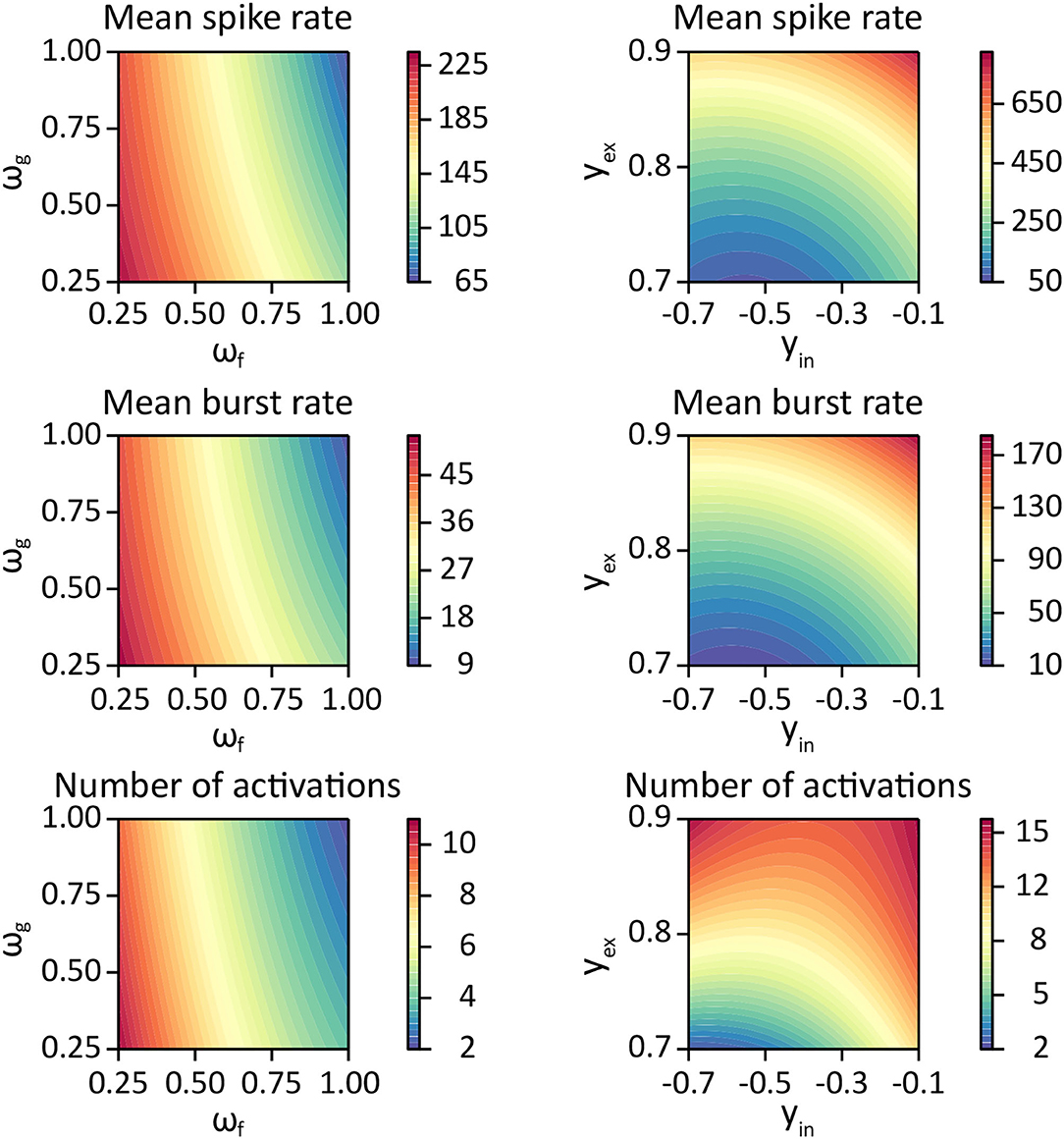
Figure 5. Contour plots for each response variable as a function of glutamate dynamics parameters ω_f, ω_g (left column) using parameter estimates listed in Table 5, and as a function of the synaptic weight bound parameters y_in, y_ex (right column) using the parameter estimates from Table 6.

3.4. Hypothesis 4: Higher Network Activity When Increasing Synaptic Weight Parameters

In this section, we computationally investigated the neuronal and astrocytic response to synaptic perturbations caused by SCZ. Figure 6A depicts the behaviour of the three response variables while changing either the maximum inhibitory synaptic weight $Y_{max}^{-}$ or in the maximum excitatory synaptic weight $Y_{max}^{+}$. Increases in $Y_{max}^{-}$ and $Y_{max}^{+}$ yielded in elevated response variables. The relationship between the parameter distortion and the effect on the observation variables were consistent among the three networks (A, B, C) and their corresponding connectivities (1, 2, 3). However, network B showed a comparatively reduced response to deviations in $Y_{max}^{-}$. The variance induced by alterations of $Y_{max}^{+}$ was higher than the inter-network and the inter-connectivity variance. This was not the case for the variance induced by deviating $Y_{max}^{-}$, which was due the lower number of inhibitory cells in the networks. Moreover, compared to the unmodified parameter configuration ($Y_{max}^{-}=-0.7$ and $Y_{max}^{+}=0.7$), the response variables from the distorted parameter configurations showed higher variances in most of the cases.

FIGURE 6

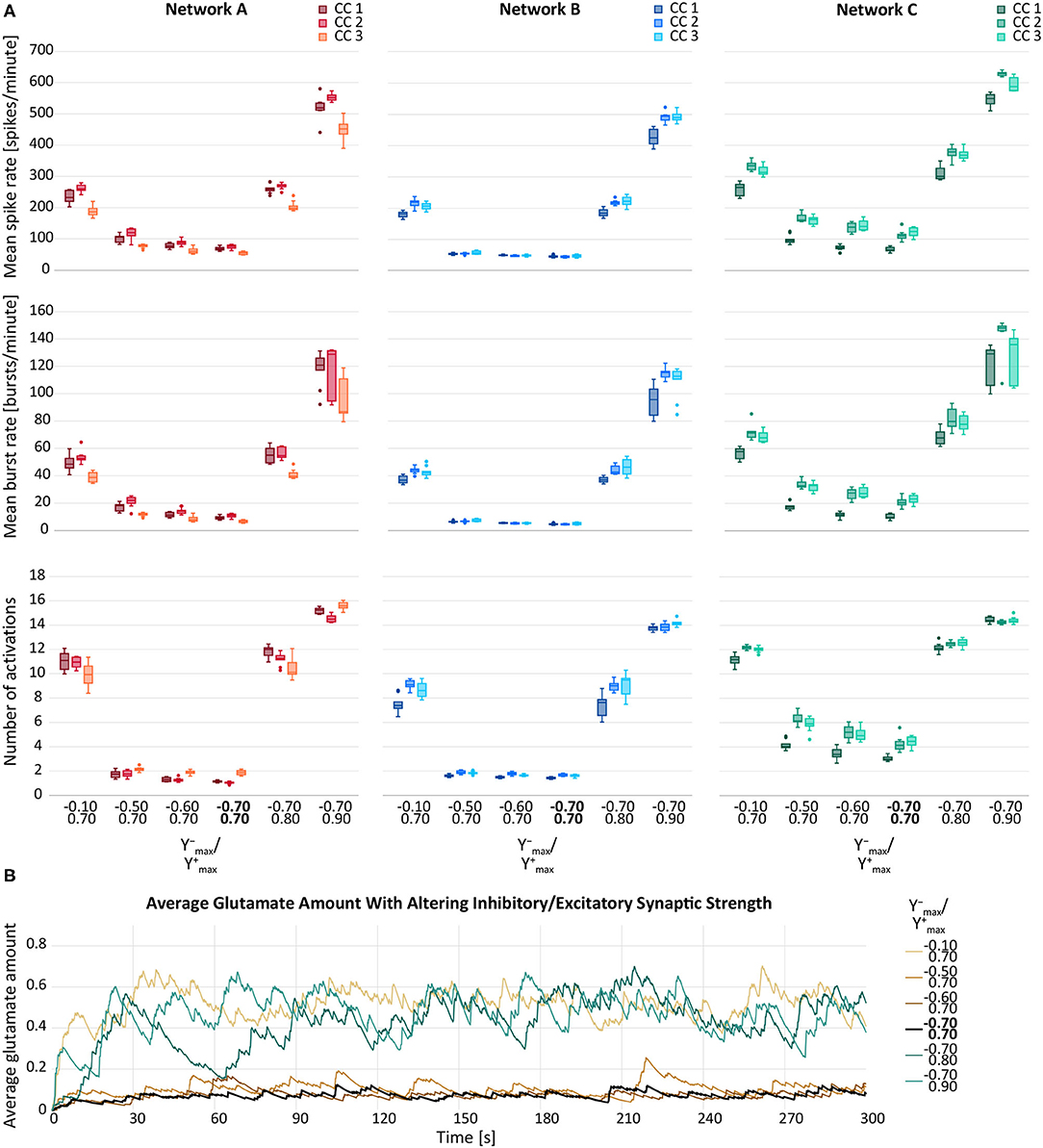
Figure 6. (A) Mean spike rate (top), mean burst rate (middle) and mean number of activations per astrocyte (bottom) for varying maximum inhibitory ($Y_{max}^{-}$) and maximum excitatory synaptic weight ($Y_{max}^{+}$) of neurons for networks A–C and their connectivity configurations CC 1, 2, 3. The default values are indicated in bold. (B) Average glutamate amount in astrocytes when altering the inhibitory and excitatory synaptic weights. The black line resembled the activity from the default network B, CC 1. The brown lines represent the changes of $Y_{max}^{-}$ and the blue lines the changes in $Y_{max}^{+}$.

In Figure 6B, the average glutamate amount in all astrocytes is plotted against time for varying $Y_{max}^{-}$ and $Y_{max}^{+}$. We noted that a change in the glutamate behaviour was achieved by all deviation levels of $Y_{max}^{+}$. For $Y_{max}^{-}$, a large deviation from the default values was required to see a change in the average glutamate levels. The smaller deviations of $Y_{max}^{-}$ did not yield a notable elevation of neither the response variables (Figure 6A) nor the time course of the average glutamate level (Figure 6B).

The parameter estimates of the corresponding statistical LME analysis are listed in Table 6. We refer to the average μ of the response variable when setting parameter values y_in, y_ex to zero as the baseline activity. Comparing the parameter estimates in Table 6 to the data in Figure 6A, we observe that the estimated baseline activity $\widehat{\mu }$ is significantly larger than the average response. This effect is compensated by large values of parameters ${\widehat{\beta }}_{in}$,${\widehat{\beta }}_{ex}$,${\widehat{\beta }}_{{in}^2}$,${\widehat{\beta }}_{{ex}^2}$ and ${\widehat{\beta }}_{in,ex}$. Thus, to analyse the magnitude of the standard deviation terms, we refer to Figure 6A. We observed that the estimated residual standard deviation $\widehat{\sigma }$ was at around 1/10 to 1/2 of the average response value. The confidence intervals for σ_net were wide, so the random effect due to different network connectivities was not clear. However, across all experiments, ${\widehat{\sigma }}_{net}$ was estimated to be smaller than $\widehat{\sigma }$. Thus, it is likely that on average, responses vary more significantly for different repetitions than between networks with different connectivities. Further, we observed relatively wide confidence intervals for all fitted coefficients, indicating that the model fit and the provided estimates have limited expressiveness. Contour plots of the response variables derived from the LME model fit are shown in Figure 5.

TABLE 6

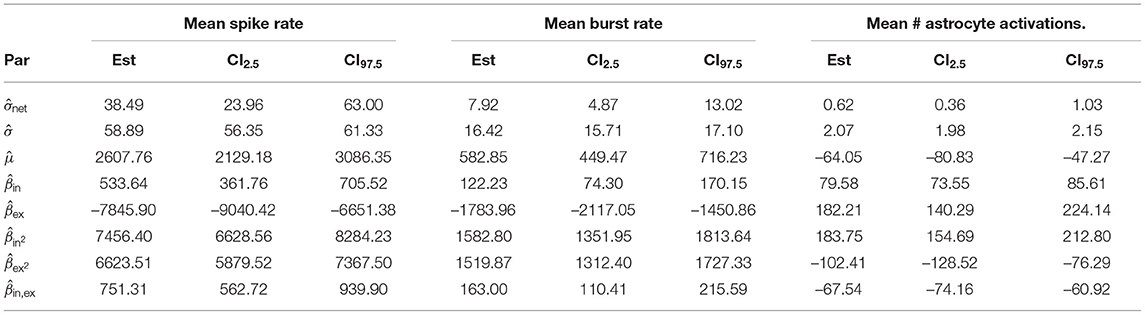
Table 6. Restricted maximum likelihood estimates, lower and upper ends of 95% confidence intervals for the synaptic weight parameter experiments.

4. Discussion

Schizophrenia is characterised by diverse dysregulations and malfunctions in neurons and astrocytes (Takahashi and Sakurai, 2013; Moraga-Amaro et al., 2014; Mei et al., 2018). In astrocytes, the pathology is among others indicated by a higher GFAP expression, an altered morphology, loss of gap junctions between cells, and an elevated glutamate release (Mitterauer, 2009; Catts et al., 2014; Mei et al., 2018). In neurons, SCZ is indicated by morphological alterations, reductions in cell density, and excessive glutamate release, which is due to the hypofunction of NMDA receptors (Cotter et al., 2001; Mei et al., 2018). Spontaneous neuronal activity is a fine balance between excitation and inhibition (Lisman, 2012; Sohal and Rubenstein, 2019), which is between 30 and 200 spikes per minute in healthy human stem cell-derived neurons (Tukker et al., 2018; Kizner et al., 2019). However, it is disputed whether SCZ causes an increase or a decrease in neuronal and astrocytic activity (Mei et al., 2018; Naujock et al., 2020).

Computational models can support the understanding of biophysical pathways when experiments are not realisable or too expensive. So far, a multitude of biophysical (bottom-up) and symptom focused (top-down) models have been developed. According to the reviews by Rolls et al. (2008) and Valton et al. (2017), top-down models mostly support the dopamine hypothesis. For example, Hoffman and McGlashan (2006) explored the effects of neuronal pruning and excessive dopamine. Using a recurrent backpropagation model of working memory, they showed how neuron reduction or hyperdopamigenic systems can produce spontaneous percepts simulating hallucinated speech. Furthermore, they were able provide an explanation for the onset of SCZ in late adolescence. For the glutamate hypothesis, only a few computational models are available (Valton et al., 2017). The models mostly focused on excitatory and inhibitory neurons, showing that deficits in glutamatergic or GABAergic activity lead to impairments in working-memory and other cognitive processing (Valton et al., 2017).

In the last few years, attempts were made to simulate SCZ using the Bayesian inference hypothesis. This hypothesis assumes that the brain combines sensory evidence together with prior knowledge and expectation to interpret a stimulus. In SCZ, different delusions bias the expected value, leading to stronger perceptual biases in the future. So far, the hypothesis has mostly been tested for illusions (Valton et al., 2017). One of the first computational models in that area was made by Adams et al. (2013). Using a biological predictive coding scheme, they showed that psychosis in SCZ can be accounted by an increased prior precision and trait abnormalities (e.g., abnormalities of smooth pursuit eye movements, event-related brain potentials or anhedonia) by a decrease in prior precision.

The loss of gap junctions in astrocytes can be a hallmark in SCZ (Mitterauer, 2009). Using the INEXA model, Genocchi et al. (2020) studied the effect of gap junction uncoupling on the neuronal activity. Additionally, Lenk et al. (2021) showed that larger distances between astrocytes, and thus, less gap junctions, seem to centralise the information transmission in astrocytes. The spike rate and burst rate increased until a cell-cell distance of 100 μm and then decreased again.

In this paper, we investigated the effect resulting from four different hypotheses of SCZ on neuronal and astrocytic activity. Using the computational network model by Lenk et al. (2020), we separately examined the neuronal and astrocytic dynamics depending on (1) the neuron and astrocyte density in the network, (2) the depressing effect of astrocytes on excitatory neurons, (3) the glutamate release from the presynapse and the glutamate uptake by the adjacent astrocyte, and (4) the excitatory and/or inhibitory synaptic weight between neurons. Furthermore, we applied a set of statistical models to quantify the effect of these pathological changes.

Several studies report that the neuronal and astrocytic density decreases in several brain regions in SCZ (Cotter et al., 2001; Brennand et al., 2011; Williams et al., 2013), which may be caused by excessive glutamate levels (Drouin-Ouellet et al., 2011). Wagenaar et al. (2006) studied the effect of neuronal cell density on the spike and burst behaviour recorded with MEAs. They found that sparser cultures exhibit a lower spike rate as well as delayed network development. In our simulated experiments, we found that reducing the number of neurons or astrocytes by 25% (hypothesis (1)) causes a significant decrease in neuronal and astrocytic activity. In the original paper of our computational model (Lenk et al., 2020), the number of astrocytes was increased, which led to an elevation of the neuronal activity. Conversely, this means that when astrocytes and their connections are eliminated, neuronal activity also decreases. Astrocytes are assumed to have a homeostatic effect on neurons, they can both enhance and dampen neuronal activity (Santello et al., 2019). Additionally, we found that the effect of reducing astrocytes or neurons can vary significantly for different network connectivity configurations. While the effect on the mean spike rate is robust to varying network connectivity configurations, the mean burst rate and the number of astrocyte activations are not. This might be useful for relating the behaviours of networks with the same number of cells, but different or unknown network configurations.

Furthermore, we have studied the effect of ATP release from the astrocyte on the postsynapse [hypothesis (2)]. Lalo et al. (2016) have demonstrated that ATP activates postsynaptic P2XRs resulting in a downregulation of neuronal NMDARs. This negative feedback mechanism might prevent cell damage due to excessive Ca²⁺ and glutamate concentrations (Singh and Abraham, 2017). By the regulation of NMDARs, P2XRs might also be involved in synaptic plasticity and long-term potentiation (LTP) (Moraga-Amaro et al., 2014; Lalo et al., 2016; Singh and Abraham, 2017). This receptor type could even have a protective role by avoiding excitotoxicity and excessive LTP (Lalo et al., 2016).

An increase in neuronal and astrocytic activity was observed when altering the rate of presynaptic facilitation and the recovery rate of mGluRs [hypothesis (3)]. The decreased facilitation rate increases the amount of neurotransmitters ready for release to the synaptic cleft, thereby increasing the release probability and spike rate. Similarly, decreasing the recovery rate of gliotransmitter receptors results in a higher presynaptic potentiation (Helen et al., 1992; Agulhon et al., 2008). Subsequently, this leads to an increase of the neuronal activity.

According to the glutamate hypothesis of SCZ, NMDARs undergo a hypofunction leading to an excessive glutamate release (Mei et al., 2018). The changes in the NMDAR function may be caused by D-serine (Takahashi and Sakurai, 2013; Cohen et al., 2015; Mei et al., 2018), which we implicitly modelled by increasing the excitatory synaptic weights. In the future, we aim to add D-serine explicitly to the INEXA model for investigating its role in long-term potentiation and thus memory (Henneberger et al., 2010). Furthermore, GABAergic interneurons (Uhlhaas and Singer, 2010) might be impacted by SCZ due to reaction to the alterations in the NMDARs and an impaired synthesis and reuptake of GABA into the cell (Uhlhaas and Singer, 2010; Moghaddam and Javitt, 2012; Mei et al., 2018). When investigating hypothesis (4), the results show a higher neuronal and astrocytic activity, when increasing the inhibitory or excitatory synaptic weights (both yields in a neuronal excitation).

Further experimental observations are coherent with our modelling results. In SCZ, glutamine synthetase, which catalyzes glutamate, was shown to have reduced activity leading to higher levels of intracellular astrocytic glutamate, and thus, result in a neuronal hyperexcitability (Hu et al., 2015; Mei et al., 2018). This observation is in agreement with the results of our simulated experiments from hypotheses (3) and (4). The accumulation of glutamate was most pronounced in simulated experiments with a decreased mGluR recovery rate. In these experiments, glutamate accumulated quickly before stabilizing at an extremely high level. As to be expected, the neuronal activity increased with dysinhibition of the GABAergic neurons or the excitation of the glutamatergic neurons.

In the INEXA model, we mainly concentrated on the IP₃-dependent Ca²⁺ dynamics. Srinivasan et al. (2015) showed that somatic calcium is abolished in adult Ip3r2^−/− mice. In the future, we intend to extend the model by adding astrocytic NMDARs and α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) receptors as well as the glutamate transporter-dependent pathway to gain further insights into the possible dysfunctions in schizophrenia.

Dynamical causal modeling (DCM), a framework using Bayesian statistics to compare competing models (Friston et al., 2003), has given rise to differential diagnosis methods for psychiatric diseases (Stephan et al., 2017). In the future, we will apply Bayesian inference to obtain posterior distributions of certain astrocytic parameters from INEXA, building the basis for Bayesian model selection among competing disease mechanisms linked to astrocyte malfunction.

Data Availability Statement

The datasets for this study can be found in Github: https://github.com/kerstinlenk/INEXA_SCZ/.

Author Contributions

KL wrote the first draft of the manuscript. LF, JL, and FS collected simulation data. LF, FS, and KL visualized the results. FS designed and performed the statistical analysis. All authors designed and performed research and contributed to the manuscript writing and revision. In addition, they have read and approved the submitted version.

Funding

KL was funded by the Academy of Finland (decision nos. 314647 and 326452).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Barbara Priwitzer for the discussion about the statistical analysis. Furthermore, we want to thank the Statistical Consulting Service at ETH Zurich, especially Chiara Vanetta for her advice on the statistical models and their interpretation.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fncel.2021.718459/full#supplementary-material

References

Adams, R., Stephan, K., Brown, H., Frith, C., and Friston, K. (2013). The computational anatomy of psychosis. Front. Psychiatry 4:47. doi: 10.3389/fpsyt.2013.00047

PubMed Abstract | CrossRef Full Text | Google Scholar

Agulhon, C., Petravicz, J., McMullen, A. B., Sweger, E. J., Minton, S. K., Taves, S. R., et al. (2008). What is the role of astrocyte calcium in neurophysiology? Neuron 59, 932–946. doi: 10.1016/j.neuron.2008.09.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Araque, A., Parpura, V., Sanzgiri, R. P., and Haydon, P. G. (1999). Tripartite synapses: glia, the unacknowledged partner. Trends Neurosci. 22, 208–215. doi: 10.1016/S0166-2236(98)01349-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Bates, D., Mchler, M., Bolker, B., and Walker, S. (2015). Fitting linear mixed-effects models using lme4. J. Stat. Softw. Articles 67, 1–48. doi: 10.18637/jss.v067.i01

CrossRef Full Text

Brennand, K. J., Simone, A., Jou, J., Gelboin-Burkhart, C., Tran, N., Sangar, S., et al. (2011). Modelling schizophrenia using human induced pluripotent stem cells. Nature 473, 221–225. doi: 10.1038/nature09915

PubMed Abstract | CrossRef Full Text | Google Scholar

Catts, V. S., Wong, J., Fillman, S. G., Fung, S. J., and Shannon Weickert, C. (2014). Increased expression of astrocyte markers in schizophrenia: association with neuroinflammation. Aust. N. Z. J. Psychiatry 48, 722–734. doi: 10.1177/0004867414531078

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen, S. M., Tsien, R. W., Goff, D. C., and Halassa, M. M. (2015). The impact of NMDA receptor hypofunction on GABAergic neurons in the pathophysiology of schizophrenia. Schizophr. Res. 167, 98–107. doi: 10.1016/j.schres.2014.12.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Cotter, D., Mackay, D., Landau, S., Kerwin, R., and Everall, I. (2001). Reduced glial cell density and neuronal size in the anterior cingulate cortex in major depressive disorder. Arch. Gen. Psychiatry 58, 545–553. doi: 10.1001/archpsyc.58.6.545

PubMed Abstract | CrossRef Full Text | Google Scholar

Danbolt, N. C. (2001). Glutamate uptake. Progr. Neurobiol. 65, 1–105. doi: 10.1016/S0301-0082(00)00067-8

PubMed Abstract | CrossRef Full Text | Google Scholar

de Bartolomeis, A., Fiore, G., and Iasevoli, F. (2005). Dopamine-glutamate interaction and antipsychotics mechanism of action: implication for new pharmacological strategies in psychosis. Curr. Pharm. Des. 11, 3561–3594. doi: 10.2174/138161205774414538

PubMed Abstract | CrossRef Full Text | Google Scholar

Dietz, A. G., Goldman, S. A., and Nedergaard, M. (2020). Glial cells in schizophrenia: a unified hypothesis. Lancet Psychiatry 7, 272–281. doi: 10.1016/S2215-0366(19)30302-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Drouin-Ouellet, J., Brownell, A. L., Saint-Pierre, M., Fasano, C., Emond, V., Trudeau, L. E., et al. (2011). Neuroinflammation is associated with changes in glial mGluR5 expression and the development of neonatal excitotoxic lesions. Glia 59, 188–199. doi: 10.1002/glia.21086

PubMed Abstract | CrossRef Full Text | Google Scholar

Friston, K., Harrison, L., and Penny, W. (2003). Dynamic causal modelling. Neuroimage 19, 1273–1302. doi: 10.1016/S1053-8119(03)00202-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Genocchi, B., Lenk, K., and Hyttinen, J. (2020). “Influence of astrocytic gap junction coupling on in silico neuronal network activity,” in MEDICON 2019, IFMBE Proceedings (Cham: Springer Nature Switzerland AG 2020), 480–487.

Google Scholar

Gramowski, A., Jügelt, K., Juegelt, K., Stuewe, S., Schulze, R., McGregor, G. P., et al. (2006). Functional screening of traditional antidepressants with primary cortical neuronal networks grown on multielectrode neurochips. Eur. J. Neurosci. 24, 455–465. doi: 10.1111/j.1460-9568.2006.04892.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Grnder, G., and Cumming, P. (2016). “Chapter 7-the dopamine hypothesis of schizophrenia: current status,” in The Neurobiology of Schizophrenia, eds T. Abel and T. Nickl-Jockschat (San Diego, CA: Academic Press), 109–124.

Google Scholar

Helen, C., Kastritsis, C., Salm, A. K., and McCarthy, K. (1992). Stimulation of the P 2Y Purinergic Receptor on Type 1 astroglia results in inositol phosphate formation and calcium mobilization. J. Neurochem. 58, 1277–1284. doi: 10.1111/j.1471-4159.1992.tb11339.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Henneberger, C., Papouin, T., Oliet, S. H. R., and Rusakov, D. A. (2010). Long-term potentiation depends on release of d-serine from astrocytes. Nature 463, 232–236. doi: 10.1038/nature08673

PubMed Abstract | CrossRef Full Text | Google Scholar

Herman, E., Bubser, M., Conn, P., and Jones, C. (2012). “Metabotropic glutamate receptors for new treatments in schizophrenia,” lems in psychiatry, in Novel Antischizophrenia Treatments, Vol. 213 of Handbook of Experimental Pharmacology, eds M. A. Geyer and G. Gross (Berlin; Heidelberg: Springer Berlin Heidelberg), 297–365.

Google Scholar

Hoffman, R., and McGlashan, T. (2006). Using a speech perception neural network computer simulation to contrast neuroanatomic versus neuromodulatory models of auditory hallucinations. Pharmacopsychiatry 39(Suppl. 1), S54–S64. doi: 10.1055/s-2006-931496

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, W., MacDonald, M. L., Elswick, D. E., and Sweet, R. A. (2015). The glutamate hypothesis of schizophrenia: evidence from human brain tissue studies. Ann. N. Y. Acad. Sci. 1338, 38–57. doi: 10.1111/nyas.12547

PubMed Abstract | CrossRef Full Text | Google Scholar

Jenkinson, S. P., Grandgirard, D., Heidemann, M., Tscherter, A., Avondet, M.-A., and Leib, S. L. (2017). Embryonic stem cell-derived neurons grown on multi-electrode arrays as a novel in vitro bioassay for the detection of clostridium botulinum neurotoxins. Front. Pharmacol. 8:73. doi: 10.3389/fphar.2017.00073

PubMed Abstract | CrossRef Full Text | Google Scholar

Kapucu, F., Tanskanen, J., Mikkonen, J. E., Ylä-Outinen, L., Narkilahti, S., and Hyttinen, J. A. K. (2012). Burst analysis tool for developing neuronal networks exhibiting highly varying action potential dynamics. Front. Comput. Neurosci. 6, 1–14. doi: 10.3389/fncom.2012.00038

PubMed Abstract | CrossRef Full Text | Google Scholar

Kizner, V., Fischer, S., and Naujock, M. (2019). “Multielectrode Array (MEA)-based detection of spontaneous network activity in human iPSC-derived cortical neurons,” in Cell-Based Assays Using iPSCs for Drug Development and Testing, Vol. 1994, eds C. F. Mandenius and J. Ross (New York, NY: Springer Science+Business Media), 209–216.

PubMed Abstract | Google Scholar

Kondziella, D., Brenner, E., Eyjolfsson, E. M., and Sonnewald, U. (2007). How do glial-neuronal interactions fit into current neurotransmitter hypotheses of schizophrenia? Neurochem Int. 50, 291–301. doi: 10.1016/j.neuint.2006.09.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Koskuvi, M., Lehtonen, S., Trontti, K., Keuters, M., Wu, Y. C., Koivisto, H., et al. (2020). Patient iPSC-astrocytes show transcriptional and functional dysregulation in schizophrenia. Bioarxiv, 1–45. doi: 10.1101/2020.10.23.350413

CrossRef Full Text | Google Scholar

Kosten, L., Verhaeghe, J., Verkerk, R., Thomae, D., De Picker, L., Wyffels, L., et al. (2016). Multiprobe molecular imaging of an NMDA receptor hypofunction rat model for glutamatergic dysfunction. Psychiatry Res. Neuroimaging 248, 1–11. doi: 10.1016/j.pscychresns.2016.01.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Lalo, U., Palygin, O., Verkhratsky, A., Grant, S. G. N., and Pankratov, Y. (2016). ATP from synaptic terminals and astrocytes regulates NMDA receptors and synaptic plasticity through PSD-95 multi-protein complex. Sci. Rep. 6, 33609. doi: 10.1038/srep33609

PubMed Abstract | CrossRef Full Text | Google Scholar

Lenk, K., Genocchi, B., Barros, M. T., and Hyttinen, J. A. (2021). Larger connection radius increases hub astrocyte number in a 3D neuron-astrocyte network model. IEEE Trans. Mol. Biol. Multiscale Commun. 7, 83–88. doi: 10.1109/TMBMC.2021.3054890

CrossRef Full Text | Google Scholar

Lenk, K., Satuvuori, E., Lallouette, J., Ladrón-de Guevara, A., Berry, H., and Hyttinen, J. A. K. A. (2020). A computational model of interactions between neuronal and astrocytic networks: the role of astrocytes in the stability of the neuronal firing rate. Front. Comput. Neurosci. 13:92. doi: 10.3389/fncom.2019.00092

PubMed Abstract | CrossRef Full Text | Google Scholar

Lisman, J. (2012). Excitation, inhibition, local oscillations, or large-scale loops: what causes the symptoms of schizophrenia? Curr. Opin. Neurobiol. 22, 537–544. doi: 10.1016/j.conb.2011.10.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Mahdavi, A., Bahrami, F., and Janahmadi, M. (2014). “Studying the effect of dysregulation of NMDA receptors function in schizophrenia,” in 22nd Iranian Conference on Electrical Engineering, ICEE 2014, number ICEE (Tehran: IEEE), 1990–1995.

Google Scholar

Manninen, T., Havela, R., and Linne, M.-L. (2018). Computational models for calcium-mediated astrocyte functions. Front. Compu.t Neurosci. 12:14. doi: 10.3389/fncom.2018.00014

PubMed Abstract | CrossRef Full Text | Google Scholar

Mei, Y.-Y., Wu, D. C., and Zhou, N. (2018). Astrocytic regulation of glutamate transmission in schizophrenia. Front. Psychiatry 9:544. doi: 10.3389/fpsyt.2018.00544

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitterauer, B. (2009). Loss of function of glial gap junctions may cause severe cognitive impairments in schizophrenia. Med. Hypotheses. 73, 393–397. doi: 10.1016/j.mehy.2009.04.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Moghaddam, B., and Javitt, D. (2012). From revolution to evolution: the glutamate hypothesis of schizophrenia and its implication for treatment. Neuropsychopharmacology 37, 4–15. doi: 10.1038/npp.2011.181

PubMed Abstract | CrossRef Full Text | Google Scholar

Moraga-Amaro, R., Jerez-Baraona, J., Simon, F., and Stehberg, J. (2014). Role of astrocytes in memory and psychiatric disorders. J. Physiol. Paris 108, 240–251. doi: 10.1016/j.jphysparis.2014.08.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Moran, R., Stephan, K. E., Botvinick, M., Breakspear, M., Carter, C. S., Kalivas, P. W., et al. (2016). “Candidate examples for a computational approach to address practical problems in psychiatry,” in Computational Psychiatry: New Perspectives on Mental Illness, Vol. 20, Chapter 12, eds A. D. R. Gordon (Cambridge, MA: The MIT Press), 223–245.

Google Scholar

Naujock, M., Speidel, A., Fischer, S., Kizner, V., Dorner-Ciossek, C., and Gillardon, F. (2020). Neuronal differentiation of induced pluripotent stem cells from schizophrenia patients in two-dimensional and in three-dimensional cultures reveals increased expression of the Kv4.2 subunit DPP6 that contributes to decreased neuronal activity. Stem. Cells Dev. 29, 1577–1587. doi: 10.1089/scd.2020.0082

PubMed Abstract | CrossRef Full Text | Google Scholar

Oehlert, G. W. (2010). A First Course in Design and Analysis of Experiments. University of Minnesota Digital Conservancy. Available online at: https://hdl.handle.net/11299/168002

Google Scholar

Ohnuma, T., Augood, S. J., Arai, H., McKenna, P. J., and Emson, P. C. (1998). Expression of the human excitatory amino acid transporter 2 and metabotropic glutamate receptors 3 and 5 in the prefrontal cortex from normal individuals and patients with schizophrenia. Mol. Brain Res. 56, 207–217. doi: 10.1016/S0169-328X(98)00063-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Oschmann, F., Berry, H., Obermayer, K., and Lenk, K. (2018). From in silico astrocyte cell models to neuron-astrocyte network models: a review. Brain Res Bull. 136, 76–84. doi: 10.1016/j.brainresbull.2017.01.027

PubMed Abstract | CrossRef Full Text | Google Scholar

Rolls, E. T., Loh, M., Deco, G., and Winterer, G. (2008). Computational models of schizophrenia and dopamine modulation in the prefrontal cortex. Nat. Rev. Neurosci. 9, 696–709. doi: 10.1038/nrn2462

PubMed Abstract | CrossRef Full Text | Google Scholar

Santello, M., Toni, N., and Volterra, A. (2019). Astrocyte function from information processing to cognition and cognitive impairment. Nat. Neurosci. 22, 154–166. doi: 10.1038/s41593-018-0325-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Schobel, S. A., Chaudhury, N. H., Khan, U. A., Paniagua, B., Styner, M. A., Asllani, I., et al. (2013). Imaging patients with psychosis and a mouse model establishes a spreading pattern of hippocampal dysfunction and implicates glutamate as a driver. Neuron 78, 81–93. doi: 10.1016/j.neuron.2013.02.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Siekmeier, P. J., and Hoffman, R. E. (2002). Enhanced semantic priming in schizophrenia: a computer model based on excessive pruning of local connections in association cortex. Br. J. Psychiatry 180, 345–350. doi: 10.1192/bjp.180.4.345

PubMed Abstract | CrossRef Full Text | Google Scholar

Singh, A., and Abraham, W. C. (2017). Astrocytes and synaptic plasticity in health and disease. Exp. Brain Res. 235, 1645–1655. doi: 10.1007/s00221-017-4928-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Sohal, V. S., and Rubenstein, J. L. R. (2019). Excitation-inhibition balance as a framework for investigating mechanisms in neuropsychiatric disorders. Mol. Psychiatry 24, 1248–1257. doi: 10.1038/s41380-019-0426-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Srinivasan, R., Huang, B. S., Venugopal, S., Johnston, A. D., Chai, H., Zeng, H., et al. (2015). Ca²⁺ signaling in astrocytes from Ip3r2^−/− mice in brain slices and during startle responses in vivo. Nat. Neurosci. 18, 708–717. doi: 10.1038/nn.4001

PubMed Abstract | CrossRef Full Text | Google Scholar

Stephan, K., Schlagenhauf, F., Huys, Q., Raman, S., Aponte, E., Brodersen, K., et al. (2017). Computational neuroimaging strategies for single patient predictions. Neuroimage 145, 180–199. doi: 10.1016/j.neuroimage.2016.06.038

PubMed Abstract | CrossRef Full Text | Google Scholar

Stephan, K. E., Bach, D. R., Fletcher, P. C., Flint, J., Frank, M. J., Friston, K. J., et al. (2016). Charting the landscape of priority problems in psychiatry, part 1: classification and diagnosis. Lancet Psychiatry 3, 77–83. doi: 10.1016/S2215-0366(15)00361-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Takahashi, N., and Sakurai, T. (2013). Roles of glial cells in schizophrenia: Possible targets for therapeutic approaches. Neurobiol. Dis. 53, 49–60. doi: 10.1016/j.nbd.2012.11.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Tukker, A. M., Wijnolts, F. M., de Groot, A., and Westerink, R. H. (2018). Human iPSC-derived neuronal models for in vitro neurotoxicity assessment. Neurotoxicology 67, 215–225. doi: 10.1016/j.neuro.2018.06.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Uhlhaas, P. J., and Singer, W. (2010). Abnormal neural oscillations and synchrony in schizophrenia. Nat. Rev. Neurosci. 11, 100–113. doi: 10.1038/nrn2774

PubMed Abstract | CrossRef Full Text | Google Scholar

Välkki, I. A., Lenk, K., Mikkonen, J. E., Kapucu, F. E., and Hyttinen, J. A. K. (2017). Network-wide adaptive burst detection depicts neuronal activity with improved accuracy. Front. Comput. Neurosci. 11:40. doi: 10.3389/fncom.2017.00040

PubMed Abstract | CrossRef Full Text | Google Scholar

Valton, V., Romaniuk, L., Douglas Steele, J., Lawrie, S., and Seriès, P. (2017). Comprehensive review: computational modelling of schizophrenia. Neurosci. Biobehav. Rev. 83, 631–646. doi: 10.1016/j.neubiorev.2017.08.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Wagenaar, D. A., Pine, J., and Potter, S. S. M. (2006). An extremely rich repertoire of bursting patterns during the development of cortical cultures. BMC Neurosci. 7:11. doi: 10.1186/1471-2202-7-11

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, M. R., Hampton, T., Pearce, R. K., Hirsch, S. R., Ansorge, O., Thom, M., et al. (2013). Astrocyte decrease in the subgenual cingulate and callosal genu in schizophrenia. Eur. Arch. Psychiatry Clin. Neurosci. 263, 41–52. doi: 10.1007/s00406-012-0328-5

PubMed Abstract | CrossRef Full Text | Google Scholar