Ih Equalizes Membrane Input Resistance in a Heterogeneous Population of Fusiform Neurons in the Dorsal Cochlear Nucleus

In a neuronal population, several combinations of its ionic conductances are used to attain a specific firing phenotype. Some neurons present heterogeneity in their firing, generally produced by expression of a specific conductance, but how additional conductances vary along in order to homeostatically regulate membrane excitability is less known. Dorsal cochlear nucleus principal neurons, fusiform neurons, display heterogeneous spontaneous action potential activity and thus represent an appropriate model to study the role of different conductances in establishing firing heterogeneity. Particularly, fusiform neurons are divided into quiet, with no spontaneous firing, or active neurons, presenting spontaneous, regular firing. These modes are determined by the expression levels of an intrinsic membrane conductance, an inwardly rectifying potassium current (I_Kir). In this work, we tested whether other subthreshold conductances vary homeostatically to maintain membrane excitability constant across the two subtypes. We found that I_h expression covaries specifically with I_Kir in order to maintain membrane resistance constant. The impact of I_h on membrane resistance is dependent on the level of I_Kir expression, being much smaller in quiet neurons with bigger I_Kir, but I_h variations are not relevant for creating the quiet and active phenotypes. Finally, we demonstrate that the individual proportion of each conductance, and not their absolute conductance, is relevant for determining the neuronal firing mode. We conclude that in fusiform neurons the variations of their different subthreshold conductances are limited to specific conductances in order to create firing heterogeneity and maintain membrane homeostasis.

Introduction

Theoretical and experimental evidence suggests that the expression levels of different ion channels and conductances vary across individual neurons with similar firing properties (Prinz et al., 2004; Marder and Goaillard, 2006; Goaillard et al., 2009), showing that similar firing properties can be achieved by different combinations of ion channel densities. On the other hand, specific and coordinated correlations of ion channels can be used to maintain constant neuronal behavior (Goldman et al., 2001; Schulz et al., 2006, 2007; Sobie, 2009; Taylor et al., 2009; Grashow et al., 2010; Khurana et al., 2011; Ransdell et al., 2013) suggesting that compensatory mechanisms act to maintain stable physiological properties (O’Leary et al., 2013). Additionally, the role of a specific conductance on the membrane excitability and passive properties depends on the dynamics of the other conductances expressed in the neuron (Ma and Koester, 1996; Swensen and Bean, 2003; Day et al., 2005; Marder et al., 2014). Thus, the modulation of a specific conductance can impact the neuronal membrane properties depending on the environment it is included (Marder et al., 2014). However, if the levels of different conductances in a neuron follow specific rules to maintain stable electrophysiological properties or the neuron can attain the same membrane characteristics using several combinations of densities of different ion channels is still a matter of debate.

To address this question, we studied the principal neuron of the dorsal cochlear nucleus (DCN) (Zhang and Oertel, 1994), the fusiform neuron. Fusiform neurons are divided in two populations based on their firing properties: one presenting spontaneous firing at rest, termed active, and another one which does not produce spontaneous firing, named quiet (Leao et al., 2012; Zugaib et al., 2016). These two firing states are produced by differential expression of an intrinsic ionic conductance (Leao et al., 2012) namely, the differential expression of an inwardly rectifying potassium current (I_Kir), which sets the resting membrane potential (RMP) at different voltage determining whether fusiform neurons fire spontaneously or not. Therefore, in the DCN fusiform neurons intrinsic variations of a specific conductance creates firing heterogeneity, and not diverse variations of different conductances in individual neurons. On the other hand, we demonstrated experimentally and theoretically that variations in the expression of a persistent sodium current (I_NaP), are not relevant for the creation of these two firing modes (Leao et al., 2012). However, we do not know how the other subthreshold conductances present in the DCN fusiform neuron affect the membrane properties of this neuron, more specifically, if variations in their expression correlates with the firing mode and subthreshold membrane properties.

To address this question, we attempted to investigate the role of the two other subthreshold conductances expressed by the DCN fusiform neurons, the hyperpolarization activated cationic current (I_h) and the background leak conductance (I_leak), on the membrane properties and on the creation of the firing modes of these neurons. Additionally using an improved computer model of the fusiform neuron, and quantifying conductance variations on individual neurons, we analyzed the impact of the combination of different sets of conductances on the membrane of the fusiform neurons and how they vary together in order to create the quiet and active phenotypes. We found a specific role of I_h in equalizing membrane input resistance in these neurons, in response to variations of I_Kir, generating distinct firing modes with similar membrane input resistances.

Materials and Methods

Brainstem Slices Preparation and Electrophysiology

ICR or Swiss mice (P17–P25) animals were sacrificed after isoflurane inhalation, according to methods approved by the Institutional Animal Care and Use Committee of the University of Pittsburgh and the Committee on Ethics in Animal Experimentation (CETEA) from the University of São Paulo. Coronal slices containing DCN were obtained as in Zugaib et al. (2016). Briefly brains were removed and cut in cold solution whose composition in mM was: NaCl (87), NaHCO₃ (25), KCl (2.5), NaH₂PO₄ (1.25), CaCl₂ (0.5), MgCl₂ (7), glucose (25), sucrose (75), 335 mOsm/kgH₂O, pH 7.4 when bubbled with carbogenic mixture (95% O₂ and 5% CO₂). Before removing the brain from the skull, the vestibulocochlear nerve (VIII cranial nerve) was cut to prevent damage to the DCN. Coronal slices (200 μm thick) containing the three layers of the DCN with its basic circuit (Oertel and Young, 2004) were obtained on a vibratome (Vibratome 1000 Plus) and incubated at 35°C for 45 min and subsequently at room temperature in recording solution [artificial cerebrospinal fluid (aCSF)], whose composition in mM was: NaCl (125), KCl (2.5), NaHCO₃ (25), NaH₂PO₄ (1.25), glucose (10), CaCl₂ (2), MgCl₂ (1), 305 mOsm/kgH₂O, pH 7.4 when bubbled with carbogenic mixture (95% O₂ and 5% CO₂). Alternatively, slices were obtained using a Leica 1000S vibratome in warm (35°C) aCSF, stored at this temperature for 1 h and then at room temperature as in Tzounopoulos et al. (2004). No difference was observed between the protocols or mice strain. Single cells were visualized with IR interference contrast optics and recorded using patch pipettes in either voltage- or current-clamp modes. Fusiform neurons were identified based on their electrophysiological and morphological characteristics (for more details see Tzounopoulos et al., 2004; Zugaib et al., 2016). Pipettes were filled with a K⁺-based internal solution containing (in mM): 113 K-gluconate, 4.5 MgCl₂, 14 tris-phosphocreatine, 9 HEPES, 0.1 EGTA, 4 Na-ATP, 0.3 tris-GTP, 10 sucrose, pH 7.3, ∼300 mOsmol. In some experiments external sodium chloride was replaced by N-methyl-D-glucamine chloride (NMDG-Cl).

Whole-cell recordings were performed at 33–36°C using an inline heating system (Warner Instruments) and perfused with aCSF at a rate of approximately 1 ml/min. Data was acquired at 10 or 20 kHz and low-pass filtered at 3 kHz (Bessel) using a MultiClamp 700B connected to a Digidata 1440A board (Axon Instruments) or an EPC-10 amplifier (HEKA Elecktronics). Voltage clamp experiments were performed at a holding potential of -65 mV, while current-clamp experiments were performed at I = 0 in quiet neurons and after injection of negative DC current (-20 to -200 pA) in active neurons. Acceptable access resistance was considered to be below 20 MΩ and was monitored during the whole experiment.

Computer Simulations

A single compartment model of the fusiform cell was built using a standard Hodgkin–Huxley formalism. It is based on a previous model reported in Leao et al. (2012) containing the following ionic conductances: I_Na (fast sodium current), I_Kd (delayed rectifier potassium current), I_h, I_NaP, I_Kir, and an I_leak. The kinetics of time and voltage-dependent parameters were determined by activation and inactivation gating variables as described in Leao et al. (2012). The maximal conductance densities of I_Na and I_Kd were adjusted in order to set firing frequencies closer to the experimental observations (Leao et al., 2012), with values of g_Na = 80 mS/cm² and g_Kd = 20 mS/cm². The other conductance densities were: g_NaP = 0.1, g_h = 0.54, and g_leak = 0.15 mS/cm². g_Kir was set at 0.5 mS/cm² for active neurons and at 1 mS/cm² for quiet neurons. The reversal potentials were set at 50 mV for E_Na, -81.5 mV for E_K, -43 mV for E_h, and -51.32 mV for E_leak. The K_IR time constant used was 0.5 ms.

I_h was built on a previous description of the current (Nagtegaal and Borst, 2010). We used two activation variables (A_h1 and A_h2) that were described with same steady state dynamics (A_h^∞) (Leao et al., 2012) but different voltage dependence of time constant (τ_h1 and τ_h2). The two activation time constants were used as in Destexhe and Babloyantz (1993). The kinetic equations were as follows

$I_{\mathrm{h}}=g_{\mathrm{h}}\mathrm{(}0.5*A_{\mathrm{h}1}+0.5*A_{\mathrm{h}2}\mathrm{)}*\mathrm{(}V-E_{\mathrm{h}}\mathrm{)}$

$A_{\mathrm{h}1}^{\infty }=A_{\mathrm{h}2}^{\infty }=\frac{1}{1+{\mathrm{e}}^{(V+\mathrm{87})/8.9}}$

${\tau }_{\mathrm{h}1}=100+{\mathrm{e}}^{(V+183.6)/30.48}$

${\tau }_{\mathrm{h}2}=700\frac{{\mathrm{e}}^{(V+188.6)/11}}{1+{\mathrm{e}}^{(V+105)/5.5}}$

Based on the experimental data (Leao et al., 2012), the model cell for the quiet versus spontaneously active states differed only in the maximum conductance of I_Kir. The geometry of the model was a cylinder 20 μm of diameter and 20 μm of length. The cell specific capacitance was set at 1 μF/cm². Simulations were run using the NEURON simulator, version7.1, in an 8-core Intel7 processor. The time step was 0.1 ms and the initial membrane potential -65 mV. All measurements were done after waiting 4 s to achieve steady state values. Parameter spaces were obtained varying only two parameters at a time, with the conductance values in the range between 0 and twice their original values. Data was saved and analyzed using MATLAB. In order to determine the regions in parameter space where active and quiet neurons were placed, 1 s of spontaneous activity (i.e., without injected current) was measured. To determine the RMP both sodium conductances (g_NaP and g_Na) were set to 0 and the RMP was measured at the end of a 1 s sweep over the range of values with no injected current.

The model and simulation files are available for public download on the freely available repository ModelDB¹.

Dynamic Clamp

We simulated I_h using the Real Time Application Interface for Linux-based (RTAI²) dynamic clamp (Dagostin et al., 2015). Two computers were used, one for data acquisition running PatchMaster (Heka Elecktronics), and a second ‘dynamic-clamp’ computer that reads voltage from the patch-clamp amplifier (EPC-10, HEKA Elecktronics) and generates current commands in real-time every 50 μs. The ‘dynamic-clamp’ computer is an x86 architecture computer (Pentium 4, Intel) with a PCI-6036E data acquisition card (National Instruments) for reading voltage and generating current commands to the clamped neuron. The real-time dynamic clamp software was written (by Dr. R. N. Leao, Federal University of Rio Grande do Norte, Brazil) in GNU-C, and routines for data acquisition were programmed using the Linux Control and Measurement Device Interface (COMEDI³).

Data Analysis

All data are corrected for a measured liquid junction potential of 10 mV. Active and quiet neurons were classified as in Leao et al. (2012). Fusiform neurons were classified as active when their spontaneous action potential firing rate was >0.5 Hz. Fusiform neurons that did not display any spontaneous firing or that displayed sparse spontaneous firing, with rates below 0.5 Hz, were classified as quiet. RMP was determined in the presence of TTX. The depolarization sag of the membrane was the difference between the steady state and the hyperpolarization peak (Figure 1A).

FIGURE 1

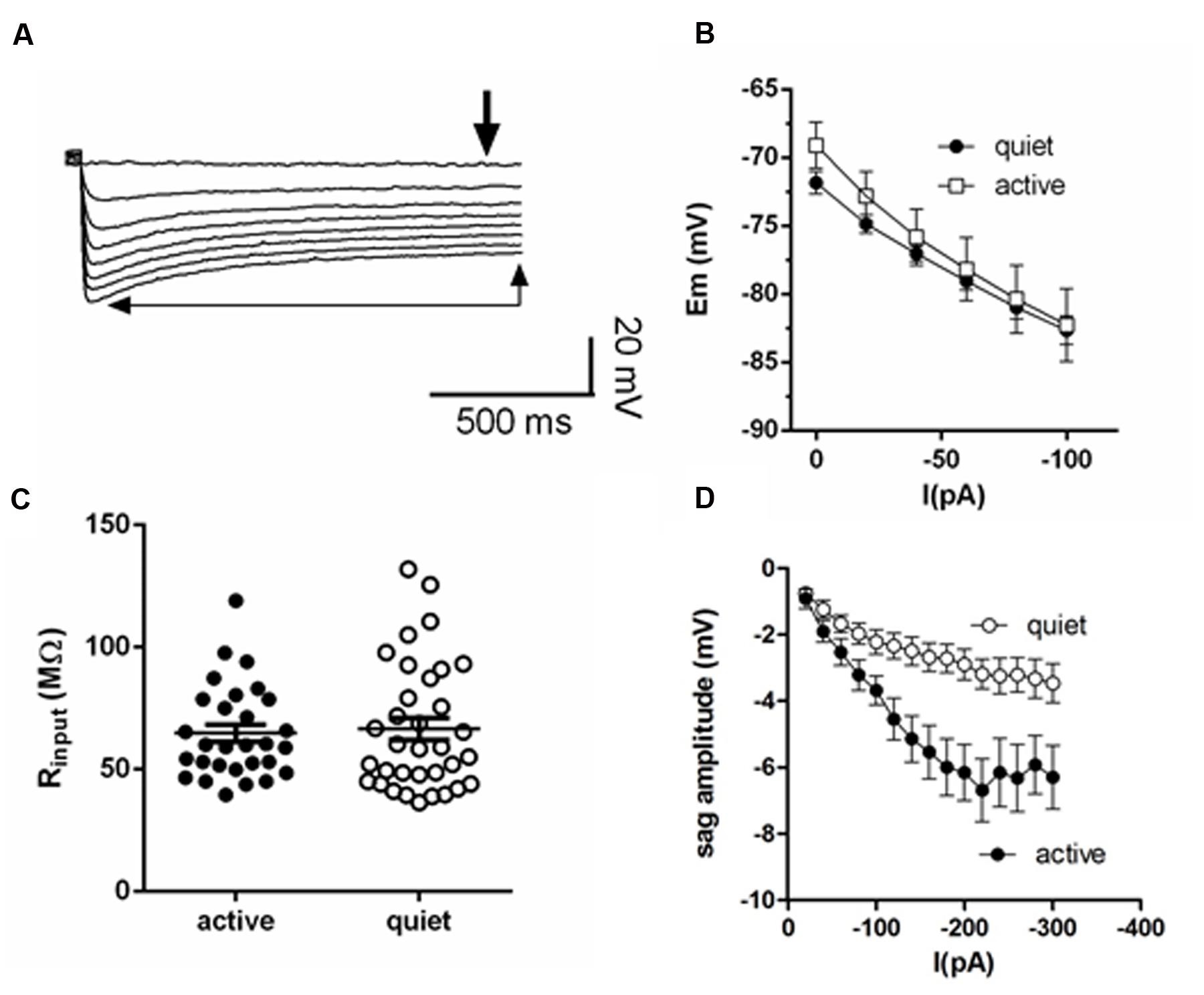
FIGURE 1. Membrane input resistance is similar in quiet and active fusiform neurons. (A) Example of the membrane response of a fusiform neuron to hyperpolarizations. The thick arrow shows the point where we measured the membrane potential used to calculate membrane input resistance. The thin arrows show the steady-state level of the membrane potential used to calculate the depolarization sag of the membrane. (B) Graph showing the steady-state response of the membrane potential to injected negative DC current in quiet (n = 16) and active (n = 14) fusiform neurons. (C) Summary of the membrane input resistance obtained by the linear regression of the data in (B). (D) Graph showing the dependence of the membrane sag amplitude to the current injected. n = 15 each.

The inward rectifying cationic current (I_h) was elicited by 4 s hyperpolarizations from -65 to -120 mV (in some cells we used -20 mV step hyperpolarizations from -60 to -120 mV) and quantified by subtracting the currents before and after the application of ZD7288 (20 μM). I_h was measured at the steady state current at the end of the hyperpolarization pulse. Alternatively, I_h was estimated as the difference between the onset and steady-state current. The conductances obtained using these two approaches were not significantly different (p > 0.05). The activation and deactivation of I_h was measured fitting a double exponential function to the current activation and tail current deactivation. The voltage dependence of g_h was calculated using the peak amplitude of the tail currents elicited after a repolarization to -65 mV and fitted with a Boltzmann function. Leak currents were defined as the currents left after blocking I_h and I_Kir with ZD7288 (20 μM) and Ba⁺⁺ (200 μM), respectively, and I_NaP with TTX (1 μM) (Leao et al., 2012). The slope conductance was determined using the linear part of the subthreshold IV relationship. Membrane input resistance was calculated both in current-clamp mode as the slope of the VI curves in response to -20 pA steps from 0 to -100 pA (Figure 1A), and in voltage-clamp mode as the inverse of the slope of the IV curves from -65 to -80 mV, values close to the RMP of the fusiform neurons (-60 to -80 mV; Leao et al., 2012).

Drugs

Drugs were prepared from 1000 × stock solutions and diluted before applications. ZD7288 was obtained from Tocris and Ascent Scientific. N-methyl D-glucamine-Cl (NMDG), BaCl₂ and tetrodotoxin (TTX) were purchased from Sigma.

Statistics

The membrane input resistances were submitted to a normality test (D′Agostino and Pearson) and they were not considered to represent a normal distribution (p < 0.0001, n = 120) so they were analyzed using a non-parametric test (Mann–Whitney). The other parameters had less data than necessary to apply normality tests (<<100) and were treated as having a normal distribution and their means compared with paired and unpaired t-test. However, comparing the data using both parametric and non-parametric tests did not affect our conclusions. Multiple comparisons were performed with one-way ANOVA and a Tukey’s multiple comparison test. Two-tailed significance level was set below 0.05. Correlations were determined using a linear regression fit. Statistics was performed using GraphPad Prism.

Results

Active and Quiet Neurons Have Similar Membrane Input Resistances

Quiet fusiform neurons display increased expression of I_Kir, which would produce a smaller membrane input resistance when compared with the input resistance of active neurons. However, we observed that both quiet and active neurons have similar membrane input resistances when measured both in current clamp (quiet: 77.8 ± 8 MΩ; active: 89.1 ± 9 MΩ; p = 0.36; n = 37 and 36, respectively. Figures 1B,C) and in voltage-clamp mode (quiet: 95 ± 12 MΩ; active 77.1 ± 10 MΩ; p = 0.09; n = 21 and 26, respectively) suggesting the presence of differential expression of compensating conductances that maintain the input resistance constant.

Fusiform Neurons Express a More Robust I_h in Active than in Quiet Neurons

Consistent with this hypothesis, we found that active neurons show bigger hyperpolarization sag of the membrane potential (peak sag: -2.9 ± 0.5 mV, quiet; -6.2 ± 0.8 mV, active; p < 0.01; n = 15 each; Figure 1D). Because this sag is inhibited by the hyperpolarization-activated cationic current (I_h) antagonist ZD7288 (not shown), this suggests the presence of a bigger I_h in these neurons that may normalize the input resistance of quiet and active neurons.

To further test this hypothesis, we measured I_h in active and quiet neurons to compare this conductance in both neuronal types. In accordance with the presence of the h current we observed after applying successive hyperpolarizations, a gradual slow developing inward current that reached a steady state in ∼3 s, which was inhibited by ZD7288 (Figure 2A). The current-voltage (IV) relationship of the ZD-sensitive current of both quiet and active neurons is shown in Figure 2B which shows that the I_h in quiet and active neurons have similar IV relationships. Using the tail currents we calculated the activation curves of I_h and they presented similar parameters (quiet neurons had a V₅₀ of -86.7 ± 4.6 mV and a slope of 8.2 ± 4 while I_h from active neurons had a V₅₀ of -81.5 ± 5 mV and a slope of 7.1 ± 4, p = 0.98). We also calculated the activation and deactivation time constants (fast and slow) of I_h from quiet and active neurons between -100 and -120 mV. Because we did not observe differences of the time constants in these potentials, we averaged the results from these potentials. Except for the fast component of the activation, none of the other parameters was different between quiet and active neurons (Table 1).

FIGURE 2

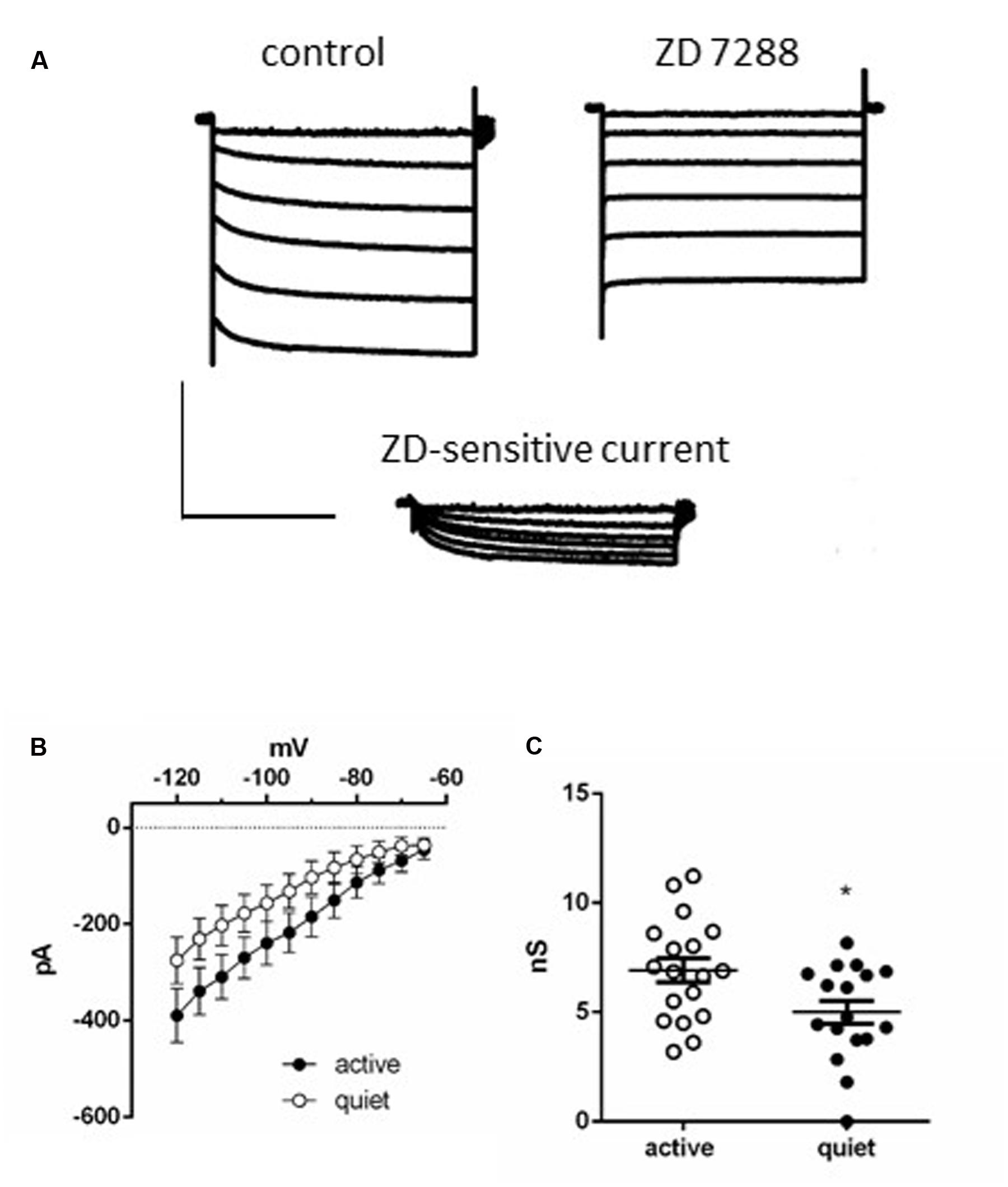
FIGURE 2. I_h in DCN fusiform neurons. (A) Example of currents activated by a membrane hyperpolarization before (left) and after (middle) application of ZD7288 (20 μM). Bottom: subtraction of the control currents by the same currents after application of ZD 7288. (B) Current-voltage relationships of the ZD 7288 sensitive current (I_h) in quiet and active fusiform neurons. (C) Summary of the slope conductances of I_h in quiet and active fusiform neurons. ^∗p < 0.05.

TABLE 1

TABLE 1. Activation and deactivation time constants of I_h from quiet and active neurons.

While I_h from quiet and active neurons are similar in its kinetics, active neurons presented a bigger slope conductance of h current (measured between -75 and -100 mV) than quiet neurons (quiet: 5.0 ± 0.5 nS; active: 6.9 ± 0.5 nS; p = 0.02, unpaired t-test n = 17 and 18, respectively; Figure 2C). Our data show that on the average active fusiform neurons express a bigger I_h than quiet neurons.

A Depolarizing Leak Current Generates a Depolarized RMP after I_Kir, I_h, and I_NaP Blockage, and Is Expressed Equally in Active and Quiet Neurons

To characterize all conductances affecting membrane input resistance, we looked at the background leak currents of the DCN fusiform neuron, which are traditional regulators of membrane passive properties (Enyedi and Czirják, 2010; Renigunta et al., 2015). After inhibition of I_Kir and I_h with Ba⁺⁺ (200 μM) and ZD7288, and I_NaP with TTX (1 μM), a residual current remains in both quiet and active neurons. This current is linear in the range of subthreshold potentials tested, and will be referred as a leak current (Figure 3A). Remarkably, this current had a depolarized reversal potential (-49.3 ± 4 mV; n = 22). Accordingly, the RMP measured after blockage of I_NaP, I_h, and I_Kir by TTX, ZD, and Ba⁺⁺, respectively, was similarly depolarized (-49.7 ± 1.7 mV; n = 12). These values are considerably above the calculated equilibrium potential of the potassium ions (-84 mV) suggesting that this leak conductance is permeable to cations other than K⁺. Accordingly, perfusion of a low-sodium solution (sodium replaced by NMDG-Cl: [Na⁺]_o = 32 mM, E_rev Na⁺ = 42.6 mV) inhibited the current in all potentials (p < 0.001), shifting the reversal potential of the leak current from -49.7 ± 7.3 to -66.2 ± 2.2 mV (Figure 3B; n = 6) and hyperpolarized RMP from -48.2 ± 3.5 to -60.3 ± 0.9 mV (n = 5; p = 0.012; Figure 3C). We conclude that DCN fusiform neurons express a leak current with Na⁺ permeability that would be capable of depolarizing the membrane potential generating a tonic depolarization if it were not counterbalanced by K_ir currents.

FIGURE 3

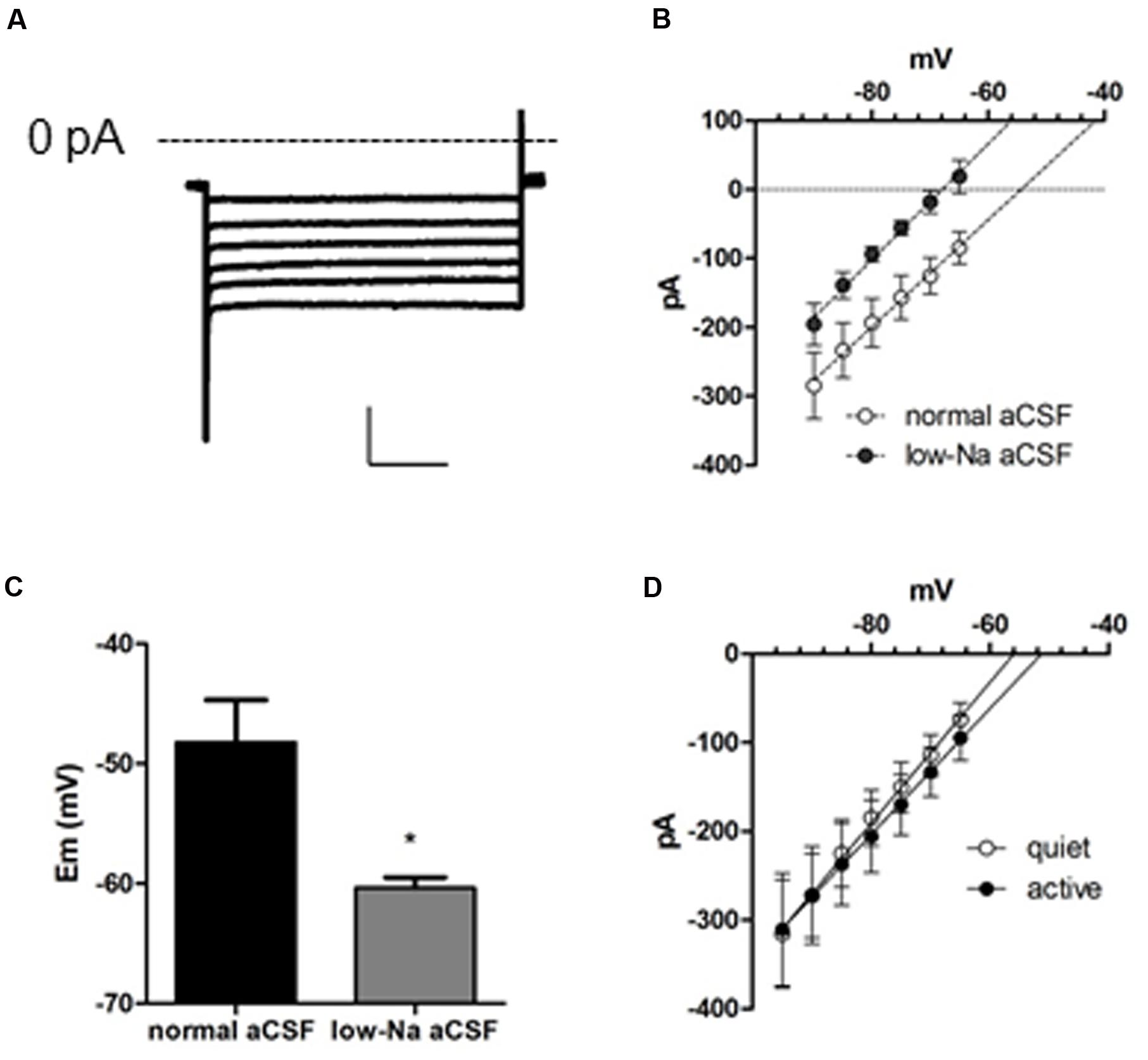
FIGURE 3. A background conductance tonically depolarizes quiet and active fusiform neurons. (A) Example of the subthreshold currents evoked by membrane hyperpolarizations after blocking I_Kir, I_h, and I_NaP with Ba⁺⁺ (200 μM), ZD7288 (20 μM), and TTX (1 μM). (B) IV plot of the membrane currents of fusiform neurons recorded in the presence of Ba⁺⁺ (200 μM), ZD7288 (20 μM), and TTX (1 μM) in control aCSF and in low-sodium aCSF. The lines are linear regressions to the data. (C) Summary of the effect of a low-sodium aCSF on the resting membrane potential (RMP) of fusiform neurons recorded in the presence of Ba⁺⁺ (200 μM), ZD7288 (20 μM), and TTX (1 μM). ^∗p <0.05, paired t-test. (D) Plot of the membrane currents of quiet and active fusiform neurons recorded in the presence of Ba⁺⁺ (200 μM), ZD7288 (20 μM), and TTX (1 μM).

To determine whether variations on this background conductance could offset the effect on membrane input resistance produced by the smaller I_Kir in active neurons, we compared this current in quiet and active neurons. We found that both quiet and active neurons presented leak currents of similar magnitudes and reversal potentials (leak conductance: quiet: 8.0 ± 1.7 nS; active: 7.1 ± 1.5 nS; p = 0.7; I_leak reversal: quiet: -52.7 ± 4.9 mV; active: -46.0 ± 6.2 mV; p = 0.4; n = 13 and 9, respectively; Figure 3D). This shows that these background conductances are similar in both fusiform neuronal types and are probably not compensating the difference in membrane input resistance produced by the differential expression of I_Kir.

I_h Inhibition Affects RMP Equally in Quiet and Active Neurons but Increases Input Resistance More Prominently in Active Neurons

So far, our results suggest that active neurons express a more robust I_h in order to compensate for their smaller I_Kir maintaining a similar input resistance than quiet neurons. If this were true, inhibition of I_h would reveal a bigger input resistance in active neurons. Also the more depolarized RMP of active neurons (Leao et al., 2012) could be accountable by their bigger I_h. Therefore, we tested the effect of the application of ZD7288 on the RMP and membrane input resistance of quiet and active fusiform neurons.

We found that application of ZD7288 affected equally the RMP (measured in the presence of TTX) of active and quiet neurons, hyperpolarizing then by the same amount (quiet: -72.1 ± 0.9 to -79.1 ± 1.3 mV; active: -63 ± 1.5 to -69.6 ± 1.8 mV; differences: quiet: -6.79 ± 1.4 mV; active: -7.6 ± 1.05 mV; p = 0.65; n = 10 and 7, respectively), maintaining the same difference in RMP in quiet and active neurons observed originally (Figure 4A). Experiments performed in the absence of TTX showed that inhibition of I_h by ZD7288 is efficient in decreasing the spontaneous firing of active neurons (from 16.2 ± 4.5 to 8.9 ± 7 Hz; n = 10; p < 0.01, paired t-test; Figure 4B), but unable to convert them to quiet neurons. We conclude that despite the differences in g_h in active and quiet neurons it does not participate in setting up the RMP differences observed in fusiform quiet and active neurons, and does not define the firing mode of fusiform neurons.

FIGURE 4

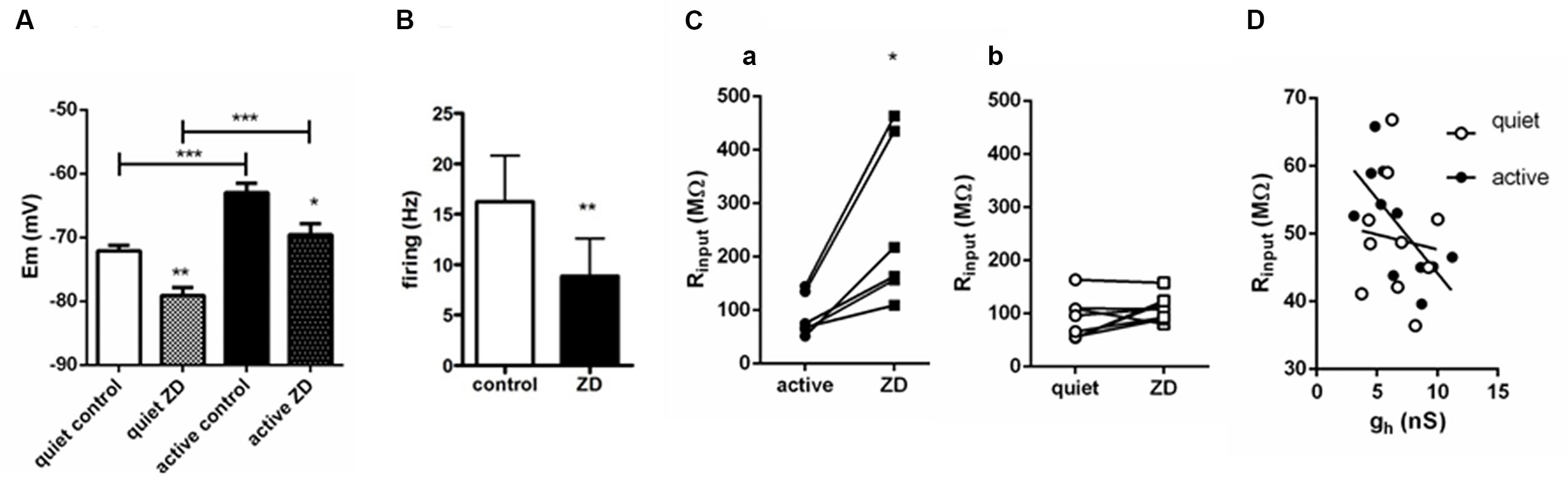
FIGURE 4. Influence of I_h on RMP, firing and input resistance of quiet and active fusiform neurons. (A) Effects of ZD 7288 (20 μM) on the RMP of quiet and active fusiform neurons. ^∗∗p < 0.01; paired t-test (compared with active control) and unpaired t-test (compared quiet and active ZD); ^∗∗∗p <0.001, paired t-test (compared with quiet control). (B) Summary of the effect of ZD 7288 on the intrinsic firing of fusiform active neurons. ^∗∗p < 0.01, paired t-test. (C) Effect of blocking I_h with ZD7288 on the membrane input resistance measured in voltage-clamp in quiet (a) and active (b) DCN fusiform neurons. ^∗p < 0.05, paired t-test. (D) Change of membrane input resistance produced by ZD7288 in quiet (n = 10) and active neurons (n = 7). ^∗∗p < 0.01, unpaired t-test. (E) Correlation of membrane input resistance with g_h conductance of quiet and active neurons.

We then measured input resistance of quiet and active neurons before and after application of ZD7288. Because the VI curve of fusiform neurons has a small rectification around -70/-80 mV and the RMP of active and quiet neurons varied at these potentials and is affected by ZD7288, we performed measurements of input resistance in voltage-clamp mode. We found that in contrast to its effect on RMP, ZD7288 had a differential effect on input resistance on quiet and active neurons. While ZD7288 significantly increased R_input in active neurons (from 121.6 ± 35 to 314.8 ± 8 MΩ; p = 0.007, paired t-test, n = 7; Figure 4Ca), it did not increase significantly membrane input resistance in quiet neurons (from 106.7 ± 22 to 148.5 ± 39 MΩ; p = 0.1, paired t-test, n = 9; Figure 4Cb). We conclude that while I_h has a similar small influence on the RMP of quiet and active neurons, it has, consistent to our prediction, a bigger influence on the membrane input resistance of active neurons.

We previously found that g_Kir correlates positively with RMP in fusiform neurons, in accordance to its major role in regulating membrane potential. If g_h is used to compensate for the increased input resistance created by the smaller g_Kir in active neurons, it is plausible that this conductance would correlate with input resistance in these neurons. In fact, when we correlated g_h and input resistance in quiet and active neurons we found that g_h correlated positively only in active neurons (quiet: r² = 0.01, p = 0.77; active: r² = 0.46, p = 0.02; Figure 4D).

These results show that in active neurons variations in g_h offsets the difference in the input resistance produced by their smaller expression of g_Kir and have a membrane input resistance more sensitive to g_h inhibition than quiet neurons. But despite the difference in g_h seen in quiet and active neurons its inhibition affected RMP equally in both neurons.

Active Neurons Are More Sensitive to Artificially Increasing g_h than Quiet Neurons

The bigger sensitivity of the membrane input resistance of active neurons to ZD7288 suggests they are more sensitive to changes in I_h than quiet neurons. If this were true, the membrane input resistance of active neurons would be more sensitive to increases in I_h than in quiet neurons. To test this hypothesis more directly we roughly doubled g_h by injected an artificial g_h (5 nS) in both quiet and active neurons (Figure 5A) and measured their membrane input resistance before and after artificially increasing g_h in both neuronal types. We found a significant decrease in membrane input resistance in active neurons (Figure 5B; p = 0.0004, Wilcoxon matched-pairs signed rank test; n = 7) while it did not affect significantly the membrane input resistance of quiet neurons (Figure 5C; p = 0.16, Wilcoxon matched-pairs signed rank test; n = 7). No change in input resistance was observed when we measured the input resistance at the onset of the hyperpolarization pulses (Figure 5D) accordingly to what is expected for an effect produced by I_h.

FIGURE 5

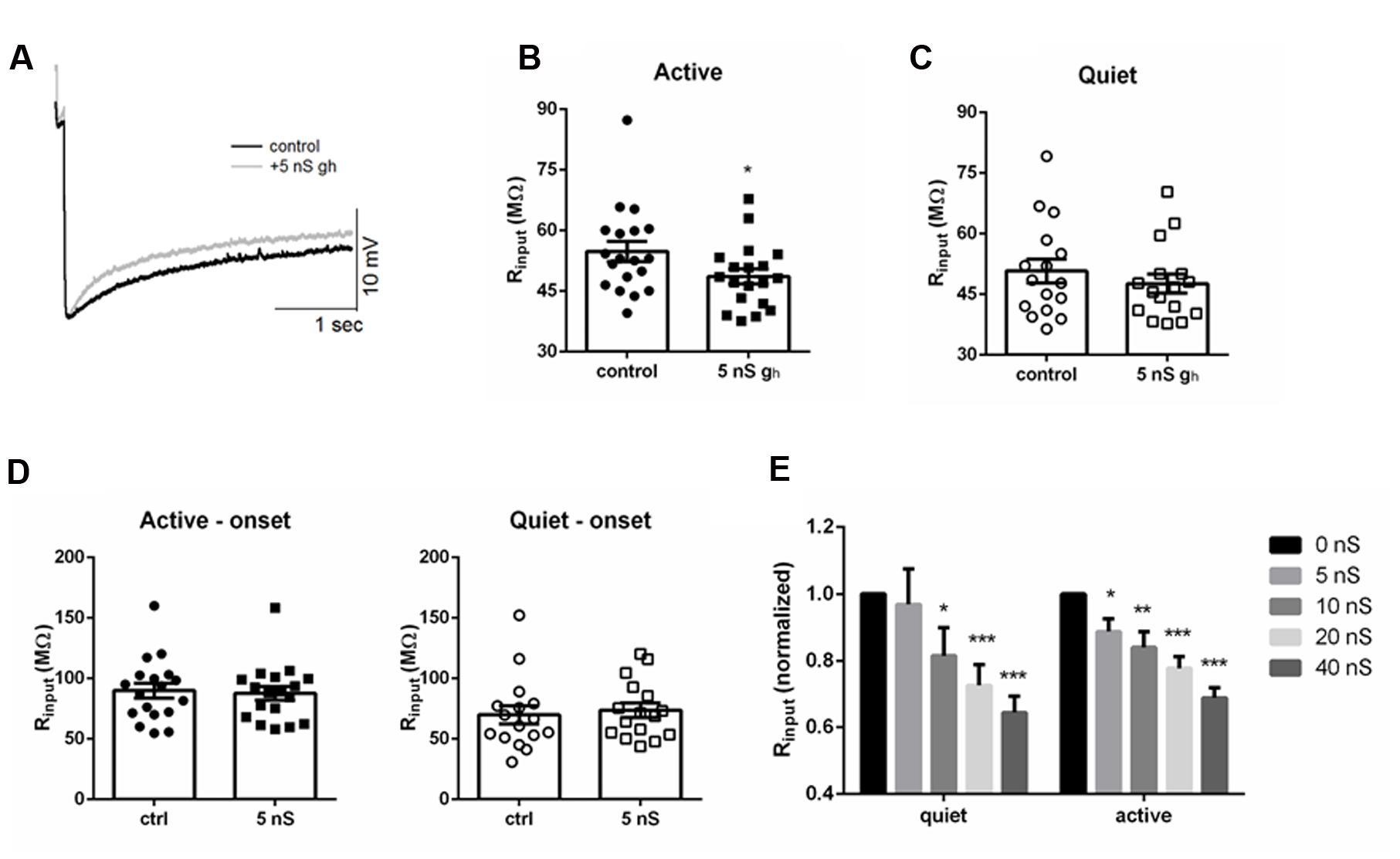
FIGURE 5. Injecting artificial g_h affects differentially membrane input resistance of DCN fusiform quiet and active neurons. (A) Example of the effect of injecting 5 nS of artificial g_h on the response to hyperpolarizing current in a fusiform neuron. (B) Summary of the effect of injecting 5 nS of artificial g_h on the membrane input resistance of DCN fusiform active neurons. ^∗p < 0.05. (C) Summary of the effect of injecting 5 nS of artificial g_h on the membrane input resistance of DCN fusiform quiet neurons. (D) Effect of 5 nS artificial g_h on the immediate membrane input resistance of fusiform neurons. (E) Effect of application of increasing artificial g_h on the normalized membrane input resistance of quiet and active neurons (n = 7 each). ^∗∗p < 0.01; ^∗∗∗p < 0.005.

We then tested how further injection of subsequent bigger artificial g_h could affect membrane input resistance of quiet and active neurons. Curiously, doubling g_h to 10 nS was effective in decreasing input resistance in quiet neurons (Figure 5E). When we normalized the input resistance and examined the effect of increasing g_h, we found that the drop in input resistance produced by increasing g_h was similar in quiet and active neurons above 10 nS (Figure 5E), reaching around 70% of the original value at 40 nS of g_h. Interestingly, injection 40 nS of artificial g_h in quiet neurons produced a small depolarization of the membrane potential (from -58.7 ± 2 to -54.2 ± 1 mV; p < 0.05, paired t-test; n = 7), but did not produce spontaneous firing, showing that I_h is not effective in depolarizing the membrane to values sufficient to produce spontaneous firing in fusiform neurons.

We conclude that the membrane input resistance of active neurons is very sensitive to adding 5 nS of g_h, roughly doubling g_h, while this did not affect significantly the membrane input resistance of quiet neurons. On the other hand, membrane input resistance of quiet and active neurons is equally sensitive to further applications of increasing artificial g_h.

A Computer Model Shows that RMP is Strongly Influenced by I_Kir and I_Leak, and Input Resistance by I_h

We found that the difference of g_h of quiet and active neurons is not very big and its inhibition affected their RMP similarly, but membrane input resistance after ZD7288 is considerably bigger in active neurons. This is in accordance with a bigger sensitivity of membrane input resistance of active neurons to variations in g_h. Accordingly, g_h only correlated with input resistance in active neurons, suggesting that variations in this conductance are used by active neurons to compensate for their smaller g_Kir and maintain homeostatic control of membrane input resistance. Additionally, this difference in g_h seems to not to affect the RMP on quiet and active neurons differentially. It seems that the effects of variations of g_h on membrane properties depend on the level of other conductances differentially expressed in quiet and active neurons. To understand how concerted variations in these currents affect subthreshold membrane properties and the transition quiet to active and membrane input resistance, we used a computer model containing the identified subthreshold conductances (g_Kir, g_h, g_leak) of the fusiform cell (Figure 6A).

FIGURE 6

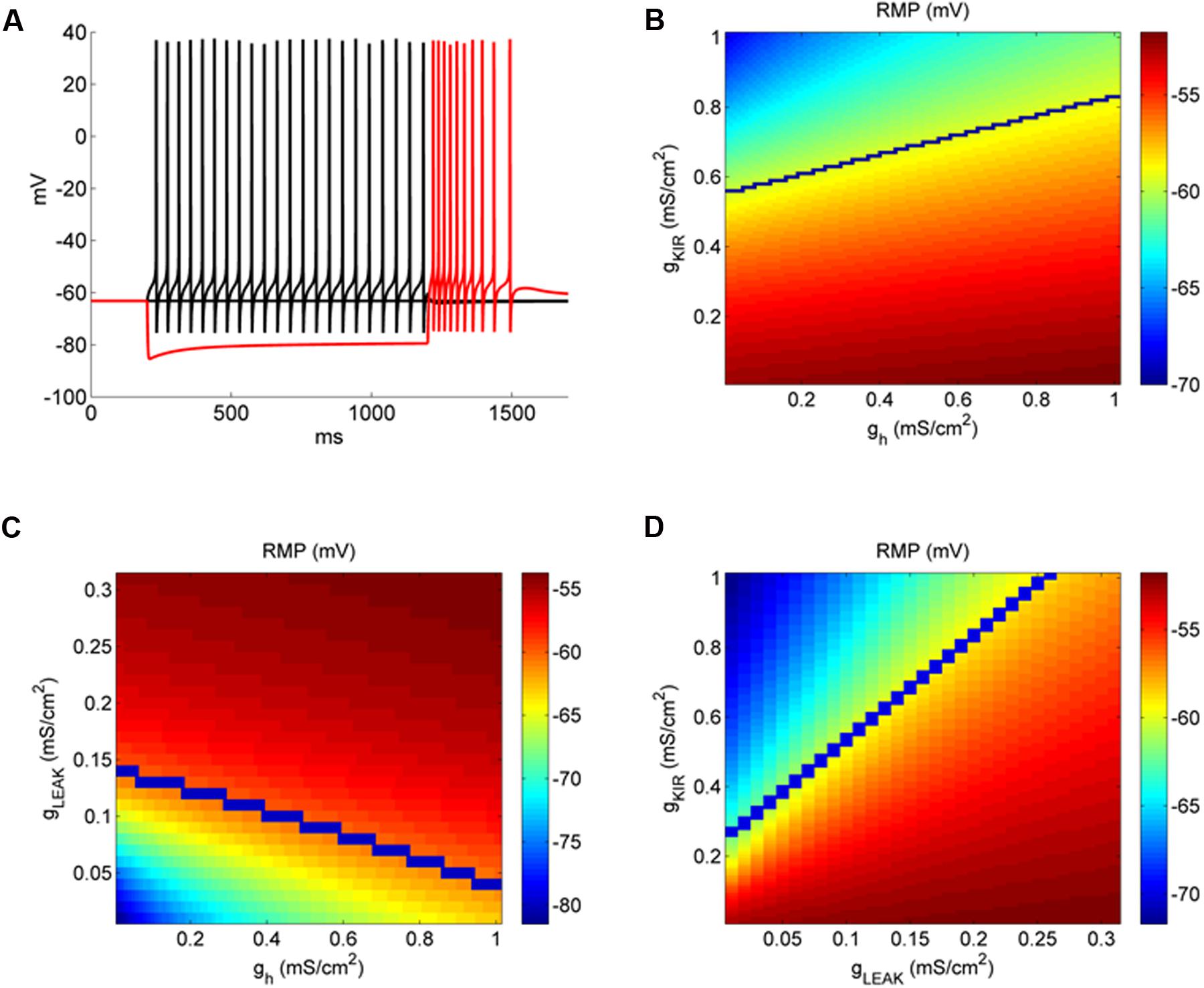
FIGURE 6. I_Kir affects more RMP than I_h in a model of DCN fusiform neuron. (A) Example of the behavior of the fusiform neuron model to membrane hyperpolarization and depolarization. (B) Conductance space of g_h versus g_Kir affecting RMP (color coded). The blue line represents the transition from quiet (above) to active (below) firing modes. (C) Conductance space of g_Leak versus g_h affecting RMP (color coded). The blue line represents the transition from quiet (above) to active (below) firing modes. (D) Conductance space of g_Kir versus g_Leak affecting RMP (color coded). The blue line represents the transition from quiet (above) to active (below) firing modes.

We found previously (Leao et al., 2012) that RMP of fusiform neurons is very sensitive to I_Kir inhibition by Ba⁺⁺ 200 μM, and that the differences in its magnitude create the differences of RMP which creates the firing modes of the fusiform neuron. On the other hand, even with a bigger I_h found in active neurons, its inhibition was not sufficient to change differently the RMP of active and quiet neurons. We then compared how changing g_h and g_Kir in our model influenced RMP. In Figure 6B we see the effect on RMP of the changing g_Kir and g_h. It is clear that RMP is much more sensitive to changing in g_Kir than in g_h. For instance, for a given g_h (0.5 mS cm^-2), RMP changes from -52.1 to -63.4 mV varying g_Kir from 0 to 1 mS cm^-2, while varying g_h from the same amount only changed RMP from -58.5 to -55.6 mV from a g_Kir of 0.5 mS cm^-2. We also can see that accordingly to its effect on RMP, g_Kir affects strongly the transition to quiet to active (blue line) in contrast to g_h. Interestingly, it can be seen that the impact of g_h on RMP is bigger in quiet than active neurons (compare the area above and below the blue line), which is different from what we observed experimentally by inhibiting I_h with ZD7288 (Figure 4A). In Figure 6C we analyzed the variations of g_leak and g_h (keeping g_Kir at 0.5 mS cm^-2). Again, variations of g_h are less effective in affecting RMP when compared with variations of g_leak, especially in active neurons (region above the blue line, with bigger values of g_leak). Finally we compared the impact of varying g_leak and g_Kir on the RMP and quiet-active transition (Figure 6D). We see that while increasing g_Kir can hyperpolarize the RMP, g_lleak is very effective in depolarize RMP, because we needed around 4–5 times more g_Kir to counteract the effect of g_leak, and produce a quiet neuron (above the blue line).

Our model showed that the depolarizing g_leak has a strong depolarizing effect on RMP. To evaluate the interaction of the reversal potential of the leak current and its conductance in RMP we varied both conductance and reversal potential of g_leak in model neurons with values of g_Kir typical of an active and a quiet neuron. Figure 7 shows that only with a reversal potential around -50 mV we were able to reach the values of activity threshold set by the I_NaP (-59/-57 mV). Also at values of E_rev below -65 mV the RMP becomes almost insensitive to variations of g_leak, especially in quiet neurons. Although a bigger I_Kir, as seen in quiet neurons, reduces the impact of g_lleak on depolarizing RMP, it does not prevent its effect on creating active firing in high conductances of g_leak (Figure 7B). We concluded that the presence of a sodium component that increases the reversal potential of g_leak is fundamental to depolarize the membrane allowing spontaneous firing in DCN fusiform neurons.

FIGURE 7

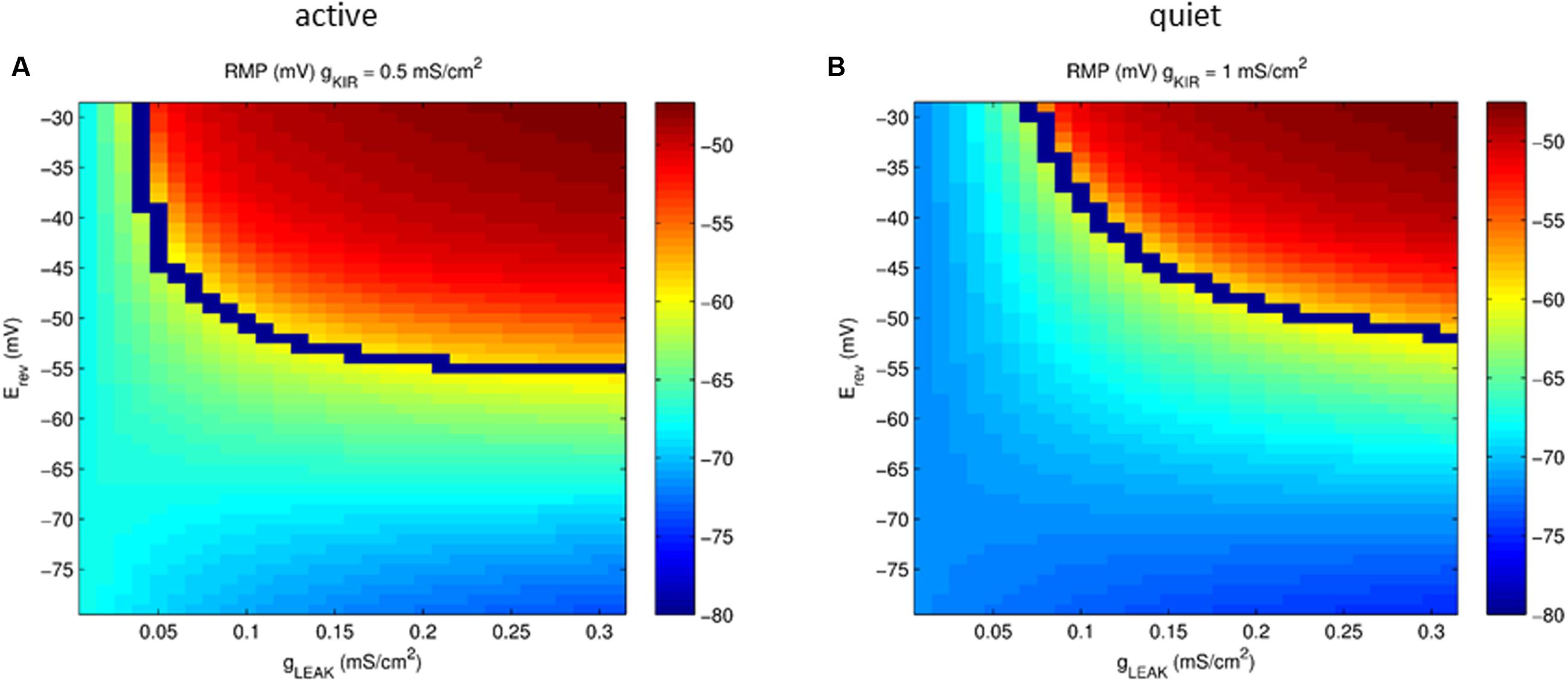
FIGURE 7. Plot of the parameter space of the leak conductance versus reversal potential affecting RMP (color coded) in a model neuron with g_Kir conductances typical of an active (A) and quiet (B) neuron. The blue line represents the transition from quiet (below) to active (above) firing modes.

We then studied the relationship of variations of g_h and g_Kir on the membrane input resistance of fusiform neurons (Figure 8A). The model showed that, similarly to what we observed experimentally, the bigger g_Kir, the smaller the effect of g_h on membrane input resistance (Figure 8B). Figure 8C shows the relationship of membrane input resistance and g_h in two situations: with a low g_Kir typical of active neurons, and a big g_Kir typical of quiet neurons. In accordance to what was observed experimentally, g_h has a more pronounced impact in the membrane input resistance in the model active neuron than in the model quiet neuron. We also observed a smaller depolarizing sag of the membrane potential after hyperpolarization in quiet neurons. This might be caused by a reduced g_h in these neurons, but because the differences observed in g_h between quiet and active neurons were not very pronounced, we decided to test if the bigger g_Kir of quiet neurons dampens the depolarization sag in these neurons. In fact, our model shows that the influence of g_h in producing the sag is diminished when g_Kir is bigger (Figures 8C–E). Our model and experimental data show that the g_h and g_Kir interaction not only controls the membrane input resistance, but also affects dynamic responses of the membrane during hyperpolarization.

FIGURE 8

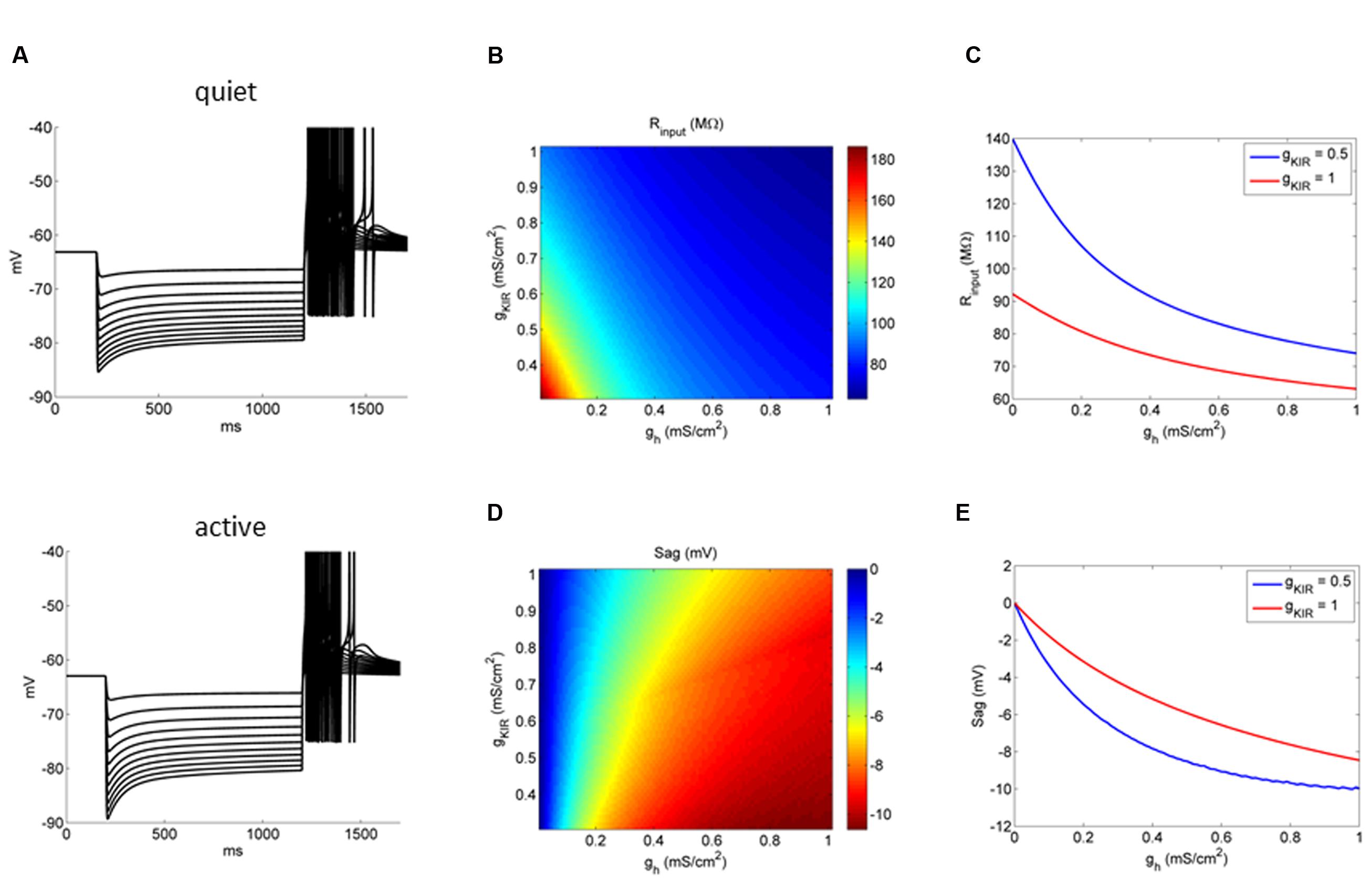
FIGURE 8. Influence of g_Kir on the impact of g_h on the membrane input resistance and response to hyperpolarizations. (A) Example of the behavior of a quiet and active fusiform neuron model to successive hyperpolarizations. (B) Conductance space of g_h versus g_Kir affecting membrane input resistance (color coded). (C) Two examples showing the effect of increasing g_h on the membrane input resistance in two models: one with a g_Kir typical of quiet neurons (red) and the other with a g_Kir typical of active neurons (blue). (D) Conductance space of g_h versus g_Kir affecting membrane depolarization sag (color coded). (E) Two examples showing the effect of increasing g_h on the membrane depolarization sag in two models: one with a g_Kir typical of quiet neurons (red) and the other with a g_Kir typical of active neurons (blue).

In the Same Cell, g_h Increases Proportionally as g_Kir Decreases, Keeping Membrane Resistance Constant

Our model predicts that in a neuron with more prominent g_Kir, g_h has less impact on membrane input resistance. Accordingly, we found that the membrane input resistance of quiet neurons, which had been shown to express a bigger g_Kir, is less sensitive to inhibition and enhancement of g_h. However, we do not know how exactly both conductances interact in a single cell to produce their effects in the RMP and input resistance. In order to evaluate how these individual conductances, plus g_leak, behave in a single neuron, we compared the subthreshold conductances g_Kir, g_h, and g_leak in the same neurons (six quiet and six active), by applying in sequence ZD7288 and Ba⁺⁺ in order to compare the proportions of these conductances in the same neuron.

We found, as previously, that g_Kir was significantly different in quiet and active neurons (Figure 9A). g_h was bigger in active neurons, but the value did not achieve significance (Figure 9A). Surprisingly, the absolute values of g_Kir and g_h (or g_leak) did not correlate inversely as would be expected if g_h (or g_leak) increased as g_Kir decreased in order to keep input resistance similar in the two types (Figures 9B,C). However, we found that the proportion of the total subthreshold conductances (g_Kir + g_h + g_leak) of g_Kir and g_h varied inversely significantly both in quiet and active neurons while g_Kir and g_leak did not (Figures 9D,E). Accordingly, when we analyzed the proportion of the subthreshold hyperpolarizing conductance (g_Kir) and the depolarizing conductances (g_h + g_leak), we found that when g_Kir is responsible for 50% or more of the total subthreshold conductances, the neurons is quiet, while when g_Kir represents 50% or less of these conductances the neuron is active (Figure 9F). We conclude that while the absolute individual values of g_h and g_Kir are not inversely correlated in an individual fusiform neuron, their individual proportions vary inversely in order to keep membrane input resistance constant in quiet and active neurons.

FIGURE 9

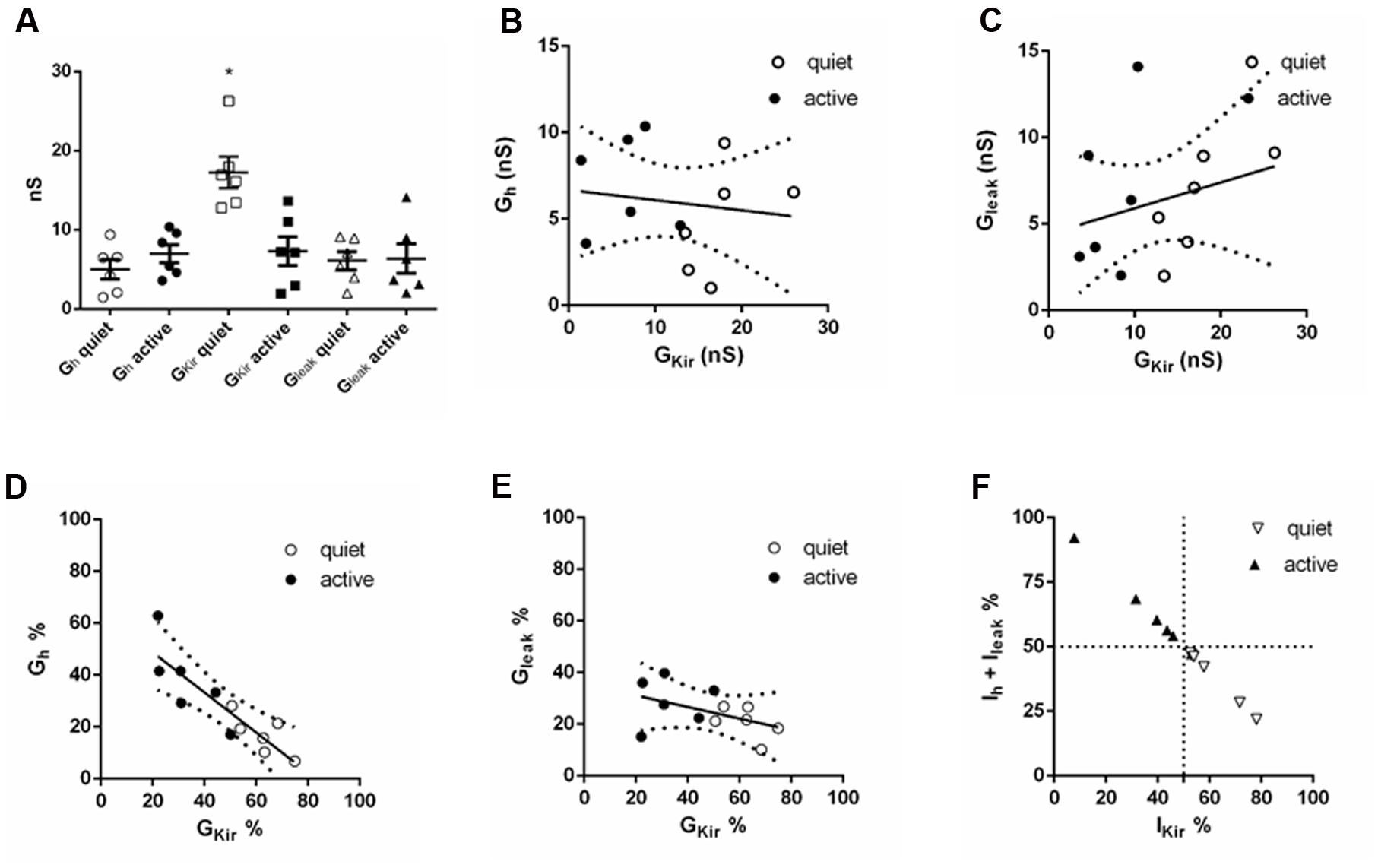
FIGURE 9. Comparison of subthreshold conductances in the same neuron. (A) Individual values of g_h, g_Kir and g_leak in six quiet and six active neurons. ^∗p < 0.05, unpaired t-test (compared with g_Kir active). (B) Correlation of g_h with g_Kir; r² = 0.02, p = 0.66. (C) Correlation of g_leak with g_Kir; r² = 0.07, p = 0.39. (D) Correlation of g_h% with g_Kir%; r² = 0.77, p = 0.0002. (E) Correlation of g_leak% with g_Kir%; r² = 0.22, p = 0.12. (F) Distribution of quiet and active neurons regarding to the proportion of g_{h +} g_leak with g_Kir.

Discussion

Our previous study (Leao et al., 2012) demonstrated that the expression of a large potassium inwardly rectifying current (I_Kir) is necessary to set the membrane potential below the activity threshold, in order to avoid spontaneous firing at rest in quiet neurons. In active neurons, a diminished I_Kir allowed the RMP to cross the activity threshold producing the spontaneous firing at rest characteristic of active neurons. Therefore, I_Kir determines the state of the fusiform neuron: quiet or active. Here, we showed that coordinated variations in I_h keep membrane input resistance constant in quiet and active neurons. We also identified a background depolarizing leak conductance, which consistently depolarizes the membrane of fusiform neurons, producing the depolarization driving of the spontaneous firing of fusiform neurons. However, variations in these two conductances are not important for creating the quiet and active types. Our data show that in DCN fusiform neurons, variations in specific subthreshold conductances contribute differentially to specific features of its excitability.

I_h is a subthreshold cationic current, produced by HCN channels, which depolarizes the membrane potential when the membrane is hyperpolarized. I_h can control RMP (Doan and Kunze, 1999; Bal and Oertel, 2000) and rate of firing in several neuronal types (McCormick and Huguenard, 1992; Maccaferri and McBain, 1996; Rodrigues and Oertel, 2006). DCN fusiform neurons of the rat express HCN2 subunit but not HCN1 (Koch et al., 2004), which is consistent with the slow activation of I_h we found in fusiform neurons. We found that I_h is not necessary for both spontaneous firing and the depolarized RMP after blocking I_Kir, the latter caused by the presence of a background Na⁺ current. Even though I_h can modulate the firing of active neurons and the RMP of active and quiet neurons, it could not define a firing type (quiet or active) since I_h inhibition could not transform an active to a quiet neuron and injection up to 40 nS of an artificial I_h did not transform a quiet neuron to a firing one. Our computer model demonstrated that I_h is more appropriate for offsetting membrane input resistance than I_leak, since it affects less RMP, so variations in this conductance will have less impact on the active/quiet transition, than variations in I_leak, which affect more prominently RMP. Thus, variations in I_h are more appropriate to offset the differences in input resistance caused by variations of I_Kir in quiet and active neurons, because it does not affect their firing mode.

We found that a modest bigger I_h in active neurons does not affect substantially RMP but can diminish input resistance enough to compensate for the smaller I_Kir in active neurons. This can be understood if we take into account the activation of I_h by hyperpolarization and its reversal potential above RMP. First, the activation of I_h results of a depolarization of the membrane, but because I_h deactivates before the current reaches the reversal potential this creates a negative feedback shunting the effect of I_h in depolarizing the membrane. Additionally since active neurons have a more depolarized RMP than quiet neurons, a smaller percentage of I_h is activated in active neurons than in quiet ones, which offsets the difference in I_h magnitude between the neuronal types. On the other hand, because input resistance was measured by hyperpolarizations this effect did not affect this parameter.

On the other hand, our model predicted that I_h would have a bigger impact on the RMP of quiet neurons, what we did not observe experimentally with ZD7288. Because RMP is much more affected by I_Kir and I_leak than I_h, the variations on the RMP produced by variations of these conductances can mask the differential effect of inhibiting I_h on RMP of quiet and active neurons. Additionally we found in our model that differences in the V_1/2 of I_h affects the impact of I_h on the RMP (not shown), and variations on this parameter are possibly another source of variability. We conclude that although our model still does not explain completely the influence of I_h on RMP in quiet and active neurons, it is in accordance to most of our experimental observations about the impact of I_h, I_Kir, and I_leak on the subthreshold properties of the DCN fusiform neurons.

In several neuronal types it has been observed that different conductances can vary differentially in order to attain a homeostatic balance of neuronal excitability (Marder and Prinz, 2002; O’Leary et al., 2013). More specifically a certain neuronal population can maintain a stable firing pattern and specific passive membrane properties across its individual neurons expressing different magnitudes of opposing conductances. For instance in crab stomatogastric neurons concerted variation of I_h and I_KA produces changes in gain control maintaining a stable firing pattern (MacLean et al., 2003; Burdakov, 2005). In cerebellar Purkinje neurons there are diverse levels of expression of different conductances producing a similar firing output (Swensen and Bean, 2005). In the auditory system it has been observed that stable firing pattern and RMP can be obtained in neurons from the ventral cochlear nucleus (VCN) by coordinated expression of the opposing h current and a low-threshold potassium current (Cao and Oertel, 2011). Similarly, in dopaminergic midbrain neurons I_h and A-type potassium currents presented a coordinated variation of their conductances in order to stabilize rebound firing (Amendola et al., 2012). On the other hand, we observed that in DCN principal neurons variations in I_h are used not to create differences in membrane potential or produce active firing, but to stabilize membrane resistance, a likely homeostatic compensation for the differences in the I_Kir magnitude in quiet and active neurons (Leao et al., 2012). This was clearly visible when we compared the percentage of each conductance in individual neurons. We found that the percentage of g_h expressed in an individual neuron varied inversely with the percentage of g_Kir, while g_leak did not correlate well with both conductances. Thus, in DCN fusiform neurons we have a concerted variation of specific conductances, one to establish different neuronal behaviors (I_Kir) while other (I_h) to keep membrane resistance stable while varying RMP across the fusiform neuronal population. This compensation is important for keeping similar responses to synaptic inputs in both active and quiet neurons, and specially for maintaining similar integration time windows of EPSPs and IPSPs, which are fundamental for expressing long-term plasticity in these neurons (Doiron et al., 2011). Consistent with this, in hippocampal organotypical cultures, chronic inhibition of inhibitory or excitatory neurotransmission homeostatically increases and decreases I_h expression, respectively, affecting membrane input resistance and EPSP temporal summation and stabilizing long-term potentiation induction in these conditions (Gasselin et al., 2015). Therefore, we propose that the increased I_h in active neurons is a homeostatic adaptation aimed at equalizing the membrane resistance of both types of fusiform neurons in order to keep membrane responses to synaptic currents similar in both types. Interestingly, down-regulation of I_h and consequent increased membrane input resistance and more hyperpolarized membrane potential, has been implicated to resilience to tinnitus in noise-exposed mice, while mice which fusiform neurons with decreased KCNQ channel current, but normal I_h, developed tinnitus (Li et al., 2015). This suggests that alterations in the homeostatic control of membrane parameters can affect the response of fusiform neurons to intense sound stimulation and be decisive for the development of tinnitus.

Both our computer model and our experimental data showed that the effect of g_h in affecting membrane input resistance and the depolarization sag are dependent on the magnitude of g_Kir, more specifically in quiet neurons with a bigger g_Kir, the impact of g_h on these parameters is smaller than in active neurons. Our data shows that the impact of a specific conductance on the membrane properties is strongly dependent on the membrane “environment” of other conductances. Although this is not a new concept, for instance is well-known how I_h affects the membrane response to synaptic currents (Magee, 1998; Masi et al., 2015), it is many times overlooked in studies analyzing the impact of a specific conductance on membrane properties. Also, our data shows that the magnitude of the depolarization sag cannot be a reliably parameter to quantify I_h without knowing the other subthreshold conductances. Similarly, we showed that more important than analyzing the absolute value of the conductance is to measure it in conjunction with other conductances. This was clear when we compared proportions of the conductances in a single neuron, instead of absolute values, that there was a threshold of 50% of the hyperpolarizing conductance (g_Kir) to change the phenotype of the neuron from quiet to active.

Finally, both our data and our model established that the main depolarization drive of DCN fusiform neurons is a linear background current, which presents a fraction permeable to Na⁺. Replacing of most external Na⁺ hyperpolarized drastically the membrane (after I_Kir blockage) and shifted the reversal potential of the background current accordingly. Sodium permeable leak currents have been identified in several types of neurons (Raman et al., 2000; Lu et al., 2007; Khaliq and Bean, 2010; Lazarenko et al., 2010; Lu and Feng, 2011) driving pacemaker activity by keeping the RMP constantly depolarized. Interestingly neurons from the deep cerebellar nucleus, which would be the cerebellar equivalent of DCN fusiform neurons (Oertel and Young, 2004), also present a Na⁺-permeable background current that keeps the membrane depolarized sustaining spontaneous firing (Raman et al., 2000). A channel that has the properties of a Na⁺ background current has been identified (NALCN; Lu et al., 2007; Ren, 2011), and is a likely candidate for the sodium component of the leak conductance in DCN fusiform neurons. But, because the Na-leak current strongly affects RMP, it could not change with I_Kir to equalize membrane input resistance without changing the firing mode of the fusiform neuron, which is in accordance with the observation that variations of this conductance do not correlate with the quiet and active modes of firing. However, our model showed that variations in both conductance and reversal potential of this current can produce quiet and active neurons in values of g_Kir typical of these states. This shows that, physiologically, the parameter space of the variations of g_leak (and its reversal potential) are probably limited to values which do not affect the firing mode of the DCN fusiform neuron.

We conclude that the DCN fusiform neuron vary their intrinsic subthreshold conductances accordingly to their roles in creating the firing modes, maintaining membrane resistance constant and depolarizing the membrane potential. Our findings show that the “instructions” for creating quiet and active fusiform neurons, follow specific rules, rather than using selected random variations of these conductances resulting in the final “desired” phenotype.

Author Contributions

RL, TT, and CC designed experiments; RL, CC, and SL performed experiments; CC and AR developed the computational model; RL, CC, and SL analyzed data; RL, CC, AR, and TT wrote the manuscript. All authors approved the final version.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Work supported by NIH Grant R01-DC007905 (to TT), FAPESP (2012/09426-1) and CNPq (470745/2012-6) grants (to RL) and FAPESP (2013/07699-0) and CNPq (306251/2014-0) grants (to AR). CC is a Ph.D. doctorate scholarship recipient from CAPES.

Footnotes

1. ^https://senselab.med.yale.edu/ModelDB/showmodel.cshtml?model=206252
2. ^http://www.rtai.org
3. ^http://www.comedi.org

References

Amendola, J., Woodhouse, A., Martin-Eauclaire, M. F., and Goaillard, J. M. (2012). Ca²⁺/cAMP-sensitive covariation of I(A) and I(H) voltage dependences tunes rebound firing in dopaminergic neurons. J. Neurosci. 32, 2166–2181. doi: 10.1523/JNEUROSCI.5297-11.2012

CrossRef Full Text | Google Scholar

Bal, R., and Oertel, D. (2000). Hyperpolarization-activated, mixed-cation current (I(h)) in octopus cells of the mammalian cochlear nucleus. J. Neurophysiol. 84, 806–817.

Google Scholar

Burdakov, D. (2005). Gain control by concerted changes in I_A and I_H conductances. Neural Comput. 17, 991–995. doi: 10.1162/0899766053491841

CrossRef Full Text | Google Scholar

Cao, X. J., and Oertel, D. (2011). The magnitudes of hyperpolarization-activated and low-voltage-activated potassium currents co-vary in neurons of the ventral cochlear nucleus. J. Neurophysiol. 106, 630–640. doi: 10.1152/jn.00015.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Dagostin, A. A., Lovell, P. V., Hilscher, M. M., Mello, C. V., and Leão, R. M. (2015). Control of phasic firing by a background leak current in avian forebrain auditory neurons. Front. Cell Neurosci. 10:471. doi: 10.3389/fncel.2015.00471

PubMed Abstract | CrossRef Full Text | Google Scholar

Day, M., Carr, D. B., Ulrich, S., Ilijic, E., Tkatch, T., and Surmeier, D. J. (2005). Dendritic excitability of mouse frontal cortex pyramidal neurons is shaped by the interaction among HCN, Kir2, and Kleak channels. J. Neurosci. 25, 8776–8787. doi: 10.1523/JNEUROSCI.2650-05.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Destexhe, A., and Babloyantz, A. (1993). A model of the inward current Ih and its possible role in thalamocortical oscillations. Neuroreport 4, 223–226. doi: 10.1097/00001756-199302000-00028

PubMed Abstract | CrossRef Full Text | Google Scholar

Doan, T. N., and Kunze, D. L. (1999). Contribution of the hyperpolarization-activated current to the resting membrane potential of rat nodose sensory neurons. J. Physiol. 514, 125–138. doi: 10.1111/j.1469-7793.1999.125af.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Doiron, B., Zhao, Y., and Tzounopoulos, T. (2011). Combined LTP and LTD of modulatory inputs controls neuronal processing of primary sensory inputs. J. Neurosci. 31, 10579–10592. doi: 10.1523/JNEUROSCI.1592-11.2011

PubMed Abstract | CrossRef Full Text | Google Scholar

Enyedi, P., and Czirják, G. (2010). Molecular background of leak K+ currents: two-pore domain potassium channels. Physiol. Rev. 90, 559–605. doi: 10.1152/physrev.00029.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Gasselin, C., Inglebert, Y., and Debanne, D. (2015). Homeostatic regulation of h-conductance controls intrinsic excitability and stabilizes the threshold for synaptic modification in CA1 neurons. J. Physiol. 593, 4855–4869. doi: 10.1113/JP271369

PubMed Abstract | CrossRef Full Text | Google Scholar

Goaillard, J.-M., Taylor, A. L., Schulz, D. J., and Marder, E. (2009). Functional consequences of animal-to-animal variation in circuit parameters. Nat. Neurosci. 12, 1424–1430. doi: 10.1038/nn.2404

PubMed Abstract | CrossRef Full Text | Google Scholar

Goldman, M. S., Golowasch, J., Marder, E., and Abbott, L. F. (2001). Global structure, robustness, and modulation of neuronal models. J. Neurosci. 21, 5229–5238.

Google Scholar

Grashow, R., Brookings, T., and Marder, E. (2010). Compensation for variable intrinsic neuronal excitability by circuit-synaptic interactions. J. Neurosci. 30, 9145–9156. doi: 10.1523/JNEUROSCI.0980-10.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Khaliq, Z. M., and Bean, B. P. (2010). Pacemaking in dopaminergic ventral tegmental area neurons: depolarizing drive from background and voltage-dependent sodium conductances. J. Neurosci. 30, 7401–7413. doi: 10.1523/JNEUROSCI.0143-10.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Khurana, S., Remme, M. W., Rinzel, J., and Golding, N. L. (2011). Dynamic interaction of Ih and IK-LVA during trains of synaptic potentials in principal neurons of the medial superior olive. J. Neurosci. 31, 8936–8947. doi: 10.1523/JNEUROSCI.1079-11.2011

PubMed Abstract | CrossRef Full Text | Google Scholar

Koch, U., Braun, M., Kapfer, C., and Grothe, B. (2004). Distribution of HCN1 and HCN2 in rat auditory brainstem nuclei. Eur. J. Neurosci. 20, 79–91. doi: 10.1111/j.0953-816X.2004.03456.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lazarenko, R. M., Fortuna, M. G., Shi, Y., Mulkey, D. K., Takakura, A. C., Moreira, T. S., et al. (2010). Anesthetic activation of central respiratory chemoreceptor neurons involves inhibition of a THIK-1-like background K(+) current. J. Neurosci. 30, 9324–9334. doi: 10.1523/JNEUROSCI.1956-10.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Leao, R. M., Li, S., Doiron, B., and Tzounopoulos, T. (2012). Diverse levels of an inwardly rectifying potassium conductance generate heterogeneous neuronal behavior in a population of dorsal cochlear nucleus pyramidal neurons. J. Neurophysiol. 107, 3008–3019. doi: 10.1152/jn.00660.2011

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, S., Kalappa, B. I., and Tzounopoulos, T. (2015). Noise-induced plasticity of KCNQ2/3 and HCN channels underlies vulnerability and resilience to tinnitus. Elife 27:4. doi: 10.7554/eLife.07242

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, B., Su, Y., Das, S., Liu, J., Xia, J., and Ren, D. (2007). The neuronal channel NALCN contributes resting sodium permeability and is required for normal respiratory rhythm. Cell 129, 371–383. doi: 10.1016/j.cell.2007.02.041

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, T. Z., and Feng, Z. P. (2011). A sodium leak current regulates pacemaker activity of adult central pattern generator neurons in Lymnaea stagnalis. PLoS ONE 6:e18745. doi: 10.1371/journal.pone.0018745

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, M., and Koester, J. (1996). The role of potassium currents in frequency-dependent spike broadening in Aplysia R20 neurons: a dynamic clamp analysis. J. Neurosci. 16, 4089–4101.

PubMed Abstract | Google Scholar

Maccaferri, G., and McBain, C. J. (1996). The hyperpolarization-activated current (Ih) and its contribution to pacemaker activity in rat CA1 hippocampal stratum oriens-alveus interneurones. J. Physiol. 497, 119–130. doi: 10.1113/jphysiol.1996.sp021754

PubMed Abstract | CrossRef Full Text | Google Scholar

MacLean, J. N., Zhang, Y., Johnson, B. R., and Harris-Warrick, R. M. (2003). Activity-independent homeostasis in rhythmically active neurons. Neuron 37, 109–120. doi: 10.1016/S0896-6273(02)01104-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Magee, J. C. (1998). Dendritic hyperpolarization-activated currents modify the integrative properties of hippocampal CA1 pyramidal neurons. J. Neurosci. 18, 7613–7624.

PubMed Abstract | Google Scholar

Marder, E., and Prinz, A. A. (2002). Modeling stability in neuron and network function: the role of activity in homeostasis. Bioessays 24, 1145–1154. doi: 10.1002/bies.10185

PubMed Abstract | CrossRef Full Text | Google Scholar

Marder, E., and Goaillard, J. M. (2006). Variability, compensation and homeostasis in neuron and network function. Nat. Rev. Neurosci. 7, 563–574. doi: 10.1038/nrn1949

PubMed Abstract | CrossRef Full Text | Google Scholar

Marder, E., O’Leary, T., and Shruti, S. (2014). Neuromodulation of circuits with variable parameters: single neurons and small circuits reveal principles of state-dependent and robust neuromodulation. Annu. Rev. Neurosci. 37, 329–346. doi: 10.1146/annurev-neuro-071013-013958

PubMed Abstract | CrossRef Full Text | Google Scholar

Masi, A., Narducci, R., Resta, F., Carbone, C., Kobayashi, K., and Mannaioni, G. (2015). Differential contribution of Ih to the integration of excitatory synaptic inputs in substantia nigra pars compacta and ventral tegmental area dopaminergic neurons. Eur. J. Neurosci. 42, 2699–2706. doi: 10.1111/ejn.13066

PubMed Abstract | CrossRef Full Text | Google Scholar

McCormick, D. A., and Huguenard, J. R. (1992). A model of the electrophysiological properties of thalamocortical relay neurons. J. Neurophysiol. 68, 1384–1400.

Google Scholar

Nagtegaal, A. P., and Borst, J. G. (2010). In vivo dynamic clamp study of I(h) in the mouse inferior colliculus. J. Neurophysiol. 104, 940–948. doi: 10.1152/jn.00264.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Oertel, D., and Young, E. D. (2004). What’s a cerebellar circuit doing in the auditory system? Trends Neurosci. 27, 104–110. doi: 10.1016/j.tins.2003.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Leary, T., Williams, A. H., Caplan, J. S., and Marder, E. (2013). Correlations in ion channel expression emerge from homeostatic tuning rules. Proc. Natl. Acad. Sci. U.S.A. 110, E2645–E2654. doi: 10.1073/pnas.1309966110

PubMed Abstract | CrossRef Full Text | Google Scholar

Prinz, A. A., Bucher, D., and Marder, E. (2004). Similar network activity from disparate circuit parameters. Nat. Neurosci. 7, 1345–1352. doi: 10.1038/nn1352

PubMed Abstract | CrossRef Full Text | Google Scholar

Raman, I. M., Gustafson, A. E., and Padgett, D. (2000). Ionic currents and spontaneous firing in neurons isolated from the cerebellar nuclei. J. Neurosci. 20, 9004–9016.

PubMed Abstract | Google Scholar

Ransdell, J. L., Nair, S. S., and Schulz, D. J. (2013). Neurons within the same network independently achieve conserved output by differentially balancing variable conductance magnitudes. J. Neurosci. 33, 9950–9956. doi: 10.1523/JNEUROSCI.1095-13.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

Ren, D. (2011). Sodium leak channels in neuronal excitability and rhythmic behaviors. Neuron 72, 899–911. doi: 10.1016/j.neuron.2011.12.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Renigunta, V., Schlichthörl, G., and Daut, J. (2015). Much more than a leak: structure and function of K2p-channels. Pflugers Arch. 467, 867–894. doi: 10.1007/s00424-015-1703-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Rodrigues, A. R., and Oertel, D. (2006). Hyperpolarization-activated currents regulate excitability in stellate cells of the mammalian ventral cochlear nucleus. J. Neurophysiol. 95, 76–87. doi: 10.1152/jn.00624.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

Schulz, D. J., Goaillard, J. M., and Marder, E. (2006). Variable channel expression in identified single and electrically coupled neurons in different animals. Nat. Neurosci. 9, 356–362. doi: 10.1038/nn1639

PubMed Abstract | CrossRef Full Text | Google Scholar

Schulz, D. J., Goaillard, J. M., and Marder, E. E. (2007). Quantitative expression profiling of identified neurons reveals cell-specific constraints on highly variable levels of gene expression. Proc. Natl. Acad. Sci. U.S.A. 104, 13187–13191. doi: 10.1073/pnas.0705827104

PubMed Abstract | CrossRef Full Text | Google Scholar

Sobie, E. A. (2009). Parameter sensitivity analysis in electrophysiological models using multivariable regression. Biophys. J. 96, 1264–1274. doi: 10.1016/j.bpj.2008.10.056

PubMed Abstract | CrossRef Full Text | Google Scholar

Swensen, A. M., and Bean, B. P. (2003). Ionic mechanisms of burst firing in dissociated Purkinje neurons. J. Neurosci. 23, 9650–9663.

PubMed Abstract | Google Scholar

Swensen, A. M., and Bean, B. P. (2005). Robustness of burst firing in dissociated purkinje neurons with acute or long-term reductions in sodium conductance. J. Neurosci. 25, 3509–3520. doi: 10.1523/JNEUROSCI.3929-04.2005

CrossRef Full Text | Google Scholar

Taylor, A. L., Goaillard, J. M., and Marder, E. (2009). How multiple conductances determine electrophysiological properties in a multicompartment model. J. Neurosci. 29, 5573–5586. doi: 10.1523/JNEUROSCI.4438-08.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Tzounopoulos, T., Kim, Y., Oertel, D., and Trussell, L. O. (2004). Cell-specific, spike timing-dependent plasticities in the dorsal cochlear nucleus. Nat. Neurosci. 7, 719–725. doi: 10.1038/nn1272

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, S., and Oertel, D. (1994). Neuronal circuits associated with the output of the dorsal cochlear nucleus through fusiform cells. J. Neurophysiol. 71, 914–930.

Google Scholar

Zugaib, J., Ceballos, C. C., and Leão, R. M. (2016). High doses of salicylate reduces glycinergic inhibition in the dorsal cochlear nucleus of the rat. Hear. Res. 332, 188–198. doi: 10.1016/j.heares.2015.10.008

PubMed Abstract | CrossRef Full Text | Google Scholar