Commentary: Chloride Regulation: A Dynamic Equilibrium Crucial for Synaptic Inhibition

A commentary on
Chloride Regulation: A Dynamic Equilibrium Crucial for Synaptic Inhibition

by Doyon, N., Vinay, L., Prescott, S. A., and De Koninck, Y. (2016). Neuron 89, 1157-1172.

The recent review by Doyon et al. (2016) is for the main part an excellent description of many important aspects of neuronal chloride regulation and will be of good use to many scientists interested in synaptic function. Nevertheless, some information given on the role of the K⁺ Cl⁻ cotransporter 2 (KCC2) is likely to be misleading. While proposing an explanation for the controversial findings by Glykys et al. (2014) that blockers of cation-chloride cotransporters did not affect the basal intracellular Cl⁻ concentration ([Cl⁻]_i), contrary to expectations from previous transporter manipulations (see e.g., references in Ben-Ari, 2014; Kaila et al., 2014), Doyon et al. (2016) suggest that this may be due to the small degree of inhibitory synaptic activity in the preparation used, with extremely low Cl⁻ load. In their explanation, they give an equation for the equilibrium relation between Cl⁻ flux through an inhibitory (Cl⁻) conductance (g_inh) and the Cl⁻ transported by KCC2. On basis of this equation, the conclusion is that the Cl⁻ equilibrium potential “E_Cl is sensitive to changes in KCC2 activity (g_KCC2) only when Cl⁻ load (g_inh) is large.” This conclusion, however, cannot be justified on basis of the relation between Cl⁻ flux through channels and Cl⁻ transported by KCC2. (The equation given by Doyon et al. is not correctly formulated, although the reason for their claim may not depend on this mistake).

For an explanation of our point of view, consider a hypothetical cell with Cl⁻ transport across the outer membrane only via Cl⁻ selective channels and KCC2. At equilibrium, the amount (mol/s) of Cl⁻ transported by the channels must be equal, but opposite, to that transported by KCC2. We thus formulate the relation:

$\begin{array}{cc}{\text{I}}_{\text{Cl}}/\text{F }={\text{ g}}_{\text{KCC}2}{\text{U}}_{\text{KCC}2}& (1)\end{array}$

where I_Cl is Cl⁻ current, F is the Faraday constant and U_KCC2 is the driving force for transport by KCC2. g_KCC2 is a proportionality factor that may be thought of as an “apparent conductance,” and should reflect the number of transporters in the membrane as well as the transport rate of the individual transporter molecules at fixed K⁺ and Cl⁻ concentrations, similarly as I_Cl depends on the Cl⁻ conductance (g_Cl) which reflects the number of Cl⁻ channels as well as the conductance of individual channels. (g_KCC2 is, however, not a conductance in the usual electrical sense). Equation (1) may be reformulated, in several steps, for clarity:

$\begin{array}{cc}{\text{g}}_{\text{Cl}}({\text{V}}_{\text{m}}-{\text{E}}_{\text{Cl}})/\text{F}={\text{g}}_{\text{KCC}2}(\text{RT}\text{ln}({[{\text{Cl}}^{-}]}_{\text{i}}/{[{\text{Cl}}^{-}]}_{\text{o}})+\text{RT}\text{ln}({[{\text{K}}^{+}]}_{\text{i}}/{[{\text{K}}^{+}]}_{\text{o}}))& (2)\end{array}$

$\begin{array}{cc}{\text{g}}_{\text{Cl}}({\text{V}}_{\text{m}}-{\text{E}}_{\text{Cl}})/{\text{F = g}}_{\text{KCC}2}\text{F}({\text{E}}_{\text{Cl}}-{\text{E}}_{\text{K}})& (3)\end{array}$

$\begin{array}{cc}\begin{array}{l}{\text{E}}_{\text{Cl}}=({\text{g}}_{\text{KCC}2}{\text{F}}^2{\text{E}}_{\text{K}}+{\text{g}}_{\text{Cl}}{\text{V}}_{\text{m}})/\hfill \\ ({\text{g}}_{\text{KCC}2}{\text{F}}^2+{\text{g}}_{\text{Cl}})\hfill \end{array}& (4)\end{array}$

where V_m is membrane potential, R the gas constant, T temperature (in K), E_K the K⁺ equilibrium potential and Cl⁻ and K⁺ concentrations are given within brackets with subscripts i and o for inside and outside, respectively.

We may use Equation (4) to illustrate the relation between E_Cl and g_KCC2 at various levels of g_Cl. (Assume that K⁺ concentrations and membrane potential are fixed, as controlled by other factors, such as the cellular Na⁺-K⁺-ATPase, not discussed here). As can be seen in Figure 1A, contrary to the claim by Doyon et al. (2016), E_Cl is only weakly dependent on KCC2 transport capacity at high Cl⁻ conductance, while it depends strongly on KCC2 when Cl⁻ conductance is low. At the extremes, when g_KCC2 = 0, then E_Cl = V_m and when g_Cl = 0, then E_Cl = E_K.

FIGURE 1

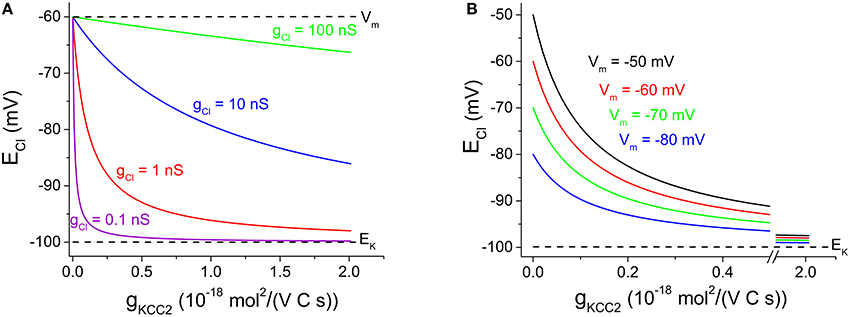
Figure 1. Cl⁻ equilibrium potential — dependence on KCC2 transporter capacity at various Cl⁻ conductance and various membrane potentials. (A) E_Cl vs. g_KCC2 with E_K fixed at −100 mV and V_m at −60 mV. g_Cl as indicated. Note that E_Cl dependence on g_KCC2 is reduced with increased g_Cl. (B) E_Cl vs. g_KCC2 with E_K fixed at −100 mV and g_Cl at 1 nS. V_m as indicated. Note that E_Cl dependence on g_KCC2 increases when V_m changes in positive direction. Note the x-axis break between 0.5 and 1.9 10⁻¹⁸ mol²/(V C s), to clearer illustrate the steeply decaying region of the curves. Justification of illustrated parameter ranges: The g_Cl range (in A) was chosen to include cells with a low g_Cl as evident from the high membrane resistance (Johansson et al., 1995) as well as cells with a high g_Cl (very low input resistance dominated by inhibitory conductances; Destexhe et al., 2003). The g_KCC2 range (in A,B) shown likely covers the capacity for most central neurons: When g_KCC2 = 1 10⁻¹⁸ mol²/(V C s), KCC2-mediated transport modeled as described by Karlsson et al. (2011) may reduce [Cl⁻]_i from 20 mM to ~5 mM with approximated time constants of 0.85, 6.8, and 55 s for spherical cells of radius 5, 10, and 20 μm, respectively, assuming 50% cytosolic volume and no other Cl⁻ transport/leak. Experimentally observed [Cl⁻]_i recovery is slower or comparable (Berglund et al., 2006; Lee et al., 2011; Pellegrino et al., 2011).

The relation between E_Cl (and thus [Cl⁻]_i) and transporter capacity has some bearing for the interpretation of the controversial findings by Glykys et al. (2014). Contrary to the suggestion by Doyon et al. (2016), Figure 1A shows that transporter block is expected to affect basal [Cl⁻]_i especially under conditions when g_Cl is low. Thus, other explanations than a low g_Cl must be sought for the controversial findings of Glykys et al. (2014). An increased g_Cl, perhaps due to increased non-specific leak, could in theory contribute to the limited effect of KCC2 blocker on [Cl⁻]_i.

On the other hand, the lack of excitatory synaptic input may contribute to a reduced sensitivity to transport block. In equation (4) above, a steady excitatory input may be represented simply by a more positive V_m, if we assume that E_K is still maintained (by the cellular Na⁺-K⁺-ATPase). Figure 1B shows that although E_Cl is more positive, the dependence of E_Cl on g_KCC2 is clearly stronger at more positive V_m.

As described, an increased g_Cl (Figure 1A) or a more positive V_m (Figure 1B) will change E_Cl in positive direction. This may be exploited experimentally e.g., by combining GABA or glycine application with depolarization to achieve a dramatic change in E_Cl and rise in [Cl⁻]_i (Karlsson et al., 2011). With such manipulations, it is obvious that the neuronal transporter capacity cannot prevent the changes in E_Cl and in steady-state [Cl⁻]_i.

Doyon et al. (2016) also note the neglected problem of apparent (illusory) conductance decrease based on recordings at different holding potentials when [Cl⁻]_i is changing, a problem which has recently been described in more detail by Yelhekar et al. (2016). It may be noted that experimentally, the effects of a changing [Cl⁻]_i on apparent conductance may be separated from true changes in conductance by using rapid voltage-ramp techniques (Karlsson et al., 2011; Yelhekar et al., 2016).

Author Contributions

SJ made the computations and paper writing. SJ, TY, and MD contributed to the ideas and final content.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Our studies are supported by the Swedish Research Council (grant no. 22292), by Gunvor och Josef Anérs Stiftelse and by Umeå University Medical Faculty (Insamlingsstiftelsen, Karin och Harald Silvanders fond, and Leila och Bertil Ehrengrens fond).

References

Ben-Ari, Y. (2014). The GABA excitatory/inhibitory developmental sequence: a personal journey. Neuroscience 279, 187–219. doi: 10.1016/j.neuroscience.2014.08.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Berglund, K., Schleich, W., Krieger, P., Loo, L. S., Wang, D., Cant, N. B., et al. (2006). Imaging synaptic inhibition in transgenic mice expressing the chloride indicator, Clomeleon. Brain Cell Biol. 35, 207–228. doi: 10.1007/s11068-008-9019-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Destexhe, A., Rudolph, M., and Paré, D. (2003). The high-conductance state of neocortical neurons in vivo. Nat. Rev. Neurosci. 4, 739–751. doi: 10.1038/nrn1198

PubMed Abstract | CrossRef Full Text | Google Scholar

Doyon, N., Vinay, L., Prescott, S. A., and De Koninck, Y. (2016). Chloride regulation: a dynamic equilibrium crucial for synaptic inhibition. Neuron 89, 1157–1172. doi: 10.1016/j.neuron.2016.02.030

PubMed Abstract | CrossRef Full Text | Google Scholar

Glykys, J., Dzhala, V., Egawa, K., Balena, T., Saponjian, Y., Kuchibhotla, K. V., et al. (2014). Local impermeant anions establish the neuronal chloride concentration. Science 343, 670–675. doi: 10.1126/science.1245423

PubMed Abstract | CrossRef Full Text | Google Scholar

Johansson, S., Sundgren, A., and Klimenko, V. (1995). Graded action potentials generated by neurons in rat hypothalamic slices. Brain Res. 700, 240–244. doi: 10.1016/0006-8993(95)00969-W

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaila, K., Price, T. J., Payne, J. A., Puskarjov, M., and Voipio, J. (2014). Cation-chloride cotransporters in neuronal development, plasticity and disease. Nat. Rev. Neurosci. 15, 637–654. doi: 10.1038/nrn3819

PubMed Abstract | CrossRef Full Text | Google Scholar

Karlsson, U., Druzin, M., and Johansson, S. (2011). Cl⁻ concentration changes and desensitization of GABA_A and glycine receptors. J. Gen. Physiol. 138, 609–626. doi: 10.1085/jgp.201110674

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, H. H. C., Deeb, T. Z., Walker, J. A., Davies, P. A., and Moss, S. J. (2011). NMDA receptor activity downregulates KCC2 resulting in depolarizing GABA_A receptor–mediated currents. Nat. Neurosci. 14, 736–743. doi: 10.1038/nn.2806

PubMed Abstract | CrossRef Full Text | Google Scholar

Pellegrino, C., Gubkina, O., Schaefer, M., Becq, H., Ludwig, A., Mukhtarov, M., et al. (2011). Knocking down of the KCC2 in rat hippocampal neurons increases intracellular chloride concentration and compromises neuronal survival. J. Physiol. 589, 2475–2496. doi: 10.1113/jphysiol.2010.203703

PubMed Abstract | CrossRef Full Text | Google Scholar

Yelhekar, T. D., Druzin, M., Karlsson, U., Blomqvist, E., and Johansson, S. (2016). How to properly measure a current-voltage relation? - Interpolation vs. ramp methods applied to studies of GABA_A receptors. Front. Cell. Neurosci. 10:10. doi: 10.3389/fncel.2016.00010

PubMed Abstract | CrossRef Full Text | Google Scholar