- 1Cell Biology of Organelle Networks Team, Tumor Cell Dynamics Unit, Inserm U1279 Gustave Roussy Institute, Université Paris-Saclay, Villejuif, France
- 2Centre National de la Recherche Scientifique (CNRS), Paris, France
- 3Institut Jacques Monod, Université de Paris, Paris, France
Intracellular trafficking supports all cell functions maintaining the exchange of material between membrane-bound organelles and the plasma membrane during endocytosis, cargo sorting, and exocytosis/secretion. Several proteins of the intracellular trafficking machinery are deregulated in diseases, particularly cancer. This complex and deadly disease stays a heavy burden for society, despite years of intense research activity. Here, we give an overview about trafficking proteins and highlight that in addition to their molecular functions, they contribute to the emergence of intracellular organelle landscapes. We review recent evidence of organelle landscape alterations in cancer. We argue that focusing on organelles, which represent the higher-order, cumulative behavior of trafficking regulators, could help to better understand, describe and fight cancer. In particular, we propose adopting a physical framework to describe the organelle landscape, with the goal of identifying the key parameters that are crucial for a stable and non-random organelle organization characteristic of healthy cells. By understanding these parameters, we may gain insights into the mechanisms that lead to a pathological organelle spatial organization, which could help explain the plasticity of cancer cells.
Introduction
Intracellular trafficking can be described as a dynamic exchange between membrane-bound organelles and/or the plasma membrane of eukaryotic cells. This exchange concerns transmembrane or membrane-bound proteins, such as channels or receptors and their bound ligands as well as macromolecules that are taken up or secreted by the cell. Trafficking is generally classified into two major pathways: the secretory pathway from the endoplasmic reticulum (ER) to the Golgi complex and plasma membrane for neosynthesized macromolecules, and the endocytic pathway from the plasma membrane to endosomes and lysosomes or to the Golgi complex and ER (Scott et al., 2014). Several additional trafficking pathways have been identified, e.g., unconventional secretion from endosomal compartments (Rabouille, 2017) or the various exchanges between different organelles (López-Doménech et al., 2018; Quidwai et al., 2021; Baltrusaitis et al., 2023) Some cell types additionally reveal different types of secretory granules in the cytoplasm that originate from the same pathway as the secretory vesicles however are sorted differently at the Golgi complex.
Trafficking relies on transport carriers that are characterized by vesicular-tubular intermediates and is supported by a complex machinery made of several families of proteins (Figure 1A; Box 1). The budding of vesicular-tubular transport carriers from a donor membrane requires the recruitment of membrane-deforming proteins, membrane-constricting proteins and coating proteins. Once the scission with the donor-membrane is completed, vesicular-tubular transport carriers are transported along the cytoskeleton with the help of motor proteins and fuse with a receiving membrane. Different types of adapter molecules connect motor proteins to transport carriers during trafficking. The fusion with a receiving membrane is initiated by tethering molecules and facilitated by a fusion machinery. The different steps of trafficking are regulated by small GTPases of different families that by themselves are regulated by Guanine Nucleotide Exchange Factors (GEFs) and GTPase Activating Proteins (GAPs).
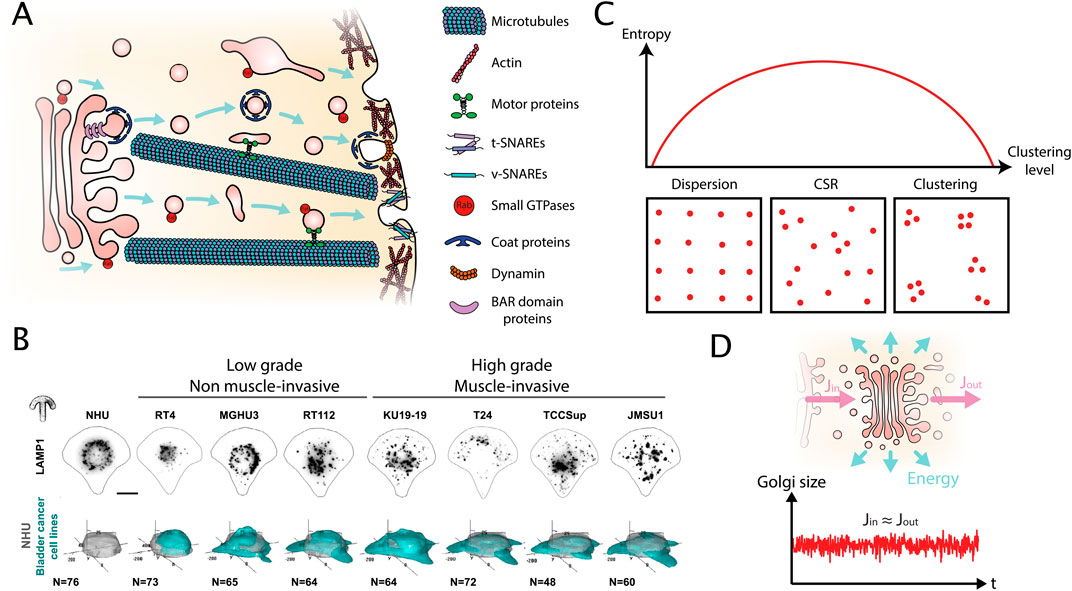
Figure 1. Key properties of intracellular organelle organization resulting from the trafficking activity. (A) Schema of ‘intracellular trafficking,’ a dynamic exchange between donor and acceptor membranes of eukaryotic cells. It relies on transport carriers that are characterized by vesicular-tubular intermediates and is supported by a complex machinery made of several families of proteins (Box 1). (B) Single cell immunofluorescent images of the ‘lysosome’ organelle in normal human urothelium (NHU) cells as well as cell lines representing ‘low grade,’ non-muscle invasive and ‘high grade,’ muscle invasive bladder cancer on crossbow-shaped micropatterns to facilitate their comparison (upper panel). Quantification of lysosome positioning by 3D density maps, a method from the spatial statistics toolbox, of N > 45 cells from (lower panel) Mathur et al. (2023). (C) Relationship between the entropy associated to a point pattern and the clustering level of the point pattern. The inserts illustrate the three archetypical point patterns: dispersion, Complete Spatial Randomness (CSR) and clustering. Because there are many ways to obtain a CSR pattern, but less possibilities for a dispersed or clustered one, the entropy is maximal in case of CSR. (D) The Golgi complex receives an inward flux (Jin) and an outward flux (Jout). Then the inward and outward fluxes are equal, the derivative of the Golgi mass is close to zero, and the Golgi size does not change significantly. Thus, considering the Golgi as stationary is a good approximation at short time scales. However, because the active fluxes dissipate energy, the system is out of the thermodynamic equilibrium, it defines a Non-Equilibrium Steady State (NESS).
Many genes coding for the trafficking machinery are deregulated in cancer. Yet, despite decades of study, there is no general description of their contribution to carcinogenesis: indeed whereas some members of the trafficking machinery can be downregulated in some cancers, they are upregulated in others, e.g., Caveolin-1 expression is upregulated in pancreatic and prostate cancer while downregulated in lung and breast cancer (Chatterjee et al., 2015; Thompson et al., 2009; Volonte et al., 2017; Wang et al., 2020). The last decades have shown that trafficking can adopt to different perturbations and change in response to cues from the environment and due to genetic or epigenetic modifications. The adaptability of trafficking pathways supports cell plasticity, a major characteristic of cancer cells (Muthuswamy and Bin, 2012). Very little trafficking proteins have been therapeutically targeted due to their critical physiological roles (Di Marco et al., 2020). To gain a deeper understanding of the role of trafficking in cancer, we propose to zoom out to a higher level: Trafficking pathways shape intracellular patterns, which we recognize as organelles. Indeed, the ability to create patterns spontaneously is one outstanding conserved feature of life. Jacques Monod even included this criterion in his definition of life under the name of autonomous morphogenesis (Monod, 1970). Pattern formation in living matter appears at many scales and has been well described on the organism level, e.g., during development (Belintsev et al., 1987). Intriguingly, much less is known about intracellular pattern formation of organelles through trafficking processes. Here, we will discuss organelle patterns as a superior scale of trafficking in the context of cancer.
Intracellular organelle patterns are different between healthy and transformed cells and correlate with cancer aggressiveness
Although widescale efforts have been made to establish atlases of genomic and proteomic alteration in cancer, no atlas of organelle-level changes has been profiled till date. Systematic studies on intracellular organelles are difficult, because, on the one hand, in vivo approaches are limited by the access of the samples and the lack of subcellular resolution, and on the other hand, in vitro cultured cells display a dynamic shape and strong morphological cell-to-cell variation. To address these limitations we and others have employed novel bioengineering and image analysis approaches: normalized cell culture conditions on adhesive micropatterns have been combined with spatial statistics approaches based on probabilistic mapping (Schauer et al., 2010; Jerabkova-Roda et al., 2023), or novel artificial intelligence (AI) methodology (Wang et al., 2023) has been implemented in order to quantify organelle spatial organization and topology. Using these technologies, the hypothesis was tested that organelle patterns in cancer cells are different from those of normal cells and change during aggressiveness (Mathur et al., 2023; Jerabkova-Roda et al., 2023; Wang et al., 2023). The rationale of this was that the observed vast alterations in trafficking processes in cancer cells will give rise to altered patterns of organelles as organelle emerge from trafficking.
First, using a bladder cancer model and well-controlled culture conditions, lysosomes of normal human urothelium (NHU) were compared to invasive and non-invasive bladder cancer cell lines that represented low-grade and high-grade bladder cancer, respectively. Lysosomes are dynamic, acidic organelles for cell clearance and recycling of macromolecules and act as cellular hub for metabolism and signaling. While in NHU cells lysosomes were positioned centrally, they were peripherally dispersed in bladder cancer cells with a stronger phenotype in ‘high-grade’ cell lines (Mathur et al., 2023) (Figure 1B). Similarly, lysosome positioning was altered in patient-derived melanoma cells and patient biopsies, scaling with and supporting melanoma aggressiveness (Jerabkova-Roda et al., 2023). Interestingly, the team of M. Barroso recently integrated artificial intelligence (AI) and imaging quantification to analyze organelle spatial distribution in the breast cancer model. They found that organelle topology allows for a highly precise differentiation between cell lines of different subtypes and aggressiveness (Wang et al., 2023).
Together, these results indicate that alterations of organelle patterns correlate with transformation and aggressiveness of cancer cells. Moreover, when lysosomal perinuclear clustering was induced experimentally in patient-derived melanoma cells, we observed significant reduction of invasive outgrowth in mouse and zebrafish models (Jerabkova-Roda et al., 2023). This study provided a direct demonstration that lysosomal positioning controls cell invasion, illustrating the importance of organelle adaptation in carcinogenesis. Thus, we argue that the patterning of organelles, which represents trafficking collectively, could potentially not only be used as a biomarker in the future, but should also to be considered to better understand, describe and fight cancer. In the next sections, we focus on a physics description of the organelle landscape to identify critical parameters for a stable and non-random organelle organization characteristic of healthy cells.
How to describe organelle organization?
Based on experimental data, we argue that organelle organization has three key properties: non-random distribution, Non-Equilibrium Steady-State (NESS) and self-organization.
Non-random distribution
When organelles are observed in cells, a fundamental question is whether their positioning is random or not. A distribution of organelles can be simplified as a point pattern if the typical size of the object is small compared to the distances between objects (Schauer et al., 2010). In spatial statistics, a “uniformly random” distribution of points is described as a Complete Spatial Randomness (CSR). Formally, a CSR is defined by the fact that i) each point’s location is independent of the other points, and ii) the probability of finding a point in a sub-region only depends on the ratio between this sub-region volume (or area in 2D) and the total volume (or area). Diggle (2013) defined two primary deviations from this CSR pattern: i) clustering (i.e., aggregation) and ii) dispersion (i.e., points repel each other mutually forming a regular grid), (Figure 1C). Spatial statistics provides tools to quantify the level of organization of point patterns (Box 2) (Dixon, 2014). Interestingly, these tools have been used extensively for Single Molecule Localization Microscopy (SMLM) (Khater et al., 2020) or to describe exocytosis distributions (Sebastian et al., 2006; Yuan et al., 2015; Urbina et al., 2018; Lachuer et al., 2023), but were rarely applied to organelles with few notable exceptions (Schauer et al., 2010; Ba et al., 2018).
A CSR pattern is expected as a result of the diffusion that maximizes the entropy of the system (Figure 1C). However, many examples of a non-random organization are found in cells: for instance, organelles such as lysosomes and mitochondria often accumulate perinuclearly (Collins et al., 2002; Jongsma et al., 2016). A systematic analysis revealed that diverse organelles (early endosomes, lysosomes, multivesicular bodies, etc.) have a unique and well-defined distribution (Schauer et al., 2010; Duong et al., 2012). More recently, using spatial statistics, it has been demonstrated that lysosomes are not randomly distributed at the whole cell scale (Ba et al., 2018). It demonstrates that mechanisms are at place that actively counterbalance diffusion to shape the organelle landscape. The resulting non-random organization of cellular structures can be understood as an adaptation to support a function: a spatial-organization function relationship (Bergeijk et al., 2016; Vaidžiulytė et al., 2019). Indeed, it has been widely documented that organelles dynamically adopt their intracellular positioning to various stimuli, such as pH, nutrient availability or their microenvironment. For example, the spatial organization of lysosomes is influenced by cholesterol concentrations (Rocha et al., 2009), intracellular pH (Walton et al., 2018) or extracellular matrix elasticity (Wang and Galli, 2018), (see Table 1 for a non-exhaustive list). The underlying cellular mechanisms and proteins that regulate organelle positioning have been reviewed extensively (e.g., endolysosomal compartment (Bonifacino and Neefjes, 2017); Golgi complex (Brownhill et al., 2009); mitochondria (Kruppa and Folma, 2021). Non-random organization allows for high local concentrations and the possibility of segregating incompatible biochemical reactions.
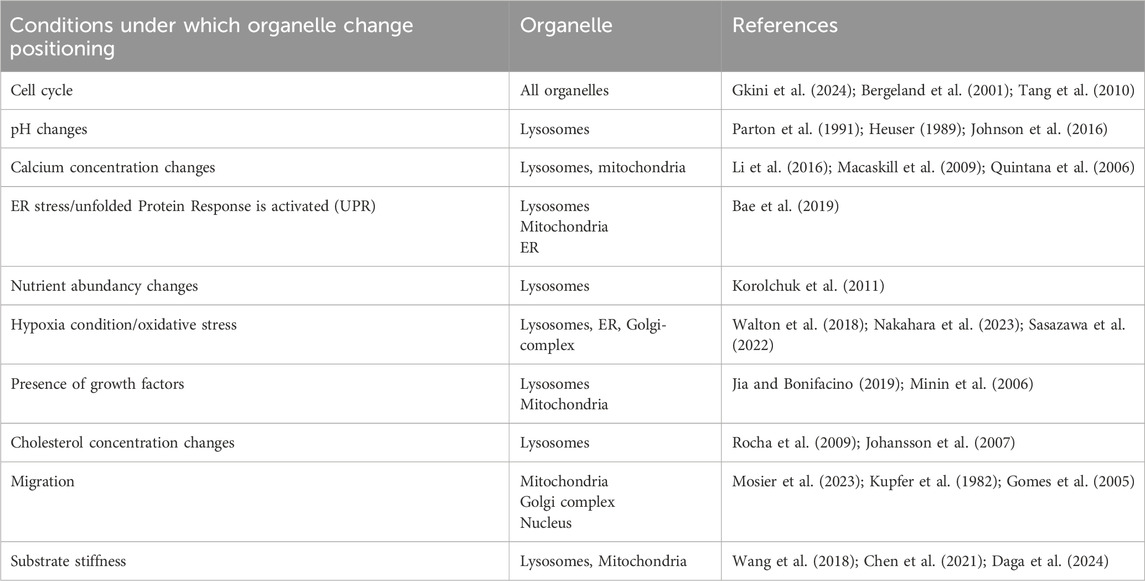
Table 1. Conditions under which changes in organelle positioning have been observed. Here we provide a non-exhaustive list of conditions during which organelle positioning changes have been documented.
Intriguingly, the non-random positioning of organelles could stem from the non-independent nature of organelles that need connectivity. It has emerged during the last few years that the organelle landscape is defined by numerous organelle membrane contact sites (MCS). This leads us to think of organelles as a network that constantly communicates, exchanges material, and changes topology. Indeed, it has been demonstrated that this organelle network is not randomly established (Valm et al., 2017), confirming a non-random spatial organization of each organelle. For example, it has been reported that mitochondria and ER structures are close to secretory sites, probably because they play a role in regulating exocytosis by Ca2+ signaling (Villanueva et al., 2014; Griesche et al., 2019). Interestingly, a feedback regulation between MCS and cellular organization has been proposed. For example, the spatial organization of lysosomes determines its MCSs with ER (Ba et al., 2018), and in return, MCSs are able to control the positioning of lysosomes (Pu et al., 2016; Jongsma et al., 2016; Bonifacino and Neefjes, 2017; Neefjes et al., 2017; Cabukusta and Neefjes, 2018).
Non-equilibrium steady state
Organelle patterns are often described as a steady state, meaning that they remain relatively constant over time (Figure 1D), (Pelham, 1996; Schauer et al., 2010). However, this steady state statement is limited, because the cell organization shows small random fluctuations around a steady state. In addition, at longer time scales, the cell organization cannot be seen any more as a steady state. Indeed, cell organization dynamically changes, for instance, during the cell cycle or in response to a variation in the environment (see Table 1). Therefore, the steady state statement is a good approximation at short time scales, i.e., time scales shorter than the cell cycle (typically <10 h in eukaryotic cells). For example, it has been demonstrated that lysosomal organization in classical petri-dish conditions is at a steady state during a time window of several minutes to hours (Pelham, 1996; Ba et al., 2018; Guardia et al., 2019; Duong et al., 2012). At steady state, spatial parameters such as distance to the nucleus, inter-organelle distance, and nearest-neighbor distance (and Ripley’s K function, see Box 2) have a constant distribution. Additionally, the organelle connections, especially MCS defining the organelle network, have been found to be stable for at least several minutes (Valm et al., 2017). Importantly, steady state should not be understood as the immobility of individual organelles but as the conservation of global organization despite individual organelle movements consuming energy. Due to these dynamics based on trafficking processes, the system is out of equilibrium: it consumes energy. Such a system is called a Non-Equilibrium Steady State (NESS) that is typical for biological samples.
Interestingly, after a reversible perturbation of the endomembrane organization, the cell spontaneously converges to its physiological steady state organization. For example, after a reversible coupling of lysosomes to classical anterograde kinesin or to the unconventional retrograde kinesin 14 (KIFC1), forcing respectively a peripheral or central clustering, lysosomes can spontaneously re-find their original steady state organization in a dozen of minutes (Guardia et al., 2019). Similar effects have been observed with changes of environmental cues, e.g., such as pH. After a perturbation, the system converges toward a reference state. In accordance to experimental observations, computational models of organelle organization often converge to a steady state (Dinh et al., 2006; Birbaumer and Schweitzer, 2011; Gou et al., 2014). In other models, the steady state is expected and used as a hypothesis that significantly facilitates the resolution of differential equations (Higuchi et al., 2014; Lin et al., 2016).
Self-organization
Self-organization is the emergence of a spatio-temporal organization resulting only from the interactions of the individual components (Karsenti, 2008). Contrarily to self-assembly, self-organization involves energy consumption (Misteli, 2001; Wedlich-Söldner and Betz, 2018). The importance of self-organization has been discussed in the context of cellular architecture (Misteli, 2001; Wedlich-Söldner and Betz, 2018). Authors argue that forming distinct organelles is self-organized. For example, the Golgi complex spontaneously reassembles after mitosis (Wei and Seemann, 2017) suggesting a self-organization property also predicted by theoretical models (Vagne et al., 2020; Tachikawa, 2023). It is also thought that MTOC are self-organized (Pereira et al., 2021) although a full centriole reconstruction has not been achieved yet in vitro, successful attempts have been reported for critical components of centrioles (Guichard et al., 2017). Interestingly, once assembled, the MTOC can autonomously find the center of the cytoplasm (Malikov et al., 2005) demonstrating the self-organization of its spatial localization. Future work in artificial cells could formally test the hierarchy in self-organization processes between the organelle network and the cytoskeleton and identify the minimal components that are necessary to recapitulate the organelle spatial organization in an in vitro system.
How is a non-random steady state self-organization within cells achieved and maintained?
One main challenge is understanding how cell compartments’ non-random steady state self-organization is achieved and maintained from intracellular trafficking. In this respect, no single gene, or not even one gene regulatory network, organizes the cell, instead, organelle organization emerges from many genes. Thus, a comprehensive understanding of intracellular organization requires the investigation of the interactions between genes and the resulting emerging laws. In the next section, we propose to consider biophysical models that describe pattern formation. We review how these models were applied in the context of trafficking proteins to explain pattern formation of organelles. Due to their bacterial origin, mitochondria are special organelles that are distinct in their participation in the cellular trafficking pathways (Baum and Baum, 2014) and can undergo fusion/fission. Similarly, membrane-less organelles such as stress granules, P-bodies, etc., which are biological condensates formed by liquid phase separations, rely less on classical trafficking machinery described in Box 1. Thus, their pattern formation could be described by different models than whose used for instance for endosomes or Golgi complex.
Chain of interactions
The interactions between molecules can lead to distinct forms of clustering: a cellular component that has a stable distribution will dictate its spatial structure to its bonded partners. This process creates a chain of interactions where spatial structure is conserved (Figure 2A). For example, Pangarkar et al. have studied the distribution of early endosomes in mammalian cells. They report a juxta-nuclear accumulation of endosome despite an unbiased bidirectional movement (Pangarkar et al., 2005). Authors explain this result by the aster structure of microtubules. Because the local density of microtubules is higher at the center of the aster, the local density of binding sites for endosome is also higher. This creates a central accumulation. This could also explain why a perinuclear cloud of lysosomes is observed (Jongsma et al., 2016). Thus, microtubules function as a brick for a chain of interactions that transfers spatial structure. Similar behavior has been proposed for the ER to organize spatial distribution of P-bodies or lipid droplets (Lee et al., 2020; Guyard et al., 2022). This mode to create non CSR pattern can be seen as a special case of a chain of interactions where a network transmits a spatial pattern to all its interacting proteins and organelles.
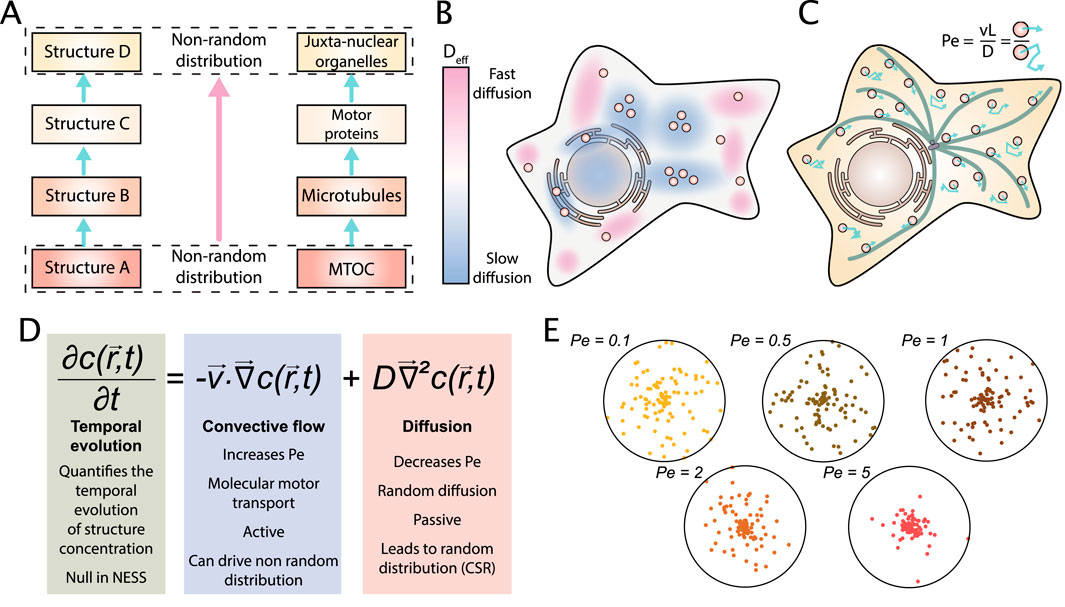
Figure 2. How is a non-random steady state self-organization within cells achieved and maintained? (A) Chain of interactions: Structures with a non-random distribution can transmit their spatial organization via molecular interactions. For example, the centrosomal Microtubule Organizing Center (MTOC) typically nucleates microtubules in an aster geometry. Motor proteins (kinesins and dyneins) bind organelles and attach them to the microtubule network, transmitting its spatial organization. Because of the aster geometry, microtubule concentration is higher close to the MTOC entailing a juxta-nuclear organization of organelles. (B) Heterogeneous diffusion: because the cytoplasm is heterogeneous and anisotropic (in terms of viscosity as well as molecular activity), there are regions of high and low diffusivity, characterized by different effective diffusion coefficients Deff of diffusing particles. Regions of different diffusivity can create local clustering patterns. (C) Convective flow: Energy is used to create a convective flow. For example, motor proteins use ATP to transport particles on microtubules. A system dominated by convective flow is characterized by a high Péclet number and is susceptible to create spatial patterns. Thus, energy consumption balances random distribution driven by diffusion. (D) The Fokker-Planck equation represents the temporal evolution of the concentration c of a particle as a function of the convective flow controlled by the speed v and the Brownian motion controlled by diffusion coefficient D. In NESS, the temporal evolution is null by definition. (E) We model the particle concentration c from steady-state solution of the Fokker-Planck equation with a centripetal flow. Five results are represented obtained in simulations for 2D disk cells and different Péclet Numbers. The degree of clustering correlates with the Péclet Number.
Plasma membrane subdomains seem also to function as a common first brick for chains of interactions (Dykstra et al., 2003; Simons and Toomre, 2000). For example, it has been shown that H-Ras clusters in lipid rafts, similar to the GLU/GLUT4-cluster at the plasma membrane that is lipid-raft dependent, probably because of a direct interaction (Prior et al., 2003; Gao et al., 2017; Yan et al., 2018). Interestingly, spatial statistics of proteins associated with lipid rafts have been used to test the validity of different raft models (Plowman et al., 2005). Chains of interactions could be a major mechanism of spatial organization in the cell. However, this mechanism is not sufficient to explain non-CSR distribution, because it postulates that the first element of the chain has already a special distribution. Moreover, some patterns seem totally independent of other proteins. For example, the plasma membrane-anchored kinase Lck clustering seems to be independent of the association with molecular networks or with lipid domains (Rossy et al., 2013). Moreover, the cell can rely on the geometry of its micro-environment as a first instructing brick to create a chain of interactions. For example, it has been observed that a grid of rigid micro-pillars can spatially organize the formation of podosome-like structures in dendritic cells (Rathar et al., 2024).
Heterogeneous diffusion
All small particles such as molecules, protein complexes, and small organelles are subject to thermal diffusion (also called Brownian motion). The diffusion coefficient D characterizes the diffusion process and is given by the Stokes-Einstein equation
Convective flow
The passive mobility from thermal diffusion of small particles can be counteracted by an active convective flow. In cells, the convective flow mobility is achieved by molecular motors (kinesin, dynein and myosin) and creates a directed flow. The speed v of the flow characterizes the convective transport. Whereas diffusion leads to a Complete Spatial Randomness (CSR) distribution, convective flow can create specific patterns. Thus, convective flow could allow the cell to achieve a non CSR distribution. The archetypal example of this is the anterograde secretion pathway (Figure 1D). The relative importance of convection flow on diffusion is quantified by the Péclet number Pe (Pe = vL/D where L is a characteristic length) (Figure 2C). Thereby, a low Péclet number corresponds to a cell with a low rate of directional transport leading to a CSR distribution, and a high Péclet number leads to the pattern formation. The resulting distribution of particles can be described by the Fokker-Planck equation (also called advection-diffusion equation) (Figure 2D).
Combinatory models: reaction-convection-diffusion model
The different ways to create patterns are not mutually exclusive, but rather are working in combination with a strong interplay between them. Indeed, particles such as protein complexes or organelles could shuttle between heterogeneous diffusion in the cytosol, tethering to the cytoskeleton due to a chain of interactions, and convective motion driven by molecular motors walking on cytoskeleton. Building on the idea that particles can switch from one state to another, models have been proposed that couple different states leading to the addition of reaction terms. These seminal models for spatial distribution of particles are reaction-diffusion-convection models. Often they can be reduced to a simpler diffusion-convection model thanks to an approximation on the different time scales of these processes. The simplification relies on the hypothesis that the reaction timescales are small compared to convection/diffusion timescales. For example, an organelle distribution model with three states: i) diffusion ii) microtubule (+) transport and iii) microtubule (−) transport that can be modeled by a set of Partial Differential Equations (PDEs), (Figure 2D). The first part is driven by thermal fluctuations and characterized by its diffusion coefficient. In contrast, the second and third parts are mainly achieved by energy-consuming processes relying on molecular motors that create an emerging convective flow characterized by a velocity. As an illustration, simulated organelle distributions are shown based on a convection-diffusion equation in 2D disk cells for different Péclet numbers (Figure 2E). This simulation illustrates that the clustering increases with the Péclet number. Some other scholars rely on reaction-diffusion models, since the seminal Turing paper of 1952 (Turing, 1952). The Turing model can reproduce complex self-organized morphogenesis patterns (Kondo and Miura, 2010) in a wide variety of situations (Kondo and Asai, 1995; Jacobo and Hudspeth, 2014; Blagodatski et al., 2015; Sekimura et al., 2015; Fofonjka and Milinkovitch, 2021). It has been recently proposed that the Turing model is a general principle of cellular self-organization at the molecular scale (Halatek et al., 2018). However, the Turing model has a robustness problem, because diverse variations in parameters, such as initial conditions, presence of noise, or delay can vanish the pattern (Bard and Lauder, 1974; Murray, 1982; Maini et al., 2012) while experimental work indicates that organelle landscape is robust (Duong et al., 2012; Guardia et al., 2019). Moreover, neglecting the convective flow seems accurate for chemical systems, but is too simplistic for organelle patterning that clearly relies on motor-driven transport.
A lot of work on the experimental and theoretical part of the analysis of organelle distribution has been performed in hyphae of the filamentous fungi Ustilago maydis (Lin and Steinberg, 2017; Gou et al., 2014; Higuchi et al., 2014; Lin et al., 2016). The efficiency of modeling in hyphae is due to its constant and simple cylindrical morphology. Some modeling has also been performed on animal cells. For example, the distribution of endosomes (Pangarkar et al., 2005) and lipid droplets in embryonic Drosophila cells (Maly, 2002), as well as endocytosed virus (Lagache and Holcman, 2008; Lagache et al., 2009) was efficiently modeled by the Fokker Planck equation. Thus, convection-diffusion models are able to reproduce the spatial organization of organelles in a large diversity of situations, and a general model of organelle distribution has been proposed (Dinh et al., 2006). According to the chosen parameters, this model generates different kind of organizations. Surprisingly, this simple model can produce patterns similar to a good range of experimental data.
Some papers use the full reaction-diffusion-convection model (Smith and Simmons, 2001; Dinh et al., 2005). For example, 4-states models using reaction-diffusion-convection propose that melanosome distribution is controlled mainly by microtubule binding rate (Slepchenko et al., 2007). Another paper proposes that endosome clustering is controlled by a Péclet number and an organelle interaction coefficient (Pangarkar et al., 2012). The common point of these models is that they do not generate instability or oscillations, confirming the stabilization effect of convection.
Can physical models potentially reveal critical parameters of carcinogenesis?
Based on recent observations of organelle changes in cancer we argue that carcinogenesis could be seen as a loss of a reference steady state organization. In this context, the increasing mutations in diverse genes, including trafficking proteins, either could support the loss of the reference state or could compensate this loss. Interestingly, organelle steady state dynamically changes during cell division (see Table 1): it seems to oscillate along the cell cycle when observed at longer time scales (Carlton et al., 2020). Notably, daughter cells re-find a comparable steady state as the mother cell after cell division under homeostasis (Figures 3A-D). Contrary, cancer cells seem to change at these time scales (Figure 3C). Thus, whereas healthy, differentiated cells could be described as being in an oscillatory state at long time scales, cancer cells can neither be considered as steady nor oscillatory (Figure 3D). Cancer cells seem instead to diverge versus a dynamic state that we define as plasticity.
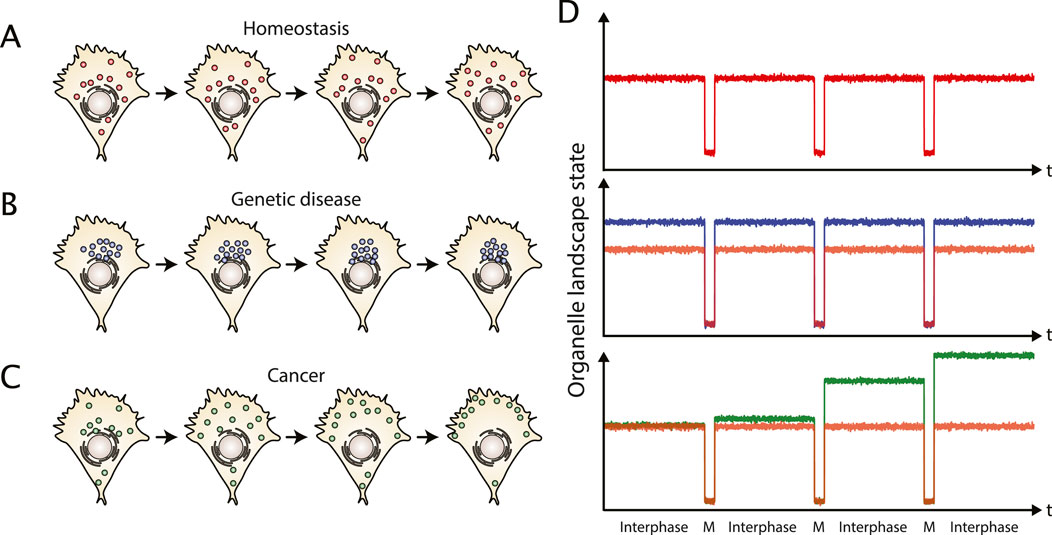
Figure 3. Organelle landscape dynamics at long time scales in healthy and pathological contexts. (A) The statistical properties of the organelle landscape in a healthy cell are preserved over several divisions. (B) Genetic diseases based on finite mutations can exhibit a pathological organelle landscape, but it is still constant over divisions. For example, Huntington’s disease is associated with a perinuclear clustering of lysosomes. (C) In cancer, the spatial organization is not preserved over divisions. While the cancer cell accumulates mutations, the organelle landscape is perturbed accordingly. (D) The organelle landscape of a healthy cell (red) is in a steady state during interphase with random fluctuations, while at longer time scales, the system can be seen as oscillatory, switching from an interphase state to a mitotic (M) state. Cells with a genetic disease (blue) are at a different steady state than healthy cells (depicted by the red curve for comparison), but reveal similar oscillations at longer time scales. Cancer cells (green) typically accumulate mutations that keep changing their organelle landscapes over divisions. The system cannot be regarded as oscillating anymore contrarily to healthy cell (depicted in red for comparison).
Notably, a chaotic regime seems to be easily achieved in biological systems, as both oscillations and chaos can emerge in a non-linear system with time delay (Mackey and Glass, 1977). Oscillations/chaos have been observed in many biochemical reactions (Sel'kov, 1968; Aon et al., 2011; Benincà et al., 2015; Olsen and Degn, 1977; Decroly and Goldbeter, 1982; Olsen and Degn, 1985; Baier and Sahle, 1998). However, chaotic regimes have not yet been observed for the organelle landscape. Future investigations could reveal whether cells have mechanisms to avoid chaotic regimes altogether, or if these regimes exist but have not been observed due to the lack of quantitative measures at the appropriate time scales. This question is especially relevant for cancer cells that randomly accumulate mutations, making their organelle landscape potentially unstable. Alternatively, intra-tumoral natural selection could stabilize whose organelle landscapes that correlate with the most aggressive cell behavior.
Modeling results illustrate that cell organization can be described by general physical principles. Thanks to this biophysical description, loss of organization could be considered as a stability problem of physical models. Interestingly, modeling allows to identify properties that contribute to stability. For instance, it is well known that the Turing model has a robustness problem (Bard and Lauder, 1974; Murray, 1982; Maini et al., 2012), but can be stabilized by the addition of convection. As convection often is represented by molecular motor activity, we speculate that the increased expression of motor proteins seen in melanoma could be interpreted as a compensation for the loss of stable organelle positioning at long time scales that is observed in aggressive melanoma cells (Jerabkova-Roda et al., 2023). Alternatively, active supply with ATP due to increased energy production, as often observed in cancer cells, could increase the convective flow indirectly.
Further, from the theoretical part, boundary conditions can also have an impact on the stability of the system. For example, it has been reported that Dirichlet boundary condition (i.e., fixed concentrations at boundaries) enhances stability of the Turing model (Dillon et al., 1994). It will be interesting to explore whether cancer cell interactions with their microenvironment including other cell types could represent some boundary conditions for organelle distribution. Indeed, the effects of boundary conditions have not yet been extensively studied in the context of organelle distribution.
Finally, it could be considered that alterations of specific gene families contribute in different ways to instability. For instance, Ras alterations could potentially contribute to organelle distribution changes through the induction of a strong chain of interactions, whereas motor proteins could contribute through changes in convection. Changes in families that regulate lipid composition of membranes or cell crowding could alter the diffusion behavior of membrane proteins or cellular macromolecules, and could contribute to organelle alteration through the diffusion term.
Different from cancer, genetic diseases based on finite mutations, such as lysosomal storage disorders or Huntington’s disease (Erie et al., 2015), could be characterized by a transition from one steady state organization versus a new pathological organization sustaining harmful functions (Figures 3B, D). In this case, the loss of the physiological steady state organization could be described as a modification in the parameters of these models. For example, mutations in motor proteins would change the Péclet number or their kinetic rate changing the reaction terms in the models without leading to instability.
Conclusion/outlook
Here, we zoomed out from the molecular functions of trafficking proteins and looked at one level above: the intracellular patterns of organelles that represent the integrated behavior of cellular trafficking activity. The rationale of this is that cancer cells reveal an altered intracellular organization of organelles at long time scales, and we argue that these changes in organelle patterning need to be considered to better understand, describe and fight cancer. Based on the fact that organization can be described by biophysical models, we propose to consider physical emerging properties such as instability of organization as an interesting but unexplored property of cancer cells. In the future, it could be propitious to perform rigorous stability analyses of different models to further identify sources of loss of the stable organization as seen in cancer cells at long time scales.
Of course, there are several limits of the discussed Partial Differentiation Equitation models due to several assumption that are made for simplification. These include the i) well-mixed system approximation that cytosol is homogeneous, ii) linear kinetics hypothesis that binding/unbinding processes can be modeled by first order reactions and iii) the choice of boundary conditions that are often under-estimated. Alternatively, some authors proposed an agent-based approach to model organelle dynamics (Mayorga et al., 2018). In agent-based modeling, the system is modeled by a set of discrete entities called agents. Each agent behaves according to a set of predefined rules. Emerging effects can appear from individual behavior of agents. These models are stochastic and more apt to describe local regulations (Dalmasso et al., 2017; Dinh et al., 2007) or feedbacks (Mayorga et al., 2017). Unfortunately, these models have not been used extensively to investigate the spatial distribution of organelles. Future work should show if they are consistent with models based on PDE, how they compare to these and which properties of complex systems we can learn from them. These models should be investigated and compared in normal versus pathological cell conditions such as cancer.
Investigating the dynamic intracellular landscape of organelles, showing fascinating pattern alterations, could allow the establishment of novel biomarker. Potentially, alterations in organelle patterns could show less heterogeneity than gene/protein expression profiles of different cancers. This could potentially facilitate the prediction of cancer progression or cell responses to drug treatment and resistance.
Finally, organelle patterns could also help reveal the cancer microenvironment and identify cancer cell addictions that make them more vulnerable to treatment than healthy cells. Intriguingly, organelle positioning strongly correlates with environmental cues (see Table 1). Therefore, changes in organelle landscapes observed in cancer could indicate which alterations are found in their microenvironment. For instance, peripheral lysosome trafficking in tumor cells was found to result from acidic extracellular pH, inducing cathepsin B secretion and tumor invasion. This behavior was reversed by inhibitors of sodium-proton exchangers (NHE) that induced a time-dependent retrograde aggregation of lysosomes (Steffan and Cardelli, 2010). More recently, in Glioblastoma stem-like cells (GSCs), organelle alterations have been linked to cholesterol addiction that revealed a vulnerability of glioblastoma to cholesterol-lowering drugs such as statins, particularly in conditions in which organelle alterations were aggravated (Maghe et al., 2024). Thus, interfering with cancer cell addictions, revealed by changes in cellular organization, could emerge as an effective strategy for cancer cell elimination.
The contribution of organelle dynamics in cell homeostasis and disease is still understudied due to lack of resolution, accessibility and cell-to-cell heterogeneity observed in classical cell models. Therefore, novel tools from mathematics, physics and engineering are urgently needed to study organelles under controlled culture conditions in higher dimensions. The focus on intracellular organelles constitutes a novel effort addressing cell perturbation beyond individual gene modification that will open exciting perspectives in the understanding, diagnostics and therapeutics of multifactorial diseases such as cancer.
Box 1 | Proteins of the trafficking machinery
Coat proteins: The main studied coat protein is clathrin (Ungewickell and Branton, 1981). Three heavy and three light chains of clathrin form a triskele (Heuser and Steer, 1989), whose repeat assembly leads to membrane curvature. The resulting hexagonal cage around the invaginated budding structure is called clathrin coated pit. Caveolins are around 20 kDa proteins known to be involve in the formation of cavolae, which are membrane invaginations enriched in proteins and distinct lipids (e.g., cholesterol, sphingolipids). Two caveolin isoforms are ubiquitously expressed, Cav1 and Cav2, whereas Cav3 is only found in muscle cells. Caveolins interact with cavins to bend membranes and to form the invaginating caveolae (Vinten et al., 2005; Hill et al., 2008). To transport cargos from the Golgi complex to the ER, the coat protein complex I (COPI) is recruited to Golgi complex membranes. This complex is composed of seven subunits: α-COP, β-COP, β′-COP, γ-COP, δ-COP, ε-COP, and ζ-COP. The induced extreme curvature of the membrane will allow the COPI coated vesicles to detach from the Golgi membrane (Tomás et al., 2010). The coat protein complex II (COPII) generates vesicles mediating protein transport from the ER to the Golgi complex. COPII complex is composed of SEC23, SEC24, SEC13, SEC31 and the small GTPase SAR1A. COPII coat is responsible for direct capture of cargo proteins and for the physical deformation of the ER membrane (Farmaki et al., 1999).
Cytoskeleton: Actin is the most abundant protein in the cell and forms filaments (F-actin for filamentous) by the polymerization of globular actin (G-actin for globular). Actin filaments are oriented with barbed end (called plus end) bound to ATP making them more stable, therefore having a faster rate of polymerization. On the other hand, the pointed end (minus end) bound with ADP making them more susceptible to disassemble (Kirschner, 1980). Microtubules form the other dynamic cytoskeleton network. These filaments made of dimers of α and β tubulin, radiate from the Microtubules Organizing Center (MTOC). The major MTOC is the centrosome, a structure composed of two centriole surrounded by pericentriolar material, but non-centriolar MTOC exists such as the ones at the Golgi apparatus (Zhu and Irina, 2013; McGill and Brinkley, 1975). Inside the centrosomal MTOC,
Motor proteins: There are different families of motor proteins that bind to either the microtubule cytoskeleton, called kinesins and dyneins, or the actin cytoskeleton, called myosins. Kinesins mostly facilitate movement towards the plus end of microtubules (Hirokawa et al., 1991) with the exception of the retrograde kinesins 14 (KIFC1,2,3), whereas dyneins facilitate movement towards the minus end of microtubules, thus often the centrosomal MTOC (Hirokawa et al., 1990). Myosins bind to actin forming actomyosin which has contractile properties (Bárány, 1967).
Membrane bending proteins: BAR-domain containing proteins (e.g., Bin/Amphiphysin/Rvs167 (Lee et al., 2002)) form dimeric banana-shaped alpha-helix coiled-coils and bind to cellular membranes facilitating membranes deformations. BAR domains can be classified into several subgroups: classical BAR/N-BAR, F-BAR, and I-BAR. N-BAR domain containing proteins are characterized by an additional N-terminal helix which promotes membrane curvature (Gallop et al., 2006). F-BAR domains are flatter than classical BAR domains allowing them to bind to larger liposomes (Frost et al., 2008). I-BAR (for Inverse BAR) domains facilitate negative membrane curvature (Mattila et al., 2007).
Membrane-constricting proteins: To pinch off an invagination from the rest of the membrane dynamin facilitates the constriction at the tubular neck of the invagination (Shpetner and Vallee, 1989). Dynamin is a GTPase that binds to membranes through a PH domain (Downing et al., 1994). Membrane fission is catalyzed through GTP hydrolysis (Mears et al., 2007).
Fusion machinery: Membrane fusion relies on SNAREs that are evolutionary-conserved molecules sharing a SNARE domain (also called SNARE motif) of about 60 residues constituting an α-helix (Weimbs et al., 1997). SNAREs are functionally classified as t-SNAREs localized on the target membrane and v-SNAREs localized on the vesicle (MSöllner et al., 1993). The interaction of t-SNAREs and v-SNAREs creates a so-called trans-SNARE complex (or SNAREpin) that is made of 4 SNARE motifs in a parallel four-helical bundle structure. The full zipping of the SNARE complex catalyzes the membrane fusion. After fusion, the zippered SNARE complex (so-called cis-SNARE) complex is disassembled by the N-ethylmaleimide-sensitive factor (NSF) and α-soluble NSF-attachment protein (α-SNAP) through ATP hydrolysis (Ma et al., 2016). The recycling of v-SNAREs by vesicle budding closes the cycle (Rizo and Südhof, 2002).
Tethering/adapter molecules: The recruitment of molecular motors to membranes is performed through dedicated adaptors. Note that many adapter molecules interact with motors of both kinesin and dynein families (e.g., JIP4 (Willett et al., 2017), RILP, BicD2, FIPs). Accumulated evidence indicates that this step is regulated by small GTPases of the Rab family (see below). For instance, Rab11& Rab4 on recycling endosomes recruit FIP (Shiba et al., 2006) and WIP (Gryaznova et al., 2018), respectively; Rab5 on early endosomes recruits Rabaptin-5 (Stenmark et al., 1995); Rab27 on MVB/melanosomes recruits melanophilin that recruits the actin-dependent motor Myo5a (Strom et al., 2002); Rab7 on lysosomes recruits RILP (Cantalupo et al., 2001); Rab6 on the Golgi complex recruits BicD2 as well as the molecular motors KIF20A (rabkinesin) and MYH9 (myosin IIA), and Rab3 recruits synaptotagmin-like protein 4a (Slp4-a) that recruits MYH9 (Encarnação et al., 2016).
Small GTPases: Intracellular trafficking is regulated by several families of small GTPases, including the RAB, ARF, RHO, RAC family. These enzymes are anchored to membranes via a post-translational lipidation. Guanosine nucleotide Dissociation Inhibitors (GDIs) cover the lipid species of the GTPase in its GDP-, non-membrane-bound form. In their active, GTP-bound form, they recruit different effectors to membranes. They are activated by Guanine Nucleotide Exchange Factors (GEFs) that exchange a GDP to a GTP (Cherfils and Chardin, 1999), and deactivated by GTPase-Activating Protein (GAPs) that facilitate GTP hydrolysis to GDP (Das et al., 2001).
Box 2 | Quantifying the organelle landscape
Point pattern representing organelles in the cell, trees in the forest or stars in the galaxy, arise regularly in science. One of the fundamental questions about these point patterns is to infer the rules shaping their spatial structures and especially if they are uniformly randomly distributed, i.e., CSR. Spatial statistics tackle this challenge providing plethora of tools and among them the Ripley K function, is undoubtedly the queen (Dixon, 2014). It quantifies the average number of neighbors in a radius
Author contributions
JP: Visualization, Writing–original draft, Funding acquisition. KS: Conceptualization, Funding acquisition, Supervision, Writing–original draft, Writing–review and editing, Visualization. HL: Conceptualization, Writing–original draft, Writing–review and editing, Visualization.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by ARC (Association pour la Recherche sur le Cancer) PhD fellowship, FRM (Fondation Recherche Médicale) PhD extension fellowship, the ITMO Nanotumor and the “La Ligue Contre le Cancer” grants to KS.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aher, A., Urnavicius, L., Xue, A., Neselu, K., and Kapoor, T. M. (2024). Structure of the γ-tubulin ring complex-capped microtubule. Nat. Struct. and Mol. Biol. 31 (7), 1124–1133. doi:10.1038/s41594-024-01264-z
Aon, M. A., Cortassa, S., and Lloyd, D. (2011). Chaos in Biochemistry and Physiology. Rev. Cell Biol. Mol. Med. doi:10.1002/3527600906.mcb.201100001
Ba, Q., Raghavan, G., Kiselyov, K., and Yang, G. (2018). Whole-cell scale dynamic organization of lysosomes revealed by spatial statistical analysis. Cell Rep. 23 (12), 3591–3606. doi:10.1016/j.celrep.2018.05.079
Baddeley, A., Rubak, E., and Turner, R. (2016). Spatial point patterns methodology and applications with R. Champan&Hall. doi:10.1201/b19708
Bae, D., Moore, K. A., Mella, J. M., Hayashi, S. Y., and Hollien, J. (2019). Degradation of Blos1 mRNA by IRE1 repositions lysosomes and protects cells from stress. J. Cell Biol. 218 (4), 1118–1127. doi:10.1083/jcb.201809027
Baier, G., and Sahle, S. (1998). Homogeneous and spatio-temporal chaos in biochemical reactions with feedback inhibition. J. Theor. Biol. 193 (2), 233–242. doi:10.1006/jtbi.1998.0695
Baltrusaitis, E. E., Ravitch, E. E., Fenton, A. R., Perez, T. A., Holzbaur, E. L. F., and Dominguez, R. (2023). Interaction between the mitochondrial adaptor MIRO and the motor adaptor TRAK. J. Biol. Chem. 299 (12), 105441. doi:10.1016/j.jbc.2023.105441
Bárány, M. (1967). ATPase activity of myosin correlated with speed of muscle shortening. J. General Physiology 50 (6), 197–218. doi:10.1085/jgp.50.6.197
Bard, J., and Lauder, I. (1974). How well does turing’s theory of morphogenesis work? J. Theor. Biol. 45 (2), 501–531. doi:10.1016/0022-5193(74)90128-3
Baum, D. A., and Baum, B. (2014). An inside-out origin for the eukaryotic cell. BMC Biol. 12 (October), 76. doi:10.1186/s12915-014-0076-2
Belintsev, B. N., Beloussov, L. V., and Zaraisky, A. G. (1987). Model of pattern formation in epithelial morphogenesis. J. Theor. Biol. 129 (4), 369–394. doi:10.1016/S0022-5193(87)80019-X
Benincà, E., Ballantine, B., and Ellner, S. P. (2015). Huisman J. Species fluctuations sustained by a cyclic succession at the edge of chaos. Proc. Natl. Acad. Sci. U. S. A. 112 (20), 6389–6394. doi:10.1073/pnas.1421968112
Bergeijk, P. van, Hoogenraad, C. C., and Kapitein, L. C. (2016). Right time, right place: probing the functions of organelle positioning. Trends Cell Biol. 26 (2), 121–134. doi:10.1016/j.tcb.2015.10.001
Bergeland, T., Widerberg, J., Bakke, O., and Nordeng, T. W. (2001). Mitotic partitioning of endosomes and lysosomes. Curr. Biol. 11 (9), 644–651. doi:10.1016/S0960-9822(01)00177-4
Birbaumer, M., and Schweitzer, F. (2011). Agent-based modeling of intracellular transport. Eur. Phys. J. B 82 (3), 245–255. doi:10.1140/epjb/e2011-20283-x
Blagodatski, A., Sergeev, A., Kryuchkov, M., Lopatina, Y., and Katanaev, V. L. (2015). Diverse set of Turing nanopatterns coat corneae across insect lineages. Proc. Natl. Acad. Sci. U. S. A. 112 (34), 10750–10755. doi:10.1073/pnas.1505748112
Bonifacino, J. S., and Neefjes, J. (2017). Moving and positioning the endolysosomal system. Curr. Opin. Cell Biol. 47 (August), 1–8. doi:10.1016/j.ceb.2017.01.008
Brangwynne, C. P., Koenderink, G. H., MacKintosh, F. C., and Weitz, D. A. (2009). Intracellular transport by active diffusion. Trends Cell Biol. 19 (9), 423–427. doi:10.1016/j.tcb.2009.04.004
Brownhill, K., Wood, L., and Allan, V. (2009). Molecular motors and the Golgi complex: staying put and moving through. Seminars Cell and Dev. Biol. 20 (7), 784–792. doi:10.1016/j.semcdb.2009.03.019
Cabukusta, B., and Neefjes, J. (2018). Mechanisms of lysosomal positioning and movement. Traffic Copenhagen, Den. 19 (10), 761–769. doi:10.1111/tra.12587
Cantalupo, G., Alifano, P., Roberti, V., Bruni, C. B., and Bucci, C. (2001). Rab-interacting lysosomal protein (RILP): the Rab7 effector required for transport to lysosomes. EMBO J. 20 (4), 683–693. doi:10.1093/emboj/20.4.683
Carlton, J. G., Jones, H., and Eggert, U. S. (2020). Membrane and organelle dynamics during cell division. Nat. Rev. Mol. Cell Biol. 21 (3), 151–166. doi:10.1038/s41580-019-0208-1
Chatterjee, M., Ben-Josef, E., Thomas, D. G., Morgan, M. A., Zalupski, M. M., Khan, G., et al. (2015). Caveolin-1 is associated with tumor progression and confers a multi-modality resistance phenotype in pancreatic cancer. Sci. Rep. 5 (1), 10867. doi:10.1038/srep10867
Chen, K., Wang, Y., Deng, X., Guo, L., and Wu, C. (2021). Extracellular matrix stiffness regulates mitochondrial dynamics through PINCH-1- and kindlin-2-mediated signalling. Curr. Res. Cell Biol. 2 (January), 100008. doi:10.1016/j.crcbio.2021.100008
Cherfils, J., and Chardin, P. (1999). GEFs: structural basis for their activation of small GTP-binding proteins. Trends Biochem. Sci. 24 (8), 306–311. doi:10.1016/s0968-0004(99)01429-2
Collins, T. J., Berridge, M. J., Lipp, P., and Bootman, M. D. (2002). Mitochondria are morphologically and functionally heterogeneous within cells. EMBO J. 21 (7), 1616–1627. doi:10.1093/emboj/21.7.1616
Daga, P., Thurakkal, B., Rawal, S., and Das, T. (2024). Matrix stiffening promotes perinuclear clustering of mitochondria. Mol. Biol. Cell 35 (7), ar91. doi:10.1091/mbc.E23-04-0139
Dalmasso, G., Zapata, P. A. M., Ryan Brady, N., and Hamacher-Brady, A. (2017). Agent-based modeling of mitochondria links sub-cellular dynamics to cellular homeostasis and heterogeneity. PLOS ONE 12 (1), e0168198. doi:10.1371/journal.pone.0168198
Das, S., Ghosh, R., and Maitra, U. (2001). Eukaryotic translation initiation factor 5 functions as a GTPase-activating protein. J. Biol. Chem. 276 (9), 6720–6726. doi:10.1074/jbc.M008863200
Decroly, O., and Goldbeter, A. (1982). Birhythmicity, chaos, and other patterns of temporal self-organization in a multiply regulated biochemical system. Proc. Natl. Acad. Sci. U.S.A. 79 (22), 6917–6921. doi:10.1073/pnas.79.22.6917
Diggle, P. J., Chetwynd, A. G., Häggkvist, R., and Morris, S. E. (1995). Second-order analysis of space-time clustering. Stat. Methods Med. Res. 4 (2), 124–136. doi:10.1177/096228029500400203
Diggle, P. J. (2013). Statistical analysis of spatial and spatio-temporal point patterns. 3rd Edn. New York, NY: Chapman and Hall/CRC. doi:10.1201/b15326
Dillon, R., Maini, P. K., and Othmer, H. G. (1994). Pattern Formation in generalized turing systems. J. Math. Biol. 32 (4), 345–393. doi:10.1007/BF00160165
Di Marco, T., Bianchi, F., Sfondrini, L., Todoerti, K., Bongarzone, I., Margherita Maffioli, E., et al. (2020). COPZ1 depletion in thyroid tumor cells triggers type I IFN response and immunogenic cell death. Cancer Lett. 476 (April), 106–119. doi:10.1016/j.canlet.2020.02.011
Dinh, A.-T., Pangarkar, C., Theofanous, T., and Mitragotri, S. (2006). Theory of spatial patterns of intracellular organelles. Biophysical J. 90 (10), L67–L69. doi:10.1529/biophysj.106.082875
Dinh, A.-T., Pangarkar, C., Theofanous, T., and Mitragotri, S. (2007). Understanding intracellular transport processes pertinent to synthetic gene delivery via stochastic simulations and sensitivity analyses. Biophysical J. 92 (3), 831–846. doi:10.1529/biophysj.106.095521
Dinh, A.-T., Theofanous, T., and Mitragotri, S. (2005). A model for intracellular trafficking of adenoviral vectors. Biophysical J. 89 (3), 1574–1588. doi:10.1529/biophysj.105.059477
Dixon, P. M. (2014). “Ripley’s K function,” in Wiley StatsRef: statistics reference online (John Wiley and Sons, Ltd).
Downing, A. K., Driscoll, P. C., Gout, I., Salim, K., Zvelebil, M. J., and Waterfield, M. D. (1994). Three-dimensional solution structure of the pleckstrin homology domain from dynamin. Curr. Biol. CB 4 (10), 884–891. doi:10.1016/s0960-9822(00)00197-4
Duong, T., Bruno, G., and Schauer, K. (2012). Closed-form density-based framework for automatic detection of cellular morphology changes. Proc. Natl. Acad. Sci. U. S. A. 109 (22), 8382–8387. doi:10.1073/pnas.1117796109
Dykstra, M., Cherukuri, A., Sohn, H. W., Shiang-Jong, T., and Pierce, S. K. (2003). Location is everything: lipid rafts and immune cell signaling. Annu. Rev. Immunol. 21, 457–481. doi:10.1146/annurev.immunol.21.120601.141021
Encarnação, M., Espada, L., Escrevente, C., Mateus, D., Ramalho, J., Michelet, X., et al. (2016). A rab3a-dependent complex essential for lysosome positioning and plasma membrane repair. J. Cell Biol. 213 (6), 631–640. doi:10.1083/jcb.201511093
Erie, C., Sacino, M., Houle, L., Lu, M. L., and Jianning, W. (2015). Altered lysosomal positioning affects lysosomal functions in a cellular model of Huntington’s disease. Eur. J. Neurosci. 42 (3), 1941–1951. doi:10.1111/ejn.12957
Farmaki, T., Ponnambalam, S., Prescott, A. R., Clausen, H., Tang, B.-L., Hong, W., et al. (1999). Forward and retrograde trafficking in mitotic animal cells ER-golgi transport arrest restricts protein export from the ER into COPII-coated structures. J. Cell Sci. 112 (5), 589–600. doi:10.1242/jcs.112.5.589
Fofonjka, F., and Milinkovitch, M. C. (2021). Reaction-diffusion in a growing 3D domain of skin scales generates a discrete cellular automaton. Nat. Commun. 12 (1), 2433. doi:10.1038/s41467-021-22525-1
Frost, A., Perera, R., Roux, A., Spasov, K., Destaing, O., Egelman, E. H., et al. (2008). Structural basis of membrane invagination by F-BAR domains. Cell 132 (5), 807–817. doi:10.1016/j.cell.2007.12.041
Gallop, J. L., Jao, C. C., Kent, H. M., Butler, P. J. G., Evans, P. R., Langen, R., et al. (2006). Mechanism of endophilin N-BAR domain-mediated membrane curvature. EMBO J. 25 (12), 2898–2910. doi:10.1038/sj.emboj.7601174
Gao, L., Chen, J., Gao, J., Wang, H., and Xiong, W. (2017). Super-resolution microscopy reveals the insulin-resistance-regulated reorganization of GLUT4 on plasma membranes. J. Cell Sci. 130 (2), 396–405. doi:10.1242/jcs.192450
Garner, R. M., Arthur, T. M., Theriot, J. A., and Chang, F. (2023). Vast heterogeneity in cytoplasmic diffusion rates revealed by nanorheology and doppelgänger simulations. Biophysical J. 122 (5), 767–783. doi:10.1016/j.bpj.2023.01.040
Gkini, V., Gómez-Lozano, I., Heikinheimo, O., and Namba, T. (2024). Dynamic changes in mitochondrial localization in human neocortical basal radial glial cells during cell cycle. J. Comp. Neurology 532 (6), e25630. doi:10.1002/cne.25630
Gomes, E. R., Jani, S., and Gundersen, G. G. (2005). Nuclear movement regulated by Cdc42, MRCK, myosin, and actin flow establishes MTOC polarization in migrating cells. Cell 121 (3), 451–463. doi:10.1016/j.cell.2005.02.022
Gou, J., Edelstein-Keshet, L., and Allard, J. (2014). Mathematical model with spatially uniform regulation explains long-range bidirectional transport of early endosomes in fungal hyphae. Mol. Biol. Cell 25 (16), 2408–2415. doi:10.1091/mbc.e14-03-0826
Griesche, N., Sanchez, G., Hermans, C., and Idevall-Hagren, O. (2019). Cortical mitochondria regulate insulin secretion by local Ca2+ buffering in rodent beta cells. J. Cell Sci. 132 (9), jcs228544. doi:10.1242/jcs.228544
Gryaznova, T., Gubar, O., Burdyniuk, M., Kropyvko, S., and Rynditch, A. (2018). WIP/ITSN1 complex is involved in cellular vesicle trafficking and formation of filopodia-like protrusions. Gene 674 (October), 49–56. doi:10.1016/j.gene.2018.06.078
Guardia, C. M., De Pace, R., Sen, A., Saric, A., Jarnik, M., Kolin, D. A., et al. (2019). Reversible association with motor proteins (ramp): a streptavidin-based method to manipulate organelle positioning. PLoS Biol. 17 (5), e3000279. doi:10.1371/journal.pbio.3000279
Guichard, P., Hamel, V., Le Guennec, M., Banterle, N., Iacovache, I., Nemčíková, V., et al. (2017). Cell-free reconstitution reveals centriole cartwheel assembly mechanisms. Nat. Commun. 8 (1), 14813. doi:10.1038/ncomms14813
Guyard, V., Monteiro-Cardoso, V. F., Omrane, M., Sauvanet, C., Houcine, A., Boulogne, C., et al. (2022). ORP5 and ORP8 orchestrate lipid droplet biogenesis and maintenance at ER-mitochondria contact sites. J. Cell Biol. 221 (9), e202112107. doi:10.1083/jcb.202112107
Halatek, J., and Frey, E. (2018). Rethinking pattern formation in reaction–diffusion systems. Nature Phys. 14, 507–514. doi:10.1038/s41567-017-0040-5
Hall, D., and Minton, A. P. (2003). Macromolecular crowding: qualitative and semiquantitative successes, quantitative challenges. Biochimica Biophysica Acta 1649 (2), 127–139. doi:10.1016/s1570-9639(03)00167-5
Heuser, J. (1989). Changes in lysosome shape and distribution correlated with changes in cytoplasmic pH. J. Cell Biol. 108 (3), 855–864. doi:10.1083/jcb.108.3.855
Heuser, J., and Steer, C. J. (1989). Trimeric binding of the 70-kD uncoating ATPase to the vertices of clathrin triskelia: a candidate intermediate in the vesicle uncoating reaction. J. Cell Biol. 109 (4 Pt 1), 1457–1466. doi:10.1083/jcb.109.4.1457
Higuchi, Y., Ashwin, P., Roger, Y., and Steinberg, G. (2014). Early endosome motility spatially organizes polysome distribution. J. Cell Biol. 204 (3), 343–357. doi:10.1083/jcb.201307164
Hill, M. M., Bastiani, M., Luetterforst, R., Kirkham, M., Kirkham, A., Nixon, S. J., et al. (2008). PTRF-cavin, a conserved cytoplasmic protein required for caveola formation and function. Cell 132 (1), 113–124. doi:10.1016/j.cell.2007.11.042
Hirokawa, N., Sato-Yoshitake, R., Kobayashi, N., Pfister, K. K., Bloom, G. S., and Brady, S. T. (1991). Kinesin associates with anterogradely transported membranous organelles in vivo. J. Cell Biol. 114 (2), 295–302. doi:10.1083/jcb.114.2.295
Hirokawa, N., Sato-Yoshitake, R., Yoshida, T., and Kawashima, T. (1990). Brain dynein (MAP1C) localizes on both anterogradely and retrogradely transported membranous organelles in vivo. J. Cell Biol. 111 (3), 1027–1037. doi:10.1083/jcb.111.3.1027
Jacobo, A., and Hudspeth, A. J. (2014). Reaction–diffusion model of hair-bundle morphogenesis. Proc. Natl. Acad. Sci. U.S.A. 111 (43), 15444–15449. doi:10.1073/pnas.1417420111
Jerabkova-Roda, K., Mousson, A., Peralta, M., Karali, R., Justiniano, H., Lisii, L. M., et al. (2023). Peripheral positioning of lysosomes supports melanoma aggressiveness. bioRXiv, 548108. doi:10.1101/2023.07.07.548108
Jia, R., and Bonifacino, J. S. (2019). Lysosome positioning influences mTORC2 and AKT signaling. Mol. Cell 75 (1), 26–38.e3. doi:10.1016/j.molcel.2019.05.009
Johannes, L., Pezeshkian, W., Ipsen, J. H., and Shillcock, J. C. (2018). Clustering on membranes: fluctuations and more. Trends Cell Biol. 28 (5), 405–415. doi:10.1016/j.tcb.2018.01.009
Johansson, M., Rocha, N., Zwart, W., Jordens, I., Janssen, L., Kuijl, C., et al. (2007). Activation of endosomal dynein motors by stepwise assembly of Rab7-RILP-p150Glued, ORP1L, and the receptor betalll spectrin. J. Cell Biol. 176 (4), 459–471. doi:10.1083/jcb.200606077
Johnson, D. E., Ostrowski, P., Jaumouillé, V., and Grinstein, S. (2016). The position of lysosomes within the cell determines their luminal pH. J. Cell Biol. 212 (6), 677–692. doi:10.1083/jcb.201507112
Jongsma, M. L. M., Berlin, I., Wijdeven, R. H. M., Janssen, L., Janssen, G. M. C., Garstka, M. A., et al. (2016). An ER-associated pathway defines endosomal architecture for controlled cargo transport. Cell 166 (1), 152–166. doi:10.1016/j.cell.2016.05.078
Karsenti, E. (2008). Self-organization in cell biology: a brief history. Nat. Rev. Mol. Cell Biol. 9 (3), 255–262. doi:10.1038/nrm2357
Khater, I. M., Nabi, I. R., and Hamarneh, G. (2020). A review of super-resolution single-molecule localization microscopy cluster analysis and quantification methods. Patterns 1 (3), 100038. doi:10.1016/j.patter.2020.100038
Kirschner, M. W. (1980). Implications of treadmilling for the stability and polarity of actin and tubulin polymers in vivo. J. Cell Biol. 86 (1), 330–334. doi:10.1083/jcb.86.1.330
Kondo, S., and Miura, T. (2010). Reaction-diffusion model as a framework for understanding biological pattern formation. Science 329 (5999), 1616–1620. doi:10.1126/science.1179047
Kondo, S., and Asai, R. (1995). A reaction–diffusion wave on the skin of the marine angelfish Pomacanthus. Nature 376, 765–768. doi:10.1038/376765a0
Korolchuk, V. I., Saiki, S., Lichtenberg, M., Siddiqi, F. H., Roberts, E. A., Imarisio, S., et al. (2011). Lysosomal positioning coordinates cellular nutrient responses. Nat. Cell Biol. 13 (4), 453–460. doi:10.1038/ncb2204
Kruppa, A. J., and Folma, B. (2021). Motor proteins at the mitochondria–cytoskeleton interface. J. Cell Sci. 134 (7), jcs226084. doi:10.1242/jcs.226084
Kuimova, M. K. (2012). Mapping viscosity in cells using molecular rotors. Phys. Chem. Chem. Phys. 14 (37), 12671–12686. doi:10.1039/C2CP41674C
Kupfer, A., Louvard, D., and Singer, S. J. (1982). Polarization of the Golgi apparatus and the microtubule-organizing center in cultured fibroblasts at the edge of an experimental wound. Proc. Natl. Acad. Sci. 79 (8), 2603–2607. doi:10.1073/pnas.79.8.2603
Lachuer, H., Laurent, L., Lévêque-Fort, S., Goud, B., and Schauer, K. (2023). Spatial organization of lysosomal exocytosis relies on membrane tension gradients. Proc. Natl. Acad. Sci. U. S. A. 120 (8), e2207425120. doi:10.1073/pnas.2207425120
Lagache, T., Dauty, E., and Holcman, D. (2009). Quantitative analysis of virus and plasmid trafficking in cells. Phys. Rev. E 79 (1), 011921. doi:10.1103/PhysRevE.79.011921
Lagache, T., and Holcman, D. (2008). Quantifying intermittent transport in cell cytoplasm. Phys. Rev. E 77 (3), 030901. doi:10.1103/PhysRevE.77.030901
Lee, E., Marcucci, M., Daniell, L., Pypaert, M., Weisz, O. A., Ochoa, G.-C., et al. (2002). Amphiphysin 2 (Bin1) and T-tubule biogenesis in muscle. Sci. (New York, N.Y.) 297 (5584), 1193–1196. doi:10.1126/science.1071362
Lee, J. E., Cathey, P. I., Wu, H., Parker, R., and Voeltz, G. K. (2020). Endoplasmic reticulum contact sites regulate the dynamics of membraneless organelles. Sci. (New York, N.Y.) 367 (6477), eaay7108. doi:10.1126/science.aay7108
Li, X., Rydzewski, N., Hider, A., Zhang, X., Yang, J., Wang, W., et al. (2016). A molecular mechanism to regulate lysosome motility for lysosome positioning and tubulation. Nat. Cell Biol. 18 (4), 404–417. doi:10.1038/ncb3324
Lin, C., Schuster, M., Guimaraes, S. C., Ashwin, P., Schrader, M., Metz, J., et al. (2016). Active diffusion and microtubule-based transport oppose myosin forces to position organelles in cells. Nat. Commun. 7 (1), 11814. doi:10.1038/ncomms11814
Lin, C., and Steinberg, G. (2017). Spatial organization of organelles in fungi: insights from mathematical modelling. Fungal Genet. Biol. FG and B 103 (June), 55–59. doi:10.1016/j.fgb.2017.03.006
Lonhus, K., Rychtáriková, R., Ali, G., and Štys, D. (2021). Estimation of rheological parameters for unstained living cells. Eur. Phys. J. Special Top. 230 (4), 1105–1112. doi:10.1140/epjs/s11734-021-00084-2
López-Doménech, G., Covill-Cooke, C., Ivankovic, D., Halff, E. F., Sheehan, D. F., Norkett, R., et al. (2018). Miro proteins coordinate microtubule- and actin-dependent mitochondrial transport and distribution. EMBO J. 37 (3), 321–336. doi:10.15252/embj.201696380
Luby-Phelps, K., Castle, P. E., Taylor, D. L., and Lanni, F. (1987). Hindered diffusion of inert tracer particles in the cytoplasm of mouse 3T3 cells. Proc. Natl. Acad. Sci. U. S. A. 84 (14), 4910–4913. doi:10.1073/pnas.84.14.4910
Ma, L., Kang, Y., Jiao, J., Rebane, A. A., Cha, H. K., Xi, Z., et al. (2016). α-SNAP enhances SNARE zippering by stabilizing the SNARE four-helix bundle. Cell Rep. 15 (3), 531–539. doi:10.1016/j.celrep.2016.03.050
Macaskill, A. F., Rinholm, J. E., Twelvetrees, A. E., Lorena Arancibia-Carcamo, I., Muir, J., Fransson, A., et al. (2009). Miro1 is a calcium sensor for glutamate receptor-dependent localization of mitochondria at synapses. Neuron 61 (4), 541–555. doi:10.1016/j.neuron.2009.01.030
Mackey, M. C., and Glass, L. (1977). Oscillation and chaos in physiological control systems. Science 197 (4300), 287–289. doi:10.1126/science.267326
Maghe, C., Trillet, K., André-Grégoire, G., Kerhervé, M., Merlet, L., Jacobs, K. A., et al. (2024). The paracaspase MAL controls cholesterol homeostasis in glioblastoma stem-like cells through lysosome proteome shaping. Cell Rep. 43 (1), 113631. doi:10.1016/j.celrep.2023.113631
Maini, P. K., Woolley, T. E., Baker, R. E., Gaffney, E. A., and Seirin Lee, S. (2012). Turing’s model for biological pattern formation and the robustness problem. Interface Focus 2 (4), 487–496. doi:10.1098/rsfs.2011.0113
Malikov, V., Cytrynbaum, E. N., Kashina, A., Mogilner, A., and Rodionov, V. (2005). Centering of a radial microtubule array by translocation along microtubules spontaneously nucleated in the cytoplasm. Nat. Cell Biol. 7 (12), 1213–1218. doi:10.1038/ncb1332
Maly, IVAN V. (2002). A stochastic model for patterning of the cytoplasm by the saltatory movement. J. Theor. Biol. 216 (1), 59–71. doi:10.1006/jtbi.2002.2531
Mandal, K., Asnacios, A., Goud, B., and Manneville, J.-B. (2016). Mapping intracellular mechanics on micropatterned substrates. Proc. Natl. Acad. Sci. U. S. A. 113 (46), E7159–E7168. doi:10.1073/pnas.1605112113
Mathur, P., De Barros Santos, C., Lachuer, H., Patat, J., Latgé, B., Radvanyi, F., et al. (2023). Transcription factor EB regulates phosphatidylinositol-3-phosphate levels that control lysosome positioning in the bladder cancer model. Commun. Biol. 6 (January), 114. doi:10.1038/s42003-023-04501-1
Mattila, P. K., Pykäläinen, A., Saarikangas, J., Paavilainen, V. O., Vihinen, H., Jokitalo, E., et al. (2007). Missing-in-Metastasis and IRSp53 deform PI(4,5)P2-rich membranes by an Inverse BAR domain–like mechanism. J. Cell Biol. 176 (7), 953–964. doi:10.1083/jcb.200609176
Mayorga, L. S., Cebrian, I., Verma, M., Hoops, S., and Bassaganya-Riera, J. (2018). Reconstruction of endosomal organization and function by a combination of ODE and agent-based modeling strategies. Biol. Direct 13 (1), 25. doi:10.1186/s13062-018-0227-4
Mayorga, L. S., Verma, M., Hontecillas, R., Hoops, S., and Bassaganya-Riera, J. (2017). Agents and networks to model the dynamic interactions of intracellular transport. Cell. Logist. 7 (4), e1392401. doi:10.1080/21592799.2017.1392401
McGill, M., and Brinkley, B. R. (1975). Human chromosomes and centrioles as nucleating sites for the in vitro assembly of microtubules from bovine brain tubulin. J. Cell Biol. 67 (1), 189–199. doi:10.1083/jcb.67.1.189
Mears, J. A., Ray, P., and Hinshaw, J. E. (2007). A corkscrew model for dynamin constriction. Struct. Lond. Engl. 1993 15 (10), 1190–1202. doi:10.1016/j.str.2007.08.012
Minin, A. A., Kulik, A. V., Gyoeva, F. K., Li, Y., Goshima, G., and Gelfand, V. I. (2006). Regulation of mitochondria distribution by RhoA and formins. J. Cell Sci. 119 (4), 659–670. doi:10.1242/jcs.02762
Misteli, T. (2001). The concept of self-organization in cellular architecture. J. Cell Biol. 155 (2), 181–185. doi:10.1083/jcb.200108110
Monod, J. (1970). Le Hasard et La Nécessité: Essai Sur La Philosophie Naturelle de La Biologie Moderne. Paris: Seuil.
Mosier, J. A., Fabiano, E. D., Ludolph, C. M., White, A. E., and Reinhart-King, C. A. (2023). Confinement primes cells for faster migration by polarizing active mitochondria. Nanoscale Adv. 6 (1), 209–220. doi:10.1039/D3NA00478C
Murray, J. D. (1982). Parameter space for turing instability in reaction diffusion mechanisms: a comparison of models. J. Theor. Biol. 98 (1), 143–163. doi:10.1016/0022-5193(82)90063-7
Muthuswamy, S. K., and Bin, X. (2012). Cell polarity as a regulator of cancer cell behavior plasticity. Annu. Rev. Cell Dev. Biol. 28, 599–625. doi:10.1146/annurev-cellbio-092910-154244
Nakahara, R., Aki, S., Sugaya, M., Hirose, H., Kato, M., Maeda, K., et al. (2023). Hypoxia activates SREBP2 through Golgi disassembly in bone marrow-derived monocytes for enhanced tumor growth. EMBO J. 42 (22), e114032. doi:10.15252/embj.2023114032
Neefjes, J., Jongsma, M. M. L., and Berlin, I. (2017). Stop or go? Endosome positioning in the establishment of compartment architecture, dynamics, and function. Trends Cell Biol. 27 (8), 580–594. doi:10.1016/j.tcb.2017.03.002
Olsen, L., and Degn, H. (1977). Chaos in an enzyme reaction. Nature 267, 177–178. doi:10.1038/267177a0
Olsen, L. F., and Degn, H. (1985). Chaos in biological systems. Q Rev. Biophys. 18 (2), 165–225. doi:10.1017/s0033583500005175
Owen, D. M., Williamson, D. J., Magenau, A., and Gaus, K. (2012). Sub-resolution lipid domains exist in the plasma membrane and regulate protein diffusion and distribution. Nat. Commun. 3 (1), 1256. doi:10.1038/ncomms2273
Pangarkar, C., Dinh, A. T., and Mitragotri, S. (2005). Dynamics and spatial organization of endosomes in mammalian cells. Phys. Rev. Lett. 95 (15), 158101. doi:10.1103/PhysRevLett.95.158101
Pangarkar, C., Dinh, A.-T., and Mitragotri, S. (2012). Endocytic pathway rapidly delivers internalized molecules to lysosomes: an analysis of vesicle trafficking, clustering and mass transfer. J. Control. Release 162 (1), 76–83. doi:10.1016/j.jconrel.2012.05.022
Parton, R. G., Dotti, C. G., Bacallao, R., Kurtz, I., Simons, K., and Prydz, K. (1991). pH-induced microtubule-dependent redistribution of late endosomes in neuronal and epithelial cells. J. Cell Biol. 113 (2), 261–274. doi:10.1083/jcb.113.2.261
Pelham, H. R. B. (1996). The dynamic organisation of the secretory pathway. Cell Struct. Funct. 21 (5), 413–419. doi:10.1247/csf.21.413
Pereira, S. G., Dias Louro, M. A., and Bettencourt-Dias, M. (2021). Biophysical and quantitative principles of centrosome biogenesis and structure. Annu. Rev. Cell Dev. Biol. 37, 43–63. doi:10.1146/annurev-cellbio-120219-051400
Plowman, S. J., Muncke, C., Parton, R. G., and Hancock, J. F. (2005). H-ras, K-Ras, and inner plasma membrane raft proteins operate in nanoclusters with differential dependence on the actin cytoskeleton. Proc. Natl. Acad. Sci. U. S. A. 102 (43), 15500–15505. doi:10.1073/pnas.0504114102
Prior, I. A., Muncke, C., Parton, R. G., and Hancock, J. F. (2003). Direct visualization of Ras proteins in spatially distinct cell surface microdomains. J. Cell Biol. 160 (2), 165–170. doi:10.1083/jcb.200209091
Pu, J., Guardia, C. M., Keren-Kaplan, T., and Bonifacino, J. S. (2016). Mechanisms and functions of lysosome positioning. J. Cell Sci. 129 (23), 4329–4339. doi:10.1242/jcs.196287
Quidwai, T., Wang, J., Hall, E. A., Petriman, N. A., Leng, W., Kiesel, P., et al. (2021). A WDR35-dependent coat protein complex transports ciliary membrane cargo vesicles to cilia. eLife 10, e69786. doi:10.7554/eLife.69786
Quintana, A., Schwarz, E. C., Schwindling, C., Lipp, P., Kaestner, L., and Hoth, M. (2006). Sustained activity of calcium release-activated calcium channels requires translocation of mitochondria to the plasma membrane. J. Biol. Chem. 281 (52), 40302–40309. doi:10.1074/jbc.M607896200
Rabouille, C. (2017). Pathways of unconventional protein secretion. Trends Cell Biol. 27 (3), 230–240. doi:10.1016/j.tcb.2016.11.007
Raja, V., Achuthan, , Le, K. H., Weld, D. M., and Brandman, O. (2024). Diffusive lensing as a mechanism of intracellular transport and compartmentalization. eLife 12 (June), RP89794. doi:10.7554/eLife.89794
Rathar, R., Sanchez-Fuentes, D., Lachuer, H., Meire, V., Boulay, A., Desgarceaux, R., et al. (2024). Tuning the immune cell response through surface nanotopography engineering. Small Sci. 4 (9), 2400227. doi:10.1002/smsc.202400227
Rizo, J., and Südhof, T. C. (2002). Snares and Munc18 in synaptic vesicle fusion. Nat. Rev. Neurosci. 3 (8), 641–653. doi:10.1038/nrn898
Rocha, N., Kuijl, C., van der Kant, R., Janssen, L., Houben, D., Janssen, H., et al. (2009). Cholesterol sensor ORP1L contacts the ER protein VAP to control rab7-RILP-P150 glued and late endosome positioning. J. Cell Biol. 185 (7), 1209–1225. doi:10.1083/jcb.200811005
Rossy, J., Owen, D. M., Williamson, D. J., Yang, Z., and Gaus, K. (2013). Conformational states of the kinase lck regulate clustering in early T cell signaling. Nat. Immunol. 14 (1), 82–89. doi:10.1038/ni.2488
Sasazawa, Y., Souma, S., Furuya, N., Miura, Y., Kazuno, S., Kakuta, S., et al. (2022). Oxidative stress-induced phosphorylation of JIP4 regulates lysosomal positioning in coordination with TRPML1 and ALG2. EMBO J. 41 (22), e111476. doi:10.15252/embj.2022111476
Schauer, K., Duong, T., Bleakley, K., Bardin, S., Bornens, M., and Bruno, G. (2010). Probabilistic density maps to study global endomembrane organization. Nat. Methods 7 (7), 560–566. doi:10.1038/nmeth.1462
Scott, C. C., Vacca, F., and Jean, G. (2014). Endosome maturation, transport and functions. Seminars Cell and Dev. Biol. Endosome Dyn. and Tubulogenesis 31 (July), 2–10. doi:10.1016/j.semcdb.2014.03.034
Sebastian, R., Diaz, M.-E., Ayala, G., Letinic, K., Moncho-Bogani, J., and Toomre, D. (2006). Spatio-temporal analysis of constitutive exocytosis in epithelial cells. IEEE/ACM Trans. Comput. Biol. Bioinforma. 3 (1), 17–32. doi:10.1109/TCBB.2006.11
Sekimura, T., Venkataraman, C., and Madzvamuse, A. (2015). A model for selection of eyespots on butterfly wings. PLoS One 10 (11), e0141434. doi:10.1371/journal.pone.0141434
Sel'kov, E. E. (1968). Self-oscillations in glycolysis. 1. A simple kinetic model. Eur. J. Biochem. 4 (1), 79–86. doi:10.1111/j.1432-1033.1968.tb00175.x
Shiba, T., Koga, H., Shin, H.-W., Kawasaki, M., Kato, R., Nakayama, K., et al. (2006). Structural basis for rab11-dependent membrane recruitment of a family of rab11-interacting protein 3 (FIP3)/arfophilin-1. Proc. Natl. Acad. Sci. U. S. A. 103 (42), 15416–15421. doi:10.1073/pnas.0605357103
Shpetner, H. S., and Vallee, R. B. (1989). Identification of dynamin, a novel mechanochemical enzyme that mediates interactions between microtubules. Cell 59 (3), 421–432. doi:10.1016/0092-8674(89)90027-5
Simons, K., and Toomre, D. (2000). Lipid rafts and signal transduction. Nat. Rev. Mol. Cell Biol. 1 (1), 31–39. doi:10.1038/35036052
Slepchenko, B. M., Semenova, I., Zaliapin, I., and Rodionov, V. (2007). Switching of membrane organelles between cytoskeletal transport systems is determined by regulation of the microtubule-based transport. J. Cell Biol. 179 (4), 635–641. doi:10.1083/jcb.200705146
Smith, D. A., and Simmons, R. M. (2001). Models of motor-assisted transport of intracellular particles. Biophysical J. 80 (1), 45–68. doi:10.1016/S0006-3495(01)75994-2
Söllner, T., Whiteheart, S. W., Brunner, M., Erdjument-Bromage, H., Geromanos, S., Tempst, P., et al. (1993). SNAP receptors implicated in vesicle targeting and fusion. Nature 362 (6418), 318–324. doi:10.1038/362318a0
Steffan, J. J., and Cardelli, J. A. (2010). Thiazolidinediones induce rab7-RILP-MAPK-dependent juxtanuclear lysosome aggregation and reduce tumor cell invasion. Traffic Copenhagen, Den. 11 (2), 274–286. doi:10.1111/j.1600-0854.2009.01012.x
Stenmark, H., Vitale, G., Ullrich, O., and Zerial, M. (1995). Rabaptin-5 is a direct effector of the small GTPase Rab5 in endocytic membrane fusion. Cell 83 (3), 423–432. doi:10.1016/0092-8674(95)90120-5
Strom, M., Hume, A. N., Tarafder, A. K., Barkagianni, E., and Seabra, M. C. (2002). A family of rab27-binding proteins. Melanophilin links Rab27a and myosin va function in melanosome transport. J. Biol. Chem. 277 (28), 25423–25430. doi:10.1074/jbc.M202574200
Tachikawa, M. (2023). Theoretical approaches for understanding the self-organized formation of the Golgi apparatus. DGD 65 (3), 161–166. doi:10.1111/dgd.12842
Tang, D., Yuan, H., and Wang, Y. (2010). The role of GRASP65 in Golgi cisternal stacking and cell cycle progression. Traffic Copenhagen, Den. 11 (6), 827–842. doi:10.1111/j.1600-0854.2010.01055.x
Thompson, T. C., Tahir, S. A., Li, L., Watanabe, M., Naruishi, K., Yang, G., et al. (2009). The role of caveolin-1 in prostate cancer: clinical implications. Prostate Cancer Prostatic Dis. 13 (1), 6–11. doi:10.1038/pcan.2009.29
Tomás, M., Martínez-Alonso, E., Ballesta, J., and Martínez-Menárguez, J. A. (2010). Regulation of ER–golgi intermediate compartment tubulation and mobility by COPI coats, motor proteins and microtubules. Traffic 11 (5), 616–625. doi:10.1111/j.1600-0854.2010.01047.x
Turing, A. M. (1952). The chemical basis of morphogenesis. Philos. Trans. R. Soc., B 237, 641. doi:10.1098/rstb.1952.0012
Ungewickell, E., and Branton, D. (1981). Assembly units of clathrin coats. Nature 289 (5796), 420–422. doi:10.1038/289420a0
Urbina, F. L., Gomez, S. M., and Gupton, S. L. (2018). Spatiotemporal organization of exocytosis emerges during neuronal shape change. J. Cell Biol. 217 (3), 1113–1128. doi:10.1083/jcb.201709064
Vagne, Q., Vrel, J.-P., and Sens, P. (2020). “A minimal self-organisation model of the Golgi apparatus.” in Elife Edited by R. E. Goldstein, S. R. Pfeffer, and J. Kondev 9 (August):e47318.
Vaidžiulytė, K., Coppey, M., and Schauer, K. (2019). Intracellular organization in cell polarity – placing organelles into the polarity loop. J. Cell Sci. 132 (24), jcs230995. doi:10.1242/jcs.230995
Valm, A. M., Cohen, S., Legant, W. R., Melunis, J., Hershberg, U., Wait, E., et al. (2017). Applying systems-level spectral imaging and analysis to reveal the organelle interactome. Nature 546 (7656), 162–167. doi:10.1038/nature22369
Villanueva, J., Viniegra, S., Gimenez-Molina, Y., García-Martinez, V., Expósito-Romero, G., del Mar Frances, M., et al. (2014). The position of mitochondria and ER in relation to that of the secretory sites in chromaffin cells. J. Cell Sci. 127 (Pt 23), 5105–5114. doi:10.1242/jcs.160242
Vinten, J., Johnsen, A. H., Roepstorff, P., Harpøth, J., and Tranum-Jensen, J. (2005). Identification of a major protein on the cytosolic face of caveolae. Biochimica Biophysica Acta 1717 (1), 34–40. doi:10.1016/j.bbamem.2005.09.013
Volonte, D., Vyas, A. R., Chen, C., Dacic, S., Stabile, L. P., Kurland, B. F., et al. (2017). Caveolin-1 promotes the tumor suppressor properties of oncogene-induced cellular senescence. J. Biol. Chem. 293 (5), 1794–1809. doi:10.1074/jbc.M117.815902
Walton, Z. E., Patel, C. H., Brooks, R. C., Yu, Y., Ibrahim-Hashim, A., Riddle, M., et al. (2018). Acid suspends the circadian clock in hypoxia through inhibition of mTOR. Cell 174 (1), 72–87.e32. doi:10.1016/j.cell.2018.05.009
Wang, G., and Galli, T. (2018). Reciprocal link between cell biomechanics and exocytosis. Traffic 19 (10), 741–749. doi:10.1111/tra.12584
Wang, G., Nola, S., Bovio, S., Bun, P., Coppey-Moisan, M., Lafont, F., et al. (2018). Biomechanical control of lysosomal secretion via the VAMP7 hub: a tug-of-war between varp and LRRK1. iScience 4 (June), 127–143. doi:10.1016/j.isci.2018.05.016
Wang, L., Goldwag, J., Bouyea, M., Barra, J., Matteson, K., Maharjan, N., et al. (2023). Spatial topology of organelle is a new breast cancer cell classifier. iScience 26 (7), 107229. doi:10.1016/j.isci.2023.107229
Wang, S., Wang, N., Zheng, Y., Yang, B., Liu, P., Zhang, F., et al. (2020). Caveolin-1 inhibits breast cancer stem cells via c-myc-mediated metabolic reprogramming. Cell Death and Dis. 11 (6), 450. doi:10.1038/s41419-020-2667-x
Wedlich-Söldner, R., and Betz, T. (2018). Self-organization: the fundament of cell biology. Philosophical Trans. R. Soc. B Biol. Sci. 373 (1747), 20170103. doi:10.1098/rstb.2017.0103
Wei, J.-H., and Seemann, J. (2017). Golgi ribbon disassembly during mitosis, differentiation and disease progression. Curr. Opin. Cell Biol. 47 (August), 43–51. doi:10.1016/j.ceb.2017.03.008
Weimbs, T., Low, S. H., Chapin, S. J., Mostov, K. E., Bucher, P., and Hofmann, K. (1997). A conserved domain is present in different families of vesicular fusion proteins: a new superfamily. Proc. Natl. Acad. Sci. U. S. A. 94 (7), 3046–3051. doi:10.1073/pnas.94.7.3046
Willett, R., Martina, J. A., Zewe, J. P., Wills, R., Hammond, G. R. V., and Puertollano, R. (2017). TFEB regulates lysosomal positioning by modulating TMEM55B expression and JIP4 recruitment to lysosomes. Nat. Commun. 8 (November), 1580. doi:10.1038/s41467-017-01871-z
Yan, Q., Lu, Y., Zhou, L., Chen, J., Xu, H., Cai, M., et al. (2018). Mechanistic insights into GLU activation and clustering revealed by super-resolution imaging. Proc. Natl. Acad. Sci. U. S. A. 115 (27), 7033–7038. doi:10.1073/pnas.1803859115
Yuan, T., Lu, J., Zhang, J., Zhang, Y., and Chen, L. (2015). Spatiotemporal detection and analysis of exocytosis reveal fusion ‘hotspots’ organized by the cytoskeleton in endocrine cells. Biophysical J. 108 (2), 251–260. doi:10.1016/j.bpj.2014.11.3462
Keywords: organelle distribution, self-organization, non-random positioning, non-equilibrium steady-state (NESS), lysosomes
Citation: Patat J, Schauer K and Lachuer H (2025) Trafficking in cancer: from gene deregulation to altered organelles and emerging biophysical properties. Front. Cell Dev. Biol. 12:1491304. doi: 10.3389/fcell.2024.1491304
Received: 04 September 2024; Accepted: 10 December 2024;
Published: 20 January 2025.
Edited by:
Stephane Gasman, Université de Strasbourg, FranceReviewed by:
Paolo Maiuri, Federico II University, ItalyTania López-Hernández, University of Barcelona, Spain
Copyright © 2025 Patat, Schauer and Lachuer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kristine Schauer, a3Jpc3RpbmUuc2NoYXVlckBndXN0YXZlcm91c3N5LmZy
 Julie Patat
Julie Patat Kristine Schauer
Kristine Schauer Hugo Lachuer
Hugo Lachuer