- Research Institute for Electronic Science, Hokkaido University, Sapporo, Japan
Many fundamental biological processes are dependent on cellular migration. Although the mechanical mechanisms of single-cell migration are relatively well understood, those underlying migration of multiple cells adhered to each other in a cluster, referred to as cluster migration, are poorly understood. A key reason for this knowledge gap is that many forces—including contraction forces from actomyosin networks, hydrostatic pressure from the cytosol, frictional forces from the substrate, and forces from adjacent cells—contribute to cell cluster movement, making it challenging to model, and ultimately elucidate, the final result of these forces. This paper describes a two-dimensional cell membrane model that represents cells on a substrate with polygons and expresses various mechanical forces on the cell surface, keeping these forces balanced at all times by neglecting cell inertia. The model is discrete but equivalent to a continuous model if appropriate replacement rules for cell surface segments are chosen. When cells are given a polarity, expressed by a direction-dependent surface tension reflecting the location dependence of contraction and adhesion on a cell boundary, the cell surface begins to flow from front to rear as a result of force balance. This flow produces unidirectional cell movement, not only for a single cell but also for multiple cells in a cluster, with migration speeds that coincide with analytical results from a continuous model. Further, if the direction of cell polarity is tilted with respect to the cluster center, surface flow induces cell cluster rotation. The reason why this model moves while keeping force balance on cell surface (i.e., under no net forces from outside) is because of the implicit inflow and outflow of cell surface components through the inside of the cell. An analytical formula connecting cell migration speed and turnover rate of cell surface components is presented.
1 Introduction
Cellular migration is a key component of numerous biological processes, including the morphogenesis of multicellular organisms, wound healing, and cancer metastasis (Friedl and Gilmour, 2009; Scarpa and Mayor, 2016; Bodor et al., 2020). Consequently, elucidating the molecular and biophysical mechanisms that control cell movement can provide fundamental insight to enhance our understanding of these critical processes. Notably, although the mechanisms controlling single-cell migration are relatively well understood (Bodor et al., 2020), those underlying multiple-cell migration, wherein cells adhere to each other and form a cluster, prior to undergoing unidirectional (Haas and Gilmour, 2006; Weijer, 2009; Haigo and Bilder, 2011; Montell et al., 2012; Kuwayama and Ishida, 2013; Pagès et al., 2022) and rotational motion (Founounou et al., 2021), referred to as cluster migration, remain unclear. One reason for this is that the phenomenon of cluster migration involves what is known as a many-body problem. That is, within cells, there are many forces related to cell movement, such as contraction forces coming from actomyosin, adhesion forces between cells, hydrostatic pressure from cytosol, and forces from adjacent cells; cell movement is a result of balance between these forces. Thus, whereas it is challenging to determine how cell membranes move under this force balance even for a single cell, it is even more difficult in the case of multiple cells, particularly when trying to understand how multiple cells coordinately move. In such complex scenarios, mechanical modeling approaches may be useful, given that these methods guarantee force balance for every element and hence, generate results that can be relied upon with some conviction.
Cell movements are mainly classified into one of two types (Callan-Jones and Voituriez, 2016). In mesenchymal migration, the cell attaches to a substrate at focal adhesions and extends its body at the leading edge by forming lamellipodia and filopodia (Innocenti, 2018). During this process, a retrograde flow of actin filaments is observed beneath the plasma membrane of the cell (Haas and Gilmour, 2006; Case and Waterman, 2015). The second type of cell movement is amoeboid migration; in this case, specific adhesion to the substrate is not necessarily required, but, nonspecific friction between the cell membrane and the surrounding matrix is thought to be sufficient for migration (Lämmermann et al., 2008; Reversat et al., 2020; O'Neill et al., 2018; Farutin et al., 2019). By contracting the rear part of the cell body via a force generated from the actomyosin meshwork under the plasma membrane, the cell increases hydrostatic pressure within the cytosol and produces blebs at the leading edge to extend its body forward (Paluch and Raz, 2013). During ameboid migration, cortical flow from front to rear is observed inside the cell, which is believed to play an important role in this process (Bergert et al., 2015). The shapes of cells undergoing each mode of migration are also different. That is, cells performing amoeboid migration are relatively rounded, whereas those engaging in mesenchymal migration are relatively elongated (Haas and Gilmour, 2006). Recent studies, however, have begun to suggest that this concept of cell movement involving two distinct migration modes is too limited and does not allow the rigorous classification of all cell movements (Bodor et al., 2020). Indeed, some cells exhibit both mesenchymal and amoeboid-like movement modes and plastically switch between these, depending on the environmental conditions (Bergert et al., 2012; Ruprecht et al., 2015). Thus, some investigators have initiated studies aimed at identifying shared universal mechanisms underlying all cell migration.
From a mechanical modeling viewpoint, a number of common features present in both the mesenchymal and amoeboid modes of migration can be identified. For example, bleb formation in amoeboid migration and lamellipodia formation in mesenchymal migration are similar, given that, in both cases, the membrane in the front region of the cell tends to expand. Mechanically, this behavior of the cell membrane at the leading edge is expressed by weak surface tension. Strong attachment between membrane and substrate in mesenchymal migration and nonspecific friction in amoeboid migration are also expressed by one parameter of a mechanical model. That is, strong attachment is expressed by a large friction coefficient value between membrane and substrate, whereas weak nonspecific friction is expressed by a small friction coefficient value. Moreover, in both modes, contractions at the trailing end of the cell membrane are expressed by a strong surface tension in that region. These observations highlight the common mechanistic features underlying all forms of cell migration. Further, in both migration modes, cortical flow beneath the plasma membrane is present and is thought to play an important role in cell movement (Bray and White, 1988; Salbreux et al., 2012). However, as noted above, because there are many forces within cells, even if we focus only on the cell membrane, it is very hard to anticipate how cell membranes move and how cells ultimately move eventually under these myriad forces. Therefore, to better understand the mechanical mechanisms underlying cell migration, mechanical models that appropriately express forces within the cells and keep these forces balanced at each point on the cell membrane are needed.
A number of mechanical models for cell migration that satisfy these conditions have been developed. For example, some groups have proposed excellent three-dimensional (3D) surface models, in which directed surface flow and cell division are reproduced (Mietke et al., 2019; Bächer et al., 2021; Okuda et al., 2022). However, 3D mechanical models require a long computational time and are not appropriate for dealing with multiple cells simultaneously. In 2D cases, cellular vertex models are frequently used for describing multiple cell dynamics, wherein cells are approximated by polygons, and cell boundaries between adjacent cells are represented by straight segments (Fletcher et al., 2014). This model have succeeded in explaining important phenomena in epithelial sheets (Farhadifar et al., 2007; Rauzi et al., 2008; Aigouy et al., 2010; Fletcher et al., 2014; Sato et al., 2015a). However, if we extend this 2D cellular vertex model and try to more precisely describe cell surface dynamics on the substrate, some problems arise. One minor problem is that because the cell boundary between adjacent cells is represented by a straight segment, the model does not appropriately express the curvature of the cell boundary. This can be overcome relatively easily, however, by adding vertices to split the straight segment into multiple segments.
If we try to extend the 2D cellular vertex model to deal with curved cell boundaries with multiple segments, the expression of frictional force can be a major problem. In the current vertex model, only the vertices of polygons experience friction forces from the surrounding objects (Fletcher et al., 2014). This means that if a cell boundary is divided into some number of segments to express its curvature more smoothly, the friction forces on the cell boundary can change depending on the number of segments. For example, let us consider the case where we represent a straight boundary between cells A and B in two ways. One is that the cell boundary is represented by one segment specified by vertices 1 and 2. The other is that we add a new vertex 3 to the segment 12 and split the segment into two segments (i.e., the cell boundary is now represented by two segments, segment 13 and segment 32). Then, we consider the case where the cell boundary shifts slightly. In that motion, the latter representation of the cell boundary obviously experiences a larger friction force than the former representation if the friction coefficients are the same, because the latter representation has three vertices whereas the former representation has two vertices. Friction force on the cell boundary should not depend on discretization of the cell boundary, but instead, should satisfy a continuous limit (i.e., the frictional force is expressed by a quantity per unit length of the cell boundary). Recently a 2D continuous mathematical model has been proposed that successfully reproduces the adhesion-independent movement of a single cell confined in a 3D space under axisymmetric conditions (Jankowiak et al., 2020). However, this model can assess only one cell. To comprehensively investigate cell migration, mechanical models capable of treating multiple cells that adhere to each other and satisfying force balance on the cell surface are necessary.
Here, we present a 2D cell membrane model, in which cells on a substrate are represented by polygons, and various forces on the cell surface, including contraction forces from actomyosin, adhesion between cells, and hydrostatic pressure from the cytosol, are implemented and balanced on the surface at all times. This model is equivalent to a continuous model if the lengths of segments representing the cell surface are kept within an appropriate range, using defined replacement rules, as described below. Cell clusters are represented by allowing a common surface between adjacent cells. We show that if cells in this model have a polarity expressed by direction-dependent surface tension, this causes the cell surface to flow from front to rear, and that flow induces unidirectional cell movement, not only for a single cell but also for a cluster of cells. In addition, if the surface-tension polarities of cells within the cluster are tilted with respect to the center of the cluster, the clusters rotate around the cluster center. This mechanical model produces movement while keeping forces balanced on the cell surface due to the inflow and outflow of cell surface components from inside the cell. The relationship between cell migration speed and turnover rate of cell surface components is discussed in Section 3.5.
2 Model
2.1 The situations treated by the mechanical model
We consider situations where cells are on a substrate; some cells exist individually on the substrate, while other cells are attached to each other to form a cluster. We focus on the dynamics of the peripheries of the cells, which movements are determined by force balance on the cell boundaries. Each cell has a polarity, and depending on the direction of the polarity, each cell changes the strength of contraction force on the cell boundary. We are concerned with two setups of cell polarity. One is that there is a chemoattractant gradient in a definite direction on the substrate, say the x-direction, and all cells have polarity in the x direction (Sections 3.2–3.6). The other is that cells that form a cluster have different directions of polarity. To be specific, the direction of polarity of each cell tilts with respect to the center of the cluster (Section 3.7). This tilted polarity may be achieved by chance or by using chirality of the cells (Taniguchi et al., 2011; Tee et al., 2015; Wan et al., 2016). A characteristic point of our model is that force balance holds at any parts of the cell boundaries at any time.
2.2 Setup of the model
In our model, cells on a substrate are represented by polygons; specifically, the

FIGURE 1. Setup for the two-dimensional (2D) cell membrane model of cell migration. (A) In this model, cells on a substrate are represented by polygons. If a cell adheres to an adjacent cell, the two cells share the segments and nodes on the joint boundary. The cell surface experiences various mechanical forces that are expressed by W and U in Eqs. 1, 2, respectively. These forces are balanced at all times on the cell surface, as shown in Eq. 3. (B) Replacement rules for cell boundary segments are as follows. When the length
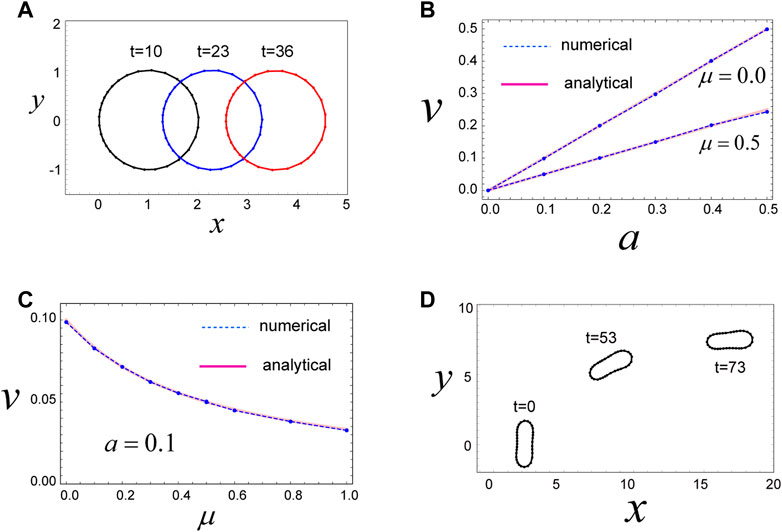
FIGURE 2. Mechanism for migration of a circular and non-circular cell. (A) A circular cell migrates in the x-direction due to the direction-dependent surface tension in Eq. 4, which generates a continuous flow of cell surface from front to rear. The cell movement is maintained as long as the cell has the polarity expressed by Eq. 4. Parameters used are as follows:
Cell boundaries experience two types of forces: one is the frictional forces that are expressed by the dissipation function given in Eq. 1, and the other is the mechanical forces that are expressed by a potential function
Here,
The frictional coefficients
The other mechanical forces on the cell surface, such as contraction forces coming from the actomyosin network beneath the plasma membrane and hydrostatic pressure from the cytosol, are represented by the following effective potential U, as follows:
where
The first term in Eq. 2 represents a pressure acting on the segments arising from the area difference between the current area of the cell,
Using this value of
In this model, we assume that the inertial force of the cell surface is negligible compared with the mechanical forces in question, and thus, all forces acting on the
holds for all i’s at any given time. Here, the symbol
2.3 Methods for numerical simulations
To numerically solve Eq. 3, we first nondimensionalize the variables and parameters appearing in the equation, using the following units: length,
3 Results
3.1 A case in which a circular cell isotropically shrinks with a constant surface tension
To test our model, we first determine whether the dissipation function W given in Eq. 1 appropriately expresses the frictional forces on the cell surface. For this we consider a case where a circular cell has a constant surface tension
3.2 A circular cell migrates due to direction-dependent surface tension
Next, we investigate a more realistic case wherein the cell under consideration is circular with a constant area
where
We then examined the steady state of the cell with these model parameters. Numerical simulations reveal that the cell moves in the positive x-direction, with a constant speed, while keeping a circular shape in the steady state (Figure 2A). The driving force for this movement is the direction-dependent surface tension in Eq. 4 and the resulting cell surface flow from the front to the rear (Supplementary Movie S1). That is, in the front region of the cell, surface tension is relatively weak due to the parameters of Eq. 4, such that the surface in the front region tends to expand. In contrast, surface tension in the rear region of the cell is relatively strong, and hence, the surface in this region tends to shrink. This surface tension-dependent tendency of the cell surface to expand or shrink produces a flow of cell membrane, in which the front region is always expanding (in some sense, blebbing is continuously occurring in front of the cell), whereas the rear region is always shrinking (Supplementary Movie S1). These behaviors act as a source and sink of cell surface and yield a flow of cell surface from front to rear. In addition, within this system, there is a frictional force between the cell surface and the substrate. Thus, if the cell surface moves in some direction, the whole cell experiences forces that move it in the opposite direction, based on the action–reaction principle.
The velocity
where
3.3 An elongated cell migrates due to direction-dependent surface tension
We further find that single-cell migration induced by direction-dependent surface tension, described in Eq. 4, occurs even when the cell shape is elliptical (Figure 2D). We can model an elliptical-shaped cell using finite values for
3.4 A case in which a cell is sandwiched by two walls
Motivated by results from published experiments (Bergert et al., 2015; Liu et al., 2015; Sakamoto et al., 2022), we next examined the scenario in which a cell is sandwiched by two parallel walls. In this case, the wall is expressed using the potential
where
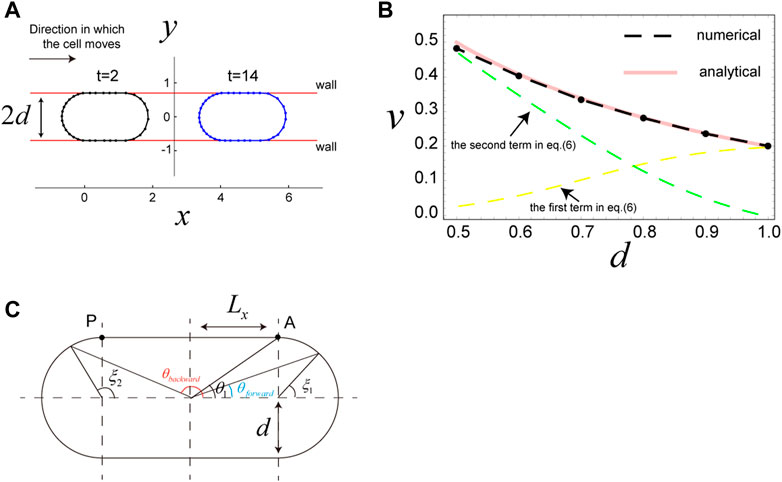
FIGURE 3. Migration of a cell sandwiched by two walls. (A) Snapshots of a cell sandwiched by two walls, which migrates in the x-direction due to surface flow resulting from the direction-dependent surface tension in Eq. 4. The distance between the two walls is
Results from analytical expression Eq. 6 are in good agreement with the results of numerical simulations (Figure 3B). Thus, we use Eq. 6 to interpret the cell speed in this scenario. The first term in Eq. 6 is the contribution from surface flow on the two semicircles of the cell, and the second term is the contribution from surface flow on the straight parts of the cell. When
3.5 Properties of surface flow-mediated cell migration
To better understand why and how cells move due to surface flow while keeping the forces balanced at all times, we surveyed the properties of cell movement observed in this model. Although these properties derived below are provided in a continuous form, it is not difficult to translate them into a discrete form. As noted above, our model neglects all inertia of the cell surface, so that the forces on any element of the cell surface are balanced at any time, and more importantly, the total force on the cell surface from the substrate must vanish at any time. Because the force on the cell surface from the external object—the substrate—is friction only, we have the following equality:
at any time
With this situation, let us consider the time evolution of the cell surface density,
Where
which describes the relationship between
Interestingly,
where
Inserting Eqs. 12–12.1 into Eq 11 gives
where we have used
3.6 Multiple cells in a cluster also move via direction-dependent surface tension
The above simulations focus on migration of individual cells; however, cells often move together with other cells. Therefore, we next examined whether cell migration due to direction-dependent surface tension occurs even when multiple cells are attached to each other, forming a cluster. Specifically, we investigated the case where the number
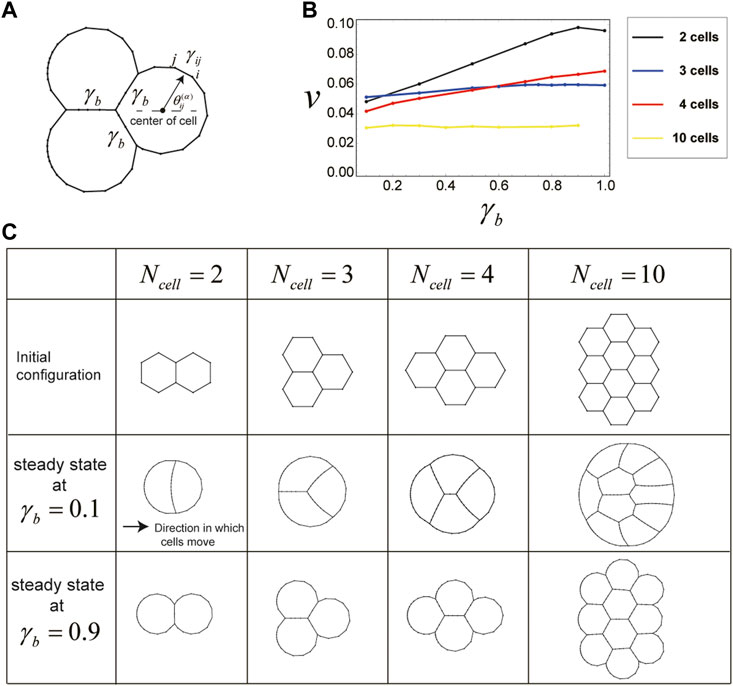
FIGURE 4. Cells in a cluster also migrate due to direction-dependent surface tension. (A) Setup for the surface tension of cells in a cluster. The boundaries between any two cells in the cluster have a constant surface tension
The shape and velocity of the cluster during this movement depend on the value of
The slow cluster movement speed at small
3.7 Cell clusters rotate when cell direction is tilted with respect to the center of a cluster
To this point, we have examined only scenarios in which all cells on a substrate have the same direction of polarity (e.g., the x-direction). However, because clustered cells may also show distinct polarities, we next investigated the case wherein direction of polarity for individual cells within a cluster differs from cell to cell. In particular, we considered four cells comprising a cluster, in which each individual cell has a polarity that is directed perpendicular to the direction from the center of the cell to that of the cell cluster (Figure 5A). Surface tension for cells within this situation is expressed as
where
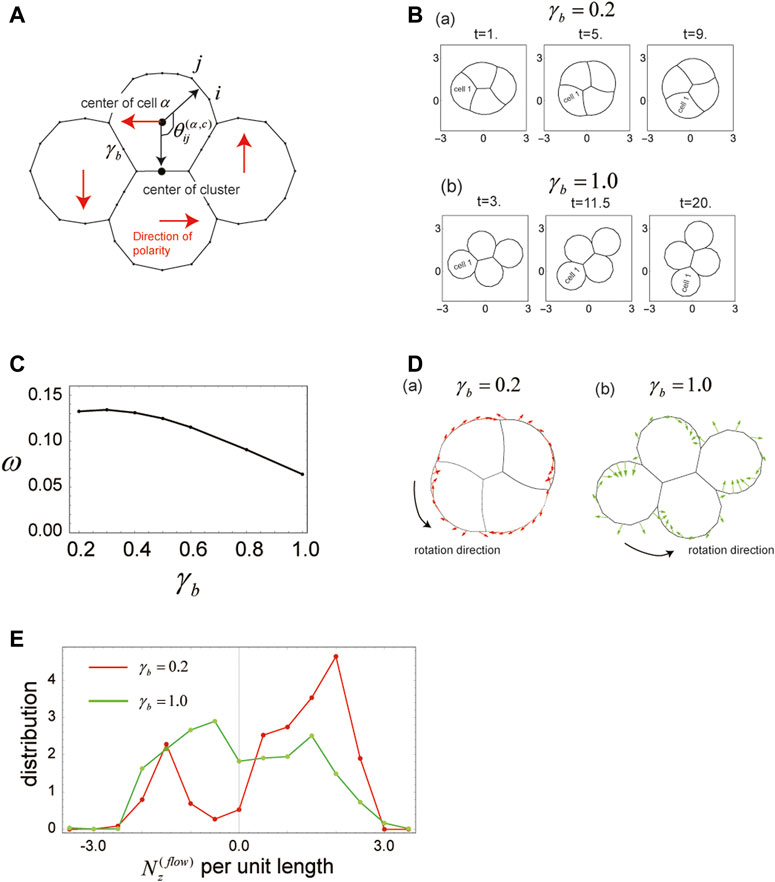
FIGURE 5. Cells in a cluster rotate when the polarity of each cell is tilted with respect to the cluster center. (A) Geometrical explanation of the angle
The initial configuration of the cell cluster is the same as in Figure 4C (
As in the case of single-polarity cluster migration examined in Section 3.6, shape and rotational velocity of the cell cluster change with
The faster rotation of the cell cluster at small
4 Discussion
In this study, we have developed a 2D cell membrane model, described by Eqs 1–3, which shows that cells on a substrate migrate due to direction-dependent surface tension, represented by Eq. 4. Notably, this is true, not only for a single cell but also for multiple cells that adhere to one another and form a cluster. Moreover, if we change the direction of cell polarity within a cell cluster, such that polarity varies from cell to cell, as in Eq. 13, the cell cluster rotates due to direction-dependent surface tension. A key point of emphasis is that, because this model neglects any inertia of the cell surface and ensures that forces are balanced on the cell surface at all times, the total force exerted on each cell from outside objects, such as the substrate and neighboring cells, always vanishes. That is, the cell movement in this situation is, what we call, “force free”, and this is driven by the inflow and outflow of cell membrane components from inside the cell, as discussed in Section 3.5.
Although this is a 2D model, it is expected that the cell movement we observe herein, namely, single-cell migration, cluster migration, and cluster rotation, may also be present in 3D models, because the mechanism of movement (i.e., direction-dependent surface tension) is likely applicable to 3D cases. Indeed, single-cell migration due to direction-dependent surface tension has been demonstrated in a previously published study (Okuda et al., 2022), for a spherical cell migrating with a constant velocity in 3D space. Thus, we anticipate that cluster migration and rotation will be shown in well-implemented 3D models.
We further expect this model may reveal relevant information for better understanding cell shape and cortical flow during cell movement in real-life situations. This is because, as previously emphasized, our model satisfies force balance on the cell membrane at all times, and hence, the cell shapes appearing in this model are the results of that force balance on cell surface during cell migration (e.g., see Figures 2D, 4C). Thus, if a parameter set in our model mimics the cell shapes and cell movement observed in experiments, we can expect which part of the cell experiences strong contractile forces and which part of the cell membrane has strong stiffness by looking at the experimental results. In addition, this mechanical model provides the speed of cell movement. Thus, with these properties we can address the relationship between cell shape and cell velocity, which is proposed in the existing works (Ohta and Ohkuma, 2009) by using a symmetry argument. We can examine the relationship between shape and speed of cells by the cell-level model. In addition, by regarding the segments in our model as the cortex in cells, we are able to investigate cortical flow within moving cells, as in previously published studies (Jankowiak et al., 2020). A key point of the present model is that due to the discreteness of this model, we can easily set the parameter values that specify key characteristics of the cells we are modeling. For example, we can change the strength of contractile and frictional forces, as well as the stiffness of the cortex, by changing
In our model, as already mentioned in Section 2.1, we focused on the dynamics of the cell peripheries. However, in many real-life cases, cells are attached to the substrate at some focal adhesions, and the two-dimensional flow of the cortex at the bottom region of the cells is also important for cell movement. Therefore, it would be a good strategy to extend the presented cortex model to a model that expresses the two-dimensional flow on the plane. This will be a target of future work. In addition, it has been observed that the plasma membrane and the cortex beneath the plasma membrane move separately during cell movement (Taniguchi et al., 2023). This observation implies that it is more realistic for a model of cell movement to describe the dynamics of two components, the plasma membrane and the cortex. This will also be a target of future research.
In the current remodeling rules for segments that represent cell boundaries, given in Section 2.2, the attachment and detachment of cells, which are important processes for considering more general movement of cells, are not described. In fact, by adding only some rules to the current setup, we can describe the attachment and detachment of cells. An example of it is as follows. When two separated cells are close to each other and the distance between some parts of two cell surfaces becomes shorter than some critical distance, then the parts of cell surfaces are merged and becomes one segment. This setup describes the attachment of two cells. In addition, when the common cell boundary between two adhered cells becomes shorter than some critical length, then the common cell boundary is split into two cell boundaries and two cell are separated. This situation represents the detachment of two cells. By introducing this rule into the current version, we can investigate more complex behaviors of cells on a substrate.
In the present paper, we have assumed that cell polarity is represented by the direction dependence of
In the present paper cell polarity was a priori given as in Eqs. 4, 13. But in reality, the direction of cell polarity dynamically changes with time depending on the environment surrounding the cell and the state of itself. Many possible ways for describing the time evolution of cell polarity have been proposed (Camley et al., 2014). By introducing proposed descriptions of cell polarity into our mechanical model and comparing the results obtained by the model to experiments, we might be able to determine which time evolution rule for cell polarity is most appropriate.
The phenomenon of cells migrating on a substrate, while forming a cluster, has been observed during development of the zebrafish lateral line (Haas and Gilmour, 2006; Lecaudey et al., 2008) and by the amoeba Dictyostelium discoideum (Hirose et al., 2011; Hayakawa et al., 2020). In addition, some clusters of epithelial cells were found to rotate 90° within an epithelial sheet during Drosophila eye development (Mlodzik, 1999; Mirkovic and Mlodzik, 2006; Jenny, 2010; Founounou et al., 2021). Although there are many possible explanations for such collective behavior (Haas and Gilmour, 2006; Lecaudey et al., 2008), it has been difficult to understand from a mechanistic standpoint, due to the many-body problem inherent in analyzing complex systems. In this regard, mechanical models are useful to better understand the forces that drive multi-cell behavior as noted in the Introduction, and the mechanism presented in this paper represents one possible explanation for such collective cell movement. By comparing experimental results, such as the spatial distribution of actomyosin and adhesion molecules in cells and observed cell shapes, with the results from our numerical simulations, we may uncover new insights into the complex patterns of cell movement observed in living systems.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
The author was the sole contributor of this work and approved the submitted version for publication.
Funding
This work was supported by a JSPS KAKENHI Grant Number JP20K03871, 23H04300 and 21H05310, the “Dynamic Alliance for Open Innovation Bridging Human, Environment and Materials” of the Ministry of Education, Culture, Sports, Science and Technology of Japan, and the Global Station for Soft Matter at Hokkaido University.
Acknowledgments
We would like to thank T. Nakagaki, H. Orihara, N. Nishigami, M. Nishikawa, M. Akiyama, M. Kimura, and Y. Tanaka for their valuable comments and discussions.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcell.2023.1126819/full#supplementary-material
References
Aigouy, B., Farhadifar, R., Staple, D. B., Sagner, A., Röper, J. C., Jülicher, F., et al. (2010). Cell flow reorients the axis of planar polarity in the wing epithelium of Drosophila. Cell. 142(5), 773–786. doi:10.1016/j.cell.2010.07.042
Bächer, C., Khoromskaia, D., Salbreux, G., and Gekle, S. (2021). A three- dimensional numerical model of an active cell cortex in the viscous limit. Front. Phys. 9, 753230. doi:10.3389/fphy.2021.753230
Bergert, M., Chandradoss, S. D., Desai, R. A., and Paluch, E. (2012). Cell mechanics control rapid transitions between blebs and lamellipodia during migration. Proc. Natl. Acad. Sci. U. S. A. 109 (36), 14434–14439. doi:10.1073/pnas.1207968109
Bergert, M., Erzberger, A., Desai, R. A., Aspalter, I. M., Oates, A. C., Charras, G., et al. (2015). Force transmission during adhesion-independent migration. Nat. Cell. Biol. 17 (4), 524–529. doi:10.1038/ncb3134
Bodor, D. L., Pönisch, W., Endres, R. G., and Paluch, E. K. (2020). Of cell shapes and motion: The physical basis of animal cell migration. Dev. Cell. 52 (5), 550–562. doi:10.1016/j.devcel.2020.02.013
Bray, D., and White, J. G. (1988). Cortical flow in animal cells. Science 239 (4842), 883–888. doi:10.1126/science.3277283
Callan-Jones, A. C., and Voituriez, R. (2016). Actin flows in cell migration: From locomotion and polarity to trajectories. Curr. Opin. Cell. Biol. 38, 12–17. doi:10.1016/j.ceb.2016.01.003
Camley, B. A., Zhang, Y., Zhao, Y., Li, B., Ben-Jacob, E., Levine, H., et al. (2014). Polarity mechanisms such as contact inhibition of locomotion regulate persistent rotational motion of mammalian cells on micropatterns. Proc. Natl. Acad. Sci. U. S. A. 111 (41), 14770–14775. doi:10.1073/pnas.1414498111
Case, L. B., and Waterman, C. M. (2015)). Integration of actin dynamics and cell adhesion by a three-dimensional, mechanosensitive molecular clutch. Nat. Cell. Biol. 17 (8), 955–963. doi:10.1038/ncb3191
Farhadifar, R., Roper, J. C., Aigouy, B., Eaton, S., and Julicher, F. (2007). The influence of cell mechanics, cell-cell interactions, and proliferation on epithelial packing. Curr. Biol. 17, 2095–2104. doi:10.1016/j.cub.2007.11.049
Farutin, A., Étienne, J., Misbah, C., and Recho, P. (2019). Crawling in a fluid. Phys. Rev. Lett. 123 (11), 118101. doi:10.1103/PhysRevLett.123.118101
Fletcher, A. G., Osterfield, M., Baker, R. E., and Shvartsman, S. Y. (2014). Vertex models of epithelial morphogenesis. Biophys. J. 106, 2291–2304. doi:10.1016/j.bpj.2013.11.4498
Founounou, N., Farhadifar, R., Collu, G. M., Weber, U., Shelley, M. J., and Mlodzik, M. (2021). Tissue fluidity mediated by adherens junction dynamics promotes planar cell polarity-driven ommatidial rotation. Nat. Commun. 12 (1), 6974. doi:10.1038/s41467-021-27253-0
Friedl, P., and Gilmour, D. (2009). Collective cell migration in morphogenesis, regeneration and cancer. Nat. Rev. Mol. Cel. Biol. 10 (7), 445–457. doi:10.1038/nrm2720
Haas, P., and Gilmour, D. (2006)). Chemokine signaling mediates self-organizing tissue migration in the zebrafish lateral line. Dev. Cell. 10 (5), 673–680. doi:10.1016/j.devcel.2006.02.019
Haigo, S. L., and Bilder, D. (2011). Global tissue revolutions in a morphogenetic movement controlling elongation. Science 331 (6020), 1071–1074. doi:10.1126/science.1199424
Hayakawa, M., Hiraiwa, T., Wada, Y., Kuwayama, H., and Shibata, T. (2020). Polar pattern formation induced by contact following locomotion in a multicellular system. Elife 9, e53609. doi:10.7554/eLife.53609
Hirose, S., Benabentos, R., Ho, H. I., Kuspa, A., and Shaulsky, G. (2011). Self-recognition in social amoebae is mediated by allelic pairs of tiger genes. Science 333 (6041), 467–470. doi:10.1126/science.1203903
Innocenti, M. (2018). New insights into the formation and the function of lamellipodia and ruffles in mesenchymal cell migration. Cell. Adh Migr. 12 (5), 401–416. doi:10.1080/19336918.2018.1448352
Jankowiak, G., Peurichard, D., Reversat, A., Schmeiser, C., and Sixt, M. (2020). Modeling adhesion-independent cell migration. Math. Models Methods Appl. Sci. 30, 513–537. doi:10.1142/S021820252050013X
Jenny, A. (2010). Planar cell polarity signaling in the Drosophila eye. Curr. Top. Dev. Biol. 93, 189–227. doi:10.1016/B978-0-12-385044-7.00007-2
Kuwayama, H., and Ishida, S. (2013). Biological soliton in multicellular movement. Sci. Rep. 3, 2272. doi:10.1038/srep02272
Lämmermann, T., Bader, B. L., Monkley, S. J., Worbs, T., Wedlich-Söldner, R., Hirsch, K., et al. (2008). Rapid leukocyte migration by integrin-independent flowing and squeezing. Nature 453 (7191), 51–55. doi:10.1038/nature06887
Landau, L. D., and Lifshitz, E. M. (1976). “Mechanics,” in Course of theoretical physics. 3rd edn. Volume 1 (Oxford: Butterworth- Heinemann).
Lecaudey, V., Cakan-Akdogan, G., Norton, W. H., and Gilmour, D. (2008). Dynamic Fgf signaling couples morphogenesis and migration in the zebrafish lateral line primordium. Development 135 (16), 2695–2705. doi:10.1242/dev.025981
Liu, Y. J., Le Berre, M., Lautenschlaeger, F., Maiuri, P., Callan-Jones, A., Heuzé, M., et al. (2015). Confinement and low adhesion induce fast amoeboid migration of slow mesenchymal cells. Cell. 160 (4), 659–672. doi:10.1016/j.cell.2015.01.007
Lo, C. M., Wang, H. B., Dembo, M., and Wang, Y. L. (2000). Cell movement is guided by the rigidity of the substrate. Biophys. J. 79 (1), 144–152. doi:10.1016/S0006-3495(00)76279-5
Mietke, A., Jülicher, F., and Sbalzarini, I. F. (2019). Self-organized shape dynamics of active surfaces. Proc. Natl. Acad. Sci. U. S. A. 116 (1), 29–34. doi:10.1073/pnas.1810896115
Mirkovic, I., and Mlodzik, M. (2006). Cooperative activities of drosophila DE-cadherin and DN-cadherin regulate the cell motility process of ommatidial rotation. Development 133 (17), 3283–3293. doi:10.1242/dev.02468
Mlodzik, M. (1999). Planar polarity in the Drosophila eye: A multifaceted view of signaling specificity and cross-talk. EMBO J. 18 (24), 6873–6879. doi:10.1093/emboj/18.24.6873
Montell, D. J., Yoon, W. H., and Starz-Gaiano, M. (2012)). Group choreography: Mechanisms orchestrating the collective movement of border cells. Nat. Rev. Mol. Cell. Biol. 13 (10), 631–645. doi:10.1038/nrm3433
Moure, A., and Gomez, H. (2020). Dual role of the nucleus in cell migration on planar substrates. Biomech. Model. Mechanobiol. 19 (5), 1491–1508. doi:10.1007/s10237-019-01283-6
O'Neill, P. R., Castillo-Badillo, J. A., Meshik, X., Kalyanaraman, V., Melgarejo, K., and Gautam, N. (2018). Membrane flow drives an adhesion-independent amoeboid cell migration mode. Dev. Cell. 46 (1), 9–22.e4. doi:10.1016/j.devcel.2018.05.029
Ohta, T., and Ohkuma, T. (2009). Deformable self-propelled particles. Phys. Rev. Lett. 102 (15), 154101. doi:10.1103/PhysRevLett.102.154101
Okuda, S., Sato, K., and Hiraiwa, T. (2022). Continuum modeling of non-conservative fluid membrane for simulating long-term cell dynamics. Eur. Phys. J. E 45, 69. doi:10.1140/epje/s10189-022-00223-0
Pagès, D. L., Dornier, E., de Seze, J., Gontran, E., Maitra, A., Maciejewski, A., et al. (2022). Cell clusters adopt a collective amoeboid mode of migration in confined nonadhesive environments. Sci. Adv. 8 (39), eabp8416. doi:10.1126/sciadv.abp8416
Paluch, E. K., and Raz, E. (2013). The role and regulation of blebs in cell migration. Curr. Opin. Cell. Biol. 25 (5), 582–590. doi:10.1016/j.ceb.2013.05.005
Rauzi, M., Verant, P., Lecuit, T., and Lenne, P. F. (2008). Nature and anisotropy of cortical forces orienting Drosophila tissue morphogenesis. Nat. Cell. Biol. 10, 1401–1410. doi:10.1038/ncb1798
Reversat, A., Gaertner, F., Merrin, J., Stopp, J., Tasciyan, S., Aguilera, J., et al. (2020). Cellular locomotion using environmental topography. Nature 582 (7813), 582–585. doi:10.1038/s41586-020-2283-z
Ruprecht, V., Wieser, S., Callan-Jones, A., Smutny, M., Morita, H., Sako, K., et al. (2015). Cortical contractility triggers a stochastic switch to fast amoeboid cell motility. Cell. 160 (4), 673–685. doi:10.1016/j.cell.2015.01.008
Sakamoto, R., Izri, Z., Shimamoto, Y., Miyazaki, M., and Maeda, Y. T. (2022). Geometric trade-off between contractile force and viscous drag determines the actomyosin-based motility of a cell-sized droplet. Proc. Natl. Acad. Sci. U. S. A. 119 (30), e2121147119. doi:10.1073/pnas.2121147119
Salbreux, G., Charras, G., and Paluch, E. (2012). Actin cortex mechanics and cellular morphogenesis. Trends Cell. Biol. 22 (10), 536–545. doi:10.1016/j.tcb.2012.07.001
Sato, K. (2017). Direction-dependent contraction forces on cell boundaries induce collective migration of epithelial cells within their sheet. Dev. Growth Differ. 59 (5), 317–328. doi:10.1111/dgd.12361
Sato, K., Hiraiwa, T., Maekawa, E., Isomura, A., Shibata, T., and Kuranaga, E. (2015). Left-right asymmetric cell intercalation drives directional collective cell movement in epithelial morphogenesis. Nat. Commun. 6, 10074. doi:10.1038/ncomms10074Refstyled
Sato, K., Hiraiwa, T., and Shibata, T. (2015). Cell chirality induces collective cell migration in epithelial sheets. Phys. Rev. Lett. 115, 188102. doi:10.1103/PhysRevLett.115.188102
Scarpa, E., and Mayor, R. (2016). Collective cell migration in development. J. Cell. Biol. 212 (2), 143–155. doi:10.1083/jcb.201508047
Taniguchi, A., Nishigami, Y., Kajiura-Kobayashi, H., Takao, D., Tamaoki, D., Nakagaki, T., et al. (2023). Light-sheet microscopy reveals dorsoventral asymmetric membrane dynamics of Amoeba proteus during pressure-driven locomotion. Biol. Open 12 (2), bio059671. doi:10.1242/bio.059671
Taniguchi, K., Maeda, R., Ando, T., Okumura, T., Nakazawa, N., Hatori, R., et al. (2011). Chirality in planar cell shape contributes to left-right asymmetric epithelial morphogenesis. Science 333 (6040), 339–341. doi:10.1126/science.1200940
Tee, Y. H., Shemesh, T., Thiagarajan, V., Hariadi, R. F., Anderson, K. L., Page, C., et al. (2015). Cellular chirality arising from the self-organization of the actin cytoskeleton. Nat. Cell. Biol. 17 (4), 445–457. doi:10.1038/ncb3137
Wan, L. Q., Chin, A. S., Worley, K. E., and Ray, P. (2016). Cell chirality: Emergence of asymmetry from cell culture. Philos. Trans. R. Soc. Lond B Biol. Sci. 371 (1710), 20150413. doi:10.1098/rstb.2015.0413
Keywords: force balance, surface flow, cell cluster migration, cell cluster rotation, analytical formula for cell migration, mechanical model
Citation: Sato K (2023) A cell membrane model that reproduces cortical flow-driven cell migration and collective movement. Front. Cell Dev. Biol. 11:1126819. doi: 10.3389/fcell.2023.1126819
Received: 19 December 2022; Accepted: 30 May 2023;
Published: 23 June 2023.
Edited by:
Namrata Gundiah, Indian Institute of Science (IISc), IndiaCopyright © 2023 Sato. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Katsuhiko Sato, a2F0c3VoaWtvX3NhdG9AZXMuaG9rdWRhaS5hYy5qcA==
 Katsuhiko Sato
Katsuhiko Sato